4BA6 - Topic 4 Dr. Steven Collins. Chap. 5 3D Viewing and Projections
|
|
|
- Brenda Taylor
- 10 years ago
- Views:
Transcription
1 4BA6 - Topic 4 Dr. Steven Collins Chap. 5 3D Viewing and Projections
2 References Computer graphics: principles & practice, Fole, vandam, Feiner, Hughes, S-LEN M23*;-6 (has a good appendix on linear algebra) Advanced Animation and Rendering Techniques, Watt and Watt, S-LEN 5.8 N26;2-5 The OpenGL Programming Guide, Woo, Neider & Davis, S- LEN 5.8 N72;-2 Interactive Computer Graphics, Edward Angel 2
3 OpenGL Geometr Pipeline x z w original vertex MODELVIEW matrix x z w ee ee ee ee vertex in the ee coordinate space PROJECTION matrix x w proj proj proj 2D projection of vertex onto viewing plane perspective division x dev dev normalised device coordinates (foreshortened) viewport transformation x win win final window coordinates 3
4 The Camera Sstem To create a view of a scene we need: a description of the scene geometr a camera or view definition Default OpenGL camera is located at the origin looking down the -z axis. The camera definition allows projection of the 3D scene geometr onto a 2D surface for displa. This projection can take a number of forms: orthographic (parallel lines preserved) perspective (foreshortening): -point, 2-point or 3-point skewed orthographic 4
5 Camera Tpes Before generating an image we must choose our viewer: The pinhole camera model is most widel used: infinite depth of field (everthing is in focus) Advanced rendering sstems model the camera double gauss lens as used in man professional cameras model depth of field and non-linear optics (including lens flare) Photorealistic rendering sstems often emplo a phsical model of the ee for rendering images model the ees response to varing brightness and colour levels model the internal optics of the ee itself (diffraction b lens fibres etc.) 5
6 Pinhole Camera Model 6
7 Modeling the Ee s Response Adaptation Glare & Diffraction 7
8 Camera Sstems A camera model implemented in Princeton Universit (995) 8
9 Viewing Sstem We are onl concerned with the geometr of viewing at this stage. The camera s position and orientation define a viewvolume or view-frustrum. objects completel or partiall within this volume are potentiall visible on the viewport. objects full outside this volume cannot be seen clipped clipped view frustrum clipping planes 9
10 Camera Models CTM= Current Transformation Matrix Each vertex in our model must be projected onto the 2D camera viewport plane in order to be displa on the screen. The CTM is emploed to determine the location of each vertex in the camera coordinate sstem: x = MCTM x We then emplo a projection matrix defined b GL_PROJECTION to map this to a 2D viewport coordinate. Finall, this 2D coordinate is mapped to device coordinates using the viewport definition (given b glviewport()).
11 Camera Modeling in OpenGL camera coordinate sstem viewport coordinate sstem device/screen coordinate sstem glmatrixmode(gl_modelview)... glviewport(,,xres,res) glmatrixmode(gl_projection)...
12 3D 2D Projection Tpe of projection depends on a number of factors: location and orientation of the viewing plane (viewport) direction of projection (described b a vector) projection tpe: Projection Perspective Parallel -point Orthographic 2-point Axonometric 3-point Oblique 2
13 Parallel Projections axonometric orthographic oblique 3
14 Perspective Projections 3-point perspective -point perspective 2-point perspective 4
15 5 Orthogonal Projections The simplest of all projections, parallel project onto viewplane. Usuall view-plane is axis aligned (often at z=) = = where M MP P x z x
16 Multiple Projections It is often useful to have multiple projections available at an given time usuall: plan (top) view, front & left or right elevation (side) view Perspective Top Front Right 6
17 Orthogonal Projections The result is an orthographic projection if the object is axis aligned, otherwise it is an axonometric projection. If the projection plane intersects the principle axes at the same distance from the origin the projection is isometric. x + + z = 7
18 Parallel Projections in OpenGL glortho(xmin, xmax, min, max, zmin, zmax); Note: we alwas view in -z direction need to transform world in order to view in other arbitrar directions. 8
19 Perspective Projections Perspective projections are more complex and exhibit foreshortening (parallel appear to converge at points). Parameters: centre of projection (COP) field of view (θ,φ) projection direction up direction 9
20 2 Perspective Projections Consider a perspective projection with the viewpoint at the origin and a viewing direction oriented along the positive -z axis and the view-plane located at z = -d p d z d z P P = = -z d = = z x d d z z x d d z d z x z x P P P divide b homogenous ordinate to map back to 3D space a similar construction for x p
21 2 Perspective Projections Details = d z z x d d z d z x z x P P P = z x z x Flip z to transform to a left handed co-ordinate sstem increasing z values mean increasing distance from the viewer. PROJECTION matrix perspective division
22 Perspective Projection Depending on the application we can use different mechanisms to specif a perspective view. Example: the field of view angles ma be derived if the distance to the viewing plane is known. Example: the viewing direction ma be obtained if a point in the scene is identified that we wish to look at. OpenGL supports this b providing different methods of specifing the perspective view: glulookat, glfrustrum and gluperspective 22
23 Perspective Projections glfrustrum(xmin, xmax, min, max, zmin, zmax); 23
24 glfrustrum Note that all points on the line defined b (xmin,min,- zmin) and COP are mapped to the lower left point on the viewport. Also all points on the line defined b (xmax,max,-zmin) and COP are mapped to the upper right corner of the viewport. The viewing direction is alwas parallel to -z It is not necessar to have a smmetric frustrum like: glfrustrum(-.,., -.,., 5., 5.); Non smmetric frustrums introduce obliqueness into the projection. zmin and zmax are specified as positive distances along -z 24
25 Perspective Projections gluperspective(fov, aspect, near, far); h 2 θ = tan h = 2near tan θ near
26 gluperspective A utilit function to simplif the specification of perspective views. Onl allows creation of smmetric frustrums. Viewpoint is at the origin and the viewing direction is the -z axis. The field of view angle, fov, must be in the range [..8] aspect allows the creation of a view frustrum that matches the aspect ratio of the viewport to eliminate distortion. 26
27 Perspective Projections 27
28 Lens Configurations mm Lens (fov = 22 ) 2mm Lens (fov = 84 ) 35mm Lens (fov = 54 ) 2mm Lens (fov = ) 28
29 Positioning the Camera The previous projections had limitations: usuall fixed origin and fixed projection direction To obtain arbitrar camera orientations and positions we manipulate the MODELVIEW matrix prior to creation of the models. This positions the camera w.r.t. the model. We wish to position the camera at (, 2, ) w.r.t. the world Two possibilities: transform the world prior to creation of objects using translatef and rotatef: gltranslatef(-, -2, -); use glulookat to position the camera with respect to the world co-ordinate sstem: glulookat(, 2,, ); Both are equivalent. 29
30 Positioning the Camera glulookat(eex, ee, eez, lookx, look, lookz, upx, up, upz); equivalent to: gltranslatef(-eex, -ee, -eez); glrotatef(theta,.,.,.); glrotatef(phi,.,.,.); 3
31 Projection window The projection matrix defines the mapping from a 3D world co-ordinate to a 2D viewport co-ordinate. The window extents are defined as a parameter of the projection: glfrustrum(l,r,b,t,n,f) (r,t,-n) (l,b,-n) (w,h,-n) gluperspective(f,a,n,f) (-w,-h,-n) h w f = n tan 2 = h a 3
32 Projection window We need to associate the 2D window co-ordinate sstem with the viewport co-ordinate sstem in order to determine the correct pixel associated with each vertex. normalised device co-ordinates viewport co-ordinates 32
33 Window to Viewport Transformation: review An affine planar transformation is used. After projection to the window, all points are transformed to normalised device co-ordinates: [-,]x[,] x n n x = 2 x max = 2 p p max x x min min min min glviewport used to relate the co-ordinate sstems: glviewport(int x, int, int width, int height); 33
34 Window to Viewport Transformation: review (x,) = location of bottom left of viewport within the window width,height = dimension in pixels of the viewport x w = width + 2 height + 2 ( x + ) x = ( + ) n w n normall we re-create the window after a window resize event to ensure a correct mapping between window and viewport dimensions: static void reshape(int width, int height) { glviewport(,, width, height); glmatrixmode(gl_projection); glloadidentit(); gluperspective(85.,., 5, 5); } 34
35 Aspect Ratio The aspect ratio defines the relationship between the width and height of an image. Using gluperspective an viewport aspect ratio ma be explicitl provided, otherwise the aspect ratio is a function of the supplied viewport width and height. The aspect ratio of the window (defined b the user) must match the viewport aspect ratio to prevent unwanted affine distortion: aspect ratio =.25 aspect ratio =.5 35
36 Sample Viewport Application // top left: top view glviewport(, win_height/2, win_width/2, win_height/2); glmatrixmode(gl_projection); glloadidentit(); glortho(-3., 3., -3., 3.,., 5.); glulookat(., 5.,.,.,.,.,.,., -.); glmatrixmode(gl_modelview); glloadidentit(); glcalllist(object); // top right: right view glviewport(win_width/2, win_height/2, win_width/2, win_height/2); glmatrixmode(gl_projection); glloadidentit(); glortho(-3., 3., -3., 3.,., 5.); glulookat(5.,.,.,.,.,.,.,.,.); glmatrixmode(gl_modelview); glloadidentit(); glcalllist(object); // bottom left: front view glviewport(,, win_width/2, win_height/2); glmatrixmode(gl_projection); glloadidentit(); glortho(-3., 3., -3., 3.,., 5.); glulookat(.,., 5.,.,.,.,.,.,.); glmatrixmode(gl_modelview); glloadidentit(); glcalllist(object); // bottom right: rotating perspective view glviewport(win_width/2,, win_width/2, win_height/2); glmatrixmode(gl_projection); glloadidentit(); gluperspective(7.,.,, 5); glulookat(.,., 5.,.,.,.,.,.,.); glmatrixmode(gl_modelview); glloadidentit(); glrotatef(3.,.,.,.); glrotatef(angle,.,.,.); glcalllist(object); 36
Realtime 3D Computer Graphics Virtual Reality
 Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
Transformations in the pipeline
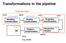 Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
Basic Problem: Map a 3D object to a 2D display surface. Analogy - Taking a snapshot with a camera
 3D Viewing Basic Problem: Map a 3D object to a 2D display surface Analogy - Taking a snapshot with a camera Synthetic camera virtual camera we can move to any location & orient in any way then create a
3D Viewing Basic Problem: Map a 3D object to a 2D display surface Analogy - Taking a snapshot with a camera Synthetic camera virtual camera we can move to any location & orient in any way then create a
3D Viewing. Chapter 7. Projections. 3D clipping. OpenGL viewing functions and clipping planes
 3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Sample Exam Questions 2007
 Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 2D and 3D Transformations Doug Bowman Adapted from notes by Yong Cao Virginia Tech 1 Transformations What are they? changing something to something else via rules mathematics:
CS 4204 Computer Graphics 2D and 3D Transformations Doug Bowman Adapted from notes by Yong Cao Virginia Tech 1 Transformations What are they? changing something to something else via rules mathematics:
2D Geometrical Transformations. Foley & Van Dam, Chapter 5
 2D Geometrical Transformations Fole & Van Dam, Chapter 5 2D Geometrical Transformations Translation Scaling Rotation Shear Matri notation Compositions Homogeneous coordinates 2D Geometrical Transformations
2D Geometrical Transformations Fole & Van Dam, Chapter 5 2D Geometrical Transformations Translation Scaling Rotation Shear Matri notation Compositions Homogeneous coordinates 2D Geometrical Transformations
Geometric Camera Parameters
 Geometric Camera Parameters What assumptions have we made so far? -All equations we have derived for far are written in the camera reference frames. -These equations are valid only when: () all distances
Geometric Camera Parameters What assumptions have we made so far? -All equations we have derived for far are written in the camera reference frames. -These equations are valid only when: () all distances
The Geometry of Perspective Projection
 The Geometry o Perspective Projection Pinhole camera and perspective projection - This is the simplest imaging device which, however, captures accurately the geometry o perspective projection. -Rays o
The Geometry o Perspective Projection Pinhole camera and perspective projection - This is the simplest imaging device which, however, captures accurately the geometry o perspective projection. -Rays o
INTRODUCTION TO RENDERING TECHNIQUES
 INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
Android and OpenGL. Android Smartphone Programming. Matthias Keil. University of Freiburg
 Android and OpenGL Android Smartphone Programming Matthias Keil Institute for Computer Science Faculty of Engineering 16. Dezember 2013 Outline 1 OpenGL Introduction 2 Displaying Graphics 3 Interaction
Android and OpenGL Android Smartphone Programming Matthias Keil Institute for Computer Science Faculty of Engineering 16. Dezember 2013 Outline 1 OpenGL Introduction 2 Displaying Graphics 3 Interaction
521493S Computer Graphics. Exercise 2 & course schedule change
 521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
521493S Computer Graphics Exercise 2 & course schedule change Course Schedule Change Lecture from Wednesday 31th of March is moved to Tuesday 30th of March at 16-18 in TS128 Question 2.1 Given two nonparallel,
Geometry for Computer Graphics
 Computer Graphics and Visualisation Geometry for Computer Graphics Student Notes Developed by F Lin K Wyrwas J Irwin C Lilley W T Hewitt T L J Howard Computer Graphics Unit Manchester Computing Centre
Computer Graphics and Visualisation Geometry for Computer Graphics Student Notes Developed by F Lin K Wyrwas J Irwin C Lilley W T Hewitt T L J Howard Computer Graphics Unit Manchester Computing Centre
SOEM 024: Computer Aided Design. E. Rozos
 SOEM 024: Computer Aided Design E. Rozos 3D Design with AutoCAD 2002 Isometric Drawings 3D coordinates, views Wire-frame 3D modelling, extruding Primitive objects Boolean operators Terminology Boolean
SOEM 024: Computer Aided Design E. Rozos 3D Design with AutoCAD 2002 Isometric Drawings 3D coordinates, views Wire-frame 3D modelling, extruding Primitive objects Boolean operators Terminology Boolean
Image Processing and Computer Graphics. Rendering Pipeline. Matthias Teschner. Computer Science Department University of Freiburg
 Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
From 3D to 2D: Orthographic and Perspective Projection Part 1
 From 3D to 2D: Orthographic and Perspective Projection Part 1 History Geometrical Constructions Types of Projection Projection in Computer Graphics Andries van Dam September 13, 2001 3D Viewing I 1/34
From 3D to 2D: Orthographic and Perspective Projection Part 1 History Geometrical Constructions Types of Projection Projection in Computer Graphics Andries van Dam September 13, 2001 3D Viewing I 1/34
2D Geometric Transformations
 2D Geometric Transformations (Chapter 5 in FVD) 2D Geometric Transformations Question: How do we represent a geometric object in the plane? Answer: For now, assume that objects consist of points and lines.
2D Geometric Transformations (Chapter 5 in FVD) 2D Geometric Transformations Question: How do we represent a geometric object in the plane? Answer: For now, assume that objects consist of points and lines.
Lecture 3: Coordinate Systems and Transformations
 Lecture 3: Coordinate Systems and Transformations Topics: 1. Coordinate systems and frames 2. Change of frames 3. Affine transformations 4. Rotation, translation, scaling, and shear 5. Rotation about an
Lecture 3: Coordinate Systems and Transformations Topics: 1. Coordinate systems and frames 2. Change of frames 3. Affine transformations 4. Rotation, translation, scaling, and shear 5. Rotation about an
Computer Graphics Labs
 Computer Graphics Labs Abel J. P. Gomes LAB. 2 Department of Computer Science and Engineering University of Beira Interior Portugal 2011 Copyright 2009-2011 All rights reserved. LAB. 2 1. Learning goals
Computer Graphics Labs Abel J. P. Gomes LAB. 2 Department of Computer Science and Engineering University of Beira Interior Portugal 2011 Copyright 2009-2011 All rights reserved. LAB. 2 1. Learning goals
w = COI EYE view direction vector u = w ( 010,, ) cross product with y-axis v = w u up vector
 . w COI EYE view direction vector u w ( 00,, ) cross product with -ais v w u up vector (EQ ) Computer Animation: Algorithms and Techniques 29 up vector view vector observer center of interest 30 Computer
. w COI EYE view direction vector u w ( 00,, ) cross product with -ais v w u up vector (EQ ) Computer Animation: Algorithms and Techniques 29 up vector view vector observer center of interest 30 Computer
Affine Transformations
 A P P E N D I X C Affine Transformations CONTENTS C The need for geometric transformations 335 C2 Affine transformations 336 C3 Matri representation of the linear transformations 338 C4 Homogeneous coordinates
A P P E N D I X C Affine Transformations CONTENTS C The need for geometric transformations 335 C2 Affine transformations 336 C3 Matri representation of the linear transformations 338 C4 Homogeneous coordinates
How to read Plans and Do Basic Drawings
 How to read Plans and Do Basic Drawings Workshop session W1 10.00 Site Orientation Exercise 10.10 Drawing Conventions 10.45 Can drawings Distort the Truth? 11.30 Summary + Coffee 11.45 Simple Drawing Techniques
How to read Plans and Do Basic Drawings Workshop session W1 10.00 Site Orientation Exercise 10.10 Drawing Conventions 10.45 Can drawings Distort the Truth? 11.30 Summary + Coffee 11.45 Simple Drawing Techniques
Introduction to Computer Graphics
 Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 [email protected] www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 [email protected] www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Introduction to Computer Graphics. Reading: Angel ch.1 or Hill Ch1.
 Introduction to Computer Graphics Reading: Angel ch.1 or Hill Ch1. What is Computer Graphics? Synthesis of images User Computer Image Applications 2D Display Text User Interfaces (GUI) - web - draw/paint
Introduction to Computer Graphics Reading: Angel ch.1 or Hill Ch1. What is Computer Graphics? Synthesis of images User Computer Image Applications 2D Display Text User Interfaces (GUI) - web - draw/paint
Aston University. School of Engineering & Applied Science
 CS2150 Aston University School of Engineering & Applied Science CS2150: Computer Graphics January Examinations 2010 Date: XXX Time: XXX Instructions to Candidates: 1. Answer Question ONE and any other
CS2150 Aston University School of Engineering & Applied Science CS2150: Computer Graphics January Examinations 2010 Date: XXX Time: XXX Instructions to Candidates: 1. Answer Question ONE and any other
SketchUp Instructions
 SketchUp Instructions Every architect needs to know how to use SketchUp! SketchUp is free from Google just Google it and download to your computer. You can do just about anything with it, but it is especially
SketchUp Instructions Every architect needs to know how to use SketchUp! SketchUp is free from Google just Google it and download to your computer. You can do just about anything with it, but it is especially
Chapter 8. Lines and Planes. By the end of this chapter, you will
 Chapter 8 Lines and Planes In this chapter, ou will revisit our knowledge of intersecting lines in two dimensions and etend those ideas into three dimensions. You will investigate the nature of planes
Chapter 8 Lines and Planes In this chapter, ou will revisit our knowledge of intersecting lines in two dimensions and etend those ideas into three dimensions. You will investigate the nature of planes
An introduction to 3D draughting & solid modelling using AutoCAD
 An introduction to 3D draughting & solid modelling using AutoCAD Faculty of Technology University of Plymouth Drake Circus Plymouth PL4 8AA These notes are to be used in conjunction with the AutoCAD software
An introduction to 3D draughting & solid modelling using AutoCAD Faculty of Technology University of Plymouth Drake Circus Plymouth PL4 8AA These notes are to be used in conjunction with the AutoCAD software
Graphics Pipeline in a Nutshell
 Graphics Pipeline in a Nutshell How do we create a rendering such as this? CS334 Spring 2008 Design the scene (technical drawing in wireframe ) Apply perspective transformations to the scene geometry for
Graphics Pipeline in a Nutshell How do we create a rendering such as this? CS334 Spring 2008 Design the scene (technical drawing in wireframe ) Apply perspective transformations to the scene geometry for
Traditional Drawing Tools
 Engineering Drawing Traditional Drawing Tools DRAWING TOOLS DRAWING TOOLS 1. T-Square 2. Triangles DRAWING TOOLS HB for thick line 2H for thin line 3. Adhesive Tape 4. Pencils DRAWING TOOLS 5. Sandpaper
Engineering Drawing Traditional Drawing Tools DRAWING TOOLS DRAWING TOOLS 1. T-Square 2. Triangles DRAWING TOOLS HB for thick line 2H for thin line 3. Adhesive Tape 4. Pencils DRAWING TOOLS 5. Sandpaper
Creating 2D Drawings from 3D AutoCAD Models
 Creating 2D Drawings from 3D AutoCAD Models David Piggott CrWare, LP GD205-2P This class explores the various techniques in creating 2D part and assembly drawings from 3D AutoCAD models. As part of the
Creating 2D Drawings from 3D AutoCAD Models David Piggott CrWare, LP GD205-2P This class explores the various techniques in creating 2D part and assembly drawings from 3D AutoCAD models. As part of the
Pro/ENGINEER Wildfire 4.0 Basic Design
 Introduction Datum features are non-solid features used during the construction of other features. The most common datum features include planes, axes, coordinate systems, and curves. Datum features do
Introduction Datum features are non-solid features used during the construction of other features. The most common datum features include planes, axes, coordinate systems, and curves. Datum features do
Lecture 2: Homogeneous Coordinates, Lines and Conics
 Lecture 2: Homogeneous Coordinates, Lines and Conics 1 Homogeneous Coordinates In Lecture 1 we derived the camera equations λx = P X, (1) where x = (x 1, x 2, 1), X = (X 1, X 2, X 3, 1) and P is a 3 4
Lecture 2: Homogeneous Coordinates, Lines and Conics 1 Homogeneous Coordinates In Lecture 1 we derived the camera equations λx = P X, (1) where x = (x 1, x 2, 1), X = (X 1, X 2, X 3, 1) and P is a 3 4
TABLE OF CONTENTS. INTRODUCTION... 5 Advance Concrete... 5 Where to find information?... 6 INSTALLATION... 7 STARTING ADVANCE CONCRETE...
 Starting Guide TABLE OF CONTENTS INTRODUCTION... 5 Advance Concrete... 5 Where to find information?... 6 INSTALLATION... 7 STARTING ADVANCE CONCRETE... 7 ADVANCE CONCRETE USER INTERFACE... 7 Other important
Starting Guide TABLE OF CONTENTS INTRODUCTION... 5 Advance Concrete... 5 Where to find information?... 6 INSTALLATION... 7 STARTING ADVANCE CONCRETE... 7 ADVANCE CONCRETE USER INTERFACE... 7 Other important
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
2.1 Three Dimensional Curves and Surfaces
 . Three Dimensional Curves and Surfaces.. Parametric Equation of a Line An line in two- or three-dimensional space can be uniquel specified b a point on the line and a vector parallel to the line. The
. Three Dimensional Curves and Surfaces.. Parametric Equation of a Line An line in two- or three-dimensional space can be uniquel specified b a point on the line and a vector parallel to the line. The
Section 11.4: Equations of Lines and Planes
 Section 11.4: Equations of Lines and Planes Definition: The line containing the point ( 0, 0, 0 ) and parallel to the vector v = A, B, C has parametric equations = 0 + At, = 0 + Bt, = 0 + Ct, where t R
Section 11.4: Equations of Lines and Planes Definition: The line containing the point ( 0, 0, 0 ) and parallel to the vector v = A, B, C has parametric equations = 0 + At, = 0 + Bt, = 0 + Ct, where t R
Understand the Sketcher workbench of CATIA V5.
 Chapter 1 Drawing Sketches in Learning Objectives the Sketcher Workbench-I After completing this chapter you will be able to: Understand the Sketcher workbench of CATIA V5. Start a new file in the Part
Chapter 1 Drawing Sketches in Learning Objectives the Sketcher Workbench-I After completing this chapter you will be able to: Understand the Sketcher workbench of CATIA V5. Start a new file in the Part
Kankakee Community College
 Kankakee Community College Course prefix and number: DRFT 2134 Course title: AutoCAD III Semester: Fall 2014 Credit hours: 4 Lecture hours: 2.5 Lab hours: 3 Catalog description: Prerequisite: DRFT 2114,
Kankakee Community College Course prefix and number: DRFT 2134 Course title: AutoCAD III Semester: Fall 2014 Credit hours: 4 Lecture hours: 2.5 Lab hours: 3 Catalog description: Prerequisite: DRFT 2114,
Introduction to Matrices for Engineers
 Introduction to Matrices for Engineers C.T.J. Dodson, School of Mathematics, Manchester Universit 1 What is a Matrix? A matrix is a rectangular arra of elements, usuall numbers, e.g. 1 0-8 4 0-1 1 0 11
Introduction to Matrices for Engineers C.T.J. Dodson, School of Mathematics, Manchester Universit 1 What is a Matrix? A matrix is a rectangular arra of elements, usuall numbers, e.g. 1 0-8 4 0-1 1 0 11
Methodology for Lecture. Review of Last Demo
 Basic Geometry Setup Methodology for Lecture Make mytest1 more ambitious Sequence of steps Demo Review of Last Demo Changed floor to all white, added global for teapot and teapotloc, moved geometry to
Basic Geometry Setup Methodology for Lecture Make mytest1 more ambitious Sequence of steps Demo Review of Last Demo Changed floor to all white, added global for teapot and teapotloc, moved geometry to
Teacher Page. 1. Reflect a figure with vertices across the x-axis. Find the coordinates of the new image.
 Teacher Page Geometr / Da # 10 oordinate Geometr (5 min.) 9-.G.3.1 9-.G.3.2 9-.G.3.3 9-.G.3. Use rigid motions (compositions of reflections, translations and rotations) to determine whether two geometric
Teacher Page Geometr / Da # 10 oordinate Geometr (5 min.) 9-.G.3.1 9-.G.3.2 9-.G.3.3 9-.G.3. Use rigid motions (compositions of reflections, translations and rotations) to determine whether two geometric
Computer Graphics. Introduction. Computer graphics. What is computer graphics? Yung-Yu Chuang
 Introduction Computer Graphics Instructor: Yung-Yu Chuang ( 莊 永 裕 ) E-mail: [email protected] Office: CSIE 527 Grading: a MatchMove project Computer Science ce & Information o Technolog og Yung-Yu Chuang
Introduction Computer Graphics Instructor: Yung-Yu Chuang ( 莊 永 裕 ) E-mail: [email protected] Office: CSIE 527 Grading: a MatchMove project Computer Science ce & Information o Technolog og Yung-Yu Chuang
An Introduction to. Graphics Programming
 An Introduction to Graphics Programming with Tutorial and Reference Manual Toby Howard School of Computer Science University of Manchester V3.3, January 13, 2010 Contents 1 About this manual 1 1.1 How
An Introduction to Graphics Programming with Tutorial and Reference Manual Toby Howard School of Computer Science University of Manchester V3.3, January 13, 2010 Contents 1 About this manual 1 1.1 How
4. CAMERA ADJUSTMENTS
 4. CAMERA ADJUSTMENTS Only by the possibility of displacing lens and rear standard all advantages of a view camera are fully utilized. These displacements serve for control of perspective, positioning
4. CAMERA ADJUSTMENTS Only by the possibility of displacing lens and rear standard all advantages of a view camera are fully utilized. These displacements serve for control of perspective, positioning
CATIA Drafting TABLE OF CONTENTS
 TABLE OF CONTENTS Introduction...1 Drafting...2 Drawing Screen...3 Pull-down Menus...4 File...4 Edit...5 View...6 Insert...7 Tools...8 Drafting Workbench...9 Views and Sheets...9 Dimensions and Annotations...10
TABLE OF CONTENTS Introduction...1 Drafting...2 Drawing Screen...3 Pull-down Menus...4 File...4 Edit...5 View...6 Insert...7 Tools...8 Drafting Workbench...9 Views and Sheets...9 Dimensions and Annotations...10
CATIA V5 Tutorials. Mechanism Design & Animation. Release 18. Nader G. Zamani. University of Windsor. Jonathan M. Weaver. University of Detroit Mercy
 CATIA V5 Tutorials Mechanism Design & Animation Release 18 Nader G. Zamani University of Windsor Jonathan M. Weaver University of Detroit Mercy SDC PUBLICATIONS Schroff Development Corporation www.schroff.com
CATIA V5 Tutorials Mechanism Design & Animation Release 18 Nader G. Zamani University of Windsor Jonathan M. Weaver University of Detroit Mercy SDC PUBLICATIONS Schroff Development Corporation www.schroff.com
Freehand Sketching. Sections
 3 Freehand Sketching Sections 3.1 Why Freehand Sketches? 3.2 Freehand Sketching Fundamentals 3.3 Basic Freehand Sketching 3.4 Advanced Freehand Sketching Key Terms Objectives Explain why freehand sketching
3 Freehand Sketching Sections 3.1 Why Freehand Sketches? 3.2 Freehand Sketching Fundamentals 3.3 Basic Freehand Sketching 3.4 Advanced Freehand Sketching Key Terms Objectives Explain why freehand sketching
OD1641 PRINCIPLES OF DRAFTING AND SHOP DRAWINGS
 SUBCOURSE OD1641 EDITION 8 PRINCIPLES OF DRAFTING AND SHOP DRAWINGS US ARMY REPAIR SHOP TECHNICIAN WARRANT OFFICER ADVANCED CORRESPONDENCE COURSE MOS/SKILL LEVEL: 441A PRINCIPLES OF DRAFTING AND SHOP
SUBCOURSE OD1641 EDITION 8 PRINCIPLES OF DRAFTING AND SHOP DRAWINGS US ARMY REPAIR SHOP TECHNICIAN WARRANT OFFICER ADVANCED CORRESPONDENCE COURSE MOS/SKILL LEVEL: 441A PRINCIPLES OF DRAFTING AND SHOP
INVESTIGATIONS AND FUNCTIONS 1.1.1 1.1.4. Example 1
 Chapter 1 INVESTIGATIONS AND FUNCTIONS 1.1.1 1.1.4 This opening section introduces the students to man of the big ideas of Algebra 2, as well as different was of thinking and various problem solving strategies.
Chapter 1 INVESTIGATIONS AND FUNCTIONS 1.1.1 1.1.4 This opening section introduces the students to man of the big ideas of Algebra 2, as well as different was of thinking and various problem solving strategies.
Welcome to Corel DESIGNER, a comprehensive vector-based drawing application for creating technical graphics.
 Importing 3D models Welcome to Corel DESIGNER, a comprehensive vector-based drawing application for creating technical graphics. In this tutorial, you will modify a three-dimensional model of a transmission
Importing 3D models Welcome to Corel DESIGNER, a comprehensive vector-based drawing application for creating technical graphics. In this tutorial, you will modify a three-dimensional model of a transmission
Essential Mathematics for Computer Graphics fast
 John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
Advanced Computer Graphics (2IV40) ~ 3D Transformations. Types (geometric) Types (algebraic) 3D Transformations. y + c 1. x = a 1.
 Advanced Computer Graphics (2IV40) ~ 3D Transformations Kees Huiing Huub van de Wetering Winter 2005/6 Tpes (geometric) maintain distances & orientation (LH/RH): rigid bod transforms (rotations, translations)
Advanced Computer Graphics (2IV40) ~ 3D Transformations Kees Huiing Huub van de Wetering Winter 2005/6 Tpes (geometric) maintain distances & orientation (LH/RH): rigid bod transforms (rotations, translations)
Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings
 Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings By Wayne and Cheryl Renshaw. Although it is centuries old, the art of street painting has been going through a resurgence.
Anamorphic Projection Photographic Techniques for setting up 3D Chalk Paintings By Wayne and Cheryl Renshaw. Although it is centuries old, the art of street painting has been going through a resurgence.
Scan-Line Fill. Scan-Line Algorithm. Sort by scan line Fill each span vertex order generated by vertex list
 Scan-Line Fill Can also fill by maintaining a data structure of all intersections of polygons with scan lines Sort by scan line Fill each span vertex order generated by vertex list desired order Scan-Line
Scan-Line Fill Can also fill by maintaining a data structure of all intersections of polygons with scan lines Sort by scan line Fill each span vertex order generated by vertex list desired order Scan-Line
SEMTech Solutions. Leaders in Refurbished SEMs. SEMTech Solutions Windows 7 SOFTWARE CONTROL SYSTEM
 SEMTech Solutions Leaders in Refurbished SEMs SEMTech Solutions Windows 7 SOFTWARE CONTROL SYSTEM Recertification Process Our Goal: Value Added Technologies Demo Outgoing Inspection Can Include: New PC
SEMTech Solutions Leaders in Refurbished SEMs SEMTech Solutions Windows 7 SOFTWARE CONTROL SYSTEM Recertification Process Our Goal: Value Added Technologies Demo Outgoing Inspection Can Include: New PC
Lecture Notes. Fundamentals of Computer Graphics. Prof. Michael Langer School of Computer Science McGill University
 COMP 557 Winter 2015 Lecture Notes Fundamentals of Computer Graphics Prof. Michael Langer School of Computer Science McGill University NOTE: These lecture notes are dynamic. The initial version of the
COMP 557 Winter 2015 Lecture Notes Fundamentals of Computer Graphics Prof. Michael Langer School of Computer Science McGill University NOTE: These lecture notes are dynamic. The initial version of the
Geometric Optics Converging Lenses and Mirrors Physics Lab IV
 Objective Geometric Optics Converging Lenses and Mirrors Physics Lab IV In this set of lab exercises, the basic properties geometric optics concerning converging lenses and mirrors will be explored. The
Objective Geometric Optics Converging Lenses and Mirrors Physics Lab IV In this set of lab exercises, the basic properties geometric optics concerning converging lenses and mirrors will be explored. The
x y The matrix form, the vector form, and the augmented matrix form, respectively, for the system of equations are
 Solving Sstems of Linear Equations in Matri Form with rref Learning Goals Determine the solution of a sstem of equations from the augmented matri Determine the reduced row echelon form of the augmented
Solving Sstems of Linear Equations in Matri Form with rref Learning Goals Determine the solution of a sstem of equations from the augmented matri Determine the reduced row echelon form of the augmented
basicdim DGC Compact control module
 luxctrol lighting control sstem DGC Compact control module Product description Compact dimensions for luminaire installation For up to 0 DSI or LI ballasts ( per output channel) LI IN input LI/DSI output
luxctrol lighting control sstem DGC Compact control module Product description Compact dimensions for luminaire installation For up to 0 DSI or LI ballasts ( per output channel) LI IN input LI/DSI output
GeoGebra. 10 lessons. Gerrit Stols
 GeoGebra in 10 lessons Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It was developed by Markus Hohenwarter
GeoGebra in 10 lessons Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It was developed by Markus Hohenwarter
B2.53-R3: COMPUTER GRAPHICS. NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions.
 B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
LIST OF CONTENTS CHAPTER CONTENT PAGE DECLARATION DEDICATION ACKNOWLEDGEMENTS ABSTRACT ABSTRAK
 vii LIST OF CONTENTS CHAPTER CONTENT PAGE DECLARATION DEDICATION ACKNOWLEDGEMENTS ABSTRACT ABSTRAK LIST OF CONTENTS LIST OF TABLES LIST OF FIGURES LIST OF NOTATIONS LIST OF ABBREVIATIONS LIST OF APPENDICES
vii LIST OF CONTENTS CHAPTER CONTENT PAGE DECLARATION DEDICATION ACKNOWLEDGEMENTS ABSTRACT ABSTRAK LIST OF CONTENTS LIST OF TABLES LIST OF FIGURES LIST OF NOTATIONS LIST OF ABBREVIATIONS LIST OF APPENDICES
The mouse callback. Positioning. Working with Callbacks. Obtaining the window size. Objectives
 Objectives Working with Callbacks Learn to build interactive programs using GLUT callbacks - Mouse - Keyboard - Reshape Introduce menus in GLUT The mouse callback glutmousefunc(mymouse) void mymouse(glint
Objectives Working with Callbacks Learn to build interactive programs using GLUT callbacks - Mouse - Keyboard - Reshape Introduce menus in GLUT The mouse callback glutmousefunc(mymouse) void mymouse(glint
Math, Trigonometry and Vectors. Geometry. Trig Definitions. sin(θ) = opp hyp. cos(θ) = adj hyp. tan(θ) = opp adj. Here's a familiar image.
 Math, Trigonometr and Vectors Geometr Trig Definitions Here's a familiar image. To make predictive models of the phsical world, we'll need to make visualizations, which we can then turn into analtical
Math, Trigonometr and Vectors Geometr Trig Definitions Here's a familiar image. To make predictive models of the phsical world, we'll need to make visualizations, which we can then turn into analtical
A Short Introduction to Computer Graphics
 A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
3D Drawing. Single Point Perspective with Diminishing Spaces
 3D Drawing Single Point Perspective with Diminishing Spaces The following document helps describe the basic process for generating a 3D representation of a simple 2D plan. For this exercise we will be
3D Drawing Single Point Perspective with Diminishing Spaces The following document helps describe the basic process for generating a 3D representation of a simple 2D plan. For this exercise we will be
Given a point cloud, polygon, or sampled parametric curve, we can use transformations for several purposes:
 3 3.1 2D Given a point cloud, polygon, or sampled parametric curve, we can use transformations for several purposes: 1. Change coordinate frames (world, window, viewport, device, etc). 2. Compose objects
3 3.1 2D Given a point cloud, polygon, or sampled parametric curve, we can use transformations for several purposes: 1. Change coordinate frames (world, window, viewport, device, etc). 2. Compose objects
Relating Vanishing Points to Catadioptric Camera Calibration
 Relating Vanishing Points to Catadioptric Camera Calibration Wenting Duan* a, Hui Zhang b, Nigel M. Allinson a a Laboratory of Vision Engineering, University of Lincoln, Brayford Pool, Lincoln, U.K. LN6
Relating Vanishing Points to Catadioptric Camera Calibration Wenting Duan* a, Hui Zhang b, Nigel M. Allinson a a Laboratory of Vision Engineering, University of Lincoln, Brayford Pool, Lincoln, U.K. LN6
A System for Capturing High Resolution Images
 A System for Capturing High Resolution Images G.Voyatzis, G.Angelopoulos, A.Bors and I.Pitas Department of Informatics University of Thessaloniki BOX 451, 54006 Thessaloniki GREECE e-mail: [email protected]
A System for Capturing High Resolution Images G.Voyatzis, G.Angelopoulos, A.Bors and I.Pitas Department of Informatics University of Thessaloniki BOX 451, 54006 Thessaloniki GREECE e-mail: [email protected]
Manual for simulation of EB processing. Software ModeRTL
 1 Manual for simulation of EB processing Software ModeRTL How to get results. Software ModeRTL. Software ModeRTL consists of five thematic modules and service blocks. (See Fig.1). Analytic module is intended
1 Manual for simulation of EB processing Software ModeRTL How to get results. Software ModeRTL. Software ModeRTL consists of five thematic modules and service blocks. (See Fig.1). Analytic module is intended
B4 Computational Geometry
 3CG 2006 / B4 Computational Geometry David Murray [email protected] www.robots.o.ac.uk/ dwm/courses/3cg Michaelmas 2006 3CG 2006 2 / Overview Computational geometry is concerned with the derivation
3CG 2006 / B4 Computational Geometry David Murray [email protected] www.robots.o.ac.uk/ dwm/courses/3cg Michaelmas 2006 3CG 2006 2 / Overview Computational geometry is concerned with the derivation
Section V.2: Magnitudes, Directions, and Components of Vectors
 Section V.: Magnitudes, Directions, and Components of Vectors Vectors in the plane If we graph a vector in the coordinate plane instead of just a grid, there are a few things to note. Firstl, directions
Section V.: Magnitudes, Directions, and Components of Vectors Vectors in the plane If we graph a vector in the coordinate plane instead of just a grid, there are a few things to note. Firstl, directions
Projective Geometry. Projective Geometry
 Euclidean versus Euclidean geometry describes sapes as tey are Properties of objects tat are uncanged by rigid motions» Lengts» Angles» Parallelism Projective geometry describes objects as tey appear Lengts,
Euclidean versus Euclidean geometry describes sapes as tey are Properties of objects tat are uncanged by rigid motions» Lengts» Angles» Parallelism Projective geometry describes objects as tey appear Lengts,
Chapter 2 - Graphics Programming with JOGL
 Chapter 2 - Graphics Programming with JOGL Graphics Software: Classification and History JOGL Hello World Program 2D Coordinate Systems in JOGL Dealing with Window Reshaping 3D Coordinate Systems in JOGL
Chapter 2 - Graphics Programming with JOGL Graphics Software: Classification and History JOGL Hello World Program 2D Coordinate Systems in JOGL Dealing with Window Reshaping 3D Coordinate Systems in JOGL
SkillsUSA 2014 Contest Projects 3-D Visualization and Animation
 SkillsUSA Contest Projects 3-D Visualization and Animation Click the Print this Section button above to automatically print the specifications for this contest. Make sure your printer is turned on before
SkillsUSA Contest Projects 3-D Visualization and Animation Click the Print this Section button above to automatically print the specifications for this contest. Make sure your printer is turned on before
Technical Regulations 2015-2016
 F1 in Schools - 2014 World Finals Technical Regulations Technical Regulations 2015-2016 2013 - F1 in Schools Ltd. Page 1 of 27 3 September 2015 CONTENTS PREFACE SUMMARY OF MAIN REVISIONS FROM 2013 REGULATIONS...
F1 in Schools - 2014 World Finals Technical Regulations Technical Regulations 2015-2016 2013 - F1 in Schools Ltd. Page 1 of 27 3 September 2015 CONTENTS PREFACE SUMMARY OF MAIN REVISIONS FROM 2013 REGULATIONS...
MMGD0203 Multimedia Design MMGD0203 MULTIMEDIA DESIGN. Chapter 3 Graphics and Animations
 MMGD0203 MULTIMEDIA DESIGN Chapter 3 Graphics and Animations 1 Topics: Definition of Graphics Why use Graphics? Graphics Categories Graphics Qualities File Formats Types of Graphics Graphic File Size Introduction
MMGD0203 MULTIMEDIA DESIGN Chapter 3 Graphics and Animations 1 Topics: Definition of Graphics Why use Graphics? Graphics Categories Graphics Qualities File Formats Types of Graphics Graphic File Size Introduction
Quick Start Tutorial Metric version
 Quick Start Tutorial Metric version 1996-2009 Cadsoft Corporation. No part of this guide or the accompanying software may be reproduced or transmitted, electronically or mechanically, without written permission
Quick Start Tutorial Metric version 1996-2009 Cadsoft Corporation. No part of this guide or the accompanying software may be reproduced or transmitted, electronically or mechanically, without written permission
MAT 1341: REVIEW II SANGHOON BAEK
 MAT 1341: REVIEW II SANGHOON BAEK 1. Projections and Cross Product 1.1. Projections. Definition 1.1. Given a vector u, the rectangular (or perpendicular or orthogonal) components are two vectors u 1 and
MAT 1341: REVIEW II SANGHOON BAEK 1. Projections and Cross Product 1.1. Projections. Definition 1.1. Given a vector u, the rectangular (or perpendicular or orthogonal) components are two vectors u 1 and
F1 in Schools - 2014 World Finals Technical Regulations. 2014 WORLD FINALS Technical Regulations
 2014 WORLD FINALS Technical Regulations Refer also to the 2014 World Finals Competition Regulations. For World Finals use only. 2013 - F1 in Schools Ltd. Page 1 of 23 13 August 2014 Front Cover A1 Racing
2014 WORLD FINALS Technical Regulations Refer also to the 2014 World Finals Competition Regulations. For World Finals use only. 2013 - F1 in Schools Ltd. Page 1 of 23 13 August 2014 Front Cover A1 Racing
Introduction to CATIA V5
 Introduction to CATIA V5 Release 16 (A Hands-On Tutorial Approach) Kirstie Plantenberg University of Detroit Mercy SDC PUBLICATIONS Schroff Development Corporation www.schroff.com www.schroff-europe.com
Introduction to CATIA V5 Release 16 (A Hands-On Tutorial Approach) Kirstie Plantenberg University of Detroit Mercy SDC PUBLICATIONS Schroff Development Corporation www.schroff.com www.schroff-europe.com
SECTION 7-4 Algebraic Vectors
 7-4 lgebraic Vectors 531 SECTIN 7-4 lgebraic Vectors From Geometric Vectors to lgebraic Vectors Vector ddition and Scalar Multiplication Unit Vectors lgebraic Properties Static Equilibrium Geometric vectors
7-4 lgebraic Vectors 531 SECTIN 7-4 lgebraic Vectors From Geometric Vectors to lgebraic Vectors Vector ddition and Scalar Multiplication Unit Vectors lgebraic Properties Static Equilibrium Geometric vectors
IES <Virtual Environment> Tutorial. ModelIT (Version 6.0)
 IES Tutorial ModelIT (Version 6.0) 1 Introduction: ModelIT Tutorial This document shows you how to use ModelIT, IES s 3D building geometry modelling tool. The tutorial is intended
IES Tutorial ModelIT (Version 6.0) 1 Introduction: ModelIT Tutorial This document shows you how to use ModelIT, IES s 3D building geometry modelling tool. The tutorial is intended
sin(θ) = opp hyp cos(θ) = adj hyp tan(θ) = opp adj
 Math, Trigonometr and Vectors Geometr 33º What is the angle equal to? a) α = 7 b) α = 57 c) α = 33 d) α = 90 e) α cannot be determined α Trig Definitions Here's a familiar image. To make predictive models
Math, Trigonometr and Vectors Geometr 33º What is the angle equal to? a) α = 7 b) α = 57 c) α = 33 d) α = 90 e) α cannot be determined α Trig Definitions Here's a familiar image. To make predictive models
Microsoft Picture Manager. Picture Manager
 Picture Manager Picture Manager allows you to easily edit and organize the pictures on your computer. Picture Manager is an application that was included with Microsoft Office suite for Windows 2003 and
Picture Manager Picture Manager allows you to easily edit and organize the pictures on your computer. Picture Manager is an application that was included with Microsoft Office suite for Windows 2003 and
MAT188H1S Lec0101 Burbulla
 Winter 206 Linear Transformations A linear transformation T : R m R n is a function that takes vectors in R m to vectors in R n such that and T (u + v) T (u) + T (v) T (k v) k T (v), for all vectors u
Winter 206 Linear Transformations A linear transformation T : R m R n is a function that takes vectors in R m to vectors in R n such that and T (u + v) T (u) + T (v) T (k v) k T (v), for all vectors u
Image Formation. 7-year old s question. Reference. Lecture Overview. It receives light from all directions. Pinhole
 Image Formation Reerence http://en.wikipedia.org/wiki/lens_(optics) Reading: Chapter 1, Forsyth & Ponce Optional: Section 2.1, 2.3, Horn. The slides use illustrations rom these books Some o the ollowing
Image Formation Reerence http://en.wikipedia.org/wiki/lens_(optics) Reading: Chapter 1, Forsyth & Ponce Optional: Section 2.1, 2.3, Horn. The slides use illustrations rom these books Some o the ollowing
LEAVING CERT DCG SCHEME OF WORK
 2010-11 LEAVING CERT DCG SCHEME OF WORK ST OLIVER S COMMUNITY COLLEGE Mission statement The technology department aspires to provide a safe, stimulating environment where all students can develop their
2010-11 LEAVING CERT DCG SCHEME OF WORK ST OLIVER S COMMUNITY COLLEGE Mission statement The technology department aspires to provide a safe, stimulating environment where all students can develop their
CATIA for Design and Engineering. Version 5 Releases 14 & 15. David S. Kelley. Central Michigan University SDC
 CATIA for Design and Engineering ersion 5 Releases 4 & 5 David S. Kelley Central Michigan University SDC PUBLICATIONS Schroff Development Corporation www.schroff.com www.schroff-europe.com TUTORIAL Extruded
CATIA for Design and Engineering ersion 5 Releases 4 & 5 David S. Kelley Central Michigan University SDC PUBLICATIONS Schroff Development Corporation www.schroff.com www.schroff-europe.com TUTORIAL Extruded
Light and its effects
 Light and its effects Light and the speed of light Shadows Shadow films Pinhole camera (1) Pinhole camera (2) Reflection of light Image in a plane mirror An image in a plane mirror is: (i) the same size
Light and its effects Light and the speed of light Shadows Shadow films Pinhole camera (1) Pinhole camera (2) Reflection of light Image in a plane mirror An image in a plane mirror is: (i) the same size
Producing 2D Documentation from 3D Models in AutoCAD
 Producing 2D Documentation from 3D Models in AutoCAD David Cohn 4D Technologies AC4689 Modeling in 3D is fine, but eventually you need to produce 2D drawings. In this class, you will learn about tools
Producing 2D Documentation from 3D Models in AutoCAD David Cohn 4D Technologies AC4689 Modeling in 3D is fine, but eventually you need to produce 2D drawings. In this class, you will learn about tools
Technical Drawing. MEC1000 Spring 2006 Instructor: David Anderson
 Technical Drawing MEC1000 Spring 2006 Instructor: David Anderson Topics Drawing Views Drawing Standards Best Practices Creating Drawings in SolidWorks Spring 2006 MEC1000 Technical Drawing - D. Anderson
Technical Drawing MEC1000 Spring 2006 Instructor: David Anderson Topics Drawing Views Drawing Standards Best Practices Creating Drawings in SolidWorks Spring 2006 MEC1000 Technical Drawing - D. Anderson
