COMPLEX NUMBERS AND PHASORS
|
|
|
- Melvin Bond
- 9 years ago
- Views:
Transcription
1 COMPLEX NUMBERS AND PHASORS 1 Professor Andrew E. Yagle, EECS 206 Instructor, Fall 2005 Dept. of EECS, The University of Michigan, Ann Arbor, MI I. Abstract The purpose of this document is to introduce EECS 206 students to the concept of phasors complex numbers used to represent sinusoids, to simplify the math of manipulating sinusoids. Phasors will be used again in EECS 215 and 314. It also includes a brief primer on complex numbers and their manipulations. A. Table of contents by sections: 1. Abstract (you re reading this now) 2. Complex numbers: Magnitude, phase, real and imaginary parts 3. Complex numbers: Polar-to-Rectangular conversion and vice-versa 4. Complex numbers: Addition, subtraction, multiplication, division 5. Complex numbers: More complex manipulations 6. Phasors: Phasor-to-sinusoid conversions and vice-versa 7. Phasors: Real-world applications (borrowing from EECS 215) B. Motivation for using Phasors (other than against the EECS 206 instructor) What do complex numbers have to do with electrical engineering? What good are they? Before you say, Beam me up, Scotty, consider the following circuits problem: Circuits problem: A voltage source 5 cos(6t) is connected in series with a 4Ω resistor and a 1 2 H inductor. The goal is to compute the current i(t) which flows through all three devices. Hard Way: In EECS 215 or 314 you will learn that Kirchoff s voltage law leads to 5 cos(6t) 4i 1 2 dt = 0. In Math 216 you will learn to solve this using the trial solution i(t) = Acos(6t) + B sin(6t). Substituting this gives 5 cos(6t) 4Acos(6t) 4B sin(6t) Asin(6t) 1 26B cos(6t) = 0. Collecting terms gives [5 4A 3B] cos(6t) + [ 4B + 3A] sin(6t) = 0. Set t = 0 and t = π 12 5 = 4A + 3B and 0 = 3A 4B. Solving A = 0.8 and B = 0.6, so that i(t) = 0.8 cos(6t) sin(6t). Using the cosine addition formula three times, this simplifies to the answer i(t) = cos(6t 37 o ). Are we having fun yet? But if we use complex numbers and phasors, we can solve the problem this way: Easy Way: Phasor I = 5/[4 + j(6)(1/2)] = 5/(4 + j3) = 1e j37o i(t) = cos(6t 37 o ). Hard way or easy way? You make the call! Want to learn more about the easy way? Read on... di
2 2 II. Complex numbers: Magnitude, phase, real and imaginary parts A. You re in EECS Now! You ve seen complex numbers before. For example, solving the quadratic equation z 2 6z + 13 = 0 using the quadratic formula results in the complex number 3 + 2j and its complex conjugate 3 2j where... Wait a minute! j? It should be i! Wrong. You re in EECS now, and in EECS i denotes current and j = 1 (note the problem in the section above). Get used to it! Fortunately, Matlab accepts either i or j as 1. We now return you to your regularly scheduled program of complex numbers review. B. Euler s formula (Leonhard) Euler s formula relates complex exponentials and trig functions. It states that e jθ = cosθ + j sinθ (1) The easiest way to derive it is to set x = jθ in the power series for e x : e jθ = 1+(jθ)+ (jθ)2 2! + (jθ)3 3! + (jθ) = 1 θ2 4! 2! +θ4 4! θ6 6! This isn t a rigorous derivation, but it will do for EECS 206. ( ) θ +...+j 1! θ3 3! + θ5 5! +... = cosθ+j sin θ (2) Note the following immediate implications (these are worth writing on your exam cheat sheet): e jπ/2 = j and e j3π/2 = e jπ/2 = j (to visualize this, see below on Argand diagrams); e jπ = 1 and e jπ + 1 = 0 cogently relates the five most important numbers in mathematics; A few people wax rhapsodic about this formula (I think they need to get lives). C. Definitions of Sine and Cosine in Terms of e jθ By adding and subtracting Euler s formula and its complex conjugate, we get cosθ = 1 2 (ejθ + e jθ ); sin θ = 1 2j (ejθ e jθ ) (3) These are called the inverse Euler formulae in the official EECS 206 lecture notes. A mathematician would call them definitions of cosθ and sinθ (never mind all that opposite-over-hypotenuse stuff...) These are important formulae of which you will make extensive use in EECS 206. To remember them: cosθ is an even (symmetric) function of θ, so changing the sign of θ should not change the definition; sinθ is an odd (anti-symmetric) function, so changing the sign of θ should change the sign in the definition; The j in the denominator of sinθ is tricky; you simply have to remember it.
3 3 D. Polar and Rectangular Forms of Complex Numbers Multiplying Euler s formula by a constant M > 0 yields the two forms of complex numbers: POLAR { }} { { }} { z = }{{} M }{{} e jθ = M cosθ MAG ARG RECTANGULAR } {{ } REAL +j M sinθ } {{ } IMAG (4) This allows us to define two ways of representing a complex number: Its polar form z = Me jθ, in which M=its magnitude and θ=its phase; and Its rectangular form z = M cosθ + jm sin θ = x + jy, in which: x = M cos θ=its real part and y = M sin θ=its imaginary part. The following notation is used to represent the above four parts of a complex number z: Magnitude: M = z. Phase: θ = arg[z] (argument of z is another term for phase of z) Real part: x = Re[z]. Imaginary part: y = Im[z]. Warning: Im[3 + j4] = 4 NOT j4! Polar form is sometimes written using: z = Me jθ = M θ (this is easier to read since θ is larger). III. Complex numbers: Polar-to-Rectangular Conversion and vice-versa A. Procedures: Polar-to-Rectangular Conversion and vice-versa The above equation allows easy conversion between the polar and rectangular forms of a complex number: Given the polar form z = Me jθ, its rectangular form z = x + jy is computed using: x = M cosθ = Re[z]=real part of z; y = M sinθ = Im[z]=imaginary part of z. Given the rectangular form z = x + jy, its polar form z = Me jθ is computed using: M = x 2 + y 2 = z =magnitude of z; θ = arctan( y x ) = tan 1 ( y x )=phase of z. IF x < 0 then use θ = arctan( y x ) + π = tan 1 ( y x ) + π. What s this about x < 0? Try converting z = 1 j to polar form: M = ( 1) 2 + ( 1) 2 = 2 and θ = arctan( 1 1 ) = π 4 1 j = 2e jπ/4. NOT! (try P R). The problem is that there are two solutions to the always-correct tan θ = y x, 180o apart. You have to choose the correct one. The sign of the real part x tells you which one is correct. Your calculator has, somewhere on it, both an R P key or function and a P R key or function. Please don t ask me to find it for you; some of your calculators look like the dashboard on the space shuttle! Find them, and learn to use them you will use them a lot in EECS 206 and 215 or 314. B. Examples: Polar-to-Rectangular Conversion and vice-versa 3 + j4 = 5e j0.927 : 3 = 5 cos(0.927) 4 = 5 sin(0.927) 5 = = arctan( 4 3 ) 1 + j = 2e j0.785 : 1 = 2cos(0.785) 1 = 2sin(0.785) 2 = = arctan( 1 1 ) 5 + j12 = 13e j1.966 : 5 = 13 cos(1.966) 12 = 13 sin(1.966) 13 = = arctan( 12 5 ) + π
4 4 You can visualize these using an Argand diagram, which is just a plot of imaginary part vs. real part of a complex number. For example, z = 3 + j4 = 5e j0.927 is plotted at rectangular coordinates (3, 4) and polar coordinates (5, 0.927), where is the angle in radians measured counterclockwise from the positive real axis (try it). This is an excellent way of picking up errors, especially in the phase being off by π radians=180. o IV. Complex numbers: Addition, subtraction, multiplication, division So why bother with rectangular-to-polar or polar-to-rectangular conversions? Here s why: To multiply or divide complex numbers, convert them to polar form and use Me jθ Ne jφ = (MN)e j(θ+φ) ; In particular, note that the magnitude of a product is the product of the magnitudes; To add or subtract, convert to rectangular form and use (a + jb) + (c + jd) = (a + c) + j(b + d). The following two examples (side-by-side) show how to do this: 5e j e j0.785 = 6.4e j j4 1 + j = 1 + j7 P R P R R P R P R P P R 3 + j j = 4 + j5 5e j e j0.785 = 5 2e j1.71 add in rectangular form multiply in polar form Note that we have already seen all of the P R and R P conversions used here. Yes, for this simple example you could compute (3 + j4)(1 + j) = ((3 1) (4 1)) + j((4 1) + (3 1)) = 1 + j7 (5) but for more complicated examples you won t want to do this. Another example (from the official lecture notes): Compute 2 3e jπ/6 + 2e jπ/3 by converting polar to rectangular : = 2 3 cos(π/6) + j2 3sin(π/6) + 2 cos(π/3) + j2 sin( π/3) = 2 3( 3/2) + j2 3(1/2) + 2(1/2) j2( 3/2) = 4(!) (6) Another example, entirely in the polar domain: A. Complex Conjugates (2 3e jπ/6 )/(2e jπ/3 ) = ej(π/6 ( π/3)) = 3e jπ/2 = j 3 (7) V. Complex numbers: Complex Manipulations The complex conjugate z of z is z = x jy = Me jθ = M θ. This turns out to be useful: Re[z] = 1 2 (z + z ): We can get the real part by adding the complex conjugate and halving;
5 5 z 2 = zz : We can get magnitude by multiplying by the complex conjugate and taking a square root; e j2arg[z] = z z : We can get the phase by dividing by the complex conjugate and taking half the log; Also, z = z ; arg[z ] = arg[z]; z = Me jθ z = Me jθ ; 1 z = 1 M e jθ ; z = Me j(θ±π). B. Complex Expressions Try this: compute 5(8+j)(8+j6)(5+j12)(5+j10) 26(7+j4)(7+j24)(2+j11) (!) Are you kidding me? And yet it s quite easy: 5(8 + j)(8 + j6)(5 + j12)(5 + j10) 26(7 + j4)(7 + j24)(2 + j11) = j 8 + j6 5 + j j j4 7 + j j11 Two very important rules (they will be even more important in EECS 215 and 314): Magnitude of the product of complex numbers is product of magnitudes. Argument of the product of complex numbers is the sum of arguments. = (25)(65)(100)(169)(125) (26) 2 = 1 (65)(625)(125) (8) The following identity is true to an overall sign. Why? (Try doing this solely in rectangular form!) (a + jb)(c + jd) (e + jf)(g + jh) = (a 2 + b 2 )(c 2 + d 2 ) (e 2 + f 2 )(g 2 + h 2 ) exp j[tan 1 (b/a) + tan 1 (d/c) tan 1 (f/e) tan 1 (h/g)] (9) VI. Phasors: Phasor-to-sinusoid conversions and vice-versa A. Procedures: Phasor-to-sinusoid conversions and vice-versa The bottom line: A phasor is a complex number used to represent a sinusoid. In particular: sinusoid x(t) = M cos(ωt + θ), < t < functionof time phasor X = Me jθ = M cosθ + jm sin θ complexnumber What do these two things have to do with each other? Consider the following: x(t) = Re[Xe jωt ] = Re[Me jθ e jωt ] = Re[Me j(ωt+θ) ] = M cos(ωt + θ). This relates the phasor X with the sinusoidal signal x(t). Now apply this trick to the sum of two sinusoids at the same frequency: Acos(ωt + θ) + B cos(ωt + φ) = Re[Ae j(ωt+θ) + Be j(ωt+φ) ] = Re[e jωt (Ae jθ + Be jφ )] Note the crucial step: The complex exponential e jωt factors out of the sum! Now let Ae jθ + Be jφ = Ce jψ for some C and ψ (as we were doing before). Then: Re[e jωt (Ae jθ + Be jφ )] = Re[e jωt (Ce jψ )] = C cos(ωt + ψ). The trigonometry equation Acos(ωt + θ) + B cos(ωt + φ) = C cos(ωt + ψ) (ugh) Is equivalent to the complex number equation Ae jθ + Be jφ = Ce jψ (OK!) How does this work in practice? Try some examples:
6 6 B. Examples: Phasor-to-sinusoid conversions and vice-versa Example #1: Simplify 5 cos(ωt + 53 o ) + 2cos(ωt + 45 o ) The hard way: Use the cosine addition formula three times (the third time to simplify the result)(ugh). The easy way: Phasors: 5e j53o + 2e j45o = (3 + j4) + (1 + j) = (4 + j5) = 6.4e j51o. So 5 cos(ωt + 53 o ) + 2cos(ωt + 45 o ) = 6.4 cos(ωt + 51 o ). Example #2: Simplify cos(ωt + 30 o ) + cos(ωt o )) + cos(ωt 90 o ). The hard way: Use the cosine addition formula three times (the third time to simplify the result)(ugh). The easy way: Phasors: e j30o + e j150o + e j90o = 0 (think resultant; draw an Argand diagram). So cos(ωt + 30 o ) + cos(ωt o )) + cos(ωt 90 o ) = 0. You didn t even need your calculator! This fact is used in three-phase current (still used in some rural areas) so current flow is conserved. I could have made it a little harder by making the last term sin(ωt) = cos(ωt 90 o ). Use the trig identity sin(ωt + θ) = cos(ωt + θ π/2) as a definition, as necessary. VII. Phasors: Real-world applications (borrowing from EECS 215) Don t panic these won t be on any EECS 206 exams! (But they WILL be on EECS 215 or 314 exams.) In EECS 215 or 314 you will encounter a lot of circuits problems like this: Problem #1: A voltage source 26 cos(50t) is connected to a small motor. The motor is modelled by a 12Ω resistor (coil resistance) in series with a 0.1H inductor (coil inductance effects). Compute the current i(t) passing through the motor and the average power dissipated in the motor. In EECS 215 or 314, you will learn that the current phasor I and average power P can be written as: I = 26+j0 12+j50(0.1) = o = o i(t) = 2 cos(50t 22.6 o ). Peak current=2 amps (a lot!) P = 1 2 Re[V I ] = 1 2 Re[26( o )] = 26 cos(22.6 o ) = 24 watts. This next problem is about power factor correction, which uses lots of complex numbers and phasors: Problem #2: A blender motor is modelled by a 30Ω resistor (modelling the coil resistance) in series with a H inductor (modelling the inductive effects of the coil). What power is dissipated by the motor? The blender is plugged into a wall socket which delivers a sinusoidal voltage at 120 volts rms at 60 Hertz. This implies an amplitude of A = volts (did you know that peak voltage is 170 volts, not 120?) and a frequency of ω = 2π RAD SEC. Tell your aunt/uncle engineer you know about the number j0 rms current phasor = I = 30+j(2π60)(40/377) = 120+j0 30+j40 = o i(t) = cos(377t 53 o ). Average power dissipated = P = Re[V rms I rms] = Re[(120)(2.4e j53o )] = watts. Problem: The voltage and current are 53 o out of phase, so the motor draws more current than it should.
7 7 So what? Detroit Edison will charge you big-time for this! And they will be right! Why? Detroit Edison s generators need to generate more current than they should have to; Need physically bigger (thicker and heavier) transmission lines to carry the current; More current greater losses and heating (power dissipation) due to line resistance; Hotter transmission lines expand and sag, touching something; this causes blackouts. So what do we do? Hook a capacitor C in parallel with the motor. RMS current phasor: I rms = 120[1/(30 + j40) + j2π(60)c)] (see EECS 215 or 314 when you study admittance). What value of C makes the phase of I rms zero? You should obtain C = = 42.4µF. Then I rms = and average power dissipated=re[v rms Irms ] = (120)(1.44) = watts. But note: The current amplitude has dropped from amps to amps! We have almost halved the peak current, while maintaining average power=172.8 watts. A. Miscellaneous Problems The above problem shows why you care about problems like these: Problem #1: 2 cos(ωt + π 3 ) + Acos(ωt + 5π 4 ) = B cos(ωt) for what value of A? That is, what should the amplitude A be to make the left side be in phase with a pure cosine? Phasors: 2e jπ/3 + Ae j5π/4 = B 0 = Im[2e jπ/3 + Ae j5π/4 ] = 2 sin( π 3 ) + Asin(5π 4 ) A = 6. Note this is the same problem as this: For what A is 2e jπ/3 + Ae j5π/4 purely real? Problem #2: The amplitude of 5 cos(7t ) + Asin(7t) is 3 for what value of A? Phasors: 5e j Ae jπ/2 = 3e jθ (3 + j4) ja = 3 + j(4 A) has magnitude=3 only if A = 4. Note that in general this type of problem will have two solutions or none. Problem #3: Derive the trig identity cos(3θ) = cos 3 θ 3 cosθ sin 2 θ without using any trig. Cube Euler s formula: e j3θ = (cosθ + j sin θ) 3 = cos 3 θ + 3j cos 2 θ sinθ 3 cosθ sin 2 θ j sin 3 θ. Equating real parts gives the desired trig identity. Also: try equating imaginary parts. Problem #4: Compute and put in rectangular form ( 2 ( 2 ) (1 + j) = (1e jπ/4 ) 1003 = e j1000π/4 e j3π/4 = e j3π/4 = (1 + j) ) This is a stunt, ( 1 + j). but illustrative. Problem #5: Compute the five 5 th roots of 32, i.e., the five solutions of z 5 32 = 0. {2e j2π1/5, 2e j2π2/5, 2e j2π3/5, 2e j2π4/5, 2e j2π5/5 = 2}. HINT: Draw an Argand diagram. We will use this result for comb filters later on in EECS 206.
Introduction to Complex Numbers in Physics/Engineering
 Introduction to Complex Numbers in Physics/Engineering ference: Mary L. Boas, Mathematical Methods in the Physical Sciences Chapter 2 & 14 George Arfken, Mathematical Methods for Physicists Chapter 6 The
Introduction to Complex Numbers in Physics/Engineering ference: Mary L. Boas, Mathematical Methods in the Physical Sciences Chapter 2 & 14 George Arfken, Mathematical Methods for Physicists Chapter 6 The
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT
 EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
2.2 Magic with complex exponentials
 2.2. MAGIC WITH COMPLEX EXPONENTIALS 97 2.2 Magic with complex exponentials We don t really know what aspects of complex variables you learned about in high school, so the goal here is to start more or
2.2. MAGIC WITH COMPLEX EXPONENTIALS 97 2.2 Magic with complex exponentials We don t really know what aspects of complex variables you learned about in high school, so the goal here is to start more or
A few words about imaginary numbers (and electronics) Mark Cohen [email protected]
 A few words about imaginary numbers (and electronics) Mark Cohen mscohen@guclaedu While most of us have seen imaginary numbers in high school algebra, the topic is ordinarily taught in abstraction without
A few words about imaginary numbers (and electronics) Mark Cohen mscohen@guclaedu While most of us have seen imaginary numbers in high school algebra, the topic is ordinarily taught in abstraction without
Phasors. Phasors. by Prof. Dr. Osman SEVAİOĞLU Electrical and Electronics Engineering Department. ^ V cos (wt + θ) ^ V sin (wt + θ)
 V cos (wt θ) V sin (wt θ) by Prof. Dr. Osman SEVAİOĞLU Electrical and Electronics Engineering Department EE 209 Fundamentals of Electrical and Electronics Engineering, Prof. Dr. O. SEVAİOĞLU, Page 1 Vector
V cos (wt θ) V sin (wt θ) by Prof. Dr. Osman SEVAİOĞLU Electrical and Electronics Engineering Department EE 209 Fundamentals of Electrical and Electronics Engineering, Prof. Dr. O. SEVAİOĞLU, Page 1 Vector
ANALYTICAL METHODS FOR ENGINEERS
 UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
CIRCUITS LABORATORY EXPERIMENT 3. AC Circuit Analysis
 CIRCUITS LABORATORY EXPERIMENT 3 AC Circuit Analysis 3.1 Introduction The steady-state behavior of circuits energized by sinusoidal sources is an important area of study for several reasons. First, the
CIRCUITS LABORATORY EXPERIMENT 3 AC Circuit Analysis 3.1 Introduction The steady-state behavior of circuits energized by sinusoidal sources is an important area of study for several reasons. First, the
Unit2: Resistor/Capacitor-Filters
 Unit2: Resistor/Capacitor-Filters Physics335 Student October 3, 27 Physics 335-Section Professor J. Hobbs Partner: Physics335 Student2 Abstract Basic RC-filters were constructed and properties such as
Unit2: Resistor/Capacitor-Filters Physics335 Student October 3, 27 Physics 335-Section Professor J. Hobbs Partner: Physics335 Student2 Abstract Basic RC-filters were constructed and properties such as
Algebra. Exponents. Absolute Value. Simplify each of the following as much as possible. 2x y x + y y. xxx 3. x x x xx x. 1. Evaluate 5 and 123
 Algebra Eponents Simplify each of the following as much as possible. 1 4 9 4 y + y y. 1 5. 1 5 4. y + y 4 5 6 5. + 1 4 9 10 1 7 9 0 Absolute Value Evaluate 5 and 1. Eliminate the absolute value bars from
Algebra Eponents Simplify each of the following as much as possible. 1 4 9 4 y + y y. 1 5. 1 5 4. y + y 4 5 6 5. + 1 4 9 10 1 7 9 0 Absolute Value Evaluate 5 and 1. Eliminate the absolute value bars from
1 Introduction. 2 Complex Exponential Notation. J.L. Kirtley Jr.
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.06 Introduction to Power Systems Class Notes Chapter AC Power Flow in Linear Networks J.L. Kirtley Jr.
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.06 Introduction to Power Systems Class Notes Chapter AC Power Flow in Linear Networks J.L. Kirtley Jr.
Alternating-Current Circuits
 hapter 1 Alternating-urrent ircuits 1.1 A Sources... 1-1. Simple A circuits... 1-3 1..1 Purely esistive load... 1-3 1.. Purely Inductive oad... 1-5 1..3 Purely apacitive oad... 1-7 1.3 The Series ircuit...
hapter 1 Alternating-urrent ircuits 1.1 A Sources... 1-1. Simple A circuits... 1-3 1..1 Purely esistive load... 1-3 1.. Purely Inductive oad... 1-5 1..3 Purely apacitive oad... 1-7 1.3 The Series ircuit...
Chapter 12 Driven RLC Circuits
 hapter Driven ircuits. A Sources... -. A ircuits with a Source and One ircuit Element... -3.. Purely esistive oad... -3.. Purely Inductive oad... -6..3 Purely apacitive oad... -8.3 The Series ircuit...
hapter Driven ircuits. A Sources... -. A ircuits with a Source and One ircuit Element... -3.. Purely esistive oad... -3.. Purely Inductive oad... -6..3 Purely apacitive oad... -8.3 The Series ircuit...
THE COMPLEX EXPONENTIAL FUNCTION
 Math 307 THE COMPLEX EXPONENTIAL FUNCTION (These notes assume you are already familiar with the basic properties of complex numbers.) We make the following definition e iθ = cos θ + i sin θ. (1) This formula
Math 307 THE COMPLEX EXPONENTIAL FUNCTION (These notes assume you are already familiar with the basic properties of complex numbers.) We make the following definition e iθ = cos θ + i sin θ. (1) This formula
L and C connected together. To be able: To analyse some basic circuits.
 circuits: Sinusoidal Voltages and urrents Aims: To appreciate: Similarities between oscillation in circuit and mechanical pendulum. Role of energy loss mechanisms in damping. Why we study sinusoidal signals
circuits: Sinusoidal Voltages and urrents Aims: To appreciate: Similarities between oscillation in circuit and mechanical pendulum. Role of energy loss mechanisms in damping. Why we study sinusoidal signals
SIGNAL PROCESSING & SIMULATION NEWSLETTER
 1 of 10 1/25/2008 3:38 AM SIGNAL PROCESSING & SIMULATION NEWSLETTER Note: This is not a particularly interesting topic for anyone other than those who ar e involved in simulation. So if you have difficulty
1 of 10 1/25/2008 3:38 AM SIGNAL PROCESSING & SIMULATION NEWSLETTER Note: This is not a particularly interesting topic for anyone other than those who ar e involved in simulation. So if you have difficulty
2 Session Two - Complex Numbers and Vectors
 PH2011 Physics 2A Maths Revision - Session 2: Complex Numbers and Vectors 1 2 Session Two - Complex Numbers and Vectors 2.1 What is a Complex Number? The material on complex numbers should be familiar
PH2011 Physics 2A Maths Revision - Session 2: Complex Numbers and Vectors 1 2 Session Two - Complex Numbers and Vectors 2.1 What is a Complex Number? The material on complex numbers should be familiar
Electrical Resonance
 Electrical Resonance (R-L-C series circuit) APPARATUS 1. R-L-C Circuit board 2. Signal generator 3. Oscilloscope Tektronix TDS1002 with two sets of leads (see Introduction to the Oscilloscope ) INTRODUCTION
Electrical Resonance (R-L-C series circuit) APPARATUS 1. R-L-C Circuit board 2. Signal generator 3. Oscilloscope Tektronix TDS1002 with two sets of leads (see Introduction to the Oscilloscope ) INTRODUCTION
Week 13 Trigonometric Form of Complex Numbers
 Week Trigonometric Form of Complex Numbers Overview In this week of the course, which is the last week if you are not going to take calculus, we will look at how Trigonometry can sometimes help in working
Week Trigonometric Form of Complex Numbers Overview In this week of the course, which is the last week if you are not going to take calculus, we will look at how Trigonometry can sometimes help in working
7. Beats. sin( + λ) + sin( λ) = 2 cos(λ) sin( )
 34 7. Beats 7.1. What beats are. Musicians tune their instruments using beats. Beats occur when two very nearby pitches are sounded simultaneously. We ll make a mathematical study of this effect, using
34 7. Beats 7.1. What beats are. Musicians tune their instruments using beats. Beats occur when two very nearby pitches are sounded simultaneously. We ll make a mathematical study of this effect, using
Trigonometry for AC circuits
 Trigonometry for AC circuits This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Trigonometry for AC circuits This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
COMPLEX NUMBERS. a bi c di a c b d i. a bi c di a c b d i For instance, 1 i 4 7i 1 4 1 7 i 5 6i
 COMPLEX NUMBERS _4+i _-i FIGURE Complex numbers as points in the Arg plane i _i +i -i A complex number can be represented by an expression of the form a bi, where a b are real numbers i is a symbol with
COMPLEX NUMBERS _4+i _-i FIGURE Complex numbers as points in the Arg plane i _i +i -i A complex number can be represented by an expression of the form a bi, where a b are real numbers i is a symbol with
Lecture - 4 Diode Rectifier Circuits
 Basic Electronics (Module 1 Semiconductor Diodes) Dr. Chitralekha Mahanta Department of Electronics and Communication Engineering Indian Institute of Technology, Guwahati Lecture - 4 Diode Rectifier Circuits
Basic Electronics (Module 1 Semiconductor Diodes) Dr. Chitralekha Mahanta Department of Electronics and Communication Engineering Indian Institute of Technology, Guwahati Lecture - 4 Diode Rectifier Circuits
Chapter 35 Alternating Current Circuits
 hapter 35 Alternating urrent ircuits ac-ircuits Phasor Diagrams Resistors, apacitors and nductors in ac-ircuits R ac-ircuits ac-ircuit power. Resonance Transformers ac ircuits Alternating currents and
hapter 35 Alternating urrent ircuits ac-ircuits Phasor Diagrams Resistors, apacitors and nductors in ac-ircuits R ac-ircuits ac-ircuit power. Resonance Transformers ac ircuits Alternating currents and
ε: Voltage output of Signal Generator (also called the Source voltage or Applied
 Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Using the Impedance Method
 Using the Impedance Method The impedance method allows us to completely eliminate the differential equation approach for the determination of the response of circuits. In fact the impedance method even
Using the Impedance Method The impedance method allows us to completely eliminate the differential equation approach for the determination of the response of circuits. In fact the impedance method even
GRE Prep: Precalculus
 GRE Prep: Precalculus Franklin H.J. Kenter 1 Introduction These are the notes for the Precalculus section for the GRE Prep session held at UCSD in August 2011. These notes are in no way intended to teach
GRE Prep: Precalculus Franklin H.J. Kenter 1 Introduction These are the notes for the Precalculus section for the GRE Prep session held at UCSD in August 2011. These notes are in no way intended to teach
Trigonometry Hard Problems
 Solve the problem. This problem is very difficult to understand. Let s see if we can make sense of it. Note that there are multiple interpretations of the problem and that they are all unsatisfactory.
Solve the problem. This problem is very difficult to understand. Let s see if we can make sense of it. Note that there are multiple interpretations of the problem and that they are all unsatisfactory.
Euler s Formula Math 220
 Euler s Formula Math 0 last change: Sept 3, 05 Complex numbers A complex number is an expression of the form x+iy where x and y are real numbers and i is the imaginary square root of. For example, + 3i
Euler s Formula Math 0 last change: Sept 3, 05 Complex numbers A complex number is an expression of the form x+iy where x and y are real numbers and i is the imaginary square root of. For example, + 3i
Current and Temperature Ratings
 Document 361-1 Current and Temperature Ratings Introduction This application note describes: How to interpret Coilcraft inductor current and temperature ratings Our current ratings measurement method and
Document 361-1 Current and Temperature Ratings Introduction This application note describes: How to interpret Coilcraft inductor current and temperature ratings Our current ratings measurement method and
Solutions to Exercises, Section 5.1
 Instructor s Solutions Manual, Section 5.1 Exercise 1 Solutions to Exercises, Section 5.1 1. Find all numbers t such that ( 1 3,t) is a point on the unit circle. For ( 1 3,t)to be a point on the unit circle
Instructor s Solutions Manual, Section 5.1 Exercise 1 Solutions to Exercises, Section 5.1 1. Find all numbers t such that ( 1 3,t) is a point on the unit circle. For ( 1 3,t)to be a point on the unit circle
LABORATORY 10 TIME AVERAGES, RMS VALUES AND THE BRIDGE RECTIFIER. Bridge Rectifier
 LABORATORY 10 TIME AVERAGES, RMS VALUES AND THE BRIDGE RECTIFIER Full-wave Rectification: Bridge Rectifier For many electronic circuits, DC supply voltages are required but only AC voltages are available.
LABORATORY 10 TIME AVERAGES, RMS VALUES AND THE BRIDGE RECTIFIER Full-wave Rectification: Bridge Rectifier For many electronic circuits, DC supply voltages are required but only AC voltages are available.
Signal Processing First Lab 01: Introduction to MATLAB. 3. Learn a little about advanced programming techniques for MATLAB, i.e., vectorization.
 Signal Processing First Lab 01: Introduction to MATLAB Pre-Lab and Warm-Up: You should read at least the Pre-Lab and Warm-up sections of this lab assignment and go over all exercises in the Pre-Lab section
Signal Processing First Lab 01: Introduction to MATLAB Pre-Lab and Warm-Up: You should read at least the Pre-Lab and Warm-up sections of this lab assignment and go over all exercises in the Pre-Lab section
SOLVING TRIGONOMETRIC EQUATIONS
 Mathematics Revision Guides Solving Trigonometric Equations Page 1 of 17 M.K. HOME TUITION Mathematics Revision Guides Level: AS / A Level AQA : C2 Edexcel: C2 OCR: C2 OCR MEI: C2 SOLVING TRIGONOMETRIC
Mathematics Revision Guides Solving Trigonometric Equations Page 1 of 17 M.K. HOME TUITION Mathematics Revision Guides Level: AS / A Level AQA : C2 Edexcel: C2 OCR: C2 OCR MEI: C2 SOLVING TRIGONOMETRIC
Equivalent Circuits and Transfer Functions
 R eq isc Equialent Circuits and Transfer Functions Samantha R Summerson 14 September, 009 1 Equialent Circuits eq ± Figure 1: Théenin equialent circuit. i sc R eq oc Figure : Mayer-Norton equialent circuit.
R eq isc Equialent Circuits and Transfer Functions Samantha R Summerson 14 September, 009 1 Equialent Circuits eq ± Figure 1: Théenin equialent circuit. i sc R eq oc Figure : Mayer-Norton equialent circuit.
Solutions for Math 311 Assignment #1
 Solutions for Math 311 Assignment #1 (1) Show that (a) Re(iz) Im(z); (b) Im(iz) Re(z). Proof. Let z x + yi with x Re(z) and y Im(z). Then Re(iz) Re( y + xi) y Im(z) and Im(iz) Im( y + xi) x Re(z). () Verify
Solutions for Math 311 Assignment #1 (1) Show that (a) Re(iz) Im(z); (b) Im(iz) Re(z). Proof. Let z x + yi with x Re(z) and y Im(z). Then Re(iz) Re( y + xi) y Im(z) and Im(iz) Im( y + xi) x Re(z). () Verify
TRIGONOMETRY Compound & Double angle formulae
 TRIGONOMETRY Compound & Double angle formulae In order to master this section you must first learn the formulae, even though they will be given to you on the matric formula sheet. We call these formulae
TRIGONOMETRY Compound & Double angle formulae In order to master this section you must first learn the formulae, even though they will be given to you on the matric formula sheet. We call these formulae
PHASOR DIAGRAMS HANDS-ON RELAY SCHOOL WSU PULLMAN, WA. RON ALEXANDER - BPA
 PHASOR DIAGRAMS HANDS-ON RELAY SCHOOL WSU PULLMAN, WA. RON ALEXANDER - BPA What are phasors??? In normal practice, the phasor represents the rms maximum value of the positive half cycle of the sinusoid
PHASOR DIAGRAMS HANDS-ON RELAY SCHOOL WSU PULLMAN, WA. RON ALEXANDER - BPA What are phasors??? In normal practice, the phasor represents the rms maximum value of the positive half cycle of the sinusoid
Direction of Induced Current
 Direction of Induced Current Bar magnet moves through coil Current induced in coil A S N v Reverse pole Induced current changes sign B N S v v Coil moves past fixed bar magnet Current induced in coil as
Direction of Induced Current Bar magnet moves through coil Current induced in coil A S N v Reverse pole Induced current changes sign B N S v v Coil moves past fixed bar magnet Current induced in coil as
Mathematics. (www.tiwariacademy.com : Focus on free Education) (Chapter 5) (Complex Numbers and Quadratic Equations) (Class XI)
 ( : Focus on free Education) Miscellaneous Exercise on chapter 5 Question 1: Evaluate: Answer 1: 1 ( : Focus on free Education) Question 2: For any two complex numbers z1 and z2, prove that Re (z1z2) =
( : Focus on free Education) Miscellaneous Exercise on chapter 5 Question 1: Evaluate: Answer 1: 1 ( : Focus on free Education) Question 2: For any two complex numbers z1 and z2, prove that Re (z1z2) =
Lecturer: James Grimbleby URL: http://www.personal.rdg.ac.uk/~stsgrimb/ email: j.b.grimbleby reading.ac.uk
 AC Circuit Analysis Module: SEEA5 Systems and Circuits Lecturer: UL: http://www.personal.rdg.ac.uk/~stsgrimb/ email:.b.grimbleby reading.ac.uk Number of Lectures: ecommended text book: David Irwin and
AC Circuit Analysis Module: SEEA5 Systems and Circuits Lecturer: UL: http://www.personal.rdg.ac.uk/~stsgrimb/ email:.b.grimbleby reading.ac.uk Number of Lectures: ecommended text book: David Irwin and
Electromagnetism Laws and Equations
 Electromagnetism Laws and Equations Andrew McHutchon Michaelmas 203 Contents Electrostatics. Electric E- and D-fields............................................. Electrostatic Force............................................2
Electromagnetism Laws and Equations Andrew McHutchon Michaelmas 203 Contents Electrostatics. Electric E- and D-fields............................................. Electrostatic Force............................................2
Trigonometry Review with the Unit Circle: All the trig. you ll ever need to know in Calculus
 Trigonometry Review with the Unit Circle: All the trig. you ll ever need to know in Calculus Objectives: This is your review of trigonometry: angles, six trig. functions, identities and formulas, graphs:
Trigonometry Review with the Unit Circle: All the trig. you ll ever need to know in Calculus Objectives: This is your review of trigonometry: angles, six trig. functions, identities and formulas, graphs:
4.1. COMPLEX NUMBERS
 4.1. COMPLEX NUMBERS What You Should Learn Use the imaginary unit i to write complex numbers. Add, subtract, and multiply complex numbers. Use complex conjugates to write the quotient of two complex numbers
4.1. COMPLEX NUMBERS What You Should Learn Use the imaginary unit i to write complex numbers. Add, subtract, and multiply complex numbers. Use complex conjugates to write the quotient of two complex numbers
COMPLEX NUMBERS AND SERIES. Contents
 COMPLEX NUMBERS AND SERIES MIKE BOYLE Contents 1. Complex Numbers Definition 1.1. A complex number is a number z of the form z = x + iy, where x and y are real numbers, and i is another number such that
COMPLEX NUMBERS AND SERIES MIKE BOYLE Contents 1. Complex Numbers Definition 1.1. A complex number is a number z of the form z = x + iy, where x and y are real numbers, and i is another number such that
FUNDAMENTALS OF ENGINEERING (FE) EXAMINATION REVIEW
 FE: Electric Circuits C.A. Gross EE1-1 FUNDAMENTALS OF ENGINEERING (FE) EXAMINATION REIEW ELECTRICAL ENGINEERING Charles A. Gross, Professor Emeritus Electrical and Comp Engineering Auburn University Broun
FE: Electric Circuits C.A. Gross EE1-1 FUNDAMENTALS OF ENGINEERING (FE) EXAMINATION REIEW ELECTRICAL ENGINEERING Charles A. Gross, Professor Emeritus Electrical and Comp Engineering Auburn University Broun
MAC 1114. Learning Objectives. Module 10. Polar Form of Complex Numbers. There are two major topics in this module:
 MAC 1114 Module 10 Polar Form of Complex Numbers Learning Objectives Upon completing this module, you should be able to: 1. Identify and simplify imaginary and complex numbers. 2. Add and subtract complex
MAC 1114 Module 10 Polar Form of Complex Numbers Learning Objectives Upon completing this module, you should be able to: 1. Identify and simplify imaginary and complex numbers. 2. Add and subtract complex
BASIC ELECTRONICS AC CIRCUIT ANALYSIS. December 2011
 AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure 2. R. Figure 1.
 Examples of Transient and RL Circuits. The Series RLC Circuit Impulse response of Circuit. Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure.
Examples of Transient and RL Circuits. The Series RLC Circuit Impulse response of Circuit. Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure.
Frequency Response of FIR Filters
 Frequency Response of FIR Filters Chapter 6 This chapter continues the study of FIR filters from Chapter 5, but the emphasis is frequency response, which relates to how the filter responds to an input
Frequency Response of FIR Filters Chapter 6 This chapter continues the study of FIR filters from Chapter 5, but the emphasis is frequency response, which relates to how the filter responds to an input
AC CIRCUITS - CAPACITORS AND INDUCTORS
 EXPRIMENT#8 AC CIRCUITS - CAPACITORS AND INDUCTORS NOTE: Two weeks are allocated for this experiment. Before performing this experiment, review the Proper Oscilloscope Use section of Experiment #7. Objective
EXPRIMENT#8 AC CIRCUITS - CAPACITORS AND INDUCTORS NOTE: Two weeks are allocated for this experiment. Before performing this experiment, review the Proper Oscilloscope Use section of Experiment #7. Objective
First Order Circuits. EENG223 Circuit Theory I
 First Order Circuits EENG223 Circuit Theory I First Order Circuits A first-order circuit can only contain one energy storage element (a capacitor or an inductor). The circuit will also contain resistance.
First Order Circuits EENG223 Circuit Theory I First Order Circuits A first-order circuit can only contain one energy storage element (a capacitor or an inductor). The circuit will also contain resistance.
Math Placement Test Practice Problems
 Math Placement Test Practice Problems The following problems cover material that is used on the math placement test to place students into Math 1111 College Algebra, Math 1113 Precalculus, and Math 2211
Math Placement Test Practice Problems The following problems cover material that is used on the math placement test to place students into Math 1111 College Algebra, Math 1113 Precalculus, and Math 2211
Positive Feedback and Oscillators
 Physics 3330 Experiment #6 Fall 1999 Positive Feedback and Oscillators Purpose In this experiment we will study how spontaneous oscillations may be caused by positive feedback. You will construct an active
Physics 3330 Experiment #6 Fall 1999 Positive Feedback and Oscillators Purpose In this experiment we will study how spontaneous oscillations may be caused by positive feedback. You will construct an active
The D.C Power Supply
 The D.C Power Supply Voltage Step Down Electrical Isolation Converts Bipolar signal to Unipolar Half or Full wave Smoothes the voltage variation Still has some ripples Reduce ripples Stabilize the output
The D.C Power Supply Voltage Step Down Electrical Isolation Converts Bipolar signal to Unipolar Half or Full wave Smoothes the voltage variation Still has some ripples Reduce ripples Stabilize the output
DIODE CIRCUITS LABORATORY. Fig. 8.1a Fig 8.1b
 DIODE CIRCUITS LABORATORY A solid state diode consists of a junction of either dissimilar semiconductors (pn junction diode) or a metal and a semiconductor (Schottky barrier diode). Regardless of the type,
DIODE CIRCUITS LABORATORY A solid state diode consists of a junction of either dissimilar semiconductors (pn junction diode) or a metal and a semiconductor (Schottky barrier diode). Regardless of the type,
Reading assignment: All students should read the Appendix about using oscilloscopes.
 10. A ircuits* Objective: To learn how to analyze current and voltage relationships in alternating current (a.c.) circuits. You will use the method of phasors, or the vector addition of rotating vectors
10. A ircuits* Objective: To learn how to analyze current and voltage relationships in alternating current (a.c.) circuits. You will use the method of phasors, or the vector addition of rotating vectors
www.mathsbox.org.uk ab = c a If the coefficients a,b and c are real then either α and β are real or α and β are complex conjugates
 Further Pure Summary Notes. Roots of Quadratic Equations For a quadratic equation ax + bx + c = 0 with roots α and β Sum of the roots Product of roots a + b = b a ab = c a If the coefficients a,b and c
Further Pure Summary Notes. Roots of Quadratic Equations For a quadratic equation ax + bx + c = 0 with roots α and β Sum of the roots Product of roots a + b = b a ab = c a If the coefficients a,b and c
Exponents and Radicals
 Exponents and Radicals (a + b) 10 Exponents are a very important part of algebra. An exponent is just a convenient way of writing repeated multiplications of the same number. Radicals involve the use of
Exponents and Radicals (a + b) 10 Exponents are a very important part of algebra. An exponent is just a convenient way of writing repeated multiplications of the same number. Radicals involve the use of
Evaluating trigonometric functions
 MATH 1110 009-09-06 Evaluating trigonometric functions Remark. Throughout this document, remember the angle measurement convention, which states that if the measurement of an angle appears without units,
MATH 1110 009-09-06 Evaluating trigonometric functions Remark. Throughout this document, remember the angle measurement convention, which states that if the measurement of an angle appears without units,
Area and Arc Length in Polar Coordinates
 Area and Arc Length in Polar Coordinates The Cartesian Coordinate System (rectangular coordinates) is not always the most convenient way to describe points, or relations in the plane. There are certainly
Area and Arc Length in Polar Coordinates The Cartesian Coordinate System (rectangular coordinates) is not always the most convenient way to describe points, or relations in the plane. There are certainly
= V peak 2 = 0.707V peak
 BASIC ELECTRONICS - RECTIFICATION AND FILTERING PURPOSE Suppose that you wanted to build a simple DC electronic power supply, which operated off of an AC input (e.g., something you might plug into a standard
BASIC ELECTRONICS - RECTIFICATION AND FILTERING PURPOSE Suppose that you wanted to build a simple DC electronic power supply, which operated off of an AC input (e.g., something you might plug into a standard
Elementary Functions
 Chapter Three Elementary Functions 31 Introduction Complex functions are, of course, quite easy to come by they are simply ordered pairs of real-valued functions of two variables We have, however, already
Chapter Three Elementary Functions 31 Introduction Complex functions are, of course, quite easy to come by they are simply ordered pairs of real-valued functions of two variables We have, however, already
580.439 Course Notes: Linear circuit theory and differential equations
 58.439 ourse Notes: Linear circuit theory and differential equations eading: Koch, h. ; any text on linear signal and system theory can be consulted for more details. These notes will review the basics
58.439 ourse Notes: Linear circuit theory and differential equations eading: Koch, h. ; any text on linear signal and system theory can be consulted for more details. These notes will review the basics
Trigonometric Functions and Triangles
 Trigonometric Functions and Triangles Dr. Philippe B. Laval Kennesaw STate University August 27, 2010 Abstract This handout defines the trigonometric function of angles and discusses the relationship between
Trigonometric Functions and Triangles Dr. Philippe B. Laval Kennesaw STate University August 27, 2010 Abstract This handout defines the trigonometric function of angles and discusses the relationship between
Solving Rational Equations
 Lesson M Lesson : Student Outcomes Students solve rational equations, monitoring for the creation of extraneous solutions. Lesson Notes In the preceding lessons, students learned to add, subtract, multiply,
Lesson M Lesson : Student Outcomes Students solve rational equations, monitoring for the creation of extraneous solutions. Lesson Notes In the preceding lessons, students learned to add, subtract, multiply,
Power measurement in balanced 3 phase circuits and power factor improvement. 1 Power in Single Phase Circuits. Experiment no 1
 Experiment no 1 Power measurement in balanced 3 phase circuits and power factor improvement 1 Power in Single Phase Circuits Let v = m cos(ωt) = cos(ωt) is the voltage applied to a R-L circuit and i =
Experiment no 1 Power measurement in balanced 3 phase circuits and power factor improvement 1 Power in Single Phase Circuits Let v = m cos(ωt) = cos(ωt) is the voltage applied to a R-L circuit and i =
RLC Resonant Circuits
 C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
Higher Education Math Placement
 Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
BASIC MATHEMATICS FOR ELECTRICITY
 MEBA Engineering School BASIC MATHEMATICS FOR ELECTRICITY (Revised: January 2002) This book belongs to: math\cover.vsd (yellow) 01/01/2002 This page is intentionally left blank. Preface Most of this material
MEBA Engineering School BASIC MATHEMATICS FOR ELECTRICITY (Revised: January 2002) This book belongs to: math\cover.vsd (yellow) 01/01/2002 This page is intentionally left blank. Preface Most of this material
SAT Subject Math Level 2 Facts & Formulas
 Numbers, Sequences, Factors Integers:..., -3, -2, -1, 0, 1, 2, 3,... Reals: integers plus fractions, decimals, and irrationals ( 2, 3, π, etc.) Order Of Operations: Arithmetic Sequences: PEMDAS (Parentheses
Numbers, Sequences, Factors Integers:..., -3, -2, -1, 0, 1, 2, 3,... Reals: integers plus fractions, decimals, and irrationals ( 2, 3, π, etc.) Order Of Operations: Arithmetic Sequences: PEMDAS (Parentheses
AP PHYSICS C Mechanics - SUMMER ASSIGNMENT FOR 2016-2017
 AP PHYSICS C Mechanics - SUMMER ASSIGNMENT FOR 2016-2017 Dear Student: The AP physics course you have signed up for is designed to prepare you for a superior performance on the AP test. To complete material
AP PHYSICS C Mechanics - SUMMER ASSIGNMENT FOR 2016-2017 Dear Student: The AP physics course you have signed up for is designed to prepare you for a superior performance on the AP test. To complete material
Transmission Lines. Smith Chart
 Smith Chart The Smith chart is one of the most useful graphical tools for high frequency circuit applications. The chart provides a clever way to visualize complex functions and it continues to endure
Smith Chart The Smith chart is one of the most useful graphical tools for high frequency circuit applications. The chart provides a clever way to visualize complex functions and it continues to endure
1 TRIGONOMETRY. 1.0 Introduction. 1.1 Sum and product formulae. Objectives
 TRIGONOMETRY Chapter Trigonometry Objectives After studying this chapter you should be able to handle with confidence a wide range of trigonometric identities; be able to express linear combinations of
TRIGONOMETRY Chapter Trigonometry Objectives After studying this chapter you should be able to handle with confidence a wide range of trigonometric identities; be able to express linear combinations of
Critical thin-film processes such as deposition and etching take place in a vacuum
 WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
Solution Derivations for Capa #11
 Solution Derivations for Capa #11 Caution: The symbol E is used interchangeably for energy and EMF. 1) DATA: V b = 5.0 V, = 155 Ω, L = 8.400 10 2 H. In the diagram above, what is the voltage across the
Solution Derivations for Capa #11 Caution: The symbol E is used interchangeably for energy and EMF. 1) DATA: V b = 5.0 V, = 155 Ω, L = 8.400 10 2 H. In the diagram above, what is the voltage across the
Ver 3537 E1.1 Analysis of Circuits (2014) E1.1 Circuit Analysis. Problem Sheet 1 (Lectures 1 & 2)
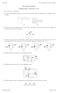 Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
Oscillations. Vern Lindberg. June 10, 2010
 Oscillations Vern Lindberg June 10, 2010 You have discussed oscillations in Vibs and Waves: we will therefore touch lightly on Chapter 3, mainly trying to refresh your memory and extend the concepts. 1
Oscillations Vern Lindberg June 10, 2010 You have discussed oscillations in Vibs and Waves: we will therefore touch lightly on Chapter 3, mainly trying to refresh your memory and extend the concepts. 1
Algebra Practice Problems for Precalculus and Calculus
 Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
Algebra and Geometry Review (61 topics, no due date)
 Course Name: Math 112 Credit Exam LA Tech University Course Code: ALEKS Course: Trigonometry Instructor: Course Dates: Course Content: 159 topics Algebra and Geometry Review (61 topics, no due date) Properties
Course Name: Math 112 Credit Exam LA Tech University Course Code: ALEKS Course: Trigonometry Instructor: Course Dates: Course Content: 159 topics Algebra and Geometry Review (61 topics, no due date) Properties
POLYNOMIAL FUNCTIONS
 POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus
 South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
[ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
The Method of Partial Fractions Math 121 Calculus II Spring 2015
 Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Low Pass Filter Rise Time vs Bandwidth
 AN121 Dataforth Corporation Page 1 of 7 DID YOU KNOW? The number googol is ten raised to the hundredth power or 1 followed by 100 zeros. Edward Kasner (1878-1955) a noted mathematician is best remembered
AN121 Dataforth Corporation Page 1 of 7 DID YOU KNOW? The number googol is ten raised to the hundredth power or 1 followed by 100 zeros. Edward Kasner (1878-1955) a noted mathematician is best remembered
Complex Algebra. What is the identity, the number such that it times any number leaves that number alone?
 Complex Algebra When the idea of negative numbers was broached a couple of thousand years ago, they were considered suspect, in some sense not real. Later, when probably one of the students of Pythagoras
Complex Algebra When the idea of negative numbers was broached a couple of thousand years ago, they were considered suspect, in some sense not real. Later, when probably one of the students of Pythagoras
Inductors in AC Circuits
 Inductors in AC Circuits Name Section Resistors, inductors, and capacitors all have the effect of modifying the size of the current in an AC circuit and the time at which the current reaches its maximum
Inductors in AC Circuits Name Section Resistors, inductors, and capacitors all have the effect of modifying the size of the current in an AC circuit and the time at which the current reaches its maximum
Circuits with inductors and alternating currents. Chapter 20 #45, 46, 47, 49
 Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
10.3. The Exponential Form of a Complex Number. Introduction. Prerequisites. Learning Outcomes
 The Exponential Form of a Complex Number 10.3 Introduction In this Section we introduce a third way of expressing a complex number: the exponential form. We shall discover, through the use of the complex
The Exponential Form of a Complex Number 10.3 Introduction In this Section we introduce a third way of expressing a complex number: the exponential form. We shall discover, through the use of the complex
Thnkwell s Homeschool Precalculus Course Lesson Plan: 36 weeks
 Thnkwell s Homeschool Precalculus Course Lesson Plan: 36 weeks Welcome to Thinkwell s Homeschool Precalculus! We re thrilled that you ve decided to make us part of your homeschool curriculum. This lesson
Thnkwell s Homeschool Precalculus Course Lesson Plan: 36 weeks Welcome to Thinkwell s Homeschool Precalculus! We re thrilled that you ve decided to make us part of your homeschool curriculum. This lesson
Magnetic Field of a Circular Coil Lab 12
 HB 11-26-07 Magnetic Field of a Circular Coil Lab 12 1 Magnetic Field of a Circular Coil Lab 12 Equipment- coil apparatus, BK Precision 2120B oscilloscope, Fluke multimeter, Wavetek FG3C function generator,
HB 11-26-07 Magnetic Field of a Circular Coil Lab 12 1 Magnetic Field of a Circular Coil Lab 12 Equipment- coil apparatus, BK Precision 2120B oscilloscope, Fluke multimeter, Wavetek FG3C function generator,
Rectifier circuits & DC power supplies
 Rectifier circuits & DC power supplies Goal: Generate the DC voltages needed for most electronics starting with the AC power that comes through the power line? 120 V RMS f = 60 Hz T = 1667 ms) = )sin How
Rectifier circuits & DC power supplies Goal: Generate the DC voltages needed for most electronics starting with the AC power that comes through the power line? 120 V RMS f = 60 Hz T = 1667 ms) = )sin How
Lecture L3 - Vectors, Matrices and Coordinate Transformations
 S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
45. The peak value of an alternating current in a 1500-W device is 5.4 A. What is the rms voltage across?
 PHYS Practice Problems hapters 8- hapter 8. 45. The peak value of an alternating current in a 5-W device is 5.4 A. What is the rms voltage across? The power and current can be used to find the peak voltage,
PHYS Practice Problems hapters 8- hapter 8. 45. The peak value of an alternating current in a 5-W device is 5.4 A. What is the rms voltage across? The power and current can be used to find the peak voltage,
Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor)
 Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor) Concept: circuits Time: 30 m SW Interface: 750 Windows file: RLC.SWS EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage
Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor) Concept: circuits Time: 30 m SW Interface: 750 Windows file: RLC.SWS EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage
13.4 THE CROSS PRODUCT
 710 Chapter Thirteen A FUNDAMENTAL TOOL: VECTORS 62. Use the following steps and the results of Problems 59 60 to show (without trigonometry) that the geometric and algebraic definitions of the dot product
710 Chapter Thirteen A FUNDAMENTAL TOOL: VECTORS 62. Use the following steps and the results of Problems 59 60 to show (without trigonometry) that the geometric and algebraic definitions of the dot product
UNIVERSITY OF CALIFORNIA AT BERKELEY College of Engineering Department of Electrical Engineering and Computer Sciences. EE105 Lab Experiments
 UNIVERSITY OF CALIFORNIA AT BERKELEY College of Engineering Department of Electrical Engineering and Computer Sciences EE15 Lab Experiments Bode Plot Tutorial Contents 1 Introduction 1 2 Bode Plots Basics
UNIVERSITY OF CALIFORNIA AT BERKELEY College of Engineering Department of Electrical Engineering and Computer Sciences EE15 Lab Experiments Bode Plot Tutorial Contents 1 Introduction 1 2 Bode Plots Basics
Georgia Department of Education Kathy Cox, State Superintendent of Schools 7/19/2005 All Rights Reserved 1
 Accelerated Mathematics 3 This is a course in precalculus and statistics, designed to prepare students to take AB or BC Advanced Placement Calculus. It includes rational, circular trigonometric, and inverse
Accelerated Mathematics 3 This is a course in precalculus and statistics, designed to prepare students to take AB or BC Advanced Placement Calculus. It includes rational, circular trigonometric, and inverse
Vector Math Computer Graphics Scott D. Anderson
 Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
DOE FUNDAMENTALS HANDBOOK ELECTRICAL SCIENCE Volume 3 of 4
 DOE-HDBK-1011/3-92 JUNE 1992 DOE FUNDAMENTALS HANDBOOK ELECTRICAL SCIENCE Volume 3 of 4 U.S. Department of Energy Washington, D.C. 20585 FSC-6910 Distribution Statement A. Approved for public release;
DOE-HDBK-1011/3-92 JUNE 1992 DOE FUNDAMENTALS HANDBOOK ELECTRICAL SCIENCE Volume 3 of 4 U.S. Department of Energy Washington, D.C. 20585 FSC-6910 Distribution Statement A. Approved for public release;
