Course Notes: Linear circuit theory and differential equations
|
|
|
- Abel Hines
- 7 years ago
- Views:
Transcription
1 ourse Notes: Linear circuit theory and differential equations eading: Koch, h. ; any text on linear signal and system theory can be consulted for more details. These notes will review the basics of linear discrete-element modeling, which can be considered to have three components: ) generating models for the individual components of systems; 2) combining those component models into network models to represent a system; and 3) solving the resulting model equations in specific cases of interest. Linear electrical circuits will be considered, because these are usually the basis for neural membrane models. These notes will be most useful to persons who have not had a course in electrical circuit theory. t is assumed that readers are familiar with solution methods for linear differential equations. Modeling the components of electrical circuits Electrical circuits are built up of individual components, each of which is a two-port, as illustrated at right. That is, components have two connections or ports through which they exchange electrical signals with the rest of the system. Such a component can be characterized by the relationship between the current flowing through the device () and the electrical potential difference across the device (). urrent is the flow of electrical charge, measured in amperes, equal to coulombs/second, and electrical potential is measured in volts. The voltage is the potential across the device, meaning, in this case, the potential at the top connection minus the potential at the bottom connection. By convention, the voltage arrowhead is at the positive end of the voltage difference. By convention, the current is positive when it flows in the direction indicated by the current arrows and current is positive when it flows through the component from the positive side of the voltage arrow, as in Fig.. For practical circuits, charge cannot be created or destroyed within the component, so the current into one connection is exactly equal to the current leaving the other connection, as shown. This assumption will always be made. Analysis of electrical circuits is based on accurate models for the relationship between voltage and current in the two-port models of the components of the system (some electrical circuit components have more than two ports, requiring more complex models, but those objects are not of interest here). The three common circuit elements and their current-voltage models are shown in Fig. 2. n the resistor (at left), the current and voltage are proportional, with constant, the resistance (units of ohms), which characterizes the device. This model is called Ohms Law and is also frequently written as Fig. Two port model for an electric circuit component (the box) Fig. 2 Two port models for three common electrical circuit elements. From left to right they are a resistor, a capacitor, and an inductor. The definitions of current and voltage are the same for all three and are shown only for the resistor. G, where the conductance G is /. The middle device is a capacitor, which stores charge on two parallel plates separated by an insulator. The voltage across a capacitor is related to the charge Q d dt L d dt
2 2 stored as Q. The current through the capacitor is equal to dq/dt, and the two-port model of the capacitor given in Fig. 2 can be derived by differentiating. A capacitor is characterized by its capacitance, in units of farads. The third model is for an inductor, a coil of wire, whose two port model is like that of a capacitor, except that it is current which is differentiated. The inductor is characterized by its inductance L, in units of henrys. For linear circuits, the parameters, G,, and L are constants. However in nerve membrane, the resistances (conductances) are not constant, and many of the interesting properties of neurons derive from the properties of these resistances. Derivations of the two-port models from the physics of these components can be found in most undergraduate physics texts. Question: The two-port models in Fig. 2 are given as differential equations. onsider how to write them as integral equations, i.e. write as a function of for the capacitor. To do this, you will have to introduce an initial condition on. This topic will be important later. The final two components that are important are ideal sources, a voltage source and a current source, shown in Fig. 3. The voltage source (left) produces a certain voltage across its terminals, regardless of the amount of current it must provide. The current source (right) similarly forces a certain current to flow through it, regardless of the rest of the circuit. These are obviously idealizations and real devices, like batteries, only approximate ideal sources. Additional components can be added in series or parallel with ideal sources to account for the limited ability of realworld sources to maintain a certain voltage or current. Fig. 3 deal sources: voltage source at left and current source at right. ombining components into networks Figure 4 shows three basic electrical networks. The principles that underlie solving for the various currents and voltages in these networks allow for networks of arbitrary complexity to be worked out. There are more powerful techniques than those presented here, which can be found in any electrical circuit theory book. However, for membrane models, it is not necessary to develop the subject of network theory in detail. A B Fig. 4 Basic electrical circuits. Figure 4A shows a simple circuit with a voltage source and a resistor connected in a series loop. There is a single current which flows in a loop in the direction of the arrow through both the
3 3 voltage source and the resistor. The voltage across the resistor is given by, from the two-port model in Fig. 2. learly the voltage across the current source must equal the voltage across the resistor, so that. From this equation, the current through the resistor is /. This is the first application of one of the two basic laws of circuits, Kirchoff s voltage law (KL), or the loop law: KL: the sum of the voltages around any closed loop in a circuit is zero. The transit around the loop must be made in one direction and the voltages must be added in a consistent way. n the case of Fig. 4A, going around the loop clockwise gives the result -. The signs on and must be opposite because the voltage arrows are transited in opposite directions. From this loop sum, we get the intuitively satisfying result that, as used above. A final point is that it is assumed in circuit theory that there is no voltage drop across the connections between elements. That is, in transiting a loop, there are voltage changes only across the components of the circuit, not the connections between components. Note that no account was made of the current through the voltage source. This is because an ideal voltage source always has a voltage across its terminals, regardless of the current flow through it. Figure 4B shows a series circuit, in which two resistors are placed in series with each other. Again there is only one current and the currents flowing through the three components of the circuit are the same. Applying KL and Ohms law gives: and ( ) 2 2 () (2) Note that Eqn. 2 is an expression of Ohms Law again, but with a resistor S 2. From this result, we can conclude that the circuits in Figs. 4A and 4B are essentially identical; two resistors in series, as in Fig. 4B, are equivalent to one resistor S whose resistance is equal to the sum of the two resistances. Series resistances: two resistors in series are equivalent to a single resistor with resistance equal to the sum of the two individual resistances. A series pair of resistors form a voltage divider, i.e. part of the voltage appears across resistor in Fig. 4B and part appears across resistor 2. Given the solution for current implicit in Eqn. 2, it is possible to write the following equations for the voltage across the two resistors: oltage divider relationship 2 and 2 2 (3) 2 2
4 4 Equation 3 gives the voltage divider relationships for the two resistors, which say simply that the voltage across one resistor in a series of resistors is equal to the same fraction of the voltage across the whole circuit as that resistor s resistance bears to the total resistance of the series. Figure 4 shows a third situation, parallel combination of two resistors. onsidering first the voltages in the network, it should be clear from KL that and the voltages across the two resistors are equal, both. This is done by applying KL twice, once to the loop involving the voltage source and and once to the loop involving and 2. There are now three currents, and 2. Based on the principle that current cannot be created or destroyed in connections among elements, it is clear that current must divide into two parts, not necessarily equal, and 2, and that 2. This is a special case of Kirchoff s current law: KL: The sum of the currents flowing into a node must be zero. Alternatively, the sum of the currents flowing out of a node must equal the sum of the currents flowing into the node. A node is a point in the circuit at which connections among components meet. n the circuit of Fig. 4 there are two nodes, one at the top of the circuit and one at the bottom. n the circuit of Fig. 4B, there are three nodes, two between the voltage source and the two resistors (top and bottom) and one between the resistors. KL applied to the circuit in Fig. 4B leads to the conclusion that the currents through all three elements are equal, as was assumed above. eturning to the parallel circuit in Fig. 4, the facts that the voltages across the components are equal (Eqn. 4) and the application of KL to the top node (Eqn. 5) gives: (4) (5) (6) Equation 6 is, once again, an expression of Ohms law. Apparently the parallel combination of two resistors can also be expressed as a single resistance P, where P 2. (7) 2 Parallel resistances: two resistors and 2 in parallel are equivalent to a single resistor, with the resistance given in Eqn. 7. Alternatively, two conductances G and G 2 in parallel are equivalent to a single conductance equal to the sum of the individual conductances (G P G G 2 ). The rule stated above about conductances can be seen from Eqn. 5. ecalling that conductance G is equal to the inverse of resistance, Eqn. 5 can be rewritten as: ( G G2 ) (5a)
5 5 from which the parallel conductance law follows. n parallel circuits, it is usually more convenient to solve problems using conductance, as opposed to resisitance. A final point about Fig. 4 is the way the current divides between the two resistors. By substituting Eqn. 6 into Eqn. 4, the relationship between the currents in Fig. 4 can be solved as follows: urrent divider relationships 2 and similarly, (8) (9) The current divider relationships can be written in a form identical to the voltage divider relationships by converting resistances to conductances. eplacing in Eqns. 8 and 9 with /G gives G G G 2 G2 and 2 () G G 2 Question : onsider the circuit in Fig. 5. By working out successive series and parallel circuits and using voltage and current divider relationships, solve for current 3 and voltage 5 in terms of source voltage and the resistances. The approach to solving such a problem is using KL and KL to write a linearly independent set of equations to solve. However, not all the equations resulting from KL loops are independent and there is one fewer independent KL equation than there are nodes in the network. There are formal methods for properly setting up these problems, which will not be considered here. There is an infinite variety of problems like this. Make some up yourself to practice Fig. 5 Mixed series-parallel circuit. Question 2: The circuit in Fig. 6 is often used to model the ionic currents through nerve membrane. What is the membrane potential m in terms of the individual ionic potentials Na, K, and l? Notice that the problem is stated in terms of conductances, not resistances, which is typical for nerve membrane models. Fig. 6. Parallel combination of three sources. With the addition of a capacitor, this circuit is a model for nerve membrane. G Na G K m G l Na K l
6 6 A useful technique for solving problems like that posed in Question 2, when there are multiple sources in the network, is to solve the network for each source individually and then sum the solutions. For example, in the circuit in Fig. 6, one can solve for m with K l, then solve for m again with Na l, and then solve a third time with Na K and then add the three solutions. Note that setting a voltage source to zero means replacing it with a simple connection, a short circuit, which is an element with zero voltage change across it. This superposition principle works because circuit problems of the kind considered so far are linear, meaning that the solution will always be expressed as a weighted linear sum of the sources. The previous statement can be proved formally, but to see that it is true, consider that the solution to network problems means applying KL and KL to the nodes and loops in the circuit. Each of the resulting equations is a linear equation in terms of the source voltages and currents and the unknown voltages and currents. Thus network problems of the kind considered so far (with constant resistances) will always lead to simultaneous sets of linear equations and the solutions will be linear sums of the sources. To apply the superposition technique when there are current sources in the system, the current sources that are to be set to zero are simply removed from the circuit, leaving an open circuit (i.e. a connection through which zero current flows). Question 3: A ladder network is a semiinfinite circuit like the one drawn in Fig. 7. With the addition of capacitors, this circuit is used to S S S model the dendrites of neurons, the so-called cable theory. This question demonstrates some interesting properties of ladder networks with resistor circuits. The system consists of series resistors S and parallel resistors P. The ladder is driven by a voltage source at one end and is infinitely long at the other end. The problem is to P P P show that the potential decays exponentially along the ladder, that is if n is the potential at the n th Fig. 7 First three sections of a semi-infinite ladder network. node, the first three of which are labeled in Fig. 7, then n a, where a is the attenuation from node to node and is defined to be. Potential arrows are not drawn in Fig. 7, but all potentials are assumed to be measured with respect to the node at the bottom of the circuit, the ground or reference node, indicated by the symbol. Show that the potential decays exponentially and compute a. Do this in two steps: n 2 3 a) A ladder network has a characteristic resistance L which is the input resistance looking into the left end of the network (i.e. the whole ladder of resistors can be replaced by a single resistor L ). ompute L. Hint: argue that the input resistance (i.e. the resistance looking into the left end of the finite network in Fig. 7a) should be L. Part of your argument should be that the original network is semi-infinite. b) Using the result in a), compute a in terms of L, S, and P. L P Fig. 7a The semi-infinite network can be replaced by a characteristic resistance L. L
7 7 Source equivalents A circuit containing resistors and sources can be replaced by an identical equivalent circuit, containing either one voltage source in series with one resistor (Thévenin equivalent) or one current source in parallel with one resistor (Norton equivalent). The circuits are equivalent in the sense that they behave exactly the same if connected in the same way to any external circuit. Two examples are shown in Fig. 8. A equiv B S P equiv P S equiv equiv Fig. 8 A. Thévenin equivalent of a two-resistor circuit. B. Norton equivalent of another circuit. n Fig. 8A, the two circuits are equivalent for any load (i.e. any circuit containing resistors and sources) connected between the terminals on the right (i.e. where the small circles are). Similarly, the two circuits in Fig. 8B are equivalent for any load connected between the terminals. The loads connected to the terminals can be any electrical circuit. By equivalent is meant that the voltages and currents in the external circuit would be the same, regardless of which of the two equivalent circuits it is connected to. To find the Thévenin equivalent, proceed as follows: Thévenin equivalent: equiv is the open circuit voltage across the load terminals (i.e. with no load connected); equiv is the resistance presented at the load terminals with all sources in the circuit set to zero. For the example in Fig. 8A, these rules give equiv P ( S P ) and equiv S P ( S P ). For the Norton equivalent: Norton equivalent: equiv is the short circuit current obtained when the load terminals are shorted together. equiv is the resistance presented at the load terminals with all sources in the circuit set to zero. For the example in Fig. 8B, these rules give /( ) and. equiv P S P equiv S P The proof of these rules is straightforward, but will not be given. However, you can easily verify that they work by trying a few simple examples. These equivalent circuits can often be used to simplify circuit problems considerably. The discussion above is stated in terms of resistors and sources, but the circuit can contain capacitors and inductors as well and the procedures are the same except that impedance (see below) is substituted for resistance.
8 8 Question 4: Derive the Norton and Thévenin equivalents of the circuits in Questions (at the terminals of 5 ) and 2 (at the terminals of m ) and in Fig. 8. With regard to Fig. 8, what is the relationship between the Norton and Thévenin equivalents of the same circuit? Question 4.5: One real-world approximation of an ideal voltage source is a battery. However, a battery is not a true voltage source in that the voltage at the battery terminals varies with the current through the battery. What is a model for a battery? Make a plot of the voltage at the battery terminals in the model, as a function of the current provided by the battery. Differential equations for circuits with Ls and s eal membrane circuits contain capacitors and (less often) inductors. For example, nerve membrane has a capacitance of about µfd/cm 2, and a complete model of nerve membrane must have a capacitor in parallel with the ionic conductances of Fig. 6. The methods for dealing with networks of capacitors and inductors are the same as for resistors, except that the concept of resistance has to be extended slightly to accommodate the fact that the two-port models for inductors and capacitors are differential equations and not algebraic equations. For linear systems, the differential equations are usually solved by transforming them (Laplace or Fourier), so the equations end up algebraic in the end. As a result, the principles of network analysis discussed above apply essentially without change. Figure 9 shows an example of a circuit containing a capacitor and two resistors. The goal is to solve for the voltage in terms of the other parameters of the circuit. The two-port rules for the capacitor and resistors plus KL give 2 d dt, and ( ) () 2 Fig. 9 ircuit involving a capacitor. KL at the junction of the components gives d dt 2 (2) Eliminating between Eqns. and 2 gives d ( dt ) (3) 2 d dt 2 (4) Equation 4 is a differential equation which relates the unknown voltage to the input voltage. Notice that this equation is linear in the voltage variables. onsideration of the process that was used to derive Eqn. 4 suggests that this will always be so. That is, the procedure for setting up the
9 9 equations in a circuit problem consists of applying KL, KL, and the two-port equations for the components of the circuit. Each of these procedures will always produce an equation that is linear in the voltages and currents (i.e. terms like 2,, 2, /, / etc. will not occur). Thus the solution of a circuit problem will always involve eliminating unknown voltages and currents among simultaneous sets of linear differential equations, which will always give a differential equation that is linear in the voltages and currents. nitial conditions To obtain a solution to a differential equation like Eqn. 4 requires boundary conditions; for a first order equation like this, one boundary condition must be specified. n circuit theory (and neural modeling) problems, it is usually appropriate to specify an initial value, i.e. a value of one of the variables at some time t. The solution is then the response of the system for time t>t. n Eqn. 4 it is the initial value of which must be specified. This turns out to be a general rule for systems containing capacitors. The differential equations will always require that the initial voltages across the capacitors be specified. Similarly, for circuits with inductors, it is the initial current through the inductor that must be specified. To understand why initial values for these variables must be set, consider that the voltage across a capacitor is the time integral of the current through the capacitor, i.e. if is the voltage across a capacitor and is the current through it, then t t () ( ) dt (5) Equation 5 follows from the two-port model for the capacitor in Fig. 2. This equation is merely a way of saying that the voltage across a capacitor is proportional to the charge stored in the capacitor, since the charge is the time integral of the current through the capacitor (refer to the discussion of Fig. 2). Now, because it is the result of an integration, cannot change instantaneously in time, assuming that is finite; that is, (t) cannot have any discontinuities, because the properties of integration imply that the integral cannot have a step change if the integrand is finite. Moreover, the value of at time t must depend on (), i.e. on the initial value of, as in Eqn. 5. This is equivalent to saying that the circuit adds or subtracts charge from the amount of charge stored in the capacitor initially and the total charge after a period of addition and subtraction depends on how much charge was there initially. ariables with this property are called state variables. State variables always require initial conditions in the equations for a system. nitial conditions: the initial conditions on linear circuit problems will always reduce to specifying the voltages across capacitors and current through inductors. Solutions to circuit differential equations The solution to Eqn. 4 can be obtained by several methods. For the problems typical of network theory, the values of the of the state variables are specified at some time t and the solution is computed for time t>t. For example, suppose that (). To simplify the notation, rewrite Eqn. 4 as
10 d dt 2 where τ2 (6) τ The term τ 2 is the product of a resistance and a capacitance; it has units of seconds and is called a time constant. The solution to Eqn. 6 can be found by multiplying both sides of the equation by the integrating factor exp( t / τ 2 ) e d dt e τ 2 t / τ t / τ 2 2 d dt e t τ [ e ] / t / τ 2 2 (7) (8) Now the equation can be integrated from the initial time (t) to time t giving t [ ] d du e u/ τ u du 2 u/ τ2 ( ) ue ( ) du t t / τ 2 e t ue u/ τ2 ds () ( ) ( ) t t t/ τ2 t/ τ2 u/ τ2 t e e ue () ( ) ( ) du (9) (2) (2) An instructive case occurs when a constant. Then t/ τ τ 2 2 t e e t/ τ2 () ( ) ( ) t/ τ 2 2 t e e t/ τ2 () ( ) ( ) 2 (22) (23) The voltage across the capacitor and 2 moves smoothly from the initial condition ( ()) to the final value 2 /( 2 ), as shown in Fig.. The transition occurs as an exponential decay with time constant τ 2 ; that is, the contribution of the initial value () decays exponentially to zero (first term in Eqn. 23) and the contribution of the steady state voltage increases exponentially (sescond term in Eqn. 23). onsider first the steady state value where d /dt; this occurs for times large compared to τ 2. n this case there will be no current through the capacitor, from the capacitor s two-port model, so the circuit behaves as if the capacitor is not present. f the capacitor is removed from the circuit in Fig. 9, then the potential is 3 2 () Time, ms Fig. Waveform of the voltage change of Eqn. 23 for the case where (), steady state voltage is 3, and the time constant is 5 ms.
11 just 2 /( 2 ), from the voltage divider relationship. What happens with the capacitor present is that current is driven into the capacitor to charge it up from () to potential 2 /( 2 ), which occurs exponentially with time constant τ 2. A circuit consisting of one capacitor and a group of resistors and sources will always behave in this way, i.e. the potential across the capacitor will change exponentially in time from its initial value to a final value set by the resistors and sources. The time constant τ 2 is a fundamental characteristic of such circuits and will always be equal to the product of the capacitance and the resistance seen from the capacitor s terminals with the sources set to zero. The circuit of Fig. 9 is a simple model for the membrane properties of a neuron. The capacitor represents the membrane capacitance, resistor 2 represents the resting resistance of the channels in the membrane, and the voltage source and resistor represent some external source applied to the membrane. harging curves like Fig. are seen in neurons when a step curent is injected into the cell body. The time constant is an important property of the cell which will be discussed in more detail later in the course. Question 5: onsider the circuit in Fig. which models a nerve membrane with capacitance and resting conductance G. The resting potential of the cell is represented by the source E. The particular arrangement of G and E will be explained in a later set of notes. The current source ext represents a current injected into the cell through an electrode. ompute the membrane potential m with ext and initial condition m (). Then compute the membrane potential as a function of time with ext, a constant, and m () equal to the steady state value found with ext. This models injecting a step of current into the ext cell, which is the experiment usually done to determine membrane time constant. Fig. Model of a nerve cell with external current injection. G E m Question 6: The circuit in Fig. 2 models a nerve membrane (G, E, and ) with a synapse attached (E S, G S ). When the synapse is activated, the switch closes for about ms, temporarily connecting the synapse circuit to the membrane circuit. First compute the steady state membrane potentials m with the switch open and closed. Second, compute the membrane potential versus time for a ms switch closure, assuming that the membrane potential starts at E, i.e. that m () E. (Be careful here, ms is considerably shorter than the membrane time constant with switch open or closed). m G E G S E S Fig. 2 Model of a nerve cell with a synapse. losing the switch models activating the synapse. Transformed differential equations, complex impedance For linear systems with constant coefficients (i.e., G,, and L that are constants, not dependent on time, voltage or current) it is usually most convenient to solve differential equations
12 2 like Eqn. 6 using the Laplace transform. This method is appropriate for initial value problems of the type considered above. The Laplace transform is defined as follows: st s () L[ t ()] te () dt (24) (t) is a function of time, say a voltage in a circuit, and () s is its Laplace transform. The transform is a function of the complex number s, called the Laplace transform variable. An important property of the transform is that it is unique and invertable, that is, given a transform (), s it is always possible to find the corresponding time function. The useful properties of Laplace transforms derive from their effect on differentiation. onsider the Laplace transform of d/dt: L d dt d st st t st e dt () t e se dt t dt [ ] (25) ( ) s( s) (26) Equation 25 results from applying integration by parts and Eqn. 26 follows from the assumption, necessary to the existence of the Laplace transform integral in Eqn. 24 and to the invertability of the transform, that e[s]>, so that e -st (t) evaluated as t approaches is zero. This result shows that taking a derivative in the time domain is equivalent to multiplying by s in the Laplace domain (and subtracting the initial value). This process can be extended to higher derivatives, giving the general rule n L d n ss () dt n n n k k s k d k dt t (27) Because of the derivative properties in Eqns. 26 and 27, the Laplace transform reduces a differential equation to an algebraic equation in s. The initial conditions of the problem are also incorporated into the algebraic equation. Using the example above and applying the Laplace transform to both sides of Eqn. 6 gives Eqn. 28: s ( ) τ 2 () s () () s s τ s τ 2 2 (28) (29) Equation 29 is the Laplace transform of the desired solution function (t), written in terms of the Laplace transform of the input voltage () s and the initial condition (). The time function for (t) can be recovered from Eqn. 29 using standard methods of transform inversion, which will not be covered here. n the case of a constant input, as in Eqns. 22 and 23, () s s and the solution is the same as Eqn. 23.
13 3 The real advantage of using the Laplace transform technique is that one can avoid entirely deriving differential equations like Eqn. 6 by Laplace transforming the two-port models of the circuit components directly. Figure 3 shows the two-port models in the Laplace transform domain. These are obtained by Laplace transforming the two-port relationships in Fig. 2. Fig. 3 Two port models for circuit components, in the Laplace transform domain. (s) (s) (s) - () s s (s) (s) sl (s) - L () gnoring the initial conditions (i.e. assuming that they are zero), these are all Ohms-law type statements. n each case, the two-port model takes the form Z(), s where Z(s) is for a resistor, /s for a capacitor, and sl for an inductor. Z is called the impedance of the element and is a function of the Laplace transform variable s. mpedance is a generalization of resistance for networks containing capacitors and inductors; the inverse of impedance, analogous to conductance, is admittance, usually denoted Y(s). Network models can be derived for circuits containing capacitors and inductors using the impedance relationships in Fig. 3 in exactly the same way as was done for resistors in the first few sections of these notes. The result will be exactly the same as the result of deriving the differential equation first in the time domain (as was done for Eqn. 6) and then Laplace transforming it. Question 7: Derive Eqn. 6 entirely in the Laplace domain, beginning with the two port models in Fig. 3 and verify that the result is the same. Question 8: Find the Thévenin equivalent of the circuit in Fig. 9 (at the terminals of ). For this, use a generalized definition of Thévenin equivalent in which there is a source and a series impedance (not resistance). Express both the source and impedance in the Laplace domain. Question 9: The initial conditions can be considered to be voltage or current sources in the Laplace-domain two-port models. onvince yourself that the initial condition for the capacitor is equivalent to a voltage source in series with the capacitor with a value of ()/s in the Laplace domain, or ()u(t) in the time domain. (u(t) is the unit step, equal to for t< and equal to for t>. ts Laplace transform is /s, which follows directly from Eqn. 24.) Similarly the initial condition for the inductor is equivalent to a voltage source in series with the inductor with value L() in the Laplace domain or L()δ(t), where δ(t) is the impulse, equal to the time derivative of u(t), in the time domain. The Laplace transform of δ(t) is. Question : Show that initial conditions can also be represented as current sources in parallel with the circuit elements. Question : Make a basic table of Laplace transforms by working out the transform of the following signals using Eqn. 24.
14 4 a) u(t), the unit step, defined as t < ut () t > (3) b) δ(t), the impulse or Dirac delta function. nformally, the impulse can be thought of as the derivative of u(t). More formally, the impulse can be defined as the limit of a function, like a square pulse, whose amplitude is /T and whose width is T as T approaches. Note that the area under the function stays constant at. For the present purposes, it is sufficient to say that δ(t) for t and f ( u ) δ ( u ) du f ( ) (3) (Hint: the impulse is assumed to be included in the integral in Eqn. 24.) c) e -at u(t) d) t u(t) e) (-e -at )u(t)/a. (Hint: you should be able to derive this one from a) and c).) f) te -at u(t) g) sin(ωt) u(t) (Hint: remember that sin(ωt) (e jωτ -e -jωτ )/2, for j- /2 ) h) e -at sin(ωt) u(t) (Same hint) As a final example, consider the circuit in Fig. 4. This circuit comes up in a model for subthreshold oscillations in nerve membrane which will be considered later in the course. Proceeding as above using the two-port impedance models and KL for the top node gives: Fig. 4 Second order circuit consisting of a parallel combination of three circuit elements driven by a current source (t) L
15 5 s L sl s L sl s 2 s s s L sl (32) (33) (34) Equation 32 gives the two-port models for the components in the Laplace domain, assuming zero initial conditions. Equation 33 expresses KL at the top node in the circuit. Equation 34 is a rearrangement in Ohms Law form expressing the Laplace transform of the voltage in terms of the Laplace transform of the current and the impedance of the circuit. t is instructive to try to derive the differential equation corresponding to Eqn. 34 in the time domain; the Laplace method is much easier. To illustrate the standard method of inverting a Laplace transform, consider the response of the circuit in Fig. 4 to an impulse of current δ(t). The Laplace transform of (t) is just and it is desired to find the voltage whose Laplace transform is as follows (from Eqn. 34): () s s 2 s s L (34a) The transform in Eqn. 34a is typical of transforms that arise in electrical circuits in that it is a ratio of polynomials in s. The usual strategy in inverting such transforms is to break them down into sums of terms of the form a /(sb), which is the transform of the exponential ae -bt (see Question ). The form of the inverse of Eqn. 34a depends on the roots of the polynomial in the denominator. f they are real, it will be a sum of exponentials. f they are complex, it will involve sines and cosines. t is instructive for this example to assume that the roots are complex. ewrite Eqn. 34a in the following factored form: () s s 2 s s 2 2δs ω ( s δ jω )( s δ jω ) (35) where j(-) /2, δ/(2) is called the damping coefficient and ω /(L) /2 is called the resonant frequency. The reason for these names will be apparent below. To make the factoring correct, ω 2 ω 2 δ 2. The transform can now be broken into two parts, a process called partial fraction expansion, as follows: () s 2 jω δ jω s δ jω δ jω s δ jω (36)
16 6 This decomposition is done by straightforward algebraic methods and can always be accomplished. You should verify that Eqns. 35 and 36 are the same. The goal is to express the transform as the sum of rational fractions with first or second order denominator polynomials, i.e. in terms of transforms whose inverses are known (as in Question ). The inverse Laplace transform of /(sa) is e -at u(t) (see Question ), so the inverse transform of the right hand side of Eqn. 37 is the sum of two exponentials: [ ] ( j ) t ( j ) t t () ( j ) e ( j ) e u() t 2 jω δ ω δ ω δ ω δ ω (37) which can be rearranged as follows: t e t j t j t j j t j t δ δ ω ω ω ω ω () ( e e ) ( e e ) u() t 2jω j 2 ω e t sin( t ) cos( t δ δ ω ) u ( t ω ) ω (38) (39) where use has been made of the following property of the complex exponential: jωt e cos( ωt) jsin( ωt) (4) Note that the final result in Eqn. 39 is entirely real, the imaginary components of previous expressions ultimately cancelled out. The solution in Eqn. 39 is a damped sinusoid, a sinusoidal term (in brackets) which oscillates at frequency ω and decays exponentially with a time constant /δ. The voltage transient is plotted in Fig. 5, for a particular choice of component values. Note that the oscillation is at frequency ω which is related to the parameters of the circuit by (t) / e -dt δ t time, sec. Fig. 5 oltage transient across the parallel L circuit in Fig. 4 for an impulse of current. Solid line is the voltage, dashed line is the exponential envelope. oltage plotted as /. n this case, L and, so that δ.5, ω, and ω.998. e 2 2 ω ω δ ω δ ω 2 2 if << (4) L 4 L
17 7 The approximation δ<<ω is true in resonant circuits, those in which the value of is large. n this case, the circuit will ring or oscillate at its resonant frequency ω ω for a long time if disturbed, as by an impulse in this example. Question 2: Show using trigonometric identities that the final expression in Eqn. 39 can be expressed as (const)e δt cos(ω tφ), for a constant phase φ, Question 3: Suppose the roots of the denominator polynomial in Eqn. 34a are real and negative. What will be the form of the inverse Laplace transform? (e.g. for.33, L, and.) efer back to this question after you have read the last section below and studied Fig. 6. Question 4: nvert the Laplace transform in Eqn. 29 using the method above and show that it gives the same solution as Eqn. 23 (Hint: () s / s in this case.) The sinusoidal steady state and frequency response The system considered in Fig. 4 and Eqn. 34 can be analyzed another way which provides further insight into its properties. n this case, we assume that the input current is a sinusoidal function of time, say cos(ωt). The system is assumed to have been allowed to run for a long time so that transient responses to the turning-on of the current have died down. Such transient responses will take the form of Eqn. 39, which is the transient response to an impulse. The transients for the sinusoidal input case can be computed directly from the Laplace transform in Eqn. 34 by letting s () be equal to the Laplace transform of cos(ωt)u(t). The solution will be the sum of the transients, which will decay as e δ t, and a steady-state sinusoidal component of the form Acos( ωt φ). After a time long compared to /δ, only the sinusoidal component will survive. Thus, it is reasonable to assume that the steady-state voltage (t) will be a sinusoidal function of time at the same frequency ω as the excitation. With the assumption of sinusoidal steady state, all signals in the circuit will take the form A cos(ωtφ) where A is the amplitude and φ is the phase (or time shift) of the signal. Different signals will have different amplitudes and phases, and the goal of the analysis is to find these values. t is convenient to represent such signals in exponential form as j( ωt φ) j( ωt φ) Acos( ωt φ) A e e 2 (42) which follows from Eqn. 4. n analyzing the sinusoidal steady state, it is sufficient to compute the responses of the circuit to the complex exponential e jωt since real signals can be computed from it using Eqn. 42. The sinusoidal steady state has properties similar to those of the Laplace transform domain, in that differential equations are reduced to algebraic equations. For example, the two-port models for circuit components take the following form:
18 resistor: capacitor: inductor: 8 becomes d dt becomes jω L d becomes jω L dt (43) (44) (45) These equations follow because for any signal of the form Ae j( ωt φ), differentiation with respect to t is the same as multiplying by jω. n the sinusoidal steady state, the term jω has the same role as s in the Laplace domain. The only difference is that there are no initial conditions to deal with. As discussed above, the initial conditions are so far in the past that they have no effect. The two-port models in the sinusoidal steady state (Eqns ) again take the form of Ohms law relationships; they can all be written as Z( jω ), where Z is the complex impedance, equal to for a resistor, /jω for a capacitor, and jωl for an inductor. The same methods that were used in Eqns can now be used again to derive the relationship between the sinusoidal steady state voltage and current in the circuit of Fig. 4. Because the two-port models take the same form, with s replaced by jω, the net result is simply to replace the s variables in Eqn. 34 with jω, giving jω 2 ω jω L (46) Equation 46 expresses the relationship between voltage and current in this circuit when the current excitation is sinusoidal. To see how this relationship is useful, assume that e jω t. The voltage can then be expressed as Ae j ( ω t φ ), where the unknown amplitude A and phase φ are obtained as follows: j( ωt φ) jωt 2 Ae e jω ω jω L (47) Ae jφ jω ω jω L 2 (48) A jω jω and φ ω jω L ω jω L 2 2 (49) Equation 47 is a restatement of Eqn. 46 with the exponential signals given explicitly. n Eqn. 48, the common component ( e jω t ) has been cancelled leaving only the amplitude and phase of the voltage on the left hand side. Equation 49 provides expressions for the amplitude and phase of the voltage in terms of the amplitude and phase of the complex number on the right hand side of Eqn. 48. Equation 49 is the frequency response of the system. t describes, in this case, how the amplitude A and phase
19 Fig. 6 Amplitude of the sinusoidal voltage across the parallel circuit of Fig. 4 versus radian frequency. L as before and results are shown for five values of, corresponding to damping δ.5,.7,.5,.7, and 5. φ of the voltage in the system of Fig. 4 change as the frequency of the sinusoidal excitation current changes. 9 A / Figure 6 shows a plot of the. amplitude of the frequency response.. of this system, i.e. a plot of A / Frequency, radians versus radian frequency ω. Again it is useful to recast the relevant expression in terms of ω and δ, the parameters derived above. When this is done, the amplitude becomes A jω 2 2 ( ω ω ) jω2δ ω ( ω ω ) 4ω δ (5) At low frequencies, the amplitude goes to zero due to the ω term in the numerator of Eqn. 5. At high frequencies, the denominator becomes approximately ω 2 and the amplitude again goes to zero as /ω. n between there is a resonance, a frequency at which the response is a peak. When the damping δ is small ( large), the resonance occurs near ωω radian, where the denominator of Eqn. 5 has a minimum. The amplitude when ωω is /(2δ), so the amplitude is larger as the damping decreases. Note that the axes in Fig. 6 are plotted logarithmically, so the gain change is substantial. When the resistor is large, the circuit in Fig. 4 is a resonator, meaning that it gives a large response to currents at frequencies near radian and smaller responses at other frequencies. Question 5: Find the frequency response of the circuit in Fig. 9, for the ratio. Plot it in a plot like Fig. 6 for the following values, typical of nerve membrane: µfd/cm 2, 2 KΩ. cm 2, and 2. Question 6: The development of Eqns and Fig. 6 assumed that the signals in the system are complex exponentials e jω t and Ae j ( ω t φ ). Show that if the signals are real, cos(ωt) and Acos(ωt), the same solutions are obtained for A and φ. Hint: obtain solutions for e j ω t and e j ω t and use the fact that the system is linear to compute the response to cos(ωt). (f the system is linear, then the response y to inputs x x 2 is equal to the sum of the individual responses y to x and y 2 to x 2, that is yy y 2.)
20 2 This section contains only an introductory view of the subject of the frequency response of systems. The subject is much more extensive and allows analysis of signals and systems in many useful ways. n particular, the subject of the Fourier transform, which is closely related to the frequency response, has not been mentioned. However, the material presented above is sufficient for neural modeling and more detailed treatments of these issues can be found in any book on signal theory.
Using the Impedance Method
 Using the Impedance Method The impedance method allows us to completely eliminate the differential equation approach for the determination of the response of circuits. In fact the impedance method even
Using the Impedance Method The impedance method allows us to completely eliminate the differential equation approach for the determination of the response of circuits. In fact the impedance method even
Introduction to Complex Numbers in Physics/Engineering
 Introduction to Complex Numbers in Physics/Engineering ference: Mary L. Boas, Mathematical Methods in the Physical Sciences Chapter 2 & 14 George Arfken, Mathematical Methods for Physicists Chapter 6 The
Introduction to Complex Numbers in Physics/Engineering ference: Mary L. Boas, Mathematical Methods in the Physical Sciences Chapter 2 & 14 George Arfken, Mathematical Methods for Physicists Chapter 6 The
Alternating-Current Circuits
 hapter 1 Alternating-urrent ircuits 1.1 A Sources... 1-1. Simple A circuits... 1-3 1..1 Purely esistive load... 1-3 1.. Purely Inductive oad... 1-5 1..3 Purely apacitive oad... 1-7 1.3 The Series ircuit...
hapter 1 Alternating-urrent ircuits 1.1 A Sources... 1-1. Simple A circuits... 1-3 1..1 Purely esistive load... 1-3 1.. Purely Inductive oad... 1-5 1..3 Purely apacitive oad... 1-7 1.3 The Series ircuit...
Chapter 12 Driven RLC Circuits
 hapter Driven ircuits. A Sources... -. A ircuits with a Source and One ircuit Element... -3.. Purely esistive oad... -3.. Purely Inductive oad... -6..3 Purely apacitive oad... -8.3 The Series ircuit...
hapter Driven ircuits. A Sources... -. A ircuits with a Source and One ircuit Element... -3.. Purely esistive oad... -3.. Purely Inductive oad... -6..3 Purely apacitive oad... -8.3 The Series ircuit...
CIRCUITS LABORATORY EXPERIMENT 3. AC Circuit Analysis
 CIRCUITS LABORATORY EXPERIMENT 3 AC Circuit Analysis 3.1 Introduction The steady-state behavior of circuits energized by sinusoidal sources is an important area of study for several reasons. First, the
CIRCUITS LABORATORY EXPERIMENT 3 AC Circuit Analysis 3.1 Introduction The steady-state behavior of circuits energized by sinusoidal sources is an important area of study for several reasons. First, the
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT
 EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
Positive Feedback and Oscillators
 Physics 3330 Experiment #6 Fall 1999 Positive Feedback and Oscillators Purpose In this experiment we will study how spontaneous oscillations may be caused by positive feedback. You will construct an active
Physics 3330 Experiment #6 Fall 1999 Positive Feedback and Oscillators Purpose In this experiment we will study how spontaneous oscillations may be caused by positive feedback. You will construct an active
The Time Constant of an RC Circuit
 The Time Constant of an RC Circuit 1 Objectives 1. To determine the time constant of an RC Circuit, and 2. To determine the capacitance of an unknown capacitor. 2 Introduction What the heck is a capacitor?
The Time Constant of an RC Circuit 1 Objectives 1. To determine the time constant of an RC Circuit, and 2. To determine the capacitance of an unknown capacitor. 2 Introduction What the heck is a capacitor?
The Membrane Equation
 The Membrane Equation Professor David Heeger September 5, 2000 RC Circuits Figure 1A shows an RC (resistor, capacitor) equivalent circuit model for a patch of passive neural membrane. The capacitor represents
The Membrane Equation Professor David Heeger September 5, 2000 RC Circuits Figure 1A shows an RC (resistor, capacitor) equivalent circuit model for a patch of passive neural membrane. The capacitor represents
Understanding Poles and Zeros
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Understanding Poles and Zeros 1 System Poles and Zeros The transfer function
MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Understanding Poles and Zeros 1 System Poles and Zeros The transfer function
W03 Analysis of DC Circuits. Yrd. Doç. Dr. Aytaç Gören
 W03 Analysis of DC Circuits Yrd. Doç. Dr. Aytaç Gören ELK 2018 - Contents W01 Basic Concepts in Electronics W02 AC to DC Conversion W03 Analysis of DC Circuits (self and condenser) W04 Transistors and
W03 Analysis of DC Circuits Yrd. Doç. Dr. Aytaç Gören ELK 2018 - Contents W01 Basic Concepts in Electronics W02 AC to DC Conversion W03 Analysis of DC Circuits (self and condenser) W04 Transistors and
Lecture - 4 Diode Rectifier Circuits
 Basic Electronics (Module 1 Semiconductor Diodes) Dr. Chitralekha Mahanta Department of Electronics and Communication Engineering Indian Institute of Technology, Guwahati Lecture - 4 Diode Rectifier Circuits
Basic Electronics (Module 1 Semiconductor Diodes) Dr. Chitralekha Mahanta Department of Electronics and Communication Engineering Indian Institute of Technology, Guwahati Lecture - 4 Diode Rectifier Circuits
L and C connected together. To be able: To analyse some basic circuits.
 circuits: Sinusoidal Voltages and urrents Aims: To appreciate: Similarities between oscillation in circuit and mechanical pendulum. Role of energy loss mechanisms in damping. Why we study sinusoidal signals
circuits: Sinusoidal Voltages and urrents Aims: To appreciate: Similarities between oscillation in circuit and mechanical pendulum. Role of energy loss mechanisms in damping. Why we study sinusoidal signals
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
[ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
ANALYTICAL METHODS FOR ENGINEERS
 UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
Transistor amplifiers: Biasing and Small Signal Model
 Transistor amplifiers: iasing and Small Signal Model Transistor amplifiers utilizing JT or FT are similar in design and analysis. Accordingly we will discuss JT amplifiers thoroughly. Then, similar FT
Transistor amplifiers: iasing and Small Signal Model Transistor amplifiers utilizing JT or FT are similar in design and analysis. Accordingly we will discuss JT amplifiers thoroughly. Then, similar FT
LAB 7 MOSFET CHARACTERISTICS AND APPLICATIONS
 LAB 7 MOSFET CHARACTERISTICS AND APPLICATIONS Objective In this experiment you will study the i-v characteristics of an MOS transistor. You will use the MOSFET as a variable resistor and as a switch. BACKGROUND
LAB 7 MOSFET CHARACTERISTICS AND APPLICATIONS Objective In this experiment you will study the i-v characteristics of an MOS transistor. You will use the MOSFET as a variable resistor and as a switch. BACKGROUND
Part IB Paper 6: Information Engineering LINEAR SYSTEMS AND CONTROL Dr Glenn Vinnicombe HANDOUT 3. Stability and pole locations.
 Part IB Paper 6: Information Engineering LINEAR SYSTEMS AND CONTROL Dr Glenn Vinnicombe HANDOUT 3 Stability and pole locations asymptotically stable marginally stable unstable Imag(s) repeated poles +
Part IB Paper 6: Information Engineering LINEAR SYSTEMS AND CONTROL Dr Glenn Vinnicombe HANDOUT 3 Stability and pole locations asymptotically stable marginally stable unstable Imag(s) repeated poles +
Chapter 35 Alternating Current Circuits
 hapter 35 Alternating urrent ircuits ac-ircuits Phasor Diagrams Resistors, apacitors and nductors in ac-ircuits R ac-ircuits ac-ircuit power. Resonance Transformers ac ircuits Alternating currents and
hapter 35 Alternating urrent ircuits ac-ircuits Phasor Diagrams Resistors, apacitors and nductors in ac-ircuits R ac-ircuits ac-ircuit power. Resonance Transformers ac ircuits Alternating currents and
EE 1202 Experiment #4 Capacitors, Inductors, and Transient Circuits
 EE 1202 Experiment #4 Capacitors, Inductors, and Transient Circuits 1. Introduction and Goal: Exploring transient behavior due to inductors and capacitors in DC circuits; gaining experience with lab instruments.
EE 1202 Experiment #4 Capacitors, Inductors, and Transient Circuits 1. Introduction and Goal: Exploring transient behavior due to inductors and capacitors in DC circuits; gaining experience with lab instruments.
J.L. Kirtley Jr. Electric network theory deals with two primitive quantities, which we will refer to as: 1. Potential (or voltage), and
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.061 Introduction to Power Systems Class Notes Chapter 1: eiew of Network Theory J.L. Kirtley Jr. 1 Introduction
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.061 Introduction to Power Systems Class Notes Chapter 1: eiew of Network Theory J.L. Kirtley Jr. 1 Introduction
A few words about imaginary numbers (and electronics) Mark Cohen mscohen@g.ucla.edu
 A few words about imaginary numbers (and electronics) Mark Cohen mscohen@guclaedu While most of us have seen imaginary numbers in high school algebra, the topic is ordinarily taught in abstraction without
A few words about imaginary numbers (and electronics) Mark Cohen mscohen@guclaedu While most of us have seen imaginary numbers in high school algebra, the topic is ordinarily taught in abstraction without
ε: Voltage output of Signal Generator (also called the Source voltage or Applied
 Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Chapter 7 Direct-Current Circuits
 Chapter 7 Direct-Current Circuits 7. Introduction...7-7. Electromotive Force...7-3 7.3 Resistors in Series and in Parallel...7-5 7.4 Kirchhoff s Circuit Rules...7-7 7.5 Voltage-Current Measurements...7-9
Chapter 7 Direct-Current Circuits 7. Introduction...7-7. Electromotive Force...7-3 7.3 Resistors in Series and in Parallel...7-5 7.4 Kirchhoff s Circuit Rules...7-7 7.5 Voltage-Current Measurements...7-9
ES250: Electrical Science. HW7: Energy Storage Elements
 ES250: Electrical Science HW7: Energy Storage Elements Introduction This chapter introduces two more circuit elements, the capacitor and the inductor whose elements laws involve integration or differentiation;
ES250: Electrical Science HW7: Energy Storage Elements Introduction This chapter introduces two more circuit elements, the capacitor and the inductor whose elements laws involve integration or differentiation;
Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure 2. R. Figure 1.
 Examples of Transient and RL Circuits. The Series RLC Circuit Impulse response of Circuit. Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure.
Examples of Transient and RL Circuits. The Series RLC Circuit Impulse response of Circuit. Let s examine the response of the circuit shown on Figure 1. The form of the source voltage Vs is shown on Figure.
Basic Op Amp Circuits
 Basic Op Amp ircuits Manuel Toledo INEL 5205 Instrumentation August 3, 2008 Introduction The operational amplifier (op amp or OA for short) is perhaps the most important building block for the design of
Basic Op Amp ircuits Manuel Toledo INEL 5205 Instrumentation August 3, 2008 Introduction The operational amplifier (op amp or OA for short) is perhaps the most important building block for the design of
Partial Fractions: Undetermined Coefficients
 1. Introduction Partial Fractions: Undetermined Coefficients Not every F(s) we encounter is in the Laplace table. Partial fractions is a method for re-writing F(s) in a form suitable for the use of the
1. Introduction Partial Fractions: Undetermined Coefficients Not every F(s) we encounter is in the Laplace table. Partial fractions is a method for re-writing F(s) in a form suitable for the use of the
CHAPTER 28 ELECTRIC CIRCUITS
 CHAPTER 8 ELECTRIC CIRCUITS 1. Sketch a circuit diagram for a circuit that includes a resistor R 1 connected to the positive terminal of a battery, a pair of parallel resistors R and R connected to the
CHAPTER 8 ELECTRIC CIRCUITS 1. Sketch a circuit diagram for a circuit that includes a resistor R 1 connected to the positive terminal of a battery, a pair of parallel resistors R and R connected to the
12.4 UNDRIVEN, PARALLEL RLC CIRCUIT*
 + v C C R L - v i L FIGURE 12.24 The parallel second-order RLC circuit shown in Figure 2.14a. 12.4 UNDRIVEN, PARALLEL RLC CIRCUIT* We will now analyze the undriven parallel RLC circuit shown in Figure
+ v C C R L - v i L FIGURE 12.24 The parallel second-order RLC circuit shown in Figure 2.14a. 12.4 UNDRIVEN, PARALLEL RLC CIRCUIT* We will now analyze the undriven parallel RLC circuit shown in Figure
Electrical Resonance
 Electrical Resonance (R-L-C series circuit) APPARATUS 1. R-L-C Circuit board 2. Signal generator 3. Oscilloscope Tektronix TDS1002 with two sets of leads (see Introduction to the Oscilloscope ) INTRODUCTION
Electrical Resonance (R-L-C series circuit) APPARATUS 1. R-L-C Circuit board 2. Signal generator 3. Oscilloscope Tektronix TDS1002 with two sets of leads (see Introduction to the Oscilloscope ) INTRODUCTION
EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP
 1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
BASIC ELECTRONICS AC CIRCUIT ANALYSIS. December 2011
 AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
Oscillations. Vern Lindberg. June 10, 2010
 Oscillations Vern Lindberg June 10, 2010 You have discussed oscillations in Vibs and Waves: we will therefore touch lightly on Chapter 3, mainly trying to refresh your memory and extend the concepts. 1
Oscillations Vern Lindberg June 10, 2010 You have discussed oscillations in Vibs and Waves: we will therefore touch lightly on Chapter 3, mainly trying to refresh your memory and extend the concepts. 1
Reading assignment: All students should read the Appendix about using oscilloscopes.
 10. A ircuits* Objective: To learn how to analyze current and voltage relationships in alternating current (a.c.) circuits. You will use the method of phasors, or the vector addition of rotating vectors
10. A ircuits* Objective: To learn how to analyze current and voltage relationships in alternating current (a.c.) circuits. You will use the method of phasors, or the vector addition of rotating vectors
Lecture 7 Circuit analysis via Laplace transform
 S. Boyd EE12 Lecture 7 Circuit analysis via Laplace transform analysis of general LRC circuits impedance and admittance descriptions natural and forced response circuit analysis with impedances natural
S. Boyd EE12 Lecture 7 Circuit analysis via Laplace transform analysis of general LRC circuits impedance and admittance descriptions natural and forced response circuit analysis with impedances natural
Measurement of Capacitance
 Measurement of Capacitance Pre-Lab Questions Page Name: Class: Roster Number: Instructor:. A capacitor is used to store. 2. What is the SI unit for capacitance? 3. A capacitor basically consists of two
Measurement of Capacitance Pre-Lab Questions Page Name: Class: Roster Number: Instructor:. A capacitor is used to store. 2. What is the SI unit for capacitance? 3. A capacitor basically consists of two
= (0.400 A) (4.80 V) = 1.92 W = (0.400 A) (7.20 V) = 2.88 W
 Physics 2220 Module 06 Homework 0. What are the magnitude and direction of the current in the 8 Ω resister in the figure? Assume the current is moving clockwise. Then use Kirchhoff's second rule: 3.00
Physics 2220 Module 06 Homework 0. What are the magnitude and direction of the current in the 8 Ω resister in the figure? Assume the current is moving clockwise. Then use Kirchhoff's second rule: 3.00
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS
 MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS Systems of Equations and Matrices Representation of a linear system The general system of m equations in n unknowns can be written a x + a 2 x 2 + + a n x n b a
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS Systems of Equations and Matrices Representation of a linear system The general system of m equations in n unknowns can be written a x + a 2 x 2 + + a n x n b a
3.1. RATIONAL EXPRESSIONS
 3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
3.1. RATIONAL EXPRESSIONS RATIONAL NUMBERS In previous courses you have learned how to operate (do addition, subtraction, multiplication, and division) on rational numbers (fractions). Rational numbers
DIODE CIRCUITS LABORATORY. Fig. 8.1a Fig 8.1b
 DIODE CIRCUITS LABORATORY A solid state diode consists of a junction of either dissimilar semiconductors (pn junction diode) or a metal and a semiconductor (Schottky barrier diode). Regardless of the type,
DIODE CIRCUITS LABORATORY A solid state diode consists of a junction of either dissimilar semiconductors (pn junction diode) or a metal and a semiconductor (Schottky barrier diode). Regardless of the type,
Critical thin-film processes such as deposition and etching take place in a vacuum
 WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
LABORATORY 10 TIME AVERAGES, RMS VALUES AND THE BRIDGE RECTIFIER. Bridge Rectifier
 LABORATORY 10 TIME AVERAGES, RMS VALUES AND THE BRIDGE RECTIFIER Full-wave Rectification: Bridge Rectifier For many electronic circuits, DC supply voltages are required but only AC voltages are available.
LABORATORY 10 TIME AVERAGES, RMS VALUES AND THE BRIDGE RECTIFIER Full-wave Rectification: Bridge Rectifier For many electronic circuits, DC supply voltages are required but only AC voltages are available.
10.450 Process Dynamics, Operations, and Control Lecture Notes - 11 Lesson 11. Frequency response of dynamic systems.
 Lesson. Frequency response of dynamic systems..0 Context We have worked with step, pulse, and sine disturbances. Of course, there are many sine disturbances, because the applied frequency may vary. Surely
Lesson. Frequency response of dynamic systems..0 Context We have worked with step, pulse, and sine disturbances. Of course, there are many sine disturbances, because the applied frequency may vary. Surely
Integrals of Rational Functions
 Integrals of Rational Functions Scott R. Fulton Overview A rational function has the form where p and q are polynomials. For example, r(x) = p(x) q(x) f(x) = x2 3 x 4 + 3, g(t) = t6 + 4t 2 3, 7t 5 + 3t
Integrals of Rational Functions Scott R. Fulton Overview A rational function has the form where p and q are polynomials. For example, r(x) = p(x) q(x) f(x) = x2 3 x 4 + 3, g(t) = t6 + 4t 2 3, 7t 5 + 3t
Bode Diagrams of Transfer Functions and Impedances ECEN 2260 Supplementary Notes R. W. Erickson
 Bode Diagrams of Transfer Functions and Impedances ECEN 2260 Supplementary Notes. W. Erickson In the design of a signal processing network, control system, or other analog system, it is usually necessary
Bode Diagrams of Transfer Functions and Impedances ECEN 2260 Supplementary Notes. W. Erickson In the design of a signal processing network, control system, or other analog system, it is usually necessary
Inrush Current. Although the concepts stated are universal, this application note was written specifically for Interpoint products.
 INTERPOINT Although the concepts stated are universal, this application note was written specifically for Interpoint products. In today s applications, high surge currents coming from the dc bus are a
INTERPOINT Although the concepts stated are universal, this application note was written specifically for Interpoint products. In today s applications, high surge currents coming from the dc bus are a
Circuits with inductors and alternating currents. Chapter 20 #45, 46, 47, 49
 Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Unit2: Resistor/Capacitor-Filters
 Unit2: Resistor/Capacitor-Filters Physics335 Student October 3, 27 Physics 335-Section Professor J. Hobbs Partner: Physics335 Student2 Abstract Basic RC-filters were constructed and properties such as
Unit2: Resistor/Capacitor-Filters Physics335 Student October 3, 27 Physics 335-Section Professor J. Hobbs Partner: Physics335 Student2 Abstract Basic RC-filters were constructed and properties such as
Line Reactors and AC Drives
 Line Reactors and AC Drives Rockwell Automation Mequon Wisconsin Quite often, line and load reactors are installed on AC drives without a solid understanding of why or what the positive and negative consequences
Line Reactors and AC Drives Rockwell Automation Mequon Wisconsin Quite often, line and load reactors are installed on AC drives without a solid understanding of why or what the positive and negative consequences
Preamble. Kirchoff Voltage Law (KVL) Series Resistors. In this section of my lectures we will be. resistor arrangements; series and
 Preamble Series and Parallel Circuits Physics, 8th Edition Custom Edition Cutnell & Johnson Chapter 0.6-0.8, 0.0 Pages 60-68, 69-6 n this section of my lectures we will be developing the two common types
Preamble Series and Parallel Circuits Physics, 8th Edition Custom Edition Cutnell & Johnson Chapter 0.6-0.8, 0.0 Pages 60-68, 69-6 n this section of my lectures we will be developing the two common types
Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor)
 Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor) Concept: circuits Time: 30 m SW Interface: 750 Windows file: RLC.SWS EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage
Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor) Concept: circuits Time: 30 m SW Interface: 750 Windows file: RLC.SWS EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage
Switch Mode Power Supply Topologies
 Switch Mode Power Supply Topologies The Buck Converter 2008 Microchip Technology Incorporated. All Rights Reserved. WebSeminar Title Slide 1 Welcome to this Web seminar on Switch Mode Power Supply Topologies.
Switch Mode Power Supply Topologies The Buck Converter 2008 Microchip Technology Incorporated. All Rights Reserved. WebSeminar Title Slide 1 Welcome to this Web seminar on Switch Mode Power Supply Topologies.
Second Order Linear Nonhomogeneous Differential Equations; Method of Undetermined Coefficients. y + p(t) y + q(t) y = g(t), g(t) 0.
 Second Order Linear Nonhomogeneous Differential Equations; Method of Undetermined Coefficients We will now turn our attention to nonhomogeneous second order linear equations, equations with the standard
Second Order Linear Nonhomogeneous Differential Equations; Method of Undetermined Coefficients We will now turn our attention to nonhomogeneous second order linear equations, equations with the standard
Scaling and Biasing Analog Signals
 Scaling and Biasing Analog Signals November 2007 Introduction Scaling and biasing the range and offset of analog signals is a useful skill for working with a variety of electronics. Not only can it interface
Scaling and Biasing Analog Signals November 2007 Introduction Scaling and biasing the range and offset of analog signals is a useful skill for working with a variety of electronics. Not only can it interface
RC & RL Transient Response
 EE 2006 University of Minnesota Duluth ab 8 1. Introduction R & R Transient Response The student will analyze series R and R circuits. A step input will excite these respective circuits, producing a transient
EE 2006 University of Minnesota Duluth ab 8 1. Introduction R & R Transient Response The student will analyze series R and R circuits. A step input will excite these respective circuits, producing a transient
is identically equal to x 2 +3x +2
 Partial fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as 1 + 3
Partial fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. 4x+7 For example it can be shown that has the same value as 1 + 3
SCHWEITZER ENGINEERING LABORATORIES, COMERCIAL LTDA.
 Pocket book of Electrical Engineering Formulas Content 1. Elementary Algebra and Geometry 1. Fundamental Properties (real numbers) 1 2. Exponents 2 3. Fractional Exponents 2 4. Irrational Exponents 2 5.
Pocket book of Electrical Engineering Formulas Content 1. Elementary Algebra and Geometry 1. Fundamental Properties (real numbers) 1 2. Exponents 2 3. Fractional Exponents 2 4. Irrational Exponents 2 5.
V out. Figure 1: A voltage divider on the left, and potentiometer on the right.
 Living with the Lab Fall 202 Voltage Dividers and Potentiometers Gerald Recktenwald v: November 26, 202 gerry@me.pdx.edu Introduction Voltage dividers and potentiometers are passive circuit components
Living with the Lab Fall 202 Voltage Dividers and Potentiometers Gerald Recktenwald v: November 26, 202 gerry@me.pdx.edu Introduction Voltage dividers and potentiometers are passive circuit components
Method To Solve Linear, Polynomial, or Absolute Value Inequalities:
 Solving Inequalities An inequality is the result of replacing the = sign in an equation with ,, or. For example, 3x 2 < 7 is a linear inequality. We call it linear because if the < were replaced with
Solving Inequalities An inequality is the result of replacing the = sign in an equation with ,, or. For example, 3x 2 < 7 is a linear inequality. We call it linear because if the < were replaced with
DIGITAL-TO-ANALOGUE AND ANALOGUE-TO-DIGITAL CONVERSION
 DIGITAL-TO-ANALOGUE AND ANALOGUE-TO-DIGITAL CONVERSION Introduction The outputs from sensors and communications receivers are analogue signals that have continuously varying amplitudes. In many systems
DIGITAL-TO-ANALOGUE AND ANALOGUE-TO-DIGITAL CONVERSION Introduction The outputs from sensors and communications receivers are analogue signals that have continuously varying amplitudes. In many systems
Capacitors in Circuits
 apacitors in ircuits apacitors store energy in the electric field E field created by the stored charge In circuit apacitor may be absorbing energy Thus causes circuit current to be reduced Effectively
apacitors in ircuits apacitors store energy in the electric field E field created by the stored charge In circuit apacitor may be absorbing energy Thus causes circuit current to be reduced Effectively
Trigonometry for AC circuits
 Trigonometry for AC circuits This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Trigonometry for AC circuits This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Equivalent Circuits and Transfer Functions
 R eq isc Equialent Circuits and Transfer Functions Samantha R Summerson 14 September, 009 1 Equialent Circuits eq ± Figure 1: Théenin equialent circuit. i sc R eq oc Figure : Mayer-Norton equialent circuit.
R eq isc Equialent Circuits and Transfer Functions Samantha R Summerson 14 September, 009 1 Equialent Circuits eq ± Figure 1: Théenin equialent circuit. i sc R eq oc Figure : Mayer-Norton equialent circuit.
Ver 3537 E1.1 Analysis of Circuits (2014) E1.1 Circuit Analysis. Problem Sheet 1 (Lectures 1 & 2)
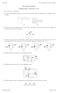 Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
1 Introduction. 2 Complex Exponential Notation. J.L. Kirtley Jr.
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.06 Introduction to Power Systems Class Notes Chapter AC Power Flow in Linear Networks J.L. Kirtley Jr.
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.06 Introduction to Power Systems Class Notes Chapter AC Power Flow in Linear Networks J.L. Kirtley Jr.
AC CIRCUITS - CAPACITORS AND INDUCTORS
 EXPRIMENT#8 AC CIRCUITS - CAPACITORS AND INDUCTORS NOTE: Two weeks are allocated for this experiment. Before performing this experiment, review the Proper Oscilloscope Use section of Experiment #7. Objective
EXPRIMENT#8 AC CIRCUITS - CAPACITORS AND INDUCTORS NOTE: Two weeks are allocated for this experiment. Before performing this experiment, review the Proper Oscilloscope Use section of Experiment #7. Objective
BJT Amplifier Circuits
 JT Amplifier ircuits As we have developed different models for D signals (simple large-signal model) and A signals (small-signal model), analysis of JT circuits follows these steps: D biasing analysis:
JT Amplifier ircuits As we have developed different models for D signals (simple large-signal model) and A signals (small-signal model), analysis of JT circuits follows these steps: D biasing analysis:
Homework Assignment 03
 Question 1 (2 points each unless noted otherwise) Homework Assignment 03 1. A 9-V dc power supply generates 10 W in a resistor. What peak-to-peak amplitude should an ac source have to generate the same
Question 1 (2 points each unless noted otherwise) Homework Assignment 03 1. A 9-V dc power supply generates 10 W in a resistor. What peak-to-peak amplitude should an ac source have to generate the same
BJT Amplifier Circuits
 JT Amplifier ircuits As we have developed different models for D signals (simple large-signal model) and A signals (small-signal model), analysis of JT circuits follows these steps: D biasing analysis:
JT Amplifier ircuits As we have developed different models for D signals (simple large-signal model) and A signals (small-signal model), analysis of JT circuits follows these steps: D biasing analysis:
Basic Electronics Prof. Dr. Chitralekha Mahanta Department of Electronics and Communication Engineering Indian Institute of Technology, Guwahati
 Basic Electronics Prof. Dr. Chitralekha Mahanta Department of Electronics and Communication Engineering Indian Institute of Technology, Guwahati Module: 2 Bipolar Junction Transistors Lecture-2 Transistor
Basic Electronics Prof. Dr. Chitralekha Mahanta Department of Electronics and Communication Engineering Indian Institute of Technology, Guwahati Module: 2 Bipolar Junction Transistors Lecture-2 Transistor
3.6. Partial Fractions. Introduction. Prerequisites. Learning Outcomes
 Partial Fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. For 4x + 7 example it can be shown that x 2 + 3x + 2 has the same
Partial Fractions 3.6 Introduction It is often helpful to break down a complicated algebraic fraction into a sum of simpler fractions. For 4x + 7 example it can be shown that x 2 + 3x + 2 has the same
2.2 Magic with complex exponentials
 2.2. MAGIC WITH COMPLEX EXPONENTIALS 97 2.2 Magic with complex exponentials We don t really know what aspects of complex variables you learned about in high school, so the goal here is to start more or
2.2. MAGIC WITH COMPLEX EXPONENTIALS 97 2.2 Magic with complex exponentials We don t really know what aspects of complex variables you learned about in high school, so the goal here is to start more or
Frequency response: Resonance, Bandwidth, Q factor
 Frequency response: esonance, Bandwidth, Q factor esonance. Let s continue the exploration of the frequency response of circuits by investigating the series circuit shown on Figure. C + V - Figure The
Frequency response: esonance, Bandwidth, Q factor esonance. Let s continue the exploration of the frequency response of circuits by investigating the series circuit shown on Figure. C + V - Figure The
MATH10212 Linear Algebra. Systems of Linear Equations. Definition. An n-dimensional vector is a row or a column of n numbers (or letters): a 1.
 MATH10212 Linear Algebra Textbook: D. Poole, Linear Algebra: A Modern Introduction. Thompson, 2006. ISBN 0-534-40596-7. Systems of Linear Equations Definition. An n-dimensional vector is a row or a column
MATH10212 Linear Algebra Textbook: D. Poole, Linear Algebra: A Modern Introduction. Thompson, 2006. ISBN 0-534-40596-7. Systems of Linear Equations Definition. An n-dimensional vector is a row or a column
6.4 Normal Distribution
 Contents 6.4 Normal Distribution....................... 381 6.4.1 Characteristics of the Normal Distribution....... 381 6.4.2 The Standardized Normal Distribution......... 385 6.4.3 Meaning of Areas under
Contents 6.4 Normal Distribution....................... 381 6.4.1 Characteristics of the Normal Distribution....... 381 6.4.2 The Standardized Normal Distribution......... 385 6.4.3 Meaning of Areas under
Network Theory Question Bank
 Network Theory Question Bank Unit-I JNTU SYLLABUS: Three Phase Circuits Three phase circuits: Phase sequence Star and delta connection Relation between line and phase voltages and currents in balanced
Network Theory Question Bank Unit-I JNTU SYLLABUS: Three Phase Circuits Three phase circuits: Phase sequence Star and delta connection Relation between line and phase voltages and currents in balanced
6 Series Parallel Circuits
 6 Series Parallel Circuits This work is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/. Air Washington
6 Series Parallel Circuits This work is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/. Air Washington
The Method of Partial Fractions Math 121 Calculus II Spring 2015
 Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
Rational functions. as The Method of Partial Fractions Math 11 Calculus II Spring 015 Recall that a rational function is a quotient of two polynomials such f(x) g(x) = 3x5 + x 3 + 16x x 60. The method
CHAPTER 6 Frequency Response, Bode Plots, and Resonance
 ELECTRICAL CHAPTER 6 Frequency Response, Bode Plots, and Resonance 1. State the fundamental concepts of Fourier analysis. 2. Determine the output of a filter for a given input consisting of sinusoidal
ELECTRICAL CHAPTER 6 Frequency Response, Bode Plots, and Resonance 1. State the fundamental concepts of Fourier analysis. 2. Determine the output of a filter for a given input consisting of sinusoidal
Lecture 22: Class C Power Amplifiers
 Whites, EE 322 Lecture 22 Page 1 of 13 Lecture 22: lass Power Amplifiers We discovered in Lecture 18 (Section 9.2) that the maximum efficiency of lass A amplifiers is 25% with a resistive load and 50%
Whites, EE 322 Lecture 22 Page 1 of 13 Lecture 22: lass Power Amplifiers We discovered in Lecture 18 (Section 9.2) that the maximum efficiency of lass A amplifiers is 25% with a resistive load and 50%
EE301 Lesson 14 Reading: 10.1-10.4, 10.11-10.12, 11.1-11.4 and 11.11-11.13
 CAPACITORS AND INDUCTORS Learning Objectives EE301 Lesson 14 a. Define capacitance and state its symbol and unit of measurement. b. Predict the capacitance of a parallel plate capacitor. c. Analyze how
CAPACITORS AND INDUCTORS Learning Objectives EE301 Lesson 14 a. Define capacitance and state its symbol and unit of measurement. b. Predict the capacitance of a parallel plate capacitor. c. Analyze how
SERIES-PARALLEL DC CIRCUITS
 Name: Date: Course and Section: Instructor: EXPERIMENT 1 SERIES-PARALLEL DC CIRCUITS OBJECTIVES 1. Test the theoretical analysis of series-parallel networks through direct measurements. 2. Improve skills
Name: Date: Course and Section: Instructor: EXPERIMENT 1 SERIES-PARALLEL DC CIRCUITS OBJECTIVES 1. Test the theoretical analysis of series-parallel networks through direct measurements. 2. Improve skills
S-Parameters and Related Quantities Sam Wetterlin 10/20/09
 S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
Partial Fractions. Combining fractions over a common denominator is a familiar operation from algebra:
 Partial Fractions Combining fractions over a common denominator is a familiar operation from algebra: From the standpoint of integration, the left side of Equation 1 would be much easier to work with than
Partial Fractions Combining fractions over a common denominator is a familiar operation from algebra: From the standpoint of integration, the left side of Equation 1 would be much easier to work with than
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS. + + x 2. x n. a 11 a 12 a 1n b 1 a 21 a 22 a 2n b 2 a 31 a 32 a 3n b 3. a m1 a m2 a mn b m
 MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS 1. SYSTEMS OF EQUATIONS AND MATRICES 1.1. Representation of a linear system. The general system of m equations in n unknowns can be written a 11 x 1 + a 12 x 2 +
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS 1. SYSTEMS OF EQUATIONS AND MATRICES 1.1. Representation of a linear system. The general system of m equations in n unknowns can be written a 11 x 1 + a 12 x 2 +
The Importance of the X/R Ratio in Low-Voltage Short Circuit Studies
 The Importance of the X/R Ratio in Low-Voltage Short Circuit Studies DATE: November 17, 1999 REVISION: AUTHOR: John Merrell Introduction In some short circuit studies, the X/R ratio is ignored when comparing
The Importance of the X/R Ratio in Low-Voltage Short Circuit Studies DATE: November 17, 1999 REVISION: AUTHOR: John Merrell Introduction In some short circuit studies, the X/R ratio is ignored when comparing
Direct-Current Circuits
 8 Direct-Current Circuits Clicker Questions Question N.0 Description: Understanding circuits with parallel resistances. Question A battery is used to light a bulb as shown. A second bulb is connected by
8 Direct-Current Circuits Clicker Questions Question N.0 Description: Understanding circuits with parallel resistances. Question A battery is used to light a bulb as shown. A second bulb is connected by
SECTION 2 Transmission Line Theory
 SEMICONDUCTOR DESIGN GUIDE Transmission Line Theory SECTION 2 Transmission Line Theory Introduction The ECLinPS family has pushed the world of ECL into the realm of picoseconds. When output transitions
SEMICONDUCTOR DESIGN GUIDE Transmission Line Theory SECTION 2 Transmission Line Theory Introduction The ECLinPS family has pushed the world of ECL into the realm of picoseconds. When output transitions
Slide 1 / 26. Inductance. 2011 by Bryan Pflueger
 Slide 1 / 26 Inductance 2011 by Bryan Pflueger Slide 2 / 26 Mutual Inductance If two coils of wire are placed near each other and have a current passing through them, they will each induce an emf on one
Slide 1 / 26 Inductance 2011 by Bryan Pflueger Slide 2 / 26 Mutual Inductance If two coils of wire are placed near each other and have a current passing through them, they will each induce an emf on one
Circuit Analysis using the Node and Mesh Methods
 Circuit Analysis using the Node and Mesh Methods We have seen that using Kirchhoff s laws and Ohm s law we can analyze any circuit to determine the operating conditions (the currents and voltages). The
Circuit Analysis using the Node and Mesh Methods We have seen that using Kirchhoff s laws and Ohm s law we can analyze any circuit to determine the operating conditions (the currents and voltages). The
2.6 The driven oscillator
 2.6. THE DRIVEN OSCILLATOR 131 2.6 The driven oscillator We would like to understand what happens when we apply forces to the harmonic oscillator. That is, we want to solve the equation M d2 x(t) 2 + γ
2.6. THE DRIVEN OSCILLATOR 131 2.6 The driven oscillator We would like to understand what happens when we apply forces to the harmonic oscillator. That is, we want to solve the equation M d2 x(t) 2 + γ
Series and Parallel Resistive Circuits
 Series and Parallel Resistive Circuits The configuration of circuit elements clearly affects the behaviour of a circuit. Resistors connected in series or in parallel are very common in a circuit and act
Series and Parallel Resistive Circuits The configuration of circuit elements clearly affects the behaviour of a circuit. Resistors connected in series or in parallel are very common in a circuit and act
Elementary Functions
 Chapter Three Elementary Functions 31 Introduction Complex functions are, of course, quite easy to come by they are simply ordered pairs of real-valued functions of two variables We have, however, already
Chapter Three Elementary Functions 31 Introduction Complex functions are, of course, quite easy to come by they are simply ordered pairs of real-valued functions of two variables We have, however, already
Chapter 7. DC Circuits
 Chapter 7 DC Circuits 7.1 Introduction... 7-3 Example 7.1.1: Junctions, branches and loops... 7-4 7.2 Electromotive Force... 7-5 7.3 Electrical Energy and Power... 7-9 7.4 Resistors in Series and in Parallel...
Chapter 7 DC Circuits 7.1 Introduction... 7-3 Example 7.1.1: Junctions, branches and loops... 7-4 7.2 Electromotive Force... 7-5 7.3 Electrical Energy and Power... 7-9 7.4 Resistors in Series and in Parallel...
Transistor Amplifiers
 Physics 3330 Experiment #7 Fall 1999 Transistor Amplifiers Purpose The aim of this experiment is to develop a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must accept input
Physics 3330 Experiment #7 Fall 1999 Transistor Amplifiers Purpose The aim of this experiment is to develop a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must accept input
Series and Parallel Circuits
 Direct Current (DC) Direct current (DC) is the unidirectional flow of electric charge. The term DC is used to refer to power systems that use refer to the constant (not changing with time), mean (average)
Direct Current (DC) Direct current (DC) is the unidirectional flow of electric charge. The term DC is used to refer to power systems that use refer to the constant (not changing with time), mean (average)
Chapter 11. Inductors ISU EE. C.Y. Lee
 Chapter 11 Inductors Objectives Describe the basic structure and characteristics of an inductor Discuss various types of inductors Analyze series inductors Analyze parallel inductors Analyze inductive
Chapter 11 Inductors Objectives Describe the basic structure and characteristics of an inductor Discuss various types of inductors Analyze series inductors Analyze parallel inductors Analyze inductive
