A simple algorithm to generate the minimal separators and the maximal cliques of a chordal graph
|
|
|
- Martin McCormick
- 9 years ago
- Views:
Transcription
1 A smpl lgortm to gnrt t mnml sprtors nd t mxml lqus o ordl grp Ann Brry 1 Romn Pogorlnk 1 Rsr Rport LMOS/RR Fbrury 11, 20 1 LMOS UMR CNRS 6158, Ensmbl Sntqu ds Cézux, F Aubèr, Frn, [email protected]
2 Abstrt W prsnt smpl und lgortm pross w uss tr LxBFS or MCS on ordl grp to gnrt t mnml sprtors nd t mxml lqus n lnr tm n sngl pss. Kywords: MCS, LxBFS, mnml sprtor, mxml lqu, ordl grp. 1
3 1 ntroduton Gnrtng t mnml sprtors nd t mxml lqus o ordl grp s smpl wt t lp o sp sr lgortms. Cordl grps (w r t grps wt no ordlss yl on our or mor vrts), wr rtrzd by Fulkrson nd Gross [7] s t grps or w on n rptdly nd smpll vrtx (.. vrtx wos ngborood s lqu) nd rmov t rom t grp, untl no vrtx s lt; ts pross, lld smpll lmnton, dns n ordrng α on t vrts lld prt lmnton ordrng (po). (α() dnots t vrtx brng numbr, nd α 1 (x) t numbr o vrtx x). At stp o t lmnton pross, nw trnstory grp s dnd. Ros [] sowd tt or ny gvn po α o ordl grp, ny mnml sprtor o t grp s dnd n t ours o t smpll lmnton pross s t trnstory ngborood o som vrtx. Morovr, t s sy to s tt n ny mxml lqu K, t vrtx y o smllst numbr by α dns K s ts trnstory losd ngborood. n t rst, w wll ll su vrts gnrtors, nd our gol wll b to dtt ts gnrtors ntly. W wll us grp sr lgortms LxBFS [10] nd MCS [11], bot tlord to gnrt po o ordl grp. T d bnd ts s qut smpl. Bot lgortms numbr t vrts rom n to 1 (n s t numbr o vrts o t grp). E vrtx brs lbl, w my b modd s t lgortm prods. At stp, nw vrtx s osn to b numbrd. t lbl o ts nw vrtx x s not lrgr tt t lbl o t prvous vrtx x +1, tn w know tt x gnrts mnml sprtor o t grp. T vrts o ts mnml sprtor r t lrdy numbrd ngbors o x. W lso know tt t prvously numbrd vrtx, x +1, gnrts mxml lqu: x +1, togtr wt ts lrdy numbrd ngbors (xludng x ), dn mxml lqu o t grp. Tus t lbls o lgortms LxBFS nd MCS nbl t usr to dtt ts gnrtors s soon s ty r numbrd. T mnml sprtors nd mxml lqus n b ound on-ln, wtout rqurng prlmnry pss o t lgortm to numbr ll t vrts. T orrspondng rsults v bn provd or MCS n two sprt pprs. Blr nd Pyton [5], wl studyng ow MCS dns lqu tr o ordl grp, sowd ow to gnrt t mxml lqus (w r t nods o t lqu tr), usng t MCS lbls. Kumr nd Mdvn [8] sowd ow to gnrt t mnml sprtors o ordl grp, gvn n MCS ordrng. 2
4 Howvr, ltoug mnml sprtor nd mxml lqu gnrtor r tully dttd t t sm stp o t lgortm, ts rsults v not bn und. Morovr, [8] us po s nput, but t mnml sprtors s wll s t mxml lqus n b omputd durng t xuton, w my b n mportnt tur wn ndlng vry lrg grps, sn globl pr-numbrng o t vrts s not nssry or vn usul. LxBFS, s w wll sow, xbts t sm proprty s MCS rgrdng ts gnrtors. Our m s to prsnt smpl und sngl-pss lgortm w gnrts t mnml sprtors nd t mxml lqus o ordl grp. T ppr s orgnzd s ollows: n Ston 2, w gv som prlmnry rsults nd dntons. n Ston 3, w prsnt our mn torm, w dsrbs ow t gnrtors r dttd, nd dsuss ts proo or LxBFS. Ston 4 prsnts our lgortm nd provds n xmpl. 2 Prlmnrs n t rst, w wll onsdr ll grps to b onntd (or dsonntd grp, t prosss w dsrb n b ppld ndpndntly to onntd omponnt). A grp s dnotd G = (V, E), V = n, E = m. Vrts x nd y r djnt xy E. For X V, G(X) dnots t subgrp ndud by X. T ngborood N G (x) o vrtx x n grp G s N G (x) = {y x xy E} (subsrpts wll b omttd wn t s lr w grp w work on). T losd ngborood s N G [x] = {x N(x)}. T ngborood o vrtx st X V s N G (X) = x X N G (x) X. A subst X o vrts s lld modul t vrts o X sr t sm xtrnl ngborood: x X, N(x) X = N(X). A lqu s st o prws djnt vrts. A subst S o vrts o onntd grp G s lld sprtor G(V S) s not onntd. A sprtor S s lld n xy-sprtor x nd y l n drnt onntd omponnts o G(V S), mnml xy-sprtor S s n xy-sprtor nd no propr subst o S s n xy-sprtor. A sprtor S s mnml sprtor, tr s som pr {x, y} su tt S s mnml xy-sprtor. Altrntly, S s n mnml sprtor nd only G(V S) s t lst 2 onntd omponnts C 1 nd C 2 su tt N(C 1 ) = N(C 2 ) = S; su omponnts r lld ull omponnts o S n G, nd S s tn mnml xy-sprtor or ny {x, y} wt x C 1 nd y C 2. LxBFS [10] nd MCS [11] r bot lnr-tm sr lgortms w numbr t vrts rom n to 1, trby dnng po. E vrtx x brs lbl w orrsponds to t lst o numbrs o t ngbors o x wt 3
5 gr numbr tn tt o x (LxBFS) or to t rdnlty o ts lst (MCS). Bot lgortms r rlld blow. Algortm LxBFS (Lxogrp Brdt-Frst Sr)[10] nput : A grp G = (V, E). output: An ordrng α o V. ntlz ll lbls s t mpty strng; or n to 1 do Pk n unnumbrd vrtx v wos lbl s mxml undr lxogrp ordr; α() v ; or unnumbrd vrtx w djnt to v do ppnd to lbl(w); Algortm MCS (Mxml Crdnlty Sr)[11] nput : A grp G = (V, E). output: An ordrng α o V. ntlz ll lbls s 0; or n to 1 do Pk n unnumbrd vrtx v wt mxmum lbl; α() v ; or unnumbrd vrtx w djnt to v do lbl(w) lbl(w) + 1; 3 Mn Torm W wll now prsnt our mn torm, rom w our lgortm s drvd. W wll nd t ollowng dntons: Dnton 3.1 Gvn ordl grp G nd po α o G, or ny vrtx x, Mdj(x) s t st o ngbors o x wt numbr gr tn tt o x: Mdj(x) = {y N(x) α 1 (y) > α 1 (x)}. Dnton 3.2 Gvn ordl grp G nd po α o G, w wll ll: 4
6 mnml sprtor gnrtor ny vrtx x wt numbr by α, su tt Mdj(x ) s mnml sprtor o G nd lbl(x ) lbl(x +1 ), wr x +1 = α( + 1). mxml lqu gnrtor vrtx y su tt Mdj(y) {y} s mxml lqu o G. Our mn rsult s t ollowng: Torm 3.3 Lt α b po dnd by tr LxBFS or MCS, lt x b t vrtx o numbr, lt x +1 b t vrtx o numbr + 1. ) x s mnml sprtor gnrtor nd only lbl(x ) lbl(x +1 ). b) x +1 s mxml lqu gnrtor nd only lbl(x ) lbl(x +1 ) or = 1. W wll now dsuss t proo o Torm 3.3. W wll rst prsnt moplx lmnton, w s pross tt xplns ow bot MCS nd LxBFS sn t mnml sprtors nd t mxml lqus o ordl grp, tn prov Torm 3.3 or LxBFS. 3.1 Moplx lmnton W wll us t noton o moplx, ntrodud by [1]: Dnton 3.4 [1] A moplx s lqu X su tt X s modul nd N(X) s mnml sprtor. W xtnd ts dnton to lqu wos ngborood s mpty. A smpll moplx s moplx wos vrts r ll smpll. [1] provd: Proprty 3.5 [1] Any ordl grp w s not lqu s t lst two non-djnt smpll moplxs. From ts, ty drvd vrnt o t rtrzton o Fulkrson nd Gross or ordl grps by smpll lmnton o vrts: Crtrzton 3.6 [1] A grp s ordl nd only on n rptdly dlt smpll moplx untl t grp s lqu (w w wll ll t trmnl moplx ). W ll ts pross moplx lmnton. 5
7 Not tt moplx lmnton on ordl grp s spl s o smpll lmnton, sn t stp st o smpll vrts s lmntd. Not lso tt or onntd grp G, t trnstory lmnton grp obtnd t t nd o stp rmns onntd. Moplx lmnton dns n ordrd prtton (X 1, X 2,..., X k ) o t vrts o t grp nto t sussv moplxs w r dnd n t sussv trnstory lmnton grps. W wll ll ts prtton moplx ordrng. Our bs rsult s t ollowng: Torm Lt G b ordl grp, lt (X 1, X 2,..., X k ) b moplx ordrng o G. At stp < k o t lmnton pross ndng moplx X n trnstory grp G, N G (X ) s mnml sprtor o G. X N G (X ) s mxml lqu o G. T trmnl moplx X k s mxml lqu. Tr r no otr mnml sprtors or mxml lqus n G. To prov ts, w wll rst rll t rsult rom Ros []: Proprty 3.8 [] Lt G b ordl grp, lt α b po o G, lt S b mnml sprtor o G. Tn tr s som vrtx x su tt Mdj(x) = S. From Proprty 3.8, t s sy to ddu t ollowng wll-known proprty: Proprty 3. [] Lt G b ordl grp, lt S b mnml sprtor o G. Tn n vry ull omponnt C o S, tr s som vrtx x su tt S N(x) (su vrtx s lld onlun pont o C). Lt us now prov Torm 3.7. Proo: (o Torm 3.7) Lt us rst prov tt N G (X ) s mnml sprtor o G. n trnstory grp G, N G (X ) s by dnton mnml sprtor S o G, wt t lst two ull omponnts C 1 nd C 2, ontnng onlun pont, w w wll ll x 1 nd x 2. Suppos S s not mnml sprtor o G. Tn tr must b ordlss pt rom x 1 to x 2 n G w ontns no vrtx o S. Lt y b t rst vrtx o ts pt to b lmntd, t 1 T rsults provd n ts subston wr brly prsntd n [2]. 6
8 stp j < ; y must b smpll n G j, but ts s mpossbl, sn y s two non-djnt ngbors on t pt. Tus vry N G (X ) ( < k) s mnml sprtor o G, nd by Proprty 3.8, ll t mnml sprtors o G v tus bn nountrd. Lt us now prov tt X N G (X ) s mxml lqu o G, by nduton on. Clrly, X 1 N G (X 1 ) s mxml lqu o G. Lt us xmn X N G (X ): t s mxml lqu o G nd tus lqu o G. Suppos t s not mxml lqu o G, nd lt y b vrtx blongng to lrgr lqu o G ontnng X N G (X ). Sn N G (X ) s mnml sprtor o G, y must blong to t sm ull omponnt o N G (X ) s t vrts o X. But tn y blongs to t sm mxml lqu modul s X, ontrdton. T trmnl moplx X k s by dnton lqu; suppos t s not mxml lqu: tn t n b ugmntd wt som vrtx y, w blongs to som moplx X. By Torm 3.7, S = N G (X ) s mnml sprtor o G. Lt C 1,..., C t b t ull omponnts o S n G, nd lt z b t onlun pont blongng to t moplx o gst numbr X j. n G j, S nnot b mnml sprtor, sn ll t otr ull omponnts o S v bn lmntd rom G j. Tror, X j N Gj (X j ) must b t trmnl moplx, ontrdton. Not tt or gvn ordl grp G, tr my b mny drnt moplx ordrngs, but tr s lwys t sm numbr o moplxs, sn ts s t numbr o mxml lqus o t grp. Wt ny moplx ordrng (X 1, X 2,..., X k ), w n ssot po α by prossng t moplxs rom 1 to n nd gvng onsutv numbrs to t vrts o gvn moplx. Usng α, w n dn t mnml sprtors nd mxml lqus s vrtx ngboroods: Proprty 3.10 Lt G b ordl grp, lt (X 1, X 2,..., X k ) b moplx ordrng o G, lt α b po ssotd wt ts moplx ordrng. Tn n t ours o moplx lmnton, t stp, prossng moplx X, T vrtx x o moplx X wos numbr s t smllst by α dns mxml lqu {x} Mdj(x) o G. T vrtx y o moplx X wos numbr s t gst by α dns mnml sprtor Mdj(y) o G. 7
9 3.2 Gnrtors o LxBFS LxBFS dns moplx ordrng nd n ssotd po: [1] sowd tt LxBFS lwys numbrs s 1 vrtx blongng to moplx (w w wll ll X 1 ). Ty lso provd tt t vrts o X 1 rv onsutv numbrs by LxBFS. Ts proprts r tru t stp o LxBFS n t trnstory lmnton grp. Tror, LxBFS dns moplx lmnton (X 1,..., X k ), by numbrng onsutvly t vrts o X 1, tn numbrng onsutvly t vrts o X 2, nd so ort: Torm 3.11 n ordl grp, LxBFS dns moplx ordrng. Not tt t s sy to ddu rom [5] tt MCS lso dns moplx ordrng. Exmpl 3.12 Fgur 1 sows t numbrs nd lbls o LxBFS xuton on ordl grp. moplx mnml sprtor mxml lqu X 1 = {g} {b, } {b,, g} X 2 = {} {b,, d} {, b,, d} X 3 = {d, } {b, } {b,, d, } X 4 = {} {b, } {b,, } X 5 = {b,, } - {b,, } 2 [6,5,4] [] 8 [8,7] 6 b [7,6] 5 [6,5] 4 d 7 [8] g 1 [6,5] [6,5,4] 3 Fgur 1: Numbrs nd lbls o LxBFS xuton on ordl grp. Sn t vrts o ny trnstory moplx X r numbrd onsutvly, t lbls wll nrs w.r.t. lxogrp ordr untl t ntr moplx s bn numbrd, nd tn wll stop nrsng. Mor prsly, wn 8
10 runnng LxBFS (numbrng t vrts rom n to 1), s long s t lbls nrs, w r dnng moplx, X. Wn t lbls stop nrsng (wn numbrng vrtx y), tn w v strtd nw moplx X 1 w wll ontn y. Usng Proprty 3.10, w n ddu tt LxBFS gnrts t mnml sprtors nd t mxml lqus ordng to Torm 3.3. Tus t s sy, usng LxBFS ordrng, to dn wt sngl pss t mnml sprtors o G t mxml lqus o G t orrspondng moplx ordrng 4 Algortm W n now drv rom Torm 3.3 gnrlzd lgortm to gnrt t mnml sprtors nd t mxml lqus o ordl grp. n t lgortm blow, t s onsdrd tt tr LxBFS or MCS s usd. Us to nrmnt t lbl o y s trnsltd s dd to lbl o y or LxBFS nd s dd 1 to t lbl o y or MCS. T lbls r ll onsdrd ntlzd t t bgnnng, s or LxBFS nd s 0 or MCS. G NUM G NUM +{x } s sortnd or V NUM V NUM +{x }; G NUM G(V NUM ). n t sm son, G ELM G ELM {x } s sortnd or V ELM V ELM {x } ; G ELM G(V ELM ) ; Symbol + dnots dsjont unon. Not tt or LxBFS, x s mnml sprtor gnrtor, tn t lbl o x gvs t sprtor drtly., or nstn, lbl(x ) = (, 7, 6), tn t mnml sprtor w x gnrts wll b {x, x 7, x 6 }.
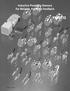
11 Algortm Mnsps-Mxlqus nput : A ordl grp G = (V, E). output: St S o mnml sprtors o G ; St S o mnml sprtor gnrtors o G ; St K o mxml lqus o G ; St K o mxml lqu gnrtors o G ; nt: G NUM G( ); G ELM G ; S ; S ; K ; K ; or =n downto 1 do Coos vrtx x o G ELM o mxmum lbl ; G NUM G NUM + {x } ; n nd lbl(x ) λ tn //x s mn. sp. gnrtor nd x +1 s mx. lqu gnrtor S S + {x } ; S S {N GNUM (x )} ; K K + {x +1 } ; K K + {(N GNUM (x ) {x }}; λ lbl(x ) ; or y N GELM (x ) do Us to nrmnt t lbl o y ; G ELM G ELM {x } ; K K + {x 1 } ; K K + {N G (x 1 )} ; T omplxty o t bov lgortm s t sm s or LxBFS or MCS, w s lnr (O(n + m)) tm. Exmpl 4.1 Fgur 4 blow gvs stp-by-stp xmpl usng MCS. St o mnml sprtors: S = {{}, {g, }, {d}}. St o mnml sprtor gnrtors: S = {d,, }. St o mxml lqus: K = {{, b, }, {, d, g, }, {g,, }, {d,, }}. St o mxml lqu gnrtors: K = {,,, }. Wn prossng vrtx x 6, x 6 = d s dnd s mnml sprtor gnrtor or {} nd tus x 7 = s mxml lqu gnrtor or {, b, }. Wn prossng vrtx x 3, x 3 = s dnd s mnml sprtor gnrtor or {g, }, so x 4 = s mxml lqu gnrtor, or {, d, g, }. Wn prossng vrtx x 2, x 2 = s dnd s mnml sprtor gnrtor or {d}, so x 3 = s mxml lqu gnrtor or {g,, }. 10
12 At t nd, x 1 = s dnd mxml lqu gnrtor, or {d,, }. b d 8 b d 7 8 b d g g g Prossng Prossng 8 Prossng b d b d b d 6 g 5 g 5 g 4 Prossng 6 Prossng 5 Prossng b d 6 5 g b d g b d g Prossng 3 Prossng 2 Prossng 1 3 Fgur 2: A stp by stp xuton usng MCS. T dsd vrtx numbrs rprsnt t mnml sprtor gnrtors, nd t rld vrtx sts r t mnml sprtors. 4.1 Multplty o t gnrtd mnml sprtors A mnml sprtor my b gnrtd svrl tms, dpndng on t numbr o ull omponnts t dns: Proprty 4.2 Lt α b po dnd by LxBFS or MCS, lt S b mnml sprtor, lt k b t numbr o ull omponnts o S. Tn S s k 1 gnrtors by α. 11
13 Proo: n t ours o smpll lmnton pross on smpll vrts, bor ny vrtx s o mnml sprtor S n b lmntd, ll t ull omponnts o S (xpt on) must v bn lmntd, ls s nnot b smpll, s s ss t onlun ponts o rmnng ull omponnt. T lst vrtx lmntd rom ts ull omponnts gnrts S. Wn ll ull omponnts (xpt on) v bn lmntd, S s no longr mnml sprtor. Tror S s k ull omponnts, t s gnrtd xtly k 1 tms. Not tt [8] gvs n O(n + mlogn) pross to nd t multplty o mnml sprtor (wt MCS). Howvr, ty lso prov tt wt LxBFS, gvn t mnml sprtor gnrtor o lowst numbr w gnrts S, wtn t subst o mnml sprtor gnrtors w dn mnml sprtor o sz S, ll t gnrtors o S r onsutv. n t ours o n xuton o LxBFS, on n stor t lbls o t gnrtors n drnt lsts ordng to t sz o t mnml sprtor ty gnrt. Tn on n run troug lst, tstng or onsutv ourrns o gvn mnml sprtor. Ts n b don n lnr tm, s by Torm 3.7, t sum o t szs o t mnml sprtors s lss tn m. 5 Conluson n ts ppr, w prsnt smpl nd optml pross w gnrts t mnml sprtors nd mxml lqus o ordl grp n sngl pss o tr LxBFS or MCS, wtout rqurng t prlmnry omputton o po. Toug bot LxBFS nd MCS yld n optml lnr-tm pross or ts problm, t s mportnt to not tt ty dn drnt st o pos o ordl grp [4], nd xbt drnt lol bvors [3]. t my b mportnt to us on or t otr, dpndng on t ntndd pplton. W wll nd ts ppr by notng tt two rntly ntrodud sr lgortms, LxDFS nd MNS [6] l to bv n t sm son. A ountr-xmpl or MNS s gvn blow (T MNS lbls r t sts o gr-numbrd ngbors, omprd by st nluson): wn vrtx 2 s numbrd, ts lbl s not grtr tn tt o vrtx 3; owvr, Mdj(3) = {3, 4} s not mxml lqu.. 12
14 {4} 3 {5} {5} 1 {4,3} Fgur 3: MNS dos not gnrt t mxml lqus. Rrns [1] A. Brry, J.-P. Bordt Sprblty gnrlzs Dr s torm. Dsrt Appld Mtmts, 84(1-3):43 53, 18. [2] A. Brry, J.-P. Bordt Moplx lmnton ordrngs. Eltron Nots n Dsrt Mtmts, 8:6, 20. [3] A. Brry, J. R. S. Blr, J.-P. Bordt, nd G. Smont. Grp xtrmts dnd by sr lgortms. Rsr rport, LMOS, RR-07-05, 2007, to ppr n Algortms. [4] A. Brry, R. Krugr, G. Smont Gnvèv Smont. Mxml lbl sr lgortms to omput prt nd mnml lmnton ordrngs. SAM J. Dsrt Mt., 23(1): , 200. [5] J. R. S. Blr nd B. W. Pyton. An ntroduton to ordl grps nd lqu trs. Grp Tory nd Sprs Mtrx Computton. [6] D. G. Cornl, R. Krugr A und vw o grp srng. SAM J. Dsrt Mt., 22(4): , [7] D. R. Fulkrson nd O. A. Gross. ndn mtrs nd ntrvl grps. P Journl o Mtmts, 28: , 16. [8] P. Srnvs Kumr nd C. E. Vn Mdvn. Mnml vrtx sprtors o ordl grps. Dsrt Appld Mtmts, 8(1-3): , 18. [] D. J. Ros. Trngultd grps nd t lmnton pross. Journl o Mtmtl Anlyss nd Appltons,. [10] D. J. Ros, R. E. Trjn, nd G. S. Lukr. Algortm spts o vrtx lmnton on grps. SAM J. Comput., 5(2): ,
15 [11] R. E. Trjn nd M. Ynnkks. Smpl lnr-tm lgortms to tst ordlty o grps, tst ylty o yprgrps, nd sltvly rdu yl yprgrps. SAM J. Comput., 13(3):566 57,
Recall from Last Time: Disjoint Set ADT
 Ltur 21: Unon n Fn twn Up-Trs Toy s An: Plntn n rown orst o Up-Trs Unon-n n Fn-n Extn xmpl Implmntn Unon/Fn Smrt Unon n Fn Unon-y-sz/t n Pt Comprsson Run Tm Anlyss s tou s t ts! Covr n Cptr 8 o t txtook
Ltur 21: Unon n Fn twn Up-Trs Toy s An: Plntn n rown orst o Up-Trs Unon-n n Fn-n Extn xmpl Implmntn Unon/Fn Smrt Unon n Fn Unon-y-sz/t n Pt Comprsson Run Tm Anlyss s tou s t ts! Covr n Cptr 8 o t txtook
A New Efficient Distributed Load Balancing Algorithm for OTIS-Star Networks
 Int'l Con. Pr. n Dst. Pro. T. n Appl. PDPTA' A Nw Ent Dstrut Lo Blnn Alortm or OTIS-Str Ntwors A. Aww 1, J. Al-S 1 Dprtmnt o CS, Unvrsty o Ptr, Ammn, Jorn Dprtmnt o ITC, Ar Opn Unvrsty, Ammn, Jorn Astrt
Int'l Con. Pr. n Dst. Pro. T. n Appl. PDPTA' A Nw Ent Dstrut Lo Blnn Alortm or OTIS-Str Ntwors A. Aww 1, J. Al-S 1 Dprtmnt o CS, Unvrsty o Ptr, Ammn, Jorn Dprtmnt o ITC, Ar Opn Unvrsty, Ammn, Jorn Astrt
4.1 Interval Scheduling. Chapter 4. Greedy Algorithms. Interval Scheduling. Interval Scheduling: Greedy Algorithms
 1 ptr 4 41 Intrvl Suln ry lortms Sls y Kvn Wyn opyrt 5 Prson-son Wsly ll rts rsrv Intrvl Suln Intrvl Suln: ry lortms Intrvl suln Jo strts t s n nss t Two os omptl ty on't ovrlp ol: n mxmum sust o mutully
1 ptr 4 41 Intrvl Suln ry lortms Sls y Kvn Wyn opyrt 5 Prson-son Wsly ll rts rsrv Intrvl Suln Intrvl Suln: ry lortms Intrvl suln Jo strts t s n nss t Two os omptl ty on't ovrlp ol: n mxmum sust o mutully
MPLS FOR MISSION-CRITICAL MICROWAVE NETWORKS BUILDING A HIGHLY RESILIENT MICROWAVE NETWORK WITH MULTI-RING TOPOLOGY
 MPLS FOR MISSION-CRITICAL MICROWAVE NETWORKS BUILDING A HIGHLY RESILIENT MICROWAVE NETWORK WITH MULTI-RING TOPOLOGY TECHNICAL WHITE PAPER H rslny n srv vllty r ky sn onsrtons wn uln msson-rtl mrowv ntworks.
MPLS FOR MISSION-CRITICAL MICROWAVE NETWORKS BUILDING A HIGHLY RESILIENT MICROWAVE NETWORK WITH MULTI-RING TOPOLOGY TECHNICAL WHITE PAPER H rslny n srv vllty r ky sn onsrtons wn uln msson-rtl mrowv ntworks.
Reading. Minimum Spanning Trees. Outline. A File Sharing Problem. A Kevin Bacon Problem. Spanning Trees. Section 9.6
 Rin Stion 9.6 Minimum Spnnin Trs Outlin Minimum Spnnin Trs Prim s Alorithm Kruskl s Alorithm Extr:Distriut Shortst-Pth Alorithms A Fil Shrin Prolm Sy unh o usrs wnt to istriut il monst thmslvs. Btwn h
Rin Stion 9.6 Minimum Spnnin Trs Outlin Minimum Spnnin Trs Prim s Alorithm Kruskl s Alorithm Extr:Distriut Shortst-Pth Alorithms A Fil Shrin Prolm Sy unh o usrs wnt to istriut il monst thmslvs. Btwn h
Cloud and Big Data Summer School, Stockholm, Aug., 2015 Jeffrey D. Ullman
 Cloud and Big Data Summr Scool, Stockolm, Aug., 2015 Jffry D. Ullman Givn a st of points, wit a notion of distanc btwn points, group t points into som numbr of clustrs, so tat mmbrs of a clustr ar clos
Cloud and Big Data Summr Scool, Stockolm, Aug., 2015 Jffry D. Ullman Givn a st of points, wit a notion of distanc btwn points, group t points into som numbr of clustrs, so tat mmbrs of a clustr ar clos
Authenticated Encryption. Jeremy, Paul, Ken, and Mike
 uthntcatd Encrypton Jrmy Paul Kn and M Objctvs Examn thr mthods of authntcatd ncrypton and dtrmn th bst soluton consdrng prformanc and scurty Basc Componnts Mssag uthntcaton Cod + Symmtrc Encrypton Both
uthntcatd Encrypton Jrmy Paul Kn and M Objctvs Examn thr mthods of authntcatd ncrypton and dtrmn th bst soluton consdrng prformanc and scurty Basc Componnts Mssag uthntcaton Cod + Symmtrc Encrypton Both
Constrained Renewable Resource Allocation in Fuzzy Metagraphs via Min- Slack
 Intrntonl Journl of ppld Oprtonl Rsrch Vol 1, No 1, pp 7-17, Summr 011 Journl hompg: wwworlur Constrnd Rnwl Rsourc llocton n Fuzzy Mtgrphs v Mn- Slck S S Hshmn* Rcvd: Jnury 31, 011 ; ccptd: My 1, 011 strct
Intrntonl Journl of ppld Oprtonl Rsrch Vol 1, No 1, pp 7-17, Summr 011 Journl hompg: wwworlur Constrnd Rnwl Rsourc llocton n Fuzzy Mtgrphs v Mn- Slck S S Hshmn* Rcvd: Jnury 31, 011 ; ccptd: My 1, 011 strct
Change Your History How Can Soccer Knowledge Improve Your Business Processes?
 Symposium Inuurl Lctur o Hjo Rijrs, VU, 26-6-2015 Chn Your History How Cn Soccr Knowl Improv Your Businss Procsss? Wil vn r Alst TU/ n DSC/ 1970 born Oostrbk 1988-1992 CS TU/ 1992-1994 TS TU/ 1994-1996
Symposium Inuurl Lctur o Hjo Rijrs, VU, 26-6-2015 Chn Your History How Cn Soccr Knowl Improv Your Businss Procsss? Wil vn r Alst TU/ n DSC/ 1970 born Oostrbk 1988-1992 CS TU/ 1992-1994 TS TU/ 1994-1996
CPS 220 Theory of Computation REGULAR LANGUAGES. Regular expressions
 CPS 22 Thory of Computation REGULAR LANGUAGES Rgular xprssions Lik mathmatical xprssion (5+3) * 4. Rgular xprssion ar built using rgular oprations. (By th way, rgular xprssions show up in various languags:
CPS 22 Thory of Computation REGULAR LANGUAGES Rgular xprssions Lik mathmatical xprssion (5+3) * 4. Rgular xprssion ar built using rgular oprations. (By th way, rgular xprssions show up in various languags:
QUANTITATIVE METHODS CLASSES WEEK SEVEN
 QUANTITATIVE METHODS CLASSES WEEK SEVEN Th rgrssion modls studid in prvious classs assum that th rspons variabl is quantitativ. Oftn, howvr, w wish to study social procsss that lad to two diffrnt outcoms.
QUANTITATIVE METHODS CLASSES WEEK SEVEN Th rgrssion modls studid in prvious classs assum that th rspons variabl is quantitativ. Oftn, howvr, w wish to study social procsss that lad to two diffrnt outcoms.
Roof Terraces. Structural assemblies 04-2012
 C Roo Trrs Strutur ssms 04-2012 Prt soutons rom n xprt sour Sütr-Systms s n rn nm or ntnt strutur ssms on ons n trrs sn 1983. Tt yr, Wrnr Sütr nvnt t Sütr -TROBA mt, t rst rn mt or t r rn o ons n trrs.
C Roo Trrs Strutur ssms 04-2012 Prt soutons rom n xprt sour Sütr-Systms s n rn nm or ntnt strutur ssms on ons n trrs sn 1983. Tt yr, Wrnr Sütr nvnt t Sütr -TROBA mt, t rst rn mt or t r rn o ons n trrs.
Uses for Binary Trees -- Binary Search Trees
 CS122 Algorithms n Dt Struturs MW 11:00 m 12:15 pm, MSEC 101 Instrutor: Xio Qin Ltur 10: Binry Srh Trs n Binry Exprssion Trs Uss or Binry Trs Binry Srh Trs n Us or storing n rtriving inormtion n Insrt,
CS122 Algorithms n Dt Struturs MW 11:00 m 12:15 pm, MSEC 101 Instrutor: Xio Qin Ltur 10: Binry Srh Trs n Binry Exprssion Trs Uss or Binry Trs Binry Srh Trs n Us or storing n rtriving inormtion n Insrt,
tis, cis cunc - cunc - tis, cis tis, cis cunc - tis, func - def - def - tis, U func - def - func - tis, pa - tri pa - tri pa - tri tu - per - tu -
 1 B Ihsu dulcs cuncts [Supr 1] [Supr 2] Tnr B B B B - B - B - Ih - Ih - Ih - su su su cs cs cs cunc - cunc - cunc - Amns, Bblthèqu Cntl L Agn, ms 162 D, ff 2v-10 ts, ts, ts, E-tr - E-tr - E-tr - n p n
1 B Ihsu dulcs cuncts [Supr 1] [Supr 2] Tnr B B B B - B - B - Ih - Ih - Ih - su su su cs cs cs cunc - cunc - cunc - Amns, Bblthèqu Cntl L Agn, ms 162 D, ff 2v-10 ts, ts, ts, E-tr - E-tr - E-tr - n p n
Matching Execution Histories of Program Versions
 Mt Exuto Hstors o Prorm Vrsos Xyu Z Rv Gupt Dprtmt o Computr S T Uvrsty o Arzo Tuso, Arzo 85721 {xyz,upt}@s.rzo.u ABSTRACT W vlop mto or mt ym stors o prorm xutos o two prorm vrsos. T mts prou usul my
Mt Exuto Hstors o Prorm Vrsos Xyu Z Rv Gupt Dprtmt o Computr S T Uvrsty o Arzo Tuso, Arzo 85721 {xyz,upt}@s.rzo.u ABSTRACT W vlop mto or mt ym stors o prorm xutos o two prorm vrsos. T mts prou usul my
Operation Transform Formulae for the Generalized. Half Canonical Sine Transform
 Appl Mhmcl Scnc Vol 7 3 no 33-4 HIKARI L wwwm-hrcom Opron rnorm ormul or h nrl Hl Cnoncl Sn rnorm A S uh # n A V Joh * # ov Vrh Inu o Scnc n Humn Amrv M S In * Shnrll Khnlwl Coll Aol - 444 M S In luh@mlcom
Appl Mhmcl Scnc Vol 7 3 no 33-4 HIKARI L wwwm-hrcom Opron rnorm ormul or h nrl Hl Cnoncl Sn rnorm A S uh # n A V Joh * # ov Vrh Inu o Scnc n Humn Amrv M S In * Shnrll Khnlwl Coll Aol - 444 M S In luh@mlcom
Managing Multiple Outsourcing: Service Quality and Volume Issues
 Prodngs of th 4 Intrntonl Confrn on Industrl Engnrng nd Oprtons Mngmnt l Indons Jnury 7 9 4 Mngng Multpl Outsourng: Srv ulty nd Volum Issus Smr K Mukhopdhyy SungKyunKwn Unvrsty GS Jongnogu Soul Kor -745
Prodngs of th 4 Intrntonl Confrn on Industrl Engnrng nd Oprtons Mngmnt l Indons Jnury 7 9 4 Mngng Multpl Outsourng: Srv ulty nd Volum Issus Smr K Mukhopdhyy SungKyunKwn Unvrsty GS Jongnogu Soul Kor -745
ELECTRICAL CAPACITY SYMBOL EQUIPMENT TYPE LOCATION / SERVING MFR MODEL (GALLONS) VOLTS PH AMPS WATTS
 OT: This is a stadard symbol list ad ot all items listed may be used. bbreviatios () XT OV OOR OW OOR P OW PRVTR OT R OT. OTTO V VV W O WTR R OT TR OW T TR O OOR OT OOR R T T O P O PR OR P O PR T W R WT,
OT: This is a stadard symbol list ad ot all items listed may be used. bbreviatios () XT OV OOR OW OOR P OW PRVTR OT R OT. OTTO V VV W O WTR R OT TR OW T TR O OOR OT OOR R T T O P O PR OR P O PR T W R WT,
11 + Non-verbal Reasoning
 Prti Tst + Non-vrl Rsoning R th instrutions rfully. Do not gin th tst or opn th ooklt until tol to o so. Work s quikly n s rfully s you n. Cirl th orrt lttr from th options givn to nswr h qustion. You
Prti Tst + Non-vrl Rsoning R th instrutions rfully. Do not gin th tst or opn th ooklt until tol to o so. Work s quikly n s rfully s you n. Cirl th orrt lttr from th options givn to nswr h qustion. You
CCD CHARGE TRANSFER EFFICIENCY (CTE) DERIVED FROM SIGNAL VARIANCE IN FLAT FIELD IMAGES The CVF method
 CCD CHARGE TRANSFER EFFICIENCY (CTE) DERIVED FROM SIGNAL VARIANCE IN FLAT FIELD IMAGES Th CVF mthod Fbrc Chrstn 1, Konrd Kujkn 1,, Dtrch Bd 3, Cyrl Cvdor 4, Sbstn Drs 3, Olf Iwrt 3. 1 Kptyn Astronomcl
CCD CHARGE TRANSFER EFFICIENCY (CTE) DERIVED FROM SIGNAL VARIANCE IN FLAT FIELD IMAGES Th CVF mthod Fbrc Chrstn 1, Konrd Kujkn 1,, Dtrch Bd 3, Cyrl Cvdor 4, Sbstn Drs 3, Olf Iwrt 3. 1 Kptyn Astronomcl
Online Load Balancing and Correlated Randomness
 Onln Load Balancng and Corrlatd Randomnss Sharayu Moharr, Sujay Sanghav Wrlss Ntworng and Communcatons Group (WNCG) Dpartmnt of Elctrcal & Computr Engnrng Th Unvrsty of Txas at Austn Austn, TX 787, USA
Onln Load Balancng and Corrlatd Randomnss Sharayu Moharr, Sujay Sanghav Wrlss Ntworng and Communcatons Group (WNCG) Dpartmnt of Elctrcal & Computr Engnrng Th Unvrsty of Txas at Austn Austn, TX 787, USA
Form: Parental Consent for Blood Donation
 A R C Wt, C 20006 Ptl Ct f B i Ifi T f t y t ll f i y tl t q y t l A R C ly. Pl ll 1-800-RE-CROSS (1-800-733-2767) v. if y v q r t t i I iv t f yr,, t, y v t t: 1. Y y t t l i ly, 2. Y y t t t l i ( k
A R C Wt, C 20006 Ptl Ct f B i Ifi T f t y t ll f i y tl t q y t l A R C ly. Pl ll 1-800-RE-CROSS (1-800-733-2767) v. if y v q r t t i I iv t f yr,, t, y v t t: 1. Y y t t l i ly, 2. Y y t t t l i ( k
ANALYSIS OF ORDER-UP-TO-LEVEL INVENTORY SYSTEMS WITH COMPOUND POISSON DEMAND
 8 th Intrnatonal Confrnc of Modlng and Smulaton - MOSIM - May -2, 2 - Hammamt - Tunsa Evaluaton and optmzaton of nnovatv producton systms of goods and srvcs ANALYSIS OF ORDER-UP-TO-LEVEL INVENTORY SYSTEMS
8 th Intrnatonal Confrnc of Modlng and Smulaton - MOSIM - May -2, 2 - Hammamt - Tunsa Evaluaton and optmzaton of nnovatv producton systms of goods and srvcs ANALYSIS OF ORDER-UP-TO-LEVEL INVENTORY SYSTEMS
Example A rectangular box without lid is to be made from a square cardboard of sides 18 cm by cutting equal squares from each corner and then folding
 1 Exmple A rectngulr box without lid is to be mde from squre crdbord of sides 18 cm by cutting equl squres from ech corner nd then folding up the sides. 1 Exmple A rectngulr box without lid is to be mde
1 Exmple A rectngulr box without lid is to be mde from squre crdbord of sides 18 cm by cutting equl squres from ech corner nd then folding up the sides. 1 Exmple A rectngulr box without lid is to be mde
Hermes: Dynamic Partitioning for Distributed Social Network Graph Databases
 Hrms: Dynm Prttonn or Dstrut Sol Ntwork Grph Dtss Dnl Nor Unvrsty o Wtrloo [email protected] Shhn Kml Unvrsty o Wtrloo s3kml@uwtrloo. Khuzm Duj Unvrsty o Wtrloo kuj@uwtrloo. L Chn HKUST [email protected] ABSTRACT
Hrms: Dynm Prttonn or Dstrut Sol Ntwork Grph Dtss Dnl Nor Unvrsty o Wtrloo [email protected] Shhn Kml Unvrsty o Wtrloo s3kml@uwtrloo. Khuzm Duj Unvrsty o Wtrloo kuj@uwtrloo. L Chn HKUST [email protected] ABSTRACT
Link-Disjoint Paths for Reliable QoS Routing
 Link-Disjoint Pths or Rlil QoS Routing Yuhun Guo, Frnno Kuiprs n Pit Vn Mighm # Shool o Eltril n Inormtion Enginring, Northrn Jiotong Univrsity, Bijing, 000, P.R. Chin Fulty o Inormtion Thnology n Systms,
Link-Disjoint Pths or Rlil QoS Routing Yuhun Guo, Frnno Kuiprs n Pit Vn Mighm # Shool o Eltril n Inormtion Enginring, Northrn Jiotong Univrsity, Bijing, 000, P.R. Chin Fulty o Inormtion Thnology n Systms,
Victims Compensation Claim Status of All Pending Claims and Claims Decided Within the Last Three Years
 Claim#:021914-174 Initials: J.T. Last4SSN: 6996 DOB: 5/3/1970 Crime Date: 4/30/2013 Status: Claim is currently under review. Decision expected within 7 days Claim#:041715-334 Initials: M.S. Last4SSN: 2957
Claim#:021914-174 Initials: J.T. Last4SSN: 6996 DOB: 5/3/1970 Crime Date: 4/30/2013 Status: Claim is currently under review. Decision expected within 7 days Claim#:041715-334 Initials: M.S. Last4SSN: 2957
Binary Search Trees. Definition Of Binary Search Tree. Complexity Of Dictionary Operations get(), put() and remove()
 Binary Sar Trs Compxity O Ditionary Oprations t(), put() and rmov() Ditionary Oprations: ƒ t(ky) ƒ put(ky, vau) ƒ rmov(ky) Additiona oprations: ƒ asnd() ƒ t(indx) (indxd inary sar tr) ƒ rmov(indx) (indxd
Binary Sar Trs Compxity O Ditionary Oprations t(), put() and rmov() Ditionary Oprations: ƒ t(ky) ƒ put(ky, vau) ƒ rmov(ky) Additiona oprations: ƒ asnd() ƒ t(indx) (indxd inary sar tr) ƒ rmov(indx) (indxd
PRESENTED TO. Data Leakage Worldwide: The Effectiveness of Corporate Security Policies
 PRSNTD TO Dt Lk Worlw: T tvnss o Corport Surty Pols UUST 2008 Ovrvw Rsr Otvs Cso ontrt nst xprss to xut n ntrntonl survy wt ous on t ollown otvs: xplor mploy us o ompny vs, nlun ommunton srvs n vs us,
PRSNTD TO Dt Lk Worlw: T tvnss o Corport Surty Pols UUST 2008 Ovrvw Rsr Otvs Cso ontrt nst xprss to xut n ntrntonl survy wt ous on t ollown otvs: xplor mploy us o ompny vs, nlun ommunton srvs n vs us,
Upward Planar Drawings of Series-Parallel Digraphs with Maximum Degree Three
 Upwr Plnr Drwins of ris-prlll Dirps wit Mximum Dr Tr (Extn Astrt) M. Aul Hssn m n M. iur Rmn Dprtmnt of Computr in n Eninrin, Bnls Univrsity of Eninrin n Tnoloy (BUET). {sm,siurrmn}@s.ut.. Astrt. An upwr
Upwr Plnr Drwins of ris-prlll Dirps wit Mximum Dr Tr (Extn Astrt) M. Aul Hssn m n M. iur Rmn Dprtmnt of Computr in n Eninrin, Bnls Univrsity of Eninrin n Tnoloy (BUET). {sm,siurrmn}@s.ut.. Astrt. An upwr
Term Structure of Interest Rates: The Theories
 Handou 03 Econ 333 Abdul Munasb Trm Srucur of Inrs Ras: Th Thors Trm Srucur Facs Lookng a Fgur, w obsrv wo rm srucur facs Fac : Inrs ras for dffrn maurs nd o mov oghr ovr m Fac : Ylds on shor-rm bond mor
Handou 03 Econ 333 Abdul Munasb Trm Srucur of Inrs Ras: Th Thors Trm Srucur Facs Lookng a Fgur, w obsrv wo rm srucur facs Fac : Inrs ras for dffrn maurs nd o mov oghr ovr m Fac : Ylds on shor-rm bond mor
WAVEGUIDES (& CAVITY RESONATORS)
 CAPTR 3 WAVGUIDS & CAVIT RSONATORS AND DILCTRIC WAVGUIDS OPTICAL FIBRS 導 波 管 & 共 振 腔 與 介 質 導 波 管 光 纖 W t rqu is t irowv rg >4 G? t losss o wv i two-odutor trsissio li du to iprt odutor d loss diltri o
CAPTR 3 WAVGUIDS & CAVIT RSONATORS AND DILCTRIC WAVGUIDS OPTICAL FIBRS 導 波 管 & 共 振 腔 與 介 質 導 波 管 光 纖 W t rqu is t irowv rg >4 G? t losss o wv i two-odutor trsissio li du to iprt odutor d loss diltri o
Schedule C. Notice in terms of Rule 5(10) of the Capital Gains Rules, 1993
 (Rul 5(10)) Shul C Noti in trms o Rul 5(10) o th Cpitl Gins Ruls, 1993 Sttmnt to sumitt y trnsror o shrs whr thr is trnsr o ontrolling intrst Prt 1 - Dtils o Trnsror Nm Arss ROC No (ompnis only) Inom Tx
(Rul 5(10)) Shul C Noti in trms o Rul 5(10) o th Cpitl Gins Ruls, 1993 Sttmnt to sumitt y trnsror o shrs whr thr is trnsr o ontrolling intrst Prt 1 - Dtils o Trnsror Nm Arss ROC No (ompnis only) Inom Tx
Finite Dimensional Vector Spaces.
 Lctur 5. Ft Dmsoal Vctor Spacs. To b rad to th musc of th group Spac by D.Maruay DEFINITION OF A LINEAR SPACE Dfto: a vctor spac s a st R togthr wth a oprato calld vctor addto ad aothr oprato calld scalar
Lctur 5. Ft Dmsoal Vctor Spacs. To b rad to th musc of th group Spac by D.Maruay DEFINITION OF A LINEAR SPACE Dfto: a vctor spac s a st R togthr wth a oprato calld vctor addto ad aothr oprato calld scalar
Sun Synchronous Orbits for the Earth Solar Power Satellite System
 Sun Synchrnus Orbts fr th Earth Sar Pwr Satt Systm Sm f th mst prmsng rbts fr th Earth Sar Pwr Systm ar crcuar Sun synchrnus rbts whch nvr ntr Earth's shaw. In ths rbts, gravty grant stabz "pwr twrs" w
Sun Synchrnus Orbts fr th Earth Sar Pwr Satt Systm Sm f th mst prmsng rbts fr th Earth Sar Pwr Systm ar crcuar Sun synchrnus rbts whch nvr ntr Earth's shaw. In ths rbts, gravty grant stabz "pwr twrs" w
Econ 371: Answer Key for Problem Set 1 (Chapter 12-13)
 con 37: Answr Ky for Problm St (Chaptr 2-3) Instructor: Kanda Naknoi Sptmbr 4, 2005. (2 points) Is it possibl for a country to hav a currnt account dficit at th sam tim and has a surplus in its balanc
con 37: Answr Ky for Problm St (Chaptr 2-3) Instructor: Kanda Naknoi Sptmbr 4, 2005. (2 points) Is it possibl for a country to hav a currnt account dficit at th sam tim and has a surplus in its balanc
Distributed Systems Principles and Paradigms. Chapter 11: Distributed File Systems. Distributed File Systems. Example: NFS Architecture
 Distriut Systms Prinipls n Prigms Mrtn vn Stn VU mstrm, Dpt. Computr Sin [email protected] Chptr 11: Vrsion: Dmr 10, 2012 1 / 14 Gnrl gol Try to mk fil systm trnsprntly vill to rmot lints. 1. Fil mov to lint
Distriut Systms Prinipls n Prigms Mrtn vn Stn VU mstrm, Dpt. Computr Sin [email protected] Chptr 11: Vrsion: Dmr 10, 2012 1 / 14 Gnrl gol Try to mk fil systm trnsprntly vill to rmot lints. 1. Fil mov to lint
Fundamentals of Tensor Analysis
 MCEN 503/ASEN 50 Chptr Fundmntls of Tnsor Anlysis Fll, 006 Fundmntls of Tnsor Anlysis Concpts of Sclr, Vctor, nd Tnsor Sclr α Vctor A physicl quntity tht cn compltly dscrid y rl numr. Exmpl: Tmprtur; Mss;
MCEN 503/ASEN 50 Chptr Fundmntls of Tnsor Anlysis Fll, 006 Fundmntls of Tnsor Anlysis Concpts of Sclr, Vctor, nd Tnsor Sclr α Vctor A physicl quntity tht cn compltly dscrid y rl numr. Exmpl: Tmprtur; Mss;
(Analytic Formula for the European Normal Black Scholes Formula)
 (Analytic Formula for th Europan Normal Black Schols Formula) by Kazuhiro Iwasawa Dcmbr 2, 2001 In this short summary papr, a brif summary of Black Schols typ formula for Normal modl will b givn. Usually
(Analytic Formula for th Europan Normal Black Schols Formula) by Kazuhiro Iwasawa Dcmbr 2, 2001 In this short summary papr, a brif summary of Black Schols typ formula for Normal modl will b givn. Usually
Traffic Flow Analysis (2)
 Traffic Flow Analysis () Statistical Proprtis. Flow rat distributions. Hadway distributions. Spd distributions by Dr. Gang-Ln Chang, Profssor Dirctor of Traffic safty and Oprations Lab. Univrsity of Maryland,
Traffic Flow Analysis () Statistical Proprtis. Flow rat distributions. Hadway distributions. Spd distributions by Dr. Gang-Ln Chang, Profssor Dirctor of Traffic safty and Oprations Lab. Univrsity of Maryland,
NON-CONSTANT SUM RED-AND-BLACK GAMES WITH BET-DEPENDENT WIN PROBABILITY FUNCTION LAURA PONTIGGIA, University of the Sciences in Philadelphia
 To appear n Journal o Appled Probablty June 2007 O-COSTAT SUM RED-AD-BLACK GAMES WITH BET-DEPEDET WI PROBABILITY FUCTIO LAURA POTIGGIA, Unversty o the Scences n Phladelpha Abstract In ths paper we nvestgate
To appear n Journal o Appled Probablty June 2007 O-COSTAT SUM RED-AD-BLACK GAMES WITH BET-DEPEDET WI PROBABILITY FUCTIO LAURA POTIGGIA, Unversty o the Scences n Phladelpha Abstract In ths paper we nvestgate
Vectors 2. 1. Recap of vectors
 Vectors 2. Recp of vectors Vectors re directed line segments - they cn be represented in component form or by direction nd mgnitude. We cn use trigonometry nd Pythgors theorem to switch between the forms
Vectors 2. Recp of vectors Vectors re directed line segments - they cn be represented in component form or by direction nd mgnitude. We cn use trigonometry nd Pythgors theorem to switch between the forms
NEGLIGENT INFLICTION OF EMOTIONAL DISTRESS IS STILL ALIVE IN TEXAS
 NEGLIGENT INFLICTION OF EMOTIONAL DISTRESS IS STILL ALIVE IN TEXAS (I H Oy B Sy W) By F A. Sp 1 G W. (W) Hz 2 M Tx wy w p v w w Sp C Tx b 1993 By v. K. 3 Hwv, b Tx k k. T y b pp, b vb, y. I Tx p b by jy
NEGLIGENT INFLICTION OF EMOTIONAL DISTRESS IS STILL ALIVE IN TEXAS (I H Oy B Sy W) By F A. Sp 1 G W. (W) Hz 2 M Tx wy w p v w w Sp C Tx b 1993 By v. K. 3 Hwv, b Tx k k. T y b pp, b vb, y. I Tx p b by jy
Algorithmic Aspects of Access Networks Design in B3G/4G Cellular Networks
 Algorithmi Aspts o Ass Ntworks Dsign in BG/G Cllulr Ntworks Dvi Amzllg, Josph (Si) Nor,DnnyRz Computr Sin Dprtmnt Thnion, Hi 000, Isrl {mzllg,nny}@s.thnion..il Mirosot Rsrh On Mirosot Wy, Rmon, WA 980
Algorithmi Aspts o Ass Ntworks Dsign in BG/G Cllulr Ntworks Dvi Amzllg, Josph (Si) Nor,DnnyRz Computr Sin Dprtmnt Thnion, Hi 000, Isrl {mzllg,nny}@s.thnion..il Mirosot Rsrh On Mirosot Wy, Rmon, WA 980
Attorney Directory. Prepared for on 12/8/2008. Helping you balance work and life. To use your plan:
 Prepared for on 12/8/2008 ttorney irectory R PRT elping you balance work and life elow is a list of etwork ttorneys with offices located near you. You can save money on legal services by using a etwork
Prepared for on 12/8/2008 ttorney irectory R PRT elping you balance work and life elow is a list of etwork ttorneys with offices located near you. You can save money on legal services by using a etwork
1.- L a m e j o r o p c ió n e s c l o na r e l d i s co ( s e e x p li c a r á d es p u é s ).
 PROCEDIMIENTO DE RECUPERACION Y COPIAS DE SEGURIDAD DEL CORTAFUEGOS LINUX P ar a p od e r re c u p e ra r nu e s t r o c o rt a f u e go s an t e un d es a s t r e ( r ot u r a d e l di s c o o d e l a
PROCEDIMIENTO DE RECUPERACION Y COPIAS DE SEGURIDAD DEL CORTAFUEGOS LINUX P ar a p od e r re c u p e ra r nu e s t r o c o rt a f u e go s an t e un d es a s t r e ( r ot u r a d e l di s c o o d e l a
MAXIMAL CHAINS IN THE TURING DEGREES
 MAXIMAL CHAINS IN THE TURING DEGREES C. T. CHONG AND LIANG YU Abstract. W study th problm of xistnc of maximal chains in th Turing dgrs. W show that:. ZF + DC+ Thr xists no maximal chain in th Turing dgrs
MAXIMAL CHAINS IN THE TURING DEGREES C. T. CHONG AND LIANG YU Abstract. W study th problm of xistnc of maximal chains in th Turing dgrs. W show that:. ZF + DC+ Thr xists no maximal chain in th Turing dgrs
Higher. Exponentials and Logarithms 160
 hsn uknt Highr Mthmtics UNIT UTCME Eponntils nd Logrithms Contnts Eponntils nd Logrithms 6 Eponntils 6 Logrithms 6 Lws of Logrithms 6 Eponntils nd Logrithms to th Bs 65 5 Eponntil nd Logrithmic Equtions
hsn uknt Highr Mthmtics UNIT UTCME Eponntils nd Logrithms Contnts Eponntils nd Logrithms 6 Eponntils 6 Logrithms 6 Lws of Logrithms 6 Eponntils nd Logrithms to th Bs 65 5 Eponntil nd Logrithmic Equtions
Targeted Cancer Gene Analysis For Research Use Only - Not Intended for Clinical Use
 Targeted Cancer Gene Analysis For Research Use Only - Not Intended for Clinical Use PGDX ID Sample ID Mutation Position Nucleotide (genomic) Amino Acid (protein) Mutation Type Consequence PGDX2163N_NotchCp
Targeted Cancer Gene Analysis For Research Use Only - Not Intended for Clinical Use PGDX ID Sample ID Mutation Position Nucleotide (genomic) Amino Acid (protein) Mutation Type Consequence PGDX2163N_NotchCp
The example is taken from Sect. 1.2 of Vol. 1 of the CPN book.
 Rsourc Allocation Abstract This is a small toy xampl which is wll-suitd as a first introduction to Cnts. Th CN modl is dscribd in grat dtail, xplaining th basic concpts of C-nts. Hnc, it can b rad by popl
Rsourc Allocation Abstract This is a small toy xampl which is wll-suitd as a first introduction to Cnts. Th CN modl is dscribd in grat dtail, xplaining th basic concpts of C-nts. Hnc, it can b rad by popl
Yuriy Alyeksyeyenkov 1
 Çanaa Ünvrss Fn-Eba Faüs Journa of Ars an Sns Sa : 9 / a s 8 Cauaon of Sgna Sours Coornas In D An D Spa ur Asnov Absra hos of auaons of oorna of sgna sours whh ar nassb an r masurmn of hr proprs s mpossb
Çanaa Ünvrss Fn-Eba Faüs Journa of Ars an Sns Sa : 9 / a s 8 Cauaon of Sgna Sours Coornas In D An D Spa ur Asnov Absra hos of auaons of oorna of sgna sours whh ar nassb an r masurmn of hr proprs s mpossb
Inductive Proximity Sensors For Reliable Precision Feedback
 Inutv Proxmty Snsors For R Prson F Sut to n 21 Inutv Proxmty Snsors Contnts Tn Dt... 24-27 Apptons... 28 Orrn Inormton... 29 Inutv Proxmty Snsors Ovrvw... 30-31 DC Inutv Proxmty Snsors Cynr/Tr Brr Dsn
Inutv Proxmty Snsors For R Prson F Sut to n 21 Inutv Proxmty Snsors Contnts Tn Dt... 24-27 Apptons... 28 Orrn Inormton... 29 Inutv Proxmty Snsors Ovrvw... 30-31 DC Inutv Proxmty Snsors Cynr/Tr Brr Dsn
Section 2.2 Future Value of an Annuity
 Secton 2.2 Future Value of an Annuty Annuty s any sequence of equal perodc payments. Depost s equal payment each nterval There are two basc types of annutes. An annuty due requres that the frst payment
Secton 2.2 Future Value of an Annuty Annuty s any sequence of equal perodc payments. Depost s equal payment each nterval There are two basc types of annutes. An annuty due requres that the frst payment
VOL. 25, NÚM. 54, EDICIÓN JUNIO 2007 PP. 122-155
 Ensayos sobr POÍTICA ECONÓMICA PENSION FUND MANAGERS AND THE STRUCTURE OF THE FOREIGN EXCHANGE MARKET HERNANDO VARGAS YANNETH ROCÍO BETANCOURT ENSAYOS SOBRE POÍTICA ECONÓMICA, VO. 25, NÚM. 54, EDICIÓN
Ensayos sobr POÍTICA ECONÓMICA PENSION FUND MANAGERS AND THE STRUCTURE OF THE FOREIGN EXCHANGE MARKET HERNANDO VARGAS YANNETH ROCÍO BETANCOURT ENSAYOS SOBRE POÍTICA ECONÓMICA, VO. 25, NÚM. 54, EDICIÓN
Applying the actuarial control cycle in private health insurance
 Applyng th cturl control cycl n prvt hlth nsurnc Bn Oo FIAA Prsntd to th Insttut o Acturs o Austrl 2005 Bnnl Convnton 8 My 11 My 2005 Ths ppr hs bn prprd or th Insttut o Acturs o Austrl s (Insttut) Bnnl
Applyng th cturl control cycl n prvt hlth nsurnc Bn Oo FIAA Prsntd to th Insttut o Acturs o Austrl 2005 Bnnl Convnton 8 My 11 My 2005 Ths ppr hs bn prprd or th Insttut o Acturs o Austrl s (Insttut) Bnnl
Business rules FATCA V. 02/11/2015
 Elmnt Attribut Siz InputTyp Rquirmnt BUSINESS RULES TYPE ERROR ACK Xpath I.Mssag Hadr FATCA_OECD Vrsion xsd: string = Validation WrongVrsion ftc:fatca_oecd/vrsion SndingCompanyIN Unlimit d xsd: string
Elmnt Attribut Siz InputTyp Rquirmnt BUSINESS RULES TYPE ERROR ACK Xpath I.Mssag Hadr FATCA_OECD Vrsion xsd: string = Validation WrongVrsion ftc:fatca_oecd/vrsion SndingCompanyIN Unlimit d xsd: string
December Homework- Week 1
 Dcmbr Hmwrk- Wk 1 Mth Cmmn Cr Stndrds: K.CC.A.1 - Cunt t 100 by ns nd by tns. K.CC.A.2 - Cunt frwrd bginning frm givn numbr within th knwn squnc (instd f hving t bgin t 1). K.CC.B.4.A - Whn cunting bjcts,
Dcmbr Hmwrk- Wk 1 Mth Cmmn Cr Stndrds: K.CC.A.1 - Cunt t 100 by ns nd by tns. K.CC.A.2 - Cunt frwrd bginning frm givn numbr within th knwn squnc (instd f hving t bgin t 1). K.CC.B.4.A - Whn cunting bjcts,
MODULE 3. 0, y = 0 for all y
 Topics: Inner products MOULE 3 The inner product of two vectors: The inner product of two vectors x, y V, denoted by x, y is (in generl) complex vlued function which hs the following four properties: i)
Topics: Inner products MOULE 3 The inner product of two vectors: The inner product of two vectors x, y V, denoted by x, y is (in generl) complex vlued function which hs the following four properties: i)
SecurView 6-0-6 Antivirus Software Installation
 SurViw 6-0-6 Antivirus Sotwr Instlltion 1. Introdution Antivirus sotwr is n tiv wy to ombt omputr viruss, trojns, worms, nd othr mliious sotwr tht my ttmpt to ompromis th intgrity o systm. It is ssntil
SurViw 6-0-6 Antivirus Sotwr Instlltion 1. Introdution Antivirus sotwr is n tiv wy to ombt omputr viruss, trojns, worms, nd othr mliious sotwr tht my ttmpt to ompromis th intgrity o systm. It is ssntil
 C o a t i a n P u b l i c D e b tm a n a g e m e n t a n d C h a l l e n g e s o f M a k e t D e v e l o p m e n t Z a g e bo 8 t h A p i l 2 0 1 1 h t t pdd w w wp i j fp h D p u b l i c2 d e b td S t
C o a t i a n P u b l i c D e b tm a n a g e m e n t a n d C h a l l e n g e s o f M a k e t D e v e l o p m e n t Z a g e bo 8 t h A p i l 2 0 1 1 h t t pdd w w wp i j fp h D p u b l i c2 d e b td S t
www.breaking News English.com Ready-to-Use English Lessons by Sean Banville Level 6 Students sell bodies and gamble to survive
 www.breaking News English.com Ready-to-Use English Lessons by Sean Banville 1,000 IDEAS & ACTIVITIES FOR LANGUAGE TEACHERS www.breakingnewsenglish.com/book.html Thousands more free lessons from Sean's
www.breaking News English.com Ready-to-Use English Lessons by Sean Banville 1,000 IDEAS & ACTIVITIES FOR LANGUAGE TEACHERS www.breakingnewsenglish.com/book.html Thousands more free lessons from Sean's
Quality and Pricing for Outsourcing Service: Optimal Contract Design
 Qulity nd Pricing for Outsourcing Srvic: Optiml Contrct Dsign Smr K. Mukhopdhyy Univrsity of Wisconsin-Milwuk Co-uthor: Xiowi Zhu, Wst Chstr Univrsity of PA Third nnul confrnc, POMS Collg of Srvic Oprtions
Qulity nd Pricing for Outsourcing Srvic: Optiml Contrct Dsign Smr K. Mukhopdhyy Univrsity of Wisconsin-Milwuk Co-uthor: Xiowi Zhu, Wst Chstr Univrsity of PA Third nnul confrnc, POMS Collg of Srvic Oprtions
No 28 Xianning West Road, Xi an No 70 Yuhua East Road, Shijiazhuang. [email protected]
 On-Ln Dynamc Cabl Ratng for Undrground Cabls basd on DTS and FEM Y.C.Lang *, Y.M.L School of Elctrcal Engnrng * Dpartmnt of Elctrcal and Informaton X an Jaotong Unvrsty Hb Unvrsty of Scnc and Tchnology
On-Ln Dynamc Cabl Ratng for Undrground Cabls basd on DTS and FEM Y.C.Lang *, Y.M.L School of Elctrcal Engnrng * Dpartmnt of Elctrcal and Informaton X an Jaotong Unvrsty Hb Unvrsty of Scnc and Tchnology
Section 3: Logistic Regression
 Scton 3: Logstc Rgrsson As our motvaton for logstc rgrsson, w wll consdr th Challngr dsastr, th sx of turtls, collg math placmnt, crdt card scorng, and markt sgmntaton. Th Challngr Dsastr On January 28,
Scton 3: Logstc Rgrsson As our motvaton for logstc rgrsson, w wll consdr th Challngr dsastr, th sx of turtls, collg math placmnt, crdt card scorng, and markt sgmntaton. Th Challngr Dsastr On January 28,
SAN JOSE UNIFIED RETURNING VOLUNTEER DRIVER PACKET
 SAN JOSE UNIFIED ETUNING VOLUNTEE DIVE PACKET VOLUNTEE DIVE S NAME: STUDENT NAME /ID# SCHOOL: SPOT/ACTIVITY: STUDENT NAME /ID# SCHOOL: SPOT/ACTIVITY: STUDENT NAME /ID# SCHOOL: SPOT/ACTIVITY: STUDENT NAME
SAN JOSE UNIFIED ETUNING VOLUNTEE DIVE PACKET VOLUNTEE DIVE S NAME: STUDENT NAME /ID# SCHOOL: SPOT/ACTIVITY: STUDENT NAME /ID# SCHOOL: SPOT/ACTIVITY: STUDENT NAME /ID# SCHOOL: SPOT/ACTIVITY: STUDENT NAME
Graph Theoretical Analysis and Design of Multistage Interconnection Networks
 637 I TRNSTIONS ON OMPUTRS, VOL. -32, NO. 7, JULY 1983 [39].. svnt,.. jski, n. J. Kuck, "utomtic sign wit pnnc grps," in Proc. 17t s. utomt. on, I omput. Soc. TMSI, 1980, pp. 506-515. [40] M.. Mcrln, "
637 I TRNSTIONS ON OMPUTRS, VOL. -32, NO. 7, JULY 1983 [39].. svnt,.. jski, n. J. Kuck, "utomtic sign wit pnnc grps," in Proc. 17t s. utomt. on, I omput. Soc. TMSI, 1980, pp. 506-515. [40] M.. Mcrln, "
Mathematics. Vectors. hsn.uk.net. Higher. Contents. Vectors 128 HSN23100
 hsn.uk.net Higher Mthemtics UNIT 3 OUTCOME 1 Vectors Contents Vectors 18 1 Vectors nd Sclrs 18 Components 18 3 Mgnitude 130 4 Equl Vectors 131 5 Addition nd Subtrction of Vectors 13 6 Multipliction by
hsn.uk.net Higher Mthemtics UNIT 3 OUTCOME 1 Vectors Contents Vectors 18 1 Vectors nd Sclrs 18 Components 18 3 Mgnitude 130 4 Equl Vectors 131 5 Addition nd Subtrction of Vectors 13 6 Multipliction by
Binary Search Trees. Definition Of Binary Search Tree. The Operation ascend() Example Binary Search Tree
 Binary Sar Trs Compxity O Ditionary Oprations t(), put() and rmov() Ditionary Oprations: ƒ t(ky) ƒ put(ky, vau) ƒ rmov(ky) Additiona oprations: ƒ asnd() ƒ t(indx) (indxd inary sar tr) ƒ rmov(indx) (indxd
Binary Sar Trs Compxity O Ditionary Oprations t(), put() and rmov() Ditionary Oprations: ƒ t(ky) ƒ put(ky, vau) ƒ rmov(ky) Additiona oprations: ƒ asnd() ƒ t(indx) (indxd inary sar tr) ƒ rmov(indx) (indxd
Important result on the first passage time and its integral functional for a certain diffusion process
 Lcturs Mtmátics Volumn 22 (21), págins 5 9 Importnt rsult on th first pssg tim nd its intgrl functionl for crtin diffusion procss Yousf AL-Zlzlh nd Bsl M. AL-Eidh Kuwit Univrsity, Kuwit Abstrct. In this
Lcturs Mtmátics Volumn 22 (21), págins 5 9 Importnt rsult on th first pssg tim nd its intgrl functionl for crtin diffusion procss Yousf AL-Zlzlh nd Bsl M. AL-Eidh Kuwit Univrsity, Kuwit Abstrct. In this
A Place to Choose Quality, Affordable Health Insurance
 MI O A ʼ H A L HI U R A C X C H A G mp w n gm n n af a m ma k a h a b u h a m a M nn ha h n u an x hangw mp v mp nbyn u ag ng n u andha h a p v d p a g a unqua yanda dab y M nn a am w avv $1b nbyu ng hx
MI O A ʼ H A L HI U R A C X C H A G mp w n gm n n af a m ma k a h a b u h a m a M nn ha h n u an x hangw mp v mp nbyn u ag ng n u andha h a p v d p a g a unqua yanda dab y M nn a am w avv $1b nbyu ng hx
Earthquake Hazard Zones: The relative risk of damage to Canadian buildings
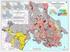 Earthquake Hazard Zones: The relative risk of damage to Canadian buildings by Paul Kovacs Executive Director, Institute for Catastrophic Loss Reduction Adjunct Research Professor, Economics, Univ. of Western
Earthquake Hazard Zones: The relative risk of damage to Canadian buildings by Paul Kovacs Executive Director, Institute for Catastrophic Loss Reduction Adjunct Research Professor, Economics, Univ. of Western
A Formal Model for Data Flow Diagram Rules
 Volum No. MAY 0 ARPN Journal o Sytm and Sotwar 00- AJSS Journal. All rght rrvd htt://www.cntc-ournal.org A Formal Modl or Data Flow Dagram Rul Rozat Ibrahm Sow Yn Yn Dartmnt o Sotwar Engnrng Unvrty Tun
Volum No. MAY 0 ARPN Journal o Sytm and Sotwar 00- AJSS Journal. All rght rrvd htt://www.cntc-ournal.org A Formal Modl or Data Flow Dagram Rul Rozat Ibrahm Sow Yn Yn Dartmnt o Sotwar Engnrng Unvrty Tun
Sharp bounds for Sándor mean in terms of arithmetic, geometric and harmonic means
 Qian t al. Journal of Inqualitis and Applications (015) 015:1 DOI 10.1186/s1660-015-0741-1 R E S E A R C H Opn Accss Sharp bounds for Sándor man in trms of arithmtic, gomtric and harmonic mans Wi-Mao Qian
Qian t al. Journal of Inqualitis and Applications (015) 015:1 DOI 10.1186/s1660-015-0741-1 R E S E A R C H Opn Accss Sharp bounds for Sándor man in trms of arithmtic, gomtric and harmonic mans Wi-Mao Qian
OHIM SEARCH TOOLS: TMVIEW, DSVIEW AND TMCLASS. Making trade mark and design information readily available for users
 OHIM SEARCH TOOLS: TMVIEW, DSVIEW AND TMCLASS Making trade mark and design information readily available for users Mariano Riccheri Moscow, 24 September 2015 INTERNATIONAL COOPERATION AREA European Cooperation:
OHIM SEARCH TOOLS: TMVIEW, DSVIEW AND TMCLASS Making trade mark and design information readily available for users Mariano Riccheri Moscow, 24 September 2015 INTERNATIONAL COOPERATION AREA European Cooperation:
- ASSEMBLY AND INSTALLATION -
 - SSEMLY ND INSTLLTION - Sliin Door Stm Mot Importnt! Ti rmwork n ml to uit 100 mm ini wll tikn (75 mm tuwork) or 125 mm ini wll tikn (100 mm tuwork) HOWEVER t uppli jm kit i pii to itr 100 mm or 125 mm
- SSEMLY ND INSTLLTION - Sliin Door Stm Mot Importnt! Ti rmwork n ml to uit 100 mm ini wll tikn (75 mm tuwork) or 125 mm ini wll tikn (100 mm tuwork) HOWEVER t uppli jm kit i pii to itr 100 mm or 125 mm
1.5 / 1 -- Communication Networks II (Görg) -- www.comnets.uni-bremen.de. 1.5 Transforms
 .5 / -- Communication Networks II (Görg) -- www.comnets.uni-bremen.de.5 Transforms Using different summation and integral transformations pmf, pdf and cdf/ccdf can be transformed in such a way, that even
.5 / -- Communication Networks II (Görg) -- www.comnets.uni-bremen.de.5 Transforms Using different summation and integral transformations pmf, pdf and cdf/ccdf can be transformed in such a way, that even
DYNAMIC PROGRAMMING APPROACH TO TESTING RESOURCE ALLOCATION PROBLEM FOR MODULAR SOFTWARE
 DYAMIC PROGRAMMIG APPROACH TO TESTIG RESOURCE ALLOCATIO PROBLEM FOR MODULAR SOFTWARE P.K. Kpur P.C. Jh A.K. Brdh Astrct Tstg phs of softwr gs wth modul tstg. Durg ths prod moduls r tstd dpdtly to rmov
DYAMIC PROGRAMMIG APPROACH TO TESTIG RESOURCE ALLOCATIO PROBLEM FOR MODULAR SOFTWARE P.K. Kpur P.C. Jh A.K. Brdh Astrct Tstg phs of softwr gs wth modul tstg. Durg ths prod moduls r tstd dpdtly to rmov
Menu Structure. Section 5. Introduction. General Functions Menu
 Menu Structure Section 5 Introduction General Functions Menu Most workstation functions are accessed by menu selections. This section explains the menu structure and provides a tree structured view of
Menu Structure Section 5 Introduction General Functions Menu Most workstation functions are accessed by menu selections. This section explains the menu structure and provides a tree structured view of
CHAPTER FIVE. Solutions for Section 5.1. Skill Refresher. Exercises
 CHAPTER FIVE 5.1 SOLUTIONS 265 Solutions for Section 5.1 Skill Refresher S1. Since 1,000,000 = 10 6, we have x = 6. S2. Since 0.01 = 10 2, we have t = 2. S3. Since e 3 = ( e 3) 1/2 = e 3/2, we have z =
CHAPTER FIVE 5.1 SOLUTIONS 265 Solutions for Section 5.1 Skill Refresher S1. Since 1,000,000 = 10 6, we have x = 6. S2. Since 0.01 = 10 2, we have t = 2. S3. Since e 3 = ( e 3) 1/2 = e 3/2, we have z =
With Rejoicing Hearts/ Con Amor Jovial. A Fm7 B sus 4 B Cm Cm7/B
 for uli With Rejoic Herts/ on mor ol dition # 10745-Z1 ime ortez Keyord ccompniment y effy Honoré INTRO With energy ( = c 88) Keyord * m7 B sus 4 B 7/B mj 9 /B SMPL B 7 *Without percussion, egin he 1995,
for uli With Rejoic Herts/ on mor ol dition # 10745-Z1 ime ortez Keyord ccompniment y effy Honoré INTRO With energy ( = c 88) Keyord * m7 B sus 4 B 7/B mj 9 /B SMPL B 7 *Without percussion, egin he 1995,
 α α λ α = = λ λ α ψ = = α α α λ λ ψ α = + β = > θ θ β > β β θ θ θ β θ β γ θ β = γ θ > β > γ θ β γ = θ β = θ β = θ β = β θ = β β θ = = = β β θ = + α α α α α = = λ λ λ λ λ λ λ = λ λ α α α α λ ψ + α =
α α λ α = = λ λ α ψ = = α α α λ λ ψ α = + β = > θ θ β > β β θ θ θ β θ β γ θ β = γ θ > β > γ θ β γ = θ β = θ β = θ β = β θ = β β θ = = = β β θ = + α α α α α = = λ λ λ λ λ λ λ = λ λ α α α α λ ψ + α =
Elements from Another Universe: Understanding the Beauty of the Periodic Table
 Elements from Another Universe: Understanding the Beauty of the Periodic Table Learning Objectives: The students will examine the properties of make believe elements, arrange these elements so as to create
Elements from Another Universe: Understanding the Beauty of the Periodic Table Learning Objectives: The students will examine the properties of make believe elements, arrange these elements so as to create
Back left Back right Front left Front right. Blue Shield of California. Subscriber JOHN DOE. a b c d
 Smpl ID r n sription o trms Bk lt Bk right Front lt Front right Provirs: Pls il ll lims with your lol BluCross BluShil lins in whos srvi r th mmr riv srvis or, whn Mir is primry, il ll Mir lims with Mir.
Smpl ID r n sription o trms Bk lt Bk right Front lt Front right Provirs: Pls il ll lims with your lol BluCross BluShil lins in whos srvi r th mmr riv srvis or, whn Mir is primry, il ll Mir lims with Mir.
Factoring Polynomials: Factoring by Grouping
 OpenStax-CNX module: m21901 1 Factoring Polynomials: Factoring by Grouping Wade Ellis Denny Burzynski This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0
OpenStax-CNX module: m21901 1 Factoring Polynomials: Factoring by Grouping Wade Ellis Denny Burzynski This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0
C e r t ifie d Se c u r e W e b
 C r t ifi d S c u r W b Z r t ifizi r t Sic h r h it im W b 1 D l gat s N ic o las M ay n c o u r t, C EO, D r am lab T c h n o lo gi s A G M ar c -A n d r é B c k, C o n su lt an t, D r am lab T c h n
C r t ifi d S c u r W b Z r t ifizi r t Sic h r h it im W b 1 D l gat s N ic o las M ay n c o u r t, C EO, D r am lab T c h n o lo gi s A G M ar c -A n d r é B c k, C o n su lt an t, D r am lab T c h n
SE3BB4: Software Design III Concurrent System Design. Sample Solutions to Assignment 1
 SE3BB4: Softwre Design III Conurrent System Design Winter 2011 Smple Solutions to Assignment 1 Eh question is worth 10pts. Totl of this ssignment is 70pts. Eh ssignment is worth 9%. If you think your solution
SE3BB4: Softwre Design III Conurrent System Design Winter 2011 Smple Solutions to Assignment 1 Eh question is worth 10pts. Totl of this ssignment is 70pts. Eh ssignment is worth 9%. If you think your solution
The Mathematics of Sudoku
 T Mtmts o Suoku Tom Dvs [email protected] ttp://www.omtr.or/mtrls (Prlmnry) Sptmr, 0 Introuton Suoku s puzzl prsnt on squr r tt s usully, ut s somtms or otr szs. In ts oumnt, w wll onsr only t s, ltou lmost
T Mtmts o Suoku Tom Dvs [email protected] ttp://www.omtr.or/mtrls (Prlmnry) Sptmr, 0 Introuton Suoku s puzzl prsnt on squr r tt s usully, ut s somtms or otr szs. In ts oumnt, w wll onsr only t s, ltou lmost
5.4 Exponential Functions: Differentiation and Integration TOOTLIFTST:
 .4 Eponntial Functions: Diffrntiation an Intgration TOOTLIFTST: Eponntial functions ar of th form f ( ) Ab. W will, in this sction, look at a spcific typ of ponntial function whr th bas, b, is.78.... This
.4 Eponntial Functions: Diffrntiation an Intgration TOOTLIFTST: Eponntial functions ar of th form f ( ) Ab. W will, in this sction, look at a spcific typ of ponntial function whr th bas, b, is.78.... This
Evobike 2014 Árak szerzõdött partnereink számára Mounty
 Evobike 2014 Árak szerzõdött partnereink számára Mounty Cikksz. Termék neve Szerzõdött árak (Ft) nettó Szerzõdött árak (Ft) bruttó Fogyasztói ár (Ft) 0713 MOUNTY LITE-PEDAL 6126 7780 10427 0713COMP MOUNTY
Evobike 2014 Árak szerzõdött partnereink számára Mounty Cikksz. Termék neve Szerzõdött árak (Ft) nettó Szerzõdött árak (Ft) bruttó Fogyasztói ár (Ft) 0713 MOUNTY LITE-PEDAL 6126 7780 10427 0713COMP MOUNTY
Criminal Offenses - On campus
 14 Campus Saf and Scuri Survy Instituti: Main Campus (164933001) Scrning Qustis Plas answr ths qustis carfully. Th answrs you provid will dtrmin which scrns you will b askd to complt for this data collcti.
14 Campus Saf and Scuri Survy Instituti: Main Campus (164933001) Scrning Qustis Plas answr ths qustis carfully. Th answrs you provid will dtrmin which scrns you will b askd to complt for this data collcti.
Modern Portfolio Theory (MPT) Statistics
 Modrn Portfolo Thory (MPT) Statstcs Mornngstar Mthodology Papr Novmr 30, 007 007 Mornngstar, Inc. All rghts rsrvd. Th nformaton n ths documnt s th proprty of Mornngstar, Inc. Rproducton or transcrpton
Modrn Portfolo Thory (MPT) Statstcs Mornngstar Mthodology Papr Novmr 30, 007 007 Mornngstar, Inc. All rghts rsrvd. Th nformaton n ths documnt s th proprty of Mornngstar, Inc. Rproducton or transcrpton
Connector and Cable Diagrams (Pinout Charts)
 Connector and Cable Diagrams (Pinout Charts) These pinout charts provide wire color and connector pin numbers for Crossover Cable Pinouts Circuit Pack and Auxiliary Equipment Leads (Pinout Charts), includes
Connector and Cable Diagrams (Pinout Charts) These pinout charts provide wire color and connector pin numbers for Crossover Cable Pinouts Circuit Pack and Auxiliary Equipment Leads (Pinout Charts), includes
Engineering. Installation Manager. Installations Manager (Gas Qualified) Whole House Assessors. Whole House Assessors (Gas Qualified)
 Apply via Engineering Role title BG12451 Installation Manager BG13779 Installations Manager (Gas Qualified) BG12450 Whole House Assessors BG13931 Whole House Assessors (Gas Qualified) BG12544 BMS Commissioning
Apply via Engineering Role title BG12451 Installation Manager BG13779 Installations Manager (Gas Qualified) BG12450 Whole House Assessors BG13931 Whole House Assessors (Gas Qualified) BG12544 BMS Commissioning
Path-dependent options
 Chapter 5 Path-dependent options The contracts we have seen so far are the most basic and important derivative products. In this chapter, we shall discuss some complex contracts, including barrier options,
Chapter 5 Path-dependent options The contracts we have seen so far are the most basic and important derivative products. In this chapter, we shall discuss some complex contracts, including barrier options,
Director s Statement
 " b f u gh Th ngb h f h h y ung h h n f h n y p h ChGu m nwh nh d' T u n b nd n ' " A W k, h, ThC Pu p O F F C A L S E L E C T O N S u F mf 2 9 P C n : m z @m y b f nk m m 415 5 48 6 4 MAY BE FRANK Fnk
" b f u gh Th ngb h f h h y ung h h n f h n y p h ChGu m nwh nh d' T u n b nd n ' " A W k, h, ThC Pu p O F F C A L S E L E C T O N S u F mf 2 9 P C n : m z @m y b f nk m m 415 5 48 6 4 MAY BE FRANK Fnk
