4 Annuities and Loans
|
|
|
- Annis Gardner
- 8 years ago
- Views:
Transcription
1 4 Annuities and Loans 4.1 Introduction In previous section, we discussed different methods for crediting interest, and we claimed that compound interest is the correct way to credit interest. This section is concerned with valuing a large number of cash flows. 4.2 Loans Toward the end of the last section we solved some time value of money problems which involved several cash flows. We approached those problems by applying compound interest to each individual cash flow, then we added or subtracted the results. This works well for a small number of payments, but can be very tedious when many payments are involved. Example 11 (A loan with very few payments). Jill borrows $1000 today. She will repay the loan by making four equal payments over the next year. The payments will be made at the end of every third month. The interest is 3.2% APR compounded quarterly. Determine the size of Jill s level payments. Solution: ( ) Let R denote size of level payments. The discount factor for a single quarter is = (1.008) 1. The present value of the payments is then Factor out the R and compute: R(1.008) 1 + R(1.008) 2 + R(1.008) 3 + R(1.008) 4 R ( (1.008) 1 + (1.008) 2 + (1.008) 3 + (1.008) 4) = R R is to be set so that this payment stream has the same present value as the loan principal, $1000, so R = $1000 so R = $1000/ = $ Example 12 (Loan with a lot of payments). Bryan takes out a home loan worth $250, 000 today. He will repay the loan by making equal payments at the end of each month for the next 30 years. The interest is 6.0% APR compounded monthly. Determine the size of Bryan s level payments. We can try to set this up like the previous problem. However, the previous problem involved adding four payments together, whereas this problem will involve adding together = 360 payments! A loan involves making payments of equal size at equally spaced intervals of time. If the interest rate remains constant of the entire period of the loan, then we will be able to compute 20
2 the present value of the loan using a simple formula. The advantage of this formula is that valuing a loan with 4 payments or 4000 payments will require about the same amount of computational effort. Formula for Present Value of a Loan or Annuity P denotes the principal of a loan (how much was borrowed) R denotes the payment size t the number of years (the term of the loan) r is the nominal interest rate per year m is the number of conversion periods per year i is the interest rate per period, so i = r/m n is the number of conversion periods in the term, so n = t m Then P = R 1 (1 + i) n i Jill s loan, revisited: Jill borrows $1000 today. She will repay the loan by making four equal payments over the next year. The payments will be made at the end of every third month. The interest is 3.2% APR compounded quarterly. Determine the size of her level payments. In this case, we have the following: We wish to find R. So, P = 1000 t = 1 m = 4 n = 4 1 = 4 r = i = = = R 1 (1.008) = R Solving for R gives R = = , same as what we found without the formula. The real advantage of the formula will become clear when we revisit Bryan s loan. 21
3 Bryan takes out a home loan worth $250, 000 today. He will repay the loan by making equal payments at the end of each month for the next 30 years. The interest is 6.0% APR compounded monthly. Determine the size of the level payments. In this case, we have the following: We wish to find R. P = 250, 000 t = 30 m = 12 n = = 360 r = 0.06 i = = Solving for R gives 250, 000 = R 1 (1.005) = R R = = 1, Without the loan formula, we would have had to add together 360 individual payments! Bryan borrowed $250, 000 and paid this back by making 360 payments of $ But wait, this means he pays back = 539, Doesn t that mean his payments were too large? NO! The First Principle of Financial Mathematics insists that figure of $539, is somewhat meaningless, as it is formed by adding together dollar figures at different times. Does the $539, have any meaning? Yes. The difference $539, $250, 000 = $289, can be interpreted as the interest paid. Think of this as saying $289, is the cost of borrowing $250, 000 for 30 years. 4.3 Understanding the Present Value of a Loan So we have a formula involving the present value of a loan, and we can do some computations with it. This is only useful if we understand what it is that we are computing. At the very beginning of the loan, the present value of the loan represents the principal of the loan, namely, how much we borrowed. The next few examples will try to give meaning to the present value of a loan when that present value is valued at a later date. 22
4 Example 13 (More on Bryan s Loan). Exactly 10 years after Bryan took out his home loan, he strikes it rich. First thing he wants to do is pay off the remaining balance on his home loan. How much will he need to pay? Solution: He has 20 years remaining on the loan, so = 240 payments left. compute the PV of the loan 10 years into the loan. We P = $ (1.005) = $209, This present value represents how much it would cost to pay off the loan in full at that point in time. Real world finance is never quite this simple, as Bryan may have to put up with early payment fees, etc. We will generally ignore such fees in this course. What are the advantages to Bryan paying off the loan early? Bryan had already made 120 payments of 1, , so total repaid is 120 $ = $179, He then pays $209, to settle the remainder of the loan. Total amount paid by Bryan is $209, $179, = $389, He borrowed $250, 000, so the total interest charge is $389, $250, 000 = $139, Had he continued to make regular payments for the full term of the loan, his total interest expense would have been $289, By paying off the loan early, he saved $289, $139, = $150, Most loans will lock you in at a fixed interest rate for the entire term of the loan. In order to take advantage of changing interest rates, one may need to refinance. Suppose Dana takes out a home loan with $300, 000 principal. She makes payments at the end of each month for 30 years. The interest is 8.4% APR compounded monthly. (Note that Dana s monthly interest rate is i = = ) First, lets determine her payment size. so R = $2, $300, 000 = R 1 (1.007)
5 Next, determine the interest charges on this loan. She pays back $ = $822, Subtracting the principal leaves $522, (Notice the interest charge is almost twice the total amount that she borrowed!) After five years, interest rates drop to 6% APR compounded monthly. Dana wants to refinance 10 her home loan to take advantage of this lower interest rate. How can she do this? We ll need to determine Dana s outstanding balance after 5 years. $2, = $286, She currently owes $286, Suppose that, in addition to taking advantage of the lower interest rate, Dana chooses to shorten the term of her loan when she refinances. In particular, she refinances to a 20 year loan with 6% APR compounded monthly. Lets determine her new payment size. $286, = R so R = $ Notice that upon refinancing, her payment size decreased AND the number of payments decreased! Next, lets determine Dana s total interest expense under the re-financing. We need to be sure to include the interest expense of the first 5 years of the original loan! $ $ = $137, $492, = $629, 295 is the total repaid. Subtracting principal leaves $329, 295 in interest expenses. Finally, lets determine Dana s savings in interest charges due to refinancing With out refinancing: $522, With refinancing: $329, Interest savings: $193, Dana saves $193, by refinancing! While in theory, it is advantageous to refinance whenever interest rates drop, in practice it is usually only advantageous to refinance if the interest rate changes by a lot. Why? In the real world, refinancing involves extra bank fees and transaction costs. 10 What does refinance mean? Basically, she takes out a new loan. The principal of the new loan is equal to the balance of the existing loan. The principal of the new loan is then used to pay off the outstanding balance of original. 24
6 4.4 Understanding Loan Payments and Interest Suppose you take out a loan of $10, 000 at 5% APR compounded annually for an unspecified amount of time. You are required to make a payment at the end of each year, but the size of the payment is up to you. The loan will be settled as soon as the present value of all of your payments is equal to the principal of the loan, where the present value is valued at the beginning of the loan. At the very least, you should pay back at least $500 each year. Why? At the end of one year, the outstanding balance has grown to $10, 000 (1.005) = $10, If you pay back $500, your balance drops back down to $10, 000, in which case you will never payoff the loan. The outstanding balance (right after payment) will always be $10, 000. In this case, your payment size is just large enough to cover the accrued interest. This is referred to as a perpetuity. Payments continue forever. What happens if you pay back only $400 each year? At the end of the first year, your outstanding balance is $10, 500. You pay back $400 leaving you with a balance of $10, 100. Your payment was not even large enough to cover that year s interest expense. After another year, the balance grows to $10, = $10, 605, which is reduced to $10, 205 after the $400 payment is applied. The outstanding balance is moving in the wrong direction! Each year, you are further in debt! What happens if you pay back more than the $500? For concreteness, suppose you pay back $800 at the end of each year. Over the course of the first year, the balance of $10, 000 grows to $10, 500, and after the payment of $800, the balance is knocked down to $9, 700. The interest expense in the first year is $500 and the $800 payment can be broken up as $800 = $500 + $300 where the $500 is applied towards interest and the $300 is applied towards the principal. Roughly, how long will it take to repay this loan? Principal fell $300 after the first year s payment. If it falls by same amount each year, then it will require 10, 000/300 = payments. In actual fact, the loan will be paid off in fewer than payments. We ll see that with each passing payment, more and more of the payment is applied to the principal. Over the second year the outstanding balance grows from $9, 700 to 9700 (1.05) = $10, 185. The interest expense in second year is 5% of $9, 700 or $485. You still make a payment 25
7 of $800, but now only $485 is eaten up by interest. The remaining $800 $485 = $315 is applied towards principal. What happens in the third year? At beginning of third year, outstanding balance is $10, 185 $800 = $9, 385. Interest charge over the year is 5% of $9, 385, so $ Amount towards principal is therefore $800 $ = $ For first three years, amount towards principal are $300, $315, $ Look at the consecutive ratios: = 1.05 and = Indeed, the amount applied toward principal is an exponential function in terms of the number of payments, and the base of the exponential function is the accumulation factor for this interest rate. 4.5 The Effect of Large Payments This section investigates the effect of paying more than the requested loan payment amount. Why would you want to pay more? By making larger payments, you will pay off the loan with fewer payments. In fact, we ll see that you can potentially save a lot by making larger payments. For example, if a loan requires 60 payments of $100 then it should take fewer than 20 payments of $300 to pay off the loan. Lets look at a concrete example. Example 14. Gil recently purchased a car, and he took out an car loan for $7500. The loan is to be repaid with payments at the end of each month, for 48 months at 2.4% APR compounded monthly. What is Gil s interest expense? Lets determine the size of Gil s monthly payments. Self Check 3. Determine Gil s monthly payments. 11 Now that we know Gil s monthly payments are $164.03, let s determine Gil s interest expense. He makes 48 payments of $ in order to pay back $7500, so his interest expense is 48 $ $7500 = $ Example 15 (More on Gil s loan). Suppose Gil decides to double the size of his payments, in order to pay off the loan more quickly. How many payments will he need to make? 11 $7500 = R 1 (1.002) 48, giving monthly payments of R = $
8 His payment size is now $ = $ The loan formula now reads $7500 = $ (1.002) n Notice the unknown is stuck up in the exponent. Most financial calculators will compute the term of a loan for you, but we ll review the algebra for those who want to see it. First divide both sides by to get = n Subtract n from both sides then subtract from both sides to get Now take the reciprocal of each side: n = n = Take logarithms on both sides and use laws of logarithms to get n ln (1.002) = ln ( ). Finally, divide both sides by ln (1.002) and evaluate the natural logarithms: n = ln ( ) ln (1.002) = Thus, if Gil doubles his payments, then he will need to make payments. ( Hmmm... how can he make of a payment? We ll fix this in a minute, but for the moment assume that if makes sense to make fractional a fractional payment.) By doubling his payments, Gil pays back $ = $7, and so he pays $ to interest. Notice that, by doubling the size of his payments, the total time to pay off the loan is less than half that it would be had he made regular payments and the amount he pays to interest is less than half of what he would pay if he had made regular payments. But how can he make payments? He can t. He will either make 23 or 24 payments. In either case, the size of the last payment won t be the same as the other payments. Lets determine how much he will owe immediately after the 23rd payment. First, we ll find the time 0 present value of the 23 payments: $ = $ But the.002 principal is $7500 so $7500 $ = $ is the time 0 value of the balance remaining immediately after the 23rd payment. Now we need to apply an accumulation factor to push the $ months forward: $ (1.002) 23 = $ Gil now has two options. 27
9 (a.) Gil could settle the loan in 23 payments if his first 22 payments are $ and his 23rd payment includes the remaining balance 12, $ $ = $ His interest expense is then 22 $ $ $7500 = $ (b.) Gil could settle the loan with 24 payments by making 23 payments of $ and then the 24th payment will be smaller than normal. The remaining $ will accrue interest for one more month, so his 24th payment would be $ (1.002) = $ In this case, his interest expense is $ $ $7500 = $ Why does doubling payments have a super-linear effect on paying off the loan? Look at first month s payment. Balance grew from $7500 to $7500 (1.002) = $ Regardless of the size of the payment, the first $15 of the payment will pay off the accrued interest, and the remaining payment is applied towards the principal. If Gil pays normal payment of $164.03, then $15 is applied to interest and the remaining $ is applied towards principal. The outstanding balance is then $ The interest accrued in the second period is then $ = $ If Gil doubles his payment to $328.06, then as before, the first $15 is applied towards the interest, and the remaining $ $15 = $ applies towards principal. The outstanding balance is now $ The interest accrued in the second period is then $ = $14.37, which is $0.33 less than previously. Making larger than expected payments causes the principal to shrink more quickly. In turn, this causes the accrued interest per period to shrink more quickly, which in turn means that even more of the next payment will be applied to the principal. Through this feedback mechanism, the effect of large and early payments is greatly amplified. 12 This is referred to as a balloon payment 28
3 More on Accumulation and Discount Functions
 3 More on Accumulation and Discount Functions 3.1 Introduction In previous section, we used 1.03) # of years as the accumulation factor. This section looks at other accumulation factors, including various
3 More on Accumulation and Discount Functions 3.1 Introduction In previous section, we used 1.03) # of years as the accumulation factor. This section looks at other accumulation factors, including various
CHAPTER 5 INTRODUCTION TO VALUATION: THE TIME VALUE OF MONEY
 CHAPTER 5 INTRODUCTION TO VALUATION: THE TIME VALUE OF MONEY 1. The simple interest per year is: $5,000.08 = $400 So after 10 years you will have: $400 10 = $4,000 in interest. The total balance will be
CHAPTER 5 INTRODUCTION TO VALUATION: THE TIME VALUE OF MONEY 1. The simple interest per year is: $5,000.08 = $400 So after 10 years you will have: $400 10 = $4,000 in interest. The total balance will be
DISCOUNTED CASH FLOW VALUATION and MULTIPLE CASH FLOWS
 Chapter 5 DISCOUNTED CASH FLOW VALUATION and MULTIPLE CASH FLOWS The basic PV and FV techniques can be extended to handle any number of cash flows. PV with multiple cash flows: Suppose you need $500 one
Chapter 5 DISCOUNTED CASH FLOW VALUATION and MULTIPLE CASH FLOWS The basic PV and FV techniques can be extended to handle any number of cash flows. PV with multiple cash flows: Suppose you need $500 one
CHAPTER 6 DISCOUNTED CASH FLOW VALUATION
 CHAPTER 6 DISCOUNTED CASH FLOW VALUATION Answers to Concepts Review and Critical Thinking Questions 1. The four pieces are the present value (PV), the periodic cash flow (C), the discount rate (r), and
CHAPTER 6 DISCOUNTED CASH FLOW VALUATION Answers to Concepts Review and Critical Thinking Questions 1. The four pieces are the present value (PV), the periodic cash flow (C), the discount rate (r), and
CHAPTER 5 INTRODUCTION TO VALUATION: THE TIME VALUE OF MONEY
 CHAPTER 5 INTRODUCTION TO VALUATION: THE TIME VALUE OF MONEY Answers to Concepts Review and Critical Thinking Questions 1. The four parts are the present value (PV), the future value (FV), the discount
CHAPTER 5 INTRODUCTION TO VALUATION: THE TIME VALUE OF MONEY Answers to Concepts Review and Critical Thinking Questions 1. The four parts are the present value (PV), the future value (FV), the discount
CHAPTER 1. Compound Interest
 CHAPTER 1 Compound Interest 1. Compound Interest The simplest example of interest is a loan agreement two children might make: I will lend you a dollar, but every day you keep it, you owe me one more penny.
CHAPTER 1 Compound Interest 1. Compound Interest The simplest example of interest is a loan agreement two children might make: I will lend you a dollar, but every day you keep it, you owe me one more penny.
Chapter 6. Learning Objectives Principles Used in This Chapter 1. Annuities 2. Perpetuities 3. Complex Cash Flow Streams
 Chapter 6 Learning Objectives Principles Used in This Chapter 1. Annuities 2. Perpetuities 3. Complex Cash Flow Streams 1. Distinguish between an ordinary annuity and an annuity due, and calculate present
Chapter 6 Learning Objectives Principles Used in This Chapter 1. Annuities 2. Perpetuities 3. Complex Cash Flow Streams 1. Distinguish between an ordinary annuity and an annuity due, and calculate present
Chapter 6 Contents. Principles Used in Chapter 6 Principle 1: Money Has a Time Value.
 Chapter 6 The Time Value of Money: Annuities and Other Topics Chapter 6 Contents Learning Objectives 1. Distinguish between an ordinary annuity and an annuity due, and calculate present and future values
Chapter 6 The Time Value of Money: Annuities and Other Topics Chapter 6 Contents Learning Objectives 1. Distinguish between an ordinary annuity and an annuity due, and calculate present and future values
FIN 3000. Chapter 6. Annuities. Liuren Wu
 FIN 3000 Chapter 6 Annuities Liuren Wu Overview 1. Annuities 2. Perpetuities 3. Complex Cash Flow Streams Learning objectives 1. Distinguish between an ordinary annuity and an annuity due, and calculate
FIN 3000 Chapter 6 Annuities Liuren Wu Overview 1. Annuities 2. Perpetuities 3. Complex Cash Flow Streams Learning objectives 1. Distinguish between an ordinary annuity and an annuity due, and calculate
CHAPTER 4 DISCOUNTED CASH FLOW VALUATION
 CHAPTER 4 DISCOUNTED CASH FLOW VALUATION Answers to Concepts Review and Critical Thinking Questions 1. Assuming positive cash flows and interest rates, the future value increases and the present value
CHAPTER 4 DISCOUNTED CASH FLOW VALUATION Answers to Concepts Review and Critical Thinking Questions 1. Assuming positive cash flows and interest rates, the future value increases and the present value
Pre-Session Review. Part 2: Mathematics of Finance
 Pre-Session Review Part 2: Mathematics of Finance For this section you will need a calculator with logarithmic and exponential function keys (such as log, ln, and x y ) D. Exponential and Logarithmic Functions
Pre-Session Review Part 2: Mathematics of Finance For this section you will need a calculator with logarithmic and exponential function keys (such as log, ln, and x y ) D. Exponential and Logarithmic Functions
10.6 Functions - Compound Interest
 10.6 Functions - Compound Interest Objective: Calculate final account balances using the formulas for compound and continuous interest. An application of exponential functions is compound interest. When
10.6 Functions - Compound Interest Objective: Calculate final account balances using the formulas for compound and continuous interest. An application of exponential functions is compound interest. When
Check off these skills when you feel that you have mastered them.
 Chapter Objectives Check off these skills when you feel that you have mastered them. Know the basic loan terms principal and interest. Be able to solve the simple interest formula to find the amount of
Chapter Objectives Check off these skills when you feel that you have mastered them. Know the basic loan terms principal and interest. Be able to solve the simple interest formula to find the amount of
1. If you wish to accumulate $140,000 in 13 years, how much must you deposit today in an account that pays an annual interest rate of 14%?
 Chapter 2 - Sample Problems 1. If you wish to accumulate $140,000 in 13 years, how much must you deposit today in an account that pays an annual interest rate of 14%? 2. What will $247,000 grow to be in
Chapter 2 - Sample Problems 1. If you wish to accumulate $140,000 in 13 years, how much must you deposit today in an account that pays an annual interest rate of 14%? 2. What will $247,000 grow to be in
The Basics of Interest Theory
 Contents Preface 3 The Basics of Interest Theory 9 1 The Meaning of Interest................................... 10 2 Accumulation and Amount Functions............................ 14 3 Effective Interest
Contents Preface 3 The Basics of Interest Theory 9 1 The Meaning of Interest................................... 10 2 Accumulation and Amount Functions............................ 14 3 Effective Interest
CHAPTER 4 DISCOUNTED CASH FLOW VALUATION
 CHAPTER 4 DISCOUNTED CASH FLOW VALUATION Solutions to Questions and Problems NOTE: All-end-of chapter problems were solved using a spreadsheet. Many problems require multiple steps. Due to space and readability
CHAPTER 4 DISCOUNTED CASH FLOW VALUATION Solutions to Questions and Problems NOTE: All-end-of chapter problems were solved using a spreadsheet. Many problems require multiple steps. Due to space and readability
5. Time value of money
 1 Simple interest 2 5. Time value of money With simple interest, the amount earned each period is always the same: i = rp o We will review some tools for discounting cash flows. where i = interest earned
1 Simple interest 2 5. Time value of money With simple interest, the amount earned each period is always the same: i = rp o We will review some tools for discounting cash flows. where i = interest earned
How To Calculate A Balance On A Savings Account
 319 CHAPTER 4 Personal Finance The following is an article from a Marlboro, Massachusetts newspaper. NEWSPAPER ARTICLE 4.1: LET S TEACH FINANCIAL LITERACY STEPHEN LEDUC WED JAN 16, 2008 Boston - Last week
319 CHAPTER 4 Personal Finance The following is an article from a Marlboro, Massachusetts newspaper. NEWSPAPER ARTICLE 4.1: LET S TEACH FINANCIAL LITERACY STEPHEN LEDUC WED JAN 16, 2008 Boston - Last week
Introduction to the Hewlett-Packard (HP) 10BII Calculator and Review of Mortgage Finance Calculations
 Introduction to the Hewlett-Packard (HP) 10BII Calculator and Review of Mortgage Finance Calculations Real Estate Division Sauder School of Business University of British Columbia Introduction to the Hewlett-Packard
Introduction to the Hewlett-Packard (HP) 10BII Calculator and Review of Mortgage Finance Calculations Real Estate Division Sauder School of Business University of British Columbia Introduction to the Hewlett-Packard
CHAPTER 5. Interest Rates. Chapter Synopsis
 CHAPTER 5 Interest Rates Chapter Synopsis 5.1 Interest Rate Quotes and Adjustments Interest rates can compound more than once per year, such as monthly or semiannually. An annual percentage rate (APR)
CHAPTER 5 Interest Rates Chapter Synopsis 5.1 Interest Rate Quotes and Adjustments Interest rates can compound more than once per year, such as monthly or semiannually. An annual percentage rate (APR)
The time value of money: Part II
 The time value of money: Part II A reading prepared by Pamela Peterson Drake O U T L I E 1. Introduction 2. Annuities 3. Determining the unknown interest rate 4. Determining the number of compounding periods
The time value of money: Part II A reading prepared by Pamela Peterson Drake O U T L I E 1. Introduction 2. Annuities 3. Determining the unknown interest rate 4. Determining the number of compounding periods
5 More on Annuities and Loans
 5 More on Annuities and Loans 5.1 Introduction This section introduces Annuities. Much of the mathematics of annuities is similar to that of loans. Indeed, we will see that a loan and an annuity are just
5 More on Annuities and Loans 5.1 Introduction This section introduces Annuities. Much of the mathematics of annuities is similar to that of loans. Indeed, we will see that a loan and an annuity are just
International Financial Strategies Time Value of Money
 International Financial Strategies 1 Future Value and Compounding Future value = cash value of the investment at some point in the future Investing for single period: FV. Future Value PV. Present Value
International Financial Strategies 1 Future Value and Compounding Future value = cash value of the investment at some point in the future Investing for single period: FV. Future Value PV. Present Value
Chapter 6. Discounted Cash Flow Valuation. Key Concepts and Skills. Multiple Cash Flows Future Value Example 6.1. Answer 6.1
 Chapter 6 Key Concepts and Skills Be able to compute: the future value of multiple cash flows the present value of multiple cash flows the future and present value of annuities Discounted Cash Flow Valuation
Chapter 6 Key Concepts and Skills Be able to compute: the future value of multiple cash flows the present value of multiple cash flows the future and present value of annuities Discounted Cash Flow Valuation
Section 5.1 - Compound Interest
 Section 5.1 - Compound Interest Simple Interest Formulas If I denotes the interest on a principal P (in dollars) at an interest rate of r (as a decimal) per year for t years, then we have: Interest: Accumulated
Section 5.1 - Compound Interest Simple Interest Formulas If I denotes the interest on a principal P (in dollars) at an interest rate of r (as a decimal) per year for t years, then we have: Interest: Accumulated
Annuities Certain. 1 Introduction. 2 Annuities-immediate. 3 Annuities-due
 Annuities Certain 1 Introduction 2 Annuities-immediate 3 Annuities-due Annuities Certain 1 Introduction 2 Annuities-immediate 3 Annuities-due General terminology An annuity is a series of payments made
Annuities Certain 1 Introduction 2 Annuities-immediate 3 Annuities-due Annuities Certain 1 Introduction 2 Annuities-immediate 3 Annuities-due General terminology An annuity is a series of payments made
Vilnius University. Faculty of Mathematics and Informatics. Gintautas Bareikis
 Vilnius University Faculty of Mathematics and Informatics Gintautas Bareikis CONTENT Chapter 1. SIMPLE AND COMPOUND INTEREST 1.1 Simple interest......................................................................
Vilnius University Faculty of Mathematics and Informatics Gintautas Bareikis CONTENT Chapter 1. SIMPLE AND COMPOUND INTEREST 1.1 Simple interest......................................................................
Present Value Concepts
 Present Value Concepts Present value concepts are widely used by accountants in the preparation of financial statements. In fact, under International Financial Reporting Standards (IFRS), these concepts
Present Value Concepts Present value concepts are widely used by accountants in the preparation of financial statements. In fact, under International Financial Reporting Standards (IFRS), these concepts
Chapter 4. The Time Value of Money
 Chapter 4 The Time Value of Money 1 Learning Outcomes Chapter 4 Identify various types of cash flow patterns Compute the future value and the present value of different cash flow streams Compute the return
Chapter 4 The Time Value of Money 1 Learning Outcomes Chapter 4 Identify various types of cash flow patterns Compute the future value and the present value of different cash flow streams Compute the return
UNIT 6 2 The Mortgage Amortization Schedule
 UNIT 6 2 The Mortgage Amortization Schedule A home mortgage is a contract that requires the homeowner to make a fixed number of monthly payments over the life of the mortgage. The duration, or length of
UNIT 6 2 The Mortgage Amortization Schedule A home mortgage is a contract that requires the homeowner to make a fixed number of monthly payments over the life of the mortgage. The duration, or length of
Business 2019. Fundamentals of Finance, Chapter 6 Solution to Selected Problems
 Business 209 Fundamentals of Finance, Chapter 6 Solution to Selected Problems 8. Calculating Annuity Values You want to have $50,000 in your savings account five years from now, and you re prepared to
Business 209 Fundamentals of Finance, Chapter 6 Solution to Selected Problems 8. Calculating Annuity Values You want to have $50,000 in your savings account five years from now, and you re prepared to
Chapter 22: Borrowings Models
 October 21, 2013 Last Time The Consumer Price Index Real Growth The Consumer Price index The official measure of inflation is the Consumer Price Index (CPI) which is the determined by the Bureau of Labor
October 21, 2013 Last Time The Consumer Price Index Real Growth The Consumer Price index The official measure of inflation is the Consumer Price Index (CPI) which is the determined by the Bureau of Labor
Compound Interest Formula
 Mathematics of Finance Interest is the rental fee charged by a lender to a business or individual for the use of money. charged is determined by Principle, rate and time Interest Formula I = Prt $100 At
Mathematics of Finance Interest is the rental fee charged by a lender to a business or individual for the use of money. charged is determined by Principle, rate and time Interest Formula I = Prt $100 At
Finding the Payment $20,000 = C[1 1 / 1.0066667 48 ] /.0066667 C = $488.26
![Finding the Payment $20,000 = C[1 1 / 1.0066667 48 ] /.0066667 C = $488.26 Finding the Payment $20,000 = C[1 1 / 1.0066667 48 ] /.0066667 C = $488.26](/thumbs/17/134163.jpg) Quick Quiz: Part 2 You know the payment amount for a loan and you want to know how much was borrowed. Do you compute a present value or a future value? You want to receive $5,000 per month in retirement.
Quick Quiz: Part 2 You know the payment amount for a loan and you want to know how much was borrowed. Do you compute a present value or a future value? You want to receive $5,000 per month in retirement.
1 Interest rates, and risk-free investments
 Interest rates, and risk-free investments Copyright c 2005 by Karl Sigman. Interest and compounded interest Suppose that you place x 0 ($) in an account that offers a fixed (never to change over time)
Interest rates, and risk-free investments Copyright c 2005 by Karl Sigman. Interest and compounded interest Suppose that you place x 0 ($) in an account that offers a fixed (never to change over time)
5.5 The Opportunity Cost of Capital
 Problems 161 The correct discount rate for a cash flow is the expected return available in the market on other investments of comparable risk and term. If the interest on an investment is taxed at rate
Problems 161 The correct discount rate for a cash flow is the expected return available in the market on other investments of comparable risk and term. If the interest on an investment is taxed at rate
Time Value of Money. Work book Section I True, False type questions. State whether the following statements are true (T) or False (F)
 Time Value of Money Work book Section I True, False type questions State whether the following statements are true (T) or False (F) 1.1 Money has time value because you forgo something certain today for
Time Value of Money Work book Section I True, False type questions State whether the following statements are true (T) or False (F) 1.1 Money has time value because you forgo something certain today for
Example. L.N. Stout () Problems on annuities 1 / 14
 Example A credit card charges an annual rate of 14% compounded monthly. This month s bill is $6000. The minimum payment is $5. Suppose I keep paying $5 each month. How long will it take to pay off the
Example A credit card charges an annual rate of 14% compounded monthly. This month s bill is $6000. The minimum payment is $5. Suppose I keep paying $5 each month. How long will it take to pay off the
The Time Value of Money
 The Time Value of Money Time Value Terminology 0 1 2 3 4 PV FV Future value (FV) is the amount an investment is worth after one or more periods. Present value (PV) is the current value of one or more future
The Time Value of Money Time Value Terminology 0 1 2 3 4 PV FV Future value (FV) is the amount an investment is worth after one or more periods. Present value (PV) is the current value of one or more future
2.1 The Present Value of an Annuity
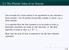 2.1 The Present Value of an Annuity One example of a fixed annuity is an agreement to pay someone a fixed amount x for N periods (commonly months or years), e.g. a fixed pension It is assumed that the
2.1 The Present Value of an Annuity One example of a fixed annuity is an agreement to pay someone a fixed amount x for N periods (commonly months or years), e.g. a fixed pension It is assumed that the
MAT116 Project 2 Chapters 8 & 9
 MAT116 Project 2 Chapters 8 & 9 1 8-1: The Project In Project 1 we made a loan workout decision based only on data from three banks that had merged into one. We did not consider issues like: What was the
MAT116 Project 2 Chapters 8 & 9 1 8-1: The Project In Project 1 we made a loan workout decision based only on data from three banks that had merged into one. We did not consider issues like: What was the
Chapter 4: Time Value of Money
 FIN 301 Homework Solution Ch4 Chapter 4: Time Value of Money 1. a. 10,000/(1.10) 10 = 3,855.43 b. 10,000/(1.10) 20 = 1,486.44 c. 10,000/(1.05) 10 = 6,139.13 d. 10,000/(1.05) 20 = 3,768.89 2. a. $100 (1.10)
FIN 301 Homework Solution Ch4 Chapter 4: Time Value of Money 1. a. 10,000/(1.10) 10 = 3,855.43 b. 10,000/(1.10) 20 = 1,486.44 c. 10,000/(1.05) 10 = 6,139.13 d. 10,000/(1.05) 20 = 3,768.89 2. a. $100 (1.10)
Credit Card Loans. Student Worksheet
 Student Worksheet Credit Card Loans Name: Recall the formula for simple interest where, I is the interest owed P is the principal amount outstanding r is the interest rate t is the time in years. Note:
Student Worksheet Credit Card Loans Name: Recall the formula for simple interest where, I is the interest owed P is the principal amount outstanding r is the interest rate t is the time in years. Note:
Future Value. Basic TVM Concepts. Chapter 2 Time Value of Money. $500 cash flow. On a time line for 3 years: $100. FV 15%, 10 yr.
 Chapter Time Value of Money Future Value Present Value Annuities Effective Annual Rate Uneven Cash Flows Growing Annuities Loan Amortization Summary and Conclusions Basic TVM Concepts Interest rate: abbreviated
Chapter Time Value of Money Future Value Present Value Annuities Effective Annual Rate Uneven Cash Flows Growing Annuities Loan Amortization Summary and Conclusions Basic TVM Concepts Interest rate: abbreviated
CHAPTER 4. The Time Value of Money. Chapter Synopsis
 CHAPTER 4 The Time Value of Money Chapter Synopsis Many financial problems require the valuation of cash flows occurring at different times. However, money received in the future is worth less than money
CHAPTER 4 The Time Value of Money Chapter Synopsis Many financial problems require the valuation of cash flows occurring at different times. However, money received in the future is worth less than money
Statistical Models for Forecasting and Planning
 Part 5 Statistical Models for Forecasting and Planning Chapter 16 Financial Calculations: Interest, Annuities and NPV chapter 16 Financial Calculations: Interest, Annuities and NPV Outcomes Financial information
Part 5 Statistical Models for Forecasting and Planning Chapter 16 Financial Calculations: Interest, Annuities and NPV chapter 16 Financial Calculations: Interest, Annuities and NPV Outcomes Financial information
CHAPTER 2. Time Value of Money 2-1
 CHAPTER 2 Time Value of Money 2-1 Time Value of Money (TVM) Time Lines Future value & Present value Rates of return Annuities & Perpetuities Uneven cash Flow Streams Amortization 2-2 Time lines 0 1 2 3
CHAPTER 2 Time Value of Money 2-1 Time Value of Money (TVM) Time Lines Future value & Present value Rates of return Annuities & Perpetuities Uneven cash Flow Streams Amortization 2-2 Time lines 0 1 2 3
3. Time value of money. We will review some tools for discounting cash flows.
 1 3. Time value of money We will review some tools for discounting cash flows. Simple interest 2 With simple interest, the amount earned each period is always the same: i = rp o where i = interest earned
1 3. Time value of money We will review some tools for discounting cash flows. Simple interest 2 With simple interest, the amount earned each period is always the same: i = rp o where i = interest earned
Time Value Conepts & Applications. Prof. Raad Jassim
 Time Value Conepts & Applications Prof. Raad Jassim Chapter Outline Introduction to Valuation: The Time Value of Money 1 2 3 4 5 6 7 8 Future Value and Compounding Present Value and Discounting More on
Time Value Conepts & Applications Prof. Raad Jassim Chapter Outline Introduction to Valuation: The Time Value of Money 1 2 3 4 5 6 7 8 Future Value and Compounding Present Value and Discounting More on
Bond Price Arithmetic
 1 Bond Price Arithmetic The purpose of this chapter is: To review the basics of the time value of money. This involves reviewing discounting guaranteed future cash flows at annual, semiannual and continuously
1 Bond Price Arithmetic The purpose of this chapter is: To review the basics of the time value of money. This involves reviewing discounting guaranteed future cash flows at annual, semiannual and continuously
Discounted Cash Flow Valuation
 BUAD 100x Foundations of Finance Discounted Cash Flow Valuation September 28, 2009 Review Introduction to corporate finance What is corporate finance? What is a corporation? What decision do managers make?
BUAD 100x Foundations of Finance Discounted Cash Flow Valuation September 28, 2009 Review Introduction to corporate finance What is corporate finance? What is a corporation? What decision do managers make?
Present Value (PV) Tutorial
 EYK 15-1 Present Value (PV) Tutorial The concepts of present value are described and applied in Chapter 15. This supplement provides added explanations, illustrations, calculations, present value tables,
EYK 15-1 Present Value (PV) Tutorial The concepts of present value are described and applied in Chapter 15. This supplement provides added explanations, illustrations, calculations, present value tables,
Finance 197. Simple One-time Interest
 Finance 197 Finance We have to work with money every day. While balancing your checkbook or calculating your monthly expenditures on espresso requires only arithmetic, when we start saving, planning for
Finance 197 Finance We have to work with money every day. While balancing your checkbook or calculating your monthly expenditures on espresso requires only arithmetic, when we start saving, planning for
Discounted Cash Flow Valuation
 6 Formulas Discounted Cash Flow Valuation McGraw-Hill/Irwin Copyright 2008 by The McGraw-Hill Companies, Inc. All rights reserved. Chapter Outline Future and Present Values of Multiple Cash Flows Valuing
6 Formulas Discounted Cash Flow Valuation McGraw-Hill/Irwin Copyright 2008 by The McGraw-Hill Companies, Inc. All rights reserved. Chapter Outline Future and Present Values of Multiple Cash Flows Valuing
Chapter F: Finance. Section F.1-F.4
 Chapter F: Finance Section F.1-F.4 F.1 Simple Interest Suppose a sum of money P, called the principal or present value, is invested for t years at an annual simple interest rate of r, where r is given
Chapter F: Finance Section F.1-F.4 F.1 Simple Interest Suppose a sum of money P, called the principal or present value, is invested for t years at an annual simple interest rate of r, where r is given
Introduction to Real Estate Investment Appraisal
 Introduction to Real Estate Investment Appraisal Maths of Finance Present and Future Values Pat McAllister INVESTMENT APPRAISAL: INTEREST Interest is a reward or rent paid to a lender or investor who has
Introduction to Real Estate Investment Appraisal Maths of Finance Present and Future Values Pat McAllister INVESTMENT APPRAISAL: INTEREST Interest is a reward or rent paid to a lender or investor who has
About Compound Interest
 About Compound Interest TABLE OF CONTENTS About Compound Interest... 1 What is COMPOUND INTEREST?... 1 Interest... 1 Simple Interest... 1 Compound Interest... 1 Calculations... 3 Calculating How Much to
About Compound Interest TABLE OF CONTENTS About Compound Interest... 1 What is COMPOUND INTEREST?... 1 Interest... 1 Simple Interest... 1 Compound Interest... 1 Calculations... 3 Calculating How Much to
Chapter 4 Time Value of Money ANSWERS TO END-OF-CHAPTER QUESTIONS
 Chapter 4 Time Value of Money ANSWERS TO END-OF-CHAPTER QUESTIONS 4-1 a. PV (present value) is the value today of a future payment, or stream of payments, discounted at the appropriate rate of interest.
Chapter 4 Time Value of Money ANSWERS TO END-OF-CHAPTER QUESTIONS 4-1 a. PV (present value) is the value today of a future payment, or stream of payments, discounted at the appropriate rate of interest.
MATHEMATICS OF FINANCE AND INVESTMENT
 MATHEMATICS OF FINANCE AND INVESTMENT G. I. FALIN Department of Probability Theory Faculty of Mechanics & Mathematics Moscow State Lomonosov University Moscow 119992 g.falin@mail.ru 2 G.I.Falin. Mathematics
MATHEMATICS OF FINANCE AND INVESTMENT G. I. FALIN Department of Probability Theory Faculty of Mechanics & Mathematics Moscow State Lomonosov University Moscow 119992 g.falin@mail.ru 2 G.I.Falin. Mathematics
Lecture Notes on the Mathematics of Finance
 Lecture Notes on the Mathematics of Finance Jerry Alan Veeh February 20, 2006 Copyright 2006 Jerry Alan Veeh. All rights reserved. 0. Introduction The objective of these notes is to present the basic aspects
Lecture Notes on the Mathematics of Finance Jerry Alan Veeh February 20, 2006 Copyright 2006 Jerry Alan Veeh. All rights reserved. 0. Introduction The objective of these notes is to present the basic aspects
This is Time Value of Money: Multiple Flows, chapter 7 from the book Finance for Managers (index.html) (v. 0.1).
 This is Time Value of Money: Multiple Flows, chapter 7 from the book Finance for Managers (index.html) (v. 0.1). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Time Value of Money: Multiple Flows, chapter 7 from the book Finance for Managers (index.html) (v. 0.1). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
Lecture Notes on Actuarial Mathematics
 Lecture Notes on Actuarial Mathematics Jerry Alan Veeh May 1, 2006 Copyright 2006 Jerry Alan Veeh. All rights reserved. 0. Introduction The objective of these notes is to present the basic aspects of the
Lecture Notes on Actuarial Mathematics Jerry Alan Veeh May 1, 2006 Copyright 2006 Jerry Alan Veeh. All rights reserved. 0. Introduction The objective of these notes is to present the basic aspects of the
PowerPoint. to accompany. Chapter 5. Interest Rates
 PowerPoint to accompany Chapter 5 Interest Rates 5.1 Interest Rate Quotes and Adjustments To understand interest rates, it s important to think of interest rates as a price the price of using money. When
PowerPoint to accompany Chapter 5 Interest Rates 5.1 Interest Rate Quotes and Adjustments To understand interest rates, it s important to think of interest rates as a price the price of using money. When
The Institute of Chartered Accountants of India
 CHAPTER 4 SIMPLE AND COMPOUND INTEREST INCLUDING ANNUITY APPLICATIONS SIMPLE AND COMPOUND INTEREST INCLUDING ANNUITY- APPLICATIONS LEARNING OBJECTIVES After studying this chapter students will be able
CHAPTER 4 SIMPLE AND COMPOUND INTEREST INCLUDING ANNUITY APPLICATIONS SIMPLE AND COMPOUND INTEREST INCLUDING ANNUITY- APPLICATIONS LEARNING OBJECTIVES After studying this chapter students will be able
Percent, Sales Tax, & Discounts
 Percent, Sales Tax, & Discounts Many applications involving percent are based on the following formula: Note that of implies multiplication. Suppose that the local sales tax rate is 7.5% and you purchase
Percent, Sales Tax, & Discounts Many applications involving percent are based on the following formula: Note that of implies multiplication. Suppose that the local sales tax rate is 7.5% and you purchase
Interest Rates: Loans, Credit Cards, and Annuties. Interest Rates: Loans, Credit Cards, and Annuties 1/43
 Interest Rates: Loans, Credit Cards, and Annuties Interest Rates: Loans, Credit Cards, and Annuties 1/43 Last Time Last time we discussed compound interest and saw that money can grow very large given
Interest Rates: Loans, Credit Cards, and Annuties Interest Rates: Loans, Credit Cards, and Annuties 1/43 Last Time Last time we discussed compound interest and saw that money can grow very large given
APPENDIX. Interest Concepts of Future and Present Value. Concept of Interest TIME VALUE OF MONEY BASIC INTEREST CONCEPTS
 CHAPTER 8 Current Monetary Balances 395 APPENDIX Interest Concepts of Future and Present Value TIME VALUE OF MONEY In general business terms, interest is defined as the cost of using money over time. Economists
CHAPTER 8 Current Monetary Balances 395 APPENDIX Interest Concepts of Future and Present Value TIME VALUE OF MONEY In general business terms, interest is defined as the cost of using money over time. Economists
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 Ch. 5 Mathematics of Finance 5.1 Compound Interest SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Provide an appropriate response. 1) What is the effective
Ch. 5 Mathematics of Finance 5.1 Compound Interest SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Provide an appropriate response. 1) What is the effective
How to calculate present values
 How to calculate present values Back to the future Chapter 3 Discounted Cash Flow Analysis (Time Value of Money) Discounted Cash Flow (DCF) analysis is the foundation of valuation in corporate finance
How to calculate present values Back to the future Chapter 3 Discounted Cash Flow Analysis (Time Value of Money) Discounted Cash Flow (DCF) analysis is the foundation of valuation in corporate finance
Solutions to Problems: Chapter 5
 Solutions to Problems: Chapter 5 P5-1. Using a time line LG 1; Basic a, b, and c d. Financial managers rely more on present value than future value because they typically make decisions before the start
Solutions to Problems: Chapter 5 P5-1. Using a time line LG 1; Basic a, b, and c d. Financial managers rely more on present value than future value because they typically make decisions before the start
HOW TO CALCULATE PRESENT VALUES
 Chapter 2 HOW TO CALCULATE PRESENT VALUES Brealey, Myers, and Allen Principles of Corporate Finance 11th Edition McGraw-Hill/Irwin Copyright 2014 by The McGraw-Hill Companies, Inc. All rights reserved.
Chapter 2 HOW TO CALCULATE PRESENT VALUES Brealey, Myers, and Allen Principles of Corporate Finance 11th Edition McGraw-Hill/Irwin Copyright 2014 by The McGraw-Hill Companies, Inc. All rights reserved.
How To Calculate The Value Of A Project
 Chapter 02 How to Calculate Present Values Multiple Choice Questions 1. The present value of $100 expected in two years from today at a discount rate of 6% is: A. $116.64 B. $108.00 C. $100.00 D. $89.00
Chapter 02 How to Calculate Present Values Multiple Choice Questions 1. The present value of $100 expected in two years from today at a discount rate of 6% is: A. $116.64 B. $108.00 C. $100.00 D. $89.00
Mathematics. Rosella Castellano. Rome, University of Tor Vergata
 and Loans Mathematics Rome, University of Tor Vergata and Loans Future Value for Simple Interest Present Value for Simple Interest You deposit E. 1,000, called the principal or present value, into a savings
and Loans Mathematics Rome, University of Tor Vergata and Loans Future Value for Simple Interest Present Value for Simple Interest You deposit E. 1,000, called the principal or present value, into a savings
Chapter 3 Mathematics of Finance
 Chapter 3 Mathematics of Finance Section 3 Future Value of an Annuity; Sinking Funds Learning Objectives for Section 3.3 Future Value of an Annuity; Sinking Funds The student will be able to compute the
Chapter 3 Mathematics of Finance Section 3 Future Value of an Annuity; Sinking Funds Learning Objectives for Section 3.3 Future Value of an Annuity; Sinking Funds The student will be able to compute the
Finance CHAPTER OUTLINE. 5.1 Interest 5.2 Compound Interest 5.3 Annuities; Sinking Funds 5.4 Present Value of an Annuity; Amortization
 CHAPTER 5 Finance OUTLINE Even though you re in college now, at some time, probably not too far in the future, you will be thinking of buying a house. And, unless you ve won the lottery, you will need
CHAPTER 5 Finance OUTLINE Even though you re in college now, at some time, probably not too far in the future, you will be thinking of buying a house. And, unless you ve won the lottery, you will need
2 The Mathematics. of Finance. Copyright Cengage Learning. All rights reserved.
 2 The Mathematics of Finance Copyright Cengage Learning. All rights reserved. 2.3 Annuities, Loans, and Bonds Copyright Cengage Learning. All rights reserved. Annuities, Loans, and Bonds A typical defined-contribution
2 The Mathematics of Finance Copyright Cengage Learning. All rights reserved. 2.3 Annuities, Loans, and Bonds Copyright Cengage Learning. All rights reserved. Annuities, Loans, and Bonds A typical defined-contribution
How to Calculate Present Values
 How to Calculate Present Values Michael Frantz, 2010-09-22 Present Value What is the Present Value The Present Value is the value today of tomorrow s cash flows. It is based on the fact that a Euro tomorrow
How to Calculate Present Values Michael Frantz, 2010-09-22 Present Value What is the Present Value The Present Value is the value today of tomorrow s cash flows. It is based on the fact that a Euro tomorrow
PRESENT VALUE ANALYSIS. Time value of money equal dollar amounts have different values at different points in time.
 PRESENT VALUE ANALYSIS Time value of money equal dollar amounts have different values at different points in time. Present value analysis tool to convert CFs at different points in time to comparable values
PRESENT VALUE ANALYSIS Time value of money equal dollar amounts have different values at different points in time. Present value analysis tool to convert CFs at different points in time to comparable values
If P = principal, r = annual interest rate, and t = time (in years), then the simple interest I is given by I = P rt.
 13 Consumer Mathematics 13.1 The Time Value of Money Start with some Definitions: Definition 1. The amount of a loan or a deposit is called the principal. Definition 2. The amount a loan or a deposit increases
13 Consumer Mathematics 13.1 The Time Value of Money Start with some Definitions: Definition 1. The amount of a loan or a deposit is called the principal. Definition 2. The amount a loan or a deposit increases
Simple Interest. and Simple Discount
 CHAPTER 1 Simple Interest and Simple Discount Learning Objectives Money is invested or borrowed in thousands of transactions every day. When an investment is cashed in or when borrowed money is repaid,
CHAPTER 1 Simple Interest and Simple Discount Learning Objectives Money is invested or borrowed in thousands of transactions every day. When an investment is cashed in or when borrowed money is repaid,
TIME VALUE OF MONEY. Return of vs. Return on Investment: We EXPECT to get more than we invest!
 TIME VALUE OF MONEY Return of vs. Return on Investment: We EXPECT to get more than we invest! Invest $1,000 it becomes $1,050 $1,000 return of $50 return on Factors to consider when assessing Return on
TIME VALUE OF MONEY Return of vs. Return on Investment: We EXPECT to get more than we invest! Invest $1,000 it becomes $1,050 $1,000 return of $50 return on Factors to consider when assessing Return on
Level Annuities with Payments More Frequent than Each Interest Period
 Level Annuities with Payments More Frequent than Each Interest Period 1 Examples 2 Annuity-immediate 3 Annuity-due Level Annuities with Payments More Frequent than Each Interest Period 1 Examples 2 Annuity-immediate
Level Annuities with Payments More Frequent than Each Interest Period 1 Examples 2 Annuity-immediate 3 Annuity-due Level Annuities with Payments More Frequent than Each Interest Period 1 Examples 2 Annuity-immediate
Chapter The Time Value of Money
 Chapter The Time Value of Money PPT 9-2 Chapter 9 - Outline Time Value of Money Future Value and Present Value Annuities Time-Value-of-Money Formulas Adjusting for Non-Annual Compounding Compound Interest
Chapter The Time Value of Money PPT 9-2 Chapter 9 - Outline Time Value of Money Future Value and Present Value Annuities Time-Value-of-Money Formulas Adjusting for Non-Annual Compounding Compound Interest
Compounding Quarterly, Monthly, and Daily
 126 Compounding Quarterly, Monthly, and Daily So far, you have been compounding interest annually, which means the interest is added once per year. However, you will want to add the interest quarterly,
126 Compounding Quarterly, Monthly, and Daily So far, you have been compounding interest annually, which means the interest is added once per year. However, you will want to add the interest quarterly,
Calculations for Time Value of Money
 KEATMX01_p001-008.qxd 11/4/05 4:47 PM Page 1 Calculations for Time Value of Money In this appendix, a brief explanation of the computation of the time value of money is given for readers not familiar with
KEATMX01_p001-008.qxd 11/4/05 4:47 PM Page 1 Calculations for Time Value of Money In this appendix, a brief explanation of the computation of the time value of money is given for readers not familiar with
Ordinary Annuities Chapter 10
 Ordinary Annuities Chapter 10 Learning Objectives After completing this chapter, you will be able to: > Define and distinguish between ordinary simple annuities and ordinary general annuities. > Calculate
Ordinary Annuities Chapter 10 Learning Objectives After completing this chapter, you will be able to: > Define and distinguish between ordinary simple annuities and ordinary general annuities. > Calculate
Chapter 03 - Basic Annuities
 3-1 Chapter 03 - Basic Annuities Section 7.0 - Sum of a Geometric Sequence The form for the sum of a geometric sequence is: Sum(n) a + ar + ar 2 + ar 3 + + ar n 1 Here a = (the first term) n = (the number
3-1 Chapter 03 - Basic Annuities Section 7.0 - Sum of a Geometric Sequence The form for the sum of a geometric sequence is: Sum(n) a + ar + ar 2 + ar 3 + + ar n 1 Here a = (the first term) n = (the number
HOW TO CALCULATE PRESENT VALUES
 Chapter 2 HOW TO CALCULATE PRESENT VALUES Brealey, Myers, and Allen Principles of Corporate Finance 11 th Global Edition McGraw-Hill Education Copyright 2014 by The McGraw-Hill Companies, Inc. All rights
Chapter 2 HOW TO CALCULATE PRESENT VALUES Brealey, Myers, and Allen Principles of Corporate Finance 11 th Global Edition McGraw-Hill Education Copyright 2014 by The McGraw-Hill Companies, Inc. All rights
Fin 3312 Sample Exam 1 Questions
 Fin 3312 Sample Exam 1 Questions Here are some representative type questions. This review is intended to give you an idea of the types of questions that may appear on the exam, and how the questions might
Fin 3312 Sample Exam 1 Questions Here are some representative type questions. This review is intended to give you an idea of the types of questions that may appear on the exam, and how the questions might
2. How would (a) a decrease in the interest rate or (b) an increase in the holding period of a deposit affect its future value? Why?
 CHAPTER 3 CONCEPT REVIEW QUESTIONS 1. Will a deposit made into an account paying compound interest (assuming compounding occurs once per year) yield a higher future value after one period than an equal-sized
CHAPTER 3 CONCEPT REVIEW QUESTIONS 1. Will a deposit made into an account paying compound interest (assuming compounding occurs once per year) yield a higher future value after one period than an equal-sized
Finance Unit 8. Success Criteria. 1 U n i t 8 11U Date: Name: Tentative TEST date
 1 U n i t 8 11U Date: Name: Finance Unit 8 Tentative TEST date Big idea/learning Goals In this unit you will study the applications of linear and exponential relations within financing. You will understand
1 U n i t 8 11U Date: Name: Finance Unit 8 Tentative TEST date Big idea/learning Goals In this unit you will study the applications of linear and exponential relations within financing. You will understand
UNIT AUTHOR: Elizabeth Hume, Colonial Heights High School, Colonial Heights City Schools
 Money & Finance I. UNIT OVERVIEW & PURPOSE: The purpose of this unit is for students to learn how savings accounts, annuities, loans, and credit cards work. All students need a basic understanding of how
Money & Finance I. UNIT OVERVIEW & PURPOSE: The purpose of this unit is for students to learn how savings accounts, annuities, loans, and credit cards work. All students need a basic understanding of how
Time Value of Money 1
 Time Value of Money 1 This topic introduces you to the analysis of trade-offs over time. Financial decisions involve costs and benefits that are spread over time. Financial decision makers in households
Time Value of Money 1 This topic introduces you to the analysis of trade-offs over time. Financial decisions involve costs and benefits that are spread over time. Financial decision makers in households
Discounted Cash Flow Valuation
 Discounted Cash Flow Valuation Chapter 5 Key Concepts and Skills Be able to compute the future value of multiple cash flows Be able to compute the present value of multiple cash flows Be able to compute
Discounted Cash Flow Valuation Chapter 5 Key Concepts and Skills Be able to compute the future value of multiple cash flows Be able to compute the present value of multiple cash flows Be able to compute
Compound Interest. Invest 500 that earns 10% interest each year for 3 years, where each interest payment is reinvested at the same rate:
 Compound Interest Invest 500 that earns 10% interest each year for 3 years, where each interest payment is reinvested at the same rate: Table 1 Development of Nominal Payments and the Terminal Value, S.
Compound Interest Invest 500 that earns 10% interest each year for 3 years, where each interest payment is reinvested at the same rate: Table 1 Development of Nominal Payments and the Terminal Value, S.
Key Concepts and Skills. Multiple Cash Flows Future Value Example 6.1. Chapter Outline. Multiple Cash Flows Example 2 Continued
 6 Calculators Discounted Cash Flow Valuation Key Concepts and Skills Be able to compute the future value of multiple cash flows Be able to compute the present value of multiple cash flows Be able to compute
6 Calculators Discounted Cash Flow Valuation Key Concepts and Skills Be able to compute the future value of multiple cash flows Be able to compute the present value of multiple cash flows Be able to compute
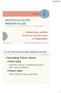
F V P V = F V = P (1 + r) n. n 1. FV n = C (1 + r) i. i=0. = C 1 r. (1 + r) n 1 ]
![F V P V = F V = P (1 + r) n. n 1. FV n = C (1 + r) i. i=0. = C 1 r. (1 + r) n 1 ] F V P V = F V = P (1 + r) n. n 1. FV n = C (1 + r) i. i=0. = C 1 r. (1 + r) n 1 ]](/thumbs/25/5828485.jpg) 1 Week 2 1.1 Recap Week 1 P V = F V (1 + r) n F V = P (1 + r) n 1.2 FV of Annuity: oncept 1.2.1 Multiple Payments: Annuities Multiple payments over time. A special case of multiple payments: annuities
1 Week 2 1.1 Recap Week 1 P V = F V (1 + r) n F V = P (1 + r) n 1.2 FV of Annuity: oncept 1.2.1 Multiple Payments: Annuities Multiple payments over time. A special case of multiple payments: annuities
Midterm 1 Practice Problems
 Midterm 1 Practice Problems 1. Calculate the present value of each cashflow using a discount rate of 7%. Which do you most prefer most? Show and explain all supporting calculations! Cashflow A: receive
Midterm 1 Practice Problems 1. Calculate the present value of each cashflow using a discount rate of 7%. Which do you most prefer most? Show and explain all supporting calculations! Cashflow A: receive
