FreeFem++, a tools to solving complex problem like Bose Einstein Condensate
|
|
|
- Gillian Heath
- 10 years ago
- Views:
Transcription
1 FreeFem++, a tools to solving complex problem like Bose Einstein Condensate equation or a melting problem. F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France with I. Danaila, S. Auliac, O. Pironneau mailto:[email protected]
2 Outline Introduction History The main characteristics Academic Examples Weak form Poisson Equation Tools Anisotropic Mesh adaptation 3d Poisson equation with mesh adaptation Build mesh from image Optimization Tools Ipopt interface Bose Einstein Condensate Phase change with Natural Convection Ground water elasticity equation Linear elasticity equation Hyper elasticity equation Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 2/41
3 News : FreeFem++ pass 10 9 unknowns The message from Pierre Jolivet (june 2012) Machine: Curie Thin Node@CEA Financement: PRACE project HPC-PDE (number ) Nombre de coeurs: 6144 Mémoire par coeurs: 4 Go Eléments finis: P3 Dimension: 2D Précision: 1e-08 Nombres d inconnues: Méthode de résolution: GMRES préconditionné par une méthode de décomposition de domaine à deux niveaux Nombre d itérations: 18 Temps de résolution: 2 minutes Type de problème: équation de diffusion avec coefficients très hétérogènes (5 ordres de grandeur de variation) The FreeFem++ days, the December 6th and 7th 2012, UPMC, Jussieu, Paris, France Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 3/41
4 Introduction FreeFem++ is a software to solve numerically partial differential equations (PDE) in IR 2 ) and in IR 3 ) with finite elements methods. We used a user language to set and control the problem. The FreeFem++ language allows for a quick specification of linear PDE s, with the variational formulation of a linear steady state problem and the user can write they own script to solve no linear problem and time depend problem. You can solve coupled problem or problem with moving domain or eigenvalue problem, do mesh adaptation, compute error indicator, etc... By the way, FreeFem++ is build to play with abstract linear, bilinear form on Finite Element Space and interpolation operator. FreeFem++ is a freeware and this run on Mac, Unix and Window architecture, in parallel with MPI. Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 4/41
5 History 1987 MacFem/PCFem les ancêtres (O. Pironneau en Pascal) payant FreeFem réécriture de C++ (P1,P0 un maillage) O. Pironneau, D. Bernardi, F. Hecht, C. Prudhomme (adaptation Maillage, bamg) FreeFem+ réécriture de C++ (P1,P0 plusieurs maillages) O. Pironneau, D. Bernardi, F. Hecht (algèbre de fonction) FreeFem++ réécriture avec autre noyau élément fini, et un autre langage utilisateur ; F. Hecht, O. Pironneau, K.Ohtsuka FreeFem 3d (S. Del Pino), Une première version de freefem en 3d avec des méthodes de domaine fictif FreeFem++ v3 réécriture du noyau élément fini pour prendre en compte les cas multidimensionnels : 1d,2d,3d... Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 5/41
6 For who, for what! For what 1. R&D 2. Academic Research, 3. Teaching of FEM, PDE, Weak form and variational form 4. Algorithmes prototyping 5. Numerical experimentation 6. Scientific computing and Parallel computing For who : the researcher, engineer, professor, student... The mailing list mailto:[email protected] with 377 members with a flux of 5-20 messages per day. More than 1000 true Users ( more than 200 download / month) Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 6/41
7 The main characteristics I/II (2D)(3D) Wide range of finite elements : continuous P1,P2 elements, discontinuous P0, P1, RT0,RT1,BDM1, elements,edge element, vectorial element, mini-element,... Automatic interpolation of data from a mesh to an other one ( with matrix construction if need), so a finite element function is view as a function of (x, y, z) or as an array. Definition of the problem (complex or real value) with the variational form with access to the vectors and the matrix. Discontinuous Galerkin formulation (only in 2d to day). LU, Cholesky, Crout, CG, GMRES, UMFPack, SuperLU, MUMPS, HIPS, SUPERLU_DIST, PASTIX.... sparse linear solver ; eigenvalue and eigenvector computation with ARPACK. Online graphics with OpenGL/GLUT/VTK, C++ like syntax. An integrated development environment FreeFem++-cs Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 7/41
8 The main characteristics II/II (2D)(3D) Analytic description of boundaries, with specification by the user of the intersection of boundaries in 2d. Automatic mesh generator, based on the Delaunay-Voronoï algorithm. (2d,3d (tetgen) ) load and save Mesh, solution Mesh adaptation based on metric, possibly anisotropic (only in 2d), with optional automatic computation of the metric from the Hessian of a solution. (2d,3d). Link with other soft : parview, gmsh, vtk, medit, gnuplot Dynamic linking to add plugin. Full MPI interface Nonlinear Optimisation tools : CG, Ipopt, NLOpt, stochastic Wide range of examples : Navier-Stokes 3d, elasticity 3d, Shell, fluid structure, eigenvalue problem, Schwarz domain decomposition algorithm, residual error indicator... Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 8/41
9 Laplace equation, weak form Let a domain Ω with a partition of Ω in Γ 2, Γ e. Find u a solution in such that : u = 1 in Ω, u = 2 on Γ 2, u n = 0 on Γ e (1) Denote V g = {v H 1 (Ω)/v Γ2 = g}. The Basic variationnal formulation with is : find u V 2 (Ω), such that u u. v = 1v+ n v, v V 0(Ω) (2) Ω Ω The finite element method is just : replace V g with a finite element space, and the FreeFem++ code : Γ Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 9/41
10 Poisson equation in a fish with FreeFem++ The finite element method is just : replace V g with a finite element space, and the FreeFem++ code : mesh3 Th("fish-3d.msh"); // read a mesh 3d fespace Vh(Th,P1); // define the P1 EF space Vh u,v; // set test and unknown function in Vh. macro Grad(u) [dx(u),dy(u),dz(u)] // EOM Grad def solve laplace(u,v,solver=cg) = int3d(th)( Grad(u) *Grad(v) ) - int3d(th) ( 1*v) + on(2,u=2); // int on γ 2 plot(u,fill=1,wait=1,value=0,wait=1); Run:fish.edp Run:fish3d.edp Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 10/41
11 Mesh adaptation : Metric / unit Mesh In Euclidean geometry the length γ of a curve γ of R d parametrized by γ(t) t=0..1 is γ = 1 0 (γ (t), γ (t)) R d dt We introduce the metric as a field x M x of d d symmetric definite > 0 matrices, and the length l of Γ w.r.t M is : l = 1 0 (γ (t), M γ(t) γ (t)) R d dt The key-idea is to construct a mesh where the lengths of the edges are close to 1 accordingly to M. Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 11/41
12 Mesh adaptation : Metrix intersection The unit ball BM in a metric M plot the maximum mesh size on all the direction, is a ellipse. If you we have two unknowns u and v, we just compute the metric M u and M v, find a metric M uv call intersection with the biggest ellipse such that : B(M v ) B(M u ) B(M v ) Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 12/41
13 Build of the metric form the solution u Optimal metric norm for interpolation error (function adaptmesh in freefem++) for P 1 continuous Lagrange finite element L : M = 1 ε u = 1 H where H = u ε L p : M = 1 ε det(h) 1 2p+2 H (result of F. Alauzet, A. Dervieux) In Norm W 1,p, the optimal metric M l for the P l Lagrange finite element, Optimal is given by (with only acute triangle) (thank J-M. Mirebeau) and (see MetricPk plugin and function ) M l,p = 1 ε (detm l) 1 lp+2 Ml for P 1 : M 1 = H 2 (sub optimal with acute triangle take H) (a ) 2 ( ) 2 b b c for P 2 : M 2 = 3 + with b c c a D (3) u(x, y) = (ax 3 + 3bx 2 y + 3cxy 2 + dy 3 )/3!, Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 13/41
14 Mesh adaptation : Example of mesh Enter? for help Enter? for help Enter? for help u = (10x 3 + y 3 ) + atan2(0.001, (sin(5y) 2x)) v = (10y 3 + x 3 ) + atan2(0.01, (sin(5x) 2y)). Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 14/41
15 A corner singularity adaptation with metric The domain is an L-shaped polygon Ω =]0, 1[ 2 \[ 1 2, 1]2 and the PDE is Find u H0 1 (Ω) such that u = 1 in Ω, The solution has a singularity at the reentrant angle and we wish to capture it numerically. example of Mesh adaptation Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 15/41
16 FreeFem++ corner singularity program int[int] lab=[1,1,1,1]; mesh Th = square(6,6,label=lab); Th=trunc(Th,x<0.5 y<0.5, label=1); fespace Vh(Th,P1); Vh u,v; real error=0.1; problem Probem1(u,v,solver=CG,eps=1.0e-6) = int2d(th)( dx(u)*dx(v) + dy(u)*dy(v)) - int2d(th)( v) + on(1,u=0); for (int i=0;i< 7;i++) { Probem1; // solving the pde Th=adaptmesh(Th,u,err=error,nbvx=100000); // the adaptation with Hessian of u plot(th,u,wait=1,fill=1); u=u; error = error/ (1000.^(1./7.)) ; } ; Run:CornerLap.edp Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 16/41
17 Poisson equation with 3d mesh adaptation load "msh3" load "tetgen" load "mshmet" load "medit" int nn = 6; int[int] l1111=[1,1,1,1],l01=[0,1],l11=[1,1]; // label numbering mesh3 Th3=buildlayers(square(nn,nn,region=0,label=l1111), nn, zbound=[0,1], labelmid=l11,labelup = l01,labeldown = l01); Th3=trunc(Th3,(x<0.5) (y < 0.5) (z < 0.5),label=1); // remove ]0.5, 1[ 3 fespace Vh(Th3,P1); Vh u,v; // FE. space definition macro Grad(u) [dx(u),dy(u),dz(u)] // EOM problem Poisson(u,v,solver=CG) = int3d(th3)( Grad(u) *Grad(v) ) -int3d(th3)( 1*v ) + on(1,u=0); real errm=1e-2; // level of error for(int ii=0; ii<5; ii++) { Poisson; Vh h; h[]=mshmet(th3,u,normalization=1,aniso=0,nbregul=1,hmin=1e-3, hmax=0.3,err=errm); errm*= 0.8; // change the level of error Th3=tetgreconstruction(Th3,switch="raAQ",sizeofvolume=h*h*h/6.); medit("u-adap-iso-"+ii,th3,u,wait=1); } Run:Laplace-Adapt-3d.edp Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 17/41
18 Build mesh from image 1/2 load "ppm2rnm" load "isoline" real[int,int] Curves(3,1); int[int] be(1); int nc; // nb of curve { real[int,int] ff1("lac-tyyppalanjarvi.pgm"); int nx = ff1.n, ny=ff1.m; // grey value [0,1] mesh Th=square(nx-1,ny-1, [(nx-1)*(x),(ny-1)*(1-y)]); fespace Vh(Th,P1); Vh f1; f1[]=ff1; nc=isoline(th,f1,iso=0.75,close=0, Curves,beginend=be, smoothing=.1,ratio=0.5); } Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 18/41
19 Build mesh from image 2/2 border Curve0(t=0,1) // the extern boundary { int c =0; // component 0 int i0 = be[2*c], i1 = be[2*c+1]-1; P=Curve(xy,i0,i1,t); // Curve 0 label=1; }... plot(curve1(100)); // show curve. mesh Th= buildmesh(curve1(-100)); // plot(th,wait=1); // Run:lac.edp (a local lac Jyväskylä) Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 19/41
20 Ipopt The IPOPT optimizer in a FreeFem++ script is done with the IPOPT function included in the ff-ipopt dynamic library. IPOPT is designed to solve constrained minimization problem in the form : find s.t. x 0 = argminf(x) { x R n i n, x lb i x i x ub i i m, c lb i c i (x) c ub i (simple bounds) (constraints functions) Where ub and lb stand for "upper bound" and "lower bound". If for some i, 1 i m we have c lb i = c ub i, it means that c i is an equality constraint, and an inequality one if < c ub c lb i i. Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 20/41
21 Ipopt interface load "ff-ipopt" varf vp([u1,u2],[v1,v2]) = int2d(th)(grad(u1) *Grad(v1)+ Grad(u2) *Grad(v2)) - int2d(th)(f1*v1+f2*v2); IPOPT([b,A],CC,ui1[],lb=lb1[],clb=cl[],ub=ub1[],warmstart=iter>1,uz=uzi[],lz=lzi[],lm=lmi matrix A = vp(vh,vh); // Fitness function matrix... real[int] b = vp(0,vh); // and linear form int[int] II1=[0],II2=[1]; // Constraints matrix matrix C1 = interpolate (Wh,Vh, U2Vc=II1); matrix C2 = interpolate (Wh,Vh, U2Vc=II2); matrix CC = -1*C1 + C2; // u2 - u1 >0 Wh cl=0; // constraints lower bounds (no upper bounds) varf vgamma([u1,u2],[v1,v2]) = on(1,2,3,4,u1=1,u2=1); real[int] ongamma=vgamma(0,vh); Vh [ub1,ub2]=[g1,g2]; Vh [lb1,lb2]=[g1,g2]; ub1[] = ongamma? ub1[] : 1e19 ; // Unbounded in interior lb1[] = ongamma? lb1[] : -1e19 ; Vh [uzi,uzi2]=[uz,uz2],[lzi,lzi2]=[lz,lz2],[ui1,ui2]=[u1,u2];; Wh lmi=lm; Run:IpoptLap.edp Run:IpoptVI2.edp Run:IpoptMinSurfVol.edp Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 21/41
22 Bose Einstein Condensate Just a direct use of Ipopt interface (2 day of works) The problem is find a complex field u on domain D such that : 1 u = argmin u =1 D 2 u 2 + V trap u 2 + g 2 u 4 Ωiu (( ) ) y x. u to code that in FreeFem++ use Ipopt interface ( Adaptation de maillage Run:BEC.edp Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 22/41
23 Phase change with Natural Convection The starting point of the problem is Brainstorming session (part I) of the third FreeFem++ days in december 2011, this is almost the Orange Problem is describe in web page fr/~hecht/ftp/ff++days/2011/orange-problem.pdf. The coupling of natural convection modeled by the Boussinesq approximation and liquid to solid phase change in Ω =]0, 1[ 2, No slip condition for the fluid are applied at the boundary and adiabatic condition on upper and lower boundary and given temperature θ r (resp θ l ) at the right and left boundaries. The model is : find the field : the velocity u = (u 1, u 2 ), the pressure p and temperature θ : u given in Ω s t u + (u )u +.µ u + p = c T e 2 in Ω f.u = 0 in Ω f t θ + (u )θ +.k T θ = t S(T ) in Ω Where Ω f is the fluid domain and the solid domain is Ω s = Ω \ Ω f. (3) Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 23/41
24 Phase change with Natural Convection The enthalpy of the change of phase is given by the function S ; µ is the relative viscosity, k T the thermal diffusivity. In Ω f = {x Ω; θ > θ f }, with θ m the melting temperature the solid has melt. We modeled, the solid phase as a fluid with huge viscosity, so : { θ < θf 10 µ = 6 θ θ m 1 Re, The Stefan enthalpy S c with defined by S c (θ) = H(θ)/S th where S the is the stefan number, and H is the Heaviside function with use the following smooth the enthalpy : S(θ) = tanh(50(θ θ m))) 2S te. Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 24/41
25 The true device Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 25/41
26 the Algorithm We apply a fixed point algorithm for the phase change part (the domain Ω f is fixed at each iteration) and a full no-linear Euler implicit scheme with a fixed domain for the rest. We use a Newton method to solve the non-linearity. if we don t make mesh adaptation, the Newton method do not converge if we use explicit method diverge too, if we implicit the dependance in Ω s the method also diverge. This is a really difficult problem. Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 26/41
27 the Algorithm, implementation The finite element space to approximate u1, u2, p, θ is defined by fespace Wh(Th,[P2,P2,P1,P1]); We do mesh adaptation a each time step, with the following code : Ph ph = S(T), pph=s(tp); Th= adaptmesh(th,t,tp,ph,pph,[u1,u2],err=errh, hmax=hmax,hmin=hmax/100,ratio = 1.2); This mean, we adapt with all variable plus the 2 melting phase a time n + 1 and n and we smooth the metric with a ratio of 1.2 to account for the movement of the melting front. Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 27/41
28 The Newton loop the fixed point are implemented as follows real err=1e100,errp ; for(int kk=0;kk<2;++kk) // 2 step of fixe point on Ω s { nu = nut; // recompute the viscosity in Ω s, Ω f for(int niter=0;niter<20; ++ niter) // newton loop { BoussinesqNL; err = u1w[].linfty; cout << niter << " err NL " << err <<endl; u1[] -= u1w[]; if(err < tolnewton) break; }// convergence.. } Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 28/41
29 The linearized problem problem BoussinesqNL([u1w,u2w,pw,Tw],[v1,v2,q,TT]) = int2d(th) ( [u1w,u2w,tw] *[v1,v2,tt]*cdt + UgradV(u1,u2,u1w,u2w,Tw) * [v1,v2,tt] + UgradV(u1w,u2w,u1,u2,T) * [v1,v2,tt] + ( Grad(u1w,u2w) *Grad(v1,v2)) * nu + ( Grad(u1,u2) *Grad(v1,v2)) * dnu* Tw + cmt*tw*v2 + grad(tw) *grad(tt)*kt - div(u1w,u2w)*q -div(v1,v2)*pw - eps*pw*q + ds(t)*tw*tt*cdt ) - int2d(th)( [u1,u2,t] *[v1,v2,tt]*cdt + UgradV(u1,u2,u1,u2,T) * [v1,v2,tt] + ( Grad(u1,u2) *Grad(v1,v2)) * nu + cmt*t*v2 - eps*p*q + grad(t) *grad(tt)*kt - div(u1,u2)*q -div(v1,v2)*p + S(T)*TT*cdt - [u1p,u2p,tp] *[v1,v2,tt]*cdt - S(Tp)*cdt*TT) + on(1,2,3,4, u1w=0,u2w=0)+on(2,tw=0)+on(4,tw=0) ; Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 29/41
30 The parameters of the computation take case 2 from Shimin Wang, Amir Faghri, and Theodore L. Bergman. A comprehensive numerical model for melting with natural convection. International Journal of Heat and Mass Transfer, January θ m = 0, Re = 1, S te = 0.045, P r = 56.2, R a = , θ l = 1, θ r = 0.1 so in this case cmt = c T = R a /P r, kt = k T = 1/P r, eps = 10 6, time step δt = 10 1, cdt = 1/δt, at time t = 80 and we get a good agreement with the article. Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 30/41
31 Phase change with Natural Convection Temperature Field at time=80s Velocity field So now, a real problem, get the physical parameter of the real experiment. Run:Orange-Newton.edp Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 31/41
32 A Free Boundary problem, (phreatic water) Let a trapezoidal domain Ω defined in FreeFem++ : real L=10; // Width real h=2.1; // Left height real h1=0.35; // Right height border a(t=0,l){x=t;y=0;label=1;}; // impermeable Γ a border b(t=0,h1){x=l;y=t;label=2;}; // the source Γ b border f(t=l,0){x=t;y=t*(h1-h)/l+h;label=3;}; // Γ f border d(t=h,0){x=0;y=t;label=4;}; // Left impermeable Γ d int n=10; mesh Th=buildmesh (a(l*n)+b(h1*n)+f(sqrt(l^2+(h-h1)^2)*n)+d(h*n)); plot(th,ps="dth.eps"); Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 32/41
33 The initial mesh The problem is : find p and Ω such that : p = 0 in Ω p = y on Γ b p n = 0 on Γ d Γ a p n = q K n x on Γ f (Neumann) p = y on Γ f (Dirichlet) where the input water flux is q = 0.02, and K = 0.5. The velocity u of the water is given by u = p. Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 33/41
34 algorithm We use the following fix point method : (with bad main B.C. Execute freeboundarypb.edp ) let be, k = 0, Ω k = Ω. First step, we forgot the Neumann BC and we solve the problem : Find p in V = H 1 (Ω k ), such p = y on Γ k b et on Γk f Ω k p p = 0, p V with p = 0 on Γ k b Γk f With the residual of the Neumann boundary condition we build a domain transformation F(x, y) = [x, y v(x)] where v is solution of : v V, such than v = 0 on Γ k a (bottom) v v = Ω k Γ k f ( p n q K n x)v, remark : we can use the previous equation to evaluate p n v = p v Ω k Γ k v V with v = 0 sur Γ k a Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 34/41
35 Implementation The new domain is : Ω k+1 = F(Ω k ) Warning if is the movement is too large we can have triangle overlapping. problem Pp(p,pp,solver=CG) = int2d(th)( dx(p)*dx(pp)+dy(p)*dy(pp)) + on(b,f,p=y) ; problem Pv(v,vv,solver=CG) = int2d(th)( dx(v)*dx(vv)+dy(v)*dy(vv)) + on (a, v=0) + int1d(th,f)(vv* ((Q/K)*N.y-(dx(p)*N.x+dy(p)*N.y))); while(errv>1e-6) { j++; Pp; Pv; errv=int1d(th,f)(v*v); coef = 1; // Here french cooking if overlapping see the example Th=movemesh(Th,[x,y-coef*v]); // deformation } Execute freeboundary.edp Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 35/41
36 Linear Lame equation, weak form Let a domain Ω R d with a partition of Ω in Γ d, Γ n. Find the displacement u field such that :.σ(u) = f in Ω, u = 0 on Γ d, σ(u).n = 0 on Γ n (4) Where ε(u) = 1 2 ( u + t u) and σ(u) = Aε(u) with A the linear positif operator on symmetric d d matrix corresponding to the material propriety. Denote V g = {v H 1 (Ω) d /v Γd = g}. The Basic displacement variational formulation is : find u V 0 (Ω), such that : ε(v) : Aε(u) = v.f+ ((Aε(u)).n).v, v V 0 (Ω) (5) Ω Ω Γ Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 36/41
37 Linear elasticity equation, in FreeFem++ fespace Vh(Th,[P1,P1,P1]); Vh [u1,u2,u3], [v1,v2,v3]; macro Strain(u1,u2,u3) [ dx(u1), dy(u2), dz(u3), (dz(u2) +dy(u3)), (dz(u1)+dx(u3)), (dy(u1)+dx(u2)) ] // EOM solve Lame([u1,u2,u3],[v1,v2,v3])= int3d(th)( Strain(v1,v2,v3) *(Aalu*Strain(u1,u2,u3)) ) - int3d(th) ( rhoalu*gravity*v3) + on(1,u1=0,u2=0,u3=0) ; real coef= 0.1/u1[].linfty; int[int] ref2=[1,0,2,0]; mesh3 Thm=movemesh3(Th, transfo=[x+u1*coef,y+u2*coef,z+u3*coef], label=ref2); plot(th,thm, wait=1,cmm="coef amplification = "+coef ); medit("th-thm",th,thm); Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 37/41
38 Lame equation / figure Run:beam-3d.edp Run:beam-EV-3d.edp Run:beam-3d-Adapt.edp Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 38/41
39 Hyper elasticity equation The Hyper elasticity problem is the minimization of the energy W (I 1, I 2, I 3 ) where I 1, I 2, I 3 are the 3 invariants. For example The Ciarlet Geymonat energy model is W = κ 1 (J 1 3) + κ 2 (J 2 3) + κ(j 1) κ ln(j) where J 1 = I 1 I 1 3 3, J 2 = I 2 I 2 3 3,J = I 1 2 3, let u the deplacement, when F = I d + u C = t F F I 1 = tr(c) I 2 = 1 2 (tr(c)2 tr(c 2 )) I 3 = det(c) The problem is find u = argmin W (I 1, I 2, I 3 ) u Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 39/41
40 Hyper elasticity equation fespace Wh(Th,[P2,P2]); // methode de Newton.. Wh [d1,d2]=[0,0]; Wh [w1,w2],[v1,v2]; for(int i=0;i<nnewton;++i) { solve dww([w1,w2],[v1,v2]) = int2d(th)( ddw2d([d1,d2],[w1,w2],[v1,v2]) ) - int2d(th)( dw2d([d1,d2],[v1,v2]) -[v1,v2] *[f1,f2] ) + on(1,w1=0,w2=0); } d1[] -= w1[]; real err = w1[].linfty; if(err< epsnewton) break; Run:Hyper-Elasticity-2d.edp show:elasticlaw2d.idp show:ciarletgemona.idp Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 40/41
41 Conclusion/Future Freefem++ v3 is very good tool to solve non standard PDE in 2D/3D to try new domain decomposition domain algorithm The the future we try to do : Build more graphic with VTK, paraview,... (in progress) Add Finite volume facility for hyperbolic PDE (just begin C.F. FreeVol Projet) 3d anisotrope mesh adaptation automate the parallel tool Thank for you attention. Journée Interfaces des Mathématiques, 13 nov. 2012, Rouen, France 41/41
Modélisation de problèmes spécifiques avec le logiciel libre FreeFem++
 Modélisation de problèmes spécifiques avec le logiciel libre FreeFem++ F. Hecht LJLL, UPMC Alpines, INRIA Rocquencourt with S. Auliac, I. Danaila P. Jolivet, A Le Hyaric, F. Nataf, O. Pironneau, P-H. Tournier
Modélisation de problèmes spécifiques avec le logiciel libre FreeFem++ F. Hecht LJLL, UPMC Alpines, INRIA Rocquencourt with S. Auliac, I. Danaila P. Jolivet, A Le Hyaric, F. Nataf, O. Pironneau, P-H. Tournier
An Introduction to FreeFem++ UPMC, September 2010 O. Pantz. CMAP, Ecole Polytechnique.
 An Introduction to FreeFem++ UPMC, September 2010 O. Pantz CMAP, Ecole Polytechnique. FreeFem++ What is it? FreeFEM++ is a Free software to solve PDE using the Finite Element Method. It runs on Windows,
An Introduction to FreeFem++ UPMC, September 2010 O. Pantz CMAP, Ecole Polytechnique. FreeFem++ What is it? FreeFEM++ is a Free software to solve PDE using the Finite Element Method. It runs on Windows,
Freefem++ F. Hecht. Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France
 Freefem++ F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France with A. Le Hyaric, S. Auliac, P. Jolivet,I. Danaila, O. Pironneau http://www.freefem.org Cours Freefem++,
Freefem++ F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France with A. Le Hyaric, S. Auliac, P. Jolivet,I. Danaila, O. Pironneau http://www.freefem.org Cours Freefem++,
Error indicator and mesh adaption, in FreeFem++
 Error indicator and mesh adaption, in FreeFem++ F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France http://www.freefem.org mailto:[email protected] Marmern, Pau,
Error indicator and mesh adaption, in FreeFem++ F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France http://www.freefem.org mailto:[email protected] Marmern, Pau,
FreeFem++-cs, the FreeFem++ Graphical Interface
 FreeFem++-cs, the FreeFem++ Graphical Interface Antoine Le Hyaric Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Antoine.Le [email protected] December 10, 2014 1 / 54 FreeFem++-cs How to
FreeFem++-cs, the FreeFem++ Graphical Interface Antoine Le Hyaric Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Antoine.Le [email protected] December 10, 2014 1 / 54 FreeFem++-cs How to
Domain decomposition techniques for interfacial discontinuities
 Domain decomposition techniques for interfacial discontinuities Geordie McBain Institut Jean le Rond d Alembert December 5, 2012 Connexion and substructuring Two ways to look at domain decomposition Decomposing
Domain decomposition techniques for interfacial discontinuities Geordie McBain Institut Jean le Rond d Alembert December 5, 2012 Connexion and substructuring Two ways to look at domain decomposition Decomposing
Introduction to the Finite Element Method
 Introduction to the Finite Element Method 09.06.2009 Outline Motivation Partial Differential Equations (PDEs) Finite Difference Method (FDM) Finite Element Method (FEM) References Motivation Figure: cross
Introduction to the Finite Element Method 09.06.2009 Outline Motivation Partial Differential Equations (PDEs) Finite Difference Method (FDM) Finite Element Method (FEM) References Motivation Figure: cross
TWO-DIMENSIONAL FINITE ELEMENT ANALYSIS OF FORCED CONVECTION FLOW AND HEAT TRANSFER IN A LAMINAR CHANNEL FLOW
 TWO-DIMENSIONAL FINITE ELEMENT ANALYSIS OF FORCED CONVECTION FLOW AND HEAT TRANSFER IN A LAMINAR CHANNEL FLOW Rajesh Khatri 1, 1 M.Tech Scholar, Department of Mechanical Engineering, S.A.T.I., vidisha
TWO-DIMENSIONAL FINITE ELEMENT ANALYSIS OF FORCED CONVECTION FLOW AND HEAT TRANSFER IN A LAMINAR CHANNEL FLOW Rajesh Khatri 1, 1 M.Tech Scholar, Department of Mechanical Engineering, S.A.T.I., vidisha
Feature Commercial codes In-house codes
 A simple finite element solver for thermo-mechanical problems Keywords: Scilab, Open source software, thermo-elasticity Introduction In this paper we would like to show how it is possible to develop a
A simple finite element solver for thermo-mechanical problems Keywords: Scilab, Open source software, thermo-elasticity Introduction In this paper we would like to show how it is possible to develop a
1 Finite difference example: 1D implicit heat equation
 1 Finite difference example: 1D implicit heat equation 1.1 Boundary conditions Neumann and Dirichlet We solve the transient heat equation ρc p t = ( k ) (1) on the domain L/2 x L/2 subject to the following
1 Finite difference example: 1D implicit heat equation 1.1 Boundary conditions Neumann and Dirichlet We solve the transient heat equation ρc p t = ( k ) (1) on the domain L/2 x L/2 subject to the following
AN INTRODUCTION TO NUMERICAL METHODS AND ANALYSIS
 AN INTRODUCTION TO NUMERICAL METHODS AND ANALYSIS Revised Edition James Epperson Mathematical Reviews BICENTENNIAL 0, 1 8 0 7 z ewiley wu 2007 r71 BICENTENNIAL WILEY-INTERSCIENCE A John Wiley & Sons, Inc.,
AN INTRODUCTION TO NUMERICAL METHODS AND ANALYSIS Revised Edition James Epperson Mathematical Reviews BICENTENNIAL 0, 1 8 0 7 z ewiley wu 2007 r71 BICENTENNIAL WILEY-INTERSCIENCE A John Wiley & Sons, Inc.,
FEM Software Automation, with a case study on the Stokes Equations
 FEM Automation, with a case study on the Stokes Equations FEM Andy R Terrel Advisors: L R Scott and R C Kirby Numerical from Department of Computer Science University of Chicago March 1, 2006 Masters Presentation
FEM Automation, with a case study on the Stokes Equations FEM Andy R Terrel Advisors: L R Scott and R C Kirby Numerical from Department of Computer Science University of Chicago March 1, 2006 Masters Presentation
Domain Decomposition Methods. Partial Differential Equations
 Domain Decomposition Methods for Partial Differential Equations ALFIO QUARTERONI Professor ofnumericalanalysis, Politecnico di Milano, Italy, and Ecole Polytechnique Federale de Lausanne, Switzerland ALBERTO
Domain Decomposition Methods for Partial Differential Equations ALFIO QUARTERONI Professor ofnumericalanalysis, Politecnico di Milano, Italy, and Ecole Polytechnique Federale de Lausanne, Switzerland ALBERTO
SIXTY STUDY QUESTIONS TO THE COURSE NUMERISK BEHANDLING AV DIFFERENTIALEKVATIONER I
 Lennart Edsberg, Nada, KTH Autumn 2008 SIXTY STUDY QUESTIONS TO THE COURSE NUMERISK BEHANDLING AV DIFFERENTIALEKVATIONER I Parameter values and functions occurring in the questions belowwill be exchanged
Lennart Edsberg, Nada, KTH Autumn 2008 SIXTY STUDY QUESTIONS TO THE COURSE NUMERISK BEHANDLING AV DIFFERENTIALEKVATIONER I Parameter values and functions occurring in the questions belowwill be exchanged
How To Calculate Energy From Water
 A bi-projection method for Bingham type flows Laurent Chupin, Thierry Dubois Laboratoire de Mathématiques Université Blaise Pascal, Clermont-Ferrand Ecoulements Gravitaires et RIsques Naturels Juin 2015
A bi-projection method for Bingham type flows Laurent Chupin, Thierry Dubois Laboratoire de Mathématiques Université Blaise Pascal, Clermont-Ferrand Ecoulements Gravitaires et RIsques Naturels Juin 2015
FINITE ELEMENT : MATRIX FORMULATION. Georges Cailletaud Ecole des Mines de Paris, Centre des Matériaux UMR CNRS 7633
 FINITE ELEMENT : MATRIX FORMULATION Georges Cailletaud Ecole des Mines de Paris, Centre des Matériaux UMR CNRS 76 FINITE ELEMENT : MATRIX FORMULATION Discrete vs continuous Element type Polynomial approximation
FINITE ELEMENT : MATRIX FORMULATION Georges Cailletaud Ecole des Mines de Paris, Centre des Matériaux UMR CNRS 76 FINITE ELEMENT : MATRIX FORMULATION Discrete vs continuous Element type Polynomial approximation
Class Meeting # 1: Introduction to PDEs
 MATH 18.152 COURSE NOTES - CLASS MEETING # 1 18.152 Introduction to PDEs, Fall 2011 Professor: Jared Speck Class Meeting # 1: Introduction to PDEs 1. What is a PDE? We will be studying functions u = u(x
MATH 18.152 COURSE NOTES - CLASS MEETING # 1 18.152 Introduction to PDEs, Fall 2011 Professor: Jared Speck Class Meeting # 1: Introduction to PDEs 1. What is a PDE? We will be studying functions u = u(x
Mean value theorem, Taylors Theorem, Maxima and Minima.
 MA 001 Preparatory Mathematics I. Complex numbers as ordered pairs. Argand s diagram. Triangle inequality. De Moivre s Theorem. Algebra: Quadratic equations and express-ions. Permutations and Combinations.
MA 001 Preparatory Mathematics I. Complex numbers as ordered pairs. Argand s diagram. Triangle inequality. De Moivre s Theorem. Algebra: Quadratic equations and express-ions. Permutations and Combinations.
AN INTERFACE STRIP PRECONDITIONER FOR DOMAIN DECOMPOSITION METHODS
 AN INTERFACE STRIP PRECONDITIONER FOR DOMAIN DECOMPOSITION METHODS by M. Storti, L. Dalcín, R. Paz Centro Internacional de Métodos Numéricos en Ingeniería - CIMEC INTEC, (CONICET-UNL), Santa Fe, Argentina
AN INTERFACE STRIP PRECONDITIONER FOR DOMAIN DECOMPOSITION METHODS by M. Storti, L. Dalcín, R. Paz Centro Internacional de Métodos Numéricos en Ingeniería - CIMEC INTEC, (CONICET-UNL), Santa Fe, Argentina
FreeFem++, 2d, 3d tools for PDE simulation
 FreeFem++, 2d, 3d tools for PDE simulation F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France with O. Pironneau, J. Morice http://www.freefem.org mailto:[email protected]
FreeFem++, 2d, 3d tools for PDE simulation F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France with O. Pironneau, J. Morice http://www.freefem.org mailto:[email protected]
FUNDAMENTAL FINITE ELEMENT ANALYSIS AND APPLICATIONS
 FUNDAMENTAL FINITE ELEMENT ANALYSIS AND APPLICATIONS With Mathematica and MATLAB Computations M. ASGHAR BHATTI WILEY JOHN WILEY & SONS, INC. CONTENTS OF THE BOOK WEB SITE PREFACE xi xiii 1 FINITE ELEMENT
FUNDAMENTAL FINITE ELEMENT ANALYSIS AND APPLICATIONS With Mathematica and MATLAB Computations M. ASGHAR BHATTI WILEY JOHN WILEY & SONS, INC. CONTENTS OF THE BOOK WEB SITE PREFACE xi xiii 1 FINITE ELEMENT
OpenFOAM Optimization Tools
 OpenFOAM Optimization Tools Henrik Rusche and Aleks Jemcov [email protected] and [email protected] Wikki, Germany and United Kingdom OpenFOAM Optimization Tools p. 1 Agenda Objective Review optimisation
OpenFOAM Optimization Tools Henrik Rusche and Aleks Jemcov [email protected] and [email protected] Wikki, Germany and United Kingdom OpenFOAM Optimization Tools p. 1 Agenda Objective Review optimisation
Module 1 : Conduction. Lecture 5 : 1D conduction example problems. 2D conduction
 Module 1 : Conduction Lecture 5 : 1D conduction example problems. 2D conduction Objectives In this class: An example of optimization for insulation thickness is solved. The 1D conduction is considered
Module 1 : Conduction Lecture 5 : 1D conduction example problems. 2D conduction Objectives In this class: An example of optimization for insulation thickness is solved. The 1D conduction is considered
Express Introductory Training in ANSYS Fluent Lecture 1 Introduction to the CFD Methodology
 Express Introductory Training in ANSYS Fluent Lecture 1 Introduction to the CFD Methodology Dimitrios Sofialidis Technical Manager, SimTec Ltd. Mechanical Engineer, PhD PRACE Autumn School 2013 - Industry
Express Introductory Training in ANSYS Fluent Lecture 1 Introduction to the CFD Methodology Dimitrios Sofialidis Technical Manager, SimTec Ltd. Mechanical Engineer, PhD PRACE Autumn School 2013 - Industry
Høgskolen i Narvik Sivilingeniørutdanningen STE6237 ELEMENTMETODER. Oppgaver
 Høgskolen i Narvik Sivilingeniørutdanningen STE637 ELEMENTMETODER Oppgaver Klasse: 4.ID, 4.IT Ekstern Professor: Gregory A. Chechkin e-mail: [email protected] Narvik 6 PART I Task. Consider two-point
Høgskolen i Narvik Sivilingeniørutdanningen STE637 ELEMENTMETODER Oppgaver Klasse: 4.ID, 4.IT Ekstern Professor: Gregory A. Chechkin e-mail: [email protected] Narvik 6 PART I Task. Consider two-point
Iterative Solvers for Linear Systems
 9th SimLab Course on Parallel Numerical Simulation, 4.10 8.10.2010 Iterative Solvers for Linear Systems Bernhard Gatzhammer Chair of Scientific Computing in Computer Science Technische Universität München
9th SimLab Course on Parallel Numerical Simulation, 4.10 8.10.2010 Iterative Solvers for Linear Systems Bernhard Gatzhammer Chair of Scientific Computing in Computer Science Technische Universität München
Introduction Our choice Example Problem Final slide :-) Python + FEM. Introduction to SFE. Robert Cimrman
 Python + FEM Introduction to SFE Robert Cimrman Department of Mechanics & New Technologies Research Centre University of West Bohemia Plzeň, Czech Republic April 3, 2007, Plzeň 1/22 Outline 1 Introduction
Python + FEM Introduction to SFE Robert Cimrman Department of Mechanics & New Technologies Research Centre University of West Bohemia Plzeň, Czech Republic April 3, 2007, Plzeň 1/22 Outline 1 Introduction
Finite Element Formulation for Plates - Handout 3 -
 Finite Element Formulation for Plates - Handout 3 - Dr Fehmi Cirak (fc286@) Completed Version Definitions A plate is a three dimensional solid body with one of the plate dimensions much smaller than the
Finite Element Formulation for Plates - Handout 3 - Dr Fehmi Cirak (fc286@) Completed Version Definitions A plate is a three dimensional solid body with one of the plate dimensions much smaller than the
Heat Transfer by Free Convection
 Heat Transfer by Free Convection Introduction This example describes a fluid flow problem with heat transfer in the fluid. An array of heating tubes is submerged in a vessel with fluid flow entering at
Heat Transfer by Free Convection Introduction This example describes a fluid flow problem with heat transfer in the fluid. An array of heating tubes is submerged in a vessel with fluid flow entering at
Optimization of Supply Chain Networks
 Optimization of Supply Chain Networks M. Herty TU Kaiserslautern September 2006 (2006) 1 / 41 Contents 1 Supply Chain Modeling 2 Networks 3 Optimization Continuous optimal control problem Discrete optimal
Optimization of Supply Chain Networks M. Herty TU Kaiserslautern September 2006 (2006) 1 / 41 Contents 1 Supply Chain Modeling 2 Networks 3 Optimization Continuous optimal control problem Discrete optimal
Paper Pulp Dewatering
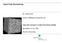 Paper Pulp Dewatering Dr. Stefan Rief [email protected] Flow and Transport in Industrial Porous Media November 12-16, 2007 Utrecht University Overview Introduction and Motivation Derivation
Paper Pulp Dewatering Dr. Stefan Rief [email protected] Flow and Transport in Industrial Porous Media November 12-16, 2007 Utrecht University Overview Introduction and Motivation Derivation
Ravi Kumar Singh*, K. B. Sahu**, Thakur Debasis Mishra***
 Ravi Kumar Singh, K. B. Sahu, Thakur Debasis Mishra / International Journal of Engineering Research and Applications (IJERA) ISSN: 48-96 www.ijera.com Vol. 3, Issue 3, May-Jun 3, pp.766-77 Analysis of
Ravi Kumar Singh, K. B. Sahu, Thakur Debasis Mishra / International Journal of Engineering Research and Applications (IJERA) ISSN: 48-96 www.ijera.com Vol. 3, Issue 3, May-Jun 3, pp.766-77 Analysis of
Simulation of Fluid-Structure Interactions in Aeronautical Applications
 Simulation of Fluid-Structure Interactions in Aeronautical Applications Martin Kuntz Jorge Carregal Ferreira ANSYS Germany D-83624 Otterfing [email protected] December 2003 3 rd FENET Annual Industry
Simulation of Fluid-Structure Interactions in Aeronautical Applications Martin Kuntz Jorge Carregal Ferreira ANSYS Germany D-83624 Otterfing [email protected] December 2003 3 rd FENET Annual Industry
Basin simulation for complex geological settings
 Énergies renouvelables Production éco-responsable Transports innovants Procédés éco-efficients Ressources durables Basin simulation for complex geological settings Towards a realistic modeling P. Havé*,
Énergies renouvelables Production éco-responsable Transports innovants Procédés éco-efficients Ressources durables Basin simulation for complex geological settings Towards a realistic modeling P. Havé*,
C3.8 CRM wing/body Case
 C3.8 CRM wing/body Case 1. Code description XFlow is a high-order discontinuous Galerkin (DG) finite element solver written in ANSI C, intended to be run on Linux-type platforms. Relevant supported equation
C3.8 CRM wing/body Case 1. Code description XFlow is a high-order discontinuous Galerkin (DG) finite element solver written in ANSI C, intended to be run on Linux-type platforms. Relevant supported equation
Renormalization of the Numerical Diffusion for an Upwind Finite Volume Method. Application to the Simulation of Kelvin-Helmholtz Instability
 5th International Symposium on Finite Volumes for Complex Applications. - Problems and Perspectives June 08-13, 008 Aussois, France Renormalization of the Numerical Diffusion for an Upwind Finite Volume
5th International Symposium on Finite Volumes for Complex Applications. - Problems and Perspectives June 08-13, 008 Aussois, France Renormalization of the Numerical Diffusion for an Upwind Finite Volume
ME6130 An introduction to CFD 1-1
 ME6130 An introduction to CFD 1-1 What is CFD? Computational fluid dynamics (CFD) is the science of predicting fluid flow, heat and mass transfer, chemical reactions, and related phenomena by solving numerically
ME6130 An introduction to CFD 1-1 What is CFD? Computational fluid dynamics (CFD) is the science of predicting fluid flow, heat and mass transfer, chemical reactions, and related phenomena by solving numerically
CAE -Finite Element Method
 16.810 Engineering Design and Rapid Prototyping Lecture 3b CAE -Finite Element Method Instructor(s) Prof. Olivier de Weck January 16, 2007 Numerical Methods Finite Element Method Boundary Element Method
16.810 Engineering Design and Rapid Prototyping Lecture 3b CAE -Finite Element Method Instructor(s) Prof. Olivier de Weck January 16, 2007 Numerical Methods Finite Element Method Boundary Element Method
Laminar Flow and Heat Transfer of Herschel-Bulkley Fluids in a Rectangular Duct; Finite-Element Analysis
 Tamkang Journal of Science and Engineering, Vol. 12, No. 1, pp. 99 107 (2009) 99 Laminar Flow and Heat Transfer of Herschel-Bulkley Fluids in a Rectangular Duct; Finite-Element Analysis M. E. Sayed-Ahmed
Tamkang Journal of Science and Engineering, Vol. 12, No. 1, pp. 99 107 (2009) 99 Laminar Flow and Heat Transfer of Herschel-Bulkley Fluids in a Rectangular Duct; Finite-Element Analysis M. E. Sayed-Ahmed
Finite Difference Approach to Option Pricing
 Finite Difference Approach to Option Pricing February 998 CS5 Lab Note. Ordinary differential equation An ordinary differential equation, or ODE, is an equation of the form du = fut ( (), t) (.) dt where
Finite Difference Approach to Option Pricing February 998 CS5 Lab Note. Ordinary differential equation An ordinary differential equation, or ODE, is an equation of the form du = fut ( (), t) (.) dt where
Design and Optimization of OpenFOAM-based CFD Applications for Hybrid and Heterogeneous HPC Platforms
 Design and Optimization of OpenFOAM-based CFD Applications for Hybrid and Heterogeneous HPC Platforms Amani AlOnazi, David E. Keyes, Alexey Lastovetsky, Vladimir Rychkov Extreme Computing Research Center,
Design and Optimization of OpenFOAM-based CFD Applications for Hybrid and Heterogeneous HPC Platforms Amani AlOnazi, David E. Keyes, Alexey Lastovetsky, Vladimir Rychkov Extreme Computing Research Center,
Computer Graphics. Geometric Modeling. Page 1. Copyright Gotsman, Elber, Barequet, Karni, Sheffer Computer Science - Technion. An Example.
 An Example 2 3 4 Outline Objective: Develop methods and algorithms to mathematically model shape of real world objects Categories: Wire-Frame Representation Object is represented as as a set of points
An Example 2 3 4 Outline Objective: Develop methods and algorithms to mathematically model shape of real world objects Categories: Wire-Frame Representation Object is represented as as a set of points
Mixed Precision Iterative Refinement Methods Energy Efficiency on Hybrid Hardware Platforms
 Mixed Precision Iterative Refinement Methods Energy Efficiency on Hybrid Hardware Platforms Björn Rocker Hamburg, June 17th 2010 Engineering Mathematics and Computing Lab (EMCL) KIT University of the State
Mixed Precision Iterative Refinement Methods Energy Efficiency on Hybrid Hardware Platforms Björn Rocker Hamburg, June 17th 2010 Engineering Mathematics and Computing Lab (EMCL) KIT University of the State
Scientic Computing 2013 Computer Classes: Worksheet 11: 1D FEM and boundary conditions
 Scientic Computing 213 Computer Classes: Worksheet 11: 1D FEM and boundary conditions Oleg Batrashev November 14, 213 This material partially reiterates the material given on the lecture (see the slides)
Scientic Computing 213 Computer Classes: Worksheet 11: 1D FEM and boundary conditions Oleg Batrashev November 14, 213 This material partially reiterates the material given on the lecture (see the slides)
Derive 5: The Easiest... Just Got Better!
 Liverpool John Moores University, 1-15 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de Technologie Supérieure, Canada Email; [email protected] 1. Introduction Engineering
Liverpool John Moores University, 1-15 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de Technologie Supérieure, Canada Email; [email protected] 1. Introduction Engineering
This makes sense. t 2 1 + 1/t 2 dt = 1. t t 2 + 1dt = 2 du = 1 3 u3/2 u=5
 1. (Line integrals Using parametrization. Two types and the flux integral) Formulas: ds = x (t) dt, d x = x (t)dt and d x = T ds since T = x (t)/ x (t). Another one is Nds = T ds ẑ = (dx, dy) ẑ = (dy,
1. (Line integrals Using parametrization. Two types and the flux integral) Formulas: ds = x (t) dt, d x = x (t)dt and d x = T ds since T = x (t)/ x (t). Another one is Nds = T ds ẑ = (dx, dy) ẑ = (dy,
How To Solve The Pde Problem On A Mesh With A Freefem++ (Freefemplest) On A Computer Or A Computer (For Freefems)
 FreeFem++ Manual version 1.42 (Under construction) http://www.freefem.org http://www.ann.jussieu.fr/ hecht/freefem++.htm F. Hecht 1, O. Pironneau 2, Université Pierre et Marie Curie, Laboratoire Jacques-Louis
FreeFem++ Manual version 1.42 (Under construction) http://www.freefem.org http://www.ann.jussieu.fr/ hecht/freefem++.htm F. Hecht 1, O. Pironneau 2, Université Pierre et Marie Curie, Laboratoire Jacques-Louis
NUMERICAL ANALYSIS OF THE EFFECTS OF WIND ON BUILDING STRUCTURES
 Vol. XX 2012 No. 4 28 34 J. ŠIMIČEK O. HUBOVÁ NUMERICAL ANALYSIS OF THE EFFECTS OF WIND ON BUILDING STRUCTURES Jozef ŠIMIČEK email: [email protected] Research field: Statics and Dynamics Fluids mechanics
Vol. XX 2012 No. 4 28 34 J. ŠIMIČEK O. HUBOVÁ NUMERICAL ANALYSIS OF THE EFFECTS OF WIND ON BUILDING STRUCTURES Jozef ŠIMIČEK email: [email protected] Research field: Statics and Dynamics Fluids mechanics
Overset Grids Technology in STAR-CCM+: Methodology and Applications
 Overset Grids Technology in STAR-CCM+: Methodology and Applications Eberhard Schreck, Milovan Perić and Deryl Snyder [email protected] [email protected] [email protected]
Overset Grids Technology in STAR-CCM+: Methodology and Applications Eberhard Schreck, Milovan Perić and Deryl Snyder [email protected] [email protected] [email protected]
The Fourth International DERIVE-TI92/89 Conference Liverpool, U.K., 12-15 July 2000. Derive 5: The Easiest... Just Got Better!
 The Fourth International DERIVE-TI9/89 Conference Liverpool, U.K., -5 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de technologie supérieure 00, rue Notre-Dame Ouest Montréal
The Fourth International DERIVE-TI9/89 Conference Liverpool, U.K., -5 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de technologie supérieure 00, rue Notre-Dame Ouest Montréal
A CODE VERIFICATION EXERCISE FOR THE UNSTRUCTURED FINITE-VOLUME CFD SOLVER ISIS-CFD
 European Conference on Computational Fluid Dynamics ECCOMAS CFD 2006 P. Wesseling, E. Oñate and J. Périaux (Eds) c TU Delft, The Netherlands, 2006 A CODE VERIFICATION EXERCISE FOR THE UNSTRUCTURED FINITE-VOLUME
European Conference on Computational Fluid Dynamics ECCOMAS CFD 2006 P. Wesseling, E. Oñate and J. Périaux (Eds) c TU Delft, The Netherlands, 2006 A CODE VERIFICATION EXERCISE FOR THE UNSTRUCTURED FINITE-VOLUME
Part II: Finite Difference/Volume Discretisation for CFD
 Part II: Finite Difference/Volume Discretisation for CFD Finite Volume Metod of te Advection-Diffusion Equation A Finite Difference/Volume Metod for te Incompressible Navier-Stokes Equations Marker-and-Cell
Part II: Finite Difference/Volume Discretisation for CFD Finite Volume Metod of te Advection-Diffusion Equation A Finite Difference/Volume Metod for te Incompressible Navier-Stokes Equations Marker-and-Cell
Effect of Aspect Ratio on Laminar Natural Convection in Partially Heated Enclosure
 Universal Journal of Mechanical Engineering (1): 8-33, 014 DOI: 10.13189/ujme.014.00104 http://www.hrpub.org Effect of Aspect Ratio on Laminar Natural Convection in Partially Heated Enclosure Alireza Falahat
Universal Journal of Mechanical Engineering (1): 8-33, 014 DOI: 10.13189/ujme.014.00104 http://www.hrpub.org Effect of Aspect Ratio on Laminar Natural Convection in Partially Heated Enclosure Alireza Falahat
Introduction to COMSOL. The Navier-Stokes Equations
 Flow Between Parallel Plates Modified from the COMSOL ChE Library module rev 10/13/08 Modified by Robert P. Hesketh, Chemical Engineering, Rowan University Fall 2008 Introduction to COMSOL The following
Flow Between Parallel Plates Modified from the COMSOL ChE Library module rev 10/13/08 Modified by Robert P. Hesketh, Chemical Engineering, Rowan University Fall 2008 Introduction to COMSOL The following
How To Find Out How Roots Of A Polynome Are Calculated
 Localisation des racines d un polynome et de ses dérivées, étude statistique André Galligo Laboratoire J.-A. Dieudonné UMR CNRS 6621 Université de Nice - Sophia Antipolis, France et projet-commun Galaad
Localisation des racines d un polynome et de ses dérivées, étude statistique André Galligo Laboratoire J.-A. Dieudonné UMR CNRS 6621 Université de Nice - Sophia Antipolis, France et projet-commun Galaad
Lecture 6 - Boundary Conditions. Applied Computational Fluid Dynamics
 Lecture 6 - Boundary Conditions Applied Computational Fluid Dynamics Instructor: André Bakker http://www.bakker.org André Bakker (2002-2006) Fluent Inc. (2002) 1 Outline Overview. Inlet and outlet boundaries.
Lecture 6 - Boundary Conditions Applied Computational Fluid Dynamics Instructor: André Bakker http://www.bakker.org André Bakker (2002-2006) Fluent Inc. (2002) 1 Outline Overview. Inlet and outlet boundaries.
Model of a flow in intersecting microchannels. Denis Semyonov
 Model of a flow in intersecting microchannels Denis Semyonov LUT 2012 Content Objectives Motivation Model implementation Simulation Results Conclusion Objectives A flow and a reaction model is required
Model of a flow in intersecting microchannels Denis Semyonov LUT 2012 Content Objectives Motivation Model implementation Simulation Results Conclusion Objectives A flow and a reaction model is required
Numerical Methods for Differential Equations
 Numerical Methods for Differential Equations Course objectives and preliminaries Gustaf Söderlind and Carmen Arévalo Numerical Analysis, Lund University Textbooks: A First Course in the Numerical Analysis
Numerical Methods for Differential Equations Course objectives and preliminaries Gustaf Söderlind and Carmen Arévalo Numerical Analysis, Lund University Textbooks: A First Course in the Numerical Analysis
Finite Element Method
 16.810 (16.682) Engineering Design and Rapid Prototyping Finite Element Method Instructor(s) Prof. Olivier de Weck [email protected] Dr. Il Yong Kim [email protected] January 12, 2004 Plan for Today FEM Lecture
16.810 (16.682) Engineering Design and Rapid Prototyping Finite Element Method Instructor(s) Prof. Olivier de Weck [email protected] Dr. Il Yong Kim [email protected] January 12, 2004 Plan for Today FEM Lecture
An Additive Neumann-Neumann Method for Mortar Finite Element for 4th Order Problems
 An Additive eumann-eumann Method for Mortar Finite Element for 4th Order Problems Leszek Marcinkowski Department of Mathematics, University of Warsaw, Banacha 2, 02-097 Warszawa, Poland, [email protected]
An Additive eumann-eumann Method for Mortar Finite Element for 4th Order Problems Leszek Marcinkowski Department of Mathematics, University of Warsaw, Banacha 2, 02-097 Warszawa, Poland, [email protected]
Mesh Generation and Load Balancing
 Mesh Generation and Load Balancing Stan Tomov Innovative Computing Laboratory Computer Science Department The University of Tennessee April 04, 2012 CS 594 04/04/2012 Slide 1 / 19 Outline Motivation Reliable
Mesh Generation and Load Balancing Stan Tomov Innovative Computing Laboratory Computer Science Department The University of Tennessee April 04, 2012 CS 594 04/04/2012 Slide 1 / 19 Outline Motivation Reliable
Reference: Introduction to Partial Differential Equations by G. Folland, 1995, Chap. 3.
 5 Potential Theory Reference: Introduction to Partial Differential Equations by G. Folland, 995, Chap. 3. 5. Problems of Interest. In what follows, we consider Ω an open, bounded subset of R n with C 2
5 Potential Theory Reference: Introduction to Partial Differential Equations by G. Folland, 995, Chap. 3. 5. Problems of Interest. In what follows, we consider Ω an open, bounded subset of R n with C 2
MEL 807 Computational Heat Transfer (2-0-4) Dr. Prabal Talukdar Assistant Professor Department of Mechanical Engineering IIT Delhi
 MEL 807 Computational Heat Transfer (2-0-4) Dr. Prabal Talukdar Assistant Professor Department of Mechanical Engineering IIT Delhi Time and Venue Course Coordinator: Dr. Prabal Talukdar Room No: III, 357
MEL 807 Computational Heat Transfer (2-0-4) Dr. Prabal Talukdar Assistant Professor Department of Mechanical Engineering IIT Delhi Time and Venue Course Coordinator: Dr. Prabal Talukdar Room No: III, 357
820446 - ACMSM - Computer Applications in Solids Mechanics
 Coordinating unit: 820 - EUETIB - Barcelona College of Industrial Engineering Teaching unit: 737 - RMEE - Department of Strength of Materials and Structural Engineering Academic year: Degree: 2015 BACHELOR'S
Coordinating unit: 820 - EUETIB - Barcelona College of Industrial Engineering Teaching unit: 737 - RMEE - Department of Strength of Materials and Structural Engineering Academic year: Degree: 2015 BACHELOR'S
Introduction to Algebraic Geometry. Bézout s Theorem and Inflection Points
 Introduction to Algebraic Geometry Bézout s Theorem and Inflection Points 1. The resultant. Let K be a field. Then the polynomial ring K[x] is a unique factorisation domain (UFD). Another example of a
Introduction to Algebraic Geometry Bézout s Theorem and Inflection Points 1. The resultant. Let K be a field. Then the polynomial ring K[x] is a unique factorisation domain (UFD). Another example of a
3 Concepts of Stress Analysis
 3 Concepts of Stress Analysis 3.1 Introduction Here the concepts of stress analysis will be stated in a finite element context. That means that the primary unknown will be the (generalized) displacements.
3 Concepts of Stress Analysis 3.1 Introduction Here the concepts of stress analysis will be stated in a finite element context. That means that the primary unknown will be the (generalized) displacements.
The simulation of machine tools can be divided into two stages. In the first stage the mechanical behavior of a machine tool is simulated with FEM
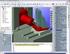 1 The simulation of machine tools can be divided into two stages. In the first stage the mechanical behavior of a machine tool is simulated with FEM tools. The approach to this simulation is different
1 The simulation of machine tools can be divided into two stages. In the first stage the mechanical behavior of a machine tool is simulated with FEM tools. The approach to this simulation is different
Introduction to the Finite Element Method (FEM)
 Introduction to the Finite Element Method (FEM) ecture First and Second Order One Dimensional Shape Functions Dr. J. Dean Discretisation Consider the temperature distribution along the one-dimensional
Introduction to the Finite Element Method (FEM) ecture First and Second Order One Dimensional Shape Functions Dr. J. Dean Discretisation Consider the temperature distribution along the one-dimensional
A gentle introduction to the Finite Element Method. Francisco Javier Sayas
 A gentle introduction to the Finite Element Method Francisco Javier Sayas 2008 An introduction If you haven t been hiding under a stone during your studies of engineering, mathematics or physics, it is
A gentle introduction to the Finite Element Method Francisco Javier Sayas 2008 An introduction If you haven t been hiding under a stone during your studies of engineering, mathematics or physics, it is
Solved with COMSOL Multiphysics 4.3
 Vibrating String Introduction In the following example you compute the natural frequencies of a pre-tensioned string using the 2D Truss interface. This is an example of stress stiffening ; in fact the
Vibrating String Introduction In the following example you compute the natural frequencies of a pre-tensioned string using the 2D Truss interface. This is an example of stress stiffening ; in fact the
Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows
 Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows 3.- 1 Basics: equations of continuum mechanics - balance equations for mass and momentum - balance equations for the energy and the chemical
Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows 3.- 1 Basics: equations of continuum mechanics - balance equations for mass and momentum - balance equations for the energy and the chemical
A Simultaneous Solution for General Linear Equations on a Ring or Hierarchical Cluster
 Acta Technica Jaurinensis Vol. 3. No. 1. 010 A Simultaneous Solution for General Linear Equations on a Ring or Hierarchical Cluster G. Molnárka, N. Varjasi Széchenyi István University Győr, Hungary, H-906
Acta Technica Jaurinensis Vol. 3. No. 1. 010 A Simultaneous Solution for General Linear Equations on a Ring or Hierarchical Cluster G. Molnárka, N. Varjasi Széchenyi István University Győr, Hungary, H-906
Best practices for efficient HPC performance with large models
 Best practices for efficient HPC performance with large models Dr. Hößl Bernhard, CADFEM (Austria) GmbH PRACE Autumn School 2013 - Industry Oriented HPC Simulations, September 21-27, University of Ljubljana,
Best practices for efficient HPC performance with large models Dr. Hößl Bernhard, CADFEM (Austria) GmbH PRACE Autumn School 2013 - Industry Oriented HPC Simulations, September 21-27, University of Ljubljana,
HEAT TRANSFER ANALYSIS IN A 3D SQUARE CHANNEL LAMINAR FLOW WITH USING BAFFLES 1 Vikram Bishnoi
 HEAT TRANSFER ANALYSIS IN A 3D SQUARE CHANNEL LAMINAR FLOW WITH USING BAFFLES 1 Vikram Bishnoi 2 Rajesh Dudi 1 Scholar and 2 Assistant Professor,Department of Mechanical Engineering, OITM, Hisar (Haryana)
HEAT TRANSFER ANALYSIS IN A 3D SQUARE CHANNEL LAMINAR FLOW WITH USING BAFFLES 1 Vikram Bishnoi 2 Rajesh Dudi 1 Scholar and 2 Assistant Professor,Department of Mechanical Engineering, OITM, Hisar (Haryana)
CFD SIMULATION OF SDHW STORAGE TANK WITH AND WITHOUT HEATER
 International Journal of Advancements in Research & Technology, Volume 1, Issue2, July-2012 1 CFD SIMULATION OF SDHW STORAGE TANK WITH AND WITHOUT HEATER ABSTRACT (1) Mr. Mainak Bhaumik M.E. (Thermal Engg.)
International Journal of Advancements in Research & Technology, Volume 1, Issue2, July-2012 1 CFD SIMULATION OF SDHW STORAGE TANK WITH AND WITHOUT HEATER ABSTRACT (1) Mr. Mainak Bhaumik M.E. (Thermal Engg.)
Visualization of 2D Domains
 Visualization of 2D Domains This part of the visualization package is intended to supply a simple graphical interface for 2- dimensional finite element data structures. Furthermore, it is used as the low
Visualization of 2D Domains This part of the visualization package is intended to supply a simple graphical interface for 2- dimensional finite element data structures. Furthermore, it is used as the low
Introduction to Engineering System Dynamics
 CHAPTER 0 Introduction to Engineering System Dynamics 0.1 INTRODUCTION The objective of an engineering analysis of a dynamic system is prediction of its behaviour or performance. Real dynamic systems are
CHAPTER 0 Introduction to Engineering System Dynamics 0.1 INTRODUCTION The objective of an engineering analysis of a dynamic system is prediction of its behaviour or performance. Real dynamic systems are
The Application of a Black-Box Solver with Error Estimate to Different Systems of PDEs
 The Application of a Black-Bo Solver with Error Estimate to Different Systems of PDEs Torsten Adolph and Willi Schönauer Forschungszentrum Karlsruhe Institute for Scientific Computing Karlsruhe, Germany
The Application of a Black-Bo Solver with Error Estimate to Different Systems of PDEs Torsten Adolph and Willi Schönauer Forschungszentrum Karlsruhe Institute for Scientific Computing Karlsruhe, Germany
Numerical Methods for Engineers
 Steven C. Chapra Berger Chair in Computing and Engineering Tufts University RaymondP. Canale Professor Emeritus of Civil Engineering University of Michigan Numerical Methods for Engineers With Software
Steven C. Chapra Berger Chair in Computing and Engineering Tufts University RaymondP. Canale Professor Emeritus of Civil Engineering University of Michigan Numerical Methods for Engineers With Software
Which strategy to move the mesh in the Computational Fluid Dynamic code OpenFOAM
 Which strategy to move the mesh in the Computational Fluid Dynamic code OpenFOAM Christophe Kassiotis April 12, 2008 École Normale Supérieure de Cachan, Laboratoire de Mécanique et Technologies (LMT) Secteur
Which strategy to move the mesh in the Computational Fluid Dynamic code OpenFOAM Christophe Kassiotis April 12, 2008 École Normale Supérieure de Cachan, Laboratoire de Mécanique et Technologies (LMT) Secteur
Yousef Saad University of Minnesota Computer Science and Engineering. CRM Montreal - April 30, 2008
 A tutorial on: Iterative methods for Sparse Matrix Problems Yousef Saad University of Minnesota Computer Science and Engineering CRM Montreal - April 30, 2008 Outline Part 1 Sparse matrices and sparsity
A tutorial on: Iterative methods for Sparse Matrix Problems Yousef Saad University of Minnesota Computer Science and Engineering CRM Montreal - April 30, 2008 Outline Part 1 Sparse matrices and sparsity
Giorgio Bornia. Research statement. Primary interests
 Giorgio Bornia Research statement 2500 Broadway and Boston 79409-1042 Lubbock, TX +1 806 834 8754 +1 806 742 1112 [email protected] http://www.math.ttu.edu/~gbornia Primary interests My main research
Giorgio Bornia Research statement 2500 Broadway and Boston 79409-1042 Lubbock, TX +1 806 834 8754 +1 806 742 1112 [email protected] http://www.math.ttu.edu/~gbornia Primary interests My main research
CFD Based Air Flow and Contamination Modeling of Subway Stations
 CFD Based Air Flow and Contamination Modeling of Subway Stations Greg Byrne Center for Nonlinear Science, Georgia Institute of Technology Fernando Camelli Center for Computational Fluid Dynamics, George
CFD Based Air Flow and Contamination Modeling of Subway Stations Greg Byrne Center for Nonlinear Science, Georgia Institute of Technology Fernando Camelli Center for Computational Fluid Dynamics, George
(Quasi-)Newton methods
 (Quasi-)Newton methods 1 Introduction 1.1 Newton method Newton method is a method to find the zeros of a differentiable non-linear function g, x such that g(x) = 0, where g : R n R n. Given a starting
(Quasi-)Newton methods 1 Introduction 1.1 Newton method Newton method is a method to find the zeros of a differentiable non-linear function g, x such that g(x) = 0, where g : R n R n. Given a starting
Finite Element Method (ENGC 6321) Syllabus. Second Semester 2013-2014
 Finite Element Method Finite Element Method (ENGC 6321) Syllabus Second Semester 2013-2014 Objectives Understand the basic theory of the FEM Know the behaviour and usage of each type of elements covered
Finite Element Method Finite Element Method (ENGC 6321) Syllabus Second Semester 2013-2014 Objectives Understand the basic theory of the FEM Know the behaviour and usage of each type of elements covered
Plates and Shells: Theory and Computation - 4D9 - Dr Fehmi Cirak (fc286@) Office: Inglis building mezzanine level (INO 31)
 Plates and Shells: Theory and Computation - 4D9 - Dr Fehmi Cirak (fc286@) Office: Inglis building mezzanine level (INO 31) Outline -1-! This part of the module consists of seven lectures and will focus
Plates and Shells: Theory and Computation - 4D9 - Dr Fehmi Cirak (fc286@) Office: Inglis building mezzanine level (INO 31) Outline -1-! This part of the module consists of seven lectures and will focus
Customer Training Material. Lecture 2. Introduction to. Methodology ANSYS FLUENT. ANSYS, Inc. Proprietary 2010 ANSYS, Inc. All rights reserved.
 Lecture 2 Introduction to CFD Methodology Introduction to ANSYS FLUENT L2-1 What is CFD? Computational Fluid Dynamics (CFD) is the science of predicting fluid flow, heat and mass transfer, chemical reactions,
Lecture 2 Introduction to CFD Methodology Introduction to ANSYS FLUENT L2-1 What is CFD? Computational Fluid Dynamics (CFD) is the science of predicting fluid flow, heat and mass transfer, chemical reactions,
Advanced CFD Methods 1
 Advanced CFD Methods 1 Prof. Patrick Jenny, FS 2014 Date: 15.08.14, Time: 13:00, Student: Federico Danieli Summary The exam took place in Prof. Jenny s office, with his assistant taking notes on the answers.
Advanced CFD Methods 1 Prof. Patrick Jenny, FS 2014 Date: 15.08.14, Time: 13:00, Student: Federico Danieli Summary The exam took place in Prof. Jenny s office, with his assistant taking notes on the answers.
INTRODUCTION TO THE FINITE ELEMENT METHOD
 INTRODUCTION TO THE FINITE ELEMENT METHOD G. P. Nikishkov 2004 Lecture Notes. University of Aizu, Aizu-Wakamatsu 965-8580, Japan [email protected] 2 Updated 2004-01-19 Contents 1 Introduction 5 1.1 What
INTRODUCTION TO THE FINITE ELEMENT METHOD G. P. Nikishkov 2004 Lecture Notes. University of Aizu, Aizu-Wakamatsu 965-8580, Japan [email protected] 2 Updated 2004-01-19 Contents 1 Introduction 5 1.1 What
CAE -Finite Element Method
 16.810 Engineering Design and Rapid Prototyping CAE -Finite Element Method Instructor(s) Prof. Olivier de Weck January 11, 2005 Plan for Today Hand Calculations Aero Æ Structures FEM Lecture (ca. 45 min)
16.810 Engineering Design and Rapid Prototyping CAE -Finite Element Method Instructor(s) Prof. Olivier de Weck January 11, 2005 Plan for Today Hand Calculations Aero Æ Structures FEM Lecture (ca. 45 min)
Modeling of Earth Surface Dynamics and Related Problems Using OpenFOAM
 CSDMS 2013 Meeting Modeling of Earth Surface Dynamics and Related Problems Using OpenFOAM Xiaofeng Liu, Ph.D., P.E. Assistant Professor Department of Civil and Environmental Engineering University of Texas
CSDMS 2013 Meeting Modeling of Earth Surface Dynamics and Related Problems Using OpenFOAM Xiaofeng Liu, Ph.D., P.E. Assistant Professor Department of Civil and Environmental Engineering University of Texas
Science Intensive Development (SID)
 Science Intensive Development (SID) At, we develop custom software that requires specific scientific knowledge. We are experienced in realizing projects that had been considered impossible. The main guarantee
Science Intensive Development (SID) At, we develop custom software that requires specific scientific knowledge. We are experienced in realizing projects that had been considered impossible. The main guarantee
Keywords: Heat transfer enhancement; staggered arrangement; Triangular Prism, Reynolds Number. 1. Introduction
 Heat transfer augmentation in rectangular channel using four triangular prisms arrange in staggered manner Manoj Kumar 1, Sunil Dhingra 2, Gurjeet Singh 3 1 Student, 2,3 Assistant Professor 1.2 Department
Heat transfer augmentation in rectangular channel using four triangular prisms arrange in staggered manner Manoj Kumar 1, Sunil Dhingra 2, Gurjeet Singh 3 1 Student, 2,3 Assistant Professor 1.2 Department
Proposal 1: Model-Based Control Method for Discrete-Parts machining processes
 Proposal 1: Model-Based Control Method for Discrete-Parts machining processes Proposed Objective: The proposed objective is to apply and extend the techniques from continuousprocessing industries to create
Proposal 1: Model-Based Control Method for Discrete-Parts machining processes Proposed Objective: The proposed objective is to apply and extend the techniques from continuousprocessing industries to create
COMPUTATIONAL FLUID DYNAMICS (CFD) ANALYSIS OF INTERMEDIATE PRESSURE STEAM TURBINE
 Research Paper ISSN 2278 0149 www.ijmerr.com Vol. 3, No. 4, October, 2014 2014 IJMERR. All Rights Reserved COMPUTATIONAL FLUID DYNAMICS (CFD) ANALYSIS OF INTERMEDIATE PRESSURE STEAM TURBINE Shivakumar
Research Paper ISSN 2278 0149 www.ijmerr.com Vol. 3, No. 4, October, 2014 2014 IJMERR. All Rights Reserved COMPUTATIONAL FLUID DYNAMICS (CFD) ANALYSIS OF INTERMEDIATE PRESSURE STEAM TURBINE Shivakumar
