Паралельність і перпендикулярність прямих і площин у просторі
|
|
|
- Василий Зузин
- 7 years ago
- Views:
Transcription
1 Паралельність і перпендикулярність прямих і площин у просторі Частина перша. Бічні сторони трапеції паралельні площині. Яке взаємне розміщення площини і площини трапеції? А)паралельні; Б) перетинаються; В)встановити неможливо; Г) збігаються..2 Дано трикутник АВС. Площина, паралельна прямій АВ, перетинає сторону Ас у точці М, а сторону ВС у точці К. Як довжина відрізка МК, якщо точка М середина АС, точка К середина ВС і АВ = 6 см? А) 4 см; Б) 6 см; В) 8 см; Г) 2 см..3 На рисунку зображено куб ABCDA BC D. Укажіть пряму перетину площини ABD і площини грані CCD D. А) DD CD ; Б) ; В) CD ; Г) площини не перетинаються..4 Точка А лежить в одній із граней двогранного кута, зображеного на рисунку. З точки А опущено перпендикуляр АВ на ребро двогранного кута і перпендикуляр АС на другу грань кута, АВ = 4 см, АС = 7 см. Знайдіть величину двогранного кута. А) 60 ; Б) 45 ; В) 30 ; Г) Точка А лежить в одній із площин, зображених на рисунку. З точки А опущено перпендикуляр АВ на лінію перетину площин і перпендикуляр АС на другу площину, АВ = 4 см, АС = 7 см. Знайдіть величину кута АВС. А)60 ; Б) 45 ; В)30 ; Г)90.
2 .6 Дано паралельні прямі a і b. Скільки існує площин, які проходять через пряму a і паралельні прямій b? А) одна; Б)дві; В)безліч; Г) жодної..7 Пряма МВ перпендикулярна до площини квадрата ABCD, зображеного на рисунку. Укажіть кут між прямою MD і площиною квадрата. А) MDA ; Б) MDB ; В) MDC ; Г) MBD..8 Точки А, В і С такі, що АВ = см, ВС = 2 см, АС = 3 см. Скільки існує площин, які містять точки А, В, С? А) одна; Б) дві; В)жодної; Г) безліч..9 Пряма проходить через середину сторони АВ трикутника АВС. Яке взаємне розташування прямих m і ВС, якщо пряма m не лежить у площині АВС? А) мимобіжні; Б) перетинаються; В) паралельні; Г) встановити неможливо..0 Трикутник ABC і площина розташовані так, що пряма AB паралельна площині і пряма AC паралельна площині. Яке взаємне розташування прямої BC і площини? А) пряма паралельна площині; Б) пряма належить площині; В) пряма перетинає площину; Г) встановити неможливо.. Точка M лежить поза площиною трикутника ABC. Яке взаємне розташування прямих AB і MC? А) перетинаються; Б) паралельні; В) мимобіжні; Г) встановити неможливо..2 Відрізок AB не перетинає площину, точки А і В віддалені від цієї площини на 7 см і см відповідно. Чому дорівнює відстань від середини відрізка АВ до площини? А) 8 см; Б) 2 см; В) 8 см; Г) 9 см..3 Яке з тверджень є правильним? А) якщо пряма a не паралельна прямій b, яка лежить у площині, то пряма a обов язково не паралельна площині ;
3 Б) якщо пряма a, яка не лежить у площині, паралельна прямій b цієї площини, то пряма a обов язково паралельна площині a ; В) якщо пряма a перетинає площину, а пряма b належить площині, то пряма a обов язково перетинає пряму b ; Г) якщо дві прямі у просторі не мають спільних точок, то вони паралельні..4 Точка A віддалена від площини на 2 см. З цієї точки проведено до площини похилу AB завдовжки 3 см. Знайдіть довжину проекції похилої AB на площину. А) 4 см; Б) 5 см; В) 6 см; Г) 9 см..5 З точки B, яка лежить в одній з граней двогранного кута, зображеного на рисунку, опущено перпендикуляр BA на ребро MK двогранного кута і перпендикуляр BC на іншу грань. Знайдіть величину двогранного кута, якщо AB 4 3 см, BC 6 см. А) 90 ; Б) 60 ; В) 45 ; Г) З точки B, яка лежить в одній з площин, зображених на рисунку, опущено перпендикуляр BA на лінію перетину площин MK і перпендикуляр BC на іншу площину. Знайдіть величину кута ВАС, якщо AB 4 3 см, BC 6 см. А) 90 ; Б) 60 ; В) 45 ; Г) Сторона AC трикутника ABC, зображеного на рисунку, належить площині, точки Mi - середини сторін AB i BC трикутника відповідно, точка B знаходиться поза площиною. Яке взаємне розташування прямої MK і площини? А) пряма і площина перетинаються; Б) пряма і площина паралельні; В) пряма належить площині; Г) встановити неможливо.
4 .8 Діагоналі паралелограма паралельні площині. Яке взаємне розміщення площини і площини паралелограма? А) збігаються; Б) перетинаються; В) встановити неможливо; Г) паралельні..9 Дано трикутник ABC. Площина, паралельна прямій AC, перетинає сторону AB у точці E, а сторону BC - у точці F. Яка довжина відрізка AC, якщо точка E - середина AB, точка F - середина BC і EF 2 см? А) 6 см; Б) 2 см; В) 8 см; Г) 24 см..20 На рисунку зображено куб ABCDA BC D. Укажіть пряму перетину площини ABC і площини грані AAD D. А) AD ; Б) AD ; В) AA ; Г) площини не перетинаються..2 Точка A лежить в одній з граней двогранного кута, зображеного на рисунку. З точки A опущено перпендикуляр AB на ребро двогранного кута і перпендикуляр ФС на другу грань кута, AB 6 2 см, BC 6 см. Знайдіть величину двогранного кута. А) 60 ; Б) 45 ; В) 30 ; Г) Точка A лежить в одній з площин, зображених на рисунку. З точки A опущено перпендикуляр AB на лінію перетину площин і перпендикуляр АС на другу площину, AB 6 2 см, BC 6 см. Знайдіть величину кута АВС. А) 60 ; Б) 45 ; В) 30 ; Г) Дано мимобіжні прямі a і b. Скільки існує площин, які проходять пряму a і паралельні прямій b? А) одна; Б) дві; В) безліч; Г) жодної..24 Пряма KO перпендикулярна до площини ромба DLTF, зображеного на рисунку.
5 Укажіть кут між прямою KF і площиною ромба. А) KOF ; Б) KFD ; В) KFT ; Г) KFO..25 Прямі a і b паралельні. Як розташована пряма a відносно площини, якщо пряма b перетинає площину? А) перетинає площину ; Б) паралельна площині ; В) належить площині ; Г) встановити неможливо..26 Пряма m паралельна стороні FK трикутника DFK. Яке взаємне розташування прямих m і DK, якщо пряма m не лежить у площині DFK? А) паралельні; Б) мимобіжні; В) встановити неможливо; Г) перетинаються..27 Дано паралелограм ABCD і площину, прямі AC і BD паралельні площині. Яке взаємне розташування прямої AB і площини? А) пряма перетинає площину; Б) пряма належить площині; В) пряма паралельна площині; Г) встановити неможливо..28 Точка M лежить поза площиною трикутника ABC. Яке взаємне розташування прямих BC і МА? А)встановити неможливо; Б)паралельні; В) перетинаються; Г) мимобіжні..29 Точка M - середина відрізка AB, який не перетинає площину. Точка А віддалена від площини на 6 см, а точка М на 4 см. Чому дорівнює відстань від точки B до площини? А) 8 см; Б) 20 см; В) 22 см; Г) 24 см..30 Яке з тверджень є правильним? А) якщо пряма в просторі перетинає одну з двох паралельних прямих, то вона перетинає й другу пряму; Б)якщо пряма паралельна площині, то вона паралельа будь-якій прямій цієї площини; В) якщо пряма перетинає одну з двох паралальних площин, то вона перетинає й другу площину; Г) якщо дві прямі в просторі не перетинаються, то вони не лежать в одній пложині.
6 .3 Точка М віддалена під площини на 5 см. З цієї точки проведено до площини похилу MK. Знайдіть довжину цієї похилої, якщо її проекція на площину дорівнює 8 см. А) 6 см; Б) 7 см; В) 9 см; Г) 23 см..32 З точки B, яка лежить в одній із граней двогранного кута, зображеного на рисунку, опущено перпендикуляр BA на ребро MK двогранного кута і перпендикуляр ВС на іншу грань. Знайдіть величину двогранного кута, якщо BC 2 3 см, АС=2 см. А) 30 ; Б) 45 ; В) 60 ; Г) З точки B, яка лежить в одній із площин, зображених на рисунку, опущено перпендикуляр BA на лінію перетину площин MK двогранного кута і перпендикуляр ВС на іншу площину. Знайдіть величину кута ВАС, якщо BC 2 3 см, АС=2 см. А) 30 ; Б) 45 ; В) 60 ; Г) Основа AD трапеції ABCD, зображеної на рисунку, належить площині, а основа BC не належить цій площині. Точки M і N - середини бічних сторін трапеції. Яке взаємне розташування прямої MN і площини? А) пряма і площина перетинаються; Б) пряма і площина паралельні; В) пряма належить площині; Г) встановити неможливо. Частина друга.35. З точки D, що лежить поза прямою n, проведено до цієї прямої похилі DK і DB, які утворюють із нею кути 45 і 60 відповідно. Знайдіть довжину проекції похилої DK на пряму n, якщо DB 0 3 см.
7 .36. Через гіпотенузу прямокутного рівнобедреного трикутника проведено площину, яка утворює з площиною трикутника кут 45. Знайдіть кути, які утворюють катети трикутника з цією площиною..37. З точки A до площини проведено похилі AB і AC, які утворюють з площиною кути по 60. Знайдіть відстань між точками B і C, якщо BAC 90, а відстань від точки A до площини дорівнює 3 см..38. З точки до прямої проведено дві похилі, проекції яких на пряму дорівнюють 9 см і 6 см. Знайдіть відстань від даної точки до прямої, якщо одна з похилих на 5 см більша за другу..39. Точка A знаходиться на відстані 9 см від площини. Похилі AB і AC утворюють із площиною кути 45 і 60 відповідно, а кут між проекціями похилих на площину дорівнює 50. Знайдіть відстань між точками B і C..40. З точки A до площини проведено похилі AB і AC, довжини яких 5 см і 20 см відповідно. Знайдіть відстань від точки A до площини, якщо проекції похилих на цю площину відносяться як 9:6..4. З точки A, що лежить поза прямою m, проведено до цієї прямої похилі AC і AD, які утворюють з нею кути 45 і 60 відповідно. Знайдіть довжину проекції похилої AD на пряму m, якщо AC = 4 2 см..42. Через сторону квадрата проведено площину, яка утворює з площиною квадрата кут 45. Знайдіть кут між діагоналлю квадрата і цією площиною..43. З точки до прямої проведено дві похилі завдовжки 25 см і 7 см. Знайдіть довжини проекцій цих похилих на дану пряму, якщо вони відносяться як 5: З точки К, що лежить поза прямою a, проведено до цієї прямої похилі КА і KB, які утворюють з нею кути 45 і 30 відповідно. Знайдіть довжину проекції похилої KB на пряму a, якщо KA 8 6 см..45. Через сторону правильного трикутника проведено площину, яка утворює з двома іншими сторонами трикутника кути по 45. Знайдіть кут між площиною трикутника і проведеною площиною..46. У рівнобедреному трикутнику ABC AB BC 3 см, AC 24 см. Пряма паралельна основі трикутника, перетинає сторони AB і BC у точках F і N відповідно і розбиває даний трикутник на дві
8 рівновеликі частини. Знайдіть радіус кола, вписаного в трикутник FBN..47. Через катет прямокутного рівнобедреного трикутника проведено площину, яка утворює з площиною трикутника кут 60. Знайдіть кути, які утворюють дві інші сторони трикутника з цією площиною..48. З точки M до площини проведено похилі MB і MC, які утворюють з площиною кути по 30. Знайдіть відстань від точки M до площини, якщо MBC 90, а довжина відрізка BC дорівнює 8 см..49. З точки до прямої проведено дві похилі завдовжки 3 см і 5 см. Знайдіть відстань від даної точки до прямої, якщо різниця проекцій похилих на цю пряму дорівнює 4 см..50. Точка K знаходиться на відстані 2 см від площини. Похилі KA і KB утворюють відповідно з площиною кути 45 і 30, а кут між похилими дорівнює 35. Знайдіть відстань між точками A і B..5. З точки M до площини проведено похилі MN і MK, довжини яких відносяться як 25: 26. Знайдіть відстань від точки M до площини, якщо довжини проекцій похилих MN і MK на цю площину дорівнюють 7 см і 0 см..52. З точки M, що лежить поза прямою l, проведено до цієї прямої похилі MN і MK, які утворюють з нею кути 30 і 45 відповідно. Знайдіть довжину похилої MK, якщо довжина проекції похилої MN на пряму l дорівнює 4 3 см..53. Через сторону квадрата проведено площину, яка утворює з його діагоналлю кут 30. Знайдіть кут між площиною квадрата і проведеною площиною..54. З точки до прямої проведено дві похилі, довжини проекцій яких на цю пряму дорівнюють 6 см і 5 см. Знайдіть довжини цих похилих, якщо вони відносяться к 0:7.
Online EFFECTIVE AS OF JANUARY 2013
 2013 A and C Session Start Dates (A-B Quarter Sequence*) 2013 B and D Session Start Dates (B-A Quarter Sequence*) Quarter 5 2012 1205A&C Begins November 5, 2012 1205A Ends December 9, 2012 Session Break
2013 A and C Session Start Dates (A-B Quarter Sequence*) 2013 B and D Session Start Dates (B-A Quarter Sequence*) Quarter 5 2012 1205A&C Begins November 5, 2012 1205A Ends December 9, 2012 Session Break
Problem A. Nanoassembly
 Problem A. Nanoassembly 2.5 seconds One of the problems of creating elements of nanostructures is the colossal time necessary for the construction of nano-parts from separate atoms. Transporting each of
Problem A. Nanoassembly 2.5 seconds One of the problems of creating elements of nanostructures is the colossal time necessary for the construction of nano-parts from separate atoms. Transporting each of
Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation
 988 Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation High School of Transport "Todor Kableshkov" 1574 Sofia, 158 Geo Milev str. Ivan Velev Abstract
988 Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation High School of Transport "Todor Kableshkov" 1574 Sofia, 158 Geo Milev str. Ivan Velev Abstract
The European Ombudsman
 Overview The European Ombudsman Е в р о п е й с к и о м б у д с м а н E l D e f e n s o r d e l P u e b l o E u r o p e o E v r o p s k ý v e ř e j n ý o c h r á n c e p r á v D e n E u r o p æ i s k e
Overview The European Ombudsman Е в р о п е й с к и о м б у д с м а н E l D e f e n s o r d e l P u e b l o E u r o p e o E v r o p s k ý v e ř e j n ý o c h r á n c e p r á v D e n E u r o p æ i s k e
Visa Smart Debit/Credit Certificate Authority Public Keys
 CHIP AND NEW TECHNOLOGIES Visa Smart Debit/Credit Certificate Authority Public Keys Overview The EMV standard calls for the use of Public Key technology for offline authentication, for aspects of online
CHIP AND NEW TECHNOLOGIES Visa Smart Debit/Credit Certificate Authority Public Keys Overview The EMV standard calls for the use of Public Key technology for offline authentication, for aspects of online
Russian Introductory Course
 Russian Introductory Course Natasha Bershadski Learn another language the way you learnt your own Succeed with the and learn another language the way you learnt your own Developed over 50 years, the amazing
Russian Introductory Course Natasha Bershadski Learn another language the way you learnt your own Succeed with the and learn another language the way you learnt your own Developed over 50 years, the amazing
UNDERGRADUATE STUDY SKILLS GUIDE 2014-15
 SCHOOL OF SLAVONIC AND EAST EUROPEAN STUDIES UNDERGRADUATE STUDY SKILLS GUIDE 2014-15 ECONOMICS AND BUSINESS HISTORY LANGUAGES AND CULTURE POLITICS AND SOCIOLOGY 1 1. AN INTRODUCTION TO STUDY SKILLS 5
SCHOOL OF SLAVONIC AND EAST EUROPEAN STUDIES UNDERGRADUATE STUDY SKILLS GUIDE 2014-15 ECONOMICS AND BUSINESS HISTORY LANGUAGES AND CULTURE POLITICS AND SOCIOLOGY 1 1. AN INTRODUCTION TO STUDY SKILLS 5
Unit 3 Boolean Algebra (Continued)
 Unit 3 Boolean Algebra (Continued) 1. Exclusive-OR Operation 2. Consensus Theorem Department of Communication Engineering, NCTU 1 3.1 Multiplying Out and Factoring Expressions Department of Communication
Unit 3 Boolean Algebra (Continued) 1. Exclusive-OR Operation 2. Consensus Theorem Department of Communication Engineering, NCTU 1 3.1 Multiplying Out and Factoring Expressions Department of Communication
How to bet using different NairaBet Bet Combinations (Combo)
 How to bet using different NairaBet Bet Combinations (Combo) SINGLES Singles consists of single bets. I.e. it will contain just a single selection of any sport. The bet slip of a singles will look like
How to bet using different NairaBet Bet Combinations (Combo) SINGLES Singles consists of single bets. I.e. it will contain just a single selection of any sport. The bet slip of a singles will look like
A usage coverage based approach for assessing product family design
 A usage coverage based approach for assessing product family design Jiliang Wang To cite this version: Jiliang Wang. A usage coverage based approach for assessing product family design. Other. Ecole Centrale
A usage coverage based approach for assessing product family design Jiliang Wang To cite this version: Jiliang Wang. A usage coverage based approach for assessing product family design. Other. Ecole Centrale
Lecture 24: Saccheri Quadrilaterals
 Lecture 24: Saccheri Quadrilaterals 24.1 Saccheri Quadrilaterals Definition In a protractor geometry, we call a quadrilateral ABCD a Saccheri quadrilateral, denoted S ABCD, if A and D are right angles
Lecture 24: Saccheri Quadrilaterals 24.1 Saccheri Quadrilaterals Definition In a protractor geometry, we call a quadrilateral ABCD a Saccheri quadrilateral, denoted S ABCD, if A and D are right angles
IС A A RT 2013. Proceedings Volume 2. 5th International Conference on Agents and Artificial Intelligence. Barcelona, Spain 15-18 February, 2013
 «'.''«ИЧИЧГШ ИШ М Ш * /////>. л ъ и г ш я ш и ъ в т ъ т ', : 4 р * т Ъ ъ ^ Х 'Ш У Л *а * 1 ЛЧй==:й?й!^'ййй IС A A RT 2013. *»ф«ч>»д* 'И И в Я в З Г З г И Ж /а 1 * icw-ia & «:*>if E M e i i i i y. x '-
«'.''«ИЧИЧГШ ИШ М Ш * /////>. л ъ и г ш я ш и ъ в т ъ т ', : 4 р * т Ъ ъ ^ Х 'Ш У Л *а * 1 ЛЧй==:й?й!^'ййй IС A A RT 2013. *»ф«ч>»д* 'И И в Я в З Г З г И Ж /а 1 * icw-ia & «:*>if E M e i i i i y. x '-
Boolean Algebra (cont d) UNIT 3 BOOLEAN ALGEBRA (CONT D) Guidelines for Multiplying Out and Factoring. Objectives. Iris Hui-Ru Jiang Spring 2010
 Boolean Algebra (cont d) 2 Contents Multiplying out and factoring expressions Exclusive-OR and Exclusive-NOR operations The consensus theorem Summary of algebraic simplification Proving validity of an
Boolean Algebra (cont d) 2 Contents Multiplying out and factoring expressions Exclusive-OR and Exclusive-NOR operations The consensus theorem Summary of algebraic simplification Proving validity of an
Quadrilateral Geometry. Varignon s Theorem I. Proof 10/21/2011 S C. MA 341 Topics in Geometry Lecture 19
 Quadrilateral Geometry MA 341 Topics in Geometry Lecture 19 Varignon s Theorem I The quadrilateral formed by joining the midpoints of consecutive sides of any quadrilateral is a parallelogram. PQRS is
Quadrilateral Geometry MA 341 Topics in Geometry Lecture 19 Varignon s Theorem I The quadrilateral formed by joining the midpoints of consecutive sides of any quadrilateral is a parallelogram. PQRS is
PRIMARY CONTENT MODULE Algebra I -Linear Equations & Inequalities T-71. Applications. F = mc + b.
 PRIMARY CONTENT MODULE Algebra I -Linear Equations & Inequalities T-71 Applications The formula y = mx + b sometimes appears with different symbols. For example, instead of x, we could use the letter C.
PRIMARY CONTENT MODULE Algebra I -Linear Equations & Inequalities T-71 Applications The formula y = mx + b sometimes appears with different symbols. For example, instead of x, we could use the letter C.
1. Find the length of BC in the following triangles. It will help to first find the length of the segment marked X.
 1 Find the length of BC in the following triangles It will help to first find the length of the segment marked X a: b: Given: the diagonals of parallelogram ABCD meet at point O The altitude OE divides
1 Find the length of BC in the following triangles It will help to first find the length of the segment marked X a: b: Given: the diagonals of parallelogram ABCD meet at point O The altitude OE divides
SERVER CERTIFICATES OF THE VETUMA SERVICE
 Page 1 Version: 3.4, 19.12.2014 SERVER CERTIFICATES OF THE VETUMA SERVICE 1 (18) Page 2 Version: 3.4, 19.12.2014 Table of Contents 1. Introduction... 3 2. Test Environment... 3 2.1 Vetuma test environment...
Page 1 Version: 3.4, 19.12.2014 SERVER CERTIFICATES OF THE VETUMA SERVICE 1 (18) Page 2 Version: 3.4, 19.12.2014 Table of Contents 1. Introduction... 3 2. Test Environment... 3 2.1 Vetuma test environment...
DEFINITIONS. Perpendicular Two lines are called perpendicular if they form a right angle.
 DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
IMO Geomety Problems. (IMO 1999/1) Determine all finite sets S of at least three points in the plane which satisfy the following condition:
 IMO Geomety Problems (IMO 1999/1) Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points A and B in S, the perpendicular bisector
IMO Geomety Problems (IMO 1999/1) Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points A and B in S, the perpendicular bisector
Exercise Set 3. Similar triangles. Parallel lines
 Exercise Set 3. Similar triangles Parallel lines Note: The exercises marked with are more difficult and go beyond the course/examination requirements. (1) Let ABC be a triangle with AB = AC. Let D be an
Exercise Set 3. Similar triangles Parallel lines Note: The exercises marked with are more difficult and go beyond the course/examination requirements. (1) Let ABC be a triangle with AB = AC. Let D be an
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Thursday, August 16, 2012 8:30 to 11:30 a.m.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 16, 2012 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of your
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 16, 2012 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of your
Section 8.8. 1. The given line has equations. x = 3 + t(13 3) = 3 + 10t, y = 2 + t(3 + 2) = 2 + 5t, z = 7 + t( 8 7) = 7 15t.
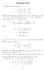 . The given line has equations Section 8.8 x + t( ) + 0t, y + t( + ) + t, z 7 + t( 8 7) 7 t. The line meets the plane y 0 in the point (x, 0, z), where 0 + t, or t /. The corresponding values for x and
. The given line has equations Section 8.8 x + t( ) + 0t, y + t( + ) + t, z 7 + t( 8 7) 7 t. The line meets the plane y 0 in the point (x, 0, z), where 0 + t, or t /. The corresponding values for x and
San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS
 San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS Recall that the bisector of an angle is the ray that divides the angle into two congruent angles. The most important results about angle bisectors
San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS Recall that the bisector of an angle is the ray that divides the angle into two congruent angles. The most important results about angle bisectors
Name Date Class. Lines and Segments That Intersect Circles. AB and CD are chords. Tangent Circles. Theorem Hypothesis Conclusion
 Section. Lines That Intersect Circles Lines and Segments That Intersect Circles A chord is a segment whose endpoints lie on a circle. A secant is a line that intersects a circle at two points. A tangent
Section. Lines That Intersect Circles Lines and Segments That Intersect Circles A chord is a segment whose endpoints lie on a circle. A secant is a line that intersects a circle at two points. A tangent
CH3 Boolean Algebra (cont d)
 CH3 Boolean Algebra (cont d) Lecturer: 吳 安 宇 Date:2005/10/7 ACCESS IC LAB v Today, you ll know: Introduction 1. Guidelines for multiplying out/factoring expressions 2. Exclusive-OR and Equivalence operations
CH3 Boolean Algebra (cont d) Lecturer: 吳 安 宇 Date:2005/10/7 ACCESS IC LAB v Today, you ll know: Introduction 1. Guidelines for multiplying out/factoring expressions 2. Exclusive-OR and Equivalence operations
Practical Geometry CHAPTER. 4.1 Introduction DO THIS
 PRACTICAL GEOMETRY 57 Practical Geometry CHAPTER 4 4.1 Introduction You have learnt how to draw triangles in Class VII. We require three measurements (of sides and angles) to draw a unique triangle. Since
PRACTICAL GEOMETRY 57 Practical Geometry CHAPTER 4 4.1 Introduction You have learnt how to draw triangles in Class VII. We require three measurements (of sides and angles) to draw a unique triangle. Since
Geometry Regents Review
 Name: Class: Date: Geometry Regents Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. If MNP VWX and PM is the shortest side of MNP, what is the shortest
Name: Class: Date: Geometry Regents Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. If MNP VWX and PM is the shortest side of MNP, what is the shortest
Projective Geometry - Part 2
 Projective Geometry - Part 2 Alexander Remorov alexanderrem@gmail.com Review Four collinear points A, B, C, D form a harmonic bundle (A, C; B, D) when CA : DA CB DB = 1. A pencil P (A, B, C, D) is the
Projective Geometry - Part 2 Alexander Remorov alexanderrem@gmail.com Review Four collinear points A, B, C, D form a harmonic bundle (A, C; B, D) when CA : DA CB DB = 1. A pencil P (A, B, C, D) is the
Blue Pelican Geometry Theorem Proofs
 Blue Pelican Geometry Theorem Proofs Copyright 2013 by Charles E. Cook; Refugio, Tx (All rights reserved) Table of contents Geometry Theorem Proofs The theorems listed here are but a few of the total in
Blue Pelican Geometry Theorem Proofs Copyright 2013 by Charles E. Cook; Refugio, Tx (All rights reserved) Table of contents Geometry Theorem Proofs The theorems listed here are but a few of the total in
Geometry Handout 2 ~ Page 1
 1. Given: a b, b c a c Guidance: Draw a line which intersects with all three lines. 2. Given: a b, c a a. c b b. Given: d b d c 3. Given: a c, b d a. α = β b. Given: e and f bisect angles α and β respectively.
1. Given: a b, b c a c Guidance: Draw a line which intersects with all three lines. 2. Given: a b, c a a. c b b. Given: d b d c 3. Given: a c, b d a. α = β b. Given: e and f bisect angles α and β respectively.
The course of understanding British and American prose and poetry by future managers
 4. Полат Е. С. Новые педагогические и информационные технологии в системе образования. М.: Просвещение, 2000. 5. Гальцова Н. П., Мезенцева Т. И., Швадленко И. А. Использование электронных информационно-образовательных
4. Полат Е. С. Новые педагогические и информационные технологии в системе образования. М.: Просвещение, 2000. 5. Гальцова Н. П., Мезенцева Т. И., Швадленко И. А. Использование электронных информационно-образовательных
MARI-ENGLISH DICTIONARY
 MARI-ENGLISH DICTIONARY This project was funded by the Austrian Science Fund (FWF) 1, grant P22786-G20, and carried out at the Department of Finno-Ugric Studies 2 at the University of Vienna 3. Editors:
MARI-ENGLISH DICTIONARY This project was funded by the Austrian Science Fund (FWF) 1, grant P22786-G20, and carried out at the Department of Finno-Ugric Studies 2 at the University of Vienna 3. Editors:
Calculation of Valu-Trac Statuses
 Calculation of Intrinsic Value Yield Latest Cash Earnings (Net Income + Depreciation and Amortization) (put aside) Dividend (subtract) Provision for Depreciation (Net Assets x Inflation Rate) (subtract)
Calculation of Intrinsic Value Yield Latest Cash Earnings (Net Income + Depreciation and Amortization) (put aside) Dividend (subtract) Provision for Depreciation (Net Assets x Inflation Rate) (subtract)
Algebraic Properties and Proofs
 Algebraic Properties and Proofs Name You have solved algebraic equations for a couple years now, but now it is time to justify the steps you have practiced and now take without thinking and acting without
Algebraic Properties and Proofs Name You have solved algebraic equations for a couple years now, but now it is time to justify the steps you have practiced and now take without thinking and acting without
SERVER CERTIFICATES OF THE VETUMA SERVICE
 Page 1 Version: 3.5, 4.11.2015 SERVER CERTIFICATES OF THE VETUMA SERVICE 1 (18) Page 2 Version: 3.5, 4.11.2015 Table of Contents 1. Introduction... 3 2. Test Environment... 3 2.1 Vetuma test environment...
Page 1 Version: 3.5, 4.11.2015 SERVER CERTIFICATES OF THE VETUMA SERVICE 1 (18) Page 2 Version: 3.5, 4.11.2015 Table of Contents 1. Introduction... 3 2. Test Environment... 3 2.1 Vetuma test environment...
COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES
 Margaryta I. Skrypnyk, Mykola M. Matiukha COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES The article studies the correspondence of management accounting structure when using of
Margaryta I. Skrypnyk, Mykola M. Matiukha COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES The article studies the correspondence of management accounting structure when using of
Vehicle Identification Numbering System 00.03
 Vehicle Identification Numbering System 00.03 IMPORTANT: See Subject 050 for the vehicle identification numbering system for vehicles built before May 1, 2000. Federal Motor Vehicle Safety Standard 115
Vehicle Identification Numbering System 00.03 IMPORTANT: See Subject 050 for the vehicle identification numbering system for vehicles built before May 1, 2000. Federal Motor Vehicle Safety Standard 115
Benchmark Databases for Testing Big-Data Analytics In Cloud Environments
 North Carolina State University Graduate Program in Operations Research Benchmark Databases for Testing Big-Data Analytics In Cloud Environments Rong Huang Rada Chirkova Yahya Fathi ICA CON 2012 April
North Carolina State University Graduate Program in Operations Research Benchmark Databases for Testing Big-Data Analytics In Cloud Environments Rong Huang Rada Chirkova Yahya Fathi ICA CON 2012 April
Database Design and Normalization
 Database Design and Normalization Chapter 10 (Week 11) EE562 Slides and Modified Slides from Database Management Systems, R. Ramakrishnan 1 Computing Closure F + Example: List all FDs with: - a single
Database Design and Normalization Chapter 10 (Week 11) EE562 Slides and Modified Slides from Database Management Systems, R. Ramakrishnan 1 Computing Closure F + Example: List all FDs with: - a single
You must have: Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser, calculator. Tracing paper may be used.
 Write your name here Surname Other names Edexcel IGCSE Mathematics B Paper 1 Centre Number Candidate Number Monday 6 June 2011 Afternoon Time: 1 hour 30 minutes Paper Reference 4MB0/01 You must have: Ruler
Write your name here Surname Other names Edexcel IGCSE Mathematics B Paper 1 Centre Number Candidate Number Monday 6 June 2011 Afternoon Time: 1 hour 30 minutes Paper Reference 4MB0/01 You must have: Ruler
BES-III distributed computing status
 КОМПЬЮТЕРНЫЕ ИССЛЕДОВАНИЯ И МОДЕЛИРОВАНИЕ 2015 Т. 7 3 С. 469 473 СЕКЦИОННЫЕ ДОКЛАДЫ УДК: 004.75, 004.052.2, 004.052.32 BES-III distributed computing status S. Belov 1, Z. Deng 2, W. Li 2, T. Lin 2, I.
КОМПЬЮТЕРНЫЕ ИССЛЕДОВАНИЯ И МОДЕЛИРОВАНИЕ 2015 Т. 7 3 С. 469 473 СЕКЦИОННЫЕ ДОКЛАДЫ УДК: 004.75, 004.052.2, 004.052.32 BES-III distributed computing status S. Belov 1, Z. Deng 2, W. Li 2, T. Lin 2, I.
US Code (Unofficial compilation from the Legal Information Institute)
 US Code (Unofficial compilation from the Legal Information Institute) TITLE 26 - INTERNAL REVENUE CODE Subtitle D - Miscellaneous Excise Taxes CHAPTER 43 QUALIFIED PENSION, ETC., PLANS Please Note: This
US Code (Unofficial compilation from the Legal Information Institute) TITLE 26 - INTERNAL REVENUE CODE Subtitle D - Miscellaneous Excise Taxes CHAPTER 43 QUALIFIED PENSION, ETC., PLANS Please Note: This
COMMERCIAL AIRLINE FACT SHEET
 COMMERCIAL AIRLINE FACT SHEET PASSENGER 100% Process LIFEJACKETS Black ame: SURVITECpos_PMS.eps Colourway: 100% Pantone PMS 158c RFD 102 Mk 2BA (00002136) Demo model (40982001) RFD 102 Mk 3 (00002256)
COMMERCIAL AIRLINE FACT SHEET PASSENGER 100% Process LIFEJACKETS Black ame: SURVITECpos_PMS.eps Colourway: 100% Pantone PMS 158c RFD 102 Mk 2BA (00002136) Demo model (40982001) RFD 102 Mk 3 (00002256)
The common ratio in (ii) is called the scaled-factor. An example of two similar triangles is shown in Figure 47.1. Figure 47.1
 47 Similar Triangles An overhead projector forms an image on the screen which has the same shape as the image on the transparency but with the size altered. Two figures that have the same shape but not
47 Similar Triangles An overhead projector forms an image on the screen which has the same shape as the image on the transparency but with the size altered. Two figures that have the same shape but not
TIgeometry.com. Geometry. Angle Bisectors in a Triangle
 Angle Bisectors in a Triangle ID: 8892 Time required 40 minutes Topic: Triangles and Their Centers Use inductive reasoning to postulate a relationship between an angle bisector and the arms of the angle.
Angle Bisectors in a Triangle ID: 8892 Time required 40 minutes Topic: Triangles and Their Centers Use inductive reasoning to postulate a relationship between an angle bisector and the arms of the angle.
1.4. Removing Brackets. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Removing Brackets 1. Introduction In order to simplify an expression which contains brackets it is often necessary to rewrite the expression in an equivalent form but without any brackets. This process
Removing Brackets 1. Introduction In order to simplify an expression which contains brackets it is often necessary to rewrite the expression in an equivalent form but without any brackets. This process
MB2-707: Version: Microsoft Dynamics CRM Customization. and Configuration. Demo
 MB2-707: Version: Microsoft Dynamics CRM Customization and Configuration Demo 1. You are a Microsoft Dynamics CRM consultant. You are assigned a new implementation. Before you configure the customer's
MB2-707: Version: Microsoft Dynamics CRM Customization and Configuration Demo 1. You are a Microsoft Dynamics CRM consultant. You are assigned a new implementation. Before you configure the customer's
Pipe fittings plant in Kolpino, Leningrad Regions
 1 Pipe fittings plant in Kolpino, Leningrad Regions ROOST Group of companies is a fast growing association with a long history. Synergy of the ROOST Group companies gives an opportunity to keep leading
1 Pipe fittings plant in Kolpino, Leningrad Regions ROOST Group of companies is a fast growing association with a long history. Synergy of the ROOST Group companies gives an opportunity to keep leading
http://www.castlelearning.com/review/teacher/assignmentprinting.aspx 5. 2 6. 2 1. 10 3. 70 2. 55 4. 180 7. 2 8. 4
 of 9 1/28/2013 8:32 PM Teacher: Mr. Sime Name: 2 What is the slope of the graph of the equation y = 2x? 5. 2 If the ratio of the measures of corresponding sides of two similar triangles is 4:9, then the
of 9 1/28/2013 8:32 PM Teacher: Mr. Sime Name: 2 What is the slope of the graph of the equation y = 2x? 5. 2 If the ratio of the measures of corresponding sides of two similar triangles is 4:9, then the
DevOps & WebSphere: Experiences in Chef enabling the IBM WebSphere Liberty Profile
 Jm h WbSh S d dm 5 h h 4 DO & WbSh: Ex Chf b h IB WbSh Lb f 4 IB C 4 IB C L Dm IB C 4 Rh Rd h fm d h b dd f fm Wh ff w md f h m d f h fm d h b, dd S IS wh w f kd, x md I dd, h fm bd IB d d, whh b h b IB
Jm h WbSh S d dm 5 h h 4 DO & WbSh: Ex Chf b h IB WbSh Lb f 4 IB C 4 IB C L Dm IB C 4 Rh Rd h fm d h b dd f fm Wh ff w md f h m d f h fm d h b, dd S IS wh w f kd, x md I dd, h fm bd IB d d, whh b h b IB
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Thursday, August 13, 2015 8:30 to 11:30 a.m., only.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 13, 2015 8:30 to 11:30 a.m., only Student Name: School Name: The possession or use of any communications
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 13, 2015 8:30 to 11:30 a.m., only Student Name: School Name: The possession or use of any communications
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Wednesday, January 29, 2014 9:15 a.m. to 12:15 p.m.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, January 29, 2014 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, January 29, 2014 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
Community College of Philadelphia Calling Code 218 Employer Scan Client Approved: November 17, 2005 Region (CIRCLE) City MSA
 Community College of Philadelphia Calling Code 218 Employer Scan Client Approved: November 17, 2005 Region (CIRCLE) City MSA Zip V0 V1 V2 Month/ Day/ Year of Contact: Business Name: Address: V3 City: V4
Community College of Philadelphia Calling Code 218 Employer Scan Client Approved: November 17, 2005 Region (CIRCLE) City MSA Zip V0 V1 V2 Month/ Day/ Year of Contact: Business Name: Address: V3 City: V4
Angles in a Circle and Cyclic Quadrilateral
 130 Mathematics 19 Angles in a Circle and Cyclic Quadrilateral 19.1 INTRODUCTION You must have measured the angles between two straight lines, let us now study the angles made by arcs and chords in a circle
130 Mathematics 19 Angles in a Circle and Cyclic Quadrilateral 19.1 INTRODUCTION You must have measured the angles between two straight lines, let us now study the angles made by arcs and chords in a circle
CHAPTER 1. LINES AND PLANES IN SPACE
 CHAPTER 1. LINES AND PLANES IN SPACE 1. Angles and distances between skew lines 1.1. Given cube ABCDA 1 B 1 C 1 D 1 with side a. Find the angle and the distance between lines A 1 B and AC 1. 1.2. Given
CHAPTER 1. LINES AND PLANES IN SPACE 1. Angles and distances between skew lines 1.1. Given cube ABCDA 1 B 1 C 1 D 1 with side a. Find the angle and the distance between lines A 1 B and AC 1. 1.2. Given
Victims Compensation Claim Status of All Pending Claims and Claims Decided Within the Last Three Years
 Claim#:021914-174 Initials: J.T. Last4SSN: 6996 DOB: 5/3/1970 Crime Date: 4/30/2013 Status: Claim is currently under review. Decision expected within 7 days Claim#:041715-334 Initials: M.S. Last4SSN: 2957
Claim#:021914-174 Initials: J.T. Last4SSN: 6996 DOB: 5/3/1970 Crime Date: 4/30/2013 Status: Claim is currently under review. Decision expected within 7 days Claim#:041715-334 Initials: M.S. Last4SSN: 2957
DATING YOUR GUILD 1952-1960
 DATING YOUR GUILD 1952-1960 YEAR APPROXIMATE LAST SERIAL NUMBER PRODUCED 1953 1000-1500 1954 1500-2200 1955 2200-3000 1956 3000-4000 1957 4000-5700 1958 5700-8300 1959 12035 1960-1969 This chart displays
DATING YOUR GUILD 1952-1960 YEAR APPROXIMATE LAST SERIAL NUMBER PRODUCED 1953 1000-1500 1954 1500-2200 1955 2200-3000 1956 3000-4000 1957 4000-5700 1958 5700-8300 1959 12035 1960-1969 This chart displays
FEDERAL BUREAU OF INVESTIGATION FOIA/PA DELETED PAGE INFORMATION SHEET
 5 Page(s) withheld entirely at this location in the file. One or more of the following El(b)(1) (b)(7)(a) (05) (b)(2) (b)(7)(b) 0)(2 ) (b)(3) (b)(7)(c) (k)(1) (b)(7)(d) (k)(2) Eg(b)(7)(E) (k)(3) (b)(7)(f)
5 Page(s) withheld entirely at this location in the file. One or more of the following El(b)(1) (b)(7)(a) (05) (b)(2) (b)(7)(b) 0)(2 ) (b)(3) (b)(7)(c) (k)(1) (b)(7)(d) (k)(2) Eg(b)(7)(E) (k)(3) (b)(7)(f)
CROSS REFERENCE. Cross Reference Index 110-122. Cast ID Number 110-111 Connector ID Number 111 Engine ID Number 112-122. 2015 Ford Motor Company 109
 CROSS REFERENCE Cross Reference Index 110-122 Cast ID Number 110-111 Connector ID Number 111 112-122 2015 Ford Motor Company 109 CROSS REFERENCE Cast ID Number Cast ID Ford Service # MC Part # Part Type
CROSS REFERENCE Cross Reference Index 110-122 Cast ID Number 110-111 Connector ID Number 111 112-122 2015 Ford Motor Company 109 CROSS REFERENCE Cast ID Number Cast ID Ford Service # MC Part # Part Type
ISSN 0975-413X CODEN (USA): PCHHAX. The study of dissolution kinetics of drugs with riboxinum (inosine)
 Available online at www.derpharmachemica.com ISSN 0975-413X CODEN (USA): PCHHAX Der Pharma Chemica, 2016, 8(1):412-416 (http://derpharmachemica.com/archive.html) The study of dissolution kinetics of drugs
Available online at www.derpharmachemica.com ISSN 0975-413X CODEN (USA): PCHHAX Der Pharma Chemica, 2016, 8(1):412-416 (http://derpharmachemica.com/archive.html) The study of dissolution kinetics of drugs
Collinearity and concurrence
 Collinearity and concurrence Po-Shen Loh 23 June 2008 1 Warm-up 1. Let I be the incenter of ABC. Let A be the midpoint of the arc BC of the circumcircle of ABC which does not contain A. Prove that the
Collinearity and concurrence Po-Shen Loh 23 June 2008 1 Warm-up 1. Let I be the incenter of ABC. Let A be the midpoint of the arc BC of the circumcircle of ABC which does not contain A. Prove that the
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B. KITCHENS
 December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
United States Naval Academy Electrical and Computer Engineering Department. EC262 Exam 1
 United States Naval Academy Electrical and Computer Engineering Department EC262 Exam 29 September 2. Do a page check now. You should have pages (cover & questions). 2. Read all problems in their entirety.
United States Naval Academy Electrical and Computer Engineering Department EC262 Exam 29 September 2. Do a page check now. You should have pages (cover & questions). 2. Read all problems in their entirety.
Mathematics (Project Maths Phase 3)
 2014. M328 Coimisiún na Scrúduithe Stáit State Examinations Commission Leaving Certificate Examination 2014 Mathematics (Project Maths Phase 3) Paper 2 Ordinary Level Monday 9 June Morning 9:30 12:00 300
2014. M328 Coimisiún na Scrúduithe Stáit State Examinations Commission Leaving Certificate Examination 2014 Mathematics (Project Maths Phase 3) Paper 2 Ordinary Level Monday 9 June Morning 9:30 12:00 300
QUADRILATERALS CHAPTER 8. (A) Main Concepts and Results
 CHAPTER 8 QUADRILATERALS (A) Main Concepts and Results Sides, Angles and diagonals of a quadrilateral; Different types of quadrilaterals: Trapezium, parallelogram, rectangle, rhombus and square. Sum of
CHAPTER 8 QUADRILATERALS (A) Main Concepts and Results Sides, Angles and diagonals of a quadrilateral; Different types of quadrilaterals: Trapezium, parallelogram, rectangle, rhombus and square. Sum of
www.pioneermathematics.com
 Problems and Solutions: INMO-2012 1. Let ABCD be a quadrilateral inscribed in a circle. Suppose AB = 2+ 2 and AB subtends 135 at the centre of the circle. Find the maximum possible area of ABCD. Solution:
Problems and Solutions: INMO-2012 1. Let ABCD be a quadrilateral inscribed in a circle. Suppose AB = 2+ 2 and AB subtends 135 at the centre of the circle. Find the maximum possible area of ABCD. Solution:
AA Literature Order Form June 2014
 GENERAL SERVICE OFFICE OF ALCOHOLICS ANONYMOUS Unit 2, Block C, Santry Business Park, Swords Road, Dublin 9. Tel: 01-8420700 / Fax: 01-8420703 Email: gso@alcoholicsanonymous.ie Website: www.alcoholicsanonymous.ie
GENERAL SERVICE OFFICE OF ALCOHOLICS ANONYMOUS Unit 2, Block C, Santry Business Park, Swords Road, Dublin 9. Tel: 01-8420700 / Fax: 01-8420703 Email: gso@alcoholicsanonymous.ie Website: www.alcoholicsanonymous.ie
Service Instruction. 1.0 SUBJECT: ECi Accessory Cases for Lycoming 4-Cylinder engines with single magneto configurations and TITAN 361 Engines
 Title: Service Instruction ECi Accessory Cases Installed on Engines S.I. No.: 03-1 Page: 1 of 7 Issued: 2/28/2003 Revision: 2 (4/13/2009) Technical Portions are FAA DER Approved. 1.0 SUBJECT: ECi Accessory
Title: Service Instruction ECi Accessory Cases Installed on Engines S.I. No.: 03-1 Page: 1 of 7 Issued: 2/28/2003 Revision: 2 (4/13/2009) Technical Portions are FAA DER Approved. 1.0 SUBJECT: ECi Accessory
Most popular response to
 Class #33 Most popular response to What did the students want to prove? The angle bisectors of a square meet at a point. A square is a convex quadrilateral in which all sides are congruent and all angles
Class #33 Most popular response to What did the students want to prove? The angle bisectors of a square meet at a point. A square is a convex quadrilateral in which all sides are congruent and all angles
CIRCLE THEOREMS. Edexcel GCSE Mathematics (Linear) 1MA0
 Edexcel GCSE Mathematics (Linear) 1MA0 CIRCLE THEOREMS Materials required for examination Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser. Tracing paper may
Edexcel GCSE Mathematics (Linear) 1MA0 CIRCLE THEOREMS Materials required for examination Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser. Tracing paper may
Montgomery GI Bill Selected Reserve (MGIB-SR) Command/Servicing Personnel Office Review
 Overview Montgomery GI Bill Selected Reserve (MGIB-SR) Command/Servicing Personnel Office Review Introduction This transaction is used to record a Reserve member s Montgomery GI Bill-SR (MGIB-SR) eligibility
Overview Montgomery GI Bill Selected Reserve (MGIB-SR) Command/Servicing Personnel Office Review Introduction This transaction is used to record a Reserve member s Montgomery GI Bill-SR (MGIB-SR) eligibility
a.) Write the line 2x - 4y = 9 into slope intercept form b.) Find the slope of the line parallel to part a
 Bellwork a.) Write the line 2x - 4y = 9 into slope intercept form b.) Find the slope of the line parallel to part a c.) Find the slope of the line perpendicular to part b or a May 8 7:30 AM 1 Day 1 I.
Bellwork a.) Write the line 2x - 4y = 9 into slope intercept form b.) Find the slope of the line parallel to part a c.) Find the slope of the line perpendicular to part b or a May 8 7:30 AM 1 Day 1 I.
South Texas Educational Technologies, Inc. TEL (956)969-3092 FAX (956)969-8614 Tomorrow s Education Today... 519 S. TEXAS BLVD WESLACO, TX 78596
 South Texas Educational Technologies, Inc. TEL (956)969-3092 FAX (956)969-8614 Tomorrow s Education Today... 519 S. TEXAS BLVD WESLACO, TX 78596 The following documents are required for employment consideration.
South Texas Educational Technologies, Inc. TEL (956)969-3092 FAX (956)969-8614 Tomorrow s Education Today... 519 S. TEXAS BLVD WESLACO, TX 78596 The following documents are required for employment consideration.
Geometry First Semester Final Exam Review
 Name: Class: Date: ID: A Geometry First Semester Final Exam Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find m 1 in the figure below. PQ parallel.
Name: Class: Date: ID: A Geometry First Semester Final Exam Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find m 1 in the figure below. PQ parallel.
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Tuesday, August 13, 2013 8:30 to 11:30 a.m., only.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Tuesday, August 13, 2013 8:30 to 11:30 a.m., only Student Name: School Name: The possession or use of any communications
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Tuesday, August 13, 2013 8:30 to 11:30 a.m., only Student Name: School Name: The possession or use of any communications
5.1 Midsegment Theorem and Coordinate Proof
 5.1 Midsegment Theorem and Coordinate Proof Obj.: Use properties of midsegments and write coordinate proofs. Key Vocabulary Midsegment of a triangle - A midsegment of a triangle is a segment that connects
5.1 Midsegment Theorem and Coordinate Proof Obj.: Use properties of midsegments and write coordinate proofs. Key Vocabulary Midsegment of a triangle - A midsegment of a triangle is a segment that connects
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, June 20, 2012 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, June 20, 2012 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
THE INFLUENCE OF POLITICAL ADVERTISING ON STUDENTS PREFERENCES AND THEIR POLITICAL CHOICE
 UDK 159.94 Garkavets S.A., Zhadan O.А., Kushnarenko V. I. THE INFLUENCE OF POLITICAL ADVERTISING ON STUDENTS PREFERENCES AND THEIR POLITICAL CHOICE The article considers the features of influence political
UDK 159.94 Garkavets S.A., Zhadan O.А., Kushnarenko V. I. THE INFLUENCE OF POLITICAL ADVERTISING ON STUDENTS PREFERENCES AND THEIR POLITICAL CHOICE The article considers the features of influence political
NOTICE TO MEMBERS No. 2005 047 May 10, 2005
 NOTICE TO MEMBERS No. 2005 047 May 10, 2005 SYMBOL CONVERSION LONG-TERM EQUITY OPTIONS EXPIRING IN JANUARY Bourse de Montréal Inc. (the Bourse) and Canadian Derivatives Clearing Corporation (CDCC) hereby
NOTICE TO MEMBERS No. 2005 047 May 10, 2005 SYMBOL CONVERSION LONG-TERM EQUITY OPTIONS EXPIRING IN JANUARY Bourse de Montréal Inc. (the Bourse) and Canadian Derivatives Clearing Corporation (CDCC) hereby
Section IV.21. The Field of Quotients of an Integral Domain
 IV.21 Field of Quotients 1 Section IV.21. The Field of Quotients of an Integral Domain Note. This section is a homage to the rational numbers! Just as we can start with the integers Z and then build the
IV.21 Field of Quotients 1 Section IV.21. The Field of Quotients of an Integral Domain Note. This section is a homage to the rational numbers! Just as we can start with the integers Z and then build the
Equation of a Line. Chapter H2. The Gradient of a Line. m AB = Exercise H2 1
 Chapter H2 Equation of a Line The Gradient of a Line The gradient of a line is simpl a measure of how steep the line is. It is defined as follows :- gradient = vertical horizontal horizontal A B vertical
Chapter H2 Equation of a Line The Gradient of a Line The gradient of a line is simpl a measure of how steep the line is. It is defined as follows :- gradient = vertical horizontal horizontal A B vertical
Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING MANAGEMENT FOR PROVISION PROCESS
 444 JOURNAL Vol. 10 ( 4). December 2011 P u b l i c a t i o n o f T e r n o p i l N a t i o n a l E c o n o m i c U n i v e r s i t y Microeconomics Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING
444 JOURNAL Vol. 10 ( 4). December 2011 P u b l i c a t i o n o f T e r n o p i l N a t i o n a l E c o n o m i c U n i v e r s i t y Microeconomics Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Theory behind Normalization & DB Design. Satisfiability: Does an FD hold? Lecture 12
 Theory behind Normalization & DB Design Lecture 12 Satisfiability: Does an FD hold? Satisfiability of FDs Given: FD X Y and relation R Output: Does R satisfy X Y? Algorithm: a.sort R on X b.do all the
Theory behind Normalization & DB Design Lecture 12 Satisfiability: Does an FD hold? Satisfiability of FDs Given: FD X Y and relation R Output: Does R satisfy X Y? Algorithm: a.sort R on X b.do all the
CHAPTER 8 QUADRILATERALS. 8.1 Introduction
 CHAPTER 8 QUADRILATERALS 8.1 Introduction You have studied many properties of a triangle in Chapters 6 and 7 and you know that on joining three non-collinear points in pairs, the figure so obtained is
CHAPTER 8 QUADRILATERALS 8.1 Introduction You have studied many properties of a triangle in Chapters 6 and 7 and you know that on joining three non-collinear points in pairs, the figure so obtained is
"HIGHER EDUCATION VALUES AND OPINIONS SURVEY" ADVANCED PLACEMENT TEACHERS and GUIDANCE COUNSELORS May-June 1994
 "HIGHER EDUCATION VALUES AND OPINIONS SURVEY" ADVANCED PLACEMENT TEACHERS and GUIDANCE COUNSELORS May-June 1994 VARIABLE SURVEY ANSWER NAME QUESTION CATEGORIES Facsimile the original mail questionnaire
"HIGHER EDUCATION VALUES AND OPINIONS SURVEY" ADVANCED PLACEMENT TEACHERS and GUIDANCE COUNSELORS May-June 1994 VARIABLE SURVEY ANSWER NAME QUESTION CATEGORIES Facsimile the original mail questionnaire
www.sakshieducation.com
 LENGTH OF THE PERPENDICULAR FROM A POINT TO A STRAIGHT LINE AND DISTANCE BETWEEN TWO PAPALLEL LINES THEOREM The perpendicular distance from a point P(x 1, y 1 ) to the line ax + by + c 0 is ax1+ by1+ c
LENGTH OF THE PERPENDICULAR FROM A POINT TO A STRAIGHT LINE AND DISTANCE BETWEEN TWO PAPALLEL LINES THEOREM The perpendicular distance from a point P(x 1, y 1 ) to the line ax + by + c 0 is ax1+ by1+ c
Chapter 7. Matrices. Definition. An m n matrix is an array of numbers set out in m rows and n columns. Examples. ( 1 1 5 2 0 6
 Chapter 7 Matrices Definition An m n matrix is an array of numbers set out in m rows and n columns Examples (i ( 1 1 5 2 0 6 has 2 rows and 3 columns and so it is a 2 3 matrix (ii 1 0 7 1 2 3 3 1 is a
Chapter 7 Matrices Definition An m n matrix is an array of numbers set out in m rows and n columns Examples (i ( 1 1 5 2 0 6 has 2 rows and 3 columns and so it is a 2 3 matrix (ii 1 0 7 1 2 3 3 1 is a
Quadrilaterals. Definition
 Quadrilaterals Definition A quadrilateral is a four-sided closed figure in a plane that meets the following conditions: Each side has its endpoints in common with an endpoint of two adjacent sides. Consecutive
Quadrilaterals Definition A quadrilateral is a four-sided closed figure in a plane that meets the following conditions: Each side has its endpoints in common with an endpoint of two adjacent sides. Consecutive
Baltic Way 1995. Västerås (Sweden), November 12, 1995. Problems and solutions
 Baltic Way 995 Västerås (Sweden), November, 995 Problems and solutions. Find all triples (x, y, z) of positive integers satisfying the system of equations { x = (y + z) x 6 = y 6 + z 6 + 3(y + z ). Solution.
Baltic Way 995 Västerås (Sweden), November, 995 Problems and solutions. Find all triples (x, y, z) of positive integers satisfying the system of equations { x = (y + z) x 6 = y 6 + z 6 + 3(y + z ). Solution.
2 : two cube. 5 : five cube. 10 : ten cube.
 Math 105 TOPICS IN MATHEMATICS REVIEW OF LECTURES VI Instructor: Line #: 52920 Yasuyuki Kachi 6 Cubes February 2 Mon, 2015 We can similarly define the notion of cubes/cubing Like we did last time, 3 2
Math 105 TOPICS IN MATHEMATICS REVIEW OF LECTURES VI Instructor: Line #: 52920 Yasuyuki Kachi 6 Cubes February 2 Mon, 2015 We can similarly define the notion of cubes/cubing Like we did last time, 3 2
Data Mining Apriori Algorithm
 10 Data Mining Apriori Algorithm Apriori principle Frequent itemsets generation Association rules generation Section 6 of course book TNM033: Introduction to Data Mining 1 Association Rule Mining (ARM)
10 Data Mining Apriori Algorithm Apriori principle Frequent itemsets generation Association rules generation Section 6 of course book TNM033: Introduction to Data Mining 1 Association Rule Mining (ARM)
Section 5.3. Section 5.3. u m ] l jj. = l jj u j + + l mj u m. v j = [ u 1 u j. l mj
![Section 5.3. Section 5.3. u m ] l jj. = l jj u j + + l mj u m. v j = [ u 1 u j. l mj Section 5.3. Section 5.3. u m ] l jj. = l jj u j + + l mj u m. v j = [ u 1 u j. l mj](/thumbs/31/14930763.jpg) Section 5. l j v j = [ u u j u m ] l jj = l jj u j + + l mj u m. l mj Section 5. 5.. Not orthogonal, the column vectors fail to be perpendicular to each other. 5..2 his matrix is orthogonal. Check that
Section 5. l j v j = [ u u j u m ] l jj = l jj u j + + l mj u m. l mj Section 5. 5.. Not orthogonal, the column vectors fail to be perpendicular to each other. 5..2 his matrix is orthogonal. Check that
Unit 10 Geometry Circles. NAME Period
 Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
Geo, Chap 4 Practice Test, EV Ver 1
 Class: Date: Geo, Chap 4 Practice Test, EV Ver 1 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. (4-3) In each pair of triangles, parts are congruent as
Class: Date: Geo, Chap 4 Practice Test, EV Ver 1 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. (4-3) In each pair of triangles, parts are congruent as
Finding the Measure of Segments Examples
 Finding the Measure of Segments Examples 1. In geometry, the distance between two points is used to define the measure of a segment. Segments can be defined by using the idea of betweenness. In the figure
Finding the Measure of Segments Examples 1. In geometry, the distance between two points is used to define the measure of a segment. Segments can be defined by using the idea of betweenness. In the figure
CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES. Karen Gevorgyan 1
 CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES Karen Gevorgyan 1 For decades, international law and public law aspects of the concept of sovereignty were in the center of attention of the representatives
CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES Karen Gevorgyan 1 For decades, international law and public law aspects of the concept of sovereignty were in the center of attention of the representatives
HOW TO USE MINITAB: DESIGN OF EXPERIMENTS. Noelle M. Richard 08/27/14
 HOW TO USE MINITAB: DESIGN OF EXPERIMENTS 1 Noelle M. Richard 08/27/14 CONTENTS 1. Terminology 2. Factorial Designs When to Use? (preliminary experiments) Full Factorial Design General Full Factorial Design
HOW TO USE MINITAB: DESIGN OF EXPERIMENTS 1 Noelle M. Richard 08/27/14 CONTENTS 1. Terminology 2. Factorial Designs When to Use? (preliminary experiments) Full Factorial Design General Full Factorial Design
5 VECTOR GEOMETRY. 5.0 Introduction. Objectives. Activity 1
 5 VECTOR GEOMETRY Chapter 5 Vector Geometry Objectives After studying this chapter you should be able to find and use the vector equation of a straight line; be able to find the equation of a plane in
5 VECTOR GEOMETRY Chapter 5 Vector Geometry Objectives After studying this chapter you should be able to find and use the vector equation of a straight line; be able to find the equation of a plane in

