Ngoc-Minh DANG CONTRÔLE STOCHASTIQUE APPLIQUÉ À LA FINANCE
|
|
|
- Hollie Manning
- 8 years ago
- Views:
Transcription
1 UNIVERSITÉ PARIS DAUPHINE - PARIS 9 U.F.R. DE MATHÉMATIQUES DE LA DÉCISION N o attribué par la bibliothèque THÈSE pour obtenir le grade de DOCTEUR ÈS-SCIENCES SPÉCIALITÉ MATHÉMATIQUES APPLIQUÉES Ngoc-Minh DANG 2011 sous le titre CONTRÔLE STOCHASTIQUE APPLIQUÉ À LA FINANCE Directeur de Thèse M. Bruno BOUCHARD JURY M. Frédéric ABERGEL, École Centrale Paris M. Bruno BOUCHARD, Université Paris-Dauphine M. Jim GATHERAL, Baruch College M. Charles-Albert LEHALLE, Crédit Agricole Cheuvreux M. Gilles PAGÈS, Université Paris VI M. Mathieu ROSENBAUM, École Polytechnique M. Nizar TOUZI, École Polytechnique
2 ii
3 A mes parents
4 Remerciements Je souhaite exprimer ma plus profonde gratitude à Bruno Bouchard pour son encadrement scientifique, sa confiance et son soutien. Le temps et la disponibilité qu il m a réservés étaient indispensables pour finir cette thèse. Mes plus vifs remerciements vont aussi à l entreprise Crédit Agricole Cheuvreux qui m a ouvert ses portes, et plus particulièrement à Charles-Albert Lehalle qui m a encadré et accueilli au sens de son équipe. J ai vraiment apprécié ses conseils, son ouverture et sa patience. Je remercie très sincèrement Nizar Touzi et Frédéric Abergel d avoir accepté de rapporter ce manuscrit. Leur remarques pertinentes et leur intérêt pour mon travail me font l honneur. Les travaux de Jim Gatheral sont à la base de la première partie de ce travail. Je lui suis particulièrement reconnaissant d avoir accepté de faire partie de mon jury. Je tiens à remercier chaleureusement Gilles Pagès qui m a permit de faire mes premiers pas d étude de mathématiques financières dans le cadre du DEA de Paris VI. Sa présence dans mon jury est très symbolique pour moi. Les discussions avec Mathieu Rosenbaum étaient très intéressantes pour moi. Je suis très heureux qu il accepte d être un membre du jury. J adresse mes plus sincères remerciements à mes amis de chez Crédit Agricole Cheuvreux. Merci donc à Julien Razamafinana, Romain Burgot, Dana Croizé, Nicolas Joseph, Silviu Vlasceanu, Vincent Leclerc, Benoit Carre. Je remercie également mes amis Romuald Elie, Jean-François Chassagneux, Moreau Ludovic, Adrien Nguyen-Huu et Thanh-Nam Vu pour les bons moments que l on a eu pendant ces trois années.
5 Je souhaite en fin remercier mes grand-parents, mes parents et toute ma famille qui m ont toujours soutenu. Je n oublierai jamais les difficultés qu ils ont surmontées pour m élever, pour me permettre de poursuivre mes études jusqu aujourd hui. Un grand merci de tout mon cœur à tous ceux qui m ont supporté pendant les moments difficiles.
6 Résumé Cette thèse traite des problèmes de trading optimal avec une approche de contrôle stochastique et se compose de quatre parties. On commence, dans la première partie, par une étude de l impact du volume sur le prix. Pour cela, on introduit un modèle structurel en temps discret dont le changement de prix est dû aux impacts de tous les volumes, affaiblis par un facteur de decay. En utilisant une version continue du modèle précédent, on obtient une condition nécessaire sur les stratégies minimisant une fonctionnelle de type moyenne-variance. Cette équation intégrale de Fredholm du premier type est résolue numériquement et on obtient des stratégies optimales. Ces travaux généralisent le modèle d Almgren-Chriss très utilisé en pratique. Dans la seconde partie, on propose un modèle générique permettant d optimiser l utilisation d algorithmes de trading. En nous basant sur des techniques de contrôle impulsionnel, on modélise l exécution d un large ordre par une séquence de variables (τ i, δ i, E i ) i de contrôle, définies de telle sort que la i-ième slice est exécutée dans [τ i, τ i + δ i ] avec le paramètre E i envoyé aux robots de trading. On caractérise la fonction valeur comme solution de viscosité d un système d EDP. On fournit un schéma numérique et on prouve dont la convergence. L approche est illustrée par un exemple numérique correspondant à un cas réel, calibré sur données financières. On s intéresse ensuite à la notion d évaluation d option sur liquidation de book dans un modèle à facteur d impact, pour lequel les notions habituelles d évaluation par mesure risque neutre ne font plus sens. On commence par traiter un cadre abstrait qui généralise les travaux de Bouchard-Elie-Touzi (2008), puis on l applique à l évaluation de garanties de type VWAP. On établit dans la dernière partie un résultat d équivalence entre problèmes de cibles stochastiques et problèmes de contrôle optimal sous forme standard. On montre comment retrouver l équation d Hamilton-Jacobi-Bellman à partir des équations obtenues par l approche de cibles stochastiques. Cette partie est déconnectée des autres mais est intéressante car elle apporte un nouvel éclairage sur le contrôle optimal.
7 Abstract This PhD thesis considers the optimal trading problem from the stochastic control approach and consists of four parts. In the first part, we begin with the study of the impacts generated by volumes on the price process. To do so, we introduce a structural model in which price movements are due to not only the last trade s volume but also to those of earlier trades, weakened by a decay factor. Considering a similar continuous version, we provide a condition ensuring the optimality of a strategy for the minimization of the execution cost in a mean-variance framework. We provide a numerical method to solve this condition, which is known as the Fredholm equation of the first kind. This work generalizes the previous model proposed by Almgren-Chriss and used extensively in trading. In the second part, we propose a general model to optimize the way trading algorithms are used. Using an impulse control approach we model the execution of a large order by a sequence of triple (τ i, δ i, E i ) i, which is defined so that the i-th slice is executed in [τ i, τ i + δ i ] with parameter E i sent to the trading robots. We characterize the value function as a viscosity solution of a system of PDE. We provide a numerical scheme and prove its convergence. Numerical illustrations are given for a real case, which has been calibrated on financial data. We deal with the problem of pricing an option on the book liquidation in presence of impact where the classical pricing by neutral risk measure fails. We begin with an abstract model generalized from the work of Bouchard- Eile-Touzi (2008), and then apply to compute the price of a VWAP guaranteed contract. We establish in the last part an equivalence result between stochastic target problems and standard optimal control. We derive the classical Hamilton- Jacobi-Bellman from the PDE obtained in the stochastic target framework. This part is disconnected from the trading problem discussed above but is of interest in the optimal control literature.
8 vi
9 Contents Introduction xi 1 Introduction xi 2 Première partie : modèle d impact et trading optimal xiii 3 Deuxième partie : modèle général pour modéliser le contrôle d algorithmes de trading xvii 4 Troisième partie : modèle de cible stochastique généralisée et applications au trading xix 5 Quatrième partie : un résultat d équivalence xxi 6 Quelques repères bibliographiques pour les applications du contrôle optimal au trading xxii I Market impact and optimal trading 1 1 Post-trade market impact model 5 1 Introduction A simple typology of impacts Model with decayed price impact Model description Model calibration Practical applications Post-impact estimation Explanatory capability of post-trade market impact estimation. 11 vii
10 CONTENTS 2 Optimal strategies with transient impact 17 1 Introduction Problem description Special cases Instantaneous impact Permanent impact Optimal condition with transient impact Calculus of variations for integral depending on convolution products Optimal condition Numerical results Discretization method Optimal strategies Proof of Lemma I II Optimal trading with general impulse control approach 27 3 General impulse control approach 31 1 Introduction Problem formulation Control policies Output of the trading algorithm Gain function Examples Viscosity characterization of the value function Proof of the viscosity characterization Dynamic programming Viscosity properties Supersolution property Subsolution property A comparison result viii
11 CONTENTS 4 Numerical results 63 1 Numerical approximation Space discretization Finite difference approximation Approximation scheme of (II.19) and convergence Numerical illustration - Theoretical case Numerical illustrations - Real case III Optimal trading with generalized stochastic target approach 75 5 Generalized stochastic target problems: abstract model 79 1 Introduction Abstract formulation and dynamic programming The general singular stochastic target problem with state constraints Examples of application Dynamic programming PDE characterization in the abstract model Formal derivation Interior of the domain Space boundary Terminal condition Main results Proof of the viscosity property in the abstract model Viscosity solution property on [0, T ) Supersolution property on [0, T ) Subsolution property on [0, T ) Viscosity solution property at T Application in optimal book liquidation Introduction Model description PDE characterization ix
12 CONTENTS 3.1 Value function and problem reduction Additional assumptions and a priori estimates Main results Comparison principle and uniqueness IV Optimal control versus stochastic target problems: an equivalence result Introduction The equivalence result Example References 133 x
13 Introduction 1 Introduction Ce travail a pour objectif d apporter des éléments de réponse à des questions de trading optimal sous l angle du contrôle optimal. Plus concrètement, on considère le cas d un broker qui doit exécuter un ordre d achat ou de vente d un client, souvent de taille impotante, pendant une durée de temps fixé à l avance par le client. Dans ce contexte, on répond aux questions suivantes : Comment l exécution d un tel ordre influence sur le processus de formation de prix? On considère un modèle où les changements de prix sont dûs aux impacts générés par les transactions, affaiblis par un factor de decay. Comment l impact influence le profile d exécution optimal? On se place dans un modèle où l impact est soit temporaire, soit permanent ou transient, et on dérive la courbe de trading optimale minimisant le coût d exécution au sens moyennevariance. Comment la nature discrète du problème d exécution peut-elle être prise en compte? On introduit un cadre général utilisant une approche par contrôle impulsionnel, qui consiste à contrôler des algorithmes de trading. Comment évaluer et gérer un actif contingent dans les modèles à facteur d impact? On propose un cadre de travail général de type cible stochastique à contrôle à variation totale bornée. Un exemple d application à l évaluation des contrats de type VWAP 1 -guaranteed est détaillée. 1 Volume Weighted Average Price xi
14 INTRODUCTION Dans la première partie, on traite les deux premières questions. Pour cela, on s inspire du modèle proposé par Bouchaud, Gefen, Potters & Wyart [21] (version discrète) et par Gatheral [33] (version continue). Plus précisément, on propose une forme alternative de ces modèles dans un cas discret, dans laquelle l incrément de prix comporte deux composantes : la somme cumulée des impacts qui décroissent avec le temps et qui sont générés par toutes les transactions précédentes, plus un bruit. On utilise ce modèle pour mesurer l impact post-trade d une séquence de transactions. On reconsidère le modèle continu de Gatheral [33] pour lequel on donne une condition d optimalité sur les stratégies pour un critère moyenne-variance. Celle-ci prend la forme d une équation intégrale de Fredholm du premier type. La solution est obtenue grâce à un algorithme numérique. On retrouve également les solutions explicites de Gatheral, Schied & Slynko [34] lorsque le coefficient d aversion au risk est nul. La troisième question est considérée dans la deuxième partie. On utilise une approche de type contrôle impulsionnel pour modéliser un méta-algorithme de trading qui luimême passe des ordre à des sous-robots : une séquence de slices est envoyées à des robots avec différents paramètres et durées d activité imposées. Il s agit de maximizer une fonction objective qui est la somme des gains courants et finaux. On caractérise la fonction valeur comme la solution de viscosité d un système d EDP et on donne également un schéma numérique pour le résoudre. Grâce à un théorème de comparaison on montre la convergence de ce schéma. On présente une application numérique sur un cas réel. On s intéresse ensuite à la notion d évaluation d option sur liquidation de book dans un modèle à facteur d impact, pour lequel les notions habituelles d évaluation par mesure risque neutre ne font plus sens. On utilise l approche par cible stochastique en moments proposée par Bouchard-Elie-Touzi (2008). Ceci revient à rechercher le plus petit prix assurant que le P&L final de l opération satisfont une contrainte de risque fixée à l avance. On commence par traiter un cadre abstrait qui généralise les travaux de Bouchard-Elie-Touzi (2008), puis on l applique à l évaluation de guarantees de type VWAP. xii
15 2 Première partie : modèle d impact et trading optimal Finalement, on termine ce travail par une partie qui est déconnectée de la problématique initiale où l on montre l équivalence entre problèmes de cible stochastique et problèmes contrôle optimal sous forme standard. 2 Première partie : modèle d impact et trading optimal Dans un problème de trading on s intéresse à la façon de diviser le volume total à passer sur le marché en plusieurs morceaux, et d exécuter ces derniers au cours du temps. Suivant la nature du modèle considéré pour le prix et le volume, on peut distinguer deux approches : l une est discrète, l autre est continue. Les premiers modèles sont de nature discrète. Ils ont été proposés tout d abord par Bertsimas & Lo [11], et puis par Almgren & Chriss [7]. Cette approche consiste à diviser l horizon de trading [0, T ], où T est un temps fixé, en N intervalles de longueur τ = T/N. Une courbe de trading est une séquence {x n } N n=0 où x n est le nombre d actions à vendre ou acheter à la date t n = nτ. Le prix de l action suit un modèle de mouvement Brownien arithmétique, auquel se rajoute un impact permanent : S n = S n 1 + σ τ + impact permanent. Dans la formule précédente l impact est permanent car il influence directement le prix. Le prix final obtenu par le broker est le prix courant auquel s ajoute un impact temporaire qui lui est propre S n = S n 1 + impact temporaire. Les deux impacts sont des fonctions du volume écoulé sur cet intervalle (x n x n 1 ) et de la duration τ. Il existe un autre type de formulation, toujour de nature discrète, où la dynamique du prix obtenue est dérivée à partir d un modèle de carnet d ordres. Premièrement proposée par Obizhaeva & Wang [46] et puis reprise dans Alfonsi & Schied [1], Alfonsi et al. [2], cette formulation consiste à modéliser les dynamiques des ordres d achat ou de vente limités. Le carnet d ordres est déformé quand un ordre est exécuté, puis revient à son point d équilibre après une certaine période de temps. xiii
16 INTRODUCTION L approche continue consiste à modéliser le prix de l action S et le volume restant x par des processus continus. Dans cette version, l impact est une fonction de la vitesse à laquelle on envoie des ordres au marché. Le modèle de Gatheral [33] est suffisamment riche pour discuter l influence de l impact sur le trading optimal. Il postule la dynamique suivante pour le prix d une action S S x (t) = S 0 + t 0 f(v x (s))g(t s)ds + t 0 σ(s)dw s, (.1) où la fonction f désigne l impact généré par un algorithme de trading dont la vitesse de trading est v x (s) = dx/ds (.2) et affaibli par un facteur de decay G, x étant la quantité restante à exécuter, x(0) = X, x(t ) = 0. Au travers des derniers paragraphes, on peut se poser les questions suivantes : Pourquoi doit-on diviser un ordre en plusieurs morceaux? Que signifie la notion d impact apparaissant dans la dynamique du prix? D où vient le facteur de decay G? Les deux premières questions partagent une même réponse (parmi plusieurs réponses possibles) : la liquidité offerte dans chaque intervalle de temps est limitée. Souvent, les quantités disponibles à chaque niveau de prix dans le carnet d ordres sont de taille négligeable devant la quantité totale que l on veut vendre ou acheter. Par conséquent, le trader doit acheter plus chère où vendre moins chère s il veut réaliser son volume dans un court délai. Ce dernier effet est appelé impact du volume sur le prix et peut être interprété comme le prime de liquidité qu un trader doit payer pour attirer la liquidité. Pour un ordre de taille faible (de l ordre d une dizaine d ATS 1 ) ce coût est négligeable, mais pour un ordre institutionnel (de l ordre d une dizaine % d ADV 2 ), il est considérable car influence directement et essentiellement le profit d un broker. 1 Average Trade Size 2 Average Daily Volume xiv
17 2 Première partie : modèle d impact et trading optimal Figure.1: Un carnet d ordres La raison donnée ci-dessus est celle d un broker. Il existe un autre type de raisonnement sur la notion impact donné par une approche empirique, par exemple Bouchaud et ses coauteurs [20, 21]. Il est évident que, qualitativement, conditionnellement à un ordre d achat (ou de vente), le cours d un actif a tendance à monter (ou à diminuer), i.e. un ordre a une influence sur le prix. En analysant des bases de données gigantesque des transactions enregistrées au cours des années, la fonction d impact est estimée quantitativement et on trouve typiquement une fonction puissance liant l impact généré et le volume traité : f(v) v ψ. De plus, en se basant sur l absence de manipulation de prix, on peut montrer que les impacts ne doivent pas être permanents. Ils sont de fait transients, i.e. ils diminuent au cours du temps selon un facteur de decay G, qui est aussi typiquement une fonction puissance. Il en résulte de ces observations le modèle suivant pour le prix n S n = S + f(v l )G(l l 0 ), l= i.e. S n = S n 1 + f(v n )G(n l 0 ), où l indice n désigne la n-ième transaction. On se place dans un cadre assez similaire sauf que l on considère maintenant que les xv
18 INTRODUCTION transactions passées peuvent avoir un impact sur toutes les variations futures du prix. où les (ξ n ) n sont i.i.d. additionnel. S n+1 = S n + n f(v l )G(n l) + ξ n+1, l=1 de loi N (0, σ 2 ) correspondent à un bruit de microstructure On s intéresse en effet à la quantification des impacts d une séquence de transactions par rapport à une date donnée. Afin de simplifier la discussion on considère uniquement le cas où f(v) v, G(l) l 1. On estime ce modèle et on définit une mesure de post-trade de l impact associé à une séquence de transactions. On obtient les résultats suivants sur les données. Résultat 1. Utilisant cette mesure on observe sur les données réelles que : L impact d une séquence de transactions depend des conditions d exécution (par exemple, le taux de participation) et des contextes du marché (par exemple la symétrique du volume disponible au bid/à l ask). L exécution d un ordre d achat dans une journée de trend positif engendre un impact plus important que celui obtenu dans une journée où il n y a pas de trend. Dans un second temps, on reprend le modèle de Gatheral [33] décrit précédemment et on considère le problème de minimization du coût d exécution dans un cadre moyennevariance. Etant donnée un coefficient d aversion au risque λ 0, on cherche à résoudre où C x est défini par C x := min x( ) (J λ[x] := E [C x ] + λvar [C x ]), T 0 S x (t)v x (t)dt X S 0, voir (.1) et (.2). Notre deuxième résultat donne une condition d optimalité caractérisant la stratégie optimale x. Résultat 2. Soient f C 1 (R), G L 1 ([0, T ]), il existe une constante c telle que x résoud l équation intégrale suivante : t 0 f(x (s))g(t s)ds + 2λ t 0 T σ 2 (s)x(s)ds + f (x (t)) x (s)g(s t)ds = c pour tout t [0, T ]. t xvi
19 3 Deuxième partie : modèle général pour modéliser le contrôle d algorithmes de trading Quelques résultats déjà existant dans la littérature sont retrouvés en faisant des choix spécifiques pour f, G et λ : le modèle d Almgren [6, 7]: f(v) = ηv, G(t) = δ t (pour impact temporaire) et G 1 (pour impact permanent). le modèle de Gatheral [33, 34]: G : (0, ) [0, ) non-constante, non-croissante, convexe et 1 0 G(t)dt <. On propose un schéma numérique pour calculer la solution de l équation précédente, les résultats trouvés nous aident à comprendre l influence de f, G, λ et σ sur la stratégie optimale. 3 Deuxième partie : modèle général pour modéliser le contrôle d algorithmes de trading On a présenté dans la section précédente deux approches pour traiter le problème de trading optimal. Elles peuvent bien évidemment servir de benchmark à la construction d algorithms. Mais malheureusement aucune de ces approches ne correspond pas à la réalité actuelle du trading, qui consiste à envoyer de manière discrète des ordres partiels à des robots. Prenons par exemple l exécution d un ordre sur le marché par un broker. Elle consiste à définir plusieurs intervalles actifs, séparés par des intervalles dits passifs. Dans chaque intervalle actif, il choisit d exécuter une partie de l ordre initial, à la fin de cet intervalle il devient systématiquement inactif avant de redevenir de nouveau actif. Cette séquence est répétée au passage complet de l ordre global. Le choix des intervalles dépend de l état actuel de l exécution et est déterminé en temps réel. Quant à l exécution de chaque slice, le trader doit décider également des paramètres de l algorithme de trading automatique (robot) qu il utilise. En dehors des paramètres usuels comme le volume, on peut aussi choisir le type d algorithmes, la distance par rapport au meilleur prix de l ordre limité, etc... D après cette description, on voit immédiatement que l approche continue ne convient pas à la réalité. L approche discrète semble mieux adaptée mais en effet, comme celle-ci n autorise que des transactions à de dates déterministes et pré-fixées, elle est également limitée. xvii
20 INTRODUCTION Pour tenter de modéliser tous les algorithmes de trading, tout en évitant les inconvénients ci-dessus, il est nécessaire de construire un modèle de contrôle suffisamment riche. Une solution naturelle consiste à utiliser une approche de type contrôle impulsionnel. On propose le modèle suivant : un algorithme de trading est déterminé par une séquence de (τi ν, δν i, Eν i ) i où τ ν i δ ν i est la date à laquelle on envoie la i-ième slice; est la date de fin de cette slice; Ei ν est le paramètre (peut être multi-dimensionnel) avec lequel la slice est exécutée par les robots. Dans ce modèle, ν est la variable de contrôle, qui prend la valeur du paramètre E i dans l intervalle [τi ν, τ i ν + δi ν ] et ϖ est un paramètre spécial qui signifie que l algorithme est inactif. (voir la figure ci-dessous) ν Ei+1 ν [ [ δν i+1 E ν i [ [ ν t ϖ τ ν i δν i [ τ ν i + δ ν i [ τ ν i+1 t τ ν i+1 + δν i+1 temps Il s agit d un modèle de contrôle impulsionnel, mais non-classique du fait de la présence de la variable δi ν. Cette variable nous permet de séparer l algorithme père des algorithmes fils (des slices), il n est pas nécessaire de surveiller un algorithme fils d une façon continue mais uniquement à la fin de la période décidée par l optimiseur. Les sorties de l exécution sont regroupées dans un processus de type d Ito Xt,x(s) ν = x+1 s t s t b(x ν t,x(r), ν r )dr + s t a(xt,x(r), ν ν r )dw r + β(xt,x(τ ν i ν ), Ei ν, δi ν )1 t<τ ν i s. i 1 xviii
21 4 Troisième partie : modèle de cible stochastique généralisée et applications au trading Le contrôleur a pour l objectif de maximizer la fonctionnelle de gain, qui s écrit comme la somme des gains intermédiaires et d un gain final V (t, x, δ, e) := sup E [Π t,x (ν)] ν St,δ,e a où Π t,x (ν) := f(xt,x(τ ν i ν + δi ν ), Ei ν ) + g(xt,x(t ν )). i I ν t,t On peut identifier de la description précédente deux régions : une active, quand une slice est en train d être exécutée, et une passive quand aucune slice n est passée sur le marché. A la fin d une phase d activité (δ 0), on peut soit lancer une nouvelle slice, et par conséquent rester dans la zone active, ou bien on entre systématiquement dans la zone passive. La même décision doit se faire quand on est dans la zone passive. En explicitant les conditions spécifiques dans chaque cas, on obtient un résultat caractérisant la fonction valeur V dans les zones identifiées. Résultat 3. La fonction valeur V est solution viscosité d un système d EDP. Pour montrer cette caractérisation on a utilisé le nouveau principe de programmation dynamique de Bouchard & Touzi [15]. Afin de compléter cette caractérisation, on montre l unicité de V par un résultat de comparaison. Résultat 4. Un théorème de comparaison est vérifié sous certaines hypothèses. On fournit également une méthode pour discrétiser le système d EDP et on vérifie la convergence du schéma proposé. Résultat 5. La fonction V peut être approchée par Ṽn, solution numérique du système discrétisé. 4 Troisième partie : modèle de cible stochastique généralisée et applications au trading Le problème de trading consiste à vendre ou acheter une quantité d actions pendant un interval de temps fini. Il est naturel de considérer la somme algébrique cumulée des volumes associés à chaque type d ordres L v (pour les ordres de vente) et L a (pour les ordres d achat). Dans un cadre de trading agency, chaque ordre est de signe constant, i.e., pour un ordre d achat on a L a 0 = K < 0 et La T = 0, en plus, l interdiction de + xix
22 INTRODUCTION vente à découverte impose que ce processus doit être non décroissant. Dans le cas le plus général, la somme cumulée des volumes passés est la somme des deux processus : L = L a + L v. La dernière décomposition implique que L est un processus à variation totale bornée. Dans tous les problèmes de trading optimal considérés, les stratégies optimales sont obtenues en minimisant une fonctionnelle du coût d exécution. On cherche alors à déterminer la prime initiale à faire payer au client de manière à ce que cette fonctionnelle ne dépasse pas un certain niveau fixé à l avance. Une approche directe permettant de résoudre ce type de problèmes est l approche par cible stochastique en moment initiée par Bouchard, Elie & Touzi [18]. On se place dans le cadre de Bouchard, Elie & Touzi [18] auquel on ajoute un nouveau contrôle de type processus à variation totale bornée. Soit un contrôle φ = (ν, L) A, la dynamique des processus contrôlés est la suivante s X φ t,x (s) = x + µ X (X φ (r))dr + Y φ t s t,y (s) = y + µ Y (Z φ (r))dr + t s t s t σ X (X φ (r))dw r + σ Y (Z φ (r))dw r + s t s t β X (X φ (r))dl r β Y (Z φ (r))dl r. Ce type de modèle permet de tenir compte un impact linéaire du volume écoulé sur la dynamique du prix. On donne également d autres exemples d application intéressants, par exemple dans les modèles avec coûts de transactions proportionnels. Dans le cadre original de Soner & Touzi [52], les auteurs ne considèrent qu une contrainte à la date finale T. Afin de traiter une contrainte de type américain : Z φ t,x,y O(s) pour tout s [t, T ], on utilise la version introduite par Bouchard & Vu [16]. Une telle contrainte est motivée par le fait qu un broker cherche à imposer des bornes limitant la somme cumulée de volume passé L [Λ, Λ]. En se plaçant tout d abord dans un cadre abstrait, on montre le résultat suivant. Résultat 6. La fonction valeur v est solution viscosité d un système d EDP. Dans un cas plus concret, on traite le problème de valorisation d un contrat de type VWAP garantit, où un broker garantit un prix d exécution (mesuré par le VWAP 1 ) en 1 Volume Weighted Average Price xx
23 5 Quatrième partie : un résultat d équivalence fonction du marché. Par rapport au cas abstrait, on obtient en plus l unicité de v grâce au résultat suivant. Résultat 7. Sous quelques hypothèses de régularité, l EDP vérifie un théorème de comparaison. Ceci ouvre la voie à des applications numériques. 5 Quatrième partie : un résultat d équivalence Cette dernière partie porte sur un thème déjà évoqué mais reste assez déconnectée de nos problématiques de trading optimal : l approche par cible stochastique. La forme la plus basique d un problème de cible est la suivante : Soit une valeur initiale z = (x, y) d un processus contrôlé Z ν t,x,y = ( X ν t,x, Y ν t,y), déterminer l ensemble S(t) des valeurs de z telles que Ψ ( Z ν t,z(t ) ) 0 P a.s. pour un certain contrôle ν. La version relaxée de ce problème est proposée par Bouchard, Elie & Touzi [18], où la contrainte presque sûre a été remplacée par une contrainte en moment de la forme E [ Ψ ( Z ν t,z(t ) )] p. Cette relaxation permet de traiter de nombreux problèmes de mathématiques financières dont l un est présenté dans la troisième partie de ce travail. La caractérisation de la fonction valeur dans cette approche se base sur le Principe de Programmation Dynamique Géométrique, initialement proposé par Soner & Touzi [52] S(t) = { (x, y) : ν tel que Z ν t,x,y(θ) S(θ) } pour tout temps d arrêt θ prenant des valeurs dans [t, T ]. Cette formulation est a priori très différente de celle du principe de programmation dynamique pour les problèmes sous forme standard, ce qui laisse penser que problèmes de contrôle stochastique sous forme standard et problèmes cible stochastique doivent être traités séparément. On montre que, en effet, les deux approches sont équivalentes. Plus précisément, on a le résultat suivant. Résultat 8. Tout problème de contrôle optimal sous forme standard peut se représenter sous la forme d un problème de cible stochastique. On montre également comment passer des EDP associés à l un et à l autre problèmes. xxi
24 INTRODUCTION 6 Quelques repères bibliographiques pour les applications du contrôle optimal au trading Le problème de trading optimal a été considéré depuis les années 90 (Almgren & Chriss [7], Bertsimas & Lo [11]), initialement sous la forme discrète et puis continue dans Almgren [6]. L optimisation en présence d un carnet d ordres a été premièrement traité par Obizhaeva & Wang [46], suivi par Alfonsi et al. [2], Hewlett [37] et récemment par Predoiu, Shaikhet & Shreve [47]. Pour trading en présence d un risque d inventaire, voir Avellaneda & Stoikov [8] ou Guéant, Lehalle & Fernandez Tapia [35]. Laruelle, Lehalle & Pagès [42] a considéré la distribution d un ordre aux plusieurs sources de liquidité, dont des dark pools. Les modèles d impact étaient bien considérés via une approche empirique, voir e.g. Bouchaud [20] et les références citées. La viabilité d un modèle d impact était étudiée tout d abord par Huberman & Stanzl [38] et récemment par Gatheral [33], Alfonsi & Schied [1]. Les modèles non-linéaire peuvent se trouver dans Almgren [6], avec un facteur de decay dans Gatheral [33], Gatheral, Schied & Slynko [34]. Se positionnant dans le framework classique, des stratégies optimales étaient dérivées sous des conditions particulières, par exemple Almgren & Lorenz [5] (avec un a priori croyance sur le drift), Lehalle [44] (effet de retour à la moyenne). Les problèmes de cible stochastique étaient premièrement proposés par Soner & Touzi [52] et étudiés plus profond par Bouchard & Touzi [14], Touzi [56]. De nombreuses contributions ont été apportées par Bouchard [12] (processus avec sauts), Bouchard, Elie & Touzi [18] (approche de type perte contrôlée) ou Moreau [45]. xxii
25 6 Quelques repères bibliographiques pour les applications du contrôle optimal au trading Liste des articles ayant contribué à la rédaction de la thèse Optimal control of trading algorithms: a general impulse control approach, B. Bouchard, N.-M. Dang, C.-A. Lehalle, à paraître dans SIAM Journal on Financial Mathematics; Generalized stochastic target problems for pricing and partial hedging under loss constraints - Application in optimal book liquidation, B. Bouchard, N.-M. Dang, soumis à Finance and Stochastics; Optimal control versus stochastic target problems: an equivalence result, B. Bouchard, N-M. Dang, soumis à Systems and Control Letters; Rigorous post-trade market impact measurement and the price formation process, C.-A. Lehalle, N.-M. Dang, Trading, 2010(1), ; Optimal trading with transient impact model, N.-M. Dang, document de travail. xxiii
26 INTRODUCTION xxiv
27 Part I Market impact and optimal trading 1
28
29 Abstract We model the price process by a structural model n S n+1 = S n + f(v l )G(n l) + ξ n+1, l=1 with (S n, v n ) n the price and the volume of the n-th trade, f and G are the impact and the decay function, respectively. We calibrate the model in a simple case with f(v) v, G(l) l 1 and use it to quantify the post-trade impact of a trading strategy. We propose a way to measure the impact and verify on empirical data it reproduces some intuitive effects. In the second part, we consider the Gatheral model S(t) = S 0 + t 0 f(v(s))g(t s)ds + t 0 σ(s)dw (s), where W is a Brownian motion and v is the trading rate, defined by v(t) = dx/dt where x is the remaining volume, x(0) = X, x(t ) = 0. We minimize the mean-variance functional of the execution cost C = T 0 S(t)v(t)dt X S 0. We obtain an integral equation characterizing the optimal strategy x and propose a numerical scheme to compute it. Keywords: market impact, transient impact, Fredholm integral equation. Note The first chapter of this part is based on an article in Trading, 2010(1).
30 4
31 Chapter 1 Post-trade market impact model 1 Introduction Even many contributions have been made since the inception of the first model in Kyle s article [40], there is still no unique interpretation of price impact. One of fairly comprehensible definitions is the following: price impact refers to the correlation between an incomping order (to buy or to sell) and the subsequent price change, from Bouchaud [20]. Among many reasons given to explain for impact s origin, the most intuitive one is: impact is due to the limit of liquidity in maket. It is crucial to understand this notion in view of an optimization in trading problems. Actually, execution of large market order is more difficult than small ones, hence traders often must move prices to fill their orders, consequently impact should increases with order size, hence, is the most significant cost of trading (large) orders (Harris [36]). The usual measure of price impact is the expectation of the normalized price move (S t+ S t )ε t, conditioning on the volume v t = v c.g. Bouchaud [20]: R (, v) = E [(S t+ S t )ε t v t = v], where ε t is the order s sign ε t = 1 buy order 1 sell order. It is reported that the impact function is power-law dependent with respect to volume, where the power depends on the time scale = δt R ( = δt, v) v ψ(δt), 5
32 POST-TRADE MARKET IMPACT MODEL This statistical fact allows one to postulate the following structural model N 1 S T S 0 = λ ε n vn ψ, which decomposes the price process between 0 and T = Nδt as the sum of all impacts n=0 generated by aggregated trades at the frequence δt. Beside providing the empirical support, Bouchaud et al. [21] argued that, an unpredictable price changes imposes a transient nature to impacts, i.e., the previous model should takes the following form N 1 S T S 0 = λ G(N n)ε n vn ψ. n=0 (I.1) In the above model, the impact from the latest trade v n is disgested immediately in the price process, hence influents uniquely price between nδt and (n + 1)δt: (S n+1 S n ) ε n v ψ n, where for ease of notations we write S n for S nδt. In this chapter we consider a structural model in which each price move is mainly explained by not only the market impact of the last trade but also those of earlier trades weakened by a decay factor S n+1 S n = n f(v n )G(n l) + ξ n+1. l=1 (I.2) Each ξ n follows a centered normal distribution with variance σ 2. We postulate that both f and G are linear, and estimate the unknown parameter over transaction data. We make use of this model to estimate a post-trade impact of a sequence of trade, and we illustrate its dependence versus the market context. 2 A simple typology of impacts Figure I.1 comes from simple simulations; it shows three kinds of market impact: the first one is passive market impact. It typically occurs when an investor sends a steady stream of passive orders to the market (in this example, it is a sequence of buy orders 6
33 2 A simple typology of impacts Figure I.1: From top to bottom: diagrams of the market impact induced by a passive order, an aggressive order and an execution in a dark pool; solid lines are the observed price, dotted lines what it would have been. 7
34 POST-TRADE MARKET IMPACT MODEL during trades 60 to 91), which prevents the price from moving in one direction, and when the investor stops sending such orders the price slowly returns to a level that would have been obtained without his sequence. In the example, we can see how the solid line reconverges with the dotted line: we created a resistance. The second simulation is aggressive market impact : a sequence of small orders is sent to the market aggressively. After a small sustained jump and a period of decay, the price returns to the level it would have achieved sooner. And the last simulation is the impact of execution in a dark pool: a large passive order was available in a dark pool. If nobody consumes it, it will have to go to the market at least passively, or it will be slowly consumed by smart order routers pinging the dark. Without being withdrawn from the market, it would have a passive market impact inducing the dotted lines of the last chart. Following the consumption of such an order in the dark by a sell, the price formation process will show behaviour close to the solid line. The sell order, despite being in the dark, will consequently have a market impact that can be read by comparing the solid line to the dotted one. These three examples show that the market impact cannot be considered outside the whole price formation process: the quantity that is removed from a pool will certainly be missing in the future as a counterpart to other trades. A quantity that is accepted by a counterpart will be added to its inventory, possibly triggering some limits in the future that could generate an impact on the price. 3 Model with decayed price impact 3.1 Model description During a trading day where N transactions occur with quantities (v n ) n=1,...,n ; the moves in the price are mostly driven by the market impact of the quantities (v n ) n=1,...,n, plus an uncertainty level that is modelled by a Brownian motion: n 1 S n = S n 1 + ξ n + f(v k )G(n k) Each ξ n follows a centered normal distribution with variance σ 2. The two functions f and G are called the price impact function and the decay kernel, respectively. k=1 8
35 4 Practical applications In such a model, the portion of the moves in the price coming from ξ is low: the moves in the price essentially come from the impact of the trades. Sometimes buy orders are followed by sell orders that offset the former, leading to small oscillations in the price, but sometimes a majority of consecutive orders will come from buyers, leading to an increase in the price. It is worth noting that the volume sequence (v n ) n is signed, i.e., takes a positive value if it is a buy order and a negative one otherwise. Let us define the total turnover W as the sum of (unsigned) cash exchanged during the whole day. Then it is possible to show that the following variable M := 1 V 1 [W N 1 n=1 ( N n l=1 G(l)V l+n ) f(v n ) ] (I.3) is a normal distribution random variable with mean S 1 and standard deviation σ M = σ N n=2 V2 n/v 1, V n is the sum of all (unsigned) transaction volumes from the n-th transaction up to the end of the day. 3.2 Model calibration The variable M given in (I.3) is defined with a general price impact function f and a decay kernel G. In order to simplify and to focus on the main idea of this work, let us take a linear function for the impact, f(v) = ηv and suppose the impact decays linearly with time, G(l) = l 1. We shall proceed to compute the unknown coefficient η by the least-squares method in presence of known covariance. The results of the calibration on CAGR.PA are shown in Figure I.2. 4 Practical applications 4.1 Post-impact estimation Now we discuss the main application of our model, given a trading strategy, what is its impact at the end of a trading day and how much does it depend on external conditions? Let us justify these questions with a very simple example. Given a trading day where transactions take place consecutively. It is possible to localise some small period where the price is increasing. It is quite natural to argue that trades 9
36 POST-TRADE MARKET IMPACT MODEL Figure I.2: Model calibration for CAGR.PA: slopes are illustrated by the solid line (without data trimming) and the dashed line (with data trimming). The right-hand panel shows the relative error and the standard error (scaled up by factor 100) using the estimated value. 10
37 4 Practical applications occurring during the beginning of this period contribute to the overall impact differently than those occurring at the end. We use equation (I.3) to calculate strategy s own impact without noise. By trading strategy we mean a sequence of transactions, representable by a set of indexes S, subset of {1,..., N} indicating that the trades S are the ones we focus on, the post-impact of this strategy is defined by I(S) := N 1 n=1 ( N n l=1 G(l) V l+n V 1 ) f(v n )1 n S (I.4) Thanks to this formula, it is now possible to estimate the market impact of a subset of trades during a post-trade analysis. The successive steps proposed to estimate market impact at post-trade are: Calibrate the parameter η of the impact function and θ of the decay kernel using all trades of the day. Compute I(S) given subset S of trades of interest that is thus a denoised estimate of their impact. It follows immediately from (I.4) that: The post-impact is a linear function with respect to the strategy: for two disjuncted strategies (S 1, S 2 ), then the total impact is thus the sum of the two impacts. Thanks to this property the computation for a pool of strategies can be handled very fast, which is essential during the post-trade analysis. In the case of a linear impact, it is not necessary to know the value of η to compare impacts. 4.2 Explanatory capability of post-trade market impact estimation It is natural to assume that execution conditions (for example, a strategy s participation rate) and market context (for example, volume imbalance) have an influence on the impact of a given trade. Our market impact estimate allows us to qualify these dependencies. To do so, we follow a method which is a mix of the Monte Carlo simulation and the bootstrapping approach. In order to be comparable, we shall impose certain conditions during the simulation step. The methodology consists of the following steps: 11
38 POST-TRADE MARKET IMPACT MODEL Choose some conditions that each simulated strategy must verify; in our case, we fix the participation rate, i.e., the required volume to be p% of market volume, where p is thus the participation rate. Given a sequence of transactions, by combining them we generate different strategies {S k } k=1,...,k where each strategy verifies the above conditions. For each generated sequence we use (I.4) to estimate the contributed impact. Repeating this sampling for different trading days, we ultimately obtain a large sample of market impact realisations in function of execution conditions and market context. We shall analyse the dependence between impact characteristics versus execution conditions and market context. Impact compensation: First of all, let us remark that the impact characteristic should be compensated for by other measures before being compared to others. Only by compensating for the market buy impact can we isolate the pure contribution of the strategy. Note also that the last measure is thus homogeneous among impacts. In view of this discussion, let us define the intrinsic impact as Intrinsic-Impact = Impact Buy Impact. Moreover, from the additivity of the market impact, the total market impact is now the sum of the buy-side impact (positive sign) and the sell-side impact (negative sign). It is intuitive that in a buy-initiated dominant day, the impact of a buy strategy is lower than usual. To distinguish days with buy-initiated dominance from those with sell-initiated dominance we propose to use the criterion Impact-Imbalance = Buy Impact Buy Impact + Sell Impact. Finally, considering some classical measures, for example trend measure (intra-day return) and volume imbalance measure, recall that Volume-Imbalance = Buy Volume Buy Volume + Sell Volume. 12
39 4 Practical applications What do we learn from these impacts? For the illustration we use CAGR.PA, the coefficient η is estimated to be 4.93e 7 using data from Jan. 1, 2010 to Feb. 15, As a first very intuitive result, we find that the intrinsic impact is proportional to the participation rate. Such a relationship is expected; recall that we consider only buy strategies. We also find out that this criterion is decreasing with the volume imbalance, as shown in Figure I.3 (left). Even if it is an expected behaviour it is still interesting because it thus justifies our impact notion. In fact, it says that we trigger less impact in a day when there are more volumes on our side. Figure I.3: Left: Intrinsic-Impact decreasing with Volume-Imbalance, p = 20%. This implies that the impact is less important in a day where there is more buy volume than sell volume. Right: Impact-Imbalance strengthens the stock trend. The most interesting result that we observe is the fact that impacts do influence the stock price in Figure I.3 (right). By definition this is the case, but we now provide a method to affirm this fact not only qualitatively but also quantitatively. Focus on best practices: from market impact to price formation process We now turn to a more interesting question: how does a particular algorithm impact the market? For a given strategy, our estimate helps us identify automatically the worst or the best market conditions, under which the impact is bad or good respectively. Here 13
40 POST-TRADE MARKET IMPACT MODEL we took the simple example of TWAP 1, i.e., the algorithm executes volume linearly. The sampling is done similarly to like in the previous section, but for each day we compute the mean value of the simulated strategies impact. A small mean value indicates that the day in question is favourable for this algorithm and vice versa. The distribution of all mean values is shown in Figure I.4. The chosen data set includes all trading days in Figure I.4: Distribution of impact mean value. We focus on two extreme values, in fact Aug. 03, 2009 is a day corresponding to a large impact, while for Sept. 7, 2009 the impact is much less important. Figure I.5 plots the complete transaction data of these two days. We can conclude from the first figure that, when an imbalance exists on the market, if you follow this imbalance then your impact really changes the stock price. In general, when there is no imbalance between buy and sell orders, then the price should follow a random walk, providing that there is no correlation between buy and sell orders. On the other hand, a large imbalance between buy and sell orders drives the price formation process to a trend; if you contribute to this imbalance, then you are responsible for it, or in other words: your impact is high! 1 Time Weighted Average Price 14
41 4 Practical applications Figure I.5: Left: Maximal impact in a positive trend day. Right: Minimal impact day in a no trend day, self diffusion of price process (reminder: buy order). Conversely, as suggested by the second figure, if the balance between buy and sell orders is maintained, then your impact is compensated for by other trades and therefore has little influence on the trend. Ultimately, this approach allows us to estimate the market impact of a strategy as a component of the whole price formation process of a day. It encompasses all the moves in the price, including systematic and specific ones, because in this view of the market each move in the price is mainly explained by the market impact of the last trade or that of an earlier trade weakened by a decay factor. This allows a post-trade estimation of the intrinsic market impact, i.e., a better understanding of the interactions of a strategy with the market. 15
42 POST-TRADE MARKET IMPACT MODEL 16
43 Chapter 2 Optimal strategies with transient impact 1 Introduction Bouchaud et al. [21] proposed a discrete-time model in which each trade of size v n generates an impact which is power-low in volume, and decays over time according to a decaying shape G: N 1 S T S 0 = λ G(N n)ε n vn ψ. Gatheral [33] has recently reconsidered a continuous-time version of this model S(t) = S 0 + t 0 n=0 f(v(s))g(t s)ds + t 0 σ(s)dw s, (I.1) where the previous power-law function λv ψ is replaced by a more general form f(v), v being the instantaneous trading rate. Then he provided conditions on f and G under which there is absence of price manipulations. For instance, if f(v) = v ψ and G(l) = l β, then the condition β +ψ 1 is sufficient to exclude any price manipulation. Using the same model, Gatheral, Schied & Slynko [34] obtained the optimal conditions, derived the explicit form of the optimal strategy in a expected cost minimization problem. In this chapter, we generalize this approach with a more general mean-variance optimization criteria, we obtain a similar characteristic for optimal strategies using another method. We describe and implement a numerical scheme to compute the optimal solution. 17
44 OPTIMAL STRATEGIES WITH TRANSIENT IMPACT 2 Problem description We are interested in a problem which consists in buying X shares, between t = 0 and t = T. A trading strategy is a real-valued function x with x(0) = X and x(t ) = 0, representing the number of remaining shares to buy. We consider only the class of strategies that are differentiable, so that we can define the corresponding trading rate v x (t) = dx/dt = x. We consider the Gatheral model (I.1) where W is a standard Brownian motion, σ is the volatility of the stock. The impact of trading at time s < t is given by f( x (s)) and decays with a factor G(t s). Under this model the implementation shortfall trading cost is C x = T 0 S x (t)v x (t)dt X S 0, where we now write S x to insist on the fact that the stock price is influenced by the strategy. Our trading goal is to determine a strategy that minimizes the following functional, given a risk-aversion coefficient λ 0 min x( ) (J λ[x] := E [C x ] + λvar [C x ]). A straightforward computation, recall (I.1) shows that T ( t ) J λ [x] = x (t) f( x (s))g(t s)ds + λx 2 (t)σ 2 (t) dt, 0 } 0 {{ } =:F (t,x(t),x (t),p x (t)) (I.2) (I.3) where F (t, y, d, p) := dp + λy 2 σ 2 (t) and p x (t) := t 0 f( x (s))g(t s)ds. 3 Special cases Depending on the form of the decay kernel G, denote t the time elapses since the trade was placed, then we distinguish the following cases G( t) = δ : instantaneous impact, G( t) 1 : permanent impact, G ( t) 0, G( t) t 0 : transient impact. 18
45 3 Special cases 3.1 Instantaneous impact In this case, the market impact decays instantaneously, for the analytic form of the market impact, let us take the following function in Almgren [6] where the impact is a power function of the trading intensity f(v(t)) = η(t)(v(t)) ψ ; G(t s) = δ t s, where η and σ are deterministic function. The functional F takes the following form F (t, x(t), x (t), p x (t)) F (x(t), x (t)) = η ( x (t)) ψ+1 + λσ 2 x 2 (t). The optimal trajectory verifies the Euler-Lagrange equation for the variational problem (I.2): d F dt p ( t, x(t), x (t), p x (t) ) F y ( t, x(t), x (t), p x (t) ) = 0 for all t [0, T ], (I.4) that is simplified in (ψ + 1) d dt (ˆη(t)( x (t)) ψ ) + 2λσ 2 (t)x(t) = 0. (I.5) Comparison with discrete-time scheme. Under a linear market impact model ψ = 1, Equation (I.5) becomes λσ 2 (t)x(t) = d dt ( ) ˆη(t)x (t). We now use a first-order finite difference scheme, we discretize the time by N intervals, whose endpoints are (t n = nh) n=0,...,n with h = T N. We approximate (x, x ) by (x n, x n) defined as the value of (x, x ) evaluated at t = t n, then λσnx 2 n = h 1 ( η n x n η n 1 x ) n 1 ) = h (η 2 n (x n+1 x n ) η n 1 (x n x n 1 ), where σ n := σ(t n ), η n := η(t n ). This leads to x n+1 = ( ) 1 + η n 1 η n + λh 2 σn 2 ηn x n η n 1 η n x n 1 for n = 1,..., N 1, x 0 = X, x N = 0. 19
46 OPTIMAL STRATEGIES WITH TRANSIENT IMPACT Let us remark that, it is suggested in Lehalle [43] that η n = η Σn V n where (Σ n, V n ) are the volatitlity and market volume of the n-th period. The discrete-time model in this case takes the following form: S n+1 = S n + Σ n hξn+1 where (ξ n ) n i.i.d. N (0, σ 2 ξ ). Hence, we have the relation hσ 2 n = h 2 σ 2 n between Σ n and σ n, this leads to the following recursive relation: x n+1 = ( 1 + Σ n 1V n + λh ) Σ n V n 1 η Σ nv n x n Σ n 1V n x n 1, Σ n V n 1 which is the usual form found in many articles, for instance see Almgren [6]. In the same article, explicit solutions are given with η n η. Explicit ODE. second-order differential equation: If we continue with (I.5), we obtain the homogeneous non-linear (ψ + 1)ψη(t)x (t)( x (t)) ψ 1 (ψ + 1)η (t)( x (t)) ψ 2λσ 2 (t)x(t) = 0. (I.6) In order to solve this equation, one can rely on methods proposed in Press, Teukolsky, Vetterling & Flannery [48]. 3.2 Permanent impact With a linear impact f( v) = βv where β > 0, (I.3) takes the following form J λ [x] = T 0 [ x (t) t which by integration by parts can be rewritten as ( λx 2 (t)σ 2 (t) βx(t) J λ [x] = βg(0)x2 2 T + dt 0 0 ] βx (s)g(t s)ds + λx 2 (t)σ 2 (t) dt, When the impact is permanent, G(t s) 1 and G (t s) 0, J λ [x] = βx2 2 t T + λ σ 2 (t)x 2 (t)dt. 0 0 ) ds x (s)g (t s). (I.7) For this case the expectation of the execution cost is independent of the strategy, only its variance depends on the strategy. The optimal strategy is L-shaped, i.e., it is optimal to trade all at the beginning. 20
47 4 Optimal condition with transient impact 4 Optimal condition with transient impact In this case the decay kernel G is no-longer impulsive and we have a non-classical calculus of variations problem, for instance the integral term contains a convolution product. 4.1 Calculus of variations for integral depending on convolution products We give here a lemma, obtained as a direct extension of a theorem in [49], which provides a necessary condition for the optimal function. The proof is given in Section 6. Lemma I.1. Given (t, y, d, p) R 4 F (t, y, d, p) a continuous function, satisfying F y is continuous and uniformly bounded, and F d, F p are uniformly bounded and integrable on < t <. Given f C 1 (R), g L 1 ([0, T ]), we consider the class K f,g (assumed nonempty) of functions x on [0, T ], satisfying (i) x is absolutely continuous on (0, T ), (ii) f x L 1 ([0, T ]), (iii) x(0) = X, x(t ) = 0, and (iv) F [, x( ), x ( ), p( )] L 1 ([0, T ]), where p is defined as p( ) := (f x ) g = 0 f(x (s))g( s)ds. Let I be defined by I[x] := T 0 F [t, x(t), x (t), p(t)]dt. Suppose x 0 K f,g is a minimum of I in K f,g. Then, there exists c R such that for all t (0, T ), the following holds: F d (t, x 0 (t), x 0(t), p(t)) t 0 F y (t, x o (t), x 0(t), p(t))ds + f (x 0 (t)) T t F p (t, x 0 (t), x 0(t), p(t)) g(s t)ds = c. (I.8) 21
48 OPTIMAL STRATEGIES WITH TRANSIENT IMPACT 4.2 Optimal condition In the general case (I.3), the functional F takes the form F (t, y, d, p) = dp + λσ 2 y 2 and the optimal condition (I.8) reads t 0 ˆf(x (s))g(t s)ds + 2λ where ˆf(x) = f( x). equation reads: t 0 f(v(s))g(t s)ds + 2λ t 0 σ 2 (s)x(s)ds + ˆf (x (t)) T t x (s)g(s t)ds = c, In terms of the instantaneous rate v(s) = x (s), the above t 0 T σ 2 (s)x(s)ds + f (v(t)) v(s)g(s t)ds = c. t (I.9) Remark I.1. Minimizing only expected trading cost is equivalent to using λ = 0, in this case we retrieve the optimal condition as given in Gatheral, Schied & Slynko [34]. 5 Numerical results 5.1 Discretization method The optimal condition (I.9) is equivalent to where T 0 f t (v(s))g( t s )ds + 2λ t 0 σ 2 (s)x(s)ds = c for all t [0, T ], (I.10) f t (v(s)) := f(v(s))1 s t + v(s)f (v(t))1 s t. To discretize this equation, we use the Nystrom method which extends Simson s 3/8 rule to arbitrary weight functions w (c.f. Press, Teukolsky, Vetterling & Flannery [48], page ). In our case, using N points of an evently spaced grid {t i } N 1 i=0 with t i = it/(n 1), the coefficients W (w, i, j) are computed such that tj t i where v k = v(t k ). w(s)v(s)ds can be approximated by j W k (w, i, j)v k k=i Discretization of the first term: For each value t = t i, 0 i N 1 we discretize the first term of (I.10) as follows: T 0 f t (v(s))g( t s )ds N 1 k=0 f ti (v k )Wk i (G, 0, N 1), 22
49 5 Numerical results where the superscript i shows that t i is taken as the lower limit of integration. Discretization of the second term: Using the same discretization grid, from the definition of x we approximate x(t j ) = T t j v(s)ds N 1 k=j The second term is now discretized as follows: ti i σ 2 (s)x(s)ds W j (σ 2, 0, i)x(t j ) 0 = = W k (1, j, N 1)v k, j = 0,..., N 1. (I.11) j=0 i j=0 N 1 W j (σ 2, 0, i) W k (1, j, N 1)v k N 1 v k k=0 j k i k=j W k (1, j, N 1)W j (σ 2, 0, i). Equation (I.10) is discretized as follows, for all 0 i N 1, N 1 k=0 N 1 f ti (v k )Wk i (G, 0, N 1) + 2λ v k k=0 j k i W k (1, j, N 1)W j (σ 2, 0, i) = c. (I.12) The difficulty comes from the non-linearity of f and f, we cannot solve (I.12) directly to obtain {v i } i=0 N 1. We propose the following algorithm to overcome this obstacle. Algorithm: 1. An initial estimate v (0) is defined by v (0) i v, solution of: v f N 1 (v) Wk 0 (G, 0, N 1) = c. k=0 2. Compute the Newton iterates {v (m) } m as follows: v (m+1) is the solution of Equation (I.12) where the following approximations have been made ( ) f(v (m+1) (m) k ) f(v k ) + v (m+1) k v (m) k f (v (m) k ) and f (v (m+1) i ) f (v (m) i ). This step consists in solving the following equation, obtained by substituting the above approximation in Equation (I.12) K v (m+1) = c, 23
50 OPTIMAL STRATEGIES WITH TRANSIENT IMPACT where K = (K ij ) 0 i,j N 1 and [ K ij = Wj i (G, 0, N 1) f (v (m) j )1 j<i + f ] (v (m) i )1 j i + 2λ W k (σ 2, 0, i)w j (1, k, N 1) k i j i [ ] c i = c Wj i (m) (G, 0, i) f(v j ) v (m) j f (v (m) j ). j=0 Once obtained {v i } 0 i N 1, we use (I.11) to compute ˆx(0), the value of the constant c is such that ˆx(0) = X. 5.2 Optimal strategies Figure I.1: λ = 0, G(t) = t 0.4, f(v) = v 1.1 In Figure I.1 we minimize only the expectation of cost (λ = 0). Using a non-linear 24
51 6 Proof of Lemma I.1 Figure I.2: λ = 3, G(t) = t 0.4, f(v) = v 1.1, σ(t) = cos(πt) impact function f(v) = v 1.1 and a decay factor G(t) = t 0.4, we obtain a curve which is similar to the linear case s solution (c.f. Gatheral, Schied & Slynko [34]). The strategy in Figure I.2 is obtained by using a coefficient λ = 3, a U-shape volatility function σ(t) = cos(πt) and the same function f and G. We observe that the trading rate is of important value in the beginning of the period, increasing in the middle where there is less volatility and finally increasing at the end. 6 Proof of Lemma I.1 We introduce the class of variations N made of function eta satisfying (i) η is absolutely continuous and has compact support in (0, T ), (ii) η(0) = η(t ) = 0 and (iii) η 25
52 OPTIMAL STRATEGIES WITH TRANSIENT IMPACT L 1 ([0, T ]). The function φ(ε) := I[x 0 + εη] may be written φ(ε) = T 0 F [t, x 0 (t) + εη(t), x 0(t) + εη (t), ( f(x 0 + εη ) g ) (t)]dt. For ε sufficiently small, the function x 0,ε = x 0 +εη is in K f,g, and there exists a positive number M such that φ ε M [ η + η + η f(x 0) g ]. Under the assumptions on the class N and by the fact that the convolution of two functions belonging to L 1 ([0, T ]) is also in L 1 ([0, T ]), the above expression is integrable on (0, T ), hence φ (0) exists and is given almost everywhere on (0, T ) by φ (0) = T 0 [ ( F d (t, x 0 (t), x 0(t), p(t)) t where the usual integration by parts was performed. follows that φ (0) = 0 almost everywhere on (0, T ). 0 ) F x (s, x 0 (s), x 0(s), p(s))ds η (t) + F p (t, x 0 (t), x 0(t), p(t)) ( η f (x 0 ) g ) ] (t) dt, Since I[x 0 ] is an extremum it Moreover, the last expression in the brackets is absolutely integrable on (0, T ), hence an interchange of limits of integration is justified and we have T 0 [ F d (t, x 0 (t), x 0(t), p(t)) + f (x 0 (t)) t 0 T t F x (s, x 0 (s), x 0(s), p(s))ds ] F p (s, x 0 (s), x 0(s), p(s))g(s t)ds η (t)dt = 0. By arbitrariness of η, this implies that the expression in brackets is equal to a constant c almost everywhere on (0, T ). 26
53 Part II Optimal trading with general impulse control approach 27
54
55 Abstract We propose a general framework for intra-day trading based on the control of trading algorithms. Given a set of generic parameterized algorithms (which have to be specified by the controller ex-ante), our aim is to optimize the dates (τ i ) i at which they are launched, the length (δ i ) i of the trading period and the value of the parameters (E i ) i kept during the time interval [τ i, τ i + δ i ). This provides to the financial agent a decision tool for selecting which algorithm (and for which set of parameters and time length) should be used in the different phases of the trading period. From the mathematical point of view, this gives rise to a non-classical impulse control problem where not only the regime E i but also the period [τ i, τ i + δ i ) have to be determined by the controller at the impulse time τ i. We adapt the weak dynamic programming principle of Bouchard and Touzi (2009) to our context to provide a characterization of the associated value function as a discontinuous viscosity solution of a system of PDEs with appropriate boundary conditions, for which we prove a comparison principle. We also propose a numerical scheme for the resolution of the above system and show that it is convergent. We finally provide a simple example of application to a problem of optimal stock trading with a non-linear market impact function. This shows how parameters adapt to the market. Key words: optimal impulse control, discontinuous viscosity solutions, intra-day trading. Note This part is based on an article to appear in SIAM Jounal on Financial Mathematics.
56 30
57 Chapter 3 General impulse control approach 1 Introduction Trading algorithms are nowadays widely spread among financial agents. They are typically used for high frequency intra-day trading purposes, e.g. for statistical arbitrage or for the execution of large orders by brokers. In both cases, the use of robots is justified by the fact that orders have to be executed very quickly, in order to make profit of good prices, and, typically for brokers, by the large size of the portfolios to be handled by a limited number of traders. A lot of efforts have been devoted these last years to build efficient trading algorithms, taking all possible market features into account, and in particular the so-called market impact effect. Some of the most popular ones have been proposed by academics, see e.g. [3], [4], [7], [11] and [42], a lot of them are developed in research divisions of brokers or investment banks, and are somehow kept secret as fundamental building blocks of their everyday business. One could expect that these algorithms correspond to global optimization problems and are run on the whole trading period without interruption. In practice, this is often not the case, in particular among brokers. In fact the way brokers execute large orders is typically as follows: they split the global number of assets to be bought or sold into small pieces, called slices, and then use robots to execute these different slices one by one. Each time a new slice is launched, the trader tunes the parameters of the algorithm (and possibly the size of the slice) depending on the evolution of the market s conditions. He can even decide to use a 31
58 GENERAL IMPULSE CONTROL APPROACH different algorithm from one slice to the other (which can actually also be viewed as changing the parameters of a single robot, at least from the mathematical point of view). The real life situation is thus the following: given a bunch of trading algorithms, the trader decides how to slice the order (i.e. divide the global order in smaller parts), at what time each slice is launched, and with which algorithm and values of the parameters. Moreover, he also decides how long he should let the algorithm run. In practice, there exists a minimal time period during which each algorithm is executed. One reason for this is simply that the trader can not practically monitor all the algorithms that are running for different purposes at the same time. Another one is that it makes no sense (in practice) to launch an algorithm for less than, say, one second. The aim of this work is to provide a decision tool for traders given the above described practical situation. Namely, we propose a rigorous framework for the optimal control of trading algorithms: how does one decide optimally of the times at which algorithms are launched, what parameters to use, for how long? Obviously, one could argue that it would be better to discuss a global optimization problem, i.e. discuss the optimal control problem associated to the global trading agenda. This is not the aim of this work. Most practitioners have their own algorithms and do not want to have the same as the others. Our approach allows us to adapt to the algorithms each trader wants to use (optimal or not), and help them to use these algorithms in an optimal way, and in particular to tune the parameters. Exactly like the computation of greeks serves as a reference for the hedging policy of an option, which is then more or less followed by the trader depending on his own feeling of the market s conditions (and because he can in practice only discretely rebalanced his portfolio), we aim at providing on-line values of the parameters that should be optimal in some sense and therefore should serve as references for the trader in the way he launches the different slices. We are therefore not interested here in the trading algorithms themselves. The aim of this work is not to come up with a new algorithm but to provide a rigorous decision tool for the use of already existing trading algorithms. From the mathematical point of view, it gives rise to a non-classical impulse control problem. As for standard impulse control problems, see e.g. the reference book [10], one chooses the times at which impulses are given (times at which an algorithm is 32
59 1 Introduction launched) and the size of the impulse (the value of the parameters). The novelty comes from the fact that one also chooses a time period during which no new impulse can be given (the period during which the algorithm runs). To the best of our knowledge, such problems have never been discussed in the mathematical literature on optimal impulse control. In this chapter, we provide a rigorous characterization of the value function as a discontinuous viscosity solution of a partial differential equation (PDE), together with suitable boundary conditions. To this end, we adapt the approach of [15] who proposes a weak version of the dynamic programming principle. The main advantage of this weak formulation is that it does not require any a priori continuity of the value function. It is the first time this approach is used in the context of impulse control problems, and this requires some non-trivial modifications of the arguments of [15]. Our PDE characterization reads as follows. When the current regime is the passive one, i.e. no trading algorithm is running, the controller can launch one at any moment τ i with a given set of parameters E i and for a period of length δ i. This gives rise to a standard quasi-variational inequality in the region corresponding to the passive regime. However, once the algorithm is launched, no change in the value of the parameters can be made before the end of the period [τ i, τ i + δ i ). This implies that the value function satisfies a linear parabolic equation on the active region. We also provide a comparison principle for the above equations and construct a finite difference numerical scheme, which we prove to be convergent. The rest of this chapter is organized as follows. The model is described in Section 2. In Section 3, we provide the PDE characterization of the value function and the associated comparison principle. The proofs of these results are given in Section 4. The numerical scheme is studied in Section 1. In the last section, we discuss a very simple numerical example of application to a particular model of optimal stock acquisition. It shows how the proposed framework naturally allows a real-time adaptive control of the trading algorithm, by switching optimally after the end of each slice given the current state of the market. Notation: All over this chapter, we shall use the following notations. Given x R k, for k given by the context, we denote by x its Euclidean norm and by B r (x) the open ball of center x and radius r > 0. The scalar product is denoted by,. Given a set A R k, we denote by A its boundary. Given d N, we denote by M d the set of 33
60 GENERAL IMPULSE CONTROL APPROACH d-dimensional square matrices. For M M d, M is the associated transposed matrix. For a function (t, x, y) R + R d R k ϕ(t, x, y), we denote by Dϕ and D 2 ϕ its gradient and Hessian matrix with respect to x, whenever they are well defined. The other partial derivatives will be written by using standard notations. 2 Problem formulation Let (Ω, F, P) be a probability space supporting a d-dimensional Brownian motion W, d 1. Let F := (F t ) t 0 denote the right-continuous complete filtration generated by W, and let T > 0 be a finite time horizon. 2.1 Control policies We first describe how the trading algorithms are controlled, precise dynamics will be imposed in Section 2.2 below. Note that different algorithms can be viewed as a single parameterized one. In what follow, we therefore consider that we have only one algorithm. A control policy of the trading algorithm is described by a non-decreasing sequence of stopping times (τ i ) i 1 and a sequence of [δ, ) E-valued random variables (δ i, E i ) i 1. The stopping times τ i describe the times at which an order is given to the algorithm, E i is the value of the parameters with which the algorithm is run and δ i the length of the period (latency period) during which it is run with the value E i. The set E is a compact subset of R d, which represents the possible values of the parameters, the quantity 0 < δ < T denotes the minimum length of the time period during which the algorithm can be run. To be consistent we impose that τ i + δ i τ i+1 and (δ i > 0 τ i + δ i T ), i 1. (II.1) The first condition expresses the fact that a new order can not be given before the end of the time period associated to the previous order. The second one means that an order should be given only if it ends before the final time horizon T. 34
61 2 Problem formulation Remark II The minimal duration constraint, δ i δ with δ > 0, has been justified from a practical point of view in the introduction. From the mathematical point of view, the problem described in Sections 2.2 and 2.3 below would not make sense without this condition, if no additional cost related to launching the algorithm with new parameters is introduced. Indeed, for δ = 0, and without additional costs, the controller could, at the limit, control the parameters continuously, and this would actually certainly be optimal. The controller will then act, at the limit, as a trader acting continuously on the market. 2. Models with δ = 0 and with an additional cost (paid each time the algorithm is launched with new parameters) could be discussed by following the lines of this chapter. Such a cost is actually already embedded in the general dynamics of Section 2.2, up to an additional assumption on the function β, see Example II.10 below. This would however require to justify this cost, and to evaluate it in practice. Moreover, certain bounds like the one stated in Remark II.2 below would not be true anymore and other conditions would be required to retrieve the estimates of Remark II.5 below. For sake of simplicity, we therefore stick to the case δ > 0 which corresponds more, from our point of view, to practical situations. 3. In the absence of a cost penalizing frequent changes in the parameters, it may be optimal to choose δ i = δ most of the time (depending whether δ is small or not). However, other values of δ i may also be optimal. Our algorithm provides a way to select the maximal optimal value, the one for which the trader changes the parameters the least often (which is desirable in practice). As usual the value of the parameters and the size of the latency period can not be chosen in some anticipative way, i.e. we impose that (δ i, E i ) is F τi -measurable, i 1. (II.2) At time t [τ i, τ i + δ i ), the value of the parameter of the trading algorithm is denoted by ν t. For t A((τ i, δ i ) i 1 ), defined as A((τ i, δ i ) i 1 ) := R + \ i 1[τ i, τ i + δ i ), we set ν t = ϖ, where ϖ R d \ E can be viewed as a cemetery point, recall that E is compact. 35
62 GENERAL IMPULSE CONTROL APPROACH It follows that the value of the parameters of the trading algorithm ν can be written as ν t = ϖ1 t A((τi,δ i ) i 1 ) + i 1 E i 1 t [τi,τ i +δ i ), t [0, T ], (II.3) where ν t = ϖ means that the algorithm is not running at time t. In the following, we denote by S the set of adapted processes ν that can be written in the form (II.3) for some sequence of stopping times (τ i ) i 1 and of [δ, ) E-valued random variables (δ i, E i ) i 1 satisfying (II.1) and (II.2). For ease of notations, we shall now write (τ ν i, δ ν i, E ν i ) i 1 the sequence associated to ν S, and define, for all stopping times ϑ 1 and ϑ 2 satisfying ϑ 1 ϑ 2 P a.s., the set of indices corresponding to orders whose execution ends between ϑ 1 and ϑ 2 : I ν ϑ 1,ϑ 2 := {i 1 : ϑ 1 < τ ν i + δ ν i ϑ 2 }. Remark II.2. Note that the constraint δ ν i δ for all i 1 and ν S implies that card(i ν 0,T ) card ({τ ν i T, i 1}) T/δ. For ease of notations, we also set Ē := E {ϖ} R d, and introduce the process ν ν t := i 1[τ ν i + δ ν i t] + 1 t τ ν i, t [0, T ]. The quantity ν t denotes the remaining latency period during which no new order can be passed to the algorithm. When ν t > 0, the algorithm is running with a value of the parameters ν t. When ν t = 0, the algorithm is not running anymore, ν t = ϖ, and a new order can be passed. The following picture sums up the dynamics of the control. 36
63 2 Problem formulation ν Ei+1 ν [ [ δν i+1 E ν i [ [ ν t ϖ τ ν i δν i [ τ ν i + δ ν i [ τ ν i+1 t τ ν i+1 + δν i+1 time 2.2 Output of the trading algorithm Given some initial data (t, x) [0, T ] R d, the output of the trading algorithm associated to some control policy ν S is defined as the strong solution Xt,x ν on [0, T ] of the stochastic differential equation ( s Xt,x(s) ν = x + 1 s t b(xt,x(r), ν ν r )dr + a(xt,x(r), ν ν r )dw r t t + ) β(xt,x(τ ν i ν ), Ei ν, δi ν )1 t<τ ν i s, (II.4) i 1 s where β : R d Ē [δ, T ] Rd and (b, a) : R d Ē Rd M d are continuous functions such that there exists K > 0 for which, for all x, x R d, e, e Ē, δ, δ [δ, T ], ψ(x, e, δ) ψ(x, e, δ) ) K x x ψ(x, e, δ) K(1 + x ) for ψ = b, a, β. (II.5) ψ(x, e, δ) ψ(x, e, δ ) K(1 + x )( e e + δ δ ) We do not differentiate here between the components that correspond to real outputs of the algorithm (cumulated gains, cumulated volumes executed by the algorithm, etc...) and others that simply describe the evolution of financial data or market factors (prices of the traded assets, global traded volumes on the markets, volatilities, etc...). The jumps on the dynamics are introduced to model the changes in the initial conditions on the variables of interest for the trading algorithm when it is launched (e.g. volume to be executed between τ ν i and τi ν + δi ν ), see Example II.7 below. 37
64 GENERAL IMPULSE CONTROL APPROACH Moreover, there is no loss of generality in assuming that X, W and ν have the same dimension d. One can always reduce more general situations to this case by playing with the coefficients b, a, β and with the choice of E. Time dependent coefficients can similarly be considered by putting the first line of a and β equal to 0, and the first component of b equal to 1, so that the first component of X actually coincides with the time parameter. We refer to Section 2.4 for the description of simple examples of application which illustrate the flexibility of the above model. We conclude this section with two technical remarks that will be used later on. Remark II.3. Observe that X ν does not jump when the regime is switched to the passive regime ϖ. Remark II.4. Note that (II.5), the fact that E is bounded and Remark II.2 imply that, for all t [0, T ], x R d and ν S, E [ ] sup Xt,x(s) ν p C p K (1 + x p ) (II.6) s [t,t ] where C p K depends only on K and p Gain function The aim of the controller is to maximize the expected value of the gain functional ν S Π t,x (ν) := g(xt,x(t ν )) + f(xt,x(τ ν i ν + δi ν ), Ei ν ), i I ν t,t with the usual convention = 0, among the set S t,δ,e := { { ν S : νs = e for s [t, t + δ) and ν t+δ = 0} if e ϖ and δ > 0 {ν S : ν t = ϖ} otherwise, where (δ, e) R + Ē denotes the initial state of the remaining latency time and value of the parameters. Here, g and f are assumed to be continuous on R d Ē and to satisfy, for some γ > 0, f(x, e) + g(x) sup (x,e) R d E 1 + x γ <, f(, ϖ) = 0. (II.7) 38
65 2 Problem formulation In view of (II.6), this ensures that the quantity is well defined for all ν S and satisfies J(t, x; ν) := E [Π t,x (ν)] J(t, x; ν) C γ K (1 + x γ ) (II.8) where C γ K depends only on K and γ. For technical reasons related to the dynamic programming principle, see [15] and the proof of Lemma II.1 below, we shall restrict to admissible trading strategies ν S t,δ,e such that ν is independent on F t, see Remark 5.2 in [15]. associated set of controls and therefore define the value function as: V (t, x, δ, e) := sup E [Π t,x (ν)]. ν St,δ,e a We denote by S a t,δ,e the We refer to Section 2.4 for examples of application, and to Section 2 for a numerical illustration. Remark II.5. It follows from (II.8) that there exists C γ K K and γ such that > 0 which depends only on V (t, x, δ, e) C γ K (1 + x γ ) for all (t, x, δ, e) [0, T ] R d R + Ē s.t. Sa t,δ,e. Note that for δ = T t and e E, (II.1) implies that V (t, x, T t, e) = V(t, x, e) := E [ g(x e t,x(t )) + f(x e t,x(t ), e) ], (II.9) where Xt,x e is the solution of X e t,x(s) = x + s t b(x e t,x(r), e)dr + s t a(x e t,x(r), e)dw r, s [t, T ]. (II.10) Remark II.6. Under (II.5), the continuity assumption on f, g and (II.7), it follows from standard arguments that the auxiliary value function V is continuous, and that, for each e E, it is a viscosity solution of L e ϕ(t, x) = 0 on [0, T ) R d, ϕ(t, x) = g(x) + f(x, e) on R d, (II.11) where, for e Ē, and a smooth function ϕ, L e ϕ(t, x) := t ϕ(t, x) + b(x, e), Dϕ(t, x) Tr [ aa (x, e)d 2 ϕ(t, x) ]. (II.12) 39
66 GENERAL IMPULSE CONTROL APPROACH 2.4 Examples Before to go on with the presentation of our general problem, let us describe simple application examples that illustrate the flexibility of the above model. For sake of simplicity, we restrict ourselves to the case of a single parameterized algorithm. Example II.7. As a first example, we consider the case where the aim of the controller is to sell a number Q 0 of one stock S between 0 and T > 0. We denote by V t the volume instantaneously traded on the market at time t, by the other participants to the market. The dynamics of (S, V ) is given by the strong solution of the SDE S t = S 0 + V t = V 0 + t 0 t 0 µ S (r, S r, V r )dr + µ V (r, S r, V r )dr + t 0 t 0 σ S (r, S r, V r )dw r, σ V (r, S r, V r )dw r, where W denotes a two dimensional standard Brownian motion, and (µ S, σ S, µ V, σ V ) are Lipschitz continuous. We implicitly assume here that the above SDE has nonnegative solutions whatever the initial conditions are. A control ν S is identified to a sequence (τi ν, δν i, Eν i ) i 1 S as in Section 2. Here E ν i stands for the proportion of the remaining number of shares that have to be sold, Q ν τi ν, which will be traded on [τ i ν, τ i ν + δi ν ). We assume that this quantity is sold uniformly on the corresponding time interval. Namely, we sell Ei νqν τ i /δi ν dt on [t, t + dt] for t [τi ν, τ i ν + δi ν). This means that the dynamics of the remaining number of stocks to sell is given by Q ν t = Q 0 i 1 τ ν i +δ ν i τ ν i 1 s t E ν i Q ν τ ν i /δν i ds. Clearly, E has to be contained in [0, 1]. Note that in order to ensure that the dynamics of the system is Markovian, we need to introduce two additional processes which coincide with Q ν τi ν and δi ν on [τi ν, τ i ν + δi ν]. This is done by considering the process ( Q ν, δ ν ) defined by the dynamics Q ν t := (Q ν τi ν Q ν τi ν )1 τ ν i t and δ t ν := i i 1 i 1(δ ν δ τ ν i ν )1 τ ν i t with the convention Q ν 0 = δ 0 ν = 0. This explains why jumps have been introduced in the general dynamics (II.4). It follows that Q ν t = Q 0 t 0 q(ν s, δ ν s ) Q ν sds. 40
67 2 Problem formulation where q(e, δ) := e/δ if e ϖ and δ > 0, q(e, δ) = 0 otherwise. Due to the impact of the strategy on the market, the price obtained for the volume executed under the regime Ei ν is S t = S t η(ei ν Q ν τi ν /δν i, S t, V t ), t [τi ν, τi ν + δi ν ) where η is some market impact function and is assumed to be Lipschitz continuous. It follows that the cumulated wealth s dynamic is t Yt ν = 0 + S r q(ν r, δ r ν ) Q ν rdr. 0 The remaining part Q ν T is instantaneously sold on the market at a price: S T c(q ν T, S T, V T ), for some Lipschitz continuous function c. The total gain after the final transaction is thus given by: Y ν T + (S T c(q ν T, S T, V T )) (Q ν T ) +. The aim of the controller is to maximize the expectation of the quantity g(y ν T + (S T c(q ν T, S T, V T )) (Q ν T ) + ) for some concave function g with polynomial growth. In this model, the process X coincides with (S, V, Y, Q, Q, δ). Only Q and δ have jumps. Example II.8. As a second example, we consider the case where the aim of the controller is to buy a number Q 0 of one stock S between 0 and T > 0. The dynamics of (S, V ) is given as in the previous example. Here Ei ν stands for the intensity at which the stocks are bought, i.e. the algorithm buys a number Ei νdt = ν t1 νt ϖdt of stocks on [t, t + dt], t [τi ν, τ i ν + δi ν ). The dynamics of the remaining number of stocks to be bought before T is thus given by: Q ν t = Q 0 t 0 q(ν s )ds where q is now defined as q(e) = e1 e ϖ. It follows that the cumulated wealth s dynamic is t Yt ν = 0 + S r q(ν r )dr = where η is a given market impact function. t 0 (S r + η(ν r, S r, V r ))q(ν r )dr, 41
68 GENERAL IMPULSE CONTROL APPROACH If the number Q 0 of shares is not liquidated at time T, the remaining part Q ν T is instantaneously bought on the market at the price S T +c(q ν T, S T, V T ), for some Lipschitz continuous function c. The total cost after the final transaction is thus given by: Y ν T + (S T + c(q ν T, S T, V T )) (Q ν T ) +. The aim of the controller is to minimize the expectation of the quantity l(y ν T + (S T + c(q ν T, S T, V T )) (Q ν T ) + ) for some convex function l with polynomial growth. A numerical application within the above framework is presented in Section 2. Example II.9. We now consider a similar situation as in the previous example except that the controller has an incentive to buy the shares more or less quickly. This can be modeled by adding a process Z ν corresponding to the number of stocks sold during a trading period. Namely, Z ν t := i 1 t 1 t [τ ν i,τi ν+δν i ) ν s ds = τ ν i t 0 ν s 1 νs ϖds i 1 Z ν τ ν i 1 τ ν i t. The aim of the controller is then to minimize E l(y T ν + (S T + c(q ν T, S T, V T )) (Q ν T ) + ) + f(t, (Q ν T ) + ) + 1 τ ν i +δi ν T f(τi ν + δi ν, Zτ ν i +δ i ) i 1 where the dependence of f in time means that the controller prefers to buy quickly, i.e. f is increasing in time, or take more time, i.e. f is decreasing in time. Example II.10. We finally explain how to incorporate a cost paid each time the algorithm is launched with new parameters. It suffices to consider an additional process C ν t := i 1 λ1 τ ν i t, for some λ > 0, and to consider a reward function which is non-increasing in C ν T. Obviously, one can let λ depend on other variables of interest. 42
69 3 Viscosity characterization of the value function 3 Viscosity characterization of the value function The aim of this section is to provide a PDE characterization of the value function V. Before to state our main result, we need to introduce some additional notations and definitions. In view of (II.1), (II.9) and the constraint that the latency period should be greater than δ, the natural domain of definition of the value function V is D := { } (t, x, δ, e) [0, T ) R d (((0, ) E) {(0, ϖ)}) : δ t + δ < T or e = ϖ, which can be decomposed in two main regions. We call the active region, the region where δ > 0 and e ϖ: D E,>0 := { } (t, x, δ, e) [0, T ) R d (0, ) E : δ t + δ < T. (II.13) It corresponds to the set of initial conditions where the algorithm is running and the controller has to wait the end of the latency period before passing a new order. We call the passive region, the region where e = ϖ, and therefore δ = 0: D ϖ := [0, T ) R d {(0, ϖ)}. (II.14) It corresponds to the set of initial conditions where the algorithm is not running and can be launched immediately with a new set of parameters. These two regions are complemented by the natural boundaries of the active region when δ 0 and t+δ T : D E,0 := [δ, T ) R d {0} E (II.15) { } D E,T := (t, x, δ, e) [0, T ) R d (0, ) E : δ t + δ = T, (II.16) and by the time boundary: D T := {T } R d R + Ē. (II.17) The closure of the natural domain of definition of the value function V is therefore } D := {(t, x, δ, e) [0, T ] R d R + Ē : δ t + δ T or e = ϖ. 43
70 GENERAL IMPULSE CONTROL APPROACH As usual, we shall rely on the dynamic programming principle, see Lemma II.1 below for a precise statement, to deduce the behavior of the value function on each component of D: V (t, x, δ, e) = sup ν S a t,δ,e for any [t, T ]-valued stopping time ϑ. E V (ϑ, Xt,x(ϑ), ν ν ϑ, ν ϑ) + f(xt,x(τ ν i ν + δi ν ), Ei ν ), (II.18) i I ν t,ϑ In the passive region. For (t, x, δ, e) D ϖ, the controller can immediately launch the trading algorithm with a new set of parameters (δ, e ) [δ, T t] E. Taking ϑ = t in (II.18) thus implies that where M[V ](t, x) := V (t, x, 0, ϖ) M[V ](t, x) sup V (t, x + β(x, e, δ ), δ, e ), (δ,e ) [δ,t t] E with the usual convention sup =. The controller can also decide to wait before passing a new order to the algorithm, i.e. choose ν = ϖ on some time interval [t, t + δ ) with δ > 0. In view of (II.18) applied to an arbitrarily small stopping time ϑ < t + δ, this implies that L ϖ V (t, x, 0, ϖ) 0. The dynamic programming principle (II.18) formally implies that one of the two above choices should be optimal, i.e. In the active region. min { L ϖ V (t, x, 0, ϖ) ; V (t, x, 0, ϖ) M[V ](t, x)} = 0. For (t, x, δ, e) D E,>0, the controller can not change the parameter of the algorithm before the end of the initial latency period δ > 0. Choosing ϑ arbitrarily small in (II.18) thus implies that V should satisfy ( L e + ) V (t, x, δ, e) = 0, δ where (t, x) L e V (t, x, δ, e) is defined as in (II.12) for (δ, e) taken as parameters. It is naturally complemented with the boundary conditions V (t, x, δ, e) = V (t, x, 0, ϖ) + f(x, e), if (t, x, δ, e) D E,0, 44
71 3 Viscosity characterization of the value function and V (t, x, δ, e) = V(t, x, e), if (t, x, δ, e) D E,T, recall (II.9). Terminal boundary condition. As usual, the boundary condition as t T should be given by the terminal condition: V (t, x, δ, e) = g(x) + f(x, e), if (t, x, δ, e) D T, where we recall that f(, ϖ) = 0 by convention. The above discussion shows that V should solve the equation Hϕ = 0 (II.19) on D, where, for a smooth function ϕ defined on D, ( L e + ) δ ϕ(t, x, δ, e) on DE,>0, ϕ(t, x, δ, e) ϕ(t, x, 0, ϖ) f(x, e) on D E,0, Hϕ(t, x, δ, e) := ϕ(t, x, δ, e) V(t, x, e) on D E,T, min { L ϖ ϕ(t, x, δ, e) ; ϕ(t, x, δ, e) M[ϕ](t, x) } on D ϖ, ϕ(t, x, δ, e) g(x) f(x, e) on D T. However, since V may not be smooth, it has to be stated in terms of viscosity solutions, see [24], in the following sense. Definition II.1. We say that a lower-semicontinuous (resp. upper-semicontinuous) function U on D is a viscosity supersolution (resp. subsolution) of (II.19) on D if for any function ϕ C 1,2,1,0 ([0, T ] R d R + Ē) and (t 0, x 0, δ 0, e 0 ) D, which achieves a global minimum (resp. maximum) of U ϕ on D such that (U ϕ)(t 0, x 0, δ 0, e 0 ) = 0, we have Hϕ(t 0, x 0, δ 0, e 0 ) 0 ( resp. Hϕ(t 0, x 0, δ 0, e 0 ) 0). If U is continuous, we say that it is a viscosity solution of (II.19) if it is a super- and a subsolution. In all this chapter, we shall say that a function ϕ is smooth if it belongs to C 1,2,1,0 ([0, T ] R d R + Ē). As usual, showing that V is a-priori continuous is a rather difficult task. As a first step, we shall therefore prove the super- and subsolution property only for the upper- 45
72 GENERAL IMPULSE CONTROL APPROACH and lower-semicontinuous enveloppes V and V of V defined as V (t, x, δ, e) := lim sup V (t, x, δ, e ) (t,x,δ,e ) D (t,x,δ,e) V (t, x, δ, e) := lim inf (t,x,δ,e ) D (t,x,δ,e) V (t, x, δ, e ), (t, x, δ, e) D. Theorem II.2. The function V (resp. V ) is a viscosity supersolution (resp. subsolution) of (II.19) on D. The following comparison result combined with Remark II.5 insures a posteriori that V is continuous and that it is the unique viscosity solution of (II.19) on D with polynomial growth. Theorem II.3. Let u and v be respectively a lower semicontinuous viscosity supersolution of (II.19) on D and a upper-semicontinuous viscosity subsolution of (II.19) on D. Assume that v + and u have polynomial growth. Then, u v on D. 4 Proof of the viscosity characterization 4.1 Dynamic programming As usual, the derivation of the partial differential equation relies on the so-called dynamic programming principle, a formal version of which is given in (II.18) above. In this section, we provide a rigorous formulation which follows ideas introduced in [15]. Namely, we only provide a weak formulation in terms of test functions. The main advantage of this approach is that it does not require any regularity on the value function V itself, but only some lower-semicontinuity of the objective function J( ; ν), see below. We refer to [15] for a general discussion. Lemma II.1 (Weak Dynamic Programming Principle). Fix (t, x, δ, e) D and let {ϑ ν, ν S a t,δ,e } be a family of [t, T ]-valued stopping times independent of F t. Then, we have V (t, x, δ, e) sup ν S a t,δ,e E [V, g](ϑ ν, Xt,x(ϑ ν ν ), ν ϑ ν, ν ϑ ν ) + f(xt,x(τ ν i ν + δi ν ), Ei ν ), i I ν t,ϑ ν (II.20) 46
73 4 Proof of the viscosity characterization where [V, g](s, ) := V (s, )1 s<t + g1 s=t, and sup E ϕ(ϑ ν, Xt,x(ϑ ν ν ), ν ν St,δ,e a ϑ ν, ν ϑ ν ) + f(xt,x(τ ν i ν + δi ν ), Ei ν ) V (t, x, δ, e) (II.21) i I ν t,ϑ ν for all upper semi-continuous function ϕ such that V ϕ on D. As in [15], the proof of the above result relies on some lower-semicontinuity property of the function J. Because of the latency time δ, we can however not apply their result directly and need to adapt their arguments by exploiting the lower-semicontinuity of the map where, for s 1 s 2 [0, T ], (t, x, δ, e, ν) D S J(t, x, P e t,t+δ (ν)) P e s 1,s 2 : ν S P e s 1,s 2 (ν) := e1 [0,s1 ) + ϖ1 [s1,s 2 ) + ν1 [s2,t ]. Lemma II.2. Fix (t, x, δ, e) D and ν S t,δ,e. Let (t n, x n, δ n, e n ) n 1 be a sequence in D such that (t n, x n, δ n, e n ) (t, x, δ, e) as n and t n t and t n + δ n t + δ for all n 1. (II.22) Then, lim inf J(t n, x n ; P en n t n+δ n,t+δ (ν)) J(t, x; ν). Proof. We only prove the result in the case where δ > 0. The case δ = 0 can be handled similarly. In this case we have t n t < t n + δ n t + δ for n large enough since t n t and δ n δ > 0. For ease of notations, we set X := Xt,x ν and X n := Xt νn n,x n where ν n := P en t n+δ n,t+δ (ν). In all this proof, we let C > 0 denote a generic constant which does not depend on n but takes value which may change from line to line. 1. We first prove that, for any fixed integer p 1: [ lim E n ] sup X n (s) X(s) 2p = 0. (II.23) t s T First note that ν n = ν on [t + δ, T ]. Since the size of the possible jump of X and X n at time t + δ, recall (II.4), depends on ν t+δ = νt+δ n, standard computations based on Burkholder-Davis-Gundy s inequality, Gronwall s Lemma and the Lipschitz continuity of b, a and β, we thus deduce that [ E ] sup X n (s) X(s) 2p C E [ X n (t + δ ) X(t + δ ) 2p]. t+δ s T 47
74 GENERAL IMPULSE CONTROL APPROACH Since (ν n, ν) = (ϖ, e) on [t n + δ n, t + δ) and no jump occurs on this time interval, the Lipschitz continuity of b and a implies that [ E ] sup X n (s) X(s) 2p C ( t + δ t n δ n p + E [ X n (t n + δ n ) X(t n + δ n ) 2p]). t n+δ n s<t+δ We similarly have, since (ν n, ν) = (e n, e) on [t, t n + δ n ) and (X n, X) does not jump on this time interval, that: [ E sup X n (s) X(s) 2p t s t n+δ n ] C ( e n e 2p + E [ X n (t) x 2p]). Finally, by the linear growth condition on b and a, the fact that ν n = e n on [t n, t) and that X n does not jump at time t, [ ] E sup X n (s) x 2p t n s t C ( [ ]) x n x 2p + E sup X n (s) x n 2p t n s t C ( x n x 2p + t n t p). 2. We now use the above estimate to conclude the proof. We first note that ( ) Π tn,xn (ν n ) Π t,x (ν) = g(x n (T )) g(x(t )) ( + f(x n (τi n + δi n ), Ei n ) ) f(x(τi ν + δi ν ), Ei ν ), (II.24) i I νn tn,t i I ν t,t with (τ n, δ n, E n ) := (τ νn, δ νn, E νn ). In view of (II.23), we can assume that sup X(s) X n (s) 0 P a.s. t s T (II.25) after possibly passing to a subsequence. Similar estimates show that, after possibly passing to a subsequence, X n (t n + δ n ) X n (t + δ ) 0 P a.s. and in L p, p 1. (II.26) Since g is continuous, it follows that lim n g(xn (T )) = g(x(t )) P a.s. (II.27) Moreover, by definition of ν n, we have i I νn tn,t f(x n (τ n i + δ n i ), E n i ) = f(x n (t n + δ n ), e n ) + i I ν t+δ,t f(x n (τ ν i + δ ν i ), E ν i ). 48
75 4 Proof of the viscosity characterization It then follows from the continuity of f, (II.25) and (II.26) that lim f(x n (τi n + δi n ), Ei n ) = f(x(t + δ ), e) + n i I νn tn,t = i I ν t,t i I ν t+δ,t f(x(τ ν i + δ ν i ), E ν i ) P a.s. f(x(τ ν i + δ ν i ), E ν i ) (II.28) The required result then follows from (II.27), (II.28), (II.7), and Fatou s Lemma combined with (II.23) and (II.6) which insure that the sequence (Π tn,x n (ν n ) ) n 1 is uniformly integrable. We now turn to the proof of the dynamic programming principle. Proof. [Lemma II.1] In this proof, we consider (Ω, F, F, P) as the d-dimensional canonical filtered space equipped with the Wiener measure and denote by ω or ω a generic point. The Brownian motion is thus defined as W (ω) = (ω t ) t 0. For ω Ω and r 0, we set ω r := ω. r and T r (ω) := ω.+r ω r. In the following, we omit the dependence of ϑ ν with respect to ν and simply write ϑ, for ease of notations. 1. The proof of (II.20) is standard and is based on the observation that, for all ν St,δ,e a, J(t, x; ν) = E E g(x t,x(t ν )) + f(xt,x(τ ν i ν + δi ν ), Ei ν ) F ϑ (II.29) + E i I ν ϑ,t f(xt,x(τ ν i ν + δi ν ), Ei ν ) i I ν t,ϑ where, by the flow property of X ν, E g(x t,x(t ν )) + f(xt,x(τ ν i ν + δi ν ), Ei ν ) F ϑ (ω) = J(ϑ(ω), Xt,x(ϑ)(ω); ν ν ω ) with, for each ω Ω, i I ν ϑ,t (II.30) ν ω : ω Ω ν ω ( ω) = ν(ω ϑ(ω) + T ϑ(ω) ( ω)) which can be viewed, for each ω Ω, as a control independent of F ϑ(ω). Since the dynamic of X νω ϑ(ω),xt,x ν (ϑ)(ω) depends on ν ω only through its path after ϑ(ω), this implies that, for each ω Ω, { } J(ϑ(ω), Xt,x(ϑ)(ω); ν ν ω ) sup J(ϑ(ω), Xt,x(ϑ)(ω); ν ν), ν Sϑ(ω), a ν ϑ (ω),ν ϑ(ω) [V, g](ϑ(ω), X ν t,x(ϑ)(ω), ν ϑ (ω), ν ϑ(ω)), 49
76 GENERAL IMPULSE CONTROL APPROACH and the result follows from (II.29) and (II.30). 2. We now prove the second inequality. 2.a. We first show that, for any ε > 0, we can find two sequences (t n, x n, δ n, e n, A n ) n 1 in D B D and (ν n ) n 1 in S such that (A n ) n 1 forms a partition of D and, for each n, ν n S a t n,δ n,e n and J(t, x ; P e t +δ,t n+δ n (ν n )) ϕ(t, x, δ, e ) 3ε for all (t, x, δ, e ) A n A n Q rn (t n, x n, δ n, e n ) D for some r n > 0, where we use the notation { } Q r ( t, x, δ, e) := (t, x, δ, e ) B r ( t, x, δ, e) : t t, t + δ t + δ. (II.31) By definition of V ϕ, for each ( t, x, δ, e) D and ε > 0, we can find ν = ν ( t, x, δ, e),ε in S such that ν S å t, δ, e and J( t, x; ν) V ( t, x, δ, e) ε ϕ( t, x, δ, e) ε. (II.32) Moreover, it follows from Lemma II.2 and the upper-semicontinuity of ϕ that we can find r = r ( t, x, δ, e) in (0, ) such that J(t, x ; P e t +δ, t+ δ ( ν)) J( t, x; ν) ε and ϕ( t, x, δ, e) ϕ(t, x, δ, e ) ε (II.33) for all (t, x, δ, e ) Q r ( t, x, δ, e). Clearly {Q r ( t, x, δ, e) : ( t, x, δ, e) D, 0 < r r ( t, x, δ, e) } forms a Vitali covering of D. It then follows from the Vitali s covering Theorem, see e.g. Lemma 1.9 p10 in [29], that we can find a countable sequence (t n, x n, δ n, e n, r n ) n 1 of elements of D R, with 0 < r n < r (tn,x n,δ n,e n) for all n 1, such that D n 1 Q rn (t n, x n, δ n, e n ). We finally construct the sequence (A n ) n 1 by setting A 1 := Q r1 (t 1, x 1, e 1, δ 1 ) D, C 0 = and A n := (Q rn (t n, x n, δ n, e n ) D) \C n 1, C n 1 := C n 2 A n 1 for n 2. The sequence (ν n ) n 1 is defined by ν n := ν (tn,xn,δn,en),ε for all n. 2.b. We are now in position to prove (II.21). Let ν be a arbitrary element of S a t,δ,e and define ˆν := ν1 [0,ϑ) + 1 [ϑ,t ] n 1 P ν ϑ ϑ+ ν ϑ,tn+δn(νn )1 (ϑ,x ν t,x (ϑ), ν ϑ,ν ϑ) A n. 50
77 4 Proof of the viscosity characterization Since ν S a t,δ,e, we have (ϑ, Xν t,x(ϑ), ν ϑ, ν ϑ) D = n 1 A n. Moreover, on {(ϑ, X ν t,x(ϑ), ν ϑ, ν ϑ) A n }, we have ϑ + ν ϑ t n + δ n. It follows that ˆν St,δ,e a, and therefore V (t, x, δ, e) J(t, x; ˆν) = E g(xt,x(t ˆν )) + i Iˆν ϑ,t f(x ˆν t,x(τ ˆν i + δˆν i ), E ˆν i ) + i Iˆν t,ϑ f(xt,x(τ ˆν i ˆν + δˆν i ), Ei ˆν ), where, by the flow property of X ˆν, the fact that ν n is independent of F tn ϑ t n on {(ϑ, Xt,x(ϑ), ν ν ϑ, ν ϑ) A n }, [ ] ( ) E g(xt,x(t ˆν )) = g X νω( ω) ϑ(ω),xt,x ν (ϑ)(ω)(t )( ω) dp( ω)dp(ω) and that and E f(xt,x(τ ˆν i ˆν + δˆν i ), Ei ˆν ) i Iˆν ϑ,t = where, for ω Ω, ν ω i I νω( ω) ϑ(ω),t f(x νω( ω) ϑ(ω),xt,x ν νω (ϑ)(ω)((τi : ω Ω ν(ω)1 [0,ϑ(ω)) + 1 [ϑ(ω),t ] n 1 + δ νω i ) T )( ω), E νω i ( ω))dp( ω)dp(ω) P ν ϑ(ω) ϑ(ω)+ ν ϑ (ω),tn+δn(νn ( ω))1 (ϑ(ω),x ν t,x (ϑ)(ω), ν ϑ (ω),ν ϑ(ω)) A n. Hence, (II.31) implies that V (t, x, δ, e) E J(ϑ, Xt,x(ϑ); ˆν ˆν) + f(xt,x(τ ˆν i ˆν + δˆν i ), Ei ˆν ) i Iˆν t,ϑ = E J(ϑ, Xt,x(ϑ); ν P ν ϑ ϑ+ ν ϑ,tn+δn(νn ))1 (ϑ,x ν t,x (ϑ), ν ϑ,ν ϑ) A n n 1 + E f(xt,x(τ ν i ν + δi ν ), Ei ν ) i I ν t,ϑ E ϕ(ϑ, Xt,x(ϑ), ν ν ϑ, ν ϑ) + i I ν t,ϑ f(xt,x(τ ν i ν + δi ν ), Ei ν ) 3ε. By arbitrariness of ε > 0 and ν St,δ,e a, this proves the required inequality. 51
78 GENERAL IMPULSE CONTROL APPROACH Remark II.1. Note that, by replacing ϕ in (II.21) by a sequence (ϕ k ) k 1 of upper semi-continuous functions satisfying sup ν S a t,δ,e ϕ k V and ϕ k [V, g] on D, we can deduce a stronger version of (II.21): E [V, g](ϑ ν, Xt,x(ϑ ν ν ), ν ϑ ν, ν ϑ ν ) + f(xt,x(τ ν i ν + δi ν ), Ei ν ) V (t, x, δ, e), i I ν t,ϑ where [V, g](s, ) := V (s, )1 s<t + g1 s=t. In particular, if V is continuous, combining (II.20) and the previous inequality leads to the classical version of the dynamic programming principle (II.18). 4.2 Viscosity properties Now we are in position to prove Theorem II.2. We split the proof in different propositions Supersolution property We start with the supersolution property in the domain D = D E,>0 D ϖ, recall the definitions (II.13)-(II.14). Proposition II.2. The function V is a viscosity supersolution of (II.19) on D. Proof. The proof follows from standard arguments except that we use the non classical formulation of the dynamic programming principle (II.21). Fix (t 0, x 0, δ 0, e 0 ) D and let ϕ be a smooth function such that (t 0, x 0, δ 0, e 0 ) achieves a (global) minimum of V ϕ on D such that 0 = (V ϕ)(t 0, x 0, δ 0, e 0 ). Let (t k, x k, δ k, e k ) k 1 be a sequence in D such that (t k, x k, δ k, e k ) (t 0, x 0, δ 0, e 0 ) and V (t k, x k, δ k, e k ) V (t 0, x 0, δ 0, e 0 ) as k, (II.34) and observe that (ϕ V )(t k, x k, δ k, e k ) 0 when k. (II.35) 52
79 4 Proof of the viscosity characterization Case 1. that We first assume that (t 0, x 0, δ 0, e 0 ) D E,>0, recall the definition (II.13), and L e 0 ϕ(t 0, x 0, δ 0, e 0 ) + δ ϕ(t 0, x 0, δ 0, e 0 ) =: 2ε < 0, (II.36) and work towards a contradiction. Define the function ϕ by ϕ(t, x, δ, e) := ϕ(t, x, δ, e) x x 0 4 t t 0 2 δ δ 0 2, (II.37) so that ϕ also satisfies (II.36). By continuity of b and a, we can find r > 0 such that ( L e ϕ + δ ϕ ) (t, x, δ, e) 0 for (t, x, δ, e) B := B r (t 0, x 0, δ 0, e 0 ) D E,>0.(II.38) Given k large enough so that (t k, x k, δ k, e k ) B, let ν k be any control in S a t k,δ k,e k. Set (X k, k ) := (X νk t k,x k, νk ) and define θ k := inf{s t k : (s, X k (s), k s, ν k s ) / B}. For r small enough we have νk > 0 and therefore ν k = e θ k k on [t k, θ k ]. Using Itô s Lemma, (II.38) and the definition of ϕ, we thus obtain that [ ] [ ] ϕ(t k, x k, δ k, e k ) E ϕ(θ k, X k (θ k ), k θ, e k k ) E ϕ(θ k, X k (θ k ), k θ, ν k k θ ) η k where η := inf{ x x t t δ δ 0 2, (t, x, δ, e k ) B r (t 0, x 0, δ 0, e 0 ), k 1} > 0, observe that e k e 0 < r. Since I νk t k,θ k =, the above inequality combined with (II.35) and (II.37) contradict (II.21) for k large enough. Case 2. We now assume that (t 0, x 0, δ 0, e 0 ) D ϖ, recall the definition (II.14). Since E is closed and ϖ / E, (II.34) implies that (δ k, e k ) = (0, ϖ) for k large enough. (II.39) We now assume that min { L ϖ ϕ(t 0, x 0, 0, ϖ), ϕ(t 0, x 0, 0, ϖ) M[ϕ](t 0, x 0 )} =: 2ε < 0, (II.40) and work toward a contradiction. If L ϖ ϕ(t 0, x 0, 0, ϖ) = 2ε < 0, 53
80 GENERAL IMPULSE CONTROL APPROACH we can argue as above to obtain a contradiction to (II.21). If ϕ(t 0, x 0, 0, ϖ) M[ϕ](t 0, x 0 ) =: 2ε < 0, we can find (ˆδ, ê) [δ, T t 0 ) E and r > 0 such that ϕ(t, x, 0, ϖ) ϕ(t, x + β(x, ê, ˆδ), ˆδ, ê) ε, for (t, x) B := B r (t 0, x 0 ). (II.41) Let ν denote the constant control that takes the value ϖ on [0, T ], set X k := X ν t k,x k and θ k := inf{s t k : (s, X k (s)) / B} (t k + k 1 ). Note that for k large enough, we have t k +k 1 + ˆδ T. We can then define ν k by ν k t := ê1 t [θ k,θ k +ˆδ) + ϖ1 t/ [θ k,θ k +ˆδ), t T, S a t k,0,ϖ and set (X k, k ) := (Xt νk k,x k, νk ). Using Ito s Lemma and (II.41), we obtain that [ ] ϕ(t k, x k, 0, ϖ) E ϕ(θ k, X k (θ k ), k θ, ν k k θ ) ε + C/k, k for some C > 0 which does not depend on k. The above inequality combined with (II.35) contradict (II.21) for k large enough. We now turn to the proof of the boundary conditions. We refer to (II.15)-(II.16)-(II.17) for the definitions of D E,0, D E,T and D T. Proposition II.3. Fix (t 0, x 0, δ 0, e 0 ) D. Then, Proof. V (t 0, x 0, 0, e 0 ) V (t 0, x 0, 0, ϖ) + f(x 0, e 0 ) if (t 0, x 0, δ 0, e 0 ) D E,0 V(t 0, x 0, e 0 ) if (t 0, x 0, δ 0, e 0 ) D E,T g(x 0 ) + f(x 0, e 0 ) if (t 0, x 0, δ 0, e 0 ) D T. We only prove the first inequality. The two other ones follow from similar arguments. Let (t k, x k, δ k, e k ) k 1 be a sequence in D such that (t k, x k, δ k, e k ) (t 0, x 0, 0, e 0 ) and V (t k, x k, δ k, e k ) V (t 0, x 0, 0, e 0 ) as k. For each k 1, define ν k := ϖ1 [0,tk +δ k ) + e k 1 [tk +δ k,t ] S a t k,δ k,e k, (II.42) 54
81 4 Proof of the viscosity characterization and set X k := Xt νk k,x k. It follows from Remark II.1 that [ ] V (t k, x k, δ k, e k ) E V (t k + δ k, X k (t k + δ k ), 0, ϖ) + f(x k (t k + δ k ), e k ), k 1. Using standard estimates, see e.g. (II.43) the proof of Lemma II.2, one easily checks that X k (t k + δ k ) x 0 in L p for all p 1, and in particular P a.s., after possibly passing to a subsequence. It thus follows from the lower-semicontinuity of V and f that, up to a subsequence, lim inf k V (t k +δ k, X k (t k +δ k ), 0, ϖ)+f(x k (t k +δ k ), e k ) V (t 0, x 0, 0, ϖ)+f(x 0, e 0 ) P a.s. The required result then follows from (II.42), (II.43), and the last inequality combined with polynomial growth property of f and V, see Remark II.5, and Fatou s Lemma Subsolution property We start with the subsolution property in the domain D = D E,>0 D ϖ, recall the definitions in (II.13)-(II.14). Proposition II.4. The function V is a viscosity subsolution of (II.19) on D. Proof. Fix (t 0, x 0, δ 0, e 0 ) D and let ϕ be a smooth function such that (t 0, x 0, δ 0, e 0 ) achieves a (global) maximum of V ϕ such that 0 = (V ϕ)(t 0, x 0, δ 0, e 0 ). In the following, we denote by (t k, x k, δ k, e k ) k 1 a sequence in D satisfying (t k, x k, δ k, e k ) (t 0, x 0, δ 0, e 0 ) and V (t k, x k, δ k, e k ) V (t 0, x 0, δ 0, e 0 ) as k. Case 1. We first assume that (t 0, x 0, δ 0, e 0 ) D E,>0 and that L e 0 ϕ(t 0, x 0, δ 0, e 0 ) + δ ϕ(t 0, x 0, δ 0, e 0 ) =: 2ε > 0, (II.44) and work towards a contradiction. By continuity of b and a, we can find r > 0 such that ( L e ϕ + δ ϕ ) (t, x, δ, e) ε for (t, x, δ, e) B := B r (t 0, x 0, δ 0, e 0 ) D E,>0. (II.45) 55
82 GENERAL IMPULSE CONTROL APPROACH Moreover, we can always assume that (t 0, x 0, δ 0, e 0 ) achieves a strict local maximum, so that after possibly changing the value of ε, we have sup(v ϕ) =: ε < 0, (II.46) pb where p B is the parabolic boundary of B. Fix ν k S tk,δ k,e k and set θ k := inf{s t k : (s, X k (s), k s, ν k s ) / B}, where (X k, k ) := (X νk t k,x k, νk ). Observe that, for r small enough, k θ k > 0 and therefore ν k = e k on [t k, θ k ]. Applying Ito s Lemma to ϕ and using (II.45) and (II.46), we deduce that [ ] [ ] ϕ(t k, x k, δ k, e k ) E ϕ(θ k, X k (θ k ), k θ, ν k θ k) E V (θ k, X k (θ k ), k θ, ν k θ k) + ε. Since I νk t k,θ k =, this contradicts (II.20) for k large enough, recall (II.44). Case 2. We now assume that (t 0, x 0, δ 0, e 0 ) = (t 0, x 0, 0, ϖ) D ϖ and min{ L ϖ ϕ(t 0, x 0, 0, ϖ), ϕ(t 0, x 0, 0, ϖ) M[ϕ](t 0, x 0 )} =: 2ε > 0, and work towards a contradiction. By continuity of b and a, we can find r > 0 such that min{ L ϖ ϕ(, 0, ϖ), ϕ(, 0, ϖ) M[ϕ]} ε on B := B r (t 0, x 0 ) ([0, T ) R d ). (II.47) Moreover, without loss of generality we can assume that (t 0, x 0 ) achieves a strict local maximum, so that after possibly changing the value of ε sup(v (, 0, ϖ) ϕ(, 0, ϖ)) =: ε < 0, (II.48) pb where p B is the parabolic boundary of B. Also observe that, since E is closed and ϖ / E, (II.44) implies that (δ k, e k ) = (0, ϖ) for k large enough. (II.49) Let ν k St a k,0,ϖ = Sa t k,δ k,e k be arbitrary, set (X k, k, (τi k) i 1) := (Xt νk k,x k, νk, (τi νk ) i 1 ) and define θ k := inf{s t k : (s, X k (s)) / B}, ϑ k := inf{τ k i, i 1 s.t. τ k i t k } and ξ k := θ k ϑ k. 56
83 4 Proof of the viscosity characterization Applying Itô s Lemma to ϕ, using (II.47), (II.48), and recalling (II.49) lead to [ ] ϕ(t k, x k, δ k, e k ) E ϕ(ξ k, X k (ξ k ), 0, ϖ) ] [ϕ(ξ k, X k (ξ k ), k ξ, ν k k ξ ) + ε1 k ξ k =ϑ k E E [ ] V (ξ k, X k (ξ k ), k ξ, ν k k ξ ) + ε. k In view of (II.44) this leads to a contradiction with (II.20) for k large enough. We now turn to the boundary condition δ 0. Recall the definition of D E,0 in (II.15). Proposition II.5. For all (t 0, x 0, δ 0, e 0 ) D E,0, we have Proof. V (t 0, x 0, 0, e 0 ) V (t 0, x 0, 0, ϖ) + f(x 0, e 0 ). By following similar arguments as in the second step of the proof of Proposition II.4 above, one easily checks that, for any smooth function ϕ such that (t 0, x 0, 0, e 0 ) achieves a global maximum of V ϕ satisfying (V ϕ)(t 0, x 0, 0, e 0 ) = 0, we have { min L e0 ϕ(t 0, x 0, 0, e 0 ) + } δ ϕ(t 0, x 0, 0, e 0 ), ϕ(t 0, x 0, 0, e 0 ) ϕ(t 0, x 0, 0, ϖ) f(x 0, e 0 ) 0. Let now ϕ be a smooth function such that (t 0, x 0, 0, e 0 ) achieves a global maximum of V ϕ satisfying (V ϕ)(t 0, x 0, 0, e 0 ) = 0, and consider the function ϕ ε defined as ϕ ε (t, x, δ, e) := ϕ(t, x, δ, e) + ε + δ ε for some ε > 0. Observe that (t 0, x 0, 0, e 0 ) achieves a global maximum of V ϕ ε. It thus follows that either ϕ ε (t 0, x 0, 0, e 0 ) ϕ ε (t 0, x 0, 0, ϖ) f(x 0, e 0 ) 0 or L e0 ϕ ε (t 0, x 0, 0, e 0 ) + δ ϕ ε(t 0, x 0, 0, e 0 ) + ε Clearly, the second assertion can not hold for ε > 0 small enough. It follows that ϕ ε (t 0, x 0, 0, e 0 ) ϕ ε (t 0, x 0, 0, ϖ) f(x 0, e 0 ) 0 for all ε > 0 small enough, which provides the required result. We next consider the boundary conditions as t+δ T and t = T. Recall the definitions of D E,T and D T in (II.16)-(II.17). 57
84 GENERAL IMPULSE CONTROL APPROACH Proposition II.6. For all (t 0, x 0, δ 0, e 0 ) D E,T, we have V (t 0, x 0, δ 0, e 0 ) V(t 0, x 0, e 0 ). For all (T, x 0, δ 0, e 0 ) D T, we have V (T, x 0, δ 0, e 0 ) g(x 0 ) + f(x 0, e). Proof. We only prove the first assertion, the second one using the same kind of arguments. Let (t k, x k, δ k, e k ) k 1 be a sequence in D satisfying (t k, x k, δ k, e k ) (t 0, x 0, δ 0, e 0 ) and V (t k, x k, δ k, e k ) V (t 0, x 0, δ 0, e 0 ) as k. For k large enough, we have t k + δ k > T δ so that, for any ν k S a t k,δ k,e k, we have ν k = e k on [t k, t k + δ k ) and ν k = ϖ on [t k + δ k, T ], recall (II.1). It follows that [ ] V (t k, x k, δ k, e k ) = E g(xt νk k,x k (T )) + f(x e k t k,x k (t k + δ k ), e k ) recall the definition of X in (II.10). Moreover, since t k + δ k t 0 + δ 0 = T, standard estimates based on (II.5) and Remark II.3 imply that (Xt νk k,x k (T ), X e k t k,x k (t k + δ k )) (X e 0 t 0,x 0 (T ), X e 0 t 0,x 0 (t 0 + δ 0 )) as k in L p for all p 1. The result then follows by taking the limsup as k in the above equality and using (II.7) as well as the dominated convergence theorem., 4.3 A comparison result In this section, we provide the proof of Theorem II.3. We first show that (II.19) admits a classical strict supersolution in the following sense: Proposition II.7. For any integer p γ, there exists a function Λ on R d R + Ē and ϱ > 0 satisfying (i) Λ C 2,1,0 (R d R + Ē), (ii) Λ g + + f + + V +, (iii) inf Λ(x, δ, e)/ x p as x, (δ,e) [0,T ] Ē (iv) b, DΛ Tr[aa D 2 Λ] ϱλ and Λ/ δ + b, DΛ Tr[aa D 2 Λ] ϱλ on R d R + Ē, 58
85 4 Proof of the viscosity characterization (v) Λ(x, 0, e) f(x, e) q(x) Λ(x, 0, ϖ) Λ(x + β(x, e, δ), δ, e) + δ for all x R d, δ [δ, T ] and e E, where q is a continuous and (strictly) positive function on R d. Proof. Let ϕ be a C 1 (R + ) function with bounded first derivative such that ϕ 0, ϕ(0) = 1 and ϕ(δ) = 0 for δ δ and let Λ be defined by: Λ(x, δ, e) = µ (1 + x 2p )(1 + κ1 e=ϖ ) + ( 2κµ (1 + x 2p ) δ ) ϕ(δ)1 e ϖ for some κ > 0 and µ > T such that f(x, e) + + g(x) + + V(t, x, e) + µ (1 + x 2p ), recall (II.7) and Remark II.5. The first three assertions clearly hold for µ large enough, recall that ϖ / E where E is closed. As for the fourth assertion, we recall that b and a are uniformly Lipschitz, so that the left-hand side is of order (1+ x 2p ), which is dominated by ϱλ for ϱ large enough. The right-hand side inequality holds for ϱ large enough by similar arguments. Finally, recalling (II.5), we observe that, for µ and κ large enough, Λ(x, 0, e) f(x, e) Λ(x, 0, ϖ) = κµ (1 + x 2p ) f(x, e) µ (1 + x 2p ), Λ(x, 0, ϖ) Λ(x + β(x, e, δ), δ, e) = µ (1 + x 2p )(1 + κ) µ (1 + x + β(x, e, δ) 2p ) µκ/2 δ for all x R d, δ δ T and e E, which provides the last assertion for q(x) := µ (1 + x 2p ). We can now provide the proof of Theorem II.3. Proof. [Theorem II.3] Let u and v be as in Theorem II.3 and let p γ be large enough so that [v(t, x, δ, e) u(t, x, δ, e)] + C(1 + x p ) on D (II.50) for some C > 0. We assume that and work toward a contradiction. sup(v u) 2η for some η > 0 (II.51) D 1. Let ϱ > 0 and Λ be as in Proposition II.7 for p γ satisfying (II.50). It follows from (II.51) that for λ (0, 1) small enough there is some (t λ, x λ, δ λ, e λ ) D such that max(ṽ w) = (ṽ w)(t λ, x λ, δ λ, e λ ) η > 0, (II.52) D 59
86 GENERAL IMPULSE CONTROL APPROACH where for a map ϕ on D, we write ϕ(t, x, δ, e) for e ϱt ϕ(t, x, δ, e), and w := (1 λ)u+λλ. Observe that ũ, ṽ are super- and subsolution of Hϕ = 0 (II.53) on D, where, for a smooth function ϕ defined on D, ( ϱ t Le + ) δ ϕ(t, x, δ, e) on DE,>0, ϕ(t, x, δ, e) ϕ(t, x, 0, ϖ) f(x, e) on D E,0, Hϕ(t, x, δ, e) := ϕ(t, x, δ, e) Ṽ(t, x, e) on D E,T, min { (ϱ t Lϖ )ϕ(t, x, δ, e) ; ϕ(t, x, δ, e) M[ϕ](t, x) } on D ϖ, ϕ(t, x, δ, e) g(x) f(x, e) on D T. (II.54) Also note that (t λ, x λ, δ λ, e λ ) / D E,T D T (II.55) since otherwise the super- and subsolution property of u and v would imply (v w)(t λ, x λ, δ λ, e λ ) λ (V(t λ, x λ, e λ ) (g(x λ ) + f(x λ, e λ )) Λ(t λ, x λ, δ λ, e λ )) which, in view of (ii) in Proposition II.7, would contradict (II.52). 2. For (t, x, δ, e) D and n 1, we now set Γ(t, x, y, δ, e) := ṽ(t, x, δ, e) w(t, y, δ, e) Θ n (t, x, y, δ, e) := Γ(t, x, y, δ, e) ϕ n (t, x, y, δ, e), where ϕ n (t, x, y, δ, e) := n x y 2p + x x λ 2p+2 + t t λ 2 + δ δ λ 2 + e e λ. By the growth assumption on v, u and the fact that Ē is compact, there is (t n, x n, y n, δ n, e n ) D 2, with D 2 := {(t, x, y, δ, e) : ((t, x, δ, e), (t, y, δ, e)) D D}, such that max Θ n = Θ n (t n, x n, y n, δ n, e n ). D 2 60
87 4 Proof of the viscosity characterization Since Γ(t n, x n, y n, δ n, e n ) Θ n (t n, x n, y n, δ n, e n ) (ṽ w)(t λ, x λ, δ λ, e λ ), it follows from the growth condition on v and u, (iii) of Proposition II.7 and the uppersemicontinuity of Λ that, up to a subsequence, (t n, x n, y n, δ n, e n ) (t λ, x λ, x λ, δ λ, e λ ) (II.56) ϕ n (t n, x n, y n, δ n, e n ) 0 (II.57) Γ(t n, x n, y n, δ n, e n ) Γ(t λ, x λ, x λ, δ λ, e λ ). (II.58) 3. It follows from (II.55) and (II.56) that, after possibly passing to a subsequence, (t n, x n, δ n, e n ) / D E,T D T for all n 1. (II.59) 3.1. We now assume that, up to a subsequence, e n ϖ for all n 1. If {n : δ n = 0} =, then we can assume that, up to a subsequence, δ n = 0, i.e., (t n, x n, δ n, e n ) D E,0 for all n 1. It then follows from the super- and subsolution property of ũ and ṽ, and (v) of Proposition II.7, that ṽ(t n, x n, 0, e n ) ṽ(t n, x n, 0, ϖ) + f(x n, e n ) ũ(t n, y n, 0, e n ) ũ(t n, y n, 0, ϖ) + f(y n, e n ) Λ(y n, 0, e n ) Λ(y n, 0, ϖ) + f(y n, e n ) + e ϱtn q(y n ), and therefore ( Γ(t n, x n, y n, 0, e n ) Γ(t n, x n, y n, 0, ϖ) + f(xn, e n ) f(y ) n, e n ) λe ϱtn q(y n ). (II.60) Sending n and using (II.56) and (II.58) leads to Γ(t λ, x λ, x λ, δ λ, e λ ) Γ(t λ, x λ, x λ, 0, ϖ) λe ϱt λ q(y λ ) which, recalling that q > 0 on R d, contradicts (II.52). It follows from the above arguments that {n : δ n = 0} <. In this case, (t n, x n, δ n, e n ) D E,>0 for all n 1 large enough, recall (II.59). Using the viscosity property of ũ and ṽ, (iv) in Proposition II.7, and standard arguments based on Ishii s Lemma, see [24], together with (II.56) allows us to deduce that ϱγ(t n, x n, y n, δ n, e n ) O λ (n 1 ), 61
88 GENERAL IMPULSE CONTROL APPROACH where O λ (n 1 ) 0 as n. Since ϱ > 0, combining the above inequality with (II.58) leads to a contradiction to (II.52) We now assume that, up to a subsequence, e n = ϖ, so that (t n, x n, δ n, e n ) D ϖ for all n 1. Note that we can not have ṽ(t n, x n, 0, ϖ) sup (δ,e) [δ,t t n] E ṽ(t n, x n, δ, e) 0 along a subsequence, since otherwise the supersolution property of ũ and (v) of Proposition II.7 would imply Γ(t n, x n, y n, 0, ϖ) sup Γ(t n, x n, y n, δ, e) λe ϱtn δ, (δ,e) [δ,t t n] E which would contradict (II.52) for n large enough, recall (II.56), (II.58) and the fact that δ > 0. We can thus assume that ṽ(t n, x n, 0, ϖ) sup (δ,e) [δ,t tn] E ṽ(t n, x n, δ, e) > 0 for n large enough. Using again the viscosity properties of ũ and ṽ, (iv) of Proposition II.7, standard arguments based on Ishii s Lemma, see [24], and (II.56) then leads ϱγ(t n, x n, y n, δ n, e n ) O λ (n 1 ), where O λ (n 1 ) 0 as n. As above, this leads to a contradiction. 62
89 Chapter 4 Numerical results 1 Numerical approximation In this section, we construct a finite difference scheme to solve the PDE (II.19) numerically, and prove the convergence of the numerical scheme. 1.1 Space discretization Given a positive integer N, we discretize the set T := {(t, δ) [0, T ] R + : δ t + δ T } in T N := {(ih N T, (i + j)h N ), i = 0,..., N and j = 0,..., N i} where h N := T/N. We next fix a positive integer M and R > 0 and approximate R d R := B R(0) R d by R d MR := { R + kh MR, k = 0,..., 2M} d where h MR := R/M. We finally consider an increasing sequence (E L ) L 1 of finite subsets of E such that L 1 E L = E. 63
90 NUMERICAL RESULTS For ease of notations, we set { D NM RL := (t, x, δ, e) D } : (t, δ) T N, x R d MR, e E L {ϖ} 1.2 Finite difference approximation From now on, we denote by x i the i-th component of a vector x R d, and by A ij the (i, j)-component of a matrix A M d. We use the notation l i for the unit vector of R d in the i th coordinate direction. We use the standard finite difference approximation, see [41] for a full description.. Space component: ψ (t, x, δ, e) xi ψ(t,x+h MR l i,δ,e) ψ(t,x,δ,e) h MR =: h MR+ x i ψ(t, x, δ, e) if b i (x, e) 0 ψ(t,x,δ,e) ψ(t,x h MR l i,δ,e) h MR =: h MR x i ψ(t, x, δ, e) if b i (x, e) < 0, 2 ψ x 2 (t, x, δ, e) ψ(t, x + h MRl i, δ, e) 2ψ(t, x, δ, e) + ψ(t, x h MR l i, δ, e) i h 2 =: h MRψ(t, x, δ, e). x i x i MR If a ij (x, e) 0, i j, then 2 ψ x i x j (t, x, δ, e) 2ψ(t, x, δ, e) + ψ(t, x + h MR(l i + l j ), δ, e) + ψ(t, x h MR (l i + l j ), δ, e) h 2 MR ψ(t, x + h MRl i, δ, e) + ψ(t, x h MR l i, δ, e) 2h 2 MR ψ(t, x + h MRl j, δ, e) + ψ(t, x h MR l j, δ, e) 2h 2 MR =: h MR+ ψ(t, x, δ, e). x i x j If a ij (x, e) < 0, i j, then 2 ψ x i x j (t, x, δ, e) [2ψ(t, x, δ, e) + ψ(t, x + h MR(l i l j ), δ, e) + ψ(t, x h MR (l i l j ), δ, e)] h 2 MR + ψ(t, x + h MRl i, δ, e) + ψ(t, x h MR l i, δ, e) 2h 2 MR + ψ(t, x + h MRl j, δ, e) + ψ(t, x h MR l j, δ, e) 2h 2 MR =: h MR ψ(t, x, δ, e). x i x j 64
91 1 Numerical approximation For ease of notations we write: ( h MR x ψ(t, x, δ, e) := and ( h MR xx ψ := h MR+ x i x j Time component: Latency duration: h MR+ x i ) ψ(t, x, δ, e)1 b i (x,e) 0 + h MR ψ(t, x, δ, e)1 x i b i (x,e)<0 i d Rd ) ψ(t, x, δ, e)1 a ij (x,e) 0 + h MR ψ(t, x, δ, e)1 x i x j a ij (x,e)<0 i,j d Md. ψ t (t, x, δ, e) ψ(t + h N, x, δ, e) ψ(t, x, δ, e) =: h N h t ψ(t, x, δ, e). N ψ δ (t, x, δ, e) ψ(t, x, δ, e) ψ(t, x, δ h N, e) =: h N h δ ψ(t, x, δ, e). N 1.3 Approximation scheme of (II.19) and convergence We now define Ṽ R NM as the solution on D RL NM of: H RL NMϕ(t, x, δ, e)1 x/ R d R + (ϕ(t, x, δ, e) g(x)) 1 x R d R = 0 where HNM RL ϕ(t, x, δ, e) is given by ( ) L R,e NM + h N δ ϕ(t, x, δ, e) ϕ(t + h N, x, 0, ϖ) f(x, e) on DRL ϕ(t, x, δ, e) on DRL NM D E,>0, NM D E,0, ϕ(t, x, δ, e) V(t, x, e) on DRL NM D E,T, min { (II.1) L ϖ NM ϕ(t, x, δ, e), ϕ(t, x, δ, e) MR LM [ϕ](t, x)} on DRL NM D ϖ, ϕ(t, x, δ, e) g(x) f(x, e) on DRL NM D T, with MN ϕ(t, x, δ, e) := h N t ϕ(t, x, δ, e) + b(x, e), h MR x ϕ(t, x, δ, e) + 1 [ ] 2 Tr aa (x, e) h MR xx ϕ(t, x) L R,e M R LM[ϕ](t, x) := max {δ,e ) ([δ,t t] {ih N } 1 i N ) E L ϕ(t, Π R M(x + β(x, e, δ )), δ, e ).. Here, Π R M denotes the projection operator on Rd MR with [ ] denoting the integer part. Π R M(x) := ( [( R x i R)/M]M ) i d, 65
92 NUMERICAL RESULTS From now on, we write Ṽn for Ṽ RnLn N nm n positive integers such that where (N n, M n, R n, L n ) n 1 is a sequence of N n, M n, R n, L n as n, and we denote by V and V the relaxed semilimits of Ṽn: V (t, x, δ, e) := lim sup (i h h N, i xh MR, i δ h N, e ) D (t, x, δ, e) n V (t, x, δ, e) := lim inf (i h h N, i xh MR, i δ h N, e ) D (t, x, δ, e) n Ṽ n (i h h N, i x h MR, i δ h N, e ) Ṽ n (i h h N, i x h MR, i δ h N, e ). One easily checks that the above scheme is monotone, in the terminology of [9]. Moreover, recalling (II.7) and (II.8), easy computations based on a induction argument also lead to the following uniform polynomial control on V and V under the additional classical condition: h 2 MR = h N. (II.2) Proposition II.1. The above scheme is monotone. If the condition (II.2), then there exists a constant C > 0, independent on N, M, L and R, such that V (t, x, δ, e) + V (t, x, δ, e) C(1 + x γ ) on D. Using the fact that f(, ϖ) = 0 and V(T, ) = g + f, recall (II.7) and Remark II.6, we now observe that, if a function ϕ satisfies max {ϕ V, ϕ ϕ(, 0, ϖ) f, ϕ g f} 1 e ϖ + (ϕ g f) 1 e=ϖ 0 on D T, then it also satisfies ϕ g f 0 on D T. Similarly, if it satisfies min {ϕ V, ϕ ϕ(, 0, ϖ) f, ϕ g f} 1 e ϖ + (ϕ g f) 1 e=ϖ 0 on D T, then it also satisfies ϕ g f 0 on D T. 66
93 1 Numerical approximation It then follows from the arguments of [9], and the continuity of f, g and V, see Remark II.6, that V is a supersolution on D of H ϕ = 0 and that V is a subsolution on D of H ϕ = 0 where H ϕ := H E,>0 ϕ := ( L e + δ ) ϕ on DE,>0, max {H E,>0 ϕ, ϕ ϕ(, 0, ϖ) f} on D E,0, max {H E,>0 ϕ, ϕ V} on D E,T, H ϖ ϕ := max { L ϖ ϕ ; ϕ M[ϕ] } on D ϖ, max { H E,>0 ϕ1 E + H ϖ ϕ1 {ϖ}, ϕ g f } on D T. (II.3) and H ϕ := H E,>0 ϕ := ( L e + δ ) ϕ on DE,>0, min {H E,>0 ϕ, ϕ ϕ(, 0, ϖ) f} on D E,0, min {H E,>0 ϕ, ϕ V} on D E,T, H ϖ ϕ := min { L ϖ ϕ ; ϕ M[ϕ] } on D ϖ, min { H E,>0 ϕ1 E + H ϖ ϕ1 {ϖ}, ϕ g f } on D T. (II.4) In order to conclude that V = V = V on D, it remains to prove the following result. Proposition II.2. Let ψ be lower-semicontinuous function with polynomial growth. If ψ is a viscosity supersolution (resp. subsolution) of H ϕ = 0 (resp. H ϕ = 0) on D, then ψ is a viscosity supersolution (resp. subsolution) of Hϕ = 0. Proof. We only prove the supersolution property, the subsolution property being proved by similar arguments. Let ψ be a supersolution of H ϕ = 0. Let (t 0, x 0, δ 0, e 0 ) D and let ϕ be a smooth function such that (t 0, x 0, δ 0, e 0 ) achieves a (global) minimum of ψ ϕ satisfying (ψ ϕ)(t 0, x 0, δ 0, e 0 ) = 0. If (t 0, x 0, δ 0, e 0 ) D E,>0 D ϖ then Hϕ(t 0, x 0, δ 0, e 0 ) 0. If (t 0, x 0, δ 0, e 0 ) D E,0 D T, then similar arguments as in the proof of Proposition II.5 shows that Hϕ(t 0, x 0, δ 0, e 0 ) 0 too. It remains to study the case where (t 0, x 0, δ 0, e 0 ) D E,T. (t, x) [0, T ) R d ψ(t, x, T t, e 0 ) is a supersolution of with the terminal condition max { L e 0 ϕ, ϕ V} (, e 0 ) 0 on [0, T ) R d max {ϕ g f, ϕ V} (T,, e 0 ) 0 on R d. We claim that, the map Since V is a subsolution of the same equation, recall Remark II.6, applying a standard comparison principle (recall our Lipschitz continuity and growth assumptions and see e.g. [24]), will readily implies that ψ V. 67
94 NUMERICAL RESULTS We conclude this proof by proving the above claim. Fix e 0 E, and let (t 0, x 0 ) [0, T ] R d and ϕ be smooth function such that (t 0, x 0 ) achieves a global minimum (equal to 0) of (t, x) ψ(t, x, T t, e 0 ) ϕ(t, x). For n 1, we define ϕ n by ϕ n (t, x, δ, e) := ϕ(t, x) n(t t δ) t t 0 2p x x 0 2p e e 0 2p, for p 1 such that (t, x, δ, e) D ψ(t, x, δ, e) /(1+ x p ) is bounded. Let (t n, x n, δ n, e n ) n be a global minimum point of ψ ϕ n. Writing that ψ(t 0, x 0, T t 0, e 0 ) ϕ(t 0, x 0 ) (ψ ϕ n )(t n, x n, δ n, e n ) one easily checks that = (ψ ϕ)(t n, x n, δ n, e n ) + n(t t n δ n ) + t n t 0 2p + x n x 0 2p + e n e 0 2p (ψ ϕ)(t n, x n, δ n, e n ) (t n, x n, e n ) (t 0, x 0, e 0 ), n(t t n δ n ) 0 and ψ(t n, x n, δ n, e n ) ψ(t 0, x 0, T t 0, e 0 ). (II.5) Note that, since e 0 E, we have e n ϖ for n large enough. Moreover, the supersolution property of ψ implies that H ϕ n (t n, x n, δ n, e n ) 0. Since ϕ n / t + ϕ n / δ = ϕ/ t + 2p(t n t 0 ) 2p 1, it follows from (II.5) that, for n large enough, L en ϕ(t n, x n ) ε n if (t n, x n, δ n, e n ) D E,>0, L en ϕ (ϕ V) (t n, x n, e n ) ε n if (t n, x n, δ n, e n ) D E,T, L en ϕ (ϕ g f) (t n, x n, e n ) ε n if (t n, x n, δ n, e n ) D T, (II.6) where ε n 0 as n. Taking the limit as n and using (II.5) then implies that max { L e 0 ϕ, ϕ V} (t 0, x 0, e 0 ) 0 if t 0 < T and max { L e 0 ϕ, ϕ g f, ϕ V} (t 0, x 0, e 0 ) 0 if t 0 = T which, by similar arguments as in the proof of Proposition II.5, implies that max {ϕ g f, ϕ V} (t 0, x 0, e 0 ) 0 if t 0 = T. We can now conclude by using the comparison principle of Theorem II.3, recall Proposition II.2, Proposition II.1, Theorem II.2 and Remark II.5. Theorem II.3. We have: V = V = V on D. 68
95 2 Numerical illustration - Theoretical case 2 Numerical illustration - Theoretical case As a numerical illustration, we consider the algorithm presented in Example II.8 above. Clearly, it is too simplistic for practical purposes. Our aim is not to demonstrate its superiority with respect to other well-known algorithms, but only to show how the control adapts automatically to the market conditions each time a new slice is launched, on a simple case where its behavior is predictable. We consider the following set of parameters. The trading period corresponds to a period of 3 hours. The price process is assumed to follow a Black and Scholes dynamics with zero drift S t = S 0 e 1 2 σ2 t+σw t, where S 0 := 13 and the annualized volatility is 25%. Adding a drift would only change the optimal strategy in an obvious manner, depending on its sign. We assume a deterministic evolution of the instantaneous volume traded on the market (V t ) t T as given below. It corresponds to an intensity in minutes. The impact function η is given by η(e, v) = 0.4(e/v) 1.1. This coincides with plausible calibrated data. We take δ = 5 minutes. For this numerical test, we restrict to values of the latency time in the set 5, 10,..., 60 minutes. The different values of the buying rate are 50, 100, 150,..., 500. It correspond to numbers of bought stocks per minute. The final cost is given by c(q, v) = η(q/(0.417v)), which implicitly means that the trader has 25 seconds to finalize the operation, i.e. he must buy Q in minutes at a rate Q/ We consider two different types of functions l: either l is the identity, l(r) = r, or l is of exponential type, l(r) = e 10 5r 100. The value 100 corresponds to more than four times the cost evaluated with the exponential function r e 10 5r of the operation which consists in buying stocks with a constant rate, assuming that the market volume takes the minimal value corresponding to the U-shaped path defined below, and for a constant stock price equal to 26. This is an extreme scenario. However, truncating the exponential function is needed in order to ensure that the value function is finite, since a log normal distribution does not admit exponential moments. We first consider the case where l is linear. In this case, the controller is risk neutral so that he has no incentive to buy the stock quickly because of a risk of increase of the price (recall that here the price is a martingale). In Figure II.1 and Figure II.2, we compare the case where the market volume is constant V t = 50000, on the left, to the case where the market volume is strongly U-shaped: V t = 50000( sin(πt/t )) 69
96 NUMERICAL RESULTS with T = 180 minutes. This volume is also given per minutes. Both figures provide the optimal buying rate in terms of the remaining time T t and the remaining quantity to buy Q t, for S t = S 0. A typical path has to be read from north-west to south-east, since Q decreases as time goes buy. As expected, when the path of the market volume is U- shaped the optimal rate strongly decreases in the middle of the period, when the market volume is low and the impact on the price of the stock is high. This is compensated by a higher rate at the beginning of the period. In Figure II.5 and Figure II.6, we provide the maximal value of the optimal latency time δ. Recall that the existence of multiple optima is possible since there is no additional cost related to the launching of a new slice, see Remark II.1. In most cases, the maximal value is strictly above the minimal threshold of 5 minutes. This support our choice of considering the latency time as a control, even in the absence of a cost associated to a change of parameters: when a latency time of, e.g., 15 minutes is optimal, the trader can let the algorithm run for this time period without having to launch it again every 5 minutes, and thus take care of his other positions. In the case where the market volume is strongly U-shaped, it is smaller at the beginning of the trading period, in comparison to the constant volume case. This is due to the fact that the algorithm knows that the market volume is going to decrease strongly (since it is deterministic) and that he will need to reduce the buying rate. It is small near the terminal time because of the constraint t+δ T. When looking at the picture backward in time, i.e. as T t increases, we see that the maximal value first increases and then drops down very quickly. The first phenomena is due to the fact that the buying rate is essentially kept constant at its maximal value near the terminal time. Then, this rate decreases as the algorithm has more time to buy the shares. The period during which the algorithm reduces the buying rate naturally coincides with a lower latency time. We next consider the case where l is of exponential type. The optimal buying rates are reported in Figures II.3-II.4. Because the controller is now risk adverse, he has an incentive to buy the stocks more quickly in order to avoid an increase of the price. This can be seen by comparing Figures II.3-II.4 with Figures II.1-II.2. However, we do not observe significant changes in the maximal optimal latency times. 70
97 2 Numerical illustration - Theoretical case Figure II.1: Buying rate - flat volume - Linear cost Figure II.2: Buying rate - U-shaped volume - Linear cost Figure II.3: Buying rate - flat volume - Exponential cost Figure II.4: Buying rate - U-shaped volume - Exponential cost 71
98 NUMERICAL RESULTS Figure II.5: Latency period - flat volume - Linear cost Figure II.6: Latency period - U-shaped volume - Linear cost Figure II.7: Latency period - flat volume - Exponential cost Figure II.8: Latency period - U-shaped volume - Exponential cost 3 Numerical illustrations - Real case We consider the problem is a real case, where the volume curve and the volatility curve are estimated from real data. The dataset consists of all transactions from January to December 2008 of France Telecom, we normalize the volume such that average daily volume =
Introduction. GEAL Bibliothèque Java pour écrire des algorithmes évolutionnaires. Objectifs. Simplicité Evolution et coévolution Parallélisme
 GEAL 1.2 Generic Evolutionary Algorithm Library http://dpt-info.u-strasbg.fr/~blansche/fr/geal.html 1 /38 Introduction GEAL Bibliothèque Java pour écrire des algorithmes évolutionnaires Objectifs Généricité
GEAL 1.2 Generic Evolutionary Algorithm Library http://dpt-info.u-strasbg.fr/~blansche/fr/geal.html 1 /38 Introduction GEAL Bibliothèque Java pour écrire des algorithmes évolutionnaires Objectifs Généricité
Parallel Discrepancy-based Search
 Parallel Discrepancy-based Search T. Moisan, J. Gaudreault, C.-G. Quimper Université Laval, FORAC research consortium February 21 th 2014 T. Moisan, J. Gaudreault, C.-G. Quimper Parallel Discrepancy-based
Parallel Discrepancy-based Search T. Moisan, J. Gaudreault, C.-G. Quimper Université Laval, FORAC research consortium February 21 th 2014 T. Moisan, J. Gaudreault, C.-G. Quimper Parallel Discrepancy-based
General Certificate of Education Advanced Level Examination June 2012
 General Certificate of Education Advanced Level Examination June 2012 French Unit 4 Speaking Test Candidate s Material To be conducted by the teacher examiner between 7 March and 15 May 2012 (FRE4T) To
General Certificate of Education Advanced Level Examination June 2012 French Unit 4 Speaking Test Candidate s Material To be conducted by the teacher examiner between 7 March and 15 May 2012 (FRE4T) To
Méthodes ensemblistes pour une localisation robuste de robots sous-marins
 Méthodes ensemblistes pour une localisation robuste de robots sous-marins Jan Sliwka To cite this version: Jan Sliwka. Méthodes ensemblistes pour une localisation robuste de robots sous-marins. Automatique
Méthodes ensemblistes pour une localisation robuste de robots sous-marins Jan Sliwka To cite this version: Jan Sliwka. Méthodes ensemblistes pour une localisation robuste de robots sous-marins. Automatique
BILL C-665 PROJET DE LOI C-665 C-665 C-665 HOUSE OF COMMONS OF CANADA CHAMBRE DES COMMUNES DU CANADA
 C-665 C-665 Second Session, Forty-first Parliament, Deuxième session, quarante et unième législature, HOUSE OF COMMONS OF CANADA CHAMBRE DES COMMUNES DU CANADA BILL C-665 PROJET DE LOI C-665 An Act to
C-665 C-665 Second Session, Forty-first Parliament, Deuxième session, quarante et unième législature, HOUSE OF COMMONS OF CANADA CHAMBRE DES COMMUNES DU CANADA BILL C-665 PROJET DE LOI C-665 An Act to
Optimal order placement in a limit order book. Adrien de Larrard and Xin Guo. Laboratoire de Probabilités, Univ Paris VI & UC Berkeley
 Optimal order placement in a limit order book Laboratoire de Probabilités, Univ Paris VI & UC Berkeley Outline 1 Background: Algorithm trading in different time scales 2 Some note on optimal execution
Optimal order placement in a limit order book Laboratoire de Probabilités, Univ Paris VI & UC Berkeley Outline 1 Background: Algorithm trading in different time scales 2 Some note on optimal execution
Memory Eye SSTIC 2011. Yoann Guillot. Sogeti / ESEC R&D yoann.guillot(at)sogeti.com
 Memory Eye SSTIC 2011 Yoann Guillot Sogeti / ESEC R&D yoann.guillot(at)sogeti.com Y. Guillot Memory Eye 2/33 Plan 1 2 3 4 Y. Guillot Memory Eye 3/33 Memory Eye Analyse globale d un programme Un outil pour
Memory Eye SSTIC 2011 Yoann Guillot Sogeti / ESEC R&D yoann.guillot(at)sogeti.com Y. Guillot Memory Eye 2/33 Plan 1 2 3 4 Y. Guillot Memory Eye 3/33 Memory Eye Analyse globale d un programme Un outil pour
AgroMarketDay. Research Application Summary pp: 371-375. Abstract
 Fourth RUFORUM Biennial Regional Conference 21-25 July 2014, Maputo, Mozambique 371 Research Application Summary pp: 371-375 AgroMarketDay Katusiime, L. 1 & Omiat, I. 1 1 Kampala, Uganda Corresponding
Fourth RUFORUM Biennial Regional Conference 21-25 July 2014, Maputo, Mozambique 371 Research Application Summary pp: 371-375 AgroMarketDay Katusiime, L. 1 & Omiat, I. 1 1 Kampala, Uganda Corresponding
International Diversification and Exchange Rates Risk. Summary
 International Diversification and Exchange Rates Risk Y. K. Ip School of Accounting and Finance, University College of Southern Queensland, Toowoomba, Queensland 4350, Australia Summary The benefits arisen
International Diversification and Exchange Rates Risk Y. K. Ip School of Accounting and Finance, University College of Southern Queensland, Toowoomba, Queensland 4350, Australia Summary The benefits arisen
Audit de sécurité avec Backtrack 5
 Audit de sécurité avec Backtrack 5 DUMITRESCU Andrei EL RAOUSTI Habib Université de Versailles Saint-Quentin-En-Yvelines 24-05-2012 UVSQ - Audit de sécurité avec Backtrack 5 DUMITRESCU Andrei EL RAOUSTI
Audit de sécurité avec Backtrack 5 DUMITRESCU Andrei EL RAOUSTI Habib Université de Versailles Saint-Quentin-En-Yvelines 24-05-2012 UVSQ - Audit de sécurité avec Backtrack 5 DUMITRESCU Andrei EL RAOUSTI
AP FRENCH LANGUAGE 2008 SCORING GUIDELINES
 AP FRENCH LANGUAGE 2008 SCORING GUIDELINES Part A (Essay): Question 31 9 Demonstrates STRONG CONTROL Excellence Ease of expression marked by a good sense of idiomatic French. Clarity of organization. Accuracy
AP FRENCH LANGUAGE 2008 SCORING GUIDELINES Part A (Essay): Question 31 9 Demonstrates STRONG CONTROL Excellence Ease of expression marked by a good sense of idiomatic French. Clarity of organization. Accuracy
Level 2 French, 2014
 91121 911210 2SUPERVISOR S Level 2 French, 2014 91121 Demonstrate understanding of a variety of written and / or visual French text(s) on familiar matters 9.30 am Wednesday 26 November 2014 Credits: Five
91121 911210 2SUPERVISOR S Level 2 French, 2014 91121 Demonstrate understanding of a variety of written and / or visual French text(s) on familiar matters 9.30 am Wednesday 26 November 2014 Credits: Five
Office of the Auditor General / Bureau du vérificateur général FOLLOW-UP TO THE 2010 AUDIT OF COMPRESSED WORK WEEK AGREEMENTS 2012 SUIVI DE LA
 Office of the Auditor General / Bureau du vérificateur général FOLLOW-UP TO THE 2010 AUDIT OF COMPRESSED WORK WEEK AGREEMENTS 2012 SUIVI DE LA VÉRIFICATION DES ENTENTES DE SEMAINE DE TRAVAIL COMPRIMÉE
Office of the Auditor General / Bureau du vérificateur général FOLLOW-UP TO THE 2010 AUDIT OF COMPRESSED WORK WEEK AGREEMENTS 2012 SUIVI DE LA VÉRIFICATION DES ENTENTES DE SEMAINE DE TRAVAIL COMPRIMÉE
Note concernant votre accord de souscription au service «Trusted Certificate Service» (TCS)
 Note concernant votre accord de souscription au service «Trusted Certificate Service» (TCS) Veuillez vérifier les éléments suivants avant de nous soumettre votre accord : 1. Vous avez bien lu et paraphé
Note concernant votre accord de souscription au service «Trusted Certificate Service» (TCS) Veuillez vérifier les éléments suivants avant de nous soumettre votre accord : 1. Vous avez bien lu et paraphé
Qu est-ce que le Cloud? Quels sont ses points forts? Pourquoi l'adopter? Hugues De Pra Data Center Lead Cisco Belgium & Luxemburg
 Qu est-ce que le Cloud? Quels sont ses points forts? Pourquoi l'adopter? Hugues De Pra Data Center Lead Cisco Belgium & Luxemburg Agenda Le Business Case pour le Cloud Computing Qu est ce que le Cloud
Qu est-ce que le Cloud? Quels sont ses points forts? Pourquoi l'adopter? Hugues De Pra Data Center Lead Cisco Belgium & Luxemburg Agenda Le Business Case pour le Cloud Computing Qu est ce que le Cloud
FOR TEACHERS ONLY The University of the State of New York
 FOR TEACHERS ONLY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION F COMPREHENSIVE EXAMINATION IN FRENCH Friday, June 16, 2006 1:15 to 4:15 p.m., only SCORING KEY Updated information
FOR TEACHERS ONLY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION F COMPREHENSIVE EXAMINATION IN FRENCH Friday, June 16, 2006 1:15 to 4:15 p.m., only SCORING KEY Updated information
Processus de Lévy en Finance: Modélisation de Dépendance
 Thèse présentée pour obtenir le titre de DOCTEUR DE L ECOLE POLYTECHNIQUE specialité: Mathématiques Appliquées par Peter TANKOV Processus de Lévy en Finance: Problèmes Inverses et Modélisation de Dépendance
Thèse présentée pour obtenir le titre de DOCTEUR DE L ECOLE POLYTECHNIQUE specialité: Mathématiques Appliquées par Peter TANKOV Processus de Lévy en Finance: Problèmes Inverses et Modélisation de Dépendance
STUDENT APPLICATION FORM (Dossier d Inscription) ACADEMIC YEAR 2010-2011 (Année Scolaire 2010-2011)
 Institut d Administration des Entreprises SOCRATES/ERASMUS APPLICATION DEADLINE : 20th November 2010 OTHER (Autre) STUDENT APPLICATION FORM (Dossier d Inscription) ACADEMIC YEAR 2010-2011 (Année Scolaire
Institut d Administration des Entreprises SOCRATES/ERASMUS APPLICATION DEADLINE : 20th November 2010 OTHER (Autre) STUDENT APPLICATION FORM (Dossier d Inscription) ACADEMIC YEAR 2010-2011 (Année Scolaire
Statistiques en grande dimension
 Statistiques en grande dimension Christophe Giraud 1,2 et Tristan Mary-Huart 3,4 (1) Université Paris-Sud (2) Ecole Polytechnique (3) AgroParistech (4) INRA - Le Moulon M2 MathSV & Maths Aléa C. Giraud
Statistiques en grande dimension Christophe Giraud 1,2 et Tristan Mary-Huart 3,4 (1) Université Paris-Sud (2) Ecole Polytechnique (3) AgroParistech (4) INRA - Le Moulon M2 MathSV & Maths Aléa C. Giraud
How To Become A Foreign Language Teacher
 Université d Artois U.F.R. de Langues Etrangères MASTER A DISTANCE Master Arts, Lettres et Langues Spécialité «CLE/ CLS en milieu scolaire» Voie Professionnelle ou Voie Recherche University of Artois Faculty
Université d Artois U.F.R. de Langues Etrangères MASTER A DISTANCE Master Arts, Lettres et Langues Spécialité «CLE/ CLS en milieu scolaire» Voie Professionnelle ou Voie Recherche University of Artois Faculty
Finding a research subject in educational technology
 Finding a research subject in educational technology Finding a research subject in educational technology thesis-subject (version 1.0, 1/4/05 ) Code: thesis-subject Daniel K. Schneider, TECFA, University
Finding a research subject in educational technology Finding a research subject in educational technology thesis-subject (version 1.0, 1/4/05 ) Code: thesis-subject Daniel K. Schneider, TECFA, University
Execution Costs. Post-trade reporting. December 17, 2008 Robert Almgren / Encyclopedia of Quantitative Finance Execution Costs 1
 December 17, 2008 Robert Almgren / Encyclopedia of Quantitative Finance Execution Costs 1 Execution Costs Execution costs are the difference in value between an ideal trade and what was actually done.
December 17, 2008 Robert Almgren / Encyclopedia of Quantitative Finance Execution Costs 1 Execution Costs Execution costs are the difference in value between an ideal trade and what was actually done.
Survey on Conference Services provided by the United Nations Office at Geneva
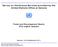 Survey on Conference Services provided by the United Nations Office at Geneva Trade and Development Board, fifty-eighth session Geneva, 12-23 September 2011 Contents Survey contents Evaluation criteria
Survey on Conference Services provided by the United Nations Office at Geneva Trade and Development Board, fifty-eighth session Geneva, 12-23 September 2011 Contents Survey contents Evaluation criteria
Office of the Auditor General / Bureau du vérificateur général FOLLOW-UP TO THE 2007 AUDIT OF THE DISPOSAL OF PAVEMENT LINE MARKER EQUIPMENT 2009
 Office of the Auditor General / Bureau du vérificateur général FOLLOW-UP TO THE 2007 AUDIT OF THE DISPOSAL OF PAVEMENT LINE MARKER EQUIPMENT 2009 SUIVI DE LA VÉRIFICATION DE L ALIÉNATION D UNE TRACEUSE
Office of the Auditor General / Bureau du vérificateur général FOLLOW-UP TO THE 2007 AUDIT OF THE DISPOSAL OF PAVEMENT LINE MARKER EQUIPMENT 2009 SUIVI DE LA VÉRIFICATION DE L ALIÉNATION D UNE TRACEUSE
Open call for tenders n SCIC C4 2014/01
 EUROPEAN COMMISSION DIRECTORATE GENERAL FOR INTERPRETATION RESOURCES AND SUPPORT DIRECTORATE Open call for tenders n SCIC C4 2014/01 Accident and sickness insurance for Conference Interpreting Agents Questions
EUROPEAN COMMISSION DIRECTORATE GENERAL FOR INTERPRETATION RESOURCES AND SUPPORT DIRECTORATE Open call for tenders n SCIC C4 2014/01 Accident and sickness insurance for Conference Interpreting Agents Questions
Les Cahiers du GERAD ISSN: 0711 2440
 Les Cahiers du GERAD ISSN: 0711 2440 Filtering for Detecting Multiple Targets Trajectories on a One-Dimensional Torus Ivan Gentil Bruno Rémillard G 2003 09 February 2003 Les textes publiés dans la série
Les Cahiers du GERAD ISSN: 0711 2440 Filtering for Detecting Multiple Targets Trajectories on a One-Dimensional Torus Ivan Gentil Bruno Rémillard G 2003 09 February 2003 Les textes publiés dans la série
Évariste Galois and Solvable Permutation Groups
 Évariste Galois and Solvable Permutation Groups David A. Cox Department of Mathematics Amherst College dac@math.amherst.edu Bilbao May 2012 Prologue Most mathematicians know about Galois: He introduced
Évariste Galois and Solvable Permutation Groups David A. Cox Department of Mathematics Amherst College dac@math.amherst.edu Bilbao May 2012 Prologue Most mathematicians know about Galois: He introduced
Archived Content. Contenu archivé
 ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
FE570 Financial Markets and Trading. Stevens Institute of Technology
 FE570 Financial Markets and Trading Lecture 13. Execution Strategies (Ref. Anatoly Schmidt CHAPTER 13 Execution Strategies) Steve Yang Stevens Institute of Technology 11/27/2012 Outline 1 Execution Strategies
FE570 Financial Markets and Trading Lecture 13. Execution Strategies (Ref. Anatoly Schmidt CHAPTER 13 Execution Strategies) Steve Yang Stevens Institute of Technology 11/27/2012 Outline 1 Execution Strategies
Sun StorEdge A5000 Installation Guide
 Sun StorEdge A5000 Installation Guide for Windows NT Server 4.0 Sun Microsystems, Inc. 901 San Antonio Road Palo Alto, CA 94303-4900 USA 650 960-1300 Fax 650 969-9131 Part No. 805-7273-11 October 1998,
Sun StorEdge A5000 Installation Guide for Windows NT Server 4.0 Sun Microsystems, Inc. 901 San Antonio Road Palo Alto, CA 94303-4900 USA 650 960-1300 Fax 650 969-9131 Part No. 805-7273-11 October 1998,
COLLABORATIVE LCA. Rachel Arnould and Thomas Albisser. Hop-Cube, France
 COLLABORATIVE LCA Rachel Arnould and Thomas Albisser Hop-Cube, France Abstract Ecolabels, standards, environmental labeling: product category rules supporting the desire for transparency on products environmental
COLLABORATIVE LCA Rachel Arnould and Thomas Albisser Hop-Cube, France Abstract Ecolabels, standards, environmental labeling: product category rules supporting the desire for transparency on products environmental
AP FRENCH LANGUAGE AND CULTURE 2013 SCORING GUIDELINES
 AP FRENCH LANGUAGE AND CULTURE 2013 SCORING GUIDELINES Interpersonal Writing: E-mail Reply 5: STRONG performance in Interpersonal Writing Maintains the exchange with a response that is clearly appropriate
AP FRENCH LANGUAGE AND CULTURE 2013 SCORING GUIDELINES Interpersonal Writing: E-mail Reply 5: STRONG performance in Interpersonal Writing Maintains the exchange with a response that is clearly appropriate
Performance Modeling of TCP/IP in a Wide-Area Network
 INSTITUT NATIONAL DE RECHERCHE EN INFORMATIQUE ET EN AUTOMATIQUE Performance Modeling of TCP/IP in a Wide-Area Network Eitan Altman, Jean Bolot, Philippe Nain, Driss Elouadghiri, Mohammed Erramdani, Patrick
INSTITUT NATIONAL DE RECHERCHE EN INFORMATIQUE ET EN AUTOMATIQUE Performance Modeling of TCP/IP in a Wide-Area Network Eitan Altman, Jean Bolot, Philippe Nain, Driss Elouadghiri, Mohammed Erramdani, Patrick
SIXTH FRAMEWORK PROGRAMME PRIORITY [6
 Key technology : Confidence E. Fournier J.M. Crepel - Validation and certification - QA procedure, - standardisation - Correlation with physical tests - Uncertainty, robustness - How to eliminate a gateway
Key technology : Confidence E. Fournier J.M. Crepel - Validation and certification - QA procedure, - standardisation - Correlation with physical tests - Uncertainty, robustness - How to eliminate a gateway
How To Find Out How Roots Of A Polynome Are Calculated
 Localisation des racines d un polynome et de ses dérivées, étude statistique André Galligo Laboratoire J.-A. Dieudonné UMR CNRS 6621 Université de Nice - Sophia Antipolis, France et projet-commun Galaad
Localisation des racines d un polynome et de ses dérivées, étude statistique André Galligo Laboratoire J.-A. Dieudonné UMR CNRS 6621 Université de Nice - Sophia Antipolis, France et projet-commun Galaad
Sun Management Center Change Manager 1.0.1 Release Notes
 Sun Management Center Change Manager 1.0.1 Release Notes Sun Microsystems, Inc. 4150 Network Circle Santa Clara, CA 95054 U.S.A. Part No: 817 0891 10 May 2003 Copyright 2003 Sun Microsystems, Inc. 4150
Sun Management Center Change Manager 1.0.1 Release Notes Sun Microsystems, Inc. 4150 Network Circle Santa Clara, CA 95054 U.S.A. Part No: 817 0891 10 May 2003 Copyright 2003 Sun Microsystems, Inc. 4150
 Rio de Janeiro. Tout simplement, HISTORIQUE! RESULTATS SPORTIFS Christophe PINNA NICE ELITE SPORT 21, bd Carnot 06300 Nice Tél. : +33 (0)6 08 45 80 07 Fax : +33 (0)4 93 56 78 77 Email : c.pinna@wanadoo.fr
Rio de Janeiro. Tout simplement, HISTORIQUE! RESULTATS SPORTIFS Christophe PINNA NICE ELITE SPORT 21, bd Carnot 06300 Nice Tél. : +33 (0)6 08 45 80 07 Fax : +33 (0)4 93 56 78 77 Email : c.pinna@wanadoo.fr
Enterprise Risk Management & Board members. GUBERNA Alumni Event June 19 th 2014 Prepared by Gaëtan LEFEVRE
 Enterprise Risk Management & Board members GUBERNA Alumni Event June 19 th 2014 Prepared by Gaëtan LEFEVRE Agenda Introduction Do we need Risk Management? The 8 th EU Company Law Directive Art 41, 2b Three
Enterprise Risk Management & Board members GUBERNA Alumni Event June 19 th 2014 Prepared by Gaëtan LEFEVRE Agenda Introduction Do we need Risk Management? The 8 th EU Company Law Directive Art 41, 2b Three
ANIMATION OF CONTINUOUS COMPUTER SIMULATIONS C.M. Woodside and Richard Mallet Computer Center, Carleton University ABSTRACT
 19.1 ANIMATION OF CONTINUOUS COMPUTER SIMULATIONS C.M. Woodside and Richard Mallet Computer Center, Carleton University ABSTRACT A block-oriented graphics program called ANIM8 has been developed for animating
19.1 ANIMATION OF CONTINUOUS COMPUTER SIMULATIONS C.M. Woodside and Richard Mallet Computer Center, Carleton University ABSTRACT A block-oriented graphics program called ANIM8 has been developed for animating
Advanced Software Engineering Agile Software Engineering. Version 1.0
 Advanced Software Engineering Agile Software Engineering 1 Version 1.0 Basic direction A agile method has to be A method is called agile if it follows Incremental the principles of the agile manifest.
Advanced Software Engineering Agile Software Engineering 1 Version 1.0 Basic direction A agile method has to be A method is called agile if it follows Incremental the principles of the agile manifest.
Guidance on Extended Producer Responsibility (EPR) Analysis of EPR schemes in the EU and development of guiding principles for their functioning
 (EPR) Analysis of in the EU and development of guiding principles for their functioning In association with: ACR+ SITA LUNCH DEBATE 25 September 2014 Content 1. Objectives and 2. General overview of in
(EPR) Analysis of in the EU and development of guiding principles for their functioning In association with: ACR+ SITA LUNCH DEBATE 25 September 2014 Content 1. Objectives and 2. General overview of in
EPREUVE D EXPRESSION ORALE. SAVOIR et SAVOIR-FAIRE
 EPREUVE D EXPRESSION ORALE SAVOIR et SAVOIR-FAIRE Pour présenter la notion -The notion I m going to deal with is The idea of progress / Myths and heroes Places and exchanges / Seats and forms of powers
EPREUVE D EXPRESSION ORALE SAVOIR et SAVOIR-FAIRE Pour présenter la notion -The notion I m going to deal with is The idea of progress / Myths and heroes Places and exchanges / Seats and forms of powers
In-Home Caregivers Teleconference with Canadian Bar Association September 17, 2015
 In-Home Caregivers Teleconference with Canadian Bar Association September 17, 2015 QUESTIONS FOR ESDC Temporary Foreign Worker Program -- Mr. Steve WEST *Answers have been updated following the conference
In-Home Caregivers Teleconference with Canadian Bar Association September 17, 2015 QUESTIONS FOR ESDC Temporary Foreign Worker Program -- Mr. Steve WEST *Answers have been updated following the conference
N1 Grid Service Provisioning System 5.0 User s Guide for the Linux Plug-In
 N1 Grid Service Provisioning System 5.0 User s Guide for the Linux Plug-In Sun Microsystems, Inc. 4150 Network Circle Santa Clara, CA 95054 U.S.A. Part No: 819 0735 December 2004 Copyright 2004 Sun Microsystems,
N1 Grid Service Provisioning System 5.0 User s Guide for the Linux Plug-In Sun Microsystems, Inc. 4150 Network Circle Santa Clara, CA 95054 U.S.A. Part No: 819 0735 December 2004 Copyright 2004 Sun Microsystems,
Archived Content. Contenu archivé
 ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
Altiris Patch Management Solution for Windows 7.6 from Symantec Third-Party Legal Notices
 Appendix A Altiris Patch Management Solution for Windows 7.6 from Symantec Third-Party Legal Notices This appendix includes the following topics: Third-Party Legal Attributions CabDotNet MICROSOFT PLATFORM
Appendix A Altiris Patch Management Solution for Windows 7.6 from Symantec Third-Party Legal Notices This appendix includes the following topics: Third-Party Legal Attributions CabDotNet MICROSOFT PLATFORM
Introduction au BIM. ESEB 38170 Seyssinet-Pariset Economie de la construction email : contact@eseb.fr
 Quel est l objectif? 1 La France n est pas le seul pays impliqué 2 Une démarche obligatoire 3 Une organisation plus efficace 4 Le contexte 5 Risque d erreur INTERVENANTS : - Architecte - Économiste - Contrôleur
Quel est l objectif? 1 La France n est pas le seul pays impliqué 2 Une démarche obligatoire 3 Une organisation plus efficace 4 Le contexte 5 Risque d erreur INTERVENANTS : - Architecte - Économiste - Contrôleur
Sun Enterprise Optional Power Sequencer Installation Guide
 Sun Enterprise Optional Power Sequencer Installation Guide For the Sun Enterprise 6500/5500 System Cabinet and the Sun Enterprise 68-inch Expansion Cabinet Sun Microsystems, Inc. 901 San Antonio Road Palo
Sun Enterprise Optional Power Sequencer Installation Guide For the Sun Enterprise 6500/5500 System Cabinet and the Sun Enterprise 68-inch Expansion Cabinet Sun Microsystems, Inc. 901 San Antonio Road Palo
Le projet européen ECOLABEL
 4/02/2015 Le projet européen ECOLABEL Agnès JULLIEN (Ifsttar) WP1 leader (key performance indicators) agnes.jullien@ifsttar.fr ECOLABEL PROJECT PROPOSED METHODOLOGY and KPIs Main concepts Development of
4/02/2015 Le projet européen ECOLABEL Agnès JULLIEN (Ifsttar) WP1 leader (key performance indicators) agnes.jullien@ifsttar.fr ECOLABEL PROJECT PROPOSED METHODOLOGY and KPIs Main concepts Development of
Archived Content. Contenu archivé
 ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
TIMISKAMING FIRST NATION
 Post-Secondary Financial Assistance Forms TFN EDUCATION 2014-05-01 TIMISKAMING FIRST NATION 0 Education Dept. Application Check List Please enclose the following when applying: Form: Statement of Intent
Post-Secondary Financial Assistance Forms TFN EDUCATION 2014-05-01 TIMISKAMING FIRST NATION 0 Education Dept. Application Check List Please enclose the following when applying: Form: Statement of Intent
The Need For Speed. leads to PostgreSQL. Dimitri Fontaine dimitri@2ndquadrant.fr. 28 Mars 2013
 The Need For Speed leads to PostgreSQL Dimitri Fontaine dimitri@2ndquadrant.fr 28 Mars 2013 Dimitri Fontaine dimitri@2ndquadrant.fr The Need For Speed 28 Mars 2013 1 / 23 Dimitri Fontaine 2ndQuadrant France
The Need For Speed leads to PostgreSQL Dimitri Fontaine dimitri@2ndquadrant.fr 28 Mars 2013 Dimitri Fontaine dimitri@2ndquadrant.fr The Need For Speed 28 Mars 2013 1 / 23 Dimitri Fontaine 2ndQuadrant France
ENABLING OBJECTIVE AND TEACHING POINTS. DRILL: 401.02 5. TIME: One 30 minutes period. 6. METHOD/APPROACH: a. demonstration; and. b. performance.
 CHAPTER 4: LESSON SPECIFICATIONS COURSE TITLE: GREEN STAR COURSE ENABLING OBJECTIVE AND TEACHING POINTS CTS NUMBER: A-CR-CCP-116/PC-001 TRAINING DETAILS DRILL: 401.02 5. TIME: One 30 minutes period. 1.
CHAPTER 4: LESSON SPECIFICATIONS COURSE TITLE: GREEN STAR COURSE ENABLING OBJECTIVE AND TEACHING POINTS CTS NUMBER: A-CR-CCP-116/PC-001 TRAINING DETAILS DRILL: 401.02 5. TIME: One 30 minutes period. 1.
-Duplication of Time-Varying Graphs
 -Duplication of Time-Varying Graphs François Queyroi Sorbonne Universités, UPMC Univ Paris 06, UMR 7606, LIP6, F-75005, Paris CNRS, UMR 7606, LIP6, F-75005, Paris, France francois.queyroi@lip6.fr ABSTRACT.
-Duplication of Time-Varying Graphs François Queyroi Sorbonne Universités, UPMC Univ Paris 06, UMR 7606, LIP6, F-75005, Paris CNRS, UMR 7606, LIP6, F-75005, Paris, France francois.queyroi@lip6.fr ABSTRACT.
Marks Communication /10 Range and Accuracy of Language /10 Pronunciation and Intonation /5 Interaction and Fluency /5 TOTAL /30
 Controlled Speaking Assessment Preparation Once you have prepared your answers to the questions record your answers and listen back to them as you listen, complete the check sheet below : Time it to ensure
Controlled Speaking Assessment Preparation Once you have prepared your answers to the questions record your answers and listen back to them as you listen, complete the check sheet below : Time it to ensure
Altiris Patch Management Solution for Windows 7.5 SP1 from Symantec Third-Party Legal Notices
 Appendix A Altiris Patch Management Solution for Windows 7.5 SP1 from Symantec Third-Party Legal Notices This appendix includes the following topics: Third-Party Legal Attributions CabDotNet XML-RPC.NET
Appendix A Altiris Patch Management Solution for Windows 7.5 SP1 from Symantec Third-Party Legal Notices This appendix includes the following topics: Third-Party Legal Attributions CabDotNet XML-RPC.NET
MD. ALI KHAN. and THE MINISTER OF CITIZENSHIP AND IMMIGRATION REASONS FOR ORDER AND ORDER
 Federal Court Cour fédérale Date: 20101001 Docket: IMM-1196-10 Citation: 2010 FC 983 St. John s, Newfoundland and Labrador, October 1, 2010 PRESENT: The Honourable Madam Justice Heneghan BETWEEN: MD. ALI
Federal Court Cour fédérale Date: 20101001 Docket: IMM-1196-10 Citation: 2010 FC 983 St. John s, Newfoundland and Labrador, October 1, 2010 PRESENT: The Honourable Madam Justice Heneghan BETWEEN: MD. ALI
HEALTH CARE DIRECTIVES ACT
 A11 HEALTH CARE DIRECTIVES ACT Advances in medical research and treatments have, in many cases, enabled health care professionals to extend lives. Most of these advancements are welcomed, but some people
A11 HEALTH CARE DIRECTIVES ACT Advances in medical research and treatments have, in many cases, enabled health care professionals to extend lives. Most of these advancements are welcomed, but some people
---------------------------------------------------------------------------------
 Hume Fogg Academic Magnet Summer Review for Students Entering AP French Language Student Name --------------------------------------------------------------------------------- Teacher: Jessica Sexton Email:
Hume Fogg Academic Magnet Summer Review for Students Entering AP French Language Student Name --------------------------------------------------------------------------------- Teacher: Jessica Sexton Email:
Il est repris ci-dessous sans aucune complétude - quelques éléments de cet article, dont il est fait des citations (texte entre guillemets).
 Modélisation déclarative et sémantique, ontologies, assemblage et intégration de modèles, génération de code Declarative and semantic modelling, ontologies, model linking and integration, code generation
Modélisation déclarative et sémantique, ontologies, assemblage et intégration de modèles, génération de code Declarative and semantic modelling, ontologies, model linking and integration, code generation
From Support Vector Machines to Hybrid System Identification
 From Support Vector Machines to Hybrid System Identification Fabien Lauer To cite this version: Fabien Lauer. From Support Vector Machines to Hybrid System Identification. Automatic. Université Henri Poincaré
From Support Vector Machines to Hybrid System Identification Fabien Lauer To cite this version: Fabien Lauer. From Support Vector Machines to Hybrid System Identification. Automatic. Université Henri Poincaré
ACP-EU Cooperation Programme in Science and Technology (S&T II) / Programme de Coopération ACP-UE pour la Science et la Technologie
 ACP Science and Technologie Programme Programme Management Unit ACP-EU Cooperation Programme in Science and Technology (S&T II) / Programme de Coopération ACP-UE pour la Science et la Technologie EuropeAid/133437/D/ACT/ACPTPS
ACP Science and Technologie Programme Programme Management Unit ACP-EU Cooperation Programme in Science and Technology (S&T II) / Programme de Coopération ACP-UE pour la Science et la Technologie EuropeAid/133437/D/ACT/ACPTPS
Competitive Intelligence en quelques mots
 Competitive Intelligence en quelques mots Henri Dou douhenri@yahoo.fr http://www.ciworldwide.org Professeur des Universités Directeur d Atelis (Intelligence Workroom) Groupe ESCEM Consultant WIPO (World
Competitive Intelligence en quelques mots Henri Dou douhenri@yahoo.fr http://www.ciworldwide.org Professeur des Universités Directeur d Atelis (Intelligence Workroom) Groupe ESCEM Consultant WIPO (World
FATMAS : A Methodology to Design Fault-tolerant Multi-agent Systems
 SEHL MELLOULI FATMAS : A Methodology to Design Fault-tolerant Multi-agent Systems Thèse présentée à la Faculté des études supérieures de l Université Laval dans le cadre du programme de doctorat en Informatique
SEHL MELLOULI FATMAS : A Methodology to Design Fault-tolerant Multi-agent Systems Thèse présentée à la Faculté des études supérieures de l Université Laval dans le cadre du programme de doctorat en Informatique
EFFECTS OF FORCE LEVEL AND TIME LAPSES AFTER TASK PERFORMANCE ON THE ACCURACY OF FORCE MATCHING IN A POWER-GRIP TRACKING TASK
 EFFECTS OF FORCE LEVEL AND TIME LAPSES AFTER TASK PERFORMANCE ON THE ACCURACY OF FORCE MATCHING IN A POWER-GRIP TRACKING TASK LAING, ANDREW C.T. Ergonomics Initiative in Injury Prevention. Faculty of Applied
EFFECTS OF FORCE LEVEL AND TIME LAPSES AFTER TASK PERFORMANCE ON THE ACCURACY OF FORCE MATCHING IN A POWER-GRIP TRACKING TASK LAING, ANDREW C.T. Ergonomics Initiative in Injury Prevention. Faculty of Applied
«Environnement Economique de l Entreprise»
 MASTER Administration des Entreprises Apprentissage Stéphane Saussier Saussier@univ-paris1.fr «Environnement Economique de l Entreprise» Séance 5 - Incentives in Organization - SSA 2015-1 Incentive Theory
MASTER Administration des Entreprises Apprentissage Stéphane Saussier Saussier@univ-paris1.fr «Environnement Economique de l Entreprise» Séance 5 - Incentives in Organization - SSA 2015-1 Incentive Theory
Measuring Policing Complexity: A Research Based Agenda
 ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
Bayesian Adaptive Trading with a Daily Cycle
 Bayesian Adaptive Trading with a Daily Cycle Robert Almgren and Julian Lorenz July 28, 26 Abstract Standard models of algorithmic trading neglect the presence of a daily cycle. We construct a model in
Bayesian Adaptive Trading with a Daily Cycle Robert Almgren and Julian Lorenz July 28, 26 Abstract Standard models of algorithmic trading neglect the presence of a daily cycle. We construct a model in
Archived Content. Contenu archivé
 ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
FOR TEACHERS ONLY The University of the State of New York
 FOR TEACHERS ONLY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION F COMPREHENSIVE EXAMINATION IN FRENCH Wednesday, June 22, 2011 9:15 a.m. to 12:15 p.m., only SCORING KEY Updated
FOR TEACHERS ONLY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION F COMPREHENSIVE EXAMINATION IN FRENCH Wednesday, June 22, 2011 9:15 a.m. to 12:15 p.m., only SCORING KEY Updated
F.S. Hillier & G.T Lierberman Introduction to Operations Research McGraw-Hill, 2004
 Recherche opérationnelle. Master 1 - Esa Si vous souhaitez prendre connaissance des questions traitées dans le cours de recherche opérationnelle du Master 1 ESA, je vous recommande cet ouvrage. F.S. Hillier
Recherche opérationnelle. Master 1 - Esa Si vous souhaitez prendre connaissance des questions traitées dans le cours de recherche opérationnelle du Master 1 ESA, je vous recommande cet ouvrage. F.S. Hillier
Problèmes de non arbitrage, de recouvrement et d optimisation de consommation dans un marché financier avec coûts de transactions.
 Problèmes de non arbitrage, de recouvrement et d optimisation de consommation dans un marché financier avec coûts de transactions. Dimitri De Vallière To cite this version: Dimitri De Vallière. Problèmes
Problèmes de non arbitrage, de recouvrement et d optimisation de consommation dans un marché financier avec coûts de transactions. Dimitri De Vallière To cite this version: Dimitri De Vallière. Problèmes
Service Level Definitions and Interactions
 Service Level Definitions and Interactions By Adrian Cockcroft - Enterprise Engineering Sun BluePrints OnLine - April 1999 http://www.sun.com/blueprints Sun Microsystems, Inc. 901 San Antonio Road Palo
Service Level Definitions and Interactions By Adrian Cockcroft - Enterprise Engineering Sun BluePrints OnLine - April 1999 http://www.sun.com/blueprints Sun Microsystems, Inc. 901 San Antonio Road Palo
«Object-Oriented Multi-Methods in Cecil» Craig Chambers (Cours IFT6310, H08)
 «Object-Oriented Multi-Methods in Cecil» Craig Chambers (Cours IFT6310, H08) Mathieu Lemoine 2008/02/25 Craig Chambers : Professeur à l Université de Washington au département de Computer Science and Engineering,
«Object-Oriented Multi-Methods in Cecil» Craig Chambers (Cours IFT6310, H08) Mathieu Lemoine 2008/02/25 Craig Chambers : Professeur à l Université de Washington au département de Computer Science and Engineering,
Langages Orientés Objet Java
 Langages Orientés Objet Java Exceptions Arnaud LANOIX Université Nancy 2 24 octobre 2006 Arnaud LANOIX (Université Nancy 2) Langages Orientés Objet Java 24 octobre 2006 1 / 32 Exemple public class Example
Langages Orientés Objet Java Exceptions Arnaud LANOIX Université Nancy 2 24 octobre 2006 Arnaud LANOIX (Université Nancy 2) Langages Orientés Objet Java 24 octobre 2006 1 / 32 Exemple public class Example
Sun StorEdge RAID Manager 6.2.21 Release Notes
 Sun StorEdge RAID Manager 6.2.21 Release Notes formicrosoftwindowsnt Sun Microsystems, Inc. 901 San Antonio Road Palo Alto, CA 94303-4900 USA 650 960-1300 Fax 650 969-9131 Part No. 805-6890-11 November
Sun StorEdge RAID Manager 6.2.21 Release Notes formicrosoftwindowsnt Sun Microsystems, Inc. 901 San Antonio Road Palo Alto, CA 94303-4900 USA 650 960-1300 Fax 650 969-9131 Part No. 805-6890-11 November
Keep in touch FINANCIAL COMMUNICATIONS. Thierry Prévot Group General Manager, Financial Communications & Strategic Prospective Analysis
 FINANCIAL COMMUNICATIONS Keep in touch with a complete range of devices and publications Thierry Prévot Group General Manager, Financial Communications & Strategic Prospective Analysis 1 Websites loreal.com
FINANCIAL COMMUNICATIONS Keep in touch with a complete range of devices and publications Thierry Prévot Group General Manager, Financial Communications & Strategic Prospective Analysis 1 Websites loreal.com
Reconstruction d un modèle géométrique à partir d un maillage 3D issu d un scanner surfacique
 Reconstruction d un modèle géométrique à partir d un maillage 3D issu d un scanner surfacique Silvère Gauthier R. Bénière, W. Puech, G. Pouessel, G. Subsol LIRMM, CNRS, Université Montpellier, France C4W,
Reconstruction d un modèle géométrique à partir d un maillage 3D issu d un scanner surfacique Silvère Gauthier R. Bénière, W. Puech, G. Pouessel, G. Subsol LIRMM, CNRS, Université Montpellier, France C4W,
This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and
 This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and education use, including for instruction at the authors institution
This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and education use, including for instruction at the authors institution
«Théories Economiques de L Entreprise» Séance 4 La théorie des incitations : L entreprise comme nœud de contrats MASTER RECHERCHE
 MASTER RECHERCHE Stéphane Saussier Saussier@univ-paris1.fr «Théories Economiques de L Entreprise» Slides disponibles : http://www.webssa.net Séance 4 La théorie des incitations : L entreprise comme nœud
MASTER RECHERCHE Stéphane Saussier Saussier@univ-paris1.fr «Théories Economiques de L Entreprise» Slides disponibles : http://www.webssa.net Séance 4 La théorie des incitations : L entreprise comme nœud
THÈSE. présentée. devant l Université de Rennes 1. pour obtenir. par
 N o d ordre: 3243 THÈSE présentée devant l Université de Rennes 1 pour obtenir le grade de : DOCTEUR DE L UNIVERSITÉ DE RENNES 1 Mention INFORMATIQUE par Martín VARELA RICO Équipe d accueil : ARMOR - IRISA
N o d ordre: 3243 THÈSE présentée devant l Université de Rennes 1 pour obtenir le grade de : DOCTEUR DE L UNIVERSITÉ DE RENNES 1 Mention INFORMATIQUE par Martín VARELA RICO Équipe d accueil : ARMOR - IRISA
Archived Content. Contenu archivé
 ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
First-half 2012 Results. August 29 th, 2012. Jean-Paul AGON. Chairman and CEO
 First-half 2012 Results August 29 th, 2012 Jean-Paul AGON Chairman and CEO First-half 2012 Results +11.4% +10.8% Operating profit 1,702.3 1,896.5 Net profit after non-controlling interests 1,625.2 1,466.6
First-half 2012 Results August 29 th, 2012 Jean-Paul AGON Chairman and CEO First-half 2012 Results +11.4% +10.8% Operating profit 1,702.3 1,896.5 Net profit after non-controlling interests 1,625.2 1,466.6
Finance immobilière Essais sur la gestion de portefeuille et des risques
 UNIVERSITÉ DE CERGY-PONTOISE E.D. ÉCONOMIE, MANAGEMENT, MATHÉMATIQUES CERGY LABORATOIRE DE RECHERCHE THEMA Thèse pour obtenir le grade de Docteur en Sciences de Gestion de l Université de Cergy-Pontoise
UNIVERSITÉ DE CERGY-PONTOISE E.D. ÉCONOMIE, MANAGEMENT, MATHÉMATIQUES CERGY LABORATOIRE DE RECHERCHE THEMA Thèse pour obtenir le grade de Docteur en Sciences de Gestion de l Université de Cergy-Pontoise
Fixed Income Asset Liability Management. summary
 Fixed Income Asset Liability Management Cees L. Dert (1,2) & Alexander H. G. Rinnooy Kan (2) (1) Pacific Investments Research Institute, Herengracht 500, NL-1010 CB Amsterdam, The (2) Econometric Netherlands
Fixed Income Asset Liability Management Cees L. Dert (1,2) & Alexander H. G. Rinnooy Kan (2) (1) Pacific Investments Research Institute, Herengracht 500, NL-1010 CB Amsterdam, The (2) Econometric Netherlands
Dental Insurance Claims Identification of Atypical Claims Activity
 Member s Paper Dental Insurance Claims Identification of Atypical Claims Activity By Barry Senensky, BSc, FCIA, FSA Jonathan Polon, BSc, FSA Any opinions expressed in this paper are those of the author
Member s Paper Dental Insurance Claims Identification of Atypical Claims Activity By Barry Senensky, BSc, FCIA, FSA Jonathan Polon, BSc, FSA Any opinions expressed in this paper are those of the author
Optimal trading? In what sense?
 Optimal trading? In what sense? Market Microstructure in Practice 3/3 Charles-Albert Lehalle Senior Research Advisor, Capital Fund Management, Paris April 2015, Printed the April 13, 2015 CA Lehalle 1
Optimal trading? In what sense? Market Microstructure in Practice 3/3 Charles-Albert Lehalle Senior Research Advisor, Capital Fund Management, Paris April 2015, Printed the April 13, 2015 CA Lehalle 1
Troncatures dans les modèles linéaires simples et à effets mixtes sous R
 Troncatures dans les modèles linéaires simples et à effets mixtes sous R Lyon, 27 et 28 juin 2013 D.Thiam, J.C Thalabard, G.Nuel Université Paris Descartes MAP5 UMR CNRS 8145 IRD UMR 216 2èmes Rencontres
Troncatures dans les modèles linéaires simples et à effets mixtes sous R Lyon, 27 et 28 juin 2013 D.Thiam, J.C Thalabard, G.Nuel Université Paris Descartes MAP5 UMR CNRS 8145 IRD UMR 216 2èmes Rencontres
ON CERTAIN SUMS RELATED TO MULTIPLE DIVISIBILITY BY THE LARGEST PRIME FACTOR
 Ann. Sci. Math. Québec 29 2005, no. 2, 3 45. ON CERTAIN SUMS RELATED TO MULTIPLE DIVISIBILITY BY THE LARGEST PRIME FACTOR WILLIAM D. BANKS, FLORIAN LUCA AND IGOR E. SHPARLINSKI RÉSUMÉ. Pour un nombre entier
Ann. Sci. Math. Québec 29 2005, no. 2, 3 45. ON CERTAIN SUMS RELATED TO MULTIPLE DIVISIBILITY BY THE LARGEST PRIME FACTOR WILLIAM D. BANKS, FLORIAN LUCA AND IGOR E. SHPARLINSKI RÉSUMÉ. Pour un nombre entier
Another way to look at the Project Une autre manière de regarder le projet. Montpellier 23 juin - 4 juillet 2008 Gourlot J.-P.
 Another way to look at the Project Une autre manière de regarder le projet Montpellier 23 juin - 4 juillet 2008 Gourlot J.-P. Plan of presentation Plan de présentation Introduction Components C, D The
Another way to look at the Project Une autre manière de regarder le projet Montpellier 23 juin - 4 juillet 2008 Gourlot J.-P. Plan of presentation Plan de présentation Introduction Components C, D The
Archived Content. Contenu archivé
 ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
ARCHIVED - Archiving Content ARCHIVÉE - Contenu archivé Archived Content Contenu archivé Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject
Unrealized Gains in Stocks from the Viewpoint of Investment Risk Management
 Unrealized Gains in Stocks from the Viewpoint of Investment Risk Management Naoki Matsuyama Investment Administration Department, The Neiji Mutual Life Insurance Company, 1-1 Marunouchi, 2-chome, Chiyoda-ku,
Unrealized Gains in Stocks from the Viewpoint of Investment Risk Management Naoki Matsuyama Investment Administration Department, The Neiji Mutual Life Insurance Company, 1-1 Marunouchi, 2-chome, Chiyoda-ku,
CFT 100000930 ICT review Questions/Answers
 CFT 100000930 ICT review Questions/Answers 1. Est-ce que la stratégie métier est formalisée dans un document détaillant les priorités? Yes, there are two strategic documents, the STRATEGIC ORIENTATIONS
CFT 100000930 ICT review Questions/Answers 1. Est-ce que la stratégie métier est formalisée dans un document détaillant les priorités? Yes, there are two strategic documents, the STRATEGIC ORIENTATIONS
Michael Gendron & Denis Moffet. Départment de Finance et d Assurance, Université Laval, Cité Universitaire, 7P4, Canada. Summary
 On the Coexistence of Mutualist and Capitalist Shareholders in Insurance Companies Ownership Considerations in a New Legal Structure of Life Insurance Companies Michael Gendron & Denis Moffet Départment
On the Coexistence of Mutualist and Capitalist Shareholders in Insurance Companies Ownership Considerations in a New Legal Structure of Life Insurance Companies Michael Gendron & Denis Moffet Départment
Solaris 10 Documentation README
 Solaris 10 Documentation README Sun Microsystems, Inc. 4150 Network Circle Santa Clara, CA 95054 U.S.A. Part No: 817 0550 10 January 2005 Copyright 2005 Sun Microsystems, Inc. 4150 Network Circle, Santa
Solaris 10 Documentation README Sun Microsystems, Inc. 4150 Network Circle Santa Clara, CA 95054 U.S.A. Part No: 817 0550 10 January 2005 Copyright 2005 Sun Microsystems, Inc. 4150 Network Circle, Santa
Processed weight to live-weight conversion factors for Atlantic halibut (Hippoglossus hippoglossus) of the Scotian Shelf and Southern Grand Banks
 Fisheries and Oceans Canada Pêches et Océans Canada Canadian Stock Assessment Secretariat Research Document 99/157 Not to be cited without permission of the authors 1 Secrétariat canadien pour l évaluation
Fisheries and Oceans Canada Pêches et Océans Canada Canadian Stock Assessment Secretariat Research Document 99/157 Not to be cited without permission of the authors 1 Secrétariat canadien pour l évaluation
Formulaire de Modification de Données de l Emploi/Job Data Change Form France
 Formulaire de Modification de Données de l Emploi/Job Data Change Form France Instructions du Formulaire de Modification de données de l emploi / JOB DATA CHANGE FORM INSTRUCTIONS Ce formulaire est à l'usage
Formulaire de Modification de Données de l Emploi/Job Data Change Form France Instructions du Formulaire de Modification de données de l emploi / JOB DATA CHANGE FORM INSTRUCTIONS Ce formulaire est à l'usage
DIRECTIVE ON ACCOUNTABILITY IN CONTRACT MANAGEMENT FOR PUBLIC BODIES. An Act respecting contracting by public bodies (chapter C-65.1, a.
 DIRECTIVE ON ACCOUNTABILITY IN CONTRACT MANAGEMENT FOR PUBLIC BODIES An Act respecting contracting by public bodies (chapter C-65.1, a. 26) SUBJECT 1. The purpose of this directive is to establish the
DIRECTIVE ON ACCOUNTABILITY IN CONTRACT MANAGEMENT FOR PUBLIC BODIES An Act respecting contracting by public bodies (chapter C-65.1, a. 26) SUBJECT 1. The purpose of this directive is to establish the
This document is a preview generated by EVS
 INTERNATIONAL STANDARD NORME INTERNATIONALE IEC 62325-451-5 Edition 1.0 2015-02 colour inside Framework for energy market communications Part 451-5: Problem statement and status request business processes,
INTERNATIONAL STANDARD NORME INTERNATIONALE IEC 62325-451-5 Edition 1.0 2015-02 colour inside Framework for energy market communications Part 451-5: Problem statement and status request business processes,
