How To Understand How A Protein Folds
|
|
|
- Myrtle Mitchell
- 3 years ago
- Views:
Transcription
1 Chapter 1 Protein folding and stability 1.1 The protein folding problem One of the great challenges in protein science is the folding problem, that is the task to predict the protein native structure solely from the amino acid sequence. This has become a major research field as a consequence of the increasing amount of sequence data acquired by DNA analysis and various genome projects. The acquisition of sequence information is a fast and straightforward procedure. On the other hand the experimental determination of the three dimensional structure assumed by a protein is slow and limited to proteins that can be crystallized in a suitable form or are sufficiently small to be solved by solution or solid state NMR. Therefore, algorithms capable to translate the linear information given by the protein sequence into the spatial information defining the structure are required. Besides structure prediction, the other fundamental issue pursued by protein science is the de novo design of proteins and enzymes with specified activities. This design problem is related to the folding problem. Both tasks are based on finding the most stable fold of a sequence, natural or designed. Furthermore, this fold must be kinetically accessible. If an enzyme is designed, the active site must possess all features required for specific binding, without compromising stability. The so called Levinthal paradox [1] is traditionally invoked to explain why the protein folding problem is so challenging. Considering, according to Anfinsen s hypothesis [2] (see section 1.3), that the native state of a protein corresponds to a global free energy minimum, folding amounts to find this minimum among a huge number of conformations. One can estimate that for a protein given by 100 amino acids, if each amino acid can assume for instance three different conformations, there are or states available. If the protein should find its native state by random search, visiting one state each picosecond, this search could take longer than the age of universe. Proteins usually fold in a time range from microseconds to seconds. Theory is still far from solving the protein folding problem in general, because of an intrinsic 5
2 6 Chapter 1. Protein folding and stability limit beyond computational capability. One could formulate the Levinthal paradox in terms of computing power. If the computation of the energy of one single conformation took one picosecond, the native state of a protein could not be calculated by random search. However, there has been a significant progress in protein science since the pioneering work of the early 70s and the current view of the folding problem suggests a solution of the Levinthal paradox [3]. The theoretical approach to protein folding aims at finding simplified descriptions of proteins which take into account only the important degrees of freedom. On the other hand protein engineering offers an effective experimental route to describe factors which govern protein stability. In this chapter the basic concepts both from the experimental and theoretical point of view will be outlined. 1.2 Native and denatured state The native state of a globular protein is defined as the small ensemble of compact conformations, reached under folding conditions in vivo or in vitro, in which the protein is stable and performs its action. This state is characterized by a low amount of entropy, because all protein atoms are kept by mutual interaction in a well defined geometry. Intramolecular enthalpy is also relatively low because many attractive interactions are satisfied. Solvent molecules surrounding the folded protein in its native state take instead advantage of a large amount of entropy, since they are not involved in interactions with the hydrophobic protein interior. By perturbing the folding conditions in some way, like increasing temperature, changing the solvent ph or adding a chemical denaturant, the protein unfolds and reaches a much more complex and heterogeneous ensemble of conformations, which is called the denatured or unfolded state. It is difficult to characterize the structural properties of the denatured state, since it strongly depends on the unfolding conditions. One can describe the ensemble by means of parameters like the radius of gyration or the hydrodynamic volume, which both define the average compactness. Experimental techniques like infrared and circular dichroism spectroscopy provide information on secondary structure elements. When a high percentage of secondary structure is lost, which is the case under strong unfolding conditions, the unfolded state assumes a random coil structure. The denatured state is characterized by a high conformational entropy, because native interactions are lost and residues are free to assume a large set of arrangements. Intramolecular enthalpy may be higher because of loss of native interactions. The solvent molecules get in contact with hydrophobic parts of the protein chain which were buried in the native state. This fact causes water molecules to assume more ordered conformations in order to minimize the contact with nonpolar groups, what reduces the entropy of the solvent relatively to the folded state. Therefore, one can understand the entropy increase as a driving force for folding [4]. When restoring the folding conditions in vitro, the spontaneous refolding of a denatured protein is usually initiated. This means that the molecule is able to find the native state spontaneously.
3 1.3. Thermodynamics of protein folding 7 However, this may not be the case for some large multidomain proteins, which cannot refold without assistance. Many proteins show folding intermediates, which are non native in structure, but rather compact and partly folded. They are characterized by a reduced amount of tertiary interactions, by a rather large content of secondary structure, and a fluctuating hydrophobic core. Such states are termed molten globule states and are formed rather early during refolding, for instance in the dead time (< 1 ms) of a stopped-flow mixing experiment under refolding conditions. 1.3 Thermodynamics of protein folding In 1973 Anfinsen [2] formulated the thermodynamic hypothesis for protein folding, stating that under physiological conditions the native state of a protein is stable since it is a global minimum of the free energy. Under denaturing conditions of increasing strength, this is not true anymore and the native state is destabilized. The concentration of native protein decreases until a point is reached, where the unfolded state dominates and is more populated and more stable. Both states, unfolded and folded, can be characterized at equilibrium at temperature T by their Gibbs free energy (see section 3.6): G i = H i TS i + pv i (1.1) where i can be the native state N or the unfolded state D. The free energy is given by three terms: enthalpy H, the product of entropy S and temperature T and the product of pressure and volume. The last term is usually constant under experimental conditions. Therefore, it can be neglected when calculating differences. The free energy of folding is defined as difference of the Gibbs free energies between the denatured and the native state G f olding (T) = H D N (T) T S D N (T) (1.2) If this difference is positive, the native state is favored, else the unfolded state is more populated. One should keep in mind that not only the polypeptide chain, but also the surrounding solvent molecules contribute to the Gibbs free energy (see section 3.6). For instance the stabilizing entropy contribution due to the solvent is larger in the folded than in the unfolded state, as already mentioned. Another effect due to water is the increase upon unfolding of the specific heat at constant pressure, C p. To a rough approximation, the value of C p of unfolding is about 12 cal/k mol per residue [5]. This increase is again due to the interaction between water molecules and non polar protein residues in the unfolded state, which causes the formation of ordered water structures like ice. The specific heat change C p rules the temperature dependence of both enthalpy and entropy of folding. Namely, given H D N (T 1 ) and S D N (T 1 ),
4 8 Chapter 1. Protein folding and stability changing the temperature to the value T 2 one can write: H D N (T 2 ) = H D N (T 1 )+ C p (T 2 T 1 ) (1.3) S D N (T 2 ) = S D N (T 1 )+ C p ln T 2 T 1 (1.4) such that the free energy of folding at temperature T 2 becomes: [ G f olding (T 2 ) = H D N (T 1 )+ C p (T 2 T 1 ) T 2 S D N (T 1 )+ C p ln T ] 2 T 1 (1.5) The unfolding transition Protein denaturation is a process in which, starting from physiological folding conditions, the environment is progressively altered, for instance by increasing temperature, changing ph or adding a chemical denaturant like urea to the solution. This leads to a transition from the native state to a denatured state, dependent on the denaturation procedure. As mentioned above, the denaturation is usually reversible, that is the protein spontaneously returns to the original native structure when the folding conditions are restored. However, it can be irreversible for large multidomain proteins. A first order transition from state A to state B is defined such that at each point of the transition both species are present at changing concentrations. The interconversion from one state to the other happens cooperatively, that is all parts contribute at the same time to the reaction. If concentration of one species is plotted to show the progress of the transition with changing conditions, the shape of the plot is sigmoidal. Unfolding and refolding of small proteins are typically first order transitions, with A and B being the native and the unfolded state. This statement is made under the assumption that the reaction between native and unfolded state is a simple two-state equilibrium, for which no intermediates are present. A two-state transition can be identified in experiments if all spectroscopic probes, like circular dichroism, fluorescence and UV spectra, change simultaneously [4] as the equilibrium changes. Calorimetric measurements can detect intermediates. There are also cases of apparent twostate transitions, where stable intermediates exist at low concentration of denaturant and are not observed by spectroscopic methods [6]. Some typical unfolding techniques are listed and briefly discussed here. Thermal unfolding The free energy of folding in eq. (1.2) is under folding conditions positive, such that the native state is favored. If temperature increases, according to eq. (1.5), the negative part, proportional to entropy, will dominate when T 2 is sufficiently high, such that G f olding becomes negative, leading to unfolding. The melting temperature T m
5 1.3. Thermodynamics of protein folding 9 is the temperature at which the free energy of folding, eq. (1.2), becomes zero: T m = H D N(T m ) S D N (T m ) (1.6) Thermal unfolding can be measured by differential scanning calorimetry. Solvent denaturation The effect of denaturants like urea or GdmCl is that they solubilize the protein chain, backbone and hydrophobic side chains. This is due to a double action of the denaturant. On one hand, it directly interacts with the protein groups; on the other hand, denaturant molecules also perturb the water solvent, which in turn alters the waterprotein interaction [7]. To a first approximation the free energy of transfer of side chains and polypeptide backbone from water to a denaturating solvent is linear with respect to the concentration of denaturant [8]: G D N = G H 2O D N m D N[denaturant] (1.7) The denatured state is more exposed to solvent than the native state. Therefore, the former is stabilized by the presence of denaturant, that is, the denaturant energy coefficient m D N is positive. Each residue of the protein contributes to the value of m D N according to its fraction of solvent exposure gained by denaturation. Thus, the coefficient is an extensive quantity and is correspondingly larger for larger proteins with more residues. A small value of m D N indicates that the surface area of the protein is not strongly changing upon denaturation, which means that the protein is not fully unfolded. ph induced denaturation Acidic and basic residues buried in proteins have often altered pk a s values, due to the strong interactions with other charges in a low dielectric medium like the protein interior (see chapter 3). For instance an acidic side chain involved in a salt bridge with a basic residue might have a pk a far below the standard solution value. Nevertheless, when the ph of the solution decreases, at some point the acidic group becomes protonated, which may favor unfolding. Given a single titratable group in the protein, the relationship between its dissociation constant and the folding equilibrium can be described by a thermodynamic cycle (see fig. (1.1)). If the proton dissociation constant of the titratable group in the native state is K N a and in the denatured state is KD a, and the equilibrium constant for folding in the unprotonated state is K N D and in the protonated state is K N D(H + ), then the equilibrium constants are related by: K N D(H + ) K N D = KN a K D a (1.8) The thermodynamic cycle must be expanded if more titratable groups are present. The contribution to the free energy of folding due to changes in the protonation state of titratable groups can be written as follows, if the mutual interaction of the titratable residues
6 10 Chapter 1. Protein folding and stability can be ignored : G D N ph = 2.3RT[Q D(pH) Q N (ph)] (1.9) where Q i (ph) is the number of bound protons in the i-th state of the protein [8]. Destabilization at low ph also occurs because the protein increases its net positive charge, which may provide additional repulsive electrostatic interactions. Figure 1.1: Thermodynamic cycle explaining ph induced unfolding. From [4]. 1.4 Folding kinetics When no folding intermediates are present, or if they are not detectable, a protein folds showing a monoexponential time evolution, typical for a two state kinetics. This is usually the case for small globular proteins with less than 100 amino acids [9, 10]. The equilibrium constant K D for the folding-unfolding reaction: N D K D = [N] [D] (1.10) is equal to the ratio of the microscopic rate constants for unfolding (k ND ) and for refolding (k DN ): Therefore, protein stability is related to the folding rate: K D = [N] [D] = k ND k DN (1.11) G unfolding = RT lnk D = RT ln k ND k DN (1.12) and the observed rate constant, which is inverse of the decay time τ, is defined: k obs = 1 τ = k ND + k DN (1.13) Denaturants affect the rate constants for folding and unfolding. The logarithm of the rate
7 1.5. Transition state and Φ-value analysis 11 constant for unfolding k ND is found to change linearly with the concentration of denaturant at [denaturant] > [denaturant] 50% at concentration higher than 50% : lnk ND = lnk H 2O ND + m D[denaturant] (1.14) while for some proteins [4] the rate constant for folding k DN follows a similar relationship for low concentration [denaturant] < [denaturant] 50% : lnk DN = lnk H 2O DN m N[denaturant] (1.15) These two equations form a V-shaped kinetic curve, called chevron plot, constructed by combining the two rate constants: lnk obs = ln(k ND + k DN ) = ln[k H 2O DN exp( m N[denaturant])+k H 2O ND exp(+m D[denaturant])] (1.16) Figure 1.2: A chevron plot, showing the linear dependence of observed rate of folding or unfolding on denaturant concentration. The data refer to cold shock protein CspB from Therotoga maritima in GdmCl. From [11]. 1.5 Transition state and Φ-value analysis Given a monoexponential reaction scheme, the reactants must overcome a barrier to be transformed into the products. All treatments of chemical kinetics base on the hypothesis that the reaction rate depends on the height of this free energy or enthalpy barrier E A, and on a probability factor that accounts for the number of accessible states for the molecule in the ground state versus the transition state. Since thermal motion is required to cross the energy barrier, the reaction rate is proportional to a Boltzmann factor.
8 12 Chapter 1. Protein folding and stability According to the transition state theory the activated state is a quasi-thermodynamic state, named transition state, which is in a sort of fast equilibrium with the ground state [12]. The rate constant is given by the corresponding virtual equilibrium constant, multiplied by the frequency (ν) of the ground state and by the transmission coefficient (κ) of passing over the energy barrier. If the activated or transition state X has a free energy which is higher than the ground state by an amount G X D, the rate constant is given by: k DN = κνexp( G X D /RT) (1.17) Transition state theory was originally developed for reactions of small molecules in the gas phase, and it has been questioned whether it is well suited for describing reactions that occur in solution and involve the simultaneous formation and breakage of many weak interactions, as in protein folding [13]. Kramers theory [14] provides an alternative formalism specifically for reactions in solution. A chemical reaction from a reactant D over the activated state X to the product N is modeled as a diffusive passage over a barrier: k DN = τnx 1 exp( V/RT) (1.18) The Boltzmann factor in the rate expression in (1.18) depends on the height of the potential energy barrier and not on the free energy. The prefactor τ NX depends on the frequency of the system in the ground state N and the frequency of escape from the activated state X, which reflects the local mobility of the system in X. This mobility depends on the friction with the solvent, represented by the macroscopic viscosity η. Therefore, if a reaction is modeled according to Kramers theory, the rate depends on solvent viscosity. In the simplest case the dependence is inversely linear: k 1 η (1.19) It is a matter of debate whether the folding reaction is diffusion controlled, that is rate-limited by the diffusion of the polypeptide parts [12]. In such a case the folding rate should depend on the solvent viscosity. The folding of the bacterial cold shock protein CspB was proposed to be a diffusional process [13], due to the observed inverse dependence of folding rate on viscosity. On the other hand such a dependence may arise also from frictional effects at the transition state instead of being due to the global chain collapse [15]. The transition state theory provides a direct relationship between rate constant for folding and free energy differences between the ground and the activated state (see eq. 1.17). The main use of this formalism is related to the comparison of folding rates between wild type proteins and mutants. When calculating activation free energy changes upon mutation the prefactor κν cancels. If a protein folds with a rate k f and a mutant with a rate k f, then the change in
9 1.5. Transition state and Φ-value analysis 13 activation free energy is given by: G X D = G X D G X D = RT ln k f k f (1.20) The method of Φ-value analysis, introduced by Fersht [16] and currently used in a wide range of experiments, is based on eq. (1.20). This procedure is aimed at obtaining the transition state structure for folding at the level of individual residues, by comparing the activation energies and the free energies of folding of different mutants of a protein. A single mutation of a protein that reduces its stability leads to a decrease -in absolute value- of the free energy of folding. Also the folding kinetics of the mutant protein can be monitored to determine the folding and unfolding rates and to provide activation energies. An increase of activation energy of folding upon mutation is related to a destabilization of the transition state. In fact, if the native state and the transition state are destabilized by the same energy amount, one can suppose that the mutated residue in the wild type protein is involved in native interactions which are already formed at the transition state. This can be confirmed if also the neighboring residues show upon mutation a similar behavior. If instead no change in transition state stability is produced by a mutation, which affects the stability of the native state, the native contacts of that residues are likely to be formed after passing the activation barrier during folding. This analysis is formalized in terms of Φ-values [4]. Let us suppose that the mutation destabilizes the folded structure by G N D, measured relative to the unfolded state. Then, if the free energy of a transition state, measured relative to the unfolded state, changes by G X D, Φ F is defined as: Φ F = G k RT ln f X D k f = (1.21) G N D G N D with the expression on the right derived from eq. (1.20). Let us suppose that upon mutation the energy of native, denatured and transition state changes in the following way: G D G D = G D + α G N G N = G N + β G X G X = G X + γ (1.22) Then one has: Φ F = G D G X G D + G X G D G N G D + G N = α γ α β (1.23) A Φ F value of 0 means that the energy of the transition state is affected by the mutation by the same amount as the denatured state (α = γ). This situation is described in the left diagram in fig. (1.3). One can infer that in this case the protein structure in the neighborhood of the mutated residue is unfolded at the transition state. On the other hand, a Φ F value of 1 means that the energy of the transition state is affected by the same amount as the native state (or γ = β,
10 14 Chapter 1. Protein folding and stability see right diagram in fig. (1.3)). This means that the structure made by the mutated residue is folded at the transition state as much as it is in the native state. Fractional Φ F values, and even values larger than 1 or smaller than 0 may also occur and are usually more difficult to interpret. Fractional Φ F values between 0 and 1 can result either from specific residue interactions that are weaker in the mutant at the transition state or from the presence of a mixture of states, some with the interactions fully formed, others with the interactions fully broken. A number of point mutations is then required in order to discriminate between these two possibilities. Another problem is that, in general, there is no linear relationship between a Φ F value and the extent of structure formation. From a fractional Φ F value, one can only conclude that the native structure is basically present, although weakened. Despite these aspects, the method is in practice very efficient in determining structural properties of the transition state of folding proteins. Figure 1.3: Φ-value analysis. From [4]. Free energy diagrams showing two possible scenarios for the effect of a single mutation on a folding protein. The energies of the denatured state for wild type and mutant are superimposed in the plot, but this does not affect the analysis [4]. On the left the mutation affects the transition state as much as it affects the denatured state (this is shown as no change at the transition state due to the superposition of energies for wild type and mutant denatured state). This leads to a Φ F value of 0. On the right, the mutation affects transition and native state by nearly the same amount, which gives a Φ F value of 1.
11 1.6. Folding mechanisms Folding mechanisms The Levinthal paradox suggested that an unbiased search for the native conformation through an astronomical number of states would never be successful. Therefore, it was argued that there must be specific pathways to reduce the large number of possibilities during folding. The main problem in folding theories was how to reconcile the simultaneous formation of stable secondary and tertiary structure. Three mechanisms were proposed to explain how the route to the native state proceeds. All of them simplify the scheme by decoupling the building of secondary structure elements from the collapse to the three dimensional structure. They are presented here: The nucleation model [17] A group of neighboring residues starts forming native secondary structure, which propagates to the whole chain in a stepwise manner. Tertiary structure arises then as a consequence of secondary structure. The diffusion-collision model [18] The secondary structure elements form early during folding and independently from tertiary structure. These elements then diffuse until they collide and successively coalesce to give the tertiary structure. The hydrophobic collapse model [19, 20] The first event during folding is the collapse of the polypeptide chain, driven by the hydrophobic effect. After collapsing, the chain rearranges locally to form the native secondary structure. First and second approach are both framework models [21], in which the formation of the correct secondary structure drives the subsequent arrangement of the tertiary conformation. The hydrophobic collapse model is at the other extreme: secondary structure forms as a consequence of the spatial collapse. A synthesis between these two classical views is provided by the nucleation-condensation model, which was proposed as folding mechanism for many small proteins after experiments on chymotrypsin inhibitor CI2. This was the second protein, after barnase, for which extensive investigation using Φ values analysis was done [21, 4]. The transition state of CI2 turned out to be an expanded structure in which secondary and tertiary structure are formed in parallel and there are no fully formed secondary structure elements yet. Molecular dynamics calculations also confirmed this picture [21]. The nucleation-condensation approach involves a nucleus consisting of neighboring residues, which forms a pre-native structure, subsequently stabilized by non-local interactions, i.e. interactions among residues that are far away from each other in sequence. This nucleus may be not present in the denatured state and does not need be completely formed in the transition state. The residues involved in the nucleus are identified by their Φ values, which are close to 1. Since proteins largely differ in structure and size, folding mechanisms are likely to vary among different protein classes. Nevertheless, many small proteins, like for instance SH3 spectrin domain [12], seem to fold according to the nucleation-condensation mechanism. Also in more
12 16 Chapter 1. Protein folding and stability complex multidomain systems secondary and tertiary structure may form in a concerted way via multiple transition states [22]. 1.7 Energy landscape and funnel theory The new theoretical approach to protein folding, which eventually leads to a solution of the Levinthal paradox, was developed in analogy to spin glass theory and polymer physics [23, 24, 25]. A folding protein is characterized by the coexistence of many competing interactions among amino acids. This leads to a situation called frustration, because the protein is not able to satisfy all interactions at the same time. The most stable state is then the structure maximizing the fraction of attractive interactions, which is the minimally frustrated structure. A useful concept related to this view is the energy landscape description. Given a set of coordinates describing the dependence on energy of a conformation, the free energy of the solvated protein as function of these coordinates defines a hypersurface, or energy landscape. A conformational transition of the protein, like the folding event, is then given by a specific trajectory or bundle of trajectories on this energy landscape. A smooth energy landscape allows rapid transitions, whereas a rugged energy surface has kinetic traps which slow down folding. Frustration is associated with a rugged energy landscape. The picture offered by the Levinthal paradox is, in terms of landscape, a flat energy surface with a single narrow absolute minimum representing the native state, similarly to a golf course with a single hole. A random search through the flat surface, without any bias, would be successful in finite time only with an extremely low probability. A different extreme is represented by a rugged landscape with many maxima and minima without a preferred conformation: this would be the case of a random heteropolymer. The energy landscape of a folding protein is described as a rugged surface sloped down from all directions into a global minimum, representing the native state (see fig. 1.4). It is explicitly assumed that there is a kinetic flow through a series of states that are progressively lower in energy. At the top of the funnel the protein exists in a number of random states that have relatively high entropy and high enthalpy. Progress down the funnel is given by collapse and reconfiguration. The reconfiguration occurs as a motion through adjacent, thus geometrically similar, conformations, by a Brownian-like motion. The acquisition of native structure reduces the free energy and drives the protein towards the bottom of the funnel, while enthalpy is progressively reduced. The driving force is working against entropy, which decreases simultaneously with entropy. The progress of folding can be described by the parameter Q i, the fraction of native contacts in the state i: Q i = C(i) C(n) (1.24)
13 1.7. Energy landscape and funnel theory 17 Figure 1.4: The folding funnel, from [23]. The height of the funnel represents enthalpy, which decreases going downhill (here referred to as energy, left arrow). The width of the funnel represents entropy. On the right the decrease of the fraction of native contacts Q is given by an arrow. The molten globule (see section 1.2) represents a compact denatured state. It is separated from the native state by an energy gap which guarantees the stability of the native structure. where C(n) is the number of contacts formed by residue pairs in the native state and C(i) is the number of such contacts conserved in state i. The molten globule state is rather compact but still highly non-native. The transition state is located at a higher value of Q i, thus closer to the native structure. If Q does not increase uniformly, but in few large steps, then the protein folding occurs through nucleation. After passing through the transition state, there is a single low energy state corresponding to the native conformation. This drives the protein to fold completely, while the absence of other relevant minima prevents from misfolding.
Review of Chemical Equilibrium 7.51 September 1999. free [A] (µm)
![Review of Chemical Equilibrium 7.51 September 1999. free [A] (µm) Review of Chemical Equilibrium 7.51 September 1999. free [A] (µm)](/thumbs/40/21435474.jpg) Review of Chemical Equilibrium 7.51 September 1999 Equilibrium experiments study how the concentration of reaction products change as a function of reactant concentrations and/or reaction conditions. For
Review of Chemical Equilibrium 7.51 September 1999 Equilibrium experiments study how the concentration of reaction products change as a function of reactant concentrations and/or reaction conditions. For
Protein Melting Curves
 Protein Melting Curves In previous classes we talked a lot about what aspects of a protein structure stabilize a protein and what aspects destabilize it. But how would one actually test such predictions?
Protein Melting Curves In previous classes we talked a lot about what aspects of a protein structure stabilize a protein and what aspects destabilize it. But how would one actually test such predictions?
CHEMISTRY STANDARDS BASED RUBRIC ATOMIC STRUCTURE AND BONDING
 CHEMISTRY STANDARDS BASED RUBRIC ATOMIC STRUCTURE AND BONDING Essential Standard: STUDENTS WILL UNDERSTAND THAT THE PROPERTIES OF MATTER AND THEIR INTERACTIONS ARE A CONSEQUENCE OF THE STRUCTURE OF MATTER,
CHEMISTRY STANDARDS BASED RUBRIC ATOMIC STRUCTURE AND BONDING Essential Standard: STUDENTS WILL UNDERSTAND THAT THE PROPERTIES OF MATTER AND THEIR INTERACTIONS ARE A CONSEQUENCE OF THE STRUCTURE OF MATTER,
Chapter 6 An Overview of Organic Reactions
 John E. McMurry www.cengage.com/chemistry/mcmurry Chapter 6 An Overview of Organic Reactions Why this chapter? To understand organic and/or biochemistry, it is necessary to know: -What occurs -Why and
John E. McMurry www.cengage.com/chemistry/mcmurry Chapter 6 An Overview of Organic Reactions Why this chapter? To understand organic and/or biochemistry, it is necessary to know: -What occurs -Why and
Built from 20 kinds of amino acids
 Built from 20 kinds of amino acids Each Protein has a three dimensional structure. Majority of proteins are compact. Highly convoluted molecules. Proteins are folded polypeptides. There are four levels
Built from 20 kinds of amino acids Each Protein has a three dimensional structure. Majority of proteins are compact. Highly convoluted molecules. Proteins are folded polypeptides. There are four levels
Lecture 11 Enzymes: Kinetics
 Lecture 11 Enzymes: Kinetics Reading: Berg, Tymoczko & Stryer, 6th ed., Chapter 8, pp. 216-225 Key Concepts Kinetics is the study of reaction rates (velocities). Study of enzyme kinetics is useful for
Lecture 11 Enzymes: Kinetics Reading: Berg, Tymoczko & Stryer, 6th ed., Chapter 8, pp. 216-225 Key Concepts Kinetics is the study of reaction rates (velocities). Study of enzyme kinetics is useful for
Hydrogen Bonds The electrostatic nature of hydrogen bonds
 Hydrogen Bonds Hydrogen bonds have played an incredibly important role in the history of structural biology. Both the structure of DNA and of protein a-helices and b-sheets were predicted based largely
Hydrogen Bonds Hydrogen bonds have played an incredibly important role in the history of structural biology. Both the structure of DNA and of protein a-helices and b-sheets were predicted based largely
Topic 2: Energy in Biological Systems
 Topic 2: Energy in Biological Systems Outline: Types of energy inside cells Heat & Free Energy Energy and Equilibrium An Introduction to Entropy Types of energy in cells and the cost to build the parts
Topic 2: Energy in Biological Systems Outline: Types of energy inside cells Heat & Free Energy Energy and Equilibrium An Introduction to Entropy Types of energy in cells and the cost to build the parts
Topic 3b: Kinetic Theory
 Topic 3b: Kinetic Theory What is temperature? We have developed some statistical language to simplify describing measurements on physical systems. When we measure the temperature of a system, what underlying
Topic 3b: Kinetic Theory What is temperature? We have developed some statistical language to simplify describing measurements on physical systems. When we measure the temperature of a system, what underlying
Lecture 3: Models of Solutions
 Materials Science & Metallurgy Master of Philosophy, Materials Modelling, Course MP4, Thermodynamics and Phase Diagrams, H. K. D. H. Bhadeshia Lecture 3: Models of Solutions List of Symbols Symbol G M
Materials Science & Metallurgy Master of Philosophy, Materials Modelling, Course MP4, Thermodynamics and Phase Diagrams, H. K. D. H. Bhadeshia Lecture 3: Models of Solutions List of Symbols Symbol G M
Studying an Organic Reaction. How do we know if a reaction can occur? And if a reaction can occur what do we know about the reaction?
 Studying an Organic Reaction How do we know if a reaction can occur? And if a reaction can occur what do we know about the reaction? Information we want to know: How much heat is generated? How fast is
Studying an Organic Reaction How do we know if a reaction can occur? And if a reaction can occur what do we know about the reaction? Information we want to know: How much heat is generated? How fast is
Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Two Forms of Energy
 Module 2D - Energy and Metabolism Objective # 19 All living organisms require energy for survival. In this module we will examine some general principles about chemical reactions and energy usage within
Module 2D - Energy and Metabolism Objective # 19 All living organisms require energy for survival. In this module we will examine some general principles about chemical reactions and energy usage within
18.2 Protein Structure and Function: An Overview
 18.2 Protein Structure and Function: An Overview Protein: A large biological molecule made of many amino acids linked together through peptide bonds. Alpha-amino acid: Compound with an amino group bonded
18.2 Protein Structure and Function: An Overview Protein: A large biological molecule made of many amino acids linked together through peptide bonds. Alpha-amino acid: Compound with an amino group bonded
CHM333 LECTURE 13 14: 2/13 15/12 SPRING 2012 Professor Christine Hrycyna
 INTRODUCTION TO ENZYMES Enzymes are usually proteins (some RNA) In general, names end with suffix ase Enzymes are catalysts increase the rate of a reaction not consumed by the reaction act repeatedly to
INTRODUCTION TO ENZYMES Enzymes are usually proteins (some RNA) In general, names end with suffix ase Enzymes are catalysts increase the rate of a reaction not consumed by the reaction act repeatedly to
Signal to Noise Instrumental Excel Assignment
 Signal to Noise Instrumental Excel Assignment Instrumental methods, as all techniques involved in physical measurements, are limited by both the precision and accuracy. The precision and accuracy of a
Signal to Noise Instrumental Excel Assignment Instrumental methods, as all techniques involved in physical measurements, are limited by both the precision and accuracy. The precision and accuracy of a
Protein Dynamics Intro
 Protein Dynamics Intro From rigid structures to motions on energy landscapes Do you all remember Anfinsen? What concept now associated with his name made Anfinsen famous? Right, it is the concept that
Protein Dynamics Intro From rigid structures to motions on energy landscapes Do you all remember Anfinsen? What concept now associated with his name made Anfinsen famous? Right, it is the concept that
CHM333 LECTURE 13 14: 2/13 15/13 SPRING 2013 Professor Christine Hrycyna
 INTRODUCTION TO ENZYMES Enzymes are usually proteins (some RNA) In general, names end with suffix ase Enzymes are catalysts increase the rate of a reaction not consumed by the reaction act repeatedly to
INTRODUCTION TO ENZYMES Enzymes are usually proteins (some RNA) In general, names end with suffix ase Enzymes are catalysts increase the rate of a reaction not consumed by the reaction act repeatedly to
Thermodynamics. Thermodynamics 1
 Thermodynamics 1 Thermodynamics Some Important Topics First Law of Thermodynamics Internal Energy U ( or E) Enthalpy H Second Law of Thermodynamics Entropy S Third law of Thermodynamics Absolute Entropy
Thermodynamics 1 Thermodynamics Some Important Topics First Law of Thermodynamics Internal Energy U ( or E) Enthalpy H Second Law of Thermodynamics Entropy S Third law of Thermodynamics Absolute Entropy
CHAPTER 6 AN INTRODUCTION TO METABOLISM. Section B: Enzymes
 CHAPTER 6 AN INTRODUCTION TO METABOLISM Section B: Enzymes 1. Enzymes speed up metabolic reactions by lowering energy barriers 2. Enzymes are substrate specific 3. The active site in an enzyme s catalytic
CHAPTER 6 AN INTRODUCTION TO METABOLISM Section B: Enzymes 1. Enzymes speed up metabolic reactions by lowering energy barriers 2. Enzymes are substrate specific 3. The active site in an enzyme s catalytic
Combinatorial Biochemistry and Phage Display
 Combinatorial Biochemistry and Phage Display Prof. Valery A. Petrenko Director - Valery Petrenko Instructors Galina Kouzmitcheva and I-Hsuan Chen Auburn 2006, Spring semester COMBINATORIAL BIOCHEMISTRY
Combinatorial Biochemistry and Phage Display Prof. Valery A. Petrenko Director - Valery Petrenko Instructors Galina Kouzmitcheva and I-Hsuan Chen Auburn 2006, Spring semester COMBINATORIAL BIOCHEMISTRY
Gibbs Free Energy and Chemical Potential. NC State University
 Chemistry 433 Lecture 14 Gibbs Free Energy and Chemical Potential NC State University The internal energy expressed in terms of its natural variables We can use the combination of the first and second
Chemistry 433 Lecture 14 Gibbs Free Energy and Chemical Potential NC State University The internal energy expressed in terms of its natural variables We can use the combination of the first and second
Nuclear Physics. Nuclear Physics comprises the study of:
 Nuclear Physics Nuclear Physics comprises the study of: The general properties of nuclei The particles contained in the nucleus The interaction between these particles Radioactivity and nuclear reactions
Nuclear Physics Nuclear Physics comprises the study of: The general properties of nuclei The particles contained in the nucleus The interaction between these particles Radioactivity and nuclear reactions
States of Matter CHAPTER 10 REVIEW SECTION 1. Name Date Class. Answer the following questions in the space provided.
 CHAPTER 10 REVIEW States of Matter SECTION 1 SHORT ANSWER Answer the following questions in the space provided. 1. Identify whether the descriptions below describe an ideal gas or a real gas. ideal gas
CHAPTER 10 REVIEW States of Matter SECTION 1 SHORT ANSWER Answer the following questions in the space provided. 1. Identify whether the descriptions below describe an ideal gas or a real gas. ideal gas
Chapter 8: An Introduction to Metabolism
 Chapter 8: An Introduction to Metabolism Name Period Concept 8.1 An organism s metabolism transforms matter and energy, subject to the laws of thermodynamics 1. Define metabolism. The totality of an organism
Chapter 8: An Introduction to Metabolism Name Period Concept 8.1 An organism s metabolism transforms matter and energy, subject to the laws of thermodynamics 1. Define metabolism. The totality of an organism
Chapter 8: Energy and Metabolism
 Chapter 8: Energy and Metabolism 1. Discuss energy conversions and the 1 st and 2 nd law of thermodynamics. Be sure to use the terms work, potential energy, kinetic energy, and entropy. 2. What are Joules
Chapter 8: Energy and Metabolism 1. Discuss energy conversions and the 1 st and 2 nd law of thermodynamics. Be sure to use the terms work, potential energy, kinetic energy, and entropy. 2. What are Joules
MULTIPLE CHOICE QUESTIONS
 MULTIPLE CHOICE QUESTIONS 1. Most components of energy conversion systems evolved very early; thus, the most fundamental aspects of energy metabolism tend to be: A. quite different among a diverse group
MULTIPLE CHOICE QUESTIONS 1. Most components of energy conversion systems evolved very early; thus, the most fundamental aspects of energy metabolism tend to be: A. quite different among a diverse group
Reaction Rates and Chemical Kinetics. Factors Affecting Reaction Rate [O 2. CHAPTER 13 Page 1
 CHAPTER 13 Page 1 Reaction Rates and Chemical Kinetics Several factors affect the rate at which a reaction occurs. Some reactions are instantaneous while others are extremely slow. Whether a commercial
CHAPTER 13 Page 1 Reaction Rates and Chemical Kinetics Several factors affect the rate at which a reaction occurs. Some reactions are instantaneous while others are extremely slow. Whether a commercial
1. A covalent bond between two atoms represents what kind of energy? a. Kinetic energy b. Potential energy c. Mechanical energy d.
 1. A covalent bond between two atoms represents what kind of energy? a. Kinetic energy b. Potential energy c. Mechanical energy d. Solar energy A. Answer a is incorrect. Kinetic energy is the energy of
1. A covalent bond between two atoms represents what kind of energy? a. Kinetic energy b. Potential energy c. Mechanical energy d. Solar energy A. Answer a is incorrect. Kinetic energy is the energy of
Why? Intermolecular Forces. Intermolecular Forces. Chapter 12 IM Forces and Liquids. Covalent Bonding Forces for Comparison of Magnitude
 1 Why? Chapter 1 Intermolecular Forces and Liquids Why is water usually a liquid and not a gas? Why does liquid water boil at such a high temperature for such a small molecule? Why does ice float on water?
1 Why? Chapter 1 Intermolecular Forces and Liquids Why is water usually a liquid and not a gas? Why does liquid water boil at such a high temperature for such a small molecule? Why does ice float on water?
CHAPTER 4: Enzyme Structure ENZYMES
 CHAPTER 4: ENZYMES Enzymes are biological catalysts. There are about 40,000 different enzymes in human cells, each controlling a different chemical reaction. They increase the rate of reactions by a factor
CHAPTER 4: ENZYMES Enzymes are biological catalysts. There are about 40,000 different enzymes in human cells, each controlling a different chemical reaction. They increase the rate of reactions by a factor
Protein Folding. The resulting three-dimensional structure is determined by the amino acid sequence (Anfinsen's dogma).
 Protein Folding Protein folding is the physical process by which a polypeptide folds into its characteristic and functional three-dimensional structure from random coil. Each protein exists as an unfolded
Protein Folding Protein folding is the physical process by which a polypeptide folds into its characteristic and functional three-dimensional structure from random coil. Each protein exists as an unfolded
Amino Acids. Amino acids are the building blocks of proteins. All AA s have the same basic structure: Side Chain. Alpha Carbon. Carboxyl. Group.
 Protein Structure Amino Acids Amino acids are the building blocks of proteins. All AA s have the same basic structure: Side Chain Alpha Carbon Amino Group Carboxyl Group Amino Acid Properties There are
Protein Structure Amino Acids Amino acids are the building blocks of proteins. All AA s have the same basic structure: Side Chain Alpha Carbon Amino Group Carboxyl Group Amino Acid Properties There are
Standard Free Energies of Formation at 298 K. Average Bond Dissociation Energies at 298 K
 1 Thermodynamics There always seems to be at least one free response question that involves thermodynamics. These types of question also show up in the multiple choice questions. G, S, and H. Know what
1 Thermodynamics There always seems to be at least one free response question that involves thermodynamics. These types of question also show up in the multiple choice questions. G, S, and H. Know what
Disulfide Bonds at the Hair Salon
 Disulfide Bonds at the Hair Salon Three Alpha Helices Stabilized By Disulfide Bonds! In order for hair to grow 6 inches in one year, 9 1/2 turns of α helix must be produced every second!!! In some proteins,
Disulfide Bonds at the Hair Salon Three Alpha Helices Stabilized By Disulfide Bonds! In order for hair to grow 6 inches in one year, 9 1/2 turns of α helix must be produced every second!!! In some proteins,
Energy & Enzymes. Life requires energy for maintenance of order, growth, and reproduction. The energy living things use is chemical energy.
 Energy & Enzymes Life requires energy for maintenance of order, growth, and reproduction. The energy living things use is chemical energy. 1 Energy exists in two forms - potential and kinetic. Potential
Energy & Enzymes Life requires energy for maintenance of order, growth, and reproduction. The energy living things use is chemical energy. 1 Energy exists in two forms - potential and kinetic. Potential
Chapter 2 Polar Covalent Bonds; Acids and Bases
 John E. McMurry http://www.cengage.com/chemistry/mcmurry Chapter 2 Polar Covalent Bonds; Acids and Bases Javier E. Horta, M.D., Ph.D. University of Massachusetts Lowell Polar Covalent Bonds: Electronegativity
John E. McMurry http://www.cengage.com/chemistry/mcmurry Chapter 2 Polar Covalent Bonds; Acids and Bases Javier E. Horta, M.D., Ph.D. University of Massachusetts Lowell Polar Covalent Bonds: Electronegativity
Molecular Spectroscopy
 Molecular Spectroscopy UV-Vis Spectroscopy Absorption Characteristics of Some Common Chromophores UV-Vis Spectroscopy Absorption Characteristics of Aromatic Compounds UV-Vis Spectroscopy Effect of extended
Molecular Spectroscopy UV-Vis Spectroscopy Absorption Characteristics of Some Common Chromophores UV-Vis Spectroscopy Absorption Characteristics of Aromatic Compounds UV-Vis Spectroscopy Effect of extended
ENZYME SCIENCE AND ENGINEERING PROF. SUBHASH CHAND DEPARTMENT OF BIOCHEMICAL ENGINEERING AND BIOTECHNOLOGY IIT DELHI LECTURE 4 ENZYMATIC CATALYSIS
 ENZYME SCIENCE AND ENGINEERING PROF. SUBHASH CHAND DEPARTMENT OF BIOCHEMICAL ENGINEERING AND BIOTECHNOLOGY IIT DELHI LECTURE 4 ENZYMATIC CATALYSIS We will continue today our discussion on enzymatic catalysis
ENZYME SCIENCE AND ENGINEERING PROF. SUBHASH CHAND DEPARTMENT OF BIOCHEMICAL ENGINEERING AND BIOTECHNOLOGY IIT DELHI LECTURE 4 ENZYMATIC CATALYSIS We will continue today our discussion on enzymatic catalysis
Enzymes. Enzyme Structure. Enzyme Classification. CHEM464/Medh, J.D. Reaction Rate and Enzyme Activity
 Enzymes Enzymes are biological catalysts They are not consumed or altered during the reaction They do not change the equilibrium, just reduce the time required to reach equilibrium. They increase the rate
Enzymes Enzymes are biological catalysts They are not consumed or altered during the reaction They do not change the equilibrium, just reduce the time required to reach equilibrium. They increase the rate
Reading: Moore chapter 18, sections 18.6-18.11 Questions for Review and Thought: 62, 69, 71, 73, 78, 83, 99, 102.
 Thermodynamics 2: Gibbs Free Energy and Equilibrium Reading: Moore chapter 18, sections 18.6-18.11 Questions for Review and Thought: 62, 69, 71, 73, 78, 83, 99, 102. Key Concepts and skills: definitions
Thermodynamics 2: Gibbs Free Energy and Equilibrium Reading: Moore chapter 18, sections 18.6-18.11 Questions for Review and Thought: 62, 69, 71, 73, 78, 83, 99, 102. Key Concepts and skills: definitions
Enzymes. Enzymes are characterized by: Specificity - highly specific for substrates
 Enzymes Enzymes are characterized by: Catalytic Power - rates are 10 6-10 12 greater than corresponding uncatalyzed reactions Specificity - highly specific for substrates Regulation - acheived in many
Enzymes Enzymes are characterized by: Catalytic Power - rates are 10 6-10 12 greater than corresponding uncatalyzed reactions Specificity - highly specific for substrates Regulation - acheived in many
Two-photon FCS Tutorial. Berland Lab Department of Physics Emory University
 Two-photon FCS Tutorial Berland Lab Department of Physics Emory University What is FCS? FCS : Fluorescence Correlation Spectroscopy FCS is a technique for acquiring dynamical information from spontaneous
Two-photon FCS Tutorial Berland Lab Department of Physics Emory University What is FCS? FCS : Fluorescence Correlation Spectroscopy FCS is a technique for acquiring dynamical information from spontaneous
Nafith Abu Tarboush DDS, MSc, PhD natarboush@ju.edu.jo www.facebook.com/natarboush
 Nafith Abu Tarboush DDS, MSc, PhD natarboush@ju.edu.jo www.facebook.com/natarboush α-keratins, bundles of α- helices Contain polypeptide chains organized approximately parallel along a single axis: Consist
Nafith Abu Tarboush DDS, MSc, PhD natarboush@ju.edu.jo www.facebook.com/natarboush α-keratins, bundles of α- helices Contain polypeptide chains organized approximately parallel along a single axis: Consist
Thermochemistry. r2 d:\files\courses\1110-20\99heat&thermorans.doc. Ron Robertson
 Thermochemistry r2 d:\files\courses\1110-20\99heat&thermorans.doc Ron Robertson I. What is Energy? A. Energy is a property of matter that allows work to be done B. Potential and Kinetic Potential energy
Thermochemistry r2 d:\files\courses\1110-20\99heat&thermorans.doc Ron Robertson I. What is Energy? A. Energy is a property of matter that allows work to be done B. Potential and Kinetic Potential energy
The first law: transformation of energy into heat and work. Chemical reactions can be used to provide heat and for doing work.
 The first law: transformation of energy into heat and work Chemical reactions can be used to provide heat and for doing work. Compare fuel value of different compounds. What drives these reactions to proceed
The first law: transformation of energy into heat and work Chemical reactions can be used to provide heat and for doing work. Compare fuel value of different compounds. What drives these reactions to proceed
Chapter 3. Protein Structure and Function
 Chapter 3 Protein Structure and Function Broad functional classes So Proteins have structure and function... Fine! -Why do we care to know more???? Understanding functional architechture gives us POWER
Chapter 3 Protein Structure and Function Broad functional classes So Proteins have structure and function... Fine! -Why do we care to know more???? Understanding functional architechture gives us POWER
KINETIC THEORY OF MATTER - molecules in matter are always in motion - speed of molecules is proportional to the temperature
 1 KINETIC TERY F MATTER - molecules in matter are always in motion - speed of molecules is proportional to the temperature TE STATES F MATTER 1. Gas a) ideal gas - molecules move freely - molecules have
1 KINETIC TERY F MATTER - molecules in matter are always in motion - speed of molecules is proportional to the temperature TE STATES F MATTER 1. Gas a) ideal gas - molecules move freely - molecules have
Paper: 6 Chemistry 2.130 University I Chemistry: Models Page: 2 of 7. 4. Which of the following weak acids would make the best buffer at ph = 5.0?
 Paper: 6 Chemistry 2.130 University I Chemistry: Models Page: 2 of 7 4. Which of the following weak acids would make the best buffer at ph = 5.0? A) Acetic acid (Ka = 1.74 x 10-5 ) B) H 2 PO - 4 (Ka =
Paper: 6 Chemistry 2.130 University I Chemistry: Models Page: 2 of 7 4. Which of the following weak acids would make the best buffer at ph = 5.0? A) Acetic acid (Ka = 1.74 x 10-5 ) B) H 2 PO - 4 (Ka =
A. A peptide with 12 amino acids has the following amino acid composition: 2 Met, 1 Tyr, 1 Trp, 2 Glu, 1 Lys, 1 Arg, 1 Thr, 1 Asn, 1 Ile, 1 Cys
 Questions- Proteins & Enzymes A. A peptide with 12 amino acids has the following amino acid composition: 2 Met, 1 Tyr, 1 Trp, 2 Glu, 1 Lys, 1 Arg, 1 Thr, 1 Asn, 1 Ile, 1 Cys Reaction of the intact peptide
Questions- Proteins & Enzymes A. A peptide with 12 amino acids has the following amino acid composition: 2 Met, 1 Tyr, 1 Trp, 2 Glu, 1 Lys, 1 Arg, 1 Thr, 1 Asn, 1 Ile, 1 Cys Reaction of the intact peptide
Chemical Bonds. Chemical Bonds. The Nature of Molecules. Energy and Metabolism < < Covalent bonds form when atoms share 2 or more valence electrons.
 The Nature of Molecules Chapter 2 Energy and Metabolism Chapter 6 Chemical Bonds Molecules are groups of atoms held together in a stable association. Compounds are molecules containing more than one type
The Nature of Molecules Chapter 2 Energy and Metabolism Chapter 6 Chemical Bonds Molecules are groups of atoms held together in a stable association. Compounds are molecules containing more than one type
Viscoelasticity of Polymer Fluids.
 Viscoelasticity of Polymer Fluids. Main Properties of Polymer Fluids. Entangled polymer fluids are polymer melts and concentrated or semidilute (above the concentration c) solutions. In these systems polymer
Viscoelasticity of Polymer Fluids. Main Properties of Polymer Fluids. Entangled polymer fluids are polymer melts and concentrated or semidilute (above the concentration c) solutions. In these systems polymer
8/20/2012 H C OH H R. Proteins
 Proteins Rubisco monomer = amino acids 20 different amino acids polymer = polypeptide protein can be one or more polypeptide chains folded & bonded together large & complex 3-D shape hemoglobin Amino acids
Proteins Rubisco monomer = amino acids 20 different amino acids polymer = polypeptide protein can be one or more polypeptide chains folded & bonded together large & complex 3-D shape hemoglobin Amino acids
Biochemistry 462a Hemoglobin Structure and Function Reading - Chapter 7 Practice problems - Chapter 7: 1-6; Proteins extra problems
 Biochemistry 462a Hemoglobin Structure and Function Reading - Chapter 7 Practice problems - Chapter 7: 1-6; Proteins extra problems Myoglobin and Hemoglobin Oxygen is required for oxidative metabolism
Biochemistry 462a Hemoglobin Structure and Function Reading - Chapter 7 Practice problems - Chapter 7: 1-6; Proteins extra problems Myoglobin and Hemoglobin Oxygen is required for oxidative metabolism
Chemistry. The student will be able to identify and apply basic safety procedures and identify basic equipment.
 Chemistry UNIT I: Introduction to Chemistry The student will be able to describe what chemistry is and its scope. a. Define chemistry. b. Explain that chemistry overlaps many other areas of science. The
Chemistry UNIT I: Introduction to Chemistry The student will be able to describe what chemistry is and its scope. a. Define chemistry. b. Explain that chemistry overlaps many other areas of science. The
Thermodynamics of Mixing
 Thermodynamics of Mixing Dependence of Gibbs energy on mixture composition is G = n A µ A + n B µ B and at constant T and p, systems tend towards a lower Gibbs energy The simplest example of mixing: What
Thermodynamics of Mixing Dependence of Gibbs energy on mixture composition is G = n A µ A + n B µ B and at constant T and p, systems tend towards a lower Gibbs energy The simplest example of mixing: What
Chemical Basis of Life Module A Anchor 2
 Chemical Basis of Life Module A Anchor 2 Key Concepts: - Water is a polar molecule. Therefore, it is able to form multiple hydrogen bonds, which account for many of its special properties. - Water s polarity
Chemical Basis of Life Module A Anchor 2 Key Concepts: - Water is a polar molecule. Therefore, it is able to form multiple hydrogen bonds, which account for many of its special properties. - Water s polarity
Study the following diagrams of the States of Matter. Label the names of the Changes of State between the different states.
 Describe the strength of attractive forces between particles. Describe the amount of space between particles. Can the particles in this state be compressed? Do the particles in this state have a definite
Describe the strength of attractive forces between particles. Describe the amount of space between particles. Can the particles in this state be compressed? Do the particles in this state have a definite
VAPORIZATION IN MORE DETAIL. Energy needed to escape into gas phase GAS LIQUID. Kinetic energy. Average kinetic energy
 30 VAPORIZATION IN MORE DETAIL GAS Energy needed to escape into gas phase LIQUID Kinetic energy Average kinetic energy - For a molecule to move from the liquid phase to the gas phase, it must acquire enough
30 VAPORIZATION IN MORE DETAIL GAS Energy needed to escape into gas phase LIQUID Kinetic energy Average kinetic energy - For a molecule to move from the liquid phase to the gas phase, it must acquire enough
Myoglobin and Hemoglobin
 Myoglobin and Hemoglobin Myoglobin and hemoglobin are hemeproteins whose physiological importance is principally related to their ability to bind molecular oxygen. Myoglobin (Mb) The oxygen storage protein
Myoglobin and Hemoglobin Myoglobin and hemoglobin are hemeproteins whose physiological importance is principally related to their ability to bind molecular oxygen. Myoglobin (Mb) The oxygen storage protein
7. DYNAMIC LIGHT SCATTERING 7.1 First order temporal autocorrelation function.
 7. DYNAMIC LIGHT SCATTERING 7. First order temporal autocorrelation function. Dynamic light scattering (DLS) studies the properties of inhomogeneous and dynamic media. A generic situation is illustrated
7. DYNAMIC LIGHT SCATTERING 7. First order temporal autocorrelation function. Dynamic light scattering (DLS) studies the properties of inhomogeneous and dynamic media. A generic situation is illustrated
RNA Structure and folding
 RNA Structure and folding Overview: The main functional biomolecules in cells are polymers DNA, RNA and proteins For RNA and Proteins, the specific sequence of the polymer dictates its final structure
RNA Structure and folding Overview: The main functional biomolecules in cells are polymers DNA, RNA and proteins For RNA and Proteins, the specific sequence of the polymer dictates its final structure
Lecture 24 - Surface tension, viscous flow, thermodynamics
 Lecture 24 - Surface tension, viscous flow, thermodynamics Surface tension, surface energy The atoms at the surface of a solid or liquid are not happy. Their bonding is less ideal than the bonding of atoms
Lecture 24 - Surface tension, viscous flow, thermodynamics Surface tension, surface energy The atoms at the surface of a solid or liquid are not happy. Their bonding is less ideal than the bonding of atoms
Modern Construction Materials Prof. Ravindra Gettu Department of Civil Engineering Indian Institute of Technology, Madras
 Modern Construction Materials Prof. Ravindra Gettu Department of Civil Engineering Indian Institute of Technology, Madras Module - 2 Lecture - 2 Part 2 of 2 Review of Atomic Bonding II We will continue
Modern Construction Materials Prof. Ravindra Gettu Department of Civil Engineering Indian Institute of Technology, Madras Module - 2 Lecture - 2 Part 2 of 2 Review of Atomic Bonding II We will continue
ENTROPY AND THE SECOND LAW OF THERMODYNAMICS
 ENTROPY AND THE SECOND LAW OF THERMODYNAMICS Energy Reservoir The system consists of the red circles in the blue box. Energy and entropy fl ow out of the system. TIME Additional Energy is added to the
ENTROPY AND THE SECOND LAW OF THERMODYNAMICS Energy Reservoir The system consists of the red circles in the blue box. Energy and entropy fl ow out of the system. TIME Additional Energy is added to the
1 Introduction. Taking the logarithm of both sides of Equation 1.1:
 j1 1 Introduction The aim of this book is to provide an understanding of the basic processes, at the atomic or molecular level, which are responsible for kinetic processes at the microscopic and macroscopic
j1 1 Introduction The aim of this book is to provide an understanding of the basic processes, at the atomic or molecular level, which are responsible for kinetic processes at the microscopic and macroscopic
3. Diodes and Diode Circuits. 3. Diodes and Diode Circuits TLT-8016 Basic Analog Circuits 2005/2006 1
 3. Diodes and Diode Circuits 3. Diodes and Diode Circuits TLT-8016 Basic Analog Circuits 2005/2006 1 3.1 Diode Characteristics Small-Signal Diodes Diode: a semiconductor device, which conduct the current
3. Diodes and Diode Circuits 3. Diodes and Diode Circuits TLT-8016 Basic Analog Circuits 2005/2006 1 3.1 Diode Characteristics Small-Signal Diodes Diode: a semiconductor device, which conduct the current
Carbohydrates, proteins and lipids
 Carbohydrates, proteins and lipids Chapter 3 MACROMOLECULES Macromolecules: polymers with molecular weights >1,000 Functional groups THE FOUR MACROMOLECULES IN LIFE Molecules in living organisms: proteins,
Carbohydrates, proteins and lipids Chapter 3 MACROMOLECULES Macromolecules: polymers with molecular weights >1,000 Functional groups THE FOUR MACROMOLECULES IN LIFE Molecules in living organisms: proteins,
[Image removed due to copyright concerns]
![[Image removed due to copyright concerns] [Image removed due to copyright concerns]](/thumbs/40/21531271.jpg) Radiation Chemistry Ionizing radiation produces abundant secondary electrons that rapidly slow down (thermalize) to energies below 7.4 ev, the threshold to produce electronic transitions in liquid water.
Radiation Chemistry Ionizing radiation produces abundant secondary electrons that rapidly slow down (thermalize) to energies below 7.4 ev, the threshold to produce electronic transitions in liquid water.
The strength of the interaction
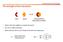 The strength of the interaction Host Guest Supramolecule (host-guest complex) When is the host capable to recognize the guest? How do we define selectivity Which element will we use to design the host
The strength of the interaction Host Guest Supramolecule (host-guest complex) When is the host capable to recognize the guest? How do we define selectivity Which element will we use to design the host
Chapter NP-5. Nuclear Physics. Nuclear Reactions TABLE OF CONTENTS INTRODUCTION OBJECTIVES 1.0 NUCLEAR REACTIONS 2.0 NEUTRON INTERACTIONS
 Chapter NP-5 Nuclear Physics Nuclear Reactions TABLE OF CONTENTS INTRODUCTION OBJECTIVES 1.0 2.0 NEUTRON INTERACTIONS 2.1 ELASTIC SCATTERING 2.2 INELASTIC SCATTERING 2.3 RADIATIVE CAPTURE 2.4 PARTICLE
Chapter NP-5 Nuclear Physics Nuclear Reactions TABLE OF CONTENTS INTRODUCTION OBJECTIVES 1.0 2.0 NEUTRON INTERACTIONS 2.1 ELASTIC SCATTERING 2.2 INELASTIC SCATTERING 2.3 RADIATIVE CAPTURE 2.4 PARTICLE
Biological Molecules
 Biological Molecules I won t lie. This is probably the most boring topic you have ever done in any science. It s pretty much as simple as this: learn the material deal with it. Enjoy don t say I didn t
Biological Molecules I won t lie. This is probably the most boring topic you have ever done in any science. It s pretty much as simple as this: learn the material deal with it. Enjoy don t say I didn t
Lecture 3: Enzyme kinetics
 Computational Systems Biology Lecture 3: Enzyme kinetics Fri 19 Jan 2009 1 Images from: D. L. Nelson, Lehninger Principles of Biochemistry, IV Edition, W. H. Freeman ed. A. Cornish-Bowden Fundamentals
Computational Systems Biology Lecture 3: Enzyme kinetics Fri 19 Jan 2009 1 Images from: D. L. Nelson, Lehninger Principles of Biochemistry, IV Edition, W. H. Freeman ed. A. Cornish-Bowden Fundamentals
Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows
 Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows 3.- 1 Basics: equations of continuum mechanics - balance equations for mass and momentum - balance equations for the energy and the chemical
Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows 3.- 1 Basics: equations of continuum mechanics - balance equations for mass and momentum - balance equations for the energy and the chemical
Define the notations you are using properly. Present your arguments in details. Good luck!
 Umeå Universitet, Fysik Vitaly Bychkov Prov i fysik, Thermodynamics, 0-0-4, kl 9.00-5.00 jälpmedel: Students may use any book(s) including the textbook Thermal physics. Minor notes in the books are also
Umeå Universitet, Fysik Vitaly Bychkov Prov i fysik, Thermodynamics, 0-0-4, kl 9.00-5.00 jälpmedel: Students may use any book(s) including the textbook Thermal physics. Minor notes in the books are also
Chemical Kinetics. 2. Using the kinetics of a given reaction a possible reaction mechanism
 1. Kinetics is the study of the rates of reaction. Chemical Kinetics 2. Using the kinetics of a given reaction a possible reaction mechanism 3. What is a reaction mechanism? Why is it important? A reaction
1. Kinetics is the study of the rates of reaction. Chemical Kinetics 2. Using the kinetics of a given reaction a possible reaction mechanism 3. What is a reaction mechanism? Why is it important? A reaction
Peptide bonds: resonance structure. Properties of proteins: Peptide bonds and side chains. Dihedral angles. Peptide bond. Protein physics, Lecture 5
 Protein physics, Lecture 5 Peptide bonds: resonance structure Properties of proteins: Peptide bonds and side chains Proteins are linear polymers However, the peptide binds and side chains restrict conformational
Protein physics, Lecture 5 Peptide bonds: resonance structure Properties of proteins: Peptide bonds and side chains Proteins are linear polymers However, the peptide binds and side chains restrict conformational
Aspects of an introduction to photochemistry
 Aspects of an introduction to photochemistry Ground state reactants Excited state reactants Reaction Intermediates Ground state products Orbital occupancy Carbonyl photochemistry Vibrational structure
Aspects of an introduction to photochemistry Ground state reactants Excited state reactants Reaction Intermediates Ground state products Orbital occupancy Carbonyl photochemistry Vibrational structure
Chemical Exchange in NMR Spectroscopy
 COURSE#1022: Biochemical Applications of NMR Spectroscopy http://www.bioc.aecom.yu.edu/labs/girvlab/nmr/course/ Chemical Exchange in NMR Spectroscopy LAST UPDATE: 3/28/2012 1 References Bain, A. D. (2003).
COURSE#1022: Biochemical Applications of NMR Spectroscopy http://www.bioc.aecom.yu.edu/labs/girvlab/nmr/course/ Chemical Exchange in NMR Spectroscopy LAST UPDATE: 3/28/2012 1 References Bain, A. D. (2003).
INTRODUCTION TO PROTEIN STRUCTURE
 Name Class: Partner, if any: INTRODUCTION TO PROTEIN STRUCTURE PRIMARY STRUCTURE: 1. Write the complete structural formula of the tripeptide shown (frame 10). Circle and label the three sidechains which
Name Class: Partner, if any: INTRODUCTION TO PROTEIN STRUCTURE PRIMARY STRUCTURE: 1. Write the complete structural formula of the tripeptide shown (frame 10). Circle and label the three sidechains which
Protein Physics. A. V. Finkelstein & O. B. Ptitsyn LECTURE 1
 Protein Physics A. V. Finkelstein & O. B. Ptitsyn LECTURE 1 PROTEINS Functions in a Cell MOLECULAR MACHINES BUILDING BLOCKS of a CELL ARMS of a CELL ENZYMES - enzymatic catalysis of biochemical reactions
Protein Physics A. V. Finkelstein & O. B. Ptitsyn LECTURE 1 PROTEINS Functions in a Cell MOLECULAR MACHINES BUILDING BLOCKS of a CELL ARMS of a CELL ENZYMES - enzymatic catalysis of biochemical reactions
Thermodynamics of glycolysis. Chemistry 433. The role of enzymes. Phosphorylation of glucose. Question. Question
 hemistry 433 Lecture 15 pplications of Free Energy N State University hermodynamics of glycolysis Reaction kj/mol D-glucose P D-glucose-6-phosphate DP Δ o = -16.7 D-glucose-6-phosphate D-fructose-6-phosphate
hemistry 433 Lecture 15 pplications of Free Energy N State University hermodynamics of glycolysis Reaction kj/mol D-glucose P D-glucose-6-phosphate DP Δ o = -16.7 D-glucose-6-phosphate D-fructose-6-phosphate
Chapter 5: Diffusion. 5.1 Steady-State Diffusion
 : Diffusion Diffusion: the movement of particles in a solid from an area of high concentration to an area of low concentration, resulting in the uniform distribution of the substance Diffusion is process
: Diffusion Diffusion: the movement of particles in a solid from an area of high concentration to an area of low concentration, resulting in the uniform distribution of the substance Diffusion is process
Introduction, Noncovalent Bonds, and Properties of Water
 Lecture 1 Introduction, Noncovalent Bonds, and Properties of Water Reading: Berg, Tymoczko & Stryer: Chapter 1 problems in textbook: chapter 1, pp. 23-24, #1,2,3,6,7,8,9, 10,11; practice problems at end
Lecture 1 Introduction, Noncovalent Bonds, and Properties of Water Reading: Berg, Tymoczko & Stryer: Chapter 1 problems in textbook: chapter 1, pp. 23-24, #1,2,3,6,7,8,9, 10,11; practice problems at end
Lecture 15: Enzymes & Kinetics Mechanisms
 ROLE OF THE TRANSITION STATE Lecture 15: Enzymes & Kinetics Mechanisms Consider the reaction: H-O-H + Cl - H-O δ- H Cl δ- HO - + H-Cl Reactants Transition state Products Margaret A. Daugherty Fall 2004
ROLE OF THE TRANSITION STATE Lecture 15: Enzymes & Kinetics Mechanisms Consider the reaction: H-O-H + Cl - H-O δ- H Cl δ- HO - + H-Cl Reactants Transition state Products Margaret A. Daugherty Fall 2004
IV. -Amino Acids: carboxyl and amino groups bonded to -Carbon. V. Polypeptides and Proteins
 IV. -Amino Acids: carboxyl and amino groups bonded to -Carbon A. Acid/Base properties 1. carboxyl group is proton donor! weak acid 2. amino group is proton acceptor! weak base 3. At physiological ph: H
IV. -Amino Acids: carboxyl and amino groups bonded to -Carbon A. Acid/Base properties 1. carboxyl group is proton donor! weak acid 2. amino group is proton acceptor! weak base 3. At physiological ph: H
EXIT TIME PROBLEMS AND ESCAPE FROM A POTENTIAL WELL
 EXIT TIME PROBLEMS AND ESCAPE FROM A POTENTIAL WELL Exit Time problems and Escape from a Potential Well Escape From a Potential Well There are many systems in physics, chemistry and biology that exist
EXIT TIME PROBLEMS AND ESCAPE FROM A POTENTIAL WELL Exit Time problems and Escape from a Potential Well Escape From a Potential Well There are many systems in physics, chemistry and biology that exist
VTT TECHNICAL RESEARCH CENTRE OF FINLAND
 Figure from: http://www.embl.de/nmr/sattler/teaching Why NMR (instead of X ray crystallography) a great number of macromolecules won't crystallize) natural environmant (water) ligand binding and inter
Figure from: http://www.embl.de/nmr/sattler/teaching Why NMR (instead of X ray crystallography) a great number of macromolecules won't crystallize) natural environmant (water) ligand binding and inter
TEACHER BACKGROUND INFORMATION THERMAL ENERGY
 TEACHER BACKGROUND INFORMATION THERMAL ENERGY In general, when an object performs work on another object, it does not transfer all of its energy to that object. Some of the energy is lost as heat due to
TEACHER BACKGROUND INFORMATION THERMAL ENERGY In general, when an object performs work on another object, it does not transfer all of its energy to that object. Some of the energy is lost as heat due to
Amino Acids and Proteins
 Amino Acids and Proteins Proteins are composed of amino acids. There are 20 amino acids commonly found in proteins. All have: N2 C α R COO Amino acids at neutral p are dipolar ions (zwitterions) because
Amino Acids and Proteins Proteins are composed of amino acids. There are 20 amino acids commonly found in proteins. All have: N2 C α R COO Amino acids at neutral p are dipolar ions (zwitterions) because
BIOLOGICAL MEMBRANES: FUNCTIONS, STRUCTURES & TRANSPORT
 BIOLOGICAL MEMBRANES: FUNCTIONS, STRUCTURES & TRANSPORT UNIVERSITY OF PNG SCHOOL OF MEDICINE AND HEALTH SCIENCES DISCIPLINE OF BIOCHEMISTRY AND MOLECULAR BIOLOGY BMLS II / B Pharm II / BDS II VJ Temple
BIOLOGICAL MEMBRANES: FUNCTIONS, STRUCTURES & TRANSPORT UNIVERSITY OF PNG SCHOOL OF MEDICINE AND HEALTH SCIENCES DISCIPLINE OF BIOCHEMISTRY AND MOLECULAR BIOLOGY BMLS II / B Pharm II / BDS II VJ Temple
ENZYMES. Serine Proteases Chymotrypsin, Trypsin, Elastase, Subtisisin. Principle of Enzyme Catalysis
 ENZYMES Serine Proteases Chymotrypsin, Trypsin, Elastase, Subtisisin Principle of Enzyme Catalysis Linus Pauling (1946) formulated the first basic principle of enzyme catalysis Enzyme increase the rate
ENZYMES Serine Proteases Chymotrypsin, Trypsin, Elastase, Subtisisin Principle of Enzyme Catalysis Linus Pauling (1946) formulated the first basic principle of enzyme catalysis Enzyme increase the rate
Ann.wellhouse@TouchStoneScience.net 1. Enzyme Function
 Ann.wellhouse@TouchStoneScience.net 1 Enzyme Function National Science Standards Science as Inquiry: Content Standard A: As a result of activities in grades 9-12, all students should develop: Abilities
Ann.wellhouse@TouchStoneScience.net 1 Enzyme Function National Science Standards Science as Inquiry: Content Standard A: As a result of activities in grades 9-12, all students should develop: Abilities
INFRARED SPECTROSCOPY (IR)
 INFRARED SPECTROSCOPY (IR) Theory and Interpretation of IR spectra ASSIGNED READINGS Introduction to technique 25 (p. 833-834 in lab textbook) Uses of the Infrared Spectrum (p. 847-853) Look over pages
INFRARED SPECTROSCOPY (IR) Theory and Interpretation of IR spectra ASSIGNED READINGS Introduction to technique 25 (p. 833-834 in lab textbook) Uses of the Infrared Spectrum (p. 847-853) Look over pages
Rate Equations and Detailed Balance
 Rate Equations and Detailed Balance Initial question: Last time we mentioned astrophysical masers. Why can they exist spontaneously? Could there be astrophysical lasers, i.e., ones that emit in the optical?
Rate Equations and Detailed Balance Initial question: Last time we mentioned astrophysical masers. Why can they exist spontaneously? Could there be astrophysical lasers, i.e., ones that emit in the optical?
General Properties Protein Nature of Enzymes Folded Shape of Enzymes H-bonds complementary
 Proteins that function as biological catalysts are called enzymes. Enzymes speed up specific metabolic reactions. Low contamination, low temperature and fast metabolism are only possible with enzymes.
Proteins that function as biological catalysts are called enzymes. Enzymes speed up specific metabolic reactions. Low contamination, low temperature and fast metabolism are only possible with enzymes.
FUNDAMENTALS OF ENGINEERING THERMODYNAMICS
 FUNDAMENTALS OF ENGINEERING THERMODYNAMICS System: Quantity of matter (constant mass) or region in space (constant volume) chosen for study. Closed system: Can exchange energy but not mass; mass is constant
FUNDAMENTALS OF ENGINEERING THERMODYNAMICS System: Quantity of matter (constant mass) or region in space (constant volume) chosen for study. Closed system: Can exchange energy but not mass; mass is constant
3.4 BRØNSTED LOWRY ACIDS AND BASES
 96 CAPTER 3 ACIDS AND BASES. TE CURVED-ARROW NOTATION and that the unshared electron pair (and negative charge) is shared equally by the two terminal carbons. C L C A C 1 allyl anion (c) Using the curved-arrow
96 CAPTER 3 ACIDS AND BASES. TE CURVED-ARROW NOTATION and that the unshared electron pair (and negative charge) is shared equally by the two terminal carbons. C L C A C 1 allyl anion (c) Using the curved-arrow
Exergy: the quality of energy N. Woudstra
 Exergy: the quality of energy N. Woudstra Introduction Characteristic for our society is a massive consumption of goods and energy. Continuation of this way of life in the long term is only possible if
Exergy: the quality of energy N. Woudstra Introduction Characteristic for our society is a massive consumption of goods and energy. Continuation of this way of life in the long term is only possible if
KINETIC MOLECULAR THEORY OF MATTER
 KINETIC MOLECULAR THEORY OF MATTER The kinetic-molecular theory is based on the idea that particles of matter are always in motion. The theory can be used to explain the properties of solids, liquids,
KINETIC MOLECULAR THEORY OF MATTER The kinetic-molecular theory is based on the idea that particles of matter are always in motion. The theory can be used to explain the properties of solids, liquids,
How To Understand Enzyme Kinetics
 Chapter 12 - Reaction Kinetics In the last chapter we looked at enzyme mechanisms. In this chapter we ll see how enzyme kinetics, i.e., the study of enzyme reaction rates, can be useful in learning more
Chapter 12 - Reaction Kinetics In the last chapter we looked at enzyme mechanisms. In this chapter we ll see how enzyme kinetics, i.e., the study of enzyme reaction rates, can be useful in learning more
