RF Engineering Basic Concepts
|
|
|
- August Jacobs
- 10 years ago
- Views:
Transcription
1 RF Engineering Basic Concepts Fritz Caspers, Peter McIntosh, Tom Kroyer CAS 2007, Daresbury
2 Contents S parameters Signal flow graph Properties of the S matrix of an N-port Basic properties of striplines, microstrip- and slotlines Application of the Smith Chart 2
3 S-parameters (1) The abbreviation S has been derived from the word scattering. For high frequencies, it is convenient to describe a given network in terms of waves rather than voltages or currents. This permits an easier definition of reference planes. For practical reasons, the description in terms of in- and outgoing waves has been introduced. Now, a 4-pole network becomes a 2-port and a 2n-pole becomes an n-port. In the case of an odd pole number (e.g. 3-pole), a common reference point may be chosen, attributing one pole equally to two ports. Then a 3-pole is converted into a (3+1) pole corresponding to a 2-port. As a general conversion rule for an odd pole number one more pole is added. 3
4 S-parameters (2) Fig. 1 2-port network Let us start by considering a simple 2-port network consisting of a single impedance Z connected in series (Fig. 1). The generator and load impedances are Z G and Z L, respectively. If Z = 0 and Z L = Z G (for real Z G ) we have a matched load, i.e. maximum available power goes into the load and U 1 = U 2 = U 0 /2. Please note that all the voltages and currents are peak values. The lines connecting the different elements are supposed to have zero electrical length. Connections with a finite electrical length are drawn as double lines or as heavy lines. Now we need to relate U 0, U 1 and U 2 with a and b. 4
5 Definition of power waves (1) The waves going towards the n-port are a = (a 1, a 2,..., a n ), the waves travelling away from the n-port are b = (b 1, b 2,..., b n ). By definition currents going into the n-port are counted positively and currents flowing out of the n-port negatively. The wave a 1 is going into the n-port at port 1 is derived from the voltage wave going into a matched load. In order to make the definitions consistent with the conservation of energy, the voltage is normalized to. Z 0 is in general an arbitrary reference impedance, but usually the characteristic impedance of a line (e.g. Z 0 = 50 Ω) is used and very often Z G = Z L = Z 0. In the following we assume Z 0 to be real. The definitions of the waves a 1 and b 1 are (2.1) Note that a and b have the dimension [1]. 5
6 Definition of power waves (2) The power travelling towards port 1, P 1 inc, is simply the available power from the source, while the power coming out of port 1, P 1 refl, is given by the reflected voltage wave. (2.2) Please note the factor 2 in the denominator, which comes from the definition of the voltages and currents as peak values ( European definition ). In the US definition effective values are used and the factor 2 is not present, so for power calculations it is important to check how the voltages are defined. For most applications, this difference does not play a role since ratios of waves are used. In the case of a mismatched load Z L there will be some power reflected towards the 2-port from Z L (2.3) 6
7 Definition of power waves (3) There is also the outgoing wave of port 2 which may be considered as the superimposition of a wave that has gone through the 2-port from the generator and a reflected part from the mismatched load. We have defined with the incident voltage wave U inc. In analogy to that we can also quote with the incident current wave I inc. We obtain the general definition of the waves a i travelling into and b i travelling out of an n-port: Solving these two equations, U i and I i can be obtained for a given a i and b i as (2.4) (2.5) For a harmonic excitation u(t) = Re{U e jωt } the power going into port i is given by (2.6) The term (a i * b i a i b i * ) is a purely imaginary number and vanishes when the real part is taken 7
8 The S-Matrix S (1) The relation between a i and b i (i = l...n) can be written as a system of n linear equations (a i being the independent variable, b i the dependent variable) (2.7) Or in matrix formulation (2.8) The physical meaning of S 11 is the input reflection coefficient with the output of the network terminated by a matched load (a 2 = 0). S 21 is the forward transmission (from port 1 to port 2), S 12 the reverse transmission (from port 2 to port 1) and S 22 the output reflection coefficient. When measuring the S parameter of an n-port, all n ports must be terminated by a matched load (not necessarily equal value for all ports), including the port connected to the generator (matched generator). Using Eqs. 2.4 and 2.7 we find the reflection coefficient of a single impedance Z L connected to a generator of source impedance Z 0 (Fig. 1, case Z G = Z 0 and Z = 0) (2.9) which is the familiar formula for the reflection coefficient ρ (often also denoted Γ). 8
9 The S-Matrix S (2) Let us now determine the S parameters of the impedance Z in Fig. 1, assuming again Z G = Z L = Z 0. From the definition of S 11 we have (2.10) and in a similar fashion we get (2.11) Due to the symmetry of the element S 22 = S 22 and S 12 = S 21. Please note that for this case we obtain S 11 + S 21 = 1. The full S matrix of the element is then (2.12) 9
10 The transfer matrix (T-matrix) The S matrix introduced in the previous section is a very convenient way to describe an n-port in terms of waves. It is very well adapted to measurements. However, it is not well suited to for characterizing the response of a number of cascaded 2-ports. A very straightforward manner for the problem is possible with the T matrix (transfer matrix), which directly relates the waves on the input and on the output [2] (2.10) The conversion formulae between S and T matrix are given in Appendix I. While the S matrix exists for any 2-port, in certain cases, e.g. no transmission between port 1 and port 2, the T matrix is not defined. The T matrix T M of m cascaded 2-ports is given by (as in [2, 3]): (2.11) Note that in the literature different definitions of the T matrix can be found and the individual matrix elements depend on the definition used. 10
11 The signal flow graph The SFG is a graphical representation of a system of linear equations having the general form: y = Mx + M y M and M are square matrices with n rows and columns x represent the n independent variables (sources) and y the n dependent variables. The elements of M and M appear as transmission coefficients of the signal path. When there are no direct signal loops, this simplifies to y = Mx, which is equivalent to the usual S parameter definition b = Sa 11
12 Drawing the SFG The SFG can be drawn as a directed graph. Each wave a i and b i is represented by a node, each arrow stands for an S parameter Nodes with no arrows pointing towards them are source noses. All other nodes are dependent signal nodes. Example: A 2-port with given S ij. At port 2 a not matched load ρ L is connected. Question: What is the input reflection coefficient S 11 of this circuit? a 1 ρ L 12
13 Simplifying the signal flow graph For general problems the SFG can be solved for applying Mason s rule (see Appendix of lecture notes). For not too complicated circuits there is a more intuitive way by simplifying the SFG according to three rules 1. Add the signal of parallel branches 2. Multiply the signals of cascaded branches 3. Resolve loops x x y x y y x+y xy x/(1-xy) 1. Parallel branches 2. Cascaded signal paths 3. Loops 13
14 Solving problems with the SFG The loop at port 2 involving S 22 and ρ L can be resolved. It gives a branch from b 2 to a 2 with the coefficient ρ L /(1-ρ L *S 22 ) Applying the cascading rule to the right path and finally the parallel branch rule we get b 1 L = S11 + S21 S L More complicated problem are usually solved by computer code using the matrix formulations mentioned before ρ a S ρ a 1 ρ L 14
15 Properties of the S matrix of an N-portN A generalized n-port has n 2 scattering coefficients. While the S ij may be all independent, in general due to symmetries etc the number of independent coefficients is much smaller. An n-port is reciprocal when S ij = S ji for all i and j. Most passive components are reciprocal, active components such as amplifiers are generally non-reciprocal. A two-port is symmetric, when it is reciprocal (S 21 = S 12 ) and when the input and output reflection coefficients are equal (S 22 = S 11 ). An N-port is passive and lossless if is S matrix is unitary, i.e. S S = 1, where x = (x*) T is the conjugate transpose of x. 15
16 Unitarity of an N-portN For a two-port the unitarity condition gives * * * S 1 0 ( ) = 11 S21 S 11 S12 S T S = S S which yields the three conditions S S * S S S * = 1 = 1 From the last equation we get, writing out amplitude and phase arg S 11 S 11 and combining the equations for the modulus (amplitude) Thus any lossless two-port can be characterized by one amplitude and three phases * 12 + * = 0 S S S S S 12 + arg S 12 = S 21 S 22 = arg S 21 S = S, S = S S S and arg S = 1 S π 1
17 General properties In general the S parameters are complex and frequency dependent. Their phases change when the reference plane is moved. Therefore it is important to clearly define the reference planes used For a given structure, often the S parameters can be determined from considering mechanical symmetries and, in case of lossless networks, from energy conservation. 17
18 Examples of S matrices: 1-ports1 Simple lumped elements are 1-ports, but also cavities with one test port, long transmission lines or antennas can be considered as 1-ports 1-ports are characterized by their reflection coefficient ρ, or in terms of S parameters, by S 11. Ideal short: S 11 = -1 Ideal termination: S 11 = 0 Active termination (reflection amplifier): S11 > 1 18
19 Examples of S matrices: 2-ports 2 (1) Ideal transmission line of length l S where γ = α + jβ is the complex propagation constant, α the line attenuation in [Neper/m] and β = 2π/λ with the wavelength λ. For a lossless line S 21 = 1. Ideal phase shifter S 0 e = γl e 0 = jϕ 21 e γl 0 e jϕ 0 12 For a reciprocal phase shifter ϕ 12 = ϕ 21, while for the gyrator ϕ 12 = ϕ 21 + π. An ideal gyrator is lossless (S S = 1), but it is not reciprocal. Gyrators are often implemented using active electronic components, however in the microwave range passive gyrators can be realized using magnetically saturated ferrite elements. 19
20 Examples of S matrices: 2-ports 2 (2) Ideal, reciprocal attenuator with the attenuation α in Neper. The attenuation in Decibel is given by A = -20*log 10 (S 21 ), 1 Np = db. An attenuator can be realized e.g. with three resistors in a T circuit or with resistive material in a waveguide. Ideal isolator The isolator allows transmission in one directly only, it is used e.g. to avoid reflections from a load back to the generator. Ideal amplifier S 0 e = α 0 S = 1 0 S = G e with the voltage gain G > 1. Please note the similarity between an ideal amplifier and an ideal isolator! α
21 Examples of S matrices: 3-ports 3 (2) It can be shown that a 3-port cannot be lossless, reciprocal and matched at all three ports at the same time. The following components have two of the above characteristics. Resistive power divider: It consists of a resistor network and is reciprocal, matched at all ports but lossy. It can be realized with three resistors in a triangle configuration. S = The T splitter is reciprocal and lossless but not matched at all ports. Using the losslessness condition and symmetry considerations one finds for E and H plane splitters S H = S E = H-plane splitter E-plane splitter 21
22 Circulators The ideal circulator is lossless, matched at all ports, but not reciprocal. A signal entering the ideal circulator at one port is transmitted exclusively to the next port in the sense of the arrow isolator circulator Its S matrix has a very simple form: 0 S = When port 3 of the circulator is terminated with a matched load we get a two-port called isolator, which lets power pass only from port 1 to port 2 22
23 Ferrites for circulators A circulator, like the gyrator and other passive non-reciprocal elements contains a volume of ferrite. This ferrite is normally magnetized into saturation by an external magnetic field. The magnetic properties of a saturated RF ferrite have to be characterized by a μ-tensor. The real and imaginary part of each complex element μ are μ and μ. They are strongly dependent on the bias field. The μ+ and μ- represent the permeability seen by a right- and lefthand circular polarized wave traversing the ferrite real part of μ imag part of μ 23
24 Practical Implementations of circulators The magnetically polarized ferrite provides the required nonreciprocal properties. As a result, power is only transmitted from port 1 to port 2, from port 2 to port 3 and from port 3 to port 1. Circulators can be built with e.g. with waveguides (left) or with striplines (right) 24
25 The Faraday isolator The Faraday isolator is based on the Faraday rotation of a polarized wave in the presence of a magnetically polarized ferrite Running along the ferrite the TE 10 wave coming from left is rotated counterclockwise by 45 degrees. It can then enter unhindered the waveguide on the right A wave coming from the right is rotated clockwise (as seen from the right); the wave then has the wrong polarization. It gets damped by the horizontal damping foil. 25
26 The Magic T A combination of a E-plane and H-plane waveguide T is a very special 4- port: A magic T. The coefficients of the S matrix can be found by using the unitary condition and mechanical symmetries. S = Ideally there is no transmission between port 3 and port 4 nor between port 1 and port 2, even though you can look straight through it! Magic Ts are often produced as coaxial lines and printed circuits. They can be used taking the sum or difference of two signals. The bandwidth of a waveguide magic T is around one octave or the equivalent H10-mode waveguide band. Broadband versions of 180 hybrids may have a frequency range from a few MHz to some GHz. 26
27 The directional coupler (1) Another very important 4-port is the directional coupler. General principle: We have two transmission lines, and a coupling mechanism is adjusted such that part of the power in line 1 is transferred to line 2. The coupler is directional when the power in line 2 travels mainly in one direction. In order to get directionality at least two coupling mechanisms are necessary, i.e. many holes or electric and magnetic coupling, as in the Bethe coupler. The λ/4 coupler has two holes at a distance λ/4. The two backwards coupled waves cancel while the forward coupled waves add up in phase Directional couplers with coupling holes in waveguide technology Bethe coupler λ/4 coupler multiple hole coupler 27
28 The directional coupler (2) The directivity is defined as the ratio of the desired over the undesired coupled wave. For a forward coupler, in decibel, S α d = 20 log S Practical numbers for the coupling are 3 db, 6 db, 10 db, and 20 db with directivities usually better than 20 db The S matrix of the 3 db coupler (π/2-hybrid) can be derived as S 3dB = 0 1 ± j ± j 2 ± j ± j 1 0 Please note that this element is lossless, reciprocal and matched at all ports. This is possible for 4-ports. 28
29 General N-portsN A general N-ports may included ports in different technologies, i.e. waveguides, coaxial lines, microstrip lines etc. In a given frequency range different modes may propagate at each physical port, e.g. several waveguide modes in a rectangular waveguide or higher order modes on a coaxial line. Each mode must then be represented by a distinct port. The number of ports needed generally increases with frequency, as more waveguide modes can propagate. In numerical simulations neglecting higher order modes in the model can lead to questionable results. 29
30 Directional couplers in microstrip technology Most of the RF elements shown can be produced at low price in printed circuit technology Magic T 90 3-dB coupler (rat-race 180 ) 30
31 Striplines (1) A stripline is a flat conductor between a top and bottom ground plane. The space around this conductor is filled with a homogeneous dielectric material. This line propagates a pure TEM mode. With the static capacity per unit length, C, the static inductance per unit length, L, the relative permittivity of the dielectric, ε r and the speed of light c the characteristic impedance Z 0 of the line is given by (5.1) Fig 19: char.impedance of striplines 31
32 Striplines (2) For a mathematical treatment, the effect of the fringing fields may be described in terms of static capacities (see Fig. 20) [14]. The total capacity is the sum of the principal and fringe capacities C p and C f. (5.2) Fig. 20: Design, dimensions and characteristics for offset center-conductor strip transmission line [14] For striplines with an homogeneous dielectric the phase velocity is the same, and frequency independent, for all TEM-modes. A configuration of two coupled striplines (3-conductor system) may have two independent TEM-modes, an odd mode and an even mode (Fig. 21). Fig. 21: Even and odd mode in coupled striplines [14] 32
33 Striplines (3) The analysis of coupled striplines is required for the design of directional couplers. Besides the phase velocity the odd and even mode impedances Z 0,odd and Z 0,even must be known. They are given as a good approximation for the side coupled structure (Fig. 22, left) [14]. They are valid as a good approximation for the structure shown in Fig. 22. (5.3) Fig. 22: Types of coupled striplines [14]: left: side coupled parallel lines, right: broadcoupled parallel lines 33
34 Striplines (4) A graphical presentation of Equations 5.3 is also known as the Cohn nomographs [14]. For a quarter-wave directional coupler (single section in Fig. 16) very simple design formulae can be given (5.4) where C 0 is the voltage coupling ratio of the λ/4 coupler. In contrast to the 2-hole waveguide coupler this type couples backwards, i.e. the coupled wave leaves the coupler in the direction opposite to the incoming wave. The stripline coupler technology is rather widespread by now, and very cheap high quality elements are available in a wide frequency range. An even simpler way to make such devices is to use a section of shielded 2-wire cable. 34
35 Microstrip (1) A microstripline may be visualized as a stripline with the top cover and the top dielectric layer taken away (Fig. 23). It is thus an asymmetric open structure, and only part of its cross section is filled with a dielectric material. Since there is a transversely inhomogeneous dielectric, only a quasi-tem wave exists. This has several implications such as a frequency-dependent characteristic impedance and a considerable dispersion (Fig. 24). Fig.23 Microstripline: left: Mechanical construction, right: static field approximation [16]. CAS, Daresbury, September 2007 RF Basic Concepts, Caspers, McIntosh, Kroyer 35
36 Microstrip (2) An exact field analysis for this line is rather complicated and there exist a considerable number of books and other publications on the subject [16, 17]. Due to the dispersion of the microstrip, the calculation of coupled lines and thus the design of couplers and related structures is also more complicated than in the case of the stripline. Microstrips tend to radiate at all kind of discontinuities such as bends, changes in width, through holes etc. With all the disadvantages mentioned above in mind, one may question why they are used at all. The mains reasons are the cheap production, once a conductor pattern has been defined, and easy access to the surface for the integration of active elements. Microstrip circuits are also known as Microwave Integrated Circuits (MICs). A further technological step is the MMIC (Monolithic Microwave Integrated Circuit) where active and passive elements are integrated on the same semiconductor substrate. In Figs. 25 and 26 various planar printed transmission lines are depicted. The microstrip with overlay is relevant for MMICs and the strip dielectric wave guide is a printed optical fibre for millimeterwaves and integrated optics [17]. CAS, Daresbury, September 2007 RF Basic Concepts, Caspers, McIntosh, Kroyer 36
37 Microstrip (3) ε Fig. 24: Characteristic impedance (current/power definition) and effective permittivity of a microstrip line [16] CAS, Daresbury, September 2007 RF Basic Concepts, Caspers, McIntosh, Kroyer 37
38 Microstrip (4) Fig. 25 (left): Planar transmission lines used in MICs; Fig 26 (right): various Transmission lines derived from microstrip CAS, Daresbury, September 2007 RF Basic Concepts, Caspers, McIntosh, Kroyer 38
39 Slotlines (1) The slotline may be considered as the dual structure of the microstrip. It is essentially a slot in the metallization of a dielectric substrate as shown in Fig. 27. The characteristic impedance and the effective dielectric constant exhibit similar dispersion properties to those of the microstrip line. A unique feature of the slotline is that it may be combined with microstrip lines on the same substrate. This, in conjunction with through holes, permits interesting topologies such as pulse inverters in sampling heads (e.g. for sampling scopes). Fig 27 part 1: Slotlines a) Mechanical construction, b) Field pattern (TE-approximation) CAS, Daresbury, September 2007 RF Basic Concepts, Caspers, McIntosh, Kroyer 39
40 Slotlines (2) Fig 27 part 2: c) Longitudinal and transverse current densities, d) Magnetic line current model. Reproduced from [16] with permission of the author. CAS, Daresbury, September 2007 RF Basic Concepts, Caspers, McIntosh, Kroyer 40
41 Slotlines (3) Fig. 28 shows a broadband (decade bandwidth) pulse inverter. Assuming the upper microstrip to be the input, the signal leaving the circuit on the lower microstrip is inverted since this microstrip ends on the opposite side of the slotline compared to the input. Printed slotlines are also used for broadband pickups in the GHz range, e.g. for stochastic cooling [15]. Fig 28. Two microstrip-slotline transitions connected back to back for 180 phase change [17] CAS, Daresbury, September 2007 RF Basic Concepts, Caspers, McIntosh, Kroyer 41
42 The Smith Chart - definition The Smith Chart is a very handy tool for visualizing and solving RF problems It indicates in the plane of the complex reflection coefficient ρ the corresponding value of the complex impedance Z = R + jx. Often the normalized impedance z is used, with z = Z/Z 0, where Z 0 is a an arbitrary characteristic impedance, e.g. Z 0 = 50 Ω. The reflection coefficient is given as Z Z 0 z 1 ρ = = Z + Z z + 1 (6.1) 0 or in terms of admittance Y = 1/Z = G + jb, with the normalized admittance y = Y/Y 0, where Y 0 = 1/Z 0 Y ρ = Y Y + Y 0 Equations 6.1 and 6.2 define conformal mappings from the z and the y plane to the ρ plane. 0 = y y (6.2) 42
43 The Smith Chart - construction A very basic use of the Smith Chart is to graphically convert values of ρ into z and vice versa. To this purpose in the ρ plane a grid is drawn that allows to find the value of z at a given point ρ. An important property of conformal mappings is that general circles are mapped to general circles. Straight lines are considered as circle with infinite radius Below the loci of constant resistance and constant reactance are drawn in the ρ plane The origin of the ρ plane is marked with a red dot, the diameter of the largest circle is ρ =1 ρ plane constant resistance circles constant reactance circles 43
44 LOAD <Ð The Smith Chart circumference ρ = ITIV E SUSCEPTA NCE (+jb/ Yo) COMPONENT (+jx/ Zo), OR CAPAC matched load ρ = 0 IN DU CTIV E REA CTA N CE 0.47 GEN ERA TOR Ð > The Smith Chart is simply the ρ plane with overlaid circles that help to find the z for each point. The radius in is general ρ = TOW A RD ± A N GL E OF REFL ECTION C OEFFIC IEN T IN DEGR EES A N GL E OF TRAN SMISSION 0.49 Ð > W A V EL EN GTH S Important points: COEFFICIEN T IN DEGREES RESISTANCE COMPONENT (R/Zo),OR CONDUCTANCE COMPONENT (G/Yo) Center of the Smith Chart: matched load. ρ = 0, z = 1 Open circuit: ρ = +1, z = Short circuit: ρ = -1, z = 0 TOW A RD <Ð W A V EL EN GTH S CA PA CITIV E REA CTA N CE COMPONENT (-jx/ Zo), OR INDUCTIVE SUSCEPTANCE(-jB/Yo) short, ρ = -1 open, ρ = Lossless elements lie on the circle ρ =1; active elements, such as reflection amplifiers, lie outside this circle ATTEN. [db] S.W. LOSS C OEFF R FL. LOSS [db] S.W. PEAK (CONST. P) TRANSM. C OEFF, P RADIALLY SCALED PARAMETERS TOWARD LOAD Ð > <Ð TOWARD GENERATOR TRANSM. COEFF, E or I SWR dbs RTN. LOSS [db] R FL. COEFF, P R FL. COEFF, E or I CENTER ORIGIN Downloaded from 44
45 Navigation in the Smith Chart 1 When a lossless element is added in series to an impedance z, one moves along the constant resistance circles (R = const) When a lossless element is added in parallel (shunt) to an impedance z, one moves along the circles conductance (G = const) Shunt L z Series L Up Down Series C Shunt C Black circles Series L Series C Blue circles Shunt L Shunt C 45
46 Navigation in the Smith Chart 2 An ideal lossless transmission line only changes the phase of ρ => a transmission line gives a rotation about the center of the Smith Chart For a line of length λ/4 we get a rotation by 180 degrees => a short circuit is converted into an open circuit and vice versa. Such a line is called λ/4 transformer. G R Toward load z Toward generator Red arcs Resistance R in series Blue arcs Conductance G in parallel Concentric circle Transmission line going Toward load Toward generator 46
47 The quality factor The quality (Q) factor of a resonant circuit is defined as the ratio of the stored energy W over the energy dissipated P in one cycle. Q = ωw P Q 0 : Unloaded Q factor of the unperturbed system, e.g. a closed cavity Q L : Loaded Q factor with measurement circuits etc connected Q ext : External Q factor of the measurement circuits etc These Q factors are related by 1 Q 1 = Q + 1 L 0 Q ext The Q factor of a resonance peak or dip can be calculated from the center frequency f 0 and the 3 db bandwidth Δf as Q f = 0 Δ f 47
48 Q factor measurement in the Smith Chart The typical locus of a resonant circuit in the Smith chart is illustrated as the dashed red circle From the different marked frequency points the 3 db bandwidth and thus the quality factors Q 0, Q L and Q ext can be determined (see lecture notes) The larger the circle, the stronger the coupling In practise, the circle may be rotated around the origin due to transmission lines between the resonant circuit and the measurement device 48
49 Q factor measurement in the Smith Chart 2 f 0 gives the center frequency of the resonator. Condition: S 11 min. Procedure in Smith Chart: Resonator in detuned short position Marker format: S 11 (amplitude and phase) Search for the minimum of S 11 Read f 0 and the resonator shunt impedance R = Re{S 11 } The unloaded Q 0 can be determined from f 5 and f 6. Condition: Re{Z} = Im{Z} in detuned short position. Resonator in detuned short position Marker format: Z Search for the two points where Re{Z} = Im{Z} f 5 and f 6 The loaded Q L can be calculated from the half-power points f 1 and f 2. Condition: Im{S 11 } max Resonator in detuned short position Marker format: Re{S 11 } + jim{s 11 } Search for the two points where Im{S 11 } max f 1 and f 2 The external Q E can be calculated from f 3 and f 4. Condition: Z = ±j in detuned open position Resonator in detuned open position Marker format: Z Search for the two points where Z = ±j f 3 and f 4 49
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis. Application Note
 Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
Keysight Technologies Understanding the Fundamental Principles of Vector Network Analysis Application Note Introduction Network analysis is the process by which designers and manufacturers measure the
Agilent De-embedding and Embedding S-Parameter Networks Using a Vector Network Analyzer. Application Note 1364-1
 Agilent De-embedding and Embedding S-Parameter Networks Using a Vector Network Analyzer Application Note 1364-1 Introduction Traditionally RF and microwave components have been designed in packages with
Agilent De-embedding and Embedding S-Parameter Networks Using a Vector Network Analyzer Application Note 1364-1 Introduction Traditionally RF and microwave components have been designed in packages with
Experiment 7: Familiarization with the Network Analyzer
 Experiment 7: Familiarization with the Network Analyzer Measurements to characterize networks at high frequencies (RF and microwave frequencies) are usually done in terms of scattering parameters (S parameters).
Experiment 7: Familiarization with the Network Analyzer Measurements to characterize networks at high frequencies (RF and microwave frequencies) are usually done in terms of scattering parameters (S parameters).
APPLICATION NOTES POWER DIVIDERS. Things to consider
 Internet Copy Rev A Overview Various RF applications require power to be distributed among various paths. The simplest way this can be done is by using a power splitter/divider. Power dividers are reciprocal
Internet Copy Rev A Overview Various RF applications require power to be distributed among various paths. The simplest way this can be done is by using a power splitter/divider. Power dividers are reciprocal
RF measurements, tools and equipment E. B. Boskamp, A. Nabetani, J. Tropp ([email protected])
 RF measurements, tools and equipment E. B. Boskamp, A. Nabetani, J. Tropp ([email protected]) INTRODUCTION I am often asked by researchers what kind of equipment is needed to set up an RF lab. The
RF measurements, tools and equipment E. B. Boskamp, A. Nabetani, J. Tropp ([email protected]) INTRODUCTION I am often asked by researchers what kind of equipment is needed to set up an RF lab. The
Agilent AN 154 S-Parameter Design Application Note
 Agilent AN 154 S-Parameter Design Application Note Introduction The need for new high-frequency, solid-state circuit design techniques has been recognized both by microwave engineers and circuit designers.
Agilent AN 154 S-Parameter Design Application Note Introduction The need for new high-frequency, solid-state circuit design techniques has been recognized both by microwave engineers and circuit designers.
Understanding the Fundamental Principles of Vector Network Analysis. Application Note 1287-1. Table of Contents. Page
 Understanding the Fundamental Principles of Vector Network Analysis Application Note 1287-1 Table of Contents Page Introduction 2 Measurements in Communications Systems 2 Importance of Vector Measurements
Understanding the Fundamental Principles of Vector Network Analysis Application Note 1287-1 Table of Contents Page Introduction 2 Measurements in Communications Systems 2 Importance of Vector Measurements
An equivalent circuit of a loop antenna.
 3.2.1. Circuit Modeling: Loop Impedance A loop antenna can be represented by a lumped circuit when its dimension is small with respect to a wavelength. In this representation, the circuit parameters (generally
3.2.1. Circuit Modeling: Loop Impedance A loop antenna can be represented by a lumped circuit when its dimension is small with respect to a wavelength. In this representation, the circuit parameters (generally
Understanding SWR by Example
 Understanding SWR by Example Take the mystery and mystique out of standing wave ratio. Darrin Walraven, K5DVW It sometimes seems that one of the most mysterious creatures in the world of Amateur Radio
Understanding SWR by Example Take the mystery and mystique out of standing wave ratio. Darrin Walraven, K5DVW It sometimes seems that one of the most mysterious creatures in the world of Amateur Radio
Connectivity in a Wireless World. Cables Connectors 2014. A Special Supplement to
 Connectivity in a Wireless World Cables Connectors 204 A Special Supplement to Signal Launch Methods for RF/Microwave PCBs John Coonrod Rogers Corp., Chandler, AZ COAX CABLE MICROSTRIP TRANSMISSION LINE
Connectivity in a Wireless World Cables Connectors 204 A Special Supplement to Signal Launch Methods for RF/Microwave PCBs John Coonrod Rogers Corp., Chandler, AZ COAX CABLE MICROSTRIP TRANSMISSION LINE
S-Parameters and Related Quantities Sam Wetterlin 10/20/09
 S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
Antenna Properties and their impact on Wireless System Performance. Dr. Steven R. Best. Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013
 Antenna Properties and their impact on Wireless System Performance Dr. Steven R. Best Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013 Phone (603) 627-7877 FAX: (603) 627-1764 Email: [email protected]
Antenna Properties and their impact on Wireless System Performance Dr. Steven R. Best Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013 Phone (603) 627-7877 FAX: (603) 627-1764 Email: [email protected]
Impedance Matching. Using transformers Using matching networks
 Impedance Matching The plasma industry uses process power over a wide range of frequencies: from DC to several gigahertz. A variety of methods are used to couple the process power into the plasma load,
Impedance Matching The plasma industry uses process power over a wide range of frequencies: from DC to several gigahertz. A variety of methods are used to couple the process power into the plasma load,
Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Z +
 Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Quick Review of Reflection Coefficient The Smith chart is a method of graphing reflection coefficients and impedance, and is often useful
Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Quick Review of Reflection Coefficient The Smith chart is a method of graphing reflection coefficients and impedance, and is often useful
Copyright 1996 IEEE. Reprinted from IEEE MTT-S International Microwave Symposium 1996
 Copyright 1996 IEEE Reprinted from IEEE MTT-S International Microwave Symposium 1996 This material is posted here with permission of the IEEE. Such permission of the IEEE does not in any way imply IEEE
Copyright 1996 IEEE Reprinted from IEEE MTT-S International Microwave Symposium 1996 This material is posted here with permission of the IEEE. Such permission of the IEEE does not in any way imply IEEE
Transmission Lines. Smith Chart
 Smith Chart The Smith chart is one of the most useful graphical tools for high frequency circuit applications. The chart provides a clever way to visualize complex functions and it continues to endure
Smith Chart The Smith chart is one of the most useful graphical tools for high frequency circuit applications. The chart provides a clever way to visualize complex functions and it continues to endure
Vector Network Analyzer Techniques to Measure WR340 Waveguide Windows
 LS-296 Vector Network Analyzer Techniques to Measure WR340 Waveguide Windows T. L. Smith ASD / RF Group Advanced Photon Source Argonne National Laboratory June 26, 2002 Table of Contents 1) Introduction
LS-296 Vector Network Analyzer Techniques to Measure WR340 Waveguide Windows T. L. Smith ASD / RF Group Advanced Photon Source Argonne National Laboratory June 26, 2002 Table of Contents 1) Introduction
6 J - vector electric current density (A/m2 )
 Determination of Antenna Radiation Fields Using Potential Functions Sources of Antenna Radiation Fields 6 J - vector electric current density (A/m2 ) M - vector magnetic current density (V/m 2 ) Some problems
Determination of Antenna Radiation Fields Using Potential Functions Sources of Antenna Radiation Fields 6 J - vector electric current density (A/m2 ) M - vector magnetic current density (V/m 2 ) Some problems
Applications in EMC testing. Outline. Antennas for EMC Testing. Terminology
 Antennas for EMC Testing Zhong Chen ETS-Lindgren 1301 Arrow Point Drive Cedar Park, TX 78613 [email protected] Outline EMC Terms and Definitions Typical EMC Antennas Calibration of EMC Antennas
Antennas for EMC Testing Zhong Chen ETS-Lindgren 1301 Arrow Point Drive Cedar Park, TX 78613 [email protected] Outline EMC Terms and Definitions Typical EMC Antennas Calibration of EMC Antennas
A wave lab inside a coaxial cable
 INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
Characterization of Spatial Power Waveguide Amplifiers
 Characterization of Spatial Power Waveguide Amplifiers Authored by: Matthew H. Commens Ansoft Corporation Ansoft 003 / Global Seminars: Delivering Performance Presentation # Outline What is a Spatial Waveguide
Characterization of Spatial Power Waveguide Amplifiers Authored by: Matthew H. Commens Ansoft Corporation Ansoft 003 / Global Seminars: Delivering Performance Presentation # Outline What is a Spatial Waveguide
Impedance Matching and Matching Networks. Valentin Todorow, December, 2009
 Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Current Probes, More Useful Than You Think
 Current Probes, More Useful Than You Think Training and design help in most areas of Electrical Engineering Copyright 1998 Institute of Electrical and Electronics Engineers. Reprinted from the IEEE 1998
Current Probes, More Useful Than You Think Training and design help in most areas of Electrical Engineering Copyright 1998 Institute of Electrical and Electronics Engineers. Reprinted from the IEEE 1998
CHAPTER4 GENERAL ASPECTS OF MUTUAL
 CHAPTER4 GENERAL ASPECTS OF MUTUAL ADMITTANCE OF CPW-FED TWIN SLOTS ON CONDUCTOR-BACKED TWO-LAYER SUBSTRATES 4.1 INTRODUCTORY REMARKS The present chapter is concerned with an exploratory investigation
CHAPTER4 GENERAL ASPECTS OF MUTUAL ADMITTANCE OF CPW-FED TWIN SLOTS ON CONDUCTOR-BACKED TWO-LAYER SUBSTRATES 4.1 INTRODUCTORY REMARKS The present chapter is concerned with an exploratory investigation
WAVEGUIDE-COAXIAL LINE TRANSITIONS
 WAVEGUIDE-COAXIAL LINE TRANSITIONS 1. Overview Equipment at microwave frequencies is usually based on a combination of PCB and waveguide components. Filters and antennas often use waveguide techniques,
WAVEGUIDE-COAXIAL LINE TRANSITIONS 1. Overview Equipment at microwave frequencies is usually based on a combination of PCB and waveguide components. Filters and antennas often use waveguide techniques,
2/20/2009 3 Transmission Lines and Waveguides.doc 1/3. and Waveguides. Transmission Line A two conductor structure that can support a TEM wave.
 2/20/2009 3 Transmission Lines and Waveguides.doc 1/3 Chapter 3 Transmission Lines and Waveguides First, some definitions: Transmission Line A two conductor structure that can support a TEM wave. Waveguide
2/20/2009 3 Transmission Lines and Waveguides.doc 1/3 Chapter 3 Transmission Lines and Waveguides First, some definitions: Transmission Line A two conductor structure that can support a TEM wave. Waveguide
ECE 435 INTRODUCTION TO THE MICROWAVE NETWORK ANALYZER
 ECE 435 INTRODUCTION TO THE MICROWAVE NETWORK ANALYZER Latest revision: October 1999 Introduction A vector network analyzer (VNA) is a device capable of measuring both the magnitude and phase of a sinusoidal
ECE 435 INTRODUCTION TO THE MICROWAVE NETWORK ANALYZER Latest revision: October 1999 Introduction A vector network analyzer (VNA) is a device capable of measuring both the magnitude and phase of a sinusoidal
PHY3128 / PHYM203 (Electronics / Instrumentation) Transmission Lines. Repeated n times I L
 Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
A PRACTICAL MINIATURIZED U-SLOT PATCH ANTENNA WITH ENHANCED BANDWIDTH
 Progress In Electromagnetics Research B, Vol. 3, 47 62, 2008 A PRACTICAL MINIATURIZED U-SLOT PATCH ANTENNA WITH ENHANCED BANDWIDTH G. F. Khodaei, J. Nourinia, and C. Ghobadi Electrical Engineering Department
Progress In Electromagnetics Research B, Vol. 3, 47 62, 2008 A PRACTICAL MINIATURIZED U-SLOT PATCH ANTENNA WITH ENHANCED BANDWIDTH G. F. Khodaei, J. Nourinia, and C. Ghobadi Electrical Engineering Department
Shielding Effectiveness Test Method. Harbour s LL, SB, and SS Coaxial Cables. Designs for Improved Shielding Effectiveness
 Shielding Effectiveness Test Method Harbour s LL, SB, and SS Coaxial Cables Designs for Improved Shielding Effectiveness Harbour Industries 4744 Shelburne Road Shelburne Vermont 05482 USA 802-985-3311
Shielding Effectiveness Test Method Harbour s LL, SB, and SS Coaxial Cables Designs for Improved Shielding Effectiveness Harbour Industries 4744 Shelburne Road Shelburne Vermont 05482 USA 802-985-3311
Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad
 International Journal of Scientific & Engineering Research Volume 3, Issue 8, August-2012 1 Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad Abstract-Parallel
International Journal of Scientific & Engineering Research Volume 3, Issue 8, August-2012 1 Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad Abstract-Parallel
Extending Rigid-Flex Printed Circuits to RF Frequencies
 Extending -Flex Printed Circuits to RF Frequencies Robert Larmouth Teledyne Electronic Technologies 110 Lowell Rd., Hudson, NH 03051 (603) 889-6191 Gerald Schaffner Schaffner Consulting 10325 Caminito
Extending -Flex Printed Circuits to RF Frequencies Robert Larmouth Teledyne Electronic Technologies 110 Lowell Rd., Hudson, NH 03051 (603) 889-6191 Gerald Schaffner Schaffner Consulting 10325 Caminito
Planar Inter Digital Capacitors on Printed Circuit Board
 1 Planar Inter Digital Capacitors on Printed Circuit Board Ajayan K.R., K.J.Vinoy Department of Electrical Communication Engineering Indian Institute of Science, Bangalore, India 561 Email {ajayanr jvinoy}
1 Planar Inter Digital Capacitors on Printed Circuit Board Ajayan K.R., K.J.Vinoy Department of Electrical Communication Engineering Indian Institute of Science, Bangalore, India 561 Email {ajayanr jvinoy}
Digital Systems Ribbon Cables I CMPE 650. Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip.
 Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
RLC Resonant Circuits
 C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
SECTION 2 Transmission Line Theory
 SEMICONDUCTOR DESIGN GUIDE Transmission Line Theory SECTION 2 Transmission Line Theory Introduction The ECLinPS family has pushed the world of ECL into the realm of picoseconds. When output transitions
SEMICONDUCTOR DESIGN GUIDE Transmission Line Theory SECTION 2 Transmission Line Theory Introduction The ECLinPS family has pushed the world of ECL into the realm of picoseconds. When output transitions
Transmission Line Transformers
 Radio Frequency Circuit Design. W. Alan Davis, Krishna Agarwal Copyright 2001 John Wiley & Sons, Inc. Print ISBN 0-471-35052-4 Electronic ISBN 0-471-20068-9 CHAPTER SIX Transmission Line Transformers 6.1
Radio Frequency Circuit Design. W. Alan Davis, Krishna Agarwal Copyright 2001 John Wiley & Sons, Inc. Print ISBN 0-471-35052-4 Electronic ISBN 0-471-20068-9 CHAPTER SIX Transmission Line Transformers 6.1
RF Network Analyzer Basics
 RF Network Analyzer Basics A tutorial, information and overview about the basics of the RF Network Analyzer. What is a Network Analyzer and how to use them, to include the Scalar Network Analyzer (SNA),
RF Network Analyzer Basics A tutorial, information and overview about the basics of the RF Network Analyzer. What is a Network Analyzer and how to use them, to include the Scalar Network Analyzer (SNA),
S-Band Low Noise Amplifier Using the ATF-10136. Application Note G004
 S-Band Low Noise Amplifier Using the ATF-10136 Application Note G004 Introduction This application note documents the results of using the ATF-10136 in low noise amplifier applications at S band. The ATF-10136
S-Band Low Noise Amplifier Using the ATF-10136 Application Note G004 Introduction This application note documents the results of using the ATF-10136 in low noise amplifier applications at S band. The ATF-10136
National Laboratory of Antennas and Microwave Technology Xidian University Xi an, Shaanxi 710071, China
 Progress In Electromagnetics Research, PIER 76, 237 242, 2007 A BROADBAND CPW-FED T-SHAPE SLOT ANTENNA J.-J. Jiao, G. Zhao, F.-S. Zhang, H.-W. Yuan, and Y.-C. Jiao National Laboratory of Antennas and Microwave
Progress In Electromagnetics Research, PIER 76, 237 242, 2007 A BROADBAND CPW-FED T-SHAPE SLOT ANTENNA J.-J. Jiao, G. Zhao, F.-S. Zhang, H.-W. Yuan, and Y.-C. Jiao National Laboratory of Antennas and Microwave
100 ADS Design Examples A Design Approach Using (ADS)
 100 ADS Design Examples A Design Approach Using (ADS) Chapter 2: Transmission Line Components Ali Behagi 2 100 ADS Design Examples 100 ADS Design Examples A Design Approach Using (ADS) Chapter 2: Transmission
100 ADS Design Examples A Design Approach Using (ADS) Chapter 2: Transmission Line Components Ali Behagi 2 100 ADS Design Examples 100 ADS Design Examples A Design Approach Using (ADS) Chapter 2: Transmission
Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014. Striplines and Microstrips (PCB Transmission Lines)
 Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014 Striplines and Microstrips (PCB Transmission Lines) Disclaimer: This presentation is merely a compilation of information from public
Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014 Striplines and Microstrips (PCB Transmission Lines) Disclaimer: This presentation is merely a compilation of information from public
RADIATION PATTERNS. The half-power (-3 db) beamwidth is a measure of the directivity of the antenna.
 RADIATION PATTERNS The radiation pattern is a graphical depiction of the relative field strength transmitted from or received by the antenna. Antenna radiation patterns are taken at one frequency, one
RADIATION PATTERNS The radiation pattern is a graphical depiction of the relative field strength transmitted from or received by the antenna. Antenna radiation patterns are taken at one frequency, one
An octave bandwidth dipole antenna
 An octave bandwidth dipole antenna Abstract: Achieving wideband performance from resonant structures is challenging because their radiation properties and impedance characteristics are usually sensitive
An octave bandwidth dipole antenna Abstract: Achieving wideband performance from resonant structures is challenging because their radiation properties and impedance characteristics are usually sensitive
CONCEPT-II. Overview of demo examples
 CONCEPT-II CONCEPT-II is a frequency domain method of moment (MoM) code, under development at the Institute of Electromagnetic Theory at the Technische Universität Hamburg-Harburg (www.tet.tuhh.de). Overview
CONCEPT-II CONCEPT-II is a frequency domain method of moment (MoM) code, under development at the Institute of Electromagnetic Theory at the Technische Universität Hamburg-Harburg (www.tet.tuhh.de). Overview
Review Paper for Broadband CPW-Fed T-Shape Slot Antenna
 Review Paper for Broadband CPW-Fed T-Shape Slot Antenna Shahpure Sana 1, Bharate Rajashri 2, Prof. Jadhav D.A. 3 1,2 BE, Dept. of E&TC, Brahmdevdada Mane Institute of Technology, Dist. Solapur (Maharashtra)
Review Paper for Broadband CPW-Fed T-Shape Slot Antenna Shahpure Sana 1, Bharate Rajashri 2, Prof. Jadhav D.A. 3 1,2 BE, Dept. of E&TC, Brahmdevdada Mane Institute of Technology, Dist. Solapur (Maharashtra)
Time and Frequency Domain Analysis for Right Angle Corners on Printed Circuit Board Traces
 Time and Frequency Domain Analysis for Right Angle Corners on Printed Circuit Board Traces Mark I. Montrose Montrose Compliance Services 2353 Mission Glen Dr. Santa Clara, CA 95051-1214 Abstract: For years,
Time and Frequency Domain Analysis for Right Angle Corners on Printed Circuit Board Traces Mark I. Montrose Montrose Compliance Services 2353 Mission Glen Dr. Santa Clara, CA 95051-1214 Abstract: For years,
Since any real component also has loss due to the resistive component, the average power dissipated is 2 2R
 Quality factor, Q Reactive components such as capacitors and inductors are often described with a figure of merit called Q. While it can be defined in many ways, it s most fundamental description is: Q
Quality factor, Q Reactive components such as capacitors and inductors are often described with a figure of merit called Q. While it can be defined in many ways, it s most fundamental description is: Q
2 Port Parameters I 1. ECE145A/218A Notes Set #4 1. Two-ways of describing device: A. Equivalent - Circuit-Model
 ECE45A/8A Notes et #4 Port Parameters Two-ways of describing device: A. Equivalent - Circuit-Model Physically based Includes bias dependence Includes frequency dependence Includes size dependence - scalability
ECE45A/8A Notes et #4 Port Parameters Two-ways of describing device: A. Equivalent - Circuit-Model Physically based Includes bias dependence Includes frequency dependence Includes size dependence - scalability
Preface Acknowledgments Acronyms
 Contents Preface Acknowledgments Acronyms xi xiii xv 1 Introduction 1 1.1 The history of Antennas and Antenna Analysis 1 1.2 Antenna Synthesis 5 1.3 Approximate Antenna Modeling 7 1.4 Organization of the
Contents Preface Acknowledgments Acronyms xi xiii xv 1 Introduction 1 1.1 The history of Antennas and Antenna Analysis 1 1.2 Antenna Synthesis 5 1.3 Approximate Antenna Modeling 7 1.4 Organization of the
Standex-Meder Electronics. Custom Engineered Solutions for Tomorrow
 Standex-Meder Electronics Custom Engineered Solutions for Tomorrow RF Reed Relays Part II Product Training Copyright 2013 Standex-Meder Electronics. All rights reserved. Introduction Purpose Designing
Standex-Meder Electronics Custom Engineered Solutions for Tomorrow RF Reed Relays Part II Product Training Copyright 2013 Standex-Meder Electronics. All rights reserved. Introduction Purpose Designing
Introduction to acoustic imaging
 Introduction to acoustic imaging Contents 1 Propagation of acoustic waves 3 1.1 Wave types.......................................... 3 1.2 Mathematical formulation.................................. 4 1.3
Introduction to acoustic imaging Contents 1 Propagation of acoustic waves 3 1.1 Wave types.......................................... 3 1.2 Mathematical formulation.................................. 4 1.3
Enhanced Stripline Scanning Array B.M. Cahill and J.C. Batchelor
 Enhanced Stripline Scanning Array B.M. Cahill and J.C. Batchelor This paper is a postprint of a paper submitted to and accepted for publication in IET Microwaves, Antennas and Propagation and is subject
Enhanced Stripline Scanning Array B.M. Cahill and J.C. Batchelor This paper is a postprint of a paper submitted to and accepted for publication in IET Microwaves, Antennas and Propagation and is subject
2. The Vector Network Analyzer
 ECE 584 Laboratory Experiments 2. The Vector Network Analyzer Introduction: In this experiment we will learn to use a Vector Network Analyzer to measure the magnitude and phase of reflection and transmission
ECE 584 Laboratory Experiments 2. The Vector Network Analyzer Introduction: In this experiment we will learn to use a Vector Network Analyzer to measure the magnitude and phase of reflection and transmission
Co-simulation of Microwave Networks. Sanghoon Shin, Ph.D. RS Microwave
 Co-simulation of Microwave Networks Sanghoon Shin, Ph.D. RS Microwave Outline Brief review of EM solvers 2D and 3D EM simulators Technical Tips for EM solvers Co-simulated Examples of RF filters and Diplexer
Co-simulation of Microwave Networks Sanghoon Shin, Ph.D. RS Microwave Outline Brief review of EM solvers 2D and 3D EM simulators Technical Tips for EM solvers Co-simulated Examples of RF filters and Diplexer
Broadband Slotted Coaxial Broadcast Antenna Technology
 Broadband Slotted Coaxial Broadcast Antenna Technology Summary Slotted coaxial antennas have many advantages over traditional broadband panel antennas including much smaller size and wind load, higher
Broadband Slotted Coaxial Broadcast Antenna Technology Summary Slotted coaxial antennas have many advantages over traditional broadband panel antennas including much smaller size and wind load, higher
Broadband Push-Pull Power Amplifier Design at Microwave Frequencies
 Broadband Push-Pull Power Amplifier Design at Microwave Frequencies Robert Smith and Prof. Steve Cripps Centre for High Frequency Engineering, Cardiff University [email protected] A broadband, high
Broadband Push-Pull Power Amplifier Design at Microwave Frequencies Robert Smith and Prof. Steve Cripps Centre for High Frequency Engineering, Cardiff University [email protected] A broadband, high
Insight on mobile phones and communication system:
 Introduction: Rapid progresses are being made in wireless communications to make interactive voice, data and even video services available anytime and anyplace. Nowadays mobile phones are becoming ubiquitous.
Introduction: Rapid progresses are being made in wireless communications to make interactive voice, data and even video services available anytime and anyplace. Nowadays mobile phones are becoming ubiquitous.
Selecting Receiving Antennas for Radio Tracking
 Selecting Receiving Antennas for Radio Tracking Larry B Kuechle, Advanced Telemetry Systems, Inc. Isanti, Minnesota 55040 [email protected] The receiving antenna is an integral part of any radio location
Selecting Receiving Antennas for Radio Tracking Larry B Kuechle, Advanced Telemetry Systems, Inc. Isanti, Minnesota 55040 [email protected] The receiving antenna is an integral part of any radio location
Impedance 50 (75 connectors via adapters)
 VECTOR NETWORK ANALYZER PLANAR TR1300/1 DATA SHEET Frequency range: 300 khz to 1.3 GHz Measured parameters: S11, S21 Dynamic range of transmission measurement magnitude: 130 db Measurement time per point:
VECTOR NETWORK ANALYZER PLANAR TR1300/1 DATA SHEET Frequency range: 300 khz to 1.3 GHz Measured parameters: S11, S21 Dynamic range of transmission measurement magnitude: 130 db Measurement time per point:
3.3 Calibration standards
 C ALIBRATION STANDARDS Fig. 3.2.3 Location of the reference plane in the N-type connector. Fig. 3.2.4 Location of the reference plane in the connector types PC3.5, 2.4 mm and 1.85 mm. 3.3 Calibration standards
C ALIBRATION STANDARDS Fig. 3.2.3 Location of the reference plane in the N-type connector. Fig. 3.2.4 Location of the reference plane in the connector types PC3.5, 2.4 mm and 1.85 mm. 3.3 Calibration standards
1. The Slotted Line. ECE 584 Microwave Engineering Laboratory Experiments. Introduction:
 ECE 584 Microwave Engineering Laboratory Experiments 1. The Slotted Line Introduction: In this experiment we will use a waveguide slotted line to study the basic behavior of standing waves and to measure
ECE 584 Microwave Engineering Laboratory Experiments 1. The Slotted Line Introduction: In this experiment we will use a waveguide slotted line to study the basic behavior of standing waves and to measure
Phase Shifters. Relation between Propagation Constant, Phase Shift, Delay, and Wavelength
 Phase Shifters Iulian Rosu, YO3DAC / VA3IUL, http://www.qsl.net/va3iul/ Phase Shifters are devices, in which the phase of an electromagnetic wave of a given frequency can be shifted when propagating through
Phase Shifters Iulian Rosu, YO3DAC / VA3IUL, http://www.qsl.net/va3iul/ Phase Shifters are devices, in which the phase of an electromagnetic wave of a given frequency can be shifted when propagating through
Microwave Measurements. 3rd Edition. Edited by RJ. Collier and A.D. Skinner. The Institution of Engineering and Technology
 Microwave Measurements 3rd Edition Edited by RJ. Collier and A.D. Skinner The Institution of Engineering and Technology Contents List of contributors Preface xvii xix 1 Transmission lines - basic principles
Microwave Measurements 3rd Edition Edited by RJ. Collier and A.D. Skinner The Institution of Engineering and Technology Contents List of contributors Preface xvii xix 1 Transmission lines - basic principles
MEASUREMENT SET-UP FOR TRAPS
 Completed on 26th of June, 2012 MEASUREMENT SET-UP FOR TRAPS AUTHOR: IW2FND Attolini Lucio Via XXV Aprile, 52/B 26037 San Giovanni in Croce (CR) - Italy [email protected] Trappole_01_EN 1 1 DESCRIPTION...3
Completed on 26th of June, 2012 MEASUREMENT SET-UP FOR TRAPS AUTHOR: IW2FND Attolini Lucio Via XXV Aprile, 52/B 26037 San Giovanni in Croce (CR) - Italy [email protected] Trappole_01_EN 1 1 DESCRIPTION...3
Analysis of Broadband Slot Cut Semi-Circular Microstrip Antennas
 Analysis of Broadband Slot Cut Semi-Circular Microstrip Antennas Amit A. Deshmukh EXTC, DJSCOE Vile Parle (W), Mumbai, India Ankita R. Jain EXTC, DJSCOE Vile Parle (W), Mumbai, India Apurva A. Joshi EXTC,
Analysis of Broadband Slot Cut Semi-Circular Microstrip Antennas Amit A. Deshmukh EXTC, DJSCOE Vile Parle (W), Mumbai, India Ankita R. Jain EXTC, DJSCOE Vile Parle (W), Mumbai, India Apurva A. Joshi EXTC,
Compact Tunable and Dual band Circular Microstrip Antenna for GSM and Bluetooth Applications
 205 Compact Tunable and Dual band Circular Microstrip Antenna for GSM and Bluetooth Applications *K. P. Ray 1, S. Nikhil 2 and A. Nair 2 1 SAMEER, IIT Campus, Powai, Mumbai 400 076, India 2 K.J.Somaiya
205 Compact Tunable and Dual band Circular Microstrip Antenna for GSM and Bluetooth Applications *K. P. Ray 1, S. Nikhil 2 and A. Nair 2 1 SAMEER, IIT Campus, Powai, Mumbai 400 076, India 2 K.J.Somaiya
Grounding Demystified
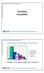 Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Lecture 20: Transmission (ABCD) Matrix.
 Whites, EE 48/58 Lecture 0 Page of 7 Lecture 0: Transmission (ABC) Matrix. Concerning the equivalent port representations of networks we ve seen in this course:. Z parameters are useful for series connected
Whites, EE 48/58 Lecture 0 Page of 7 Lecture 0: Transmission (ABC) Matrix. Concerning the equivalent port representations of networks we ve seen in this course:. Z parameters are useful for series connected
When designing. Inductors at UHF: EM Simulation Guides Vector Network Analyzer. measurement. EM SIMULATION. There are times when it is
 Inductors at UHF: EM Simulation Guides Vector Network Analyzer Measurements John B. Call Thales Communications Inc., USA When designing There are times when it is circuits for necessary to measure a operation
Inductors at UHF: EM Simulation Guides Vector Network Analyzer Measurements John B. Call Thales Communications Inc., USA When designing There are times when it is circuits for necessary to measure a operation
SAR ASSOCIATED WITH THE USE OF HANDS-FREE MOBILE TELEPHONES
 SAR ASSOCIATED WITH THE USE OF HANDS-FREE MOBILE TELEPHONES S.J. Porter, M.H. Capstick, F. Faraci, I.D. Flintoft and A.C. Marvin Department of Electronics, University of York Heslington, York, YO10 5DD,
SAR ASSOCIATED WITH THE USE OF HANDS-FREE MOBILE TELEPHONES S.J. Porter, M.H. Capstick, F. Faraci, I.D. Flintoft and A.C. Marvin Department of Electronics, University of York Heslington, York, YO10 5DD,
Investigations on Critical Higher Order Modes in CEBAF Upgrade Cavities
 Investigations on Critical Higher Order Modes in CEBAF Upgrade Cavities F. Marhauser Thanks also to H. Wang and K. Tian 27. August 2009 How HOMs are excited and why they are important - Wakefields- some
Investigations on Critical Higher Order Modes in CEBAF Upgrade Cavities F. Marhauser Thanks also to H. Wang and K. Tian 27. August 2009 How HOMs are excited and why they are important - Wakefields- some
potential in the centre of the sphere with respect to infinity.
 Umeå Universitet, Fysik 1 Vitaly Bychkov Prov i fysik, Electricity and Waves, 2006-09-27, kl 16.00-22.00 Hjälpmedel: Students can use any book. Define the notations you are using properly. Present your
Umeå Universitet, Fysik 1 Vitaly Bychkov Prov i fysik, Electricity and Waves, 2006-09-27, kl 16.00-22.00 Hjälpmedel: Students can use any book. Define the notations you are using properly. Present your
S-parameter Simulation and Optimization
 S-parameter Simulation and Optimization Slide 5-1 S-parameters are Ratios Usually given in db as 20 log of the voltage ratios of the waves at the ports: incident, reflected, or transmitted. S-parameter
S-parameter Simulation and Optimization Slide 5-1 S-parameters are Ratios Usually given in db as 20 log of the voltage ratios of the waves at the ports: incident, reflected, or transmitted. S-parameter
The waveguide adapter consists of a rectangular part smoothly transcending into an elliptical part as seen in Figure 1.
 Waveguide Adapter Introduction This is a model of an adapter for microwave propagation in the transition between a rectangular and an elliptical waveguide. Such waveguide adapters are designed to keep
Waveguide Adapter Introduction This is a model of an adapter for microwave propagation in the transition between a rectangular and an elliptical waveguide. Such waveguide adapters are designed to keep
Copyright 2000 IEEE. Reprinted from IEEE MTT-S International Microwave Symposium 2000
 Copyright 2000 IEEE Reprinted from IEEE MTT-S International Microwave Symposium 2000 This material is posted here with permission of the IEEE. Such permission of the IEEE does not in any way imply IEEE
Copyright 2000 IEEE Reprinted from IEEE MTT-S International Microwave Symposium 2000 This material is posted here with permission of the IEEE. Such permission of the IEEE does not in any way imply IEEE
2.1 Introduction. 2.2 Terms and definitions
 .1 Introduction An important step in the procedure for solving any circuit problem consists first in selecting a number of independent branch currents as (known as loop currents or mesh currents) variables,
.1 Introduction An important step in the procedure for solving any circuit problem consists first in selecting a number of independent branch currents as (known as loop currents or mesh currents) variables,
Engineering Sciences 151. Electromagnetic Communication Laboratory Assignment 3 Fall Term 1998-99
 Engineering Sciences 151 Electromagnetic Communication Laboratory Assignment 3 Fall Term 1998-99 WAVE PROPAGATION II: HIGH FREQUENCY SLOTTED LINE AND REFLECTOMETER MEASUREMENTS OBJECTIVES: To build greater
Engineering Sciences 151 Electromagnetic Communication Laboratory Assignment 3 Fall Term 1998-99 WAVE PROPAGATION II: HIGH FREQUENCY SLOTTED LINE AND REFLECTOMETER MEASUREMENTS OBJECTIVES: To build greater
Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device. Application: Radiation
 Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device Application: adiation Introduction An antenna is designed to radiate or receive electromagnetic
Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device Application: adiation Introduction An antenna is designed to radiate or receive electromagnetic
Performing Amplifier Measurements with the Vector Network Analyzer ZVB
 Product: Vector Network Analyzer R&S ZVB Performing Amplifier Measurements with the Vector Network Analyzer ZVB Application Note This document describes typical measurements that are required to be made
Product: Vector Network Analyzer R&S ZVB Performing Amplifier Measurements with the Vector Network Analyzer ZVB Application Note This document describes typical measurements that are required to be made
Syntactic Foam - A New Dielectric
 Syntactic Foam - A New Dielectric for Beam Forming Networks in Space Applications Peter Uhlig, Jens Leiß, Dietmar Köther IMST GmbH VDE ITG DISKUSSIONSSITZUNG ZUM THEMA MATERIALCHARAKTERISIERUNG RUHR-UNIVERSITÄT
Syntactic Foam - A New Dielectric for Beam Forming Networks in Space Applications Peter Uhlig, Jens Leiß, Dietmar Köther IMST GmbH VDE ITG DISKUSSIONSSITZUNG ZUM THEMA MATERIALCHARAKTERISIERUNG RUHR-UNIVERSITÄT
Ampere's Law. Introduction. times the current enclosed in that loop: Ampere's Law states that the line integral of B and dl over a closed path is 0
 1 Ampere's Law Purpose: To investigate Ampere's Law by measuring how magnetic field varies over a closed path; to examine how magnetic field depends upon current. Apparatus: Solenoid and path integral
1 Ampere's Law Purpose: To investigate Ampere's Law by measuring how magnetic field varies over a closed path; to examine how magnetic field depends upon current. Apparatus: Solenoid and path integral
Network Analysis. Specifying calibration standards for the HP 8510 network analyzer Product Note 8510-5A
 Network Analysis Specifying calibration standards for the HP 8510 network analyzer Product Note 8510-5A 2 Known devices called calibration standards provide the measurement reference for network analyzer
Network Analysis Specifying calibration standards for the HP 8510 network analyzer Product Note 8510-5A 2 Known devices called calibration standards provide the measurement reference for network analyzer
T = 1 f. Phase. Measure of relative position in time within a single period of a signal For a periodic signal f(t), phase is fractional part t p
 Data Transmission Concepts and terminology Transmission terminology Transmission from transmitter to receiver goes over some transmission medium using electromagnetic waves Guided media. Waves are guided
Data Transmission Concepts and terminology Transmission terminology Transmission from transmitter to receiver goes over some transmission medium using electromagnetic waves Guided media. Waves are guided
L stub Z A = Z 0 Z R Z 0S. Single stub impedance matching
 Single stub impedance matching Impedance matching can be achieved by inserting another transmission line (stub) as shown in the diagram below Z A = Z 0 Z 0 Z R Z 0S d stub L stub Amanogawa, 006 Digital
Single stub impedance matching Impedance matching can be achieved by inserting another transmission line (stub) as shown in the diagram below Z A = Z 0 Z 0 Z R Z 0S d stub L stub Amanogawa, 006 Digital
Comparative analysis for Bandwidth Enhancement of RMPA using EBG and varying feed line lengths
 Comparative analysis for Bandwidth Enhancement of RMPA using EBG and varying feed line lengths Tripti Basedia 1 1 EC Deptt., SRIT, India, Jabalpur Rahul Koshtha 2 EC Deptt., SRIT, India, Jabalpur ---------------------------------------------------------------------***---------------------------------------------------------------------
Comparative analysis for Bandwidth Enhancement of RMPA using EBG and varying feed line lengths Tripti Basedia 1 1 EC Deptt., SRIT, India, Jabalpur Rahul Koshtha 2 EC Deptt., SRIT, India, Jabalpur ---------------------------------------------------------------------***---------------------------------------------------------------------
Embedded FM/TV Antenna System
 1 Embedded FM/TV Antenna System Final Report Prepared for By January 21, 2011 2 Table of Contents 1 Introduction... 5 2 Technical Specification... 6 3 Prototype Antenna... 7 4 FASTROAD Active module fabrication...
1 Embedded FM/TV Antenna System Final Report Prepared for By January 21, 2011 2 Table of Contents 1 Introduction... 5 2 Technical Specification... 6 3 Prototype Antenna... 7 4 FASTROAD Active module fabrication...
Electronic filters design tutorial -2
 In the first part of this tutorial we explored the bandpass filters designed with lumped elements, namely inductors and capacitors. In this second part we will design filters with distributed components
In the first part of this tutorial we explored the bandpass filters designed with lumped elements, namely inductors and capacitors. In this second part we will design filters with distributed components
Critical thin-film processes such as deposition and etching take place in a vacuum
 WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
WHITEPAPER INTRODUCING POWER SUPPLIES AND PLASMA Critical thin-film processes such as deposition and etching take place in a vacuum SYSTEMS chamber in the presence of a plasma. A plasma is an electrically
A Dual-Band Beam-Switched Slot Array for GSM 900/1800MHz
 Proceedings of Asia-Pacific Microwave Conference 2006 A Dual-Band Beam-Switched Slot Array for GSM 900/1800MHz Yijun Liu, Zhongxiang Shen, Boyu Zheng and Weihua Tan School of Electrical and Electronic
Proceedings of Asia-Pacific Microwave Conference 2006 A Dual-Band Beam-Switched Slot Array for GSM 900/1800MHz Yijun Liu, Zhongxiang Shen, Boyu Zheng and Weihua Tan School of Electrical and Electronic
ANALYSIS AND VERIFICATION OF A PROPOSED ANTENNA DESIGN FOR AN IMPLANTABLE. RFID TAG AT 915 MHz RAHUL BAKORE
 ANALYSIS AND VERIFICATION OF A PROPOSED ANTENNA DESIGN FOR AN IMPLANTABLE RFID TAG AT 915 MHz By RAHUL BAKORE Bachelor of Engineering in Electronics and Communication University Of Rajasthan Jaipur, Rajasthan,
ANALYSIS AND VERIFICATION OF A PROPOSED ANTENNA DESIGN FOR AN IMPLANTABLE RFID TAG AT 915 MHz By RAHUL BAKORE Bachelor of Engineering in Electronics and Communication University Of Rajasthan Jaipur, Rajasthan,
Oscar E. Morel UtilX Corporation
 Oscar E. Morel UtilX Corporation Time Domain Reflectometry (TDR) has been the preferred technique to assess: Cable length Splice number and spatial location, and Metallic neutral condition Tests for neutral
Oscar E. Morel UtilX Corporation Time Domain Reflectometry (TDR) has been the preferred technique to assess: Cable length Splice number and spatial location, and Metallic neutral condition Tests for neutral
Crosstalk effects of shielded twisted pairs
 This article deals with the modeling and simulation of shielded twisted pairs with CST CABLE STUDIO. The quality of braided shields is investigated with respect to perfect solid shields. Crosstalk effects
This article deals with the modeling and simulation of shielded twisted pairs with CST CABLE STUDIO. The quality of braided shields is investigated with respect to perfect solid shields. Crosstalk effects
Application Note Noise Frequently Asked Questions
 : What is? is a random signal inherent in all physical components. It directly limits the detection and processing of all information. The common form of noise is white Gaussian due to the many random
: What is? is a random signal inherent in all physical components. It directly limits the detection and processing of all information. The common form of noise is white Gaussian due to the many random
a 1 a 2 2 Port b 2 b 1 Multi-Port Handset Switch S-Parameters Application Note AN20 Seven-Port S-Parameter Definition Introduction Summary:
 AN2 Multi-Port Handset Switch S-Parameters Introduction High-power UltraCMOS switches are the nextgeneration solution for wireless handset power amplifiers and antenna switch modules. Most multi-throw
AN2 Multi-Port Handset Switch S-Parameters Introduction High-power UltraCMOS switches are the nextgeneration solution for wireless handset power amplifiers and antenna switch modules. Most multi-throw
Software for Design NMR Probes Using the Shielded Split Ring and the Shielded Symmetrical Band Resonators
 Software for Design NMR Probes Using the Shielded Split Ring and the Shielded Symmetrical Band Resonators Nasreddine Benahmed University of Tlemcen, Algeria ABSTRACT This article presents a software (NMR
Software for Design NMR Probes Using the Shielded Split Ring and the Shielded Symmetrical Band Resonators Nasreddine Benahmed University of Tlemcen, Algeria ABSTRACT This article presents a software (NMR
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Pri Eðlisfræði 2, vor 2007 28. Sources of Magnetic Field Assignment is due at 2:00am on Wednesday, March 7, 2007 Credit for problems submitted late will decrease to 0% after the deadline
[ Assignment View ] [ Pri Eðlisfræði 2, vor 2007 28. Sources of Magnetic Field Assignment is due at 2:00am on Wednesday, March 7, 2007 Credit for problems submitted late will decrease to 0% after the deadline
Antenna Basic Concepts
 ANTENNA An antenna is a device to transmit and/or receive electromagnetic waves. Electromagnetic waves are often referred to as radio waves. Most antennas are resonant devices, which operate efficiently
ANTENNA An antenna is a device to transmit and/or receive electromagnetic waves. Electromagnetic waves are often referred to as radio waves. Most antennas are resonant devices, which operate efficiently
UNDERSTANDING NOISE PARAMETER MEASUREMENTS (AN-60-040)
 UNDERSTANDING NOISE PARAMETER MEASUREMENTS (AN-60-040 Overview This application note reviews noise theory & measurements and S-parameter measurements used to characterize transistors and amplifiers at
UNDERSTANDING NOISE PARAMETER MEASUREMENTS (AN-60-040 Overview This application note reviews noise theory & measurements and S-parameter measurements used to characterize transistors and amplifiers at
RF-Microwaves formulas - 1-port systems
 RF-Microwaves formulas - -port systems s-parameters: Considering a voltage source feeding into the DUT with a source impedance of. E i E r DUT The voltage into the DUT is composed of 2 parts, an incident
RF-Microwaves formulas - -port systems s-parameters: Considering a voltage source feeding into the DUT with a source impedance of. E i E r DUT The voltage into the DUT is composed of 2 parts, an incident
