Positive Integral Operators With Analytic Kernels
|
|
|
- Justin Green
- 8 years ago
- Views:
Transcription
1 Çnky Ünverte Fen-Edeyt Fkülte, Journl of Art nd Scence Sy : 6 / Arl k 006 Potve ntegrl Opertor Wth Anlytc Kernel Cn Murt D KMEN Atrct n th pper we contruct exmple of potve defnte ntegrl kernel whch re lo nlytc Key word: ntegrl opertor, Cuchy ntegrl formul, Potve defnte kernel, Atrct Bu çl flmd yn zmnd nltk oln poztf tn ml ntegrl çekrdek örneklern oluflturc z Anhtr Kelmeler: ntegrl opertörler, Cuchy ntegrl formülü, Poztf tn ml çekrdekler NTRODUCTON To contruct exmple of potve defnte ntegrl kernel whch re lo nlytc, we need to recll the followng defnton (ee [], [3], [4], [5]) Throughout, let u denote the nner proct on ny complex Hlert pce H y, We let / f, f f nd cll t the norm of f Defnton () Let denote ny ntervl (fnte or nfnte) on the rel lne L () the pce of Leegue meurle complex vlued functon f : C Krelm Ünverte, Fen Edeyt Fkülte, Mtemtk Bölümü, Zonguldk e-ml: cnmurtdkmen@krelmetr 63
![Cuchy ntegrl formülü, Poztf tn ml çekrdekler NTRODUCTON To contruct exmple of potve defnte ntegrl kernel whch re lo nlytc, we need to recll the followng defnton (ee [], [3], [4], [5]) Throughout, let](/docs-images/54/10476901/images/page_1.jpg "u denote the nner proct on ny complex Hlert pce H y, We let / f, f f nd cll t the norm of f Defnton () Let denote ny ntervl (fnte or nfnte) on the rel lne L () the pce of Leegue meurle complex vlued")
2 Potve ntegrl Opertor wth Anlytc Kernel whch re qure ntegrle, n the ene tht operton nd nner proct f, g f( t) g( t) dt So the norm of f f f() t dt () Gven two ntervl, functon k on J uch tht k(, u) d J J L J f() t dt, wth pontwe = ll meurle complex vlued Defnton Let H, H e Hlert pce A lner opertor S: H H ounded f there ext ome M R uch tht Sf M f for ll f H ( fn) A lner opertor S: H H, there ext uequence ( ), H compct f gven ounded equence f f g H uch tht nr Sfn r g We ue B( H, H) nd K( H, H) for the pce of ll ounded lner opertor nd for ll compct opertor from H nto H repectvely Theorem f S B( H, H), there ext unque S B( H, H), clled djont of S, uch tht Sf, gh f, S g H f H H nd S S, then S clled elf-djont or ymmetrc Defnton 3 Let T e elf-djont lner opertor on Hlert pce H,, Then T clled potve, wrtten T 0, f Tf, f 0 for ll f H Defnton 4 Let, J e ntervl nd uppoe formul Sf () k(, u) f () u J where, f L ( J), defne compct lner opertor S mppng nto L ( ) The djont S : L ( ) L ( J) gven y Sgu ( ) gtktudt ( ) (, ) R n kl ( J), then the L ( J ) 64
3 Cn Murt D KMEN So f g L ( ) SS g() S g()(, u k u) J J g( t) k( t, u) k(, u) dt gtktdt ( ) (, ) where Kt (,) kuktut (, )(, ), J Sg L ( J) f S S g L ( ) t T SS Fgure Sf L ( ) t well known tht, ecue kl ( J), nterchngng the order of ntegrl legtmte nd tht KL Theorem Here T SS necerly potve wrtten T 0 menng tht Tf, f 0 for ll f H Proof: Tg, g SS g, g S g, S g S g 0 L ( ) L ( ) L ( J) L ( J) Smlrly SS potve opertor on L ( J ) Th gve u method of contructng exmple of potve ntegrl opertor on L ( ) Whenever kl ( J), T SS wll e potve ntegrl opertor on L ( ) wth kernel Kt (,) kuktu (, )(, ) J 65
4 Potve ntegrl Opertor wth Anlytc Kernel Defnton 5 Here k clled kernel of S nd K clled the kernel of T Remrk 3 f ku (, ) luhu (, ) ( ) where hu ( ) then J kuktu (, )(, ) lultu (, )(, ) J Remrk 4 A reult nlogou to theorem true f the Leeque meure on J multpled y potve contnt m (uully / ) n th ce we hve Sf () k(, u) f ()( u m) J where, f L ( J) nd Sgu ( ) kugtdt (, ) ( ) where uj, t nd g L ( ) Tf () SS f () K(,) t g() t dt where Kt (,) kuktu (, )(, )( m) J Now, we wll ue th theorem to gve exmple of potve defnte kernel K ung kernel k whch re n nturl wy n mthemtcl nly Specfclly we conder k ' whch re from Cuchy' ntegrl formul (CF) A equel we hope to gve ome more exmple ung me technque conderng the Fourer trnformton nd the Lplce trnform (ee []) n ll ce K wll e n nlytc kernel of nd t Exmple uggeted y CF n th ecton we wll gve ome exmple of potve ntegrl opertor uggeted y Cuchy' ntegrl formul whch were otned rng my MSc tudy (ee [] ) We recll the prmeterzed Cuchy' ntegrl formul We prmeterze the ntegrl y tkng z ( u) 66
5 Cn Murt D KMEN D C ( u) u Fgure Here potvely orented rectfle Jordn curve nd D t nner domn Let f e n nlytc neghorhood of D nd D f( z) f() dz z f( ( u)) ( u) ( u) J Exmple Suppoe the unt crcle, [, ] (,) Here we hll tke [, ] z e Fgure 67
6 Potve ntegrl Opertor wth Anlytc Kernel We wrte the Cuchy' ntegrl formul (CF) to get our ntegrl kernel f( z) f ( ) dz ( ) z f we uttute z e then dz e d nd f( e ) e f() d e Th ugget the lner opertor S L L defned y : ([, ]) ( ) d Sf ( ) f ( ) k(, ) e e Hence Here Sg( ) gt ( ) dt kt (, ) e t e t k L J e (, ) ( ) For th we need to how tht they re qure ntegrle: dd () e Then, equton () true nce k (, ) contnuou on J So kt (, ) So SS h kernel Kt (,) ktkt (,)(, ) d e e t d () 68
7 Cn Murt D KMEN n generl, f h functon on then o tht he ( ) e d = hz ( ) dz dz he ( ) d = hz ( ) z (3) Now f we ue (3) n (), then we get dz Kt (,) z z t z dz z zt The pole of ntegrnd re t z nd z / t Snce t,, / t Then we hve only one pole t z Therefore, Kt (,) zt dz Re f(), z z t, we know tht Snce K the kernel of SS, K potve defnte on L ( ) where (,) Now we wll fnd nother potve defnte kernel for vertcl trp Exmple Let R nd let D e the open hlf-plne zc :Re z Let e the oundry lne of D nd uppoe [, ] D, (e ), o tht t, where t, L ( ) whoe kernel derved We hll now contruct potve ntegrl opertor on from the Cuchy ntegrl formul for functon nlytc n neghorhood of D 69
8 Potve ntegrl Opertor wth Anlytc Kernel D R Fgure 3 We cn prmeterze y ( u) u, ( u) u Then we hve y CF f( z) f( u) f () dz= z u Th ugget u the opertor S: L (R)( ) L ( ) uch tht Sf Sf () () = R f( u) u o we hve ku (, ) u Here we hve tht (, ) L( ) ku ( x R), ecue R R d d d u (β + ) + uu 70
9 Cn Murt D KMEN Snce the neret pont of to the lne, we hve tht for ll Then, ( ) ( ) R R d d d (β + ) u + u u = R ( ) u Hence K (,) t R R u tu ( ) ( ) u u t ( t) R ( ) Fgure 4 The pole n the upper hlf plne t ( t) Sy hu ( ) u( ) u( t) 7
10 Potve ntegrl Opertor wth Anlytc Kernel then K (, t) Re ( h( u), ( t)) ( t ) ( ) t Snce K (,) t the kernel of SS, (4) potve defnte on L ( ) Suppoe now u, u nd D ll pont to the left of, tht D z :Re z nd tht [, ] D(e ) R D u Fgure 5 n th ce CF red f( z) f( u) f () dz= z u whch ugget the lner opertor S L : (R) ) L ( ) uch tht f( u) Sf Sf() () u = R 7
![the left of, tht D z :Re z nd tht [, ] D(e ) R D u Fgure 5 n th ce CF red f( z) f( u)](/docs-images/54/10476901/images/page_10.jpg "f () dz= z u whch ugget the lner opertor S L : (R) ) L ( ) uch tht f( u) Sf Sf() () u")
11 Cn Murt D KMEN Then we hve k(, u), u u R Here k (, u ) L ( (,u) L ( x R), ecue R R d d d u (β + ) u+ u d R d (β + ) u+ u = R ( ) u So KK (,t) (,) t= R = R u u t ( ) ( ) u u t ( ) ( t) R Fgure 6 The pole n the upper hlf plne ( ) Sy hu ( ) u( ) u( t) 73
12 Potve ntegrl Opertor wth Anlytc Kernel then K (, t ) Re ( h ( u ), ( )) Hence K(,) t t (5) Snce K kernel of SS, (5) potve defnte on L ( ) For the lt prt of our exmple we ue the fct tht the um of two potve opertor potve So f 0 nd [, ] (, ), we otn potve opertor on L ( ) wth kernel Kt (,) whch nlytc n D D u D u 0 Fgure 7 Hence we hve Kt (,) K(,) tk(,) t t 4 4 ( t) (6) Agn nce K kernel of SS SS, (6) potve defnte on L ( ) We now gve nother exmple whch mlr to the lt one Th tme D wll e the horzontl trp 74
13 Cn Murt D KMEN Exmple 3 Let 0 nd let D e the open hlf-plne z :mz D nd uppoe [, ] D,, t We hll now contruct potve ntegrl opertor on L ( ) Let e the oundry lne of whoe kernel derved from the Cuchy ntegrl formul for functon nlytc n neghorhood of D D 0 Fgure 8 Th tme CF red f () f( zf(z) ) dz dz R+β zz f we put z u then dz, then we get f( f(β + uu) ) f() R β + uu ) Th ugget the lner opertor S: L ((R) ) L ( ) defned y f( u) Sf () u Sf () = R Hence gt () Sgu ( ) dt ut 75
14 Potve ntegrl Opertor wth Anlytc Kernel Then we hve k(, t) nd k( u, t) u u t Here k u (, ) L ( ) ( x R),, ecue R = R d d u u Let u tn nd ec d Then, R u / ec d / / / dd tn dd ( ) d Then we hve K (,t) (,) t= R = R u ut ( ) ( ) u u t t R Fgure 9 76
15 Cn Murt D KMEN The pole n the upper hlf plne t Then, K(, t) Re ( h( u), t ) t t t t 4 Hence t ( ) K(,) t K (,) t ( t) 4 Here K (,) t ymmetrc nd potve defnte For the econd prt of our exmple we gn let 0 nd let D e the open hlf-plne z :mz Let e the oundry lne of D nd uppoe [, ] D,, t We hll now contruct potve ntegrl opertor on L ( ) whoe kernel derved from the Cuchy formul for functon nlytc n neghorhood of D 0 D Fgure 0 We put z ( u) u nd dz n CF 77
![hlf-plne z :mz Let e the oundry lne of D nd uppoe [, ] D,, t We hll now contruct potve ntegrl opertor on L ( )](/docs-images/54/10476901/images/page_15.jpg "whoe kernel derved from the Cuchy formul for functon nlytc n neghorhood of D 0 D Fgure 0 We put z ( u) u nd dz n")
16 Potve ntegrl Opertor wth Anlytc Kernel f( f (-β u+ ) u) f() β u+ u Th ugget the lner opertor S: L ((R) ) L ( ) uch tht f( u) Sf () = R ( ) u Here k (, u ) ( ) ( ) u L ( x R),, ecue d d d < y (,7) y (,7) ( ) u u(u ) + β Then, R R = R R K(,) t ( ) ( ) u t u (R Fgure The pole n the upper hlf plne Then, K(, t) Re ( h( u), ) ( t) t ( ) t K ( t, ) t 4 t 78
17 Cn Murt D KMEN Here K (,) t ymmetrc nd potve defnte on L ( ) For the lt prt of our exmple, we gn ue the fct tht the um of two potve opertor potve So f 0 nd [, ] R, we otn potve opertor on L ( ) wth kernel Kt (,) 0 D Fgure t ( ) t ( ) Kt (,) ( t) 4 ( t) ( t) (8) Then (8) potve defnte on L ( ) We wll now conder more generl hlf-plne Exmple 34 Let 0 / We defne the two hlf plne y D z : rgz D z : rgz D D [, ], 0 o Let D, D We cn prmeterze y ( u) u, u (R nd put e 79
18 Potve ntegrl Opertor wth Anlytc Kernel D 0 R Fgure 3 So CF for D cn e wrtten f( u) f() f () π R u where we do not conder nd / nce from Remrk 3 nd Remrk 4 Th ugget the lner opertor S : L ( ) L ( ) (R) defned y Sf() f ( u) () = R u Then, k u ( x R),ecue u (, ) L ( ) 80
19 Cn Murt D KMEN R = R d d d u u u co co θ u n n θ = R R u u d co d u co ( ) R ( ) (co ) u So tht we hve K (,) t = R = R ( u)( ut) ( u)( ut) 0 t Fgure 4 R 8
20 Potve ntegrl Opertor wth Anlytc Kernel The pole n the upper hlf plne Then, K(, t) Re ( h( u), ) t ( t)co ( t)n ( t)n ( t)co ( t)n ( t)co K ( t, ) ( t) n ( t) co Then we know tht K (,) t ymmetrc nd potve defnte on L ( ) Now we wll contruct our kernel for D We cn prmeterze y ( u) u, u R D 0 R Fgure 5 8
21 Cn Murt D KMEN So CF for D cn e wrtten f( u) f () = f () π R u Th ugget u the opertor S from L ( (R) ) to L ( ) uch tht R f ( u) Sf Sf ()() = u Hence Smlrly gt () S g( u) dt u t k(, u) L (x R) u Then we hve K K(,t) (,) t= R = R ( u)( ut) ( u)( ut) 0 t Fgure 6 R 83
22 Potve ntegrl Opertor wth Anlytc Kernel The pole n the upper hlf plne t Then, K(, t) Re ( h( u), t) t ( t)co ( t)n ( t)n ( t)co ( t)n ( t)co K ( t, ) ( t) n ( t) co Then, we know tht K (,) t ymmetrc nd potve defnte on L ( ) Now for the lt prt of the exmple we ue the fct tht the um of two potve opertor potve D 0 Fgure 7 84
23 Cn Murt D KMEN BBLOGRAPHY CMDkmen, Potve ntegrl Opertor wth Anlytc Kernel MSc The, The Unverty of Mncheter, 997 NYoung An ntrocton to Hlert pce Cmrdge Unverty Pre, Cmrdge, 988 WRudn Rel nd Complex Anly McGrw-Hll Book Compny, New York, 966 HHochtdt ntegrl Equton John Wley & Son nc, New York, 973 Mtrnovc, S Drgolv The Cuchy Method of Ree DRedel Pulhng Compny, Dordrecht,
Example A rectangular box without lid is to be made from a square cardboard of sides 18 cm by cutting equal squares from each corner and then folding
1 Exmple A rectngulr box without lid is to be mde from squre crdbord of sides 18 cm by cutting equl squres from ech corner nd then folding up the sides. 1 Exmple A rectngulr box without lid is to be mde
Lecture 5. Inner Product
Lecture 5 Inner Product Let us strt with the following problem. Given point P R nd line L R, how cn we find the point on the line closest to P? Answer: Drw line segment from P meeting the line in right
WHAT HAPPENS WHEN YOU MIX COMPLEX NUMBERS WITH PRIME NUMBERS?
WHAT HAPPES WHE YOU MIX COMPLEX UMBERS WITH PRIME UMBERS? There s n ol syng, you n t pples n ornges. Mthemtns hte n t; they love to throw pples n ornges nto foo proessor n see wht hppens. Sometmes they
Solution to Problem Set 1
CSE 5: Introduction to the Theory o Computtion, Winter A. Hevi nd J. Mo Solution to Prolem Set Jnury, Solution to Prolem Set.4 ). L = {w w egin with nd end with }. q q q q, d). L = {w w h length t let
and thus, they are similar. If k = 3 then the Jordan form of both matrices is
Homework ssignment 11 Section 7. pp. 249-25 Exercise 1. Let N 1 nd N 2 be nilpotent mtrices over the field F. Prove tht N 1 nd N 2 re similr if nd only if they hve the sme miniml polynomil. Solution: If
Vector Geometry for Computer Graphics
Vector Geometry for Computer Grphcs Bo Getz Jnury, 7 Contents Prt I: Bsc Defntons Coordnte Systems... Ponts nd Vectors Mtrces nd Determnnts.. 4 Prt II: Opertons Vector ddton nd sclr multplcton... 5 The
5.2. LINE INTEGRALS 265. Let us quickly review the kind of integrals we have studied so far before we introduce a new one.
5.2. LINE INTEGRALS 265 5.2 Line Integrls 5.2.1 Introduction Let us quickly review the kind of integrls we hve studied so fr before we introduce new one. 1. Definite integrl. Given continuous rel-vlued
8.5 UNITARY AND HERMITIAN MATRICES. The conjugate transpose of a complex matrix A, denoted by A*, is given by
6 CHAPTER 8 COMPLEX VECTOR SPACES 5. Fnd the kernel of the lnear transformaton gven n Exercse 5. In Exercses 55 and 56, fnd the mage of v, for the ndcated composton, where and are gven by the followng
4.11 Inner Product Spaces
314 CHAPTER 4 Vector Spces 9. A mtrix of the form 0 0 b c 0 d 0 0 e 0 f g 0 h 0 cnnot be invertible. 10. A mtrix of the form bc d e f ghi such tht e bd = 0 cnnot be invertible. 4.11 Inner Product Spces
v a 1 b 1 i, a 2 b 2 i,..., a n b n i.
SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 455 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces we have studed thus far n the text are real vector spaces snce the scalars are
Recurrence. 1 Definitions and main statements
Recurrence 1 Defntons and man statements Let X n, n = 0, 1, 2,... be a MC wth the state space S = (1, 2,...), transton probabltes p j = P {X n+1 = j X n = }, and the transton matrx P = (p j ),j S def.
Chapter 6 Best Linear Unbiased Estimate (BLUE)
hpter 6 Bet Lner Unbed Etmte BLUE Motvton for BLUE Except for Lner Model ce, the optml MVU etmtor mght:. not even ext. be dffcult or mpoble to fnd Reort to ub-optml etmte BLUE one uch ub-optml etmte Ide
Integration by Substitution
Integrtion by Substitution Dr. Philippe B. Lvl Kennesw Stte University August, 8 Abstrct This hndout contins mteril on very importnt integrtion method clled integrtion by substitution. Substitution is
1 Example 1: Axis-aligned rectangles
COS 511: Theoretcal Machne Learnng Lecturer: Rob Schapre Lecture # 6 Scrbe: Aaron Schld February 21, 2013 Last class, we dscussed an analogue for Occam s Razor for nfnte hypothess spaces that, n conjuncton
LINEAR TRANSFORMATIONS AND THEIR REPRESENTING MATRICES
LINEAR TRANSFORMATIONS AND THEIR REPRESENTING MATRICES DAVID WEBB CONTENTS Liner trnsformtions 2 The representing mtrix of liner trnsformtion 3 3 An ppliction: reflections in the plne 6 4 The lgebr of
EN3: Introduction to Engineering. Teach Yourself Vectors. 1. Definition. Problems
EN3: Introducton to Engneerng Tech Yourself Vectors Dvson of Engneerng Brown Unversty. Defnton vector s mthemtcl obect tht hs mgntude nd drecton, nd stsfes the lws of vector ddton. Vectors re used to represent
MODULE 3. 0, y = 0 for all y
Topics: Inner products MOULE 3 The inner product of two vectors: The inner product of two vectors x, y V, denoted by x, y is (in generl) complex vlued function which hs the following four properties: i)
Luby s Alg. for Maximal Independent Sets using Pairwise Independence
Lecture Notes for Randomzed Algorthms Luby s Alg. for Maxmal Independent Sets usng Parwse Independence Last Updated by Erc Vgoda on February, 006 8. Maxmal Independent Sets For a graph G = (V, E), an ndependent
Newton-Raphson Method of Solving a Nonlinear Equation Autar Kaw
Newton-Rphson Method o Solvng Nonlner Equton Autr Kw Ater redng ths chpter, you should be ble to:. derve the Newton-Rphson method ormul,. develop the lgorthm o the Newton-Rphson method,. use the Newton-Rphson
We are now ready to answer the question: What are the possible cardinalities for finite fields?
Chapter 3 Fnte felds We have seen, n the prevous chapters, some examples of fnte felds. For example, the resdue class rng Z/pZ (when p s a prme) forms a feld wth p elements whch may be dentfed wth the
Extending Probabilistic Dynamic Epistemic Logic
Extendng Probablstc Dynamc Epstemc Logc Joshua Sack May 29, 2008 Probablty Space Defnton A probablty space s a tuple (S, A, µ), where 1 S s a set called the sample space. 2 A P(S) s a σ-algebra: a set
BERNSTEIN POLYNOMIALS
On-Lne Geometrc Modelng Notes BERNSTEIN POLYNOMIALS Kenneth I. Joy Vsualzaton and Graphcs Research Group Department of Computer Scence Unversty of Calforna, Davs Overvew Polynomals are ncredbly useful
Example 27.1 Draw a Venn diagram to show the relationship between counting numbers, whole numbers, integers, and rational numbers.
2 Rtionl Numbers Integers such s 5 were importnt when solving the eqution x+5 = 0. In similr wy, frctions re importnt for solving equtions like 2x = 1. Wht bout equtions like 2x + 1 = 0? Equtions of this
PERRON FROBENIUS THEOREM
PERRON FROBENIUS THEOREM R. CLARK ROBINSON Defnton. A n n matrx M wth real entres m, s called a stochastc matrx provded () all the entres m satsfy 0 m, () each of the columns sum to one, m = for all, ()
n + d + q = 24 and.05n +.1d +.25q = 2 { n + d + q = 24 (3) n + 2d + 5q = 40 (2)
MATH 16T Exam 1 : Part I (In-Class) Solutons 1. (0 pts) A pggy bank contans 4 cons, all of whch are nckels (5 ), dmes (10 ) or quarters (5 ). The pggy bank also contans a con of each denomnaton. The total
Basically, logarithmic transformations ask, a number, to what power equals another number?
Wht i logrithm? To nwer thi, firt try to nwer the following: wht i x in thi eqution? 9 = 3 x wht i x in thi eqution? 8 = 2 x Biclly, logrithmic trnformtion k, number, to wht power equl nother number? In
Ring structure of splines on triangulations
www.oeaw.ac.at Rng structure of splnes on trangulatons N. Vllamzar RICAM-Report 2014-48 www.rcam.oeaw.ac.at RING STRUCTURE OF SPLINES ON TRIANGULATIONS NELLY VILLAMIZAR Introducton For a trangulated regon
Lecture 3: Force of Interest, Real Interest Rate, Annuity
Lecture 3: Force of Interest, Real Interest Rate, Annuty Goals: Study contnuous compoundng and force of nterest Dscuss real nterest rate Learn annuty-mmedate, and ts present value Study annuty-due, and
Math 135 Circles and Completing the Square Examples
Mth 135 Circles nd Completing the Squre Exmples A perfect squre is number such tht = b 2 for some rel number b. Some exmples of perfect squres re 4 = 2 2, 16 = 4 2, 169 = 13 2. We wish to hve method for
Netherlands Published online: 27 Jun 2013.
Th artcle wa downloaded by: [Bblotheek TU Delft] On: 04 Noveber 2013, At: 08:09 Publher: Routledge Infora Ltd Regtered n England and Wale Regtered Nuber: 1072954 Regtered offce: Morter Houe, 37-41 Morter
Rate Monotonic (RM) Disadvantages of cyclic. TDDB47 Real Time Systems. Lecture 2: RM & EDF. Priority-based scheduling. States of a process
Dsadvantages of cyclc TDDB47 Real Tme Systems Manual scheduler constructon Cannot deal wth any runtme changes What happens f we add a task to the set? Real-Tme Systems Laboratory Department of Computer
Answer: A). There is a flatter IS curve in the high MPC economy. Original LM LM after increase in M. IS curve for low MPC economy
4.02 Quz Solutons Fall 2004 Multple-Choce Questons (30/00 ponts) Please, crcle the correct answer for each of the followng 0 multple-choce questons. For each queston, only one of the answers s correct.
Regular Sets and Expressions
Regulr Sets nd Expressions Finite utomt re importnt in science, mthemtics, nd engineering. Engineers like them ecuse they re super models for circuits (And, since the dvent of VLSI systems sometimes finite
9.3. The Scalar Product. Introduction. Prerequisites. Learning Outcomes
The Sclr Product 9.3 Introduction There re two kinds of multipliction involving vectors. The first is known s the sclr product or dot product. This is so-clled becuse when the sclr product of two vectors
. At first sight a! b seems an unwieldy formula but use of the following mnemonic will possibly help. a 1 a 2 a 3 a 1 a 2
7 CHAPTER THREE. Cross Product Given two vectors = (,, nd = (,, in R, the cross product of nd written! is defined to e: " = (!,!,! Note! clled cross is VECTOR (unlike which is sclr. Exmple (,, " (4,5,6
Use Geometry Expressions to create a more complex locus of points. Find evidence for equivalence using Geometry Expressions.
Lerning Objectives Loci nd Conics Lesson 3: The Ellipse Level: Preclculus Time required: 120 minutes In this lesson, students will generlize their knowledge of the circle to the ellipse. The prmetric nd
Lecture 3 Gaussian Probability Distribution
Lecture 3 Gussin Probbility Distribution Introduction l Gussin probbility distribution is perhps the most used distribution in ll of science. u lso clled bell shped curve or norml distribution l Unlike
The invention of line integrals is motivated by solving problems in fluid flow, forces, electricity and magnetism.
Instrutor: Longfei Li Mth 43 Leture Notes 16. Line Integrls The invention of line integrls is motivted by solving problems in fluid flow, fores, eletriity nd mgnetism. Line Integrls of Funtion We n integrte
Review guide for the final exam in Math 233
Review guide for the finl exm in Mth 33 1 Bsic mteril. This review includes the reminder of the mteril for mth 33. The finl exm will be cumultive exm with mny of the problems coming from the mteril covered
Chapter 7 Kinetic energy and work
Chpter 7 Kc energy nd wor I. Kc energy. II. or. III. or - Kc energy theorem. IV. or done by contnt orce - Grttonl orce V. or done by rble orce. VI. Power - Sprng orce. - Generl. D-Anly 3D-Anly or-kc Energy
Distributions. (corresponding to the cumulative distribution function for the discrete case).
Distributions Recll tht n integrble function f : R [,] such tht R f()d = is clled probbility density function (pdf). The distribution function for the pdf is given by F() = (corresponding to the cumultive
What is Candidate Sampling
What s Canddate Samplng Say we have a multclass or mult label problem where each tranng example ( x, T ) conssts of a context x a small (mult)set of target classes T out of a large unverse L of possble
2005-06 Second Term MAT2060B 1. Supplementary Notes 3 Interchange of Differentiation and Integration
Source: http://www.mth.cuhk.edu.hk/~mt26/mt26b/notes/notes3.pdf 25-6 Second Term MAT26B 1 Supplementry Notes 3 Interchnge of Differentition nd Integrtion The theme of this course is bout vrious limiting
Boolean Algebra. ECE 152A Winter 2012
Boolen Algebr ECE 52A Wnter 22 Redng Assgnent Brown nd Vrnesc 2 Introducton to Logc Crcuts 2.5 Boolen Algebr 2.5. The Venn Dgr 2.5.2 Notton nd Ternology 2.5.3 Precedence of Opertons 2.6 Synthess Usng AND,
Mean Molecular Weight
Mean Molecular Weght The thermodynamc relatons between P, ρ, and T, as well as the calculaton of stellar opacty requres knowledge of the system s mean molecular weght defned as the mass per unt mole of
Support Vector Machines
Support Vector Machnes Max Wellng Department of Computer Scence Unversty of Toronto 10 Kng s College Road Toronto, M5S 3G5 Canada wellng@cs.toronto.edu Abstract Ths s a note to explan support vector machnes.
Vectors 2. 1. Recap of vectors
Vectors 2. Recp of vectors Vectors re directed line segments - they cn be represented in component form or by direction nd mgnitude. We cn use trigonometry nd Pythgors theorem to switch between the forms
ARTICLE IN PRESS. JID:COMAID AID:1153 /FLA [m3g; v 1.79; Prn:21/02/2009; 14:10] P.1 (1-13) Computer Aided Geometric Design ( )
![ARTICLE IN PRESS. JID:COMAID AID:1153 /FLA [m3g; v 1.79; Prn:21/02/2009; 14:10] P.1 (1-13) Computer Aided Geometric Design ( )](/thumbs/27/10357589.jpg "ARTICLE IN PRESS. JID:COMAID AID:1153 /FLA [m3g; v 1.79; Prn:21/02/2009; 14:10] P.1 (1-13) Computer Aided Geometric Design ( )")
COMAID:5 JID:COMAID AID:5 /FLA [mg; v 79; Prn:/0/009; 4:0] P -) Computer Aded Geometrc Degn ) Content lt avalable at ScenceDrect Computer Aded Geometrc Degn wwwelevercom/locate/cagd Fat approach for computng
RIGHT TRIANGLES AND THE PYTHAGOREAN TRIPLETS
RIGHT TRIANGLES AND THE PYTHAGOREAN TRIPLETS Known for over 500 yers is the fct tht the sum of the squres of the legs of right tringle equls the squre of the hypotenuse. Tht is +b c. A simple proof is
Vectors. The magnitude of a vector is its length, which can be determined by Pythagoras Theorem. The magnitude of a is written as a.
Vectors mesurement which onl descries the mgnitude (i.e. size) of the oject is clled sclr quntit, e.g. Glsgow is 11 miles from irdrie. vector is quntit with mgnitude nd direction, e.g. Glsgow is 11 miles
Alternatives to an Inefficient International Telephony. Settlement System
Alterntve to n Ineffent Interntonl Telephony Settlement Sytem Alterntve to n Ineffent Interntonl Telephony Settlement Sytem Koj Domon Shool of Sol Sene Wed Unverty -6- Nh-Wed Shnjuku-ku Tokyo 69-8050 JAPAN
21 Vectors: The Cross Product & Torque
21 Vectors: The Cross Product & Torque Do not use our left hand when applng ether the rght-hand rule for the cross product of two vectors dscussed n ths chapter or the rght-hand rule for somethng curl
s-domain Circuit Analysis
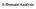S-Doman naly -Doman rcut naly Tme doman t doman near rcut aplace Tranform omplex frequency doman doman Tranformed rcut Dfferental equaton lacal technque epone waveform aplace Tranform nvere Tranform -
The remaining two sides of the right triangle are called the legs of the right triangle.
10 MODULE 6. RADICAL EXPRESSIONS 6 Pythgoren Theorem The Pythgoren Theorem An ngle tht mesures 90 degrees is lled right ngle. If one of the ngles of tringle is right ngle, then the tringle is lled right
Irregular Repeat Accumulate Codes 1
Irregulr epet Accumulte Codes 1 Hu Jn, Amod Khndekr, nd obert McElece Deprtment of Electrcl Engneerng, Clforn Insttute of Technology Psden, CA 9115 USA E-ml: {hu, mod, rjm}@systems.cltech.edu Abstrct:
The OC Curve of Attribute Acceptance Plans
The OC Curve of Attrbute Acceptance Plans The Operatng Characterstc (OC) curve descrbes the probablty of acceptng a lot as a functon of the lot s qualty. Fgure 1 shows a typcal OC Curve. 10 8 6 4 1 3 4
DATABASDESIGN FÖR INGENJÖRER - 1056F
DATABASDESIGN FÖR INGENJÖRER - 06F Sommr 00 En introuktionskurs i tssystem http://user.it.uu.se/~ul/t-sommr0/ lt. http://www.it.uu.se/eu/course/homepge/esign/st0/ Kjell Orsorn (Rusln Fomkin) Uppsl Dtse
Chapter 7: Answers to Questions and Problems
19. Based on the nformaton contaned n Table 7-3 of the text, the food and apparel ndustres are most compettve and therefore probably represent the best match for the expertse of these managers. Chapter
COLLOQUIUM MATHEMATICUM
COLLOQUIUM MATHEMATICUM VOL. 74 997 NO. TRANSFERENCE THEORY ON HARDY AND SOBOLEV SPACES BY MARIA J. CARRO AND JAVIER SORIA (BARCELONA) We show that the transference method of Cofman and Wess can be extended
PHY 140A: Solid State Physics. Solution to Homework #2
PHY 140A: Solid Stte Physics Solution to Homework # TA: Xun Ji 1 October 14, 006 1 Emil: jixun@physics.ucl.edu Problem #1 Prove tht the reciprocl lttice for the reciprocl lttice is the originl lttice.
CURVES ANDRÉ NEVES. that is, the curve α has finite length. v = p q p q. a i.e., the curve of smallest length connecting p to q is a straight line.
CURVES ANDRÉ NEVES 1. Problems (1) (Ex 1 of 1.3 of Do Crmo) Show tht the tngent line to the curve α(t) (3t, 3t 2, 2t 3 ) mkes constnt ngle with the line z x, y. (2) (Ex 6 of 1.3 of Do Crmo) Let α(t) (e
FINANCIAL MATHEMATICS. A Practical Guide for Actuaries. and other Business Professionals
FINANCIAL MATHEMATICS A Practcal Gude for Actuares and other Busness Professonals Second Edton CHRIS RUCKMAN, FSA, MAAA JOE FRANCIS, FSA, MAAA, CFA Study Notes Prepared by Kevn Shand, FSA, FCIA Assstant
PROF. BOYAN KOSTADINOV NEW YORK CITY COLLEGE OF TECHNOLOGY, CUNY
MAT 0630 INTERNET RESOURCES, REVIEW OF CONCEPTS AND COMMON MISTAKES PROF. BOYAN KOSTADINOV NEW YORK CITY COLLEGE OF TECHNOLOGY, CUNY Contents 1. ACT Compss Prctice Tests 1 2. Common Mistkes 2 3. Distributive
Solution: Let i = 10% and d = 5%. By definition, the respective forces of interest on funds A and B are. i 1 + it. S A (t) = d (1 dt) 2 1. = d 1 dt.
Chapter 9 Revew problems 9.1 Interest rate measurement Example 9.1. Fund A accumulates at a smple nterest rate of 10%. Fund B accumulates at a smple dscount rate of 5%. Fnd the pont n tme at whch the forces
Binary Representation of Numbers Autar Kaw
Binry Representtion of Numbers Autr Kw After reding this chpter, you should be ble to: 1. convert bse- rel number to its binry representtion,. convert binry number to n equivlent bse- number. In everydy
Simple Interest Loans (Section 5.1) :
Chapter 5 Fnance The frst part of ths revew wll explan the dfferent nterest and nvestment equatons you learned n secton 5.1 through 5.4 of your textbook and go through several examples. The second part
Certificate No. 68613082 ONTARIO COURT (PROVINCIAL DIVISION) - versus - PAULO RAPOSO TRANSCRIPT OF PROCEEDINGS
Certfcate No. 686182 ONTARIO COURT (PROVINCIAL DIVISION) HER MAJESTY THE QUEEN - versus - PAULO RAPOSO TRANSCRIPT OF PROCEEDINGS Heard before The Honourable Mr. Justce D. Cooper at Hamlton, Ontaro on Aprl
On Lockett pairs and Lockett conjecture for π-soluble Fitting classes
On Lockett pars and Lockett conjecture for π-soluble Fttng classes Lujn Zhu Department of Mathematcs, Yangzhou Unversty, Yangzhou 225002, P.R. Chna E-mal: ljzhu@yzu.edu.cn Nanyng Yang School of Mathematcs
Generalizing the degree sequence problem
Mddlebury College March 2009 Arzona State Unversty Dscrete Mathematcs Semnar The degree sequence problem Problem: Gven an nteger sequence d = (d 1,...,d n ) determne f there exsts a graph G wth d as ts
INTERCHANGING TWO LIMITS. Zoran Kadelburg and Milosav M. Marjanović
THE TEACHING OF MATHEMATICS 2005, Vol. VIII, 1, pp. 15 29 INTERCHANGING TWO LIMITS Zorn Kdelburg nd Milosv M. Mrjnović This pper is dedicted to the memory of our illustrious professor of nlysis Slobodn
Abstract. 2.2. Adjusted PPM.
Effectvene of Avance an Authentcate Packet Markng Scheme for Traceback of Denal of Servce Attack Blal Rzv an Emmanuel Fernánez-Gaucheran Department of Electrcal & Computer Engneerng &Computer Scence Unverty
Section 5.4 Annuities, Present Value, and Amortization
Secton 5.4 Annutes, Present Value, and Amortzaton Present Value In Secton 5.2, we saw that the present value of A dollars at nterest rate per perod for n perods s the amount that must be deposted today
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan 3 Binary Operations We are used to addition and multiplication of real numbers. These operations combine two real numbers
Production. 2. Y is closed A set is closed if it contains its boundary. We need this for the solution existence in the profit maximization problem.
Producer Theory Producton ASSUMPTION 2.1 Propertes of the Producton Set The producton set Y satsfes the followng propertes 1. Y s non-empty If Y s empty, we have nothng to talk about 2. Y s closed A set
CANKAYA UNIVERSITY FACULTY OF ENGINEERING MECHANICAL ENGINEERING DEPARTMENT ME 212 THERMODYNAMICS II HW# 11 SOLUTIONS
CNKY UNIVESIY FCULY OF ENGINEEING MECHNICL ENGINEEING DEMEN ME HEMODYNMICS II HW# SOLUIONS Deterne te ulton reure of wter or t -60 0 C ung dt lle n te te tle. Soluton Ste tle do not ge turton reure for
Resistive Network Analysis. The Node Voltage Method - 1
esste Network Anlyss he nlyss of n electrcl network conssts of determnng ech of the unknown rnch currents nd node oltges. A numer of methods for network nlyss he een deeloped, sed on Ohm s Lw nd Krchoff
Algebra Review. How well do you remember your algebra?
Algebr Review How well do you remember your lgebr? 1 The Order of Opertions Wht do we men when we write + 4? If we multiply we get 6 nd dding 4 gives 10. But, if we dd + 4 = 7 first, then multiply by then
Causal, Explanatory Forecasting. Analysis. Regression Analysis. Simple Linear Regression. Which is Independent? Forecasting
Causal, Explanatory Forecastng Assumes cause-and-effect relatonshp between system nputs and ts output Forecastng wth Regresson Analyss Rchard S. Barr Inputs System Cause + Effect Relatonshp The job of
Factoring Polynomials
Fctoring Polynomils Some definitions (not necessrily ll for secondry school mthemtics): A polynomil is the sum of one or more terms, in which ech term consists of product of constnt nd one or more vribles
Lectures 8 and 9 1 Rectangular waveguides
1 Lectures 8 nd 9 1 Rectngulr wveguides y b x z Consider rectngulr wveguide with 0 < x b. There re two types of wves in hollow wveguide with only one conductor; Trnsverse electric wves
Least Squares Fitting of Data
Least Squares Fttng of Data Davd Eberly Geoetrc Tools, LLC http://www.geoetrctools.co/ Copyrght c 1998-2016. All Rghts Reserved. Created: July 15, 1999 Last Modfed: January 5, 2015 Contents 1 Lnear Fttng
Optimal Pricing Scheme for Information Services
Optml rcng Scheme for Informton Servces Shn-y Wu Opertons nd Informton Mngement The Whrton School Unversty of ennsylvn E-ml: shnwu@whrton.upenn.edu e-yu (Shron) Chen Grdute School of Industrl Admnstrton
Calculation of Sampling Weights
Perre Foy Statstcs Canada 4 Calculaton of Samplng Weghts 4.1 OVERVIEW The basc sample desgn used n TIMSS Populatons 1 and 2 was a two-stage stratfed cluster desgn. 1 The frst stage conssted of a sample
Unit 11 Using Linear Regression to Describe Relationships
Unit 11 Uing Linear Regreion to Decribe Relationhip Objective: To obtain and interpret the lope and intercept of the leat quare line for predicting a quantitative repone variable from a quantitative explanatory
benefit is 2, paid if the policyholder dies within the year, and probability of death within the year is ).
REVIEW OF RISK MANAGEMENT CONCEPTS LOSS DISTRIBUTIONS AND INSURANCE Loss and nsurance: When someone s subject to the rsk of ncurrng a fnancal loss, the loss s generally modeled usng a random varable or
How To Understand The Recipe Notes Of A Recipe Card
Audo Engneerng Socety Conventon per reented t the th Conventon 6 My 3 r, Frnce Th conventon pper h been reproduced fro the uthor' dvnce nucrpt, wthout edtng, correcton, or conderton by the Revew Bord.
Sequences and Series
Secto 9. Sequeces d Seres You c thk of sequece s fucto whose dom s the set of postve tegers. f ( ), f (), f (),... f ( ),... Defto of Sequece A fte sequece s fucto whose dom s the set of postve tegers.
Appendix D: Completing the Square and the Quadratic Formula. In Appendix A, two special cases of expanding brackets were considered:
Appendi D: Completing the Squre nd the Qudrtic Formul Fctoring qudrtic epressions such s: + 6 + 8 ws one of the topics introduced in Appendi C. Fctoring qudrtic epressions is useful skill tht cn help you
How fast can we sort? Sorting. Decision-tree model. Decision-tree for insertion sort Sort a 1, a 2, a 3. CS 3343 -- Spring 2009
CS 4 -- Spring 2009 Sorting Crol Wenk Slides courtesy of Chrles Leiserson with smll chnges by Crol Wenk CS 4 Anlysis of Algorithms 1 How fst cn we sort? All the sorting lgorithms we hve seen so fr re comprison
EASY RECEPTION TASKS FOR USE IN THE LITERACY HOUR. S t e p h e n s t e. Jigsaw names of self and friends.
EASY RECEPTION TASKS FOR USE IN THE LITERACY HOUR Own Nme Tk Mtching letter underneth nme crd. S t e p h e n t e B e n Mtching mgnetic letter under nme crd p t t h o n Jigw nme of elf nd friend. T r c
9 CONTINUOUS DISTRIBUTIONS
9 CONTINUOUS DISTIBUTIONS A rndom vrible whose vlue my fll nywhere in rnge of vlues is continuous rndom vrible nd will be ssocited with some continuous distribution. Continuous distributions re to discrete
How To Assemble The Tangent Spaces Of A Manfold Nto A Coherent Whole
CHAPTER 7 VECTOR BUNDLES We next begn addressng the queston: how do we assemble the tangent spaces at varous ponts of a manfold nto a coherent whole? In order to gude the decson, consder the case of U
Faraday's Law of Induction
Introducton Faraday's Law o Inducton In ths lab, you wll study Faraday's Law o nducton usng a wand wth col whch swngs through a magnetc eld. You wll also examne converson o mechanc energy nto electrc energy
REGULAR MULTILINEAR OPERATORS ON C(K) SPACES
REGULAR MULTILINEAR OPERATORS ON C(K) SPACES FERNANDO BOMBAL AND IGNACIO VILLANUEVA Abstract. The purpose of ths paper s to characterze the class of regular contnuous multlnear operators on a product of
Drawing Diagrams From Labelled Graphs
Drwing Digrms From Lbelled Grphs Jérôme Thièvre 1 INA, 4, venue de l Europe, 94366 BRY SUR MARNE FRANCE Anne Verroust-Blondet 2 INRIA Rocquencourt, B.P. 105, 78153 LE CHESNAY Cedex FRANCE Mrie-Luce Viud
Mathematics. Vectors. hsn.uk.net. Higher. Contents. Vectors 128 HSN23100
hsn.uk.net Higher Mthemtics UNIT 3 OUTCOME 1 Vectors Contents Vectors 18 1 Vectors nd Sclrs 18 Components 18 3 Mgnitude 130 4 Equl Vectors 131 5 Addition nd Subtrction of Vectors 13 6 Multipliction by
Section 7-4 Translation of Axes
62 7 ADDITIONAL TOPICS IN ANALYTIC GEOMETRY Section 7-4 Trnsltion of Aes Trnsltion of Aes Stndrd Equtions of Trnslted Conics Grphing Equtions of the Form A 2 C 2 D E F 0 Finding Equtions of Conics In the
SPEE Recommended Evaluation Practice #6 Definition of Decline Curve Parameters Background:
SPEE Recommended Evaluaton Practce #6 efnton of eclne Curve Parameters Background: The producton hstores of ol and gas wells can be analyzed to estmate reserves and future ol and gas producton rates and
Series Solutions of ODEs 2 the Frobenius method. The basic idea of the Frobenius method is to look for solutions of the form 3
Royal Holloway Unversty of London Department of Physs Seres Solutons of ODEs the Frobenus method Introduton to the Methodology The smple seres expanson method works for dfferental equatons whose solutons
Section 5.3 Annuities, Future Value, and Sinking Funds
Secton 5.3 Annutes, Future Value, and Snkng Funds Ordnary Annutes A sequence of equal payments made at equal perods of tme s called an annuty. The tme between payments s the payment perod, and the tme