Networks, instruments and data centres: what does your seismic (meta-) data really mean? Joachim Wassermann (LMU Munich)
|
|
|
- Derek Hodge
- 10 years ago
- Views:
Transcription
1 Networks, instruments and data centres: what does your seismic (meta-) data really mean? Joachim Wassermann (LMU Munich) Quest Workshop, Hveragerdi 2011
2 Why an issue? Seismic Networks: Data Exchange many different data formats are existing, but uniform standard exists to send the data to DCs meta data of special importance! possibility to form virtual networks - especially important for regional events or earthquakes located close to a border region increasing the value of the network owners (more use gives more credits) simulating instruments is sometimes easier than correcting real data to true ground motion (relevant for synthetics) 2
3 SEED What is SEED? SEED is an international standard for the exchange of digital seismological data SEED was designed for use by the earthquake research community, primarily for the exchange between institutions of unprocessed earth motion data SEED is a format for digital data measured at one point in space and at equal intervals of time. 3
4 SEED in Practice recordings of digital time-series data (seismic waveforms) exchange of waveform data (real-time, archive) archiving of digital waveform data (IRIS-DMC, ODC, EIDA...) storage of meta-data (information about the data, e.g. station information, sensor) end user (analysis software) not for non-time series data not for unequal time-interval sampled data (except logs) not designed for processed or synthetic data, but possible (IRIS already use it!) parametric data possible (e.g. phase readings) but never used; IASPEI Seismic Format (ISF) 4
5 SEED Structure control headers dataless SEED ascii waveform data raw data and embedded auxiliary information (full) SEED volume mini-seed binary (+ ascii) 5
6 SEED: Metadata and System Response All site characteristics: Latitude, longitude, elevation All instrument characteristics: Detailed responses - calibration, transfer functions Sensor External Preamp and Filter Datalogger Orientation angles and depth of emplacement Serial numbers Instrument type Effective date/time 6
7 System Response or: Filters and Their Description J. Wassermann (LMU - Munich) F. Scherbaum (Univ. Potsdam)
8 From source to receiver... Fig. 1.1 Signal distortion during wave propagation from the earthquake source to the surface.
9 Influence of recording system Fig. 1.2 Vertical component record of the Izmit earthquake in Turkey (1999/08/17) recorded at station MA13 of the University of Potsdam during a field experiment in Northern Norway. Shown from top to bottom are the vertical component records for a: Wood-Anderson, a WWSSN SP, and a WWSSN LP instrument simulation.
10 Sampling process precursory signals Fig. 1.3 Impulse response of stage 3 of the two-sided decimation filter incorporated in the Quanterra QDP 380 system (top trace). The bottom trace shows a filter response with an identical amplitude but different phase response.
11 Seismogram Fig System diagram of a seismogram
12 Seismogram This part is covered by SEED
13 SEED response information Sampling Decimation Seismometer Amplifier AAA filter DAA filter Analog LTI system Poles and Zeros Digital LTI system FIR - Filter
14 Seismometer # << IRIS SEED Reader, Release 4.4 >> # # ======== CHANNEL RESPONSE DATA ======== B050F03 Station: RJOB B050F16 Network: BW B052F03 Location:?? B052F04 Channel: EHZ B052F22 Start date: 2007,199 B052F23 End date: No Ending Time # ======================================= # # + Response (Poles & Zeros), RJOB ch EHZ + # # B053F03 Transfer function type: A [Laplace Transform (Rad/sec)] B053F04 Stage sequence number: 1 B053F05 Response in units lookup: M/S - Velocity in Meters per Second B053F06 Response out units lookup: V - Volts B053F07 A0 normalization factor: E+07 B053F08 Normalization frequency: 1 B053F09 Number of zeroes: 2 B053F14 Number of poles: 5 # Complex zeroes: # i real imag real_error imag_error B053F E E E E+00 B053F E E E E+00 # Complex poles: # i real imag real_error imag_error B053F E E E E+00 B053F E E E E+00 B053F E E E E+00 B053F E E E E+00 B053F E E E E+00
15 Definition Filters or systems are, in the most general sense, devices (in the physical world) or algorithms (in the mathematical world) which act on some input signal to produce a - possibly different - output signal.
16 RC filter
17 Differential equation R x(t) C y(t)
18 Differential equation x(t) R C y(t) Voltage balance?
19 Differential equation x(t) R C y(t) Voltage balance?
20 Differential equation x(t) R C y(t) Voltage balance? Current through resistor R and capacitance C:
21 Differential equation x(t) R C y(t) Voltage balance? Current through resistor R and capacitance C:
22 Differential equation x(t) R C y(t) Voltage balance? Current through resistor R and capacitance C:
23 Differential equation x(t) R C y(t) Voltage balance? Current through resistor R and capacitance C: First order linear differential equation
24 Harmonic input signals
25 Harmonic input signals for harmonic input signal x(t)
26 Harmonic input signals Harmonic input signal: for harmonic input signal x(t)
27 Harmonic input signals for harmonic input signal x(t) Harmonic input signal: x(t) = A i e jωt
28 Harmonic input signals for harmonic input signal x(t) Harmonic input signal: x(t) = A i e jωt Ansatz for the output signal:
29 Harmonic input signals for harmonic input signal x(t) Harmonic input signal: Ansatz for the output signal: x(t) = A i e jωt y(t) = A o e jωt y(t) = jωa o e jωt
30 Harmonic input signals for harmonic input signal x(t) Harmonic input signal: Ansatz for the output signal: x(t) = A i e jωt y(t) = A o e jωt y(t) = jωa o e jωt A o e jωt (RCjω + 1) = A i e jωt
31 Harmonic input signals for harmonic input signal x(t) Harmonic input signal: Ansatz for the output signal: x(t) = A i e jωt y(t) = A o e jωt y(t) = jωa o e jωt A o e jωt (RCjω + 1) = A i e jωt A o A i = 1 RCjω + 1 = T ( jω)
32 Harmonic input signals for harmonic input signal x(t) Harmonic input signal: Ansatz for the output signal: x(t) = A i e jωt y(t) = A o e jωt y(t) = jωa o e jωt A o e jωt (RCjω + 1) = A i e jωt A o A i = 1 RCjω + 1 = T ( jω) Frequency response function
33 Input/output relation A o = T ( jω) A i
34 Input/output relation A o = T ( jω) A i Definition The frequency response function T(jω) is defined as the Fourier transform of the output signal divided by the Fourier transform of the input signal.
35 Input/output relation A o = T ( jω) A i Definition The frequency response function T(jω) is defined as the Fourier transform of the output signal divided by the Fourier transform of the input signal. The frequency response function can be measured by comparing output and input signals to the system without further knowledge of the physics going on inside the filter!
36 Transfer function and Laplace transform Bilateral Laplace transform of f(t): L [ f (t)] = f (t)e st dt with the complex variable s = σ + jω
37 Transfer function and Laplace transform Bilateral Laplace transform of f(t): L [ f (t)] = f (t)e st dt with the complex variable s = σ + jω L [ f (t)] will be written as F(s).
38 Transfer function and Laplace transform Bilateral Laplace transform of f(t): L [ f (t)] = f (t)e st dt with the complex variable s = σ + jω L [ f (t)] will be written as F(s). Property: L f (t) = s F(s)
39 Transfer function and Laplace transform
40 Transfer function and Laplace transform Transforming equation using L f (t) = s F(s) we obtain:
41 Transfer function and Laplace transform Transforming equation using L f (t) = s F(s) we obtain:
42 Transfer function and Laplace transform Transforming equation using L f (t) = s F(s) we obtain: with Y(s) and X(s) being the Laplace transforms of y(t) and x(t), respectively.
43 Transfer function and Laplace transform Transforming equation using L f (t) = s F(s) we obtain: with Y(s) and X(s) being the Laplace transforms of y(t) and x(t), respectively. T (s) = Y (s) X(s) = 1 1+ src = 1 1+ sτ
44 Transfer function and Laplace transform Transforming equation using L f (t) = s F(s) we obtain: with Y(s) and X(s) being the Laplace transforms of y(t) and x(t), respectively. T (s) = Y (s) X(s) = 1 1+ src = 1 1+ sτ transfer function
45 Transfer function and Laplace transform Transforming equation using L f (t) = s F(s) we obtain: with Y(s) and X(s) being the Laplace transforms of y(t) and x(t), respectively. T (s) = Y (s) X(s) = 1 1+ src = 1 1+ sτ transfer function s = -1/τ pole of the transfer function
46 The frequency response function and the pole position jω ρ(ω) Θ σ 1 / τ Fig Representation of the RC filter in the s plane. The pole location at -1/τ is marked by an X. Transfer function RC filter: T (s) = sτ = 1 1 τ (1 / τ ) + s For s = j ω, ω moves along the imaginary axis 1/τ+jω represents the vector ρ(jω) which is pointing from the pole position towards the actual frequency on the imaginary axis. T ( jω) = 1 1 τ (1 / τ ) + jω
47 General linear time invariant systems
48 General linear time invariant systems Generalization of concepts
49 General linear time invariant systems Generalization of concepts Rewrite the differential equation for the RC filter: RC y(t) + y(t) x(t) = α 1 d dt y(t) + α 0 y(t) + β 0 x(t) = 0
50 General linear time invariant systems Generalization of concepts Rewrite the differential equation for the RC filter: RC y(t) + y(t) x(t) = α 1 d dt y(t) + α 0 y(t) + β 0 x(t) = 0 RC filter special case of Nth order LTI system
51 General linear time invariant systems Generalization of concepts Rewrite the differential equation for the RC filter: RC y(t) + y(t) x(t) = α 1 d dt y(t) + α 0 y(t) + β 0 x(t) = 0 N k =0 RC filter special case of Nth order LTI system d k L α k dt y(t) + d k β k dt x(t) = 0 k =0
52 General linear time invariant systems Generalization of concepts Rewrite the differential equation for the RC filter: d RC y(t) + y(t) x(t) = α 1 dt y(t) + α y(t) + β x(t) = N k =0 RC filter special case of Nth order LTI system WHAT IS IT GOOD FOR???? d k L α k dt y(t) + d k β k dt x(t) = 0 k =0
53 Seismometer
54 Seismometer The inertia of the mass
55 Seismometer The inertia of the mass The spring
56 Seismometer The inertia of the mass The spring The dashpot
57 Seismometer The inertia of the mass The spring The dashpot
58 Seismometer The inertia of the mass The spring The dashpot 2nd order LTI!!
59 Seismometer Transfer function Laplace transform of x r ( t) + 2εx r ( t) + ω 2 0 x r ( t) = u g ( t)
60 Seismometer Transfer function Laplace transform of x r ( t) + 2εx r ( t) + ω 2 0 x r ( t) = u g ( t) s 2 X r ( s) + 2εsX r ( s ) + ω 2 0 X r ( s) = s 2 U g ( s)
61 Seismometer Transfer function Laplace transform of x r ( t) + 2εx r ( t) + ω 2 0 x r ( t) = u g ( t) s 2 X r ( s) + 2εsX r ( s ) + ω 2 0 X r ( s) = s 2 U g ( s) Transfer function: T( s) X r ( s) = = U g ( s) s s 2 + 2εs + ω 2 0
62 Seismometer Transfer function Laplace transform of x r ( t) + 2εx r ( t) + ω 2 0 x r ( t) = u g ( t) s 2 X r ( s) + 2εsX r ( s ) + ω 2 0 X r ( s) = s 2 U g ( s) Transfer function: T( s) X r ( s) = = U g ( s) s s 2 + 2εs + ω 2 0 Since a quadratic equation x 2 + bx + c = 0 has the roots x 1,2 = b 2 ± b2 4 c
63 pole positions p 1,2 : p 1,2 = ε ± ε 2 ω 0 2 = hω 0 ± ω 0 h 2 1 = ( h ± h 2 1)ω 0
64 pole positions p 1,2 : p 1,2 = ε ± ε 2 ω 0 2 = hω 0 ± ω 0 h 2 1 = ( h ± h 2 1)ω 0 For the underdamped case (h < 1) the pole position becomes p 1,2 = ( h ± j 1 h 2 )ω 0
65 pole positions p 1,2 : p 1,2 = ε ± ε 2 ω 0 2 = hω 0 ± ω 0 h 2 1 = ( h ± h 2 1)ω 0 For the underdamped case (h < 1) the pole position becomes p 1,2 = ( h ± j 1 h 2 )ω 0 with the pole distance from the origin p 1,2 = ( h ± j 1 h 2 ) ω 0 = h 2 + (1 h 2 ) ω 0 = ω 0
66 pole positions p 1,2 : p 1,2 = ε ± ε 2 ω 0 2 = hω 0 ± ω 0 h 2 1 = ( h ± h 2 1)ω 0 For the underdamped case (h < 1) the pole position becomes p 1,2 = ( h ± j 1 h 2 )ω 0 with the pole distance from the origin p 1,2 = ( h ± j 1 h 2 ) ω 0 = h 2 + (1 h 2 ) ω 0 = ω 0 Therefore, the poles of an underdamped seismometer are located in the left half of the s plane in a distance of ω0 from the the origin. The quantity h ω0 gives the distance from the imaginary axis.
67 Consequences of transition from single pole to general N-th order system No major change in concept Zeros in addition to poles Can be treated in very similar way
68 Graphical estimation of the frequency response function jω ρ p (ω) ρ 0 (ω) Fig. 3.2 Complex s plane representation of a system with a single pole and zero. The pole and zero locations are marked by an X, and a 0, respectively. Θ p X 0 Θ 0 σ
69 Graphical estimation of the frequency response function jω ρ p (ω) ρ 0 (ω) Fig. 3.2 Complex s plane representation of a system with a single pole and zero. The pole and zero locations are marked by an X, and a 0, respectively. Transfer function: Θ p X 0 Θ 0 σ s 0 and s p : position of the zero and the pole, respectively.
70 Graphical estimation of the frequency response function jω ρ p (ω) ρ 0 (ω) Fig. 3.2 Complex s plane representation of a system with a single pole and zero. The pole and zero locations are marked by an X, and a 0, respectively. Transfer function: Θ p X 0 Θ 0 σ s 0 and s p : position of the zero and the pole, respectively. Frequency response function: (s = jω) T ( jω) = jω s 0 jω s p
71 Graphical estimation of the frequency response function jω ρ p (ω) ρ 0 (ω) Fig. 3.2 Complex s plane representation of a system with a single pole and zero. The pole and zero locations are marked by an X, and a 0, respectively. Transfer function: Θ p X 0 Θ 0 σ s 0 and s p : position of the zero and the pole, respectively. Frequency response function: (s = jω) T ( jω) = jω s 0 jω s p jω s p vector ρ p (ω) jω s 0 vector ρ 0 (ω)
72 Graphical estimation of the frequency response function jω ρ p (ω) ρ 0 (ω) Fig. 3.2 Complex s plane representation of a system with a single pole and zero. The pole and zero locations are marked by an X, and a 0, respectively. Transfer function: Θ p X 0 Θ 0 σ s 0 and s p : position of the zero and the pole, respectively. Frequency response function: (s = jω) T ( jω) = jω s 0 jω s p jω s p vector ρ p (ω) jω s 0 vector ρ 0 (ω) T ( jω) = ρ 0 (ω) e jθ 0 1 ρ p (ω) e jθ p
73 Simulation Process
74 Inverse and simulation filtering! of digital seismograms
75 Inverse and simulation filtering! of digital seismograms NEXT: From filter problem to the simulation problem - the conversion of digital (broad-band) records into those from different seismograph systems.
76 Inverse and simulation filtering! of digital seismograms NEXT: From filter problem to the simulation problem - the conversion of digital (broad-band) records into those from different seismograph systems. REASON: Signal amplitudes or onset time determination in a manner consistent with other observatories. Simulated systems will most commonly belong to the standard classes of instruments described by Willmore (1979) because there is no single, optimum class of instruments for the detection and analysis of different types of seismic waves. The different seismic magnitude definitions are based on different instruments!
77 Stability problems Noise free situation * source spectrum recording system! recorded spectrum *! log f log f Fig. 9.3 Recording the displacement spectrum of an idealized earthquake source. Recovery of source spectrum: log f * recorded spectrum inverse filter! source spectrum *! log f log f log f Fig. 9.4 Recovering the source spectrum by inverse filtering in the noisefree case.
78 Noisy situation noisy spectrum * inverse filter! noisy source spectrum noise noise amplification *! valid frequency band log f log f log f Fig. 9.5 Noise amplification by inverse filtering. The solid line in the left panel shows the signal plus noise while the noisefree signal is shown by the dashed line.
79 Noisy situation
80 Noisy situation Problem: Decrease of signal-to-noise ratio (SNR) outside the passband of the recording instrument magnification of the inverse filter is largest where SNR is smallest. Thus, noise in this frequency band will be amplified (instability!).
81 Noisy situation Problem: Decrease of signal-to-noise ratio (SNR) outside the passband of the recording instrument magnification of the inverse filter is largest where SNR is smallest. Thus, noise in this frequency band will be amplified (instability!). Consequence: The instrument response can only be deconvolved within a certain valid frequency band in the presence of noise. The valid frequency band depends on both the signal-to noise ratio and the slope of the frequency response function of the recording systems.
82 Example Station Pruhonice (PRU) of the Czech Academy of Sciences. noise Fig. 9.6 Vertical component record of an mb = 7.5 earthquake (1994 April 4) in the Kurile islands (upper panel). The units are counts with offset removed. The lower panel shows the corresponding amplitude spectrum. Notice the noise at both the low frequency and high frequency ends of the amplitude spectrum.
83 Amplitude spectrum and displacement frequency response function of the recording system. Fig. 9.7 Amplitude spectrum from Fig. 9.6 compared to the modulus of the displacement frequency response function at station PRU (lower panel).
84 Frequency domain results Fig. 9.9 Deconvolution illustrated in the frequency domain. From top to bottom, the amplitude spectrum of the observed trace, the frequency response function of the inverse filter, and the amplitude spectrum of the deconvolved trace are displayed.
85 Waterlevel correction Fig Deconvolution by spectral division using a waterlevel stabilization of 80 db (top trace) and 60 db (second trace) of the signal shown in Fig The corresponding amplitude spectra are shown in the two bottom traces.
86 Simulation = Deconvolution + Filtering Be aware that in the digital world you have to change from s- to z-transform Y sim ( z) T syn ( z) = ! Y T act ( z) a ct ( z) = T sim ( z)! Y a ct ( z) = transfer function of actual recording system = transfer function of the instrument to be synthesized = z- transform of the recorded seismogram = z- transform of the simulated seismogram
87 FIR - Filter Effects Sampling Decimation Seismometer Amplifier AAA filter DAA filter Analog LTI system Digital LTI system
88 What is the reason for doing FIR filtering and decimating? Nearly all seismic recorders use the oversampling technique to increase the resolution of recordings. In order to achieve an optimum valid frequency band, the filters are very steep. Besides its advantages this also bears new problems.
89 DAA filter # # + FIR response, RJOB ch EHZ + # # B061F03 Stage sequence number: 3 B061F05 Symmetry type: A B061F06 Response in units lookup: COUNTS - Digital Counts B061F07 Response out units lookup: COUNTS - Digital Counts B061F08 Number of numerators: 96 # Numerator coefficients: # i, coefficient B061F E-09 B061F E-07 B061F E-06 B061F E-06 B061F E-06 B061F E-06 B061F E-06 B061F E-05 # # # + Decimation, RJOB ch EHZ + # # B057F03 Stage sequence number: 4 B057F04 Input sample rate: E+03 B057F05 Decimation factor: 5 B057F06 Decimation offset: 0 B057F07 Estimated delay (seconds): E-01 B057F08 Correction applied (seconds): E+00
90 Linear Difference Equation N a y [ n k ] b k 0 = k = M l 0 = l x [ n l ] Infinite Impulse Response: ak 0 Finite Impulse Response: a0 = 1; ak 0 = 0
91
92
93 a) b)
94 Routine Quality Control at DCs
95 Why Routine Control? The sooner problems are detected the sooner they can be fixed Sensor malfunctions, misconfigurations, aging Digitizer & recorder malfunctions Vault problems: tilting, settling, etc Cable & connection problems Telemetry issues Timing problems Many, many other potential issues
96 Quick Checks: Polarization The quadrant method allows an analyst to perform a rough check of 3-component sensor horizontal polarity. Compare the P wave first motion of a relatively large event between the 3 components to determine back azimuth: 0 N out Z out 270º 90º All in phase E out Aluetian Island event :: Texas, USA station (BA: ~317 ) 180º * Assumes Z component polarity is correct. 48
97 Quack (IRIS DMC) Automated QC measurements for incoming real-time data at the DMC: Tracks a number of simple parameters (signal RMS, mean, gaps, overlaps, etc.) in addition to more complicated analyses (PSD/ PDF, STA/LTA) Generates daily reports, using thresholds to control what information is included in the report in order to reduce the number of issues that need attention 49
98 RMS values 50
99 STA/LTA 51
100 Prob. Density of Power Spectra 52
101 Missing: Timing Problems problem if digitizer don t report (GPS) timing problems miniseed has only restricted possibilities for reporting timing problems Way out by stacked cross correlation of noise between distant stations (by-product of cross correlating diffusive wave field) 53
102 Two Stations CrossCorrelation 54
Network of European Research Infrastructures for Earthquake Risk Assessment and Mitigation. Report
 Network of European Research Infrastructures for Earthquake Risk Assessment and Mitigation Report Automatic data QC and distribution statistics for data providers Activity: Activity number: Expanding access
Network of European Research Infrastructures for Earthquake Risk Assessment and Mitigation Report Automatic data QC and distribution statistics for data providers Activity: Activity number: Expanding access
Bandwidth-dependent transformation of noise data from frequency into time domain and vice versa
 Topic Bandwidth-dependent transformation of noise data from frequency into time domain and vice versa Authors Peter Bormann (formerly GeoForschungsZentrum Potsdam, Telegrafenberg, D-14473 Potsdam, Germany),
Topic Bandwidth-dependent transformation of noise data from frequency into time domain and vice versa Authors Peter Bormann (formerly GeoForschungsZentrum Potsdam, Telegrafenberg, D-14473 Potsdam, Germany),
ANALYZER BASICS WHAT IS AN FFT SPECTRUM ANALYZER? 2-1
 WHAT IS AN FFT SPECTRUM ANALYZER? ANALYZER BASICS The SR760 FFT Spectrum Analyzer takes a time varying input signal, like you would see on an oscilloscope trace, and computes its frequency spectrum. Fourier's
WHAT IS AN FFT SPECTRUM ANALYZER? ANALYZER BASICS The SR760 FFT Spectrum Analyzer takes a time varying input signal, like you would see on an oscilloscope trace, and computes its frequency spectrum. Fourier's
Probability and Random Variables. Generation of random variables (r.v.)
 Probability and Random Variables Method for generating random variables with a specified probability distribution function. Gaussian And Markov Processes Characterization of Stationary Random Process Linearly
Probability and Random Variables Method for generating random variables with a specified probability distribution function. Gaussian And Markov Processes Characterization of Stationary Random Process Linearly
BSEE Degree Plan Bachelor of Science in Electrical Engineering: 2015-16
 BSEE Degree Plan Bachelor of Science in Electrical Engineering: 2015-16 Freshman Year ENG 1003 Composition I 3 ENG 1013 Composition II 3 ENGR 1402 Concepts of Engineering 2 PHYS 2034 University Physics
BSEE Degree Plan Bachelor of Science in Electrical Engineering: 2015-16 Freshman Year ENG 1003 Composition I 3 ENG 1013 Composition II 3 ENGR 1402 Concepts of Engineering 2 PHYS 2034 University Physics
b 1 is the most significant bit (MSB) The MSB is the bit that has the most (largest) influence on the analog output
 CMOS Analog IC Design - Chapter 10 Page 10.0-5 BLOCK DIAGRAM OF A DIGITAL-ANALOG CONVERTER b 1 is the most significant bit (MSB) The MSB is the bit that has the most (largest) influence on the analog output
CMOS Analog IC Design - Chapter 10 Page 10.0-5 BLOCK DIAGRAM OF A DIGITAL-ANALOG CONVERTER b 1 is the most significant bit (MSB) The MSB is the bit that has the most (largest) influence on the analog output
Department of Electrical and Computer Engineering Ben-Gurion University of the Negev. LAB 1 - Introduction to USRP
 Department of Electrical and Computer Engineering Ben-Gurion University of the Negev LAB 1 - Introduction to USRP - 1-1 Introduction In this lab you will use software reconfigurable RF hardware from National
Department of Electrical and Computer Engineering Ben-Gurion University of the Negev LAB 1 - Introduction to USRP - 1-1 Introduction In this lab you will use software reconfigurable RF hardware from National
Vector Spaces; the Space R n
 Vector Spaces; the Space R n Vector Spaces A vector space (over the real numbers) is a set V of mathematical entities, called vectors, U, V, W, etc, in which an addition operation + is defined and in which
Vector Spaces; the Space R n Vector Spaces A vector space (over the real numbers) is a set V of mathematical entities, called vectors, U, V, W, etc, in which an addition operation + is defined and in which
Seismic Sensors and their Calibration
 CHAPTER 5 Seismic Sensors and their Calibration 5.1 Overview Erhard Wielandt There are two basic types of seismic sensors: inertial seismometers which measure ground motion relative to an inertial reference
CHAPTER 5 Seismic Sensors and their Calibration 5.1 Overview Erhard Wielandt There are two basic types of seismic sensors: inertial seismometers which measure ground motion relative to an inertial reference
NRZ Bandwidth - HF Cutoff vs. SNR
 Application Note: HFAN-09.0. Rev.2; 04/08 NRZ Bandwidth - HF Cutoff vs. SNR Functional Diagrams Pin Configurations appear at end of data sheet. Functional Diagrams continued at end of data sheet. UCSP
Application Note: HFAN-09.0. Rev.2; 04/08 NRZ Bandwidth - HF Cutoff vs. SNR Functional Diagrams Pin Configurations appear at end of data sheet. Functional Diagrams continued at end of data sheet. UCSP
SUMMARY OF MAGNITUDE WORKING GROUP RECOMMENDATIONS ON DETERMINING EARTHQUAKE MAGNITUDES FROM DIGITAL DATA
 B SUMMARY OF MAGNITUDE WORKING GROUP RECOMMENDATIONS ON DETERMINING EARTHQUAKE MAGNITUDES FROM DIGITAL DATA The Working Group on Magnitudes (Magnitude WG) of the International Association of Seismology
B SUMMARY OF MAGNITUDE WORKING GROUP RECOMMENDATIONS ON DETERMINING EARTHQUAKE MAGNITUDES FROM DIGITAL DATA The Working Group on Magnitudes (Magnitude WG) of the International Association of Seismology
Determination of source parameters from seismic spectra
 Topic Determination of source parameters from seismic spectra Authors Michael Baumbach, and Peter Bormann (formerly GeoForschungsZentrum Potsdam, Telegrafenberg, D-14473 Potsdam, Germany); E-mail: [email protected]
Topic Determination of source parameters from seismic spectra Authors Michael Baumbach, and Peter Bormann (formerly GeoForschungsZentrum Potsdam, Telegrafenberg, D-14473 Potsdam, Germany); E-mail: [email protected]
Impedance 50 (75 connectors via adapters)
 VECTOR NETWORK ANALYZER PLANAR TR1300/1 DATA SHEET Frequency range: 300 khz to 1.3 GHz Measured parameters: S11, S21 Dynamic range of transmission measurement magnitude: 130 db Measurement time per point:
VECTOR NETWORK ANALYZER PLANAR TR1300/1 DATA SHEET Frequency range: 300 khz to 1.3 GHz Measured parameters: S11, S21 Dynamic range of transmission measurement magnitude: 130 db Measurement time per point:
Earthquake Magnitude
 Earthquake Magnitude Earthquake magnitude scales: Logarithmic measure of earthquake size amplitude of biggest wave: Magnitude 6 quake 10 * Magnitude 5 energy: Magnitude 6 quake is about 32 * Magnitude
Earthquake Magnitude Earthquake magnitude scales: Logarithmic measure of earthquake size amplitude of biggest wave: Magnitude 6 quake 10 * Magnitude 5 energy: Magnitude 6 quake is about 32 * Magnitude
Network Analyzer Operation
 Network Analyzer Operation 2004 ITTC Summer Lecture Series John Paden Purposes of a Network Analyzer Network analyzers are not about computer networks! Purposes of a Network Analyzer Measures S-parameters
Network Analyzer Operation 2004 ITTC Summer Lecture Series John Paden Purposes of a Network Analyzer Network analyzers are not about computer networks! Purposes of a Network Analyzer Measures S-parameters
MODULATION Systems (part 1)
 Technologies and Services on Digital Broadcasting (8) MODULATION Systems (part ) "Technologies and Services of Digital Broadcasting" (in Japanese, ISBN4-339-62-2) is published by CORONA publishing co.,
Technologies and Services on Digital Broadcasting (8) MODULATION Systems (part ) "Technologies and Services of Digital Broadcasting" (in Japanese, ISBN4-339-62-2) is published by CORONA publishing co.,
chapter Introduction to Digital Signal Processing and Digital Filtering 1.1 Introduction 1.2 Historical Perspective
 Introduction to Digital Signal Processing and Digital Filtering chapter 1 Introduction to Digital Signal Processing and Digital Filtering 1.1 Introduction Digital signal processing (DSP) refers to anything
Introduction to Digital Signal Processing and Digital Filtering chapter 1 Introduction to Digital Signal Processing and Digital Filtering 1.1 Introduction Digital signal processing (DSP) refers to anything
MATRIX TECHNICAL NOTES
 200 WOOD AVENUE, MIDDLESEX, NJ 08846 PHONE (732) 469-9510 FAX (732) 469-0418 MATRIX TECHNICAL NOTES MTN-107 TEST SETUP FOR THE MEASUREMENT OF X-MOD, CTB, AND CSO USING A MEAN SQUARE CIRCUIT AS A DETECTOR
200 WOOD AVENUE, MIDDLESEX, NJ 08846 PHONE (732) 469-9510 FAX (732) 469-0418 MATRIX TECHNICAL NOTES MTN-107 TEST SETUP FOR THE MEASUREMENT OF X-MOD, CTB, AND CSO USING A MEAN SQUARE CIRCUIT AS A DETECTOR
Agilent Time Domain Analysis Using a Network Analyzer
 Agilent Time Domain Analysis Using a Network Analyzer Application Note 1287-12 0.0 0.045 0.6 0.035 Cable S(1,1) 0.4 0.2 Cable S(1,1) 0.025 0.015 0.005 0.0 1.0 1.5 2.0 2.5 3.0 3.5 4.0 Frequency (GHz) 0.005
Agilent Time Domain Analysis Using a Network Analyzer Application Note 1287-12 0.0 0.045 0.6 0.035 Cable S(1,1) 0.4 0.2 Cable S(1,1) 0.025 0.015 0.005 0.0 1.0 1.5 2.0 2.5 3.0 3.5 4.0 Frequency (GHz) 0.005
TCOM 370 NOTES 99-4 BANDWIDTH, FREQUENCY RESPONSE, AND CAPACITY OF COMMUNICATION LINKS
 TCOM 370 NOTES 99-4 BANDWIDTH, FREQUENCY RESPONSE, AND CAPACITY OF COMMUNICATION LINKS 1. Bandwidth: The bandwidth of a communication link, or in general any system, was loosely defined as the width of
TCOM 370 NOTES 99-4 BANDWIDTH, FREQUENCY RESPONSE, AND CAPACITY OF COMMUNICATION LINKS 1. Bandwidth: The bandwidth of a communication link, or in general any system, was loosely defined as the width of
T = 1 f. Phase. Measure of relative position in time within a single period of a signal For a periodic signal f(t), phase is fractional part t p
 Data Transmission Concepts and terminology Transmission terminology Transmission from transmitter to receiver goes over some transmission medium using electromagnetic waves Guided media. Waves are guided
Data Transmission Concepts and terminology Transmission terminology Transmission from transmitter to receiver goes over some transmission medium using electromagnetic waves Guided media. Waves are guided
Understanding Poles and Zeros
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Understanding Poles and Zeros 1 System Poles and Zeros The transfer function
MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Understanding Poles and Zeros 1 System Poles and Zeros The transfer function
Data in seismology: networks, instruments, current problems
 Data in seismology: networks, instruments, current problems Seismic networks, data centres, instruments Seismic Observables and their interrelations Seismic data acquisition parameters (sampling rates,
Data in seismology: networks, instruments, current problems Seismic networks, data centres, instruments Seismic Observables and their interrelations Seismic data acquisition parameters (sampling rates,
Instrumentation. Earthquake Seismology
 Instrumentation in Earthquake Seismology Jens Havskov, Institute of Solid Earth Physics University of Bergen Norway and Gerardo Alguacil Instituto Andaluz de Geofisica University of Granada Spain Preliminary
Instrumentation in Earthquake Seismology Jens Havskov, Institute of Solid Earth Physics University of Bergen Norway and Gerardo Alguacil Instituto Andaluz de Geofisica University of Granada Spain Preliminary
5 Signal Design for Bandlimited Channels
 225 5 Signal Design for Bandlimited Channels So far, we have not imposed any bandwidth constraints on the transmitted passband signal, or equivalently, on the transmitted baseband signal s b (t) I[k]g
225 5 Signal Design for Bandlimited Channels So far, we have not imposed any bandwidth constraints on the transmitted passband signal, or equivalently, on the transmitted baseband signal s b (t) I[k]g
FREQUENCY RESPONSE ANALYZERS
 FREQUENCY RESPONSE ANALYZERS Dynamic Response Analyzers Servo analyzers When you need to stabilize feedback loops to measure hardware characteristics to measure system response BAFCO, INC. 717 Mearns Road
FREQUENCY RESPONSE ANALYZERS Dynamic Response Analyzers Servo analyzers When you need to stabilize feedback loops to measure hardware characteristics to measure system response BAFCO, INC. 717 Mearns Road
12.510 Introduction to Seismology Spring 2008
 MIT OpenCourseWare http://ocw.mit.edu 12.510 Introduction to Seismology Spring 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 04/30/2008 Today s
MIT OpenCourseWare http://ocw.mit.edu 12.510 Introduction to Seismology Spring 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 04/30/2008 Today s
AVR127: Understanding ADC Parameters. Introduction. Features. Atmel 8-bit and 32-bit Microcontrollers APPLICATION NOTE
 Atmel 8-bit and 32-bit Microcontrollers AVR127: Understanding ADC Parameters APPLICATION NOTE Introduction This application note explains the basic concepts of analog-to-digital converter (ADC) and the
Atmel 8-bit and 32-bit Microcontrollers AVR127: Understanding ADC Parameters APPLICATION NOTE Introduction This application note explains the basic concepts of analog-to-digital converter (ADC) and the
Email: [email protected]
 USE OF VIRTUAL INSTRUMENTS IN RADIO AND ATMOSPHERIC EXPERIMENTS P.N. VIJAYAKUMAR, THOMAS JOHN AND S.C. GARG RADIO AND ATMOSPHERIC SCIENCE DIVISION, NATIONAL PHYSICAL LABORATORY, NEW DELHI 110012, INDIA
USE OF VIRTUAL INSTRUMENTS IN RADIO AND ATMOSPHERIC EXPERIMENTS P.N. VIJAYAKUMAR, THOMAS JOHN AND S.C. GARG RADIO AND ATMOSPHERIC SCIENCE DIVISION, NATIONAL PHYSICAL LABORATORY, NEW DELHI 110012, INDIA
Digital Transmission (Line Coding)
 Digital Transmission (Line Coding) Pulse Transmission Source Multiplexer Line Coder Line Coding: Output of the multiplexer (TDM) is coded into electrical pulses or waveforms for the purpose of transmission
Digital Transmission (Line Coding) Pulse Transmission Source Multiplexer Line Coder Line Coding: Output of the multiplexer (TDM) is coded into electrical pulses or waveforms for the purpose of transmission
SEED. Reference Manual. Standard for the Exchange of Earthquake Data. SEED Format Version 2.4 August, 2012
 SEED Reference Manual Standard for the Exchange of Earthquake Data SEED Format Version 2.4 August, 2012 International Federation of Digital Seismograph Networks Incorporated Research Institutions for Seismology
SEED Reference Manual Standard for the Exchange of Earthquake Data SEED Format Version 2.4 August, 2012 International Federation of Digital Seismograph Networks Incorporated Research Institutions for Seismology
1. Oscilloscope is basically a graph-displaying device-it draws a graph of an electrical signal.
 CHAPTER 3: OSCILLOSCOPE AND SIGNAL GENERATOR 3.1 Introduction to oscilloscope 1. Oscilloscope is basically a graph-displaying device-it draws a graph of an electrical signal. 2. The graph show signal change
CHAPTER 3: OSCILLOSCOPE AND SIGNAL GENERATOR 3.1 Introduction to oscilloscope 1. Oscilloscope is basically a graph-displaying device-it draws a graph of an electrical signal. 2. The graph show signal change
Earthquake Magnitude Calculator for the AS-1 Seismograph 1
 Magnitude calculator for the AS-1 Page 1 of 23 Earthquake Magnitude Calculator for the AS-1 Seismograph 1 Lawrence W. Braile and Saptarshi Dasgupta, Purdue University SKIP TO CALCULATORS Introduction:
Magnitude calculator for the AS-1 Page 1 of 23 Earthquake Magnitude Calculator for the AS-1 Seismograph 1 Lawrence W. Braile and Saptarshi Dasgupta, Purdue University SKIP TO CALCULATORS Introduction:
Enhancing the SNR of the Fiber Optic Rotation Sensor using the LMS Algorithm
 1 Enhancing the SNR of the Fiber Optic Rotation Sensor using the LMS Algorithm Hani Mehrpouyan, Student Member, IEEE, Department of Electrical and Computer Engineering Queen s University, Kingston, Ontario,
1 Enhancing the SNR of the Fiber Optic Rotation Sensor using the LMS Algorithm Hani Mehrpouyan, Student Member, IEEE, Department of Electrical and Computer Engineering Queen s University, Kingston, Ontario,
Frequency Response of FIR Filters
 Frequency Response of FIR Filters Chapter 6 This chapter continues the study of FIR filters from Chapter 5, but the emphasis is frequency response, which relates to how the filter responds to an input
Frequency Response of FIR Filters Chapter 6 This chapter continues the study of FIR filters from Chapter 5, but the emphasis is frequency response, which relates to how the filter responds to an input
Manual Analysis Software AFD 1201
 AFD 1200 - AcoustiTube Manual Analysis Software AFD 1201 Measurement of Transmission loss acc. to Song and Bolton 1 Table of Contents Introduction - Analysis Software AFD 1201... 3 AFD 1200 - AcoustiTube
AFD 1200 - AcoustiTube Manual Analysis Software AFD 1201 Measurement of Transmission loss acc. to Song and Bolton 1 Table of Contents Introduction - Analysis Software AFD 1201... 3 AFD 1200 - AcoustiTube
Nearly real-time monitoring system of TABOO seismic network activity.
 Nearly real-time monitoring system of TABOO seismic network activity. Marzorati S.* and TABOO working group * National Earthquake Centre, Ancona Istituto Nazionale di Geofisica e Vulcanologia Nearly real-time
Nearly real-time monitoring system of TABOO seismic network activity. Marzorati S.* and TABOO working group * National Earthquake Centre, Ancona Istituto Nazionale di Geofisica e Vulcanologia Nearly real-time
Sensor Performance Metrics
 Sensor Performance Metrics Michael Todd Professor and Vice Chair Dept. of Structural Engineering University of California, San Diego [email protected] Email me if you want a copy. Outline Sensors as dynamic
Sensor Performance Metrics Michael Todd Professor and Vice Chair Dept. of Structural Engineering University of California, San Diego [email protected] Email me if you want a copy. Outline Sensors as dynamic
USB 3.0 CDR Model White Paper Revision 0.5
 USB 3.0 CDR Model White Paper Revision 0.5 January 15, 2009 INTELLECTUAL PROPERTY DISCLAIMER THIS WHITE PAPER IS PROVIDED TO YOU AS IS WITH NO WARRANTIES WHATSOEVER, INCLUDING ANY WARRANTY OF MERCHANTABILITY,
USB 3.0 CDR Model White Paper Revision 0.5 January 15, 2009 INTELLECTUAL PROPERTY DISCLAIMER THIS WHITE PAPER IS PROVIDED TO YOU AS IS WITH NO WARRANTIES WHATSOEVER, INCLUDING ANY WARRANTY OF MERCHANTABILITY,
AVX EMI SOLUTIONS Ron Demcko, Fellow of AVX Corporation Chris Mello, Principal Engineer, AVX Corporation Brian Ward, Business Manager, AVX Corporation
 AVX EMI SOLUTIONS Ron Demcko, Fellow of AVX Corporation Chris Mello, Principal Engineer, AVX Corporation Brian Ward, Business Manager, AVX Corporation Abstract EMC compatibility is becoming a key design
AVX EMI SOLUTIONS Ron Demcko, Fellow of AVX Corporation Chris Mello, Principal Engineer, AVX Corporation Brian Ward, Business Manager, AVX Corporation Abstract EMC compatibility is becoming a key design
Introduction to acoustic imaging
 Introduction to acoustic imaging Contents 1 Propagation of acoustic waves 3 1.1 Wave types.......................................... 3 1.2 Mathematical formulation.................................. 4 1.3
Introduction to acoustic imaging Contents 1 Propagation of acoustic waves 3 1.1 Wave types.......................................... 3 1.2 Mathematical formulation.................................. 4 1.3
RLC Resonant Circuits
 C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
Author: Dr. Society of Electrophysio. Reference: Electrodes. should include: electrode shape size use. direction.
 Standards for Reportin ng EMG Data Author: Dr. Roberto Merletti, Politecnico di Torino, Italy The Standards for Reporting EMG Data, written by Dr. Robertoo Merletti, are endorsed by the International Society
Standards for Reportin ng EMG Data Author: Dr. Roberto Merletti, Politecnico di Torino, Italy The Standards for Reporting EMG Data, written by Dr. Robertoo Merletti, are endorsed by the International Society
Reading: HH Sections 4.11 4.13, 4.19 4.20 (pgs. 189-212, 222 224)
 6 OP AMPS II 6 Op Amps II In the previous lab, you explored several applications of op amps. In this exercise, you will look at some of their limitations. You will also examine the op amp integrator and
6 OP AMPS II 6 Op Amps II In the previous lab, you explored several applications of op amps. In this exercise, you will look at some of their limitations. You will also examine the op amp integrator and
MPC 4. Machinery Protection Card Type MPC 4 FEATURES. Continuous on-line Machinery Protection Card
 Machinery Protection Card Type FEATURES Continuous on-line Machinery Protection Card Real-time measurement and monitoring using state-of-the-art DSP techniques Fully VME-compatible slave interface Fully
Machinery Protection Card Type FEATURES Continuous on-line Machinery Protection Card Real-time measurement and monitoring using state-of-the-art DSP techniques Fully VME-compatible slave interface Fully
ε: Voltage output of Signal Generator (also called the Source voltage or Applied
 Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
telemetry Rene A.J. Chave, David D. Lemon, Jan Buermans ASL Environmental Sciences Inc. Victoria BC Canada [email protected] I.
 Near real-time transmission of reduced data from a moored multi-frequency sonar by low bandwidth telemetry Rene A.J. Chave, David D. Lemon, Jan Buermans ASL Environmental Sciences Inc. Victoria BC Canada
Near real-time transmission of reduced data from a moored multi-frequency sonar by low bandwidth telemetry Rene A.J. Chave, David D. Lemon, Jan Buermans ASL Environmental Sciences Inc. Victoria BC Canada
SOFTWARE FOR GENERATION OF SPECTRUM COMPATIBLE TIME HISTORY
 3 th World Conference on Earthquake Engineering Vancouver, B.C., Canada August -6, 24 Paper No. 296 SOFTWARE FOR GENERATION OF SPECTRUM COMPATIBLE TIME HISTORY ASHOK KUMAR SUMMARY One of the important
3 th World Conference on Earthquake Engineering Vancouver, B.C., Canada August -6, 24 Paper No. 296 SOFTWARE FOR GENERATION OF SPECTRUM COMPATIBLE TIME HISTORY ASHOK KUMAR SUMMARY One of the important
EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP
 1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
1 EXPERIMENT NUMBER 8 CAPACITOR CURRENT-VOLTAGE RELATIONSHIP Purpose: To demonstrate the relationship between the voltage and current of a capacitor. Theory: A capacitor is a linear circuit element whose
Making Accurate Voltage Noise and Current Noise Measurements on Operational Amplifiers Down to 0.1Hz
 Author: Don LaFontaine Making Accurate Voltage Noise and Current Noise Measurements on Operational Amplifiers Down to 0.1Hz Abstract Making accurate voltage and current noise measurements on op amps in
Author: Don LaFontaine Making Accurate Voltage Noise and Current Noise Measurements on Operational Amplifiers Down to 0.1Hz Abstract Making accurate voltage and current noise measurements on op amps in
Physics 9e/Cutnell. correlated to the. College Board AP Physics 1 Course Objectives
 Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus
 South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
Agilent PN 89400-13 Extending Vector Signal Analysis to 26.5 GHz with 20 MHz Information Bandwidth
 Agilent PN 89400-13 Extending Vector Signal Analysis to 26.5 GHz with 20 MHz Information Bandwidth Product Note The Agilent Technologies 89400 series vector signal analyzers provide unmatched signal analysis
Agilent PN 89400-13 Extending Vector Signal Analysis to 26.5 GHz with 20 MHz Information Bandwidth Product Note The Agilent Technologies 89400 series vector signal analyzers provide unmatched signal analysis
Solutions to Exam in Speech Signal Processing EN2300
 Solutions to Exam in Speech Signal Processing EN23 Date: Thursday, Dec 2, 8: 3: Place: Allowed: Grades: Language: Solutions: Q34, Q36 Beta Math Handbook (or corresponding), calculator with empty memory.
Solutions to Exam in Speech Signal Processing EN23 Date: Thursday, Dec 2, 8: 3: Place: Allowed: Grades: Language: Solutions: Q34, Q36 Beta Math Handbook (or corresponding), calculator with empty memory.
Pulsed Fourier Transform NMR The rotating frame of reference. The NMR Experiment. The Rotating Frame of Reference.
 Pulsed Fourier Transform NR The rotating frame of reference The NR Eperiment. The Rotating Frame of Reference. When we perform a NR eperiment we disturb the equilibrium state of the sstem and then monitor
Pulsed Fourier Transform NR The rotating frame of reference The NR Eperiment. The Rotating Frame of Reference. When we perform a NR eperiment we disturb the equilibrium state of the sstem and then monitor
Active Vibration Isolation of an Unbalanced Machine Spindle
 UCRL-CONF-206108 Active Vibration Isolation of an Unbalanced Machine Spindle D. J. Hopkins, P. Geraghty August 18, 2004 American Society of Precision Engineering Annual Conference Orlando, FL, United States
UCRL-CONF-206108 Active Vibration Isolation of an Unbalanced Machine Spindle D. J. Hopkins, P. Geraghty August 18, 2004 American Society of Precision Engineering Annual Conference Orlando, FL, United States
RECOMMENDED STANDARDS FOR DIGITAL TAPE FORMATS 1
 This document has been converted from the original publication: Barry, K. M., Cavers, D. A. and Kneale, C. W., 1975, Report on recommended standards for digital tape formats: Geophysics, 40, no. 02, 344-352.
This document has been converted from the original publication: Barry, K. M., Cavers, D. A. and Kneale, C. W., 1975, Report on recommended standards for digital tape formats: Geophysics, 40, no. 02, 344-352.
Application Report. 1 Introduction. 2 Resolution of an A-D Converter. 2.1 Signal-to-Noise Ratio (SNR) Harman Grewal... ABSTRACT
 Application Report SLAA323 JULY 2006 Oversampling the ADC12 for Higher Resolution Harman Grewal... ABSTRACT This application report describes the theory of oversampling to achieve resolutions greater than
Application Report SLAA323 JULY 2006 Oversampling the ADC12 for Higher Resolution Harman Grewal... ABSTRACT This application report describes the theory of oversampling to achieve resolutions greater than
Laboratory Manual and Supplementary Notes. CoE 494: Communication Laboratory. Version 1.2
 Laboratory Manual and Supplementary Notes CoE 494: Communication Laboratory Version 1.2 Dr. Joseph Frank Dr. Sol Rosenstark Department of Electrical and Computer Engineering New Jersey Institute of Technology
Laboratory Manual and Supplementary Notes CoE 494: Communication Laboratory Version 1.2 Dr. Joseph Frank Dr. Sol Rosenstark Department of Electrical and Computer Engineering New Jersey Institute of Technology
ELECTRICAL ENGINEERING
 EE ELECTRICAL ENGINEERING See beginning of Section H for abbreviations, course numbers and coding. The * denotes labs which are held on alternate weeks. A minimum grade of C is required for all prerequisite
EE ELECTRICAL ENGINEERING See beginning of Section H for abbreviations, course numbers and coding. The * denotes labs which are held on alternate weeks. A minimum grade of C is required for all prerequisite
Chapter 8 - Power Density Spectrum
 EE385 Class Notes 8/8/03 John Stensby Chapter 8 - Power Density Spectrum Let X(t) be a WSS random process. X(t) has an average power, given in watts, of E[X(t) ], a constant. his total average power is
EE385 Class Notes 8/8/03 John Stensby Chapter 8 - Power Density Spectrum Let X(t) be a WSS random process. X(t) has an average power, given in watts, of E[X(t) ], a constant. his total average power is
Jitter Measurements in Serial Data Signals
 Jitter Measurements in Serial Data Signals Michael Schnecker, Product Manager LeCroy Corporation Introduction The increasing speed of serial data transmission systems places greater importance on measuring
Jitter Measurements in Serial Data Signals Michael Schnecker, Product Manager LeCroy Corporation Introduction The increasing speed of serial data transmission systems places greater importance on measuring
30. Bode Plots. Introduction
 0. Bode Plots Introduction Each of the circuits in this problem set is represented by a magnitude Bode plot. The network function provides a connection between the Bode plot and the circuit. To solve these
0. Bode Plots Introduction Each of the circuits in this problem set is represented by a magnitude Bode plot. The network function provides a connection between the Bode plot and the circuit. To solve these
Introduction to Digital Filters
 CHAPTER 14 Introduction to Digital Filters Digital filters are used for two general purposes: (1) separation of signals that have been combined, and (2) restoration of signals that have been distorted
CHAPTER 14 Introduction to Digital Filters Digital filters are used for two general purposes: (1) separation of signals that have been combined, and (2) restoration of signals that have been distorted
Sample Questions for the AP Physics 1 Exam
 Sample Questions for the AP Physics 1 Exam Sample Questions for the AP Physics 1 Exam Multiple-choice Questions Note: To simplify calculations, you may use g 5 10 m/s 2 in all problems. Directions: Each
Sample Questions for the AP Physics 1 Exam Sample Questions for the AP Physics 1 Exam Multiple-choice Questions Note: To simplify calculations, you may use g 5 10 m/s 2 in all problems. Directions: Each
Introduction to IQ-demodulation of RF-data
 Introduction to IQ-demodulation of RF-data by Johan Kirkhorn, IFBT, NTNU September 15, 1999 Table of Contents 1 INTRODUCTION...3 1.1 Abstract...3 1.2 Definitions/Abbreviations/Nomenclature...3 1.3 Referenced
Introduction to IQ-demodulation of RF-data by Johan Kirkhorn, IFBT, NTNU September 15, 1999 Table of Contents 1 INTRODUCTION...3 1.1 Abstract...3 1.2 Definitions/Abbreviations/Nomenclature...3 1.3 Referenced
Radar Systems Engineering Lecture 6 Detection of Signals in Noise
 Radar Systems Engineering Lecture 6 Detection of Signals in Noise Dr. Robert M. O Donnell Guest Lecturer Radar Systems Course 1 Detection 1/1/010 Block Diagram of Radar System Target Radar Cross Section
Radar Systems Engineering Lecture 6 Detection of Signals in Noise Dr. Robert M. O Donnell Guest Lecturer Radar Systems Course 1 Detection 1/1/010 Block Diagram of Radar System Target Radar Cross Section
Frequency response. Chapter 1. 1.1 Introduction
 Chapter Frequency response. Introduction The frequency response of a system is a frequency dependent function which expresses how a sinusoidal signal of a given frequency on the system input is transferred
Chapter Frequency response. Introduction The frequency response of a system is a frequency dependent function which expresses how a sinusoidal signal of a given frequency on the system input is transferred
Advanced Signal Processing and Digital Noise Reduction
 Advanced Signal Processing and Digital Noise Reduction Saeed V. Vaseghi Queen's University of Belfast UK WILEY HTEUBNER A Partnership between John Wiley & Sons and B. G. Teubner Publishers Chichester New
Advanced Signal Processing and Digital Noise Reduction Saeed V. Vaseghi Queen's University of Belfast UK WILEY HTEUBNER A Partnership between John Wiley & Sons and B. G. Teubner Publishers Chichester New
Estimated Pre Calculus Pacing Timeline
 Estimated Pre Calculus Pacing Timeline 2010-2011 School Year The timeframes listed on this calendar are estimates based on a fifty-minute class period. You may need to adjust some of them from time to
Estimated Pre Calculus Pacing Timeline 2010-2011 School Year The timeframes listed on this calendar are estimates based on a fifty-minute class period. You may need to adjust some of them from time to
Grounding Demystified
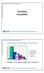 Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
SEISMIC MONITORING & PROTECTION SYSTEMS
 SEISMIC MONITORING & PROTECTION SYSTEMS PRODUCT GUIDE Seismic Transducers & Switches Nuclear Infrastructure Protection Structural & Environmental Monitoring Data Capture & Analysis 25 YEARS 1978-2003 PROTECTING
SEISMIC MONITORING & PROTECTION SYSTEMS PRODUCT GUIDE Seismic Transducers & Switches Nuclear Infrastructure Protection Structural & Environmental Monitoring Data Capture & Analysis 25 YEARS 1978-2003 PROTECTING
Performance of Quasi-Constant Envelope Phase Modulation through Nonlinear Radio Channels
 Performance of Quasi-Constant Envelope Phase Modulation through Nonlinear Radio Channels Qi Lu, Qingchong Liu Electrical and Systems Engineering Department Oakland University Rochester, MI 48309 USA E-mail:
Performance of Quasi-Constant Envelope Phase Modulation through Nonlinear Radio Channels Qi Lu, Qingchong Liu Electrical and Systems Engineering Department Oakland University Rochester, MI 48309 USA E-mail:
Lab #9: AC Steady State Analysis
 Theory & Introduction Lab #9: AC Steady State Analysis Goals for Lab #9 The main goal for lab 9 is to make the students familar with AC steady state analysis, db scale and the NI ELVIS frequency analyzer.
Theory & Introduction Lab #9: AC Steady State Analysis Goals for Lab #9 The main goal for lab 9 is to make the students familar with AC steady state analysis, db scale and the NI ELVIS frequency analyzer.
AN1200.04. Application Note: FCC Regulations for ISM Band Devices: 902-928 MHz. FCC Regulations for ISM Band Devices: 902-928 MHz
 AN1200.04 Application Note: FCC Regulations for ISM Band Devices: Copyright Semtech 2006 1 of 15 www.semtech.com 1 Table of Contents 1 Table of Contents...2 1.1 Index of Figures...2 1.2 Index of Tables...2
AN1200.04 Application Note: FCC Regulations for ISM Band Devices: Copyright Semtech 2006 1 of 15 www.semtech.com 1 Table of Contents 1 Table of Contents...2 1.1 Index of Figures...2 1.2 Index of Tables...2
Name: Date: Class: Finding Epicenters and Measuring Magnitudes Worksheet
 Example Answers Name: Date: Class: Finding Epicenters and Measuring Magnitudes Worksheet Objective: To use seismic data and an interactive simulation to triangulate the location and measure the magnitude
Example Answers Name: Date: Class: Finding Epicenters and Measuring Magnitudes Worksheet Objective: To use seismic data and an interactive simulation to triangulate the location and measure the magnitude
Lecture 14. Point Spread Function (PSF)
 Lecture 14 Point Spread Function (PSF), Modulation Transfer Function (MTF), Signal-to-noise Ratio (SNR), Contrast-to-noise Ratio (CNR), and Receiver Operating Curves (ROC) Point Spread Function (PSF) Recollect
Lecture 14 Point Spread Function (PSF), Modulation Transfer Function (MTF), Signal-to-noise Ratio (SNR), Contrast-to-noise Ratio (CNR), and Receiver Operating Curves (ROC) Point Spread Function (PSF) Recollect
ANALYTICAL METHODS FOR ENGINEERS
 UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
Time Series Analysis: Introduction to Signal Processing Concepts. Liam Kilmartin Discipline of Electrical & Electronic Engineering, NUI, Galway
 Time Series Analysis: Introduction to Signal Processing Concepts Liam Kilmartin Discipline of Electrical & Electronic Engineering, NUI, Galway Aims of Course To introduce some of the basic concepts of
Time Series Analysis: Introduction to Signal Processing Concepts Liam Kilmartin Discipline of Electrical & Electronic Engineering, NUI, Galway Aims of Course To introduce some of the basic concepts of
PRAKlA SEISMDS "V V PRAKLA-SEISMOS AG
 !\ PRAKlA SEISMDS "V V PRAKLA-SEISMOS AG 1 Bridge - all conlrols and video screens are within easy reach Mast lable to lit various antennae 01 radio survey systems in one beamline THE ESSENTIAL INSTRUMENTATION
!\ PRAKlA SEISMDS "V V PRAKLA-SEISMOS AG 1 Bridge - all conlrols and video screens are within easy reach Mast lable to lit various antennae 01 radio survey systems in one beamline THE ESSENTIAL INSTRUMENTATION
A wave lab inside a coaxial cable
 INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
Taking the Mystery out of the Infamous Formula, "SNR = 6.02N + 1.76dB," and Why You Should Care. by Walt Kester
 ITRODUCTIO Taking the Mystery out of the Infamous Formula, "SR = 6.0 + 1.76dB," and Why You Should Care by Walt Kester MT-001 TUTORIAL You don't have to deal with ADCs or DACs for long before running across
ITRODUCTIO Taking the Mystery out of the Infamous Formula, "SR = 6.0 + 1.76dB," and Why You Should Care by Walt Kester MT-001 TUTORIAL You don't have to deal with ADCs or DACs for long before running across
Application Note Noise Frequently Asked Questions
 : What is? is a random signal inherent in all physical components. It directly limits the detection and processing of all information. The common form of noise is white Gaussian due to the many random
: What is? is a random signal inherent in all physical components. It directly limits the detection and processing of all information. The common form of noise is white Gaussian due to the many random
Lock - in Amplifier and Applications
 Lock - in Amplifier and Applications What is a Lock in Amplifier? In a nut shell, what a lock-in amplifier does is measure the amplitude V o of a sinusoidal voltage, V in (t) = V o cos(ω o t) where ω o
Lock - in Amplifier and Applications What is a Lock in Amplifier? In a nut shell, what a lock-in amplifier does is measure the amplitude V o of a sinusoidal voltage, V in (t) = V o cos(ω o t) where ω o
RANDOM VIBRATION AN OVERVIEW by Barry Controls, Hopkinton, MA
 RANDOM VIBRATION AN OVERVIEW by Barry Controls, Hopkinton, MA ABSTRACT Random vibration is becoming increasingly recognized as the most realistic method of simulating the dynamic environment of military
RANDOM VIBRATION AN OVERVIEW by Barry Controls, Hopkinton, MA ABSTRACT Random vibration is becoming increasingly recognized as the most realistic method of simulating the dynamic environment of military
EE 179 April 21, 2014 Digital and Analog Communication Systems Handout #16 Homework #2 Solutions
 EE 79 April, 04 Digital and Analog Communication Systems Handout #6 Homework # Solutions. Operations on signals (Lathi& Ding.3-3). For the signal g(t) shown below, sketch: a. g(t 4); b. g(t/.5); c. g(t
EE 79 April, 04 Digital and Analog Communication Systems Handout #6 Homework # Solutions. Operations on signals (Lathi& Ding.3-3). For the signal g(t) shown below, sketch: a. g(t 4); b. g(t/.5); c. g(t
FFT Spectrum Analyzers
 FFT Spectrum Analyzers SR760 and SR770 100 khz single-channel FFT spectrum analyzers SR760 & SR770 FFT Spectrum Analyzers DC to 100 khz bandwidth 90 db dynamic range Low-distortion source (SR770) Harmonic,
FFT Spectrum Analyzers SR760 and SR770 100 khz single-channel FFT spectrum analyzers SR760 & SR770 FFT Spectrum Analyzers DC to 100 khz bandwidth 90 db dynamic range Low-distortion source (SR770) Harmonic,
The Effect of Network Cabling on Bit Error Rate Performance. By Paul Kish NORDX/CDT
 The Effect of Network Cabling on Bit Error Rate Performance By Paul Kish NORDX/CDT Table of Contents Introduction... 2 Probability of Causing Errors... 3 Noise Sources Contributing to Errors... 4 Bit Error
The Effect of Network Cabling on Bit Error Rate Performance By Paul Kish NORDX/CDT Table of Contents Introduction... 2 Probability of Causing Errors... 3 Noise Sources Contributing to Errors... 4 Bit Error
Understanding Dynamic Range in Acceleration Measurement Systems. February 2013 By: Bruce Lent
 in Acceleration Measurement Systems February 2013 By: Bruce Lent Topics to discuss Definition of dynamic range The effective range Making full use of the high level Using filters to improve dynamic range
in Acceleration Measurement Systems February 2013 By: Bruce Lent Topics to discuss Definition of dynamic range The effective range Making full use of the high level Using filters to improve dynamic range
Positive Feedback and Oscillators
 Physics 3330 Experiment #6 Fall 1999 Positive Feedback and Oscillators Purpose In this experiment we will study how spontaneous oscillations may be caused by positive feedback. You will construct an active
Physics 3330 Experiment #6 Fall 1999 Positive Feedback and Oscillators Purpose In this experiment we will study how spontaneous oscillations may be caused by positive feedback. You will construct an active
Agilent Creating Multi-tone Signals With the N7509A Waveform Generation Toolbox. Application Note
 Agilent Creating Multi-tone Signals With the N7509A Waveform Generation Toolbox Application Note Introduction Of all the signal engines in the N7509A, the most complex is the multi-tone engine. This application
Agilent Creating Multi-tone Signals With the N7509A Waveform Generation Toolbox Application Note Introduction Of all the signal engines in the N7509A, the most complex is the multi-tone engine. This application
Propagation Channel Emulator ECP_V3
 Navigation simulators Propagation Channel Emulator ECP_V3 1 Product Description The ECP (Propagation Channel Emulator V3) synthesizes the principal phenomena of propagation occurring on RF signal links
Navigation simulators Propagation Channel Emulator ECP_V3 1 Product Description The ECP (Propagation Channel Emulator V3) synthesizes the principal phenomena of propagation occurring on RF signal links
Application of Virtual Instrumentation for Sensor Network Monitoring
 Application of Virtual Instrumentation for Sensor etwor Monitoring COSTATI VOLOSECU VICTOR MALITA Department of Automatics and Applied Informatics Politehnica University of Timisoara Bd. V. Parvan nr.
Application of Virtual Instrumentation for Sensor etwor Monitoring COSTATI VOLOSECU VICTOR MALITA Department of Automatics and Applied Informatics Politehnica University of Timisoara Bd. V. Parvan nr.
PCM Encoding and Decoding:
 PCM Encoding and Decoding: Aim: Introduction to PCM encoding and decoding. Introduction: PCM Encoding: The input to the PCM ENCODER module is an analog message. This must be constrained to a defined bandwidth
PCM Encoding and Decoding: Aim: Introduction to PCM encoding and decoding. Introduction: PCM Encoding: The input to the PCM ENCODER module is an analog message. This must be constrained to a defined bandwidth
Review of Fourier series formulas. Representation of nonperiodic functions. ECE 3640 Lecture 5 Fourier Transforms and their properties
 ECE 3640 Lecture 5 Fourier Transforms and their properties Objective: To learn about Fourier transforms, which are a representation of nonperiodic functions in terms of trigonometric functions. Also, to
ECE 3640 Lecture 5 Fourier Transforms and their properties Objective: To learn about Fourier transforms, which are a representation of nonperiodic functions in terms of trigonometric functions. Also, to
Agilent PN 8753-1 RF Component Measurements: Amplifier Measurements Using the Agilent 8753 Network Analyzer. Product Note
 Agilent PN 8753-1 RF Component Measurements: Amplifier Measurements Using the Agilent 8753 Network Analyzer Product Note 2 3 4 4 4 4 6 7 8 8 10 10 11 12 12 12 13 15 15 Introduction Table of contents Introduction
Agilent PN 8753-1 RF Component Measurements: Amplifier Measurements Using the Agilent 8753 Network Analyzer Product Note 2 3 4 4 4 4 6 7 8 8 10 10 11 12 12 12 13 15 15 Introduction Table of contents Introduction
Plate waves in phononic crystals slabs
 Acoustics 8 Paris Plate waves in phononic crystals slabs J.-J. Chen and B. Bonello CNRS and Paris VI University, INSP - 14 rue de Lourmel, 7515 Paris, France [email protected] 41 Acoustics 8 Paris We
Acoustics 8 Paris Plate waves in phononic crystals slabs J.-J. Chen and B. Bonello CNRS and Paris VI University, INSP - 14 rue de Lourmel, 7515 Paris, France [email protected] 41 Acoustics 8 Paris We
Voice---is analog in character and moves in the form of waves. 3-important wave-characteristics:
 Voice Transmission --Basic Concepts-- Voice---is analog in character and moves in the form of waves. 3-important wave-characteristics: Amplitude Frequency Phase Voice Digitization in the POTS Traditional
Voice Transmission --Basic Concepts-- Voice---is analog in character and moves in the form of waves. 3-important wave-characteristics: Amplitude Frequency Phase Voice Digitization in the POTS Traditional
Calibration and Use of a Strain-Gage-Instrumented Beam: Density Determination and Weight-Flow-Rate Measurement
 Chapter 2 Calibration and Use of a Strain-Gage-Instrumented Beam: Density Determination and Weight-Flow-Rate Measurement 2.1 Introduction and Objectives This laboratory exercise involves the static calibration
Chapter 2 Calibration and Use of a Strain-Gage-Instrumented Beam: Density Determination and Weight-Flow-Rate Measurement 2.1 Introduction and Objectives This laboratory exercise involves the static calibration
