РОЗРАХУНКИ БРУСА ПРИ ПРОСТИХ ВИДАХ ДЕФОРМУВАННЯ
|
|
|
- Станислав Князев
- 7 years ago
- Views:
Transcription
1 МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ «Харківський політехнічний інститут» Конкін В.М., Конохов В.І., Шергін С.Ю., Кравцова Н.В. РОЗРАХУНКИ БРУСА ПРИ ПРОСТИХ ВИДАХ ДЕФОРМУВАННЯ Навчально-методичний посібник з курсу Опір матеріалів для студентів машинобудівних спеціальностей заочної форми навчання Затверджено редакційно-видавничою радою університету, протокол від 07..0р. Харків НТУ «ХПІ» 0
2 УДК 60.7 ББК 0. Р64 Рецензенти: В.Г.Сукіасов, канд-т техн. наук, доц., Національний технічний університет Харківський політехнічний інститут ; О.О.Чупринін, канд-т техн. наук, доц., Харківська державна академія міського господарства Авторський колектив: Конкін В.М., Конохов В.І., Шергін С.Ю., Кравцова Н.В. Р64 Розрахунки бруса при простих видах деформування: н.-метод. посіб. з курсу Опір матеріалів для студентів машинобудівних спеціальностей заочної форми навчання/ Конкін В.М., Конохов В.І., Шергін С.Ю., Кравцова Н.В. Харків: НТУ ХПІ, 0 4 с. ISBN Посібник містить розрахунки прямолінійних стержнів на розтягання стискання, прямий поперечний згин та кручення. Призначено для студентів машинобудівних спеціальностей заочної форми навчання. Може бути корисним для викладачів, а також для аспірантів та наукових працівників. Іл. 4. Табл. 7. Бібліогр.: 5 назв. УДК 60.7 ББК 0. В.М. Конкін, В.І. Конохов, ISBN С.Ю. Шергін, Н.В. Кравцова, 0
3 Вступ Сучасний етап науково-технічного розвитку потребує удосконалення методів розрахунків на міцність з метою впровадження нових технологій, підвищення надійності та довговічності машин, оскільки конкурентоспроможність продукції машинобудування на світовому ринку неможлива без різкого підвищення якості машин, що випускаються. Навчально-методичний посібник є одним з серії навчальнометодичної літератури, підготованої на кафедрі опору матеріалів НТУ ХПІ для студентів заочної форми навчання, зокрема, з курсу Опір матеріалів та розрахунки на міцність у машинобудуванні. Посібник охоплює три важливих розділи загального курсу опору матеріалів, а саме, розрахунки на розтягання стискання, згин, кручення і призначений для засвоєння студентами загальних положень теорії простих видів деформування, ознайомлення з наведеними прикладами. У першому розділі посібника розглянуто теорію та приклади розрахунків на центральний розтягання стискання стержнів. У другому розділі розглянуто згинання прямолінійних стержнів, наведено визначення внутрішніх силових факторів при прямому поперечному згинанні, визначення нормальних напружень при чистому згинанні, дотичних напружень при поперечному згинанні балок, наведено розрахунки на міцність з урахуванням нормальних і дотичних напружень. У третьому розділі розглянуто кручення валів круглого та прямокутного поперечного перерізів. У кожному розділі надаються розрахункові схеми та числові дані для виконання індивідуальних розрахунково-проектувальних завдань, а також приклади їх розв язання та оформлення.
4 . РОЗТЯГАННЯ СТИСКАННЯ При розрахунках на міцність, жорсткість та стійкість багатьох елементів машинобудівних конструкцій зустрічається такий вид простого деформування, як розтягання стискання стержнів... Центральне розтягання та стискання прямолінійних стержнів... Внутрішня поздовжня сила Центральне розтягання стискання у брусі виникає в тому випадку, коли зовнішні навантаження діють по його осі (осьові зовнішні сили), чи приводяться до осьових сил. У цьому випадку у перерізі виникає єдиний внутрішній силовий фактор внутрішня поздовжня сила. Брус, що знаходиться під дією розтягання стискання, називається стержнем. Проаналізуємо розподіл внутрішньої поздовжньої сили. Графічне представлення розподілу поздовжньої сили N по довжині стержня називається епюрою поздовжньої сили N. Розглянемо стержень, навантажений двома осьовими силами F і F (рис..). Використовуючи метод перерізів, визначимо значення поздовжньої сили на першій та другій ділянках стержня відповідно у перерізах z і z N z, N z. Відкидаючи праві частини стержня у кожному випадку та замінивши дію відкинутої частини на залишену поздовжніми силами N z і N z, записуємо рівняння рівноваги для кожної ділянки F iz 0. Одержуємо наступні рівняння для визначення поздовжньої сили на кожній ділянці стержня: для першої ділянки (перерізи його потрапляють у діапазон 0 z ) F N z 0 4,
5 Рисунок. для другої ділянки ( z ) F F Nz 0. Звідси значення поздовжніх сил на кожній ділянці: Nz F, Nz F F. Узагальнюючи наведене вище, можна сформулювати правило для визначення поздовжньої сили у перерізі з поточною координатою z. Поздовжня сила N z в довільному перерізі чисельно дорівнює алгебраїчній сумі проекцій на вісь стержня (вісь Z) зовнішніх сил, які розташовані по один бік від перерізу (всіх однобічних сил). Правило знаків: поздовжня сила приймається позитивною (додатною), якщо викликає деформацію розтягання, і негативною (від'ємною), якщо викликає деформацію стискання.... Побудова епюри внутрішньої поздовжньої сили Порядок побудови епюри внутрішньої поздовжньої сили покажемо на прикладі стержня, наведеного на рис.... Визначаємо значення опорної реакції H з умови статичної рівноваги системи зовнішніх сил F iz 0: 5
6 F i z H q b c F F 0, звідси H 0, кh. Рисунок.. Розбиваємо стержень на ділянки, границі яких збігаються з перерізами, де прикладені зосереджені сили (у даному випадку сили F і F ), а також з перерізами, де починаються і закінчуються розподілені навантаження.. Записуємо вирази для поздовжньої сили у поточному перерізі, що визначається координатою z i на кожній ділянці з урахуванням прийнятого правила знаків та визначаємо її значення: 0 z с; Nz F qz; лінійна функція с Nz F F ; z с b; 0 z a; qz лінійна функція N0 0кН; N0,5 5кН. N0,5 5кН; N, 4кН. Nz H const N 0 N0,4 4 кh. За отриманими даними у масштабі будуємо епюру внутрішніх поздовжніх сил N z. 4. Перевірка правильності побудови епюр. а) На ділянці з рівномірно розподіленим навантаженням q епюра N z є лінійною (описується рівнянням прямої лінії, нахиленої до нульо- 6
7 вої), якщо 0 ділянках q, то N z const N z є лінійною, на третьому постійна.. У нашому випадку на першій і другій б) У перерізах, де прикладені зосереджені сили ( F і F та реакція H ), на епюрі N z спостерігаються стрибки на величини цих сил.... Напруження при центральному розтяганні стисканні Розглянемо розтягання прямолінійного стержня довільного поперечного перерізу під дією двох рівних по величині та протилежно спрямованих сил (рис.. а). У довільному місці стержня уявно проведемо поперечний переріз, відкинемо праву частину, дію відкинутої частини на ту, що залишилася, замінимо внутрішнім зусиллям N z, що з рівняння статичної рівноваги F iz 0 визначиться як Nz F (рис.. б). Поздовжня сила N z є рівнодіючою (результуючою) внутрішніх зусиль, які довільним образом розподілені по точках перерізу, та нормальні до нього. Тобто при центральному розтяганні - стисканні у поперечному перерізі виникає тільки нормальне напруження (рис.. в). Рисунок. 7
8 Очевидно, що на елементарну площадку d діє елементарна поздовжня сила dn d. Звідси одержуємо рівняння в інтегральному вигляді: N d. (.) Вирішити це рівняння неможливо, тому що невідомий закон розподілу по перерізу напруження. Щоб описати закон розподілу напружень по поперечному перерізу, звернемося до досліду. Як показують експерименти, при центральному розтяганні стисканні однакові подовжні відрізки ac і bd стержня одержують однакові подовження (рис.. г): a c ac b d bd. Лінії на бічній поверхні стержня, що являють собою сліди поперечних перерізів, рівнобіжні до деформування, залишаються рівнобіжними й у процесі деформування: ab a b і cd c d. Це дозволяє вважати, що при центральному розтяганні стисканні виконується гіпотеза плоских перерізів: переріз плоский та нормальний до осі (поперечний переріз) до деформації залишається плоским та нормальним до осі в процесі деформації, тобто переміщуючись, переріз залишається паралельним (рівнобіжним) самому собі. Якщо уявити модель стержня, що складається з окремих подовжніх волокон, то при розтяганні кожне волокно подовжується на одну і ту ж величину. Отже, у кожному подовжньому волокні діє однакове зусилля. Цей висновок дозволяє вважати, що при центральному розтяганні стисканні нормальне напруження по поперечному перерізу розподіляється рівномірно, тобто const. Тоді з рівняння (.) маємо: N d, звідси нормальне напруження для всіх точок перерізу при центральному розтяганні стисканні буде однаковим, і визначиться формулою N. (.) У розглянутому випадку напруження залишаються постійними як по перерізу, так і по довжині (якщо повздовжня сила та площа поперечного перерізу постійні), тобто по всьому обсягу стержня. Такий напружений стан називається однорідним. 8
9 Максимальні розрахункові нормальні напруження, обчислені за формулою (.), повинні зіставлятися з гранично допустимими напруженнями для матеріалу стержня, що забезпечують безпечну експлуатацію. Ці на-. пруження називаються допустимими напруженнями Сформулюємо умову міцності при центральному розтяганні стисканні, яка повинна виконуватись в кожній точці поперечних перерізів даного стержня: N. (.) Для матеріалів, що мають неоднакові характеристики при розтяганні та стисканні, умова міцності (.) набуває вигляд: Nроз роз роз ; (.4) Nст ст ст, де роз та ст найбільші нормальні напруження при розтяганні та стисканні відповідно. Переріз стержня, у якому виникає найбільше нормальне напруження, є небезпечним. Напруження, що допускається (допустиме напруження), визначається як небезпечне напруження для даного матеріалу, поділене на нормативний коефіцієнт запасу н n, тобто н н н. Для пластичних матері- n алів за небезпечне напруження приймається границя текучості т, а для крихких тимчасовий опір в...4. Види розрахунків за допустимим напруженням Покажемо основні види розрахунків, які виконуються з використанням умови міцності (.) (розрахунки за допустимим напруженням) Перевірочний розрахунок Основна мета перевірочного розрахунку полягає в зіставленні максимальних розрахункових та допустимого напруження. У цьому розрахун- 9
10 ку відомою вважається вся вхідна інформація про стержень, що включає три групи даних: про зовнішні сили: значення навантажень та координати точок на осі бруса, де прикладенні ці навантаження, про геометричні розміри стержня: площа поперечного перерізу, про механічні властивості матеріалу стержня: допустиме напруження. За формулою (.) обчислюємо максимальні напруження порівнюємо з допустимим. Якщо 0 ma та ma міцність стержня забезпечена (допускається відхилення до 5% в бік перебільшення у значенні над ). При ma стержень вважається недовантаженим, ma що приводить до перевитрати матеріалу. У випадку, ma стержень перевантажений, що приводить до необхідності переглянути вихідну розрахункову схему чи вибрати інший матеріал Проектувальний розрахунок (підбор площі поперечного перерізу) Мета цього розрахунку полягає у визначені безпечних з точки зору міцності розмірів перерізу стержня. Відомими вважаються: зовнішні сили: значення навантажень і координати точок на осі бруса, де прикладенні ці навантаження, механічні властивості матеріалу стержня: допустиме напруження. Після побудови епюри внутрішніх поздовжніх сил, обирається переріз з максимальним значенням N. ma З умови міцності (.) площу небезпечного поперечного перерізу обчислюємо за формулою N ma Визначення максимально допустимого зовнішнього навантаження Мета цього розрахунку полягає у визначені безпечного з точки зору
11 міцності зовнішнього навантаження стержня. Розрахунок проводиться за допомогою умови міцності (.). Відомими вважаються: геометричні розміри стержня: площа поперечного перерізу, механічні властивості матеріалу стержня: допустиме напруження. Будується епюра внутрішньої поздовжньої сили в загальному виді. З умови міцності (.) визначається N, з якої далі знаходиться навантаження, що допускається. ma..5. Деформації та переміщення при розтяганні стисканні. Закон Гука. Модуль пружності. Коефіцієнт Пуассона Розглянемо розтягнутий силою F стержень довжиною 0 та площею поперечного перерізу (рис..4). Рисунок.4 Під дією зовнішнього розтягувального навантаження поздовжній розмір стержня збільшується до. Зміна довжини 0 називається абсолютним подовженням стержня, або абсолютною поздовжньою деформацією. Відношення (.5) 0 називається відносною поздовжньою деформацією (чи просто поздовжньою деформацією). Якщо в стержні виникає неоднорідний напружений стан, деформація в точці a визначається шляхом граничного переходу до нескінченно малого елемента довжиною dz :
12 dz. dz Відносна поздовжня деформація вважається додатною при розтяганні і від ємною при стисканні. При цьому необхідно зазначити, що в лінійних пружних системах існує прямопропорційна залежність між напруженнями та деформаціями. E. Це співвідношення називається законом Гука при центральному розтяганні стисканні (одновісному напруженому стані). Коефіцієнт пропорційності E модуль пружності (поздовжньої пружності) фізична постійна матеріалу. Орієнтовні величини модуля пружності для деяких матеріалів мають значення: сталь E = (...,)0 5 МПа; мідь і сплави міді E = (...,)0 5 МПа; алюміній і сплави алюмінію E = (0,7...0,7)0 5 МПа. Враховуючи (.) та (.5), залежність між навантаженням та подовженням при однорідному напруженому стані визначається співвідношенням N, E де E називається жорсткістю стержня при розтяганні. Якщо N та змінюються по довжині стержня, то абсолютне подовження стержня довжиною 0 визначається за формулою: 0 0 N( z) dz. E Крім поздовжніх деформацій у стержні виникають і поперечні деформації. Різниця b b b0 (рис..4) називається абсолютною поперечною деформацією. Відношення b b 0 ' називається відносною поперечною деформацією. Відносна поперечна деформація має протилежний знак від відносної поздовжньої деформації. При цьому існує прямопропор-
13 ційна залежність між відносною поздовжньою та відносною поперечною деформаціями: '. Абсолютна величина відношення відносної поперечної деформації до відносної поздовжньої називається коефіцієнтом Пуассона, тобто. Значення коефіцієнта Пуассона для деяких матеріалів, що використовуються у машинобудуванні, знаходяться у діапазоні: 0 0, 5: для каучуку близько до 0,5; для сталі = 0,5...0,; для міді = 0,...0,5; для алюмінію = 0,...0,6. Коефіцієнт Пуассона, також як і модуль поздовжньої пружності E, є фізичними константами матеріалу та характеризують його пружні властивості... Статично невизначувані системи при розтяганні стисканні... Основні поняття та визначення У практиці розрахунків при розтяганні стисканні зустрічаються розрахункові схеми, для яких при відомих активних зовнішніх зусиллях рівнянь статичної рівноваги недостатньо для визначення реактивних зусиль і внутрішніх зусиль. Такі системи прийнято називати статично невизначуваними. Статично невизначуваною називається кінематично незмінна система, у якої число невідомих зусиль, включаючи реакції опор та внутрішні сили, більше числа рівнянь статики, які можна скласти для даної системи чи її частини. Різниця між кількістю невідомих зусиль та кількістю незалежних рівнянь статичної рівноваги, що можна записати для всієї системи або її частини, називається ступенем статичної невизначеності системи. Це число показує скільки додаткових рівнянь у геометричному аналізі процесу деформування системи необхідно скласти, щоб можна було '
14 вирішити задачу. Розкриття статичної невизначуваності таких систем складається з чотирьох основних етапів. Загальний план рішення таких задач полягає в наступному.. Статична сторона задачі (ССЗ). Визначаємо напрямок реакцій зв'язків, внутрішніх зусиль у стержнях, складаємо рівняння рівноваги, визначаємо ступінь статичної невизначуваності задачі.. Геометрична сторона задачі (ГСЗ). Установлюємо зв'язок між переміщеннями окремих перерізів конструкції, виходячи з умови спільності переміщень. Складаємо необхідну кількість рівнянь зв язку між переміщеннями. Число таких рівність повинно дорівнювати ступеню статичної невизначуваності системи. Отримані рівняння називаються рівняннями спільності переміщень.. Фізична сторона задачі (ФСЗ). У рівняннях спільності переміщень для окремих елементів їхні переміщення виражаємо на підставі закону Гука через діючі в них невідомі зусилля. 4. Синтез. Вирішуємо отриману систему рівнянь щодо невідомих зусиль. Розглянемо розрахунки статично невизначуваних задач при центральному розтяганні стисканні на прикладах.... Жорстко закріплений стержень під дією зосередженої сили Жорстко закріплений обома кінцями стержень площею поперечного перерізу навантажений силою F (рис..5). Модуль пружності матеріалу E. Визначити опорні реакції та побудувати епюру поздовжніх сил. Рисунок.5 4
15 . ССЗ. Показуємо опорні реакції R C і R B. Записуємо єдину умову рівноваги, яку можна скласти для даної задачі Fzi RC RB F 0. (.6) Це рівняння має дві невідомі, тому ступінь статичної невизначеності дорівнює: n.. ГСЗ. Так як опори жорсткі, то повне подовження стержня дорівнює нулю, тобто 0. Один з підходів реалізації цієї умови такий. Відкидаємо одну з опор та послідовно прикладаємо зовнішні сили і невідому реакцію у відкинутій опорі. Повне подовження стержня зобразиться як сума подовжень від зовнішнього навантаження F ( F ) і реакції RC ( ): R C F RC 0.. ФСЗ. Подовження від зовнішнього зусилля у розглянутому випадку складає: F, укорочення від реакції: C (a b) Fa R R E C. E 4. Синтез. Повна деформація стержня виявляється рівною: Fa RC(a b) 0. (.7) E E a З рівняння (.7) одержуємо R C F, а з рівняння (.6) випливає: RB F RC F. Розбиваємо стержень на дві ділянки та запи- a b b a b суємо значення поздовжньої сили на кожній ділянці: a а ділянка: 0 z b : N( z ) RC F ; a b b а ділянка: 0 z a : N( z ) RB F. a b По отриманим рівнянням будуємо епюру поздовжніх сил.... Жорстко закріплений стержень під дією температурного навантаження Особливий інтерес викликають задачі розрахунків статично невизначуваних систем при термосиловому навантаженні. У статично невизначу- 5
16 ваних стержнях і стержньових системах навіть невеликі перепади температур приводять до появи помітних величин напружень. Доповнимо вище розглянутий приклад розрахунком температурних напружень. Будемо вважати, що стержень нагрітий на t С (рис..6).. Записуємо єдину умо- t. ССЗ. Показуємо опорні реакції R C і ву рівноваги, яку можна скласти для даної задачі zi t C t B F R R 0 ; R t C t R B R t B R t t Реакції RC і R B, що виникають у защемленнях, рівні між собою та спрямовані в протилежні сторони. t Рисунок.6. ГСЗ. Повне подовження стержня складеться з суми подовжень вільного температурного розширення стержня та укорочення від реакції t RC Rt (див. рис..6), тобто 0, t Rt. ФСЗ. Укорочення від реакції, як і в попередньому прикладі, дорівнює: RC t (a b) R C, E а температурне розширення стержня 6
17 t t (а b) t ( t температурний коефіцієнт лінійного розширення). 4. Синтез. З рішення системи рівнянь одержуємо реакції опор t t t E RC RB Rt tet a b та значення поздовжньої сили, яке на всіх ділянках стержня є постійним: N ( z ) N ( z R Et. t t ) Температурні напруження у перерізі стержня t t Nt t Et і не залежать від площі поперечного перерізу. При охолодженні стержня план рішення не змінюється, а результат задачі відрізняється тільки знаком (стержень розтягується)...4. Урахування недосконалості виготовлення (монтажний фактор) Аналогічно температурній розглядається задача визначення монтажних напружень, які викликані наявністю недосконалості виготовлення стержня. Стержень виготовлено більше номінального розміру на величину (рис..7). При монтуванні його стискають та закріплюють в опорах, де виникають реакції R C і R B. t Рисунок.7 7
18 .ССЗ. Записуємо єдину умову рівноваги, яку можна скласти для даної задачі Реакції RC C B F R R 0 ; і zi R B R C R B R, що виникають у защемленнях, рівні між собою та спрямовані в протилежні сторони..гсз. Повне подовження стержня складеться з суми подовжень: недосконалості та укорочення від реакції R C R (див. рис..7), тобто R 0.. ФСЗ. Укорочення від реакції, як і в попередньому прикладі, дорівнює: R C (a b) R C, E 4. Синтез. З рішення системи рівнянь одержуємо реакції опор E RC RB R a b та значення поздовжньої сили, яке на всіх ділянках стержня є постійним: N ( z ) N ( z) R. У цьому випадку монтажні напруження у перерізі стержня N E і не залежать від площі поперечного перерізу. a b Якщо стержень виготовлено менше номінального розміру, то при монтуванні його розтягують. План рішення задачі не змінюється, а результат відрізняється тільки знаком (стержень розтягається)... Розрахунково-проектувальне завдання При вивчені розділу Розтягання стискання в курсі Опір матеріалів ставиться мета навчити студентів основам інженерного розрахунку елементів конструкцій машин і механізмів на міцність і жорсткість при навантаженні, що діє вздовж осі стержня (поздовжньої сили), з урахуванням 8
19 при цьому умов роботи, властивостей матеріалів та різноманітних типів поперечних перерізів. Для кращої організації і більш ефективної самостійної роботи студентів, згідно з вимогами програми курсу Опір матеріалів, студентам пропонується до виконання розрахунково-проектувальне завдання (РПЗ) по темі Розрахунки на міцність при центральному розтяганні стисканні. Виконуючи цю роботу, студент практично знайомиться з методами обчислення внутрішніх поздовжніх сил, побудови епюр цих сил, розрахунку нормальних напружень та переміщень, визначення розмірів поперечного перерізу для різноманітних схем, що забезпечують умови міцності.... Склад розрахунково-проектувального завдання Розрахунково-проектувальне завдання складається з трьох етапів:. Рішення запропонованих викладачем задач для певних варіантів розрахункових схем і вихідних даних, оформлення їх за вимогами кафедри Опору матеріалів.. Написання контрольних робіт за темою РПЗ.. Захист РПЗ. Захист включає в себе пояснення методів і принципів розв'язання задач і відповідь на контрольні теоретичні запитання. Кількість та об єм цих запитань визначається викладачем індивідуально для кожного студента. Мета завдання проведення перевірочних, проектувальних розрахунків для визначення розмірів поперечного перерізу та грузонавантаження конструкції с заданим коефіцієнтом запасу. Дано:. Розрахункова схема заданої системи з вказаними довжинами дільниць і видом зовнішнього навантаження.. Чисельні дані.. Механічні характеристики деяких марок сталі таблиця Д.4. РПЗ складається з трьох обов язкових для рішення задач:. Перевірочний розрахунок. Для заданої схеми навантаження стержня ступінчатої зміни площі поперечного перерізу побудувати епюри внутрішніх поздовжніх сил, нормальних напружень, переміщень та перевірити міцність стержня. 9
20 Варіанти розрахункових схем наведені в додатку., а чисельні дані в таблиці Д. та Д.4.. Визначення максимально допустимого навантаження. Для заданої схеми стержньової системи визначити з умови міцності допустиме значення зовнішньої сили F. Варіанти розрахункових схем наведені в додатку., а чисельні дані в таблиці Д. та Д.4.. Проектувальний розрахунок. Для заданої статично невизначуваної системи з послідовним розташуванням ділянок стержня з розрахунку на міцність визначити площу поперечних перерізів на всіх ділянках стержня і побудувати епюру поздовжніх сил та нормальних напружень. Для цієї ж розрахункової схеми провести розрахунки для визначення впливу температурного навантаження та недосконалості виготовлення на напружений стан. Перевірити міцність конструкції від дії зовнішнього навантаження, температури та недосконалості виготовлення. Варіанти розрахункових схем наведені в додатку., а чисельні дані в таблиці Д. та Д Порядок виконання завдання Задача. Для статично визначуваного стержня з послідовно розташованими ділянками різної площі поперечного перерізу, навантаженого зосередженими поздовжніми силами та розподільним навантаженням побудувати епюри внутрішніх поздовжніх сил, нормальних напружень, переміщень, перевірити міцність.. Виписати для заданого варіанту чисельні дані. В певному масштабі накреслити схему заданої системи з зазначенням її лінійних розмірів і зовнішніх навантажень.. Визначити значення внутрішньої поздовжньої сили в перерізах на ділянках стержня та побудувати для заданої схеми епюру внутрішніх поздовжніх сил.. Обчислити нормальні напруження на різних ділянках стержня, побудувати епюру нормальних напружень та перевірити виконання умови міцності. 4. Побудувати епюру поздовжніх переміщень перерізів стержня. 0
21 Задача. Для заданої статично визначуваної стержньової системи визначити допустиме навантаження (значення зосередженої зовнішньої сили F ).. Виписати для заданого варіанту чисельні дані. В певному масштабі накреслити схему заданої системи з зазначенням її лінійних розмірів і зовнішнього навантаження.. Визначити значення поздовжніх сил в певних перерізах стержнів в долях зовнішньої сили F. З умови міцності для кожного з стержнів визначити значення допустимого навантаження F для всієї системи.. Обчислити нормальні напруження в стержнях. Задача. Для статично невизначуваного стержня при центральному розтяганні стисканні з умови міцності визначити параметр А площі поперечного перерізу. Провести розрахунки з урахуванням додаткового фактора (зміни температури та недосконалості виготовлення).. Для заданого варіанту завдання виписати чисельні дані і в певному масштабі накреслити схему заданої системи з зазначенням лінійних розмірів і зовнішніх навантажень.. Встановити ступінь статичної невизначуваності системи.. Статичний аспект задачі. Скласти і записати рівняння статики. Вибрати основну статично визначувану систему, уявно відкинувши одну з опор і замінивши її реакцією опори. 4. Геометричний аспект задачі. Розглянути сумісне деформування основної системи. Записати рівняння сумісності переміщень. Сумарне переміщення на відкинутій опорі від дії зовнішніх сил та реактивного зусилля повинно дорівнювати нулю. 5. Фізичний аспект задачі. Використати закон Гука для запису виразів для переміщень як абсолютних деформацій стержня. 6. Сумісне рішення отриманих рівнянь. Визначити значення реактивних зусиль в опорах. 7. Побудувати епюру поздовжніх сил. 8. З умови міцності для максимально напружених ділянок визначити параметр площі поперечного перерізу. 9. Побудувати епюри нормальних напружень для усіх ділянок схеми. 0. Побудувати епюру переміщень і зробити деформаційну перевірку.
22 . Для наданої розрахункової схеми провести розрахунок статично невизначуваного стержня з урахуванням зміни температури. Побудувати епюри внутрішніх поздовжніх сил та нормальних напружень від дії цього додаткового фактора.. Для наданої розрахункової схеми провести розрахунок статично невизначуваного стержня з урахуванням недосконалості виготовлення конструкції. Побудувати епюри внутрішніх поздовжніх сил та нормальних напружень від дії цього додаткового фактора.. Визначити сумарні напруження від дії зовнішнього навантаження, дії температури та недосконалості виготовлення, побудувати епюру цих напружень та перевірити міцність стержня.... Приклади розв язання задач Зразок виконання задачі Дано: 5 0,5 0 м ; E 0 МПа; т 40 МПа; nт,6; F 400 кh; 0, м; F 00 кh; 0,4 м; кh q 500 ; м 0,5 м. Допустиме напруження: т 50 МПа. n Необхідно:. Визначити внутрішні зусилля на ділянках стержня та побудувати епюру внутрішніх поздовжніх сил N.. Визначити нормальні напруження на ділянках стержня та побудувати епюру напружень. Перевірити міцність стержня.. Визначити абсолютні деформації ділянок стержня та побудувати епюру поздовжніх переміщень поперечних перерізів W. Рішення: т. Визначення реакції H. F z ; H F q 0; H F q F 400кH. 0 F
23 . Побудова епюри внутрішніх зусиль N. 0 z N z H 400 кh N. z z H F N N N 0. z z F qz, F 00 кh; F q 0. 0 z N 4 4 z4 F 00 кh.. Визначення нормальних напружень на ділянках стержня та побудова епюри. N Па 80 МПа; 0,5 0 N 0; N Па 0 МПа; 0,5 0 N 0; N Па 4 0, МПа. Максимальне по абсолютному значенню нормальне напруження досягається на першій ділянці.
24 80 МПа 50 МПа умова міцності виконується. ma 4. Визначення абсолютних деформацій ділянок стержня та побудова епюри переміщень W. N E N E E E 0 F z 5 0 N , ,5 0 0; z dz F qz E F dz 0,5 0 q z dz 000 E z q F q E 5 0, dz м; 0,4 0 м; 4 N4 E , ,5 0 м; W W W W 4 W W W м; м ; м м. Зразок виконання задачі Дано: a,0 м; c,5 м; h,5 м. т 40 МПа; nт,. 4 4 ;
25 Допустиме напруження: т 00 МПа. n Необхідно:. Виразити значення внутрішніх зусиль в стержнях системи через параметр навантаження F.. З умови міцності стержнів визначити допустиме навантаження.. Визначити напруження в стержнях системи. т Рішення:. Визначаємо геометричні параметри конструкції: площі поперечних перерізів стержнів та довжину стержня :,0 см ; 6 d,0 см ; ; 4 4,96 9,8 см a h, м.. Знаходимо внутрішні зусилля в стержнях. Для цього розрізаємо стержень та окремо розглядаємо рівновагу верхньої та нижньої частин конструкції. Для нижньої частини визначаємо залежність внутрішньої поздовжньої сили N від зовнішньої сили F. Запишемо рівняння статичної рівноваги: B 0, або N Fc a c a c Fc ; N 0,4. 0 F 5
26 Для верхньої частини знаходимо залежність внутрішніх поздовжніх сил N та N через N, а згодом, через силу F. Запишемо рівняння статичної рівноваги: N F iy 0; N N sin 0; N 0,55F. sin F ix 0; N N cos 0; N 0, 4F, де h a sin 0,78; cos 0, Визначаємо чисельне значення параметра навантаження F з умови міцності кожного стержня: для першого: N 0,4F 000,0 0 F 0,4 0,4 для другого стержня: N 0,55F ; 000 6,0 0 F 0,55 0,55 для третього стержня N 0,4F ; F 0, ,8 0 0,4 ; , 0 58, , 0 H 558,кH. H 58,8 кh. H 747,кH. Остаточно обираємо допустиме значення сили F, як найменше з обчислених: 558, кh. F min F ; F ; F
27 5. Визначаємо напруження в стержнях: 00 МПа ; N N 0,55558, 0 4 6,0 0 0,4558, 0 4 9,8 0 9 МПа; 96 МПа. Умова міцності виконана, оскільки напруження в усіх стержнях не перевищує допустимого напруження. Зразок виконання задачі Дано: F 00 кh; F 500 кh; 0,4 м; 0,4 м; 0,м; 0, мм; E 0 5 t МПа; 40 т O C; 40 МПа;,5 0 t n т 6,6. ; град Допустиме напруження: т 50 МПа. n Необхідно:. Розкрити статичну невизначуваність стержня при дії зовнішніх сил, побудувати епюру внутрішніх поздовжніх сил. З умови міцності визначити розміри поперечного перерізу (параметр площі ). Визначити напруження на ділянках стержня, побудувати епюру напружень від дії зовнішнього навантаження.. Розкрити статичну невизначуваність конструкції при наявності недосконалості виготовлення стержня. Визначити монтажні напруження в частинах стержня, побудувати епюру монтажних напружень.. Розкрити статичну невизначуваність конструкції при наявності зміни температури. Визначити температурні напруження в частинах стержня, побудувати епюру температурних напружень. 4. Побудувати епюру сумарних напружень. Перевірити виконання умови міцності стержня. т 7
28 Рішення: Урахування дії зовнішніх сил. Визначення розмірів поперечних перерізів. Встановлюємо ступінь статичної невизначеності n.. Статична сторона задачі. Рівняння статики Z ; R R F F 0. 0 B C. Геометрична сторона задачі. Рівняння сумісності переміщень F F R 0 С С. С С C 5. Фізична сторона задачі F F F C F ; C F E E E RC RC C RC. E E 6. Сумісне рішення рівнянь: F F F RC RC E E E E Звідси ; E 0. 8
29 R C F R F F ,0 B RC F F кн. 7. Будуємо епюру поздовжніх зусиль: 60 кh. C 0 z 0 z z ; ; ; N N N z RC z RC F z R 40 кh. B 60 кh. 40 кh. 8. Проводимо деформаційну перевірку побудови епюри N. z Nz Nz N E E 0 600,4 400,4 400, 0 E E E Визначаємо небезпечну ділянку стержня, порівнюючи напруження, які обчислюються на ділянках з точністю до параметру площі : N z 60 0 ; Nz 40 0 ; Nz 40. Небезпечною є перша ділянка. 0. Визначаємо параметр площі з умови міцності для першої ділянки: Nz ma, звідси N z 0, м. 9
30 . Будуємо епюру нормальних напружень від дії зовнішнього навантаження: 0 z ; 50МПа, 0 z z ; ; z N N z 400 0, ,870 Урахування недосконалості виготовлення. Статична сторона задачі. Рівняння статики: 9 МПа, 46 МПа. Z 0; RB RC 0; RB RC.. Геометрична сторона задачі. Рівняння сумісності переміщень: С С. Фізична сторона задачі: R 0. C RC RC R. C C E 4. Сумісне рішення рівнянь: RC E RC E 0. E R C E 0, ,0 6 0, кh. R B RC 70 кh. 5. Будуємо епюру поздовжніх зусиль: z z z ; ; ; N N N z RC 70 кh. z RC 70 кh. z R 70 кh. B 0
31 C N 6. Проводимо деформаційну перевірку побудови епюри z E 0, E 0, 0 N 0. 0,4 z N z E 0,4 0, E 7. Будуємо епюру монтажних напружень: N z ; z 0, z 0 z ; ; N z N z 700 0, ,87 0 0, 0 N 40 МПа, 40 МПа, 80 МПа.
32 Урахування температурного навантаження. Статична сторона задачі. Рівняння статики: Z 0; R t B R t C 0; R t B R. Геометрична сторона задачі. Рівняння сумісності переміщень: t C t 0. С С RC t. Фізична сторона задачі. Обчислимо скорочення незакріпленого стержня при його охолодженні: t t 6 t,5 0 0,5 40 0,50 м та його подовження під дією реакції опори: C C E 4. Сумісне рішення рівнянь: t t t R C RC R. RC t E t. E E t RC 0.,
33 87 кh.,0 0 0, ,5 6 5 E R t t C 87 кh. t C t B R R 5. Будуємо епюру поздовжніх зусиль:. 87 кh ; 0 87 кh. ; 87 кh. ; 0 t B t t C t t C t R z N z R z N z R z N z 6. Проводимо деформаційну перевірку побудови епюри t N : ,5 0 0,5 0 0,5 0, 0,4 0, E E z N E z N E z N t t t t t C 7. Будуємо епюру температурних напружень: 00 МПа. 0 0, ; 0 50 МПа, 0 0, ; 50 МПа, 0 0, ; 0 z N z z N z z N z t t t t t t
34 Визначення сумарних напружень t t t МПа, МПа, МПа. Максимальне напруження по абсолютному значенню на другій ділянці. ma 49 МПа 50 МПа. Умова міцності виконана. 4
35 ..4. Розрахункові схеми та чисельні дані Додаток. Задача. Статично визначуваний стержень 5
36 Продовження додатка. 6
37 Таблиця Д. Вхідні дані до задачі вар. F кh F кh q кh/м м м м ,5 0,4 0,,90, ,4 0,5 0,6,75, , 0,4 0,5,00, , 0, 0,4,0, ,4 0, 0,5,80, , 0,5 0,4,50, ,6 0,4 0,5,60, ,5 0, 0,4,90, ,4 0, 0,,75, ,5 0,4 0,,00, ,4 0, 0,5,90, ,5 0,6 0,4,75, ,4 0,5 0,,00, , 0,4 0,,0, , 0,5 0,4,80, ,5 0,4 0,,50, ,4 0,5 0,6,60, , 0,4 0,5,90, , 0, 0,4,75, ,4 0, 0,5,00, ,4 0,5 0,6,75, , 0, 0,4,0, ,6 0,4 0,5,60, ,4 0, 0,5,00,4 м n т 7
38 Додаток. Задача. Статично визначувана стержньова система
39 Продовження додатка
40 Продовження додатка
41 Таблиця Д. Вхідні дані до задачі вар Переріз Переріз a, м b, м c, м n т. 0 d=4 см,5,0,8,. d=4 см,6,8,0,4. 5,6/4 d=4 см,8,0,6, d=5 см,4,6,8,6 5. d=5 см,0,8,6,8 6. 6,5/6,,0,8, 7. d=4 см 6,8,5,0,4 8. d=4 см,0,6,8,5 9. 5/4 4,6,8,0,6 0. d=4 см 0,8,4,6,8. d=4 см,6,0,8,. d=4 см 5,6/4,8,,0,4. d=5 см 6,5,0,8,5 4. d=5 см,6,8,0,6 5. 6,5/6,8,0,6, d=4 см,4,6,8, 7. d=4 см,0,8,6, /4,,0,8, d=4 см,8,5,0, d=5 см,0,6,8,8. d=4 см,6,8,0,. 5,6/4 d=4 см,8,4,6,4. 6 4,6,0,8,5 4. d=5 см,8,,0,6 4
42 Додаток. Задача. Статично невизначуваний стержень 4
43 Продовження додатка. 4
44 Таблиця Д. Вхідні дані до задачі вар F, кh F, кh, м, м 44, м 0 t, C, мм n т ,5 0,4 0, 0-0,, ,4 0,5 0,6 5-0,4, , 0,4 0,5 0-0,, , 0, 0,4-0 0,, ,4 0, 0,5-5 0,, , 0,5 0,4-0 0,, ,6 0,4 0,5 5-0,, ,5 0, 0,4 0-0,4, ,4 0, 0, -0-0,, ,5 0,4 0, -5 0,, ,4 0, 0,5 0 0,, ,5 0,6 0,4 5 0,, ,4 0,5 0, 0-0,, , 0,4 0, -0 0,, , 0,5 0,4-5 0,, ,5 0,4 0, -0 0,, ,4 0,5 0,6 5-0,, , 0,4 0,5 0-0,4, , 0, 0,4-0 -0,, ,4 0, 0,5-5 0,, ,4 0,5 0,6 0 0,, , 0, 0,4-0 -0,4, ,6 0,4 0,5 5-0,, ,4 0, 0,5 0 0,,4
45 Додаток.4. Таблиця Д.4 Механічні характеристики сталей Марка сталі Модуль пружності, E 0 5, МПа Границя текучості, т, МПа Температурний коефіцієнт лінійного розширення, 0 6, t град. Ст 0,0 0,6. Ст 0, 50,. Ст 5,98 80, 4. Ст 0,00 00,6 5. Ст 5,06 0,9 6. Ст 40, 40,4 7. Ст 45,00 60,7 8. Ст 50,6 80,0 9. Ст 55,0 90,0 0. Ст 60,04 40,. Ст 0Г,04 80,. Ст 0Г,04 0,6. Ст 50Г,6 400,6 4. Ст 0Х,6 650, 5. Ст 40Х,4 800,4 6. Ст 45Х,06 850,8 7. Ст 0ХМ,0 750, 8. Ст 5ХМ,04 850, 9. Ст 40ХН,00 800,8 0. Ст 50ХН,00 900,8. Ст 5ХФ,06 550,0. Ст 40ХФА,00 750,0. Ст 0ХГСА,96 650,0 4. Ст 0ХГC,94 850,0 45
46 Додаток.5 Основні поняття, позначення, формули, формулювання та правила з теми «Розтягання стискання стержнів» Позначення та формули Одиниця виміру Назва 0 м (метр) абсолютна поздовжня деформація b b b 0 м (метр) абсолютна поперечна деформація відносна поздовжня деформація 0 ' b відносна поперечна деформація b 0 ' коефіцієнт Пуассона N Н (ньютон) внутрішня поздовжня сила А Fiz d м площа поперечного перерізу N Па (паскаль) нормальне напруження E Па (паскаль) модуль пружності (поздовжньої пружності) E. закон Гука N умова міцності при центральному розтяганні-стисканні N E Поздовжня сила умова жорсткості при центральному розтяганні-стисканні N z в довільному перерізі чисельно дорівнює алгебраїчній сумі проекцій на вісь стержня (вісь Z) зовнішніх сил, які розташовані по один бік від перерізу (всіх однобічних сил). Правило знаків: поздовжня сила приймається позитивною (додатною), якщо викликає деформацію розтягання, і негативною (від'ємною), якщо викликає деформацію стискання. 46
47 Контрольні питання. Що називається центральним розтяганням стисканням?. Які внутрішні силові фактори мають місце в перерізах стержня при центральному розтяганні стисканні?. Сформулюйте правила побудови епюри внутрішньої поздовжньої сили. 4. У чому полягає суть гіпотези плоских перерізів в умовах центрального розтягання? 5. За якою формулою обчислюються нормальні напруження при центральному розтяганні стисканні? Який вигляд має умова міцності? 6. Які види розрахунків можливі за умовою міцності? 7. Який вигляд має закон Гука при центральному розтяганні стисканні? 8. Чи всі матеріали підкоряються закону Гука? 9. Що таке модуль пружності матеріалу? 0. Що таке коефіцієнт Пуассона?.За якою формулою обчислюються абсолютні деформації стержнів при центральному розтяганні стисканні?. Які геометричні характеристики використовуються в розрахунках на міцність при центральному розтяганні стисканні?. Що називається жорсткістю стержня при розтяганні стисканні? 4.Який вигляд має умова жорсткості? 5. Які напруження виникають при центральному розтяганні стисканні на похилих площадках? 6. У якому перерізі стержня при центральному розтяганні стисканні виникають максимальні нормальні напруження і у якому перерізі максимальні дотичні напруження? 7. У чому полягає закон парності дотичних напружень? 8. Які системи називаються статично невизначуваними? 9. Які додаткові рівняння окрім рівнянь статичної рівноваги необхідно скласти для вирішення статично невизначуваних задач? 0. В якому порядку виконується розрахунок статично невизначуваних систем при центральному розтяганні стисканні?. В чому полягає деформаційна перевірка правильності розкриття статичної невизначуваності при центральному розтяганні стисканні? 47
48 . ЗГИНАННЯ.. Згинання прямолінійних стержнів... Класифікація згинання та типи опор Згинанням називається тип деформування стержня, при якому в його поперечних перерізах виникають згинальні моменти. Класифікація згинання. Згинання підрозділяється на поперечне (зовнішнє навантаження діє в напрямку, перпендикулярному осі стержня), поздовжнє (зовнішні сили діють уздовж осі стержня) та поздовжньо-поперечне. Поперечне згинання підрозділяється на плоске, при якому згинальні сили лежать в одній площині, та просторове, при якому зовнішні згинальні сили довільно орієнтовані у просторі. Плоске згинання підрозділяється на пряме та косе. У випадку прямого згинання площина дії згинальних навантажень збігається з однією з головних площин стержня. На рис.. показаний випадок навантаження стержня при прямому поперечному згинанні. Зовнішні сили розташовані у площині УОZ, що збігається з головною віссю перерізу Y. При косому згинанні площина дії згинальних навантажень не збігається з жодною з головних площин. Рисунок. 48
49 y Чисте згинання такий випадок згинання, при якому поперечна сила Q дорівнює нулю, а згинальний момент є єдиним внутрішнім силовим фактором у перерізі стержня і виявляється постійним на ділянці стержня. Розглянемо згинання балок. Балкою називається прямолінійний стержень, що працює на згинання. Балки закріплені на опорах, які забороняють переміщення балки як твердого цілого. Види опор та реактивні зусилля в них показані на рис... Рисунок. У шарнірно-рухомій опорі (рис.. а) виникає одна реактивна сила R, що діє перпендикулярно поверхні опори (у напрямку показаного зв'язку). У шарнірно-нерухомій опорі (рис.. б) виникають дві складових реакції: вертикальна R і горизонтальна H. У затисненні (жорсткому затисненні) (рис.. в), виникають три складові: вертикальна R, горизонтальна H і момент. Рисунок. Для кінематичної незмінюваності плоских балок необхідна кількість зовнішніх зв'язків дорівнює трьом. Але при плоскому згинанні горизонтальна складова H реакції в шарнірно-нерухомій опорі тотожно дорівнює 49
50 нулю, тому надалі для визначення реакцій опор використовуємо два рівняння статики. Якщо кількість зовнішніх поперечних зв'язків більше двох, то така балка називається статично невизначуваною (багатоопорною). Типи і найменування балок, що зустрічаються, показані на рис Поперечна сила Q y та згинальний момент, як внутрішні силові фактори при згинанні Проаналізуємо внутрішні силові фактори у поперечному перерізі балки при прямому поперечному згинанні, а потім сформулюємо основні правила побудови епюр Q і. y Розглянемо консольний стержень з затисненим правим торцем та навантажений силами F і F (рис..4). Нехай F > F. Рисунок.4 Згідно методу перерізів розріжемо балку на першій і другій ділянках, покажемо відсічені частини, замінимо дію відкинутих частин на залишену внутрішніми силовими факторами Q і. З умов статики визначимо їхні значення: y 50
51 перша ділянка: F i = F Q y (z ) = 0, звідки Q y (z ) = F ; i = F z + (z ) = 0, звідки друга ділянка: F i = F + F Q (z ) = 0, звідки i = F z F (z ) + (z ) = 0, звідки y (z ) = F z. Q y (z ) = F + F ; (z )= F z + F (z a). Використовуючи такі позначення, сформулюємо наступні правила для визначення поперечної сили та згинального моменту при згинанні. Поперечна сила в даному перерізі Q чисельно дорівнює алгебраїчній сумі проекцій на нормаль (вісь Y) до осі стержня сил, розташованих по одну сторону від перерізу (всіх однобічних сил), та утворює заміну діі відкинутої частини на залишену. Правило знаків для Q : поперечна сила вважається позитивною y (додатною), якщо обертає розглянуту відсічену частину балки відносно центра ваги перерізу за годинниковою стрілкою, та негативною (від ємною) якщо проти годинникової стрілки. Згинальний момент в даному перерізі z чисельно дорівнює алгебраїчній сумі моментів щодо поперечної осі перерізу сил, які розташовані по одну сторону від цього перерізу (всіх однобічних сил). Правило знаків для : згинальний момент вважається позитивним (додатним), якщо відсічена частина згинається опуклістю вниз (стиснуте волокно вгорі, розтягнуте внизу), та негативним (від ємним) якщо навпаки. Таким чином, епюра згинальних моментів будується з боку стиснутих волокон. Схематично прийняті правила знаків виглядають так: y Рисунок.5 5
52 ... Диференціальні залежності при згинанні Розглянемо балку, навантажену довільним розподіленим навантаженням q(z) (рис..6 а). В перерізі на відстані z виділимо елемент довжиною dz. В перерізі I діють внутрішні силові фактори Q y і, в перерізі II на відстані dz від першого діють внутрішні зусилля Qy dqy і + d. У межах нескінченно малого dz навантаження q(z) можна вважати рівномірно розподіленим та рівним q. Рисунок.6 Оскільки балка під дією зовнішнього навантаження знаходиться в рівновазі, то і кожен її елемент під дією зовнішніх та внутрішніх зусиль також знаходиться в рівновазі (рис..6 б). Запишемо рівняння статики:. F y 0; Qy Q y dqy qdz 0, отже. 0 ; dz q dz ( Q y dq dqy q (.) dz y ) dz d 0, приводячи подібні члени та зневажаючи нескінченно малими другого порядку, одержимо: Q dz d 0, звідки: y d Qy. (.) dz. Підставимо вираз (.) у залежність (.), одержимо : dq y d q. (.) dz dz 5
53 ..4. Приклади побудови епюр поперечних сил Q y та згинальних моментів Приклад. Розглянемо консольну балку з рівномірно розподіленим навантаженням q (рис..7). Показуємо поточний переріз з координатою z, межі її зміни, записуємо функції Q y і. Рівномірно розподілене навантаження q замінюємо зосередженою силою ( q z ), яку прикладено посередині ділянки (плече зосередженої сили 0,5 z). z 0 z Q y ( z) q z ; ( z) q. Далі обчислюємо значення Qy і : z 0Qy 0 ; 0; z Qy q ; q. Рисунок.7 З побудованих епюр, використовуючи правила перевірки, визначаємо опорні реакції R і. Реакція R q дорівнює величині стрибка на епюрі y Q в цьому перерізі та спрямована нагору, тому що Q y позитивна. З умов статики Fyi R q 0 одержуємо те ж саме значення R q. 5
54 На епюрі q в затиcненні скачок моменту дорівнює. Через те що в затисненні негативний, то q, отже повинний бути спрямований проти годинникової стрілки. З умови статики i q 0 одержуємо те ж саме значення: q. Приклад. Розглянемо двохопорну однопролітну балку з рівномірно розподіленим навантаженням q (рис..8). Рисунок.8. Визначаємо опорні реакції. 0, R q 0 B, звідки: R q B. B 0, R q 0, звідки: R q. q q Перевірка: F yi 0, R RB q q 0. Те, що реакції однакові та рівні половині зовнішнього навантаження, є наслідком симетрії задачі. 54
55 . Показуємо поточний переріз з координатою z, межі її зміни та записуємо функції Q y і : 0 z Q ( z) q z R q q z y B ; z z ( z) q RB z q q z. Далі обчислюємо значення Q y і : q q z 0 Qy, 0, z Qy, 0. Звертаємо увагу, що в точці, де q Q qz 0 y, згинальний момент повинен мати екстремальне значення. Таким чином, при qz q q q q ma z Приклад. Розглянемо двохопорну однопролітну балку, яка симетрично навантажена двома зосередженими силами F (рис..9). z Рисунок.9 55
56 У зв язку з симетрією задачі R R F. Запишемо функції і визначимо характерні значення перша ділянка: Q y і B для ділянок: 0 z a Qy ( z) R F; ( z) R z; z ; 0 0 z a Fa. друга ділянка: a z ( a) Q ( z ) R F F F 0. Поперечна сила на ділянці дорівнює нулю, отже y, ( z) Rz F( z a) Fz Fz Fa Fa. const, ділянка зазнає чисте згинання. третя ділянка: 0 z a Q ( z ) R F ; z ) R ; z y B ; ( B z 0 0 z a Fa. Приклад 4. Розглянемо двоконсольну балку (рис..0). Рисунок.0. Визначаємо опорні реакції: 0; q 4 F 5 RB 4 0; звідки RB 6кН. B 0; q 4 F R 4 0; звідки R 4 кн. Перевірка: F R R q 4 F y B 56
57 . Побудуємо епюри внутрішніх зусиль. Для цього розбиваємо балку на ділянки, показуємо перерізи на кожній з них, вказуємо межі зміни координати z i, визначаємо й обчислюємо функції Q y і. Перша ділянка: 0 z Q y ( z ) 0; ( z ) кнм. y ( Друга ділянка: z 5 Q z ) R q ( z ) 4 ( z ) ; ( z ) R ( z ) q( z ( z ) ) ( z ) 4 ( ) z ; z Q 4 кн; кнм; z 5 Q 4 кн; кнм. y На другій ділянці поперечна сила досягає максимального значення при z визначиться з умови: Q y ( z ) 4 ( z ) 0, звідки z м, 8 4 кнм. ma y Q змінює знак, а згинальний момент y z z. Координата Третя ділянка: 0 z Qy ( z ) F кн; ( z ) Fz ; z 0 0; z кнм...5. Правила побудови та перевірки епюр і Вищенаведені приклади та диференціальні залежності (.) і (.) дозволяють установити закономірності розподілів поперечних сил та згинальних моментів по довжині балки.. На ділянках, де розподілене навантаження відсутнє ( q 0 ), епю- Q y постійна, а епюра ра представляє лінійну функцію (рис..9).. На ділянках з рівномірно розподіленим навантаженням q епюра Q y лінійна, а епюра Q y квадратична парабола, причому опуклість парабо-ли спрямована в протилежну сторону дії розподіленого навантаження (рис..7). У точці z z, де поперечна сила Q y ( z ) 0 (змінює знак), момент.8). досягає екстремального значення ( ) (рис. ma, min 57
58 . На ділянках, де Q 0, епюра постійна. y 4. На ділянці, де поперечна сила Q y позитивна, епюра моменту зростає, і убуває якщо Q y негативна (у випадку руху зліва направо). 5. У перерізі, де до балки прикладена зосереджена сила F: на епюрі Q y спостерігається стрибок на величину F у напрямку прикладеної сили; на епюрі з'являється злам, причому вістря зламу спрямоване проти дії зосередженої сили. 6. У перерізах, де до балки прикладено зосереджений момент, на епюрі спостерігається стрибок на величину цього моменту... Напруження при поперечному згинанні При прямому поперечному згинанні в перерізі виникають поперечна сила Q, що викликає деформацію зсуву і появу дотичних напружень, та y згинальний момент, що викликає деформацію згинання і нормальні напруження у перерізі балки.... Нормальні напруження при чистому згинанні Розглянемо випадок чистого згинання, коли в перерізі виникає тільки згинальний момент. Покажемо стержень до його деформування (рис.. а) та після навантаження згинальними моментами (рис.. б). Спостерігаючи за деформацією ортогональної сітки, попередньо нанесеної на бічну поверхню балки до і після навантаження (рис.. а, рис.. б), відзначимо, що подовжні лінії при чистому згинанні викривляються по дузі кола, а контури поперечних перерізів залишаються плоскими та перетинають подовжні лінії під прямими кутами. У стиснутій області (у даному випадку внизу) волокна коротшають, а в зоні розтягання (угорі) подовжуються. Існує поздовжній шар, довжина якого при чистому згинанні залишається незмінною. Цей шар називається нейтральним, його радіус кривизни позначимо. 58
59 Рисунок. Поперечний переріз балки перетинається з нейтральним шаром по прямій, яка називається нейтральною лінією перерізу. Відзначені обставини дозволяють ввести наступні гіпотези: при чистому згинанні дотримується гіпотеза плоских перерізів: усі поперечні перерізи стержня при чистому згинанні не викривляються, а лише повертаються один відносно одного навколо осі X; поздовжні волокна не тиснуть одне на одне; по ширині перерізу нормальні напруження не змінюються. Логічно припустити, що в точках поперечного перерізу при чистому згинанні виникають тільки нормальні напруження, що приводять до інтегрального внутрішнього силового фактора згинального момента. Через відсутність поперечних сил у напрямку осі Y, очевидно, що в точках перерізу дотичні напруження відсутні. Розглянемо прямолінійний стержень довільного поперечного перерізу площею з віссю симетрії Y при чистому згинанні (рис.. а), тоді вісь Y головна центральна, а вісь X збігається з нейтральною лінією. У перерізі з координатою z визначимо внутрішній згинальний момент (рис.. б). Момент дорівнює сумі моментів від розподілених внутрішніх зусиль. 59
60 Задача про визначення внутрішніх зусиль відноситься до класу статично невизначених задач, тому далі застосовуємо схему рішення таких задач. Статична сторона задачі. Із шести рівнянь статичної рівноваги три рівняння F, F 0, 0 i 0 iy iz виконуються тотожно. Виділимо елемент площі d з координатами (, y ) (рис.. в). Елементарна сила в осьовому напрямку, що діє на площадку d дорівнює dn d, а результуюча сила знайдеться як N d. Рисунок. Елементарний момент сили dn щодо осей X і Y запишеться як d dn y та d y dn. Відповідно згинаючі моменти: dn y y d; y dn d. Таким чином, умови статики приймуть вигляд: 60
61 F iz 0; d 0; (.4) iy 0 ; d 0; (.5) i 0; y d 0. (.6) Відзначимо невідомі: нормальне напруження (величина та закон його розподілу за висотою перерізу); радіус кривизни нейтрального шару; положення нейтральної лінії в перерізі. Геометрична сторона задачі. Розглянемо деформацію елемента довжиною dz. Нехай волокно OO належить нейтральному шару. Виділимо на відстані y від нього волокно ab (рис..). Первісна довжина волокна 0 ab OO d, тому що волокно OO не деформується. Після деформування волокно ab перетворюється на дугу a b з радіусом кривизни та довжиною: Рисунок. a b d ( y) d. Визначимо відносну деформацію волокна ab : ab ab ( y) d d d Така залежність має місце для будь-якого волокна: y. 6
62 y. (.7) Фізична сторона задачі. При чистому згинанні поздовжні волокна піддаються розтяганню стисканню, тому закон Гука запишемо як E. Після підстановки значення з виразу (.7) маємо: y E. (.8) Підставляючи (.8) послідовно в рівняння (.4), (.5), (.6), одержимо наступне: y E E. d E d yd S 0. Таким чином, статичний момент площі S 0, тому що модуль поздовжньої пружності E та радіус кривизни є ненульовими. Отже, нейтральна лінія при чистому згинанні проходить через центр ваги поперечного перерізу. y E E. d E d yd I 0. Таким чином відцентровий момент інерції I y щодо центральних осей дорівнює нулю, тому осі Х, У є головними центральними осями інерції. При прямому згинанні силова лінія (вісь Y) перпендикулярна нейтральної лінії (вісь Х).. yd E yd E I 0, y y E y d звідси кривизна нейтрального поздовжнього шару визначається виразом:, (.9) EI де y d I осьовий момент інерції перерізу, а EI жорсткість стержня при згинанні. 6
63 Порівнюючи значення кривизни з рівнянь (.8) і (.9) одержимо: Ey. Ey EI EI Формула для визначення нормальних напружень в довільній точці перерізу набуває вигляду: y. (.0) I ma З отриманої формули випливає, що нормальні напруження по висоті перерізу змінюються лінійно. На рис..4 показані розподіли нормальних напружень по висоті для різних за формою перерізів. Максимальні напруження виникають у найбільш віддалених точках від нейтральної лінії при y yma, тобто y ma ma. I Рисунок.4 Умова міцності при згинанні набуває вигляду: 6
64 ma yma ma. (.) I y ma Ця умова використовується для розрахунку перерізів, що мають одну вісь симетрії (рис..4 б). Для перерізів із двома осями симетрії (рис..4 а), I враховуючи, що W осьовий момент опору, зручніше використовувати умову міцності при згинанні у вигляді: Коли поперечна сила ma ma. (.) W y Q не дорівнює нулю, відбувається скривлення поперечних перерізів, і гіпотеза плоских перерізів не дотримується. Як показують дослідження, при відношенні довжини стержня до висоти h поперечного перерізу 8 (що має місце для більшості балок) можна h вважати, що поперечний переріз практично не скривляється, тоді формула (.0) для визначення нормальних напружень при чистому згинанні справедлива і при поперечному згинанні. Приклад. Визначити розміри різних форм поперечних перерізів, якщо згинальний момент в перерізі 80кНм, допустиме напруження при згинанні 60 МПа. З умови міцності (.) осьовий момент опору перерізу ma 800 W 0,5 0 м =500 см Далі розраховуємо геометричні параметри перерізів:. Прямокутний переріз (рис..5 а), для якого повинне задаватися відношення h b (візьмемо h b ). Осьовий момент опору bh W b 500 см, звідки b 750 9см. Висота перерізу 6 h 8см, площа поперечного перерізу bh b 6 см. 64
65 . Прямокутний переріз з відношенням (рис..5 б). Ось- bh b овий момент опору W 500см, звідси 6 4 h b b 000,8 см, h, 4см,,8,4 60 см.. Круглий суцільній переріз діаметром d (рис..5 в). Осьовий d момент опору W 0,d 500 см, звідси діаметр перерізу d 7, d , см; площа см. 4. Кільцевий переріз (рис..5 г). Задаємо відношення діаметрів d c 0,8. Осьовий момент опору для цього перерізу D D 4 4 W ( c ) 0,D ( c ) 500 см Тоді D 0, 4 4 0,8 см, d 0,4 0,8 6, см. D 0,4 Площа перерізу ( c ) ( 0,8 ) 5см Двотавровий переріз (рис..5 д). За ГОСТ підбираємо номер двотавра з найближчим більшим значенням осьового моменту опору до розрахункового. Так, для двотавра 0а: W 58см, 50см. Визначимо коефіцієнт перевитрати матеріалу як відношення окремих площ до площі раціонального поперечного перерізу (двотавр). Скла- i демо таблицю (рис..5), з якої робимо висновок, що раціональним є двотавровий переріз з найменшою витратою матеріалу. 65
66 Рисунок.5... Дотичні напруження при поперечному згинанні Дія в перерізі поперечної сили Q y викликає дотичні напруження, що збігаються по напрямку з нею. Дотичні напруження по ширині перерізу не змінюються та визначаються за формулою Д.І.Журавського: де y відс Q y поперечна сила, що діє в перерізі; QyS b I, (.) перерізу щодо центральної осі X (нейтральної лінії); I осьовий момент інерції b y ширина перерізу на тім рівні у від нейтральної лінії, де визначаються дотичні напруження; S відс відс y c абсолютне значення статичного моменту щодо центральної осі X частини перерізу, що лежить вище (чи нижче) того рівня, де визначаються дотичні напруження. Умова міцності по дотичним напруженням при поперечному згинанні записується у вигляді: ma Q y ma b y S відс ma I [ ]. (.4) 66
67 Таким чином, при поперечному згинанні маємо умови міцності по нормальним та дотичним напруженням. Основним вважається умова міцності по нормальним напруженням, а умова (.4) по дотичним напруженням, як правило, перевіряється. Q y (рис..6). Оскільки... Розподіл дотичних напружень для прямокутного перерізу В перерізі діють момент М х і поперечна сила Q y, ширина перерізу b y b та осьовий момент інерції bh I є постійними величинами, то дотичні напруження змінюються за таким же законом, що і статичний момент відсіченої частини площі S відс. Рисунок.6 Визначаємо дотичні напруження на довільному рівні y. Площа відсіченої відс h bh y частини перерізу b y, положення її центра h h y h h y h y ваги y c. 4 4 h Статичний момент відсіченої частини площі: відс відс bh y h y bh y Sх yc. h 4 h 8 h Таким чином, дотичні напруження змінюються за законом квадратичної параболи. Максимальні дотичні напруження виникають на 67
68 нейтральній лінії, де нормальні напруження дорівнюють нулю. Для визначення ma необхідно обчислити статичний момент половини площі перерізу відс bh S ma. Тоді маємо: 8 Qy bh 8 Qy Qy ma. b bh bh... Розподіл дотичних напружень для двотаврового перерізу В перерізі діють згинальний момент М х та поперечна сила Q y (рис..7). Використовуючи вираз (.) для дотичних напружень, визначимо їхні значення в характерних точках перерізу. З достатнім ступенем точності можна замінити реальну форму полиці і стінки на прямокутники. Рисунок.7 Точка : 0 S відс (вище рівня відсічена площа відсутня)., тому що 0 Точки,. Ці точки мають однакову координату y, але належать полиці та стінці одночасно, тобто різній ширині b =b; b =d. Тому в місці переходу полки в стінку виникає скачок дотичних напружень. Точка (приналежна полиці): 68
69 Qy h t Qyt h t bt. b I I Точка (приналежна стінці): Qy h t bt. d I Точка 4: h Qy t h t h відс QyS bt d t ma 4 bi d I. відс S ma статичний момент щодо центральної осі половини площі перерізу (для стандартних профілів приведений у таблицях сортаменту). Графік розподілу дотичних напружень приведено на рис Порядок виконання проектувального розрахунку при згинанні. З умови міцності по нормальним напруженням визначаємо осьовий момент опору поперечного перерізу, тобто W, та проек- ma [ ] туємо переріз.. Перевіряємо переріз по дотичним напруженням. Якщо [ ] то розрахунок закінчений. Якщо [ ] ma 69, ma (перевищення більш 5%), то розміри перерізу визначаються з умови міцності по дотичним напруженням. Приклад. Визначити розміри двотаврового поперечного перерізу балки (рис..8), якщо допустиме нормальне напруження [ ] 50 МПа, дотичне [ ] 00 МПа.. Визначаємо реакції: Fa F a) R 0, R 45кН; B ( B B ( a) Fa R 0, R F 45кН. Перевірка: F F F R R 0. y B
70 . Розбиваємо балку на три ділянки та записуємо для поточного перерізу на кожній ділянці вирази для Q і : 0 z a ; Q y F 0кН; F z ; y 0 z ; Q F R 5кН; F( z R z ; a) 0 z a ; Q y F 0 кн; F z. Обчислюємо Q y і в характерних перерізах та будуємо епюри.. З побудованих епюр видно, що небезпечними є перерізи на обох опорах (де =4 кнм), та будь-який переріз на консолях (де ma Q y ma =0 кн). 4. З умови міцності по нормальним напруженням визначаємо осьо- ma 4 0 вий момент опору: W 0,6 0 м = 60см. [ ] По таблицях ГОСТ обираємо двотавр 8а, для якого 59см, що незначно менше розрахункового значення. W y Рисунок.8 Інші необхідні для розрахунку параметри двотавру: А 5, 4см, I 40см 4 ; d 5, мм, S 89, 8 см. відс ma 70
71 5. Перевіряємо виконання умови міцності по дотичним напруженням: відс Q 6 ys ma 00 89,8 0 6 ma 6,9 0 d I 8 5, Па =6,9 МПа < []. Умова міцності виконується і розрахунок закінчено. Приклад. Для даної схеми навантаження дерев'яної балки перекриття (рис..9) визначити розміри прямокутного перерізу, якщо відношення h сторін прямокутника ; допустиме нормальне напруження b [ ] 0 МПа, дотичне [ ], 5МПа. Оскільки навантаження симетричне, опорні реакції однакові і дорівнюють половині зовнішнього навантаження, тобто R R 40кН. B. Визначаємо поперечні сили та згинальні моменти по ділянкам. Перша ділянка: 0 z a ; Q y F 40 кн; F z. Друга ділянка: 0 z ; Q F R 0; R z F z a) 40z 40 a 40z 40 a 4 кнм. ( Третя ділянка: y 0 z а ; Q y F 40 кн; F z. З епюр (рис..9) видно, що небезпечними є перерізи на обох опорах, де Q y та одночасно приймають максимальні значення ( Qy ma 40 кн, ma 4 кнм). 7 Рисунок.9
72 . З умови міцності по нормальним напруженням знаходимо осьовий момент опору перерізу: ma 4 0 0,4 0 6 W м = 400 см. [ ] 0 0 bh Як відомо, для прямокутника W b 400см, 6 звідки обчислюємо розміри його сторін та площу: b 400 8,4 см, h b 6, 8см, bh b 8,4 4см. Перевіримо виконання умови міцності по дотичним напруженням. Максимальне дотичне напруження для прямокутного перерізу дорівнює: Q y ma ma 4, Па = 4, МПа, що 4 0 перевищує допустиме напруження =,5МПа умова міцності не виконується. Визначаємо розміри поперечного перерізу з умови міцності по дотичним напруженням:, звідки знаходимо площу поперечного перерізу: ma Q y ma Q y ma м = 40 см. [ ],5 0 Площа bh b 40см, звідки ширина перерізу: b 0 см, а висота h см. Таким чином, умова міцності по дотичним напруженням виявилась більш строгою, тому остаточно обираємо такі сторони прямокутника: h см, b см... Розрахунково-проектувальне завдання Для засвоєння матеріалу розділу «Згинання прямолінійних стержнів» студенти повинні виконати навчальне завдання. Для цього необхідно: вивчити теоретичний матеріал відповідного розділу курсу; проаналізувати вихідні дані і постановку задачі і намітити план її виконання;
73 намалювати схему балки, записати необхідні для рішення задачі формули і рівняння (рівняння статичної рівноваги і т.д.). оформити задачу в чернетці і, у разі потреби, проконсультуватися у викладача. Розрахунки необхідно робити в загальному виді з проміжними викладеннями в звичайних чи десяткових дробах, зберігаючи усюди дві значущі цифри. Для побудови епюр внутрішніх силових факторів, напружень і переміщень необхідно правильно вибрати масштаб по координатних осях, проставити позначення відповідного параметра і його розмірність, а потім по необхідному числу крапок побудувати графік. Завдання підлягає заліку при виконанні наступних умов: здано чистовий варіант розрахунково-проектувального завдання і дані правильні відповіді на контрольні питання; вирішено контрольні задачі на консультаціях.... Склад та порядок виконання розрахунковопроектувального завдання Студенти повинні виконати чотири розрахункові задачі. Схеми навантаження балок наведені в додатку., а величини зовнішніх сил та геометричні розміри балок, межа текучості матеріалу балки, коефіцієнт запасу міцності n т у додатку.. При виконанні завдання необхідно:. Побудувати епюри внутрішніх поперечних сил і згинальних моментів до усіх розрахункових схем балок.. Для четвертої розрахункової схеми підібрати згідно з умовою міцності за нормальними напруженнями ряд простих перерізів та зробити порівняльний аналіз ступеня їх раціональності. План розвязання ) Відповідно до заданого варіанта накреслити розрахункові схеми балок разом з їх навантаженням, додержуючись певного масштабу. ) Для кожної балки визначити опорні реакції, скласти вирази і підрахувати внутрішні зусилля Q y і на усіх ділянках, накреслити їх епюри та перевірити відповідність епюр до диференціальних співвідношеннь між силовими факторами при згині. т 7
74 ) Для кожної балки знайти небезпечний переріз (де діє максимальний за модулем згинальний момент ). ma 4) Обчислити допустиме напруження т. n 5) Для розрахункової схеми балки 4 визначити осьовий момент опору перерізу W з умови міцності по нормальним напруженням та підібрати розміри наступних перерізів (див. рис..5): прямокутника із співвідношенням сторін h / b ; прямокутника із співвідношенням сторін h / b 0, 5; кола; кільця, у якому c d / D 0. 8; двотавра. 6) Обчислити площу перерізів. Одержані результати подати у вигляді таблиці. Для двотаврової балки побудувати епюри розподілу нормальних і дотичних напружень у небезпечних перерізах з максимальними значеннями внутрішніх зусиль.... Приклад виконання завдання... Послідовність виконання завдання Будуємо епюри внутрішніх силових факторів для чотирьох балок свого варіанту завдання. Визначаємо небезпечний переріз, в якому діє максимальний за модулем внутрішній момент згину. т ma Умова міцності за нормальними напруженнями для перерізів, які симетричні відносно нейтральної лінії має вигляд: ma. W Звідси знаходимо осьовий момент опору перерізу: ma W, де допустиме напруження визначається за формулою: т. n т 74
75 Підбір необхідних розмірів перерізів балки виконується таким чином: для двотавра номер профілю визначається з порівняння знайденого моменту опору із даними сортаменту (ГОСТ 89-89) для прямокутника осьовий момент опору визначається за розмі- bh рами сторін h та b : W, де h бік прямокутника, перпендикулярний нейтральній осі 6 X. Позначимо h k b, ( k =; 0,5 ), тоді b h k і W h 6 k звідки h 6kW, а площа перерізу дорівнює b h; d 0,d, тоді d 0W, а площа перері- зу для кола d. 4 W D 4 4 для кільця с 0,D с W, де с d ; D d, D внутрішній і зовнішній діаметри кільця відповідно. Площа кільця D с. 4 Графіки розподілу нормальних і дотичних напружень треба збудувати тільки для балки двотаврового перерізу. Епюри нормальних напружень визначити у перерізі, де діє, а розподіл дотичних напружень ma знайти для перерізу з максимальною за модулем поперечною силою Q yma. На епюрі зазначити зони розтягу та стиску, а на епюрі напрям вектора дотичних напружень. Підрахунок дотичних напружень провести за формулою Д.І.Журавського (.). Визначити дотичні напруження в характерних точках перерізу: найбільш віддалених від нейтральної осі; що лежать на стику полки двотавра зі стінкою; що лежать на нейтральній осі перерізу. 75
76 ... Зразок виконання завдання 4 76
77 77 Розрахунок на міцність балки 4:. Визначення реакцій опор: 50 кн. 0)/ 0 4 (0 0 ; 4 0 ; 0 кн ; 0)/ 0 0 ( 0 ; 0 ; B B B R q R F R R q F Перевірка: ; ; 0 q F R R F B iy. Визначення поперечних зусиль Q y та моментів згину : 0 кhм ; 0; ; ) ( 0 кh ; ) ( м 0 м 0 z z y z F z F z Q z ;,5 кhм.5 0,5 50,5 0,5 м ; ) / ( 0 ; ) ( ) ( ) ( 0 ; ; 0 кнм 0 ; ) ( ) ( ) ( 0 кh ; кh ; 50 0 ; ) ( ) ( м м,5м м м м м z y z z z y z y y q q R F z z q R F z Q z z q z R z F z Q Q z q R F z Q z 0 кhм. 0; ; ) ( 0 кh ; ) ( м 0 м 0 z z B B y z R z R z Q z. Підбір перерізів з умови міцності: ; МПа 00,5 00 ] [ ] [ ]; [ т т ma ma ma n σ ; W W σ X
78 W см Для двотавра згідно з додатком 4 приймаємо Ι 6: I 87 см 4, W 09 см, 0, см, S ma 6,см, h 6 см, d 5 мм, t 7,8 мм, b 8 мм. Як відомо, для прямокутного перерізу bh W, тоді 6 при відношенні сторін прямокутника h b h, W h h ,6 см, 00 см Для прямокутника з відношенням сторін h b h, W h h ,7 см,, b 5, см, b h 56 см 00 см, b,4 см,. bh 90 см. Для круга d W d 0,d см, см, d 78,5 см. 4 78
79 Для кільця W D D ( с 4 ) 0, D ( с ) 00 см 0 00 см, d с D 0,8 9,6 см, 4 ( 0,8 ) с 40 см D. 4 Зробимо порівняльний аналіз перерізів: 4, А i,см 0, ,5 40 А i /А min,8 4,5,9 4. Визначимо нормальні та дотичні напруження у двотаврі ma отс Qy S y ;,5 0 ; b I, МПа ; МПа ; 870 h bt ; отс t S y( ) 7, , ,4 0 0 МПа ; , , , МПа. 79
80 Додаток. Розрахункові схеми 80
81 Продовження додатка. 8
82 Продовження додатка. 8
83 Продовження додатка. 8
84 Продовження додатка. 84
85 Продовження додатка. 85
86 Варіант Додаток. Вхідні дані F F F q q кн кн кнм м n т a b c ,7,5,0, ,4,0,5, ,5,5,5, ,6,5,5, ,8,0,0, ,0,5,0, ,8,5,0, ,6,0,0, ,5,0,5, ,4,5,5, ,6,5,0, ,4,5,0, ,5,0,5, ,6,5,, ,8,5,0, ,7,5,0, ,4,0,5, ,5,5,5, ,6,5,5, ,8,0,0, ,0,5,0, ,8,5,0, ,6,0,0, ,5,0,5,5 м Примітка. Матеріал сталь Ст. 0: т = 00 МПа. 86
87 Додаток. Основні поняття, позначення, формули, формулювання та правила з теми «Згинання стержнів» Позначення та Одиниця виміру Назва формули Q y Fiy Н (ньютон) внутрішня поперечна сила Нм внутрішній згинальний момент i y Па (паскаль) нормальне напруження I ma ma Па W QyS відс Па b y I умова міцності за нормальними напруженнями умова міцності за дотичними напруженнями I W y I y ma d м 4 м осьовий момент інерції осьовий момент опору Поперечна сила в даному перерізі Q y чисельно дорівнює алгебраїчній сумі проекцій на нормаль (вісь Y) до осі стержня сил, розташованих по одну сторону від перерізу (всіх однобічних сил), та утворює заміну діі відкинутої частини на залишену. Згинальний момент в даному перерізі z чисельно дорівнює алгебраїчній сумі моментів щодо поперечної осі перерізу сил, які розташовані по одну сторону від цього перерізу (всіх однобічних сил). Правила знаків : 87
88 Контрольні питання. Що називається згинанням балок?. Класифікація згинання.. Як знайти внутрішній згинальний момент у довільному перерізі балки? 4. Правило знаків для згинального моменту. 5. Як знайти внутрішню поперечну силу в довільному перерізі балки? 6. Правило знаків для поперечної сили. 7. Диференційні залежності при згинанні. 8. Правила побудови та перевірки епюр внутрішніх силових факторів. 9. Як визначити нормальні напруження при чистому згинанні? 0. Що таке нейтральна лінія і де вона знаходиться?. У яких точках перерізу виникають максимальні нормальні напруження?. Умова міцності по нормальним напруженням при згинанні.. Яку форму мають раціональні перерізи при згинанні? 4. Як визначити дотичні напруження при поперечному згинанні? 5. У яких точках перерізу виникають максимальні дотичні напруження? 6. Умова міцності по дотичним напруженням при згинанні. 88
89 . КРУЧЕННЯ В даному розділі посібника розглядаються два основних види деформації стержня: зсув (зріз) та кручення. Зсув або зріз виникає тоді, коли зовнішні сили зміщують два паралельні плоскі перерізи стержня один відносно одного при незмінній відстані між ними. Кручення виникає при дії на стержень зовнішніх сил, які утворюють момент відносно осі стержня. Деформація кручення супроводжується поворотом поперечних перерізів стержня один відносно одного навколо його осі... Зсув Деформація зсуву відбувається тоді, коли з шести компонент головного вектора сил та головного вектора моменту внутрішніх зусиль не дорівнюють нулю тільки поперечні сили Q або Q.... Основні поняття та визначення Деформація зсуву виникає при дії на площадках виділеного елемента тільки дотичних напружень. Такий напружений стан називається чистим зсувом (рис..). х у Рисунок. 89
90 Деформація зсуву може бути отримана (приблизно), коли на стержень діють дві рівні по величині і протилежно спрямовані сили, перпендикулярні до осі стержня. Прикладом такої дії сил на брус може бути різання ножицями металевих прутків (рис.. а). Рисунок. Через те, що між діючими силами існує деяка відстань, то, звичайно, деформація зсуву супроводжується іншими видами деформацій, найчастіше деформацією згинання (рис.. б). Розглянемо короткий прямокутний елемент, затиснений одним кінцем, під дією сили Q (рис..). Рисунок. Дія сили Q викликає зсув елемента. Так як відстань між площинами, що зсуваються, мала, то виникаючим згинальним моментом зневажаємо. З рис.. неважко переконатися, що BB S. Величина S називається абсолютним зсувом. При деформації прямокутного елемента прямі кути змінюються на 90
91 S величину, тангенс якого tg. Через малість кута tg, тоді a S називають відносним зсувом (кут зсуву, зрушення), що являє a собою відношення абсолютного зсуву S до відстані a між площинами. Використовуючи метод перерізів (рис..4 а), визначимо напруження, що виникають при зсуві. Візьмемо переріз і розглянемо рівновагу відсіченої частини (рис..4 б), для чого складемо рівняння F 0: yi Q d 0. Це рівняння не може бути вирішене без геометричного аналізу деформування (невідомі величина та закон зміни ). Рисунок.4 При розрахунках на зсув умовно приймається рівномірний закон розподілу по перерізу, тобто const. Тоді: Q, (.) з де з площа зрізу. Як і при будь-якому розрахунку опору матеріалів напруження в матеріалі повинні зіставлятися з напруженням, що допускається (допустиме напруження), тобто умова міцності на зріз має вигляд: Q. (.) Допустиме напруження приймається рівним :,5 0, 6 з 9 0. Дослідне вивчення зсуву в матеріалах проводиться на спеціальних тонкостінних трубках, що навантажуються крутним моментом до руйнування. У результаті цього одержують діаграму зсуву, що для пластично-
92 го матеріалу має вид (рис..5). По діаграмі можна визначити характеристики міцності матеріалу при зсуві (зрізі). Рисунок.5 Межа (границя) пропорційності пц матеріалу при зсуві це найбільше напруження, до якого виконується закон Гука (точка ). Межа (границя) текучості т це найменше напруження, при якому відносний зсув зростає при практично постійному навантаженні (т. ). Межа (границя) міцності в при зсуві це максимальне напруження в матеріалі, при якому не настає руйнування (точка ).... Закон Гука при зсуві При центральному розтяганні стисканні між нормальним напруженням, відносною деформацією та модулем подовжньої пружності Е існує залежність E, що називається законом Гука при розтяганні стисканні. Аналогічна залежність, як показують експерименти, також існує між дотичним напруженням, відносним зсувом та модулем зсуву G, тобто закон Гука при зсуві: G. (.) Зв'язок трьох пружних постійних для ізотропного матеріалу (модуля поздовжньої пружності E, модуля зсуву G і коефіцієнта Пуассона ) визначається залежністю //: E G (.4). Таким чином, модуль поздовжньої пружності E, модуль зсуву G і коефіцієнт Пуассона характеризують пружні властивості матеріалу. 9
93 .. Розрахунки на міцність і жорсткість при крученні... Основні поняття та визначення Розповсюдженим стержневим елементом конструкцій машин, що працюють на кручення, є вал. Якщо навантаження на прямолінійний стержень (вал) складається тільки з моментів, площини дії яких перпендикулярні до осі стержня, то із шести внутрішніх зусиль та моментів у довільному перерізі залишається лише один внутрішній крутний момент. Відзначимо, що крутний момент, наприклад, виникає у валах, що обертаються з кутовою швидкістю n [об/хв] та передають потужність K [квт] розподільні та передавальні вали зубчатих, пасових передач. У цьому випадку на валу в місцях посадки зубчатих коліс, шківів виникає зовнішній зосереджений крутний момент, кhм : 9 к К к 9, 55. n Визначення внутрішніх крутних моментів та побудова епюр ґрунтуються на методі перерізів: внутрішній крутний момент к z у даному перерізі чисельно дорівнює алгебраїчній сумі зовнішніх крутних моментів, що розташовані по один бік від перерізу. Правило знаків: Зовнішній крутний момент вважається додатним, якщо при спостеріганні з боку перерізу вздовж осі вала він намагається обертати відсічену частину проти годинникової стрілки. Сформулюємо правила для побудови і перевірки правильності епюр крутних моментів:. При побудові епюр необхідно перевіряти рівновагу вала, тобто zi 0.. На ділянці з інтенсивністю розподіленого моменту m const епюра лінійна, а якщо 0 по довжині вала є кусоч- к m, то епюра к но-постійною по ділянках вала, тобто const. кi. У точці прикладення зосередженого моменту на епюрі к спостерігається стрибок на величину зовнішнього моменту. Експериментально встановлено, що при дії на вал двох протилежно спрямованих крутних моментів (рис..6) одні перерізи вала будуть к
94 повертатися щодо інших навколо осі, у той час як довжина вала залишається незмінною. Рисунок.6 Якщо закручувати вал аж до руйнування і представити графічно залежність крутного моменту від кута закручування то одержимо діаграму кручення, що у випадку пластичного матеріалу має вид діаграми, показаної на рис..7. На цій діаграмі також, як і на діаграмі розтягання, можна відзначити ряд характерних точок, що відповідають характеристикам матеріалу при крученні: точка відповідає максимальному значенню моменту, до якого зберігається лінійна залежність між навантаженням к пц і кутом закручування ; у точці спостерігається явище текучості матеріалу при крученні, коли при практично постійному моменті М т збільшується кут закручування; точка відповідає максимальному значенню моменту, при якому відбувається руйнування зразка. ma Рисунок.7 94
95 ... Дотичні напруження при крученні стержнів круглого та кільцевого перерізів На валу з круглим перерізом (рис..8 а) відзначимо утворюючі (меридіани) та поперечні перерізи (паралелі) та розглянемо експериментальні результати його кручення: Рисунок.8. При крученні поперечні перерізи стержня повертаються навколо його осі і відносно один одного.. Утворюючі повертаються на один і той же кут. Прямокутники перетворюються в паралелограми, прямі кути змінюються, як і у випадку чистого зсуву (рис..8 а). Це свідчить про те, що виділений елементарний обсяг будь-якого шару вала знаходиться в умовах чистого зсуву.. При крученні стержня круглого перерізу дотримується гіпотеза плоских перерізів: переріз плоский і нормальний до осі перед деформуванням залишається плоским і нормальним до осі в процесі деформівання. 4. Відстані між перерізами в процесі деформації не змінюються ( a const ), це підтверджує відсутність у перерізі нормальних напружень. 5. Довжина і прямолінійність радіусів перерізів не порушується, тобто дотичні напруження у будь-якій точці перерізу перпендикулярні радіусу (рис..8 б). Розглянемо стержень діаметром d, довжиною, що навантажений моментом (рис..9 а). На відстані z від правого краю виділимо елемент довжиною dz і розглянемо його рівновагу (рис..9 б). Вважаючи, що початок координат співпадає з центром ваги О перерізу, запишемо рівняння статичної рівноваги елементу dz : z к d 0. (.5) 95
96 Рисунок.9 Проведемо геометричний аналіз деформацій при крученні. Для цього з нескінченно малої ділянки вала довжиною dz виділимо трубку, перерізом якої є нескінченно тонке кільце товщиною d (рис..9 в). Умовно вважаємо, що лівий переріз нерухомий. Правий переріз повернеться навколо осі z на кут d, причому назвемо абсолютним кутом закручування. Утворюючі ab і cd на бічній поверхні циліндра переміщаються в положення ab і cd відповідно, зміщаючись на кут зсуву. Обчислимо довжину дуги b b (рис..9 в), розглядаючи спочатку криволінійний трикутник аbb : bb dz tg dz, а потім трикутник Оbb : bb d d (для малих кутів tg ). Зневажаючи не- скінченно малими величинами другого порядку, одержуємо d dz d, звідки. dz Введемо поняття відносного кута закручування: d, (.6) dz тоді : 96
97 . (.7) Так як в нескінченно малому елементі abcd виникає напружений стан чистого зсуву (рис..9 г), то в межах малих деформацій виконується закон Гука при зсуві: G. (.8) З виразів (.7), (.8) одержимо: G. (.9) Остання залежність виражає закон Гука при крученні, на підставі якого можна зробити висновок про те, що дотичні напруження вздовж радіуса переріза змінюються по лінійному закону. Підставимо залежність (.9) у рівняння (.5) та одержимо наступне: к G d к G d к де d Ip полярний момент інерції перерізу. Це дає можливість визначити відносний кут закручування: Величина G I p 0, к. (.0) G I G Ip називається жорсткістю вала при крученні. З виразів (.9), (.0) одержуємо формулу для визначення дотичних напружень при крученні вала круглого чи кільцевого перерізів: к. (.) I З рівняння (.6) з урахуванням виразу (.0) кут закручування дорівнює: p p Якщо к, к dz dz. G I 0 0 p G Ip є постійними величинами, то абсолютний кут закручування вала можна обчислити за формулою: к. (.) G I p 97
98 ... Розрахунок на міцність при крученні стержня круглого та кільцевого перерізу З рівняння (.) випливає, що дотичні напруження по радіусу перерізу розподіляються лінійно, тому максимальні дотичні напруження виникають у крайніх точках перерізу, де ma I p к : ma ma. (.) Епюри дотичних напружень для круглого та кільцевого перерізів наведені на рис..0. Рисунок.0 З огляду на те, що величина 98 I p ma W p є полярним моментом опору перерізу, умова міцності при крученні запишеться у вигляді: к, (.) W де т ma т допустиме дотичне напруження ( т n p границя текучості матеріалу, nт коефіцієнт запасу міцності). Значення полярного моменту опору круглого перерізу дорівнює: а для кільцевого перерізу: W d p 0, d, 6
99 4 4 c 0, D c D Wp d, де с. 6 D Діаметр вала круглого перерізу обчислюється з умови міцності (.) за формулою: 6 к к d, а зовнішній діаметр кільцевого перерізу: D 6 0, к к 4 4 c 0, c..4. Розрахунок на жорсткість при крученні стержня круглого та кільцевого перерізу Крім розрахунку на міцність вали розраховуються на жорсткість. Умова жорсткості має вигляд: ma к G I p., (.) де допустимий відносний кут закручування, що вимірюється у [рад/м]. Полярний момент інерції для круглого перерізу визначається як а для кільцевого: 4 I 4 d p 0, 4 d, c 0, D c D Ip. Тоді, з умови жорсткості, діаметр вала круглого перерізу дорівнює: G 4 к 4 к d. 0, G Для кільцевого перерізу зовнішній діаметр визначається як: D 4 G к к с 0, G с. 99
100 Приклад З умов міцності та жорсткості визначити діаметр вала круглого перерізу (рис..) при таких значеннях крутних моментів: 0,6 кhм ; 0,8 кhм ;,0 кhм ; 4 0,6 кhм. Рисунок. 0 МПа, допустимий відносний кут закру- Допустиме напруження чування 0,5 град/м Модуль пружності сталі при зсуві 0,5 /80 4,4 0 - G 0,80 МПа. 5 рад/м. З епюри крутних моментів визначаємо небезпечну ділянку, де діє М 0,6 0,8,4. найбільший момент: кhм d міцн. кр ma Доберемо діаметр вала з умови міцності: 6 к 0, к,4 0 0, 00 Тепер доберемо діаметр вала з умови жорсткості: 4 d жорст. 0, 0,8 0 4 к G 4, ,4 0 6 к 0, G 0,0705 м 70,5 мм. 0,0794 м 79,4 мм. міцн. жорст. Із двох діаметрів слід вибрати більший, знайдений з умови жорсткості та округлити його в більшу сторону до найближчого стандартного значення: d ma d ; d 80 мм. При цьому, максимальні дотичні напруження будуть на другій ділянці валу: ma W кр p,4 0 0,80 0 9,67 МПа. 00
101 ..5. Кручення стержнів прямокутного перерізу При крученні стержнів некруглого перерізу (прямокутних, трикутних, еліптичних, прокатних, тонкостінних і ін.) гіпотеза плоских перерізів не виконується. Поперечні перерізи не залишаються плоскими, окремі точки виходять із площини перерізи піддаються депланації. При крученні стержня постійного перерізу крутними моментами, прикладеними до вільних його кінців, депланація всіх поперечних перерізів виявляється однаковою. При рівномірній депланації нормальні напруження в поперечних перерізах не виникають. Такий вид кручення називається чистим (вільним) крученням, при якому величини і характер розподілу дотичних напружень в усіх перерізах однаковий. Рішення задачі про чисте кручення некруглих стержнів методами опору матеріалів неможливо. Точні рішення задач про кручення стержнів некруглого перерізу отримані в теорії пружності. Остаточні формули для визначення максимальних дотичних напружень ma, відносного кута закручування і абсолютного кута закручування стержня довжиною, як і для стержнів круглого перерізу, мають вигляд: де к к к ma ; ;, W G I G I W к момент опору на кручення, к к к I момент інерції на кручення. Розподіл дотичних напружень для прямокутного перерізу приведене на рис... Найбільші напруження виникають на серединах довгих сторін перерізу (точки А и В). Дотичні напруження на серединах коротких сторін (точки С,D) визначаються за формулою. Момент опору на кручення прямокутного перерізу мають вигляд: к ma к ma W і момент інерції на кручення I к для Wк hb, Iк hb. Коефіцієнти,, визначаються в залежності від відношення довгої сторони h прямокутника до короткої сторони b і наведені в таблиці.. 0
102 Рисунок. Умова міцності при крученні стержня прямокутного перерізу має вигляд: к. W ma Умова жорсткості при крученні приймається для відносного кута закручування: к G I або для абсолютного кута закручування: к к, к G I к. 0
103 Таблиця. Кручення призматичного стержня прямокутного перерізу (таблиця коефіцієнтів,, ) h b,00 0,08 0,4,000,05 0, 0,47 0,98,0 0,4 0,54 0,96,5 0,7 0,60 0,946,0 0,9 0,66 0,9,5 0, 0,7 0,96,0 0, 0,77 0,90,5 0,5 0,8 0,89,40 0,7 0,87 0,879,45 0,9 0,9 0,869,50 0, 0,96 0,859,55 0, 0,00 0,850,60 0,4 0,04 0,84,65 0,6 0,07 0,84,70 0,7 0, 0,87,75 0,9 0,4 0,8,80 0,40 0,7 0,85,85 0,4 0,0 0,809,90 0,4 0, 0,804,95 0,45 0,6 0,800,00 0,46 0,9 0,795,0 0,48 0,4 0,787,5 0,5 0,40 0,778,50 0,58 0,49 0,766,75 0,6 0,57 0,759,00 0,67 0,6 0,75,5 0,7 0,69 0,750,50 0,75 0,7 0,748,75 0,79 0,77 0,746 4,00 0,8 0,8 0,745 5,00 0,9 0,9 0,74 6,00 0,98 0,98 0,74 7,00 0,0 0,0 0,74 8,00 0,07 0,07 0,74 0, 0, 0,74 0
104 .. Статично невизначувані системи при крученні Статично невизначуваною називається кінематично незмінна система, у якої число невідомих зусиль, включаючи реакції опор і внутрішні силові фактори (крутні моменти), більше числа рівнянь статики, які можна скласти для даної задачі. Порядок рішення статично невизначуваних задач розглянемо на прикладі. Приклад Розкрити статичну невизначеність стержня (рис..), побудувати епюру крутних моментів та визначити параметр d круглих поперечних перерізів стержня з умови міцності. Статична сторона задачі Складемо єдине можливе рівняння рівноваги з двома невідомими,, тому задача є один раз статично невизначеною: C B 0. (.4) z C B C B Рисунок. 04
105 C Геометрична сторона задачі Для розкриття статичної невизначуваності необхідно скласти одне рівняння спільності переміщень. Умовно відкинемо праве затиснення, а його дію замінимо моментом, при цьому задача стає статично визначуваною. Момент визначається з умови, що поворот правого торцевого перерізу щодо лівого під дією моментів C,, дорівнює нулю: 0. (.5) CВ C C Фізична сторона задачі Скористаємося законом Гука при крученні для кутів закручування. Момент закручує в напрямку проти руху часової стрілки весь стержень; момент в напрямку за рухом часової стрілки частину стержня між лівим затисненням та місцем розташування ; момент проти руху часової стрілки тільки першу ділянку стержня: 4 C p C а C а, G I G I p а а, (.6) G I G I G I p p а, 4 d де Ip D d, Ip 6 6 Ip полярні моменти інерції круглого перерізу першої та другої половини стержня. Спільне рішення рівнянь Підставимо (.6) в (.5): СВ С З обліком того, що а С а а G I G I G I p p p 4 p а а G I G I p p C 0. 4,, а Ip 6 Ip, одержимо: 05
106 звідки: 7 С. 7 С , З рівняння рівноваги (.4) знаходимо момент в лівому затисненні: 7 58 B С. 7 7 Побудова епюри крутних моментів Обчислюємо значення внутрішніх крутних моментів по ділянках стержня, які показані на рис..: 7 к z С ; 7 0 к z С ; 7 58 к z B. 7 Перевіряємо правильність рішення задачі, для чого обчислимо кут повороту правого торцевого перерізу щодо лівого затиснення, який повинен дорівнювати нулю: СВ СВ 7 а 7GI p 0 а 0 а 7GI 7G 6I p p 58 а 7G 6I а а 7G 6Ip 7G 6Ip p Визначення розмірів поперечного перерізу Обчислення параметру d поперечного перерізу проводимо в найбільш напруженій ділянці стержня. Для цього здійснюємо порівняльний аналіз найбільших дотичних напружень на чотирьох ділянках згідно виразу (.): 7 -а ділянка діаметром d : ma ; 7W 06 p
107 0 -а ділянка діаметром d : ma ; 7W -я ділянка діаметром D : p 0 0,5 ma ; 7W 7 8W 7W 58 7,5 4-а ділянка діаметром D : ma. 7W 7W У вищенаведених виразах полярні моменти опору перерізів окремих ділянок стержня дорівнюють: W p p p d D d, Wp 8 8Wp Порівнюючи результати аналізу, робимо висновок, що найбільш навантаженою є друга ділянка стержня діаметром d. 0 6 З умови міцності (.) к ( z) ma 7, W d одержимо: d р p p p..4. Розрахунково-проектувальне завдання При вивченні розділів Зсув та Кручення в курсі Опір матеріалів ставиться мета навчити студентів основам інженерного розрахунку елементів конструкцій машин і механізмів на міцність і жорсткість з урахуванням умов роботи, властивостей матеріалів та різноманітних типів поперечних перерізів. Для кращої організації і більш ефективної самостійної роботи студентів, згідно з вимогами програми курсу, студентам пропонується до виконання задачі по темі Розрахунки на міцність та жорсткість при крученні. Виконуючи цю роботу, студент практично знайомиться з методами обчислення крутних моментів, побудови епюр моментів та напружень, визначення розмірів та форми поперечного перерізу для різноманітних схем, що забезпечують умови міцності та жорсткості. 07
108 .4.. Склад розрахунково-проектувального завдання Розрахунково-проектувальне завдання складається з трьох етапів:. Рішення запропонованих викладачем задач для певних варіантів розрахункових схем і вихідних даних, оформлення їх за вимогами кафедри Опору матеріалів.. Написання контрольних робіт.. Захист завдання. Захист включає в себе пояснення методів і принципів розв'язання задач і відповідь на контрольні теоретичні запитання. Кількість та об єм цих запитань визначається викладачем індивідуально для кожного студента. Мета роботи проведення проектувального розрахунку для визначення розмірів поперечного перерізу з умов міцності та жорсткості. Для цього задані:. Схема заданої системи з вказівкою довжин дільниць і зовнішнього навантаження.. Форма і співвідношення розмірів поперечного перерізу., допустимий відносний кут. Допустиме дотичне напруження закручування, модуль зсуву матеріалу G. Завдання складається з двох обов язкових для рішення задач: Задача : З умов міцності та жорсткості обрати розміри поперечних перерізів (діаметр круглого і кільцевого валів) для статично визначуваної системи. Порівняти їхні ваги. Варіанти розрахункових схем наведені в додатку., а чисельні дані в таблиці Д.. Задача : Для заданої статично невизначуваної системи з послідовним розташуванням ділянок стержня з розрахунку на міцність визначити розміри поперечних перерізів на всіх ділянках стержня і побудувати епюру кутів закручування, порівнявши їх значення з допустимим значенням кута закручування. В разі потреби відшукати розміри поперечних перерізів стержня з умови жорсткості. Варіанти розрахункових схем наведені в додатку., а чисельні дані в таблиці Д Порядок виконання завдання Задача. Для статично визначуваного валу, який навантажено крутними моментами, з умови міцності та жорсткості визначити розміри поперечного перерізу. 08
109 . Виписати для заданого варіанту чисельні дані. В певному масштабі накреслити схему заданої системи з зазначенням її лінійних розмірів і зовнішніх навантажень.. Визначити значення зовнішніх крутних моментів на шківах.. Побудувати для заданої схеми епюри крутних моментів. 4. Визначити діаметр суцільного круглого валу з умови міцності. 5. Розташувати шківи раціонально і для цього випадку побудувати епюру крутних моментів. 6. Визначити розміри поперечного перерізу (діаметри суцільного і трубчастого валів) для раціонального розташування шківів з умов міцності та жорсткості. 7. Обчислити дотичні напруження на різних ділянках валу відповідно зі значеннями епюри крутних моментів і побудувати епюру дотичних напружень для вала круглого перерізу. 8. Порівняти ваги валу для заданої системи і валу при раціональному розташуванні шківів. Також для раціонального розташування шківів порівняти ваги валів суцільного і трубчастого перерізів. 9. Побудувати епюру кутів закручування раціонального суцільного валу. 0. Побудувати епюри дотичних напружень для різних видів поперечних перерізів. Задача. Для статично невизначуваної системи при крученні з умови міцності та жорсткості визначити розміри поперечного перерізу.. Для заданого варіанту завдання виписати чисельні дані і в певному масштабі накреслити схему заданої системи з зазначенням лінійних розмірів і зовнішніх навантажень.. Встановити ступінь статичної невизначуваності системи.. Визначити геометричні характеристики круглого, кільцевого та прямокутного поперечних перерізів через значення параметру d діаметру круглого перерізу. 4. Статичний аспект задачі. Скласти і записати рівняння статики. Замінити початкову систему статично визначуваною системою, уявно відкинувши одну з опор і замінивши її дію крутним моментом. 5. Геометричний аспект задачі. Записати рівняння сумісності кутів закручування всіх ділянок стержня кут повороту правого перерізу відносно лівого перерізу дорівнює нулю. 09
110 6. Фізичний аспект задачі. Використати закон Гука для запису виразів кутів закручування. 7. Знайти крутні моменти на опорах з рішення системи рівнянь, що складені в п.5, п Побудувати епюру крутних моментів. 9. З умови міцності визначити розміри поперечних перерізів. 0. Побудувати епюри максимальних дотичних напружень для всіх ділянок стержня.. Побудувати епюру кутів закручування і зробити перевірку умови жорсткості..4.. Приклади розв`язання задач.4... Зразок виконання задачі Рисунок.4 Потужність, що передається шківами, дорівнює: N 0 квт; N 5 квт; N 40 квт; N при частоті обертання: n 478 об / хв квт, Довжини ділянок валу: 0,5 м ; 0,4 м ; 0, м ; 4 0, м. Допустимі дотичні навантаження: 50 МПа. Допустимий відносний кут закру- град / м. чування: 0 80 Модуль зсуву 0,05 рад / м; G 0, 80 МПа. 5 0
Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation
 988 Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation High School of Transport "Todor Kableshkov" 1574 Sofia, 158 Geo Milev str. Ivan Velev Abstract
988 Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation High School of Transport "Todor Kableshkov" 1574 Sofia, 158 Geo Milev str. Ivan Velev Abstract
Problem A. Nanoassembly
 Problem A. Nanoassembly 2.5 seconds One of the problems of creating elements of nanostructures is the colossal time necessary for the construction of nano-parts from separate atoms. Transporting each of
Problem A. Nanoassembly 2.5 seconds One of the problems of creating elements of nanostructures is the colossal time necessary for the construction of nano-parts from separate atoms. Transporting each of
UNDERGRADUATE STUDY SKILLS GUIDE 2014-15
 SCHOOL OF SLAVONIC AND EAST EUROPEAN STUDIES UNDERGRADUATE STUDY SKILLS GUIDE 2014-15 ECONOMICS AND BUSINESS HISTORY LANGUAGES AND CULTURE POLITICS AND SOCIOLOGY 1 1. AN INTRODUCTION TO STUDY SKILLS 5
SCHOOL OF SLAVONIC AND EAST EUROPEAN STUDIES UNDERGRADUATE STUDY SKILLS GUIDE 2014-15 ECONOMICS AND BUSINESS HISTORY LANGUAGES AND CULTURE POLITICS AND SOCIOLOGY 1 1. AN INTRODUCTION TO STUDY SKILLS 5
IС A A RT 2013. Proceedings Volume 2. 5th International Conference on Agents and Artificial Intelligence. Barcelona, Spain 15-18 February, 2013
 «'.''«ИЧИЧГШ ИШ М Ш * /////>. л ъ и г ш я ш и ъ в т ъ т ', : 4 р * т Ъ ъ ^ Х 'Ш У Л *а * 1 ЛЧй==:й?й!^'ййй IС A A RT 2013. *»ф«ч>»д* 'И И в Я в З Г З г И Ж /а 1 * icw-ia & «:*>if E M e i i i i y. x '-
«'.''«ИЧИЧГШ ИШ М Ш * /////>. л ъ и г ш я ш и ъ в т ъ т ', : 4 р * т Ъ ъ ^ Х 'Ш У Л *а * 1 ЛЧй==:й?й!^'ййй IС A A RT 2013. *»ф«ч>»д* 'И И в Я в З Г З г И Ж /а 1 * icw-ia & «:*>if E M e i i i i y. x '-
Russian Introductory Course
 Russian Introductory Course Natasha Bershadski Learn another language the way you learnt your own Succeed with the and learn another language the way you learnt your own Developed over 50 years, the amazing
Russian Introductory Course Natasha Bershadski Learn another language the way you learnt your own Succeed with the and learn another language the way you learnt your own Developed over 50 years, the amazing
The European Ombudsman
 Overview The European Ombudsman Е в р о п е й с к и о м б у д с м а н E l D e f e n s o r d e l P u e b l o E u r o p e o E v r o p s k ý v e ř e j n ý o c h r á n c e p r á v D e n E u r o p æ i s k e
Overview The European Ombudsman Е в р о п е й с к и о м б у д с м а н E l D e f e n s o r d e l P u e b l o E u r o p e o E v r o p s k ý v e ř e j n ý o c h r á n c e p r á v D e n E u r o p æ i s k e
ISSN 0975-413X CODEN (USA): PCHHAX. The study of dissolution kinetics of drugs with riboxinum (inosine)
 Available online at www.derpharmachemica.com ISSN 0975-413X CODEN (USA): PCHHAX Der Pharma Chemica, 2016, 8(1):412-416 (http://derpharmachemica.com/archive.html) The study of dissolution kinetics of drugs
Available online at www.derpharmachemica.com ISSN 0975-413X CODEN (USA): PCHHAX Der Pharma Chemica, 2016, 8(1):412-416 (http://derpharmachemica.com/archive.html) The study of dissolution kinetics of drugs
MARI-ENGLISH DICTIONARY
 MARI-ENGLISH DICTIONARY This project was funded by the Austrian Science Fund (FWF) 1, grant P22786-G20, and carried out at the Department of Finno-Ugric Studies 2 at the University of Vienna 3. Editors:
MARI-ENGLISH DICTIONARY This project was funded by the Austrian Science Fund (FWF) 1, grant P22786-G20, and carried out at the Department of Finno-Ugric Studies 2 at the University of Vienna 3. Editors:
Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING MANAGEMENT FOR PROVISION PROCESS
 444 JOURNAL Vol. 10 ( 4). December 2011 P u b l i c a t i o n o f T e r n o p i l N a t i o n a l E c o n o m i c U n i v e r s i t y Microeconomics Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING
444 JOURNAL Vol. 10 ( 4). December 2011 P u b l i c a t i o n o f T e r n o p i l N a t i o n a l E c o n o m i c U n i v e r s i t y Microeconomics Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING
Pipe fittings plant in Kolpino, Leningrad Regions
 1 Pipe fittings plant in Kolpino, Leningrad Regions ROOST Group of companies is a fast growing association with a long history. Synergy of the ROOST Group companies gives an opportunity to keep leading
1 Pipe fittings plant in Kolpino, Leningrad Regions ROOST Group of companies is a fast growing association with a long history. Synergy of the ROOST Group companies gives an opportunity to keep leading
EFFICIENCY OF SOLAR ROOF WITH TRANSPARENT COVER FOR HEATING SUPPLY OF BUILDINGS
 Budownictwo o zoptymalizowanym potencjale energetycznym 2(14) 2014, s. 117-124 Orest VOZNYAK, Stepan SHAPOVAL, Ostap PONA, Maryana KASYNETS Lviv Polytechnic National University, Ukraine EFFICIENCY OF SOLAR
Budownictwo o zoptymalizowanym potencjale energetycznym 2(14) 2014, s. 117-124 Orest VOZNYAK, Stepan SHAPOVAL, Ostap PONA, Maryana KASYNETS Lviv Polytechnic National University, Ukraine EFFICIENCY OF SOLAR
COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES
 Margaryta I. Skrypnyk, Mykola M. Matiukha COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES The article studies the correspondence of management accounting structure when using of
Margaryta I. Skrypnyk, Mykola M. Matiukha COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES The article studies the correspondence of management accounting structure when using of
The course of understanding British and American prose and poetry by future managers
 4. Полат Е. С. Новые педагогические и информационные технологии в системе образования. М.: Просвещение, 2000. 5. Гальцова Н. П., Мезенцева Т. И., Швадленко И. А. Использование электронных информационно-образовательных
4. Полат Е. С. Новые педагогические и информационные технологии в системе образования. М.: Просвещение, 2000. 5. Гальцова Н. П., Мезенцева Т. И., Швадленко И. А. Использование электронных информационно-образовательных
MasterCard Titanium a special card... exceptional benefits. MasterCard Titanium Credit Card
 fjт OQcSe bh MasterCard Titanium Credit Card КС Тс К СуСЖ КСт КС КУТ т тлсм МСОКТ ЖР ткт ОКР ткм ЛсКЛ Ж КТЖУт. fjт OQcSe...Z bh FSG gjge Ahli United Bank and The Sultan Center present the MasterCard Titanium
fjт OQcSe bh MasterCard Titanium Credit Card КС Тс К СуСЖ КСт КС КУТ т тлсм МСОКТ ЖР ткт ОКР ткм ЛсКЛ Ж КТЖУт. fjт OQcSe...Z bh FSG gjge Ahli United Bank and The Sultan Center present the MasterCard Titanium
FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina
 FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina Москва Издательство Российского университета дружбы народов 2002 FUNCTIONS OF THE MODAL
FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina Москва Издательство Российского университета дружбы народов 2002 FUNCTIONS OF THE MODAL
BES-III distributed computing status
 КОМПЬЮТЕРНЫЕ ИССЛЕДОВАНИЯ И МОДЕЛИРОВАНИЕ 2015 Т. 7 3 С. 469 473 СЕКЦИОННЫЕ ДОКЛАДЫ УДК: 004.75, 004.052.2, 004.052.32 BES-III distributed computing status S. Belov 1, Z. Deng 2, W. Li 2, T. Lin 2, I.
КОМПЬЮТЕРНЫЕ ИССЛЕДОВАНИЯ И МОДЕЛИРОВАНИЕ 2015 Т. 7 3 С. 469 473 СЕКЦИОННЫЕ ДОКЛАДЫ УДК: 004.75, 004.052.2, 004.052.32 BES-III distributed computing status S. Belov 1, Z. Deng 2, W. Li 2, T. Lin 2, I.
Online EFFECTIVE AS OF JANUARY 2013
 2013 A and C Session Start Dates (A-B Quarter Sequence*) 2013 B and D Session Start Dates (B-A Quarter Sequence*) Quarter 5 2012 1205A&C Begins November 5, 2012 1205A Ends December 9, 2012 Session Break
2013 A and C Session Start Dates (A-B Quarter Sequence*) 2013 B and D Session Start Dates (B-A Quarter Sequence*) Quarter 5 2012 1205A&C Begins November 5, 2012 1205A Ends December 9, 2012 Session Break
Chronic Fatigue Syndrome
 256 Srp Arh Celok Lek. 2011 Mar-Apr;139(3-4):256-261 ПРЕГЛЕД ЛИТЕРАТУРЕ / REVIEW ARTICLE DOI: 10.2298/SARH1104256B Chronic Fatigue Syndrome Snežana Brkić, Slavica Tomić, Maja Ružić, Daniela Marić Hospital
256 Srp Arh Celok Lek. 2011 Mar-Apr;139(3-4):256-261 ПРЕГЛЕД ЛИТЕРАТУРЕ / REVIEW ARTICLE DOI: 10.2298/SARH1104256B Chronic Fatigue Syndrome Snežana Brkić, Slavica Tomić, Maja Ružić, Daniela Marić Hospital
THE INFLUENCE OF POLITICAL ADVERTISING ON STUDENTS PREFERENCES AND THEIR POLITICAL CHOICE
 UDK 159.94 Garkavets S.A., Zhadan O.А., Kushnarenko V. I. THE INFLUENCE OF POLITICAL ADVERTISING ON STUDENTS PREFERENCES AND THEIR POLITICAL CHOICE The article considers the features of influence political
UDK 159.94 Garkavets S.A., Zhadan O.А., Kushnarenko V. I. THE INFLUENCE OF POLITICAL ADVERTISING ON STUDENTS PREFERENCES AND THEIR POLITICAL CHOICE The article considers the features of influence political
SOCIAL-MEDIA PLATFORMS AND ITS EFFECT ON DIGITAL MARKETING ACTIVITIES
 УДК 339.138:659.1 Lesidrenska Svetlana, PhD., Associate Professor, Head of the Economics and Management Department at Technical University of Varna, (Bulgaria); Dicke Philipp, Ph.D. Student at University
УДК 339.138:659.1 Lesidrenska Svetlana, PhD., Associate Professor, Head of the Economics and Management Department at Technical University of Varna, (Bulgaria); Dicke Philipp, Ph.D. Student at University
MATH 381 HOMEWORK 2 SOLUTIONS
 MATH 38 HOMEWORK SOLUTIONS Question (p.86 #8). If g(x)[e y e y ] is harmonic, g() =,g () =, find g(x). Let f(x, y) = g(x)[e y e y ].Then Since f(x, y) is harmonic, f + f = and we require x y f x = g (x)[e
MATH 38 HOMEWORK SOLUTIONS Question (p.86 #8). If g(x)[e y e y ] is harmonic, g() =,g () =, find g(x). Let f(x, y) = g(x)[e y e y ].Then Since f(x, y) is harmonic, f + f = and we require x y f x = g (x)[e
Odessa National Academy of Telecommunications named after O.S. Popov, Odessa 2
 Системи обробки інформації, 015, випуск 1 (137) ISSN 1681-7710 UDC 61.391 Nameer Qasim 1, Ali Al-Anssari 1, Moath Talat Ramadan Salah 1 Odessa National Academy of Telecommunications named after O.S. Popov,
Системи обробки інформації, 015, випуск 1 (137) ISSN 1681-7710 UDC 61.391 Nameer Qasim 1, Ali Al-Anssari 1, Moath Talat Ramadan Salah 1 Odessa National Academy of Telecommunications named after O.S. Popov,
TERMINOLOGY OF KOGNITIVE LINGUISTICS: CONCEPTUAL SYSTEM AND CONCEPTUAL PICTURE OF THE WORLD
 UDC 811.161.1' 1(082) M. V. PIMENOVA (Kemerovo, Russia) TERMINOLOGY OF KOGNITIVE LINGUISTICS: CONCEPTUAL SYSTEM AND CONCEPTUAL PICTURE OF THE WORLD The article deals with the determination of the terms
UDC 811.161.1' 1(082) M. V. PIMENOVA (Kemerovo, Russia) TERMINOLOGY OF KOGNITIVE LINGUISTICS: CONCEPTUAL SYSTEM AND CONCEPTUAL PICTURE OF THE WORLD The article deals with the determination of the terms
L 2 : x = s + 1, y = s, z = 4s + 4. 3. Suppose that C has coordinates (x, y, z). Then from the vector equality AC = BD, one has
 The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
DEFINITION 5.1.1 A complex number is a matrix of the form. x y. , y x
 Chapter 5 COMPLEX NUMBERS 5.1 Constructing the complex numbers One way of introducing the field C of complex numbers is via the arithmetic of matrices. DEFINITION 5.1.1 A complex number is a matrix of
Chapter 5 COMPLEX NUMBERS 5.1 Constructing the complex numbers One way of introducing the field C of complex numbers is via the arithmetic of matrices. DEFINITION 5.1.1 A complex number is a matrix of
CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES. Karen Gevorgyan 1
 CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES Karen Gevorgyan 1 For decades, international law and public law aspects of the concept of sovereignty were in the center of attention of the representatives
CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES Karen Gevorgyan 1 For decades, international law and public law aspects of the concept of sovereignty were in the center of attention of the representatives
Czech Technical University in Prague, Faculty of Transportation Science, Praha, Czech Republic CRISIS MANAGEMENT PRINCIPLES AND COMPETENT CRISIS PLAN
 Безпека критичних інфраструктур 23 UDC 005.8:005.931.11:005.521 D. PROCHAZKOVA, J. PROCHAZKA Czech Technical University in Prague, Faculty of Transportation Science, Praha, Czech Republic CRISIS MANAGEMENT
Безпека критичних інфраструктур 23 UDC 005.8:005.931.11:005.521 D. PROCHAZKOVA, J. PROCHAZKA Czech Technical University in Prague, Faculty of Transportation Science, Praha, Czech Republic CRISIS MANAGEMENT
Joong-Seok Cho 1 THE RELATION BETWEEN ACCOUNTING QUALITY AND SECURITY ANALYSTS' TARGET PRICE FORECAST PERFORMANCE
 НОВИНИ СВІТОВОЇ НАУКИ 503 Joong-Seok Cho 1 THE RELATION BETWEEN ACCOUNTING QUALITY AND SECURITY ANALYSTS' TARGET PRICE FORECAST PERFORMANCE Using a sample of the US security analysts' target price forecasts
НОВИНИ СВІТОВОЇ НАУКИ 503 Joong-Seok Cho 1 THE RELATION BETWEEN ACCOUNTING QUALITY AND SECURITY ANALYSTS' TARGET PRICE FORECAST PERFORMANCE Using a sample of the US security analysts' target price forecasts
STARTING SYSTEM OPERATION IN THE STARTER-GENERATOR
 International Journal on Technical and Physical Problems of Engineering (IJTPE) Published by International Organization on TPE (IOTPE) ISSN 077-358 IJTPE Journal www.iotpe.com ijtpe@iotpe.com March 00
International Journal on Technical and Physical Problems of Engineering (IJTPE) Published by International Organization on TPE (IOTPE) ISSN 077-358 IJTPE Journal www.iotpe.com ijtpe@iotpe.com March 00
5.3 Improper Integrals Involving Rational and Exponential Functions
 Section 5.3 Improper Integrals Involving Rational and Exponential Functions 99.. 3. 4. dθ +a cos θ =, < a
Section 5.3 Improper Integrals Involving Rational and Exponential Functions 99.. 3. 4. dθ +a cos θ =, < a
 1 D e r 1. S c h u l t a g M a l e a u s. S c h re i b e d e i n e n N a m e n u n t e r e i n K i n d. 1 2 D a s b i n i c h M a l e d i c h s e l b e r. 2 3 F re u n d e M a l e d i c h u n d d e i n
1 D e r 1. S c h u l t a g M a l e a u s. S c h re i b e d e i n e n N a m e n u n t e r e i n K i n d. 1 2 D a s b i n i c h M a l e d i c h s e l b e r. 2 3 F re u n d e M a l e d i c h u n d d e i n
INTEGRATION SDN CONTROLLERS INTO OPENSTACK. EVALUITION OF PERFORMANCE AND RELIABILITY
 Системи обробки інформації, 2015, випуск 10 (135) ISSN 16817710 УДК 621.372 O.B. Tkachova 1, Mohammed Jamal Salim 2, Raed Yahya Abdulghafoor 2 1 Kharkiv National University of Radio Electronics, Kharkiv
Системи обробки інформації, 2015, випуск 10 (135) ISSN 16817710 УДК 621.372 O.B. Tkachova 1, Mohammed Jamal Salim 2, Raed Yahya Abdulghafoor 2 1 Kharkiv National University of Radio Electronics, Kharkiv
A COURSE IN MODERN ENGLISH LEXICOLOGY
 R. S. Ginzburg, S. S. Khidekel, G. Y. Knyazeva, A. A. Sankin A COURSE IN MODERN ENGLISH LEXICOLOGY SECOND EDITION Revised and Enlarged Допущено Министерством высшего и среднего специального образования
R. S. Ginzburg, S. S. Khidekel, G. Y. Knyazeva, A. A. Sankin A COURSE IN MODERN ENGLISH LEXICOLOGY SECOND EDITION Revised and Enlarged Допущено Министерством высшего и среднего специального образования
SHORT RUSSIAN PHRASEBOOK FOR ENGLISH-SPEAKING TRAVELERS FREE DOWNLOAD. EDITION 4.0
 SHORT RUSSIAN PHRASEBOOK FOR ENGLISH-SPEAKING TRAVELERS FREE DOWNLOAD. EDITION 4.0 Common Russian phrases. Russian alphabet and sounds Knowing how to pronounce Russian letters will facilitate your conversation.
SHORT RUSSIAN PHRASEBOOK FOR ENGLISH-SPEAKING TRAVELERS FREE DOWNLOAD. EDITION 4.0 Common Russian phrases. Russian alphabet and sounds Knowing how to pronounce Russian letters will facilitate your conversation.
бы appleы х нfi йтхыкы, за шы зхт зт тсыхн, Bayerische Julius- Maximilians UniversitДt, WЭrzburg, бзл с. 2
 appleтн ы шы шк шбсрс лб шанобхшх н с л о мк лб шс шлfi тзт тсыхн бз appleб н х абсбхтappleо шыхн : с йтз т appleбзхappleыршб с сшы сы ст з к, 1 сск ко бз к, 2 лappleзт тот лк, 3 хоо ы ок, 4 хнfiо т з
appleтн ы шы шк шбсрс лб шанобхшх н с л о мк лб шс шлfi тзт тсыхн бз appleб н х абсбхтappleо шыхн : с йтз т appleбзхappleыршб с сшы сы ст з к, 1 сск ко бз к, 2 лappleзт тот лк, 3 хоо ы ок, 4 хнfiо т з
Solutions by: KARATUĞ OZAN BiRCAN. PROBLEM 1 (20 points): Let D be a region, i.e., an open connected set in
 KOÇ UNIVERSITY, SPRING 2014 MATH 401, MIDTERM-1, MARCH 3 Instructor: BURAK OZBAGCI TIME: 75 Minutes Solutions by: KARATUĞ OZAN BiRCAN PROBLEM 1 (20 points): Let D be a region, i.e., an open connected set
KOÇ UNIVERSITY, SPRING 2014 MATH 401, MIDTERM-1, MARCH 3 Instructor: BURAK OZBAGCI TIME: 75 Minutes Solutions by: KARATUĞ OZAN BiRCAN PROBLEM 1 (20 points): Let D be a region, i.e., an open connected set
A. I. KUBARKO, T. G. SEVERINA NORMAL PHYSIOLOGY
 A. I. KUBARKO, T. G. SEVERINA NORMAL PHYSIOLOGY Minsk BSMU 2015 МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ КАФЕДРА НОРМАЛЬНОЙ ФИЗИОЛОГИИ А. И.
A. I. KUBARKO, T. G. SEVERINA NORMAL PHYSIOLOGY Minsk BSMU 2015 МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ КАФЕДРА НОРМАЛЬНОЙ ФИЗИОЛОГИИ А. И.
Functionalized molecules - synthesis, properties and application
 Functionalized molecules - synthesis, properties and application Edited by Volodymyr I. ybachenko Functionalized molecules - synthesis, properties and application Edited by Volodymyr I. ybachenko Donetsk
Functionalized molecules - synthesis, properties and application Edited by Volodymyr I. ybachenko Functionalized molecules - synthesis, properties and application Edited by Volodymyr I. ybachenko Donetsk
Visa Smart Debit/Credit Certificate Authority Public Keys
 CHIP AND NEW TECHNOLOGIES Visa Smart Debit/Credit Certificate Authority Public Keys Overview The EMV standard calls for the use of Public Key technology for offline authentication, for aspects of online
CHIP AND NEW TECHNOLOGIES Visa Smart Debit/Credit Certificate Authority Public Keys Overview The EMV standard calls for the use of Public Key technology for offline authentication, for aspects of online
UNIVERSITY OF ILUNOхS LIBRARY AT URBANA-CHAMPA1GN AGR1CULT-"'J?'-
 ' UNVRSTY F NхS LBRARY AT URBANA-HAMPA1GN AGR1ULT-"'J?'- igitied by the nternet Arhive 2012 ith fndg frm University f llis Urbn-hmpign http://.rhive.rg/detils/illismmeri1982med s 8 h U p m UU t g 5. -
' UNVRSTY F NхS LBRARY AT URBANA-HAMPA1GN AGR1ULT-"'J?'- igitied by the nternet Arhive 2012 ith fndg frm University f llis Urbn-hmpign http://.rhive.rg/detils/illismmeri1982med s 8 h U p m UU t g 5. -
BASICS OF ENGLISH PHONETICS. (course of lectures)
 BASICS OF ENGLISH PHONETICS (course of lectures) Contents 1. Lecture I. Phonetics as a science 2. Lecture II. The classification of English consonants 3. Lecture III. The English vowel system 4. Lecture
BASICS OF ENGLISH PHONETICS (course of lectures) Contents 1. Lecture I. Phonetics as a science 2. Lecture II. The classification of English consonants 3. Lecture III. The English vowel system 4. Lecture
The relationship between managers' leadership styles in physical education offices universities and sport volunteers' satisfaction
 ПЕДАГОГІКА ПСИХОЛОГІЯ та медико-біологічні проблеми фізичного виховання і спорту The relationship between managers' leadership styles in physical education offices universities and sport volunteers' satisfaction
ПЕДАГОГІКА ПСИХОЛОГІЯ та медико-біологічні проблеми фізичного виховання і спорту The relationship between managers' leadership styles in physical education offices universities and sport volunteers' satisfaction
ENEOLITHIC CERAMIC TABLETS (ALTARS) FROM BULGARIA
 ENEOLITHIC CERAMIC TABLETS (ALTARS) FROM BULGARIA Dimitar CHERNAKOV (Bulgaria) Whenever a research on various prehistoric sites has been carried findings of non utility comprise a considerably large share
ENEOLITHIC CERAMIC TABLETS (ALTARS) FROM BULGARIA Dimitar CHERNAKOV (Bulgaria) Whenever a research on various prehistoric sites has been carried findings of non utility comprise a considerably large share
розумінню впливу соціального середовища на здоров'я людини. УДК 316.614-056 Brouchatskaya Elina Riga Anastasia-Valentini
 SECTION 2. SOCIAL PROBLEMS IN THE CONTEXT OF BRANCH SOCIOLOGYS. 2.9 SOCIOLOGY OF HEALTH. MEDICINE SOCIOLOGY/ РАЗДЕЛ 2. СОЦИАЛЬНЫЕ ПРОБЛЕМЫ В КОНТЕКСТЕ ОТРАСЛЕВЫХ СОЦИОЛОГИЙ. 2.9 СОЦИОЛОГИЯ ЗДОРОВЬЯ. СОЦИОЛОГИЯ
SECTION 2. SOCIAL PROBLEMS IN THE CONTEXT OF BRANCH SOCIOLOGYS. 2.9 SOCIOLOGY OF HEALTH. MEDICINE SOCIOLOGY/ РАЗДЕЛ 2. СОЦИАЛЬНЫЕ ПРОБЛЕМЫ В КОНТЕКСТЕ ОТРАСЛЕВЫХ СОЦИОЛОГИЙ. 2.9 СОЦИОЛОГИЯ ЗДОРОВЬЯ. СОЦИОЛОГИЯ
OFFSHORE TERRITORIES: BASIC CONCEPTS OF FUNCTIONING
 УДК 339.9:336.564.2 M. V. Kleshcheeva, Student of Donetsk National Ttechnical University, Ukraine OFFSHORE TERRITORIES: BASIC CONCEPTS OF FUNCTIONING Formulation of the problem. At this point in time offshore
УДК 339.9:336.564.2 M. V. Kleshcheeva, Student of Donetsk National Ttechnical University, Ukraine OFFSHORE TERRITORIES: BASIC CONCEPTS OF FUNCTIONING Formulation of the problem. At this point in time offshore
CROSS REFERENCE. Cross Reference Index 110-122. Cast ID Number 110-111 Connector ID Number 111 Engine ID Number 112-122. 2015 Ford Motor Company 109
 CROSS REFERENCE Cross Reference Index 110-122 Cast ID Number 110-111 Connector ID Number 111 112-122 2015 Ford Motor Company 109 CROSS REFERENCE Cast ID Number Cast ID Ford Service # MC Part # Part Type
CROSS REFERENCE Cross Reference Index 110-122 Cast ID Number 110-111 Connector ID Number 111 112-122 2015 Ford Motor Company 109 CROSS REFERENCE Cast ID Number Cast ID Ford Service # MC Part # Part Type
DIFFERENTIATION MATRICES FOR MEROMORPHIC FUNCTIONS
 Bol. Soc. Mat. Mexicana (3 Vol. 1, 006 DIFFERETIATIO MATRICES FOR MEROMORPHIC FUCTIOS RAFAEL G. CAMPOS AD CLAUDIO MEESES Abstract. A procedure for obtaining differentiation matrices is extended straightforwardly
Bol. Soc. Mat. Mexicana (3 Vol. 1, 006 DIFFERETIATIO MATRICES FOR MEROMORPHIC FUCTIOS RAFAEL G. CAMPOS AD CLAUDIO MEESES Abstract. A procedure for obtaining differentiation matrices is extended straightforwardly
1 Homework 1. [p 0 q i+j +... + p i 1 q j+1 ] + [p i q j ] + [p i+1 q j 1 +... + p i+j q 0 ]
![1 Homework 1. [p 0 q i+j +... + p i 1 q j+1 ] + [p i q j ] + [p i+1 q j 1 +... + p i+j q 0 ] 1 Homework 1. [p 0 q i+j +... + p i 1 q j+1 ] + [p i q j ] + [p i+1 q j 1 +... + p i+j q 0 ]](/thumbs/40/21231772.jpg) 1 Homework 1 (1) Prove the ideal (3,x) is a maximal ideal in Z[x]. SOLUTION: Suppose we expand this ideal by including another generator polynomial, P / (3, x). Write P = n + x Q with n an integer not
1 Homework 1 (1) Prove the ideal (3,x) is a maximal ideal in Z[x]. SOLUTION: Suppose we expand this ideal by including another generator polynomial, P / (3, x). Write P = n + x Q with n an integer not
BLAST-FURNACE EQUIPMENT
 BLAST-FURNACE EQUIPMENT HOT METAL LADLE CAR Standard series: Г-1-50, Г-100,Г-1-140. Hot metal ladle car is designed for transportation of hot metal from furnace to casting machines, mixers and steelmaking
BLAST-FURNACE EQUIPMENT HOT METAL LADLE CAR Standard series: Г-1-50, Г-100,Г-1-140. Hot metal ladle car is designed for transportation of hot metal from furnace to casting machines, mixers and steelmaking
VENTILATION AIR CONDITIONING HEATING AIR HANDLING UNITS TECHNICAL CATALOGUE
 VENTILATION AIR CONDITIONING HEATING 6 AIR HANDLING UNITS TECHNICAL CATALOGUE AIR HANDLING UNITS CONTENTS 06.01-01 AHU - AIR HANDLING UNITS 3 06.01-02 DESCRIPTION ON TYPES OF SECTIONS 4 06.01-06 HORIZONTAL
VENTILATION AIR CONDITIONING HEATING 6 AIR HANDLING UNITS TECHNICAL CATALOGUE AIR HANDLING UNITS CONTENTS 06.01-01 AHU - AIR HANDLING UNITS 3 06.01-02 DESCRIPTION ON TYPES OF SECTIONS 4 06.01-06 HORIZONTAL
The invention of line integrals is motivated by solving problems in fluid flow, forces, electricity and magnetism.
 Instrutor: Longfei Li Mth 43 Leture Notes 16. Line Integrls The invention of line integrls is motivted by solving problems in fluid flow, fores, eletriity nd mgnetism. Line Integrls of Funtion We n integrte
Instrutor: Longfei Li Mth 43 Leture Notes 16. Line Integrls The invention of line integrls is motivted by solving problems in fluid flow, fores, eletriity nd mgnetism. Line Integrls of Funtion We n integrte
RAJALAKSHMI ENGINEERING COLLEGE MA 2161 UNIT I - ORDINARY DIFFERENTIAL EQUATIONS PART A
 RAJALAKSHMI ENGINEERING COLLEGE MA 26 UNIT I - ORDINARY DIFFERENTIAL EQUATIONS. Solve (D 2 + D 2)y = 0. 2. Solve (D 2 + 6D + 9)y = 0. PART A 3. Solve (D 4 + 4)x = 0 where D = d dt 4. Find Particular Integral:
RAJALAKSHMI ENGINEERING COLLEGE MA 26 UNIT I - ORDINARY DIFFERENTIAL EQUATIONS. Solve (D 2 + D 2)y = 0. 2. Solve (D 2 + 6D + 9)y = 0. PART A 3. Solve (D 4 + 4)x = 0 where D = d dt 4. Find Particular Integral:
Algebraic Structures II
 MAS 305 Algebraic Structures II Notes 12 Autumn 2006 Factorization in integral domains Lemma If a, b, c are elements of an integral domain R and ab = ac then either a = 0 R or b = c. Proof ab = ac a(b
MAS 305 Algebraic Structures II Notes 12 Autumn 2006 Factorization in integral domains Lemma If a, b, c are elements of an integral domain R and ab = ac then either a = 0 R or b = c. Proof ab = ac a(b
VILLAGE TOURISM OF SERBIA
 VILLGE TOURISM OF SERBI H U N R Y G SUBOTIC R Senta SOMBOR Č V O SERBI T J N N O Bački Petrovac U M sa V Ti I C R O T D K P B B U KIKIND D V I NOVI SD N ZRENJNIN N Beočin Irig E M iš R m Ta S Kovačica
VILLGE TOURISM OF SERBI H U N R Y G SUBOTIC R Senta SOMBOR Č V O SERBI T J N N O Bački Petrovac U M sa V Ti I C R O T D K P B B U KIKIND D V I NOVI SD N ZRENJNIN N Beočin Irig E M iš R m Ta S Kovačica
Computational Physics
 Computational Physics Sheet 6, Computational Physics Course 17105 Professor: H. Ruhl, Exercises: N. Moschüring and N. Elkina Discussion of Solutions: Dec 03, 01, Room A49 Problem 1: Yee solver for Schrödinger
Computational Physics Sheet 6, Computational Physics Course 17105 Professor: H. Ruhl, Exercises: N. Moschüring and N. Elkina Discussion of Solutions: Dec 03, 01, Room A49 Problem 1: Yee solver for Schrödinger
План урока London sightseeing tour Гуськов Александр Игоревич МАУ СОШ 36
 План урока London sightseeing tour Гуськов Александр Игоревич МАУ СОШ 36 Основная цель урока: - создать условия для формирования социокультурной компетенции. Образовательный аспект цели: - проверить умение
План урока London sightseeing tour Гуськов Александр Игоревич МАУ СОШ 36 Основная цель урока: - создать условия для формирования социокультурной компетенции. Образовательный аспект цели: - проверить умение
Section 8.8. 1. The given line has equations. x = 3 + t(13 3) = 3 + 10t, y = 2 + t(3 + 2) = 2 + 5t, z = 7 + t( 8 7) = 7 15t.
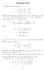 . The given line has equations Section 8.8 x + t( ) + 0t, y + t( + ) + t, z 7 + t( 8 7) 7 t. The line meets the plane y 0 in the point (x, 0, z), where 0 + t, or t /. The corresponding values for x and
. The given line has equations Section 8.8 x + t( ) + 0t, y + t( + ) + t, z 7 + t( 8 7) 7 t. The line meets the plane y 0 in the point (x, 0, z), where 0 + t, or t /. The corresponding values for x and
LG-Ericsson TSP (ip-ldk, ipecs) User Guide. Issue 4.1Ac
 LG-Ericsson TSP (ip-ldk, ipecs) User Guide Issue 4.1Ac REVISION HISTORY Version Date Description of Change S/W Version Issue 3.7Aa SEP 12, 2007 Initial Release Issue 4.0Aa JUN 27, 2009 Add ipecs-50a/50b/micro/1200
LG-Ericsson TSP (ip-ldk, ipecs) User Guide Issue 4.1Ac REVISION HISTORY Version Date Description of Change S/W Version Issue 3.7Aa SEP 12, 2007 Initial Release Issue 4.0Aa JUN 27, 2009 Add ipecs-50a/50b/micro/1200
SERVER CERTIFICATES OF THE VETUMA SERVICE
 Page 1 Version: 3.5, 4.11.2015 SERVER CERTIFICATES OF THE VETUMA SERVICE 1 (18) Page 2 Version: 3.5, 4.11.2015 Table of Contents 1. Introduction... 3 2. Test Environment... 3 2.1 Vetuma test environment...
Page 1 Version: 3.5, 4.11.2015 SERVER CERTIFICATES OF THE VETUMA SERVICE 1 (18) Page 2 Version: 3.5, 4.11.2015 Table of Contents 1. Introduction... 3 2. Test Environment... 3 2.1 Vetuma test environment...
Solutions for Math 311 Assignment #1
 Solutions for Math 311 Assignment #1 (1) Show that (a) Re(iz) Im(z); (b) Im(iz) Re(z). Proof. Let z x + yi with x Re(z) and y Im(z). Then Re(iz) Re( y + xi) y Im(z) and Im(iz) Im( y + xi) x Re(z). () Verify
Solutions for Math 311 Assignment #1 (1) Show that (a) Re(iz) Im(z); (b) Im(iz) Re(z). Proof. Let z x + yi with x Re(z) and y Im(z). Then Re(iz) Re( y + xi) y Im(z) and Im(iz) Im( y + xi) x Re(z). () Verify
RESOURCE-EFFICIENT ALLOCATION HEURISTICS FOR MANAGEMENT OF DATA CENTERS FOR CLOUD COMPUTING
 V. Litvinov, K. Matsueva. Resource-efficient allocation heuristics for management of data centers for cloud computing 113 UDC 004.7:004942(045) Vitaliy Litvinov 1 Karyna Matsueva 2 RESOURCE-EFFICIENT ALLOCATION
V. Litvinov, K. Matsueva. Resource-efficient allocation heuristics for management of data centers for cloud computing 113 UDC 004.7:004942(045) Vitaliy Litvinov 1 Karyna Matsueva 2 RESOURCE-EFFICIENT ALLOCATION
2D Geometrical Transformations. Foley & Van Dam, Chapter 5
 2D Geometrical Transformations Fole & Van Dam, Chapter 5 2D Geometrical Transformations Translation Scaling Rotation Shear Matri notation Compositions Homogeneous coordinates 2D Geometrical Transformations
2D Geometrical Transformations Fole & Van Dam, Chapter 5 2D Geometrical Transformations Translation Scaling Rotation Shear Matri notation Compositions Homogeneous coordinates 2D Geometrical Transformations
ROLLS FOR ROLLING MILLS
 ROLLS FOR ROLLING MILLS The Uralmashplant JSC, is a key equipment supplier for basic industry sectors: mining, metallurgical, and oil-and-gas industries. In 2013 the Uralmashplant marked its 80s anniversary.
ROLLS FOR ROLLING MILLS The Uralmashplant JSC, is a key equipment supplier for basic industry sectors: mining, metallurgical, and oil-and-gas industries. In 2013 the Uralmashplant marked its 80s anniversary.
Value aspects of modern Ukrainian advertising discourses
 Lviv National Polytechnic University. MEDIA I SPOŁECZEŃSTWO... MEDIOZNAWSTWO KOMUNIKOLOGIA SEMIOLOGIA SOCJOLOGIA MEDIÓW MEDIA A PEDAGOGIKA Value aspects of modern Ukrainian advertising discourses nr 4/2014
Lviv National Polytechnic University. MEDIA I SPOŁECZEŃSTWO... MEDIOZNAWSTWO KOMUNIKOLOGIA SEMIOLOGIA SOCJOLOGIA MEDIÓW MEDIA A PEDAGOGIKA Value aspects of modern Ukrainian advertising discourses nr 4/2014
SERVER CERTIFICATES OF THE VETUMA SERVICE
 Page 1 Version: 3.4, 19.12.2014 SERVER CERTIFICATES OF THE VETUMA SERVICE 1 (18) Page 2 Version: 3.4, 19.12.2014 Table of Contents 1. Introduction... 3 2. Test Environment... 3 2.1 Vetuma test environment...
Page 1 Version: 3.4, 19.12.2014 SERVER CERTIFICATES OF THE VETUMA SERVICE 1 (18) Page 2 Version: 3.4, 19.12.2014 Table of Contents 1. Introduction... 3 2. Test Environment... 3 2.1 Vetuma test environment...
MATH 52: MATLAB HOMEWORK 2
 MATH 52: MATLAB HOMEWORK 2. omplex Numbers The prevalence of the complex numbers throughout the scientific world today belies their long and rocky history. Much like the negative numbers, complex numbers
MATH 52: MATLAB HOMEWORK 2. omplex Numbers The prevalence of the complex numbers throughout the scientific world today belies their long and rocky history. Much like the negative numbers, complex numbers
MATH 102 College Algebra
 FACTORING Factoring polnomials ls is simpl the reverse process of the special product formulas. Thus, the reverse process of special product formulas will be used to factor polnomials. To factor polnomials
FACTORING Factoring polnomials ls is simpl the reverse process of the special product formulas. Thus, the reverse process of special product formulas will be used to factor polnomials. To factor polnomials
Futó Z. Károly Róbert College, Fleischmann Rudolf Research Institute
 УДК 631.8:632:633.854:665.3 2014 Futó Z. Károly Róbert College, Fleischmann Rudolf Research Institute THE EFFECT OF NUTRIENT SUPPLY AND PLANT PROTECTION IN YIELD AND OIL CONTENT OF SUNFLOWER (Helianthus
УДК 631.8:632:633.854:665.3 2014 Futó Z. Károly Róbert College, Fleischmann Rudolf Research Institute THE EFFECT OF NUTRIENT SUPPLY AND PLANT PROTECTION IN YIELD AND OIL CONTENT OF SUNFLOWER (Helianthus
THERMOELECTRIC CONVERTERS OF ELECTRICAL AND OPTICAL SIGNALS-NEW CLASS OF THERMOELECTRIC DEVICES
 THERMOELECTRIC CONVERTERS OF ELECTRICAL AND OPTICAL SIGNALS-NEW CLASS OF THERMOELECTRIC DEVICES E.M. Sher E.M. Sher (Physics and Technical Institute, Saint-Petersburg, Russia) The new class of thermoelectric
THERMOELECTRIC CONVERTERS OF ELECTRICAL AND OPTICAL SIGNALS-NEW CLASS OF THERMOELECTRIC DEVICES E.M. Sher E.M. Sher (Physics and Technical Institute, Saint-Petersburg, Russia) The new class of thermoelectric
4.2. LINE INTEGRALS 1. 2 2 ; z = t. ; y = sin
 4.2. LINE INTEGRALS 1 4.2 Line Integrals MATH 294 FALL 1982 FINAL # 7 294FA82FQ7.tex 4.2.1 Consider the curve given parametrically by x = cos t t ; y = sin 2 2 ; z = t a) Determine the work done by the
4.2. LINE INTEGRALS 1 4.2 Line Integrals MATH 294 FALL 1982 FINAL # 7 294FA82FQ7.tex 4.2.1 Consider the curve given parametrically by x = cos t t ; y = sin 2 2 ; z = t a) Determine the work done by the
FACTORS INFLUENCING THE FORMATION OF HUMAN RESOURCES
 Nataliia Hunko 65 Nataliia Hunko, Factors Influencing the Formation of Human Resources,, pp. 65-72. DOI: 10.14254/2071-789X.2013/6-2/6 Nataliia Hunko Assistant Department of Management National University
Nataliia Hunko 65 Nataliia Hunko, Factors Influencing the Formation of Human Resources,, pp. 65-72. DOI: 10.14254/2071-789X.2013/6-2/6 Nataliia Hunko Assistant Department of Management National University
So far, we have looked at homogeneous equations
 Chapter 3.6: equations Non-homogeneous So far, we have looked at homogeneous equations L[y] = y + p(t)y + q(t)y = 0. Homogeneous means that the right side is zero. Linear homogeneous equations satisfy
Chapter 3.6: equations Non-homogeneous So far, we have looked at homogeneous equations L[y] = y + p(t)y + q(t)y = 0. Homogeneous means that the right side is zero. Linear homogeneous equations satisfy
AGRITOURISM AS THE BEST FORM OF ENTERPRENEURSHIP IN THE POLISH COUTRYSIDE. Anita Szygula
 . с. 125 132 Visnyk of the lviv University. series international relations. 2014. Issue 34. p. 125 132 125 УДК 338.48-44(438-22) AGRITOURISM AS THE BEST FORM OF ENTERPRENEURSHIP IN THE POLISH COUTRYSIDE
. с. 125 132 Visnyk of the lviv University. series international relations. 2014. Issue 34. p. 125 132 125 УДК 338.48-44(438-22) AGRITOURISM AS THE BEST FORM OF ENTERPRENEURSHIP IN THE POLISH COUTRYSIDE
Review Sheet for Test 1
 Review Sheet for Test 1 Math 261-00 2 6 2004 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And
Review Sheet for Test 1 Math 261-00 2 6 2004 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And
Introduction to Complex Numbers in Physics/Engineering
 Introduction to Complex Numbers in Physics/Engineering ference: Mary L. Boas, Mathematical Methods in the Physical Sciences Chapter 2 & 14 George Arfken, Mathematical Methods for Physicists Chapter 6 The
Introduction to Complex Numbers in Physics/Engineering ference: Mary L. Boas, Mathematical Methods in the Physical Sciences Chapter 2 & 14 George Arfken, Mathematical Methods for Physicists Chapter 6 The
PALAEONTOLOGIA POLQNICA 'Ъ-Ь
 PALAEONTOLOGIA POLQNICA 'Ъ-Ь mm P O L T S H A C A D E M Y O F S C I E N C E S INSTITUTE OF PALEOBIOLOGY PALAEONTOLOGIA POLONICA No. 50, 1990 t h e a l b ia w AMMONITES OF POLAND (A M Q N ITY A L B U POLS
PALAEONTOLOGIA POLQNICA 'Ъ-Ь mm P O L T S H A C A D E M Y O F S C I E N C E S INSTITUTE OF PALEOBIOLOGY PALAEONTOLOGIA POLONICA No. 50, 1990 t h e a l b ia w AMMONITES OF POLAND (A M Q N ITY A L B U POLS
Complex Numbers. w = f(z) z. Examples
 omple Numbers Geometrical Transformations in the omple Plane For functions of a real variable such as f( sin, g( 2 +2 etc ou are used to illustrating these geometricall, usuall on a cartesian graph. If
omple Numbers Geometrical Transformations in the omple Plane For functions of a real variable such as f( sin, g( 2 +2 etc ou are used to illustrating these geometricall, usuall on a cartesian graph. If
General Theory of Differential Equations Sections 2.8, 3.1-3.2, 4.1
 A B I L E N E C H R I S T I A N U N I V E R S I T Y Department of Mathematics General Theory of Differential Equations Sections 2.8, 3.1-3.2, 4.1 Dr. John Ehrke Department of Mathematics Fall 2012 Questions
A B I L E N E C H R I S T I A N U N I V E R S I T Y Department of Mathematics General Theory of Differential Equations Sections 2.8, 3.1-3.2, 4.1 Dr. John Ehrke Department of Mathematics Fall 2012 Questions
RISK MANAGEMENT OF LEASING COMPANY
 УДК 005:658.91 O. A. Saenko, Ph.D. (economics), Luhansk Taras Shevchenko National University RISK MANAGEMENT OF LEASING COMPANY Problem statement. In economic terms, risk is the likelihood / possibility
УДК 005:658.91 O. A. Saenko, Ph.D. (economics), Luhansk Taras Shevchenko National University RISK MANAGEMENT OF LEASING COMPANY Problem statement. In economic terms, risk is the likelihood / possibility
The General Cauchy Theorem
 Chapter 3 The General Cauchy Theorem In this chapter, we consider two basic questions. First, for a given open set Ω, we try to determine which closed paths in Ω have the property that f(z) dz = 0for every
Chapter 3 The General Cauchy Theorem In this chapter, we consider two basic questions. First, for a given open set Ω, we try to determine which closed paths in Ω have the property that f(z) dz = 0for every
econstor zbw www.econstor.eu
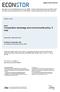 econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Siebert,
econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Siebert,
Industrial Metrology and Interchangeable Manufacturing under the Viewpoint of Nanotechnology and Nanometrology
 БЪЛГАРСКА АКАДЕМИЯ НА НАУКИТЕ BULGARIAN ACADEMY OF SCIENCES ПРОБЛЕМИ НА ТЕХНИЧЕСКАТА КИБЕРНЕТИКА И РОБОТИКАТА, 59 PROBLEMS OF ENGINEERING CYBERNETICS AND ROBOTICS, 59 София 2008 Sofia Industrial Metrology
БЪЛГАРСКА АКАДЕМИЯ НА НАУКИТЕ BULGARIAN ACADEMY OF SCIENCES ПРОБЛЕМИ НА ТЕХНИЧЕСКАТА КИБЕРНЕТИКА И РОБОТИКАТА, 59 PROBLEMS OF ENGINEERING CYBERNETICS AND ROBOTICS, 59 София 2008 Sofia Industrial Metrology
On Supervised and Unsupervised Discretization 1
 БЪЛГАРСКА АКАДЕМИЯ НА НАУКИТЕ. BULGARIAN ACADEMY OF SCIENCES КИБЕРНЕТИКА И ИНФОРМАЦИОННИ ТЕХНОЛОГИИ Том 2, 2 CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 2, No 2 София. 2002. Sofia On Supervised and
БЪЛГАРСКА АКАДЕМИЯ НА НАУКИТЕ. BULGARIAN ACADEMY OF SCIENCES КИБЕРНЕТИКА И ИНФОРМАЦИОННИ ТЕХНОЛОГИИ Том 2, 2 CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 2, No 2 София. 2002. Sofia On Supervised and
Steel Fury: Kharkov 1942. User's manual
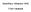 Steel Fury: Kharkov 1942 User's manual CONTENT 2 LIST OF USED REDUCTIONS...3 1 SYSTEM REQUIREMENTS...4 2 GAME INSTALLATION, START AND UNINSTALL...5 3 MAIN MENU......6 3.1 Player selection......7 3.2 Company......8
Steel Fury: Kharkov 1942 User's manual CONTENT 2 LIST OF USED REDUCTIONS...3 1 SYSTEM REQUIREMENTS...4 2 GAME INSTALLATION, START AND UNINSTALL...5 3 MAIN MENU......6 3.1 Player selection......7 3.2 Company......8
NOTES FOR MATH 520: COMPLEX ANALYSIS
 NOTES FOR MATH 520: COMPLEX ANALYSIS KO HONDA 1. Complex numbers 1.1. Definition of C. As a set, C = R 2 = {(x, y) x, y R}. In other words, elements of C are pairs of real numbers. C as a field: C can
NOTES FOR MATH 520: COMPLEX ANALYSIS KO HONDA 1. Complex numbers 1.1. Definition of C. As a set, C = R 2 = {(x, y) x, y R}. In other words, elements of C are pairs of real numbers. C as a field: C can
Appropriate Modifier Usage
 Anatomical modifiers Anesthesia modifiers EA, EB and EC FB, FC and FD Anatomical modifiers are used to indicate that a procedure or service was performed at a specific anatomic site or to indicate that
Anatomical modifiers Anesthesia modifiers EA, EB and EC FB, FC and FD Anatomical modifiers are used to indicate that a procedure or service was performed at a specific anatomic site or to indicate that
FACTORING ANGLE EQUATIONS:
 FACTORING ANGLE EQUATIONS: For convenience, algebraic names are assigned to the angles comprising the Standard Hip kernel. The names are completely arbitrary, and can vary from kernel to kernel. On the
FACTORING ANGLE EQUATIONS: For convenience, algebraic names are assigned to the angles comprising the Standard Hip kernel. The names are completely arbitrary, and can vary from kernel to kernel. On the
C relative to O being abc,, respectively, then b a c.
 2 EP-Program - Strisuksa School - Roi-et Math : Vectors Dr.Wattana Toutip - Department of Mathematics Khon Kaen University 200 :Wattana Toutip wattou@kku.ac.th http://home.kku.ac.th/wattou 2. Vectors A
2 EP-Program - Strisuksa School - Roi-et Math : Vectors Dr.Wattana Toutip - Department of Mathematics Khon Kaen University 200 :Wattana Toutip wattou@kku.ac.th http://home.kku.ac.th/wattou 2. Vectors A
USI Master Policy Information
 Policy I.D. Gender A.B. (#327) M 86 United of Omaha $ 1,000,000.00 A.B. (#430) - (#436) M 86 Metlife $ 2,000,000.00 A.G. #1 (#371), (#610), (#624) M Conseco Life $ 3,125,000.00 10/Apr/10 A.G. #2 (#380),
Policy I.D. Gender A.B. (#327) M 86 United of Omaha $ 1,000,000.00 A.B. (#430) - (#436) M 86 Metlife $ 2,000,000.00 A.G. #1 (#371), (#610), (#624) M Conseco Life $ 3,125,000.00 10/Apr/10 A.G. #2 (#380),
Evolution of the Ideas about Creativity in Psychological and Pedagogical Concepts of 19 th -20 th century
 Nr 6 (2) 2013 Kultura i Wychowanie Evolution of the Ideas about Creativity in Psychological and Pedagogical Concepts of 19 th -20 th century Olexander Didenko Khmelnytskyi city, Ukraine didenko12.69@mail.ru
Nr 6 (2) 2013 Kultura i Wychowanie Evolution of the Ideas about Creativity in Psychological and Pedagogical Concepts of 19 th -20 th century Olexander Didenko Khmelnytskyi city, Ukraine didenko12.69@mail.ru
Side reactions of onium coupling reagents BOP and HBTU in the synthesis of silica polymer supports
 Ukrainica Bioorganica Acta 1 (2005) 13 19 Side reactions of onium coupling reagents BP and HBTU in the synthesis of silica polymer supports L. V. Dubey, I. Ya. Dubey* Institute of Molecular Biology and
Ukrainica Bioorganica Acta 1 (2005) 13 19 Side reactions of onium coupling reagents BP and HBTU in the synthesis of silica polymer supports L. V. Dubey, I. Ya. Dubey* Institute of Molecular Biology and
B4 Computational Geometry
 3CG 2006 / B4 Computational Geometry David Murray david.murray@eng.o.ac.uk www.robots.o.ac.uk/ dwm/courses/3cg Michaelmas 2006 3CG 2006 2 / Overview Computational geometry is concerned with the derivation
3CG 2006 / B4 Computational Geometry David Murray david.murray@eng.o.ac.uk www.robots.o.ac.uk/ dwm/courses/3cg Michaelmas 2006 3CG 2006 2 / Overview Computational geometry is concerned with the derivation
Lecture Notes on Polynomials
 Lecture Notes on Polynomials Arne Jensen Department of Mathematical Sciences Aalborg University c 008 Introduction These lecture notes give a very short introduction to polynomials with real and complex
Lecture Notes on Polynomials Arne Jensen Department of Mathematical Sciences Aalborg University c 008 Introduction These lecture notes give a very short introduction to polynomials with real and complex
PRODUCTIVITY, ADAPTABILITY AND GRAIN QUALITY OF MODERN UKRAINIAN WINTER TRITICALE CULTIVARS*
 464 Вавиловский журнал генетики и селекции, 2012, Том 16, 2 УДК 631.524.83:631.524.85:633.112.1«324» PRODUCTIVITY, ADAPTABILITY AND GRAIN QUALITY OF MODERN UKRAINIAN WINTER TRITICALE CULTIVARS* 2012 г.
464 Вавиловский журнал генетики и селекции, 2012, Том 16, 2 УДК 631.524.83:631.524.85:633.112.1«324» PRODUCTIVITY, ADAPTABILITY AND GRAIN QUALITY OF MODERN UKRAINIAN WINTER TRITICALE CULTIVARS* 2012 г.
Maria Skublewska-Paszkowska 1 COMPARISON OF ARM ANIMATION. Марія Скублевска-Пашковська ПОРІВНЯННЯ МЕТОДІВ АНІМАЦІЇ РУХУ РУКИ
 НОВИНИ СВІТОВОЇ НАУКИ 505 Maria Skublewska-Paszkowska COMPARISON OF ARM ANIMATION 3D animation is a complex task which involves many methods used to create a moving object. The article presents two techniques
НОВИНИ СВІТОВОЇ НАУКИ 505 Maria Skublewska-Paszkowska COMPARISON OF ARM ANIMATION 3D animation is a complex task which involves many methods used to create a moving object. The article presents two techniques
Baltic Way 1995. Västerås (Sweden), November 12, 1995. Problems and solutions
 Baltic Way 995 Västerås (Sweden), November, 995 Problems and solutions. Find all triples (x, y, z) of positive integers satisfying the system of equations { x = (y + z) x 6 = y 6 + z 6 + 3(y + z ). Solution.
Baltic Way 995 Västerås (Sweden), November, 995 Problems and solutions. Find all triples (x, y, z) of positive integers satisfying the system of equations { x = (y + z) x 6 = y 6 + z 6 + 3(y + z ). Solution.
XLPE рower cables. 2 Modern solutions for power cables I Estralin HVC
 XLPE рower cables...2 Production technology...3 Estralin HVC a pioneer in Russia s XLPE cable production...4 Main types of products and services...5 Markings...6 XLPE cables 6-35 kv...7 Comparative characteristics
XLPE рower cables...2 Production technology...3 Estralin HVC a pioneer in Russia s XLPE cable production...4 Main types of products and services...5 Markings...6 XLPE cables 6-35 kv...7 Comparative characteristics
Future Trends in Airline Pricing, Yield. March 13, 2013
 Future Trends in Airline Pricing, Yield Management, &AncillaryFees March 13, 2013 THE OPPORTUNITY IS NOW FOR CORPORATE TRAVEL MANAGEMENT BUT FIRST: YOU HAVE TO KNOCK DOWN BARRIERS! but it won t hurt much!
Future Trends in Airline Pricing, Yield Management, &AncillaryFees March 13, 2013 THE OPPORTUNITY IS NOW FOR CORPORATE TRAVEL MANAGEMENT BUT FIRST: YOU HAVE TO KNOCK DOWN BARRIERS! but it won t hurt much!
The Archaeological Map of Nymphaion (PI. 72)
 Tomasz Schöll The Archaeological Map of Nymphaion (PI. 72) О ne of the main tasks fulfilled within the boundaries of the international project Nymphaion - the History and Structure of a Greek polis", carried
Tomasz Schöll The Archaeological Map of Nymphaion (PI. 72) О ne of the main tasks fulfilled within the boundaries of the international project Nymphaion - the History and Structure of a Greek polis", carried
GCDs and Relatively Prime Numbers! CSCI 2824, Fall 2014!
 GCDs and Relatively Prime Numbers! CSCI 2824, Fall 2014!!! Challenge Problem 2 (Mastermind) due Fri. 9/26 Find a fourth guess whose scoring will allow you to determine the secret code (repetitions are
GCDs and Relatively Prime Numbers! CSCI 2824, Fall 2014!!! Challenge Problem 2 (Mastermind) due Fri. 9/26 Find a fourth guess whose scoring will allow you to determine the secret code (repetitions are
