Modelling The Claims Development Result For Solvency Purposes
|
|
|
- Bryce Lambert
- 10 years ago
- Views:
Transcription
1 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes Mchael Merz Maro V. Wüthrch Abstract We assume that the clams lablty process satses the dstrbuton-ree chan-ladder model assumptons. For clams reservng at tme we predct the total ultmate clam wth the normaton avalable at tme and smlarly at tme we predct the same total ultmate clam wth the (updated) normaton avalable at tme. The clams development result at tme or accountng year ( ] s then dened to be the derence between these two successve predctons or the total ultmate clam. n [6 0] we have analyzed ths clams development result and we have quanted ts predcton uncertanty. Here we smply mody and llustrate the results obtaned n [6 0]. We emphasze that these results have drect consequences or solvency consderatons and were (under the new rs-adusted solvency regulaton) already mplemented n ndustry. Keywords. tochastc lams Reservng han-ladder Method lams evelopment Result Loss Experence ncurred Losses Pror Accdent Years olvency Mean quare Error o Predcton.. NTROUTON We consder the problem o quantyng the uncertanty assocated wth the development o clams reserves or pror accdent years n general nsurance. We assume that we are at tme and we predct the total ultmate clam at tme (wth the avalable normaton up to tme ) and one perod later at tme we predct the same total ultmate clam wth the updated normaton avalable at tme. The derence between these two successve predctons s the so-called clams development result or accountng year ( ]. The realzaton o ths clams development result has a drect mpact on the prot & loss (P&L) statement and on the nancal strength o the nsurance company. Thereore t also needs to be studed or solvency purposes. Here we analyze the predcton o the clams development result and the possble luctuatons around ths predcton (predcton uncertanty). Bascally we answer two questons that are o practcal relevance: asualty Actuaral ocety E-Forum Fall
2 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes (a) n general one predcts the clams development result or accountng year ( ] n the budget statement at tme by 0. We analyze the uncertanty n ths predcton. Ths s a prospectve vew: how ar can the realzaton o the clams development result devate rom 0? Remar: we dscuss below why the clams development result s predcted by 0. (b) n the P&L statement at tme one then obtans an observaton or the clams development result. We analyze whether ths observaton s wthn a reasonable range around 0 or whether t s an outler. Ths s a retrospectve vew. Moreover we dscuss the possble categorzaton o ths uncertanty. o let us start wth the descrpton o the budget statement and o the P&L statement or an example we reer to Table. The budget values at an. year are predcted values or the next accountng year ( ] o ths accountng year ( ].. The P&L statement are then the observed values at the end Postons a) and b) correspond to the premum ncome and ts assocated clams (generated by the premum lablty). Poston d) corresponds to expenses such as acquston expenses head oce expenses etc. Poston e) corresponds to the nancal returns generated on the balance sheet/assets. All these postons are typcally well-understood. They are predcted at an. year (budget values) and one has ther observatons at ec. 3 year n the P&L statement whch descrbes the nancal closng o the nsurance company or accountng year ( ]. asualty Actuaral ocety E-Forum Fall
3 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes budget values at an. year P&L statement at ec. 3 year a) premums earned b) clams ncurred current accdent year c) loss experence pror accdent years d) underwrtng and other expenses e) nvestment ncome ncome beore taxes Table : ncome statement n $ 000 However poston c) loss experence pror accdent years s oten much less understood. t corresponds to the derence between the clams reserves at tme t and at tme t adusted or the clam payments durng accountng year ( ] or clams wth accdent years pror to accountng year. n the sequel we wll denote ths poston by the clams development result (R). We analyze ths poston wthn the ramewor o the dstrbuton-ree chan-ladder (L) method. Ths s descrbed below. hort-term vs. long-term vew n the classcal clams reservng lterature one usually studes the total uncertanty n the clams development untl the total ultmate clam s nally settled. For the dstrbuton-ree L method ths has rst been done by Mac [7]. The study o the total uncertanty o the ull run-o s a long-term vew. Ths classcal vew n clams reservng s very mportant or solvng solvency questons and almost all stochastc clams reservng methods whch have been proposed up to now concentrate on ths long term vew (see Wüthrch-Merz [9]). However n the present wor we concentrate on a second mportant vew the short-term vew. The short-term vew s mportant or a varety o reasons: asualty Actuaral ocety E-Forum Fall
4 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes the short-term behavour s not adequate the company may smply not get to the long-term because t wll be declared nsolvent beore t gets to the long term. A short-term vew s relevant or management decsons as actons need to be taen on a regular bass. Note that most actons n an nsurance company are usually done on a yearly bass. These are or example nancal closngs prcng o nsurance products premum adustments etc. Relected through the annual nancal statements and reports the short-term perormance o the company s o nterest and mportance to regulators clents nvestors ratng agences stoc-marets etc. ts consstency wll ultmately have an mpact on the nancal strength and the reputaton o the company n the nsurance maret. Hence our goal s to study the development o the clams reserves on a yearly bass where we assume that the clams development process satses the assumptons o the dstrbutonree chan-ladder model. Our man results Results and 3.5 below gve an mproved verson o the results obtaned n [6 0]. e Felce-Morcon [4] have mplemented smlar deas reerrng to the random varable representng the Year-End Oblgatons o the nsurer nstead o the R. They obtaned smlar ormulas or the predcton error and vered the numercal results wth the help o the bootstrap method. They have notced that ther results or aggregated accdent years always le below the analytcal ones obtaned n [6]. The reason or ths s that there s one redundant term n (4.5) o [6]. Ths s now corrected see ormula (A.4) below. Let us menton that the deas presented n [6 0] were already successully mplemented n practce. Predcton error estmates o Year-End Oblgatons n the overdspersed Posson model have been derved by VAP [5] n a eld study on a large sample o talan MTPL companes. A eld study n lne wth [6 0] has been publshed by AAM-AME []. Moreover we would also le to menton that durng the wrtng o ths paper we have learned that smultaneously smlar deas have been developed by Böhm- Glaab []. asualty Actuaral ocety E-Forum Fall
5 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes. METHOOLOGY. Notaton We denote cumulatve payments or accdent year { 0 K } { 0 K } untl development year by. Ths means that the ultmate clam or accdent year s gven by. For smplcty we assume that (note that all our results can be generalzed to the case > ). Then the outstandng loss labltes or accdent year { 0 K } at tme t are gven by and at tme t they are gven by R (.) R. (.) Let denote the clams data avalable at tme { ; and } (.3) t and { and } { } ; ; (.4) denote the clams data avalable one perod later at tme t. That s we go one step ahead n tme rom to we obtan new observatons { } ; on the new dagonal o the clams development trangle (c. Fgure ). More ormally ths means that we get an enlargement o the -eld generated by the observatons generated by the observatons.e. ( ) ( ) to the -eld. (.5). strbuton-ree chan-ladder method asualty Actuaral ocety E-Forum Fall
6 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes We study the clams development process and the R wthn the ramewor o the wellnown dstrbuton-ree L method. That s we assume that the cumulatve payments satsy the assumptons o the dstrbuton-ree L model. The dstrbuton-ree L model has been ntroduced by Mac [7] and has been used by many other actuares. t s probably the most popular clams reservng method because t s smple and t delvers n general very accurate results. accdent development year accdent development year year 0 K K year 0 K K 0 0 M M M M Fgure : Loss development trangle at tme t and t Model Assumptons. umulatve payments n derent accdent years { 0 K } are ndependent. ( ) 0 are Marov processes and there exst constants > 0 > 0 such that or all and 0 we have [ ] E (.6) asualty Actuaral ocety E-Forum Fall
7 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes ( ) Var. (.7) Remars. n the orgnal wor o Mac [7] there were weaer assumptons or the denton o the dstrbuton-ree L model namely the Marov process assumpton was replaced by an assumpton only on the rst two moments (see also Wüthrch-Merz [9]). The dervaton o an estmate or the estmaton error n [0] was done n a tmeseres ramewor. Ths mposes stronger model assumptons. Note also that n (.7) we requre that the cumulatve clams are postve n order to get a meanngul varance assumpton. Model Assumptons. mply (usng the tower property o condtonal expectatons) [ ] E and [ ] E. (.8) Ths means that or nown L actors we are able to calculate the condtonally expected ultmate clam gven the normaton and respectvely. O course n general the L actors ramewor o the L method ths s done as ollows: are not nown and need to be estmated. Wthn the. At tme t gven normaton the L actors are estmated by 0 where. (.9) 0. At tme t gven normaton the L actors are estmated by asualty Actuaral ocety E-Forum Fall
8 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes where 0 0. (.0) Ths means the L estmates at tme use the ncrease n normaton about the clams development process n the new observed accountng year ( ] based on the addtonal observaton. and are thereore Mac [7] proved that these are unbased estmators or and moreover that m and m l ( m or ) are uncorrelated random varables or l (see Theorem n Mac [7] and Lemma.5 n [9]). Ths mples that gven s an unbased estmator or [ ] L (.) E wth and gven L (.) s an unbased estmator or [ ] E wth. Remars.3 The realzatons o the estmators realzatons o 0 K are nown at tme t but the 0 K are unnown snce the observatons K durng the accountng year ( ] are unnown at tme. asualty Actuaral ocety E-Forum Fall
9 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes When ndces o accdent and development years are such that there are no actor products n (.) or (.) an empty product s replaced by. For example and. The estmators are based on the L estmators at tme and thereore use the ncrease n normaton gven by the new observatons n the accountng year rom to..3 ondtonal mean square error o predcton Assume that we are at tme that s we have normaton and our goal s to predct the random varable. Then gven n (.) s a -measurable predctor or. At tme we measure the predcton uncertanty wth the so-called condtonal mean square error o predcton (MEP) whch s dened by E (.3) That s we measure the predcton uncertanty n the L ( P[ ]) -dstance. Because s -measurable ths can easly be decoupled nto process varance and estmaton error: ( ) ( [ ] Var E ). (.4) Ths means that s used as predctor or the random varable and as estmator or the expected value [ ] [ ] E at tme. O course the condtonal expectaton E s nown at tme (.e. the L actors are nown) t s used as predctor asualty Actuaral ocety E-Forum Fall
10 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes or and the estmaton error term vanshes. For more normaton on condtonal and uncondtonal MEP s we reer to hapter 3 n [9]:.4 lams development result (R) We gnore any prudental margn and assume that clams reserves are set equal to the expected outstandng loss labltes condtonal on the avalable normaton at tme and respectvely. That s n our understandng best estmate clams reserves correspond to condtonal expectatons whch mples a sel-nancng property (see orollary.6 n [8]). For nown L actors thereore used as predctor or expectaton [ ] the condtonal expectaton [ ] E s used as predctor or result (true R) or accountng year ( ] E s nown and s at tme. mlarly at tme the condtonal s dened as ollows.. Then the true clams development enton.4 (True clams development result) The true R or accdent year { K } n accountng year ( ] s gven by ( ) E [ R ] ( X E [ R ] ) E [ ] E [ ] R (.5) where by X denotes the ncremental payments. Furthermore the true aggregate s gven R ( ). (.6) Usng the martngale property we see that asualty Actuaral ocety E-Forum Fall
11 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes [ R ( ) ] 0 E. (.7) Ths means that or nown L actors equal to zero. Thereore or nown L actors the expected true R (vewed rom tme ) s we reer to ( ) R as the true R. Ths also ustes the act that n the budget values o the ncome statement poston c) loss experence pror accdent years s predcted by $0 (see poston c) n Table ). The predcton uncertanty o ths predcton 0 can then easly be calculated namely R ( 0) Var R ( ) ( ) E [ ]. (.8) For a proo we reer to ormula (5.5) n [0] (apply recursvely the model assumptons) and the aggregaton o accdent years can easly be done because accdent years are ndependent accordng to Model Assumptons.. Unortunately the L actors are n general not nown and thereore the true R s not observable. Replacng the unnown actors by ther estmators.e. replacng the expected ultmate clams E [ ] and E [ ] wth ther estmates and respectvely the true R or accdent year ( ) n accountng year ( ] predcted/estmated n the L method by: s enton.5 (Observable clams development result) The observable R or accdent year { K } n accountng year ( ] ( ) R X R R s gven by (.9) asualty Actuaral ocety E-Forum Fall
12 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes where R and aggregate R s gven by R are dened below by (.) and (.) respectvely. Furthermore the observable ( ) R. (.0) Note that under the Model Assumptons. gven R s an unbased estmator or [ R ] s an unbased estmator or [ R ] ( ) (.) E and gven R ( ) (.) E. Remars.6 We pont out the (non-observable) true clams development result ( ) approxmated by an observable clams development result R ( ) R s. n the next secton we quanty the qualty o ths approxmaton (retrospectve vew). Moreover the observable clams development result R ( ) s the poston that occurs n the P&L statement at ec. 3 year. Ths poston s n the budget statement predcted by 0. n the next secton we also measure the qualty o ths predcton whch determnes the solvency requrements (prospectve vew). We emphasze that such a solvency consderaton s only a one-year vew. The remanng run-o can or example be treated wth a cost-o-captal loadng that s asualty Actuaral ocety E-Forum Fall
13 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes based on the one-year observable clams development result (ths has or example been done n the wss olvency Test). 3. MEP OF THE LAM EVELOPMENT REULT Our goal s to quanty the ollowng two quanttes: R ( ) E R ( ) 0 (3.) R 0 R ( ) ( ( E R )) R. (3.) The rst condtonal MEP gves the prospectve solvency pont o vew. t quantes the predcton uncertanty n the budget value 0 or the observable clams development result at the end o the accountng perod. n the solvency margn we need to hold rs captal or possble negatve devatons o ( ) R rom 0. The second condtonal MEP gves a retrospectve pont o vew. t analyzes the dstance between the true R and the observable R. t may or example answer the queston whether the true R could also be postve ( we would now the true L actors) when we have an observable R gven by $ (see Table ). Hence the retrospectve vew separates pure randomness (process varance) rom parameter estmaton uncertantes. n order to quanty the condtonal MEP s we need an estmator or the varance parameters. An unbased estmate or s gven by (see Lemma 3.5 n [9]) 0. (3.3) asualty Actuaral ocety E-Forum Fall
14 Modellng The lams evelopment Result For olvency Purposes 3. ngle accdent year n ths secton we gve estmators or the two condtonal MEP s dened n (3.)-(3.). For ther dervaton we reer to the appendx. We dene Δ (3.4) Φ (3.5) Ψ (3.6) and Φ Ψ Φ Γ. (3.7) We are now ready to gve estmators or all the error terms. Frst o all the varance o the true R gven n (.8) s estmated by R ar V Ψ. (3.8) The estmator or the condtonal MEP s are then gven by: Modelng the lams evelopment Result For olvency Purposes asualty Actuaral ocety E-Forum Fall
15 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes Result 3. (ondtonal ME estmator or a sngle accdent year) We estmate the condtonal MEP s gven n (3.)-(3.) by R ( 0) ( ) ( ) Γ Δ (3.9) R ( ) ( Φ Δ ) R ( ). (3.0) Ths mmedately mples that we have ( 0) R ( ) R Var R ( ) ( R ) ( ) R R. (3.) Note that ths s ntutvely clear snce the true and the observable R should move nto the same drecton accordng to the observatons n accountng year ( ]. However the rst lne n (3.) s slghtly msleadng. Note that we have derved estmators whch gve an equalty on the rst lne o (3.). However ths equalty holds true only or our estmators where we neglect uncertantes n hgher order terms. Note as already mentoned or typcal real data examples hgher order terms are o neglgble order whch means that we get an approxmate equalty on the rst lne o (3.) (see also dervaton n (A.)). Ths s smlar to the ndngs presented n hapter 3 o [9]. 3. Aggregaton over pror accdent years When aggregatng over pror accdent years one has to tae nto account the correlatons between derent accdent years snce the same observatons are used to estmate the L actors and are then appled to derent accdent years (see also ecton 3..4 n [9]). Based on the denton o the condtonal MEP or the true aggregate R around the aggregated observable R the ollowng estmator s obtaned: asualty Actuaral ocety E-Forum Fall
16 Modellng The lams evelopment Result For olvency Purposes Result 3. (ondtonal MEP or aggregated accdent years part ) For aggregated accdent years we obtan the ollowng estmator R R sep m (3.) > > Λ Φ R R 0 wth Λ. (3.3) For the condtonal MEP o the aggregated observable R around 0 we need an addtonal denton. Φ Φ Ξ. (3.4) Result 3.3 (ondtonal MEP or aggregated accdent years part ) For aggregated accdent years we obtan the ollowng estmator 0 R sep m (3.5) > > Λ Ξ R 0 0. Note that (3.5) can be rewrtten as ollows: Modelng the lams evelopment Result For olvency Purposes asualty Actuaral ocety E-Forum Fall
17 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes ( 0) m sep (3.6) R ( ) R ( ) R ( ) Var ( R ( ) ) > > 0 ( ) R R ( ). ( Ξ Φ ) Hence we obtan the same decouplng or aggregated accdent years as or sngle accdent years. Remars 3.4 (omparson to the classcal Mac [7] ormula) n Results we have obtaned a natural splt nto process varance and estmaton error. However ths splt has no longer ths clear dstncton as t appears. The reason s that the process varance also nluences the volatlty o and hence s part o the estmaton error. n other approaches one may obtan other splts e.g. n the credblty chan ladder method (see Bühlmann et al. [3]) one obtans a derent splt. Thereore we mody Results whch leads to a ormula that gves nterpretatons n terms o the classcal Mac [7] ormula see also (4.)-(4.3) below. Result 3.5 asualty Actuaral ocety E-Forum Fall
18 Modellng The lams evelopment Result For olvency Purposes For sngle accdent years we obtan rom Result 3. R 0 Δ Γ (3.7). / / / For aggregated accdent years we obtan rom Result 3.3 R R ) ( (0) 0 (3.8). / / 0 > > We compare ths now to the classcal Mac [7] ormula. For sngle accdent years the condtonal MEP o the predctor or the ultmate clam s gven n Theorem 3 n Mac [7] (see also Estmator 3. n [9]). We see rom (3.7) that the condtonal MEP o the R consders only the rst term o the process varance o the classcal Mac [7] ormula and or the estmaton error the next dagonal s ully consdered ) ( but all remanng runo cells ) ( are scaled by /. For aggregated accdent years the condtonal MEP o the predctor or the ultmate clam s gven on page 0 n Mac [7] (see also Estmator 3.6 n [9]). We see rom (3.8) that the condtonal MEP o the R or aggregated accdent years consders the estmaton error or the next accountng year ) ( and all other accountng years ) ( are scaled by /. Hence we have obtaned a derent splt that allows or easy nterpretatons n terms o the Mac [7] ormula. However note that these nterpretatons only hold true or lnear approxmatons (A.) otherwse the pcture s more nvolved. Modelng the lams evelopment Result For olvency Purposes asualty Actuaral ocety E-Forum Fall
19 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes 4. NUMERAL EXAMPLE AN ONLUON For our numercal example we use the dataset gven n Table. The table contans cumulatve payments or accdent years { 0 K8} at tme 8 and at tme 9. Hence ths allows or an explctly calculaton o the observable clams development result Table : Run-o trangle (cumulatve payments n $ 000) or tme 8 and 9 asualty Actuaral ocety E-Forum Fall
20 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes Table summarzes the L estmates and o the age-to-age actors as well as the varance estmates or 0 K 7. nce we do not have enough data to estmate Usng the estmates clams labltes 7 (recall and R at tme ) we use the extrapolaton gven n Mac [7]: 4 { }. (4.) 7 mn we calculate the clams reserves R or the outstandng t and X R or X R at tme t respectvely. Ths then gves realzatons o the observable R or sngle accdent years and or aggregated accdent years (see Table 3). Observe that we have a negatve observable aggregate R at tme o about $ (whch corresponds to poston c) n the P&L statement n Table ). R X R R ( ) Total Table 3: Realzaton o the observable R at tme t n $ 000 The queston whch we now have s whether the true aggregate R could also be postve we had nown the true L actors at tme t (retrospectve vew). We thereore asualty Actuaral ocety E-Forum Fall
21 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes perorm the varance and MEP analyss usng the results o ecton 3. Table 4 provdes the estmates or sngle and aggregated accdent years. On the other hand we would le to now how ths observaton o $ corresponds to the predcton uncertanty n the budget values where we have predcted that the R s $ 0 (see poston c) n Table ). Ths s the prospectve (solvency) vew. We observe that the estmated standard devaton o the true aggregate R s equal to $ 65 4 whch means that t s not unlely to have the true aggregate R n the range o about $ ± Moreover we see that the square root o the estmate or the MEP between true and observable R s o sze $ (see Table 4) ths means that t s lely that the true R has the same sgn as the observable R whch s $ Thereore also the nowledge o the true L actors would probably have led to a negatve clams development experence. Moreover note that the predcton 0 n the budget values has a predcton uncertanty relatve to the observable R o $ whch means that t s not unlely to have an observable R o $ n other words the solvency captal/rs margn or the R should drectly be related to ths value o $ R V ar ( R) m sep R R cov Total Table 4: Volatltes o the estmates n $ 000 wth: Mac asualty Actuaral ocety E-Forum Fall
22 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes R estmated reserves at tme t c. (.) V ar estmated std. dev. o the true R c. (3.8) ( R) estmated R (3.0) and (3.) between true and observable R c. m predcton std. dev. o 0 compared to R ( ) sep R 0 Mac c. (3.9) and (3.5) o the ultmate clam c. Mac [7] and (4.3) Note that we only consder the one-year uncertanty o the clams reserves run-o. Ths s exactly the short term vew/pcture that should loo ne to get to the long term. n order to treat the ull run-o one can then add or example a cost-o-captal margn to the remanng run-o whch ensures that the uture solvency captal can be nanced. We emphasze that t s mportant to add a margn whch ensures the smooth run-o o the whole labltes ater the next accountng year. Fnally these results are compared to the classcal Mac ormula [7] or the estmate o the condtonal MEP o the ultmate clam by n the dstrbuton-ree L model. The Mac ormula [7] gves the total uncertanty o the ull run-o (long term vew) whch estmates Mac ( ) E (4.) and Mac E (4.3) see also Estmator 3.6 n [9]. Notce that the normaton n the next accountng year (dagonal ) contrbutes substantally to the total uncertanty o the total ultmate clam over pror accdent years. That s the uncertanty n the next accountng year s $ and asualty Actuaral ocety E-Forum Fall
23 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes the total uncertanty s $ Note that we have chosen a short-taled lne o busness so t s clear that a lot o uncertanty s already contaned n the next accountng year. Generally speang the porton o uncertanty whch s already contaned n the next accountng year s larger or short-taled busness than or long-taled busness snce n long-taled busness the adverse movements n the clams reserves emerge slowly over many years. one chooses long-taled lnes o busness then the one-year rs s about /3 o the ull run-o rs. Ths observaton s nlne wth a European eld study n derent companes see AAM-AME []. APPENX A. PROOF AN ERVATON Assume that a are postve constants wth >> a then we have ( ) a a (A.) where the rght-hand sde s a lower bound or the let-hand sde. Usng the above ormula we wll approxmate all product terms rom our prevous wor [0] by summatons. ervaton o Result 3.. We rst gve the dervaton o Result 3. or a sngle accdent year. Note that the term Δ s gven n ormula (3.0) o [0]. Henceorth there remans to derve the terms Φ and Γ. For the term Φ we obtan rom ormula (3.9) n [0] ( ) ( ) asualty Actuaral ocety E-Forum Fall
24 Modellng The lams evelopment Result For olvency Purposes (A.) Φ where the approxmatons are accurate because >> or typcal clams reservng data. For the term Γ we obtan rom (3.6) n [0] (A.3) Γ Φ Ψ. Henceorth Result 3. s obtaned rom (3.8) (3.4) and (3.5) n [0]. ervatons o Results 3. and 3.3. We now turn to Result 3.. All that remans to derve are the correlaton terms. We start wth the dervaton o Λ (ths ders rom the calculaton n [6]). From (4.4)- (4.5) n [6] we see that or < the cross covarance term o the estmaton error [ ] [ ] R E R E s estmated by resampled values gven whch mples Modelng the lams evelopment Result For olvency Purposes asualty Actuaral ocety E-Forum Fall
25 Modellng The lams evelopment Result For olvency Purposes E (A.4) E E E E. Note that the last two lnes der rom (4.5) n [6]. Ths last expresson s now equal to (see also ecton 4.. n [6]). Next we use (A.) so we see that the last lne can be approxmated by Modelng the lams evelopment Result For olvency Purposes asualty Actuaral ocety E-Forum Fall
26 Modellng The lams evelopment Result For olvency Purposes. Next we note that hence ths last term s equal to. Hence pluggng n the estmators or and at tme yelds the clam. Hence there remans to calculate the second term n Result 3.. From (3.3) n [0] we agan obtan the clam usng that >> or typcal clams reservng data. o there remans to derve Result 3.3. The proo s completely analogous the term contanng Λ was obtaned above. The term Ξ s obtaned rom (3.7) n [0] analogous to (A.3). Ths completes the dervatons. 5. REFERENE [] AAM-AME (007). AAM-AME study on non-le long tal labltes. Reserve rs and rs margn assessment under olvency. October [] Böhm H. Glaab H. (006). Modellerung des Kalenderahr-Rsos m addtven und multplatven chadenreserverungsmodell. Tal presented at the German ATN olloquum. [3] Bühlmann H. e Felce M. Gsler A. Morcon F. Wüthrch M.V. (008). Recursve credblty ormula or chan ladder actors and the clams development result. Preprnt ETH Zurch. [4] e Felce M. Morcon F. (006). Process error and estmaton error o year-end reserve estmaton n the dstrbuton ree chan-ladder model. Ale Worng Paper Rome November 006. Modelng the lams evelopment Result For olvency Purposes asualty Actuaral ocety E-Forum Fall
27 Modelng the lams evelopment Result For olvency Purposes Modellng The lams evelopment Result For olvency Purposes [5] VAP (006). Reserves requrements and captal requrements n non-le nsurance. An analyss o the talan MTPL nsurance maret by stochastc clams reservng models. Report prepared by e Felce M. Morcon F. Matarazzo L. avastracc. and Pasqualn. October 006. [6] Merz M. Wüthrch M.V. (007). Predcton error o the expected clams development result n the chan ladder method. Bulletn o wss Assocaton o Actuares No [7] Mac T. (993). strbuton-ree calculaton o the standard error o chan ladder reserve estmates. Astn Bulletn Vol. 3 No [8] Wüthrch M.V. Bühlmann H. Furrer H. (008). onsstent Actuaral Valuaton. prnger Berln. [9] Wüthrch M.V. Merz M. (008). tochastc lams Reservng Methods n nsurance. Wley Fnance. [0] Wüthrch M.V. Merz M. Lyseno N. (008). Uncertanty n the clams development result n the chan ladder method. Accepted or publcaton n cand. Act.. Bographes o the Authors Merz Mchael s Assstant Proessor or tatstcs Rs and nsurance at Unversty o Tübngen (Germany). He was awarded n 004 wth the OR Actuaral Prze or hs doctoral thess n rs theory. Wüthrch Maro V. s enor Researcher and Lecturer at ETH Zurch (wtzerland) n the eld actuaral and nancal mathematcs. He holds a Ph n Mathematcs rom ETH Zurch and serves on the board o the wss Assocaton o Actuares. Unversty Tübngen Faculty o Economcs Tübngen Germany. [email protected] ETH Zurch epartment o Mathematcs H-809 Zurch wtzerland. [email protected] asualty Actuaral ocety E-Forum Fall
Analysis of Premium Liabilities for Australian Lines of Business
 Summary of Analyss of Premum Labltes for Australan Lnes of Busness Emly Tao Honours Research Paper, The Unversty of Melbourne Emly Tao Acknowledgements I am grateful to the Australan Prudental Regulaton
Summary of Analyss of Premum Labltes for Australan Lnes of Busness Emly Tao Honours Research Paper, The Unversty of Melbourne Emly Tao Acknowledgements I am grateful to the Australan Prudental Regulaton
Cost-of-Capital Margin for a General Insurance Liability Runoff
 Cost-of-Captal Margn for a General Insurance Lablty Runoff Robert Salzmann and Maro V Wüthrch Abstract Under new solvency regulatons, general nsurance companes need to calculate a rsk margn to cover possble
Cost-of-Captal Margn for a General Insurance Lablty Runoff Robert Salzmann and Maro V Wüthrch Abstract Under new solvency regulatons, general nsurance companes need to calculate a rsk margn to cover possble
Prediction of Disability Frequencies in Life Insurance
 Predcton of Dsablty Frequences n Lfe Insurance Bernhard Köng Fran Weber Maro V. Wüthrch October 28, 2011 Abstract For the predcton of dsablty frequences, not only the observed, but also the ncurred but
Predcton of Dsablty Frequences n Lfe Insurance Bernhard Köng Fran Weber Maro V. Wüthrch October 28, 2011 Abstract For the predcton of dsablty frequences, not only the observed, but also the ncurred but
Istituto Italiano degli Attuari Riunione di Seminario Attuariale. A Collective Risk Model for Claims Reserve Distribution
 Isttuto Italano degl Attuar Runone d Semnaro Attuarale Unverstà Cattolca del Sacro Cuore Mlano, 12 Maggo 2011 A Collectve Rsk Model for Clams Reserve Dstrbuton no Savell Full Professor of Rsk Theory Catholc
Isttuto Italano degl Attuar Runone d Semnaro Attuarale Unverstà Cattolca del Sacro Cuore Mlano, 12 Maggo 2011 A Collectve Rsk Model for Clams Reserve Dstrbuton no Savell Full Professor of Rsk Theory Catholc
Stochastic Claims Reserving under Consideration of Various Different Sources of Information
 Stochastc Clams Reservng under Consderaton of Varous Dfferent Sources of Informaton Dssertaton Zur Erlangung der Würde des Dotors der Wrtschaftswssenschaften der Unverstät Hamburg vorgelegt von Sebastan
Stochastc Clams Reservng under Consderaton of Varous Dfferent Sources of Informaton Dssertaton Zur Erlangung der Würde des Dotors der Wrtschaftswssenschaften der Unverstät Hamburg vorgelegt von Sebastan
Solution: Let i = 10% and d = 5%. By definition, the respective forces of interest on funds A and B are. i 1 + it. S A (t) = d (1 dt) 2 1. = d 1 dt.
 Chapter 9 Revew problems 9.1 Interest rate measurement Example 9.1. Fund A accumulates at a smple nterest rate of 10%. Fund B accumulates at a smple dscount rate of 5%. Fnd the pont n tme at whch the forces
Chapter 9 Revew problems 9.1 Interest rate measurement Example 9.1. Fund A accumulates at a smple nterest rate of 10%. Fund B accumulates at a smple dscount rate of 5%. Fnd the pont n tme at whch the forces
Stress test for measuring insurance risks in non-life insurance
 PROMEMORIA Datum June 01 Fnansnspektonen Författare Bengt von Bahr, Younes Elonq and Erk Elvers Stress test for measurng nsurance rsks n non-lfe nsurance Summary Ths memo descrbes stress testng of nsurance
PROMEMORIA Datum June 01 Fnansnspektonen Författare Bengt von Bahr, Younes Elonq and Erk Elvers Stress test for measurng nsurance rsks n non-lfe nsurance Summary Ths memo descrbes stress testng of nsurance
benefit is 2, paid if the policyholder dies within the year, and probability of death within the year is ).
 REVIEW OF RISK MANAGEMENT CONCEPTS LOSS DISTRIBUTIONS AND INSURANCE Loss and nsurance: When someone s subject to the rsk of ncurrng a fnancal loss, the loss s generally modeled usng a random varable or
REVIEW OF RISK MANAGEMENT CONCEPTS LOSS DISTRIBUTIONS AND INSURANCE Loss and nsurance: When someone s subject to the rsk of ncurrng a fnancal loss, the loss s generally modeled usng a random varable or
Traffic-light a stress test for life insurance provisions
 MEMORANDUM Date 006-09-7 Authors Bengt von Bahr, Göran Ronge Traffc-lght a stress test for lfe nsurance provsons Fnansnspetonen P.O. Box 6750 SE-113 85 Stocholm [Sveavägen 167] Tel +46 8 787 80 00 Fax
MEMORANDUM Date 006-09-7 Authors Bengt von Bahr, Göran Ronge Traffc-lght a stress test for lfe nsurance provsons Fnansnspetonen P.O. Box 6750 SE-113 85 Stocholm [Sveavägen 167] Tel +46 8 787 80 00 Fax
How To Calculate The Accountng Perod Of Nequalty
 Inequalty and The Accountng Perod Quentn Wodon and Shlomo Ytzha World Ban and Hebrew Unversty September Abstract Income nequalty typcally declnes wth the length of tme taen nto account for measurement.
Inequalty and The Accountng Perod Quentn Wodon and Shlomo Ytzha World Ban and Hebrew Unversty September Abstract Income nequalty typcally declnes wth the length of tme taen nto account for measurement.
Traffic-light extended with stress test for insurance and expense risks in life insurance
 PROMEMORIA Datum 0 July 007 FI Dnr 07-1171-30 Fnansnspetonen Författare Bengt von Bahr, Göran Ronge Traffc-lght extended wth stress test for nsurance and expense rss n lfe nsurance Summary Ths memorandum
PROMEMORIA Datum 0 July 007 FI Dnr 07-1171-30 Fnansnspetonen Författare Bengt von Bahr, Göran Ronge Traffc-lght extended wth stress test for nsurance and expense rss n lfe nsurance Summary Ths memorandum
Joe Pimbley, unpublished, 2005. Yield Curve Calculations
 Joe Pmbley, unpublshed, 005. Yeld Curve Calculatons Background: Everythng s dscount factors Yeld curve calculatons nclude valuaton of forward rate agreements (FRAs), swaps, nterest rate optons, and forward
Joe Pmbley, unpublshed, 005. Yeld Curve Calculatons Background: Everythng s dscount factors Yeld curve calculatons nclude valuaton of forward rate agreements (FRAs), swaps, nterest rate optons, and forward
Recurrence. 1 Definitions and main statements
 Recurrence 1 Defntons and man statements Let X n, n = 0, 1, 2,... be a MC wth the state space S = (1, 2,...), transton probabltes p j = P {X n+1 = j X n = }, and the transton matrx P = (p j ),j S def.
Recurrence 1 Defntons and man statements Let X n, n = 0, 1, 2,... be a MC wth the state space S = (1, 2,...), transton probabltes p j = P {X n+1 = j X n = }, and the transton matrx P = (p j ),j S def.
DEFINING %COMPLETE IN MICROSOFT PROJECT
 CelersSystems DEFINING %COMPLETE IN MICROSOFT PROJECT PREPARED BY James E Aksel, PMP, PMI-SP, MVP For Addtonal Informaton about Earned Value Management Systems and reportng, please contact: CelersSystems,
CelersSystems DEFINING %COMPLETE IN MICROSOFT PROJECT PREPARED BY James E Aksel, PMP, PMI-SP, MVP For Addtonal Informaton about Earned Value Management Systems and reportng, please contact: CelersSystems,
An Alternative Way to Measure Private Equity Performance
 An Alternatve Way to Measure Prvate Equty Performance Peter Todd Parlux Investment Technology LLC Summary Internal Rate of Return (IRR) s probably the most common way to measure the performance of prvate
An Alternatve Way to Measure Prvate Equty Performance Peter Todd Parlux Investment Technology LLC Summary Internal Rate of Return (IRR) s probably the most common way to measure the performance of prvate
Luby s Alg. for Maximal Independent Sets using Pairwise Independence
 Lecture Notes for Randomzed Algorthms Luby s Alg. for Maxmal Independent Sets usng Parwse Independence Last Updated by Erc Vgoda on February, 006 8. Maxmal Independent Sets For a graph G = (V, E), an ndependent
Lecture Notes for Randomzed Algorthms Luby s Alg. for Maxmal Independent Sets usng Parwse Independence Last Updated by Erc Vgoda on February, 006 8. Maxmal Independent Sets For a graph G = (V, E), an ndependent
THE DISTRIBUTION OF LOAN PORTFOLIO VALUE * Oldrich Alfons Vasicek
 HE DISRIBUION OF LOAN PORFOLIO VALUE * Oldrch Alfons Vascek he amount of captal necessary to support a portfolo of debt securtes depends on the probablty dstrbuton of the portfolo loss. Consder a portfolo
HE DISRIBUION OF LOAN PORFOLIO VALUE * Oldrch Alfons Vascek he amount of captal necessary to support a portfolo of debt securtes depends on the probablty dstrbuton of the portfolo loss. Consder a portfolo
Section 5.4 Annuities, Present Value, and Amortization
 Secton 5.4 Annutes, Present Value, and Amortzaton Present Value In Secton 5.2, we saw that the present value of A dollars at nterest rate per perod for n perods s the amount that must be deposted today
Secton 5.4 Annutes, Present Value, and Amortzaton Present Value In Secton 5.2, we saw that the present value of A dollars at nterest rate per perod for n perods s the amount that must be deposted today
What is Candidate Sampling
 What s Canddate Samplng Say we have a multclass or mult label problem where each tranng example ( x, T ) conssts of a context x a small (mult)set of target classes T out of a large unverse L of possble
What s Canddate Samplng Say we have a multclass or mult label problem where each tranng example ( x, T ) conssts of a context x a small (mult)set of target classes T out of a large unverse L of possble
CHAPTER 14 MORE ABOUT REGRESSION
 CHAPTER 14 MORE ABOUT REGRESSION We learned n Chapter 5 that often a straght lne descrbes the pattern of a relatonshp between two quanttatve varables. For nstance, n Example 5.1 we explored the relatonshp
CHAPTER 14 MORE ABOUT REGRESSION We learned n Chapter 5 that often a straght lne descrbes the pattern of a relatonshp between two quanttatve varables. For nstance, n Example 5.1 we explored the relatonshp
The Cox-Ross-Rubinstein Option Pricing Model
 Fnance 400 A. Penat - G. Pennacc Te Cox-Ross-Rubnsten Opton Prcng Model Te prevous notes sowed tat te absence o arbtrage restrcts te prce o an opton n terms o ts underlyng asset. However, te no-arbtrage
Fnance 400 A. Penat - G. Pennacc Te Cox-Ross-Rubnsten Opton Prcng Model Te prevous notes sowed tat te absence o arbtrage restrcts te prce o an opton n terms o ts underlyng asset. However, te no-arbtrage
BERNSTEIN POLYNOMIALS
 On-Lne Geometrc Modelng Notes BERNSTEIN POLYNOMIALS Kenneth I. Joy Vsualzaton and Graphcs Research Group Department of Computer Scence Unversty of Calforna, Davs Overvew Polynomals are ncredbly useful
On-Lne Geometrc Modelng Notes BERNSTEIN POLYNOMIALS Kenneth I. Joy Vsualzaton and Graphcs Research Group Department of Computer Scence Unversty of Calforna, Davs Overvew Polynomals are ncredbly useful
Institute of Informatics, Faculty of Business and Management, Brno University of Technology,Czech Republic
 Lagrange Multplers as Quanttatve Indcators n Economcs Ivan Mezník Insttute of Informatcs, Faculty of Busness and Management, Brno Unversty of TechnologCzech Republc Abstract The quanttatve role of Lagrange
Lagrange Multplers as Quanttatve Indcators n Economcs Ivan Mezník Insttute of Informatcs, Faculty of Busness and Management, Brno Unversty of TechnologCzech Republc Abstract The quanttatve role of Lagrange
Causal, Explanatory Forecasting. Analysis. Regression Analysis. Simple Linear Regression. Which is Independent? Forecasting
 Causal, Explanatory Forecastng Assumes cause-and-effect relatonshp between system nputs and ts output Forecastng wth Regresson Analyss Rchard S. Barr Inputs System Cause + Effect Relatonshp The job of
Causal, Explanatory Forecastng Assumes cause-and-effect relatonshp between system nputs and ts output Forecastng wth Regresson Analyss Rchard S. Barr Inputs System Cause + Effect Relatonshp The job of
Using Series to Analyze Financial Situations: Present Value
 2.8 Usng Seres to Analyze Fnancal Stuatons: Present Value In the prevous secton, you learned how to calculate the amount, or future value, of an ordnary smple annuty. The amount s the sum of the accumulated
2.8 Usng Seres to Analyze Fnancal Stuatons: Present Value In the prevous secton, you learned how to calculate the amount, or future value, of an ordnary smple annuty. The amount s the sum of the accumulated
The Application of Fractional Brownian Motion in Option Pricing
 Vol. 0, No. (05), pp. 73-8 http://dx.do.org/0.457/jmue.05.0..6 The Applcaton of Fractonal Brownan Moton n Opton Prcng Qng-xn Zhou School of Basc Scence,arbn Unversty of Commerce,arbn [email protected]
Vol. 0, No. (05), pp. 73-8 http://dx.do.org/0.457/jmue.05.0..6 The Applcaton of Fractonal Brownan Moton n Opton Prcng Qng-xn Zhou School of Basc Scence,arbn Unversty of Commerce,arbn [email protected]
THE METHOD OF LEAST SQUARES THE METHOD OF LEAST SQUARES
 The goal: to measure (determne) an unknown quantty x (the value of a RV X) Realsaton: n results: y 1, y 2,..., y j,..., y n, (the measured values of Y 1, Y 2,..., Y j,..., Y n ) every result s encumbered
The goal: to measure (determne) an unknown quantty x (the value of a RV X) Realsaton: n results: y 1, y 2,..., y j,..., y n, (the measured values of Y 1, Y 2,..., Y j,..., Y n ) every result s encumbered
How To Understand The Results Of The German Meris Cloud And Water Vapour Product
 Ttel: Project: Doc. No.: MERIS level 3 cloud and water vapour products MAPP MAPP-ATBD-ClWVL3 Issue: 1 Revson: 0 Date: 9.12.1998 Functon Name Organsaton Sgnature Date Author: Bennartz FUB Preusker FUB Schüller
Ttel: Project: Doc. No.: MERIS level 3 cloud and water vapour products MAPP MAPP-ATBD-ClWVL3 Issue: 1 Revson: 0 Date: 9.12.1998 Functon Name Organsaton Sgnature Date Author: Bennartz FUB Preusker FUB Schüller
A Novel Methodology of Working Capital Management for Large. Public Constructions by Using Fuzzy S-curve Regression
 Novel Methodology of Workng Captal Management for Large Publc Constructons by Usng Fuzzy S-curve Regresson Cheng-Wu Chen, Morrs H. L. Wang and Tng-Ya Hseh Department of Cvl Engneerng, Natonal Central Unversty,
Novel Methodology of Workng Captal Management for Large Publc Constructons by Usng Fuzzy S-curve Regresson Cheng-Wu Chen, Morrs H. L. Wang and Tng-Ya Hseh Department of Cvl Engneerng, Natonal Central Unversty,
1. Measuring association using correlation and regression
 How to measure assocaton I: Correlaton. 1. Measurng assocaton usng correlaton and regresson We often would lke to know how one varable, such as a mother's weght, s related to another varable, such as a
How to measure assocaton I: Correlaton. 1. Measurng assocaton usng correlaton and regresson We often would lke to know how one varable, such as a mother's weght, s related to another varable, such as a
Answer: A). There is a flatter IS curve in the high MPC economy. Original LM LM after increase in M. IS curve for low MPC economy
 4.02 Quz Solutons Fall 2004 Multple-Choce Questons (30/00 ponts) Please, crcle the correct answer for each of the followng 0 multple-choce questons. For each queston, only one of the answers s correct.
4.02 Quz Solutons Fall 2004 Multple-Choce Questons (30/00 ponts) Please, crcle the correct answer for each of the followng 0 multple-choce questons. For each queston, only one of the answers s correct.
NON-CONSTANT SUM RED-AND-BLACK GAMES WITH BET-DEPENDENT WIN PROBABILITY FUNCTION LAURA PONTIGGIA, University of the Sciences in Philadelphia
 To appear n Journal o Appled Probablty June 2007 O-COSTAT SUM RED-AD-BLACK GAMES WITH BET-DEPEDET WI PROBABILITY FUCTIO LAURA POTIGGIA, Unversty o the Scences n Phladelpha Abstract In ths paper we nvestgate
To appear n Journal o Appled Probablty June 2007 O-COSTAT SUM RED-AD-BLACK GAMES WITH BET-DEPEDET WI PROBABILITY FUCTIO LAURA POTIGGIA, Unversty o the Scences n Phladelpha Abstract In ths paper we nvestgate
A Model of Private Equity Fund Compensation
 A Model of Prvate Equty Fund Compensaton Wonho Wlson Cho Andrew Metrck Ayako Yasuda KAIST Yale School of Management Unversty of Calforna at Davs June 26, 2011 Abstract: Ths paper analyzes the economcs
A Model of Prvate Equty Fund Compensaton Wonho Wlson Cho Andrew Metrck Ayako Yasuda KAIST Yale School of Management Unversty of Calforna at Davs June 26, 2011 Abstract: Ths paper analyzes the economcs
Portfolio Loss Distribution
 Portfolo Loss Dstrbuton Rsky assets n loan ortfolo hghly llqud assets hold-to-maturty n the bank s balance sheet Outstandngs The orton of the bank asset that has already been extended to borrowers. Commtment
Portfolo Loss Dstrbuton Rsky assets n loan ortfolo hghly llqud assets hold-to-maturty n the bank s balance sheet Outstandngs The orton of the bank asset that has already been extended to borrowers. Commtment
ENTERPRISE RISK MANAGEMENT IN INSURANCE GROUPS: MEASURING RISK CONCENTRATION AND DEFAULT RISK
 ETERPRISE RISK MAAGEMET I ISURACE GROUPS: MEASURIG RISK COCETRATIO AD DEFAULT RISK ADIE GATZERT HATO SCHMEISER STEFA SCHUCKMA WORKIG PAPERS O RISK MAAGEMET AD ISURACE O. 35 EDITED BY HATO SCHMEISER CHAIR
ETERPRISE RISK MAAGEMET I ISURACE GROUPS: MEASURIG RISK COCETRATIO AD DEFAULT RISK ADIE GATZERT HATO SCHMEISER STEFA SCHUCKMA WORKIG PAPERS O RISK MAAGEMET AD ISURACE O. 35 EDITED BY HATO SCHMEISER CHAIR
8 Algorithm for Binary Searching in Trees
 8 Algorthm for Bnary Searchng n Trees In ths secton we present our algorthm for bnary searchng n trees. A crucal observaton employed by the algorthm s that ths problem can be effcently solved when the
8 Algorthm for Bnary Searchng n Trees In ths secton we present our algorthm for bnary searchng n trees. A crucal observaton employed by the algorthm s that ths problem can be effcently solved when the
Efficient Project Portfolio as a tool for Enterprise Risk Management
 Effcent Proect Portfolo as a tool for Enterprse Rsk Management Valentn O. Nkonov Ural State Techncal Unversty Growth Traectory Consultng Company January 5, 27 Effcent Proect Portfolo as a tool for Enterprse
Effcent Proect Portfolo as a tool for Enterprse Rsk Management Valentn O. Nkonov Ural State Techncal Unversty Growth Traectory Consultng Company January 5, 27 Effcent Proect Portfolo as a tool for Enterprse
Scale Dependence of Overconfidence in Stock Market Volatility Forecasts
 Scale Dependence of Overconfdence n Stoc Maret Volatlty Forecasts Marus Glaser, Thomas Langer, Jens Reynders, Martn Weber* June 7, 007 Abstract In ths study, we analyze whether volatlty forecasts (judgmental
Scale Dependence of Overconfdence n Stoc Maret Volatlty Forecasts Marus Glaser, Thomas Langer, Jens Reynders, Martn Weber* June 7, 007 Abstract In ths study, we analyze whether volatlty forecasts (judgmental
The OC Curve of Attribute Acceptance Plans
 The OC Curve of Attrbute Acceptance Plans The Operatng Characterstc (OC) curve descrbes the probablty of acceptng a lot as a functon of the lot s qualty. Fgure 1 shows a typcal OC Curve. 10 8 6 4 1 3 4
The OC Curve of Attrbute Acceptance Plans The Operatng Characterstc (OC) curve descrbes the probablty of acceptng a lot as a functon of the lot s qualty. Fgure 1 shows a typcal OC Curve. 10 8 6 4 1 3 4
7.5. Present Value of an Annuity. Investigate
 7.5 Present Value of an Annuty Owen and Anna are approachng retrement and are puttng ther fnances n order. They have worked hard and nvested ther earnngs so that they now have a large amount of money on
7.5 Present Value of an Annuty Owen and Anna are approachng retrement and are puttng ther fnances n order. They have worked hard and nvested ther earnngs so that they now have a large amount of money on
On the Optimal Control of a Cascade of Hydro-Electric Power Stations
 On the Optmal Control of a Cascade of Hydro-Electrc Power Statons M.C.M. Guedes a, A.F. Rbero a, G.V. Smrnov b and S. Vlela c a Department of Mathematcs, School of Scences, Unversty of Porto, Portugal;
On the Optmal Control of a Cascade of Hydro-Electrc Power Statons M.C.M. Guedes a, A.F. Rbero a, G.V. Smrnov b and S. Vlela c a Department of Mathematcs, School of Scences, Unversty of Porto, Portugal;
Module 2 LOSSLESS IMAGE COMPRESSION SYSTEMS. Version 2 ECE IIT, Kharagpur
 Module LOSSLESS IMAGE COMPRESSION SYSTEMS Lesson 3 Lossless Compresson: Huffman Codng Instructonal Objectves At the end of ths lesson, the students should be able to:. Defne and measure source entropy..
Module LOSSLESS IMAGE COMPRESSION SYSTEMS Lesson 3 Lossless Compresson: Huffman Codng Instructonal Objectves At the end of ths lesson, the students should be able to:. Defne and measure source entropy..
Estimation of Dispersion Parameters in GLMs with and without Random Effects
 Mathematcal Statstcs Stockholm Unversty Estmaton of Dsperson Parameters n GLMs wth and wthout Random Effects Meng Ruoyan Examensarbete 2004:5 Postal address: Mathematcal Statstcs Dept. of Mathematcs Stockholm
Mathematcal Statstcs Stockholm Unversty Estmaton of Dsperson Parameters n GLMs wth and wthout Random Effects Meng Ruoyan Examensarbete 2004:5 Postal address: Mathematcal Statstcs Dept. of Mathematcs Stockholm
Risk Model of Long-Term Production Scheduling in Open Pit Gold Mining
 Rsk Model of Long-Term Producton Schedulng n Open Pt Gold Mnng R Halatchev 1 and P Lever 2 ABSTRACT Open pt gold mnng s an mportant sector of the Australan mnng ndustry. It uses large amounts of nvestments,
Rsk Model of Long-Term Producton Schedulng n Open Pt Gold Mnng R Halatchev 1 and P Lever 2 ABSTRACT Open pt gold mnng s an mportant sector of the Australan mnng ndustry. It uses large amounts of nvestments,
Multiple-Period Attribution: Residuals and Compounding
 Multple-Perod Attrbuton: Resduals and Compoundng Our revewer gave these authors full marks for dealng wth an ssue that performance measurers and vendors often regard as propretary nformaton. In 1994, Dens
Multple-Perod Attrbuton: Resduals and Compoundng Our revewer gave these authors full marks for dealng wth an ssue that performance measurers and vendors often regard as propretary nformaton. In 1994, Dens
STAMP DUTY ON SHARES AND ITS EFFECT ON SHARE PRICES
 STAMP UTY ON SHARES AN ITS EFFECT ON SHARE PRICES Steve Bond Mke Hawkns Alexander Klemm THE INSTITUTE FOR FISCAL STUIES WP04/11 STAMP UTY ON SHARES AN ITS EFFECT ON SHARE PRICES Steve Bond (IFS and Unversty
STAMP UTY ON SHARES AN ITS EFFECT ON SHARE PRICES Steve Bond Mke Hawkns Alexander Klemm THE INSTITUTE FOR FISCAL STUIES WP04/11 STAMP UTY ON SHARES AN ITS EFFECT ON SHARE PRICES Steve Bond (IFS and Unversty
Experiment 5 Elastic and Inelastic Collisions
 PHY191 Experment 5: Elastc and Inelastc Collsons 8/1/014 Page 1 Experment 5 Elastc and Inelastc Collsons Readng: Bauer&Westall: Chapter 7 (and 8, or center o mass deas) as needed 1. Goals 1. Study momentum
PHY191 Experment 5: Elastc and Inelastc Collsons 8/1/014 Page 1 Experment 5 Elastc and Inelastc Collsons Readng: Bauer&Westall: Chapter 7 (and 8, or center o mass deas) as needed 1. Goals 1. Study momentum
Staff Paper. Farm Savings Accounts: Examining Income Variability, Eligibility, and Benefits. Brent Gloy, Eddy LaDue, and Charles Cuykendall
 SP 2005-02 August 2005 Staff Paper Department of Appled Economcs and Management Cornell Unversty, Ithaca, New York 14853-7801 USA Farm Savngs Accounts: Examnng Income Varablty, Elgblty, and Benefts Brent
SP 2005-02 August 2005 Staff Paper Department of Appled Economcs and Management Cornell Unversty, Ithaca, New York 14853-7801 USA Farm Savngs Accounts: Examnng Income Varablty, Elgblty, and Benefts Brent
Statistical Methods to Develop Rating Models
 Statstcal Methods to Develop Ratng Models [Evelyn Hayden and Danel Porath, Österrechsche Natonalbank and Unversty of Appled Scences at Manz] Source: The Basel II Rsk Parameters Estmaton, Valdaton, and
Statstcal Methods to Develop Ratng Models [Evelyn Hayden and Danel Porath, Österrechsche Natonalbank and Unversty of Appled Scences at Manz] Source: The Basel II Rsk Parameters Estmaton, Valdaton, and
Modelling the Claims Development Result for Solvency Purposes
 Modelling the Claims Development Result for Solvency Purposes Michael Merz, Mario V. Wüthrich Version: June 10, 008 Abstract We assume that the claims liability process satisfies the distribution-free
Modelling the Claims Development Result for Solvency Purposes Michael Merz, Mario V. Wüthrich Version: June 10, 008 Abstract We assume that the claims liability process satisfies the distribution-free
 Dscrete-Tme Approxmatons of the Holmstrom-Mlgrom Brownan-Moton Model of Intertemporal Incentve Provson 1 Martn Hellwg Unversty of Mannhem Klaus M. Schmdt Unversty of Munch and CEPR Ths verson: May 5, 1998
Dscrete-Tme Approxmatons of the Holmstrom-Mlgrom Brownan-Moton Model of Intertemporal Incentve Provson 1 Martn Hellwg Unversty of Mannhem Klaus M. Schmdt Unversty of Munch and CEPR Ths verson: May 5, 1998
ECONOMICS OF PLANT ENERGY SAVINGS PROJECTS IN A CHANGING MARKET Douglas C White Emerson Process Management
 ECONOMICS OF PLANT ENERGY SAVINGS PROJECTS IN A CHANGING MARKET Douglas C Whte Emerson Process Management Abstract Energy prces have exhbted sgnfcant volatlty n recent years. For example, natural gas prces
ECONOMICS OF PLANT ENERGY SAVINGS PROJECTS IN A CHANGING MARKET Douglas C Whte Emerson Process Management Abstract Energy prces have exhbted sgnfcant volatlty n recent years. For example, natural gas prces
Forecasting the Direction and Strength of Stock Market Movement
 Forecastng the Drecton and Strength of Stock Market Movement Jngwe Chen Mng Chen Nan Ye [email protected] [email protected] [email protected] Abstract - Stock market s one of the most complcated systems
Forecastng the Drecton and Strength of Stock Market Movement Jngwe Chen Mng Chen Nan Ye [email protected] [email protected] [email protected] Abstract - Stock market s one of the most complcated systems
Number of Levels Cumulative Annual operating Income per year construction costs costs ($) ($) ($) 1 600,000 35,000 100,000 2 2,200,000 60,000 350,000
 Problem Set 5 Solutons 1 MIT s consderng buldng a new car park near Kendall Square. o unversty funds are avalable (overhead rates are under pressure and the new faclty would have to pay for tself from
Problem Set 5 Solutons 1 MIT s consderng buldng a new car park near Kendall Square. o unversty funds are avalable (overhead rates are under pressure and the new faclty would have to pay for tself from
PSYCHOLOGICAL RESEARCH (PYC 304-C) Lecture 12
 14 The Ch-squared dstrbuton PSYCHOLOGICAL RESEARCH (PYC 304-C) Lecture 1 If a normal varable X, havng mean µ and varance σ, s standardsed, the new varable Z has a mean 0 and varance 1. When ths standardsed
14 The Ch-squared dstrbuton PSYCHOLOGICAL RESEARCH (PYC 304-C) Lecture 1 If a normal varable X, havng mean µ and varance σ, s standardsed, the new varable Z has a mean 0 and varance 1. When ths standardsed
Can Auto Liability Insurance Purchases Signal Risk Attitude?
 Internatonal Journal of Busness and Economcs, 2011, Vol. 10, No. 2, 159-164 Can Auto Lablty Insurance Purchases Sgnal Rsk Atttude? Chu-Shu L Department of Internatonal Busness, Asa Unversty, Tawan Sheng-Chang
Internatonal Journal of Busness and Economcs, 2011, Vol. 10, No. 2, 159-164 Can Auto Lablty Insurance Purchases Sgnal Rsk Atttude? Chu-Shu L Department of Internatonal Busness, Asa Unversty, Tawan Sheng-Chang
1 Example 1: Axis-aligned rectangles
 COS 511: Theoretcal Machne Learnng Lecturer: Rob Schapre Lecture # 6 Scrbe: Aaron Schld February 21, 2013 Last class, we dscussed an analogue for Occam s Razor for nfnte hypothess spaces that, n conjuncton
COS 511: Theoretcal Machne Learnng Lecturer: Rob Schapre Lecture # 6 Scrbe: Aaron Schld February 21, 2013 Last class, we dscussed an analogue for Occam s Razor for nfnte hypothess spaces that, n conjuncton
Brigid Mullany, Ph.D University of North Carolina, Charlotte
 Evaluaton And Comparson Of The Dfferent Standards Used To Defne The Postonal Accuracy And Repeatablty Of Numercally Controlled Machnng Center Axes Brgd Mullany, Ph.D Unversty of North Carolna, Charlotte
Evaluaton And Comparson Of The Dfferent Standards Used To Defne The Postonal Accuracy And Repeatablty Of Numercally Controlled Machnng Center Axes Brgd Mullany, Ph.D Unversty of North Carolna, Charlotte
Simple Interest Loans (Section 5.1) :
 Chapter 5 Fnance The frst part of ths revew wll explan the dfferent nterest and nvestment equatons you learned n secton 5.1 through 5.4 of your textbook and go through several examples. The second part
Chapter 5 Fnance The frst part of ths revew wll explan the dfferent nterest and nvestment equatons you learned n secton 5.1 through 5.4 of your textbook and go through several examples. The second part
THE USE OF RISK ADJUSTED CAPITAL TO SUPPORT BUSINESS DECISION-MAKING
 THE USE OF RISK ADJUSTED CAPITAL TO SUPPORT BUSINESS DECISION-MAKING By Gary Patrk Stefan Bernegger Marcel Beat Rüegg Swss Rensurance Company Casualty Actuaral Socety and Casualty Actuares n Rensurance
THE USE OF RISK ADJUSTED CAPITAL TO SUPPORT BUSINESS DECISION-MAKING By Gary Patrk Stefan Bernegger Marcel Beat Rüegg Swss Rensurance Company Casualty Actuaral Socety and Casualty Actuares n Rensurance
The impact of hard discount control mechanism on the discount volatility of UK closed-end funds
 Investment Management and Fnancal Innovatons, Volume 10, Issue 3, 2013 Ahmed F. Salhn (Egypt) The mpact of hard dscount control mechansm on the dscount volatlty of UK closed-end funds Abstract The mpact
Investment Management and Fnancal Innovatons, Volume 10, Issue 3, 2013 Ahmed F. Salhn (Egypt) The mpact of hard dscount control mechansm on the dscount volatlty of UK closed-end funds Abstract The mpact
An Evaluation of the Extended Logistic, Simple Logistic, and Gompertz Models for Forecasting Short Lifecycle Products and Services
 An Evaluaton of the Extended Logstc, Smple Logstc, and Gompertz Models for Forecastng Short Lfecycle Products and Servces Charles V. Trappey a,1, Hsn-yng Wu b a Professor (Management Scence), Natonal Chao
An Evaluaton of the Extended Logstc, Smple Logstc, and Gompertz Models for Forecastng Short Lfecycle Products and Servces Charles V. Trappey a,1, Hsn-yng Wu b a Professor (Management Scence), Natonal Chao
Vasicek s Model of Distribution of Losses in a Large, Homogeneous Portfolio
 Vascek s Model of Dstrbuton of Losses n a Large, Homogeneous Portfolo Stephen M Schaefer London Busness School Credt Rsk Electve Summer 2012 Vascek s Model Important method for calculatng dstrbuton of
Vascek s Model of Dstrbuton of Losses n a Large, Homogeneous Portfolo Stephen M Schaefer London Busness School Credt Rsk Electve Summer 2012 Vascek s Model Important method for calculatng dstrbuton of
v a 1 b 1 i, a 2 b 2 i,..., a n b n i.
 SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 455 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces we have studed thus far n the text are real vector spaces snce the scalars are
SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 455 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces we have studed thus far n the text are real vector spaces snce the scalars are
Course outline. Financial Time Series Analysis. Overview. Data analysis. Predictive signal. Trading strategy
 Fnancal Tme Seres Analyss Patrck McSharry [email protected] www.mcsharry.net Trnty Term 2014 Mathematcal Insttute Unversty of Oxford Course outlne 1. Data analyss, probablty, correlatons, vsualsaton
Fnancal Tme Seres Analyss Patrck McSharry [email protected] www.mcsharry.net Trnty Term 2014 Mathematcal Insttute Unversty of Oxford Course outlne 1. Data analyss, probablty, correlatons, vsualsaton
The Current Employment Statistics (CES) survey,
 Busness Brths and Deaths Impact of busness brths and deaths n the payroll survey The CES probablty-based sample redesgn accounts for most busness brth employment through the mputaton of busness deaths,
Busness Brths and Deaths Impact of busness brths and deaths n the payroll survey The CES probablty-based sample redesgn accounts for most busness brth employment through the mputaton of busness deaths,
8.5 UNITARY AND HERMITIAN MATRICES. The conjugate transpose of a complex matrix A, denoted by A*, is given by
 6 CHAPTER 8 COMPLEX VECTOR SPACES 5. Fnd the kernel of the lnear transformaton gven n Exercse 5. In Exercses 55 and 56, fnd the mage of v, for the ndcated composton, where and are gven by the followng
6 CHAPTER 8 COMPLEX VECTOR SPACES 5. Fnd the kernel of the lnear transformaton gven n Exercse 5. In Exercses 55 and 56, fnd the mage of v, for the ndcated composton, where and are gven by the followng
How Sets of Coherent Probabilities May Serve as Models for Degrees of Incoherence
 1 st Internatonal Symposum on Imprecse Probabltes and Ther Applcatons, Ghent, Belgum, 29 June 2 July 1999 How Sets of Coherent Probabltes May Serve as Models for Degrees of Incoherence Mar J. Schervsh
1 st Internatonal Symposum on Imprecse Probabltes and Ther Applcatons, Ghent, Belgum, 29 June 2 July 1999 How Sets of Coherent Probabltes May Serve as Models for Degrees of Incoherence Mar J. Schervsh
IDENTIFICATION AND CORRECTION OF A COMMON ERROR IN GENERAL ANNUITY CALCULATIONS
 IDENTIFICATION AND CORRECTION OF A COMMON ERROR IN GENERAL ANNUITY CALCULATIONS Chrs Deeley* Last revsed: September 22, 200 * Chrs Deeley s a Senor Lecturer n the School of Accountng, Charles Sturt Unversty,
IDENTIFICATION AND CORRECTION OF A COMMON ERROR IN GENERAL ANNUITY CALCULATIONS Chrs Deeley* Last revsed: September 22, 200 * Chrs Deeley s a Senor Lecturer n the School of Accountng, Charles Sturt Unversty,
Methods for Calculating Life Insurance Rates
 World Appled Scences Journal 5 (4): 653-663, 03 ISSN 88-495 IDOSI Pulcatons, 03 DOI: 0.589/dos.wasj.03.5.04.338 Methods for Calculatng Lfe Insurance Rates Madna Movsarovna Magomadova Chechen State Unversty,
World Appled Scences Journal 5 (4): 653-663, 03 ISSN 88-495 IDOSI Pulcatons, 03 DOI: 0.589/dos.wasj.03.5.04.338 Methods for Calculatng Lfe Insurance Rates Madna Movsarovna Magomadova Chechen State Unversty,
Pragmatic Insurance Option Pricing
 Paper to be presented at the XXXVth ASTIN Colloquum, Bergen, 6 9th June 004 Pragmatc Insurance Opton Prcng by Jon Holtan If P&C Insurance Company Ltd Oslo, Norway Emal: [email protected] Telephone: +47960065
Paper to be presented at the XXXVth ASTIN Colloquum, Bergen, 6 9th June 004 Pragmatc Insurance Opton Prcng by Jon Holtan If P&C Insurance Company Ltd Oslo, Norway Emal: [email protected] Telephone: +47960065
Transition Matrix Models of Consumer Credit Ratings
 Transton Matrx Models of Consumer Credt Ratngs Abstract Although the corporate credt rsk lterature has many studes modellng the change n the credt rsk of corporate bonds over tme, there s far less analyss
Transton Matrx Models of Consumer Credt Ratngs Abstract Although the corporate credt rsk lterature has many studes modellng the change n the credt rsk of corporate bonds over tme, there s far less analyss
NPAR TESTS. One-Sample Chi-Square Test. Cell Specification. Observed Frequencies 1O i 6. Expected Frequencies 1EXP i 6
 PAR TESTS If a WEIGHT varable s specfed, t s used to replcate a case as many tmes as ndcated by the weght value rounded to the nearest nteger. If the workspace requrements are exceeded and samplng has
PAR TESTS If a WEIGHT varable s specfed, t s used to replcate a case as many tmes as ndcated by the weght value rounded to the nearest nteger. If the workspace requrements are exceeded and samplng has
Implied (risk neutral) probabilities, betting odds and prediction markets
 Impled (rsk neutral) probabltes, bettng odds and predcton markets Fabrzo Caccafesta (Unversty of Rome "Tor Vergata") ABSTRACT - We show that the well known euvalence between the "fundamental theorem of
Impled (rsk neutral) probabltes, bettng odds and predcton markets Fabrzo Caccafesta (Unversty of Rome "Tor Vergata") ABSTRACT - We show that the well known euvalence between the "fundamental theorem of
CHOLESTEROL REFERENCE METHOD LABORATORY NETWORK. Sample Stability Protocol
 CHOLESTEROL REFERENCE METHOD LABORATORY NETWORK Sample Stablty Protocol Background The Cholesterol Reference Method Laboratory Network (CRMLN) developed certfcaton protocols for total cholesterol, HDL
CHOLESTEROL REFERENCE METHOD LABORATORY NETWORK Sample Stablty Protocol Background The Cholesterol Reference Method Laboratory Network (CRMLN) developed certfcaton protocols for total cholesterol, HDL
Financial Mathemetics
 Fnancal Mathemetcs 15 Mathematcs Grade 12 Teacher Gude Fnancal Maths Seres Overvew In ths seres we am to show how Mathematcs can be used to support personal fnancal decsons. In ths seres we jon Tebogo,
Fnancal Mathemetcs 15 Mathematcs Grade 12 Teacher Gude Fnancal Maths Seres Overvew In ths seres we am to show how Mathematcs can be used to support personal fnancal decsons. In ths seres we jon Tebogo,
CHAPTER 5 RELATIONSHIPS BETWEEN QUANTITATIVE VARIABLES
 CHAPTER 5 RELATIONSHIPS BETWEEN QUANTITATIVE VARIABLES In ths chapter, we wll learn how to descrbe the relatonshp between two quanttatve varables. Remember (from Chapter 2) that the terms quanttatve varable
CHAPTER 5 RELATIONSHIPS BETWEEN QUANTITATIVE VARIABLES In ths chapter, we wll learn how to descrbe the relatonshp between two quanttatve varables. Remember (from Chapter 2) that the terms quanttatve varable
OLA HÖSSJER, BENGT ERIKSSON, KAJSA JÄRNMALM AND ESBJÖRN OHLSSON ABSTRACT
 ASSESSING INDIVIDUAL UNEXPLAINED VARIATION IN NON-LIFE INSURANCE BY OLA HÖSSJER, BENGT ERIKSSON, KAJSA JÄRNMALM AND ESBJÖRN OHLSSON ABSTRACT We consder varaton of observed clam frequences n non-lfe nsurance,
ASSESSING INDIVIDUAL UNEXPLAINED VARIATION IN NON-LIFE INSURANCE BY OLA HÖSSJER, BENGT ERIKSSON, KAJSA JÄRNMALM AND ESBJÖRN OHLSSON ABSTRACT We consder varaton of observed clam frequences n non-lfe nsurance,
+ + + - - This circuit than can be reduced to a planar circuit
 MeshCurrent Method The meshcurrent s analog of the nodeoltage method. We sole for a new set of arables, mesh currents, that automatcally satsfy KCLs. As such, meshcurrent method reduces crcut soluton to
MeshCurrent Method The meshcurrent s analog of the nodeoltage method. We sole for a new set of arables, mesh currents, that automatcally satsfy KCLs. As such, meshcurrent method reduces crcut soluton to
Forecasting the Demand of Emergency Supplies: Based on the CBR Theory and BP Neural Network
 700 Proceedngs of the 8th Internatonal Conference on Innovaton & Management Forecastng the Demand of Emergency Supples: Based on the CBR Theory and BP Neural Network Fu Deqang, Lu Yun, L Changbng School
700 Proceedngs of the 8th Internatonal Conference on Innovaton & Management Forecastng the Demand of Emergency Supples: Based on the CBR Theory and BP Neural Network Fu Deqang, Lu Yun, L Changbng School
Calculating the high frequency transmission line parameters of power cables
 < ' Calculatng the hgh frequency transmsson lne parameters of power cables Authors: Dr. John Dcknson, Laboratory Servces Manager, N 0 RW E B Communcatons Mr. Peter J. Ncholson, Project Assgnment Manager,
< ' Calculatng the hgh frequency transmsson lne parameters of power cables Authors: Dr. John Dcknson, Laboratory Servces Manager, N 0 RW E B Communcatons Mr. Peter J. Ncholson, Project Assgnment Manager,
Estimating Total Claim Size in the Auto Insurance Industry: a Comparison between Tweedie and Zero-Adjusted Inverse Gaussian Distribution
 Avalable onlne at http:// BAR, Curtba, v. 8, n. 1, art. 3, pp. 37-47, Jan./Mar. 2011 Estmatng Total Clam Sze n the Auto Insurance Industry: a Comparson between Tweede and Zero-Adjusted Inverse Gaussan
Avalable onlne at http:// BAR, Curtba, v. 8, n. 1, art. 3, pp. 37-47, Jan./Mar. 2011 Estmatng Total Clam Sze n the Auto Insurance Industry: a Comparson between Tweede and Zero-Adjusted Inverse Gaussan
The Cross Section of Foreign Currency Risk Premia and Consumption Growth Risk
 The Cross Secton of Foregn Currency Rsk Prema and Consumpton Growth Rsk By HANNO LUSTIG AND ADRIEN VERDELHAN* Aggregate consumpton growth rsk explans why low nterest rate currences do not apprecate as
The Cross Secton of Foregn Currency Rsk Prema and Consumpton Growth Rsk By HANNO LUSTIG AND ADRIEN VERDELHAN* Aggregate consumpton growth rsk explans why low nterest rate currences do not apprecate as
Support Vector Machines
 Support Vector Machnes Max Wellng Department of Computer Scence Unversty of Toronto 10 Kng s College Road Toronto, M5S 3G5 Canada [email protected] Abstract Ths s a note to explan support vector machnes.
Support Vector Machnes Max Wellng Department of Computer Scence Unversty of Toronto 10 Kng s College Road Toronto, M5S 3G5 Canada [email protected] Abstract Ths s a note to explan support vector machnes.
Stochastic epidemic models revisited: Analysis of some continuous performance measures
 Stochastc epdemc models revsted: Analyss of some contnuous performance measures J.R. Artalejo Faculty of Mathematcs, Complutense Unversty of Madrd, 28040 Madrd, Span A. Economou Department of Mathematcs,
Stochastc epdemc models revsted: Analyss of some contnuous performance measures J.R. Artalejo Faculty of Mathematcs, Complutense Unversty of Madrd, 28040 Madrd, Span A. Economou Department of Mathematcs,
1 De nitions and Censoring
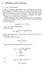 De ntons and Censorng. Survval Analyss We begn by consderng smple analyses but we wll lead up to and take a look at regresson on explanatory factors., as n lnear regresson part A. The mportant d erence
De ntons and Censorng. Survval Analyss We begn by consderng smple analyses but we wll lead up to and take a look at regresson on explanatory factors., as n lnear regresson part A. The mportant d erence
Survival analysis methods in Insurance Applications in car insurance contracts
 Survval analyss methods n Insurance Applcatons n car nsurance contracts Abder OULIDI 1 Jean-Mare MARION 2 Hervé GANACHAUD 3 Abstract In ths wor, we are nterested n survval models and ther applcatons on
Survval analyss methods n Insurance Applcatons n car nsurance contracts Abder OULIDI 1 Jean-Mare MARION 2 Hervé GANACHAUD 3 Abstract In ths wor, we are nterested n survval models and ther applcatons on
A Binary Particle Swarm Optimization Algorithm for Lot Sizing Problem
 Journal o Economc and Socal Research 5 (2), -2 A Bnary Partcle Swarm Optmzaton Algorthm or Lot Szng Problem M. Fath Taşgetren & Yun-Cha Lang Abstract. Ths paper presents a bnary partcle swarm optmzaton
Journal o Economc and Socal Research 5 (2), -2 A Bnary Partcle Swarm Optmzaton Algorthm or Lot Szng Problem M. Fath Taşgetren & Yun-Cha Lang Abstract. Ths paper presents a bnary partcle swarm optmzaton
On the pricing of illiquid options with Black-Scholes formula
 7 th InternatonalScentfcConferenceManagngandModellngofFnancalRsks Ostrava VŠB-TU Ostrava, Faculty of Economcs, Department of Fnance 8 th 9 th September2014 On the prcng of llqud optons wth Black-Scholes
7 th InternatonalScentfcConferenceManagngandModellngofFnancalRsks Ostrava VŠB-TU Ostrava, Faculty of Economcs, Department of Fnance 8 th 9 th September2014 On the prcng of llqud optons wth Black-Scholes
When Talk is Free : The Effect of Tariff Structure on Usage under Two- and Three-Part Tariffs
 0 When Talk s Free : The Effect of Tarff Structure on Usage under Two- and Three-Part Tarffs Eva Ascarza Ana Lambrecht Naufel Vlcassm July 2012 (Forthcomng at Journal of Marketng Research) Eva Ascarza
0 When Talk s Free : The Effect of Tarff Structure on Usage under Two- and Three-Part Tarffs Eva Ascarza Ana Lambrecht Naufel Vlcassm July 2012 (Forthcomng at Journal of Marketng Research) Eva Ascarza
