The Trans-Atlantic Cable
|
|
|
- Moris McCarthy
- 10 years ago
- Views:
Transcription
1 The Trans-Atlantic Cable Charles Byrne (Charles Department of Mathematical Sciences University of Massachusetts Lowell Lowell, MA 01854, USA (The most recent version is available as a pdf file at October 14, 2010 Abstract In 1815, at the end of the war with England, the US was a developing country, with most people living on small farms, eating whatever they could grow themselves. Only those living near navigable water could market their crops. Poor transportation and communication kept them isolated. By 1848, at the end of the next war, this time with Mexico, things were different. The US was a transcontinental power, integrated by railroads, telegraph, steamboats, the Erie Canal, and innovations in mass production and agriculture. In 1828, the newly elected President, Andrew Jackson, arrived in Washington by horsedrawn carriage; he left in 1837 by train. The most revolutionary change was in communication, where the recent advances in understanding electromagnetism produced the telegraph. It wasn t long before efforts began to lay a telegraph cable under the Atlantic Ocean, even though some wondered what England and the US could possibly have to say to one another. The laying of the trans-atlantic cable was, in many ways, the 19th century equivalent of landing a man on the moon, involving, as it did, considerable expense, too frequent failure, and a level of precision in engineering design and manufacturing never before attempted. From a scientific perspective, it was probably more difficult, given that the study of electromagnetism was in its infancy at the time. In this note we discuss the efforts to develop an accurate mathematical model for transmission of signals through a long underwater cable, the leading role this model played in inspiring the technological innovation that eventually led to the success of the enormous effort, and the partial differential equation on which so much money depended. 1
2 1 Introduction In 1815, at the end of the war with England, the US was a developing country, with most people living on small farms, eating whatever they could grow themselves. Only those living near navigable water could market their crops. Poor transportation and communication kept them isolated. By 1848, at the end of the next war, this time with Mexico, things were different. The US was a transcontinental power, integrated by railroads, telegraph, steamboats, the Erie Canal, and innovations in mass production and agriculture. In 1828, the newly elected President, Andrew Jackson, arrived in Washington by horse-drawn carriage; he left in 1837 by train. The most revolutionary change was in communication, where the recent advances in understanding electromagnetism produced the telegraph. It wasn t long before efforts began to lay a telegraph cable under the Atlantic Ocean, even though some wondered what England and the US could possibly have to say to one another. The laying of the trans-atlantic cable was, in many ways, the 19th century equivalent of landing a man on the moon, involving, as it did, considerable expense, too frequent failure, and a level of precision in engineering design and manufacturing never before attempted. From a scientific perspective, it was probably more difficult, given that the study of electromagnetism was in its infancy at the time. Early on, Faraday and others worried that sending a message across a vast distance would take a long time, but they reasoned, incorrectly, that this would be similar to filling a very long hose with water. What they did not realize initially was that, as William Thomson was to discover, the transmission of a pulse through an undersea cable was described more by a heat equation than a wave equation. This meant that a signal that started out as a sharp pulse would be spread out as time went on, making communication extremely slow. The problem was the increased capacitance with the ground. Somewhat later, Oliver Heaviside realized that, when all four of the basic elements of the electrical circuit, the inductance, the resistance, the conductance to the ground and the capacitance to the ground, were considered together, it might be possible to adjust these parameters, in particular, to increase the inductance, so as to produce undistorted signals. Heaviside died in poverty, but his ideas eventually were adopted. In 1859 Queen Victoria sent President Buchanan a 99 word greeting using an early version of the cable, but the message took over sixteen hours to be received. By 1866 one could transmit eight words a minute along a cable that stretched from Ireland to Newfoundland, at a cost of about 1500 dollars per word in today s money. 2
3 With improvements in insulation, using gutta percha, a gum from a tropical tree also used to make golf balls, and the development of magnetic alloys that increased the inductance of the cable, messages could be sent faster and more cheaply. In this note we survey the development of the mathematics of the problem. We focus, in particular, on the partial differential equations that were used to describe the transmission problem. What we give here is a brief glimpse; more detailed discussion of this problem is found in the books by Körner [2], Gonzalez-Velasco [1], and Wylie [3]. 2 The Electrical Circuit ODE We begin with the ordinary differential equation that describes the horizontal motion of a block of wood attached to a spring. We let x(t) be the position of the block relative to the equilibrium position x = 0, with x(0) and x (0) denoting the initial position and velocity of the block. When an external force f(t) is imposed, a portion of this force is devoted to overcoming the inertia of the block, a portion to compressing or stretching the spring, and the remaining portion to resisting friction. Therefore, the differential equation describing the motion is mx (t) + ax (t) + kx(t) = f(t), (2.1) where m is the mass of the block, a the coefficient of friction, and k the spring constant. The charge Q(t) deposited on a capacitor in an electrical circuit due to an imposed electromotive force E(t) is similarly described by the ordinary differential equation LQ (t) + RQ (t) + 1 Q(t) = E(t). (2.2) C The first term, containing the inductance coefficient L, describes the portion of the force E(t) devoted to overcoming the effect of a change in the current I(t) = Q (t); here L is analogous to the mass m. The second term, containing the resistance coefficient R, describes that portion of the force E(t) needed to overcome resistance to the current I(t); now R is analogous to the friction coefficient a. Finally, the third term, containing the reciprocal of the capacitance C, describes the portion of E(t) used to store charge on the capacitor; now 1 C is analogous to k, the spring constant. 3
4 3 The Telegraph Equation The objective here is to describe the behavior of u(x, t), the voltage at location x along the cable, at time t. In the beginning, it was believed that the partial differential equation describing the voltage would be the wave equation If this were the case, an initial pulse u xx = α 2 u tt. E(t) = H(t) H(t T ) would move along the cable undistorted; here H(t) is the Heaviside function that is zero for t < 0 and one for t 0. Thomson (later Sir William Thomson, and even later, Lord Kelvin) thought otherwise. Thomson argued that there would be a voltage drop over an interval [x, x + x] due to resistance to the current i(x, t) passing through the cable, so that u(x + x, t) u(x, t) = Ri(x, t) x, and so u x = Ri. He also argued that there would be capacitance to the ground, made more significant under water. Since the apparent change in current due to the changing voltage across the capacitor is i(x + x, t) i(x, t) = Cu t (x, t) x, we have i x Eliminating the i(x, t), we can write = C u t. which is the heat equation, not the wave equation. u xx (x, t) = CRu t (x, t), (3.1) 4 Consequences of Thomson s Model To see what Thomson s model predicts, we consider the following problem. Suppose we have a semi-infinite cable, that the voltage is u(x, t) for x 0, and t 0, and that 4
5 u(0, t) = E(t). Let U(x, s) be the Laplace transform of u(x, t), viewed as a function of t. Then, from Thomson s model we have U(x, s) = L(E)(s)e CRsx, where L(E)(s) denotes the Laplace transform of E(t). Since U(x, s) is the product of two functions of s, the convolution theorem applies. But first, it is helpful to find out which function has for its Laplace transform the function e αx s. The answer comes from the following fact: the function be b2 /4t /2 πt 3/2 has for its Laplace transform the function e b s. Therefore, we can write u(x, t) = CRx 2 π t 0 E(t τ) e CRx2 /4τ τ τ dτ. Now we consider two special cases. 4.1 Special Case 1: E(t) = H(t) Suppose now that E(t) = H(t), the Heaviside function. Using the substitution we find that The function z = CRx 2 /4τ, u(x, t) = 1 2 CRx/2 π π 0 erf(r) = 2 π r is the well known error function, so we can write 0 e z2 dz e z2 dz. (4.1) u(x, t) = 1 erf ( CRx 2 ). (4.2) t 4.2 Special Case 2: E(t) = H(t) H(t T ) Now suppose that E(t) is the pulse H(t) H(t T ). Using the results from the previous subsection, we find that, for t > T, u(x, t) = erf ( CRx 2 t T 5 ) ( CRx erf 2 ). (4.3) t
6 For fixed x, u(x, t) is proportional to the area under the function e z2, over an interval that, as time goes on, moves steadily to the left and decreases in length. For small t the interval involves only large z, where the function e z2 is nearly zero and the integral is nearly zero. As t increases, the interval of integration moves to the left, so that the integrand grows larger, but the length of the interval grows smaller. The net effect is that the voltage at x increases gradually over time, and then decreases gradually; the sharp initial pulse is smoothed out in time. 5 Heaviside to the Rescue It seemed that Thomson had solved the mathematical problem and discovered why the behavior was not wave-like. Since it is not really possible to reduce the resistance along the cable, and capacitance to the ground would probably remain a serious issue, particularly under water, it appeared that little could be done to improve the situation. But Heaviside had a solution. Heaviside argued that Thomson had ignored two other circuit components, the leakage of current to the ground, and the self-inductance of the cable. He revised Thomson s equations, obtaining u x = Li t Ri, and i x = Cu t Gu, where L is the inductance and G is the coefficient of leakage of current to the ground. The partial differential equation governing u(x, t) now becomes u xx = LCu tt + (LG + RC)u t + RGu, (5.1) which is the formulation used by Kirchhoff. As Körner remarks, never before had so much money been riding on the solution of one partial differential equation. 5.1 A Special Case: G = 0 If we take G = 0, thereby assuming that no current passes into the ground, the partial differential equation becomes u xx = LCu tt + RCu t, (5.2) or 1 CL u xx = u tt + R L u t. (5.3) 6
7 If R/L could be made small, we would have a wave equation again, but with a propagation speed of 1/ CL. This suggested to Heaviside that one way to obtain undistorted signaling would be to increase L, since we cannot realistically hope to change R. He argued for years for the use of cables with higher inductance, which eventually became the practice, helped along by the invention of new materials, such as magnetic alloys, that could be incorporated into the cables. 5.2 Another Special Case Assume now that E(t) is the pulse. Applying the Laplace transform method described earlier to Equation (5.1), we obtain from which we get U xx (x, s) = (Cs + G)(Ls + R)U(x, s) = λ 2 U(x, s), U(x, s) = A(s)e λx + ( 1 s (1 e T s ) A(s) ) e λx. If it happens that GL = CR, we can solve easily for λ: λ = CLs + GR. Then we have U(x, s) = e GRx 1 s (1 e T s )e CLxs, so that u(x, t) = e ( GRx H(t x CL) H(t T x CL) ). (5.4) This tells us that we have an undistorted pulse that arrives at the point x at the time t = x CL. In order to have GL = CR, we need L = CR/G. Since C and R are more or less fixed, and G is typically reduced by insulation, L will need to be large. Again, this argues for increasing the inductance in the cable. References [1] Gonzalez-Velasco, E. (1996) Fourier Analysis and Boundary Value Problems. Academic Press. [2] Körner, T. (1988) Fourier Analysis. Cambridge, UK: Cambridge University Press. 7
8 [3] Wylie, C.R. (1966) Advanced Engineering Mathematics. New York: McGraw- Hill. 8
Applications of Second-Order Differential Equations
 Applications of Second-Order Differential Equations Second-order linear differential equations have a variety of applications in science and engineering. In this section we explore two of them: the vibration
Applications of Second-Order Differential Equations Second-order linear differential equations have a variety of applications in science and engineering. In this section we explore two of them: the vibration
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
[ Assignment View ] [ Print ] Eðlisfræði 2, vor 2007 30. Inductance Assignment is due at 2:00am on Wednesday, March 14, 2007 Credit for problems submitted late will decrease to 0% after the deadline has
Objectives. Capacitors 262 CHAPTER 5 ENERGY
 Objectives Describe a capacitor. Explain how a capacitor stores energy. Define capacitance. Calculate the electrical energy stored in a capacitor. Describe an inductor. Explain how an inductor stores energy.
Objectives Describe a capacitor. Explain how a capacitor stores energy. Define capacitance. Calculate the electrical energy stored in a capacitor. Describe an inductor. Explain how an inductor stores energy.
Nikki Tarolla. Paper Category
 1 Nikki Tarolla Paper Category 2 The Transatlantic Cable was a revolution to technology that was used to unite the continents. Although it took many tries to establish a connection with all the continents,
1 Nikki Tarolla Paper Category 2 The Transatlantic Cable was a revolution to technology that was used to unite the continents. Although it took many tries to establish a connection with all the continents,
A wave lab inside a coaxial cable
 INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
INSTITUTE OF PHYSICS PUBLISHING Eur. J. Phys. 25 (2004) 581 591 EUROPEAN JOURNAL OF PHYSICS PII: S0143-0807(04)76273-X A wave lab inside a coaxial cable JoãoMSerra,MiguelCBrito,JMaiaAlves and A M Vallera
Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014. Striplines and Microstrips (PCB Transmission Lines)
 Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014 Striplines and Microstrips (PCB Transmission Lines) Disclaimer: This presentation is merely a compilation of information from public
Eatman Associates 2014 Rockwall TX 800-388-4036 rev. October 1, 2014 Striplines and Microstrips (PCB Transmission Lines) Disclaimer: This presentation is merely a compilation of information from public
Midterm Solutions. mvr = ω f (I wheel + I bullet ) = ω f 2 MR2 + mr 2 ) ω f = v R. 1 + M 2m
 Midterm Solutions I) A bullet of mass m moving at horizontal velocity v strikes and sticks to the rim of a wheel a solid disc) of mass M, radius R, anchored at its center but free to rotate i) Which of
Midterm Solutions I) A bullet of mass m moving at horizontal velocity v strikes and sticks to the rim of a wheel a solid disc) of mass M, radius R, anchored at its center but free to rotate i) Which of
The Original Transatlantic Communication
 Menooa Badalian [email protected] The Original Transatlantic Communication Abstract: The Transatlantic cable, running under the Atlantic Ocean, is the groundbreaking achievement of the late 19 th century.
Menooa Badalian [email protected] The Original Transatlantic Communication Abstract: The Transatlantic cable, running under the Atlantic Ocean, is the groundbreaking achievement of the late 19 th century.
Second Order Linear Partial Differential Equations. Part I
 Second Order Linear Partial Differential Equations Part I Second linear partial differential equations; Separation of Variables; - point boundary value problems; Eigenvalues and Eigenfunctions Introduction
Second Order Linear Partial Differential Equations Part I Second linear partial differential equations; Separation of Variables; - point boundary value problems; Eigenvalues and Eigenfunctions Introduction
An Introduction to Partial Differential Equations
 An Introduction to Partial Differential Equations Andrew J. Bernoff LECTURE 2 Cooling of a Hot Bar: The Diffusion Equation 2.1. Outline of Lecture An Introduction to Heat Flow Derivation of the Diffusion
An Introduction to Partial Differential Equations Andrew J. Bernoff LECTURE 2 Cooling of a Hot Bar: The Diffusion Equation 2.1. Outline of Lecture An Introduction to Heat Flow Derivation of the Diffusion
PHY3128 / PHYM203 (Electronics / Instrumentation) Transmission Lines. Repeated n times I L
 Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
Transmission Lines Introduction A transmission line guides energy from one place to another. Optical fibres, waveguides, telephone lines and power cables are all electromagnetic transmission lines. are
ENERGY TRANSFER SYSTEMS AND THEIR DYNAMIC ANALYSIS
 ENERGY TRANSFER SYSTEMS AND THEIR DYNAMIC ANALYSIS Many mechanical energy systems are devoted to transfer of energy between two points: the source or prime mover (input) and the load (output). For chemical
ENERGY TRANSFER SYSTEMS AND THEIR DYNAMIC ANALYSIS Many mechanical energy systems are devoted to transfer of energy between two points: the source or prime mover (input) and the load (output). For chemical
AS COMPETITION PAPER 2008
 AS COMPETITION PAPER 28 Name School Town & County Total Mark/5 Time Allowed: One hour Attempt as many questions as you can. Write your answers on this question paper. Marks allocated for each question
AS COMPETITION PAPER 28 Name School Town & County Total Mark/5 Time Allowed: One hour Attempt as many questions as you can. Write your answers on this question paper. Marks allocated for each question
Chapter 11. Inductors ISU EE. C.Y. Lee
 Chapter 11 Inductors Objectives Describe the basic structure and characteristics of an inductor Discuss various types of inductors Analyze series inductors Analyze parallel inductors Analyze inductive
Chapter 11 Inductors Objectives Describe the basic structure and characteristics of an inductor Discuss various types of inductors Analyze series inductors Analyze parallel inductors Analyze inductive
MATH 425, PRACTICE FINAL EXAM SOLUTIONS.
 MATH 45, PRACTICE FINAL EXAM SOLUTIONS. Exercise. a Is the operator L defined on smooth functions of x, y by L u := u xx + cosu linear? b Does the answer change if we replace the operator L by the operator
MATH 45, PRACTICE FINAL EXAM SOLUTIONS. Exercise. a Is the operator L defined on smooth functions of x, y by L u := u xx + cosu linear? b Does the answer change if we replace the operator L by the operator
HEAVISIDE CABLE, THOMSON CABLE AND THE BEST CONSTANT OF A SOBOLEV-TYPE INEQUALITY. Received June 1, 2007; revised September 30, 2007
 Scientiae Mathematicae Japonicae Online, e-007, 739 755 739 HEAVISIDE CABLE, THOMSON CABLE AND THE BEST CONSTANT OF A SOBOLEV-TYPE INEQUALITY Yoshinori Kametaka, Kazuo Takemura, Hiroyuki Yamagishi, Atsushi
Scientiae Mathematicae Japonicae Online, e-007, 739 755 739 HEAVISIDE CABLE, THOMSON CABLE AND THE BEST CONSTANT OF A SOBOLEV-TYPE INEQUALITY Yoshinori Kametaka, Kazuo Takemura, Hiroyuki Yamagishi, Atsushi
High Voltage Transient Analysis
 High Voltage Transient Analysis 4. Surges on Transmission Lines Due to a variety of reasons, such as a direct stroke of lightning on the line, or by indirect strokes, or by switching operations or by faults,
High Voltage Transient Analysis 4. Surges on Transmission Lines Due to a variety of reasons, such as a direct stroke of lightning on the line, or by indirect strokes, or by switching operations or by faults,
19.7. Applications of Differential Equations. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Applications of Differential Equations 19.7 Introduction Blocks 19.2 to 19.6 have introduced several techniques for solving commonly-occurring firstorder and second-order ordinary differential equations.
Applications of Differential Equations 19.7 Introduction Blocks 19.2 to 19.6 have introduced several techniques for solving commonly-occurring firstorder and second-order ordinary differential equations.
C B A T 3 T 2 T 1. 1. What is the magnitude of the force T 1? A) 37.5 N B) 75.0 N C) 113 N D) 157 N E) 192 N
 Three boxes are connected by massless strings and are resting on a frictionless table. Each box has a mass of 15 kg, and the tension T 1 in the right string is accelerating the boxes to the right at a
Three boxes are connected by massless strings and are resting on a frictionless table. Each box has a mass of 15 kg, and the tension T 1 in the right string is accelerating the boxes to the right at a
Physics 41 HW Set 1 Chapter 15
 Physics 4 HW Set Chapter 5 Serway 8 th OC:, 4, 7 CQ: 4, 8 P: 4, 5, 8, 8, 0, 9,, 4, 9, 4, 5, 5 Discussion Problems:, 57, 59, 67, 74 OC CQ P: 4, 5, 8, 8, 0, 9,, 4, 9, 4, 5, 5 Discussion Problems:, 57, 59,
Physics 4 HW Set Chapter 5 Serway 8 th OC:, 4, 7 CQ: 4, 8 P: 4, 5, 8, 8, 0, 9,, 4, 9, 4, 5, 5 Discussion Problems:, 57, 59, 67, 74 OC CQ P: 4, 5, 8, 8, 0, 9,, 4, 9, 4, 5, 5 Discussion Problems:, 57, 59,
Physics 9e/Cutnell. correlated to the. College Board AP Physics 1 Course Objectives
 Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
The Heat Equation. Lectures INF2320 p. 1/88
 The Heat Equation Lectures INF232 p. 1/88 Lectures INF232 p. 2/88 The Heat Equation We study the heat equation: u t = u xx for x (,1), t >, (1) u(,t) = u(1,t) = for t >, (2) u(x,) = f(x) for x (,1), (3)
The Heat Equation Lectures INF232 p. 1/88 Lectures INF232 p. 2/88 The Heat Equation We study the heat equation: u t = u xx for x (,1), t >, (1) u(,t) = u(1,t) = for t >, (2) u(x,) = f(x) for x (,1), (3)
Dynamic Process Modeling. Process Dynamics and Control
 Dynamic Process Modeling Process Dynamics and Control 1 Description of process dynamics Classes of models What do we need for control? Modeling for control Mechanical Systems Modeling Electrical circuits
Dynamic Process Modeling Process Dynamics and Control 1 Description of process dynamics Classes of models What do we need for control? Modeling for control Mechanical Systems Modeling Electrical circuits
Problem Solving 8: RC and LR Circuits
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Problem Solving 8: RC and LR Circuits Section Table and Group (e.g. L04 3C ) Names Hand in one copy per group at the end of the Friday Problem
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Problem Solving 8: RC and LR Circuits Section Table and Group (e.g. L04 3C ) Names Hand in one copy per group at the end of the Friday Problem
Chapter 4. Forces and Newton s Laws of Motion. continued
 Chapter 4 Forces and Newton s Laws of Motion continued 4.9 Static and Kinetic Frictional Forces When an object is in contact with a surface forces can act on the objects. The component of this force acting
Chapter 4 Forces and Newton s Laws of Motion continued 4.9 Static and Kinetic Frictional Forces When an object is in contact with a surface forces can act on the objects. The component of this force acting
ENCOURAGING THE INTEGRATION OF COMPLEX NUMBERS IN UNDERGRADUATE ORDINARY DIFFERENTIAL EQUATIONS
 Texas College Mathematics Journal Volume 6, Number 2, Pages 18 24 S applied for(xx)0000-0 Article electronically published on September 23, 2009 ENCOURAGING THE INTEGRATION OF COMPLEX NUMBERS IN UNDERGRADUATE
Texas College Mathematics Journal Volume 6, Number 2, Pages 18 24 S applied for(xx)0000-0 Article electronically published on September 23, 2009 ENCOURAGING THE INTEGRATION OF COMPLEX NUMBERS IN UNDERGRADUATE
Physics 6C, Summer 2006 Homework 2 Solutions
 Physics 6C, Summer 006 Homework Solutions All problems are from the nd edition of Walker. Numerical values are different for each student. Chapter 3 Problems. Figure 3-30 below shows a circuit containing
Physics 6C, Summer 006 Homework Solutions All problems are from the nd edition of Walker. Numerical values are different for each student. Chapter 3 Problems. Figure 3-30 below shows a circuit containing
Circuits with inductors and alternating currents. Chapter 20 #45, 46, 47, 49
 Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Induced voltages and Inductance Faraday s Law
 Induced voltages and Inductance Faraday s Law concept #1, 4, 5, 8, 13 Problem # 1, 3, 4, 5, 6, 9, 10, 13, 15, 24, 23, 25, 31, 32a, 34, 37, 41, 43, 51, 61 Last chapter we saw that a current produces a magnetic
Induced voltages and Inductance Faraday s Law concept #1, 4, 5, 8, 13 Problem # 1, 3, 4, 5, 6, 9, 10, 13, 15, 24, 23, 25, 31, 32a, 34, 37, 41, 43, 51, 61 Last chapter we saw that a current produces a magnetic
An Introduction to Core-conductor Theory
 An Introduction to Core-conductor Theory I often say when you can measure what you are speaking about and express it in numbers you know something about it; but when you cannot measure it, when you cannot
An Introduction to Core-conductor Theory I often say when you can measure what you are speaking about and express it in numbers you know something about it; but when you cannot measure it, when you cannot
Grounding Demystified
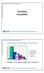 Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
Grounding Demystified 3-1 Importance Of Grounding Techniques 45 40 35 30 25 20 15 10 5 0 Grounding 42% Case 22% Cable 18% Percent Used Filter 12% PCB 6% Grounding 42% Case Shield 22% Cable Shielding 18%
DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING
 SESSION WEEK COURSE: Physics II DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING DESCRIPTION GROUPS (mark ) Indicate YES/NO If the session needs 2
SESSION WEEK COURSE: Physics II DEGREE: Bachelor's Degree in Industrial Electronics and Automation COURSE: 1º TERM: 2º WEEKLY PLANNING DESCRIPTION GROUPS (mark ) Indicate YES/NO If the session needs 2
Principles of Electromechanical Energy Conversion
 Principles of Electromechanical Energy Conversion Why do we study this? Electromechanical energy conversion theory is the cornerstone for the analysis of electromechanical motion devices. The theory allows
Principles of Electromechanical Energy Conversion Why do we study this? Electromechanical energy conversion theory is the cornerstone for the analysis of electromechanical motion devices. The theory allows
EE301 Lesson 14 Reading: 10.1-10.4, 10.11-10.12, 11.1-11.4 and 11.11-11.13
 CAPACITORS AND INDUCTORS Learning Objectives EE301 Lesson 14 a. Define capacitance and state its symbol and unit of measurement. b. Predict the capacitance of a parallel plate capacitor. c. Analyze how
CAPACITORS AND INDUCTORS Learning Objectives EE301 Lesson 14 a. Define capacitance and state its symbol and unit of measurement. b. Predict the capacitance of a parallel plate capacitor. c. Analyze how
College of the Holy Cross, Spring 2009 Math 373, Partial Differential Equations Midterm 1 Practice Questions
 College of the Holy Cross, Spring 29 Math 373, Partial Differential Equations Midterm 1 Practice Questions 1. (a) Find a solution of u x + u y + u = xy. Hint: Try a polynomial of degree 2. Solution. Use
College of the Holy Cross, Spring 29 Math 373, Partial Differential Equations Midterm 1 Practice Questions 1. (a) Find a solution of u x + u y + u = xy. Hint: Try a polynomial of degree 2. Solution. Use
N 1. (q k+1 q k ) 2 + α 3. k=0
 Teoretisk Fysik Hand-in problem B, SI1142, Spring 2010 In 1955 Fermi, Pasta and Ulam 1 numerically studied a simple model for a one dimensional chain of non-linear oscillators to see how the energy distribution
Teoretisk Fysik Hand-in problem B, SI1142, Spring 2010 In 1955 Fermi, Pasta and Ulam 1 numerically studied a simple model for a one dimensional chain of non-linear oscillators to see how the energy distribution
Slide 1 / 26. Inductance. 2011 by Bryan Pflueger
 Slide 1 / 26 Inductance 2011 by Bryan Pflueger Slide 2 / 26 Mutual Inductance If two coils of wire are placed near each other and have a current passing through them, they will each induce an emf on one
Slide 1 / 26 Inductance 2011 by Bryan Pflueger Slide 2 / 26 Mutual Inductance If two coils of wire are placed near each other and have a current passing through them, they will each induce an emf on one
SECTION 2 Transmission Line Theory
 SEMICONDUCTOR DESIGN GUIDE Transmission Line Theory SECTION 2 Transmission Line Theory Introduction The ECLinPS family has pushed the world of ECL into the realm of picoseconds. When output transitions
SEMICONDUCTOR DESIGN GUIDE Transmission Line Theory SECTION 2 Transmission Line Theory Introduction The ECLinPS family has pushed the world of ECL into the realm of picoseconds. When output transitions
ACCELERATION DUE TO GRAVITY
 EXPERIMENT 1 PHYSICS 107 ACCELERATION DUE TO GRAVITY Skills you will learn or practice: Calculate velocity and acceleration from experimental measurements of x vs t (spark positions) Find average velocities
EXPERIMENT 1 PHYSICS 107 ACCELERATION DUE TO GRAVITY Skills you will learn or practice: Calculate velocity and acceleration from experimental measurements of x vs t (spark positions) Find average velocities
S. Boyd EE102. Lecture 1 Signals. notation and meaning. common signals. size of a signal. qualitative properties of signals.
 S. Boyd EE102 Lecture 1 Signals notation and meaning common signals size of a signal qualitative properties of signals impulsive signals 1 1 Signals a signal is a function of time, e.g., f is the force
S. Boyd EE102 Lecture 1 Signals notation and meaning common signals size of a signal qualitative properties of signals impulsive signals 1 1 Signals a signal is a function of time, e.g., f is the force
Equations, Inequalities & Partial Fractions
 Contents Equations, Inequalities & Partial Fractions.1 Solving Linear Equations 2.2 Solving Quadratic Equations 1. Solving Polynomial Equations 1.4 Solving Simultaneous Linear Equations 42.5 Solving Inequalities
Contents Equations, Inequalities & Partial Fractions.1 Solving Linear Equations 2.2 Solving Quadratic Equations 1. Solving Polynomial Equations 1.4 Solving Simultaneous Linear Equations 42.5 Solving Inequalities
www.mathsbox.org.uk Displacement (x) Velocity (v) Acceleration (a) x = f(t) differentiate v = dx Acceleration Velocity (v) Displacement x
 Mechanics 2 : Revision Notes 1. Kinematics and variable acceleration Displacement (x) Velocity (v) Acceleration (a) x = f(t) differentiate v = dx differentiate a = dv = d2 x dt dt dt 2 Acceleration Velocity
Mechanics 2 : Revision Notes 1. Kinematics and variable acceleration Displacement (x) Velocity (v) Acceleration (a) x = f(t) differentiate v = dx differentiate a = dv = d2 x dt dt dt 2 Acceleration Velocity
The integrating factor method (Sect. 2.1).
 The integrating factor method (Sect. 2.1). Overview of differential equations. Linear Ordinary Differential Equations. The integrating factor method. Constant coefficients. The Initial Value Problem. Variable
The integrating factor method (Sect. 2.1). Overview of differential equations. Linear Ordinary Differential Equations. The integrating factor method. Constant coefficients. The Initial Value Problem. Variable
BASIC ELECTRONICS AC CIRCUIT ANALYSIS. December 2011
 AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
AM 5-202 BASIC ELECTRONICS AC CIRCUIT ANALYSIS December 2011 DISTRIBUTION RESTRICTION: Approved for Pubic Release. Distribution is unlimited. DEPARTMENT OF THE ARMY MILITARY AUXILIARY RADIO SYSTEM FORT
minimal polyonomial Example
 Minimal Polynomials Definition Let α be an element in GF(p e ). We call the monic polynomial of smallest degree which has coefficients in GF(p) and α as a root, the minimal polyonomial of α. Example: We
Minimal Polynomials Definition Let α be an element in GF(p e ). We call the monic polynomial of smallest degree which has coefficients in GF(p) and α as a root, the minimal polyonomial of α. Example: We
You re One in Seven Billion!
 You re One in Seven Billion! We ve all heard the expression, You re one in a million!. With the ever-growing number of people on the planet, it might be more accurate to say, You re one in seven billion!
You re One in Seven Billion! We ve all heard the expression, You re one in a million!. With the ever-growing number of people on the planet, it might be more accurate to say, You re one in seven billion!
Waves. Wave Parameters. Krauss Chapter Nine
 Waves Krauss Chapter Nine Wave Parameters Wavelength = λ = Length between wave crests (or troughs) Wave Number = κ = 2π/λ (units of 1/length) Wave Period = T = Time it takes a wave crest to travel one
Waves Krauss Chapter Nine Wave Parameters Wavelength = λ = Length between wave crests (or troughs) Wave Number = κ = 2π/λ (units of 1/length) Wave Period = T = Time it takes a wave crest to travel one
ELECTRICAL ENGINEERING
 EE ELECTRICAL ENGINEERING See beginning of Section H for abbreviations, course numbers and coding. The * denotes labs which are held on alternate weeks. A minimum grade of C is required for all prerequisite
EE ELECTRICAL ENGINEERING See beginning of Section H for abbreviations, course numbers and coding. The * denotes labs which are held on alternate weeks. A minimum grade of C is required for all prerequisite
RAJALAKSHMI ENGINEERING COLLEGE MA 2161 UNIT I - ORDINARY DIFFERENTIAL EQUATIONS PART A
 RAJALAKSHMI ENGINEERING COLLEGE MA 26 UNIT I - ORDINARY DIFFERENTIAL EQUATIONS. Solve (D 2 + D 2)y = 0. 2. Solve (D 2 + 6D + 9)y = 0. PART A 3. Solve (D 4 + 4)x = 0 where D = d dt 4. Find Particular Integral:
RAJALAKSHMI ENGINEERING COLLEGE MA 26 UNIT I - ORDINARY DIFFERENTIAL EQUATIONS. Solve (D 2 + D 2)y = 0. 2. Solve (D 2 + 6D + 9)y = 0. PART A 3. Solve (D 4 + 4)x = 0 where D = d dt 4. Find Particular Integral:
A Mathematical Model for Online Electrical Characterization of Thermoelectric Generators using the P-I Curves at Different Temperatures
 A Mathematical Model for Online Electrical Characterization of Thermoelectric Generators using the P-I Curves at Different Temperatures Eduardo I. Ortiz-Rivera, Member IEEE Email: [email protected]
A Mathematical Model for Online Electrical Characterization of Thermoelectric Generators using the P-I Curves at Different Temperatures Eduardo I. Ortiz-Rivera, Member IEEE Email: [email protected]
Spring Simple Harmonic Oscillator. Spring constant. Potential Energy stored in a Spring. Understanding oscillations. Understanding oscillations
 Spring Simple Harmonic Oscillator Simple Harmonic Oscillations and Resonance We have an object attached to a spring. The object is on a horizontal frictionless surface. We move the object so the spring
Spring Simple Harmonic Oscillator Simple Harmonic Oscillations and Resonance We have an object attached to a spring. The object is on a horizontal frictionless surface. We move the object so the spring
Nonlinear Systems of Ordinary Differential Equations
 Differential Equations Massoud Malek Nonlinear Systems of Ordinary Differential Equations Dynamical System. A dynamical system has a state determined by a collection of real numbers, or more generally
Differential Equations Massoud Malek Nonlinear Systems of Ordinary Differential Equations Dynamical System. A dynamical system has a state determined by a collection of real numbers, or more generally
Carbon Cable. Sergio Rubio Carles Paul Albert Monte
 Carbon Cable Sergio Rubio Carles Paul Albert Monte Carbon, Copper and Manganine PhYsical PropERTieS CARBON PROPERTIES Carbon physical Properties Temperature Coefficient α -0,0005 ºC-1 Density D 2260 kg/m3
Carbon Cable Sergio Rubio Carles Paul Albert Monte Carbon, Copper and Manganine PhYsical PropERTieS CARBON PROPERTIES Carbon physical Properties Temperature Coefficient α -0,0005 ºC-1 Density D 2260 kg/m3
LeaPS Workshop March 12, 2010 Morehead Conference Center Morehead, KY
 LeaPS Workshop March 12, 2010 Morehead Conference Center Morehead, KY Word Bank: Acceleration, mass, inertia, weight, gravity, work, heat, kinetic energy, potential energy, closed systems, open systems,
LeaPS Workshop March 12, 2010 Morehead Conference Center Morehead, KY Word Bank: Acceleration, mass, inertia, weight, gravity, work, heat, kinetic energy, potential energy, closed systems, open systems,
6.041/6.431 Spring 2008 Quiz 2 Wednesday, April 16, 7:30-9:30 PM. SOLUTIONS
 6.4/6.43 Spring 28 Quiz 2 Wednesday, April 6, 7:3-9:3 PM. SOLUTIONS Name: Recitation Instructor: TA: 6.4/6.43: Question Part Score Out of 3 all 36 2 a 4 b 5 c 5 d 8 e 5 f 6 3 a 4 b 6 c 6 d 6 e 6 Total
6.4/6.43 Spring 28 Quiz 2 Wednesday, April 6, 7:3-9:3 PM. SOLUTIONS Name: Recitation Instructor: TA: 6.4/6.43: Question Part Score Out of 3 all 36 2 a 4 b 5 c 5 d 8 e 5 f 6 3 a 4 b 6 c 6 d 6 e 6 Total
L stub Z A = Z 0 Z R Z 0S. Single stub impedance matching
 Single stub impedance matching Impedance matching can be achieved by inserting another transmission line (stub) as shown in the diagram below Z A = Z 0 Z 0 Z R Z 0S d stub L stub Amanogawa, 006 Digital
Single stub impedance matching Impedance matching can be achieved by inserting another transmission line (stub) as shown in the diagram below Z A = Z 0 Z 0 Z R Z 0S d stub L stub Amanogawa, 006 Digital
Scientific Programming
 1 The wave equation Scientific Programming Wave Equation The wave equation describes how waves propagate: light waves, sound waves, oscillating strings, wave in a pond,... Suppose that the function h(x,t)
1 The wave equation Scientific Programming Wave Equation The wave equation describes how waves propagate: light waves, sound waves, oscillating strings, wave in a pond,... Suppose that the function h(x,t)
Laminar and Turbulent flow. Flow Sensors. Reynolds Number. Thermal flow Sensor. Flow and Flow rate. R = Mass Flow controllers
 Flow and Flow rate. Laminar and Turbulent flow Laminar flow: smooth, orderly and regular Mechanical sensors have inertia, which can integrate out small variations due to turbulence Turbulent flow: chaotic
Flow and Flow rate. Laminar and Turbulent flow Laminar flow: smooth, orderly and regular Mechanical sensors have inertia, which can integrate out small variations due to turbulence Turbulent flow: chaotic
How Rockets Work Newton s Laws of Motion
 How Rockets Work Whether flying a small model rocket or launching a giant cargo rocket to Mars, the principles of how rockets work are exactly the same. Understanding and applying these principles means
How Rockets Work Whether flying a small model rocket or launching a giant cargo rocket to Mars, the principles of how rockets work are exactly the same. Understanding and applying these principles means
The two dimensional heat equation
 The two dimensional heat equation Ryan C. Trinity University Partial Differential Equations March 6, 2012 Physical motivation Consider a thin rectangular plate made of some thermally conductive material.
The two dimensional heat equation Ryan C. Trinity University Partial Differential Equations March 6, 2012 Physical motivation Consider a thin rectangular plate made of some thermally conductive material.
AS COMPETITION PAPER 2007 SOLUTIONS
 AS COMPETITION PAPER 2007 Total Mark/50 SOLUTIONS Section A: Multiple Choice 1. C 2. D 3. B 4. B 5. B 6. A 7. A 8. C 1 Section B: Written Answer Question 9. A mass M is attached to the end of a horizontal
AS COMPETITION PAPER 2007 Total Mark/50 SOLUTIONS Section A: Multiple Choice 1. C 2. D 3. B 4. B 5. B 6. A 7. A 8. C 1 Section B: Written Answer Question 9. A mass M is attached to the end of a horizontal
Power Electronics. Prof. K. Gopakumar. Centre for Electronics Design and Technology. Indian Institute of Science, Bangalore.
 Power Electronics Prof. K. Gopakumar Centre for Electronics Design and Technology Indian Institute of Science, Bangalore Lecture - 1 Electric Drive Today, we will start with the topic on industrial drive
Power Electronics Prof. K. Gopakumar Centre for Electronics Design and Technology Indian Institute of Science, Bangalore Lecture - 1 Electric Drive Today, we will start with the topic on industrial drive
General Framework for an Iterative Solution of Ax b. Jacobi s Method
 2.6 Iterative Solutions of Linear Systems 143 2.6 Iterative Solutions of Linear Systems Consistent linear systems in real life are solved in one of two ways: by direct calculation (using a matrix factorization,
2.6 Iterative Solutions of Linear Systems 143 2.6 Iterative Solutions of Linear Systems Consistent linear systems in real life are solved in one of two ways: by direct calculation (using a matrix factorization,
Beginner Modeling Exercises Section 2 Mental Simulation of Simple Positive Feedback
 D-4487 Beginner Modeling Exercises Section 2 Mental Simulation of Simple Positive Feedback Stock Flow Growth Factor Prepared for the MIT System Dynamics in Education Project Under the Supervision of Dr.
D-4487 Beginner Modeling Exercises Section 2 Mental Simulation of Simple Positive Feedback Stock Flow Growth Factor Prepared for the MIT System Dynamics in Education Project Under the Supervision of Dr.
Physics 2048 Test 1 Solution (solutions to problems 2-5 are from student papers) Problem 1 (Short Answer: 20 points)
 Physics 248 Test 1 Solution (solutions to problems 25 are from student papers) Problem 1 (Short Answer: 2 points) An object's motion is restricted to one dimension along the distance axis. Answer each
Physics 248 Test 1 Solution (solutions to problems 25 are from student papers) Problem 1 (Short Answer: 2 points) An object's motion is restricted to one dimension along the distance axis. Answer each
The one dimensional heat equation: Neumann and Robin boundary conditions
 The one dimensional heat equation: Neumann and Robin boundary conditions Ryan C. Trinity University Partial Differential Equations February 28, 2012 with Neumann boundary conditions Our goal is to solve:
The one dimensional heat equation: Neumann and Robin boundary conditions Ryan C. Trinity University Partial Differential Equations February 28, 2012 with Neumann boundary conditions Our goal is to solve:
a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2.
 Chapter 1 LINEAR EQUATIONS 1.1 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,..., a n, b are given
Chapter 1 LINEAR EQUATIONS 1.1 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,..., a n, b are given
Slope and Rate of Change
 Chapter 1 Slope and Rate of Change Chapter Summary and Goal This chapter will start with a discussion of slopes and the tangent line. This will rapidly lead to heuristic developments of limits and the
Chapter 1 Slope and Rate of Change Chapter Summary and Goal This chapter will start with a discussion of slopes and the tangent line. This will rapidly lead to heuristic developments of limits and the
Convolution, Correlation, & Fourier Transforms. James R. Graham 10/25/2005
 Convolution, Correlation, & Fourier Transforms James R. Graham 10/25/2005 Introduction A large class of signal processing techniques fall under the category of Fourier transform methods These methods fall
Convolution, Correlation, & Fourier Transforms James R. Graham 10/25/2005 Introduction A large class of signal processing techniques fall under the category of Fourier transform methods These methods fall
Copyright 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley.
 Chapter 20. Traveling Waves You may not realize it, but you are surrounded by waves. The waviness of a water wave is readily apparent, from the ripples on a pond to ocean waves large enough to surf. It
Chapter 20. Traveling Waves You may not realize it, but you are surrounded by waves. The waviness of a water wave is readily apparent, from the ripples on a pond to ocean waves large enough to surf. It
Students Manual for the Exam. General Engineering and Electrical Civil Engineering Discipline
 Students Manual for the Exam General Engineering and Electrical Civil Engineering Discipline -- October March 2014 2013 -- COPYRIGHT NOTICE COPYRIGHTS 2013 NATIONAL CENTER FOR ASSESSMENT IN HIGHER EDUCATION
Students Manual for the Exam General Engineering and Electrical Civil Engineering Discipline -- October March 2014 2013 -- COPYRIGHT NOTICE COPYRIGHTS 2013 NATIONAL CENTER FOR ASSESSMENT IN HIGHER EDUCATION
Limits and Continuity
 Math 20C Multivariable Calculus Lecture Limits and Continuity Slide Review of Limit. Side limits and squeeze theorem. Continuous functions of 2,3 variables. Review: Limits Slide 2 Definition Given a function
Math 20C Multivariable Calculus Lecture Limits and Continuity Slide Review of Limit. Side limits and squeeze theorem. Continuous functions of 2,3 variables. Review: Limits Slide 2 Definition Given a function
Assessment Plan for Learning Outcomes for BA/BS in Physics
 Department of Physics and Astronomy Goals and Learning Outcomes 1. Students know basic physics principles [BS, BA, MS] 1.1 Students can demonstrate an understanding of Newton s laws 1.2 Students can demonstrate
Department of Physics and Astronomy Goals and Learning Outcomes 1. Students know basic physics principles [BS, BA, MS] 1.1 Students can demonstrate an understanding of Newton s laws 1.2 Students can demonstrate
CURRENT ELECTRICITY INTRODUCTION TO RESISTANCE, CAPACITANCE AND INDUCTANCE
 CURRENT ELECTRICITY INTRODUCTION TO RESI STANCE, CAPACITANCE AND INDUCTANCE P R E A M B L E This problem is adapted from an on-line knowledge enhancement module for a PGCE programme. It is used to cover
CURRENT ELECTRICITY INTRODUCTION TO RESI STANCE, CAPACITANCE AND INDUCTANCE P R E A M B L E This problem is adapted from an on-line knowledge enhancement module for a PGCE programme. It is used to cover
The Membrane Equation
 The Membrane Equation Professor David Heeger September 5, 2000 RC Circuits Figure 1A shows an RC (resistor, capacitor) equivalent circuit model for a patch of passive neural membrane. The capacitor represents
The Membrane Equation Professor David Heeger September 5, 2000 RC Circuits Figure 1A shows an RC (resistor, capacitor) equivalent circuit model for a patch of passive neural membrane. The capacitor represents
Viscoelasticity of Polymer Fluids.
 Viscoelasticity of Polymer Fluids. Main Properties of Polymer Fluids. Entangled polymer fluids are polymer melts and concentrated or semidilute (above the concentration c) solutions. In these systems polymer
Viscoelasticity of Polymer Fluids. Main Properties of Polymer Fluids. Entangled polymer fluids are polymer melts and concentrated or semidilute (above the concentration c) solutions. In these systems polymer
Modeling Mechanical Systems
 chp3 1 Modeling Mechanical Systems Dr. Nhut Ho ME584 chp3 2 Agenda Idealized Modeling Elements Modeling Method and Examples Lagrange s Equation Case study: Feasibility Study of a Mobile Robot Design Matlab
chp3 1 Modeling Mechanical Systems Dr. Nhut Ho ME584 chp3 2 Agenda Idealized Modeling Elements Modeling Method and Examples Lagrange s Equation Case study: Feasibility Study of a Mobile Robot Design Matlab
ORDINARY DIFFERENTIAL EQUATIONS
 ORDINARY DIFFERENTIAL EQUATIONS GABRIEL NAGY Mathematics Department, Michigan State University, East Lansing, MI, 48824. SEPTEMBER 4, 25 Summary. This is an introduction to ordinary differential equations.
ORDINARY DIFFERENTIAL EQUATIONS GABRIEL NAGY Mathematics Department, Michigan State University, East Lansing, MI, 48824. SEPTEMBER 4, 25 Summary. This is an introduction to ordinary differential equations.
Application of Fourier Transform to PDE (I) Fourier Sine Transform (application to PDEs defined on a semi-infinite domain)
 Application of Fourier Transform to PDE (I) Fourier Sine Transform (application to PDEs defined on a semi-infinite domain) The Fourier Sine Transform pair are F. T. : U = 2/ u x sin x dx, denoted as U
Application of Fourier Transform to PDE (I) Fourier Sine Transform (application to PDEs defined on a semi-infinite domain) The Fourier Sine Transform pair are F. T. : U = 2/ u x sin x dx, denoted as U
L and C connected together. To be able: To analyse some basic circuits.
 circuits: Sinusoidal Voltages and urrents Aims: To appreciate: Similarities between oscillation in circuit and mechanical pendulum. Role of energy loss mechanisms in damping. Why we study sinusoidal signals
circuits: Sinusoidal Voltages and urrents Aims: To appreciate: Similarities between oscillation in circuit and mechanical pendulum. Role of energy loss mechanisms in damping. Why we study sinusoidal signals
The Technical Archer. Austin Wargo
 The Technical Archer Austin Wargo May 14, 2010 Abstract A mathematical model of the interactions between a long bow and an arrow. The model uses the Euler-Lagrange formula, and is based off conservation
The Technical Archer Austin Wargo May 14, 2010 Abstract A mathematical model of the interactions between a long bow and an arrow. The model uses the Euler-Lagrange formula, and is based off conservation
DIFFERENTIABILITY OF COMPLEX FUNCTIONS. Contents
 DIFFERENTIABILITY OF COMPLEX FUNCTIONS Contents 1. Limit definition of a derivative 1 2. Holomorphic functions, the Cauchy-Riemann equations 3 3. Differentiability of real functions 5 4. A sufficient condition
DIFFERENTIABILITY OF COMPLEX FUNCTIONS Contents 1. Limit definition of a derivative 1 2. Holomorphic functions, the Cauchy-Riemann equations 3 3. Differentiability of real functions 5 4. A sufficient condition
AP Physics 1 and 2 Lab Investigations
 AP Physics 1 and 2 Lab Investigations Student Guide to Data Analysis New York, NY. College Board, Advanced Placement, Advanced Placement Program, AP, AP Central, and the acorn logo are registered trademarks
AP Physics 1 and 2 Lab Investigations Student Guide to Data Analysis New York, NY. College Board, Advanced Placement, Advanced Placement Program, AP, AP Central, and the acorn logo are registered trademarks
Chapter 4: Newton s Laws: Explaining Motion
 Chapter 4: Newton s Laws: Explaining Motion 1. All except one of the following require the application of a net force. Which one is the exception? A. to change an object from a state of rest to a state
Chapter 4: Newton s Laws: Explaining Motion 1. All except one of the following require the application of a net force. Which one is the exception? A. to change an object from a state of rest to a state
e.g. arrival of a customer to a service station or breakdown of a component in some system.
 Poisson process Events occur at random instants of time at an average rate of λ events per second. e.g. arrival of a customer to a service station or breakdown of a component in some system. Let N(t) be
Poisson process Events occur at random instants of time at an average rate of λ events per second. e.g. arrival of a customer to a service station or breakdown of a component in some system. Let N(t) be
Free Fall: Observing and Analyzing the Free Fall Motion of a Bouncing Ping-Pong Ball and Calculating the Free Fall Acceleration (Teacher s Guide)
 Free Fall: Observing and Analyzing the Free Fall Motion of a Bouncing Ping-Pong Ball and Calculating the Free Fall Acceleration (Teacher s Guide) 2012 WARD S Science v.11/12 OVERVIEW Students will measure
Free Fall: Observing and Analyzing the Free Fall Motion of a Bouncing Ping-Pong Ball and Calculating the Free Fall Acceleration (Teacher s Guide) 2012 WARD S Science v.11/12 OVERVIEW Students will measure
AP Physics C. Oscillations/SHM Review Packet
 AP Physics C Oscillations/SHM Review Packet 1. A 0.5 kg mass on a spring has a displacement as a function of time given by the equation x(t) = 0.8Cos(πt). Find the following: a. The time for one complete
AP Physics C Oscillations/SHM Review Packet 1. A 0.5 kg mass on a spring has a displacement as a function of time given by the equation x(t) = 0.8Cos(πt). Find the following: a. The time for one complete
WORK DONE BY A CONSTANT FORCE
 WORK DONE BY A CONSTANT FORCE The definition of work, W, when a constant force (F) is in the direction of displacement (d) is W = Fd SI unit is the Newton-meter (Nm) = Joule, J If you exert a force of
WORK DONE BY A CONSTANT FORCE The definition of work, W, when a constant force (F) is in the direction of displacement (d) is W = Fd SI unit is the Newton-meter (Nm) = Joule, J If you exert a force of
Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Z +
 Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Quick Review of Reflection Coefficient The Smith chart is a method of graphing reflection coefficients and impedance, and is often useful
Introduction to the Smith Chart for the MSA Sam Wetterlin 10/12/09 Quick Review of Reflection Coefficient The Smith chart is a method of graphing reflection coefficients and impedance, and is often useful
The Time Constant of an RC Circuit
 The Time Constant of an RC Circuit 1 Objectives 1. To determine the time constant of an RC Circuit, and 2. To determine the capacitance of an unknown capacitor. 2 Introduction What the heck is a capacitor?
The Time Constant of an RC Circuit 1 Objectives 1. To determine the time constant of an RC Circuit, and 2. To determine the capacitance of an unknown capacitor. 2 Introduction What the heck is a capacitor?
3.1. Solving linear equations. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Solving linear equations 3.1 Introduction Many problems in engineering reduce to the solution of an equation or a set of equations. An equation is a type of mathematical expression which contains one or
Solving linear equations 3.1 Introduction Many problems in engineering reduce to the solution of an equation or a set of equations. An equation is a type of mathematical expression which contains one or
Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows
 Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows 3.- 1 Basics: equations of continuum mechanics - balance equations for mass and momentum - balance equations for the energy and the chemical
Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows 3.- 1 Basics: equations of continuum mechanics - balance equations for mass and momentum - balance equations for the energy and the chemical
Section 15.1 Energy and Its Forms (pages 446 452)
 Section 15.1 and Its Forms (pages 446 452) This section describes how energy and work are related. It defines kinetic energy and potential energy, and gives examples for calculating these forms of energy.
Section 15.1 and Its Forms (pages 446 452) This section describes how energy and work are related. It defines kinetic energy and potential energy, and gives examples for calculating these forms of energy.
Physics: Principles and Applications, 6e Giancoli Chapter 4 Dynamics: Newton's Laws of Motion
 Physics: Principles and Applications, 6e Giancoli Chapter 4 Dynamics: Newton's Laws of Motion Conceptual Questions 1) Which of Newton's laws best explains why motorists should buckle-up? A) the first law
Physics: Principles and Applications, 6e Giancoli Chapter 4 Dynamics: Newton's Laws of Motion Conceptual Questions 1) Which of Newton's laws best explains why motorists should buckle-up? A) the first law
Digital Systems Ribbon Cables I CMPE 650. Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip.
 Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
Ribbon Cables A ribbon cable is any cable having multiple conductors bound together in a flat, wide strip. Each dielectric configuration has different high-frequency characteristics. All configurations
The Fourth International DERIVE-TI92/89 Conference Liverpool, U.K., 12-15 July 2000. Derive 5: The Easiest... Just Got Better!
 The Fourth International DERIVE-TI9/89 Conference Liverpool, U.K., -5 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de technologie supérieure 00, rue Notre-Dame Ouest Montréal
The Fourth International DERIVE-TI9/89 Conference Liverpool, U.K., -5 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de technologie supérieure 00, rue Notre-Dame Ouest Montréal
Candidate Number. General Certificate of Education Advanced Level Examination June 2014
 entre Number andidate Number Surname Other Names andidate Signature General ertificate of Education dvanced Level Examination June 214 Physics PHY4/1 Unit 4 Fields and Further Mechanics Section Wednesday
entre Number andidate Number Surname Other Names andidate Signature General ertificate of Education dvanced Level Examination June 214 Physics PHY4/1 Unit 4 Fields and Further Mechanics Section Wednesday
