This page left blank for double-sided printing
|
|
|
- Kristian Bond
- 10 years ago
- Views:
Transcription
1
2 This page left blank for double-sided printing
3 A COMPARISON OF LUNAR LANDING TRAJECTORY STRATEGIES USING NUMERICAL SIMULATIONS Mike Loucks 1, John Carrico 2, Timothy Carrico 2, Chuck Deiterich 3 1 Space Exploration Engineering Co.687 Chinook Way, Friday Harbor WA [email protected] 2 Analytical Graphics Inc. 220 Valley Creek Blvd. Exton, PA [email protected], [email protected] 3 Applied Technology and Engineering. P.O. Box 476, Bertram, TX [email protected] Abstract The authors present several lunar landing trajectory strategies, including those used on the Apollo, Ranger and Surveyor programs; some planned for a commercial lunar mission; and some new techniques based on artificial intelligence. The paper describes the complete strategies for trajectory design from Earth-launch to Lunar landing. This includes a comparison between using Earth and Lunar orbit strategies versus direct ascent and direct descent methods. Closed-loop landing controls for the descent to the Lunar surface are also discussed. Each of these cases is modeled with a high-precision numerical integrator using full force models. The authors document and compare the maneuvers, fuel use, and other parameters affecting the transfer and landing trajectories. In addition, the authors discuss methods to expand the launch window. The fully integrated end-to-end trajectory ephemerides are available from the authors in electronic ASCII text by request. Background The work presented in this paper originally started in support of developing a software framework in response to the NASA Space Exploration Initiative 1. In developing the software framework, it became apparent that there was not a lot of recent literature on the methods of Lunar landing. This current work is the result of investigating how Lunar landings were achieved on previous missions, and modeling these techniques with modern software. The results of modeling previous techniques with high-precision numerical integration are presented. In addition, some work has been done to use new methods, and a subset of that work is also presented. Earth-to-Moon Transfers Earth-to-Moon transfer trajectories can be described in three major phases: Leaving the Earth, transferring from the Earth to the proximity of the Moon, and approaching the Moon. Leaving the Earth There are two main ways to launch from the Earth into a transfer trajectory: either by direct ascent into the trans-lunar trajectory or by first inserting into an Earth parking-orbit and then, after a specified coast time, executing a Trans-Lunar injection (TLI) maneuver. This second method is sometimes called Launch-Coast-Burn. Often the choice between the two methods is International Lunar Conference September 2005 Page 1
4 simply based on the capabilities of the launch vehicle. A review of the early missions seems to indicate that the first missions were direct ascents, but soon the launch-coast-burn was used when the technology became available. The Soviet Luna missions 1-3 used direct ascent 2, but most if not all the Luna missions afterwards used launch-coast-burn. The Soviet Zond 4 3 used launch-coast-burn., as did the Ranger 7-9 missions. An early NASA technical report entitled Surveyor Project Final Report 4 states: Surveyors I, II, and IV were injected into translunar trajectories via the direct-ascent mode; Surveyors III, V, VI, and VII used the parking-orbit ascent mode. The parkingorbit ascent mode was clearly superior from a mission design standpoint, since, using a parking-orbit ascent, it was geometrically possible to launch on any day of the month. Indeed, using the launch-coast-burn method allows transfers to the Moon on any day of the month. The maneuver magnitude ( burn ) has complete responsibility for establishing the apogee at or near the Lunar orbit distance from the Earth. The Launch time has total control over and establishes the right ascension of the ascending node (RAAN), and the coast time establishes the direction of the line-of-apsides. Using the launch time to control the RAAN allows the orbit plane to be rotated so as to contain the Moon at Lunar encounter. The coast time is adjusted to put the apogee of the transfer orbit near the Moon s orbit. Combined, these controls allow the transfer trajectory to encounter the Moon at any day of the month. All the trajectories produced for this study use a launch-coast-burn ascent from Earth. Transfer Trajectories There are several types of transfers from the Earth to the Moon. Most missions flown up to this point have used a simple ballistic transfer that can be thought of as a very eccentric Earth-centered ellipse with its apogee at the Moon. (This description, of course, doesn t account for the gravity of the Moon, but remains useful.) If the apogee is just at the Moon s distance, the transfer time will be about 5 days. If the TLI is greater, then the apogee will be beyond the Moon, and will require a greater Lunar Orbit Insertion (LOI) maneuver to capture at the Moon. Four examples are shown in Figure 1: A 5 day transfer, a 4-day, a 3-Day, and a 34 hour (1.4 Day), the last being the time-of-flight used for the Luna-1 mission 2, the first mission to the Moon. Figure 1: Ballistic Transfer is Earth-Centered Inertial Coordinates It is often more insightful to plot the trajectories in a rotating system, with the Earth-Moon line fixed. These same examples are shown in Figure 2. The Soviet Luna 1 flew a 34 hour (1.4 day) International Lunar Conference September 2005 Page 2
5 transfer 2. Luna 9, the first spacecraft to perform a soft landing on the Moon, used a 3 day 7 hour transfer 2. Apollo 11 used a 72 hour (3.0 day) transfer 5. Lunar Prospector 6 flew a 105 hour (4.375 day) transfer. 34-Hour 3-Day 4-Day 5-Day In order to expand the launch window, several missions have added phasing loops before the final transfer from the Earth to the Moon. Clementine 7,8,9,10 used 2½ phasing loops, which could be adjusted in orbit period with perigee maneuvers to allow for more launch days per month while maintaining the same arrival day (to meet lunar lighting conditions.) An example from the present work, with 3½ phasing loops, is shown in Figure 3. This figure is shown in the Sun-Earth rotating coordinate system which separates the phasing loops, making it easier to understand and analyze. The use of rotating coordinates is common practice, and each system has its own purpose. Figure 2: Ballistic Transfers in Earth-Moon Rotating Coordinates Another method of Lunar transfer is the Weak Stability Boundary (WSB) transfer 11,12,13,14,15,16. The transfer trajectory leaves the Earth with an apogee around 1.5x10 6 km, and falls back into Earth orbit, but with a radius of perigee increased by the Sun s perturbations so that it co-orbits the Earth with the Moon. As a result, the spacecraft can enter lunar orbit with no maneuver, although it is a highly unstable orbit, and must be controlled. This is shown in Figure 4 in Earth Inertial coordinates and Figure 5 in Sun-Earth rotating coordinates ½ Figure 3: 3½ Phasing Loop Transfer in Sun- Earth Rotating Coordinates Although the TLI maneuver for the WSB is greater than for the standard ballistic transfer, there can be a lunar capture V savings of about 25% when capturing into a Lunar orbit. The Hiten mission 17 (originally called Muses-A) performed such a capture in October, International Lunar Conference September 2005 Page 3
6 Figure 4: WSB in Earth Inertial Coordinates Figure 5: WSB in Sun-Earth Rotating Coordinates There have also been proposals and studies of first transferring to a Lissajous orbit at the Earth- Moon L1 point, possibly rendezvousing with a space station there, and then continuing on to Lunar orbit 18,19,20,21,22. This is sometimes referred to as an L1 Gateway trajectory. Transfer trajectories have also been proposed that first transfer to the Earth-Moon L2 libration point, possibly rendezvousing with a space station there 23, before descent to the Moon. Smart-1 is a unique mission in that it used a low-thrust ion engine to transfer from a geostationary transfer orbit to Lunar orbit. From a NASA Lunar mission webpage 2 : The SMART-1 spacecraft launched on 27 September 2003 from Kourou, French Guiana as an auxiliary passenger on an Ariane-5 Cyclade which launched two other large satellites as its primary payload. It was put into a geostationary transfer orbit, 742 x 36,016 km, inclined at 7 degrees to the equator. The spacecraft used its ion drive over a period of 14 months to elongate its Earth orbit and utilized three lunar resonance maneuvers in August, September, and October 2004 to minimize propellant use. Its final continuous thrust maneuver took place over 100 hours from 10 to 14 October Lunar orbit capture occurred on 13 November 2004 at a distance of 60,000 km from the lunar surface. The ion engine began firing in orbit at 05:24 UT (12:24 a.m. EST) on 15 November to start a 4.5 day period of thrust to lower the orbit. The first perilune took place on 15 November at 17:48 UTC (12:48 p.m. EST) at an altitude of about 5000 km above the lunar surface. The engine was then used to lower the initial 4962 x km altitude, 5 day, 9 hour period, 81 degree inclination orbit, putting SMART-1 into a 300 x 3000 km polar orbit. Approaching the Moon This study compares two methods of approaching the Moon. The first is a direct Lunar descent, in which the transfer trajectory from the Earth is targeted to a direct Lunar landing. The second method involves capturing into a Lunar parking-orbit from the translunar trajectory by executing a retrograde Lunar Orbit Insertion (LOI) maneuver at or near periselene. After orbiting in the capture orbit for one or more orbits, a Descent Orbit Insertion (DOI) maneuver is performed to International Lunar Conference September 2005 Page 4
7 lower periselene and start the descent to the Lunar surface. For this study, a circular Lunar parking-orbit based on the Apollo missions of 60 nm (111 km) altitude is used. Mission Examples When researching the present work, the study of previous missions was invaluable. In particular, the Surveyor missions were helpful for the direct Lunar descent trajectories, and the Apollo missions were the model for the Lunar parking-orbit. The final Apollo descent was also the model for the approach and landing maneuvers, and is described in greater detail later. Surveyor 1 was launched directly into a lunar impact trajectory. A staged solid retro-rocket was used to slow the spacecraft as it approached the Lunar surface, that is, without inserting into a lunar parking-orbit. It then used vernier engines to affect a soft landing. Surveyor 3 used a launch-coast-burn ascent to achieve a Lunar transfer trajectory. The descent to the Lunar surface was achieved using the same technique as Surveyor 1. This site was later visited by Apollo 12. Surveyor 5 also used the launch-coast-burn ascent, and then during operations the trajectory was modified to compensate for an onboard failure. Surveyor 6 had the same trajectory profile as Surveyor 3, but performed a pre-planned hop on the Lunar surface. A Proposed Commercial Mission: Blastoff! Some of the work presented in this study was originally investigated for a proposed mission that never flew. Blastoff! was a commercial entity funded by Idealabs! in The company planned a commercial mission to the Moon that would have placed rovers near the Apollo landing sites. Nominal Blastoff! trajectories used the Lunar Surveyor direct descent approach, with 2 stacked solid motors: a Star 37 and a Star 20. The Star 37 was to be used to perform the TLI out of Earth orbit, and the Star 20 would have been used to slow the Moon-centered-fixed velocity above the Lunar surface prior to landing engine ignition. The Lander was then to use a mono-propellant hydrazine propulsion system to control the vertical drop rates. This trajectory is numerically simulated with a closed-loop feedback control that counters the Moon s gravity to achieve a constant descent rate. The direct descent design of the Blastoff! mission was driven by the need to minimize financial cost and achieve Lunar landing as soon as possible after launch. It was quicker and cheaper to acquire solid engines than to build a bipropellant system from scratch and this design enabled the company owners to meet their schedule. The spacecraft would have been launched on an Athena II Launch vehicle, and the monopropellant landing system would have also been used for midcourse control during the cruise phase. Blastoff! considered a classic 3.5 phasing loop approach where the first loop was slightly stunted, as performed by Clementine. A single phasing loop was also considered. In addition, another approach considered was to use 1 phasing loop with a 3 phasing loop backup: If the launch dispersions were too great to perform the mission, a 3 phasing loop strategy allowed the spacecraft to coast until the next month, in which case the transfer could be completed, although to an alternate landing site. International Lunar Conference September 2005 Page 5
8 Trajectory Examples Several trajectories for this study were calculated, and are described in detail in the following sections. The same numerical methods were used to calculate all trajectories. Numerical Methods The trajectories presented have been calculated using numerical integration with full-precision force models, including the effects of the gravity of the Earth, Moon, and Sun, as well as nonspherical gravity of the central body: a 21x21 Earth gravity field near the Earth, an 8x8 Earth gravity field in cislunar space, and an 8x8 Lunar field when near or around the Moon. During the low-earth parking-orbit, the translunar trajectory, and the Lunar parking-orbits, an error controlled dual-order variable-step Runge-Kutta algorithm was used to propagate the trajectories using Cowell s formulation of the equations of motion. During the closed-loop control of the final descent phase the same numerical integrator was used, but the maximum step size was set to 1.0 second for some runs, and to 0.1 second for others (as discussed below). The software used for these studies is the Satellite Tool Kit/Astrogator module 24 written by Analytical Graphics, Inc. 25 in cooperation with the NASA Goddard Space Flight Center (GSFC) Flight Dynamics Analysis Branch (FDAB). STK/Astrogator was first used to analyze and plan maneuvers operationally for the WMAP mission 26. Astrogator is the commercialized version of Swingby 27 developed at the NASA GSFC Flight Dynamics Division (now the FDAB), which was used to analyze and plan maneuvers operationally for Clementine (DSPSE) 28, Lunar Prospector 6, WIND 29,30,31, SOHO 32, and ACE 33. The first commercialized version before Astrogator was called Navigator which was used to fly the AsiaSat-3 rescue mission around the Moon 34. For trajectory design and maneuver planning, Astrogator uses an iterative differential correction method to solve a series of targeting problems. These targeting problems are set up (or profiled ) and called automatically, allowing sequential problems to be solved, such as coarse, fine, and very fine targeting problems. The user sets up the profiles, selecting the controls and desired constraints for each, and specifies other parameters such as step-sizes and convergence tolerances. Astrogator can also be used with optimization methods, such as STK/Analyzer, although this was not needed for the current analysis. For the closed-loop control analysis described in the Lunar Descent section, Astrogator s extensible functionality was used. Specifically, some custom plug-in engine models were written in VBScript, which Astrogator can call at run-time without the need to modify Astrogator itself. This plug-in capability is documented in the Astrogator on-line help system. Transfer Trajectory Simulations For comparison purposes, all the following trajectories were targeted to achieve a landing at the same landing site (latitude 10 deg, longitude 340 deg) on 24 February :00 UTC. The V values reported for each transfer trajectory include the impulsive and finite maneuvers needed to descend to the lunar surface. The details of the powered descent modeling is describe later in the paper, and only one method is used in this section for reporting, the kinetic landing algorithm. International Lunar Conference September 2005 Page 6
9 5-day Transfer to Lunar Parking-Orbit The first trajectory is a standard 5-day transfer from the Earth to the Moon, and is the 5-day transfer shown in Figure 1 and Figure 2. Other than a longer time-of-flight, it is very similar to the Apollo trajectories. A multi-profile targeting sequence was used to design this trajectory. Using a first guess for the initial TLI maneuver based on previous studies (3.14 km/s), the Launch and Coast were varied so that when the spacecraft was at approximately Lunar orbit distance (400,000 km form Earth) the difference between the spacecraft s Right Ascension and Declination compared to the Moon s same parameters are both zero. We call this -RA -Dec targeting. When this targeting profile has converged, then the Launch time, Coast time, and TLI V are simultaneously adjusted to achieve a guess at the B-Plane 35 parameters B T and B R ( km, 5000 km), as well as time of flight. After this, the launch-coast-burn parameters are adjusted to achieve a periselene altitude of 60 nm (111 km), an inclination of 165 degrees (similar to Apollo), and a 5 day time-of-flight. (5 days is approximately the value that yields minimum TLI and LOI V.) After this, the LOI maneuver is targeted to achieve a circular Lunar parking-orbit, which at 60 nm has a period of about 2 hours. About two revolutions after the LOI, the trajectory passes over the landing site, and the descent phase was computed, as described later. The descent phase includes a DOI maneuver of about 29 m/s, and the integrated V of the powered descent to the surface. Table 1 summarizes the major features of this trajectory. Launch Coast TLI LOI DOI Powered Descent V 19 Feb :23 UTC 35 min km/s 816 m/s 29 m/s 1915 m/s Table 1: 5-Day Transfer to Lunar Orbit Mission Summary 5-day Transfer to Direct Lunar Descent A 5-day transfer to a direct Lunar descent is shown in Figure 6. The trajectory is shown in the Moon-Fixed coordinate system. Targeting this trajectory starts off very similar to the previous. The initial -RA -Dec targeting is followed by B-Plane targeting with a time of flight (TOF) constraint. However, in this case, B- Plane values are used that would cause the trajectory to impact the Moon (3000 km, 128 km). The trajectory never hits the Moon, however, as the propagation is stopped at a radius of 50,000 km from the Moon s center. Figure 6: Direct Lunar Descent After the B-plane targeting has converged with a TOF constraint a staged braking maneuver is inserted, and is targeted to burn until only a specified Moon-centered-fixed excess velocity of International Lunar Conference September 2005 Page 7
10 1500 m/s remains. The closed-loop descent control law is also added (as described later.) Then the launch-coast-burn values are varied to achieve the desired latitude, longitude, and epoch of landing. Each iteration of the targeter includes a complete numerical simulation of the Lunar descent. Astrogator s homotopy search method was useful in solving this non-linear problem in some cases. After each time the trajectory converges, the altitude of the braking maneuver and residual excess velocity are adjusted until the Lander has minimal fuel when landed. Table 2 summarizes the major features of this trajectory, including the integrated powered decent V. Launch Coast TLI Staged braking maneuver Powered Descent V Altitude of braking maneuver start 19 Feb :14 UTC 19 min km/s 846 m/s 2362 m/s 324 km Table 2: 5-Day to Direct Lunar Descent Mission Summary 3.5 Phasing Loop to Direct Lunar Descent The 5-day transfer described above was augmented with 3 phasing loops, and re-targeted, and shown in Figure 3. The method was very similar to the 5-day transfer, except that a maneuver at the 3 rd perigee (P3), just before the final transfer to the Moon, was needed to raise the apogee to reach the Moon. Table 3 summarizes the major features of this trajectory. Launch Coast TLI P3 maneuver Staged braking maneuver Powered Descent V Altitude of braking maneuver 2 Feb :44 UTC 35 min km/s 41 m/s 832 m/s 2350 m/s 324 km Table 3: 3.5 Phasing Loop to Direct Lunar Descent Mission Summary Weak Stability Boundary Transfer For this study previous WSB trajectories 14,15 were analyzed and the geometry used as a first guess for targeting. The launch-coast-burn parameters were varied to achieve a line-of-apsides with a right ascension of 250 deg and a declination of -26 degrees, measured in the Sun-Earth rotating coordinate system. The TLI was varied to achieve C 3 energy of km 2 /s 2 in order to produce a radius of apogee at about 1.37x10 6 km. After this was achieved, the launch-coastburn parameters were varied to achieve a desired epoch and X value, measured at the X-Z plane crossing in the Sun-Earth rotating frame. In the Sun-Earth rotating frame, X is defined as the axis aligned from the Sun to the Earth, and Z is constrained towards the ecliptic s normal vector. The trajectory is shown in this frame in Figure 7. The line to the left of the Earth is the Sun-Earth line, which remains fixed in this coordinate system. International Lunar Conference September 2005 Page 8
11 After this initial targeting, the same launch-coast-burn parameters were refined to achieve a desired velocity component in the X direction, this time measured in the Earth-Moon rotating frame instead. As shown in the literature 15, these two X axes line up at this transition. After the trajectory has been targeted this far, a maneuver is inserted back at apogee, and the three components of the V are used as controls to target the constraints set to the Moon-centered fixed Cartesian position of the landing site, in X, Y, and Z (all km). These are evaluated after stopping propagation on a Lunar altitude of zero. The next step is to refine the apogee maneuver to target on the latitude and longitude of the landing site, stopping at 200 km altitude, with the desired epoch as an additional constraint. Figure 7: WSB Transfer in Sun-Earth Rotating Coordinates When this has converged, a braking maneuver is inserted at 400 km altitude, and is targeted to leave an excess Moon-centered fixed velocity of 1500 m/s, to be consistent with the previously described direct descents. After the braking maneuver, the closed-loop descent control law is added. At this point the altitude of the braking maneuver and residual excess velocity could be adjusted to minimize the amount of fuel when landed, however, these first guesses based on the previous trajectories worked well. Table 4 summarizes the major features of this trajectory. Launch Coast TLI Apogee maneuver Staged braking maneuver Powered Descent V 26 Nov :41 UTC 78 min km/s 42 m/s 670 m/s 2331 m/s Table 4: Weak Stability Boundary Transfer Mission Summary This WSB trajectory has been targeted without any optimization, and was constrained to a specific landing date. Based on previous work, it may be possible to lower the V needed for this trajectory. The WSB LOI is a sensitive function of the landing date because landing date is directly correlated with the relative Sun-Earth-Moon geometry at encounter. WSB trajectories with unconstrained geometry at encounter can be optimized to minimize the orbital energy at periselene, which would minimize the LOI maneuver needed to enter a circular orbit. Earth to Earth-Moon L1 to Lunar Orbit Transfer This transfer involves first transferring the spacecraft from Earth to the Earth-Moon L1 point, staying in an L1 Lissajous orbit for two revolutions, transferring into Lunar parking-orbit, and International Lunar Conference September 2005 Page 9
12 finally the descent. For this study an L1 Lissajous orbit with Z amplitude of about 20,000 km was chosen. The trajectory is shown in Figure 8. To target the Earth-Moon L1 orbit the launch-coast-burn parameters were varied to achieve a Cartesian position of (0 km,0 km,10,000 km), measured in L1-centered Earth-Moon rotating libration-point coordinates. When this is converged, an L1 Orbit Insertion maneuver (L1OI) is inserted at the X-Z plane crossing, and targeted to achieve a subsequent perpendicular X-Z plane crossing. To target this, a constraint that the X component of velocity, V X, must be zero is imposed. V x is measured at the X-Z plane crossings in the L1-centered Earth-Moon rotating libration point coordinate system. After the first plane crossings converge to be perpendicular, the propagation is increased to the next X-Z plane crossing, and targeted to cross perpendicularly. When converged, the process is repeated, for several revolutions. As subsequent plane crossings are targeted, the previous crossings are not constrained to be perpendicular, and they vary slightly from this. At some point the magnitude of the corrections to the maneuver become un-physically small, and a station keeping maneuver can be used instead of the L1OI maneuver. The station-keeping maneuver is inserted several revolutions before the last targeted crossing, which minimizes the maneuver. Figure 8: Earth to L1 to Lunar Landing in Earth-Moon Rotating Coordinates The next step is to target the departure maneuver, after the number of desired revolutions in the Lissajous orbit. For this study, two revolutions in the Lissajous orbit were used from L1OI to the last plane crossing, lasting 22.5 days. A maneuver is used at an X-Z plane crossing a few revolutions before the desired departure time. As a coarse targeting step, the maneuver is first targeted like a station-keeping maneuver, which is to target subsequent perpendicular plane crossings. After this, the final crossing, two revolutions after the maneuver, is targeted with a slight velocity component towards the Moon. For this study, a V X of 80 m/s worked well. This L1 departure V was calculated to be 3 m/s. After the departure maneuver, the trajectory heads towards the Moon. After Lunar closest approach (periselene at 7377 km altitude), a maneuver is performed at the next aposelene to lower periselene to 60 nm (111 km). The aposelene maneuver is also used to change the inclination of the Lunar orbit, so that, after a LOI circularization maneuver at periselene, the resulting Lunar parking-orbit passes over the desired landing site after 4 revolutions. (The Lunar International Lunar Conference September 2005 Page 10
13 parking-orbit inclination in this case turned out to be 10 degrees.) Table 5 summarizes the major features of this trajectory. Launch Coast TLI L1 orbit insertion maneuver L1 departure maneuver Perigee Lowering Maneuver Apogee Lowering maneuver (Circularize) DOI Powered Descent V 22 Jan :47 UTC 31 min m/s 706 m/s 3 m/s 212 m/s 623 m/s 22 m/s 1952 m/s Table 5: Earth to Earth-Moon L1 to Lunar Orbit Transfer Mission Summary Transfer Trajectory Summary and Comparison Table 6 displays the major features of the 5 transfer trajectories. The TOF for each is given, as measured from launch to landing. Note that the L1 transfer included an arbitrary 2 Lissajous orbits at the L1 point, so the TOF is given with the time spent at L1 included. The total spacecraft (s/c) V is the sum of all the maneuvers not including the TLI, since the TLI is usually performed by the upper stage of the launch vehicle. The V without the powered descent is also given because there was no attempt to optimize the landings, and these could be lowered by further studies. 5-Day to 5-Day to Direct 3.5 Phasing WSB L1 Lunar Orbit Descent Loop Launch (UTC) 19 Feb Feb Feb Nov Jan :23 05:14 01:44 04:41 01:47 TOF (days) (10.7) TLI s/c V w/o descent Total s/c V Table 6: Transfer Trajectory Comparison The time of flight is only 10.7 days, when the 22.5 days spent in the Lissajous orbit at L1 is not included The quickest transfers are the 5-Day transfers, as expected, and would presumably be more desirable for manned missions. A transfer to a station at the L1 point only takes about 10 days, not including the time at the station. Targeting Specific Landing Sites All trajectories were targeted to achieve the same landing site (latitude 10 deg, longitude 340 deg) on 24 February :00 UTC. In order to affect a landing at this site without using too much fuel, the pre-landing trajectory, modeled as if the landing segment was not executed, should pass over the landing site. While this is a straightforward task for the direct descent trajectories, which can target the landing site directly, it is more complicated for trajectories that enter a Lunar parking-orbit prior to landing. International Lunar Conference September 2005 Page 11
14 The Lunar orbit plane has a RAAN relative to the Earth-Moon line based on the TOF, as shown in Figure 9. Note that the 5-Day transfer has a relative RAAN of about 90 degrees to the Earth- Moon line, and as TOF is lowered, the trajectory approaches the Earth-Moon line. The most straightforward method to cause the initial Lunar parking-orbit to pass over the landing site is to adjust the TOF. However, this can raise the TLI and LOI Vs, as well as possibly violate other mission requirements. Instead, it is sometimes possible to adjust the Lunar inclination. Another option is to stay in Lunar orbit until the natural precession of the orbit with respect to the Moon s surface causes the orbit to over-fly the landing site. If it does not fly over exactly, slight changes to the Lunar inclination, and possibly the orbit period can be made. 5-Day 4-Day 3-Day 34-hour Earth-Moon line Figure 9: Different relative RAANs vs. Time-of-Flight in Earth-Moon Rotating Coordinates For some of the trajectories above a simple adjustment of the inclination was enough, while others required several phasing orbits. For these, the number of orbits was increased until the ground track passed over the desired landing spot. (For this initial study the tolerance on the landing site was loose enough that this was not a hard task.) When such an orbit is identified, then the true anomaly of the DOI maneuver is adjusted to achieve the exact landing spot, usually by targeting on the exact desired latitude. Lunar Powered Descent Trajectories This section describes the powered descent methods, and is roughly based on the Apollo Lunar Module (LM) capabilities and landing strategy. From the NASA technical memorandum Apollo Lunar Descent and Ascent Trajectories 36 : The LM powered descent trajectory design was established as a three phase maneuver to satisfy the operational requirements imposed of such a maneuver. The first phase, called the braking phase, is designed primarily for the efficient propellant usage while reducing orbit velocity and guiding to high gate conditions for initiation of the second phase, called the approach phase. The term high gate is derived from aircraft pilot terminology for beginning the approach to an airport. The approach phase is designed for pilot visual (out the window) monitoring of the approach to the lunar surface. The final (or landing) phase, which begins at low gate conditions (again from pilot terminology), is designed to provide continual visual assessment of the landing site and to provide compatibility for the pilot takeover from automatic control for the final touchdown on the surface. International Lunar Conference September 2005 Page 12
15 This study uses the Apollo 37 missions as reference and as a baseline from which future studies can be compared. The technique in this study 38 was to attempt to match certain Apollo velocities at their respective altitudes. The mass and propulsion properties for the Lander, dubbed Ke-V for this study 39, were also based on the Apollo LM Descent System, as shown in Table 7. Fuel Mass Dry Mass Specific Impulse, I sp Maximum Thrust 8165 kg (18,000 lbm) 6531 kg (14398 lbm) 311 s N (9900 lbf) Table 7: Lander Mass and Propulsion Values Braking Phase For the transfer trajectories that include a direct Lunar descent, a staged braking maneuver is used to achieved the typical Apollo high-gate 500 ft/s velocity at 7000 ft. For the trajectories that include a Lunar parking-orbit before the descent, there are a series of braking maneuvers previous to 7000 ft that give a velocity of 500 ft/s at 7000 feet. This is shown schematically in the appendix. Screen captures from the numerical simulations in STK during the braking phase are shown in Figure 10 and a close-up in Figure 11. Figure 10: Screen Capture of Braking Phase from Numerical Simulation International Lunar Conference September 2005 Page 13
16 Figure 11: Screen capture of Ke-V during Descent Phase Numerical Simulation After the standard Apollo lunar parking-orbit (60 x 60 nm altitude), the DOI maneuver lowers periselene to 50,000 ft (8.3 nm, or 15 km). At periselene, the Lander starts the retrograde braking maneuvers. The Apollo LM could not throttle continuously from full thrust to zero. The engine was not throttleable in the range from 60% to 90%. As a result, the controls laws for the LM accounted for this. In this study we model an engine with full throttle range. The braking phase begins at periselene and the first maneuver lasts 26 seconds. The maneuver s thrust (the direction opposite the flames) is aligned about 5 degrees above the anti-velocity vector (measured in Moon centered fixed), and the throttle is at 10%. For Apollo, this maneuver gave time for the engine gimbal to align with the center-of-mass before maximum throttle was commanded. After this, a full throttle maneuver is executed for 150 seconds, with the thrust aligned 11 degrees above the anti-velocity vector. Then the LM executed a series of different maneuvers and attitude changes for about the next 6 minutes until the high gate at 7000 ft. This study approximated this by varying a constant thrust efficiency to achieve a constraint of 500 ft/s at 7000 ft altitude, and used a constant attitude. The result of this study was a thrust efficiency of about 70% for this segment of the trajectory. Approach and Landing Phases The Approach phase begins at the high gate altitude of 7000 ft with a Moon-fixed velocity of 500 ft/s. This study compares two different closed-loop control laws used to model a soft landing on the Lunar surface, starting at the high gate. The two control laws are used to control the thrust of the descent engine. The first control law is based on using the landing thruster to affect a constant velocity descent rate. The second algorithm uses a Fuzzy Logic rule-based algorithm to control descent. Figure 12 is a screen capture from the Landing simulation. International Lunar Conference September 2005 Page 14
17 Figure 12: Screen Capture of Ke-V from Landing Numerical Simulation Kinetic Controller The first control law, dubbed the Kinetic Controller, varies the throttle value continuously to achieve a -4 ft/s Moon-fixed velocity at the low gate (150 ft). At 150 ft, a different algorithm is used to maintain a -3 ft/s altitude rate until landing. The Kinetic Controller uses a simple algorithm to compute the necessary thrust. The controller is called between each propagation step, and the step size was limited to a constant. Every time the controller is called, it uses the current altitude, velocity, and mass to determine the appropriate thrust. Some studies used a constant one second step (yielding 1 Hz), and this was compared with using a constant 0.1 second step (10 Hz). The fuel consumption differences were insignificant (about 0.02%). To calculate the thrust, the time-independent equation of motion from classical physics is used: a d = ( V V f 2 ) / ( 2 ( H 0 - H f ) ) where H 0 and V 0 are the current displacement (altitude) and velocity, respectively. H f is the altitude at low gate (150 ft), and V f the desired rate at that point (-4 ft/s). The result then, a d, is the desired acceleration. However, the commanded acceleration must also counter the gravitational acceleration of the Moon, g M. Therefore the commanded thrust is calculated by adding the accelerations and multiplying by the total mass of the Lander: Thrust = ( a d + g M ) Mass Total If the calculated thrust value is larger than the maximum thrust available for the landing engine, the maximum thrust is used. Once the Lander reaches low-gate, a different control law is used, International Lunar Conference September 2005 Page 15
18 based on the altitude rate. It is a simple ratio of the current altitude rate, u 0, to the desired rate, u d, multiplied by the gravitational acceleration and the mass. Thrust = ( u 0 / u d ) g M Mass Total This control worked well to affect a soft landing in about 107 seconds from 7000 ft, and used about 1784 lb of fuel (811 kg). Figure 13 shows the altitude, velocity, and thrust over time as a result of running the simulation. K1 - Kinetic Landing Alt (ft) & Velocity (ft/s) Lunar_Altitude (ft) Lunar_V_fixed_mag (ft/sec) Thrust_Mag (N) Thrust (N) 0 Seconds Figure 13: Altitude, Velocity, and Thrust Magnitude Fuzzy Logic Controller Fuzzy Logic was selected as the second mathematical model for calculating the requisite accelerations to land on the surface of the Moon. Fuzzy Logic is a proven method for the development of control laws in man-rated and other critical systems. It has also been implemented in various NASA systems and cited in numerous research and academic papers related to autonomous control in space. Fuzzy Logic control is an evolution of the concepts defined by Lotfi Zadeh in his paper entitled Fuzzy Sets, Information and Control. 40 Applied to control law development, it provides a method for the computation of linguistic control decision terms, such as Near, Far, Slow, and Fast and the transitions between. Used in a rule base, control laws can be developed such as: IF spacecraft is NEAR the Lunar Surface AND is going FAST THEN a LARGE ACCELERATION is required in the direction of the velocity vector. This method provides an understandable, maintainable method to encode subject matter expertise of astrodynamics specialists. With a significant cost associated with creating, constantly modifying and maintaining complex spacecraft control algorithms in a R & D environment, Fuzzy Logic provides an open dialog on descent trajectory analysis between astrodynamic specialists and software engineers, quite literally allowing for real time rule modification during 0 International Lunar Conference September 2005 Page 16
19 observation of the trajectories in 3D. This proved to be a powerful and time saving construct for analysis. This paper discusses engine burns along the fixed Moon velocity vector for the Lunar landing sequence which alone is perfectly suitable for traditional control law methods. However, Fuzzy Logic provides a rapid means to modify and analyze various engine burn strategies and can be extended to simultaneously control spacecraft horizontal, vertical and attitude control to land in a desired location 1 allowing for analysis of highly complex, non-linear, multi-axis maneuvering, an area difficult to mathematically model. The purpose of this research was to purport an analysis approach and environment for Lunar landing, not to seek adoption of any one technique or specific control law development. However, employing a set of standard tools, we were able to devise a method of Fuzzy Logic control that promises to offer a great deal of flexibility, simplicity and insight into Lunar landing behavior. The authors hope this contribution will lend itself to advanced engine, sensor design and mission planning. Fuzzy Logic Determination of Requisite Acceleration for Lunar Landing The Satellite Tool Kit was used as the Lunar landing simulation environment. With the Astrogator module, spacecraft can be modeled to a high level of fidelity and set into an accurate physics environment which includes gravitational forces, solar pressure and other space environmental conditions related to the Lunar mission. Astrogator is designed to model the physics of spacecraft flight and can fire engines based on various conditions or via external algorithms as in a closed-loop control law process. Controlling the engines in this simulation environment allows for accurate physics, numerous analytical tools and data outputs such as fuel consumption, burn rate and range rate. The authors extended the engine model in STK to call an external Fuzzy Logic algorithm. The algorithm was developed in a commercial software product, FuzzyTech 41, and compiled into a callable library which received real numbers regarding velocity and range and returned acceleration. The desired acceleration was compared to the available thrust on the Lander and engines fired in STK to affect the maneuver. In this closed-loop process, the control algorithm is called every propagation step with relative speed and distance data. The algorithm calculates the acceleration required from the spacecraft s engine to achieve desired velocity and returns this value in ft/s 2. Acceleration was chosen over an earlier model returning thrust to provide an analysis environment independent of engine size. The Fuzzy Logic model consists of a compiled algorithm designed in one commercial off the shelf (COTS) product, FuzzyTech, linked to another COTS product STK. To link these together, the authors coded a software component (COM Object) that is used to communicate between 1 The authors assert, and intend to further study the notion of best ephemeris to landing by simultaneously controlling attitude, vertical and horizontal in response to a Fuzzy Logic analysis of the closing surface. Amplifying geographic information provided to the spacecraft as it descends regarding topography will allow small engine burns to adjust the trajectory early, alleviating larger, more costly burns closer to landing. International Lunar Conference September 2005 Page 17
20 STK and the compiled algorithm, providing Fuzzy Logic I/O, performing various low level calculations, report writing and management of a waypoint to waypoint targeted velocity landing profile. The landing profile, loaded once at run time, is persisted in an Extensible Markup Language (XML) format, allowing the analyst to specify desired velocity/altitude pairs by simply editing a text document then propagating the descent trajectory. This is shown in Figure 14. XML will also lend itself to automation for trade studies on descent trajectory strategies. Figure 14: XML Lunar Landing Flight Profile The Fuzzy Logic algorithm consists of two input sets, a rule set and an output set, which is shown in Figure 15. Each input in value is a real number that is converted into an element in one or more sets. However, unlike bivalent set logic, where a value belongs to a set or not (true/false), Fuzzy Logic membership in a set can be true, false, or somewhere in between. Figure 15: Lunar Landing Fuzzy Logic System For this analysis each set s universe of discourse was defined in ranges representative of Apollo Lunar descent trajectories 36. Review and modeling of the Apollo descent trajectories offered insight into the relationships between distances, velocities and thrust and baseline initial state values, providing a stepping off point for a Fuzzy Logic system design. For the purpose of this International Lunar Conference September 2005 Page 18
21 analysis, this proved to be a suitable range providing a great deal of flexibility and acute control over the Lander as Fuzzy Logic took control at high gate. The ranges for sets, rules and acceleration output can be quickly modified to scale up or down to represent significantly different landing vehicles. Input Fuzzy Set: Altitude Δ Altitude Δ is the difference between the Lander s current altitude and the target altitude for the next altitude/velocity pair waypoint. For this analysis three overlapping sets were created to represent the concepts of far, near and at altitude. This is shown in Figure 16. Figure 16: Fuzzy Input Set Altitude Δ The shape of these sets provides the greatest range of values falling into the far set for all values greater than 50 ft. The geometric shape of far, with a wide range of values having membership value of 1.0 along the right side shoulder, provides for coarse control with few rules and little variation as it comes into a range where more acute control is desired. The shouldered sets also account for spacecraft conditions outside of the operating range of the controller. Input Fuzzy Set: Velocity Δ Velocity Δ is the difference between the Lander s current vertical velocity and the target velocity for the next altitude/velocity pair waypoint. The Fuzzy Logic algorithm uses Velocity (Moon Fixed) to calculate acceleration. At 7000 ft this value (in the simulation) is about 500 ft/s. The altitude rate at this point is 200 ft/s. As the trajectory approaches a more vertical orientation these numbers become near equal. By creating the simulation control on Velocity (Moon Fixed) the thrust removes the transverse rate of the Lander. Similar to the altitude Δ Fuzzy set, velocity is represented by three overlapping sets, the shape providing a shouldered region for general control and velocities less than -75 ft/s (i.e., greater in magnitude), while more acute control over velocity occurs when greater than -75 ft/s (i.e., when at a slower landing speed). This is shown in Figure 17. International Lunar Conference September 2005 Page 19
22 Figure 17: Fuzzy Input Set Velocity Δ To illustrate how real numbers from STK are converted into Fuzzy Set values, the example below converts -60 ft/s into a Fuzzy Set value. The value from STK indicates a -60 ft/s Δ in the speed of the Lander compared to the current target velocity some distance away (Altitude Δ). The number is passed into the algorithm and is converted into set membership values as shown in Table 8: Real # Input from STK Velocity Δ Degree of Membership -60 ft/s Very Fast 0.77 Fast 0.23 Target Velocity 0.00 Table 8: Velocity input set membership This can be read as: The velocity Δ -60 ft/s is a member of the VeryFast variable to a degree of 77% and is a member of the Fast variable to a degree of 23% and is a member of the Target_Velocity variable to a degree of 0%. Geometrically, the real number input value is represented in Figure 18: Figure 18: Fuzzy Input Set Velocity Δ for -60 ft/s from STK Simulation Vertical Acceleration Rule Base The inference rule set determines the acceleration set output and consists of antecedent and consequent (If, Then) statements. The rules are shown in Figure 19. (Note that deltas in velocity International Lunar Conference September 2005 Page 20
23 and altitude were modeled to control the spacecraft, not with respect to the Lunar surface, but to specified points along the spacecraft s descent trajectory, allowing for comparative analysis.) Figure 19: Fuzzy Inference Rule Set for Acceleration These rules fire in parallel in response to input from STK. For example, if altitude Δ is far, rules 7, 8 and 9 will fire. Since the output Vert_Accel is another Fuzzy Set, the inference rules provide membership values to the Vert_Acel set for calculation of a real number. For this analysis, the membership in the output was calculated using a MIN function which sets the value of membership for a specific rule consequent by taking the minimum membership value of the altitude Δ and velocity Δ IF Altitude Δ is far (1.00) and Velocity Δ is very_fast (.85) THEN Vert_Accel is medium (.85) Output Fuzzy Set: Vert_Accel This output set models the acceleration required to arrive at the desired velocity for a given altitude as specified velocity/altitude waypoints in the XML file. This set is shown in Figure 20. As discussed in the previous paragraphs on rules, vertical acceleration is also a fuzzy set. However, STK requires a real number to calculate the engine thrust so a process called Defuzzification is required to convert the set membership into a real number for the simulation. International Lunar Conference September 2005 Page 21
24 Figure 20: Fuzzy Output Set Vertical Acceleration There are numerous methods available to calculate such a real number, for this paper the authors chose the Center of Maximum method (CoM). The CoM method of Defuzzification provides the best compromise for a real number output by calculating a weighted mean of the most typical (maximum) values for Acceleration by the inference results. For example, the following conditions for spacecraft Δ altitude and Δ velocity return 3.78 ft/s 2 to STK which is converted into thrust (Thrust = mass x acceleration). The most typical values for acceleration in this model are: Zero = 0 Small = 2 Medium = 3 Large = 5 which result in a CoM Defuzzification of: ( 0.00 * * * * 5 ) / ( ) = 3.78 Analysis of Fuzzy Logic Two basic landing profiles where calculated using the Fuzzy Logic controlled velocity at velocity/altitude pairs, and are named F1 and F2 in this study. (The previous Kinetic lander is called K1. ) The calculated throttle value was updated at a rate of 1 Hz and 0.1 Hz to compare trajectory and fuel consumption. For the velocities in this research, the difference was negligible, as shown in Table 9. International Lunar Conference September 2005 Page 22
25 Fuel Use (lbs) 1 Hz 0.1 Hz F F K Table 9: Fuel Use as a Function of Simulation Step Size Further analysis will be pursued on the update cycle rate to include broader control cycle ranges and velocities. This is important to tie the research to sensor and computer processing design. Details on descent trajectory, acceleration and fuel are provided below. Fuzzy Logic Landing Control Profiles To understand the effect of the rules, 5 different simulations were run, as detailed in Table 10. Flight Description Simulation F1 Altitude Velocity pairs taken from Apollo 17 Mission Report 42 F2 Single Waypoint at landing F2 Mod 1 Single Waypoint at landing Rule Mod 1 F2 Mod 2 Single Waypoint at landing Rule Mod 2 F2 Mod 3 Single Waypoint at landing Rule Mod 1 Table 10: Fuzzy Rule Set Simulations F2 used a single waypoint target of 12 ft and -3 ft/s. A single rule in the F2 simulation was further modified to compare flight profiles and fuel consumption, and were named F2 Mod 1, F2 Mod 2, and F2 Mod 3. The rule that was modified was Rule 7: IF Far AND Very Fast THEN Large. The consequent statement (THEN) was modified from Large to Medium and the Degree of Support (DoS) from 100% to 20%. DoS is an inference method which allows rules themselves to be weighted from 0 to 100 when the antecedent conditions are met. Table 11 shows Rule 7 in simulation F2 and three modifications to the rule, simulations F2 Mod 1 to 3. Flight Simulation IF AND THEN Degree of Support F2 Altitude Velocity Δ =Very Vertical Acceleration = Large 100% F2 Mod 1 Δ =Far Fast Vertical Acceleration = Medium 100% F2 Mod 2 Vertical Acceleration = Medium 50% F2 Mod 3 Vertical Acceleration = Medium 20% Table 11: Rule 7 Modifications This rule modification resulted in different landing profiles and fuel consumption. By modifying this single rule we adjusted the amount of acceleration to be used when at high altitude. Since the rules are independent from one another, and fire in parallel, other rules respond to the excess velocity as altitude decreases. International Lunar Conference September 2005 Page 23
26 Removing velocity too early causes greater fuel consumption. Firing the engine Large at a Far distant to the surface, as in Simulation F2, removes the velocity early, resulting in a near constant velocity until an increase in thrust adjusts the velocity for targeted landing at -3 ft/s. This altitude, velocity, and mass flow rate history from this simulation are shown in Figure 21. (The mass flow rate is shown as negative in this figure representing the loss of mass as the Lander burns fuel.) Figure 21: Simulation F2 (100% DoS at Higher Altitude) By contrast, adjusting the rule to fire Medium to 20% at a Far altitude, as in Simulation F2 Mod 3, yields a more rapid overall descent with a much larger mass flow rate to adjust the velocity for landing. The results from this are shown in Figure 22. International Lunar Conference September 2005 Page 24
27 Figure 22: Simulation F2 Mod 3 (20% DoS at Higher Altitude) Fuel consumption decreased the more the single rule was modified to decrease the application of thrust from a Far altitude. Switching the rule from Medium to Small resulted in too high a velocity for the closer rules to adequately remove. Table 12 shows the fuels use for each simulation, and these data are shown graphically in Figure 23 Flight Simulation Fuel Consumption (lbs) F F F2 Mod F2 Mod F2 Mod K Table 12: Fuel Use for each Simulation International Lunar Conference September 2005 Page 25
28 Fuel Consumption from 7000 ft Lbs F1 F2 F2 Mod 1 F2 Mod 2 F2 Mod 3 K1 Simulations Figure 23: Fuel consumption comparison for Fuzzy Logic F2 Flights from 7000 ft F2 was a single waypoint descent profile. Observing the data from modification of a single rule provided insight into Δ velocity timing and has suggested further research into a more complex rule system that can take into account mass, human physical and mental comfort (g-force) to analyze these bumps in the graph where thrust is applied. The dramatic difference in fuel consumption (~1000 lbs) evidenced by moving these applications of thrust by modifying rules alone invites further refinement and analysis of the fuzzy input sets (altitude Δ and velocity Δ) where the shapes of the sets can further tune control. Conclusions The current study has resulted in fully numerically integrated trajectories from the Earth to a soft landing on the Moon. Several different types of transfer trajectories have been modeled, two types of Lunar approaches (Direct and Lunar parking-orbit), and two different control laws used for landing. These landings were based on Apollo strategies, and were successfully modeled using both a kinetic controller and a fuzzy logic controller. The Fuzzy-Logic controller used about the same fuel as the Kinetic, and was sensitive to various parameters. This study has demonstrated that the current software trajectory and control technology is readily available and applicable to current analyses. International Lunar Conference September 2005 Page 26
29 Future work Now that the baseline trajectories have been calculated, the transfer trajectories can be optimized, and powered descent trajectories can be computed, and these compared with the baseline. The effect of constraining the epoch of landing and methods to achieve specific landing sites using the WSB transfer require further investigation. The affect of other mission constraints during landing, such as lighting conditions and obstacle avoidance must also be addressed. These other mission requirements may affect the control law formulation and it is expected that the Fuzzy-Logic controller will be well-suited to account for these. These preliminary results also indicate that changing the current fuzzy sets and other parameters may reduce the fuel use. In addition, the Fuzzy Logic model may be extended to receive dynamic mass information which is expected to provide a more efficient method of timing the removal of velocity with respect to the next waypoint. Considerations will also being given to the difference of the determination of requisite acceleration magnitude and timing in terms of human comfort, pilot visibility and g- force limitations. Because the overall goal of this work is to create an accurate physics-based environment and software framework to support Lunar trajectory design and control, future work will include support additional workflow and numerical simulation requirements. International Lunar Conference September 2005 Page 27
30 Appendix International Lunar Conference September 2005 Page 28
31 References 1 NASA Space Exploration Initiative, announced at NASA Headquarters, Washington D.C., U.S. President Bush, 14 January, NASA National Space Science Data Center (NSSDC) Lunar and Planetary Home Page ( specifically the link off this to the Moon home page ( September, David Darling, The Encyclopedia of Astrobiology, Astronomy, and Spaceflight, ( September, Jet Propulsion Laboratory Surveyor Project Final Report, NASA Technical Report , 1 July, R. Godwin, (editor), Apollo 11 - The NASA Mission Reports, Vol. I, p. 225, Apogee Books, L. Lozier, K. Galal,, D. Folta, M. Beckman, Lunar Prospector Mission Design and Trajectory Support,, AAS , K.V. Richon, L.K Newman, Flight Dynamics Support for the Clementine Deep Space Program Science Experiment (DSPSE) Mission, AAS D. Carrington, J. Carrico, J. Jen, C. Roberts, A. Seacord, P. Sharer, L. Newman, K. Richon, B. Kaufman, J. Middour, M. Soyka, Trajectory Design for the Deep Space Program Science Experiment (DSPSE) Mission, AAS , Proceedings of the AAS/NASA International Symposium, Greenbelt, Maryland, April J. Carrico, D. Carrington, M. Hametz, P. Jordan, D. Peters, C. Schiff, K. Richon, L. Newman, Maneuver Planning and Results for Clementine (The Deep Space Program Science Experiment), Paper No. AAS , AAS/AIAA Spaceflight Mechanics Meeting, Albuquerque, New Mexico, USA, February D.W. Dunham, R.W. Farquhar, Trajectory Design for a Lunar Mapping and Near-Earth-Asteroid Flyby Mission, AAS , Spaceflight Mechanics 1993, Vol. 82, Advances in the Astronautical Sciences, ed. R. Melton, pp E.A. Belbruno, Lunar Capture Orbits, A Method of Constructing Earth-Moon Trajectories and the Lunar GAS Mission, in: Proceedings of AIAA/DGLR/JSASS Inter. Propl. Conf., AIAA Paper No , (May 1987) 12 E.A. Belbruno, The Dynamical Mechanism of Ballistic Lunar Capture Transfers in the Four-Body Problem from the Perspective of Invariant Manifolds and Hill's Regions, Institut D'Estudis Catalans, CRM Research Report No. 270, (November 1994) 13 E.A. Belbruno, R. Humble, J. Coil, Ballistic Capture Lunar Transfer Determination for the U.S. Air Force Academy Blue Moon Mission, Advances in Astronautical Science, Spaceflight Mechanics, 95, AAS Publ., Paper No. AAS , (1997) 14 E. Belbruno, J. Carrico, Calculation of Weak Stability Boundary Ballistic Lunar Transfer Trajectories, Paper No. AIAA , AIAA/AAS Astrodynamics Specialist Conference in Denver, Colorado, USA, August W.S. Koon, M.W. Lo, J.E. Marsden, S.D. Ross, Shoot the Moon, Spaceflight Mechanics,, AAS Vol.105 Part II, , W.S. Koon, M.W. Lo, J.E. Marsden, S.D. Ross, Low Energy Transfer to the Moon, Celestial Mechanics and Dynamical Astronomy, 81, H. Yamakawa, J. Kawaguchi, N. Ishii, H. Matsuo, On Earth-Moon Transfer Trajectory with Gravitational Capture, in: Proceedings AAS/AIAA Astrodynamics Specialists Conf., Paper No. AAS , (August 1993) 18 R. Farquhar, D. Dunham, "Libration-Point Staging Concepts for Earth-Mars Transportation," Manned Mars Missions: Working Group Papers, NASA M002, Vol. 1, NASA/LANL, June 1986, pp ; proceedings of a workshop at NASA Marshall Space Flight Center, Huntsville, Alabama, June 10-14, R.W. Farquhar, D.W. Dunham, Y. Guo, J.V. McAdams, Utilization of Libration Points for Human Exploration in the Sun-Earth-Moon System and Beyond, Proceedings of the 54th International Astronautical Congress of the International Astronautical Federation, Bremen, Germany, September-October 2003 (also: Acta Astronautica 55 (2004), pp ) 20 W. Huntress, R. Farquhar, D. Stetson, B. Clark, J. Zimmerman, W. O'Neil, R. Bourke, "The Next Steps in Exploring Space" A Study by the International Academy of Astronautics, July 9, G.L. Condon, C.L. Ranieri, C. Ocampo, Earth-Moon Libration Point (L1) Gateway Station. Lunar Transfer Vehicle Kickstage Disposal Options, Libration Point Orbits And Applications, Parador d'aiguablava, Girona, Spain, June 2002 International Lunar Conference September 2005 Page 29
32 22 G.L. Condon, D.J. Pearson, The Role of Humans in Libration Point Missions With Specific Application to an Earth-Moon Libration Point Gateway Station (AAS ), Advances in the Astronautical Sciences, Volume 109, Astrodynamics, p95, R. Farquhar, "A Halo-Orbit Lunar Station," Astronautics & Aeronautics, June 1972, pp J. Carrico, E. Fletcher, Software Architecture and Use of Satellite Tool Kit s Astrogator Module for Libration Point Orbit Missions, Libration Point Orbits And Applications, Parador d'aiguablava, Girona, Spain, June Analytical Graphics, Inc., 220 Valley Creek Blvd., Exton, PA 19341, USA, Phone: , [email protected], 26 M. Mesarch, S. Andrews, The Maneuver Planning Process for the Microwave Anisotropy Probe (MAP) Mission, AIAA , AIAA/AAS Astrodynamics Specialist Conference, Monterey, CA, USA 27 J. Carrico, C. Schiff, L. Roszman, H.L. Hooper, D. Folta, K. Richon, An Interactive Tool for Design and Support of Lunar, Gravity Assist, and Libration Point Trajectories, Paper No. AIAA , AIAA/AHS/ASEE Aerospace Design Conference, Irvine, California, USA, February J. Carrico, D. Conway, D. Ginn, D. Folta, K. Richon, Operational Use of Swingby an Interactive Trajectory Design and Maneuver Planning Tool for Missions to the Moon and Beyond, Paper No. AAS , AAS/AIAA Astrodynamics Specialist Conference, Halifax, Nova Scotia, Canada, August P. Sharer,, H. Franz,, Folta, D., WIND Trajectory Design and Control, Paper No. MS95/032, CNES International Symposium on Space Dynamics, Toulouse, France, June H. Franz, WIND Nominal Mission Performance and Extended Mission Design, AIAA , August H. Franz, WIND Lunar Backflip and Distant Prograde Orbit Implementation, AAS , AAS/AIAA Spaceflight Mechanics Meeting, Santa Barbara, California, USA, February D.W. Dunham, S.J. Jen, C.E. Roberts, A.W. Seacord, Transfer Trajectory Design for the SOHO Libration-Point Mission, IAF , 43rd Congress of the International Astronautical Federation, Washington, D.C., USA, August/September, P. Sharer, T. Harrington, Trajectory Optimization for the ACE Halo Orbit Mission, AIAA CP (1996). 34 J. Salvatore, C. Ocampo, Mission Design and Orbit Operations for the First Lunar Flyby Rescue Mission, IAF-99-A.2.01, 50th International Astronautical Congress, Amsterdam, The Netherlands, October W. Kizner, A Method of Describing Miss Distances for Lunar and Interplanetary Trajectories, Ballistic Missile and Space Technology, III, Apollo Lunar Descent and Ascent Trajectories, NASA technical memorandum, NASA TM X-58040, March 1970, presented to the AIAA 8 th Aerospace Sciences Meeting, NY, NY, January, Floyd V. Bennett, Apollo Experience Report - Mission Planning for Lunar Module Ascent and Descent, NASA TN D-6846, June M. Loucks, J. Carrico, T. Carrico, C. Deiterich, A Comparison Of Lunar Landing Trajectory Strategies Using Numerical Simulations, International Lunar Conference, Toronto, CA, Kevin Carrico, Impact Creative Services, Lotfi A. Zadeh Fuzzy Sets, Information and Control, FuzzyTech, INFORM GmbH, Pascalstrasse 23, D Aachen, GERMANY, Phone: , [email protected], 42 R. Godwin, (editor), Apollo 17 - The NASA Mission Reports, Volume 1, Apogee Books, 2002 International Lunar Conference September 2005 Page 30
Section 4: The Basics of Satellite Orbits
 Section 4: The Basics of Satellite Orbits MOTION IN SPACE VS. MOTION IN THE ATMOSPHERE The motion of objects in the atmosphere differs in three important ways from the motion of objects in space. First,
Section 4: The Basics of Satellite Orbits MOTION IN SPACE VS. MOTION IN THE ATMOSPHERE The motion of objects in the atmosphere differs in three important ways from the motion of objects in space. First,
Orbital Mechanics and Space Geometry
 Orbital Mechanics and Space Geometry AERO4701 Space Engineering 3 Week 2 Overview First Hour Co-ordinate Systems and Frames of Reference (Review) Kepler s equations, Orbital Elements Second Hour Orbit
Orbital Mechanics and Space Geometry AERO4701 Space Engineering 3 Week 2 Overview First Hour Co-ordinate Systems and Frames of Reference (Review) Kepler s equations, Orbital Elements Second Hour Orbit
Penn State University Physics 211 ORBITAL MECHANICS 1
 ORBITAL MECHANICS 1 PURPOSE The purpose of this laboratory project is to calculate, verify and then simulate various satellite orbit scenarios for an artificial satellite orbiting the earth. First, there
ORBITAL MECHANICS 1 PURPOSE The purpose of this laboratory project is to calculate, verify and then simulate various satellite orbit scenarios for an artificial satellite orbiting the earth. First, there
Lecture L17 - Orbit Transfers and Interplanetary Trajectories
 S. Widnall, J. Peraire 16.07 Dynamics Fall 008 Version.0 Lecture L17 - Orbit Transfers and Interplanetary Trajectories In this lecture, we will consider how to transfer from one orbit, to another or to
S. Widnall, J. Peraire 16.07 Dynamics Fall 008 Version.0 Lecture L17 - Orbit Transfers and Interplanetary Trajectories In this lecture, we will consider how to transfer from one orbit, to another or to
Orbital Mechanics. Angular Momentum
 Orbital Mechanics The objects that orbit earth have only a few forces acting on them, the largest being the gravitational pull from the earth. The trajectories that satellites or rockets follow are largely
Orbital Mechanics The objects that orbit earth have only a few forces acting on them, the largest being the gravitational pull from the earth. The trajectories that satellites or rockets follow are largely
Mission Design for the Lunar Reconnaissance Orbiter
 AAS 07-057 Mission Design for the Lunar Reconnaissance Orbiter Mark Beckman Goddard Space Flight Center, Code 595 29th ANNUAL AAS GUIDANCE AND CONTROL CONFERENCE February 4-8, 2006 Breckenridge, Colorado
AAS 07-057 Mission Design for the Lunar Reconnaissance Orbiter Mark Beckman Goddard Space Flight Center, Code 595 29th ANNUAL AAS GUIDANCE AND CONTROL CONFERENCE February 4-8, 2006 Breckenridge, Colorado
Astrodynamics (AERO0024)
 Astrodynamics (AERO0024) 6. Interplanetary Trajectories Gaëtan Kerschen Space Structures & Systems Lab (S3L) Course Outline THEMATIC UNIT 1: ORBITAL DYNAMICS Lecture 02: The Two-Body Problem Lecture 03:
Astrodynamics (AERO0024) 6. Interplanetary Trajectories Gaëtan Kerschen Space Structures & Systems Lab (S3L) Course Outline THEMATIC UNIT 1: ORBITAL DYNAMICS Lecture 02: The Two-Body Problem Lecture 03:
G U I D E T O A P P L I E D O R B I T A L M E C H A N I C S F O R K E R B A L S P A C E P R O G R A M
 G U I D E T O A P P L I E D O R B I T A L M E C H A N I C S F O R K E R B A L S P A C E P R O G R A M CONTENTS Foreword... 2 Forces... 3 Circular Orbits... 8 Energy... 10 Angular Momentum... 13 FOREWORD
G U I D E T O A P P L I E D O R B I T A L M E C H A N I C S F O R K E R B A L S P A C E P R O G R A M CONTENTS Foreword... 2 Forces... 3 Circular Orbits... 8 Energy... 10 Angular Momentum... 13 FOREWORD
Can Hubble be Moved to the International Space Station? 1
 Can Hubble be Moved to the International Space Station? 1 On January 16, NASA Administrator Sean O Keefe informed scientists and engineers at the Goddard Space Flight Center (GSFC) that plans to service
Can Hubble be Moved to the International Space Station? 1 On January 16, NASA Administrator Sean O Keefe informed scientists and engineers at the Goddard Space Flight Center (GSFC) that plans to service
RS platforms. Fabio Dell Acqua - Gruppo di Telerilevamento
 RS platforms Platform vs. instrument Sensor Platform Instrument The remote sensor can be ideally represented as an instrument carried by a platform Platforms Remote Sensing: Ground-based air-borne space-borne
RS platforms Platform vs. instrument Sensor Platform Instrument The remote sensor can be ideally represented as an instrument carried by a platform Platforms Remote Sensing: Ground-based air-borne space-borne
Name: Earth 110 Exploration of the Solar System Assignment 1: Celestial Motions and Forces Due in class Tuesday, Jan. 20, 2015
 Name: Earth 110 Exploration of the Solar System Assignment 1: Celestial Motions and Forces Due in class Tuesday, Jan. 20, 2015 Why are celestial motions and forces important? They explain the world around
Name: Earth 110 Exploration of the Solar System Assignment 1: Celestial Motions and Forces Due in class Tuesday, Jan. 20, 2015 Why are celestial motions and forces important? They explain the world around
Trajectory Design with STK/Astrogator. New Horizons Mission Tutorial
 Trajectory Design with STK/Astrogator New Horizons Mission Tutorial STK/Astrogator New Horizons Mission Tutorial Page 2 Mission Overview In this tutorial, we will model a Mission to Pluto. Starting from
Trajectory Design with STK/Astrogator New Horizons Mission Tutorial STK/Astrogator New Horizons Mission Tutorial Page 2 Mission Overview In this tutorial, we will model a Mission to Pluto. Starting from
Spacecraft Dynamics and Control. An Introduction
 Brochure More information from http://www.researchandmarkets.com/reports/2328050/ Spacecraft Dynamics and Control. An Introduction Description: Provides the basics of spacecraft orbital dynamics plus attitude
Brochure More information from http://www.researchandmarkets.com/reports/2328050/ Spacecraft Dynamics and Control. An Introduction Description: Provides the basics of spacecraft orbital dynamics plus attitude
Trajectory design for the Solar Orbiter mission
 Monografías de la Real Academia de Ciencias de Zaragoza. 25: 177 218, (2004). Trajectory design for the Solar Orbiter mission G. Janin European Space Operations Centre. European Space Agency. 64293 Darmstadt,
Monografías de la Real Academia de Ciencias de Zaragoza. 25: 177 218, (2004). Trajectory design for the Solar Orbiter mission G. Janin European Space Operations Centre. European Space Agency. 64293 Darmstadt,
2. Orbits. FER-Zagreb, Satellite communication systems 2011/12
 2. Orbits Topics Orbit types Kepler and Newton laws Coverage area Influence of Earth 1 Orbit types According to inclination angle Equatorial Polar Inclinational orbit According to shape Circular orbit
2. Orbits Topics Orbit types Kepler and Newton laws Coverage area Influence of Earth 1 Orbit types According to inclination angle Equatorial Polar Inclinational orbit According to shape Circular orbit
MISSION DESIGN AND OPERATIONS CONSIDERATIONS FOR NASA S LUNAR RECONNAISSANCE ORBITER
 MISSION DESIGN AND OPERATIONS CONSIDERATIONS FOR NASA S LUNAR RECONNAISSANCE ORBITER Mr. Martin B. Houghton NASA's Goddard Space Flight Center, Greenbelt, Maryland USA [email protected] Mr. Craig
MISSION DESIGN AND OPERATIONS CONSIDERATIONS FOR NASA S LUNAR RECONNAISSANCE ORBITER Mr. Martin B. Houghton NASA's Goddard Space Flight Center, Greenbelt, Maryland USA [email protected] Mr. Craig
Does currently available technology have the capacity to facilitate a manned mission to Mars?
 Furze Platt Senior School Does currently available technology have the capacity to facilitate a manned mission to Mars? Daniel Messias Date: 8/03/2015 Candidate Number: 7158 Centre Number: 51519 Contents
Furze Platt Senior School Does currently available technology have the capacity to facilitate a manned mission to Mars? Daniel Messias Date: 8/03/2015 Candidate Number: 7158 Centre Number: 51519 Contents
Analysis on the Long-term Orbital Evolution and Maintenance of KOMPSAT-2
 Analysis on the Long-term Orbital Evolution and Maintenance of KOMPSAT-2 Ok-Chul Jung 1 Korea Aerospace Research Institute (KARI), 45 Eoeun-dong, Daejeon, South Korea, 305-333 Jung-Hoon Shin 2 Korea Advanced
Analysis on the Long-term Orbital Evolution and Maintenance of KOMPSAT-2 Ok-Chul Jung 1 Korea Aerospace Research Institute (KARI), 45 Eoeun-dong, Daejeon, South Korea, 305-333 Jung-Hoon Shin 2 Korea Advanced
Flight and Orbital Mechanics
 Flight and Orbital Mechanics Lecture slides Challenge the future 1 Material for exam: this presentation (i.e., no material from text book). Sun-synchronous orbit: used for a variety of earth-observing
Flight and Orbital Mechanics Lecture slides Challenge the future 1 Material for exam: this presentation (i.e., no material from text book). Sun-synchronous orbit: used for a variety of earth-observing
Halliday, Resnick & Walker Chapter 13. Gravitation. Physics 1A PHYS1121 Professor Michael Burton
 Halliday, Resnick & Walker Chapter 13 Gravitation Physics 1A PHYS1121 Professor Michael Burton II_A2: Planetary Orbits in the Solar System + Galaxy Interactions (You Tube) 21 seconds 13-1 Newton's Law
Halliday, Resnick & Walker Chapter 13 Gravitation Physics 1A PHYS1121 Professor Michael Burton II_A2: Planetary Orbits in the Solar System + Galaxy Interactions (You Tube) 21 seconds 13-1 Newton's Law
Satellite Posi+oning. Lecture 5: Satellite Orbits. Jan Johansson [email protected] Chalmers University of Technology, 2013
 Lecture 5: Satellite Orbits Jan Johansson [email protected] Chalmers University of Technology, 2013 Geometry Satellite Plasma Posi+oning physics Antenna theory Geophysics Time and Frequency GNSS
Lecture 5: Satellite Orbits Jan Johansson [email protected] Chalmers University of Technology, 2013 Geometry Satellite Plasma Posi+oning physics Antenna theory Geophysics Time and Frequency GNSS
Chapter 2. Mission Analysis. 2.1 Mission Geometry
 Chapter 2 Mission Analysis As noted in Chapter 1, orbital and attitude dynamics must be considered as coupled. That is to say, the orbital motion of a spacecraft affects the attitude motion, and the attitude
Chapter 2 Mission Analysis As noted in Chapter 1, orbital and attitude dynamics must be considered as coupled. That is to say, the orbital motion of a spacecraft affects the attitude motion, and the attitude
Coverage Characteristics of Earth Satellites
 Coverage Characteristics of Earth Satellites This document describes two MATLAB scripts that can be used to determine coverage characteristics of single satellites, and Walker and user-defined satellite
Coverage Characteristics of Earth Satellites This document describes two MATLAB scripts that can be used to determine coverage characteristics of single satellites, and Walker and user-defined satellite
Correct Modeling of the Indirect Term for Third-Body Perturbations
 AAS 07-47 Correct Modeling of the Indirect Term for Third-Body Perturbations Matthew M. Berry * Vincent T. Coppola The indirect term in the formula for third body perturbations models the acceleration
AAS 07-47 Correct Modeling of the Indirect Term for Third-Body Perturbations Matthew M. Berry * Vincent T. Coppola The indirect term in the formula for third body perturbations models the acceleration
State Newton's second law of motion for a particle, defining carefully each term used.
 5 Question 1. [Marks 28] An unmarked police car P is, travelling at the legal speed limit, v P, on a straight section of highway. At time t = 0, the police car is overtaken by a car C, which is speeding
5 Question 1. [Marks 28] An unmarked police car P is, travelling at the legal speed limit, v P, on a straight section of highway. At time t = 0, the police car is overtaken by a car C, which is speeding
Forces on the Rocket. Rocket Dynamics. Equation of Motion: F = Ma
 Rocket Dynamics orces on the Rockets - Drag Rocket Stability Rocket Equation Specific Impulse Rocket otors Thrust orces on the Rocket Equation of otion: = a orces at through the Center of ass Center of
Rocket Dynamics orces on the Rockets - Drag Rocket Stability Rocket Equation Specific Impulse Rocket otors Thrust orces on the Rocket Equation of otion: = a orces at through the Center of ass Center of
USE OF SCILAB FOR SPACE MISSION ANALYSIS AND FLIGHT DYNAMICS ACTIVITIES
 USE OF SCILAB FOR SPACE MISSION ANALYSIS AND FLIGHT DYNAMICS ACTIVITIES Thierry Martin CNES Scilabtec 09 Use of Scilab for space mission analysis Page 1 Use of Scilab in CNES Scilab is now widely used
USE OF SCILAB FOR SPACE MISSION ANALYSIS AND FLIGHT DYNAMICS ACTIVITIES Thierry Martin CNES Scilabtec 09 Use of Scilab for space mission analysis Page 1 Use of Scilab in CNES Scilab is now widely used
Development of a Sun Synchronous. Conjunctions
 Development of a Sun Synchronous Zoning Architecture to Minimize Conjunctions Kevin Shortt Brian Weeden Secure World Foundation www.secureworldfoundation.org Overview Current Situation in Sun synchronous
Development of a Sun Synchronous Zoning Architecture to Minimize Conjunctions Kevin Shortt Brian Weeden Secure World Foundation www.secureworldfoundation.org Overview Current Situation in Sun synchronous
WEIGHTLESS WONDER Reduced Gravity Flight
 WEIGHTLESS WONDER Reduced Gravity Flight Instructional Objectives Students will use trigonometric ratios to find vertical and horizontal components of a velocity vector; derive a formula describing height
WEIGHTLESS WONDER Reduced Gravity Flight Instructional Objectives Students will use trigonometric ratios to find vertical and horizontal components of a velocity vector; derive a formula describing height
Satellite technology
 Satellite technology Overview What is a satellite? The key elements of orbital position Satellite manufacturers and design The components of a satellite: payload and bus Digital versus analogue How do
Satellite technology Overview What is a satellite? The key elements of orbital position Satellite manufacturers and design The components of a satellite: payload and bus Digital versus analogue How do
Interaction of Energy and Matter Gravity Measurement: Using Doppler Shifts to Measure Mass Concentration TEACHER GUIDE
 Interaction of Energy and Matter Gravity Measurement: Using Doppler Shifts to Measure Mass Concentration TEACHER GUIDE EMR and the Dawn Mission Electromagnetic radiation (EMR) will play a major role in
Interaction of Energy and Matter Gravity Measurement: Using Doppler Shifts to Measure Mass Concentration TEACHER GUIDE EMR and the Dawn Mission Electromagnetic radiation (EMR) will play a major role in
Lecture 07: Work and Kinetic Energy. Physics 2210 Fall Semester 2014
 Lecture 07: Work and Kinetic Energy Physics 2210 Fall Semester 2014 Announcements Schedule next few weeks: 9/08 Unit 3 9/10 Unit 4 9/15 Unit 5 (guest lecturer) 9/17 Unit 6 (guest lecturer) 9/22 Unit 7,
Lecture 07: Work and Kinetic Energy Physics 2210 Fall Semester 2014 Announcements Schedule next few weeks: 9/08 Unit 3 9/10 Unit 4 9/15 Unit 5 (guest lecturer) 9/17 Unit 6 (guest lecturer) 9/22 Unit 7,
Space Shuttle Mission SPACE SHUTTLE SYSTEM. Operation. Luca d Agostino, Dipartimento di Ingegneria Aerospaziale, Università di Pisa, 2010/11.
 Space Shuttle Mission SPACE SHUTTLE SYSTEM Operation SPACE SHUTTLE SYSTEM Operation The flight plan and operation of the Space Shuttle differs markedly from that of the now-familiar launch procedures and
Space Shuttle Mission SPACE SHUTTLE SYSTEM Operation SPACE SHUTTLE SYSTEM Operation The flight plan and operation of the Space Shuttle differs markedly from that of the now-familiar launch procedures and
Lecture 13. Gravity in the Solar System
 Lecture 13 Gravity in the Solar System Guiding Questions 1. How was the heliocentric model established? What are monumental steps in the history of the heliocentric model? 2. How do Kepler s three laws
Lecture 13 Gravity in the Solar System Guiding Questions 1. How was the heliocentric model established? What are monumental steps in the history of the heliocentric model? 2. How do Kepler s three laws
Celestial Sphere. Celestial Coordinates. Lecture 3: Motions of the Sun and Moon. ecliptic (path of Sun) ecliptic (path of Sun)
 Lecture 3: Motions of the and Moon ecliptic (path of ) ecliptic (path of ) The 23.5 degree tilt of Earth s spin axis relative to its orbital axis around the causes the seasons Celestial Sphere Celestial
Lecture 3: Motions of the and Moon ecliptic (path of ) ecliptic (path of ) The 23.5 degree tilt of Earth s spin axis relative to its orbital axis around the causes the seasons Celestial Sphere Celestial
Physics 9e/Cutnell. correlated to the. College Board AP Physics 1 Course Objectives
 Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Sun Earth Relationships
 1 ESCI-61 Introduction to Photovoltaic Technology Sun Earth Relationships Ridha Hamidi, Ph.D. Spring (sun aims directly at equator) Winter (northern hemisphere tilts away from sun) 23.5 2 Solar radiation
1 ESCI-61 Introduction to Photovoltaic Technology Sun Earth Relationships Ridha Hamidi, Ph.D. Spring (sun aims directly at equator) Winter (northern hemisphere tilts away from sun) 23.5 2 Solar radiation
Exam # 1 Thu 10/06/2010 Astronomy 100/190Y Exploring the Universe Fall 11 Instructor: Daniela Calzetti
 Exam # 1 Thu 10/06/2010 Astronomy 100/190Y Exploring the Universe Fall 11 Instructor: Daniela Calzetti INSTRUCTIONS: Please, use the `bubble sheet and a pencil # 2 to answer the exam questions, by marking
Exam # 1 Thu 10/06/2010 Astronomy 100/190Y Exploring the Universe Fall 11 Instructor: Daniela Calzetti INSTRUCTIONS: Please, use the `bubble sheet and a pencil # 2 to answer the exam questions, by marking
DEVELOPMENT OF AN ARCHITECTURE OF SUN-SYNCHRONOUS ORBITAL SLOTS TO MINIMIZE CONJUNCTIONS. Brian Weeden Secure World Foundation
 DEVELOPMENT OF AN ARCHITECTURE OF SUN-SYNCHRONOUS ORBITAL SLOTS TO MINIMIZE CONJUNCTIONS Brian Weeden Secure World Foundation Sun-synchronous orbit (SSO) satellites serve many important functions, primarily
DEVELOPMENT OF AN ARCHITECTURE OF SUN-SYNCHRONOUS ORBITAL SLOTS TO MINIMIZE CONJUNCTIONS Brian Weeden Secure World Foundation Sun-synchronous orbit (SSO) satellites serve many important functions, primarily
Physics 2A, Sec B00: Mechanics -- Winter 2011 Instructor: B. Grinstein Final Exam
 Physics 2A, Sec B00: Mechanics -- Winter 2011 Instructor: B. Grinstein Final Exam INSTRUCTIONS: Use a pencil #2 to fill your scantron. Write your code number and bubble it in under "EXAM NUMBER;" an entry
Physics 2A, Sec B00: Mechanics -- Winter 2011 Instructor: B. Grinstein Final Exam INSTRUCTIONS: Use a pencil #2 to fill your scantron. Write your code number and bubble it in under "EXAM NUMBER;" an entry
EN4 Dynamics and Vibrations. Design Project. Orbital Design for a Lunar Impact Mission. Synopsis
 EN4 Dynamics and Vibrations Design Project Orbital Design for a Lunar Impact Mission Synopsis NASA has identified a need for a low-cost mission to launch a satellite that will impact the moon. You will
EN4 Dynamics and Vibrations Design Project Orbital Design for a Lunar Impact Mission Synopsis NASA has identified a need for a low-cost mission to launch a satellite that will impact the moon. You will
Discrete mechanics, optimal control and formation flying spacecraft
 Discrete mechanics, optimal control and formation flying spacecraft Oliver Junge Center for Mathematics Munich University of Technology joint work with Jerrold E. Marsden and Sina Ober-Blöbaum partially
Discrete mechanics, optimal control and formation flying spacecraft Oliver Junge Center for Mathematics Munich University of Technology joint work with Jerrold E. Marsden and Sina Ober-Blöbaum partially
Iodine RF Ion Thruster Development Busek Co. Inc. Vlad Hruby PhD, President
 Iodine RF Ion Thruster Development Busek Co. Inc. Vlad Hruby PhD, President Mike Tsay PhD busek.com 2015 Busek Co. Inc. All Rights Reserved. Iodine RF Ion Thruster Development Status Briefing NASA NRA
Iodine RF Ion Thruster Development Busek Co. Inc. Vlad Hruby PhD, President Mike Tsay PhD busek.com 2015 Busek Co. Inc. All Rights Reserved. Iodine RF Ion Thruster Development Status Briefing NASA NRA
Note S1: Eclipses & Predictions
 The Moon's Orbit The first part of this note gives reference information and definitions about eclipses [14], much of which would have been familiar to ancient Greek astronomers, though not necessarily
The Moon's Orbit The first part of this note gives reference information and definitions about eclipses [14], much of which would have been familiar to ancient Greek astronomers, though not necessarily
Herschel, Planck and GAIA Orbit Design. Martin Hechler, Jordi Cobos
 Herschel, Planck and GAIA Orbit Design Martin Hechler, Jordi Cobos Mission Analysis Section, ESA/ESOC, D-64293 Darmstadt, Germany TERMA, Flight Dynamics Division, ESA/ESOC, Darmstadt, Germany 7th International
Herschel, Planck and GAIA Orbit Design Martin Hechler, Jordi Cobos Mission Analysis Section, ESA/ESOC, D-64293 Darmstadt, Germany TERMA, Flight Dynamics Division, ESA/ESOC, Darmstadt, Germany 7th International
Mission Spacecraft and Operations Overview MAVEN Science Community Workshop December 2, 2012
 Mars Atmosphere and Volatile EvolutioN (MAVEN) Mission Mission Spacecraft and Operations Overview MAVEN Science Community Workshop December 2, 2012 Chris Waters Spacecraft Design Lead Lockheed Martin MAVEN
Mars Atmosphere and Volatile EvolutioN (MAVEN) Mission Mission Spacecraft and Operations Overview MAVEN Science Community Workshop December 2, 2012 Chris Waters Spacecraft Design Lead Lockheed Martin MAVEN
CELESTIAL CLOCK - THE SUN, THE MOON, AND THE STARS
 INTRODUCTION CELESTIAL CLOCK - THE SUN, THE MOON, AND THE STARS This is a scientific presentation to provide you with knowledge you can use to understand the sky above in relation to the earth. Before
INTRODUCTION CELESTIAL CLOCK - THE SUN, THE MOON, AND THE STARS This is a scientific presentation to provide you with knowledge you can use to understand the sky above in relation to the earth. Before
The µtorque Momentum-Exchange Tether Experiment
 The µtorque Momentum-Exchange Tether Experiment Robert P. Hoyt Tethers Unlimited, Inc., 19011 36 h Ave. W., Suite F, Lynnwood, WA 98036-5752 (425) 744-0400 [email protected] Abstract. Long, high-strength
The µtorque Momentum-Exchange Tether Experiment Robert P. Hoyt Tethers Unlimited, Inc., 19011 36 h Ave. W., Suite F, Lynnwood, WA 98036-5752 (425) 744-0400 [email protected] Abstract. Long, high-strength
STEREO Guidance & Control
 STEREO Guidance & Control J. Courtney Ray [email protected] J. C. Ray 98/11/19 1 STEREO G&C Requirements Baseline System Software Some Analysis J. C. Ray 98/11/19 2 G&C Requirements - Drivers Spacecraft
STEREO Guidance & Control J. Courtney Ray [email protected] J. C. Ray 98/11/19 1 STEREO G&C Requirements Baseline System Software Some Analysis J. C. Ray 98/11/19 2 G&C Requirements - Drivers Spacecraft
Attitude and Orbit Dynamics of High Area-to-Mass Ratio (HAMR) Objects and
 Attitude and Orbit Dynamics of High Area-to-Mass Ratio (HAMR) Objects and Carolin Früh National Research Council Postdoctoral Fellow, AFRL, [email protected] Orbital Evolution of Space Debris Objects Main
Attitude and Orbit Dynamics of High Area-to-Mass Ratio (HAMR) Objects and Carolin Früh National Research Council Postdoctoral Fellow, AFRL, [email protected] Orbital Evolution of Space Debris Objects Main
Satellites and Space Stations
 Satellites and Space Stations A satellite is an object or a body that revolves around another object, which is usually much larger in mass. Natural satellites include the planets, which revolve around
Satellites and Space Stations A satellite is an object or a body that revolves around another object, which is usually much larger in mass. Natural satellites include the planets, which revolve around
KINEMATICS OF PARTICLES RELATIVE MOTION WITH RESPECT TO TRANSLATING AXES
 KINEMTICS OF PRTICLES RELTIVE MOTION WITH RESPECT TO TRNSLTING XES In the previous articles, we have described particle motion using coordinates with respect to fixed reference axes. The displacements,
KINEMTICS OF PRTICLES RELTIVE MOTION WITH RESPECT TO TRNSLTING XES In the previous articles, we have described particle motion using coordinates with respect to fixed reference axes. The displacements,
Artificial Satellites Earth & Sky
 Artificial Satellites Earth & Sky Name: Introduction In this lab, you will have the opportunity to find out when satellites may be visible from the RPI campus, and if any are visible during the activity,
Artificial Satellites Earth & Sky Name: Introduction In this lab, you will have the opportunity to find out when satellites may be visible from the RPI campus, and if any are visible during the activity,
Chapter 5: Circular Motion, the Planets, and Gravity
 Chapter 5: Circular Motion, the Planets, and Gravity 1. Earth s gravity attracts a person with a force of 120 lbs. The force with which the Earth is attracted towards the person is A. Zero. B. Small but
Chapter 5: Circular Motion, the Planets, and Gravity 1. Earth s gravity attracts a person with a force of 120 lbs. The force with which the Earth is attracted towards the person is A. Zero. B. Small but
Free Fall: Observing and Analyzing the Free Fall Motion of a Bouncing Ping-Pong Ball and Calculating the Free Fall Acceleration (Teacher s Guide)
 Free Fall: Observing and Analyzing the Free Fall Motion of a Bouncing Ping-Pong Ball and Calculating the Free Fall Acceleration (Teacher s Guide) 2012 WARD S Science v.11/12 OVERVIEW Students will measure
Free Fall: Observing and Analyzing the Free Fall Motion of a Bouncing Ping-Pong Ball and Calculating the Free Fall Acceleration (Teacher s Guide) 2012 WARD S Science v.11/12 OVERVIEW Students will measure
AIDA: Asteroid Impact & Deflection Assessment A Joint ESA-NASA Mission. Joint ESA NASA AIDA Team
 AIDA: Asteroid Impact & Deflection Assessment A Joint ESA-NASA Mission Joint ESA NASA AIDA Team Chelyabinsk Meteor on 15 February 2013 AIDA Asteroid Deflection Test AIDA international cooperation First
AIDA: Asteroid Impact & Deflection Assessment A Joint ESA-NASA Mission Joint ESA NASA AIDA Team Chelyabinsk Meteor on 15 February 2013 AIDA Asteroid Deflection Test AIDA international cooperation First
DIRECT ORBITAL DYNAMICS: USING INDEPENDENT ORBITAL TERMS TO TREAT BODIES AS ORBITING EACH OTHER DIRECTLY WHILE IN MOTION
 1 DIRECT ORBITAL DYNAMICS: USING INDEPENDENT ORBITAL TERMS TO TREAT BODIES AS ORBITING EACH OTHER DIRECTLY WHILE IN MOTION Daniel S. Orton email: [email protected] Abstract: There are many longstanding
1 DIRECT ORBITAL DYNAMICS: USING INDEPENDENT ORBITAL TERMS TO TREAT BODIES AS ORBITING EACH OTHER DIRECTLY WHILE IN MOTION Daniel S. Orton email: [email protected] Abstract: There are many longstanding
Section 2. Satellite Orbits
 Section 2. Satellite Orbits References Kidder and Vonder Haar: chapter 2 Stephens: chapter 1, pp. 25-30 Rees: chapter 9, pp. 174-192 In order to understand satellites and the remote sounding data obtained
Section 2. Satellite Orbits References Kidder and Vonder Haar: chapter 2 Stephens: chapter 1, pp. 25-30 Rees: chapter 9, pp. 174-192 In order to understand satellites and the remote sounding data obtained
Quasi-Synchronous Orbits
 Quasi-Synchronous Orbits and Preliminary Mission Analysis for Phobos Observation and Access Orbits Paulo J. S. Gil Instituto Superior Técnico Simpósio Espaço 50 anos do 1º Voo Espacial Tripulado 12 de
Quasi-Synchronous Orbits and Preliminary Mission Analysis for Phobos Observation and Access Orbits Paulo J. S. Gil Instituto Superior Técnico Simpósio Espaço 50 anos do 1º Voo Espacial Tripulado 12 de
Where On Earth Will Three Different Satellites Provide Simultaneous Coverage?
 Where On Earth Will Three Different Satellites Provide Simultaneous Coverage? In this exercise you will use STK/Coverage to model and analyze the quality and quantity of coverage provided by the Earth
Where On Earth Will Three Different Satellites Provide Simultaneous Coverage? In this exercise you will use STK/Coverage to model and analyze the quality and quantity of coverage provided by the Earth
CHAPTER 1 INTRODUCTION
 CHAPTER 1 INTRODUCTION 1.1 Background of the Research Agile and precise maneuverability of helicopters makes them useful for many critical tasks ranging from rescue and law enforcement task to inspection
CHAPTER 1 INTRODUCTION 1.1 Background of the Research Agile and precise maneuverability of helicopters makes them useful for many critical tasks ranging from rescue and law enforcement task to inspection
Dynamics of Iain M. Banks Orbitals. Richard Kennaway. 12 October 2005
 Dynamics of Iain M. Banks Orbitals Richard Kennaway 12 October 2005 Note This is a draft in progress, and as such may contain errors. Please do not cite this without permission. 1 The problem An Orbital
Dynamics of Iain M. Banks Orbitals Richard Kennaway 12 October 2005 Note This is a draft in progress, and as such may contain errors. Please do not cite this without permission. 1 The problem An Orbital
Solar System. 1. The diagram below represents a simple geocentric model. Which object is represented by the letter X?
 Solar System 1. The diagram below represents a simple geocentric model. Which object is represented by the letter X? A) Earth B) Sun C) Moon D) Polaris 2. Which object orbits Earth in both the Earth-centered
Solar System 1. The diagram below represents a simple geocentric model. Which object is represented by the letter X? A) Earth B) Sun C) Moon D) Polaris 2. Which object orbits Earth in both the Earth-centered
Halliday, Resnick & Walker Chapter 13. Gravitation. Physics 1A PHYS1121 Professor Michael Burton
 Halliday, Resnick & Walker Chapter 13 Gravitation Physics 1A PHYS1121 Professor Michael Burton II_A2: Planetary Orbits in the Solar System + Galaxy Interactions (You Tube) 21 seconds 13-1 Newton's Law
Halliday, Resnick & Walker Chapter 13 Gravitation Physics 1A PHYS1121 Professor Michael Burton II_A2: Planetary Orbits in the Solar System + Galaxy Interactions (You Tube) 21 seconds 13-1 Newton's Law
Actuator Constrained Optimal Control of Formations Near the Libration Points
 Background Actuator Constrained Optimal Control of Formations Near the Libration Points Capt Stuart A. Stanton Dr. Belinda G. Marchand Department of Aerospace Engineering and Engineering Mechanics The
Background Actuator Constrained Optimal Control of Formations Near the Libration Points Capt Stuart A. Stanton Dr. Belinda G. Marchand Department of Aerospace Engineering and Engineering Mechanics The
Newton s Law of Gravity
 Gravitational Potential Energy On Earth, depends on: object s mass (m) strength of gravity (g) distance object could potentially fall Gravitational Potential Energy In space, an object or gas cloud has
Gravitational Potential Energy On Earth, depends on: object s mass (m) strength of gravity (g) distance object could potentially fall Gravitational Potential Energy In space, an object or gas cloud has
4.1.6. Interplanetary Travel. Outline. In This Section You ll Learn to...
 Interplanetary Travel 4.1.6 In This Section You ll Learn to... Describe the basic steps involved in getting from one planet in the solar system to another Explain how we can use the gravitational pull
Interplanetary Travel 4.1.6 In This Section You ll Learn to... Describe the basic steps involved in getting from one planet in the solar system to another Explain how we can use the gravitational pull
The Four Seasons. A Warm Up Exercise. A Warm Up Exercise. A Warm Up Exercise. The Moon s Phases
 The Four Seasons A Warm Up Exercise What fraction of the Moon s surface is illuminated by the Sun (except during a lunar eclipse)? a) Between zero and one-half b) The whole surface c) Always half d) Depends
The Four Seasons A Warm Up Exercise What fraction of the Moon s surface is illuminated by the Sun (except during a lunar eclipse)? a) Between zero and one-half b) The whole surface c) Always half d) Depends
Local Sidereal Time is the hour angle of the First Point of Aries, and is equal to the hour angle plus right ascension of any star.
 1 CHAPTER 7 TIME In this chapter we briefly discuss the several time scales that are in use in astronomy, such as Universal Time, Mean Solar Time, Ephemeris Time, Terrestrial Dynamical Time, and the several
1 CHAPTER 7 TIME In this chapter we briefly discuss the several time scales that are in use in astronomy, such as Universal Time, Mean Solar Time, Ephemeris Time, Terrestrial Dynamical Time, and the several
Projectile Motion 1:Horizontally Launched Projectiles
 A cannon shoots a clown directly upward with a speed of 20 m/s. What height will the clown reach? How much time will the clown spend in the air? Projectile Motion 1:Horizontally Launched Projectiles Two
A cannon shoots a clown directly upward with a speed of 20 m/s. What height will the clown reach? How much time will the clown spend in the air? Projectile Motion 1:Horizontally Launched Projectiles Two
SUN-SYNCHRONOUS ORBIT SLOT ARCHITECTURE ANALYSIS AND DEVELOPMENT. A Thesis. Presented to. the Faculty of California Polytechnic State University
 SUN-SYNCHRONOUS ORBIT SLOT ARCHITECTURE ANALYSIS AND DEVELOPMENT A Thesis Presented to the Faculty of California Polytechnic State University San Luis Obispo In Partial Fulfillment of the Requirements
SUN-SYNCHRONOUS ORBIT SLOT ARCHITECTURE ANALYSIS AND DEVELOPMENT A Thesis Presented to the Faculty of California Polytechnic State University San Luis Obispo In Partial Fulfillment of the Requirements
Robotic Pre-Cursor Contribution to Human NEA Mission. H. Kuninaka JSPEC/JAXA
 Robotic Pre-Cursor Contribution to Human NEA Mission H. Kuninaka JSPEC/JAXA Asteroid Explorer Hayabusa Dimensions 1.0m x 1.6m x 1.1m Weight : 380kg(Dry) Chemical Fuel 70kg Xe Propellant 60kg Total 510kg
Robotic Pre-Cursor Contribution to Human NEA Mission H. Kuninaka JSPEC/JAXA Asteroid Explorer Hayabusa Dimensions 1.0m x 1.6m x 1.1m Weight : 380kg(Dry) Chemical Fuel 70kg Xe Propellant 60kg Total 510kg
Physics Kinematics Model
 Physics Kinematics Model I. Overview Active Physics introduces the concept of average velocity and average acceleration. This unit supplements Active Physics by addressing the concept of instantaneous
Physics Kinematics Model I. Overview Active Physics introduces the concept of average velocity and average acceleration. This unit supplements Active Physics by addressing the concept of instantaneous
Satellite Mission Analysis
 CARLETON UNIVERSITY SPACECRAFT DESIGN PROJECT 2004 FINAL DESIGN REPORT Satellite Mission Analysis FDR Reference Code: FDR-SAT-2004-3.2.A Team/Group: Satellite Mission Analysis Date of Submission: April
CARLETON UNIVERSITY SPACECRAFT DESIGN PROJECT 2004 FINAL DESIGN REPORT Satellite Mission Analysis FDR Reference Code: FDR-SAT-2004-3.2.A Team/Group: Satellite Mission Analysis Date of Submission: April
Astromechanics Two-Body Problem (Cont)
 5. Orbit Characteristics Astromechanics Two-Body Problem (Cont) We have shown that the in the two-body problem, the orbit of the satellite about the primary (or vice-versa) is a conic section, with the
5. Orbit Characteristics Astromechanics Two-Body Problem (Cont) We have shown that the in the two-body problem, the orbit of the satellite about the primary (or vice-versa) is a conic section, with the
TIDES. 1. Tides are the regular rise and fall of sea level that occurs either once a day (every 24.8 hours) or twice a day (every 12.4 hours).
 TIDES What causes tides? How are tides predicted? 1. Tides are the regular rise and fall of sea level that occurs either once a day (every 24.8 hours) or twice a day (every 12.4 hours). Tides are waves
TIDES What causes tides? How are tides predicted? 1. Tides are the regular rise and fall of sea level that occurs either once a day (every 24.8 hours) or twice a day (every 12.4 hours). Tides are waves
Lecture L6 - Intrinsic Coordinates
 S. Widnall, J. Peraire 16.07 Dynamics Fall 2009 Version 2.0 Lecture L6 - Intrinsic Coordinates In lecture L4, we introduced the position, velocity and acceleration vectors and referred them to a fixed
S. Widnall, J. Peraire 16.07 Dynamics Fall 2009 Version 2.0 Lecture L6 - Intrinsic Coordinates In lecture L4, we introduced the position, velocity and acceleration vectors and referred them to a fixed
SPECIAL PERTURBATIONS UNCORRELATED TRACK PROCESSING
 AAS 07-228 SPECIAL PERTURBATIONS UNCORRELATED TRACK PROCESSING INTRODUCTION James G. Miller * Two historical uncorrelated track (UCT) processing approaches have been employed using general perturbations
AAS 07-228 SPECIAL PERTURBATIONS UNCORRELATED TRACK PROCESSING INTRODUCTION James G. Miller * Two historical uncorrelated track (UCT) processing approaches have been employed using general perturbations
Spacecraft orbits and missions
 General Astrophysics and Space Research Course 210142, Space Physics Module Spring 2009, Joachim Vogt Spacecraft orbits and missions Topics of this lecture Basics of celestial mechanics Geocentric orbits
General Astrophysics and Space Research Course 210142, Space Physics Module Spring 2009, Joachim Vogt Spacecraft orbits and missions Topics of this lecture Basics of celestial mechanics Geocentric orbits
Tropical Horticulture: Lecture 2
 Lecture 2 Theory of the Tropics Earth & Solar Geometry, Celestial Mechanics The geometrical relationship between the earth and sun is responsible for the earth s climates. The two principal movements of
Lecture 2 Theory of the Tropics Earth & Solar Geometry, Celestial Mechanics The geometrical relationship between the earth and sun is responsible for the earth s climates. The two principal movements of
CBERS Program Update Jacie 2011. Frederico dos Santos Liporace AMS Kepler [email protected]
 CBERS Program Update Jacie 2011 Frederico dos Santos Liporace AMS Kepler [email protected] Overview CBERS 3 and 4 characteristics Differences from previous CBERS satellites (CBERS 1/2/2B) Geometric
CBERS Program Update Jacie 2011 Frederico dos Santos Liporace AMS Kepler [email protected] Overview CBERS 3 and 4 characteristics Differences from previous CBERS satellites (CBERS 1/2/2B) Geometric
Work, Power, Energy Multiple Choice. PSI Physics. Multiple Choice Questions
 Work, Power, Energy Multiple Choice PSI Physics Name Multiple Choice Questions 1. A block of mass m is pulled over a distance d by an applied force F which is directed in parallel to the displacement.
Work, Power, Energy Multiple Choice PSI Physics Name Multiple Choice Questions 1. A block of mass m is pulled over a distance d by an applied force F which is directed in parallel to the displacement.
circular motion & gravitation physics 111N
 circular motion & gravitation physics 111N uniform circular motion an object moving around a circle at a constant rate must have an acceleration always perpendicular to the velocity (else the speed would
circular motion & gravitation physics 111N uniform circular motion an object moving around a circle at a constant rate must have an acceleration always perpendicular to the velocity (else the speed would
TOPO Trajectory Operations Officer
 ISS Live! was developed at NASA s Johnson Space Center (JSC) under NASA Contracts NNJ14RA02C and NNJ11HA14C wherein the U.S. Government retains certain rights. Console Handbook TOPO Trajectory Operations
ISS Live! was developed at NASA s Johnson Space Center (JSC) under NASA Contracts NNJ14RA02C and NNJ11HA14C wherein the U.S. Government retains certain rights. Console Handbook TOPO Trajectory Operations
5. Forces and Motion-I. Force is an interaction that causes the acceleration of a body. A vector quantity.
 5. Forces and Motion-I 1 Force is an interaction that causes the acceleration of a body. A vector quantity. Newton's First Law: Consider a body on which no net force acts. If the body is at rest, it will
5. Forces and Motion-I 1 Force is an interaction that causes the acceleration of a body. A vector quantity. Newton's First Law: Consider a body on which no net force acts. If the body is at rest, it will
EDMONDS COMMUNITY COLLEGE ASTRONOMY 100 Winter Quarter 2007 Sample Test # 1
 Instructor: L. M. Khandro EDMONDS COMMUNITY COLLEGE ASTRONOMY 100 Winter Quarter 2007 Sample Test # 1 1. An arc second is a measure of a. time interval between oscillations of a standard clock b. time
Instructor: L. M. Khandro EDMONDS COMMUNITY COLLEGE ASTRONOMY 100 Winter Quarter 2007 Sample Test # 1 1. An arc second is a measure of a. time interval between oscillations of a standard clock b. time
USING MS EXCEL FOR DATA ANALYSIS AND SIMULATION
 USING MS EXCEL FOR DATA ANALYSIS AND SIMULATION Ian Cooper School of Physics The University of Sydney [email protected] Introduction The numerical calculations performed by scientists and engineers
USING MS EXCEL FOR DATA ANALYSIS AND SIMULATION Ian Cooper School of Physics The University of Sydney [email protected] Introduction The numerical calculations performed by scientists and engineers
Data Review and Analysis Program (DRAP) Flight Data Visualization Program for Enhancement of FOQA
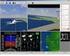 86 Data Review and Analysis Program (DRAP) Flight Data Visualization Program for Enhancement of FOQA Koji MURAOKA and Noriaki OKADA, Flight Systems Research Center, E-mail: [email protected] Keywords:
86 Data Review and Analysis Program (DRAP) Flight Data Visualization Program for Enhancement of FOQA Koji MURAOKA and Noriaki OKADA, Flight Systems Research Center, E-mail: [email protected] Keywords:
Newton s Law of Universal Gravitation
 Newton s Law of Universal Gravitation The greatest moments in science are when two phenomena that were considered completely separate suddenly are seen as just two different versions of the same thing.
Newton s Law of Universal Gravitation The greatest moments in science are when two phenomena that were considered completely separate suddenly are seen as just two different versions of the same thing.
Rotation: Moment of Inertia and Torque
 Rotation: Moment of Inertia and Torque Every time we push a door open or tighten a bolt using a wrench, we apply a force that results in a rotational motion about a fixed axis. Through experience we learn
Rotation: Moment of Inertia and Torque Every time we push a door open or tighten a bolt using a wrench, we apply a force that results in a rotational motion about a fixed axis. Through experience we learn
Mechanics lecture 7 Moment of a force, torque, equilibrium of a body
 G.1 EE1.el3 (EEE1023): Electronics III Mechanics lecture 7 Moment of a force, torque, equilibrium of a body Dr Philip Jackson http://www.ee.surrey.ac.uk/teaching/courses/ee1.el3/ G.2 Moments, torque and
G.1 EE1.el3 (EEE1023): Electronics III Mechanics lecture 7 Moment of a force, torque, equilibrium of a body Dr Philip Jackson http://www.ee.surrey.ac.uk/teaching/courses/ee1.el3/ G.2 Moments, torque and
APP Aircraft Performance Program Demo Notes Using Cessna 172 as an Example
 APP Aircraft Performance Program Demo Notes Using Cessna 172 as an Example Prepared by DARcorporation 1. Program Layout & Organization APP Consists of 8 Modules, 5 Input Modules and 2 Calculation Modules.
APP Aircraft Performance Program Demo Notes Using Cessna 172 as an Example Prepared by DARcorporation 1. Program Layout & Organization APP Consists of 8 Modules, 5 Input Modules and 2 Calculation Modules.
Atlas Emergency Detection System (EDS)
 Atlas Emergency Detection System (EDS) Jeff A. Patton 1 United Launch Alliance, Littleton, Colorado, 80127-7005 [Abstract] The Atlas Expendable Launch Vehicle Program has been studying safe abort requirements
Atlas Emergency Detection System (EDS) Jeff A. Patton 1 United Launch Alliance, Littleton, Colorado, 80127-7005 [Abstract] The Atlas Expendable Launch Vehicle Program has been studying safe abort requirements
Motion & The Global Positioning System (GPS)
 Grade Level: K - 8 Subject: Motion Prep Time: < 10 minutes Duration: 30 minutes Objective: To learn how to analyze GPS data in order to track an object and derive its velocity from positions and times.
Grade Level: K - 8 Subject: Motion Prep Time: < 10 minutes Duration: 30 minutes Objective: To learn how to analyze GPS data in order to track an object and derive its velocity from positions and times.
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Fluid Mechanics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur
 Fluid Mechanics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture - 20 Conservation Equations in Fluid Flow Part VIII Good morning. I welcome you all
Fluid Mechanics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture - 20 Conservation Equations in Fluid Flow Part VIII Good morning. I welcome you all
Reasons for Seasons. Question: TRUE OR FALSE. Question: TRUE OR FALSE? What causes the seasons? What causes the seasons?
 Reasons for Seasons Question: TRUE OR FALSE? Earth is closer to the Sun in summer and farther from the Sun in winter. Question: TRUE OR FALSE? Earth is closer to the Sun in summer and farther from the
Reasons for Seasons Question: TRUE OR FALSE? Earth is closer to the Sun in summer and farther from the Sun in winter. Question: TRUE OR FALSE? Earth is closer to the Sun in summer and farther from the
About the NeuroFuzzy Module of the FuzzyTECH5.5 Software
 About the NeuroFuzzy Module of the FuzzyTECH5.5 Software Ágnes B. Simon, Dániel Biró College of Nyíregyháza, Sóstói út 31, [email protected], [email protected] Abstract: Our online edition of the software
About the NeuroFuzzy Module of the FuzzyTECH5.5 Software Ágnes B. Simon, Dániel Biró College of Nyíregyháza, Sóstói út 31, [email protected], [email protected] Abstract: Our online edition of the software
State Newton's second law of motion for a particle, defining carefully each term used.
 5 Question 1. [Marks 20] An unmarked police car P is, travelling at the legal speed limit, v P, on a straight section of highway. At time t = 0, the police car is overtaken by a car C, which is speeding
5 Question 1. [Marks 20] An unmarked police car P is, travelling at the legal speed limit, v P, on a straight section of highway. At time t = 0, the police car is overtaken by a car C, which is speeding
