Hypothetical Syllogisms 1
|
|
|
- Elinor Short
- 7 years ago
- Views:
Transcription
1 Phil 2302 Intro to Logic Dr. Naugle Hypothetical Syllogisms 1 Compound syllogisms are composed of different kinds of sentences in their premises and conclusions (not just categorical propositions, statements or sentences). Compound syllogisms are more familiar and are more often used than categorical syllogisms, and the rules of their uses are much easier to grasp. There are several kinds of compound syllogisms including hypothetical, disjunctive, conjunctive, dilemmas, and sorites. Today, hypothetical syllogisms (and a little symbolic logic as well). I. Hypothetical Syllogisms A. Definition A hypothetical syllogism is built around a hypothetical statement which takes the form: "IF... THEN." Hypothetical syllogisms are not entirely hypothetical, but one of its premises is. Three hypothetical statements would not lead to any conclusion! "IF... THEN." "IF... THEN." Therefore, "IF... THEN." Rather, this kind of syllogism must be constructed of a conditional major premise, and an unconditional minor premise leading to an unconditional conclusion. 1. A conditional major premise. 2. An unconditional minor premise. 3. An unconditional conclusion. Rather than having three terms as categorical syllogisms do, a hypothetical syllogism has only two terms. Instead of talking about subjects and predicates, here we will be talking about antecedents and consequents. * The antecedent is the "IF" part of the statement. It states the condition under which the "THEN" part is true. 1 NB: This material is taken from several logic texts authored by N. Geisler, H. Kahane, and others. I make no claim to originality in this material.
2 * The consequent is the "THEN" part, the consequence of or what follows from the antecedent if the "IF" part is true. All the minor premise has to do is say that the "IF" part "is" (modus ponens) or the "THEN" part "is not" (modus tollens). Either way, the conclusion is valid. IF (antecedent; first term)... then (consequent; second term). B. MODUS PONENS: Affirming the Antecedent 1. Definition The first way to get a valid conclusion from a hypothetical or conditional premise is to affirm the antecedent, which in Latin is called modus ponens (lit. way of affirmation). That is, the minor or second premise will assert that the antecedent or "if" is not just a speculation, but a reality. And if the "if" is true, then the "then" has to follow, and that becomes the conclusion. In symbolic logic (which simply uses symbols instead of words to indicate relations), the sideways horseshoe indicates and "if,... then" relation. If P, then Q P Therefore, Q P... Q P Q 2. Examples of valid modus ponens syllogisms (see fallacies below): 1. If you can put an argument into symbolic logic that looks like this (P), then you have a modus ponens argument (Q). 2. You can put an argument into symbolic logic that looks like this (P). 3. Therefore, you have a modus ponens argument (Q)! 1. If Jesus Christ arose from the dead (P), then he is the Son of God (Q). 2. Jesus Christ arose from the dead (P). 3. Therefore He is the Son of God (Q). 1. If a contingent being exists (P), then a necessary being must exist as its cause (Q). 2. A contingent being exists (P). 3. Therefore, a necessary being must exist as its cause (Q).
3 1. If there is design in the universe (d), then there must have been a Designer (D) 2. There is design in the universe (d). 3. Therefore, there must have been a designer (D). 2. I am Chinese. 3. Therefore, I am human. C. MODUS TOLLENS: Denying the Consequent 1. Definition: The other valid form of the hypothetical syllogism is to deny that the consequent is true. Modus ponens in Latin means "the way of affirmation," and, correspondingly, modus tollens in Latin means to "the way of negation" Hence, the hypothetical modus tollens syllogistic arguments are those which deny the consequent of a hypothetical statement, thereby negating the antecedent as well. If there is a real connection between the antecedent and the consequent (the "if" and the "then,"), and the consequent is false, then the antecedent must be false also. Denying the consequent also involves the denial of the antecedent as well. So modus tollens is the reverse of modus ponens. If the antecedent were true, then so would the consequent (that's what modus ponens said!). If P, then Q Not Q Therefore, not P. P... Q ~ Q ~ P 1. If anyone is born of God, then he loves his brothers. 2. Adolph does not love his brothers. 3. Therefore, Adolph is not born of God. 1. If the president acts forcefully, he will gain in the polls. 2. He is not gaining in the polls. 3. Therefore, the president is not acting forcefully. 1. If the national debt is paid off with inflated money, then borrowers will benefit and lenders will be harmed. 2. Borrowers are not benefited, and lenders are not harmed. 3. Therefore, the national debt is not being paid off with inflated money.
4 1. If a world government is established, wars will cease. 2. Wars are not ceasing. 3. Therefore, a world government is not being established. 1. If I have cash, I will loan you money. 2. I am not loaning you money. 3. Therefore, I do not have cash. 2. I am not human. 3. Therefore, I am not Chinese. II. Fallacies of the Hypothetical Syllogism A valid hypothetical syllogism either denies the consequent (modus tollensm.t.d.c.) or affirms the antecedent (modus ponens-m.p.a.a.) of the major premise; it does not deny the antecedent or affirm the consequent. A. Denying the Antecedent: That a particular condition is not fulfilled is not any proof that the consequent has not occurred since some other condition with which the consequent may be connected may be the cause of its fulfillment. 1. If abortion is murder, then it is wrong. 2. But abortion isn't murder. 3. Therefore, it is not wrong. 1. If Tom is late for work, then he will not attend the meeting. 2. Tom is not late for work. 3. Therefore, Tom will attend the meeting. 2. I am not Chinese. 3. Therefore, I am not human. 1. If my name is Archibald, I am male. 2. My name is not Archibald. 3. Therefore, I am not male. 1. If Hawaii is ready for statehood, then Alaska is ready for statehood. 2. Hawaii is not ready for statehood. 3. Therefore, Alaska is not ready for statehood.
5 B. Affirming the Consequent: The connection of a consequent with a condition (or antecedent) does not preclude the possibility that there are other conditions upon which the same consequent may follow. To affirm the consequent is no guarantee that the specified condition produced it. The fact that the consequent may have occurred is no proof or guarantee of that particular condition or antecedent. 1. If a member of the House of Commons is declared bankrupt, he loses his seat. 2. He has lost his seat. 3. Therefore, he is declared bankrupt. 1. If reincarnation is true, then past life regression therapy will work. 2. Past life regression therapy works. 3. Therefore, reincarnation is true. 1. If Reagan is still president, then a liar is in the White House. 2. A liar is in the White House. 3. Therefore, Reagan is president. 2. I am human 3. Therefore, I am Chinese 1. If my name is Archibald, I am male. 2. I am male 3. Therefore, my name is Archibald. 1. If Hawaii is ready for statehood, then Alaska is ready for statehood. 2. Alaska is ready for statehood. 3. Therefore, Hawaii is ready for statehood. Conclusion: When you spot a conditional argument, you can test its validity very easily. First, make sure you know what the conditional or major premise is. Second, see whether the minor premise affirms or denies the antecedent or consequent in the major premise. If it affirms the antecedent or denies the consequent, a conclusion can be drawn and it is valid. Otherwise not.
def: An axiom is a statement that is assumed to be true, or in the case of a mathematical system, is used to specify the system.
 Section 1.5 Methods of Proof 1.5.1 1.5 METHODS OF PROOF Some forms of argument ( valid ) never lead from correct statements to an incorrect. Some other forms of argument ( fallacies ) can lead from true
Section 1.5 Methods of Proof 1.5.1 1.5 METHODS OF PROOF Some forms of argument ( valid ) never lead from correct statements to an incorrect. Some other forms of argument ( fallacies ) can lead from true
Likewise, we have contradictions: formulas that can only be false, e.g. (p p).
 CHAPTER 4. STATEMENT LOGIC 59 The rightmost column of this truth table contains instances of T and instances of F. Notice that there are no degrees of contingency. If both values are possible, the formula
CHAPTER 4. STATEMENT LOGIC 59 The rightmost column of this truth table contains instances of T and instances of F. Notice that there are no degrees of contingency. If both values are possible, the formula
1.2 Forms and Validity
 1.2 Forms and Validity Deductive Logic is the study of methods for determining whether or not an argument is valid. In this section we identify some famous valid argument forms. Argument Forms Consider
1.2 Forms and Validity Deductive Logic is the study of methods for determining whether or not an argument is valid. In this section we identify some famous valid argument forms. Argument Forms Consider
CHAPTER 3. Methods of Proofs. 1. Logical Arguments and Formal Proofs
 CHAPTER 3 Methods of Proofs 1. Logical Arguments and Formal Proofs 1.1. Basic Terminology. An axiom is a statement that is given to be true. A rule of inference is a logical rule that is used to deduce
CHAPTER 3 Methods of Proofs 1. Logical Arguments and Formal Proofs 1.1. Basic Terminology. An axiom is a statement that is given to be true. A rule of inference is a logical rule that is used to deduce
DISCRETE MATH: LECTURE 3
 DISCRETE MATH: LECTURE 3 DR. DANIEL FREEMAN 1. Chapter 2.2 Conditional Statements If p and q are statement variables, the conditional of q by p is If p then q or p implies q and is denoted p q. It is false
DISCRETE MATH: LECTURE 3 DR. DANIEL FREEMAN 1. Chapter 2.2 Conditional Statements If p and q are statement variables, the conditional of q by p is If p then q or p implies q and is denoted p q. It is false
Rules of Inference Friday, January 18, 2013 Chittu Tripathy Lecture 05
 Rules of Inference Today s Menu Rules of Inference Quantifiers: Universal and Existential Nesting of Quantifiers Applications Old Example Re-Revisited Our Old Example: Suppose we have: All human beings
Rules of Inference Today s Menu Rules of Inference Quantifiers: Universal and Existential Nesting of Quantifiers Applications Old Example Re-Revisited Our Old Example: Suppose we have: All human beings
Beyond Propositional Logic Lukasiewicz s System
 Beyond Propositional Logic Lukasiewicz s System Consider the following set of truth tables: 1 0 0 1 # # 1 0 # 1 1 0 # 0 0 0 0 # # 0 # 1 0 # 1 1 1 1 0 1 0 # # 1 # # 1 0 # 1 1 0 # 0 1 1 1 # 1 # 1 Brandon
Beyond Propositional Logic Lukasiewicz s System Consider the following set of truth tables: 1 0 0 1 # # 1 0 # 1 1 0 # 0 0 0 0 # # 0 # 1 0 # 1 1 1 1 0 1 0 # # 1 # # 1 0 # 1 1 0 # 0 1 1 1 # 1 # 1 Brandon
Lecture 2: Moral Reasoning & Evaluating Ethical Theories
 Lecture 2: Moral Reasoning & Evaluating Ethical Theories I. Introduction In this ethics course, we are going to avoid divine command theory and various appeals to authority and put our trust in critical
Lecture 2: Moral Reasoning & Evaluating Ethical Theories I. Introduction In this ethics course, we are going to avoid divine command theory and various appeals to authority and put our trust in critical
DEDUCTIVE & INDUCTIVE REASONING
 DEDUCTIVE & INDUCTIVE REASONING Expectations 1. Take notes on inductive and deductive reasoning. 2. This is an information based presentation -- I simply want you to be able to apply this information to
DEDUCTIVE & INDUCTIVE REASONING Expectations 1. Take notes on inductive and deductive reasoning. 2. This is an information based presentation -- I simply want you to be able to apply this information to
Phil 2302 Intro to Logic. Introduction to Induction i
 Phil 2302 Intro to Logic Introduction to Induction i "The object of reasoning is to find out, from the consideration of what we already know, something else which we do not know. Consequently, reasoning
Phil 2302 Intro to Logic Introduction to Induction i "The object of reasoning is to find out, from the consideration of what we already know, something else which we do not know. Consequently, reasoning
INTRODUCTION TO LOGIC
 INTRODUCTION TO LOGIC A. Basic Concepts 1. Logic is the science of the correctness or incorrectness of reasoning, or the study of the evaluation of arguments. 2. A statement is a declarative sentence,
INTRODUCTION TO LOGIC A. Basic Concepts 1. Logic is the science of the correctness or incorrectness of reasoning, or the study of the evaluation of arguments. 2. A statement is a declarative sentence,
Deductive versus Inductive Reasoning
 Deductive Arguments 1 Deductive versus Inductive Reasoning Govier has pointed out that there are four basic types of argument: deductive, inductive generalization, analogical, and conductive. For our purposes,
Deductive Arguments 1 Deductive versus Inductive Reasoning Govier has pointed out that there are four basic types of argument: deductive, inductive generalization, analogical, and conductive. For our purposes,
Predicate logic Proofs Artificial intelligence. Predicate logic. SET07106 Mathematics for Software Engineering
 Predicate logic SET07106 Mathematics for Software Engineering School of Computing Edinburgh Napier University Module Leader: Uta Priss 2010 Copyright Edinburgh Napier University Predicate logic Slide 1/24
Predicate logic SET07106 Mathematics for Software Engineering School of Computing Edinburgh Napier University Module Leader: Uta Priss 2010 Copyright Edinburgh Napier University Predicate logic Slide 1/24
Syllogisms and Fallacies 101
 1 Syllogisms and Fallacies 101 This isn t a course in logic, but all educated people should know the basic vocabulary and the basic underlying logic of the syllogism. Major premise: No reptiles have fur.
1 Syllogisms and Fallacies 101 This isn t a course in logic, but all educated people should know the basic vocabulary and the basic underlying logic of the syllogism. Major premise: No reptiles have fur.
Kant s deontological ethics
 Michael Lacewing Kant s deontological ethics DEONTOLOGY Deontologists believe that morality is a matter of duty. We have moral duties to do things which it is right to do and moral duties not to do things
Michael Lacewing Kant s deontological ethics DEONTOLOGY Deontologists believe that morality is a matter of duty. We have moral duties to do things which it is right to do and moral duties not to do things
Handout #1: Mathematical Reasoning
 Math 101 Rumbos Spring 2010 1 Handout #1: Mathematical Reasoning 1 Propositional Logic A proposition is a mathematical statement that it is either true or false; that is, a statement whose certainty or
Math 101 Rumbos Spring 2010 1 Handout #1: Mathematical Reasoning 1 Propositional Logic A proposition is a mathematical statement that it is either true or false; that is, a statement whose certainty or
WELCOME TO GOD S FAMILY
 WELCOME TO GOD S FAMILY To all who received him, to those who believed in his name, he gave the right to become children of God children born not of natural descent, nor of human decision or a husband
WELCOME TO GOD S FAMILY To all who received him, to those who believed in his name, he gave the right to become children of God children born not of natural descent, nor of human decision or a husband
LOGIC AND SETS CLAST MATHEMATICS COMPETENCIES
 5 LOGIC AND SETS CLAST MATHEMATICS COMPETENCIES IE1: IIE1: IIE2: IIE3: IIE4: IIIE1: IIIE2: IVE1: Deduce facts of set inclusion or set non-inclusion from a diagram Identify statements equivalent to the
5 LOGIC AND SETS CLAST MATHEMATICS COMPETENCIES IE1: IIE1: IIE2: IIE3: IIE4: IIIE1: IIIE2: IVE1: Deduce facts of set inclusion or set non-inclusion from a diagram Identify statements equivalent to the
Slippery Slopes and Vagueness
 Slippery Slopes and Vagueness Slippery slope reasoning, typically taken as a fallacy. But what goes wrong? Is it always bad reasoning? How should we respond to a slippery slope argument and/or guard against
Slippery Slopes and Vagueness Slippery slope reasoning, typically taken as a fallacy. But what goes wrong? Is it always bad reasoning? How should we respond to a slippery slope argument and/or guard against
Predicate Logic. Example: All men are mortal. Socrates is a man. Socrates is mortal.
 Predicate Logic Example: All men are mortal. Socrates is a man. Socrates is mortal. Note: We need logic laws that work for statements involving quantities like some and all. In English, the predicate is
Predicate Logic Example: All men are mortal. Socrates is a man. Socrates is mortal. Note: We need logic laws that work for statements involving quantities like some and all. In English, the predicate is
Math 3000 Section 003 Intro to Abstract Math Homework 2
 Math 3000 Section 003 Intro to Abstract Math Homework 2 Department of Mathematical and Statistical Sciences University of Colorado Denver, Spring 2012 Solutions (February 13, 2012) Please note that these
Math 3000 Section 003 Intro to Abstract Math Homework 2 Department of Mathematical and Statistical Sciences University of Colorado Denver, Spring 2012 Solutions (February 13, 2012) Please note that these
How s Your Love Life? (A Superlative Witness You Belong to Jesus) 1 John 3:11-18
 1 How s Your Love Life? (A Superlative Witness You Belong to Jesus) 1 John 3:11-18 Introduction: 1) One of the most effective ways of teaching is using contrast and comparisons. For example if I say male
1 How s Your Love Life? (A Superlative Witness You Belong to Jesus) 1 John 3:11-18 Introduction: 1) One of the most effective ways of teaching is using contrast and comparisons. For example if I say male
CHAPTER 2. Logic. 1. Logic Definitions. Notation: Variables are used to represent propositions. The most common variables used are p, q, and r.
 CHAPTER 2 Logic 1. Logic Definitions 1.1. Propositions. Definition 1.1.1. A proposition is a declarative sentence that is either true (denoted either T or 1) or false (denoted either F or 0). Notation:
CHAPTER 2 Logic 1. Logic Definitions 1.1. Propositions. Definition 1.1.1. A proposition is a declarative sentence that is either true (denoted either T or 1) or false (denoted either F or 0). Notation:
God is Love. 1 John 4:7-11
 God is Love 1 John 4:7-11 Introduction: As we move into a new section of the book of 1 John, I would like for us to read the entirety of 1 John 4:7-21. Over the next three weeks, we will be covering these
God is Love 1 John 4:7-11 Introduction: As we move into a new section of the book of 1 John, I would like for us to read the entirety of 1 John 4:7-21. Over the next three weeks, we will be covering these
CATECHISM (adopted 2008) FOR CUMBERLAND PRESBYTERIAN CONFESSION OF FAITH
 (from 2008 preliminary minutes page 183) CATECHISM (adopted 2008) FOR CUMBERLAND PRESBYTERIAN CONFESSION OF FAITH 1. Who is God? God is the one living, active Creator of all that is, seen and unseen. 2.
(from 2008 preliminary minutes page 183) CATECHISM (adopted 2008) FOR CUMBERLAND PRESBYTERIAN CONFESSION OF FAITH 1. Who is God? God is the one living, active Creator of all that is, seen and unseen. 2.
Invalidity in Predicate Logic
 Invalidity in Predicate Logic So far we ve got a method for establishing that a predicate logic argument is valid: do a derivation. But we ve got no method for establishing invalidity. In propositional
Invalidity in Predicate Logic So far we ve got a method for establishing that a predicate logic argument is valid: do a derivation. But we ve got no method for establishing invalidity. In propositional
Development of a computer system to support knowledge acquisition of basic logical forms using fairy tale "Alice in Wonderland"
 Development of a computer system to support knowledge acquisition of basic logical forms using fairy tale "Alice in Wonderland" Antonija Mihaljević Španjić *, Alen Jakupović *, Matea Tomić * * Polytechnic
Development of a computer system to support knowledge acquisition of basic logical forms using fairy tale "Alice in Wonderland" Antonija Mihaljević Španjić *, Alen Jakupović *, Matea Tomić * * Polytechnic
1/9. Locke 1: Critique of Innate Ideas
 1/9 Locke 1: Critique of Innate Ideas This week we are going to begin looking at a new area by turning our attention to the work of John Locke, who is probably the most famous English philosopher of all
1/9 Locke 1: Critique of Innate Ideas This week we are going to begin looking at a new area by turning our attention to the work of John Locke, who is probably the most famous English philosopher of all
Philosophy 120: Introductory Logic Summer 2007
 Class: Date: Philosophy 120: Introductory Logic Summer 2007 Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. INSTRUCTIONS: The following selections
Class: Date: Philosophy 120: Introductory Logic Summer 2007 Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. INSTRUCTIONS: The following selections
Logic in general. Inference rules and theorem proving
 Logical Agents Knowledge-based agents Logic in general Propositional logic Inference rules and theorem proving First order logic Knowledge-based agents Inference engine Knowledge base Domain-independent
Logical Agents Knowledge-based agents Logic in general Propositional logic Inference rules and theorem proving First order logic Knowledge-based agents Inference engine Knowledge base Domain-independent
How To Proofread
 GRADE 8 English Language Arts Proofreading: Lesson 6 Read aloud to the students the material that is printed in boldface type inside the boxes. Information in regular type inside the boxes and all information
GRADE 8 English Language Arts Proofreading: Lesson 6 Read aloud to the students the material that is printed in boldface type inside the boxes. Information in regular type inside the boxes and all information
Phil 1010, Practice Final Exam George Rainbolt s Section, Fall 2008
 Phil 1010, Practice Final Exam George Rainbolt s Section, Fall 2008 I. Statement Types: for each of the following statements, identify its type. If a statement contains two or more types, choose the type
Phil 1010, Practice Final Exam George Rainbolt s Section, Fall 2008 I. Statement Types: for each of the following statements, identify its type. If a statement contains two or more types, choose the type
PHILOSOPHY 101: CRITICAL THINKING
 PHILOSOPHY 101: CRITICAL THINKING [days and times] [classroom] [semester] 20YY, [campus] [instructor s name] [office hours: days and times] [instructor s e-mail] COURSE OBJECTIVES AND OUTCOMES 1. Identify
PHILOSOPHY 101: CRITICAL THINKING [days and times] [classroom] [semester] 20YY, [campus] [instructor s name] [office hours: days and times] [instructor s e-mail] COURSE OBJECTIVES AND OUTCOMES 1. Identify
Examination paper for MA0301 Elementær diskret matematikk
 Department of Mathematical Sciences Examination paper for MA0301 Elementær diskret matematikk Academic contact during examination: Iris Marjan Smit a, Sverre Olaf Smalø b Phone: a 9285 0781, b 7359 1750
Department of Mathematical Sciences Examination paper for MA0301 Elementær diskret matematikk Academic contact during examination: Iris Marjan Smit a, Sverre Olaf Smalø b Phone: a 9285 0781, b 7359 1750
Cosmological Arguments for the Existence of God S. Clarke
 Cosmological Arguments for the Existence of God S. Clarke [Modified Fall 2009] 1. Large class of arguments. Sometimes they get very complex, as in Clarke s argument, but the basic idea is simple. Lets
Cosmological Arguments for the Existence of God S. Clarke [Modified Fall 2009] 1. Large class of arguments. Sometimes they get very complex, as in Clarke s argument, but the basic idea is simple. Lets
The Reaffirmation of Baptismal Faith Including the Use of Water
 The Reaffirmation of Baptismal Faith Including the Use of Water INTRODUCTION Baptism is an unrepeatable sacrament of entry into the One Holy Catholic and Apostolic Church, of which the Methodist Church
The Reaffirmation of Baptismal Faith Including the Use of Water INTRODUCTION Baptism is an unrepeatable sacrament of entry into the One Holy Catholic and Apostolic Church, of which the Methodist Church
Who is Satan Today? Knowing & Understanding Our Enemy Ken Birks, Pastor/Teacher
 Who is Satan Today? Knowing & Understanding Our Enemy Ken Birks, Pastor/Teacher I. Introductory Remarks. As people who have been born again of God's Spirit, we have been delivered from the power of darkness.
Who is Satan Today? Knowing & Understanding Our Enemy Ken Birks, Pastor/Teacher I. Introductory Remarks. As people who have been born again of God's Spirit, we have been delivered from the power of darkness.
HUMN-218 COURSE SYLLABUS FOR LOGIC AND CRITICAL THINKING. Jill R. Wood Instructor
 Coffeyville Community College HUMN-218 COURSE SYLLABUS FOR LOGIC AND CRITICAL THINKING Jill R. Wood Instructor COURSE NUMBER: HUMN-218 COURSE TITLE: Logic and Critical Thinking CREDIT HOURS: 3 INSTRUCTOR:
Coffeyville Community College HUMN-218 COURSE SYLLABUS FOR LOGIC AND CRITICAL THINKING Jill R. Wood Instructor COURSE NUMBER: HUMN-218 COURSE TITLE: Logic and Critical Thinking CREDIT HOURS: 3 INSTRUCTOR:
Atheism. Richland Creek Community Church
 Atheism Richland Creek Community Church The Existence of God: Does America believe in God? Google - What percentage of Americans believe in God? = well over 90%. In fact, over the past 50 years of research
Atheism Richland Creek Community Church The Existence of God: Does America believe in God? Google - What percentage of Americans believe in God? = well over 90%. In fact, over the past 50 years of research
What Is Induction and Why Study It?
 1 What Is Induction and Why Study It? Evan Heit Why study induction, and indeed, why should there be a whole book devoted to the study of induction? The first reason is that inductive reasoning corresponds
1 What Is Induction and Why Study It? Evan Heit Why study induction, and indeed, why should there be a whole book devoted to the study of induction? The first reason is that inductive reasoning corresponds
Mathematical Induction
 Mathematical Induction In logic, we often want to prove that every member of an infinite set has some feature. E.g., we would like to show: N 1 : is a number 1 : has the feature Φ ( x)(n 1 x! 1 x) How
Mathematical Induction In logic, we often want to prove that every member of an infinite set has some feature. E.g., we would like to show: N 1 : is a number 1 : has the feature Φ ( x)(n 1 x! 1 x) How
Boolean Design of Patterns
 123 Boolean Design of Patterns Basic weave structures interlacement patterns can be described in many ways, but they all come down to representing the crossings of warp and weft threads. One or the other
123 Boolean Design of Patterns Basic weave structures interlacement patterns can be described in many ways, but they all come down to representing the crossings of warp and weft threads. One or the other
What Is Circular Reasoning?
 What Is Circular Reasoning? Logical fallacies are a type of error in reasoning, errors which may be recognized and corrected by observant thinkers. There are a large number of informal fallacies that are
What Is Circular Reasoning? Logical fallacies are a type of error in reasoning, errors which may be recognized and corrected by observant thinkers. There are a large number of informal fallacies that are
Truth Focus Statements for the Twelve Healing Code Categories
 Truth Focus Statements for the Twelve Healing Code Categories The following are suggested Truth Focus Statements that can be used when doing The Healing Code, as outlined in The Healing Code book. They
Truth Focus Statements for the Twelve Healing Code Categories The following are suggested Truth Focus Statements that can be used when doing The Healing Code, as outlined in The Healing Code book. They
Philosophical argument
 Michael Lacewing Philosophical argument At the heart of philosophy is philosophical argument. Arguments are different from assertions. Assertions are simply stated; arguments always involve giving reasons.
Michael Lacewing Philosophical argument At the heart of philosophy is philosophical argument. Arguments are different from assertions. Assertions are simply stated; arguments always involve giving reasons.
Who Is Your Defense Attorney? 1 John 2:1-2. The text for this sermon, the theme of which is, Who Is Your Defense
 Easter 2 B Who Is Your Defense Attorney? 1 John 2:1-2 The text for this sermon, the theme of which is, Who Is Your Defense Attorney?, is 1 John 2:1-2 My little children, I am writing these things to you
Easter 2 B Who Is Your Defense Attorney? 1 John 2:1-2 The text for this sermon, the theme of which is, Who Is Your Defense Attorney?, is 1 John 2:1-2 My little children, I am writing these things to you
Introduction to Logic: Argumentation and Interpretation. Vysoká škola mezinárodních a veřejných vztahů PhDr. Peter Jan Kosmály, Ph.D. 9. 3.
 Introduction to Logic: Argumentation and Interpretation Vysoká škola mezinárodních a veřejných vztahů PhDr. Peter Jan Kosmály, Ph.D. 9. 3. 2016 tests. Introduction to Logic: Argumentation and Interpretation
Introduction to Logic: Argumentation and Interpretation Vysoká škola mezinárodních a veřejných vztahů PhDr. Peter Jan Kosmály, Ph.D. 9. 3. 2016 tests. Introduction to Logic: Argumentation and Interpretation
Logic Appendix. Section 1 Truth Tables CONJUNCTION EXAMPLE 1
 Logic Appendix T F F T Section 1 Truth Tables Recall that a statement is a group of words or symbols that can be classified collectively as true or false. The claim 5 7 12 is a true statement, whereas
Logic Appendix T F F T Section 1 Truth Tables Recall that a statement is a group of words or symbols that can be classified collectively as true or false. The claim 5 7 12 is a true statement, whereas
Lighting the Advent Wreath
 Lighting the Advent Wreath Advent comes from the Latin word 'adventus' meaning 'Coming.' Advent begins the church year starting four Sundays before Christmas. The season of Advent has been set aside as
Lighting the Advent Wreath Advent comes from the Latin word 'adventus' meaning 'Coming.' Advent begins the church year starting four Sundays before Christmas. The season of Advent has been set aside as
Divine command theory
 Today we will be discussing divine command theory. But first I will give a (very) brief overview of the semester, and the discipline of philosophy. Why do this? One of the functions of an introductory
Today we will be discussing divine command theory. But first I will give a (very) brief overview of the semester, and the discipline of philosophy. Why do this? One of the functions of an introductory
ON WHITCOMB S GROUNDING ARGUMENT FOR ATHEISM Joshua Rasmussen Andrew Cullison Daniel Howard-Snyder
 ON WHITCOMB S GROUNDING ARGUMENT FOR ATHEISM Joshua Rasmussen Andrew Cullison Daniel Howard-Snyder Abstract: Dennis Whitcomb argues that there is no God on the grounds that (i) God is omniscient, yet (ii)
ON WHITCOMB S GROUNDING ARGUMENT FOR ATHEISM Joshua Rasmussen Andrew Cullison Daniel Howard-Snyder Abstract: Dennis Whitcomb argues that there is no God on the grounds that (i) God is omniscient, yet (ii)
The History of Logic. Aristotle (384 322 BC) invented logic.
 The History of Logic Aristotle (384 322 BC) invented logic. Predecessors: Fred Flintstone, geometry, sophists, pre-socratic philosophers, Socrates & Plato. Syllogistic logic, laws of non-contradiction
The History of Logic Aristotle (384 322 BC) invented logic. Predecessors: Fred Flintstone, geometry, sophists, pre-socratic philosophers, Socrates & Plato. Syllogistic logic, laws of non-contradiction
Peter: I think it's ridiculous. Almost as ridiculous as believing in the Tooth Fairy, or the Easter Bunny, or Santa Claus.
 The following dialogue is partially edited/modified to reduce length. The material is from Peter Kreeft s (1984) The Best Things in Life. Socrates: Are you looking for me, Peter? Peter: As a matter of
The following dialogue is partially edited/modified to reduce length. The material is from Peter Kreeft s (1984) The Best Things in Life. Socrates: Are you looking for me, Peter? Peter: As a matter of
Predicate Logic. For example, consider the following argument:
 Predicate Logic The analysis of compound statements covers key aspects of human reasoning but does not capture many important, and common, instances of reasoning that are also logically valid. For example,
Predicate Logic The analysis of compound statements covers key aspects of human reasoning but does not capture many important, and common, instances of reasoning that are also logically valid. For example,
KJV. King James Bible Study Correspondence Course An Outreach of Highway Evangelistic Ministries 5311 Windridge lane ~ Lockhart, Florida 32810 ~ USA
 BAPTISM Lesson 3 Return pages 6 & 7 11 "Now That I Am Saved, Where Do I Start? Water baptism is an important step of obedience in the life of a Christian. At the beginning of this study, one must realize
BAPTISM Lesson 3 Return pages 6 & 7 11 "Now That I Am Saved, Where Do I Start? Water baptism is an important step of obedience in the life of a Christian. At the beginning of this study, one must realize
II CORINTHIANS 5:11-21
 II CORINTHIANS 5:11-21 Lesson 11 FIRST DAY: Review and Overview 1. Share a verse or thought from II Corinthians 5:1-10 that continues to minister to you today. a. How does living in a tent affect your
II CORINTHIANS 5:11-21 Lesson 11 FIRST DAY: Review and Overview 1. Share a verse or thought from II Corinthians 5:1-10 that continues to minister to you today. a. How does living in a tent affect your
THE LAW OF SPIRIT OF LIFE HAS SET ME FREE!
 THE LAW OF SPIRIT OF LIFE HAS SET ME FREE! (Romans 8:1-4) INTRODUCTION To many Bible students Romans 8 is the high water mark of the book of Romans. In fact to some it is the high water mark of the Bible.
THE LAW OF SPIRIT OF LIFE HAS SET ME FREE! (Romans 8:1-4) INTRODUCTION To many Bible students Romans 8 is the high water mark of the book of Romans. In fact to some it is the high water mark of the Bible.
21. What was the original sin? A. It was Adam and Eve=s sin of pride and disobedience to God=s law. 22. When did you receive a share in God=s life
 92 Questions 1. How many Gods are there? A. One. 2. How many Persons are there in God? A. Three persons in God. 3. Who are they? What are their names? A. God the Father, God the Son, and God the Holy Spirit.
92 Questions 1. How many Gods are there? A. One. 2. How many Persons are there in God? A. Three persons in God. 3. Who are they? What are their names? A. God the Father, God the Son, and God the Holy Spirit.
Chapter 5: Fallacies. 23 February 2015
 Chapter 5: Fallacies 23 February 2015 Plan for today Talk a bit more about arguments notice that the function of arguments explains why there are lots of bad arguments Turn to the concept of fallacy and
Chapter 5: Fallacies 23 February 2015 Plan for today Talk a bit more about arguments notice that the function of arguments explains why there are lots of bad arguments Turn to the concept of fallacy and
3. Mathematical Induction
 3. MATHEMATICAL INDUCTION 83 3. Mathematical Induction 3.1. First Principle of Mathematical Induction. Let P (n) be a predicate with domain of discourse (over) the natural numbers N = {0, 1,,...}. If (1)
3. MATHEMATICAL INDUCTION 83 3. Mathematical Induction 3.1. First Principle of Mathematical Induction. Let P (n) be a predicate with domain of discourse (over) the natural numbers N = {0, 1,,...}. If (1)
Propositional Logic. A proposition is a declarative sentence (a sentence that declares a fact) that is either true or false, but not both.
 irst Order Logic Propositional Logic A proposition is a declarative sentence (a sentence that declares a fact) that is either true or false, but not both. Are the following sentences propositions? oronto
irst Order Logic Propositional Logic A proposition is a declarative sentence (a sentence that declares a fact) that is either true or false, but not both. Are the following sentences propositions? oronto
Lecture Notes in Discrete Mathematics. Marcel B. Finan Arkansas Tech University c All Rights Reserved
 Lecture Notes in Discrete Mathematics Marcel B. Finan Arkansas Tech University c All Rights Reserved 2 Preface This book is designed for a one semester course in discrete mathematics for sophomore or junior
Lecture Notes in Discrete Mathematics Marcel B. Finan Arkansas Tech University c All Rights Reserved 2 Preface This book is designed for a one semester course in discrete mathematics for sophomore or junior
8 THE TWISTED THINKING OF LOGICAL FALLACIES (CHAPTER 5)
 8 THE TWISTED THINKING OF LOGICAL FALLACIES (CHAPTER 5) Overview Statement: To be good critical thinkers, leaders must study logical fallacies, both so they can avoid using them and spot them in others.
8 THE TWISTED THINKING OF LOGICAL FALLACIES (CHAPTER 5) Overview Statement: To be good critical thinkers, leaders must study logical fallacies, both so they can avoid using them and spot them in others.
WALKING AFTER THE SPIRIT A Study on Romans 8:5-13. by Dr. Jack L. Arnold
 IIIM Magazine Online, Volume 2, Number 11, March 13 to March 19, 2000 WALKING AFTER THE SPIRIT A Study on Romans 8:5-13 by Dr. Jack L. Arnold A number of years ago I preached through Romans 8, and at that
IIIM Magazine Online, Volume 2, Number 11, March 13 to March 19, 2000 WALKING AFTER THE SPIRIT A Study on Romans 8:5-13 by Dr. Jack L. Arnold A number of years ago I preached through Romans 8, and at that
Logical Fallacies in Attacks Against the Bible: Eleven Examples
 Logical Fallacies in Attacks Against the Bible: Eleven Examples Edwin K. P. Chong Version: August 26, 2003 In this essay, I describe, by way of examples, eleven fallacies of logic and their use in attacking
Logical Fallacies in Attacks Against the Bible: Eleven Examples Edwin K. P. Chong Version: August 26, 2003 In this essay, I describe, by way of examples, eleven fallacies of logic and their use in attacking
FOUNDATIONS OF FORGIVENESS LESSON #1 I. GOD S FORGIVENESS IS
 FOUNDATIONS OF FORGIVENESS LESSON #1 Intro. Tonight we re going to open our series the foundations of forgiveness concentrating on God s forgiveness to us. In the upcoming weeks we ll look at our forgiveness
FOUNDATIONS OF FORGIVENESS LESSON #1 Intro. Tonight we re going to open our series the foundations of forgiveness concentrating on God s forgiveness to us. In the upcoming weeks we ll look at our forgiveness
True Worship. Douglas L. Crook
 True Worship by Douglas L. Crook True Worship John 4:24...must worship Him in spirit and in truth Let s consider this phrase and its meaning. To understand the concept of worshipping God in spirit and
True Worship by Douglas L. Crook True Worship John 4:24...must worship Him in spirit and in truth Let s consider this phrase and its meaning. To understand the concept of worshipping God in spirit and
CSL105: Discrete Mathematical Structures. Ragesh Jaiswal, CSE, IIT Delhi
 Propositional Logic: logical operators Negation ( ) Conjunction ( ) Disjunction ( ). Exclusive or ( ) Conditional statement ( ) Bi-conditional statement ( ): Let p and q be propositions. The biconditional
Propositional Logic: logical operators Negation ( ) Conjunction ( ) Disjunction ( ). Exclusive or ( ) Conditional statement ( ) Bi-conditional statement ( ): Let p and q be propositions. The biconditional
Solutions Q1, Q3, Q4.(a), Q5, Q6 to INTLOGS16 Test 1
 Solutions Q1, Q3, Q4.(a), Q5, Q6 to INTLOGS16 Test 1 Prof S Bringsjord 0317161200NY Contents I Problems 1 II Solutions 3 Solution to Q1 3 Solutions to Q3 4 Solutions to Q4.(a) (i) 4 Solution to Q4.(a)........................................
Solutions Q1, Q3, Q4.(a), Q5, Q6 to INTLOGS16 Test 1 Prof S Bringsjord 0317161200NY Contents I Problems 1 II Solutions 3 Solution to Q1 3 Solutions to Q3 4 Solutions to Q4.(a) (i) 4 Solution to Q4.(a)........................................
What Good Things Can We Do With the Tongue?
 TONGUE What Good Things Can We Do With the Tongue? 1 What Good Things Can We Do With the Tongue? 2 Timothy 1:13 INTRODUCTION: A. Lesson Texts: 1. 2 Timothy 1:13 Hold fast the pattern of sound words which
TONGUE What Good Things Can We Do With the Tongue? 1 What Good Things Can We Do With the Tongue? 2 Timothy 1:13 INTRODUCTION: A. Lesson Texts: 1. 2 Timothy 1:13 Hold fast the pattern of sound words which
What happens when logic and psychology meet?
 Logic meets psychology 1 What happens when logic and psychology meet? 27 September 2005 Core Logic Logic and Cognition Group m.e.counihan@uva.nl kamer 218 (Vendelstraat 8) tel. 020-525 4531 Logic meets
Logic meets psychology 1 What happens when logic and psychology meet? 27 September 2005 Core Logic Logic and Cognition Group m.e.counihan@uva.nl kamer 218 (Vendelstraat 8) tel. 020-525 4531 Logic meets
Inductive Reasoning Page 1 of 7. Inductive Reasoning
 Inductive Reasoning Page 1 of 7 Inductive Reasoning We learned that valid deductive thinking begins with at least one universal premise and leads to a conclusion that is believed to be contained in the
Inductive Reasoning Page 1 of 7 Inductive Reasoning We learned that valid deductive thinking begins with at least one universal premise and leads to a conclusion that is believed to be contained in the
PRAYER SERVICE FOR THE YEAR OF MERCY
 PRAYER SERVICE FOR THE YEAR OF MERCY DECEMBER 8, 2015 NOVEMBER 20, 2016 This brief prayer service may be used in any number of contexts (parish meetings, small groups, family prayer, etc.), and may be
PRAYER SERVICE FOR THE YEAR OF MERCY DECEMBER 8, 2015 NOVEMBER 20, 2016 This brief prayer service may be used in any number of contexts (parish meetings, small groups, family prayer, etc.), and may be
Society tells us otherwise. Our broke family and friends tell us otherwise.
 Breaking the Bondage of Debt Text: Proverbs 22:7 I. Intro a. You can t believe everything you hear. Think about it for a second: Who taught you that borrowing money was a good idea? i. Was it your broke
Breaking the Bondage of Debt Text: Proverbs 22:7 I. Intro a. You can t believe everything you hear. Think about it for a second: Who taught you that borrowing money was a good idea? i. Was it your broke
A FAMILY GUIDE TO SAVING FOR COLLEGE
 START SMART A FAMILY GUIDE TO SAVING FOR COLLEGE SCHOLASTIC and associated logos are trademarks and/or registered trademarks of Scholastic Inc. All rights reserved. WELCOME, PARENT OF A FUTURE COLLEGE
START SMART A FAMILY GUIDE TO SAVING FOR COLLEGE SCHOLASTIC and associated logos are trademarks and/or registered trademarks of Scholastic Inc. All rights reserved. WELCOME, PARENT OF A FUTURE COLLEGE
BORROWING MONEY FOR YOUR BUSINESS
 BORROWING MONEY FOR YOUR BUSINESS Disclaimer: There are thousands of books and websites that provide a great depth of information about how to finance a business with loans. This document provides a quick
BORROWING MONEY FOR YOUR BUSINESS Disclaimer: There are thousands of books and websites that provide a great depth of information about how to finance a business with loans. This document provides a quick
Main Point: Jesus is the one who is faithful. Main Application: Remember that Jesus is faithful even when we are not.
 Week 27, John 18:12 27 Hook Main Point: Jesus is the one who is faithful. Main Application: Remember that Jesus is faithful even when we are not. Discussion Questions: What is the biggest promise that
Week 27, John 18:12 27 Hook Main Point: Jesus is the one who is faithful. Main Application: Remember that Jesus is faithful even when we are not. Discussion Questions: What is the biggest promise that
WHERE IS The GOSPEL?
 Even the most confident man will not stand apart from Jesus GRADESCHOOL Pray with children to start class. THE STORY Teaching Points for Class Discussion: Peter s first denial Peter and another disciple
Even the most confident man will not stand apart from Jesus GRADESCHOOL Pray with children to start class. THE STORY Teaching Points for Class Discussion: Peter s first denial Peter and another disciple
WHERE DO OUR MORALS COME FROM? Moral relativism and self-interest theory
 WHERE DO OUR MORALS COME FROM? Moral relativism and self-interest theory In pairs, discuss the following questions: Are there any other living creatures that live moral lives? Discuss. Where does morality
WHERE DO OUR MORALS COME FROM? Moral relativism and self-interest theory In pairs, discuss the following questions: Are there any other living creatures that live moral lives? Discuss. Where does morality
Read this syllabus very carefully. If there are any reasons why you cannot comply with what I am requiring, then talk with me about this at once.
 LOGIC AND CRITICAL THINKING PHIL 2020 Maymester Term, 2010 Daily, 9:30-12:15 Peabody Hall, room 105 Text: LOGIC AND RATIONAL THOUGHT by Frank R. Harrison, III Professor: Frank R. Harrison, III Office:
LOGIC AND CRITICAL THINKING PHIL 2020 Maymester Term, 2010 Daily, 9:30-12:15 Peabody Hall, room 105 Text: LOGIC AND RATIONAL THOUGHT by Frank R. Harrison, III Professor: Frank R. Harrison, III Office:
A. Arguments are made up of statements, which can be either true or false. Which of the following are statements?
 Critical Thinking University of St Andrews March 2007 Bullet point material is not on the students copies. Feel free to use the material as you see fit, depending on timing, ability, enthusiasm etc. Good
Critical Thinking University of St Andrews March 2007 Bullet point material is not on the students copies. Feel free to use the material as you see fit, depending on timing, ability, enthusiasm etc. Good
Life Insurance Buyer's Guide
 Life Insurance Buyer's Guide This guide can help you when you shop for life insurance. It discusses how to: Find a Policy That Meets Your Needs and Fits Your Budget Decide How Much Insurance You Need Make
Life Insurance Buyer's Guide This guide can help you when you shop for life insurance. It discusses how to: Find a Policy That Meets Your Needs and Fits Your Budget Decide How Much Insurance You Need Make
What is the Church? Matthew 16:18
 THE CHURCH What is the Church? 1 What is the Church? Matthew 16:18 INTRODUCTION: A. Matthew 16:18... And on this rock I will build My church. What is the church? 1. The prophets of old prophesied about
THE CHURCH What is the Church? 1 What is the Church? Matthew 16:18 INTRODUCTION: A. Matthew 16:18... And on this rock I will build My church. What is the church? 1. The prophets of old prophesied about
The Cathedral of the Immaculate Conception
 The Cathedral of the Immaculate Conception Second Readings- Taken from the New Testament Please make your choices from the following readings and refer to the reading number in the box above the reading:
The Cathedral of the Immaculate Conception Second Readings- Taken from the New Testament Please make your choices from the following readings and refer to the reading number in the box above the reading:
LESSON TITLE: The Great Commandment. THEME: Love is the fulfillment of the Law. SCRIPTURE: Mark 12:28-34 CHILDREN S DEVOTIONS FOR THE WEEK OF:
 Devotion NT264 CHILDREN S DEVOTIONS FOR THE WEEK OF: LESSON TITLE: The Great Commandment THEME: Love is the fulfillment of the Law. SCRIPTURE: Mark 12:28-34 Dear Parents Welcome to Bible Time for Kids.
Devotion NT264 CHILDREN S DEVOTIONS FOR THE WEEK OF: LESSON TITLE: The Great Commandment THEME: Love is the fulfillment of the Law. SCRIPTURE: Mark 12:28-34 Dear Parents Welcome to Bible Time for Kids.
The Mathematics of GIS. Wolfgang Kainz
 The Mathematics of GIS Wolfgang Kainz Wolfgang Kainz Department of Geography and Regional Research University of Vienna Universitätsstraße 7, A-00 Vienna, Austria E-Mail: wolfgang.kainz@univie.ac.at Version.
The Mathematics of GIS Wolfgang Kainz Wolfgang Kainz Department of Geography and Regional Research University of Vienna Universitätsstraße 7, A-00 Vienna, Austria E-Mail: wolfgang.kainz@univie.ac.at Version.
Borrowing Money Standard 7 Assessment
 1 Name: Class Period: Borrowing Money Directions: Match each description in the column below with the CORRECT term from the list. Write the letter of the term in the space provided. A. Interest B. Interest
1 Name: Class Period: Borrowing Money Directions: Match each description in the column below with the CORRECT term from the list. Write the letter of the term in the space provided. A. Interest B. Interest
{ Put Your Armor On! }
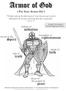 { Put Your Armor On! } Therefore take up the whole armor of God, that you may be able to withstand in the evil day, and having done all, to stand firm. helmet of salvation A study of the Armor of God from
{ Put Your Armor On! } Therefore take up the whole armor of God, that you may be able to withstand in the evil day, and having done all, to stand firm. helmet of salvation A study of the Armor of God from
God Hears and Answers"" 7/10/11 1 John 5:13-15
 God Hears and Answers"" 7/10/11 1 John 5:13-15 Introduction I'd like to begin by asking you a question. What are the five most significant prayers that you've ever prayed? To clarify the question, when
God Hears and Answers"" 7/10/11 1 John 5:13-15 Introduction I'd like to begin by asking you a question. What are the five most significant prayers that you've ever prayed? To clarify the question, when
Arguments and Dialogues
 ONE Arguments and Dialogues The three goals of critical argumentation are to identify, analyze, and evaluate arguments. The term argument is used in a special sense, referring to the giving of reasons
ONE Arguments and Dialogues The three goals of critical argumentation are to identify, analyze, and evaluate arguments. The term argument is used in a special sense, referring to the giving of reasons
How to Get Your Prayers Answered. By Dr. Roger Sapp
 How to Get Your Prayers Answered By Dr. Roger Sapp There are many good Christians who pray daily with diligence and with discipline but seem to struggle to get their prayers answered by the Father. On
How to Get Your Prayers Answered By Dr. Roger Sapp There are many good Christians who pray daily with diligence and with discipline but seem to struggle to get their prayers answered by the Father. On
The Disciple Driven Church
 The Disciple Driven Church An Old Expression of Faith in a Fresh New Way Contributors: Dr. Terry & Suzette Goodwin What is Different About the Disciple Driven Church? Question? Is your faith focused more
The Disciple Driven Church An Old Expression of Faith in a Fresh New Way Contributors: Dr. Terry & Suzette Goodwin What is Different About the Disciple Driven Church? Question? Is your faith focused more
Chapter 1. Use the following to answer questions 1-5: In the questions below determine whether the proposition is TRUE or FALSE
 Use the following to answer questions 1-5: Chapter 1 In the questions below determine whether the proposition is TRUE or FALSE 1. 1 + 1 = 3 if and only if 2 + 2 = 3. 2. If it is raining, then it is raining.
Use the following to answer questions 1-5: Chapter 1 In the questions below determine whether the proposition is TRUE or FALSE 1. 1 + 1 = 3 if and only if 2 + 2 = 3. 2. If it is raining, then it is raining.
Understanding Regulation U
 Understanding Regulation U What every deal lawyer needs to know about the margin regulations November 17, 2011 Craig Unterberg David Aman Federal Margin Regulations Background Authorized under Section
Understanding Regulation U What every deal lawyer needs to know about the margin regulations November 17, 2011 Craig Unterberg David Aman Federal Margin Regulations Background Authorized under Section
WRITING PROOFS. Christopher Heil Georgia Institute of Technology
 WRITING PROOFS Christopher Heil Georgia Institute of Technology A theorem is just a statement of fact A proof of the theorem is a logical explanation of why the theorem is true Many theorems have this
WRITING PROOFS Christopher Heil Georgia Institute of Technology A theorem is just a statement of fact A proof of the theorem is a logical explanation of why the theorem is true Many theorems have this
CONTEMPORARY MORAL PROBLEMS LECTURE 9 ABORTION PART 1 THE MAIN ISSUE. Is abortion morally permissible? Let us avoid:
 CONTEMPORARY MORAL PROBLEMS LECTURE 9 ABORTION PART 1 1 THE MAIN ISSUE Is abortion morally permissible? Let us avoid: 1. Loaded labels such as "pro-choice," "antichoice," "pro-life," "pro-abortion" 2.
CONTEMPORARY MORAL PROBLEMS LECTURE 9 ABORTION PART 1 1 THE MAIN ISSUE Is abortion morally permissible? Let us avoid: 1. Loaded labels such as "pro-choice," "antichoice," "pro-life," "pro-abortion" 2.
Faith is the Victory In Overcoming Sin
 FAITH Faith is the Victory In Overcoming Sin 1 Faith is the Victory In Overcoming Sin 1 John 5:4-5 INTRODUCTION: A. The theme of this series is Faith is the Victory!, with our basic text found in 1 John
FAITH Faith is the Victory In Overcoming Sin 1 Faith is the Victory In Overcoming Sin 1 John 5:4-5 INTRODUCTION: A. The theme of this series is Faith is the Victory!, with our basic text found in 1 John
plain talk about life insurance The right life insurance can have an enormous effect on your life and the lives of those you love.
 plain talk about life insurance The right life insurance can have an enormous effect on your life and the lives of those you love. Thinking about life insurance? You re not alone. Canadians generally agree
plain talk about life insurance The right life insurance can have an enormous effect on your life and the lives of those you love. Thinking about life insurance? You re not alone. Canadians generally agree
A simple solution to the hardest logic puzzle ever
 a simple solution to the hardest logic puzzle ever 105 11 Potts, C. 2005. The Logic of Conventional Implicatures. Oxford: Oxford University Press. Searle, J. R. and D. Vanderveken. 1985. Foundations of
a simple solution to the hardest logic puzzle ever 105 11 Potts, C. 2005. The Logic of Conventional Implicatures. Oxford: Oxford University Press. Searle, J. R. and D. Vanderveken. 1985. Foundations of
P1. All of the students will understand validity P2. You are one of the students -------------------- C. You will understand validity
 Validity Philosophy 130 O Rourke I. The Data A. Here are examples of arguments that are valid: P1. If I am in my office, my lights are on P2. I am in my office C. My lights are on P1. He is either in class
Validity Philosophy 130 O Rourke I. The Data A. Here are examples of arguments that are valid: P1. If I am in my office, my lights are on P2. I am in my office C. My lights are on P1. He is either in class
