Unit. Area Model Factoring. Research-based National Science Foundation-funded. Learning transforms lives.
|
|
|
- Willa Ross
- 8 years ago
- Views:
Transcription
1 Unit 10 Area Model Factoring Research-based National Science Foundation-funded Learning transforms lives.
2 Dear Student, When we multiply two factors, we get their product. If we start with the product, we can undo the multiplication to find the factors. The process of discovering the factors that can be multiplied to give a number or epression is called factoring = ( + _ )( + _) Unit 10 uses area models to make sense of factoring. You ve already learned how to multiply two algebraic epressions using an area model: ( + 7)( 2) = We can also use area models to un-multiply, to start with an algebraic epression and factor it, that is, find two other epressions whose product is that original epression. _ 2 _ = ( + _ )( + _) Unit 10 shows how multiplication, division, and factoring are all related, how division and factoring are like opposites of multiplication, and how we can use area models to reason about all three. The Authors
3 Lesson 3: Factoring IMPORTANT STUFF Problems 1 and 2 ask about the equation ( 2)( 5) = and its area model. 1 What calculation creates the 10 in ? -2 _ 2 What calculation creates the -7 in ? -2 + _ Problems 3 and 4 ask about the equation ( + 3)( 8) = and its area model shown below What calculation creates the -24 in ? 4 What calculation creates the -5 in ? 5 List all the pairs of integers (positive or negative) whose product is Which pair has a sum of 7? 7 Which pair has a sum of 8? 8 Which pair has a sum of 13? 9 Which pair has a sum of -7? Use an area model to factor. Complete each model and equation = = = = Unit 10: Area Model Factoring
4 Complete the model and finish Jay s thought = ( ) ( ) 2 2 Thinking out Loud Jay: I can tell from the equation that I need a pair of numbers whose product is 2 and whose sum is. The numbers are and so the factors must be and. 15 List all the pairs of integers (positive or negative) whose product is Which pair has a sum of 11? 17 Which pair has a sum of -13? 18 Which pair has a sum of 31? 19 Which pair has a sum of -17? Use an area model to factor. Complete each model and equation = = = = Who Am I? t + u = 10 tu = 21 t > u t u 25 Who Am I? t + u = 10 tu = 25 t u 26 Who Am I? t + u = 11 tu = 30 u > t t u 27 Who Am I? t + u = 12 tu = Who Am I? t u t u t + u = 11 tu = 24 t < u 29 Who Am I? tu = 81 t + u = 18 t u Lesson 3: Factoring 13
5 STUFF TO MAKE YOU THINK For some epressions, factoring with the area model doesn t give any new information. b For eample, it s not helpful to fill in the outside of this model _ 1 b because b 2 and 4 have no common factors besides An epression like b that cannot be factored (that is, has no factors other than itself and 1) is called prime, just like a number whose only factors are itself and 1! Determine if it makes sense to factor each epression. If so, complete the area model. If not, cross it out and label it prime. a b c 2h 9 _ 6p 60 _ 4w 2 _ 8w d 8w 2 _ 3 e 10m 2 30m 80 f g _ c 2 8c _ 3c 24 h _ 30a 2 7w _ 15a _ 25b 2 _ 5c 31 Here are four ways to set up the epression n 2 + 9n + 14 in a model. Three of the ways don t help or don t work when you try to fill out the outside. Cross out the three that don t help or don t work, complete the one that does, and write an equation to match it. a n 2 9n 14 b _ n 2 9n _ 0 14 c d _ n 2 7n _ 2n 14 _ n 2 3n _ 6n Unit 10: Area Model Factoring
6 Imagine you have been asked to help design a village. The people only want roads that travel northsouth, or east-west, so that their intersections form right angles like this: and not like this:. All of the north-south roads must cross all the east-west roads. W N E 32 Draw how you would arrange 5 roads so there are 33 Sketch a village map in which 7 roads 6 intersections in the village. form 10 intersections. S 34 Factor the epression r 2 + 5r Factor the epression r 2 + 7r r 2 6 ( )( ) r Suppose the people said they wanted 12 intersections but didn t care how many roads they had. How many different possible arrangements could you make? Draw the maps. What is the smallest number of roads that will still give them 12 intersections? 37 With eactly 10 roads, what is the smallest number of intersections there can be? What is the greatest number of intersections? TOUGH STUFF Factoring doesn t always work out into neat and tidy factors. You may have to try a lot of different ways = ( ) ( ) = ( ) ( ) Lesson 3: Factoring 15
7 Additional Practice Factor each epression. A a a + 56 = B y y + 42 = a 2 7a y There is no squared term here C = D = _ ( ) E z z + 72 = F = z G q 2 + 4q + bq = q b H y = 6 y 4q 7 2 I = J = K k 2 + 2k 48 = L r 2 + 8r + 7 = Draw your own area models. 16 Unit 10: Area Model Factoring
8 For these problems, only the inside of the area model is filled in. Find a way to complete the outside of the model and use your work to write at least one equation (using multiplication or division) that is represented by the area model. M _ 9y 45 N _ 2n 2 16n O 10a 2 P _ 6a Q _ p 2 2p R ac 3a 4a 2 _ 10p 20 S Here are four ways to set up the epression w w + 30 inside an area model. Three of the ways don t help or don t work when you try to fill out the outside. Cross out the three that don t help or don t work, complete the one that does, and write an equation to match it. i w 2 11w 30 ii _ w 2 11w _ iii _ w 2 10w _ w 30 iv _ w 2 6w _ 5w 30 Lesson 3: Factoring 17
9 TEACHING GUIDE Area Model Factoring Unit 10 Teaching Guide Unit 10 June Mark E. Paul Goldenberg Mary Fries Jane M. Kang Tracy Cordner Unit 10 Area Model Factoring HEINEMANN Portsmouth, NH Research-based National Science Foundation-funded Learning transforms lives.
10 firsthand An imprint of Heinemann 361 Hanover Street Portsmouth, NH Offices and agents throughout the world Education Development Center, Inc. 43 Foundry Avenue Waltham, MA by Education Development Center, Inc. Co-Principal Investigators and Project Directors: E. Paul Goldenberg and June Mark Development and Research Team: Tracy Cordner, Mary Fries, Mari Halladay, Jane M. Kang, and Josephine Louie Contributors: Cindy Carter, Susan Creighton, Jeff Downin, Doreen Kilday, Deborah Spencer, and Yu Yan Xu This material is based on work supported by the National Science Foundation under Grant No. ESI Opinions epressed are those of the authors and not necessarily those of the Foundation. All rights reserved. No part of this book may be reproduced in any form or by any electronic or mechanical means, including information storage and retrieval systems, without permission in writing from the publisher, ecept by a reviewer, who may quote brief passages in a review, and with the eception of reproducible pages, which are identified by the Transition to Algebra copyright line, and may be photocopied for classroom use only. Dedicated to Teachers is a trademark of Greenwood Publishing Group, Inc. Due to a printing error, the area model on the front cover of the Student Worktet may be colored incorrectly; the shading on the lower half of the model may be missing. (Compare the Worktets covers to the Answer Key cover, which has the correct shading.) If your students have mis-printed copies, you may wish to discuss and have students color the model to complete an ( + 3)( + 2) model. Transition to Algebra, Unit 10: Area Model Factoring Teaching Guide ISBN-13: Transition to Algebra Teacher Resources ISBN-13: Transition to Algebra, Unit 10 Student Worktets 10-pack ISBN-13: Transition to Algebra Student Worktets, 10 Sets of All 12 Units ISBN-13: Printed in the United States of America on acid-free paper RRD
11 Unit 10 Area Model Factoring CONTENTS T4 Unit Introduction T7 Lesson 1: Division Undoes Multiplication T10 Lesson 2: Area Model Inside Out T13 Lesson 3: Factoring T16 Student Reflections & Snapshot Check-in T17 Lesson 4: Products, Sums, and Signs T20 Lesson 5: Zero Product Property T22 Lesson 6: Solving by Factoring T25 Student Reflections & Unit Assessment T26 Eploration: Area Model Cutouts T29 Eploration: Signed Area Model Cutouts T31 Activity: Area Model Puzzles RESOURCES T32 Finding Pairs Cutout (Lesson 5) T33 Snapshot Check-in T34 Snapshot Check-in Answer Key T35 Unit Assessment T36 Unit Assessment Answer Key T37 MENTAL MATHEMATICS Factors, products & sums and percentage calculations T38 Finding factor pairs T39 Finding factor pairs with negatives T40 Product and sum T41 Finding factors using products and sums T42 Finding factors using sums and products T43 10% of a number T44 20% of a number T45 Finding 5% and 15% of a number T46 10% off T47 10% more T48 20% off T3
12 2/6/14 3:43 PM Unit 10 Area Model Factoring UNIT 10 Area Model Research-based National Science Foundation-funded Learning transforms lives. Factoring Learning Goals By the end of Unit 10, students should be able to: Understand both division and factoring as ways of undoing multiplication. Understand how a single area model can represent multiplication, division, or factoring depending on which pieces are given and which pieces are sought. Factor monic quadratic trinomials by finding the two numbers with a given sum and product. Use the zero product property to solve quadratic equations. Factoring can be a difficult concept for introductory algebra students to learn and master. This unit presents factoring as a kind of un-multiplying, building on the ideas of Unit 4: Area and Multiplication, which introduced the area model as a tool for organizing multiplication of numbers and polynomials. In this unit, students first consider division with area models, working with a given area (the product of the multiplication being undone) and one side length of the area model (a factor) to find the other length (the other factor of the original multiplication). Students then connect the models to corresponding multiplication and division equations and eplore area model puzzles that provide enough information about the factors and product to find the missing terms. This supports students in understanding the roles of and relationships between the pieces of the area model and their corresponding equations and in thinking fleibly with the model in preparation for factoring. The factoring problems in this unit focus primarily on epressing trinomial products as two binomial factors. Students also practice finding sums for pairs of numbers with a given product and build logic about the zero product property and its role in solving equations by factoring. Factoring and Area Models As in distribution, where multiplying 2(n + 3) can appear to students to be a different process from multiplying ( + 3)( 4), where the FOIL (first, outer, inner, last) approach is often used, factoring can also be seen as several different processes. For instance, factoring can appear altogether different from simplifying 9h + 6h a rational epression like 3h or solving an equation like 2 8 = 0. Factor = ( 7)( + 11) T4 Transition to Algebra Unit 10: Area Model Factoring TEACHING GUIDE
13 The area model provides a contet in which students can unify their understanding of these seemingly different processes with a single tool. Simplify 3 2 3h 9h 6h 9h + 6h 3h 9h + 6h 3h = 3h(3 + 2) Area Model Puzzles As Unit 4 did to some etent, this unit presents area model problems in the form of puzzles. Parts of the product are shown, parts of the factors are shown, and students need to treat these problems much the way they d treat any puzzle by first looking to see what empty space(s) they can fill in with certainty. Then, they can chase other empty spaces around the puzzle until they ve filled in all the blanks. This is, of course, neither a case of pure division, where the product and one of the factors are completely known, nor a case of pure factoring, where only the product is known and one has no knowledge about the factors. In pure division, the puzzle is simpler: one knows eactly where to start. In a pure factoring problem, the puzzle might take a bit of eperimentation before chasing the empty spaces around, but the process of using logic together with the known structure of the area model to find the remaining pieces is the same. Lesson 2 introduces area model puzzles to focus attention on the roles of different parts of the area model and how these pieces relate within a given model and to the problem at hand. Factoring Puzzles MysteryGrid puzzles requiring numerical factoring appear in the Stuff to Make You Think and Tough Stuff problems in Lessons 1 and 2; then in these same sections of Lesson 4, students confront MysteryGrid puzzles with polynomial elements and clues that require factoring. MysteryGrid 5, 6, 7, 8 12, + 48, 2 8 = = ( 8) = 0 Either = 0 or 8 = 0 _ 5 3m 6mj MysteryGrid 0, 1,, 2 2, , + _ 14j 35 Seeking and Using Structure In this unit, students use the Algebraic Habits of Mind familiar structure of the area model and its relationship to multiplication to strengthen and build an intuitive understanding of the necessary computational skills for factoring algebraic epressions and solving equations by factoring. Equations such as ( 1)( + 2) = 0 are viewed as two separate chunks of information: either 1 = 0 or + 2 = 0 (or both). This relies on an understanding of the zero product property and supports solving quadratic equations by factoring. Using Tools Strategically As students etend their use of area models to the division and factoring of polynomials, they have to be strategic about their placement of the given information in the model. Students also use tables to organize their search for pairs of numbers with a given sum and product. Puzzling and Persevering All of the puzzles in Unit 10 MysteryGrids, Who Am I? puzzles, Mystery Number puzzles, and area model puzzles are designed to engage students in mathematics related to factoring. These puzzles offer a natural contet for perseverance in factoring, as students must look around, make sense of given information, identify a reasonable starting place, consider potential solving strategies, identify reasonable net steps, and determine when the puzzle is solved. 56, 30, 40, 2, + 42, 0, 1, + 14, + 35, 2 + 1, + T5
14 Who Am I? puzzles in the Additional Practice of Lessons 2 and 4 and in the Important Stuff of Lesson 3 require students to consider pairs of numbers with a given product and sum. Mystery Number puzzles, such as the problem with butterflies shown here, appear as contets for using the zero product property to solve systems of equations in Lessons 5 and 6. Who Am I? t + u = 10 tu = 21 t > u = + = t u = A monic quadratic trinomial is a polynomial with three terms (trinomial) with a highest power of two (quadratic) and a coefficient of 1 on the leading term (monic). For eample, the epression is a monic quadratic trinomial. Mental Mathematics: Factors, Products & Sums and Percentage Calculations There are two strands of Mental Mathematics for this unit. The first strand connects directly to the mathematical content of Unit 10; students consider the factor pairs of a given number, calculate the product and sum for pairs of numbers, and identify which pair of numbers will yield a given product and sum. These activities support the factoring of monic quadratic trinomials presented in the lessons. The second strand of Mental Mathematics in this unit builds on students eperiences multiplying and dividing by 10, 2, and 5 in Units 1, 4, and 5, etending these ideas to calculations with percentages. Students calculate 5%, 10%, 15%, and 20% of given numbers and later also percent off, which requires subtraction. These ideas are likely to be relevant contets for mental mathematics in students lives. Eplorations The two Eplorations in this unit, Area Model Cutouts and Signed Area Model Cutouts, support greater understanding of factoring with quadratic polynomials through a hands-on activity. Students arrange 2,, and square unit paper cutouts into rectangles and record their results using area models and equations. Related Activity In the Related Activity, Area Model Puzzles, students build and share their own area model puzzles, reinforcing the structure and function of the area model and giving students an opportunity to create their own mathematics. T6 Transition to Algebra Unit 10: Area Model Factoring TEACHING GUIDE
15 Lesson 3: Factoring PURPOSE This lesson introduces factoring monic quadratic trinomials by identifying which calculations result in which pieces of the product and by considering how finding sums and products relates to factoring. By eploring equations of the form 2 + _ + 12 and finding that there is only one possible factor pair for a given middle term, students prepare for the product/sum search involved in factoring. Mental Mathematics Begin each day with five minutes of Mental Mathematics (pages T37 T48). In today s lesson, students will see how to use both products and sums in factoring quadratic trinomials. Launch: The Roles of Sums and Products Allow time for students to consider PROBLEMS 1 4 in the Student Worktet. Lesson at a Glance Mental Mathematics (5 min) Launch: The Roles of Sums and Products (10 min) Students work through the first four problems in the Student Worktet and discuss the roles of sums and products in factoring trinomials into binomial pairs. Student Problem Solving and Discussion (20 min) Allow time for students to work through the Important Stuff and eplore additional problems. Students identify pairs of numbers with a given product and then pairs with given sums, and they use this information to factor several epressions. Reflection and Assessment (10 min) Snapshot Check-in Unit 10 Related Activity: Area Model Puzzles (See page T31 and Student Worktet page 37.) Problems 1 and 2 ask about the equation ( 2)( 5) = and its area model. 1 What calculation creates the 10 in ? -2 _ 2 What calculation creates the -7 in ? -2 + _ Then bring the group together to discuss student responses. Net, draw this problem on the board.? What if... What if students suggest something like this? = Discuss the form that the factors will take: ( + _) ( + _). Remind students that not all trinomials are factorable, but for now, we will be looking only at ones that are. Ask students to identify the calculations in the model that result in the 18 and 9 terms, and work together to identify pairs of numbers with a product of 18 and a sum of 9. Write the factors out, and verify that these are the correct factors by completing the model. As students offer suggestions for filling in the empty spaces, challenge them to eplain their reasoning. Draw students attention to the term on the outside left. This term requires that any term in that row have a factor of as well (unless the other factor had a term with an in the denominator, but this is not common in introductory algebra). Then ask students to identify the term that must go at the top of the rightmost column. Likely, someone will notice that the 3 actually belongs there. Lesson 3: Factoring T13
16 Student Problem Solving and Discussion Allow time for students to work on the problems in the Student Worktet. Listen for students describing two things: The coefficient of the term is the sum of the two numbers in the factors. The number (the constant term) at the end of the trinomial is the product of these same two numbers. If some students don t complete the Thinking Out Loud bo on page 13, spend some time analyzing the model using Jay s thoughts: talk about the model, how it works, why it works that way, where there are factors, products, sums, and terms, and how they relate. Ask about this model and others on this page. Ask students to tell you which models they ve understood, and then help them connect what they understand to this model. Starting with an epression and using the area model to find the original factors is what has been called un-multiplying. Feel free to use this term as a way to help students see the interconnectedness between multiplication, division, and factoring. In PROBLEMS 5 13, students list all of the integer pairs that result in the product 12, then identify which pairs have various sums, and complete area models to factor trinomials of the form 2 + b + 12, where b varies among the sums. Students then, in PROBLEM 14, complete a statement of reasoning about the process before working through a similar set of problems with a product of 30. Complete the model and finish Jay s thought = ( ) ( ) 2 2 Thinking Out Loud Jay: I can tell from the equation that I need a pair of numbers whose product is 2 and whose sum is. The numbers are and, so the factors must be and. PROBLEMS feature Who Am I? puzzles in which students search for numbers with a particular product and sum. 24 Who Am I? t + u = 10 tu = 21 t > u t u 25 Who Am I? t + u = 10 tu = 25 t u In the Stuff to Make You Think, students consider problems in which it is not helpful to factor, which arrangements of terms in area models are helpful, and several perpendicular street diagrams that use similar sum and product reasoning to that in the lesson. PROBLEMS can be completed with manipulatives like toothpicks or popsicle sticks. Tough Stuff PROBLEMS 38 & 39 feature more difficult trinomial factoring, such as an epression with a fractional coefficient and a non-monic trinomial = ( ) ( ) = ( ) ( ) Questions such as the following can support discussion:»» If you know that the area model for will look like this (show the model at right), how can you determine what goes in the other two boes? 2 24 T14 Transition to Algebra Unit 10: Area Model Factoring TEACHING GUIDE
17 Listen for students who use the model to eplain why the two missing pieces of the factors will have a product of 24 and a sum of 11. Students should be able to describe that because the area of the lower right rectangle is 24, the two side lengths will have a product of 24 and because the remaining two pieces of area will each have one factor of, the coefficients of these two like terms will have to sum to 11.»» How do the Mental Mathematics activities we ve been doing in this unit relate to factoring? Listen for students who identify the connection between finding the pair of numbers with a given product and sum and the thinking required for factoring.»» How can we determine what size area model will best help us factor an epression? Remind students that not all epressions are factorable and factoring often does require some trial and error. Present epressions like y 25, , and Whenever there is a common factor among all the terms in the epression (such as 5 in the first epression), it is helpful to use a 1 something model (in this case, 1 3) to factor out the common factor; then additional factoring can take place from there as needed. In the epressions and 2 25, however, students may identify that there is no common factor, so using a 2 2 model allows for the 2 term and the constant term to be placed in different rows and columns. Lesson 3: Factoring T15
18 CHECK IN Student Reflections & Snapshot Check-in Ask students to reflect on their learning: What are some things you ve learned so far in this unit? What questions do you still have? Assess student understanding of the ideas presented so far in the unit with the Snapshot Check-in on page T33. Use student performance on this assessment to guide students to select targeted Additional Practice problems from this or prior lessons as necessary. So far in Unit 10, students have: Translated area models into algebraic equations showing multiplication and division. Used area models to divide algebraic epressions by a factor. Completed area model puzzles with various pieces of information omitted. Considered the use of factoring in simplifying rational epressions. Used area models to factor monic quadratic trinomials. Students have been developing the following Algebraic Habits of Mind: Puzzling and Persevering Students have worked through area models inside out, using available clues to work out the missing information. They have also solved Who Am I? number puzzles that require thinking similar to factoring finding two numbers with a given product and sum. Using Tools Strategically Students have etended their use of the area models to support their thinking about division and factoring. Seeking and Using Structure Students have connected the structure of the information provided in or found using area models to the structure of algebraic equations involving multiplicative operations with polynomials. T16 Transition to Algebra Unit 10: Area Model Factoring TEACHING GUIDE
19 Snapshot Check-in Name: Use the area model to write three equations: one using multiplication and two using division Draw an area model and use it to answer this division problem. 2 12w 20 4 = _ Fill in the missing information to complete this area model and the equation that goes with it. 3 v 2 2v 5v 10 4 v = 5 List all the pairs of integers (positive or negative) whose product is -15. Use an area model to factor. Complete the model and equation = by Heinemann and Education Development Center, Inc., from Transition to Algebra (Portsmouth, NH: Heinemann). This page may be reproduced for classroom use only. Unit 10: Area Model Factoring Snapshot Check-in R5 Snapshot Check-in 2014 by Heinemann and Education Development Center, Inc., from Transition to Algebra (Portsmouth, NH: Heinemann). This page may be reproduced for classroom use only. T33
20 Snapshot Check-in Name: ANSWER KEY Use the area model to write three equations: one using multiplication and two using division ( 4) = = = 2 Draw an area model and use it to answer this division problem. 2 12w 20 4 = _ 3w 5 3w w -20 Fill in the missing information to complete this area model and the equation that goes with it. 3 v v 2 2v 5 v 2 5v v (v + 5)(v + 2) v = 5 List all the pairs of integers (positive or negative) whose product is Use an area model to factor. Complete the model and equation = ( 5)( + 3) (Factors can be written in either order.) 2014 by Heinemann and Education Development Center, Inc., from Transition to Algebra (Portsmouth, NH: Heinemann). This page may be reproduced for classroom use only. Unit 10: Area Model Factoring Snapshot Check-in R6 Transition to Algebra Unit 10: Area Model Factoring TEACHING GUIDE T by Heinemann and Education Development Center, Inc., from Transition to Algebra (Portsmouth, NH: Heinemann). This page may be reproduced for classroom use only.
21 Unit 10 Mental Mathematics Factors, products & sums and percentage calculations The two mental mathematics activities in this unit are not related to each other but are both useful in high school mathematics. Students work with number pairs corresponding to specific products and sums, which supports the product-sum search in factoring quadratic trinomials. The structure of these activities differs in format from the previous ones in that inputs and outputs comprise multiple pieces of information. Then students review common percentages. Students make mental calculations, such as finding 20% off prices epressed in dollar amounts. The percentage activities serve multiple purposes: they re-animate skills and associations students have already developed, and they give the opportunity for the lively, fast-paced back-and-forth that students may have been missing in the first five activities. In nearly all of these mental mathematics activities, students enact a function : an input-output rule is established at the outset, and students give the output for each input they hear. Each function rule focuses on a key mathematical idea or property (e.g. complements or the distributive property) that students begin to feel intuitively. After introducing the day s task, the teacher deliberately does not reiterate the task but says only the input numbers for students to transform. Minimizing words lets students focus on the numerical pattern of the activity, helping them perceive the structure behind the mathematics. A lively pace maimizes practice and keeps students engaged. T37
22 $90 $81 Mental Mathematics Activity 9 10% off PURPOSE Students keep mental track of two processes: they find 10% of a given number and then they subtract it from the original number. 10% off is a familiar sight for students and one worth understanding. Do not pressure students to stop verbalizing the value for 10%. Encourage them, always, to whisper intermediate steps to themselves if they find that helps. Competent mathematicians will do the same! The easiest way to calculate a 90% off sale is to take 10% of the price! Introduce: When you see a sale that says 10% off, do you know what that means? It s not the same as 10% of. Let students respond. Sure, you look at the price, figure out 10% of it, and then subtract that from the original price. Today, you ll take 10% off every price I name. So, if I say $200, what would you say? Start by first saying softly to yourself what 10% of that is. Right, $20. Now subtract that from $200. Right, $180. What if I said $400? You d say... yes, $40, then $360. You ve got it. Let s keep going! About this sequence: Calculating 10% off is different from anything students have been asked to mentally calculate before, so both steps consist mostly of inputs that are deliberately easy calculations. Step 1: Have students find 10% off each price you give. Use multiples of 10 and 100, and encourage students to verbalize (softly) their calculation of 10% before calling out their final answer. Input 10% Output (Input minus 10%) $10 $1 $9 $300 $30 $270 $500 $50 $450 $20 $2 $18 $80 $8 $72 $2000 $200 $1800 Step 2: Encourage students to keep whispering the interim step (finding 10%) to themselves, but have them say only the final result (10% off) out loud. Include some values that are not multiples of 10. $80 $72 $20 $18 $4 $3.60 $10 $9 $200 $180 $400 $360 $450 $405 $70 $63 $25 $22.50 $75 $67.50 $300 $270 $90 $81 $4000 $3600 $170 $153 $5 $4.50 $220 $198 $150 $135 $6.99 $6.29 $230 $207 $1.99 $1.79 T46 Transition to Algebra Unit 10: Area Model Factoring TEACHING GUIDE
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
A.3. Polynomials and Factoring. Polynomials. What you should learn. Definition of a Polynomial in x. Why you should learn it
 Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Section 5.0A Factoring Part 1
 Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
Section 5.0A Factoring Part 1 I. Work Together A. Multiply the following binomials into trinomials. (Write the final result in descending order, i.e., a + b + c ). ( 7)( + 5) ( + 7)( + ) ( + 7)( + 5) (
SUNY ECC. ACCUPLACER Preparation Workshop. Algebra Skills
 SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
SUNY ECC ACCUPLACER Preparation Workshop Algebra Skills Gail A. Butler Ph.D. Evaluating Algebraic Epressions Substitute the value (#) in place of the letter (variable). Follow order of operations!!! E)
Using the Area Model to Teach Multiplying, Factoring and Division of Polynomials
 visit us at www.cpm.org Using the Area Model to Teach Multiplying, Factoring and Division of Polynomials For more information about the materials presented, contact Chris Mikles mikles@cpm.org From CCA
visit us at www.cpm.org Using the Area Model to Teach Multiplying, Factoring and Division of Polynomials For more information about the materials presented, contact Chris Mikles mikles@cpm.org From CCA
Factoring Quadratic Trinomials
 Factoring Quadratic Trinomials Student Probe Factor x x 3 10. Answer: x 5 x Lesson Description This lesson uses the area model of multiplication to factor quadratic trinomials. Part 1 of the lesson consists
Factoring Quadratic Trinomials Student Probe Factor x x 3 10. Answer: x 5 x Lesson Description This lesson uses the area model of multiplication to factor quadratic trinomials. Part 1 of the lesson consists
How To Factor Quadratic Trinomials
 Factoring Quadratic Trinomials Student Probe Factor Answer: Lesson Description This lesson uses the area model of multiplication to factor quadratic trinomials Part 1 of the lesson consists of circle puzzles
Factoring Quadratic Trinomials Student Probe Factor Answer: Lesson Description This lesson uses the area model of multiplication to factor quadratic trinomials Part 1 of the lesson consists of circle puzzles
A Concrete Introduction. to the Abstract Concepts. of Integers and Algebra using Algebra Tiles
 A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
10.1. Solving Quadratic Equations. Investigation: Rocket Science CONDENSED
 CONDENSED L E S S O N 10.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations
CONDENSED L E S S O N 10.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations
A Quick Algebra Review
 1. Simplifying Epressions. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Eponents 9. Quadratics 10. Rationals 11. Radicals
1. Simplifying Epressions. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Eponents 9. Quadratics 10. Rationals 11. Radicals
FACTORING ax 2 bx c WITH a 1
 296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
The majority of college students hold credit cards. According to the Nellie May
 CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
Chris Yuen. Algebra 1 Factoring. Early High School 8-10 Time Span: 5 instructional days
 1 Chris Yuen Algebra 1 Factoring Early High School 8-10 Time Span: 5 instructional days Materials: Algebra Tiles and TI-83 Plus Calculator. AMSCO Math A Chapter 18 Factoring. All mathematics material and
1 Chris Yuen Algebra 1 Factoring Early High School 8-10 Time Span: 5 instructional days Materials: Algebra Tiles and TI-83 Plus Calculator. AMSCO Math A Chapter 18 Factoring. All mathematics material and
Five 5. Rational Expressions and Equations C H A P T E R
 Five C H A P T E R Rational Epressions and Equations. Rational Epressions and Functions. Multiplication and Division of Rational Epressions. Addition and Subtraction of Rational Epressions.4 Comple Fractions.
Five C H A P T E R Rational Epressions and Equations. Rational Epressions and Functions. Multiplication and Division of Rational Epressions. Addition and Subtraction of Rational Epressions.4 Comple Fractions.
CAHSEE on Target UC Davis, School and University Partnerships
 UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
UC Davis, School and University Partnerships CAHSEE on Target Mathematics Curriculum Published by The University of California, Davis, School/University Partnerships Program 006 Director Sarah R. Martinez,
FACTORING QUADRATICS 8.1.1 through 8.1.4
 Chapter 8 FACTORING QUADRATICS 8.. through 8..4 Chapter 8 introduces students to rewriting quadratic epressions and solving quadratic equations. Quadratic functions are any function which can be rewritten
Chapter 8 FACTORING QUADRATICS 8.. through 8..4 Chapter 8 introduces students to rewriting quadratic epressions and solving quadratic equations. Quadratic functions are any function which can be rewritten
6706_PM10SB_C4_CO_pp192-193.qxd 5/8/09 9:53 AM Page 192 192 NEL
 92 NEL Chapter 4 Factoring Algebraic Epressions GOALS You will be able to Determine the greatest common factor in an algebraic epression and use it to write the epression as a product Recognize different
92 NEL Chapter 4 Factoring Algebraic Epressions GOALS You will be able to Determine the greatest common factor in an algebraic epression and use it to write the epression as a product Recognize different
a. You can t do the simple trick of finding two integers that multiply to give 6 and add to give 5 because the a (a = 4) is not equal to one.
 FACTORING TRINOMIALS USING THE AC METHOD. Factoring trinomial epressions in one unknown is an important skill necessary to eventually solve quadratic equations. Trinomial epressions are of the form a 2
FACTORING TRINOMIALS USING THE AC METHOD. Factoring trinomial epressions in one unknown is an important skill necessary to eventually solve quadratic equations. Trinomial epressions are of the form a 2
Multiplying Binomials and Factoring Trinomials Using Algebra Tiles and Generic Rectangles
 Multiplying Binomials Standard: Algebra 10.0 Time: 55 mins. Multiplying Binomials and Factoring Trinomials Using Algebra Tiles and s Materials: Class set of Algebra Tiles or access to a computer for each
Multiplying Binomials Standard: Algebra 10.0 Time: 55 mins. Multiplying Binomials and Factoring Trinomials Using Algebra Tiles and s Materials: Class set of Algebra Tiles or access to a computer for each
Polynomial and Synthetic Division. Long Division of Polynomials. Example 1. 6x 2 7x 2 x 2) 19x 2 16x 4 6x3 12x 2 7x 2 16x 7x 2 14x. 2x 4.
 _.qd /7/5 9: AM Page 5 Section.. Polynomial and Synthetic Division 5 Polynomial and Synthetic Division What you should learn Use long division to divide polynomials by other polynomials. Use synthetic
_.qd /7/5 9: AM Page 5 Section.. Polynomial and Synthetic Division 5 Polynomial and Synthetic Division What you should learn Use long division to divide polynomials by other polynomials. Use synthetic
Using Algebra Tiles from Polynomials to Factoring
 Using Algebra Tiles from Polynomials to Factoring For more information about the materials you find in this packet, contact: Chris Mikles (888) 808-4276 mikles@cpm.org CPM Educational Program 203, all
Using Algebra Tiles from Polynomials to Factoring For more information about the materials you find in this packet, contact: Chris Mikles (888) 808-4276 mikles@cpm.org CPM Educational Program 203, all
Polynomial Degree and Finite Differences
 CONDENSED LESSON 7.1 Polynomial Degree and Finite Differences In this lesson you will learn the terminology associated with polynomials use the finite differences method to determine the degree of a polynomial
CONDENSED LESSON 7.1 Polynomial Degree and Finite Differences In this lesson you will learn the terminology associated with polynomials use the finite differences method to determine the degree of a polynomial
2.4. Factoring Quadratic Expressions. Goal. Explore 2.4. Launch 2.4
 2.4 Factoring Quadratic Epressions Goal Use the area model and Distributive Property to rewrite an epression that is in epanded form into an equivalent epression in factored form The area of a rectangle
2.4 Factoring Quadratic Epressions Goal Use the area model and Distributive Property to rewrite an epression that is in epanded form into an equivalent epression in factored form The area of a rectangle
Answers to Basic Algebra Review
 Answers to Basic Algebra Review 1. -1.1 Follow the sign rules when adding and subtracting: If the numbers have the same sign, add them together and keep the sign. If the numbers have different signs, subtract
Answers to Basic Algebra Review 1. -1.1 Follow the sign rules when adding and subtracting: If the numbers have the same sign, add them together and keep the sign. If the numbers have different signs, subtract
Mathematics More Visual Using Algebra Tiles
 www.cpm.org Chris Mikles CPM Educational Program A California Non-profit Corporation 33 Noonan Drive Sacramento, CA 958 (888) 808-76 fa: (08) 777-8605 email: mikles@cpm.org An Eemplary Mathematics Program
www.cpm.org Chris Mikles CPM Educational Program A California Non-profit Corporation 33 Noonan Drive Sacramento, CA 958 (888) 808-76 fa: (08) 777-8605 email: mikles@cpm.org An Eemplary Mathematics Program
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
What are the place values to the left of the decimal point and their associated powers of ten?
 The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
The verbal answers to all of the following questions should be memorized before completion of algebra. Answers that are not memorized will hinder your ability to succeed in geometry and algebra. (Everything
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
Pre-Calculus II Factoring and Operations on Polynomials
 Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
Factoring... 1 Polynomials...1 Addition of Polynomials... 1 Subtraction of Polynomials...1 Multiplication of Polynomials... Multiplying a monomial by a monomial... Multiplying a monomial by a polynomial...
CPM Educational Program
 CPM Educational Program A California, Non-Profit Corporation Chris Mikles, National Director (888) 808-4276 e-mail: mikles @cpm.org CPM Courses and Their Core Threads Each course is built around a few
CPM Educational Program A California, Non-Profit Corporation Chris Mikles, National Director (888) 808-4276 e-mail: mikles @cpm.org CPM Courses and Their Core Threads Each course is built around a few
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c
 Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
FACTORISATION YEARS. A guide for teachers - Years 9 10 June 2011. The Improving Mathematics Education in Schools (TIMES) Project
 9 10 YEARS The Improving Mathematics Education in Schools (TIMES) Project FACTORISATION NUMBER AND ALGEBRA Module 33 A guide for teachers - Years 9 10 June 2011 Factorisation (Number and Algebra : Module
9 10 YEARS The Improving Mathematics Education in Schools (TIMES) Project FACTORISATION NUMBER AND ALGEBRA Module 33 A guide for teachers - Years 9 10 June 2011 Factorisation (Number and Algebra : Module
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
POLYNOMIAL FUNCTIONS
 POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
POLYNOMIAL FUNCTIONS Polynomial Division.. 314 The Rational Zero Test.....317 Descarte s Rule of Signs... 319 The Remainder Theorem.....31 Finding all Zeros of a Polynomial Function.......33 Writing a
VISUAL ALGEBRA FOR COLLEGE STUDENTS. Laurie J. Burton Western Oregon University
 VISUAL ALGEBRA FOR COLLEGE STUDENTS Laurie J. Burton Western Oregon University VISUAL ALGEBRA FOR COLLEGE STUDENTS TABLE OF CONTENTS Welcome and Introduction 1 Chapter 1: INTEGERS AND INTEGER OPERATIONS
VISUAL ALGEBRA FOR COLLEGE STUDENTS Laurie J. Burton Western Oregon University VISUAL ALGEBRA FOR COLLEGE STUDENTS TABLE OF CONTENTS Welcome and Introduction 1 Chapter 1: INTEGERS AND INTEGER OPERATIONS
USING ALGEBRA TILES EFFECTIVELY
 MATHEMATICS USING ALGEBRA TILES EFFECTIVELY TOOLS FOR UNDERSTANDING by Bettye C. Hall Reviewers James Gates, Ed.D. Yvonne S. Gentzler, Ph.D. AUTHOR Bettye C. Hall is the former Director of Mathematics
MATHEMATICS USING ALGEBRA TILES EFFECTIVELY TOOLS FOR UNDERSTANDING by Bettye C. Hall Reviewers James Gates, Ed.D. Yvonne S. Gentzler, Ph.D. AUTHOR Bettye C. Hall is the former Director of Mathematics
Lesson 9.1 Solving Quadratic Equations
 Lesson 9.1 Solving Quadratic Equations 1. Sketch the graph of a quadratic equation with a. One -intercept and all nonnegative y-values. b. The verte in the third quadrant and no -intercepts. c. The verte
Lesson 9.1 Solving Quadratic Equations 1. Sketch the graph of a quadratic equation with a. One -intercept and all nonnegative y-values. b. The verte in the third quadrant and no -intercepts. c. The verte
4/27/2010 ALGEBRA 1 CHAPTER 8 FACTORING. PAR Activities Cara Boening
 4/27/2010 ALGEBRA 1 CHAPTER 8 FACTORING PAR Activities Cara Boening Table of Contents Preparation Strategies... 3 Scavenger Hunt... 4 Graphic Organizer Chapter 8.... 6 Word Inventory... 8 TEASE... 12 Anticipation
4/27/2010 ALGEBRA 1 CHAPTER 8 FACTORING PAR Activities Cara Boening Table of Contents Preparation Strategies... 3 Scavenger Hunt... 4 Graphic Organizer Chapter 8.... 6 Word Inventory... 8 TEASE... 12 Anticipation
Factors and Products
 CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
EAP/GWL Rev. 1/2011 Page 1 of 5. Factoring a polynomial is the process of writing it as the product of two or more polynomial factors.
 EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: Set the factors of a polynomial equation (as opposed to an
Polynomials and Quadratics
 Polynomials and Quadratics Want to be an environmental scientist? Better be ready to get your hands dirty!.1 Controlling the Population Adding and Subtracting Polynomials............703.2 They re Multiplying
Polynomials and Quadratics Want to be an environmental scientist? Better be ready to get your hands dirty!.1 Controlling the Population Adding and Subtracting Polynomials............703.2 They re Multiplying
If A is divided by B the result is 2/3. If B is divided by C the result is 4/7. What is the result if A is divided by C?
 Problem 3 If A is divided by B the result is 2/3. If B is divided by C the result is 4/7. What is the result if A is divided by C? Suggested Questions to ask students about Problem 3 The key to this question
Problem 3 If A is divided by B the result is 2/3. If B is divided by C the result is 4/7. What is the result if A is divided by C? Suggested Questions to ask students about Problem 3 The key to this question
Review of Intermediate Algebra Content
 Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS
 (Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
(Section 0.6: Polynomial, Rational, and Algebraic Expressions) 0.6.1 SECTION 0.6: POLYNOMIAL, RATIONAL, AND ALGEBRAIC EXPRESSIONS LEARNING OBJECTIVES Be able to identify polynomial, rational, and algebraic
Factoring ax 2 + bx + c - Teacher Notes
 Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
Southern Nevada Regional Professi onal D evel opment Program VOLUME 1, ISSUE 8 MAY 009 A N ewsletter from the Sec ondary Mathematic s Team Factoring ax + bx + c - Teacher Notes Here we look at sample teacher
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
The GMAT Guru. Prime Factorization: Theory and Practice
 . Prime Factorization: Theory and Practice The following is an ecerpt from The GMAT Guru Guide, available eclusively to clients of The GMAT Guru. If you would like more information about GMAT Guru services,
. Prime Factorization: Theory and Practice The following is an ecerpt from The GMAT Guru Guide, available eclusively to clients of The GMAT Guru. If you would like more information about GMAT Guru services,
Math Review. for the Quantitative Reasoning Measure of the GRE revised General Test
 Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
Math 0980 Chapter Objectives. Chapter 1: Introduction to Algebra: The Integers.
 Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Vocabulary Words and Definitions for Algebra
 Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
The program also provides supplemental modules on topics in geometry and probability and statistics.
 Algebra 1 Course Overview Students develop algebraic fluency by learning the skills needed to solve equations and perform important manipulations with numbers, variables, equations, and inequalities. Students
Algebra 1 Course Overview Students develop algebraic fluency by learning the skills needed to solve equations and perform important manipulations with numbers, variables, equations, and inequalities. Students
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
7.7 Solving Rational Equations
 Section 7.7 Solving Rational Equations 7 7.7 Solving Rational Equations When simplifying comple fractions in the previous section, we saw that multiplying both numerator and denominator by the appropriate
Section 7.7 Solving Rational Equations 7 7.7 Solving Rational Equations When simplifying comple fractions in the previous section, we saw that multiplying both numerator and denominator by the appropriate
SECTION P.5 Factoring Polynomials
 BLITMCPB.QXP.0599_48-74 /0/0 0:4 AM Page 48 48 Chapter P Prerequisites: Fundamental Concepts of Algebra Technology Eercises Critical Thinking Eercises 98. The common cold is caused by a rhinovirus. The
BLITMCPB.QXP.0599_48-74 /0/0 0:4 AM Page 48 48 Chapter P Prerequisites: Fundamental Concepts of Algebra Technology Eercises Critical Thinking Eercises 98. The common cold is caused by a rhinovirus. The
Answer Key for California State Standards: Algebra I
 Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
Algebra Practice Problems for Precalculus and Calculus
 Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
Algebra Practice Problems for Precalculus and Calculus Solve the following equations for the unknown x: 1. 5 = 7x 16 2. 2x 3 = 5 x 3. 4. 1 2 (x 3) + x = 17 + 3(4 x) 5 x = 2 x 3 Multiply the indicated polynomials
2-5 Rational Functions
 -5 Rational Functions Find the domain of each function and the equations of the vertical or horizontal asymptotes, if any 1 f () = The function is undefined at the real zeros of the denominator b() = 4
-5 Rational Functions Find the domain of each function and the equations of the vertical or horizontal asymptotes, if any 1 f () = The function is undefined at the real zeros of the denominator b() = 4
Students will be able to simplify and evaluate numerical and variable expressions using appropriate properties and order of operations.
 Outcome 1: (Introduction to Algebra) Skills/Content 1. Simplify numerical expressions: a). Use order of operations b). Use exponents Students will be able to simplify and evaluate numerical and variable
Outcome 1: (Introduction to Algebra) Skills/Content 1. Simplify numerical expressions: a). Use order of operations b). Use exponents Students will be able to simplify and evaluate numerical and variable
Unit 7 The Number System: Multiplying and Dividing Integers
 Unit 7 The Number System: Multiplying and Dividing Integers Introduction In this unit, students will multiply and divide integers, and multiply positive and negative fractions by integers. Students will
Unit 7 The Number System: Multiplying and Dividing Integers Introduction In this unit, students will multiply and divide integers, and multiply positive and negative fractions by integers. Students will
Factoring Flow Chart
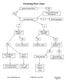 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Introduction Assignment
 PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
IOWA End-of-Course Assessment Programs. Released Items ALGEBRA I. Copyright 2010 by The University of Iowa.
 IOWA End-of-Course Assessment Programs Released Items Copyright 2010 by The University of Iowa. ALGEBRA I 1 Sally works as a car salesperson and earns a monthly salary of $2,000. She also earns $500 for
IOWA End-of-Course Assessment Programs Released Items Copyright 2010 by The University of Iowa. ALGEBRA I 1 Sally works as a car salesperson and earns a monthly salary of $2,000. She also earns $500 for
Unit 1 Number Sense. In this unit, students will study repeating decimals, percents, fractions, decimals, and proportions.
 Unit 1 Number Sense In this unit, students will study repeating decimals, percents, fractions, decimals, and proportions. BLM Three Types of Percent Problems (p L-34) is a summary BLM for the material
Unit 1 Number Sense In this unit, students will study repeating decimals, percents, fractions, decimals, and proportions. BLM Three Types of Percent Problems (p L-34) is a summary BLM for the material
A. Factoring out the Greatest Common Factor.
 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
LAKE ELSINORE UNIFIED SCHOOL DISTRICT
 LAKE ELSINORE UNIFIED SCHOOL DISTRICT Title: PLATO Algebra 1-Semester 2 Grade Level: 10-12 Department: Mathematics Credit: 5 Prerequisite: Letter grade of F and/or N/C in Algebra 1, Semester 2 Course Description:
LAKE ELSINORE UNIFIED SCHOOL DISTRICT Title: PLATO Algebra 1-Semester 2 Grade Level: 10-12 Department: Mathematics Credit: 5 Prerequisite: Letter grade of F and/or N/C in Algebra 1, Semester 2 Course Description:
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
MTH124: Honors Algebra I
 MTH124: Honors Algebra I This course prepares students for more advanced courses while they develop algebraic fluency, learn the skills needed to solve equations, and perform manipulations with numbers,
MTH124: Honors Algebra I This course prepares students for more advanced courses while they develop algebraic fluency, learn the skills needed to solve equations, and perform manipulations with numbers,
Unit 6 Number and Operations in Base Ten: Decimals
 Unit 6 Number and Operations in Base Ten: Decimals Introduction Students will extend the place value system to decimals. They will apply their understanding of models for decimals and decimal notation,
Unit 6 Number and Operations in Base Ten: Decimals Introduction Students will extend the place value system to decimals. They will apply their understanding of models for decimals and decimal notation,
COLLEGE ALGEBRA. Paul Dawkins
 COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
9.3 OPERATIONS WITH RADICALS
 9. Operations with Radicals (9 1) 87 9. OPERATIONS WITH RADICALS In this section Adding and Subtracting Radicals Multiplying Radicals Conjugates In this section we will use the ideas of Section 9.1 in
9. Operations with Radicals (9 1) 87 9. OPERATIONS WITH RADICALS In this section Adding and Subtracting Radicals Multiplying Radicals Conjugates In this section we will use the ideas of Section 9.1 in
Solving Rational Equations
 Lesson M Lesson : Student Outcomes Students solve rational equations, monitoring for the creation of extraneous solutions. Lesson Notes In the preceding lessons, students learned to add, subtract, multiply,
Lesson M Lesson : Student Outcomes Students solve rational equations, monitoring for the creation of extraneous solutions. Lesson Notes In the preceding lessons, students learned to add, subtract, multiply,
A positive exponent means repeated multiplication. A negative exponent means the opposite of repeated multiplication, which is repeated
 Eponents Dealing with positive and negative eponents and simplifying epressions dealing with them is simply a matter of remembering what the definition of an eponent is. division. A positive eponent means
Eponents Dealing with positive and negative eponents and simplifying epressions dealing with them is simply a matter of remembering what the definition of an eponent is. division. A positive eponent means
Teaching Algebra with Manipulatives. For use with Glencoe Algebra 1 Glencoe Algebra 2
 Teaching Algebra with Manipulatives For use with Glencoe Algebra 1 Glencoe Algebra 2 Manipulatives Glencoe offers three types of kits to enhance the use of manipulatives in your Pre-Algebra classroom.
Teaching Algebra with Manipulatives For use with Glencoe Algebra 1 Glencoe Algebra 2 Manipulatives Glencoe offers three types of kits to enhance the use of manipulatives in your Pre-Algebra classroom.
Polynomials and Factoring. Unit Lesson Plan
 Polynomials and Factoring Unit Lesson Plan By: David Harris University of North Carolina Chapel Hill Math 410 Dr. Thomas, M D. 2 Abstract This paper will discuss, and give, lesson plans for all the topics
Polynomials and Factoring Unit Lesson Plan By: David Harris University of North Carolina Chapel Hill Math 410 Dr. Thomas, M D. 2 Abstract This paper will discuss, and give, lesson plans for all the topics
CHAPTER 7: FACTORING POLYNOMIALS
 CHAPTER 7: FACTORING POLYNOMIALS FACTOR (noun) An of two or more quantities which form a product when multiplied together. 1 can be rewritten as 3*, where 3 and are FACTORS of 1. FACTOR (verb) - To factor
CHAPTER 7: FACTORING POLYNOMIALS FACTOR (noun) An of two or more quantities which form a product when multiplied together. 1 can be rewritten as 3*, where 3 and are FACTORS of 1. FACTOR (verb) - To factor
INVESTIGATIONS AND FUNCTIONS 1.1.1 1.1.4. Example 1
 Chapter 1 INVESTIGATIONS AND FUNCTIONS 1.1.1 1.1.4 This opening section introduces the students to man of the big ideas of Algebra 2, as well as different was of thinking and various problem solving strategies.
Chapter 1 INVESTIGATIONS AND FUNCTIONS 1.1.1 1.1.4 This opening section introduces the students to man of the big ideas of Algebra 2, as well as different was of thinking and various problem solving strategies.
MTH-4106-1. actoring. and. Algebraic Fractions
 MTH-4106-1 C1-C4 Factorization 1/31/12 11:38 AM Page 1 F MTH-4106-1 actoring and Algebraic Fractions FACTORING AND ALGEBRAIC FUNCTIONS Project Coordinator: Jean-Paul Groleau Authors: Nicole Perreault
MTH-4106-1 C1-C4 Factorization 1/31/12 11:38 AM Page 1 F MTH-4106-1 actoring and Algebraic Fractions FACTORING AND ALGEBRAIC FUNCTIONS Project Coordinator: Jean-Paul Groleau Authors: Nicole Perreault
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
In this section, you will develop a method to change a quadratic equation written as a sum into its product form (also called its factored form).
 CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
Unit 12: Introduction to Factoring. Learning Objectives 12.2
 Unit 1 Table of Contents Unit 1: Introduction to Factoring Learning Objectives 1. Instructor Notes The Mathematics of Factoring Teaching Tips: Challenges and Approaches Additional Resources Instructor
Unit 1 Table of Contents Unit 1: Introduction to Factoring Learning Objectives 1. Instructor Notes The Mathematics of Factoring Teaching Tips: Challenges and Approaches Additional Resources Instructor
Chapter 3 Section 6 Lesson Polynomials
 Chapter Section 6 Lesson Polynomials Introduction This lesson introduces polynomials and like terms. As we learned earlier, a monomial is a constant, a variable, or the product of constants and variables.
Chapter Section 6 Lesson Polynomials Introduction This lesson introduces polynomials and like terms. As we learned earlier, a monomial is a constant, a variable, or the product of constants and variables.
MATH 0110 Developmental Math Skills Review, 1 Credit, 3 hours lab
 MATH 0110 Developmental Math Skills Review, 1 Credit, 3 hours lab MATH 0110 is established to accommodate students desiring non-course based remediation in developmental mathematics. This structure will
MATH 0110 Developmental Math Skills Review, 1 Credit, 3 hours lab MATH 0110 is established to accommodate students desiring non-course based remediation in developmental mathematics. This structure will
Determinants can be used to solve a linear system of equations using Cramer s Rule.
 2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
2.6.2 Cramer s Rule Determinants can be used to solve a linear system of equations using Cramer s Rule. Cramer s Rule for Two Equations in Two Variables Given the system This system has the unique solution
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Year 9 set 1 Mathematics notes, to accompany the 9H book.
 Part 1: Year 9 set 1 Mathematics notes, to accompany the 9H book. equations 1. (p.1), 1.6 (p. 44), 4.6 (p.196) sequences 3. (p.115) Pupils use the Elmwood Press Essential Maths book by David Raymer (9H
Part 1: Year 9 set 1 Mathematics notes, to accompany the 9H book. equations 1. (p.1), 1.6 (p. 44), 4.6 (p.196) sequences 3. (p.115) Pupils use the Elmwood Press Essential Maths book by David Raymer (9H
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Contents. How You May Use This Resource Guide
 Contents How You May Use This Resource Guide ii 7 Factoring and Algebraic Fractions 1 Worksheet 7.1: The Box Problem......................... 4 Worksheet 7.2: Multiplying and Factoring Polynomials with
Contents How You May Use This Resource Guide ii 7 Factoring and Algebraic Fractions 1 Worksheet 7.1: The Box Problem......................... 4 Worksheet 7.2: Multiplying and Factoring Polynomials with
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
PERT Mathematics Test Review
 PERT Mathematics Test Review Prof. Miguel A. Montañez ESL/Math Seminar Math Test? NO!!!!!!! I am not good at Math! I cannot graduate because of Math! I hate Math! Helpful Sites Math Dept Web Site Wolfson
PERT Mathematics Test Review Prof. Miguel A. Montañez ESL/Math Seminar Math Test? NO!!!!!!! I am not good at Math! I cannot graduate because of Math! I hate Math! Helpful Sites Math Dept Web Site Wolfson
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
HIBBING COMMUNITY COLLEGE COURSE OUTLINE
 HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
HIBBING COMMUNITY COLLEGE COURSE OUTLINE COURSE NUMBER & TITLE: - Beginning Algebra CREDITS: 4 (Lec 4 / Lab 0) PREREQUISITES: MATH 0920: Fundamental Mathematics with a grade of C or better, Placement Exam,
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
