= = GM. v 1 = Ωa 1 sin i.
|
|
|
- Polly Pitts
- 10 years ago
- Views:
Transcription
1 1 Binary Stars Consider a binary composed of two stars of masses M 1 and We define M = M 1 + and µ = M 1 /M If a 1 and a 2 are the mean distances of the stars from the center of mass, then M 1 a 1 = a 2 The mean separation of the stars is a = a 1 + a 2 If the orbit is elliptical with eccentricity e, then the separation at periastron is a1 e) and at apastron it is a1 + e) The total energy and angular momentum of the binary are E = 1 GM 1 J = µ GaM 1 e 2 a 2) = µωa 2 1 e 2 Kepler s Law is ) Ω 2 2π 2 = = GM P a 3 The projected orbital velocity of star 1 is The quantity v 1 = Ωa 1 sin i f 1 M 1,,i) = sin i) 3 = v3 1 GΩ is known as the mass function since it depends only on observables v 1,P If Doppler shifts from star 2 are measured, then f 2 M 1,,i) = M 1 sin i) 3 = v3 2 GΩ can also be found Then = v 1 M 1 v 2 independent of i If the binary is eclipsing, the angle i can be determined and the masses individually determined as well Mass Transfer and Roche Lobes The total potential of a binary is Φ = GM 1 + G + 1 r 1 r 2 2 d2 Ω 2, where r 1 and r 2 are the distances to stars 1 and 2 and d is the distance to the rotation axis Restricting ourselves to the orbital plane, with the origin at the center of mass, GM Φx,y) = 1 GM x 1 x 2 + y 2) GM a 1 ) 2 + y 2 x + a 2 ) 2 + y 2 2 a 3
2 2 In dimensionless coordinates x = x/a, ȳ = y/a, m 1 = M 1 /M, m 2 = /M: Φ x,ȳ) = GM m 1 m a x 1 x 2 + ȳ 2) m 2 ) 2 + ȳ 2 x + m 1 ) 2 + ȳ 2 2 Contours of constant Φ are shown in the figure There are deep minima at the stellar centers, and maxima at five so-called Lagrangian points The L 1 point between the stars is significant because if a star expands and reaches the potential surface passing through it, mass can be transferred to its companion The equipotential surface that passes through L 1 is called the Roche lobe, and its size depends upon the mass ratio of the binary Kopal 1959) gives for the radius R R with nearly the same volume as the Roche lobe: A better fit is by Eggleton: [ R R /a = R R a = 046 M1 M1 M ) 2/3 ln ) 1/3 1) 1 + M1 ) 1/3 )] 1 2)
3 3 Assume the binary is circular Then MJ 2 ) 2a 2M1 M a = GM1 2 M, da = 1) M 1 M M 1 ) dm 1, 3) if dm = dj = 0 This shows that if < M 1, transferring mass from M 1 to results in a shrinkage of the orbit Am episode of conservative mass transfer in a binary results in a final = a initial M1,initial,initial M 1,final,final ) 2 Eq 3) implies that in terms of the mass ratio of the binary, q = /M 1, da = 2a ) q 1 dq, 4) q 1 + q or a 1 + q) 4 q 2 Expressing Eq 1) in terms of q, then taking the derivative and combining with Eq 4), da dr L = R L a R [ ) ] L dq 2 q q = R 1 L dq q 1 + q q) This implies that the Roche lobe size reaches its minimum value when q = 6/5, or M 1 = 5M/11 On the other hand, suppose that mass is lost from one star in the form of a wind and is not accreted onto the companion Then we might expect that M a final = a initial M, and mass loss will cause an increase in a binary s separation Now consider mass transfer when star 1 fills its Roche lobe Stable mass transfer occurs when the change in radius of star 1 after transferring an increment of mass through the inner Lagrangian point is not offset by a corresponding change in the Roche radius, triggered by the new mass ratio of the binary This requires that the logarithmic change of radius with mass for star 1 satisfies dln R α dln R R = dln a + 1 ) 2M1 dln M 1 dln M 1 dlnm 1 3 = 2 M + 1 M M 1 3
4 4 In an equal mass binary, the first term vanishes Generally, we can expect that this condition is generally satisfied It is not, however, for a star with a convective envelope, for which γ = 5/3 and R M 1/3 In some situations, mass transfer will be driven by losses of orbital angular momentum The primary sources of angular momentum loss are magnetic braking and gravitational radiation We have ȧ a = 2 J J 2 1 M 1 ), where the donor star is taken to be 2, so that M 2 < 0 Using the simple Roche lobe formula, Ṙ R = 2 J R R J 2 1 M ) 2 M M 2 M 1 3 Assume that Ṙ2/R 2 = α M 2 /, where α = 1/3 for a non-relativistic degenerate, or convective, star, and α = 1 for a main sequence star For stable mass transfer, R 2 should remain equal to R R Then we have J J = α 2 M 1 ) Since both sides of this equation must be negative, we find M α 2 When α = 1/31), /M 1 2/34/3) Gravitational radiation leads to J J = 32G3 5c 5 M 1 M 1 + ) a 4 s 1 5) Explosive Mass Loss Another case of mass transfer occurs after a supernova explosion, but here the mass loss is sudden and catastrophic and the companion does not accept the mass If too much mass is lost from the system, the binary will be disrupted The survival of the binary depends on the amount of mass loss, the phase of the binary ie, is it near periastron a more stable situation) or apastron a less stable situation)), and the magnitude and direction of any kick imparted to the supernova remnant star If the explosion is
5 5 perfectly symmetric, the kick velocity is zero However, if the explosion is asymmetric, the kick velocity is determined by momentum conservation A 1% asymmetry in the neutrinos released in a supernova could impart a kick velocity of approximately V = E M ns c 360 kms 1 assuming a neutron star mass of M ns = 14 M and E = erg This, in many cases, exceeds the relative orbital velocities of the stars prior to the explosion As we will see, a kick in the direction of orbital motion of the remnant destabilizes the system, but a reverse kick can stabilize it Following J Hills, Ap J ) 322, the total energy of the binary prior to the explosion is E o = GMo 1 = GMo 1 2a o r µ ov 2 o where the subscript o refers to the initial system r is the instantaneous separation of the two stars equal to a o if the orbit is circular) At periastron, r = a o 1 e o ) and at apastron, r = a o 1 + e o ) µ o = M1 o/ is the reduced mass and is the initial total mass V o is the initial relative velocities of the two stars We can furthermore define a parameter Vc 2 = G/a o as the relative velocity in the circular orbit case Immediately after the explosion, if the orbit is still bound, we have E = GM 1 2a = GM 1 r µv 2 by comparison, where µ = M 1 /M Defining = 1 M 1 = M, it is straightforward to demonstrate that a a o = 1 / 1 2a o /r)/ ) + V 2 o V 2) /Vc 2 In order to remain bound, it is therefore necessary that a <, or < r 1 V o 2 V 2 ) 2a o Vc 2 Several cases can now be considered If the explosion occurs on a timescale short compared to the orbital period, and if no kick is imparted
6 6 to the supernova remnant star, it is reasonable to assume that V = V o, ie, the relative velocities of the two stars remains the same In this case, the condition for stability becomes < r 2a o If the orbit is initially circular, the RHS of the above is simply 1/2 If the initial orbit is elliptical, the RHS of the above is in the range 1 e o )/2 1 + e o )/2, depending on the precise value of r when the explosion occurs In the limit that the initial eccentricity is unity, it is therefore possible both that very little mass loss could disrupt the orbit, if the stars are near apastron, or that the binary could remain stable in spite of losing almost all the binary s mass, if the stars are near periastron If the supernova remnant star receives a kick velocity, which is directed at an angle of cosθ with respect to V o, we find V = V o + V, V V = V 2 = V 2 o + 2V o V + V ) 2 Therefore, the condition for stability becomes < r 2a o [ 1 V V + 2V o cos θ) V 2 c In the case that the kick is exactly mis)aligned with V o, we have that cos θ = +1 1) Comparing the limiting amounts of mass loss for stability in the two cases, denoted + and, respectively, we find + = 2r a o V o V V 2 c < 0 This means that a kick in the same direction as the orbital motion tends to destabilize the orbit, while a misaligned kick stabilizes the orbit In the case of a circular initial orbit and a misaligned kick, one has = 1 2 [ 1 + V V 2 c ] 2V c V ) If the kick velocity magnitude is comparable to the relative orbital speed in this case, one has < for stability, ie, no amount of mass loss can disrupt the orbit! An oppositely directed kick of this size, however, always disrupts the binary ]
Neutron Stars. How were neutron stars discovered? The first neutron star was discovered by 24-year-old graduate student Jocelyn Bell in 1967.
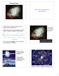 Neutron Stars How were neutron stars discovered? The first neutron star was discovered by 24-year-old graduate student Jocelyn Bell in 1967. Using a radio telescope she noticed regular pulses of radio
Neutron Stars How were neutron stars discovered? The first neutron star was discovered by 24-year-old graduate student Jocelyn Bell in 1967. Using a radio telescope she noticed regular pulses of radio
Dynamics of Iain M. Banks Orbitals. Richard Kennaway. 12 October 2005
 Dynamics of Iain M. Banks Orbitals Richard Kennaway 12 October 2005 Note This is a draft in progress, and as such may contain errors. Please do not cite this without permission. 1 The problem An Orbital
Dynamics of Iain M. Banks Orbitals Richard Kennaway 12 October 2005 Note This is a draft in progress, and as such may contain errors. Please do not cite this without permission. 1 The problem An Orbital
DYNAMICS OF GALAXIES
 DYNAMICS OF GALAXIES 2. and stellar orbits Piet van der Kruit Kapteyn Astronomical Institute University of Groningen the Netherlands Winter 2008/9 and stellar orbits Contents Range of timescales Two-body
DYNAMICS OF GALAXIES 2. and stellar orbits Piet van der Kruit Kapteyn Astronomical Institute University of Groningen the Netherlands Winter 2008/9 and stellar orbits Contents Range of timescales Two-body
This paper is also taken for the relevant Examination for the Associateship. For Second Year Physics Students Wednesday, 4th June 2008: 14:00 to 16:00
 Imperial College London BSc/MSci EXAMINATION June 2008 This paper is also taken for the relevant Examination for the Associateship SUN, STARS, PLANETS For Second Year Physics Students Wednesday, 4th June
Imperial College London BSc/MSci EXAMINATION June 2008 This paper is also taken for the relevant Examination for the Associateship SUN, STARS, PLANETS For Second Year Physics Students Wednesday, 4th June
The Orbital Period Distribution of Wide Binary Millisecond Pulsars
 Binary Radio Pulsars ASP Conference Series, Vol. 328, 2005 F. A. Rasio and I. H. Stairs The Orbital Period Distribution of Wide Binary Millisecond Pulsars B. Willems Northwestern University, Department
Binary Radio Pulsars ASP Conference Series, Vol. 328, 2005 F. A. Rasio and I. H. Stairs The Orbital Period Distribution of Wide Binary Millisecond Pulsars B. Willems Northwestern University, Department
A. 81 2 = 6561 times greater. B. 81 times greater. C. equally strong. D. 1/81 as great. E. (1/81) 2 = 1/6561 as great.
 Q12.1 The mass of the Moon is 1/81 of the mass of the Earth. Compared to the gravitational force that the Earth exerts on the Moon, the gravitational force that the Moon exerts on the Earth is A. 81 2
Q12.1 The mass of the Moon is 1/81 of the mass of the Earth. Compared to the gravitational force that the Earth exerts on the Moon, the gravitational force that the Moon exerts on the Earth is A. 81 2
Section 4: The Basics of Satellite Orbits
 Section 4: The Basics of Satellite Orbits MOTION IN SPACE VS. MOTION IN THE ATMOSPHERE The motion of objects in the atmosphere differs in three important ways from the motion of objects in space. First,
Section 4: The Basics of Satellite Orbits MOTION IN SPACE VS. MOTION IN THE ATMOSPHERE The motion of objects in the atmosphere differs in three important ways from the motion of objects in space. First,
DIRECT ORBITAL DYNAMICS: USING INDEPENDENT ORBITAL TERMS TO TREAT BODIES AS ORBITING EACH OTHER DIRECTLY WHILE IN MOTION
 1 DIRECT ORBITAL DYNAMICS: USING INDEPENDENT ORBITAL TERMS TO TREAT BODIES AS ORBITING EACH OTHER DIRECTLY WHILE IN MOTION Daniel S. Orton email: [email protected] Abstract: There are many longstanding
1 DIRECT ORBITAL DYNAMICS: USING INDEPENDENT ORBITAL TERMS TO TREAT BODIES AS ORBITING EACH OTHER DIRECTLY WHILE IN MOTION Daniel S. Orton email: [email protected] Abstract: There are many longstanding
Figure 1.1 Vector A and Vector F
 CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
Orbital Mechanics. Angular Momentum
 Orbital Mechanics The objects that orbit earth have only a few forces acting on them, the largest being the gravitational pull from the earth. The trajectories that satellites or rockets follow are largely
Orbital Mechanics The objects that orbit earth have only a few forces acting on them, the largest being the gravitational pull from the earth. The trajectories that satellites or rockets follow are largely
Extra-solar massive planets with small semi-major axes?
 Monografías de la Real Academia de Ciencias de Zaragoza. 25: 115 120, (2004). Extra-solar massive planets with small semi-major axes? S. Fernández, D. Giuliodori and M. A. Nicotra Observatorio Astronómico.
Monografías de la Real Academia de Ciencias de Zaragoza. 25: 115 120, (2004). Extra-solar massive planets with small semi-major axes? S. Fernández, D. Giuliodori and M. A. Nicotra Observatorio Astronómico.
Problem 6.40 and 6.41 Kleppner and Kolenkow Notes by: Rishikesh Vaidya, Physics Group, BITS-Pilani
 Problem 6.40 and 6.4 Kleppner and Kolenkow Notes by: Rishikesh Vaidya, Physics Group, BITS-Pilani 6.40 A wheel with fine teeth is attached to the end of a spring with constant k and unstretched length
Problem 6.40 and 6.4 Kleppner and Kolenkow Notes by: Rishikesh Vaidya, Physics Group, BITS-Pilani 6.40 A wheel with fine teeth is attached to the end of a spring with constant k and unstretched length
EDMONDS COMMUNITY COLLEGE ASTRONOMY 100 Winter Quarter 2007 Sample Test # 1
 Instructor: L. M. Khandro EDMONDS COMMUNITY COLLEGE ASTRONOMY 100 Winter Quarter 2007 Sample Test # 1 1. An arc second is a measure of a. time interval between oscillations of a standard clock b. time
Instructor: L. M. Khandro EDMONDS COMMUNITY COLLEGE ASTRONOMY 100 Winter Quarter 2007 Sample Test # 1 1. An arc second is a measure of a. time interval between oscillations of a standard clock b. time
Eðlisfræði 2, vor 2007
 [ Assignment View ] [ Pri Eðlisfræði 2, vor 2007 28. Sources of Magnetic Field Assignment is due at 2:00am on Wednesday, March 7, 2007 Credit for problems submitted late will decrease to 0% after the deadline
[ Assignment View ] [ Pri Eðlisfræði 2, vor 2007 28. Sources of Magnetic Field Assignment is due at 2:00am on Wednesday, March 7, 2007 Credit for problems submitted late will decrease to 0% after the deadline
Halliday, Resnick & Walker Chapter 13. Gravitation. Physics 1A PHYS1121 Professor Michael Burton
 Halliday, Resnick & Walker Chapter 13 Gravitation Physics 1A PHYS1121 Professor Michael Burton II_A2: Planetary Orbits in the Solar System + Galaxy Interactions (You Tube) 21 seconds 13-1 Newton's Law
Halliday, Resnick & Walker Chapter 13 Gravitation Physics 1A PHYS1121 Professor Michael Burton II_A2: Planetary Orbits in the Solar System + Galaxy Interactions (You Tube) 21 seconds 13-1 Newton's Law
Notes: Most of the material in this chapter is taken from Young and Freedman, Chap. 13.
 Chapter 5. Gravitation Notes: Most of the material in this chapter is taken from Young and Freedman, Chap. 13. 5.1 Newton s Law of Gravitation We have already studied the effects of gravity through the
Chapter 5. Gravitation Notes: Most of the material in this chapter is taken from Young and Freedman, Chap. 13. 5.1 Newton s Law of Gravitation We have already studied the effects of gravity through the
G U I D E T O A P P L I E D O R B I T A L M E C H A N I C S F O R K E R B A L S P A C E P R O G R A M
 G U I D E T O A P P L I E D O R B I T A L M E C H A N I C S F O R K E R B A L S P A C E P R O G R A M CONTENTS Foreword... 2 Forces... 3 Circular Orbits... 8 Energy... 10 Angular Momentum... 13 FOREWORD
G U I D E T O A P P L I E D O R B I T A L M E C H A N I C S F O R K E R B A L S P A C E P R O G R A M CONTENTS Foreword... 2 Forces... 3 Circular Orbits... 8 Energy... 10 Angular Momentum... 13 FOREWORD
The Two-Body Problem
 The Two-Body Problem Abstract In my short essay on Kepler s laws of planetary motion and Newton s law of universal gravitation, the trajectory of one massive object near another was shown to be a conic
The Two-Body Problem Abstract In my short essay on Kepler s laws of planetary motion and Newton s law of universal gravitation, the trajectory of one massive object near another was shown to be a conic
Evolution of Close Binary Systems
 Evolution of Close Binary Systems Before going on to the evolution of massive stars and supernovae II, we ll think about the evolution of close binary systems. There are many multiple star systems in the
Evolution of Close Binary Systems Before going on to the evolution of massive stars and supernovae II, we ll think about the evolution of close binary systems. There are many multiple star systems in the
Specific Intensity. I ν =
 Specific Intensity Initial question: A number of active galactic nuclei display jets, that is, long, nearly linear, structures that can extend for hundreds of kiloparsecs. Many have two oppositely-directed
Specific Intensity Initial question: A number of active galactic nuclei display jets, that is, long, nearly linear, structures that can extend for hundreds of kiloparsecs. Many have two oppositely-directed
White Dwarf Properties and the Degenerate Electron Gas
 White Dwarf Properties and the Degenerate Electron Gas Nicholas Rowell April 10, 2008 Contents 1 Introduction 2 1.1 Discovery....................................... 2 1.2 Survey Techniques..................................
White Dwarf Properties and the Degenerate Electron Gas Nicholas Rowell April 10, 2008 Contents 1 Introduction 2 1.1 Discovery....................................... 2 1.2 Survey Techniques..................................
Lecture 13. Gravity in the Solar System
 Lecture 13 Gravity in the Solar System Guiding Questions 1. How was the heliocentric model established? What are monumental steps in the history of the heliocentric model? 2. How do Kepler s three laws
Lecture 13 Gravity in the Solar System Guiding Questions 1. How was the heliocentric model established? What are monumental steps in the history of the heliocentric model? 2. How do Kepler s three laws
Solution of the Gaussian Transfer Orbit Equations of Motion
 Mechanics and Mechanical Engineering Vol. 15, No. 1 (011) 39 46 c Technical University of Lodz Solution of the Gaussian Transfer Orbit Equations of Motion Osman M. Kamel Astronomy and Space Science Dept.
Mechanics and Mechanical Engineering Vol. 15, No. 1 (011) 39 46 c Technical University of Lodz Solution of the Gaussian Transfer Orbit Equations of Motion Osman M. Kamel Astronomy and Space Science Dept.
Class 2 Solar System Characteristics Formation Exosolar Planets
 Class 1 Introduction, Background History of Modern Astronomy The Night Sky, Eclipses and the Seasons Kepler's Laws Newtonian Gravity General Relativity Matter and Light Telescopes Class 2 Solar System
Class 1 Introduction, Background History of Modern Astronomy The Night Sky, Eclipses and the Seasons Kepler's Laws Newtonian Gravity General Relativity Matter and Light Telescopes Class 2 Solar System
Torque Analyses of a Sliding Ladder
 Torque Analyses of a Sliding Ladder 1 Problem Kirk T. McDonald Joseph Henry Laboratories, Princeton University, Princeton, NJ 08544 (May 6, 2007) The problem of a ladder that slides without friction while
Torque Analyses of a Sliding Ladder 1 Problem Kirk T. McDonald Joseph Henry Laboratories, Princeton University, Princeton, NJ 08544 (May 6, 2007) The problem of a ladder that slides without friction while
Carol and Charles see their pencils fall exactly straight down.
 Section 24-1 1. Carol is in a railroad car on a train moving west along a straight stretch of track at a constant speed of 120 km/h, and Charles is in a railroad car on a train at rest on a siding along
Section 24-1 1. Carol is in a railroad car on a train moving west along a straight stretch of track at a constant speed of 120 km/h, and Charles is in a railroad car on a train at rest on a siding along
(Long-Baseline) Interferometric Measurements of Binary Stars
 (Long-Baseline) Interferometric Measurements of Binary Stars A. Boden MSC/Caltech & GSU C. Hummel USNO/ESO G. Torres & D. Latham CfA H. McAlister CHARA/GSU Outline Introduction: Why study binary stars
(Long-Baseline) Interferometric Measurements of Binary Stars A. Boden MSC/Caltech & GSU C. Hummel USNO/ESO G. Torres & D. Latham CfA H. McAlister CHARA/GSU Outline Introduction: Why study binary stars
Binary Stars. Kepler s Laws of Orbital Motion
 Binary Stars Kepler s Laws of Orbital Motion Kepler s Three Laws of orbital motion result from the solution to the equation of motion for bodies moving under the influence of a central 1/r 2 force gravity.
Binary Stars Kepler s Laws of Orbital Motion Kepler s Three Laws of orbital motion result from the solution to the equation of motion for bodies moving under the influence of a central 1/r 2 force gravity.
Orbital Dynamics with Maple (sll --- v1.0, February 2012)
 Orbital Dynamics with Maple (sll --- v1.0, February 2012) Kepler s Laws of Orbital Motion Orbital theory is one of the great triumphs mathematical astronomy. The first understanding of orbits was published
Orbital Dynamics with Maple (sll --- v1.0, February 2012) Kepler s Laws of Orbital Motion Orbital theory is one of the great triumphs mathematical astronomy. The first understanding of orbits was published
Problem Set V Solutions
 Problem Set V Solutions. Consider masses m, m 2, m 3 at x, x 2, x 3. Find X, the C coordinate by finding X 2, the C of mass of and 2, and combining it with m 3. Show this is gives the same result as 3
Problem Set V Solutions. Consider masses m, m 2, m 3 at x, x 2, x 3. Find X, the C coordinate by finding X 2, the C of mass of and 2, and combining it with m 3. Show this is gives the same result as 3
Physics Notes Class 11 CHAPTER 3 MOTION IN A STRAIGHT LINE
 1 P a g e Motion Physics Notes Class 11 CHAPTER 3 MOTION IN A STRAIGHT LINE If an object changes its position with respect to its surroundings with time, then it is called in motion. Rest If an object
1 P a g e Motion Physics Notes Class 11 CHAPTER 3 MOTION IN A STRAIGHT LINE If an object changes its position with respect to its surroundings with time, then it is called in motion. Rest If an object
Halliday, Resnick & Walker Chapter 13. Gravitation. Physics 1A PHYS1121 Professor Michael Burton
 Halliday, Resnick & Walker Chapter 13 Gravitation Physics 1A PHYS1121 Professor Michael Burton II_A2: Planetary Orbits in the Solar System + Galaxy Interactions (You Tube) 21 seconds 13-1 Newton's Law
Halliday, Resnick & Walker Chapter 13 Gravitation Physics 1A PHYS1121 Professor Michael Burton II_A2: Planetary Orbits in the Solar System + Galaxy Interactions (You Tube) 21 seconds 13-1 Newton's Law
Newton s Law of Gravity
 Gravitational Potential Energy On Earth, depends on: object s mass (m) strength of gravity (g) distance object could potentially fall Gravitational Potential Energy In space, an object or gas cloud has
Gravitational Potential Energy On Earth, depends on: object s mass (m) strength of gravity (g) distance object could potentially fall Gravitational Potential Energy In space, an object or gas cloud has
Development of an automated satellite network management system
 Development of an automated satellite network management system Iasonas Kytros Christos Porios Nikitas Terzoudis Varvara Chatzipavlou Coach: Sitsanlis Ilias February 2013 Abstract In this paper we present
Development of an automated satellite network management system Iasonas Kytros Christos Porios Nikitas Terzoudis Varvara Chatzipavlou Coach: Sitsanlis Ilias February 2013 Abstract In this paper we present
Orbital Dynamics in Terms of Spacetime Angular Momentum
 Chapter 4 Orbital Dynamics in Terms of Spacetime Angular Momentum by Myron W. Evans 1 and H. Eckardt 2 Alpha Institute for Advanced Study (AIAS) (www.aias.us, www.atomicprecision.com) Abstract Planar orbital
Chapter 4 Orbital Dynamics in Terms of Spacetime Angular Momentum by Myron W. Evans 1 and H. Eckardt 2 Alpha Institute for Advanced Study (AIAS) (www.aias.us, www.atomicprecision.com) Abstract Planar orbital
Candidate Number. General Certificate of Education Advanced Level Examination June 2010
 entre Number andidate Number Surname Other Names andidate Signature General ertificate of Education dvanced Level Examination June 1 Physics PHY4/1 Unit 4 Fields and Further Mechanics Section Friday 18
entre Number andidate Number Surname Other Names andidate Signature General ertificate of Education dvanced Level Examination June 1 Physics PHY4/1 Unit 4 Fields and Further Mechanics Section Friday 18
8.012 Physics I: Classical Mechanics Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
(Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7)
 Chapter 4. Lagrangian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7 4.1 Important Notes on Notation In this chapter, unless otherwise stated, the following
Chapter 4. Lagrangian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7 4.1 Important Notes on Notation In this chapter, unless otherwise stated, the following
Astromechanics Two-Body Problem (Cont)
 5. Orbit Characteristics Astromechanics Two-Body Problem (Cont) We have shown that the in the two-body problem, the orbit of the satellite about the primary (or vice-versa) is a conic section, with the
5. Orbit Characteristics Astromechanics Two-Body Problem (Cont) We have shown that the in the two-body problem, the orbit of the satellite about the primary (or vice-versa) is a conic section, with the
Lesson 3: Isothermal Hydrostatic Spheres. B68: a self-gravitating stable cloud. Hydrostatic self-gravitating spheres. P = "kt 2.
 Lesson 3: Isothermal Hydrostatic Spheres B68: a self-gravitating stable cloud Bok Globule Relatively isolated, hence not many external disturbances Though not main mode of star formation, their isolation
Lesson 3: Isothermal Hydrostatic Spheres B68: a self-gravitating stable cloud Bok Globule Relatively isolated, hence not many external disturbances Though not main mode of star formation, their isolation
Lecture 07: Work and Kinetic Energy. Physics 2210 Fall Semester 2014
 Lecture 07: Work and Kinetic Energy Physics 2210 Fall Semester 2014 Announcements Schedule next few weeks: 9/08 Unit 3 9/10 Unit 4 9/15 Unit 5 (guest lecturer) 9/17 Unit 6 (guest lecturer) 9/22 Unit 7,
Lecture 07: Work and Kinetic Energy Physics 2210 Fall Semester 2014 Announcements Schedule next few weeks: 9/08 Unit 3 9/10 Unit 4 9/15 Unit 5 (guest lecturer) 9/17 Unit 6 (guest lecturer) 9/22 Unit 7,
Elliptical Galaxies. Houjun Mo. April 19, 2004. Basic properties of elliptical galaxies. Formation of elliptical galaxies
 Elliptical Galaxies Houjun Mo April 19, 2004 Basic properties of elliptical galaxies Formation of elliptical galaxies Photometric Properties Isophotes of elliptical galaxies are usually fitted by ellipses:
Elliptical Galaxies Houjun Mo April 19, 2004 Basic properties of elliptical galaxies Formation of elliptical galaxies Photometric Properties Isophotes of elliptical galaxies are usually fitted by ellipses:
Central configuration in the planar n + 1 body problem with generalized forces.
 Monografías de la Real Academia de Ciencias de Zaragoza. 28: 1 8, (2006). Central configuration in the planar n + 1 body problem with generalized forces. M. Arribas, A. Elipe Grupo de Mecánica Espacial.
Monografías de la Real Academia de Ciencias de Zaragoza. 28: 1 8, (2006). Central configuration in the planar n + 1 body problem with generalized forces. M. Arribas, A. Elipe Grupo de Mecánica Espacial.
Penn State University Physics 211 ORBITAL MECHANICS 1
 ORBITAL MECHANICS 1 PURPOSE The purpose of this laboratory project is to calculate, verify and then simulate various satellite orbit scenarios for an artificial satellite orbiting the earth. First, there
ORBITAL MECHANICS 1 PURPOSE The purpose of this laboratory project is to calculate, verify and then simulate various satellite orbit scenarios for an artificial satellite orbiting the earth. First, there
Chapter 2. Mission Analysis. 2.1 Mission Geometry
 Chapter 2 Mission Analysis As noted in Chapter 1, orbital and attitude dynamics must be considered as coupled. That is to say, the orbital motion of a spacecraft affects the attitude motion, and the attitude
Chapter 2 Mission Analysis As noted in Chapter 1, orbital and attitude dynamics must be considered as coupled. That is to say, the orbital motion of a spacecraft affects the attitude motion, and the attitude
Orbits of the Lennard-Jones Potential
 Orbits of the Lennard-Jones Potential Prashanth S. Venkataram July 28, 2012 1 Introduction The Lennard-Jones potential describes weak interactions between neutral atoms and molecules. Unlike the potentials
Orbits of the Lennard-Jones Potential Prashanth S. Venkataram July 28, 2012 1 Introduction The Lennard-Jones potential describes weak interactions between neutral atoms and molecules. Unlike the potentials
Practice Problems on the Navier-Stokes Equations
 ns_0 A viscous, incompressible, Newtonian liquid flows in stead, laminar, planar flow down a vertical wall. The thickness,, of the liquid film remains constant. Since the liquid free surface is eposed
ns_0 A viscous, incompressible, Newtonian liquid flows in stead, laminar, planar flow down a vertical wall. The thickness,, of the liquid film remains constant. Since the liquid free surface is eposed
Lecture L17 - Orbit Transfers and Interplanetary Trajectories
 S. Widnall, J. Peraire 16.07 Dynamics Fall 008 Version.0 Lecture L17 - Orbit Transfers and Interplanetary Trajectories In this lecture, we will consider how to transfer from one orbit, to another or to
S. Widnall, J. Peraire 16.07 Dynamics Fall 008 Version.0 Lecture L17 - Orbit Transfers and Interplanetary Trajectories In this lecture, we will consider how to transfer from one orbit, to another or to
VELOCITY, ACCELERATION, FORCE
 VELOCITY, ACCELERATION, FORCE velocity Velocity v is a vector, with units of meters per second ( m s ). Velocity indicates the rate of change of the object s position ( r ); i.e., velocity tells you how
VELOCITY, ACCELERATION, FORCE velocity Velocity v is a vector, with units of meters per second ( m s ). Velocity indicates the rate of change of the object s position ( r ); i.e., velocity tells you how
Vector Algebra II: Scalar and Vector Products
 Chapter 2 Vector Algebra II: Scalar and Vector Products We saw in the previous chapter how vector quantities may be added and subtracted. In this chapter we consider the products of vectors and define
Chapter 2 Vector Algebra II: Scalar and Vector Products We saw in the previous chapter how vector quantities may be added and subtracted. In this chapter we consider the products of vectors and define
Physics 9e/Cutnell. correlated to the. College Board AP Physics 1 Course Objectives
 Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Chapter 15.3 Galaxy Evolution
 Chapter 15.3 Galaxy Evolution Elliptical Galaxies Spiral Galaxies Irregular Galaxies Are there any connections between the three types of galaxies? How do galaxies form? How do galaxies evolve? P.S. You
Chapter 15.3 Galaxy Evolution Elliptical Galaxies Spiral Galaxies Irregular Galaxies Are there any connections between the three types of galaxies? How do galaxies form? How do galaxies evolve? P.S. You
Planetesimal Dynamics Formation of Terrestrial Planets from Planetesimals
 Planetesimal Dynamics Formation of Terrestrial Planets from Planetesimals Protoplanetary disk Gas/Dust Planetesimals...... 10 6 yr 10 5-6 yr Protoplanets 10 7-8 yr Terrestrial planets Eiichiro Kokubo National
Planetesimal Dynamics Formation of Terrestrial Planets from Planetesimals Protoplanetary disk Gas/Dust Planetesimals...... 10 6 yr 10 5-6 yr Protoplanets 10 7-8 yr Terrestrial planets Eiichiro Kokubo National
Chapter 6. Work and Energy
 Chapter 6 Work and Energy The concept of forces acting on a mass (one object) is intimately related to the concept of ENERGY production or storage. A mass accelerated to a non-zero speed carries energy
Chapter 6 Work and Energy The concept of forces acting on a mass (one object) is intimately related to the concept of ENERGY production or storage. A mass accelerated to a non-zero speed carries energy
Data Provided: A formula sheet and table of physical constants is attached to this paper. DARK MATTER AND THE UNIVERSE
 Data Provided: A formula sheet and table of physical constants is attached to this paper. DEPARTMENT OF PHYSICS AND ASTRONOMY Autumn Semester (2014-2015) DARK MATTER AND THE UNIVERSE 2 HOURS Answer question
Data Provided: A formula sheet and table of physical constants is attached to this paper. DEPARTMENT OF PHYSICS AND ASTRONOMY Autumn Semester (2014-2015) DARK MATTER AND THE UNIVERSE 2 HOURS Answer question
Parametric Curves. (Com S 477/577 Notes) Yan-Bin Jia. Oct 8, 2015
 Parametric Curves (Com S 477/577 Notes) Yan-Bin Jia Oct 8, 2015 1 Introduction A curve in R 2 (or R 3 ) is a differentiable function α : [a,b] R 2 (or R 3 ). The initial point is α[a] and the final point
Parametric Curves (Com S 477/577 Notes) Yan-Bin Jia Oct 8, 2015 1 Introduction A curve in R 2 (or R 3 ) is a differentiable function α : [a,b] R 2 (or R 3 ). The initial point is α[a] and the final point
Some Comments on the Derivative of a Vector with applications to angular momentum and curvature. E. L. Lady (October 18, 2000)
 Some Comments on the Derivative of a Vector with applications to angular momentum and curvature E. L. Lady (October 18, 2000) Finding the formula in polar coordinates for the angular momentum of a moving
Some Comments on the Derivative of a Vector with applications to angular momentum and curvature E. L. Lady (October 18, 2000) Finding the formula in polar coordinates for the angular momentum of a moving
Chapter 5: Circular Motion, the Planets, and Gravity
 Chapter 5: Circular Motion, the Planets, and Gravity 1. Earth s gravity attracts a person with a force of 120 lbs. The force with which the Earth is attracted towards the person is A. Zero. B. Small but
Chapter 5: Circular Motion, the Planets, and Gravity 1. Earth s gravity attracts a person with a force of 120 lbs. The force with which the Earth is attracted towards the person is A. Zero. B. Small but
The Hidden Lives of Galaxies. Jim Lochner, USRA & NASA/GSFC
 The Hidden Lives of Galaxies Jim Lochner, USRA & NASA/GSFC What is a Galaxy? Solar System Distance from Earth to Sun = 93,000,000 miles = 8 light-minutes Size of Solar System = 5.5 light-hours What is
The Hidden Lives of Galaxies Jim Lochner, USRA & NASA/GSFC What is a Galaxy? Solar System Distance from Earth to Sun = 93,000,000 miles = 8 light-minutes Size of Solar System = 5.5 light-hours What is
RS platforms. Fabio Dell Acqua - Gruppo di Telerilevamento
 RS platforms Platform vs. instrument Sensor Platform Instrument The remote sensor can be ideally represented as an instrument carried by a platform Platforms Remote Sensing: Ground-based air-borne space-borne
RS platforms Platform vs. instrument Sensor Platform Instrument The remote sensor can be ideally represented as an instrument carried by a platform Platforms Remote Sensing: Ground-based air-borne space-borne
Solar System Fundamentals. What is a Planet? Planetary orbits Planetary temperatures Planetary Atmospheres Origin of the Solar System
 Solar System Fundamentals What is a Planet? Planetary orbits Planetary temperatures Planetary Atmospheres Origin of the Solar System Properties of Planets What is a planet? Defined finally in August 2006!
Solar System Fundamentals What is a Planet? Planetary orbits Planetary temperatures Planetary Atmospheres Origin of the Solar System Properties of Planets What is a planet? Defined finally in August 2006!
Practice Final Math 122 Spring 12 Instructor: Jeff Lang
 Practice Final Math Spring Instructor: Jeff Lang. Find the limit of the sequence a n = ln (n 5) ln (3n + 8). A) ln ( ) 3 B) ln C) ln ( ) 3 D) does not exist. Find the limit of the sequence a n = (ln n)6
Practice Final Math Spring Instructor: Jeff Lang. Find the limit of the sequence a n = ln (n 5) ln (3n + 8). A) ln ( ) 3 B) ln C) ln ( ) 3 D) does not exist. Find the limit of the sequence a n = (ln n)6
Testing dark matter halos using rotation curves and lensing
 Testing dark matter halos using rotation curves and lensing Darío Núñez Instituto de Ciencias Nucleares, UNAM Instituto Avanzado de Cosmología A. González, J. Cervantes, T. Matos Observational evidences
Testing dark matter halos using rotation curves and lensing Darío Núñez Instituto de Ciencias Nucleares, UNAM Instituto Avanzado de Cosmología A. González, J. Cervantes, T. Matos Observational evidences
2. Orbits. FER-Zagreb, Satellite communication systems 2011/12
 2. Orbits Topics Orbit types Kepler and Newton laws Coverage area Influence of Earth 1 Orbit types According to inclination angle Equatorial Polar Inclinational orbit According to shape Circular orbit
2. Orbits Topics Orbit types Kepler and Newton laws Coverage area Influence of Earth 1 Orbit types According to inclination angle Equatorial Polar Inclinational orbit According to shape Circular orbit
Magnetism. d. gives the direction of the force on a charge moving in a magnetic field. b. results in negative charges moving. clockwise.
 Magnetism 1. An electron which moves with a speed of 3.0 10 4 m/s parallel to a uniform magnetic field of 0.40 T experiences a force of what magnitude? (e = 1.6 10 19 C) a. 4.8 10 14 N c. 2.2 10 24 N b.
Magnetism 1. An electron which moves with a speed of 3.0 10 4 m/s parallel to a uniform magnetic field of 0.40 T experiences a force of what magnitude? (e = 1.6 10 19 C) a. 4.8 10 14 N c. 2.2 10 24 N b.
Equations Involving Lines and Planes Standard equations for lines in space
 Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
Astronomy 1140 Quiz 1 Review
 Astronomy 1140 Quiz 1 Review Prof. Pradhan September 15, 2015 What is Science? 1. Explain the difference between astronomy and astrology. (a) Astrology: nonscience using zodiac sign to predict the future/personality
Astronomy 1140 Quiz 1 Review Prof. Pradhan September 15, 2015 What is Science? 1. Explain the difference between astronomy and astrology. (a) Astrology: nonscience using zodiac sign to predict the future/personality
Name: Earth 110 Exploration of the Solar System Assignment 1: Celestial Motions and Forces Due in class Tuesday, Jan. 20, 2015
 Name: Earth 110 Exploration of the Solar System Assignment 1: Celestial Motions and Forces Due in class Tuesday, Jan. 20, 2015 Why are celestial motions and forces important? They explain the world around
Name: Earth 110 Exploration of the Solar System Assignment 1: Celestial Motions and Forces Due in class Tuesday, Jan. 20, 2015 Why are celestial motions and forces important? They explain the world around
Mechanics 1: Conservation of Energy and Momentum
 Mechanics : Conservation of Energy and Momentum If a certain quantity associated with a system does not change in time. We say that it is conserved, and the system possesses a conservation law. Conservation
Mechanics : Conservation of Energy and Momentum If a certain quantity associated with a system does not change in time. We say that it is conserved, and the system possesses a conservation law. Conservation
Force on Moving Charges in a Magnetic Field
 [ Assignment View ] [ Eðlisfræði 2, vor 2007 27. Magnetic Field and Magnetic Forces Assignment is due at 2:00am on Wednesday, February 28, 2007 Credit for problems submitted late will decrease to 0% after
[ Assignment View ] [ Eðlisfræði 2, vor 2007 27. Magnetic Field and Magnetic Forces Assignment is due at 2:00am on Wednesday, February 28, 2007 Credit for problems submitted late will decrease to 0% after
PHYSICS FOUNDATIONS SOCIETY THE DYNAMIC UNIVERSE TOWARD A UNIFIED PICTURE OF PHYSICAL REALITY TUOMO SUNTOLA
 PHYSICS FOUNDATIONS SOCIETY THE DYNAMIC UNIVERSE TOWARD A UNIFIED PICTURE OF PHYSICAL REALITY TUOMO SUNTOLA Published by PHYSICS FOUNDATIONS SOCIETY Espoo, Finland www.physicsfoundations.org Printed by
PHYSICS FOUNDATIONS SOCIETY THE DYNAMIC UNIVERSE TOWARD A UNIFIED PICTURE OF PHYSICAL REALITY TUOMO SUNTOLA Published by PHYSICS FOUNDATIONS SOCIETY Espoo, Finland www.physicsfoundations.org Printed by
Faraday s Law of Induction
 Chapter 10 Faraday s Law of Induction 10.1 Faraday s Law of Induction...10-10.1.1 Magnetic Flux...10-3 10.1. Lenz s Law...10-5 10. Motional EMF...10-7 10.3 Induced Electric Field...10-10 10.4 Generators...10-1
Chapter 10 Faraday s Law of Induction 10.1 Faraday s Law of Induction...10-10.1.1 Magnetic Flux...10-3 10.1. Lenz s Law...10-5 10. Motional EMF...10-7 10.3 Induced Electric Field...10-10 10.4 Generators...10-1
Lecture 7 Formation of the Solar System. Nebular Theory. Origin of the Solar System. Origin of the Solar System. The Solar Nebula
 Origin of the Solar System Lecture 7 Formation of the Solar System Reading: Chapter 9 Quiz#2 Today: Lecture 60 minutes, then quiz 20 minutes. Homework#1 will be returned on Thursday. Our theory must explain
Origin of the Solar System Lecture 7 Formation of the Solar System Reading: Chapter 9 Quiz#2 Today: Lecture 60 minutes, then quiz 20 minutes. Homework#1 will be returned on Thursday. Our theory must explain
11. Rotation Translational Motion: Rotational Motion:
 11. Rotation Translational Motion: Motion of the center of mass of an object from one position to another. All the motion discussed so far belongs to this category, except uniform circular motion. Rotational
11. Rotation Translational Motion: Motion of the center of mass of an object from one position to another. All the motion discussed so far belongs to this category, except uniform circular motion. Rotational
astronomy 2008 1. A planet was viewed from Earth for several hours. The diagrams below represent the appearance of the planet at four different times.
 1. A planet was viewed from Earth for several hours. The diagrams below represent the appearance of the planet at four different times. 5. If the distance between the Earth and the Sun were increased,
1. A planet was viewed from Earth for several hours. The diagrams below represent the appearance of the planet at four different times. 5. If the distance between the Earth and the Sun were increased,
Problem Set #8 Solutions
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department 8.01L: Physics I November 7, 2015 Prof. Alan Guth Problem Set #8 Solutions Due by 11:00 am on Friday, November 6 in the bins at the intersection
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department 8.01L: Physics I November 7, 2015 Prof. Alan Guth Problem Set #8 Solutions Due by 11:00 am on Friday, November 6 in the bins at the intersection
Orbital Mechanics and Space Geometry
 Orbital Mechanics and Space Geometry AERO4701 Space Engineering 3 Week 2 Overview First Hour Co-ordinate Systems and Frames of Reference (Review) Kepler s equations, Orbital Elements Second Hour Orbit
Orbital Mechanics and Space Geometry AERO4701 Space Engineering 3 Week 2 Overview First Hour Co-ordinate Systems and Frames of Reference (Review) Kepler s equations, Orbital Elements Second Hour Orbit
ADVANCED TOPICS IN ASTRODYNAMICS GRAVITATIONAL ASSISTED TRAJECTORIES
 ADVANCED TOPICS IN ASTRODYNAMICS SUMMER COURSE BARCELONA, JULY 2004 NOTES FOR THE GRAVITATIONAL ASSISTED TRAJECTORIES LECTURES E. Barrabés, G. Gómez and J. Rodríguez-Canabal Contents 1 Introduction 3 1.1
ADVANCED TOPICS IN ASTRODYNAMICS SUMMER COURSE BARCELONA, JULY 2004 NOTES FOR THE GRAVITATIONAL ASSISTED TRAJECTORIES LECTURES E. Barrabés, G. Gómez and J. Rodríguez-Canabal Contents 1 Introduction 3 1.1
Newton s Law of Motion
 chapter 5 Newton s Law of Motion Static system 1. Hanging two identical masses Context in the textbook: Section 5.3, combination of forces, Example 4. Vertical motion without friction 2. Elevator: Decelerating
chapter 5 Newton s Law of Motion Static system 1. Hanging two identical masses Context in the textbook: Section 5.3, combination of forces, Example 4. Vertical motion without friction 2. Elevator: Decelerating
On a Flat Expanding Universe
 Adv. Studies Theor. Phys., Vol. 7, 2013, no. 4, 191-197 HIKARI Ltd, www.m-hikari.com On a Flat Expanding Universe Bo Lehnert Alfvén Laboratory Royal Institute of Technology, SE-10044 Stockholm, Sweden
Adv. Studies Theor. Phys., Vol. 7, 2013, no. 4, 191-197 HIKARI Ltd, www.m-hikari.com On a Flat Expanding Universe Bo Lehnert Alfvén Laboratory Royal Institute of Technology, SE-10044 Stockholm, Sweden
Nuclear fusion in stars. Collapse of primordial density fluctuations into galaxies and stars, nucleosynthesis in stars
 Nuclear fusion in stars Collapse of primordial density fluctuations into galaxies and stars, nucleosynthesis in stars The origin of structure in the Universe Until the time of formation of protogalaxies,
Nuclear fusion in stars Collapse of primordial density fluctuations into galaxies and stars, nucleosynthesis in stars The origin of structure in the Universe Until the time of formation of protogalaxies,
Celestial mechanics: The perturbed Kepler problem.
 Celestial mechanics: The perturbed Kepler problem. László Árpád Gergely1,2 1 Department of Theoretical Physics, University of Szeged, Tisza Lajos krt 84-86, Szeged 6720, Hungary 2 Department of Experimental
Celestial mechanics: The perturbed Kepler problem. László Árpád Gergely1,2 1 Department of Theoretical Physics, University of Szeged, Tisza Lajos krt 84-86, Szeged 6720, Hungary 2 Department of Experimental
Physics 1A Lecture 10C
 Physics 1A Lecture 10C "If you neglect to recharge a battery, it dies. And if you run full speed ahead without stopping for water, you lose momentum to finish the race. --Oprah Winfrey Static Equilibrium
Physics 1A Lecture 10C "If you neglect to recharge a battery, it dies. And if you run full speed ahead without stopping for water, you lose momentum to finish the race. --Oprah Winfrey Static Equilibrium
All About Motion - Displacement, Velocity and Acceleration
 All About Motion - Displacement, Velocity and Acceleration Program Synopsis 2008 20 minutes Teacher Notes: Ian Walter Dip App Chem; GDipEd Admin; TTTC This program explores vector and scalar quantities
All About Motion - Displacement, Velocity and Acceleration Program Synopsis 2008 20 minutes Teacher Notes: Ian Walter Dip App Chem; GDipEd Admin; TTTC This program explores vector and scalar quantities
State of Stress at Point
 State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
Chapter 3.8 & 6 Solutions
 Chapter 3.8 & 6 Solutions P3.37. Prepare: We are asked to find period, speed and acceleration. Period and frequency are inverses according to Equation 3.26. To find speed we need to know the distance traveled
Chapter 3.8 & 6 Solutions P3.37. Prepare: We are asked to find period, speed and acceleration. Period and frequency are inverses according to Equation 3.26. To find speed we need to know the distance traveled
Notes on Elastic and Inelastic Collisions
 Notes on Elastic and Inelastic Collisions In any collision of 2 bodies, their net momentus conserved. That is, the net momentum vector of the bodies just after the collision is the same as it was just
Notes on Elastic and Inelastic Collisions In any collision of 2 bodies, their net momentus conserved. That is, the net momentum vector of the bodies just after the collision is the same as it was just
Modeling Galaxy Formation
 Galaxy Evolution is the study of how galaxies form and how they change over time. As was the case with we can not observe an individual galaxy evolve but we can observe different galaxies at various stages
Galaxy Evolution is the study of how galaxies form and how they change over time. As was the case with we can not observe an individual galaxy evolve but we can observe different galaxies at various stages
AP1 Oscillations. 1. Which of the following statements about a spring-block oscillator in simple harmonic motion about its equilibrium point is false?
 1. Which of the following statements about a spring-block oscillator in simple harmonic motion about its equilibrium point is false? (A) The displacement is directly related to the acceleration. (B) The
1. Which of the following statements about a spring-block oscillator in simple harmonic motion about its equilibrium point is false? (A) The displacement is directly related to the acceleration. (B) The
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Exam in: FYS 310 Classical Mechanics and Electrodynamics Day of exam: Tuesday June 4, 013 Exam hours: 4 hours, beginning at 14:30 This examination
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Exam in: FYS 310 Classical Mechanics and Electrodynamics Day of exam: Tuesday June 4, 013 Exam hours: 4 hours, beginning at 14:30 This examination
Columbia University Department of Physics QUALIFYING EXAMINATION
 Columbia University Department of Physics QUALIFYING EXAMINATION Monday, January 13, 2014 1:00PM to 3:00PM Classical Physics Section 1. Classical Mechanics Two hours are permitted for the completion of
Columbia University Department of Physics QUALIFYING EXAMINATION Monday, January 13, 2014 1:00PM to 3:00PM Classical Physics Section 1. Classical Mechanics Two hours are permitted for the completion of
Practice final for Basic Physics spring 2005 answers on the last page Name: Date:
 Practice final for Basic Physics spring 2005 answers on the last page Name: Date: 1. A 12 ohm resistor and a 24 ohm resistor are connected in series in a circuit with a 6.0 volt battery. Assuming negligible
Practice final for Basic Physics spring 2005 answers on the last page Name: Date: 1. A 12 ohm resistor and a 24 ohm resistor are connected in series in a circuit with a 6.0 volt battery. Assuming negligible
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics. 8.02 Spring 2013 Conflict Exam Two Solutions
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics 802 Spring 2013 Conflict Exam Two Solutions Problem 1 (25 points): answers without work shown will not be given any credit A uniformly charged
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics 802 Spring 2013 Conflict Exam Two Solutions Problem 1 (25 points): answers without work shown will not be given any credit A uniformly charged
SPINDLE ERROR MOVEMENTS MEASUREMENT ALGORITHM AND A NEW METHOD OF RESULTS ANALYSIS 1. INTRODUCTION
 Journal of Machine Engineering, Vol. 15, No.1, 2015 machine tool accuracy, metrology, spindle error motions Krzysztof JEMIELNIAK 1* Jaroslaw CHRZANOWSKI 1 SPINDLE ERROR MOVEMENTS MEASUREMENT ALGORITHM
Journal of Machine Engineering, Vol. 15, No.1, 2015 machine tool accuracy, metrology, spindle error motions Krzysztof JEMIELNIAK 1* Jaroslaw CHRZANOWSKI 1 SPINDLE ERROR MOVEMENTS MEASUREMENT ALGORITHM
Mechanics lecture 7 Moment of a force, torque, equilibrium of a body
 G.1 EE1.el3 (EEE1023): Electronics III Mechanics lecture 7 Moment of a force, torque, equilibrium of a body Dr Philip Jackson http://www.ee.surrey.ac.uk/teaching/courses/ee1.el3/ G.2 Moments, torque and
G.1 EE1.el3 (EEE1023): Electronics III Mechanics lecture 7 Moment of a force, torque, equilibrium of a body Dr Philip Jackson http://www.ee.surrey.ac.uk/teaching/courses/ee1.el3/ G.2 Moments, torque and
