CHAPTER 31 CAPACITOR
|
|
|
- Nelson Parks
- 9 years ago
- Views:
Transcription
1 . Given tht Numer of eletron HPTER PITOR Net hrge Q The net potentil ifferene L..6 pitne v F.. r 5 m. m F... Let the rius of the is R re R D mm m 8.85 r r m.5 m mm. m V 6V Q? Q V 6.8. W Q V J. 5. Plte re 5 m.5 m Seprtion mm m Potentil v v () We now v () Then erese to mm mm m v m 6 Km F The extr hrge given to plte (.65.).. 6. F, 4 F, 6 F V V 4 6 F 6 F 4, 4 48, m. m mm V
2 pitor 7. F F 4 F V V The euivlent pity () Let Euivlent hrge t the pitor 4 9. F 6 V V 9. on eh. s this is series omintion, the hrge on eh pitor is sme s the euivlent hrge whih is. () Let the wor one y the ttery W V W W V 6. J F, 4 F, 4 F e ( ) F 6 Sine & re prllel & re in series with So, () V 4 F 8 F 4 F 4 6, re series &, re series s the V is sme t p &. So no urrent pss through p &. p 4 F n 6 F p 5 F () 4 F, 6 F, In se of p &, p 4 F p 6 F & 5 F & 5 F The eution of pitor 5 5 F. R S
3 pitor. V v e [ They re prllel] 5 6 F V. The pitne of the outer sphere. F. F Potentil, V v Let the hrge given to iniviul yliner. V 5 F V 6 F 5 6 V. F The totl hrge given to the inner yliner 44 F. V, Now V R K So, K / R K R 4 R. Similrly 4 R The omintion is neessrily prllel. Hene e 4 R 4 R 4 (R R ) F In this system the pitne re rrnge in series. Then the pitne is prllel to eh other. () The eution of pitne in one row () n three pitne of pity re onnete in prllel The eution of pitne F s the volt pitne on eh row re sme n the iniviul is No. of Totl 6 V pitne 4. Let there re x no of pitors in series ie in row So, x 5 x 4 pitors. Effetive pitne in row 4 Now, let there re y suh rows, So, y 4 y 4 pitor. So, the omintions of four rows eh of 4 pitors..
4 pitor 5. 4 F 8 F F D 6 F 4 F F D 8 F 6 F 4 F 8 F F D 6 F 5 5 () pitor n F 6 8 (i) The hrge on the pitne 8 F 8 4 Q 5 4 The potentil t 4 F 4 4 t 8 F The Potentil ifferene V 6 (ii) Hene the effetive hrge t F 5 F Potentil t F Differene ; Potentil t 6 F 6 5 V 6 5 The potentil t & D is V P R () S It is lne. So from it is lere tht the whet str rige lne. So the potentil t the point & D re sme. So no urrent flow through the point & D. So if we onnet nother pitor t the point & D the hrge on the pitor is zero. 6. e etween & / (The three re prllel) 7. In the figure the three pitors re rrnge in prllel. ll hve sme surfe re First pitne n pitne r pitne e ( ) ( ).4 E / D
5 pitor ( ) ( ) ( )( ) ( ) ( ) ( )( ) 6 8. () ( )( ) In(R L /R ) e In [In.69] PF () Sme s R /R will e sme. 9. Given tht PF F PF F V 4 V 4 4? Let The new hrge PF V The Voltge. Let the new potentil is V fter the flow of hrge, potentil is sme in the two pitor V V 6 S / V Initilly when s is not onnete, 5 eff fter the swith is me on, Then eff 5 Q Now, the initil hrge will remin store in the store in the short pitor Hene net hrge flowing
6 pitor. V.4 F P.4 F Given tht mss of prtile m mg hrge. m Let potentil V.4 The Eution pitne. F The prtile my e in euilirium, so tht the wt. of the prtile ting own wr, must e lne y the eletri fore ting up wr. E Mg Eletri fore E V E mg QV mg.. V 8.85 V. 98 where V Potentil, seprtion of oth the pltes V.4 4 MV.. Let mss of eletron hrge eletron e We now, For hrge prtile to e projete in sie to pltes of prllel plte pitor with eletri fiel E, y E x m where y Vertil istne overe or x Horizontl istne overe Initil veloity From the given t, y V, E R For pitor V s Here hre on pitor., x,? V where Euivlent pitne of the totl rrngement So, V me.6
7 pitor Hene E V ( ) V ( ) Sustituting the t in the nown eution, we get, e V ( )m u u Ve m( ) u Ve m( ) /. The elertion of eletron e eme Me pe The elertion of proton p Mp The istne trvelle y proton X pt () m e e x E E ep x p E The istne trvelle y eletron () From () n () X t x t 4. () x x x M x M p p pe Mp F M x x x F F F F 6 F 6 s the rige in lne there is no urrent through the 5 F pitor So, it reues to similr in the se of () & () s n lso e written s. 6 6 e.5 F () y loop metho pplition in the lose iruit D Q Q Q () F F 4F In the lose iruit D Q Q F 4F Q () From () n () Q Q 48 () n Q 48 n sutrting Q 4Q, n sustitution in eution Q F F 5 F F 6 F F F Q 4 F (Q Q ) 4 F D.7
8 pitor 48 Q Q 48 8 Q Q 48 Q 48, V () Q 4F F 48 4 V V 4 F F V 4 F 4 V 4 V The potentil 4 ( 4) Potentil ifferene V 4 The V V 8 V Left Right () V V 48 8 V 6 F F From the figure it is lere tht the left n right rnh re symmetry n reverse, so the urrent go towrs E from FE sme s the urrent from EDE. The net hrge Q V Q V The potentil t K is zero. () 6 V 4 F E F D V 4 V F F The net potentil V V. V 6. () Net hrge Net pitne / V F 4 F F /8 4/8 /8 /8 F F 4/8 /8 / / y str Delt onversion eff 8 F F F 6 F F.8
9 pitor () F F F 4 F F 4 F F /8 f /8 f 4/8 f f f F / f y str Delt onvensor /8 f / f /8 f 4/8 f f f /8 f /8 f / f /8 f / f 4 f 4 f f /8 f () F 4 F 4/ F 5 F 8/ F 4 F 8 F 4 F 4 F 4 8 ef 4 () 8 F f 4 f 6 f f 4 f 4 f 4 f 6 f 8 f 8 f 4 f 4 f 8 f 8 f 6 f f 4 f f 4 f 8/6 f / f / f 8/6 f ef f.9
10 pitor 7. f f f f n re in series e This is prllel to 6 Whih is series to Whih is prllel to 7 Whih is series to Whih is prllel to 8 This is series to 4 Fig F f Fig 9. Let the euivlent pitne e. Sine it is n infinite series. So, there will e negligile hnge if the rrngement is one n in Fig e ( ) ( ) ( ) (Impossile) So, F 4 f 4 f 4 f 4 f f f f f n 4 f re in series 4 So, 4 Then n f re prllel f f The vlue of is 4 f 6 6.
11 F. 9 F net 8. V.5 V 9.. Given tht pitne F hrge The effetive hrge 8 F V V V. 6. F 7 F 6 net ( ) Potentil V 5 V 7 5 ut potentil n never e ( )ve. So, V 5 V. Here three pitors re forme n eh of x pitor x x 96 f.m. 4 mm 4 m pitne of pitor F. s three pitor re rrnge is series 4 So, e The totl hrge to pitor The hrge of single Plte () When hrge of is introue to the plte, we lso get.5 hrge on the upper surfe of Plte. () Given 5 F 5 9 F 5 8 F Now hrge.5 6 V F V 5. Here given, pitne of eh pitor, 5 f.5 f hrge Q F whih is given to upper plte.5 hrge pper on outer n inner sie of upper plte n.5 of hrge lso see on the mile. () hrge of eh plte.5 pitne.5 f
12 pitor.5 V v V. 5 () The hrge on lower plte lso.5 pitne.5 F.5 V V V. 5 The potentil in V 6. PF F, 5 PF 5 F Effetive 5 5 hrge F V V V V Energy store in eh pitor E (/) V (/) (4.84) PJ E (/) V (/) 5 (.7) PJ 7. 4 F, 6 F, V V E. pitor e The E pitne e.5 F The energy supplie y the ttery to eh plte E (/) V (/).4 48 J The energy supplies y the ttery to pitor J 8. F 6 F For & F E For & 4 4 e 5 F 8 J 8 mj 4 f 6 f V V V V E (/) v (/) 5 () J mj 9. Store energy of pitor 4. J 4. J When then onnete, the hrge shre So tht the energy shoul ivie. The totl energy store in the two pitors eh is J..
13 4. Initil hrge store V Let the hrges on & 4 pitors e & respetively There, V 4. or E (/) V 8 (/) E (/) V 8 (/) hrge Q Rius of sphere R pitne of the sphere 4 R Energy Q 4. Q V 4 R V E E Q 4 R Q 8 R 6 J 8 J [ in spheril shell 4 R] 6 R V 4 R 4. 4 /m m m The energy store in the plne RV [ of igger shell 4 R] 6 m 4 ( ) The neessry eletro stti energy store in uil volume of ege m infront of the plne J 44. re m m seprtion mm m i i 4 So, flown out. ie, i f. () So, () Energy sore y ttery uring the proess v.6.7 J () efore the proess E i (/) i v (/) J fter the fore E i (/) f v (/) J () Worone Fore Distne (e) pitor From () n () we hve lulte, the energy loss y the seprtion of pltes is eul to the wor one y the mn on plte. Hene no het is proue in trnsformer. Q R
14 pitor 45. () efore reonnetion f V 4 V V 4 (efore reonnetion) fter onnetion When f V V V (fter onnetion) (), V V V v () We now V W W v 44 J 4.4 mj The wor one on the ttery. () Initil eletrostti fiel energy Ui (/) V Finl Eletrostti fiel energy U (/) V Derese in Eletrostti Fiel energy (/) V (/) V (/) (V V ) (/) (576 44) 6J Energy 6 j.6 mj (e)fter reonnetion, V v The energy ppere (/) V (/) 44 7 J 7. mj This mount of energy is evelope s het when the hrge flow through the pitor. 46. () Sine the swith ws open for long time, hene the hrge flown must e ue to the oth, when the swith is lose. ef / So E () Worone v () E i E E f (/) E E E E E 4 E E E i E f 4 () The net hrge in the energy is wste s het f V 4 V V 5 4 n 6 f V R V 6 7 Energy store on first pitor E i () Energy store on n pitor E (7) 6 44 J.44 mj 4 J 4. mj E.4
15 pitor 48. () V V Let the effetive potentil V V V V The new hrge V n V () U (/) V U (/) V U f (/) V ( ) (/) (4.6) (5 6) J.45 mj ut U i The loss in KE mj 5 f 4 v 6 f v (i) (ii) When the pitor is onnete to the ttery, hrge Q E ppers on one plte n Q on the other. When the polrity is reverse, hrge Q ppers on the first plte n Q on the seon. hrge Q, therefore psses through the ttery from the negtive to the positive terminl. The ttery oes wor. W Q E QE E In this proess. The energy store in the pitor is the sme in the two ses. Thus the worone y ttery ppers s het in the onneting wires. The het proue is therefore, E J.44 mj [hve 5 f V E V] 49. m m 4 m m m 4 t t 8.85 t F.4 nf 5. Dieletri onst. 4 F.4 nf, V 6 V hrge supplie V hrge Inue ( /) (.5) n Net hrge ppering on one ote surfe 5. Here Plte re m m Seprtion.5 m 5 m Thiness of metl t.4 m 4 m 8.5. n 4.5 m pf t t t (5 4) Here the pitne is inepenent of the position of metl. t ny position the net seprtion is t. s is the seprtion n t is the thiness. m t.4 m m mm m.5
16 5. Initil hrge store 5 Let the ieletri onstnt of the mteril inue e. Now, when the extr hrge flown through ttery is. So, net hrge store in pitor 5 Now or or, V V Deviing () n () we get () () f V 6 V mm m. () the hrge on the ve plte V 5 f 6 V () E V 6V () m t m 5 or m V/M 5 6 When the ieletri ple on it t t () 5 6 f. V 6 V Q V 5 f f 8. 6 f V 6 V Q V F hrge flown Q Q F Let the pitnes e & net pitne Now p m 4 m m m V 6 V t m F. 4 m pitor 5 6 mm 4 mm.6
17 pitor t t 56. () re Seprtion / () similrly / ( ( ) ) ( ) K K ( ) 57. () x ( ) x tn X x tn onsier n elementl pitor of with x our t istne x from one en. It is onstitute of two pitor elements of ieletri onstnts n with plte seprtion xtn n xtn respetively in series R R x x tn ( x tn ) or R x tn x tn (x) (x) ( x )x tn [log e ( ) x tn] tn ( ) [log e ( ) tn log e ] tn ( ) tn n.7
18 pitor R R ( ) ( ) loge loge 58. R ( ) / In s V I. Initilly when swith s is lose Totl Initil Energy (/) V (/) V V () II. When swith is open the pitne in eh of pitors vries, hene the energy lso vries. i.e. in se of, the hrge remins Sme i.e. v eff E In se of eff v v 6 E eff v v v Totl finl energy v 6 Initil Energy Now, Finl Energy 59. efore inserting fter inserting v v v 6 Q Q V v 6 The hrge flown through the power supply Q Q Q V V V ( ) Worone hrge in emf V ( ) ( ) V V ( ) K.8
19 6. pitne F 4 F P. V () V m Dieletri onstnt.5 () New F New p V. [ remins sme fter isonnetion of ttery] () In the sene of the ieletri sl, the hrge tht must hve proue V 4 m () hrge inue t surfe of the ieletri sl ( /) (where ieletri onstnt, hrge of plte) 5 5 m Here we shoul onsier pitor n in series 4 ( ) 4 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 4 6. These three metlli hollow spheres form two spheril pitors, whih re onnete in series. Solving them iniviully, for () n () 4 ( for spheril pitor forme y two spheres of rii R > R ) 4RR R R Similrly for () n () eff 4 4 (4 ) ( )( ) ( ) ( ) 4 ( )( ) 4 ( ) 4 6. Here we shoul onsier two spheril pitor of pitne n in series 4 ( ) 4 ( ) pitor.9
20 pitor 64. Q V V 4 ( ) ( ) v 6 v m V (v / ) 6 Q v 6 ( ) ( ) m 8 f ( ) ( ) f m m 66. m m V 4 V The pitne m The energy store (/) V (/) (4) The fore ttrtion etween the pltes N. K M We nows In this prtiulr se the eletrifiel ttrts the ieletri into the pitor with fore Where With of pltes Dieletri onstnt Seprtion etween pltes V E Potentil ifferene. Hene in this se the surfes re fritionless, this fore is ounterte y the weight. So, M E ( ) Mg E ( ) g V ( ).
21 pitor 67. l l K K n n () onsier the left sie The plte re of the prt with the ieletri is y its pitne x n with out ieletri These re onnete in prllel [L x( )] Let the potentil V (L x) U (/) V v L x( ) () Suppose ieletri sl is ttrte y eletri fiel n n externl fore F onsier the prt x whih mes insie further, s the potentil ifferene remins onstnt t V. The hrge supply, () v to the pitor The wor one y the ttery is w v. () v The externl fore F oes wor w e ( f.x) uring smll isplement The totl wor one in the pitor is w w e () v fx This shoul e eul to the inrese v in the store energy. Thus (/) ()v () v fx f v x from eution () v F ( ) V F V ( ) F ( ) For the right sie, V V V F ( ) F ( ) V V F ( ) The rtio of the emf of the left ttery to the right ttery.
22 68. pitne of the portion with ieletris, pitne of the portion without ieletris, ( ) Net pitne ( ) ( ) onsier the motion of ieletri in the pitor. Let it further move istne x, whih uses n inrese of pitne y Q () E The wor one y the ttery w Vg E () E E Let fore ting on it e f Wor one y the fore uring the isplement, x fx Inrese in energy store in the pitor (/) () E () E fx fx (/) () E f ( ) E x ( ) x f E x m f t ( ) E ( ) E ( ) m ( ) ( )m E ( ) (here x ) (l ) t 4m( ) E ( ) E l K pitor l Time perio t 8m( ) E ( ).
Practice Test 2. a. 12 kn b. 17 kn c. 13 kn d. 5.0 kn e. 49 kn
Prtie Test 2 1. A highwy urve hs rdius of 0.14 km nd is unnked. A r weighing 12 kn goes round the urve t speed of 24 m/s without slipping. Wht is the mgnitude of the horizontl fore of the rod on the r?
Volumes by Cylindrical Shells: the Shell Method
olumes Clinril Shells: the Shell Metho Another metho of fin the volumes of solis of revolution is the shell metho. It n usull fin volumes tht re otherwise iffiult to evlute using the Dis / Wsher metho.
Answer, Key Homework 10 David McIntyre 1
Answer, Key Homework 10 Dvid McIntyre 1 This print-out should hve 22 questions, check tht it is complete. Multiple-choice questions my continue on the next column or pge: find ll choices efore mking your
c b 5.00 10 5 N/m 2 (0.120 m 3 0.200 m 3 ), = 4.00 10 4 J. W total = W a b + W b c 2.00
Chter 19, exmle rolems: (19.06) A gs undergoes two roesses. First: onstnt volume @ 0.200 m 3, isohori. Pressure inreses from 2.00 10 5 P to 5.00 10 5 P. Seond: Constnt ressure @ 5.00 10 5 P, isori. olume
Module 5. Three-phase AC Circuits. Version 2 EE IIT, Kharagpur
Module 5 Three-hse A iruits Version EE IIT, Khrgur esson 8 Three-hse Blned Suly Version EE IIT, Khrgur In the module, ontining six lessons (-7), the study of iruits, onsisting of the liner elements resistne,
Vectors Summary. Projection vector AC = ( Shortest distance from B to line A C D [OR = where m1. and m
. Slr prout (ot prout): = osθ Vetors Summry Lws of ot prout: (i) = (ii) ( ) = = (iii) = (ngle etween two ientil vetors is egrees) (iv) = n re perpeniulr Applitions: (i) Projetion vetor: B Length of projetion
50 MATHCOUNTS LECTURES (10) RATIOS, RATES, AND PROPORTIONS
0 MATHCOUNTS LECTURES (0) RATIOS, RATES, AND PROPORTIONS BASIC KNOWLEDGE () RATIOS: Rtios re use to ompre two or more numers For n two numers n ( 0), the rtio is written s : = / Emple : If 4 stuents in
Maximum area of polygon
Mimum re of polygon Suppose I give you n stiks. They might e of ifferent lengths, or the sme length, or some the sme s others, et. Now there re lots of polygons you n form with those stiks. Your jo is
SOLUTIONS TO CONCEPTS CHAPTER 5
1. m k S 10m Let, ccelertion, Initil velocity u 0. S ut + 1/ t 10 ½ ( ) 10 5 m/s orce: m 5 10N (ns) 40000. u 40 km/hr 11.11 m/s. 3600 m 000 k ; v 0 ; s 4m v u ccelertion s SOLUIONS O CONCEPS CHPE 5 0 11.11
How To Balance Power In A Distribution System
NTERNATONA JOURNA OF ENERG, ssue 3, ol., 7 A dynmilly S bsed ompt ontrol lgorithm for lod blning in distribution systems A. Kzemi, A. Mordi Koohi nd R. Rezeipour Abstrt An lgorithm for pplying fixed pitor-thyristorontrolled
Unit 5 Section 1. Mortgage Payment Methods & Products (20%)
Unit 5 Setion 1 Mortgge Pyment Methos & Prouts (20%) There re tully only 2 mortgge repyment methos ville CAPITAL REPAYMENT n INTEREST ONLY. Cpitl Repyment Mortgge Also lle Cpitl & Interest mortgge or repyment
Angles 2.1. Exercise 2.1... Find the size of the lettered angles. Give reasons for your answers. a) b) c) Example
2.1 Angles Reognise lternte n orresponing ngles Key wors prllel lternte orresponing vertilly opposite Rememer, prllel lines re stright lines whih never meet or ross. The rrows show tht the lines re prllel
The remaining two sides of the right triangle are called the legs of the right triangle.
10 MODULE 6. RADICAL EXPRESSIONS 6 Pythgoren Theorem The Pythgoren Theorem An ngle tht mesures 90 degrees is lled right ngle. If one of the ngles of tringle is right ngle, then the tringle is lled right
2 DIODE CLIPPING and CLAMPING CIRCUITS
2 DIODE CLIPPING nd CLAMPING CIRCUITS 2.1 Ojectives Understnding the operting principle of diode clipping circuit Understnding the operting principle of clmping circuit Understnding the wveform chnge of
, and the number of electrons is -19. e e 1.60 10 C. The negatively charged electrons move in the direction opposite to the conventional current flow.
Prolem 1. f current of 80.0 ma exists in metl wire, how mny electrons flow pst given cross section of the wire in 10.0 min? Sketch the directions of the current nd the electrons motion. Solution: The chrge
Ratio and Proportion
Rtio nd Proportion Rtio: The onept of rtio ours frequently nd in wide vriety of wys For exmple: A newspper reports tht the rtio of Repulins to Demorts on ertin Congressionl ommittee is 3 to The student/fulty
MATH PLACEMENT REVIEW GUIDE
MATH PLACEMENT REVIEW GUIDE This guie is intene s fous for your review efore tking the plement test. The questions presente here my not e on the plement test. Although si skills lultor is provie for your
1. Definition, Basic concepts, Types 2. Addition and Subtraction of Matrices 3. Scalar Multiplication 4. Assignment and answer key 5.
. Definition, Bsi onepts, Types. Addition nd Sutrtion of Mtries. Slr Multiplition. Assignment nd nswer key. Mtrix Multiplition. Assignment nd nswer key. Determinnt x x (digonl, minors, properties) summry
Further applications of area and volume
2 Further pplitions of re n volume 2A Are of prts of the irle 2B Are of omposite shpes 2C Simpson s rule 2D Surfe re of yliners n spheres 2E Volume of omposite solis 2F Error in mesurement Syllus referene
1 Fractions from an advanced point of view
1 Frtions from n vne point of view We re going to stuy frtions from the viewpoint of moern lger, or strt lger. Our gol is to evelop eeper unerstning of wht n men. One onsequene of our eeper unerstning
Rotating DC Motors Part II
Rotting Motors rt II II.1 Motor Equivlent Circuit The next step in our consiertion of motors is to evelop n equivlent circuit which cn be use to better unerstn motor opertion. The rmtures in rel motors
Hydromagnetic Unsteady Mixed Convection Flow Past an Infinite Vertical Porous Plate
pplie Mthemtis. ; (): 39-45 DO:.593/j.m..5 Hyromgneti Unstey Mixe Convetion Flo Pst n nfinite ertil Porous Plte B.. Shrm T. Chn R. C. Chuhry Deprtment of Mthemtis Birl nstitute of Tehnology & Siene Pilni
Words Symbols Diagram. abcde. a + b + c + d + e
Logi Gtes nd Properties We will e using logil opertions to uild mhines tht n do rithmeti lultions. It s useful to think of these opertions s si omponents tht n e hooked together into omplex networks. To
Week 11 - Inductance
Week - Inductnce November 6, 202 Exercise.: Discussion Questions ) A trnsformer consists bsiclly of two coils in close proximity but not in electricl contct. A current in one coil mgneticlly induces n
Visualization of characteristics of the contact network between spheres in 3D assembly
Int. Agrophys., 2013, 27, 275-281 oi: 10.2478/v10247-012-0095-6 INTERNATIONAL Agrophysis www.interntionl-grophysis.org Visuliztion of hrteristis of the ontt network etween spheres in 3D ssemly R. Koy³k*
THE LONGITUDINAL FIELD IN THE GTEM 1750 AND THE NATURE OF THE TERMINATION.
THE LONGITUDINAL FIELD IN THE GTEM 175 AND THE NATURE OF THE TERMINATION. Benjmin Guy Loder Ntionl Physil Lbortory, Queens Rod, Teddington, Middlesex, Englnd. TW11 LW Mrtin Alexnder Ntionl Physil Lbortory,
Capacitance and Dielectrics
2.2 This is the Nerest One He 803 P U Z Z L E R Mny electronic components crry wrning lel like this one. Wht is there insie these evices tht mkes them so ngerous? Why wouln t you e sfe if you unplugge
Chapter. Contents: A Constructing decimal numbers
Chpter 9 Deimls Contents: A Construting deiml numers B Representing deiml numers C Deiml urreny D Using numer line E Ordering deimls F Rounding deiml numers G Converting deimls to frtions H Converting
Radius of the Earth - Radii Used in Geodesy James R. Clynch Naval Postgraduate School, 2002
dius of the Erth - dii Used in Geodesy Jmes. Clynh vl Postgrdute Shool, 00 I. Three dii of Erth nd Their Use There re three rdii tht ome into use in geodesy. These re funtion of ltitude in the ellipsoidl
StyleView SV32 Change Power System Batteries
F the ltest User Instlltion Guie n StyleLink Softwre Downlo plese visit: Enontrrá l versión más reiente el mnul e instlión el usurio y el softwre e StyleLink en: Si vous souhitez téléhrger le ernier mnuel
Cypress Creek High School IB Physics SL/AP Physics B 2012 2013 MP2 Test 1 Newton s Laws. Name: SOLUTIONS Date: Period:
Nme: SOLUTIONS Dte: Period: Directions: Solve ny 5 problems. You my ttempt dditionl problems for extr credit. 1. Two blocks re sliding to the right cross horizontl surfce, s the drwing shows. In Cse A
CS99S Laboratory 2 Preparation Copyright W. J. Dally 2001 October 1, 2001
CS99S Lortory 2 Preprtion Copyright W. J. Dlly 2 Octoer, 2 Ojectives:. Understnd the principle of sttic CMOS gte circuits 2. Build simple logic gtes from MOS trnsistors 3. Evlute these gtes to oserve logic
SECTION 7-2 Law of Cosines
516 7 Additionl Topis in Trigonometry h d sin s () tn h h d 50. Surveying. The lyout in the figure t right is used to determine n inessile height h when seline d in plne perpendiulr to h n e estlished
1. In the Bohr model, compare the magnitudes of the electron s kinetic and potential energies in orbit. What does this imply?
Assignment 3: Bohr s model nd lser fundmentls 1. In the Bohr model, compre the mgnitudes of the electron s kinetic nd potentil energies in orit. Wht does this imply? When n electron moves in n orit, the
(Ch. 22.5) 2. What is the magnitude (in pc) of a point charge whose electric field 50 cm away has a magnitude of 2V/m?
Em I Solutions PHY049 Summe 0 (Ch..5). Two smll, positively chged sphees hve combined chge of 50 μc. If ech sphee is epelled fom the othe by n electosttic foce of N when the sphees e.0 m pt, wht is the
Lesson 2.1 Inductive Reasoning
Lesson.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 1, 16,,. 400, 00, 100, 0,,,. 1 8, 7, 1, 4,, 4.,,, 1, 1, 0,,. 60, 180, 10,
Orthopoles and the Pappus Theorem
Forum Geometriorum Volume 4 (2004) 53 59. FORUM GEOM ISSN 1534-1178 Orthopoles n the Pppus Theorem tul Dixit n Drij Grinerg strt. If the verties of tringle re projete onto given line, the perpeniulrs from
COMPONENTS: COMBINED LOADING
LECTURE COMPONENTS: COMBINED LOADING Third Edition A. J. Clrk School of Engineering Deprtment of Civil nd Environmentl Engineering 24 Chpter 8.4 by Dr. Ibrhim A. Asskkf SPRING 2003 ENES 220 Mechnics of
If two triangles are perspective from a point, then they are also perspective from a line.
Mth 487 hter 4 Prtie Prolem Solutions 1. Give the definition of eh of the following terms: () omlete qudrngle omlete qudrngle is set of four oints, no three of whih re olliner, nd the six lines inident
EQUATIONS OF LINES AND PLANES
EQUATIONS OF LINES AND PLANES MATH 195, SECTION 59 (VIPUL NAIK) Corresponding mteril in the ook: Section 12.5. Wht students should definitely get: Prmetric eqution of line given in point-direction nd twopoint
H SERIES. Area and Perimeter. Curriculum Ready. www.mathletics.com
Are n Perimeter Curriulum Rey www.mthletis.om Copyright 00 3P Lerning. All rights reserve. First eition printe 00 in Austrli. A tlogue reor for this ook is ville from 3P Lerning Lt. ISBN 78--86-30-7 Ownership
The art of Paperarchitecture (PA). MANUAL
The rt of Pperrhiteture (PA). MANUAL Introution Pperrhiteture (PA) is the rt of reting three-imensionl (3D) ojets out of plin piee of pper or ror. At first, esign is rwn (mnully or printe (using grphil
Lesson 1: Getting started
Answer key 0 Lesson 1: Getting strte 1 List the three min wys you enter t in QuikBooks. Forms, lists, registers 2 List three wys to ess fetures in QuikBooks. Menu r, Ion Br, Centers, Home pge 3 Wht ookkeeping
UNCORRECTED SAMPLE PAGES
6 Chpter Length, re, surfe re n volume Wht you will lern 6A Length n perimeter 6B Cirumferene of irles n perimeter of setors 6C Are of qurilterls n tringles 6D Are of irles 6E Perimeter n re of omposite
End of term: TEST A. Year 4. Name Class Date. Complete the missing numbers in the sequences below.
End of term: TEST A You will need penil nd ruler. Yer Nme Clss Dte Complete the missing numers in the sequenes elow. 8 30 3 28 2 9 25 00 75 25 2 Put irle round ll of the following shpes whih hve 3 shded.
Calculating Principal Strains using a Rectangular Strain Gage Rosette
Clulting Prinipl Strins using Retngulr Strin Gge Rosette Strin gge rosettes re used often in engineering prtie to determine strin sttes t speifi points on struture. Figure illustrtes three ommonly used
AAPT UNITED STATES PHYSICS TEAM AIP 2010
2010 F = m Exm 1 AAPT UNITED STATES PHYSICS TEAM AIP 2010 Enti non multiplicnd sunt preter necessittem 2010 F = m Contest 25 QUESTIONS - 75 MINUTES INSTRUCTIONS DO NOT OPEN THIS TEST UNTIL YOU ARE TOLD
α. Figure 1(iii) shows the inertia force and
CHPTER DYNMIC ORCE NLYSIS Whe the ierti fores re osiere i the lysis of the mehism, the lysis is kow s ymi fore lysis. Now pplyig D lemert priiple oe my reue ymi system ito equivlet stti system use the
6.5 - Areas of Surfaces of Revolution and the Theorems of Pappus
Lecture_06_05.n 1 6.5 - Ares of Surfces of Revolution n the Theorems of Pppus Introuction Suppose we rotte some curve out line to otin surfce, we cn use efinite integrl to clculte the re of the surfce.
Swelling and Mechanical Properties of Hydrogels Composed of. Binary Blends of Inter-linked ph-responsive Microgel Particles
Eletroi Supplemetry Mteril (ESI) for Soft Mtter. This jourl is The Royl Soiety of Chemistry 205 SUPPLEMENTARY INFRMATIN Swellig Mehil Properties of Hyrogels Compose of Biry Bles of Iter-like ph-resposive
MA 15800 Lesson 16 Notes Summer 2016 Properties of Logarithms. Remember: A logarithm is an exponent! It behaves like an exponent!
MA 5800 Lesson 6 otes Summer 06 Rememer: A logrithm is n eponent! It ehves like n eponent! In the lst lesson, we discussed four properties of logrithms. ) log 0 ) log ) log log 4) This lesson covers more
Geometry 7-1 Geometric Mean and the Pythagorean Theorem
Geometry 7-1 Geometric Men nd the Pythgoren Theorem. Geometric Men 1. Def: The geometric men etween two positive numers nd is the positive numer x where: = x. x Ex 1: Find the geometric men etween the
Boğaziçi University Department of Economics Spring 2016 EC 102 PRINCIPLES of MACROECONOMICS Problem Set 5 Answer Key
Boğziçi University Deprtment of Eonomis Spring 2016 EC 102 PRINCIPLES of MACROECONOMICS Prolem Set 5 Answer Key 1. One yer ountry hs negtive net exports. The next yer it still hs negtive net exports n
SE3BB4: Software Design III Concurrent System Design. Sample Solutions to Assignment 1
SE3BB4: Softwre Design III Conurrent System Design Winter 2011 Smple Solutions to Assignment 1 Eh question is worth 10pts. Totl of this ssignment is 70pts. Eh ssignment is worth 9%. If you think your solution
Fluent Merging: A General Technique to Improve Reachability Heuristics and Factored Planning
Fluent Merging: A Generl Tehnique to Improve Rehility Heuristis n Ftore Plnning Menkes vn en Briel Deprtment of Inustril Engineering Arizon Stte University Tempe AZ, 85287-8809 [email protected] Suro Kmhmpti
Reasoning to Solve Equations and Inequalities
Lesson4 Resoning to Solve Equtions nd Inequlities In erlier work in this unit, you modeled situtions with severl vriles nd equtions. For exmple, suppose you were given usiness plns for concert showing
JCM TRAINING OVERVIEW Multi-Download Module 2
Multi-Downlo Moule 2 JCM Trining Overview Mrh, 2012 Mrh, 2012 CLOSING THE MDM2 APPLICATION To lose the MDM2 Applition proee s follows: 1. Mouse-lik on the 'File' pullown Menu (See Figure 35 ) on the MDM2
Or more simply put, when adding or subtracting quantities, their uncertainties add.
Propgtion of Uncertint through Mthemticl Opertions Since the untit of interest in n eperiment is rrel otined mesuring tht untit directl, we must understnd how error propgtes when mthemticl opertions re
OxCORT v4 Quick Guide Revision Class Reports
OxCORT v4 Quik Guie Revision Clss Reports This quik guie is suitble for the following roles: Tutor This quik guie reltes to the following menu options: Crete Revision Clss Reports pg 1 Crete Revision Clss
DECLARATION OF PERFORMANCE NO. HU-DOP_TN-212-25_001
NO. HU-DOP_TN-212-25_001 Product type 212 (TN) 3,5x25 mm EN 14566:2008+A1:2009 NO. HU-DOP_TN-212-35_001 Product type 212 (TN) 3,5x35 mm EN 14566:2008+A1:2009 NO. HU-DOP_TN-212-45_001 Product type 212 (TN)
Unit 6: Exponents and Radicals
Eponents nd Rdicls -: The Rel Numer Sstem Unit : Eponents nd Rdicls Pure Mth 0 Notes Nturl Numers (N): - counting numers. {,,,,, } Whole Numers (W): - counting numers with 0. {0,,,,,, } Integers (I): -
On Equivalence Between Network Topologies
On Equivlene Between Network Topologies Tre Ho Deprtment of Eletril Engineering Cliforni Institute of Tehnolog [email protected]; Mihelle Effros Deprtments of Eletril Engineering Cliforni Institute of Tehnolog
Evaluation of chemical and biological consequences of soil sterilization methods
Cspin J. Env. Si. 27, Vol. 5 No.2 pp. 87~91 Copyright y The University of Guiln, Printe in I.R. Irn [Reserh] CJES Cspin Journl of Environmentl Sienes Evlution of hemil n iologil onsequenes of soil steriliztion
PROBLEMS 13 - APPLICATIONS OF DERIVATIVES Page 1
PROBLEMS - APPLICATIONS OF DERIVATIVES Pge ( ) Wter seeps out of conicl filter t the constnt rte of 5 cc / sec. When the height of wter level in the cone is 5 cm, find the rte t which the height decreses.
OUTLINE SYSTEM-ON-CHIP DESIGN. GETTING STARTED WITH VHDL August 31, 2015 GAJSKI S Y-CHART (1983) TOP-DOWN DESIGN (1)
August 31, 2015 GETTING STARTED WITH VHDL 2 Top-down design VHDL history Min elements of VHDL Entities nd rhitetures Signls nd proesses Dt types Configurtions Simultor sis The testenh onept OUTLINE 3 GAJSKI
Warm-up for Differential Calculus
Summer Assignment Wrm-up for Differentil Clculus Who should complete this pcket? Students who hve completed Functions or Honors Functions nd will be tking Differentil Clculus in the fll of 015. Due Dte:
Corrigendum-II Dated:19.05.2011
10(21)/2010-NICSI NATIONAL INFORMATICS CENTRE SERVICES In. (NICSI) (A Government of Ini Enterprise uner NIC) Ministry of Communition & Informtion Tehnology Hll 2 & 3, 6 th Floor, NBCC Tower 15, Bhikiji
HW 9. Problem 14.5. a. To Find:
HW 9 Problem 14.5. To Find: ( The number-verge moleulr weight (b The weight-verge moleulr weight ( The degree of polymeriztion for the given polypropylene mteril Moleulr Weight Rnge (g/mol x i w i 8,000
CHAPTER 9: Moments of Inertia
HPTER 9: Moments of nerti! Moment of nerti of res! Second Moment, or Moment of nerti, of n re! Prllel-is Theorem! Rdius of Grtion of n re! Determintion of the Moment of nerti of n re ntegrtion! Moments
ERmet ZD Application Note Version 1.1
ERmet ZD Applition Note Version. Generl The ERmet ZD is speiilly esigne or high spee ierentil signling in teleom pplitions t t rtes o up to 5 Git/s. This roust, high perormne, moulr onnetor system is lso
GENERAL OPERATING PRINCIPLES
KEYSECUREPC USER MANUAL N.B.: PRIOR TO READING THIS MANUAL, YOU ARE ADVISED TO READ THE FOLLOWING MANUAL: GENERAL OPERATING PRINCIPLES Der Customer, KeySeurePC is n innovtive prout tht uses ptente tehnology:
INSTALLATION, OPERATION & MAINTENANCE
DIESEL PROTECTION SYSTEMS Exhust Temperture Vlves (Mehnil) INSTALLATION, OPERATION & MAINTENANCE Vlve Numer TSZ-135 TSZ-150 TSZ-200 TSZ-275 TSZ-392 DESCRIPTION Non-eletril temperture vlves mnuftured in
Arc-Consistency for Non-Binary Dynamic CSPs
Ar-Consisteny for Non-Binry Dynmi CSPs Christin Bessière LIRMM (UMR C 9928 CNRS / Université Montpellier II) 860, rue de Sint Priest 34090 Montpellier, Frne Emil: [email protected] Astrt. Constrint stisftion
Released Assessment Questions, 2015 QUESTIONS
Relesed Assessmet Questios, 15 QUESTIONS Grde 9 Assessmet of Mthemtis Ademi Red the istrutios elow. Alog with this ooklet, mke sure you hve the Aswer Booklet d the Formul Sheet. You my use y spe i this
Seeking Equilibrium: Demand and Supply
SECTION 1 Seeking Equilirium: Demnd nd Supply OBJECTIVES KEY TERMS TAKING NOTES In Setion 1, you will explore mrket equilirium nd see how it is rehed explin how demnd nd supply intert to determine equilirium
Foreign Debt and The Gold Standard: Comparing Russian and Japanese Experience in Late XIX Century Ivan Medovikov
Foreign Det n The Gol Stnr: Compring Russin n Jpnese Experiene in Lte XIX Century Ivn Meovikov Astrt The following work will exmine risk premiums on government et issue y Russin n Jpnese governments in
Interior and exterior angles add up to 180. Level 5 exterior angle
22 ngles n proof Ientify interior n exterior ngles in tringles n qurilterls lulte interior n exterior ngles of tringles n qurilterls Unerstn the ie of proof Reognise the ifferene etween onventions, efinitions
Physics 43 Homework Set 9 Chapter 40 Key
Physics 43 Homework Set 9 Chpter 4 Key. The wve function for n electron tht is confined to x nm is. Find the normliztion constnt. b. Wht is the probbility of finding the electron in. nm-wide region t x
SUPPLEMENTARY MATERIAL
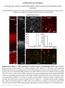SUPPLEMENTARY MATERIAL Lyer-speifi exittory iruits differentilly ontrol reurrent network dynmis in the neoortex Rirdo Beltrmo, Giuli D Urso, Mro Dl Mshio, Psqulin Frisello, Seren Bovetti, Yonne Clovis,
Quick Guide to Lisp Implementation
isp Implementtion Hndout Pge 1 o 10 Quik Guide to isp Implementtion Representtion o si dt strutures isp dt strutures re lled S-epressions. The representtion o n S-epression n e roken into two piees, the
European Convention on Social and Medical Assistance
Europen Convention on Soil nd Medil Assistne Pris, 11.XII.1953 Europen Trety Series - No. 14 The governments signtory hereto, eing memers of the Counil of Europe, Considering tht the im of the Counil of
Review guide for the final exam in Math 233
Review guide for the finl exm in Mth 33 1 Bsic mteril. This review includes the reminder of the mteril for mth 33. The finl exm will be cumultive exm with mny of the problems coming from the mteril covered
How To Organize A Meeting On Gotomeeting
NOTES ON ORGANIZING AND SCHEDULING MEETINGS Individul GoToMeeting orgnizers my hold meetings for up to 15 ttendees. GoToMeeting Corporte orgnizers my hold meetings for up to 25 ttendees. GoToMeeting orgnizers
Fundamentals of transformer design
Fundmentls of trnsformer design y H du Preez, onsultnt trnsformer is stti piee of equipment with omplited eletromgneti iruit. The eletril energy is trnsferred from one eletril iruit to nother through mgneti
SINCLAIR COMMUNITY COLLEGE DAYTON, OHIO DEPARTMENT SYLLABUS FOR COURSE IN MAT 1355 - INTERMEDIATE ALGEBRA I (3 CREDIT HOURS)
SINCLAIR COMMUNITY COLLEGE DAYTON OHIO DEPARTMENT SYLLABUS FOR COURSE IN MAT 1355 - INTERMEDIATE ALGEBRA I (3 CREDIT HOURS) 1. COURSE DESCRIPTION: Ftorig; opertios with polyoils d rtiol expressios; solvig
How To Find The Re Of Tringle
Heron s Formul for Tringulr Are y Christy Willims, Crystl Holom, nd Kyl Gifford Heron of Alexndri Physiist, mthemtiin, nd engineer Tught t the museum in Alexndri Interests were more prtil (mehnis, engineering,
v T R x m Version PREVIEW Practice 7 carroll (11108) 1
Version PEVIEW Prctice 7 crroll (08) his print-out should he 5 questions. Multiple-choice questions y continue on the next colun or pge find ll choices before nswering. Atwood Mchine 05 00 0.0 points A
2. Properties of Functions
2. PROPERTIES OF FUNCTIONS 111 2. Properties of Funtions 2.1. Injetions, Surjetions, an Bijetions. Definition 2.1.1. Given f : A B 1. f is one-to-one (short han is 1 1) or injetive if preimages are unique.
15.6. The mean value and the root-mean-square value of a function. Introduction. Prerequisites. Learning Outcomes. Learning Style
The men vlue nd the root-men-squre vlue of function 5.6 Introduction Currents nd voltges often vry with time nd engineers my wish to know the verge vlue of such current or voltge over some prticulr time
PHY 222 Lab 8 MOTION OF ELECTRONS IN ELECTRIC AND MAGNETIC FIELDS
PHY 222 Lb 8 MOTION OF ELECTRONS IN ELECTRIC AND MAGNETIC FIELDS Nme: Prtners: INTRODUCTION Before coming to lb, plese red this pcket nd do the prelb on pge 13 of this hndout. From previous experiments,
The Pythagorean Theorem
The Pythgoren Theorem Pythgors ws Greek mthemtiin nd philosopher, orn on the islnd of Smos (. 58 BC). He founded numer of shools, one in prtiulr in town in southern Itly lled Crotone, whose memers eventully
Practical Problems in Voltammetry: 4. Preparation of Working Electrodes
Prtil Prolems in Voltmmetry: 4. Preprtion of Working Eletrodes Adrin W. Bott, Ph.D. Bionlytil Systems, In. West Lfyette, IN 4796-1382 E-mil: [email protected] The ondition of the surfe of the working eletrode
Section 5-4 Trigonometric Functions
5- Trigonometric Functions Section 5- Trigonometric Functions Definition of the Trigonometric Functions Clcultor Evlution of Trigonometric Functions Definition of the Trigonometric Functions Alternte Form