LECTURE 18: Horn Antennas (Rectangular horn antennas. Circular apertures.)
|
|
|
- Kristopher Osborne
- 9 years ago
- Views:
Transcription
1 LCTUR 18: Horn Antennas (Rectangular horn antennas. Circular apertures.) 1 Rectangular Horn Antennas Horn antennas are popular in the microwave band (above 1 GHz). Horns provide high gain, low VSWR (with waveguide feeds), relatively wide bandwidth, and they are not difficult to make. There are three basic types of rectangular horns. The horns can be also flared exponentially. This provides better matching in a broad frequency band, but is technologically more difficult and expensive. The rectangular horns are ideally suited for rectangular waveguide feeders. The horn acts as a gradual transition from a waveguide mode to a free-space mode of the M wave. When the feeder is a cylindrical waveguide, the antenna Nikolova 14 1
2 is usually a conical horn. Why is it necessary to consider the horns separately instead of applying the theory of waveguide aperture antennas directly? It is because the so-called phase error occurs due to the difference between the lengths from the center of the feeder to the center of the horn aperture and the horn edge. This makes the uniform-phase aperture results invalid for the horn apertures. 1.1 The H-plane sectoral horn The geometry and the respective parameters shown in the figure below are used often in the subsequent analysis. l H R x a a H R A z R H H-plane (x-z) cut of an H-plane sectoral horn a l H H A = R +, (18.1) A = arctan lh RH = ( A a) A R, (18.) 1 4. (18.3) Nikolova 14
3 The two fundamental dimensions for the construction of the horn are A and R H. The tangential field arriving at the input of the horn is composed of the transverse field components of the waveguide dominant mode T 1 : where Z g = η λ 1 a λ βg = β 1 a π y( x) = cos x e a H ( x) = ( x)/ Z x y g jβ z is the wave impedance of the T 1 mode; g is the propagation constant of the T 1 mode. (18.4) Here, β = ω µε = π / λ, and λ is the free-space wavelength. The field that is illuminating the aperture of the horn is essentially a spatially expanded version of the waveguide field. Note that the wave impedance of the flared waveguide (the horn) gradually approaches the intrinsic impedance of open space η, as A (the H-plane width) increases. The complication in the analysis arises from the fact that the waves arriving at the horn aperture are not in phase due to the different path lengths from the horn apex. The aperture phase variation is given by e j β ( R R ). (18.5) Since the aperture is not flared in the y-direction, the phase is uniform in this direction. We first approximate the path of the wave in the horn: x 1 x R= R + x = R 1+ R 1 R + R. (18.6) The last approximation holds if x R, or A/ R. Then, we can assume that Nikolova 14 3
4 1 x R R. (18.7) R Using (18.7), the field at the aperture is approximated as π a ( x) cos x e y A β j x R. (18.8) The field at the aperture plane outside the aperture is assumed equal to zero. The field expression (18.8) is substituted in the integral I y (see Lecture 17): I = ( x, y ) e dx dy, (18.9) jβ( x sinθcosj y sinθsin j) y a + S A y + A/ b + b/ j x I = x e R e jbx sinθcosjdx e jby sinθsinjdy y π cos A. (18.1) (((((( (((((( A/ b/ I ( θj, ) The second integral has been already encountered. The first integral is cumbersome and the final result only is given below: where and bb sin sinθsinϕ 1 π R Iy = I( θϕ, ) b, (18.11) b bb sinθsinϕ R π j βsinθcosj+ β A R π j βsinθcosj β A [ 1 1 ] I( θj, ) = e C( s ) js( s ) C( s ) + js( s ) [ ( ) ( ) ( 1 ) ( 1 )] + e C t js t C t + js t 1 βa πr s1 = Rβ u πβ R A ; 1 βa πr s = + Rβ u πβ R A ; (18.1) Nikolova 14 4
5 t1 = 1 βa πr Rβ u+ πβ R A ; t = 1 βa πr + Rβ u+ πβ R A ; u = sinθcosϕ. Cx ( ) and Sx ( ) are Fresnel integrals, which are defined as x π ( ) cos τ τ ; ( ) ( ), Cx= d C x= Cx x ( ) sin ; ( ) ( ). π Sx= τ d τ S x= Sx (18.13) More accurate evaluation of I y can be obtained if the approximation in (18.6) is not made, and is substituted in (18.9) as or ay ( ) π π a ( x) = cos x e e cos x e y = A A + jβ R β jβ R + x R j R + x The far field can be now calculated as (see Lecture 17): e jβ r (1 cos )sin θ = jβ + θ j Iy, 4π r e jβ r j (1 cos )cos I j = β + θ j y, 4π r bb sin sinθsinj πr j r e b 1 cosθ + = jb b b 4πr bb sinθsinj ( θˆ + φˆ ) I( θj, ) sinj cos j.. (18.14) (18.15) (18.16) Nikolova 14 5
6 The amplitude pattern of the H-plane sectoral horn is obtained as Principal-plane patterns -plane ( ϕ = 9 ): bb sin sinθsinϕ 1 cosθ + = I( θϕ, ). (18.17) bb sinθsinϕ F bb sin sinθsinϕ 1 cosθ + ( θ ) = bb sinθsinϕ (18.18) The second factor in (18.18) is exactly the pattern of a uniform line source of length b along the y-axis. H-plane ( ϕ = ): 1+ cosθ FH( θ) = fh( θ) = (18.19) 1+ cos θ I( θϕ, = ) = I( θ =, ϕ = ) The H-plane pattern in terms of the I( θϕ, ) integral is an approximation, which is a consequence of the phase approximation made in (18.7). Accurate value for fh ( θ ) is found by integrating numerically the field as given in (18.14), i.e., + A/ π x fh ( θ ) cos e e dx A jβ R + x jβx sinθ. (18.) A/ Nikolova 14 6
7 - AND H-PLAN PATTRN OF H-PLAN SCTORAL HORN Fig. 13-1, Balanis, p. 674 Nikolova 14 7
8 The directivity of the H-plane sectoral horn is calculated by the general directivity expression for apertures (for derivation, see Lecture 17): D 4π = λ S a S A ads A. (18.1) ds The integral in the denominator is proportional to the total radiated power, + b/ + A/ π ds x dx dy ηπ rad = a = cos = A S b/ A/ A Ab. (18.) In the solution of the integral in the numerator of (18.1), the field is substituted with its phase approximated as in (18.8). The final result is where ε t = 8 ; π D H b 3 A 4p = εh ph = εε t λp λ λ H ph {[ ( ] [ ] } 1 ) ( ) ( 1 ) ( ) p ε H ph = C p C p + S p S p ; 64t 1 1 p1 = t 1 +, p = t 1+ 8t 8t ; 1 A 1 t =. 8 λ R / λ ( Ab), (18.3) The factor ε t explicitly shows the aperture efficiency associated with the aperture cosine taper. The factor ε H ph is the aperture efficiency associated with the aperture phase distribution. A family of universal directivity curves is given below. From these curves, it is obvious that for a given axial length R and at a given wavelength, there is an optimal aperture width A corresponding to the maximum directivity. Nikolova 14 8
9 R = 1λ [Stutzman] It can be shown that the optimal directivity is obtained if the relation between A and R is or A= 3λR, (18.4) A R = 3. (18.5) λ λ Nikolova 14 9
10 1. The -plane sectoral horn l R y b a R B z R -plane (y-z) cut of an -plane sectoral horn The geometry of the -plane sectoral horn in the -plane (y-z plane) is analogous to that of the H-plane sectoral horn in the H-plane. The analysis is following the same steps as in the previous section. The field at the aperture is approximated by [compare with (18.8)] Here, the approximations and π a = cos x e y a β j y R y 1 y R= R + y = R 1+ R 1 R + R. (18.6) are made, which are analogous to (18.6) and (18.7). (18.7) 1 y R R (18.8) R Nikolova 14 1
11 The radiation field is obtained as 4 j r βr βb a π R e β j sinθsinj ˆ ˆ ( sin cos ) = jβ e θ j + φ j π β 4πr βa cos sinθcosj (1 + cos θ ) [ C( r) js( r) C( r1) + js( r1) ]. βa 1 sinθcosj The arguments of the Fresnel integrals used in (18.9) are r β B βb = R sinθsin ϕ, 1 π R r β B βb = + R sinθsin ϕ. π R (18.9) (18.3) Principal-plane patterns The normalized H-plane pattern is found by substituting ϕ = in (18.9): βa cos sinθ 1 cosθ + H ( θ ) =. (18.31) βa 1 sinθ The second factor in this expression is the pattern of a uniform-phase cosineamplitude tapered line source. The normalized -plane pattern is found by substituting ϕ = 9 in (18.9): [ Cr ( ) Cr ( 1) ] + [ Sr ( ) Sr ( 1) ] (1+ cos θ) (1+ cos θ) ( θ) = f ( θ) = 4 C( r θ= ) + S ( rθ= ) Here, the arguments of the Fresnel integrals are calculated for ϕ = 9 :. (18.3) Nikolova 14 11
12 and r β B βb = R sin θ, 1 π R r β B βb = + R sin θ, π R (18.33) B β rθ = = r( θ = ) =. (18.34) π R Similar to the H-plane sectoral horn, the principal -plane pattern can be accurately calculated if no approximation of the phase distribution is made. Then, the function f ( θ ) has to be calculated by numerical integration of (compare with (18.)) B/ jβ R ( ) + y f j sin y θ e e β θ dy. (18.35) B/ Nikolova 14 1
13 - AND H-PLAN PATTRN OF -PLAN SCTORAL HORN Fig. 13.4, Balanis, p. 66 Nikolova 14 13
14 Directivity The directivity of the -plane sectoral horn is found in a manner analogous to the H-plane sectoral horn: where ε t 8 =, ε π ph D = a 3 B 4p ε ph εε t phab λp λ = λ, (18.36) + = =. λr C( q) S( q) B, q q A family of universal directivity curves λd / a vs. B/ λ with R being a parameter is given below. R = 1λ Nikolova 14 14
15 The optimal relation between the flared height B and the horn apex length R that produces the maximum possible directivity is B= λr. (18.37) 1.3 The pyramidal horn The pyramidal horn is probably the most popular antenna in the microwave frequency ranges (from 1 GHz up to 18 GHz). The feeding waveguide is flared in both directions, the -plane and the H-plane. All results are combinations of the -plane sectoral horn and the H-plane sectoral horn analyses. The field distribution at the aperture is approximated as π a cos x e y A β x y j + R H R. (18.38) The -plane principal pattern of the pyramidal horn is the same as the -plane principal pattern of the -plane sectoral horn. The same holds for the H-plane patterns of the pyramidal horn and the H-plane sectoral horn. The directivity of the pyramidal horn can be found by introducing the phase efficiency factors of both planes and the taper efficiency factor of the H-plane: where ε t 8 = ; π D 4p = εε ε ( AB), (18.39) λ H P t ph ph {[ ( ] [ ] } 1 ) ( ) ( 1 ) ( ) p ε H ph = C p C p + S p S p ; 64t 1 1 p1 = t 1 +, p = t 1 +, 8t 8t ε ph C( q) + S( q) B, q q λr = =. 1 A 1 t = ; 8 λ R / λ The gain of a horn is usually very close to its directivity because the radiation Nikolova H
16 efficiency is very good (low losses). The directivity as calculated with (18.39) is very close to measurements. The above expression is a physical optics approximation, and it does not take into account only multiple diffractions, and the diffraction at the edges of the horn arising from reflections from the horn interior. These phenomena, which are unaccounted for, lead to only very minor fluctuations of the measured results about the prediction of (18.39). That is why horns are often used as gain standards in antenna measurements. The optimal directivity of an -plane horn is achieved at q = 1 [see also (18.37)], ε ph =.8. The optimal directivity of an H-plane horn is achieved at t = 3/8 [see also (18.4)], ε H ph =.79. Thus, the optimal horn has a phase aperture efficiency of ε P = ε Hε =.63. (18.4) ph ph ph The total aperture efficiency includes the taper factor, too: εp = εεhε = =.51. (18.41) ph t ph ph Therefore, the best achievable directivity for a rectangular waveguide horn is about half that of a uniform rectangular aperture. We reiterate that best accuracy is achieved if ε ph H and ε ph are calculated numerically without using the second-order phase approximations in (18.7) and (18.8). Optimum horn design Usually, the optimum (from the point of view of maximum gain) design of a horn is desired because it results in the shortest axial length. The whole design can be actually reduced to the solution of a single fourth-order equation. For a horn to be realizable, the following must be true: R = RH = RP. (18.4) The figures below summarize the notations used in describing the horn s geometry. Nikolova 14 16
17 b α R y B α α H H R x A z R R H It can be shown that RH A/ A = = R A/ a/ A a, (18.43) H R B/ B = = R B/ b/ B b. (18.44) The optimum-gain condition in the -plane (18.37) is substituted in (18.44) to produce B bb λr =. (18.45) There is only one physically meaningful solution to (18.45): ( 8λ ) 1 B= b+ b + R. (18.46) Similarly, the maximum-gain condition for the H-plane of (18.4) together with (18.43) yields Since R H R H A a A ( A a) = A A 3λ =. (18.47) 3λ = R must be fulfilled, (18.47) is substituted in (18.46), which gives Nikolova 14 17
18 1 8 AA ( a) B= b b + +. (18.48) 3 Substituting in the expression for the horn s gain, 4p G = ε ap AB, (18.49) λ gives the relation between A, the gain G, and the aperture efficiency ε ap : 4p 1 8 Aa ( a) G = ε ap A b+ b +, (18.5) λ 3 + 3bGλ 3G λ =. (18.51) 4 A4 aa3 A 8pε 3 ap p ε ap quation (18.51) is the optimum pyramidal horn design equation. The optimum-gain value of ε ap =.51 is usually used, which makes the equation a fourth-order polynomial equation in A. Its roots can be found analytically (which is not particularly easy) and numerically. In a numerical solution, the first guess is usually set at A () =.45λ G. Once A is found, B can be computed from (18.48) and R = RH is computed from (18.47). Sometimes, an optimal horn is desired for a known axial length R. In this case, there is no need for nonlinear-equation solution. The design procedure follows the steps: (a) find A from (18.4), (b) find B from (18.37), and (c) calculate the gain G using (18.49) where ε ap =.51. Horn antennas operate well over a bandwidth of 5%. However, gain performance is optimal only at a given frequency. To understand better the frequency dependence of the directivity and the aperture efficiency, the plot of these curves for an X-band (8. GHz to 1.4 GHz) horn fed by WR9 waveguide is given below ( a =.9 in. =.86 cm and b =.4 in. = 1.16 cm). Nikolova 14 18
19 The gain increases with frequency, which is typical for aperture antennas. However, the curve shows saturation at higher frequencies. This is due to the decrease of the aperture efficiency, which is a result of an increased phase difference in the field distribution at the aperture. Nikolova 14 19
20 The pattern of a large pyramidal horn ( f = 1.55 GHz, feed is waveguide WR9): Nikolova 14
21 Comparison of the -plane patterns of a waveguide open end, small pyramidal horn and large pyramidal horn: Nikolova 14 1
22 Note the multiple side lobes and the significant back lobe. They are due to diffraction at the horn edges, which are perpendicular to the field. To reduce edge diffraction, enhancements are proposed for horn antennas such as corrugated horns aperture-matched horns The corrugated horns achieve tapering of the field in the vertical direction, thus, reducing the side-lobes and the diffraction from the top and bottom edges. The overall main beam becomes smooth and nearly rotationally symmetrical (esp. for A B). This is important when the horn is used as a feed to a reflector antenna. Nikolova 14
23 Nikolova 14 3
24 Comparison of the H-plane patterns of a waveguide open end, small pyramidal horn and large pyramidal horn: Nikolova 14 4
25 Circular apertures.1 A uniform circular aperture The uniform circular aperture is approximated by a circular opening in a ground plane illuminated by a uniform plane wave normally incident from behind. x z a y The field distribution is described as a = x ˆ, ρ a. (18.5) The radiation integral is ˆ I j x e β ds S = a rr. (18.53) The integration point is at ρ = xˆρ cosϕ + y ˆρ sinϕ. (18.54) In (18.54), cylindrical coordinates are used, therefore, ρˆ ρ = ρ sin θ(cosϕcosϕ + sinϕsin ϕ ) = ρ sinθcos( ϕ ϕ ). (18.55) Hence, (18.53) becomes a π a I j sin cos( ) x = e βρ θ j j dj ρ dρ = π ρ J( βρ sin θ) dρ. (18.56) Here, J is the Bessel function of the first kind of order zero. Applying the identity Nikolova 14 5
26 to (18.56) leads to xj ( x ) dx = xj 1( x ) (18.57) a I x = π J1( βasin θ) βsinθ. (18.58) Note that in this case the equivalent magnetic current formulation of the equivalence principle is used [see Lecture 17]. The far field is obtained as ( ˆ cos ˆ cos sin ) e jβ r = θ j φ θ j jβ I x = π r j r 1( sin ) ( ˆ e β J βa θ = θcosj φˆ cosθsin j) jβπa. πr βasinθ Principal-plane patterns -plane ( ϕ = ): θ (18.59) J1( βasin θ) ( θ ) = βasinθ (18.6) H-plane ( ϕ = 9 ): ϕ J1( βasin θ) ( θ) = cosθ βasinθ (18.61) The 3-D amplitude pattern: J 1( βasin θ) ( θϕ, ) = 1 sin θsin ϕ (( βa sin ( θ ( f ( θ ) (18.6) The larger the aperture, the less significant the cosθ factor is in (18.61) because the main beam in the θ = direction is very narrow and in this small solid angle cosθ 1. Thus, the 3-D pattern of a large circular aperture features a fairly symmetrical beam. Nikolova 14 6
27 xample plot of the principal-plane patterns for a = 3λ : 1.9 -plane H-plane *pi*sin(theta) The half-power angle for the f ( θ ) factor is obtained at βasinθ = 1.6. So, the HPBW for large apertures (a λ ) is given by λ HPBW = θ1/. arcsin 58.4 βa =, deg. (18.63) βa a For example, if the diameter of the aperture is a = 1λ, then HPBW = The side-lobe level of any uniform circular aperture is.133 (-17.5 db). Any uniform aperture has unity taper aperture efficiency, and its directivity can be found directly in terms of its physical area, 4p 4p Du A p a λ λ = p =. (18.64) Nikolova 14 7
28 . Tapered circular apertures Many practical circular aperture antennas can be approximated as radially symmetric apertures with field amplitude distribution, which is tapered from the center toward the aperture edge. Then, the radiation integral (18.56) has a more general form: a I = π ( ρ ) ρ J ( βρ sin θ) dρ. (18.65) x In (18.65), we still assume that the field has axial symmetry, i.e., it does not depend on ϕ. Often used approximation is the parabolic taper of order n: a ρ ( ρ ) = 1 a n (18.66) where is a constant. This is substituted in (18.65) to calculate the respective component of the radiation integral: n a ρ Ix ( θ) = π 1 ρ J( βρ sin θ) dρ a. (18.67) The following relation is used to solve (18.67): 1 n n! (1 x) nxj( bx) dx = J 1 n 1( b) bn+ + a b= ba θ. Then, I x ( ) π a I x ( θ) = f( θ, n) In our case, x= ρ / and sin where. (18.68) n + 1 n+ 1( n+ 1)! Jn+ 1( βasin θ) n+ 1 ( βasinθ) θ reduces to, (18.69) f( θ, n) = (18.7) is the normalized pattern (neglecting the angular factors such as cosϕ and cosθsinϕ). The aperture taper efficiency is calculated to be Nikolova 14 8
29 εt = C 1 C C + n + 1 C(1 C) (1 C) + + n+ 1 n+ 1. (18.71) Here, C denotes the pedestal height. The pedestal height is the edge field illumination relative to the illumination at the center. The properties of several common tapers are given in the tables below. The parabolic taper ( n = 1) provides lower side lobes in comparison with the uniform distribution ( n = ) but it has a broader main beam. There is always a trade-off between low side-lobe levels and high directivity (small HPBW). More or less optimal solution is provided by the parabolic-on-pedestal aperture distribution. Moreover, this distribution approximates very closely the real case of circular reflector antennas, where the feed antenna pattern is intercepted by the reflector only out to the reflector rim. Nikolova 14 9
30 Nikolova 14 3
New Method for Optimum Design of Pyramidal Horn Antennas
 66 New Method for Optimum Design of Pyramidal Horn Antennas Leandro de Paula Santos Pereira, Marco Antonio Brasil Terada Antenna Group, Electrical Engineering Dept., University of Brasilia - DF [email protected]
66 New Method for Optimum Design of Pyramidal Horn Antennas Leandro de Paula Santos Pereira, Marco Antonio Brasil Terada Antenna Group, Electrical Engineering Dept., University of Brasilia - DF [email protected]
Rec. ITU-R F.699-5 1 RECOMMENDATION ITU-R F.699-5 *
 Rec. ITU-R F.699-5 1 RECOMMENATION ITU-R F.699-5 * REFERENCE RAIATION PATTERNS FOR LINE-OF-SIGHT RAIO-RELAY SYSTEM ANTENNAS FOR USE IN COORINATION STUIES AN INTERFERENCE ASSESSMENT IN THE FREQUENCY RANGE
Rec. ITU-R F.699-5 1 RECOMMENATION ITU-R F.699-5 * REFERENCE RAIATION PATTERNS FOR LINE-OF-SIGHT RAIO-RELAY SYSTEM ANTENNAS FOR USE IN COORINATION STUIES AN INTERFERENCE ASSESSMENT IN THE FREQUENCY RANGE
Chapter 11 PARABOLIC DISH FEEDS PERFORMANCE ANALYSIS Paul Wade N1BWT 1997,1998
 Chapter 11 PARABOLIC DISH FEEDS PERFORMANCE ANALYSIS Paul Wade N1BWT 1997,1998 Achieving optimum performance from a microwave dish antenna requires that the feed antenna be matched to the parabolic reflector.
Chapter 11 PARABOLIC DISH FEEDS PERFORMANCE ANALYSIS Paul Wade N1BWT 1997,1998 Achieving optimum performance from a microwave dish antenna requires that the feed antenna be matched to the parabolic reflector.
Antennas. Antennas are transducers that transfer electromagnetic energy between a transmission line and free space. Electromagnetic Wave
 Antennas Transmitter I Transmitting Antenna Transmission Line Electromagnetic Wave I Receiver I Receiving Antenna Transmission Line Electromagnetic Wave I Antennas are transducers that transfer electromagnetic
Antennas Transmitter I Transmitting Antenna Transmission Line Electromagnetic Wave I Receiver I Receiving Antenna Transmission Line Electromagnetic Wave I Antennas are transducers that transfer electromagnetic
Antenna Glossary Before we talk about specific antennas, there are a few common terms that must be defined and explained:
 Antenna Basics Introduction Antennas are a very important component of communication systems. By definition, an antenna is a device used to transform an RF signal, traveling on a conductor, into an electromagnetic
Antenna Basics Introduction Antennas are a very important component of communication systems. By definition, an antenna is a device used to transform an RF signal, traveling on a conductor, into an electromagnetic
ASTRA 3B HORN ANTENNA DESIGN
 ASTRA 3B HORN ANTENNA DESIGN Jorge Teniente and Carlos del-río Grupo de Antenas, Universidad Pública de Navarra, Campus Arrosadía s/n, 31006 Spain, Email: [email protected], [email protected]
ASTRA 3B HORN ANTENNA DESIGN Jorge Teniente and Carlos del-río Grupo de Antenas, Universidad Pública de Navarra, Campus Arrosadía s/n, 31006 Spain, Email: [email protected], [email protected]
2/20/2009 3 Transmission Lines and Waveguides.doc 1/3. and Waveguides. Transmission Line A two conductor structure that can support a TEM wave.
 2/20/2009 3 Transmission Lines and Waveguides.doc 1/3 Chapter 3 Transmission Lines and Waveguides First, some definitions: Transmission Line A two conductor structure that can support a TEM wave. Waveguide
2/20/2009 3 Transmission Lines and Waveguides.doc 1/3 Chapter 3 Transmission Lines and Waveguides First, some definitions: Transmission Line A two conductor structure that can support a TEM wave. Waveguide
Two primary advantages of radars: all-weather and day /night imaging
 Lecture 0 Principles of active remote sensing: Radars. Objectives: 1. Radar basics. Main types of radars.. Basic antenna parameters. Required reading: G: 8.1, p.401-40 dditional/advanced reading: Online
Lecture 0 Principles of active remote sensing: Radars. Objectives: 1. Radar basics. Main types of radars.. Basic antenna parameters. Required reading: G: 8.1, p.401-40 dditional/advanced reading: Online
Section 5.0 : Horn Physics. By Martin J. King, 6/29/08 Copyright 2008 by Martin J. King. All Rights Reserved.
 Section 5. : Horn Physics Section 5. : Horn Physics By Martin J. King, 6/29/8 Copyright 28 by Martin J. King. All Rights Reserved. Before discussing the design of a horn loaded loudspeaker system, it is
Section 5. : Horn Physics Section 5. : Horn Physics By Martin J. King, 6/29/8 Copyright 28 by Martin J. King. All Rights Reserved. Before discussing the design of a horn loaded loudspeaker system, it is
ELECTROMAGNETIC ANALYSIS AND COLD TEST OF A DISTRIBUTED WINDOW FOR A HIGH POWER GYROTRON
 ELECTROMAGNETIC ANALYSIS AND COLD TEST OF A DISTRIBUTED WINDOW FOR A HIGH POWER GYROTRON M.A.Shapiro, C.P.Moeller, and R.J.Temkin Plasma Science and Fusion Ceer, Massachusetts Institute of Technology,
ELECTROMAGNETIC ANALYSIS AND COLD TEST OF A DISTRIBUTED WINDOW FOR A HIGH POWER GYROTRON M.A.Shapiro, C.P.Moeller, and R.J.Temkin Plasma Science and Fusion Ceer, Massachusetts Institute of Technology,
Lecture L5 - Other Coordinate Systems
 S. Widnall, J. Peraire 16.07 Dynamics Fall 008 Version.0 Lecture L5 - Other Coordinate Systems In this lecture, we will look at some other common systems of coordinates. We will present polar coordinates
S. Widnall, J. Peraire 16.07 Dynamics Fall 008 Version.0 Lecture L5 - Other Coordinate Systems In this lecture, we will look at some other common systems of coordinates. We will present polar coordinates
Area and Arc Length in Polar Coordinates
 Area and Arc Length in Polar Coordinates The Cartesian Coordinate System (rectangular coordinates) is not always the most convenient way to describe points, or relations in the plane. There are certainly
Area and Arc Length in Polar Coordinates The Cartesian Coordinate System (rectangular coordinates) is not always the most convenient way to describe points, or relations in the plane. There are certainly
Chapter 2 ELECTROMAGNETIC HORN ANTENNAS Paul Wade N1BWT 1994,1998
 Chapter 2 ELECTROMAGNETIC HORN ANTENNAS Paul Wade N1BWT 1994,1998 A horn antenna is the ideal choice for a rover station. It offers moderate gain in a small, rugged package with no adjustments needed,
Chapter 2 ELECTROMAGNETIC HORN ANTENNAS Paul Wade N1BWT 1994,1998 A horn antenna is the ideal choice for a rover station. It offers moderate gain in a small, rugged package with no adjustments needed,
Fraunhofer Diffraction
 Physics 334 Spring 1 Purpose Fraunhofer Diffraction The experiment will test the theory of Fraunhofer diffraction at a single slit by comparing a careful measurement of the angular dependence of intensity
Physics 334 Spring 1 Purpose Fraunhofer Diffraction The experiment will test the theory of Fraunhofer diffraction at a single slit by comparing a careful measurement of the angular dependence of intensity
Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad
 International Journal of Scientific & Engineering Research Volume 3, Issue 8, August-2012 1 Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad Abstract-Parallel
International Journal of Scientific & Engineering Research Volume 3, Issue 8, August-2012 1 Mode Patterns of Parallel plates &Rectangular wave guides Mr.K.Chandrashekhar, Dr.Girish V Attimarad Abstract-Parallel
Lecture L3 - Vectors, Matrices and Coordinate Transformations
 S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND
 DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND THE THREE-DIMENSIONAL DISTRIBUTION OF THE RADIANT FLUX DENSITY AT THE FOCUS OF A CONVERGENCE BEAM
DOING PHYSICS WITH MATLAB COMPUTATIONAL OPTICS RAYLEIGH-SOMMERFELD DIFFRACTION INTEGRAL OF THE FIRST KIND THE THREE-DIMENSIONAL DISTRIBUTION OF THE RADIANT FLUX DENSITY AT THE FOCUS OF A CONVERGENCE BEAM
Pillbox Antenna for 5.6 GHz Band Dragoslav Dobričić, YU1AW [email protected]
 Pillbox Antenna for 5.6 GHz Band Dragoslav Dobričić, YU1AW [email protected] Introduction The pillbox or cheese antenna is made of two parallel plates which are connected to the narrow strip of parabolic
Pillbox Antenna for 5.6 GHz Band Dragoslav Dobričić, YU1AW [email protected] Introduction The pillbox or cheese antenna is made of two parallel plates which are connected to the narrow strip of parabolic
Antenna Properties and their impact on Wireless System Performance. Dr. Steven R. Best. Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013
 Antenna Properties and their impact on Wireless System Performance Dr. Steven R. Best Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013 Phone (603) 627-7877 FAX: (603) 627-1764 Email: [email protected]
Antenna Properties and their impact on Wireless System Performance Dr. Steven R. Best Cushcraft Corporation 48 Perimeter Road Manchester, NH 03013 Phone (603) 627-7877 FAX: (603) 627-1764 Email: [email protected]
RADIATION PATTERNS. The half-power (-3 db) beamwidth is a measure of the directivity of the antenna.
 RADIATION PATTERNS The radiation pattern is a graphical depiction of the relative field strength transmitted from or received by the antenna. Antenna radiation patterns are taken at one frequency, one
RADIATION PATTERNS The radiation pattern is a graphical depiction of the relative field strength transmitted from or received by the antenna. Antenna radiation patterns are taken at one frequency, one
Diffraction of a Circular Aperture
 Diffraction of a Circular Aperture Diffraction can be understood by considering the wave nature of light. Huygen's principle, illustrated in the image below, states that each point on a propagating wavefront
Diffraction of a Circular Aperture Diffraction can be understood by considering the wave nature of light. Huygen's principle, illustrated in the image below, states that each point on a propagating wavefront
1 Symmetries of regular polyhedra
 1230, notes 5 1 Symmetries of regular polyhedra Symmetry groups Recall: Group axioms: Suppose that (G, ) is a group and a, b, c are elements of G. Then (i) a b G (ii) (a b) c = a (b c) (iii) There is an
1230, notes 5 1 Symmetries of regular polyhedra Symmetry groups Recall: Group axioms: Suppose that (G, ) is a group and a, b, c are elements of G. Then (i) a b G (ii) (a b) c = a (b c) (iii) There is an
Solutions to Homework 10
 Solutions to Homework 1 Section 7., exercise # 1 (b,d): (b) Compute the value of R f dv, where f(x, y) = y/x and R = [1, 3] [, 4]. Solution: Since f is continuous over R, f is integrable over R. Let x
Solutions to Homework 1 Section 7., exercise # 1 (b,d): (b) Compute the value of R f dv, where f(x, y) = y/x and R = [1, 3] [, 4]. Solution: Since f is continuous over R, f is integrable over R. Let x
Interference and Diffraction
 Chapter 14 nterference and Diffraction 14.1 Superposition of Waves... 14-14. Young s Double-Slit Experiment... 14-4 Example 14.1: Double-Slit Experiment... 14-7 14.3 ntensity Distribution... 14-8 Example
Chapter 14 nterference and Diffraction 14.1 Superposition of Waves... 14-14. Young s Double-Slit Experiment... 14-4 Example 14.1: Double-Slit Experiment... 14-7 14.3 ntensity Distribution... 14-8 Example
Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device. Application: Radiation
 Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device Application: adiation Introduction An antenna is designed to radiate or receive electromagnetic
Antenna A mean for radiating and receiving radio waves Transitional structure between free-space and a guiding device Application: adiation Introduction An antenna is designed to radiate or receive electromagnetic
Review B: Coordinate Systems
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of hysics 8.02 Review B: Coordinate Systems B.1 Cartesian Coordinates... B-2 B.1.1 Infinitesimal Line Element... B-4 B.1.2 Infinitesimal Area Element...
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of hysics 8.02 Review B: Coordinate Systems B.1 Cartesian Coordinates... B-2 B.1.1 Infinitesimal Line Element... B-4 B.1.2 Infinitesimal Area Element...
Mathematical Induction
 Mathematical Induction (Handout March 8, 01) The Principle of Mathematical Induction provides a means to prove infinitely many statements all at once The principle is logical rather than strictly mathematical,
Mathematical Induction (Handout March 8, 01) The Principle of Mathematical Induction provides a means to prove infinitely many statements all at once The principle is logical rather than strictly mathematical,
WAVELENGTH OF LIGHT - DIFFRACTION GRATING
 PURPOSE In this experiment we will use the diffraction grating and the spectrometer to measure wavelengths in the mercury spectrum. THEORY A diffraction grating is essentially a series of parallel equidistant
PURPOSE In this experiment we will use the diffraction grating and the spectrometer to measure wavelengths in the mercury spectrum. THEORY A diffraction grating is essentially a series of parallel equidistant
Solutions for Review Problems
 olutions for Review Problems 1. Let be the triangle with vertices A (,, ), B (4,, 1) and C (,, 1). (a) Find the cosine of the angle BAC at vertex A. (b) Find the area of the triangle ABC. (c) Find a vector
olutions for Review Problems 1. Let be the triangle with vertices A (,, ), B (4,, 1) and C (,, 1). (a) Find the cosine of the angle BAC at vertex A. (b) Find the area of the triangle ABC. (c) Find a vector
Understanding Poles and Zeros
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Understanding Poles and Zeros 1 System Poles and Zeros The transfer function
MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Understanding Poles and Zeros 1 System Poles and Zeros The transfer function
Design and Electromagnetic Modeling of E-Plane Sectoral Horn Antenna For Ultra Wide Band Applications On WR-137 & WR- 62 Waveguides
 International Journal of Engineering Science Invention ISSN (Online): 2319 6734, ISSN (Print): 2319 6726 Volume 3 Issue 7ǁ July 2014 ǁ PP.11-17 Design and Electromagnetic Modeling of E-Plane Sectoral Horn
International Journal of Engineering Science Invention ISSN (Online): 2319 6734, ISSN (Print): 2319 6726 Volume 3 Issue 7ǁ July 2014 ǁ PP.11-17 Design and Electromagnetic Modeling of E-Plane Sectoral Horn
Lecture 9. Poles, Zeros & Filters (Lathi 4.10) Effects of Poles & Zeros on Frequency Response (1) Effects of Poles & Zeros on Frequency Response (3)
 Effects of Poles & Zeros on Frequency Response (1) Consider a general system transfer function: zeros at z1, z2,..., zn Lecture 9 Poles, Zeros & Filters (Lathi 4.10) The value of the transfer function
Effects of Poles & Zeros on Frequency Response (1) Consider a general system transfer function: zeros at z1, z2,..., zn Lecture 9 Poles, Zeros & Filters (Lathi 4.10) The value of the transfer function
Designing Log Periodic Antennas
 Designing Log Periodic Antennas By Glen Dash, Ampyx LLC, GlenDash at alum.mit.edu Copyright 2000, 2005 Ampyx LLC Lightweight and precise, the log periodic has become a favorite among EMC engineers. In
Designing Log Periodic Antennas By Glen Dash, Ampyx LLC, GlenDash at alum.mit.edu Copyright 2000, 2005 Ampyx LLC Lightweight and precise, the log periodic has become a favorite among EMC engineers. In
Chapter 22: Electric Flux and Gauss s Law
 22.1 ntroduction We have seen in chapter 21 that determining the electric field of a continuous charge distribution can become very complicated for some charge distributions. t would be desirable if we
22.1 ntroduction We have seen in chapter 21 that determining the electric field of a continuous charge distribution can become very complicated for some charge distributions. t would be desirable if we
Applications in EMC testing. Outline. Antennas for EMC Testing. Terminology
 Antennas for EMC Testing Zhong Chen ETS-Lindgren 1301 Arrow Point Drive Cedar Park, TX 78613 [email protected] Outline EMC Terms and Definitions Typical EMC Antennas Calibration of EMC Antennas
Antennas for EMC Testing Zhong Chen ETS-Lindgren 1301 Arrow Point Drive Cedar Park, TX 78613 [email protected] Outline EMC Terms and Definitions Typical EMC Antennas Calibration of EMC Antennas
arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014
![arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014 arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014](/thumbs/39/19151390.jpg) Theory of Electromagnetic Fields Andrzej Wolski University of Liverpool, and the Cockcroft Institute, UK arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014 Abstract We discuss the theory of electromagnetic
Theory of Electromagnetic Fields Andrzej Wolski University of Liverpool, and the Cockcroft Institute, UK arxiv:1111.4354v2 [physics.acc-ph] 27 Oct 2014 Abstract We discuss the theory of electromagnetic
Laboratory #6: Dipole and Monopole Antenna Design
 EEE 171 Lab #6 1 Laboratory #6: Dipole and Monopole Antenna Design I. OBJECTIVES Design several lengths of dipole antennas. Design appropriate impedance matching networks for those antennas. The antennas
EEE 171 Lab #6 1 Laboratory #6: Dipole and Monopole Antenna Design I. OBJECTIVES Design several lengths of dipole antennas. Design appropriate impedance matching networks for those antennas. The antennas
W1GHZ W1GHZ W1GHZ W1GHZ W1GHZ W1GHZ W1GHZ W1GHZ
 Online Online Online Online Online Online Online Antenna Book Antenna BookOnline Antenna Book Antenna Book Antenna Book Antenna Book Antenna Book Antenna Book Chapter 7 Slot Antennas Paul Wade 2000,2001
Online Online Online Online Online Online Online Antenna Book Antenna BookOnline Antenna Book Antenna Book Antenna Book Antenna Book Antenna Book Antenna Book Chapter 7 Slot Antennas Paul Wade 2000,2001
Magnetic Field of a Circular Coil Lab 12
 HB 11-26-07 Magnetic Field of a Circular Coil Lab 12 1 Magnetic Field of a Circular Coil Lab 12 Equipment- coil apparatus, BK Precision 2120B oscilloscope, Fluke multimeter, Wavetek FG3C function generator,
HB 11-26-07 Magnetic Field of a Circular Coil Lab 12 1 Magnetic Field of a Circular Coil Lab 12 Equipment- coil apparatus, BK Precision 2120B oscilloscope, Fluke multimeter, Wavetek FG3C function generator,
CHAPTER4 GENERAL ASPECTS OF MUTUAL
 CHAPTER4 GENERAL ASPECTS OF MUTUAL ADMITTANCE OF CPW-FED TWIN SLOTS ON CONDUCTOR-BACKED TWO-LAYER SUBSTRATES 4.1 INTRODUCTORY REMARKS The present chapter is concerned with an exploratory investigation
CHAPTER4 GENERAL ASPECTS OF MUTUAL ADMITTANCE OF CPW-FED TWIN SLOTS ON CONDUCTOR-BACKED TWO-LAYER SUBSTRATES 4.1 INTRODUCTORY REMARKS The present chapter is concerned with an exploratory investigation
Selecting Receiving Antennas for Radio Tracking
 Selecting Receiving Antennas for Radio Tracking Larry B Kuechle, Advanced Telemetry Systems, Inc. Isanti, Minnesota 55040 [email protected] The receiving antenna is an integral part of any radio location
Selecting Receiving Antennas for Radio Tracking Larry B Kuechle, Advanced Telemetry Systems, Inc. Isanti, Minnesota 55040 [email protected] The receiving antenna is an integral part of any radio location
Diffraction and Young s Single Slit Experiment
 Diffraction and Young s Single Slit Experiment Developers AB Overby Objectives Preparation Background The objectives of this experiment are to observe Fraunhofer, or far-field, diffraction through a single
Diffraction and Young s Single Slit Experiment Developers AB Overby Objectives Preparation Background The objectives of this experiment are to observe Fraunhofer, or far-field, diffraction through a single
Fiber Optics: Fiber Basics
 Photonics Technical Note # 21 Fiber Optics Fiber Optics: Fiber Basics Optical fibers are circular dielectric wave-guides that can transport optical energy and information. They have a central core surrounded
Photonics Technical Note # 21 Fiber Optics Fiber Optics: Fiber Basics Optical fibers are circular dielectric wave-guides that can transport optical energy and information. They have a central core surrounded
Interference. Physics 102 Workshop #3. General Instructions
 Interference Physics 102 Workshop #3 Name: Lab Partner(s): Instructor: Time of Workshop: General Instructions Workshop exercises are to be carried out in groups of three. One report per group is due by
Interference Physics 102 Workshop #3 Name: Lab Partner(s): Instructor: Time of Workshop: General Instructions Workshop exercises are to be carried out in groups of three. One report per group is due by
Introduction to Complex Numbers in Physics/Engineering
 Introduction to Complex Numbers in Physics/Engineering ference: Mary L. Boas, Mathematical Methods in the Physical Sciences Chapter 2 & 14 George Arfken, Mathematical Methods for Physicists Chapter 6 The
Introduction to Complex Numbers in Physics/Engineering ference: Mary L. Boas, Mathematical Methods in the Physical Sciences Chapter 2 & 14 George Arfken, Mathematical Methods for Physicists Chapter 6 The
The Vector or Cross Product
 The Vector or ross Product 1 ppendix The Vector or ross Product We saw in ppendix that the dot product of two vectors is a scalar quantity that is a maximum when the two vectors are parallel and is zero
The Vector or ross Product 1 ppendix The Vector or ross Product We saw in ppendix that the dot product of two vectors is a scalar quantity that is a maximum when the two vectors are parallel and is zero
Unified Lecture # 4 Vectors
 Fall 2005 Unified Lecture # 4 Vectors These notes were written by J. Peraire as a review of vectors for Dynamics 16.07. They have been adapted for Unified Engineering by R. Radovitzky. References [1] Feynmann,
Fall 2005 Unified Lecture # 4 Vectors These notes were written by J. Peraire as a review of vectors for Dynamics 16.07. They have been adapted for Unified Engineering by R. Radovitzky. References [1] Feynmann,
A PRACTICAL MINIATURIZED U-SLOT PATCH ANTENNA WITH ENHANCED BANDWIDTH
 Progress In Electromagnetics Research B, Vol. 3, 47 62, 2008 A PRACTICAL MINIATURIZED U-SLOT PATCH ANTENNA WITH ENHANCED BANDWIDTH G. F. Khodaei, J. Nourinia, and C. Ghobadi Electrical Engineering Department
Progress In Electromagnetics Research B, Vol. 3, 47 62, 2008 A PRACTICAL MINIATURIZED U-SLOT PATCH ANTENNA WITH ENHANCED BANDWIDTH G. F. Khodaei, J. Nourinia, and C. Ghobadi Electrical Engineering Department
Vector surface area Differentials in an OCS
 Calculus and Coordinate systems EE 311 - Lecture 17 1. Calculus and coordinate systems 2. Cartesian system 3. Cylindrical system 4. Spherical system In electromagnetics, we will often need to perform integrals
Calculus and Coordinate systems EE 311 - Lecture 17 1. Calculus and coordinate systems 2. Cartesian system 3. Cylindrical system 4. Spherical system In electromagnetics, we will often need to perform integrals
CHAPTER 8, GEOMETRY. 4. A circular cylinder has a circumference of 33 in. Use 22 as the approximate value of π and find the radius of this cylinder.
 TEST A CHAPTER 8, GEOMETRY 1. A rectangular plot of ground is to be enclosed with 180 yd of fencing. If the plot is twice as long as it is wide, what are its dimensions? 2. A 4 cm by 6 cm rectangle has
TEST A CHAPTER 8, GEOMETRY 1. A rectangular plot of ground is to be enclosed with 180 yd of fencing. If the plot is twice as long as it is wide, what are its dimensions? 2. A 4 cm by 6 cm rectangle has
The elements used in commercial codes can be classified in two basic categories:
 CHAPTER 3 Truss Element 3.1 Introduction The single most important concept in understanding FEA, is the basic understanding of various finite elements that we employ in an analysis. Elements are used for
CHAPTER 3 Truss Element 3.1 Introduction The single most important concept in understanding FEA, is the basic understanding of various finite elements that we employ in an analysis. Elements are used for
Helical Feed Antennas Paul Wade W1GHZ 2002 [email protected]
 Helical Feed Antennas Paul Wade W1GHZ 22 [email protected] Helical antennas have long been popular in applications from VHF to microwaves requiring circular polarization, since they have the unique property
Helical Feed Antennas Paul Wade W1GHZ 22 [email protected] Helical antennas have long been popular in applications from VHF to microwaves requiring circular polarization, since they have the unique property
ANALYTICAL METHODS FOR ENGINEERS
 UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
UNIT 1: Unit code: QCF Level: 4 Credit value: 15 ANALYTICAL METHODS FOR ENGINEERS A/601/1401 OUTCOME - TRIGONOMETRIC METHODS TUTORIAL 1 SINUSOIDAL FUNCTION Be able to analyse and model engineering situations
WAVEGUIDE-COAXIAL LINE TRANSITIONS
 WAVEGUIDE-COAXIAL LINE TRANSITIONS 1. Overview Equipment at microwave frequencies is usually based on a combination of PCB and waveguide components. Filters and antennas often use waveguide techniques,
WAVEGUIDE-COAXIAL LINE TRANSITIONS 1. Overview Equipment at microwave frequencies is usually based on a combination of PCB and waveguide components. Filters and antennas often use waveguide techniques,
Design & Simulation of 8-Shape Slotted Microstrip Patch Antenna
 World Applied Sciences Journal 31 (6): 1065-1071, 2014 ISSN 1818-4952 IDOSI Publications, 2014 DOI: 10.5829/idosi.wasj.2014.31.06.1462 Design & Simulation of 8-Shape Slotted Microstrip Patch Antenna Sohag
World Applied Sciences Journal 31 (6): 1065-1071, 2014 ISSN 1818-4952 IDOSI Publications, 2014 DOI: 10.5829/idosi.wasj.2014.31.06.1462 Design & Simulation of 8-Shape Slotted Microstrip Patch Antenna Sohag
Simplified procedure for evaluating the coverage area of a multifeed shaped antenna Application to the planning of a broadcasting satellite system
 Simplified procedure for evaluating the coverage area of a multifeed shaped antenna Application to the planning of a broadcasting satellite system L. Tomati (RAI) M. D Onofrio (RAI) G. Carere (RAI) Shaped
Simplified procedure for evaluating the coverage area of a multifeed shaped antenna Application to the planning of a broadcasting satellite system L. Tomati (RAI) M. D Onofrio (RAI) G. Carere (RAI) Shaped
Analysis of Broadband Slot Cut Semi-Circular Microstrip Antennas
 Analysis of Broadband Slot Cut Semi-Circular Microstrip Antennas Amit A. Deshmukh EXTC, DJSCOE Vile Parle (W), Mumbai, India Ankita R. Jain EXTC, DJSCOE Vile Parle (W), Mumbai, India Apurva A. Joshi EXTC,
Analysis of Broadband Slot Cut Semi-Circular Microstrip Antennas Amit A. Deshmukh EXTC, DJSCOE Vile Parle (W), Mumbai, India Ankita R. Jain EXTC, DJSCOE Vile Parle (W), Mumbai, India Apurva A. Joshi EXTC,
Design of a Planar Omnidirectional Antenna for Wireless Applications
 Design of a Planar Omnidirectional Antenna for Wireless Applications Randy Bancroft and Blaine Bateman Centurion Wireless Technologies Westminster, Colorado Abstract Omnidirectional antennas are of great
Design of a Planar Omnidirectional Antenna for Wireless Applications Randy Bancroft and Blaine Bateman Centurion Wireless Technologies Westminster, Colorado Abstract Omnidirectional antennas are of great
Antenna Patterns and Their Meaning
 Antenna Patterns and Their Meaning Much can be learned about how an antenna performs from its patterns. This paper describes many of the common antenna parameters that can be understood from the patterns.
Antenna Patterns and Their Meaning Much can be learned about how an antenna performs from its patterns. This paper describes many of the common antenna parameters that can be understood from the patterns.
Chapter 6 Circular Motion
 Chapter 6 Circular Motion 6.1 Introduction... 1 6.2 Cylindrical Coordinate System... 2 6.2.1 Unit Vectors... 3 6.2.2 Infinitesimal Line, Area, and Volume Elements in Cylindrical Coordinates... 4 Example
Chapter 6 Circular Motion 6.1 Introduction... 1 6.2 Cylindrical Coordinate System... 2 6.2.1 Unit Vectors... 3 6.2.2 Infinitesimal Line, Area, and Volume Elements in Cylindrical Coordinates... 4 Example
Transmission Line and Back Loaded Horn Physics
 Introduction By Martin J. King, 3/29/3 Copyright 23 by Martin J. King. All Rights Reserved. In order to differentiate between a transmission line and a back loaded horn, it is really important to understand
Introduction By Martin J. King, 3/29/3 Copyright 23 by Martin J. King. All Rights Reserved. In order to differentiate between a transmission line and a back loaded horn, it is really important to understand
3.5.4.2 One example: Michelson interferometer
 3.5.4.2 One example: Michelson interferometer mirror 1 mirror 2 light source 1 2 3 beam splitter 4 object (n object ) interference pattern we either observe fringes of same thickness (parallel light) or
3.5.4.2 One example: Michelson interferometer mirror 1 mirror 2 light source 1 2 3 beam splitter 4 object (n object ) interference pattern we either observe fringes of same thickness (parallel light) or
The Math Circle, Spring 2004
 The Math Circle, Spring 2004 (Talks by Gordon Ritter) What is Non-Euclidean Geometry? Most geometries on the plane R 2 are non-euclidean. Let s denote arc length. Then Euclidean geometry arises from the
The Math Circle, Spring 2004 (Talks by Gordon Ritter) What is Non-Euclidean Geometry? Most geometries on the plane R 2 are non-euclidean. Let s denote arc length. Then Euclidean geometry arises from the
Antenna design for Space Applications M. Sabbadini European Space Agency, Noordwijk, The Netherlands [email protected]
 Antenna design for Space Applications M. Sabbadini European Space Agency, Noordwijk, The Netherlands [email protected] Day 2 overview Satellite communications Communication satellite antenna design
Antenna design for Space Applications M. Sabbadini European Space Agency, Noordwijk, The Netherlands [email protected] Day 2 overview Satellite communications Communication satellite antenna design
How To Understand The Physics Of Metasurfing
 ASI, ROMA, 4 Novembre, 13 Acknowledgements A Toccafondi (Associate Professor) M. Albani (Assistant Professor) Modulated Metasurface Antennas S. Maci Dept. Information Engineering and Math Science, University
ASI, ROMA, 4 Novembre, 13 Acknowledgements A Toccafondi (Associate Professor) M. Albani (Assistant Professor) Modulated Metasurface Antennas S. Maci Dept. Information Engineering and Math Science, University
Chapter 1 ANTENNA FUNDAMENTALS. Paul Wade W1GHZ (ex-n1bwt) 1994,1997,1998 ANTENNA BASICS
 Chapter 1 ANTENNA FUNDAMENTALS Paul Wade W1GHZ (ex-n1bwt) 1994,1997,1998 Introduction Antenna gain is essential for microwave communication since it helps both transmitting and receiving, it is doubly
Chapter 1 ANTENNA FUNDAMENTALS Paul Wade W1GHZ (ex-n1bwt) 1994,1997,1998 Introduction Antenna gain is essential for microwave communication since it helps both transmitting and receiving, it is doubly
Physics 41 Chapter 38 HW Key
 Physics 41 Chapter 38 HW Key 1. Helium neon laser light (63..8 nm) is sent through a 0.300-mm-wide single slit. What is the width of the central imum on a screen 1.00 m from the slit? 7 6.38 10 sin θ.11
Physics 41 Chapter 38 HW Key 1. Helium neon laser light (63..8 nm) is sent through a 0.300-mm-wide single slit. What is the width of the central imum on a screen 1.00 m from the slit? 7 6.38 10 sin θ.11
REPORT ITU-R BO.2029. Broadcasting-satellite service earth station antenna pattern measurements and related analyses
 Rep. ITU-R BO.229 1 REPORT ITU-R BO.229 Broadcasting-satellite service earth station antenna pattern measurements and related analyses (Question ITU-R 93/11) (22) 1 Introduction Recommendation ITU-R BO.1443
Rep. ITU-R BO.229 1 REPORT ITU-R BO.229 Broadcasting-satellite service earth station antenna pattern measurements and related analyses (Question ITU-R 93/11) (22) 1 Introduction Recommendation ITU-R BO.1443
PROBLEM SET. Practice Problems for Exam #1. Math 1352, Fall 2004. Oct. 1, 2004 ANSWERS
 PROBLEM SET Practice Problems for Exam # Math 352, Fall 24 Oct., 24 ANSWERS i Problem. vlet R be the region bounded by the curves x = y 2 and y = x. A. Find the volume of the solid generated by revolving
PROBLEM SET Practice Problems for Exam # Math 352, Fall 24 Oct., 24 ANSWERS i Problem. vlet R be the region bounded by the curves x = y 2 and y = x. A. Find the volume of the solid generated by revolving
2 Port Parameters I 1. ECE145A/218A Notes Set #4 1. Two-ways of describing device: A. Equivalent - Circuit-Model
 ECE45A/8A Notes et #4 Port Parameters Two-ways of describing device: A. Equivalent - Circuit-Model Physically based Includes bias dependence Includes frequency dependence Includes size dependence - scalability
ECE45A/8A Notes et #4 Port Parameters Two-ways of describing device: A. Equivalent - Circuit-Model Physically based Includes bias dependence Includes frequency dependence Includes size dependence - scalability
2 Session Two - Complex Numbers and Vectors
 PH2011 Physics 2A Maths Revision - Session 2: Complex Numbers and Vectors 1 2 Session Two - Complex Numbers and Vectors 2.1 What is a Complex Number? The material on complex numbers should be familiar
PH2011 Physics 2A Maths Revision - Session 2: Complex Numbers and Vectors 1 2 Session Two - Complex Numbers and Vectors 2.1 What is a Complex Number? The material on complex numbers should be familiar
RF-Microwaves formulas - 1-port systems
 RF-Microwaves formulas - -port systems s-parameters: Considering a voltage source feeding into the DUT with a source impedance of. E i E r DUT The voltage into the DUT is composed of 2 parts, an incident
RF-Microwaves formulas - -port systems s-parameters: Considering a voltage source feeding into the DUT with a source impedance of. E i E r DUT The voltage into the DUT is composed of 2 parts, an incident
Math 1B, lecture 5: area and volume
 Math B, lecture 5: area and volume Nathan Pflueger 6 September 2 Introduction This lecture and the next will be concerned with the computation of areas of regions in the plane, and volumes of regions in
Math B, lecture 5: area and volume Nathan Pflueger 6 September 2 Introduction This lecture and the next will be concerned with the computation of areas of regions in the plane, and volumes of regions in
Trigonometric Functions: The Unit Circle
 Trigonometric Functions: The Unit Circle This chapter deals with the subject of trigonometry, which likely had its origins in the study of distances and angles by the ancient Greeks. The word trigonometry
Trigonometric Functions: The Unit Circle This chapter deals with the subject of trigonometry, which likely had its origins in the study of distances and angles by the ancient Greeks. The word trigonometry
A Novel Multi Frequency Rectangular Microstrip Antenna with Dual T Shaped Slots for UWB Applications
 IOSR Journal of Electronics and Communication Engineering (IOSR-JECE) e-issn: 2278-2834,p- ISSN: 2278-8735.Volume 9, Issue 1, Ver. VI (Feb. 2014), PP 120-124 A Novel Multi Frequency Rectangular Microstrip
IOSR Journal of Electronics and Communication Engineering (IOSR-JECE) e-issn: 2278-2834,p- ISSN: 2278-8735.Volume 9, Issue 1, Ver. VI (Feb. 2014), PP 120-124 A Novel Multi Frequency Rectangular Microstrip
TWO-DIMENSIONAL TRANSFORMATION
 CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
CHAPTER 2 TWO-DIMENSIONAL TRANSFORMATION 2.1 Introduction As stated earlier, Computer Aided Design consists of three components, namely, Design (Geometric Modeling), Analysis (FEA, etc), and Visualization
Method of Green s Functions
 Method of Green s Functions 8.303 Linear Partial ifferential Equations Matthew J. Hancock Fall 006 We introduce another powerful method of solving PEs. First, we need to consider some preliminary definitions
Method of Green s Functions 8.303 Linear Partial ifferential Equations Matthew J. Hancock Fall 006 We introduce another powerful method of solving PEs. First, we need to consider some preliminary definitions
A Method for Measuring Amplitude and Phase of Each Radiating Element of a Phased Array Antenna
 Electronics and Communications in Japan, Vol. 65-B, No. 5, 1982 A Method for Measuring Amplitude and Phase of Each Radiating Element of a Phased Array Antenna Seiji Mano and Takashi Katagi, Regular Members
Electronics and Communications in Japan, Vol. 65-B, No. 5, 1982 A Method for Measuring Amplitude and Phase of Each Radiating Element of a Phased Array Antenna Seiji Mano and Takashi Katagi, Regular Members
GLOBAL COLLEGE OF ENGINEERING &TECHNOLOGY: YSR DIST. Unit VII Fiber Optics Engineering Physics
 Introduction Fiber optics deals with the light propagation through thin glass fibers. Fiber optics plays an important role in the field of communication to transmit voice, television and digital data signals
Introduction Fiber optics deals with the light propagation through thin glass fibers. Fiber optics plays an important role in the field of communication to transmit voice, television and digital data signals
Chapter 17. Orthogonal Matrices and Symmetries of Space
 Chapter 17. Orthogonal Matrices and Symmetries of Space Take a random matrix, say 1 3 A = 4 5 6, 7 8 9 and compare the lengths of e 1 and Ae 1. The vector e 1 has length 1, while Ae 1 = (1, 4, 7) has length
Chapter 17. Orthogonal Matrices and Symmetries of Space Take a random matrix, say 1 3 A = 4 5 6, 7 8 9 and compare the lengths of e 1 and Ae 1. The vector e 1 has length 1, while Ae 1 = (1, 4, 7) has length
Review Paper for Broadband CPW-Fed T-Shape Slot Antenna
 Review Paper for Broadband CPW-Fed T-Shape Slot Antenna Shahpure Sana 1, Bharate Rajashri 2, Prof. Jadhav D.A. 3 1,2 BE, Dept. of E&TC, Brahmdevdada Mane Institute of Technology, Dist. Solapur (Maharashtra)
Review Paper for Broadband CPW-Fed T-Shape Slot Antenna Shahpure Sana 1, Bharate Rajashri 2, Prof. Jadhav D.A. 3 1,2 BE, Dept. of E&TC, Brahmdevdada Mane Institute of Technology, Dist. Solapur (Maharashtra)
Examples of Uniform EM Plane Waves
 Examples of Uniform EM Plane Waves Outline Reminder of Wave Equation Reminder of Relation Between E & H Energy Transported by EM Waves (Poynting Vector) Examples of Energy Transport by EM Waves 1 Coupling
Examples of Uniform EM Plane Waves Outline Reminder of Wave Equation Reminder of Relation Between E & H Energy Transported by EM Waves (Poynting Vector) Examples of Energy Transport by EM Waves 1 Coupling
Physics 235 Chapter 1. Chapter 1 Matrices, Vectors, and Vector Calculus
 Chapter 1 Matrices, Vectors, and Vector Calculus In this chapter, we will focus on the mathematical tools required for the course. The main concepts that will be covered are: Coordinate transformations
Chapter 1 Matrices, Vectors, and Vector Calculus In this chapter, we will focus on the mathematical tools required for the course. The main concepts that will be covered are: Coordinate transformations
PLANE TRUSSES. Definitions
 Definitions PLANE TRUSSES A truss is one of the major types of engineering structures which provides a practical and economical solution for many engineering constructions, especially in the design of
Definitions PLANE TRUSSES A truss is one of the major types of engineering structures which provides a practical and economical solution for many engineering constructions, especially in the design of
Parabolic Equations. Chapter 5. Contents. 5.1.2 Well-Posed Initial-Boundary Value Problem. 5.1.3 Time Irreversibility of the Heat Equation
 7 5.1 Definitions Properties Chapter 5 Parabolic Equations Note that we require the solution u(, t bounded in R n for all t. In particular we assume that the boundedness of the smooth function u at infinity
7 5.1 Definitions Properties Chapter 5 Parabolic Equations Note that we require the solution u(, t bounded in R n for all t. In particular we assume that the boundedness of the smooth function u at infinity
Proposal for a Slot Pair Array Having an Invariant Main Beam Direction with a Cosecant Radiation Pattern Using a Post-Wall Waveguide
 176 IEICE TRANS. ELECTRON., VOL.E86 C, NO.2 FEBRUARY 2003 PAPER Special Issue on Circuit and Device Technology for High-Speed Wireless Communication Proposal for a Slot Pair Array Having an Invariant Main
176 IEICE TRANS. ELECTRON., VOL.E86 C, NO.2 FEBRUARY 2003 PAPER Special Issue on Circuit and Device Technology for High-Speed Wireless Communication Proposal for a Slot Pair Array Having an Invariant Main
Oscillations. Vern Lindberg. June 10, 2010
 Oscillations Vern Lindberg June 10, 2010 You have discussed oscillations in Vibs and Waves: we will therefore touch lightly on Chapter 3, mainly trying to refresh your memory and extend the concepts. 1
Oscillations Vern Lindberg June 10, 2010 You have discussed oscillations in Vibs and Waves: we will therefore touch lightly on Chapter 3, mainly trying to refresh your memory and extend the concepts. 1
Analysis of the G3LTF Dual Band Feed for 23cm and 13cm Paul Wade W1GHZ 2004 [email protected]
 Analysis of the G3LTF Dual Band Feed for 23cm and 13cm Paul Wade W1GHZ 2004 [email protected] In the March 2004 edition of the RSGB Microwave Newsletter, G3LTF described 1 a dual band feed for the 23 cm and
Analysis of the G3LTF Dual Band Feed for 23cm and 13cm Paul Wade W1GHZ 2004 [email protected] In the March 2004 edition of the RSGB Microwave Newsletter, G3LTF described 1 a dual band feed for the 23 cm and
Printed Dipole Array Fed with Parallel Stripline for Ku-band Applications
 Printed Dipole Array Fed with Parallel Stripline for Ku-band Applications M. Dogan 1, 3,K. Özsoy 1, 2, and I.Tekin 1, 1 Electronics Engineering, Sabanci University, Istanbul, Turkey 2 Vestek Electronic
Printed Dipole Array Fed with Parallel Stripline for Ku-band Applications M. Dogan 1, 3,K. Özsoy 1, 2, and I.Tekin 1, 1 Electronics Engineering, Sabanci University, Istanbul, Turkey 2 Vestek Electronic
Transmission Lines. Smith Chart
 Smith Chart The Smith chart is one of the most useful graphical tools for high frequency circuit applications. The chart provides a clever way to visualize complex functions and it continues to endure
Smith Chart The Smith chart is one of the most useful graphical tools for high frequency circuit applications. The chart provides a clever way to visualize complex functions and it continues to endure
6) How wide must a narrow slit be if the first diffraction minimum occurs at ±12 with laser light of 633 nm?
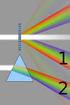 Test IV Name 1) In a single slit diffraction experiment, the width of the slit is 3.1 10-5 m and the distance from the slit to the screen is 2.2 m. If the beam of light of wavelength 600 nm passes through
Test IV Name 1) In a single slit diffraction experiment, the width of the slit is 3.1 10-5 m and the distance from the slit to the screen is 2.2 m. If the beam of light of wavelength 600 nm passes through
Antennas & Propagation. CS 6710 Spring 2010 Rajmohan Rajaraman
 Antennas & Propagation CS 6710 Spring 2010 Rajmohan Rajaraman Introduction An antenna is an electrical conductor or system of conductors o Transmission - radiates electromagnetic energy into space o Reception
Antennas & Propagation CS 6710 Spring 2010 Rajmohan Rajaraman Introduction An antenna is an electrical conductor or system of conductors o Transmission - radiates electromagnetic energy into space o Reception
Analysis of Radiation Patterns of Log-Periodic Dipole Array Using Transmission Line Matrix Model
 Analysis of Radiation Patterns of Log-Periodic Dipole Array Using Transmission Line Matrix Model Surender Daasari 1, Suresh Thallapelli 2 Department of ECE, Kamala Institute of Technlogy & Science, Singapuram,
Analysis of Radiation Patterns of Log-Periodic Dipole Array Using Transmission Line Matrix Model Surender Daasari 1, Suresh Thallapelli 2 Department of ECE, Kamala Institute of Technlogy & Science, Singapuram,
FOOTING DESIGN EXAMPLE
 County: Any Design: BRG Date: 10/007 Hwy: Any Ck Dsn: BRG Date: 10/007 FOOTING DESIGN EXAMPLE Design: Based on AASHTO LRFD 007 Specifications, TxDOT LRFD Bridge Design Manual, and TxDOT Project 0-4371
County: Any Design: BRG Date: 10/007 Hwy: Any Ck Dsn: BRG Date: 10/007 FOOTING DESIGN EXAMPLE Design: Based on AASHTO LRFD 007 Specifications, TxDOT LRFD Bridge Design Manual, and TxDOT Project 0-4371
1. Introduction sine, cosine, tangent, cotangent, secant, and cosecant periodic
 1. Introduction There are six trigonometric functions: sine, cosine, tangent, cotangent, secant, and cosecant; abbreviated as sin, cos, tan, cot, sec, and csc respectively. These are functions of a single
1. Introduction There are six trigonometric functions: sine, cosine, tangent, cotangent, secant, and cosecant; abbreviated as sin, cos, tan, cot, sec, and csc respectively. These are functions of a single
Log-Periodic Loop Antennas
 Log-Periodic Loop Antennas by Jeong Il Kim Thesis submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Master
Log-Periodic Loop Antennas by Jeong Il Kim Thesis submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Master
Linear algebra and the geometry of quadratic equations. Similarity transformations and orthogonal matrices
 MATH 30 Differential Equations Spring 006 Linear algebra and the geometry of quadratic equations Similarity transformations and orthogonal matrices First, some things to recall from linear algebra Two
MATH 30 Differential Equations Spring 006 Linear algebra and the geometry of quadratic equations Similarity transformations and orthogonal matrices First, some things to recall from linear algebra Two
G. GRAPHING FUNCTIONS
 G. GRAPHING FUNCTIONS To get a quick insight int o how the graph of a function looks, it is very helpful to know how certain simple operations on the graph are related to the way the function epression
G. GRAPHING FUNCTIONS To get a quick insight int o how the graph of a function looks, it is very helpful to know how certain simple operations on the graph are related to the way the function epression
Antenna Basic Concepts
 ANTENNA An antenna is a device to transmit and/or receive electromagnetic waves. Electromagnetic waves are often referred to as radio waves. Most antennas are resonant devices, which operate efficiently
ANTENNA An antenna is a device to transmit and/or receive electromagnetic waves. Electromagnetic waves are often referred to as radio waves. Most antennas are resonant devices, which operate efficiently
www.sakshieducation.com
 LENGTH OF THE PERPENDICULAR FROM A POINT TO A STRAIGHT LINE AND DISTANCE BETWEEN TWO PAPALLEL LINES THEOREM The perpendicular distance from a point P(x 1, y 1 ) to the line ax + by + c 0 is ax1+ by1+ c
LENGTH OF THE PERPENDICULAR FROM A POINT TO A STRAIGHT LINE AND DISTANCE BETWEEN TWO PAPALLEL LINES THEOREM The perpendicular distance from a point P(x 1, y 1 ) to the line ax + by + c 0 is ax1+ by1+ c
