Générer des graphiques 3D - Cours Université de Sfax
|
|
|
- Hector Anthony
- 10 years ago
- Views:
Transcription
1 Générer des graphiques 3D - Cours Université de Sfa Marc Girondot Januar 24, 2013 Générer des données 3D > librar(fields) > essai <- function(, ) return (^2+^2+runif(1, min=1, ma=3)) > essai(1, 2) [1] > <- seq(from=-10, to=10, b=0.5) > <- seq(from=-10, to=10, b=0.5) > z <- outer(,, essai) > str(z) num [1:41, 1:41]
2 Utilisation de image.plot La fonction image.plot est disponible dans le package fields. Draws image plot with a legend strip for the color scale based on either a regular grid or a grid of quadrilaterals. Description This function combines the R image function with some automatic placement of a legend. This is done b splitting the plotting region into two parts. Putting the image in one and the legend in the other. It also allows for plotting quadrilateral cells in the image format that often arise from regular grids transformed with a map projection. Usage image.plot(..., Arguments add = FALSE, nlevel = 64, horizontal = FALSE, legend.shrink = 0.9, legend.width = 1.2, legend.mar = ifelse(horizontal, 3.1, 5.1), legend.lab = NULL, graphics.reset = FALSE, bigplot = NULL, smallplot = NULL, legend.onl = FALSE, col = tim.colors(nlevel), lab.breaks = NULL, ais.args = NULL, legend.args = NULL, midpoint=false, border=na, lwd=1.0)... The usual arguments to the image function as,,or z or as a list with,,z as components. One can also include a breaks argument for an unequal color scale with color scale boundaries at the breaks (see eample below). If a quadrilatera l grid, arguments must be eplicitl, and z with, and being matrices of dimension equal or one more than z giving the grid locations. The basic concept is that the coordinates of and still define a grid but the image cells are general quadrilaterals rather than being restricted to rectangles. See details below as to how one handles whether the quads are specified b their vertices or b their midpoints. add If true add image and a legend strip to the eisting plot. nlevel Number of color levels used in legend strip legend.shrink 2
3 Amount to shrink the size of legend relative to the full height or width of the plot. legend.width Width in characters of the legend strip. Default is 1.2, a little bigger that the width of a character. legend.mar Width in characters of legend margin that has the ais. Default is 5.1 for a vertical legend and 3.1 for a horizontal legend. legend.lab Label for the ais of the color legend. Default is no label as this is usual evident from the plot title. graphics.reset If FALSE (default) the plotting region ( plt in par) will not be reset and one can add more information onto the image plot. (e.g. using functions such as points or lines.) If TRUE will reset plot parameters to the values before entering the function. horizontal If false (default) legend will be a vertical strip on the right side. If true the legend strip will be along the bottom. bigplot Plot coordinates for image plot. If not passed these will be determined within the function. smallplot Plot coordinates for legend strip. If not passed these will be determined within the function. Be sure to leave room for the ais labels. For eample, if the legend is on the right side smallplot= c(.85,.9,0,1) will leave (.1 in plot coordinates) for the ais labels to the right of the color strip. This argument is useful for drawing a plot with the legend that is the same size as the plots without legends. legend.onl If TRUE just add the legend to a the plot in the plot region defined b the coordinates in smallplot. In the absence of other information the range for the legend is determined from the zlim argument. col Color table to use for image ( see help file on image for details). Default is a pleasing range of 64 divisions suggested b Tim Hoar and is similar to the MATLAB (TM) jet color scheme. 3
4 lab.breaks If breaks are supplied these are tet string labels to put at each break value. This is intended to label ais on a transformed scale such as logs. ais.args Additional arguments for the ais function used to create the legend ais. (See eample below adding a log scaling.) legend.args Arguments for a complete specification of the legend label. This is in the form of list and is just passed to the mtet function. Usuall this will not be needed. (See eample below.) midpoint This option for the case of unequall spaced grids with and being matrices of grid point locations. If FALSE (default) the quadralaterals will be etended to surround the z locations as midpoints. If TRUE z values will be averaged to ield a midpoint value and the original grid points be used to define the quadralaterals. (See help on pol.image for details). In most cases midpoint should be FALSE to preserve eact values for z and let the grid polgons be modified. border This onl works if and are matrices - if NA the quadralaterals will have a border color that is the same as the interior color. Otherwise this specifies the color to use. lwd Line width of borders around piels. This might need to be set less than 1.0 to avoid visible rounding of the piel corners. 4
5 > image.plot(,, z, col=tim.colors(16)) > image.plot(,, z, col=tim.colors(128))
6 > image.plot(,, z, col=heat.colors(16)) > image.plot(,, z, col=heat.colors(128))
7 > image.plot(,, z, col=rainbow(16)) > image.plot(,, z, col=rainbow(128))
8 Utilisation de persp persp est disponible dans le package graphics. Perspective Plots Description This function draws perspective plots of a surface over the - plane. persp is a generic function. Usage persp(,...) ## Default S3 method: persp( = seq(0, 1, length.out = nrow(z)), = seq(0, 1, length.out = ncol(z)), z, lim = range(), lim = range(), zlim = range(z, na.rm = TRUE), lab = NULL, lab = NULL, zlab = NULL, main = NULL, sub = NULL, theta = 0, phi = 15, r = sqrt(3), d = 1, scale = TRUE, epand = 1, col = "white", border = NULL, ltheta = -135, lphi = 0, shade = NA, bo = TRUE, aes = TRUE, nticks = 5, ticktpe = "simple",...) Arguments, locations of grid lines at which the values in z are measured. These must be in ascending order. B default, equall spaced values from 0 to 1 are used. If is a list, its components $ and $ are used for and, respectivel. z a matri containing the values to be plotted (NAs are allowed). Note that can be used instead of z for convenience. lim, lim, zlim -, - and z-limits. These should be chosen to cover the range of values of the surface: see 'Details'. lab, lab, zlab titles for the aes. N.B. These must be character strings; epressions are not accepted. Numbers will be coerced to character strings. 8
9 main, sub main and sub title, as for title. theta, phi angles defining the viewing direction. theta gives the azimuthal direction and phi the colatitude. r the distance of the eepoint from the centre of the plotting bo. d a value which can be used to var the strength of the perspective transformation. Values of d greater than 1 will lessen the perspective effect and values less and 1 will eaggerate it. scale before viewing the, and z coordinates of the points defining the surface are transformed to the interval [0,1]. If scale is TRUE the, and z coordinates are transformed separatel. If scale is FALSE the coordinates are scaled so that aspect ratios are retained. This is useful for rendering things like DEM information. epand a epansion factor applied to the z coordinates. Often used with 0 < epand < 1 to shrink the plotting bo in the z direction. col the color(s) of the surface facets. Transparent colours are ignored. This is reccled to the (n-1)(n-1) facets. border the color of the line drawn around the surface facets. The default, NULL, corresponds to par("fg"). A value of NA will disable the drawing of borders: this is sometimes useful when the surface is shaded. ltheta, lphi if finite values are specified for ltheta and lphi, the surface is shaded as though it was being illuminated from the direction specified b azimuth ltheta and colatitude lphi. shade the shade at a surface facet is computed as ((1+d)/2)^shade, where d is the dot product of a unit vector normal to the facet and a unit vector in the direction of a light source. Values of shade close to one ield shading similar to a point light source model and values close to zero produce no shading. Values in the range 0.5 to 0.75 provide an approimation to dalight illumination. 9
10 bo should the bounding bo for the surface be displaed. The default is TRUE. aes should ticks and labels be added to the bo. The default is TRUE. If bo is FALSE then no ticks or labels are drawn. ticktpe character: "simple" draws just an arrow parallel to the ais to indicate direction of increase; "detailed" draws normal ticks as per 2D plots. nticks the (approimate) number of tick marks to draw on the aes. Has no effect if ticktpe is "simple".... additional graphical parameters (see par). Couleur des facettes fonction du niveau La commande z[-1, -1] permet de prendre tous les points sauf le point de coordonnée 1, 1. Dans z, il a la couleur au point d intersection et. Si on travaille sur des surfaces, il a donc une surface de moins que d intersection à la fois sur et sur. Dans zfacet, il a donc la valeur de z au centre de l élément. La fonction cut() permet de discrétiser un objet continu. 10
11 z z Effet du paramètre theta > persp(,, z, theta=0) > persp(,, z, theta=30) 11
12 z z > persp(,, z, theta=45) > persp(,, z, theta=90) 12
13 z Effet du paramètre phi > persp(,, z, phi=0) z > persp(,, z, phi=15) 13
14 > persp(,, z, phi=45) z 14
15 z z Graphique d une couleur homogène avec ou sans ombrage > persp(,, z, phi=15, col = "lightblue") > persp(,, z, phi=15, col = "lightblue", shade=0.5) 15
16 z > nrz <- nrow(z) > ncz <- ncol(z) > nbcol <- 128 > zfacet <- (z[-1, -1] + z[-1, -ncz] + z[-nrz, -1] + z[-nrz, -ncz])/4 > facetcol <- cut(zfacet, nbcol) > color <- heat.colors(nbcol) > persp(,, z, col=color[facetcol], phi=15, theta=0) > persp(,, z, col=color[facetcol], phi=90, theta=0, d=100) 16 z
17 z Couleur des facettes selon un arc en ciel > color <- rainbow(nbcol) > persp(,, z, col=color[facetcol], phi=15, theta=0) > persp(,, z, col=color[facetcol], phi=90, theta=0, d=100) z 17
18 z Couleur des facettes selon un dégradé du bleu vers le vert > jet.colors <- colorramppalette( c("blue", "green") ) > color <- jet.colors(nbcol) > persp(,, z, col=color[facetcol], phi=15, theta=0) > persp(,, z, col=color[facetcol], phi=90, theta=0, d=100) 18 z
19 Représentation grâce à levelplot levelplot du package lattice permet aussi de représenter une surface avec des niveau de couleur proportionnel à une valeur. > librar("lattice") > grid <- epand.grid(=, =) > levelplot(z~*, grid, cuts = 64, lab="", lab="", main="", colorke = TRUE, region = TRU
Each function call carries out a single task associated with drawing the graph.
 Chapter 3 Graphics with R 3.1 Low-Level Graphics R has extensive facilities for producing graphs. There are both low- and high-level graphics facilities. The low-level graphics facilities provide basic
Chapter 3 Graphics with R 3.1 Low-Level Graphics R has extensive facilities for producing graphs. There are both low- and high-level graphics facilities. The low-level graphics facilities provide basic
MATHEMATICS Y6 Geometry 6750 Use co-ordinates and extend to 4 quadrants Equipment MathSphere www.mathsphere.co.uk
 MATHEMATICS Y6 Geometry 675 Use co-ordinates and etend to quadrants Paper, pencil, ruler Equipment MathSphere 675 Use co-ordinates and etend to quadrants. Page Concepts Children should be familiar with
MATHEMATICS Y6 Geometry 675 Use co-ordinates and etend to quadrants Paper, pencil, ruler Equipment MathSphere 675 Use co-ordinates and etend to quadrants. Page Concepts Children should be familiar with
x y The matrix form, the vector form, and the augmented matrix form, respectively, for the system of equations are
 Solving Sstems of Linear Equations in Matri Form with rref Learning Goals Determine the solution of a sstem of equations from the augmented matri Determine the reduced row echelon form of the augmented
Solving Sstems of Linear Equations in Matri Form with rref Learning Goals Determine the solution of a sstem of equations from the augmented matri Determine the reduced row echelon form of the augmented
By Clicking on the Worksheet you are in an active Math Region. In order to insert a text region either go to INSERT -TEXT REGION or simply
 Introduction and Basics Tet Regions By Clicking on the Worksheet you are in an active Math Region In order to insert a tet region either go to INSERT -TEXT REGION or simply start typing --the first time
Introduction and Basics Tet Regions By Clicking on the Worksheet you are in an active Math Region In order to insert a tet region either go to INSERT -TEXT REGION or simply start typing --the first time
In this this review we turn our attention to the square root function, the function defined by the equation. f(x) = x. (5.1)
 Section 5.2 The Square Root 1 5.2 The Square Root In this this review we turn our attention to the square root function, the function defined b the equation f() =. (5.1) We can determine the domain and
Section 5.2 The Square Root 1 5.2 The Square Root In this this review we turn our attention to the square root function, the function defined b the equation f() =. (5.1) We can determine the domain and
Teacher Page. 1. Reflect a figure with vertices across the x-axis. Find the coordinates of the new image.
 Teacher Page Geometr / Da # 10 oordinate Geometr (5 min.) 9-.G.3.1 9-.G.3.2 9-.G.3.3 9-.G.3. Use rigid motions (compositions of reflections, translations and rotations) to determine whether two geometric
Teacher Page Geometr / Da # 10 oordinate Geometr (5 min.) 9-.G.3.1 9-.G.3.2 9-.G.3.3 9-.G.3. Use rigid motions (compositions of reflections, translations and rotations) to determine whether two geometric
Graphing Linear Equations
 6.3 Graphing Linear Equations 6.3 OBJECTIVES 1. Graph a linear equation b plotting points 2. Graph a linear equation b the intercept method 3. Graph a linear equation b solving the equation for We are
6.3 Graphing Linear Equations 6.3 OBJECTIVES 1. Graph a linear equation b plotting points 2. Graph a linear equation b the intercept method 3. Graph a linear equation b solving the equation for We are
Solving Quadratic Equations by Graphing. Consider an equation of the form. y ax 2 bx c a 0. In an equation of the form
 SECTION 11.3 Solving Quadratic Equations b Graphing 11.3 OBJECTIVES 1. Find an ais of smmetr 2. Find a verte 3. Graph a parabola 4. Solve quadratic equations b graphing 5. Solve an application involving
SECTION 11.3 Solving Quadratic Equations b Graphing 11.3 OBJECTIVES 1. Find an ais of smmetr 2. Find a verte 3. Graph a parabola 4. Solve quadratic equations b graphing 5. Solve an application involving
D.3. Angles and Degree Measure. Review of Trigonometric Functions
 APPENDIX D Precalculus Review D7 SECTION D. Review of Trigonometric Functions Angles and Degree Measure Radian Measure The Trigonometric Functions Evaluating Trigonometric Functions Solving Trigonometric
APPENDIX D Precalculus Review D7 SECTION D. Review of Trigonometric Functions Angles and Degree Measure Radian Measure The Trigonometric Functions Evaluating Trigonometric Functions Solving Trigonometric
Chapter 8. Lines and Planes. By the end of this chapter, you will
 Chapter 8 Lines and Planes In this chapter, ou will revisit our knowledge of intersecting lines in two dimensions and etend those ideas into three dimensions. You will investigate the nature of planes
Chapter 8 Lines and Planes In this chapter, ou will revisit our knowledge of intersecting lines in two dimensions and etend those ideas into three dimensions. You will investigate the nature of planes
GeoGebra. 10 lessons. Gerrit Stols
 GeoGebra in 10 lessons Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It was developed by Markus Hohenwarter
GeoGebra in 10 lessons Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It was developed by Markus Hohenwarter
Web - Travaux Pratiques 1
 Web - Travaux Pratiques 1 Pour rappel, le squelette d une page HTML5 est la suivante : Syntaxe ... ... Une fois qu une page est terminée,
Web - Travaux Pratiques 1 Pour rappel, le squelette d une page HTML5 est la suivante : Syntaxe ... ... Une fois qu une page est terminée,
Answer Key for the Review Packet for Exam #3
 Answer Key for the Review Packet for Eam # Professor Danielle Benedetto Math Ma-Min Problems. Show that of all rectangles with a given area, the one with the smallest perimeter is a square. Diagram: y
Answer Key for the Review Packet for Eam # Professor Danielle Benedetto Math Ma-Min Problems. Show that of all rectangles with a given area, the one with the smallest perimeter is a square. Diagram: y
Affine Transformations
 A P P E N D I X C Affine Transformations CONTENTS C The need for geometric transformations 335 C2 Affine transformations 336 C3 Matri representation of the linear transformations 338 C4 Homogeneous coordinates
A P P E N D I X C Affine Transformations CONTENTS C The need for geometric transformations 335 C2 Affine transformations 336 C3 Matri representation of the linear transformations 338 C4 Homogeneous coordinates
6. The given function is only drawn for x > 0. Complete the function for x < 0 with the following conditions:
 Precalculus Worksheet 1. Da 1 1. The relation described b the set of points {(-, 5 ),( 0, 5 ),(,8 ),(, 9) } is NOT a function. Eplain wh. For questions - 4, use the graph at the right.. Eplain wh the graph
Precalculus Worksheet 1. Da 1 1. The relation described b the set of points {(-, 5 ),( 0, 5 ),(,8 ),(, 9) } is NOT a function. Eplain wh. For questions - 4, use the graph at the right.. Eplain wh the graph
ACT Math Vocabulary. Altitude The height of a triangle that makes a 90-degree angle with the base of the triangle. Altitude
 ACT Math Vocabular Acute When referring to an angle acute means less than 90 degrees. When referring to a triangle, acute means that all angles are less than 90 degrees. For eample: Altitude The height
ACT Math Vocabular Acute When referring to an angle acute means less than 90 degrees. When referring to a triangle, acute means that all angles are less than 90 degrees. For eample: Altitude The height
Licence Informatique Année 2005-2006. Exceptions
 Université Paris 7 Java Licence Informatique Année 2005-2006 TD n 8 - Correction Exceptions Exercice 1 La méthode parseint est spécifiée ainsi : public static int parseint(string s) throws NumberFormatException
Université Paris 7 Java Licence Informatique Année 2005-2006 TD n 8 - Correction Exceptions Exercice 1 La méthode parseint est spécifiée ainsi : public static int parseint(string s) throws NumberFormatException
Package tagcloud. R topics documented: July 3, 2015
 Package tagcloud July 3, 2015 Type Package Title Tag Clouds Version 0.6 Date 2015-07-02 Author January Weiner Maintainer January Weiner Description Generating Tag and Word Clouds.
Package tagcloud July 3, 2015 Type Package Title Tag Clouds Version 0.6 Date 2015-07-02 Author January Weiner Maintainer January Weiner Description Generating Tag and Word Clouds.
Section V.2: Magnitudes, Directions, and Components of Vectors
 Section V.: Magnitudes, Directions, and Components of Vectors Vectors in the plane If we graph a vector in the coordinate plane instead of just a grid, there are a few things to note. Firstl, directions
Section V.: Magnitudes, Directions, and Components of Vectors Vectors in the plane If we graph a vector in the coordinate plane instead of just a grid, there are a few things to note. Firstl, directions
Modifier le texte d'un élément d'un feuillet, en le spécifiant par son numéro d'index:
 Bezier Curve Une courbe de "Bézier" (fondé sur "drawing object"). select polygon 1 of page 1 of layout "Feuillet 1" of document 1 set class of selection to Bezier curve select Bezier curve 1 of page 1
Bezier Curve Une courbe de "Bézier" (fondé sur "drawing object"). select polygon 1 of page 1 of layout "Feuillet 1" of document 1 set class of selection to Bezier curve select Bezier curve 1 of page 1
When I was 3.1 POLYNOMIAL FUNCTIONS
 146 Chapter 3 Polnomial and Rational Functions Section 3.1 begins with basic definitions and graphical concepts and gives an overview of ke properties of polnomial functions. In Sections 3.2 and 3.3 we
146 Chapter 3 Polnomial and Rational Functions Section 3.1 begins with basic definitions and graphical concepts and gives an overview of ke properties of polnomial functions. In Sections 3.2 and 3.3 we
10.1. Solving Quadratic Equations. Investigation: Rocket Science CONDENSED
 CONDENSED L E S S O N 10.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations
CONDENSED L E S S O N 10.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations
Core Maths C2. Revision Notes
 Core Maths C Revision Notes November 0 Core Maths C Algebra... Polnomials: +,,,.... Factorising... Long division... Remainder theorem... Factor theorem... 4 Choosing a suitable factor... 5 Cubic equations...
Core Maths C Revision Notes November 0 Core Maths C Algebra... Polnomials: +,,,.... Factorising... Long division... Remainder theorem... Factor theorem... 4 Choosing a suitable factor... 5 Cubic equations...
Double Integrals in Polar Coordinates
 Double Integrals in Polar Coordinates. A flat plate is in the shape of the region in the first quadrant ling between the circles + and +. The densit of the plate at point, is + kilograms per square meter
Double Integrals in Polar Coordinates. A flat plate is in the shape of the region in the first quadrant ling between the circles + and +. The densit of the plate at point, is + kilograms per square meter
Petrel TIPS&TRICKS from SCM
 Petrel TIPS&TRICKS from SCM Maps: Knowledge Worth Sharing Map Annotation A map is a graphic representation of some part of the earth. In our industry, it may represent either the surface or sub surface;
Petrel TIPS&TRICKS from SCM Maps: Knowledge Worth Sharing Map Annotation A map is a graphic representation of some part of the earth. In our industry, it may represent either the surface or sub surface;
Students Currently in Algebra 2 Maine East Math Placement Exam Review Problems
 Students Currently in Algebra Maine East Math Placement Eam Review Problems The actual placement eam has 100 questions 3 hours. The placement eam is free response students must solve questions and write
Students Currently in Algebra Maine East Math Placement Eam Review Problems The actual placement eam has 100 questions 3 hours. The placement eam is free response students must solve questions and write
Personnalisez votre intérieur avec les revêtements imprimés ALYOS design
 Plafond tendu à froid ALYOS technology ALYOS technology vous propose un ensemble de solutions techniques pour vos intérieurs. Spécialiste dans le domaine du plafond tendu, nous avons conçu et développé
Plafond tendu à froid ALYOS technology ALYOS technology vous propose un ensemble de solutions techniques pour vos intérieurs. Spécialiste dans le domaine du plafond tendu, nous avons conçu et développé
Using the Area Model to Teach Multiplying, Factoring and Division of Polynomials
 visit us at www.cpm.org Using the Area Model to Teach Multiplying, Factoring and Division of Polynomials For more information about the materials presented, contact Chris Mikles [email protected] From CCA
visit us at www.cpm.org Using the Area Model to Teach Multiplying, Factoring and Division of Polynomials For more information about the materials presented, contact Chris Mikles [email protected] From CCA
1. a. standard form of a parabola with. 2 b 1 2 horizontal axis of symmetry 2. x 2 y 2 r 2 o. standard form of an ellipse centered
 Conic Sections. Distance Formula and Circles. More on the Parabola. The Ellipse and Hperbola. Nonlinear Sstems of Equations in Two Variables. Nonlinear Inequalities and Sstems of Inequalities In Chapter,
Conic Sections. Distance Formula and Circles. More on the Parabola. The Ellipse and Hperbola. Nonlinear Sstems of Equations in Two Variables. Nonlinear Inequalities and Sstems of Inequalities In Chapter,
Tutorial 3: Graphics and Exploratory Data Analysis in R Jason Pienaar and Tom Miller
 Tutorial 3: Graphics and Exploratory Data Analysis in R Jason Pienaar and Tom Miller Getting to know the data An important first step before performing any kind of statistical analysis is to familiarize
Tutorial 3: Graphics and Exploratory Data Analysis in R Jason Pienaar and Tom Miller Getting to know the data An important first step before performing any kind of statistical analysis is to familiarize
5.1. A Formula for Slope. Investigation: Points and Slope CONDENSED
 CONDENSED L E S S O N 5.1 A Formula for Slope In this lesson ou will learn how to calculate the slope of a line given two points on the line determine whether a point lies on the same line as two given
CONDENSED L E S S O N 5.1 A Formula for Slope In this lesson ou will learn how to calculate the slope of a line given two points on the line determine whether a point lies on the same line as two given
Polynomial Degree and Finite Differences
 CONDENSED LESSON 7.1 Polynomial Degree and Finite Differences In this lesson you will learn the terminology associated with polynomials use the finite differences method to determine the degree of a polynomial
CONDENSED LESSON 7.1 Polynomial Degree and Finite Differences In this lesson you will learn the terminology associated with polynomials use the finite differences method to determine the degree of a polynomial
Addition and Subtraction of Vectors
 ddition and Subtraction of Vectors 1 ppendi ddition and Subtraction of Vectors In this appendi the basic elements of vector algebra are eplored. Vectors are treated as geometric entities represented b
ddition and Subtraction of Vectors 1 ppendi ddition and Subtraction of Vectors In this appendi the basic elements of vector algebra are eplored. Vectors are treated as geometric entities represented b
North Carolina Community College System Diagnostic and Placement Test Sample Questions
 North Carolina Communit College Sstem Diagnostic and Placement Test Sample Questions 0 The College Board. College Board, ACCUPLACER, WritePlacer and the acorn logo are registered trademarks of the College
North Carolina Communit College Sstem Diagnostic and Placement Test Sample Questions 0 The College Board. College Board, ACCUPLACER, WritePlacer and the acorn logo are registered trademarks of the College
POB-JAVA Documentation
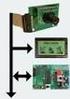 POB-JAVA Documentation 1 INTRODUCTION... 4 2 INSTALLING POB-JAVA... 5 Installation of the GNUARM compiler... 5 Installing the Java Development Kit... 7 Installing of POB-Java... 8 3 CONFIGURATION... 9
POB-JAVA Documentation 1 INTRODUCTION... 4 2 INSTALLING POB-JAVA... 5 Installation of the GNUARM compiler... 5 Installing the Java Development Kit... 7 Installing of POB-Java... 8 3 CONFIGURATION... 9
Algebra II. Administered May 2013 RELEASED
 STAAR State of Teas Assessments of Academic Readiness Algebra II Administered Ma 0 RELEASED Copright 0, Teas Education Agenc. All rights reserved. Reproduction of all or portions of this work is prohibited
STAAR State of Teas Assessments of Academic Readiness Algebra II Administered Ma 0 RELEASED Copright 0, Teas Education Agenc. All rights reserved. Reproduction of all or portions of this work is prohibited
DISTANCE, CIRCLES, AND QUADRATIC EQUATIONS
 a p p e n d i g DISTANCE, CIRCLES, AND QUADRATIC EQUATIONS DISTANCE BETWEEN TWO POINTS IN THE PLANE Suppose that we are interested in finding the distance d between two points P (, ) and P (, ) in the
a p p e n d i g DISTANCE, CIRCLES, AND QUADRATIC EQUATIONS DISTANCE BETWEEN TWO POINTS IN THE PLANE Suppose that we are interested in finding the distance d between two points P (, ) and P (, ) in the
D.2. The Cartesian Plane. The Cartesian Plane The Distance and Midpoint Formulas Equations of Circles. D10 APPENDIX D Precalculus Review
 D0 APPENDIX D Precalculus Review SECTION D. The Cartesian Plane The Cartesian Plane The Distance and Midpoint Formulas Equations of Circles The Cartesian Plane An ordered pair, of real numbers has as its
D0 APPENDIX D Precalculus Review SECTION D. The Cartesian Plane The Cartesian Plane The Distance and Midpoint Formulas Equations of Circles The Cartesian Plane An ordered pair, of real numbers has as its
Chapter 6 Quadratic Functions
 Chapter 6 Quadratic Functions Determine the characteristics of quadratic functions Sketch Quadratics Solve problems modelled b Quadratics 6.1Quadratic Functions A quadratic function is of the form where
Chapter 6 Quadratic Functions Determine the characteristics of quadratic functions Sketch Quadratics Solve problems modelled b Quadratics 6.1Quadratic Functions A quadratic function is of the form where
Liste d'adresses URL
 Liste de sites Internet concernés dans l' étude Le 25/02/2014 Information à propos de contrefacon.fr Le site Internet https://www.contrefacon.fr/ permet de vérifier dans une base de donnée de plus d' 1
Liste de sites Internet concernés dans l' étude Le 25/02/2014 Information à propos de contrefacon.fr Le site Internet https://www.contrefacon.fr/ permet de vérifier dans une base de donnée de plus d' 1
Visualization of 2D Domains
 Visualization of 2D Domains This part of the visualization package is intended to supply a simple graphical interface for 2- dimensional finite element data structures. Furthermore, it is used as the low
Visualization of 2D Domains This part of the visualization package is intended to supply a simple graphical interface for 2- dimensional finite element data structures. Furthermore, it is used as the low
More Equations and Inequalities
 Section. Sets of Numbers and Interval Notation 9 More Equations and Inequalities 9 9. Compound Inequalities 9. Polnomial and Rational Inequalities 9. Absolute Value Equations 9. Absolute Value Inequalities
Section. Sets of Numbers and Interval Notation 9 More Equations and Inequalities 9 9. Compound Inequalities 9. Polnomial and Rational Inequalities 9. Absolute Value Equations 9. Absolute Value Inequalities
CSS : petits compléments
 CSS : petits compléments Université Lille 1 Technologies du Web CSS : les sélecteurs 1 au programme... 1 ::before et ::after 2 compteurs 3 media queries 4 transformations et transitions Université Lille
CSS : petits compléments Université Lille 1 Technologies du Web CSS : les sélecteurs 1 au programme... 1 ::before et ::after 2 compteurs 3 media queries 4 transformations et transitions Université Lille
Detection of water leakage using laser images from 3D laser scanning data
 Detection of water leakage using laser images from 3D laser scanning data QUANHONG FENG 1, GUOJUAN WANG 2 & KENNERT RÖSHOFF 3 1 Berg Bygg Konsult (BBK) AB,Ankdammsgatan 20, SE-171 43, Solna, Sweden (e-mail:[email protected])
Detection of water leakage using laser images from 3D laser scanning data QUANHONG FENG 1, GUOJUAN WANG 2 & KENNERT RÖSHOFF 3 1 Berg Bygg Konsult (BBK) AB,Ankdammsgatan 20, SE-171 43, Solna, Sweden (e-mail:[email protected])
Graphics in R. Biostatistics 615/815
 Graphics in R Biostatistics 615/815 Last Lecture Introduction to R Programming Controlling Loops Defining your own functions Today Introduction to Graphics in R Examples of commonly used graphics functions
Graphics in R Biostatistics 615/815 Last Lecture Introduction to R Programming Controlling Loops Defining your own functions Today Introduction to Graphics in R Examples of commonly used graphics functions
15.1. Exact Differential Equations. Exact First-Order Equations. Exact Differential Equations Integrating Factors
 SECTION 5. Eact First-Order Equations 09 SECTION 5. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Section 5.6, ou studied applications of differential
SECTION 5. Eact First-Order Equations 09 SECTION 5. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Section 5.6, ou studied applications of differential
Section 11.4: Equations of Lines and Planes
 Section 11.4: Equations of Lines and Planes Definition: The line containing the point ( 0, 0, 0 ) and parallel to the vector v = A, B, C has parametric equations = 0 + At, = 0 + Bt, = 0 + Ct, where t R
Section 11.4: Equations of Lines and Planes Definition: The line containing the point ( 0, 0, 0 ) and parallel to the vector v = A, B, C has parametric equations = 0 + At, = 0 + Bt, = 0 + Ct, where t R
2D Geometrical Transformations. Foley & Van Dam, Chapter 5
 2D Geometrical Transformations Fole & Van Dam, Chapter 5 2D Geometrical Transformations Translation Scaling Rotation Shear Matri notation Compositions Homogeneous coordinates 2D Geometrical Transformations
2D Geometrical Transformations Fole & Van Dam, Chapter 5 2D Geometrical Transformations Translation Scaling Rotation Shear Matri notation Compositions Homogeneous coordinates 2D Geometrical Transformations
The following is an overview of lessons included in the tutorial.
 Chapter 2 Tutorial Tutorial Introduction This tutorial is designed to introduce you to some of Surfer's basic features. After you have completed the tutorial, you should be able to begin creating your
Chapter 2 Tutorial Tutorial Introduction This tutorial is designed to introduce you to some of Surfer's basic features. After you have completed the tutorial, you should be able to begin creating your
Connecting Transformational Geometry and Transformations of Functions
 Connecting Transformational Geometr and Transformations of Functions Introductor Statements and Assumptions Isometries are rigid transformations that preserve distance and angles and therefore shapes.
Connecting Transformational Geometr and Transformations of Functions Introductor Statements and Assumptions Isometries are rigid transformations that preserve distance and angles and therefore shapes.
Excel 2007 - Using Pivot Tables
 Overview A PivotTable report is an interactive table that allows you to quickly group and summarise information from a data source. You can rearrange (or pivot) the table to display different perspectives
Overview A PivotTable report is an interactive table that allows you to quickly group and summarise information from a data source. You can rearrange (or pivot) the table to display different perspectives
Find the Relationship: An Exercise in Graphing Analysis
 Find the Relationship: An Eercise in Graphing Analsis Computer 5 In several laborator investigations ou do this ear, a primar purpose will be to find the mathematical relationship between two variables.
Find the Relationship: An Eercise in Graphing Analsis Computer 5 In several laborator investigations ou do this ear, a primar purpose will be to find the mathematical relationship between two variables.
Physics 53. Kinematics 2. Our nature consists in movement; absolute rest is death. Pascal
 Phsics 53 Kinematics 2 Our nature consists in movement; absolute rest is death. Pascal Velocit and Acceleration in 3-D We have defined the velocit and acceleration of a particle as the first and second
Phsics 53 Kinematics 2 Our nature consists in movement; absolute rest is death. Pascal Velocit and Acceleration in 3-D We have defined the velocit and acceleration of a particle as the first and second
ANIMATION OF CONTINUOUS COMPUTER SIMULATIONS C.M. Woodside and Richard Mallet Computer Center, Carleton University ABSTRACT
 19.1 ANIMATION OF CONTINUOUS COMPUTER SIMULATIONS C.M. Woodside and Richard Mallet Computer Center, Carleton University ABSTRACT A block-oriented graphics program called ANIM8 has been developed for animating
19.1 ANIMATION OF CONTINUOUS COMPUTER SIMULATIONS C.M. Woodside and Richard Mallet Computer Center, Carleton University ABSTRACT A block-oriented graphics program called ANIM8 has been developed for animating
Understand the Sketcher workbench of CATIA V5.
 Chapter 1 Drawing Sketches in Learning Objectives the Sketcher Workbench-I After completing this chapter you will be able to: Understand the Sketcher workbench of CATIA V5. Start a new file in the Part
Chapter 1 Drawing Sketches in Learning Objectives the Sketcher Workbench-I After completing this chapter you will be able to: Understand the Sketcher workbench of CATIA V5. Start a new file in the Part
Introduction to Autodesk Inventor for F1 in Schools
 Introduction to Autodesk Inventor for F1 in Schools F1 in Schools Race Car In this course you will be introduced to Autodesk Inventor, which is the centerpiece of Autodesk s digital prototyping strategy
Introduction to Autodesk Inventor for F1 in Schools F1 in Schools Race Car In this course you will be introduced to Autodesk Inventor, which is the centerpiece of Autodesk s digital prototyping strategy
Linear Equations in Two Variables
 Section. Sets of Numbers and Interval Notation 0 Linear Equations in Two Variables. The Rectangular Coordinate Sstem and Midpoint Formula. Linear Equations in Two Variables. Slope of a Line. Equations
Section. Sets of Numbers and Interval Notation 0 Linear Equations in Two Variables. The Rectangular Coordinate Sstem and Midpoint Formula. Linear Equations in Two Variables. Slope of a Line. Equations
LINEAR FUNCTIONS OF 2 VARIABLES
 CHAPTER 4: LINEAR FUNCTIONS OF 2 VARIABLES 4.1 RATES OF CHANGES IN DIFFERENT DIRECTIONS From Precalculus, we know that is a linear function if the rate of change of the function is constant. I.e., for
CHAPTER 4: LINEAR FUNCTIONS OF 2 VARIABLES 4.1 RATES OF CHANGES IN DIFFERENT DIRECTIONS From Precalculus, we know that is a linear function if the rate of change of the function is constant. I.e., for
Introduction to Autodesk Inventor for F1 in Schools
 F1 in Schools race car Introduction to Autodesk Inventor for F1 in Schools In this course you will be introduced to Autodesk Inventor, which is the centerpiece of Autodesk s Digital Prototyping strategy
F1 in Schools race car Introduction to Autodesk Inventor for F1 in Schools In this course you will be introduced to Autodesk Inventor, which is the centerpiece of Autodesk s Digital Prototyping strategy
Advanced Microsoft Excel 2010
 Advanced Microsoft Excel 2010 Table of Contents THE PASTE SPECIAL FUNCTION... 2 Paste Special Options... 2 Using the Paste Special Function... 3 ORGANIZING DATA... 4 Multiple-Level Sorting... 4 Subtotaling
Advanced Microsoft Excel 2010 Table of Contents THE PASTE SPECIAL FUNCTION... 2 Paste Special Options... 2 Using the Paste Special Function... 3 ORGANIZING DATA... 4 Multiple-Level Sorting... 4 Subtotaling
10.0-2. Finite Element Modeling
 What s New in FEMAP FEMAP 10.0 and 10.0.1 include enhancements and new features in: User Interface on page 3 Meshing on page 23 Mesh Associativity on page 33 Properties on page 33 Functions on page 35
What s New in FEMAP FEMAP 10.0 and 10.0.1 include enhancements and new features in: User Interface on page 3 Meshing on page 23 Mesh Associativity on page 33 Properties on page 33 Functions on page 35
Calcul parallèle avec R
 Calcul parallèle avec R ANF R Vincent Miele CNRS 07/10/2015 Pour chaque exercice, il est nécessaire d ouvrir une fenètre de visualisation des processes (Terminal + top sous Linux et Mac OS X, Gestionnaire
Calcul parallèle avec R ANF R Vincent Miele CNRS 07/10/2015 Pour chaque exercice, il est nécessaire d ouvrir une fenètre de visualisation des processes (Terminal + top sous Linux et Mac OS X, Gestionnaire
1.6. Piecewise Functions. LEARN ABOUT the Math. Representing the problem using a graphical model
 . Piecewise Functions YOU WILL NEED graph paper graphing calculator GOAL Understand, interpret, and graph situations that are described b piecewise functions. LEARN ABOUT the Math A cit parking lot uses
. Piecewise Functions YOU WILL NEED graph paper graphing calculator GOAL Understand, interpret, and graph situations that are described b piecewise functions. LEARN ABOUT the Math A cit parking lot uses
Thursday, February 7, 2013. DOM via PHP
 DOM via PHP Plan PHP DOM PHP : Hypertext Preprocessor Langage de script pour création de pages Web dynamiques Un ficher PHP est un ficher HTML avec du code PHP
DOM via PHP Plan PHP DOM PHP : Hypertext Preprocessor Langage de script pour création de pages Web dynamiques Un ficher PHP est un ficher HTML avec du code PHP
Tutorials. If you have any questions, comments, or suggestions about these lessons, don't hesitate to contact us at [email protected].
 Tutorials The lesson schedules for these tutorials were installed when you installed Milestones Professional 2010. They can be accessed under File Open a File Lesson Chart. If you have any questions, comments,
Tutorials The lesson schedules for these tutorials were installed when you installed Milestones Professional 2010. They can be accessed under File Open a File Lesson Chart. If you have any questions, comments,
Graphing Piecewise Functions
 Graphing Piecewise Functions Course: Algebra II, Advanced Functions and Modeling Materials: student computers with Geometer s Sketchpad, Smart Board, worksheets (p. -7 of this document), colored pencils
Graphing Piecewise Functions Course: Algebra II, Advanced Functions and Modeling Materials: student computers with Geometer s Sketchpad, Smart Board, worksheets (p. -7 of this document), colored pencils
Introduction to the TI-Nspire CX
 Introduction to the TI-Nspire CX Activity Overview: In this activity, you will become familiar with the layout of the TI-Nspire CX. Step 1: Locate the Touchpad. The Touchpad is used to navigate the cursor
Introduction to the TI-Nspire CX Activity Overview: In this activity, you will become familiar with the layout of the TI-Nspire CX. Step 1: Locate the Touchpad. The Touchpad is used to navigate the cursor
Enterprise Risk Management & Board members. GUBERNA Alumni Event June 19 th 2014 Prepared by Gaëtan LEFEVRE
 Enterprise Risk Management & Board members GUBERNA Alumni Event June 19 th 2014 Prepared by Gaëtan LEFEVRE Agenda Introduction Do we need Risk Management? The 8 th EU Company Law Directive Art 41, 2b Three
Enterprise Risk Management & Board members GUBERNA Alumni Event June 19 th 2014 Prepared by Gaëtan LEFEVRE Agenda Introduction Do we need Risk Management? The 8 th EU Company Law Directive Art 41, 2b Three
Largest Fixed-Aspect, Axis-Aligned Rectangle
 Largest Fixed-Aspect, Axis-Aligned Rectangle David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: February 21, 2004 Last Modified: February
Largest Fixed-Aspect, Axis-Aligned Rectangle David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: February 21, 2004 Last Modified: February
ColdGuard Bi-PARTING DOOR INSTALLATION INSTRUCTIONS
 EHD TRACK LEVEL, (SET LEVEL ON PLASTIC HEADER. DO NOT PLACE LEVEL ON ALUMINUM TRACK.) TRACK IS FLUSH WITH TOP OF HEADER JUNCTION BOX IDLER PULLEY LOCATOR PINS LOCATOR PINS OPERATOR DOOR STOP JUNCTION BOX
EHD TRACK LEVEL, (SET LEVEL ON PLASTIC HEADER. DO NOT PLACE LEVEL ON ALUMINUM TRACK.) TRACK IS FLUSH WITH TOP OF HEADER JUNCTION BOX IDLER PULLEY LOCATOR PINS LOCATOR PINS OPERATOR DOOR STOP JUNCTION BOX
RAPPORT FINANCIER ANNUEL PORTANT SUR LES COMPTES 2014
 RAPPORT FINANCIER ANNUEL PORTANT SUR LES COMPTES 2014 En application de la loi du Luxembourg du 11 janvier 2008 relative aux obligations de transparence sur les émetteurs de valeurs mobilières. CREDIT
RAPPORT FINANCIER ANNUEL PORTANT SUR LES COMPTES 2014 En application de la loi du Luxembourg du 11 janvier 2008 relative aux obligations de transparence sur les émetteurs de valeurs mobilières. CREDIT
Create Charts in Excel
 Create Charts in Excel Table of Contents OVERVIEW OF CHARTING... 1 AVAILABLE CHART TYPES... 2 PIE CHARTS... 2 BAR CHARTS... 3 CREATING CHARTS IN EXCEL... 3 CREATE A CHART... 3 HOW TO CHANGE THE LOCATION
Create Charts in Excel Table of Contents OVERVIEW OF CHARTING... 1 AVAILABLE CHART TYPES... 2 PIE CHARTS... 2 BAR CHARTS... 3 CREATING CHARTS IN EXCEL... 3 CREATE A CHART... 3 HOW TO CHANGE THE LOCATION
Lines & Planes. Packages: linalg, plots. Commands: evalm, spacecurve, plot3d, display, solve, implicitplot, dotprod, seq, implicitplot3d.
 Lines & Planes Introduction and Goals: This lab is simply to give you some practice with plotting straight lines and planes and how to do some basic problem solving with them. So the exercises will be
Lines & Planes Introduction and Goals: This lab is simply to give you some practice with plotting straight lines and planes and how to do some basic problem solving with them. So the exercises will be
2.1 Three Dimensional Curves and Surfaces
 . Three Dimensional Curves and Surfaces.. Parametric Equation of a Line An line in two- or three-dimensional space can be uniquel specified b a point on the line and a vector parallel to the line. The
. Three Dimensional Curves and Surfaces.. Parametric Equation of a Line An line in two- or three-dimensional space can be uniquel specified b a point on the line and a vector parallel to the line. The
Metes and Bounds Help
 Metes and Bounds Help Topics: Drawing Wizard Data Entry o Entering Metes and Bounds Data o Entering Section Call Data Layers o Layer Options o Analyze Layer Closing Error Tabs Drawing Options o Drawing
Metes and Bounds Help Topics: Drawing Wizard Data Entry o Entering Metes and Bounds Data o Entering Section Call Data Layers o Layer Options o Analyze Layer Closing Error Tabs Drawing Options o Drawing
WEB TRADER USER MANUAL
 WEB TRADER USER MANUAL Web Trader... 2 Getting Started... 4 Logging In... 5 The Workspace... 6 Main menu... 7 File... 7 Instruments... 8 View... 8 Quotes View... 9 Advanced View...11 Accounts View...11
WEB TRADER USER MANUAL Web Trader... 2 Getting Started... 4 Logging In... 5 The Workspace... 6 Main menu... 7 File... 7 Instruments... 8 View... 8 Quotes View... 9 Advanced View...11 Accounts View...11
Circles - Past Edexcel Exam Questions
 ircles - Past Edecel Eam Questions 1. The points A and B have coordinates (5,-1) and (13,11) respectivel. (a) find the coordinates of the mid-point of AB. [2] Given that AB is a diameter of the circle,
ircles - Past Edecel Eam Questions 1. The points A and B have coordinates (5,-1) and (13,11) respectivel. (a) find the coordinates of the mid-point of AB. [2] Given that AB is a diameter of the circle,
R Graphics Cookbook. Chang O'REILLY. Winston. Tokyo. Beijing Cambridge. Farnham Koln Sebastopol
 R Graphics Cookbook Winston Chang Beijing Cambridge Farnham Koln Sebastopol O'REILLY Tokyo Table of Contents Preface ix 1. R Basics 1 1.1. Installing a Package 1 1.2. Loading a Package 2 1.3. Loading a
R Graphics Cookbook Winston Chang Beijing Cambridge Farnham Koln Sebastopol O'REILLY Tokyo Table of Contents Preface ix 1. R Basics 1 1.1. Installing a Package 1 1.2. Loading a Package 2 1.3. Loading a
Plane Stress Transformations
 6 Plane Stress Transformations ASEN 311 - Structures ASEN 311 Lecture 6 Slide 1 Plane Stress State ASEN 311 - Structures Recall that in a bod in plane stress, the general 3D stress state with 9 components
6 Plane Stress Transformations ASEN 311 - Structures ASEN 311 Lecture 6 Slide 1 Plane Stress State ASEN 311 - Structures Recall that in a bod in plane stress, the general 3D stress state with 9 components
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Millier Dickinson Blais
 Research Report Millier Dickinson Blais 2007-2008 National Survey of the Profession September 14, 2008 Contents 1 Introduction & Methodology... 3 2 National Results... 5 3 Regional Results... 6 3.1 British
Research Report Millier Dickinson Blais 2007-2008 National Survey of the Profession September 14, 2008 Contents 1 Introduction & Methodology... 3 2 National Results... 5 3 Regional Results... 6 3.1 British
http://school-maths.com Gerrit Stols
 For more info and downloads go to: http://school-maths.com Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It
For more info and downloads go to: http://school-maths.com Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It
Drawing a histogram using Excel
 Drawing a histogram using Excel STEP 1: Examine the data to decide how many class intervals you need and what the class boundaries should be. (In an assignment you may be told what class boundaries to
Drawing a histogram using Excel STEP 1: Examine the data to decide how many class intervals you need and what the class boundaries should be. (In an assignment you may be told what class boundaries to
KaleidaGraph Quick Start Guide
 KaleidaGraph Quick Start Guide This document is a hands-on guide that walks you through the use of KaleidaGraph. You will probably want to print this guide and then start your exploration of the product.
KaleidaGraph Quick Start Guide This document is a hands-on guide that walks you through the use of KaleidaGraph. You will probably want to print this guide and then start your exploration of the product.
Introduction to ANSYS ICEM CFD
 Workshop 8.2 3D Pipe Junction 14.5 Release Introduction to ANSYS ICEM CFD 2012 ANSYS, Inc. April 1, 2013 1 Release 14.5 3D Pipe Junction 3D Pipe Junction This is a simple 4-way pipe intersection with two
Workshop 8.2 3D Pipe Junction 14.5 Release Introduction to ANSYS ICEM CFD 2012 ANSYS, Inc. April 1, 2013 1 Release 14.5 3D Pipe Junction 3D Pipe Junction This is a simple 4-way pipe intersection with two
Numéro de projet CISPR 16-1-4 Amd 2 Ed. 3.0. IEC/TC or SC: CISPR/A CEI/CE ou SC: Date of circulation Date de diffusion 2015-10-30
 PRIVATE CIRCULATION GEL/210/11_15_0275 For comment/vote - Action Due Date: 2016/01/08 Submitted for parallel voting in CENELEC Soumis au vote parallèle au CENELEC Also of interest to the following committees
PRIVATE CIRCULATION GEL/210/11_15_0275 For comment/vote - Action Due Date: 2016/01/08 Submitted for parallel voting in CENELEC Soumis au vote parallèle au CENELEC Also of interest to the following committees
Excel 2013 - Using Pivot Tables
 Overview A PivotTable report is an interactive table that allows you to quickly group and summarise information from a data source. You can rearrange (or pivot) the table to display different perspectives
Overview A PivotTable report is an interactive table that allows you to quickly group and summarise information from a data source. You can rearrange (or pivot) the table to display different perspectives
Régression logistique : introduction
 Chapitre 16 Introduction à la statistique avec R Régression logistique : introduction Une variable à expliquer binaire Expliquer un risque suicidaire élevé en prison par La durée de la peine L existence
Chapitre 16 Introduction à la statistique avec R Régression logistique : introduction Une variable à expliquer binaire Expliquer un risque suicidaire élevé en prison par La durée de la peine L existence
1.5 SOLUTION SETS OF LINEAR SYSTEMS
 1-2 CHAPTER 1 Linear Equations in Linear Algebra 1.5 SOLUTION SETS OF LINEAR SYSTEMS Many of the concepts and computations in linear algebra involve sets of vectors which are visualized geometrically as
1-2 CHAPTER 1 Linear Equations in Linear Algebra 1.5 SOLUTION SETS OF LINEAR SYSTEMS Many of the concepts and computations in linear algebra involve sets of vectors which are visualized geometrically as
SolidWorks Implementation Guides. Sketching Concepts
 SolidWorks Implementation Guides Sketching Concepts Sketching in SolidWorks is the basis for creating features. Features are the basis for creating parts, which can be put together into assemblies. Sketch
SolidWorks Implementation Guides Sketching Concepts Sketching in SolidWorks is the basis for creating features. Features are the basis for creating parts, which can be put together into assemblies. Sketch
Roots of equation fx are the values of x which satisfy the above expression. Also referred to as the zeros of an equation
 LECTURE 20 SOLVING FOR ROOTS OF NONLINEAR EQUATIONS Consider the equation f = 0 Roots of equation f are the values of which satisfy the above epression. Also referred to as the zeros of an equation f()
LECTURE 20 SOLVING FOR ROOTS OF NONLINEAR EQUATIONS Consider the equation f = 0 Roots of equation f are the values of which satisfy the above epression. Also referred to as the zeros of an equation f()
Pro/ENGINEER Wildfire 4.0 Basic Design
 Introduction Datum features are non-solid features used during the construction of other features. The most common datum features include planes, axes, coordinate systems, and curves. Datum features do
Introduction Datum features are non-solid features used during the construction of other features. The most common datum features include planes, axes, coordinate systems, and curves. Datum features do
Colegio del mundo IB. Programa Diploma REPASO 2. 1. The mass m kg of a radio-active substance at time t hours is given by. m = 4e 0.2t.
 REPASO. The mass m kg of a radio-active substance at time t hours is given b m = 4e 0.t. Write down the initial mass. The mass is reduced to.5 kg. How long does this take?. The function f is given b f()
REPASO. The mass m kg of a radio-active substance at time t hours is given b m = 4e 0.t. Write down the initial mass. The mass is reduced to.5 kg. How long does this take?. The function f is given b f()
Processing the Image or Can you Believe what you see? Light and Color for Nonscientists PHYS 1230
 Processing the Image or Can you Believe what you see? Light and Color for Nonscientists PHYS 1230 Optical Illusions http://www.michaelbach.de/ot/mot_mib/index.html Vision We construct images unconsciously
Processing the Image or Can you Believe what you see? Light and Color for Nonscientists PHYS 1230 Optical Illusions http://www.michaelbach.de/ot/mot_mib/index.html Vision We construct images unconsciously
COMPONENTS OF VECTORS
 COMPONENTS OF VECTORS To describe motion in two dimensions we need a coordinate sstem with two perpendicular aes, and. In such a coordinate sstem, an vector A can be uniquel decomposed into a sum of two
COMPONENTS OF VECTORS To describe motion in two dimensions we need a coordinate sstem with two perpendicular aes, and. In such a coordinate sstem, an vector A can be uniquel decomposed into a sum of two
Sun Management Center Change Manager 1.0.1 Release Notes
 Sun Management Center Change Manager 1.0.1 Release Notes Sun Microsystems, Inc. 4150 Network Circle Santa Clara, CA 95054 U.S.A. Part No: 817 0891 10 May 2003 Copyright 2003 Sun Microsystems, Inc. 4150
Sun Management Center Change Manager 1.0.1 Release Notes Sun Microsystems, Inc. 4150 Network Circle Santa Clara, CA 95054 U.S.A. Part No: 817 0891 10 May 2003 Copyright 2003 Sun Microsystems, Inc. 4150
Shake, Rattle and Roll
 00 College Board. All rights reserved. 00 College Board. All rights reserved. SUGGESTED LEARNING STRATEGIES: Shared Reading, Marking the Tet, Visualization, Interactive Word Wall Roller coasters are scar
00 College Board. All rights reserved. 00 College Board. All rights reserved. SUGGESTED LEARNING STRATEGIES: Shared Reading, Marking the Tet, Visualization, Interactive Word Wall Roller coasters are scar
7.7 Solving Rational Equations
 Section 7.7 Solving Rational Equations 7 7.7 Solving Rational Equations When simplifying comple fractions in the previous section, we saw that multiplying both numerator and denominator by the appropriate
Section 7.7 Solving Rational Equations 7 7.7 Solving Rational Equations When simplifying comple fractions in the previous section, we saw that multiplying both numerator and denominator by the appropriate
