Introduction: what is quantum field theory?
|
|
|
- Gilbert Elliott
- 9 years ago
- Views:
Transcription
1 Introduction: what is quantum field theory? Asaf Pe er 1 January 13, 2015 This part of the course is based on Ref. [1] 1. Relativistic quantum mechanics By the mid 1920 s, the basics of quantum mechanics were already discovered by people like de Broglie, Bohr, Schrödinger, Pauli and Heisenberg. However, in its basic form, quantum mechanics is inconsistent with the already known theory of special relativity. Therearevariousways toseethis: for example, theamplitudefor afreeparticletopropagate from x 0 to x is U(t) = x e iht x 0, (1) which is nonzero for all x and t, indicating that a particle can propagate between any two points at arbitrary short time; this is in contradiction, of course, to the requirement set by special relativity, that nothing travels faster than the speed of light, c. Thus, Schrödinger equation needs to be replaced by a relativistic equation (known as Klein-Gordon equation). A different, yet related question is the question of particle interaction. Schrödinger equation, for example, explains how a single particle evolves under the influence of an external potential; however, it does not describe interactions between particles, such as electronphoton scattering (Compton scattering), or the production of new particles that take place when relativistic particles interact. A classical example is the prediction of the anti-electron particle (the positron) by Dirac in 1928, that results when two energetic photons interact (γ +γ e + +e ). The positron was discovered by Anderson in In following years, a plethora of new particles were discovered. 2. The electron-photon duality The concept of wave-particle duality tells us that the properties of electrons and photons are fundamentally very similar. Despite obvious differences in their mass and charge, under the right circumstances both suffer wave-like diffraction and both behave like particle. 1 Physics Dep., University College Cork
2 2 Yet the appearance of these objects in classical physics is very different. Electrons and other matter particles are postulated to be elementary constituents of Nature. In contrast, light is a derived concept: in classical EM, the fundamental entities are the electromagnetic fields. Maxwell thought of photons as a ripple of these fields. Ifphotonsandparticlesaretruelytobeplacedonequalfooting, howshouldwereconcile this difference in the quantum world? One possibility is that we view particle as fundamental, with the electromagnetic field arising only in some classical limit from a collection of quantum photons. Alternatively, we may consider field as fundamental, with the photon appearing only when we correctly treat the field in a manner consistent with quantum theory. In this case, we may want to introduce an analogue electron field, whose ripples give rise to particles with mass and charge. But why then didn t Faraday, Maxwell and other classical physicists find it useful to introduce the concept of matter fields, analogous to the electromagnetic field? In this course, we will take the second viewpoint, namely that the field is primary and particles are derived concepts, appearing only after quantization. We will show how photons arise from the quantization of the electromagnetic field and how massive, charged particles such as electrons arise from the quantization of matter fields. We will learn that in order to describe the fundamental laws of Nature, we must in fact introduce a field to every fundamental particle in nature: not only introduce electron fields, but also quark fields, neutrino fields, gluon fields, W and Z-boson fields, Higgs fields and a whole slew of others. The advantage of the field is fundamental view point can be understood as due to the following reasons: (1) locality; (2) the ability to create and annihilate particles; and (3) the fact that all particles of the same type are identical. 3. Locality One key concept which I am afraid is not properly emphasized is the concept that the laws of nature are local. The old laws of Coulomb and Newton involve action at a distance. This means that the force felt by an electron (or planet) changes immediately if a distant proton (or star) moves. This is wrong!!. It is both philosophically unsatisfactory, and, more importantly, experimentally wrong - it is inconsistent with the basic concept that no signal can travel faster than the speed of light, which is finite. Thus, we are seeking a theory in which all interactions are mediated in a local fashion by the field.
3 3 4. Particle number is not conserved Another reason to treat the field, rather than the particle as the fundamental quantity is the experimental fact that when particles interact, new particles can be created (or annihilated) - the particle number is not conserved. This fact is demonstrated at a daily basis in CERN and other accelerators. It is a direct consequence of the combination of quantum mechanics and special relativity. Particles are not indestructible objects, made at the beginning of the universe and here for good. They can be created and destroyed. They are, in fact, mostly ephemeral and fleeting. This experimentally verified fact was first predicted by Dirac who understood how relativity implies the necessity of anti-particles. We will review Dirac s argument for anti-particles later in this course, together with the better understanding that we get from viewing particles in the framework of quantum field theory. For now, we will quickly sketch the circumstances in which we expect the number of particles to change. Consider a particle of mass m trapped in a box of size L. Heisenberg tells us that the uncertainty in the momentum is p /L. In a relativistic setting, momentum and energy are on an equivalent footing, so we should also have an uncertainty in the energy of order E c/l. When the uncertainty in the energy exceeds E = 2mc 2, we cross the barrier to pop particle anti-particle pairs out of the vacuum. We learn that particle-anti-particle pairs are expected to be important when a particle of mass m is localized within a distance of order λ = mc. (2) The distance λ is called Compton wavelength. At distances shorter than this, there is a high probability that we will detect particle- anti-particle pairs swarming around the original particle that we put in. Note that Compton wavelength is always smaller than the de Broglie wavelength, λ db = h/ p : the de Broglie wavelength indicates the distance at which the wave nature of the particle becomes apparent, while Compton wavelength is the distance at which the concept of a single pointlike particle breaks down completely. The presence of a multitude of particles and antiparticles at short distances implies that any attempt to write down a relativistic version of the one-particle Schrödinger equation is doomed to failure. There is no mechanism in standard non-relativistic quantum mechanics to deal with changes in the particle number. We thus need a new formalism to treat states with an unspecified number of particles, as is expected in the relativistic regime. This formalism is quantum field theory (QFT).
4 4 5. All particles of the same type are the same A third reason to treat fields as the fundamental physical quantity is that all particles of the same type are the same. This is much more serious than it initially sounds. For example, two electrons are identical in every way, regardless of where they came from and what they ve been through. The same is true of every other fundamental particle. Suppose we capture a proton from a cosmic ray which we identify as coming from a supernova lying 8 billion lightyears away. We compare this proton with one freshly minted in a particle accelerator here on Earth. And the two are exactly the same! How is this possible? Why aren t there errors in proton production? How can two objects, manufactured so far apart in space and time, be identical in all respects? One explanation that might be offered is that there s a sea of proton stuff filling the universe and when we make a proton we somehow dip our hand into this stuff and from it mould a proton. Then its not surprising that protons produced in different parts of the universe are identical: they are made of the same stuff. It turns out that this is roughly what happens. The stuff is the proton field or, if you look closely enough, the quark field. In fact, there is more to this tale. Being the same in the quantum world is not like being the same in the classical world: quantum particles that are the same are truely indistinguishable. Swapping two particles around leaves the state completely unchanged - apart from a possible minus sign. This minus sign determines the statistics of the particle. In quantum mechanics you have to put these statistics in by hand and, to agree with experiment, should choose Bose statistics (no minus sign) for integer spin particles, and Fermi statistics (yes minus sign) for half-integer spin particles. In quantum field theory, this relationship between spin and statistics is not something that you have to put in by hand. Rather, it is a consequence of the framework. 6. What is quantum field theory? After (hopefully) convincing you that QFT is necessary, it is time to define it. The clue is in the name: it is the quantization of a classical field, the most familiar example of which is the electromagnetic field. In standard quantum mechanics, we are taught to take the classical degrees of freedom and promote them to operators acting on a Hilbert space. In QFT, we are doing essentially the same - for fields. Thus the basic degrees of freedom in quantum field theory are operator valued functions of space and time. Classically, every point in space has a field value associated with it; in QFT, every point in space has an operator associated with it. These operators are going to operate on
5 5 Hilbert space. This means that we are dealing with an infinite number of degrees of freedom - at least one for every point in space, and there are infinite number of such points. This infinity will come back to bite on several occasions. It will turn out that the possible interactions in quantum field theory are governed by a few basic principles: locality, symmetry and renormalization group flow (the decoupling of short distance phenomena from physics at larger scales). These ideas make QFT a very robust framework: given a set of fields there is very often an almost unique way to couple them together. As it turns out, QFT is an extremely useful tool not only for relativistic systems (where it is necessary), but also for non-relativistic systems with many particles, such as in condensed matter physics (where collective excitations, known as phonons exist). It is obviously the fundamental basis for particle physics, high energy physics, and plays a major role in quantum gravity and cosmology - as well as in pure mathematics. 7. Units and scales Nature presents us with three fundamental dimensionful constants; the speed of light c, Planck s constant (divided by 2π), and Newton s gravitation constant G. They have dimensions: [c] = LT 1 [ ] = L 2 MT 1 (3) [G] = L 3 M 1 T 2 (L - length, T - time and M - mass). Throughout this course, we will work with natural units, defined by c = = 1 (4) which allows us to express all dimensionful quantities in terms of a single scale which we choose to be mass or, equivalently, energy (since E = mc 2 has become E = m). The usual choice of energy unit is ev, the electron volt or, more often GeV = 10 9 ev or TeV = ev. To convert the unit of energy back to a unit of length or time, we need to insert the relevant powers of c and. For example, the length scale λ associated to a mass m is the Compton wavelength λ = mc. (5) With this conversion factor, the electron mass m e = ev translates to a length scale λ e = cm.
6 6 Throughout this course we will refer to the dimension of a quantity, meaning the mass dimension. If X has dimensions of (mass) d we will write [X] = d. In particular, the surviving natural quantity G has dimensions [G] = 2 and defines a mass scale, G = c M 2 p = 1 M 2 p (6) where M p GeV is the Planck scale. It corresponds to a length l p cm. The Planck scale is thought to be the smallest length scale that makes sense: beyond this quantum gravity effects become important and it is no longer clear that the concept of spacetime makes sense. The largest length scale we can talk of is the size of the cosmological horizon, roughly l p. Fig. 1. Energy and distance scales in the known universe Some useful scales in the universe are shown in Figure 1. This is a logarithmic plot, with energy increasing to the right and, correspondingly, length increasing to the left. The smallest and largest scales known are shown on the figure, together with other relevant energy scales. The standard model of particle physics is expected to hold up to about the TeV energies. This is precisely the regime that is currently being probed by the Large Hadron Collider (LHC) at CERN. There is a general belief that the framework of quantum field theory will continue to hold to energy scales only slightly below the Planck scale - for example, there are experimental hints that the coupling constants of electromagnetism, and the weak and strong forces unify at around GeV. For comparison, the rough masses of some elementary (and not so elementary) particles are shown in the table:
7 7 Particle photon neutrino electron Muon Pions Proton, Neutron W,Z Bosons Higgs Boson Mass < ev 10 2 ev 0.5 MeV 100 MeV 140 MeV 1 GeV GeV 125 GeV REFERENCES [1] D. Tong, Lectures on Quantum Field Theory (
Concepts in Theoretical Physics
 Concepts in Theoretical Physics Lecture 6: Particle Physics David Tong e 2 The Structure of Things 4πc 1 137 e d ν u Four fundamental particles Repeated twice! va, 9608085, 9902033 Four fundamental forces
Concepts in Theoretical Physics Lecture 6: Particle Physics David Tong e 2 The Structure of Things 4πc 1 137 e d ν u Four fundamental particles Repeated twice! va, 9608085, 9902033 Four fundamental forces
REALIZING EINSTEIN S DREAM Exploring Our Mysterious Universe
 REALIZING EINSTEIN S DREAM Exploring Our Mysterious Universe The End of Physics Albert A. Michelson, at the dedication of Ryerson Physics Lab, U. of Chicago, 1894 The Miracle Year - 1905 Relativity Quantum
REALIZING EINSTEIN S DREAM Exploring Our Mysterious Universe The End of Physics Albert A. Michelson, at the dedication of Ryerson Physics Lab, U. of Chicago, 1894 The Miracle Year - 1905 Relativity Quantum
Theory of electrons and positrons
 P AUL A. M. DIRAC Theory of electrons and positrons Nobel Lecture, December 12, 1933 Matter has been found by experimental physicists to be made up of small particles of various kinds, the particles of
P AUL A. M. DIRAC Theory of electrons and positrons Nobel Lecture, December 12, 1933 Matter has been found by experimental physicists to be made up of small particles of various kinds, the particles of
STRING THEORY: Past, Present, and Future
 STRING THEORY: Past, Present, and Future John H. Schwarz Simons Center March 25, 2014 1 OUTLINE I) Early History and Basic Concepts II) String Theory for Unification III) Superstring Revolutions IV) Remaining
STRING THEORY: Past, Present, and Future John H. Schwarz Simons Center March 25, 2014 1 OUTLINE I) Early History and Basic Concepts II) String Theory for Unification III) Superstring Revolutions IV) Remaining
Feynman diagrams. 1 Aim of the game 2
 Feynman diagrams Contents 1 Aim of the game 2 2 Rules 2 2.1 Vertices................................ 3 2.2 Anti-particles............................. 3 2.3 Distinct diagrams...........................
Feynman diagrams Contents 1 Aim of the game 2 2 Rules 2 2.1 Vertices................................ 3 2.2 Anti-particles............................. 3 2.3 Distinct diagrams...........................
Where is Fundamental Physics Heading? Nathan Seiberg IAS Apr. 30, 2014
 Where is Fundamental Physics Heading? Nathan Seiberg IAS Apr. 30, 2014 Disclaimer We do not know what will be discovered. This is the reason we perform experiments. This is the reason scientific research
Where is Fundamental Physics Heading? Nathan Seiberg IAS Apr. 30, 2014 Disclaimer We do not know what will be discovered. This is the reason we perform experiments. This is the reason scientific research
1 Introduction. 1 There may, of course, in principle, exist other universes, but they are not accessible to our
 1 1 Introduction Cosmology is the study of the universe as a whole, its structure, its origin, and its evolution. Cosmology is soundly based on observations, mostly astronomical, and laws of physics. These
1 1 Introduction Cosmology is the study of the universe as a whole, its structure, its origin, and its evolution. Cosmology is soundly based on observations, mostly astronomical, and laws of physics. These
Particle Physics. The Standard Model. A New Periodic Table
 5 Particle Physics This lecture is about particle physics, the study of the fundamental building blocks of Nature and the forces between them. We call our best theory of particle physics the Standard Model
5 Particle Physics This lecture is about particle physics, the study of the fundamental building blocks of Nature and the forces between them. We call our best theory of particle physics the Standard Model
The Higgs Boson. Linac08 Victoria BC, Canada CANADA S NATIONAL LABORATORY FOR PARTICLE AND NUCLEAR PHYSICS
 CANADA S NATIONAL LABORATORY FOR PARTICLE AND NUCLEAR PHYSICS Owned and operated as a joint venture by a consortium of Canadian universities via a contribution through the National Research Council Canada
CANADA S NATIONAL LABORATORY FOR PARTICLE AND NUCLEAR PHYSICS Owned and operated as a joint venture by a consortium of Canadian universities via a contribution through the National Research Council Canada
Chapter 18: The Structure of the Atom
 Chapter 18: The Structure of the Atom 1. For most elements, an atom has A. no neutrons in the nucleus. B. more protons than electrons. C. less neutrons than electrons. D. just as many electrons as protons.
Chapter 18: The Structure of the Atom 1. For most elements, an atom has A. no neutrons in the nucleus. B. more protons than electrons. C. less neutrons than electrons. D. just as many electrons as protons.
THE MEANING OF THE FINE STRUCTURE CONSTANT
 THE MEANING OF THE FINE STRUCTURE CONSTANT Robert L. Oldershaw Amherst College Amherst, MA 01002 USA [email protected] Abstract: A possible explanation is offered for the longstanding mystery surrounding
THE MEANING OF THE FINE STRUCTURE CONSTANT Robert L. Oldershaw Amherst College Amherst, MA 01002 USA [email protected] Abstract: A possible explanation is offered for the longstanding mystery surrounding
Introduction to Elementary Particle Physics. Note 01 Page 1 of 8. Natural Units
 Introduction to Elementary Particle Physics. Note 01 Page 1 of 8 Natural Units There are 4 primary SI units: three kinematical (meter, second, kilogram) and one electrical (Ampere 1 ) It is common in the
Introduction to Elementary Particle Physics. Note 01 Page 1 of 8 Natural Units There are 4 primary SI units: three kinematical (meter, second, kilogram) and one electrical (Ampere 1 ) It is common in the
Generally Covariant Quantum Mechanics
 Chapter 15 Generally Covariant Quantum Mechanics by Myron W. Evans, Alpha Foundation s Institutute for Advance Study (AIAS). ([email protected], www.aias.us, www.atomicprecision.com) Dedicated to the Late
Chapter 15 Generally Covariant Quantum Mechanics by Myron W. Evans, Alpha Foundation s Institutute for Advance Study (AIAS). ([email protected], www.aias.us, www.atomicprecision.com) Dedicated to the Late
Evolution of the Universe from 13 to 4 Billion Years Ago
 Evolution of the Universe from 13 to 4 Billion Years Ago Prof. Dr. Harold Geller [email protected] http://physics.gmu.edu/~hgeller/ Department of Physics and Astronomy George Mason University Unity in the
Evolution of the Universe from 13 to 4 Billion Years Ago Prof. Dr. Harold Geller [email protected] http://physics.gmu.edu/~hgeller/ Department of Physics and Astronomy George Mason University Unity in the
How To Understand General Relativity
 Chapter S3 Spacetime and Gravity What are the major ideas of special relativity? Spacetime Special relativity showed that space and time are not absolute Instead they are inextricably linked in a four-dimensional
Chapter S3 Spacetime and Gravity What are the major ideas of special relativity? Spacetime Special relativity showed that space and time are not absolute Instead they are inextricably linked in a four-dimensional
University of Cambridge Part III Mathematical Tripos
 Preprint typeset in JHEP style - HYPER VERSION Michaelmas Term, 2006 and 2007 Quantum Field Theory University of Cambridge Part III Mathematical Tripos Dr David Tong Department of Applied Mathematics and
Preprint typeset in JHEP style - HYPER VERSION Michaelmas Term, 2006 and 2007 Quantum Field Theory University of Cambridge Part III Mathematical Tripos Dr David Tong Department of Applied Mathematics and
0.33 d down 1 1. 0.33 c charm + 2 3. 0 0 1.5 s strange 1 3. 0 0 0.5 t top + 2 3. 0 0 172 b bottom 1 3
 Chapter 16 Constituent Quark Model Quarks are fundamental spin- 1 particles from which all hadrons are made up. Baryons consist of three quarks, whereas mesons consist of a quark and an anti-quark. There
Chapter 16 Constituent Quark Model Quarks are fundamental spin- 1 particles from which all hadrons are made up. Baryons consist of three quarks, whereas mesons consist of a quark and an anti-quark. There
Atomic Structure: Chapter Problems
 Atomic Structure: Chapter Problems Bohr Model Class Work 1. Describe the nuclear model of the atom. 2. Explain the problems with the nuclear model of the atom. 3. According to Niels Bohr, what does n stand
Atomic Structure: Chapter Problems Bohr Model Class Work 1. Describe the nuclear model of the atom. 2. Explain the problems with the nuclear model of the atom. 3. According to Niels Bohr, what does n stand
Pearson Physics Level 30 Unit VIII Atomic Physics: Chapter 17 Solutions
 Pearson Physics Level 30 Unit VIII Atomic Physics: Chapter 17 Solutions Student Book page 831 Concept Check Since neutrons have no charge, they do not create ions when passing through the liquid in a bubble
Pearson Physics Level 30 Unit VIII Atomic Physics: Chapter 17 Solutions Student Book page 831 Concept Check Since neutrons have no charge, they do not create ions when passing through the liquid in a bubble
Wave Function, ψ. Chapter 28 Atomic Physics. The Heisenberg Uncertainty Principle. Line Spectrum
 Wave Function, ψ Chapter 28 Atomic Physics The Hydrogen Atom The Bohr Model Electron Waves in the Atom The value of Ψ 2 for a particular object at a certain place and time is proportional to the probability
Wave Function, ψ Chapter 28 Atomic Physics The Hydrogen Atom The Bohr Model Electron Waves in the Atom The value of Ψ 2 for a particular object at a certain place and time is proportional to the probability
Chapter 1 Units, Physical Quantities, and Vectors
 Chapter 1 Units, Physical Quantities, and Vectors 1 The Nature of Physics Physics is an experimental science. Physicists make observations of physical phenomena. They try to find patterns and principles
Chapter 1 Units, Physical Quantities, and Vectors 1 The Nature of Physics Physics is an experimental science. Physicists make observations of physical phenomena. They try to find patterns and principles
Theoretical Particle Physics FYTN04: Oral Exam Questions, version ht15
 Theoretical Particle Physics FYTN04: Oral Exam Questions, version ht15 Examples of The questions are roughly ordered by chapter but are often connected across the different chapters. Ordering is as in
Theoretical Particle Physics FYTN04: Oral Exam Questions, version ht15 Examples of The questions are roughly ordered by chapter but are often connected across the different chapters. Ordering is as in
Chapter 23 The Beginning of Time
 Chapter 23 The Beginning of Time 23.1 The Big Bang Our goals for learning What were conditions like in the early universe? What is the history of the universe according to the Big Bang theory? What were
Chapter 23 The Beginning of Time 23.1 The Big Bang Our goals for learning What were conditions like in the early universe? What is the history of the universe according to the Big Bang theory? What were
A Theory for the Cosmological Constant and its Explanation of the Gravitational Constant
 A Theory for the Cosmological Constant and its Explanation of the Gravitational Constant H.M.Mok Radiation Health Unit, 3/F., Saiwanho Health Centre, Hong Kong SAR Govt, 8 Tai Hong St., Saiwanho, Hong
A Theory for the Cosmological Constant and its Explanation of the Gravitational Constant H.M.Mok Radiation Health Unit, 3/F., Saiwanho Health Centre, Hong Kong SAR Govt, 8 Tai Hong St., Saiwanho, Hong
13- What is the maximum number of electrons that can occupy the subshell 3d? a) 1 b) 3 c) 5 d) 2
 Assignment 06 A 1- What is the energy in joules of an electron undergoing a transition from n = 3 to n = 5 in a Bohr hydrogen atom? a) -3.48 x 10-17 J b) 2.18 x 10-19 J c) 1.55 x 10-19 J d) -2.56 x 10-19
Assignment 06 A 1- What is the energy in joules of an electron undergoing a transition from n = 3 to n = 5 in a Bohr hydrogen atom? a) -3.48 x 10-17 J b) 2.18 x 10-19 J c) 1.55 x 10-19 J d) -2.56 x 10-19
Cross section, Flux, Luminosity, Scattering Rates
 Cross section, Flux, Luminosity, Scattering Rates Table of Contents Paul Avery (Andrey Korytov) Sep. 9, 013 1 Introduction... 1 Cross section, flux and scattering... 1 3 Scattering length λ and λ ρ...
Cross section, Flux, Luminosity, Scattering Rates Table of Contents Paul Avery (Andrey Korytov) Sep. 9, 013 1 Introduction... 1 Cross section, flux and scattering... 1 3 Scattering length λ and λ ρ...
DO PHYSICS ONLINE FROM QUANTA TO QUARKS QUANTUM (WAVE) MECHANICS
 DO PHYSICS ONLINE FROM QUANTA TO QUARKS QUANTUM (WAVE) MECHANICS Quantum Mechanics or wave mechanics is the best mathematical theory used today to describe and predict the behaviour of particles and waves.
DO PHYSICS ONLINE FROM QUANTA TO QUARKS QUANTUM (WAVE) MECHANICS Quantum Mechanics or wave mechanics is the best mathematical theory used today to describe and predict the behaviour of particles and waves.
University of Cambridge Part III Mathematical Tripos
 Preprint typeset in JHEP style - HYPER VERSION Michaelmas Term, 2006 and 2007 Quantum Field Theory University of Cambridge Part III Mathematical Tripos Dr David Tong Department of Applied Mathematics and
Preprint typeset in JHEP style - HYPER VERSION Michaelmas Term, 2006 and 2007 Quantum Field Theory University of Cambridge Part III Mathematical Tripos Dr David Tong Department of Applied Mathematics and
Basic Nuclear Concepts
 Section 7: In this section, we present a basic description of atomic nuclei, the stored energy contained within them, their occurrence and stability Basic Nuclear Concepts EARLY DISCOVERIES [see also Section
Section 7: In this section, we present a basic description of atomic nuclei, the stored energy contained within them, their occurrence and stability Basic Nuclear Concepts EARLY DISCOVERIES [see also Section
Masses in Atomic Units
 Nuclear Composition - the forces binding protons and neutrons in the nucleus are much stronger (binding energy of MeV) than the forces binding electrons to the atom (binding energy of ev) - the constituents
Nuclear Composition - the forces binding protons and neutrons in the nucleus are much stronger (binding energy of MeV) than the forces binding electrons to the atom (binding energy of ev) - the constituents
Atomic Structure Ron Robertson
 Atomic Structure Ron Robertson r2 n:\files\courses\1110-20\2010 possible slides for web\atomicstructuretrans.doc I. What is Light? Debate in 1600's: Since waves or particles can transfer energy, what is
Atomic Structure Ron Robertson r2 n:\files\courses\1110-20\2010 possible slides for web\atomicstructuretrans.doc I. What is Light? Debate in 1600's: Since waves or particles can transfer energy, what is
Periodic Table of Particles/Forces in the Standard Model. Three Generations of Fermions: Pattern of Masses
 Introduction to Elementary Particle Physics. Note 01 Page 1 of 8 Periodic Table of Particles/Forces in the Standard Model Three Generations of Fermions: Pattern of Masses 1.0E+06 1.0E+05 1.0E+04 1.0E+03
Introduction to Elementary Particle Physics. Note 01 Page 1 of 8 Periodic Table of Particles/Forces in the Standard Model Three Generations of Fermions: Pattern of Masses 1.0E+06 1.0E+05 1.0E+04 1.0E+03
Level 3 Achievement Scale
 Unit 1: Atoms Level 3 Achievement Scale Can state the key results of the experiments associated with Dalton, Rutherford, Thomson, Chadwick, and Bohr and what this lead each to conclude. Can explain that
Unit 1: Atoms Level 3 Achievement Scale Can state the key results of the experiments associated with Dalton, Rutherford, Thomson, Chadwick, and Bohr and what this lead each to conclude. Can explain that
How To Teach Physics At The Lhc
 LHC discoveries and Particle Physics Concepts for Education Farid Ould- Saada, University of Oslo On behalf of IPPOG EPS- HEP, Vienna, 25.07.2015 A successful program LHC data are successfully deployed
LHC discoveries and Particle Physics Concepts for Education Farid Ould- Saada, University of Oslo On behalf of IPPOG EPS- HEP, Vienna, 25.07.2015 A successful program LHC data are successfully deployed
TIME, SYMMETRY OF. Although everyday experience leads us to believe that time "flows" in one direction, the
 TIME, SYMMETRY OF Although everyday experience leads us to believe that time "flows" in one direction, the equations of both classical and modern physics work equally well in either time direction. Since
TIME, SYMMETRY OF Although everyday experience leads us to believe that time "flows" in one direction, the equations of both classical and modern physics work equally well in either time direction. Since
PX408: Relativistic Quantum Mechanics
 January 2016 PX408: Relativistic Quantum Mechanics Tim Gershon ([email protected]) Handout 1: Revision & Notation Relativistic quantum mechanics, as its name implies, can be thought of as the bringing
January 2016 PX408: Relativistic Quantum Mechanics Tim Gershon ([email protected]) Handout 1: Revision & Notation Relativistic quantum mechanics, as its name implies, can be thought of as the bringing
23. The Beginning of Time. Agenda. Agenda. ESA s Venus Express. Conditions in the Early Universe. 23.1 Running the Expansion Backward
 23. The Beginning of Time Somewhere, something incredible is waiting to be known. Agenda Announce: Solar Altitude Lab (#2) due today Read Ch. 24 for Thursday Observation make-up next week Project Presentations
23. The Beginning of Time Somewhere, something incredible is waiting to be known. Agenda Announce: Solar Altitude Lab (#2) due today Read Ch. 24 for Thursday Observation make-up next week Project Presentations
Curriculum for Excellence. Higher Physics. Success Guide
 Curriculum for Excellence Higher Physics Success Guide Electricity Our Dynamic Universe Particles and Waves Electricity Key Area Monitoring and Measuring A.C. Monitoring alternating current signals with
Curriculum for Excellence Higher Physics Success Guide Electricity Our Dynamic Universe Particles and Waves Electricity Key Area Monitoring and Measuring A.C. Monitoring alternating current signals with
Pretest Ch 20: Origins of the Universe
 Name: _Answer key Pretest: _2_/ 58 Posttest: _58_/ 58 Pretest Ch 20: Origins of the Universe Vocab/Matching: Match the definition on the left with the term on the right by placing the letter of the term
Name: _Answer key Pretest: _2_/ 58 Posttest: _58_/ 58 Pretest Ch 20: Origins of the Universe Vocab/Matching: Match the definition on the left with the term on the right by placing the letter of the term
PHOTOELECTRIC EFFECT AND DUAL NATURE OF MATTER AND RADIATIONS
 PHOTOELECTRIC EFFECT AND DUAL NATURE OF MATTER AND RADIATIONS 1. Photons 2. Photoelectric Effect 3. Experimental Set-up to study Photoelectric Effect 4. Effect of Intensity, Frequency, Potential on P.E.
PHOTOELECTRIC EFFECT AND DUAL NATURE OF MATTER AND RADIATIONS 1. Photons 2. Photoelectric Effect 3. Experimental Set-up to study Photoelectric Effect 4. Effect of Intensity, Frequency, Potential on P.E.
Your years of toil Said Ryle to Hoyle Are wasted years, believe me. The Steady State Is out of date Unless my eyes deceive me.
 Your years of toil Said Ryle to Hoyle Are wasted years, believe me. The Steady State Is out of date Unless my eyes deceive me. My telescope Has dashed your hope; Your tenets are refuted. Let me be terse:
Your years of toil Said Ryle to Hoyle Are wasted years, believe me. The Steady State Is out of date Unless my eyes deceive me. My telescope Has dashed your hope; Your tenets are refuted. Let me be terse:
Particle Physics. Michaelmas Term 2011 Prof Mark Thomson. Handout 7 : Symmetries and the Quark Model. Introduction/Aims
 Particle Physics Michaelmas Term 2011 Prof Mark Thomson Handout 7 : Symmetries and the Quark Model Prof. M.A. Thomson Michaelmas 2011 206 Introduction/Aims Symmetries play a central role in particle physics;
Particle Physics Michaelmas Term 2011 Prof Mark Thomson Handout 7 : Symmetries and the Quark Model Prof. M.A. Thomson Michaelmas 2011 206 Introduction/Aims Symmetries play a central role in particle physics;
Chapter 15 Cosmology: Will the universe end?
 Cosmology: Will the universe end? 1. Who first showed that the Milky Way is not the only galaxy in the universe? a. Kepler b. Copernicus c. Newton d. Hubble e. Galileo Ans: d 2. The big bang theory and
Cosmology: Will the universe end? 1. Who first showed that the Milky Way is not the only galaxy in the universe? a. Kepler b. Copernicus c. Newton d. Hubble e. Galileo Ans: d 2. The big bang theory and
Astronomy 110 Homework #04 Assigned: 02/06/2007 Due: 02/13/2007. Name:
 Astronomy 110 Homework #04 Assigned: 02/06/2007 Due: 02/13/2007 Name: Directions: Listed below are twenty (20) multiple-choice questions based on the material covered by the lectures this past week. Choose
Astronomy 110 Homework #04 Assigned: 02/06/2007 Due: 02/13/2007 Name: Directions: Listed below are twenty (20) multiple-choice questions based on the material covered by the lectures this past week. Choose
TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES. PHYS 3650, Exam 2 Section 1 Version 1 October 31, 2005 Total Weight: 100 points
 TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES PHYS 3650, Exam 2 Section 1 Version 1 October 31, 2005 Total Weight: 100 points 1. Check your examination for completeness prior to starting.
TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES PHYS 3650, Exam 2 Section 1 Version 1 October 31, 2005 Total Weight: 100 points 1. Check your examination for completeness prior to starting.
Objectives 404 CHAPTER 9 RADIATION
 Objectives Explain the difference between isotopes of the same element. Describe the force that holds nucleons together. Explain the relationship between mass and energy according to Einstein s theory
Objectives Explain the difference between isotopes of the same element. Describe the force that holds nucleons together. Explain the relationship between mass and energy according to Einstein s theory
Unification - The Standard Model
 Unification - The Standard Model Information on Physics level 4 Undergraduate Course PT.4.6 K.S. Stelle, Office Huxley 519 November 9, 2015 Rapid Feedback to be handed in to the UG office Level 3 (day
Unification - The Standard Model Information on Physics level 4 Undergraduate Course PT.4.6 K.S. Stelle, Office Huxley 519 November 9, 2015 Rapid Feedback to be handed in to the UG office Level 3 (day
The Birth of the Universe Newcomer Academy High School Visualization One
 The Birth of the Universe Newcomer Academy High School Visualization One Chapter Topic Key Points of Discussion Notes & Vocabulary 1 Birth of The Big Bang Theory Activity 4A the How and when did the universe
The Birth of the Universe Newcomer Academy High School Visualization One Chapter Topic Key Points of Discussion Notes & Vocabulary 1 Birth of The Big Bang Theory Activity 4A the How and when did the universe
Origins of the Cosmos Summer 2016. Pre-course assessment
 Origins of the Cosmos Summer 2016 Pre-course assessment In order to grant two graduate credits for the workshop, we do require you to spend some hours before arriving at Penn State. We encourage all of
Origins of the Cosmos Summer 2016 Pre-course assessment In order to grant two graduate credits for the workshop, we do require you to spend some hours before arriving at Penn State. We encourage all of
Boardworks AS Physics
 Boardworks AS Physics Vectors 24 slides 11 Flash activities Prefixes, scalars and vectors Guide to the SI unit prefixes of orders of magnitude Matching powers of ten to their SI unit prefixes Guide to
Boardworks AS Physics Vectors 24 slides 11 Flash activities Prefixes, scalars and vectors Guide to the SI unit prefixes of orders of magnitude Matching powers of ten to their SI unit prefixes Guide to
PEDAGOGY: THE BUBBLE ANALOGY AND THE DIFFERENCE BETWEEN GRAVITATIONAL FORCES AND ROCKET THRUST IN SPATIAL FLOW THEORIES OF GRAVITY *
 PEDAGOGY: THE BUBBLE ANALOGY AND THE DIFFERENCE BETWEEN GRAVITATIONAL FORCES AND ROCKET THRUST IN SPATIAL FLOW THEORIES OF GRAVITY * Tom Martin Gravity Research Institute Boulder, Colorado 80306-1258 [email protected]
PEDAGOGY: THE BUBBLE ANALOGY AND THE DIFFERENCE BETWEEN GRAVITATIONAL FORCES AND ROCKET THRUST IN SPATIAL FLOW THEORIES OF GRAVITY * Tom Martin Gravity Research Institute Boulder, Colorado 80306-1258 [email protected]
Calculating particle properties of a wave
 Calculating particle properties of a wave A light wave consists of particles (photons): The energy E of the particle is calculated from the frequency f of the wave via Planck: E = h f (1) A particle can
Calculating particle properties of a wave A light wave consists of particles (photons): The energy E of the particle is calculated from the frequency f of the wave via Planck: E = h f (1) A particle can
Selected Topics in Elementary Particle Physics ( Haupt-Seminar )
 Selected Topics in Elementary Particle Physics ( Haupt-Seminar ) Paola Avella, Veronika Chobanova, Luigi Li Gioi, Christian Kiesling, Hans-Günther Moser, Martin Ritter, Pit Vanhoefer Time: Do, 12 ct -14
Selected Topics in Elementary Particle Physics ( Haupt-Seminar ) Paola Avella, Veronika Chobanova, Luigi Li Gioi, Christian Kiesling, Hans-Günther Moser, Martin Ritter, Pit Vanhoefer Time: Do, 12 ct -14
Does Quantum Mechanics Make Sense? Size
 Does Quantum Mechanics Make Sense? Some relatively simple concepts show why the answer is yes. Size Classical Mechanics Quantum Mechanics Relative Absolute What does relative vs. absolute size mean? Why
Does Quantum Mechanics Make Sense? Some relatively simple concepts show why the answer is yes. Size Classical Mechanics Quantum Mechanics Relative Absolute What does relative vs. absolute size mean? Why
Light as a Wave. The Nature of Light. EM Radiation Spectrum. EM Radiation Spectrum. Electromagnetic Radiation
 The Nature of Light Light and other forms of radiation carry information to us from distance astronomical objects Visible light is a subset of a huge spectrum of electromagnetic radiation Maxwell pioneered
The Nature of Light Light and other forms of radiation carry information to us from distance astronomical objects Visible light is a subset of a huge spectrum of electromagnetic radiation Maxwell pioneered
Nanoelectronics. Chapter 2 Classical Particles, Classical Waves, and Quantum Particles. [email protected]@2015.3
 Nanoelectronics Chapter 2 Classical Particles, Classical Waves, and Quantum Particles [email protected]@2015.3 1 Electron Double-Slit Experiment [email protected]@2015.3 2 2.1 Comparison of Classical and
Nanoelectronics Chapter 2 Classical Particles, Classical Waves, and Quantum Particles [email protected]@2015.3 1 Electron Double-Slit Experiment [email protected]@2015.3 2 2.1 Comparison of Classical and
7. A UNIFICATION OF ELECTROSTATIC AND GRAVITATIONAL FORCES. Abstract
 7. A UNIFICATION OF ELECTROSTATIC AND RAVITATIONAL FORCES Abstract The gravitational force of attraction F between two bodies, distance apart, one of mass M 1 containing N 1 positive and negative electric
7. A UNIFICATION OF ELECTROSTATIC AND RAVITATIONAL FORCES Abstract The gravitational force of attraction F between two bodies, distance apart, one of mass M 1 containing N 1 positive and negative electric
Big Bang Cosmology. Big Bang vs. Steady State
 Big Bang vs. Steady State Big Bang Cosmology Perfect cosmological principle: universe is unchanging in space and time => Steady-State universe - Bondi, Hoyle, Gold. True? No! Hubble s Law => expansion
Big Bang vs. Steady State Big Bang Cosmology Perfect cosmological principle: universe is unchanging in space and time => Steady-State universe - Bondi, Hoyle, Gold. True? No! Hubble s Law => expansion
Review D: Potential Energy and the Conservation of Mechanical Energy
 MSSCHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics 8.01 Fall 2005 Review D: Potential Energy and the Conservation of Mechanical Energy D.1 Conservative and Non-conservative Force... 2 D.1.1 Introduction...
MSSCHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics 8.01 Fall 2005 Review D: Potential Energy and the Conservation of Mechanical Energy D.1 Conservative and Non-conservative Force... 2 D.1.1 Introduction...
Remodelling the Big Bang
 Remodelling the Big Bang Dewey B. Larson Unquestionably, the most significant development that has taken place in cosmology in recent years is the replacement of the original Big Bang theory by a totally
Remodelling the Big Bang Dewey B. Larson Unquestionably, the most significant development that has taken place in cosmology in recent years is the replacement of the original Big Bang theory by a totally
Physics 111 Homework Solutions Week #9 - Tuesday
 Physics 111 Homework Solutions Week #9 - Tuesday Friday, February 25, 2011 Chapter 22 Questions - None Multiple-Choice 223 A 224 C 225 B 226 B 227 B 229 D Problems 227 In this double slit experiment we
Physics 111 Homework Solutions Week #9 - Tuesday Friday, February 25, 2011 Chapter 22 Questions - None Multiple-Choice 223 A 224 C 225 B 226 B 227 B 229 D Problems 227 In this double slit experiment we
Recent developments in Electromagnetic Hadron Form Factors
 Recent developments in Electromagnetic Hadron Form Factors (JOH7RPDVL*XVWDIVVRQ '$31,$63K16DFOD\ :KDW are Form Factors? :K\ to measure? +RZ to measure? :KDWLVQHZ" Consequences, Conclusions 6SRNHSHUVR QV
Recent developments in Electromagnetic Hadron Form Factors (JOH7RPDVL*XVWDIVVRQ '$31,$63K16DFOD\ :KDW are Form Factors? :K\ to measure? +RZ to measure? :KDWLVQHZ" Consequences, Conclusions 6SRNHSHUVR QV
PHYSICS FOUNDATIONS SOCIETY THE DYNAMIC UNIVERSE TOWARD A UNIFIED PICTURE OF PHYSICAL REALITY TUOMO SUNTOLA
 PHYSICS FOUNDATIONS SOCIETY THE DYNAMIC UNIVERSE TOWARD A UNIFIED PICTURE OF PHYSICAL REALITY TUOMO SUNTOLA Published by PHYSICS FOUNDATIONS SOCIETY Espoo, Finland www.physicsfoundations.org Printed by
PHYSICS FOUNDATIONS SOCIETY THE DYNAMIC UNIVERSE TOWARD A UNIFIED PICTURE OF PHYSICAL REALITY TUOMO SUNTOLA Published by PHYSICS FOUNDATIONS SOCIETY Espoo, Finland www.physicsfoundations.org Printed by
x 1 ' = x 1 vt 1 x 1 ' = 4.0 m t 1 = 1.0 s x 2 vt 2 ' = 4.0 m t 2 ' = x 2 = 3.0 s x 1 = x 2 x 1 ' + vt 1 ' + vt 2 v (t 1 t 2 ) = x 2 ' x 1 ' = x 2
 Physics 2220 Module 16 Homework 01. A firecracker explodes in reference frame S at t 1 1.0 seconds. A second firecracker explodes at the same position at t 2 3.0 seconds. In reference frame S', which moves
Physics 2220 Module 16 Homework 01. A firecracker explodes in reference frame S at t 1 1.0 seconds. A second firecracker explodes at the same position at t 2 3.0 seconds. In reference frame S', which moves
Transcript 22 - Universe
 Transcript 22 - Universe A few introductory words of explanation about this transcript: This transcript includes the words sent to the narrator for inclusion in the latest version of the associated video.
Transcript 22 - Universe A few introductory words of explanation about this transcript: This transcript includes the words sent to the narrator for inclusion in the latest version of the associated video.
Chapters 21-29. Magnetic Force. for a moving charge. F=BQvsinΘ. F=BIlsinΘ. for a current
 Chapters 21-29 Chapter 21:45,63 Chapter 22:25,49 Chapter 23:35,38,53,55,58,59 Chapter 24:17,18,20,42,43,44,50,52,53.59,63 Chapter 26:27,33,34,39,54 Chapter 27:17,18,34,43,50,51,53,56 Chapter 28: 10,11,28,47,52
Chapters 21-29 Chapter 21:45,63 Chapter 22:25,49 Chapter 23:35,38,53,55,58,59 Chapter 24:17,18,20,42,43,44,50,52,53.59,63 Chapter 26:27,33,34,39,54 Chapter 27:17,18,34,43,50,51,53,56 Chapter 28: 10,11,28,47,52
Spontaneous symmetry breaking in particle physics: a case of cross fertilization
 Spontaneous symmetry breaking in particle physics: a case of cross fertilization Yoichiro Nambu lecture presented by Giovanni Jona-Lasinio Nobel Lecture December 8, 2008 1 / 25 History repeats itself 1960
Spontaneous symmetry breaking in particle physics: a case of cross fertilization Yoichiro Nambu lecture presented by Giovanni Jona-Lasinio Nobel Lecture December 8, 2008 1 / 25 History repeats itself 1960
GRAVITY CONCEPTS. Gravity is the universal force of attraction between all matter
 IT S UNIVERSAL GRAVITY CONCEPTS Gravity is the universal force of attraction between all matter Weight is a measure of the gravitational force pulling objects toward Earth Objects seem weightless when
IT S UNIVERSAL GRAVITY CONCEPTS Gravity is the universal force of attraction between all matter Weight is a measure of the gravitational force pulling objects toward Earth Objects seem weightless when
A Short Guide to Significant Figures
 A Short Guide to Significant Figures Quick Reference Section Here are the basic rules for significant figures - read the full text of this guide to gain a complete understanding of what these rules really
A Short Guide to Significant Figures Quick Reference Section Here are the basic rules for significant figures - read the full text of this guide to gain a complete understanding of what these rules really
The origin of neutrino mass
 New experimental data, which show that neutrinos have mass, are forcing theorists to revise the Standard Model of particle physics The origin of neutrino mass IF WE look deep into the universe, we see
New experimental data, which show that neutrinos have mass, are forcing theorists to revise the Standard Model of particle physics The origin of neutrino mass IF WE look deep into the universe, we see
Three Pictures of Quantum Mechanics. Thomas R. Shafer April 17, 2009
 Three Pictures of Quantum Mechanics Thomas R. Shafer April 17, 2009 Outline of the Talk Brief review of (or introduction to) quantum mechanics. 3 different viewpoints on calculation. Schrödinger, Heisenberg,
Three Pictures of Quantum Mechanics Thomas R. Shafer April 17, 2009 Outline of the Talk Brief review of (or introduction to) quantum mechanics. 3 different viewpoints on calculation. Schrödinger, Heisenberg,
Losing energy in classical, relativistic and quantum mechanics
 Losing energy in classical, relativistic and quantum mechanics David Atkinson ABSTRACT A Zenonian supertask involving an infinite number of colliding balls is considered, under the restriction that the
Losing energy in classical, relativistic and quantum mechanics David Atkinson ABSTRACT A Zenonian supertask involving an infinite number of colliding balls is considered, under the restriction that the
Physics for the 21 st Century. Unit 1: The Basic Building Blocks of Matter. Bonnie Fleming and Mark Kruse
 Physics for the 21 st Century Unit 1: The Basic Building Blocks of Matter Bonnie Fleming and Mark Kruse What are the basic building blocks that make up all matter? BONNIE FLEMING: The basic building blocks
Physics for the 21 st Century Unit 1: The Basic Building Blocks of Matter Bonnie Fleming and Mark Kruse What are the basic building blocks that make up all matter? BONNIE FLEMING: The basic building blocks
Solutions to Problems in Goldstein, Classical Mechanics, Second Edition. Chapter 7
 Solutions to Problems in Goldstein, Classical Mechanics, Second Edition Homer Reid April 21, 2002 Chapter 7 Problem 7.2 Obtain the Lorentz transformation in which the velocity is at an infinitesimal angle
Solutions to Problems in Goldstein, Classical Mechanics, Second Edition Homer Reid April 21, 2002 Chapter 7 Problem 7.2 Obtain the Lorentz transformation in which the velocity is at an infinitesimal angle
Introduction to Netlogo: A Newton s Law of Gravity Simulation
 Introduction to Netlogo: A Newton s Law of Gravity Simulation Purpose Netlogo is an agent-based programming language that provides an all-inclusive platform for writing code, having graphics, and leaving
Introduction to Netlogo: A Newton s Law of Gravity Simulation Purpose Netlogo is an agent-based programming language that provides an all-inclusive platform for writing code, having graphics, and leaving
Universe. Can scientists theory of everything really explain all the weirdness the universe displays? /// BY EDWARD WITTEN
 Can scientists theory of everything really explain all the weirdness the universe displays? /// BY EDWARD WITTEN Astronomers have wrapped up cosmic history in a neat package. Or so it might seem. Some
Can scientists theory of everything really explain all the weirdness the universe displays? /// BY EDWARD WITTEN Astronomers have wrapped up cosmic history in a neat package. Or so it might seem. Some
High Energy Physics. Lecture 4 More kinematics and a picture show of particle collisions
 High Energy Physics Lecture 4 More kinematics and a picture show of particle collisions 1 Recall from the previous lecture: the momentum of the scattered Particle in an elastic collision is given by p
High Energy Physics Lecture 4 More kinematics and a picture show of particle collisions 1 Recall from the previous lecture: the momentum of the scattered Particle in an elastic collision is given by p
Gravity and running coupling constants
 Gravity and running coupling constants 1) Motivation and history 2) Brief review of running couplings 3) Gravity as an effective field theory 4) Running couplings in effective field theory 5) Summary 6)
Gravity and running coupling constants 1) Motivation and history 2) Brief review of running couplings 3) Gravity as an effective field theory 4) Running couplings in effective field theory 5) Summary 6)
PHY1020 BASIC CONCEPTS IN PHYSICS I
 PHY1020 BASIC CONCEPTS IN PHYSICS I Jackson Levi Said 14 lectures/tutorials/past paper session Project on one of the interesting fields in physics (30%) Exam in January/February (70%) 1 The Course RECOMMENDED
PHY1020 BASIC CONCEPTS IN PHYSICS I Jackson Levi Said 14 lectures/tutorials/past paper session Project on one of the interesting fields in physics (30%) Exam in January/February (70%) 1 The Course RECOMMENDED
The Standard Model and the LHC! in the Higgs Boson Era Juan Rojo!
 The Standard Model and the LHC in the Higgs Boson Era Juan Rojo Saturday Mornings of Theoretical Physics Rudolf Peierls Center for Theoretical Physics Oxford, 07/02/2015 1 The Standard Model of Particle
The Standard Model and the LHC in the Higgs Boson Era Juan Rojo Saturday Mornings of Theoretical Physics Rudolf Peierls Center for Theoretical Physics Oxford, 07/02/2015 1 The Standard Model of Particle
Lecture 09 Nuclear Physics Part 1
 Lecture 09 Nuclear Physics Part 1 Structure and Size of the Nucleus Νuclear Masses Binding Energy The Strong Nuclear Force Structure of the Nucleus Discovered by Rutherford, Geiger and Marsden in 1909
Lecture 09 Nuclear Physics Part 1 Structure and Size of the Nucleus Νuclear Masses Binding Energy The Strong Nuclear Force Structure of the Nucleus Discovered by Rutherford, Geiger and Marsden in 1909
Final. Mark Scheme. Physics A PHYA1. (Specification 2450) Unit 1: Particles, quantum phenomena and electricity
 Version.0 General Certificate of Education (A-level) June 0 Physics A PHYA (Specification 450) Unit : Particles, quantum phenomena and electricity Final Mark Scheme Mark schemes are prepared by the Principal
Version.0 General Certificate of Education (A-level) June 0 Physics A PHYA (Specification 450) Unit : Particles, quantum phenomena and electricity Final Mark Scheme Mark schemes are prepared by the Principal
Modified Gravity and the CMB
 Modified Gravity and the CMB Philippe Brax, IphT Saclay, France arxiv:1109.5862 PhB, A.C. Davis Work in progress PhB, ACD, B. Li Minneapolis October 2011 PLANCK will give us very precise information on
Modified Gravity and the CMB Philippe Brax, IphT Saclay, France arxiv:1109.5862 PhB, A.C. Davis Work in progress PhB, ACD, B. Li Minneapolis October 2011 PLANCK will give us very precise information on
1 Quantifying gravity
 1 Quantifying gravity We have introduced a network of point masses to satisfy a vanishing energy condition for each point. The next step is to replace the pure point by a fundamental neutral bound system,
1 Quantifying gravity We have introduced a network of point masses to satisfy a vanishing energy condition for each point. The next step is to replace the pure point by a fundamental neutral bound system,
Build Your Own Universe
 Build Your Own Universe You will need: At least 10,000,000,000,000,00 0,000,000,000,000,000,000,00 0,000,000,000,000,000,000,00 0,000,000,000,000,000,000,00 0,000 x Down quarks At least 10,000,000,000,000,000,
Build Your Own Universe You will need: At least 10,000,000,000,000,00 0,000,000,000,000,000,000,00 0,000,000,000,000,000,000,00 0,000,000,000,000,000,000,00 0,000 x Down quarks At least 10,000,000,000,000,000,
Chemistry 2 Chapter 13: Electrons in Atoms Please do not write on the test Use an answer sheet! 1 point/problem 45 points total
 Chemistry 2 Chapter 13: Electrons in Atoms Please do not write on the test Use an answer sheet! 1 point/problem 45 points total 1. Calculate the energy in joules of a photon of red light that has a frequency
Chemistry 2 Chapter 13: Electrons in Atoms Please do not write on the test Use an answer sheet! 1 point/problem 45 points total 1. Calculate the energy in joules of a photon of red light that has a frequency
2. Spin Chemistry and the Vector Model
 2. Spin Chemistry and the Vector Model The story of magnetic resonance spectroscopy and intersystem crossing is essentially a choreography of the twisting motion which causes reorientation or rephasing
2. Spin Chemistry and the Vector Model The story of magnetic resonance spectroscopy and intersystem crossing is essentially a choreography of the twisting motion which causes reorientation or rephasing
The Elegant Universe Teacher s Guide
 The Elegant Universe Teacher s Guide On the Web It s the holy grail of physics the search for the ultimate explanation of how the universe works. And in the past few years, excitement has grown among scientists
The Elegant Universe Teacher s Guide On the Web It s the holy grail of physics the search for the ultimate explanation of how the universe works. And in the past few years, excitement has grown among scientists
Unamended Quantum Mechanics Rigorously Implies Awareness Is Not Based in the Physical Brain
 Unamended Quantum Mechanics Rigorously Implies Awareness Is Not Based in the Physical Brain Casey Blood, PhD Professor Emeritus of Physics, Rutgers University www.quantummechanicsandreality.com [email protected]
Unamended Quantum Mechanics Rigorously Implies Awareness Is Not Based in the Physical Brain Casey Blood, PhD Professor Emeritus of Physics, Rutgers University www.quantummechanicsandreality.com [email protected]
Photons. ConcepTest 27.1. 1) red light 2) yellow light 3) green light 4) blue light 5) all have the same energy. Which has more energy, a photon of:
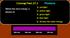 ConcepTest 27.1 Photons Which has more energy, a photon of: 1) red light 2) yellow light 3) green light 4) blue light 5) all have the same energy 400 nm 500 nm 600 nm 700 nm ConcepTest 27.1 Photons Which
ConcepTest 27.1 Photons Which has more energy, a photon of: 1) red light 2) yellow light 3) green light 4) blue light 5) all have the same energy 400 nm 500 nm 600 nm 700 nm ConcepTest 27.1 Photons Which
Advanced Quantum Physics
 Advanced Quantum Physics Aim of the course Building upon the foundations of wave mechanics, this course will introduce and develop the broad field of quantum physics including: Quantum mechanics of point
Advanced Quantum Physics Aim of the course Building upon the foundations of wave mechanics, this course will introduce and develop the broad field of quantum physics including: Quantum mechanics of point
Appendix A: Science Practices for AP Physics 1 and 2
 Appendix A: Science Practices for AP Physics 1 and 2 Science Practice 1: The student can use representations and models to communicate scientific phenomena and solve scientific problems. The real world
Appendix A: Science Practices for AP Physics 1 and 2 Science Practice 1: The student can use representations and models to communicate scientific phenomena and solve scientific problems. The real world
About the Author. journals as Physics Letters, Nuclear Physics and The Physical Review.
 About the Author Dr. John Hagelin is Professor of Physics and Director of the Doctoral Program in Physics at Maharishi International University. Dr. Hagelin received his A.B. Summa Cum Laude from Dartmouth
About the Author Dr. John Hagelin is Professor of Physics and Director of the Doctoral Program in Physics at Maharishi International University. Dr. Hagelin received his A.B. Summa Cum Laude from Dartmouth
Assessment Plan for Learning Outcomes for BA/BS in Physics
 Department of Physics and Astronomy Goals and Learning Outcomes 1. Students know basic physics principles [BS, BA, MS] 1.1 Students can demonstrate an understanding of Newton s laws 1.2 Students can demonstrate
Department of Physics and Astronomy Goals and Learning Outcomes 1. Students know basic physics principles [BS, BA, MS] 1.1 Students can demonstrate an understanding of Newton s laws 1.2 Students can demonstrate
