The basis functions of normalized simplex splines are then defined
|
|
|
- Myles Lloyd
- 10 years ago
- Views:
Transcription
1 ACM Symposium on Solid Modeling and Applications (2004) G. Elber, N. Patrikalakis, P. Brunet (Editors) Multiresolution Heterogeneous Solid Modeling and Visualization Using Trivariate Simplex Splines Jing Hua, Ying He, and Hong Qin Center for Visual Computing (CVC) and Department of Computer Science State University of New York at Stony Brook, Stony Brook, NY Abstract This paper presents a new and powerful heterogeneous solid modeling paradigm for representing, modeling, and rendering of multi-dimensional, physical attributes across any volumetric objects. The modeled solid can be of complicated geometry and arbitrary topology. It is formulated using a trivariate simplex spline defined over a tetrahedral decomposition of any 3D domain. Heterogeneous material attributes associated with solid geometry can be modeled and edited by manipulating the control vectors and/or associated knots of trivariate simplex splines easily. The multiresolution capability is achieved by interactively subdividing any regions of interest and allocating more knots and control vectors accordingly. We also develop a feature-sensitive fitting algorithm that can reconstruct a more compact, continuous trivariate simplex spline from structured or unstructured volumetric grids. This multiresolution representation results from the adaptive and progressive tetrahedralization of the 3D domain. In addition, based on the simplex spline theory, we derive several theoretical formula and propose a fast direct rendering algorithm for interactive data analysis and visualization of the simplex spline volumes. Our experiments demonstrate that the proposed paradigm augments the current modeling and visualization techniques with the new and unique advantages. Categories and Subject Descriptors (according to ACM CCS): I.3.5 [Computer Graphics]: Computational Geometry and Object Modeling 1. Introduction and Motivation New and powerful solid representations underpin the success of solid modeling and relevant applications. With the advent of everincreasing computing power and more advanced data acquisition technologies, solid geometry has quickly gained popularity as an intuitive and natural paradigm for representing, modeling, and simulating three-dimensional real-world objects in interactive graphics, simulation, scientific visualization, and virtual environments. To date, the vast majority of popular solid modeling approaches, as well as commonly-used solid modeling systems, are built upon the following geometric foundations: constructive solid geometry (CSG), boundary representation (B-reps), and cell decomposition. When our goals are to reconstruct heterogeneous models of physical objects with continuous properties, and further model and visualize the objects, prior representations and the current state-of-theart in solid modeling fall short in offering designers an integrated paradigm to represent complex solid geometry, arbitrary topology, and continuously-varying material attributes in a single framework simultaneously, since solid geometry and heterogeneous attributes are usually considered separately. In sharp contrast to the previously-mentioned modeling challenges, research in visualization areas is mainly concerned with the underlying attribute fields purely for the display and visualization purpose. The representations prevalently used are oftentimes discrete in nature (e.g., voxel-based regular grids or unstructured point samples). Geometry of an underlying volume is implicitly defined in the scalar field. Historically, volumetric primitives have been based on uniform or rectilinear grid, where the data is often regularly spaced along grid lines. In the past few years, an unstructured volume representation has started to emerge as a viable modeling tool, where a tetrahedral mesh is exploited to dictate the domain of a volume [CDM 94, THJ99, CCM 00, RN00]. This type of representation is expected to be more and more popular as the irregular, adaptive 3D scanning technologies becomes commonplace. However, from a pure visualization s point of view, tetrahedra are mainly exploited as rendering primitives, i.e., they serve as a good discrete representation for visualization. This kind of tetrahedral mesh representation is only C 0. It is less suitable for modeling continuouslyvarying material attributes without resorting to approximation. To satisfy the modeling requirement of high-order continuity, volumetric modeling based on splines such as B-splines or NURBS [RE99, HQ01, SPS01, MC01] appears to be more appropriate. Nonetheless, modeling with B-splines or NURBS has severe shortcomings. Its modeling scope is extremely constrained in term of geometric, topological, and attribute aspects. First, B-spline and NURBS are defined over a regular, tensor-product domain. A single
2 B-spline or NURBS can not represent volumes of arbitrary topology without patching or trimming operations. Furthermore, patching multiple B-splines or NURBS to form arbitrary topology is not easy to control at all. Second, tensor-product splines are essentially smooth everywhere. It is difficult to model high-frequency features. Third, when refining a region of interest in a tensor-product spline patch, it will introduce too many extra degrees of freedom in other less-interesting regions nearby in order to retain its regular structure. Attractive properties such as local adaptivity and multiresolution are rather difficult to achieve. To overcome the above difficulties in both modeling and visualization, in this paper we propose an integrated approach for representing, modeling, and rendering of multi-dimensional, physical attributes across any volumetric objects. We consider modeling both the geometry and the attributes carried by the volume. In particular, we develop a trivariate simplex spline model that is defined over a tetrahedral decomposition of any 3D domain. The modeled volume can be of complicated geometry and arbitrary topology. Our goal is to demonstrate that the trivariate simplex spline is a promising primitive for both visualization and modeling tasks, especially for representing and visualizing heterogeneous models of physical objects and their material properties. Our model makes use of a more general and flexible tetrahedral domain and offers a compact continuous representation at the same time. It unifies geometry and attribute properties over domains of arbitrary topology. It is possible to represent a complicated heterogeneous object with a single trivariate simplex spline without any additional operations of trimming or patching, while the geometry of the object is explicitly represented by the spline. The trivariate simplex spline based representation offers a single, compact analytic representation, because it is a piecewise polynomial of the lowest possible degree and the highest possible continuity everywhere across the entire tetrahedral domain. For example, given a degree n for the trivarite DMS spline which use simplex spline as basis functions, the representation scheme can achieve C n 1 continuity over smooth regions. Meanwhile, by placing control points and their associated knots in certain locations, variable continuity is readily accomplished including a C 0 continuity that defines sharp features. This property is ideal for data reduction when reverse-engineering a continuous spline model from the discretized data inputs. Since we develop the trivariate simplex spline for both solid geometry and the material attributes associated with the solid geometry simultaneously, it facilitates the modeling of heterogeneous objects. The feature-sensitive fitting algorithm that we develop can reconstruct a more compact trivariate simplex spline from a structured or arbitrary unstructured volume. It reconstructs the geometry and the associated material attributes simultaneously. The C n 1 continuity and C 0 continuity can both be modeled with ease. Such flexibility allows us to model continuously-varying material distribution. It may be noted that, in our framework we use time-varying knots instead of fixed knots, which offers more freedom and improves accuracy for approximation. The knots are explicitly and automatically determined by optimizing a specific objective function. Unlike frequently used B-spline, our new algorithm can avoid the complicated procedures of trimming and patching when dealing with these cases. This representation can also enable the strong multiresolution modeling capability through interactively subdividing any region of interest, allocating more knots and control points accordingly. Other modeling advantages such as local adaptivity and free-form deformation are also apparent by means of displacing control points, direct manipulation of control coefficients, and adjustment of free knots. In addition, based on the simplex spline theory, we derive several theoretical formula and propose a fast direct rendering algorithm for interactive data analysis and visualization of the simplex spline volumes. When visualizing this type of solids, resampling or interpolation process is no longer necessary at all. It (including position, derivative, etc.) can be evaluated anywhere analytically and computed efficiently for volume rendering. We conduct extensive experiments and our empirical results demonstrate that the proposed paradigm significantly augments the currently existing techniques in modeling and visualization research areas. The applications of our techniques are diverse, including solid modeling of arbitrary topological types, material editing and reconstruction, volume simplification, and data exploration and visualization in bio-medical and geological fields. 2. Related Work Research on volume modeling using B-splines or NURBS has received much attention in the modeling community in recent years. Raviv and Elber [RE99] presented a 3D interactive sculpting paradigm that employed a set of scalar uniform trivariate B-spline functions as object representations. Schmitt and Pasko [SPS01] presented an approach for constructive modeling of FRep solids defined by real-valued functions using 4D uniform rational cubic B- spline volumes as primitives. Hua and Qin [HQ01, HQ02] presented a haptics-based direct manipulation and exploration of scalar B- spline volumes. Martin and Cohen [MC01] presented a completed mathematical framework for representing and extracting volumetric attributes using trivariate NURBS. In the visualization community, volume modeling and rendering via tetrahedral mesh has recently gained more popularity as well. Primarily, researchers are interested in constructing or using tetrahedral mesh of volume dataset to achieve better rendering effects. Cignoni et. al [CDM 94] proposed a multiresolution model for the representation and visualization of unstructured volumetric datasets based on a decomposition of the three-dimensional domain into tetrahedra. Later, they presented a tetrahedral mesh simplification approach based on accurate error evaluation [CCM 00]. Roxborough and Nielson [RN00] presented a method for visualization of freehand collected three-dimensional ultrasound data based on adaptive, progressive construction of the tetrahedral mesh. Yao and Taylor [YT00] adopted a tetrahedral mesh structure to represent anatomical structures. They proposed an efficient and automatic algorithm to construct a tetrahedral mesh from contours in CT images. A rich body of previous work on tetrahedral meshes suggest that a simplicial complex is potentially promising to serve for both visualization and modeling. Multivariate simplex splines for approximation theory have been extensively investigated in mathematical science for many years. Motivated by an idea of Curry and Schoenberg for a geometric interpretation of univariate B-splines, de Boor [db76] first presented a brief description of multivariate simplex splines. Since then, their theoretical aspects have been explored extensively. From the point of view of blossoming, Dahmen et. al [DMS92] proposed triangular B-splines. In sharp contrast to the theoretical advances, the
3 application of multivariate simplex splines has been severely underexplored. Greiner and Seidel [GS94] demonstrated the practical feasibility of multivariate B-spline algorithms in graphics and shape design. Pfeifle and Seidel proposed a faster evaluation technique for quadratic bivariate DMS-spline surfaces [PS94] and demonstrated the fitting of triangular B-spline surfaces to scattered data through the use of least squares and optimization techniques [PS95]. Qin and Terzopoulos [QT97] presented dynamic triangular NURBS, a freeform shape model. Most recently, He and Qin [HQ04] presented a new approach for reconstructing a triangular B-spline surface from a set of scanned 3D points. To the authors best knowledge, there are no existing research work, which applies multivariate simplex splines to represent solid geometry, model its heterogeneous material attributes, and reconstruct continuous volumetric splines from discretized volumetric inputs via data fitting. 3. Trivariate DMS-spline Volumes Analogous to a tensor-product, trivariate B-spline volume [RE99, MC01], we can instead use simplex splines to model volumetric objects. To motivate our rationales, we have detailed some major advantages of multivariate simplex spline volumes over conventional tensor-product B-spline volumes in Section Trivariate Simplex Splines Throughout this paper, we employ a trivariate simplex spline to represent and extract both solid geometry and its volumetric attributes. Now we shall review the formulation of the trivariate simplex splines and summarize their analytic and geometric properties. A degree n trivariate simplex spline, M(x x 0,,x n+3 ), can be defined as a function of x R 3 over the half open convex hull of a point set V =[x 0,,x n+3 ), depending on the n + 4 knots x i R 3,i = 0,,n + 3. The basis function of trivariate simplex splines may be formulated recursively, which facilitates point evaluation and its derivative and gradient computation. When n = 0, { 1 M(x x 0,,x 3 )= Vol R 3 (x 0,,x 3 ), x [x 0,,x 3 ), 0, otherwise, and when n > 0, select four points W = {x k0,x k1,x k2,x k3 } from V, such that W is affinely independent, then 3 M(x x 0,,x n+3 )= λ j (x W)M(x V \{x k j }), (1) j=0 where 3 j=0 λ j(x W)=1 and 3 j=0 λ j(x W)x k j = x. The directional derivative of M(x V) with respect to a vector v is defined as follows: 3 D v M(x V)=n µ j (v W)M(x V \{x k j }), (2) j=0 where v = 3 j=0 µ j(v W)x k j and 3 j=0 µ j(v W)=0. In the interest of space, more theoretical discussions can be found elsewhere Trivariate DMS-spline Volumes In [DMS92], Dahmen, Micchelli and Seidel presented a multivariate B-spline scheme, called DMS-spline, based on blending functions and control vectors. The surface scheme is also called triangular B-spline, which has been studied in [GS94, PS94, PS95, QT96, SV94]. We apply the trivariate DMS-spline to represent both solid geometry and its associated physical attributes in this paper. Let Ω be an arbitrary proper tetrahedralization of R 3 or some bounded domain D R 3. Here, Proper means that every pair of domain tetrahedra are disjoint, or share exactly one vertex, one edge, or one face. To each vertex t of the tetrahedralization, we assign a knot cloud, which is a sequence of points [t 0,t 1,,t n ], where t 0 t. For every tetrahedron I =(p, q, r, s), we require all the tetrahedra [p i,q j,r k,s l ] with i + j + k + l n are nondegenerate. the set interior( i+ j+k+l n [p i,q j,r k,s l ]) (3) is not empty. if I has a boundary triangle, the knots associated to the boundary triangle must lie outside of Ω. We then define, for each tetrahedron I and i+ j +k +l = n (in the following, we use β to denote 4-tuple (i, j,k,l)), the knot sets Vβ I =[p 0,,p i,q 0,,q j,r 0,,r k,s 0,,s l ]. (4) The basis functions of normalized simplex splines are then defined as Nβ I (u)= d(p i,q j,r k,s l ) M(u Vβ I ), (5) where d(p i,q j,r k,s l ) is six times of the volume of (p i,q j,r k,s l ). Like the ordinary tensor-product B-spline, a trivariate simplex spline volume of degree n over arbitrary tetrahedral domain is the combination of a set of basis functions with control vectors c I β : s(u)= c I β NI β (u). (6) I Ω β =n Like B-splines, the nonnegative basis functions of simplex spline volume sum to unity. They have a number of nice properties, such as the convex hull property, local support, affine invariance. Shape design based on trivariate DMS-spline volume includes the specification of a domain tetrahedralization, knot sequences, and control points to generate an initial shape. The initial shape is then refined into the final desired shape through interactive adjustment of domain tetrahedralization, control points, and knots. The geometric flexibility of simplex spline volumes provides great power on its shape editing. Figure 1 show a cubic trivariate DMS-spline solid corresponding to a domain with a single tetrahedron. Note that our trivariate DMS volumes represent not only boundary geometry, but also interior solid geometry. They can represent physical or material attributes over the entire solid as well. Figure 1 shows scaled tetrahedra of the solid in order to emphasize its non-empty solid interior geometry. For a general trivariate DMS-spline volume, each domain tetrahedron I has its own set of control points c I β. However, in this paper, we consider a more restricted class of volumes by sharing respective control points along common triangles of two adjacent tetrahedra in parametric tetrahedralization. Splines with shared control points have a direct visual effect in geometric and solid modeling. More importantly, as proved by Dahmen et. al [DMS92], a degree
4 Figure 1: A cubic trivariate DMS-spline solid corresponding to a single tetrahedral domain with 20 control points. The tetrahedra of the designed solid object are scaled to show the interior of the solid. n trivariate DMS-spline with shared control points can be evaluated with the efficiency of a degree n 1 spline. s(u)= ĉ I β (u)ni β (u) I Ω β =n 1 where ĉ I β (u)= 3 m=0c I β+e mλ m(u p i,q j,r k,s l ) and e m =(δ i,m ) 3 i=0, m = 0,1,2 as the coordinate vectors. This property can significantly improve the software system for rendering a DMS-spline volume. It also implies that the knots {t i,n i N} has no effect on the value of s(u). Note that for our trivariate DMS spline volumes, the used tetrahedral domain is not necessary to undergo a separate parameterization process, because it is already conforming to the three-dimensional physical domain for material attributes. The generalized control vectors are now (n+3) vectors, including control points (p x, p y, p z ) for the solid geometry, and control coefficients (g 1,,g n ) for the attributes, where n denotes the number of attributes associated with the geometry Coupling Solid Geometry and Physical Attributes In our framework, we consider a control coefficient (and possibly other vector-based quantities with n components) is associated with a corresponding control point and evaluated with the geometry simultaneously based on the same tetrahedral domain. In this way, we shall generalize DMS spline technique from geometric domains to visual or material domains. Typical material-oriented examples include: mass, damping, stiffness (such as strain and stress), and displacement for solid physics; or density, velocity, and pressure for fluid mechanics, etc. These attributes may be assigned at the control points or fitted by using both control vectors and knots. Other commonly-used visual information include: color, texture, intensity, opacity, transparency, etc. This flexibility permits our paradigm to be employed in a wide variety of applications involving continuous domains, such as finite element analysis, virtual sculpting, and computational fluid simulation. Consider that control coefficients g I β are associated with control points p I β (gi β may be a multi-dimensional vector). Besides solid geometry, a material (e.g., density) function over s(x) can be simultaneously defined as [ ] [ ] g g I s (x)= β p I Nβ I (x), (7) i β where g can be color, texture, mass, temperature, or other visual or material functions as stated above. Visual and material modeling is indispensable for computerized virtual environments. Besides commonly-used material distributions in classical mechanics, it can be generalized to heat transfer, electricity, and beyond. The diverse set of these novel solid models are unique and invaluable because they can potentially unify geometric, topological, kinematic, material, and dynamic properties. The field attributes can be modified by directly changing the control coefficients stored at the control points. In addition, by moving the control points, we can perform FFD of the underlying geometric space. As a result, this procedure deforms the field properties and provides an alternate interaction mechanism. The geometric space over which the field is defined can be of arbitrary topology, which adds further shape editing flexibility. 4. Multiresolution Modeling Based on the flexible simplex splines, we can easily achieve multiresolution modeling of heterogeneous solid objects. The multiresolution capability is achieved by interactively subdividing any region of interest and allocating more knots and control vectors accordingly Interactive Tetrahedralization We use Delaunay tetrahedralization to construct a tetrahedral domain, which serves as the tetrahedral domain of the trivariate simplex spline. In fact, the scalar simplex splines lend itself well appropriate for an unstructured grid volume representation. For constructing Delaunay tetrahedralization for a 3D point set, we make use of the incremental flip algorithm proposed in [Joe91, ES92]. The procedure to update a tetrahedralization is to insert one new vertex at each step. Then, a sequence of actions are applied to modify the tetrahedralization locally. Each flip action consists of replacing one, two, or three adjacent tetrahedra with four, three, or two new tetrahedra, respectively. When the new vertex lies either on a triangular face or on an edge of the current tetrahedralization, other face flips may be needed. When performing Delaunay tetrahedralization, the user have an option to enforce the quality constraints (including volume of tetrahedron, etc.). The user can also interactively specify boundary constraints (such as points, edges, polygons, or cells). We implement the boundary conforming Delaunay tetrahedralization [She97], which tries to recover the missing boundary edges of the piecewise linear complexes from its current Delaunay tetrahedralization by inserting new points Geometric Editing Using Control Points With this flexible modeling technique, we can easily design solid geometric shapes with sharp features and associated high frequency material properties. Since the control vectors include the position
5 of control points and associated control coefficients, editing of control points and/or control coefficients offer more powerful modeling capabilities. Based on our experiments, we observe that associating control points to a domain in such a way: locating control points at the edges of tetrahedra of the domain, can well preserve the shape and features represented by the original domain. The difference between the geometry of the domain and the resulting DMS solid object is very small. Moving control points around can lead to a desired deformation of the underlying model easily. Figure 2 shows an example. Figure 2 shows the domain of the cubic DMS solid, which is a torus. The user moves the control points to the new locations as shown in the solid mesh in Figure 2. Six very sharp corners are formed on the original solid object. its quality conforming Delaunay mesh. Badly shaped elements from the mesh are eliminated and replaced with well shaped ones. This is done by automatically inserting additional points into current mesh. From Figure 4, we can see that more knots are generated around feature edges. By associating control points with the defined domain, all the features are preserved in the resulting DMS solid of degree 4. Please refer to Figure 4(d). Figure 2: The domain is a torus. The deformation of the object is achieved by moving the control points to the new locations. The mesh shows a part of control nets, while the flat shaded surface indicates the resulting solid objects. Usually when the number of control points is very large, it is tedious and relatively difficult to manipulate the control points individually. In our system we provide Free-Form Deformation (FFD) tools to allow users to move control points. Figure 3 shows another example, where the domain is 5 separated tori as shown in Figure 3, and the DMS solid is quadratic. After the initial control points are generated, the user employ the bending FFD tool to relocate the control points to achieve the design shown in Figure 3. Note that, it is almost impossible for B-splines to model such objects whose domain is of non-trivial topology. Figure 3: The domain consists of 5 separated tori, which is of non-trivial topology. The deformation of the object is achieved by bending the control net. Figure 4 shows another example. The user first builds a 3D piecewise linear complex as shown in Figure 4, then our system generates (c) Figure 4: The piecewise linear boundary constraints that the user specifies. The multiresolution tetrahedralization conforming to the piecewise linear boundary constraints. (c) The color map of material distribution of the designed object. (d) Volume rendering of the designed object, where we can see that all the geometric shape features are preserved Attribute Editing Using Control Coefficients or Control Points Besides modeling solid geometry, the user can easily edit associated physical or material attributes as well. This is achieved by editing control coefficients at the corresponding control points, because the underlying material distribution is in fact a trivariate simplex spline defined over the same tetrahedralization. In the most simple form, the (multi-dimensional) control coefficients can be in one-to-one correspondence to their control-point counterparts which are used to define arbitrarily curved solid geometry over the same parametric domain (which is the initial tetrahedralization). However, local refinements for material modeling are frequently desirable in order to represent high-frequency features in the material domain. Our system allows users to interactively sketch skeletons. Each skeletal element is then associated with a locally defined implicit function; individual functions are blended using a polynomial weighting function that can be controlled by the user. After specifying these, the scalar control coefficients of the DMS-spline solid are assigned as the evaluations of the blending of field functions g i of a set of skeletons s i (i = 1,,N) at the positions of corresponding control points, N f (x,y,z)= g i (x,y,z), (8) i=1 where the skeletons s i can be any geometric primitive admitting a well defined distance function: points, curves, parametric surfaces, (d)
6 simple volumes, etc. The field functions g i are decreasing functions of the distance to the associated skeleton, g i (x,y,z)=g i (d(x,y,z,s i )), (9) where d(x,y,z,s i ) is the distance between (x,y,z) and s i, and G i can be defined by pieces of polynomials or by more sophisticated anisotropic functions. Therefore, the user may enforce global and local control of an underlying scalar field in three separate ways: (1) defining or manipulating of the skeleton, (2) defining or adjusting those implicit functions defined for each skeletal element, and (3) defining a blending function to weight the individual implicit functions. Figure 4 shows an example, where the user uses a mouse to freely sketch a curve inside the engineering part and defines an implicit function, f (d) = 1, to associate with the skeleton. Then the 1+d 2 scalar control coefficients at the control points are assigned according to the skeleton function. The resulting material distribution is shown in Figure 4(c)(d). As shown in Figure 5, the user sketches a solid modeling conference logo, SM, with free hand inside a domain, which is a torus. After associating control points with the torus domain and assigning control coefficients according to the distance function to the sketched curve logo, the resulting geometry and its associated scalar field can be easily generated. In this example, we use a trivariate DMS-spline of degree 4. Figure 5 shows the volume rendering of the entire object. We can clearly see the resulting geometry and its associated attribute field. In Figure 5, the shaded surface shows the isosurface of the attribute field of the solid torus, which is generated using Marching Tetrahedra Method that we developed (We will discuss it in Section 6.2). Figure 5: Editing attributes inside the tetrahedral domain of the torus model. From the direct volume rendering, we can clearly see the geometric boundary of the torus and the highlighted attributes. Marching tetrahedra rendering of an isosurface of the resulting attribute field over the torus model. The greyscale background shows the torus geometry. In Figure 6, the user is trying to design a digest system of the bunny model. The user draws a ellipsoid like shape to represent its stomach and two pipes adjacent to it (Illustrated in Figure 6). Figure 6 shows the tetrahedralization of the bunny, which serves as the domain. In this example, we use a quadratic trivariate DMSspline. After associating control points with the domain, the resulting geometry and its associated attribute field can be easily generated. Please see Figure 6(c)(d). (c) Figure 6: Define a skeleton inside the Stanford bunny model for material editing. The generated tetrahedral mesh of the Stanford bunny model. (c) Direct volume rendering of the resulting attribute field over the bunny model. (d) The color map of one slice of the bunny model shows the resulting attribute distribution. By aligning free knots along the feature lines/faces in the domain, sharp features in both geometric and attribute fields can be modeled. As we state in Section 4.2, associating control points to the edges of tetrahedra of a domain can also well preserve the shape and features represented by the original domain. Let us see Figure 4 as an example. All the geometric features shown in the original domain are well preserved in the final resulting geometric object as shown in Figure 4(d). In addition, by moving the control points, we can perform FFD of the underlying geometric object. As a result, this procedure deforms the associated attribute field. This is an alternate interaction mechanism for editing attributes. 5. Feature Sensitive Data Fitting To model data or attribute over the simplex spline based volume, it is much more desirable to have a fitting tool in addition to modeling tools as presented above. In this section, we propose a feature sensitive data fitting algorithm. That means the fitting algorithm can represent the data over the volume accurately and recover all the features with as few control vectors and bases as possible. Also the geometry of the volume is recovered simultaneously. Note that in the following section, we mainly discuss how to fit an unstructured volume. In fact, it can be any format, consisting of a set of points with associated attributes (i.e., (x,y,z,d 1,,d n )). Figure 7 shows the spx model from the fluid dynamics research community. In order better to show the advantages of our fitting algorithm. We upsample the spx dataset from 2896 sampling points to points. (d)
7 points is finite. The number of tetrahedra needed for fitting at the desired accuracy depends on the user-specified error bound and the datasets Finding a Good Initial Tetrahedralization Figure 7: The point view of the spx dataset, where the color indicates the density difference. Volume rendering of the spx dataset The Fitting Algorithm The problem of fitting volume data can be stated as follows: given asetp = {p i } m i=1 of points p i =(x i,y i,z i,d i ) R 4, find a trivariate DMS volume s : R 3 R 4 that approximates P. Unlike the existing fitting algorithms with parametric representations which usually find a one-to-one mapping between the data points and the points in the parametric space, our method skips this parameterization procedure. As stated before, we first build up a tetrahedralization parametric domain which is close to the original geometry of the tobe-fitted dataset. This domain serves for fitting both geometry and attributes. We use the position (x i,y i,z i ) of the data point p i as its parametric value. Therefore, we need to minimize the following objective function: m mine = (p i s(x i,y i,z i )) 2. (10) i=1 Our fitting algorithm treats both control vectors and knots as free variables. In this way, it can greatly reduce the approximation error given the same number of control vectors and knots. The tight coupling of both geometry and attributes during data fitting enables further editing on the continuous representation by means of moving control points, FFD, or changing control coefficients as we discussed in the Section 4, even after the fitting process is done. We first give an overview of our fitting algorithm. Then we will discuss some related issues in detail. 1. Create a tetrahedral domain for the entire volume domain, which fully contains the fitted volumetric object; 2. Solve Equation 10 by treating control vectors as free variables. 3. for each node t i of the tetrahedralization, if the fitting error in its 1-ring neighboring tetrahedra is larger than a user-specified value, solve Equation 10 by treating the knots associated to t i as free variables. 4. For each tetrahedron, if its fitting error is larger than a threshold ε, then subdivide it into four tetrahedra and repeat (2-4) until the fitting error of every tetrahedron is less than ε This algorithm will not stop until the fitting error in each tetrahedron is less than the user-specified error bound. Then the discrete point set with the associated attribute field is converted to a continuous spline-based volumetric implicit function, which can be evaluated at arbitrary sampling resolution and rendered with the direct volume rendering or the Marching Tetrahedra algorithm. The fitting algorithm is guaranteed to converge since the number of sampling As we can see from the fitting algorithm, a good initial basis will save a lot of time of performing recursive refinement and local fitting. More important, it can help to preserve geometric features of the original volume datasets. Essentially, there should be more primary knots distributed in the region containing features. Therefore, the dataset will undergo a preprocessing stage before fitting. First we have to find the proper tetrahedralization of the point sets. We perform the Delaunay tetrahedralization of the point set. Now we have to consider how to remove those tetrahedra which are outside the actual object. We place a ball at every point, whose radius is equal to the shortest distance from this point to its one-ring neighbors. Then, we perform the union of balls to obtain an occupancy map, which can roughly indicates the boundary of the actual object. Figure 8 illustrates the occupancy map of the point set of the spx dataset. Third, we check each tetrahedron to see if all the center points of its six edges are inside this occupancy map. If not, this tetrahedron is clipped away. Figure 8 shows the occupancy map and the Delaunay tetrahedralization together, where we can see some of tetrahedra are outside the occupancy map. From Figure 8(c), we can see that all the outside tetrahedra are removed and the final tetrahedralization of the point set is obtained. In this paper, we consider the fact that the real datasets to be fitted are usually densely sampled. This algorithm does not work well for very scattered datasets. Note that, this preprocessing is to produce a tetrahedral domain, not to generate the tetrahedralization of the object. The domain tetrahedralization should be much coarser than the tetrahedralization of the object as shown in Figure 8(c). (c) Figure 8: Occupance map of the point set. The Delaunay tetrahedralization of the point set. (c) The final tetrahedralization after removing the outside tetrahedra. In order to let the generated tetrahedral domain faithfully reflect the nature of the object, the features should be considered in tetrahedralization. Essentially, we have two types of features since we consider both the geometry and physical attributes. Geometric features are one category and field features belongs to another category. Geometric features mean those regions where C 0 continuity occurs. We use an efficient algorithm to classify the boundary vertices. The boundary vertices are identified as corner vertex, curve vertex, and general boundary vertex. The classification algorithm is based on the solid angle at each vertex. The solid angle α i of
8 tetrahedron I(p 0,p 1,p 2,p 3 ) at vertex p 0 is defined to be the surface area formed by projecting each point on the face not containing p 0 to a unit sphere centered at p 0. An equation for the computation of solid angle α i is given by Liu et al.[lj94]: sin α i 2 = 12v/ 1 i< j< 3 [(l i0 + l j0 ) 2 lij 2 ], where v is the volume of T, and l ij is the length of the edge connecting vertices p i and p j.the solid angle α at the vertex p 0 is the sum of the solid angles in all tetrahedra incident at p 0. For an interior vertex, the solid angle is 4π, while the boundary vertex is less than 4π. We identify the type of p 0 as follows [HK03]: p 0 is a corner boundary vertex if α π 2 or 4π α π 2 p 0 is a curve boundary vertex if π 2 < α 3π 2 or π 2 < 4π α 3π 2 otherwise, p 0 is a general boundary vertex Once the vertices are classified, we can extract feature lines from those corner boundary vertices and curve boundary vertices. Starting from a corner vertex, p i, we can link adjacent edge vertices by examining each of its neighbor vertices, which are either corner boundary vertices or curve boundary vertices, and see if they have similar normal orientation N(p i ) N(p j ) A for some angular threshold A. Once the link is established, we start to traverse the neighbor one, p j, until it reaches another corner boundary points or it cannot proceed. The sharp feature lines of Spx dataset are shown in Figure 9 in red. We sample the feature lines based on their curvature and a userspecified sampling rate. As a result, all these feature lines are well preserved as the piecewise linear boundary of the initial tetrahedralization to represent the shape of the to-be-fitted object. We also check the curvature of boundary surfaces according to the classified general boundary vertices to determine the placement of primary knots on those boundary surfaces for the initial tetrahedralization. For the interior vertices, we can distribute the initial primary knots according to the density of the original sampling points of the dataset. After all the primary knots have been determined, we can perform constrained tetrahedralization to obtain the initial tetrahedralization. Figure 9 shows the constructed initial tetrahedralization. critical points, field discontinuity, high frequency region, etc. Ideally, these features should be detected and explicitly represented for constructing a feature-based tetrahedralization. However, it is still a challenging research problem in computer vision to find all the high level features such as surfaces, field discontinuity, and so on. That research topic is beyond the scope of this paper. In practice we simply employ a very straightforward method. We just allocate more primary knots in the region where the deviation of gradients is high. Based on the tetrahedralization constructed purely according to the geometric information, we calculate the deviation of gradients for each tetrahedron. If the deviation is greater than a threshold, we insert a new vertex into the tetrahedron, where the gradient magnitude is maximal in this tetrahedron. Then we split the tetrahedron locally to incorporate the vertex. After several iterations of such split operation, the final initial tetrahedralization is constructed Trivariate DMS-spline Fitting with Free Knots If only the control vectors are treated as variables in Equation 10, it falls into a very special category of nonlinear programming, i.e., unconstrained convex quadratic programming. where x =(...,c I β,...)t, Q = E = 1 2 xt Qx + c T x + f, m i=1 NI β (x i,y i,z i )N I β (x i,y i,z i )...., m c =(..., 2 p i Nβ I (x i,y i,z i ),...) T, i=1 and f = m i=1 p i 2. Note that, Q is a positive definite, symmetric and sparse matrix. Interior-point method can solve this problem very efficiently. When considering the knots as free variables in Equation 10, we need calculate the gradient with respect to knots. We derive the formula of the directional derivative of trivariate DMS-spline s(u) with respect to a knot t p,l (p N,0 l < n) along the direction v: where D tp,l,vs(u)=d v G(u)+H(u,v), (11) G(u)= 1 n + 1 c I β e jn(u V β I ), I Ω,i j =p β =n+1,β j l Figure 9: Geometric features of the spx dataset. The finally constructed initial tetrahedralization. and H(u, v)= µ j (v Xβ I )ci β N(u V β I ), I Ω,i j =p β =n,β j =l V I β = {...,t p,0,...,t p,l 1,t p,l,t p,l,t p,l+1,...,t p,n,...,}. So far the initial tetrahedralization only considers the explicit geometric features of the object. Features of its attribute field have not been taken into account. In a nutshell, field features include Note that the i j in above equation is the j-th element of 4-tuple I = (i 0,...,i 3 ) which represents the vertex indices of a tetrahedron I. We also need to pay special attention to the positions of knots.
9 To describe clearly, we classify the knots into two categories: the primary knots {t s,0 s N} and the sub-knots {t s,l s N,1 l n}. The primary knots must yield valid tetrahedralization in Ω and the sub-knots must satisfy Equation 3. Especially, the sub-knots on the boundary must lie outside of Ω. To prevent degeneracy, we also set the restriction to the minimal length between any two knots (either primary knots or sub-knots). Therefore, Equation 10 is a typical large-scale constrained nonlinear programming problem. It is usually very time consuming for solve this kind of problem. To simplify our implementation and improve the performance, we solve this problem locally, i.e., for each node t i of the tetrahedralization, if the fitting error in its 1-ring neighboring tetrahedra is larger than a user-specified value, then we solve Equation 10 by treating the knots associated to t i as free variables. Since all other knots are fixed, we can deal with a sub-problem of Equation 10, in which only {p j p j is in 1-ring neighboring of t i } are considered Local Adaptive Refinement The above volume data fitting procedure attempts to minimize the total squared distance of the volume data points p i to the DMSspline s. For some regions with dense points or sharp features, it is often desirable to introduce new degrees of freedom into the spline representation in order to improve the fitting quality. The goal of this refinement is to subdivide any domain tetrahedron whose fitting error is greater than a threshold. Essentially, this step is the knot insertion for DMS-spline. Seidel et al. [SV94] proved that the new control vectors of the refined domain can be computed with the polar form. To simplify our implementation, in this paper we simply treat all the control vectors as variables and solve Equation 10 again. Intuitively, local adaptive refinement is a further action for allocating tetrahedra around the feature parts. Error characterization and evaluation is an important issue at this step. In the adaptive refinement, both geometric features and field features are considered. For attribute data fitting, if the error metric inside a tetrahedron is greater than a user-specified value, a new knot is inserted at the location, where the gradient magnitude is largest inside the tetrahedron. For solid geometry fitting, a new inserted knot should be placed on the feature line. During the optimization, the primary knots can only move along the sharp feature. This is explicitly enforced since the feature lines have been detected. The sub-knots must lie on the feature line segment between two adjacent primary knots. Figure 10 shows the fitting results for the spx model. Figure 10 and shows the fitting with control vectors only, while Figure 10(c) and (d) shows the final fitting results with both control vectors and knots. Apparently, adjusting knots can greatly reduce the fitting error and achieve a better effect. Figure 11 shows the fitting results for a smooth engineering part, router. Figure 11 is the original data set. Figure 11 shows the final fitting result, which is fitted using both control vectors and knots. Figure 12 shows the fitting results for two separated engineering parts. Figure 12 shows the original data set. Figure 12 shows the final fitting result, which is fitted with both control vectors and knots. (c) Figure 10: - Fitting with control vectors only (front view and side view). (c)-(d) Fitting with both control vectors and knots (front view and side view). Figure 11: The original dataset, router, in point view, where the color indicates the attribute value. Fitting with both control vectors and knots. The final result is rendered using our marching tetrahedra algorithm. 6. Visualization Techniques 6.1. Direct Volume Rendering (d) Attribute distribution on a 3D solid object can be visualized in a number of ways, for example by color contours on a 2D slice, or by a polygonal approximation to a contour surface. Direct volume rendering refers to techniques which produce a projected image directly from the volume data, without intermediate constructs such as contour surface polygons. Among the direct volume rendering techniques, the ray casting approach typically casts rays from pixels in the screen into a volumetric dataset. The quantity that is accumulated for each ray originating in each pixel is converted into color or intensity and is assigned to the pixel. It assumes datasets scatter, occlude, generate, and reflect light. Volume rendering enhances three dimensional visualization of imaged tissue by providing translucent rendering. In addition to the standard 3D image analysis tools, volc The Eurographics Association 2004.
10 Figure 12: The original dataset, crosscube, in point view, where the color indicates the attribute value. Fitting with both control vectors and knots. The final result is rendered using the direct volume rendering algorithm. ume rendering allows the user to interactively define thresholds for opacity, color application, and brightness. Translucent rendering of volumetric data provides more information about a spatial relationship of different structures than standard 3D surface rendering. Direct volume rendering affords to quickly isolate tissue of interest, and quickly provides 3D spatial information for enhanced diagnostic confidence, improves surgical and treatment planning, and aids in education. In the proposed approach, we only consider absorption nature of the dataset. That is to say that the object is visualized by integrating the density of the trivariate simplex functions along the path of each casted ray as in [RE01]. The intensity of light passing through translucent material decreases exponentially. Therefore, I(a, b) = exp( g I β NI β (u(t))dt) 0 I Ω β =n = exp( g I β Nβ I (u(t))dt). I Ω β =n 0 The proposed direct rendering of scalar simplex spline functions is able to incrementally update complex volumetric data sets at interactive rates of several frames per second. Assume a control coefficient g I β changes with gi β. Then the new intensity of the pixel will be: I new (a,b)=i old (a,b)exp( g I β 0 Nβ I (u(t))dt). (12) Since Nβ I (u(t)) = d(p i,q j,r k,s l ) M(u(t) V I β ) as shown in Equation 5, the problem becomes how to evaluate R L 0 M(u(t) V I β )dt efficiently. Grounded on the theory of simplex splines, we derive the following analytic solution to compute the integral in a recursive fashion. In the following derivation, the notations has the same meanings as in 3.1. In order to save space, we abbreviate V I β to V. Suppose that u(t)=x c +td c, where x c and d c are constant vectors, which denote the starting point of a casted ray and the unit direction of the ray, respectively. Then when n > 0, using the linear decomposition, we can obtain: 3 M(u(t) V)dt = λ(x c +td c )M(x c +td c V \{x k j })dt 0 0 j=0 3 3 = ( λ(x c )+t µ(d c ))M(x c +td c V \{x k j })dt, 0 j=0 j=0 (13) where λ and µ have the same meaning as in Equation 1 and 2. Due to the existing of Equation 2 and D dc M(x c +td c V)=d c M(x c +td c V)= dm(x c +td c V),(14) dt then performing integration by parts, we can obtain, 3 t µ(d c )M(x c +td c V \{x k j })dt 0 j=0 = 1 td dc M(x c +td c V)dt n 0 = tm(x c +td c V) L 0 1 M(x c +td c V)dt n 0 = 1 M(x c +td c V)dt. (15) n 0 Replacing Equation 15 in Equation 13, we can obtain the following equation: M(x c +td c V)dt = 0 When n = 0, n n j=0 λ(x c ) M(x c +td c V\{x k j })dt. 0 (16) M(x c +td c V)dt = L 0 Vol(V). With the above equation, we can efficiently evaluate the integral of densities along a casted line. Besides the X-ray volume rendering, we can also perform general ray casting. Since the solid object is represented by a single trivariate DMS-spline, our ray casting avoids resampling and interpolation problems Marching Tetrahedra Isosurfacing Since the resulting heterogeneous solid object consists of tetrahedra, it is easy to perform marching tetrahedra isosurfacing to extract an isosurface of its associated field. Please refer to [CDM 94] for the detail of a marching tetrahedra algorithm. It is important to note that, based on the geometry of the primary knots, the samples may be spaced at non-unit intervals or distributed very irregularly. Our approach does not require resampling onto a regular voxel raster, which would introduce error. Furthermore, along tetrahedron edges, the process of isosurface extraction employs the original trivariate DMS-spline interpolation, which has the potential to avoid introducing sampling artifacts. Since traditional voxel-based sculpting systems employ trilinear interpolation, they exhibit aliasing when the voxel grid is scaled or deformed. Aliasing must then be eliminated by filtering most or all of the voxel grid. We avoid this problem by using what is essentially a higher-order C n 1 trivariate spline. If the objects modeled by our approach are originally smooth, they will remain smooth even if the control lattice is arbitrarily scaled or even deformed. If they contain C 0 or discontinuity region, these features will be preserved as well. A key aspect of isosurface extraction is normal vector computation. With our polynomial-based approach, it can be determined
11 Model data pts domain tetra control pts knots geometric fitting error field fitting error spx cubecross router Table 1: Statistics of Data fitting. analytically. Furthermore, the local evaluation can lead to multiresolution isosurface extraction. When a tetrahedron of the object is determined cross the isosurface of its associated field, and its size is larger than a specified threshold, we can evaluate the trivariate DMS-spline and upsample it locally to increase the resolution and then perform isosurfacing on those smaller cells. Please see the illustration in Figure 13. else some locations of the geometric object may not have attribute properties, or attribute properties are assigned to the locations outside the geometric object. When using the decoupling scheme, it is possible to model any number of attribute properties over the geometric object. Complicated geometries with simple attributes, and vice versa, may be represented at the resolution that best suits them. The gain may be a large savings in storage and execution time. Furthermore, noise is an important variable in any visualization involving measured data. Simplex splines generally provide a robust representation for a signal containing moderate noise. Compared with polygons, or higher dimensional analogues such as voxels, simplex splines generally represent a smooth function with fewer points. However, with our knots manipulation technique they can represent higher frequency features as well. Figure 13: The single tetrahedron in the solid object is larger than the specified size and is needed to be upsampled. Based on the corresponding domain tetrahedron (as shown in mesh), the tetrahedron in the solid object is upsampled. Each cell is scaled a little in order to clearly observe the upsampling result. 7. Implementation and Discussion We have implemented a prototype system on a PC with 3.0 GHz P4 CPU and 2GB of RAM. The system is written in C++ and OpenGL. In our system we incorporate the Phantom 1.0 device from Sensable Technologies into our user interface. Users can use a mouse or the Phantom to manipulate the control points or sketch the skeletons. Table 1 shows the statistics of the performance of our fitting algorithm on several datasets, where the fitting error is the mean square error. As one can see, we couple geometric and attribute representation together in order to provide a unified paradigm to explicitly model geometry, topology, and its associated attribute properties. However, one weak point of this representation is that if the geometric features and attribute field features are not conforming to each other, we have to select the higher resolution to model both, even though it might not necessary for one of them to have such a high resolution. A potential solution for this case is to decouple geometric and attribute representations. Thus, it offers more flexibility to construct different resolution of tetrahedralization of a domain to fit the geometry and attribute distribution, respectively. But special care of aligning the boundaries of two domains exactly the same must be taken, or 8. Conclusion In this paper we have articulated a new integral approach for representing, modeling, reconstructing, and visualizing multidimensional, physical attributes across any volumetric objects. In particular, we employ a trivariate simplex spline model that is defined over a tetrahedral decomposition of any 3D domain. The modeled volume can be of complicated geometry and arbitrary topology. The trivariate simplex spline model ideally serves the pressing needs of both visualization and modeling communities since the model makes use of a more general and flexible tetrahedral domain and offers a compact continuous representation at the same time. More importantly, it integrates geometry and attribute properties over domains of arbitrary topology, by modeling a complicated heterogeneous object with a single trivariate simplex spline without any additional operations of trimming or patching. All of the above attractive characteristics result from many appealing properties of trivariate simplex splines such as piecewise polynomials of low degree, high-order continuity, and sharp feature modeling through different knot placements. In addition, we have developed a feature-sensitive fitting algorithm that can reconstruct a more compact trivariate simplex spline from a structured or unstructured volume. It reconstructs the geometry and the associated material attributes simultaneously, satisfying various continuity requirements set by the user. Such flexibility allows us to model continuous or discontinuous material distribution with ease. Our new representation can also facilitate multiresolution, local adaptive subdivision, free-form deformation, both isosurface and volume rendering, as well as other modeling and visualization functionalities. This is mainly because many of its nice analytical properties and associated computational tools. Based on our extensive experiments on using the trivariate simplex spline, we believe that our new paradigm can significantly advance the current state of the
12 knowledge in modeling and visualizing heterogeneous models of physical objects and their material properties. Besides solid modeling and volume visualization, in the near future we are pursuing other application directions including general data modeling, material editing and reconstruction, geometric processing of bio-medical and geological datasets, dynamic simulation and analysis of multiresolution, heterogeneous objects, etc. References [CCM 00] CIGNONI P., CONSTANZA D., MONTANI C., ROC- CHINI C., SCOPIGNO R.: Simplification of tetrahedral meshes with accurate error evaluation. In Proceedings of the conference on Visualization 00 (2000), pp [CDM 94] CIGNONI P., DE FLORIANI L., MONTANI C., PUPPO E., SCOPIGNO R.: Multiresolution modeling and visualization of volume data based on simplicial complexes. In Proceedings of the 1994 symposium on Volume visualization (1994), pp [db76] DE BOOR C.: Splines as linear combinations of B- splines. In Approximation Theory II (1976), Academic Press, New York, pp [DMS92] DAHMEN W., MICCHELLI C. A., SEIDEL H.-P.: Blossoming begets B-spline bases buit better by b- patches. Mathematics of Computation 59, 199 (1992), [ES92] EDELSBRUNNER H., SHAH N. R.: Incremental topological flipping works for regular triangulations. In Proceedings of 8th Annual ACM Symposium on Computational Geometry (1992), pp [GS94] GREINER G., SEIDEL H. P.: Modeling with triangular B-splines. IEEE Computer Graphics and Applications 14, 2 (1994), [HK03] HONG W., KAUFMAN A.: Feature preserved volume simplification. In Proceedings of the Eighth ACM Symposium on Solid Modeling and Applications (2003), pp [HQ01] HUA J., QIN H.: Haptic sculpting of volumetric implicit functions. In Proceedings of 9th Pacific Conference on Computer Graphics and Applications (2001), pp [HQ02] HUA J., QIN H.: Haptics-based volumetric modeling using dynamic spline-based implicit functions. In Proceedings of IEEE Symposium on Volume Visualization and Graphics (2002), pp [HQ04] HE Y., QIN H.: Surface reconstruction with triangular B-splines. In Proceedings of Geometric Modeling and Processing, (2004). [Joe91] JOE B.: Construction of three-dimensional triangulations using local transformations. Computer Aided Geometric Design 8 (1991), [LJ94] LIU A., JOE B.: Relationship between tetrahedron shape measures. BIT 34, 2 (1994), [MC01] MARTIN W., COHEN E.: Representation and extraction of volumetric attributes using trivariate splines: A mathematical framework. In Proceedings of the 7th ACM Symposium on Solid Modeling and Applications (2001), pp [PS94] PFEIFLE R., SEIDEL H.-P.: Faster evaluation of quadratic bivariate dms spline surfaces. In Proceedings of Graphics Interface 94 (1994), pp [PS95] PFEIFLE R., SEIDEL H.-P.: Fitting triangular B-splines to functional scattered data. In Proceedings of Graphics Interface 95 (1995), pp [QT96] QIN H., TERZOPOULOS D.: D-NURBS: A physicsbased framework for geometric design. IEEE Trans. on Visualization and Computer Graphics 2, 1 (1996), [QT97] QIN H., TERZOPOULOS D.: Triangular NURBS and their dynamic generalizations. Computer Aided Geometric Design 14, 4 (1997), [RE99] RAVIV A., ELBER G.: Three dimensioinal freeform sculpting via zero sets of scalar trivariate functions. In Proceedings of 5th ACM Symposium on Solid Modeling and Applications (1999), pp [RE01] RAVIV A., ELBER G.: Interactive direct rendering of trivariate B-spline scalar functions. IEEE Transactions on Visualization and Computer Graphics 7, 2 (2001), [RN00] ROXBOROUGH T., NIELSON G. M.: Tetrahedron based, least squares, progressive volume models with application to freehand ultrasound data. In Proceedings of the conference on Visualization 00 (2000), pp [She97] SHEWCHUK J. R.: Delaunay Refinement Mesh Generation. PhD thesis, School of Computer Science, Carnegie Mellon University, [SPS01] SCHMITT B., PASKO A., SCHLICK C.: Constructive modeling of frep solids using spline volumes. In Proceedings of the 6th ACM symposium on Solid modeling and applications (2001), pp [SV94] SEIDEL H.-P., VERMEULEN A. H.: Simplex splines support surprisingly strong symmetric structures and subdivision. In Curves and Surfaces II. AK Peters, 1994, pp [THJ99] TROTTS I. J., HAMANN B., JOY K. I.: Simplification of tetrahedral meshes with error bounds. IEEE Trans. on Visualization and Computer Graphics 5, 3 (1999), [YT00] YAO J., TAYLOR R. H.: Tetrahedral mesh modeling of density data for anatomical atlases and intensitybased registration. In Proceedings of the third International Conference on Medical Image Computing and Computer-Assisted Intervention (2000), pp
Computer Graphics. Geometric Modeling. Page 1. Copyright Gotsman, Elber, Barequet, Karni, Sheffer Computer Science - Technion. An Example.
 An Example 2 3 4 Outline Objective: Develop methods and algorithms to mathematically model shape of real world objects Categories: Wire-Frame Representation Object is represented as as a set of points
An Example 2 3 4 Outline Objective: Develop methods and algorithms to mathematically model shape of real world objects Categories: Wire-Frame Representation Object is represented as as a set of points
Constrained Tetrahedral Mesh Generation of Human Organs on Segmented Volume *
 Constrained Tetrahedral Mesh Generation of Human Organs on Segmented Volume * Xiaosong Yang 1, Pheng Ann Heng 2, Zesheng Tang 3 1 Department of Computer Science and Technology, Tsinghua University, Beijing
Constrained Tetrahedral Mesh Generation of Human Organs on Segmented Volume * Xiaosong Yang 1, Pheng Ann Heng 2, Zesheng Tang 3 1 Department of Computer Science and Technology, Tsinghua University, Beijing
We can display an object on a monitor screen in three different computer-model forms: Wireframe model Surface Model Solid model
 CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
CHAPTER 1 Splines and B-splines an Introduction
 CHAPTER 1 Splines and B-splines an Introduction In this first chapter, we consider the following fundamental problem: Given a set of points in the plane, determine a smooth curve that approximates the
CHAPTER 1 Splines and B-splines an Introduction In this first chapter, we consider the following fundamental problem: Given a set of points in the plane, determine a smooth curve that approximates the
Geometric Modelling & Curves
 Geometric Modelling & Curves Geometric Modeling Creating symbolic models of the physical world has long been a goal of mathematicians, scientists, engineers, etc. Recently technology has advanced sufficiently
Geometric Modelling & Curves Geometric Modeling Creating symbolic models of the physical world has long been a goal of mathematicians, scientists, engineers, etc. Recently technology has advanced sufficiently
A Short Introduction to Computer Graphics
 A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
Computer Graphics CS 543 Lecture 12 (Part 1) Curves. Prof Emmanuel Agu. Computer Science Dept. Worcester Polytechnic Institute (WPI)
 Computer Graphics CS 54 Lecture 1 (Part 1) Curves Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) So Far Dealt with straight lines and flat surfaces Real world objects include
Computer Graphics CS 54 Lecture 1 (Part 1) Curves Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) So Far Dealt with straight lines and flat surfaces Real world objects include
Part-Based Recognition
 Part-Based Recognition Benedict Brown CS597D, Fall 2003 Princeton University CS 597D, Part-Based Recognition p. 1/32 Introduction Many objects are made up of parts It s presumably easier to identify simple
Part-Based Recognition Benedict Brown CS597D, Fall 2003 Princeton University CS 597D, Part-Based Recognition p. 1/32 Introduction Many objects are made up of parts It s presumably easier to identify simple
The Essentials of CAGD
 The Essentials of CAGD Chapter 2: Lines and Planes Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/essentials-cagd c 2000 Farin & Hansford
The Essentials of CAGD Chapter 2: Lines and Planes Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/essentials-cagd c 2000 Farin & Hansford
CSE 167: Lecture 13: Bézier Curves. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011
 CSE 167: Introduction to Computer Graphics Lecture 13: Bézier Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Homework project #6 due Friday, Nov 18
CSE 167: Introduction to Computer Graphics Lecture 13: Bézier Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Homework project #6 due Friday, Nov 18
Volume visualization I Elvins
 Volume visualization I Elvins 1 surface fitting algorithms marching cubes dividing cubes direct volume rendering algorithms ray casting, integration methods voxel projection, projected tetrahedra, splatting
Volume visualization I Elvins 1 surface fitting algorithms marching cubes dividing cubes direct volume rendering algorithms ray casting, integration methods voxel projection, projected tetrahedra, splatting
An Overview of the Finite Element Analysis
 CHAPTER 1 An Overview of the Finite Element Analysis 1.1 Introduction Finite element analysis (FEA) involves solution of engineering problems using computers. Engineering structures that have complex geometry
CHAPTER 1 An Overview of the Finite Element Analysis 1.1 Introduction Finite element analysis (FEA) involves solution of engineering problems using computers. Engineering structures that have complex geometry
Degree Reduction of Interval SB Curves
 International Journal of Video&Image Processing and Network Security IJVIPNS-IJENS Vol:13 No:04 1 Degree Reduction of Interval SB Curves O. Ismail, Senior Member, IEEE Abstract Ball basis was introduced
International Journal of Video&Image Processing and Network Security IJVIPNS-IJENS Vol:13 No:04 1 Degree Reduction of Interval SB Curves O. Ismail, Senior Member, IEEE Abstract Ball basis was introduced
Figure 2.1: Center of mass of four points.
 Chapter 2 Bézier curves are named after their inventor, Dr. Pierre Bézier. Bézier was an engineer with the Renault car company and set out in the early 196 s to develop a curve formulation which would
Chapter 2 Bézier curves are named after their inventor, Dr. Pierre Bézier. Bézier was an engineer with the Renault car company and set out in the early 196 s to develop a curve formulation which would
Finite Element Formulation for Plates - Handout 3 -
 Finite Element Formulation for Plates - Handout 3 - Dr Fehmi Cirak (fc286@) Completed Version Definitions A plate is a three dimensional solid body with one of the plate dimensions much smaller than the
Finite Element Formulation for Plates - Handout 3 - Dr Fehmi Cirak (fc286@) Completed Version Definitions A plate is a three dimensional solid body with one of the plate dimensions much smaller than the
Dual Marching Cubes: Primal Contouring of Dual Grids
 Dual Marching Cubes: Primal Contouring of Dual Grids Scott Schaefer and Joe Warren Rice University 6100 Main St. Houston, TX 77005 [email protected] and [email protected] Abstract We present a method for
Dual Marching Cubes: Primal Contouring of Dual Grids Scott Schaefer and Joe Warren Rice University 6100 Main St. Houston, TX 77005 [email protected] and [email protected] Abstract We present a method for
Point Lattices in Computer Graphics and Visualization how signal processing may help computer graphics
 Point Lattices in Computer Graphics and Visualization how signal processing may help computer graphics Dimitri Van De Ville Ecole Polytechnique Fédérale de Lausanne Biomedical Imaging Group [email protected]
Point Lattices in Computer Graphics and Visualization how signal processing may help computer graphics Dimitri Van De Ville Ecole Polytechnique Fédérale de Lausanne Biomedical Imaging Group [email protected]
Multiphysics Software Applications in Reverse Engineering
 Multiphysics Software Applications in Reverse Engineering *W. Wang 1, K. Genc 2 1 University of Massachusetts Lowell, Lowell, MA, USA 2 Simpleware, Exeter, United Kingdom *Corresponding author: University
Multiphysics Software Applications in Reverse Engineering *W. Wang 1, K. Genc 2 1 University of Massachusetts Lowell, Lowell, MA, USA 2 Simpleware, Exeter, United Kingdom *Corresponding author: University
From Scattered Samples to Smooth Surfaces
 From Scattered Samples to Smooth Surfaces Kai Hormann 1 California Institute of Technology (a) (b) (c) (d) Figure 1: A point cloud with 4,100 scattered samples (a), its triangulation with 7,938 triangles
From Scattered Samples to Smooth Surfaces Kai Hormann 1 California Institute of Technology (a) (b) (c) (d) Figure 1: A point cloud with 4,100 scattered samples (a), its triangulation with 7,938 triangles
3. Interpolation. Closing the Gaps of Discretization... Beyond Polynomials
 3. Interpolation Closing the Gaps of Discretization... Beyond Polynomials Closing the Gaps of Discretization... Beyond Polynomials, December 19, 2012 1 3.3. Polynomial Splines Idea of Polynomial Splines
3. Interpolation Closing the Gaps of Discretization... Beyond Polynomials Closing the Gaps of Discretization... Beyond Polynomials, December 19, 2012 1 3.3. Polynomial Splines Idea of Polynomial Splines
How To Create A Surface From Points On A Computer With A Marching Cube
 Surface Reconstruction from a Point Cloud with Normals Landon Boyd and Massih Khorvash Department of Computer Science University of British Columbia,2366 Main Mall Vancouver, BC, V6T1Z4, Canada {blandon,khorvash}@cs.ubc.ca
Surface Reconstruction from a Point Cloud with Normals Landon Boyd and Massih Khorvash Department of Computer Science University of British Columbia,2366 Main Mall Vancouver, BC, V6T1Z4, Canada {blandon,khorvash}@cs.ubc.ca
Curves and Surfaces. Goals. How do we draw surfaces? How do we specify a surface? How do we approximate a surface?
 Curves and Surfaces Parametric Representations Cubic Polynomial Forms Hermite Curves Bezier Curves and Surfaces [Angel 10.1-10.6] Goals How do we draw surfaces? Approximate with polygons Draw polygons
Curves and Surfaces Parametric Representations Cubic Polynomial Forms Hermite Curves Bezier Curves and Surfaces [Angel 10.1-10.6] Goals How do we draw surfaces? Approximate with polygons Draw polygons
A Generalized Marching Cubes Algorithm Based On Non-Binary Classifications
 Konrad-Zuse-Zentrum fu r Informationstechnik Berlin Takustraße 7 D-14195 Berlin-Dahlem Germany HANS-CHRISTIAN HEGE DETLEV STALLING MARTIN SEEBASS MALTE ZOCKLER A Generalized Marching Cubes Algorithm Based
Konrad-Zuse-Zentrum fu r Informationstechnik Berlin Takustraße 7 D-14195 Berlin-Dahlem Germany HANS-CHRISTIAN HEGE DETLEV STALLING MARTIN SEEBASS MALTE ZOCKLER A Generalized Marching Cubes Algorithm Based
the points are called control points approximating curve
 Chapter 4 Spline Curves A spline curve is a mathematical representation for which it is easy to build an interface that will allow a user to design and control the shape of complex curves and surfaces.
Chapter 4 Spline Curves A spline curve is a mathematical representation for which it is easy to build an interface that will allow a user to design and control the shape of complex curves and surfaces.
Lecture 7 - Meshing. Applied Computational Fluid Dynamics
 Lecture 7 - Meshing Applied Computational Fluid Dynamics Instructor: André Bakker http://www.bakker.org André Bakker (2002-2006) Fluent Inc. (2002) 1 Outline Why is a grid needed? Element types. Grid types.
Lecture 7 - Meshing Applied Computational Fluid Dynamics Instructor: André Bakker http://www.bakker.org André Bakker (2002-2006) Fluent Inc. (2002) 1 Outline Why is a grid needed? Element types. Grid types.
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
EECS 556 Image Processing W 09. Interpolation. Interpolation techniques B splines
 EECS 556 Image Processing W 09 Interpolation Interpolation techniques B splines What is image processing? Image processing is the application of 2D signal processing methods to images Image representation
EECS 556 Image Processing W 09 Interpolation Interpolation techniques B splines What is image processing? Image processing is the application of 2D signal processing methods to images Image representation
Volumetric Meshes for Real Time Medical Simulations
 Volumetric Meshes for Real Time Medical Simulations Matthias Mueller and Matthias Teschner Computer Graphics Laboratory ETH Zurich, Switzerland [email protected], http://graphics.ethz.ch/ Abstract.
Volumetric Meshes for Real Time Medical Simulations Matthias Mueller and Matthias Teschner Computer Graphics Laboratory ETH Zurich, Switzerland [email protected], http://graphics.ethz.ch/ Abstract.
NEW YORK STATE TEACHER CERTIFICATION EXAMINATIONS
 NEW YORK STATE TEACHER CERTIFICATION EXAMINATIONS TEST DESIGN AND FRAMEWORK September 2014 Authorized for Distribution by the New York State Education Department This test design and framework document
NEW YORK STATE TEACHER CERTIFICATION EXAMINATIONS TEST DESIGN AND FRAMEWORK September 2014 Authorized for Distribution by the New York State Education Department This test design and framework document
Model Repair. Leif Kobbelt RWTH Aachen University )NPUT $ATA 2EMOVAL OF TOPOLOGICAL AND GEOMETRICAL ERRORS !NALYSIS OF SURFACE QUALITY
 )NPUT $ATA 2ANGE 3CAN #!$ 4OMOGRAPHY 2EMOVAL OF TOPOLOGICAL AND GEOMETRICAL ERRORS!NALYSIS OF SURFACE QUALITY 3URFACE SMOOTHING FOR NOISE REMOVAL 0ARAMETERIZATION 3IMPLIFICATION FOR COMPLEXITY REDUCTION
)NPUT $ATA 2ANGE 3CAN #!$ 4OMOGRAPHY 2EMOVAL OF TOPOLOGICAL AND GEOMETRICAL ERRORS!NALYSIS OF SURFACE QUALITY 3URFACE SMOOTHING FOR NOISE REMOVAL 0ARAMETERIZATION 3IMPLIFICATION FOR COMPLEXITY REDUCTION
Segmentation of building models from dense 3D point-clouds
 Segmentation of building models from dense 3D point-clouds Joachim Bauer, Konrad Karner, Konrad Schindler, Andreas Klaus, Christopher Zach VRVis Research Center for Virtual Reality and Visualization, Institute
Segmentation of building models from dense 3D point-clouds Joachim Bauer, Konrad Karner, Konrad Schindler, Andreas Klaus, Christopher Zach VRVis Research Center for Virtual Reality and Visualization, Institute
Modelling, Extraction and Description of Intrinsic Cues of High Resolution Satellite Images: Independent Component Analysis based approaches
 Modelling, Extraction and Description of Intrinsic Cues of High Resolution Satellite Images: Independent Component Analysis based approaches PhD Thesis by Payam Birjandi Director: Prof. Mihai Datcu Problematic
Modelling, Extraction and Description of Intrinsic Cues of High Resolution Satellite Images: Independent Component Analysis based approaches PhD Thesis by Payam Birjandi Director: Prof. Mihai Datcu Problematic
2.5 Physically-based Animation
 2.5 Physically-based Animation 320491: Advanced Graphics - Chapter 2 74 Physically-based animation Morphing allowed us to animate between two known states. Typically, only one state of an object is known.
2.5 Physically-based Animation 320491: Advanced Graphics - Chapter 2 74 Physically-based animation Morphing allowed us to animate between two known states. Typically, only one state of an object is known.
A matrix method for degree-raising of B-spline curves *
 VOI. 40 NO. 1 SCIENCE IN CHINA (Series E) February 1997 A matrix method for degree-raising of B-spline curves * QIN Kaihuai (%*>/$) (Department of Computer Science and Technology, Tsinghua University,
VOI. 40 NO. 1 SCIENCE IN CHINA (Series E) February 1997 A matrix method for degree-raising of B-spline curves * QIN Kaihuai (%*>/$) (Department of Computer Science and Technology, Tsinghua University,
Mean Value Coordinates
 Mean Value Coordinates Michael S. Floater Abstract: We derive a generalization of barycentric coordinates which allows a vertex in a planar triangulation to be expressed as a convex combination of its
Mean Value Coordinates Michael S. Floater Abstract: We derive a generalization of barycentric coordinates which allows a vertex in a planar triangulation to be expressed as a convex combination of its
Algebra 1 2008. Academic Content Standards Grade Eight and Grade Nine Ohio. Grade Eight. Number, Number Sense and Operations Standard
 Academic Content Standards Grade Eight and Grade Nine Ohio Algebra 1 2008 Grade Eight STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express
Academic Content Standards Grade Eight and Grade Nine Ohio Algebra 1 2008 Grade Eight STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express
Constrained curve and surface fitting
 Constrained curve and surface fitting Simon Flöry FSP-Meeting Strobl (June 20, 2006), [email protected], Vienna University of Technology Overview Introduction Motivation, Overview, Problem
Constrained curve and surface fitting Simon Flöry FSP-Meeting Strobl (June 20, 2006), [email protected], Vienna University of Technology Overview Introduction Motivation, Overview, Problem
(Refer Slide Time: 1:42)
 Introduction to Computer Graphics Dr. Prem Kalra Department of Computer Science and Engineering Indian Institute of Technology, Delhi Lecture - 10 Curves So today we are going to have a new topic. So far
Introduction to Computer Graphics Dr. Prem Kalra Department of Computer Science and Engineering Indian Institute of Technology, Delhi Lecture - 10 Curves So today we are going to have a new topic. So far
Computer Applications in Textile Engineering. Computer Applications in Textile Engineering
 3. Computer Graphics Sungmin Kim http://latam.jnu.ac.kr Computer Graphics Definition Introduction Research field related to the activities that includes graphics as input and output Importance Interactive
3. Computer Graphics Sungmin Kim http://latam.jnu.ac.kr Computer Graphics Definition Introduction Research field related to the activities that includes graphics as input and output Importance Interactive
Introduction to the Finite Element Method (FEM)
 Introduction to the Finite Element Method (FEM) ecture First and Second Order One Dimensional Shape Functions Dr. J. Dean Discretisation Consider the temperature distribution along the one-dimensional
Introduction to the Finite Element Method (FEM) ecture First and Second Order One Dimensional Shape Functions Dr. J. Dean Discretisation Consider the temperature distribution along the one-dimensional
Introduction to the Finite Element Method
 Introduction to the Finite Element Method 09.06.2009 Outline Motivation Partial Differential Equations (PDEs) Finite Difference Method (FDM) Finite Element Method (FEM) References Motivation Figure: cross
Introduction to the Finite Element Method 09.06.2009 Outline Motivation Partial Differential Equations (PDEs) Finite Difference Method (FDM) Finite Element Method (FEM) References Motivation Figure: cross
Introduction to Computer Graphics
 Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 [email protected] www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 [email protected] www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Tetrahedron Meshes. Linh Ha
 Tetrahedron Meshes Linh Ha Overview Fundamental Tetrahedron meshing Meshing polyhedra Tetrahedral shape Delaunay refinements Removing silver Variational Tetrahedral Meshing Meshing Polyhedra Is that easy?
Tetrahedron Meshes Linh Ha Overview Fundamental Tetrahedron meshing Meshing polyhedra Tetrahedral shape Delaunay refinements Removing silver Variational Tetrahedral Meshing Meshing Polyhedra Is that easy?
Efficient Storage, Compression and Transmission
 Efficient Storage, Compression and Transmission of Complex 3D Models context & problem definition general framework & classification our new algorithm applications for digital documents Mesh Decimation
Efficient Storage, Compression and Transmission of Complex 3D Models context & problem definition general framework & classification our new algorithm applications for digital documents Mesh Decimation
Topographic Change Detection Using CloudCompare Version 1.0
 Topographic Change Detection Using CloudCompare Version 1.0 Emily Kleber, Arizona State University Edwin Nissen, Colorado School of Mines J Ramón Arrowsmith, Arizona State University Introduction CloudCompare
Topographic Change Detection Using CloudCompare Version 1.0 Emily Kleber, Arizona State University Edwin Nissen, Colorado School of Mines J Ramón Arrowsmith, Arizona State University Introduction CloudCompare
OpenFOAM Optimization Tools
 OpenFOAM Optimization Tools Henrik Rusche and Aleks Jemcov [email protected] and [email protected] Wikki, Germany and United Kingdom OpenFOAM Optimization Tools p. 1 Agenda Objective Review optimisation
OpenFOAM Optimization Tools Henrik Rusche and Aleks Jemcov [email protected] and [email protected] Wikki, Germany and United Kingdom OpenFOAM Optimization Tools p. 1 Agenda Objective Review optimisation
2.2 Creaseness operator
 2.2. Creaseness operator 31 2.2 Creaseness operator Antonio López, a member of our group, has studied for his PhD dissertation the differential operators described in this section [72]. He has compared
2.2. Creaseness operator 31 2.2 Creaseness operator Antonio López, a member of our group, has studied for his PhD dissertation the differential operators described in this section [72]. He has compared
Robust NURBS Surface Fitting from Unorganized 3D Point Clouds for Infrastructure As-Built Modeling
 81 Robust NURBS Surface Fitting from Unorganized 3D Point Clouds for Infrastructure As-Built Modeling Andrey Dimitrov 1 and Mani Golparvar-Fard 2 1 Graduate Student, Depts of Civil Eng and Engineering
81 Robust NURBS Surface Fitting from Unorganized 3D Point Clouds for Infrastructure As-Built Modeling Andrey Dimitrov 1 and Mani Golparvar-Fard 2 1 Graduate Student, Depts of Civil Eng and Engineering
In mathematics, there are four attainment targets: using and applying mathematics; number and algebra; shape, space and measures, and handling data.
 MATHEMATICS: THE LEVEL DESCRIPTIONS In mathematics, there are four attainment targets: using and applying mathematics; number and algebra; shape, space and measures, and handling data. Attainment target
MATHEMATICS: THE LEVEL DESCRIPTIONS In mathematics, there are four attainment targets: using and applying mathematics; number and algebra; shape, space and measures, and handling data. Attainment target
Current Standard: Mathematical Concepts and Applications Shape, Space, and Measurement- Primary
 Shape, Space, and Measurement- Primary A student shall apply concepts of shape, space, and measurement to solve problems involving two- and three-dimensional shapes by demonstrating an understanding of:
Shape, Space, and Measurement- Primary A student shall apply concepts of shape, space, and measurement to solve problems involving two- and three-dimensional shapes by demonstrating an understanding of:
Draft Martin Doerr ICS-FORTH, Heraklion, Crete Oct 4, 2001
 A comparison of the OpenGIS TM Abstract Specification with the CIDOC CRM 3.2 Draft Martin Doerr ICS-FORTH, Heraklion, Crete Oct 4, 2001 1 Introduction This Mapping has the purpose to identify, if the OpenGIS
A comparison of the OpenGIS TM Abstract Specification with the CIDOC CRM 3.2 Draft Martin Doerr ICS-FORTH, Heraklion, Crete Oct 4, 2001 1 Introduction This Mapping has the purpose to identify, if the OpenGIS
HIGH AND LOW RESOLUTION TEXTURED MODELS OF COMPLEX ARCHITECTURAL SURFACES
 HIGH AND LOW RESOLUTION TEXTURED MODELS OF COMPLEX ARCHITECTURAL SURFACES E. K. Stathopoulou a, A. Valanis a, J. L. Lerma b, A. Georgopoulos a a Laboratory of Photogrammetry, National Technical University
HIGH AND LOW RESOLUTION TEXTURED MODELS OF COMPLEX ARCHITECTURAL SURFACES E. K. Stathopoulou a, A. Valanis a, J. L. Lerma b, A. Georgopoulos a a Laboratory of Photogrammetry, National Technical University
Back to Elements - Tetrahedra vs. Hexahedra
 Back to Elements - Tetrahedra vs. Hexahedra Erke Wang, Thomas Nelson, Rainer Rauch CAD-FEM GmbH, Munich, Germany Abstract This paper presents some analytical results and some test results for different
Back to Elements - Tetrahedra vs. Hexahedra Erke Wang, Thomas Nelson, Rainer Rauch CAD-FEM GmbH, Munich, Germany Abstract This paper presents some analytical results and some test results for different
Mathematics Course 111: Algebra I Part IV: Vector Spaces
 Mathematics Course 111: Algebra I Part IV: Vector Spaces D. R. Wilkins Academic Year 1996-7 9 Vector Spaces A vector space over some field K is an algebraic structure consisting of a set V on which are
Mathematics Course 111: Algebra I Part IV: Vector Spaces D. R. Wilkins Academic Year 1996-7 9 Vector Spaces A vector space over some field K is an algebraic structure consisting of a set V on which are
PATTERN RECOGNITION AND MACHINE LEARNING CHAPTER 4: LINEAR MODELS FOR CLASSIFICATION
 PATTERN RECOGNITION AND MACHINE LEARNING CHAPTER 4: LINEAR MODELS FOR CLASSIFICATION Introduction In the previous chapter, we explored a class of regression models having particularly simple analytical
PATTERN RECOGNITION AND MACHINE LEARNING CHAPTER 4: LINEAR MODELS FOR CLASSIFICATION Introduction In the previous chapter, we explored a class of regression models having particularly simple analytical
Visualization and Feature Extraction, FLOW Spring School 2016 Prof. Dr. Tino Weinkauf. Flow Visualization. Image-Based Methods (integration-based)
 Visualization and Feature Extraction, FLOW Spring School 2016 Prof. Dr. Tino Weinkauf Flow Visualization Image-Based Methods (integration-based) Spot Noise (Jarke van Wijk, Siggraph 1991) Flow Visualization:
Visualization and Feature Extraction, FLOW Spring School 2016 Prof. Dr. Tino Weinkauf Flow Visualization Image-Based Methods (integration-based) Spot Noise (Jarke van Wijk, Siggraph 1991) Flow Visualization:
Section 1.1. Introduction to R n
 The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
Customer Training Material. Lecture 2. Introduction to. Methodology ANSYS FLUENT. ANSYS, Inc. Proprietary 2010 ANSYS, Inc. All rights reserved.
 Lecture 2 Introduction to CFD Methodology Introduction to ANSYS FLUENT L2-1 What is CFD? Computational Fluid Dynamics (CFD) is the science of predicting fluid flow, heat and mass transfer, chemical reactions,
Lecture 2 Introduction to CFD Methodology Introduction to ANSYS FLUENT L2-1 What is CFD? Computational Fluid Dynamics (CFD) is the science of predicting fluid flow, heat and mass transfer, chemical reactions,
Image Segmentation and Registration
 Image Segmentation and Registration Dr. Christine Tanner ([email protected]) Computer Vision Laboratory, ETH Zürich Dr. Verena Kaynig, Machine Learning Laboratory, ETH Zürich Outline Segmentation
Image Segmentation and Registration Dr. Christine Tanner ([email protected]) Computer Vision Laboratory, ETH Zürich Dr. Verena Kaynig, Machine Learning Laboratory, ETH Zürich Outline Segmentation
Automatic 3D Reconstruction via Object Detection and 3D Transformable Model Matching CS 269 Class Project Report
 Automatic 3D Reconstruction via Object Detection and 3D Transformable Model Matching CS 69 Class Project Report Junhua Mao and Lunbo Xu University of California, Los Angeles [email protected] and lunbo
Automatic 3D Reconstruction via Object Detection and 3D Transformable Model Matching CS 69 Class Project Report Junhua Mao and Lunbo Xu University of California, Los Angeles [email protected] and lunbo
Direct Volume Rendering Elvins
 Direct Volume Rendering Elvins 1 Principle: rendering of scalar volume data with cloud-like, semi-transparent effects forward mapping object-order backward mapping image-order data volume screen voxel
Direct Volume Rendering Elvins 1 Principle: rendering of scalar volume data with cloud-like, semi-transparent effects forward mapping object-order backward mapping image-order data volume screen voxel
H.Calculating Normal Vectors
 Appendix H H.Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use the OpenGL lighting facility, which is described in Chapter
Appendix H H.Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use the OpenGL lighting facility, which is described in Chapter
Anatomic Modeling from Unstructured Samples Using Variational Implicit Surfaces
 Studies in Health Technology and Informatics, vol. 81 (Proceedings of Medicine Meets Virtual Reality 2001. J. D. Westwood, et al., eds.), Amsterdam: IOS Press, pp. 594-600. Anatomic Modeling from Unstructured
Studies in Health Technology and Informatics, vol. 81 (Proceedings of Medicine Meets Virtual Reality 2001. J. D. Westwood, et al., eds.), Amsterdam: IOS Press, pp. 594-600. Anatomic Modeling from Unstructured
Recovering Primitives in 3D CAD meshes
 Recovering Primitives in 3D CAD meshes Roseline Bénière a,c, Gérard Subsol a, Gilles Gesquière b, François Le Breton c and William Puech a a LIRMM, Univ. Montpellier 2, CNRS, 161 rue Ada, 34392, France;
Recovering Primitives in 3D CAD meshes Roseline Bénière a,c, Gérard Subsol a, Gilles Gesquière b, François Le Breton c and William Puech a a LIRMM, Univ. Montpellier 2, CNRS, 161 rue Ada, 34392, France;
Compact Representations and Approximations for Compuation in Games
 Compact Representations and Approximations for Compuation in Games Kevin Swersky April 23, 2008 Abstract Compact representations have recently been developed as a way of both encoding the strategic interactions
Compact Representations and Approximations for Compuation in Games Kevin Swersky April 23, 2008 Abstract Compact representations have recently been developed as a way of both encoding the strategic interactions
Optical Design Tools for Backlight Displays
 Optical Design Tools for Backlight Displays Introduction Backlights are used for compact, portable, electronic devices with flat panel Liquid Crystal Displays (LCDs) that require illumination from behind.
Optical Design Tools for Backlight Displays Introduction Backlights are used for compact, portable, electronic devices with flat panel Liquid Crystal Displays (LCDs) that require illumination from behind.
Arrangements And Duality
 Arrangements And Duality 3.1 Introduction 3 Point configurations are tbe most basic structure we study in computational geometry. But what about configurations of more complicated shapes? For example,
Arrangements And Duality 3.1 Introduction 3 Point configurations are tbe most basic structure we study in computational geometry. But what about configurations of more complicated shapes? For example,
Module1. x 1000. y 800.
 Module1 1 Welcome to the first module of the course. It is indeed an exciting event to share with you the subject that has lot to offer both from theoretical side and practical aspects. To begin with,
Module1 1 Welcome to the first module of the course. It is indeed an exciting event to share with you the subject that has lot to offer both from theoretical side and practical aspects. To begin with,
Intersection of a Line and a Convex. Hull of Points Cloud
 Applied Mathematical Sciences, Vol. 7, 213, no. 13, 5139-5149 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.12988/ams.213.37372 Intersection of a Line and a Convex Hull of Points Cloud R. P. Koptelov
Applied Mathematical Sciences, Vol. 7, 213, no. 13, 5139-5149 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.12988/ams.213.37372 Intersection of a Line and a Convex Hull of Points Cloud R. P. Koptelov
Selective Degree Elevation for Multi-Sided Bézier Patches
 EUROGRAPHICS 2015 / O. Sorkine-Hornung and M. Wimmer (Guest Editors) Volume 34 (2015), Number 2 Selective Degree Elevation for Multi-Sided Bézier Patches J. Smith 1 and S. Schaefer 1 1 Texas A&M University
EUROGRAPHICS 2015 / O. Sorkine-Hornung and M. Wimmer (Guest Editors) Volume 34 (2015), Number 2 Selective Degree Elevation for Multi-Sided Bézier Patches J. Smith 1 and S. Schaefer 1 1 Texas A&M University
4.1 Learning algorithms for neural networks
 4 Perceptron Learning 4.1 Learning algorithms for neural networks In the two preceding chapters we discussed two closely related models, McCulloch Pitts units and perceptrons, but the question of how to
4 Perceptron Learning 4.1 Learning algorithms for neural networks In the two preceding chapters we discussed two closely related models, McCulloch Pitts units and perceptrons, but the question of how to
Seminar. Path planning using Voronoi diagrams and B-Splines. Stefano Martina [email protected]
 Seminar Path planning using Voronoi diagrams and B-Splines Stefano Martina [email protected] 23 may 2016 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International
Seminar Path planning using Voronoi diagrams and B-Splines Stefano Martina [email protected] 23 may 2016 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International
NEW MEXICO Grade 6 MATHEMATICS STANDARDS
 PROCESS STANDARDS To help New Mexico students achieve the Content Standards enumerated below, teachers are encouraged to base instruction on the following Process Standards: Problem Solving Build new mathematical
PROCESS STANDARDS To help New Mexico students achieve the Content Standards enumerated below, teachers are encouraged to base instruction on the following Process Standards: Problem Solving Build new mathematical
APPLYING COMPUTER VISION TECHNIQUES TO TOPOGRAPHIC OBJECTS
 APPLYING COMPUTER VISION TECHNIQUES TO TOPOGRAPHIC OBJECTS Laura Keyes, Adam Winstanley Department of Computer Science National University of Ireland Maynooth Co. Kildare, Ireland [email protected], [email protected]
APPLYING COMPUTER VISION TECHNIQUES TO TOPOGRAPHIC OBJECTS Laura Keyes, Adam Winstanley Department of Computer Science National University of Ireland Maynooth Co. Kildare, Ireland [email protected], [email protected]
Introduction to Computer Graphics Marie-Paule Cani & Estelle Duveau
 Introduction to Computer Graphics Marie-Paule Cani & Estelle Duveau 04/02 Introduction & projective rendering 11/02 Prodedural modeling, Interactive modeling with parametric surfaces 25/02 Introduction
Introduction to Computer Graphics Marie-Paule Cani & Estelle Duveau 04/02 Introduction & projective rendering 11/02 Prodedural modeling, Interactive modeling with parametric surfaces 25/02 Introduction
MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem
 MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem David L. Finn November 30th, 2004 In the next few days, we will introduce some of the basic problems in geometric modelling, and
MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem David L. Finn November 30th, 2004 In the next few days, we will introduce some of the basic problems in geometric modelling, and
Estimated Pre Calculus Pacing Timeline
 Estimated Pre Calculus Pacing Timeline 2010-2011 School Year The timeframes listed on this calendar are estimates based on a fifty-minute class period. You may need to adjust some of them from time to
Estimated Pre Calculus Pacing Timeline 2010-2011 School Year The timeframes listed on this calendar are estimates based on a fifty-minute class period. You may need to adjust some of them from time to
Computational Geometry Lab: FEM BASIS FUNCTIONS FOR A TETRAHEDRON
 Computational Geometry Lab: FEM BASIS FUNCTIONS FOR A TETRAHEDRON John Burkardt Information Technology Department Virginia Tech http://people.sc.fsu.edu/ jburkardt/presentations/cg lab fem basis tetrahedron.pdf
Computational Geometry Lab: FEM BASIS FUNCTIONS FOR A TETRAHEDRON John Burkardt Information Technology Department Virginia Tech http://people.sc.fsu.edu/ jburkardt/presentations/cg lab fem basis tetrahedron.pdf
Academic Standards for Mathematics
 Academic Standards for Grades Pre K High School Pennsylvania Department of Education INTRODUCTION The Pennsylvania Core Standards in in grades PreK 5 lay a solid foundation in whole numbers, addition,
Academic Standards for Grades Pre K High School Pennsylvania Department of Education INTRODUCTION The Pennsylvania Core Standards in in grades PreK 5 lay a solid foundation in whole numbers, addition,
P. Lu, Sh. Huang and K. Jiang
 416 Rev. Adv. Mater. Sci. 33 (2013) 416-422 P. Lu, Sh. Huang and K. Jiang NUMERICAL ANALYSIS FOR THREE-DIMENSIONAL BULK METAL FORMING PROCESSES WITH ARBITRARILY SHAPED DIES USING THE RIGID/VISCO-PLASTIC
416 Rev. Adv. Mater. Sci. 33 (2013) 416-422 P. Lu, Sh. Huang and K. Jiang NUMERICAL ANALYSIS FOR THREE-DIMENSIONAL BULK METAL FORMING PROCESSES WITH ARBITRARILY SHAPED DIES USING THE RIGID/VISCO-PLASTIC
Introduction to ANSYS
 Lecture 3 Introduction to ANSYS Meshing 14. 5 Release Introduction to ANSYS Meshing 2012 ANSYS, Inc. March 27, 2014 1 Release 14.5 Introduction to ANSYS Meshing What you will learn from this presentation
Lecture 3 Introduction to ANSYS Meshing 14. 5 Release Introduction to ANSYS Meshing 2012 ANSYS, Inc. March 27, 2014 1 Release 14.5 Introduction to ANSYS Meshing What you will learn from this presentation
Modelling with Implicit Surfaces that Interpolate
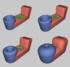 Modelling with Implicit Surfaces that Interpolate Greg Turk GVU Center, College of Computing Georgia Institute of Technology James F O Brien EECS, Computer Science Division University of California, Berkeley
Modelling with Implicit Surfaces that Interpolate Greg Turk GVU Center, College of Computing Georgia Institute of Technology James F O Brien EECS, Computer Science Division University of California, Berkeley
Bernice E. Rogowitz and Holly E. Rushmeier IBM TJ Watson Research Center, P.O. Box 704, Yorktown Heights, NY USA
 Are Image Quality Metrics Adequate to Evaluate the Quality of Geometric Objects? Bernice E. Rogowitz and Holly E. Rushmeier IBM TJ Watson Research Center, P.O. Box 704, Yorktown Heights, NY USA ABSTRACT
Are Image Quality Metrics Adequate to Evaluate the Quality of Geometric Objects? Bernice E. Rogowitz and Holly E. Rushmeier IBM TJ Watson Research Center, P.O. Box 704, Yorktown Heights, NY USA ABSTRACT
The Scientific Data Mining Process
 Chapter 4 The Scientific Data Mining Process When I use a word, Humpty Dumpty said, in rather a scornful tone, it means just what I choose it to mean neither more nor less. Lewis Carroll [87, p. 214] In
Chapter 4 The Scientific Data Mining Process When I use a word, Humpty Dumpty said, in rather a scornful tone, it means just what I choose it to mean neither more nor less. Lewis Carroll [87, p. 214] In
animation animation shape specification as a function of time
 animation animation shape specification as a function of time animation representation many ways to represent changes with time intent artistic motion physically-plausible motion efficiency control typically
animation animation shape specification as a function of time animation representation many ways to represent changes with time intent artistic motion physically-plausible motion efficiency control typically
Clustering & Visualization
 Chapter 5 Clustering & Visualization Clustering in high-dimensional databases is an important problem and there are a number of different clustering paradigms which are applicable to high-dimensional data.
Chapter 5 Clustering & Visualization Clustering in high-dimensional databases is an important problem and there are a number of different clustering paradigms which are applicable to high-dimensional data.
11.1. Objectives. Component Form of a Vector. Component Form of a Vector. Component Form of a Vector. Vectors and the Geometry of Space
 11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
Lecture Notes to Accompany. Scientific Computing An Introductory Survey. by Michael T. Heath. Chapter 10
 Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Chapter 10 Boundary Value Problems for Ordinary Differential Equations Copyright c 2001. Reproduction
Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Chapter 10 Boundary Value Problems for Ordinary Differential Equations Copyright c 2001. Reproduction
Essential Mathematics for Computer Graphics fast
 John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
John Vince Essential Mathematics for Computer Graphics fast Springer Contents 1. MATHEMATICS 1 Is mathematics difficult? 3 Who should read this book? 4 Aims and objectives of this book 4 Assumptions made
Topological Data Analysis Applications to Computer Vision
 Topological Data Analysis Applications to Computer Vision Vitaliy Kurlin, http://kurlin.org Microsoft Research Cambridge and Durham University, UK Topological Data Analysis quantifies topological structures
Topological Data Analysis Applications to Computer Vision Vitaliy Kurlin, http://kurlin.org Microsoft Research Cambridge and Durham University, UK Topological Data Analysis quantifies topological structures
Finite Elements for 2 D Problems
 Finite Elements for 2 D Problems General Formula for the Stiffness Matrix Displacements (u, v) in a plane element are interpolated from nodal displacements (ui, vi) using shape functions Ni as follows,
Finite Elements for 2 D Problems General Formula for the Stiffness Matrix Displacements (u, v) in a plane element are interpolated from nodal displacements (ui, vi) using shape functions Ni as follows,
MODERN VOXEL BASED DATA AND GEOMETRY ANALYSIS SOFTWARE TOOLS FOR INDUSTRIAL CT
 MODERN VOXEL BASED DATA AND GEOMETRY ANALYSIS SOFTWARE TOOLS FOR INDUSTRIAL CT C. Reinhart, C. Poliwoda, T. Guenther, W. Roemer, S. Maass, C. Gosch all Volume Graphics GmbH, Heidelberg, Germany Abstract:
MODERN VOXEL BASED DATA AND GEOMETRY ANALYSIS SOFTWARE TOOLS FOR INDUSTRIAL CT C. Reinhart, C. Poliwoda, T. Guenther, W. Roemer, S. Maass, C. Gosch all Volume Graphics GmbH, Heidelberg, Germany Abstract:
2.3 Convex Constrained Optimization Problems
 42 CHAPTER 2. FUNDAMENTAL CONCEPTS IN CONVEX OPTIMIZATION Theorem 15 Let f : R n R and h : R R. Consider g(x) = h(f(x)) for all x R n. The function g is convex if either of the following two conditions
42 CHAPTER 2. FUNDAMENTAL CONCEPTS IN CONVEX OPTIMIZATION Theorem 15 Let f : R n R and h : R R. Consider g(x) = h(f(x)) for all x R n. The function g is convex if either of the following two conditions
Robert Collins CSE598G. More on Mean-shift. R.Collins, CSE, PSU CSE598G Spring 2006
 More on Mean-shift R.Collins, CSE, PSU Spring 2006 Recall: Kernel Density Estimation Given a set of data samples x i ; i=1...n Convolve with a kernel function H to generate a smooth function f(x) Equivalent
More on Mean-shift R.Collins, CSE, PSU Spring 2006 Recall: Kernel Density Estimation Given a set of data samples x i ; i=1...n Convolve with a kernel function H to generate a smooth function f(x) Equivalent
C O M P U C O M P T U T E R G R A E R G R P A H I C P S Computer Animation Guoying Zhao 1 / 66 /
 Computer Animation Guoying Zhao 1 / 66 Basic Elements of Computer Graphics Modeling construct the 3D model of the scene Rendering Render the 3D model, compute the color of each pixel. The color is related
Computer Animation Guoying Zhao 1 / 66 Basic Elements of Computer Graphics Modeling construct the 3D model of the scene Rendering Render the 3D model, compute the color of each pixel. The color is related
