An Introduction to FreeFem++ UPMC, September 2010 O. Pantz. CMAP, Ecole Polytechnique.
|
|
|
- Coral Hodge
- 10 years ago
- Views:
Transcription
1 An Introduction to FreeFem++ UPMC, September 2010 O. Pantz CMAP, Ecole Polytechnique.
2 FreeFem++ What is it? FreeFEM++ is a Free software to solve PDE using the Finite Element Method. It runs on Windows, Linux and Mac OS. What does it do? Mesh generation; Automatic Building of Mass/Rigid Matrices and second member; Diverse Linear Solvers integrated; Works for 2d or 3d problems; Generates Graphic/Text/File outputs; and a lot more...
3 Download page How to start? How does it work? Write your script using a raw text editor Notepad++ under Windows, plenty of choices under Linux; Save it with file extension.edp; Run it : Just clic on the file under Windows/Mac OS. Execute command FreeFem++ MyScript.edp under Linux. Getting Help Full documentation and many examples included in FeeFem++. Subscribe to the mailing list. Syntax YOU KNOW what a Variational Formulation is? YOU KNOW some C++? Then YOU KNOW FeeFem++!
4 Outline... First Example: Poisson Equation Mesh; Finite Elements; Save and Read. Second Example: Elasticity Make it simple: use Macros. Third Example: Stokes Matrices: build and solve; Forth Example: Navier Stokes Convection; Fifth Example: Coupled systems Boundary Elements.
5 First Example: POISSON. Build a mesh, Define a problem, Solve and Save.
6 where S h is a regular mesh of Ω and Π 1 := space of polynomals whose degree is lower or equal to one. Let s Start! Poisson Equation Find u : Ω :=]0, 1[ 2 R such that { u = f on Ω u = 0 on Ω. Variational Formulation Find u H 1 0 (Ω) such that for all v H1 0 (Ω), Ω u v dx Ω fv dx = 0. Galerkin Approximation Using P1 Finite Elements Find u h V h such that for all v h V h, Ω u h v h dx Ω fv h dx = 0, V h = {v h H 1 0 (Ω) : v h T Π 1, for any T S h },
7 Poisson.edp mesh Sh= square(10,10); // mesh generation of a square fespace Vh(Sh,P1); // space of P1 Finite Elements Vh u,v; // u and v belongs to Vh func f=cos(x)*y; // f is a function of x and y problem Poisson(u,v)= // Definition of the problem int2d(sh)(dx(u)*dx(v)+dy(u)*dy(v)) // bilinear form -int2d(sh)(f*v) // linear form +on(1,2,3,4,u=0); // Dirichlet Conditions Poisson; // Solve Poisson Equation plot(u); // Plot the result
8 Save and Read Save.edp include "Poisson.edp"; // include previous script plot(u,ps="result.eps"); // Generate eps output savemesh(sh,"sh.msh"); // Save the Mesh ofstream file("potential.txt"); file<<u[]; Read.edp mesh Sh=readmesh("Sh.msh"); // Read the Mesh fespace Vh(Sh,P1); Vh u=0; ifstream file("potential.txt"); file>>u[]; // Read the potential plot(u,cmm="the result was correctly saved :)");
9 More mesh Generation Keyword square only allows for the generation of structured meshes. More general meshes can be generated by using keywords border and buildmesh. It enables you to define mesh for open sets whose boundaries are described by parametrized curves. Mesh.edp border a(t=0,2.*pi){x=cos(t);y=sin(t);}; mesh Sh1=buildmesh(a(20)); plot(sh1,wait=1,cmm="the unit disk"); border b(t=0,2.*pi){x=0.2*cos(t)+0.3;y=sin(t)* ;}; mesh Sh2=buildmesh(a(20)+b(-20)); plot(sh2,wait=1,cmm="the unit disk with a hole"); mesh Sh3=buildmesh(a(20)+b(20)); plot(sh3,wait=1,cmm="the unit disk with an inclusion");
10 Poisson2.edp int Dirichlet=1; // For label definition border a(t=0,2.*pi){x=cos(t);y=sin(t); label=dirichlet;}; border b(t=0,2.*pi){x=0.2*cos(t)+0.3;y=sin(t)* ; label=dirichlet;}; mesh Sh=buildmesh(a(80)+b(-20)); // The Unit Disk with a hole fespace Vh(Sh,P1); Vh u,v; func f=cos(x)*y; problem Poisson(u,v)= int2d(sh)(dx(u)*dx(v)+dy(u)*dy(v)) -int2d(sh)(f*v) +on(dirichlet,u=0); // u=0 label=dirichlet=1 Poisson; plot(u);
11 Limit Conditions Find u : Ω :=]0, 1[ 2 R such that u = f on Ω, u n = g on Γ N, u = u D on Γ D. Variational Formulation Find u V := {v H 1 (Ω) : v = u d on Γ D }, such that for all v V D := {v H 1 (Ω) : v = 0 on Γ D }, Ω Ω u v dx fv dx gv ds = 0. Γ N Galerkin Approximation Using P1 Finite Elements Find u h V h such that for all v h V D h, Ω u h v h dx Ω fv h Γ N gv h ds dx = 0, V h = {v h V : v h T Π 1, for any T S h }, V D h = {v h V D : v h T Π 1, for any T S h }.
12 Poisson3.edp int Dirichlet=1,Neumann=2; // For label definition border a(t=0,2.*pi){x=cos(t);y=sin(t);label=dirichlet;}; border b(t=0,2.*pi){x=0.2*cos(t)+0.3;y=sin(t)* ;label=neumann;}; mesh Sh=buildmesh(a(80)+b(-20)); fespace Vh(Sh,P1); Vh u,v; func f=cos(x)*y; func ud=x; func g=1.; problem Poisson(u,v)= int2d(sh)(dx(u)*dx(v)+dy(u)*dy(v)) +int1d(sh,neumann)(g*v) -int2d(sh)(f*v) +on(dirichlet,u=ud); // u=ud on label=dirichlet=1 Poisson; plot(u);
13 Mesh adaptation Mesh could be adapted with respect to a given finite element with the keyword adaptmesh. Poisson4.edp int Dirichlet=1,Neumann=2; border a(t=0,2.*pi){x=cos(t);y=sin(t);label=dirichlet;}; border b(t=0,2.*pi){x=0.2*cos(t)+0.3;y=sin(t)* ;label=neumann;}; mesh Sh=buildmesh(a(80)+b(-20)); fespace Vh(Sh,P1); Vh u,v; func f=cos(x)*y; func ud=x; func g=1.; problem Poisson(u,v)= int2d(sh)(dx(u)*dx(v)+dy(u)*dy(v)) -int1d(sh,neumann)(g*v)-int2d(sh)(f*v) +on(dirichlet,u=ud); Poisson;plot(Sh,cmm="Initial Mesh",wait=1);plot(u,wait=1); Sh=adaptmesh(Sh,u,err=1.e-3); Poisson;plot(Sh,cmm="Adapted Mesh",wait=1);plot(u);
14 P1... int Dirichlet=1,Neumann=2; border a(t=0,2.*pi){x=cos(t);y=sin(t);label=dirichlet;}; border b(t=0,2.*pi){x=0.2*cos(t)+0.3;y=sin(t)* ;label=neumann;}; mesh Sh=buildmesh(a(10)+b(-5)); func f=cos(x)*y; func ud=x; func g=1.; fespace Vh1(Sh,P1);Vh1 u1,v1; problem Poisson1(u1,v1)= int2d(sh)(dx(u1)*dx(v1)+dy(u1)*dy(v1)) -int1d(sh,neumann)(g*v1)-int2d(sh)(f*v1) +on(dirichlet,u1=ud); //...
15 .. versus P2... fespace Vh2(Sh,P2);Vh2 u2,v2; problem Poisson2(u2,v2)= int2d(sh)(dx(u2)*dx(v2)+dy(u2)*dy(v2)) -int1d(sh,neumann)(g*v2)-int2d(sh)(f*v2) +on(dirichlet,u2=ud); //...
16 ... versus P3 P3 finite elements are not avaiable by default. They have to be loaded first (in fact, you can even define your own elements). load "Element_P3"; // load P3 finite elements fespace Vh3(Sh,P3);Vh3 u3,v3; problem Poisson3(u3,v3)= int2d(sh)(dx(u3)*dx(v3)+dy(u3)*dy(v3)) -int1d(sh,neumann)(g*v3)-int2d(sh)(f*v3) +on(dirichlet,u3=ud); //...
17 Solve it all and plot! Poisson5.edp Poisson1;Poisson2;Poisson3; plot(u1,cmm="with P1 finite elements",wait=1); plot(u2,cmm="with P2 finite elements",wait=1); plot(u3,cmm="with P3 finite elements"); WARNING VERY BAD SCRIPT!!! As we will see there is smarter ways to do this by using macro or varf.
18 What have I learned About Meshes mesh = Type for... meshes; square = To create structured meshes; savemesh = To save a mesh in a file; readmesh = To read mesh previously saved; border = Type for parametrized curves; buildmesh = Build a mesh with parametrized boundaries; adaptmesh = To refine a mesh. About Variational Formulations fespace = Type for Finite Element Spaces; problem =Type for a Variational Problem; P1,P2,P3 = Lagrange Elements; int2d = Integration over a domain; int1d = Integration over part of the boundary; on = To impose Boundary Conditions.
19 What have I learned Misc... func = Type for a function of x and y; int = Type for integers; plot = Just guess; include = To include a script into another; ofstream = To direct the output to a file; ifstream = To get the input from a file. cos = All classical maths functions could be used;
20 Second Example: ELASTICITY. Macros are beautiful.
21 More tricky: Linear Elasticity The Variationnal Formulation Find u X := {v H 1 (Ω) 2 : v = 0 on Γ D }, such that for all v X, Ω Ae(u) e(v) dx with where for any symetric matrix ξ, Γ N v g ds = 0, e(u) = ( u + u T )/2, Aξ ξ = 2µ ξ 2 + λ(tr(ξ)) 2.
22 If you are a barbarian elasticity1.edp real L=10,H=1,dn=5; mesh Sh=square(L*dn,H*dn,[x*L,y*H]); // square OK of rectangles real mu=1,lambda=1; fespace Vh(Sh,P1); Vh u1,u2,v1,v2; // One for each component func g1=0;func g2=-1.; problem elasticity(u1,u2,v1,v2)= int2d(sh)(2.*mu* (dx(u1)*dx(v1)+dy(u2)*dy(v2)+(dy(u1)+dx(u2))*(dy(v1)+dx(v2))/2.) + lambda*(dx(u1)+dy(u2))*(dx(v1)+dy(v2))) -int1d(sh,2)(g1*v1+g2*v2) // ARGH... +on(4,u1=0,u2=0); plot([u1,u2],wait=1); // you can plot vectors :)
23 If you are civilized: Use Macros elasticity2.edp real L=10,H=1,dn=5; mesh Sh=square(L*dn,H*dn,[x*L,y*H]); real mu=1,lambda=1; fespace Vh(Sh,[P1,P1]); // vectorial FE space macro u [u1,u2] // end of macro macro v [v1,v2] // end of macro macro e(u) [dx(u[0]),(dx(u[1])+dy(u[0]))/ sqrt(2),dy(u[1])] // macro A [[2.*mu+lambda,0,lambda],[0,2.*mu,0],[lambda,0,2.*mu+lambda]] // macro g [0,-1.] // Vh u,v; // One for each component problem elasticity(u,v)= int2d(sh)((a*e(u)) *e(v))-int1d(sh,2)(g *v) +on(4,u1=0,u2=0); elasticity;plot(u,wait=1);
24 Don t like the output? Try This: elasticity3.edp include "elasticity2.edp"; fespace Vh0(Sh,P0); Vh0 sigma=(a*e(u)) *e(u); plot(sigma,fill=1,cmm="constraints",wait=1); real delta=1.e-3; mesh Th=movemesh(Sh,[x+delta*u1,y+delta*u2]); plot(th,cmm="deformed configuration",wait=1); fespace Wh0(Th,P0); Wh0 tau=0; tau[]=sigma[]; plot(tau,fill=1,cmm="constraints on deformed configuration");
25 Time, it is Time Wave equation Looking for u C 1 ([0, T ], L 2 (Ω) 2 ) C 0 ([0, T ], X) such that for all v X := {v H 1 (Ω) : v = 0 on Γ D }, Ω 2 u t 2 v dx + Ω Ae(u) e(v) dx = 0, u(t = 0) = u 0, and Time Discretization u t (t = 0) = v 0. Ω u n+1 2u n + u n 1 t 2 v dx + Ω Ae(un+1 ) e(v) dx = 0.
26 Parameters and Macros real T=5000.,dt=5.; // Finale Time and time step macro v0 [0,-1.] // Intial velocity mesh Sh; // Building the mesh real L=10,H=1,dn=5;Sh=square(L*dn,H*dn,[x*L,y*H]); macro u [u1,u2] // state macro up [up1,up2] // previous state macro upp [upp1,upp2] // previous previous state macro v [v1,v2] // end of macro macro e(u) [dx(u[0]),(dx(u[1])+dy(u[0]))/ sqrt(2),dy(u[1])] // macro A [[2.*mu+lambda,0,lambda],[0,2.*mu,0],[lambda,0,2.*mu+lambda]] //...
27 Definition of the problem fespace Vh(Sh,[P1,P1]); // vectorial FE space Vh u,up,upp,v; real mu=1,lambda=1; real t; problem OneStepElasticity(u,v,init=t)= int2d(sh)((u *v)/(dt^2)+(a*e(u)) *e(v)) +int2d(sh)((upp *v-2.*(up *v))/(dt^2)) +on(4,u1=0,u2=0); upp=[0.,0.]; // Initialization of states up=upp+[dt*v0[0],dt*v0[1]];
28 Loops look like C++ Evolution.edp real delta=0.05; // exageration of the displacement for(t=0;t<t;t+=dt){ mesh Th=movemesh(Sh,[x+delta*u[0],y+delta*u[1]]); plot(th,bb=[[0,-3.*h],[l*1.3,4.*h]]); OneStepElasticity; upp=up;up=u; }
29 What have I learned macro = To define a macro, ends with a commentary; for = To make a loop; [P1,P1]= Product of FE spaces; P0 = P0 Finite Elements; movemesh = To move a mesh; init = Build the matrix or Not?; real = Type for reals; fill = Fill between isolines; cmm = Comments for plot; wait = Wait before next plot; u[] = If u is a Finite Element, return the values of u at each degree of freedom.
30 Third Example: STOKES. Be Free: Use Matrices and Vectors.
31 Stokes Let V = H 1 (Ω) 2, V 0 = H0 1(Ω)2, and R = L 2 (Ω). Stokes problem consists in finding (u, p, c) V R R, such that and u = u d on Ω, where a(u, v) + b(p, v) = 0 for all v V, b(q, u) + cm(q) = 0, for all q R, a(u, v) = m(p) = 0, b(p, u) = Ω m(p) = µe(u) e(v) dx, Ω div(u)p dx, Ω p dx.
32 Let s rock... real u1d=1.; // velocity of the upper face mesh Sh; // Definition of the mesh { int n=30; Sh=square(n,n); } fespace Vh(Sh,[P1b,P1b]); // Definition of the FE spaces fespace Rh(Sh,P1); macro u [u1,u2] // Some macros macro v [v1,v2] // macro e(u) [dx(u[0]),(dx(u[1])+dy(u[0]))/sqrt(2.),dy(u[1])] // macro div(u) (dx(u[0])+dy(u[1])) //...
33 real mu=1.; // Viscosity // Definition of the linear/bilinear forms varf a(u,v)=int2d(sh)(mu*(e(u) *e(v)))+on(1,2,3,4,u1=0,u2=0); varf b([p],u)=int2d(sh)(div(u)*p); varf m(p,q)=int2d(sh)(q); varf bc(u,v)=on(3,u1=u1d,u2=0); matrix M; // Building the System real[int] L(Vh.ndof+Rh.ndof+1); { matrix A=a(Vh,Vh); matrix B=b(Rh,Vh); real[int] C=m(0,Rh); M=[[A,B,0], [B,0,C], [0,C,0]]; L=0; L(0:Vh.ndof-1)=bc(0,Vh);} //...
34 stokes.edp Vh u; Rh p; // Solving the system { set(m,solver=umfpack); real[int] sol=m^-1*l; u=[0,0];p=0; u1[]=sol(0:vh.ndof-1); p[]=sol(vh.ndof:vh.ndof+rh.ndof-1); } plot(u,p); // Display the result
35 What have I learned matrix = Sparse Matrix; real[int] = array of reals; M = Transposed Matrix; M=[[A,B],[C,D]] = Matrix defined by bloc; M=a(Vh,Wh) = Build Matrix Associated to the Bilinear part of a; L=a(0,Wh) = Build vector Associated to the Linear part of a; varf = bilinear form+linear form; set(,solver= ) = Define the solver associate to a matrix; s=m^-1*l = Solve Ms=L.
36 Fourth Example: Navier Stokes. Recipe for NS: Take Stokes, Add Convection.
37 Navier Stokes Let s try to solve the NS equation u t + u u µ e(u) + p = 0 in Ω, u = 0 in Ω, u = u D on Ω Time Discretization u n+1 u n X n ( dt) dt µ e(u n ) + p n = 0 in Ω, u n = 0 in Ω, u n = u D on Ω, with Ẋ n = u n X n and X n (t = 0) = Id.
38 Variational Fromulation Using the same notation than for Stokes, N.S. problem consists in finding for each n, (u n+1, p n+1, c n+1 ) V R R, such that with r( un+1 u n c dt, v) + a(u n+1, v) + b(p n+1, v) = 0 for all v V, u n c = u n X n ( dt), and r(u, v) = Ω uv dx.
39 Parameters/mesh and macros real T=0.1,dt=0.005,u1d=1.; real mu=1.,rho=1.; mesh Sh; { int n=30; Sh=square(n,n); } fespace Vh(Sh,[P1b,P1b]); fespace Rh(Sh,P1); macro u [u1,u2] // macro up [up1,up2] // macro v [v1,v2] // macro e(u) [dx(u[0]),(dx(u[1])+dy(u[0]))/sqrt(2.),dy(u[1])] // macro div(u) (dx(u[0])+dy(u[1])) // macro Convect(u,dt,v) [convect(u,dt,v[0]),convect(u,dt,v[1])] // Vector convection...
40 Linear and Bilinear forms Vh u,up;rh p; // definition of the linear/bilinear forms (same than for Stokes) varf a(u,v)=int2d(sh)(mu*(e(u) *e(v)))+on(1,2,3,4,u1=0,u2=0); varf b([p],u)=int2d(sh)(div(u)*p); varf m(p,q)=int2d(sh)(q); varf bc(u,v)=on(3,u1=u1d,u2=0); varf r(u,v)=int2d(sh)((rho/dt)*(u *v)); // For the inertial terms varf conv(u,v)=int2d(sh)((rho/dt)*(convect(up,(-dt),up) *v)); //...
41 Building the System matrix M; real[int] L(Vh.ndof+Rh.ndof+1);L=0; real[int] L0=bc(0,Vh); { matrix A0=a(Vh,Vh); matrix A1=r(Vh,Vh); matrix A=A0+A1; matrix B=b(Rh,Vh); real[int] C=m(0,Rh); M=[[A,B,0], [B,0,C], [0,C,0]]; } set(m,solver=umfpack); //...
42 NS.edp real[int] viso=[0.,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.]; // For the output up=[0.,0.];u=[0,0];p=0; for(real t=0;t<t;t+=dt){ real[int] L1=conv(0,Vh); L(0:Vh.ndof-1)=L0+L1; real[int] sol=m^-1*l; // Solving the system u1[]=sol(0:vh.ndof-1); p[]=sol(vh.ndof:vh.ndof+rh.ndof-1); plot(u,viso=viso); // Display the result up=u; }
43 Fifth Example: COUPLED SYSTEMS. Boundary Elements
44 What have I learned convect = Compute Characteristics; viso = Option in plot to set the values of the isolines displayed.
45 Couples Let s now try to couple two systems... Could be wathever you want, but let s consider two Poisson equations. For i = 1, 2, k i u i = f i in Ω i u 1 = u 2 on Γ = Ω 1 Ω 2 u i = 0 on Γ i = Ω i \ Γ.
46 Find Variational Formulation u i V i := {v H 1 (Ω i ) : u 1 = 0 on Γ i }, and p H 1/2 (Γ) such that for all (v 1, v 2, q) V 1 V 2 H 1/2 (Γ), a 1 (u 1, v 1 ) + b(p, v 1 ) = L 1 (v 1 ) and a 2 (u 2, v 2 ) b(p, v 2 ) = L 2 (v 2 ), b(q, u 1 u 2 ) = 0, where and a i (u i, v i ) = b(q, u) = Ω i (k i u i v i ), Γ qu ds.
47 Parameters, mesh and macro int n1=10,n2=25; real k1=1,k2=2; real f1=1,f2=1; mesh Sh1=square(n1,n1); mesh Sh2=square(n2,n2,[x+1.,y]); mesh Sh=emptymesh(Sh1); // mesh for the Lagrange Multiplier macro grad(u) [dx(u),dy(u)] //
48 Linear,Bilinear Forms,Spaces varf a1(u,v)=int2d(sh1)(k1*(grad(u) *grad(v)))+on(1,3,4,u=0); varf a2(u,v)=int2d(sh2)(k2*(grad(u) *grad(v)))+on(1,2,3,u=0); varf b1(q,u)=int1d(sh,2)(q*u); varf b2(q,u)=int1d(sh,2)(-q*u); varf pen(p,q)=int1d(sh,1,3,4)(-p*q); // penalization of the unused terms varf L1(u,v)=int2d(Sh1)(f1*v); varf L2(u,v)=int2d(Sh2)(f2*v); fespace Vh1(Sh1,P2),Vh2(Sh2,P1),Rh(Sh,P1);
49 Build Sytem matrix M;{ matrix A1=a1(Vh1,Vh1); matrix A2=a2(Vh2,Vh2); matrix B1=b1(Rh,Vh1); matrix B2=b2(Rh,Vh2); // Cool: Automatic interpolation matrix P=pen(Rh,Rh); M=[[A1,0,B1], [0,A2,B2], [B1,B2,P ]];} real[int] L(Vh1.ndof+Vh2.ndof+Rh.ndof);{ real[int] L10=a1(0,Vh1);real[int] L11=L1(0,Vh1); real[int] L1=L10+L11; real[int] L20=a2(0,Vh2);real[int] L21=L2(0,Vh2); real[int] L2=L20+L21; L=0;L(0:Vh1.ndof-1)=L1;L(Vh1.ndof:Vh1.ndof+Vh2.ndof-1)=L2;} //...
50 Coupled.edp set(m,solver=umfpack); real[int] sol=m^-1*l; Vh1 u1=0; Vh2 u2=0; u1[]=sol(0:vh1.ndof-1); u2[]=sol(vh1.ndof:vh1.ndof+vh2.ndof-1); plot(sh1,sh2,wait=1); plot(u1,u2);
51 What have I learned emptymesh = To create a mesh with all nodes on the boundary; Interpolation between different mesh works!
52 THANK YOU FOR OUR ATTENTION.
Domain decomposition techniques for interfacial discontinuities
 Domain decomposition techniques for interfacial discontinuities Geordie McBain Institut Jean le Rond d Alembert December 5, 2012 Connexion and substructuring Two ways to look at domain decomposition Decomposing
Domain decomposition techniques for interfacial discontinuities Geordie McBain Institut Jean le Rond d Alembert December 5, 2012 Connexion and substructuring Two ways to look at domain decomposition Decomposing
FreeFem++-cs, the FreeFem++ Graphical Interface
 FreeFem++-cs, the FreeFem++ Graphical Interface Antoine Le Hyaric Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Antoine.Le [email protected] December 10, 2014 1 / 54 FreeFem++-cs How to
FreeFem++-cs, the FreeFem++ Graphical Interface Antoine Le Hyaric Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Antoine.Le [email protected] December 10, 2014 1 / 54 FreeFem++-cs How to
FEM Software Automation, with a case study on the Stokes Equations
 FEM Automation, with a case study on the Stokes Equations FEM Andy R Terrel Advisors: L R Scott and R C Kirby Numerical from Department of Computer Science University of Chicago March 1, 2006 Masters Presentation
FEM Automation, with a case study on the Stokes Equations FEM Andy R Terrel Advisors: L R Scott and R C Kirby Numerical from Department of Computer Science University of Chicago March 1, 2006 Masters Presentation
How High a Degree is High Enough for High Order Finite Elements?
 This space is reserved for the Procedia header, do not use it How High a Degree is High Enough for High Order Finite Elements? William F. National Institute of Standards and Technology, Gaithersburg, Maryland,
This space is reserved for the Procedia header, do not use it How High a Degree is High Enough for High Order Finite Elements? William F. National Institute of Standards and Technology, Gaithersburg, Maryland,
DYNAMIC ANALYSIS OF THICK PLATES SUBJECTED TO EARTQUAKE
 DYNAMIC ANALYSIS OF THICK PLATES SUBJECTED TO EARTQUAKE ÖZDEMİR Y. I, AYVAZ Y. Posta Adresi: Department of Civil Engineering, Karadeniz Technical University, 68 Trabzon, TURKEY E-posta: [email protected]
DYNAMIC ANALYSIS OF THICK PLATES SUBJECTED TO EARTQUAKE ÖZDEMİR Y. I, AYVAZ Y. Posta Adresi: Department of Civil Engineering, Karadeniz Technical University, 68 Trabzon, TURKEY E-posta: [email protected]
Introduction to the Finite Element Method
 Introduction to the Finite Element Method 09.06.2009 Outline Motivation Partial Differential Equations (PDEs) Finite Difference Method (FDM) Finite Element Method (FEM) References Motivation Figure: cross
Introduction to the Finite Element Method 09.06.2009 Outline Motivation Partial Differential Equations (PDEs) Finite Difference Method (FDM) Finite Element Method (FEM) References Motivation Figure: cross
Høgskolen i Narvik Sivilingeniørutdanningen STE6237 ELEMENTMETODER. Oppgaver
 Høgskolen i Narvik Sivilingeniørutdanningen STE637 ELEMENTMETODER Oppgaver Klasse: 4.ID, 4.IT Ekstern Professor: Gregory A. Chechkin e-mail: [email protected] Narvik 6 PART I Task. Consider two-point
Høgskolen i Narvik Sivilingeniørutdanningen STE637 ELEMENTMETODER Oppgaver Klasse: 4.ID, 4.IT Ekstern Professor: Gregory A. Chechkin e-mail: [email protected] Narvik 6 PART I Task. Consider two-point
Visualization of 2D Domains
 Visualization of 2D Domains This part of the visualization package is intended to supply a simple graphical interface for 2- dimensional finite element data structures. Furthermore, it is used as the low
Visualization of 2D Domains This part of the visualization package is intended to supply a simple graphical interface for 2- dimensional finite element data structures. Furthermore, it is used as the low
FreeFem++, a tools to solving complex problem like Bose Einstein Condensate
 FreeFem++, a tools to solving complex problem like Bose Einstein Condensate equation or a melting problem. F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France with I.
FreeFem++, a tools to solving complex problem like Bose Einstein Condensate equation or a melting problem. F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France with I.
Feature Commercial codes In-house codes
 A simple finite element solver for thermo-mechanical problems Keywords: Scilab, Open source software, thermo-elasticity Introduction In this paper we would like to show how it is possible to develop a
A simple finite element solver for thermo-mechanical problems Keywords: Scilab, Open source software, thermo-elasticity Introduction In this paper we would like to show how it is possible to develop a
Finite Elements for 2 D Problems
 Finite Elements for 2 D Problems General Formula for the Stiffness Matrix Displacements (u, v) in a plane element are interpolated from nodal displacements (ui, vi) using shape functions Ni as follows,
Finite Elements for 2 D Problems General Formula for the Stiffness Matrix Displacements (u, v) in a plane element are interpolated from nodal displacements (ui, vi) using shape functions Ni as follows,
Computational Physics
 Computational Physics Sheet 6, Computational Physics Course 17105 Professor: H. Ruhl, Exercises: N. Moschüring and N. Elkina Discussion of Solutions: Dec 03, 01, Room A49 Problem 1: Yee solver for Schrödinger
Computational Physics Sheet 6, Computational Physics Course 17105 Professor: H. Ruhl, Exercises: N. Moschüring and N. Elkina Discussion of Solutions: Dec 03, 01, Room A49 Problem 1: Yee solver for Schrödinger
Finite Element Formulation for Beams - Handout 2 -
 Finite Element Formulation for Beams - Handout 2 - Dr Fehmi Cirak (fc286@) Completed Version Review of Euler-Bernoulli Beam Physical beam model midline Beam domain in three-dimensions Midline, also called
Finite Element Formulation for Beams - Handout 2 - Dr Fehmi Cirak (fc286@) Completed Version Review of Euler-Bernoulli Beam Physical beam model midline Beam domain in three-dimensions Midline, also called
1 Finite difference example: 1D implicit heat equation
 1 Finite difference example: 1D implicit heat equation 1.1 Boundary conditions Neumann and Dirichlet We solve the transient heat equation ρc p t = ( k ) (1) on the domain L/2 x L/2 subject to the following
1 Finite difference example: 1D implicit heat equation 1.1 Boundary conditions Neumann and Dirichlet We solve the transient heat equation ρc p t = ( k ) (1) on the domain L/2 x L/2 subject to the following
FINITE ELEMENT : MATRIX FORMULATION. Georges Cailletaud Ecole des Mines de Paris, Centre des Matériaux UMR CNRS 7633
 FINITE ELEMENT : MATRIX FORMULATION Georges Cailletaud Ecole des Mines de Paris, Centre des Matériaux UMR CNRS 76 FINITE ELEMENT : MATRIX FORMULATION Discrete vs continuous Element type Polynomial approximation
FINITE ELEMENT : MATRIX FORMULATION Georges Cailletaud Ecole des Mines de Paris, Centre des Matériaux UMR CNRS 76 FINITE ELEMENT : MATRIX FORMULATION Discrete vs continuous Element type Polynomial approximation
TWO-DIMENSIONAL FINITE ELEMENT ANALYSIS OF FORCED CONVECTION FLOW AND HEAT TRANSFER IN A LAMINAR CHANNEL FLOW
 TWO-DIMENSIONAL FINITE ELEMENT ANALYSIS OF FORCED CONVECTION FLOW AND HEAT TRANSFER IN A LAMINAR CHANNEL FLOW Rajesh Khatri 1, 1 M.Tech Scholar, Department of Mechanical Engineering, S.A.T.I., vidisha
TWO-DIMENSIONAL FINITE ELEMENT ANALYSIS OF FORCED CONVECTION FLOW AND HEAT TRANSFER IN A LAMINAR CHANNEL FLOW Rajesh Khatri 1, 1 M.Tech Scholar, Department of Mechanical Engineering, S.A.T.I., vidisha
Mean Value Coordinates
 Mean Value Coordinates Michael S. Floater Abstract: We derive a generalization of barycentric coordinates which allows a vertex in a planar triangulation to be expressed as a convex combination of its
Mean Value Coordinates Michael S. Floater Abstract: We derive a generalization of barycentric coordinates which allows a vertex in a planar triangulation to be expressed as a convex combination of its
Code Generation Tools for PDEs. Matthew Knepley PETSc Developer Mathematics and Computer Science Division Argonne National Laboratory
 Code Generation Tools for PDEs Matthew Knepley PETSc Developer Mathematics and Computer Science Division Argonne National Laboratory Talk Objectives Introduce Code Generation Tools - Installation - Use
Code Generation Tools for PDEs Matthew Knepley PETSc Developer Mathematics and Computer Science Division Argonne National Laboratory Talk Objectives Introduce Code Generation Tools - Installation - Use
820446 - ACMSM - Computer Applications in Solids Mechanics
 Coordinating unit: 820 - EUETIB - Barcelona College of Industrial Engineering Teaching unit: 737 - RMEE - Department of Strength of Materials and Structural Engineering Academic year: Degree: 2015 BACHELOR'S
Coordinating unit: 820 - EUETIB - Barcelona College of Industrial Engineering Teaching unit: 737 - RMEE - Department of Strength of Materials and Structural Engineering Academic year: Degree: 2015 BACHELOR'S
INTRODUCTION TO THE FINITE ELEMENT METHOD
 INTRODUCTION TO THE FINITE ELEMENT METHOD G. P. Nikishkov 2004 Lecture Notes. University of Aizu, Aizu-Wakamatsu 965-8580, Japan [email protected] 2 Updated 2004-01-19 Contents 1 Introduction 5 1.1 What
INTRODUCTION TO THE FINITE ELEMENT METHOD G. P. Nikishkov 2004 Lecture Notes. University of Aizu, Aizu-Wakamatsu 965-8580, Japan [email protected] 2 Updated 2004-01-19 Contents 1 Introduction 5 1.1 What
Modélisation de problèmes spécifiques avec le logiciel libre FreeFem++
 Modélisation de problèmes spécifiques avec le logiciel libre FreeFem++ F. Hecht LJLL, UPMC Alpines, INRIA Rocquencourt with S. Auliac, I. Danaila P. Jolivet, A Le Hyaric, F. Nataf, O. Pironneau, P-H. Tournier
Modélisation de problèmes spécifiques avec le logiciel libre FreeFem++ F. Hecht LJLL, UPMC Alpines, INRIA Rocquencourt with S. Auliac, I. Danaila P. Jolivet, A Le Hyaric, F. Nataf, O. Pironneau, P-H. Tournier
How To Solve The Pde Problem On A Mesh With A Freefem++ (Freefemplest) On A Computer Or A Computer (For Freefems)
 FreeFem++ Manual version 1.42 (Under construction) http://www.freefem.org http://www.ann.jussieu.fr/ hecht/freefem++.htm F. Hecht 1, O. Pironneau 2, Université Pierre et Marie Curie, Laboratoire Jacques-Louis
FreeFem++ Manual version 1.42 (Under construction) http://www.freefem.org http://www.ann.jussieu.fr/ hecht/freefem++.htm F. Hecht 1, O. Pironneau 2, Université Pierre et Marie Curie, Laboratoire Jacques-Louis
Nonlinear Modal Analysis of Mechanical Systems with Frictionless Contact Interfaces
 Nonlinear Modal Analysis of Mechanical Systems with Frictionless Contact Interfaces Denis Laxalde, Mathias Legrand and Christophe Pierre Structural Dynamics and Vibration Laboratory Department of Mechanical
Nonlinear Modal Analysis of Mechanical Systems with Frictionless Contact Interfaces Denis Laxalde, Mathias Legrand and Christophe Pierre Structural Dynamics and Vibration Laboratory Department of Mechanical
FUNDAMENTAL FINITE ELEMENT ANALYSIS AND APPLICATIONS
 FUNDAMENTAL FINITE ELEMENT ANALYSIS AND APPLICATIONS With Mathematica and MATLAB Computations M. ASGHAR BHATTI WILEY JOHN WILEY & SONS, INC. CONTENTS OF THE BOOK WEB SITE PREFACE xi xiii 1 FINITE ELEMENT
FUNDAMENTAL FINITE ELEMENT ANALYSIS AND APPLICATIONS With Mathematica and MATLAB Computations M. ASGHAR BHATTI WILEY JOHN WILEY & SONS, INC. CONTENTS OF THE BOOK WEB SITE PREFACE xi xiii 1 FINITE ELEMENT
AMATH 352 Lecture 3 MATLAB Tutorial Starting MATLAB Entering Variables
 AMATH 352 Lecture 3 MATLAB Tutorial MATLAB (short for MATrix LABoratory) is a very useful piece of software for numerical analysis. It provides an environment for computation and the visualization. Learning
AMATH 352 Lecture 3 MATLAB Tutorial MATLAB (short for MATrix LABoratory) is a very useful piece of software for numerical analysis. It provides an environment for computation and the visualization. Learning
Domain Decomposition Methods. Partial Differential Equations
 Domain Decomposition Methods for Partial Differential Equations ALFIO QUARTERONI Professor ofnumericalanalysis, Politecnico di Milano, Italy, and Ecole Polytechnique Federale de Lausanne, Switzerland ALBERTO
Domain Decomposition Methods for Partial Differential Equations ALFIO QUARTERONI Professor ofnumericalanalysis, Politecnico di Milano, Italy, and Ecole Polytechnique Federale de Lausanne, Switzerland ALBERTO
Plates and Shells: Theory and Computation - 4D9 - Dr Fehmi Cirak (fc286@) Office: Inglis building mezzanine level (INO 31)
 Plates and Shells: Theory and Computation - 4D9 - Dr Fehmi Cirak (fc286@) Office: Inglis building mezzanine level (INO 31) Outline -1-! This part of the module consists of seven lectures and will focus
Plates and Shells: Theory and Computation - 4D9 - Dr Fehmi Cirak (fc286@) Office: Inglis building mezzanine level (INO 31) Outline -1-! This part of the module consists of seven lectures and will focus
This makes sense. t 2 1 + 1/t 2 dt = 1. t t 2 + 1dt = 2 du = 1 3 u3/2 u=5
 1. (Line integrals Using parametrization. Two types and the flux integral) Formulas: ds = x (t) dt, d x = x (t)dt and d x = T ds since T = x (t)/ x (t). Another one is Nds = T ds ẑ = (dx, dy) ẑ = (dy,
1. (Line integrals Using parametrization. Two types and the flux integral) Formulas: ds = x (t) dt, d x = x (t)dt and d x = T ds since T = x (t)/ x (t). Another one is Nds = T ds ẑ = (dx, dy) ẑ = (dy,
Introduction to COMSOL. The Navier-Stokes Equations
 Flow Between Parallel Plates Modified from the COMSOL ChE Library module rev 10/13/08 Modified by Robert P. Hesketh, Chemical Engineering, Rowan University Fall 2008 Introduction to COMSOL The following
Flow Between Parallel Plates Modified from the COMSOL ChE Library module rev 10/13/08 Modified by Robert P. Hesketh, Chemical Engineering, Rowan University Fall 2008 Introduction to COMSOL The following
Variable Base Interface
 Chapter 6 Variable Base Interface 6.1 Introduction Finite element codes has been changed a lot during the evolution of the Finite Element Method, In its early times, finite element applications were developed
Chapter 6 Variable Base Interface 6.1 Introduction Finite element codes has been changed a lot during the evolution of the Finite Element Method, In its early times, finite element applications were developed
15.062 Data Mining: Algorithms and Applications Matrix Math Review
 .6 Data Mining: Algorithms and Applications Matrix Math Review The purpose of this document is to give a brief review of selected linear algebra concepts that will be useful for the course and to develop
.6 Data Mining: Algorithms and Applications Matrix Math Review The purpose of this document is to give a brief review of selected linear algebra concepts that will be useful for the course and to develop
Introduction Our choice Example Problem Final slide :-) Python + FEM. Introduction to SFE. Robert Cimrman
 Python + FEM Introduction to SFE Robert Cimrman Department of Mechanics & New Technologies Research Centre University of West Bohemia Plzeň, Czech Republic April 3, 2007, Plzeň 1/22 Outline 1 Introduction
Python + FEM Introduction to SFE Robert Cimrman Department of Mechanics & New Technologies Research Centre University of West Bohemia Plzeň, Czech Republic April 3, 2007, Plzeň 1/22 Outline 1 Introduction
Finite Element Formulation for Plates - Handout 3 -
 Finite Element Formulation for Plates - Handout 3 - Dr Fehmi Cirak (fc286@) Completed Version Definitions A plate is a three dimensional solid body with one of the plate dimensions much smaller than the
Finite Element Formulation for Plates - Handout 3 - Dr Fehmi Cirak (fc286@) Completed Version Definitions A plate is a three dimensional solid body with one of the plate dimensions much smaller than the
Lecture 10. Finite difference and finite element methods. Option pricing Sensitivity analysis Numerical examples
 Finite difference and finite element methods Lecture 10 Sensitivities and Greeks Key task in financial engineering: fast and accurate calculation of sensitivities of market models with respect to model
Finite difference and finite element methods Lecture 10 Sensitivities and Greeks Key task in financial engineering: fast and accurate calculation of sensitivities of market models with respect to model
Calculation of Eigenmodes in Superconducting Cavities
 Calculation of Eigenmodes in Superconducting Cavities W. Ackermann, C. Liu, W.F.O. Müller, T. Weiland Institut für Theorie Elektromagnetischer Felder, Technische Universität Darmstadt Status Meeting December
Calculation of Eigenmodes in Superconducting Cavities W. Ackermann, C. Liu, W.F.O. Müller, T. Weiland Institut für Theorie Elektromagnetischer Felder, Technische Universität Darmstadt Status Meeting December
EFFECTS ON NUMBER OF CABLES FOR MODAL ANALYSIS OF CABLE-STAYED BRIDGES
 EFFECTS ON NUMBER OF CABLES FOR MODAL ANALYSIS OF CABLE-STAYED BRIDGES Yang-Cheng Wang Associate Professor & Chairman Department of Civil Engineering Chinese Military Academy Feng-Shan 83000,Taiwan Republic
EFFECTS ON NUMBER OF CABLES FOR MODAL ANALYSIS OF CABLE-STAYED BRIDGES Yang-Cheng Wang Associate Professor & Chairman Department of Civil Engineering Chinese Military Academy Feng-Shan 83000,Taiwan Republic
Overset Grids Technology in STAR-CCM+: Methodology and Applications
 Overset Grids Technology in STAR-CCM+: Methodology and Applications Eberhard Schreck, Milovan Perić and Deryl Snyder [email protected] [email protected] [email protected]
Overset Grids Technology in STAR-CCM+: Methodology and Applications Eberhard Schreck, Milovan Perić and Deryl Snyder [email protected] [email protected] [email protected]
MATLAB DFS. Interface Library. User Guide
 MATLAB DFS Interface Library User Guide DHI Water Environment Health Agern Allé 5 DK-2970 Hørsholm Denmark Tel: +45 4516 9200 Fax: +45 4516 9292 E-mail: [email protected] Web: www.dhigroup.com 2007-03-07/MATLABDFS_INTERFACELIBRARY_USERGUIDE.DOC/JGR/HKH/2007Manuals/lsm
MATLAB DFS Interface Library User Guide DHI Water Environment Health Agern Allé 5 DK-2970 Hørsholm Denmark Tel: +45 4516 9200 Fax: +45 4516 9292 E-mail: [email protected] Web: www.dhigroup.com 2007-03-07/MATLABDFS_INTERFACELIBRARY_USERGUIDE.DOC/JGR/HKH/2007Manuals/lsm
Dispersion diagrams of a water-loaded cylindrical shell obtained from the structural and acoustic responses of the sensor array along the shell
 Dispersion diagrams of a water-loaded cylindrical shell obtained from the structural and acoustic responses of the sensor array along the shell B.K. Jung ; J. Ryue ; C.S. Hong 3 ; W.B. Jeong ; K.K. Shin
Dispersion diagrams of a water-loaded cylindrical shell obtained from the structural and acoustic responses of the sensor array along the shell B.K. Jung ; J. Ryue ; C.S. Hong 3 ; W.B. Jeong ; K.K. Shin
Computation of crystal growth. using sharp interface methods
 Efficient computation of crystal growth using sharp interface methods University of Regensburg joint with John Barrett (London) Robert Nürnberg (London) July 2010 Outline 1 Curvature driven interface motion
Efficient computation of crystal growth using sharp interface methods University of Regensburg joint with John Barrett (London) Robert Nürnberg (London) July 2010 Outline 1 Curvature driven interface motion
Lecture Notes to Accompany. Scientific Computing An Introductory Survey. by Michael T. Heath. Chapter 10
 Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Chapter 10 Boundary Value Problems for Ordinary Differential Equations Copyright c 2001. Reproduction
Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Chapter 10 Boundary Value Problems for Ordinary Differential Equations Copyright c 2001. Reproduction
Mesh Discretization Error and Criteria for Accuracy of Finite Element Solutions
 Mesh Discretization Error and Criteria for Accuracy of Finite Element Solutions Chandresh Shah Cummins, Inc. Abstract Any finite element analysis performed by an engineer is subject to several types of
Mesh Discretization Error and Criteria for Accuracy of Finite Element Solutions Chandresh Shah Cummins, Inc. Abstract Any finite element analysis performed by an engineer is subject to several types of
Finite cloud method: a true meshless technique based on a xed reproducing kernel approximation
 INTERNATIONAL JOURNAL FOR NUMERICAL METHODS IN ENGINEERING Int. J. Numer. Meth. Engng 2001; 50:2373 2410 Finite cloud method: a true meshless technique based on a xed reproducing kernel approximation N.
INTERNATIONAL JOURNAL FOR NUMERICAL METHODS IN ENGINEERING Int. J. Numer. Meth. Engng 2001; 50:2373 2410 Finite cloud method: a true meshless technique based on a xed reproducing kernel approximation N.
Finite Difference Approach to Option Pricing
 Finite Difference Approach to Option Pricing February 998 CS5 Lab Note. Ordinary differential equation An ordinary differential equation, or ODE, is an equation of the form du = fut ( (), t) (.) dt where
Finite Difference Approach to Option Pricing February 998 CS5 Lab Note. Ordinary differential equation An ordinary differential equation, or ODE, is an equation of the form du = fut ( (), t) (.) dt where
CHAPTER 3. INTRODUCTION TO MATRIX METHODS FOR STRUCTURAL ANALYSIS
 1 CHAPTER 3. INTRODUCTION TO MATRIX METHODS FOR STRUCTURAL ANALYSIS Written by: Sophia Hassiotis, January, 2003 Last revision: February, 2015 Modern methods of structural analysis overcome some of the
1 CHAPTER 3. INTRODUCTION TO MATRIX METHODS FOR STRUCTURAL ANALYSIS Written by: Sophia Hassiotis, January, 2003 Last revision: February, 2015 Modern methods of structural analysis overcome some of the
Your FEMLAB Trial: An Introduction to FEMLAB s Multiphysics Modeling Capabilities
 Your FEMLAB Trial: An Introduction to FEMLAB s Multiphysics Modeling Capabilities 1 Preface. This manual gives you an introduction to modeling in FEMLAB by taking you through the basic steps of the modeling
Your FEMLAB Trial: An Introduction to FEMLAB s Multiphysics Modeling Capabilities 1 Preface. This manual gives you an introduction to modeling in FEMLAB by taking you through the basic steps of the modeling
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B. KITCHENS
 December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
Introduction to Solid Modeling Using SolidWorks 2012 SolidWorks Simulation Tutorial Page 1
 Introduction to Solid Modeling Using SolidWorks 2012 SolidWorks Simulation Tutorial Page 1 In this tutorial, we will use the SolidWorks Simulation finite element analysis (FEA) program to analyze the response
Introduction to Solid Modeling Using SolidWorks 2012 SolidWorks Simulation Tutorial Page 1 In this tutorial, we will use the SolidWorks Simulation finite element analysis (FEA) program to analyze the response
Class Meeting # 1: Introduction to PDEs
 MATH 18.152 COURSE NOTES - CLASS MEETING # 1 18.152 Introduction to PDEs, Fall 2011 Professor: Jared Speck Class Meeting # 1: Introduction to PDEs 1. What is a PDE? We will be studying functions u = u(x
MATH 18.152 COURSE NOTES - CLASS MEETING # 1 18.152 Introduction to PDEs, Fall 2011 Professor: Jared Speck Class Meeting # 1: Introduction to PDEs 1. What is a PDE? We will be studying functions u = u(x
CAE -Finite Element Method
 16.810 Engineering Design and Rapid Prototyping Lecture 3b CAE -Finite Element Method Instructor(s) Prof. Olivier de Weck January 16, 2007 Numerical Methods Finite Element Method Boundary Element Method
16.810 Engineering Design and Rapid Prototyping Lecture 3b CAE -Finite Element Method Instructor(s) Prof. Olivier de Weck January 16, 2007 Numerical Methods Finite Element Method Boundary Element Method
The elements used in commercial codes can be classified in two basic categories:
 CHAPTER 3 Truss Element 3.1 Introduction The single most important concept in understanding FEA, is the basic understanding of various finite elements that we employ in an analysis. Elements are used for
CHAPTER 3 Truss Element 3.1 Introduction The single most important concept in understanding FEA, is the basic understanding of various finite elements that we employ in an analysis. Elements are used for
Stress and deformation of offshore piles under structural and wave loading
 Stress and deformation of offshore piles under structural and wave loading J. A. Eicher, H. Guan, and D. S. Jeng # School of Engineering, Griffith University, Gold Coast Campus, PMB 50 Gold Coast Mail
Stress and deformation of offshore piles under structural and wave loading J. A. Eicher, H. Guan, and D. S. Jeng # School of Engineering, Griffith University, Gold Coast Campus, PMB 50 Gold Coast Mail
RF-thermal-structural-RF coupled analysis on the travelling wave disk-loaded accelerating structure
 RF-thermal-structural-RF coupled analysis on the travelling wave disk-loaded accelerating structure PEI Shi-Lun( 裴 士 伦 ) 1) CHI Yun-Long( 池 云 龙 ) ZHANG Jing-Ru( 张 敬 如 ) HOU Mi( 侯 汨 ) LI Xiao-Ping( 李 小
RF-thermal-structural-RF coupled analysis on the travelling wave disk-loaded accelerating structure PEI Shi-Lun( 裴 士 伦 ) 1) CHI Yun-Long( 池 云 龙 ) ZHANG Jing-Ru( 张 敬 如 ) HOU Mi( 侯 汨 ) LI Xiao-Ping( 李 小
Finite Element Method
 16.810 (16.682) Engineering Design and Rapid Prototyping Finite Element Method Instructor(s) Prof. Olivier de Weck [email protected] Dr. Il Yong Kim [email protected] January 12, 2004 Plan for Today FEM Lecture
16.810 (16.682) Engineering Design and Rapid Prototyping Finite Element Method Instructor(s) Prof. Olivier de Weck [email protected] Dr. Il Yong Kim [email protected] January 12, 2004 Plan for Today FEM Lecture
Automated moving mesh techniques in CFD
 Unione Europea Repubblica Italiana Regione Autonoma della Sardegna Automated moving mesh techniques in CFD Application to fluid-structure interactions and rigid motions problems MANUELA PROFIR [email protected]
Unione Europea Repubblica Italiana Regione Autonoma della Sardegna Automated moving mesh techniques in CFD Application to fluid-structure interactions and rigid motions problems MANUELA PROFIR [email protected]
List of Problems Solved Introduction p. 1 Concept p. 1 Nodes p. 3 Elements p. 4 Direct Approach p. 5 Linear Spring p. 5 Heat Flow p.
 Preface p. v List of Problems Solved p. xiii Introduction p. 1 Concept p. 1 Nodes p. 3 Elements p. 4 Direct Approach p. 5 Linear Spring p. 5 Heat Flow p. 6 Assembly of the Global System of Equations p.
Preface p. v List of Problems Solved p. xiii Introduction p. 1 Concept p. 1 Nodes p. 3 Elements p. 4 Direct Approach p. 5 Linear Spring p. 5 Heat Flow p. 6 Assembly of the Global System of Equations p.
GeoGebra. 10 lessons. Gerrit Stols
 GeoGebra in 10 lessons Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It was developed by Markus Hohenwarter
GeoGebra in 10 lessons Gerrit Stols Acknowledgements GeoGebra is dynamic mathematics open source (free) software for learning and teaching mathematics in schools. It was developed by Markus Hohenwarter
The Fourth International DERIVE-TI92/89 Conference Liverpool, U.K., 12-15 July 2000. Derive 5: The Easiest... Just Got Better!
 The Fourth International DERIVE-TI9/89 Conference Liverpool, U.K., -5 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de technologie supérieure 00, rue Notre-Dame Ouest Montréal
The Fourth International DERIVE-TI9/89 Conference Liverpool, U.K., -5 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de technologie supérieure 00, rue Notre-Dame Ouest Montréal
Modeling with Python
 H Modeling with Python In this appendix a brief description of the Python programming language will be given plus a brief introduction to the Antimony reaction network format and libroadrunner. Python
H Modeling with Python In this appendix a brief description of the Python programming language will be given plus a brief introduction to the Antimony reaction network format and libroadrunner. Python
To define concepts such as distance, displacement, speed, velocity, and acceleration.
 Chapter 7 Kinematics of a particle Overview In kinematics we are concerned with describing a particle s motion without analysing what causes or changes that motion (forces). In this chapter we look at
Chapter 7 Kinematics of a particle Overview In kinematics we are concerned with describing a particle s motion without analysing what causes or changes that motion (forces). In this chapter we look at
FINAL EXAM SOLUTIONS Math 21a, Spring 03
 INAL EXAM SOLUIONS Math 21a, Spring 3 Name: Start by printing your name in the above box and check your section in the box to the left. MW1 Ken Chung MW1 Weiyang Qiu MW11 Oliver Knill h1 Mark Lucianovic
INAL EXAM SOLUIONS Math 21a, Spring 3 Name: Start by printing your name in the above box and check your section in the box to the left. MW1 Ken Chung MW1 Weiyang Qiu MW11 Oliver Knill h1 Mark Lucianovic
440 Geophysics: Heat flow with finite differences
 440 Geophysics: Heat flow with finite differences Thorsten Becker, University of Southern California, 03/2005 Some physical problems, such as heat flow, can be tricky or impossible to solve analytically
440 Geophysics: Heat flow with finite differences Thorsten Becker, University of Southern California, 03/2005 Some physical problems, such as heat flow, can be tricky or impossible to solve analytically
An Object-Oriented class design for the Generalized Finite Element Method programming
 10(2013) 1267 1291 An Object-Oriented class design for the Generalized Finite Element Method programming Abstract The Generalized Finite Element Method (GFEM) is a numerical method based on the Finite
10(2013) 1267 1291 An Object-Oriented class design for the Generalized Finite Element Method programming Abstract The Generalized Finite Element Method (GFEM) is a numerical method based on the Finite
A gentle introduction to the Finite Element Method. Francisco Javier Sayas
 A gentle introduction to the Finite Element Method Francisco Javier Sayas 2008 An introduction If you haven t been hiding under a stone during your studies of engineering, mathematics or physics, it is
A gentle introduction to the Finite Element Method Francisco Javier Sayas 2008 An introduction If you haven t been hiding under a stone during your studies of engineering, mathematics or physics, it is
FreeFem++, 2d, 3d tools for PDE simulation
 FreeFem++, 2d, 3d tools for PDE simulation F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France with O. Pironneau, J. Morice http://www.freefem.org mailto:[email protected]
FreeFem++, 2d, 3d tools for PDE simulation F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France with O. Pironneau, J. Morice http://www.freefem.org mailto:[email protected]
Computational Geometry Lab: FEM BASIS FUNCTIONS FOR A TETRAHEDRON
 Computational Geometry Lab: FEM BASIS FUNCTIONS FOR A TETRAHEDRON John Burkardt Information Technology Department Virginia Tech http://people.sc.fsu.edu/ jburkardt/presentations/cg lab fem basis tetrahedron.pdf
Computational Geometry Lab: FEM BASIS FUNCTIONS FOR A TETRAHEDRON John Burkardt Information Technology Department Virginia Tech http://people.sc.fsu.edu/ jburkardt/presentations/cg lab fem basis tetrahedron.pdf
Scientic Computing 2013 Computer Classes: Worksheet 11: 1D FEM and boundary conditions
 Scientic Computing 213 Computer Classes: Worksheet 11: 1D FEM and boundary conditions Oleg Batrashev November 14, 213 This material partially reiterates the material given on the lecture (see the slides)
Scientic Computing 213 Computer Classes: Worksheet 11: 1D FEM and boundary conditions Oleg Batrashev November 14, 213 This material partially reiterates the material given on the lecture (see the slides)
FUNCTIONAL DATA ANALYSIS: INTRO TO R s FDA
 FUNCTIONAL DATA ANALYSIS: INTRO TO R s FDA EXAMPLE IN R...fda.txt DOCUMENTATION: found on the fda website, link under software (http://www.psych.mcgill.ca/misc/fda/) Nice 2005 document with examples, explanations.
FUNCTIONAL DATA ANALYSIS: INTRO TO R s FDA EXAMPLE IN R...fda.txt DOCUMENTATION: found on the fda website, link under software (http://www.psych.mcgill.ca/misc/fda/) Nice 2005 document with examples, explanations.
The simulation of machine tools can be divided into two stages. In the first stage the mechanical behavior of a machine tool is simulated with FEM
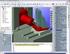 1 The simulation of machine tools can be divided into two stages. In the first stage the mechanical behavior of a machine tool is simulated with FEM tools. The approach to this simulation is different
1 The simulation of machine tools can be divided into two stages. In the first stage the mechanical behavior of a machine tool is simulated with FEM tools. The approach to this simulation is different
Freefem++ F. Hecht. Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France
 Freefem++ F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France with A. Le Hyaric, S. Auliac, P. Jolivet,I. Danaila, O. Pironneau http://www.freefem.org Cours Freefem++,
Freefem++ F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France with A. Le Hyaric, S. Auliac, P. Jolivet,I. Danaila, O. Pironneau http://www.freefem.org Cours Freefem++,
Navier-Stokes Equation Solved in Comsol 4.1. Copyright Bruce A. Finlayson, 2010 See also Introduction to Chemical Engineering Computing, Wiley (2006).
 Introduction to Chemical Engineering Computing Copyright, Bruce A. Finlayson, 2004 1 Navier-Stokes Equation Solved in Comsol 4.1. Copyright Bruce A. Finlayson, 2010 See also Introduction to Chemical Engineering
Introduction to Chemical Engineering Computing Copyright, Bruce A. Finlayson, 2004 1 Navier-Stokes Equation Solved in Comsol 4.1. Copyright Bruce A. Finlayson, 2010 See also Introduction to Chemical Engineering
Linear Static Analysis of a Cantilever Beam Using Beam Library (SI Units)
 APPENDIX A Linear Static Analysis of a Cantilever Beam Using Beam Library (SI Units) Objectives: Create a geometric representation of a cantilever beam. Use the geometry model to define an MSC.Nastran
APPENDIX A Linear Static Analysis of a Cantilever Beam Using Beam Library (SI Units) Objectives: Create a geometric representation of a cantilever beam. Use the geometry model to define an MSC.Nastran
CFD modelling of floating body response to regular waves
 CFD modelling of floating body response to regular waves Dr Yann Delauré School of Mechanical and Manufacturing Engineering Dublin City University Ocean Energy Workshop NUI Maynooth, October 21, 2010 Table
CFD modelling of floating body response to regular waves Dr Yann Delauré School of Mechanical and Manufacturing Engineering Dublin City University Ocean Energy Workshop NUI Maynooth, October 21, 2010 Table
Solutions for Review Problems
 olutions for Review Problems 1. Let be the triangle with vertices A (,, ), B (4,, 1) and C (,, 1). (a) Find the cosine of the angle BAC at vertex A. (b) Find the area of the triangle ABC. (c) Find a vector
olutions for Review Problems 1. Let be the triangle with vertices A (,, ), B (4,, 1) and C (,, 1). (a) Find the cosine of the angle BAC at vertex A. (b) Find the area of the triangle ABC. (c) Find a vector
CUDA for Real Time Multigrid Finite Element Simulation of
 CUDA for Real Time Multigrid Finite Element Simulation of SoftTissue Deformations Christian Dick Computer Graphics and Visualization Group Technische Universität München, Germany Motivation Real time physics
CUDA for Real Time Multigrid Finite Element Simulation of SoftTissue Deformations Christian Dick Computer Graphics and Visualization Group Technische Universität München, Germany Motivation Real time physics
Computational fluid dynamics (CFD) 9 th SIMLAB Course
 Computational fluid dnamics (CFD) 9 th SIMLAB Course Janos Benk October 3-9, Janos Benk: Computational fluid dnamics (CFD) www5.in.tum.de/wiki/inde.php/lab_course_computational_fluid_dnamics_-_summer_
Computational fluid dnamics (CFD) 9 th SIMLAB Course Janos Benk October 3-9, Janos Benk: Computational fluid dnamics (CFD) www5.in.tum.de/wiki/inde.php/lab_course_computational_fluid_dnamics_-_summer_
A new Feynman-Kac-formula for option pricing in Lévy models
 A new Feynman-Kac-formula for option pricing in Lévy models Kathrin Glau Department of Mathematical Stochastics, Universtity of Freiburg (Joint work with E. Eberlein) 6th World Congress of the Bachelier
A new Feynman-Kac-formula for option pricing in Lévy models Kathrin Glau Department of Mathematical Stochastics, Universtity of Freiburg (Joint work with E. Eberlein) 6th World Congress of the Bachelier
Notes for AA214, Chapter 7. T. H. Pulliam Stanford University
 Notes for AA214, Chapter 7 T. H. Pulliam Stanford University 1 Stability of Linear Systems Stability will be defined in terms of ODE s and O E s ODE: Couples System O E : Matrix form from applying Eq.
Notes for AA214, Chapter 7 T. H. Pulliam Stanford University 1 Stability of Linear Systems Stability will be defined in terms of ODE s and O E s ODE: Couples System O E : Matrix form from applying Eq.
Computational Mathematics with Python
 Boolean Arrays Classes Computational Mathematics with Python Basics Olivier Verdier and Claus Führer 2009-03-24 Olivier Verdier and Claus Führer Computational Mathematics with Python 2009-03-24 1 / 40
Boolean Arrays Classes Computational Mathematics with Python Basics Olivier Verdier and Claus Führer 2009-03-24 Olivier Verdier and Claus Führer Computational Mathematics with Python 2009-03-24 1 / 40
Høgskolen i Narvik Sivilingeniørutdanningen
 Høgskolen i Narvik Sivilingeniørutdanningen Eksamen i Faget STE66 ELASTISITETSTEORI Klasse: 4.ID Dato: 7.0.009 Tid: Kl. 09.00 1.00 Tillatte hjelpemidler under eksamen: Kalkulator Kopi av Boken Mechanics
Høgskolen i Narvik Sivilingeniørutdanningen Eksamen i Faget STE66 ELASTISITETSTEORI Klasse: 4.ID Dato: 7.0.009 Tid: Kl. 09.00 1.00 Tillatte hjelpemidler under eksamen: Kalkulator Kopi av Boken Mechanics
SIMULATION SOFTWARE AND NUMERICAL ISSUES. Alexander L. Pugh Massachusetts Institute of Technology, Cambridge, USA
 SIMULATION SOFTWARE AND NUMERICAL ISSUES Alexander L. Pugh Massachusetts Institute of Technology, Cambridge, USA Keywords: Adams integration method, adaptive integration methods, Euler integration method,
SIMULATION SOFTWARE AND NUMERICAL ISSUES Alexander L. Pugh Massachusetts Institute of Technology, Cambridge, USA Keywords: Adams integration method, adaptive integration methods, Euler integration method,
Laminar Flow and Heat Transfer of Herschel-Bulkley Fluids in a Rectangular Duct; Finite-Element Analysis
 Tamkang Journal of Science and Engineering, Vol. 12, No. 1, pp. 99 107 (2009) 99 Laminar Flow and Heat Transfer of Herschel-Bulkley Fluids in a Rectangular Duct; Finite-Element Analysis M. E. Sayed-Ahmed
Tamkang Journal of Science and Engineering, Vol. 12, No. 1, pp. 99 107 (2009) 99 Laminar Flow and Heat Transfer of Herschel-Bulkley Fluids in a Rectangular Duct; Finite-Element Analysis M. E. Sayed-Ahmed
3 Orthogonal Vectors and Matrices
 3 Orthogonal Vectors and Matrices The linear algebra portion of this course focuses on three matrix factorizations: QR factorization, singular valued decomposition (SVD), and LU factorization The first
3 Orthogonal Vectors and Matrices The linear algebra portion of this course focuses on three matrix factorizations: QR factorization, singular valued decomposition (SVD), and LU factorization The first
The finite element immersed boundary method: model, stability, and numerical results
 Te finite element immersed boundary metod: model, stability, and numerical results Lucia Gastaldi Università di Brescia ttp://dm.ing.unibs.it/gastaldi/ INdAM Worksop, Cortona, September 18, 2006 Joint
Te finite element immersed boundary metod: model, stability, and numerical results Lucia Gastaldi Università di Brescia ttp://dm.ing.unibs.it/gastaldi/ INdAM Worksop, Cortona, September 18, 2006 Joint
An introduction to Code_Aster. Daniele Colombo An introduction to Code_Aster
 An introduction to Code_Aster Goals and basic knowledge Goals of this short course: give you basic knowledge on how Code_Aster works give you an overview on how you can use Code_Aster with the pre/post
An introduction to Code_Aster Goals and basic knowledge Goals of this short course: give you basic knowledge on how Code_Aster works give you an overview on how you can use Code_Aster with the pre/post
www.integratedsoft.com Electromagnetic Sensor Design: Key Considerations when selecting CAE Software
 www.integratedsoft.com Electromagnetic Sensor Design: Key Considerations when selecting CAE Software Content Executive Summary... 3 Characteristics of Electromagnetic Sensor Systems... 3 Basic Selection
www.integratedsoft.com Electromagnetic Sensor Design: Key Considerations when selecting CAE Software Content Executive Summary... 3 Characteristics of Electromagnetic Sensor Systems... 3 Basic Selection
Programming a truss finite element solver in C
 CHAPTER 4 Programming a truss finite element solver in C In this section, some C functions are developed that allow to compute displacements and internal efforts of a two-dimensional truss structure. 4.1
CHAPTER 4 Programming a truss finite element solver in C In this section, some C functions are developed that allow to compute displacements and internal efforts of a two-dimensional truss structure. 4.1
Multigrid preconditioning for nonlinear (degenerate) parabolic equations with application to monument degradation
 Multigrid preconditioning for nonlinear (degenerate) parabolic equations with application to monument degradation M. Donatelli 1 M. Semplice S. Serra-Capizzano 1 1 Department of Science and High Technology
Multigrid preconditioning for nonlinear (degenerate) parabolic equations with application to monument degradation M. Donatelli 1 M. Semplice S. Serra-Capizzano 1 1 Department of Science and High Technology
Survey, Statistics and Psychometrics Core Research Facility University of Nebraska-Lincoln. Log-Rank Test for More Than Two Groups
 Survey, Statistics and Psychometrics Core Research Facility University of Nebraska-Lincoln Log-Rank Test for More Than Two Groups Prepared by Harlan Sayles (SRAM) Revised by Julia Soulakova (Statistics)
Survey, Statistics and Psychometrics Core Research Facility University of Nebraska-Lincoln Log-Rank Test for More Than Two Groups Prepared by Harlan Sayles (SRAM) Revised by Julia Soulakova (Statistics)
Error indicator and mesh adaption, in FreeFem++
 Error indicator and mesh adaption, in FreeFem++ F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France http://www.freefem.org mailto:[email protected] Marmern, Pau,
Error indicator and mesh adaption, in FreeFem++ F. Hecht Laboratoire Jacques-Louis Lions Université Pierre et Marie Curie Paris, France http://www.freefem.org mailto:[email protected] Marmern, Pau,
(a) We have x = 3 + 2t, y = 2 t, z = 6 so solving for t we get the symmetric equations. x 3 2. = 2 y, z = 6. t 2 2t + 1 = 0,
 Name: Solutions to Practice Final. Consider the line r(t) = 3 + t, t, 6. (a) Find symmetric equations for this line. (b) Find the point where the first line r(t) intersects the surface z = x + y. (a) We
Name: Solutions to Practice Final. Consider the line r(t) = 3 + t, t, 6. (a) Find symmetric equations for this line. (b) Find the point where the first line r(t) intersects the surface z = x + y. (a) We
Domain Decomposition Methods for Elastic Materials with Compressible and Almost Incompressible Components
 Domain Decomposition Methods for Elastic Materials with Compressible and Almost Incompressible Components Sabrina Gippert geboren in Neuss Fakultät für Mathematik Universität Duisburg-Essen November 01
Domain Decomposition Methods for Elastic Materials with Compressible and Almost Incompressible Components Sabrina Gippert geboren in Neuss Fakultät für Mathematik Universität Duisburg-Essen November 01
AN INTRODUCTION TO NUMERICAL METHODS AND ANALYSIS
 AN INTRODUCTION TO NUMERICAL METHODS AND ANALYSIS Revised Edition James Epperson Mathematical Reviews BICENTENNIAL 0, 1 8 0 7 z ewiley wu 2007 r71 BICENTENNIAL WILEY-INTERSCIENCE A John Wiley & Sons, Inc.,
AN INTRODUCTION TO NUMERICAL METHODS AND ANALYSIS Revised Edition James Epperson Mathematical Reviews BICENTENNIAL 0, 1 8 0 7 z ewiley wu 2007 r71 BICENTENNIAL WILEY-INTERSCIENCE A John Wiley & Sons, Inc.,
