Inverse Kinematic Problem Solving: A Symbolic Approach Using MapleSim and Maple

Transcription

1 Inverse Kinematic Problem Solving: A Symbolic Approach Using MapleSim and Maple 4 High-Performance Physical Modeling and Simulation

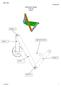
2 Inverse Kinematic Problem Solving: A Symbolic Approach Using MapleSim and Maple In multibody mechanics, the motion analysis for a platform (the kinematics problem) can be classified into two cases: the forward kinematics problem and the inverse kinematics problem. For the forward kinematics problem, the trajectory of a point on a mechanism (for example, the end effector of a robot arm or the center of a platform support by a parallel link manipulator) is computed as a function of the joint motions. In the inverse kinematics case, the problem is reversed: the goal is to compute the joint motions necessary to achieve a prescribed end effector trajectory. In general, given the mechanism geometry, it is pretty straightforward to solve the forward kinematics problem both numerically and symbolically. In contrast, solving for the inverse kinematics problem typically involves solving a nonlinear system of equations with trigonometric functions. Issues such as singularity, multiple (non-unique) solutions (as in the case of elbow up and elbow down configurations for a robot arm), and no solution (as in the case in which the specified trajectory goes beyond the workspace of the mechanism) can often come up, further complicating the solution process. The complexity in the inverse kinematics problem is compounded even more for parallel link manipulators. Because of the complexity involved, the inverse kinematics problem is often solved numerically through iterations, and is computationally expensive. With a numeric approach, however, information about the motion of the mechanism is often lost. In this paper, we will describe how to obtain a symbolic solution to the inverse kinematics problem for a Stewart-Gough parallel link manipulator using tools available in MapleSim TM. In particular, we will show how having access to the symbolic Jacobian of the constraint equations allows us to inspect and exploit the underlying matrix structure, which leads to a simplified solution process for obtaining the symbolic solution. An advantage of having a symbolic solution to the inverse kinematics problem is the possibility of codegenerating the symbolic solution so that it can be embedded in real-time hardware-in-theloop (HIL) applications. This approach can be contrasted with a purely numerical approach where the iterative solution process makes it difficult to use in real-time applications. Figure 1: Stewart-Gough Platform in MapleSim Inverse Kinematic Problem Solving: A Symbolic Approach Using MapleSim and Maple

3 Figure 2: Platform Leg Structure Figure 3: Platform Leg Parameters A Stewart-Gough manipulator is generally referred to as a six degrees-of-freedom (DOF) parallel linkage mechanism. There are several variations in the leg configurations of a Stewart- Gough platform. In this paper, we will be looking at a Stewart-Gough platform (see Figure 1) whose motion is provided through six prismatic joints; each is anchored with a universal joint (two cascaded revolute joints) on one end and a spherical (ball) joint on the other end (see Figure 2). Each of the platform legs is defined with five parameters, specifying the x-y offset of the two anchor points (Xg, Yg, Xp, and Yp) and the base anchor rotation angle offset (Ang). See Figure 3. The inverse kinematics problem in this case is to find the length of each of the six prismatic joints that will result in a desired motion trajectory for the supported platform. In symbolic terms, this means we want to obtain the expressions for the prismatic joint lengths as a function of the desired position. The tight integration between MapleSim and Maple TM offers users a unique feature: access to the underlying symbolic system equations. The advantage of having access to the symbolic equations is clearly illustrated when solving the inverse kinematics problem. Information can be obtained by observing the structure of the symbolic system of equations, which can assist in obtaining the solution to the problem. Here, we will use the Multibody Analysis template provided with MapleSim to retrieve the symbolic system equations for the Stewart- Gough platform (see Figure 4). At the top of the template, there are some setup steps that lead to a call to the command BuildEQs. The result of executing BuildEQs is a data record (with a default name of MB) containing information about the multibody system defined within the MapleSim model. Information available in this data record includes state variable and parameter

4 Figure 4: Multibody Analysis Template Figure 5: Multibody System Information definitions, inertia properties (inertial matrix), dynamic equations, constraint (kinematic) equations, as well as Jacobian matrices of the constraint equations. In general, to solve the inverse kinematics problem, we would take the position constraint equations for the platform and try to solve for the length of each leg given the desired platform location. In the case of the Stewart- Gough platform, this represents solving a set of 18 positional constraint equations for the six prismatic joint lengths, plus 12 revolute joint angles for the orientation of the legs. In addition to being a nontrivial problem to solve, the sheer size of this inverse problem implies that even with numeric iterations, the calculations involved are still quite intense. Further, the numeric solution would not provide any insights into the structure of the problem that might be exploited for design or performance considerations. As it turns out, for this particular leg configuration, a structural property can be exploited to simplify the solution of the inverse kinematic problem so that a closed-form symbolic solution can be obtained. The 18 positional constraint equations come from the spherical joints that are used to attach each leg to the platform, which result from enforcing the x, y, z position of each leg s end to be coincident with a given point on the platform. Such structural properties can be observed from the definition of the state vector and the position constraint Jacobian matrix of the system. The generalized coordinate definition for the Stewart-Gough platform can be accessed from the vq field of the system data record MB (in Maple syntax, MB:-vQ). The default compact display from Maple (see Figure 5) shows that, in this case, there are 24 generalized coordinates or states for the platform system. The ordering and names of the individual state variables can be inspected by double-clicking on the compact vector summary, represented by the blue text enclosed within the square brackets, which opens the Matrix/Vector browser (see Figure 6). From the Vector browser, the state vector is ordered such that the position of the platform center (named x_platform_rb4(t), y_platform_ RB4(t), and z_platform_rb4(t)) is at the top. The length variable of each prismatic joint from s_splc1_leg_p1(t) to s_splc6_ Leg_P1(t) is next. This value is followed by the variables for the orientation of the platform (zeta_platform_rb4(t), eta_platform_ Inverse Kinematic Problem Solving: A Symbolic Approach Using MapleSim and Maple

5 Figure 6: State Vector Definition RB4(t), and xi_platform_rb4(t)). Finally, six pairs of joint angles for the two revolute joints at the base anchor of each leg (theta_splc#_ Leg_R1(t) and theta_splc#_leg_r2(t), where # ranges from 1 to 6) fill in the rest of the state vector. A structural breakdown of the state vector is shown below: Platform Position Variables (3) Leg Length Variables (6) Platform Orientation Variables (3) Leg Orientation Variables (2 x 6 = 12) The Jacobian matrix for the position constraints is defined as the partial derivatives of the positional constraint equations (accessible through the MB:-GetPosCons() command, see Figure 5) with respect to the state variables. In this case, it is a matrix (for 18 constraints and 24 states). Its structure describes the relationships between the constraint equations and the state variables: a zero entry in the (i,j) element of the Jacobian matrix means that the i th positional constraint is independent of the j th state variable. Once again, to inspect the Jacobian matrix, we will open the Matrix browser by double-clicking the result returned by the xjacpos field of the MB record (MB:-xJacPos in Figure 5). In addition to seeing the symbolic entries of the Jacobian, the overall structural information can be visualized graphically as an image by clicking the Image tab of the Matrix browser window (see Figure 7). By using the image option, we can visualize either the magnitude or the structure of the matrix under examination. In this case, we select the structure option in the Display list

6 Figure 7: Position Constraint Jacobian (Table View) Figure 8: Position Constraint Jacobian (Image View) near the bottom of the window (see Figure 8). The colormap is chosen such that the white areas represent structural zero entries (that is, the entry is exactly zero for all times) and the black areas represent nonzero entries. Relating the Matrix browser image back to the state vector definition, we can see that the two bands of nonzero columns in the image correspond to the platform position and orientation variables. This means that all of the constraints are dependent on these platform variables as expected. On the other hand, an interesting pattern has emerged relating the constraint equations to the leg length and orientation variables. This pattern reveals that the constraint equations (within the constraint equation vector, obtained from the call to the MB:-GetPosCons command - see Figure 5) are bundled into six groups that correspond to the variables associated with each of the six legs in the system. For example, the first three constraint equations form a bundle that describes the constraints for the first leg, the second bundle of three for the second leg, and so on. This implies that the kinematics constraints for each leg can be solved independently and with only a subset of the constraint equations. With this information, we can now effectively transform the original problem of solving 18 nonlinear constraint equations into a problem of solving six sets of three nonlinear constraint equations independently. Furthermore, because of the symmetry and the parametric nature of the leg component, the solution obtained for one leg is expressed with respect to the leg parameters, as defined in Figure 3. This means the same solution is applicable to all six legs, given the appropriate leg parameter values. So, the overall inverse kinematics problem is stripped down to solving a subset of three positional constraint equations, representing a significant reduction in the problem complexity. We obtained the reduced set of position constraint equations, shown in Figure 9, by taking the position constraint equations corresponding to the first leg of the platform. For compactness, we renamed state variables with shorter names as follows: s for the leg length, a and for the revolute joint angles at the base anchor point, and X, Y, Z for the position variables. For this particular example, we specified a fixed orientation (0 rad rotation about all three axes) for the platform when solving the inverse kinematics problem below, which will keep the platform level. With this simplified problem, we can now use the Maple solve command to obtain the symbolic expression for the leg length s. From the result, we obtain the solution as a function f of the platform position (X, Y, Z) and the leg parameters (Xg, Yg, Xp, Ang) in the following form: s = f (X, Y, Z, Xg, Yg, Xp, Yp, Ang) Now, we can take this symbolic solution for s and implement it as a custom component in MapleSim to obtain an inverse kinematics simulation. The result of the simulation is shown in Figure 10. Inverse Kinematic Problem Solving: A Symbolic Approach Using MapleSim and Maple

7 In conclusion, we have taken advantage of the ability to access the underlying symbolic system equations to help reduce the size of the inverse kinematics problem by exploiting the symbolic structure of the Jacobian matrix. It should be noted that the same problem can also be solved numerically within MapleSim (to obtain the plot shown in Figure 10) by simply applying enforced motion to the platform by using the Prescribed Translation motion driver component. However, such a purely numerical solution does not have the same flexibility as the symbolic solution presented in this paper. Using the symbolic solution obtained here and MapleSim s code generation feature, you can embed the code into other platforms, unlocking the possibility for real-time application without the need for an iterative solver. Figure 9: A Subset of Position Constraints Figure 10: Inverse Kinematics Solution

8 Toll-free: (US & Canada) Direct: Maplesoft, a division of Waterloo Maple Inc., Maplesoft, Maple, MapleSim, are trademarks of Waterloo Maple Inc. All other trademarks are the property of their respective owners.