Students difficulties in problems that involve unit-vector notation
|
|
|
- Briana Holland
- 8 years ago
- Views:
Transcription
1 Students difficulties in problems that involve unit-vector notation Pablo Barniol, Genaro Zavala Physics Education Research and Innovation Group. Department of Physics, Tecnológico de Monterrey, Campus Monterrey, E. Garza Sada 2501, Monterrey, N. L México (Received 11 June 2014, accepted 26 November 2014). Abstract Many researchers have analyzed students understanding of vector concepts. However, at the moment there is a need in the physics education research area for a study that presents a complete analysis of students difficulties with problems that involve unit-vector notation. This article responds to this need. We administered a test with open-ended problems to a total of 972 students who had completed the required introductory physics courses at a large private Mexican university. We found frequent errors when students sketched a vector written in the unit-vector notation and calculated direction, magnitude, sum, subtraction, scalar multiplication, dot product and cross product in problems that involve this notation. These errors persist even after instruction and have not been reported in the literature. The results of this research can help guide the development of new instructional materials that will attempt to improve students understanding of problems involving unit-vector notation. Keywords: vector, students difficulties, unit-vector notation. Resumen Muchos investigadores han analizado la comprensión de los conceptos de vectores de los estudiantes. Sin embargo, en este momento hay necesidad en el área de la investigación en educación física, para un estudio que presente un análisis completo de las dificultades de los estudiantes con problemas que implican la notación unidad en vectores. Este artículo responde a esta necesidad. Administramos una prueba con problemas de composición abierta para un total de 972 estudiantes, quienes habían completado los cursos de introducción a la física requeridos para una gran universidad privada mexicana. Encontramos errores frecuentes cuando los estudiantes esbozaron un vector escrito en la notación de unidad-vector y dirección calculada, en magnitud, en suma, en resta, en multiplicación escalar, en producto escalar y en producto vectorial, en problemas que involucran esta notación. Estos errores persisten incluso después de la instrucción, no se han reportado en la literatura. Los resultados de esta investigación pueden ayudar a guiar el desarrollo de nuevos materiales de instrucción, que intentarán mejorar la comprensión de los estudiantes en los problemas que implican la notación en unidad-vectores. Palabras clave: vector, dificultades de los estudiantes, notación de unidad-vector. PACS: Fk, G ISSN I. INTRODUCTION primary reason for the vague usage of the field concept in answering some electricity and magnetism conceptual Vector concepts are very important in physics, since many problems. physical quantities are defined as vectors. For example force, Although many studies have centered on students velocity and acceleration are defined as vectors, and electric difficulties with vector concepts in problems with and magnetic field are defined as vector fields. mathematic and physical context, only a few of them have Many researchers have analyzed misconceptions of these focused on students difficulties in problems that involve types of physical quantities [1], and some of them have unit-vector notation. This is remarkable because this notation described the relationship between these misconceptions and is commonly used in the introductory physics university students difficulties with vector concepts [2, 3]. Flores et al. courses. This article seeks to address this need. [2] mentioned that after traditional instruction in mechanics Therefore, the objective of this study is to analyze the many students lack the ability to reason about vectors that difficulties that students who have completed their represent forces and kinematic quantities. Moreover, introductory physics university courses still have with Saarelainen et al. [3] established that the absence of problems that involve the unit-vector notation. appropriate vector thinking in the case of the fields was the Lat. Am. J. Phys. Educ. Vol.8, No. 4, Dec
2 Pablo Barniol and Genaro Zavala II. PREVIOUS RESEARCH therefore, we believe that this vacuum justifies the present research. The previous studies that analyze students understanding of vectors concepts can be clustered in three groups: 1) studies that analyze students understanding of vectors concepts in problems with no physical context [4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15], 2) studies that investigate students understanding in problems with a physical context [2, 3, 6, 7, 9, 15, 16, 17, 18, 19, 20], and 3) studies that compare students performance on solving problems with physical context and problems with no physical context [6, 7, 9, 13, 15, 19]. Results of the present study were used, following the recommendations of Beichner [21], to build five items of our reliable 20-item multiple choice vector concept test (Test of Understanding of Vectors, TUV) that was presented briefly in a short paper [22]. The results of some of our other works presented elsewhere [8, 9, 10, 14, 15] were used to build the other items of the test that evaluate the students understanding of vector concepts posed in graphical form. Finally, some previous studies from this journal [23, 24] have presented new technology based instructional strategies to teach vector concept. Note that some of these studies pertain to more than one group. The present study is classified within the first group since III. METHODOLOGY it is a report on students understanding of problems with no physical context. This first group can also be divided in two subgroups: a) studies that focus on students understanding of problems that involve unit-vector notation [4, 6], b) studies that focus on students understanding of problems in which the vectors are presented in graphical form (the rest of This study was conducted at a large private Mexican university. In this institution the textbooks used in the physics courses are Physics for Scientists and Engineers by Serway and Jewett [25] and Tutorials in Introductory Physics by McDermott and Shaffer [26]. the reports). From this subdivision, we can note that only two studies analyze students understanding of problems A. Design of the open-ended problems with unit-vector notation. Next we describe briefly what is established in the two articles that focus on problems that involve unit-vector notation. In the first report, Knight [4] designed an open-ended problem test, and administered it to students who entered the university before receiving any instruction in vectors. He found that 50% of these students had no useful vector knowledge at all. In the designed test, four problems involve the unit-vector notation. The first problem asks the student to establish the y-component of the vector 3i-2j+3k. Knight found two frequent errors: 1) students would exclude the negative sign and 2) they would include the unit vector in the answer (2j). The second problem asks them to write, in unit-vector notation, the vector -3i+2j which is presented in graphical form. The author found that some students frequently made the error of writing the vector as 3x+2y. The third problem asks for the addition of two vectors written in the unit-vector notation, and the fourth problem asks to calculate the dot product of two vectors written in this notation. In these two We decided to use open-ended problems because they have been used to identify students difficulties in vector concepts [4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14].To establish these problems, we asked physics faculty members in interviews about the vector properties and operations in this notation and after that, we arrived to a consensus of eight problems that are used in this study. In the Appendix of this article, we show these eight problems, in which students are asked to: 1) sketch a vector, 2) calculate the direction of a vector, 3) calculate the magnitude of a vector, 4) add two vectors, 5) subtract two vectors, 6) perform a negative scalar multiplication of a vector, 7) calculate the dot product of two vectors, and 8) calculate the cross product of two vectors. Note that in the analysis of each of the problems we will describe briefly the background that the students must have to answer each of the items correctly. problems, the author didn t detect any frequent errors. In the second work, Van Deventer [6] compared B. Study Participants students performance in isomorphic ( same form ) problems with physical and no-physical context. The author carried out eleven interviews with university students who had taken the introductory physics courses, in order to identify the frequent errors. Three interviewee s problems involved unit-vector notation. In the addition and subtraction problems, the researcher didn t find any errors. On the other hand, in the dot product the author found one error: some students believed that the dot product of vector 3i and vector 4j was12ij. After this synthetic view of these two studies, we can see that so far, the studies that have focused on students difficulties in problems that involve unit-vector notation are only partial. There are no other studies, to our knowledge; The objective of the study allows us to choose the participants of this study. In this institution the students who are completing their introductory physics university courses are students who had finished the calculus-based Electricity and Magnetism course. There were a population of 972 students; however, we had some limitations. The first limitation was temporal since we were limited by the time it takes students for a diagnostic of open-ended problems. The second limitation was based on the fact that many of the problems that we wanted to administer were highly related to each other (for example: the dot product and the cross product, the addition and the subtraction, and the direction and the magnitude). Some authors (i.e. Gray [27]) have Lat. Am. J. Phys. Educ. Vol.8, No. 4, Dec
3 pointed that solving a problem when a related problem is solved previously could influence the answer. Due to time limitations and to avoid any possible influence between related problems we decided to randomly divide the sample into six different groups, following the methodology by Barniol & Zavala [8]. The six groups of students were divided as follow: 143 students did Problem 1 (graphic representation of a vector), 197 did Problems 2 and 5 (direction of a vector and subtraction), 139 did Problem 3 (magnitude of a vector), 202 did Problem 4 and 6 (addition and scalar multiplication), 143 did Problem 7 (dot product) and 148 students did Problem 8 (cross product). C. Analysis of students answers Students difficulties in problems that involve unit-vector notation Vector from (-2,0) to (-2,3) 1% Others 5% FIGURE 1. Frequent errors in problem 1. To analyze students answers in the open-ended problems we use a codification process established by Hernandez Sampieri et al. [28]. According to these authors, this process consists in finding and naming similar answers, then listing them, and finally establishing the proportions of each answer. In the analysis of each of the problems we first codify the most common errors in a table and then in the analysis of these errors we describe the reasoning or procedures that lead students to make these errors. IV. RESULTS In the following subsections, we present the results of students answers to each of the problems. In each case we present the most common errors and their distribution. Then we describe in detail what students did in each of the errors. A. Graphical representation of a vector written in the unit-vector notation We designed Problem 1 (shown in the Appendix) to analyze students difficulties in sketching a vector written in the unitvector notation. Students are asked to sketch a vector in a grid with coordinate axis. The statement of this problem is: Draw in the grid the vector A=-2i+3j. As mentioned before, 143 students answered this problem. To answer this problem correctly students should know that this vector have a negative x-component of two units and a positive y- component of three units. Therefore, they should sketch the vector from the origin (0, 0) to the point (-2, 3). Table 1 shows the proportion of the answers given by the students, and Figure 1 shows the errors graphically. In Table 1, we notice that 81% of students correctly represented vector -2i+3j. We found three errors. TABLE I. Answers given for Problem 1: Graphic representation of vector -2i+3j. Correct 81% Vector from (-2,0) to (0,3) 7% Vector in point (-2,3) 6% 1) Students sketched a vector from point (-2, 0) to point (0, 3).These students drew the components of the vector (from the origin in a tail-to-tail representation) and then sketched vector -2i+3j from the head of vector -2i to the head of vector 3j. This error seems to be related to the tail-to-tail error identified by Knight [4] in vector addition problems. 2) Students identified correctly the point (-2, 3), but instead of drawing vector -2i+3j from point (0, 0) to this point, students incorrectly sketched the vector at this point. The drawn vectors have different magnitudes and directions, but approximately one third of the students sketched a vector -i+j at this point (as shown in Figure 1). 3) Students drew a vector from point (-2, 0) to point (-2, 3). These students correctly identified these two points (-2, 0) and (-2, 3), which is one step of the correct procedure; however, they made the mistake of sketching the vector between these two points (as shown in Figure 1). If we analyze these three errors as a group we note that they have in common that students identify points that are part of the correct procedure but make errors in the interpretation of the role of these points in the correct procedure. B. Direction of a vector written in the unit-vector notation To analyze students difficulties with the direction calculation of a vector written in the unit-vector notation, we designed Problem 2 (shown in the Appendix) that asks students to calculate the direction of a vector. The statement of this problem is: Consider vector A=-3i+4j. Calculate the direction of this vector measured from the positive x-axis. As mentioned before, 197 students answered this problem. There are different procedures to answer this problem; however, a common correct procedure is that students visualize that vector A is in the third quadrant with its tail in the origin and with a negative x-component of three units and a positive y-component of four units. Then students realize that the direction of a vector is calculated as an angle in counterclockwise direction from the axis, x-axis, in this case. Students then calculate the angle between vector A and its x-component using the equation tan -1 (4/3) and finally they subtract this value to 180 obtaining an angle of Lat. Am. J. Phys. Educ. Vol. 8, No. 4, Dec
4 Pablo Barniol and Genaro Zavala Table II shows the answers and distributions given by the students. TABLE II. Answers given for Problem 2: Calculation of the direction of vector -3î+4ĵ. Correct ( ) 17% Presents only a correct sketch of the vector 18% Presents only an incorrect sketch of the vector 6% Considers that the direction is in the negative direction of x-axis and in the positive direction of 7% y-axis Considers that the direction is in the negative direction of x-axis 7% Magnitude of the vector (5) 5% Unit vector in the direction of vector A 5% % % % 135 1% No answer 11% Others 11% calculated the unit vector in the direction of vector A, as the direction of this vector. It seems that these students have difficulties in understanding the meaning of the unit vector (we will also see this difficulty in the next problem). Finally, we detected four errors in the calculation of the correct angle: 1) Students (5%) incorrectly answered These students directly calculated the direction as tan -1 (4/3). 2) Students (4%) incorrectly established that the direction is 53.13, calculating it as tan -1 (4/3). 3) Students (3%) answered These students calculated first a angle (as tan -1 (4/3)) and then incorrectly added a 90 angle to this value. 4) Students established that the direction of the vector is 135. These students incorrectly believed that the vector makes an exact negative 45 angle with the negative x-axis. C. Magnitude of a vector written in the unit-vector notation We designed Problem 3 (shown in the Appendix) to analyze students difficulties with the magnitude calculation of a As we can see in Table II, only 17% of the students correctly vector written in the unit-vector notation. established that the direction of the vector is When The statement of this problem is this: Consider vector we analyzed students answers, we found that a considerable A= 2i+2j. Calculate the magnitude of this vector. As proportion (38%) of students didn t calculate the direction of mentioned before, 139 students answered this problem. To vector A but presented a sketch of the vector or used a answer this problem correctly students should calculate the qualitative description when answering the question. We magnitude of vector A using the Pythagorean Theorem found that 24% of students presented a sketched of a vector, ( ( )) obtaining 8. Table III shows the answers and usually in a coordinate system: 18% presented a correct distributions given by the students. drawing of the vector and 6% of the students presented an We notice from Table 3 that 74% correctly answered incorrect drawing of the vector, such as the one shown in the Problem 3 as 8. These students correctly used the analysis of the previous problem. Pythagorean Theorem A= ( ). We found four frequent We also found that 14% used a qualitative description. errors: 7% of the students answered that the direction of vector A is 1) Students unexpectedly concluded that the magnitude in the negative direction of the x-axis and in the positive of vector A is the unit vector in the direction of vector A direction of the y-axis. Some students stated that explicitly, (2i/ 8+2j/ 8). As mentioned in the previous analysis, and some others referred to directions as to the northwest students seem to have difficulties in understanding the or to the second quadrant. This incorrect conception was meaning of this vector. also detected in a previous report from us with a problem 2) Students calculated the magnitude of vector A as 4. that asked students to identify (in a graphic) vectors with the These students made a calculation error, because they same direction [8]. We also found that 7% of the students incorrectly calculated ( ) as 4. thought that the direction of vector -3i+4j (measured from 3) Students considered that the magnitude of the vector is positive x-axis) was in the negative direction of the x-axis. 2. Some students applied the Pythagorean theorem The most frequent answers in this category were: -3i, incorrectly as A= (2+2). 3 units to the left, and to the left. 4) Students believed that the magnitude of the vector was It seems very probable that these students have 8. Some of these students also incorrectly applied the difficulties with the phrase measured from the positive x- theorem as A 2 = ( ). axis, and believe that the requested direction is the one of the x-component of the vector. As noticed before, about 38% of students presented a sketch or used a qualitative TABLE III. Answers given for Problem 3: Calculation of the description. It is interesting to mention that Aguirre and magnitude of vector 2i+2j. Erickson [16] also found in an interview-based study that, when students are asked to calculate the direction of a vector, Correct ( 8) 74% a significant number of them used qualitative instead of 2i/ 8+2j/ 8 4% quantitative descriptions when answering the question. 4 3% We also discovered that 7% of students incorrectly stated 2 1% that the direction of vector A is 5, confusing direction with 8 1% magnitude. Moreover, we found that 5% of students No answers 9% Others 8% Lat. Am. J. Phys. Educ. Vol.8, No. 4, Dec
5 D. Addition of vectors written in unit-vector notation To analyze students difficulties with the addition of vectors written in the unit-vector notation, we designed Problem 4 (shown in the Appendix). The statement of this problem is: Consider vectors A=3i+4j and B=2i-3j. Find the vector sum R=A+B. As mentioned before, 202 students answered this problem. To answer this problem correctly students must add the x-components and the y-components of both vectors to obtain the components of the vector sum 5i+j. Table 4 shows the distribution of answers given by students. TABLE IV. Answers given for Problem 4: Addition of vectors 3i+4j and 2i-3j. Correct (5i+j) 88% 5i-j 7% No answer 1% Others 4% Students difficulties in problems that involve unit-vector notation y-components (j). Students added the y-components. It seems that the negative sign of the y-component of vector B confused them. F. Scalar multiplication of a vector written in unit-vector notation We designed Problem 6 (shown in the Appendix) to analyze students difficulties with the scalar multiplication of a vector written in the unit-vector notation. The statement of this problem is: Consider vector A=-2i+6j. Find vector T=-3A. As mentioned before, 202 students answered this problem. To answer this problem correctly students should multiply the x- and y-components of vector A by -3 obtaining the vector 6i-18j. Table 6 shows the answers and distributions given by students. TABLE VI. Answers given for Problem 6: Scalar multiplication -3(-2i+6j). In Table 4 we notice that 88% of the students correctly answered this problem. We only found one significant error (7%) in which students incorrectly answered 5i-j. These students correctly added the x-components of the vectors (5i), but incorrectly added the y-components (-j) since they included an incorrect negative sign for the answer. E. Subtraction of vectors written in unit-vector notation To investigate students difficulties with the subtraction of vectors written in the unit-vector notation, we designed Problem 5 (shown in the Appendix). The statement of this problem is: Consider vectors A=3i+4j and B=2i-3j. Find the vector difference T=A-B. As mentioned before, 197 students answered this problem. To answer this problem correctly students should subtract the x-component of vector B from the x-component of vector A and the y-component of vector B from the y-component of vector A obtaining the vector difference i+7j. Table 5 shows the answers and distributions given by students. TABLE V. Answers given for Problem 5: Subtraction of vectors (3i+4j) (2i-3j). Correct (i+7j) 75% i+j 8% No answer 8% Others 9% Table 5 shows that 75% of the students answered this problem correctly. As in the addition problem, we found only one significant error (8%) in which students incorrectly answered i+j. These students correctly subtracted the x- components of the vectors (i), but incorrectly subtracted the Correct (6i-18j) 87% -6i+18j 4% No answer 4% Others 5% We see from this table that 87% of the students answered Problem 6 correctly. In this problem we also found only one significant error (4%): students incorrectly answered - 6i+18j. These students had difficulties with the negative signs since they found the correct absolute value of the components but incorrectly established the sign of both components. It seems probable that these students performed the operation using a multiplier of +3 instead of -3. G. Dot product of vectors written in unit-vector notation To analyze students difficulties with the dot product of vectors written in the unit-vector notation, we designed Problem 7 (shown in the Appendix). The statement of this problem is: Consider vectors A=1i+3j and B=5i. Calculate the dot product (A B). As mentioned before, 143 students answered this problem. One way to answer this problem correctly is to calculate the dot product of the x-component of vector A with the x-component of vector B obtaining 5, i.e. the angle between these vector components is 0, and to calculate the dot product of the y-component of vector A with the x-component of vector B which is zero because the angle between these vector components is 90. Finally the answer is adding the results of the dot product which is 5. Table 7 shows the answers and distributions given by students. Lat. Am. J. Phys. Educ. Vol. 8, No. 4, Dec
6 Pablo Barniol and Genaro Zavala TABLE VII. Answers given for Problem 7: Dot product (1i+3j) 5i. Correct (5) 35% 5i 20% 5i+3j 14% 15k 6% 6i+3j 4% -15k 3% No answers 4% Others 14% Unlike the previous three problems, in Table 7 we see that a small proportion of students (35%) answered Problem 7 correctly. In this Problem we found five frequent errors: 1) Students (20%) answered 5i. These students correctly multiplied the magnitude of the x-components of the vectors but incorrectly added the i-unit vector to that answer. 2) Students (14%) established that the answer is 5i+3j. These students made the same error as in the previous problem to obtain the 5i, and then they also incorrectly added the y-component vector of vector A (3j). 3) Other students (6%) confused the dot product with the cross product answering 15k. The great majority of students established explicitly in their procedure that they added the k-unit vector, forming the cross product j i. (Note that the cross product is actually -15k, so there is also a sign error). 4) Students (4%) added incorrectly both vector (6i+3j). 5) Students (3%) answered -15k. These students also confused the dot product with the cross product but without the sign error. It is interesting to analyze as a group the five frequent errors found in this problem that sum up to 47%. We first note that all of these students have difficulties to interpret the result of a dot product as a scalar since all of the answers represented vectors. Moreover, students who answer 6i+3j or 5i+3j (an additionally 20%) incorrectly use additional procedures in this problem. About this issue it s worth noting that investigations that analyze students difficulties in the interpretation of the dot product have found that students interpret the dot product of two vectors as a vector between both vectors [6, 10]. Finally, the students who answer 15k or -15k (9%) confuse the dot product with the cross product. H. Cross product of vectors written in unit-vector notation the right hand rule and because the angle between these vector components is 90. Finally students add these two results obtaining -15k. Table 8 shows the answers given by students. TABLE VIII. Answers given for Problem 8: Cross product (1i+3j) 5i. Correct (-15k) 61% +15k 10% 5i+3j 5% 6i+3j 2% 5i+15k 2% -15j 2% No answers 3% Others 15% We note from this table that 61% of students correctly answered Problem 7 (-15k). There were five errors. 1) The most frequent error (10%) was to omit the negative sign in the answer (+15k). 2) Students (5%) answered 5i+3j. As in the dot product problem, these students multiplied the magnitudes of the x-components of the vectors, including the i-unit vector in this answer (5i) and added the y-component vector of vector A (3j). 3) Students (2%) added the vectors (6i+3j). 4) Students (2%) answered 5i+15k. These students obtained the 5i as did the students of the second error, and obtained the 15k of their answer, performing a cross product of the y-component of vector A (3j) with the x-component of vector A (5i). (Note that they also made a sign error in the cross product). 5) Finally, a few students (2%) gave -15j as the answer. As we can see, these students included the j-unit vector instead of the k-unit vector. It is interesting to analyze as a group the five frequent errors found in this problem that sums up to 47%. We first note that the most frequent error +15k is a sign error. Scaiffe and Heckler [29] mention that this sign error is due to confusion about the execution and choice of the righthand rule and lack of recognition that the cross product is no commutative. Moreover, the students who answer 6i+3j and 5i+3j (7%) incorrectly use additional procedures in this problem. V. DISCUSSION To analyze students difficulties with the cross product of vectors written in the unit-vector notation, we designed In the following section, we perform several analyses. First, Problem 8 (shown in the Appendix). The statement of this we perform an overview analysis of students difficulties problem is: Consider vectors A=1i+3j and B=5i. Calculate with the eight problems. Then, we classify these difficulties the cross product (A B). As mentioned before, 148 according to their type. Finally, we compare our results with students answered this problem. previous research studies. To answer this problem correctly students first calculate the cross product of the x-component of vector A with the x- A. Overview analysis of students difficulties component of vector B obtaining 0 because the angle between these vector components is 0. Then students First we perform an overview analysis of students calculate the cross product of the y-component of vector A difficulties in the eight problems. We cluster the eight with the x-component of vector B obtaining -15k applying problems used in this study according to their difficulty Lat. Am. J. Phys. Educ. Vol.8, No. 4, Dec
7 level. The three most difficult problems are: Calculation of the direction of a vector (Problem 2, 17%), calculation of the dot product of two vectors (Problem 7, 35%), and calculation of the cross product of two vectors (Problem 8, 61%). We note that the proportions of the correct answers of these problems are less than 70%. Therefore, students difficulties are concentrated in these three problems. On the other hand, the rest of the problems show a low difficulty level with a correct proportion that is higher than 70%: Problems 1, 3-6. B. Classification of students difficulties by type We classified the students difficulties by type: (1) difficulties with the graphical interpretation of vectors, (2) difficulties with operational manipulation of vectors, and (3) difficulties with the interpretation of the operation. B1. Difficulties with the graphical interpretation of vectors There is only one problem (Problem 1) that explicitly asks students to make a graphical interpretation of a vector in unit-vector notation. However, in Problem 2, students also used graphs to try to answer the question, so we can analyze these difficulties in both problems. First we analyze Problem 1. 19% of students answered this problem incorrectly. The two most common errors (that add up to 13%) are important to note, since without being able to make a graphical interpretation of a vector written in unit-vector notation correctly, students will not be able to solve problems in other advanced courses where they are required to use a mental view of vectors representing a physical quantity. In the first error, students thought that the vector -2i+3j goes from the x-axis (point -2, 0) to the y-axis (point 0, 3), and in the second case they thought that the vector -2i+3j is a vector with its tail in point (-2, 3). In both mistakes, students correctly identified the points that needed to be recognized in the process in order to correctly draw the vector -2i+3j, however they didn t have the necessary knowledge to be certain about where the vector must start and end. In Problem 2 we also detected that 6% of the students presented incorrect sketches of the required vector similar to the one analyzed in Problem 1. In this problem, we also observed other difficulties with the graphical interpretation of the direction concept of a vector. The first difficulty is that a considerable proportion of students (14%) don t interpret the direction of a vector as an angle; they think of it only as a description (i.e. in the negative direction of the x-axis, negative x-direction and positive y-direction.) The second difficulty is with their comprehension of the graphical representation of the angle s general characteristics when measured from the positive x-axis. In the analysis of Problem 2, we observed that 9% of students incorrectly calculated the angle as ± From a quick visualization of the requested vector -3i+4j, we can establish that the direction of this vector has to be between 90 and 180. Students difficulties in problems that involve unit-vector notation Therefore, it is clear these students don t know or are unable to apply this general notion of the direction of a vector. B2. Difficulties with operational manipulation of vectors The majority of the problems (problems 3 to 8) ask students to make calculations of vectors in the unit-vector notation. For these problems, students might only need to remember the definition of the mathematical operations to answer the problems correctly. It seems however, that in some cases the interpretation of the calculations plays a role in students answers. In this section we analyze the difficulties with operational manipulation of vectors and in the next section we study the difficulties with the interpretation of the operation. In problems 4 (addition of vectors), 5 (subtraction of vectors) 6 (scalar multiplication of a vector) most students respond to the problems correctly and their answers do not show many problems with interpretation. In these three problems the main mistakes come from sign errors. These mistakes seem to be more algebraic in nature than due to vector-related problems. In both problems (the subtraction and multiplication by a scalar, for instance), students made the mistake of not multiplying the negative sign on the operation to the second term of the two components. In Problem 3 (magnitude of a vector) 5% of the students calculated the magnitude of the vector 2i+2j as 2, 4 or 8, incorrectly applying the Pythagorean Theorem. These mistakes seem to also be more caused by operational calculation errors than interpretation mistakes. However, in Problem 3 as well as in Problems 7 and 8, both types of errors might play a role in the results. In Problem 7, there are mistakes in which the dot multiplication of vectors A=1i+3j and B=5i can be thought of as calculation problems, since some students multiply the components but leave the unit vectors. This also happens in Problem 8, in which some students answered in a similar way, cross multiplying components and leaving the same unit vectors. Students seem to have problems learning the rules of the dot and cross multiplications. However, as mentioned above, interpretation issues might play a role and we discuss this in the following subsection. B3. Difficulties with the interpretation of the operation In Problems 2 (direction of a vector), 3 (magnitude of a vector), 7 (dot product) and 8 (cross product) we find that there are definitely interpretation problems. In Problem 3, although most students answer this question correctly, there are some students (4%) who calculate the unit vector in the direction of the given vector as the magnitude of the vector. We believe that this mistake is related to misconceptions related to a confusion between direction and magnitude. The evidence for this is that not only 4% of students calculate the unit vector when they are asked to calculate the magnitude, but also 7% of students calculate the magnitude of the vector when they are asked in Problem 2 to calculate the direction of the vector. Lat. Am. J. Phys. Educ. Vol. 8, No. 4, Dec
8 Pablo Barniol and Genaro Zavala Another clear problem of interpretation is what occurs in Problem 7 (dot product) and Problem 8 (cross product). In Problem 7, students are asked to calculate the dot product between two vectors. They have to understand that the result should be a scalar. However, 47% of students answered with a vector instead. This is clear evidence that they do not understand the interpretation of a dot product. Moreover, they not only confuse the dot product with the cross product (9% in Problem 7 and 7% in Problem 8) but also confuse these operations with the addition of vectors (4% in Problem 7 and 2% in Problem 8). These examples clearly show that some of the students difficulties are the result of their problems with the interpretation of the operation. B4. Comparison of the results with previous research Finally, we compare our results with those of previous researchers. In the previous research section, we saw that no study had analyzed students difficulties with problems similar to Problems 1 to 6 and 8. This is the first analysis of students answers to these types of problems. We also observed that only Problem 7 (dot product problem) is related to an open-ended problem designed by Van Deventer [6], and it is the only one administered in interviews. As mentioned before, the only error detected in his study was the incorrect calculation of the dot product of vectors 3i and 4j as 12ij. It is interesting to note that we didn t find this error in our analysis of Problem 7 (Table 7). We believe that this could be due to the differences in the samples analyzed. Van Deventer s sample included students that had finished their first introductory physics course. In our study we analyzed the responses of students who had finished their third introductory university physics courses. We believe that the error 12ij reported before is a lower cognitive level error which advanced students typically do not make. It s worth noting that our analysis of Problem 7 is the first analysis that presents a complete taxonomy of students difficulties in an open-ended dot product s calculation problem. VI. CONCLUSSIONS after having completed three introductory university physics courses. Next we establish the most frequent error in each of the eight problems. In Problem 1 we found that the most frequent error is to incorrectly sketch vector -2i+3j from the point (-2, 0) to the point (0, 3). In Problem 2 (direction s calculation) we found that a significant proportion of students consider that the direction of vector -3i+4j measured from the positive x-axis is in the negative direction of x-axis, and in the calculation of an angle, we found that the most common error is to state that the direction of this vector is On the other hand, in Problem 3 (magnitude s calculation) we detected that the most frequent error is to believe that the unit vector in the direction of vector A is the magnitude of vector A. In Problems 4-6 (addition, subtraction and negative scalar multiplication of a vector) we found difficulties with the signs in the calculations. Finally, in Problem 7 (dot product s calculation) we discovered that the most frequent error is to calculate the dot product of vectors A=1i+3j and B=5i as 5i, and in Problem 8 (cross product s calculation) it is to report the incorrect sign for the answer. These frequent errors have not been previously reported in the literature. In the Discussion section, we first performed an overview analysis and a classification of the difficulties. In the overview analysis of the eight problems, we observed that the three most difficult problems were: Calculation of the direction of a vector (Problem 2, 17%), calculation of the dot product of two vectors (Problem 7, 35%), and calculation of the cross product of two vector (Problem 8, 61%). Then, in order to understand the types of difficulties that students have with unit-vector notation, we classified those difficulties according to their type. The analysis showed that students have difficulties with the graphical interpretation of vectors when they are explicitly asked to make a sketch or when the solution of the problem leads them to do so. Students also have difficulties with mathematical operations of vectors in which sometimes they forget the rules of the operations or they carry their difficulties with algebra into the vector operations. Others have difficulties with the interpretation of the operations because they confuse magnitude with direction or dot product with cross product. Finally, it is important to mention that following the process to increase students understanding established by McDermott [30], the results of this research can help to guide the development of new instructional materials (second stage of the cycle) that attempt to increase students understanding of problems that involve unit-vector notation. This development must explicitly address the most frequent error in each of the problems and focus especially on the three problems that are most difficult for the students (calculation of the direction of a vector, calculation of dot product, and calculation of cross product). In this study, we present a complete analysis of frequent errors in problems that involve unit-vector notation by students who have completed all of their introductory university physics courses. McDermott [30] established a process to increase students understanding developing new instructional material based on research. In the first stage the researchers need to identify students conceptual difficulties in a specific concept. Then in the second stage the researches use these finding to guide the development of new instructional material. The present study is an investigation of student understanding (first stage of the cycle) in problems that involve unit-vector notation. In the Results section of this article, we detected and described frequent errors that the students had in the eight problems included in this study. It s important to mention that these difficulties persist in the students responses, even Lat. Am. J. Phys. Educ. Vol.8, No. 4, Dec
9 ACKNOWLEDGEMENTS The authors acknowledge the support received through grant number CAT140. REFERENCES [1] McDermott, L. C. & Redish, E. F., Resource letter PER- 1: Physics education research, Am. J. Phys. 67, (1999). [2] Flores, S., Kanim, S. E. & Kautz, C. H., Student use of vectors in introductory mechanics, Am. J. Phys. 72, (2004). [3] Saarelainen, M., Laaksonen, A. & Hirvonen, P. E., Students' initial knowledge of electric and magnetic fields - More profound explanations and reasoning models for undesired conceptions, European Journal of Physics 28, (2007). [4] Knight, R. D., Vector knowledge of beginning physics students, The Physics Teacher 33, (1995). [5] Nguyen, N. & Meltzer, D., Initial understanding of vector concepts among students in introductory physics courses, Am. J. Phys. 71, (2003). [6] Van Deventer, J., Comparing student performance on isomorphic and physics vector representations, The University of Maine. Department of Physics, Master s Thesis (2008). Unpublished. Available in: < edu/center/files/2009/12/vandeventer_thesis.pdf>. [7] Van Deventer, J. & Wittmann, M. C., Comparing student use of mathematical and physical vector representations, AIP Conference Proceedings 951, (2007). [8] Barniol, P. & Zavala, G., Investigation of students preconceptions and difficulties with the vector direction concept at a Mexican university, AIP Conference Proceedings 1179, (2009). [9] Barniol, P. & Zavala, G., Vector addition: Effect of the context and position of the vectors, AIP Conference Proceedings 1289, (2010). [10] Zavala, G. & Barniol, P., Students' understanding of the concepts of vector components and vector products, AIP Conference Proceedings 1289, (2010). [11] Hawkins, J. M., Thompson, J. R., Wittmann, M. C., Sayre, E. C. & Frank, B. W., Students responses to different representations of a vector addition question, AIP Conference Proceedings 1289, (2010). [12] Hinrichs, B. E., Writing position vectors in 3-d space: A student difficulty with spherical unit vectors in intermediate E&M, AIP Conference Proceedings 1289, (2010). [13] Wang, T. & Sayre, E. C., Maximum likelihood estimation (MLE) of students understanding of vector subtraction, AIP Conference Proceedings 1289, (2010). [14] Barniol, P. & Zavala, G., Students difficulties with unit vectors and scalar multiplication of a vector, AIP Conference Proceedings 1413, (2012). [15] Zavala, G. & Barniol, P., Students understanding of dot product as a projection in no-context, work and electric flux Students difficulties in problems that involve unit-vector notation problems, AIP Conference Proceedings, 1513, (2013). [16] Aguirre, J. M. & Erickson, G., Students' conceptions about the vector characteristics of three physics concepts. Journal of Research in Science Teaching 21, (1984). [17] Aguirre, J. M., Student preconceptions about vector kinematics, Physics Teacher 26, (1988). [18] Aguirre, J. M. & Rankin, G., College students' conceptions about vector kinematics, Physics Education 24, (1989). [19] Shaffer, P. S & McDermott, L. C., A research-based approach to improving student understanding of the vector nature of kinematical concepts, Am. J. Phys. 73, (2005). [20] Barniol, P., Zavala, G. & Hinojosa, C., Students difficulties in interpreting the torque vector in a physical situation, AIP Conference Proceedings 1513, (2013). [21] Beichner, R., Testing student interpretation of kinematic graphs, Am. J. Phys. 62, (1994). [22] Barniol, P. & Zavala, G., Testing students understanding of vector concepts, Physics Education Research Conference, Portland: USA (2013). [23] Tsegaye K., Baylie D. & Dejine S., Computer based teaching aid for basic vector operations in higher institution Physics, Latin American Journal of Physics Education 4, 1-6 (2012). [24] Orozco Martínez, J., Mora, C. & Sánchez Sánchez, R., Using the cellphone in an interactive lecture demostration in the subject Vector Algebra, addition and subtraction of vectors, Latin American Journal of Physics Education 6, (2012). [25] Serway, R. A. & Jewett J. W., Fisica para Ciencias e Ingenieria [Physics for Scientists and Engineers], (Cengage Learning, Mexico, 2008). [26] McDermott, L. C. & Shaffer, P., Tutoriales para Fisica Introductoria [Tutorials in Introductory Physics], (Pearson Education, Buenos Aires, 2001). [27] Gray, K., Rebello, N. and Zollman, D., The effect of question order on responses to multiple-choice questions presented at the Physics Education Research Conference, Boise: USA, [28] Hernandez Sampieri, R., Fernadez-Collado, C. & Baptista Lucio, P., Metodologia de la investigacion [Methodolgy of investigation], (McGrawHill, México, 2006). [29] Scaife, T. M., & Heckler, A. F., Student understanding of the direction of the magnetic force on a charged particle, Am. J. Phys. 78, (2010). [30] McDermott, L. C., Oersted medal lecture 2001: "Physics education research - The key to student learning", Am. J. Phys. 69, (2001). APPENDIX The eight problems used in this study: 1. Draw in the grid the vector A=-2i+3j. Lat. Am. J. Phys. Educ. Vol. 8, No. 4, Dec
10 Pablo Barniol and Genaro Zavala 3. Consider vector A= 2i+2j. Calculate the magnitude of this vector. 4. Consider vectors A=3i+4j and B=2i-3j. Find the vector sum R=A+B. 5. Consider vectors A=3i+4j and B=2i-3j. Find the vector difference T=A-B. 6. Consider vector A=2i+6j. Find vector T=-3A. 7. Consider vectors A=1i+3j and B=5i. Calculate the dot product (A B). 8. Consider vectors A=1i+3j and B=5i. Calculate the cross product (A B). 2. Consider vector A=-3i+4j. Calculate the direction of this vector measured from the positive x-axis. Lat. Am. J. Phys. Educ. Vol.8, No. 4, Dec
PHYSICS 151 Notes for Online Lecture #6
 PHYSICS 151 Notes for Online Lecture #6 Vectors - A vector is basically an arrow. The length of the arrow represents the magnitude (value) and the arrow points in the direction. Many different quantities
PHYSICS 151 Notes for Online Lecture #6 Vectors - A vector is basically an arrow. The length of the arrow represents the magnitude (value) and the arrow points in the direction. Many different quantities
How do the Students Describe the Quantum Mechanics and Classical Mechanics?
 How do the Students Describe the Quantum Mechanics and Classical Mechanics? Özgür Özcan Department of Physics Education, Hacettepe University, 06800, Beytepe, Ankara, Turkey. E-mail: ozcano@hacettepe.edu.tr
How do the Students Describe the Quantum Mechanics and Classical Mechanics? Özgür Özcan Department of Physics Education, Hacettepe University, 06800, Beytepe, Ankara, Turkey. E-mail: ozcano@hacettepe.edu.tr
A vector is a directed line segment used to represent a vector quantity.
 Chapters and 6 Introduction to Vectors A vector quantity has direction and magnitude. There are many examples of vector quantities in the natural world, such as force, velocity, and acceleration. A vector
Chapters and 6 Introduction to Vectors A vector quantity has direction and magnitude. There are many examples of vector quantities in the natural world, such as force, velocity, and acceleration. A vector
Figure 1.1 Vector A and Vector F
 CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
Students difficulties with tension in massless strings. Part I.
 ENSEÑANZA REVISTA MEXICANA DE FÍSICA E 55 (1) 21 33 JUNIO 2009 Students difficulties with tension in massless strings. Part I. S. Flores-García, L.L. Alfaro-Avena, J.E. Chávez-Pierce, J. Estrada, and J.V.
ENSEÑANZA REVISTA MEXICANA DE FÍSICA E 55 (1) 21 33 JUNIO 2009 Students difficulties with tension in massless strings. Part I. S. Flores-García, L.L. Alfaro-Avena, J.E. Chávez-Pierce, J. Estrada, and J.V.
Vector has a magnitude and a direction. Scalar has a magnitude
 Vector has a magnitude and a direction Scalar has a magnitude Vector has a magnitude and a direction Scalar has a magnitude a brick on a table Vector has a magnitude and a direction Scalar has a magnitude
Vector has a magnitude and a direction Scalar has a magnitude Vector has a magnitude and a direction Scalar has a magnitude a brick on a table Vector has a magnitude and a direction Scalar has a magnitude
11.1. Objectives. Component Form of a Vector. Component Form of a Vector. Component Form of a Vector. Vectors and the Geometry of Space
 11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
Pre-Calculus Unit Plan: Vectors and their Applications. Dr. Mohr-Schroeder. Fall 2012. University of Kentucky. Jessica Doering.
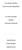 Pre-Calculus Unit Plan: Vectors and their Applications Dr. Mohr-Schroeder Fall 2012 University of Kentucky Jessica Doering Andrea Meadors Stephen Powers Table of Contents Narrative and Overview of Unit
Pre-Calculus Unit Plan: Vectors and their Applications Dr. Mohr-Schroeder Fall 2012 University of Kentucky Jessica Doering Andrea Meadors Stephen Powers Table of Contents Narrative and Overview of Unit
Chapter 3B - Vectors. A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University
 Chapter 3B - Vectors A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University 2007 Vectors Surveyors use accurate measures of magnitudes and directions to
Chapter 3B - Vectors A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University 2007 Vectors Surveyors use accurate measures of magnitudes and directions to
Units, Physical Quantities, and Vectors
 Chapter 1 Units, Physical Quantities, and Vectors PowerPoint Lectures for University Physics, Thirteenth Edition Hugh D. Young and Roger A. Freedman Lectures by Wayne Anderson Goals for Chapter 1 To learn
Chapter 1 Units, Physical Quantities, and Vectors PowerPoint Lectures for University Physics, Thirteenth Edition Hugh D. Young and Roger A. Freedman Lectures by Wayne Anderson Goals for Chapter 1 To learn
Plotting and Adjusting Your Course: Using Vectors and Trigonometry in Navigation
 Plotting and Adjusting Your Course: Using Vectors and Trigonometry in Navigation ED 5661 Mathematics & Navigation Teacher Institute August 2011 By Serena Gay Target: Precalculus (grades 11 or 12) Lesson
Plotting and Adjusting Your Course: Using Vectors and Trigonometry in Navigation ED 5661 Mathematics & Navigation Teacher Institute August 2011 By Serena Gay Target: Precalculus (grades 11 or 12) Lesson
Lab 2: Vector Analysis
 Lab 2: Vector Analysis Objectives: to practice using graphical and analytical methods to add vectors in two dimensions Equipment: Meter stick Ruler Protractor Force table Ring Pulleys with attachments
Lab 2: Vector Analysis Objectives: to practice using graphical and analytical methods to add vectors in two dimensions Equipment: Meter stick Ruler Protractor Force table Ring Pulleys with attachments
Review A: Vector Analysis
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics 8.02 Review A: Vector Analysis A... A-0 A.1 Vectors A-2 A.1.1 Introduction A-2 A.1.2 Properties of a Vector A-2 A.1.3 Application of Vectors
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics 8.02 Review A: Vector Analysis A... A-0 A.1 Vectors A-2 A.1.1 Introduction A-2 A.1.2 Properties of a Vector A-2 A.1.3 Application of Vectors
Mechanics 1: Vectors
 Mechanics 1: Vectors roadly speaking, mechanical systems will be described by a combination of scalar and vector quantities. scalar is just a (real) number. For example, mass or weight is characterized
Mechanics 1: Vectors roadly speaking, mechanical systems will be described by a combination of scalar and vector quantities. scalar is just a (real) number. For example, mass or weight is characterized
2 Session Two - Complex Numbers and Vectors
 PH2011 Physics 2A Maths Revision - Session 2: Complex Numbers and Vectors 1 2 Session Two - Complex Numbers and Vectors 2.1 What is a Complex Number? The material on complex numbers should be familiar
PH2011 Physics 2A Maths Revision - Session 2: Complex Numbers and Vectors 1 2 Session Two - Complex Numbers and Vectors 2.1 What is a Complex Number? The material on complex numbers should be familiar
9 Multiplication of Vectors: The Scalar or Dot Product
 Arkansas Tech University MATH 934: Calculus III Dr. Marcel B Finan 9 Multiplication of Vectors: The Scalar or Dot Product Up to this point we have defined what vectors are and discussed basic notation
Arkansas Tech University MATH 934: Calculus III Dr. Marcel B Finan 9 Multiplication of Vectors: The Scalar or Dot Product Up to this point we have defined what vectors are and discussed basic notation
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus
 South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
South Carolina College- and Career-Ready (SCCCR) Pre-Calculus Key Concepts Arithmetic with Polynomials and Rational Expressions PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR.7 Standards Know
Section V.3: Dot Product
 Section V.3: Dot Product Introduction So far we have looked at operations on a single vector. There are a number of ways to combine two vectors. Vector addition and subtraction will not be covered here,
Section V.3: Dot Product Introduction So far we have looked at operations on a single vector. There are a number of ways to combine two vectors. Vector addition and subtraction will not be covered here,
Section 9.1 Vectors in Two Dimensions
 Section 9.1 Vectors in Two Dimensions Geometric Description of Vectors A vector in the plane is a line segment with an assigned direction. We sketch a vector as shown in the first Figure below with an
Section 9.1 Vectors in Two Dimensions Geometric Description of Vectors A vector in the plane is a line segment with an assigned direction. We sketch a vector as shown in the first Figure below with an
13.4 THE CROSS PRODUCT
 710 Chapter Thirteen A FUNDAMENTAL TOOL: VECTORS 62. Use the following steps and the results of Problems 59 60 to show (without trigonometry) that the geometric and algebraic definitions of the dot product
710 Chapter Thirteen A FUNDAMENTAL TOOL: VECTORS 62. Use the following steps and the results of Problems 59 60 to show (without trigonometry) that the geometric and algebraic definitions of the dot product
NEW YORK STATE TEACHER CERTIFICATION EXAMINATIONS
 NEW YORK STATE TEACHER CERTIFICATION EXAMINATIONS TEST DESIGN AND FRAMEWORK September 2014 Authorized for Distribution by the New York State Education Department This test design and framework document
NEW YORK STATE TEACHER CERTIFICATION EXAMINATIONS TEST DESIGN AND FRAMEWORK September 2014 Authorized for Distribution by the New York State Education Department This test design and framework document
INTRODUCING THE NORMAL DISTRIBUTION IN A DATA ANALYSIS COURSE: SPECIFIC MEANING CONTRIBUTED BY THE USE OF COMPUTERS
 INTRODUCING THE NORMAL DISTRIBUTION IN A DATA ANALYSIS COURSE: SPECIFIC MEANING CONTRIBUTED BY THE USE OF COMPUTERS Liliana Tauber Universidad Nacional del Litoral Argentina Victoria Sánchez Universidad
INTRODUCING THE NORMAL DISTRIBUTION IN A DATA ANALYSIS COURSE: SPECIFIC MEANING CONTRIBUTED BY THE USE OF COMPUTERS Liliana Tauber Universidad Nacional del Litoral Argentina Victoria Sánchez Universidad
Section 1.1. Introduction to R n
 The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
The Calculus of Functions of Several Variables Section. Introduction to R n Calculus is the study of functional relationships and how related quantities change with each other. In your first exposure to
Section 10.4 Vectors
 Section 10.4 Vectors A vector is represented by using a ray, or arrow, that starts at an initial point and ends at a terminal point. Your textbook will always use a bold letter to indicate a vector (such
Section 10.4 Vectors A vector is represented by using a ray, or arrow, that starts at an initial point and ends at a terminal point. Your textbook will always use a bold letter to indicate a vector (such
Grade 6 Mathematics Assessment. Eligible Texas Essential Knowledge and Skills
 Grade 6 Mathematics Assessment Eligible Texas Essential Knowledge and Skills STAAR Grade 6 Mathematics Assessment Mathematical Process Standards These student expectations will not be listed under a separate
Grade 6 Mathematics Assessment Eligible Texas Essential Knowledge and Skills STAAR Grade 6 Mathematics Assessment Mathematical Process Standards These student expectations will not be listed under a separate
Chapter 3 Vectors. m = m1 + m2 = 3 kg + 4 kg = 7 kg (3.1)
 COROLLARY I. A body, acted on by two forces simultaneously, will describe the diagonal of a parallelogram in the same time as it would describe the sides by those forces separately. Isaac Newton - Principia
COROLLARY I. A body, acted on by two forces simultaneously, will describe the diagonal of a parallelogram in the same time as it would describe the sides by those forces separately. Isaac Newton - Principia
Vector Algebra II: Scalar and Vector Products
 Chapter 2 Vector Algebra II: Scalar and Vector Products We saw in the previous chapter how vector quantities may be added and subtracted. In this chapter we consider the products of vectors and define
Chapter 2 Vector Algebra II: Scalar and Vector Products We saw in the previous chapter how vector quantities may be added and subtracted. In this chapter we consider the products of vectors and define
MATH 0110 Developmental Math Skills Review, 1 Credit, 3 hours lab
 MATH 0110 Developmental Math Skills Review, 1 Credit, 3 hours lab MATH 0110 is established to accommodate students desiring non-course based remediation in developmental mathematics. This structure will
MATH 0110 Developmental Math Skills Review, 1 Credit, 3 hours lab MATH 0110 is established to accommodate students desiring non-course based remediation in developmental mathematics. This structure will
Example SECTION 13-1. X-AXIS - the horizontal number line. Y-AXIS - the vertical number line ORIGIN - the point where the x-axis and y-axis cross
 CHAPTER 13 SECTION 13-1 Geometry and Algebra The Distance Formula COORDINATE PLANE consists of two perpendicular number lines, dividing the plane into four regions called quadrants X-AXIS - the horizontal
CHAPTER 13 SECTION 13-1 Geometry and Algebra The Distance Formula COORDINATE PLANE consists of two perpendicular number lines, dividing the plane into four regions called quadrants X-AXIS - the horizontal
The Dot and Cross Products
 The Dot and Cross Products Two common operations involving vectors are the dot product and the cross product. Let two vectors =,, and =,, be given. The Dot Product The dot product of and is written and
The Dot and Cross Products Two common operations involving vectors are the dot product and the cross product. Let two vectors =,, and =,, be given. The Dot Product The dot product of and is written and
Unified Lecture # 4 Vectors
 Fall 2005 Unified Lecture # 4 Vectors These notes were written by J. Peraire as a review of vectors for Dynamics 16.07. They have been adapted for Unified Engineering by R. Radovitzky. References [1] Feynmann,
Fall 2005 Unified Lecture # 4 Vectors These notes were written by J. Peraire as a review of vectors for Dynamics 16.07. They have been adapted for Unified Engineering by R. Radovitzky. References [1] Feynmann,
3. KINEMATICS IN TWO DIMENSIONS; VECTORS.
 3. KINEMATICS IN TWO DIMENSIONS; VECTORS. Key words: Motion in Two Dimensions, Scalars, Vectors, Addition of Vectors by Graphical Methods, Tail to Tip Method, Parallelogram Method, Negative Vector, Vector
3. KINEMATICS IN TWO DIMENSIONS; VECTORS. Key words: Motion in Two Dimensions, Scalars, Vectors, Addition of Vectors by Graphical Methods, Tail to Tip Method, Parallelogram Method, Negative Vector, Vector
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
AP Physics - Vector Algrebra Tutorial
 AP Physics - Vector Algrebra Tutorial Thomas Jefferson High School for Science and Technology AP Physics Team Summer 2013 1 CONTENTS CONTENTS Contents 1 Scalars and Vectors 3 2 Rectangular and Polar Form
AP Physics - Vector Algrebra Tutorial Thomas Jefferson High School for Science and Technology AP Physics Team Summer 2013 1 CONTENTS CONTENTS Contents 1 Scalars and Vectors 3 2 Rectangular and Polar Form
Two vectors are equal if they have the same length and direction. They do not
 Vectors define vectors Some physical quantities, such as temperature, length, and mass, can be specified by a single number called a scalar. Other physical quantities, such as force and velocity, must
Vectors define vectors Some physical quantities, such as temperature, length, and mass, can be specified by a single number called a scalar. Other physical quantities, such as force and velocity, must
High School Algebra Reasoning with Equations and Inequalities Solve equations and inequalities in one variable.
 Performance Assessment Task Quadratic (2009) Grade 9 The task challenges a student to demonstrate an understanding of quadratic functions in various forms. A student must make sense of the meaning of relations
Performance Assessment Task Quadratic (2009) Grade 9 The task challenges a student to demonstrate an understanding of quadratic functions in various forms. A student must make sense of the meaning of relations
Student Performance Q&A:
 Student Performance Q&A: 2008 AP Calculus AB and Calculus BC Free-Response Questions The following comments on the 2008 free-response questions for AP Calculus AB and Calculus BC were written by the Chief
Student Performance Q&A: 2008 AP Calculus AB and Calculus BC Free-Response Questions The following comments on the 2008 free-response questions for AP Calculus AB and Calculus BC were written by the Chief
A simple application of the implicit function theorem
 Boletín de la Asociación Matemática Venezolana, Vol. XIX, No. 1 (2012) 71 DIVULGACIÓN MATEMÁTICA A simple application of the implicit function theorem Germán Lozada-Cruz Abstract. In this note we show
Boletín de la Asociación Matemática Venezolana, Vol. XIX, No. 1 (2012) 71 DIVULGACIÓN MATEMÁTICA A simple application of the implicit function theorem Germán Lozada-Cruz Abstract. In this note we show
The Force Table Introduction: Theory:
 1 The Force Table Introduction: "The Force Table" is a simple tool for demonstrating Newton s First Law and the vector nature of forces. This tool is based on the principle of equilibrium. An object is
1 The Force Table Introduction: "The Force Table" is a simple tool for demonstrating Newton s First Law and the vector nature of forces. This tool is based on the principle of equilibrium. An object is
DRAFT. New York State Testing Program Grade 8 Common Core Mathematics Test. Released Questions with Annotations
 DRAFT New York State Testing Program Grade 8 Common Core Mathematics Test Released Questions with Annotations August 2014 Developed and published under contract with the New York State Education Department
DRAFT New York State Testing Program Grade 8 Common Core Mathematics Test Released Questions with Annotations August 2014 Developed and published under contract with the New York State Education Department
Mathematics Notes for Class 12 chapter 10. Vector Algebra
 1 P a g e Mathematics Notes for Class 12 chapter 10. Vector Algebra A vector has direction and magnitude both but scalar has only magnitude. Magnitude of a vector a is denoted by a or a. It is non-negative
1 P a g e Mathematics Notes for Class 12 chapter 10. Vector Algebra A vector has direction and magnitude both but scalar has only magnitude. Magnitude of a vector a is denoted by a or a. It is non-negative
28 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE. v x. u y v z u z v y u y u z. v y v z
 28 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE 1.4 Cross Product 1.4.1 Definitions The cross product is the second multiplication operation between vectors we will study. The goal behind the definition
28 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE 1.4 Cross Product 1.4.1 Definitions The cross product is the second multiplication operation between vectors we will study. The goal behind the definition
Lecture L3 - Vectors, Matrices and Coordinate Transformations
 S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between
Worksheet to Review Vector and Scalar Properties
 Worksheet to Review Vector and Scalar Properties 1. Differentiate between vectors and scalar quantities 2. Know what is being requested when the question asks for the magnitude of a quantity 3. Define
Worksheet to Review Vector and Scalar Properties 1. Differentiate between vectors and scalar quantities 2. Know what is being requested when the question asks for the magnitude of a quantity 3. Define
Common Core Unit Summary Grades 6 to 8
 Common Core Unit Summary Grades 6 to 8 Grade 8: Unit 1: Congruence and Similarity- 8G1-8G5 rotations reflections and translations,( RRT=congruence) understand congruence of 2 d figures after RRT Dilations
Common Core Unit Summary Grades 6 to 8 Grade 8: Unit 1: Congruence and Similarity- 8G1-8G5 rotations reflections and translations,( RRT=congruence) understand congruence of 2 d figures after RRT Dilations
Physics demonstration of sound waves using Visual Analyser
 Physics demonstration of sound waves using Visual Analyser Shahrul Kadri, Rosly Jaafar, Wan Zul Adli and Anis Nazihah Department of Physics, Universiti Pendidikan Sultan Idris, 35900 Tanjong Malim, Perak
Physics demonstration of sound waves using Visual Analyser Shahrul Kadri, Rosly Jaafar, Wan Zul Adli and Anis Nazihah Department of Physics, Universiti Pendidikan Sultan Idris, 35900 Tanjong Malim, Perak
Review of Vector Analysis in Cartesian Coordinates
 R. evicky, CBE 6333 Review of Vector Analysis in Cartesian Coordinates Scalar: A quantity that has magnitude, but no direction. Examples are mass, temperature, pressure, time, distance, and real numbers.
R. evicky, CBE 6333 Review of Vector Analysis in Cartesian Coordinates Scalar: A quantity that has magnitude, but no direction. Examples are mass, temperature, pressure, time, distance, and real numbers.
Vectors VECTOR PRODUCT. Graham S McDonald. A Tutorial Module for learning about the vector product of two vectors. Table of contents Begin Tutorial
 Vectors VECTOR PRODUCT Graham S McDonald A Tutorial Module for learning about the vector product of two vectors Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk 1. Theory 2. Exercises
Vectors VECTOR PRODUCT Graham S McDonald A Tutorial Module for learning about the vector product of two vectors Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk 1. Theory 2. Exercises
Polynomial Operations and Factoring
 Algebra 1, Quarter 4, Unit 4.1 Polynomial Operations and Factoring Overview Number of instructional days: 15 (1 day = 45 60 minutes) Content to be learned Identify terms, coefficients, and degree of polynomials.
Algebra 1, Quarter 4, Unit 4.1 Polynomial Operations and Factoring Overview Number of instructional days: 15 (1 day = 45 60 minutes) Content to be learned Identify terms, coefficients, and degree of polynomials.
How Old Are They? This problem gives you the chance to: form expressions form and solve an equation to solve an age problem. Will is w years old.
 How Old Are They? This problem gives you the chance to: form expressions form and solve an equation to solve an age problem Will is w years old. Ben is 3 years older. 1. Write an expression, in terms of
How Old Are They? This problem gives you the chance to: form expressions form and solve an equation to solve an age problem Will is w years old. Ben is 3 years older. 1. Write an expression, in terms of
Georgia Standards of Excellence Frameworks. Mathematics. GSE Pre-Calculus Unit 7: Vectors
 Georgia Standards of Excellence Frameworks Mathematics GSE Pre-Calculus Unit 7: Vectors These materials are for nonprofit educational purposes only. Any other use may constitute copyright infringement.
Georgia Standards of Excellence Frameworks Mathematics GSE Pre-Calculus Unit 7: Vectors These materials are for nonprofit educational purposes only. Any other use may constitute copyright infringement.
Vector Spaces; the Space R n
 Vector Spaces; the Space R n Vector Spaces A vector space (over the real numbers) is a set V of mathematical entities, called vectors, U, V, W, etc, in which an addition operation + is defined and in which
Vector Spaces; the Space R n Vector Spaces A vector space (over the real numbers) is a set V of mathematical entities, called vectors, U, V, W, etc, in which an addition operation + is defined and in which
High School Functions Interpreting Functions Understand the concept of a function and use function notation.
 Performance Assessment Task Printing Tickets Grade 9 The task challenges a student to demonstrate understanding of the concepts representing and analyzing mathematical situations and structures using algebra.
Performance Assessment Task Printing Tickets Grade 9 The task challenges a student to demonstrate understanding of the concepts representing and analyzing mathematical situations and structures using algebra.
Physics 235 Chapter 1. Chapter 1 Matrices, Vectors, and Vector Calculus
 Chapter 1 Matrices, Vectors, and Vector Calculus In this chapter, we will focus on the mathematical tools required for the course. The main concepts that will be covered are: Coordinate transformations
Chapter 1 Matrices, Vectors, and Vector Calculus In this chapter, we will focus on the mathematical tools required for the course. The main concepts that will be covered are: Coordinate transformations
AP Physics 1 and 2 Lab Investigations
 AP Physics 1 and 2 Lab Investigations Student Guide to Data Analysis New York, NY. College Board, Advanced Placement, Advanced Placement Program, AP, AP Central, and the acorn logo are registered trademarks
AP Physics 1 and 2 Lab Investigations Student Guide to Data Analysis New York, NY. College Board, Advanced Placement, Advanced Placement Program, AP, AP Central, and the acorn logo are registered trademarks
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 9/24/12, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.1-14.3. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241fa12/241.html)
Math 241, Exam 1 Information. 9/24/12, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.1-14.3. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241fa12/241.html)
Chapter 111. Texas Essential Knowledge and Skills for Mathematics. Subchapter B. Middle School
 Middle School 111.B. Chapter 111. Texas Essential Knowledge and Skills for Mathematics Subchapter B. Middle School Statutory Authority: The provisions of this Subchapter B issued under the Texas Education
Middle School 111.B. Chapter 111. Texas Essential Knowledge and Skills for Mathematics Subchapter B. Middle School Statutory Authority: The provisions of this Subchapter B issued under the Texas Education
Section V.2: Magnitudes, Directions, and Components of Vectors
 Section V.: Magnitudes, Directions, and Components of Vectors Vectors in the plane If we graph a vector in the coordinate plane instead of just a grid, there are a few things to note. Firstl, directions
Section V.: Magnitudes, Directions, and Components of Vectors Vectors in the plane If we graph a vector in the coordinate plane instead of just a grid, there are a few things to note. Firstl, directions
Student Conceptions of Integration and Accumulation. Jason Samuels City University of New York BMCC
 Student Conceptions of Integration and Accumulation Brian Fisher Lubbock Christian University Jason Samuels City University of New York BMCC Aaron Wangberg Winona State University Prior research has shown
Student Conceptions of Integration and Accumulation Brian Fisher Lubbock Christian University Jason Samuels City University of New York BMCC Aaron Wangberg Winona State University Prior research has shown
GRADES 7, 8, AND 9 BIG IDEAS
 Table 1: Strand A: BIG IDEAS: MATH: NUMBER Introduce perfect squares, square roots, and all applications Introduce rational numbers (positive and negative) Introduce the meaning of negative exponents for
Table 1: Strand A: BIG IDEAS: MATH: NUMBER Introduce perfect squares, square roots, and all applications Introduce rational numbers (positive and negative) Introduce the meaning of negative exponents for
ex) What is the component form of the vector shown in the picture above?
 Vectors A ector is a directed line segment, which has both a magnitude (length) and direction. A ector can be created using any two points in the plane, the direction of the ector is usually denoted by
Vectors A ector is a directed line segment, which has both a magnitude (length) and direction. A ector can be created using any two points in the plane, the direction of the ector is usually denoted by
Evaluation of an exercise for measuring impact in e-learning: Case study of learning a second language
 Evaluation of an exercise for measuring impact in e-learning: Case study of learning a second language J.M. Sánchez-Torres Universidad Nacional de Colombia Bogotá D.C., Colombia jmsanchezt@unal.edu.co
Evaluation of an exercise for measuring impact in e-learning: Case study of learning a second language J.M. Sánchez-Torres Universidad Nacional de Colombia Bogotá D.C., Colombia jmsanchezt@unal.edu.co
Algebra Unpacked Content For the new Common Core standards that will be effective in all North Carolina schools in the 2012-13 school year.
 This document is designed to help North Carolina educators teach the Common Core (Standard Course of Study). NCDPI staff are continually updating and improving these tools to better serve teachers. Algebra
This document is designed to help North Carolina educators teach the Common Core (Standard Course of Study). NCDPI staff are continually updating and improving these tools to better serve teachers. Algebra
Vector Math Computer Graphics Scott D. Anderson
 Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
Vector Math Computer Graphics Scott D. Anderson 1 Dot Product The notation v w means the dot product or scalar product or inner product of two vectors, v and w. In abstract mathematics, we can talk about
AP PHYSICS C Mechanics - SUMMER ASSIGNMENT FOR 2016-2017
 AP PHYSICS C Mechanics - SUMMER ASSIGNMENT FOR 2016-2017 Dear Student: The AP physics course you have signed up for is designed to prepare you for a superior performance on the AP test. To complete material
AP PHYSICS C Mechanics - SUMMER ASSIGNMENT FOR 2016-2017 Dear Student: The AP physics course you have signed up for is designed to prepare you for a superior performance on the AP test. To complete material
Extracting the roots of septics by polynomial decomposition
 Lecturas Matemáticas Volumen 29 (2008), páginas 5 12 ISSN 0120 1980 Extracting the roots of septics by polynomial decomposition Raghavendra G. Kulkarni HMC Division, Bharat Electronics Ltd., Bangalore,
Lecturas Matemáticas Volumen 29 (2008), páginas 5 12 ISSN 0120 1980 Extracting the roots of septics by polynomial decomposition Raghavendra G. Kulkarni HMC Division, Bharat Electronics Ltd., Bangalore,
Prentice Hall: Middle School Math, Course 1 2002 Correlated to: New York Mathematics Learning Standards (Intermediate)
 New York Mathematics Learning Standards (Intermediate) Mathematical Reasoning Key Idea: Students use MATHEMATICAL REASONING to analyze mathematical situations, make conjectures, gather evidence, and construct
New York Mathematics Learning Standards (Intermediate) Mathematical Reasoning Key Idea: Students use MATHEMATICAL REASONING to analyze mathematical situations, make conjectures, gather evidence, and construct
Physics Midterm Review Packet January 2010
 Physics Midterm Review Packet January 2010 This Packet is a Study Guide, not a replacement for studying from your notes, tests, quizzes, and textbook. Midterm Date: Thursday, January 28 th 8:15-10:15 Room:
Physics Midterm Review Packet January 2010 This Packet is a Study Guide, not a replacement for studying from your notes, tests, quizzes, and textbook. Midterm Date: Thursday, January 28 th 8:15-10:15 Room:
Algebra 1 Course Information
 Course Information Course Description: Students will study patterns, relations, and functions, and focus on the use of mathematical models to understand and analyze quantitative relationships. Through
Course Information Course Description: Students will study patterns, relations, and functions, and focus on the use of mathematical models to understand and analyze quantitative relationships. Through
Mathematics Scoring Guide for Sample Test 2005
 Mathematics Scoring Guide for Sample Test 2005 Grade 5 Contents Strand and Performance Indicator Map with Answer Key................. 2 Holistic Rubrics......................................................
Mathematics Scoring Guide for Sample Test 2005 Grade 5 Contents Strand and Performance Indicator Map with Answer Key................. 2 Holistic Rubrics......................................................
State of Stress at Point
 State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
Algebra 1 2008. Academic Content Standards Grade Eight and Grade Nine Ohio. Grade Eight. Number, Number Sense and Operations Standard
 Academic Content Standards Grade Eight and Grade Nine Ohio Algebra 1 2008 Grade Eight STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express
Academic Content Standards Grade Eight and Grade Nine Ohio Algebra 1 2008 Grade Eight STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express
MP4, MP7 1.NBT.1 MP4, MP7 1.NBT.1 MP4, MP7 1.MD.4 4 1.4 Collect 20 Together MP4, MP7 1.NBT.1
 Unit 1 Common Core Mathematical Practices (MP) Domains Operations and Algebraic Thinking (OA) Number and Operations in Base Ten (NBT) Measurement and Data (MD) INVESTIG ATION 1 Counting and Quantity Teach
Unit 1 Common Core Mathematical Practices (MP) Domains Operations and Algebraic Thinking (OA) Number and Operations in Base Ten (NBT) Measurement and Data (MD) INVESTIG ATION 1 Counting and Quantity Teach
N Q.3 Choose a level of accuracy appropriate to limitations on measurement when reporting quantities.
 Performance Assessment Task Swimming Pool Grade 9 The task challenges a student to demonstrate understanding of the concept of quantities. A student must understand the attributes of trapezoids, how to
Performance Assessment Task Swimming Pool Grade 9 The task challenges a student to demonstrate understanding of the concept of quantities. A student must understand the attributes of trapezoids, how to
Chapter 5A. Torque. A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University
 Chapter 5A. Torque A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University 2007 Torque is a twist or turn that tends to produce rotation. * * * Applications
Chapter 5A. Torque A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University 2007 Torque is a twist or turn that tends to produce rotation. * * * Applications
Three-dimensional figure showing the operation of the CRT. The dotted line shows the path traversed by an example electron.
 Physics 241 Lab: Cathode Ray Tube http://bohr.physics.arizona.edu/~leone/ua/ua_spring_2010/phys241lab.html NAME: Section 1: 1.1. A cathode ray tube works by boiling electrons off a cathode heating element
Physics 241 Lab: Cathode Ray Tube http://bohr.physics.arizona.edu/~leone/ua/ua_spring_2010/phys241lab.html NAME: Section 1: 1.1. A cathode ray tube works by boiling electrons off a cathode heating element
Chapter 11 Equilibrium
 11.1 The First Condition of Equilibrium The first condition of equilibrium deals with the forces that cause possible translations of a body. The simplest way to define the translational equilibrium of
11.1 The First Condition of Equilibrium The first condition of equilibrium deals with the forces that cause possible translations of a body. The simplest way to define the translational equilibrium of
PROBLEM-BASED LEARNING IN MATERIALS AND MANUFACTURING ENGINEERING EDUCATION ACCORDING TO THE ITESM-2015
 PROBLEM-BASED LEARNING IN MATERIALS AND MANUFACTURING ENGINEERING EDUCATION ACCORDING TO THE ITESM-2015 Eduardo Cárdenas Alemán, César Alberto Núñez López, Juan Oscar Molina Solís Monterrey Institute of
PROBLEM-BASED LEARNING IN MATERIALS AND MANUFACTURING ENGINEERING EDUCATION ACCORDING TO THE ITESM-2015 Eduardo Cárdenas Alemán, César Alberto Núñez López, Juan Oscar Molina Solís Monterrey Institute of
Performance Assessment Task Bikes and Trikes Grade 4. Common Core State Standards Math - Content Standards
 Performance Assessment Task Bikes and Trikes Grade 4 The task challenges a student to demonstrate understanding of concepts involved in multiplication. A student must make sense of equal sized groups of
Performance Assessment Task Bikes and Trikes Grade 4 The task challenges a student to demonstrate understanding of concepts involved in multiplication. A student must make sense of equal sized groups of
High School Algebra Reasoning with Equations and Inequalities Solve systems of equations.
 Performance Assessment Task Graphs (2006) Grade 9 This task challenges a student to use knowledge of graphs and their significant features to identify the linear equations for various lines. A student
Performance Assessment Task Graphs (2006) Grade 9 This task challenges a student to use knowledge of graphs and their significant features to identify the linear equations for various lines. A student
Thnkwell s Homeschool Precalculus Course Lesson Plan: 36 weeks
 Thnkwell s Homeschool Precalculus Course Lesson Plan: 36 weeks Welcome to Thinkwell s Homeschool Precalculus! We re thrilled that you ve decided to make us part of your homeschool curriculum. This lesson
Thnkwell s Homeschool Precalculus Course Lesson Plan: 36 weeks Welcome to Thinkwell s Homeschool Precalculus! We re thrilled that you ve decided to make us part of your homeschool curriculum. This lesson
6. Vectors. 1 2009-2016 Scott Surgent (surgent@asu.edu)
 6. Vectors For purposes of applications in calculus and physics, a vector has both a direction and a magnitude (length), and is usually represented as an arrow. The start of the arrow is the vector s foot,
6. Vectors For purposes of applications in calculus and physics, a vector has both a direction and a magnitude (length), and is usually represented as an arrow. The start of the arrow is the vector s foot,
In order to describe motion you need to describe the following properties.
 Chapter 2 One Dimensional Kinematics How would you describe the following motion? Ex: random 1-D path speeding up and slowing down In order to describe motion you need to describe the following properties.
Chapter 2 One Dimensional Kinematics How would you describe the following motion? Ex: random 1-D path speeding up and slowing down In order to describe motion you need to describe the following properties.
Appendix A: Science Practices for AP Physics 1 and 2
 Appendix A: Science Practices for AP Physics 1 and 2 Science Practice 1: The student can use representations and models to communicate scientific phenomena and solve scientific problems. The real world
Appendix A: Science Practices for AP Physics 1 and 2 Science Practice 1: The student can use representations and models to communicate scientific phenomena and solve scientific problems. The real world
How To Complete The College Readiness Math Mooc
 College Readiness Math MOOC Instructor Information: Dr. Jennifer Kosiak, jkosiak@uwlax.edu General email: mathmooc@uwlax.edu Mathematics Department, University of Wisconsin- La Crosse Description: The
College Readiness Math MOOC Instructor Information: Dr. Jennifer Kosiak, jkosiak@uwlax.edu General email: mathmooc@uwlax.edu Mathematics Department, University of Wisconsin- La Crosse Description: The
Temperature Scales. The metric system that we are now using includes a unit that is specific for the representation of measured temperatures.
 Temperature Scales INTRODUCTION The metric system that we are now using includes a unit that is specific for the representation of measured temperatures. The unit of temperature in the metric system is
Temperature Scales INTRODUCTION The metric system that we are now using includes a unit that is specific for the representation of measured temperatures. The unit of temperature in the metric system is
Adding vectors We can do arithmetic with vectors. We ll start with vector addition and related operations. Suppose you have two vectors
 1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
DELAWARE MATHEMATICS CONTENT STANDARDS GRADES 9-10. PAGE(S) WHERE TAUGHT (If submission is not a book, cite appropriate location(s))
 Prentice Hall University of Chicago School Mathematics Project: Advanced Algebra 2002 Delaware Mathematics Content Standards (Grades 9-10) STANDARD #1 Students will develop their ability to SOLVE PROBLEMS
Prentice Hall University of Chicago School Mathematics Project: Advanced Algebra 2002 Delaware Mathematics Content Standards (Grades 9-10) STANDARD #1 Students will develop their ability to SOLVE PROBLEMS
Week 13 Trigonometric Form of Complex Numbers
 Week Trigonometric Form of Complex Numbers Overview In this week of the course, which is the last week if you are not going to take calculus, we will look at how Trigonometry can sometimes help in working
Week Trigonometric Form of Complex Numbers Overview In this week of the course, which is the last week if you are not going to take calculus, we will look at how Trigonometry can sometimes help in working
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA MECHANICAL PRINCIPLES AND APPLICATIONS NQF LEVEL 3 OUTCOME 1 - LOADING SYSTEMS
 EDEXCEL NATIONAL CERTIFICATE/DIPLOMA MECHANICAL PRINCIPLES AND APPLICATIONS NQF LEVEL 3 OUTCOME 1 - LOADING SYSTEMS TUTORIAL 1 NON-CONCURRENT COPLANAR FORCE SYSTEMS 1. Be able to determine the effects
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA MECHANICAL PRINCIPLES AND APPLICATIONS NQF LEVEL 3 OUTCOME 1 - LOADING SYSTEMS TUTORIAL 1 NON-CONCURRENT COPLANAR FORCE SYSTEMS 1. Be able to determine the effects
PES 1110 Fall 2013, Spendier Lecture 27/Page 1
 PES 1110 Fall 2013, Spendier Lecture 27/Page 1 Today: - The Cross Product (3.8 Vector product) - Relating Linear and Angular variables continued (10.5) - Angular velocity and acceleration vectors (not
PES 1110 Fall 2013, Spendier Lecture 27/Page 1 Today: - The Cross Product (3.8 Vector product) - Relating Linear and Angular variables continued (10.5) - Angular velocity and acceleration vectors (not
Mechanics lecture 7 Moment of a force, torque, equilibrium of a body
 G.1 EE1.el3 (EEE1023): Electronics III Mechanics lecture 7 Moment of a force, torque, equilibrium of a body Dr Philip Jackson http://www.ee.surrey.ac.uk/teaching/courses/ee1.el3/ G.2 Moments, torque and
G.1 EE1.el3 (EEE1023): Electronics III Mechanics lecture 7 Moment of a force, torque, equilibrium of a body Dr Philip Jackson http://www.ee.surrey.ac.uk/teaching/courses/ee1.el3/ G.2 Moments, torque and
TECHNOLOGY AND SEMIOTIC REPRESENTATIONS IN LEARNING MATHEMATICS. Jose Luis Lupiáñez Gómez University of Cantabria, Spain. Abstract
 1 TECHNOLOGY AND SEMIOTIC REPRESENTATIONS IN LEARNING MATHEMATICS Jose Luis Lupiáñez Gómez University of Cantabria, Spain Abstract New technologies modify the socioculturals environments. The educational
1 TECHNOLOGY AND SEMIOTIC REPRESENTATIONS IN LEARNING MATHEMATICS Jose Luis Lupiáñez Gómez University of Cantabria, Spain Abstract New technologies modify the socioculturals environments. The educational
Performance Assessment Task Which Shape? Grade 3. Common Core State Standards Math - Content Standards
 Performance Assessment Task Which Shape? Grade 3 This task challenges a student to use knowledge of geometrical attributes (such as angle size, number of angles, number of sides, and parallel sides) to
Performance Assessment Task Which Shape? Grade 3 This task challenges a student to use knowledge of geometrical attributes (such as angle size, number of angles, number of sides, and parallel sides) to
Vectors Math 122 Calculus III D Joyce, Fall 2012
 Vectors Math 122 Calculus III D Joyce, Fall 2012 Vectors in the plane R 2. A vector v can be interpreted as an arro in the plane R 2 ith a certain length and a certain direction. The same vector can be
Vectors Math 122 Calculus III D Joyce, Fall 2012 Vectors in the plane R 2. A vector v can be interpreted as an arro in the plane R 2 ith a certain length and a certain direction. The same vector can be
Glencoe. correlated to SOUTH CAROLINA MATH CURRICULUM STANDARDS GRADE 6 3-3, 5-8 8-4, 8-7 1-6, 4-9
 Glencoe correlated to SOUTH CAROLINA MATH CURRICULUM STANDARDS GRADE 6 STANDARDS 6-8 Number and Operations (NO) Standard I. Understand numbers, ways of representing numbers, relationships among numbers,
Glencoe correlated to SOUTH CAROLINA MATH CURRICULUM STANDARDS GRADE 6 STANDARDS 6-8 Number and Operations (NO) Standard I. Understand numbers, ways of representing numbers, relationships among numbers,
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c
 Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
Worksheet 1. What You Need to Know About Motion Along the x-axis (Part 1)
 Worksheet 1. What You Need to Know About Motion Along the x-axis (Part 1) In discussing motion, there are three closely related concepts that you need to keep straight. These are: If x(t) represents the
Worksheet 1. What You Need to Know About Motion Along the x-axis (Part 1) In discussing motion, there are three closely related concepts that you need to keep straight. These are: If x(t) represents the
Tennessee Department of Education. Task: Sally s Car Loan
 Tennessee Department of Education Task: Sally s Car Loan Sally bought a new car. Her total cost including all fees and taxes was $15,. She made a down payment of $43. She financed the remaining amount
Tennessee Department of Education Task: Sally s Car Loan Sally bought a new car. Her total cost including all fees and taxes was $15,. She made a down payment of $43. She financed the remaining amount
2-1 Position, Displacement, and Distance
 2-1 Position, Displacement, and Distance In describing an object s motion, we should first talk about position where is the object? A position is a vector because it has both a magnitude and a direction:
2-1 Position, Displacement, and Distance In describing an object s motion, we should first talk about position where is the object? A position is a vector because it has both a magnitude and a direction:
