JOINT IMPORTANCE MEASURES IN NETWORK SYSTEM
|
|
|
- Silvia McKenzie
- 10 years ago
- Views:
Transcription
1 V CHACKO ANOHARAN JOINT IPORTANCE EASRES IN NETWORK SYSTE RT&A # 04 (3) (Vo) 0 December JOINT IPORTANCE EASRES IN NETWORK SYSTE V Chaco and anoharan Deartment of Stattc StThoma Coege Thrur-68000Keraa Inda Deartment of Stattc nverty of Cacut Keraa Inda e-ma: chacovm@gmacom Abtract: any rea word ytem (eectrc ower tranortaton teecommuncaton etc) are muttate ytem comoed of muttate comonent n whch ytem reabty can be comuted n term reabte of t comonent Such ytem may be regarded a fow networ whoe arc (comonent) have ndeendent dcrete and mut-vaued random caacte An arc can at dfferent condton be characterzed by dfferent erformance eve caung networ ytem to wor wth dfferent eve of outut erformance The crtcaty of uch arc mut be meaured wth reference to ther erformance eve and reabty and t contrbuton to the overa ytem outut erformance meaure(op) In th aer we ntroduce a generazed concet of mortance meaure and ont mortance meaure for the fow networ made u of muttate arc wth reect to outut erformance meaure (exected erformance reabty and avaabty) An aroach baed on the unvera generatng functon (GF) for the evauaton of the rooed ont mortance meaure ntroduced An utratve exame gven Keyword: Networ reabty avaabty dcrete tate arc ont mortance meaure GF SC B5 90B5 Introducton Snce the very eary tme of reabty engneerng the networ reabty one of the man ubect of reearch The networ reabty theory ha been aed extenvey n many rea-word ytem uch a comuter and communcaton ytem ower tranmon and dtrbuton ytem tranortaton ytem o/ga roducton ytem etc [8] Networ reabty evauaton aroache exot a varety of too for ytem modeng and reabty ndex cacuaton Networ reabty robem are generay cafed baed on the method ued to tranfer the fow (or gna) and how the fow conervaton aw atfed Tycay there are two categore; the muttate arc networ (AN) and the muttate node networ (NN) In AN each arc ha a non-negatve nteger vaued dcrete random varabe caacty (muttate arc) and a fow n the networ obey the conervaton aw Aarenty n NN each node a muttate node wth dcrete tate determned by a et of node recevng the gna drecty from t wthout atfyng conervaton aw Both have ther own acaton; for exame eectrca ower dtrbuton ytem can be modeed by AN and comuter networ or ceuar hone networ can be modeed a NN The tandard mathematca and tattca theory of ytem reabty aume both ytem and comonent behavor are of bnary nature functonng (tate ) and faed (tate 0) [] However n ome ytem when comonent may be oeratng n a degraded tate the ytem may be oeratng n degraded tate and the ytem may t rovde an accetabe eve of ervce [] The networ reabty evauaton for comex degn ree on enumeratve technque [] The fow reabty robem for the drected caacted-fow networ n whch the caacty of each arc ha + vaue from ource to n generazed a a muttate ytem mode [0] A grah theoretc method ued for the reabty evauaton of muttage nterconnecton networ wth muttate eement [4] 9
2 V CHACKO ANOHARAN JOINT IPORTANCE EASRES IN NETWORK SYSTE RT&A # 04 (3) (Vo) 0 December Imortance meaure (I) quantfe the crtcaty of a artcuar comonent wthn a ytem degn They have been wdey ued a too for dentfyng ytem weane and to rortze reabty mrovement actvte [6] They can ao rovde vauabe nformaton for the afety and effcent oeraton of the ytem In muttate ytem (SS) I characterze for a gven comonent the mot mortant comonent tate wth regard to t mact on ytem reabty The nowedge about the I can be ued a a gude to rovde redundancy o that ytem reabty ncreaed Thu meaure that can dfferentate uch an mact are hghy derabe In genera there are two way to mrove the reabty of a bnary ytem ) ncreae the reabty of ndvdua comonent and/or ) add redundant comonent to the ytem Comote mortance meaure are deveoed wth the am of dentfyng and ranng artcuar arc (comonent) n a networ ytem deendng on ther mact on the muttate networ reabty behavor [3] Jont reabty mortance (JRI) of two or more comonent a quanttatve meaure of the nteracton of two or more comonent or tate of two or more comonent [5] It nvetgated to rovde nformaton on the tye and degree of nteracton between two or more comonent by dentfyng the gn and ze of t [55] The vaue of JRI rereent the degree of nteracton between two or more comonent wth reect to ytem reabty Jont tructura mortance (JSI) ued when the comonent reabte are not avaabe [5] Jont tructura and ont reabty mortance meaure for any number of muttate comonent n the SS are uefu for the degn engneer [5] [7] For the SS wth muttate comonent the robem reated to SS reabty mrovement t evovng The robem of fndng the ont mortance of more than two arc n a networ ytem wth varou outut erformance meaure (eg reabty avaabty etc) t reman unoved To ove th robem method deendent on the nformaton obtaned from muttate I and ont mortance meaure(ji) can be deveoed for effcent reource aocaton any of the engneerng ytem are modeed by networ (eectrc ower generaton ytem tranortaton ytem teecommuncaton networ ytem etc) (ee [7] [0] and [4]) hence the deveoment of ont mortance meaure of two or more arc wth dfferent outut erformance (eg roductvty caacty etc) n a drected networ wth muttate erformance eve qute derabe In order to anwer th robem we ntroduce the JI of two or more arc n muttate drected networ ytem wth varou outut erformance meaure (exected erformance reabty and avaabty) We rovde an agorthm baed on unvera generatng functon (GF) for the evauaton of ont mortance meaure when networ ytem ha dfferent outut erformance Th aer organzed a foow In ecton we defne the JI n networ ytem wth varou outut erformance meaure (exected erformance reabty and avaabty) Secton 3 conder the acaton of GF for the JI evauaton Iutraton gven n ecton 4 foowed by concuon n the at ecton Jont mortance meaure of arc n muttate networ ytem Conder a drected muttate networ made u of n arc Each arc may be n one of tate { 0 } { n } Let W (t) outut erformance of the muttate networ at tme t whch tae the vaue w =0 where max{ } deendng on the ytem tate at tme t The two vector of the ytem erformance reazaton w={w 0 } and of the ytem tate robabte ={ 0 } defne the ytem outut erformance dtrbuton Let (t) the tate of the SS at tme t We ue ome meaure of the erformance of a SS for obtanng ont mortance meaure The teady-tate the robabty dtrbuton of the ytem tate : m Pr{ (t) } m Pr{ W ( t) w } 0 t t 30
3 V CHACKO ANOHARAN JOINT IPORTANCE EASRES IN NETWORK SYSTE RT&A # 04 (3) (Vo) 0 December An aocated me meaure of ytem outut erformance t exected vaue of ytem tate defned n the teady-tate a: E [ ( t )] A mar meaure of ytem outut erformance t exected vaue of ytem outut erformance n the teady-tate a: E w When aed to SS the concet of avaabty reated to the abty of the ytem to meet a requred demand w correondng to tate The genera defnton of ntantaneou muttate ytem avaabty then: A( t) Pr{ ( t) } Pr{ W ( t) w} If the ytem under oeraton wthout brea u to tme t then A ( t ) the ytem reabty: R( t) Pr{ ( t) } Pr{ W ( t) w} The SS tatonary avaabty defned a A 0 (w w ) Let G ( N A) rereent a tochatc caacted networ wth nown demand d from a ecfed ource node to a ecfed n node t N rereent the et of a node and A { a n} rereent the et of a arc The current tate (caacty) of arc a rereented by x { 0 } the range of tate of arc a The vector ( 0 ) rereent the robabty aocated to each of the vaue taen by x The ytem tate vector x ( x x xn) denote the tate of a the arc of the networ ytem Functon ( x) : n where { 0 } max{ } ma the ytem tate vector nto ytem tate That (x) the networ caacty from ource to n under ytem tate vector x whch rereent a muttate tructure functon [] Networ reabty may be defned a the robabty that a demand of d unt can be ued from ource to n through the muttate arc We ha mae the foowng aumton for the networ reabty ytem Arc tate are tochatcay ndeendent The tructure functon (x) tattcay coherent That mrovng an arc erformance cannot caue to degrade the erformance of the networ ytem and a arc are reevant Jont reabty mortance (JRI) of the two edge n an undrected networ n bnary nature an extenon of the margna reabty mortance (RI) of edge [6] In an undrected networ reabty the robabty that ource and termna are connected by worng edge [6] For an undrected tochatc networ G ( N E) where E { e n} et of a edge N the et of node et R (G) rereent the robabty that the ource and termna are connected by worng edge and q ( q q qn ) where q Pr{ e E worng } RI of edge e n an R( G ) undrected networ defned a I G( ) [6] Agan JRI of two edge defned a foow q 3
4 V CHACKO ANOHARAN JOINT IPORTANCE EASRES IN NETWORK SYSTE RT&A # 04 (3) (Vo) 0 December Defnton The JRI of two edge e and e the econd order arta dervatve of reabty of an undrected networ wth reect to reabte of both edge: R( G) IG ( ) qq An exct exreon for th JRI of two edge * * * * ( ) R( G ) R( G ) R( G ) R( G ) I G * where G rereent G wth edge e contracted and edge e deeted The JRI exreed n term of RI of edge n ame ub-grah a IG ( ) I * ( ) IG ( ) G and IG ( ) I * ( ) IG ( ) G Aternatvey the foowng reatonh are obtaned IG( ) IG ( ) IG( ) IG ( ) IG ( ) and IG ( ) We now roceed wth the robem of meaurng ont mortance n the drected networ ytem wth reect to exected erformance Frt we fnd the JRI of any number of arc n the networ where the arc caacty rereented a fnte dcrete tate n nature That each arc can tae the vaue n a dcrete tate ace { 0 } where rereent the maxmum fow (bet tate) through the arc For fndng the JRI of more than two arc we foow the method for fndng JRI n SS [5] Suoe for ntance the robabty dtrbuton of each arc unnown then we ue the ont tructura mortance of muttate ytem (JSI) of more than two comonent [5] The JSI ( ) for two comonent and gven by JSI( ) m q ( ( m { SI(;m ) SI(;m )} ) X where SI ( ;m ) = n ( ) X ( m X ) q ) m m and X ( x x m xn ) the tate ace vector of ytem comonent Here χ(true)= and χ(fae)=0 ( m X ) ( m X ) q determne the crtca ath vector to the eve wth tate m of comonent The JSI () for three comonent JSI( r ) r nm { JSI( r;mn ) JSI( r;mn )} where JSI( r;mn ) SI( r;mn ) SI(r;m n ) So n order to fnd the JSI of three arc we have to fnd JSI of two arc for each tate of thrd arc and tae ucceve dfference and tota um Agan the change n JSI of three comonent wth fourth comonent rovde JSI of four comonent Thu roceedng e th we can fnd JSI of any number of arc Suoe that the arc robabte are nown Then to fnd the ont reabty mortance of more than two muttate arc for the networ one may roceed a foow The ont reabty mortance (JRI) of SS for comonent defned a foow [5] The ont reabty mortance of tate b of comonent a tate b of comonent a tate b of the comonent a ( n) of the SS 3
5 V CHACKO ANOHARAN JOINT IPORTANCE EASRES IN NETWORK SYSTE RT&A # 04 (3) (Vo) 0 December JRI( a a ; b b ) R a E b R b R a a n b where E the exected erformance of ytem and { } P( ( x ) ) 0 Ra b P( xa b ) are the comonent reabte Thu n fndng the JRI of muttate arc we have to fnd the th arta dervatve of the overa exected erformance of networ wth reect to the reabte of each arc under conderaton For ntance we conder the JRI of tate of three comonent Let Pmn P( ( m nr X r ) ) and m P( X m ) For =3 e dfferentatng E artay wth reect to and we get m 3 E [ P P mn m n rn P mn Pmn Pmn Pm n P m m n P m n rn ] [ P But oberve that JRI of tate of two comonent when thrd comonent n tate n Therefore JRI of tate three comonent are exreed n term of JRI of tate of two comonent a foow: 3 E E E [ ] n [ ] r n R m R R n R m R R m R r r R( G) JRI worng tate for edge can be wrtten a where R It how that the R R above reut hod wth bnary nature of edge e = Hence the reut of JRI of two edge n a bnary networ [5] can be condered a a generazaton of the reut JRI [6] to any number of bnary and muttate edge when conderng undrected networ ytem Thu we have the foowng theorem for three arc of a drected networ ytem Theorem The ont reabty mortance of three arc n a muttate networ wth muttate arc m n P m n P 3 r r E E ([ ] n r m n R m R R r n m n R m R E the exected outut erformance of networ R m R and Rrn where m n P m n E [ R m R ] ] n r are the reabte of arc and r wth reect to erformance eve m and n reectvey In the above dcued ont reabty mortance meaure and ont tructura mortance meaure we ued the exected erformance of the networ a outut erformance meaure But n order to fnd the JI wth reect to other outut erformance meaure reabty and avaabty of the muttate networ ytem we roceed a foow When the generc -th muttate arc condered one can ntroduce a erformance threhod and dvde the comete ordered et of t tate nto two ordered ubet correondng to the arc erformance above and beow the eve reectvey By o dong we re-ntroduce a coectvey bnary ogc for the arc tate Let arc be contraned to erformance beow whe the ret of arc of the networ ytem are not contraned: we denote by the networ ytem OP (reabty or avaabty) obtaned n th tuaton Smary we denote by the networ ytem OP reutng from the dua tuaton n whch arc contraned to erformance ) 33
6 V CHACKO ANOHARAN JOINT IPORTANCE EASRES IN NETWORK SYSTE RT&A # 04 (3) (Vo) 0 December above The networ ytem erformance meaure o ntroduced rey on a retrcton of the achevabe erformance of the networ arc Dfferent modeng aumton n the enforcement of th retrcton w ead to dfferent erformance vaue ng the meaure and we can defne Brnubaum mortance meaure for muttate eement Suoe that rereent the Brnubaum mortance of the comonent when comonent retrcted to the erformance above eve Smary defne the Brnubaum mortance of the comonent when comonent retrcted to beow eve Thu we can defne the ont mortance of two comonent and to the networ ytem erformance a Smary we can obtan the hgher order ont mortance meaure for more than two arc e for exame to meaure the mrovement of ont mortance of two arc wth reect to the nteractve effect of more than two arc at frt we ha cacuate change n the ont mortance of two arc wth reect to the change of thrd arc If there any change n the ont mortance of two arc due to change n erformance of thrd arc from uer tate to ower tate we can ay that there an nteractve effect for three arc for the networ OP mrovement We ha fnd the ont mortance meaure at teady tate ytem erformance n the foowng ecton 3 Acaton of GF In SS modeed by networ wth reect to varou outut erformance we modfy the above ont mortance meaure The GF found to be a uefu too n aement of outut erformance meaure of the networ ytem [] The method of GF generaze the technque that baed on ung a we nown ordnary generatng functon The bac dea are ntroduced by haov n 987 [] The aroach roved to be very convenent for numerca reazaton It requre reatvey ma comutatona reource for evauatng SS reabty ndce and therefore can be ued n comex reabty oeraton Imortance meaure evauaton n SS ung GF can be ee n Ref [9] The SS mode ncude the erformance dtrbuton of a arc and the ytem tructure functon: x n ( x x xn ) where any ytem eement can have fnte number of dcrete tate and t erformance dtrbuton rereented by ordered et x : ( x x x ) and : ( ) that reate the robabty of each tate wth erformance correondng to th tate The GF of a dcrete varabe X correondng to the tate of an arc defned a the oynoma ( ) 0 x where the dcrete random varabe X ha obe vaue and the robabty that X equa to x In order to rereent a the obe combnaton of tate of the two arc a and a one ha to reate the correondng robabte of tate of two muttate arc ubytem wth vaue of the vector ( xa xa ) n thee tate For thee uroe we conder a comoton oerator Ω over GF of ndvdua muttate arc whch tae the foowng form for a ar ( ) of muttate arc 34
7 V CHACKO ANOHARAN JOINT IPORTANCE EASRES IN NETWORK SYSTE RT&A # 04 (3) (Vo) 0 December ( ) ( ( ) ( )) ( x n n x n ) n n ( x xn ) The reutng oynoma ( ) rereent the robabty dtrbuton of the ubytem contanng arc and + Ayng the oerator Ω to a other arc one by one we get the reutng oynoma that tae the form n ( ) 0 The oynoma rereent dtrbuton of tate of connecton between ource and n of the entre networ Th oynoma reate the robabte of a the obe tate of whoe networ q wth the outut erformance correondng to thee tate y Thu we can obtan the reabty of networ a R 0 q I( demand of d unt u ed from to t ) where I () the ndcator functon To evauate the ont mortance meaure we need the teady tate dtrbuton of the oberved erformance of the networ ytem under ome contrant In order to ue the GF n ont mortance meaure evauaton we ue the foowng aroach Let O be the outut erformance of muttate networ ytem when arc n fxed tate whe the ret of the arc evove tochatcay among ther correondng tate wth teady-tate erformance dtrbuton { x } n 0 Aume that the arc n one of t tate wth erformance not greater than We denote by the tate n the ordered et of tate of arc whoe erformance x equa or mmedatey beow e x x The condtona robabty of the arc beng n a generc tate characterzed by a erformance X not greater than a re-ecfed eve threhod ) : x q y ( * x ] r 0 r Smary the condtona robabty of arc beng n a tate when t nown that x ] * Pr[ ] r r Now conder the ont robabty dtrbuton of two arc and for X x X x h gven four addtona retrcton () h h () h h (3) h h and (4) h h Thu now under the conderaton that the arc are ndeendent we coud arrve at robabty dtrbuton gven beow That can be comuted a earer reut for ndeendent arc a foow Let h x X x h h h ] h h r r 0 m 0 m 35
8 V CHACKO ANOHARAN JOINT IPORTANCE EASRES IN NETWORK SYSTE RT&A # 04 (3) (Vo) 0 December x X x h h h ] h h r m r 0 m h x X x h h h ] 3 h h h r r m 0 m and x X x h h h ] 4 h h r m r m h Smary we can fnd ont dtrbuton of any number of arc wth the ecfed retrcton We defne a the networ outut erformance meaure ( eg reabty or avaabty) obtaned when arc forced to vt ony tate wth erformance not greater than : O 0 Smary we defne a the networ outut erformance meaure obtaned under the condton that the arc tay ony n tate wth erformance greater than : O Thu the Brnubaum mortance tae the form In order to comute the ont mortance of two arc and e et denote the ont mortance of two arc wth reect to the networ outut erformance meaure then e h h ho h ho h 0h 0 0h h h 0 3 h O h 4 h h h O h 36
9 V CHACKO ANOHARAN JOINT IPORTANCE EASRES IN NETWORK SYSTE RT&A # 04 (3) (Vo) 0 December Smary by fndng change n ont mortance of two arc wth reect to thrd arc we get the ont mortance of three arc Contnung e th we get the ont mortance of any number of arc wth reect to networ outut erformance meaure and tate ace retrcted robabte of a arc In order to obtan the tate ace retrcted meaure one ha to modfy the GF of arc a foow ( ) ( ) 0 hh x x ( ) 0 ( h x x ) h0 h h x x h ( x x h h h ( ) h0 0 h0 ) h h x xh ( x x h) h h ( ) h0 h0 x h ( x x h x h h ( ) hh h h ) and x h x h h ( x x h ) ( ) 0 hh 0hh when evauatng GF of foowng agorthm for evauaton of and and We ue the Obtan the u-functon of a of the ytem eement If the ytem contan a ar of eement connected n arae or n ere reace th ar wth an equvaent macro-eement wth u-functon obtaned by um or mn oerator for ( ) If the ytem contan more than one eement do t agan and agan Then determne the u-functon of the entre ere-arae ytem a the u-functon of the remanng nge equvaent macro-eement The ytem robabty and erformance dtrbuton are rereented by the coeffcent and exonent of th u-functon correondng to the tate robabte and erformance eve reectvey Comute the ytem OP for the gven eve wth the gven vector of the tate robabte and erformance eve 4 Iutratve exame For the networ n fgure t dered to obtan the robabty that a demand of 0 unt can be ued from ource to n [3] Here the ytem can be condered a the SS n Ref [5] Tabe reent arc robabte In tabe we comuted JRI of ar of arc wth α= β= whch nfuence ytem mot wth reect to ytem outut met the demand or not 37
10 V CHACKO ANOHARAN JOINT IPORTANCE EASRES IN NETWORK SYSTE RT&A # 04 (3) (Vo) 0 December It how the ar (89) ha arget JRI wth reect to ytem reabty 4 Concuon In th aer ont mortance meaure of two or more arc n muttate arc networ wth varou outut erformance meaure are deveoed The rocedure of evauatng ont mortance meaure ung GF rooed The rooed meaure can be ued n any ytem modeed a muttate networ havng varou outut erformance meaure wth muttate arc Tabe Arc State State robabte Tabe Par () (89) (4) (6) JRI
11 V CHACKO ANOHARAN JOINT IPORTANCE EASRES IN NETWORK SYSTE RT&A # 04 (3) (Vo) 0 December Reference [] R E Barow and F Prochan Stattca theory of reabty and fe tetng Hot Rnheart NewYor975 [] R E Barow and A Wu Coherent ytem wth muttate comonent ath Oer Re 3 (978) 75-8 [3] W Brnbaum On the mortance of dfferent comonent n a mut-comonent ytem P R Krhnaah (Ed) utvarate anay II Acadamc Pre NewYor 969 [4] V C Bueno On the mortance of comonent for muttate monotone ytem Stat Prob Lett 7 (989) 5-59 [5] V Chaco and anoharan Jont mortance meaure for the muttate ytem Advance n Performance and Safety of Comex ytem A KVerma P K Kaur and S G Ghadge (Ed) acman Inda 008 [6] J S Hong and C H Le Jont reabty mortance of two edge n an undrected networ IEEE Tran Reab 47 (993) 97-0 [7] G Levtn Otma reabty enhancement for muttate tranmon networ wth fxed tranmon tme Reab Eng Syt Saft76 (00) [8] G Levtn Reabty of acycc muttate networ wth contant tranmon charactertc of ne Reab Eng Syt Saft 78 (00) [9] G Levtn and A Lnan Imortance and entvty anay of muttate ytem ung the unvera generatng functon Reab Eng Syt Saf 65 (999) 7-8 [0] Y K Ln ng mnma cut to tudy the ytem caacty for a tochatc fow networ n two-commodty cae Comuter and Oer Reer 30 (003) [] A Lnan and G Levtn uttate Sytem Reabty-aement otmzaton and evauaton Word Scentfc Sngaore 003 [] S Patra and R B ra Evauaton of robabty ma functon of fow n a communcaton networ conderng a muttate mode of networ n croereab36 (996) 45-6 [3] J E Ramrez-arquez and D W Cot uttate comonent crtcaty anay n muttate ytem Adv Saf Reab (Ed K Koowroc) Tayor and Franc grou London 005 [4] C R Thrathy S Patra R B ra and N ahaatra Reabty evauaton of muttate nterconnecton networ wth muttate eement croereab 36 (996)43-48 [5] S Wu Jont mortance of muttate ytem Com Indut Eng 49 (005) [6] W C Yeh The -out-of-n acycc muttate node networ reabty evauaton ung unvera generatng functon method Reab Eng Syt Saf 9 (006) [7] V Chaco and anoharan Jont mortance meaure for muttate reabty ytem OPSEARCH Voume 48 Number DOI: 0007/ z 39
PERFORMANCE ANALYSIS OF PARALLEL ALGORITHMS
 Software Analye PERFORMANCE ANALYSIS OF PARALLEL ALGORIHMS Felcan ALECU PhD, Unverty Lecturer, Economc Informatc Deartment, Academy of Economc Stude, Bucharet, Romana E-mal: [email protected] Abtract:
Software Analye PERFORMANCE ANALYSIS OF PARALLEL ALGORIHMS Felcan ALECU PhD, Unverty Lecturer, Economc Informatc Deartment, Academy of Economc Stude, Bucharet, Romana E-mal: [email protected] Abtract:
Hospital care organisation in Italy: a theoretical assessment of the reform
 Dartmento d Scenze Economche Unvertà d Breca Va S. Fautno 7/b 5 BESCIA Tel. 3 98885 Fax. 3 988837 e-mal: [email protected] otal care organaton n Italy: a theoretcal aement of the reform oella evagg Abtract.
Dartmento d Scenze Economche Unvertà d Breca Va S. Fautno 7/b 5 BESCIA Tel. 3 98885 Fax. 3 988837 e-mal: [email protected] otal care organaton n Italy: a theoretcal aement of the reform oella evagg Abtract.
Mathematical model of service quality performance s computing of multiservice network
 Mathematca mode of erce quaty performance computng of muterce networ Tuemoa Gufarda, Internatona academy of bune, maty, Kazahtan btract Th artce deoted to effectene of muterce networ functonng n order
Mathematca mode of erce quaty performance computng of muterce networ Tuemoa Gufarda, Internatona academy of bune, maty, Kazahtan btract Th artce deoted to effectene of muterce networ functonng n order
CRIMINAL MAPPING BASED ON FORENSIC EVIDENCES USING GENERALIZED GAUSSIAN MIXTURE MODEL
 Voume No. 4 June 202 ISSN 2278-080 The Internatona Journa of Computer Scence & Appcaton TIJCSA RESEARCH AER Avaabe Onne at http://www.journaofcomputercence.com/ CRIMINAL MAING BASED ON FORENSIC EVIDENCES
Voume No. 4 June 202 ISSN 2278-080 The Internatona Journa of Computer Scence & Appcaton TIJCSA RESEARCH AER Avaabe Onne at http://www.journaofcomputercence.com/ CRIMINAL MAING BASED ON FORENSIC EVIDENCES
8.5 UNITARY AND HERMITIAN MATRICES. The conjugate transpose of a complex matrix A, denoted by A*, is given by
 6 CHAPTER 8 COMPLEX VECTOR SPACES 5. Fnd the kernel of the lnear transformaton gven n Exercse 5. In Exercses 55 and 56, fnd the mage of v, for the ndcated composton, where and are gven by the followng
6 CHAPTER 8 COMPLEX VECTOR SPACES 5. Fnd the kernel of the lnear transformaton gven n Exercse 5. In Exercses 55 and 56, fnd the mage of v, for the ndcated composton, where and are gven by the followng
THE ANALYSIS AND OPTIMIZATION OF SURVIVABILITY OF MPLS NETWORKS. Mohammadreza Mossavari, Yurii Zaychenko
 Internatonal Journal "Informaton Theore & Applcaton" Vol5 / 28 253 TE ANALYSIS AND OTIMIATION OF SURVIVABILITY OF MLS NETWORS Mohammadreza Moavar, Yur aychenko Abtract: The problem of MLS network urvvablty
Internatonal Journal "Informaton Theore & Applcaton" Vol5 / 28 253 TE ANALYSIS AND OTIMIATION OF SURVIVABILITY OF MLS NETWORS Mohammadreza Moavar, Yur aychenko Abtract: The problem of MLS network urvvablty
Development and use of prediction models in Building Acoustics as in EN 12354. 1 Introduction. 2 EN 12354, part 1 & 2. 2.2 Lightweight single elements
 evelopment and ue of predcton model n Buldng Acoutc a n EN 1354 Eddy TNO Scence and Indutry, P.O. Box 155, N-600 A elft, The Netherland, [email protected] Improvng the acoutc clmate n buldng an mportant
evelopment and ue of predcton model n Buldng Acoutc a n EN 1354 Eddy TNO Scence and Indutry, P.O. Box 155, N-600 A elft, The Netherland, [email protected] Improvng the acoutc clmate n buldng an mportant
Optimum Design of Magnetic Inductive Energy Harvester and its AC-DC Converter
 Otmum Degn of Magnetc nductve Energy Harveter and t AC-DC Converter Qan Sun, Sumeet Patl, Stehen Stoute, Nan-Xang Sun, Brad Lehman Deartment of Electrcal and Comuter Engneerng Northeatern Unverty Boton,
Otmum Degn of Magnetc nductve Energy Harveter and t AC-DC Converter Qan Sun, Sumeet Patl, Stehen Stoute, Nan-Xang Sun, Brad Lehman Deartment of Electrcal and Comuter Engneerng Northeatern Unverty Boton,
Luby s Alg. for Maximal Independent Sets using Pairwise Independence
 Lecture Notes for Randomzed Algorthms Luby s Alg. for Maxmal Independent Sets usng Parwse Independence Last Updated by Erc Vgoda on February, 006 8. Maxmal Independent Sets For a graph G = (V, E), an ndependent
Lecture Notes for Randomzed Algorthms Luby s Alg. for Maxmal Independent Sets usng Parwse Independence Last Updated by Erc Vgoda on February, 006 8. Maxmal Independent Sets For a graph G = (V, E), an ndependent
A Study on Secure Data Storage Strategy in Cloud Computing
 Journal of Convergence Informaton Technology Volume 5, Number 7, Setember 00 A Study on Secure Data Storage Strategy n Cloud Comutng Danwe Chen, Yanjun He, Frst Author College of Comuter Technology, Nanjng
Journal of Convergence Informaton Technology Volume 5, Number 7, Setember 00 A Study on Secure Data Storage Strategy n Cloud Comutng Danwe Chen, Yanjun He, Frst Author College of Comuter Technology, Nanjng
Approximation Algorithms for Data Distribution with Load Balancing of Web Servers
 Approxmaton Agorthms for Data Dstrbuton wth Load Baancng of Web Servers L-Chuan Chen Networkng and Communcatons Department The MITRE Corporaton McLean, VA 22102 chen@mtreorg Hyeong-Ah Cho Department of
Approxmaton Agorthms for Data Dstrbuton wth Load Baancng of Web Servers L-Chuan Chen Networkng and Communcatons Department The MITRE Corporaton McLean, VA 22102 chen@mtreorg Hyeong-Ah Cho Department of
Dynamic Virtual Network Allocation for OpenFlow Based Cloud Resident Data Center
 56 IEICE TRANS. COMMUN., VOL.E96 B, NO. JANUARY 203 PAPER Speca Secton on Networ Vrtuazaton, and Fuson Patform of Computng and Networng Dynamc Vrtua Networ Aocaton for OpenFow Based Coud Resdent Data Center
56 IEICE TRANS. COMMUN., VOL.E96 B, NO. JANUARY 203 PAPER Speca Secton on Networ Vrtuazaton, and Fuson Patform of Computng and Networng Dynamc Vrtua Networ Aocaton for OpenFow Based Coud Resdent Data Center
s-domain Circuit Analysis
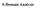 S-Doman naly -Doman rcut naly Tme doman t doman near rcut aplace Tranform omplex frequency doman doman Tranformed rcut Dfferental equaton lacal technque epone waveform aplace Tranform nvere Tranform -
S-Doman naly -Doman rcut naly Tme doman t doman near rcut aplace Tranform omplex frequency doman doman Tranformed rcut Dfferental equaton lacal technque epone waveform aplace Tranform nvere Tranform -
DEFINING %COMPLETE IN MICROSOFT PROJECT
 CelersSystems DEFINING %COMPLETE IN MICROSOFT PROJECT PREPARED BY James E Aksel, PMP, PMI-SP, MVP For Addtonal Informaton about Earned Value Management Systems and reportng, please contact: CelersSystems,
CelersSystems DEFINING %COMPLETE IN MICROSOFT PROJECT PREPARED BY James E Aksel, PMP, PMI-SP, MVP For Addtonal Informaton about Earned Value Management Systems and reportng, please contact: CelersSystems,
Modeling ISP Tier Design
 Modelng ISP Ter Degn We Da School of Informaton and Computer Scence Unverty of Calforna, Irvne Irvne, CA, US [email protected] Scott Jordan School of Informaton and Computer Scence Unverty of Calforna, Irvne
Modelng ISP Ter Degn We Da School of Informaton and Computer Scence Unverty of Calforna, Irvne Irvne, CA, US [email protected] Scott Jordan School of Informaton and Computer Scence Unverty of Calforna, Irvne
A Novel Architecture Design of Large-Scale Distributed Object Storage System
 Internatonal Journal of Grd Dtrbuton Computng Vol.8, No.1 (2015), pp.25-32 http://dx.do.org/10.14257/gdc.2015.8.1.03 A Novel Archtecture Degn of Large-Scale Dtrbuted Obect Storage Sytem Shan Yng 1 and
Internatonal Journal of Grd Dtrbuton Computng Vol.8, No.1 (2015), pp.25-32 http://dx.do.org/10.14257/gdc.2015.8.1.03 A Novel Archtecture Degn of Large-Scale Dtrbuted Obect Storage Sytem Shan Yng 1 and
v a 1 b 1 i, a 2 b 2 i,..., a n b n i.
 SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 455 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces we have studed thus far n the text are real vector spaces snce the scalars are
SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 455 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces we have studed thus far n the text are real vector spaces snce the scalars are
PID Control of Heat Exchanger System
 Volume 8 No.6, October 00 PID Control of Heat Exchanger Sytem Yuvraj Bhuhan Khare Yaduvr Sngh Deartment of Electrcal & Intrumentaton Engneerng Thaar Unverty, Patala, 4700, Punjab, Inda ABSTRACT Heat exchanger
Volume 8 No.6, October 00 PID Control of Heat Exchanger Sytem Yuvraj Bhuhan Khare Yaduvr Sngh Deartment of Electrcal & Intrumentaton Engneerng Thaar Unverty, Patala, 4700, Punjab, Inda ABSTRACT Heat exchanger
BERNSTEIN POLYNOMIALS
 On-Lne Geometrc Modelng Notes BERNSTEIN POLYNOMIALS Kenneth I. Joy Vsualzaton and Graphcs Research Group Department of Computer Scence Unversty of Calforna, Davs Overvew Polynomals are ncredbly useful
On-Lne Geometrc Modelng Notes BERNSTEIN POLYNOMIALS Kenneth I. Joy Vsualzaton and Graphcs Research Group Department of Computer Scence Unversty of Calforna, Davs Overvew Polynomals are ncredbly useful
SIMPLIFYING NDA PROGRAMMING WITH PROt SQL
 SIMPLIFYING NDA PROGRAMMING WITH PROt SQL Aeen L. Yam, Besseaar Assocates, Prnceton, NJ ABSRACf The programmng of New Drug Appcaton (NDA) Integrated Summary of Safety (ISS) usuay nvoves obtanng patent
SIMPLIFYING NDA PROGRAMMING WITH PROt SQL Aeen L. Yam, Besseaar Assocates, Prnceton, NJ ABSRACf The programmng of New Drug Appcaton (NDA) Integrated Summary of Safety (ISS) usuay nvoves obtanng patent
The Shrinking Hand: Why Information Technology Leads to Smaller Firms
 Th paper can e downoaded wthout charge from the Soca Scence Reearch Network eectronc rary at: http://rn.com/atract=1601193 It ha een puhed n reved form n The Internatona Journa of the Economc of Bune,
Th paper can e downoaded wthout charge from the Soca Scence Reearch Network eectronc rary at: http://rn.com/atract=1601193 It ha een puhed n reved form n The Internatona Journa of the Economc of Bune,
Recurrence. 1 Definitions and main statements
 Recurrence 1 Defntons and man statements Let X n, n = 0, 1, 2,... be a MC wth the state space S = (1, 2,...), transton probabltes p j = P {X n+1 = j X n = }, and the transton matrx P = (p j ),j S def.
Recurrence 1 Defntons and man statements Let X n, n = 0, 1, 2,... be a MC wth the state space S = (1, 2,...), transton probabltes p j = P {X n+1 = j X n = }, and the transton matrx P = (p j ),j S def.
+ + + - - This circuit than can be reduced to a planar circuit
 MeshCurrent Method The meshcurrent s analog of the nodeoltage method. We sole for a new set of arables, mesh currents, that automatcally satsfy KCLs. As such, meshcurrent method reduces crcut soluton to
MeshCurrent Method The meshcurrent s analog of the nodeoltage method. We sole for a new set of arables, mesh currents, that automatcally satsfy KCLs. As such, meshcurrent method reduces crcut soluton to
The issue of whether the Internet will permanently destroy the news media is currently a
 Wll the Internet etroy the New Meda? or Can Onlne Advertng Market Save the Meda? by Suan Athey, Emlo Calvano and Johua S. Gan * Frt raft: October, 009 Th Veron: November, 00 PRELIMINARY PLEASE O NOT QUOTE
Wll the Internet etroy the New Meda? or Can Onlne Advertng Market Save the Meda? by Suan Athey, Emlo Calvano and Johua S. Gan * Frt raft: October, 009 Th Veron: November, 00 PRELIMINARY PLEASE O NOT QUOTE
Lecture #21. MOS Capacitor Structure
 Lecture #21 OUTLINE The MOS apactor Electrotatc Readng: oure Reader EE130 Lecture 21, Slde 1 MOS apactor Structure MOS capactor (croectonal vew _ TE x EE130 Lecture 21, Slde 2 Typcal MOS capactor and trantor
Lecture #21 OUTLINE The MOS apactor Electrotatc Readng: oure Reader EE130 Lecture 21, Slde 1 MOS apactor Structure MOS capactor (croectonal vew _ TE x EE130 Lecture 21, Slde 2 Typcal MOS capactor and trantor
Impact of the design method of permanent magnets synchronous generators for small direct drive wind turbines for battery operation
 Impact o the degn method o permanent magnet ynchronou generator or mall drect drve wnd turbne or battery operaton Mha PREDESCU, Dr. eng.*, Aurelan CRǍCIUNESCU, Pro. Dr. **, Andre BEJINARIU, Eng.*, Octavan
Impact o the degn method o permanent magnet ynchronou generator or mall drect drve wnd turbne or battery operaton Mha PREDESCU, Dr. eng.*, Aurelan CRǍCIUNESCU, Pro. Dr. **, Andre BEJINARIU, Eng.*, Octavan
The Dynamics of Wealth and Income Distribution in a Neoclassical Growth Model * Stephen J. Turnovsky. University of Washington, Seattle
 The Dynamcs of Weath and Income Dstrbuton n a Neocassca Growth Mode * Stephen J. Turnovsy Unversty of Washngton, Seatte Ceca García-Peñaosa CNRS and GREQAM March 26 Abstract: We examne the evouton of the
The Dynamcs of Weath and Income Dstrbuton n a Neocassca Growth Mode * Stephen J. Turnovsy Unversty of Washngton, Seatte Ceca García-Peñaosa CNRS and GREQAM March 26 Abstract: We examne the evouton of the
Module 2 LOSSLESS IMAGE COMPRESSION SYSTEMS. Version 2 ECE IIT, Kharagpur
 Module LOSSLESS IMAGE COMPRESSION SYSTEMS Lesson 3 Lossless Compresson: Huffman Codng Instructonal Objectves At the end of ths lesson, the students should be able to:. Defne and measure source entropy..
Module LOSSLESS IMAGE COMPRESSION SYSTEMS Lesson 3 Lossless Compresson: Huffman Codng Instructonal Objectves At the end of ths lesson, the students should be able to:. Defne and measure source entropy..
1. Fundamentals of probability theory 2. Emergence of communication traffic 3. Stochastic & Markovian Processes (SP & MP)
 6.3 / -- Communcaton Networks II (Görg) SS20 -- www.comnets.un-bremen.de Communcaton Networks II Contents. Fundamentals of probablty theory 2. Emergence of communcaton traffc 3. Stochastc & Markovan Processes
6.3 / -- Communcaton Networks II (Görg) SS20 -- www.comnets.un-bremen.de Communcaton Networks II Contents. Fundamentals of probablty theory 2. Emergence of communcaton traffc 3. Stochastc & Markovan Processes
How To Calculate The Accountng Perod Of Nequalty
 Inequalty and The Accountng Perod Quentn Wodon and Shlomo Ytzha World Ban and Hebrew Unversty September Abstract Income nequalty typcally declnes wth the length of tme taen nto account for measurement.
Inequalty and The Accountng Perod Quentn Wodon and Shlomo Ytzha World Ban and Hebrew Unversty September Abstract Income nequalty typcally declnes wth the length of tme taen nto account for measurement.
Netherlands Published online: 27 Jun 2013.
 Th artcle wa downloaded by: [Bblotheek TU Delft] On: 04 Noveber 2013, At: 08:09 Publher: Routledge Infora Ltd Regtered n England and Wale Regtered Nuber: 1072954 Regtered offce: Morter Houe, 37-41 Morter
Th artcle wa downloaded by: [Bblotheek TU Delft] On: 04 Noveber 2013, At: 08:09 Publher: Routledge Infora Ltd Regtered n England and Wale Regtered Nuber: 1072954 Regtered offce: Morter Houe, 37-41 Morter
Linear Circuits Analysis. Superposition, Thevenin /Norton Equivalent circuits
 Lnear Crcuts Analyss. Superposton, Theenn /Norton Equalent crcuts So far we hae explored tmendependent (resste) elements that are also lnear. A tmendependent elements s one for whch we can plot an / cure.
Lnear Crcuts Analyss. Superposton, Theenn /Norton Equalent crcuts So far we hae explored tmendependent (resste) elements that are also lnear. A tmendependent elements s one for whch we can plot an / cure.
ITS-90 FORMULATIONS FOR VAPOR PRESSURE, FROSTPOINT TEMPERATURE, DEWPOINT TEMPERATURE, AND ENHANCEMENT FACTORS IN THE RANGE 100 TO +100 C.
 ITS-90 FORMULATIONS FOR VAPOR PRESSURE, FROSTPOINT TEMPERATURE, DEWPOINT TEMPERATURE, AND ENHANCEMENT FACTORS IN THE RANGE 100 TO +100 C Bob Hardy Thunder Scentfc Corporaton, Albuquerque, NM, USA Abtract:
ITS-90 FORMULATIONS FOR VAPOR PRESSURE, FROSTPOINT TEMPERATURE, DEWPOINT TEMPERATURE, AND ENHANCEMENT FACTORS IN THE RANGE 100 TO +100 C Bob Hardy Thunder Scentfc Corporaton, Albuquerque, NM, USA Abtract:
A Simple Congestion-Aware Algorithm for Load Balancing in Datacenter Networks
 A Smpe Congeston-Aware Agorthm for Load Baancng n Datacenter Networs Mehrnoosh Shafee, and Javad Ghader, Coumba Unversty Abstract We study the probem of oad baancng n datacenter networs, namey, assgnng
A Smpe Congeston-Aware Agorthm for Load Baancng n Datacenter Networs Mehrnoosh Shafee, and Javad Ghader, Coumba Unversty Abstract We study the probem of oad baancng n datacenter networs, namey, assgnng
Multifunction Phased Array Radar Resource Management: Real-Time Scheduling Algorithm
 Journal of Computatonal Informaton Sytem 7:2 (211) 385-393 Avalable at http://www.jofc.com Multfuncton Phaed Array Radar Reource Management: Real-me Schedulng Algorm Janbn LU 1,, Hu XIAO 2, Zemn XI 1,
Journal of Computatonal Informaton Sytem 7:2 (211) 385-393 Avalable at http://www.jofc.com Multfuncton Phaed Array Radar Reource Management: Real-me Schedulng Algorm Janbn LU 1,, Hu XIAO 2, Zemn XI 1,
QoS-based Virtual Private Network Design for an MPLS network
 QoS-bae Virtua Private Networ Deign for an MPLS networ Anotai Sriitja an Davi Tier Det. of Information Science an Teecommunication Univerity of Pittburgh 5 N. Beefie Avenue, Pittburgh, PA 560 emai: [email protected],
QoS-bae Virtua Private Networ Deign for an MPLS networ Anotai Sriitja an Davi Tier Det. of Information Science an Teecommunication Univerity of Pittburgh 5 N. Beefie Avenue, Pittburgh, PA 560 emai: [email protected],
Multi-agent System for Custom Relationship Management with SVMs Tool
 Mut-agent System for Custom Reatonshp Management wth SVMs oo Yanshan Xao, Bo Lu, 3, Dan Luo, and Longbng Cao Guangzhou Asan Games Organzng Commttee, Guangzhou 5063, P.R. Chna Facuty of Informaton echnoogy,
Mut-agent System for Custom Reatonshp Management wth SVMs oo Yanshan Xao, Bo Lu, 3, Dan Luo, and Longbng Cao Guangzhou Asan Games Organzng Commttee, Guangzhou 5063, P.R. Chna Facuty of Informaton echnoogy,
Portfolio Loss Distribution
 Portfolo Loss Dstrbuton Rsky assets n loan ortfolo hghly llqud assets hold-to-maturty n the bank s balance sheet Outstandngs The orton of the bank asset that has already been extended to borrowers. Commtment
Portfolo Loss Dstrbuton Rsky assets n loan ortfolo hghly llqud assets hold-to-maturty n the bank s balance sheet Outstandngs The orton of the bank asset that has already been extended to borrowers. Commtment
ACTION: Breaking the Privacy Barrier for RFID Systems
 ACTION: Breaking the Privacy Barrier for RFID Sytem Li Lu, Jinong Han, Renyi Xiao, and Yunhao Liu Deartment of Comuter Science & Engineering, Hong Kong Univerity of Science & Technoogy, Hong Kong, China
ACTION: Breaking the Privacy Barrier for RFID Sytem Li Lu, Jinong Han, Renyi Xiao, and Yunhao Liu Deartment of Comuter Science & Engineering, Hong Kong Univerity of Science & Technoogy, Hong Kong, China
Predicting Advertiser Bidding Behaviors in Sponsored Search by Rationality Modeling
 Predctng Advertser Bddng Behavors n Sponsored Search by Ratonaty Modeng Hafeng Xu Centre for Computatona Mathematcs n Industry and Commerce Unversty of Wateroo Wateroo, ON, Canada [email protected] Dy
Predctng Advertser Bddng Behavors n Sponsored Search by Ratonaty Modeng Hafeng Xu Centre for Computatona Mathematcs n Industry and Commerce Unversty of Wateroo Wateroo, ON, Canada [email protected] Dy
GRADIENT METHODS FOR BINARY INTEGER PROGRAMMING
 Proceedns of the 4st Internatona Conference on Computers & Industra Enneern GRADIENT METHODS FOR BINARY INTEGER PROGRAMMING Chen-Yuan Huan¹, Ta-Chun Wan² Insttute of Cv Avaton, Natona Chen Kun Unversty,
Proceedns of the 4st Internatona Conference on Computers & Industra Enneern GRADIENT METHODS FOR BINARY INTEGER PROGRAMMING Chen-Yuan Huan¹, Ta-Chun Wan² Insttute of Cv Avaton, Natona Chen Kun Unversty,
Chapter 4 ECONOMIC DISPATCH AND UNIT COMMITMENT
 Chapter 4 ECOOMIC DISATCH AD UIT COMMITMET ITRODUCTIO A power system has several power plants. Each power plant has several generatng unts. At any pont of tme, the total load n the system s met by the
Chapter 4 ECOOMIC DISATCH AD UIT COMMITMET ITRODUCTIO A power system has several power plants. Each power plant has several generatng unts. At any pont of tme, the total load n the system s met by the
Optimal maintenance of a production-inventory system with continuous repair times and idle periods
 Proceedngs o the 3 Internatonal Conerence on Aled Mathematcs and Comutatonal Methods Otmal mantenance o a roducton-nventory system wth contnuous rear tmes and dle erods T. D. Dmtrakos* Deartment o Mathematcs
Proceedngs o the 3 Internatonal Conerence on Aled Mathematcs and Comutatonal Methods Otmal mantenance o a roducton-nventory system wth contnuous rear tmes and dle erods T. D. Dmtrakos* Deartment o Mathematcs
Calculation of Sampling Weights
 Perre Foy Statstcs Canada 4 Calculaton of Samplng Weghts 4.1 OVERVIEW The basc sample desgn used n TIMSS Populatons 1 and 2 was a two-stage stratfed cluster desgn. 1 The frst stage conssted of a sample
Perre Foy Statstcs Canada 4 Calculaton of Samplng Weghts 4.1 OVERVIEW The basc sample desgn used n TIMSS Populatons 1 and 2 was a two-stage stratfed cluster desgn. 1 The frst stage conssted of a sample
A Resources Allocation Model for Multi-Project Management
 A Resources Aocaton Mode for Mut-Proect Management Hamdatou Kane, Aban Tsser To cte ths verson: Hamdatou Kane, Aban Tsser. A Resources Aocaton Mode for Mut-Proect Management. 9th Internatona Conference
A Resources Aocaton Mode for Mut-Proect Management Hamdatou Kane, Aban Tsser To cte ths verson: Hamdatou Kane, Aban Tsser. A Resources Aocaton Mode for Mut-Proect Management. 9th Internatona Conference
Applied Research Laboratory. Decision Theory and Receiver Design
 Decson Theor and Recever Desgn Sgnal Detecton and Performance Estmaton Sgnal Processor Decde Sgnal s resent or Sgnal s not resent Nose Nose Sgnal? Problem: How should receved sgnals be rocessed n order
Decson Theor and Recever Desgn Sgnal Detecton and Performance Estmaton Sgnal Processor Decde Sgnal s resent or Sgnal s not resent Nose Nose Sgnal? Problem: How should receved sgnals be rocessed n order
VRT012 User s guide V0.1. Address: Žirmūnų g. 27, Vilnius LT-09105, Phone: (370-5) 2127472, Fax: (370-5) 276 1380, Email: info@teltonika.
 VRT012 User s gude V0.1 Thank you for purchasng our product. We hope ths user-frendly devce wll be helpful n realsng your deas and brngng comfort to your lfe. Please take few mnutes to read ths manual
VRT012 User s gude V0.1 Thank you for purchasng our product. We hope ths user-frendly devce wll be helpful n realsng your deas and brngng comfort to your lfe. Please take few mnutes to read ths manual
TOPOLOGICAL DESIGN OF MULTIPLE VPNS OVER MPLS NETWORK Anotai Srikitja David Tipper
 TOPOLOGICAL DESIGN OF MULTIPLE VPNS OVER MPLS NETWORK Anotai Sriitja David Tier Det. of Information Science and Teecommunications University of Pittsburgh N. Beefied Avenue, Pittsburgh, PA 60 ABSTRACT
TOPOLOGICAL DESIGN OF MULTIPLE VPNS OVER MPLS NETWORK Anotai Sriitja David Tier Det. of Information Science and Teecommunications University of Pittsburgh N. Beefied Avenue, Pittsburgh, PA 60 ABSTRACT
Simple Interest Loans (Section 5.1) :
 Chapter 5 Fnance The frst part of ths revew wll explan the dfferent nterest and nvestment equatons you learned n secton 5.1 through 5.4 of your textbook and go through several examples. The second part
Chapter 5 Fnance The frst part of ths revew wll explan the dfferent nterest and nvestment equatons you learned n secton 5.1 through 5.4 of your textbook and go through several examples. The second part
PSYCHOLOGICAL RESEARCH (PYC 304-C) Lecture 12
 14 The Ch-squared dstrbuton PSYCHOLOGICAL RESEARCH (PYC 304-C) Lecture 1 If a normal varable X, havng mean µ and varance σ, s standardsed, the new varable Z has a mean 0 and varance 1. When ths standardsed
14 The Ch-squared dstrbuton PSYCHOLOGICAL RESEARCH (PYC 304-C) Lecture 1 If a normal varable X, havng mean µ and varance σ, s standardsed, the new varable Z has a mean 0 and varance 1. When ths standardsed
A note on profit maximization and monotonicity for inbound call centers
 A note on profit maximization and monotonicity for inbound call center Ger Koole & Aue Pot Department of Mathematic, Vrije Univeriteit Amterdam, The Netherland 23rd December 2005 Abtract We conider an
A note on profit maximization and monotonicity for inbound call center Ger Koole & Aue Pot Department of Mathematic, Vrije Univeriteit Amterdam, The Netherland 23rd December 2005 Abtract We conider an
A Secure Password-Authenticated Key Agreement Using Smart Cards
 A Secure Password-Authentcated Key Agreement Usng Smart Cards Ka Chan 1, Wen-Chung Kuo 2 and Jn-Chou Cheng 3 1 Department of Computer and Informaton Scence, R.O.C. Mltary Academy, Kaohsung 83059, Tawan,
A Secure Password-Authentcated Key Agreement Usng Smart Cards Ka Chan 1, Wen-Chung Kuo 2 and Jn-Chou Cheng 3 1 Department of Computer and Informaton Scence, R.O.C. Mltary Academy, Kaohsung 83059, Tawan,
XAC08-6 Professional Project Management
 1 XAC08-6 Professona Project anagement Ths Lecture: Tte s so manager shoud ncude a s management pan a document that gudes any experts agree Some faure project to Ba, ba, ba, ba Communcaton anagement Wee
1 XAC08-6 Professona Project anagement Ths Lecture: Tte s so manager shoud ncude a s management pan a document that gudes any experts agree Some faure project to Ba, ba, ba, ba Communcaton anagement Wee
Coordinate System for 3-D Model Used in Robotic End-Effector
 AU JT 8(: 8 (Apr Codnate Sytem f D Model Ued n Robot EndEffer ulfqar Al Soomro Shool of Advaned Stude, Aan Inttute of Tehnology Pathum Than, Thaland Abtrat Th paper reve the onept of odnate ytem on new
AU JT 8(: 8 (Apr Codnate Sytem f D Model Ued n Robot EndEffer ulfqar Al Soomro Shool of Advaned Stude, Aan Inttute of Tehnology Pathum Than, Thaland Abtrat Th paper reve the onept of odnate ytem on new
ESSAYS IN RENEWABLE ENERGY AND EMISSIONS TRADING
 ESSAYS IN RENEWABLE ENERGY AND EMISSIONS TRADING By JOSHUA D. KNEIFEL A DISSERTATION PRESENTED TO THE GRADUATE SCHOOL OF THE UNIVERSITY OF FLORIDA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE
ESSAYS IN RENEWABLE ENERGY AND EMISSIONS TRADING By JOSHUA D. KNEIFEL A DISSERTATION PRESENTED TO THE GRADUATE SCHOOL OF THE UNIVERSITY OF FLORIDA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE
21 Vectors: The Cross Product & Torque
 21 Vectors: The Cross Product & Torque Do not use our left hand when applng ether the rght-hand rule for the cross product of two vectors dscussed n ths chapter or the rght-hand rule for somethng curl
21 Vectors: The Cross Product & Torque Do not use our left hand when applng ether the rght-hand rule for the cross product of two vectors dscussed n ths chapter or the rght-hand rule for somethng curl
Efficient Project Portfolio as a tool for Enterprise Risk Management
 Effcent Proect Portfolo as a tool for Enterprse Rsk Management Valentn O. Nkonov Ural State Techncal Unversty Growth Traectory Consultng Company January 5, 27 Effcent Proect Portfolo as a tool for Enterprse
Effcent Proect Portfolo as a tool for Enterprse Rsk Management Valentn O. Nkonov Ural State Techncal Unversty Growth Traectory Consultng Company January 5, 27 Effcent Proect Portfolo as a tool for Enterprse
What is Candidate Sampling
 What s Canddate Samplng Say we have a multclass or mult label problem where each tranng example ( x, T ) conssts of a context x a small (mult)set of target classes T out of a large unverse L of possble
What s Canddate Samplng Say we have a multclass or mult label problem where each tranng example ( x, T ) conssts of a context x a small (mult)set of target classes T out of a large unverse L of possble
JCM_VN_AM003_ver01.0 Sectoral scope: 03
 Sectoral scoe: 03 Jont Credtng Mechansm Aroved Methodology VN_AM003 Imrovng the energy effcency of commercal buldngs by utlzaton of hgh effcency equment A. Ttle of the methodology Imrovng the energy effcency
Sectoral scoe: 03 Jont Credtng Mechansm Aroved Methodology VN_AM003 Imrovng the energy effcency of commercal buldngs by utlzaton of hgh effcency equment A. Ttle of the methodology Imrovng the energy effcency
Measuring adverse selection in managed health care
 Ž. Journal of Health Economc 19 2000 829 854 www.elever.nlrlocatereconbae Meaurng advere electon n managed health care Rchard G. Frank a,), Jacob Glazer b, Thoma G. McGure c a HarÕard UnÕerty, HarÕard
Ž. Journal of Health Economc 19 2000 829 854 www.elever.nlrlocatereconbae Meaurng advere electon n managed health care Rchard G. Frank a,), Jacob Glazer b, Thoma G. McGure c a HarÕard UnÕerty, HarÕard
Generalizing the degree sequence problem
 Mddlebury College March 2009 Arzona State Unversty Dscrete Mathematcs Semnar The degree sequence problem Problem: Gven an nteger sequence d = (d 1,...,d n ) determne f there exsts a graph G wth d as ts
Mddlebury College March 2009 Arzona State Unversty Dscrete Mathematcs Semnar The degree sequence problem Problem: Gven an nteger sequence d = (d 1,...,d n ) determne f there exsts a graph G wth d as ts
1 Example 1: Axis-aligned rectangles
 COS 511: Theoretcal Machne Learnng Lecturer: Rob Schapre Lecture # 6 Scrbe: Aaron Schld February 21, 2013 Last class, we dscussed an analogue for Occam s Razor for nfnte hypothess spaces that, n conjuncton
COS 511: Theoretcal Machne Learnng Lecturer: Rob Schapre Lecture # 6 Scrbe: Aaron Schld February 21, 2013 Last class, we dscussed an analogue for Occam s Razor for nfnte hypothess spaces that, n conjuncton
Extending Probabilistic Dynamic Epistemic Logic
 Extendng Probablstc Dynamc Epstemc Logc Joshua Sack May 29, 2008 Probablty Space Defnton A probablty space s a tuple (S, A, µ), where 1 S s a set called the sample space. 2 A P(S) s a σ-algebra: a set
Extendng Probablstc Dynamc Epstemc Logc Joshua Sack May 29, 2008 Probablty Space Defnton A probablty space s a tuple (S, A, µ), where 1 S s a set called the sample space. 2 A P(S) s a σ-algebra: a set
benefit is 2, paid if the policyholder dies within the year, and probability of death within the year is ).
 REVIEW OF RISK MANAGEMENT CONCEPTS LOSS DISTRIBUTIONS AND INSURANCE Loss and nsurance: When someone s subject to the rsk of ncurrng a fnancal loss, the loss s generally modeled usng a random varable or
REVIEW OF RISK MANAGEMENT CONCEPTS LOSS DISTRIBUTIONS AND INSURANCE Loss and nsurance: When someone s subject to the rsk of ncurrng a fnancal loss, the loss s generally modeled usng a random varable or
The Greedy Method. Introduction. 0/1 Knapsack Problem
 The Greedy Method Introducton We have completed data structures. We now are gong to look at algorthm desgn methods. Often we are lookng at optmzaton problems whose performance s exponental. For an optmzaton
The Greedy Method Introducton We have completed data structures. We now are gong to look at algorthm desgn methods. Often we are lookng at optmzaton problems whose performance s exponental. For an optmzaton
RESEARCH ON DUAL-SHAKER SINE VIBRATION CONTROL. Yaoqi FENG 1, Hanping QIU 1. China Academy of Space Technology (CAST) yaoqi.feng@yahoo.
 ICSV4 Carns Australa 9- July, 007 RESEARCH ON DUAL-SHAKER SINE VIBRATION CONTROL Yaoq FENG, Hanpng QIU Dynamc Test Laboratory, BISEE Chna Academy of Space Technology (CAST) [email protected] Abstract
ICSV4 Carns Australa 9- July, 007 RESEARCH ON DUAL-SHAKER SINE VIBRATION CONTROL Yaoq FENG, Hanpng QIU Dynamc Test Laboratory, BISEE Chna Academy of Space Technology (CAST) [email protected] Abstract
How Sets of Coherent Probabilities May Serve as Models for Degrees of Incoherence
 1 st Internatonal Symposum on Imprecse Probabltes and Ther Applcatons, Ghent, Belgum, 29 June 2 July 1999 How Sets of Coherent Probabltes May Serve as Models for Degrees of Incoherence Mar J. Schervsh
1 st Internatonal Symposum on Imprecse Probabltes and Ther Applcatons, Ghent, Belgum, 29 June 2 July 1999 How Sets of Coherent Probabltes May Serve as Models for Degrees of Incoherence Mar J. Schervsh
Expressive Negotiation over Donations to Charities
 Expressve Negotaton over Donatons to Chartes Vncent Contzer Carnege Meon Unversty 5000 Forbes Avenue Pttsburgh, PA 523, USA [email protected] Tuomas Sandhom Carnege Meon Unversty 5000 Forbes Avenue Pttsburgh,
Expressve Negotaton over Donatons to Chartes Vncent Contzer Carnege Meon Unversty 5000 Forbes Avenue Pttsburgh, PA 523, USA [email protected] Tuomas Sandhom Carnege Meon Unversty 5000 Forbes Avenue Pttsburgh,
Mall Cell Network - Power, Memory and Networking
 Slow admon and power control for mall cell network va dtrbuted optmzaton Sew Eng Na, Tony Q.S. Quek, Mérouane Debbah To cte th veron: Sew Eng Na, Tony Q.S. Quek, Mérouane Debbah. Slow admon and power control
Slow admon and power control for mall cell network va dtrbuted optmzaton Sew Eng Na, Tony Q.S. Quek, Mérouane Debbah To cte th veron: Sew Eng Na, Tony Q.S. Quek, Mérouane Debbah. Slow admon and power control
Feature selection for intrusion detection. Slobodan Petrović NISlab, Gjøvik University College
 Feature selecton for ntruson detecton Slobodan Petrovć NISlab, Gjøvk Unversty College Contents The feature selecton problem Intruson detecton Traffc features relevant for IDS The CFS measure The mrmr measure
Feature selecton for ntruson detecton Slobodan Petrovć NISlab, Gjøvk Unversty College Contents The feature selecton problem Intruson detecton Traffc features relevant for IDS The CFS measure The mrmr measure
Section 5.3 Annuities, Future Value, and Sinking Funds
 Secton 5.3 Annutes, Future Value, and Snkng Funds Ordnary Annutes A sequence of equal payments made at equal perods of tme s called an annuty. The tme between payments s the payment perod, and the tme
Secton 5.3 Annutes, Future Value, and Snkng Funds Ordnary Annutes A sequence of equal payments made at equal perods of tme s called an annuty. The tme between payments s the payment perod, and the tme
Solved Problems Chapter 3: Mechanical Systems
 ME 43: Sytem Dynamic and Contro Probem A-3-8- Soved Probem Chapter 3: Mechanica Sytem In Figure 3-3, the impe penduum hown conit of a phere of ma m upended by a tring of negigibe ma. Negecting the eongation
ME 43: Sytem Dynamic and Contro Probem A-3-8- Soved Probem Chapter 3: Mechanica Sytem In Figure 3-3, the impe penduum hown conit of a phere of ma m upended by a tring of negigibe ma. Negecting the eongation
The Design of Reliable Trust Management Systems for Electronic Trading Communities
 The Degn of Relale Trut Management Sytem for Electronc Tradng Communte Chryantho Dellaroca Sloan School of Management Maachuett Inttute of Technology Room E53-315 Camrdge, MA 02139 [email protected] Atract:
The Degn of Relale Trut Management Sytem for Electronc Tradng Communte Chryantho Dellaroca Sloan School of Management Maachuett Inttute of Technology Room E53-315 Camrdge, MA 02139 [email protected] Atract:
Can Auto Liability Insurance Purchases Signal Risk Attitude?
 Internatonal Journal of Busness and Economcs, 2011, Vol. 10, No. 2, 159-164 Can Auto Lablty Insurance Purchases Sgnal Rsk Atttude? Chu-Shu L Department of Internatonal Busness, Asa Unversty, Tawan Sheng-Chang
Internatonal Journal of Busness and Economcs, 2011, Vol. 10, No. 2, 159-164 Can Auto Lablty Insurance Purchases Sgnal Rsk Atttude? Chu-Shu L Department of Internatonal Busness, Asa Unversty, Tawan Sheng-Chang
Ring structure of splines on triangulations
 www.oeaw.ac.at Rng structure of splnes on trangulatons N. Vllamzar RICAM-Report 2014-48 www.rcam.oeaw.ac.at RING STRUCTURE OF SPLINES ON TRIANGULATIONS NELLY VILLAMIZAR Introducton For a trangulated regon
www.oeaw.ac.at Rng structure of splnes on trangulatons N. Vllamzar RICAM-Report 2014-48 www.rcam.oeaw.ac.at RING STRUCTURE OF SPLINES ON TRIANGULATIONS NELLY VILLAMIZAR Introducton For a trangulated regon
ARTICLE IN PRESS. JID:COMAID AID:1153 /FLA [m3g; v 1.79; Prn:21/02/2009; 14:10] P.1 (1-13) Computer Aided Geometric Design ( )
![ARTICLE IN PRESS. JID:COMAID AID:1153 /FLA [m3g; v 1.79; Prn:21/02/2009; 14:10] P.1 (1-13) Computer Aided Geometric Design ( ) ARTICLE IN PRESS. JID:COMAID AID:1153 /FLA [m3g; v 1.79; Prn:21/02/2009; 14:10] P.1 (1-13) Computer Aided Geometric Design ( )](/thumbs/27/10357589.jpg) COMAID:5 JID:COMAID AID:5 /FLA [mg; v 79; Prn:/0/009; 4:0] P -) Computer Aded Geometrc Degn ) Content lt avalable at ScenceDrect Computer Aded Geometrc Degn wwwelevercom/locate/cagd Fat approach for computng
COMAID:5 JID:COMAID AID:5 /FLA [mg; v 79; Prn:/0/009; 4:0] P -) Computer Aded Geometrc Degn ) Content lt avalable at ScenceDrect Computer Aded Geometrc Degn wwwelevercom/locate/cagd Fat approach for computng
A hybrid global optimization algorithm based on parallel chaos optimization and outlook algorithm
 Avalable onlne www.ocpr.com Journal of Chemcal and Pharmaceutcal Research, 2014, 6(7):1884-1889 Research Artcle ISSN : 0975-7384 CODEN(USA) : JCPRC5 A hybrd global optmzaton algorthm based on parallel
Avalable onlne www.ocpr.com Journal of Chemcal and Pharmaceutcal Research, 2014, 6(7):1884-1889 Research Artcle ISSN : 0975-7384 CODEN(USA) : JCPRC5 A hybrd global optmzaton algorthm based on parallel
A Structure Preserving Database Encryption Scheme
 A Structure Preservng Database Encryton Scheme Yuval Elovc, Ronen Wasenberg, Erez Shmuel, Ehud Gudes Ben-Guron Unversty of the Negev, Faculty of Engneerng, Deartment of Informaton Systems Engneerng, Postfach
A Structure Preservng Database Encryton Scheme Yuval Elovc, Ronen Wasenberg, Erez Shmuel, Ehud Gudes Ben-Guron Unversty of the Negev, Faculty of Engneerng, Deartment of Informaton Systems Engneerng, Postfach
Clustering based Two-Stage Text Classification Requiring Minimal Training Data
 OI: 10.2298/CSIS120130044Z Custerng based Two-Stage Text Cassfcaton Requrng Mnma Tranng ata Xue Zhang 1,2 and Wangxn Xao 3,4 1 Key Laboratory of Hgh Confdence Software Technooges, Mnstry of Educaton, Pekng
OI: 10.2298/CSIS120130044Z Custerng based Two-Stage Text Cassfcaton Requrng Mnma Tranng ata Xue Zhang 1,2 and Wangxn Xao 3,4 1 Key Laboratory of Hgh Confdence Software Technooges, Mnstry of Educaton, Pekng
Relay Secrecy in Wireless Networks with Eavesdropper
 Relay Secrecy n Wreless Networks wth Eavesdropper Parvathnathan Venktasubramanam, Tng He and Lang Tong School of Electrcal and Computer Engneerng Cornell Unversty, Ithaca, NY 14853 Emal : {pv45, th255,
Relay Secrecy n Wreless Networks wth Eavesdropper Parvathnathan Venktasubramanam, Tng He and Lang Tong School of Electrcal and Computer Engneerng Cornell Unversty, Ithaca, NY 14853 Emal : {pv45, th255,
Factored Conditional Restricted Boltzmann Machines for Modeling Motion Style
 Factored Condtona Restrcted Botzmann Machnes for Modeng Moton Stye Graham W. Tayor [email protected] Geoffrey E. Hnton [email protected] Department of Computer Scence, Unversty of Toronto, Toronto,
Factored Condtona Restrcted Botzmann Machnes for Modeng Moton Stye Graham W. Tayor [email protected] Geoffrey E. Hnton [email protected] Department of Computer Scence, Unversty of Toronto, Toronto,
Section 5.4 Annuities, Present Value, and Amortization
 Secton 5.4 Annutes, Present Value, and Amortzaton Present Value In Secton 5.2, we saw that the present value of A dollars at nterest rate per perod for n perods s the amount that must be deposted today
Secton 5.4 Annutes, Present Value, and Amortzaton Present Value In Secton 5.2, we saw that the present value of A dollars at nterest rate per perod for n perods s the amount that must be deposted today
Support Vector Machines
 Support Vector Machnes Max Wellng Department of Computer Scence Unversty of Toronto 10 Kng s College Road Toronto, M5S 3G5 Canada [email protected] Abstract Ths s a note to explan support vector machnes.
Support Vector Machnes Max Wellng Department of Computer Scence Unversty of Toronto 10 Kng s College Road Toronto, M5S 3G5 Canada [email protected] Abstract Ths s a note to explan support vector machnes.
CHOLESTEROL REFERENCE METHOD LABORATORY NETWORK. Sample Stability Protocol
 CHOLESTEROL REFERENCE METHOD LABORATORY NETWORK Sample Stablty Protocol Background The Cholesterol Reference Method Laboratory Network (CRMLN) developed certfcaton protocols for total cholesterol, HDL
CHOLESTEROL REFERENCE METHOD LABORATORY NETWORK Sample Stablty Protocol Background The Cholesterol Reference Method Laboratory Network (CRMLN) developed certfcaton protocols for total cholesterol, HDL
Modeling and Prediction of Pedestrian Behavior based on the Sub-goal Concept
 Modelng and Predcton of Pedestran Behavor based on the Sub-goal Concet Tetsush Ieda, Yoshhro Chgodo, Danel Rea, Francesco Zanlungo, Masahro Shom, Taayu Kanda Intellgent Robotcs and Communcaton Laboratores,
Modelng and Predcton of Pedestran Behavor based on the Sub-goal Concet Tetsush Ieda, Yoshhro Chgodo, Danel Rea, Francesco Zanlungo, Masahro Shom, Taayu Kanda Intellgent Robotcs and Communcaton Laboratores,
Imperial College London
 F. Fang 1, C.C. Pan 1, I.M. Navon 2, M.D. Pggott 1, G.J. Gorman 1, P.A. Allson 1 and A.J.H. Goddard 1 1 Appled Modellng and Computaton Group Department of Earth Scence and Engneerng Imperal College London,
F. Fang 1, C.C. Pan 1, I.M. Navon 2, M.D. Pggott 1, G.J. Gorman 1, P.A. Allson 1 and A.J.H. Goddard 1 1 Appled Modellng and Computaton Group Department of Earth Scence and Engneerng Imperal College London,
A Comprehensive Analysis of Bandwidth Request Mechanisms in IEEE 802.16 Networks
 A Comrehensve Analyss of Bandwdth Reuest Mechansms n IEEE 802.6 Networks Davd Chuck, Kuan-Yu Chen and J. Morrs Chang Deartment of Electrcal and Comuter Engneerng Iowa State Unversty, Ames, Iowa 500, USA
A Comrehensve Analyss of Bandwdth Reuest Mechansms n IEEE 802.6 Networks Davd Chuck, Kuan-Yu Chen and J. Morrs Chang Deartment of Electrcal and Comuter Engneerng Iowa State Unversty, Ames, Iowa 500, USA
Vasicek s Model of Distribution of Losses in a Large, Homogeneous Portfolio
 Vascek s Model of Dstrbuton of Losses n a Large, Homogeneous Portfolo Stephen M Schaefer London Busness School Credt Rsk Electve Summer 2012 Vascek s Model Important method for calculatng dstrbuton of
Vascek s Model of Dstrbuton of Losses n a Large, Homogeneous Portfolo Stephen M Schaefer London Busness School Credt Rsk Electve Summer 2012 Vascek s Model Important method for calculatng dstrbuton of
