RevisedJanuary26,
|
|
|
- Stewart Butler
- 10 years ago
- Views:
Transcription
1 EarliestEligibleVirtualDeadlineFirst:AFlexible andaccuratemechanismforproportionalshare DepartmentofComputerScience,OldDominionUniversity ResourceAllocation IonStoica,HusseinAbdel-Wahab Norfolk,Virginia, TR tobegrantedinarbitrarilysmallintervalsoftime.mainly,weshowthatinsteadyconditionsour denethenotionoffairnessinthecontextofanidealizedsysteminwhichtheresourceisassumed Weassumethattheresourceisallocatedintimequantaofsizeq.Toeachclient,weassociatea weightwhichdeterminestherelativesharefromtheresourcethattheclientshouldreceive.we algorithmguaranteesthatthedierencebetweentheservicetimethataclientshouldreceiveinthe Weproposeandanalyzeanewproportionalshareallocationalgorithmfortimesharedresources. Abstract ofatimequantum.thealgorithmprovidessupportfordynamicoperations,suchasaclientjoining orleavingthecompetition(fortheresource),andchangingaclient'sweight.byusinganecient idealizedsystemandtheservicetimeitactuallyreceivesintherealsystemisboundedbythesizeq representsthenumberofclientscompetingfortheresource. augmentedbinarysearchtreedatastructureweimplementtheseoperationsino(logn),wheren RevisedJanuary26,
2 1Introduction Oneofthemostchallengingproblemsinmodernoperatingsystemsistodesignexibleandaccurate inapredictableandresponsiveway.inaddition,ageneral-purposeoperatingsystemshouldseamlessly algorithmstoallocateresourcesamongcompetingclients.thisissuehasbecomemoreimportantwith constraints.inordertomeettheseconstraintstheunderlyingoperatingsystemshouldallocateresources integratethesenewtypesofapplicationswithconventionalinteractiveandbatchapplications. theemergenceofnewtypesofreal-timeapplicationssuchasmultimediawhichhavewelldenedtime thesecondclientshouldreceive75%oftheresource.real-timeschedulersarebasedonanevent-driven theshareoftheresourcethattheclientshouldreceive.theschedulertriestoallocatetheresource ulers[20,21,22].inproportionalsharealgorithmseachclienthasassociatedaweightwhichdetermines theseschedulersfallintwocategories:proportionalshare[2,26,28,29,30],andreal-time1basedsched- and3,respectivelythatcompeteforthesameresource.thentherstclientshouldreceive25%,while amongcompetingclientsinproportiontotheirshare.forexample,considertwoclientswithweights1 Manyschedulershavetried,andinparthavesucceeded,toaddresstheserequirements.Generally, policies,theseschedulersguaranteethatalleventsareprocessedbeforetheirdeadlines.whileingeneral loadsituations,real-timebasedschedulerstendtooerbetterguaranteesforapplicationswithtimeliness modelinwhichaclientischaracterizedbyasetofeventsarrivinginacertainpattern(usuallyperiodic), theproportionalshareschedulerstendtobemoreexibleandtoensureagracefuldegradationinover- andbyapredictedservicetimeandadeadlineassociatedtoeachevent.byimposingstrictadmission extendedtosupportbatchapplications.themainreasonisthatwhilemultimediaandinteractive constraints,suchasmultimedia. applicationsttheevent-drivenmodelimplicitlyassumedbytheseschedulers,batchapplicationsdonot. isthetimeatwhichthenextframeshouldarrive.similarly,aninteractiveapplication(suchasaneditor) Forexample,avideoapplicationcanbemodeledasaperiodicprocess,whereaneventrepresentsthe arrivalofaframe,itsservicetimeisthetimerequiredtoprocessanddisplaytheframe2,anditsdeadline canbemodeledasanaperiodicprocess,whereaneventisgeneratedasaresultoftheuserpressingakey, Althoughreal-timebasedschedulersprovidebettersupportformultimedia,theycannotbeeasily inmanysituationsitisdiculttoaccuratelydeterminethisservicetime.themainreasonisthat,evenfor thesameapplication,theservicetimemayhavelargevariations,andthesevariationsarehardtopredict. Forexample,theservicetimerequiredbyacompilermayvarysignicantlyevenforthesameprogram, isgivenbythelargestacceptabledelaybetweenthemomentwhenthekeyispressedandthemoment whenthecharacterisdisplayed.incontrasttobothmultimediaandinteractiveapplications,batch theservicetimeisthetimerequiredtoprocessanddisplaythecorrespondingcharacter,andthedeadline thatusereal-timeschemesforschedulingcontinuousmediaalsoemployconventionalalgorithms(e.g., dependingonhowmanymodulesarerecompiled.forthesereasonsmanygeneralpurposeschedulers applicationsareusuallycharacterizedbyonlyoneparameter,i.e.,therequestedservicetime.moreover, restrictive.thus,ausercanbeinthesituationinwhichhecannotrunanewapplication,althoughhe mightbewillingtoacceptadegradationinperformanceofotherapplicationsinordertoaccommodate in[18]:ratemonotonicandearlydeadlinerst. inordertosatisfystrongtimeconstraints,theyimposestrictadmissionpolicieswhichmakethemfairly round-robin)forschedulingbatchapplications.anotherdrawbackofreal-timebasedschedulersisthat, 1Usually,theseschedulersarebasedontwowell-knownreal-timealgorithmsproposedandanalyzedbyLiuandLayland 2Dependingonthedesiredqualitythiscanbeeithertheworstcase,orastatisticalaverageservicetime. 2
3 guaranteesfortheservicetimereceivedbyaclient.inthisway,ouralgorithmprovidesauniedapproach forschedulingcontinuousmedia,interactiveandbatchapplications.inpart,thealgorithmbuildson which,whileretainingalltheadvantagesoftheproportionalshareschedulers,providesstrongtimeliness forexample,whenanapplicationterminatesitisdiculttodistributerapidlyitsshareamongtheother applicationsthatarestillcompetingfortheresource. thenewone.finally,inahighlydynamicenvironmenttheseschedulersdonotprovideenoughexibility; tracktheworkprogressinanidealuid-owbasedsystem.toeachclientweassociateaweightwhich ideasfoundinpreviousnetworkfair-queueingalgorithms[23,31],andgeneral-purposeproportionalshare allocationalgorithms[29,30].asin[23,31],andsimilarto[29,30]weusethenotionofvirtualtimeto Inthispaperweproposeanewscheduler(calledEarliestEligibleVirtualDeadlineFirst{EEVDF) andavirtualdeadlinewhicharethecorrespondingstartingandnishingtimesofservicingtherequest determinestherelativeshareoftheresourcethattheclientshouldreceive.theclientrequirementsare uniformlytranslatedinasequenceofrequestsfortheresource.theserequestsareeitherissuedexplicitly bytheclients,orbythescheduleritselfonbehalfoftheclients.inthiswaybatchactivitiesaretreated thecurrentvirtualtime.thealgorithmsimplyallocatesanewtimequantumtotheclientthathasthe eligiblerequestwiththeearliestvirtualdeadline.wenotethatwhiletheconceptofvirtualdeadlineis alsoemployedbyotherproportional-sharealgorithms[23,31,29,30],theconceptofeligibletimeisa intheuid-owmodel.arequestissaidtobeeligibleifitsvirtualeligibletimeislessthanorequalto uniformlywithmultimediaandinteractiveactivities.basedontheclientshareandontheservicetime uniquefeatureofouralgorithm(which,aswewillshow,playsadecisiveroleinimprovingtheallocation thattheclienthasalreadyreceived,theschedulerassociatestoeachclient'srequestavirtualeligibletime accuracy). allocations,higherlevelresourceabstractionsareneededtospecifytheapplications'requirements.we noteherethatmanyoftheexistingabstractions,suchasticketsandcurrencies(developedbywaldspurger andweihl[28,30]),andprocessorcapacityreserves(proposedbymercer,savageandtokuda[20])are bedirectlytranslatedintotheweightassociatedtothatclientintheeevdfalgorithm.byeciently implementingdynamicoperations,theeevdfprovidesdirectsupportforhigherlevelmechanismssuch easilysupportedbyeevdf.forexample,inlotteryschedulingthenumberofticketsheldbyaclientcould WhileEEVDFimplementsaexibleandaccuratelow-levelmechanismforproportionalshareresource asticketstransferandinationemployedbylotteryscheduling[28,30].throughoutthispaperwewill notdiscussfurtherotherhigherlevelresourceabstractions;instead,wewillimplicitlyassumethatoneof concludesthepaper. thebasiceevdfalgorithm.section4discussestheconceptoffairnessindynamicsystems,whilesection 5presentsthreestrategiesforimplementingtheEEVDFalgorithm.InSection6wegivethefairness theexistingabstractionsisimplementedontopofeevdf.therefore,inthispaperwewillnotaddress problemsthatareusuallyhandledbythishigherlevel(e.g.,priorityinversion). analysisofthealgorithm.finally,insection7wegiveanoverviewoftherelatedwork,andsection8 Thispaperisorganizedasfollows.Thenextsectiondiscussesourassumptions,andSection3presents 2Assumptions Weconsiderasetofclientsthatcompeteforatimesharedresource(e.g.,processor,communication bandwidth).weassumethattheresourceisallocatedintimequantaofsizeatmostq.atthebeginning 3
4 asprocessorandcommunicationbandwidth.forexample,inmanypreemptiveoperatingsystems(e.g., simple,thismodelcapturesthebasicmechanismstraditionallyusedforsharingcommonresources,such higherprioritybecomesactive,oritmayvoluntarilyreleasethecpuwhileitiswaitingforaneventto useiteitherfortheentiretimequantum,oritmayreleaseitbeforethetimequantumexpires.although thesamefashion:aprocessusesthecpuuntilitstimequantumexpiresoranotherprocesswitha UNIX,Windows-NT),theCPUschedulerallocatestheprocessingtimeamongcompetingprocessesin ofeachtimequantumaclientisselectedtousetheresource.oncetheclientacquirestheresource,itmay outputlink.thus,inthiscase,thesizeqofatimequantumrepresentsthetimerequiredtosendapacket multiplexesasetofincomingsessionsonapacket-by-packetbasis.sinceusuallythetransmissionofa ofmaximumlength. packetcannotbepreempted,wetakeatimequantumtobethetimerequiredtosendapacketonthe itshouldreceive.theshareiscomputedastheratiobetweentheclient'sweightandthetotalsumover occur(e.g.,ani/ooperationtocomplete).asanotherexample,consideracommunicationswitchthat ofallclientsactiveattimet.thentheshareofclientiattimet,denotedfi(t),isdenedas: theweightsofallactiveclients.aclientissaidtobeactivewhileitiscompetingfortheresource,and passiveotherwise.moreformally,letwidenotetheweightassociatedtoclienti,andleta(t)betheset Further,weassociatetoeachclientaweightthatdeterminestherelativeshareoftheresourcethat usetheresourceforfi(t)ttimeunits.ingeneral,whentheclientsharevariesovertime,theservice Ideally,iftheclientshareremainsconstantduringatimeinterval[t;t+t],thenclientiisentitledto timethatclientishouldreceiveinaperfectfairsystemwhilebeingactiveduringatimeinterval[t0;t1] is Si(t0;t1)=Zt1 fi(t)=wi Pj2A(t)wj: (1) timeunits.theaboveequationcorrespondstoanidealuid-owsysteminwhichtheresourcecanbe quantacannotbetakenarbitrarilysmall.oneofthereasonsistheoverheadintroducedbythescheduling algorithmandtheoverheadinswitchingfromoneclienttoanother:takingtimequantaofthesameorder grantedinarbitrarilysmallintervalsoftime.inourcase,thisisequivalenttothesituationinwhich thesizeofatimequantumapproacheszero(q!0).3unfortunately,inmanypracticalsituations,time t0fi()d (2) ofmagnitudeastheseoverheadscoulddrasticallyreducetheresourceutilization.forexample,itwould beunacceptableforacputospendmoretimeinschedulinganewprocess,andcontextswitching betweentheprocesses,thandoingusefulcomputation.anotherreasonisthatsomeoperationscannot communicationswitchbeginstosendapacketforonesession,itcannotserveanyothersessionuntilthe beinterrupted,i.e.,oncestartedtheymustcompleteinthesametimequanta.forexample,oncea entirepacketissent. inours),itisnotpossibleforaclienttoalwaysreceiveexactlytheservicetimeitisentitledto.the dierencebetweentheservicetimethataclientshouldreceiveatatimet,andtheservicetimeitactually receivesiscalledservicetimelag.moreprecisely,letti0beatimeatwhichclientibecomesactive,and letsi(ti0;t)betheservicetimetheclientreceivesintheinterval[ti0;t](here,weassumethatclientiis activeintheentireinterval[ti0;t]).thentheservicetimelagofclientiattimetis 3AsimilarmodelwasusedbyDemersetalinstudyingfair-queuingalgorithmsincommunicationnetworks[9]. Duetoquantization,inasysteminwhichtheresourceisallocatedindiscretetimequanta(asitis 4
5 useitasthemainparameterincharacterizingourproportionalresourceallocationalgorithm. 3TheEEVDFAlgorithm Sincetheservicetimelagdeterminesboththethroughputaccuracyandthesystempredictability,we lagi(t)=si(ti0;t)?si(ti0;t): (3) case,therequestduration(length)iseitherspeciedbytheclient,orotherwisetheschedulerassumes processorcase,thescheduleritselfcouldbetheonetoissuetherequestsonbehalfoftheclient.inthis Inordertoobtainaccesstotheresource,aclientmustissuearequestwhichspeciesthedurationofthe a\default"duration.thisallowsustotreatallcontinuousmedia,interactive,andbatchactivitiesina request,andtobepassiveotherwise.foruniformity,throughoutthispaperweassumethattheclientis servicetimeitneeds.onceaclient'srequestisfullled,itmayeitherissueanewrequest,orotherwisethe consistentway. clientbecomespassive.noticethatwecanalternatelydeneaclienttobeactivewhileithasapending thesoleinitiatoroftherequests.however,inpracticethisisnotnecessarilytrue.forexample,inthe fewerlongerrequests,ormanyshorterones.forexample,aclientmayaskfor1mincomputationtime, itstimeexpires.noticethataclientmayrequestthesameamountofservicetimebygeneratingeither eitherbyissuing60requestswithadurationof1seceach,orbyissuing600requestswithadurationof expires,theclientispreemptedandthenexttimequantumcanbeallocatedtoanotherclient).whena atimequantum,thentheservicetimemightnotbeallocatedcontinuously(i.e.,whenatimequantum clientrequeststheresourceforlessthanonetimequantum,theschedulersimplypreemptstheclientonce Forexibilityweallowrequeststohaveanyduration.Ifthedurationoftherequestislargerthan 100mseceach.AswewillshowinSection6,shorterrequestsguaranteebetterallocationaccuracy,while longerrequestsdecreasethesystemoverhead.inthiswayaclientcouldtradebetweentheallocation byaxedintervaloftimebetweentwoconsecutiveevents,calledperiodanddenotedbyt,andby themaximumservicetimerrequiredtoprocessanevent.wheneveraneventoccurs,thetasksimply accuracyandtheschedulingoverhead. knownproblemofschedulingperiodictasksinareal-timesystem[18].aperiodictaskischaracterized thatthecurrenteventshouldbeprocessedbeforethenexteventoccurs.noticethatthisrequirement guaranteesthatthetaskreceivesasmuchasrservicetimeunitsduringeveryperiodt.consequently, requestsrservicetimeunitsforprocessingthatevent.acentralrequirementinreal-timesystemsis Toclarifytheideaswebrieypointoutthesimilaritiesanddierencesbetweenourmodelandthewell- beexpressedast+rf.similarly,inourmodel,bygivingthetimetatwhicharequestismadeand isidenticaltotheexpressionoftherequest'sdeadlineinthecaseofschedulingperiodictasks.asamajor servicetimerandthetimetatwhichtheeventoccurs,thedeadlineofthecorrespondingrequestcan anidealsystembysolvingtheequationr=s(t;d).ifthesharefoftheclientdoesnotchangeinthe itsdurationr,weobtainthetimedbeforewhichtheclientshouldreceivetherequestedservicetimein interval[t;d),thenfromeq.(2)followsthats(t;d)=f(d?t),andfurtherweobtaind=t+rf,which inthiscasethetaskreceivesasharef=rtoftheresource.thus,bygivingthesharef,therequested assumedtobegeneratedasaresultofanexternalevent(e.g.,apacketarrival,atime-out),inourmodel dierencebetweenourmodelandareal-timesystem,wenotethatwhileinareal-timesystemarequestis 5
6 asaresultofaninternalevent(whentheclientgeneratesanewrequestafterthecurrentonehasbeen arequestiseithergeneratedasresultofanexternalevent(whenthecliententersthecompetition),or continuousmediaandinteractiveapplications,andforconventionalbatch-applications. fullled).inthiswayourmodelprovidesintegratedsupportforbotheventdrivenapplications,suchas Similarlyto[31]and[23]wedenethesystemvirtualtimeas intheinterval[t1;t2)as BycombiningEq.(1)and(2)wecanexpresstheservicetimethatanactiveclientishouldreceive Si(t1;t2)=wiZt2 V(t)=Zt 01 Pj2A()wjd: Pj2A()wjd: 1 (4) inthecorrespondinguid-owsystemeachactiveclientireceiveswireal-timeunitsduringonevirtual allactiveclientsinonevirtualtimeunit.thatis,thesizeofavirtualtimeunitismodiedsuchthat competitiondecreasesitaccelerates.intuitively,theowofthevirtualtimechangesto\accommodate" activeclients.noticethatwhenthecompetitionincreasesthevirtualtimeslowsdown,whilewhenthe Wenotethatthevirtualtimeincreasesatarateinverseproportionaltothesumoftheweightsofall (5) Thus,ineachvirtualtimeunitthetwoclientsshouldreceivew1=2,andw2=3timeunits.Next,from timeunit.forexample,considertwoclientswithweightsw1=2andw2=3.thentherateatwhich Eq.(4)and(5)itfollowsthatSi(t1;t2)=wi(V(t2)?V(t1)): thevirtualtimeincreasesis1 w1+w2=0:2,andthereforeavirtualtimeunitequalsvereal-timeunits. ofactiveclientsisconstantandthesumoftheirweightsisone(pi2awi=1),i.e.,theshareofa clientiisfi=wi.thentheservicetimethatclientishouldreceiveduringaninterval[t1;t2)issimply virtualtimesv(t1)andv(t2)wearriveateq.(6).thus,eq.(6)canbeviewedasadirectgeneralization Si(t1;t2)=wi(t2?t1).Next,noticethatbyreplacingtherealtimest1andt2withthecorresponding Tobetterinterprettheaboveequationitisusefultoconsideramuchsimplermodelinwhichthenumber (6) ofcomputingtheservicetimesi(t1;t2)inadynamicsystem. deadlined.arequestofanactiveclientbecomeseligibleattimeewhentheservicetimethattheclient shouldreceiveinthecorrespondinguid-owsystemequalstheservicetimethattheclienthasalready received(intherealsystem)beforeissuingthecurrentrequest.letti0bethetimeatwhichclienti servicetimethanitwassupposedtoreceive(i.e.,itslagisnegativeattimet),thentheclientshouldwait newrequestischosensuchthatsi(ti0;e)=si(ti0;t).noticethatifattimetclientihasreceivedmore becomesactive,andlettbethetimeatwhichitinitiatesanewrequest.thentheeligibletimeeofthe Thebasicideabehindouralgorithmissimple.Weassociatetoeachrequestaneligibletimeeanda untiltimeebeforethenewrequestbecomeseligible.inthiswayaclientthathasreceivedmoreservice timethanitsshareis\sloweddown",whilegivingtheotheractiveclientstheopportunityto\catchup". alwayspositive.byusingeq.(6)wecanexpressthevirtualeligibletimev(e)as Ontheotherhand,ifattimetclientihasreceivedlessservicetimethanitwassupposedtoreceive(i.e., timethattheclientshouldhavereceivedattimeeitfollowsthattheclient'slagattimee(lagi(e))is Sinceineithercasetheservicetimethattheclienthasreceivedattimeeisnogreaterthantheservice itslagispositive),thenwehavee<t,andthereforethenewrequestisimmediatelyeligibleattimet. 6
7 whererrepresentsthelengthofthenewrequest.further,byusingagaineq.(6),wederivethevirtual betweentheeligibletimeeandthedeadlinedequalstheservicetimeofthenewrequest,i.e.,si(e;d)=r, deadlinev(d)as Next,thedeadlineoftherequestischosensuchthattheservicetimethattheclientshouldreceive V(e)=V(ti0)+si(ti0;t) wi: (7) inwhicheislargerthanthecurrenttimet.thenecannotbecomputedexactlyfromeq.(5)and(7), V(d),theydonotnecessarilygiveusthevaluesoftherealtimeseandd!Toseewhy,considerthecase havinganemptyreservoirinwhichwecollectwaterfromaspring.althoughwecandeneamarkto sincewedonotknowhowtheslopeofvwillvaryinthefuture.intuitively,thesituationissimilarto NoticethatalthoughEq.(7)and(8)giveusthevirtualeligibletimeV(e)andthevirtualdeadline V(d)=V(e)+rwi: (8) springmayvaryinthefuture.thereforewewillformulateouralgorithmintermsofvirtualeligibletimes indicatewhenthereservoirisfull,wecannotsayexactlywhenthiswillhappensincetheow-rateofthe earliestvirtualdeadline. anddeadlinesandnotoftherealtimes.withthistheearliesteligiblevirtualdeadlinefirst(eevdf) algorithmcanbesimplystatedasfollows: EEVDFAlgorithm.Anewquantumisallocatedtotheclientthathastheeligiblerequestwiththe doesnotcompromisethefairness.intuitively,thisresultsfromthedenitionofthevirtualeligibleeligible exactlytheamountofservicetimeaclientwillactuallyuse.however,aswewillshowinsection6,this thisisarealisticassumption4,forprocessorschedulingitismuchharder(andoftenimpossible)topredict allocatingbandwidthincommunicationnetworks[9,12,23],whichassumethatthelengthofapacket requested.thisisanimportantfeaturethatdierentiatesitfromthefairqueueingalgorithmsusedfor (andthereforetheservicetime)isknownwhenthepacketarrives.althoughincommunicationnetworks TheEEVDFalgorithmdoesnotassumethataclientwillalwaysusealltheservicetimeithas eligibletimeandthedeadlinearenotgiven.letr(k)denotethelengthofthekthrequestmadebyclienti, vdtodenotethevirtualeligibletimeandvirtualdeadlinerespectively,wheneverthecorrespondingreal andletve(k)andvd(k)denotethevirtualeligibletimeandthevirtualdeadlineassociatedtothisrequest. fornon-uniformquanta.5 time:wheneveraclientuseslessservicetimethanithasrequested,thevirtualeligibletimeofthenext Iftheclientuseseachtimetheentireservicetimeithasrequested,thenbyusingEq.(7)and(8)we requestispushedbackwards(suchthatthelagtobezero).inthiswayeevdfprovidesdirectsupport eachrequest: obtainthefollowingreccurencewhichcomputesboththevirtualeligibletimeandthevirtualdeadlineof SinceEEVDFisformulatedintermsofvirtualtimes,intheremainingofthispaperweuseveand received. rstcasethefractionfromthetimequantum(thattheclientwillactuallyuse)isassumedtobeknowninadvance,inthe tothedesiredfractionofatimequantum.thedierencebetweenfractionalandnon-uniformquantaisthatwhileinthe non-uniformquantacasethisfractionisnotknown. 5NoticethatEEVDFalsoprovidessupportforfractionalquantabysimplytakingthetimeoftherequesttobeequal 4Usually,thesealgorithmstakethepacketarrivaltimetobethetimeatwhichthelastbitfromthepackethasbeen 7
8 Figure1:AnexampleofEEVDFschedulinginvolvingtwoclientswithequalweightsw1=w2=2.All 1 time 0:5).Thearrowsrepresentthetimeswhentherequestsareinitiated(thepairassociatedtoeacharrow therequestsgeneratedbyclient1havelength2,andalloftherequestsgeneratedbyclient2areoflength (0, 1) (1, 2) (2, 3) representsthevirtualeligibletimeandthevirtualdeadlineofthecorrespondingrequest). 1.Client1becomesactiveattime0(virtualtime0),whileclient2becomesactiveattime1(virtualtime 2 time (0.5, 1) (1, 1.5) (1.5, 2) (2, 2.5) virtual time vd(k)=ve(k)+r(k) wi; (10) time onlythecasewhentheclientusestheresourceforlesstimethanrequested.letu(k)denotetheservice ithasrequested.sinceaclientneverreceivesmoreservicetimethanrequested,weneedtoconsider timethatclientiactuallyreceivesduringkthrequest.thentheonlychangeineq.(9){(11),willbein computingtheeligibletimeofanewrequest.specically,eq.(11)isreplacedby Next,letusconsiderthemoregeneralcaseinwhichtheclientdoesnotusetheentireservicetime t0=0.thus,accordingtoeq.(9)and(10)thevirtualeligibletimefortherstrequestofclient1 timequantumisofunitsize(q=1)andthatclient1istherstonewhichenterscompetitionattime w1=w2=2thatissuerequestswithlengthsr1=2,andr2=1,respectively.weassumethatthe Toclarifytheideas,letustakeasimpleexample(seeFigure1).Considertwoclientswithweights ve(k+1)=ve(k)+u(k) isve=0,whileitsvirtualdeadlineisvd=1.beingthesingleclientthathasanoutstandingeligible wi: (12) functionbecomes1 virtualdeadline1(whichwaitsforanothertimequantumtofulllitsrequest),andonefromclient2 whichhasthesamevirtualdeadlinei.e.,1.inthissituationwearbitrarilybreakthetieinthefavor secondquantumisallocated.thenatt=1therearetwopendingrequests:onefromclient1withthe isv(1)=r101 request,client1receivestherstquantum.attimet=1,client2entersthecompetition.sincethe virtualtimeincreasesataconstantrateduringtheinterval[0;1)(i.e.,1 ofclient2,whichthereforereceivesthesecondquantumupontermination.sincethisquantumfullls w1d=0:5.afterthesecondcliententersthecompetitiontheslopeofthevirtualtime w1+w2=0:25.next,letusassumethatclient2makesitsrstrequestbeforethe w1=0:5),itsvalueattimet=1 thecurrentrequestofclient2,client2issuesanewonewiththevirtualeligibletime1andthevirtual 8 ve(k+1)=vd(k): ve(1)=v(ti0); (11) (9)
9 deadline1:5.thus,attimet=2thesingleeligiblerequestistheoneofclient1,whichthereforereceives thenextquantum.further,att=3thereareagaintwoeligiblerequests:theoneofclient2thathas justbecomeeligible,andthenewrequestissuedbyclient1.sincethedeadlineofthesecondclient's request(1.5)isearlierthantheoneoftherstclient(2),thefourthquantumisallocatedtotheclient2. tion,clientleavingthecompetition,andchangingtheclient'sweight.inanidealizeduid-owsystem, thatadynamicsystemprovidessupportforthefollowingthreeoperations:clientjoiningthecompeti- 4FairnessinDynamicSystems Inthissectionweaddresstheissueoffairnessindynamicsystems.Throughoutthispaper,weassume Further,Figure1showshowthenextthreequantaareallocated. considerthefollowingtwoquestions: supportingdynamicoperationsistrivialsinceatanymomentoftimethelagofanyactiveclientiszero. true.intheremainingofthissectionwediscusshowthisaectsthefairnessinadynamicsystem6.we Unfortunately,inasysteminwhichtheservicetimeisallocatedindiscretetimequanta,thisisnolonger competitionwithanegativelag,i.e.,afterithasreceivedmoreservicetimethanitwasentitledto.as 1.Whatistheimpactofaclientwithnon-zerolagleaving,joining,orchangingitsweightonthe 2.Whenaclientwithnon-zerolagleavesthecompetition,whatshouldbeitslagwhenitrejoinsthe Inansweringtherstquestion,westartwithasimpleexample.Letusassumethataclientleavesthe otherclients? isequaltotheservicetimethattheclientsshouldreceive.therefore,ifaclientleavesthecompetition wewillshowinsection6,duringanytimeinterval,thetotalservicetimeallocatedtoallactiveclients withanegativelag,theremainingclientsshouldhavereceivedlessservicetimethantheywereentitled competition? to.inshort,againforoneclienttranslatesintoalossfortheotheractiveclients.inthiscase,the WaldspurgerandWeihlintheirstrideschedulingalgorithm[29,30],thetwopoliciesarenotequivalent. simplyupdatingthevirtualtime.wenotethatalthoughthispolicyissimilartotheoneemployedby activeclients.inotherwords,eachactiveclientwillinheritagain/lossproportionaltoitsweight.besides itsintuitiveappeal,aswewillshow,thispolicyhasanotheradvantage:itcanbeeasilyimplementedby operationtakesplace,theeect(i.e.,theresultinggainorloss)isproportionallydistributedamongall activeclientsinordertoattainfairness?weanswerthisquestionbyassumingthatwheneveradynamic questionweneedtoansweristhefollowing:howshouldthelossbedistributedamongtheremaining othertwoclients. competition(seefigure2).further,wediscusstheimpactofclient3leavingthecompetitiononthe Thedierenceconsistsinthewayinwhichthevirtualtimeisupdatedwhenaclientleavesorjoinsthe Supposethatthreeclientswithzerolagsbecomeactiveattimet0,andattimetclient3leavesthe competition:whileinstrideschedulingonlytheslopeofthevirtualtime7isupdated,inouralgorithm thevalueofthevirtualtimeisupdatedaswell(seeeq.18,19,20inthissection). 7Insteadvirtualtime,strideschedulingusesanequivalentconcept,calledglobalpass. 6TheseissueswerealsoaddressedbyWaldspurgerandWeihlinthecontextoftheirstrideschedulingalgorithm[30]. Tobetterunderstandourreasonsinconsideringtheabovepolicy,letusconsiderthefollowingexample. 9
10 Figure2:Thethreeclientsbecomeactiveattimet0.Attimet,client3leavesthecompetition. 1 2 SinceEEVDFisawork-conserving8algorithm,thetotalservicetimereceivedbyallactiveclientsduring Next,weturnourattentiontotheclients1and2whichremainactiveafterclient3leavesthecompetition. ofthevirtualtimeduringthisintervalisconstantandequalto1 thelagofeachclientattimetis Sincethenumberofactiveclientsandtheirsharesdonotchangeduringtheinterval[t0;t),theslope lagi(t)=wit?t0 w1+w2+w3.thenfromeq.(3)and(6), 3 t t thisintervalcanbeexpressedast?t0?s3(t0;t).lett+bethetimeimmediatelyafterclient3leaves theinterval[t0;t)isequaltot?t0.fromhere,theservicetimeallocatedtothersttwoclientsduring thecompetition,wherebyneglectingtheleavingoperationoverhead,wehavet+!t. 0 w1+w2+w3?si(t0;t);i=1;2;3: (13) Wenotethatiflag3(t)6=0,thenthisresultisdierentfromtheservicetimeeachclientshouldhave receivedjustbeforethedepartureofclient3,i.e.,(t?t0)wi t?t0?s3(t0;t))proportionaltotheclients'weights,i.e., andintuitiveapproachwouldbetosimplydividetheentireservicetimereceivedbybothclients(i.e., Now,whatistheservicetimethatclients1and2shouldhavereceivedattimet+?Anatural client3leaves,theremainingtwoclientswillproportionallysupporttheeventuallossorgaininthe thevirtualtime.byreplacings3(t0;t)fromeq.(13)intoeq.(14),weobtain servicetime.next,weshowthatintheeevdfalgorithmthisisequivalenttoasimpletranslationof Si(t0;t+)=(t?t0?s3(t0;t))wi w1+w2;i=1;2; w1+w2+w3(i=1;2;3).thisisbecauseonce (14) Finally,fromEq.(6)and(15)itfollowsthat Si(t0;t+)=(t?t0)wi V(t+)=V(t)+lag3(t) =wi(v(t)?v(t0))+wilag3(t) w1+w2+w3+wilag3(t) w1+w2;i=1;2: w1+w2;i=1;2: (16) (15) Thus,tomaintainthefairnessamongtheremainingclients,thevirtualtimeshouldbeupdatedaccording tothelagoftheclientwhichleavesthecompetition(asshownbytheaboveequation).sincet+is client(seesection6fordetails). becomputedas ithasreceivedattimet(i.e.,si(t0;t)=si(t0;t+)).fromhere,thelagsofthersttwoclientsatt+can asymptoticallyclosetot,theservicetimereceivedbyanyclientattimet+isequaltotheservicetime 8Aschedulingalgorithmissaidtobework-conservingiftheresourcecannotbeidlewhilethereisatleastoneactive lagi(t+)=wi(v(t+)?v(t0))?si(t0;t+)=lagi(t)+wilag3(t) 10 w1+w2;i=1;2: (17)
11 Thereforewhenclient3leaves,itslagisproportionallydistributedamongtheremainingclients,which Correspondingly,whenaclientjjoinsthecompetitionattimet,thevirtualtimeisupdatedasfollows updatingruleforthevirtualtimewhenaclientjleavesthecompetitionattimet isinaccordancewithourinterpretationoffairness.bygeneralizingeq.(16),wederivethefollowing V(t)=V(t)?lagj(t) V(t)=V(t)+lagj(t) Pi2A(t+)wi: Pi2A(t+)wi; (18) byupdatingthevirtualtimeaccordingtoeq.(18)and(19)weensurethatthesumoverthelagsofall activeclientsisalwayszero.thiscanbeviewedasaconservationpropertyoftheservicetime,i.e.,any representsthelagwithwhichclientjjoinsthecompetition.althoughitmightnotbeclearatthispoint, timeaclientreceivesmoreservicetimethanitsshare,thereisatleastanotherclientthatreceivesless. wherea(t+)containsalltheactiveclientsimmediatelyafterclientjjoinsthecompetition,andlagj(t) (19) weobtain timet,andrejoinsitimmediately(atthesametimet)havingweightw0j.byaddingeq.(18)and(19), fromwjtow0j.thenthisisequivalenttothefollowingtwooperations:clientjleavesthecompetitionat (18)and(19)thevirtualtimedoesnotchange.9 Wenotethatifthelagoftheclientthatleavesorjoinsthecompetitioniszero,thenaccordingtoEq. thattakeplaceatthesametime.tobespecic,supposethatattimettheweightofclientjischanged Wenotethatchangingtheweightofanactiveclientisequivalenttoaleaveandarejoinoperation clientwithzerolagismodied.thus,inasysteminwhichanyclientisallowedtojoin,leave,orchange Asforjoinandleaveoperations,noticethatthevirtualtimedoesnotchangewhentheweightofa V(t)=V(t)+lagj(t) (Pi2A(t)wi)?wj?(Pi2A(t)wi)?wj+w0j: lagj(t) becomespassivewithoutusingitsentiresharecoulduseitwhenitagainbecomesactivenexttime,and itsweightonlywhenitslagiszero,thevariationofthevirtualtimeiscontinuous. Nowletusturnourattentiontothesecondquestion.Weneedtodecidewhetheraclientthat (20) whetheraclientthatleavesthecompetitionafterithasusedmoreservicetimethanitsshareshouldbe penalizedwhenitrejoinsthecompetition.tobespecic,consideraclientthatleavesthecompetition considerthefollowingexample.supposethatbeforetimettherearetwoactiveclients1and2,andat aclientforthelostservicewhenitrejoinsthecompetition,thismighthamperotherclients.toseewhy, accumulateovermultipleperiodsofactivity,andconsequently,overlargeintervalsoftimetheclientmay iswhethertheclientshouldreceiveanycompensationwhenitrejoinsthecompetition.unfortunately, receivesignicantlylessservicetimethanitisentitledto.ontheotherhand,ifwedecidetocompensate thereisnosimpleanswertothisquestion.ifwedecidenottocompensate,thenthelostservicetimemay withapositivelag(i.e.,afterithasreceivedlessservicetimethanitwasentitledto).thenthequestion timetclient2becomespassivewithapositivelag,lag2(t)>0.next,assumethatatasubsequenttime t0client2rejoinsthecompetition,whileanotherclient3isactive(weassumethatatthistimeclient1 isnolongeractive).thenclient2willhavetorecovertheservicetimethatithaslosttoclient1,atthe expenseofclient3!consequently,client3willindirectlylosesomeservicetimebecauseclient2hasnot useditsentireservicetimewhileitwaspreviouslyactive,whichisnotfair. 9However,noticethattheslopeofthevirtualtimechanges. 11
12 ofaclientwhenitrejoinsthecompetition,inthissectionwepresentthreestrategiesforimplementing clientreceivescompensationoritispenalizedwhenitrejoinsthecompetition. theeevdfalgorithm.thecharacteristicsofthesestrategiesaredictatedbythedecisiononwhethera clientcouldleave,join,orchangeitsweightwhenitslagisnon-zero,andbythedecisiononwhethera 5AlgorithmImplementation Strategy1.Inthisstrategyaclientmayleaveorjointhecompetitionatanytime,anddependingon Since,aswehaveseenintheprevioussection,thereisnoclearansweronwhatisfairtodowiththelag occurs(e.g.,aclientjoining,leaving,orchangingtheweightofaclient),thevirtualtimeisupdated itslagitiseitherpenalizedoritreceivescompensationwhenitrejoinsthecompetition.moreprecisely, accordingtoeq.(18),(19),and(20)respectively.finally,wenotethatthisstrategyisappropriatefor iftheclientleavesthecompetitionattimet,andrejoinsatt0,thenlag(t)=lag(t0).eachtimeanevent notpreservedafteraclientleavesthecompetition,i.e.,anyclientthat(re)joinsthecompetitionhaszero lag.thisstrategyisappropriateforthosesystemsinwhichtheeventsthatcausetheclientstobecome activeareindependent.thisissimilartoareal-timesysteminwhichtheprocessingtimerequiredbyan wegiveanexampleofhowthisstrategymightbeactuallyimplemented. Strategy2.Thisstrategyissimilartothepreviousonewiththeonlydierencebeingthatthelagis systemswhereitisdesirabletomaintainfairnessovermultipleperiodsofclientactivity.inappendixa iszero.thus,inthiscase,thereisnoneedtoupdatethevirtualtimewhenadynamicoperationtakes Strategy3.Inthisstrategyaclientisallowedtoleave,join,orchangeitsweight,onlywhenitslag place.ontheotherhand,somecomplexityisaddedinensuringthatwhentheseeventsoccurthelag eventisassumedtobeindependentoftheprocessingtimerequiredbyanyotherevent. isindeedzero.inordertoensurethatalleventsinvolveonlyclientswithzerolag,weneedtoupdate implementingthisstrategyistoupdatetheslopeofthevirtualtimewhenaclientleavesthecompetition theslopeofthevirtualtimeatthecorrespondingtimesintheuid-owsystem.themainproblemin mayinvolveahighoverhead.insolvingthisproblem,weassumethatnoeventoccursduringanytime veryexpensivetoimplement;itrequirestostoretheeventhistoryand,inaddition,the\undo"operation allthemodicationsinthesystemthatoccurredbetweenthetimewhentheclientshouldleavethe owsystemissmallerthanthecorrespondingtimeintherealsystem.asolutionwouldbeto\undo" withapositivelag.10inthiscasethetimeatwhichtheclientshouldleavethecompetitionintheuidcase,thisisarealisticassumptionsince,ingeneral,theschedulingalgorithmexecutesonlybetweentime theservicetime(i.e.,transmissiontime)isassumedtobeknown,beforetherequestisinitiated.the quantum.wenotethatthisassumptionisnotasrestrictiveasitappears.forexample,intheprocessor quanta.ontheotherhand,incommunicationnetworkswedonotneedtoenforcethisassumptionsince competitionintheuid-owsystemandthetimewhenitactuallyleaves.unfortunately,thissolutionis wecancomputethevirtualtimewhentheclientshouldleaveintheuid-owsystemasthevirtualdeadlineoftheclient's timequantumisgivenbelow. basicmechanismstoimplementthisstrategy,undertheassumptionthatnoeventcanoccurduringa algorithm[23]. lastrequest.thisistheapproachusedbyparekhandgallagerintheirpacket-by-packetgeneralizedprocessorshare ideaissimplytodelaytheclientuntilitslagbecomeszero.thisisdonebyissuingadummyrequestof 10Wenotethatinasysteminwhichtheclientalwaysusestheentireservicetimeithasrequested,byusingEq.(9){(11) First,assumethataclientwantstoleavethecompetitionwhenitslagisnegative.Inthiscase,the 12
13 zerolength.thisapproachismotivatedbythefactthat,inthiscase,theeligibletimeisalwayschosen nolatterthanatimequantumafteritsdeadline.thus,betweenthemomentwhenthelagoftheclient suchthatthelagiszero.sincearequestcannotbeprocessedbeforeitbecomeseligible,andsincethe becomeszero,andthemomentwhentherequestisfullled,noothertimequantaareallocated.since lagandthereforewefurtherconsideronlythelatercase.aswewillshowinsection6,inasystemin whichthevirtualtimevariescontinuously(suchasinoursystem),arequestisguaranteedtobefullled caseofaclientwhichleaveswithanegativelagtothecaseofaclientwhichleaveswithanonnegative virtualeligibletimeofthedummyrequestisequaltoitsdeadline(seeeq.(10)),itfollowsthatthis noeventoccursduringthistimequantum,itwillnotmakeanydierencewhetherweupdatethevirtual requestwillbeprocessedafteritsdeadline.thus,byusingarequestofzerolength,wehavereducedthe timeafterthetimequantumexpires,insteadofexactlywhenthelagbecomeszero. clientleavesbeforeitslastrequesthasbeenfullled.herewetakethesimplestapproach:theextra timequantathatarenolongerusedbytheclientarerandomlyallocatedtootheractiveclientswithout chargingthem,i.e.,theirreceivedservicetimesandtheirslagsarenotupdated.althoughmorecomplex allocationschemesmightbedevised,theyarenotnecessarytoachievethegoalofthisstrategywhichis toguaranteethataslongasaclientcompetesfortheresourceitwillreceiveatleastitsshare. Asecondquestionregardingthisstrategyiswhattodowiththeremainingservicetimewhenthe 6FairnessAnalysisoftheEEVDFAlgorithm Inthissectionwedetermineboundsfortheservicetimelag.Firstweshowthatduringanytimeinterval inwhichthereisatleastoneactiveclient,thereisalsoatleastoneeligiblependingrequest(lemma thereisatleastoneactiveclienttheresourcecannotbeidle.byusingthisresult,intheorem1wegive 2).AdirectconsequenceofthisresultisthattheEEVDFalgorithmiswork-conserving,i.e.,aslongas tightboundsforthelagofanyclientinasteadysystem(seedenitions1and2below).finally,we showthatintheparticularcasewhenalltherequestshavedurationsnogreaterthanatimequantumq, algorithm(lemma5). ouralgorithmachievestightboundswhichareoptimalwithrespecttoanyproportionalshareallocation joiningorleavingthecompetition,andchangingtheclient'sweight,simplyasevent.weintroducenow withzerolag. somedenitionstohelpusinouranalysis. Denition1Asystemissaidtobesteadyifalltheeventsoccurringinthatsysteminvolveonlyclients Throughoutthissectionwerefertoanyeventthatcanchangethestateofthesystem,i.e.,aclient continuous.aswewillsee,thisisthebasicpropertyweusetodeterminetightboundsfortheclientlag. Recallthatinasysteminwhichalleventsinvolveonlyclientshavingzerolagsthevirtualtimeis Thefollowingdenitionrestrictsthenotionofsteadinesstoaninterval. clientswithzerolag. Denition2Anintervalissaidtobesteadyifalltheeventsoccurringinthatintervalinvolveonly Thus,inasteadysystemthelagofanyclientthatjoins,leaves,orhasitsweightchanged,iszero. issteady.thenextlemmagivestheconditionforaclientrequesttobeeligible. Wenotethatasteadysystemcouldbealternativelydenedasasystemforwhichanytimeinterval 13
14 Proof.Letrbethelengthofthependingrequestofclientkattimet(recallthatanactiveclienthas Lemma1Consideranactiveclientkwithapositivelagattimet,i.e., therequest.forthesakeofcontradiction,assumetherequestisnoteligibleattimet,i.e., Thenclientkhasapendingeligiblerequestattimet. alwaysapendingrequest),andletveandvddenotethevirtualeligibletimeandthevirtualdeadlineof lagk(t)0; (21) Lett0bethetimewhentherequestwasinitiated.ThenfromEq.(7)wehave Sincebetweent0andttherequestwasnoteligible,itfollowsthattheclienthasnotreceivedanyservice timeintheinterval[t0;t),andthereforesk(tk0;t0)=sk(tk0;t).bysubstitutingsk(tk0;t0)tosk(tk0;t)ineq. ve=v(tk0)+sk(tk0;t0) ve>v(t) wk: (22) (23)andbyusingEq.(3)and(6)weobtain lagk(t)=wk(v(t)?v(tk0))?sk(tk0;t) (24) (23) Finally,fromIneq.(22)itfollowsthatlagk(t)<0,whichcontradictsthehypothesisandthereforeproves thelemma. =wk(v(t)?v(tk0))?wk(ve?v(tk0)) followingcorollary. FromLemma1andfromthefactthatanyzerosumhasatleastanonnegativeterm,wehavethe =wk(v(t)?ve): Thenthereisatleastoneeligiblerequestattimet. Corollary1LetA(t)bethesetofallactiveclientsattimet,suchthat immediateconsequenceofthisresultandtheabovecorollaryisthatatanytimetatwhichthereisat Thenextlemmashowsthatatanytimetthesumofthelagsoverallactiveclientsiszero.An i2a(t)lagi(t)=0: X leastoneactiveclient,thereisalsoatleastonependingeligiblerequestinthesystem.thus,inthesense (25) ofthedenitiongivenin[23],theeevdfalgorithmiswork-conserving,i.e.,aslongasthereareactive clientstheresourceisbusy. Lemma2Atanymomentoftimet,thesumofthelagsofallactiveclientsiszero,i.e, i2a(t)lagi(t)=0: X14 (26)
15 Proof.Theproofgoesbyinduction.First,weassumethatattimet=0thereisnoactiveclientand thereforeeq.(26)istriviallytrue.next,fortheinductionstep,weshowthateq.(26)remainstrue aftereachoneofthefollowingeventsoccurs:(i)aclientjoinsthecompetition,(ii)aclientleavesthe competition,(iii)aclientchangesitsweight.finally,weshowthat(iv)duringanyinterval[t;t0)inwhich noneoftheaboveeventsoccursifeq.(26)holdsattimet,thenitalsoholdsattimet0. Case(i).Assumethatclientjjoinsthecompetitionattimetwithlaglagj(t).Lett?denotethetime immediatelybefore,andlett+denotethetimeimmediatelyafterclientjjoinsthecompetition,where t+andt?areasymptoticallyclosetot.next,letw(t)denotethetotalsumovertheweightsofallactive clientsattimet,i.e.,w(t)=pi2a(t)wi(t),andbyconvenienceletustakelagj(t?)=lagj(t).since t?!t+wehavesi(ti0;t?)=si(ti0;t+).thenfromeq.(3)weobtain: lagi(t+)=lagi(t?)+si(ti0;t+)?si(ti0;t?) Further,byusingEq.(6)and(19),thelagofanyactiveclientiattimet+(includingclientj)is lagi(t+)=lagi(t?)?lagj(t)wi W(t+): (27) SinceA(t+)=A(t?)[fjg,andsincefromtheinductionhypothesiswehavePi2A(t?)lagi(t?)=0,by usingeq.(27),weobtainx i2a(t+)lagi(t+)=x i2a(t+)(lagi(t?)?lagj(t)wi W(t+)) (28) =X i2a(t+)lagi(t?)?lagj(t)pi2a(t+)wi W(t+) =X i2a(t?)lagi(t?)+lagj(t?)?lagj(t)=0: Case(ii).Theproofofthiscaseisverysimilartotheoneofthepreviouscase;thereforeweomitithere. Case(iii).Changingtheweightofaclientjfromwjtow0jattimetcanbeviewedasasequenceoftwo events:rst,clientjleavesthecompetitionattimet;second,itjoinsthecompetitionatthesametime t,butwithweightw0j.thus,theproofofthiscasereducestotheprevioustwocases. Case(iv).Consideraninterval[t;t0)inwhichnoeventoccurs,i.e.,noclientleavesorjoinsthecompetition andnoweightischangedduringtheinterval[t;t0).next,assumethatpi2a(t)lagi(t)=0.thenweshall provethatpi2a(t0)lagi(t0)=0.byusingeq.(3)and(6)weobtain X i2a(t0)lagi(t0)=x i2a(t0)(si(ti0;t0)?si(ti0;t0)) (29) =X i2a(t)(si(ti0;t)?si(ti0;t))+x i2a(t)(si(t;t0)?si(t;t0)) =X i2a(t)lagi(t)+x i2a(t)si(t;t0)?x i2a(t)si(t;t0) =X i2a(t)wi(v(t0)?v(t))?x i2a(t)si(t;t0) =(t0?t)?x i2a(t)si(t;t0): Nextweshowthattheresourceisbusyduringtheentireinterval[t;t0).Forcontradictionassumethisis nottrue.letldenotetheearliesttimeintheinterval[t;t0)whentheresourceisidle.similarlytoeq. (29)wehave: 15
16 Sincetheresourceisnotidleatanytimebetweentandl,itfollowsthatthetotalservicetimeallocated toallactiveclientsduringtheinterval[t;t0)(i.e.,pi2a(t)si(t;l))isequaltol?t.further,fromthe aboveequationwehavepi2a(l)lagi(l)=0.butthenfromlemma1itfollowsthatthereisatleastone eligiblerequestattimel,andthereforetheresourcecannotbeidleattimel,whichprovesourclaim. i2a(l)lagi(l)=(l?t)?x X Further,withasimilarargument,itiseasytoshowthatPi2A(t0)lagi(t0)=0whichcompletestheproof i2a(t)si(t;l): system.wenotethatthisresultissimilartotheoneobtainedbyparekhandgallager[23]fortheir GeneralizedProcessorSharingalgorithm,i.e.,inacommunicationnetwork,apacketisguaranteednot ofthiscase. tomissitsdeadlinebymorethanthetimerequiredtosendapacketofmaximumlength. lemmafollows. Thefollowinglemmagivestheupperboundforthemaximumdelayoffulllingarequestinasteady Sincethesearetheonlycasesinwhichthelagsoftheactiveclientsmaychange,theproofofthe partitionofalltheactiveclientsattimed,intotwosetsbandc,wheresetbcontainsalltheclients Proof.Letebetheeligibletimeassociatedtotherequest(withdeadlined)ofclientk.Considerthe Lemma3Inasteadysystemanyrequestofanyactiveclientkisfulllednolaterthand+q,whered thathaveatleastadeadlineintheinterval[e;d],andsetccontainsalltheotheractiveclients(see istherequest'sdeadline,andqisthesizeofatimequantum. Case1(texists).Hereweconsidertwosub-caseswhethert2[e;d),ort<e.Firstassumethataclient any.furtherweconsidertwocaseswhethersuchatexistsornot. Figure3).LettbethelatesttimenogreaterthandatwhichaclientinCreceivesatimequantum,if increceivesatimequantumatatimet2[e;d).sinceallthedeadlinesofthependingrequestsissued byclientsincarelargerthand,thismeansthatattimetthependingrequestofclientkisalready fullled.consequently,intherstsub-casetherequestofclientkisfullledbeforetimed. noteligibleattimet,i.e.,t<ej.noticethatbesidestheclientsind(t),theotherclientsthatbelong (andthereforesmallerthananydeadlineofanyclientinc),itfollowsthatallthesependingrequestsare withthedeadlineintheinterval[t;d)(seefigure3).further,letd()denotethesubsetofdcontaining eligibletimeofitspendingrequestattimet.sincethedeadlinesoftheserequestsarenogreaterthand nootherclientwithanearlierdeadlineiseligibleatt.foranyclientjbelongingtod(t),letejbethe theactiveclientsattime.sinceatimequantumisallocatedtoaclientincattimet,itfollowsthat Forthesecondsub-case,letusDdenotealltheactiveclientsthathaveatleastoneeligiblerequest todarethosethateventuallyjointhecompetitionaftertimet.foranyclientjindthatjoinsthe itsrequests(noticethattheeligibletimeejandthedeadlinedjmightnotbeassociatedtothesame competitionaftertimet,wetakeejtobetheeligibletimeofitsrstrequest. request).fromeq.(10)iteasytoseethatafterclientjreceivessj(ej;dj)timeunits,allitsrequests intheinterval[ej;dj)arefullled.thus,theservicetimeneededtofulllalltherequestswhichhave deadlinesintheinterval[t;d)is Next,foranyclientjbelongingtoD,letdjdenotethelargestdeadlinenogreaterthandofanyof 16
17 ] ] ] ] ] client [ [ k t e B C d D(t) d + q [ [ [ ] [ Figure3:Thecurrentpendingrequestofclientkhastheeligibletimeeanddeadlined.SetBcontains alltheactiveclientsthathaveatleastonerequestwiththedeadlineintheinterval[e;d],whilesetc containsalltheotheractiveclients.timetrepresentsthelargesttimenogreaterthandatwhichaclient fromcreceivesatimequantum.finally,setd(t)containsalltheactiveclientsattimetthathaveat leastoneeligiblerequestwiththedeadlineintheinterval[t;d). Xj2DSj(ej;dj)=Xj2D(Zdj ejwj Pi2A()wid): (30) BydecomposingtheabovesumoverasetofdisjointintervalsJl=[al;bl)(1lm)covering[t;d), suchthatnointervalcontainsanyeligibletimeordeadlineofanyclientbelongingtod,wecanrewrite Eq.(30)asXj2DSj(ej;dj)=mXl=1(Zbl alpi2d(al)wi Pi2A(al)wid)<mXl=1(Zbl ald)=mxl=1(bl?al)=d?t; (31) TheaboveinequalityresultsfromthefactthatD()isapropersubsetofA()atleastforsomesubintervalsJi(otherwise,ifA()isidenticaltoD()overtheentireinterval[t;d),setsCandC0wouldbe empty). Assumethatattimed+qtherequestofclientk(havingthedeadlined)isnotfullledyet.Sinceno clientinccanbeservedbeforetherequestofclientkisfullled,itfollowsthattheservicetimebetween t+qandd+qisallocatedonlytotheclientsind.consequently,duringtheentireinterval[t+q;d+q), thereared?tservicetimeunitstobeallocatedtoallclientsind.next,recallthatanyclientjbelonging todwillnotreceiveanyothertimequantumafteritsrequesthavingdeadlinedjiseventuallyfullled,as longastherequestofclientkisnotfullled.thisissimplybecausethenextrequestofclientjwillhave adeadlinegreaterthand.butaccordingtoeq.(31)theservicetimerequiredtofulllalltherequests havingthedeadlinesintheinterval[t;d)islessthand?t,whichmeansthatatsomepointtheresource isidleduringtheinterval[t+q;d+q).butthiscontradictsthefactthateevdfiswork-conserving, andthereforeprovesthiscase. Case2.(tdoesnotexist)Inthiscasewetakettobethetimewhentherstclientjoinsthecompetition. Fromheretheproofissimilartotheonefortherstcase,withthefollowingdierence.SincesetCis empty,allthetimequantabetweentanddareallocatedtotheclientsind,andtherefore,inthiscase, weshowthatinfactclientkdoesnotmissthedeadlined. 17
18 requestsoftheclientswithnegativelagswhichareactiveatt1.thenanyrequestofanyactiveclientk isfulllednolaterthand+q,ifd2[dm;t2). Lemma4LetI=[t1;t2)beasteadyinterval,andletdmbethelargestdeadlineamongallthepending lagtojoin,leave,ortochangetheirweight,willeventuallyreachasteadystate. ofasteadyintervalthesameboundholds.thisshowsthatasystemwhichallowsclientswithnon-zero Followingwegiveasimilarresultforasteadyinterval.Mainly,weshowthatforcertainsubintervals Proof.SimilarlytotheproofofLemma3,weconsiderthepartitionofalltheactiveclientsattimed, intotwosetbandc,wheresetbcontainsalltheactiveclientsthathaveatleastadeadlineinthe interval[e;d],andsetccontainsalltheotherclients.similarly,welettdenotethelatesttimeinthe interval[t1;d)whenaclientincreceivesatimequantum,ifany.further,weconsidertwocaseswhether Case1.(texists)TheproofproceedssimilarlytotheoneforCase1inLemma3. Case2.(tdoesnotexist)Inthiscaseweconsidertwosub-setsofC:C?containingallclientsinC suchtexistsornot. allclientsinc+hadnonnegativelagsattimet1,andsincetheydonotreceiveanytimequantabetween dm)andthereforeallclientsinc?willhavenonnegativelagsattimedm.ontheotherhand,since toc?receivesanytimequantumbeforedmitfollowsthatnopendingrequestofanyclientinc?is fullledbeforeitsdeadline(recallthatthedeadlinesofalltheotherclientswithnegativelagsatt1are t1anddm,allofthemwillhavepositivelagsatdm.thus,wehave thathadnegativelagsattimet1,andc+containingalltheotherclientsinc.sincenoclientbelonging Ontheotherhand,wenotethatiftherequestofclientkisnotfullledbeforeitsdeadline,thenno karepositiveattimed,i.e., nogreaterthandisfullled.butthenfromeq.(3)itfollowsthattheirlagsaswellasthelagofclient otherclientbelongingtobwillreceiveanyothertimequantumafteritslastrequestwiththedeadline Xi2Clagi(d)>0 Xi2Blagi(d)0 (32) Further,byaddingEq.(32)and(33),weobtain i2a(d)lagi(d)>0 X (33) Theorem1Thelagofanyactiveclientkinasteadysystemisboundedasfollows, whichcontradictslemma2,andthereforecompletestheproof. Thenexttheoremgivestightboundsforaclient'slaginasteadysystem. (34) wherermaxrepresentsthemaximumdurationofanyrequestissuedbyclientk.moreover,thesebounds areasymptoticallytight.?rmax<lagk(d)<max(rmax;q); 18 (35)
19 have SinceSkincreasesmonotonicallywithaslopenogreaterthanone(seeEq.(4)),fromEq.(3)itfollows Proof.Leteanddbetheeligibletimeandthedeadlineofarequestwithdurationrissuedbyclientk. sincearequestisnotservicedbeforeitiseligible,itiseasytoseethattheminimumlagisachievedwhen minimumlagoccursattimee+r,iftherequestisfullledbythattime.further,byusingeq(3)we thatthelagofclientkdecreasesaslongasitreceivesservicetime,andincreasesotherwise.further, theclientreceivestheentirelyservicetimeassoonastherequestbecomeseligible.inotherwords,the Fromthedenitionoftheeligibletime(seeSection2)wehavelagk(e)0,andthusfromtheabove lagk(e+r)=sk(tk0;e+r)?sk(tk0;e+r) =Sk(tk0;e)+Sk(e;e+r)?(sk(tk0;e)+sk(e;e+r)) =lagk(e)+sk(e;e+r)?sk(e;e+r) (36) activewehave Sincethisisthelowerboundfortheclient'slagduringarequestwithdurationr,andsincermaxrepresents equationweobtainlagk(e+r)sk(e;e+r)?sk(e;e+r)>?sk(e;e+r)?r: themaximumdurationofanyrequestissuedbyclientk,itfollowsthatataanytimetwhileclientkis lagk(t)?rmax: (37) aslateaspossible.sinceaccordingtolemma3,therequestisfulllednolaterthand+q,itfollows thatthelatesttimewhenclientkshouldreceivetherstquantumisd+q?r.weconsidertwocases: rqandr<q.intherstcased+q?rd,andthereforeweobtainsk(e;d+q?r)<sk(e;d)=r. Lett1bethetimeatwhichtherequestisissued.Further,fromthedenitionoftheeligibletime,and Similarly,themaximumlagintheinterval[e;d)isobtainedwhentheentireservicetimeisallocated (38) fromthefactthattheclientisassumedthatitdoesnotreceiveanytimequantumduringtheinterval [t1;d+q?r),wehaveforanytimetwhiletherequestispending SincetheslopeofSkisalwaysnogreaterthanone,inthesecondcasewehaveSk(e;d+q?r)= lagk(t)sk(tk0;d+q?r)?sk(tk0;d+q?r) =(Sk(tk0;e)?sk(tk0;t1))+Sk(e;d+q?r)?sk(t1;d+q?r) =Sk(tk0;e)+Sk(e;d+q?r)?sk(tk0;t1)?sk(t1;d+q?r) =Sk(e;d+q?r)<r: (39) Finally,bycombiningEq.(39)and(40)weobtainlagk(t)<max(q;r).Thus,atanytimetwhilethe Sk(e;d)+Sk(d;d+q?r)<r+q?r=q,andfromhereweobtain clientisactivewehave lagk(t)sk(e;d+q?r)<q: lagk(t)<max(q;rmax): (40) 19 (41)
20 virtualdeadlineofthesecondclient'srequest,i.e.,t0+rmax rmaxandr0maxarechosensuchthatthevirtualdeadlineoftherstclient'srequestissmallerthanthe activeattimet0andtheirrstrequestshavethelengthsrmaxandr0max,respectively.weassumethat w1,w2betheweightsoftwoactiveclients,suchthatw1w2.next,supposethatbothclientsbecome Toshowthattheboundlagk(t)>?rmaxisasymptoticallytight,considerthefollowingexample.Let w1<t0+r0max thevirtualdeadlineoftherstrequestofclient2,suchthatclient1receivesitsentireservicetimejust consequentlylag1(rmax)approaches?rmax. However,inthiscaseweassumethatthevirtualdeadlineoftherstrequestofclient1isearlierthan entireservicetimebeforeclient2,andthusfromeq.(3)wehavelag1(rmax)=s1(t0;t0+rmax)?rmax. Next,byusingEq.(4)weobtainS1(t0;t0+rmax)=w1 Toshowthattheboundlagk(t)<max(rmax;q)isasymptoticallytight,weusethesameexample. w1+w2,whichapproacheszerowhenw1 w2.thenclient1receivesthe priortoitsdeadline.sincethedetailsoftheproofaresimilarwiththepreviouscasewedonotshow themhere. w2!1,and oftherequesttobeintheorderofseconds.ontheotherhand,inthecaseofamultimediaapplication weneedtotakethelengthofarequestnogreaterthanseveraltensofmilliseconds,duetothedelay requirements.forexample,foranintensivecomputationtaskitwouldbeacceptabletotakethelength thelengthoftheirrequests.whileshorterrequestsoerabetterallocationaccuracy,thelongerones reducethesystemoverheadsinceforthesametotalservicetimefewerrequestsneedtobegenerated. Itisthereforepossibletotradebetweentheaccuracyandthesystemoverhead,dependingontheclient NoticethattheboundsgivenbyTheorem1applyindependentlytoeachclientanddependonlyon constraints.theorem1showsthateevdfcanaccommodateclientswithdierentrequirements,while guaranteeingtightboundsforthelagofeachclientduringasteadyinterval.thefollowingcorollary followsdirectlyfromtheorem1. Corollary2Considerasteadysystemandaclientksuchthatnorequestofclientkislargerthana timequantum.thenatanytimet,thelagofclientkisboundedasfollows: holdforanyproportionalsharealgorithm. Lemma5Givenanysteadysystemwithtimequantaofsizeqandanyproportionalsharealgorithm,the lagofanyclientisboundedby?qandq. NextwegiveasimplelemmawhichshowsthattheboundsgiveninCorollary3areoptimal,i.e.,they?q<lagk(t)<q: (42) Proof.Considernclientswithequalweightsthatbecomeactiveattime0.Weconsidertwocases:(i) Similarly,thelagoftheclientwhichreceivesthenthtimequantumis(attimen?1,immediatelybefore eachclientreceivesexactlyonetimequantumoutoftherstnquanta,and(ii)thereisaclientkwhich itreceivesthetimequantum) receivesmorethanatimequanta.fromeq.(3),itiseasytoseethat,attimeq,thelagoftheclient thatreceivestherstquantumislag(q(n?1))=q?qn: lag(q)=qn?q: (43) 20 (44)
21 smallerthanq,i.e.,q?,whereisapositivereal.thenbytakingn>q,fromeq.(44),itfollowsthat lag(q(n?1))>q?whichisnotpossible.similarly,itcanbeshownthatnoalgorithmcanachievea thatthelagofclientjissmallerthan?qafteritreceivesthesecondtimequantum,andthelagofclient Forcontradiction,assumethatthereisaproportionalsharealgorithmthatachievesanupperbound anotherclientkthatdoesnotreceiveanytimequantaintherstntimeunits.thenitiseasytosee lowerboundbetterthan-q. 7RelatedWork kislargerthanqafterjustbeforereceivingitsrsttimequantum,whichcompletesourproof. Forthesecondcase(ii),noticethatsinceclientjreceivesmorethanonetimequanta,theremustbe rithmsasfollows:time-dependentpriority,real-time,fairqueueing,andproportionalshare. 7.1Time-DependentPriority Inthissectionwepresentacompressiveoverviewoftherelatedwork.Weclassifytheschedulingalgo- precedenceoveraprocesswithlowerpriority.unfortunately,thisschemesareinexibleandmaylead tostarvation[25].intryingtoovercometheseproblems,severalsolutionswereproposed.oneofthe Manyoftheexistingoperatingsystemsrelyontheconceptofprioritytoallocateprocessingtimeto competingprocesses[25].inthestaticpriorityschemes,aprocesswithhigherpriorityhasabsolute prioritiesaccordingtotheirrecentcpuusage.thispolicywasimplementedinmanyoperatingsystems, controloverresourceallocationduringshortperiodsoftime. best-knownschemesisdecayusagescheduling[13]whichtriestoensurefairnessbychangingtheprocess suchasunixbsd[16]andsystemv[1].themaindrawbackofthispolicyisthatitoersonlyacrude theschedulerensuresthattheclientwiththehighestpriorityinthatclassisalwaysatthefrontofthe ing(tfs)[11].thepriorityofaclientintfsisdenedbyatime-dependentfunction,i.e.,thepriority characteristicsandschedulingobjectives.allclientsbelongingtothesameclasshaveassociatedthesame valuewhenevertheclientisscheduled.intfsclientsarepartitionedindisjointclassesbasedontheir time-dependentfunctionandareorganizedinafcfsqueue.byservingtheminaround-robinfashion, increaseslinearlywithtimewhiletheclientwaitstobescheduled,anditisreinitializedtoapredened Recently,FongandSquillantehaveproposedanewschedulingdisciplinecalledTime-FunctionSchedul- queue.thustoselecttheclientwiththehighestoverallpriorityitisenoughtosearchamongtheclients whichareatthefrontoftheirqueues.inthisway,thedispatchoperationcanbeecientlyimplemented ino(logc),wherecrepresentsthetotalnumberofclasses.ontheotherhand,thetime-complexityof tionanditcanbeusedtoachievegeneralschedulingobjectivessuchasrelativeper-classthroughputs updatingclients'prioritiesiso(clogc).tfsprovideseectiveandexiblecontroloverresourcealloca- dependsonthefrequencyatwhichtheclients'prioritiesareupdated.sincetheupdatingoperationis andlowwaitingtimevariance.althoughsomewhatindirectly,tfscanalsoarchiveproportionalshare ratherexpensivethislimitstheallocationaccuracythatcanbeachieved. allocationbyassigninganequalsharetoeachclientinthesameclass.however,thealgorithmaccuracy antees.thesetasksarecharacterizedbyasequenceofeventsthatarriveinacertainpattern(usually 7.2Real-Time Real-timesystemswerespecicallydevelopedforcriticaltimetaskswhichrequirestrongdeadlineguar- 21
22 newrequest.moreprecisely,theedfalgorithmassignsprioritiestotaskscorrespondingtothedeadlines shouldbeprocessed. periodic).eacheventisdescribedbyitspredictedservicetimeandadeadlinebeforewhichtheevent highestpriority. prioritiesinthedecreasingorderoftheirperiods,i.e.,thetaskwiththesmallestperiodhasthehighest priority.whileinrmtheprioritiesarexed,inedftheychangedynamicallywheneverataskinitiatesa oftheircurrentrequests,i.e.,thetaskwhichhastherequestwiththeearliestdeadlineisassignedthe deadlinerst(edf),wereproposedandanalyzedbyliuandlaylandin[18].inrm,tasksareassigned Twoofthemostpopularalgorithmsforschedulingperiodictasks,ratemonotonic(RM)andearliest case,assoonasthecurrenttimequantumexpires,thenewrequestisscheduledforexecution.sincein notchange)theeevdfandedfalgorithmsareequivalent.toseewhy,considerhoweevdfbehaves whenanewrequestwithanearlierdeadlinethantheprocessthatiscurrentlyexecutingisissued.inthis anidealizeduid-owmodelthesizeofatimequantumisarbitrarilysmall,thisisequivalenttoschedule thenewrequestassoonasitarrives,whichisidenticaltothepolicyemployedbyedf. Wenoteherethatinastaticuid-owsystem(inwhichtheweightsandthenumberofactiveclientsdo admissionpolicies.specically,liuandlayland[18]haveshownthatundertheedfpolicyalltasks willmeettheirdeadlinesaslongastheprocessorisnotover-utilized(i.e.,itsutilizationis100%). givenbylehoczky,sha,anddingin[17].unfortunately,thisanalysisismoreexpensive,whichmakes utilizationof69%.foraspeciedsetoftasks,thisboundcanbeimprovedbyusingtheexactanalysis itlessappealingforpracticalimplementations.besidesensuringahigherprocessorutilization,another Similarly,fortheRMalgorithm,theyhavegivenaschedulabilitytestwiththeworstcaseprocessor Inordertoguaranteethatalltaskswillmeettheirdeadlines,bothRMandEDFimposestrict issimplerandslightlymoreecienttoimplementthanedf.finally,anotheradvantageofrmisthat RM,whichreducesthecontext-switchingoverhead.Ontheotherhand,sinceitusesxedprioritiesRM incaseofoverloadthetaskswithhigherprioritieswillstillmeettheirdeadlinesattheexpenseoftasks advantageofedfversusrmisthat,forthesamesetoftasks,itnevergeneratesmorepreemptionsthan fordistributedmultimediaapplications,coulsonetal[8]usetheedfalgorithmforprocessorscheduling. withlowerpriorities,whileundertheedfalgorithmalltaskscouldmisstheirdeadlines. processorusageinamicrokernelsystem.intheirmodel,eachclient(thread)hasassociatedareserve timeapplicationstotheexistingoperatingsystems.forexample,indesigninganapplicationplatform Mercer,Savage,andTokudaconsiderbothRMandEDFalgorithmsindevelopingaexiblehigherlevel abstraction,calledprocessorcapacityreserves[20,21],specicallydesignedformeasuringandcontrolling towhichitscomputationtimeischarged.theschedulerusestheusagemeasurementsforeachclientto BothRMandEDFwerethesolutionsofchoiceusedtoaddsupportforcontinuousmediaandreal- systemresourcesintotwovirtualmachines:onemachinerunningageneralpurposeoperatingsystem, extendingand/ormodifyingthegeneralpurposecpuschedulersintheexistingoperatingsystems,bollela andjeay[4]takeamoreradicalapproach.theirideaistopartitiontheprocessorandothershared andtheotheronerunningareal-timekernelsupport.specically,thecpuismultiplexedbetweenthe controlandenforceitsreservation. twosystems,eachoperatingsystemrunningalternativelyforapredenedtimeslice.whilethisapproach achievesahighlevelofisolationbetweengeneralpurposeandreal-timeapplications,runningtwodierent Unliketheaboveapproacheswhichtrytoaddsupportforreal-timeapplicationssuchasmultimediaby operatingsystemsincreasesboththeoverheadandtheresourcerequirementsinthesystem. 22
23 interactive,andbatchapplications.forthisreason,generalpurposeoperatingsystemsthatusereal-time basedschedulersforsupportingcontinuousmediaandinteractiveapplications,alsoemploymoreconventionalschedulers(suchasround-robin)forbatchactivities.comparedtoproportional-shareschedulers, real-timeschedulersaremorerestrictiveandlessexible.asanexample,whenanapplicationterminates itisdiculttoecientlyredistributeitsshareamongtheapplicationsthatarestillactive.finallywe notethatalthoughreal-timebasedschedulersprovidestrongertimelinessguarantees,theguaranteesofferedbytheeevdfalgorithm(i.e.,adeadlineisnevermissedbymorethanatimequantum)aregood enoughtoaccommodateabroadrangeofreal-timeapplications. rate-basedexecution(rbe)[13].inrbeaprocessischaracterizedbythreeparameters:x,y,andd, event.likeeevdf,rbedoesnotmakeanyassumptionsabouttheinterarrivaltimes,andaboutthe wherexrepresentsthenumberofeventsthatarriveduringatimeintervalwiththedurationy,andd representsthedesiredmaximumelapsedtimebetweenthedeliveryofaneventandthecompletionofthat distributionoftheprocessingtimeduringytimeunits.wenotethatspecifyingparametersxandyis equivalenttospecifyingthesharethattheprocessshouldreceiveduringatimeintervalwiththeduration Recently,JeayandBennettehaveproposedanewabstractionformultimediaapplications,called Ingeneral,real-timebasedschedulersdonotprovideanintegratedsolutionforcontinuousmedia, determinedfromtheclientshareandtherequestduration),theeevdfprovidesmoreexibilityinshare y.whilerbeprovidesbettercontroloverthemaximumelapsedtimed(intheeevdfthisisimplicitly real-timemodels,itdoesnotaddresstheproblemofsupportingbatchandmultimediaapplicationsinan integratedenvironment. allocationovertimeintervalsofarbitrarylength.moreover,althoughrbegeneralizesthetraditional translatedintoaseriesofdeadlines,whicharesimilartothedeadlinesoftheclients'requestsineevdf. associatetoeachclientaminimumexecutionratewhichisdenedasthedesiredfractionoftheprocessing timethattheclientshouldreceiveinagiveninterval.forcontinuousmediaandinteractiveapplications timediaapplicationsinageneralpurposeoperatingsystem[22].similarlytoarequestineevdf,they minimumexecutionratesexpresstheirminimumacceptableratesofforwardprogress.theseratesare theminimumexecutionratesresultdirectlyfromtheirtimeconstraints,whileforbatchapplicationsthe NiehandLamhavedevelopedanovelintegratedprocessorschedulerthatprovidessupportformul- itbehavesinahighlydynamicenvironment.forexample,itisnotclearwhatisthetrade-o(ifany) constraintsfortheclientswithhigherprioritiesattheexpenseoftheclientswithlowerpriorities. andrequestrespectively)inprovidinganintegratedsolutionforschedulingcontinuousmedia,interactive andbatchapplications.howeversincethisschedulerisbasedonasimpleedfpolicyitisnotclearhow TheschedulerattemptstomeetthesedeadlinesbyusinganEDFalgorithm.Inaddition,thescheduler betweenecientimplementationofdynamicoperations(i.e.,adjustingtheclients'minimumexecution assignstoeachactivityapriority.whenthesystemisoverloaded,theschedulertriestomeetthetime schedulermoreexibleandeectiveinsupportingabroaderrangeofapplications,thismightincrease rates)andthedegreeoffairnessensuredbythescheduler.whiletheadditionofprioritiesmakesthe WenotethatbothEEVDFandthisschedulerrelyonsimilarconcepts(i.e.,minimumexecutionrate toreceiveashareoftheresourceswhichisinferiorand/orsuperiorbounded. thecomplexityandpossiblytheschedulingoverhead.althoughineevdfwearenotprovidingsimilar supportforexpressingclients'priorities,wenotethatthissupportcanbeintegratedinhigherlevel resourceabstractionssuchasmonetaryfunds[26].11 11In[26]weconsidertwoclassesofservices:boundedandunbounded.Aclientreceivingaboundedserviceisguaranteed 23
24 7.3FairQueuing TheEEVDFalgorithmsharesmanycommoncharacteristicswiththefairqueueingalgorithmswhich wereoriginallydevelopedforbandwidthallocationincommunicationnetworks.thesealgorithmsuse thesamenotionofidealizeduid-owmodeltoexpresstheconceptoffairnessinadynamicsystem,and thenotionofvirtualtimetotracktheworkprogressinthesystem.sincetheidealizedmodelcannot Accordingtothispolicy,theorderinwhichthepacketsareservedisdenedastheorderinwhichthey beappliedinthecontextofapacket-basedtrac(whereapackettransmissioncannotbepreemptedby otherpackets)demersetalhaveintroducedanewpolicy,calledpacket-by-packetfairqueueing(pfq)[9]. totheleaky-bucketconstraints[6].namely,theyprovedthateachpacketisprocessedwithintmaxtime unitsfromthetimeatwhichthepacketwouldbeprocessedinthecorrespondingidealizedsystem,where wouldnishinthecorrespondingidealuid-owsystem. tmaxisthetransmissiontimeofthelargestpossiblepacket. ParekhandGallager[23]haveanalyzedthePFQ12schemewhentheinputtracstreamconforms belongingtothesamesessionhavebeensent.aswewillshowinthefollowingexample,thisdierence iscriticalinreducingthesessionlagfromo(n)too(1),wherenisthenumberofactivesessions(an ofthevirtualdeadlineineevdf.moreover,thepfqpolicyisverysimilartotheoneemployedbythe eligibleassoonasitarrives,whileineevdfapacketbecomeseligibleonlyafterallthepreviousmessages intheidealizedsystem.themajordierencebetweenthetwopoliciesisthatinpfqapacketbecomes EEVDFalgorithm;bothselecttosendthepacketwhichhastheearliestvirtualdeadline(nishingtime) WenotethatthecomputationofthevirtualnishingtimeinPFQisidenticaltothecomputation activesessionisdenedasasessionthathasatleastonepackettosend). interval[0;n?1),andthereforethetotalservicetimereceivedbysession1duringtheinterval[0;n?1) areeligibleattime0,therstn?1packetsofsession1willbesentwithoutinterruptionduringthetime therstpacketofanyoftheothersessionsis1.thenitiseasytoseethat,sinceinpfqallthepackets alltheothersessionshaveweightsequalto1.further,forsimplicity,assumethatallthepacketsareof virtualdeadlinesofthepacketsbelongingtosession1are:1n,2n,3n,:::,n?1 equalsizeandthetransmissionofonepackettakesonetimeunit.fromeq.(9){(11)itfollowsthatthe Letusconsideracommunicationswitchwithn+1activesessions,wheresession1hasweightn,and thelagofsession1attimen?1is iss1(0;n?1)=n?1.ontheotherhand,fromeq.(5)and(6)itfollowsthatthetotalservicetime thatsession1shouldhavereceivedduringthesameintervaliss1(0;n?1)=n?1 n,1.similarly,thedeadlineof packeteligibleatatime.moreprecisely,theeligibletimesoftherstn?1packetsofsession1are:0,1n, :::,n?2 whichprovesourpoint.wenotethatineevdfthisdoesnothappensincesession1willhaveonlyone n.thus,aftertherstpacketbelongingtosession1issent,thevirtualtimebecomes1 lag1(n?1)=s1(0;n?1)?s1(0;n?1)=?n?1 2; 2.Finally,fromEq.(3), Asanexampleconsiderareceiverthatprocessestheincomingpacketsatxedperiodsoftime.Tobe specic,assumethateverytwotimeunitsthereceiverprocessesanincomingpacketfromsession1(see interleavedwithtransmissionsofpacketsfromtheothersessions. oneoftheothernsessions.thus,ineevdfthetransmissionoftherstn?1packetsofsession1is atthistimethesecondpacketofsession1isnoteligibleyet,thenextpackettobesentwillbelongto Wenotethatguaranteeingstrongerboundsforsessionlagshelpsinreducingthebuerrequirements. 2n.Since 12IntheirworkthePFQisreferredaspacket-by-packetgeneralizedprocessorsharing(PGPS). 24
25 complexityleaving Operationjoining Quantumfractional Algorithm Lagnon-uniformYes selection LotteryChargeBITREVStridePD O(pm)O(nc)O(logw)O(lognc)O(1) Yes Yes No Yes No EEVDF changeweighto(lognc)o(nc)o(lognc)o(lognc)o(nc)o(lognc) O(lognc)O(nc)O(lognc)O(lognc)O(lognc)O(lognc) Yes O(1) Table1:ComparisonbetweenEEVDFandotherproportionalshareschedulingalgorithms:Lottery, Charge-based,BitReversal(BITREV),StrideandPD.Legend:ncdenotesthenumberofclientsthat competefortheresource,wdenotestheclientweight,andmdenotesthenumberoftimequantaallocated fromthemomentwhencliententerscompetition. theaboveexample).thenwhenusingpfq,thesizeofthebuertostoretheincomingpacketsiso(n), whilewhenusingeevdfitisonlyo(1).13 approximatesthepfqscheme.inthisschemeheusesthenotionofvirtualtimetomeasuretheprogress ofworkintheactualpacket-basedsystem,notintheidealizedone.themainadvantageofthisnew schemeisthatitdoesnotneedtoupdatethevirtualtimewheneveraneventoccursintheidealized model,andthereforecouldbemoreecientlyimplemented(althoughitstillmaintainstheo(logn) thisdoesnotcomeforfree;theboundsguaranteedbythisschemeforthesessionlagsarewithinafactor complexityforinsertionanddeletionfrompriorityqueue,wherenisthenumberofclients).however, Recently,Golestanihasproposedanewschemecalledselfclockedfairqueueing(SCFQ)[12],that approximatingthemwiththevirtualtimesintherealsystemwouldresultinanon-workconserving 7.4ProportionalShare EEVDFalgorithmwillbenetbyusingthesamenotionofvirtualtimeasinSCFQ.Thisisbecausein EEVDFtheeligibletimesarecomputedbasedonthevirtualtimesintheidealizedsystem,andtrivially oftwofromtheonesguaranteedbypfq.asanopenproblem,wenotethatitisnotclearwhetherour Recently,asignicantnumberofproportionalshareschedulingalgorithmshavebeendeveloped[2,26, algorithm,whichwillmakethealgorithmmuchhardertoanalyze,andmoreexpensivetoimplement. receiveswhilecompetingfortheresource,asdenedbyeq.(3). Quantum{Specieswhetherornotthealgorithmprovidessupportforfractionalandnon-uniform Lag{Thedierencebetweentheservicetimetheclientshouldreceiveandtheservicetimeitactually timequanta. Operationcomplexity{Timecomplexityforeachofthebasicdynamicoperationssupportedbythe 28,29,30].IncomparingthesealgorithmstoEEVDFweconsiderthefollowingcriteria(seeTable1): scheduling.intheiralgorithmtheresourcerightsareencapsulatedintolotterytickets.everyclienthas associatedacertainnumberofticketsthatdeterminestheshareoftheresourcethattheclientshould scheduler,i.e.,clientselection,joining,leaving,andchangingtheweightofaclient. 13Hereweassumethatthereceiverandsenderdonotuseanyowcontrolmechanism. WaldspurgerandWeihl[28,30]haveproposedaproportionalshareschedulingalgorithmcalledlottery 25
26 receive.atthebeginningofeverytimeslicealotteryisheldandtheclientwiththewinningticketis selectedandgrantedtousetheresource.sincetheticketnumbersarerandomlygenerated,thisscheme powerfulandexibleresourceabstractionforresourcemanagement. schedulinglaysinitssimplicity;sincethereisnoneedtoupdateanyglobalstate,dynamicoperations areeasyandecienttoimplement.inaddition,bymeansoftickets,lotteryschedulingintroducesa ofthenumberofallocatedtimequanta,thisresultisnotasgood.however,theadvantageofthelottery ensuresthat,ontheaverage,aclientreceivesanumberoftimeslicesproportionaltothefractionof allocatedquantam,i.e.,o(pm).comparedtotheotheralgorithmswhichguaranteeboundsindependent ticketsithas.asshownintable1,theclientlagisproportionaltothesquarerootofthenumberof ing[19].theschemeisbasedonchargingthreads(clients)forprocessorusage.threadsareconsidered inaround-robinorderandoccasionallysomeofthemareskippedtokeeptheirusageclosetothedesiredproportion.theclientlagisboundedbyo(nc),wherencrepresentsthenumberofactiveclients. complexityoftheotherdynamicoperationsisalsoo(nc). Maheshawarihasproposedanewdeterministicschemecalledcharged-basedproportionalschedul- Althoughtheselectionoperationisfastontheaverage,itsworstcasecomplexityisO(nc).Thetime algorithmforgeneratingthewinningnumbers[26].althoughtheyhaveinitiallyshown[26]thatthe algorithmguaranteesthattheclientlagisboundedbyo(logm),wheremrepresentsthenumberof allocatedtimequanta,morerecentresultshavereducedthisboundtoo(logw),wherewistheclient otherhand,aslotteryscheduling,itsupportsdynamicoperationseciently,i.e.,itrequiresonlyinteger weight[27].themaindrawbackofthisalgorithmisthatitdoesnotsupportnon-uniformquanta.onthe comparisons,additionsandsubtractions. Inanattempttoimprovethelotteryscheduling,StoicaandWahabhavedevelopedanewdeterministic receivesatimequantum,itspassisupdatedtoitsstride(noticethatthisissimilartocomputingthe rithms[31,23]tothedomainofprocessorscheduling.strideschedulingrelaysontheconceptofglobal pass(whichissimilartovirtualtime)tomeasuretheworkprogressinthesystem.eachclienthas associatedastridewhichisinverselyproportionaltoitsweight,andapasswhichmeasurestheprogress Thealgorithmcanbeviewedasanextensionandacross-applicationofthenetworkfair-queueingalgo- ofthatclient.thealgorithmallocatesatimequantumtotheclientwiththelowestpass.afteraclient Recently,WaldspurgerandWeihlhaveproposedanewalgorithmcalledstridescheduling[29,30]. binarytree,andrecursivelyapplyingthebasicstrideschedulingalgorithmateachlevel,waldspurgerand guaranteesaclientlagofo(nc),wherencisthenumberofactiveclients.bygroupingtheclientsina virtualdeadlinebyeq.(10),whentherequestdurationisequaltoatimequantum).thebasicalgorithm WeihlhavefurtherreducedtheclientlagtoO(lognc).Aswellasthebasicalgorithm,thehierarchical multipleresources,calledpd(from\pseudo-deadlines")[2].givenmidenticalcopiesofaresourcethe strideimplementsallthedynamicoperationsino(lognc). PDalgorithmguaranteesthattheclientlagisboundedbyonetimequantum.Inthesingleresource case,thealgorithmexhibitsao(lognc)time-complexityforclientselection,thesameaseevdf.while solvingtheproportionalshareschedulingproblemformultipleresources,pddoesnotprovideexplicit supportfordynamicoperations,andthereforetheirimplementationwouldrequireanexpensiveo(nc) pre-processingphase.moreover,thepdalgorithmlackssupportforfractionalandnon-uniformtime Baruah,Gehrke,andPlaxtonhavedevelopedapowerfulproportionalshareschedulingalgorithmfor quanta. Recently,Baruahclaimednewresultsthataddresstheproblemofsupportingdynamicoperationsin 26
27 thecontextofxedtimequanta[3].thenewalgorithmimplementsclientleavingandjoiningoperations ino(nc)timeformultipleresourcecase,andino(lognc)timeforasingleresourcecase.also,whena clientleavesthecompetition,thealgorithmprovidesano(logn)boundontheclientlag.whilethese Strategy3,theEEVDFalgorithmachievesanO(1)boundontheclientlag,whileprovidingsupportfor bothnon-uniformandfractionaltimequanta(seecorollary2). 8Conclusions Wehavedescribedanewproportionalshareresourceallocationschedulerthatprovidesaexiblecontrol, resultsimprovetheonesachievedbythepdalgorithm,wenotethatforasingleresourcecase,byusing andprovidesstrongtimelinessguaranteesfortheservicetimereceivedbyaclient.inthiswayweprovide auniedapproachforschedulingmultimedia,interactive,andbatchapplications.weachievethisby theresource.ouralgorithmguaranteesthatinsteadyconditionsthedierencebetweentheservice uniformlyconvertingtheapplicationrequirementsregardlessoftheirtypeinasequenceofrequestsfor systems.thealgorithmprovidesecientsupportfordynamicoperationssuchasclientjoiningorleaving timethataclientshouldreceiveintheidealizedsystemandtheservicetimeitactuallyreceivesinthe proportionalshareallocationofbothprocessor[29,30]andcommunicationbandwidth[23]indynamic realsystemisboundedbyonetimequantum.thisresultimprovesthepreviousknownboundsfor forbothfractionalandnon-uniformtimequanta. thecompetition(fortheresource),andchangingaclient'sweight.thescheduleralsoprovidessupport anexample,considerthecaseinwhichtheclientsaregroupedinseveralclasses.then,atahigherlevel abstractionsontopofeevdf.anexample,suchanabstractionsshouldprovideinferiorboundedservice[26],i.e.,aclientshouldbeabletospecifyaminimumfractionoftheresourceforwhichitisable torun.thisfeatureisimportantinsupportingbothmultimediaapplicationsthatrequirecertainrate objectivesandreal-timeapplicationsthathavetomeetspecieddeadlines. Second,itwillbeinterestingtoconsiderbothhierarchicalandheterogeneousschedulingschemes.As However,manyotherproblemsremainopen.First,wewouldliketoinvestigatehigherlevelresource toimplementtheirownalgorithmsformanagingthesharesoftheresourcesallocatedtothem. managementinthenewgenerationsofoperatingsystems[5,10]inwhichtheapplicationswouldbeable allocatedcputimeslicestoeachprocess,andinturn,theprocessmayselectathreadtorunbyusinga dierentpolicy.ultimately,wethinkthatthismaybeavaluableapproachtoimplementexibleresource aproportionalschedulermaybeusedtoallocateresourcesharestoeachclass,whileatalowerlevel, amongtheclientsinthesameclass,asimplescheduler(e.g.round-robin)maybeused.asasecond prototypeunderfreebsdunix.theexperimentalresultswillbereportedinaforthcomingpaper. example,considertheprocess-threadhierarchy.here,similarly,aproportionalschedulermaybeusedto Wehaveconductedextensivesimulationsandwearecurrentlyinthenalstagesofimplementinga 27
28 9AppendixA:Example:ImplementationofStrategy1 InthisappendixwegivetheANSICcodeforStrategy1.Forclarityofpresentationweusetwodistinct datastructures:aclientdatastructure(clientstruct)andarequestdatastructure(reqstruct).however,wenotethatsinceanyclienthasassociatedatmostonependingrequest,inpracticeitisenoughto useonecommondatastructureincludingalltheinformation.forsimplicity,weassumethattheduration ofanyrequestissuedbyaclientisnogreaterthanonetimequantum(i.e.,quantumsize).theclients' pendingrequestsarestoredinatree-baseddatastructurereqtree(seeappendixbfordetails)that supportsthefollowingoperations:insertion(insertreq),deletion(deletereq),andndingtheeligible requestwiththeearliestvirtualdeadline(getreq).alltheseoperationsareimplementedino(logn), wherenrepresentsthenumberofpendingrequests.noticethatsinceanyactiveclienthasexactlyone pendingrequest,nalsorepresentsthenumberofactiveclients. Whenaclientjoinsthecompetition(joinfunction),thevirtualtimeisupdatedaccordingtoEq. (19),andtheclientissuesitsrstrequest.Therequest'svirtualeligibletimeandthevirtualdeadline arecomputedaccordingtoeq.(9)and(10).similarly,whentheclientleavesthecompetition(leave function),thevirtualtimeisupdatedaccordingtoeq.(18),anditsrequestisremovedfromthetree.14 Finally,whentheweightofaclientischanged(changeweight),thevirtualtimeisupdatedaccordingto Eq.(20). Thedispatchfunction(EEVDFdispatch)ndstheeligiblerequestwiththeearliestdeadline(by invokinggetreq)andallocatestheresourcetothecorrespondingclient.sincetherequestisassumed totakeatmostonetimequantum,whentheclientreleasestheresourcetherequestisalreadyfullled, andconsequentlytheclient'slagisupdatedandanewrequestisissued.wenotethatifthedurationof therequestisgreaterthanonetimequantum,thereisnoneedtoissueanewrequestbeforethecurrent oneisfullled.inthiscasethedeletereqandissuereqfunctionsarecalledlessfrequently,whichresults inaloweroverhead.however,aswehaveshowninsection6thiscomesattheexpenseofdecreasing theallocationaccuracy.thefunctionsusedtoupdatethevirtualtime(getcurrentvt)andtheclientlag (updatelag)arenotgiven(theirimplementationbasedontheeq.(3),(5),and(6)beingstraightforward). /*clientdatastructure*/ typedefstruct_client{ intlag;/*clientlag*/ void*req;/*pendingrequest*/... }client_struct; /*requestdatastructure*/ typedefstruct_req{ time_v ve;/*virtualeligibletime*/ time_v vd;/*virtualdeadline*/ time_v min_vd;/*variableusedinaugmenteddatastructure*/ client_struct*client;/*clientwhichhasissuedrequest*/ struct_req*left,*right,*parent; }req_struct; /*globaldata*/ req_struct*reqtree=null;/*requesttree*/ time_vvirtualtime=0;/*virtualtime*/ int TotalWeight=0;/*totalweightofallactiveclients*/ 14Hereweassumethattheclientlagisupdatedbeforetheleavefunctioniscalled 28
29 /*joincompetition*/ voidjoin(client_struct*client) {/*updatetotalweightofallactiveclients*/ }/*leavecompetition*/ VirtualTime=get_current_vt()-client->lag/TotalWeight; /*updatevirtualtimeaccordingtoclientlag*/ TotalWeight+=client->weight; {/*updatetotalweightofallactiveclients*/ voidleave(client_struct*client) client->req->vd=req->ve+quantumsize/client->weight; insert_req(client->req); /*issuerequest*/ client->req->ve=virtualtime; }/*changeclientweight*/ TotalWeight-=client->weight; voidchange_weight(client_struct*client,intnew_weight) {/*partialupdatevirtualtimeaccordingtoclientlag*/ VirtualTime=get_current_vt()+client->lag/TotalWeight; /*updatevirtualtimeaccordingtoclientlag*/ /*deleterequest*/ delete_req(client->req); /*updateclient'sweight*/ client->weight=new_weight; /*updatevirtualtime*/ VirtualTime-=client->lag/TotalWeight; /*updatetotalweightofallactiveclients*/ TotalWeight+=new_weight-client->weight; VirtualTime=get_current_vt()+client->lag/(TotalWeight-client->weight); {int }/*dispatchfunction*/ voideevdf_dispatch() /*geteligiblerequestwithearliestvirtualdeadline*/ req=get_req(reqtree,get_curreent_vt()); /*allocateresourcetoclientwithearliesteligiblevirtualdeadline*/ /*updateclient'slag*/ update_lag(client,used); used=allocate(req->client); used; } delete_req(reqtree,req); /*issuenewrequest*/ client->req->ve+=used/client->weight; /*currentrequesthasbeenfullled;deleteit*/ insert_req(client->req); client->req->vd=client->req->ve+quantumsize/client->weight; 29
30 requestitrepresents.inaddition,inminvd,eachnodemaintainstheminimumvirtualdeadlineamong line(getreq).eachnodeinthetreestoresthevirtualeligibletimeve,andthevirtualdeadlinevdofthe 10AppendixB.RequestDataStructure allofthenodesinitssubtree(anode'ssubtreeconsistsofthenodeitselfandallitsdescendants).the Inthissectionweproposeanecientdatastructuretomanagetherequestsinitiatedbyactiveclients. Thedatastructureisbasedonanaugmentedbinarysearchtreeandsupportsthefollowingoperations: virtualeligibletimeveisusedasakeyinthebinarysearchtree.figure4depictsasimpleinstanceof insertion(insertreq),deletion(deletereq),andndingtheeligiblerequestwiththeearliestvirtualdead- n1)is:ve=10,vd=25,andminvd=15(noticethat,inthiscase,theminvdrepresentstheminimum ourdatastructurecontaining6nodes.asanexample,theinformationassociatedwiththeroot(node virtualdeadlineamongallthenodesinthetree). Figure4:Thependingrequestsarestoredinanaugmentedbinarysearchtree.Eachnodemaintainstwo statevariablesassociatedtotherequestitrepresents:thevirtualeligibletime(whichisalsothekeyin 10.1Searching deletereq. thetree)andthevirtualdeadline.inadditioneachnodemaintainstheminimumamongallthevirtual deadlinesstoredinthenodesofitssubtree. Figure5showstheANSICcodeofthegetreqfunction.Thefunctionacceptsasinputthecurrentvirtual timevtime,andreturnstheeligiblerequestwiththeearliestdeadline.thealgorithmstartsattheroot Theremainderofthissectiondescribesthedetailsofthethreebasicoperations:getreq,insertreq, (node),thealgorithmselectstherightchildasthenextcurrentnode,otherwisethealgorithmselectsthe leftchild.asaresult(seefigure5(a))weobtainapathfromroottooneoftheleaveswhichpartitions andgoesdownthetreeasfollows:whenevervtimeislargerthantheeligibletimeofthecurrentnode thetreeintwo:allthenodesintheleft(shaded)partitionrepresenteligiblerequests,whileallthenodes andamongthenodesintheleftpartition. thesearchingpath.thustondtheearliesteligiblerequestitisenoughtosearchonlyalongthepath eligiblerequests,besidesthenodesintheleftpartition,weneedtoconsideralsotheeligiblenodesalong intherightpartitionrepresentrequeststhatarenoteligibleyet.noticethattoobtaintheentiresetof 30 n / 25 n 15 n / 18 n 20 n 15 n / 20 8 / / / 20
31 /*geteligiblerequestwithearliestdeadline*/ {req_struct*node=root,*st_tree=null,*path_req=null; req_struct*get_req(req_struct*root,time_vvtime) while(node){ if(node->ve<=vtime){ (a) /*updatenodewithearliestdeadlinealongpath.*/ if((!path_req) (path_req->vd>node->vd)) }/*checkwhethernodewithearliestdeadlinewasalongpath*/ }else /*updaterootofsubtreecontainingearliestdeadline*/ if((!st_tree) (node->left&&st_tree->min_vd>node->left->min_vd)) node=node->left; node=node->right; path_req=node; if((!st_tree) (st_tree->min_vd>=path_req->vd)) returnpath_req; st_tree=node->left; /*returnnodewithearliestdeadlinefromsubtree*/ for(node=st_tree;node;){ }}/*ifnodefound,returnit*/ if(st_tree->min_vd==node->vd) if(node->min_vd==node->left->min_vd) else returnnode; node=node->right; node=node->left; (b)thecodeforsearchingthenodewiththeearliesteligibledeadline. Figure5:(a)Thesearchingpathinarequesttree(foreachnode,onlythevirtualeligibletimeisshown). 31 n 1 12 n2 8 vtime = 10 n3 n4 6 9
32 itsdescendantsinitsminvdeld,forndingthenodewiththeearliestdeadlineintheleftpartitionit leftpartition.thus,sincetherootofeachofthesesubtreesmaintainsthesmallestdeadlineamongall andallitsleftdescendantsareeligible(thesetofleftdescendantsconsistsofallnodesbelongingtothe subtreeofthenode'sleftchild).forexample,infigure5(a),noden2andallthedescendantsofnoden3 areeligible.further,itiseasytoseethatallthesesubtreesaredisjoint,andtheirunioncoverstheentire isenoughtosearchonlyamongthedescendantsoftherootofthesubtreewiththesmallestminvd. Next,noticethatifvtimeislargerthantheeligibletimeofthecurrentnode,thenthecurrentnode thesmallestminvdintheleftpartition.afterthenalvaluesofthesevariablesarecomputed,clearly virtualdeadlinevdissmallerthantheminvdofsttree,thenpathreqrepresentstherequestwiththe theeligiblenodewiththeearliestdeadlineiseitherpathreq,oritbelongstosttree.thus,ifthenode's theearliestdeadlineonthesearchingpath,andsttree,whichmaintainstherootofthesubtreewith earliestdeadline,andconsequentlythealgorithmreturnsit.otherwise,ifthenodewiththeearliest deadlinebelongstosttree,thealgorithmidentiesandreturnsit(thistaskisperformedbythelast10 Thesearchingalgorithmupdatestwomainvariables:pathreq,whichmaintainstheeligiblenodewith voidinsert_req(req_struct*root,req_str*req) linesofthecodeinfigure5(b)). /*insertnewrequest*/ {req_struct*node=root; while(node){ if(node->min_vd>req->vd) if(node->ve<req->ve){ /*updateminvdofcurrentnode*/ node->min_vd=req->vd; }else{ if(!node->right){ if(!node->left){ }node=node->right; node->right=req; /*insertnewrequestasrightchild*/ req->parent=node; return; }}}}node=node->left; node->left=req; /*insertnewrequestasleftchild*/ req->parent=node; return; classicalinsertionalgorithmforbinarysearchtrees[7]isthatalltheancestorsofthenewnodeeventually needtoupdatetheirminvdeld.asshowninfigure6,thisissimplydonebyupdating(theminvdof) 10.2Insertion Thecodeforinsertinganewrequest(insertreqfunction)isstraightforward.Theonlydierencefromthe Figure6:Thecodeforinsertion. 32
33 totheplacewherethenodeistobeinserted. 10.3Deletion AsshowninFigure8(a),thedeletionalgorithmconsidersthreecasesdependingonwhetherthenode allnodeswhichhavetheminvdlargerthanthevirtualdeadlineofthenewnodeonthepathfromroot voidbackward_update(req_struct*node,req_struct*root) {do{node->min_vd=node->vd; children.asinthecaseofinsertion,themaindierencefromthestandardalgorithm(see[7])consists /*updateminvdeldsofallancestorsofnode*/ inupdatingtheminvdeldsoftheancestorsofthedeletednode,whenneeded.forexample,inthetree tobedeletedis(i)aleaf,(ii)aninternalnodewithonlyonechild,or(iii)aninternalnodewithtwo fromfigure4ifnoden5isdeleted,thenitsancestorsn2andn1shouldupdatetheirminvdeldto18. }}while((node!=root)&&(node=node->parent)) /*checkforrightchild*/ if(node->right&&node->min_vd>node->right->min_vd) /*checkforleftchild*/ if(node->left&&node->min_vd>node->left->min_vd) node->min_vd=node->right->min_vd; node->min_vd=node->left->min_vd; givennodeanditerativelyadvancestotheroot.ateachlevel,itsetstheminvdofthecurrentnode allthenodesonthepathfromthatnodetotheroot(i.e.,itsancestors).thefunctionstartsfromthe takesasinputanodeandtherootofthetreethenodebelongstoandupdatestheminvdeldsof totheminimumbetweenthenode'svirtualdeadlineandtheminvd'sofitschildren.inthiswaythe Inouralgorithmthistaskisperformedbythebackwardupdatefunction(seeFigure7).Thisfunction Figure7:Thecodeforthebackwardupdatefunction. functionwiththefollowingparameters:theparentofthedeletednoden2andtherootn1.sinceafter thedeletionofn5,n2remainswithonlyonechildn4,theminvdofn2issettotheminimumbetween modicationpropagatesrecursivelytotheroot.toseehowthisprocedureworks,considerthesituation theminimumbetweenitsvirtualdeadlineandtheminvd'sofitschildren,i.e.,17. itsvirtualdeadlinevdandtheminvdofn4,i.e.,18.further,atthenextlevel,theminvdofn1issetto inwhichnoden5isremovedfromthetreeinfigure4.inthiscase,weinvokethebackwardupdate Sincethesuccessorofnodeistheleftmostnodeamongitsrightdescendants,itfollowsthatthesuccessor thenodetobedeleted(succ)andremovesitfromthetreebyrecursivelycallingthedeletereqfunction. abitmorecomplex(foracompletedescription,see[7]).first,thealgorithmndsthesuccessor15of requesttreeandthenodetobedeleted(node).inthersttwocases((i)and(ii))thenodeissimply removedanditsparentinheritsitschild,ifany.oncethisoperationisaccomplished,thealgorithm updatestheminvds'ofthenode'sancestorsbycallingthebackwardupdatefunction.thecase(iii)is Figure8showsthecodeofthedeletereqfunction.Thealgorithmtakesasinputtherootofthe example,infigure4,thesuccessoroftherootisnoden6,whichhasthekey11. 15Inabinarysearchtree,thesuccessorofanodenisdenedasthenodewiththesmallestkeygreaterthann'skey.For 33
34 req_struct*delete_req(req_struct*root,req_struct*req) 9 {req_struct*child,*succ; /*deletespeciedrequest*/ if(!req->right!req->left){/*cases(i)and(ii)*/ (a) if(child) /*getnode'schild,ifany*/ child=get_child(req); /*removenodeformtree*/ child->parent=node->parent; (i) (ii) (iii) if(req==root) }else{/*case(iii)*/ backward_update(parent,root); if(req->parent->left==req) /*updateminvdofnode'sancestors*/ returnchild; req->parent->left=child; /*deletenode'ssuccessorfromtree*/ /*getnode'ssuccessor*/ succ=get_succesor(req); req->right=delete_req(req->right,succ); req->parent->right=child; }returnroot; backward_update(req,root); swap_node(succ,req); /*updateminvdofnode'sancestors*/ /*swapnodewithitssuccessor*/ Figure8:(a)Thegenericcasesfordeletion.(b)Thecodefordeletion. 34 } (b) 20
35 entiretree.inthiswayitupdatesonlytheminvdeldsoftherightdescendantsofnode.finally,the Foreciencythisfunctionoperatesonlyonthetreecontainingnode'srightdescendantsandnotonthe oftimeateachlevelofthetree(recallthatinthecaseofdeletereq,althoughwehavearecursivecall, algorithmreplacesnodewithitssuccessor,andupdatestheminvdeldsofallitsancestorsbycalling canhaveatmostonerightchild.thereforethedeletereqfunctioniscalledrecursivelyexactlyonce. thiscallmayoccuratmostonce).thus,foratreeofheighth,thetimecomplexityofgetreq,insertreq, thebackwardupdatefunction. anddeletereqfunctionsiso(h). 10.4BalancedTrees FromFigures5(b)6,and8(b),itiseasytoseethatthatallthealgorithmsspendaconstantamount beingsimilar).sincearotationclearlytakesconstanttime,andsinceasshownin[7]thetimecomplexity Althoughabinarysearchtreeprovidesgoodperformancesontheaverage[7],intheworstcase(whenthe tobalanceatreewithnnodesiso(lgn),theoveralltimecomplexityofgetreq,insertreqanddeletereq treedegenerates)itexhibitsano(n)timecomplexityforinsertion,deletion,andsearchingoperations, functionsisalsoo(logn). oneoftheexistingbalanceddatastructures,suchasred-black[7],oravltrees[24].theprocedureto wherenrepresentsthenumberofnodesofthetree.theusualsolutiontoaddressthisproblemistouse /*leftrotation*/ voidleft_rotation(req_struct*node) balancethetreeafteraninsertionordeletionisbasedontwotypesofoperations:leftandrightrotations. {/*updateminvdelds*/ Figureshowsthecodetoupdatetheminvdeldsfortheleftrotation(thecodefortherightrotation } left->min_vd=node->min_vd; node->min_vd=min(node->min_vd,node->left->min_vd); node->min_vd=min(node->vd,left->right->min_vd); /*performrotation*/... Figure9:Thecodeforupdatingnode'sstateforaleft-rotationrotation. 35
36 References [2]S.K.Baruah,J.E.GehrkeandC.G.Plaxton,\FastSchedulingofPeriodicTasksonMultipleResources", [1]M.J.Bach.\TheDesignoftheUnixOperatingSystem,"Prentice-Hall,1986. [3]S.K.Baruah,PersonalCommunications,June1995. [4]G.BollelaandK.Jeay,\SupportforReal-TimeComputingWithinGeneralPurposeOperatingSystems", Proc.ofthe9thInternationalParallelProcessingSymposium,April1995,pp.280{288. [6]R.L.Cruz,\Acalculusfornetworkdelay.PartI:Networkelementsinisolation",IEEETransactionon [7]T.H.Cormen,C.E.LeisersonandR.L.Rivest.\IntroductiontoAlgorithms,"MITPress,1992. [5]B.N.Bershad,S.Savage,P.Pardyak,E.G.Sirer,M.Fiuczynski,D.Becker,S.EggersandC.Chambers, InformationTheory,vol.37,pp.114{131,1991. \Extensibility,SafetyandPerformanceintheSPINOperatingSystem",SOSP-15,1995. Proc.oftheIEEEReal-TimeTechnologyandApplicationsSymposium,Chicago,May1995. [8]G.CoulsonA.Campbell,P.Robin,G.Blair,M.PapathomasandD.Hutchinson,\TheDesignofaQoS [9]A.Demers,S.Keshav,andS.Shenkar,\AnalysisandSimulationofaFairQueueingAlgorithm",Proc.of ComputerScience,LancasterUniversity,1994. ControlledATMBasedCommunicationSysteminChorus",InternalReportMPG-94-05,Departmentof [11]L.L.FongandM.S.Squillante,\Time-FunctionScheduling:AGeneralApproachforControllableResource [12]S.J.Golestani,\ASelf-ClockedFairQueueingSchemeforBroadbandApplications",Proc.ofIEEEINFO- [10]D.R.Engler,M.FransKaashoekandJ.O'TooleJr,\Exokernel:AnOperatingSystemArchitecturefor Management",WorkingDraft,IBMT.J.WatsonResearchCenter,NewYork,March1995. Application-LevelResourceManagement",SOSP-15,1995. ACMSIGCOM'89,September1989,pp.1{12. [14]K.JeayandD.Bennett,\ARate-BasedExecutionAbstractionforMultimediaComputing",Proc.of [13]J.L.Hellerstein.\AchievingServiceRateObjectiveswithDecayUsageScheduling,"IEEETransactionson Durham,Appril95. thefifthinternationalworkshoponnetworkandoperatingsystemsupportfordigitalaudioandvideo, SoftwareEngineering,Vol.19,No.8,August1993,pp COM'94,April1994,pp.636{646. [16]S.J.Leer,M.K.McKusick,M.J.KarelsandJ.S.Quarterman.\TheDesignandImplementationofthe [15]J.KayandP.Lauder.\AFairShareScheduler,"CommunicationoftheACM,Vol.31,No.1,January1988, pp [18]C.L.LiuandJ.W.Layland,\SchedulingAlgorithmsforMultiprogramminginaHard-Real-TimeEnvironment",JournaloftheACM,vol.20,no.1,January1973,pp.46{ BSDUNIXOperatingSystem,"Addison-Wesley,1989. [17]J.P.Lehoczky,L.ShaandY.Ding,\TheRateMonotonicSchedulingAlgorithm:ExactCharacterization andaveragebehaviour",proc.oftheieeetenthreal-timesystemssymposium,december1989,pp. 166{
37 [19]U.Maheshwari,\Charged-basedProportionalScheduling",TechnicalMemorandumMIT/LCS/TM-529, [21]C.W.Mercer,S.Savage,andH.Tokuda,\ProcessorCapacityReserves:OperatingSystemSupportforMultimediaApplications",Proc.oftheIEEEInternationalConferenceonMultimediaComputingandSystems, May1994 ProcessorUsage",Proc.oftheFourthWorkshoponWorkstationOperatingSystems,October1993 [20]C.W.Mercer,S.Savage,andH.Tokuda\ProcessorCapacityReserves:AnAbstractionforManaging LaboratoryforCS,MIT,July1995. [22]J.Nieh,M.S.Lam,\IntegratedProcessorSchedulingforMultimedia",Proc.oftheFifthInternational [23]A.K.ParekhandR.G.Gallager,\AGeneralizedProcessorSharingApproachToFlowControlinIntegrated [25]A.SilberschatzandP.B.Galvin.\OperatingSystemsConcepts,"-fourthedition,Addison-Wesley,1994. [24]J.D.Smith,\DesignandAnalysisofAlgorithms",PWS-KENTPublishingCompany,Boston,1989. WorkshoponNetworkandOperatingSystemSupportforDigitalAudioandVideo,Durham,N.H.,April, ServicesNetworks-TheSingleNodeCase",Proc.ofIEEEINFOCOM'92,1992,pp.915{ [27]I.Stoica,Workinprogress,CSDpt.,ODU,1995. [26]I.Stoica,H.Abdel-Wahab,\Anewapproachtoimplementproportionalshareresourceallocation",Technical [28]C.A.WaldspurgerandW.E.Weihl.\LotteryScheduling:FlexibleProportional-ShareResourceManagement,"Proc.oftheFirstSymposiumonOperatingSystemDesignandImplementation,November1994,pp. 1{12. [29]C.A.WaldspurgerandW.E.Weihl.\StrideScheduling:DeterministicProportionalShareResourceMenagement,"TechnicalMemorandum,MIT/LCS/TM-528,LaboratoryforCS,MIT,July1995. PhDThesis,LaboratoryforCS,MIT,September1995. tionsoncomputersystems,vol.9,no.2,may1991,pp.101{124. ReportTR-95-05,CSDpt.,ODU,April1995. [30]C.A.Waldspurger.\LotteryandStrideScheduling:FlexibleProportional-ShareResourceManagement," [31]L.Zhang,\VirtualClock:ANewTracControlAlgorithmforPacket-SwitchedNetworks",ACMTransac- 37
Data Structures and Algorithms V22.0102. Otávio Braga
 Data Structures and Algorithms V22.0102 Otávio Braga We use a stack When an operand is read, output it When an operator is read Pop until the top of the stack has an element of lower precedence Then push
Data Structures and Algorithms V22.0102 Otávio Braga We use a stack When an operand is read, output it When an operator is read Pop until the top of the stack has an element of lower precedence Then push
The purpose of software configuration management (SCM) is to establish and
 DonnaAlbino LIS489FinalProject SoftwareConfigurationManagement Thepurposeofsoftwareconfigurationmanagement(SCM)is toestablishand maintaintheintegrityoftheproductsofthesoftwareprojectthroughoutthe project
DonnaAlbino LIS489FinalProject SoftwareConfigurationManagement Thepurposeofsoftwareconfigurationmanagement(SCM)is toestablishand maintaintheintegrityoftheproductsofthesoftwareprojectthroughoutthe project
Section IV.1: Recursive Algorithms and Recursion Trees
 Section IV.1: Recursive Algorithms and Recursion Trees Definition IV.1.1: A recursive algorithm is an algorithm that solves a problem by (1) reducing it to an instance of the same problem with smaller
Section IV.1: Recursive Algorithms and Recursion Trees Definition IV.1.1: A recursive algorithm is an algorithm that solves a problem by (1) reducing it to an instance of the same problem with smaller
fire Utrymningsplan/Evacuation plan In case of fire or other emergency Vid brand eller annan fara Rescue Call Larma Warn Varna Extinguish Evacuate
 genom telefon 2 In case of or other emergency telephone 2 the if possible and risk engineering Uppsala 08-8 58 00 205-02-25/JB Plan 3, tr genom telefon 2 In case of or other emergency telephone 2 the if
genom telefon 2 In case of or other emergency telephone 2 the if possible and risk engineering Uppsala 08-8 58 00 205-02-25/JB Plan 3, tr genom telefon 2 In case of or other emergency telephone 2 the if
Automatic Text Processing: Cross-Lingual. Text Categorization
 Automatic Text Processing: Cross-Lingual Text Categorization Dipartimento di Ingegneria dell Informazione Università degli Studi di Siena Dottorato di Ricerca in Ingegneria dell Informazone XVII ciclo
Automatic Text Processing: Cross-Lingual Text Categorization Dipartimento di Ingegneria dell Informazione Università degli Studi di Siena Dottorato di Ricerca in Ingegneria dell Informazone XVII ciclo
Analysis of Algorithms I: Optimal Binary Search Trees
 Analysis of Algorithms I: Optimal Binary Search Trees Xi Chen Columbia University Given a set of n keys K = {k 1,..., k n } in sorted order: k 1 < k 2 < < k n we wish to build an optimal binary search
Analysis of Algorithms I: Optimal Binary Search Trees Xi Chen Columbia University Given a set of n keys K = {k 1,..., k n } in sorted order: k 1 < k 2 < < k n we wish to build an optimal binary search
Wikipedia in the Tourism Industry: Forecasting Demand and Modeling Usage Behavior
 kipedia in the Tourism Industry: Forecasting Demand and Modeling Usage Behavior Pejman Khadivi Discovery Analytics Center Computer Science Department Virginia Tech, Blacksburg, Virginia Email: [email protected]
kipedia in the Tourism Industry: Forecasting Demand and Modeling Usage Behavior Pejman Khadivi Discovery Analytics Center Computer Science Department Virginia Tech, Blacksburg, Virginia Email: [email protected]
Bachelor of Science in Information Technology Program Outcome Assessment
 Program Outcome 1: Apply mathematical and computing concepts to support programming logic, functions, data structures, and database access. 10 8 85.2% 86.4% 84.8% 90.7% ITEC-2010 ITEC 2010 Application
Program Outcome 1: Apply mathematical and computing concepts to support programming logic, functions, data structures, and database access. 10 8 85.2% 86.4% 84.8% 90.7% ITEC-2010 ITEC 2010 Application
STORM: Stochastic Optimization Using Random Models Katya Scheinberg Lehigh University. (Joint work with R. Chen and M. Menickelly)
 STORM: Stochastic Optimization Using Random Models Katya Scheinberg Lehigh University (Joint work with R. Chen and M. Menickelly) Outline Stochastic optimization problem black box gradient based Existing
STORM: Stochastic Optimization Using Random Models Katya Scheinberg Lehigh University (Joint work with R. Chen and M. Menickelly) Outline Stochastic optimization problem black box gradient based Existing
Strategic planning in LTL logistics increasing the capacity utilization of trucks
 Strategic planning in LTL logistics increasing the capacity utilization of trucks J. Fabian Meier 1,2 Institute of Transport Logistics TU Dortmund, Germany Uwe Clausen 3 Fraunhofer Institute for Material
Strategic planning in LTL logistics increasing the capacity utilization of trucks J. Fabian Meier 1,2 Institute of Transport Logistics TU Dortmund, Germany Uwe Clausen 3 Fraunhofer Institute for Material
Decentralized control of stochastic multi-agent service system. J. George Shanthikumar Purdue University
 Decentralized control of stochastic multi-agent service system J. George Shanthikumar Purdue University Joint work with Huaning Cai, Peng Li and Andrew Lim 1 Many problems can be thought of as stochastic
Decentralized control of stochastic multi-agent service system J. George Shanthikumar Purdue University Joint work with Huaning Cai, Peng Li and Andrew Lim 1 Many problems can be thought of as stochastic
2015 PMB SEMESTER 2 Module timetable - PADM2B0 W2 (F) Introduction to Public Sector HR Management (Wk 30, 2015/07/19)
 Module timetable - W2 () Introduction to Public Sector HR Management (Wk 30, 2015/07/19) Mo 2015/07/21 2015/07/20 2015/07/22 Wk 30, 2015/07/22 2015/07/24 2015/07/23 Tutorial, Wk 30, 2015/07/24 Page 1,
Module timetable - W2 () Introduction to Public Sector HR Management (Wk 30, 2015/07/19) Mo 2015/07/21 2015/07/20 2015/07/22 Wk 30, 2015/07/22 2015/07/24 2015/07/23 Tutorial, Wk 30, 2015/07/24 Page 1,
Option Pricing. Chapter 12 - Local volatility models - Stefan Ankirchner. University of Bonn. last update: 13th January 2014
 Option Pricing Chapter 12 - Local volatility models - Stefan Ankirchner University of Bonn last update: 13th January 2014 Stefan Ankirchner Option Pricing 1 Agenda The volatility surface Local volatility
Option Pricing Chapter 12 - Local volatility models - Stefan Ankirchner University of Bonn last update: 13th January 2014 Stefan Ankirchner Option Pricing 1 Agenda The volatility surface Local volatility
New York Workers Compensation Trends
 New York Workers Compensation Trends June 2015 Oliver Wyman QUALIFICATIONS, ASSUMPTIONS AND LIMITING CONDITIONS This report is for the exclusive use of the Oliver Wyman client named herein. This report
New York Workers Compensation Trends June 2015 Oliver Wyman QUALIFICATIONS, ASSUMPTIONS AND LIMITING CONDITIONS This report is for the exclusive use of the Oliver Wyman client named herein. This report
How To Send An Encrypted Email In Outlook 2000 (For A Password Protected Email) On A Pc Or Macintosh (For An Ipo) On Pc Or Ipo (For Pc Or For A Password Safemail) On An Iphone Or
 Outlook 2000 1. Open Outlook 2000 and select the Tools > Options > Security. 2. Click Change Settings. 3. Under the Certificates and Algorithms, there are two Choose buttons. The first allows you to select
Outlook 2000 1. Open Outlook 2000 and select the Tools > Options > Security. 2. Click Change Settings. 3. Under the Certificates and Algorithms, there are two Choose buttons. The first allows you to select
An Enterprise Dynamic Thresholding System
 An Enterprise Dynamic Thresholding System Mazda Marvasti, Arnak Poghosyan, Ashot Harutyunyan, and Naira Grigoryan Presented by: Bob Patten, VMware 2013 2011 VMware Inc. All rights reserved Agenda Modern
An Enterprise Dynamic Thresholding System Mazda Marvasti, Arnak Poghosyan, Ashot Harutyunyan, and Naira Grigoryan Presented by: Bob Patten, VMware 2013 2011 VMware Inc. All rights reserved Agenda Modern
Evaluating Predictive Analytics for Capacity Planning. HIC 2015 Andrae Gaeth
 Evaluating Predictive Analytics for Capacity Planning HIC 2015 Andrae Gaeth What is predictive analytics? Predictive analytics is the practice of extracting information from existing data sets, and then
Evaluating Predictive Analytics for Capacity Planning HIC 2015 Andrae Gaeth What is predictive analytics? Predictive analytics is the practice of extracting information from existing data sets, and then
Security in Outsourcing of Association Rule Mining
 Security in Outsourcing of Association Rule Mining W. K. Wong The University of Hong Kong [email protected] David W. Cheung The University of Hong Kong [email protected] Ben Kao The University of Hong
Security in Outsourcing of Association Rule Mining W. K. Wong The University of Hong Kong [email protected] David W. Cheung The University of Hong Kong [email protected] Ben Kao The University of Hong
the recursion-tree method
 the recursion- method recurrence into a 1 recurrence into a 2 MCS 360 Lecture 39 Introduction to Data Structures Jan Verschelde, 22 November 2010 recurrence into a The for consists of two steps: 1 Guess
the recursion- method recurrence into a 1 recurrence into a 2 MCS 360 Lecture 39 Introduction to Data Structures Jan Verschelde, 22 November 2010 recurrence into a The for consists of two steps: 1 Guess
Estimates of Uncertainty of the Calibration of Balances
 Estimates of Uncertainty of the Calibration of Balances Chart shows the uncertainty (estimates) of the calibration of representative electronic balances. Chart. Uncertainty of calibration (estimates) Minimum
Estimates of Uncertainty of the Calibration of Balances Chart shows the uncertainty (estimates) of the calibration of representative electronic balances. Chart. Uncertainty of calibration (estimates) Minimum
A COMPARISON OF REGRESSION MODELS FOR FORECASTING A CUMULATIVE VARIABLE
 A COMPARISON OF REGRESSION MODELS FOR FORECASTING A CUMULATIVE VARIABLE Joanne S. Utley, School of Business and Economics, North Carolina A&T State University, Greensboro, NC 27411, (336)-334-7656 (ext.
A COMPARISON OF REGRESSION MODELS FOR FORECASTING A CUMULATIVE VARIABLE Joanne S. Utley, School of Business and Economics, North Carolina A&T State University, Greensboro, NC 27411, (336)-334-7656 (ext.
Periodic wave in spatial domain - length scale is wavelength Given symbol l y
 1.4 Periodic Waves Often have situations where wave repeats at regular intervals Electromagnetic wave in optical fibre Sound from a guitar string. These regularly repeating waves are known as periodic
1.4 Periodic Waves Often have situations where wave repeats at regular intervals Electromagnetic wave in optical fibre Sound from a guitar string. These regularly repeating waves are known as periodic
 I n s t r u k c j a o b s ł u g i p r o g r a m u Program Finansowo-K się gowy w e r s j a 1. 1 p o d W i n d o w s. W y d a w n i c t w o " G I D E X " S Z C Z E C I N - m a j - 2 0 0 2 W y ł ą c z n
I n s t r u k c j a o b s ł u g i p r o g r a m u Program Finansowo-K się gowy w e r s j a 1. 1 p o d W i n d o w s. W y d a w n i c t w o " G I D E X " S Z C Z E C I N - m a j - 2 0 0 2 W y ł ą c z n
Point Biserial Correlation Tests
 Chapter 807 Point Biserial Correlation Tests Introduction The point biserial correlation coefficient (ρ in this chapter) is the product-moment correlation calculated between a continuous random variable
Chapter 807 Point Biserial Correlation Tests Introduction The point biserial correlation coefficient (ρ in this chapter) is the product-moment correlation calculated between a continuous random variable
Battery Provisioning and Scheduling for a Hybrid Battery-Diesel Generator System
 attery Provisioning and Scheduling for a Hybrid attery-diesel Generator System Sahil Singla University of Waterloo [email protected] Yashar Ghiassi-Farrokhfal University of Waterloo [email protected]
attery Provisioning and Scheduling for a Hybrid attery-diesel Generator System Sahil Singla University of Waterloo [email protected] Yashar Ghiassi-Farrokhfal University of Waterloo [email protected]
timeout StoR!msg0 RtoS?ack0
 c1997kluweracademicpublishers,boston.manufacturedinthenetherlands. FormalMethodsinSystemDesign,,?{??(1997) SymbolicVericationofCommunication ProtocolswithInniteStateSpacesusingQDDs queues.itiswell-knownthatmostinterestingvericationproblems,suchasdeadlockdetection,
c1997kluweracademicpublishers,boston.manufacturedinthenetherlands. FormalMethodsinSystemDesign,,?{??(1997) SymbolicVericationofCommunication ProtocolswithInniteStateSpacesusingQDDs queues.itiswell-knownthatmostinterestingvericationproblems,suchasdeadlockdetection,
Network Intrusion Detection using Semi Supervised Support Vector Machine
 Network Intrusion Detection using Semi Supervised Support Vector Machine Jyoti Haweliya Department of Computer Engineering Institute of Engineering & Technology, Devi Ahilya University Indore, India ABSTRACT
Network Intrusion Detection using Semi Supervised Support Vector Machine Jyoti Haweliya Department of Computer Engineering Institute of Engineering & Technology, Devi Ahilya University Indore, India ABSTRACT
Functional Dependencies and Normalization
 Functional Dependencies and Normalization 5DV119 Introduction to Database Management Umeå University Department of Computing Science Stephen J. Hegner [email protected] http://www.cs.umu.se/~hegner Functional
Functional Dependencies and Normalization 5DV119 Introduction to Database Management Umeå University Department of Computing Science Stephen J. Hegner [email protected] http://www.cs.umu.se/~hegner Functional
Revenue Structure, Objectives of a Firm and. Break-Even Analysis.
 Revenue :The income receipt by way of sale proceeds is the revenue of the firm. As with costs, we need to study concepts of total, average and marginal revenues. Each unit of output sold in the market
Revenue :The income receipt by way of sale proceeds is the revenue of the firm. As with costs, we need to study concepts of total, average and marginal revenues. Each unit of output sold in the market
From CFD to computational finance (and back again?)
 computational finance p. 1/17 From CFD to computational finance (and back again?) Mike Giles [email protected] Oxford University Mathematical Institute Oxford-Man Institute of Quantitative Finance
computational finance p. 1/17 From CFD to computational finance (and back again?) Mike Giles [email protected] Oxford University Mathematical Institute Oxford-Man Institute of Quantitative Finance
The class slides, your notes, and the sample problem that we worked in class may be helpful for reference.
 Page 1 of 5 Normalization Lab 12 and Take-home Exam II Objective The goal of this lab is to give you more practice on normalizing a database. You will analyze an existing database to determine the changes
Page 1 of 5 Normalization Lab 12 and Take-home Exam II Objective The goal of this lab is to give you more practice on normalizing a database. You will analyze an existing database to determine the changes
Clock Synchronization
 Clock Synchronization Henrik Lönn Electronics & Software Volvo Technological Development Contents General Types of Synchronisation Faults and problems to cope with Example algorithms Transmission delays
Clock Synchronization Henrik Lönn Electronics & Software Volvo Technological Development Contents General Types of Synchronisation Faults and problems to cope with Example algorithms Transmission delays
HOW TO SELECT VARISTORS
 HOW TO SELECT VARISTORS We have three alternatives: - selection of the varistors suitable for the operating voltage of the application - calculating the surge current, energy absorption and average power
HOW TO SELECT VARISTORS We have three alternatives: - selection of the varistors suitable for the operating voltage of the application - calculating the surge current, energy absorption and average power
Fuel Performance Management
 O P E R AT I O N A L P E R F O R M A N C E Fuel Performance Management FUEL PERFORMANCE MANAGEMENT Boeing delivers LIFECYCLE SOLUTIONS, including products, services, and support that maximize the value
O P E R AT I O N A L P E R F O R M A N C E Fuel Performance Management FUEL PERFORMANCE MANAGEMENT Boeing delivers LIFECYCLE SOLUTIONS, including products, services, and support that maximize the value
Full and Complete Binary Trees
 Full and Complete Binary Trees Binary Tree Theorems 1 Here are two important types of binary trees. Note that the definitions, while similar, are logically independent. Definition: a binary tree T is full
Full and Complete Binary Trees Binary Tree Theorems 1 Here are two important types of binary trees. Note that the definitions, while similar, are logically independent. Definition: a binary tree T is full
Advanced Encryption Standard (AES) User's Guide
 Advanced Encryption Standard (AES) User's Guide Version 1.00 BETA For use with AES versions 1.6 and above Date: 11-Feb-2015 11:23 All rights reserved. This document and the associated software are the
Advanced Encryption Standard (AES) User's Guide Version 1.00 BETA For use with AES versions 1.6 and above Date: 11-Feb-2015 11:23 All rights reserved. This document and the associated software are the
TURNKEY 33 PROPERTY MULTIFAMILY PORTFOLIO
 LE / FOR SALE / FOR SALE / FOR SALE / FOR SALE / FOR SALE / FOR SALE / FOR SALE / FOR SALE / FOR TURNKEY 33 PROPERTY MULTIFAMILY PORTFOLIO MILWAUKEE APARTMENT PORTFOLIO, MILWAUKEE, WI 1123 NORTH WATER
LE / FOR SALE / FOR SALE / FOR SALE / FOR SALE / FOR SALE / FOR SALE / FOR SALE / FOR SALE / FOR TURNKEY 33 PROPERTY MULTIFAMILY PORTFOLIO MILWAUKEE APARTMENT PORTFOLIO, MILWAUKEE, WI 1123 NORTH WATER
Why Semantic Analysis is Better than Sentiment Analysis. A White Paper by T.R. Fitz-Gibbon, Chief Scientist, Networked Insights
 Why Semantic Analysis is Better than Sentiment Analysis A White Paper by T.R. Fitz-Gibbon, Chief Scientist, Networked Insights Why semantic analysis is better than sentiment analysis I like it, I don t
Why Semantic Analysis is Better than Sentiment Analysis A White Paper by T.R. Fitz-Gibbon, Chief Scientist, Networked Insights Why semantic analysis is better than sentiment analysis I like it, I don t
CANADIAN PAYMENTS ASSOCIATION LVTS RULE 4 COMMENCEMENT
 CANADIAN PAYMENTS ASSOCIATION LVTS RULE 4 LVTS Rule 4, December 1998: as amended July 30, 2001, November 19, 2001, October 6, 2003, November 24, 2003, March 29, 2007, December 13, 2010 and March 2, 2015.
CANADIAN PAYMENTS ASSOCIATION LVTS RULE 4 LVTS Rule 4, December 1998: as amended July 30, 2001, November 19, 2001, October 6, 2003, November 24, 2003, March 29, 2007, December 13, 2010 and March 2, 2015.
Final. 1. (2 pts) What is the expected effect on the real demand for money of an increase in the nominal interest rate? How to explain this effect?
 Name: Number: Nova School of Business and Economics Macroeconomics, 1103-1st Semester 2013-2014 Prof. André C. Silva TAs: João Vaz, Paulo Fagandini, and Pedro Freitas Final Maximum points: 20. Time: 2h.
Name: Number: Nova School of Business and Economics Macroeconomics, 1103-1st Semester 2013-2014 Prof. André C. Silva TAs: João Vaz, Paulo Fagandini, and Pedro Freitas Final Maximum points: 20. Time: 2h.
Model Based Testing for Security Checking. Wissam Mallouli and Prof. Ana Cavalli National Institute of Telecommunications, France November 21, 2007
 Model Based Testing for Security Checking Wissam Mallouli and Prof. Ana Cavalli National Institute of Telecommunications, France November 21, 2007 Outline Introduction Active/Passive Testing Active Testing
Model Based Testing for Security Checking Wissam Mallouli and Prof. Ana Cavalli National Institute of Telecommunications, France November 21, 2007 Outline Introduction Active/Passive Testing Active Testing
CS570 Data Mining Classification: Ensemble Methods
 CS570 Data Mining Classification: Ensemble Methods Cengiz Günay Dept. Math & CS, Emory University Fall 2013 Some slides courtesy of Han-Kamber-Pei, Tan et al., and Li Xiong Günay (Emory) Classification:
CS570 Data Mining Classification: Ensemble Methods Cengiz Günay Dept. Math & CS, Emory University Fall 2013 Some slides courtesy of Han-Kamber-Pei, Tan et al., and Li Xiong Günay (Emory) Classification:
What is Modeling and Simulation and Software Engineering?
 What is Modeling and Simulation and Software Engineering? V. Sundararajan Scientific and Engineering Computing Group Centre for Development of Advanced Computing Pune 411 007 [email protected] Definitions
What is Modeling and Simulation and Software Engineering? V. Sundararajan Scientific and Engineering Computing Group Centre for Development of Advanced Computing Pune 411 007 [email protected] Definitions
FY 2013 EMERGENCY MANAGEMENT PERFORMANCE GRANTS (EMPG) PROGRAM
 OMB Control Number: 1660-0126 Public reporting burden for this form is estimated to average 3 hours per response. The burden estimate includes the time for reviewing instructions, searching existing data
OMB Control Number: 1660-0126 Public reporting burden for this form is estimated to average 3 hours per response. The burden estimate includes the time for reviewing instructions, searching existing data
Quality Assessment Strategies for GIS Reference Data Used in Patient Address Geocoding
 Quality Assessment Strategies for GIS Reference Data Used in Patient Address Geocoding By C.A. Klaus and L.E. Carrasco, Ph.D. North Carolina Central Cancer Registry June 2012 The Value of GIS Reference
Quality Assessment Strategies for GIS Reference Data Used in Patient Address Geocoding By C.A. Klaus and L.E. Carrasco, Ph.D. North Carolina Central Cancer Registry June 2012 The Value of GIS Reference
Largest Fixed-Aspect, Axis-Aligned Rectangle
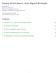 Largest Fixed-Aspect, Axis-Aligned Rectangle David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: February 21, 2004 Last Modified: February
Largest Fixed-Aspect, Axis-Aligned Rectangle David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: February 21, 2004 Last Modified: February
Determination of the normalization level of database schemas through equivalence classes of attributes
 Computer Science Journal of Moldova, vol.17, no.2(50), 2009 Determination of the normalization level of database schemas through equivalence classes of attributes Cotelea Vitalie Abstract In this paper,
Computer Science Journal of Moldova, vol.17, no.2(50), 2009 Determination of the normalization level of database schemas through equivalence classes of attributes Cotelea Vitalie Abstract In this paper,
Enhancing the relativity between Content, Title and Meta Tags Based on Term Frequency in Lexical and Semantic Aspects
 Enhancing the relativity between Content, Title and Meta Tags Based on Term Frequency in Lexical and Semantic Aspects Mohammad Farahmand, Abu Bakar MD Sultan, Masrah Azrifah Azmi Murad, Fatimah Sidi [email protected]
Enhancing the relativity between Content, Title and Meta Tags Based on Term Frequency in Lexical and Semantic Aspects Mohammad Farahmand, Abu Bakar MD Sultan, Masrah Azrifah Azmi Murad, Fatimah Sidi [email protected]
WINDEX ORIGINAL GLASS CLEANER
 1. PRODUCT AND COMPANY IDENTIFICATION Product information Trade name : Use of the : Hard Surface Cleaner Substance/Mixture Company : S.C. Johnson & Son, Inc. 1525 Howe Street Racine WI 53403-2236 Emergency
1. PRODUCT AND COMPANY IDENTIFICATION Product information Trade name : Use of the : Hard Surface Cleaner Substance/Mixture Company : S.C. Johnson & Son, Inc. 1525 Howe Street Racine WI 53403-2236 Emergency
O N L I N E B A N K I N G O N L I N E F I N A N C I A L M A N A G E M E N T. End-User Guide
 O N L I N E B A N K I N G O N L I N E F I N A N C I A L M A N A G E M E N T End-User Guide September 24, 2012 CONTENTS Overview... 1 Getting Started... 1 Dashboard... 3 Accounts... 5 Adding an Online Account...
O N L I N E B A N K I N G O N L I N E F I N A N C I A L M A N A G E M E N T End-User Guide September 24, 2012 CONTENTS Overview... 1 Getting Started... 1 Dashboard... 3 Accounts... 5 Adding an Online Account...
Multi-GPU Load Balancing for Simulation and Rendering
 Multi- Load Balancing for Simulation and Rendering Yong Cao Computer Science Department, Virginia Tech, USA In-situ ualization and ual Analytics Instant visualization and interaction of computing tasks
Multi- Load Balancing for Simulation and Rendering Yong Cao Computer Science Department, Virginia Tech, USA In-situ ualization and ual Analytics Instant visualization and interaction of computing tasks
Oscillations of the Sending Window in Compound TCP
 Oscillations of the Sending Window in Compound TCP Alberto Blanc 1, Denis Collange 1, and Konstantin Avrachenkov 2 1 Orange Labs, 905 rue Albert Einstein, 06921 Sophia Antipolis, France 2 I.N.R.I.A. 2004
Oscillations of the Sending Window in Compound TCP Alberto Blanc 1, Denis Collange 1, and Konstantin Avrachenkov 2 1 Orange Labs, 905 rue Albert Einstein, 06921 Sophia Antipolis, France 2 I.N.R.I.A. 2004
D) Marginal revenue is the rate at which total revenue changes with respect to changes in output.
 Ch. 9 1. Which of the following is not an assumption of a perfectly competitive market? A) Fragmented industry B) Differentiated product C) Perfect information D) Equal access to resources 2. Which of
Ch. 9 1. Which of the following is not an assumption of a perfectly competitive market? A) Fragmented industry B) Differentiated product C) Perfect information D) Equal access to resources 2. Which of
Euler s Method and Functions
 Chapter 3 Euler s Method and Functions The simplest method for approximately solving a differential equation is Euler s method. One starts with a particular initial value problem of the form dx dt = f(t,
Chapter 3 Euler s Method and Functions The simplest method for approximately solving a differential equation is Euler s method. One starts with a particular initial value problem of the form dx dt = f(t,
Revenue-optimal Scheduling of Solar Thermal Power Plants with integrated Thermal Storage
 OPTEC Miniworkshop on "Optimal Control for Solar Thermal Power Plants at K.U. Leuven Revenue-optimal Scheduling of Solar Thermal Power Plants with integrated Thermal Storage Michael Wittmann, DLR Overview
OPTEC Miniworkshop on "Optimal Control for Solar Thermal Power Plants at K.U. Leuven Revenue-optimal Scheduling of Solar Thermal Power Plants with integrated Thermal Storage Michael Wittmann, DLR Overview
Constant scallop-height tool path generation for three-axis sculptured surface machining
 COMPUTER-AIDED DESIGN Computer-Aided Design 34 2002) 64±654 www.elsevier.com/locate/cad Constant scallop-height tool path generation for three-axis sculptured surface machining Hsi-Yung Feng*, Huiwen Li
COMPUTER-AIDED DESIGN Computer-Aided Design 34 2002) 64±654 www.elsevier.com/locate/cad Constant scallop-height tool path generation for three-axis sculptured surface machining Hsi-Yung Feng*, Huiwen Li
Check Digit Schemes and Error Detecting Codes. By Breanne Oldham Union University
 Check Digit Schemes and Error Detecting Codes By Breanne Oldham Union University What are Check Digit Schemes? Check digit schemes are numbers appended to an identification number that allow the accuracy
Check Digit Schemes and Error Detecting Codes By Breanne Oldham Union University What are Check Digit Schemes? Check digit schemes are numbers appended to an identification number that allow the accuracy
Using Ensemble of Decision Trees to Forecast Travel Time
 Using Ensemble of Decision Trees to Forecast Travel Time José P. González-Brenes Guido Matías Cortés What to Model? Goal Predict travel time at time t on route s using a set of explanatory variables We
Using Ensemble of Decision Trees to Forecast Travel Time José P. González-Brenes Guido Matías Cortés What to Model? Goal Predict travel time at time t on route s using a set of explanatory variables We
Elucexion - Guidelines For Responding to Accidents
 EXERCISE EVALUATION GUIDE Exercise Name: Local Public Health Community Preparedness Ebola TTX Exercise Date: [Insert exercise date] Organization/Jurisdiction: [Insert organization or jurisdiction] Response
EXERCISE EVALUATION GUIDE Exercise Name: Local Public Health Community Preparedness Ebola TTX Exercise Date: [Insert exercise date] Organization/Jurisdiction: [Insert organization or jurisdiction] Response
CS 294-73 Software Engineering for Scientific Computing. http://www.cs.berkeley.edu/~colella/cs294fall2013. Lecture 16: Particle Methods; Homework #4
 CS 294-73 Software Engineering for Scientific Computing http://www.cs.berkeley.edu/~colella/cs294fall2013 Lecture 16: Particle Methods; Homework #4 Discretizing Time-Dependent Problems From here on in,
CS 294-73 Software Engineering for Scientific Computing http://www.cs.berkeley.edu/~colella/cs294fall2013 Lecture 16: Particle Methods; Homework #4 Discretizing Time-Dependent Problems From here on in,
SHOUT TRIPLE-ACTING LAUNDRY STAIN REMOVER
 1. PRODUCT AND COMPANY IDENTIFICATION Product information Trade name : Use of the : Spot & Stain Remover Substance/Mixture Company : S.C. Johnson & Son, Inc. 1525 Howe Street Racine WI 53403-2236 Emergency
1. PRODUCT AND COMPANY IDENTIFICATION Product information Trade name : Use of the : Spot & Stain Remover Substance/Mixture Company : S.C. Johnson & Son, Inc. 1525 Howe Street Racine WI 53403-2236 Emergency
SINGLE SIGN-ON MECHANISM FOR DISTRIBUTED COMPUTING SECURITY ENVIRONMENT
 SINGLE SIGN-ON MECHANISM FOR DISTRIBUTED COMPUTING SECURITY ENVIRONMENT K.karthika 1, M. Daya kanimozhi Rani 2 1 K.karthika, Assistant professor, Department of IT, Adhiyamaan College of Engineering, Hosur
SINGLE SIGN-ON MECHANISM FOR DISTRIBUTED COMPUTING SECURITY ENVIRONMENT K.karthika 1, M. Daya kanimozhi Rani 2 1 K.karthika, Assistant professor, Department of IT, Adhiyamaan College of Engineering, Hosur
All of my instructors showed a true compassion for teaching. This passion helped students enjoy every class. Amanda
 F 228 D O z F/ Fx L / H V L I & P G G F Q, z,, B, z -, q k k k FUN F x 20% 02 F 9185957834 I P G j P, E, j, k,, ; I I G F Ex 2011 H B H 2011-2012 F H E U F P G I G L L 228 D & 228 k B P 04 F 9185957834
F 228 D O z F/ Fx L / H V L I & P G G F Q, z,, B, z -, q k k k FUN F x 20% 02 F 9185957834 I P G j P, E, j, k,, ; I I G F Ex 2011 H B H 2011-2012 F H E U F P G I G L L 228 D & 228 k B P 04 F 9185957834
WINDEX ORIGINAL GLASS CLEANER WITH AMMONIA-D
 1. PRODUCT AND COMPANY IDENTIFICATION Product information Product name : WINDEX ORIGINAL GLASS CLEANER WITH AMMONIA- D Recommended use : Hard Surface Cleaner Manufacturer, importer, supplier : S.C. Johnson
1. PRODUCT AND COMPANY IDENTIFICATION Product information Product name : WINDEX ORIGINAL GLASS CLEANER WITH AMMONIA- D Recommended use : Hard Surface Cleaner Manufacturer, importer, supplier : S.C. Johnson
Congestion Notification in Ethernet: Part of the IEEE 802.1 Data Center Bridging standardization effort
 High Performance Switching and Routing Telecom Center Workshop: Sept 4, 1997. Congestion Notification in Ethernet: Part of the IEEE 802.1 Data Center Bridging standardization effort Berk Atikoglu, Balaji
High Performance Switching and Routing Telecom Center Workshop: Sept 4, 1997. Congestion Notification in Ethernet: Part of the IEEE 802.1 Data Center Bridging standardization effort Berk Atikoglu, Balaji
Systems with Persistent Memory: the Observation Inequality Problems and Solutions
 Chapter 6 Systems with Persistent Memory: the Observation Inequality Problems and Solutions Facts that are recalled in the problems wt) = ut) + 1 c A 1 s ] R c t s)) hws) + Ks r)wr)dr ds. 6.1) w = w +
Chapter 6 Systems with Persistent Memory: the Observation Inequality Problems and Solutions Facts that are recalled in the problems wt) = ut) + 1 c A 1 s ] R c t s)) hws) + Ks r)wr)dr ds. 6.1) w = w +
Pearson's Correlation Tests
 Chapter 800 Pearson's Correlation Tests Introduction The correlation coefficient, ρ (rho), is a popular statistic for describing the strength of the relationship between two variables. The correlation
Chapter 800 Pearson's Correlation Tests Introduction The correlation coefficient, ρ (rho), is a popular statistic for describing the strength of the relationship between two variables. The correlation
ISSUES IN UNIVARIATE FORECASTING
 ISSUES IN UNIVARIATE FORECASTING By Rohaiza Zakaria 1, T. Zalizam T. Muda 2 and Suzilah Ismail 3 UUM College of Arts and Sciences, Universiti Utara Malaysia 1 [email protected], 2 [email protected] and 3
ISSUES IN UNIVARIATE FORECASTING By Rohaiza Zakaria 1, T. Zalizam T. Muda 2 and Suzilah Ismail 3 UUM College of Arts and Sciences, Universiti Utara Malaysia 1 [email protected], 2 [email protected] and 3
Mixed Precision Iterative Refinement Methods Energy Efficiency on Hybrid Hardware Platforms
 Mixed Precision Iterative Refinement Methods Energy Efficiency on Hybrid Hardware Platforms Björn Rocker Hamburg, June 17th 2010 Engineering Mathematics and Computing Lab (EMCL) KIT University of the State
Mixed Precision Iterative Refinement Methods Energy Efficiency on Hybrid Hardware Platforms Björn Rocker Hamburg, June 17th 2010 Engineering Mathematics and Computing Lab (EMCL) KIT University of the State
Data Structures Fibonacci Heaps, Amortized Analysis
 Chapter 4 Data Structures Fibonacci Heaps, Amortized Analysis Algorithm Theory WS 2012/13 Fabian Kuhn Fibonacci Heaps Lacy merge variant of binomial heaps: Do not merge trees as long as possible Structure:
Chapter 4 Data Structures Fibonacci Heaps, Amortized Analysis Algorithm Theory WS 2012/13 Fabian Kuhn Fibonacci Heaps Lacy merge variant of binomial heaps: Do not merge trees as long as possible Structure:
Binary Search Trees. Data in each node. Larger than the data in its left child Smaller than the data in its right child
 Binary Search Trees Data in each node Larger than the data in its left child Smaller than the data in its right child FIGURE 11-6 Arbitrary binary tree FIGURE 11-7 Binary search tree Data Structures Using
Binary Search Trees Data in each node Larger than the data in its left child Smaller than the data in its right child FIGURE 11-6 Arbitrary binary tree FIGURE 11-7 Binary search tree Data Structures Using
Learning to Rank Revisited: Our Progresses in New Algorithms and Tasks
 The 4 th China-Australia Database Workshop Melbourne, Australia Oct. 19, 2015 Learning to Rank Revisited: Our Progresses in New Algorithms and Tasks Jun Xu Institute of Computing Technology, Chinese Academy
The 4 th China-Australia Database Workshop Melbourne, Australia Oct. 19, 2015 Learning to Rank Revisited: Our Progresses in New Algorithms and Tasks Jun Xu Institute of Computing Technology, Chinese Academy
Scheduling Aperiodic and Sporadic Jobs in Priority- Driven Systems
 Scheduling Aperiodic and Sporadic Jobs in Priority- Driven Systems Ingo Sander [email protected] Liu: Chapter 7 IL2212 Embedded Software 1 Outline l System Model and Assumptions l Scheduling Aperiodic Jobs l
Scheduling Aperiodic and Sporadic Jobs in Priority- Driven Systems Ingo Sander [email protected] Liu: Chapter 7 IL2212 Embedded Software 1 Outline l System Model and Assumptions l Scheduling Aperiodic Jobs l
Predicting Customer Default Times using Survival Analysis Methods in SAS
 Predicting Customer Default Times using Survival Analysis Methods in SAS Bart Baesens [email protected] Overview The credit scoring survival analysis problem Statistical methods for Survival
Predicting Customer Default Times using Survival Analysis Methods in SAS Bart Baesens [email protected] Overview The credit scoring survival analysis problem Statistical methods for Survival
Dynamic request management algorithms for Web-based services in Cloud computing
 Dynamic request management algorithms for Web-based services in Cloud computing Riccardo Lancellotti Mauro Andreolini Claudia Canali Michele Colajanni University of Modena and Reggio Emilia COMPSAC 2011
Dynamic request management algorithms for Web-based services in Cloud computing Riccardo Lancellotti Mauro Andreolini Claudia Canali Michele Colajanni University of Modena and Reggio Emilia COMPSAC 2011
