А. Г. Мерзляк В. Б. Полонський М. С. Якір. Підручник для 9 класу загальноосвітніх навчальних закладів
|
|
|
- Яна Скуратова
- 7 years ago
- Views:
Transcription
1 А. Г. Мерзляк В. Б. Полонський М. С. Якір ГЕОМЕТРІЯ Підручник для 9 класу загальноосвітніх навчальних закладів Рекомендовано Міністерством освіти і науки України Харків «Гімназія» 009
2 УДК 373:51 ББК.151я71 М5 Видано за рахунок державних коштів Продаж заборонено Рекомендовано Міністерством освіти і науки України (Наказ від р. 56) Відповідальні за підготовку до видання: Головний спеціаліст Міністерства освіти і науки України Н. С. Прокопенко Методист вищої категорії Інституту інноваційних технологій і змісту освіти О. О. Литвиненко Експерти, які здійснювали експертизу та рекомендували підручник до видання: О. В. Горелова, учитель-методист загальноосвітньої школи 10 м. Ізмаїла Одеської області К. М. Петечук, методист Закарпатського інституту післядипломної педагогічної освіти О. М. Сінюкова, викладач кафедри геометрії Південноукраїнського державного педагогічного університету ім. К. Д. Ушинського м. Одеси, кандидат фізико-математичних наук, доцент В. В. Шарко, завідувач відділу топології Інституту математики НАН України, доктор фізико-математичних наук, професор Т. М. Хмара, провідний науковий співробітник лабораторії математичної і фізичної освіти Інституту педагогіки АПН України, кандидат педагогічних наук ISBN А. Г. Мерзляк, В. Б. Полонський, М. С. Якір, 009 С. Е. Кулинич, художнє оформлення, 009 ТОВ ТО «Гімназія», оригінал-макет, 009
3 Від авторів Любі дев ятикласники! У цьому навчальному році ви продовжуватимете вивчати геометрію. Сподіваємося, що ви встигли полюбити цю важливу і красиву науку, а отже, з інтересом будете засвоювати нові знання. Ми маємо надію, що цьому сприятиме підручник, який ви тримаєте. Ознайомтеся, будь ласка, з його структурою. Підручник розділено на шість параграфів, кожний з яких складається з пунктів. У пунктах викладено теоретичний матеріал. Особливу увагу звертайте на текст, виділений жирним шрифтом. Також не залишайте поза увагою слова, надруковані курсивом. Зазвичай виклад теоретичного матеріалу завершується прикладами розв язування задач. Ці записи можна розглядати як один з можливих зразків оформлення розв язання. До кожного пункту підібрано задачі для самостійного розв язування, приступати до яких радимо лише після засвоєння теоретичного матеріалу. Серед завдань є як прості й середні за складністю вправи, так і складні задачі (особливо ті, які позначено зірочкою (*)). Свої знання можна перевірити, розв язуючи задачі у тестовій формі з рубрики «Перевір себе». Якщо після виконання домашніх завдань залишається вільний час і ви хочете знати більше, то рекомендуємо звернутися до рубрики «Коли зроблено уроки». Матеріал, викладений там, є непростим. Але тим цікавіше випробувати свої сили! Дерзайте! Бажаємо успіху! 3
4 Шановні колеги! Ми дуже сподіваємося, що цей підручник стане надійним помічником у вашій нелегкій і шляхетній праці, і будемо щиро раді, якщо він вам сподобається. У книзі дібрано обширний і різноманітний дидактичний матеріал. Проте за один навчальний рік усі задачі розв язати неможливо, та в цьому й немає потреби. Разом з тим набагато зручніше працювати, коли є значний запас задач. Це дає можливість реалізувати принципи рівневої диференціації та індивідуального підходу в навчанні. Червоним кольором позначено номери задач, що рекомендуються для домашньої роботи, синім кольором номери задач, які з урахуванням індивідуальних особливостей учнів класу на розсуд учителя можна розв язувати усно. Матеріал рубрики «Коли зроблено уроки» може бути використаний для організації роботи математичного гуртка і факультативних занять. Бажаємо творчого натхнення й терпіння. Умовні позначення n завдання, що відповідають початковому і середньому рівням навчальних досягнень; n завдання, що відповідають достатньому рівню на вчаль них досягнень; n завдання, що відповідають високому рівню на вчальних досягнень; n * задачі для математичних гуртків і факультативів; задачі, у яких отримано результат, що може бути використаний при розв язуванні інших задач; доведення теореми, що відповідає достатньому рівню навчальних досягнень; доведення теореми, що відповідає високому рівню навчальних досягнень; доведення теореми, не обов язкове для вивчення; закінчення доведення теореми. 4
5 Розв язування трикутників 1 У цьому параграфі ви дізнаєтесь, що являють собою синус, косинус і тангенс кута α, де 0 m α m 180. Ви навчитеся за двома сторонами трикутника і кутом між ними знаходити третю сторону, а також за стороною і двома прилеглими до неї кутами знаходити дві інші сторони трикутника. У 8 класі ви навчилися розв язувати прямокутні трикутники. Вивчивши матеріал цього параграфа, ви зможете розв язувати будь-які трикутники. Ви дізнаєтеся про нові формули, за допомогою яких можна знаходити площу трикутника. 1. Синус, косинус і тангенс кута від 0 до 180 Перед вивченням цього пункту рекомендуємо повторити зміст пункту 14 на с. 49. Поняття «синус», «косинус» і «тангенс» гострого кута вам знайомі з курсу геометрії 8 класу. Розширимо ці поняття для будь-якого кута α, де 0 m α m 180. У верхній півплощині координатної площини розглянемо півколо з центром у початку координат, радіус якого дорівнює 1 (рис. 1). Таке півколо називають одиничним. Будемо говорити, що куту α (0 m α m 180 ) відповідає точка M одиничного півкола, якщо MOA = α, де точки O і A мають відповідно координати (0; 0) і (1; 0) (рис. 1). Наприклад, на рисунку 1 куту, який дорівнює 90, відповідає точка C; куту, який дорівнює 180, точка B; куту, який дорівнює 0, точка A. Рис. 1 5
6 1. Розв язування трикутників Нехай α гострий кут. Йому відповідає деяка точка M (x; y) дуги AC (рис. ). З прямокутного трикутника OMN маємо: cos α= ON, OM sin α=mn OM. Оскільки OM = 1, ON = x, MN = y, то x = cos α, y = sin α. Отже, косинус і синус гострого кута α це відповідно абсциса і ордината точки M одиничного півкола, яка відповідає куту α. Отриманий результат підказує, як визначити синус і косинус будь-якого кута α, де 0 m α m 180. Означення. Косинусом і синусом кута α (0 m m α m 180 ) називають відповідно абсцису x і ординату y точки M одиничного півкола, яка відповідає куту α (рис. 3). Користуючись таким означенням, можна, наприклад, записати: sin 0 = 0, cos 0 = 1, sin 90 = 1, cos 90 = 0, sin 180 = 0, cos 180 = 1. Рис. Рис. 3 Якщо M (x; y) до вільна точка одиничного пів кола, то 1 m x m 1 і 0 m y m 1. Отже, для будь-якого кута α, де 0 m α m 180, маємо: 0 m sin α m 1, 1 m cos α m 1. Якщо α тупий кут, то абсциса точки одиничного півкола, що відповідає цьому куту, є від ємною. Отже, косинус тупого кута є від ємним числом. Зрозуміло, що справедли 6
7 1. Синус, косинус і тангенс кута від 0 до 180 ве і таке твердження: якщо cos α < 0, то α тупий або розгорнутий кут. Із курсу геометрії 8 класу ви знаєте, що для будь-якого гострого кута α sin (90 α) = cos α, сos (90 α) = sin α Ці формули залишаються справедливими і для α = 0, і для α = 90 (переконайтеся в цьому самостійно). Нехай кутам α і 180 α, де α 0, α 90 і α 180, відповідають точки M (x 1 ; y 1 ) і N (x ; y ) одиничного півкола (рис. 4). Рис. 4 Прямокутні трикутники OMM 1 і ONN 1 рівні за гіпотенузою і гострим кутом (ON = OM = 1, MOM 1 = NON 1 = = α). Звідси y = y 1 і x = x 1. Отже, sin (180 α) = sin α, cos (180 α) = cos α Переконайтеся самостійно, що ці рівності залишаються правильними для α = 0, α = 90, α = 180. Якщо α гострий кут, то, як ви знаєте з курсу геометрії 8 класу, справедлива тотожність sin α + cos α = 1, яка залишається правильною для α = 0, α = 90, α = 180 (переконайтеся в цьому самостійно). 7
8 1. Розв язування трикутників Нехай α тупий кут. Тоді 180 α є гострим кутом. Маємо: sin α + cos α = (sin (180 α)) + ( cos (180 α)) = = sin (180 α) + cos (180 α) = 1. Отже, рівність sin α + cos α = 1 виконується для всіх 0 m α m 180. О з н а ч е н н я. Тангенсом кута α, де 0 m α m 180 і α 90, називають відношення sin α cos α, тобто α tg α = sin cosα Оскільки cos 90 = 0, то tg α не визначений для α = 90. Очевидно, що кожному куту α (0 m α m 180 ) відповідає єдина точка одиничного півкола. Отже, кожному куту α відповідає єдине число, яке є значенням синуса (косинуса, тангенса для α 90 ). Тому залежність значень синуса (косинуса, тангенса) від величини кута є функціональною. Функції f (α) = sin α, g (α) = cos α, h (α) = tg α, які відповідають цим функціональним залежностям, називають тригонометричними функціями кута α. Задача. Доведіть, що tg (180 α) = tg α. Р о з в я з а н н я sin ( ) sin sin tg ( α ) tg cos( 180 ) = α α cos = α = = cos α. α α α Приклад. Знайдіть sin 10, cos 10, tg 10. Р о з в я з а н н я. Маємо: 3 sin10 = sin ( ) = sin 60 = ; 1 cos10 = cos ( ) = cos 60 = ; tg 10 = tg ( ) = tg 60 = 3.? 1. Яке півколо називають одиничним?. Поясніть, у якому випадку кажуть, що куту α відповідає точка M одиничного півкола. 8
9 1. Синус, косинус і тангенс кута від 0 до Що називають синусом кута α, де 0 m α m 180? 4. Що називають косинусом кута α, де 0 m α m 180? 5. Чому дорівнює sin 0? сos 0? sin 90? cos 90? sin 180? cos 180? 6. У яких межах знаходяться значення sin α, якщо 0 m α m 180? 7. У яких межах знаходяться значення cos α, якщо 0 m α m 180? 8. Яким числом, додатним чи від ємним, є синус гострого кута? синус тупого кута? косинус гострого кута? косинус тупого кута? 9. Яким кутом є кут α, якщо cos α < 0? 10. Чому дорівнює sin (180 α)? cos (180 α)? 11. Як пов язані між собою синус і косинус одного й того самого кута? 1. Що називають тангенсом кута α, де 0 m α m 180 і α 90? 13. Чому tg α не визначений для α = 90? 14. Яку загальну назву мають функції f (α) = sin α, g (α) = cos α і h (α) = tg α? Практичне завдання 1. Накресліть одиничне півколо, узявши за одиничний відрізок п ять клітинок зошита. Побудуйте кут, вершиною якого є початок координат, а однією зі сторін додатна піввісь x: 1) косинус якого дорівнює 1 5 ; ) косинус якого дорівнює 0,4; 3) синус якого дорівнює 0,6; 4) синус якого дорівнює 1; 5) косинус якого дорівнює 0; 6) косинус якого дорівнює 1. Вправи. Чому дорівнює: 1) sin (180 α), якщо sin ; α= 1 3 ) cos (180 α), якщо cos α = 0,7; 9
10 1. Розв язування трикутників 3) cos (180 α), якщо cos α= 4 ; 9 4) tg (180 α), якщо tg α = 5? 3. Кути α і β суміжні, cos α= ) Знайдіть cos β. ) Який із кутів α і β є гострим, а який тупим? 4. Знайдіть значення виразу: 1) sin cos 0 ; 4) 6 tg sin 180 ; ) 3 sin 0 5 cos 180 ; 5) cos sin 165 ; sin0 + sin 90 3) tg 3 tg 0 tg 106 ; 6). cos0 cos90 5. Обчисліть: 1) 4 cos 90 + cos 180 ; ) cos 0 cos sin Чому дорівнює синус кута, якщо його косинус дорівнює: 1) 1; ) 0? 7. Чому дорівнює косинус кута, якщо його синус дорівнює: 1) 1; ) 0? 8. Знайдіть sin 135, cos 135, tg Знайдіть sin 150, cos 150, tg Чи існує кут α, для якого: 1) sin α= 1 ; 3) cos α= 3 ; 5 5) cos α = 1,001; ) sin α = 0,3; 4) cos α = 0,99; 6) sin α= 5? 11. Знайдіть: 1) cos α, якщо sin α= 3 5 і 0 m α m 90 ; ) cos α, якщо sin α= 1 3 і 90 m α m 180 ; 3) cos α, якщо sin α= 3 ; 4 4) sin α, якщо cos α = 0,8. 1. Знайдіть: 1) cos α, якщо sin α= 5 ; 13 ) sin α, якщо cos α=
11 1. Синус, косинус і тангенс кута від 0 до Чи є правильним твердження (відповідь обґрун туй те): 1) косинус гострого кута більший за косинус тупого кута; ) існує кут, синус і косинус якого рівні; 3) існує кут, синус і косинус якого дорівнюють нулю; 4) косинус кута трикутника може дорівнювати від ємному числу; 5) синус кута трикутника може дорівнювати від ємному числу; 6) косинус кута трикутника може дорівнювати нулю; 7) синус кута трикутника може дорівнювати нулю; 8) косинус кута трикутника може дорівнювати 1; 9) синус кута трикутника може дорівнювати 1; 10) синус кута, відмінного від прямого, менший від синуса прямого кута; 11) косинус розгорнутого кута менший від косинуса кута, відмінного від розгорнутого; 1) синуси суміжних кутів рівні; 13) косинуси нерівних суміжних кутів є протилежними числами; 14) якщо косинуси двох кутів рівні, то рівні й самі кути; 15) якщо синуси двох кутів рівні, то рівні й самі кути; 16) тангенс гострого кута більший за тангенс тупого кута? 14. Порівняйте з нулем значення виразу: 1) sin 110 cos 140 ; 3) sin 18 cos 130 tg 9 ; ) sin 80 cos 100 cos 148 ; 4) sin 70 cos 90 tg У трикутнику ABC B = 60, точка O центр вписаного кола. Чому дорівнює косинус кута AOC? 16. Точка O центр кола, вписаного в трикутник ABC, 3 cos BOC =. Знайдіть кут A трикутника. 17. Знайдіть значення виразу: 1) sin cos 150 tg 135 ; ) cos 10 8 sin cos 90 cos 16 ; 3) cos 180 (sin 135 tg 60 cos 135 ). 11
12 1. Розв язування трикутників 18. Чому дорівнює значення виразу: 1) sin cos 10 ; ) sin 90 (tg 150 cos 135 tg 10 cos 135 )? 19. Знайдіть значення виразу, не користуючись таблицями і калькулятором: 1) sin 18 ; sin16 0. Обчисліть: 1) sin 8 ; sin15 ) cos 18 ; cos16 ) cos 49 ; cos131 3) tg 18. tg16 3) tg 1 tg Знайдіть суму квадратів синусів усіх кутів прямокутного трикутника.. Знайдіть суму квадратів косинусів усіх кутів прямокутного трикутника. Вправи для повторення 3. Висота паралелограма, проведена з вершини тупого кута, дорівнює 5 см і ділить сторону паралелограма навпіл. Гострий кут паралелограма дорівнює 30. Знайдіть діагональ паралелограма, проведену з вершини тупого кута, і кути, які вона утворює зі сторонами паралелограма. 4. Пряма CE паралельна бічній стороні AB трапеції ABCD і ділить основу AD на відрізки AE і DE такі, що AE = 7 см, DE = 10 см. Знайдіть середню лінію трапеції. Готуємося до вивчення нової теми 5. Дві сторони трикутника дорівнюють 8 см і 11 см. Чи може кут, протилежний стороні завдовжки 8 см, бути: 1) тупим; ) прямим? Відповідь обґрунтуйте. 6. У трикутнику ABC проведено висоту BD, A = 60, C = 45, AB = 10 см. Знайдіть сторону BC. 7. Знайдіть висоту BD трикутника ABC і проекцію сторони AB на пряму AC, якщо BAC = 150, AB = 1 см. 1
13 . Теорема косинусів 13. Теорема косинусів Із першої ознаки рівності трикутників випливає, що дві сторони і кут між ними однозначно визначають трикутник. Отже, за вказаними елементами можна знайти третю сторону трикутника. Як це зробити, показує така тео рема. Теорема.1 (теорема косинусів). Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін мінус подвоєний добуток цих сторін і косинуса кута між ними. Розглянемо трикутник ABC. Доведемо, Доведення. наприклад, що BC = AB + AC AB AC cos A. Можливі три випадки: 1) кут A гострий; ) кут A тупий; 3) кут A прямий. Розглянемо перший випадок. Якщо А < 90, тоді хоча б один з кутів B і C є гострим. Нехай, наприклад, C < 90. Проведемо висоту BD (рис. 5). З œ ABD отримуємо: BD = AB sin A, AD = AB cos A. З œ BDC отримуємо: BC = BD + CD = BD + (AC AD) = = AB sin A + (AC AB cos A) = = AB sin A + AC AC AB cos A + AB cos A = = AB (sin A + cos A) + AC AC AB cos A = = AB + AC AB AC cos A. Якщо C l 90, то B < 90. Тоді потрібно провести висоту трикутника ABC з вершини C. Далі доведення аналогічне розглянутому. Для випадку, коли кут A тупий, проведемо висоту BD трикутника ABC (рис. 6). З œ ABD отримуємо: BD = AB sin BAD = AB sin (180 BAC) = = AB sin BAC, AD = AB cos BAD = Рис. 6 B = AB cos (180 BAC) = = AB cos BAC. A D Рис. 5 C
14 B A 1. Розв язування трикутників З œ BDC отримуємо: BC = BD + CD = BD + (AC + AD) = = AB sin BAC + (AC AВ cos BAC) = = AB + AC AB AC cos BAC. Якщо кут A прямий (рис. 7), то cos A = 0. Рівність, яку потрібно довести, набуває вигляду C BC = AB + AC і виражає теорему Піфагора для трикутника ABC ( A = 90 ). Рис. 7 Та частина доведення, у якій розглянуто випадок, коли A прямий, показує, що теорема Піфагора є окремим випадком теореми коси нусів. Тому теорема косинусів є узагальненням теореми Піфа гора. Якщо скористатися позначенням для сторін і кутів трикутника ABC (див. форзац), то, наприклад, для сторони a можна записати: a = b + c bc cos α. За допомогою теореми косинусів, знаючи три сторони трикутника, можна визначити, чи є він гострокутним, тупокутним або прямокутним. Теорема. (наслідок з теореми косинусів). Нехай a, b і c сторони трикутника ABC, причому a його найбільша сторона. Якщо a < b + c, то трикутник є гострокутним. Якщо a > b + c, то трикутник є тупокутним. Якщо a = b + c, то трикутник є прямокутним. Доведення. Маємо: a = b + c bc cos α. Звідси bc cos α = b + c a. Нехай a < b + c. Тоді b + c a > 0. Отже, bc cos α > 0, тобто cos α > 0. Тому кут α гострий. Оскільки a найбільша сторона трикутника, то проти неї лежить найбільший кут, який на підставі вищедоведеного є гострим. Отже, у цьому випадку трикутник є гострокутним. Нехай a > b + c. Тоді b + c a < 0. Отже, bc cos α < < 0, тобто cos α < 0. Тому кут α тупий. 14
15 15. Теорема косинусів Нехай a = b + c. Тоді bc cos α = 0, тобто cos α = 0. Звідси α = 90. Задача. Доведіть, що сума квадратів діагоналей паралелограма дорівнює сумі квадратів усіх його сторін. Розв язання. На рисунку 8 зображено паралелограм ABCD. Нехай AB = CD = a, BC = AD = b, B b BAD = α, тоді ADC = 180 α. C З œ ABD за теоремою косинусів a a BD = a + b ab cos α. (1) З œ ACD за теоремою косинусів A b D AC = a + b ab cos (180 α) або Рис. 8 AC = a + b + ab cos α. () Додавши рівності (1) і (), отримаємо BD + AC = a + b. Приклад 1. У трикутнику ABC сторона AB на 4 см більша за сторону BC, B = 10, AC = 14 см. Знайдіть сторони AB і BC. Розв язання. За теоремою косинусів AC = AB + BC AB BC cos B. Нехай BC = x см, x > 0, тоді AB = (x + 4) см. Маємо: 14 = (x + 4) + x x (x + 4) cos 10 ; ( ) 196= x + 8x x x( x + 4) æ ; 196 = x + 8x x (x + 4); 3x + 1x 180 = 0; x + 4x 60 = 0; x 1 = 6; x = 10. Корінь x = 10 не задовольняє умову x > 0. Отже, BC = 6 см, AB = 10 см. Відповідь: 10 см, 6 см. 1 Приклад. На стороні AC трикутника ABC позначено точку D так, що CD : AD = 1 :. Знайдіть відрізок BD, якщо AB = 14 см, BC = 13 см, AC = 15 см.
16 1. Розв язування трикутників A D B M D B C Рис. 9 Рис. 10 Розв язання. За теоремою косинусів з œ ABC (рис. 9): AB = AC + BC AC BC cos C, звідси AC + BC AB cos C = = = =. ACæBC æ15æ13 æ15æ Оскільки CD : AD = 1 :, то CD = AC = 5 см. 3 Тоді з œ BCD: BD = BC + CD BCæCDæcos C = A 33 = = æ13æ5æ 18 Отже, BD = 18 = 8 (см). Відповідь: 8 см. Приклад 3. Дві сторони трикутника дорівнюють 3 см і 30 см, а медіана, проведена до більшої з відомих сторін, 10 см. Знайдіть третю сторону трикутника. Розв язання. Нехай у трикутнику ABC (рис. 10) AC = = 3 см, BC = 30 см, відрізок AM медіана, AM = 10 см. На продовженні відрізка AM за точку M відкладено відрізок MD, який дорівнює медіані AM. Тоді AD = 0 см. У чотирикутнику ABDC діагоналі AD і BC точкою M перетину діляться навпіл (BM = MC за умовою, AM = MD за побудовою). Отже, чотирикутник ABDC паралелограм. За властивістю діагоналей паралелограма маємо: AD + BC = (AB + AC ). Тоді = (AB + 3 ); = (AB + 59);. C 16
17 . Теорема косинусів AB = 11; AB = 11 см. Відповідь: 11 см.? 1. Сформулюйте теорему косинусів.. Гострокутним, прямокутним чи тупокутним є трикутник зі сторонами a, b і c, де a його найбільша сторона, якщо: 1) a < b + c ; ) a > b + c ; 3) a = b + c? 3. Як пов язані між собою діагоналі і сторони паралелограма? Вправи 8. Знайдіть невідому сторону трикутника ABC, якщо: 1) AB = 5 см, BC = 8 см, B = 60 ; ) AB = 3 см, AC = см, A = Знайдіть невідому сторону трикутника DEF, якщо: 1) DE = 4 см, DF = 3 см, D = 30 ; ) DF = 3 см, EF = 5 см, F = Сторони трикутника дорівнюють 1 см, 0 см і 8 см. Знайдіть найбільший кут трикутника. 31. Сторони трикутника дорівнюють 18 см, 5 см і 7 см. Знайдіть середній за величиною кут трикутника. 3. Установіть, гострокутним, прямокутним чи тупокутним є трикутник, сторони якого дорівнюють: 1) 5 см, 7 см і 9 см; 3) 10 см, 15 см і 18 см. ) 5 см, 1 см і 13 см; 33. Сторони трикутника дорівнюють 7 см, 8 см і 1 см. Чи є правильним твердження, що даний трикутник є гострокутним? 34. Доведіть, що трикутник зі сторонами 8 см, 15 см і 17 см є прямокутним. 35. Сторони паралелограма дорівнюють см і 5 см, а один із кутів дорівнює 45. Знайдіть діагоналі паралелограма. 17
18 1. Розв язування трикутників 36. У трапеції ABCD (BC C AD) BC = 3 см, AD = 10 см, CD = 4 см, D = 60. Знайдіть діагоналі трапеції. 37. На стороні AB рівностороннього трикутника ABC позначено точку D так, що AD : DB = : 1. Знайдіть відрізок СD, якщо AB = 6 см. 38. На гіпотенузі AB прямокутного трикутника ABC позначено точку M так, що AM : BM = 1 : 3. Знайдіть відрізок CM, якщо AC = BC = 4 см. 39. Дві сторони трикутника дорівнюють 3 см і 4 см, 35 а синус кута між ними дорівнює. Знайдіть третю сторону трикутника. Скільки розв язків має задача? У трикутнику ABC відомо, що C = 90, AC = 0 см, BC = 15 см. На стороні AB позначено точку M так, що BM = 4 см. Знайдіть довжину відрізка CM. 41. На продовженні гіпотенузи AB прямокутного рівнобедреного трикутника ABC за точку B позначено точку D так, що BD = BC. Знайдіть відрізок CD, якщо катет трикутника ABC дорівнює a. 4. У трикутнику ABC відомо, що C = 90, AB = 13 см, AC = 1 см. На продовженні гіпотенузи AB за точку B позначено точку D так, що BD = 6 см. Знайдіть довжину відрізка CD. 43. Центр кола, вписаного в прямокутний трикутник, знаходиться на відстанях a і b від кінців гіпотенузи. Знайдіть гіпотенузу трикутника. 44. Точка O центр кола, вписаного в трикутник ABC, BC = a, AC = b, AOB = 10. Знайдіть сторону AB. 45. Дві сторони трикутника, кут між якими дорівнює 60, відносяться як 5 : 8, а третя сторона дорівнює 1 см. Знайдіть невідомі сторони трикутника. 46. Дві сторони трикутника відносяться як 1 : 3 і утворюють кут у 30. Третя сторона трикутника дорівнює 7 см. Знайдіть невідомі сторони трикутника. 47. Сума двох сторін трикутника, які утворюють кут у 10, дорівнює 8 см, а довжина третьої сторони становить 7 см. Знайдіть невідомі сторони трикутника. 18
19 19. Теорема косинусів 48. Дві сторони трикутника, кут між якими дорівнює 10, відносяться як 5 : 3. Знайдіть сторони трикутника, якщо його периметр дорівнює 30 см. 49. Дві сторони трикутника дорівнюють 16 см і 14 см, а кут, протилежний меншій із відомих сторін, дорівнює 60. Знайдіть невідому сторону трикутника. 50. Дві сторони трикутника дорівнюють 15 см і 35 см, а кут, протилежний більшій із відомих сторін, дорівнює 10. Знайдіть периметр трикутника. 51. На стороні BC трикутника ABC позначено точку D так, що CD = 14 см. Знайдіть відрізок AD, якщо AB = 37 см, BC = 44 см і AC = 15 см. 5. На стороні AB трикутника ABC позначено точку K, а на продовженні сторони BC за точку C точку M. Знайдіть відрізок MK, якщо AB = 15 см, BC = 7 см, AC = 13 см, AK = 8 см, MC = 3 см. 53. Одна зі сторін трикутника у рази більша за другу, а кут між цими сторонами становить 60. Доведіть, що даний трикутник є прямокутним. 54. Доведіть, що коли квадрат сторони трикутника дорівнює неповному квадрату суми двох інших сторін, то протилежний цій стороні кут дорівнює Доведіть, що коли квадрат сторони трикутника дорівнює неповному квадрату різниці двох інших сторін, то протилежний цій стороні кут дорівнює Дві сторони паралелограма дорівнюють 7 см і 11 см, а одна з діагоналей 1 см. Знайдіть другу діагональ паралелограма. 57. Діагоналі паралелограма дорівнюють 13 см і 11 см, а одна зі сторін 9 см. Знайдіть периметр паралелограма. 58. Діагоналі паралелограма дорівнюють 8 см і 14 см, а одна зі сторін на см більша за другу. Знайдіть сторони паралелограма. 59. Сторони паралелограма дорівнюють 11 см і 3 см, а його діагоналі відносяться як : 3. Знайдіть діагоналі паралелограма.
20 1. Розв язування трикутників 60. У трапеції ABCD (AD C BC) відомо, що AB = 5 см, BC = 9 см, AD = 16 см, cos A = 1. Знайдіть сторону CD трапеції У трапеції ABCD (AD C BC) відомо, що AB = 15 см, BC = 6 см, СD = 4 см, AD = 11 см. Знайдіть косинус кута D трапеції. 6. Знайдіть діагональ AC чотирикутника ABCD, якщо навколо нього можна описати коло, і AB = 3 см, BC = 4 см, CD = 5 см, AD = 6 см. 63. Чи можна описати коло навколо чотирикутника ABCD, якщо AB = 4 см, AD = 3 см, BD = 6 см і C = 30? 64. Доведіть, що проти більшого кута паралелограма лежить більша діагональ. Сформулюйте і доведіть обернене твердження. 65. Сторони трикутника дорівнюють 1 см, 15 см і 18 см. Знайдіть бісектрису трикутника, проведену з вершини його найбільшого кута. 66. Основа рівнобедреного трикутника дорівнює 5 см, а бічна сторона 0 см. Знайдіть бісектрису трикутника, проведену з вершини кута при його основі. 67. Сторони трикутника дорівнюють 16 см, 18 см і 6 см. Знайдіть медіану трикутника, проведену до його більшої сторони. 68. Основа рівнобедреного трикутника дорівнює 4 см, а медіана, проведена до бічної сторони, 5 см. Знайдіть бічну сторону трикутника. 69. Дві сторони трикутника дорівнюють 1 см і 14 см, а медіана, проведена до третьої сторони, 7 см. Знайдіть невідому сторону трикутника. 70. У трикутнику ABC відомо, що AB = BC, ABC = = 10. На продовженні відрізка AB за точку B позначено точку D так, що BD = AB. Доведіть, що трикутник ACD рівнобедрений. 71. Доведіть, що m = 1 c a + b c, де a, b і c сторони трикутника, m c медіана трикутника, проведена до сторони c. 0
21 3. Теорема синусів Вправи для повторення 7. У колі проведено діаметр AC і хорду AB, яка дорівнює радіусу кола. Знайдіть кути трикутника ABC. 73. Один із кутів, утворених при перетині бісектриси кута паралелограма з його стороною, дорівнює одному з кутів паралелограма. Знайдіть кути паралелограма. 74. У трикутник ABC вписано паралелограм ADEF так, що кут A у них спільний, а точки D, E і F належать відповід но сторонам AB, BC і AC трикутника. Знайдіть сторони пара лелограма ADEF, якщо AB = 8 см, AC = 1 см, AD : AF = : 3. Готуємося до вивчення нової теми 75. Знайдіть кут ADC (рис. 11), якщо ABC = Знайдіть кут ABC (рис. 1), якщо ADC = 43. D B D C α B A B C A C A Рис. 11 Рис. 1 Рис Відрізок AB діаметр кола, радіус якого дорівнює R, ABC = α (рис. 13). Знайдіть хорду AC. Поновіть у пам яті зміст пункту 8 на с Теорема синусів Із другої ознаки рівності трикутників випливає, що сторона і два прилеглі до неї кути однозначно визначають трикутник. Отже, за вказаними елементами можна знайти дві інші сторони трикутника. Як це зробити, підказує така теорема. 1
22 1. Розв язування трикутників Те о р е м а 3.1 (т е о р е м а с и н у с і в). Сторони трикутника пропорційні синусам протилежних кутів. Лема. Хорда кола дорівнює добутку діаметра на синус будь-якого вписаного кута, який спирається на цю хорду. Доведення. На рисунку 14 відрізок MN хорда кола з центром у точці O. Проведемо діа P α O метр MP. Тоді MNP = 90 як α вписаний кут, що спирається на діаметр. Нехай величина вписаного кута MPN дорівнює α. Тоді M N 180 α з прямокутного трикутника MPN отримуємо Рис. 14 MN = MP sin α. (1) Усі вписані кути, які спираються на хорду MN, дорівнюють α або 180 α. Отже, їх синуси рівні. Тому отримана рівність (1) справедлива для всіх вписаних кутів, які спираються на хорду MN. Тепер ми можемо довести теорему синусів. Доведення. Нехай у трикутнику ABC відомо, що AB = c, BC = a, CA = b. Доведемо, що a b c sin A = sin B = sin C. Нехай радіус описаного кола трикутника ABC дорівнює R. Тоді за лемою a = R sin A, b = R sin B, c = R sin C. Звідси a b c = = = R sin A sin B sin C Наслідок. Радіус описаного кола трикутника можна обчислити за формулою a R = sin α, де a сторона трикутника, α протилежний їй кут.
23 3 3. Теорема синусів Приклад 1. У трикутнику ABC відомо, що AC = BC = 1 см, B = 45. Знайдіть кут A. Розв язання. За теоремою синусів Тоді маємо: BC AC sin A = sin B. sin sin sin A BC B 1æ 45 1 = = = : =. AC см, Оскільки BC < AC, то A < B. Отже, A гострий. Звідси, ураховуючи, що sin A = 1, Відповідь: 30. отримуємо A = 30. Приклад. У трикутнику ABC відомо, що AC = BC = 1 см, A = 30. Знайдіть кут B. Розв язання. Маємо: BC AC sin A = sin B, см, sin B = AC sin A =. BC Оскільки BC < AC, то A < B. Тоді кут B може бути як гострим, так і тупим. Звідси B = 45 або B = = 135. Відповідь: 45 або 135. Приклад 3. На стороні AB трикутника ABC (рис. 15) позначено точку D так, що BDC = γ, AD = m. Знайдіть BD, якщо A = α, B = β. Розв язання. BDC зовнішній кут трикутника ADC. Тоді ACD + C + A = BDC, звідси ACD = γ α. З ADC за теоремою синусів: CD AD =. sin CAD sin ACD AD sin CAD m sin α Отже, CD = = sin ACD sin( γ α). A α m D γ Рис. 15 β B
24 1. Розв язування трикутників З œ BCD: BD CD = ; sin BCD sin CBD CD sin BCD m sinαsin ( 180 ( β+ γ)) m sin α sin( β+ γ) BD = = = sin CBD sinβsin ( γ α) sinβsin ( γ α). Відповідь: m sinαsin ( β+ γ). sinβsin ( γ α) Приклад 4. Відрізок BD бісектриса трикутника ABC, B = 30, C = 105. Знайдіть радіус кола, описаного навколо трикутника ABC, якщо радіус кола, описаного навколо трикутника BDC, дорівнює 8 6 см. Розв язання. Нехай R 1 радіус кола, описаного навколо трикутника BDC (рис. 16), R 1 = 8 6 см. C 1 CBD= ABC = 15. D З œ BDC: BDC = 180 ( CBD + C) = A B = 180 ( ) = 60. Рис. 16 BC Тоді = R, sin BDC 1 звідси BC = R1 sin BDC = æ 8 6 sin 60 = 4 (см). З œ ABC: A = 180 ( ABC + C) = 180 ( ) = 45. Нехай R шуканий радіус кола, описаного навколо трикутника ABC. Тоді BC BC 4 = R, звідси R = = = 4 (см). sin A sin A sin 45 Відповідь: 4 см.? 1. Як знайти хорду кола, якщо відомо діаметр кола і вписаний кут, який спирається на цю хорду?. Сформулюйте теорему синусів. 3. Як знайти радіус кола, описаного навколо трикутника зі стороною a і протилежним цій стороні кутом α? 4
25 3. Теорема синусів Вправи 78. Знайдіть сторону BC трикутника ABC, зображеного на рисунку 17 (довжини відрізків дано в сантиметрах). 79. Знайдіть кут A трикутника ABC, зображеного на рисунку 18 (довжини відрізків дано в сантиметрах). B A C Рис. 17 Рис Знайдіть сторону AB трикутника ABC, якщо AC = 6 см, B = 10, C = У трикутнику ABC відомо, що AB = 1 см, BC = = 10 см, sin A = 0,. Знайдіть синус кута C трикутника. 8. У трикутнику DEF відомо, що DE = 16 см, F = = 50, D = 38. Знайдіть невідомі сторони трикутника. 83. У трикутнику MKP відомо, що KP = 8 см, K = = 106, P = 3. Знайдіть невідомі сторони трикутника. 84. Для знаходження відстані від точки A до дзвіниці B, яка розташована на іншому березі річки (рис. 19), за допомогою віх, рулетки і приладу для вимірювання кутів (теодоліту) позначили на місцевості точку C таку, що BAC = 4, ACB = 64, AC = 0 м. Як знайти відстань від A до B? Знайдіть цю відстань. 85. У трикутнику ABC відомо, що BС = a, A = = α, C = γ. Знайдіть AB і AC. Рис A 6 B 6 45 C
26 1. Розв язування трикутників 86. Діагональ паралелограма дорівнює d і утворює з його сторонами кути α і β. Знайдіть сторони паралелограма. 87. Знайдіть кут A трикутника ABC, якщо: 1) AC = см, BC = 1 см, B = 135 ; ) AC = см, BC = 3 см, B = 45. Скільки розв язків у кожному з випадків має задача? Відповідь обґрунтуйте. 88. Чи існує трикутник ABC такий, що sin A = 0,4, AC = 18 см, BC = 6 см? Відповідь обґрунтуйте. 89. У трикутнику DEF відомо, що DE = 8 см, sin F = 0,16. Знайдіть радіус кола, описаного навколо трикутника DEF. 90. Радіус кола, описаного навколо трикутника MKP, дорівнює 5 см, sin M = 0,7. Знайдіть сторону KP. 91. На продовженні сторони AB трикутника ABC за точку B позначено точку D. Знайдіть радіус кола, описаного навколо трикутника ACD, якщо ABC = 60, ADC = 45, а радіус кола, описаного навколо трикутника ABC, дорівнює 4 см. 9. Радіус кола, описаного навколо трикутника ABC, дорівнює 6 см. Знайдіть радіус кола, описаного навколо трикутника AOC, де O точка перетину бісектрис трикутника ABC, якщо ABC = За рисунком 0 знайдіть AD, якщо CD = a. 94. За рисунком 1 знайдіть AC, якщо BD = m. B β A C a D γ A Рис. 0 Рис На стороні AB трикутника ABC позначено точку M так, що AMC = ϕ. Знайдіть відрізок CM, якщо AB = c, A = α, ACB = γ. 96. У трикутнику ABC відомо, що A = α, B = β. На стороні BC позначено точку D так, що ADB = ϕ, AD = m. Знайдіть сторону BC. 6 C α B β m D
27 3. Теорема синусів 97. Доведіть, що бісектриса трикутника поділяє його сторону на відрізки, довжини яких обернено пропорційні синусам прилеглих до цієї сторони кутів. 98. Дві сторони трикутника дорівнюють 6 см і 1 см, а висота, проведена до третьої сторони, 4 см. Знайдіть радіус кола, описаного навколо даного трикутника. 99. Знайдіть радіус кола, описаного навколо рівно бедреного трикутника з основою 16 см і бічною стороною 10 см Сторона трикутника дорівнює 4 см, а радіус описаного кола 8 3 см. Чому дорівнює кут трикутника, протилежний даній стороні? 101. Траса для велосипедистів має форму трикутника, два кути якого дорівнюють 50 і 100. Меншу сторону цього трикутника один із велосипедистів проїжджає за 1 год. За який час він проїде всю трасу? Відповідь подайте у годинах із точністю до десятих. 10. У трикутнику ABC AC = b, A = α, C = γ. Знайдіть бісектрису BD трикутника Основа рівнобедреного трикутника дорівнює a, протилежний їй кут дорівнює α. Знайдіть бісектрису трикутника, проведену з вершини кута при основі Доведіть, користуючись теоремою синусів, що бісектриса трикутника поділяє його сторону на відрізки, довжини яких пропорційні прилеглим сторонам Основи рівнобічної трапеції дорівнюють 9 см і 1 см, а висота 8 см. Знайдіть радіус кола, описаного навколо трапеції Відрізок CD бісектриса трикутника ABC, у якому A = α, B = β. Через точку D проведено пряму, яка паралельна стороні BC і перетинає сторону AC у точці E, причому AE = a. Знайдіть CE Медіана AM трикутника ABC дорівнює m і утворює зі сторонами AB і AC кути α і β відповідно. Знайдіть сторони AB і AC. 1 Нагадаємо, що цей факт з використанням теореми про пропорційні відрізки було доведено в підручнику: А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. «Геометрія. 8 клас». Х.: Гімназія, с. 7
28 1. Розв язування трикутників 108. Медіана CD трикутника ABC утворює зі сторонами AC і BC кути α і β відповідно, BC = a. Знайдіть медіану CD Висоти гострокутного трикутника ABC перетинаються в точці H. Доведіть, що радіуси кіл, описаних навколо трикутників AHB, BHC, AHC і ABC, рівні Дороги, які сполучають села A, B і C (рис. ), утворюють трикутник, причому дорога із села A до села C заасфальтована, а дороги із села A до села B та із села B до села C ґрунтові. Дороги із села A до сіл B і C утворюють кут у 15, а дороги із села B до сіл A і C кут у 5. Швидкість руху автомобіля по асфальтованій дорозі у рази більша за швидкість його руху по ґрунтовій. Який шлях обрати водію автомобіля, щоб якнайшвидше дістатися із села A до села B? A B C Рис Дороги із сіл A і B сходяться біля розвилки C (рис. 3). Дорога із села A до розвилки утворює з дорогою в село B кут у 30, а дорога із села B з дорогою в село A кут у 70. Одночасно із села A до розвилки виїхав автомобіль зі швидкістю 90 км/год, а із села B автобус зі швидкістю 60 км/год. Хто з них першим доїде до розвилки? A B C Рис. 3 8
29 4. Розв язування трикутників Вправи для повторення 11. Бісектриси кутів B і C прямокутника ABCD перетинають сторону AD B у точках M і K відповідно. Доведіть, що F BM = CK. D M E 113. На рисунку 4 DE C AC, FK C AB. A K C Укажіть, які трикутники на цьому рисунку подібні. Рис На стороні AB квадрата ABCD позначено точку K, а на стороні CD точку M так, що AK : KB = 1 :, DM : MC = 3 : 1. Знайдіть сторону квадрата, якщо MK = 13 см. Готуємося до вивчення нової теми 115. Розв яжіть прямокутний трикутник: 1) за двома катетами a = 7 см і b = 35 см; ) за гіпотенузою c = 17 см і катетом a = 8 см; 3) за гіпотенузою c = 4 см і гострим кутом α = 50 ; 4) за катетом a = 8 см і протилежним кутом α = 4. Поновіть у пам яті зміст пункту 15 на с Розв язування трикутників Розв язати трикутник це означає знайти невідомі його сторони і кути за відомими сторонами і кутами. У 8 класі ви навчилися розв язувати прямокутні трикутники. Теореми косинусів і синусів дозволяють розв язати будь-який трикутник. b γ a П р и к л а д 1. Розв яжіть трикутник (рис. 5) за стороною a = 1 см і двома α β кутами β = 36, γ = 119. c Рис. 5 Розв язання. Маємо: α = 180 (β + γ) = = 5. 9
30 1. Розв язування трикутників За теоремою синусів: b a = sinβ sin α ; a sinβ 1 sin 36 1æ0588, b = = 16, 7 (см); sin α sin 5 0, 43 c a = sinγ sin α ; a sin γ 1 sin sin 61 1æ0875, c = = = 48, (см). sin α sin 5 sin 5 0, 43 Відповідь: b 16,7 см, c 4,8 см; α = 5. Зауважимо, що значення тригонометричних функцій знайдено за таблицею, розміщеною на с. 68 підручника. Їх також можна було знайти за допомогою мікрокалькулятора. П р и к л а д. Розв яжіть трикутник (рис. 5) за двома сторонами a = 14 см, b = 8 см і кутом γ = 38 між ними. Розв язання. За теоремою косинусів: c = a + b ab cos γ = cos ,788 = 83,488; с 9,1 см. Далі маємо: a = b + c bc cos α; b + c a cos α= 0, 338. bc Знайдемо кут α 1 такий, що cos α 1 = 0,338. Число 0,338 відсутнє в таблиці значень косинуса, найближчим до нього є число 0,34. Тоді отримуємо α Звідси α = 180 α β = 180 (α + γ) = 3. Відповідь: c 9,1 см, α 110, β 3. П р и к л а д 3. Розв яжіть трикутник (рис. 5) за трьома сторонами a = 7 см, b = см, c = 8 см. Розв язання. Маємо: a = b + c bc cos α, звідси b + c a cos α= = 0594,. Тоді α 54. bc ææ8 a b = sinα sin β, b sinα sin 54 æ0, 809 sin β = 031,. a
31 31 4. Розв язування трикутників Оскільки b є найменшою стороною даного трикутника, то кут β є гострим, β 13. Тоді γ = 180 (α + β) = 113. Відповідь: α 54, β 13, γ 113. П р и к л а д 4. Розв яжіть трикутник (рис. 5) за двома сторонами і кутом, який протилежний одній зі сторін: 1) a = 17 см, b = 6 см, α = 156 ; ) b = 7 см, c = 8 см, β = 65 ; 3) a = 6 см, b = 5 см, β = 50. Розв язання a b 1) = sinα sin β, b sinα 6 sin sin 4 6æ0, 407 sin β = = = 0144,. a Оскільки кут α даного трикутника тупий, то кут β є гострим, β 8. Тоді γ = 180 (α + β) 16. a c = sinα sin γ, a sin γ a sin 16 17æ076, c = 11, 5 (см). sin α sin , Відповідь: β 8, γ 16, c 11,5 см. b c ) = sinβ sin γ, c sinβ 8 sin 65 8æ0, 906 sin γ = = 1, 035 > 1, b 7 7 що неможливо. Відповідь: задача не має розв язку. a b 3) = sinα sin β, a sinβ 6 sin 50 6æ0, 766 sin α = = 0919,. b 5 5 Можливі два випадки: α 67 або α = 113. Розглянемо випадок, коли α 67 : γ = 180 (α + β) = 63 ; b c = sinβ sin γ, b sin γ 5sin 63 5æ0, 891 c = 58, (см). sinβ sin , При α 113 отримуємо: γ = 180 (α + β) = 17 ; b sin γ 5sin 17 5æ0, 9 c = 19, (см). sin β sin , Відповідь: α 67, γ 63, c 5,8 см або α 113, γ 17, c 1,9 см.
32 1. Розв язування трикутників? Що означає розв язати трикутник? Вправи 116. Розв яжіть трикутник за стороною і двома кутами 1 : 1) a = 10 см, β = 0, γ = 85 ; ) b = 16 см, α = 40, β = Розв яжіть трикутник за стороною і двома кутами: 1) b = 9 см, α = 35, γ = 70 ; ) c = 14 см, β = 13, γ = Розв яжіть трикутник за двома сторонами і кутом між ними: 1) b = 18 см, c = см, α = 76 ; ) a = 0 см, b = 15 см, γ = Розв яжіть трикутник за двома сторонами і кутом між ними: 1) a = 8 см, c = 6 см, β = 15 ; ) b = 7 см, c = 5 см, α = Розв яжіть трикутник за трьома сторонами: 1) a = 4 см, b = 5 см, c = 7 см; ) a = 6 см, b = 19 см, c = 4 см. 11. Розв яжіть трикутник за трьома сторонами: 1) a = 5 см, b = 6 см, c = 8 см; ) a = 1 см, b = 17 см, c = 3 см. 1. Розв яжіть трикутник, у якому: 1) a = 10 см, b = 3 см, β = 10, кут α гострий; ) a = 10 см, b = 3 см, β = 10, кут α тупий. 13. Розв яжіть трикутник за двома сторонами і кутом, який лежить проти однієї із даних сторін: 1) a = 7 см, b = 11 см, β = 46 ; ) b = 15 см, c = 17 см, β = 3 ; 3) a = 7 см, c = 3 см, γ = 7. 1 У задачах прийнято позначення: a, b і c сторони трикутника, α, β і γ кути, протилежні відповідно сторонам a, b і c. 3
33 4. Розв язування трикутників 14. Розв яжіть трикутник за двома сторонами і кутом, який лежить проти однієї із даних сторін: 1) a = 3 см, c = 30 см, γ = 10 ; ) a = 18 см, b = 5 см, α = У трикутнику ABC відомо, що AB = BC = 0 см, A = = 70. Знайдіть: 1) сторону AC; ) медіану CM; 3) бісектрису AD; 4) радіус описаного кола трикутника ABC. 16. Діагональ AC рівнобічної трапеції ABCD (BC C AD) дорівнює 8 см, CAD = 38, BAD = 7. Знайдіть: 1) сторони трапеції; ) радіус описаного кола трикутника ABC. 17. Основи трапеції дорівнюють 1 см і 16 см, а бічні сторони 7 см і 9 см. Знайдіть кути трапеції. Вправи для повторення 18. Бісектриса кута B паралелограма ABCD перетинає його сторону AD у точці M, а продовження сторони CD за точку D у точці K. Знайдіть довжину відрізка DK, якщо AM = 8 см, а периметр паралелограма дорівнює 50 см. 19. Периметр одного з двох подібних трикутників на 18 см менший від периметра другого трикутника, а найбільші сторони цих трикутників дорівнюють 5 см і 8 см. Знайдіть периметри даних трикутників. Готуємося до вивчення нової теми 130. Точка M середина сторони CD прямокутника ABCD (рис. 6), AB = 6 см, AD = 5 см. Чому дорівнює площа трикутника ACM? 131. На стороні AC трикутника ABC позначено точку D так, що ADB = α. Доведіть, що площа трикутника ABC S= 1 ACæBD sin α. B A Рис. 6 C M D Поновіть у пам яті зміст пункту 17 на с
34 1. Розв язування трикутників Коли зроблено уроки Тригонометрія наука про вимірювання трикутників Ви знаєте, що стародавні мандрівники орієнтувалися за зірками і планетами. Вони могли досить точно визначити місцезнаходження корабля в океані або каравану в пустелі за розташуванням світил на небосхилі. При цьому одним з орієнтирів була висота, на яку піднімалося над горизонтом те або інше небесне світило в даній місцевості у даний момент часу. Зрозуміло, що безпосередньо виміряти цю висоту неможливо. Тому вчені стали розробляти методи непрямих вимірювань. Тут суттєву роль відігравало розв язування трикутника, дві вершини якого лежали на поверхні Землі, а третя була зіркою або планетою (рис. 7) знайома вам задача 94. Для розв язування подібних задач стародавнім астрономам необхідно було навчитися знаходити взаємозв язки між елементами трикутника. Так виникла тригонометрія наука, яка вивчає залежність між сторонами і кутами трикутника. Термін «три го но метрія» (від грецьких слів «тригоном» трикутник і «метрео» вимірювати) означає «вимірювання три кут ників». На рисунку 8 зображено центральний кут AOB, який дорівнює α. З прямокутного трикутника OMB маємо: MB = OB sin α. Отже, якщо в одиничному колі виміряти половини довжин хорд, на які спираються центральні кути з величинами, 4, 6,..., 180, то таким чином ми обчислимо значення синусів кутів 1,, 3,..., 90 відповідно. h Вимірюючи довжини півхорд, давньогрецький астро β α γ ном Гіппарх (ІІ ст. до н. е.) A B склав перші тригонометричні Рис. 7 таблиці. 34
35 Коли зроблено уроки Поняття «синус» і «косинус» з являються в тригонометричних трактатах індійських учених у ІV V ст. У Х ст. арабські вчені оперували поняттям «тангенс», яке виникло з потреб гномоніки учення про сонячний годинник (рис. 9). A O αα M B Рис. 8 Рис. 9 У Європі перший трактат з тригонометрії «П ять книг про трикутники всіх видів», автором якого був німецький учений Регіомонтан ( ), було опубліковано в 1533 р. Він же відкрив і теорему тангенсів: a b = tg α β, a+ b α+ β tg b c = tg β γ, b+ c β+ γ tg c a = tg γ α, c+ a γ + α tg де a, b і c сторони трикутника, α, β і γ кути трикутника, протилежні відповідно сторонам a, b і c. Сучасного вигляду тригонометрія набула в роботах видатного математика Леонарда Ейлера. Леонард Ейлер ( ) Видатний математик, фізик, механік, астроном 35
36 1. Розв язування трикутників 5. Формули для знаходження площі трикутника З курсу геометрії 8 класу ви дізналися, що площу S трикутника можна обчислити за формулами S= aha = bhb = chc, де a, b і c сторони трикутника, h a, h b, h c висоти, проведені до цих сторін відповідно. Тепер у нас з явилася можливість отримати ще кілька формул для знаходження площі трикутника. Теорема 5.1. Площа трикутника дорівнює півдобутку двох його сторін і синуса кута між ними. Доведення. Доведемо, що площу S трикутника ABC можна обчислити за формулою S = 1 ab sin γ, де a і b сторони трикутника, γ кут між ними. Можливі три випадки: 1) кут γ гострий (рис. 30); ) кут γ тупий (рис. 31); 3) кут γ прямий. На рисунках 30 і 31 проведемо висоту BD трикутника 1 1 ABC. Тоді S= BDæAC= BDæ b. B B A a a γ γ 180 γ C b D A b C D Рис. 30 Рис
37 5. Формули для знаходження площі трикутника З œ BDC у першому випадку BD = a sin γ, а у другому BD = a sin (180 γ) = a sin γ. Звідси для двох перших випадків маємо S= 1 ab sin γ. Якщо кут C прямий, то sin γ = 1. Для прямокутного трикутника ABC з катетами a і b маємо: S= ab= absin90 = ab sin γ. Т е о р е м а 5. (ф о р м у л а Г е р о н а 1 ). Площу S трикутника ABC можна обчислити за формулою S = p( p a)( p b)( p c), де a, b, c сторони трикутника, p його півпе ри метр. Доведення. Маємо: S= 1 ab sin γ. 1 Звідси S = a b sin γ. 4 За теоремою косинусів c = a + b ab cos γ. a + b c Звідси cos γ=. ab Оскільки sin γ = 1 cos γ = (1 cos γ) (1 + cos γ), то маємо: 1 S = a b ( 1 cos γ)( 1+ cos γ) = 4 ( )( + ) 1 a + b c a + b c = ab 1 1 = 4 ab ab = 1 ab 4 ab a b + c ab + a + b c æ æ ab ab ( )( + ) 1 = c ( a b) ( a b) c = 16 c a+ b c+ a b a+ b c a+ b+ c = æ æ æ = = 1 Ге р о н А л е к с а н д р і й с ь к и й давньогрецький учений, який жив у І ст. н. е. 37
38 1. Розв язування трикутників ( a+ b+ c) a ( a+ b+ c) b ( a+ b+ c) c a+ b+ c = æ æ æ = = p a p b p c p æ æ æ = p( p a)( p b)( p c). Звідси S= p( p a)( p b)( p c). Т е о р е м а 5.3. Площу S трикутника ABC можна обчислити за формулою S = abc, 4 R де a, b, c сторони трикутника, R радіус описаного кола трикутника ABC. Доведення. Маємо: S= 1 bc sin α. Із леми пункту 3 випливає, що sin α= a. Тоді R a abc S= 1 1 bcsin α= bcæ =. R 4R Зауважимо, що доведена теорема дає змогу знаходити радіус описаного кола трикутника за формулою R abc = 4S Т е о р е м а 5.4. Площа трикутника дорівнює добутку його півпериметра на радіус вписаного кола. Доведення. На рисунку 3 зображено трикутник ABC, у який вписано коло радіуса r. Доведемо, що A M B P O N Рис. 3 C 38 S = pr, де S площа даного трикутника, p його півпери метр. Нехай точка O центр вписаного кола, яке дотикається до сто рін трикутника ABC у точках M, N і P. Площа трикутника ABC до
39 5. Формули для знаходження площі трикутника рівнює сумі площ трикутників AOB, BOC, COA. Це зручно записати в такій формі: S = S AOB + S BOC + S COA. Проведемо радіуси в точки дотику. Отримуємо: OM AB, ON BC, OP CA. Звідси: S = 1 AOB OM AB = 1 æ ræ AB; S = 1 BOC ON BC = 1 æ ræ BC; S = 1 COA OP AC = 1 æ ræ AC AB + BC + AC Отже, S= ræab + ræbc+ ræac = ræ = pr. Вищезазначене узагальнює така теорема. Т е о р е м а 5.5. Площа описаного многокутника дорівнює добутку його півпериметра на радіус вписаного кола. Доведіть цю теорему самостійно (рис. 33). Зауважимо, що теорема 5.5 дає змогу знаходити радіус вписаного кола многокутника за формулою r S = p З а д а ч а 1. Доведіть, що площу S паралелограма можна обчислити за формулою S = ab sin α, де a і b сусідні сторони паралелограма, α кут між ними. Розв язання. Розглянемо паралелограм ABCD, у якому AB = B C = a, AD = b, BAD = α (рис. 34). a Проведемо діагональ BD. Оскільки α œ ABD = œ CBD, то запишемо: A b D SABCD = SABD = æ 1 ab sinα = ab sin α. Рис Рис. 33
40 1. Розв язування трикутників C Задача. Доведіть, що площа B опуклого чотирикутника дорівнює півдобутку його діагоналей і синуса кута ϕ O між ними. A Розв язання. Нехай кут між діагоналями AC і BD чотирикутника ABCD D Рис. 35 дорівнює ϕ. На рисунку 35 AOB = ϕ. Тоді BOC = AOD = 180 ϕ і COD = ϕ. Маємо: S ABCD = S AOB + S BOC + S COD + S DOA = = 1 1 OBæOAæsinϕ+ OBæOCæsin ( 180 ϕ) OCæODæsinϕ+ ODæOAæsin ( 180 ϕ ) = 1 1 = OB( OA + OC) æsin ϕ+ OD( OC + OA) æsin ϕ= = 1 1 OBæACæsinϕ+ ODæACæsin ϕ= 1 1 = AC( OB + OD) æsinϕ= ACæBDæsin ϕ. Приклад. Сторони трикутника дорівнюють 17 см, 65 см і 80 см. Знайдіть найменшу висоту трикутника, радіуси його вписаного і описаного кіл. Розв язання. Нехай a = 17 см, b = 65 см, c = 80 см Півпериметр трикутника p = = 81 (см), його площа S= p( p a)( p b)( p c) = 81( 81 17)( 81 65)( 81 80) = = 81æ64æ16 = 9ææ 8 4 = 88 (см ). Найменшою висотою трикутника є висота h, проведена до його найбільшої сторони c. Оскільки S = 1 ch, то h S 88 = = æ = 7, (см). c 80 40
41 S Радіус вписаного кола r = p = = Радіус описаного кола 5. Формули для знаходження площі трикутника 3 9 (см). R abc 17æ65æ80 17æ65æ5 = = = = 4S 4æ88 4æ (см). Відповідь: 7, см, 3 9 см, см.? 1. Як можна знайти площу трикутника, якщо відомо дві його сторони і кут між ними?. Запишіть формулу Герона для обчислення площі трикутника. 3. Як можна знайти площу трикутника, якщо відомо три його сторони і радіус описаного кола? 4. Як можна знайти площу трикутника, якщо відомо три його сторони і радіус вписаного кола? 5. Як можна знайти радіус описаного кола трикутника, якщо відомо площу трикутника і його сторони? 6. Як можна знайти радіус вписаного кола трикутника, якщо відомо площу трикутника і його сторони? 7. Чому дорівнює площа описаного многокутника? Вправи 13. Знайдіть площу трикутника ABC, якщо: 1) AB = 1 см, AC = 9 см, A = 30 ; ) AC = 3 см, BC = 6 см, C = Знайдіть площу трикутника DEF, якщо: 1) DE = 7 см, DF = 8 см, D = 60 ; ) DE = 10 см, EF = 6 см, E = Площа трикутника MKN дорівнює 75 см. Знайдіть сторону MK, якщо KN = 15 см, K = Знайдіть кут між даними сторонами трикутника ABC, якщо: 1) AB = 1 см, BC = 10 см, площа трикутника дорівнює 30 3 см ; 41
42 1. Розв язування трикутників ) AB = 14 см, AC = 8 см, площа трикутника дорівнює 56 см Площа трикутника ABC дорівнює 18 см, AC = 8 см, BC = 9 см. Знайдіть кут C Знайдіть площу рівнобедреного трикутника з бічною стороною 16 см і кутом 15 при основі Знайдіть площу трикутника зі сторонами: 1) 13 см, 14 см, 15 см; ) см, 3 см, 4 см Знайдіть площу трикутника зі сторонами: 1) 9 см, 10 см, 17 см; ) 4 см, 5 см, 7 см Знайдіть найменшу висоту трикутника зі сторонами 13 см, 0 см і 1 см Знайдіть найбільшу висоту трикутника зі сторонами 11 см, 5 см і 30 см. 14. Периметр трикутника дорівнює 3 см, а радіус вписаного кола 1,5 см. Знайдіть площу трикутника Площа трикутника дорівнює 84 см, а його периметр 7 см. Знайдіть радіус вписаного кола трикутника Знайдіть радіуси вписаного та описаного кіл трикутника зі сторонами: 1) 5 см, 5 см і 6 см; ) 5 см, 9 см і 36 см Знайдіть радіуси вписаного та описаного кіл трикутника зі сторонами 6 см, 5 см і 9 см Знайдіть площу паралелограма за його сторонами a і b та кутом α між ними, якщо: 1) a = 5 см, b = 9 см, α = 45 ; ) a = 10 см, b = 18 см, α = Чому дорівнює площа паралелограма, сторони якого дорівнюють 7 см і 1 см, а один із кутів 10? 148. Знайдіть площу ромба зі стороною 9 3 см і кутом Діагоналі опуклого чотирикутника дорівнюють 8 см і 1 см, а кут між ними 30. Знайдіть площу чотирикутника Знайдіть площу опуклого чотирикутника, діагоналі якого дорівнюють 3 3 см і 4 см, а кут між ними 60. 4
Problem A. Nanoassembly
 Problem A. Nanoassembly 2.5 seconds One of the problems of creating elements of nanostructures is the colossal time necessary for the construction of nano-parts from separate atoms. Transporting each of
Problem A. Nanoassembly 2.5 seconds One of the problems of creating elements of nanostructures is the colossal time necessary for the construction of nano-parts from separate atoms. Transporting each of
Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation
 988 Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation High School of Transport "Todor Kableshkov" 1574 Sofia, 158 Geo Milev str. Ivan Velev Abstract
988 Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation High School of Transport "Todor Kableshkov" 1574 Sofia, 158 Geo Milev str. Ivan Velev Abstract
San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS
 San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS Recall that the bisector of an angle is the ray that divides the angle into two congruent angles. The most important results about angle bisectors
San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS Recall that the bisector of an angle is the ray that divides the angle into two congruent angles. The most important results about angle bisectors
CHAPTER 8 QUADRILATERALS. 8.1 Introduction
 CHAPTER 8 QUADRILATERALS 8.1 Introduction You have studied many properties of a triangle in Chapters 6 and 7 and you know that on joining three non-collinear points in pairs, the figure so obtained is
CHAPTER 8 QUADRILATERALS 8.1 Introduction You have studied many properties of a triangle in Chapters 6 and 7 and you know that on joining three non-collinear points in pairs, the figure so obtained is
Geometry Handout 2 ~ Page 1
 1. Given: a b, b c a c Guidance: Draw a line which intersects with all three lines. 2. Given: a b, c a a. c b b. Given: d b d c 3. Given: a c, b d a. α = β b. Given: e and f bisect angles α and β respectively.
1. Given: a b, b c a c Guidance: Draw a line which intersects with all three lines. 2. Given: a b, c a a. c b b. Given: d b d c 3. Given: a c, b d a. α = β b. Given: e and f bisect angles α and β respectively.
QUADRILATERALS CHAPTER 8. (A) Main Concepts and Results
 CHAPTER 8 QUADRILATERALS (A) Main Concepts and Results Sides, Angles and diagonals of a quadrilateral; Different types of quadrilaterals: Trapezium, parallelogram, rectangle, rhombus and square. Sum of
CHAPTER 8 QUADRILATERALS (A) Main Concepts and Results Sides, Angles and diagonals of a quadrilateral; Different types of quadrilaterals: Trapezium, parallelogram, rectangle, rhombus and square. Sum of
Quadrilateral Geometry. Varignon s Theorem I. Proof 10/21/2011 S C. MA 341 Topics in Geometry Lecture 19
 Quadrilateral Geometry MA 341 Topics in Geometry Lecture 19 Varignon s Theorem I The quadrilateral formed by joining the midpoints of consecutive sides of any quadrilateral is a parallelogram. PQRS is
Quadrilateral Geometry MA 341 Topics in Geometry Lecture 19 Varignon s Theorem I The quadrilateral formed by joining the midpoints of consecutive sides of any quadrilateral is a parallelogram. PQRS is
CIRCLE THEOREMS. Edexcel GCSE Mathematics (Linear) 1MA0
 Edexcel GCSE Mathematics (Linear) 1MA0 CIRCLE THEOREMS Materials required for examination Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser. Tracing paper may
Edexcel GCSE Mathematics (Linear) 1MA0 CIRCLE THEOREMS Materials required for examination Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser. Tracing paper may
Angles in a Circle and Cyclic Quadrilateral
 130 Mathematics 19 Angles in a Circle and Cyclic Quadrilateral 19.1 INTRODUCTION You must have measured the angles between two straight lines, let us now study the angles made by arcs and chords in a circle
130 Mathematics 19 Angles in a Circle and Cyclic Quadrilateral 19.1 INTRODUCTION You must have measured the angles between two straight lines, let us now study the angles made by arcs and chords in a circle
IMO Geomety Problems. (IMO 1999/1) Determine all finite sets S of at least three points in the plane which satisfy the following condition:
 IMO Geomety Problems (IMO 1999/1) Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points A and B in S, the perpendicular bisector
IMO Geomety Problems (IMO 1999/1) Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points A and B in S, the perpendicular bisector
Assignments in Mathematics Class IX (Term 2) 8. QUADRILATERALS
 Assignments in Mathematics Cass IX (Term 2) 8. QUADRILATERALS IMPORTANT TERMS, DEFINITIONS AND RESULTS Sum of the anges of a quadriatera is 360. A diagona of a paraeogram divides it into two congruent
Assignments in Mathematics Cass IX (Term 2) 8. QUADRILATERALS IMPORTANT TERMS, DEFINITIONS AND RESULTS Sum of the anges of a quadriatera is 360. A diagona of a paraeogram divides it into two congruent
http://www.castlelearning.com/review/teacher/assignmentprinting.aspx 5. 2 6. 2 1. 10 3. 70 2. 55 4. 180 7. 2 8. 4
 of 9 1/28/2013 8:32 PM Teacher: Mr. Sime Name: 2 What is the slope of the graph of the equation y = 2x? 5. 2 If the ratio of the measures of corresponding sides of two similar triangles is 4:9, then the
of 9 1/28/2013 8:32 PM Teacher: Mr. Sime Name: 2 What is the slope of the graph of the equation y = 2x? 5. 2 If the ratio of the measures of corresponding sides of two similar triangles is 4:9, then the
Class-10 th (X) Mathematics Chapter: Tangents to Circles
 Class-10 th (X) Mathematics Chapter: Tangents to Circles 1. Q. AB is line segment of length 24 cm. C is its midpoint. On AB, AC and BC semicircles are described. Find the radius of the circle which touches
Class-10 th (X) Mathematics Chapter: Tangents to Circles 1. Q. AB is line segment of length 24 cm. C is its midpoint. On AB, AC and BC semicircles are described. Find the radius of the circle which touches
Russian Introductory Course
 Russian Introductory Course Natasha Bershadski Learn another language the way you learnt your own Succeed with the and learn another language the way you learnt your own Developed over 50 years, the amazing
Russian Introductory Course Natasha Bershadski Learn another language the way you learnt your own Succeed with the and learn another language the way you learnt your own Developed over 50 years, the amazing
DEFINITIONS. Perpendicular Two lines are called perpendicular if they form a right angle.
 DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
Section 8.8. 1. The given line has equations. x = 3 + t(13 3) = 3 + 10t, y = 2 + t(3 + 2) = 2 + 5t, z = 7 + t( 8 7) = 7 15t.
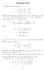 . The given line has equations Section 8.8 x + t( ) + 0t, y + t( + ) + t, z 7 + t( 8 7) 7 t. The line meets the plane y 0 in the point (x, 0, z), where 0 + t, or t /. The corresponding values for x and
. The given line has equations Section 8.8 x + t( ) + 0t, y + t( + ) + t, z 7 + t( 8 7) 7 t. The line meets the plane y 0 in the point (x, 0, z), where 0 + t, or t /. The corresponding values for x and
CHAPTER 1. LINES AND PLANES IN SPACE
 CHAPTER 1. LINES AND PLANES IN SPACE 1. Angles and distances between skew lines 1.1. Given cube ABCDA 1 B 1 C 1 D 1 with side a. Find the angle and the distance between lines A 1 B and AC 1. 1.2. Given
CHAPTER 1. LINES AND PLANES IN SPACE 1. Angles and distances between skew lines 1.1. Given cube ABCDA 1 B 1 C 1 D 1 with side a. Find the angle and the distance between lines A 1 B and AC 1. 1.2. Given
UNDERGRADUATE STUDY SKILLS GUIDE 2014-15
 SCHOOL OF SLAVONIC AND EAST EUROPEAN STUDIES UNDERGRADUATE STUDY SKILLS GUIDE 2014-15 ECONOMICS AND BUSINESS HISTORY LANGUAGES AND CULTURE POLITICS AND SOCIOLOGY 1 1. AN INTRODUCTION TO STUDY SKILLS 5
SCHOOL OF SLAVONIC AND EAST EUROPEAN STUDIES UNDERGRADUATE STUDY SKILLS GUIDE 2014-15 ECONOMICS AND BUSINESS HISTORY LANGUAGES AND CULTURE POLITICS AND SOCIOLOGY 1 1. AN INTRODUCTION TO STUDY SKILLS 5
www.pioneermathematics.com
 Problems and Solutions: INMO-2012 1. Let ABCD be a quadrilateral inscribed in a circle. Suppose AB = 2+ 2 and AB subtends 135 at the centre of the circle. Find the maximum possible area of ABCD. Solution:
Problems and Solutions: INMO-2012 1. Let ABCD be a quadrilateral inscribed in a circle. Suppose AB = 2+ 2 and AB subtends 135 at the centre of the circle. Find the maximum possible area of ABCD. Solution:
http://jsuniltutorial.weebly.com/ Page 1
 Parallelogram solved Worksheet/ Questions Paper 1.Q. Name each of the following parallelograms. (i) The diagonals are equal and the adjacent sides are unequal. (ii) The diagonals are equal and the adjacent
Parallelogram solved Worksheet/ Questions Paper 1.Q. Name each of the following parallelograms. (i) The diagonals are equal and the adjacent sides are unequal. (ii) The diagonals are equal and the adjacent
5 VECTOR GEOMETRY. 5.0 Introduction. Objectives. Activity 1
 5 VECTOR GEOMETRY Chapter 5 Vector Geometry Objectives After studying this chapter you should be able to find and use the vector equation of a straight line; be able to find the equation of a plane in
5 VECTOR GEOMETRY Chapter 5 Vector Geometry Objectives After studying this chapter you should be able to find and use the vector equation of a straight line; be able to find the equation of a plane in
Triangles. Triangle. a. What are other names for triangle ABC?
 Triangles Triangle A triangle is a closed figure in a plane consisting of three segments called sides. Any two sides intersect in exactly one point called a vertex. A triangle is named using the capital
Triangles Triangle A triangle is a closed figure in a plane consisting of three segments called sides. Any two sides intersect in exactly one point called a vertex. A triangle is named using the capital
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Thursday, January 24, 2013 9:15 a.m. to 12:15 p.m.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, January 24, 2013 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, January 24, 2013 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
How to bet using different NairaBet Bet Combinations (Combo)
 How to bet using different NairaBet Bet Combinations (Combo) SINGLES Singles consists of single bets. I.e. it will contain just a single selection of any sport. The bet slip of a singles will look like
How to bet using different NairaBet Bet Combinations (Combo) SINGLES Singles consists of single bets. I.e. it will contain just a single selection of any sport. The bet slip of a singles will look like
1. Find the length of BC in the following triangles. It will help to first find the length of the segment marked X.
 1 Find the length of BC in the following triangles It will help to first find the length of the segment marked X a: b: Given: the diagonals of parallelogram ABCD meet at point O The altitude OE divides
1 Find the length of BC in the following triangles It will help to first find the length of the segment marked X a: b: Given: the diagonals of parallelogram ABCD meet at point O The altitude OE divides
IС A A RT 2013. Proceedings Volume 2. 5th International Conference on Agents and Artificial Intelligence. Barcelona, Spain 15-18 February, 2013
 «'.''«ИЧИЧГШ ИШ М Ш * /////>. л ъ и г ш я ш и ъ в т ъ т ', : 4 р * т Ъ ъ ^ Х 'Ш У Л *а * 1 ЛЧй==:й?й!^'ййй IС A A RT 2013. *»ф«ч>»д* 'И И в Я в З Г З г И Ж /а 1 * icw-ia & «:*>if E M e i i i i y. x '-
«'.''«ИЧИЧГШ ИШ М Ш * /////>. л ъ и г ш я ш и ъ в т ъ т ', : 4 р * т Ъ ъ ^ Х 'Ш У Л *а * 1 ЛЧй==:й?й!^'ййй IС A A RT 2013. *»ф«ч>»д* 'И И в Я в З Г З г И Ж /а 1 * icw-ia & «:*>if E M e i i i i y. x '-
The European Ombudsman
 Overview The European Ombudsman Е в р о п е й с к и о м б у д с м а н E l D e f e n s o r d e l P u e b l o E u r o p e o E v r o p s k ý v e ř e j n ý o c h r á n c e p r á v D e n E u r o p æ i s k e
Overview The European Ombudsman Е в р о п е й с к и о м б у д с м а н E l D e f e n s o r d e l P u e b l o E u r o p e o E v r o p s k ý v e ř e j n ý o c h r á n c e p r á v D e n E u r o p æ i s k e
Geometry Regents Review
 Name: Class: Date: Geometry Regents Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. If MNP VWX and PM is the shortest side of MNP, what is the shortest
Name: Class: Date: Geometry Regents Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. If MNP VWX and PM is the shortest side of MNP, what is the shortest
Lecture 24: Saccheri Quadrilaterals
 Lecture 24: Saccheri Quadrilaterals 24.1 Saccheri Quadrilaterals Definition In a protractor geometry, we call a quadrilateral ABCD a Saccheri quadrilateral, denoted S ABCD, if A and D are right angles
Lecture 24: Saccheri Quadrilaterals 24.1 Saccheri Quadrilaterals Definition In a protractor geometry, we call a quadrilateral ABCD a Saccheri quadrilateral, denoted S ABCD, if A and D are right angles
Shape, Space and Measure
 Name: Shape, Space and Measure Prep for Paper 2 Including Pythagoras Trigonometry: SOHCAHTOA Sine Rule Cosine Rule Area using 1-2 ab sin C Transforming Trig Graphs 3D Pythag-Trig Plans and Elevations Area
Name: Shape, Space and Measure Prep for Paper 2 Including Pythagoras Trigonometry: SOHCAHTOA Sine Rule Cosine Rule Area using 1-2 ab sin C Transforming Trig Graphs 3D Pythag-Trig Plans and Elevations Area
The common ratio in (ii) is called the scaled-factor. An example of two similar triangles is shown in Figure 47.1. Figure 47.1
 47 Similar Triangles An overhead projector forms an image on the screen which has the same shape as the image on the transparency but with the size altered. Two figures that have the same shape but not
47 Similar Triangles An overhead projector forms an image on the screen which has the same shape as the image on the transparency but with the size altered. Two figures that have the same shape but not
Section 9-1. Basic Terms: Tangents, Arcs and Chords Homework Pages 330-331: 1-18
 Chapter 9 Circles Objectives A. Recognize and apply terms relating to circles. B. Properly use and interpret the symbols for the terms and concepts in this chapter. C. Appropriately apply the postulates,
Chapter 9 Circles Objectives A. Recognize and apply terms relating to circles. B. Properly use and interpret the symbols for the terms and concepts in this chapter. C. Appropriately apply the postulates,
Quadrilaterals. Definition
 Quadrilaterals Definition A quadrilateral is a four-sided closed figure in a plane that meets the following conditions: Each side has its endpoints in common with an endpoint of two adjacent sides. Consecutive
Quadrilaterals Definition A quadrilateral is a four-sided closed figure in a plane that meets the following conditions: Each side has its endpoints in common with an endpoint of two adjacent sides. Consecutive
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Student Name:
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, August 18, 2010 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, August 18, 2010 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of
You must have: Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser, calculator. Tracing paper may be used.
 Write your name here Surname Other names Edexcel IGCSE Mathematics B Paper 1 Centre Number Candidate Number Monday 6 June 2011 Afternoon Time: 1 hour 30 minutes Paper Reference 4MB0/01 You must have: Ruler
Write your name here Surname Other names Edexcel IGCSE Mathematics B Paper 1 Centre Number Candidate Number Monday 6 June 2011 Afternoon Time: 1 hour 30 minutes Paper Reference 4MB0/01 You must have: Ruler
Exercise Set 3. Similar triangles. Parallel lines
 Exercise Set 3. Similar triangles Parallel lines Note: The exercises marked with are more difficult and go beyond the course/examination requirements. (1) Let ABC be a triangle with AB = AC. Let D be an
Exercise Set 3. Similar triangles Parallel lines Note: The exercises marked with are more difficult and go beyond the course/examination requirements. (1) Let ABC be a triangle with AB = AC. Let D be an
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Student Name:
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, June 17, 2010 1:15 to 4:15 p.m., only Student Name: School Name: Print your name and the name of your
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, June 17, 2010 1:15 to 4:15 p.m., only Student Name: School Name: Print your name and the name of your
Test on Circle Geometry (Chapter 15)
 Test on Circle Geometry (Chapter 15) Chord Properties of Circles A chord of a circle is any interval that joins two points on the curve. The largest chord of a circle is its diameter. 1. Chords of equal
Test on Circle Geometry (Chapter 15) Chord Properties of Circles A chord of a circle is any interval that joins two points on the curve. The largest chord of a circle is its diameter. 1. Chords of equal
Unit 3 Boolean Algebra (Continued)
 Unit 3 Boolean Algebra (Continued) 1. Exclusive-OR Operation 2. Consensus Theorem Department of Communication Engineering, NCTU 1 3.1 Multiplying Out and Factoring Expressions Department of Communication
Unit 3 Boolean Algebra (Continued) 1. Exclusive-OR Operation 2. Consensus Theorem Department of Communication Engineering, NCTU 1 3.1 Multiplying Out and Factoring Expressions Department of Communication
Online EFFECTIVE AS OF JANUARY 2013
 2013 A and C Session Start Dates (A-B Quarter Sequence*) 2013 B and D Session Start Dates (B-A Quarter Sequence*) Quarter 5 2012 1205A&C Begins November 5, 2012 1205A Ends December 9, 2012 Session Break
2013 A and C Session Start Dates (A-B Quarter Sequence*) 2013 B and D Session Start Dates (B-A Quarter Sequence*) Quarter 5 2012 1205A&C Begins November 5, 2012 1205A Ends December 9, 2012 Session Break
Fundamentals of Geometry. Oleg A. Belyaev belyaev@polly.phys.msu.ru
 Fundamentals of Geometry Oleg A. Belyaev belyaev@polly.phys.msu.ru February 28, 2007 Contents I Classical Geometry 1 1 Absolute (Neutral) Geometry 3 1.1 Incidence....................................................
Fundamentals of Geometry Oleg A. Belyaev belyaev@polly.phys.msu.ru February 28, 2007 Contents I Classical Geometry 1 1 Absolute (Neutral) Geometry 3 1.1 Incidence....................................................
Database Design and Normalization
 Database Design and Normalization Chapter 10 (Week 11) EE562 Slides and Modified Slides from Database Management Systems, R. Ramakrishnan 1 Computing Closure F + Example: List all FDs with: - a single
Database Design and Normalization Chapter 10 (Week 11) EE562 Slides and Modified Slides from Database Management Systems, R. Ramakrishnan 1 Computing Closure F + Example: List all FDs with: - a single
MARI-ENGLISH DICTIONARY
 MARI-ENGLISH DICTIONARY This project was funded by the Austrian Science Fund (FWF) 1, grant P22786-G20, and carried out at the Department of Finno-Ugric Studies 2 at the University of Vienna 3. Editors:
MARI-ENGLISH DICTIONARY This project was funded by the Austrian Science Fund (FWF) 1, grant P22786-G20, and carried out at the Department of Finno-Ugric Studies 2 at the University of Vienna 3. Editors:
FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina
 FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina Москва Издательство Российского университета дружбы народов 2002 FUNCTIONS OF THE MODAL
FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina Москва Издательство Российского университета дружбы народов 2002 FUNCTIONS OF THE MODAL
Blue Pelican Geometry Theorem Proofs
 Blue Pelican Geometry Theorem Proofs Copyright 2013 by Charles E. Cook; Refugio, Tx (All rights reserved) Table of contents Geometry Theorem Proofs The theorems listed here are but a few of the total in
Blue Pelican Geometry Theorem Proofs Copyright 2013 by Charles E. Cook; Refugio, Tx (All rights reserved) Table of contents Geometry Theorem Proofs The theorems listed here are but a few of the total in
Collinearity and concurrence
 Collinearity and concurrence Po-Shen Loh 23 June 2008 1 Warm-up 1. Let I be the incenter of ABC. Let A be the midpoint of the arc BC of the circumcircle of ABC which does not contain A. Prove that the
Collinearity and concurrence Po-Shen Loh 23 June 2008 1 Warm-up 1. Let I be the incenter of ABC. Let A be the midpoint of the arc BC of the circumcircle of ABC which does not contain A. Prove that the
Contents. Problems... 2 Solutions... 6
 Contents Problems............................ Solutions............................ 6 Problems Baltic Way 014 Problems Problem 1 Show that cos(56 ) cos( 56 ) cos( 56 )... cos( 3 56 ) = 1 4. Problem Let
Contents Problems............................ Solutions............................ 6 Problems Baltic Way 014 Problems Problem 1 Show that cos(56 ) cos( 56 ) cos( 56 )... cos( 3 56 ) = 1 4. Problem Let
Visa Smart Debit/Credit Certificate Authority Public Keys
 CHIP AND NEW TECHNOLOGIES Visa Smart Debit/Credit Certificate Authority Public Keys Overview The EMV standard calls for the use of Public Key technology for offline authentication, for aspects of online
CHIP AND NEW TECHNOLOGIES Visa Smart Debit/Credit Certificate Authority Public Keys Overview The EMV standard calls for the use of Public Key technology for offline authentication, for aspects of online
You must have: Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser, calculator. Tracing paper may be used.
 Write your name here Surname Other names Edexcel IGCSE Centre Number Mathematics A Paper 3H Monday 6 June 2011 Afternoon Time: 2 hours Candidate Number Higher Tier Paper Reference 4MA0/3H You must have:
Write your name here Surname Other names Edexcel IGCSE Centre Number Mathematics A Paper 3H Monday 6 June 2011 Afternoon Time: 2 hours Candidate Number Higher Tier Paper Reference 4MA0/3H You must have:
AREAS OF PARALLELOGRAMS AND TRIANGLES
 15 MATHEMATICS AREAS OF PARALLELOGRAMS AND TRIANGLES CHAPTER 9 9.1 Introduction In Chapter 5, you have seen that the study of Geometry, originated with the measurement of earth (lands) in the process of
15 MATHEMATICS AREAS OF PARALLELOGRAMS AND TRIANGLES CHAPTER 9 9.1 Introduction In Chapter 5, you have seen that the study of Geometry, originated with the measurement of earth (lands) in the process of
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Thursday, August 16, 2012 8:30 to 11:30 a.m.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 16, 2012 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of your
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 16, 2012 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of your
Boolean Algebra (cont d) UNIT 3 BOOLEAN ALGEBRA (CONT D) Guidelines for Multiplying Out and Factoring. Objectives. Iris Hui-Ru Jiang Spring 2010
 Boolean Algebra (cont d) 2 Contents Multiplying out and factoring expressions Exclusive-OR and Exclusive-NOR operations The consensus theorem Summary of algebraic simplification Proving validity of an
Boolean Algebra (cont d) 2 Contents Multiplying out and factoring expressions Exclusive-OR and Exclusive-NOR operations The consensus theorem Summary of algebraic simplification Proving validity of an
Triangle Centers MOP 2007, Black Group
 Triangle Centers MOP 2007, Black Group Zachary Abel June 21, 2007 1 A Few Useful Centers 1.1 Symmedian / Lemmoine Point The Symmedian point K is defined as the isogonal conjugate of the centroid G. Problem
Triangle Centers MOP 2007, Black Group Zachary Abel June 21, 2007 1 A Few Useful Centers 1.1 Symmedian / Lemmoine Point The Symmedian point K is defined as the isogonal conjugate of the centroid G. Problem
Algebraic Properties and Proofs
 Algebraic Properties and Proofs Name You have solved algebraic equations for a couple years now, but now it is time to justify the steps you have practiced and now take without thinking and acting without
Algebraic Properties and Proofs Name You have solved algebraic equations for a couple years now, but now it is time to justify the steps you have practiced and now take without thinking and acting without
Mathematics 3301-001 Spring 2015 Dr. Alexandra Shlapentokh Guide #3
 Mathematics 3301-001 Spring 2015 Dr. Alexandra Shlapentokh Guide #3 The problems in bold are the problems for Test #3. As before, you are allowed to use statements above and all postulates in the proofs
Mathematics 3301-001 Spring 2015 Dr. Alexandra Shlapentokh Guide #3 The problems in bold are the problems for Test #3. As before, you are allowed to use statements above and all postulates in the proofs
GEOMETRY (Common Core)
 GEOMETRY (COMMON CORE) The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY (Common Core) Tuesday, June 2, 2015 1:15 to 4:15 p.m., only Student Name: School Name: The possession
GEOMETRY (COMMON CORE) The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY (Common Core) Tuesday, June 2, 2015 1:15 to 4:15 p.m., only Student Name: School Name: The possession
Vector Notation: AB represents the vector from point A to point B on a graph. The vector can be computed by B A.
 1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
Pipe fittings plant in Kolpino, Leningrad Regions
 1 Pipe fittings plant in Kolpino, Leningrad Regions ROOST Group of companies is a fast growing association with a long history. Synergy of the ROOST Group companies gives an opportunity to keep leading
1 Pipe fittings plant in Kolpino, Leningrad Regions ROOST Group of companies is a fast growing association with a long history. Synergy of the ROOST Group companies gives an opportunity to keep leading
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Thursday, August 13, 2015 8:30 to 11:30 a.m., only.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 13, 2015 8:30 to 11:30 a.m., only Student Name: School Name: The possession or use of any communications
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 13, 2015 8:30 to 11:30 a.m., only Student Name: School Name: The possession or use of any communications
Chronic Fatigue Syndrome
 256 Srp Arh Celok Lek. 2011 Mar-Apr;139(3-4):256-261 ПРЕГЛЕД ЛИТЕРАТУРЕ / REVIEW ARTICLE DOI: 10.2298/SARH1104256B Chronic Fatigue Syndrome Snežana Brkić, Slavica Tomić, Maja Ružić, Daniela Marić Hospital
256 Srp Arh Celok Lek. 2011 Mar-Apr;139(3-4):256-261 ПРЕГЛЕД ЛИТЕРАТУРЕ / REVIEW ARTICLE DOI: 10.2298/SARH1104256B Chronic Fatigue Syndrome Snežana Brkić, Slavica Tomić, Maja Ružić, Daniela Marić Hospital
Equation of a Line. Chapter H2. The Gradient of a Line. m AB = Exercise H2 1
 Chapter H2 Equation of a Line The Gradient of a Line The gradient of a line is simpl a measure of how steep the line is. It is defined as follows :- gradient = vertical horizontal horizontal A B vertical
Chapter H2 Equation of a Line The Gradient of a Line The gradient of a line is simpl a measure of how steep the line is. It is defined as follows :- gradient = vertical horizontal horizontal A B vertical
Lesson 13: Angle Sum of a Triangle
 Student Outcomes Students know the angle sum theorem for triangles; the sum of the interior angles of a triangle is always 180. Students present informal arguments to draw conclusions about the angle sum
Student Outcomes Students know the angle sum theorem for triangles; the sum of the interior angles of a triangle is always 180. Students present informal arguments to draw conclusions about the angle sum
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Tuesday, August 13, 2013 8:30 to 11:30 a.m., only.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Tuesday, August 13, 2013 8:30 to 11:30 a.m., only Student Name: School Name: The possession or use of any communications
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Tuesday, August 13, 2013 8:30 to 11:30 a.m., only Student Name: School Name: The possession or use of any communications
COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES
 Margaryta I. Skrypnyk, Mykola M. Matiukha COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES The article studies the correspondence of management accounting structure when using of
Margaryta I. Skrypnyk, Mykola M. Matiukha COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES The article studies the correspondence of management accounting structure when using of
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Wednesday, January 29, 2014 9:15 a.m. to 12:15 p.m.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, January 29, 2014 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, January 29, 2014 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
CH3 Boolean Algebra (cont d)
 CH3 Boolean Algebra (cont d) Lecturer: 吳 安 宇 Date:2005/10/7 ACCESS IC LAB v Today, you ll know: Introduction 1. Guidelines for multiplying out/factoring expressions 2. Exclusive-OR and Equivalence operations
CH3 Boolean Algebra (cont d) Lecturer: 吳 安 宇 Date:2005/10/7 ACCESS IC LAB v Today, you ll know: Introduction 1. Guidelines for multiplying out/factoring expressions 2. Exclusive-OR and Equivalence operations
Summer Math Packet. Post Geometry Honors
 Summer Math Packet for Post Geometry Honors (for students who have completed Geometry Honors) Name Please read the directions (separate document) completely before starting your packet Print out the packet
Summer Math Packet for Post Geometry Honors (for students who have completed Geometry Honors) Name Please read the directions (separate document) completely before starting your packet Print out the packet
CIRCUMFERENCE AND AREA OF A CIRCLE
 CIRCUMFERENCE AND AREA OF A CIRCLE 1. AC and BD are two perpendicular diameters of a circle with centre O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take = 3.14) 2. In the given
CIRCUMFERENCE AND AREA OF A CIRCLE 1. AC and BD are two perpendicular diameters of a circle with centre O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take = 3.14) 2. In the given
Question Bank Trigonometry
 Question Bank Trigonometry 3 3 3 3 cos A sin A cos A sin A 1. Prove that cos A sina cos A sina 3 3 3 3 cos A sin A cos A sin A L.H.S. cos A sina cos A sina (cosa sina) (cos A sin A cosa sina) (cosa sina)
Question Bank Trigonometry 3 3 3 3 cos A sin A cos A sin A 1. Prove that cos A sina cos A sina 3 3 3 3 cos A sin A cos A sin A L.H.S. cos A sina cos A sina (cosa sina) (cos A sin A cosa sina) (cosa sina)
Vehicle Identification Numbering System 00.03
 Vehicle Identification Numbering System 00.03 IMPORTANT: See Subject 050 for the vehicle identification numbering system for vehicles built before May 1, 2000. Federal Motor Vehicle Safety Standard 115
Vehicle Identification Numbering System 00.03 IMPORTANT: See Subject 050 for the vehicle identification numbering system for vehicles built before May 1, 2000. Federal Motor Vehicle Safety Standard 115
CHAPTER 6 LINES AND ANGLES. 6.1 Introduction
 CHAPTER 6 LINES AND ANGLES 6.1 Introduction In Chapter 5, you have studied that a minimum of two points are required to draw a line. You have also studied some axioms and, with the help of these axioms,
CHAPTER 6 LINES AND ANGLES 6.1 Introduction In Chapter 5, you have studied that a minimum of two points are required to draw a line. You have also studied some axioms and, with the help of these axioms,
Most popular response to
 Class #33 Most popular response to What did the students want to prove? The angle bisectors of a square meet at a point. A square is a convex quadrilateral in which all sides are congruent and all angles
Class #33 Most popular response to What did the students want to prove? The angle bisectors of a square meet at a point. A square is a convex quadrilateral in which all sides are congruent and all angles
FEDERAL BUREAU OF INVESTIGATION FOIA/PA DELETED PAGE INFORMATION SHEET
 5 Page(s) withheld entirely at this location in the file. One or more of the following El(b)(1) (b)(7)(a) (05) (b)(2) (b)(7)(b) 0)(2 ) (b)(3) (b)(7)(c) (k)(1) (b)(7)(d) (k)(2) Eg(b)(7)(E) (k)(3) (b)(7)(f)
5 Page(s) withheld entirely at this location in the file. One or more of the following El(b)(1) (b)(7)(a) (05) (b)(2) (b)(7)(b) 0)(2 ) (b)(3) (b)(7)(c) (k)(1) (b)(7)(d) (k)(2) Eg(b)(7)(E) (k)(3) (b)(7)(f)
ISSN 0975-413X CODEN (USA): PCHHAX. The study of dissolution kinetics of drugs with riboxinum (inosine)
 Available online at www.derpharmachemica.com ISSN 0975-413X CODEN (USA): PCHHAX Der Pharma Chemica, 2016, 8(1):412-416 (http://derpharmachemica.com/archive.html) The study of dissolution kinetics of drugs
Available online at www.derpharmachemica.com ISSN 0975-413X CODEN (USA): PCHHAX Der Pharma Chemica, 2016, 8(1):412-416 (http://derpharmachemica.com/archive.html) The study of dissolution kinetics of drugs
Testing for Congruent Triangles Examples
 Testing for Congruent Triangles Examples 1. Why is congruency important? In 1913, Henry Ford began producing automobiles using an assembly line. When products are mass-produced, each piece must be interchangeable,
Testing for Congruent Triangles Examples 1. Why is congruency important? In 1913, Henry Ford began producing automobiles using an assembly line. When products are mass-produced, each piece must be interchangeable,
Projective Geometry - Part 2
 Projective Geometry - Part 2 Alexander Remorov alexanderrem@gmail.com Review Four collinear points A, B, C, D form a harmonic bundle (A, C; B, D) when CA : DA CB DB = 1. A pencil P (A, B, C, D) is the
Projective Geometry - Part 2 Alexander Remorov alexanderrem@gmail.com Review Four collinear points A, B, C, D form a harmonic bundle (A, C; B, D) when CA : DA CB DB = 1. A pencil P (A, B, C, D) is the
MATHEMATICS Grade 12 EUCLIDEAN GEOMETRY: CIRCLES 02 JULY 2014
 EUCLIDEAN GEOMETRY: CIRCLES 02 JULY 2014 Checklist Make sure you learn proofs of the following theorems: The line drawn from the centre of a circle perpendicular to a chord bisects the chord The angle
EUCLIDEAN GEOMETRY: CIRCLES 02 JULY 2014 Checklist Make sure you learn proofs of the following theorems: The line drawn from the centre of a circle perpendicular to a chord bisects the chord The angle
Three Lemmas in Geometry Solutions Yufei Zhao Massachusetts Institute of Technology
 Three Lemmas in Geometry Solutions Yufei Zhao Massachusetts Institute of Technology yufei.zhao@gmail.com 1 Diameter of incircle 1. (IMO 1992) In the plane let C be a circle, l a line tangent to the circle
Three Lemmas in Geometry Solutions Yufei Zhao Massachusetts Institute of Technology yufei.zhao@gmail.com 1 Diameter of incircle 1. (IMO 1992) In the plane let C be a circle, l a line tangent to the circle
C relative to O being abc,, respectively, then b a c.
 2 EP-Program - Strisuksa School - Roi-et Math : Vectors Dr.Wattana Toutip - Department of Mathematics Khon Kaen University 200 :Wattana Toutip wattou@kku.ac.th http://home.kku.ac.th/wattou 2. Vectors A
2 EP-Program - Strisuksa School - Roi-et Math : Vectors Dr.Wattana Toutip - Department of Mathematics Khon Kaen University 200 :Wattana Toutip wattou@kku.ac.th http://home.kku.ac.th/wattou 2. Vectors A
The course of understanding British and American prose and poetry by future managers
 4. Полат Е. С. Новые педагогические и информационные технологии в системе образования. М.: Просвещение, 2000. 5. Гальцова Н. П., Мезенцева Т. И., Швадленко И. А. Использование электронных информационно-образовательных
4. Полат Е. С. Новые педагогические и информационные технологии в системе образования. М.: Просвещение, 2000. 5. Гальцова Н. П., Мезенцева Т. И., Швадленко И. А. Использование электронных информационно-образовательных
Data Mining Apriori Algorithm
 10 Data Mining Apriori Algorithm Apriori principle Frequent itemsets generation Association rules generation Section 6 of course book TNM033: Introduction to Data Mining 1 Association Rule Mining (ARM)
10 Data Mining Apriori Algorithm Apriori principle Frequent itemsets generation Association rules generation Section 6 of course book TNM033: Introduction to Data Mining 1 Association Rule Mining (ARM)
Name Date Class. Lines and Segments That Intersect Circles. AB and CD are chords. Tangent Circles. Theorem Hypothesis Conclusion
 Section. Lines That Intersect Circles Lines and Segments That Intersect Circles A chord is a segment whose endpoints lie on a circle. A secant is a line that intersects a circle at two points. A tangent
Section. Lines That Intersect Circles Lines and Segments That Intersect Circles A chord is a segment whose endpoints lie on a circle. A secant is a line that intersects a circle at two points. A tangent
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Tuesday, January 26, 2016 1:15 to 4:15 p.m., only.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Tuesday, January 26, 2016 1:15 to 4:15 p.m., only Student Name: School Name: The possession or use of any communications
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Tuesday, January 26, 2016 1:15 to 4:15 p.m., only Student Name: School Name: The possession or use of any communications
DATING YOUR GUILD 1952-1960
 DATING YOUR GUILD 1952-1960 YEAR APPROXIMATE LAST SERIAL NUMBER PRODUCED 1953 1000-1500 1954 1500-2200 1955 2200-3000 1956 3000-4000 1957 4000-5700 1958 5700-8300 1959 12035 1960-1969 This chart displays
DATING YOUR GUILD 1952-1960 YEAR APPROXIMATE LAST SERIAL NUMBER PRODUCED 1953 1000-1500 1954 1500-2200 1955 2200-3000 1956 3000-4000 1957 4000-5700 1958 5700-8300 1959 12035 1960-1969 This chart displays
Paper Reference. Edexcel GCSE Mathematics (Linear) 1380 Paper 4 (Calculator) Friday 10 June 2011 Morning Time: 1 hour 45 minutes
 Centre No. Candidate No. Paper Reference 1 3 8 0 4 H Paper Reference(s) 1380/4H Edexcel GCSE Mathematics (Linear) 1380 Paper 4 (Calculator) Higher Tier Friday 10 June 2011 Morning Time: 1 hour 45 minutes
Centre No. Candidate No. Paper Reference 1 3 8 0 4 H Paper Reference(s) 1380/4H Edexcel GCSE Mathematics (Linear) 1380 Paper 4 (Calculator) Higher Tier Friday 10 June 2011 Morning Time: 1 hour 45 minutes
Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING MANAGEMENT FOR PROVISION PROCESS
 444 JOURNAL Vol. 10 ( 4). December 2011 P u b l i c a t i o n o f T e r n o p i l N a t i o n a l E c o n o m i c U n i v e r s i t y Microeconomics Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING
444 JOURNAL Vol. 10 ( 4). December 2011 P u b l i c a t i o n o f T e r n o p i l N a t i o n a l E c o n o m i c U n i v e r s i t y Microeconomics Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING
Geo, Chap 4 Practice Test, EV Ver 1
 Class: Date: Geo, Chap 4 Practice Test, EV Ver 1 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. (4-3) In each pair of triangles, parts are congruent as
Class: Date: Geo, Chap 4 Practice Test, EV Ver 1 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. (4-3) In each pair of triangles, parts are congruent as
3.1 Triangles, Congruence Relations, SAS Hypothesis
 Chapter 3 Foundations of Geometry 2 3.1 Triangles, Congruence Relations, SAS Hypothesis Definition 3.1 A triangle is the union of three segments ( called its side), whose end points (called its vertices)
Chapter 3 Foundations of Geometry 2 3.1 Triangles, Congruence Relations, SAS Hypothesis Definition 3.1 A triangle is the union of three segments ( called its side), whose end points (called its vertices)
Benchmark Databases for Testing Big-Data Analytics In Cloud Environments
 North Carolina State University Graduate Program in Operations Research Benchmark Databases for Testing Big-Data Analytics In Cloud Environments Rong Huang Rada Chirkova Yahya Fathi ICA CON 2012 April
North Carolina State University Graduate Program in Operations Research Benchmark Databases for Testing Big-Data Analytics In Cloud Environments Rong Huang Rada Chirkova Yahya Fathi ICA CON 2012 April
SQA Higher Mathematics Unit 3
 SCHOLAR Study Guide SQA Higher Mathematics Unit 3 Jane Paterson Heriot-Watt University Dorothy Watson Balerno High School Heriot-Watt University Edinburgh EH14 4AS, United Kingdom. First published 2001
SCHOLAR Study Guide SQA Higher Mathematics Unit 3 Jane Paterson Heriot-Watt University Dorothy Watson Balerno High School Heriot-Watt University Edinburgh EH14 4AS, United Kingdom. First published 2001
Intermediate Math Circles October 10, 2012 Geometry I: Angles
 Intermediate Math Circles October 10, 2012 Geometry I: Angles Over the next four weeks, we will look at several geometry topics. Some of the topics may be familiar to you while others, for most of you,
Intermediate Math Circles October 10, 2012 Geometry I: Angles Over the next four weeks, we will look at several geometry topics. Some of the topics may be familiar to you while others, for most of you,
GOYAL BROTHERS PRAKASHAN
 Assignments in Mathematics Cass IX (Term ) 9. AREAS OF PARALLELOGRAMS AND TRIANGLES IMPORTANT TERMS, DEFINITIONS AND RESULTS If two figures A and B are congruent, they must have equa areas. Or, if A and
Assignments in Mathematics Cass IX (Term ) 9. AREAS OF PARALLELOGRAMS AND TRIANGLES IMPORTANT TERMS, DEFINITIONS AND RESULTS If two figures A and B are congruent, they must have equa areas. Or, if A and
HALL G 380,000 GROSS SF
 LEVEL 1 404 403 402 401 1007 1006 1005 1004 1003 1002 1001 907 906 905 904 903 902 901 807 806 805 804 803 802 801 707 706 705 704 703 702 701 607 606 605 604 603 602 601 507 506 505 504 503 502 501 GALILEO
LEVEL 1 404 403 402 401 1007 1006 1005 1004 1003 1002 1001 907 906 905 904 903 902 901 807 806 805 804 803 802 801 707 706 705 704 703 702 701 607 606 605 604 603 602 601 507 506 505 504 503 502 501 GALILEO
Geometry EOC Practice Test #4
 Class: Date: Geometry EOC Practice Test #4 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. In the diagram below, which expression represents x, the degree
Class: Date: Geometry EOC Practice Test #4 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. In the diagram below, which expression represents x, the degree
HOW TO USE MINITAB: DESIGN OF EXPERIMENTS. Noelle M. Richard 08/27/14
 HOW TO USE MINITAB: DESIGN OF EXPERIMENTS 1 Noelle M. Richard 08/27/14 CONTENTS 1. Terminology 2. Factorial Designs When to Use? (preliminary experiments) Full Factorial Design General Full Factorial Design
HOW TO USE MINITAB: DESIGN OF EXPERIMENTS 1 Noelle M. Richard 08/27/14 CONTENTS 1. Terminology 2. Factorial Designs When to Use? (preliminary experiments) Full Factorial Design General Full Factorial Design
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Student Name:
 GEOMETRY The University of the State of New Yk REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, June 17, 2010 1:15 to 4:15 p.m., only Student Name: School Name: Print your name and the name of your school
GEOMETRY The University of the State of New Yk REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, June 17, 2010 1:15 to 4:15 p.m., only Student Name: School Name: Print your name and the name of your school
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Thursday, August 13, 2009 8:30 to 11:30 a.m., only.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 13, 2009 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of your
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 13, 2009 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of your
Wednesday 15 January 2014 Morning Time: 2 hours
 Write your name here Surname Other names Pearson Edexcel Certificate Pearson Edexcel International GCSE Mathematics A Paper 4H Centre Number Wednesday 15 January 2014 Morning Time: 2 hours Candidate Number
Write your name here Surname Other names Pearson Edexcel Certificate Pearson Edexcel International GCSE Mathematics A Paper 4H Centre Number Wednesday 15 January 2014 Morning Time: 2 hours Candidate Number
egyptigstudentroom.com
 UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS International General Certificate of Secondary Education *5128615949* MATHEMATICS 0580/04, 0581/04 Paper 4 (Extended) May/June 2007 Additional Materials:
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS International General Certificate of Secondary Education *5128615949* MATHEMATICS 0580/04, 0581/04 Paper 4 (Extended) May/June 2007 Additional Materials:
Baltic Way 1995. Västerås (Sweden), November 12, 1995. Problems and solutions
 Baltic Way 995 Västerås (Sweden), November, 995 Problems and solutions. Find all triples (x, y, z) of positive integers satisfying the system of equations { x = (y + z) x 6 = y 6 + z 6 + 3(y + z ). Solution.
Baltic Way 995 Västerås (Sweden), November, 995 Problems and solutions. Find all triples (x, y, z) of positive integers satisfying the system of equations { x = (y + z) x 6 = y 6 + z 6 + 3(y + z ). Solution.
