Developing science for result-based management in fisheries - a digression?
|
|
|
- Clarence Johns
- 8 years ago
- Views:
Transcription
1 Not to be cited without prior reference to the author. 18 th August 211 ICES CM 211/P:12 Developing science for result-based management in fisheries - a digression? By, Mogens Schou Ministry of Food, Copenhagen. msc@fvm.dk; mobile Abstract Biological and economic fisheries science and advice are serving public management rather than private exploitation of fisheries resources. Management regulates the fisher s choice of methods, technology, area and level of activity with increasing detail thus fuelling the demand for such science. The main activity is aimed at reducing the gap between registered catches (landings) and total catches and at targeting larger fish. Management needs time to prepare and legislate and it regulates with rigid and uniform rules. This leaves little room for the industry to adapt to the dynamics of resource utilization opportunities. As a contrast, result-based management sets the targets (catch quotas, where all fish caught count on the fishers quota), and leave the choice of method in harvesting to the exploiter together with the obligation to fully document (by E-log and CCTV) that targets are observed. As EU considers result-based management with full catch accountability, science might look at the opportunities of such management. It is about comparing the ability of a result based management vis á vis a regulatory management to optimize food output in an environment where the ideal harvesting pattern is highly complex and variable. And it is about developing approaches and tools for the industry to continuously improve the result of the output. The paper points to possible science topics and areas that can contribute to the development and optimization of result based management, i.a. biological/hydrographic, economics/market, optimal management models and technology/methods Keywords: Result based management; Catch-Quota Management (CQM); full documentation; EU fisheries policy; CFP. Result based management for improved utilization of marine resources 1. What is result based management in fisheries I base myself on the following conditions for result based management: 1. A management strategy to ensure achievement of clearly stated results that contribute to the optimal output/impact relation. In the case of fisheries ensuring MSY and the lowest environmental impact when taxing the commercial resources.
2 2. Output targets must be measurable, considered legitimate and relevant for the industry to optimize its efforts against. The utilization of commercial stocks is a clear candidate for a result based management as catch quotas are defineable, measurable and easy to use as a production target. 3. Rules must be kept to a minimum leaving the industry with the field of opportunity and the incentive to innovate. 4. Documentation and monitoring to assess whether the result is within the targets and to generate data relevant to the continous setting and development of targets is crucial. In a result based management the exploiter must take responsibility for sufficient and correct data. 5. Why result based management? Basically the need for sustainable food production in a is better achieved by private ingenuity than by public regulation for 3 reasons. The industry is closer to the problem, the industry will develop methods and technology applicable to the situation while public management uses generally applicable rules irrespective of the concrete situation. The industry may change and develop methods and technology with short notice while public management needs time to assess, define, negotiate and legislate. 2. Introduction Utilizing the marine food potential to its full requires a high degree of knowledge, skill and technology to overcome the variability and complexities in the harvesting. Basically the present fisheries regulation is aimed at reducing the gap between registered catches (landings) and total catches and at targeting larger sized fish. To-day EU fisheries management focuses on managing the fishers use of methods, technology, fishing-area and level of activity in order to reduce the gap. A management by command and control. It is normally appreciated that wealth generation in our society is best served by market based approaches where the ingenuity and drive of the individual is allowed to unfold within certain boundaries ensuring the common interest. While a command and control approach define the acceptable actions of the individual a result based management set the boundaries and let the individual choose and develop his actions. The nature of result based management in fisheries is that science and public management set the targets and refrains from regulating how the targets should be met. He who exploits the resource has the choice of method in harvesting and the obligation to document that targets are observed. Instead of fixing landing quotas the targets are set as catch quotas.
3 Fixing the targets for the individual fish stocks takes place in an ecosystem context where primary ecosystem factors such as trophic interaction enter into the equation. The results are catch-quotas for each individual stock or stock component. All catches including possible discards count against the catch quota. This is how I understand FMSY implementation in its final form. Secondary ecosystem considerations relate to non-commercial species such as marine mammals and to habitat protection. Regulation in this area may be result-based e.g. a max quota for harbor porpoise. However, most likely result based management is not a broadly applicable option here for the time being. Especially habitat protection is most likely best served by horizontal rules as area closures and regulation of gear construction. The picture as I see it is shown in the annexed sheet. It can be expressed with a fisher representatives words: go take the fish, and don t wreck the place. My primary focus in this paper is to consider result-based management as a way to the optimal output from commercial stocks. The objective of management: Optimal utilization of fish stocks can be compared to filling out the shape of an amoeba with squares. If they are too large they either extend beyond the shape or they don t fill the shape to its boundaries. If the squares are of sufficient smallness and number they may cover the amoeba. However as the amoeba changes shape a highly dynamic adaptation of the squares is needed. Management by command and control can be compared to the amoeba illustration where the optimal exploitation requires a considerable amount of rules to cover all the decisions relevant to the stock impact that the fisher may take. An improvement of the present unsatisfactory situation will require even more management, control and science input by a system now strained on all three parameters. Three fundamental criticisms can be levied against management by command and control in a complex environment. It requires centralized knowledge of extreme quality and a regulatory framework with forbidding costs and demands for qualified administration. It does not take account of the effect on fishermen s earnings with an obvious conflict between objectives. And an amoeba changes shape by the instant while regulations are subject to knowledge gathering, negotiations and legal process completely without the dynamics needed in competitive production processes in a changing environment. In contrast, a result based management, where the fisher account for the output and not his choice of method will incentivize him to obtain the optimal output through continuous use and innovation of methods and technology. Catch-Quota Management (CQM) is a result based management with the following main features: The fisher is accountable for the result only. The result is the total catch quota he can take. All catches including by-catches must be covered by a quota and all catches of the given species, including eventual discards count on the quota.
4 In the result based management the fisher decide how to obtain the result. There are no regulations regarding methods or technology. The result is obtained at sea where no efficient public control is possible. The fisher carries the responsibility to fully document that he stays within the quotas. He must do so reliably e.g. by CCTV and sensors. If he fails to do so he is ultimately out of the catch-quota management. Seen from a public perspective the main points of interest are: Innovation, knowledge and investments will successively improve utilization with the effect that the amoeban area of opportunity is gradually filled out. TAC/Quotas can be increased as there is no need to take account of discards on public level Data for model building and advice will improve rapidly in quality. Public management and control can be reduced Promoting fish can be done in good faith and with an increasing inclusion of information that consumers may reward. Result based management not the least full documentation can produce instruments to serve the secondary ecosystem considerations too. I see no fundamental criticism to be levied against CQM as a resource management system. However, some balances and challenges are crucial. CQM and full documentation requires a transformation of management methods and investments in electronic systems and traced distribution chains. When the quota for one species in a mixed fishery is exhausted the fisher must stop the mixed fishery. To-day he can discard non quota species and still make money from the target species. That must go. Will he be able to target the fishery and obtain quotas for his catches in order to catch the quota for all species in the mixed fisheries? I believe this is the case in the North Atlantic, where supposedly relative few choke species could block for the utilization of other species. Probably this is not at present the case in highly mixed fisheries as in the Mediterranean. In addition to planning and conducting a selective fishery, the allocation of quotas between fishermen is important. As all catches must be accounted for, a high degree of transferability of quota-rights is important. Market based catch-share systems have shown to be effective in facilitating this if designed well. As mixed fisheries must stop when the least plentiful quota is exhausted it is the advice on species abundance for mixed stocks is accurate and up to date. Failure to take account of e.g. big recruiting year classes may result in inoptimal catch results. I have omitted the political and legal considerations regarding the transformation from regulatory to result based management, and it should also be noticed that CQM entails a
5 professionalization of fisheries which may put more pressure on small scale fishing if not counteracted. 3. Political background and present experience Denmark, Germany, France and UK in March 211 jointly pointed to result-based management by CQM as the basis for the revised CFP. We are convinced that genuine fully documented catch-quota systems will promote sustainable development and a sustainable approach to fishery management focussing on total removal -Ministers declaration 1 st March 211 The proposal for a CQM management is backed by extensive practical trials since 28; currently with app. 6 vessels in 5 countries participating in Catch-Quota Management (CQM) and full documentation (CCTV cameras and sensors). By the end of 21 Denmark had performed 5. hours at sea with CQM and full documentation. A workshop with the following points was held in Copenhagen 17th May 211 WS 1 A reliable data chain for management, control and advice WS 2. Smart control : Innovating control i.a. by data combining or new technology WS 3. Cost efficiency of full documentation versus traditional control WS 4. Technical rules can they be simplified under CQM The results of the workshop, papers, press clips and videos regarding CQM can be seen at The 13th July 211 the EU Commission presented its proposal for a revised CFP [COM(211) 425 Final]. The Commission i.a. propose full catch accountability with an obligation to land all fish, introduction of transferable catch concessions, full documentation to ensure all fish landed and an improved science base for management. The Commission has not, however included thoughts on the simplification of regulations and control that may flow from the proposal. The political process in Parliament and Council should lead to an adoption of the revised CFP at the end of 212. The role of science 1. A new perspective Biological and economic fisheries science and advice are serving public management rather than private exploitation of fisheries resources. Science could address the issue of optimal potential marine production and ways to support this in a result based context characterized one the one hand by catch data that are fully reliable and on the other hand a drive for innovation that stems from the fishery itself. The following science areas could be considered.
6 1. Biological/hydrographic science could, o delimitate and develop relevant output factors that constitute the basis for result based management. o improve models and concrete advice on basis of real time fully documented date. Improve analysis by making use of the industry s interpretative participation in a process where the argument is not about the figures but the reason for the figures. o develop real time or floating quota allocation models instead of present calendar year TAC/quotas. Within the calendar year concept models for year to year quota flexibility could be considered. 2. Economic/social science could focus on the cost efficiency potential of result based management for society and for the individual fisher, and it could do so in a static or dynamic perspective where innovation and technology drivers ensure successive improvement of the impact/result relationship in fishing. So far the property right question has been exercised extensively while I find little work relating the amount of fish that we can get out of the sea, e.g. with a result based management. 3. Technological science, innovation and best cases decide the speed with which the industry is able to optimize the opportunities given to them, and smart documentation, traceability and informative marketing will set the agenda for fish as a trustworthy food this issue being a serious barrier for the marketing of fish as a notoriously healthy food. 2. Possible concrete science topics The following are some incomplete illustrations of areas where science and advice could contribute to sustainability and wealth generation in a result based management. Biological/hydrographic The catch-quota may gradually as knowledge and skills develop, be defined with a higher degree of refinement, e.g. by fixing quotas for separate stock components with a view to further improving the utilization pattern and the long-term output, and reduce pressure on vulnerable components. Options and consequences of CQM in relation to more precise targeting of the individual age groups in a stock e.g. by fishing on a variety of age groups to obtain a differentiated outtake. This may lead to a more optimal output pattern, and it may reduce fishery induced evolution of the species. Consequences of multiannual quota allocations e.g. allowing a large recruiting year class to be caught the following year or to give a fisher with an individual quota to postpone his harvesting until the fish has grown into the high priced market sizes. What is the potential output of commercial stocks? In the North Sea an improvement of 1%? 5%?
7 Economics, social science and the market Most of the suggestions under biological/hydrographic have an economic dimension too: Management and control costs Costs and benefits in relation to fully documented and traced fishery products e.g. as the sustainability stamp can be integrated in the process instead of being certified by third party involvement. Economic science could focus on the cost efficiency potential of result based management for society and for the individual fisher, and it could do so in a static or dynamic perspective where innovation and technology drivers ensure successive improvement of the economic result of fishing. Optimal management Choke species CQM entails that a fishery require a catch quota for all commercial species caught in that fishery. When the least plentiful quota in a mixed fishery - the choke species - is exhausted, the fishery must stop. To-day app. 6 vessels in DK, UK and Germany fish under CQM (on a limited scale and so far only for cod) subject to this condition. The principle imply that it is better to lose some catch opportunities due to lack of quota than continue fishing and discarding the non-quota species. CQM will incentivize selective fishing and transferable quota systems. Good solutions to the choke species problem are essential for the economic result of the fishery. I am convinced that viable solutions will be gradually and quickly found in the North Atlantic while the situation in the mixed fisheries of e.g. the Mediterranean is different. In the annex professor Henrik Holm has developed an algorithmic solution to the problem. His model will make it possible when fixing TAC/quotas to assess consequences for total quota uptake of varying relationships between the least and the most plentiful species in mixed fisheries, of changes in vessels targeting ability and of changes in quota transferability. Analyses of management approaches that can handle the problem of choke-species would be relevant. Transferable-catch shares is one approach. The Danish catch share management includes privately managed pools. The pools manage a market based swapping and leasing system allowing fishermen to land fish for which they do not have a quota and to lease or swap the necessary fish afterwards. In the public management a pool is managed as one vessel allowing for great flexibility within the pool. Analyses of the pools have shown that the quotas available for swapping and leasing are plentiful. The pools have established a code that fishermen should not discard fish for non-quota reasons as long as the pool as such has quotas available. Still some upgrading may happen and the test of the flexibility should be seen in context of the CQM, where lack of quotas cannot be solved by discarding. See more at
8 Other systems as risk pools have been established. See e.g. West Coast Trawlers' Network for a risk pool agreement. The problem of choke species may also be considered in a trade-off-model where a defined overfishing for one species in a mixed fishery may be accepted in order to optimize the catch of the mixed fishery as such. Here MSY would apply on a mixed stock basis rather than on a single stock basis. Such an approach should be used with caution as it would reduce the incentive to refine the precise targeting of the individual stock or to implement a flexible quota allocation. Management based on overall quotas or year class specific quotas Is the optimal biological and economic output of a stock linked to a given minimum size of the fish caught? Year after year? And should management care whether the stipulated result in the form of a quota is taken as fish in market size 5 (the smallest) or market size 1? From a biological point of view I suggest that the optimal outtake of each year class from a given stock will vary from year to year depending on the actual relative strength of the year classes of the given stock. Why not supplement the advice on TACs with a recommended year class specific TAC? and why not tell how the optimal outtake of each year class may affect the overall TAC that can be taken? From an economic point of view a differentiated approach might also be interesting. However the adopted MSY principle work with tonnes not value. From an administrative point it is quite feasible to count a vessel s catches against its quota with a correction factor based on the market size of the fish caught. If in this way for example 25% of a fleet switched from trawl to gill netting the average size of the fish would increase and the fishing mortality decrease considerably. In a result based management it is possible to define the result on a year class level. Clearly it is possible to disincentivise catches of juveniles by a high deterrence factor. The problem of fixing the proper incentive however, may show that we try to steer a very big ship with a very small rudder. This remains to be seen. From a genetic point of view there is little doubt that fishing over a larger range of year classes will reduce the fishery induced evolution. Technology and methods CQM will induce user driven innovation in selective fishing methods to ensure that only the marketable fish are caught. Thus management should now focus on under water
9 effects not accounted for, negative effects on habitats, destroying of fish not being caught and quality deterioration on fish being caught. Pre-catch identification of quantity, size distribution and species composition.) Active selectivity and release in fishing gears Low impact -> high quality fishing The above research area is currently being explored in CRISP (Centre for Research-based Innovation in Sustainable fish capture and Pre-processing technology) Commercial use for non-targeted fish If CQM is followed by a landing obligation ( discard ban ) it will result in species and sizes of fish not previously being brought to habour must be considered as a new resource. Product development, marketing etc are required to ensure that these landings of fish become an economic benefit rather than a cost related to fishing.
10 New Fisheries Management - aligning economic forces for conservation New Fisheries Management address the objectives of optimal food output, ecosystem considerations and allocation of rights to ensure the resource is used with a balanced fleet capacity. 1. Catch-Quota Management (CQM) is a result based management. Fishermen account for the result the total outtake, of their fishery. CQM ensures the optimal utilization of commercial stocks available. The model is operational as is demonstrated by DK and UK fishing trials since 28. Full documentation is an essential element of CQM. 2. Taxing of the resource must take place in respect of the ecosystem. 3 considerations are counted 1) The trophic dynamics are integrated in the MSY set TAC/quotas 2) Reduced catch of non-target species; 3) Protection of habitats and environment. 3. Allocation of user rights must be efficient in the senses that they balance catches with the fleet in the short term and fleet with catch opportunities in the long term. Transferability or flexible allocation of user rights is essential. Go, take the fish And Don t wreck the place Take your fish Objective Maximizing the food output from commercial fish stocks by MSY. That is: TAC/Quotas based on carrying capacity of the individual stock and on direct ecosystem effects (trophic interaction ) Avoid and minimize unwanted and effects of fishing Don t wreck the place Strategy Result based management of output: (the total catch) -> Catch-Quota Management for full accountability Market based management of the rights to catch -> quota transferability to align catch with fleet + Result based management if possible (e.g. harbour porpoise) Credit schemes where science is week and species inextricable Generally applicable rules to protect habitats etc Effects Catch quota management with full documentation will: exchange incentives to discard with incentives to selective fishing and new uses for all fish landed. Ease a discard ban remove the need for detailed regulation and control Give precise data ensure compliance and market access Catch Share management with high transferability will: enable fleet/quota balance on long term allow quota adaptations to mixed species catches (e.g. Danish pool system and EU in-year transfer scheme) 1. Do we have a coherent management that optimizes the food production base in respect of the ecosystem? More at
11 Optimization in Catch Quota Management Asst. Prof. Henrik Holm Department of Basic Sciences and Environment Faculty of Life Sciences University of Copenhagen Thorvaldsensvej 4 DK-1871 Frederiksberg C Denmark hholm@life.ku.dk URL: hholm/ In a mixed fishery (we consider in this paper only mixed fisheries involving two different types of fish) managed by catch quotas (as opposed to landing quotas), a vessel must stop fishing as soon as one of the quotas in its quota portfolio has been reached. A vessel may use its equipment to influence its catch composition within a certain range, and thereby try to optimize its catch in order to maximize the income (market prices for the types of fish involved in the mixed fishery are given). A priori, a vessel s quota portfolio is given, however, it is possible to lease quotas from other vessels in order to obtain a more desirable portfolio. Therefore, a vessel fishing under catch quota management has several ways to optimize its catch and income. We shall give precise mathematical formulations of the relevant optimization problems and solve them. We illustrate with a number of concrete examples. 1 The Single Vessel Case In this section, we consider a fishery in which a single vessel 1 catches two types of fish, called type 1 and type 2, in some combination. We assume in this section that the vessel is completely isolated in the sense that fish quotas cannot be leased or bought from others vessels. We shall get rid of this restrictive assumption in Section 2. Example 1.1 Some typical type 1/type 2 fish combinations are: cod/haddock (Scottish fleet) cod/nephrops (Danish fleet) sole/plaice (Dutch fleet) Our goal in this section is, in a nutshell, to determine the type 1/type 2 catch composition that results in the maximal income given that the vessel s targetting ability may not allow it to fully utilize both catch quotas in the mixed fishery. To find the optimal catch composition, we must first give a mathematical description of the situation we are considering. 1 The single vessel under consideration could be a specific vessel in some fleet, however, it could also be an abstract vessel representing a group of actual vessels fishing under similar conditions. Another possibility is to think of the vessel as an average of an entire fleet. 1
12 1.1 Assumptions The market prices (kr/kg or kilokr/ton) of the two types of fish determine the market data: Market Data Market price of type 1 fish p 1 Market price of type 2 fish p 2 Example 1.2 Prices obtained for landed catches vary a lot. Suggestive levels are: p cod = 2 (kilokr/ton) p haddock = 14 (kilokr/ton) p nephrops = 55 (kilokr/ton) p sole = 85 (kilokr/ton) p plaice = 1 (kilokr/ton) The vessel under consideration catches fish of type 1 and type 2 in some combination determined by the catch composition parameter, c [, 1], whose value the vessel can partially influence by using various types of equipment. The catch composition parameter is simply defined as the percentage of type 2 fish in the total catch. Thus we have: The percentage of type 1 fish in the total catch is : 1 c The percentage of type 2 fish in the total catch is : c Example 1.3 The value c =.55 corresponds to a type 1/type 2 catch composition of 45%/55%. The vessel s fishing equipment allows it to vary the catch composition parameter in a certain range from a lower catch composition bound, l, to an upper catch composition bound, u. Example 1.4 The values l =.5 and u =.6 correspond to the situation where the vessel may vary its type 1/type 2 catch composition in the range from 5%/5% to 4%/6%. For the vessel in question, we assume that the bounds l and u are given. The value of the catch composition parameter c [l, u] is then to be determined such that the vessel maximizes its income. The vessel s fishery is bounded by its type 1 fish quota, Q 1, and its type 2 fish quota, Q 2 (in tonnes). In catch quota management, the vessel must stop fishing once it reaches one of these two quotas. Example 1.5 Examples of member state quotas (in tonnes) are: Scottish fleet: Q cod = 11 and Q haddock = 21 Danish fleet: Q cod = 4 and Q nephrops = 4 Dutch fleet: Q sole = 1 and Q plaice = 2 Thus, a single vessel in the Scottish fleet may have quotas Q cod = 11 and Q haddock = 21 (tonnes). 2
13 We summarize the mathematical data describing the vessel under consideration: Vessel Data Type 1 fish quota Q 1 Type 2 fish quota Q 2 Lower catch composition bound l Upper catch composition bound u Catch composition parameter c Here Q 1, Q 2, l, and u are given, whereas c is to be (optimally) determined in the range [l,u]. 1.2 The Mathematical Model Denote by t 1 and t 2 the number of tonnes of fish of type 1 and type 2 caught by the vessel. In catch quota management, both of these numbers are bounded by the vessel s given quotas, that is, t 1 Q 1 t 2 Q 2 (i) (ii) The total catch is t 1 +t 2 of which t 2, by definition of the catch composition parameter, constitutes the fraction c, that is, t 2 t 1 +t 2 = c. Equivalently, ct 1 (1 c)t 2 = (iii c ) This is a straight line in a (t 1,t 2 ) coordinate system with slope a = c 1 c and constant term b =. Since l c can vary in the interval [l,u], the slope of the line in (iii c ) can vary in the interval [ 1 l, u 1 u ]. The restrictions (i), (ii), and (iii c ) are illustrated in the following (t 1,t 2 ) coordinate system. Q 2 line with slope u 1 u Type 2 fish (tonnes) c = u line with slope l 1 l c = l Q 1 Type 1 fish (tonnes) The vessel s income for catching (and selling) t 1 tonnes of fish of type 1, and t 2 tonnes of fish of type 2 is computed from the market prices: I(t 1,t 2 ) = p 1 t 1 + p 2 t 2. 3
14 For each value of the parameter c in the interval [l,u] corresponding to a choice of type 1/type 2 catch composition within the range determined by the vessel s equipment the maximal income is found by optimizing the income function I(t 1,t 2 ) (in two variables) subject to the boundary conditions (i), (ii), and (iii c ). This optimization problem, in which the third boundary condition depends on the value of c, may be written in short form as follows. I(t 1,t 2 ) = p 1 t 1 + p 2 t 2 = Max! t 1 Q 1 t 2 Q 2 ct 1 (1 c)t 2 = The optimization problem (P c ) above is an example of a so-called linear programming problem in two variables (t 1,t 2 ), which given any specific value of c is easily solved. (P c ) Example 1.6 We consider a whitefish fishery where type 1/type 2 fish are cod/haddock. Prices and quotas are as in Examples 1.2 and 1.5, that is, p 1 = 2 Q 1 = 11 p 2 = 14 Q 2 = 21 Suppose, as in Example 1.3, that the vessel aims for cod/haddock catch composition of 45%/55% corresponding to the catch composition parameter c =.55. To maximize its income, the vessel must solve: As illustrated below, the solution to this problem is: I(t 1,t 2 ) = 2t t 2 = Max! t 1 11 t t 1.45t 2 = (t 1,t 2) (11,13.4) (tonnes). (P.55 ) Note that the ratio of t2 = 13.4 and the total catch t 1 +t 2 = 24.4 really is c =.55, and that the fishery must stop since the cod quota Q 1 = 11 has been reached. Therefore, subject to management by catch quotas, the income is: I = I(t1,t 2) = I(11,13.4) = (kilokr). Q 2 = 21 (17.2,21.) haddock (tonnes) Management by catch quotas c =.55 (11.,13.4) Q 1 = 11 Management by landing quotas cod (tonnes) 4
15 In comparison, the present management by landing quotas would generate an income of I(11,21) = = 514 (kilokr), that is, 16 (kilokr) more than under catch quota management. However, the resulting discards of cods would be = 6.2 (tonnes), which has a market value of 124 (kilokr). Thus, under management by landing quotas and with the given assumptions one must, in some sense, throw away 124 (kilokr) to earn an extra 16 (kilokr). Recall that our goal is to find the optimal catch composition, that is, the catch composition which results in the maximal income. In view of this, the example above, although illustrative, is not very informative since it requires the catch composition parameter c to be known in advance. To overcome this obstacle, we return to the optimization problem (P c ). For any given c in [l,u], we denote by the maximum point of the problem (P c ), and we let be the associated maximal income. (t 1(c),t 2(c)) I (c) = I(t 1(c),t 2(c)) = p 1 t 1(c) + p 2 t 2(c) Example 1.7 Consider the setup of Example 1.6. As seen in loc. cit., one has in this case: (t 1(.55),t 2(.55)) = (11,13.4) and I (.55) = 48. With this notation at hand, we can give a precise mathematical formulation of the vessel s incomeoptimization problem. The Single Vessel Optimization Problem. The following data are given: The market prices p 1 and p 2. The vessel s quotas Q 1 and Q 2. The vessel s lower and upper catch composition bounds l and u. To maximize its income, the vessel must find the value c [l,u] of the catch composition parameter which makes the income I (c) as large as possible, that is, I (c ) = max c [l,u] I (c). This maximal income is denoted by I, and c is called the optimal catch composition parameter. The corresponding optimal (type 1, type 2) catch composition, that is, (t 1 (c ),t 2 (c )) is denoted by (t 1,t 2 ). 1.3 Solution It takes only straightforward graphical considerations to solve the single vessel optimization problem formulated above. The precise solution presented below, which may seem a bit technical at first sight, will be important in Section 2. 5
16 Solution of the Single Vessel Optimization Problem. Depending on the three cases, Case I: Case II: Case III: Q 2 Q 1 < l 1 l l 1 l Q 2 u Q 1 1 u u 1 u < Q 2 Q 1 the optimal catch composition parameter c, the optimal catch composition (t1,t 2 ), and the maximal income I are given as follows. l (case I) c Q 2 = (case II) Q 1 + Q 2 u (case III) (1 l ) Q 2,Q 2 (case I) l (t1,t 2) = (Q 1,Q 2 ) (case II) ( u Q1, 1 u Q ) 1 (case III) ( 1 l ) p1 + p 2 Q2 (case I) l I = p 1 Q 1 + p 2 Q 2 (case II) ( u ) p1 + p 2 Q1 (case III) 1 u Example 1.8 Consider the setup in Example 1.6, that is, type 1/type 2 is cod/haddock, and p 1 = 2 Q 1 = 11 p 2 = 14 Q 2 = 21 Assume that the vessel s equipment allows it to vary its cod/haddock catch composition in the range from 5%/5% to 4%/6%. As in Example 1.4, this corresponds to the bounds: l =.5 and u =.6 The three cases I, II, and III described above are determind by the numbers l 1 l = = 1. and u 1 u = = 1.5 Since Q 2 Q 1 = > 1.5 we are in Case III. Hence, the formulae above give the optimal values: c = u =.6, (t 1,t 2) = (11,16.5), I = 451. Thus, within the possible range, it is optimal for the vessel to aim for an cod/haddock catch composition of 4%/6%, in which case the fishery stops after having caught t1 = 11 tonnes of cod and t 2 = 16.5 tonnes of haddock. The total market value for these fish are I = 451 kilokr. We note that the catch composition 45%/55% chosen in Example 1.6 is not optimal since it only generates an income of 48 (kilokr). 6
17 Suppose that next season, the vessel s haddock quota drops from Q 2 = 21 to Q 2 = 15, say. The vessel must then change its fishery accordingly, indeed, now Q 2 Q 1 = lies between 1. and 1.5 which puts us in Case II. This time, the formulae above give the optimal values: c =.58, (t 1,t 2) = (11,15), I = 43. Hence, it is now optimal for the vessel to aim for an cod/haddock catch composition of 42%/58%, in which case both quotas Q 1 = 11 and Q 2 = 15 are reached simultaneously. haddock (tonnes) Q 2 = 15 c =.58 Q 1 = cod (tonnes) As implied by the example above, the formulae in our solution of the single vessel optimization problem can also be used to assess the boundaries for the quota relation between type 1 and type 2 fish which will make it possible for the vessel to obtain full quota utilization of both species 2 The Multiple Vessel Case In this section, we expand on the situation from Section 1 by considering a mixed fishery in which two vessels 2, called vessel A and vessel B, both catch type 1 and type 2 fish in varying combinations. The vessels may may lease 3 quotas from each other in order to optimize their quota portfolios and, in turn, their income. From a mathematical point of view, the leasing aspect complicates the situation considerably compared to the single vessel case studied in Section 1. 2 The two vessels under consideration could very well be two specific vessels in some fleet. Alternatively, one might think of the two vessels as being abstract ones representing some relevant situation. For example, one vessel could represent an actual group of vessels in some fleet fishing under similar conditions, while the other vessel could represent the residual fleet, that is, the average of the remaining vessels in the fleet. 3 In real life fishery, quotas may transferred (bought or leased) in some member states. Buying of quotas is understood as permanent buying of quota shares, and consequently the quota amount released every year on account of total allowable catches (TACs) is being set accordingly. Buying typically takes place in context of structural changes, as private scrapping investments in new vessels etc. Buying is not considered here. Leasing of quotas relate to the amount in tonnes of a given stock leased for the given quota year. Leasing may take place in context of planning the fishery for the entire quota year, or it may relate to daily adaptation of vessel quotas to the development in the fishery or to cover unforeseen bycatches. The leasing element is considered here as an important tool of flexible quota management. 7
18 2.1 Assumptions In the present situation, the market is defined by the market prices (in kr/kg or kilokr/ton) of the two types of fish, and by the leasing prices (also in kr/kg or kilokr/ton) of the two types of fish quota. Market Data Market price of type 1 fish p 1 Market price of type 2 fish p 2 Leasing price of type 1 fish quota q 1 Leasing price of type 2 fish quota q 2 Example 2.1 Prices for leasing of quotas vary a lot. Suggestive levels are: q cod = 1 (kilokr/ton) q haddock = 3 (kilokr/ton) q nephrops = 3 (kilokr/ton) q sole = 6 (kilokr/ton) q plaice = 2 (kilokr/ton) Much of the data defining the two vessels under consideration are the same as described in Subsection 1.1, however, each vessel has its own quotas, its own catch composition bounds etc. Vessel A Data Type 1 fish quota Q A 1 Type 2 fish quota Q A 2 Lower catch composition bound l A Upper catch composition bound u A Catch composition parameter c A Type 1 fish quota leased from vessel B x 1 Type 2 fish quota leased from vessel B x 2 Vessel B Data Type 1 fish quota Q B 1 Type 2 fish quota Q B 2 Lower catch composition bound l B Upper catch composition bound u B Catch composition parameter c B Type 1 fish quota leased from vessel A x 1 Type 2 fish quota leased from vessel A x 2 Since the two vessels may lease quotas from each other, we must consider two additional variables, x 1 and x 2. Here x 1 and x 2 are the number (in tonnes) of type 1 and type 2 fish quotas, respectively, which vessel A leases from vessel B. Alternatively, vessel B leases x 1 and x 2 tonnes of type 1 and type 2 fish quota from vessel A. The pair (x 1,x 2 ) is called a quota leasing agreement between the vessels A and B. Example 2.2 The situation where: vessel A leases 1 tonnes of type 1 fish quota from vessel B, and vessel A leases 15 tonnes of type 2 fish quota to vessel B corresponds to the quota leasing agreement (x 1,x 2 ) = (1, 15). 2.2 The Mathematical Model Since vessel A can lease at most Q B 1 tonnes of type 1 fish quota from vessel B one has x 1 Q B 1 ; and since vessel A can lease at most Q A 1 tonnes of type 1 fish quota to vessel B one has x 1 Q A 1. 8
19 Combining this with similar considerations for the variable x 2 give the following restrictions: Q A 1 x 1 Q B 1 Q A 2 x 2 Q B 2 Once a quota leasing agreement (x 1,x 2 ) has been made, the vessels quota portfolios change as follows: Vessel A s quota portfolio changes from (Q A 1,QA 2 ) to (QA 1 + x 1,Q A 2 + x 2), and Vessel B s quota portfolio changes from (Q B 1,QB 2 ) to (QB 1 x 1,Q B 2 x 2). As in Subsection 1.2, we denote by (t1 A,tA 2 ) the number of tonnes of fish of (type 1, type 2) caught by vessel A. Similarly (t1 B,tB 2 ) denotes the number of tonnes of fish of (type 1, type 2) caught by vessel B. As described in Subsection 1.2, the catches for vessels A and B are subject to the conditions: t A 1 QA 1 + x 1 t A 2 QA 2 + x 2 c A t A 1 (1 c A)t A 2 = and t B 1 QB 1 x 1 t B 2 QB 2 x 2 c B t B 1 (1 c B)t B 2 = Since it costs money to lease quotas from the other vessel (dually, one gets paid for leasing quotas to the other vessel), the income functions for the two vessels become more complicated, in fact, they are given by: I A (t A 1,t A 2,x 1,x 2 ) = p 1 t A 1 + p 2 t A 2 q 1 x 1 q 2 x 2, I B (t B 1,t B 2,x 1,x 2 ) = p 1 t B 1 + p 2 t B 2 + q 1 x 1 + q 2 x 2. We begin by focusing on vessel A. The situation viewed from vessel B s point of view can be described similarly. For each value of the parameter c A [l A,u A ] corresponding to a choice of type 1/type 2 catch composition within the range determined by vessel A s equipment the maximal income for vessel A is found by optimizing the income function I A (t1 A,tA 2,x 1,x 2 ) (in four variables) subject to the boundary conditions above, that is, I A (t1 A,tA 2,x 1,x 2 ) = p 1 t1 A + p 2t2 A q 1x 1 q 2 x 2 = Max! t1 A QA 1 + x 1 t2 A QA 2 + x 2 c A t1 A (1 c A)t2 A = (R A c A ) Q A 1 x 1 Q B 1 Q A 2 x 2 Q B 2 If the parameter c A is given then (R A c A ) is a so-called linear programming problem in four variables (t A 1,tA 2,x 1,x 2 ), which can be solved using Dantzig s simplex algorithm. However, this is not particularly useful since we do not know the optimal catch composition parameter in advance. To overcome this difficulty, we note that for any fixed choice of quota leasing agreement (x 1,x 2 ) [ Q A 1,QB 1 ] [ QA 2,QB 2 ], the problem (R A c A ) reduces to a problem in two variables t A 1 and ta 2, namely: I A (x 1,x 2 )(t A 1,tA 2 ) = p 1t A 1 + p 2t A 2 q 1x 1 q 2 x 2 = Max! t A 1 QA 1 + x 1 t A 2 QA 2 + x 2 c A t A 1 (1 c A)t A 2 = 9
20 Note that this is nothing but the single vessel optimization problem which was formulated in Subsection 1.2 (the only difference being that Q A i is replaced by Q A i + x i) and solved in 1.3. Thus, supposing that vessel A and vessel B make the quota leasing agreement (x 1,x 2 ), then vessel A knows how to fish optimally and thus maximize its income. In fact, the following formulae are immediate from our solution of the single vessel optimization problem. Quota Leasing Agreements from the Viewpoint of Vessel A. Suppose that vessel A and vessel B make the quota leasing agreement (x 1,x 2 ), changing vessel A s quota portfolio from (Q A 1,QA 2 ) to (QA 1 + x 1,Q A 2 + x 2). Vessel A then knows Its optimal catch composition parameter c A, The corresponding optimal catch, ((t A 1 ),(t A 2 ) ), and The associated maximal income I A. In fact, depending on the three cases, Case I: Case II: Case III: Q A 2 + x 2 Q A 1 + x < l A 1 1 l A l A QA 2 + x 2 1 l A Q A 1 + x 1 u A 1 u A < QA 2 + x 2 Q A 1 + x 1 u A 1 u A one has the following formulae: l A (case I) c Q A = A 2 + x 2 Q A 1 + x 1 + Q A 2 + x (case II) 2 u A (case III) (1 l A ) (Q A 2 + x 2 ),Q A 2 + x 2 (case I) l A ((t1 A ),(t2 A ) ( ) ) = Q A 1 + x 1,Q A 2 + x 2 (case II) ( Q A u A 1 + x 1, (Q A 1 + x 1 ) ) (case III) 1 u A ( 1 l A ) p1 + p 2 (Q A l 2 + x 2 ) q 1 x 1 q 2 x 2 (case I) A I A = p 1 (Q A 1 + x 1 ) + p 2 (Q A 2 + x 2 ) q 1 x 1 q 2 x 2 (case II) ( u A ) p1 + p 2 (Q A 1 u 1 + x 1 ) q 1 x 1 q 2 x 2 (case III) A Note that c A, (t A 1 ), (t A 2 ), and I A are functions of the variables (x 1,x 2 ). Hence, for any choice of quota leasing agreement (x 1,x 2 ), vessel A s new quota portfolio (Q A 1 + x 1,Q A 2 + x 2) results in the maximal income I A(x 1,x 2 ) provided, of course, that it fishes optimally, i.e. according to the optimal catch composition parameter c A(x 1,x 2 ). Thus, seen from the viewpoint of vessel A, the optimal quota leasing agreement (x 1,x 2 ) is the one that maximizes the function I A(x 1,x 2 ). We shall return to the following example throughout the rest of this paper. 1
21 Example 2.3 The market for cods and haddocks are assumed as follows. Market Data Cod market price p 1 = 2 Haddock market price p 2 = 14 Cod quota leasing price q 1 = 1 Haddock quota leasing price q 2 = 3 The Scottish fleet s total cod and haddock quotas are 11 and 21 tonnes, respectively. Suppose that half of the fleet (vessel A) can vary its cod/haddock catch combination in the range from 5%/5% to 4%/6%, and that the other half (vessel B) in the range from 8%/2% to 2%/8%. Thus one has: Vessel A Data Cod quota Q A 1 = 55 Haddock quota Q A 2 = 15 Lower catch composition bound l A =.5 Upper catch composition bound u A =.6 Vessel B Data Cod quota Q B 1 = 55 Haddock quota Q B 2 = 15 Lower catch composition bound l B =.2 Upper catch composition bound u B =.8 If the vessels choose not to lease quotas from each other corresponding to the quota leasing agreement (x 1,x 2 ) = (,) then we may consider them as isolated. In this case, our solution to the single vessel problem in Subsection 1.3 shows that their maximal incomes are: I A = 2255 and I B = 257 As seen above, the given constants Q A 1,QA 2,QB 1,QB 2,l A,u A completely describe vessel A s maximal income I A(x 1,x 2 ) as a function of the quota leasing agreement (x 1,x 2 ) made by vessels A and B. Its graph is: 2e+5 e+ 1 x x1 Graph of income function I A(x 1,x 2 ) for vessel A It follows that the optimal quota leasing agreement for vessel A is (x1,x 2 ) = (55,6) (meaning that vessel A should try to lease 55 tonnes of cod quota and 6 tonnes of haddock quota from vessel B) resulting in the new quota portfolio (Q A 1 + x 1,Q A 2 + x 2) = (11,165) and a larger maximal income: I A(55,6) =
22 A couple of observations are in order here: If vessel A were given the quota portfolio (11, 165) to begin with, its maximal income would have been 451, cf. Example 1.8. In the present situation, vessel A must pay = 73 to obtain the quota portfolio, thus reducing its maximal income to = 378. To obtain the larger (than 2255) maximal income of 378, it is required that vessel A fishes optimally, that is, according to the optimal catch composition parameter c A(55,6) =.6, corresponding to a cod/haddock catch composition of 4%/6%. In this case, vessel A s fishery stops after having caught (t A 1 ) (55,6) = 11 tonnes of cod, and (t A 2 ) (55,6) = 165 tonnes of haddock, that is, both quotas are reached simultaneously. Of course, the quota leasing agreement (x1,x 2 ) = (55,6), which is optimal for vessel A, can never become a reality since it reduces vessel B s cod quota to zero and thus stops vessel B s fishery. The example above illustrates that we must consider the situation from the viewpoint of vessel A and vessel B simultaneously. Analogously to how we found the functions c A, (t A 1 ), (t A 2 ), and I A for vessel A, we can find the corresponding functions for vessel B. This is done below. Quota Leasing Agreements from the Viewpoint of Vessel B. Suppose that vessel A and vessel B make the quota leasing agreement (x 1,x 2 ). Depending on the following three cases, Case I: Case II: Case III: Q B 2 x 2 Q B 1 x < l B 1 1 l B l B QB 2 x 2 1 l B Q B 1 x 1 u B 1 u B < QB 2 x 2 Q B 1 x 1 u B 1 u B vessel B s optimal catch composition parameter, its optimal catch, and the associated maximal income are given by the following formulae. l B (case I) c Q B = B 2 x 2 Q B 1 x 1 + Q B 2 x (case II) 2 u B (case III) (1 l B ) (Q B 2 x 2 ),Q B 2 x 2 (case I) l B ((t1) B,(t2) B ( ) ) = Q B 1 x 1,Q B 2 x 2 (case II) ( Q B u B 1 x 1, (Q B 1 x 1 ) ) (case III) 1 u B ( 1 l B ) p1 + p 2 (Q B l 2 x 2 ) + q 1 x 1 + q 2 x 2 (case I) B I B = p 1 (Q B 1 x 1 ) + p 2 (Q B 2 x 2 ) + q 1 x 1 + q 2 x 2 (case II) ( u B ) p1 + p 2 (Q B 1 u 1 x 1 ) + q 1 x 1 + q 2 x 2 (case III) B If vessels A and B decide not to exchange any quotas corresponding to the quota leasing agreement (x 1,x 2 ) = (,) then their maximal incomes are I A(,) and I B(,), respectively. Obviously, vessel A is only interested in making a quota leasing agreement (x 1,x 2 ) if it is profitable, that is, if 12
23 it results in a larger maximal income than IA(,). Similarly for vessel B. Thus, the profitable quota leasing agreements for vessels A and B are the subsets of the square [ Q A 1,QB 1 ] [ QA 2,QB 2 ] given by P A = { (x 1,x 2 ) I A(x 1,x 2 ) IA(,) } and P B = { (x 1,x 2 ) I B(x 1,x 2 ) IB(,) }. A necessary condition for vessels A and B to make a quota leasing agreement (x 1,x 2 ) is that this agreement is profitable for both parties, that is, (x 1,x 2 ) must belong to the intersection P = P A P B. It is of interest for both vessels to find the set P of quota leasing agreements which are profitable for both of them. As illustrated by Example 2.6, there might not be any(!), however, usually there are many. In Example 2.3, vessel B is superior to vessel A in the sense that both vessels have the same number of quotas, but vessel B is more flexible in its catch composition (which ranges from 8%/2% to 2%/8%) than vessel A (which only ranges from 5%/5% to 4%/6%). However, even in this case there are many quota leasing agreements that are profitable for both vessels. This is explored in Examples 2.4 and 2.5 below. Example 2.4 Consider the setup in Example 2.3. The graphs of vessel A s and vessel B s income functions I A(x 1,x 2 ) and I B(x 1,x 2 ) are illustrated below. 4e+5 2e+5 2e+5 e+ e+ 1 1 x2 5 x2 5 x1 x Graph of income function I A(x 1,x 2 ) for vessel A Graph of income function I B(x 1,x 2 ) for vessel B From these graphs one finds the sets of profitable quota leasing agreements for vessels A and B: x 2 x The set P A of profitable quota leasing x 1 agreements for vessel A The set P B of profitable quota leasing x 1 agreements for vessel B 13
24 The set P of quota leasing agreements that are profitable for both vessels is found by intersecting the two sets P A and P B, as illustrated below x 2 x 2 V = (, ) V 1 = ( 255, 2632) V 2 = (1119, 3881) V 4 = (2343, 213) V 3 = (228, 356) The setxp 1 of quota leasing agreements that are profitable for both vessels x 1 We see that P is a polygon with vertices V,...,V 4 whose coordinates are shown in the figure above. The corresponding areas on vessel A s and B income functions are: 4e+5 2e+5 2e+5 e+ e+ 1 1 x2 5 x2 5 x1 x In general, the set P of quota leasing agreements that are profitable for both vessels is a polygon. Of course, it is possible to write down explicit formulae for the vertices V,V 1,... of this polygon in terms of the given market data p 1, p 2,q 1,q 2, and vessel data Q A 1,QA 2,l A,u A and Q B 1,QB 2,l B,u B, however, since these formulae are rarther complicated, we shall not attempt to present them here. Instead, we note that in all specific examples, one can easily find the set P, as it is done in Example 2.4. Note that the quota leasing agreements (x 1,x 2 ) corresponding to boundary points, i.e. the edges, of the polygon P are not interesting, since either vessel A or vessel B will not make (or lose) any mony from such an agreement. Hence, the interesting quota leasing agreements correspond to interior points of the set P. 14
25 Example 2.5 Consider the set P of quota leasing agreements that are profitable for both vessels, found in Example 2.4 above. The vertex V = (,) corresponds to the situation where the vessels lease no quotas from or to each other. We consider as well two other possible quota leasing agreements: V V x 2 x 2 V 1 (1, 25) V 4 V 1 (1, 2341) V 4 V 2 V 3 Quota leasing agreement (x 1,x 2 ) = (1, 25) V 2 V 3 Quota leasing agreement (x 1,x 2 ) = (1, 2341) Since (x 1,x 2 ) = x 1 (1, 25) (corresponding to the situation where x 1 vessel A leases 1 tonnes of cod quota from, and 25 tonnes of haddock quota to vessel B) and (x 1,x 2 ) = (1, 2341) are points in P, these quota leasing agreements are profitable for both vessels. However, as we shall see below, one vessel might benefit more than the other. Computing the functions I A,I B and c A,c B at the points (,), (1, 25), and (1, 2341) gives us the maximal income, and the catch composition required to obtain this, for each of the three situations. (x 1, x 2 ) Vessel A Vessel B (,) (1, 25) (1, 2341) Income Catch I A = 2255 c A =.6 (4%/6%) Income Catch I A = 235 c A =.59 (41%/59%) Income Catch I A = c A =.56 (44%/56%) Income Catch I B = 257 c B =.66 (34%/66%) Income Catch I B = 2835 c B =.71 (29%/71%) Income Catch I B = c B =.74 (26%/74%) Compared to the situation (,), where no quotas are leased, we see that if the quota leasing agreement (1, 25) is made then vessel A makes an additional 5, whereas vessel B makes an additional 265. If the quota leasing agreement (1, 2341) is made then both vessels make an additional By the end of the day, whatever quota leasing agreement is made between the two vessels depends on which has the best negotiation skills. Example 2.6 Consider the same setup as in Example 2.3, however, assume this time that vessel A s possible cod/haddock catch composition ranges from 4%/6% to 3%/7% (that is, l A =.6 and u A =.7). In this situation, the sets P A and P B have only an edge in commen, and hence there are no quota leasing agreements which are profitable for both vessels. 15 x x 1
26 Annex Boundary conditions for Optimization model for the outtake of catch quotas under result based management Prof. Henrik Holms paper is based on the boundary conditions described in this paper. 1. Optimizing the uptake of quotas under Catch Quota Management (CQM) Basis Catch-Quota Management (CQM) is a result based management with the following main features: The fisher is accountable for the total catch quota he has been given. All catches including by-catches must be covered by his quota and all catches of the given species, including eventual discards count on his quota. When the quota is exhausted the fisher must stop the fishery. If the quota for one species in a mixed fishery is exhausted fishing for all species in the fishery must stop. The fisher must optimize the utilization of his yearly vessel quota portfolio by i. Planning time and place of fishery or by using selective gear ii. Buying quota rights that covers his actual catches. The input component is the vessel with a given use of fishing gear, fishing method and composition of species caught. Vessels with similar gear and fishing pattern belong to a fleet. The main variables are 1. Fleet type. We operate with 3 fleets. Vessels of each fleet have a defined ability to control the catch composition within certain boundaries. 2. Fish catch-ability. In periods or areas fish may be more or less easy to catch. Here we consider catch-ability as an exogenous variable. 3. Quota availability. This depends on the allocation key between EU member states and on the changes in relative TAC s from year to year). We consider the availability as an exogenous variable. 4. Prices. The output component to be optimized is tonnes of fish or value of fish in DKK Problem Establish or simulate the optimal outtake for given fleets against a given quota portfolio, a given typical quota allocation for the fleet and under the given boundary conditions.
27 Note on dynamics: The quota portfolio may change from one year to the other. Also the catchability may change as an overestimation of quotas may result in low catch ability and an underestimation in high catch ability, hence closing of a mixed fisheries where the high catch-ability do not match the underestimated quota Boundary conditions 1 st boundary condition The ability of the individual fleet to target the quota for the individual species in a mixed fishery. No change of vessel quota allocation is possible Borderline case a) being that no targeting is possible in which case it is a simple (quota portfolio): (catch composition) calculation and borderline case b) that full targeting is possible in which case it cannot be considered as a mixed fishery. Comment: The targeting ability of the fleets is defined under 3; Fleet structure and fisheries 2 nd boundary condition In certain member states it is possible to lease or buy quota rights. In that case fleets can buy rights to cover their need for quotas in mixed (or portfolio) fisheries). There is a limit to buying up: If there is only one fleet type buying up is only relevant to the point where all get the same portfolio, i.e. transferability only makes sense as long as the advantage for the receiving fleet exceed a possible disadvantage for the vessels transferring the fish. And of course transferability must take place within the total quota available for the member state. Basis for simulation of quota utilization on account of vessel ability to target catch composition Simulation and optimization for vessels in the following fleets: I. Whitefish ( Scottish fleet ) (cod and haddock) a. Typical catch composition for mixed fisheries haddock 5% : cod 5% b. Function regarding fleet ability to target individual species The vessel may influence the catch composition in the range between haddock 5% : cod 5% and haddock 6% : cod 4%: c. Available quota for the vessel: cod 11 tonnes and haddock 21 tonnes II. Nephrops fishery ( Danish ) a. Typical catch composition for mixed fisheries Nephrops 8 % : cod 2 % b. Function regarding fleet ability to target individual species The vessel may influence the catch composition in the range between nephrops 9% : cod 1% and nephrops 7% : cod 3%: c. Available quota for the vessel cod 4 tonnes; Nephrops 4 tonnes
28 III. Sole/plaice fishery ( Dutch ) a. Typical catch composition for mixed fisheries Sole 2 % : plaice 8%. b. Function regarding fleet ability to target individual species Sole % : plaice 1%. Sole 2 % : plaice 8%. c. Available quota for the vessel: Sole 1 tonnes; Plaice 2 tonnes Simulation of quota utilization on account of fleet targeting ability combined with quota transferability Quota transferability increase quota utilization. In a system with transferability it is necessary to take account of the patterns of all relevant fleets in order to optimize on Member State level instead of fleet level. We may talk about 15-2 fleets with each their characteristics. For the sake of simplicity we consider for each of the above fleets only a residual fleet that encompass the average pattern of all other fleets. The figure illustrate the comfort and discomfort zones in relation quota utilization on member state level (colours should be graded if I knew how). The effect of a management with transferability is that the y-axis moves to the left, leaving a larger green area I. Member state quota availability 11. tonnes of cod; 21. tonnes of haddock 1. Whitefish (Scottish fleet) (cod and haddock) a. Starting quota 5.5 tonnes of cod and 1.5 tonnes of haddock 2. Residual fleet a. Starting quota 5.5 tonnes of cod and 1.5 tonnes of haddock b. Function regarding fleet ability to target individual species: The vessel may influence the catch composition in the range between haddock 2% : cod 8% and haddock 2% : cod 8% II. Member state quota availability 4. tonnes of cod; 4. tonnes of Nephrops 1. Nephrops fishery (Danish) a. Starting quota cod 5 tonnes; Nephrops 3.5 tonnes 2. Residual fleet a. Starting quota cod 3.5 tonnes; Nephrops 5 tonnes
The Economics of Ecosystem Based Management: The Fishery Case
 The Economics of Ecosystem Based Management: The Fishery Case Fisheries impact on marine ecosystem and policy implications Peder Andersen Co-authors: Lars Ravensbeck Hans S. Frost Department of Food and
The Economics of Ecosystem Based Management: The Fishery Case Fisheries impact on marine ecosystem and policy implications Peder Andersen Co-authors: Lars Ravensbeck Hans S. Frost Department of Food and
Skjal 2. The Faroe Plateau Ecosystem. ICES 2016
 Skjal 2. The Faroe Plateau Ecosystem. ICES 2016 ICES Advice on fishing opportunities, catch, and effort Faroes Ecoregion Published 10 June 2016 4.3.1 Cod (Gadus morhua) in Subdivision 5.b.1 (Faroe Plateau)
Skjal 2. The Faroe Plateau Ecosystem. ICES 2016 ICES Advice on fishing opportunities, catch, and effort Faroes Ecoregion Published 10 June 2016 4.3.1 Cod (Gadus morhua) in Subdivision 5.b.1 (Faroe Plateau)
COUNTRY NOTE ON NATIONAL FISHERIES MANAGEMENT SYSTEMS -- GERMANY
 COUNTRY NOTE ON NATIONAL FISHERIES MANAGEMENT SYSTEMS -- GERMANY Historical overview 1. There has been an ongoing structural change in the German fleet since the end of World War II. In the 1950s, nearly
COUNTRY NOTE ON NATIONAL FISHERIES MANAGEMENT SYSTEMS -- GERMANY Historical overview 1. There has been an ongoing structural change in the German fleet since the end of World War II. In the 1950s, nearly
6.3.2 Advice June 2014. Mixed-fisheries advice for Subarea IV (North Sea) and Divisions IIIa North (Skagerrak) and VIId (Eastern Channel)
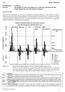 6.3.2 Advice June 2014 ECOREGION STOCK North Sea Mixed-fisheries advice for Subarea IV (North Sea) and Divisions IIIa North (Skagerrak) and VIId (Eastern Channel) Scenarios for 2015 Mixed-fisheries considerations
6.3.2 Advice June 2014 ECOREGION STOCK North Sea Mixed-fisheries advice for Subarea IV (North Sea) and Divisions IIIa North (Skagerrak) and VIId (Eastern Channel) Scenarios for 2015 Mixed-fisheries considerations
3.13.5.b Gear selectivity in the directed cod fishery (BACOMA project)
 3.13.5.b Gear selectivity in the directed cod fishery (BACOMA project) IBSFC has asked ICES to: i) evaluate the potential improvement in the gear selectivity in the directed cod fisheries as concluded
3.13.5.b Gear selectivity in the directed cod fishery (BACOMA project) IBSFC has asked ICES to: i) evaluate the potential improvement in the gear selectivity in the directed cod fisheries as concluded
6.3.27 (update) Advice November 2014
 6.3.27 (update) Advice November 2014 ECOREGION STOCK North Sea Sole in Subarea IV (North Sea) (updated) Please note: The present advice replaces the advice given for this stock in June 2014. Advice for
6.3.27 (update) Advice November 2014 ECOREGION STOCK North Sea Sole in Subarea IV (North Sea) (updated) Please note: The present advice replaces the advice given for this stock in June 2014. Advice for
8.3.18 Advice May 2014
 8.3.18 Advice May 2014 ECOREGION STOCK Baltic Sea Sprat in Subdivisions 22 32 (Baltic Sea) Advice for 2015 ICES advises on the basis of the MSY approach that catches in 2015 should be no more than 222
8.3.18 Advice May 2014 ECOREGION STOCK Baltic Sea Sprat in Subdivisions 22 32 (Baltic Sea) Advice for 2015 ICES advises on the basis of the MSY approach that catches in 2015 should be no more than 222
Final Report on the Danish Catch Quota Management Project 2010
 Final Report on the Danish Catch Quota Management Project 2010 DTU Aqua Report No 235-2011 Af Jørgen Dalskov, Kirsten Birch Håkansson and Hans Jakob Olesen Final Report on the Danish Catch Quota Management
Final Report on the Danish Catch Quota Management Project 2010 DTU Aqua Report No 235-2011 Af Jørgen Dalskov, Kirsten Birch Håkansson and Hans Jakob Olesen Final Report on the Danish Catch Quota Management
The Physical and Economic Accounts for UK Fisheries
 The Physical and Economic Accounts for UK Fisheries Report by the Office for National Statistics (ONS) March 2003 Acknowledgements The author of this report is Charles Palmer (formerly ONS). The author
The Physical and Economic Accounts for UK Fisheries Report by the Office for National Statistics (ONS) March 2003 Acknowledgements The author of this report is Charles Palmer (formerly ONS). The author
Indicator fact sheet Fishing fleet trends
 Indicator fact sheet Fishing fleet trends Key message: The big EU 15 fishing fleet (1989 2000) has decreased in numbers of vessels (10 %), in tonnage (6 %) and power (12 %) The much smaller EFTA fishing
Indicator fact sheet Fishing fleet trends Key message: The big EU 15 fishing fleet (1989 2000) has decreased in numbers of vessels (10 %), in tonnage (6 %) and power (12 %) The much smaller EFTA fishing
3.3.3 Capelin (Mallotus villosus) in Subareas I and II (Northeast Arctic), excluding Division IIa west of 5 W (Barents Sea capelin)
 ICES Advice on fishing opportunities, catch, and effort Barents Sea and Norwegian Sea Ecoregions Published 8 October 2015 3.3.3 Capelin (Mallotus villosus) in Subareas I and II (Northeast Arctic), excluding
ICES Advice on fishing opportunities, catch, and effort Barents Sea and Norwegian Sea Ecoregions Published 8 October 2015 3.3.3 Capelin (Mallotus villosus) in Subareas I and II (Northeast Arctic), excluding
How can Fisheries Management Solve the Problem of Biological Sustainability?
 How can Fisheries Management Solve the Problem of Biological Sustainability? Workshop in Akureyri Iceland 11.-12. October 2007 Niels Vestergaard Department of Environmental and Business Economics Centre
How can Fisheries Management Solve the Problem of Biological Sustainability? Workshop in Akureyri Iceland 11.-12. October 2007 Niels Vestergaard Department of Environmental and Business Economics Centre
Capacity and Efficiency in Swedish Pelagic Fisheries
 SLI WORKING PAPER 2006:1 Capacity and Efficiency in Swedish Pelagic Fisheries Staffan Waldo The Swedish Institute for Food and Agricultural Economics Capacity and Efficiency in Swedish Pelagic Fisheries
SLI WORKING PAPER 2006:1 Capacity and Efficiency in Swedish Pelagic Fisheries Staffan Waldo The Swedish Institute for Food and Agricultural Economics Capacity and Efficiency in Swedish Pelagic Fisheries
Danish Experiences with the Landing obligation in the Baltic Sea
 Danish Experiences with the Landing obligation in the Baltic Sea and industrial fisheries elsewhere DAG, London 25 November 2015 Presented by Kenn Skau Fischer Fisheries Policy advisor= lobbyist Danish
Danish Experiences with the Landing obligation in the Baltic Sea and industrial fisheries elsewhere DAG, London 25 November 2015 Presented by Kenn Skau Fischer Fisheries Policy advisor= lobbyist Danish
SURVEY OF ECONOMIC ASSISTANCE TO THE FISHING SECTOR. (Paper submitted by the Spanish authorities)
 SURVEY OF ECONOMIC ASSISTANCE TO THE FISHING SECTOR Types of measures (Paper submitted by the Spanish authorities) Several methods have been proposed for assessing economic assistance to the fishing sector,
SURVEY OF ECONOMIC ASSISTANCE TO THE FISHING SECTOR Types of measures (Paper submitted by the Spanish authorities) Several methods have been proposed for assessing economic assistance to the fishing sector,
Suggestions for simplified Fixed Capital Stock calculations at Statistics Sweden Michael Wolf, National Accounts Division Statistics Sweden
 Capital Stock Conference March 1997 Agenda Item VI Suggestions for simplified Fixed Capital Stock calculations at Statistics Sweden Michael Wolf, National Accounts Division Statistics Sweden 1 Suggestions
Capital Stock Conference March 1997 Agenda Item VI Suggestions for simplified Fixed Capital Stock calculations at Statistics Sweden Michael Wolf, National Accounts Division Statistics Sweden 1 Suggestions
Operations and Supply Chain Management Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras
 Operations and Supply Chain Management Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture - 36 Location Problems In this lecture, we continue the discussion
Operations and Supply Chain Management Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture - 36 Location Problems In this lecture, we continue the discussion
Sustainable fisheries: impact assessment. Algemene Rekenkamer Postbus 20015 2500 EA Den Haag
 Sustainable fisheries: impact assessment Algemene Rekenkamer Postbus 20015 2500 EA Den Haag 1 Beam trawler fishery for plaice and sole Plaice Sole 2 Present situation (2013) 2008 (recommendations) 2013
Sustainable fisheries: impact assessment Algemene Rekenkamer Postbus 20015 2500 EA Den Haag 1 Beam trawler fishery for plaice and sole Plaice Sole 2 Present situation (2013) 2008 (recommendations) 2013
Brexit & the EU s Common Fisheries Policy
 Brexit & the EU s Common Fisheries Policy contents Background THE BrITISH FISHIng InduSTry Eu over-centralization QuoTaS & discards SuBSIdIES BETTEr off out Background Britain joined the European union's
Brexit & the EU s Common Fisheries Policy contents Background THE BrITISH FISHIng InduSTry Eu over-centralization QuoTaS & discards SuBSIdIES BETTEr off out Background Britain joined the European union's
THE LANDING OBLIGATION AND ITS IMPLICATIONS ON THE CONTROL OF FISHERIES
 DIRECTORATE-GENERAL FOR INTERL POLICIES POLICY DEPARTMENT B: STRUCTURAL AND COHESION POLICIES FISHERIES THE LANDING OBLIGATION AND ITS IMPLICATIONS ON THE CONTROL OF FISHERIES STUDY This document was requested
DIRECTORATE-GENERAL FOR INTERL POLICIES POLICY DEPARTMENT B: STRUCTURAL AND COHESION POLICIES FISHERIES THE LANDING OBLIGATION AND ITS IMPLICATIONS ON THE CONTROL OF FISHERIES STUDY This document was requested
OPRE 6201 : 2. Simplex Method
 OPRE 6201 : 2. Simplex Method 1 The Graphical Method: An Example Consider the following linear program: Max 4x 1 +3x 2 Subject to: 2x 1 +3x 2 6 (1) 3x 1 +2x 2 3 (2) 2x 2 5 (3) 2x 1 +x 2 4 (4) x 1, x 2
OPRE 6201 : 2. Simplex Method 1 The Graphical Method: An Example Consider the following linear program: Max 4x 1 +3x 2 Subject to: 2x 1 +3x 2 6 (1) 3x 1 +2x 2 3 (2) 2x 2 5 (3) 2x 1 +x 2 4 (4) x 1, x 2
Flu Fishing - A Guide to Managing Your Fisher Catch
 The EU Discard Reduction Manual A GUIDE TO HELP FISHERMEN AND MEMBER STATES MEET THE CFP S LANDING OBLIGATION Karly McIlwain ACKNOWLEDGEMENTS Environmental Defense Fund gratefully acknowledges the Quadrivium
The EU Discard Reduction Manual A GUIDE TO HELP FISHERMEN AND MEMBER STATES MEET THE CFP S LANDING OBLIGATION Karly McIlwain ACKNOWLEDGEMENTS Environmental Defense Fund gratefully acknowledges the Quadrivium
NLD. Fleet report 2013 Vlootverslag 2013
 NLD Fleet report 2013 Vlootverslag 2013 Table of contents Summary of report 4 1 Fleets. 5 1.1 Description of fleets. 5 1.2 Link with fisheries. 5 1.3 Development in fleets. 6 1.4 Development in engine
NLD Fleet report 2013 Vlootverslag 2013 Table of contents Summary of report 4 1 Fleets. 5 1.1 Description of fleets. 5 1.2 Link with fisheries. 5 1.3 Development in fleets. 6 1.4 Development in engine
U.S./Canada Management and Special Access Programs for Sector Vessels
 U.S./Canada Management and Special Access Programs for Sector Vessels Sustainable Fisheries This summary provides a broad overview of restrictions and requirements; the regulations summarized here may
U.S./Canada Management and Special Access Programs for Sector Vessels Sustainable Fisheries This summary provides a broad overview of restrictions and requirements; the regulations summarized here may
Oligopoly: How do firms behave when there are only a few competitors? These firms produce all or most of their industry s output.
 Topic 8 Chapter 13 Oligopoly and Monopolistic Competition Econ 203 Topic 8 page 1 Oligopoly: How do firms behave when there are only a few competitors? These firms produce all or most of their industry
Topic 8 Chapter 13 Oligopoly and Monopolistic Competition Econ 203 Topic 8 page 1 Oligopoly: How do firms behave when there are only a few competitors? These firms produce all or most of their industry
Credit Card Market Study Interim Report: Annex 4 Switching Analysis
 MS14/6.2: Annex 4 Market Study Interim Report: Annex 4 November 2015 This annex describes data analysis we carried out to improve our understanding of switching and shopping around behaviour in the UK
MS14/6.2: Annex 4 Market Study Interim Report: Annex 4 November 2015 This annex describes data analysis we carried out to improve our understanding of switching and shopping around behaviour in the UK
Using Probabilistic MCB Analysis to Determine Uncertainty in a Stock Assessment
 Using the probabilistic MCB runs to set management parameters and determine stock status The existence of uncertainty is a well-accepted and thoroughly documented part of the stock assessment process in
Using the probabilistic MCB runs to set management parameters and determine stock status The existence of uncertainty is a well-accepted and thoroughly documented part of the stock assessment process in
1 Uncertainty and Preferences
 In this chapter, we present the theory of consumer preferences on risky outcomes. The theory is then applied to study the demand for insurance. Consider the following story. John wants to mail a package
In this chapter, we present the theory of consumer preferences on risky outcomes. The theory is then applied to study the demand for insurance. Consider the following story. John wants to mail a package
A. GULF OF MAINE HADDOCK ASSESSMENT SUMMARY FOR 2014
 A. GULF OF MAINE HADDOCK ASSESSMENT SUMMARY FOR 2014 State of Stock: The Gulf of Maine haddock (Melanogrammus aeglefinus) stock is not overfished and overfishing is not occurring in 2013 (Figure A1). Spawning
A. GULF OF MAINE HADDOCK ASSESSMENT SUMMARY FOR 2014 State of Stock: The Gulf of Maine haddock (Melanogrammus aeglefinus) stock is not overfished and overfishing is not occurring in 2013 (Figure A1). Spawning
Marine Stewardship Council
 Marine Stewardship Council MSC Fishery Standard Principles and Criteria for Sustainable Fishing Version 1.1 1 st May 2010 Committees responsible for this Standard This standard is intended to be used on
Marine Stewardship Council MSC Fishery Standard Principles and Criteria for Sustainable Fishing Version 1.1 1 st May 2010 Committees responsible for this Standard This standard is intended to be used on
Presentation Materials
 Economic Implications of a Strategy to Purchase Alaska Halibut Fishery Commercial Fishing Sector Quota Shares to Create a Recreational Guided Angler Sector Harvest Common Pool Presentation Materials prepared
Economic Implications of a Strategy to Purchase Alaska Halibut Fishery Commercial Fishing Sector Quota Shares to Create a Recreational Guided Angler Sector Harvest Common Pool Presentation Materials prepared
Session 19. Applying Environmental Policy Instruments: the Case of Fisheries
 Environmental Economics and Development Policy World Bank Headquarters Washington DC Session 19 Applying Environmental Policy Instruments: the Case of Fisheries John A. Dixon Kirk E. Hamilton The World
Environmental Economics and Development Policy World Bank Headquarters Washington DC Session 19 Applying Environmental Policy Instruments: the Case of Fisheries John A. Dixon Kirk E. Hamilton The World
3.3. Solving Polynomial Equations. Introduction. Prerequisites. Learning Outcomes
 Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Improving Selectivity running for a long time now and ongoing
 Improving Selectivity running for a long time now and ongoing A Dutch Flatfish Fisheries Point of View European Parliament Committee on Fisheries 13 April 2015 Pim Visser, chief executive VisNed blad 1
Improving Selectivity running for a long time now and ongoing A Dutch Flatfish Fisheries Point of View European Parliament Committee on Fisheries 13 April 2015 Pim Visser, chief executive VisNed blad 1
CEMARE Report 58 Future options for UK fish quota management. A Hatcher, S Pascoe, R Banks and R Arnason
 CEMARE Report 58 Future options for UK fish quota management A Hatcher, S Pascoe, R Banks and R Arnason Future Options for UK Fish Quota Management A Report to the Department for the Environment, Food
CEMARE Report 58 Future options for UK fish quota management A Hatcher, S Pascoe, R Banks and R Arnason Future Options for UK Fish Quota Management A Report to the Department for the Environment, Food
Moral Hazard. Itay Goldstein. Wharton School, University of Pennsylvania
 Moral Hazard Itay Goldstein Wharton School, University of Pennsylvania 1 Principal-Agent Problem Basic problem in corporate finance: separation of ownership and control: o The owners of the firm are typically
Moral Hazard Itay Goldstein Wharton School, University of Pennsylvania 1 Principal-Agent Problem Basic problem in corporate finance: separation of ownership and control: o The owners of the firm are typically
5 Year Strategic Plan
 Mid Atlantic Fishery Management Council 5 Year Strategic Plan 2014 2018 DRAFT 5/31/2013 Table of Contents Table of Contents... 1 Introduction... 2 The Mid Atlantic Fishery Management Council... 2 Rationale
Mid Atlantic Fishery Management Council 5 Year Strategic Plan 2014 2018 DRAFT 5/31/2013 Table of Contents Table of Contents... 1 Introduction... 2 The Mid Atlantic Fishery Management Council... 2 Rationale
Shark, Skate and Ray Conservation Plan
 Shark, Skate and Ray Conservation Plan Introduction Sharks, skates and rays, collectively known as elasmobranchs are caught in fisheries worldwide, including in EU and UK waters. Many have been depleted
Shark, Skate and Ray Conservation Plan Introduction Sharks, skates and rays, collectively known as elasmobranchs are caught in fisheries worldwide, including in EU and UK waters. Many have been depleted
National Marine Fisheries Service Electronic Monitoring Cooperative Research and Implementation Program
 National Marine Fisheries Service Electronic Monitoring Cooperative Research and Implementation Program Introduction This cooperative research program has been developed to be responsive both to the implementation
National Marine Fisheries Service Electronic Monitoring Cooperative Research and Implementation Program Introduction This cooperative research program has been developed to be responsive both to the implementation
The Graphical Method: An Example
 The Graphical Method: An Example Consider the following linear program: Maximize 4x 1 +3x 2 Subject to: 2x 1 +3x 2 6 (1) 3x 1 +2x 2 3 (2) 2x 2 5 (3) 2x 1 +x 2 4 (4) x 1, x 2 0, where, for ease of reference,
The Graphical Method: An Example Consider the following linear program: Maximize 4x 1 +3x 2 Subject to: 2x 1 +3x 2 6 (1) 3x 1 +2x 2 3 (2) 2x 2 5 (3) 2x 1 +x 2 4 (4) x 1, x 2 0, where, for ease of reference,
Linear Programming. Solving LP Models Using MS Excel, 18
 SUPPLEMENT TO CHAPTER SIX Linear Programming SUPPLEMENT OUTLINE Introduction, 2 Linear Programming Models, 2 Model Formulation, 4 Graphical Linear Programming, 5 Outline of Graphical Procedure, 5 Plotting
SUPPLEMENT TO CHAPTER SIX Linear Programming SUPPLEMENT OUTLINE Introduction, 2 Linear Programming Models, 2 Model Formulation, 4 Graphical Linear Programming, 5 Outline of Graphical Procedure, 5 Plotting
Review of Fundamental Mathematics
 Review of Fundamental Mathematics As explained in the Preface and in Chapter 1 of your textbook, managerial economics applies microeconomic theory to business decision making. The decision-making tools
Review of Fundamental Mathematics As explained in the Preface and in Chapter 1 of your textbook, managerial economics applies microeconomic theory to business decision making. The decision-making tools
Comments on the Green Paper for the reform of the Common Fisheries Policy
 1 Comments on the Green Paper for the reform of the Common Fisheries Policy These comments have been made in cooperation between Thorupstrand Kystfiskerlaug (in-shore fishers guild of Thorupstrand) Han
1 Comments on the Green Paper for the reform of the Common Fisheries Policy These comments have been made in cooperation between Thorupstrand Kystfiskerlaug (in-shore fishers guild of Thorupstrand) Han
CHAPTER 11: BASIC LINEAR PROGRAMMING CONCEPTS
 Linear programming is a mathematical technique for finding optimal solutions to problems that can be expressed using linear equations and inequalities. If a real-world problem can be represented accurately
Linear programming is a mathematical technique for finding optimal solutions to problems that can be expressed using linear equations and inequalities. If a real-world problem can be represented accurately
Lecture 2. Marginal Functions, Average Functions, Elasticity, the Marginal Principle, and Constrained Optimization
 Lecture 2. Marginal Functions, Average Functions, Elasticity, the Marginal Principle, and Constrained Optimization 2.1. Introduction Suppose that an economic relationship can be described by a real-valued
Lecture 2. Marginal Functions, Average Functions, Elasticity, the Marginal Principle, and Constrained Optimization 2.1. Introduction Suppose that an economic relationship can be described by a real-valued
K 1 < K 2 = P (K 1 ) P (K 2 ) (6) This holds for both American and European Options.
 Slope and Convexity Restrictions and How to implement Arbitrage Opportunities 1 These notes will show how to implement arbitrage opportunities when either the slope or the convexity restriction is violated.
Slope and Convexity Restrictions and How to implement Arbitrage Opportunities 1 These notes will show how to implement arbitrage opportunities when either the slope or the convexity restriction is violated.
Unraveling versus Unraveling: A Memo on Competitive Equilibriums and Trade in Insurance Markets
 Unraveling versus Unraveling: A Memo on Competitive Equilibriums and Trade in Insurance Markets Nathaniel Hendren January, 2014 Abstract Both Akerlof (1970) and Rothschild and Stiglitz (1976) show that
Unraveling versus Unraveling: A Memo on Competitive Equilibriums and Trade in Insurance Markets Nathaniel Hendren January, 2014 Abstract Both Akerlof (1970) and Rothschild and Stiglitz (1976) show that
The Work on Gender Mainstreaming in the Ministry of Employment by Agnete Andersen, legal adviser
 The Work on Gender Mainstreaming in the Ministry of Employment by Agnete Andersen, legal adviser Agnete Andersen The outset for the work on gender mainstreaming Gender equality is a difficult bird because
The Work on Gender Mainstreaming in the Ministry of Employment by Agnete Andersen, legal adviser Agnete Andersen The outset for the work on gender mainstreaming Gender equality is a difficult bird because
S.I. No. 176 of 2006 Fishing Effort for Vessels in the Context of the Recovery of Certain Stocks Regulations 2006
 S.I. No. 176 of 2006 Fishing Effort for Vessels in the Context of the Recovery of Certain Stocks Regulations 2006 I, John Browne, Minister of State at the Department of Communications, Marine and Natural
S.I. No. 176 of 2006 Fishing Effort for Vessels in the Context of the Recovery of Certain Stocks Regulations 2006 I, John Browne, Minister of State at the Department of Communications, Marine and Natural
Two Papers on Internet Connectivity and Quality. Abstract
 Two Papers on Internet Connectivity and Quality ROBERTO ROSON Dipartimento di Scienze Economiche, Università Ca Foscari di Venezia, Venice, Italy. Abstract I review two papers, addressing the issue of
Two Papers on Internet Connectivity and Quality ROBERTO ROSON Dipartimento di Scienze Economiche, Università Ca Foscari di Venezia, Venice, Italy. Abstract I review two papers, addressing the issue of
Project Title: Fishing Technology and Conservation Engineering to Reduce Bycatch Contact: Carwyn F. Hammond and Scott McEntire
 Project Title: Fishing Technology and Conservation Engineering to Reduce Bycatch Contact: Carwyn F. Hammond and Scott McEntire Overview: The Conservation Engineering project of the AFSC conducts an ongoing
Project Title: Fishing Technology and Conservation Engineering to Reduce Bycatch Contact: Carwyn F. Hammond and Scott McEntire Overview: The Conservation Engineering project of the AFSC conducts an ongoing
EUROPEAN SECURITIES AND MARKETS AUTHORITY (ESMA) CONSULTATION PAPER
 EUROPEAN SECURITIES AND MARKETS AUTHORITY (ESMA) CONSULTATION PAPER 22 City Road Finsbury Square London EC1Y 2AJ Tel: +44 (0) 20 7448 7100 Fax: +44 (0) 20 7638 4636 Email: info@apcims.co.uk DRAFT TECHNICAL
EUROPEAN SECURITIES AND MARKETS AUTHORITY (ESMA) CONSULTATION PAPER 22 City Road Finsbury Square London EC1Y 2AJ Tel: +44 (0) 20 7448 7100 Fax: +44 (0) 20 7638 4636 Email: info@apcims.co.uk DRAFT TECHNICAL
Review of Basic Options Concepts and Terminology
 Review of Basic Options Concepts and Terminology March 24, 2005 1 Introduction The purchase of an options contract gives the buyer the right to buy call options contract or sell put options contract some
Review of Basic Options Concepts and Terminology March 24, 2005 1 Introduction The purchase of an options contract gives the buyer the right to buy call options contract or sell put options contract some
E-fish: Regulating quantity or promoting e-quality? Foundations of a new paradigm
 CFP Reform: Resource conservation and Fleet management European Parliament Hearing 2010 E-fish Regulating quantity or promoting e-quality? Foundations of a new paradigm The value of a scarce resource:
CFP Reform: Resource conservation and Fleet management European Parliament Hearing 2010 E-fish Regulating quantity or promoting e-quality? Foundations of a new paradigm The value of a scarce resource:
1.2 Advice basis May 2014
 1.2 Advice basis May 2014 1.2.1 General context of ICES advice ICES advises competent authorities on marine policy and management issues related to the impacts of human activities on marine ecosystems
1.2 Advice basis May 2014 1.2.1 General context of ICES advice ICES advises competent authorities on marine policy and management issues related to the impacts of human activities on marine ecosystems
Electronic management and exchange of fishery information
 FLUX Electronic management and exchange of fishery information Dr Heiner Lehr heiner@syntesa.eu 1 INTRODUCTION 2 Global seafood trade Global seafood trade is estimated to be worth about 140 billion USD
FLUX Electronic management and exchange of fishery information Dr Heiner Lehr heiner@syntesa.eu 1 INTRODUCTION 2 Global seafood trade Global seafood trade is estimated to be worth about 140 billion USD
Linear Programming I
 Linear Programming I November 30, 2003 1 Introduction In the VCR/guns/nuclear bombs/napkins/star wars/professors/butter/mice problem, the benevolent dictator, Bigus Piguinus, of south Antarctica penguins
Linear Programming I November 30, 2003 1 Introduction In the VCR/guns/nuclear bombs/napkins/star wars/professors/butter/mice problem, the benevolent dictator, Bigus Piguinus, of south Antarctica penguins
AP ENVIRONMENTAL SCIENCE 2006 SCORING GUIDELINES. Question 4
 AP ENVIRONMENTAL SCIENCE 2006 SCORING GUIDELINES Question 4 (a) Identify the five-year period during which the greatest rate of decline in the fish harvest took place. For that five-year period, calculate
AP ENVIRONMENTAL SCIENCE 2006 SCORING GUIDELINES Question 4 (a) Identify the five-year period during which the greatest rate of decline in the fish harvest took place. For that five-year period, calculate
INFO1400. Define an organization and compare the technical definition of organizations with the behavioral definition.
 Chapter 3 INFO1400 Review Questions 1. Which features of organizations do managers need to know about to build and use information systems successfully? What is the impact of information systems on organizations?
Chapter 3 INFO1400 Review Questions 1. Which features of organizations do managers need to know about to build and use information systems successfully? What is the impact of information systems on organizations?
Special Situations in the Simplex Algorithm
 Special Situations in the Simplex Algorithm Degeneracy Consider the linear program: Maximize 2x 1 +x 2 Subject to: 4x 1 +3x 2 12 (1) 4x 1 +x 2 8 (2) 4x 1 +2x 2 8 (3) x 1, x 2 0. We will first apply the
Special Situations in the Simplex Algorithm Degeneracy Consider the linear program: Maximize 2x 1 +x 2 Subject to: 4x 1 +3x 2 12 (1) 4x 1 +x 2 8 (2) 4x 1 +2x 2 8 (3) x 1, x 2 0. We will first apply the
ASSESSMENT CENTER FOR IDENTIFYING POTENTIAL PROJECT MANAGERS: A CHANCE FOR SYSTEMATIC HUMAN RESOURCE DEVELOPMENT
 ASSESSMENT CENTER FOR IDENTIFYING POTENTIAL PROJECT MANAGERS: A CHANCE FOR SYSTEMATIC HUMAN RESOURCE DEVELOPMENT Dipl. Psych. Ingo Heyn, ALLIANZ LEBENSVERSICHERUNGS-AG, Germany, 1999 Paper for the 6th
ASSESSMENT CENTER FOR IDENTIFYING POTENTIAL PROJECT MANAGERS: A CHANCE FOR SYSTEMATIC HUMAN RESOURCE DEVELOPMENT Dipl. Psych. Ingo Heyn, ALLIANZ LEBENSVERSICHERUNGS-AG, Germany, 1999 Paper for the 6th
2. Simple Linear Regression
 Research methods - II 3 2. Simple Linear Regression Simple linear regression is a technique in parametric statistics that is commonly used for analyzing mean response of a variable Y which changes according
Research methods - II 3 2. Simple Linear Regression Simple linear regression is a technique in parametric statistics that is commonly used for analyzing mean response of a variable Y which changes according
Annual report on balance between fishing capacity and fishing opportunities for 2013 - Croatia
 Annual report on balance between fishing capacity and fishing opportunities for 2013 - Croatia pursuant to Article 22 of the Regulation (EU) no 1380/2013 of the European Parliament and of the Council of
Annual report on balance between fishing capacity and fishing opportunities for 2013 - Croatia pursuant to Article 22 of the Regulation (EU) no 1380/2013 of the European Parliament and of the Council of
SMART FISHING INITIATIVE RESULTS 2010 - JUNE 2016 RESULTS 2010-2016. WWF s 2020 VISION Our oceans are wellmanaged,
 Brent Stirtion/Getty Images RESULTS 2010-2016 WWF s 2020 VISION Our oceans are wellmanaged, healthy, robust and full of life, providing valuable services for the well-being of humanity. SMART FISHING INITIATIVE
Brent Stirtion/Getty Images RESULTS 2010-2016 WWF s 2020 VISION Our oceans are wellmanaged, healthy, robust and full of life, providing valuable services for the well-being of humanity. SMART FISHING INITIATIVE
A Functional Classification System for Marine Protected Areas in the United States
 A Functional Classification System for Marine Protected Areas in the United States The U.S. Classification System: An Objective Approach for Understanding the Purpose and Effects of MPAs as an Ecosystem
A Functional Classification System for Marine Protected Areas in the United States The U.S. Classification System: An Objective Approach for Understanding the Purpose and Effects of MPAs as an Ecosystem
REPORT. electronic monitoring in fisheries management
 REPORT 2015 electronic monitoring in fisheries management WWF commissioned this report as a contribution to the ongoing discussions surrounding the introduction of new CFP regulations including the Landing
REPORT 2015 electronic monitoring in fisheries management WWF commissioned this report as a contribution to the ongoing discussions surrounding the introduction of new CFP regulations including the Landing
Proposed measures for fisheries management in Natura 2000-sites in the Danish territorial area of the Kattegat and Samsø Belt
 Proposed measures for fisheries management in Natura 2000-sites in the Danish territorial area of the Kattegat and Samsø Belt Meeting at the AgriFish Agency, Copenhagen 20 March 2012 The Danish AgriFish
Proposed measures for fisheries management in Natura 2000-sites in the Danish territorial area of the Kattegat and Samsø Belt Meeting at the AgriFish Agency, Copenhagen 20 March 2012 The Danish AgriFish
INTERNATIONAL COMPARISON OF INTEREST RATE GUARANTEES IN LIFE INSURANCE
 INTERNATIONAL COMPARISON OF INTEREST RATE GUARANTEES IN LIFE INSURANCE J. DAVID CUMMINS, KRISTIAN R. MILTERSEN, AND SVEIN-ARNE PERSSON Abstract. Interest rate guarantees seem to be included in life insurance
INTERNATIONAL COMPARISON OF INTEREST RATE GUARANTEES IN LIFE INSURANCE J. DAVID CUMMINS, KRISTIAN R. MILTERSEN, AND SVEIN-ARNE PERSSON Abstract. Interest rate guarantees seem to be included in life insurance
Lessons for fisheries management from the EU cod recovery plan
 Marine Policy Volume 37, January 2013, Pages 200 213 http://dx.doi.org/10.1016/j.marpol.2012.05.002, 2013 Elsevier Lessons for fisheries management from the EU cod recovery plan Sarah B. M. Kraak 1,2,
Marine Policy Volume 37, January 2013, Pages 200 213 http://dx.doi.org/10.1016/j.marpol.2012.05.002, 2013 Elsevier Lessons for fisheries management from the EU cod recovery plan Sarah B. M. Kraak 1,2,
The Basics of Interest Theory
 Contents Preface 3 The Basics of Interest Theory 9 1 The Meaning of Interest................................... 10 2 Accumulation and Amount Functions............................ 14 3 Effective Interest
Contents Preface 3 The Basics of Interest Theory 9 1 The Meaning of Interest................................... 10 2 Accumulation and Amount Functions............................ 14 3 Effective Interest
Insurance and Public Pensions : (b) Adverse Selection
 Insurance and Public Pensions : (b) Adverse Selection Adverse selection is said to occur if potential buyers of insurance know their own probabilities of loss better than do insurance companies. So suppose
Insurance and Public Pensions : (b) Adverse Selection Adverse selection is said to occur if potential buyers of insurance know their own probabilities of loss better than do insurance companies. So suppose
How To Measure Performance
 How to Write Great Performance Measures Part of a Continuing Series on: Performance Monitoring and Program Evaluation Sponsored by NOAA s SEE Evaluation Committee John Bortniak Member, SEE Evaluation Committee
How to Write Great Performance Measures Part of a Continuing Series on: Performance Monitoring and Program Evaluation Sponsored by NOAA s SEE Evaluation Committee John Bortniak Member, SEE Evaluation Committee
The Open University s repository of research publications and other research outputs
 Open Research Online The Open University s repository of research publications and other research outputs The degree-diameter problem for circulant graphs of degree 8 and 9 Journal Article How to cite:
Open Research Online The Open University s repository of research publications and other research outputs The degree-diameter problem for circulant graphs of degree 8 and 9 Journal Article How to cite:
An Effective Marine Protected Area. Pacific Island Marine Protected Area Community (PIMPAC)
 An Effective Marine Protected Area Pacific Island Marine Protected Area Community (PIMPAC) Background: The PIMPAC initiative is designed to enhance Marine Protected Area (MPA) management effectiveness
An Effective Marine Protected Area Pacific Island Marine Protected Area Community (PIMPAC) Background: The PIMPAC initiative is designed to enhance Marine Protected Area (MPA) management effectiveness
SABLEFISH PERMIT STACKING PROGRAM- ACTION ISSUES, ELECTRONIC FISH TICKET ANALYSIS
 Agenda Item C.6.a Supplemental Attachment 3 April 2014 SABLEFISH PERMIT STACKING PROGRAM- ACTION ISSUES, ELECTRONIC FISH TICKET ANALYSIS In the Draft Council Decision Analysis Document for the sablefish
Agenda Item C.6.a Supplemental Attachment 3 April 2014 SABLEFISH PERMIT STACKING PROGRAM- ACTION ISSUES, ELECTRONIC FISH TICKET ANALYSIS In the Draft Council Decision Analysis Document for the sablefish
Maria Espinosa Romero John Driscoll
 Maria Espinosa Romero John Driscoll Fisheries management in Canada a. Traditionally done on a stock-by-stock basis; b. Canada s commitments to ecosystem approach will change this; c. Two interrelated pathways
Maria Espinosa Romero John Driscoll Fisheries management in Canada a. Traditionally done on a stock-by-stock basis; b. Canada s commitments to ecosystem approach will change this; c. Two interrelated pathways
Chapter 1: Financial Markets and Financial Derivatives
 Chapter 1: Financial Markets and Financial Derivatives 1.1 Financial Markets Financial markets are markets for financial instruments, in which buyers and sellers find each other and create or exchange
Chapter 1: Financial Markets and Financial Derivatives 1.1 Financial Markets Financial markets are markets for financial instruments, in which buyers and sellers find each other and create or exchange
THE FISHERIES REQUIREMENTS FOR AREA IN RELATION TO SEISMIC ACTIVITIES THE FISHERIES
 THE FISHERIES REQUIREMENTS FOR AREA IN RELATION TO SEISMIC ACTIVITIES THE FISHERIES The fish stocks in the Norwegian sector can be divided into two separate categories: The pelagic species comprise herring,
THE FISHERIES REQUIREMENTS FOR AREA IN RELATION TO SEISMIC ACTIVITIES THE FISHERIES The fish stocks in the Norwegian sector can be divided into two separate categories: The pelagic species comprise herring,
Income and the demand for complementary health insurance in France. Bidénam Kambia-Chopin, Michel Grignon (McMaster University, Hamilton, Ontario)
 Income and the demand for complementary health insurance in France Bidénam Kambia-Chopin, Michel Grignon (McMaster University, Hamilton, Ontario) Presentation Workshop IRDES, June 24-25 2010 The 2010 IRDES
Income and the demand for complementary health insurance in France Bidénam Kambia-Chopin, Michel Grignon (McMaster University, Hamilton, Ontario) Presentation Workshop IRDES, June 24-25 2010 The 2010 IRDES
MATH 21. College Algebra 1 Lecture Notes
 MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
Answers to Text Questions and Problems. Chapter 22. Answers to Review Questions
 Answers to Text Questions and Problems Chapter 22 Answers to Review Questions 3. In general, producers of durable goods are affected most by recessions while producers of nondurables (like food) and services
Answers to Text Questions and Problems Chapter 22 Answers to Review Questions 3. In general, producers of durable goods are affected most by recessions while producers of nondurables (like food) and services
Math Review. for the Quantitative Reasoning Measure of the GRE revised General Test
 Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
Math Review for the Quantitative Reasoning Measure of the GRE revised General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important
Building a financial perspective into an engineering program
 Building a financial perspective into an engineering program P.J.Gregory Department of Mechanical Engineering, Monash University, Clayton Campus, Victoria, Australia (Peter.gregory@eng.monash.edu.au) Abstract
Building a financial perspective into an engineering program P.J.Gregory Department of Mechanical Engineering, Monash University, Clayton Campus, Victoria, Australia (Peter.gregory@eng.monash.edu.au) Abstract
9.3.7 Advice December 2014
 9.3.7 Advice December 2014 ECOREGION STOCK Widely distributed and migratory stocks European eel Advice for 2015 The status of eel remains critical and ICES advises that all anthropogenic mortality (e.g.
9.3.7 Advice December 2014 ECOREGION STOCK Widely distributed and migratory stocks European eel Advice for 2015 The status of eel remains critical and ICES advises that all anthropogenic mortality (e.g.
A simple analysis of the TV game WHO WANTS TO BE A MILLIONAIRE? R
 A simple analysis of the TV game WHO WANTS TO BE A MILLIONAIRE? R Federico Perea Justo Puerto MaMaEuSch Management Mathematics for European Schools 94342 - CP - 1-2001 - DE - COMENIUS - C21 University
A simple analysis of the TV game WHO WANTS TO BE A MILLIONAIRE? R Federico Perea Justo Puerto MaMaEuSch Management Mathematics for European Schools 94342 - CP - 1-2001 - DE - COMENIUS - C21 University
11. Analysis of Case-control Studies Logistic Regression
 Research methods II 113 11. Analysis of Case-control Studies Logistic Regression This chapter builds upon and further develops the concepts and strategies described in Ch.6 of Mother and Child Health:
Research methods II 113 11. Analysis of Case-control Studies Logistic Regression This chapter builds upon and further develops the concepts and strategies described in Ch.6 of Mother and Child Health:
For example, estimate the population of the United States as 3 times 10⁸ and the
 CCSS: Mathematics The Number System CCSS: Grade 8 8.NS.A. Know that there are numbers that are not rational, and approximate them by rational numbers. 8.NS.A.1. Understand informally that every number
CCSS: Mathematics The Number System CCSS: Grade 8 8.NS.A. Know that there are numbers that are not rational, and approximate them by rational numbers. 8.NS.A.1. Understand informally that every number
CHAPTER 2 Estimating Probabilities
 CHAPTER 2 Estimating Probabilities Machine Learning Copyright c 2016. Tom M. Mitchell. All rights reserved. *DRAFT OF January 24, 2016* *PLEASE DO NOT DISTRIBUTE WITHOUT AUTHOR S PERMISSION* This is a
CHAPTER 2 Estimating Probabilities Machine Learning Copyright c 2016. Tom M. Mitchell. All rights reserved. *DRAFT OF January 24, 2016* *PLEASE DO NOT DISTRIBUTE WITHOUT AUTHOR S PERMISSION* This is a
A MANAGER S ROADMAP GUIDE FOR LATERAL TRANS-SHIPMENT IN SUPPLY CHAIN INVENTORY MANAGEMENT
 A MANAGER S ROADMAP GUIDE FOR LATERAL TRANS-SHIPMENT IN SUPPLY CHAIN INVENTORY MANAGEMENT By implementing the proposed five decision rules for lateral trans-shipment decision support, professional inventory
A MANAGER S ROADMAP GUIDE FOR LATERAL TRANS-SHIPMENT IN SUPPLY CHAIN INVENTORY MANAGEMENT By implementing the proposed five decision rules for lateral trans-shipment decision support, professional inventory
Fair Trade USA Data-Limited Stock Assessment Decision Tree
 Fair Trade USA Data-Limited Stock Assessment Decision Tree January 31, 2014 Introduction This stock assessment decision tree may be used to determine which data-limited stock assessment methodology is
Fair Trade USA Data-Limited Stock Assessment Decision Tree January 31, 2014 Introduction This stock assessment decision tree may be used to determine which data-limited stock assessment methodology is
1 Error in Euler s Method
 1 Error in Euler s Method Experience with Euler s 1 method raises some interesting questions about numerical approximations for the solutions of differential equations. 1. What determines the amount of
1 Error in Euler s Method Experience with Euler s 1 method raises some interesting questions about numerical approximations for the solutions of differential equations. 1. What determines the amount of
Lines & Planes. Packages: linalg, plots. Commands: evalm, spacecurve, plot3d, display, solve, implicitplot, dotprod, seq, implicitplot3d.
 Lines & Planes Introduction and Goals: This lab is simply to give you some practice with plotting straight lines and planes and how to do some basic problem solving with them. So the exercises will be
Lines & Planes Introduction and Goals: This lab is simply to give you some practice with plotting straight lines and planes and how to do some basic problem solving with them. So the exercises will be
RIR for Hagfish Collection of Information
 RIR for Hagfish Collection of Information A description of the management objectives This collection of information for the hagfish fishery is being proposed under the provisions of section 402(a) of the
RIR for Hagfish Collection of Information A description of the management objectives This collection of information for the hagfish fishery is being proposed under the provisions of section 402(a) of the
If A is divided by B the result is 2/3. If B is divided by C the result is 4/7. What is the result if A is divided by C?
 Problem 3 If A is divided by B the result is 2/3. If B is divided by C the result is 4/7. What is the result if A is divided by C? Suggested Questions to ask students about Problem 3 The key to this question
Problem 3 If A is divided by B the result is 2/3. If B is divided by C the result is 4/7. What is the result if A is divided by C? Suggested Questions to ask students about Problem 3 The key to this question
Measurement with Ratios
 Grade 6 Mathematics, Quarter 2, Unit 2.1 Measurement with Ratios Overview Number of instructional days: 15 (1 day = 45 minutes) Content to be learned Use ratio reasoning to solve real-world and mathematical
Grade 6 Mathematics, Quarter 2, Unit 2.1 Measurement with Ratios Overview Number of instructional days: 15 (1 day = 45 minutes) Content to be learned Use ratio reasoning to solve real-world and mathematical
How To Calculate A Balance On A Savings Account
 319 CHAPTER 4 Personal Finance The following is an article from a Marlboro, Massachusetts newspaper. NEWSPAPER ARTICLE 4.1: LET S TEACH FINANCIAL LITERACY STEPHEN LEDUC WED JAN 16, 2008 Boston - Last week
319 CHAPTER 4 Personal Finance The following is an article from a Marlboro, Massachusetts newspaper. NEWSPAPER ARTICLE 4.1: LET S TEACH FINANCIAL LITERACY STEPHEN LEDUC WED JAN 16, 2008 Boston - Last week
6.3 Conditional Probability and Independence
 222 CHAPTER 6. PROBABILITY 6.3 Conditional Probability and Independence Conditional Probability Two cubical dice each have a triangle painted on one side, a circle painted on two sides and a square painted
222 CHAPTER 6. PROBABILITY 6.3 Conditional Probability and Independence Conditional Probability Two cubical dice each have a triangle painted on one side, a circle painted on two sides and a square painted
ROADMAP. A. Context and problem definition
 TITLE OF THE INITIATIVE ROADMAP Commission Communication on EU Risk management and supply chain security LEAD DG RESPONSIBLE UNIT TAXUD B2 DATE OF ROADMAP 10 / 2012 This indicative roadmap is provided
TITLE OF THE INITIATIVE ROADMAP Commission Communication on EU Risk management and supply chain security LEAD DG RESPONSIBLE UNIT TAXUD B2 DATE OF ROADMAP 10 / 2012 This indicative roadmap is provided
ANOTHER PERVERSE EFFECT OF MONOPOLY POWER
 ANOTHER PERVERSE EFFECT OF MONOPOLY POWER Jean J. Gabszewicz and Xavier Y. Wauthy November 2000 Abstract We show that the simple fact that a monopolist sells a good in units which are indivisible may well
ANOTHER PERVERSE EFFECT OF MONOPOLY POWER Jean J. Gabszewicz and Xavier Y. Wauthy November 2000 Abstract We show that the simple fact that a monopolist sells a good in units which are indivisible may well
1 Solving LPs: The Simplex Algorithm of George Dantzig
 Solving LPs: The Simplex Algorithm of George Dantzig. Simplex Pivoting: Dictionary Format We illustrate a general solution procedure, called the simplex algorithm, by implementing it on a very simple example.
Solving LPs: The Simplex Algorithm of George Dantzig. Simplex Pivoting: Dictionary Format We illustrate a general solution procedure, called the simplex algorithm, by implementing it on a very simple example.
