Geometric transformations and registration of images, orthoimage generation and mosaicing

Transcription

1 Geometric transformations and registration of images, orthoimage generation and mosaicing E.P. Baltsavias Institute of Geodesy and Photogrammetry, ETHZ Zurich E.P. Baltsavias, Athens, , p.1

2 Geometric Transformations Consist of 2 steps: 1.Transformation of pixel coordinates 2.Interpolation of grey values Both steps together often called resampling. Grey value interpolation not always necessary, e.g. rotation by 90 o. Applications: Change of the images (zoom, rotation etc.), correction of geometric errors, sensor calibration, transformations from one system to another (image to image/map/vector tranformation), rectification, transformation in epipolar images (for stereo display, matching), orthoimage generation, matching, generation of synthetic 3-D scenes (animation, simulation),... Often used, very useful, algorithmically simple, computationally intensive E.P. Baltsavias, Athens, , p.2

3 Examples of geometric operations Mirroring, transposing, rotation, shear, zoom-in/zoom-out (with or without grey level interpolation) Different polynomial transformations (normallly of 1st - 3rd degree). Number of terms: (n+1) 2, with n...degree of polynomial. Important ones: - Similarity transformation (Helmert) X = V x + M cos (φ) x + sin (φ) y ; Y = V y - sin (φ) x + M cos(φ) y V x, V y...x-, y-shift ; M...x-, y-scale ; φ...rotation angle - Affine transformation X = a 0 + a 1 x + a 2 y ; Y = b 0 + b 1 x + b 2 y a 0, b 0...x-, y-shift; a 1, b 2...x-, y-scale; a 2, b 1...x-, y-shear - Bilinear transformation X = a 0 + a 1 x + a 2 y + a 3 xy ; Y = b 0 + b 1 x + b 2 y + b 3 xy E.P. Baltsavias, Athens, , p.3

4 Other transformations: - projective (8 parameters, plane to plane transformation), e.g. for rectification of fassades X = (a 1 x + a 2 y + a 3) / ( a 7 x + a 8 y + 1) Y = (a 4 x + a 5 y + a 6) / ( a 7 x + a 8 y + 1) - perspective (s. collinearity equation), e.g. for orthoimage generation E.P. Baltsavias, Athens, , p.4

5 Representation of transformations with homogeneous coordinates u v w = a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 x y z and X = u / w ; Y = v/w a 1, a 5...x-, y-scale ; a 2, a 4...x-, y-shear ; a 3, a 6...x-, y-shift a 7, a 8...x-,y- principal point coordinates (normally = 0) a 9... focal length, i.e. global scale (normally = 1) Advantage -> combination of transformations by matrix multiplication, e.g. Transformation T (= T 1 xt 2 xt 3 ) instead of each transformation T i separately E.P. Baltsavias, Athens, , p.5

6 direct method (transformation T) H indirect method (inverse transformation T -1 ) H...Grey value of background (user defined, or fixed in programme) In geometric transformations with grey level interpolation the indirect method is almost always used E.P. Baltsavias, Athens, , p.6

7 With large data sets with a regular grid structure an update philosophy can be used -> Transformation is much faster. Example: Affine Transformation X 1 = a 0 + a 1 x 1 + a 2 y 1 X 2 = a 0 + a 1 x 2 + a 2 y 2 ; Mit x 2 = x 1, y 2 = y 1 + D y X 2 = a 0 + a 1 x 1 + a 2 (y 1 + D y ) = X 1 + a 2 D y = X 1 + A D y 1 2 with A = constant -> instead of 2 additions/2 multiplications only 1 addition E.P. Baltsavias, Athens, , p.7

8 Grey Level Interpolation Polynomial of nth degree -> (n+1) 2 terms (unknown coefficients) -> (n+1) 2 observations (known grey values of neighbours) are required n = 0 -> nearest neighbour interpolation (NINT operation), 1 neighbour n = 1 -> bilinear interpolation, 2 x 2 neighbours n = 3 -> bicubic interpolation, 4 x 4 neighbours Other interpolation methods: Lagrange polynomial Lagrange: 4 x 4 neighbours, similar quality as bicubic but faster In interpolation methods with negative coefficients (e.g. bicubic) the result can be outside the range [0, 255] -> Normalisation needed -> additional computing time required E.P. Baltsavias, Athens, , p.8

9 The indirect method is used direct method indirect method E.P. Baltsavias, Athens, , p.9

10 Example of computation of the coefficients Bilinear interpolation 0,0 x 0,1 y g local coordinate system of grey values f(i,j) 1,0 1,1 g = a + b x + c y + d xy with a = f(0,0), b = (f1,0) - f(0,0), c = f(0,1) - f(0,0), d = f(1,1) + f(0,0) - f(0,1) - f(1,0) E.P. Baltsavias, Athens, , p.10

11 Computing time aspects Bilinear needs more time than nearest neighbour, bicubic significantly more than bilinear Reduction of computing time by - Update philosophy (when interpolated points are a densification of the known points and on a regular grid, e.g. DTM densification) - Use of precomputed and saved Look-Up Tables (LUTs) for computation of the coefficients (especially for the bicubic interpolation) E.P. Baltsavias, Athens, , p.11

12 Quality aspects Bilinear is clearly better than nearest neighbour (staircase effect at straight edges), bicubic a bit better than bilinear (image is more sharp, but also artifacts -> grey level oscillations ( ringing ) at high contrast edges). In most cases bilinear interpolation is used. Nearest neighbour is sometimes used in Remote Sensing -> original grey values are kept-> important for multispectral classification E.P. Baltsavias, Athens, , p.12

13 Registration of Image to Image/Map/Vectors Sometimes also called overlaying or rectification Other definitions Georeferencing: the geometric relation between image and object space (generally a map coordinate system) is known, but the image has not been transformed in the object space system Geocoding (rectification): the image is transformed in a map coordinate system (normally with a polynomial transformation) Orthoimage generation (differential rectification, orthorectification): strict transformation in a map coordinate system with help of a DTM (relief correction) Rectification without DTM used often with satellite imagery Classes of rectification - parametric, i.e. flight/orbit, sensor etc. parameters are used - nonparametric, i.e. normally 2-D polynomial transformations E.P. Baltsavias, Athens, , p.13

14 Nonparametric rectification Measurement of control points in image and the reference (image, map, vectors, GPS) Requirement: well identifiable and measurable in image and reference Measurement of x,y coordinates in the reference (easier than below) - manually (cursor, digitiser) - GPS - use of a database with known identifiable points Identification and measurement of x,y pixel coordinates in image (major problem) - manually - semiautomatically, e.g. using matching between two images (second one is reference) Control point measurement -> most important problem, time consuming, costly E.P. Baltsavias, Athens, , p.14

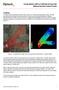
15 Difficulty of identifying and measuring control points in images - independently whether they come from topographic maps, GPS etc. - difficulty depends on image resolution. See example below (left: Landsat TM (bands 1, 2 and 3 combined as B/W) 30 m ground resolution, middle: SPOT Pan orthoimage 8.33 m, right: Ikonos GEO 1m, all in the region Luzern, Switzerland). Problems increase as ground resolution becomes coarser. E.P. Baltsavias, Athens, , p.15

16 Examples of GCP definition (identification quality) in Ikonos GEO images (Lucerne, switzerland). Top:good definition ; bottom: poor. GCPs came from 1:25,000 topographic maps and orthoimages from 1:30,000 scale aerial imagery. E.P. Baltsavias, Athens, , p.16

17 Examples of GCP definition (identification quality) in Ikonos GEO images (Nisyros volcanic isalnd, Greece). Top:good definition ; bottom: poor. GCPs came from GPS field measurements. E.P. Baltsavias, Athens, , p.17

18 Example of good GCP definition in Ikonos GEO images (Melbourne). The round-abouts were measured indirectly through measurements along the round-about perimeter. In the field with GPS, and in the images with manual measurements and ellipse fit with least squares adjustment, or least squares template matching (see next two pages). E.P. Baltsavias, Athens, , p.18

19 E.P. Baltsavias, Athens, , p.19 Measurement of GCP (round-about) with best-fit ellipse.

20 E.P. Baltsavias, Athens, , p.20 Measurement of GCPs (round-abouts) in 2 Ikonos images with least squares template matching. 3 examples. Template is always at left, 2 Ikonos images in the middle and right. Bottom rows show grey level gradients which were actually used in matching.

21 Estimation of a polynomial transformation from the reference in the image (indirect method), generally with Least Squares Adjustment (LSA) Degree of polynomial (generally 1-3) depends on terrain form and terrain area covered by image, e.g. smaller degree when terrain flat and area small After LSA the residuals are examined and eventually some points remeasured or deleted Grey level interpolation Important cases: - Image to map (or orthoimage), image to image (comparison, operations between the images, multitemporal analysis) - Often used with satellite images Factors influencing accuracy: number and quality of control points, degree of transformation, terrain roughness Image is transformed to the average plane (height) of the control points, i.e. image regions with heights far away from this plane have large image errors E.P. Baltsavias, Athens, , p.21

22 Orthoimage Generation Orthoimage -> orthogonal projection, image with map geometry Input data: DTM, digital image, sensor orientation (interior, exterior), transformation from photo- in pixel-coordinate system (only with analog images), optionally other correction values (lens distortion etc.) Generation method (coarse description) - Choice of the orthoimage grid spacing W (usually as W = D/n), D...DTM grid spacing, n...integer > 1) Rule of thumb : P/2 < W < 2P, P...pixel size of original image in object space called also pixel footprint If W >> P, subsample the original image (what other input data must be changed?) - Choice of the orthoimage region (normally in object space) - Projection of the orthoimage grid points in the digital image - Grey level interpolation E.P. Baltsavias, Athens, , p.22

23 projection center digital image transformation from photo- to pixelcoordinate system (normally affine) orthoimage regular grid E.P. Baltsavias, Athens, , p.23

24 With non area sensors (e.g. linear CCDs) the respective geometric sensor models are used With satellite imagery the strict geometric transformation is often approximated by polynomials -> 3-D to 2-D transformation (save computing time!) Orthoimage grid spacing is usually smaller than the DTM spacing. Two options exist: - DTM densified by bilinear interpolation, then all orthoimage grid points transformed in pixel coordinate system (strict solution) - DTM points treated as anchor points and transformed in pixel coordinate system. The remaining orthoimage grid points get pixel coordinates through bilinear interpolation using the known pixel coordinates of the DTM points Anchor point method is faster and results in similar accuracy as the strict solution E.P. Baltsavias, Athens, , p.24

25 Left: digital input image ; right: orthoimage. Black squares represent anchor point locations. Note that the regular grid on object space is distorted in image plane. All white squares represent orthoimage grid points whose pixel coordinates are interpolated using the known pixel coordinates of the anchor points. E.P. Baltsavias, Athens, , p.25

26 Geometric corrections (usually not made) - Lens distortion (very small in modern aerial cameras) - Atmospheric refraction (never used with satellite images) - Earth curvature (only when the imaged area is large) Estimation of the influence of these corrections on the accuracy by using approximative formulas -> decision whether necessary or not Other important factors - Scale of the input imagery (often 2-3 smaller than scale of imagery) - Pixel size used in scanning the imagery (depends on desired data size, resolution of the sensor and the film, application). Often in range microns. E.P. Baltsavias, Athens, , p.26

27 Planimetric accuracy of the orthoimage - under good conditions -> less than 1 pixel - important influence factors: DTM errors (especially at the image borders), exterior orientation accuracy (depends on control point quality and algorithm for its computation, e.g. by resection or bundle block adjustment). Geometric scanner errors are also possible. Non-DTM objects (buildings, bridges, trees etc.) - are radially displaced in orthoimages - can be corrected a posteriori, or combination of DTM with 3-D description of the visible surface of these objects and then orthoimage generation - reduction of radial displacement by using camera with 30 cm lens and/or creating orthoimage only in the central image part E.P. Baltsavias, Athens, , p.27

28 ρ = R c h -- = Z ρ -- h image r = Z r -- h Above formulas valid for vertical imagery terrain m o...scale factor of orthoimage enlargement Non-DTM objects. Radial displacement in image ( ρ) and in orthoimage ( r). E.P. Baltsavias, Athens, , p.28

29 Computing time - very little in comparison to the time needed for acquisition of data required for orthoimage generation, batch run possible - Example: 14 min CPU time, image and orthoimage 100 MB, Sun Sparc 20 E.P. Baltsavias, Athens, , p.29

30 Planimetric Accuracy Control of Orthoimages Use of well defined control points. Possible control sources: - maps and large scale plans (are they accurate enough?) - GPS (are the point well identifiable?) - photogrammetric determination using stereo pair - derivation of control points using ortherectified stereo pairs (treated later) - use of existing higher accuracy orthoimages Control should cover whole image format and all existing terrain types If orthoimage produced using a DTM (not DSM), control must lie on the ground Analysis of the residuals and plot can reveal systematic errors (e.g. in sensor orientation) Overlay of raster map layers or vectors (especially roads) on the orthoimage E.P. Baltsavias, Athens, , p.30

31 Mosaicking Prerequisite: images must be in the same geometric reference system Errors in mosaicking - geometric -> sometimes covered up by rubber-sheeting - radiometric - colour balance of the 3 channels in colour orthoimages Radiometric correction - based on equalisation of global statistical functions of the grey values (cumulative histogram, mean and standard deviation etc.) in the overlap regions - Grey level transformation for achieving this equalisation determines grey level corrections. Corrections in all overlap regions of an image are combined and applied via LUTs E.P. Baltsavias, Athens, , p.31

32 Overlap regions used in the radiometric correction can be determined automatically (e.g. a rectangle) or manually (e.g. a closed polygon line) In latter case aim -> exclude regions with differences between the images, e.g. because of clouds User determines the priority of the images -> which is up (visible)? or gives manually the seam line (polygon line) between the two images with aim to minimise geometric and radiometric differences, e.g. choice of the seam line in regions without texture or along sharp edges A linearly weighted averaging of the grey values of the overlapping images vertically to the seam line reduces radiometric and covers up geometric differences The mosaic extent can be user defined or automatically selected (minimum bounding rectangle of all images) E.P. Baltsavias, Athens, , p.32

33 Example of radiometric correction for image A using the cumulative histogram (see following figure). Procedure: A 1 B 2 3 C Find the overlapping regions of image A with all other images (in this case region 1 with image B, region 2 with image C, and region 3 with images B and C). For each region, do: E.P. Baltsavias, Athens, , p.33

34 Compute the cumulative histogram of all images in the overlap region. Define a target cumulative histogram (e.g. the histogram of one image, or the average of the three histograms) Compute transformations (corrections) to the histogram of each image, so that the actual histogram is transform to the target histogram. These corrections are saved in a LUT with 256 entries and output for 8-bit grey values. For each image do: combine the LUTs to compute the final correction LUT. The combination can be a weighted average using as weights a function of the area of each overlap region from which the LUTs were computed. Read the images from disk in the appropriate sequence, apply the correction LUT and save them. E.P. Baltsavias, Athens, , p.34

35 Problems in radiometric correction of colour images If each R,G,B channel is corrected separately, then when combining the corrected channels new unnatural colours appear (colour shift) A possible solution is to transform RGB into another colour space, e.g. IHS (intensity, hue, saturation), then do radiometric correction to the intensity channel (or if necessary to all), and then transform back to RGB. E.P. Baltsavias, Athens, , p.35

36 Example of mosaicking of false colour IR images (Maggia valley, CH) without (left) and with (right) radiometric correction E.P. Baltsavias, Athens, , p.36

37 Geometric correction of mosaics Errors mainly due to sensor orientation, but locally also due to DTM, scanner Generally only aesthetic improvement possible, or more accurate re-estimation of the sensor orientation -> to avoid re-estimation, estimate orientation from bundle adjustment with dense and acuurate tie points Reduction of misregistration errors by measuring identical points in overlap region and computing a local tranformation between the two images. The error can be divided between both images (then both transformed), or only one is transformed. The transformation should not be applied to the whole image, but starting from the seam line it should fade out after a certain distance from it. E.P. Baltsavias, Athens, , p.37

38 Accuracy evaluation of mosaics If original orthoimages not available, check planimetric accuracy as with orthoimages. Also visual control along seam lines (if visible) for radiometric and geometric differences. For latter check straight strong edges vertical to the seam lines. If original orthoimages available - check radiometry by comparing statistics of grey values (e.g. histograms) from both images in the overlap region - check geometry by measuring identical points in both orthoimages and checking the difference of their map coordinates Xi, Yi. Measure points in a quasi regular grid covering the whole overlap region. If system delivers only pixel coordinates x i, y i, then compute Xi, Yi as E.P. Baltsavias, Athens, , p.38

39 X i = x i s x + X o Y i = y i s y + Y o Xo, Yo...map coordinates of center of upper left pixel s x, s y...orthoimage pixel size in X and Y direction E.P. Baltsavias, Athens, , p.39

40 Orthoimage Maps Useful when maps do not exist or are not available, or are not accurate and/ or up-to-date, and when a fast and/or economic map production is required Have been often created from satellite imagery (esp. from SPOT in SE Asia, Eastern Europe etc.) Orthoimage maps particularly suitable for tailored specific thematic applications, e.g. forestry, hiking, touristic maps etc. Basic elements of a topographic orthoimage map: orthoimage mosaic, overlaid contours, map grid and tick marks, names, legend Additional useful elements: transportation lines, rivers and lake outlines E.P. Baltsavias, Athens, , p.40

41 Topographic features can be digitised from the mosaic or imported in vector form from other systems (photogrammetric, GIS) Orthoimage maps can be also created by combination with scanned map layers Orthoimage (maps) is printed in a larger scale than the original imagery (usually 2-5 times enlargement). The printing pixel size cannot exceed ca. 150 µm, else it is visible by human eye. The enlargement factor of the orthoimage map with respect to the original image (assuming that the orthoimage grid spacing = pixel footprint) is given by the ratio (printing pixel size) / (scan pixel size of original image) E.P. Baltsavias, Athens, , p.41

42 Correction of 3-D objects (buildings etc.) From top left clockwise: Orthoimage with no corrected buildings ; correct position of buildings ; buildings corrected, but old information partially remains (occluded areas, not visible in original aerial image) ; occluded areas filled-in from neighbouring images. E.P. Baltsavias, Athens, , p.42

43 original image orthoimage stereomate Heavy lines represent corresponding distorted and orthorectified locations. E.P. Baltsavias, Athens, , p.43