Lesson 3: Calculating Conditional Probabilities and Evaluating Independence Using Two-Way Tables
|
|
|
- Muriel Thompson
- 9 years ago
- Views:
Transcription
1 Calculating Conditional Probabilities and Evaluating Independence Using Two-Way Tables Classwork Example 1 Students at Rufus King High School were discussing some of the challenges of finding space for athletic teams to practice after school. Part of the problem, according to Kristin, is that females are more likely to be involved in an after-school athletics program than males. However, the athletic director assigns the available facilities as if males are more likely to be involved. Before suggesting changes to the assignments, the students decided to investigate. Suppose the following information is known about Rufus King High School: 40% of students are involved in one or more of the after-school athletics programs offered at the school. It is also known that 58% of the school s students are female. The students decide to construct a hypothetical 1000 two-way table, like Table 1, to organize the data. Table 1: Participation in after-school athletics programs (yes or no) by gender Females Males Yes Participate in After-School No Do Not Participate in After- Athletics Programs School Athletics Programs Cell 1 Cell 2 Cell 3 Cell 4 Cell 5 Cell 6 Cell 7 Cell 8 Cell 9 Exercises 1 6: Organizing the Data 1. What cell in Table 1 represents a hypothetical group of 1,000 students at Rufus King High School? 2. What cells in Table 1 can be filled based on the information given about the student population? Place these values in the appropriate cells of the table based on this information. Two-Way Tables S.19
2 3. Based only on the cells you completed in Exercise 2, which of the following probabilities can be calculated, and which cannot be calculated? Calculate the probability if it can be calculated. If it cannot be calculated, indicate why. a. The probability that a randomly selected student is female. b. The probability that a randomly selected student participates in an after-school athletics program. c. The probability that a randomly selected student who does not participate in an after-school athletics program is male. d. The probability that a randomly selected male student participates in an after-school athletics program. 4. The athletic director indicated that 23.2% of the students at Rufus King are females and participate in after-school athletics programs. Based on this information, complete Table Consider the cells 1, 2, 4, and 5 of Table 1. Identify which of these cells represent students who are female or who participate in after-school athletics programs. 6. What cells of the two-way table represent students who are males who do not participate in after-school athletics programs? Two-Way Tables S.20
3 Example 2 The completed hypothetical 1000 table organizes information in a way that makes it possible to answer various questions. For example, you can investigate whether females at the school are more likely to be involved in the afterschool athletic programs. Consider the following events: Let represent the event a randomly selected student is female. Let not represent the complement of. The complement of A represents the event a randomly selected student is not female, which is equivalent to the event a randomly selected student is male. Let represent the event a randomly selected student participates in an after-school athletics program. Let not represent the complement of. The complement of represents the event a randomly selected student does not participate in an after-school athletics program. Let or (described as union ) represent the event a randomly selected student is female or participates in an after-school athletics program. Let and (described as intersect ) represent the event a randomly selected student is female and participates in an after-school athletics program. Exercises Based on the descriptions above, describe the following events in words: a. Not or Not. b. and Not. 8. Based on the above descriptions and Table 1, determine the probability of each of the following events. a. b. c. Not Two-Way Tables S.21
4 d. Not e. or f. and 9. Determine the following values: a. The probability of plus the probability of Not. b. The probability of plus the probability of Not. c. What do you notice about the results of parts (a) and (b)? Explain. Example 3: Conditional Probability Another type of probability is called a conditional probability. Pulling apart the two-way table helps to define a conditional probability. Yes Participate in After-School No Do Not Participate in After- Athletics Program School Athletics Program Females Cell 1 Cell 2 Cell 3 Suppose that a randomly selected student is female. What is the probability that the selected student participates in an after-school athletics program? This probability is an example of what is called a conditional probability. This probability is calculated as the number of students who are female students and participate in an after-school athletics program (or the students in cell 1) divided by the total number of female students (or the students in cell 3). Two-Way Tables S.22
5 Exercises The following are also examples of conditional probabilities. Answer each question. a. What is the probability that if a randomly selected student is female, she participates in the after-school athletic program? b. What is the probability that if a randomly selected student is female, she does not participate in after-school athletics? 11. Describe two conditional probabilities that can be determined from the following row in Table 1. Yes Participate in After-School No Do Not Participate in After- Athletics Program School Athletics Program Males Cell 4 Cell 5 Cell Describe two conditional probabilities that can be determined from the following column in Table 1. Yes Participate in After-School Athletics Program Females Cell 1 Males Cell 4 Cell 7 Two-Way Tables S.23
6 13. Determine the following conditional probabilities. a. A randomly selected student is female. What is the probability she participates in an after-school athletics program? Explain how you determined your answer. b. A randomly selected student is male. What is the probability he participates in an after-school athletics program? c. A student is selected at random. What is the probability this student participates in an after-school athletics program? 14. Based on the answers to Exercise 13, do you think that female students are more likely to be involved in after-school athletics program? Explain your answer. 15. What might explain the concern females expressed in the beginning of this lesson about the problem of assigning space? Two-Way Tables S.24
7 Lesson Summary Data organized in a two-way frequency table can be used to calculate probabilities. Two-way frequency tables can also be used to calculate conditional probabilities. In certain problems, probabilities that are known can be used to create a hypothetical 1000 two-way table. This hypothetical population of 1,000 can be used to calculate conditional probabilities. Probabilities are always interpreted by the context of the data. Problem Set Oostburg College has a rather large marching band. Engineering majors were heard bragging that students majoring in engineering are more likely to be involved in the marching band than students from other majors. 1. If the above claim is accurate, does that mean that most of the band is engineering students? Explain your answer. 2. The following graph was prepared to investigate the above claim. Based on the graph, complete the following two-way frequency table. Engineering Major Not Engineering Major In the Marching Band Not in the Marching Band Two-Way Tables S.25
8 3. Let represent the event that a randomly selected student is in the marching band. Let represent the event that a randomly selected student is an engineering major. a. Describe the event represented by the complement of. b. Describe the event represented by the complement of. c. Describe the event and ( intersect ). d. Describe the event or ( union ). 4. Based on the completed two-way frequency table, determine the following and explain how you got your answer. a. The probability that a randomly selected student is in the marching band. b. The probability that a randomly selected student is an engineering major. c. The probability that a randomly selected student is in the marching band and an engineering major. d. The probability that a randomly selected student is in the marching band and not an engineering major. 5. Indicate if the following conditional probabilities would be calculated using the rows or the columns of the two-way frequency table. a. A randomly selected student is majoring in engineering. What is the probability this student is in the marching band? b. A randomly selected student is not in the marching band. What is the probability that this student is majoring in engineering? 6. Based on the two-way frequency table, determine the following conditional probabilities. a. A randomly selected student is majoring in engineering. What is the probability that this student is in the marching band? b. A randomly selected student is not majoring in engineering. What is the probability that this student is in the marching band? 7. The claim that started this investigation was that students majoring in engineering are more likely to be in the marching band than students from other majors. Describe the conditional probabilities that would be used to determine if this claim is accurate. 8. Based on the two-way frequency table, calculate the conditional probabilities identified in Problem Do you think the claim that students majoring in engineering are more likely to be in the marching band than students for other majors is accurate? Explain your answer. 10. There are 40 students at Oostburg College majoring in computer science. Computer science is not considered an engineering major. Calculate an estimate of the number of computer science majors you think are in the marching band. Explain how you calculated your estimate. Two-Way Tables S.26
Lesson 17: Margin of Error When Estimating a Population Proportion
 Margin of Error When Estimating a Population Proportion Classwork In this lesson, you will find and interpret the standard deviation of a simulated distribution for a sample proportion and use this information
Margin of Error When Estimating a Population Proportion Classwork In this lesson, you will find and interpret the standard deviation of a simulated distribution for a sample proportion and use this information
Class 19: Two Way Tables, Conditional Distributions, Chi-Square (Text: Sections 2.5; 9.1)
 Spring 204 Class 9: Two Way Tables, Conditional Distributions, Chi-Square (Text: Sections 2.5; 9.) Big Picture: More than Two Samples In Chapter 7: We looked at quantitative variables and compared the
Spring 204 Class 9: Two Way Tables, Conditional Distributions, Chi-Square (Text: Sections 2.5; 9.) Big Picture: More than Two Samples In Chapter 7: We looked at quantitative variables and compared the
Setting up a basic database in Access 2003
 Setting up a basic database in Access 2003 1. Open Access 2. Choose either File new or Blank database 3. Save it to a folder called customer mailing list. Click create 4. Double click on create table in
Setting up a basic database in Access 2003 1. Open Access 2. Choose either File new or Blank database 3. Save it to a folder called customer mailing list. Click create 4. Double click on create table in
Having a coin come up heads or tails is a variable on a nominal scale. Heads is a different category from tails.
 Chi-square Goodness of Fit Test The chi-square test is designed to test differences whether one frequency is different from another frequency. The chi-square test is designed for use with data on a nominal
Chi-square Goodness of Fit Test The chi-square test is designed to test differences whether one frequency is different from another frequency. The chi-square test is designed for use with data on a nominal
Blood Type Probability O 0.42 A 0.43 B 0.11 AB 0.04
 PubH 6414 Worksheet 5a: Probability Principles 1 of 6 Example 1: Distribution of Blood Types in the US Blood Type Probability O 0.42 A 0.43 B 0.11 AB 0.04 Use the distribution of blood types in the US
PubH 6414 Worksheet 5a: Probability Principles 1 of 6 Example 1: Distribution of Blood Types in the US Blood Type Probability O 0.42 A 0.43 B 0.11 AB 0.04 Use the distribution of blood types in the US
Probability. Distribution. Outline
 7 The Normal Probability Distribution Outline 7.1 Properties of the Normal Distribution 7.2 The Standard Normal Distribution 7.3 Applications of the Normal Distribution 7.4 Assessing Normality 7.5 The
7 The Normal Probability Distribution Outline 7.1 Properties of the Normal Distribution 7.2 The Standard Normal Distribution 7.3 Applications of the Normal Distribution 7.4 Assessing Normality 7.5 The
DESCRIPTIVE STATISTICS & DATA PRESENTATION*
 Level 1 Level 2 Level 3 Level 4 0 0 0 0 evel 1 evel 2 evel 3 Level 4 DESCRIPTIVE STATISTICS & DATA PRESENTATION* Created for Psychology 41, Research Methods by Barbara Sommer, PhD Psychology Department
Level 1 Level 2 Level 3 Level 4 0 0 0 0 evel 1 evel 2 evel 3 Level 4 DESCRIPTIVE STATISTICS & DATA PRESENTATION* Created for Psychology 41, Research Methods by Barbara Sommer, PhD Psychology Department
Bivariate Statistics Session 2: Measuring Associations Chi-Square Test
 Bivariate Statistics Session 2: Measuring Associations Chi-Square Test Features Of The Chi-Square Statistic The chi-square test is non-parametric. That is, it makes no assumptions about the distribution
Bivariate Statistics Session 2: Measuring Associations Chi-Square Test Features Of The Chi-Square Statistic The chi-square test is non-parametric. That is, it makes no assumptions about the distribution
STEP TWO: Highlight the data set, then select DATA PIVOT TABLE
 STEP ONE: Enter the data into a database format, with the first row being the variable names, and each row thereafter being one completed survey. For this tutorial, highlight this table, copy and paste
STEP ONE: Enter the data into a database format, with the first row being the variable names, and each row thereafter being one completed survey. For this tutorial, highlight this table, copy and paste
Is it statistically significant? The chi-square test
 UAS Conference Series 2013/14 Is it statistically significant? The chi-square test Dr Gosia Turner Student Data Management and Analysis 14 September 2010 Page 1 Why chi-square? Tests whether two categorical
UAS Conference Series 2013/14 Is it statistically significant? The chi-square test Dr Gosia Turner Student Data Management and Analysis 14 September 2010 Page 1 Why chi-square? Tests whether two categorical
UNDERSTANDING THE TWO-WAY ANOVA
 UNDERSTANDING THE e have seen how the one-way ANOVA can be used to compare two or more sample means in studies involving a single independent variable. This can be extended to two independent variables
UNDERSTANDING THE e have seen how the one-way ANOVA can be used to compare two or more sample means in studies involving a single independent variable. This can be extended to two independent variables
Chapter 4: Probability and Counting Rules
 Chapter 4: Probability and Counting Rules Learning Objectives Upon successful completion of Chapter 4, you will be able to: Determine sample spaces and find the probability of an event using classical
Chapter 4: Probability and Counting Rules Learning Objectives Upon successful completion of Chapter 4, you will be able to: Determine sample spaces and find the probability of an event using classical
AP: LAB 8: THE CHI-SQUARE TEST. Probability, Random Chance, and Genetics
 Ms. Foglia Date AP: LAB 8: THE CHI-SQUARE TEST Probability, Random Chance, and Genetics Why do we study random chance and probability at the beginning of a unit on genetics? Genetics is the study of inheritance,
Ms. Foglia Date AP: LAB 8: THE CHI-SQUARE TEST Probability, Random Chance, and Genetics Why do we study random chance and probability at the beginning of a unit on genetics? Genetics is the study of inheritance,
The Big Picture. Describing Data: Categorical and Quantitative Variables Population. Descriptive Statistics. Community Coalitions (n = 175)
 Describing Data: Categorical and Quantitative Variables Population The Big Picture Sampling Statistical Inference Sample Exploratory Data Analysis Descriptive Statistics In order to make sense of data,
Describing Data: Categorical and Quantitative Variables Population The Big Picture Sampling Statistical Inference Sample Exploratory Data Analysis Descriptive Statistics In order to make sense of data,
6 3 The Standard Normal Distribution
 290 Chapter 6 The Normal Distribution Figure 6 5 Areas Under a Normal Distribution Curve 34.13% 34.13% 2.28% 13.59% 13.59% 2.28% 3 2 1 + 1 + 2 + 3 About 68% About 95% About 99.7% 6 3 The Distribution Since
290 Chapter 6 The Normal Distribution Figure 6 5 Areas Under a Normal Distribution Curve 34.13% 34.13% 2.28% 13.59% 13.59% 2.28% 3 2 1 + 1 + 2 + 3 About 68% About 95% About 99.7% 6 3 The Distribution Since
Nonparametric Tests. Chi-Square Test for Independence
 DDBA 8438: Nonparametric Statistics: The Chi-Square Test Video Podcast Transcript JENNIFER ANN MORROW: Welcome to "Nonparametric Statistics: The Chi-Square Test." My name is Dr. Jennifer Ann Morrow. In
DDBA 8438: Nonparametric Statistics: The Chi-Square Test Video Podcast Transcript JENNIFER ANN MORROW: Welcome to "Nonparametric Statistics: The Chi-Square Test." My name is Dr. Jennifer Ann Morrow. In
Using SPSS, Chapter 2: Descriptive Statistics
 1 Using SPSS, Chapter 2: Descriptive Statistics Chapters 2.1 & 2.2 Descriptive Statistics 2 Mean, Standard Deviation, Variance, Range, Minimum, Maximum 2 Mean, Median, Mode, Standard Deviation, Variance,
1 Using SPSS, Chapter 2: Descriptive Statistics Chapters 2.1 & 2.2 Descriptive Statistics 2 Mean, Standard Deviation, Variance, Range, Minimum, Maximum 2 Mean, Median, Mode, Standard Deviation, Variance,
2.5 Conditional Probabilities and 2-Way Tables
 2.5 Conditional Probabilities and 2-Way Tables Learning Objectives Understand how to calculate conditional probabilities Understand how to calculate probabilities using a contingency or 2-way table It
2.5 Conditional Probabilities and 2-Way Tables Learning Objectives Understand how to calculate conditional probabilities Understand how to calculate probabilities using a contingency or 2-way table It
MATH 140 Lab 4: Probability and the Standard Normal Distribution
 MATH 140 Lab 4: Probability and the Standard Normal Distribution Problem 1. Flipping a Coin Problem In this problem, we want to simualte the process of flipping a fair coin 1000 times. Note that the outcomes
MATH 140 Lab 4: Probability and the Standard Normal Distribution Problem 1. Flipping a Coin Problem In this problem, we want to simualte the process of flipping a fair coin 1000 times. Note that the outcomes
Probabilities and Proportions
 CHAPTER 4 Probabilities and Proportions Chapter Overview While the graphic and numeric methods of Chapters 2 and 3 provide us with tools for summarizing data, probability theory, the subject of this chapter,
CHAPTER 4 Probabilities and Proportions Chapter Overview While the graphic and numeric methods of Chapters 2 and 3 provide us with tools for summarizing data, probability theory, the subject of this chapter,
Two-Way ANOVA Lab: Interactions
 Name Two-Way ANOVA Lab: Interactions Perhaps the most complicated situation that you face in interpreting a two-way ANOVA is the presence of an interaction. This brief lab is intended to give you additional
Name Two-Way ANOVA Lab: Interactions Perhaps the most complicated situation that you face in interpreting a two-way ANOVA is the presence of an interaction. This brief lab is intended to give you additional
NEW JERSEY VOTERS DIVIDED OVER SAME-SEX MARRIAGE. A Rutgers-Eagleton Poll on same-sex marriage, conducted in June 2006, found the state s
 - Eagleton Poll Oct. 25, 2006 CONTACTS: MURRAY EDELMAN, Ph.D., (917) 968-1299 (cell) TIM VERCELLOTTI, Ph.D., (732) 932-9384, EXT. 285; (919) 812-3452 (cell) (Note: News media covering the New Jersey Supreme
- Eagleton Poll Oct. 25, 2006 CONTACTS: MURRAY EDELMAN, Ph.D., (917) 968-1299 (cell) TIM VERCELLOTTI, Ph.D., (732) 932-9384, EXT. 285; (919) 812-3452 (cell) (Note: News media covering the New Jersey Supreme
PREA COMPLIANCE AUDIT TOOL QUESTIONS FOR INMATES. Prisons and Jails 05/03/2013
 Prisons and Jails 05/03/2013 RANDOM SAMPLE OF INMATES... 2 YOUTHFUL INMATES... 4 DISABLED AND LIMITED ENGLISH PROFICIENT INMATES... 5 TRANSGENDER AND INTERSEX INMATES; GAY, LESBIAN, AND BISEXUAL INMATES...
Prisons and Jails 05/03/2013 RANDOM SAMPLE OF INMATES... 2 YOUTHFUL INMATES... 4 DISABLED AND LIMITED ENGLISH PROFICIENT INMATES... 5 TRANSGENDER AND INTERSEX INMATES; GAY, LESBIAN, AND BISEXUAL INMATES...
CHAPTER 15 NOMINAL MEASURES OF CORRELATION: PHI, THE CONTINGENCY COEFFICIENT, AND CRAMER'S V
 CHAPTER 15 NOMINAL MEASURES OF CORRELATION: PHI, THE CONTINGENCY COEFFICIENT, AND CRAMER'S V Chapters 13 and 14 introduced and explained the use of a set of statistical tools that researchers use to measure
CHAPTER 15 NOMINAL MEASURES OF CORRELATION: PHI, THE CONTINGENCY COEFFICIENT, AND CRAMER'S V Chapters 13 and 14 introduced and explained the use of a set of statistical tools that researchers use to measure
Interview Guide of Virtual ICU Nurses
 Name of virtual ICU: Day: Nurse number: Gender: Male Female Time of interview: Beginning: End: Total duration of interview: Interviewers (circle initials): PC PH KM AK DW Introduction: Our research team
Name of virtual ICU: Day: Nurse number: Gender: Male Female Time of interview: Beginning: End: Total duration of interview: Interviewers (circle initials): PC PH KM AK DW Introduction: Our research team
The Chi-Square Test. STAT E-50 Introduction to Statistics
 STAT -50 Introduction to Statistics The Chi-Square Test The Chi-square test is a nonparametric test that is used to compare experimental results with theoretical models. That is, we will be comparing observed
STAT -50 Introduction to Statistics The Chi-Square Test The Chi-square test is a nonparametric test that is used to compare experimental results with theoretical models. That is, we will be comparing observed
How to Make APA Format Tables Using Microsoft Word
 How to Make APA Format Tables Using Microsoft Word 1 I. Tables vs. Figures - See APA Publication Manual p. 147-175 for additional details - Tables consist of words and numbers where spatial relationships
How to Make APA Format Tables Using Microsoft Word 1 I. Tables vs. Figures - See APA Publication Manual p. 147-175 for additional details - Tables consist of words and numbers where spatial relationships
Binary Adders: Half Adders and Full Adders
 Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
STAT 35A HW2 Solutions
 STAT 35A HW2 Solutions http://www.stat.ucla.edu/~dinov/courses_students.dir/09/spring/stat35.dir 1. A computer consulting firm presently has bids out on three projects. Let A i = { awarded project i },
STAT 35A HW2 Solutions http://www.stat.ucla.edu/~dinov/courses_students.dir/09/spring/stat35.dir 1. A computer consulting firm presently has bids out on three projects. Let A i = { awarded project i },
EXAMINATIONS OF THE HONG KONG STATISTICAL SOCIETY
 EXAMINATIONS OF THE HONG KONG STATISTICAL SOCIETY HIGHER CERTIFICATE IN STATISTICS, 2015 MODULE 1 : Data collection and interpretation Time allowed: One and a half hours Candidates should answer THREE
EXAMINATIONS OF THE HONG KONG STATISTICAL SOCIETY HIGHER CERTIFICATE IN STATISTICS, 2015 MODULE 1 : Data collection and interpretation Time allowed: One and a half hours Candidates should answer THREE
Association Between Variables
 Contents 11 Association Between Variables 767 11.1 Introduction............................ 767 11.1.1 Measure of Association................. 768 11.1.2 Chapter Summary.................... 769 11.2 Chi
Contents 11 Association Between Variables 767 11.1 Introduction............................ 767 11.1.1 Measure of Association................. 768 11.1.2 Chapter Summary.................... 769 11.2 Chi
Welcome back to EDFR 6700. I m Jeff Oescher, and I ll be discussing quantitative research design with you for the next several lessons.
 Welcome back to EDFR 6700. I m Jeff Oescher, and I ll be discussing quantitative research design with you for the next several lessons. I ll follow the text somewhat loosely, discussing some chapters out
Welcome back to EDFR 6700. I m Jeff Oescher, and I ll be discussing quantitative research design with you for the next several lessons. I ll follow the text somewhat loosely, discussing some chapters out
Session 7 Bivariate Data and Analysis
 Session 7 Bivariate Data and Analysis Key Terms for This Session Previously Introduced mean standard deviation New in This Session association bivariate analysis contingency table co-variation least squares
Session 7 Bivariate Data and Analysis Key Terms for This Session Previously Introduced mean standard deviation New in This Session association bivariate analysis contingency table co-variation least squares
LAB : THE CHI-SQUARE TEST. Probability, Random Chance, and Genetics
 Period Date LAB : THE CHI-SQUARE TEST Probability, Random Chance, and Genetics Why do we study random chance and probability at the beginning of a unit on genetics? Genetics is the study of inheritance,
Period Date LAB : THE CHI-SQUARE TEST Probability, Random Chance, and Genetics Why do we study random chance and probability at the beginning of a unit on genetics? Genetics is the study of inheritance,
Chapter 5 Analysis of variance SPSS Analysis of variance
 Chapter 5 Analysis of variance SPSS Analysis of variance Data file used: gss.sav How to get there: Analyze Compare Means One-way ANOVA To test the null hypothesis that several population means are equal,
Chapter 5 Analysis of variance SPSS Analysis of variance Data file used: gss.sav How to get there: Analyze Compare Means One-way ANOVA To test the null hypothesis that several population means are equal,
Math 728 Lesson Plan
 Math 728 Lesson Plan Tatsiana Maskalevich January 27, 2011 Topic: Probability involving sampling without replacement and dependent trials. Grade Level: 8-12 Objective: Compute the probability of winning
Math 728 Lesson Plan Tatsiana Maskalevich January 27, 2011 Topic: Probability involving sampling without replacement and dependent trials. Grade Level: 8-12 Objective: Compute the probability of winning
School Bullying Survey
 School Bullying Survey This survey is not required for your class. If you choose not to complete this survey, your grade in the class will not be affected in any way. If this is your decision, just leave
School Bullying Survey This survey is not required for your class. If you choose not to complete this survey, your grade in the class will not be affected in any way. If this is your decision, just leave
CALCULATIONS & STATISTICS
 CALCULATIONS & STATISTICS CALCULATION OF SCORES Conversion of 1-5 scale to 0-100 scores When you look at your report, you will notice that the scores are reported on a 0-100 scale, even though respondents
CALCULATIONS & STATISTICS CALCULATION OF SCORES Conversion of 1-5 scale to 0-100 scores When you look at your report, you will notice that the scores are reported on a 0-100 scale, even though respondents
EXAM. Exam #3. Math 1430, Spring 2002. April 21, 2001 ANSWERS
 EXAM Exam #3 Math 1430, Spring 2002 April 21, 2001 ANSWERS i 60 pts. Problem 1. A city has two newspapers, the Gazette and the Journal. In a survey of 1, 200 residents, 500 read the Journal, 700 read the
EXAM Exam #3 Math 1430, Spring 2002 April 21, 2001 ANSWERS i 60 pts. Problem 1. A city has two newspapers, the Gazette and the Journal. In a survey of 1, 200 residents, 500 read the Journal, 700 read the
33 DISCOUNTED PRESENT VALUE
 33 DISCOUNTED PRESENT VALUE Purpose: To illustrate the idea of discounted present value with computations of the value of payments to be received in the future at different rates of interest. To use discounted
33 DISCOUNTED PRESENT VALUE Purpose: To illustrate the idea of discounted present value with computations of the value of payments to be received in the future at different rates of interest. To use discounted
Contingency Tables and the Chi Square Statistic. Interpreting Computer Printouts and Constructing Tables
 Contingency Tables and the Chi Square Statistic Interpreting Computer Printouts and Constructing Tables Contingency Tables/Chi Square Statistics What are they? A contingency table is a table that shows
Contingency Tables and the Chi Square Statistic Interpreting Computer Printouts and Constructing Tables Contingency Tables/Chi Square Statistics What are they? A contingency table is a table that shows
8.3 Probability Applications of Counting Principles
 8. Probability Applications of Counting Principles In this section, we will see how we can apply the counting principles from the previous two sections in solving probability problems. Many of the probability
8. Probability Applications of Counting Principles In this section, we will see how we can apply the counting principles from the previous two sections in solving probability problems. Many of the probability
Introduction to Analysis of Variance (ANOVA) Limitations of the t-test
 Introduction to Analysis of Variance (ANOVA) The Structural Model, The Summary Table, and the One- Way ANOVA Limitations of the t-test Although the t-test is commonly used, it has limitations Can only
Introduction to Analysis of Variance (ANOVA) The Structural Model, The Summary Table, and the One- Way ANOVA Limitations of the t-test Although the t-test is commonly used, it has limitations Can only
Representing Vector Fields Using Field Line Diagrams
 Minds On Physics Activity FFá2 5 Representing Vector Fields Using Field Line Diagrams Purpose and Expected Outcome One way of representing vector fields is using arrows to indicate the strength and direction
Minds On Physics Activity FFá2 5 Representing Vector Fields Using Field Line Diagrams Purpose and Expected Outcome One way of representing vector fields is using arrows to indicate the strength and direction
Chapter 1 Section 4: Compound Linear Inequalities
 Chapter 1 Section 4: Compound Linear Inequalities Introduction Compound linear inequalities involve finding the union or intersection of solution sets of two or more linear inequalities. You ve already
Chapter 1 Section 4: Compound Linear Inequalities Introduction Compound linear inequalities involve finding the union or intersection of solution sets of two or more linear inequalities. You ve already
How To Understand And Solve A Linear Programming Problem
 At the end of the lesson, you should be able to: Chapter 2: Systems of Linear Equations and Matrices: 2.1: Solutions of Linear Systems by the Echelon Method Define linear systems, unique solution, inconsistent,
At the end of the lesson, you should be able to: Chapter 2: Systems of Linear Equations and Matrices: 2.1: Solutions of Linear Systems by the Echelon Method Define linear systems, unique solution, inconsistent,
IOWA CERTIFIED NURSING ASSISTANT WAGE AND BENEFIT SURVEY. Prepared for:
 IOWA CERTIFIED NURSING ASSISTANT WAGE AND BENEFIT SURVEY Prepared for: Iowa Commission on the Status of Women Iowa CareGivers Association Iowa Workforce Development Office of the Long Term Care Ombudsman
IOWA CERTIFIED NURSING ASSISTANT WAGE AND BENEFIT SURVEY Prepared for: Iowa Commission on the Status of Women Iowa CareGivers Association Iowa Workforce Development Office of the Long Term Care Ombudsman
CREATING A 12 TONE MATRIX: "My music is not modern, it is merely badly played." A. Schoenberg
 CREATING A 12 TONE MATRIX: "My music is not modern, it is merely badly played." A. Schoenberg WHY CREATE A 12 TONE MATRIX? Having a chart like this (12 tone matrix) showing all variants of the series at
CREATING A 12 TONE MATRIX: "My music is not modern, it is merely badly played." A. Schoenberg WHY CREATE A 12 TONE MATRIX? Having a chart like this (12 tone matrix) showing all variants of the series at
Characteristics of Binomial Distributions
 Lesson2 Characteristics of Binomial Distributions In the last lesson, you constructed several binomial distributions, observed their shapes, and estimated their means and standard deviations. In Investigation
Lesson2 Characteristics of Binomial Distributions In the last lesson, you constructed several binomial distributions, observed their shapes, and estimated their means and standard deviations. In Investigation
Statgraphics Getting started
 Statgraphics Getting started The aim of this exercise is to introduce you to some of the basic features of the Statgraphics software. Starting Statgraphics 1. Log in to your PC, using the usual procedure
Statgraphics Getting started The aim of this exercise is to introduce you to some of the basic features of the Statgraphics software. Starting Statgraphics 1. Log in to your PC, using the usual procedure
Midterm Review Problems
 Midterm Review Problems October 19, 2013 1. Consider the following research title: Cooperation among nursery school children under two types of instruction. In this study, what is the independent variable?
Midterm Review Problems October 19, 2013 1. Consider the following research title: Cooperation among nursery school children under two types of instruction. In this study, what is the independent variable?
"Statistical methods are objective methods by which group trends are abstracted from observations on many separate individuals." 1
 BASIC STATISTICAL THEORY / 3 CHAPTER ONE BASIC STATISTICAL THEORY "Statistical methods are objective methods by which group trends are abstracted from observations on many separate individuals." 1 Medicine
BASIC STATISTICAL THEORY / 3 CHAPTER ONE BASIC STATISTICAL THEORY "Statistical methods are objective methods by which group trends are abstracted from observations on many separate individuals." 1 Medicine
Chapter 7 Sampling (Reminder: Don t forget to utilize the concept maps and study questions as you study this and the other chapters.
 Chapter 7 Sampling (Reminder: Don t forget to utilize the concept maps and study questions as you study this and the other chapters.) The purpose of Chapter 7 it to help you to learn about sampling in
Chapter 7 Sampling (Reminder: Don t forget to utilize the concept maps and study questions as you study this and the other chapters.) The purpose of Chapter 7 it to help you to learn about sampling in
Meiosis is a special form of cell division.
 Page 1 of 6 KEY CONCEPT Meiosis is a special form of cell division. BEFORE, you learned Mitosis produces two genetically identical cells In sexual reproduction, offspring inherit traits from both parents
Page 1 of 6 KEY CONCEPT Meiosis is a special form of cell division. BEFORE, you learned Mitosis produces two genetically identical cells In sexual reproduction, offspring inherit traits from both parents
Lesson 5: Percent Change Bellringer
 Lesson 5: Percent Change Bellringer Find 88% of your class! Lesson 5: Percent Change Classwork Let s Think: Mrs. Accordino had you do a new sprint today on converting numbers in to percents! You compare
Lesson 5: Percent Change Bellringer Find 88% of your class! Lesson 5: Percent Change Classwork Let s Think: Mrs. Accordino had you do a new sprint today on converting numbers in to percents! You compare
Client Marketing: Sets
 Client Marketing Client Marketing: Sets Purpose Client Marketing Sets are used for selecting clients from the client records based on certain criteria you designate. Once the clients are selected, you
Client Marketing Client Marketing: Sets Purpose Client Marketing Sets are used for selecting clients from the client records based on certain criteria you designate. Once the clients are selected, you
Teaching & Learning Plans. Arithmetic Sequences. Leaving Certificate Syllabus
 Teaching & Learning Plans Arithmetic Sequences Leaving Certificate Syllabus The Teaching & Learning Plans are structured as follows: Aims outline what the lesson, or series of lessons, hopes to achieve.
Teaching & Learning Plans Arithmetic Sequences Leaving Certificate Syllabus The Teaching & Learning Plans are structured as follows: Aims outline what the lesson, or series of lessons, hopes to achieve.
Chapter 2 Quantitative, Qualitative, and Mixed Research
 1 Chapter 2 Quantitative, Qualitative, and Mixed Research This chapter is our introduction to the three research methodology paradigms. A paradigm is a perspective based on a set of assumptions, concepts,
1 Chapter 2 Quantitative, Qualitative, and Mixed Research This chapter is our introduction to the three research methodology paradigms. A paradigm is a perspective based on a set of assumptions, concepts,
Methods for Interaction Detection in Predictive Modeling Using SAS Doug Thompson, PhD, Blue Cross Blue Shield of IL, NM, OK & TX, Chicago, IL
 Paper SA01-2012 Methods for Interaction Detection in Predictive Modeling Using SAS Doug Thompson, PhD, Blue Cross Blue Shield of IL, NM, OK & TX, Chicago, IL ABSTRACT Analysts typically consider combinations
Paper SA01-2012 Methods for Interaction Detection in Predictive Modeling Using SAS Doug Thompson, PhD, Blue Cross Blue Shield of IL, NM, OK & TX, Chicago, IL ABSTRACT Analysts typically consider combinations
Getting Started with Statistics. Out of Control! ID: 10137
 Out of Control! ID: 10137 By Michele Patrick Time required 35 minutes Activity Overview In this activity, students make XY Line Plots and scatter plots to create run charts and control charts (types of
Out of Control! ID: 10137 By Michele Patrick Time required 35 minutes Activity Overview In this activity, students make XY Line Plots and scatter plots to create run charts and control charts (types of
CONTINGENCY TABLES ARE NOT ALL THE SAME David C. Howell University of Vermont
 CONTINGENCY TABLES ARE NOT ALL THE SAME David C. Howell University of Vermont To most people studying statistics a contingency table is a contingency table. We tend to forget, if we ever knew, that contingency
CONTINGENCY TABLES ARE NOT ALL THE SAME David C. Howell University of Vermont To most people studying statistics a contingency table is a contingency table. We tend to forget, if we ever knew, that contingency
Math Tools Cell Phone Plans
 NATIONAL PARTNERSHIP FOR QUALITY AFTERSCHOOL LEARNING www.sedl.org/afterschool/toolkits Math Tools Cell Phone Plans..............................................................................................
NATIONAL PARTNERSHIP FOR QUALITY AFTERSCHOOL LEARNING www.sedl.org/afterschool/toolkits Math Tools Cell Phone Plans..............................................................................................
3.4 Statistical inference for 2 populations based on two samples
 3.4 Statistical inference for 2 populations based on two samples Tests for a difference between two population means The first sample will be denoted as X 1, X 2,..., X m. The second sample will be denoted
3.4 Statistical inference for 2 populations based on two samples Tests for a difference between two population means The first sample will be denoted as X 1, X 2,..., X m. The second sample will be denoted
The first three steps in a logistic regression analysis with examples in IBM SPSS. Steve Simon P.Mean Consulting www.pmean.com
 The first three steps in a logistic regression analysis with examples in IBM SPSS. Steve Simon P.Mean Consulting www.pmean.com 2. Why do I offer this webinar for free? I offer free statistics webinars
The first three steps in a logistic regression analysis with examples in IBM SPSS. Steve Simon P.Mean Consulting www.pmean.com 2. Why do I offer this webinar for free? I offer free statistics webinars
ASSIGNMENT 4 PREDICTIVE MODELING AND GAINS CHARTS
 DATABASE MARKETING Fall 2015, max 24 credits Dead line 15.10. ASSIGNMENT 4 PREDICTIVE MODELING AND GAINS CHARTS PART A Gains chart with excel Prepare a gains chart from the data in \\work\courses\e\27\e20100\ass4b.xls.
DATABASE MARKETING Fall 2015, max 24 credits Dead line 15.10. ASSIGNMENT 4 PREDICTIVE MODELING AND GAINS CHARTS PART A Gains chart with excel Prepare a gains chart from the data in \\work\courses\e\27\e20100\ass4b.xls.
CONTINGENCY (CROSS- TABULATION) TABLES
 CONTINGENCY (CROSS- TABULATION) TABLES Presents counts of two or more variables A 1 A 2 Total B 1 a b a+b B 2 c d c+d Total a+c b+d n = a+b+c+d 1 Joint, Marginal, and Conditional Probability We study methods
CONTINGENCY (CROSS- TABULATION) TABLES Presents counts of two or more variables A 1 A 2 Total B 1 a b a+b B 2 c d c+d Total a+c b+d n = a+b+c+d 1 Joint, Marginal, and Conditional Probability We study methods
The Circumference Function
 2 Geometry You have permission to make copies of this document for your classroom use only. You may not distribute, copy or otherwise reproduce any part of this document or the lessons contained herein
2 Geometry You have permission to make copies of this document for your classroom use only. You may not distribute, copy or otherwise reproduce any part of this document or the lessons contained herein
Mind on Statistics. Chapter 15
 Mind on Statistics Chapter 15 Section 15.1 1. A student survey was done to study the relationship between class standing (freshman, sophomore, junior, or senior) and major subject (English, Biology, French,
Mind on Statistics Chapter 15 Section 15.1 1. A student survey was done to study the relationship between class standing (freshman, sophomore, junior, or senior) and major subject (English, Biology, French,
Technical Information
 Technical Information Trials The questions for Progress Test in English (PTE) were developed by English subject experts at the National Foundation for Educational Research. For each test level of the paper
Technical Information Trials The questions for Progress Test in English (PTE) were developed by English subject experts at the National Foundation for Educational Research. For each test level of the paper
Playing with Numbers
 PLAYING WITH NUMBERS 249 Playing with Numbers CHAPTER 16 16.1 Introduction You have studied various types of numbers such as natural numbers, whole numbers, integers and rational numbers. You have also
PLAYING WITH NUMBERS 249 Playing with Numbers CHAPTER 16 16.1 Introduction You have studied various types of numbers such as natural numbers, whole numbers, integers and rational numbers. You have also
Chi-square test Fisher s Exact test
 Lesson 1 Chi-square test Fisher s Exact test McNemar s Test Lesson 1 Overview Lesson 11 covered two inference methods for categorical data from groups Confidence Intervals for the difference of two proportions
Lesson 1 Chi-square test Fisher s Exact test McNemar s Test Lesson 1 Overview Lesson 11 covered two inference methods for categorical data from groups Confidence Intervals for the difference of two proportions
Solutions to Homework 10 Statistics 302 Professor Larget
 s to Homework 10 Statistics 302 Professor Larget Textbook Exercises 7.14 Rock-Paper-Scissors (Graded for Accurateness) In Data 6.1 on page 367 we see a table, reproduced in the table below that shows the
s to Homework 10 Statistics 302 Professor Larget Textbook Exercises 7.14 Rock-Paper-Scissors (Graded for Accurateness) In Data 6.1 on page 367 we see a table, reproduced in the table below that shows the
QUANTITATIVE METHODS IN BUSINESS PROBLEM #2: INTRODUCTION TO SIMULATION
 QUANTITATIVE METHODS IN BUSINESS PROBLEM #2: INTRODUCTION TO SIMULATION Dr. Arnold Kleinstein and Dr. Sharon Petrushka Introduction Simulation means imitation of reality. In this problem, we will simulate
QUANTITATIVE METHODS IN BUSINESS PROBLEM #2: INTRODUCTION TO SIMULATION Dr. Arnold Kleinstein and Dr. Sharon Petrushka Introduction Simulation means imitation of reality. In this problem, we will simulate
Standard 12: The student will explain and evaluate the financial impact and consequences of gambling.
 TEACHER GUIDE 12.1 GAMBLING PAGE 1 Standard 12: The student will explain and evaluate the financial impact and consequences of gambling. Risky Business Priority Academic Student Skills Personal Financial
TEACHER GUIDE 12.1 GAMBLING PAGE 1 Standard 12: The student will explain and evaluate the financial impact and consequences of gambling. Risky Business Priority Academic Student Skills Personal Financial
Quick Tricks for Multiplication
 Quick Tricks for Multiplication Why multiply? A computer can multiply thousands of numbers in less than a second. A human is lucky to multiply two numbers in less than a minute. So we tend to have computers
Quick Tricks for Multiplication Why multiply? A computer can multiply thousands of numbers in less than a second. A human is lucky to multiply two numbers in less than a minute. So we tend to have computers
RATIOS, PROPORTIONS, PERCENTAGES, AND RATES
 RATIOS, PROPORTIOS, PERCETAGES, AD RATES 1. Ratios: ratios are one number expressed in relation to another by dividing the one number by the other. For example, the sex ratio of Delaware in 1990 was: 343,200
RATIOS, PROPORTIOS, PERCETAGES, AD RATES 1. Ratios: ratios are one number expressed in relation to another by dividing the one number by the other. For example, the sex ratio of Delaware in 1990 was: 343,200
Importing Data from a Dat or Text File into SPSS
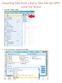 Importing Data from a Dat or Text File into SPSS 1. Select File Open Data (Using Text Wizard) 2. Under Files of type, choose Text (*.txt,*.dat) 3. Select the file you want to import. The dat or text file
Importing Data from a Dat or Text File into SPSS 1. Select File Open Data (Using Text Wizard) 2. Under Files of type, choose Text (*.txt,*.dat) 3. Select the file you want to import. The dat or text file
CHAPTER 7 INTRODUCTION TO SAMPLING DISTRIBUTIONS
 CHAPTER 7 INTRODUCTION TO SAMPLING DISTRIBUTIONS CENTRAL LIMIT THEOREM (SECTION 7.2 OF UNDERSTANDABLE STATISTICS) The Central Limit Theorem says that if x is a random variable with any distribution having
CHAPTER 7 INTRODUCTION TO SAMPLING DISTRIBUTIONS CENTRAL LIMIT THEOREM (SECTION 7.2 OF UNDERSTANDABLE STATISTICS) The Central Limit Theorem says that if x is a random variable with any distribution having
A support tool for composing questionnaires in social survey data archive SRDQ
 20th Workshop on Methodologies and Tools for Complex System Modeling and Integrated Policy Assessment (CSM2006) 2006.8.28-30: Laxenburg, Austria A support tool for composing questionnaires in social survey
20th Workshop on Methodologies and Tools for Complex System Modeling and Integrated Policy Assessment (CSM2006) 2006.8.28-30: Laxenburg, Austria A support tool for composing questionnaires in social survey
Chapter 13. Chi-Square. Crosstabs and Nonparametric Tests. Specifically, we demonstrate procedures for running two separate
 1 Chapter 13 Chi-Square This section covers the steps for running and interpreting chi-square analyses using the SPSS Crosstabs and Nonparametric Tests. Specifically, we demonstrate procedures for running
1 Chapter 13 Chi-Square This section covers the steps for running and interpreting chi-square analyses using the SPSS Crosstabs and Nonparametric Tests. Specifically, we demonstrate procedures for running
Mutual Fund Expense Information on Quarterly Shareholder Statements
 June 2005 Mutual Fund Expense Information on Quarterly Shareholder Statements You may have noticed that beginning with your March 31 quarterly statement from AllianceBernstein, two new sections have been
June 2005 Mutual Fund Expense Information on Quarterly Shareholder Statements You may have noticed that beginning with your March 31 quarterly statement from AllianceBernstein, two new sections have been
(b) You draw two balls from an urn and track the colors. When you start, it contains three blue balls and one red ball.
 Examples for Chapter 3 Probability Math 1040-1 Section 3.1 1. Draw a tree diagram for each of the following situations. State the size of the sample space. (a) You flip a coin three times. (b) You draw
Examples for Chapter 3 Probability Math 1040-1 Section 3.1 1. Draw a tree diagram for each of the following situations. State the size of the sample space. (a) You flip a coin three times. (b) You draw
Book Review of Rosenhouse, The Monty Hall Problem. Leslie Burkholder 1
 Book Review of Rosenhouse, The Monty Hall Problem Leslie Burkholder 1 The Monty Hall Problem, Jason Rosenhouse, New York, Oxford University Press, 2009, xii, 195 pp, US $24.95, ISBN 978-0-19-5#6789-8 (Source
Book Review of Rosenhouse, The Monty Hall Problem Leslie Burkholder 1 The Monty Hall Problem, Jason Rosenhouse, New York, Oxford University Press, 2009, xii, 195 pp, US $24.95, ISBN 978-0-19-5#6789-8 (Source
INTERNSHIP PROGRAMME APPLICATION FORM
 WHAT IS THE PURPOSE OF THIS FORM? To assist the National Treasury in selecting candidates for the Internship Programme. This form may be used to identify candidates to be interviewed. Since all applicants
WHAT IS THE PURPOSE OF THIS FORM? To assist the National Treasury in selecting candidates for the Internship Programme. This form may be used to identify candidates to be interviewed. Since all applicants
Section 12 Part 2. Chi-square test
 Section 12 Part 2 Chi-square test McNemar s Test Section 12 Part 2 Overview Section 12, Part 1 covered two inference methods for categorical data from 2 groups Confidence Intervals for the difference of
Section 12 Part 2 Chi-square test McNemar s Test Section 12 Part 2 Overview Section 12, Part 1 covered two inference methods for categorical data from 2 groups Confidence Intervals for the difference of
FAO Standard Seed Security Assessment CREATING MS EXCEL DATABASE
 FAO Standard Seed Security Assessment CREATING MS EXCEL DATABASE When you open a Microsoft Excel programme, a new file (book1) appears on your screen. This file normally consist of three work sheets (new
FAO Standard Seed Security Assessment CREATING MS EXCEL DATABASE When you open a Microsoft Excel programme, a new file (book1) appears on your screen. This file normally consist of three work sheets (new
Microsoft Get It Done Survey of Office Workers
 Microsoft Get It Done Survey of Office Workers Executive Summary and Survey Results Presented by: Harris Interactive Public Relations Research November 2013 About the Survey Survey Method This survey was
Microsoft Get It Done Survey of Office Workers Executive Summary and Survey Results Presented by: Harris Interactive Public Relations Research November 2013 About the Survey Survey Method This survey was
STRATIFIED SAMPLING. Edexcel GCSE Mathematics (Linear) 1MA0
 Edexcel GCSE Mathematics (Linear) 1MA0 STRATIFIED SAMPLING Materials required for examination Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser. Tracing paper
Edexcel GCSE Mathematics (Linear) 1MA0 STRATIFIED SAMPLING Materials required for examination Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser. Tracing paper
INTERSECTION MATH And more! James Tanton
 INTERSECTION MATH And more! James Tanton www.jamestanton.com The following represents a sample activity based on the December 2006 newsletter of the St. Mark s Institute of Mathematics (www.stmarksschool.org/math).
INTERSECTION MATH And more! James Tanton www.jamestanton.com The following represents a sample activity based on the December 2006 newsletter of the St. Mark s Institute of Mathematics (www.stmarksschool.org/math).
Absolute Value Equations and Inequalities
 Key Concepts: Compound Inequalities Absolute Value Equations and Inequalities Intersections and unions Suppose that A and B are two sets of numbers. The intersection of A and B is the set of all numbers
Key Concepts: Compound Inequalities Absolute Value Equations and Inequalities Intersections and unions Suppose that A and B are two sets of numbers. The intersection of A and B is the set of all numbers
Basic Probability Theory II
 RECAP Basic Probability heory II Dr. om Ilvento FREC 408 We said the approach to establishing probabilities for events is to Define the experiment List the sample points Assign probabilities to the sample
RECAP Basic Probability heory II Dr. om Ilvento FREC 408 We said the approach to establishing probabilities for events is to Define the experiment List the sample points Assign probabilities to the sample
Dolch Second Grade Sight Vocabulary Bingo. Wild West Bingo. All 46 Second Grade Dolch Sight Words. Ordered by frequency
 Wild West Bingo All 46 Second Grade Dolch Sight Words Ordered by frequency Set1 Set 2 Set 3 would off pull very cold both your tell sit its work which around first read don t does why right goes found
Wild West Bingo All 46 Second Grade Dolch Sight Words Ordered by frequency Set1 Set 2 Set 3 would off pull very cold both your tell sit its work which around first read don t does why right goes found
Probability Topics: Contingency Tables
 Connexions module: m835 Probability Topics: Contingency Tables Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
Connexions module: m835 Probability Topics: Contingency Tables Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
Life Insurance Modelling: Notes for teachers. Overview
 Life Insurance Modelling: Notes for teachers In this mathematics activity, students model the following situation: An investment fund is set up Investors pay a set amount at the beginning of 20 years.
Life Insurance Modelling: Notes for teachers In this mathematics activity, students model the following situation: An investment fund is set up Investors pay a set amount at the beginning of 20 years.

