Production Planning and Control, Vol.12, N 4, pp , 2001
|
|
|
- Janis Amberly Pitts
- 8 years ago
- Views:
Transcription
1 ACommonCycleApproachtoLotSchedulinginMultistage ManufacturingSystems LAAS-CNRS,7AvenueduColonelRoche,31077ToulouseFRANCE Jean-ClaudeHennet assumptionofconstantdemandratesforalltheend-products.underthecommoncycleapproach, productionplanningprobleminajob-shop.thecyclicnatureoftheproblemisrelatedtothea-priori ACyclicEconomicLot-SizingandSchedulingProblem(CELSP)isformulatedtosolveamultistage Abstract thedemandoverthecommoncyclehorizon.thepapershowsthattheceslpcanbesolvedina eachgenericjobconsistsofproducinganassociatedend-productinthequantityrequiredtomeet decomposedwayandthatitssolutioncaneasilybeimplementedandadjustedtolimitedvariations Multistagemanufacturingsystems,planning,scheduling,optimization. ofdemands. Keywords 1
2 describethemultistagestructureoftheproducts. 1INTRODUCTION Thisstudyisdevotedtotheorganizationofproductioninmanufacturingsystemsproducingfamilies ofproductsthroughseveralprocessingandassemblystages.aninput-outputapproachisusedto usefulforcontrollingandmonitoringthesystem,butintermsofproductionorganization,itmay points,respectivelyrelatedtoproductsandprocesses.descriptionofamanufacturingsysteminterms ofprocessesfocusesonthepropertiesoftheexistingresources,whichareforinstancethemachines, pallets,carriersandworkteams.suchadescriptionisdictatedbytheexistingfacilities.itisvery Productionactivityinamanufacturingsystemcanbedescribedfromtwocomplementaryview- improveeciencyonlymarginally. Then,inthelate1980's,Grubbstromandhisco-authors(GrubbstromandOvrin,1992;GrubbstromandMolinder,1994)haveintroducedlead-timesintheirinput-outputbasedmodels,underthe formofconstantdelays.asimilarapproachhasbeenusedbyhennet(hennet,1998;hennetand elsofproductionandinventorysystemshasbecomeclassicalsincetheworkofveinott(veinott,1969). ysisoftheproductsstructure:primaryproductsaretransformedintoend-productsthroughoneorsev- eralstageswhichcombineandtransformproducts.theuseofinput-outputanalysistoconstructmod- Aproduct-relateddescriptionofamanufacturingsystemisobtainedthroughaninput-outputanal- Barthes,1998)tobuildclosed-loopplanningpolicies. andcostparametersassociatedwiththeresources,itaimsatsolvingthecombinedlot-sizingand hasinputnodes,outputnodesandnocycle.suchadescriptioncanbeveryuseful,inparticularfor re-engineeringandre-designpurposes.thisstudyusesaninput-outputrepresentationofmultistage manufacturingsystems,todeneorre-denejobsandtaskstobeperformed.thenusingtheproperties Graphically,amultistagemanufacturingstructurecanberepresentedbyagozintograph,which schedulingproblem. iterativeresolutionofstandardjob-shopschedulingproblems. ingproblem(elmaghraby,1978)),whichisknowntobenp-hard,andforwhichthesearchforan optimalprocedureisstillanopenproblem(bourlandandyano,1997).however,underthecommoncycleapproach,themultiresourceelsphasbeenreduced(ouennicheandboctor,1998)toan ThisproblemisamultiresourceextensionoftheclassicalELSP(EconomicLotsizingandSchedul- 2
3 introducedin(bomberger,1966)tosolvetheelsp.intheccapproach,eachtaskisperformed exactlyonceineachcycle.somesucientconditionsofoptimalityoftheccassumptionhavebeen establishedin(gallego,1990).inaddition,computationalexperienceshowsthatccschedulesare closetooptimalwhenprocessingtimesarenottoodierentandthattheyoftencomparefavorably TheCommonCycle(CC)approachisthesimplestversionoftheBasicPeriod(BP)assumption, undertheassumptionofconstantdemandrates.then,itisshownthatanormalizedscheduling toheuristicsusedtosolvethemorecomplexproblemsbasedonlessrestrictivebp(basicperiod) problemcanbesolvedrst,independentlyofthevalueofthecommoncycleperiod.theoptimal assumptions. valueoftheperiodisthencomputedbyanexplicitformulaoftheeoqtype. themultiresourceelspundertheccapproach.somebasicpropertiesofthecelspareestablished, TheCyclicEconomicLotsizingandSchedulingProblem(CELSP)studiedinthispaperdescribes 2AMultistageModel problemcanbeeasilyadaptedtolimitedvariationsofthedemand. Intermsofimplementation,thecomputedsolutionofthecombinedlot-sizingandscheduling 2.1TheInput-OutputApproach ABillofMaterialscanbeconstructedtosummarizetheinputandoutputowsofamanufacturing systemoversomeworkinghorizon,t.vectortddenotesthecumulatedexternaloutputvectorand TQthecumulatedproduction/supplyvectoroverT.Then,astaticLeontief-typerepresentationof thesystemovertis: (R S)isnotfullrow-rank,itrepresentsthepossibilitytoobtainthesamecombinationofoutputs whererandsarenonnegativematrices.ristheoutputmatrix(forinternalandexternaltransformations)andsthe(internal)consumptionmatrix.thenetproductionmatrix,(r S)relatesdtoQ. Forgeneralmanufacturingsystems,matricesRandShavethesamerectangularstructure.Ifmatrix (R S)TQ=Td (1) throughdierentactivities.if(r S)isnotfullcolumn-rank,itcorrespondstothepossibilityto substitutesomeproductioninputsbysomeotherones. 3
4 ufacturingactivityhasseveralinputproducts,andproductsofthesametypemaybeusedbyseveral activities.howeverthereisaone-to-onecorrespondencebetweenoutputproductsandactivities:each productionofoneunitofproducticonsumescomponentsj=1;:::;minquantitiesji,forj=1;:::;m. manufacturingactivityhasexactlyoneoutputproduct.accordingtoagivenmanufacturingrecipe, Theproductstructuresstudiedinthispaperarerepresentedbygeneralacyclicgraphs.Eachman- Furthermore,thegraphoftheproductstructurehasnocycle. index,matrixristheidentitymatrix,i,andmatrixsisthenonnegativematrix=((ji)). whichtypicallycharacterizetheeldofapplicationofrequirementsplanning,andparticularlymrp assemblygraphsaresquarematrices.ifactivitiesandassociatedoutputproductshavethesame techniques(seee.g.(baker,1993)).theinputandoutputmatricesrepresentingsuchgeneralized SuchconvergentmanufacturingstructurescanberepresentedbyGozintographs(Vazsonyi,1955), levellforproductswhicharecomponentsofproductsoflevelsstriclylessthanlandofatleastone levell 1product.Levellsisthemaximalnumberofstagesinthemanufacturingprocess. Anexamplewithm=5,n=2isdescribedbythegozintographofFig.1. Productscanthenbepartitionedintolevels(seee.g.(Salomon,1991)).Level0isforendproducts, 1 Level 2 : primary products A B Productsbeingorderedinagreementwiththeincreasingorderoftheirlevel,theinputmatrix Figure1:Anexampleofamultistageproductstructure Level 1 : intermediate product C Level 0 : end products D E
5 isalower-triangularnonnegativematrixwithzerosonthemaindiagonal: Thefollowingresultcanthenbestated: =26400:::0 m1:::m;m : (2) Input-Outputproductionmodel: Any(nonnegative)demandvectorTdcanbesatisedoverTwithinthedomainofvalidityofthe Theorem1 (3).Thenetproductionmatrix,(I )hasallitso-diagonalelementsnonpositive.itmaybe ToprovetheTheorem,itsucestoprovetheexistenceofanonnegativevectorQsolutionofequation Proof (I )TQ=Td; (3) ofanm-matrix(alsocalledaclasskmatrix(kohleretal.,1975))tobeanessentiallynonpositive matrixwithallitsprincipalminorspositive.therefore,matrix(i )isanm-matrix(berman triangular,anditsdiagonalelementsareequalto1.therefore,det(i )=1,andmoregenerally, alltheprincipalminorsofmatrix(i )areequalto1.itisawell-knowncharacteristicproperty calledanessentiallynonpositivematrix(bermanandplemmons,1979).furthermore,itislower- (BermanandPlemmons,1979). ratedcanbefullledusingthenonnegativeproduction/supplyratevectorq,uniquelydenedby: andplemmons,1979).thisimplies,inparticular,thatitsinverse(i ) 1isanonnegativematrix Adirectconsequenceofthispropertyisthat,aslongasthemodelapplies,anynonnegativedemand Q=(I ) 1d (4) 5
6 Nonnegativityofmatrix(I ) 1canbeeasilycheckeddirectly: Thefollowingrelationsareobtained,form>2.: 8<:bi+1;i=i+1;ifori=1;:::m 1 (I ) 1=26410:::0 bm1:::bm;m 11 b bi+k;i=i+k;i+pj=1;:::;k 1i+k;i+jbi+j;ifori=1;:::m 2;k=2;:::;m i: : Fromtheserelations,itcomesbyinductionthatsincematrixisnonnegative,matrix(I ) 1is alsononnegative. mustalsotakeintoaccounttheconstraintsandcostsrelatedtotheuseofparticularresources. ofthismodelinproductionplanningisthereforeveryappealing.however,arealisticproductionplan yieldingvectorqtwithinthetimehorizont,usingtheresourcesavailable.aninput-outputanalysis thusprovidesasimplemodeltodeterminetheproductionrequirementsofalltheproducts.theuse TheLeontiefmodel(4)appliesovertimeperiodTifthereexistsafeasibleproductionschedule Theconsideredproductionplanningproblemisdescribedbythefollowingparameters: 2.2ProductionPlanning products, productsaretheend-products,andthem nremainingproductsareintermediateandprimary -,theinput-outputmatrixofthesystem,withdimensionmm -nnumberofend-products -didemandrateforend-producti(i=1;:::;n);ddenotesthedemandratevector. -mnumberofproducts(primary,intermediateandend-products).byconvention,thenrst -hjunitaryinventoryholdingcostofproductj;j=1;:::;mperunitoftime pacityconstraintsusuallyrequiresaniterativeadjustmentprocess.recently,someattemptshavebeen niques,productionandstoragearenotgloballyoptimized.inaddition,satisfactionofproductionca- -pjproductionrateofproductj;j=1;:::;m -fjsetupcostofproductj;j=1;:::;m. InMaterialRequirementPlanning(MRP)andManufacturingResourcePlanning(MRPII)tech- 6
7 madetobuildmathematicalmodelsoftherequirementplanningmethod(gravesetal.,1998;grubbstromandmolinder,1994;hennetandbarthes,1998).inparticular,thedynamicmodelof(graves etal.,1998)describestheforecastupdatingprocessinarollinghorizonframework,andthemodelin constraints(forinstancethemultilevellotsizingproblem)orintegratethemunderasimpliedform. (HennetandBarthes,1998)representsproductionplanningasatrackingproblem. Onthecontrary,problemswithsmalltimebuckets,suchastheContinuousSetupLotsizingProblem acrucialrole(salomon,1991).modelswithlargetimebucketseitherdonotintegratetheresource timeframework.inthesemodels,thelengthoftheelementaryperiod,calledthetimebucket,plays Mostdeterministiclotsizingmodelsforproductionplanninghavebeenformulatedinthediscrete (CSLP),representmoreaccuratelytheresourceconstraintsoftheschedulingproblem.Butthey rapidlybecomeuntractablewhenthetimehorizonisincreased,becauseofthelargenumberofboolean variablesinvolvedintheirformulation. addressthelotsizingandschedulingissuesthroughtheresolutionofacycliceconomiclotsizing times,whichmaybeconsideredacceptableinsomeplanningproblems,becomesclearlyunrealisticat therealtimelevel.hence,inthecontextofrepetitivemultistageproduction,itisproposedtojointly beintegratedintotheplanningmodeltoguaranteefeasibility.also,theassumptionofconstantlead- Asstressedin(Rouxetal.,1999)foramulti-sitejob-shopproblem,realschedulingdecisionsmust Muckstadt,1994).Input-outputmodelsarecombinedwithcyclicschedulingconstraintstoformulate andschedulingproblem(celsp).themodellingapproachissimilartotheoneusedin(loerchand thelot-sizingdecisionprobleminamultistagemanufacturingsystemunderfairlystabledemands.in addition,thedenitionofthecelsprequirestheknowledgeoftheresourceassignmentpolicy.the consideredmanufacturingcontextisajob-shopwhereeachproductionactivity,denedbyitsoutput product,j,withj2(1;:::;m),mustbecompletedonaparticularresource,r.aresourcemaybe assignedtoseveralactivities. forend-products.thisratherunrealisticassumptionisusedtobuildanominalproductionschedule overanoptimizedproductionperiod.theproblemofadjustmentoftherealscheduletorealdemand 3CyclicLotScheduling ThemultistageCELSPisnowadressedundertheassumptionofconstantdemandrates(di,i=1;:::;n) 7
8 study,theexistenceofsafetystocksisimplicit,andtherealdemandsforproductsmayapplytoall theproductsandmaycoversafetystocksregulationaroundtheirnominallevels,aswellasactual usefulforoptimizingthedistributionofsafetystockswithinamultistageproductionmodel.inthis isconsideredinsection4.inadditiontotheseadjusments,andtolimittheirimportance,theuseof externaldemandvariations. safetystocksisclassicaltocompensatefordemanductuations.input-outputmodelsareparticularly 3.1GenericJobsandGenericTasks whichisk-periodichasbeenprovedusingtimedpetrinets(carlierandchretienne,1988).butdueto theproblemcomplexity,manyauthorshaverestrictedtheclassofinvestigatedschedulestoperiodic(or innitelyoften.forsucharecurrentjob-shopschedulingproblem,theexistenceofanoptimalsolution overaninnitetimehorizoncanbecharacterizedbyasetofgenerictasksthathavetobeperformed Asthedemandratesaresupposedconstant,thecostminimizingsolutionofthelotschedulingproblem 1-periodic)solutions(HanenandMunier,1995).Inparticular,thecommoncycleapproachhasbeen theoperationsmustbeperformedexactlyoncewithintheselectedtimehorizon.theyarecalledthe developedforsimultaneousdeterminationoflotsizesandschedules(ouennicheandboctor,1998). sucestocharacterizetheschedulewithinonetimehorizonhavingthelengthoftheperiod,t.all Underthecommoncycleapproach,theproductionschedulingpolicyisanundenitelylongperiodical repetitionofthesamesequencesoftasksonthedierentmachines.todenesuchaschedule,it generictasks.someschedulingpropertieswillbeestablishedtosimplifythetreatmentofthismodel. therelevantentitiesforprecedenceconstraintsarethegenerictaskswithineachgenericjob,notthe Itthenbecomesnecessarytodeveloptheinput-outputgraphintosubgraphs.Eachsubgraphrepresents agenericjob. amountsofproducts.thisisparticularlyclearforintermediateproductsusedbyseveralendproducts. Whenusingtheinput-outputmodel,oneencountersadicultytoformulateschedulingconstraints: inquantitytdi.thegenerictaskswhichconstitutejobiareassociatedwithallthepathsofthe gozintographhavingproductiastheirterminalnode.thus,byconstruction,thesubgraphofeach producti,theassociatedoperationisproductionofquantityjllitdiofproductj.inthesubgraph jobisapureassemblygraph.forinstance,ifthereisapathoflength2,say(j;l;i)fromproductjto Eachgenericjobi(i=1;:::;n)isassociatedwiththeendproducti(i=1;:::;n),tobeproduced 8
9 othersublotsofthesamecomponent,andpossiblytothesublotsoftheothercomponentsproduced totheothergenerictasksofthesamejobthroughprecedenceconstraints.butitisalsorelatedtothe nentwithinaperiodissplitintosublots.anactivityproducingasublotisagenerictask.itisrelated ofjobj,thereisaprecedenceconstraintbetweenoperation(j;l;i)andoperation(l;i). bythesameresourceifthisisasharedresource. Ifseveralgenericjobsrequirethesametypeofcomponents,thentheproductionlotofthiscompo- tasks1,3,5,7,8. andcomposedoftasks2,4,6,9,10andtheotheroneassociatedwithend-product(e)andcomposedof graphoffig.2.thisdevelopedgraphdescribestwogenericjobs:oneassociatedwithend-product(d) Inagreementwiththisdenitionofgenericjobs,thegozintographofFig.1isdevelopedintothe Product A on Resource 3 Figure2:GraphdevelopingthegraphofFig.1 6 Product B Resource Product C Resource 1 disjunctiveresourcesharingconstraints:resource1isusedtoproduceproductsdande,resource2 constraintsbetweenthesublotsofthesameproduct(productsa,b,c)anddashedzonesrepresenting sentingthegozintoparameters.twotypeofdashedzonesareconsidered;dashedzonesrepresenting Inthedevelopedgraph,arcscorrespondtoprecedenceconstraints,withvaluationsstillrepre- 2 1 Product D Product E isusedtoproduceproductsbandc,andresource3isusedtoproduceproducta. 9
10 tojobiifi=j(s):itisthestartingoperationofapath(j;:::;i)endingatnodeiintheprecedence graphofgenerictasks. Letpdenotethetotalnumberofgenericmanufacturingtasks.Agenerictasks2(1;:::;p)belongs i=sinquantitydit.thedurationofterminaltasksisst,with endproductarethesame. itsassociatedpathreducestonodei.forsimplicity,theindexofaterminaltaskandoftheassociated Thus,atasks2(1;:::;n)isaterminaltask.Suchataskconsistsinproducingtheend-product Thengenerictasksproducingtheend-productsarecalledterminaltasks.Ifsisaterminaltask, isdenedbythepath(j;l;:::;i),thentask(s)isdenedby(l;:::;i).tasksconsistsinproducing thedevelopedprecedencegraph(thegraphoffig.2fortheexample).itisdenoted(s).iftasks Ifs2(n+1;:::;p),thenitisnotaterminaltask,andthereisauniquegenerictaskaftersin s=ds=psfors=1;:::;n: (5) productj=p(s)inquantityqst,withqs=jll0idi: Thedurationofgenerictasks2(n+1;:::;p)issT,with ThemainvariablesoftheCELSParethedurationofthecommoncycleperiodTand,withina 3.2ProblemFormulations=qs=pjforj=P(s): (6) typicaltimeintervalwithdurationt,thegenericperiod[0;t],thestarttimest(s)ofgenerictasks assignedtoproductionofproductj. productj:(j)=fs;p(s)=jg:thecardinalityof(j),whichisthenumberofgenerictasks producingj,isdenoted!j.theresourcer= (s)ofthegenerictasksproducingjistheresource Let(j)denotethesetofgenerictasksofproduction(orsupply)ofthesameintermediate(orprimary) s2(1;:::;p).thesubsequentdatesoftaskssimilartosaret(s)+ktwithk=1;2;:::. rg:thecardinalityoftheset(r)isdenotedr.10 taskstobecompletedonaparticularresource,r,isdenoted(r)anddenedby:(r)=fs; (s)= Resourceconstraintscanbecombinedwithdisjunctiveconstraintsonsublots.Thesetofgeneric
11 3.2.1Theproblemconstraints Constraintsareformulatedoverthegenericperiod. Resourceconstraints PrecedenceconstraintsT(s)+sTT(t)ifsprecedest,s>n Resourcesaresupposedsimpleandunitary.Resourceconstraintsapplytothegenerictasksofthe sameproductandtothegenerictasksofthevariousproductsusingthesameresource. T(s)+sTTfors2(1;:::;n) (7) (8) tointroduceauxiliarybooleanvariablesxskunderthefollowingconvention: Toobtainaconjunctivelinearformulationofsuchdisjunctiveconstraints,aclassicaltechniqueis xsk=8><>:1iftasksisinthekthposition T(s)+sT T(t)T(2 xsk xt;k+1) 8s;t; (s)= (t)=r;k=1;:::;r 1: withr 0otherwise Xk=1xsk=18ssuchthatr= (s) onresourcer= (s) (10) (11) (9) particularbyalargeconstant,usuallydenotedm.suchaformulationwitha"bigm"isoftenused attherighthandsideoftheinequality,couldbereplacedbyanypositivescalarlargerthant,in Notethatinformulation(10)ofdisjunctiveconstraints,variableTwhichappearsmultiplicatively Xs2rxsk=18r2(1;:::;R);k2(1;:::r): forresourceconstraintsinjob-shopschedulingproblems(e.g.in(ouennicheandboctor,1998)).here, (12) No-waitconstraintswithinlots theuseofvariabletinplaceofmin(10)isduetotheinterpretationoftheproblemasacyclic schedulingproblemforwhichtheheightbetweentwoinstancesofatask(denedasin(hanenand Munier,1995))isequalto1forallthegenerictasks,underthecommoncycleapproach. Withinthegenericperiod,sublotsofthesamecomponentcorrespondtoitsuseindierentstages 11
12 evaluatedin(mckoyandp.j.egbelu,1999).inparticular,ithasbeenshownthatthenon-grouping continuouslyprocessedwithinoneaggregatedlot.thesetwostrategieshavebeencomparedand strategymaynotablydecreasecycletimes,butthatthisadvantagehastobebalancedagainstthe fordierentendproducts.twodierentstrategiesmaybeinvestigatedforthesequencingofsublots: theymaybeprocessedseparately,asiftheywererelatedtodierentcomponents,ortheymaybe increaseinthenumberofsetups. Itisthusassumedthatallthesublotsofthesamelotshouldbeproducedinsequencewithout interruption,inordertohaveonlyoneset-upcostfortheconsideredproductwithineachperiod. Thissectionshowshowtheconstraintsofthegroupingstrategymaybeintegratedinthemodel. LetTb(j)denotethestartdateofproductj,possiblydenedasthelatestdatesuchthat: Theconstraintsofnon-idlingwithinlotstaketheform: andlette(j)denotethecompletiondateofproductj,possiblydenedastheearliestdatesuchthat: Te(j)T(s)+sT8s2(j): Tb(j)T(s)8s2(j); (14) (13) 3.2.2TheObjectiveFunctionTe(j) Tb(j)=TX Theobjectiveistominimizethesumofsetupcostsandinventoryholdingcostsperunitoftime.It s2(j)s: (15) canbedecomposedintothreeterms:j=c1+c2+c3 -set-upcostsperunitoftime:c1=(pmj=1fj)=t withc1;c2;c3denedasfollows: -inventoryholdingcostsforendproductsperunitoftime:c2=tk2withk2=pni=1hi(1 di=pi)di=2 -inventoryholdingcostsforintermediateandprimaryproductsperunitoftime: (16) (OuennicheandBoctor,1998). c3=pps=n+1hjqs(t((s)) T(s)+qsT=2pj qst=2pl)withj=p(s)andl=p((s)). Theexpressionsofinventoryholdingcostsperunitoftimearesimilartotheonesobtainedin 12
13 Itisproposedtoreformulatetheproblemunderthechangesofvariables: 3.3ADecomposedResolutionMethod latedasfollows: Thenewvariablesarecallednormalizeddates.Constraints(7),(8),(10),(15)arethenreformu- Z(s)=T(s)=Tfors=1;:::;p;Zb(j)=Tb(j)=T;Ze(j)=Te(j)=Tforj=1;:::;m: Z(s)+sZ(t)ifsbeforet,s2(n+1;:::;p) Z(s)+s1fors2(1;:::;n) (17) Constraints(9),(11),(12)remainunchanged.Thetermc3inJ(16)canbere-writtenintheform: Z(s)+s Z(t)(2 xsk xt;k+1)8s;t; (s)= (t)=r;k=1;:::;r 1: Ze(j) Zb(j)=X s2(j)s: (20) (18) (19) c3=tk3fork3=pps=n+1hjqs(z((s)) Z(s)+qs=2pj qs=2pl),withj=p(s)andl=p((s)). TheCELSPcanbesolvedoptimallyinadecomposedway: -solverstanormalizedschedulingproblemwithvariablesz(s)andxsk ThisnewformulationoftheconstraintsoftheCELSPallowstostatethefollowingTheorem: -computetheoptimalvalueoftbyaneoq-typeformula: Theorem2 -computetheoptimalstarttimesofoptimalproductionlotsbyt(s)=tz(s). Proof T=vut(mXj=1fj)=(k2+k3): (21) variabletdoesnotappearintheconstraintsandissimplyamultiplyingfactorinthecriterionterm thenormalizedcelsp.moreover,theonlytermofcriterionjinvolvingvariablesz(s)isc3,as VariableT>0isnotinvolvedinanyoftheconstraints(17),(18),(19),(20),(9),(11),(12)of 13
14 thefollowinglinearcriteriontobeminimized:c=pps=n+1hjqs(z((s)) Z(s)): notfeasible.asthenextstep,assumingthattheproblemisfeasible,theoptimalvalueoftcanbe c3,theoptimalsolutionofthecelspwithrespecttovariablesz(s)andxskcanbeindependently explicitelyobtainedthroughtheoptimalityconditionsofcriterionjwithrespecttot.itisthen obtainedbysolvingthenormalizedschedulingproblemdenedbytheaforelistedconstraintsandby expressedbytheeoq-typeformula(21)statedinthetheorem. InfeasibilityofthenormalizedschedulingproblemmayhappenonlyifthecompleteCELSPis parameterintheexpressionofdisjunctiveconstraintsconsiderablyimprovesthenumericalrobustness oftheresolutionprocess. problemcaneasilybesolvedbymixedlinearprogramming.thefactofavoidingtheuseofa"bigm" Asforanyjob-shopschedulingproblem,thecurseofdimensionalityimposestouseheuristics Aslongasthenumberofbooleanvariablesxskdoesnotgettoolarge,thenormalizedscheduling more. usedinthiscasebuttheoptimalityofthevalueoftcomputedbyformula(21)isnotguaranteedany numberofjobsgetslarge,asitisgenerallythecaseinpractice.thedecomposedmethodcanstillbe ratherthananoptimalresolutiontechniqueinsolvingthenormalizedschedulingproblemwhenthe Thedicultytousetheresultsoflot-sizingandschedulingoptimisationproblemsinindustrialapplicationshasbeenstressedbymanyauthors(M.Ben-Daya,1999;Brandimarteetal.,1995).Thisis oftheproblemdata.clearly,demanductuationsareanimportantcauseofchangesintheproblem data.inmanyindustries,theseuctuationsarecontrolledthroughamasterproductionschedule (MPS)overarollingtimehorizon.IncreasingthelengthofthefrozenpartoftheMPShasbeen mainlyduetothecombinedeectofthehighsensitivityofthesolutionsandofthehighvariability showntobeacriticalfactortoreducethenervousnessofthemrpsystem(zhaoandlee,1996). areretatedtomachinefailureanddeterioration,qualityinspectionandmaintenance.theimportance ofthesefactorshasbeenshowntobeparticularlyhighinmultistagemanufacturingsystems(m.ben- Apartfromvariationsofdemandratesforendproducts,someofthemainreasonsfordatachanges 4AReactiveScheduler 14
15 changesareconsidered,itispossibletoobtaingoodimplementablesolutionsbyadaptationofthe nominaloptimizedsolution. Daya,1999). 1.Theadaptedsolutionischosenperiodical,withthesameperiodTasinthenominalsolution. However,aslongasthedemandandproductionpatternremainsstationaryandthatlimiteddata thenominalone.thiscanbeachievedbyreplacing,inthenormalizedgenericschedulingproblem, constraints(19)bythesetofprecedenceconstraintsdescribingthenominalsequenceoftaskson resources. 3.Theadaptedsolutionisobtainedbysolvingthemodiednormalizedgenericschedulingproblem 2.Thesequenceoftasksoneachmachineischosenidenticalintheadaptedsolutionandin usingthecurrentdataandtheassumptionsof1and2. 5NumericalEvaluation itonlyinvolvesconjunctiveconstraintsandrealvariables. Themodiednormalizedgenericschedulingproblemismuchsimplerthantheoriginalonebecause stages.intherststage,thecompleteproblemissolvedforthenominalvaluesofdemandand Thepracticalimplementationoftheproposedlot-sizingandschedulingtechniqueproceedsintwo productionrates.thesecondstageisthereal-timeadjustmentofthesolutioninresponsetoreal uctuationsofdemandandproductionrates.suchanadjustmentispossibleonlyifproduction overload.themethodisnowillustratedonthemultistageproductstructureoffig.1andfig.2,under dierentsetsofdata. 5.1Thenominaloptimalschedule capacityovertheperiodisnotexceeded.furtheradjustmentsarerequiredinthecaseofcapacity Foreachproductj,theunitholdingcostishj=0:01. demandratesforintermediateproductsarenull,andthevectorofproductionratesis[ ]. Atthenominalpoint,demandrateforproductEisd1=0:8,demandrateforproductDisd2=0:5, 15
16 chartoffig.3,withvariablesz(q)expressedaspercentagesoftheperiod. TheoptimalnominalsolutionofthenormalizedschedulingproblemisdisplayedthroughtheGantt obtainedusingtheeoq-typeexpression(21)ist'14:0timeunits. Thesumofxedcostsforthe5productshasbeentakenequalto1000.Then,thevalueofT Figure3:Ganttchartforagenericperiod cent.thesolutionsobtainedfortheoptimalandforthesimpliedschedulingproblemarereported Inthedataofthenumericalexample,vectorsdandparenowrandomlyvariedupto10to50per 5.2Thereactiveschedule Resource 3 Resource 2 Resource % 20% 40% 60% 80% 100% time axis ontable1.maximal disturbance level 10% 20% 30% 40% 50% 16 Number of infeasible solutions 0/10 0/10 2/10 3/10 6/10 Average relative suboptimality of the schedule < 10-4 < Average relative difference in the period length 4% 7% 10% 12% 18% Suboptimality gap using the nominal period 0.1% 0.5% 0.9% 1.3% 1.7%
17 imposingthatthesequenceoftasksoneachmachineidenticaltotheoneobtainedforthenominal Twotypesofsimplicationcanbemadetoadjustthescheduletoreal-timeconstraints. Accordingtotheapproachdevelopedintheprecedingsection,therstsimplicationconsistsin Table1 setofdata.suchasimplicationleadstoconsiderablesavingsincomputationaltime.thesimplied thissimplicationismerelymarginal(lessthan1=1000inrelativevalue). schedulingproblemtobesolvedovereachperiodisastandardlinearprogramonlyhavingcontinuous variables.onthecontrary,theoriginalschedulingproblemalsoinvolvesthebooleanvariablesxsk period.fromthecomputationalviewpoints,thesavingsarenegligiblesinceagoodapproximationof denedin(9).onthesmallsizeexampleconsideredhere,thecomputationaltimeisdecreasedbya theoptimalvalueoftheperiodisobtainedbyapplyingtheeoq-typeformula(21)totheproblem factorrangingfrom20to100.itisclearfromtable1thattheaveragecriteriondeteriorationdueto dataandthesolutionofthesimpliedschedulingproblem.table1showsthatfordatavariationsup to50percent,theaveragerelativedierenceintheperiodlengthiscloseto20percent.andthatit Thesecondsimplicationconsistsofusingthenominalperiodinsteadoftheoptimaloneateach inducesasuboptimalitygapofalmost2percent.thus,fromthepureoptimalityviewpoint,itwould beecienttoadjusteachperiodandtheproductionlotsizesaccordingly.however,fromapratical viewpoint,itiscertainlypreferabletomaintaintheproductionperiodatitsnominalvalueaslongas Theproposedreactiveschedulingtechniquehastobeadjustedtodealwiththecaseswhennofeasible thechangesindataremainlowanddonotinvolveaclearstationarytrend. 5.3Adjustmenttoreal-timeconditions solutionexists.thiscasefrequentlyoccursunderimportantvariationsofdemandloadand/orproductionrates.thecomputedfrequenciesofoccurenceofsuchcasesarereportedonthesecondrow oftable1. notfeasible,and,fromthepracticalviewpointthereisnorealrestrictioninassessingfeasibilityonly solutionwhiletheoriginalschedulingproblemisfeasible,thiscasehasneverbeenencounteredinthe experiments.thus,ingeneral,bothproblemscanbesimultaneouslyconsideredaseitherfeasibleor Itisimportanttonotethat,althoughthesimpliedschedulingproblemmayhavenofeasible 17
18 orbacklogs.thecyclicapproachisnotnaturallywell-suitedfordealingwithsuchcases.however, job-shop,eitherbecauseofexcessivedemandratesorlowproductivity.ifthesystemdoesnotpossess extraresources,theonlysolutiontothisproblemistoproducelessthanthedemand,withlosssales fromthesolutionofthesimpliedproblem. theceslpcanbemodiedtotreatthiscase. Theabsenceofasolutiontothegenericschedulingproblemcorrespondstoanoverloadofthe normalizedgenericschedulingproblemisnotfeasible,afeasiblemakespanproblemcanbeformulated. thesimpliedschedulingproblem,exceptforconstraints(18),whicharereplacedby(23): Thenormalizedmakespanvalue,denoted,canbeminimisedunderalltheschedulingconstraintsof portionalityfactorleadstothereductionofallthegenerictaskdurationssbythisfactor.ifthe Itcanbeobservedfromequations(5),(6)thatreducingallthedemandratesbythesamepro- Z(s)+sZ(t)ifsbeforetinthenominalschedule,s2(n+1;:::;p) Z(s)+sfors2(1;:::;n) Minimizesubjectto (22) thereisnowaitingtimealongthispath,thevalueofthemakespancanbelimitedto1(or1 )by Theoptimalvalueofthemakespanisthelengthofthecriticalpathinthegraphoftasks.As Ze(j) Zb(j)=X s2(j)s: (24) (23) dividingallthedemandratedby(resp.by easilysolved.then,accordingtothecompanypolicy,theremainingdemandratevector,(1 )d maycorrespondtolostsalesortobacklogsforthefollowingperiod. thenbere-formulatedunderthereduceddemandrates.thisproblemisclearlyfeasibleandcanbe 1 ).Thenormalizedgenericschedulingproblemcan reliabilityoftheequipmentsandworkteams.suchdisturbancesmustbetakenintoaccountwhen 6Conclusions buildingthelot-sizingandschedulingpolicy,speciallyinthecaseofmultistageproduction,forwhich disturbancesareoftenampliedthroughtheproductstructure. Mostofthemodernmanufacturingcompaniesoperateinvariablecompetitivemarkets,withthe consequenceofhavingtoreacttouctuatingdemands.anotherfactorofdisturbancesistheimperfect 18
19 withtheadaptivityadvantageofadjustingthelengthsoftaskstotherealevolutionofdemandand productivity. Theapproachfollowedinthispapercombinestherepetitivepropertiesofcyclictasksequencing problemintoanormalizedschedulingproblem,whichcanbesolvedrstandindependently,andalot sizingproblem.itisofcurrentpracticetoseparatelytreattheproblemsoflot-sizingandscheduling, constantdemandandproductionrates.thecommoncycleapproachallowstodecomposethecyclic butusuallywiththelot-sizingproblemtreatedrst.here,byfocusingtheanalysisonstoragecosts, Anormalizedlot-sizingandschedulingproblemhasrstbeenformulatedundertheassumptionof forsolvingthehighlydisturbedcases,forwhichthemanufacturingsystemisoverloaded. ithasbeenestablishedthatschedulingdecisionshaveanimportantinuenceonlot-sizingdecisions. thenominalsequencingoftasksonresourcesbutchangingthedatesanddurationsoftasks.the eciencyofthisadjusmentschemehasbeenshownnumerically.amethodhasnallybeenproposed Arapidandecientadjustmentofthenominalscheduletorealdataisobtainedbymaintaining References Baker,K.R.(1993).Requirementsplanning.In:HandbooksinOperationsResearchandManagement Berman,A.andR.J.Plemmons(1979).NonNegativeMatricesintheMathematicalSciences.AcademicPress. Science,vol.4,S.C.Graves,A.H.G.RinnooyKan,P.H.ZipkinEds..North-Holland.pp.571{ 628. Bourland,K.E.andC.A.Yano(1997).Acomparisonofsolutionapproachesforthexed-sequence Bomberger,E.(1966).Adynamicprogrammingapproachtoalotsizeschedulingproblem.ManagementScience,Vol.12,pp Brandimarte,P.,W.UkovitchandA.Villa(1995).Factorylevelaggregatescheduling:Bridgingthe economiclotschedulingproblem.iietransactions,vol.29,pp gapbetweenoptimizedschedulingandrealtimecontrol.in:optimizationmodelsandconcepts inproductionmanagement,p.brandimarteanda.villaeds..gordonandbreachpublishers. pp.187{
20 Carlier,J.andP.Chretienne(1988).Timedpetrinetsschedules.In:AdvancesinPetriNets:Lecture Elmaghraby,S.E.(1978).Theeconomiclotschedulingproblem(elsp):reviewandextensions.ManagementScience,Vol.24,pp Gallego,G.(1990).Anextensiontotheclassofeasyeconomiclotschedulingproblems.IIETransactions,vol.22,pp NotesinComputerScience,No.340.Springer.pp.62{84. Graves,S.C.,D.B.KletterandW.B.Hetzel(1998).Adynamicmodelforrequirementplanningwith Grubbstrom,R.W.andA.Molinder(1994).Materialrequirementplanningemployinginput-output applicationtosupplychainoptimization.operationsresearch,vol.46,suppno.3,pp.s35-s49. Grubbstrom,R.W.andP.Ovrin(1992).Intertemporalgeneralizationoftherelationshipbetween analysisandlaplacetransforms.intl.j.productioneconomics,vol.35,pp Hanen,C.andA.Munier(1995).Cyclicschedulingonparallelprocessors:Anoverview.In:Scheduling materialrequirementplanningandinput-outputanalysis.intl.j.productioneconomics,vol. 26,pp Hennet,J.C.(1998).Afeedbackcontrolapproachtomultistageproductionplanningbasedoninputoutputanalysis.In:LAASReportNo98159,12thInternationalConferenceonInput-Output TheoryanditsApplications,P.Chretienne,E.G.Coman,J.K.Lenstra,Z.LiuEds.JohnWiley andsonsltd.pp.193{226. Hennet,J.C.andI.Barthes(1998).Closed-loopplanningofmulti-levelproductionunderresource Kohler,G.J.,A.B.WhinstonandG.P.Wright(1975).OptimizationoverLeontiefsubstitutionsystems. constraints.in:proceedingsoftheifacsymposiumincom'98,nancy,(france). Techniques,New-York(USA),18-22Mai1998,14p. Loerch,A.G.andJ.A.Muckstadt(1994).Anapproachtoproductionplanningandschedulingin NorthHolland/AmericanElsevier. M.Ben-Daya,A.Rahim(1999).Multi-stagelotsizingmodelswithimperfectprocessesandinspection errors.productionplanningandcontrol,vol.10,pp cyclicallyscheduledmanufacturingsystems.int.journalofproductionresearch,vol32,pp
Full and Complete Binary Trees
 Full and Complete Binary Trees Binary Tree Theorems 1 Here are two important types of binary trees. Note that the definitions, while similar, are logically independent. Definition: a binary tree T is full
Full and Complete Binary Trees Binary Tree Theorems 1 Here are two important types of binary trees. Note that the definitions, while similar, are logically independent. Definition: a binary tree T is full
If n is odd, then 3n + 7 is even.
 Proof: Proof: We suppose... that 3n + 7 is even. that 3n + 7 is even. Since n is odd, there exists an integer k so that n = 2k + 1. that 3n + 7 is even. Since n is odd, there exists an integer k so that
Proof: Proof: We suppose... that 3n + 7 is even. that 3n + 7 is even. Since n is odd, there exists an integer k so that n = 2k + 1. that 3n + 7 is even. Since n is odd, there exists an integer k so that
Discrete Structures for Computer Science
 Discrete Structures for Computer Science Adam J. Lee adamlee@cs.pitt.edu 6111 Sennott Square Lecture #20: Bayes Theorem November 5, 2013 How can we incorporate prior knowledge? Sometimes we want to know
Discrete Structures for Computer Science Adam J. Lee adamlee@cs.pitt.edu 6111 Sennott Square Lecture #20: Bayes Theorem November 5, 2013 How can we incorporate prior knowledge? Sometimes we want to know
Stochastic Models for Inventory Management at Service Facilities
 Stochastic Models for Inventory Management at Service Facilities O. Berman, E. Kim Presented by F. Zoghalchi University of Toronto Rotman School of Management Dec, 2012 Agenda 1 Problem description Deterministic
Stochastic Models for Inventory Management at Service Facilities O. Berman, E. Kim Presented by F. Zoghalchi University of Toronto Rotman School of Management Dec, 2012 Agenda 1 Problem description Deterministic
SJS DATA INTEGRATION LIMITED Financial Accounts 2013-09-30 REGISTERED NUMBER: 08214170 (England and Wales)
 SJS DATA INTEGRATION LIMITED Financial Accounts 2013-09-30 REGISTERED NUMBER: 08214170 (England and Wales) Abbreviated Unaudited Accounts for the Period 13 September 2012 to 30 September 2013 for SJS DATA
SJS DATA INTEGRATION LIMITED Financial Accounts 2013-09-30 REGISTERED NUMBER: 08214170 (England and Wales) Abbreviated Unaudited Accounts for the Period 13 September 2012 to 30 September 2013 for SJS DATA
LECTURE 5: DUALITY AND SENSITIVITY ANALYSIS. 1. Dual linear program 2. Duality theory 3. Sensitivity analysis 4. Dual simplex method
 LECTURE 5: DUALITY AND SENSITIVITY ANALYSIS 1. Dual linear program 2. Duality theory 3. Sensitivity analysis 4. Dual simplex method Introduction to dual linear program Given a constraint matrix A, right
LECTURE 5: DUALITY AND SENSITIVITY ANALYSIS 1. Dual linear program 2. Duality theory 3. Sensitivity analysis 4. Dual simplex method Introduction to dual linear program Given a constraint matrix A, right
Critical points of once continuously differentiable functions are important because they are the only points that can be local maxima or minima.
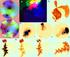 Lecture 0: Convexity and Optimization We say that if f is a once continuously differentiable function on an interval I, and x is a point in the interior of I that x is a critical point of f if f (x) =
Lecture 0: Convexity and Optimization We say that if f is a once continuously differentiable function on an interval I, and x is a point in the interior of I that x is a critical point of f if f (x) =
Rolle s Theorem. q( x) = 1
 Lecture 1 :The Mean Value Theorem We know that constant functions have derivative zero. Is it possible for a more complicated function to have derivative zero? In this section we will answer this question
Lecture 1 :The Mean Value Theorem We know that constant functions have derivative zero. Is it possible for a more complicated function to have derivative zero? In this section we will answer this question
Position Auctions with Externalities
 Position Auctions with Externalities Patrick Hummel 1 and R. Preston McAfee 2 1 Google Inc. phummel@google.com 2 Microsoft Corp. preston@mcafee.cc Abstract. This paper presents models for predicted click-through
Position Auctions with Externalities Patrick Hummel 1 and R. Preston McAfee 2 1 Google Inc. phummel@google.com 2 Microsoft Corp. preston@mcafee.cc Abstract. This paper presents models for predicted click-through
The Real Estate Enterprise Supply Chain Logistics Model Research
 , pp.75-84 http://dx.doi.org/10.14257/ijunesst.2015.8.12.08 The Real Estate Enterprise Supply Chain Logistics Model Research Jian-ping You Central South University csuyoujianping@126.com Abstract To overcome
, pp.75-84 http://dx.doi.org/10.14257/ijunesst.2015.8.12.08 The Real Estate Enterprise Supply Chain Logistics Model Research Jian-ping You Central South University csuyoujianping@126.com Abstract To overcome
Two Fundamental Theorems about the Definite Integral
 Two Fundamental Theorems about the Definite Integral These lecture notes develop the theorem Stewart calls The Fundamental Theorem of Calculus in section 5.3. The approach I use is slightly different than
Two Fundamental Theorems about the Definite Integral These lecture notes develop the theorem Stewart calls The Fundamental Theorem of Calculus in section 5.3. The approach I use is slightly different than
Figure 1.1 Vector A and Vector F
 CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
Lecture: Financing Based on Market Values II
 Lecture: Financing Based on Market Values II Lutz Kruschwitz & Andreas Löffler Discounted Cash Flow, Section 2.4.4 2.4.5, Outline 2.4.4 Miles-Ezzell- and Modigliani-Miller Miles-Ezzell adjustment Modigliani-Miller
Lecture: Financing Based on Market Values II Lutz Kruschwitz & Andreas Löffler Discounted Cash Flow, Section 2.4.4 2.4.5, Outline 2.4.4 Miles-Ezzell- and Modigliani-Miller Miles-Ezzell adjustment Modigliani-Miller
Word templates are available for many of our journals, but please check the Instructions for Authors page of the journal before you use them.
 Submitting Your Manuscript to ScholarOne Manuscripts: A Guide To submit your manuscript, you will need the following files: A Title page file with the names of all authors and co-authors* Main document
Submitting Your Manuscript to ScholarOne Manuscripts: A Guide To submit your manuscript, you will need the following files: A Title page file with the names of all authors and co-authors* Main document
AXIS AWARDS APPLICATION PREPARATION DOCUMENT
 AXIS AWARDS APPLICATION PREPARATION DOCUMENT INSTRUCTIONS PLEASE READ CAREFULLY This document lists all the questions in the online application form. Use this document to help prepare your application
AXIS AWARDS APPLICATION PREPARATION DOCUMENT INSTRUCTIONS PLEASE READ CAREFULLY This document lists all the questions in the online application form. Use this document to help prepare your application
Further Study on Strong Lagrangian Duality Property for Invex Programs via Penalty Functions 1
 Further Study on Strong Lagrangian Duality Property for Invex Programs via Penalty Functions 1 J. Zhang Institute of Applied Mathematics, Chongqing University of Posts and Telecommunications, Chongqing
Further Study on Strong Lagrangian Duality Property for Invex Programs via Penalty Functions 1 J. Zhang Institute of Applied Mathematics, Chongqing University of Posts and Telecommunications, Chongqing
CHAPTER FIVE. 5. Equations of Lines in R 3
 118 CHAPTER FIVE 5. Equations of Lines in R 3 In this chapter it is going to be very important to distinguish clearly between points and vectors. Frequently in the past the distinction has only been a
118 CHAPTER FIVE 5. Equations of Lines in R 3 In this chapter it is going to be very important to distinguish clearly between points and vectors. Frequently in the past the distinction has only been a
Retirement Financial Planning: A State/Preference Approach. William F. Sharpe 1 February, 2006
 Retirement Financial Planning: A State/Preference Approach William F. Sharpe 1 February, 2006 Introduction This paper provides a framework for analyzing a prototypical set of decisions concerning spending,
Retirement Financial Planning: A State/Preference Approach William F. Sharpe 1 February, 2006 Introduction This paper provides a framework for analyzing a prototypical set of decisions concerning spending,
Single Stage Light Business Case Template
 Better Business Cases Single Stage Light Business Case Template Prepared by: Prepared for: Date: Version: Status: Better Business Cases Single Stage Light Business Case Template Document Control Document
Better Business Cases Single Stage Light Business Case Template Prepared by: Prepared for: Date: Version: Status: Better Business Cases Single Stage Light Business Case Template Document Control Document
A Factoring and Discrete Logarithm based Cryptosystem
 Int. J. Contemp. Math. Sciences, Vol. 8, 2013, no. 11, 511-517 HIKARI Ltd, www.m-hikari.com A Factoring and Discrete Logarithm based Cryptosystem Abdoul Aziz Ciss and Ahmed Youssef Ecole doctorale de Mathematiques
Int. J. Contemp. Math. Sciences, Vol. 8, 2013, no. 11, 511-517 HIKARI Ltd, www.m-hikari.com A Factoring and Discrete Logarithm based Cryptosystem Abdoul Aziz Ciss and Ahmed Youssef Ecole doctorale de Mathematiques
The Mean Value Theorem
 The Mean Value Theorem THEOREM (The Extreme Value Theorem): If f is continuous on a closed interval [a, b], then f attains an absolute maximum value f(c) and an absolute minimum value f(d) at some numbers
The Mean Value Theorem THEOREM (The Extreme Value Theorem): If f is continuous on a closed interval [a, b], then f attains an absolute maximum value f(c) and an absolute minimum value f(d) at some numbers
A Rough-Cut Capacity Planning Model with Overlapping
 1 A Rough-Cut Capacity Planning Model with Overlapping Baydoun G. 1, Haït A. 2 and Pellerin R. 1 1 École Polytechnique de Montréal, Montréal, Canada georges.baydoun, robert.pellerin@polymlt.ca 2 University
1 A Rough-Cut Capacity Planning Model with Overlapping Baydoun G. 1, Haït A. 2 and Pellerin R. 1 1 École Polytechnique de Montréal, Montréal, Canada georges.baydoun, robert.pellerin@polymlt.ca 2 University
A Logic-Based Approach to Cloud Computing
 A Logic-Based Approach to Cloud Computing Jan Van den Bussche (Hasselt University, Belgium) joint work with Tom Ameloot and Frank Neven 1 Origins of Cloud Computing Large websites (Amazon, Google, Facebook)
A Logic-Based Approach to Cloud Computing Jan Van den Bussche (Hasselt University, Belgium) joint work with Tom Ameloot and Frank Neven 1 Origins of Cloud Computing Large websites (Amazon, Google, Facebook)
Implementations of tests on the exogeneity of selected. variables and their Performance in practice ACADEMISCH PROEFSCHRIFT
 Implementations of tests on the exogeneity of selected variables and their Performance in practice ACADEMISCH PROEFSCHRIFT ter verkrijging van de graad van doctor aan de Universiteit van Amsterdam op gezag
Implementations of tests on the exogeneity of selected variables and their Performance in practice ACADEMISCH PROEFSCHRIFT ter verkrijging van de graad van doctor aan de Universiteit van Amsterdam op gezag
Iterations of sum of powers of digits
 International Journal of Computer Discovered Mathematics Volume 0 (2015) No.0 pp.1-4 c IJCDM Received 12 June 2015. Published on-line 12 June 2015 DOI: web site: c The Author(s) 2015. This article is published
International Journal of Computer Discovered Mathematics Volume 0 (2015) No.0 pp.1-4 c IJCDM Received 12 June 2015. Published on-line 12 June 2015 DOI: web site: c The Author(s) 2015. This article is published
Green Big Data. A Green IT / Green IS Perspective on Big Data
 Green Big Data A Green IT / Green IS Perspective on Big Data Agenda 1. Starting Point and Research Question 2. Subject of Analysis 3. Research Methodology 4. Results 5. Conclusion Green Big Data 2 Starting
Green Big Data A Green IT / Green IS Perspective on Big Data Agenda 1. Starting Point and Research Question 2. Subject of Analysis 3. Research Methodology 4. Results 5. Conclusion Green Big Data 2 Starting
Danielle M. Varda, PhD University of Colorado Denver School of Public Affairs. Lead. Solve. Change
 Danielle M. Varda, PhD University of Colorado Denver School of Public Affairs Lead. Solve. Change Network Leadership/Management We need new tools/methods to evaluate partnerships. Current Assumption =
Danielle M. Varda, PhD University of Colorado Denver School of Public Affairs Lead. Solve. Change Network Leadership/Management We need new tools/methods to evaluate partnerships. Current Assumption =
6.2 Permutations continued
 6.2 Permutations continued Theorem A permutation on a finite set A is either a cycle or can be expressed as a product (composition of disjoint cycles. Proof is by (strong induction on the number, r, of
6.2 Permutations continued Theorem A permutation on a finite set A is either a cycle or can be expressed as a product (composition of disjoint cycles. Proof is by (strong induction on the number, r, of
A new continuous dependence result for impulsive retarded functional differential equations
 CADERNOS DE MATEMÁTICA 11, 37 47 May (2010) ARTIGO NÚMERO SMA#324 A new continuous dependence result for impulsive retarded functional differential equations M. Federson * Instituto de Ciências Matemáticas
CADERNOS DE MATEMÁTICA 11, 37 47 May (2010) ARTIGO NÚMERO SMA#324 A new continuous dependence result for impulsive retarded functional differential equations M. Federson * Instituto de Ciências Matemáticas
6 The Literature Review
 6 The Literature Review The literature review is important because: It describes how the proposed research is related to prior research in statistics. It shows the originality and relevance of your research
6 The Literature Review The literature review is important because: It describes how the proposed research is related to prior research in statistics. It shows the originality and relevance of your research
Breaking Generalized Diffie-Hellman Modulo a Composite is no Easier than Factoring
 Breaking Generalized Diffie-Hellman Modulo a Composite is no Easier than Factoring Eli Biham Dan Boneh Omer Reingold Abstract The Diffie-Hellman key-exchange protocol may naturally be extended to k > 2
Breaking Generalized Diffie-Hellman Modulo a Composite is no Easier than Factoring Eli Biham Dan Boneh Omer Reingold Abstract The Diffie-Hellman key-exchange protocol may naturally be extended to k > 2
. P. 4.3 Basic feasible solutions and vertices of polyhedra. x 1. x 2
 4. Basic feasible solutions and vertices of polyhedra Due to the fundamental theorem of Linear Programming, to solve any LP it suffices to consider the vertices (finitely many) of the polyhedron P of the
4. Basic feasible solutions and vertices of polyhedra Due to the fundamental theorem of Linear Programming, to solve any LP it suffices to consider the vertices (finitely many) of the polyhedron P of the
z-scores AND THE NORMAL CURVE MODEL
 z-scores AND THE NORMAL CURVE MODEL 1 Understanding z-scores 2 z-scores A z-score is a location on the distribution. A z- score also automatically communicates the raw score s distance from the mean A
z-scores AND THE NORMAL CURVE MODEL 1 Understanding z-scores 2 z-scores A z-score is a location on the distribution. A z- score also automatically communicates the raw score s distance from the mean A
Competition and Fraud in Online Advertising Markets
 Competition and Fraud in Online Advertising Markets Bob Mungamuru 1 and Stephen Weis 2 1 Stanford University, Stanford, CA, USA 94305 2 Google Inc., Mountain View, CA, USA 94043 Abstract. An economic model
Competition and Fraud in Online Advertising Markets Bob Mungamuru 1 and Stephen Weis 2 1 Stanford University, Stanford, CA, USA 94305 2 Google Inc., Mountain View, CA, USA 94043 Abstract. An economic model
AMBIGUOUS CLASSES IN QUADRATIC FIELDS
 MATHEMATICS OF COMPUTATION VOLUME, NUMBER 0 JULY 99, PAGES -0 AMBIGUOUS CLASSES IN QUADRATIC FIELDS R. A. MOLLIN Dedicated to the memory ofd. H. Lehmer Abstract. We provide sufficient conditions for the
MATHEMATICS OF COMPUTATION VOLUME, NUMBER 0 JULY 99, PAGES -0 AMBIGUOUS CLASSES IN QUADRATIC FIELDS R. A. MOLLIN Dedicated to the memory ofd. H. Lehmer Abstract. We provide sufficient conditions for the
Diesel Cycle Analysis
 Engineering Software P.O. Box 1180, Germantown, MD 20875 Phone: (301) 540-3605 FAX: (301) 540-3605 E-Mail: info@engineering-4e.com Web Site: http://www.engineering-4e.com Diesel Cycle Analysis Diesel Cycle
Engineering Software P.O. Box 1180, Germantown, MD 20875 Phone: (301) 540-3605 FAX: (301) 540-3605 E-Mail: info@engineering-4e.com Web Site: http://www.engineering-4e.com Diesel Cycle Analysis Diesel Cycle
Lectures notes on orthogonal matrices (with exercises) 92.222 - Linear Algebra II - Spring 2004 by D. Klain
 Lectures notes on orthogonal matrices (with exercises) 92.222 - Linear Algebra II - Spring 2004 by D. Klain 1. Orthogonal matrices and orthonormal sets An n n real-valued matrix A is said to be an orthogonal
Lectures notes on orthogonal matrices (with exercises) 92.222 - Linear Algebra II - Spring 2004 by D. Klain 1. Orthogonal matrices and orthonormal sets An n n real-valued matrix A is said to be an orthogonal
arxiv:1112.0829v1 [math.pr] 5 Dec 2011
![arxiv:1112.0829v1 [math.pr] 5 Dec 2011 arxiv:1112.0829v1 [math.pr] 5 Dec 2011](/thumbs/39/18839218.jpg) How Not to Win a Million Dollars: A Counterexample to a Conjecture of L. Breiman Thomas P. Hayes arxiv:1112.0829v1 [math.pr] 5 Dec 2011 Abstract Consider a gambling game in which we are allowed to repeatedly
How Not to Win a Million Dollars: A Counterexample to a Conjecture of L. Breiman Thomas P. Hayes arxiv:1112.0829v1 [math.pr] 5 Dec 2011 Abstract Consider a gambling game in which we are allowed to repeatedly
An Integrated Production Inventory System for. Perishable Items with Fixed and Linear Backorders
 Int. Journal of Math. Analysis, Vol. 8, 2014, no. 32, 1549-1559 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijma.2014.46176 An Integrated Production Inventory System for Perishable Items with
Int. Journal of Math. Analysis, Vol. 8, 2014, no. 32, 1549-1559 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijma.2014.46176 An Integrated Production Inventory System for Perishable Items with
arxiv:math/0112298v1 [math.st] 28 Dec 2001
![arxiv:math/0112298v1 [math.st] 28 Dec 2001 arxiv:math/0112298v1 [math.st] 28 Dec 2001](/thumbs/39/20405706.jpg) Annuities under random rates of interest revisited arxiv:math/0112298v1 [math.st] 28 Dec 2001 Krzysztof BURNECKI, Agnieszka MARCINIUK and Aleksander WERON Hugo Steinhaus Center for Stochastic Methods,
Annuities under random rates of interest revisited arxiv:math/0112298v1 [math.st] 28 Dec 2001 Krzysztof BURNECKI, Agnieszka MARCINIUK and Aleksander WERON Hugo Steinhaus Center for Stochastic Methods,
Using Wireless Measurements in Control Applications
 Using Wireless Measurements in Control Applications Terry Blevins, Mark Nixon, Marty Zielinski Emerson Process Management Keywords: PID Control, Industrial Control, Wireless Transmitters ABSTRACT Wireless
Using Wireless Measurements in Control Applications Terry Blevins, Mark Nixon, Marty Zielinski Emerson Process Management Keywords: PID Control, Industrial Control, Wireless Transmitters ABSTRACT Wireless
EHP Financial Assurance Calculator. User guide
 User guide Prepared by: Energy Regulation & Implementation, State of Queensland, 2014. The Queensland Government supports and encourages the dissemination and exchange of its information. The copyright
User guide Prepared by: Energy Regulation & Implementation, State of Queensland, 2014. The Queensland Government supports and encourages the dissemination and exchange of its information. The copyright
An Adaptive Decoding Algorithm of LDPC Codes over the Binary Erasure Channel. Gou HOSOYA, Hideki YAGI, Toshiyasu MATSUSHIMA, and Shigeichi HIRASAWA
 2007 Hawaii and SITA Joint Conference on Information Theory, HISC2007 Hawaii, USA, May 29 31, 2007 An Adaptive Decoding Algorithm of LDPC Codes over the Binary Erasure Channel Gou HOSOYA, Hideki YAGI,
2007 Hawaii and SITA Joint Conference on Information Theory, HISC2007 Hawaii, USA, May 29 31, 2007 An Adaptive Decoding Algorithm of LDPC Codes over the Binary Erasure Channel Gou HOSOYA, Hideki YAGI,
Access to Community Laboratory Services. Marc Chabot, MEng MBA Manager of Commercial Strategy and Customer Insight ChabotM@dynacare.
 Access to Community Laboratory Services Marc Chabot, MEng MBA Manager of Commercial Strategy and Customer Insight ChabotM@dynacare.ca Project Overview Staff, Budget & Training National collection network
Access to Community Laboratory Services Marc Chabot, MEng MBA Manager of Commercial Strategy and Customer Insight ChabotM@dynacare.ca Project Overview Staff, Budget & Training National collection network
Chapter 7. BANDIT PROBLEMS.
 Chapter 7. BANDIT PROBLEMS. Bandit problems are problems in the area of sequential selection of experiments, and they are related to stopping rule problems through the theorem of Gittins and Jones (974).
Chapter 7. BANDIT PROBLEMS. Bandit problems are problems in the area of sequential selection of experiments, and they are related to stopping rule problems through the theorem of Gittins and Jones (974).
EFFICIENT KNOWLEDGE BASE MANAGEMENT IN DCSP
 EFFICIENT KNOWLEDGE BASE MANAGEMENT IN DCSP Hong Jiang Mathematics & Computer Science Department, Benedict College, USA jiangh@benedict.edu ABSTRACT DCSP (Distributed Constraint Satisfaction Problem) has
EFFICIENT KNOWLEDGE BASE MANAGEMENT IN DCSP Hong Jiang Mathematics & Computer Science Department, Benedict College, USA jiangh@benedict.edu ABSTRACT DCSP (Distributed Constraint Satisfaction Problem) has
Differentiating under an integral sign
 CALIFORNIA INSTITUTE OF TECHNOLOGY Ma 2b KC Border Introduction to Probability and Statistics February 213 Differentiating under an integral sign In the derivation of Maximum Likelihood Estimators, or
CALIFORNIA INSTITUTE OF TECHNOLOGY Ma 2b KC Border Introduction to Probability and Statistics February 213 Differentiating under an integral sign In the derivation of Maximum Likelihood Estimators, or
BPEL disadvantage: more time to product BPEL advantage: better reusability, analysis
 Modeling Page 1 To BPEL or not to BPEL? 5:56 PM To BPEL or not to BPEL? BPEL disadvantage: more time to product BPEL advantage: better reusability, analysis Modeling Page 2 A tale of two strategies 5:57
Modeling Page 1 To BPEL or not to BPEL? 5:56 PM To BPEL or not to BPEL? BPEL disadvantage: more time to product BPEL advantage: better reusability, analysis Modeling Page 2 A tale of two strategies 5:57
Constraints and Shortfalls in Engineering Design Practice
 Constraints and Shortfalls in Engineering Design Practice Lars Hein 1, Zhun Fan 2 1 IPU, Produktionstorvet, Building 425, DK-2800 Kgs. Lyngby, Denmark. 2 Department of Mechanical Engineering, DTU, Nils
Constraints and Shortfalls in Engineering Design Practice Lars Hein 1, Zhun Fan 2 1 IPU, Produktionstorvet, Building 425, DK-2800 Kgs. Lyngby, Denmark. 2 Department of Mechanical Engineering, DTU, Nils
FACTORING AFTER DEDEKIND
 FACTORING AFTER DEDEKIND KEITH CONRAD Let K be a number field and p be a prime number. When we factor (p) = po K into prime ideals, say (p) = p e 1 1 peg g, we refer to the data of the e i s, the exponents
FACTORING AFTER DEDEKIND KEITH CONRAD Let K be a number field and p be a prime number. When we factor (p) = po K into prime ideals, say (p) = p e 1 1 peg g, we refer to the data of the e i s, the exponents
the form as set out. Full Economic Costing is not payable on these awards. Retrospective application (where the individual has already commenced
 PATHOLOGICAL SOCIETY & JEAN SHANKS FOUNDATION PATHOLOGICAL RESEARCH TRAINING FELLOWSHIPS SCHEME GUIDANCE TO APPLICANTS This is a national scheme designed to increase the research skills, ability and interest
PATHOLOGICAL SOCIETY & JEAN SHANKS FOUNDATION PATHOLOGICAL RESEARCH TRAINING FELLOWSHIPS SCHEME GUIDANCE TO APPLICANTS This is a national scheme designed to increase the research skills, ability and interest
Production and Inventory Management
 Production and Inventory Management ARNOLDO C. HAX Massachusetts Institute of Technology DAN CANDEA Polytechnic Institute of Cluj-Napoca TECHNISCHE HOCHSCHULE DARMSTADT FoaiberGirii 1 Gesam th ibl iot
Production and Inventory Management ARNOLDO C. HAX Massachusetts Institute of Technology DAN CANDEA Polytechnic Institute of Cluj-Napoca TECHNISCHE HOCHSCHULE DARMSTADT FoaiberGirii 1 Gesam th ibl iot
Batch Scheduling of Deteriorating Products
 Decision Making in Manufacturing and Services Vol. 1 2007 No. 1 2 pp. 25 34 Batch Scheduling of Deteriorating Products Maksim S. Barketau, T.C. Edwin Cheng, Mikhail Y. Kovalyov, C.T. Daniel Ng Abstract.
Decision Making in Manufacturing and Services Vol. 1 2007 No. 1 2 pp. 25 34 Batch Scheduling of Deteriorating Products Maksim S. Barketau, T.C. Edwin Cheng, Mikhail Y. Kovalyov, C.T. Daniel Ng Abstract.
Removing Partial Inconsistency in Valuation- Based Systems*
 Removing Partial Inconsistency in Valuation- Based Systems* Luis M. de Campos and Serafín Moral Departamento de Ciencias de la Computación e I.A., Universidad de Granada, 18071 Granada, Spain This paper
Removing Partial Inconsistency in Valuation- Based Systems* Luis M. de Campos and Serafín Moral Departamento de Ciencias de la Computación e I.A., Universidad de Granada, 18071 Granada, Spain This paper
Control Systems with Actuator Saturation
 Control Systems with Actuator Saturation Analysis and Design Tingshu Hu Zongli Lin With 67 Figures Birkhauser Boston Basel Berlin Preface xiii 1 Introduction 1 1.1 Linear Systems with Actuator Saturation
Control Systems with Actuator Saturation Analysis and Design Tingshu Hu Zongli Lin With 67 Figures Birkhauser Boston Basel Berlin Preface xiii 1 Introduction 1 1.1 Linear Systems with Actuator Saturation
Since [L : K(α)] < [L : K] we know from the inductive assumption that [L : K(α)] s < [L : K(α)]. It follows now from Lemma 6.
![Since [L : K(α)] < [L : K] we know from the inductive assumption that [L : K(α)] s < [L : K(α)]. It follows now from Lemma 6. Since [L : K(α)] < [L : K] we know from the inductive assumption that [L : K(α)] s < [L : K(α)]. It follows now from Lemma 6.](/thumbs/19/305510.jpg) Theorem 7.1. Let L K be a finite extension. Then a)[l : K] [L : K] s b) the extension L K is separable iff [L : K] = [L : K] s. Proof. Let M be a normal closure of L : K. Consider first the case when L
Theorem 7.1. Let L K be a finite extension. Then a)[l : K] [L : K] s b) the extension L K is separable iff [L : K] = [L : K] s. Proof. Let M be a normal closure of L : K. Consider first the case when L
15 Prime and Composite Numbers
 15 Prime and Composite Numbers Divides, Divisors, Factors, Multiples In section 13, we considered the division algorithm: If a and b are whole numbers with b 0 then there exist unique numbers q and r such
15 Prime and Composite Numbers Divides, Divisors, Factors, Multiples In section 13, we considered the division algorithm: If a and b are whole numbers with b 0 then there exist unique numbers q and r such
Section 4.2: The Division Algorithm and Greatest Common Divisors
 Section 4.2: The Division Algorithm and Greatest Common Divisors The Division Algorithm The Division Algorithm is merely long division restated as an equation. For example, the division 29 r. 20 32 948
Section 4.2: The Division Algorithm and Greatest Common Divisors The Division Algorithm The Division Algorithm is merely long division restated as an equation. For example, the division 29 r. 20 32 948
Interactive Machine Learning. Maria-Florina Balcan
 Interactive Machine Learning Maria-Florina Balcan Machine Learning Image Classification Document Categorization Speech Recognition Protein Classification Branch Prediction Fraud Detection Spam Detection
Interactive Machine Learning Maria-Florina Balcan Machine Learning Image Classification Document Categorization Speech Recognition Protein Classification Branch Prediction Fraud Detection Spam Detection
Towards Optimal Firewall Rule Ordering Utilizing Directed Acyclical Graphs
 Towards Optimal Firewall Rule Ordering Utilizing Directed Acyclical Graphs Ashish Tapdiya and Errin W. Fulp Department of Computer Science Wake Forest University Winston Salem, NC, USA nsg.cs.wfu.edu Email:
Towards Optimal Firewall Rule Ordering Utilizing Directed Acyclical Graphs Ashish Tapdiya and Errin W. Fulp Department of Computer Science Wake Forest University Winston Salem, NC, USA nsg.cs.wfu.edu Email:
KeyEscrowinMutuallyMistrustingDomains?
 KeyEscrowinMutuallyMistrustingDomains? Abstract.Inthispaperwepresentakeyescrowsystemwhichmeets L.Chen,D.GollmannandC.J.Mitchell possiblerequirementsforinternationalkeyescrow,wheredierentdomainsmaynottrusteachother.inthissystemmultiplethirdparties,
KeyEscrowinMutuallyMistrustingDomains? Abstract.Inthispaperwepresentakeyescrowsystemwhichmeets L.Chen,D.GollmannandC.J.Mitchell possiblerequirementsforinternationalkeyescrow,wheredierentdomainsmaynottrusteachother.inthissystemmultiplethirdparties,
1 Solution of Homework
 Math 3181 Dr. Franz Rothe February 4, 2011 Name: 1 Solution of Homework 10 Problem 1.1 (Common tangents of two circles). How many common tangents do two circles have. Informally draw all different cases,
Math 3181 Dr. Franz Rothe February 4, 2011 Name: 1 Solution of Homework 10 Problem 1.1 (Common tangents of two circles). How many common tangents do two circles have. Informally draw all different cases,
A Portfolio Model of Insurance Demand. April 2005. Kalamazoo, MI 49008 East Lansing, MI 48824
 A Portfolio Model of Insurance Demand April 2005 Donald J. Meyer Jack Meyer Department of Economics Department of Economics Western Michigan University Michigan State University Kalamazoo, MI 49008 East
A Portfolio Model of Insurance Demand April 2005 Donald J. Meyer Jack Meyer Department of Economics Department of Economics Western Michigan University Michigan State University Kalamazoo, MI 49008 East
Portfolio selection based on upper and lower exponential possibility distributions
 European Journal of Operational Research 114 (1999) 115±126 Theory and Methodology Portfolio selection based on upper and lower exponential possibility distributions Hideo Tanaka *, Peijun Guo Department
European Journal of Operational Research 114 (1999) 115±126 Theory and Methodology Portfolio selection based on upper and lower exponential possibility distributions Hideo Tanaka *, Peijun Guo Department
Relationship among crude oil prices, share prices and exchange rates
 Relationship among crude oil prices, share prices and exchange rates Do higher share prices and weaker dollar lead to higher crude oil prices? Akira YANAGISAWA Leader Energy Demand, Supply and Forecast
Relationship among crude oil prices, share prices and exchange rates Do higher share prices and weaker dollar lead to higher crude oil prices? Akira YANAGISAWA Leader Energy Demand, Supply and Forecast
Formal Verification Coverage: Computing the Coverage Gap between Temporal Specifications
 Formal Verification Coverage: Computing the Coverage Gap between Temporal Specifications Sayantan Das Prasenjit Basu Ansuman Banerjee Pallab Dasgupta P.P. Chakrabarti Department of Computer Science & Engineering
Formal Verification Coverage: Computing the Coverage Gap between Temporal Specifications Sayantan Das Prasenjit Basu Ansuman Banerjee Pallab Dasgupta P.P. Chakrabarti Department of Computer Science & Engineering
Portfolio Optimization
 Portfolio Optimization Jaehyun Park Ahmed Bou-Rabee Stephen Boyd EE103 Stanford University November 22, 2014 Outline Single asset investment Portfolio investment Portfolio optimization Single asset investment
Portfolio Optimization Jaehyun Park Ahmed Bou-Rabee Stephen Boyd EE103 Stanford University November 22, 2014 Outline Single asset investment Portfolio investment Portfolio optimization Single asset investment
Determination of the normalization level of database schemas through equivalence classes of attributes
 Computer Science Journal of Moldova, vol.17, no.2(50), 2009 Determination of the normalization level of database schemas through equivalence classes of attributes Cotelea Vitalie Abstract In this paper,
Computer Science Journal of Moldova, vol.17, no.2(50), 2009 Determination of the normalization level of database schemas through equivalence classes of attributes Cotelea Vitalie Abstract In this paper,
OSTROWSKI FOR NUMBER FIELDS
 OSTROWSKI FOR NUMBER FIELDS KEITH CONRAD Ostrowski classified the nontrivial absolute values on Q: up to equivalence, they are the usual (archimedean) absolute value and the p-adic absolute values for
OSTROWSKI FOR NUMBER FIELDS KEITH CONRAD Ostrowski classified the nontrivial absolute values on Q: up to equivalence, they are the usual (archimedean) absolute value and the p-adic absolute values for
Moving Target Search. 204 Automated Reasoning
 Moving Target Search Toru Ishida NTT Communications and Information Processing Laboratories 1-2356, Take, Yokosuka, 238-03, JAPAN ishida%nttkb.ntt.jp@relay.cs.net Richard E. Korf Computer Science Department
Moving Target Search Toru Ishida NTT Communications and Information Processing Laboratories 1-2356, Take, Yokosuka, 238-03, JAPAN ishida%nttkb.ntt.jp@relay.cs.net Richard E. Korf Computer Science Department
3.6 The Real Zeros of a Polynomial Function
 SECTION 3.6 The Real Zeros of a Polynomial Function 219 3.6 The Real Zeros of a Polynomial Function PREPARING FOR THIS SECTION Before getting started, review the following: Classification of Numbers (Appendix,
SECTION 3.6 The Real Zeros of a Polynomial Function 219 3.6 The Real Zeros of a Polynomial Function PREPARING FOR THIS SECTION Before getting started, review the following: Classification of Numbers (Appendix,
EQUATIONS WITH A PARAMETER
 Journal of Applied Mathematics Stochastic Analysis, 10:3 (1997), 273-278. MONOTONE ITERATIONS FOR DIFFERENTIAL EQUATIONS WITH A PARAMETER TADEUSZ JANKOWSKI Technical University of Gdansk, Department of
Journal of Applied Mathematics Stochastic Analysis, 10:3 (1997), 273-278. MONOTONE ITERATIONS FOR DIFFERENTIAL EQUATIONS WITH A PARAMETER TADEUSZ JANKOWSKI Technical University of Gdansk, Department of
Knowledge, Innovations and Technologies Integration Nurturing Electronic Insurance Business
 Račinskaja et al. Electronic Insurance Business. 15 Knowledge, Innovations and Technologies Integration Nurturing Electronic Insurance Business Irena Račinskaja 1, Asta Žalimienė 2, Jonas Žaptorius 1,2
Račinskaja et al. Electronic Insurance Business. 15 Knowledge, Innovations and Technologies Integration Nurturing Electronic Insurance Business Irena Račinskaja 1, Asta Žalimienė 2, Jonas Žaptorius 1,2
The Inversion Transformation
 The Inversion Transformation A non-linear transformation The transformations of the Euclidean plane that we have studied so far have all had the property that lines have been mapped to lines. Transformations
The Inversion Transformation A non-linear transformation The transformations of the Euclidean plane that we have studied so far have all had the property that lines have been mapped to lines. Transformations
Types, Polymorphism, and Type Reconstruction
 Types, Polymorphism, and Type Reconstruction Sources This material is based on the following sources: Pierce, B.C., Types and Programming Languages. MIT Press, 2002. Kanellakis, P.C., Mairson, H.G. and
Types, Polymorphism, and Type Reconstruction Sources This material is based on the following sources: Pierce, B.C., Types and Programming Languages. MIT Press, 2002. Kanellakis, P.C., Mairson, H.G. and
How To Solve The Online Advertising Problem
 Frequency Capping in Online Advertising Niv Buchbinder Moran Feldman Arpita Ghosh Joseph (Seffi) Naor July 2, 2014 Abstract We study the following online problem. There are n advertisers. Each advertiser
Frequency Capping in Online Advertising Niv Buchbinder Moran Feldman Arpita Ghosh Joseph (Seffi) Naor July 2, 2014 Abstract We study the following online problem. There are n advertisers. Each advertiser
 Define Current Supply (Supply Now) Define Strategic Plans Define Operational Plans Assumptions Forecast/Project Future Supply (Supply Then) Define Future Requirements (Demand Then) Calculate/ Determine
Define Current Supply (Supply Now) Define Strategic Plans Define Operational Plans Assumptions Forecast/Project Future Supply (Supply Then) Define Future Requirements (Demand Then) Calculate/ Determine
WHERE DOES THE 10% CONDITION COME FROM?
 1 WHERE DOES THE 10% CONDITION COME FROM? The text has mentioned The 10% Condition (at least) twice so far: p. 407 Bernoulli trials must be independent. If that assumption is violated, it is still okay
1 WHERE DOES THE 10% CONDITION COME FROM? The text has mentioned The 10% Condition (at least) twice so far: p. 407 Bernoulli trials must be independent. If that assumption is violated, it is still okay
Nan Kong, Andrew J. Schaefer. Department of Industrial Engineering, Univeristy of Pittsburgh, PA 15261, USA
 A Factor 1 2 Approximation Algorithm for Two-Stage Stochastic Matching Problems Nan Kong, Andrew J. Schaefer Department of Industrial Engineering, Univeristy of Pittsburgh, PA 15261, USA Abstract We introduce
A Factor 1 2 Approximation Algorithm for Two-Stage Stochastic Matching Problems Nan Kong, Andrew J. Schaefer Department of Industrial Engineering, Univeristy of Pittsburgh, PA 15261, USA Abstract We introduce
Clique coloring B 1 -EPG graphs
 Clique coloring B 1 -EPG graphs Flavia Bonomo a,c, María Pía Mazzoleni b,c, and Maya Stein d a Departamento de Computación, FCEN-UBA, Buenos Aires, Argentina. b Departamento de Matemática, FCE-UNLP, La
Clique coloring B 1 -EPG graphs Flavia Bonomo a,c, María Pía Mazzoleni b,c, and Maya Stein d a Departamento de Computación, FCEN-UBA, Buenos Aires, Argentina. b Departamento de Matemática, FCE-UNLP, La
5 Comparison with the Previous Convergence Programme and Sensitivity Analysis
 5 Comparison with the Previous Convergence Programme and Sensitivity Analysis 5.1 Comparison with the Previous Macroeconomic Scenario The differences between the macroeconomic scenarios of the current
5 Comparison with the Previous Convergence Programme and Sensitivity Analysis 5.1 Comparison with the Previous Macroeconomic Scenario The differences between the macroeconomic scenarios of the current
Who Should Sell Stocks?
 Who Should Sell Stocks? Ren Liu joint work with Paolo Guasoni and Johannes Muhle-Karbe ETH Zürich Imperial-ETH Workshop on Mathematical Finance 2015 1 / 24 Merton s Problem (1969) Frictionless market consisting
Who Should Sell Stocks? Ren Liu joint work with Paolo Guasoni and Johannes Muhle-Karbe ETH Zürich Imperial-ETH Workshop on Mathematical Finance 2015 1 / 24 Merton s Problem (1969) Frictionless market consisting
Handover parameter optimization in LTE selforganizing
 FP7 ICT-SOCRATES Handover parameter optimization in LTE selforganizing networks TD (1)168 COST 1, 1 th MCM Athens, Greece February 3 rd 5 th TUBS, Braunschweig, Germany IBBT, Ghent, Belgium VOD, Newbury,
FP7 ICT-SOCRATES Handover parameter optimization in LTE selforganizing networks TD (1)168 COST 1, 1 th MCM Athens, Greece February 3 rd 5 th TUBS, Braunschweig, Germany IBBT, Ghent, Belgium VOD, Newbury,
Department of Veterans Affairs VHA DIRECTIVE 2012-015 Veterans Health Administration Washington, DC 20420 May 4, 2012
 Department of Veterans Affairs VHA DIRECTIVE 2012-015 Veterans Health Administration Washington, DC 20420 VETERANS HEALTH ADMINISTRATION FOUR TIERED LEADERSHIP DEVELOPMENT PROGRAM: LEADERSHIP, EFFECTIVENESS,
Department of Veterans Affairs VHA DIRECTIVE 2012-015 Veterans Health Administration Washington, DC 20420 VETERANS HEALTH ADMINISTRATION FOUR TIERED LEADERSHIP DEVELOPMENT PROGRAM: LEADERSHIP, EFFECTIVENESS,
Harmonizing Objectives and Constraints or Art of Strategic Planning
 Harmonizing Objectives and Constraints or Art of Strategic Planning Ouneheuane CHITTAPHONG Deputy Director General Department of Investment Monitoring & Evaluation (DIME) Committee for Planning & Investment
Harmonizing Objectives and Constraints or Art of Strategic Planning Ouneheuane CHITTAPHONG Deputy Director General Department of Investment Monitoring & Evaluation (DIME) Committee for Planning & Investment
Quality of Service Routing in Ad-Hoc Networks Using OLSR
 Quality of Service Routing in Ad-Hoc Networks Using OLSR Ying Ge Communications Research Centre ying.ge@crc.ca Thomas Kunz Carleton University tkunz@sce.carleton.ca Louise Lamont Communications Research
Quality of Service Routing in Ad-Hoc Networks Using OLSR Ying Ge Communications Research Centre ying.ge@crc.ca Thomas Kunz Carleton University tkunz@sce.carleton.ca Louise Lamont Communications Research
Contents. 2 Lines and Circles 3 2.1 Cartesian Coordinates... 3 2.2 Distance and Midpoint Formulas... 3 2.3 Lines... 3 2.4 Circles...
 Contents Lines and Circles 3.1 Cartesian Coordinates.......................... 3. Distance and Midpoint Formulas.................... 3.3 Lines.................................. 3.4 Circles..................................
Contents Lines and Circles 3.1 Cartesian Coordinates.......................... 3. Distance and Midpoint Formulas.................... 3.3 Lines.................................. 3.4 Circles..................................
Bias of the regression estimator for experiments using clustered random assignment
 Statistics and Probability Letters 78 2008 2654 2659 Contents lists available at ScienceDirect Statistics and Probability Letters journal homepage: www.elsevier.com/locate/stapro Bias of the regression
Statistics and Probability Letters 78 2008 2654 2659 Contents lists available at ScienceDirect Statistics and Probability Letters journal homepage: www.elsevier.com/locate/stapro Bias of the regression
PVIPE MEDIA INTERNET ADVERTISING CAMPAIGNS
 PVIPE MEDIA INTERNET ADVERTISING CAMPAIGNS The following service descriptions and pricing outline specific packages focused on payper-click (PPC) advertising. PVIPE has created several tiers of services,
PVIPE MEDIA INTERNET ADVERTISING CAMPAIGNS The following service descriptions and pricing outline specific packages focused on payper-click (PPC) advertising. PVIPE has created several tiers of services,
A Numerical Study on the Wiretap Network with a Simple Network Topology
 A Numerical Study on the Wiretap Network with a Simple Network Topology Fan Cheng and Vincent Tan Department of Electrical and Computer Engineering National University of Singapore Mathematical Tools of
A Numerical Study on the Wiretap Network with a Simple Network Topology Fan Cheng and Vincent Tan Department of Electrical and Computer Engineering National University of Singapore Mathematical Tools of
Comments on \Do We Really Know that Oil Caused the Great Stag ation? A Monetary Alternative", by Robert Barsky and Lutz Kilian
 Comments on \Do We Really Know that Oil Caused the Great Stag ation? A Monetary Alternative", by Robert Barsky and Lutz Kilian Olivier Blanchard July 2001 Revisionist history is always fun. But it is not
Comments on \Do We Really Know that Oil Caused the Great Stag ation? A Monetary Alternative", by Robert Barsky and Lutz Kilian Olivier Blanchard July 2001 Revisionist history is always fun. But it is not
INTEGRATION OF CONTROL THEORY AND SCHEDULING METHODS FOR SUPPLY CHAIN MANAGEMENT. Kaushik Subramanian
 INTEGRATION OF CONTROL THEORY AND SCHEDULING METHODS FOR SUPPLY CHAIN MANAGEMENT by Kaushik Subramanian A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy
INTEGRATION OF CONTROL THEORY AND SCHEDULING METHODS FOR SUPPLY CHAIN MANAGEMENT by Kaushik Subramanian A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy
WRITING PROOFS. Christopher Heil Georgia Institute of Technology
 WRITING PROOFS Christopher Heil Georgia Institute of Technology A theorem is just a statement of fact A proof of the theorem is a logical explanation of why the theorem is true Many theorems have this
WRITING PROOFS Christopher Heil Georgia Institute of Technology A theorem is just a statement of fact A proof of the theorem is a logical explanation of why the theorem is true Many theorems have this
Open Access Numerical Analysis on Mutual Influences in Urban Subway Double-Hole Parallel Tunneling
 Send Orders for Reprints to reprints@benthamscience.ae The Open Construction and Building Technology Journal, 2014, 8, 455-462 455 Open Access Numerical Analysis on Mutual Influences in Urban Subway Double-Hole
Send Orders for Reprints to reprints@benthamscience.ae The Open Construction and Building Technology Journal, 2014, 8, 455-462 455 Open Access Numerical Analysis on Mutual Influences in Urban Subway Double-Hole
SCHEDULE 8 Generalist Project Services Framework 2015
 SCHEDULE 8 Generalist Project Services Framework 2015 Nominal Insurer And Schedule 8 (Project Services Framework) Page: 1 of 6 Schedule 8 Generalist Project Services Framework Contents Overview... 3 1.
SCHEDULE 8 Generalist Project Services Framework 2015 Nominal Insurer And Schedule 8 (Project Services Framework) Page: 1 of 6 Schedule 8 Generalist Project Services Framework Contents Overview... 3 1.
GAP ANALYSIS OF APPROACHES TO IMPLEMENTATION OF MANAGEMENT SYSTEMS
 52 PROCEEDINGS OF THE SCIENTIFIC CONFERENCE QUALITY AND LEADING INNOVATION 2014 GAP ANALYSIS OF APPROACHES TO IMPLEMENTATION OF MANAGEMENT SYSTEMS DOI: 10.12776/QALI.V1.#5 MIROSLAV HRNIAR ABSTRACT Purpose:
52 PROCEEDINGS OF THE SCIENTIFIC CONFERENCE QUALITY AND LEADING INNOVATION 2014 GAP ANALYSIS OF APPROACHES TO IMPLEMENTATION OF MANAGEMENT SYSTEMS DOI: 10.12776/QALI.V1.#5 MIROSLAV HRNIAR ABSTRACT Purpose:
Efficient Curve Fitting Techniques
 15/11/11 Life Conference and Exhibition 11 Stuart Carroll, Christopher Hursey Efficient Curve Fitting Techniques - November 1 The Actuarial Profession www.actuaries.org.uk Agenda Background Outline of
15/11/11 Life Conference and Exhibition 11 Stuart Carroll, Christopher Hursey Efficient Curve Fitting Techniques - November 1 The Actuarial Profession www.actuaries.org.uk Agenda Background Outline of
Achievable Strategies for General Secure Network Coding
 Achievable Strategies for General Secure Network Coding Tao Cui and Tracey Ho Department of Electrical Engineering California Institute of Technology Pasadena, CA 91125, USA Email: {taocui, tho}@caltech.edu
Achievable Strategies for General Secure Network Coding Tao Cui and Tracey Ho Department of Electrical Engineering California Institute of Technology Pasadena, CA 91125, USA Email: {taocui, tho}@caltech.edu
An Implementation of Software Project Scheduling and Planning using ACO & EBS
 An Implementation of Software Project Scheduling and Planning using ACO & EBS 1 Prof. DadaramJadhav, 2 Akshada Paygude, 3 Aishwarya Bhosale, 4 Rahul Bhosale SavitribaiPhule Pune University, Dept. Of Computer
An Implementation of Software Project Scheduling and Planning using ACO & EBS 1 Prof. DadaramJadhav, 2 Akshada Paygude, 3 Aishwarya Bhosale, 4 Rahul Bhosale SavitribaiPhule Pune University, Dept. Of Computer

