The Basic Practice of Statistics Fifth Edition
|
|
|
- Scot Benson
- 10 years ago
- Views:
Transcription
1 EXCEL MANUAL for Moore s The Basic Practice of Statistics Fifth Edition Betsy Greenberg University of Texas Austin with solutions by Linda Myers Harrisburg Area Community College W.H. Freeman and Company New York
2 Copyright 2010 by W.H. Freeman and Company No part of this book may be reproduced by any mechanical, photographic, or electronic process, or in the form of a phonographic recording, nor may it be stored in a retrieval system, transmitted, or otherwise copied for public or private use, without written permission from the publisher. ISBN-13: ISBN-10:
3 Contents Preface Chapter 0 Introduction 1 Chapter 1 Looking at Data: Exploring Distributions 22 Chapter 2 Looking at Data: Exploring Relationships 38 Chapter 3 Producing Data 49 Chapter 4 Probability 54 Chapter 5 Sampling Distributions 65 Chapter 6 Introduction to Inference 68 Chapter 7 Inference for Distribution s Chapter 8 Inference for Proportions 85 Chapter 9 Inference for Two-Way Tables 62 Chapter 10 Inference for Regression 98 Chapter 11 Multiple Regression 105 Chapter 12 One-Way Analysis of Variance 114 Chapter 13 Two-Way Analysis of Variance 118 Chapter 14 Bootstrap Methods and Permutation Tests 123 Chapter 15 Nonparametric Tests 130 Chapter 16 Logistic Regression 135 Chapter 17 Statistics for Quality 137 Chapter 18 Exercises Time Series Forecasting
4 PREFACE This Excel Manual is a supplement to Statistics textbooks by David S. Moore, et al. that are published by W.H. Freeman. This manual is intended to help student perform the analysis described in those textbooks. Excel is widely available as part of Microsoft Office. It contains some statistical functions in its basic installation. It also comes with statistical routines in the Data Analysis Toolpak, an add in found separately on the Microsoft Office CD. Excel is a useful teaching and learning tool, however it is not meant to replace more sophisticated statistical tools such as SPSS or SAS. People often use Excel as their everyday statistics software because they have already purchased it. This manual helps students understand the capabilities of Excel for statistical analysis. In addition to describing the standard features of Excel, this manual also illustrates the capabilities of the WHFStat Add In module. The WHFStat Add In module is available from W.H. Freeman. The module is programmed to include the following procedures and graphical analyses under the umbrella of a single menu. Descriptive statistics Probability calculations Discrete probability Distributions Estimating and Testing Means Proportion Testing Correlation and Regression Time Series Forecasting Two way table and Chi squared test Analysis of variance Graphs including normal quantile plots, boxplots, and control charts Betsy Greenberg University of Texas at Austin August 2008
5 CHAPTER 0 Introduction Microsoft Excel is a widely used spreadsheet application that millions of people use in their personal and professional lives to store, analyze, and present information. This manual describes how Microsoft Excel can be used effectively in your statistics course. Using Excel Microsoft Excel, commonly referred to as just Excel, is a spreadsheet program that organizes data in columns and rows, much like an accounting worksheet or table of data. Excel can also perform statistical analysis using built-in functions. The WHFStat Add-In software works within Excel to group all of the statistics functions into one menu. This software is described in section 0.8, and is available on StatsPortal, your Online Study Center, or packaged with this manual. 1
6 2 Chapter 0 Versions of Excel The examples in this book were written using Microsoft Excel The WHFStat Add In module operates with Excel 2003 or Excel 2007 under either the Windows Vista or Windows XP operating systems. It is also compatible with Excel 2004 for Macintosh. Versions of Excel prior to version 2003 cannot be used with this software. Prior Knowledge It is not necessary to have any prior knowledge of Excel to use this manual. However, it will be helpful to become familiar with Excel before using it for statistical analysis. Worksheet Basics When Excel is launched, a new file opens with a series of blank worksheets, also known as sheets. The file itself is called a workbook, which refers to the entire collection of spreadsheets, graphs, and user-developed programming code in the file. The figure below is a screenshot of a blank sheet in the Excel 2007 application. In the upper-right corner of the application window are three buttons that allow the user to minimize, maximize, or close the window. Notice that there are two sets of these buttons, one in the top grey portion of the window and one in the lighter blue area. This is because the Excel application is actually displaying one window within another. Clicking the middle of the three buttons (ignore the question mark button for now) in the light-blue area will make the two windows more prominent, as shown below.
7 Introduction 3 The outer window is the Excel application window, which contains all of the buttons and menus that control the functionality of the program. The inner window contains the workbook with all of its sheets. Looking more closely at this inner window reveals a number of controls that allow the user to navigate around the active worksheet or to display other sheets in the workbook.
8 4 Chapter 0 Sheet Tabs Each worksheet is labeled with a tab at the bottom of the workbook, and individual sheets are activated by clicking these tabs. More than one sheet can be activated by selecting the first sheet, holding the Control Key down, and selecting additional sheets as required. If there are too many sheet tabs to be displayed all at once, the tab scrolling buttons can be used to bring a particular tab into view. Double clicking or right-clicking the name on a tab allows the sheet to be renamed. Sheets can be rearranged by dragging and dropping a given sheet tab to a new location within the group of tabs as a whole. Clicking the Insert Worksheet button adds a new blank sheet to the workbook. The scroll bars allow the portion of the spreadsheet currently displayed to be moved left or right, up or down. Rows, Columns, and Cells Notice that the worksheet is divided into a series of columns labeled with letters at the top, and a series of rows labeled with numbers on the far left. At the intersection of any column and row is a discrete portion of the sheet called a cell. All numeric and text data for a worksheet is housed within these cells. An individual cell is identified by the row and column in which it resides. For example, the cell located at the intersection of column A and row 1 is identified as A1, which is also known as the cell s address. Selecting Cells and Ranges In order to enter data in a cell, the target cell must first be selected. A cell is selected by using the mouse to click on a specific cell s location or by typing the arrow keys until the proper cell is reached. When a cell is selected, it is surrounded by a heavy black outline and the row and column headings corresponding to that cell are highlighted, as shown for cell A1 in the picture above. The highlighted cell is known as the active cell, and any numbers or text revisions to the spreadsheet will always be added to this active cell. When a new workbook is created, cell A1 in Sheet1 is automatically selected as the active cell. Clicking and dragging across more than one cell selects all the cells across the entire region, known as a cell range. To select multiple ranges, select the first range, hold the Control key down, and select any other ranges of cells. Clicking the Select All button selects all cells in the current worksheet. The worksheet shown below illustrates four types of ranges: an individual cell, a partial row of cells, a partial column of cells, and a range crossing multiple columns and rows. A range must be a rectangular shape or a group of adjacent cells. The active cell is always the upper-left cell of the last selected range. Just like individual cells, ranges have addresses that describe the cells they contain. A range address is composed of the upper-left cell in the range, a colon, and the lower-right cell in the range. The pictured ranges have the following range addresses: B2, B5:B10, D2:H2, D4:G11. The current active cell as pictured is D4.
9 Introduction 5 Using Excel s Functionality The Ribbon Excel 2007 introduced a new interface for accessing Excel s various controls and functionality called the Ribbon. The ribbon provides a series of context specific commands, grouped together so that similar commands display at the same time. The various groups of commands are accessed by selecting a ribbon tab near the top of the ribbon. Each tab displays a series of related commands. Brief overviews of the commands available in the ribbon tabs are outlined in the table below: The most commonly used functions cut, copy, and paste; font formatting and alignment, number formats, cell background color and borders, inserting and deleting cells, sorting, filtering, and finding/replace functions Functions to insert tables, charts, artwork, graphics or specialized text
10 6 Chapter 0 Printing options, workbook themes and colors, margins, page breaks, and scaling Controls to assist the user in creating, editing, and auditing formulas and calculation options Sorting and filtering, data validation, outlining, connecting to data in external sources such as databases or the internet Spellcheck and proofing tools, protecting and sharing workbooks, adding comments, tracking changes Display the workbook in various ways, hide/display gridlines and headings, arrange and size windows The Office Button Commands to open a new or existing workbook, save changes, and print can be found by clicking the circular Office button in the upper-left corner of the application window. For users accustomed to Excel versions prior to 2007, these commands correspond to the old File menu, which is not part of the new Excel ribbon. The Quick Access Toolbar Excel 2007 also gives the user the opportunity to place some of the most commonly used commands in a special Quick Access toolbar that is always available, regardless of which ribbon tab is currently selected. It is located just right of the Office button in the upper-left corner of the application window. Saving a file, undoing or redoing a change, previewing or printing can easily be added to this menu by selecting options in the small drop-down arrow at the right end of the toolbar. Excel also provides the ability to add practically any built-in command to this toolbar, so if a particular command is frequently used, it can be added here, rather than constantly selecting it on the ribbon. The Formula Bar and Name Box Although cell contents can be edited directly in the active cell, it is generally easier to edit cell contents by using the formula bar, located below the ribbon and just above the worksheet window. This is particularly useful for long formulas or text. When cell contents are being edited, two buttons appear, which allow the user to cancel the changes being made (the Cancel button, marked with an ) or accept the changes as entered (the Enter button, marked with a check mark ). Always available is the Insert Function button, which easily allows the user to select one of many pre-existing Excel functions for use in the cell being edited (see Entering Data: Formulas below). Once a function has been selected using this tool, Excel displays a helpful interface to assist the user in building the formula correctly.
11 Introduction 7 Sometimes the data displayed in the Formula bar is too long to be displayed in a single line. The height of the formula bar can be adjusted to display multiple lines by dragging the bottom portion of the formula bar downward. Once adjusted, one can toggle between the single line and multiple line displays by clicking the double downward arrow button at the end of the Formula bar. To the left of the Formula bar is the Name box, which displays the address of the current active cell D3 in the picture above. This can also be used to quickly navigate to a specific cell by typing the cell address into the Name box and hitting Return. The requested cell is selected and the spreadsheet is scrolled to the appropriate location. When editing formulas, the Name box displays the most frequently used Excel functions, allowing the user to easily add them to the current formula by selecting from a drop-down menu.
12 8 Chapter 0 The Status Bar, Zoom Slider, and Window Size Control At the bottom of the Excel application window are several more useful features. The status bar, located at the far left, displays messages about the current status of the Excel application. Rightclicking the status bar allows the user to select a number of options for what is displayed, such as whether or not Caps Lock is turned on or quick sums, counts, and averages of the currently selected cells. Just to the right of the status bar are three buttons that allow the user to switch between Normal, Page Layout, and Page Break preview views. Just to the right is a slider that controls the current Zoom setting for the worksheet. This can be adjusted to make a greater or lesser portion of the spreadsheet be displayed in the current window. In the bottom-right corner of the window is the Window Size Control, which can be used to adjust the size of the application window. The Help Button Near the top-right corner of the application window is a blue circle containing a question mark. This Help button, activates Excel s Help system. An extensive amount of information comes pre-loaded with the Excel application. Excel also automatically searches for the most up-to-date information on Microsoft s Excel website. While this manual provides a quick summary of the most basic Excel functionality, the Help system will provide more detailed information on specific topics as you need them.
13 Introduction 9 Entering Data Three types of information can be entered into a cell: text, numeric values, and formulas. Text Text can be entered in any combination of letters, numbers, or special characters. By default, text is aligned to the left within the cell. This can be changed via the Alignment group of buttons on the Home tab of the Ribbon (Ribbon Home Alignment). Although an individual cell can contain 32,767 characters, generally large strings of text are broken up into smaller pieces and spread across multiple cells. If the text entered into a cell is longer than the width of the cell allows to be displayed, the display is truncated. The completed text is still housed within the cell, and can be viewed in the formula bar. See the appropriate section above for instructions on how to adjust the amount of lines displayed in the Formula bar. The font type, size, color, and other font formatting features are adjusted using the controls in the Ribbon Home Font group. Numeric Values Excel is used primarily to perform calculations, so typically many of the cells in a spreadsheet contain numbers. Excel can be instructed to interpret the number in a specific cell as a date or time, a fraction, an amount of currency, a percentage, a phone number, or just a regular number. This is controlled with the buttons in the Number group on the Home tab of the Ribbon (Ribbon Home Number). If you enter a number and it appears differently than expected, try changing the cell s number format settings. For example, when entering 1/4 into an unformatted cell, Excel
14 10 Chapter 0 displays this as 4-Jan. Excel has interpreted the entry as the short format for a date and displayed it in the default date format. Once the number format for a cell has been specified by the user, it retains that format until changed. By default, numbers are right aligned, but this can be changed with the Alignment controls as described above for Text entries. A few rules to keep in mind when entering numeric values: No spaces allowed, The first character of a number must be 0 through 9, +,, or $. The number can include commas, decimal points (using the period key) or forward slashes (such as with dates or fractions). Negative numbers are designated with a preceding negative sign (-) or by surrounding the number with parentheses. Numeric values that do not follow the guidelines listed above, or that contain letters or other characters are interpreted as text. To force a number to be interpreted as text, precede the number with an apostrophe (single quote). If a cell is too narrow to display the entire number it contains, Excel instead displays a series of # signs. To display the number correctly, adjust the column width as described in the Formatting a Worksheet Section below. Formulas Formulas are mathematical expressions that can use values or formulas in other cells to calculate new values. Formulas can include numbers, cell addresses, multi-cell ranges, functions, and text. Upon entering a formula into a cell, the result of the formula is displayed in the cell itself and the equation is displayed in the Formula bar. To create a formula, make sure the first character within the cell is an equal sign (=). This alerts Excel that the following data entered in the cell should be interpreted as a formula. Excel uses the following symbols for these most common mathematical operations: the plus sign (+) for addition the minus sign (-) for subtraction the asterisk (*) for multiplication the forward slash (/) for division the caret symbol (^) for exponentiation the open and close parentheses ( ) for grouping parts of the formula
15 Introduction 11 Example formula =A3+ (C5) ^2 If a formula refers to a cell address for a value, and the value in that cell is changed, the formula is automatically updated and the new value displayed. This allows the user to continually update values throughout the spreadsheet and immediately see the resulting changes in the formulas as those value changes are made. Functions Functions can be used for arithmetic, statistical, scientific, logical or financial calculations, or even to manipulate text and find values within the spreadsheet. The most common functions are SUM, COUNT, AVERAGE, MAX, and MIN, but there are hundreds of functions available for your use. The general format for a function is an equal sign (just as with any formula), the capitalized name of the function itself, an open parenthesis, one or more arguments, and a close parenthesis. Arguments are the specific pieces of data required by that function to do the calculation. For example, a formula using the AVERAGE function would typically be of the form =AVERAGE (A2:A25). We have supplied the cell range A2:A25 for the argument. The cell range can either be typed into the formula, or it can be entered by dragging the mouse across the appropriate cell range when that portion of the formula is reached. The function name itself is not case sensitive and will be capitalized automatically when entry of the formula has been completed. While a function can be typed directly into a cell, it is much easier to use the built-in Insert function button, located in the Formula bar. Clicking this displays the following interface, which guides the user through searching for an appropriate function and entering the data for any required arguments.
16 12 Chapter 0 Modifying Data Editing Once a cell s content has begun to be entered, the backspace or delete keys can be used to modify the contents. To discard the changes completely, type the ESC key or click on the Cancel button in the Formula Bar. If the cell s content has been entered previously, it can be revised by double clicking the cell and moving the cursor to the appropriate location within the contents of the cell. Cell contents can also be edited by clicking the cell and changing the contents displayed in the Formula bar. Deleting or Clearing Data To delete cell contents, select the range of cells to be deleted and type the Delete key. This does not remove the actual cell from the spreadsheet, just its contents. Any cell formatting will remain. To have the option to remove cell contents, formatting, comments, or all three at once, select the range of cells to be cleared and click the Clear button within the Editing group on the Home tab of the Ribbon (Ribbon Home Editing Clear).
17 Introduction 13 The following options will be displayed: Clears formats, contents, and comments as described below Clears any background or border coloring, specific font styles or number formats, conditional formatting, cell alignment, etc. Clears data entered in the cell, similar to typing the Delete key Removes any comments attached to the cell Inserting and Deleting Rows and Columns Sometimes after data has been entered into a series of rows, it becomes necessary to insert new data between two of the existing rows. To insert a row, click the numbered row heading of the row beneath where you want to add the row and click the Insert button within the Cells group on the Home tab (Ribbon Home Cells Insert). A row will be inserted and any data previously in the selected row or below is shifted down. To insert more than one row, click and drag on more than one row heading and click the Insert button. New rows are added and old rows are shifted as appropriate. Inserting columns functions in much the same way, except one clicks on the desired number of column lettered headings immediately to the right of where the new columns should be inserted. Clicking the same Insert button executes the action. To delete rows or columns, select the specific rows or columns to be deleted and click the Delete button (Ribbon Home Cells Delete), which is right next to the Insert button. As rows or columns are deleted, all rows beneath or all columns to the right of the deleted section are shifted to fill the gap.
18 14 Chapter 0 Moving, Copying, and Filling Information Once cells contain content, that content can easily be moved or copied to another location within the same sheet, to another sheet, to a sheet in a different workbook, or even to another application. Cut and Paste Cell Content You may be familiar with the practice of cutting and pasting data in other applications, and Excel provides this functionality as well. Select the range of cells that contain the information to be moved and click the Cut button (Ribbon Home Clipboard Cut). Alternately, after selecting the target range of cells, right-click and select Cut from the pop-up menu or type Ctrl+X. All three methods of cutting place the entire contents of the selected cell range in Excel s memory (referred to in all Microsoft Office products as the Clipboard). At this point, the data has not yet been moved from the cells, but the selected cut range is indicated with a flashing dotted line surrounding it. Next, select the upper-left cell of the new area where you want the data you have just cut to be pasted. Click the Paste button (Ribbon Home Clipboard Paste) and the data from the old cells is placed within the new ones.
19 Introduction 15 Copy and Paste Cell Content To copy a target range to another location, with the old data remaining where it was, use the same basic method as described above, but select the Copy button or menu option instead of Cut. Drag and Drop Cell Content A target range of cells can also be dragged and dropped to another location on the same sheet. To do so, select the cell range to be moved. Notice that when the mouse pointer is placed directly over the heavy black line surrounding the selected range that the pointer changes to a small cross with four arrows. When the four arrow cross is displayed, click and hold the mouse, dragging the mouse to another location on the spreadsheet. The entire selected range of cells moves along with it, including all content and formatting.
20 16 Chapter 0 AutoFill Cell Content Excel also provides a simple way to populate data or formulas across a range of cells, or to create an incremental data series. To simply copy data or a formula across a range, select the cell to be copied. Notice that there is a small square (called a fill handle ) in the bottom-right corner of the heavy line surrounding the selected cell (circled in the image to the left). When the mouse pointer is placed over this handle, the arrow pointer becomes a crosshair. As that crosshair is displayed, click on the fill handle and drag the mouse down or to the right across the cells to be filled. Upon releasing the mouse, the data or formula in the original cell is copied across the range. Any formatting in the original cell is copied as well. To create an incremental series, type the first two numbers in the series in adjacent cells. Following the same procedure as described for copying above, select the two cells containing the first two data points in the series and drag the fill handle across the appropriate number of cells for the whole series. Based upon the first two numbers entered, Excel AutoFills the remainder of the series. Excel can also AutoFill the names of months. Simply enter January or Jan, and using the AutoFill method described above, Excel fills in the remainder of the months in the format entered. After December, Excel continues on with January again, filling in each successive month over the entire dragged range.
21 Introduction 17 Formatting a Worksheet Excel provides a wealth of tools to customize the look and feel of spreadsheets. First, select a cell or a range of cells to be formatted. Using the buttons on the Home tab in the Font, Alignment, Number, Styles, and Cells groups, the background color, border colors, row height, column width, fonts styles, and size and number formats can all be changed. Individual cells can be merged using the Merge and Center options in the Alignment group. Preprogrammed formats can be applied using the Cell Styles options in the Styles group. Adjusting Column Width and Row Height The height and width of an individual row or column can be changed by clicking and dragging the line between the rows or column in their respective headers. When pointing the mouse directly at the line between row headings or column headings, the pointer arrow changes to a line with arrows pointing in two directions (see images below). With this double-arrowed pointer displaying, click and hold the mouse. Light gray lines show the current boundaries of the row or column being adjusted. Dragging the mouse widens or narrows these boundaries to display the proposed width or height. If multiple rows or columns are selected at one time, the height or width is adjusted for the entire selection. Alternately, you can double click on the line between row or column headings for a best fit option for the selection. Row or column headings can also be right-clicked to display a menu that includes a Row Height or Column Width option. Formatting Cells Many cell, font, and number formatting options are available directly from the Home tab of the Ribbon, the Format Cells feature provides additional formatting options. It can be accessed by clicking the arrow-within-square button located in the bottom right of the Font, Alignment, and Number groups on the Home tab (see the circles in the image below).
22 18 Chapter 0 Adjusting the settings in the format cells will change the format in the selected cells. Tabs at the top provide the following formatting controls: Number Alignment Font Border Fill Protection Select number format styles of general, currency, date, time, percentage, etc. Also controls the number of decimal places displayed, whether or not commas or currency symbols are displayed, and how negative values are differentiated. Horizontal and vertical text alignment, direction of text, such as at a 45º angle, whether to wrap text, indent, etc. Select font family and size, options for bold, italic, underline, strikethrough, superscript, subscript, and font color. Turn on or off borders at each of the four sides of a cell or the two diagonals. Weight, style, and color of each border segment can be adjusted independently. Control the color and pattern of cell interior backgrounds. Control whether users can edit the contents of cells or view cells formulas in the Formula bar. As with all formatting options, this can be controlled on a cell-bycell basis.
23 Introduction 19 Printing Page Setup Options Excel provides a number of tools to configure how the spreadsheet will look when it is printed. The primary printing options are located on the Page Layout tab of the Ribbon in the Page Setup group (Ribbon Page Layout Page Setup). Options include controls to adjust the page margins, page orientation, the expected size of the paper being used for printing, background images, where page breaks occur, which cells in the spreadsheet will be printed, and whether or not to repeat certain rows at the top or certain columns at the left of each page. Clicking the arrow-within-square button in the bottom right of the Page Setup group opens up a more detailed Page Setup interface with a greater level of control for these options as well as the ability to specify page headers and footers.
24 20 Chapter 0 Print, Quick Print, and Print Preview To access printing options, click the circular Office button in the top left of the Excel application window. From the Office menu, select the Print sub-menu, as displayed on the left. Selecting the Print command will display an interface that allows the user to select a printer and printing options. The Quick Print command will print the current spreadsheet using the default printer and default print options. The Print Preview command allows the user to see how the spreadsheet will appear before printing it. Using Excel s Statistical Tools Excel contains a set of pre-built statistical analysis tools as part of the Analysis Toolpak add-in included with the Excel software. For some Excel installations, it will need to be turned on. Doing so requires the following steps: 1. Click the circular Office button in the upperleft corner of the Excel application window. 2. In the light-blue border at the bottom of the Office menu, click the Excel Options button. 3. In the pop-up interface that displays, select Add-ins from the navigation bar on the left. 4. A list of available add-ins will be displayed. It may take a few moments for Excel to collect this information. At the bottom of the list, there should be a drop-down menu with add-ins selected. Click the Go button next to this. 5. Make sure that Analysis ToolPak is checked. Note: If the Analysis ToolPak is not listed, it will need to be added from the Excel installation software. Once the Analysis ToolPak add-in is installed, there should be a new analysis group available on the Data tab of the Ribbon (Ribbon Data Analysis). Click the Data Analysis button, and the following list of available analysis tools will be displayed.
25 Introduction 21 Many of the included Excel statistical analysis tools are detailed where appropriate in the exercises in the following chapters. Where appropriate, exercises taken from the textbook are solved using both the Excel analysis tools and the WHFStat add-in module packaged with this manual. The Excel solutions are identified by this icon The WHFStat solutions are identified by this icon Using the WHFStat Add-In Module WHFStat is an Excel Add-in, software that makes it easier to use Excel to do most statistical operations. The software is available on StatsPortal, your Online Study Center or packaged with this manual. Once installed, the WHFStat Add-In module will be integrated into your Excel application and will automatically load every time you open Excel. You will notice a new Add-Ins tab on the Ribbon, upon which the Menu Commands group will have a button labeled WHFStat. Clicking this will display the various menu options available for the add-in.
26 CHAPTER 1 Looking at Data: Exploring Distributions Bar Charts Excel allows us to examine the distribution of variables with graphs. Bar charts are useful for categorical data. The following data provides the tire model reported for 2969 accidents that involved Firestone tires. 22
27 Looking at Data: Exploring Distributions 23 We will use this data to make a Bar Chart with Excel. Highlight the data and select Insert Column 2 D Column as shown below. Clicking on the 2 D Column will produce the following bar chart.
28 24 Chapter 1 Pie Charts Another way to examine distributions of categorical variables is with a pie chart. We will continue to use the data from the previous example to show how to make a pie chart with Excel. To make a pie chart of the waste data, select Insert Pie 2 D Pie from the menu.
29 Looking at Data: Exploring Distributions 25 Although we highlighted three columns, Excel used only the first two when constructing the pie chart. The values in the column labeled percent can be used by changing the data. If you right click on the pie chart and choose Select data, the Select Data Source dialog box pops up. In that dialog box, you can delete the Count series so that the Percent series will be used instead. Alternatively, you can click on the graph and select the Design tab from the menu to select an alternative presentation such as the one shown below. Histograms The most common graph for the distribution of a quantitative variable is a histogram. We will illustrate this with IQ test scores for 60 fifth grade students. To create a histogram, select Data Data Analysis Histogram
30 26 Chapter 1 from the menu. In the dialog box, specify the input range to be where the data is located as shown below. If the first cell is a label, check the Labels box. The Output Range specifies where the output will be placed. Finally, check the Chart Output box and then click OK. The default histogram appears as follows. You can also specify alternative bin ranges to avoid the default values selected by Excel. It is helpful to first select Data Sort from the menu to sort the data before deciding on the Bin Ranges. The new values are then typed into a column on the Excel worksheet. If the data has a label and the Label box will be checked, then this new column should also have a label. The new column is then entered into the Histogram dialog box next to Bin Range.
31 Looking at Data: Exploring Distributions 27 The new histogram will use the selected bin ranges, but not be entirely satisfactory. For example, the bin ranges in the histogram below appear to be interval midpoints instead of cutpoints. It appears from this histogram as though there are no observations below 85, when in fact there are. The gap width between the bars can be changed or eliminated by right clicking on a bar and selecting Format Data Series and changing the option in the following dialog box.
32 28 Chapter 1 Time Series Plots When quantitative data are collected over time, it is a good idea to plot the observations in the order they were collected. For example, the following data lists the volume of water discharged by the Mississippi River in the Gulf of Mexico for each year from 1954 to Year Discharger Year Discharge Year Discharger Year Discharge To make a time series plot of this data, highlight the data and select Insert Scatter and select a graph design from the menu.
33 Looking at Data: Exploring Distributions 29 The time series plot will appear as soon as you click on the plot design of your choice. If Scatter with Straight Lines is selected, the plot will appear as follows. As usual, the plot can be altered by clicking on the graph and selecting the Design tab. Since the dates appeared in one column with the data in the next column to the right, the time plot has the dates on the x axis and the data on the y axis. If the data appears in a different or
34 30 Chapter 1 der, you can right click on a data point and choose Select Data. The dialog box that is shown below allows you to switch columns, and add or delete a series so that you can use the appropriate data. If your data is not accompanied by a column of dates, highlight only that data and select Insert Line from the menu. Select the design that you prefer to obtain a time plot. In this case, the x axis will be labeled with consecutive numbers instead of dates. Numerical measures are often used to describe distributions. Select Data Data Analysis Descriptive Statistics from the menu to obtain descriptive statistics. Enter the input range for the data. If the data includes a label in the first row, check the appropriate box. Specify where the output will appear, check the box next to Summary Statistics, and click OK in the following dialog box.
35 Looking at Data: Exploring Distributions 31 The command summarizes several different measures of both the center and spread of a distribution. The command prints the statistics Mean, Standard Error, Median, Mode, Standard Deviation, Sample Variance, Kurtosis, Skewness, Range, Minimum, Maximum, Sum, and Count, for each column specified. Count is the number of actual values in the column (missing values are not counted). Mean is the average of the values. To find the median, the data first must be ordered. If N is odd, the median is the value in the middle. If N is even, the median is the average of the two middle values. StDev is the standard deviation computed as ( ) StDev = x i x N 1 Standard Error is the standard error of the mean. It is calculated asstdev N. The same results can be obtained using functions in Excel. For example, typing =AVERAGE(A2:A61) into a cell gives the mean, =STDEV(A2:A61) gives the standard deviation, and =COUNT(A2:A61) gives the sample size. In addition, we can obtain the quartiles needed for the five number summary using the QUARTILE function. If you click on the Insert Function,, you can search for the appropriate function as shown below. 2
36 32 Chapter 1 As shown below, you can obtain the function either by typing the formula int0 an empty cell, clicking on an empty cell and then typing the formula into the formula bar to the right of the Insert Function button, or by filling in a dialog box. Either way, you must specify the Array that holds the data and then the Quart, where Quart = 0 is the minimum value, 1 is the first quartile, 2 is the median, 3 is the third quartile, and 4 is the maximum. Excel doesn t use exactly the same algorithm to calculate quartiles as your textbook, so minor differences in results will sometimes occur. The five number summary consisting of the median, quartiles, and minimum and maximum values provides a quick overall description of a distribution.
37 Looking at Data: Exploring Distributions 33 Normal Calculations Sometimes the Normal density can describe the overall pattern of a distribution. A histogram may be helpful in deciding when this is appropriate. Normal quantile plots are also useful in determining whether a distribution is approximately Normal. If the points on a Normal quantile plot lie close to a straight line, the plot indicates that the data are Normal. Excel can be used to perform Normal distribution calculations. If data in a column are Normally distributed, then the data can be standardized to obtain data with a standard Normal distribution, that is, those with mean equal to zero and standard deviation equal to one. The STANDARDIZE(x,mean,standard_dev) function can be used to do this. The function requires that you specify the x value that you want to standardize, the mean of the distribution and the standard deviation of the distribution. The function returns the standardized value, z = ( x x) s. For example, if the IQ scores are normally distributed with a mean equal to 100 and a standard deviation equal to 10, then we can standardize as shown below. If we copy the formula down the column, we can obtain the standardized values for all of the vocabulary scores. The standardized IQ scores (or z score) will tell how far above or below the mean a particular score falls. The measure is in units of standard deviations. The first student has a score of 81, a value that is below the mean (z = 1.9). Another score, 117 is above the mean (z = 1.7). We could examine the standardized values to see how well they obey the rule. Approximately 68% of the standardized values should have values between 1 and +1, 95% should have values between 2 and +2, and 99.7% should have values between 3 and +3. You can use Excel to do probability calculations for the Normal distribution using the NORMDIST(x,mean,standard_dev,cumulative) function. When cumulative=1, this function returns the normal distribution for the specified mean and standard deviation. In addition to the 1 for cumulative, you must specify the x value for the distribution along with the mean and standard deviation. For example, the heights are approximately Normal with a mean of about 64 inches and a standard deviation of 2.7 inches. To find the proportion of women who are less than 70 inches tall, we select type =NORMDIST(70,64,2.7,1) into a cell or the formula bar. Alternatively, click Function Wizard on the formula bar to select the NORMDIST function and fill in the dialog box.
38 34 Chapter 1 The result says that the proportion of women who are less than 70 inches tall is , or nearly 99%. This is slightly different from the result that would be obtained using Table A since it is not required to round the standardized value. We can also use Excel to do backward calculations. The length of human pregnancies in days from conception to birth follow approximately the N(266,16) distribution. To find the length of the longest 10% of pregnancies, we can use the NORMINV function. The function requires that we specify the appropriate probability along with the mean and standard deviation of the distribution. Since we want the value for the top 10%, the input constant is 0.9 corresponding to 90% below the calculated value. As for all functions, we click on the cell where you want the results and then type in that cell or on the formula bar as shown below, or click on the function wizard. The function returns the inverse of the normal cumulative distribution for the specified mean and standard deviation. In this example the value returned is 286.5, indicating the the longest 10% of human pregnancies last at least days.
39 CHAPTER 2 Looking at Data: Exploring Relationships Scatterplots Often we are interested in illustrating the relationships between two variables, such as the relationship between height and weight, between smoking and lung cancer, or between advertising expenditures and sales. For illustration, we will consider the relationship between the number of items sold and gross sales at Duck Worth Wearing, a shop selling high quality, second hand children s clothing, toys, and furniture. If both variables are quantitative, the most useful display of their relationship is the scatterplot. Scatterplots can be produced by highlighting the variables in the scatterplot and selecting Insert Scatter Scatter with only Markers from the menu. The explanatory variable should be plotted on the x axis and the response variable should be plotted on the y axis. The highlighted columns should have the x variable on the left and the y variable on the right, so you may need to rearrange your data. If so, you 35
40 36 Chapter 2 can highlight the column with the y variable and select Home Insert Insert Sheet Columns to add space for a column to the left of the y variable. Copy the x variable into the empty space. Once the data are correctly arranged and you click on the Scatter with only Markers button, your scatterplot will appear. Initially, your scatterplot may not look the way you want it to. If you are clicked on the chart, Chart Tools will also appear at the top of the Excel menu. These tools allow you to modify the chart. Choose layout and modify as desired. For example, select Layout Axis Titles Primary Horizontal Axis Title Title Below Axis to add an x axis title. Click the axis title and type the text that you want. The data in the scatterplot are positively associated, in a roughly linear pattern with no clear outliers.
41 Looking at Data: Exploring Relationships 37 We can add information about a third categorical variable to a scatterplot by using different symbols for different points. The Duck Worth Wearing store is open Monday through Saturday. The five Saturdays in April 2000 (04/01, 04/08, 04/15, 04/22 and 04/29) are the days with the highest numbers of items sold. We can improve the scatterplot by plotting the Saturdays with a different plot symbol. First, we add a categorical variable Saturday to the Excel spreadsheet. This variable has only two values: 1 for the Saturdays and 0 for the weekdays. The Saturday data is easily separated from the weekdays by sorting as shown. A labeled scatterplot can then be obtained by selecting Design Select Data Add to add a series with only the Saturday data..
42 38 Chapter 2 Specify the x and y values and a series name by clicking on the small spreadsheet icons. The additional series will appear in the graph. You will probably want to add a legend to the scatterplot by clicking on the chart and selecting Layout Legend. The scatterplot with Saturdays identified shows that the company is busier on Saturdays. Correlation We can compute the correlation coefficient between two quantitative variables using Excel. The correlation coefficient can be calculated by selecting
43 Looking at Data: Exploring Relationships 39 from the menu. Data Data Analysis Basic Statistics Correlation Below we illustrate a correlation calculation with bird colony data. The data gives, for 13 colonies of sparrow haws, the percent of adult birds in a colony that return from the previous year and the number of new adults that join the colony. To calculate the correlation, the input range should be the variable for which you wish you are needing the correlation. If there are labels in the first row, check the appropriate box. Select a location for the output and click on the OK button. The correlation of the two variables is shown in the table below to be If more than two variables are selected in the Input Range, Excel will include the correlation coefficients between all pairs of variables.
44 40 Chapter 2 Alternatively, the correlation of two variables can be calculated using the CORREL function. Type =CORREL(data range) into any cell or click on the Insert Function button and type CORREL to obtain the dialog box shown below. Least Squares Regression The scatterplot for Duck Worth Wearing shows that there is a strong linear relationship between the number of items sold and the gross sales. To calculate the least squares line of the form y = a + bx from data, right click on a point on the scatterplot, select Add Trendline from the list, select Linear on the Trendline Options, check the box next to Display Equation on the chart, and Display R squared value on the chart if desired.
45 Looking at Data: Exploring Relationships 41 The scatterplot now shows the least sqaures line, the equation for the line (y = 6.595x ) and that r 2 = The slope and intercept can also be found using Excel s SLOPE and INTERCEPT functions. These functions can be typed into a cell or you can click on the Insert Function button. Both SLOPE and INTERCEPT require that you specify the known values of y and x. To find the residual for each point, first calculate the fitted value for each point, then calculate the value of the residual. For each point, the fitted value, = a + bx and the residual is y. Once the residuals have been calculated, the residual plot is just a scatterplot of the residual versus the x variable.
46 42 Chapter 2 Tables for Categorical Variables We can describe relationships between two or more categorical variables using two or threeway tables in Excel. We will use the data on binge drinking by college students. In this data set, we have stored information on 17,096 students classified by gender and whether or not they are frequent binge drinkers. To make a two way table in Excel select Insert Pivot Table from the menu. In the dialog box, select the range of input data and the location where you want the Pivot Table report to be placed as shown below. Click OK and the blank Pivot Table will appear. The Pivot Table Field List will also appear as long as a cell within the Pivot Table is selected.
47 Looking at Data: Exploring Relationships 43 If we view gender as the explanatory variable and frequent binge drinking as the response variable, then we put gender in the columns and frequent binge drinking in the rows. This is easily done by dragging the word Gender into the Column Labels field and the word Drinker into the Row Labels field. Once either Gender or Drinker is dragged into the Values field, the data will appear in the Pivot Table as shown below. For three way tables, an additional variable would be included and dragged into the Report Filter field.
48 44 Chapter 2 Once the two way table has been constructed, marginal and conditional probabilities can be constructed by typing the appropriate formulas into cells. For example, to calculate the proportion of men that are frequent binge drinkers, the formula would be =D7/D8.
49 CHAPTER 3 Producing Data Random Samples Excel allows us to select a simple random sample from a population. To choose a random sample, select Data Data Analysis Sampling from the menu. Specify the input range from which you are sampling, click on the radio button for Random, specify the number of samples, and the output range. In the example below, we wish to select a sample of five randomly selected small business clients for a customer satisfaction survey. The input range for Sampling must be numeric. If you have a list of names instead of numbers, you must create a corresponding list of numbers. To enter a list of numbers into Excel, enter the first few numbers to establish the pattern. Highlight these numbers and then use the fill handle to automatically fill data in worksheet cells. The sample you select may have repeated numbers. You can select a new sample if this is not what you want or you can select a sample larger than needed so that you can skip any repeats. 45
50 46 Chapter 3 Alternatively, a sample can be chosen by assigning random numbers to each item or person in the population and then sorting the population to select the items with either the smallest or largest random numbers. To assign random numbers, select Data Data Analysis Random Number Generation from the menu. To assign a random number to each client on the list, choose Data Data Analysis Random Number Generation from the menu. Specify that you wish to select the random numbers from a the normal distribution (or uniform distribution) and specify the cells where the results will be stored as shown below.
51 Producing Data 47 Sorting Data Rather than searching through the list of random numbers to select the clients with the smallest (or largest) random numbers, it is convenient to sort the clients. Highlight the column with the random numbers and select Data Sort from the menu. This command orders the data in a column in numerical sequence. If Excel finds data next to your selected column, you will get the Sort Warning shown below and have a choice to Expand the selection or Continue with the current selection. Since you want to keep client name and number associated with the random numbers, you should select Expand the selection. If you select Continue with the current selection, only the highlighted column with be sorted and the adjacent columns will remain as they are.
52 48 Chapter 3 Randomization in Experiments Sampling can be used to randomly select treatment groups in an experiment. If you have a list of subjects and a list of treatments, random numbers can be used to reorder one of these lists to make the random assignments. For example, suppose that 60 subjects are to be assigned to 3 treatments. You could have the numbers 1 through 60 in one column and the numbers 1, 2, and 3, each repeated 20 times, listed in another column. A third column of random numbers should also be added. The random numbers can be selected by choosing Data Data Analysis Random Number Generation from the menu as explained earlier, or by using either the RAND() or RANDBETWEEN(bottom,top). RAND() returns a random number between 0 and 1, evenly distributed. Although the parenthesis are required, this function has no arguments. RANDBETWEEN(bottom,top) returns a random number between the bottom and top numbers that you specify. If you use these functions, you must copy the numbers and then do a special paste of only the values. To copy the random numbers, select the Home tab, in the Clipboard group, click Copy. Alternatively, you could select Control C or right click on the data and select Copy. To paste only the values without the formula, on the Home tab, in the Clipboard group, click Paste, and then click Paste Values. Now highlight the column with the treatments and the random numbers. Select Data Sort from the menu. In the dialog box, you will specify the column that you wish to sort. The other column that you highlighted will be carried along.
53 Producing Data 49 After sorting, the treatments will appear in a random order and the worksheet will show which subjects get each treatment.
54 CHAPTER 4 Probability Simulating Random Data Excel can be used to simulate random data. To simulate random data, select Data Data Analysis Random Number Generation from the menu. Then select a distribution from the dialog box shown on the next page. For example, if you select Bernoulli from the menu, you can generate a random sequence of 0s and 1s. In the dialog box, select the distribution. If the distribution is Bernoulli, specify also a P value (probability of success) and where the results are to be stored. For example, to simulate a sequence of 50 coin tosses (with equal probability of heads and tails), the dialog box must be filled in as shown on the following page. For example, the sequence of 0s and 1s may look like: 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0 The 1s correspond to the variable for which you input the probability of success. In this case, we may consider the 1s to be heads and the 0s to be tails. Thus, our sequence of coin flips would be: 50
55 Probability 51 H, T, H, T, T, T, H, T, H, H, H, T, T, H, H, T, T, T, T, H, H, H, T, T, H, T, H, H, H, H, T, T, H, T, H, T, H, T, H, T, T, T, H, H, H, T, H, H, H, T. To graph the proportion of heads versus the number of tosses, we need to calculate the proportion of heads as shown below. Notice that the formula includes a $ sign to indicate that the first number in the average is always in row 2, even when the formula is copied. To construct a graph of the data, highlight the entire column of proportions and select Insert Line from the menu. The proportion of tosses that give a head changes as we make tosses. Eventually, the proportion approaches 0.5.
56 52 Chapter 4 Simulating from Other Distributions In addition to Bernoulli, Excel can be used to simulate data from many other distributions. These distributions are Uniform, Normal, Bernoulli, Binomial, Poisson, Patterned, and Discrete. For example, discrete distributions can be simulated with Excel. Benford s law describes a distribution that is often observed in the first digit of numerical records. Here is the distribution for Benford s law. First digit Proportion Any discrete distribution can be specified by putting the values and corresponding probabilities into two columns. We will simulate observations from the distribution following Benford s law. First we enter the sizes and probabilities into an Excel spreadsheet as shown below. To simulate data from the specified discrete distribution, select Data Data Analysis Random Number Generation from the menu and select Discrete in the
57 Probability 53 dialog box. As shown, you must specify where the data are to be stored, the column specifying the values, and the column specifying the probabilities. Simulated data will not look exactly like the distribution from which they are selected. To see the difference between the exact distribution and the simulated data, we can compare graphs. To graph the simulated data, select Data Data Analysis Histogram from the menu. In the dialog box, select the random data for the Input Range and the column listing the first digits for the Bin Range as shown below.
58 54 Chapter 4 To compare the simulated data with the specified distribution, highlight the column of probabilities and select Insert Column from the menu. Both graphs are skewed to the right, but the simulated data in the histogram are not as smoothly distributed as the probability distribution illustrated in the following bar chart. The randomness illustrated in the histogram is typical of simulated data. To generate random numbers that are spread out uniformly between two numbers, select Data Data Analysis Random Number Generation from the menu and select Uniform in the dialog box. For example to generate 1000 random numbers uniformly across the interval from 0 to 1, the dialog box would be filled out as follows.
59 Probability 55 Select Data Data Analysis Random Number Generation from the menu and select Normal in the dialog box to simulate observations from a Normal distribution. To simulate the heights of ten young women with the N(64, 2.7) distributions, the dialog box would be filled out as follows. Probability Calculations Excel lets you perform mathematical operations and functions. The results of a calculation can be stored in a cell. For example, if we wish to calculate the probability that a first digit is equal to or greater than 6, we can use our Benford s Law data and use Excel s SUM function to add the appropriate probabilities.
60 56 Chapter 4 We can also use Excel to calculate the mean and variance of a discrete random variable using the following equations. To calculate the mean and variable of X we arrange the calculation in the form of a table as shown below. The third column gives the value of, i.e., the product of the first two columns. The values in this column are added up using the SUM function to find the mean. The next column gives. If this formula is to be copied, the value for should have $ in front of the row number so that the value doesn t change. The values in the fourth column are added up to obtain the variance. The standard deviation of X can be found using the SQRT function. Binomial Probabilities Suppose a music inspector inspects a sample of ten CDs from a shipment of 10,000 music CDs. Suppose that 10% of the CDs in the shipment are bad. The inspector will count the number X of bad CDs. Earlier in this chapter, we learned to generate random numbers for this situation by selecting Data Data Analysis Random Number Generation from the menu and selecting the Bernoulli distribution to generate a sequence of ten 1 s and 0 s to represent the bad and good CDs. If we are interested only in the number of bad CDs, we can generate the number X by selecting Data Data Analysis Random Number Generation from the menu and selecting the Binomial distribution. Instead of generating only one value for X, we can simulate a large number of repetitions of the sample.
61 Probability 57 In addition to simulating binomial data, we can use Excel to calculate exact binomial probabilities. The BINOMDIST(number_s,trials,probability_s,cumulative) function calcu lated the probability of h. Specify the number of successes, number of trials, probability of success, and 0 for the probability. For example, BINOM DIST(1,10,0.1,0) gives the value This is the probability that exactly one CD out of 10 is bad. If you want the entire probability distribution, enter the numbers 0 through 10 in a column on the Excel worksheet and use the same formula to obtain the probability of each possible outcome for a binomial distribution with n = 10 and p = 0.1 as shown below. If you enter a 1 instead of a 0 in the last position of the BINOMDIST function, Excel calculates P(X x) instead of P(X = x). If you wish to calculate P(X x), then it is necessary to realize that P(X x) = 1 P(X x 1). To graph the distribution, highlight the column of probabilities and select Insert Column 2 D Column from the menu. The default axis labels will be incorrect, so you need to click on the graph and then select Design Select Data from the menu and then edit the horizontal (category) axis labels on the right side of the dialog box.
62 58 Chapter 4 The resulting graph would look like the one below. Suppose that an opinion poll asks 2500 adults whether they agree or disagree that I like buying new clothes, but shopping is often frustrating and time consuming. Suppose also that 60% of all adult U.S. residents would say Agree. To find P(X 1520), the probability that at least 1520 adults agree, use the BINOMDIST function with Number_s set to 1520, 2500 trials, 0.6 probability of success, and Cumulative set to 1.
63 Probability 59 As shown, the result is Normal Approximation to the Binomial To illustrate the shape of the distribution on the number of adults that would say Agree out of the 2500 adults polled, enter the numbers from 1400 to 1600 in steps of 1 to be stored in a column of your choice. Remember that you can enter the first few numbers and then select these cells and drag the fill handle. down the cells that you want to fill. Next use the BINOMDIST function to compute the probability for 2500 trials with 0.6 probability of success for each value. Finally, highlight the two columns and select Insert Scatter from the menu to illustrate the shape. The numbers 1400 to 160 are the X values and the probabilities are the Y values as shown below. As the figure shows, the binomial probabilities will be approximated well by a normal distribution. The values for the mean and standard deviation are equal to μ = np = = 1500 σ = np(1 p) = =
64 60 Chapter 4 The values are easily calculated using Excel. Enter =2500*.6 into a cell for the mean or =sqrt(250*.6*.4) for the standard deviation. When np 10 and n ( 1 p) 10, we can use the normal approximation to approximate binomial probabilities. Here, we approximate the probability that at least 1520 of the people in the sample find shopping frustrating when n = 2500 and p = 0.6. We act as though the count X has the N(1500, ) distribution. To obtain the normal approximation for this example, use NORMDIST function in Excel. We let X be 1520, specify a mean equal to 1500, a standard deviation equal to , and Cumulative equal to 1. As with the binomial distribution, the cumulative probability is P(X x). To calculate P(X > x), we must subtract the result from 1. As we see from the following, the normal approximation gives P(X 1520) = , approximately the same as the exact results we obtained previously.
65 CHAPTER 5 Sampling Distributions The Central Limit Theorem We can use Excel to illustrate the central limit theorem. The time a technician takes to service an air conditioning unit is exponentially distributed with mean μ = 1 hour and standard deviation σ = 1 hour. This distribution is strongly right skewed. To generate 250 rows in 25 columns, select Data Data Analysis Random Number Generation from the menu. Specify an output location with 250 rows and 25 columns. Since the exponential distribution is not available in Excel, we will generate data from a Uniform distribution and then transform it into data that is exponentially distributed. 62
66 Sampling Distributions 63 To transform the random numbers to values from an exponential distributions, we use the simple formula Y = ln(u) where U is a uniformly distributed random variable on (0,1) and Y is an exponential random variable with mean equal to 1. For example if you type = ln(a2) into cell Z2:AX251, you will create an observation that is exponentially distributed with with mean μ = 1 hour and standard deviation σ = 1 hour. The formula can easily be copied to create 250 rows and 25 columns from this distribution. To illustrate the Central Limit Theorem, we create a column with the mean of 2 observations, the mean of 5 observations, the mean of 10 observations, and the mean of 25 observations. These are easily created using the AVERAGE function. Select Data Data Analysis Histogram from the menu to produce a histogram of the original data or the mean of 2, 5, 10, or 25 observations. The histograms illustrate the right skewness of the original data and then sample means from 2, 5, 10, and 25 observations. As n increases, the shape of the distribution becomes more Normal. The mean stays at μ = 1 and the standard deviation decreases.
67 64 Chapter 5
68 CHAPTER 6 Introduction to Inference One Sample Z Confidence Interval Confidence intervals for the population mean μ, with σ known, can be calculated in Excel using the AVERAGE and CONFIDENCE functions. This interval goes from x z * ( σ n) to x z * * + ( σ n) where x is the mean of the data, n is the sample size, and z is the critical value from the normal table corresponding to the confidence level. x is calculated using the AVER AGE function and the margin of error, z ( σ n ) *, is calculated using the CONFIDENCE function. To illustrate the confidence interval we consider biologists studying the healing of skin wounds. They measured the rate at which new cells closed a razor cut made in the skin of an anesthetized newt. Here are data from 18 newts, measured in micrometers (millionths of a meter) per hour: We want a 95% confidence interval for the mean rate μ for all newts of this species. We enter the data into column A of an Excel spreadsheet and then calculate x, the mean of these values 65
69 66 Chapter 6 using the AVERAGE function. The function arguments in the CONFIDENCE function are Alpha, Standard_dev, and Size. Alpha is 1 C, where C is the confidence level, Standard_dev is the known population standard deviation, and Size refers to the size of the sample as shown below. Excel calculates the mean to be and the margin of error to be Therefore the 95% confidence interval is (21.97, 29.36). Excel can be used to find the critical value that is used for a specific level of confidence using the NORSMINV function. The NORMSINV function finds the value of z that has a specific area below it. For a level C confidence interval, we want to have an area of ( 1 C) 2 above and below the critical value. If we want the critical value for a 75% level of confidence, a 1 (1 C) 2 = and the critical value not included in Table D, we let C = Therefore, { } value z* is One Sample Z Test As with confidence intervals, we can use Excel to do a hypothesis test for a population mean μ, with σ known. In our example, we consider sweetness loss scores for cola. Suppose we know that for any cola, the sweetness loss scores vary from taster to taster according to a Normal
70 Introduction to Inference 67 distribution with standard deviation σ = 1. The mean μ for all tasters measures loss of sweetness, and is different for different colas. Here are the sweetness losses for a new cola, as measured by 10 trained tasters: We want to determine if there is significant evidence of sweetness loss. This calls for a test of the hypothesis that μ = 0 against the alternative μ > 0. We know that for any cola, the sweetness loss scores vary from taster to taster according to a Normal distribution with standard deviation σ = 1, so we enter that value into the dialog box. To test we use Excel s ZTEST function. The function arguments are the Array or data, the X value, which is the value from the null hypothesis, and Sigma, the population standard deviation. If the lower tail or two tail P value is needed, you must subtract the calculated value and/or double the value.
71 CHAPTER 7 Inference for Distributions One Sample t Procedures An investor was concerned about the poor performance of his portfolio. The data gives the rates of returns for 39 months that the account was managed by a particular broker. Consider the 39 monthly returns as a random sample from the population of monthly returns the broker would generate if he managed the account forever To find a 95% confidence interval for the mean choose Data Data Analysis Descriptive Statistics from the menu. In the dialog box, supply the Input range for the data being analyzed. If there are labels in the first row, check the appropriate box. Indicate where you d like the output and check the Summary Statistics and Confidence Level for Mean boxes along with the confidence level. Click OK to calculate the estimate and margin of error for a 95% confidence interval. 68
72 Inference for Distributions 69 Excel gives the following output indicating that the mean is equal to 1.10 and the margin of er ror is equal to This means that the 95% confidence interval for the mean rate of return is ± 1.94, or ( 3.04, 0.84). Excel calculated the confidence interval as
73 70 Chapter 7 s s x tα to x + tα 2 2 n n where x is the mean of the data, s is the sample standard deviation, n is the sample size, and is the critical value from a t distribution with n 1 degrees of freedom. Since the sample size is equal to 39, t is the critical value from a t distribution with 38 degrees of freedom. α 2 t α 2 You can also compute a confidence interval for the mean improvement by first computing the improvement for each subject and then selecting Data Data Analysis Descriptive Statistics from the menu. The TINV function can be used to find the critical value you would use for a 95% confidence interval based on the t(38) distribution. The function arguments are the Probability, which is 0.05 for a 95% confidence interval, and the Degrees of Freedom. As shown below, the critical value from the t(38) distribution is equal to Matched Pairs In a matched pairs study, subjects are matched in pairs and the outcomes are compared within each matched pair. In this example, subjects worked a paper and pencil maze while wearing masks. Each mask was either unscented or carried a floral scent. The response variable is their mean time on three trials. Each subject worked the maze with both types of mask. The data gives the subjects average times. To assess whether the floral scent significantly improved performance, we test H 0 : μ = 0 H a : μ > 0, where μ is the mean improvement if all subjects received similar instruction.
74 Inference for Distributions 71 To do a t test for matched pairs using Excel, select Data Data Analysis t Test: Paired Two Sample for Means from the Excel menu. Since Paired t evaluates the first sample minus the second sample, we select the Unscented values for Variable 1 and the Scented for Variable 2. The Hypothesized Mean Difference is 0. The large value (0.349) given for the P value shows that the data do not support the claim that floral scents improve performance.
75 72 Chapter 7 Excel does not list a procedure for 1 Sample tests, but it is easy to use the t Test: Paired Two Sample for Means for 1 Sample. Consider the investment example from earlier in this chapter. During the same 39 months, the S&P 500 had an average return of μ = 0.95%. To see if the investors returns are compatible with the S&P 500 average for those same months, we test H 0 : μ = 0.95 H a : μ To do the hypothesis test, enter the investment data in one column and the values from the null hypothesis in another column of the same length. As with paired comparisons, select Data Data Analysis t Test: Paired Two Sample for Means from the Excel menu. Although not intended for this purpose, this works because the calculations are the same for 1 Sample and paired data. Enter the actual data for Variable 1 and the constant values for Variable 2. Check the box for labels, if appropriate, specify the location of the output, and click OK.
76 Inference for Distributions 73 Excel calculates the test statistic as x μ t = 0 s n where x is the mean of the data, s is the sample standard deviation, n is the sample size, and μ 0 is the hypothesized population mean. As shown below, the test statistic t is calculated as The P value of this test is There is strong evidence that the investor s returns were different from the S&P 500 average. We can safely reject H0. Two Sample t Procedures To perform a hypothesis test and of the difference between two population means, select from the Excel menu. Data Data Analysis t Test: Two Sample Assuming Unequal Variances The following example fits the two sample setting. A researcher buried polyester strips in the soil to see how quickly they decay. Five of the strips, chosen at random, were dug up after two weeks. Another five were dug up after 16 weeks. The breaking strength (in pounds) of all 10 strips was measured and entered into an Excel worksheet. The dialog box looks exactly the same as the one for t Test: Paired Sample for Means, however the calculations are very different. Excel calculates the Two Sample t test statistic as t = X s n 1 X s + n 2 This statistic has an approximate t distribution with degrees of freedom given by the Scatter
77 74 Chapter 7 thwaite approximation s1 s df n n = s1 1 s + n n n n Excel rounds the number to an integer, if necessary Enter the actual data for Variable 1 and the constant values for Variable 2 and the Hypothsized Mean Difference equal to 0. Check the box for labels, if appropriate, specify the location of the output, and click OK. We wish to test H 0 : μ 2 = μ16 H a : μ 2 > μ16 so we note that the mean for 2 weeks is larger than the mean for 16 weeks, and we use the 1 tail P value.
78 Inference for Distributions 75 The results show that the P value was calculated to be The experiment did not find convincing evidence that polyester decays more in 16 weeks than in 2 weeks. If a confidence interval is needed, the not equal alternative must be selected on the Options subdialog box. If a confidence interval is needed, we must calculate 2 2 s1 s2 X. 1 X 2 ± t * + n n Fortunately, this is easily down with the previous Excel output. In our example, so the confidence interval is equal to 7.4±2.777 or ( , ). If we select t Test: Two Sample Assuming Equal Variances instead of Unequal Variances, Excel uses a pooled procedure, which assumes that the two populations have equal variances and pools the two sample variances to estimate the common population variance. The test statistic has a t distribution with exactly n 1 + n2 2 degrees of freedom. The pooled procedure can be seriously in error if the variances are not equal. It is recommended that the Equal Variances procedure never be used. 1 2 The F Test for Equality of Variance Consider the experiment to compare the mean breaking strengths of polyester fabric after being buried for two weeks and for 16 weeks. We might also compare the standard deviations to see whether strength loss is more or less variable after 16 weeks. We want to test H 0 : σ 1 = σ 2 : σ σ H a The hypothesis of equal spread can be tested in Excel using an F test by selecting Data Data Analysis F Test Two Sample for Variances 1 from the menu. The F test is not recommended for distributions that are not normal. Before we 2
79 76 Chapter 7 calculate the F statistic, it is important to verify that the distributions are normal. This is done graphically by selecting Data Data Analysis Histogram from the menu. To test the equality of two variances, select Data Data Analysis F Test Two Sample for Variances and fill out the dialog box. Check Samples in one column, Samples in different columns, or Summarized data depending on the format of your data. The F statistic is the ratio of the sample variances, 2 s1 F = 2 s The one tail P value is listed as.0163, but since we are doing a two tail test, the correct P value is equal to 0.033, so the difference between the spread on the two tests is statistically significant at the 5% level. The results from the test follow. 2
80 CHAPTER 8 Inference for Proportions Confidence Intervals for a Single Proportion To compute a confidence interval and perform a hypothesis test of the proportion, select Add Ins WHFStat Proportion Testing One Sample from the menu. In the dialog box, enter the number of successful trials, the sample size, the test proportion from the null hypothesis, and the desired level of confidence. A sample survey found that 170 of a sample of 2673 adult heterosexuals had multiple partners. The sample size is n = 2673 and the count of successes is X = 170. Fill in the data in the dialog box to make a 99% confidence interval for the proportion p of all adult heterosexuals with multiple partners. Although we are not now interested in a hypothesis test, it is required to select a test proportion. 85
81 86 Chapter 8 The output that follows shows that the 99% confidence interval for the proportion of adult heterosexuals with multiple partners is ± or (0.0514, ). A more accurate confidence interval for the population proportion p can be obtained by using the plus four method. ~ X + 2 p = n + 4 This is equivalent to adding two successes and two failures to the actual data. Calculations based on the plus four method are given in the Wilson Estimate section. The confidence interval using this method is ± or ( 0.52,.076). The plus four method is always recommended and is particularly important to do if sample sizes are not large. Significance Tests for a Proportion Consider whether newborn babies are more likely to be boys than girls, presumably to compensate for higher mortality among boys in early life. A random sample found 13,173 boys among 25,468 first born children. The sample proportion of boys is p ˆ = 13,173 25,468 = Is this sample evidence that boys are more common than girls in the entire population? To answer this question we test H0: p = 0.5 Ha: p > 0.5
82 Inference for Proportions 87 In the Testing a Proportion One Sample dialog box, enter the data and the hypothesized proportion. Although we aren t interested in the confidence interval, it is also necessary to select a Confidence Level. Excel calculates the test statistic as pˆ p0 z = p0 ( 1 p0 ) n where pˆ is the observed probability equal to X/n, X is the observed number of successes in n trials, and p 0 is the hypothesized probability. The probabilities are obtained from the standard normal distribution. In other words, Excel uses tests and intervals based on the normal approximation.
83 88 Chapter 8 Excel gives the one sided P value as This means that there is very strong evidence that more than half of newborns are boys. Confidence Interval for Comparing Proportions To compute a confidence interval and perform a hypothesis test of the difference between two proportions, select Add Ins WHFStat Proportion Testing Two Samples from the menu. Enter the summary data, and the confidence level. A random sample by the National Institutes of Health concerns the number of young adults (ages 19 to 25) that still live in their parents home. Included in the sample are 2253 men and 2629 women in this age group. The survey found that 986 of the men and 923 of the women lived with their parents. Here is the data summary: Population n X pˆ = X/n 1 (men) (women) The difference p1 p 2 allows us to see how large the difference is between the proportions of young men and young women who live with their parents. To compute a 95% confidence interval for p1 p 2, select Add Ins WHFStat ProportionTesting Two Samples from the Excel menu. Enter the summarized data in the dialog box, select the 95% Confidence Level, and click OK. Excel calculates the confidence interval as pˆ 1 pˆ 1(1 pˆ ˆ ˆ 1) p2 (1 p2 ) pˆ 2 ± z * +, n n where ˆp 1 and ˆp 2 are the observed probabilities of sample one and sample two, respectively, and p ˆ = X n, where X is the observed success in n trials. 1 2
84 Inference for Proportions 89 The following results show that we are 95% confident that the percent of women living at home is somewhere between 5.9 and 11.4 percentage points lower among women than among men. More Accurate Confidence Intervals A simple modification improves the accuracy of confidence interval for comparing propositions. As with a single proportion, the interval is called the plus four interval because you add four imaginary observations, one success and one failure in each of the two samples. That is, we let ~ X1 + 1 p 1 = and ~ X p 2 = n + 2 n The confidence interval based on this modification is given in the output in the Wilson output section. For this example, the results are about the same as without the modification. The plus four interval is generally much more accurate than the large sample interval when the samples are small. 2
85 90 Chapter 8 Significance Tests for Comparing Proportions We also can use Excel to do significance tests to help us decide if the effect we see in the samples is really there in the populations. The null hypothesis says that there is no difference between the two populations: H0: p1 = p2. In the next example, researchers ask the question, Would you marry a person from a lower social class than your own? Of the 149 men in the sample, 91 said Yes. Among the 236 women, 117 said Yes. To see if there is a statistically significant difference we have a twosided alternative: H0: p1 = p2 Ha: p1 p2 Select Add Ins WHFStat Proportion Testing Two Samples to perform the significance test. Enter the summary information in the dialog box and select a Confidence Level before clicking on OK. Excel uses a pooled estimate of p for the hypothesis test and calculates z as z = pˆ 1 pˆ 2 X1 + X 2, where pˆ = 1 1 n1 + n2 pˆ(1 pˆ) + n1 n 2 Because the P value shown on the following page is equal to 0.027, the results are statistically significant at the α = 0.05 level. There is good evidence that men are more likely than women to say they will marry someone from a lower social class.
86 Inference for Proportions 91
87 CHAPTER 9 Inference for Two Way Tables The Chi Square Test We can use Excel to do a χ 2 test of the null hypothesis that there is no relationship between the column variable and the row variable in a two way table. Our example looks at the health care system in the United States and Canada. The study looked at outcomes a year after a heart attack. One outcome was the patients own assessment of their quality of life relative to what it had been before the heart attack. The data for the patients who survived a year are in an Excel worksheet with the columns Quality of Life and Country. To obtain tables of counts from this data, select Insert Pivot Table from the Excel menu. In the first dialog box enter the table range including the column titles for the variables containing the categories that define the rows and column, of the table, as shown on the following page. Also, choose where the Pivot Table will be placed and then click OK. 92
88 Inference for Two Way Tables 93 An empty Pivot Table will appear along with the Pivot Table Field List. Check variables and move them into the Row Labels and Column Labels fields. In addition, you must move one variable into the Σ Values field as shown. Click the Update button to create a table with counts. Once the data has been summarized, it is helpful to graph the data so that the reported outcomes can be compared for each country. The pivot table automatically orders the variables, in this case alphabetically. Since alphabetical ordering doesn t make sense for the quality of life outcomes, these were coded in a logical order from Much
89 94 Chapter 9 Better to Much Worse. Additionally, the counts were each divided by their column total so that the percentages in each category could be compared. As seen in the table above and the following graph, the reported outcomes look similar in Canada and the United States. The outcome About the Same is selected most frequently and Much Worse is selected the least frequently in both countries. However, there are also differences between the countries as well. In the United States, the outcomes Somewhat Worse and Much Worse are selected less often than in Canada. The chi square test will help us see whether the differences between the two countries are statistically significant. The null hypothesis, H 0 for this test is that there is no association between the row variable and the column variable. H a is that there is an association. In this example, H 0 is that there is no difference between the reported outcomes in the United States and Canada. To perform a chi square test of association between variables, expected cell counts are required. These can be calculated by first copying the row and column totals from the Pivot Table and then calculating the expected counts for the interior cells on the table. The expected count for each outcome/country combination is calculated as Expected count Row = total Column Overall total total as shown in the spreadsheet below.
90 Inference for Two Way Tables 95 Excel s CHITEST function provides the P value for the chi squared test of association between the row and column variables. The function arguments are the actual counts and the expected counts (interior cells) on the tables. The P value for this example is.0195, a small value. This means that there is a statistically significant relationship between patients assessment of their quality of life and the country where they are treated for a heart attack. The number of degrees of freedom for the χ 2 statistic is equal to (rows 1) (columns 1). For our example the degrees of freedom is equal to 4. The χ 2 statistic compares the table of observed counts with the table of expected counts.
91 96 Chapter 9 2 χ = ( observed count - expected count ) expected count 2 Excel does not provide the χ 2 statistic, but since we have the P value, we can work backward to obtain the value using the CHIINV function. The function arguments are the probability, i.e., the P value entered directly from the spreadsheet, and the degrees of freedom. The χ 2 value calculated by Excel is equal to Alternatively, you may select Add Ins WHFStat Two Way Table / Chi Squared Test from the Excel menu and fill in the dialog box as shown below. The results are identical to those described above.
92 Inference for Two Way Tables 97
93 CHAPTER 10 Inference for Regression Estimating the Regression Parameters In the following example we will examine the relationship between bank wages and length of service for 59 married women who hold customer service jobs in Indiana banks. The data are below. WAGES LOS WAGES LOS WAGES LOS WAGES LOS
94 78 Chapter 10 Before attempting inference, examine the data by (1) making a scatterplot; (2) fitting the leastsquares regression, yˆ = b0 + b1x ; (3) checking for outliers and influential observations; and (4) computing the value of r 2. These can all be done at once by making a fitted line plot. First make a scatterplot. Begin by highlighting your data with the explanatory variable to the left of the response variable. Selecting Insert Scatter Scatter with only Markers, then right click on an observation, right click on the scatterplot, select Add Trendline from the list, select Linear on the Trendline Options, check the box next to Display Equation on the chart, and Display R squared value on the chart if desired. The scatterplot shows a moderate linear relationship with no extreme outliers. The leastsquares line is given to be y = x, and r 2 = The change in wages along the regression line as length of service increases explains only about 12% of the variation. The change in wages along the regression line as length of service increases explains only about 12% of the variation. Additional Regression information can be obtained by selecting Data Data Analysis Regression from the Excel menu. The response variable (WAGES) and the explanatory variable (LOS) are entered in the dialog box in the windows labeled Input Y Range and Input X Range, respectively.
95 Inference for Regression 79 The values of b 0 and b 1 are given in the bottom section in the column labeled Coefficients. The first entry in that column is b 0, the intercept, and the second is b1, the slope. We see that b = and b = These are the estimates of β and β Therefore, the regression equation is WAGES = LOS The standard error, s = 82.23, found in the top section, is used to estimate σ, the standard deviation of responses about the true regression line.
96 80 Chapter 10 Remember that before using regression inference, the data must satisfy the regression model assumptions. Use a scatterplot to check that the true relationship is linear. The scatter of the data points about the line should be roughly the same over the entire range of the data. A plot of the residuals against x should not show any pattern. A histogram or stemplot of the residuals should not show any major departures from normality. We have fitted a regression line and we should now examine the residuals. To obtain residual plot, make sure that the Residual plots box is checked as shown on previous page. The residual plots for this data looks satisfactory. You can also check the Residuals box to obtain a list of the residuals. These can be used to make a histogram of the residuals. The assumption of normally distributed residuals also appears to be reasonable. There are no serious deviations from a Normal Distribution. This is important for the inference that follows. Confidence Intervals and Hypothesis Tests for β 0 and β 1 Confidence intervals and tests for the slope and intercept are based on the normal sampling distributions of the estimates b 0 and b 1. Since the standard deviations are not known, a t distribution is used. The value of SE b is It appears in the output from the regression to the 1 right of the estimated slope, b = Similarly, the value of SE b0 is It appears to the right of the estimated constant, b = Confidence intervals for β 0 and β 1 have the form * estimate ± t SEestimate
97 Inference for Regression 81 The TINV function can be used to find the critical value you would use for a 95% confidence interval based on the t(57) distribution. The t distributions for this problem have n 2 = 57 degrees of freedom. The function arguments are the Probability, which is 0.05 for a 95% confidence interval, and the Degrees of Freedom. As shown below, the critical value from the t(57) distribution is equal to The upper and lower bounds for the confidence interval can be calculated with Excel s calculator functions. A 95% confidence interval for β 1 is (.176, 1.005). Fortunately, this calculation isn t needed as the confidence interval is listed in the Excel output on the right side of the bottom section on the same row as the slope. The t statistic and P value for the test of H 0 : β 1 = 0 H a : β 1 0 appear in the columns labeled t Stat and P value. The t ratio can also be obtained from the formula b t = = = 2.85 SE b The P value is listed as We expect that wages will rise with length of service, so our alternative is one sided, H a : β 1 > 0. The P value for this alternative is one half the two sided value; that is, the P value is There is strong evidence that mean wages increase as length of service increases. Confidence intervals and hypothesis tests for β 0 can be obtained similarly. Inference about Prediction We found that the least squares line for predicting WAGES from LOS is y ˆ = x. Excel can be used to predict WAGES for a worker who has been with the bank 125 months either by plugging 125 into the least squares equation or using the TREND function. The
98 82 Chapter 10 function arguments are the data, i.e., the Known y s and the Known x s, and the New x, which is equal to 125 in this example. The last argument is left blank. We may be interested in predicting the mean response, the average earnings of all workers in the subpopulation with 125 months on the job, or we may be interested in predicting the earnings of one individual worker with 125 months of service. The prediction is the same for both, yˆ = dollars per week. However, the margin of error is different for the two kinds of prediction. Individual workers with 125 months of service do not all earn the same amount. So we need a larger margin of error to pin down one worker s earnings than to estimate the mean earnings of all workers who have been with their employer 125 months. The confidence interval for the mea response is y ˆ ± t *SE μˆ. The value for SE μˆ is not listed and must be calculated. The value is most easily calculated using the formula 2 s SE 2 ( ) 2 ˆ μ = + SE b x * x 1 n 2 In this example, s*= 82.23, SE b = 0.207, n = 59, x* = 125, and x = 70.49, is calculated from the 1 values of the explanatory variable (LOS.) Based on the data given below, = The value for t* for 57 degrees of freedom was found previously to be Therefore, the 95% confidence interval for the mean response is equal to ± or (392.0, 454.3). SE μˆ
99 Inference for Regression 83 The individual prediction interval will be wider than the confidence interval for the mean response. This interval is. The value of SE ˆ y is also not given on the Excel output, but it is easily obtained from the following formula SE yˆ = s ( SE ). ˆ μ The value from the formula is 83.7, giving a 95% prediction interval of ± or (255.6, 590.8). Alternatively, the value of is easily approximated by SE 2 y ˆ s + 1. n In this example, the approximation gives a value of
100 CHAPTER 11 Multiple Regression Multiple Regression Multiple regression fits the regression equation μ = β + β X + β X + y L +β k X k to data in selected response and predictor variables. We will illustrate multiple regression with the data showing characteristics of the 30 stocks in the Dow Jones Industrial Average (DJIA). We ll examine how profits are related to sales and assets. To run a multiple regression analysis using Excel, select Data Data Analysis Regression from the menu. In the dialog box, enter the response variable in the Input Y Range window and as many explanatory variables as you like in the Input X Range window. Since you need a single cell range for the x values, all of the explanatory variables must be adjacent. 84
101 Multiple Regression 85 The above output provides the estimated regression coefficients; the intercept, b 0 = , the slope for Assets, b 1 = , and the slope for Sales, b 2 = Therefore, the regression equation is Profits = Assets Sales The estimate of σ is given as s = The estimate is calculated as s = 2 Σei n p 1 where the e iʹs are the residuals and p is the number of predictor variables. In the bottom section, the column marked Standard Error gives the estimated standard errors: = , s = , and s = A level C confidence interval for β can be computed as b1 b2 j s b0
102 86 Chapter 11 b * j ± t s bj where t* is the upper ( 1 C) 2 critical value for the t ( n p 1) distribution. This is exactly the same as for simple linear regression. In that case, p = 1, so the number of degrees of freedom is n 2. 0 j = To test the hypothesis H : β 0, the value of t is computed as b. For each coefficient, the value appears in the column marked t ratio. The values are given as 3.43, 2.16, and The P values for a test against H a : β j 0 are provided in the column marked p and are from the t( n p 1) distribution. j s b j The analysis of variance table for multiple regression is illustrated below. It has the same format as for simple linear regression. The only difference is that the number of degrees of freedom for the model increases from 1 to p, reflecting the fact that there are p explanatory variables. Similarly, the number of degrees of freedom for the error decreases from n 2 to n p 1. Analysis of Variance SOURCE DF SS MS F SIGNIFICANCE F Regression p Σ ( yˆ y) 2 i MSM=SSM/DFM MSM/MSE 2 Error n p 1 Σ ( yi yˆ i ) MSE=SSE/DFE 2 Total n 1 Σ ( y i y) 2 σ The value of MSE is the estimate of. In the example above, it is given as This value could also be obtained by squaring the estimate of σ (s = 2.450). The ratio MSM/MSE is an F statistic for testing the null hypothesis H 0 : β1 = β2 = L = β p = against the alternative hypothesis β 0 for at least one j = 1,2, K, p H a : j The test statistic has the F( p, n p 1) distribution. In the example above, F = The P value listed under the column marked p is given as This means that there is strong evidence that at least one β 0. j The value of R sq is listed above as This means that the proportion of the variation in profits that is explained by assets and sales is 2 SSM R = = SST Remember that before using regression inference, the data must satisfy the regression model assumptions. The scatter of the data points about the line should be roughly the same 0
103 Multiple Regression 87 over the entire range of the data. A plot of the residuals against each explanatory variable should not show any pattern. A histogram of the residuals should not show any major departures from normality. To obtain prediction intervals for a new observation, we can plug the values of the explanatory variable into the least squares regression equation. Alternatively, we use Excel s TREND function to find the predicted value. The function arguments are the values of the response variable, the Known y s, the values of the explanatory variables, the Known x s, and the New x s. The values must be entered in the same order as in the regression equation. The values entered below correspond to Assets = 36 and Sales = 33. As shown below, the predicted value is SE ˆ y The individual prediction interval for an individual response is yˆ ± t *SE is also not given on the Excel output, but it is easily approximated by SE 2 y ˆ s + 1. n yˆ. The value of In this example, the approximation gives a value of The critical value from the t distribution with 27 degrees of freedom is obtained from the TINV function with the arguments, probability = 0.05, and degrees of freedom = 27, giving t* = Therefore, the approximate 95% prediction interval is ± or ( 1.65, 8.59). Model Building When the relationship between a response and an explanatory variable is curved, a quadratic function may be an appropriate model. The data for the following example examines the relationship between the price and size of homes.
104 88 Chapter 11 A scatterplot of the data suggests that a quadratic model may be reasonable for this data. A fitted line plot of the quadratic model is a good way to see if a quadratic relationship is reasonable. To make a fitted line plot, right click on any data point and select Add Trendline from the menu and select a polynomial, order 2 model as shown on the next page. This fits a 2 model of the form yˆ = β + β x + β x
105 Multiple Regression 89 To fully evaluate the model, make a variable for sqft squared. Then select Data Data Analysis Regression to run a regression using sqft and sqft 2.
106 90 Chapter 11 Notice that the individual t tests for both SqFt and SqFt2 are not significant, but the overall F test for the null hypothesis that both coefficients are zero is significant (P value = ). This is due to a high degree of correlation between SqFt and SqFt2. As we will keep one of SqFt and SqFt2, it is natural to keep SqFt and drop its square. When a categorical variable is used for prediction, it is usually best to made variables to indicate whether or not the value is in a particular category. In our example, the data has the number of bedrooms available to predict house prices. We define Bed1, an indicator variable that is equal to 1 if the variable bedrooms is equal to 1. Bed1 is equal to 0, otherwise. The IF function can be used to create indicator variables in Excel. The function arguments are the Logical test, in this case whether or not the variable Bedrooms is equal to 1, the Value if true, in this case, 1, and the Value if false, in this case 0. Copying the formula down the entire column will create the indicator variable.
107 Multiple Regression 91 We can create four indicator variables, Bed1, Bed2, Bed3, and Bed4, because there are four possible bedroom sizes. Alternative variables are possible. For example, we can create a variable that is equal to 1 for homes with 3 or more bedrooms and equal to 0 otherwise. Interaction effects are easily modeled by multiplying two variables together. Variable Selection Excel can help you to select a satisfactory model. Generally, you want a model for which the overall F test for the null hypothesis that all coefficients are zero is significant and all the individual t tests for the explanatory variable are significant. In choosing between different models, you want the model with the highest Adjusted R Squared value. In Excel, the easiest way to select a model is by backward elimination. Select Data Data Analysis Regression or Add Ins WHFStat Correlation and Regression Regression from the Excel menu. Begin with a model containing all the explanatory variables of interest. Then, at each step the variable with highest P value is deleted. Since you need a single cell range for the x values, all of the explanatory variables must continue to be adjacent as variables are eliminated. Continue the procedure until the overall F test is significant and all the individual t tests for the remaining explanatory variable are significant.
108 CHAPTER 12 One Way Analysis of Variance One Way Analysis of Variance Excel can perform a one way analysis of variance test to compare means of different populations. The response variable must be numeric. The data should be entered with each population in separate columns (or rows) on a worksheet. To perform a one way analysis of variance with stacked data, choose Data Data Analysis ANOVA: Single Factor from the Excel menu. Our example comes from a study conducted to compare three educational approaches (basal, DRTA, and strategies) to improve children s reading comprehension. We want to test the null hypothesis that the three groups represent three populations that all have the same mean score on the pretest. The data are given in CA14_001.MTW. The data are arranged with one row for each student. The teaching method is given in one column and the student s pretest score given in a second column. To analyze these data, select Stat ANOVA Oneway from the menu. In the dialog box enter the columns containing the test scores in the Input Range box, check the Chart Titles box, indicate where the output should go, click OK. 114
109 One Way Analysis of Variance 115 It is important to check that the assumptions of one way analysis of variance are satisfied. Specifically, the populations are normal with possibly different means and the same variance. Histogram of the variables serve to detect outliers or extreme deviations from Normality. Compute the ratio of the largest to the smallest sample standard deviation. If this ratio is less than 2 and the histograms are satisfactory, the assumptions of ANOVA are satisfied. Call the mean test scores for the three educational approaches μ 1, μ 2, and μ 3. We want to test the null hypothesis that there are no differences among the test scores for the three groups: H 0 : μ 1 = μ 2 = μ3 The alternative is that there is some difference. H a : not all of μ 1, μ 2, and μ 3 are equal
110 116 Chapter 12 The output provides the ANOVA table. The columns in this table are labeled Source of Variation, SS (sum of squares), df (degrees of freedom), MS (mean square), F, P value, and F crit. The rows in the table are labeled Between Groups, Within Groups, and Total. Consider our model DATA = FIT + RESIDUAL The Between Groups row corresponds to the FIT term, the Within Groups row corresponds to the RESIDUAL term, and the Total row corresponds to the DATA term. Notice that both the degrees of freedom and the sum of squares add to the value in the Total row. The pooled standard deviation can be computed from the ANOVA table using the sum of squares and degrees of freedom for the Within Groups row. That is, which implies that s = p s 2 p = SS DF = = The F statistic is given in the ANOVA table. If is true, the F statistic has an F(DFG,DFE) distribution, where DFG stands for degrees of freedom for groups and DFE stands for degrees of freedom for error. DFG = I 1, the number of groups minus 1. DFE = N I, the number of observations minus the number of groups. The P value for this distribution is also given above. In this example, the P value is given as A P value this large does not give us evidence against the hypothesis that the means are all equal. For information purposes, the output from one way analysis of variance provides the mean and variance for each group. Individual 95% confidence intervals for the means are of the form s p s * * p x + i t, xi t ni ni where x i and ni are the sample mean and sample size for level i, s p = Pooled StDev is the pooled estimate of the common standard deviation, and t* is the value from a t table corresponding to 95% confidence and the degrees of freedom for within groups. Alternatively, the exact same results can be obtained by selecting Add Ins WHFStat Analysis of Variance ANOVA from the Excel menu. Select the radio button for One way Analysis of Variance and fill in the dialog box as shown below. H 0
111 One Way Analysis of Variance 117
112 118 Chapter 13 CHAPTER 13 Two Way Analysis of Variance Cross Tabulation The following data is from a study by researchers conducted on students enrolled in an introductory management course at a large midwestern university. The purpose of the study is to examine if the frequency with which a supermarket product is offered at a discount and the percent reduction affect the price that customers expect to pay for the product. For 10 weeks 160 subjects received information about the products. The treatment conditions corresponded to the number of promotions during this 10 week period and the percent that the product was discounted. Ten students were randomly assigned to each treatment. The case study examines the price customers expect to pay for two levels of promotions (1 and 3) and two levels of discount (40% and 20%). Thus, we have a two way analysis of variance with each of the factors having two levels and 10 observations in each of the four treatment combinations. The data are on the following page. 118
113 Two Way Analysis of Variance 119 Number of promotions Percent discount Expected price The data must be entered with one variable for rows and the other variable for columns as shown below. The input range includes the variable titles in addition to the sample results. Since replication is allowed, you must also specify the number of rows per sample, in this case 10. Select Data Data Analysis Anova: Two Factor With Replication, fill out the Input and Output Range, the Rows per sample, and click OK. Excel provides numerical summaries of the data. The first section of the data gives the Count, Sum, and Variance of the different groups of data. The variance is the square of the sample standard deviation.
114 120 Chapter 13 Interactions Plots Interactions plots can be used to describe the interaction effects in a two way analysis of variance. The averages for the promotions and discount data can be plotted in an interactions plot. Enter the appropriate summary data in Excel, highlight the data and select Insert Line 2 D Line from the menu.
115 Two Way Analysis of Variance 121 The two lines are approximately parallel, suggesting that there is little or no interaction between promotion and discount. The ANOVA Table The results of a two way analysis of variance are given in the ANOVA table. The total variation (SS) is split among the two main effects, the interaction, and the error. The degrees of freedom (df) is split the same way. If the sample size is the same for all groups, as in our example, then SST = SSA + SSB + SSAB + SSE DFT = DFA + DFB + DBAB + DFE Where A and B are the main effects and AB is the interaction. Here is the form of the ANOVA table. Source Degrees of freedom Sum of squares Mean square A I 1 SSA SSA/DFA MSA/MSE B J 1 SSB SSB/DFB MSB/MSE AB SSAB SSAB/DFAB MSAB/MSE Error SSE SSE/DBE Total N 1 SST SST/DFT F There are three null hypotheses in two way analysis of variances, with an F test for each. We test for significance of the two main effects and the interaction. The bottom section of the Excel output provides the ANOVA output. To the right of the F column are columns labeled P value and F crit. The P value is the result of the significance test and the F crit value is the critical value from the F distribution for the selected significance level, in this case As expected, in our example, the interaction is not statistically significant (P value = ) On the other hand, the main effects of discount (sample) and promotion (columns) are significant with P values and 0.040, respectively.
116 122 Chapter 13 Alternatively, the exact same results can be obtained by selecting Add Ins WHFStat Analysis of Variance ANOVA from the Excel menu. Select the radio button for Two way Analysis of Variance and fill in the dialog box as shown below. 122
117 CHAPTER 14 Bootstrap Methods and Permutation Tests Bootstrap methods are based on resampling from data and were first introduced in 1979 for estimating the standard error of the estimate of a parameter. Resampling methods allow us to quantify uncertainty by calculating standard errors and confidence intervals and performing significance tests. They require fewer assumptions than traditional methods and generally give more accurate answers (sometimes very much more accurate). Moreover, resampling lets us tackle new inference settings easily. Resampling also helps us understand the concepts of statistical inference. The bootstrap is best carried out with specialized software that does simulation well and quickly. Excel is not well suited to large scale simulations. However, we will use Excel to demonstrate the principles of the bootstrap with small scale simulations. 123
118 124 Chapter 14 The Bootstrap Procedure Step 1 Resample. Create hundreds of new samples, called bootstrap samples or bootstrap samples resamples, by sampling with replacement from the original random sample. Each resample is the same size as the original random sample. Step 2 Calculate the bootstrap distribution. Calculate the statistic for each resample. The distribution of these resample statistics is called a bootstrap distribution. If we want to estimate the population mean μ, the statistic is the sample mean J. Step 3 Use the bootstrap distribution. The bootstrap distribution gives information about the shape, center, and spread of the sampling distribution of the statistic. The bootstrap standard error of a statistic is the standard deviation of the bootstrap distribution of that statistic. Bootstrap Distribution We show how to create a bootstrap distribution for the spending of a small sample of shoppers. Here are the dollar amounts spent by 50 consecutive shoppers at a supermarket. We are willing to regard this as an SRS of all shoppers at this market To begin with, we will select Add Ins WHFStat Graphs Histogram from the Excel menu. Alternatively, we can select Data Data Analysis Histogram. Either way, we fill in the dialog box to examine the shape of the shopping distribution. The histogram on the following page shows that the data is skewed to right.
119 Bootstrap Methods 125 To create the bootstrap distribution, we will sample with replacement 1000 times and create 1000 samples each of size 50. To sample, enter the observations into a worksheet and enter the probability of each, i.e., Select Data Data Analysis Random Number Generation from the Excel menu. Fill out the dialog box by entering the data and probabilities (without column titles) and the location of the samples. In the dialog box shown below, we choose the Output Range D2:BA1001, a range that will give us 1000 rows each of sample size 50. We calculate the sample mean for each row using Excel s AVERAGE function as shown on the following page.
120 126 Chapter 14 The central limit theorem says that the sampling distribution of the sample mean J becomes Normal as the sample size increases. To find out if the sampling distribution is Normal for n = 50, we make a histogram of the bootstrap distribution of the mean. As we can see from the following histogram, the bootstrap distribution is approximately Normal. We can calculate the mean and standard error for the bootstrap distribution using Excel s AVERAGE and STDEV function as shown below.
121 Bootstrap Methods 127 The mean of the bootstrap distribution is and the bootstrap standard error is All of these values will differ if you repeat 1000 resamples, because resamples are drawn at random. The bootstrap estimate of bias is the mean of the bootstrap distribution minus the statistic for the original data. For the shopping data the mean of the original sample is Therefore, the bootstrap estimate of bias for these resamples is When a bootstrap distribution is approximately Normal and has small bias, an approximate level C confidence interval is statistic ± t * SEboot, statistic A 95% confidence interval for the population mean for the shopping data is therefore ± 1.96(3.209) = (18.61, 41.19). Hypothesis Tests The following example considers a test to determine whether new directed reading activities improved the reading ability of elementary school students, as measured by their Degree of Reading Power (DRP) score. The study assigned students at random to either the new method (treatment group, 21 students) or traditional teaching methods (control group, 23 students). Their DRP scores are given below. Treatment group Control group The statistic that measures the success of the new method is the difference in mean DRP scores,
122 128 Chapter 14 x treatment x control. The null hypothesis is no difference between the two methods. We will use the bootstrap distribution to do a hypothesis test using Excel. To create the bootstrap distribution for the difference between the two methods, we create a discrete probability distribution using the scores for all 44 students. The simplest way is to list all 44 scores and an associated probability of 1/44.. Select Data Data Analysis Random Number Generation from the Excel menu. Fill out the dialog box by entering the data and probabilities (without column titles) and the location of the samples to create 999 resamples each of size 44 into 999 rows. The output range for our samples was D2:AV1000. Since the null hypothesis says that there is no difference between the control group and the treatment group, we arbitrarily select the first 21 columns to be the control group and the remaining 23 columns to be the treatment group. We then calculate the row mean for each group and calculate the difference for each row. That is, we calculate =AVERAGE(E2:Y2) AVERAGE(Z2:AV2) for the first sample. The formula can be copied to calculate the statistic for the remaining samples. This is the bootstrap distribution of the statistic x treatment x control under the condition that the null hypothesis is true. Select Add Ins WHFStat Graph Histogram or Data Data Analysis Histogram from the Excel menu and make a histogram of the values of the statistic. We see that the bootstrap distribution is nearly Normal. The value of the statistic actually observed in the study was x treatment x control = = 9.954
123 Bootstrap Methods 129 Count the number of values that exceed If your data is in column AW, this is easily done by entering =COUNTIF(AW2:AW1000,ʺ>9.954ʺ) into a cell. For these resamples, 17 of the 1000 resamples gave a value or larger. This value will differ if you repeat 1000 resamples, because resamples are drawn at random. The proportion of samples that exceed the observed value is 17/1000 or Recall from Chapter 8 that we can improve the estimate of a population proportion by adding two successes and two failures to the sample. We can similarly improve the estimate of the P value by adding one sample result above the observed statistic. The final bootstrap test estimate of the P value is = = This is a one sided P value. The data give good evidence that the new method beats the standard method.
124 CHAPTER 15 Individual Value Plot Nonparametric Tests The investigations in previous chapters into various methods of inference have proven to be robust and not very sensitive to a moderate lack of normality, especially when the sample size is fairly large. There are several options for dealing with nonnormal distributions. This chapter deals with nonparametric methods, defined as inference procedures that do not require any specific type of population distribution. The analysis is done using existing Excel tools only. The Wilcoxon Rank Sum Test One type of nonparametric test is based on the rank (ordered position) of each observation in the dataset. The Wilcoxon rank sum test addresses the common two sample problem. The rank tests studied in this chapter focus on the center of a population. If a population has a normal distribution, the center is the mean. For a skewed distribution, the center is best represented by the median. The hypotheses for the rank tests will replace the mean with the median as the measure of the center. Observations are ranked by sorting them in order from smallest to largest, combining observations from both datasets (for a two sample problem). The rank of each observation is its position in this ordered list, starting with rank 1 for the smallest observation. If an SRS is taken from each population, there are a total of N observations in all, where N = n 1 + n 2. The sum W of the ranks for the first sample is the Wilcoxon rank sum statistic. The mean of W is defined by: 130
125 Nonparametric Tests 131 The standard deviation is defined by: The Wilcoxon rank sum test rejects the hypothesis that the two populations have identical distributions when the rank sum W is far from its mean. The hypotheses tested are: H 0 : No difference in the distribution of yields against the one sided alternative H a : Yields are systematically higher in weed free plots. The rank sum statistic W becomes approximately Normal as the two sample sizes increase. We can form the test statistic by standardizing W. Use standard Normal probability calculations to find P values for this statistic. Because W takes only whole number values, the continuity correction improves the accuracy of the approximation. The following example follows the setting for the Wilcoxon rank sum test. A researcher planted corn in eight plots of ground, then weeded the corn to allow no weeds in four plots and exactly three weeds per meter in the other four plots. The table here shows yields of corn (bushels per acre) in each of the plots. Weeds per meter Yield (bu/acre) The Wilcoxon rank sum test assumes that the data are independent random samples from two populations that have the same shape (hence the same variance) and a scale that is at least ordinal. The data need not be from normal populations. The first step in the calculation is to sort the data as shown and provide the ranks.
126 132 Chapter 15 Formulas for the calculations are shown in the following spreadsheet. Since the ranks are a simple series, 1, 2, 3, 4,..., type 1 and 2 in the first two cells. Select the cells that contain the starting values. Drag the fill handle down to fill in the remaining ranks. The COUNTIF function counts the number of cells with 0 or 3 weeds. The ADDIF function adds the values of the ranks with 0 or 3 weeds. The test statistic is calculated using the STANDARDIZE function, and the P value is calculated using the NORMSDIST function. Since we have an upper tail test, we must subtract from one as shown below. The results determine the attained significance level of the test using a normal approximation with and without a continuity correction factor. We see from the output that follows that the sum of the ranks in the first group (0 weeds) is W = 23. The approximate P value using the continuity correction is The effect of weeds on yield is not statistically significant at the 0.05 level.
127 Nonparametric Tests 133 Wilcoxon Signed Rank Test We can use Excel to perform a one sample Wilcoxon signed rank test of the median for single samples or matched pairs. The Wilcoxon test assumes that the data are a random sample from a symmetric population that is not necessarily normal. Consider a study of early childhood education. Kindergarten students were asked to tell a fairy tale that had been read to them earlier in the week. Each child told two stories. The first had been read to them and the second had been read and also illustrated with pictures. An expert listened to a recording of the children and assigned a score for certain uses of language. Here and in EG26 06.MTW are the data for five low progress readers in a pilot study: Child Story Story Difference We will test the hypotheses H 0 : scores have the same distribution for both stories H a : scores are systematically higher for Story 2 Because these are matched pairs data, we base our inference on the differences. Enter the differences into an Excel worksheet. Calculate the absolute value of the differences as well. If there are any zero differences, remove them. Sort and then rank the absolute value of the differences. The sum W + of the ranks for the positive differences is the Wilcoxon signed rank statistic. If the distribution of the responses is not affected by the different treatments within pairs, then W + has mean and standard deviation
128 134 Chapter 15 The Wilcoxon signed rank test rejects the hypothesis that there are no systematic differences within pairs when the rank sum W + is far from its mean. Formulas for the calculations are shown in the following spreadsheet. Since the ranks are a simple series, 1, 2, 3, 4,..., type 1 and 2 in the first two cells. Select the cells that contain the starting values. Drag the fill handle down to fill in the remaining ranks. The ADDIF function adds the values of the ranks with positive differences. The test statistic with the continuity correction is calculated using the STANDARDIZE function and the P value is calculated using the NORMSDIST function. Since we have an upper tail test, we must subtract from one as shown below. The following output shows that the observed value W = 9. The Normal approximation with the continuity correction gives the approximate P value of This small sample is not statistically significant. +
129 CHAPTER 16 Logistic Regression The data for logistic regression are n independent observations each consisting of a value of the explanatory variable x and either a success or failure for each trial. Our example concerns an experiment that was designed to examine how well the insecticide rotenone kills an aphid, called Macrosiphoniella sanborni, that feeds on the chrysanthemum plant. The explanatory variable is the concentration (in log of milligrams per liter) of the insecticide. About 50 aphids were exposed to each of five concentrations. Each insect was either killed or not killed. Here are the data, along with the results of some calculations: Concentration x (log scale) Number of insects Number killed Propoertion killed A plot of the proportion killed versus x illustrates the need for logistic regression. If a line is fit to the data, values of x above 2.5 will predict proportions above 1. Similarly, values of x below 0.7 will predict proportions below
130 136 Chapter 16 The logistic regression model removes this difficulty by working with the natural logarithm of the odds, p/(1 p). We use the term log odds for this transformation. As p moves from 0 to 1, the log odds moves through all negative and positive numerical values. We model the log odds as a linear function of the explanatory variable: The plot of log odds versus log concentration is close to linear. The graph strongly suggests that insecticide concentration affects the kill rate in a way that fits the logistic regression model. Unfortunately, we cannot perform logistic regression analysis in Excel. analysis should be done in a statistical program such as SPSS, SAS, or Minitab. Complete
131 CHAPTER 17 Statistics for Quality Pareto Charts Pareto charts are bar graphs with the bars ordered by height. They are often used to isolate the vital few categories on which we should focus our attention. Consider the following example: A large medical center, financially pressed by restrictions on reimbursement by insurers and the government, looked at losses broken down by diagnosis. Government standards place cases into diagnostic related groups (DRGs). For example, major joint replacements (mostly hip and knee) are DRG 209. The data list the nine DRGs with the most losses along with the percent of losses. Since the percents are given, a Pareto chart can be constructed by highlighting the data and selecting Insert Scatter from the menu and then select a scatterplot type. Next, click on the graph and select Design Change Chart Type. In the dialog box, select the Column type. Surprisingly, this gives a different graph from the one that we obtain if we simply select the Column type to begin with. 137
132 138 Chapter 17 The advantage of this approach is that we obtain a bar chart with the DRGs on the x axis and the Percent Loss on the y axis as shown below. The categories in the bar chart above are ordered numerically instead of from most frequent to least frequent as required for a Pareto chart. To change this, highlight the data and select Data Sort from the menu. In the dialog box, specify that you wish to sort Percent Loss values from largest to smallest.
133 Statistics for Quality 139 The axis titles on the Pareto Chart can be obtained by clicking on the graph and then selecting Layout Axis Titles from the Excel menu. The chart below allows us to identify the vital few categories that contain most of the observations. Control Charts for Sample Means Our next example considers a manufacturer of computer monitors. The manufacturer measures the tension of fine wires behind the viewing screen. Tension is measured by an electrical device with output readings in millivolts (mv). The proper tension is 275 mv. Some variation is always present in the production process. When the process is operating properly, the standard deviation of the tension readings is σ = 43 mv. Four measurements are made every hour. The data contain the measurements for 20 hours. The first row of observations is from the first hour, the next row is from the second hour, and so on. There are a total of 80 observations.
134 140 Chapter 17 Excel can be used to produce control charts for sample means by selecting Add Ins WHFStat Graphs Control Chart from the menu. In the dialog box, enter the x values. These values will be plotted on the chart. In addition, a center line, an upper control limit (UCL) at 3σ above the center line, and a lower control limit (LCL) at 3σ below the center line are drawn on the chart. The parameters μ and σ must be specified from historical data by filling in the Process Mean and Process Standard Deviation in the dialog box. In the following dialog box we specify that the historical mean is equal to 275 and the historical standard deviation is equal to 43 and the sample size of 4. The center line is at m = 275 mv. The upper and lower control limits are The x chart for the mesh tension data show that no points lie outside the control limits.
135 Statistics for Quality 141 In practice, we must monitor both the process center, using an x chart, and the process spread, using a control chart for the sample standard deviation s. This is commonly done with an s chart, a chart of standard deviations against time. Usually, the x chart and the s chart will be looked at together. The x chart and s chart can be produced by selecting Add Ins WHFStat Graphs Control Chart from the menu. Check the box next to Add Standard Deviation Chart and enter the data into the dialog box as shown. The samples are of size n = 4 and the process standard deviation in control is σ = 43 mv. The centerline is therefore The control limits are
136 142 Chapter 17 as described in your text. The s chart for the mesh tension data is also in control.
137 CHAPTER 18 Time Series Forecasting Time Series Plots Consider the monthly retail sales data beginning January 1992 and ending May 2002 (125 months). Excel can be used to plot the monthly retail sales by highlighting the data and selecting Insert Scatter Scatter with Straight Lines from the menu. This command plots measurement data on the y axis versus time data on the x axis. If you only have the y axis data in the order that the values appear in the column, in equally spaced time intervals, you may want to use Insert Line to plot the y axis data versus consecutive numbers on the x axis. 143
138 144 Chapter 18 Since January 1992, overall sales have gradually increased and a distinct pattern repeats itself approximately every 12 months. Alternatively, the time series plot can be obtained by selecting Add Ins WHFStat Times Series Forecasting Times Series Scatterplot and filling out the dialog box as shown. Trend Analysis Our example discusses monthly retail sales of General Merchandise Stores beginning January 1992 and ending May 2002 (125 months). The pattern of increasing growth in the time series plot of the retail sales data is an example of a linear trend. Excel can be used to estimate the linear trend. Right click on any point in the graph and select Add Trendline from the menu as shown to fit a general trend model to time series data and provide forecasts.
139 Time Series Forecasting 145 You can choose from among a variety of time series models. Here we select Linear and check the appropriate box to display the equation on the chart. This is best done on a graph with consecutive numerical values on the x axis. Recall that this graph is obtained by highlighting only the sales data and selecting Insert Line from the menu. Excel estimates the linear trend to be yt = t
140 146 Chapter 18 where t is the number of months elapsed beginning with the first month of the time series. We can also use regression techniques to fit a linear model to the above data. This gives additional output. First, create a variable x (or t) where x is the number of months elapsed beginning with the first month of the time series. That is, x = 1 corresponds to January 1992, x = 2 corresponds to February 1992, etc. Next, select Data Data Analysis Regression from the menu. Enter Sales in the Input Y Range and t as the Input X Range. Specify that there are titles in the first row, where you want your output, and click OK. The trend only model ignores the seasonal variation in the retail sales time series. Notice that the R 2 value for the trend only model is 42.9% or To forecast sales, we can either plug in a specific value for x into the regression equation, Yt = t, or we can use Excel s TREND function. For example to forecast the sales for
141 Time Series Forecasting 147 January, we could enter =TREND(C2:C126,B2:B126,133) into a cell. The new value of x is 133, corresponding to the 133rd month, where January 2002 is considered the first month. The resulting forecast is 38,092. Selecting Add Ins WHFStat Times Series Forecasting Times Series Scatterplot and filling out the dialog box as shown gives us another way to obtain the same results. The WHFStat Add In does not require that the values of the explanatory variable be entered. As a default, these values are assumed to be 1, 2, 3,. The results are the same as shown previously, but the output is substantially different as shown below. Exponential Growth
142 148 Chapter 18 Consider the sales of DVD players since the introduction of the DVD format in March At the end of June 2002, nearly 33 million DVD players had been sold in the United States with over 18,000 titles available in the DVD format. The Consumers Electronic Association tracks monthly sales of DVD players. We can highlight the dates and units sold and select Insert Scatter Scatter with Lines from the menu to plot the DVD sales data. Alternatively, we can highlight on the units sold and select Insert Line from the menu to obtain the graph shown. The pattern of increasing growth in this plot is an example of an exponential trend. Excel can be used to estimate the exponential trend. Right click on a point in the graph and select Add Trendline from the menu. In the dialog box, under Trend/Regression Type, choose Exponential. As shown above in the trend analysis, Excel estimates the exponential trend to be yt = 29524e 0.068t where t is the number of months elapsed beginning with the first month of the time series. As with the linear trend, we can select Add Ins WHFStat Times Series Forecasting Forecast and select Exponential (Ln) for the Trendline Type to get the same results as above.
143 Time Series Forecasting 149 Seasonal Models A trend equation may be a good description of the long run behavior of the data, but we need to account for short run phenomena like seasonal variation to improve the accuracy of our forecasts. In this example, we can use indicator variables to add the seasonal pattern to the trend model for the monthly retail sales data. Name the indicator variables X1, X2,.X11. Enter data such that the value of X1 is 1 for January and 0 otherwise. Similarly, the value for X2 is 1 for February and 0 otherwise, etc. We do not need an X12 variable as it would provide the same information as X1, X2,,X11. Select Data Data Analysis Regression from the menu and enter Sales as the Input Y variable. Enter t and all 12 indicator variables as the Input X Variables and click OK. (Recall that we defined the variable x in the previous section as the number of months elapsed beginning with the first month of the time series.) We get the following output from Excel.
144 150 Chapter 18 The R 2 value for the trend and season model is 98.7%, which is a dramatic improvement over the trend only model. Recall that the R 2 value for the trend only model was 42.9%. The forecast value for January 2002 would be (133) = , since in January X1 is equal to 1 and the other indicator variables are equal to 0. A much easier alternative is available by selecting Add Ins WHFStat Times Series Forecasting Forecast and selecting Monthly under Time Periods. Unfortunately, this capability only works if you are using at most five years of data.
145 Time Series Forecasting 151 Autocorrelation The residuals from a regression model that uses time as an explanatory variable should be examined for signs of autocorrelation. Examine the residuals that result from fitting an exponential trend to the DVD player sales data. First, calculate log e (Sales). Name this column lnsales and calculate the values using Excel s LN function. Next, select Data Data Analysis Regression from the menu and regress lnsales on the predictor variable x, where x is the number of months elapsed beginning with the first month of the time series. In the dialog box, check Residual Plots box to obtain the residual plot from the exponential trend model. The pattern in the plot indicates positive autocorrelation among the residuals. An alternative plot for detecting autocorrelation is a lagged residual plot. Create a column of lagged residuals by copying the values one row down as shown. There will be one missing at the top of the output column. The lagged column should have the same number of rows as the Residual column, so the last value from the Residual column does need to be lagged.
146 152 Chapter 18 Next, highlight the residuals and lagged residuals and select Insert Scatter from the menu and plot the residuals versus the lagged residuals. The graph on the following page shows a linear pattern with positive slope. This indicates that the residuals may have positive autocorrelation. Excel can be used to calculate the autocorrelation by calculating the correlation between the residuals and the lagged residuals. This is easily done with the CORREL function. The function arguments are the two arrays of data. Make sure to enter the data from the same rows. In our example, =CORREL(H56:H117,I56:I117) results in a value of 0.616, indicating a strong autocorrelation.
147 Time Series Forecasting 153 When autocorrelation is present, an autoregressive model can be used. The first order autoregressive model specifies a linear relationship between the response variable and the lagged values of the response variable. The shorthand for this model is AR(1). The model can be found with Excel either by making a scatterplot and adding a trendline or by selecting Data Data Analysis Regression from the menu and letting the Input Y Variable be the response variable and the Input X Variable be the lagged values of the response variable. Moving average models With some time series, our forecasts can be obtained by using the average of several past time periods. Moving average models use the average of the last k values of the time series as the forecast for period t. To find the forecasts using Excel, select Data Data Analysis Moving Average from the Excel menu. Specify the values of the time series and the value for k in the dialog box as shown. If you check the Chart Output box, a graph of the time series and the moving average values is provided in addition to the calculated values. The graph for the sales data considered earlier is provided below.
148 154 Chapter 18 The moving average analysis can also be obtained by selecting Add Ins WHFStat Times Series Forecasting Moving Average from the Excel menu. In this case, the output includes the moving average for each point and the error = actual forecast for each point. Exponential smoothing models The exponential smoothing model uses a weighted average of the observed value from and the forecast value for time t 1 to calculate the forecast for time t. The weight, w, is called the smoothing constant and is a value between 0 and 1. The forecasting equation is Choosing w close to 1 puts more weight on the most recent value. = To find the forecasts using Excel, select Data Data Analysis Exponential Smoothing from the menu. Specify the values of the time series and the value for the damping factor (1 w) in the dialog box as shown.
149 Time Series Forecasting 155 If you check the Chart Output box, a graph of the time series and the forecast values is provided in addition to the calculated values. A sample graph is provided below. The exponential smoothing analysis can also be obtained by selecting Add Ins WHFStat Time Series Forecasting Exponential Smoothing from the Excel menu. In this case, the smoothed values are listed and plotted.
150 156 Chapter 1 Exercises 1.3 The rating service Arbitron places U.S. radio stations into more than 50 categories that describe the kind of programs they broadcast. Which formats attract the largest audiences? Here are Arbitronʹs measurements of the share of the listening audience (aged 12 and over) for the most popular formats Format Audience share Country 12.6% News/Talk/Information 10.4% Adult Contemporary 7.1% Pop Contemporary Hit 5.5% Classic Rock 4.7% Rhythmic Contemporary Hit 4.2% Urban Contemporary 4.1% Urban Contemporary 3.4% Oldies 3.3% Hot Adult Contemporary 3.2% Mexican Regional 3.1% (a) What is the sum of the audience shares for these formats? What percent of the radio audience listens to stations with other formats? (b) Make a bar graph to display these data. Be sure to include an ``Other formatʹʹ category. (c) Would it be correct to display these data in a pie chart? Why? 1.5 Births are not, as you might think, evenly distributed across the days of the week. Here are the average numbers of babies born on each day of the week in 2005: Day Births Sunday 7,374 Monday 11,704 Tuesday 13,169 Wednesday 13,038 Thursday 13,013 Friday 12,664 Saturday 8,459
151 157 Present these data in a well labeled bar graph. Would it also be correct to make a pie chart? Suggest some possible reasons why there are fewer births on weekends Table 1.3 shows the annual spending per person on health care in the worldʹs richer countries. Make a stemplot of the data after rounding to the nearest $100 (so that stems are thousands of dollars and leaves are hundreds of dollars). Split the stems, placing leaves 0 to 4 on the first stem and leaves 5 to 9 on the second stem of the same value. Describe the shape, center, and spread of the distribution. Which country is the high outlier? Table 1.3 Annual spending per person on health care (in U.S. dollars) Country Dollars Country Dollars Country Dollars Argentina 1067 Hungary 1269 Poland 745 Australia 2874 Iceland 3110 Portugal 1791 Austria 2306 Ireland 2496 Saudi Arabia 578 Belgium 2828 Israel 1911 Singapore 1156 Canada 2989 Italy 2266 Slovakia 777 Croatia 838 Japan 2244 Slovenia 1669 Czech Republic 1302 Korea 1074 South Africa 669 Denmark 2762 Kuwait 567 Spain 1853 Estonia 682 Lithuania 754 Sweden 2704 Finland 2108 Netherlands 2987 Switzerland 3776 France 2902 New Zealand 1893 United Kingdom 2389 Germany 3001 Norway 3809 United States 5711 Greece 1997 Oman The most popular colors for cars and light trucks change over time. Silver passed green in 2000 to become the most popular color worldwide, then gave way to shades of white in Here is the distribution of colors for vehicles sold in North America in 2007:
152 158 Color Popularity White 19% Silver 18% Black 16% Red 13% Gray 12% Blue 12% Beige, brown 5% Other Fill in the percent of vehicles that are in other colors. Make a graph to display the distribution of color popularity Among persons aged 15 to 24 years in the United States, the leading causes of death and the number of deaths in 2005 were: accidents, 15,567; homicide, 5359; suicide, 4139; cancer, 1717; heart disease, 1067; congenital defects, 483. (a) Make a bar graph to display these data. (b) To make a pie chart, you need one additional piece of information. What is it? spam is the curse of the Internet. Here is a compilation of the most common types of spam: Type of Spam Percent Adult 19 Financial 20 Health 7 Internet 7 Leisure 6 Products 25 Scams 9 Make two bar graphs of these percents, one with bars ordered as in the table (alphabetically) and the other with bars in order from tallest to shortest. Comparisons are easier if you order the bars by height.
153 Table 1.5 gives the number of active medical doctors per 100,000 people in each state. Medical doctors per 100,000 people, by state State Doctors State Doctors State Doctors Alabama 213 Louisiana 264 Ohio 261 Alaska 222 Maine 267 Oklahoma 171 Arizona 208 Maryland 411 Oregon 263 Arkansas 203 Massachusetts 450 Pennsylvania 294 California 259 Michigan 240 Rhode Island 351 Colorado 258 Minnesota 281 South Carolina 230 Connecticut 363 Mississippi 181 South Dakota 219 Delaware 248 Missouri 239 Tennessee 261 Florida 245 Montana 221 Texas 212 Georgia 220 Nebraska 239 Utah 209 Hawaii 310 Nevada 186 Vermont 362 Idaho 169 New Hampshire 260 Virginia 270 Illinois 272 New Jersey 306 Washington 265 Indiana 213 New Mexico 240 West Virginia 229 Iowa 187 New York 389 Wisconsin 254 Kansas 220 North Carolina 253 Wyoming 188 Kentucky 230 North Dakota 242 Dist. of Columbia 798 (a) Why is the number of doctors per 100,000 people a better measure of the availability of health care than a simple count of the number of doctors in a state? (b) Make a histogram that displays the distribution of doctors per 100,000 people. Write a brief description of the distribution. Are there any outliers? If so, can you explain them?
154 Recruitment, the addition of new members to a fish population, is an important measure of the health of ocean ecosystems. The table gives data on the recruitment of rock sole in the Bering Sea from 1973 to Make a stemplot to display the distribution of yearly rock sole recruitment. (Round to the nearest hundred and split the stems.) Describe the shape, center, and spread of the distribution and any striking deviations that you see. Year Recruitment (millions) Year Recruitment (millions) Year Recruitment (millions) Year Recruitment (millions) Make a time plot of the rock sole recruitment data in Exercise What does the time plot show that your stemplot in Exercise 1.37 did not show? When you have time series data, a time plot is often needed to understand what is happening Here are data on the number of people bitten by alligators in Florida over a 36 year period: Year Number Year Number Year Number Year Number
155 161 (a) Make a histogram of the counts of people bitten by alligators. The distribution has an irregular shape. What is the midpoint of the yearly counts of people bitten? (b) Make a time plot. There is great variation from year to year, but also an increasing trend. How many of the 22 years from 1986 to 2007 had more people bitten by alligators than your midpoint from (a)? The trend reflects Floridaʹs growing population, which brings more people close to alligators.
156 162 Chapter 2 Exercises 2.1 Example 1.9 (page 20) gives the breaking strength in pounds of 20 pieces of Douglas fir. Find the mean breaking strength. How many of the pieces of wood have strengths less than the mean? What feature of the stemplot (Figure 1.11, page 21) explains the fact that the mean is smaller than most of the observations? 2.3 Find the mean of the travel times to work for the 20 New York workers in Example 2.3. Compare the mean and median for these data. What general fact does your comparison illustrate? 2.5 Table 1.4 (page 33) gives the ratio of two essential fatty acids in 30 food oils. Find the mean and the median for these data. Make a histogram of the data. What feature of the distribution explains why the mean is more than 10 times as large as the median? 2.29 An alternative presentation of the flower length data in Table 2.1 reports the five number summary and uses boxplots to display the distributions. Do this. Do the boxplots fail to reveal any important information visible in the stemplots in Figure 2.5? 2.35 Here are the survival times in days of 72 guinea pigs after they were injected with infectious bacteria in a medical\ experiment. Survival times, whether of machines under stress or cancer patients after treatment, usually have distributions that are skewed to the right (a) Graph the distribution and describe its main features. Does it show the expected right skew?
157 163 (b) Which numerical summary would you choose for these data? Calculate your chosen summary. How does it reflect the skewness of the distribution? 2.37 Table 1.1 (page 12) gives the percent of foreign born residents in each of the states. For the nation as a whole, 12.5% of residents are foreign born. Find the mean of the 51 entries in Table 1.1. It is not 12.5%. Explain carefully why this happens. (Hint: The states with the largest populations are California, Texas, New York, and Florida. Look at their entries in Table 1.1.)
158 In 2007, the Boston Red Sox won the World Series for the second time in 4 years. Table 2.2 gives the salaries of the 25 players on the Red Sox World Series roster. Provide the team owner with a full description of the distribution of salaries and a brief summary of its most important features. Salaries for the 2007 Boston Red Sox World Series team Player Salary Player Salary Player Salary Josh Beckett $6,666,667 Jon Lester $384,000 Jonathan $425,000 Papelbon Alex Cora $2,000,000 Javier López $402,000 Dustin Pedroia $380,000 Coco Crisp $3,833,333 Mike Lowell $9,000,000 Manny Ramirez $17,016,381 Manny $380,000 Julio Lugo $8,250,000 Curt Schilling $13,000,000 Delcarmen J. D. Drew $14,400,000 D Matsuzaka $6,333,333 Kyle Snyder $535,000 Jacoby Ellsbury $380,000 Doug $750,000 Mike Timlin $2,800,000 Mirabelli Eric Gagné $6,000,000 Hideki $1,225,000 Jason Varitek $11,000,000 Okajimi Eric Hinske $5,725,000 David Ortiz $13,250,000 Kevin Youkilis $424,000 Bobby Kielty $2,100, Businesses know that customers often respond to background music. Do they also respond to odors? Nicolas Guéguen and his colleagues studied this question in a small pizza restaurant in France on Saturday evenings in May. On one evening, a relaxing lavender odor was spread through the restaurant; on another evening, a stimulating lemon odor; a third evening served as a control, with no odor. Table 2.3 shows the amounts (in euros) that customers spent on each of these evenings. Compare the three distributions. What effect did the two odors have on customer spending? Amount spent (euros) by customers in a restaurant when exposed to odors No odor
159 165 Lemon Odor Lavender Odor Farmers know that driving heavy equipment on wet soil compresses the soil and hinders the growth of crops. Table 2.5 gives data on the penetrability of the same soil at three levels of compression. Penetrability is a measure of the resistance plant roots meet when they grow through the soil. Low penetrability means high resistance. How does increasing compression affect penetrability? Table 2.5 Penetrability of soil at three compression levels Compressed Intermediate Loose The stemplot in Exercise 1.19 (page 26) displays the distribution of the percent of residents aged 65 and older in the states. Stemplots help you find the five number summary because they arrange the observations in increasing order. a) Five the five number summary of this distribution. b) Which observations does the 1.5 x IQR rule flag as suspected outliers? ( The rule flags several observations that are clearly not outliers. The reason is that the center half of the observations are close together, so that IQR is small. The example reminds us to use our eyes, not a rule, to spot outliers.
160 Which members of the Boston Red Sox (Table 2.2) have salaries that are suspected outliers by the 1.5 IQR rule?
161 167 Chapter 3 Exercises 3.9 The heights of women aged 20 to 29 are approximately Normal with mean 64 inches and standard deviation 2.7 inches. Men the same age have mean height 69.3 inches with standard deviation 2.8 inches. What are the z scores for a woman 6 feet tall and a man 6 feet tall? Say in simple language what information the z scores give that the actual heights do not The summer monsoon rains in India follow approximately a Normal distribution with mean 852 millimeters (mm) of rainfall and standard deviation 82 mm. (a) In the drought year 1987, 697 mm of rain fell. In what percent of all years will India have 697 mm or less of monsoon rain? (b) Normal rainfall means within 20% of the long term average, or between 683 mm and 1022 mm. In what percent of all years is the rainfall normal? 3.31 Emissions of sulfur dioxide by industry set off chemical changes in the atmosphere that result in acid rain. The acidity of liquids is measured by ph on a scale of 0 to 14. Distilled water has ph 7.0, and lower ph values indicate acidity. Normal rain is somewhat acidic, so acid rain is sometimes defined as rainfall with a ph below 5.0. The ph of rain at one location varies among rainy days according to a Normal distribution with mean 5.4 and standard deviation What proportion of rainy days have rainfall with ph below 5.0? 3.33 Automated manufacturing operations are quite precise but still vary, often with distributions that are close to Normal. The width in inches of slots cut by a milling machine follows approximately the N(0.8750,0.0012) distribution. The specifications allow slot widths between and inch. What proportion of slots meet these specifications? 3.35 The 2008 Chevrolet Malibu with a four cylinder engine has combined gas mileage 25 mpg. What percent of all vehicles have worse gas mileage than the Malibu? 3.37 The quartiles of any distribution are the values with cumulative proportions 0.25 and They span the middle half of the distribution. What are the quartiles of the distribution of gas mileage?
162 Reports on a studentʹs ACT or SAT usually give the percentile as well as the actual score. The percentile is just the cumulative proportion stated as a percent: the percent of all scores that were lower than this one. In 2007, composite ACT scores were close to Normal with mean 21.2 and standard deviation 5.0. Jacob scored 16. What was his percentile? 3.41 The heights of women aged 20 to 29 follow approximately the N(64, 2.7) distribution. Men the same age have heights distributed as N(69.3, 2.8). What percent of young women are taller than the mean height of young men? 3.43 Changing the mean and standard deviation of a Normal distribution by a moderate amount can greatly change the percent of observations in the tails. Suppose that a college is looking for applicants with SAT math scores 750 and above. (a) In 2007, the scores of men on the math SAT followed the N(533, 116) distribution. What percent of men scored 750 or better? (b) Womenʹs SAT math scores that year had the N(499, 110) distribution. What percent of women scored 750 or better? You see that the percent of men above 750 is almost three times the percent of women with such high scores. Why this is true is controversial. (On the other hand, women score higher than men on the new SAT writing test, though by a smaller amount.) 3.49 Here are the lengths in millimeters of the thorax for 49 male fruit flies: (a) Make a histogram of the distribution. Although the result depends a bit on your choice of classes, the distribution appears roughly symmetric with no outliers.
163 169 (b) Find the mean, median, standard deviation, and quartiles for these data. Comparing the mean and the median and comparing the distances of the two quartiles from the median suggest that the distribution is quite symmetric. Why? (c) If the distribution were exactly Normal with the mean and standard deviation you found in (b), what proportion of observations would lie between the two quartiles you found in (b)? What proportion of the actual observations lie between the quartiles (include observations equal to either quartile value). Despite the discrepancy, this distribution is ``close enough to Normalʹʹ for statistical work in later chapters Table 2.5 (page 65) gives data on the penetrability of soil at each of three levels of compression. We might expect the penetrability of specimens of the same soil at the same level of compression to follow a Normal distribution. Make stemplots of the data for loose and for intermediate compression. Does either sample seem roughly Normal? Does either appear distinctly non Normal? If so, what kind of departure from Normality does your stemplot show?
164 170 Chapter 4 Exercises 4.5 Airlines have increasingly outsourced the maintenance of their planes to other companies. Critics say that the maintenance may be less carefully done, so that outsourcing creates a safety hazard. As evidence, they point to government data on percent of major maintenance outsourced and percent of flight delays blamed on the airline (often due to maintenance problems): Airline Outsource percent Delay percent Airline Outsource percent Delay percent AirTran Frontier Alaska Hawaiian American JetBlue America West Northwest ATA Southwest Continental United Delta US Airways Make a scatterplot that shows how delays depend on outsourcing. 4.7 Does your plot for Exercise 4.5 show a positive association between maintenance outsourcing and delays caused by the airline? One airline is a high outlier in delay percent. Which airline is this? Aside from the outlier, does the plot show a roughly linear form? Is the relationship very strong? 4.9 The study of dieting described in Exercise 4.4 collected data on the lean body mass (in kilograms) and metabolic rate (in calories) for both female and male subjects: Sex F F F F F F F F F F Mass Rate Sex F F M M M M M M M Mass
165 171 Rate (a) Make a scatterplot of metabolic rate versus lean body mass for all 19 subjects. Use separate symbols to distinguish women and men. (b) Does the same overall pattern hold for both women and men? What is the most important difference between women and men?
166 The gas mileage of an automobile first increases and then decreases as the speed increases. Suppose that this relationship is very regular, as shown by the following data on speed (miles per hour) and mileage (miles per gallon): Speed Mileage Make a scatterplot of mileage versus speed. Show that the correlation between speed and mileage is r = 0. Explain why the correlation is 0 even though there is a strong relationship between speed and mileage Coffee is a leading export from several developing countries. When coffee prices are high, farmers often clear forest to plant more coffee trees. Here are five years of data on prices paid to coffee growers in Indonesia and the percent of forest area lost in a national park that lies in a coffee producing region: Price (cents per pound) Forest Loss (percent) (a) Make a scatterplot. Which is the explanatory variable? What kind of pattern does your plot show? (b) Find the correlation r between coffee price and forest loss. Do your scatterplot and correlation support the idea that higher coffee prices increase the loss of forest? (c) The price of coffee in international trade is given in dollars and cents. If the prices in the data were translated into the equivalent prices in euros, would the correlation between coffee price and percent of forest loss change? Explain your answer Most people dislike losses more than they like gains. In money terms, people are about as sensitive to a loss of $10 as to a gain of $20. To discover what parts of the brain are active in decisions about gain and loss, psychologists presented subjects with a series of gambles with different odds and different amounts of winnings and losses. From a subjectʹs choices, they constructed a measure of behavioral loss aversion. Higher scores show greater sensitivity to losses. Observing brain activity while subjects made their decisions pointed to
167 173 specific brain regions. Here are data for 16 subjects on behavioral loss aversion and neural loss aversion, a measure of activity in one region of the brain: Neural Behavioral Neural Behavioral (a) Make a scatterplot that shows how behavior responds to brain activity. (b) Describe the overall pattern of the data. There is one clear outlier. (c) Find the correlation r between neural and behavioral loss aversion both with and without the outlier. Does the outlier have a strong influence on the value of r? By looking at your plot, explain why adding the outlier to the other data points causes r to increase Japanese researchers measured the growth of icicles in a cold chamber under various conditions of temperature, wind, and water flow. Table 4.2 contains data produced under two sets of conditions. In both cases, there was no wind and the temperature was set at 11 C. Water flowed over the icicle at a higher rate (29.6 milligrams per second) in Run 8905 and at a slower rate (11.9 mg/s) in Run Time (min) Length (cm) Run 8903 Run 8905 Time (min) Length (cm) Time (min) Length (cm) Time (min) Length (cm)
168 174 (a) Make a scatterplot of the length of the icicle in centimeters versus time in minutes, using separate symbols for the two runs. (b) What does your plot show about the pattern of growth of icicles? What does it show about the effect of changing the rate of water flow on icicle growth? 4.33 To detect the presence of harmful insects in farm fields, we can put up boards covered with a sticky material and examine the insects trapped on the boards. Which colors attract insects best? Experimenters placed six boards of each of four colors at random locations in a field of oats and measured the number of cereal leaf beetles trapped. Here are the data: Board color Beetles trapped Blue Green White Yellow (a) Make a plot of beetles trapped against color (space the four colors equally on the horizontal axis). Which color appears best at attracting beetles? (b) Does it make sense to speak of a positive or negative association between board color and beetles trapped? Why? Is correlation r a helpful description of the relationship? Why? 4.43 We have data from a house in the Midwest that uses natural gas for heating. Will installing solar panels reduce the amount of gas consumed? Gas consumption is higher in cold weather, so the relationship between outside temperature and gas consumption is important. Here are data for 16 consecutive months: Nov. Dec. Jan. Feb. Mar. Apr. May June Degree days per day Gas used per day July Aug. Sep. Oct. Nov. Dec. Jan. Feb. Degree days per day Gas used per day Outside temperature is recorded in degree days, a common measure of demand for heating. A dayʹs degree days are the number of degrees its average
169 175 temperature falls below 65. Gas used is recorded in hundreds of cubic feet. Here are data for 23 more months after installing solar panels: Degree days Gas used Degree days Gas used What do the before and after data show about the effect of solar panels? (Start by plotting both sets of data on the same plot, using two different plotting symbols.) 4.45 We often describe our emotional reaction to social rejection as pain. Does social rejection cause activity in areas of the brain that are known to be activated by physical pain? If it does, we really do experience social and physical pain in similar ways. Psychologists first included and then deliberately excluded individuals from a social activity while they measured changes in brain activity. After each activity, the subjects filled out questionnaires that assessed how excluded they felt. Here are data for 13 subjects. The explanatory variable is social distress measured by each subjectʹs questionnaire score after exclusion relative to the score after inclusion. (So values greater than 1 show the degree of distress caused by exclusion.) The response variable is change in activity in a region of the brain that is activated by physical pain. Discuss what the data show. Subject Social distress Brain activity Subject Social distress Brain activity
170 176 Chapter 5 Exercises 5.3 An outbreak of the deadly Ebola virus in 2002 and 2003 killed 91 of the 95 gorillas in 7 home ranges in the Congo. To study the spread of the virus, measure distance by the number of home ranges separating a group of gorillas from the first group infected. Here are data on distance and number of days until deaths began in each later group: Distance Days As you saw in Exercise 4.10 (page 106), there is a linear relationship between distance x and days y. (a) Use your calculator to find the mean and standard deviation of both x and y and the correlation r between x and y. Use these basic measures to find the equation of the least squares line for predicting y from x. (b) Enter the data into your software or calculator and use the regression function to find the least squares line. The result should agree with your work in (a) up to roundoff error Exercise 4.5 (page 99) gives data for 14 airlines on the percent of major maintenance outsourced and the percent of flight delays blamed on the airline. (a) Make a scatterplot with outsourcing percent as x and delay percent as y. Hawaiian Airlines is a high outlier in the y direction. Because several other airlines have similar values of x, the influence of this outlier is unclear without actual calculation. (b) Find the correlation r with and without Hawaiian Airlines. How influential is the outlier for correlation? (c) Find the least squares line for predicting y from x with and without Hawaiian Airlines. Draw both lines on your scatterplot. Use both lines to predict the percent of delays blamed on an airline that has outsourced 76% of its major maintenance. How influential is the outlier for the least squares line?
171 Keeping water supplies clean requires regular measurement of levels of pollutants. The measurements are indirect a typical analysis involves forming a dye by a chemical reaction with the dissolved pollutant, then passing light through the solution and measuring its absorbence. To calibrate such measurements, the laboratory measures known standard solutions and uses regression to relate absorbence and pollutant concentration. This is usually done every day. Here is one series of data on the absorbence for different levels of nitrates. Nitrates are measured in milligrams per liter of water. Nitrates Absorbence (a) Chemical theory says that these data should lie on a straight line. If the correlation is not at least 0.997, something went wrong and the calibration procedure is repeated. Plot the data and find the correlation. Must the calibration be done again? (b) The calibration process sets nitrate level and measures absorbence. The linear relationship that results is used to estimate the nitrate level in water from a measurement of absorbence. What is the equation of the line used to estimate nitrate level? What is the estimated nitrate level in a water specimen with absorbence 40? (c) Do you expect estimates of nitrate level from absorbence to be quite accurate? Why? 5.37 Exercise 4.29 (page 116) describes an experiment that showed a linear relationship between how sensitive people are to monetary losses ( behavioral loss aversionʹ ) and activity in one part of their brains ( neural loss aversion ). (a) Make a scatterplot with neural loss aversion as x and behavioral loss aversion as y. One point is a high outlier in both the x and y directions. (b) Find the least squares line for predicting y from x, leaving out the outlier, and add the line to your plot. (c) The outlier lies very close to your regression line. Looking at the plot, you now expect that adding the outlier will increase the correlation but will have little effect on the least squares line. Explain why. (d) Find the correlation and the equation of the least squares line with and without the outlier. Your results verify the expectations from (c).
172 People with diabetes must manage their blood sugar levels carefully. They measure their fasting plasma glucose (FPG) several times a day with a glucose meter. Another measurement, made at regular medical checkups, is called HbA. This is roughly the percent of red blood cells that have a glucose molecule attached. It measures average exposure to glucose over a period of several months. Table 5.2 gives data on both HbA and FPG for 18 diabetics five months after they had completed a diabetes education class. Subject HbA (%) Table 5.2 Two measures of glucose level in diabetics FPG (mg/ml) Subject HbA (%) FPG (mg/ml) Subject HbA (%) FPG (mg/ml) (a) Make a scatterplot with HbA as the explanatory variable. There is a positive linear relationship, but it is surprisingly weak. (b) Subject 15 is an outlier in the y direction. Subject 18 is an outlier in the x direction. Find the correlation for all 18 subjects, for all except Subject 15, and for all except Subject 18. Are either or both of these subjects influential for the correlation? Explain in simple language why r changes in opposite directions when we remove each of these points Add three regression lines for predicting FPG from HbA to your scatterplot from Exercise 5.39: for all 18 subjects, for all except Subject 15, and for all except Subject 18. Is either Subject 15 or Subject 18 strongly influential for the leastsquares line? Explain in simple language what features of the scatterplot explain the degree of influence Do beavers benefit beetles? Researchers laid out 23 circular plots, each 4 meters in diameter, in an area where beavers were cutting down cottonwood trees. In each plot, they counted the number of stumps from trees cut by beavers and the number of clusters of beetle larvae. Ecologists think that the new sprouts
173 179 from stumps are more tender than other cottonwood growth, so that beetles prefer them. If so, more stumps should produce more beetle larvae. Here are the data: Stumps Beetle Larvae Stumps Beetle Larvae Analyze these data to see if they support the beavers benefit beetles idea Exercise 4.3 (page 121) gives monthly data on outside temperature (indegree days per day) and natural gas consumed for a house in the Midwest both before and after installing solar panels. A cold winter month in this location may average 45 degree days per day (temperature 20 o F). Use before and after regression lines to estimate the savings in gas consumption due to solar panels Exercise 4.43 (page 121) gives monthly data on outside temperature (in degree days per day) and natural gas consumed for a house in the Midwest both before and after installing solar panels. A cold winter month in this location may average 45 degree days per day (temperature 20 ). Use before and after regression lines to estimate the savings in gas consumption due to solar panels.
174 180 Chapter 6 Exercises 6.1 Recycling is supposed to save resources. Some people think recycled products are lower in quality than other products, a fact that makes recycling less practical. Here are data on attitudes toward coffee filters made of recycled paper among people who had bought these filters and people who had not: Think the quality of the recycled product is Higher The same Lower Buyers Nonbuyers (a) How many people does this table describe? How many of these were buyers of coffee filters made of recycled paper? (b) Give the marginal distribution of opinion about the quality of recycled filters. What percent of consumers think the quality of the recycled product is the same or higher than the quality of other filters? 6.3 Exercise 6.1 gives data on the opinions of people who have and have not bought coffee filters made from recycled paper. To see the relationship between opinion and experience with the product, find the conditional distributions of opinion (the response variable) for buyers and nonbuyers. What do you conclude? 6.7 Which hospital is safer? To help consumers make informed decisions about health care, the government releases data about patient outcomes in hospitals. You want to compare Hospital A and Hospital B which serve your community. The table presents data on all patients undergoing surgery in a recent time period. The data include the condition of the patient ( good or poor ) before the surgery. Survived means the patient lived at least 6 weeks after surgery. Good Condition Poor Condition Hospital A Hospital B Hospital A Hospital B Died 6 8 Died 57 8 Survived Survived Total Total
175 181 a) Compare the percents to show Hospital A gas a higher survival rate for both groups of patients. b) Combine the data into a single two way table of outcome ( survived or died ) by Hospital ( A or B ). The local paper reports just these overall survival rates. Which hospital has the higher rate? c) Explain from the data, in language a reporter can understand, how Hospital B can do better overall even though Hospital A does better for both groups of patients Will giving cocaine addicts an antidepressant drug help them break their addiction? An experiment assigned 24 chronic cocaine users to take the antidepressant drug desipramine, another 24 to take lithium, and another 24 to take a placebo. (Lithium is a standard drug to treat cocaine addiction. A placebo is a dummy pill, used so that the effect of being in the study but not taking any drug can be seen.) After three years, 14 of the 24 subjects in the desipramine group had remained free of cocaine, along with 6 of the 24 in the lithium group and 4 of the 24 in the placebo group. (a) Make up a two way table of Treatment received by whether or not the subject remained free of cocaine. (b) Compare the effectiveness of the three treatments in preventing use of cocaine by former addicts. Use percents and draw a bar graph. What do you conclude? 6.25 Discrimination? Wabash Tech has two professional schools, business and law. Here are two way tables of applicants to both schools, categorized by gender and admission decision. Business Law Admit Deny Admit Deny Male Male Female Female a) Make a two way table of gender by admission decision for the two professional schools together by summing entries in these tables. b) From the two way table, calculate the percent of male applicants who are admitted and the percent of female applicants who are admitted. Wabash admits a higher percent of male applicants.
176 182 c) Now compute separately the percents of male and female applicants admitted by the law school and the business school. Each school admits a higher percent of female applicants. d) This is Simpsons Paradox: both schools admit a higher percent of women who apply, but overall Wabash admits a lower percent of female applicants than male applicants. Explain carefully, as if speaking to a skeptical reporter, how it can happen that Wabash appears to favor males when each school individually favors females The University of Chicagoʹs General Social Survey asked a representative sample of adults this question: Which of the following statements best describes how your daily work is organized? 1: I am free to decide how my daily work is organized. 2: I can decide how my daily work is organized, within certain limits. 3: I am not free to decide how my daily work is organized. Here is a two way table of the responses for three levels of education: Highest Degree Completed Response Less than high school High school Bachelor s How does freedom to organize you work depend on level of education? 6.29 Colleges and universities across the country are grappling with the case of the mysteriously vanishing male. So said an article in the Washington Post. Here are data on the numbers of degrees earned in , as projected by the National Center for Education Statistics. The table entries are counts of degrees in thousands. Female Male Associate s Bachelor s Master s Professional Doctor s Briefly contrast the participation of men and women in earning degrees.
177 Do angry people have more heart disease? People who get angry easily tend to have more heart disease. That s the conclusion of a study that followed a random sample of 12,986 people from three locations for about four years. All subjects were free of heart disease at the beginning of the study. The subjects took the Spielberger Trait Anger Scale test, which measures how prone a person is to sudden anger. Here are data for the 8474 people in the sample who had normal blood pressure. CHD stands for Coronary Heart Disease. This includes people who had heart attacks and those who needed treatment for heart disease. Low anger Moderate High Anger Total Anger CHD No CHD Total Do these data support the study s conclusion about the relationship between anger and heart disease?
178 184 Chapter 7 Exercises 7.3 The Pew Research Center asked a random sample of adults whether they had favorable or unfavorable opinions of a number of major companies. Answers to such questions depend a lot on recent news. Here are the percents with favorable opinions for several of the companies: Company Percent Favorable Apple 71 Ben and Jerry s 59 Coors 53 Exxon/Mobil 44 Google 73 Haliburton 25 McDonald s 71 Microsoft 78 Starbucks 64 Wal Mart 68 Make a graph that displays these data. 7.5 Here are the weights (in milligrams) of 58 diamonds from a nodule carried up to the earthʹs surface in surrounding rock. This represents a single population of diamonds formed in a single event deep in the earth Make a graph that shows the distribution of weights of diamonds. Describe the shape of the distribution and any outliers. Use numerical measures appropriate for the shape to describe the center and spread. 7.9 The Aleppo pine and the Torrey pine are widely planted as ornamental trees in Southern California. Here are the lengths (centimeters) of 15 Aleppo pine needles:
179 Here are the lengths of 18 needles from Torrey pines: Use five number summaries and boxplots to compare the two distributions. Given only the length of a needle, do you think you could say which pine species it comes from? 7.11 Deleting Outliers. In exercise 7.9 you gave five number summaries for two distributions of lengths of pine needles. Do the data contain any observations that are suspected outliers by the 1.5xIQR rule? 7.15 The lengths of needles from Aleppo pines follow approximately the Normal distribution with mean 9.6 centimeters (cm) and standard deviation 1.6 cm. According to the rule, what range of lengths covers the center 95% of Aleppo pine needles? What percent of needles are less than 6.4 cm long? 7.17 Almost all medical schools in the United States require applicants to take the Medical College Admission Test (MCAT). The scores of applicants on the biological sciences part of the MCAT in 2007 were approximately Normal with mean 9.6 and standard deviation 2.2. For applicants who actually entered medical school, the mean score was 10.6 and the standard deviation was 1.7. (a) What percent of all applicants had scores higher than 13? (b) What percent of those who entered medical school had scores between 8 and 12? 7.19 From Rex Boggs in Australia comes an unusual data set: before showering in the morning, he weighed the bar of soap in his shower stall. The weight goes down as the soap is used. The data appear below (weights in grams). Notice that Mr.\ Boggs forgot to weigh the soap on some days. Day Weight Day Weight Day Weight Plot the weight of the bar of soap against day. Is the overall pattern roughly
180 186 linear? Based on your scatterplot, is the correlation between day and weight close to 1, positive but not close to 1, close to 0, negative but not close to 1, or close to 1? Explain your answer. Then find the correlation r to verify what you concluded from the graph Animals and people that take in more energy than they expend will get fatter. Here are data on 12 rhesus monkeys: 6 lean monkeys (4% to 9% body fat) and 6 obese monkeys (13% to 44% body fat). The data report the energy expended in 24 hours (kilojoules per minute) and the lean body mass (kilograms, leaving out fat) for each monkey. Lean Obese Mass Energy Mass Energy (a) What is the mean lean body mass of the lean monkeys? Of the obese monkeys? Because animals with higher lean mass usually expend more energy, we canʹt directly compare energy expended (b) Instead, look at how energy expended is related to body mass. Make a scatterplot of energy versus mass, using different plot symbols for lean and obese monkeys. Then add to the plot two regression lines, one for lean monkeys and one for obese monkeys. What do these lines suggest about the monkeys? 7.25 That animal species produce more offspring when their supply of food goes up isnʹt surprising. That some animals appear able to anticipate unusual food abundance is more surprising. Red squirrels eat seeds from pine cones, a food source that occasionally has very large crops (called seed masting). Here are data on an index of the abundance of pine cones and average number of offspring per female over 16 years: Cone Index Offspring Cone Index Offspring
181 187 Describe the relationship with both a graph and numerical measures, then summarize in words. What is striking is that the offspring are conceived in the spring, before the cones mature in the fall to feed the new young squirrels through the winter The usual way to study the brainʹs response to sounds is to have subjects listen to pure tones. The response to recognizable sounds may differ. To compare responses, researchers anesthetized macaque monkeys. They fed pure tones and also monkey calls directly to their brains by inserting electrodes. Response to the stimulus was measured by the firing rate (electrical spikes per second) of neurons in various areas of the brain. Table 7.1 contains the responses for 37 neurons. Table 7.1 Neuron response to tones and monkey calls Neuron Tone Call Neuron Tone Call Neuron Tone Call (a) One important finding is that responses to monkey calls are generally stronger than responses to pure tones. For how many of the 37 neurons is this true? (b) We might expect some neurons to have strong responses to any stimulus and others to have consistently weak responses. There would then be a strong relationship between tone response and call response. Make a scatterplot of monkey call response against pure tone response (explanatory variable). Find the correlation r between tone and call responses. How strong is the linear relationship?
182 We have 91 years of data on the date of ice breakup on the Tanana River. Describe the distribution of the breakup date with both a graph or graphs and appropriate numerical summaries. What is the median date (month and day) for ice breakup? Table 7.3 Days from April 20 for the Tanana River tripod to fall Year Day Year Day Year Day Year Day Year Day Year Day More on Global Warming. Side by side boxplots offer a different look at the data. Group the data into periods of roughly equal length: , , , and Make boxplots to compare ice breakup dates in these four time periods. Write a brief description of what the plots. Show Here is one way that nature regulates the size of animal populations: High population density attracts predators, who remove a higher proportion of the population than when the density of the prey is low. One study looked at kelp perch and their common predator, the kelp bass. The researcher set up four large circular pens on the sandy ocean bottom in southern California. He chose young perch at random from a large group and placed 10, 20, 40, and 60 perch in the four pens. Then he dropped the nets protecting the pens, allowing bass to swarm in, and counted the perch left after 2 hours. Here are data on the proportions of perch eaten in four repetitions of this setup:
183 189 Perch Proportion killed Do the data support the principle that more prey attract more predators, who drive down the number of prey? Follow the four step process (page 55) in your answer Change in the Serengeti. Long term records from the Serengeti National Park in Tanzania show interesting ecological relationships. When wildebeasts are more abundant, they graze grass more heavily, so there are fewer fires and more trees grow. Lions feed more successfully when there are more trees, so the lion population increases. Here are the data on one part of the cycle, wildebeest abundance (in thousands of animals) and the percent of grass area that burned in the same year.
184 190 Wildebeasts (1000s Percent burned Wildebeasts (1000s) Percent burned Wildebeasts (1000s) Percent burned To what extent do these data support the claim that more wildebeest reduce the percent of grassland that burn? How rapidly does burned area decrease as the number of wildebeest increases? Include a graph and suitable calculations Table 7.1 (page 188) contains data on the response of 37 monkey neurons to pure tones and to monkey calls. You made a scatterplot of these data in Exercise (a) Find the least squares line for predicting a neuronʹs call response from its pure tone response. Add the line to your scatterplot. Mark on your plot the point (call it A) with the largest residual (either positive or negative) and also the point (call it B) that is an outlier in the x direction. (b) How influential are each of these points for the correlation r? (c) How influential are each of these points for the regression line?
185 191 Chapter 8 Exercises 8.7 A firm wants to understand the attitudes of its minority managers toward its system for assessing management performance. Below is a list of all the firm s managers who are members of minority groups. Use Table B at line 139 to choose six to be interviewed in detail about the performance appraisal system. 1 Abdulhamid 8 Duncan 15 Huang 22 Puri 2 Agarwal 9 Fernandez 16 Kim 23 Richards 3 Baxter 10 Fleming 17 Lumumba 24 Rodriguez 4 Bonds 11 Gates 18 Mourning 25 Santiago 5 Brown 12 Gomez 19 Nguyen 26 Shen 6 Castro 13 Gupta 20 Peters 27 Vargas 7 Chavez 14 Hernandez 21 Peña 28 Wang 8.11 Cook County, Illinois, has the second largest population of any county in the United States (after Los Angeles County, California). Cook County has 30 suburban townships and an additional 8 townships that make up the city of Chicago. The suburban townships are Barrington Elk Grove Maine Orland Riverside Berwyn Evanston New Trier Palatine Schaumburg Bloom Hanover Niles Palos Stickney Bremen Lemont Northfield Proviso Thornton Calumet Leyden Norwood Park Rich Wheeling Cicero Lyons Oak Park River Forest Worth The Chicago townships are Hyde Park Lake North Chicago South Chicago Jefferson Lake View Rogers Park West Chicago Because city and suburban areas may differ, the first stage of a multistage sample chooses a stratified sample of 6 suburban townships and 4 of the more heavily populated Chicago townships. Use Table B or software to choose this sample. (If you use Table B, assign labels in alphabetical order and start at line 101 for the suburbs and at line 110 for Chicago.)
186 You want to ask a sample of college students the question How much do you trust information about health that you find on the Internet a great deal, somewhat, not much, or not at all? You try out this and other questions on a pilot group of 10 students chosen from your class. The class members are Anderson Deng Glaus Nguyen Samuels Arroyo De Ramos Helling Palmiero Shen Batista Drasin Husain Percival Tse Bell Eckstein Johnson Prince Velasco Burke Fernandez Kim Puri Wallace Cabrera Fullmer Molina Richards Washburn Calloway Gandhi Morgan Rider Zabidi Delluci Garcia Murphy Rodriguez Zhao Choose an SRS of 10 students. If you use Table B, start at line To gather data on a 1200 acre pine forest in Louisiana, the U.S. Forest Service laid a grid of 1410 equally spaced circular plots over a map of the forest. A ground survey visited a sample of 10% of these plots. (a) How would you label the plots? (b) Choose the first 5 plots in an SRS of 141 plots. (If you use Table B, start at line 105.) 8.39 At a large block party there are 290 men and 110 women. You want to ask opinions about how to improve the next party. To be sure that womenʹs opinions are adequately represented, you decide to choose a stratified random sample of 20 men and 20 women. Explain how you will assign labels to the names of the people at the party. Give the labels of the first 3 men and the first 3 women in your sample. If you use Table B, start at line 130.
187 193 Chapter 9 Exercises 9.9 The changing climate will probably bring more rain to California, but we donʹt know whether the additional rain will come during the winter wet season or extend into the long dry season in spring and summer. Kenwyn Suttle of the University of California at Berkeley and his coworkers carried out a randomized controlled experiment to study the effects of more rain in either season. They randomly assigned plots of open grassland to 3 treatments: added water equal to 20% of annual rainfall either during January to March (winter) or during April to June (spring), and no added water (control). Thirty six circular plots of area 70 square meters were available (see the photo), of which 18 were used for this study. One response variable was total plant biomass, in grams per square meter, produced in a plot over a year. (a) Outline the design of the experiment, following the model of Figure 9.4. (b) Number all 36 plots and choose 6 at random for each of the 3 treatments. Be sure to explain how you did the random selection Elementary schools in rural India are usually small, with a single teacher. The teachers often fail to show up for work. Here is an idea for improving attendance: give the teacher a digital camera with a tamper proof time and date stamp and ask a student to take a photo of the teacher and class at the beginning and end of the day. Offer the teacher better pay for good attendance, verified by the photos. Will this work? A randomized comparative experiment started with 120 rural schools in Rajasthan and assigned 60 to this treatment and 60 to a control group. Random checks for teacher attendance showed that 21% of teachers in the treatment group were absent, as opposed to 42% in the control group (a) Outline the design of this experiment. (b) Label the schools and choose the first 10 schools for the treatment group. If you use Table B, start at line Some people think that red wine protects moderate drinkers from heart disease better than other alcoholic beverages. This calls for a randomized comparative experiment. The subjects were healthy men aged 35 to 65. They were randomly assigned to drink red wine (9 subjects), drink white wine (9 subjects), drink white wine and also take polyphenols from red wine (6 subjects),
188 194 take polyphenols alone (9 subjects), or drink vodka and lemonade (6 subjects). Outline the design of the experiment and randomly assign the 39 subjects to the 5 groups. If you use Table B, start at line Doctors identify chronic tension type headaches as headaches that occur almost daily for at least six months. Can antidepressant medications or stress management training reduce the number and severity of these headaches? Are both together more effective than either alone? (a) Use a diagram like Figure 9.2 to display the treatments in a design with two factors: medication yes or no and stress management yes or no. Then outline the design of a completely randomized experiment to compare these treatments. (b) The headache sufferers named below have agreed to participate in the study. Randomly assign the subjects to the treatments. If you use the Simple Random Sample applet or other software, assign all the subjects. If you use Table A, start at line 130 and assign subjects to only the first treatment group. Abbott Decker Herrera Lucero Richter Abdalla Devlin Hersch Masters Riley Alawi Engel Hurwitz Morgan Samuels Broden Fuentes Irwin Nelson Smith Chai Garrett Jiang Nho Suarez Chuang Gill Kelley Ortiz Upasani Cordoba Glover Kim Ramdas Wilson Custer Hammond Landers Reed Xiang 9.41 Hereʹs the opening of a Starbucks press release: Starbucks Corp. on Monday said it would roll out a line of blended coffee drinks intended to tap into the growing popularity of reduced calorie and reduced fat menu choices for Americans. You wonder if Starbucks customers like the new ``Mocha Frappuccino Lightʹʹ as well as the regular Mocha Frappuccino coffee. (a) Describe a matched pairs design to answer this question. Be sure to include proper blinding of your subjects. (b) You have 20 regular Starbucks customers on hand. Use the Simple Random Sample applet or Table B at line 141 to do the randomization that your design requires.
189 195 Chapter 10 Exercises A couple plans to have three children. There are 8 possible arrangements of girls and boys. For example, GGB means the first two children are girls and the third child is a boy. All 8 arrangements are (approximately) equally likely. (a) Write down all 8 arrangements of the sexes of three children. What is the probability of any one of these arrangements? (b) Let X be the number of girls the couple has. What is the probability that X = 2? (c) Starting from your work in (a), find the distribution of X. That is, what values can X take, and what are the probabilities for each value? A sample survey contacted an SRS of 663 registered voters in Oregon shortly after an election and asked respondents whether they had voted. Voter records show that 56\% of registered voters had actually voted. We will see later that in this situation the proportion of the sample who voted (call this proportion V) has approximately the Normal distribution with mean μ = 0.56 and standard deviation σ = (a) If the respondents answer truthfully, what is P(0.52 V 0.60)? This is the probability that the sample proportion V estimates the population proportion 0.56 within plus or minus (b) In fact, 72% of the respondents said they had voted (V = 0.72). If respondents answer truthfully, what is P(V 0.72)? This probability is so small that it is good evidence that some people who did not vote claimed that they did vote.
190 196 Chapter 11 Exercises 11.7 Letʹs illustrate the idea of a sampling distribution in the case of a very small sample from a very small population. The population is the scores of 10 students on an exam: Student Score The parameter of interest is the mean score μ in this population. The sample is an SRS of size n = 4 drawn from the population. Because the students are labeled 0 to 9, a single random digit from Table B chooses one student for the sample. (a) Find the mean of the 10 scores in the population. This is the population mean μ (b) Use the first digits in row 116 of Table B to draw an SRS of size 4 from this population. What are the four scores in your sample? What is their mean x? This statistic is an estimate of μ. (c) Repeat this process 9 more times, using the first digits in rows 117 to 125 of Table B. Make a histogram of the 10 values of x. You are constructing the sampling distribution of x. Is the center of your histogram close to μ? 11.9 Suppose that in fact the blood cholesterol level of all men aged 20 to 34 follows the Normal distribution with mean μ = 188 milligrams per deciliter (mg/dl) and standard deviation σ = 41 mg/dl. (a) Choose an SRS of 100 men from this population. What is the sampling distribution of x? What is the probability that x takes a value between 185 and 191 mg/dl? This is the probability that x estimates μ within ± 3 mg/dl. (b) Choose an SRS of 1000 men from this population. Now what is the probability that x falls within ± 3 mg/dl of μ? The larger sample is much more likely to give an accurate estimate of μ An insurance company knows that in the entire population of millions of homeowners, the mean annual loss from fire is μ = 250 and the standard deviation of the loss is σ = The distribution of losses is strongly right
191 197 skewed: most policies have $0 loss, but a few have large losses. If the company sells 10,000 policies, can it safely base its rates on the assumption that its average loss will be no greater than $275? Follow the four step process as illustrated in Example Sheliaʹs doctor is concerned that she may suffer from gestational diabetes (high blood glucose levels during pregnancy). There is variation both in the actual glucose level and in the blood test that measures the level. A patient is classified as having gestational diabetes if the glucose level is above 140 milligrams per deciliter (mg/dl) one hour after having a sugary drink. Sheliaʹs measured glucose level one hour after the sugary drink varies according to the Normal distribution with μ = 125 mg/dl and σ = 10 mg/dl. (a) If a single glucose measurement is made, what is the probability that Shelia is diagnosed as having gestational diabetes? (b) If measurements are made on 4 separate days and the mean result is compared with the criterion 140 mg/dl, what is the probability that Shelia is diagnosed as having gestational diabetes? Sheliaʹs measured glucose level one hour after a sugary drink varies according to the Normal distribution with μ = 125 mg/dl and σ = 10 mg/dl. What is the level L such that there is probability only 0.05 that the mean glucose level of 4 test results falls above L? (Hint: This requires a backward Normal calculation. See page 83 in Chapter 3 if you need to review.) The number of accidents per week at a hazardous intersection varies with mean 2.2 and standard deviation 1.4. This distribution takes only whole number values, so it is certainly not Normal. (a) Let x be the mean number of accidents per week at the intersection during a year (52 weeks). What is the approximate distribution of x according to the central limit theorem? (b) What is the approximate probability that x is less than 2? (c) What is the approximate probability that there are fewer than 100 accidents at the intersection in a year? (Hint: Restate this event in terms of x.)
192 Andrew plans to retire in 40 years. He plans to invest part of his retirement funds in stocks, so he seeks out information on past returns. He learns that over the entire 20th century, the real (that is, adjusted for inflation) annual returns on U.S. common stocks had mean 8.7% and standard deviation 20.2%. The distribution of annual returns on common stocks is roughly symmetric, so the mean return over even a moderate number of years is close to Normal. What is the probability (assuming that the past pattern of variation continues) that the mean annual return on common stocks over the next 40 years will exceed 10%? What is the probability that the mean return will be less than 5%? Follow the four step process as illustrated in Example Unlike Joe (see the previous exercise) the operators of the numbers racket can rely on the law of large numbers. It is said that the New York City mobster Casper Holstein took as many as 25,000 bets per day in the Prohibition era. Thatʹs 150,000 bets in a week if he takes Sunday off. Casperʹs mean winnings per bet are $0.40 (he pays out 60 cents of each dollar bet to people like Joe and keeps the other 40 cents.) His standard deviation for single bets is about $18.96, the same as Joeʹs. (a) What are the mean and standard deviation of Casperʹs average winnings x on his 150,000 bets? (b) According to the central limit theorem, what is the approximate probability that Casperʹs average winnings per bet are between $0.30 and $0.50? After only a week, Casper can be pretty confident that his winnings will be quite close to $0.40 per bet.
193 199 Chapter 12 Exercises 12.9 Suppose that 10% of adults belong to health clubs, and 40% of these health club members go to the club at least twice a week. What percent of all adults go to a health club at least twice a week? Write the information given in terms of probabilities and use the general multiplication rule New York Stateʹs Quick Draw lottery moves right along. Players choose between one and ten numbers from the range 1 to 80; 20 winning numbers are displayed on a screen every four minutes. If you choose just one number, your probability of winning is 20/80, or Lester plays one number 8 times as he sits in a bar. What is the probability that all 8 bets lose? Slot machines are now video games, with outcomes determined by random number generators. In the old days, slot machines were like this: you pull the lever to spin three wheels; each wheel has 20 symbols, all equally likely to show when the wheel stops spinning; the three wheels are independent of each other. Suppose that the middle wheel has 9 cherries among its 20 symbols, and the left and right wheels have 1 cherry each. (a) You win the jackpot if all three wheels show cherries. What is the probability of winning the jackpot? (b) There are three ways that the three wheels can show two cherries and one symbol other than a cherry. Find the probability of each of these ways. (c) What is the probability that the wheels stop with exactly two cherries showing among them?
194 200 Chapter 13 Exercises 13.5 Typing errors in a text are either nonword errors (as when the is typed as teh ) or word errors that result in a real but incorrect word. Spell checking software will catch nonword errors but not word errors. Human proofreaders catch 70% of word errors. You ask a fellow student to proofread an essay in which you have deliberately made 10 word errors. (a) If the student matches the usual 70% rate, what is the distribution of the number of errors caught? What is the distribution of the number of errors missed? (b) Missing 3 or more out of 10 errors seems a poor performance. What is the probability that a proofreader who catches 70% of word errors misses exactly 3 out of 10? If you use software, also find the probability of missing 3 or more out of A small liberal arts college would like to have an entering class of 415 students next year. Past experience shows that about 27% of the students admitted will decide to attend. The college therefore plans to admit 1535 students. Suppose that students make their decisions independently and that the probability is 0.27 that a randomly chosen student will accept the offer of admission. (a) What are the mean and standard deviation of the number of students who accept the admissions offer from this college? (b) Use the Normal approximation: what is the approximate probability that the college gets more students than they want? (c) Use software to compute the exact probability that the college gets more students than they want. How good is the approximation in part (b)? A believer in the random walk theory of stock markets thinks that an index of stock prices has probability 0.65 of increasing in any year. Moreover, the change in the index in any given year is not influenced by whether it rose or fell in earlier years. Let X be the number of years among the next 5 years in which the index rises. (a) X has a binomial distribution. What are n and p? (b) What are the possible values that X can take?
195 201 (c) Find the probability of each value of X. Draw a probability histogram for the distribution of X. (See Figure 13.2 for an example of a probability histogram.) (d) What are the mean and standard deviation of this distribution? Mark the location of the mean on your histogram Many women take oral contraceptives to prevent pregnancy. Under ideal conditions, 1% of women taking the pill become pregnant within one year. In typical use, however, 5% become pregnant. Choose at random 20 women taking the pill. How many become pregnant in the next year? (a) Explain why this is a binomial setting. (b) What is the probability that at least one of the women becomes pregnant under ideal conditions? What is the probability in typical use? A study of the effectiveness of oral contraceptives interviews a random sample of 500 women who are taking the pill. (a) Based on the information about typical use in Exercise 13.27, what is the probability that at least 25 of these women become pregnant in the next year? (Check that the Normal approximation is permissible and use it to find this probability. If your software allows, find the exact binomial probability and compare the two results.) (b) We canʹt use the Normal approximation to the binomial distributions to find this probability under ideal conditions as described in Exercise Why not? According to genetic theory, the blossom color in the second generation of a certain cross of sweet peas should be red or white in a 3:1 ratio. That is, each plant has probability 3/4 of having red blossoms, and the blossom colors of separate plants are independent. (a) What is the probability that exactly 6 out of 8 of these plants have red blossoms? (b) What is the mean number of red blossomed plants when 80 plants of this type are grown from seeds? (c) What is the probability of obtaining at least 60 red blossomed plants when 80 plants are grown from seeds? Use the Normal approximation. If your software allows, find the exact binomial probability and compare the two results.
196 The Census Bureau says that 21% of Americans aged 18 to 24 do not have a high school diploma. A vocational school wants to attract young people who may enroll in order to achieve high school equivalency. The school mails an advertising flyer to 25,000 persons between the ages of 18 and 24. (a) If the mailing list can be considered a random sample of the population, what is the mean number of high school dropouts who will receive the flyer? (b) What is the approximate probability that at least 5000 dropouts will receive the flyer? Here is a simple probability model for multiple choice tests. Suppose that each student has probability p of correctly answering a question chosen at random from a universe of possible questions. (A strong student has a higher p than a weak student.) Answers to different questions are independent. (a) Jodi is a good student for whom p = Use the Normal approximation to find the probability that Jodi scores between 70% and 80% on a 100 question test. (b) If the test contains 250 questions, what is the probability that Jodi will score between 70% and 80%? You see that Jodiʹs score on the longer test is more likely to be close to her true score In 2007, Bob Jones University ended its fall semester a week early because of a whooping cough outbreak; 158 students were isolated and another 1200 given antibiotics as a precaution. Authorities react strongly to whooping cough outbreaks because the disease is so contagious. Because the effect of childhood vaccination often wears off by late adolescence, treat the Bob Jones students as if they were unvaccinated. It appears that about 1400 students were exposed. What is the probability that at least 75% of these students develop infections if not treated? (Fortunately, whooping cough is much less serious after infancy.) We would like to find the probability that exactly 2 of the 20 exposed children in the previous exercise develop whooping cough. (a) One way to get 2 infections is to get 1 among the 17 vaccinated children and 1 among the 3 unvaccinated children. Find the probability of exactly 1 infection among the 17 vaccinated children. Find the probability of exactly 1 infection
197 203 among the 3 unvaccinated children. These events are independent: what is the probability of exactly 1 infection in each group? (b) Write down all the ways in which 2 infections can be divided between the two groups of children. Follow the pattern of part (a) to find the probability of each of these possibilities. Add all of your results (including the result of part (a)) to obtain the probability of exactly 2 infections among the 20 children.
198 204 Chapter 14 Exercises 14.3 The critical value z* for confidence level 97.5% is not in Table C. Use software or Table A of standard Normal probabilities to find z*. Include in your answer a sketch like Figure 14.3 with C = and your critical value z* marked on the axis Here are the IQ test scores of 31 seventh grade girls in a Midwest school district: (a) These 31 girls are an SRS of all seventh grade girls in the school district. Suppose that the standard deviation of IQ scores in this population is known to be σ = 15. We expect the distribution of IQ scores to be close to Normal. Make a stemplot of the distribution of these 31 scores (split the stems) to verify that there are no major departures from Normality. You have now checked the simple conditions to the extent possible. (b) Estimate the mean IQ score for all seventh grade girls in the school district, using a 99% confidence interval. Follow the four step process as illustrated in Example The P value for the first cola in Example 14.7 is the probability (taking the null hypothesis μ = 0 to be true) that x takes a value at least as large as 0.3. (a) What is the sampling distribution of x when μ = 0? This distribution appears in Figure (b) Do a Normal probability calculation to find the P value. Your result should agree with Example 14.7 up to roundoff error Exercise 14.7 describes 6 measurements of the electrical conductivity of a liquid. You stated the null and alternative hypotheses in Exercise 14.9.
199 205 (a) One set of measurements has mean conductivity x = Enter this x, along with the other required information, into the P Value of a Test of Significance applet. What is the P value? Is this outcome statistically significant at the α = 0.05 level? At the α = 0.01 level? (b) Another set of measurements has x = 4.7. Use the applet to find the P value for this outcome. Is it statistically significant at the α = 0.05 level? At the α = 0.01level? (c) Explain briefly why these P values tell us that one outcome is strong evidence against the null hypothesis and that the other outcome is not.
200 Here are 6 measurements of the electrical conductivity of a liquid: The liquid is supposed to have conductivity 5. Do the measurements give good evidence that the true conductivity is not 5? The 6 measurements are an SRS from the population of all results we would get if we kept measuring conductivity forever. This population has a Normal distribution with mean equal to the true conductivity of the liquid and standard deviation 0.2. Use this information to carry out a test, following the four step process as illustrated in Example Young men in North America and Europe (but not in Asia) tend to think they need more muscle to be attractive. One study presented 200 young American men with 100 images of men with various levels of muscle. Researchers measure level of muscle in kilograms per square meter (kg/m 2 ) of fat free body mass. Typical young men have about 20 kg/m 2. Each subject chose two images, one that represented his own level of body muscle and one that he thought represented what women prefer. The mean gap between self image and what women prefer was 2.35 kg/m 2. Suppose that the ``muscle gapʹʹ in the population of all young men has a Normal distribution with standard deviation 2.5 kg/m 2. Give a 90% confidence interval for the mean amount of muscle young men think they should add to be attractive to women. (They are wrong: women actually prefer a level close to that of typical men.) If young men thought that their own level of muscle was about what women prefer, the mean muscle gap in the study described in Exercise would be 0. We suspect (before seeing the data) that young men think women prefer more muscle than they themselves have. (a) State null and alternative hypotheses for testing this suspicion. (b) What is the value of the test statistic z? (c) You can tell just from the value of z that the evidence in favor of the alternative is very strong (that is, the P value is very small). Explain why this is true.
201 Breast feeding mothers secrete calcium into their milk. Some of the calcium may come from their bones, so mothers may lose bone mineral. Researchers measured the percent change in mineral content of the spines of 47 mothers during three months of breast feeding. Here are the data: (a) The researchers are willing to consider these 47 women as an SRS from the population of all nursing mothers. Suppose that the percent change in this population has standard deviation σ = 2.5%. Make a stemplot of the data to see that they appear to follow a Normal distribution quite closely. (Donʹt forget that you need both a 0 and a 0 stem because there are both positive and negative values.) (b) Use a 99 % confidence interval to estimate the mean percent change in the population Exercise gives the percent change in the mineral content of the spine for 47 mothers during three months of nursing a baby. As in that exercise, suppose that the percent change in the population of all nursing mothers has a Normal distribution with standard deviation σ = 2.5%. Do these data give good evidence that on the average nursing mothers lose bone mineral? Athletes performing in bright sunlight often smear black eye grease under their eyes to reduce glare. Does eye grease work? In one study, 16 student subjects took a test of sensitivity to contrast after 3 hours facing into bright sun, both with and without eye grease. This is a matched pairs design. Here are the differences in sensitivity, with eye grease minus without eye grease: We want to know whether eye grease increases sensitivity on the average.
202 208 (a) What are the null and alternative hypotheses? Say in words what mean μ your hypotheses concern. (b) Suppose that the subjects are an SRS of all young people with normal vision, that contrast differences follow a Normal distribution in this population, and that the standard deviation of differences is σ = Carry out a test of significance.
203 209 Chapter 15 Exercises 15.5 Example 14.1 (page 360) described NHANES survey data on the body mass index (BMI) of 654 young women. The mean BMI in the sample was x = We treated these data as an SRS from a Normally distributed population with standard deviation σ = 7.5. (a) Suppose that we had an SRS of just 100 young women. What would be the margin of error for 95% confidence? (b) Find the margins of error for 95% confidence based on SRSs of 400 young women and 1600 young women. (c) Compare the three margins of error. How does increasing the sample size change the margin of error of a confidence interval when the confidence level and population standard deviation remain the same? 15.9 Give a 95% confidence interval for the mean ph μ for each sample size in the previous exercise. The intervals, unlike the P values, give a clear picture of what mean ph values are plausible for each sample Example 14.1 (page 360) assumed that the body mass index (BMI) of all American young women follows a Normal distribution with standard deviation σ = 7.5. How large a sample would be needed to estimate the mean BMI μ in this population to within ±1 with 95% confidence? Software can generate samples from (almost) exactly Normal distributions. Here is a random sample of size five from the Normal Distribution with mean 10 and standard deviation 2: These data match the conditions for a z test better than the real data will: the population is very close to normal and has a known standard deviation σ = 2, and the population mean is μ = 10. Test the hypotheses: H0: μ = 8 Ha: μ 8 a) What are the z statistic and its P value? Is the test significant at the 5% level? b) We know that the null hypothesis does not hold, but the test failed to give strong evidence against H0. Explain why this is not surprising.
204 210 Chapter 16 Exercises 16.5 Elephants sometimes damage crops in Africa. It turns out that elephants dislike bees. They recognize beehives in areas where they are common and avoid them. Can this be used to keep elephants away from trees? A group in Kenya placed active beehives in some trees and empty beehives in others. Will elephant damage be less in trees with hives? Will even empty hives keep elephants away? (a) Outline the design of an experiment to answer these questions using 72 acacia trees (be sure to include a control group). (b) Use software or the Simple Random Sample to choose the trees for the activehive group, or Table B at line 137 to choose the first 4 trees in that group. (c) What is the response variable in this experiment? The distribution of blood cholesterol level in the population of young men aged 20 to 34 years is close to Normal with standard deviation σ = 41 milligrams per deciliter (mg/dl). You measure the blood cholesterol of 14 cross country runners. The mean level is x =172 mg/dl. Assuming that σ is the same as in the general population, give a 90% confidence interval for the mean level μ among cross country runners How large a sample is needed to cut the margin of error in Exercise in half? How large a sample is needed to cut the margin of error to ±5 mg/dl? The level of pesticides found in the blubber of whales is a measure of pollution of the oceans by runoff from land and can also be used to identify different populations of whales. A sample of 8 male minke whales in the West Greenland area of the North Atlantic found the mean concentration of the insecticide dieldrin to be x =357 nanograms per gram of blubber (ng/g). Suppose that the concentration in all such whales varies Normally with standard deviation σ = 50 ng/g. Use a 95% confidence interval to estimate the mean level. Be sure to state your conclusion in plain language Use the information in Exercise to give an 80% confidence interval and a 90% confidence interval for the mean concentration of dieldrin in the whale population. What general fact about confidence intervals do the margins of error of your three intervals illustrate? IQ tests are scaled so that the mean score in a large population should be μ = 100. We suspect that the very low birth weight population has mean score less than 100. Does the study described in the previous exercise give good
205 211 evidence that this is true? State hypotheses, carry out a test assuming that the ``simple conditionsʹʹ (page 360) hold, and give your conclusion in plain language The time that people require to react to a stimulus usually has a right skewed distribution, as lack of attention or tiredness causes some lengthy reaction times. Reaction times for children with attention deficit hyperactivity disorder (ADHD) are more skewed, as their condition causes more frequent lack of attention. In one study, children with ADHD were asked to press the spacebar on a computer keyboard when any letter other than X appeared on the screen. With 2 seconds between letters, the mean reaction time was 445 milliseconds (ms) and the standard deviation was 82 ms. Take these values to be the population μ and σ for ADHD children. (a) What are the mean and standard deviation of the mean reaction time x for a randomly chosen group of 15 ADHD children? For a group of 150 such children? (b) The distribution of reaction time is strongly skewed. Explain briefly why we hesitate to regard x as Normally distributed for 15 children but are willing to use a Normal distribution for the mean reaction time of 150 children. (c) What is the approximate probability that the mean reaction time in a group of 150 ADHD children is greater than 450 ms? Here are the daily average body temperatures (degrees Fahrenheit) for 20 healthy adults: (a) Make stemplot of the data. The distribution is roughly symmetric and singlepeaked. There is one mild outlier. We expect the distribution of the sample mean x to be close to Normal. (b) Do these data give evidence that the mean body temperature for all healthy adults is not equal to the traditional 98.6 degrees? Follow the four step process for significance tests (page 378). (Suppose that body temperature varies Normally with standard deviation 0.7 degree.) Use the data in Exercise to estimate mean body temperature with 90% confidence. Follow the four step process for confidence intervals (page 366).
206 212 Chapter 17 Exercises 17.3 Use Table C or software to find (a) the critical value for a one sided test with level α = 0.05based on the t(5) distribution. (b) the critical value for a 98% confidence interval based on the t(21) distribution The composition of the earthʹs atmosphere may have changed over time. To try to discover the nature of the atmosphere long ago, we can examine the gas in bubbles inside ancient amber. Amber is tree resin that has hardened and been trapped in rocks. The gas in bubbles within amber should be a sample of the atmosphere at the time the amber was formed. Measurements on specimens of amber from the late Cretaceous era (75 to 95 million years ago) give these percents of nitrogen: Assume (this is not yet agreed on by experts) that these observations are an SRS from the late Cretaceous atmosphere. Use a 90% confidence interval to estimate the mean percent of nitrogen in ancient air. Follow the four step process as illustrated in Example The usual way to study the brainʹs response to sounds is to have subjects listen to pure tones. The response to recognizable sounds may differ. To compare responses, researchers anesthetized macaque monkeys. They fed pure tones and also monkey calls directly to their brains by inserting electrodes. Response to the stimulus was measured by the firing rate (electrical spikes per second) of neurons in various areas of the brain. Table 17.2 contains the responses for 37 neurons. Researchers suspected that the response to monkey calls would be stronger than the response to a pure tone. Do the data support this idea?
207 213 Table 17.2 Neuron response to tones and monkey calls Neuron Tone Call Neuron Tone Call Neuron Tone Call Complete the Plan, Solve, and Conclude steps of the four step process, following the model of Example A group of earth scientists studied the small diamonds found in a nodule of rock carried up to the earthʹs surface in surrounding rock. This is an opportunity to examine a sample from a single population of diamonds formed in a single event deep in the earth. Table 17.3 (page 460) presents data on the nitrogen content (parts per million) and the abundance of carbon 13 in these diamonds. Table 17.3 Nitrogen and carbon 13 in a sample of diamonds Diamond Nitrogen (ppm) Carbon 13 Ratio Diamond Nitrogen (ppm) Carbon 13 Ratio
208 (Carbon has several isotopes, forms with different numbers of neutrons in the nuclei of their atoms. Carbon 12 makes up almost 99% of natural carbon. The abundance of carbon 13 is measured by the ratio of carbon 13 to carbon 12, in parts per thousand more or less than a standard. The minus signs in the data mean that the ratio is smaller in these diamonds than in standard carbon.) We would like to estimate the mean abundance of both nitrogen and carbon 13 in the population of diamonds represented by this sample. Examine the data for nitrogen. Can we use a t confidence interval for mean nitrogen? Explain your answer. Give a 95% confidence interval if you think the result can be trusted You read in the report of a psychology experiment: Separate analyses for our two groups of 12 participants revealed no overall placebo effect for our student group (mean = 0.08, SD = 0.37, t(11) = 0.49) and a significant effect for our non student group (mean = 0.35, SD = 0.37, t(11) = 3.25, p < 0.01). The null hypothesis is that the mean effect is zero. What are the correct values of the two t statistics based on the means and standard deviations? Compare each correct t value with the critical values in Table C. What can you say about the two sided P value in each case? The Trial Urban District Assessment (TUDA) is a government sponsored study of student achievement in large urban school districts. TUDA gives a reading test scored from 0 to 500. A score of 243 is a basic reading level and a score of 281 is proficient. Scores for a random sample of 1470 eighth graders in Atlanta had x =240 with standard error 1.1. (a) We donʹt have the 1470 individual scores, but use of the t procedures is surely safe. Why? (b) Give a 99% confidence interval for the mean score of all Atlanta eighthgraders. (Be careful: the report gives the standard error of x, not the standard deviation s.) (c) Urban children often perform below the basic level. Is there good evidence that the mean for all Atlanta eighth graders is less than the basic level? The placebo effect is particularly strong in patients with Parkinson s disease. To understand the workings of the placebo effect, scientists measure activity at a key point in the brain when patients receive a placebo that they think is an active drug and also when no treatment is given. The same six patients are measured both with and without the placebo, at different times. (a) Explain why the proper procedure to compare the mean response to placebo with control (no treatment) is a matched pairs t test.
209 215 (b) The six differences (treatment minus control) had x = and s = Is there significant evidence of a difference between treatment and control?
210 Blissymbols are pictographs (think of Egyptian hieroglyphics) sometimes used to help learning disabled children. In a study of computer assisted learning, 12 normal ability schoolchildren were assigned at random to each of four computer learning programs. After they used the program, they attempted to recognize 24 Blissymbols. Here are the counts correct for one of the programs: (a) Make a stemplot (split the stems). Are there outliers or strong skewness that would forbid use of the t procedures? (b) Give a 90% confidence interval for the mean count correct among all children of this age who use the program Our bodies have a natural electrical field that is known to help wounds heal. Does changing the field strength slow healing? A series of experiments with newts investigated this question. In one experiment, the two hind limbs of 12 newts were assigned at random to either experimental or control groups. This is a matched pairs design. The electrical field in the experimental limbs was reduced to zero by applying a voltage. The control limbs were left alone. Here are the rates at which new cells closed a razor cut in each limb, in micrometers per hour: Newt Control limb Experimental limb (a) Make a stemplot of the differences between limbs of the same newt (control limb minus experimental limb). There is a high outlier. (b) A good way to judge the effect of an outlier is to do your analysis twice, once with the outlier and a second time without it. Carry out two t tests to see if the mean healing rate is significantly lower in the experimental limbs, one including all 12 newts and another that omits the outlier. What are the test statistics and their P values? Does the outlier have a strong influence on your conclusion? Hereʹs a new idea for treating advanced melanoma, the most serious kind of skin cancer. Genetically engineer white blood cells to better recognize and destroy cancer cells, then infuse these cells into patients. The subjects in a small initial study were 11 patients whose melanoma had not responded to existing treatments. One question was how rapidly the new cells would multiply after infusion, as measured by the doubling time in days. Here are the doubling times: (a) Examine the data. Is it reasonable to use the t procedures?
211 217 (b) Give a 90% confidence interval for the mean doubling time. Are you willing to use this interval to make an inference about the mean doubling time in a population of similar patients? The concentration of carbon dioxide (CO2) in the atmosphere is increasing rapidly due to our use of fossil fuels. Because plants use CO2 to fuel photosynthesis, more CO2 may cause trees and other plants to grow faster. An elaborate apparatus allows researchers to pipe extra CO2 to a 30 meter circle of forest. They selected two nearby circles in each of three parts of a pine forest and randomly chose one of each pair to receive extra CO2. The response variable is the mean increase in base area for 30 to 40 trees in a circle during a growing season. We measure this in percent increase per year. The following are one year s data. Pair Control plot Treatment plot (a) State the null and alternative hypotheses. Explain clearly why the investigators used a one sided alternative. (b) Carry out a test and report your conclusion in simple language. (c) The investigators used the test you just carried out. Any use of the t procedures with samples this size is risky. Why? Velvetleaf is a particularly annoying weed in cornfields. It produces lots of seeds, and the seeds wait in the soil for years until conditions are right. How many seeds do velvetleaf plants produce? Here are counts from 28 plants that came up in a cornfield when no herbicide was used: We would like to give a confidence interval for the mean number of seeds produced by velvetleaf plants. Alas, the t interval canʹt be safely used for these data. Why not? Give a 90% confidence interval for the difference in healing rates (control minus experimental) in the previous exercise The design of controls and instruments affects how easily people can use them. Timothy Sturm investigated this effect in a course project, asking 25 righthanded students to turn a knob (with their right hands) that moved an indicator by screw action. There were two identical instruments, one with a right hand thread (the knob turns clockwise) and the other with a left hand thread (the knob turns counterclockwise). Table 17.5 gives the times in seconds each subject took to move the indicator a fixed distance.
212 218 Table 17.5 Performance times (seconds) using right hand and left hand threads Subject Right Thread Left Thread Subject Right Thread Left Thread (a) Each of the 25 students used both instruments. Explain briefly how you would use randomization in arranging the experiment. (b) The project hoped to show that right handed people find right hand threads easier to use. Do an analysis that leads to a conclusion about this issue Give a 90% confidence interval for the mean time advantage of right hand over left hand threads in the setting of Exercise Do you think that the time saved would be of practical importance if the task were performed many times for example, by an assembly line worker? To help answer this question, find the mean time for right hand threads as a percent of the mean time for left hand threads.
213 219 Chapter 18 Exercises 18.5 Conservationists have despaired over destruction of tropical rain forest by logging, clearing, and burning. These words begin a report on a statistical study of the effects of logging in Borneo. Here are data on the number of tree species in 12 unlogged forest plots and 9 similar plots logged 8 years earlier: Unlogged Logged (a) The study report says, Loggers were unaware that the effects of logging would be assessed. Why is this important? The study report also explains why the plots can be considered to be randomly assigned. (b) Does logging significantly reduce the mean number of species in a plot after 8 years? Follow the four step process as illustrated in Examples 18.2 and Use the data in Exercise 18.5 to give a 90% confidence interval for the difference in mean number of species between unlogged and logged plots Businesses know that customers often respond to background music. Do they also respond to odors? One study of this question took place in a small pizza restaurant in France on Saturday evenings in May. On one of these evenings, a relaxing lavender odor was spread through the restaurant. Table 18.2 gives the time (minutes) that two samples of 30 customers spent in the restaurant and the amount they spent (in euros). The two evenings were comparable in many ways (weather, customer count, and so on), so we are willing to regard the data as independent SRSs from spring Saturday evenings at this restaurant. The authors say, Therefore at this stage it would be impossible to generalize the results to other restaurants. (a) Does a lavender odor encourage customers to stay longer in the restaurant? Examine the time data and explain why they are suitable for two sample t procedures. Use the two sample t test to answer the question posed. (b) Does a lavender odor encourage customers to spend more while in the restaurant? Examine the spending data. In what ways do these data deviate from Normality? With 30 observations, the t procedures are nonetheless reasonably accurate. Use the two sample t test to answer the question posed.
214 220 Table 18.2 Time (minutes) and spending (Euros) by restaurant customers No odor Lavender Minutes Euros Minutes Euros Equip male and female students with a small device that secretly records sound for a random 30 seconds during each 12.5 minute period over two days. Count the words each subject speaks during each recording period, and from this, estimate how many words per day each subject speaks. The published report includes a table summarizing six such studies. Here are two of the six:
215 221 Sample Size Estimated Average Number (SD) Of Words Spoken per Day Study Women Men Women Men ,177 (7520) 16,569 (9108) ,496 (7914) 12,867 (8343) Readers are supposed to understand that, for example, the 56 women in the first study had x = 16,177 and s = It is commonly thought that women talk more than men. Does either of the two samples support this idea? For each study: (a) State hypotheses in terms of the population means for men ( μ M ) and women ( μ F ). (b) Find the two sample t statistic. (c) What degrees of freedom does Option 2 use to get a conservative P value? (d) Compare your value of t with the critical values in Table C. What can you say about the P value of the test? (e) What do you conclude from the results of these two studies? In a study of the presence of whelks along the Pacific coast, investigators put down a frame that covers 0.25 square meter and counted the whelks on the sea bottom inside the frame. They did this at 7 locations in California and 6 locations in Oregon. The report says that whelk densities were twice as high in Oregon as in California (mean ± SEM, 26.9±1.56 versus 11.9±2.68 whelks per 0.25 m 2, Oregon versus California, respectively; Studentʹs t test, P < 0.001). (a) SEM stands for the standard error of the mean, s/ n.fill in the values in this summary table: Group Location n x s 1 Oregon??? 2 California??? (b) What degrees of freedom would you use in the conservative two sample t procedures to compare Oregon and California? (c) What is the two sample t test statistic for comparing the mean densities of whelks in Oregon and California? (d) Test the null hypothesis of no difference between the two population means against the two sided alternative. Use your statistic from part (c) with degrees of freedom from part (b). Does your conclusion agree with the published report?
216 The post lunch dip is the drop in mental alertness after a midday meal. Does an extract of the leaves of the ginkgo tree reduce the post lunch dip? Assign healthy people aged 18 to 40 to take either ginkgo extract or a placebo pill. After lunch, ask them to read seven pages of random letters and place an X over every e. Count the number of misses per line read. (a) What is a placebo and why was one group given a placebo? (b) What is the double blind method and why should it be used in this experiment? (c) Here are summaries of performance after 13 weeks of either ginkgo extract or placebo: Group Group size Mean Std. dev. Ginkgo Placebo Is there a significant difference between the two groups? What do these data show about the effect of ginkgo extract? The SAFE (Social, Attitudinal, Familial, and Environmental Stress) scale measures the stress level of adults adjusting to a different culture. Scores range from 1 (not stressful) to 5 (extremely stressful). In a study of stress among immigrant mothers in a university community, mothers of children between 2 and 10 years of age whose families had come to the United States for professional or academic reasons took the SAFE questionnaire. Here are summaries for mothers from Asia and Europe: Origin Sample size Mean Std. dev Asian European Is there evidence of a difference in mean stress levels between mothers from Asia and Europe? Here are the IQ test scores of 31 seventh grade girls in a Midwest school district The IQ test scores of 47 seventh grade boys in the same district are
217 (a) Make stemplots or histograms of both sets of data. Because the distributions are reasonably symmetric with no extreme outliers, the t procedures will work well. (b) Treat these data as SRSs from all seventh grade students in the district. Is there good evidence that girls and boys differ in their mean IQ scores? Use the data in Exercise to give a 95% confidence interval for the difference between the mean IQ scores of all boys and all girls in the district Of course, the reason for durable press treatment is to reduce wrinkling. ``Wrinkle recovery angleʹʹ measures how well a fabric recovers from wrinkles. Higher is better. Here are data on the wrinkle recovery angle (in degrees) for the same fabric swatches discussed in the previous exercise: Permafresh Hylite Is there a significant difference in wrinkle resistance? (a) Do the sample means suggest that one process has better wrinkle resistance? (b) Make stemplots for both samples. There are no obvious deviations from Normality. (c) Test the hypothesis H0 : μ1 = μ2 against the two sided alternative. What do you conclude from part (a) and from the result of your test? In Exercise 18.39, you found that the Hylite process results in significantly greater wrinkle resistance than the Permafresh process. How large is the difference in mean wrinkle recovery angle? Give a 90% confidence interval The investigators expected the control group to adjust the breeding date the next year, whereas the well fed supplemented group had no reasons to change. The report continues: but in the following year food supplemented females were more out of synchrony with the caterpillar peak than the controls. Here are the data (days behind the caterpillar peak): Control Supplemented
218 224 Carry out a t test and show that it leads to the quoted conclusion Kathleen Vohs of the University of Minnesota and her coworkers carried out several randomized comparative experiments on the effects of thinking about money. Hereʹs part of one such experiment. Ask student subjects to unscramble 30 sets of five words to make a meaningful phrase from four of the five words. The control group unscrambled phrases like cold it desk outside is into it is cold outside. The treatment group unscrambled phrases that lead to thinking about money, turning high a salary desk paying into a high paying salary. Then each subject worked a hard puzzle, knowing that he or she could ask for help. Here are the times in seconds until subjects asked for help, for the treatment group, and for the control group, The researchers suspected that money is connected with self sufficiency, so that the treatment group will ask for help less quickly on the average. Do the data support this idea? A subliminal message is below our threshold of awareness but may nonetheless influence us. Can subliminal messages help students learn math? A group of students who had failed the mathematics part of the City University of New York Skills Assessment Test agreed to participate in a study to find out. All received a daily subliminal message, flashed on a screen too rapidly to be consciously read. The treatment group of 10 students (chosen at random) was exposed to Each day I am getting better in math. The control group of 8 students was exposed to a neutral message, People are walking on the street. All students participated in a summer program designed to raise their math skills, and all took the assessment test again at the end of the program. Table 18.3 gives data on the subjectsʹ scores before and after the program. Is there good evidence that the treatment brought about a greater improvement in math scores than the neutral message? How large is the mean difference in gains between treatment and control? (Use 90% confidence.)
219 225 Table 18.3 Mathematics skills scores before and after a subliminal message Treatment group Control group Before After Before After Different varieties of the tropical flower Heliconia are fertilized by different species of hummingbirds. Over time, the lengths of the flowers and the forms of the hummingbirds beaks have evolved to match each other. Here are data on the lengths in millimeters of two color varieties of the same species of flower on the island of Dominica: H. caribaea red H. caribaea yellow Is there good evidence that the mean lengths of the two varieties differ? Estimate the difference between the population means. (Use 95% confidence.)
220 226 Chapter 19 Exercises 19.5 Canada has much stronger gun control laws than the United States, and Canadians support gun control more strongly than do Americans. A sample survey asked a random sample of 1505 adult Canadians, Do you agree or disagree that all firearms should be registered? Of the 1505 people in the sample, 1288 answered either Agree strongly or agree somewhat (a) The survey dialed residential telephone numbers at random in all ten Canadian provinces (omitting the sparsely populated northern territories). Based on what you know about sample surveys, what is likely to be the biggest weakness in this survey? (b) Nonetheless, act as if we have an SRS from adults in the Canadian provinces. Give a 95% confidence interval for the proportion who support registration of all firearms Sample surveys usually contact large samples, so we can use the largesample confidence interval if the sample design is close to an SRS. Scientific studies often use small samples that require the plus four method. For example, the small round holes you often see in sea shells were drilled by other sea creatures, who ate the former owners of the shells. Whelks often drill into mussels, but this behavior appears to be more or less common in different locations. Investigators collected whelk eggs from the coast of Oregon, raised the whelks in the laboratory, and then put each whelk in a container with some delicious mussels. Only 9 of 98 whelks drilled into mussels. (a) Why can t we use the large sample confidence interval for the proportion p of Oregon whelks that will spontaneously drill mussels? (b) The plus four method adds four observations, two successes and two failures. What are the sample size and the number of successes after you do this? What is the plus four estimate p% of p? (c) Give the plus four 90% confidence interval for the proportion of Oregon whelks that will spontaneously drill mussels The plus four method is particularly useful when there are no successes or no failures in the data. The study of Spanish currency described in Example 19.5 found that in Seville, all 20 of a sample of 20 euro bills had cocaine traces. (a) What is the sample proportion ˆp of contaminated bills? What is the large
221 227 sample 95% confidence interval for p? Itʹs not plausible that every bill in Seville has cocaine traces, as this interval says. (b) Find the plus four estimate p% and the plus four 95% confidence interval for p. These results are more reasonable PTC is a substance that has a strong bitter taste for some people and is tasteless for others. The ability to taste PTC is inherited. About 75% of Italians can taste PTC, for example. You want to estimate the proportion of Americans with at least one Italian grandparent who can taste PTC. Starting with the 75% estimate for Italians, how large a sample must you collect in order to estimate the proportion of PTC tasters within ± 0.04 with 90% confidence? We often judge other people by their faces. It appears that some people judge candidates for elected office by their faces. Psychologists showed headand shoulders photos of the two main candidates in 32 races for the U.S. Senate to many subjects (dropping subjects who recognized one of the candidates) to see which candidate was rated more competent based on nothing but the photos. On election day, the candidates whose faces looked more competent won 22 of the 32 contests. If faces donʹt influence voting, half of all races in the long run should be won by the candidate with the better face. Is there evidence that the candidate with the better face wins more than half the time? Follow the four step process as illustrated in Example The Harris Poll asked a sample of smokers, Do you believe that smoking will probably shorten your life, or not Of the 1010 people in the sample, 848 said Yes. (a) Harris called residential telephone numbers at random in an attempt to contact an SRS of smokers. Based on what you know about national sample surveys, what is likely to be the biggest weakness in the survey? (b) We will nonetheless act as if the people interviewed are an SRS of smokers. Give a 95% confidence interval for the percent of smokers who agree that smoking will probably shorten their lives.
222 The Pew Research Center asked a random sample of 1128 adult women, How satisfied are you with your life overall? Of these women, 56 said either Mostly dissatisfiedʹ or Very dissatisfied. (a) Pew dialed residential telephone numbers at random in the continental United States in an attempt to contact a random sample of adults. Based on what you know about national sample surveys, what is likely to be the biggest weakness in the survey? (b) Act as if the sample is an SRS. Give a large sample 90% confidence interval for the proportion p of all adult women who are mostly or very dissatisfied with their lives. (c) Give the plus four confidence interval for p. If you express the two confidence intervals in percents and round to the nearest tenth of a percent, how do they differ? (As always, the plus four method pulls results away from 0% or 100%, whichever is closer. Although the condition for the large sample interval is met, we can place more trust in the plus four interval.) Most soybeans grown in the United States are genetically modified to, for example, resist pests and so reduce use of pesticides. Because some nations do not accept genetically modified (GM) foods, grain handling facilities routinely test soybean shipments for the presence of GM beans. In a study of the accuracy of these tests, researchers submitted shipments of soybeans containing 1% of GM beans to 23 randomly selected facilities. Eighteen detected the GM beans. (a) Show that the conditions for the large sample confidence interval are not met. Show that the conditions for the plus four interval are met. (b) Use the plus four method to give a 90% confidence interval for the percent of all grain handling facilities that will correctly detect 1% of GM beans in a shipment Some shrubs have the useful ability to resprout from their roots after their tops are destroyed. Fire is a particular threat to shrubs in dry climates, as it can injure the roots as well as destroy the aboveground material. One study of resprouting took place in a dry area of Mexico. The investigators clipped the tops of samples of several species of shrubs. In some cases, they also applied a propane torch to the stumps to simulate a fire. Of 12 specimens of the shrub Krameria cytisoides, 5 resprouted after fire. Estimate with 90% confidence the proportion of all shrubs of this species that will resprout after fire.
223 A sample survey funded by the National Science Foundation asked a random sample of American adults about biological evolution. One question asked subjects to answer True, False, or Not sure to the statement Human beings, as we know them today, developed from earlier species of animals. Of the 1484 respondents, 594 said True. What can you say with 95% confidence about the percent of all American adults who think that humans developed from earlier species of animals? Does the sample in Exercise give good evidence to support the claim Fewer than half of American adults think that humans developed from earlier species of animals?
224 230 Chapter 20 Exercises 20.1 Younger people use online instant messaging (IM) more often than older people. A random sample of IM users found that 73 of the 158 people in the sample aged 18 to 27 said they used IM more often than . In the 28 to 39 age group, 26 of 143 people used IM more often than . Give a 95% confidence interval for the difference between the proportions of IM users in these age groups who use IM more often than . Follow the four step process as illustrated in Examples 20.1 and A government survey randomly selected 6889 female high school students and 7028 male high school students. Of these students, 1915 females and 3078 males met recommended levels of physical activity. (These levels are quite high: at least 60 minutes of activity that makes you breathe hard on at least 5 of the past 7 days.) Give a 99% confidence interval for the difference between the proportions of all female and male high school students who meet the recommended levels of activity We donʹt like to find broken crackers when we open the package. How can makers reduce breaking? One idea is to microwave the crackers for 30 seconds right after baking them. Breaks start as hairline cracks called checking. Assign 65 newly baked crackers to the microwave and another 65 to a control group that is not microwaved. After one day, none of the microwave group and 16 of the control group show checking. Give the 95% plus four confidence interval for the amount by which microwaving reduces the proportion of checking. The plus four method is particularly helpful when, as here, a count of successes is zero. Follow the four step process as illustrated in Example Most alpine skiers and snowboarders do not use helmets. Do helmets reduce the risk of head injuries? A study in Norway compared skiers and snowboarders who suffered head injuries with a control group who were not injured. Of 578 injured subjects, 96 had worn a helmet. Of the 2992 in the control group, 656 wore helmets. Is helmet use less common among skiers and snowboarders who have head injuries? Follow the four step process as illustrated in Example (Note that this is an observational study that compares injured and uninjured subjects. An experiment that assigned subjects to helmet and no helmet groups would be more convincing.) Many teens have posted profiles on sites such as MySpace. A sample survey asked random samples of teens with online profiles if they included false
225 231 information in their profiles. Of 170 younger teens (ages 12 to 14), 117 said Yes. Of 317 older teens (ages 15 to 17), 152 said Yes. (a) Do these samples satisfy the guidelines for the large sample confidence interval? (b) Give a 95% confidence interval for the difference between the proportions of younger and older teens who include false information in their online profiles Genetic influences on cancer can be studied by manipulating the genetic makeup of mice. One of the processes that turn genes on or off (so to speak) in particular locations is called DNA methylation. Do low levels of this process help cause tumors? Compare mice altered to have low levels with normal mice. Of 33 mice with lowered levels of DNA methylation, 23 developed tumors. None of the control group of 18 normal mice developed tumors in the same time period. (a) Explain why we cannot safely use either the large sample confidence interval or the test for comparing the proportions of normal and altered mice that develop tumors. (b) The plus four method adds two observations, a success and a failure, to each sample. What are the sample sizes and the numbers of mice with tumors after you do this? Give a plus four 99% confidence interval for the difference in the proportions of the two populations that develop tumors. (c) Based on your confidence interval, is the difference between normal and altered mice significant at the 1% level? Is there a significant difference in the proportions of papers with and without statistical help that are rejected without review? State hypotheses, find the test statistic, use software or the bottom row of Table C to get a P value, and give your conclusion. (This observational study does not establish causation, because studies that include statistical help may also be better in other ways than those that do not.) Give a 95% confidence interval for the difference between the proportions of papers rejected without review when a statistician is and is not involved in the research The North Carolina State University study in the previous exercise also looked at possible differences in the proportions of female and male students who succeeded in the course. They found that 23 of the 34 women and 60 of the
226 men succeeded. Is there evidence of a difference between the proportions of women and men who succeed? Nicotine patches are often used to help smokers quit. Does giving medicine to fight depression help? A randomized double blind experiment assigned 244 smokers who wanted to stop to receive nicotine patches and another 245 to receive both a patch and the antidepression drug bupropion. After a year, 40 subjects in the nicotine patch group and 87 in the patch plus drug group had abstained from smoking. Give a 99% confidence interval for the difference (treatment minus control) in the proportion of smokers who quit Do our emotions influence economic decisions? One way to examine the issue is to have subjects play an ultimatum game against other people and against a computer. Your partner (person or computer) gets $10, on the condition that it be shared with you. The partner makes you an offer. If you refuse, neither of you gets anything. So itʹs to your advantage to accept even the unfair offer of $2 out of the $10. Some people get mad and refuse unfair offers. Here are data on the responses of 76 subjects randomly assigned to receive an offer of $2 from either a person they were introduced to or a computer: Accept Reject Human offers Computer offers 32 6 We suspect that emotion will lead to offers from another person being rejected more often than offers from an impersonal computer. Do a test to assess the evidence for this conjecture Are shoppers more or less likely to use credit cards for impulse purchases that they decide to make on the spot, as opposed to purchases that they had in mind when they went to the store? Stop every third person leaving a department store with a purchase. (This is in effect a random sample of people who buy at that store.) A few questions allow us to classify the purchase as impulse or not. Here are the data on how the customer paid: Credit card? Yes No Impulse purchases Planned purchases 35 31
227 233 Estimate with 95% confidence the percent of all customers at this store who use a credit card. Give numerical summaries to describe the difference in credit card use between impulse and planned purchases. Is this difference statistically significant?
228 234 Chapter 21 Exercises 21.1 A sample survey of 1497 adult Internet users found that 36% consult the online collaborative encyclopedia Wikipedia. Give a 95% confidence interval for the proportion of all adult Internet users who refer to Wikipedia When the new euro coins were introduced throughout Europe in 2002, curious people tried all sorts of things. Two Polish mathematicians spun a Belgian euro (one side of the coin has a different design for each country) 250 times. They got 140 heads. Newspapers reported this result widely. Is it significant evidence that the coin is not balanced when spun? 21.5 Ask young men to estimate their own degree of body muscle by choosing from a set of 100 photos. Then ask them to choose what they think women prefer. The researchers know the actual degree of muscle, measured as kilograms per square meter of fat free mass, for each of the photos. They can therefore measure the difference between what a subject thinks women prefer and the subjectʹs own self image. Call this difference the muscle gap. Here are summary statistics for the muscle gap from two samples, one of American and European young men and the other of Chinese young men from Taiwan: Group n x s American/European Chinese Give a 95% confidence interval for the mean size of the muscle gap for all American and European young men. On the average, men think they need this much more muscle to match what women prefer Hereʹs how butterflies mate: a male passes to a female a packet of sperm called a spermatophore. Females may mate several times. Will they remate sooner if the first spermatophore they receive is small? Among 20 females who received a large spermatophore (greater than 25 milligrams), the mean time to the next mating was 5.15 days, with standard deviation 0.18 day. For 21 females who received a small spermatophore (about 7 milligrams), the mean was 4.33 days and the standard deviation was 0.31 day. Is the observed difference in means statistically significant?
229 Give a 90% confidence interval for the difference between the proportions of all Hispanic and all white young people who listen to rap every day A study of the inheritance of speed and endurance in mice found a tradeoff between these two characteristics, both of which help mice survive. To test endurance, mice were made to swim in a bucket with a weight attached to their tails. (The mice were rescued when exhausted.) Here are data on endurance in minutes for female and male mice: Group n Mean Standard Deviation Female Male (a) Both sets of endurance data are skewed to the right. Why are t procedures nonetheless reasonably accurate for these data? (b) Do the data show that female mice have significantly higher endurance on the average than male mice? Use the information in Exercise to give a 95% confidence interval for the mean difference (female minus male) in endurance times Use the information in the previous exercise to give a 99% confidence interval for the proportion of all students in 2004 who had at least one parent who graduated from college. (The sample excludes 17 year olds who had dropped out of school, so your estimate is valid for students but is probably too high for all 17 year olds.) Starting in the 1970s, medical technology allowed babies with very low birth weight (VLBW, less than 1500 grams, about 3.3 pounds) to survive without major handicaps. It was noticed that these children nonetheless had difficulties in school and as adults. A long term study has followed 242 VLBW babies to age 20 years, along with a control group of 233 babies from the same population who had normal birth weight. (a) Is this an experiment or an observational study? Why? (b) At age 20, 179 of the VLBW group and 193 of the control group had graduated from high school. Is the graduation rate among the VLBW group significantly lower than for the normal birth weight controls?
230 The Womenʹs Health Initiative is a randomized, controlled clinical trial designed to see if a low fat diet reduces the incidence of breast cancer. In all, 19,541 women were assigned at random to a low fat diet and a control group of 29,294 women were assigned to a normal diet. All the subjects were between ages 50 and 79 and had no prior breast cancer. After 8 years, 655 of the women in the low fat group and 1072 of the women in the control group had developed breast cancer. Does this clinical trial give evidence that a low fat diet reduces breast cancer? High levels of cholesterol in the blood are not healthy in either humans or dogs. Because a diet rich in saturated fats raises the cholesterol level, it is plausible that dogs owned as pets have higher cholesterol levels than dogs owned by a veterinary research clinic. Normal levels of cholesterol based on the clinicʹs dogs would then be misleading. A clinic compared healthy dogs it owned with healthy pets brought to the clinic to be neutered. The summary statistics for blood cholesterol levels (milligrams per deciliter of blood) appear below. Group n x s Pets Clinic Is there strong evidence that pets have a higher mean cholesterol level than clinic dogs? Continue your work with the information in Exercise Give a 95% confidence interval for the mean cholesterol level in pets Dogs are big and expensive. Rats are small and cheap. Might rats be trained to replace dogs in sniffing out illegal drugs? A first study of this idea trained rats to rear up on their hind legs when they smelled simulated cocaine. To see how well rats performed after training, they were let loose on a surface with many cups sunk in it, one of which contained simulated cocaine. Four out of six trained rats succeeded in 80 out of 80 trials. How should we estimate the long term success rate p of a rat that succeeds in every one of 80 trials?
231 237 (a) What is the ratʹs sample proportion p ˆ? What is the large sample 95% confidence interval for p? Itʹs not plausible that the rat will always be successful, as this interval says. (b) Find the plus four estimate p% and the plus four 95 % confidence interval for p. These results are more reasonable The color of a fabric depends on the dye used and also on how the dye is applied. This matters to clothing manufacturers, who want the color of the fabric to be just right. The study discussed in the previous exercise went on to dye fabric made of ramie with the same procion blue dye applied in two different ways. Here are the lightness scores for 8 pieces of identical fabric dyed in each way: Method B Method C (a) This is a randomized comparative experiment. Outline the design. (b) A clothing manufacturer wants to know which method gives the darker color (lower lightness score). Use sample means to answer this question. Is the difference between the two sample means statistically significant? Can you tell from just the P value whether the difference is large enough to be important in practice? We wonder what proportion of female students have at least one parent who allows them to drink around him or her. Table 21.1 contains information about a sample of 94 students. Use this sample to give a 95% confidence interval for this proportion We donʹt like to find broken crackers when we open the package. How can makers reduce breaking? One idea is to microwave the crackers for 30 seconds right after baking them. Analyze the following results from two experiments intended to examine this idea. Does microwaving significantly improve indicators of future breaking? How large is the improvement? What do you conclude about the idea of microwaving crackers? (a) The experimenter randomly assigned 65 newly baked crackers to be microwaved and another 65 to a control group that is not microwaved. Fourteen
232 238 days after baking, 3 of the 65 microwaved crackers and 57 of the 65 crackers in the control group showed visible checking, which is the starting point for breaks. (b) The experimenter randomly assigned 20 crackers to be microwaved and another 20 to a control group. After 14 days, he broke the crackers. Here are summaries of the pressure needed to break them, in pounds per square inch: Microwave Control Mean Standard deviation
233 239 Chapter 22 Exercises 22.1 The Pennsylvania State University has its main campus in University Park and more than 20 smaller commonwealth campuses around the state. The Penn State Division of Student Affairs polled a random sample of undergraduates about their use of online social networking. (The response rate was only about 20%, which casts some doubt on the usefulness of the data.) Facebook was the most popular site, with more than 80% of students having an account. Here is a comparison of Facebook use by undergraduates at the University Park and commonwealth campuses: University Park Commonwealth Do not use Facebook Several times a month or less At least once a week At least once a day (a) What percent of University Park students fall in each Facebook category? What percent of commonwealth campus students fall in each category? Each column should add to 100% (up to roundoff error). These are the conditional distributions of Facebook use given campus setting. (b) Make a bar graph that compares the two conditional distributions. What are the most important differences in Facebook use between the two campus settings? 22.3 In the setting of Exercise 22.1, we might do several significance tests to compare University Park with the commonwealth campuses. (a) Is there a significant difference between the proportions of students in the two locations who do not use Facebook? Give the P value. (b) Is there a significant difference between the proportions of students in the two locations who are in the At least once a week category? Give the P value. (c) Explain clearly why P values for individual outcomes like these canʹt tell us whether the two distributions for all four outcomes in the two locations differ significantly The two way table in Exercise 22.1 displays data on use of Facebook by two groups of Penn State students. Itʹs clear that nonusers are much more frequent at
234 240 the commonwealth campuses. Letʹs look just at students who have Facebook accounts: Use Facebook University Park Commonwealth Several times a month or less At least once a week At least once a day Total Facebook Users The null hypothesis is that there is no relationship between campus and Facebook use. (a) If this hypothesis is true, what are the expected counts for Facebook use among commonwealth campus students? This is one column of the two way table of expected counts. Find the column total and verify that it agrees with the column total for the observed counts. (b) Commonwealth campus students as a group are older and more likely to be married and employed than University Park students. What does comparing the observed and expected counts in this column show about Facebook use by these students? Many birds are injured or killed by flying into windows. It appears that birds donʹt see windows. Can tilting windows down so that they reflect earth rather than sky reduce bird strikes? Place six windows at the edge of a woods: two vertical, two tilted 20 degrees, and two tilted 40 degrees. During the next four months, there were 53 bird strikes, 31 on the vertical windows, 14 on the 20 degree windows, and 8 on the 40 degree windows. If the tilt has no effect, we expect strikes on windows with all three tilts to have equal probability. Test this null hypothesis. What do you conclude? For reasons known only to social scientists, the General Social Survey (GSS) regularly asks its subjects their astrological sign. Here are the counts of responses for the most recent GSS: Sign Aries Taurus Gemini Cancer Leo Virgo Count
235 241 Sign Libra Scorpio Sagittarius Capricorn Aquarius Pisces Count If births are spread uniformly across the year, we expect all 12 signs to be equally likely. Are they? Follow the four step process in your answer The General Social Survey (GSS) asked this question: Consider a person who believes that Blacks are genetically inferior. If such a person wanted to make a speech in your community claiming that Blacks are inferior, should he be allowed to speak, or not? Here are the responses, broken down by the race of the respondent: Black White Other Allowed Not allowed (a) Because the GSS is essentially an SRS of all adults, we can combine the races in these data and give a 99% confidence interval for the proportion of all adults who would allow a racist to speak. Do this. (b) Find the column percents and use them to compare the attitudes of the three racial groups. How significant are the differences found in the sample? The nonprofit group Public Agenda conducted telephone interviews with a stratified sample of parents of high school children. There were 202 black parents, 202 Hispanic parents, and 201 white parents. One question asked was Are the high schools in your state doing an excellent, good, fair or poor job, or donʹt you know enough to say? Here are the survey results: Black Parents Hispanic Parents White Parents Excellent Good Fair Poor Don t know Total
236 242 Are the differences in the distributions of responses for the three groups of parents statistically significant? What departures from the null hypothesis no relationship between group and response contribute most to the value of the chi square statistic? Write a brief conclusion based on your analysis Before bringing a new product to market, firms carry out extensive studies to learn how consumers react to the product and how best to advertise its advantages. Here are data from a study of a new laundry detergent. The subjects are people who donʹt currently use the established brand that the new product will compete with. Give subjects free samples of both detergents. After they have tried both for a while, ask which they prefer. The answers may depend on other facts about how people do laundry. Laundry Practices Soft water, warm wash Soft water, Hot wash Hard water, Warm wash Prefer standard product Prefer new product Hard water, Hot wash How do laundry practices (water hardness and wash temperature) influence the choice of detergent? In which settings does the new detergent do best? Are the differences between the detergents statistically significant? Make a 2 x 5 table by combining the counts in the three rows that mention Democrat and in the three rows that mention Republican and ignoring strict independents and supporters of other parties. We might think of this table as comparing all adults who lean Democrat and all adults who lean Republican. How does support for the two major parties differ among adults with different levels of education?
237 243 Chapter 23 Exercises 23.1 Ebola and gorillas. An outbreak of the deadly Ebola virus in 2002 and 2003 killed 91 of the 95 gorillas in 7 home ranges in the Congo. To study the spread of the virus, measure distance by the number of home ranges separating a group of gorillas from the first group infected. Here are data on distance and number of days until deaths began in each later group:2 Distance x Days y (a) Examine the data. Make a scatterplot with distance as the explanatory variable and find the correlation. There is a strong linear relationship Great Arctic rivers. One effect of global warming is to increase the flow of water into the Arctic Ocean from rivers. Such an increase may have major effects on the world s climate. Six rivers (Yenisey, Lena, Ob, Pechora, Kolyma, and Severnaya Dvina) drain two thirds of the Arctic in Europe and Asia. Several of these are among the largest rivers on earth. Table 23.2 presents the total discharge from these rivers each year from 1936 to Discharge is measured in cubic kilometers of water. Use software to analyze these data. (a) Make a scatterplot of river discharge against time. Is there a clear increasing trend? Calculate r 2 and briefly interpret its value. There is considerable year toyear variation, so we wonder if the trend is statistically significant. (b) As a first step, find the least squares line and draw it on your plot. Then find the regression standard error s, which measures scatter about this line. We will continue the analysis in later exercises. TABLE 23.2 Arctic river discharge (cubic kilometers), 1936 to 1999 YEAR DISCHARGE YEAR DISCHARGE YEAR DISCHARGE YEAR DISCHARGE
238 Great Arctic rivers: testing. The most important question we ask of the data in Table 23.2 is this: is the increasing trend visible in your plot (Exercise 23.3) statistically significant? If so, changes in the Arctic may already be affecting the earth s climate. Use software to answer this question. Give a test statistic, its Pvalue, and the conclusion you draw from the test Ebola and gorillas: testing correlation. Exercise 23.1 gives data showing that the delay in deaths from an Ebola outbreak in groups of gorillas increases linearly with distance from the origin of the outbreak. There are only 6 observations, so we worry that the apparent relationship may be just chance. Is the correlation significantly greater than 0? Answer this question in two ways. (a) Return to your t statistic from Exercise What is the one sided P value for this t? Apply your result to test the correlation. (b) Find the correlation r and use Table E to approximate the P value of the one sided test Ebola and gorillas: estimating slope. Exercise 23.1 presents data on distance and days until an Ebola outbreak reached six groups of gorillas. Software tells us that the least squares slope is b = with standard error SEb = Because there are only 6 observations, the observed slope b may not be an accurate estimate of the population slope β. Give a 90% confidence interval for β Great Arctic rivers: estimating slope. Use the data in Table 23.2 to give a 90% confidence interval for the slope of the population regression of Arctic river discharge on year. Does this interval convince you that discharge is actually increasing over time? Explain your answer Manatees: conditions for inference. We know that there is a strong linear relationship. Let s check the other conditions for inference. Figure includes a table of the two variables, the predicted values ˆy for each x in the data, the residuals, and related quantities. (This table is stored as ex23 29.dat on the text CD andweb site.)
239 245 (a) Round the residuals to the nearest whole number and make a stemplot. Thedistribution is single peaked and symmetric and appears close to Normal. (b) Make a residual plot, residuals against boats registered. Use a vertical scale from 25 to 25 to show the pattern more clearly. Add the residual = 0 line. There is no clearly nonlinear pattern. The spread about the line may be a bit greater for larger values of the explanatory variable, but the effect is not large. (c) It is reasonable to regard the number of manatees killed by boats in successive years as independent. The number of boats grew over time. Someone says that pollution also grew over time and may explain more manatee deaths. How would you respond to this idea? Predicting tropical storms. Exercise 5.53 (page 158) gives data on William Gray s predictions of the number of named tropical storms in Atlantic hurricane seasons from 1984 to Use these data for regression inference as follows. (a) Does Professor Gray do better than random guessing? That is, is there a significantly positive correlation between his forecasts and the actual numberof storms? (Report a t statistic from regression output and give the one sided P value.) Predicting tropical storms: residuals. Make a stemplot of the residuals (round to the nearest tenth) from your regression in Exercise Explain why your plot suggests that we should not use these data to get a prediction interval for the number of storms in a single year Our brains don t like losses. Exercise 4.29 (page 116) describes an experiment that showed a linear relationship between how sensitive people are to monetary losses ( behavioral loss aversion ) and activity in one part of their brains ( neural loss aversion ). (a) Make a scatterplot with neural loss aversion as x and behavioral loss aversion as y. One point is a high outlier in both the x and y directions. In Exercise 5.37(page 153) you found that this outlier is not influential for the least squares line. (b) The research report says that r = 0.85 and that the test for regression slope has P < Verify these results, using all of the observations.
240 246 (c) The report recognizes the outlier and says, However, this regression also remained highly significant (P = 0.004) when the extreme data point (top right corner) was removed from the analysis. Repeat your analysis omitting the outlier. Show that the outlier influences regression inference by comparing the t statistic for testing slope with and without the outlier. Then verify the report s claim about the P value of this test DNA on the ocean floor. We think of DNA as the stuff that stores the genetic code. It turns out that DNA occurs, mainly outside living cells, on the ocean floor. It is important in nourishing seafloor life. Scientists think that this DNA comes from organic matter that settles to the bottom from the top layers of the ocean. Phytopigments, which come mainly from algae, are a measure of the amount of organic matter that has settled to the bottom. The data file ex23 39.dat on the text CD and Web site contains data on concentrations of DNA and phytopigments (both in grams per square meter) in 116 ocean locations around the world. Look first at DNA alone. Describe the distribution of DNA concentration and give a confidence interval for the mean concentration. Be sure to explain why your confidence interval is trustworthy in the light of the shape of the distribution. The data show surprisingly high DNA concentration, and this by itself was an important finding Squirrels and their food supply. Exercise 7.25 (page 188) gives data on the abundance of the pine cones that red squirrels feed on and the mean number of offspring per female squirrel over 16 years. The strength of the relationship is remarkable because females produce young before the food is available. How significant is the evidence that more cones leads to more offspring? (Use a vertical scale from 2 to 2 in your residual plot to show the pattern more clearly.) Beavers and beetles. Exercise 5.51 (page 157) describes a study that found that the number of stumps from trees felled by beavers predicts the abundance of beetle larvae. Is there good evidence that more beetle larvae clusters are present when beavers have left more tree stumps? Estimate how many more clusters accompany
241 247 each additional stump, with 95% confidence DNA on the ocean floor. Another conclusion of the study introduced in Exercise was that organic matter settling down from the top layers of the ocean is the main source of DNA on the seafloor. An important piece of evidence is the relationship between DNA and phytopigments. Do the data in the file ex23 39.dat give good reason to think that phytopigment concentration helps explain DNA concentration? (Try vertical limits 1 to 1 to make the pattern of your residual plot clearer.)
242 248 Chapter 24 Exercises 24.9 Bromeliads are tropical flowering plants. Many are epiphytes that attach to trees and obtain moisture and nutrients from air and rain. Their leaf bases form cups that collect water and are home to the larvae of many insects. As a preliminary to a study of changes in the nutrient cycle, Jacqueline Ngai and Diane Srivastava examined the effects of adding nitrogen, phosphorus, or both to the cups. They randomly assigned 8 bromeliads growing in Costa Rica to each of four treatment groups, including an unfertilized control group. A monkey destroyed one of the plants in the control group, leaving 7 bromeliads in that group. Here are the numbers of new leaves on each plant over the 7 months following fertilization: Nitrogen Phosphorus Both Neither Analyze these data and discuss the results. Does nitrogen or phosphorus have a greater effect on the growth of bromeliads? Follow the four step process as illustrated in Example What conditions help overweight people exercise regularly? Subjects were randomly assigned to three treatments: a single long exercise period 5 days per week; several 10 minute exercise periods 5 days per week; and several 10 minute periods 5 days per week on a home treadmill that was provided to the subjects. The study report contains the following information about weight loss (in kilograms) after six months of treatment: Treatment n x s Long exercise periods Short exercise periods Short periods with equipment
243 249 (a) Do the standard deviations satisfy the rule of thumb for safe use of ANOVA? (b) Calculate the overall mean response x. the mean squares MSG and MSE, and the F statistic. (c) Which F distribution would you use to find the P value of the ANOVA F test? Software says that P = What do you conclude from this study? Our bodies have a natural electrical field that helps wounds heal. Might higher or lower levels speed healing? An experiment with newts investigated this question. Newts were randomly assigned to five groups. In four of the groups, an electrode applied to one hind limb (chosen at random) changed the natural field, while the other hind limb was not manipulated. Both limbs in the fifth (control) group remained in their natural state. Table 24.5 gives data from this experiment. The Group variable shows the field applied as a multiple of the natural field for each newt. For example, 0.5 is half the natural field, 1 is the natural level (the control group), and 1.5 indicates a field 1.5 times natural. Diff is the response variable, the difference in the healing rate (in micrometers per hour) of cuts made in the experimental and control limbs of that newt. Negative values mean that the experimental limb healed more slowly. The investigators conjectured that nature heals best, so that changing the field from the natural state (the 1 group) will slow healing. Do a complete analysis to see whether the groups differ in the effect of the electrical field level on healing. Follow the four step process in your work. Table 24.5 Effect of electrical field on healing rate in newts Grou p Diff Grou p Diff Grou p Diff Grou p Diff Grou p Diff
244 Durable press cotton fabrics are treated to improve their recovery from wrinkles after washing. Unfortunately, the treatment also reduces the strength of the fabric. A study compared the breaking strength of untreated fabric with that of fabrics treated by three commercial durable press processes. Five specimens of the same fabric were assigned at random to each group. Here are the data, in pounds of pull needed to tear the fabric: Untreated Permafresh Permafresh Hylite LF The untreated fabric is clearly much stronger than any of the treated fabrics. We want to know if there is a significant difference in breaking strength among the three durable press treatments. Analyze the data for the three processes and write a clear summary of your findings. Which process do you recommend if breaking strength is a main concern? Use the four step process to guide your discussion. (Although the standard deviations do not quite satisfy our rule of thumb, that rule is conservative and many statisticians would use ANOVA for these data.) Your work in Exercise shows that there were significant differences in mean plant biomass among the three treatments in Do a complete analysis of the data for 2001 and report your conclusions.
245 251 Chapter 25 Exercises Excel could not be used to solve questions in these chapters.
246 252 Chapter 26 Exercises Excel could not be used to solve questions in these chapters.
247 253 Chapter 27 Exercises The table below shows the progress of world record times (in seconds) for the 10,000 meter run for both men and women. Record year Men Time (seconds) Record year Time (seconds) Record year Women Time (seconds) (a) Make a scatterplot of world record time against year, using separate symbols for men and women. Describe the pattern for each gender. Then compare the progress of men and women. (b) Fit the model with two regression lines, one for women and one for men, and identify the estimated regression lines. (c) Women began running this long distance later than men, so we might expect their improvement to be more rapid. Moreover, it is often said that men have little advantage over women in distance running as opposed to sprints, where muscular strength plays a greater role. Do the data appear to support these claims?
248 An experiment was conducted using a Geiger Mueller tube in a physics lab. Geiger Mueller tubes respond to gamma rays and to beta particles (electrons). A pulse that corresponds to each detection of a decay product is produced, and these pulses were counted using a computer based nuclear counting board. Elapsed time (in seconds) and counts of pulses for a short lived unstable isotope of silver are shown in Table 27.5 (see page 27 36). (a) Create a scatterplot of the counts versus time and describe the pattern. (b) Since some curvature is apparent in the scatterplot, you might want to consider the quadratic model for predicting counts based on time. Fit the quadratic model and identify the estimated mean response. (c) Add the estimated mean response to your scatterplot. Would you recommend the use of the quadratic model for predicting radioactive decay in this situation? Explain. (d) Transform the counts using the natural logarithm and create a scatterplot of the transformed variable versus time. (e) Fit a simple linear regression model using the natural logarithm of the counts. Provide the estimated regression line, a scatterplot with the estimated regression line, and appropriate residual plots. (f) Does the simple linear regression model for the transformed counts fit the data better than the quadratic regression model? Explain Table 27.8 contains data on the size of perch caught in a lake in Finland. Use statistical software to help you analyze these data. (a) Use the multiple regression model with two explanatory variables, length and width, to predict the weight of a perch. Provide the estimated multiple regression equation. (b) How much of the variation in the weight of perch is explained by the model in part (a)? (c) Does the ANOVA table indicate that at least one of the explanatory variables is helpful in predicting the weight of perch? Explain. (d) Do the individual t tests indicate that both β 1 and β 2 are significantly different from zero? Explain. (e) Create a new variable, called interaction, that is the product of length and width. Use the multiple regression model with three explanatory variables, length, width, and interaction, to predict the weight of a perch. Provide the estimated multiple regression equation. (f) How much of the variation in the weight of perch is explained by the model in part (e)?
249 255 (g) Does the ANOVA table indicate that at least one of the explanatory variables is helpful in predicting the weight of perch? Explain. (h) Describe how the individual t statistics changed when the interaction term was added Use explanatory variables length, width, and interaction from Exercise (page 27 49) on the 56 perch to provide 95% confidence intervals for the mean and prediction intervals for future observations. Interpret both intervals for the 10th perch in the data set. What t distribution is used to provide both intervals? The Sanchez household is about to install solar panels to reduce the cost of heating their house. In order to know how much the solar panels help, they record their consumption of natural gas before the solar panels are installed. Gas consumption is higher in cold weather, so the relationship between outside temperature and gas consumption is important. Here are the data for 16 consecutive months: Nov. Dec. Jan. Feb. Mar. Apr. May June Degree days Gas used July Aug. Sep. Oct. Nov. Dec. Jan. Feb. Degree days Gas used Outside temperature is recorded in degree days, a common measure of demand for heating. A dayʹs degree days are the number of degrees its average temperature falls below 65ºF. Gas used is recorded in hundreds of cubic feet. (a) Create an indicator variable, say INDwinter, which is 1 for the months of November, December, January, and February. Make a plot of all the data using a different symbol for winter months. (b) Fit the model with two regression lines, one for winter months and one for other months, and identify the estimated regression lines. (c) Do you think that two regression lines were needed to explain the relationship between gas used and degree days? Explain.
250 Burning calories with exercise. Table provides data on speed and calories burned per hour for a 175 pound male using two different treadmills (a Cybex and a LifeFitness) at inclines of 0%, 2%, and 4%. (a) Create a scatterplot of calories against miles per hour using six different plotting symbols, one for each combination of incline level and machine.
251 257 Chapter 28 Exercises 28.1 The full data for the logging study appear in Table 24.2 (text page 640). The data for counts of individual trees in the plots studied also appear in the data file ex28 01.dat. Carry out data analysis and ANOVA to determine whether logging affects the mean count of individual trees in a plot Which color attracts beetles best? To detect the presence of harmful insects in farm fields, we can put up boards covered with a sticky material and examine the insects trapped on the boards. Which colors attract insects best? Experimenters placed six boards of each of four colors at random locations in a field of oats and measured the number of cereal leaf beetles trapped. Here are the data:2 Board color Beetles trapped Blue Green White Yellow Is there evidence that the colors differ in their ability to attract beetles? 28.3 If you are a dog lover, perhaps having your dog along reduces the effect of stress. To examine the effect of pets in stressful situations, researchers recruited 45 women who said they were dog lovers. The EESEE story Stress among Pets and Friends describes the results. Fifteen of the subjects were randomly assigned to each of three groups to do a stressful task alone (the control group), with a good friend present, or with their dog present. The subjectʹs mean heart rate during the task is one measure of the effect of stress. Table 28.2 displays the data. Are there significant differences among the mean heart rates under the three conditions? A student project measured the increase in the heart rates of fellow students when they stepped up and down for three minutes to the beat of a metronome. The explanatory variables are step height (Lo = 5.75 inches, Hi = 11.5 inches) and metronome beat (Slow = 14 steps/minute, Med = 21 steps/minute, Fast = 28 steps/minute). The subjectʹs heart rate was measured for
252 seconds before and after stepping. The response variable is the increase in heart rate during exercise. The data appear in Table (a) Display the 6 treatments in a two way layout. (b) Find the group means, plot the means, and discuss the interaction and the two main effects. Table 28.3 Increase in heart rate due to exercise in six treatment groups Lo/Slow Lo/Med Lo/Fast Hi/Slow Hi/Med Hi/Fast The researchers who conducted the study in the previous exercise also recorded the number of times each of three types of behavior (object play, locomotor play, and social play) occurred. The file ex28 13.dat contains the counts of social play episodes by each rat during the observation period. Use two way ANOVA to analyze the effects of gender and housing Exercise (text page 661) describes a study on the rate at which the skin of newts heals under the bodyʹs natural electrical field (the 1 group in Table 24.5) and under four levels of electric field that differ from the natural level (the 0, 0.5, 1.25, and 1.5 groups). Carry out a one way ANOVA to compare the mean healing rates. Then perform Tukey multiple comparisons for the 10 pairs of population means. Use the underline method illustrated in Example to display the complicated results. What do you conclude?
Intro to Excel spreadsheets
 Intro to Excel spreadsheets What are the objectives of this document? The objectives of document are: 1. Familiarize you with what a spreadsheet is, how it works, and what its capabilities are; 2. Using
Intro to Excel spreadsheets What are the objectives of this document? The objectives of document are: 1. Familiarize you with what a spreadsheet is, how it works, and what its capabilities are; 2. Using
Basic Excel Handbook
 2 5 2 7 1 1 0 4 3 9 8 1 Basic Excel Handbook Version 3.6 May 6, 2008 Contents Contents... 1 Part I: Background Information...3 About This Handbook... 4 Excel Terminology... 5 Excel Terminology (cont.)...
2 5 2 7 1 1 0 4 3 9 8 1 Basic Excel Handbook Version 3.6 May 6, 2008 Contents Contents... 1 Part I: Background Information...3 About This Handbook... 4 Excel Terminology... 5 Excel Terminology (cont.)...
Excel 2007 Basic knowledge
 Ribbon menu The Ribbon menu system with tabs for various Excel commands. This Ribbon system replaces the traditional menus used with Excel 2003. Above the Ribbon in the upper-left corner is the Microsoft
Ribbon menu The Ribbon menu system with tabs for various Excel commands. This Ribbon system replaces the traditional menus used with Excel 2003. Above the Ribbon in the upper-left corner is the Microsoft
Excel 2003 Tutorial I
 This tutorial was adapted from a tutorial by see its complete version at http://www.fgcu.edu/support/office2000/excel/index.html Excel 2003 Tutorial I Spreadsheet Basics Screen Layout Title bar Menu bar
This tutorial was adapted from a tutorial by see its complete version at http://www.fgcu.edu/support/office2000/excel/index.html Excel 2003 Tutorial I Spreadsheet Basics Screen Layout Title bar Menu bar
Microsoft Excel 2010 Tutorial
 1 Microsoft Excel 2010 Tutorial Excel is a spreadsheet program in the Microsoft Office system. You can use Excel to create and format workbooks (a collection of spreadsheets) in order to analyze data and
1 Microsoft Excel 2010 Tutorial Excel is a spreadsheet program in the Microsoft Office system. You can use Excel to create and format workbooks (a collection of spreadsheets) in order to analyze data and
SECTION 2-1: OVERVIEW SECTION 2-2: FREQUENCY DISTRIBUTIONS
 SECTION 2-1: OVERVIEW Chapter 2 Describing, Exploring and Comparing Data 19 In this chapter, we will use the capabilities of Excel to help us look more carefully at sets of data. We can do this by re-organizing
SECTION 2-1: OVERVIEW Chapter 2 Describing, Exploring and Comparing Data 19 In this chapter, we will use the capabilities of Excel to help us look more carefully at sets of data. We can do this by re-organizing
Microsoft Excel 2010 Part 3: Advanced Excel
 CALIFORNIA STATE UNIVERSITY, LOS ANGELES INFORMATION TECHNOLOGY SERVICES Microsoft Excel 2010 Part 3: Advanced Excel Winter 2015, Version 1.0 Table of Contents Introduction...2 Sorting Data...2 Sorting
CALIFORNIA STATE UNIVERSITY, LOS ANGELES INFORMATION TECHNOLOGY SERVICES Microsoft Excel 2010 Part 3: Advanced Excel Winter 2015, Version 1.0 Table of Contents Introduction...2 Sorting Data...2 Sorting
Scientific Graphing in Excel 2010
 Scientific Graphing in Excel 2010 When you start Excel, you will see the screen below. Various parts of the display are labelled in red, with arrows, to define the terms used in the remainder of this overview.
Scientific Graphing in Excel 2010 When you start Excel, you will see the screen below. Various parts of the display are labelled in red, with arrows, to define the terms used in the remainder of this overview.
Below is a very brief tutorial on the basic capabilities of Excel. Refer to the Excel help files for more information.
 Excel Tutorial Below is a very brief tutorial on the basic capabilities of Excel. Refer to the Excel help files for more information. Working with Data Entering and Formatting Data Before entering data
Excel Tutorial Below is a very brief tutorial on the basic capabilities of Excel. Refer to the Excel help files for more information. Working with Data Entering and Formatting Data Before entering data
Getting Started with Excel 2008. Table of Contents
 Table of Contents Elements of An Excel Document... 2 Resizing and Hiding Columns and Rows... 3 Using Panes to Create Spreadsheet Headers... 3 Using the AutoFill Command... 4 Using AutoFill for Sequences...
Table of Contents Elements of An Excel Document... 2 Resizing and Hiding Columns and Rows... 3 Using Panes to Create Spreadsheet Headers... 3 Using the AutoFill Command... 4 Using AutoFill for Sequences...
Preface of Excel Guide
 Preface of Excel Guide The use of spreadsheets in a course designed primarily for business and social science majors can enhance the understanding of the underlying mathematical concepts. In addition,
Preface of Excel Guide The use of spreadsheets in a course designed primarily for business and social science majors can enhance the understanding of the underlying mathematical concepts. In addition,
EXCEL Tutorial: How to use EXCEL for Graphs and Calculations.
 EXCEL Tutorial: How to use EXCEL for Graphs and Calculations. Excel is powerful tool and can make your life easier if you are proficient in using it. You will need to use Excel to complete most of your
EXCEL Tutorial: How to use EXCEL for Graphs and Calculations. Excel is powerful tool and can make your life easier if you are proficient in using it. You will need to use Excel to complete most of your
Basic Microsoft Excel 2007
 Basic Microsoft Excel 2007 The biggest difference between Excel 2007 and its predecessors is the new layout. All of the old functions are still there (with some new additions), but they are now located
Basic Microsoft Excel 2007 The biggest difference between Excel 2007 and its predecessors is the new layout. All of the old functions are still there (with some new additions), but they are now located
Excel 2007 Tutorials - Video File Attributes
 Get Familiar with Excel 2007 42.40 3.02 The Excel 2007 Environment 4.10 0.19 Office Button 3.10 0.31 Quick Access Toolbar 3.10 0.33 Excel 2007 Ribbon 3.10 0.26 Home Tab 5.10 0.19 Insert Tab 3.10 0.19 Page
Get Familiar with Excel 2007 42.40 3.02 The Excel 2007 Environment 4.10 0.19 Office Button 3.10 0.31 Quick Access Toolbar 3.10 0.33 Excel 2007 Ribbon 3.10 0.26 Home Tab 5.10 0.19 Insert Tab 3.10 0.19 Page
Introduction to Microsoft Excel 2010
 Introduction to Microsoft Excel 2010 Screen Elements Quick Access Toolbar The Ribbon Formula Bar Expand Formula Bar Button File Menu Vertical Scroll Worksheet Navigation Tabs Horizontal Scroll Bar Zoom
Introduction to Microsoft Excel 2010 Screen Elements Quick Access Toolbar The Ribbon Formula Bar Expand Formula Bar Button File Menu Vertical Scroll Worksheet Navigation Tabs Horizontal Scroll Bar Zoom
Appendix 2.1 Tabular and Graphical Methods Using Excel
 Appendix 2.1 Tabular and Graphical Methods Using Excel 1 Appendix 2.1 Tabular and Graphical Methods Using Excel The instructions in this section begin by describing the entry of data into an Excel spreadsheet.
Appendix 2.1 Tabular and Graphical Methods Using Excel 1 Appendix 2.1 Tabular and Graphical Methods Using Excel The instructions in this section begin by describing the entry of data into an Excel spreadsheet.
Excel 2007: Basics Learning Guide
 Excel 2007: Basics Learning Guide Exploring Excel At first glance, the new Excel 2007 interface may seem a bit unsettling, with fat bands called Ribbons replacing cascading text menus and task bars. This
Excel 2007: Basics Learning Guide Exploring Excel At first glance, the new Excel 2007 interface may seem a bit unsettling, with fat bands called Ribbons replacing cascading text menus and task bars. This
Handout: How to Use Excel 2010
 How to Use Excel 2010 Table of Contents THE EXCEL ENVIRONMENT... 4 MOVE OR SCROLL THROUGH A WORKSHEET... 5 USE THE SCROLL BARS TO MOVE THROUGH A WORKSHEET... 5 USE THE ARROW KEYS TO MOVE THROUGH A WORKSHEET...
How to Use Excel 2010 Table of Contents THE EXCEL ENVIRONMENT... 4 MOVE OR SCROLL THROUGH A WORKSHEET... 5 USE THE SCROLL BARS TO MOVE THROUGH A WORKSHEET... 5 USE THE ARROW KEYS TO MOVE THROUGH A WORKSHEET...
Using Excel for Analyzing Survey Questionnaires Jennifer Leahy
 University of Wisconsin-Extension Cooperative Extension Madison, Wisconsin PD &E Program Development & Evaluation Using Excel for Analyzing Survey Questionnaires Jennifer Leahy G3658-14 Introduction You
University of Wisconsin-Extension Cooperative Extension Madison, Wisconsin PD &E Program Development & Evaluation Using Excel for Analyzing Survey Questionnaires Jennifer Leahy G3658-14 Introduction You
Excel 2007 A Beginners Guide
 Excel 2007 A Beginners Guide Beginner Introduction The aim of this document is to introduce some basic techniques for using Excel to enter data, perform calculations and produce simple charts based on
Excel 2007 A Beginners Guide Beginner Introduction The aim of this document is to introduce some basic techniques for using Excel to enter data, perform calculations and produce simple charts based on
Excel Guide for Finite Mathematics and Applied Calculus
 Excel Guide for Finite Mathematics and Applied Calculus Revathi Narasimhan Kean University A technology guide to accompany Mathematical Applications, 6 th Edition Applied Calculus, 2 nd Edition Calculus:
Excel Guide for Finite Mathematics and Applied Calculus Revathi Narasimhan Kean University A technology guide to accompany Mathematical Applications, 6 th Edition Applied Calculus, 2 nd Edition Calculus:
Excel 2010: Create your first spreadsheet
 Excel 2010: Create your first spreadsheet Goals: After completing this course you will be able to: Create a new spreadsheet. Add, subtract, multiply, and divide in a spreadsheet. Enter and format column
Excel 2010: Create your first spreadsheet Goals: After completing this course you will be able to: Create a new spreadsheet. Add, subtract, multiply, and divide in a spreadsheet. Enter and format column
STC: Descriptive Statistics in Excel 2013. Running Descriptive and Correlational Analysis in Excel 2013
 Running Descriptive and Correlational Analysis in Excel 2013 Tips for coding a survey Use short phrases for your data table headers to keep your worksheet neat, you can always edit the labels in tables
Running Descriptive and Correlational Analysis in Excel 2013 Tips for coding a survey Use short phrases for your data table headers to keep your worksheet neat, you can always edit the labels in tables
Microsoft Excel Tutorial
 Microsoft Excel Tutorial by Dr. James E. Parks Department of Physics and Astronomy 401 Nielsen Physics Building The University of Tennessee Knoxville, Tennessee 37996-1200 Copyright August, 2000 by James
Microsoft Excel Tutorial by Dr. James E. Parks Department of Physics and Astronomy 401 Nielsen Physics Building The University of Tennessee Knoxville, Tennessee 37996-1200 Copyright August, 2000 by James
Excel. Microsoft Office s spreadsheet application can be used to track. and analyze numerical data for display on screen or in printed
 Excel Microsoft Office s spreadsheet application can be used to track and analyze numerical data for display on screen or in printed format. Excel is designed to help you record and calculate data, and
Excel Microsoft Office s spreadsheet application can be used to track and analyze numerical data for display on screen or in printed format. Excel is designed to help you record and calculate data, and
Excel Level Two. Introduction. Contents. Exploring Formulas. Entering Formulas
 Introduction Excel Level Two This workshop introduces you to formulas, functions, moving and copying data, using autofill, relative and absolute references, and formatting cells. Contents Introduction
Introduction Excel Level Two This workshop introduces you to formulas, functions, moving and copying data, using autofill, relative and absolute references, and formatting cells. Contents Introduction
Data exploration with Microsoft Excel: univariate analysis
 Data exploration with Microsoft Excel: univariate analysis Contents 1 Introduction... 1 2 Exploring a variable s frequency distribution... 2 3 Calculating measures of central tendency... 16 4 Calculating
Data exploration with Microsoft Excel: univariate analysis Contents 1 Introduction... 1 2 Exploring a variable s frequency distribution... 2 3 Calculating measures of central tendency... 16 4 Calculating
The Center for Teaching, Learning, & Technology
 The Center for Teaching, Learning, & Technology Instructional Technology Workshops Microsoft Excel 2010 Formulas and Charts Albert Robinson / Delwar Sayeed Faculty and Staff Development Programs Colston
The Center for Teaching, Learning, & Technology Instructional Technology Workshops Microsoft Excel 2010 Formulas and Charts Albert Robinson / Delwar Sayeed Faculty and Staff Development Programs Colston
Task Force on Technology / EXCEL
 Task Force on Technology EXCEL Basic terminology Spreadsheet A spreadsheet is an electronic document that stores various types of data. There are vertical columns and horizontal rows. A cell is where the
Task Force on Technology EXCEL Basic terminology Spreadsheet A spreadsheet is an electronic document that stores various types of data. There are vertical columns and horizontal rows. A cell is where the
Excel 2003 A Beginners Guide
 Excel 2003 A Beginners Guide Beginner Introduction The aim of this document is to introduce some basic techniques for using Excel to enter data, perform calculations and produce simple charts based on
Excel 2003 A Beginners Guide Beginner Introduction The aim of this document is to introduce some basic techniques for using Excel to enter data, perform calculations and produce simple charts based on
Creating and Editing Workbooks. STUDENT LEARNING OUTCOMES (SLOs) After completing this chapter, you will be able to:
 CHAPTER 1 Creating and Editing Workbooks CHAPTER OVERVIEW Microsoft Excel (Excel) is a spreadsheet program you can use to create electronic workbooks to organize numerical data, perform calculations, and
CHAPTER 1 Creating and Editing Workbooks CHAPTER OVERVIEW Microsoft Excel (Excel) is a spreadsheet program you can use to create electronic workbooks to organize numerical data, perform calculations, and
Microsoft Excel Tutorial
 Microsoft Excel Tutorial Microsoft Excel spreadsheets are a powerful and easy to use tool to record, plot and analyze experimental data. Excel is commonly used by engineers to tackle sophisticated computations
Microsoft Excel Tutorial Microsoft Excel spreadsheets are a powerful and easy to use tool to record, plot and analyze experimental data. Excel is commonly used by engineers to tackle sophisticated computations
Spreadsheet - Introduction
 CSCA0102 IT and Business Applications Chapter 6 Spreadsheet - Introduction Spreadsheet A spreadsheet (or spreadsheet program) is software that permits numerical data to be used and to perform automatic
CSCA0102 IT and Business Applications Chapter 6 Spreadsheet - Introduction Spreadsheet A spreadsheet (or spreadsheet program) is software that permits numerical data to be used and to perform automatic
Computer Training Centre University College Cork. Excel 2013 Level 1
 Computer Training Centre University College Cork Excel 2013 Level 1 Table of Contents Introduction... 1 Opening Excel... 1 Using Windows 7... 1 Using Windows 8... 1 Getting Started with Excel 2013... 2
Computer Training Centre University College Cork Excel 2013 Level 1 Table of Contents Introduction... 1 Opening Excel... 1 Using Windows 7... 1 Using Windows 8... 1 Getting Started with Excel 2013... 2
Excel Project Creating a Stock Portfolio Simulation
 Background Vocabulary Excel Project Creating a Stock Portfolio Simulation 1. What is a stock? A stock is a share in the ownership of a corporation, a large business organization. A stock, also, represents
Background Vocabulary Excel Project Creating a Stock Portfolio Simulation 1. What is a stock? A stock is a share in the ownership of a corporation, a large business organization. A stock, also, represents
Word 2007: Basics Learning Guide
 Word 2007: Basics Learning Guide Exploring Word At first glance, the new Word 2007 interface may seem a bit unsettling, with fat bands called Ribbons replacing cascading text menus and task bars. This
Word 2007: Basics Learning Guide Exploring Word At first glance, the new Word 2007 interface may seem a bit unsettling, with fat bands called Ribbons replacing cascading text menus and task bars. This
Bill Burton Albert Einstein College of Medicine [email protected] April 28, 2014 EERS: Managing the Tension Between Rigor and Resources 1
 Bill Burton Albert Einstein College of Medicine [email protected] April 28, 2014 EERS: Managing the Tension Between Rigor and Resources 1 Calculate counts, means, and standard deviations Produce
Bill Burton Albert Einstein College of Medicine [email protected] April 28, 2014 EERS: Managing the Tension Between Rigor and Resources 1 Calculate counts, means, and standard deviations Produce
Microsoft Excel 2010. Understanding the Basics
 Microsoft Excel 2010 Understanding the Basics Table of Contents Opening Excel 2010 2 Components of Excel 2 The Ribbon 3 o Contextual Tabs 3 o Dialog Box Launcher 4 o Quick Access Toolbar 4 Key Tips 5 The
Microsoft Excel 2010 Understanding the Basics Table of Contents Opening Excel 2010 2 Components of Excel 2 The Ribbon 3 o Contextual Tabs 3 o Dialog Box Launcher 4 o Quick Access Toolbar 4 Key Tips 5 The
Data exploration with Microsoft Excel: analysing more than one variable
 Data exploration with Microsoft Excel: analysing more than one variable Contents 1 Introduction... 1 2 Comparing different groups or different variables... 2 3 Exploring the association between categorical
Data exploration with Microsoft Excel: analysing more than one variable Contents 1 Introduction... 1 2 Comparing different groups or different variables... 2 3 Exploring the association between categorical
How to Use a Data Spreadsheet: Excel
 How to Use a Data Spreadsheet: Excel One does not necessarily have special statistical software to perform statistical analyses. Microsoft Office Excel can be used to run statistical procedures. Although
How to Use a Data Spreadsheet: Excel One does not necessarily have special statistical software to perform statistical analyses. Microsoft Office Excel can be used to run statistical procedures. Although
INTRODUCTION TO EXCEL
 INTRODUCTION TO EXCEL 1 INTRODUCTION Anyone who has used a computer for more than just playing games will be aware of spreadsheets A spreadsheet is a versatile computer program (package) that enables you
INTRODUCTION TO EXCEL 1 INTRODUCTION Anyone who has used a computer for more than just playing games will be aware of spreadsheets A spreadsheet is a versatile computer program (package) that enables you
Q&As: Microsoft Excel 2013: Chapter 2
 Q&As: Microsoft Excel 2013: Chapter 2 In Step 5, why did the date that was entered change from 4/5/10 to 4/5/2010? When Excel recognizes that you entered a date in mm/dd/yy format, it automatically formats
Q&As: Microsoft Excel 2013: Chapter 2 In Step 5, why did the date that was entered change from 4/5/10 to 4/5/2010? When Excel recognizes that you entered a date in mm/dd/yy format, it automatically formats
Microsoft Excel 2007 An Essential Guide (Level 1)
 IT Services Microsoft Excel 2007 An Essential Guide (Level 1) Contents Introduction...1 Starting Excel...1 The Excel Screen...1 Getting Help...2 Moving Around the Worksheet...2 Saving your Work...2 Data
IT Services Microsoft Excel 2007 An Essential Guide (Level 1) Contents Introduction...1 Starting Excel...1 The Excel Screen...1 Getting Help...2 Moving Around the Worksheet...2 Saving your Work...2 Data
PERFORMING REGRESSION ANALYSIS USING MICROSOFT EXCEL
 PERFORMING REGRESSION ANALYSIS USING MICROSOFT EXCEL John O. Mason, Ph.D., CPA Professor of Accountancy Culverhouse School of Accountancy The University of Alabama Abstract: This paper introduces you to
PERFORMING REGRESSION ANALYSIS USING MICROSOFT EXCEL John O. Mason, Ph.D., CPA Professor of Accountancy Culverhouse School of Accountancy The University of Alabama Abstract: This paper introduces you to
Microsoft Excel Basics
 COMMUNITY TECHNICAL SUPPORT Microsoft Excel Basics Introduction to Excel Click on the program icon in Launcher or the Microsoft Office Shortcut Bar. A worksheet is a grid, made up of columns, which are
COMMUNITY TECHNICAL SUPPORT Microsoft Excel Basics Introduction to Excel Click on the program icon in Launcher or the Microsoft Office Shortcut Bar. A worksheet is a grid, made up of columns, which are
How to Use Excel 2007
 How to Use Excel 2007 Table of Contents THE EXCEL ENVIRONMENT... 4 MOVE OR SCROLL THROUGH A WORKSHEET... 5 USE THE SCROLL BARS TO MOVE THROUGH A WORKSHEET... 5 USE THE ARROW KEYS TO MOVE THROUGH A WORKSHEET...
How to Use Excel 2007 Table of Contents THE EXCEL ENVIRONMENT... 4 MOVE OR SCROLL THROUGH A WORKSHEET... 5 USE THE SCROLL BARS TO MOVE THROUGH A WORKSHEET... 5 USE THE ARROW KEYS TO MOVE THROUGH A WORKSHEET...
ECDL / ICDL Spreadsheets Syllabus Version 5.0
 ECDL / ICDL Spreadsheets Syllabus Version 5.0 Purpose This document details the syllabus for ECDL / ICDL Spreadsheets. The syllabus describes, through learning outcomes, the knowledge and skills that a
ECDL / ICDL Spreadsheets Syllabus Version 5.0 Purpose This document details the syllabus for ECDL / ICDL Spreadsheets. The syllabus describes, through learning outcomes, the knowledge and skills that a
Excel 2007/2010 for Researchers. Jamie DeCoster Institute for Social Science Research University of Alabama. September 7, 2010
 Excel 2007/2010 for Researchers Jamie DeCoster Institute for Social Science Research University of Alabama September 7, 2010 I d like to thank Joe Chandler for comments made on an earlier version of these
Excel 2007/2010 for Researchers Jamie DeCoster Institute for Social Science Research University of Alabama September 7, 2010 I d like to thank Joe Chandler for comments made on an earlier version of these
3 What s New in Excel 2007
 3 What s New in Excel 2007 3.1 Overview of Excel 2007 Microsoft Office Excel 2007 is a spreadsheet program that enables you to enter, manipulate, calculate, and chart data. An Excel file is referred to
3 What s New in Excel 2007 3.1 Overview of Excel 2007 Microsoft Office Excel 2007 is a spreadsheet program that enables you to enter, manipulate, calculate, and chart data. An Excel file is referred to
Table of Contents TASK 1: DATA ANALYSIS TOOLPAK... 2 TASK 2: HISTOGRAMS... 5 TASK 3: ENTER MIDPOINT FORMULAS... 11
 Table of Contents TASK 1: DATA ANALYSIS TOOLPAK... 2 TASK 2: HISTOGRAMS... 5 TASK 3: ENTER MIDPOINT FORMULAS... 11 TASK 4: ADD TOTAL LABEL AND FORMULA FOR FREQUENCY... 12 TASK 5: MODIFICATIONS TO THE HISTOGRAM...
Table of Contents TASK 1: DATA ANALYSIS TOOLPAK... 2 TASK 2: HISTOGRAMS... 5 TASK 3: ENTER MIDPOINT FORMULAS... 11 TASK 4: ADD TOTAL LABEL AND FORMULA FOR FREQUENCY... 12 TASK 5: MODIFICATIONS TO THE HISTOGRAM...
Engineering Problem Solving and Excel. EGN 1006 Introduction to Engineering
 Engineering Problem Solving and Excel EGN 1006 Introduction to Engineering Mathematical Solution Procedures Commonly Used in Engineering Analysis Data Analysis Techniques (Statistics) Curve Fitting techniques
Engineering Problem Solving and Excel EGN 1006 Introduction to Engineering Mathematical Solution Procedures Commonly Used in Engineering Analysis Data Analysis Techniques (Statistics) Curve Fitting techniques
Data Analysis Tools. Tools for Summarizing Data
 Data Analysis Tools This section of the notes is meant to introduce you to many of the tools that are provided by Excel under the Tools/Data Analysis menu item. If your computer does not have that tool
Data Analysis Tools This section of the notes is meant to introduce you to many of the tools that are provided by Excel under the Tools/Data Analysis menu item. If your computer does not have that tool
SPSS Manual for Introductory Applied Statistics: A Variable Approach
 SPSS Manual for Introductory Applied Statistics: A Variable Approach John Gabrosek Department of Statistics Grand Valley State University Allendale, MI USA August 2013 2 Copyright 2013 John Gabrosek. All
SPSS Manual for Introductory Applied Statistics: A Variable Approach John Gabrosek Department of Statistics Grand Valley State University Allendale, MI USA August 2013 2 Copyright 2013 John Gabrosek. All
Using Excel 2003 with Basic Business Statistics
 Using Excel 2003 with Basic Business Statistics Introduction Use this document if you plan to use Excel 2003 with Basic Business Statistics, 12th edition. Instructions specific to Excel 2003 are needed
Using Excel 2003 with Basic Business Statistics Introduction Use this document if you plan to use Excel 2003 with Basic Business Statistics, 12th edition. Instructions specific to Excel 2003 are needed
Advanced Microsoft Excel 2010
 Advanced Microsoft Excel 2010 Table of Contents THE PASTE SPECIAL FUNCTION... 2 Paste Special Options... 2 Using the Paste Special Function... 3 ORGANIZING DATA... 4 Multiple-Level Sorting... 4 Subtotaling
Advanced Microsoft Excel 2010 Table of Contents THE PASTE SPECIAL FUNCTION... 2 Paste Special Options... 2 Using the Paste Special Function... 3 ORGANIZING DATA... 4 Multiple-Level Sorting... 4 Subtotaling
Microsoft Access 2010 handout
 Microsoft Access 2010 handout Access 2010 is a relational database program you can use to create and manage large quantities of data. You can use Access to manage anything from a home inventory to a giant
Microsoft Access 2010 handout Access 2010 is a relational database program you can use to create and manage large quantities of data. You can use Access to manage anything from a home inventory to a giant
EXCEL PIVOT TABLE David Geffen School of Medicine, UCLA Dean s Office Oct 2002
 EXCEL PIVOT TABLE David Geffen School of Medicine, UCLA Dean s Office Oct 2002 Table of Contents Part I Creating a Pivot Table Excel Database......3 What is a Pivot Table...... 3 Creating Pivot Tables
EXCEL PIVOT TABLE David Geffen School of Medicine, UCLA Dean s Office Oct 2002 Table of Contents Part I Creating a Pivot Table Excel Database......3 What is a Pivot Table...... 3 Creating Pivot Tables
How to make a line graph using Excel 2007
 How to make a line graph using Excel 2007 Format your data sheet Make sure you have a title and each column of data has a title. If you are entering data by hand, use time or the independent variable in
How to make a line graph using Excel 2007 Format your data sheet Make sure you have a title and each column of data has a title. If you are entering data by hand, use time or the independent variable in
MS Word 2007 practical notes
 MS Word 2007 practical notes Contents Opening Microsoft Word 2007 in the practical room... 4 Screen Layout... 4 The Microsoft Office Button... 4 The Ribbon... 5 Quick Access Toolbar... 5 Moving in the
MS Word 2007 practical notes Contents Opening Microsoft Word 2007 in the practical room... 4 Screen Layout... 4 The Microsoft Office Button... 4 The Ribbon... 5 Quick Access Toolbar... 5 Moving in the
USING EXCEL ON THE COMPUTER TO FIND THE MEAN AND STANDARD DEVIATION AND TO DO LINEAR REGRESSION ANALYSIS AND GRAPHING TABLE OF CONTENTS
 USING EXCEL ON THE COMPUTER TO FIND THE MEAN AND STANDARD DEVIATION AND TO DO LINEAR REGRESSION ANALYSIS AND GRAPHING Dr. Susan Petro TABLE OF CONTENTS Topic Page number 1. On following directions 2 2.
USING EXCEL ON THE COMPUTER TO FIND THE MEAN AND STANDARD DEVIATION AND TO DO LINEAR REGRESSION ANALYSIS AND GRAPHING Dr. Susan Petro TABLE OF CONTENTS Topic Page number 1. On following directions 2 2.
MS Excel. Handout: Level 2. elearning Department. Copyright 2016 CMS e-learning Department. All Rights Reserved. Page 1 of 11
 MS Excel Handout: Level 2 elearning Department 2016 Page 1 of 11 Contents Excel Environment:... 3 To create a new blank workbook:...3 To insert text:...4 Cell addresses:...4 To save the workbook:... 5
MS Excel Handout: Level 2 elearning Department 2016 Page 1 of 11 Contents Excel Environment:... 3 To create a new blank workbook:...3 To insert text:...4 Cell addresses:...4 To save the workbook:... 5
Introduction to Microsoft Excel 1 Part I
 Introduction to Microsoft Excel 1 Part I Objectives When you complete this workshop you will be able to: Recognize Excel s basic operations and tools; Develop simple worksheets; Use formulas; Format worksheets;
Introduction to Microsoft Excel 1 Part I Objectives When you complete this workshop you will be able to: Recognize Excel s basic operations and tools; Develop simple worksheets; Use formulas; Format worksheets;
Data Analysis. Using Excel. Jeffrey L. Rummel. BBA Seminar. Data in Excel. Excel Calculations of Descriptive Statistics. Single Variable Graphs
 Using Excel Jeffrey L. Rummel Emory University Goizueta Business School BBA Seminar Jeffrey L. Rummel BBA Seminar 1 / 54 Excel Calculations of Descriptive Statistics Single Variable Graphs Relationships
Using Excel Jeffrey L. Rummel Emory University Goizueta Business School BBA Seminar Jeffrey L. Rummel BBA Seminar 1 / 54 Excel Calculations of Descriptive Statistics Single Variable Graphs Relationships
OX Spreadsheet Product Guide
 OX Spreadsheet Product Guide Open-Xchange February 2014 2014 Copyright Open-Xchange Inc. OX Spreadsheet Product Guide This document is the intellectual property of Open-Xchange Inc. The document may be
OX Spreadsheet Product Guide Open-Xchange February 2014 2014 Copyright Open-Xchange Inc. OX Spreadsheet Product Guide This document is the intellectual property of Open-Xchange Inc. The document may be
0 Introduction to Data Analysis Using an Excel Spreadsheet
 Experiment 0 Introduction to Data Analysis Using an Excel Spreadsheet I. Purpose The purpose of this introductory lab is to teach you a few basic things about how to use an EXCEL 2010 spreadsheet to do
Experiment 0 Introduction to Data Analysis Using an Excel Spreadsheet I. Purpose The purpose of this introductory lab is to teach you a few basic things about how to use an EXCEL 2010 spreadsheet to do
Introduction to Microsoft Excel 2007/2010
 to Microsoft Excel 2007/2010 Abstract: Microsoft Excel is one of the most powerful and widely used spreadsheet applications available today. Excel's functionality and popularity have made it an essential
to Microsoft Excel 2007/2010 Abstract: Microsoft Excel is one of the most powerful and widely used spreadsheet applications available today. Excel's functionality and popularity have made it an essential
Microsoft Word 2010 Prepared by Computing Services at the Eastman School of Music July 2010
 Microsoft Word 2010 Prepared by Computing Services at the Eastman School of Music July 2010 Contents Microsoft Office Interface... 4 File Ribbon Tab... 5 Microsoft Office Quick Access Toolbar... 6 Appearance
Microsoft Word 2010 Prepared by Computing Services at the Eastman School of Music July 2010 Contents Microsoft Office Interface... 4 File Ribbon Tab... 5 Microsoft Office Quick Access Toolbar... 6 Appearance
Advanced Excel 10/20/2011 1
 Advanced Excel Data Validation Excel has a feature called Data Validation, which will allow you to control what kind of information is typed into cells. 1. Select the cell(s) you wish to control. 2. Click
Advanced Excel Data Validation Excel has a feature called Data Validation, which will allow you to control what kind of information is typed into cells. 1. Select the cell(s) you wish to control. 2. Click
Decision Support AITS University Administration. Web Intelligence Rich Client 4.1 User Guide
 Decision Support AITS University Administration Web Intelligence Rich Client 4.1 User Guide 2 P age Web Intelligence 4.1 User Guide Web Intelligence 4.1 User Guide Contents Getting Started in Web Intelligence
Decision Support AITS University Administration Web Intelligence Rich Client 4.1 User Guide 2 P age Web Intelligence 4.1 User Guide Web Intelligence 4.1 User Guide Contents Getting Started in Web Intelligence
Google Docs Basics Website: http://etc.usf.edu/te/
 Website: http://etc.usf.edu/te/ Google Docs is a free web-based office suite that allows you to store documents online so you can access them from any computer with an internet connection. With Google
Website: http://etc.usf.edu/te/ Google Docs is a free web-based office suite that allows you to store documents online so you can access them from any computer with an internet connection. With Google
ECDL. European Computer Driving Licence. Spreadsheet Software BCS ITQ Level 2. Syllabus Version 5.0
 European Computer Driving Licence Spreadsheet Software BCS ITQ Level 2 Using Microsoft Excel 2010 Syllabus Version 5.0 This training, which has been approved by BCS, The Chartered Institute for IT, includes
European Computer Driving Licence Spreadsheet Software BCS ITQ Level 2 Using Microsoft Excel 2010 Syllabus Version 5.0 This training, which has been approved by BCS, The Chartered Institute for IT, includes
Excel Basics for Account Reconciliation
 Excel Basics for Account Reconciliation Excel Basics for Acct Recon Training Guide 1 Table of Contents Introduction... 5 Overview... 5 Course objectives... 5 Lesson 1 Getting Started... 6 Overview... 6
Excel Basics for Account Reconciliation Excel Basics for Acct Recon Training Guide 1 Table of Contents Introduction... 5 Overview... 5 Course objectives... 5 Lesson 1 Getting Started... 6 Overview... 6
Kingsoft Spreadsheet 2012
 Kingsoft Spreadsheet 2012 Kingsoft Spreadsheet is a flexible and efficient commercial spreadsheet application. It is widely used by professionals in many fields such as: Business, Finance, Economics and
Kingsoft Spreadsheet 2012 Kingsoft Spreadsheet is a flexible and efficient commercial spreadsheet application. It is widely used by professionals in many fields such as: Business, Finance, Economics and
Introduction to Microsoft Word 2003
 Introduction to Microsoft Word 2003 Sabeera Kulkarni Information Technology Lab School of Information University of Texas at Austin Fall 2004 1. Objective This tutorial is designed for users who are new
Introduction to Microsoft Word 2003 Sabeera Kulkarni Information Technology Lab School of Information University of Texas at Austin Fall 2004 1. Objective This tutorial is designed for users who are new
Excel Unit 4. Data files needed to complete these exercises will be found on the S: drive>410>student>computer Technology>Excel>Unit 4
 Excel Unit 4 Data files needed to complete these exercises will be found on the S: drive>410>student>computer Technology>Excel>Unit 4 Step by Step 4.1 Creating and Positioning Charts GET READY. Before
Excel Unit 4 Data files needed to complete these exercises will be found on the S: drive>410>student>computer Technology>Excel>Unit 4 Step by Step 4.1 Creating and Positioning Charts GET READY. Before
Spreadsheets and Laboratory Data Analysis: Excel 2003 Version (Excel 2007 is only slightly different)
 Spreadsheets and Laboratory Data Analysis: Excel 2003 Version (Excel 2007 is only slightly different) Spreadsheets are computer programs that allow the user to enter and manipulate numbers. They are capable
Spreadsheets and Laboratory Data Analysis: Excel 2003 Version (Excel 2007 is only slightly different) Spreadsheets are computer programs that allow the user to enter and manipulate numbers. They are capable
Plotting: Customizing the Graph
 Plotting: Customizing the Graph Data Plots: General Tips Making a Data Plot Active Within a graph layer, only one data plot can be active. A data plot must be set active before you can use the Data Selector
Plotting: Customizing the Graph Data Plots: General Tips Making a Data Plot Active Within a graph layer, only one data plot can be active. A data plot must be set active before you can use the Data Selector
Working with Data in Microsoft Excel 2003
 Working with Data in Microsoft Excel 2003 Doc 5.94 Ver 2 March 2005 John Matthews Central Computing Services Abstract This document provides some examples of handling numeric data using the Microsoft Excel
Working with Data in Microsoft Excel 2003 Doc 5.94 Ver 2 March 2005 John Matthews Central Computing Services Abstract This document provides some examples of handling numeric data using the Microsoft Excel
To reuse a template that you ve recently used, click Recent Templates, click the template that you want, and then click Create.
 What is Excel? Applies to: Excel 2010 Excel is a spreadsheet program in the Microsoft Office system. You can use Excel to create and format workbooks (a collection of spreadsheets) in order to analyze
What is Excel? Applies to: Excel 2010 Excel is a spreadsheet program in the Microsoft Office system. You can use Excel to create and format workbooks (a collection of spreadsheets) in order to analyze
Tutorial 2: Using Excel in Data Analysis
 Tutorial 2: Using Excel in Data Analysis This tutorial guide addresses several issues particularly relevant in the context of the level 1 Physics lab sessions at Durham: organising your work sheet neatly,
Tutorial 2: Using Excel in Data Analysis This tutorial guide addresses several issues particularly relevant in the context of the level 1 Physics lab sessions at Durham: organising your work sheet neatly,
DOING MORE WITH WORD: MICROSOFT OFFICE 2010
 University of North Carolina at Chapel Hill Libraries Carrboro Cybrary Chapel Hill Public Library Durham County Public Library DOING MORE WITH WORD: MICROSOFT OFFICE 2010 GETTING STARTED PAGE 02 Prerequisites
University of North Carolina at Chapel Hill Libraries Carrboro Cybrary Chapel Hill Public Library Durham County Public Library DOING MORE WITH WORD: MICROSOFT OFFICE 2010 GETTING STARTED PAGE 02 Prerequisites
Figure 1. An embedded chart on a worksheet.
 8. Excel Charts and Analysis ToolPak Charts, also known as graphs, have been an integral part of spreadsheets since the early days of Lotus 1-2-3. Charting features have improved significantly over the
8. Excel Charts and Analysis ToolPak Charts, also known as graphs, have been an integral part of spreadsheets since the early days of Lotus 1-2-3. Charting features have improved significantly over the
How To Analyze Data In Excel 2003 With A Powerpoint 3.5
 Microsoft Excel 2003 Data Analysis Larry F. Vint, Ph.D [email protected] 815-753-8053 Technical Advisory Group Customer Support Services Northern Illinois University 120 Swen Parson Hall DeKalb, IL 60115 Copyright
Microsoft Excel 2003 Data Analysis Larry F. Vint, Ph.D [email protected] 815-753-8053 Technical Advisory Group Customer Support Services Northern Illinois University 120 Swen Parson Hall DeKalb, IL 60115 Copyright
Search help. More on Office.com: images templates. Here are some basic tasks that you can do in Microsoft Excel 2010.
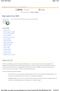 Page 1 of 8 Excel 2010 Home > Excel 2010 Help and How-to > Getting started with Excel Search help More on Office.com: images templates Basic tasks in Excel 2010 Here are some basic tasks that you can do
Page 1 of 8 Excel 2010 Home > Excel 2010 Help and How-to > Getting started with Excel Search help More on Office.com: images templates Basic tasks in Excel 2010 Here are some basic tasks that you can do
EXCEL 2007. Using Excel for Data Query & Management. Information Technology. MS Office Excel 2007 Users Guide. IT Training & Development
 Information Technology MS Office Excel 2007 Users Guide EXCEL 2007 Using Excel for Data Query & Management IT Training & Development (818) 677-1700 [email protected] http://www.csun.edu/training TABLE
Information Technology MS Office Excel 2007 Users Guide EXCEL 2007 Using Excel for Data Query & Management IT Training & Development (818) 677-1700 [email protected] http://www.csun.edu/training TABLE
Excel -- Creating Charts
 Excel -- Creating Charts The saying goes, A picture is worth a thousand words, and so true. Professional looking charts give visual enhancement to your statistics, fiscal reports or presentation. Excel
Excel -- Creating Charts The saying goes, A picture is worth a thousand words, and so true. Professional looking charts give visual enhancement to your statistics, fiscal reports or presentation. Excel
In this session, we will explain some of the basics of word processing. 1. Start Microsoft Word 11. Edit the Document cut & move
 WORD PROCESSING In this session, we will explain some of the basics of word processing. The following are the outlines: 1. Start Microsoft Word 11. Edit the Document cut & move 2. Describe the Word Screen
WORD PROCESSING In this session, we will explain some of the basics of word processing. The following are the outlines: 1. Start Microsoft Word 11. Edit the Document cut & move 2. Describe the Word Screen
Excel 2003 Tutorials - Video File Attributes
 Using Excel Files 18.00 2.73 The Excel Environment 3.20 0.14 Opening Microsoft Excel 2.00 0.12 Opening a new workbook 1.40 0.26 Opening an existing workbook 1.50 0.37 Save a workbook 1.40 0.28 Copy a workbook
Using Excel Files 18.00 2.73 The Excel Environment 3.20 0.14 Opening Microsoft Excel 2.00 0.12 Opening a new workbook 1.40 0.26 Opening an existing workbook 1.50 0.37 Save a workbook 1.40 0.28 Copy a workbook
Using Excel (Microsoft Office 2007 Version) for Graphical Analysis of Data
 Using Excel (Microsoft Office 2007 Version) for Graphical Analysis of Data Introduction In several upcoming labs, a primary goal will be to determine the mathematical relationship between two variable
Using Excel (Microsoft Office 2007 Version) for Graphical Analysis of Data Introduction In several upcoming labs, a primary goal will be to determine the mathematical relationship between two variable
Using Microsoft Excel 2010
 Unit 5 Using Microsoft Excel 2010 Unit Objectives This unit includes the knowledge and skills required to analyze information in an electronic worksheet and to format information using functions specific
Unit 5 Using Microsoft Excel 2010 Unit Objectives This unit includes the knowledge and skills required to analyze information in an electronic worksheet and to format information using functions specific
Advanced Presentation Features and Animation
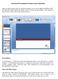 There are three features that you should remember as you work within PowerPoint 2007: the Microsoft Office Button, the Quick Access Toolbar, and the Ribbon. The function of these features will be more
There are three features that you should remember as you work within PowerPoint 2007: the Microsoft Office Button, the Quick Access Toolbar, and the Ribbon. The function of these features will be more
Enhanced Formatting and Document Management. Word 2010. Unit 3 Module 3. Diocese of St. Petersburg Office of Training Training@dosp.
 Enhanced Formatting and Document Management Word 2010 Unit 3 Module 3 Diocese of St. Petersburg Office of Training [email protected] This Page Left Intentionally Blank Diocese of St. Petersburg 9/5/2014
Enhanced Formatting and Document Management Word 2010 Unit 3 Module 3 Diocese of St. Petersburg Office of Training [email protected] This Page Left Intentionally Blank Diocese of St. Petersburg 9/5/2014
WEB TRADER USER MANUAL
 WEB TRADER USER MANUAL Web Trader... 2 Getting Started... 4 Logging In... 5 The Workspace... 6 Main menu... 7 File... 7 Instruments... 8 View... 8 Quotes View... 9 Advanced View...11 Accounts View...11
WEB TRADER USER MANUAL Web Trader... 2 Getting Started... 4 Logging In... 5 The Workspace... 6 Main menu... 7 File... 7 Instruments... 8 View... 8 Quotes View... 9 Advanced View...11 Accounts View...11
Microsoft Office. Mail Merge in Microsoft Word
 Microsoft Office Mail Merge in Microsoft Word TABLE OF CONTENTS Microsoft Office... 1 Mail Merge in Microsoft Word... 1 CREATE THE SMS DATAFILE FOR EXPORT... 3 Add A Label Row To The Excel File... 3 Backup
Microsoft Office Mail Merge in Microsoft Word TABLE OF CONTENTS Microsoft Office... 1 Mail Merge in Microsoft Word... 1 CREATE THE SMS DATAFILE FOR EXPORT... 3 Add A Label Row To The Excel File... 3 Backup
PowerPoint 2007: Basics Learning Guide
 PowerPoint 2007: Basics Learning Guide What s a PowerPoint Slide? PowerPoint presentations are composed of slides, just like conventional presentations. Like a 35mm film-based slide, each PowerPoint slide
PowerPoint 2007: Basics Learning Guide What s a PowerPoint Slide? PowerPoint presentations are composed of slides, just like conventional presentations. Like a 35mm film-based slide, each PowerPoint slide
Licensed to: CengageBrain User
 This is an electronic version of the print textbook. Due to electronic rights restrictions, some third party content may be suppressed. Editorial review has deemed that any suppressed content does not
This is an electronic version of the print textbook. Due to electronic rights restrictions, some third party content may be suppressed. Editorial review has deemed that any suppressed content does not
Ohio University Computer Services Center August, 2002 Crystal Reports Introduction Quick Reference Guide
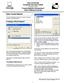 Open Crystal Reports From the Windows Start menu choose Programs and then Crystal Reports. Creating a Blank Report Ohio University Computer Services Center August, 2002 Crystal Reports Introduction Quick
Open Crystal Reports From the Windows Start menu choose Programs and then Crystal Reports. Creating a Blank Report Ohio University Computer Services Center August, 2002 Crystal Reports Introduction Quick
Microsoft Excel Training - Course Topic Selections
 Microsoft Excel Training - Course Topic Selections The Basics Creating a New Workbook Navigating in Excel Moving the Cell Pointer Using Excel Menus Using Excel Toolbars: Hiding, Displaying, and Moving
Microsoft Excel Training - Course Topic Selections The Basics Creating a New Workbook Navigating in Excel Moving the Cell Pointer Using Excel Menus Using Excel Toolbars: Hiding, Displaying, and Moving
Excel Math Project for 8th Grade Identifying Patterns
 There are several terms that we will use to describe your spreadsheet: Workbook, worksheet, row, column, cell, cursor, name box, formula bar. Today you are going to create a spreadsheet to investigate
There are several terms that we will use to describe your spreadsheet: Workbook, worksheet, row, column, cell, cursor, name box, formula bar. Today you are going to create a spreadsheet to investigate
The Basics of Microsoft Excel
 The Basics of Microsoft Excel Theresa A Scott, MS Biostatistician III Department of Biostatistics Vanderbilt University [email protected] Table of Contents 1 Introduction 1 1.1 Spreadsheet Basics..........................................
The Basics of Microsoft Excel Theresa A Scott, MS Biostatistician III Department of Biostatistics Vanderbilt University [email protected] Table of Contents 1 Introduction 1 1.1 Spreadsheet Basics..........................................
