Estimating Risk. Sukon Kanchanaraksa, PhD Johns Hopkins University
|
|
|
- Reynard Hodge
- 7 years ago
- Views:
Transcription
1 This work is licensed under a Creative Commons Attribution-onCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this site. Copyright 2008, The Johns Hopkins University and Sukon Kanchanaraksa. All rights reserved. Use of these materials permitted only in accordance with license rights granted. Materials provided AS IS ; no representations or warranties provided. User assumes all responsibility for use, and all liability related thereto, and must independently review all materials for accuracy and efficacy. May contain materials owned by others. User is responsible for obtaining permissions for use from third parties as needed.
2 stimating Risk Sukon Kanchanaraksa, PhD Johns Hopkins University
3 Section A Relative Risk
4 Risk Incidence of Disease (Attack Rate) = Absolute Risk 4
5 Attack Rates from Food-Borne Outbreak xercise Attack Rate (%) Food (1) Ate (2) ot Ate gg salad Macaroni Cottage cheese Tuna salad Ice cream Other
6 Attack Rates from Food-Borne Outbreak xercise Attack Rate (%) Difference of Attack Rates Food (1) Ate (2) ot Ate (1) (2) gg salad Macaroni Cottage cheese Tuna salad Ice cream Other
7 Attack Rates from Food-Borne Outbreak xercise Attack Rate (%) Difference of Attack Rates Ratio of Attack Rates Food (1) Ate (2) ot Ate (1) (2) (1)/(2) gg salad Macaroni Cottage cheese Tuna salad Ice cream Other
8 Approaches to the Measurement of xcess Risk Ratio of risks Risk in exposed Risk in non exposed Differences in risks (Risk in exposed) (Risk in non-exposed) 8
9 Relative Risk or Risk Ratio Relative risk (RR) = Risk in exposed Risk in non-exposed 9
10 Cohort Study First, identify Then follow to see whether Disease develops Disease does not develop Calculate and compare Totals xposed a b a+b ot exposed c d c+d Incidence of disease a a+b c c+d a a+b = Incidence in exposed c c+d = Incidence in not exposed 10
11 Cohort Study First, identify Then follow to see whether Disease develops Disease does not develop Calculate and compare Totals xposed a b a+b ot exposed a = Incidence in exposed a+b c = Incidence in not exposed c+d c d c+d Relative Risk = Incidence of disease a a+b c c+d a a+b c c+d 11
12 Cohort Study Then follow to see whether calculate First select Smoke cigarettes Do not smoke cigarettes Develop CHD Do not develop CHD Totals Incidence of disease Relative Risk = = =
13 Interpreting Relative Risk of a Disease If RR = 1 Risk in exposed = Risk in non-exposed o association If RR > 1 Risk in exposed > Risk in non-exposed Positive association;? causal If RR < 1 Risk in exposed < Risk in non-exposed egative association;? protective 13
14 Cross-Tabulation Table (Food-Borne Outbreak xercise) Attack Rates of Sore Throat gg Salad Ate Did not eat Tuna Salad Ate Did not eat 46/53 (87%) 8/12 (67%) 3/10 (30%) 3/10 (30%) 14
15 Cross-Tabulation Table (Food-Borne Outbreak xercise) Relative Risk of Sore Throat gg Salad Ate Did not eat Tuna Salad Ate Did not eat The baseline group for comparison is the no exposure group i.e., those who did not eat tuna salad and did not eat egg salad 15
16 xposure-disease Tables xpanded from the Cross- Tabulation Table (Food-Borne Outbreak xercise) Sore Throat Sore Throat Both Tuna Salad and gg Salad Yes o Total Ate Did not eat either RR = (46/53)/(3/10) =2.9 Tuna Salad Only Yes o Total Ate Did not eat either RR = (3/10)/(3/10) =1.0 Sore Throat gg Salad Only Yes o Total Ate Did not eat either RR = (8/12)/(3/10) =2.2 16
17 Relative Risk by Food Items o tuna salad Ate tuna salad 2 Relative Risk 1 +Tuna +gg o gg Salad Ate gg Salad 17
18 Relative Risk for MI and CHD Death in Men Aged in Relation to Cigarette Smoking 5 Cholesterol Levels Low 5 Blood Pressure < 130 mmhg 4 High* mmhg Relative Risk on-smoker Smoker on-smoker Smoker * High > 220 mg/100 cc Source: Doyle et al,
19 Relationship between Serum Cholesterol Levels and Risk of Coronary Heart Disease by Age and Sex Serum Men Women Cholesterol mg/dl Aged Aged Aged Aged Incidence Rates (per 1,000) < Source: Doyle et al,
20 Incidence Rates and RR of CHD in Relation to Serum Cholesterol Levels by Age and Sex Serum Men Women Cholesterol mg/dl Aged Aged Aged Aged Incidence Rates (per 1,000) < Relative Risk* < * RR of 1.0 set at level for males yrs of age with cholesterol level < 190 mg/dl. 20
21 Incidence Rates and RR of CHD in Relation to Serum Cholesterol Levels by Age and Sex Serum Men Women Cholesterol mg/dl Aged Aged Aged Aged Incidence Rates (per 1,000) < Relative Risk* < * RR of 1.0 set at level for males yrs of age with cholesterol level < 190 mg/dl. 21
22 Section B Odds Ratio
23 Interpreting Odds Odds is often known as the ratio of money that may be won versus the amount of money bet In statistics, an odds of an event is the ratio of: The probability that the event WILL occur to the probability that the event will OT occur For example, in 100 births, the probability of a delivery being a boy is 51% and being a girl is 49% The odds of a delivery being a boy is 51/49 = 1.04 In simpler term, an odds of an event can be calculated as: umber of events divided by number of non-events 23
24 Calculating Risk in a Cohort Study Develop Disease Do ot Develop Disease xposed a b on-exposed c d The probability that an exposed person develops disease = a a + b The probability that a non-exposed person develops disease = c c + d 24
25 Applying Concept of Odds Let s borrow the concept of odds and apply it to disease and non-disease So, the odds of having the disease is the ratio of the probability that the disease will occur to the probability that the disease will not occur Or, the odds of having the disease can be calculated as the number of people with the disease divided by the number of people without the disease [ote: in the exposure-disease 2x2 table, the odds of having a disease in the exposed group is the same as the odds that an exposed person develops the disease] 25
26 Calculating Odds in a Cohort Study Develop Disease Do ot Develop Disease xposed a b on-exposed c d The odds that an exposed person develops disease = a b The odds that a non-exposed person develops disease = c d 26
27 Calculating Odds in a Cohort Study Odds ratio is the ratio of the odds of disease in the exposed to the odds of disease in the non-exposed OR = Develop Disease Do ot Develop Disease xposed a b on-exposed c d odds that an exposed person develops the disease odds that a non - exposed person develops the disease = a b c d 27
28 Disease Odds Ratio in a Cohort Study OR = a b c d = a b x d c = ad bc 28
29 Calculating Odds Ratio in a Case-Control Study History of xposure o History of xposure Case a c Control b d The odds that a case was exposed = The odds that a control was exposed = a c b d 29
30 Calculating Odds Ratio in a Case-Control Study History of xposure o History of xposure Case a c Control b d Odds ratio (OR) is the ratio of the odds that a case was exposed to the odds that a control was exposed a odds that a case was exposed OR = = c odds that a control was exposed b d 30
31 xposure Odds Ratio in a Case-Control Study OR = a c b d = a c x d b = ad bc 31
32 Odds Ratio versus Relative Risk Odds ratio can be calculated in a cohort study and in a casecontrol study The exposure odds ratio is equal to the disease odds ratio Relative risk can only be calculated in a cohort study 32
33 When Is Odds Ratio a Good stimate of Relative Risk? When the cases studied are representative of all people with the disease in the population from which the cases were drawn, with regards to history of the exposure When the controls studied are representative of all people without the disease in the population from which the cases were drawn, with regards to history of exposure When the disease being studied is not a frequent one 33
34 When Is Odds Ratio a Good stimate of Relative Risk? If the incidence of the disease is low, then: a+b ~ b c+d ~ d Therefore: RR = ~ a/(a+b) c/(c+ d) a/b c/d = ad bc = OR 34
35 Comparing OR to RR: Disease Is Infrequent Develop Disease Do not Develop Disease xposed ,000 on- xposed ,000 Relative Risk = Odds Ratio = 200/10, /10, x x 9800 = 2 =
36 Comparing OR to RR: Disease Is OT Infrequent Develop Disease Do not Develop Disease xposed on- xposed Relative Risk = 50/75 50/25 50 x 75 Odds Ratio = 50 x 25 = 2 = 3 36
37 Interpreting Odds Ratio of a Disease If OR = 1 xposure is not related to disease o association; independent If OR > 1 xposure is positively related to disease Positive association;? causal If OR < 1 xposure is negatively related to disease egative association;? protective 37
38 Section C Odds Ratio in Unmatched and Matched Case-Control
39 Unmatched Case-Control Study: xample CAS COTROL Assume a study of 10 cases and 10 unmatched controls, with these findings = xposed = ot exposed 39
40 Unmatched Case-Control Study: xample CAS COTROL Thus, 6 of 10 cases were exposed, and 3 of 10 controls were exposed. In a 2x2 table, we have the following: Case Control xposed 6 3 ot xposed 4 7 = xposed = ot exposed 40
41 Unmatched Case-Control Study: xample CAS COTROL Case Control xposed 6 3 ot xposed 4 7 OR = ad bc = 6 x 7 3 x 4 = 3.5 = xposed = ot exposed 41
42 Quick Pause In a hypothetical 2x2 table with the following rows and columns, is the OR calculated correctly? Control Case xposed 8 3 ot xposed 4 7 OR = ad bc = 8 x 7 3 x 4 =
43 Quick Pause Control Case xposed 8 3 ot xposed 4 7 Incorrect! OR = ad bc = 8 x 7 3 x 4 = 4.7 Why? 43
44 Odds Ratio in a Case-Control Study OR = a c b d = a c x d b = ad bc = (# cases exposed) x (# controls not exposed) (# cases not exposed) x (# controls exposed) The numerator is the product of cases exposed and controls not exposed. 44
45 Case-Control Study: xample Cases CHD Controls (without disease) Smoked cigarettes Did not smoke cigarettes Total % Smoking cigarettes = 56% = 44% OR = ad bc = 112 x x 88 =
46 Matched Case-Control Study In a matched case-control study, one or more controls are selected to match to a case on certain characteristics, such as age, race, and gender When one control is matched to a case, the case and the matched control form a matched pair 46
47 Concordant and Discordant Pairs We can define two types of matched pairs by the similarity or difference of the exposure of the case and control in each pair Concordant pairs are: 1. Pairs in which both the case and the control were exposed, and 2. Pairs in which neither the case nor the control was exposed Discordant pairs are: 3. Pairs in which the case was exposed but the control was not, and 4. Pairs in which the control was exposed and the case was not 47
48 2x2 Table in a Matched Case-Control Study Discordant xposed Controls ot xposed Cases xposed ot xposed Concordant 48
49 2x2 Table in a Matched Case-Control Study aa = number of matched pairs 2 x aa subjects in this cell xposed Controls ot xposed Cases xposed aa bb ot xposed cc dd Total number of subjects = 2 x (aa+bb+cc+dd) 49
50 OR from 2x2 Table in a Matched Case-Control Study Odds ratio (matched) = bb cc xposed Controls ot xposed Cases xposed aa bb ot xposed cc dd ote: bb is not the product of b and b (not b x b); it is the number of pairs 50
51 Matched Case-Control Study: xample CAS COTROL Assume a study of 10 cases and 10 controls in which each control was matched to a case resulting in 10 pairs. = xposed = ot exposed 51
52 Matched Case-Control Study: xample CAS COTROL Cases xposed Controls ot xposed xposed 2 4 ot xposed 1 3 Matched OR = 4 1 = 4 = xposed = ot exposed 52
53 Review: Matched Case-Control Study Cases xposed Controls ot xposed xposed 2 4 ot xposed 1 3 Q1. How many pairs? Q2. How many subjects? Q3. What are the discordant pairs? Q4. Which is the bb cell? Q5. What is the bb cell? 53
54 Review: Unmatching a Matched 2x2 Table Matched CC Controls xposed ot xposed Cases xposed 2 4 ot xposed 1 3 Disease Unmatched Yes o 2x2 xposure xposed ot xposed 54
55 Section D Attributable Risk
56 Attributable Risk Attributable risk (AR) is a measure of excess risk that is attributed to the exposure Attributable risk in the exposed group equals the difference between the incidence in the exposed group and the incidence in the non-exposed (baseline) group 56
57 Attack Rates from Food-Borne Outbreak xercise Attack Rate (%) Difference of Attack Rates Food (1) Ate (2) ot Ate (1) (2) gg salad Macaroni Cottage cheese Tuna salad Ice cream Other
58 Risk in xposed and on-xposed Groups Background Risk xposed group on-exposed group 58
59 Risk in xposed and on-xposed Groups Incidence due to exposure Attributable risk Incidence not due to exposure Background Risk xposed group on-exposed group 59
60 Risk in xposed and on-xposed Groups 1. Incidence attributable to exposure (attributable risk) = ( Incidence in ) ( Incidence in ) exposed group non-exposed group 60
61 Risk in xposed and on-xposed Groups 1. Incidence attributable to exposure (attributable risk) = ( Incidence in ) ( Incidence in ) exposed group non-exposed group 2. Proportion of incidence attributable to exposure (proportional attributable risk) = ( Incidence in ) ( Incidence in ) exposed group non-exposed group Incidence in exposed group 61
62 xample: Cohort Study Develop CHD Do not develop CHD Totals Incidence of disease Smoke cigarettes Do not smoke cigarettes per 1, per 1,000 62
63 Attributable Risk in Smokers 1. The incidence in smokers which is attributable to their smoking = ( Incidence in ) ( Incidence in ) smokers non-smokers = = 10.6/1,000/year 63
64 Proportion Attributable Risk in Smokers 2. The proportion of the total incidence in the smokers which is attributable to their smoking = ( Incidence in ) ( Incidence in ) smokers non-smokers Incidence in smokers = = = = 37.9% 64
65 Risk in the Total Population Population is a mix of exposed and non-exposed groups 65
66 Attributable Risk in the Total Population 3. Incidence attributable to exposure = ( Incidence in ) ( Incidence in ) total population non-exposed group 66
67 Attributable Risk in the Total Population 3. Incidence attributable to exposure =( Incidence in ) ( Incidence in ) total population non-exposed group 4. Proportion of incidence attributable to exposure = ( Incidence in ) ( Incidence in ) total population non-exposed group Incidence in total population 67
68 Attributable Risk in the Total Population 3. Incidence attributable to smoking in the total population = ( Incidence in ) ( Incidence in ) total population non-exposed group 68
69 Attributable Risk in the Total Population If the incidence in the total population is unknown, it can be calculated if we know: Incidence among smokers Incidence among nonsmokers Proportion of the total population that smokes 69
70 Attributable Risk in the Total Population We know that: The incidence in smokers = 28.0/1,000/year The incidence in nonsmokers = 17.4/1,000/year From another source, we learn that: The proportion of smokers in the population is 44% So, we know that: The proportion of nonsmokers in the population is 56% 70
71 Attributable Risk in the Total Population Incidence in total population = ( Incidence) Percent smokers in in smokers population ( ) ( )+ Incidence in nonsmokers Percent non-smokers in population ( ) (28.0/1000) (.44) + (17.4/1000) (.56) = 22.1/1000/year 71
72 Attributable Risk in the Total Population 3. Incidence attributable to smoking = ( Incidence in total population ) ( Incidence in ) non-smokers (22.1/1000/year) (17.4/1000/year) = 4.7/1000/year 72
73 Attributable Risk in the Total Population 4. Proportion of incidence attributable to exposure =( Incidence in ) ( Incidence in ) total population non-smokers Incidence in total population = 21.3% 73
74 Lung Cancer, CHD Mortality in Male British Physicians Age-Adjusted Death Rates/100,000 Smokers on-smokers RR AR %AR Lung cancer % CHD % %AR = Proportion attributable risk Source: Doll and Peto (1976). BMJ, 2:
75 Lung Cancer, CHD Mortality in Male British Physicians Age-Adjusted Death Rates/100,000 Smokers on-smokers RR AR %AR Lung cancer % CHD % %AR = Proportion attributable risk Source: Doll and Peto (1976). BMJ, 2:
Use of the Chi-Square Statistic. Marie Diener-West, PhD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Cohort Studies. Sukon Kanchanaraksa, PhD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Case-Control Studies. Sukon Kanchanaraksa, PhD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Case-control studies. Alfredo Morabia
 Case-control studies Alfredo Morabia Division d épidémiologie Clinique, Département de médecine communautaire, HUG Alfredo.Morabia@hcuge.ch www.epidemiologie.ch Outline Case-control study Relation to cohort
Case-control studies Alfredo Morabia Division d épidémiologie Clinique, Département de médecine communautaire, HUG Alfredo.Morabia@hcuge.ch www.epidemiologie.ch Outline Case-control study Relation to cohort
Measures of Prognosis. Sukon Kanchanaraksa, PhD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Summary Measures (Ratio, Proportion, Rate) Marie Diener-West, PhD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
P (B) In statistics, the Bayes theorem is often used in the following way: P (Data Unknown)P (Unknown) P (Data)
 22S:101 Biostatistics: J. Huang 1 Bayes Theorem For two events A and B, if we know the conditional probability P (B A) and the probability P (A), then the Bayes theorem tells that we can compute the conditional
22S:101 Biostatistics: J. Huang 1 Bayes Theorem For two events A and B, if we know the conditional probability P (B A) and the probability P (A), then the Bayes theorem tells that we can compute the conditional
Biostatistics and Epidemiology within the Paradigm of Public Health. Sukon Kanchanaraksa, PhD Marie Diener-West, PhD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
The American Cancer Society Cancer Prevention Study I: 12-Year Followup
 Chapter 3 The American Cancer Society Cancer Prevention Study I: 12-Year Followup of 1 Million Men and Women David M. Burns, Thomas G. Shanks, Won Choi, Michael J. Thun, Clark W. Heath, Jr., and Lawrence
Chapter 3 The American Cancer Society Cancer Prevention Study I: 12-Year Followup of 1 Million Men and Women David M. Burns, Thomas G. Shanks, Won Choi, Michael J. Thun, Clark W. Heath, Jr., and Lawrence
Exercise Answers. Exercise 3.1 1. B 2. C 3. A 4. B 5. A
 Exercise Answers Exercise 3.1 1. B 2. C 3. A 4. B 5. A Exercise 3.2 1. A; denominator is size of population at start of study, numerator is number of deaths among that population. 2. B; denominator is
Exercise Answers Exercise 3.1 1. B 2. C 3. A 4. B 5. A Exercise 3.2 1. A; denominator is size of population at start of study, numerator is number of deaths among that population. 2. B; denominator is
Life Tables. Marie Diener-West, PhD Sukon Kanchanaraksa, PhD
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Lesson 14 14 Outline Outline
 Lesson 14 Confidence Intervals of Odds Ratio and Relative Risk Lesson 14 Outline Lesson 14 covers Confidence Interval of an Odds Ratio Review of Odds Ratio Sampling distribution of OR on natural log scale
Lesson 14 Confidence Intervals of Odds Ratio and Relative Risk Lesson 14 Outline Lesson 14 covers Confidence Interval of an Odds Ratio Review of Odds Ratio Sampling distribution of OR on natural log scale
Bayes Theorem & Diagnostic Tests Screening Tests
 Bayes heorem & Screening ests Bayes heorem & Diagnostic ests Screening ests Some Questions If you test positive for HIV, what is the probability that you have HIV? If you have a positive mammogram, what
Bayes heorem & Screening ests Bayes heorem & Diagnostic ests Screening ests Some Questions If you test positive for HIV, what is the probability that you have HIV? If you have a positive mammogram, what
African Americans & Cardiovascular Diseases
 Statistical Fact Sheet 2013 Update African Americans & Cardiovascular Diseases Cardiovascular Disease (CVD) (ICD/10 codes I00-I99, Q20-Q28) (ICD/9 codes 390-459, 745-747) Among non-hispanic blacks age
Statistical Fact Sheet 2013 Update African Americans & Cardiovascular Diseases Cardiovascular Disease (CVD) (ICD/10 codes I00-I99, Q20-Q28) (ICD/9 codes 390-459, 745-747) Among non-hispanic blacks age
Chapter 7: Effect Modification
 A short introduction to epidemiology Chapter 7: Effect Modification Neil Pearce Centre for Public Health Research Massey University Wellington, New Zealand Chapter 8 Effect modification Concepts of interaction
A short introduction to epidemiology Chapter 7: Effect Modification Neil Pearce Centre for Public Health Research Massey University Wellington, New Zealand Chapter 8 Effect modification Concepts of interaction
Evaluation of Diagnostic and Screening Tests: Validity and Reliability. Sukon Kanchanaraksa, PhD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Mortality Assessment Technology: A New Tool for Life Insurance Underwriting
 Mortality Assessment Technology: A New Tool for Life Insurance Underwriting Guizhou Hu, MD, PhD BioSignia, Inc, Durham, North Carolina Abstract The ability to more accurately predict chronic disease morbidity
Mortality Assessment Technology: A New Tool for Life Insurance Underwriting Guizhou Hu, MD, PhD BioSignia, Inc, Durham, North Carolina Abstract The ability to more accurately predict chronic disease morbidity
Underwriting Critical Illness Insurance: A model for coronary heart disease and stroke
 Underwriting Critical Illness Insurance: A model for coronary heart disease and stroke Presented to the 6th International Congress on Insurance: Mathematics and Economics. July 2002. Lisbon, Portugal.
Underwriting Critical Illness Insurance: A model for coronary heart disease and stroke Presented to the 6th International Congress on Insurance: Mathematics and Economics. July 2002. Lisbon, Portugal.
Confounding in Epidemiology
 The Young Epidemiology Scholars Program (YES) is supported by The Robert Wood Johnson Foundation and administered by the College Board. Confounding in Epidemiology Mona Baumgarten Department of Epidemiology
The Young Epidemiology Scholars Program (YES) is supported by The Robert Wood Johnson Foundation and administered by the College Board. Confounding in Epidemiology Mona Baumgarten Department of Epidemiology
Mind on Statistics. Chapter 4
 Mind on Statistics Chapter 4 Sections 4.1 Questions 1 to 4: The table below shows the counts by gender and highest degree attained for 498 respondents in the General Social Survey. Highest Degree Gender
Mind on Statistics Chapter 4 Sections 4.1 Questions 1 to 4: The table below shows the counts by gender and highest degree attained for 498 respondents in the General Social Survey. Highest Degree Gender
RATIOS, PROPORTIONS, PERCENTAGES, AND RATES
 RATIOS, PROPORTIOS, PERCETAGES, AD RATES 1. Ratios: ratios are one number expressed in relation to another by dividing the one number by the other. For example, the sex ratio of Delaware in 1990 was: 343,200
RATIOS, PROPORTIOS, PERCETAGES, AD RATES 1. Ratios: ratios are one number expressed in relation to another by dividing the one number by the other. For example, the sex ratio of Delaware in 1990 was: 343,200
The Young Epidemiology Scholars Program (YES) is supported by The Robert Wood Johnson Foundation and administered by the College Board.
 The Young Epidemiology Scholars Program (YES) is supported by The Robert Wood Johnson Foundation and administered by the College Board. Case Control Study Mark A. Kaelin Department of Health Professions
The Young Epidemiology Scholars Program (YES) is supported by The Robert Wood Johnson Foundation and administered by the College Board. Case Control Study Mark A. Kaelin Department of Health Professions
Andrews Publications Tobacco Litigation 2000 THEORIES FOR THE REDUCTION OF DAMAGES
 THEORIES FOR THE REDUCTION OF DAMAGES By Steven Wright Brita J. Forssberg SYNERGISM Effect of cigarette smoking is greater than that of asbestos. Synergism Synergism Lung cancer incidence rates, expressed
THEORIES FOR THE REDUCTION OF DAMAGES By Steven Wright Brita J. Forssberg SYNERGISM Effect of cigarette smoking is greater than that of asbestos. Synergism Synergism Lung cancer incidence rates, expressed
Journal Club: Niacin in Patients with Low HDL Cholesterol Levels Receiving Intensive Statin Therapy by the AIM-HIGH Investigators
 Journal Club: Niacin in Patients with Low HDL Cholesterol Levels Receiving Intensive Statin Therapy by the AIM-HIGH Investigators Shaikha Al Naimi Doctor of Pharmacy Student College of Pharmacy Qatar University
Journal Club: Niacin in Patients with Low HDL Cholesterol Levels Receiving Intensive Statin Therapy by the AIM-HIGH Investigators Shaikha Al Naimi Doctor of Pharmacy Student College of Pharmacy Qatar University
Lecture 25. December 19, 2007. Department of Biostatistics Johns Hopkins Bloomberg School of Public Health Johns Hopkins University.
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
How to Approach a Study: Concepts, Hypotheses, and Theoretical Frameworks. Lynda Burton, ScD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Estimation of the Number of Lung Cancer Cases Attributable to Asbestos Exposure
 Estimation of the Number of Lung Cancer Cases Attributable to Asbestos Exposure BC Asbestos Statistics Approximately 55,000 BC men and women exposed in 1971 in high exposed industries Significant exposure
Estimation of the Number of Lung Cancer Cases Attributable to Asbestos Exposure BC Asbestos Statistics Approximately 55,000 BC men and women exposed in 1971 in high exposed industries Significant exposure
Canadian Individual Critical Illness Insurance Morbidity Experience
 Morbidity Study Canadian Individual Critical Illness Insurance Morbidity Experience Between Policy Anniversaries in 2002 and 2007 Using Expected CIA Incidence Tables from July 2012 Individual Living Benefits
Morbidity Study Canadian Individual Critical Illness Insurance Morbidity Experience Between Policy Anniversaries in 2002 and 2007 Using Expected CIA Incidence Tables from July 2012 Individual Living Benefits
Longevity Risk in the United Kingdom
 Institut für Finanz- und Aktuarwissenschaften, Universität Ulm Longevity Risk in the United Kingdom Stephen Richards 20 th July 2005 Copyright c Stephen Richards. All rights reserved. Electronic versions
Institut für Finanz- und Aktuarwissenschaften, Universität Ulm Longevity Risk in the United Kingdom Stephen Richards 20 th July 2005 Copyright c Stephen Richards. All rights reserved. Electronic versions
The Role of Insurance in Providing Access to Cardiac Care in Maryland. Samuel L. Brown, Ph.D. University of Baltimore College of Public Affairs
 The Role of Insurance in Providing Access to Cardiac Care in Maryland Samuel L. Brown, Ph.D. University of Baltimore College of Public Affairs Heart Disease Heart Disease is the leading cause of death
The Role of Insurance in Providing Access to Cardiac Care in Maryland Samuel L. Brown, Ph.D. University of Baltimore College of Public Affairs Heart Disease Heart Disease is the leading cause of death
The Importance of Statistics Education
 The Importance of Statistics Education Professor Jessica Utts Department of Statistics University of California, Irvine http://www.ics.uci.edu/~jutts jutts@uci.edu Outline of Talk What is Statistics? Four
The Importance of Statistics Education Professor Jessica Utts Department of Statistics University of California, Irvine http://www.ics.uci.edu/~jutts jutts@uci.edu Outline of Talk What is Statistics? Four
Incorrect Analyses of Radiation and Mesothelioma in the U.S. Transuranium and Uranium Registries Joey Zhou, Ph.D.
 Incorrect Analyses of Radiation and Mesothelioma in the U.S. Transuranium and Uranium Registries Joey Zhou, Ph.D. At the Annual Meeting of the Health Physics Society July 15, 2014 in Baltimore A recently
Incorrect Analyses of Radiation and Mesothelioma in the U.S. Transuranium and Uranium Registries Joey Zhou, Ph.D. At the Annual Meeting of the Health Physics Society July 15, 2014 in Baltimore A recently
New Cholesterol Guidelines: Carte Blanche for Statin Overuse Rita F. Redberg, MD, MSc Professor of Medicine
 New Cholesterol Guidelines: Carte Blanche for Statin Overuse Rita F. Redberg, MD, MSc Professor of Medicine Disclosures & Relevant Relationships I have nothing to disclose No financial conflicts Editor,
New Cholesterol Guidelines: Carte Blanche for Statin Overuse Rita F. Redberg, MD, MSc Professor of Medicine Disclosures & Relevant Relationships I have nothing to disclose No financial conflicts Editor,
Course Notes Frequency and Effect Measures
 EPI-546: Fundamentals of Epidemiology and Biostatistics Course Notes Frequency and Effect Measures Mat Reeves BVSc, PhD Outline: I. Quantifying uncertainty (Probability and Odds) II. Measures of Disease
EPI-546: Fundamentals of Epidemiology and Biostatistics Course Notes Frequency and Effect Measures Mat Reeves BVSc, PhD Outline: I. Quantifying uncertainty (Probability and Odds) II. Measures of Disease
Two Correlated Proportions (McNemar Test)
 Chapter 50 Two Correlated Proportions (Mcemar Test) Introduction This procedure computes confidence intervals and hypothesis tests for the comparison of the marginal frequencies of two factors (each with
Chapter 50 Two Correlated Proportions (Mcemar Test) Introduction This procedure computes confidence intervals and hypothesis tests for the comparison of the marginal frequencies of two factors (each with
Indices of Morbidity and Mortality. Sukon Kanchanaraksa, PhD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
RR833. The joint effect of asbestos exposure and smoking on the risk of lung cancer mortality for asbestos workers (1971-2005)
 Health and Safety Executive The joint effect of asbestos exposure and smoking on the risk of lung cancer mortality for asbestos workers (1971-2005) Prepared by the Health and Safety Laboratory for the
Health and Safety Executive The joint effect of asbestos exposure and smoking on the risk of lung cancer mortality for asbestos workers (1971-2005) Prepared by the Health and Safety Laboratory for the
Absolute cardiovascular disease risk assessment
 Quick reference guide for health professionals Absolute cardiovascular disease risk assessment This quick reference guide is a summary of the key steps involved in assessing absolute cardiovascular risk
Quick reference guide for health professionals Absolute cardiovascular disease risk assessment This quick reference guide is a summary of the key steps involved in assessing absolute cardiovascular risk
Long-term impact of childhood bereavement
 Long-term impact of childhood bereavement Preliminary analysis of the 1970 British Cohort Study (BCS70) Samantha Parsons CWRC WORKING PAPER September 2011 Long-Term Impact of Childhood Bereavement Preliminary
Long-term impact of childhood bereavement Preliminary analysis of the 1970 British Cohort Study (BCS70) Samantha Parsons CWRC WORKING PAPER September 2011 Long-Term Impact of Childhood Bereavement Preliminary
ADVANCE: a factorial randomised trial of blood pressure lowering and intensive glucose control in 11,140 patients with type 2 diabetes
 ADVANCE: a factorial randomised trial of blood pressure lowering and intensive glucose control in 11,140 patients with type 2 diabetes Effects of a fixed combination of the ACE inhibitor, perindopril,
ADVANCE: a factorial randomised trial of blood pressure lowering and intensive glucose control in 11,140 patients with type 2 diabetes Effects of a fixed combination of the ACE inhibitor, perindopril,
Radon in Homes and Lung Cancer Risk. Sarah C Darby CTSU, University of Oxford
 Radon in Homes and Lung Cancer Risk Sarah C Darby CTSU, University of Oxford Plan of talk 1. Introduction to radon and lung cancer 2. Estimating the risk in homes 3. Reducing radon-related deaths Orion
Radon in Homes and Lung Cancer Risk Sarah C Darby CTSU, University of Oxford Plan of talk 1. Introduction to radon and lung cancer 2. Estimating the risk in homes 3. Reducing radon-related deaths Orion
HeartScore Web - based version users guide TABLE OF CONTENTS. 1. Preamble... 2. 2. Benefits of using HeartScore... 2. 3. Accessing HeartScore...
 TABLE OF CONTENTS 1. Preamble... 2 2. Benefits of using HeartScore... 2 3. Accessing HeartScore... 2 4. HeartScore Web Based Homepage... 3 5. Patient Card... 4 6. Create a new examination... 6 7. Examination
TABLE OF CONTENTS 1. Preamble... 2 2. Benefits of using HeartScore... 2 3. Accessing HeartScore... 2 4. HeartScore Web Based Homepage... 3 5. Patient Card... 4 6. Create a new examination... 6 7. Examination
Homework Help Heart Disease & Stroke
 Preventing Heart Disease & Stroke What causes heart disease and stroke? high blood pressure high cholesterol diabetes smoking stress drinking too much alcohol not being physically active being overweight
Preventing Heart Disease & Stroke What causes heart disease and stroke? high blood pressure high cholesterol diabetes smoking stress drinking too much alcohol not being physically active being overweight
Now we ve weighed up your application for our protection products, it s only fair we talk you through our assessment process. More than anything, we
 how we assess your application UNDERWRITING EXPLAINED. Now we ve weighed up your application for our protection products, it s only fair we talk you through our assessment process. More than anything,
how we assess your application UNDERWRITING EXPLAINED. Now we ve weighed up your application for our protection products, it s only fair we talk you through our assessment process. More than anything,
Chi-square test Fisher s Exact test
 Lesson 1 Chi-square test Fisher s Exact test McNemar s Test Lesson 1 Overview Lesson 11 covered two inference methods for categorical data from groups Confidence Intervals for the difference of two proportions
Lesson 1 Chi-square test Fisher s Exact test McNemar s Test Lesson 1 Overview Lesson 11 covered two inference methods for categorical data from groups Confidence Intervals for the difference of two proportions
Appendix: Description of the DIETRON model
 Appendix: Description of the DIETRON model Much of the description of the DIETRON model that appears in this appendix is taken from an earlier publication outlining the development of the model (Scarborough
Appendix: Description of the DIETRON model Much of the description of the DIETRON model that appears in this appendix is taken from an earlier publication outlining the development of the model (Scarborough
Guide to Biostatistics
 MedPage Tools Guide to Biostatistics Study Designs Here is a compilation of important epidemiologic and common biostatistical terms used in medical research. You can use it as a reference guide when reading
MedPage Tools Guide to Biostatistics Study Designs Here is a compilation of important epidemiologic and common biostatistical terms used in medical research. You can use it as a reference guide when reading
Coronary Heart Disease (CHD) Brief
 Coronary Heart Disease (CHD) Brief What is Coronary Heart Disease? Coronary Heart Disease (CHD), also called coronary artery disease 1, is the most common heart condition in the United States. It occurs
Coronary Heart Disease (CHD) Brief What is Coronary Heart Disease? Coronary Heart Disease (CHD), also called coronary artery disease 1, is the most common heart condition in the United States. It occurs
Cost-Benefit and Cost-Effectiveness Analysis. Kevin Frick, PhD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
What do we mean by cause in public health?
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
What is a P-value? Ronald A. Thisted, PhD Departments of Statistics and Health Studies The University of Chicago
 What is a P-value? Ronald A. Thisted, PhD Departments of Statistics and Health Studies The University of Chicago 8 June 1998, Corrections 14 February 2010 Abstract Results favoring one treatment over another
What is a P-value? Ronald A. Thisted, PhD Departments of Statistics and Health Studies The University of Chicago 8 June 1998, Corrections 14 February 2010 Abstract Results favoring one treatment over another
MANAGEMENT OF LIPID DISORDERS: IMPLICATIONS OF THE NEW GUIDELINES
 MANAGEMENT OF LIPID DISORDERS: IMPLICATIONS OF THE NEW GUIDELINES Robert B. Baron MD MS Professor and Associate Dean UCSF School of Medicine Declaration of full disclosure: No conflict of interest EXPLAINING
MANAGEMENT OF LIPID DISORDERS: IMPLICATIONS OF THE NEW GUIDELINES Robert B. Baron MD MS Professor and Associate Dean UCSF School of Medicine Declaration of full disclosure: No conflict of interest EXPLAINING
3.2 Conditional Probability and Independent Events
 Ismor Fischer, 5/29/2012 3.2-1 3.2 Conditional Probability and Independent Events Using population-based health studies to estimate probabilities relating potential risk factors to a particular disease,
Ismor Fischer, 5/29/2012 3.2-1 3.2 Conditional Probability and Independent Events Using population-based health studies to estimate probabilities relating potential risk factors to a particular disease,
Basic Study Designs in Analytical Epidemiology For Observational Studies
 Basic Study Designs in Analytical Epidemiology For Observational Studies Cohort Case Control Hybrid design (case-cohort, nested case control) Cross-Sectional Ecologic OBSERVATIONAL STUDIES (Non-Experimental)
Basic Study Designs in Analytical Epidemiology For Observational Studies Cohort Case Control Hybrid design (case-cohort, nested case control) Cross-Sectional Ecologic OBSERVATIONAL STUDIES (Non-Experimental)
Butler Memorial Hospital Community Health Needs Assessment 2013
 Butler Memorial Hospital Community Health Needs Assessment 2013 Butler County best represents the community that Butler Memorial Hospital serves. Butler Memorial Hospital (BMH) has conducted community
Butler Memorial Hospital Community Health Needs Assessment 2013 Butler County best represents the community that Butler Memorial Hospital serves. Butler Memorial Hospital (BMH) has conducted community
Overview of study designs
 Overview of study designs In epidemiology, measuring the occurrence of disease or other healthrelated events in a population is only a beginning. Epidemiologists are also interested in assessing whether
Overview of study designs In epidemiology, measuring the occurrence of disease or other healthrelated events in a population is only a beginning. Epidemiologists are also interested in assessing whether
Health Maintenance: Controlling Cholesterol
 Sacramento Heart & Vascular Medical Associates February 18, 2012 500 University Ave. Sacramento, CA 95825 Page 1 What is cholesterol? Cholesterol is a fatty substance. It has both good and bad effects
Sacramento Heart & Vascular Medical Associates February 18, 2012 500 University Ave. Sacramento, CA 95825 Page 1 What is cholesterol? Cholesterol is a fatty substance. It has both good and bad effects
Chapter 6. Examples (details given in class) Who is Measured: Units, Subjects, Participants. Research Studies to Detect Relationships
 Announcements: Midterm Friday. Bring calculator and one sheet of notes. Can t use the calculator on your cell phone. Assigned seats, random ID check. Review Wed. Review sheet posted on website. Fri discussion
Announcements: Midterm Friday. Bring calculator and one sheet of notes. Can t use the calculator on your cell phone. Assigned seats, random ID check. Review Wed. Review sheet posted on website. Fri discussion
PRACTICE PROBLEMS FOR BIOSTATISTICS
 PRACTICE PROBLEMS FOR BIOSTATISTICS BIOSTATISTICS DESCRIBING DATA, THE NORMAL DISTRIBUTION 1. The duration of time from first exposure to HIV infection to AIDS diagnosis is called the incubation period.
PRACTICE PROBLEMS FOR BIOSTATISTICS BIOSTATISTICS DESCRIBING DATA, THE NORMAL DISTRIBUTION 1. The duration of time from first exposure to HIV infection to AIDS diagnosis is called the incubation period.
PREFERRED UNDERWRITING
 PREFERRED UNDERWRITING For Solution 10 & Solution 20 Criteria Guide 2015 FOR ADVISOR USE ONLY Contents About this guide...1 Preferred underwriting...1 Availability...1 Risk classifications...1 Standard
PREFERRED UNDERWRITING For Solution 10 & Solution 20 Criteria Guide 2015 FOR ADVISOR USE ONLY Contents About this guide...1 Preferred underwriting...1 Availability...1 Risk classifications...1 Standard
Cardiovascular Disease Risk Factors
 Cardiovascular Disease Risk Factors Risk factors are traits and life-style habits that increase a person's chances of having coronary artery and vascular disease. Some risk factors cannot be changed or
Cardiovascular Disease Risk Factors Risk factors are traits and life-style habits that increase a person's chances of having coronary artery and vascular disease. Some risk factors cannot be changed or
Effect measure modification & Interaction. Madhukar Pai, MD, PhD McGill University madhukar.pai@mcgill.ca
 Effect measure modification & Interaction Madhukar Pai, MD, PhD McGill University madhukar.pai@mcgill.ca 1 Interaction + Effect Modification = Frustration Introduction to effect modification leaves some
Effect measure modification & Interaction Madhukar Pai, MD, PhD McGill University madhukar.pai@mcgill.ca 1 Interaction + Effect Modification = Frustration Introduction to effect modification leaves some
Best Class Criteria LIFE UNDERWRITING
 LIFE UNDERWRITING Best Class Criteria The following criteria contain key information that can help you estimate whether your life insurance clients will qualify for one of our best risk classes Super Preferred,
LIFE UNDERWRITING Best Class Criteria The following criteria contain key information that can help you estimate whether your life insurance clients will qualify for one of our best risk classes Super Preferred,
7. Relating risk factors to health outcomes
 7. Relating risk factors to health outcomes Quantifying relationships between two factors or one factor and the occurrence, presence, severity, or course of disease The Big Picture At this point in the
7. Relating risk factors to health outcomes Quantifying relationships between two factors or one factor and the occurrence, presence, severity, or course of disease The Big Picture At this point in the
Combination Birth Control Pills - FAQ
 Combination Birth Control Pills - FAQ How does the birth control pill work? prevents ovulation thickens cervical mucus, which makes it hard for sperm to enter the uterus thins the lining of the uterus,
Combination Birth Control Pills - FAQ How does the birth control pill work? prevents ovulation thickens cervical mucus, which makes it hard for sperm to enter the uterus thins the lining of the uterus,
Statistik for MPH: 2. 10. september 2015. www.biostat.ku.dk/~pka/mph15. Risiko, relativ risiko, signifikanstest (Silva: 110-133.) Per Kragh Andersen
 Statistik for MPH: 2 10. september 2015 www.biostat.ku.dk/~pka/mph15 Risiko, relativ risiko, signifikanstest (Silva: 110-133.) Per Kragh Andersen 1 Fra den. 1 uges statistikundervisning: skulle jeg gerne
Statistik for MPH: 2 10. september 2015 www.biostat.ku.dk/~pka/mph15 Risiko, relativ risiko, signifikanstest (Silva: 110-133.) Per Kragh Andersen 1 Fra den. 1 uges statistikundervisning: skulle jeg gerne
Chapter 2: Health in Wales and the United Kingdom
 Chapter 2: Health in Wales and the United Kingdom This section uses statistics from a range of sources to compare health outcomes in Wales with the remainder of the United Kingdom. Population trends Annual
Chapter 2: Health in Wales and the United Kingdom This section uses statistics from a range of sources to compare health outcomes in Wales with the remainder of the United Kingdom. Population trends Annual
HEART DISEASE AND STROKE
 GENETICS AND CRITICAL ILLNESS INSURANCE UNDERWRITING: MODELS FOR BREAST CANCER AND OVARIAN CANCER AND FOR CORONARY HEART DISEASE AND STROKE By Chessman Tavarwisa Wekwete Submitted for the Degree of Doctor
GENETICS AND CRITICAL ILLNESS INSURANCE UNDERWRITING: MODELS FOR BREAST CANCER AND OVARIAN CANCER AND FOR CORONARY HEART DISEASE AND STROKE By Chessman Tavarwisa Wekwete Submitted for the Degree of Doctor
smoking Smoking in Wales: current facts
 smoking Smoking in Wales: current facts Publication date November 7 Authors: Rachel Dolman, Rhys Gibbon, Cath Roberts The authors were supported by an editorial board consisting of Sue Leake, Chris Roberts
smoking Smoking in Wales: current facts Publication date November 7 Authors: Rachel Dolman, Rhys Gibbon, Cath Roberts The authors were supported by an editorial board consisting of Sue Leake, Chris Roberts
Glossary of Methodologic Terms
 Glossary of Methodologic Terms Before-After Trial: Investigation of therapeutic alternatives in which individuals of 1 period and under a single treatment are compared with individuals at a subsequent
Glossary of Methodologic Terms Before-After Trial: Investigation of therapeutic alternatives in which individuals of 1 period and under a single treatment are compared with individuals at a subsequent
C. The null hypothesis is not rejected when the alternative hypothesis is true. A. population parameters.
 Sample Multiple Choice Questions for the material since Midterm 2. Sample questions from Midterms and 2 are also representative of questions that may appear on the final exam.. A randomly selected sample
Sample Multiple Choice Questions for the material since Midterm 2. Sample questions from Midterms and 2 are also representative of questions that may appear on the final exam.. A randomly selected sample
Health Care Costs and Secondhand Smoke
 Health Care Costs and Secondhand Smoke As a society, we all pay the price for exposure to secondhand smoke. We know that secondhand smoke causes death and disease in people who don t smoke. New research
Health Care Costs and Secondhand Smoke As a society, we all pay the price for exposure to secondhand smoke. We know that secondhand smoke causes death and disease in people who don t smoke. New research
49. INFANT MORTALITY RATE. Infant mortality rate is defined as the death of an infant before his or her first birthday.
 49. INFANT MORTALITY RATE Wing Tam (Alice) Jennifer Cheng Stat 157 course project More Risk in Everyday Life Risk Meter LIKELIHOOD of exposure to hazardous levels Low Medium High Consequences: Severity,
49. INFANT MORTALITY RATE Wing Tam (Alice) Jennifer Cheng Stat 157 course project More Risk in Everyday Life Risk Meter LIKELIHOOD of exposure to hazardous levels Low Medium High Consequences: Severity,
People like to clump things into categories. Virtually every research
 05-Elliott-4987.qxd 7/18/2006 5:26 PM Page 113 5 Analysis of Categorical Data People like to clump things into categories. Virtually every research project categorizes some of its observations into neat,
05-Elliott-4987.qxd 7/18/2006 5:26 PM Page 113 5 Analysis of Categorical Data People like to clump things into categories. Virtually every research project categorizes some of its observations into neat,
13. Poisson Regression Analysis
 136 Poisson Regression Analysis 13. Poisson Regression Analysis We have so far considered situations where the outcome variable is numeric and Normally distributed, or binary. In clinical work one often
136 Poisson Regression Analysis 13. Poisson Regression Analysis We have so far considered situations where the outcome variable is numeric and Normally distributed, or binary. In clinical work one often
Chi Squared and Fisher's Exact Tests. Observed vs Expected Distributions
 BMS 617 Statistical Techniques for the Biomedical Sciences Lecture 11: Chi-Squared and Fisher's Exact Tests Chi Squared and Fisher's Exact Tests This lecture presents two similarly structured tests, Chi-squared
BMS 617 Statistical Techniques for the Biomedical Sciences Lecture 11: Chi-Squared and Fisher's Exact Tests Chi Squared and Fisher's Exact Tests This lecture presents two similarly structured tests, Chi-squared
Introduction to Statistics and Quantitative Research Methods
 Introduction to Statistics and Quantitative Research Methods Purpose of Presentation To aid in the understanding of basic statistics, including terminology, common terms, and common statistical methods.
Introduction to Statistics and Quantitative Research Methods Purpose of Presentation To aid in the understanding of basic statistics, including terminology, common terms, and common statistical methods.
Application of Information Systems and Secondary Data. Lynda Burton, ScD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Risk Management Plan
 Risk Management Plan Active substance: Drospirenone/ethinylestradiol Version number: 4.0 VI.2 Elements for a Public Summary VI.2.1 Overview of disease epidemiology Oral contraception Effective control
Risk Management Plan Active substance: Drospirenone/ethinylestradiol Version number: 4.0 VI.2 Elements for a Public Summary VI.2.1 Overview of disease epidemiology Oral contraception Effective control
Online Appendix for Limited Life Expectancy, Human Capital and Health Investment
 Online Appendix for Limited Life Expectancy, Human Capital and Health Investment Authors: Emily Oster, E. Ray Dorsey, Ira Shoulson Appendix A: Incentive Calculations In section 6 we calculate the elasticity
Online Appendix for Limited Life Expectancy, Human Capital and Health Investment Authors: Emily Oster, E. Ray Dorsey, Ira Shoulson Appendix A: Incentive Calculations In section 6 we calculate the elasticity
5. EPIDEMIOLOGICAL STUDIES
 5. EPIDEMIOLOGICAL STUDIES This chapter reviews observational and experimental epidemiological studies that have been conducted to determine associations between disinfected drinking-water and adverse
5. EPIDEMIOLOGICAL STUDIES This chapter reviews observational and experimental epidemiological studies that have been conducted to determine associations between disinfected drinking-water and adverse
C ohort, cross sectional, and case-control
 54 RESEARCH SERIES Observational research methods. Research design II: cohort, cross sectional, and case-control studies C J Mann... Cohort, cross sectional, and case-control studies are collectively referred
54 RESEARCH SERIES Observational research methods. Research design II: cohort, cross sectional, and case-control studies C J Mann... Cohort, cross sectional, and case-control studies are collectively referred
The Burden of Occupational Lung Cancer Paul A. Demers, PhD
 The Burden of Occupational Lung Cancer Paul A. Demers, PhD February 24 th, 2014 Measuring the Impact (burden) of Occupational Cancer Number or proportion of cancer deaths Number or proportion of new cancers
The Burden of Occupational Lung Cancer Paul A. Demers, PhD February 24 th, 2014 Measuring the Impact (burden) of Occupational Cancer Number or proportion of cancer deaths Number or proportion of new cancers
Health risk assessment: a standardized framework
 Health risk assessment: a standardized framework February 1, 2011 Thomas R. Frieden, MD, MPH Director, Centers for Disease Control and Prevention Leading causes of death in the U.S. The 5 leading causes
Health risk assessment: a standardized framework February 1, 2011 Thomas R. Frieden, MD, MPH Director, Centers for Disease Control and Prevention Leading causes of death in the U.S. The 5 leading causes
Lung Cancer. Public Outcomes Report. Submitted by Omar A. Majid, MD
 Public Outcomes Report Lung Cancer Submitted by Omar A. Majid, MD Lung cancer is the most common cancer-related cause of death among men and women. It has been estimated that there will be 226,1 new cases
Public Outcomes Report Lung Cancer Submitted by Omar A. Majid, MD Lung cancer is the most common cancer-related cause of death among men and women. It has been estimated that there will be 226,1 new cases
Lung cancer and asbestos
 Lung cancer and asbestos Bureau Veritas Training Bill Sanderson For the benefit of business and people To begin with.. There are known knowns, that is there are things we know that we know. There are known
Lung cancer and asbestos Bureau Veritas Training Bill Sanderson For the benefit of business and people To begin with.. There are known knowns, that is there are things we know that we know. There are known
Know your Numbers The D5 Goals for Diabetes Care. Shelly Hanson RN, CNS, CDE Cuyuna Regional Medical Center November 6, 2014
 Know your Numbers The D5 Goals for Diabetes Care Shelly Hanson RN, CNS, CDE Cuyuna Regional Medical Center November 6, 2014 The D5 What is it 5 different treatment goals identified for optimal diabetes
Know your Numbers The D5 Goals for Diabetes Care Shelly Hanson RN, CNS, CDE Cuyuna Regional Medical Center November 6, 2014 The D5 What is it 5 different treatment goals identified for optimal diabetes
Public Health Education
 Public Health Education University of Nevada, Reno School of Public Health Manuel Bayona EXHIBIT AA Health Care Document consists of 13 slides Entire document provided. Due to size limitations, pages provided.
Public Health Education University of Nevada, Reno School of Public Health Manuel Bayona EXHIBIT AA Health Care Document consists of 13 slides Entire document provided. Due to size limitations, pages provided.
PREDICTION OF INDIVIDUAL CELL FREQUENCIES IN THE COMBINED 2 2 TABLE UNDER NO CONFOUNDING IN STRATIFIED CASE-CONTROL STUDIES
 International Journal of Mathematical Sciences Vol. 10, No. 3-4, July-December 2011, pp. 411-417 Serials Publications PREDICTION OF INDIVIDUAL CELL FREQUENCIES IN THE COMBINED 2 2 TABLE UNDER NO CONFOUNDING
International Journal of Mathematical Sciences Vol. 10, No. 3-4, July-December 2011, pp. 411-417 Serials Publications PREDICTION OF INDIVIDUAL CELL FREQUENCIES IN THE COMBINED 2 2 TABLE UNDER NO CONFOUNDING
Biostatistics: Types of Data Analysis
 Biostatistics: Types of Data Analysis Theresa A Scott, MS Vanderbilt University Department of Biostatistics theresa.scott@vanderbilt.edu http://biostat.mc.vanderbilt.edu/theresascott Theresa A Scott, MS
Biostatistics: Types of Data Analysis Theresa A Scott, MS Vanderbilt University Department of Biostatistics theresa.scott@vanderbilt.edu http://biostat.mc.vanderbilt.edu/theresascott Theresa A Scott, MS
Table 16a Multiple Myeloma Average Annual Number of Cancer Cases and Age-Adjusted Incidence Rates* for 2002-2006
 Multiple Myeloma Figure 16 Definition: Multiple myeloma forms in plasma cells that are normally found in the bone marrow. 1 The plasma cells grow out of control and form tumors (plasmacytoma) or crowd
Multiple Myeloma Figure 16 Definition: Multiple myeloma forms in plasma cells that are normally found in the bone marrow. 1 The plasma cells grow out of control and form tumors (plasmacytoma) or crowd
Fewer people with coronary heart disease are being diagnosed as compared to the expected figures.
 JSNA Coronary heart disease 1) Key points 2) Introduction 3) National picture 4) Local picture of CHD prevalence 5) Mortality from coronary heart disease in Suffolk County 6) Trends in mortality rates
JSNA Coronary heart disease 1) Key points 2) Introduction 3) National picture 4) Local picture of CHD prevalence 5) Mortality from coronary heart disease in Suffolk County 6) Trends in mortality rates
Cancer prevention. Chapter 16
 Chapter 16 Cancer prevention 16.1 Introduction The preceding chapters of this book have focused on principles and methods needed to study the determinants of disease and their effects. The ultimate goal
Chapter 16 Cancer prevention 16.1 Introduction The preceding chapters of this book have focused on principles and methods needed to study the determinants of disease and their effects. The ultimate goal
Cardiovascular disease physiology. Linda Lowe-Krentz Bioscience in the 21 st Century October 14, 2011
 Cardiovascular disease physiology Linda Lowe-Krentz Bioscience in the 21 st Century October 14, 2011 Content Introduction The number 1 killer in America Some statistics Recommendations The disease process
Cardiovascular disease physiology Linda Lowe-Krentz Bioscience in the 21 st Century October 14, 2011 Content Introduction The number 1 killer in America Some statistics Recommendations The disease process
Calcium. 1995-2013, The Patient Education Institute, Inc. www.x-plain.com nuf40101 Last reviewed: 02/19/2013 1
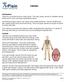 Calcium Introduction Calcium is a mineral found in many foods. The body needs calcium to maintain strong bones and to carry out many important functions. Not having enough calcium can cause many health
Calcium Introduction Calcium is a mineral found in many foods. The body needs calcium to maintain strong bones and to carry out many important functions. Not having enough calcium can cause many health
Health Profile for St. Louis City
 Health Profile for St. Louis City The health indicators of St. Louis City show that the city has many health problems. To highlight a few, the city s rates of sexually transmitted diseases (i.e., HIV/AIDS,
Health Profile for St. Louis City The health indicators of St. Louis City show that the city has many health problems. To highlight a few, the city s rates of sexually transmitted diseases (i.e., HIV/AIDS,
International Task Force for Prevention Of Coronary Heart Disease. Clinical management of risk factors. coronary heart disease (CHD) and stroke
 International Task Force for Prevention Of Coronary Heart Disease Clinical management of risk factors of coronary heart disease and stroke Economic analyses of primary prevention of coronary heart disease
International Task Force for Prevention Of Coronary Heart Disease Clinical management of risk factors of coronary heart disease and stroke Economic analyses of primary prevention of coronary heart disease
Advanced Statistical Analysis of Mortality. Rhodes, Thomas E. and Freitas, Stephen A. MIB, Inc. 160 University Avenue. Westwood, MA 02090
 Advanced Statistical Analysis of Mortality Rhodes, Thomas E. and Freitas, Stephen A. MIB, Inc 160 University Avenue Westwood, MA 02090 001-(781)-751-6356 fax 001-(781)-329-3379 trhodes@mib.com Abstract
Advanced Statistical Analysis of Mortality Rhodes, Thomas E. and Freitas, Stephen A. MIB, Inc 160 University Avenue Westwood, MA 02090 001-(781)-751-6356 fax 001-(781)-329-3379 trhodes@mib.com Abstract
Study Designs. Simon Day, PhD Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
High Blood Cholesterol
 National Cholesterol Education Program ATP III Guidelines At-A-Glance Quick Desk Reference 1 Step 1 2 Step 2 3 Step 3 Determine lipoprotein levels obtain complete lipoprotein profile after 9- to 12-hour
National Cholesterol Education Program ATP III Guidelines At-A-Glance Quick Desk Reference 1 Step 1 2 Step 2 3 Step 3 Determine lipoprotein levels obtain complete lipoprotein profile after 9- to 12-hour
