b) a) σ = σ =
|
|
|
- Darren Kelly
- 7 years ago
- Views:
Transcription
1 Bayesan parameter estmaton through varatonal methods Tomm S. Jaakkola Unversty of Calforna Santa Cruz, CA Mchael I. Jordan Massachusetts Insttute of Technology Cambrdge, MA January 21, 1998 Abstract We consder a logstc regresson model wth a Gaussan pror dstrbuton over the parameters. We show that accurate varatonal technques can be used to obtan a closed form posteror dstrbuton over the parameters gven the data thereby yeldng a posteror predctve model. The results are readly extended to bnary belef networks. For belef networks we also derve closed form posterors n the presence of ncomplete observatons through the use of addtonal varatonal technques. Fnally, we show that the dual of the regresson problem gves a latent varable densty model, the varatonal formulaton of whch leads to exactly solvable EM updates. 1 Introducton Bayesan methods have a number of vrtues, partcularly ther unform treatment of uncertanty at all levels of the modelng process. The formalsm also allows ready ncorporaton of pror knowledge and the seamless combnaton of such knowledge wth observed data (Bernardo & Smth 1994, Heckerman et al. 1995). The elegant semantcs, however, often comes at a szable computatonal cost posteror dstrbutons resultng from the ncorporaton of observed data must be represented and updated. The cost nvolved n these operatons can call nto queston the vablty of Bayesan methods even n relatvely smple settngs, such as generalzed lnear models (McCullagh & Nelder 1983). We concern ourselves n ths paper wth a partcular generalzed lnear model logstc regresson and we focus on Bayesan calculatons that are computatonally tractable. In partcular we descrbe a exble determnstc approxmaton procedure that allows the posteror dstrbuton n logstc regresson to be represented and updated ecently. We also show how our methods permt a Bayesan treatment of a more complex model a belef network n whch each node s a logstc regresson model. 1
2 The determnstc approxmaton methods that we develop n ths paper are known genercally as varatonal methods. Varatonal technques have been used extensvely n the physcs lterature (see, e.g., Pars 1988, Sakura 1985) and have also found applcatons n statstcs (Rustag 1976). Roughly speakng, the objectve of these methods s to transform the problem of nterest nto an optmzaton problem va the ntroducton of extra degrees of freedom known as varatonal parameters. For xed values of the varatonal parameters the transformed problem often has a closed form soluton, provdng an approxmate soluton to the orgnal problem. The varatonal parameters are adjusted va an optmzaton algorthm to yeld an mprovng sequence of approxmatons. Let us brey sketch the varatonal method that we develop n ths paper. We study a logstc regresson model wth a Gaussan pror on the parameter vector. Our varatonal transformaton replaces the logstc functon wth an adjustable lower bound that has a Gaussan form; that s, an exponental of a quadratc functon of the parameters. The product of the pror and the varatonally transformed lkelhood thus yelds a Gaussan expresson for the posteror, whch we optmze varatonally. Ths procedure s terated for each successve data pont. Our methods can be compared to the Laplace approxmaton for logstc regresson (cf. Spegelhalter & Laurtzen 1990), a closely related method whch also utlzes a Gaussan approxmaton to the posteror. To antcpate the dscusson n followng sectons, we wll see that the varatonal approach has an advantage over the Laplace approxmaton; n partcular, the use of varatonal parameters gves the varatonal approach greater exblty. We wll show that ths exblty translates nto mproved accuracy of the approxmaton. Varatonal methods can also be contrasted wth samplng technques, whch have become the method of choce n Bayesan statstcs (Thomas et al. 1992, Neal 1993). Samplng technques enjoy wde applcablty and can be powerful n evaluatng multdmensonal ntegrals and representng posteror dstrbutons. They do not, however, yeld closed form solutons nor do they guarantee monotoncally mprovng approxmatons. It s precsely these features that characterze varatonal methods. The paper s organzed as follows. Frst we descrbe n some detal a varatonal approxmaton method for Bayesan logstc regresson. Ths s followed by an evaluaton of the accuracy of the method and a comparson to Laplace approxmaton. We then extend the framework to belef networks, consderng both complete data and ncomplete data. Fnally, we consder the dual of the regresson problem and show that our technques lead to exactly solvable EM updates. 2
3 2 Bayesan logstc regresson We begn wth a logstc regresson model gven by: P (SjX; ) = g (2S? 1) T X ; (1) where g(x) = (1 + e?x )?1 s the logstc functon, S the bnary response varable, and X = fx 1 ; : : : ; X n g the set of explanatory varables. We represent the uncertanty n the parameter values va a pror dstrbuton P () whch we assume to be a Gaussan wth possbly full covarance structure. Our predctve dstrbuton s therefore: P (SjX) = Z P (SjX; )P ()d: (2) In order to utlze ths dstrbuton we need to be able to compute the posteror parameter dstrbuton P (jd 1 ; : : : ; D T ), where we assume that each D t = fs t ; X t 1; : : : ; X t ng s a complete observaton. Ths calculaton s ntractable for large n, thus we consder a varatonal approxmaton. Our approach nvolves ndng a varatonal transformaton of the logstc functon and usng ths transformed functon as an approxmate lkelhood. In partcular we wsh to consder transformatons that combne readly wth a Gaussan pror. We begn by symmetrzng the log logstc functon: log g(x) =? log(1 + e?x ) = x=2? log(e x=2 + e?x=2 ); (3) and notng that f(x) = log(e x=2 + e?x=2 ), s a convex functon n the varable x 2. (Ths s readly vered by takng second dervatves). Snce a tangent surface to a convex functon s a global lower bound for the functon, we can bound f(x) globally wth a rst order Taylor expanson n the varable x 2 : f(x) 2 ) (x2? 2 ) (4) =?=2 + log g() tanh(=2)(x2? 2 ): (5) Note that ths lower bound s exact whenever 2 = x 2. Combnng ths result wth Eq. (3) and exponentatng yelds the desred varatonal transformaton of the logstc functon: P (SjX; ) = g(h S ) g() exp n (H S? )=2? ()(H 2 S? 2 ) o ; (6) where H S = (2S?1) T X and () = tanh(=2)=(4). We also ntroduce the followng notaton: P (SjX; ; ) g() exp n (H S? )=2? ()(H 2 S? 2 ) o ; (7) 3
4 that s, P (SjX; ; ) denotes the varatonal lower bound on the logstc functon. For each xed value of H S we can n fact recover the exact value of the logstc functon va a partcular choce of the varatonal parameter. Indeed, maxmzng the lower bound wth respect to yelds = H S ; substtutng ths value back nto the lower bound recovers the orgnal condtonal probablty. For all other values of we obtan a lower bound. The true posteror P (jd) can be computed by normalzng P (SjX; )P (). Gven that ths calculaton s not feasble n general, we nstead form the bound: P (SjX; )P () P (SjX; ; )P () (8) and normalze the varatonal approxmaton P (SjX; ; )P (). Gven that P () s Gaussan and gven our choce of a Gaussan varatonal form for P (SjX; ; ), the normalzed varatonal dstrbuton s a Gaussan. Consequently, our approxmate Bayesan update amounts to updatng the pror mean and the pror covarance matrx nto the posteror mean and the posteror covarance matrx. Omttng the algebra we nd that the updates take the followng form:?1 p =?1 + 2() XX T (9) p = p h?1 + (S? 1=2)X (10) for a sngle data pont X = [X 1 : : : X n ] T. Successve data ponts are ncorporated nto the posteror by applyng these updates recursvely. Our work s not nshed, however, because the posteror covarance matrx depends on the varatonal parameter through () and we have yet to specfy. We choose va an optmzaton procedure; n partcular, we nd a value of that yelds a tght lower bound n eq. (8). The fact that the varatonal expresson n eq. (8) s a lower bound s mportant t allows us to use the EM algorthm to perform the optmzaton. We derve such an EM algorthm n Appendx A); the result s the followng (closed form) update equaton for : 2 = E n ( T X) 2o = X T post X + (X T post ) 2 ; (11) where the expectaton s taken wth respect to P (jd; old ), the varatonal posteror dstrbuton based on the prevous value of. Alternatng between the update for and the update for the parameters yelds a monotone mprovement to the posteror approxmaton. Emprcally we nd that ths procedure converges rapdly; only a few teratons are needed. The accuracy of the approxmaton s consdered n the followng two sectons. To summarze, the varatonal approach allows us to obtan a closed form expresson for the posteror predctve dstrbuton n logstc regresson: P (SjX; D) = Z P (SjX; )P (jd)d; (12) 4
5 where the posteror dstrbuton P (jd) comes from makng a sngle pass through the data set D = fd 1 ; : : : ; D T g, applyng the updates n eq. (9) and eq. (10) at each step. The predctve probabltes P (S t jx t ; D) take the form: log P (S t jx t ; D) = log g( t )? t =2+( t ) 2 t? 1 2 T? T t?1 t t log j tj jj ; (13) for any complete observaton D t, where and sgnfy the parameters n P (jd) and the subscrpt t refers to the posteror P (jd; D t ) found by augmentng the data set to nclude the pont D t. 3 Accuracy of the varatonal method The logstc functon s shown n Fgure 1(a), along wth a varatonal approxmaton for = 2. As we have noted, for each value of the varatonal parameter, there s a partcular pont x where the approxmaton s exact; for the remanng values of x the approxmaton s a lower bound σ = 0.50 σ = a) b) Fgure 1: a) The logstc functon (sold lne) and ts varatonal form (dashed lne) for R = 2. b) The derence between the predctve lkelhood P (S = 1jX) = g()p ()d and ts varatonal approxmaton as a functon of g(). The pror P () s Gaussan wth mean and varance 2. Integratng eq. (8) over the parameters we obtan a lower bound on the predctve probablty of an observaton. The tghtness of ths lower bound s a measure of accuracy of the approxmaton. To assess the varatonal approxmaton accordng to ths measure, we compared the lower bound to the true predctve probablty n the smple case n whch there s only one explanatory varable and the observaton s D = fs = 1; X = 1g. In ths case t s feasble to compute the true predctve probablty numercally. Fgure 1(b) shows the derence between the true predctve 5
6 probablty and the varatonal lower bound for varous settngs of the pror dstrbuton, wth optmzed separately for each derent pror dstrbuton. The fact that the approxmaton s a lower bound means that ths derence s always postve. We emphasze that the tghtness of the lower bound s not the only relevant measure of accuracy. Indeed, whle a tght lower bound on the predctve probablty assures us that the assocated posteror dstrbuton s hghly accurate, the converse s not true n general. In other words, a poor lower bound does not necessarly mply a poor approxmaton to the posteror dstrbuton, only that we no longer have any guarantees of accuracy. In practce, we expect the accuracy of the posteror to be more mportant than that of the predctve probablty snce errors n the posteror run the rsk of accumulatng n the course of the sequental estmaton procedure. We defer the evaluaton of the posteror accuracy to the followng secton where comparsons are made to related methods. 4 Comparson to other methods There are other sequental approxmaton methods that yeld closed form posteror parameter dstrbutons n logstc regresson models. The method most closely related to ours s that of Spegelhalter and Laurtzen (1990), whch we refer to as the S-L approxmaton n ths paper. Ther method s based on the Laplace approxmaton; that s, they utlze a local quadratc approxmaton to the complete log-lkelhood centered at the pror mean. The parameter updates that mplement ths approxmaton are smlar n sprt to the varatonal updates of eq. (9) and eq. (10):?1 post =?1 + ^p(1? ^p) XX T (14) post = + (S? ^p) post X (15) where ^p = g( T X). Snce there are no addtonal adjustable parameters n ths approxmaton, t s smpler than the varatonal method; however, we would expect ths lack of exblty to translate nto less accurate posteror estmates. We compared the accuracy of the posteror estmates for the two methods n the smple case where there s only one explanatory varable X = 1. The posteror of nterest was P (js = 1), computed for varous choces of values for the pror mean and the pror standard devaton. The correct posteror mean and standard devatons were obtaned numercally. Fgures 2 and 3 present the results. We plot sgned derences n comparng the obtaned posteror means to the correct ones; relatve errors were used for the posteror standard devatons. The error measures were left sgned to reveal any systematc bases. As can be seen n Fgures 2(a) and 3(a) the varatonal method yelds sgncantly more accurate estmates of the posteror means, for both values of the pror varance. For the posteror varance, 6
7 the S-L estmate and the varatonal estmate appear to yeld roughly comparable accuracy for the small value of the pror varance (Fgure 2(b)); however, for the larger pror varance, the varatonal approxmaton s superor (Fgure 3(b)). We note that the varatonal method consstently underestmates the true posteror varance; a fact that could be used to rene the approxmaton. Fnally, n terms of the KLdvergences between the approxmate and true posterors, the varatonal method and the S-L approxmaton are roughly equvalent for the small pror varance; and agan the varatonal method s superor for the larger value of the pror varance. Ths s shown n Fgure 4. error n mean 0.05 S L approxmaton Varatonal a) relatve error n stdv S L approxmaton Varatonal 0.04 b) Fgure 2: a) The errors n the posteror means as a functon of g(), where s the pror mean. Here = 1 for the pror. b) The relatve errors n the posteror standard devatons as a functon of g(). Agan = 1 for the pror dstrbuton error n mean S L approxmaton Varatonal relatve error n stdv S L approxmaton Varatonal a) b) Fgure 3: The plots are the same as n Fgure 2, but now = 2 for the pror dstrbuton. 7
8 KL dvergence S L approxmaton Varatonal KL dvergence S L approxmaton Varatonal 0 a) b) Fgure 4: KL-dvergences between the approxmate and the true posteror dstrbuton as a functon of g(). a) = 2 for the pror. b) = 3. The two approxmaton methods have (vsually) dentcal curves for = 1. 5 Extenson to belef networks A belef network s a probablstc model over a set of varables fs g that are dented wth the nodes n an acyclc drected graph. Lettng () denote the set of parents of node S n the graph, we dene the jont dstrbuton assocated wth the belef network as the followng product: P (S 1 ; : : : ; S n ) = Y P (S js ()): (16) We refer to the condtonal probabltes P (S js ()) as the \local probabltes" assocated wth the belef network. In ths secton we extend our earler work and consder belef networks n whch logstc regresson s used to dene the local probabltes. Thus we ntroduce parameter vectors, one for each varable S, and consder models n whch each local probablty P (S js (); ) s a logstc regresson of node S on ts parents S (). To smplfy the arguments n the followng sectons, we wll consder augmented belef networks n whch the parameters themselves are treated as nodes n the belef network (see Fgure 5). Ths s a standard devce n the belef network lterature and s of course natural wthn the Bayesan formalsm. 5.1 Complete cases A \complete case" refers to a data pont n whch all of the varables fs g are observed. If all of the data ponts are complete cases, then the methods that we developed n the prevous secton apply mmedately to belef networks. Ths can be seen as follows. Consder the Markov blankets assocated wth each of the parameters (Fgure 5(a)). For complete cases each of the nodes wthn the Markov blanket for 8
9 each of the parameters s observed (shaded n the dagram). By the ndependence semantcs of belef networks, ths mples that the posteror dstrbutons for the parameters are ndependent of one another (condtoned on the observed data). Thus the problem of estmatng the posteror dstrbutons for the parameters reduces to a set of n ndependent subproblems, each of whch s a Bayesan logstc regresson problem. We apply the methods developed n the prevous sectons drectly. S 1 S 2 S3 S 1 S 2 S3 θ 4 θ 4 S 4 θ 5 S 4 θ 5 a) S 5 b) S 5 Fgure 5: a) A complete observaton (shaded varables) and the Markov blanket (dashed lne) assocated wth the parameters 4. b) An observaton where the value of S 4 s mssng (unshaded n the gure). 5.2 Incomplete cases The stuaton s substantally more complex when there are ncomplete cases n the data set. Incomplete cases mply that we no longer have all the Markov blankets for the parameters n the network. Thus dependences can arse between the parameter dstrbutons n derent condtonal models. Let us consder ths stuaton n some detal. A mssng value mples that the observatons pertan to a margnal dstrbuton obtaned by summng or margnalzng over the mssng values of the unobserved varables. The margnal dstrbuton s therefore a mxture dstrbuton, where each mxture component corresponds to a partcular conguraton of the mssng varables. The weght assgned to that component s essentally the posteror probablty of the assocated conguraton (Spegelhalter & Laurtzen 1990). Note that the dependences arsng from the mssng values n the observatons can make the network qute densely connected (a mssng value for a node eectvely connects all of the neghborng nodes n the graph). The dense connectvty leaves lttle structure to be exploted n the exact probablstc computatons n these networks and tends to make exact Bayesan calculatons ntractable. Our approach to developng Bayesan methods for belef networks wth mssng varables combnes two varatonal technques. In partcular, we cope wth the de- 9
10 pendences ntroduced by the mssng data by appeal to mean eld methods (cf. Saul, Jaakkola, & Jordan 1994). We wll see that these methods, when combned wth the varatonal transformatons ntroduced earler for a sngle logstc regresson model restore the feasblty of a Bayesan approach to the logstc belef networks. Essentally the mean eld methods \ll n" the mssng values, allowng the varatonal transformaton for complete data descrbed n prevous sectons to be nvoked. The correct margnalzaton across mssng varables s a global operaton that aects all of the condtonal models that depend on the varables beng margnalzed over. Under the mean eld approxmaton, on the other hand, margnalzaton s a local operaton that acts ndvdually on the relevant condtonal models. The dervaton of the approprate margnalzaton operaton s presented n Appendx C. The results of that dervaton show that under the mean eld approxmaton, margnalzaton across a varable S 0 can be vewed as the followng transformaton of the local probabltes: P (SjS ; )! Y S 0 P (SjS ; ) q(s 0 ) (17) where q(s 0 ) s a mean eld dstrbuton over the mssng values. (Ths dstrbuton can be vewed as the \varatonal parameter" assocated wth the mean eld transformaton). We see that the transformed condtonal probabltes are a geometrc average across the mssng values wth respect to the mean eld dstrbuton. Whle the transformatons are carred out separately for each relevant condtonal model, the mean eld dstrbuton assocated wth the mssng values remans the same across such transformatons. Gven the transformaton n eq. (17), the approxmate Bayesan updates are obtaned readly. In partcular, when condtonng on a data pont that has mssng values we rst apply the mean eld transformaton. Ths eectvely lls n the mssng values, resultng n a transformed jont dstrbuton that factorzes as n the case of complete observatons. The posteror parameter dstrbutons therefore can be obtaned ndependently for the parameters assocated wth the transformed local probabltes. Two ssues reman to be consdered. Frst, the transformed condtonal probabltes (cf. Eq. (17)) are products of logstc functons and therefore more complcated than before. The varatonal method that we have proposed for the logstc functon, however, transforms each logstc functon nto an exponental wth quadratc dependence on the parameters. Products of such transforms are also exponental wth quadratc dependence on the parameters. Thus the approxmate lkelhood wll agan be Gaussan and f the pror s a multvarate Gaussan the posteror wll also be Gaussan. The second ssue s the dependence of the posteror parameter dstrbutons on the varatonal dstrbuton q. Once agan wth have to optmze the varatonal 10
11 parameters (a dstrbuton n ths case) to make our bounds as tght as possble; n partcular, we set q to the dstrbuton that maxmzes our lower bound. Ths optmzaton s carred out n conjuncton wth the optmzaton of the parameters for the transformatons of the logstc functons, whch are also lower bounds. As we show n Appendx B.3, the fact that all of our approxmatons are lower bounds mples that we can agan devse an EM algorthm to perform the maxmzaton. The resultng updates are as follows:?1 p =?1 n + 2( ) E S ()S() T h p = p?1 n + E (S? 1=2)S () where S () s the vector of parents of S, and the expectatons are taken wth respect to the varatonal dstrbuton q. 6 The dual problem o o (18) (19) (1) (2) (3) x x x... x (1) (2) (3) s s s... (1) (2) (3) s s s... θ a) b) θ θ θ (1) (2) (3)... Fgure 6: a) Bayesan regresson problem. b) The dual problem. The dual of the regresson problem (eq. (1)) s found by swtchng the roles of the explanatory varables X and the parameters. In the dual problem, we have xed parameters X and explanatory varables. Unlke before, dstnct values of may explan derent observatons whle the parameters X reman the same for all the observatons, as shown n gure 6. In order to make the dual problem of gure 6b useful as a densty model we generalze the bnary output varables S to vectors S = [S 1 ; : : : ; S n ] T where each component S has a dstnct set of parameters X = [X 1 : : : X m ] T assocated wth t. The explanatory varables reman the same for all components. Consequently, the dual of the regresson problem becomes a latent varable densty model wth a jont dstrbuton gven by P (S 1 ; : : : ; S n jx) = Z " Y P (S jx ; ) # P ()d (20) 11
12 where the condtonal probabltes are logstc regresson models P (S jx ; ) = g (2S? 1) P jx j j (21) We would lke to use the EM- algorthm for parameter estmaton n ths latent varable densty model. To acheve ths we agan explot the varatonal transformatons. The transformatons can be ntroduced for each of the condtonal probablty n the jont dstrbuton and optmzed separately for every observaton D t = fs1; t : : : ; Sng t n the database consstng only of the values of the bnary output varables. As n the logstc regresson case, the transformatons change the unweldy condtonal models nto smpler ones that depend on the parameters only quadratcally n the exponent. The varatonal evdence, whch s a product of the transformed condtonal probabltes, retans the same property. Consequently, under the varatonal approxmaton, we can compute the posteror dstrbuton over the latent varables n closed form. The mean and the covarance of ths posteror can be obtaned analogously to the regresson case gvng?1 t =?1 + X t = t "?1 + X 2() t X X T (22) # (S t? 1=2)X (23) The varatonal parameters t assocated wth each observaton and the condtonal model can be updated usng eq. (11) whenever X s replaced wth X, now the vector of parameters assocated wth the th condtonal model. We can solve the M-step of the EM-algorthm by accumulatng sucent statstcs for the parameters X ; ; based on the closed form posteror dstrbutons correspondng to the observatons n the data set. Omttng the algebra n ths regard, we get the followng explct updates for the parameters: where 1 T 1 T X t X t t (24) t (25) X A?1 b (26) A = X t b = X t 2( t ) ( t + t T t ) (27) (S t? 1=2) t (28) 12
13 and the subscrpt t denotes the quanttes pertanng to the observaton D t. Note that snce the varatonal transformatons that we expoted to arrve at these updates were all lower bounds, the M-step necessarly results n a monotoncally ncreasng lower bound on the log-probablty of the observatons. Ths desrable monotoncty property s unlkely to arse wth other types of approxmaton methods, such as the Laplace approxmaton. 7 Dscusson We have exempled the use of varatonal technques n the settng of Bayesan parameter estmaton. We found that varatonal methods can be exploted to yeld closed form expressons that approxmate the posteror dstrbutons for the parameters n logstc regresson. The methods apply mmedately to a Bayesan treatment of logstc belef networks wth complete data. We also showed how to combne mean eld theory wth our varatonal transformaton and thereby treat belef networks wth mssng data. Fnally, our varatonal technques lead to an exactly solvable EM algorthm for a latent varable densty model the dual of the logstc regresson problem. It s also of nterest to note that our varatonal method provdes an alternatve to the standard teratve Newton-Raphson method for maxmum lkelhood estmaton n logstc regresson (an algorthm known as \teratve reweghted least squares" or \IRLS"). The advantage of the varatonal approach s that t guarantees monotone mprovement n lkelhood. We present the dervaton of ths algorthm n Appendx C. Fnally, for an alternatve perspectve on the applcaton of varatonal methods to Bayesan nference, see Hnton and van Camp (1993) and MacKay (1997). These authors have developed a varatonal method known as \ensemble learnng," whch can be vewed as a mean eld approxmaton to the margnal lkelhood. References J. Bernardo and A. Smth (1994). Bayesan theory. New York: Wley. D. Heckerman, D. Geger, and D. Chckerng (1995). Learnng Bayesan networks: the combnaton of knowledge and statstcal data. Machne Learnng 20 No. 3: 197. G. Hnton and D. van Camp (1993). Keepng neural networks smple by mnmzng the descrpton length of the weghts. In Proceedngs of the 6th Annual Workshop on Computatonal Learnng Theory, ACM press. P. McCullagh & J. Nelder (1983). Generalzed lnear models. London: Chapman and Hall. 13
14 D. MacKay (1997). Ensemble learnng for hdden Markov models. Unpublshed manuscrpt. Department of Physcs, Unversty of Cambrdge. Avalable on the web at R. Neal (1992). Connectonst learnng of belef networks. Artcal Intellgence 56: R. Neal (1993). Probablstc nference usng Markov chan Monte Carlo methods. Techncal report CRG-TR-93-1, Unversty of Toronto. G. Pars (1988). Statstcal eld theory. Addson-Wesley. J. Rustag (1976). Varatonal Methods n Statstcs. Academc Press. L. Saul, T. Jaakkola, and M. Jordan (1996). Mean eld theory for sgmod belef networks. Journal of Artcal Intellgence Research 4: D. Spegelhalter and S. Laurtzen (1990). Sequental updatng of condtonal probabltes on drected graphcal structures. Networks 20: A. Thomas, D. Spegelhalter and W. Glks (1992). BUGS: A Program to Perform Bayesan Inference Usng Gbbs Samplng. In Bayesan Statstcs 4. Clarendon Press. A Optmzaton of the varatonal parameters To optmze the varatonal approxmaton of eq. (8) n the context of an observaton D = fs; X 1 ; : : : ; X n g we formulate an EM algorthm to maxmze the predctve lkelhood of ths observaton wth respect to. In other words, we nd that maxmzes the rght hand sde of Z Z P (SjX; )P ()d P (SjX; ; )P ()d (29) In the EM formalsm ths s acheved by teratvely maxmzng the expected complete log-lkelhood gven by Q(j old ) = E flog P (SjX; ; )P ()g (30) where the expectaton s over P (jd; old ). Takng the dervatve of Q wth respect to and settng t to zero Q(jold ) h E ( T X) 2? 2 = 0 14
15 As () s a monotoncally decreasng functon 1 the maxmum s obtaned at 2 = E ( T X) 2 (32) By substtutng for old above, the procedure can be repeated. Each such teraton yelds a better approxmaton n the sense of eq. (29). B Parameter posterors through mean eld Here we consder n detal the use of mean eld n llng-n the mssng values to facltate the computaton of posteror parameter dstrbutons. We start by ntroducng the mean eld approxmaton from the pont of vew that wll be most convenent for our purposes (for several other formulatons, see Pars 1988). B.1 Mean eld As mentoned n the text, mean eld can be vewed as an approxmaton to margnalzaton. Consder therefore the problem of margnalzng over the varable S 0 when the jont dstrbuton s gven by P (S 1 ; : : : ; S n j) = Y P (S js (); ) (33) If we performed the margnalzaton exactly, then the resultng dstrbuton would not retan the same factorzaton as the orgnal jont (assumng S 0 s nvolved n more than one of the condtonals) as can be seen from X Y S 0 P (S js (); ) = " Y 00 P (S 00jS ( 00); 00) # X Y S 0 0 P (S 0jS ( 0 ); 0) (34) where we have parttoned the product over the condtonals accordng to whether they depend on S 0 (ndexed by 0 ) or not (ndexed by 00 ). Margnalzaton s therefore not a local operaton. Localty s a desrable property for computatonal reasons, however, and we attempt to preserve localty under approxmate margnalzaton. The approxmaton we use for ths purpose s a varatonal transformaton based on the fact that any geometrc average 2 s always less than or equal to the usual average. By applyng ths property to the margnalzaton, we nd X X " # P (S1 ; : : : ; S P (S 1 ; : : : ; S n j) = q(s 0 n j) ) (35) q(s 0 ) S 0 S 0 1 Ths holds for 0. However, snce P (SjX; ; ) s a symmetrc functon of, assumng 0 has no eect on the qualty of the approxmaton. Q 2 A geometrc average of p ; 2 f1; : : : ; ng wth respect to the dstrbuton q s gven by pq. 15
16 Y S 0 Y = C(q) " # q(s ) P (S1 ; : : : ; S n j) 0 q(s 0 ) " Y S 0 P (S js (); ) q(s 0 ) # (36) (37) where the nequalty comes from transformng the average over the bracketed term (wth respect to the dstrbuton q) nto a geometrc average. The thrd lne follows from pluggng n the form of the jont dstrbuton and exchangng the order of the products. The multplcatve constant C(q) relates to the entropy of the varatonal dstrbuton q: C(q) = Y S 0 " 1 # q(s ) 0 q(s 0 ) and therefore log C(q) =? X S 0 q(s 0 ) log q(s 0 ) (38) Let us now make a few observatons about the result n Eq. (37). Frst, the choce of the varatonal dstrbuton q nvolves a trade-o between feasblty and accuracy. If, for example, q s set equal to the true posteror dstrbuton over the mssng values S 0, the transformaton would be exact rather than a lower bound. In cases where the correct posteror s dcult or nfeasble to compute, on the other hand, we may settle for a manageable form for q and consequently ncur the cost of obtanng a lower bound n place of the exact result. Second, for any xed q the transformed margnalzaton of Eq. (37) follows the factorzaton of the orgnal jont dstrbuton. The condtonal probabltes, however, have been moded n ths approxmaton accordng to P (S js (); )! Y S 0 P (S js (); ) q(s 0 ) (39) Ths transformaton of condtonal probabltes s a local operaton. Note that the transformaton has no eect on the condtonal probabltes that do not depend on the mssng values S 0. We note that the varatonal dstrbuton q s the same n all transformatons correspondng to the same mssng value conguraton. Let us lastly pont out that the term mean eld approxmaton tradtonally refers to the case where the varatonal dstrbuton q has a partcular parametrc form, namely the completely factorzed dstrbuton: my q(s 0 ) = q (S) 0 (40) =1 Ths smple choce may be necessary for reasons of computatonal feasblty n dense graphcal models wth a relatvely large number of mssng values. 16
17 B.2 Parameter posterors To ll-n the possble mssng values n an observaton D t = fs; t : : : ; Sng t we employ the (generalzed) mean eld approxmaton descrbed above. As a result, the jont dstrbuton after the approxmate margnalzaton factorzes as wth complete observatons. Thus the posteror dstrbutons for the parameters reman ndependent across the derent condtonal models and can be computed separately. Thus P ( jd t ; q) / " Y S 0 P (S js (); ) q(s 0 ) # P ( ) (41) The form of ths posteror, however, remans at least as unweldy as the Bayesan logstc regresson problem consdered earler n the paper. Proceedng analogously, we transform the logstc functons as n Eq. (6) correspondng to each of the condtonal probabltes n the product and obtan P ( jd t ; q; ) / = = " Y " Y " S 0 P (S js (); ; ) q(s 0 ) S 0 g( ) e # P ( ) (42) n g( ) e (H S? )=2?( )(H 2? 2) o # q(s ) 0 S P ( ) (43) n o # PS q(s ) 0 (H 0 S? )=2?( )(H 2? 2) S P ( ) (44) = h g( ) e ( EfH S g? )=2?( ) ( EfH 2 S g? 2 ) P ( ) (45) P (S js (); ; ; q)p ( ) (46) where H S = (2S?1) T S (), S () s the vector of parents of S, and the expectatons are wth respect to the varatonal dstrbuton q. For smplcty, we have not let the varatonal parameter vary ndependently wth the conguratons of the mssng values but assumed t to be the same for all such conguratons. Ths choce s naturally suboptmal but s made here prmarly for notatonal smplcty (the choce may also be necessary n cases where the number of mssng values s large). Now, snce H S s lnear n the parameters, the exponent n Eq. (45) consstng of averages over H S and ts square wth respect to the varatonal dstrbuton q, stays at most quadratc n the parameters. Ths property mples that f the pror dstrbuton s a multvarate Gaussan so wll be the posteror. The mean p and covarance p of such posteror are gven by (we omt the algebra)?1 p =?1 n + 2( ) E S ()S() T h p = p?1 n + E (S? 1=2)S () Note that ths posteror depends both on the dstrbuton q and the parameters. The optmzaton of these parameters s shown n Appendx B o o (47) (48)
18 B.3 Optmzaton of the varatonal parameters We have ntroduced two varatonal \parameters": the mean eld dstrbuton q for the mssng values, and the parameters correspondng to the logstc transformatons. The metrc for optmzng the parameters comes from the fact that the transformatons assocated wth these parameters ntroduce a lower bound on the probablty of the observatons. Thus by maxmzng ths lower bound we nd the parameter values that yeld the most accurate approxmatons. We therefore attempt to maxmze the rght hand sde of log P (D t ) log P (D t j; q) (49) = log Z = log Y P (D t j; ; q)p ()d (50) Z P (S js (); ; ; q)p ( )d + log C(q) (51) where D t contans the observed settngs of the varables. We have used the fact that the jont dstrbuton under our approxmatons factorzes as wth complete cases. Smlarly to the case of the smple Bayesan logstc regresson consdered prevously, we can devse an EM-algorthm to maxmze the varatonal lower bound wth respect to the parameters q and ; the parameters can be consdered as latent varables n ths formulaton. The E-step of the EM-algorthm,.e., ndng the posteror dstrbuton over the latent varables, has already been descrbed n Appendx B.2. Here we wll consder n detal only the M-step. For smplcty, we solve the M-step n two phases: one where the varatonal dstrbuton s kept xed and the maxmzaton s over, and the other where these roles have been reversed. We start wth the rst phase. As the varatonal jont dstrbuton factorzes, the problem of ndng the optmal parameters separates nto ndependent problems concernng each of the transformed condtonal. Thus the optmzaton becomes analogous to the smple Bayesan logstc regresson consdered earler. Two derences exst: rst, the posteror over each s now obtaned from Eq. (46); second, we have an addtonal expectaton wth respect to the varatonal dstrbuton q. Wth these derences the optmzaton s analogous to the one presented n Appendx A above and we won't repeat t here. The latter part of our two-stage M-step s new, however, and we wll consder t n detal. The objectve s to optmze q whle keepng the parameters xed to ther prevously obtaned values. Smlarly to the case we construct an EM-algorthm to perform ths nner loop optmzaton: Q(qjq old ) = E flog P (D t ; j; q)g (52) = X E n log P (S js (); ; ; q)p ( ) o + log C(q) (53) 18
19 where the rst expectaton s wth respect to P (j; q old ), whch factorzes across the condtonal probabltes as explaned prevously; the expectatons E are over the component dstrbutons P ( j ; q old ), obtaned drectly from Eq. (46). Let us now nsert the form of the transformed condtonal probabltes, P (S js (); ; ; q), nto the above denton of the Q functon. For clarty we wll omt all the terms wth no dependence on the varatonal dstrbuton q. We obtan: X Q(qjq old ) = X = E q n E Eq fh S g=2? ( ) E q fh 2 o S g + log C(q) + : : : (54) n E fh S g=2? ( ) E fh 2 o g + H(q) + : : : S (55) where E q refers to the expectaton wth respect to the varatonal dstrbuton q. The second equaton follows by exchangng the order of the (mutually ndependent) expectatons E and E q. We have also used the fact that log C(q) s the entropy H(q) of q (see Appendx B above). Recall the notaton H S = (2S? 1) T S (), where S () s a bnary vector of parents of S. Before proceedng to maxmze the Q functon wth respect to q, we explcate the averages E n the above formula: E fh S g = (2S? 1) T p S () (56) E fh 2 S g = T p S () 2 + S T () p S () (57) Here p and p are the mean and the covarance, respectvely, of the posteror P ( j ; q old ) assocated wth the th condtonal model. Smply nsertng these back nto the expresson for the Q functon we get X 2 Q(qjq old ) = E q (S? 1=2) T p S ()? ( ) T p S () o?( ) S() T p S () + H(q) + : : : (58) Now, some of the bnary varables S have a value assgnment based on the observaton D t and the remanng varables wll be averaged over the varatonal dstrbuton q. Assumng no a pror constrants on the form of the q dstrbuton, the maxmzng q s the Boltzmann dstrbuton (see e.g. Pars 1988): q(s 0 ) / exp X 2! (S? 1=2) T p S ()? ( ) T p S ()? ( ) S() T p S () Whenever the varatonal dstrbuton s constraned, however, such as n the case of a completely factorzed dstrbuton, we may no longer expect to nd the q that maxmzes eq. (58). Nevertheless, a locally optmal soluton can be found by, for example, sequentally k Q(qjq old ) = 0 (60) wth respect to each of the components q k = q k (S k = 1) n the factorzed dstrbuton. 19
20 C Techncal note: ML estmaton The standard maxmum lkelhood procedure for estmatng the parameters n logstc regresson uses an teratve Newton-Raphson method to nd the parameter values. Whle the method s fast, t s not monotonc;.e., the probablty of the observatons s not guaranteed to ncrease after any teraton. We show here how to derve a monotonc, fast estmaton procedure for logstc regresson by makng use of the varatonal transformaton n eq. (6). Let us denote H t = (2S t? 1) T X t and wrte the log-probablty of the observatons as L() = X t X t log P (S t jx t ; ) = X t log g(h t ) log g( t ) + (H t? t )=2? ( t ) H 2 t? 2 t = L(; ) (61) The varatonal lower bound s exact whenever t = H t for all t. Although the parameters cannot be solved easly from L(), L(; ) allows a closed form soluton for any xed, snce the varatonal log-probablty s a quadratc functon of. The parameters that maxmze L(; ) are gven by 0 = A?1 b where A = X t 2( t ) H t H t T and b = X t (S t? 1=2)H t (62) Successvely solvng for and updatng yelds the followng chan of nequaltes: L() = L(; ) L( 0 ; ) L( 0 ; 0 ) = L( 0 ) (63) where the prme sgnes an update and we have assumed that t = H t ntally. The combned update thus leads to a monotoncally ncreasng log-probablty. In addton, the closed form -updates make ths procedure comparable n speed to the standard Newton-Raphson alternatve. 20
What is Candidate Sampling
 What s Canddate Samplng Say we have a multclass or mult label problem where each tranng example ( x, T ) conssts of a context x a small (mult)set of target classes T out of a large unverse L of possble
What s Canddate Samplng Say we have a multclass or mult label problem where each tranng example ( x, T ) conssts of a context x a small (mult)set of target classes T out of a large unverse L of possble
CS 2750 Machine Learning. Lecture 3. Density estimation. CS 2750 Machine Learning. Announcements
 Lecture 3 Densty estmaton Mlos Hauskrecht mlos@cs.ptt.edu 5329 Sennott Square Next lecture: Matlab tutoral Announcements Rules for attendng the class: Regstered for credt Regstered for audt (only f there
Lecture 3 Densty estmaton Mlos Hauskrecht mlos@cs.ptt.edu 5329 Sennott Square Next lecture: Matlab tutoral Announcements Rules for attendng the class: Regstered for credt Regstered for audt (only f there
How To Calculate The Accountng Perod Of Nequalty
 Inequalty and The Accountng Perod Quentn Wodon and Shlomo Ytzha World Ban and Hebrew Unversty September Abstract Income nequalty typcally declnes wth the length of tme taen nto account for measurement.
Inequalty and The Accountng Perod Quentn Wodon and Shlomo Ytzha World Ban and Hebrew Unversty September Abstract Income nequalty typcally declnes wth the length of tme taen nto account for measurement.
benefit is 2, paid if the policyholder dies within the year, and probability of death within the year is ).
 REVIEW OF RISK MANAGEMENT CONCEPTS LOSS DISTRIBUTIONS AND INSURANCE Loss and nsurance: When someone s subject to the rsk of ncurrng a fnancal loss, the loss s generally modeled usng a random varable or
REVIEW OF RISK MANAGEMENT CONCEPTS LOSS DISTRIBUTIONS AND INSURANCE Loss and nsurance: When someone s subject to the rsk of ncurrng a fnancal loss, the loss s generally modeled usng a random varable or
Logistic Regression. Steve Kroon
 Logstc Regresson Steve Kroon Course notes sectons: 24.3-24.4 Dsclamer: these notes do not explctly ndcate whether values are vectors or scalars, but expects the reader to dscern ths from the context. Scenaro
Logstc Regresson Steve Kroon Course notes sectons: 24.3-24.4 Dsclamer: these notes do not explctly ndcate whether values are vectors or scalars, but expects the reader to dscern ths from the context. Scenaro
Module 2 LOSSLESS IMAGE COMPRESSION SYSTEMS. Version 2 ECE IIT, Kharagpur
 Module LOSSLESS IMAGE COMPRESSION SYSTEMS Lesson 3 Lossless Compresson: Huffman Codng Instructonal Objectves At the end of ths lesson, the students should be able to:. Defne and measure source entropy..
Module LOSSLESS IMAGE COMPRESSION SYSTEMS Lesson 3 Lossless Compresson: Huffman Codng Instructonal Objectves At the end of ths lesson, the students should be able to:. Defne and measure source entropy..
1 Example 1: Axis-aligned rectangles
 COS 511: Theoretcal Machne Learnng Lecturer: Rob Schapre Lecture # 6 Scrbe: Aaron Schld February 21, 2013 Last class, we dscussed an analogue for Occam s Razor for nfnte hypothess spaces that, n conjuncton
COS 511: Theoretcal Machne Learnng Lecturer: Rob Schapre Lecture # 6 Scrbe: Aaron Schld February 21, 2013 Last class, we dscussed an analogue for Occam s Razor for nfnte hypothess spaces that, n conjuncton
Logistic Regression. Lecture 4: More classifiers and classes. Logistic regression. Adaboost. Optimization. Multiple class classification
 Lecture 4: More classfers and classes C4B Machne Learnng Hlary 20 A. Zsserman Logstc regresson Loss functons revsted Adaboost Loss functons revsted Optmzaton Multple class classfcaton Logstc Regresson
Lecture 4: More classfers and classes C4B Machne Learnng Hlary 20 A. Zsserman Logstc regresson Loss functons revsted Adaboost Loss functons revsted Optmzaton Multple class classfcaton Logstc Regresson
1 De nitions and Censoring
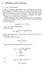 De ntons and Censorng. Survval Analyss We begn by consderng smple analyses but we wll lead up to and take a look at regresson on explanatory factors., as n lnear regresson part A. The mportant d erence
De ntons and Censorng. Survval Analyss We begn by consderng smple analyses but we wll lead up to and take a look at regresson on explanatory factors., as n lnear regresson part A. The mportant d erence
Support Vector Machines
 Support Vector Machnes Max Wellng Department of Computer Scence Unversty of Toronto 10 Kng s College Road Toronto, M5S 3G5 Canada wellng@cs.toronto.edu Abstract Ths s a note to explan support vector machnes.
Support Vector Machnes Max Wellng Department of Computer Scence Unversty of Toronto 10 Kng s College Road Toronto, M5S 3G5 Canada wellng@cs.toronto.edu Abstract Ths s a note to explan support vector machnes.
L10: Linear discriminants analysis
 L0: Lnear dscrmnants analyss Lnear dscrmnant analyss, two classes Lnear dscrmnant analyss, C classes LDA vs. PCA Lmtatons of LDA Varants of LDA Other dmensonalty reducton methods CSCE 666 Pattern Analyss
L0: Lnear dscrmnants analyss Lnear dscrmnant analyss, two classes Lnear dscrmnant analyss, C classes LDA vs. PCA Lmtatons of LDA Varants of LDA Other dmensonalty reducton methods CSCE 666 Pattern Analyss
Fisher Markets and Convex Programs
 Fsher Markets and Convex Programs Nkhl R. Devanur 1 Introducton Convex programmng dualty s usually stated n ts most general form, wth convex objectve functons and convex constrants. (The book by Boyd and
Fsher Markets and Convex Programs Nkhl R. Devanur 1 Introducton Convex programmng dualty s usually stated n ts most general form, wth convex objectve functons and convex constrants. (The book by Boyd and
An Alternative Way to Measure Private Equity Performance
 An Alternatve Way to Measure Prvate Equty Performance Peter Todd Parlux Investment Technology LLC Summary Internal Rate of Return (IRR) s probably the most common way to measure the performance of prvate
An Alternatve Way to Measure Prvate Equty Performance Peter Todd Parlux Investment Technology LLC Summary Internal Rate of Return (IRR) s probably the most common way to measure the performance of prvate
1. Fundamentals of probability theory 2. Emergence of communication traffic 3. Stochastic & Markovian Processes (SP & MP)
 6.3 / -- Communcaton Networks II (Görg) SS20 -- www.comnets.un-bremen.de Communcaton Networks II Contents. Fundamentals of probablty theory 2. Emergence of communcaton traffc 3. Stochastc & Markovan Processes
6.3 / -- Communcaton Networks II (Görg) SS20 -- www.comnets.un-bremen.de Communcaton Networks II Contents. Fundamentals of probablty theory 2. Emergence of communcaton traffc 3. Stochastc & Markovan Processes
BERNSTEIN POLYNOMIALS
 On-Lne Geometrc Modelng Notes BERNSTEIN POLYNOMIALS Kenneth I. Joy Vsualzaton and Graphcs Research Group Department of Computer Scence Unversty of Calforna, Davs Overvew Polynomals are ncredbly useful
On-Lne Geometrc Modelng Notes BERNSTEIN POLYNOMIALS Kenneth I. Joy Vsualzaton and Graphcs Research Group Department of Computer Scence Unversty of Calforna, Davs Overvew Polynomals are ncredbly useful
8.5 UNITARY AND HERMITIAN MATRICES. The conjugate transpose of a complex matrix A, denoted by A*, is given by
 6 CHAPTER 8 COMPLEX VECTOR SPACES 5. Fnd the kernel of the lnear transformaton gven n Exercse 5. In Exercses 55 and 56, fnd the mage of v, for the ndcated composton, where and are gven by the followng
6 CHAPTER 8 COMPLEX VECTOR SPACES 5. Fnd the kernel of the lnear transformaton gven n Exercse 5. In Exercses 55 and 56, fnd the mage of v, for the ndcated composton, where and are gven by the followng
Calculation of Sampling Weights
 Perre Foy Statstcs Canada 4 Calculaton of Samplng Weghts 4.1 OVERVIEW The basc sample desgn used n TIMSS Populatons 1 and 2 was a two-stage stratfed cluster desgn. 1 The frst stage conssted of a sample
Perre Foy Statstcs Canada 4 Calculaton of Samplng Weghts 4.1 OVERVIEW The basc sample desgn used n TIMSS Populatons 1 and 2 was a two-stage stratfed cluster desgn. 1 The frst stage conssted of a sample
Recurrence. 1 Definitions and main statements
 Recurrence 1 Defntons and man statements Let X n, n = 0, 1, 2,... be a MC wth the state space S = (1, 2,...), transton probabltes p j = P {X n+1 = j X n = }, and the transton matrx P = (p j ),j S def.
Recurrence 1 Defntons and man statements Let X n, n = 0, 1, 2,... be a MC wth the state space S = (1, 2,...), transton probabltes p j = P {X n+1 = j X n = }, and the transton matrx P = (p j ),j S def.
v a 1 b 1 i, a 2 b 2 i,..., a n b n i.
 SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 455 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces we have studed thus far n the text are real vector spaces snce the scalars are
SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 455 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces we have studed thus far n the text are real vector spaces snce the scalars are
Forecasting the Demand of Emergency Supplies: Based on the CBR Theory and BP Neural Network
 700 Proceedngs of the 8th Internatonal Conference on Innovaton & Management Forecastng the Demand of Emergency Supples: Based on the CBR Theory and BP Neural Network Fu Deqang, Lu Yun, L Changbng School
700 Proceedngs of the 8th Internatonal Conference on Innovaton & Management Forecastng the Demand of Emergency Supples: Based on the CBR Theory and BP Neural Network Fu Deqang, Lu Yun, L Changbng School
Mean Field Theory for Sigmoid Belief Networks. Abstract
 Journal of Artæcal Intellgence Research 4 è1996è 61 76 Submtted 11è95; publshed 3è96 Mean Feld Theory for Sgmod Belef Networks Lawrence K. Saul Tomm Jaakkola Mchael I. Jordan Center for Bologcal and Computatonal
Journal of Artæcal Intellgence Research 4 è1996è 61 76 Submtted 11è95; publshed 3è96 Mean Feld Theory for Sgmod Belef Networks Lawrence K. Saul Tomm Jaakkola Mchael I. Jordan Center for Bologcal and Computatonal
Institute of Informatics, Faculty of Business and Management, Brno University of Technology,Czech Republic
 Lagrange Multplers as Quanttatve Indcators n Economcs Ivan Mezník Insttute of Informatcs, Faculty of Busness and Management, Brno Unversty of TechnologCzech Republc Abstract The quanttatve role of Lagrange
Lagrange Multplers as Quanttatve Indcators n Economcs Ivan Mezník Insttute of Informatcs, Faculty of Busness and Management, Brno Unversty of TechnologCzech Republc Abstract The quanttatve role of Lagrange
An Analysis of Central Processor Scheduling in Multiprogrammed Computer Systems
 STAN-CS-73-355 I SU-SE-73-013 An Analyss of Central Processor Schedulng n Multprogrammed Computer Systems (Dgest Edton) by Thomas G. Prce October 1972 Techncal Report No. 57 Reproducton n whole or n part
STAN-CS-73-355 I SU-SE-73-013 An Analyss of Central Processor Schedulng n Multprogrammed Computer Systems (Dgest Edton) by Thomas G. Prce October 1972 Techncal Report No. 57 Reproducton n whole or n part
PSYCHOLOGICAL RESEARCH (PYC 304-C) Lecture 12
 14 The Ch-squared dstrbuton PSYCHOLOGICAL RESEARCH (PYC 304-C) Lecture 1 If a normal varable X, havng mean µ and varance σ, s standardsed, the new varable Z has a mean 0 and varance 1. When ths standardsed
14 The Ch-squared dstrbuton PSYCHOLOGICAL RESEARCH (PYC 304-C) Lecture 1 If a normal varable X, havng mean µ and varance σ, s standardsed, the new varable Z has a mean 0 and varance 1. When ths standardsed
Georey E. Hinton. University oftoronto. Email: zoubin@cs.toronto.edu. Technical Report CRG-TR-96-1. May 21, 1996 (revised Feb 27, 1997) Abstract
 The EM Algorthm for Mxtures of Factor Analyzers Zoubn Ghahraman Georey E. Hnton Department of Computer Scence Unversty oftoronto 6 Kng's College Road Toronto, Canada M5S A4 Emal: zoubn@cs.toronto.edu Techncal
The EM Algorthm for Mxtures of Factor Analyzers Zoubn Ghahraman Georey E. Hnton Department of Computer Scence Unversty oftoronto 6 Kng's College Road Toronto, Canada M5S A4 Emal: zoubn@cs.toronto.edu Techncal
How Sets of Coherent Probabilities May Serve as Models for Degrees of Incoherence
 1 st Internatonal Symposum on Imprecse Probabltes and Ther Applcatons, Ghent, Belgum, 29 June 2 July 1999 How Sets of Coherent Probabltes May Serve as Models for Degrees of Incoherence Mar J. Schervsh
1 st Internatonal Symposum on Imprecse Probabltes and Ther Applcatons, Ghent, Belgum, 29 June 2 July 1999 How Sets of Coherent Probabltes May Serve as Models for Degrees of Incoherence Mar J. Schervsh
The OC Curve of Attribute Acceptance Plans
 The OC Curve of Attrbute Acceptance Plans The Operatng Characterstc (OC) curve descrbes the probablty of acceptng a lot as a functon of the lot s qualty. Fgure 1 shows a typcal OC Curve. 10 8 6 4 1 3 4
The OC Curve of Attrbute Acceptance Plans The Operatng Characterstc (OC) curve descrbes the probablty of acceptng a lot as a functon of the lot s qualty. Fgure 1 shows a typcal OC Curve. 10 8 6 4 1 3 4
Solving Factored MDPs with Continuous and Discrete Variables
 Solvng Factored MPs wth Contnuous and screte Varables Carlos Guestrn Berkeley Research Center Intel Corporaton Mlos Hauskrecht epartment of Computer Scence Unversty of Pttsburgh Branslav Kveton Intellgent
Solvng Factored MPs wth Contnuous and screte Varables Carlos Guestrn Berkeley Research Center Intel Corporaton Mlos Hauskrecht epartment of Computer Scence Unversty of Pttsburgh Branslav Kveton Intellgent
Luby s Alg. for Maximal Independent Sets using Pairwise Independence
 Lecture Notes for Randomzed Algorthms Luby s Alg. for Maxmal Independent Sets usng Parwse Independence Last Updated by Erc Vgoda on February, 006 8. Maxmal Independent Sets For a graph G = (V, E), an ndependent
Lecture Notes for Randomzed Algorthms Luby s Alg. for Maxmal Independent Sets usng Parwse Independence Last Updated by Erc Vgoda on February, 006 8. Maxmal Independent Sets For a graph G = (V, E), an ndependent
Modelling high-dimensional data by mixtures of factor analyzers
 Computatonal Statstcs & Data Analyss 41 (2003) 379 388 www.elsever.com/locate/csda Modellng hgh-dmensonal data by mxtures of factor analyzers G.J. McLachlan, D. Peel, R.W. Bean Department of Mathematcs,
Computatonal Statstcs & Data Analyss 41 (2003) 379 388 www.elsever.com/locate/csda Modellng hgh-dmensonal data by mxtures of factor analyzers G.J. McLachlan, D. Peel, R.W. Bean Department of Mathematcs,
8 Algorithm for Binary Searching in Trees
 8 Algorthm for Bnary Searchng n Trees In ths secton we present our algorthm for bnary searchng n trees. A crucal observaton employed by the algorthm s that ths problem can be effcently solved when the
8 Algorthm for Bnary Searchng n Trees In ths secton we present our algorthm for bnary searchng n trees. A crucal observaton employed by the algorthm s that ths problem can be effcently solved when the
Approximating Cross-validatory Predictive Evaluation in Bayesian Latent Variables Models with Integrated IS and WAIC
 Approxmatng Cross-valdatory Predctve Evaluaton n Bayesan Latent Varables Models wth Integrated IS and WAIC Longha L Department of Mathematcs and Statstcs Unversty of Saskatchewan Saskatoon, SK, CANADA
Approxmatng Cross-valdatory Predctve Evaluaton n Bayesan Latent Varables Models wth Integrated IS and WAIC Longha L Department of Mathematcs and Statstcs Unversty of Saskatchewan Saskatoon, SK, CANADA
CHAPTER 14 MORE ABOUT REGRESSION
 CHAPTER 14 MORE ABOUT REGRESSION We learned n Chapter 5 that often a straght lne descrbes the pattern of a relatonshp between two quanttatve varables. For nstance, n Example 5.1 we explored the relatonshp
CHAPTER 14 MORE ABOUT REGRESSION We learned n Chapter 5 that often a straght lne descrbes the pattern of a relatonshp between two quanttatve varables. For nstance, n Example 5.1 we explored the relatonshp
Hallucinating Multiple Occluded CCTV Face Images of Different Resolutions
 In Proc. IEEE Internatonal Conference on Advanced Vdeo and Sgnal based Survellance (AVSS 05), September 2005 Hallucnatng Multple Occluded CCTV Face Images of Dfferent Resolutons Ku Ja Shaogang Gong Computer
In Proc. IEEE Internatonal Conference on Advanced Vdeo and Sgnal based Survellance (AVSS 05), September 2005 Hallucnatng Multple Occluded CCTV Face Images of Dfferent Resolutons Ku Ja Shaogang Gong Computer
ANALYZING THE RELATIONSHIPS BETWEEN QUALITY, TIME, AND COST IN PROJECT MANAGEMENT DECISION MAKING
 ANALYZING THE RELATIONSHIPS BETWEEN QUALITY, TIME, AND COST IN PROJECT MANAGEMENT DECISION MAKING Matthew J. Lberatore, Department of Management and Operatons, Vllanova Unversty, Vllanova, PA 19085, 610-519-4390,
ANALYZING THE RELATIONSHIPS BETWEEN QUALITY, TIME, AND COST IN PROJECT MANAGEMENT DECISION MAKING Matthew J. Lberatore, Department of Management and Operatons, Vllanova Unversty, Vllanova, PA 19085, 610-519-4390,
1. Measuring association using correlation and regression
 How to measure assocaton I: Correlaton. 1. Measurng assocaton usng correlaton and regresson We often would lke to know how one varable, such as a mother's weght, s related to another varable, such as a
How to measure assocaton I: Correlaton. 1. Measurng assocaton usng correlaton and regresson We often would lke to know how one varable, such as a mother's weght, s related to another varable, such as a
Forecasting the Direction and Strength of Stock Market Movement
 Forecastng the Drecton and Strength of Stock Market Movement Jngwe Chen Mng Chen Nan Ye cjngwe@stanford.edu mchen5@stanford.edu nanye@stanford.edu Abstract - Stock market s one of the most complcated systems
Forecastng the Drecton and Strength of Stock Market Movement Jngwe Chen Mng Chen Nan Ye cjngwe@stanford.edu mchen5@stanford.edu nanye@stanford.edu Abstract - Stock market s one of the most complcated systems
DEFINING %COMPLETE IN MICROSOFT PROJECT
 CelersSystems DEFINING %COMPLETE IN MICROSOFT PROJECT PREPARED BY James E Aksel, PMP, PMI-SP, MVP For Addtonal Informaton about Earned Value Management Systems and reportng, please contact: CelersSystems,
CelersSystems DEFINING %COMPLETE IN MICROSOFT PROJECT PREPARED BY James E Aksel, PMP, PMI-SP, MVP For Addtonal Informaton about Earned Value Management Systems and reportng, please contact: CelersSystems,
THE DISTRIBUTION OF LOAN PORTFOLIO VALUE * Oldrich Alfons Vasicek
 HE DISRIBUION OF LOAN PORFOLIO VALUE * Oldrch Alfons Vascek he amount of captal necessary to support a portfolo of debt securtes depends on the probablty dstrbuton of the portfolo loss. Consder a portfolo
HE DISRIBUION OF LOAN PORFOLIO VALUE * Oldrch Alfons Vascek he amount of captal necessary to support a portfolo of debt securtes depends on the probablty dstrbuton of the portfolo loss. Consder a portfolo
Joint Scheduling of Processing and Shuffle Phases in MapReduce Systems
 Jont Schedulng of Processng and Shuffle Phases n MapReduce Systems Fangfe Chen, Mural Kodalam, T. V. Lakshman Department of Computer Scence and Engneerng, The Penn State Unversty Bell Laboratores, Alcatel-Lucent
Jont Schedulng of Processng and Shuffle Phases n MapReduce Systems Fangfe Chen, Mural Kodalam, T. V. Lakshman Department of Computer Scence and Engneerng, The Penn State Unversty Bell Laboratores, Alcatel-Lucent
Data Visualization by Pairwise Distortion Minimization
 Communcatons n Statstcs, Theory and Methods 34 (6), 005 Data Vsualzaton by Parwse Dstorton Mnmzaton By Marc Sobel, and Longn Jan Lateck* Department of Statstcs and Department of Computer and Informaton
Communcatons n Statstcs, Theory and Methods 34 (6), 005 Data Vsualzaton by Parwse Dstorton Mnmzaton By Marc Sobel, and Longn Jan Lateck* Department of Statstcs and Department of Computer and Informaton
The Development of Web Log Mining Based on Improve-K-Means Clustering Analysis
 The Development of Web Log Mnng Based on Improve-K-Means Clusterng Analyss TngZhong Wang * College of Informaton Technology, Luoyang Normal Unversty, Luoyang, 471022, Chna wangtngzhong2@sna.cn Abstract.
The Development of Web Log Mnng Based on Improve-K-Means Clusterng Analyss TngZhong Wang * College of Informaton Technology, Luoyang Normal Unversty, Luoyang, 471022, Chna wangtngzhong2@sna.cn Abstract.
Loop Parallelization
 - - Loop Parallelzaton C-52 Complaton steps: nested loops operatng on arrays, sequentell executon of teraton space DECLARE B[..,..+] FOR I :=.. FOR J :=.. I B[I,J] := B[I-,J]+B[I-,J-] ED FOR ED FOR analyze
- - Loop Parallelzaton C-52 Complaton steps: nested loops operatng on arrays, sequentell executon of teraton space DECLARE B[..,..+] FOR I :=.. FOR J :=.. I B[I,J] := B[I-,J]+B[I-,J-] ED FOR ED FOR analyze
Project Networks With Mixed-Time Constraints
 Project Networs Wth Mxed-Tme Constrants L Caccetta and B Wattananon Western Australan Centre of Excellence n Industral Optmsaton (WACEIO) Curtn Unversty of Technology GPO Box U1987 Perth Western Australa
Project Networs Wth Mxed-Tme Constrants L Caccetta and B Wattananon Western Australan Centre of Excellence n Industral Optmsaton (WACEIO) Curtn Unversty of Technology GPO Box U1987 Perth Western Australa
Lecture 5,6 Linear Methods for Classification. Summary
 Lecture 5,6 Lnear Methods for Classfcaton Rce ELEC 697 Farnaz Koushanfar Fall 2006 Summary Bayes Classfers Lnear Classfers Lnear regresson of an ndcator matrx Lnear dscrmnant analyss (LDA) Logstc regresson
Lecture 5,6 Lnear Methods for Classfcaton Rce ELEC 697 Farnaz Koushanfar Fall 2006 Summary Bayes Classfers Lnear Classfers Lnear regresson of an ndcator matrx Lnear dscrmnant analyss (LDA) Logstc regresson
A hybrid global optimization algorithm based on parallel chaos optimization and outlook algorithm
 Avalable onlne www.ocpr.com Journal of Chemcal and Pharmaceutcal Research, 2014, 6(7):1884-1889 Research Artcle ISSN : 0975-7384 CODEN(USA) : JCPRC5 A hybrd global optmzaton algorthm based on parallel
Avalable onlne www.ocpr.com Journal of Chemcal and Pharmaceutcal Research, 2014, 6(7):1884-1889 Research Artcle ISSN : 0975-7384 CODEN(USA) : JCPRC5 A hybrd global optmzaton algorthm based on parallel
Single and multiple stage classifiers implementing logistic discrimination
 Sngle and multple stage classfers mplementng logstc dscrmnaton Hélo Radke Bttencourt 1 Dens Alter de Olvera Moraes 2 Vctor Haertel 2 1 Pontfíca Unversdade Católca do Ro Grande do Sul - PUCRS Av. Ipranga,
Sngle and multple stage classfers mplementng logstc dscrmnaton Hélo Radke Bttencourt 1 Dens Alter de Olvera Moraes 2 Vctor Haertel 2 1 Pontfíca Unversdade Católca do Ro Grande do Sul - PUCRS Av. Ipranga,
Latent Class Regression. Statistics for Psychosocial Research II: Structural Models December 4 and 6, 2006
 Latent Class Regresson Statstcs for Psychosocal Research II: Structural Models December 4 and 6, 2006 Latent Class Regresson (LCR) What s t and when do we use t? Recall the standard latent class model
Latent Class Regresson Statstcs for Psychosocal Research II: Structural Models December 4 and 6, 2006 Latent Class Regresson (LCR) What s t and when do we use t? Recall the standard latent class model
Prediction of Disability Frequencies in Life Insurance
 Predcton of Dsablty Frequences n Lfe Insurance Bernhard Köng Fran Weber Maro V. Wüthrch October 28, 2011 Abstract For the predcton of dsablty frequences, not only the observed, but also the ncurred but
Predcton of Dsablty Frequences n Lfe Insurance Bernhard Köng Fran Weber Maro V. Wüthrch October 28, 2011 Abstract For the predcton of dsablty frequences, not only the observed, but also the ncurred but
THE METHOD OF LEAST SQUARES THE METHOD OF LEAST SQUARES
 The goal: to measure (determne) an unknown quantty x (the value of a RV X) Realsaton: n results: y 1, y 2,..., y j,..., y n, (the measured values of Y 1, Y 2,..., Y j,..., Y n ) every result s encumbered
The goal: to measure (determne) an unknown quantty x (the value of a RV X) Realsaton: n results: y 1, y 2,..., y j,..., y n, (the measured values of Y 1, Y 2,..., Y j,..., Y n ) every result s encumbered
The Greedy Method. Introduction. 0/1 Knapsack Problem
 The Greedy Method Introducton We have completed data structures. We now are gong to look at algorthm desgn methods. Often we are lookng at optmzaton problems whose performance s exponental. For an optmzaton
The Greedy Method Introducton We have completed data structures. We now are gong to look at algorthm desgn methods. Often we are lookng at optmzaton problems whose performance s exponental. For an optmzaton
How To Find The Dsablty Frequency Of A Clam
 1 Predcton of Dsablty Frequences n Lfe Insurance Bernhard Köng 1, Fran Weber 1, Maro V. Wüthrch 2 Abstract: For the predcton of dsablty frequences, not only the observed, but also the ncurred but not yet
1 Predcton of Dsablty Frequences n Lfe Insurance Bernhard Köng 1, Fran Weber 1, Maro V. Wüthrch 2 Abstract: For the predcton of dsablty frequences, not only the observed, but also the ncurred but not yet
+ + + - - This circuit than can be reduced to a planar circuit
 MeshCurrent Method The meshcurrent s analog of the nodeoltage method. We sole for a new set of arables, mesh currents, that automatcally satsfy KCLs. As such, meshcurrent method reduces crcut soluton to
MeshCurrent Method The meshcurrent s analog of the nodeoltage method. We sole for a new set of arables, mesh currents, that automatcally satsfy KCLs. As such, meshcurrent method reduces crcut soluton to
Estimation of Dispersion Parameters in GLMs with and without Random Effects
 Mathematcal Statstcs Stockholm Unversty Estmaton of Dsperson Parameters n GLMs wth and wthout Random Effects Meng Ruoyan Examensarbete 2004:5 Postal address: Mathematcal Statstcs Dept. of Mathematcs Stockholm
Mathematcal Statstcs Stockholm Unversty Estmaton of Dsperson Parameters n GLMs wth and wthout Random Effects Meng Ruoyan Examensarbete 2004:5 Postal address: Mathematcal Statstcs Dept. of Mathematcs Stockholm
Enabling P2P One-view Multi-party Video Conferencing
 Enablng P2P One-vew Mult-party Vdeo Conferencng Yongxang Zhao, Yong Lu, Changja Chen, and JanYn Zhang Abstract Mult-Party Vdeo Conferencng (MPVC) facltates realtme group nteracton between users. Whle P2P
Enablng P2P One-vew Mult-party Vdeo Conferencng Yongxang Zhao, Yong Lu, Changja Chen, and JanYn Zhang Abstract Mult-Party Vdeo Conferencng (MPVC) facltates realtme group nteracton between users. Whle P2P
Addendum to: Importing Skill-Biased Technology
 Addendum to: Importng Skll-Based Technology Arel Bursten UCLA and NBER Javer Cravno UCLA August 202 Jonathan Vogel Columba and NBER Abstract Ths Addendum derves the results dscussed n secton 3.3 of our
Addendum to: Importng Skll-Based Technology Arel Bursten UCLA and NBER Javer Cravno UCLA August 202 Jonathan Vogel Columba and NBER Abstract Ths Addendum derves the results dscussed n secton 3.3 of our
Brigid Mullany, Ph.D University of North Carolina, Charlotte
 Evaluaton And Comparson Of The Dfferent Standards Used To Defne The Postonal Accuracy And Repeatablty Of Numercally Controlled Machnng Center Axes Brgd Mullany, Ph.D Unversty of North Carolna, Charlotte
Evaluaton And Comparson Of The Dfferent Standards Used To Defne The Postonal Accuracy And Repeatablty Of Numercally Controlled Machnng Center Axes Brgd Mullany, Ph.D Unversty of North Carolna, Charlotte
CHOLESTEROL REFERENCE METHOD LABORATORY NETWORK. Sample Stability Protocol
 CHOLESTEROL REFERENCE METHOD LABORATORY NETWORK Sample Stablty Protocol Background The Cholesterol Reference Method Laboratory Network (CRMLN) developed certfcaton protocols for total cholesterol, HDL
CHOLESTEROL REFERENCE METHOD LABORATORY NETWORK Sample Stablty Protocol Background The Cholesterol Reference Method Laboratory Network (CRMLN) developed certfcaton protocols for total cholesterol, HDL
Chapter 7: Answers to Questions and Problems
 19. Based on the nformaton contaned n Table 7-3 of the text, the food and apparel ndustres are most compettve and therefore probably represent the best match for the expertse of these managers. Chapter
19. Based on the nformaton contaned n Table 7-3 of the text, the food and apparel ndustres are most compettve and therefore probably represent the best match for the expertse of these managers. Chapter
An MILP model for planning of batch plants operating in a campaign-mode
 An MILP model for plannng of batch plants operatng n a campagn-mode Yanna Fumero Insttuto de Desarrollo y Dseño CONICET UTN yfumero@santafe-concet.gov.ar Gabrela Corsano Insttuto de Desarrollo y Dseño
An MILP model for plannng of batch plants operatng n a campagn-mode Yanna Fumero Insttuto de Desarrollo y Dseño CONICET UTN yfumero@santafe-concet.gov.ar Gabrela Corsano Insttuto de Desarrollo y Dseño
Risk-based Fatigue Estimate of Deep Water Risers -- Course Project for EM388F: Fracture Mechanics, Spring 2008
 Rsk-based Fatgue Estmate of Deep Water Rsers -- Course Project for EM388F: Fracture Mechancs, Sprng 2008 Chen Sh Department of Cvl, Archtectural, and Envronmental Engneerng The Unversty of Texas at Austn
Rsk-based Fatgue Estmate of Deep Water Rsers -- Course Project for EM388F: Fracture Mechancs, Sprng 2008 Chen Sh Department of Cvl, Archtectural, and Envronmental Engneerng The Unversty of Texas at Austn
On the Optimal Control of a Cascade of Hydro-Electric Power Stations
 On the Optmal Control of a Cascade of Hydro-Electrc Power Statons M.C.M. Guedes a, A.F. Rbero a, G.V. Smrnov b and S. Vlela c a Department of Mathematcs, School of Scences, Unversty of Porto, Portugal;
On the Optmal Control of a Cascade of Hydro-Electrc Power Statons M.C.M. Guedes a, A.F. Rbero a, G.V. Smrnov b and S. Vlela c a Department of Mathematcs, School of Scences, Unversty of Porto, Portugal;
Bayesian Cluster Ensembles
 Bayesan Cluster Ensembles Hongjun Wang 1, Hanhua Shan 2 and Arndam Banerjee 2 1 Informaton Research Insttute, Southwest Jaotong Unversty, Chengdu, Schuan, 610031, Chna 2 Department of Computer Scence &
Bayesan Cluster Ensembles Hongjun Wang 1, Hanhua Shan 2 and Arndam Banerjee 2 1 Informaton Research Insttute, Southwest Jaotong Unversty, Chengdu, Schuan, 610031, Chna 2 Department of Computer Scence &
Analysis of Premium Liabilities for Australian Lines of Business
 Summary of Analyss of Premum Labltes for Australan Lnes of Busness Emly Tao Honours Research Paper, The Unversty of Melbourne Emly Tao Acknowledgements I am grateful to the Australan Prudental Regulaton
Summary of Analyss of Premum Labltes for Australan Lnes of Busness Emly Tao Honours Research Paper, The Unversty of Melbourne Emly Tao Acknowledgements I am grateful to the Australan Prudental Regulaton
A Novel Methodology of Working Capital Management for Large. Public Constructions by Using Fuzzy S-curve Regression
 Novel Methodology of Workng Captal Management for Large Publc Constructons by Usng Fuzzy S-curve Regresson Cheng-Wu Chen, Morrs H. L. Wang and Tng-Ya Hseh Department of Cvl Engneerng, Natonal Central Unversty,
Novel Methodology of Workng Captal Management for Large Publc Constructons by Usng Fuzzy S-curve Regresson Cheng-Wu Chen, Morrs H. L. Wang and Tng-Ya Hseh Department of Cvl Engneerng, Natonal Central Unversty,
Linear Circuits Analysis. Superposition, Thevenin /Norton Equivalent circuits
 Lnear Crcuts Analyss. Superposton, Theenn /Norton Equalent crcuts So far we hae explored tmendependent (resste) elements that are also lnear. A tmendependent elements s one for whch we can plot an / cure.
Lnear Crcuts Analyss. Superposton, Theenn /Norton Equalent crcuts So far we hae explored tmendependent (resste) elements that are also lnear. A tmendependent elements s one for whch we can plot an / cure.
Traffic State Estimation in the Traffic Management Center of Berlin
 Traffc State Estmaton n the Traffc Management Center of Berln Authors: Peter Vortsch, PTV AG, Stumpfstrasse, D-763 Karlsruhe, Germany phone ++49/72/965/35, emal peter.vortsch@ptv.de Peter Möhl, PTV AG,
Traffc State Estmaton n the Traffc Management Center of Berln Authors: Peter Vortsch, PTV AG, Stumpfstrasse, D-763 Karlsruhe, Germany phone ++49/72/965/35, emal peter.vortsch@ptv.de Peter Möhl, PTV AG,
SPEE Recommended Evaluation Practice #6 Definition of Decline Curve Parameters Background:
 SPEE Recommended Evaluaton Practce #6 efnton of eclne Curve Parameters Background: The producton hstores of ol and gas wells can be analyzed to estmate reserves and future ol and gas producton rates and
SPEE Recommended Evaluaton Practce #6 efnton of eclne Curve Parameters Background: The producton hstores of ol and gas wells can be analyzed to estmate reserves and future ol and gas producton rates and
Evaluating credit risk models: A critique and a new proposal
 Evaluatng credt rsk models: A crtque and a new proposal Hergen Frerchs* Gunter Löffler Unversty of Frankfurt (Man) February 14, 2001 Abstract Evaluatng the qualty of credt portfolo rsk models s an mportant
Evaluatng credt rsk models: A crtque and a new proposal Hergen Frerchs* Gunter Löffler Unversty of Frankfurt (Man) February 14, 2001 Abstract Evaluatng the qualty of credt portfolo rsk models s an mportant
Variance estimation for the instrumental variables approach to measurement error in generalized linear models
 he Stata Journal (2003) 3, Number 4, pp. 342 350 Varance estmaton for the nstrumental varables approach to measurement error n generalzed lnear models James W. Hardn Arnold School of Publc Health Unversty
he Stata Journal (2003) 3, Number 4, pp. 342 350 Varance estmaton for the nstrumental varables approach to measurement error n generalzed lnear models James W. Hardn Arnold School of Publc Health Unversty
Abstract. Clustering ensembles have emerged as a powerful method for improving both the
 Clusterng Ensembles: {topchyal, Models jan, of punch}@cse.msu.edu Consensus and Weak Parttons * Alexander Topchy, Anl K. Jan, and Wllam Punch Department of Computer Scence and Engneerng, Mchgan State Unversty
Clusterng Ensembles: {topchyal, Models jan, of punch}@cse.msu.edu Consensus and Weak Parttons * Alexander Topchy, Anl K. Jan, and Wllam Punch Department of Computer Scence and Engneerng, Mchgan State Unversty
Causal, Explanatory Forecasting. Analysis. Regression Analysis. Simple Linear Regression. Which is Independent? Forecasting
 Causal, Explanatory Forecastng Assumes cause-and-effect relatonshp between system nputs and ts output Forecastng wth Regresson Analyss Rchard S. Barr Inputs System Cause + Effect Relatonshp The job of
Causal, Explanatory Forecastng Assumes cause-and-effect relatonshp between system nputs and ts output Forecastng wth Regresson Analyss Rchard S. Barr Inputs System Cause + Effect Relatonshp The job of
How To Know The Components Of Mean Squared Error Of Herarchcal Estmator S
 S C H E D A E I N F O R M A T I C A E VOLUME 0 0 On Mean Squared Error of Herarchcal Estmator Stans law Brodowsk Faculty of Physcs, Astronomy, and Appled Computer Scence, Jagellonan Unversty, Reymonta
S C H E D A E I N F O R M A T I C A E VOLUME 0 0 On Mean Squared Error of Herarchcal Estmator Stans law Brodowsk Faculty of Physcs, Astronomy, and Appled Computer Scence, Jagellonan Unversty, Reymonta
A DYNAMIC CRASHING METHOD FOR PROJECT MANAGEMENT USING SIMULATION-BASED OPTIMIZATION. Michael E. Kuhl Radhamés A. Tolentino-Peña
 Proceedngs of the 2008 Wnter Smulaton Conference S. J. Mason, R. R. Hll, L. Mönch, O. Rose, T. Jefferson, J. W. Fowler eds. A DYNAMIC CRASHING METHOD FOR PROJECT MANAGEMENT USING SIMULATION-BASED OPTIMIZATION
Proceedngs of the 2008 Wnter Smulaton Conference S. J. Mason, R. R. Hll, L. Mönch, O. Rose, T. Jefferson, J. W. Fowler eds. A DYNAMIC CRASHING METHOD FOR PROJECT MANAGEMENT USING SIMULATION-BASED OPTIMIZATION
Support vector domain description
 Pattern Recognton Letters 20 (1999) 1191±1199 www.elsever.nl/locate/patrec Support vector doman descrpton Davd M.J. Tax *,1, Robert P.W. Dun Pattern Recognton Group, Faculty of Appled Scence, Delft Unversty
Pattern Recognton Letters 20 (1999) 1191±1199 www.elsever.nl/locate/patrec Support vector doman descrpton Davd M.J. Tax *,1, Robert P.W. Dun Pattern Recognton Group, Faculty of Appled Scence, Delft Unversty
How To Calculate An Approxmaton Factor Of 1 1/E
 Approxmaton algorthms for allocaton problems: Improvng the factor of 1 1/e Urel Fege Mcrosoft Research Redmond, WA 98052 urfege@mcrosoft.com Jan Vondrák Prnceton Unversty Prnceton, NJ 08540 jvondrak@gmal.com
Approxmaton algorthms for allocaton problems: Improvng the factor of 1 1/e Urel Fege Mcrosoft Research Redmond, WA 98052 urfege@mcrosoft.com Jan Vondrák Prnceton Unversty Prnceton, NJ 08540 jvondrak@gmal.com
Optimal Customized Pricing in Competitive Settings
 Optmal Customzed Prcng n Compettve Settngs Vshal Agrawal Industral & Systems Engneerng, Georga Insttute of Technology, Atlanta, Georga 30332 vshalagrawal@gatech.edu Mark Ferguson College of Management,
Optmal Customzed Prcng n Compettve Settngs Vshal Agrawal Industral & Systems Engneerng, Georga Insttute of Technology, Atlanta, Georga 30332 vshalagrawal@gatech.edu Mark Ferguson College of Management,
Alternate Approximation of Concave Cost Functions for
 Alternate Approxmaton of Concave Cost Functons for Process Desgn and Supply Chan Optmzaton Problems Dego C. Cafaro * and Ignaco E. Grossmann INTEC (UNL CONICET), Güemes 3450, 3000 Santa Fe, ARGENTINA Department
Alternate Approxmaton of Concave Cost Functons for Process Desgn and Supply Chan Optmzaton Problems Dego C. Cafaro * and Ignaco E. Grossmann INTEC (UNL CONICET), Güemes 3450, 3000 Santa Fe, ARGENTINA Department
MARKET SHARE CONSTRAINTS AND THE LOSS FUNCTION IN CHOICE BASED CONJOINT ANALYSIS
 MARKET SHARE CONSTRAINTS AND THE LOSS FUNCTION IN CHOICE BASED CONJOINT ANALYSIS Tmothy J. Glbrde Assstant Professor of Marketng 315 Mendoza College of Busness Unversty of Notre Dame Notre Dame, IN 46556
MARKET SHARE CONSTRAINTS AND THE LOSS FUNCTION IN CHOICE BASED CONJOINT ANALYSIS Tmothy J. Glbrde Assstant Professor of Marketng 315 Mendoza College of Busness Unversty of Notre Dame Notre Dame, IN 46556
Awell-known result in the Bayesian inventory management literature is: If lost sales are not observed, the
 MANUFACTURING & SERVICE OPERATIONS MANAGEMENT Vol. 10, No. 2, Sprng 2008, pp. 236 256 ssn 1523-4614 essn 1526-5498 08 1002 0236 nforms do 10.1287/msom.1070.0165 2008 INFORMS Dynamc Inventory Management
MANUFACTURING & SERVICE OPERATIONS MANAGEMENT Vol. 10, No. 2, Sprng 2008, pp. 236 256 ssn 1523-4614 essn 1526-5498 08 1002 0236 nforms do 10.1287/msom.1070.0165 2008 INFORMS Dynamc Inventory Management
Realistic Image Synthesis
 Realstc Image Synthess - Combned Samplng and Path Tracng - Phlpp Slusallek Karol Myszkowsk Vncent Pegoraro Overvew: Today Combned Samplng (Multple Importance Samplng) Renderng and Measurng Equaton Random
Realstc Image Synthess - Combned Samplng and Path Tracng - Phlpp Slusallek Karol Myszkowsk Vncent Pegoraro Overvew: Today Combned Samplng (Multple Importance Samplng) Renderng and Measurng Equaton Random
where the coordinates are related to those in the old frame as follows.
 Chapter 2 - Cartesan Vectors and Tensors: Ther Algebra Defnton of a vector Examples of vectors Scalar multplcaton Addton of vectors coplanar vectors Unt vectors A bass of non-coplanar vectors Scalar product
Chapter 2 - Cartesan Vectors and Tensors: Ther Algebra Defnton of a vector Examples of vectors Scalar multplcaton Addton of vectors coplanar vectors Unt vectors A bass of non-coplanar vectors Scalar product
ECONOMICS OF PLANT ENERGY SAVINGS PROJECTS IN A CHANGING MARKET Douglas C White Emerson Process Management
 ECONOMICS OF PLANT ENERGY SAVINGS PROJECTS IN A CHANGING MARKET Douglas C Whte Emerson Process Management Abstract Energy prces have exhbted sgnfcant volatlty n recent years. For example, natural gas prces
ECONOMICS OF PLANT ENERGY SAVINGS PROJECTS IN A CHANGING MARKET Douglas C Whte Emerson Process Management Abstract Energy prces have exhbted sgnfcant volatlty n recent years. For example, natural gas prces
Implementation of Deutsch's Algorithm Using Mathcad
 Implementaton of Deutsch's Algorthm Usng Mathcad Frank Roux The followng s a Mathcad mplementaton of Davd Deutsch's quantum computer prototype as presented on pages - n "Machnes, Logc and Quantum Physcs"
Implementaton of Deutsch's Algorthm Usng Mathcad Frank Roux The followng s a Mathcad mplementaton of Davd Deutsch's quantum computer prototype as presented on pages - n "Machnes, Logc and Quantum Physcs"
Enabling a Powerful Marine and Offshore Decision-Support Solution Through Bayesian Network Technique
 Rsk Analyss, Vol. 26, No. 3, 2006 DOI: 10.1111/j.1539-6924.2006.00775.x Enablng a Powerful Marne and Offshore Decson-Support Soluton Through Bayesan Network Technque A. G. Eleye-Datubo, 1 A. Wall, 1 A.
Rsk Analyss, Vol. 26, No. 3, 2006 DOI: 10.1111/j.1539-6924.2006.00775.x Enablng a Powerful Marne and Offshore Decson-Support Soluton Through Bayesan Network Technque A. G. Eleye-Datubo, 1 A. Wall, 1 A.
Online Inference of Topics with Latent Dirichlet Allocation
 Onlne Inference of Topcs wth Latent Drchlet Allocaton Kevn R. Cann Computer Scence Dvson Unversty of Calforna Berkeley, CA 94720 kevn@cs.berkeley.edu Le Sh Helen Wlls Neuroscence Insttute Unversty of Calforna
Onlne Inference of Topcs wth Latent Drchlet Allocaton Kevn R. Cann Computer Scence Dvson Unversty of Calforna Berkeley, CA 94720 kevn@cs.berkeley.edu Le Sh Helen Wlls Neuroscence Insttute Unversty of Calforna
NPAR TESTS. One-Sample Chi-Square Test. Cell Specification. Observed Frequencies 1O i 6. Expected Frequencies 1EXP i 6
 PAR TESTS If a WEIGHT varable s specfed, t s used to replcate a case as many tmes as ndcated by the weght value rounded to the nearest nteger. If the workspace requrements are exceeded and samplng has
PAR TESTS If a WEIGHT varable s specfed, t s used to replcate a case as many tmes as ndcated by the weght value rounded to the nearest nteger. If the workspace requrements are exceeded and samplng has
The Application of Fractional Brownian Motion in Option Pricing
 Vol. 0, No. (05), pp. 73-8 http://dx.do.org/0.457/jmue.05.0..6 The Applcaton of Fractonal Brownan Moton n Opton Prcng Qng-xn Zhou School of Basc Scence,arbn Unversty of Commerce,arbn zhouqngxn98@6.com
Vol. 0, No. (05), pp. 73-8 http://dx.do.org/0.457/jmue.05.0..6 The Applcaton of Fractonal Brownan Moton n Opton Prcng Qng-xn Zhou School of Basc Scence,arbn Unversty of Commerce,arbn zhouqngxn98@6.com
Joe Pimbley, unpublished, 2005. Yield Curve Calculations
 Joe Pmbley, unpublshed, 005. Yeld Curve Calculatons Background: Everythng s dscount factors Yeld curve calculatons nclude valuaton of forward rate agreements (FRAs), swaps, nterest rate optons, and forward
Joe Pmbley, unpublshed, 005. Yeld Curve Calculatons Background: Everythng s dscount factors Yeld curve calculatons nclude valuaton of forward rate agreements (FRAs), swaps, nterest rate optons, and forward
Calculating the high frequency transmission line parameters of power cables
 < ' Calculatng the hgh frequency transmsson lne parameters of power cables Authors: Dr. John Dcknson, Laboratory Servces Manager, N 0 RW E B Communcatons Mr. Peter J. Ncholson, Project Assgnment Manager,
< ' Calculatng the hgh frequency transmsson lne parameters of power cables Authors: Dr. John Dcknson, Laboratory Servces Manager, N 0 RW E B Communcatons Mr. Peter J. Ncholson, Project Assgnment Manager,
Title Language Model for Information Retrieval
 Ttle Language Model for Informaton Retreval Rong Jn Language Technologes Insttute School of Computer Scence Carnege Mellon Unversty Alex G. Hauptmann Computer Scence Department School of Computer Scence
Ttle Language Model for Informaton Retreval Rong Jn Language Technologes Insttute School of Computer Scence Carnege Mellon Unversty Alex G. Hauptmann Computer Scence Department School of Computer Scence
Section 5.4 Annuities, Present Value, and Amortization
 Secton 5.4 Annutes, Present Value, and Amortzaton Present Value In Secton 5.2, we saw that the present value of A dollars at nterest rate per perod for n perods s the amount that must be deposted today
Secton 5.4 Annutes, Present Value, and Amortzaton Present Value In Secton 5.2, we saw that the present value of A dollars at nterest rate per perod for n perods s the amount that must be deposted today
Allocating Time and Resources in Project Management Under Uncertainty
 Proceedngs of the 36th Hawa Internatonal Conference on System Scences - 23 Allocatng Tme and Resources n Project Management Under Uncertanty Mark A. Turnqust School of Cvl and Envronmental Eng. Cornell
Proceedngs of the 36th Hawa Internatonal Conference on System Scences - 23 Allocatng Tme and Resources n Project Management Under Uncertanty Mark A. Turnqust School of Cvl and Envronmental Eng. Cornell
The Retail Planning Problem Under Demand Uncertainty
 Vol., No. 5, September October 013, pp. 100 113 ISSN 1059-1478 EISSN 1937-5956 13 05 100 DOI 10.1111/j.1937-5956.01.0144.x 013 Producton and Operatons Management Socety The Retal Plannng Problem Under
Vol., No. 5, September October 013, pp. 100 113 ISSN 1059-1478 EISSN 1937-5956 13 05 100 DOI 10.1111/j.1937-5956.01.0144.x 013 Producton and Operatons Management Socety The Retal Plannng Problem Under
Data Broadcast on a Multi-System Heterogeneous Overlayed Wireless Network *
 JOURNAL OF INFORMATION SCIENCE AND ENGINEERING 24, 819-840 (2008) Data Broadcast on a Mult-System Heterogeneous Overlayed Wreless Network * Department of Computer Scence Natonal Chao Tung Unversty Hsnchu,
JOURNAL OF INFORMATION SCIENCE AND ENGINEERING 24, 819-840 (2008) Data Broadcast on a Mult-System Heterogeneous Overlayed Wreless Network * Department of Computer Scence Natonal Chao Tung Unversty Hsnchu,
PERRON FROBENIUS THEOREM
 PERRON FROBENIUS THEOREM R. CLARK ROBINSON Defnton. A n n matrx M wth real entres m, s called a stochastc matrx provded () all the entres m satsfy 0 m, () each of the columns sum to one, m = for all, ()
PERRON FROBENIUS THEOREM R. CLARK ROBINSON Defnton. A n n matrx M wth real entres m, s called a stochastc matrx provded () all the entres m satsfy 0 m, () each of the columns sum to one, m = for all, ()
Statistical Methods to Develop Rating Models
 Statstcal Methods to Develop Ratng Models [Evelyn Hayden and Danel Porath, Österrechsche Natonalbank and Unversty of Appled Scences at Manz] Source: The Basel II Rsk Parameters Estmaton, Valdaton, and
Statstcal Methods to Develop Ratng Models [Evelyn Hayden and Danel Porath, Österrechsche Natonalbank and Unversty of Appled Scences at Manz] Source: The Basel II Rsk Parameters Estmaton, Valdaton, and
GRAVITY DATA VALIDATION AND OUTLIER DETECTION USING L 1 -NORM
 GRAVITY DATA VALIDATION AND OUTLIER DETECTION USING L 1 -NORM BARRIOT Jean-Perre, SARRAILH Mchel BGI/CNES 18.av.E.Beln 31401 TOULOUSE Cedex 4 (France) Emal: jean-perre.barrot@cnes.fr 1/Introducton The
GRAVITY DATA VALIDATION AND OUTLIER DETECTION USING L 1 -NORM BARRIOT Jean-Perre, SARRAILH Mchel BGI/CNES 18.av.E.Beln 31401 TOULOUSE Cedex 4 (France) Emal: jean-perre.barrot@cnes.fr 1/Introducton The
An Evaluation of the Extended Logistic, Simple Logistic, and Gompertz Models for Forecasting Short Lifecycle Products and Services
 An Evaluaton of the Extended Logstc, Smple Logstc, and Gompertz Models for Forecastng Short Lfecycle Products and Servces Charles V. Trappey a,1, Hsn-yng Wu b a Professor (Management Scence), Natonal Chao
An Evaluaton of the Extended Logstc, Smple Logstc, and Gompertz Models for Forecastng Short Lfecycle Products and Servces Charles V. Trappey a,1, Hsn-yng Wu b a Professor (Management Scence), Natonal Chao
POLYSA: A Polynomial Algorithm for Non-binary Constraint Satisfaction Problems with and
 POLYSA: A Polynomal Algorthm for Non-bnary Constrant Satsfacton Problems wth and Mguel A. Saldo, Federco Barber Dpto. Sstemas Informátcos y Computacón Unversdad Poltécnca de Valenca, Camno de Vera s/n
POLYSA: A Polynomal Algorthm for Non-bnary Constrant Satsfacton Problems wth and Mguel A. Saldo, Federco Barber Dpto. Sstemas Informátcos y Computacón Unversdad Poltécnca de Valenca, Camno de Vera s/n
