А) 12см 2 ; Б) 16см 2 ; В)24см 2 ; Г) 48см 2. Варіант 1 Частина 1 1. Різниця двох кутів паралелограма дорівнює Знайти його кути.
|
|
|
- Вячеслав Евригин
- 7 years ago
- Views:
Transcription
1 А) 12см 2 ; Б) 16см 2 ; В)24см 2 ; Г) 48см 2. Варіант 1 1. Різниця двох кутів паралелограма дорівнює Знайти його кути. А) 40 0, 140 0, 40 0, ; В) 70 0, 110 0, 70 0, ; Б) 80 0, 120 0, 80 0, ; Г) 60 0, 100 0, 60 0, Одна з основ трапеції дорівнює 5 см, а її середня лінія 8 см. Знайдіть другу основу трапеції. А) 6,5см; Б) 13 см; В) 5,5см; Г) 11см. 3. У прямокутному трикутнику дано гіпотенузу m і гострий кут α. Знайдіть катет, прилеглий до кута α Продовження бічних сторін AB і CD трапеції ABCD перетинаються в точці F, AB : BF = 3:7, AD більша основа трапеції. Різниця основ трапеції дорівнює 6 см. Знайдіть AD Перпендикуляр, опущений з точки перетину діагоналей ромба на його сторону, ділить її на відрізки 3см і 12см. Знайдіть площу ромба Вписане коло прямокутного трикутника АВС дотикається до гіпотенузи АВ у точці К. Знайдіть радіус описаного кола, якщо АК = 4см, ВК = 6см. А) mtgα; Б) msinα; В) mcosα; Г). 4. Радіус вписаного кола правильного шестикутника см. Чому дорівнює радіус описаного кола цього шестикутника? А) 6см; Б) 8см; В) 6 см; Г) 8 см. 5. У певний момент часу довжина тіні дзвіниці Софіївського собору дорівнює 19м, а довжина тіні ліхтарного стовпа, який стоїть біля дзвіниці 1,5м. яка висота дзвіниці, якщо висота стовпа дорівнює 6м? А) 76м; Б) 72м; В) 75м; Г) 80м. 6. Чому дорівнює площа трикутника, периметр якого становить 12см, а радіус вписаного кола дорівнює 4см?
2 Варіант 2 1. На рисунку зображено прямокутник ABCD, = Яка величина <AOD? В С О А А) 86 0 ; Б) 43 0 ; В) 94 0 ; Г) Сума трьох сторін паралелограма дорівнює 24см. Знайдіть сторони паралелограма, якщо його периметр становить 30см. А) 6см, 9см, 6см;9см; В) 7см; 8см; 7см; 8см; Б) 6см; 8см; 6см; 8см; Г) визначити неможливо. D А) 130см 2 ; Б) 65см 2 ; В) 60см 2 ; Г) 120см З точки до прямої проведено дві похилі завдовжки 10см і 18см, а сума їх проекцій на пряму дорівнює 16см. Знайдіть відстань від даної точки до цієї прямої Висота СК трикутника АВС поділяє сторону АВ на відрізки АК і ВК. Знайдіть сторону ВС, якщо АС = 6см, ВК = 3см, і <А = Коло, вписане в рівнобічну трапецію, ділить точкою дотику бічну сторону на відрізки завдовжки 8см і 18см. Знайдіть площу трапеції. 3. Відрізок AD бісектриса трикутника АВС, зображеного на рисунку. Чому дорівнює периметр трикутника АВС? А 12см В D 6см 8см С А) 24см; Б) 30см; В) 35см; Г) 40см. 4. Знайдіть діагональ прямокутника зі сторонами 5см і 12см. А) 13см; Б) 14см; В) 16см; Г) 17см. 5. Два кути трикутника дорівнюють 30 0 і Знайдіть його сторону, протилежну куту 30 0, якщо сторона, протилежна куту 45 0, дорівнює см. А) 3см; Б) 2см; В) ; Г) 6. Обчисліть площу рівнобедреного трикутника, бічна сторона якого дорівнює 13см, а основа 10см.
3 Варіант 3 1. Знайдіть найбільший з кутів чотирикутника, якщо вони пропорційні числам 2, 3, 7 і 8. А) 72 0 ; Б) ; В) ; Г) Чому дорівнює більша із сторін паралелограма, якщо вона на 8см більша за іншу сторону, а периметр паралелограма дорівнює 40см? А) 20см; Б) 18см; В) 16см; Г) 14см. 3. Точка знаходиться на відстані 6 см від прямої m. З цієї точки до прямої проведено похилу, яка утворює з прямою m кут Знайдіть довжину цієї похилої. А) см; Б) 12 см; В) см; Г) 6 см Діагоналі трапеції ABCD (BC AD) перетинаються в точці О, АО:ОС = 7:3, BD = 40см. Знайдіть довжину відрізка OD Висота СD трикутника ABC ділить сторону АВ на відрізки AD і BD, такі, що AD = 8см; BD = 12см. Знайдіть площу трикутника АВС, якщо <А = Сторони трикутника дорівнюють 12см, 15см і 18см. Знайдіть бісектрису трикутника, проведену з вершини його найбільшого кута. 4. Сторони трикутника відносяться як 7:6:4. Знайдіть більшу сторону подібного йому трикутника, менша сторона якого дорівнює 12см. А) 84см; Б) 56см; В) 21см; Г) 14см. 5. Катети прямокутного трикутника дорівнюють 2см і. Знайдіть синус більшого гострого кута цього трикутника. А) ; Б) ; В) ; Г) ; 6. Чому дорівнює довжина кола, яке обмежує круг площею 25π см 2? А) 5π см; Б) 10π см; В) 20π см; Г) 25π см.
4 Варіант 4 1. Кути трапеції ABCD, прилеглі до основи ВС дорівнюють 70 0 і Знайдіть кути прилеглі до основи AD. А) 20 0 і ; Б) 40 0 і ; В) 50 0 і ; Г) такої трапеції не існує. 2. Середня лінія рівнобічної трапеції, у яку можна вписати коло, дорівнює 12см. Знайдіть бічну сторону трапеції. А) 6см; Б) 12см; В) 24см; Г) не можна визначити Висота прямокутного трикутника з гострим кутом α, проведена до гіпотенузи, дорівнює h. Знайдіть гіпотенузу цього трикутника Перпендикуляр, опущений з точки кола на його діаметр, ділить діаметр на два відрізки, різниця яких дорівнює 21см. Знайдіть довжини кола, якщо довжина перпендикуляра - 10см. 3. У колі радіуса 17см проведено хорду завдовжки 16см. Знайдіть відстань від центра кола до цієї хорди. А) 9см; Б) 5см; В) 15см; Г) см. 4. Знайдіть катет прямокутного трикутника, якщо його гіпотенуза дорівнює 27см, а проекція шуканого катета на гіпотенузу 3см. А) 6см; Б) 9см; В) 18см; Г)81см. 5. У трикутнику АВС відомо, що <С = 90 0, ВС = 5см, АВ = 10см. Знайдіть <A цього трикутника. А) 90 0 ; Б) 60 0 ; В) 45 0 ; Г) Обчисліть площу ромба ABCD, якщо АС = 8см; BD = 5см. А) 10см 2 ; Б) 13см 2 ; В) 40см 2 ; Г) 20см Знайдіть площу рівнобічної трапеції, основи якої дорівнюють 9см і 19см, а бічна сторона 13см.
5 Варіант 5 1. На рисунку зображено прямокутник ABCD, <BOC = Яка величина кута <ВАО? А) 24см; Б)13,5см; В) 50/3c ; Г) 36см. 5. У трикутнику АВС відомо, що АС = 6, <В = 60 0, <А = Знайдіть сторону ВС. А) 6см; Б)12см; В) 6 см; Г) 12 см. 6. Відрізок СМ висота трикутника АВС, зображеного на рисунку. Чому дорівнює площа трикутника АВС? А) 32 0 ; Б) 64 0 ; В) 48 0 ; Г) Якою має бути довжина відрізка АО, щоб чотирикутник ABCD зображений на рисунку був паралелограмом, якщо ВО = OD, AC = 18см? А) 9см; Б) 6см; В) 12см; Г) 16см. А) 24см 2 ; Б) 32см 2 ; В) 48см 2 ; Г) 64см У рівнобічній трапеції FKPE відомо, що FK = EP = 9см, FE = 20см, КР = 8см. Знайдіть тангенс кута F трапеції У трикутник АВС вписано ромб так як показано на рисунку. Знайдіть сторони ромба, якщо АВ = 18см, АС = 12см. 3. Чому дорівнює радіус кола, описаного навколо квадрата зі стороною 8см? А) Б) 8см; В) 4см; Г) 2 см. 4. За даними наведеними на рисунку, знайдіть довжину відрізка CD (довжини відрізків наведено в сантиметрах) Центр кола, вписаного у рівнобедрений трикутник, ділить його висоту, проведену до основи, на відрізки, довжини яких дорівнюють 34см і 16см. Знайдіть площу даного трикутника. Варіант 6
6 1. Якою має бути градусна міра <ACD, щоб ромб ABCD, зображений на рисунку, був квадратом? В А) 90 0 ; Б) 60 0 ; В) 45 0 ; Г) А 2. У трикутнику АВС відомо, що АВ = 12см; ВС = 16см; АС = 20см. Точка D середина сторони АВ, точка Е середина сторони АС. Знайдіть периметр чотирикутника BDEC. А) 80см; Б) 48см; В) 24см; Г) 40см. 3. Катет прямокутного трикутника дорівнює 8см, а його проекція на гіпотенузу 4см. Знайдіть гіпотенузу даного трикутника. А) 10см; Б) 12см; В) 16см; Г) 18см. 4. З точки D, яка належить гіпотенузі АВ прямокутного трикутника АВС, зображеного на рисунку, опущено перпендикуляр DE на катет АС. Знайдіть довжину цього перпендикуляра. О Д С А) 10,5см; Б) 14см; В) 12см; Г) 16см. 5. Чому дорівнює радіус кола, вписаного в правильний трикутник зі стороною 18см? А) 18 Б) 9 см; В) 6 см; Г) см. 6. Обчисліть площу трикутника, дві сторони якого дорівнюють 3см і 2см, а кут між ними А) 2 ; Б) 3см 2 ; В) см 2 ; Г) 3 см Сторони трикутника дорівнюють 6см, 25см і 29см. Знайдіть радіус вписаного кола даного трикутника Сторони паралелограма дорівнюють 12см і 20 см, а кут між його висотами проведеними з вершини тупого кута Знайдіть площу паралелограма Сторони трикутника дорівнюють 8см, 9см і 13см. Знайдіть медіану трикутника, проведену до його найбільшої сторони.
7 Варіант 7 1. Діагоналі квадрата ABCD перетинаються в точці О, АО = 12см. Знайдіть довжину відрізка BD. А) 6см; Б) 12см; В) 18см; Г) 24см. 5. На рисунку зображено трикутники АВС і BCD такі, що <АСВ = <CBD = Знайдіть довжину відрізка CD. 2. Якою має бути градусна міра кута ACD, щоб трикутник ABC, зображений на рисунку, був правильним? А) 8см; Б) см; В) см; Г) 9см. А) 90 0 ; Б) 60 0 ; В) 45 0 ; Г) Діагональ прямокутника дорівнює 6см і утворює з його стороною кут Знайдіть більшу сторону прямокутника. А) 6 см; Б) 6см; В) 3см; Г) 3 см. 4. Основи трапеції відносяться як 3:7, а її середня лінія дорівнює 40см. Знайдіть основи трапеції. А) 12см і 28см; Б) 24см і 56см; В) 48см і 112см; Г)18см і 42см; 6. Чому дорівнює відношення площі квадрата до площі вписаного у нього круга? А) 2:π; Б) π:2; В) 4: π; Г) π: Продовження бічних сторін AB і CD трапеції ABCD перетинаються в точці К. Більша основа AD трапеції дорівнює 18см, АК = 24см, АВ = 16см. Знайдіть меншу основу трапеції Дві сторони трикутника, кут між якими дорівнює 60 0, відносяться як 5:8, а третя сторона дорівнює 21см. Знайдіть невідомі сторони трикутника Радіус кола, вписаного в рівнобедрений трикутник АВС (АВ=ВС), дорівнює 12см, а відстань від центра цього кола до вершини В 20см. Знайдіть площу даного трикутника.
8 Варіант 8 1. Кінці хорди кола ділять його на дві дуги, градусна міра однієї з них у 5 разів більша за градусну міру другої. Знайдіть градусні міри цих дуг. А) 30 0, ; Б) 60 0, ; В) 40 0, ; Г) 50 0, Відстані від точки перетину діагоналей прямокутника до його сусідніх сторін дорівнюють 6см і 12см. Знайдіть сусідні сторони прямокутника. А) 18см і 6см; Б) 16см і 8см; В) 24см і 12см; Г) 15см і 9см. 3. У колі, радіус якого дорівнює 10 см, проведено хорду, завдовжки 16 см. Чому дорівнює відстань від центра кола до даної хорди? А) 6см; Б) 8см; В) 10см; Г) 12см У коло вписано квадрат зі стороною 9 см. Знайдіть сторону правильного трикутника, описаного навколо цього кола Основа рівнобедреного трикутника відноситься до його бічної сторони як 6:5. Знайдіть периметр трикутника, якщо його висота, проведена до основи, дорівнює 8см Основи рівнобічної трапеції дорівнюють 15см і 33см, а діагональ ділить її гострий кут навпіл. Знайдіть площу трапеції. 4. У трикутнику DEF відомо, що DE = 10см, EF = 14см, DF = 18см. Точка М середина сторони DE, точка К середина сторони EF. Знайдіть периметр чотирикутника DМКF. А) 21см; Б) 30см; В) 39см; Г) 42см. 5. Електричну опору з точки, яка знаходиться на відстані 12м від її основи, видно під кутом Яка висота опори? А) 6м; Б) 12м; В) 24м; Г) установити неможливо. 6. Чому дорівнює площа паралелограма, сторони якого дорівнюють 4см і 6см, а кут між ними А) 6 см 2 ; Б) 6 см 2 ; В)12 см 2 ; Г) см 2.
Problem A. Nanoassembly
 Problem A. Nanoassembly 2.5 seconds One of the problems of creating elements of nanostructures is the colossal time necessary for the construction of nano-parts from separate atoms. Transporting each of
Problem A. Nanoassembly 2.5 seconds One of the problems of creating elements of nanostructures is the colossal time necessary for the construction of nano-parts from separate atoms. Transporting each of
Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation
 988 Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation High School of Transport "Todor Kableshkov" 1574 Sofia, 158 Geo Milev str. Ivan Velev Abstract
988 Programming the Microchip Pic 16f84a Microcontroller As a Signal Generator Frequencies in Railway Automation High School of Transport "Todor Kableshkov" 1574 Sofia, 158 Geo Milev str. Ivan Velev Abstract
Online EFFECTIVE AS OF JANUARY 2013
 2013 A and C Session Start Dates (A-B Quarter Sequence*) 2013 B and D Session Start Dates (B-A Quarter Sequence*) Quarter 5 2012 1205A&C Begins November 5, 2012 1205A Ends December 9, 2012 Session Break
2013 A and C Session Start Dates (A-B Quarter Sequence*) 2013 B and D Session Start Dates (B-A Quarter Sequence*) Quarter 5 2012 1205A&C Begins November 5, 2012 1205A Ends December 9, 2012 Session Break
The European Ombudsman
 Overview The European Ombudsman Е в р о п е й с к и о м б у д с м а н E l D e f e n s o r d e l P u e b l o E u r o p e o E v r o p s k ý v e ř e j n ý o c h r á n c e p r á v D e n E u r o p æ i s k e
Overview The European Ombudsman Е в р о п е й с к и о м б у д с м а н E l D e f e n s o r d e l P u e b l o E u r o p e o E v r o p s k ý v e ř e j n ý o c h r á n c e p r á v D e n E u r o p æ i s k e
How to bet using different NairaBet Bet Combinations (Combo)
 How to bet using different NairaBet Bet Combinations (Combo) SINGLES Singles consists of single bets. I.e. it will contain just a single selection of any sport. The bet slip of a singles will look like
How to bet using different NairaBet Bet Combinations (Combo) SINGLES Singles consists of single bets. I.e. it will contain just a single selection of any sport. The bet slip of a singles will look like
UNDERGRADUATE STUDY SKILLS GUIDE 2014-15
 SCHOOL OF SLAVONIC AND EAST EUROPEAN STUDIES UNDERGRADUATE STUDY SKILLS GUIDE 2014-15 ECONOMICS AND BUSINESS HISTORY LANGUAGES AND CULTURE POLITICS AND SOCIOLOGY 1 1. AN INTRODUCTION TO STUDY SKILLS 5
SCHOOL OF SLAVONIC AND EAST EUROPEAN STUDIES UNDERGRADUATE STUDY SKILLS GUIDE 2014-15 ECONOMICS AND BUSINESS HISTORY LANGUAGES AND CULTURE POLITICS AND SOCIOLOGY 1 1. AN INTRODUCTION TO STUDY SKILLS 5
DEFINITIONS. Perpendicular Two lines are called perpendicular if they form a right angle.
 DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
www.pioneermathematics.com
 Problems and Solutions: INMO-2012 1. Let ABCD be a quadrilateral inscribed in a circle. Suppose AB = 2+ 2 and AB subtends 135 at the centre of the circle. Find the maximum possible area of ABCD. Solution:
Problems and Solutions: INMO-2012 1. Let ABCD be a quadrilateral inscribed in a circle. Suppose AB = 2+ 2 and AB subtends 135 at the centre of the circle. Find the maximum possible area of ABCD. Solution:
Quadrilateral Geometry. Varignon s Theorem I. Proof 10/21/2011 S C. MA 341 Topics in Geometry Lecture 19
 Quadrilateral Geometry MA 341 Topics in Geometry Lecture 19 Varignon s Theorem I The quadrilateral formed by joining the midpoints of consecutive sides of any quadrilateral is a parallelogram. PQRS is
Quadrilateral Geometry MA 341 Topics in Geometry Lecture 19 Varignon s Theorem I The quadrilateral formed by joining the midpoints of consecutive sides of any quadrilateral is a parallelogram. PQRS is
Visa Smart Debit/Credit Certificate Authority Public Keys
 CHIP AND NEW TECHNOLOGIES Visa Smart Debit/Credit Certificate Authority Public Keys Overview The EMV standard calls for the use of Public Key technology for offline authentication, for aspects of online
CHIP AND NEW TECHNOLOGIES Visa Smart Debit/Credit Certificate Authority Public Keys Overview The EMV standard calls for the use of Public Key technology for offline authentication, for aspects of online
Geometry Handout 2 ~ Page 1
 1. Given: a b, b c a c Guidance: Draw a line which intersects with all three lines. 2. Given: a b, c a a. c b b. Given: d b d c 3. Given: a c, b d a. α = β b. Given: e and f bisect angles α and β respectively.
1. Given: a b, b c a c Guidance: Draw a line which intersects with all three lines. 2. Given: a b, c a a. c b b. Given: d b d c 3. Given: a c, b d a. α = β b. Given: e and f bisect angles α and β respectively.
Database Design and Normalization
 Database Design and Normalization Chapter 10 (Week 11) EE562 Slides and Modified Slides from Database Management Systems, R. Ramakrishnan 1 Computing Closure F + Example: List all FDs with: - a single
Database Design and Normalization Chapter 10 (Week 11) EE562 Slides and Modified Slides from Database Management Systems, R. Ramakrishnan 1 Computing Closure F + Example: List all FDs with: - a single
Russian Introductory Course
 Russian Introductory Course Natasha Bershadski Learn another language the way you learnt your own Succeed with the and learn another language the way you learnt your own Developed over 50 years, the amazing
Russian Introductory Course Natasha Bershadski Learn another language the way you learnt your own Succeed with the and learn another language the way you learnt your own Developed over 50 years, the amazing
Unit 3 Boolean Algebra (Continued)
 Unit 3 Boolean Algebra (Continued) 1. Exclusive-OR Operation 2. Consensus Theorem Department of Communication Engineering, NCTU 1 3.1 Multiplying Out and Factoring Expressions Department of Communication
Unit 3 Boolean Algebra (Continued) 1. Exclusive-OR Operation 2. Consensus Theorem Department of Communication Engineering, NCTU 1 3.1 Multiplying Out and Factoring Expressions Department of Communication
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Thursday, January 24, 2013 9:15 a.m. to 12:15 p.m.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, January 24, 2013 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, January 24, 2013 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
CIRCLE THEOREMS. Edexcel GCSE Mathematics (Linear) 1MA0
 Edexcel GCSE Mathematics (Linear) 1MA0 CIRCLE THEOREMS Materials required for examination Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser. Tracing paper may
Edexcel GCSE Mathematics (Linear) 1MA0 CIRCLE THEOREMS Materials required for examination Ruler graduated in centimetres and millimetres, protractor, compasses, pen, HB pencil, eraser. Tracing paper may
COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES
 Margaryta I. Skrypnyk, Mykola M. Matiukha COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES The article studies the correspondence of management accounting structure when using of
Margaryta I. Skrypnyk, Mykola M. Matiukha COMPLIANCE OF MANAGEMENT ACCOUNTING WHEN USING INFORMATION TECHNOLOGIES The article studies the correspondence of management accounting structure when using of
Benchmark Databases for Testing Big-Data Analytics In Cloud Environments
 North Carolina State University Graduate Program in Operations Research Benchmark Databases for Testing Big-Data Analytics In Cloud Environments Rong Huang Rada Chirkova Yahya Fathi ICA CON 2012 April
North Carolina State University Graduate Program in Operations Research Benchmark Databases for Testing Big-Data Analytics In Cloud Environments Rong Huang Rada Chirkova Yahya Fathi ICA CON 2012 April
CHAPTER 8 QUADRILATERALS. 8.1 Introduction
 CHAPTER 8 QUADRILATERALS 8.1 Introduction You have studied many properties of a triangle in Chapters 6 and 7 and you know that on joining three non-collinear points in pairs, the figure so obtained is
CHAPTER 8 QUADRILATERALS 8.1 Introduction You have studied many properties of a triangle in Chapters 6 and 7 and you know that on joining three non-collinear points in pairs, the figure so obtained is
Mathematics 3301-001 Spring 2015 Dr. Alexandra Shlapentokh Guide #3
 Mathematics 3301-001 Spring 2015 Dr. Alexandra Shlapentokh Guide #3 The problems in bold are the problems for Test #3. As before, you are allowed to use statements above and all postulates in the proofs
Mathematics 3301-001 Spring 2015 Dr. Alexandra Shlapentokh Guide #3 The problems in bold are the problems for Test #3. As before, you are allowed to use statements above and all postulates in the proofs
http://www.castlelearning.com/review/teacher/assignmentprinting.aspx 5. 2 6. 2 1. 10 3. 70 2. 55 4. 180 7. 2 8. 4
 of 9 1/28/2013 8:32 PM Teacher: Mr. Sime Name: 2 What is the slope of the graph of the equation y = 2x? 5. 2 If the ratio of the measures of corresponding sides of two similar triangles is 4:9, then the
of 9 1/28/2013 8:32 PM Teacher: Mr. Sime Name: 2 What is the slope of the graph of the equation y = 2x? 5. 2 If the ratio of the measures of corresponding sides of two similar triangles is 4:9, then the
IС A A RT 2013. Proceedings Volume 2. 5th International Conference on Agents and Artificial Intelligence. Barcelona, Spain 15-18 February, 2013
 «'.''«ИЧИЧГШ ИШ М Ш * /////>. л ъ и г ш я ш и ъ в т ъ т ', : 4 р * т Ъ ъ ^ Х 'Ш У Л *а * 1 ЛЧй==:й?й!^'ййй IС A A RT 2013. *»ф«ч>»д* 'И И в Я в З Г З г И Ж /а 1 * icw-ia & «:*>if E M e i i i i y. x '-
«'.''«ИЧИЧГШ ИШ М Ш * /////>. л ъ и г ш я ш и ъ в т ъ т ', : 4 р * т Ъ ъ ^ Х 'Ш У Л *а * 1 ЛЧй==:й?й!^'ййй IС A A RT 2013. *»ф«ч>»д* 'И И в Я в З Г З г И Ж /а 1 * icw-ia & «:*>if E M e i i i i y. x '-
Geometry Regents Review
 Name: Class: Date: Geometry Regents Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. If MNP VWX and PM is the shortest side of MNP, what is the shortest
Name: Class: Date: Geometry Regents Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. If MNP VWX and PM is the shortest side of MNP, what is the shortest
Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING MANAGEMENT FOR PROVISION PROCESS
 444 JOURNAL Vol. 10 ( 4). December 2011 P u b l i c a t i o n o f T e r n o p i l N a t i o n a l E c o n o m i c U n i v e r s i t y Microeconomics Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING
444 JOURNAL Vol. 10 ( 4). December 2011 P u b l i c a t i o n o f T e r n o p i l N a t i o n a l E c o n o m i c U n i v e r s i t y Microeconomics Nataliia ZARUDNA MODERN REQUIREMENTS FOR ACCOUNTING
United States Naval Academy Electrical and Computer Engineering Department. EC262 Exam 1
 United States Naval Academy Electrical and Computer Engineering Department EC262 Exam 29 September 2. Do a page check now. You should have pages (cover & questions). 2. Read all problems in their entirety.
United States Naval Academy Electrical and Computer Engineering Department EC262 Exam 29 September 2. Do a page check now. You should have pages (cover & questions). 2. Read all problems in their entirety.
http://jsuniltutorial.weebly.com/ Page 1
 Parallelogram solved Worksheet/ Questions Paper 1.Q. Name each of the following parallelograms. (i) The diagonals are equal and the adjacent sides are unequal. (ii) The diagonals are equal and the adjacent
Parallelogram solved Worksheet/ Questions Paper 1.Q. Name each of the following parallelograms. (i) The diagonals are equal and the adjacent sides are unequal. (ii) The diagonals are equal and the adjacent
MARI-ENGLISH DICTIONARY
 MARI-ENGLISH DICTIONARY This project was funded by the Austrian Science Fund (FWF) 1, grant P22786-G20, and carried out at the Department of Finno-Ugric Studies 2 at the University of Vienna 3. Editors:
MARI-ENGLISH DICTIONARY This project was funded by the Austrian Science Fund (FWF) 1, grant P22786-G20, and carried out at the Department of Finno-Ugric Studies 2 at the University of Vienna 3. Editors:
1. Find the length of BC in the following triangles. It will help to first find the length of the segment marked X.
 1 Find the length of BC in the following triangles It will help to first find the length of the segment marked X a: b: Given: the diagonals of parallelogram ABCD meet at point O The altitude OE divides
1 Find the length of BC in the following triangles It will help to first find the length of the segment marked X a: b: Given: the diagonals of parallelogram ABCD meet at point O The altitude OE divides
ISSN 0975-413X CODEN (USA): PCHHAX. The study of dissolution kinetics of drugs with riboxinum (inosine)
 Available online at www.derpharmachemica.com ISSN 0975-413X CODEN (USA): PCHHAX Der Pharma Chemica, 2016, 8(1):412-416 (http://derpharmachemica.com/archive.html) The study of dissolution kinetics of drugs
Available online at www.derpharmachemica.com ISSN 0975-413X CODEN (USA): PCHHAX Der Pharma Chemica, 2016, 8(1):412-416 (http://derpharmachemica.com/archive.html) The study of dissolution kinetics of drugs
GEOMETRY (Common Core)
 GEOMETRY (COMMON CORE) The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY (Common Core) Tuesday, June 2, 2015 1:15 to 4:15 p.m., only Student Name: School Name: The possession
GEOMETRY (COMMON CORE) The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY (Common Core) Tuesday, June 2, 2015 1:15 to 4:15 p.m., only Student Name: School Name: The possession
The course of understanding British and American prose and poetry by future managers
 4. Полат Е. С. Новые педагогические и информационные технологии в системе образования. М.: Просвещение, 2000. 5. Гальцова Н. П., Мезенцева Т. И., Швадленко И. А. Использование электронных информационно-образовательных
4. Полат Е. С. Новые педагогические и информационные технологии в системе образования. М.: Просвещение, 2000. 5. Гальцова Н. П., Мезенцева Т. И., Швадленко И. А. Использование электронных информационно-образовательных
Boolean Algebra (cont d) UNIT 3 BOOLEAN ALGEBRA (CONT D) Guidelines for Multiplying Out and Factoring. Objectives. Iris Hui-Ru Jiang Spring 2010
 Boolean Algebra (cont d) 2 Contents Multiplying out and factoring expressions Exclusive-OR and Exclusive-NOR operations The consensus theorem Summary of algebraic simplification Proving validity of an
Boolean Algebra (cont d) 2 Contents Multiplying out and factoring expressions Exclusive-OR and Exclusive-NOR operations The consensus theorem Summary of algebraic simplification Proving validity of an
Algebraic Properties and Proofs
 Algebraic Properties and Proofs Name You have solved algebraic equations for a couple years now, but now it is time to justify the steps you have practiced and now take without thinking and acting without
Algebraic Properties and Proofs Name You have solved algebraic equations for a couple years now, but now it is time to justify the steps you have practiced and now take without thinking and acting without
The common ratio in (ii) is called the scaled-factor. An example of two similar triangles is shown in Figure 47.1. Figure 47.1
 47 Similar Triangles An overhead projector forms an image on the screen which has the same shape as the image on the transparency but with the size altered. Two figures that have the same shape but not
47 Similar Triangles An overhead projector forms an image on the screen which has the same shape as the image on the transparency but with the size altered. Two figures that have the same shape but not
THE INFLUENCE OF POLITICAL ADVERTISING ON STUDENTS PREFERENCES AND THEIR POLITICAL CHOICE
 UDK 159.94 Garkavets S.A., Zhadan O.А., Kushnarenko V. I. THE INFLUENCE OF POLITICAL ADVERTISING ON STUDENTS PREFERENCES AND THEIR POLITICAL CHOICE The article considers the features of influence political
UDK 159.94 Garkavets S.A., Zhadan O.А., Kushnarenko V. I. THE INFLUENCE OF POLITICAL ADVERTISING ON STUDENTS PREFERENCES AND THEIR POLITICAL CHOICE The article considers the features of influence political
CH3 Boolean Algebra (cont d)
 CH3 Boolean Algebra (cont d) Lecturer: 吳 安 宇 Date:2005/10/7 ACCESS IC LAB v Today, you ll know: Introduction 1. Guidelines for multiplying out/factoring expressions 2. Exclusive-OR and Equivalence operations
CH3 Boolean Algebra (cont d) Lecturer: 吳 安 宇 Date:2005/10/7 ACCESS IC LAB v Today, you ll know: Introduction 1. Guidelines for multiplying out/factoring expressions 2. Exclusive-OR and Equivalence operations
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Thursday, August 16, 2012 8:30 to 11:30 a.m.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 16, 2012 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of your
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 16, 2012 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of your
MB2-707: Version: Microsoft Dynamics CRM Customization. and Configuration. Demo
 MB2-707: Version: Microsoft Dynamics CRM Customization and Configuration Demo 1. You are a Microsoft Dynamics CRM consultant. You are assigned a new implementation. Before you configure the customer's
MB2-707: Version: Microsoft Dynamics CRM Customization and Configuration Demo 1. You are a Microsoft Dynamics CRM consultant. You are assigned a new implementation. Before you configure the customer's
QUADRILATERALS CHAPTER 8. (A) Main Concepts and Results
 CHAPTER 8 QUADRILATERALS (A) Main Concepts and Results Sides, Angles and diagonals of a quadrilateral; Different types of quadrilaterals: Trapezium, parallelogram, rectangle, rhombus and square. Sum of
CHAPTER 8 QUADRILATERALS (A) Main Concepts and Results Sides, Angles and diagonals of a quadrilateral; Different types of quadrilaterals: Trapezium, parallelogram, rectangle, rhombus and square. Sum of
Section 8.8. 1. The given line has equations. x = 3 + t(13 3) = 3 + 10t, y = 2 + t(3 + 2) = 2 + 5t, z = 7 + t( 8 7) = 7 15t.
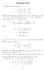 . The given line has equations Section 8.8 x + t( ) + 0t, y + t( + ) + t, z 7 + t( 8 7) 7 t. The line meets the plane y 0 in the point (x, 0, z), where 0 + t, or t /. The corresponding values for x and
. The given line has equations Section 8.8 x + t( ) + 0t, y + t( + ) + t, z 7 + t( 8 7) 7 t. The line meets the plane y 0 in the point (x, 0, z), where 0 + t, or t /. The corresponding values for x and
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Wednesday, January 29, 2014 9:15 a.m. to 12:15 p.m.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, January 29, 2014 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, January 29, 2014 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
Boolean Algebra Part 1
 Boolean Algebra Part 1 Page 1 Boolean Algebra Objectives Understand Basic Boolean Algebra Relate Boolean Algebra to Logic Networks Prove Laws using Truth Tables Understand and Use First Basic Theorems
Boolean Algebra Part 1 Page 1 Boolean Algebra Objectives Understand Basic Boolean Algebra Relate Boolean Algebra to Logic Networks Prove Laws using Truth Tables Understand and Use First Basic Theorems
Collinearity and concurrence
 Collinearity and concurrence Po-Shen Loh 23 June 2008 1 Warm-up 1. Let I be the incenter of ABC. Let A be the midpoint of the arc BC of the circumcircle of ABC which does not contain A. Prove that the
Collinearity and concurrence Po-Shen Loh 23 June 2008 1 Warm-up 1. Let I be the incenter of ABC. Let A be the midpoint of the arc BC of the circumcircle of ABC which does not contain A. Prove that the
Assignments in Mathematics Class IX (Term 2) 8. QUADRILATERALS
 Assignments in Mathematics Cass IX (Term 2) 8. QUADRILATERALS IMPORTANT TERMS, DEFINITIONS AND RESULTS Sum of the anges of a quadriatera is 360. A diagona of a paraeogram divides it into two congruent
Assignments in Mathematics Cass IX (Term 2) 8. QUADRILATERALS IMPORTANT TERMS, DEFINITIONS AND RESULTS Sum of the anges of a quadriatera is 360. A diagona of a paraeogram divides it into two congruent
Lecture Notes on Database Normalization
 Lecture Notes on Database Normalization Chengkai Li Department of Computer Science and Engineering The University of Texas at Arlington April 15, 2012 I decided to write this document, because many students
Lecture Notes on Database Normalization Chengkai Li Department of Computer Science and Engineering The University of Texas at Arlington April 15, 2012 I decided to write this document, because many students
CIRCUMFERENCE AND AREA OF A CIRCLE
 CIRCUMFERENCE AND AREA OF A CIRCLE 1. AC and BD are two perpendicular diameters of a circle with centre O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take = 3.14) 2. In the given
CIRCUMFERENCE AND AREA OF A CIRCLE 1. AC and BD are two perpendicular diameters of a circle with centre O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take = 3.14) 2. In the given
CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES. Karen Gevorgyan 1
 CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES Karen Gevorgyan 1 For decades, international law and public law aspects of the concept of sovereignty were in the center of attention of the representatives
CONCEPT OF STATE SOVEREIGNTY: MODERN ATTITUDES Karen Gevorgyan 1 For decades, international law and public law aspects of the concept of sovereignty were in the center of attention of the representatives
SERVER CERTIFICATES OF THE VETUMA SERVICE
 Page 1 Version: 3.4, 19.12.2014 SERVER CERTIFICATES OF THE VETUMA SERVICE 1 (18) Page 2 Version: 3.4, 19.12.2014 Table of Contents 1. Introduction... 3 2. Test Environment... 3 2.1 Vetuma test environment...
Page 1 Version: 3.4, 19.12.2014 SERVER CERTIFICATES OF THE VETUMA SERVICE 1 (18) Page 2 Version: 3.4, 19.12.2014 Table of Contents 1. Introduction... 3 2. Test Environment... 3 2.1 Vetuma test environment...
HALL G 380,000 GROSS SF
 LEVEL 1 404 403 402 401 1007 1006 1005 1004 1003 1002 1001 907 906 905 904 903 902 901 807 806 805 804 803 802 801 707 706 705 704 703 702 701 607 606 605 604 603 602 601 507 506 505 504 503 502 501 GALILEO
LEVEL 1 404 403 402 401 1007 1006 1005 1004 1003 1002 1001 907 906 905 904 903 902 901 807 806 805 804 803 802 801 707 706 705 704 703 702 701 607 606 605 604 603 602 601 507 506 505 504 503 502 501 GALILEO
AREAS OF PARALLELOGRAMS AND TRIANGLES
 15 MATHEMATICS AREAS OF PARALLELOGRAMS AND TRIANGLES CHAPTER 9 9.1 Introduction In Chapter 5, you have seen that the study of Geometry, originated with the measurement of earth (lands) in the process of
15 MATHEMATICS AREAS OF PARALLELOGRAMS AND TRIANGLES CHAPTER 9 9.1 Introduction In Chapter 5, you have seen that the study of Geometry, originated with the measurement of earth (lands) in the process of
А А А дламая АмАяАяАсАяАя АК А АВдлАмАК АКАВАК
 Аядл АК А АВдлАК АКАВАК 2 АяАяА АВА АсдлАя А А А длая АяАяАсАяАя АК А АВдлАК АКАВАК Ас. apple apple АУ fi applefi АвАвАУ- fi applefi - АУapple applefi apple fi fi fi applefi-. (. 2-184, 2-185) АУ apple
Аядл АК А АВдлАК АКАВАК 2 АяАяА АВА АсдлАя А А А длая АяАяАсАяАя АК А АВдлАК АКАВАК Ас. apple apple АУ fi applefi АвАвАУ- fi applefi - АУapple applefi apple fi fi fi applefi-. (. 2-184, 2-185) АУ apple
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, June 20, 2012 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, June 20, 2012 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
Data Mining Apriori Algorithm
 10 Data Mining Apriori Algorithm Apriori principle Frequent itemsets generation Association rules generation Section 6 of course book TNM033: Introduction to Data Mining 1 Association Rule Mining (ARM)
10 Data Mining Apriori Algorithm Apriori principle Frequent itemsets generation Association rules generation Section 6 of course book TNM033: Introduction to Data Mining 1 Association Rule Mining (ARM)
Chronic Fatigue Syndrome
 256 Srp Arh Celok Lek. 2011 Mar-Apr;139(3-4):256-261 ПРЕГЛЕД ЛИТЕРАТУРЕ / REVIEW ARTICLE DOI: 10.2298/SARH1104256B Chronic Fatigue Syndrome Snežana Brkić, Slavica Tomić, Maja Ružić, Daniela Marić Hospital
256 Srp Arh Celok Lek. 2011 Mar-Apr;139(3-4):256-261 ПРЕГЛЕД ЛИТЕРАТУРЕ / REVIEW ARTICLE DOI: 10.2298/SARH1104256B Chronic Fatigue Syndrome Snežana Brkić, Slavica Tomić, Maja Ružić, Daniela Marić Hospital
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Student Name:
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, August 18, 2010 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, August 18, 2010 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of
Most popular response to
 Class #33 Most popular response to What did the students want to prove? The angle bisectors of a square meet at a point. A square is a convex quadrilateral in which all sides are congruent and all angles
Class #33 Most popular response to What did the students want to prove? The angle bisectors of a square meet at a point. A square is a convex quadrilateral in which all sides are congruent and all angles
Karnaugh Maps & Combinational Logic Design. ECE 152A Winter 2012
 Karnaugh Maps & Combinational Logic Design ECE 52A Winter 22 Reading Assignment Brown and Vranesic 4 Optimized Implementation of Logic Functions 4. Karnaugh Map 4.2 Strategy for Minimization 4.2. Terminology
Karnaugh Maps & Combinational Logic Design ECE 52A Winter 22 Reading Assignment Brown and Vranesic 4 Optimized Implementation of Logic Functions 4. Karnaugh Map 4.2 Strategy for Minimization 4.2. Terminology
Practical Geometry CHAPTER. 4.1 Introduction DO THIS
 PRACTICAL GEOMETRY 57 Practical Geometry CHAPTER 4 4.1 Introduction You have learnt how to draw triangles in Class VII. We require three measurements (of sides and angles) to draw a unique triangle. Since
PRACTICAL GEOMETRY 57 Practical Geometry CHAPTER 4 4.1 Introduction You have learnt how to draw triangles in Class VII. We require three measurements (of sides and angles) to draw a unique triangle. Since
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Thursday, August 13, 2009 8:30 to 11:30 a.m., only.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 13, 2009 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of your
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 13, 2009 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of your
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Student Name:
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, June 17, 2010 1:15 to 4:15 p.m., only Student Name: School Name: Print your name and the name of your
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, June 17, 2010 1:15 to 4:15 p.m., only Student Name: School Name: Print your name and the name of your
San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS
 San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS Recall that the bisector of an angle is the ray that divides the angle into two congruent angles. The most important results about angle bisectors
San Jose Math Circle April 25 - May 2, 2009 ANGLE BISECTORS Recall that the bisector of an angle is the ray that divides the angle into two congruent angles. The most important results about angle bisectors
Lesson 13: Angle Sum of a Triangle
 Student Outcomes Students know the angle sum theorem for triangles; the sum of the interior angles of a triangle is always 180. Students present informal arguments to draw conclusions about the angle sum
Student Outcomes Students know the angle sum theorem for triangles; the sum of the interior angles of a triangle is always 180. Students present informal arguments to draw conclusions about the angle sum
HOW TO USE MINITAB: DESIGN OF EXPERIMENTS. Noelle M. Richard 08/27/14
 HOW TO USE MINITAB: DESIGN OF EXPERIMENTS 1 Noelle M. Richard 08/27/14 CONTENTS 1. Terminology 2. Factorial Designs When to Use? (preliminary experiments) Full Factorial Design General Full Factorial Design
HOW TO USE MINITAB: DESIGN OF EXPERIMENTS 1 Noelle M. Richard 08/27/14 CONTENTS 1. Terminology 2. Factorial Designs When to Use? (preliminary experiments) Full Factorial Design General Full Factorial Design
How To Solve The Pythagorean Triangle
 Name Period CHAPTER 9 Right Triangles and Trigonometry Section 9.1 Similar right Triangles Objectives: Solve problems involving similar right triangles. Use a geometric mean to solve problems. Ex. 1 Use
Name Period CHAPTER 9 Right Triangles and Trigonometry Section 9.1 Similar right Triangles Objectives: Solve problems involving similar right triangles. Use a geometric mean to solve problems. Ex. 1 Use
Vector Notation: AB represents the vector from point A to point B on a graph. The vector can be computed by B A.
 1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
Chapter 3: IP Addressing and VLSM
 Chapter 3: IP Addressing and VLSM QUESTION 54 What is the principle reason to use a private IP address on an internal network? A. Subnet strategy for private companies. B. Manage and scale the growth of
Chapter 3: IP Addressing and VLSM QUESTION 54 What is the principle reason to use a private IP address on an internal network? A. Subnet strategy for private companies. B. Manage and scale the growth of
Die Welt Multimedia-Reichweite
 Die Welt Multimedia-Reichweite 1) Background The quantification of Die Welt s average daily audience (known as Multimedia-Reichweite, MMR) has been developed by Die Welt management, including the research
Die Welt Multimedia-Reichweite 1) Background The quantification of Die Welt s average daily audience (known as Multimedia-Reichweite, MMR) has been developed by Die Welt management, including the research
Triangles. Triangle. a. What are other names for triangle ABC?
 Triangles Triangle A triangle is a closed figure in a plane consisting of three segments called sides. Any two sides intersect in exactly one point called a vertex. A triangle is named using the capital
Triangles Triangle A triangle is a closed figure in a plane consisting of three segments called sides. Any two sides intersect in exactly one point called a vertex. A triangle is named using the capital
H3C large-scale network routing
 Exam : GB0-380 Title : H3C large-scale network routing Version : DEMO 1 / 9 1.L L L L A. BGP B. RIP-1 C. RIP-2 D. IS-IS Answer: CD 2. EGP A. BGP OSPF B. OSPF RIP C. BGP RIP D. OSPF BGP Answer: A 3. 4 10.0.0.0/24
Exam : GB0-380 Title : H3C large-scale network routing Version : DEMO 1 / 9 1.L L L L A. BGP B. RIP-1 C. RIP-2 D. IS-IS Answer: CD 2. EGP A. BGP OSPF B. OSPF RIP C. BGP RIP D. OSPF BGP Answer: A 3. 4 10.0.0.0/24
Session 5 Dissections and Proof
 Key Terms for This Session Session 5 Dissections and Proof Previously Introduced midline parallelogram quadrilateral rectangle side-angle-side (SAS) congruence square trapezoid vertex New in This Session
Key Terms for This Session Session 5 Dissections and Proof Previously Introduced midline parallelogram quadrilateral rectangle side-angle-side (SAS) congruence square trapezoid vertex New in This Session
TERMINOLOGY OF KOGNITIVE LINGUISTICS: CONCEPTUAL SYSTEM AND CONCEPTUAL PICTURE OF THE WORLD
 UDC 811.161.1' 1(082) M. V. PIMENOVA (Kemerovo, Russia) TERMINOLOGY OF KOGNITIVE LINGUISTICS: CONCEPTUAL SYSTEM AND CONCEPTUAL PICTURE OF THE WORLD The article deals with the determination of the terms
UDC 811.161.1' 1(082) M. V. PIMENOVA (Kemerovo, Russia) TERMINOLOGY OF KOGNITIVE LINGUISTICS: CONCEPTUAL SYSTEM AND CONCEPTUAL PICTURE OF THE WORLD The article deals with the determination of the terms
@12 @1. G5 definition s. G1 Little devils. G3 false proofs. G2 sketches. G1 Little devils. G3 definition s. G5 examples and counters
 Class #31 @12 @1 G1 Little devils G2 False proofs G3 definition s G4 sketches G5 examples and counters G1 Little devils G2 sketches G3 false proofs G4 examples and counters G5 definition s Jacob Amanda
Class #31 @12 @1 G1 Little devils G2 False proofs G3 definition s G4 sketches G5 examples and counters G1 Little devils G2 sketches G3 false proofs G4 examples and counters G5 definition s Jacob Amanda
EFFICIENCY OF SOLAR ROOF WITH TRANSPARENT COVER FOR HEATING SUPPLY OF BUILDINGS
 Budownictwo o zoptymalizowanym potencjale energetycznym 2(14) 2014, s. 117-124 Orest VOZNYAK, Stepan SHAPOVAL, Ostap PONA, Maryana KASYNETS Lviv Polytechnic National University, Ukraine EFFICIENCY OF SOLAR
Budownictwo o zoptymalizowanym potencjale energetycznym 2(14) 2014, s. 117-124 Orest VOZNYAK, Stepan SHAPOVAL, Ostap PONA, Maryana KASYNETS Lviv Polytechnic National University, Ukraine EFFICIENCY OF SOLAR
2 : two cube. 5 : five cube. 10 : ten cube.
 Math 105 TOPICS IN MATHEMATICS REVIEW OF LECTURES VI Instructor: Line #: 52920 Yasuyuki Kachi 6 Cubes February 2 Mon, 2015 We can similarly define the notion of cubes/cubing Like we did last time, 3 2
Math 105 TOPICS IN MATHEMATICS REVIEW OF LECTURES VI Instructor: Line #: 52920 Yasuyuki Kachi 6 Cubes February 2 Mon, 2015 We can similarly define the notion of cubes/cubing Like we did last time, 3 2
Name Date Class. Lines and Segments That Intersect Circles. AB and CD are chords. Tangent Circles. Theorem Hypothesis Conclusion
 Section. Lines That Intersect Circles Lines and Segments That Intersect Circles A chord is a segment whose endpoints lie on a circle. A secant is a line that intersects a circle at two points. A tangent
Section. Lines That Intersect Circles Lines and Segments That Intersect Circles A chord is a segment whose endpoints lie on a circle. A secant is a line that intersects a circle at two points. A tangent
Geometry Module 4 Unit 2 Practice Exam
 Name: Class: Date: ID: A Geometry Module 4 Unit 2 Practice Exam Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which diagram shows the most useful positioning
Name: Class: Date: ID: A Geometry Module 4 Unit 2 Practice Exam Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which diagram shows the most useful positioning
Unit 8: Congruent and Similar Triangles Lesson 8.1 Apply Congruence and Triangles Lesson 4.2 from textbook
 Unit 8: Congruent and Similar Triangles Lesson 8.1 Apply Congruence and Triangles Lesson 4.2 from textbook Objectives Identify congruent figures and corresponding parts of closed plane figures. Prove that
Unit 8: Congruent and Similar Triangles Lesson 8.1 Apply Congruence and Triangles Lesson 4.2 from textbook Objectives Identify congruent figures and corresponding parts of closed plane figures. Prove that
Equation of a Line. Chapter H2. The Gradient of a Line. m AB = Exercise H2 1
 Chapter H2 Equation of a Line The Gradient of a Line The gradient of a line is simpl a measure of how steep the line is. It is defined as follows :- gradient = vertical horizontal horizontal A B vertical
Chapter H2 Equation of a Line The Gradient of a Line The gradient of a line is simpl a measure of how steep the line is. It is defined as follows :- gradient = vertical horizontal horizontal A B vertical
KNOWLEDGE IS POWER The BEST first-timers guide to betting on and winning at the races you ll EVER encounter
 KNOWLEDGE IS POWER The BEST first-timers guide to betting on and winning at the races you ll EVER encounter Copyright 2013 James Witherite. All Rights Reserved.. WELCOME TO THE RACES! If you re new to
KNOWLEDGE IS POWER The BEST first-timers guide to betting on and winning at the races you ll EVER encounter Copyright 2013 James Witherite. All Rights Reserved.. WELCOME TO THE RACES! If you re new to
FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina
 FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina Москва Издательство Российского университета дружбы народов 2002 FUNCTIONS OF THE MODAL
FUNCTIONS OF THE MODAL VERBS IN ENGLISH (MODAL VERBS ANALOGIES IN THE RUSSIAN LANGUAGE) Сompiled by G.V. Kuzmina Москва Издательство Российского университета дружбы народов 2002 FUNCTIONS OF THE MODAL
IMO Geomety Problems. (IMO 1999/1) Determine all finite sets S of at least three points in the plane which satisfy the following condition:
 IMO Geomety Problems (IMO 1999/1) Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points A and B in S, the perpendicular bisector
IMO Geomety Problems (IMO 1999/1) Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points A and B in S, the perpendicular bisector
GEOMETRY. Chapter 1: Foundations for Geometry. Name: Teacher: Pd:
 GEOMETRY Chapter 1: Foundations for Geometry Name: Teacher: Pd: Table of Contents Lesson 1.1: SWBAT: Identify, name, and draw points, lines, segments, rays, and planes. Pgs: 1-4 Lesson 1.2: SWBAT: Use
GEOMETRY Chapter 1: Foundations for Geometry Name: Teacher: Pd: Table of Contents Lesson 1.1: SWBAT: Identify, name, and draw points, lines, segments, rays, and planes. Pgs: 1-4 Lesson 1.2: SWBAT: Use
Inversion. Chapter 7. 7.1 Constructing The Inverse of a Point: If P is inside the circle of inversion: (See Figure 7.1)
 Chapter 7 Inversion Goal: In this chapter we define inversion, give constructions for inverses of points both inside and outside the circle of inversion, and show how inversion could be done using Geometer
Chapter 7 Inversion Goal: In this chapter we define inversion, give constructions for inverses of points both inside and outside the circle of inversion, and show how inversion could be done using Geometer
MATHEMATICS Grade 12 EUCLIDEAN GEOMETRY: CIRCLES 02 JULY 2014
 EUCLIDEAN GEOMETRY: CIRCLES 02 JULY 2014 Checklist Make sure you learn proofs of the following theorems: The line drawn from the centre of a circle perpendicular to a chord bisects the chord The angle
EUCLIDEAN GEOMETRY: CIRCLES 02 JULY 2014 Checklist Make sure you learn proofs of the following theorems: The line drawn from the centre of a circle perpendicular to a chord bisects the chord The angle
PELLISSIPPI STATE COMMUNITY COLLEGE MASTER SYLLABUS
 PELLISSIPPI STATE COMMUNITY COLLEGE MASTER SYLLABUS SMALL BUSINESS MANAGEMENT BUSN 1340 Class Hours: 3.0 Credit Hours: 3.0 Laboratory Hours: 0.0 Revised: August 23, 2013 NOTE: This course is not designed
PELLISSIPPI STATE COMMUNITY COLLEGE MASTER SYLLABUS SMALL BUSINESS MANAGEMENT BUSN 1340 Class Hours: 3.0 Credit Hours: 3.0 Laboratory Hours: 0.0 Revised: August 23, 2013 NOTE: This course is not designed
A COURSE IN MODERN ENGLISH LEXICOLOGY
 R. S. Ginzburg, S. S. Khidekel, G. Y. Knyazeva, A. A. Sankin A COURSE IN MODERN ENGLISH LEXICOLOGY SECOND EDITION Revised and Enlarged Допущено Министерством высшего и среднего специального образования
R. S. Ginzburg, S. S. Khidekel, G. Y. Knyazeva, A. A. Sankin A COURSE IN MODERN ENGLISH LEXICOLOGY SECOND EDITION Revised and Enlarged Допущено Министерством высшего и среднего специального образования
Unique column combinations
 Unique column combinations Arvid Heise Guest lecture in Data Profiling and Data Cleansing Prof. Dr. Felix Naumann Agenda 2 Introduction and problem statement Unique column combinations Exponential search
Unique column combinations Arvid Heise Guest lecture in Data Profiling and Data Cleansing Prof. Dr. Felix Naumann Agenda 2 Introduction and problem statement Unique column combinations Exponential search
Introduction. The Quine-McCluskey Method Handout 5 January 21, 2016. CSEE E6861y Prof. Steven Nowick
 CSEE E6861y Prof. Steven Nowick The Quine-McCluskey Method Handout 5 January 21, 2016 Introduction The Quine-McCluskey method is an exact algorithm which finds a minimum-cost sum-of-products implementation
CSEE E6861y Prof. Steven Nowick The Quine-McCluskey Method Handout 5 January 21, 2016 Introduction The Quine-McCluskey method is an exact algorithm which finds a minimum-cost sum-of-products implementation
Joong-Seok Cho 1 THE RELATION BETWEEN ACCOUNTING QUALITY AND SECURITY ANALYSTS' TARGET PRICE FORECAST PERFORMANCE
 НОВИНИ СВІТОВОЇ НАУКИ 503 Joong-Seok Cho 1 THE RELATION BETWEEN ACCOUNTING QUALITY AND SECURITY ANALYSTS' TARGET PRICE FORECAST PERFORMANCE Using a sample of the US security analysts' target price forecasts
НОВИНИ СВІТОВОЇ НАУКИ 503 Joong-Seok Cho 1 THE RELATION BETWEEN ACCOUNTING QUALITY AND SECURITY ANALYSTS' TARGET PRICE FORECAST PERFORMANCE Using a sample of the US security analysts' target price forecasts
2015 Chapter Competition Solutions
 05 Chapter Competition Solutions Are you wondering how we could have possibly thought that a Mathlete would be able to answer a particular Sprint Round problem without a calculator? Are you wondering how
05 Chapter Competition Solutions Are you wondering how we could have possibly thought that a Mathlete would be able to answer a particular Sprint Round problem without a calculator? Are you wondering how
The following instructions may please be noted before filling the return
 Form 223 The following instructions may please be noted before filling the return 1. Please use the correct return form. This return form is for VAT dealers who are also in the business of executing works
Form 223 The following instructions may please be noted before filling the return 1. Please use the correct return form. This return form is for VAT dealers who are also in the business of executing works
TIgeometry.com. Geometry. Angle Bisectors in a Triangle
 Angle Bisectors in a Triangle ID: 8892 Time required 40 minutes Topic: Triangles and Their Centers Use inductive reasoning to postulate a relationship between an angle bisector and the arms of the angle.
Angle Bisectors in a Triangle ID: 8892 Time required 40 minutes Topic: Triangles and Their Centers Use inductive reasoning to postulate a relationship between an angle bisector and the arms of the angle.
Fundamentals of Geometry. Oleg A. Belyaev belyaev@polly.phys.msu.ru
 Fundamentals of Geometry Oleg A. Belyaev belyaev@polly.phys.msu.ru February 28, 2007 Contents I Classical Geometry 1 1 Absolute (Neutral) Geometry 3 1.1 Incidence....................................................
Fundamentals of Geometry Oleg A. Belyaev belyaev@polly.phys.msu.ru February 28, 2007 Contents I Classical Geometry 1 1 Absolute (Neutral) Geometry 3 1.1 Incidence....................................................
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Tuesday, August 13, 2013 8:30 to 11:30 a.m., only.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Tuesday, August 13, 2013 8:30 to 11:30 a.m., only Student Name: School Name: The possession or use of any communications
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Tuesday, August 13, 2013 8:30 to 11:30 a.m., only Student Name: School Name: The possession or use of any communications
Math 531, Exam 1 Information.
 Math 531, Exam 1 Information. 9/21/11, LC 310, 9:05-9:55. Exam 1 will be based on: Sections 1A - 1F. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/531fa11/531.html)
Math 531, Exam 1 Information. 9/21/11, LC 310, 9:05-9:55. Exam 1 will be based on: Sections 1A - 1F. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/531fa11/531.html)
Combinations and Permutations Grade Eight
 Ohio Standards Connection: Data Analysis and Probability Benchmark H Use counting techniques, such as permutations and combinations, to determine the total number of options and possible outcomes. Indicator
Ohio Standards Connection: Data Analysis and Probability Benchmark H Use counting techniques, such as permutations and combinations, to determine the total number of options and possible outcomes. Indicator
TRENDS IN CLOUD COMPUTING
 TRENDS IN CLOUD COMPUTING FULL REPORT RESEARCH FOURTH ANNUAL AUGUST 2013 www.comptia.org 4 th $Annual$Trends$in$Cloud$Computing:Section1 1 AboutthisResearch CompTIA s4 th $Annual$Trends$in$Cloud$Computing$studybuildsonpreviousCompTIAresearchinthe
TRENDS IN CLOUD COMPUTING FULL REPORT RESEARCH FOURTH ANNUAL AUGUST 2013 www.comptia.org 4 th $Annual$Trends$in$Cloud$Computing:Section1 1 AboutthisResearch CompTIA s4 th $Annual$Trends$in$Cloud$Computing$studybuildsonpreviousCompTIAresearchinthe
5.1 Midsegment Theorem and Coordinate Proof
 5.1 Midsegment Theorem and Coordinate Proof Obj.: Use properties of midsegments and write coordinate proofs. Key Vocabulary Midsegment of a triangle - A midsegment of a triangle is a segment that connects
5.1 Midsegment Theorem and Coordinate Proof Obj.: Use properties of midsegments and write coordinate proofs. Key Vocabulary Midsegment of a triangle - A midsegment of a triangle is a segment that connects
Intermediate Math Circles October 10, 2012 Geometry I: Angles
 Intermediate Math Circles October 10, 2012 Geometry I: Angles Over the next four weeks, we will look at several geometry topics. Some of the topics may be familiar to you while others, for most of you,
Intermediate Math Circles October 10, 2012 Geometry I: Angles Over the next four weeks, we will look at several geometry topics. Some of the topics may be familiar to you while others, for most of you,
Warm-up Tangent circles Angles inside circles Power of a point. Geometry. Circles. Misha Lavrov. ARML Practice 12/08/2013
 Circles ARML Practice 12/08/2013 Solutions Warm-up problems 1 A circular arc with radius 1 inch is rocking back and forth on a flat table. Describe the path traced out by the tip. 2 A circle of radius
Circles ARML Practice 12/08/2013 Solutions Warm-up problems 1 A circular arc with radius 1 inch is rocking back and forth on a flat table. Describe the path traced out by the tip. 2 A circle of radius
