MHR Principles of Mathematics 10 Solutions 1
|
|
|
- Joel Sparks
- 7 years ago
- Views:
Transcription
1 Chapter 5 Quadratic Expressions Chapter 5 Get Ready Chapter 5 Get Ready Question 1 Page 08 a 3y has one term. It is a monomial. 3 b 5+ 6a has two terms. It is a binomial. c 6 x + x 1 has three terms. It is a trinomial d 8ab 6ab + ab has three terms. It is a trinomial. 3 e 5de 7ehas two terms. It is a binomial. f 19m+ 8n 3phas three terms. It is a trinomial. Chapter 5 Get Ready Question Page 08 a y 4y + y has a degree of b 8ab + 9ab 6ab has a degree of c 10xy 3x y + 5x y has a degree of 9. d 6abc 5a bc 7abc has a degree of 5. MHR Principles of Mathematics 10 Solutions 1
2 Chapter 5 Get Ready Question 3 Page 08 5x+ 7 + x 11 = 5x+ 7+ x 11 a ( ( = 7x 4 b ( 3b 8 ( 6b 7 = ( 3b 8 + ( 6b+ 7 c ( = 3b 8 6b+ 7 = 3b 1 ( x + x+ + x + x = x + x+ + x + x = x + x d ( 9y 3 7y + 6 ( 3y 3 5y + 8 = ( 9y 3 7y ( 3y 3 + 5y 8 e ( ( = y y + y + y 3 6 = y y a + a + a a = a + a + a a = a + a f ( c 3c+ 1 ( c 3c 5 = ( c 3c+ 1 + ( c + 3c+ 5 = c c+ + c + c = c MHR Principles of Mathematics 10 Solutions
3 Chapter 5 Get Ready Question 4 Page 08 7x + 3xy y + 8x xy y = 7x + 3xy y + 8x xy y a ( ( = 15x + xy 3y b ( 4g + gh 7h ( g gh+ 3h = ( 4g + gh 7h + ( g + gh 3h c ( ( = 4g + gh 7h g + gh 3h = 3g + 3gh 10h ab + a b + ab a + b = ab + a b + ab a + b = 8ab + a + 5b d ( 3cd + c + 9d ( cd + c d = ( 3cd + c + 9d + ( cd c + d e ( ( ( = cd c d cd c d = cd + 10d x + 8 6x 7 + 5x 1 = x+ 8 6x+ 7+ 5x 1 = x + 14 f ( ( ( ( ( ( 5a b + 6b a b + 7a = 5a b + 6b a + b 7a = 5a b+ 6b a b 7a = 4a + 5b b MHR Principles of Mathematics 10 Solutions 3
4 Chapter 5 Get Ready Question 5 Page 09 a 3(x + b 4(x + c x(x + 3 d 4x(x MHR Principles of Mathematics 10 Solutions
5 Chapter 5 Get Ready Question 6 Page 09 a 7m( 3m+ 8 = 7m( 3m + 7m( 8 = + 1m 56 m b 4( c+ 9 = 4( c + ( 4( 9 = 4c 36 c 5a ( 6a 8a = 5a ( 6a + 5a ( 8a = 30a 40a 4 3 d ( d d + 1 = ( d + ( d + ( 1 = + d 4d Chapter 5 Get Ready Question 7 Page 09 a V = ( x( 6x( 5x 1 = 1x ( 5x 1 = 1x ( 5x + 1x ( 1 = 60x 1x 3 b A= ( x( 6x + ( x( 5x ( x( 5x 1 = 4x + 4x( 5x 1 + 1x( 5x 1 = 4x + 4x( 5x + 4x( 1 + 1x( 5x + 1x( 1 = 4x + 0x 4x+ 60x 1x = x x Chapter 5 Get Ready Question 8 Page 09 a The factors of 10 are 1,, 5, and 10. b The factors of 4 are 1,, 3, 4, 6, 8, 1, and 4. c The factors of 16 are 1,, 4, 8, and 16. d The factors of 3 are 1,, 4, 8, 16, and 3. Chapter 5 Get Ready Question 9 Page 09 a 8= b 14 = 7 c 8 = 7 d 30 = 3 5 MHR Principles of Mathematics 10 Solutions 5
6 Chapter 5 Get Ready Question 10 Page 09 a 6= 3 9= 3 3 The GCF of 6 and 9 is 3. b 5 = = 3 5 The GCF of 15 and 5 is 5. c 4 = 3 16= The GCF of 16 and 4 is, or 8. d 0 = 5 8 = 7 The GCF of 0 and 8 is, or 4. e 36 = = 3 5 The GCF of 36 and 15 is 3. f 3= 40 = 5 The GCF of 3 and 40 is, or 8. 6 MHR Principles of Mathematics 10 Solutions
7 Chapter 5 Section 1: Multiply Polynomials Chapter 5 Section 1 Question 1 Page 17 a The model illustrates ( ( x+ 1 x+ 3 = x + 5x+ 3 b The model illustrates ( ( x+ 1 x+ 3 = x + 4x+3 c The model illustrates ( ( x+ x+ 3 = x + 4x+4 d The model illustrates ( ( x+ 3 x+ 1 = x + 7x+ 3 MHR Principles of Mathematics 10 Solutions 7
8 Chapter 5 Section 1 Question Page 17 a ( x+ 1( x+ 1 b ( x+ 4( x+ c ( x+ 1( x+ 5 8 MHR Principles of Mathematics 10 Solutions
9 + 1 3x+ d ( x ( Chapter 5 Section 1 Question 3 Page 17 a ( x+ 3( x+ 5 = x( x ( x+ 5 b ( x+ 3( x+ 4 = x( x ( x+ 4 = x + x+ x+ = x + x = x + x+ x+ = x + x c ( y+ ( y+ 4 = y( y+ 4 + ( y+ 4 d ( r+ 4( r+ = r( r+ + 4( r+ = y + y+ y+ = y + y = r + r+ r+ = r + r e ( n+ 7( n+ 1 = n( n ( n+ 1 f ( p+ 9( p+ 9 = p( p ( p+9 = n + n+ n+ = n + n = p + p+ p+ = p + p g ( w+ 7( w+ 8 = w( w ( w+ 8 h ( d + 3( d + 11 = d( d ( d + 11 = w + w+ w+ = w + w = d + d + d + = d + d MHR Principles of Mathematics 10 Solutions 9
10 Chapter 5 Section 1 Question 4 Page 17 a ( k 3( k 5 = k( k 5 3( k 5 b ( y 3( y 4 = y( y 4 3( y 4 = k k k + = k k = y y y+ = y y c ( x ( x 4 = x( x 4 ( x 4 d ( q 4( q = q( q 4( q = x x x+ = x x = q q q+ = q q e ( j 7( j 1 = j( j 1 7( j 1 f ( p 9( p 3 = p( p 3 9( p 3 = j j j+ = j j = p p p+ = p p g ( z 7x( z 8x = z( z 8x 7x( z 8x = z 8xz 7xz+ 56x = z 15xz+ 56x h ( b 3c( b 11c = b( b 11c 3c( b 11c = b 11bc 3bc+ 33c = b 14bc+ 33c Chapter 5 Section 1 Question 5 Page 18 a ( x+ 3( x 5 = x( x 5 + 3( x 5 b ( y+ 3( y 4 = y( y 4 + 3( y 4 = x x+ x = x x = y y+ y = y y c ( c ( c+ 4 = c( c+ 4 ( c+ 4 = c + c c = c + c d ( w 4( w+ = w( w+ 4( w+ = w + w w = w w e ( m+ 7( m 1 = m( m 1 + 7( m 1 f ( y 9( y+ 3 = y( y+ 3 9( y+3 = m m+ m = m + m = y + y y = y y g ( x + 7y( x 8y = x( x 8y + 7y( x 8y = x 8xy + 7xy 56y = x xy 56y h ( a+ 6b( a 10b = a( a 10b + 6b( a 10b = a 10ab+ 6ab 60b = a 4ab 60b 10 MHR Principles of Mathematics 10 Solutions
11 Chapter 5 Section 1 Question 6 Page 18 a ( ( x+ 3 x+ 4 = x + 8x+ 3x+ 1 = + + x 11x 1 y 3 5y 7 = 5y 7y 15y+ 1 b ( ( = + 5y y 1 c ( 6c 1 ( 3c+ 5 = 18c + 30c 3c 5 d = + 18c 7c 5 ( ( 7w w+ 1 = 14w + 7w 4w = + 14w 3w e ( ( 5m+ 6 5m 6 = 5m 30m+ 30m 36 = 5m 36 9y y+ = 18y + 18y 4y 4 f ( ( = + 18y 14y 4 g ( ( 7d + 5c 8d 6c = 56d 4cd + 40cd 30c = 56d cd 30c 6q+ 5r 7q 1r = 4q 7qr+ 35qr 60r h ( ( = 4q 37qr 60r Chapter 5 Section 1 Question 7 Page 18 a 3( x 5( x+ 6 = 3( x + 6x 5x 30 b ( x 7( x 9 = ( x 9x 7x+ 63 = 3( x + x 30 = ( x 16x = x + x 3 16 = x + x c ( y+ ( y 8 = ( y 8y+ y 16 d ( k + 3( k + 7 = ( k + 7k + 3k + 1 = ( y 6y 16 = ( k + 10k + 1 = + + y 6y 16 e m( m 3n( m 5n = m( m 5mn 3mn+ 15n = m( m 8mn+ 15n = m 8m n+ 15mn 3 f a( 3a+ 4b( 6a+ 7b = a( 18a + 1ab+ 4ab+ 8b = a( 18a + 45ab+ 8b = 36a + 90a b+ 56ab 3 = + + k 0k 4 MHR Principles of Mathematics 10 Solutions 11
12 Chapter 5 Section 1 Question 8 Page 18 a ( ( ( ( x+ 4 x+ 6 + x 1 x+ 7 = x + 6x+ 4x+ 4+ x + 7x x 7 = + + x 16x 17 b ( x+ 5( 3x 7 + ( 4x+ 9( x 11 = 6x 14x+ 15x 35+ ( 8x 44x+ 18x 99 = x x+ x + x x+ x = x x c 3( 6x ( 6x 1 ( x 3( 5x+ 6 = 3( 36x 6x 1x+ ( 10x + 1x 15x 18 = 336 ( x 18x+ 110 ( x 3x 18 = x 54x 6 10x 3x 18 = x x d ( x ( x 3 + ( 3x+ 5( x+ 4 = ( x 3x x+ 6 + ( 3x + 1x+ 5x+ 0 = 1( x 5x+ 6 + ( 3x + 17x+ 0 = x + x + x + x+ = x + x ( ( ( ( ( e ( x+ 4 x 4 = x+ 4 x+ 4 x 4 x 4 ( ( = x + x+ x+ x x x = x + x+ x x = x + x+ x + x = 16x f 53 ( x 1( 5x + 66 ( x+ 3( 5x = 515 ( x 6x 5x ( x 1x+ 15x 6 = 515 ( x 11x ( x + 3x 6 75x 55x x 18x 36 = = x + x 1 MHR Principles of Mathematics 10 Solutions
13 Chapter 5 Section 1 Question 9 Page 18 a h= ( d 3( d 15 ( d d d 5 ( d d = = = d + d b h = ( d 3( d 15 h = d + 36d 90 = ( 10 3( ( 10 ( 10 = 70 = = 70 Both forms of the equation predict a height of 70 m when d represents 10 m. Chapter 5 Section 1 Question 10 Page 18 a A1 = x b A = ( x+ ( x+ 3 6 c A = ( x+ 3( x+ 6 = x + 6x+ 3x+ 18 = x + 9x+ 18 d e A A1 = x + 9x+ 18 x = 9x + 18 A A1 = 9x+ 18 ( 1 = = 16 If x represents 1 m, the increase in area is 16 m. MHR Principles of Mathematics 10 Solutions 13
14 Chapter 5 Section 1 Question 11 Page 18 a i A= x( x+ 10 = x + 10x ii A = x( x = x iii A= ( x+ 5( x+ 6 = x + x+ x+ = x + x b Chapter 5 Section 1 Question 1 Page 18 a The x-intercepts of y= ( x+ 3( x 1 are 3 and 1. b y = ( x+ 3( x 1 c = x x+ x = x + x MHR Principles of Mathematics 10 Solutions
15 Chapter 5 Section 1 Question 13 Page 19 a b V = w( w+ ( c V = w( w+ ( = ww ( + = + w 4 w Chapter 5 Section 1 Question 14 Page 19 a b SA = 6( x( x 1 = 6x c SA = ( x + y 6 d SA SA1 = 6( x + y 6x ( ( = 6 x+ y x+ y 6x ( ( = 6 x + xy + xy + y 6x = 6 x + xy+ y 6x = x + xy+ y x = 1xy + 6y MHR Principles of Mathematics 10 Solutions 15
16 3 3 e V V1 = ( x+ y x ( ( ( = x+ y x+ y x+ y x ( ( ( x y( x xy y x = x+ y x + xy+ xy+ y x 3 = = x xy xy xy xy y x = 3xy+ 3xy + y 3 Chapter 5 Section 1 Question 15 Page 19 a d = 3000( v+ 0.3( 1.0 v ( v v v ( v v = = = v + v b d = v + v+ = 3000 = 100 ( 0. ( At 0. m/s, she can swim 100 m before running out of air. c She can swim a maximum of m at 0.35 m/s before running out of air. 16 MHR Principles of Mathematics 10 Solutions
17 Chapter 5 Section 1 Question 16 Page 19 a Method 1: ( ( 4 x x = 4x+ 4+ 5x = 9x + 4 Method : ( 4( 6 ( x + x+ x x+ = x + x+ x+ x x = 9x + 4 b Method 1: ( ( x x = x + 4x+ 6 Method : ( ( x x+ 7 3 x = x + 7x 3x+ 6 = x + x+ 4 6 Chapter 5 Section 1 Question 17 Page 19 a n = p n 500 = 100 p n 500 = p 100 n = p n 5 = p 100 b R = np n = n n = 5n 100 c MHR Principles of Mathematics 10 Solutions 17
18 Chapter 5 Section 1 Question 18 Page 19 s n n = + 1 Chapter 5 Section 1 Question 19 Page 19 Answers will vary. Chapter 5 Section 1 Question 0 Page 19 The number n must be 18 more than a multiple of 4. The smallest possible value for n is = 4. If 4 is divided by 8, the remainder is. Answer C 18 MHR Principles of Mathematics 10 Solutions
19 Chapter 5 Section Special Products Chapter 5 Section Question 1 Page 5 a b c d MHR Principles of Mathematics 10 Solutions 19
20 Chapter 5 Section Question Page 5 Use the appropriate pattern for squaring a binomial. a x+ 5 = x + x b ( y+ 4 = y + y ( ( ( ( ( = x + x c ( w+ 6 = ( w + ( w( 6 + ( 6 d ( = w + w e ( m+ 11 = ( m + ( m( 11 + ( 11 f ( = m + m+ 11 ( ( ( ( ( k + 7 = ( k + ( k( 7 + ( 7 c+ 10 = ( c + ( c( 10 + ( 10 g g+ 9 = g + g 9 + h ( = g + g ( ( ( ( = y + y = k + k = c + c ( ( ( ( 9 x+ 0 = x + x = x + x Chapter 5 Section Question 3 Page 5 Use the appropriate pattern for squaring a binomial. a ( x 5 = ( x ( x( 5 + ( 5 b ( = x x c ( x 9 = ( x ( x( 9 + ( 9 d ( = x x e ( v 1 = ( v ( v( 1 + ( 1 f ( = v v g ( n = ( n ( n( + ( h ( = n n+ 4 4 Chapter 5 Section Question 4 Page 5 Use the appropriate pattern for squaring a binomial. a ( x + 3y = ( x + ( x( 3y + ( 3y = x + 6xy+ 9y c ( 5c+ d = ( 5c + ( 5c( d + ( d d ( = 5c + 0cd + 4d e ( 9k + m = ( 9k + ( 9k( m + ( m f ( = 81k + 36km+ 4m 0 MHR Principles of Mathematics 10 Solutions z 3 = ( z ( z( 3 + ( 3 = z z+ 6 9 c 1 = ( c (( c 1 + ( 1 = c c+ 1 ( ( ( ( b 100 = b b = b b+ m 6 = ( m ( m( 6 + ( 6 = m m b ( x y = ( x ( x( y + ( y = 4x 4xy+ y ( ( ( ( 3a 4b = 3a 3a 4b + 4b = 9a 4ab+ 16b ( ( ( ( 4u 5v = 4u 4u 5v + 5v = 16u 40uv+ 5v
21 Chapter 5 Section Question 5 Page 5 Use the appropriate pattern for the product of a sum and a difference. a ( ( ( v+ 1 v 1 = v ( 1 b ( a 1 ( a+ 1 = ( a ( 1 = v 1 = a c ( y+ 5 ( y 5 = ( y ( 5 d ( x 7 ( x+ 7 = ( x ( 7 = y 5 e ( e 9 ( e+ 9 = ( e ( 9 f ( z+ 6 ( z 6 = ( z ( 6 = e 81 g ( x+ 1( x 1 = ( x ( 1 h ( y 3 ( y+ 3 = ( y ( 3 = x 144 Chapter 5 Section Question 6 Page 5 a ( w v( w+ v = ( w ( v b ( 3m n ( 3m+ n = ( 3m ( n c ( y+ 6x ( y 6x = ( y ( 6x d ( 3x + 4y ( 3x 4y = ( 3x ( 4y 1 = x = z Use the appropriate pattern for the product of a sum and a difference. = w v = y 36x = y 9 = 9m n = 9x 16y e ( ( + = ( ( 7g 3h 7g 3h 7g 3h = 49g 9h f ( ( + = ( ( 9x 8y 9x 8y 9x 8y = 81x 64 y MHR Principles of Mathematics 10 Solutions 1
22 Chapter 5 Section Question 7 Page 5 a ( x+ 4( x 4 = ( x ( 4 = x 16 ( x 4( x 4 ( ( + = = 1 x 16 = 16 = 1 b ( x 8 = ( x ( x( 8 + ( 8 x 16x 64 = + x ( x 8 = ( 8 = 36 ( 16x+ 64 = = 36 c ( x+ 8 = ( x + ( x( 8 + ( 8 x 16x 64 = + + x ( x + 8 = ( + 8 = 100 ( + 16x+ 64 = = 100 MHR Principles of Mathematics 10 Solutions
23 d ( x 10( x+ 10 = ( x ( 10 = x 100 ( x 10( x 10 ( 10( + = + 10 = 96 x 100 = 100 = 96 e ( x+ 11( x 11 = ( x ( 11 = x 11 ( x ( x ( ( = = 117 f x 11 = 11 = 117 ( x+ 1 = ( x + ( x( 1 + ( = x + x+ x ( x + 1 = ( + 1 = 196 ( + 4x+ 144 = = 196 g ( x 7 = ( x ( x( 7 + ( 7 = x x x ( x 7 = ( 7 = 5 ( 14x+ 49 = = 5 MHR Principles of Mathematics 10 Solutions 3
24 h ( x 30( x+ 30 = ( x ( 30 = x 900 ( x ( x ( ( = = 896 x 900 = 900 = 896 Chapter 5 Section Question 8 Page 6 ( A= π r+ k ( r ( r( k ( k = π + + ( r rk k = π + + = π r + πrk + πk Chapter 5 Section Question 9 Page 6 a b A= ( x+ 5( x+ 5 = x + x c Increase in area = x + 10x+ 5 x = 10x MHR Principles of Mathematics 10 Solutions
25 Chapter 5 Section Question 10 Page 6 a The vertex is (, 0. b y = ( x+ ( x ( x( ( = + + = x + x+ 4 4 c L.S. = y = R.S. = x + x = ( 4( = 0 L.S. = R.S The point (, 0 satisfies the equation y= x + 4x+ 4. Chapter 5 Section Question 11 Page 6 a A= ( 3x+ y( 3x y ( 3x ( y = = 9x 4y b = ( + ( ( Change in area 3x y 3x y 3x = 9x 4y 9x = 4y c A= 9x 4y ( 8 ( 5 = 9 4 = 476 Change in area = 4y = 4 ( 5 = 100 The area of the rectangle is 476 cm. The change in area is 100 cm less. MHR Principles of Mathematics 10 Solutions 5
26 Chapter 5 Section Question 1 Page 6 Method 1: A= x+ x + ( ( ( 4 ( x ( = + 8 = + x = + x Method : ( A= x + 4x ( ( ( ( = x x + + 4x x x x = x = + 4 The expressions are equivalent. Chapter 5 Section Question 13 Page 6 a b ( x ( x Exposed area = ( x ( x( 5 ( 5 ( x ( x( ( = = x + x+ x x = 1x + 1 c Exposed area = ( x+ ( x 1 ( x ( x( ( ( x ( x( 1 ( 1 = = x + x+ x + x = 1x MHR Principles of Mathematics 10 Solutions
27 Chapter 5 Section Question 14 Page 6 ( ( a 31 9 = b = = 30 1 ( ( = 60 1 = = = 899 = 3599 c = ( 100 1( = = = 9999 d = ( ( 70 1 = 70 1 = = 4899 Chapter 5 Section Question 15 Page 6 ( ( 3 8 = = 30 = = 896 ( ( a = b 35 5 = = 80 4 ( ( = 30 5 = = = 6384 = 875 c 96 = ( ( d = = = 9984 ( ( = = 80 3 = = 6391 Chapter 5 Section Question 16 Page 7 a h= 5 t b ( MHR Principles of Mathematics 10 Solutions 7
28 c h ( t = ( t (( t ( = ( t t = = + + 5t 30t = + 5t 30t 35 Chapter 5 Section Question 17 Page 7 a R= ( x( x = x + 448x+ x = x+ x b R= x+ x ( ( 000 = = The resolution of the new CCD is 14.7 megapixels. Chapter 5 Section Question 18 Page 7 Solutions for Achievement Checks are shown in the Teacher s Resource. Chapter 5 Section Question 19 Page 7 4 a ( x = ( x ( x ( x 4x 4( x 4x 4 = = x 4x + 4x 4x + 16x 16x+ 4x 16x x x x x = b ( x+ 3( x 5( 4x+ 7 = ( x+ 3( 4x + 7x 0x 35 = ( x+ 3( 4x 13x 35 = x x x+ x x = x x x MHR Principles of Mathematics 10 Solutions
29 c ( x + 5x+ 3 = ( x + 5x+ 3( x + 5x = x + x + x + x + x + x+ x + x = x + x + x + x+ 3 d ( 5x = ( 5x ( 5x ( 5x ( 5x 0x 4 = + = x 100x 0x 50x 40x 8 = x x + x Chapter 5 Section Question 0 Page a Δ E = mv m( v b Δ E = mv m( v x = mv m( v 10v = = 5mv 1.5m c Δ E = mv m( v 5 mv mv mv m 1 1 Δ E = mv m( v x 1 1 = mv m v xv + x 1 1 = = mvx 0.5mx ( mv mv mvx mx MHR Principles of Mathematics 10 Solutions 9
30 Chapter 5 Section Question 1 Page 7 a b ( + 1 ( + 1 ( +1 n n n n n n = n = ( n MHR Principles of Mathematics 10 Solutions
31 Chapter 5 Section 3 Common Factors Chapter 5 Section 3 Question 1 Page 34 a The GCF is x. b The GCF is a. c The GCF is x. d The GCF is k 4 / e The GCF is m. f The GCF is 3y. Chapter 5 Section 3 Question Page 34 a b MHR Principles of Mathematics 10 Solutions 31
32 c Chapter 5 Section 3 Question 3 Page 34 ( a 15w+ 5z = 5 3w+ 5z b 3a 11 b cannot be factored c 17ca 8cd c( 17a 8d = d 9y 8y 3 = y( 9 8y + = ( + 4g 8g + 6= ( g 4g e 1b 18b 6b b 3 f + n 5 + 1n 4 6n 3 = n 3 ( n + 6n 3 g 7h 3m 5 k cannot be factored h Chapter 5 Section 3 Question 4 Page 34 a 14x y 16xy 3 xy( 7x 8y + = + b 10km 3 6km = km ( 5k 3 ( c 8 sy+ 11 t cannot be factored d 66cde 4 cde = cde 3c 1 e 7 gh mn 13 pq cannot be factored f 5fg 5fg + 0f g = 5fg g 5+ 4f + ( g 7r s 18r 3 s 36rs 3 = 9rs ( 3r r 4s h 4n p n 4 p 1n 3 p = n p ( p+ 5n 6n 3 MHR Principles of Mathematics 10 Solutions
33 Chapter 5 Section 3 Question 5 Page 34 a 3x( x ( x+ 8 = ( x+ 8( 3x+ b c y x 5 4 x 5 cannot be factored d 5 ab ( cb ( + 1 = ( b+ 1( a+ 9c ( + ( + 4s( r+ u t( r+ u = ( r+ u( 4s t Chapter 5 Section 3 Question 6 Page 34 a mx + my + x + y = ( mx + my + ( x + y = m( x+ y + ( x+ y = ( x+ y( m+ c ay + 3ay + 4y + 1= ( ay + 3ay + ( 4y + 1 ay( y 3 4( y 3 ( y 3( ay 4 = = + + b x + 3x+ x+ 6= ( x + 3x + ( x+ 6 x( x 3 ( x 3 ( x 3( x = = + + d 6x + 9x x 3= ( 6x + 9x + ( x 3 3x( x 3 ( x 3 ( x 3( 3x 1 = + + = + e 16v 1v 1v+ 9 = ( 16v 1v + ( 1v+ 9 4v( 4v 3 3( 4v 3 ( 4v 3( 4v 3 = = ( 4v 3 = Chapter 5 Section 3 Question 7 Page 34 Answers will vary. Sample answers are shown. a 1x 18y 6( x 3 + = + y b x 3 + x + x= x( x + x+ 1 c 5y + 10y 3 = 5y ( 1+ y d ab 3 + 4ab ab 4 5 = ab 3 ( 1+ ab+ 3ab MHR Principles of Mathematics 10 Solutions 33
34 Chapter 5 Section 3 Question 8 Page 35 a b P= l+ w ( l w = + P= l+ w ( ( 9 = 15 + = 48 ( ( 15 9 ( P= l+ w = + = 4 = 48 The perimeter is 48 cm using either formula because the formulas are equivalent. Chapter 5 Section 3 Question 9 Page 35 a b SA = πr + πrh ( h = πr r+ SA = πr + πrh ( π( ( 8 = π = 66π ( ( 3( 3 8 SA = πr r + h = π + = 66π The surface area is 66π, or about 07.3 cm, using either formula because the formulas are equivalent. Chapter 5 Section 3 Question 10 Page 35 ( ( x x x + x= x + x = x( x ( 6x 9 = = x + There are four possible lengths and widths. Chapter 5 Section 3 Question 11 Page 35 a 5x( 7 y + 4( y 7 = 5x( y 7 + 4( y 7 = ( y 7( 5x+ 4 b 5y( x 1 + ( 1 x = 5y( x 1 ( x 1 = ( x 1( 5y 34 MHR Principles of Mathematics 10 Solutions
35 Chapter 5 Section 3 Question 1 Page 35 a ( ( ( SA = x 1 + x + + x + 5 b SA = ( x 1 + ( x + + ( x + 5 = 4x 4x+ 1+ 4x + 8x+ 4+ 4x + 0x+ 5 = + + 1x 4x 30 c SA = x + x ( x x = Chapter 5 Section 3 Question 13 Page 35 a A= ( 8x( 4x ( 4y( y = 3x 8y ( x y = 84 ( x y( x y = 8 + b A= πr πr ( R r = π = π( R r( R+ r Chapter 5 Section 3 Question 14 Page 35 y = x 3x ( x 3 = x The x-intercepts are 0 and 1.5. Chapter 5 Section 3 Question 15 Page a x + y = ( x + 3y b a 3 ab= a( a b km c km 4 km 3 + km = ( k 3 3m+ k This can simplify the operations when the values of the variables are known because you can wait until the last step to divide. MHR Principles of Mathematics 10 Solutions 35
36 Chapter 5 Section 3 Question 16 Page 35 3a+ 8b= 1 ( a+ b = ( a+ 40b= 60 Answer C Chapter 5 Section 3 Question 17 Page 35 Let the five consecutive numbers be x, x + 1, x +, x + 3, and x + 4. ( ( ( ( x + x+ + x+ + x+ + x+ = x + x + x+ + x + x+ + x + x+ + x + x+ 16 = + + 5x 0x 30 ( x x = The sum is divisible by MHR Principles of Mathematics 10 Solutions
37 Chapter 5 Section 4 Factor Quadratic Expressions of the Form x +bx + c Chapter 5 Section 4 Question 1 Page 40 a b = ( + 3( + 1 x + 7x+ 10= ( x+ 5( x+ x x x x c d = ( + 4( + x + 4x+ 4= ( x+ ( x+ x x x x Chapter 5 Section 4 Question Page 40 a The integers are 5 and 9. b The integers are 3 and. c The integers are and 5. d The integers are 10 and. MHR Principles of Mathematics 10 Solutions 37
38 Chapter 5 Section 4 Question 3 Page = ( + ( + j + 1 j+ 7 = ( j+ 9( j+ 3 a x 7x 10 x 5 x b c k + 5k + 4= ( k + 4( k + 1 d p + 9 p+ 1 is not factorable e w 11w 5 is not factorable f + + d + 10d + 4 = ( d + 6( d + 4 Chapter 5 Section 4 Question 4 Page 40 ( ( a m 7m+ 10= m 5 m b x 5x+ 7 is not factorable c y 5y+ 4= ( y 4( y 1 d r 16r+ 64 = ( r 8 e w 9w 4 is not factorable f + q 10q+ 9 = ( q 9( q 1 Chapter 5 Section 4 Question 5 Page 41 a a 3a 10= ( a 5( a+ b s + 3s 10= ( s ( s+ 5 c d 8d 9 ( d 9( d 1 = + d e g 5g 14 ( g 7( g = + f r f + 7 f 6 is not factorable + r 6 is not factorable g x x 4 ( x 6( x 7 + = + h b b 4 is not factorable Chapter 5 Section 4 Question 6 Page 41 x + 18x+ 80 = x+ 10 x+ 8 a ( ( x + 10 = = 5 x + 8= = 3 The length is 5 cm and the width is 3 cm. x 15x+ 50 = x 5 x 10 b ( ( x 5= 15 5 = 10 x 10 = = 5 The length is 10 cm and the width is 5 cm. 38 MHR Principles of Mathematics 10 Solutions
39 Chapter 5 Section 4 Question 7 Page 41 a 3x + 1x+ 9= 3( x + 4x+ 3 = 3( x+ 1( x+ 3 c 5z + 40z+ 60= 5( z + 8z+ 1 = 5( z+ ( z+ 6 b d d + 56 = ( d 11d + 8 = ( d 4( d 7 d 4s 8s 3= 4( s s 8 ( s ( = 4 4 s+ ( e bx + 10bx 4b = b x + 10x 4 f ( ( = b x+ 1 x ( 3 x x x x x x = = x( x+ 6( x+ 1 Chapter 5 Section 4 Question 8 Page 41 Answers may vary. For example: a b = 8 or b = 7 b b = 5 or b = 4 x + 8x+ 1= x+ x+ 6 x 5x+ 4= x 1 x 4 ( ( ( ( x x x x = ( ( ( ( 4 + 4= x x x x c b = 7 or b = d b = 9 or b = 3 x 7x 8= ( x 8( x+ 1 x + 9x 10= x 1 x+ 10 x x 8= ( x 4( x+ x + 3x 10= ( x+ 5( x ( ( Chapter 5 Section 4 Question 9 Page 41 a c = 5 or c = 9 b c = or c = 6 x + 6x+ 5= ( x+ 5( x+ 5 x + 6x+ 9= ( x+ 3( x+ 3 x x = ( x ( x+ 1 x x 6= ( x 3( x + c c = 9 or c = 0 d c = 3 or c = 8 x 8x 9= ( x 9( x+ 1 x 8x 0= ( x 10( x+ x + x 3= ( x+ 3( x 1 x + x 8= ( x+ 4( x Chapter 5 Section 4 Question 10 Page 41 x+ x+ = x + x a ( ( ( ( x + y x+ 3y = x + 4xy+ 3y c ( ( ( ( x x+ = x + x x y x+ 9y = x + 7xy 18y x+ x = x x b ( ( ( ( x + 4y x 6y = x xy 4y d ( ( ( ( x x = x x x 6y x 9y = x 15xy+ 54y The coefficients of corresponding terms in the simplified forms are the same. MHR Principles of Mathematics 10 Solutions 39
40 Chapter 5 Section 4 Question 11 Page 41 a a + 11ab+ 4b = ( a+ 3b( a+ 8b b k 11km+ 18m = ( k m( k 9m c c + 4cd 1d = ( c+ 7d( c 3d d x 6xy 16y = ( x 8y( x + y Chapter 5 Section 4 Question 1 Page 41 Answers will vary. Chapter 5 Section 4 Question 13 Page 41 x 4x 1= x 6 x+ a ( ( b The x-intercepts are and 6. c x =, (, 16 Chapter 5 Section 4 Question 14 Page 41 a h= t + t ( t t = ( t ( = 5 4 t+ 1 b The binomial factors can be used to find the t-intercepts, one of which represents when the ball will land on the ground. 40 MHR Principles of Mathematics 10 Solutions
41 Chapter 5 Section 4 Question 15 Page 41 a The equations are alike because the coefficients are the same. They are different because the degrees of the variables are different. x 4 + 9x + 0= x + 5 x + 4 b ( ( Chapter 5 Section 4 Question 16 Page = ( + 5( + 6 x 4 7xy + 1y = ( x 3y( x 4y 4 a x x x x b c x 6 3x 3 54= ( x 3 9( x ( d ( x + ( x = ( x + ( x = 3( x 5 ( x = 3( x 7( x Chapter 5 Section 4 Question 17 Page 41 3 a ( x+ = ( x+ ( x+ ( x+ ( x ( x 4x 4 = = x + 4x + 4x+ x + 8x+ 8 3 = x + 6x + 1x+ 8 b x 3 + 9x + 7x+ 7= ( x+ 3 3 c 8a a b+ 150ab + 15b 3 = ( a+ 5b 3 MHR Principles of Mathematics 10 Solutions 41
42 Chapter 5 Section 5 Factor Quadratic Expressions of the Form ax +bx + c Chapter 5 Section 5 Question 1 Page 46 a ( ( x + 5x+ 3= x+ 1 x+ 3 b ( ( 3x 7x+ 4= x+ 1 3x+ 4 c ( ( 6x + 5x+ 1= x+ 1 3x+ 1 4 MHR Principles of Mathematics 10 Solutions
43 d ( ( 6x + 11x+ 4= x+ 1 3x+ 4 Chapter 5 Section 5 Question Page 46 a x + 7x+ 5= x + x+ 5x+ 5 b ( x x ( 5x 5 = x( x 1 5( x 1 ( x 1( x 5 = = + + c 4k + 15k + 9= 4k + 1k + 3k + 9 d ( 4k 1k ( 3k 9 = k( k 3 3( k 3 ( k 3( 4k 3 = = y + y+ = y + y+ y+ ( 6y 16y ( 3y 8 = ( ( ( 3y 8( y 1 = y 3y y+ 8 = + + 3m + 10m+ 8= 3m + 6m+ 4m+ 8 ( 3m 6m ( 4m 8 = m( m 4( m ( m ( 3m 4 = = + + e 10w + 15w+ 3 is not factorable f 1q + 17q+ 6 = 1q + 9q+ 8q+ 6 ( 1q 9q ( 8q 6 = q( 4q 3 ( 4q 3 ( 4q 3( 3q = = + + MHR Principles of Mathematics 10 Solutions 43
44 Chapter 5 Section 5 Question 3 Page 46 a 4x 11x+ 6= 4x 8x 3x+ 6 b ( 4x 8x ( 3x 6 = + + 4x( x 3( x ( x ( 4x 3 = = c 6c 3c+ 1 is not factorable d 5n 11n+ 6= 5n 6n 5n+ 6 ( 5n 6n ( 5n 6 = + + n( 5n 6 1( 5n 6 ( 5n 6( n 1 = = a a+ = a a a+ ( 6a 6a ( a 1 = + + 6a( a 1 1( a 1 ( a 1( 6a 1 = = e 9b 4b+ 7= 9b 1b 3b+ 7 f 15k 19k + 6 = 15k 10k 9k + 6 ( 9b 1b ( 3b 7 = + + 3b( 3b 7 1( 3b 7 ( 3b 7( 3b 1 = = Chapter 5 Section 5 Question 4 Page 46 ( 15k 10k ( 9k 6 = + + 5k( 3k 3( 3k ( 3k ( 5k 3 = = a 3y + 4y 7= 3y 3y+ 7y 7 b ( 3y 3y ( 7y 7 = + 3y( y 1 7( y 1 ( y 1( 3y 7 = + = + m + 3m 9= m 3m+ 6m 9 ( m 3m ( 6m 9 = + m( m 3 3( m 3 ( m 3( m 3 = + = + c 8k 6k 5= 8k 10k + 4k 5 d 1 y + y 1 = 1 y + 4 y 3y 1 ( 8k 10k ( 4k 5 = + ( ( ( 4k 5( k 1 = k 4k 5 + 4k 5 = + ( 1 y 4 y ( 3y 1 = + + 4y( 3y 1 1( 3y 1 ( 3y 1( 4y 1 = + + = + e 9x 15x 4 cannot be factored f h h = h h+ h ( 5h 15h ( h 3 = + h( h ( ( h 3( 5h 1 = h 3 = + 44 MHR Principles of Mathematics 10 Solutions
45 Chapter 5 Section 5 Question 5 Page 46 a b c d e f x + xy+ y = x + xy+ xy+ y ( ( = 3x + 6xy + xy + y 3x( x y y( x y ( x y( 3x y = = + + 6m + 13mn+ n = 6m + 1mn+ mn+ n ( ( = 6m + 1mn + mn+ n 6m( m n n( m n ( m n( 6m n = = + + p pq+ q = p pq pq+ q ( ( = p 10pq pq 5q p( p 5q q( p 5q ( p 5q( p q = = = c cd d c cd cd d ( ( = 6c 1cd + 5cd 10d 6cc ( d 5dc ( d ( c d( 6c 5d = + = x xy y = x xy+ xy y ( ( = 9x 1xy + 3xy 4y 3x( 3x 4y y( 3x 4y ( 3x 4y( 3x y = + = + 6d + de e = 6d + 4de 3de e ( ( = 6d + 4de + 3de e d( 3d e e( 3d e ( 3d e( d e = + + = + MHR Principles of Mathematics 10 Solutions 45
46 Chapter 5 Section 5 Question 6 Page 46 a b c k k + = k k = k k k ( k k ( k = ( ( ( k ( k = k k 3 1 k 3 = 3 1 p + p = p + p = p + p p ( p p ( p = p( p ( p ( p ( p = = m m = m m = m m+ m ( m m ( m m( m ( m ( m ( m = = = d 10x + 15x 10 = 5 x + 3x = x + x x 5 4 ( x x ( x = x( x ( x ( x ( x = = e 10r r+ 4 = 5r 11r+ = + 5r 10r r ( r r ( r = r( r ( r ( r ( r = 5 1 = MHR Principles of Mathematics 10 Solutions
47 f 8y y+ 1= 4y 11y+ 6 = y y y ( y y ( y = y( y ( y ( y ( y = 4 3 = 4 3 Chapter 5 Section 5 Question 7 Page 46 a b 4x + 1x+ 5= 4x + 10x+ x+ 5 ( 4x 10x ( x 5 = ( ( ( x 5( x 1 = x x+ 5 + x+ 5 = + + x x+ = x x x ( 7x 1x ( x 6 = + + 7x( x 3 ( x 3 ( x 3( 7x = = ( 4x + 1x+ 5= = 45 ( x+ 5( x+ 1 = ( ( + 5 ( ( + 1 = 45 ( 7x 3x+ 6= = 1 ( x 3( 7x = (( 3 ( 7( = 1 ( ( c 15x x 8 = 15x 1x+ 10x 8 ( 15x 1x ( 10x 8 = + ( ( ( 5x 4( 3x = 3x 5x 4 + 5x 4 = + d 8x + 14x 4= ( 4x + 7x = ( 4x + 8x + ( x x( x ( x ( x ( x = = ( 15x x 8 = 15 8 = 48 ( 5x 4( 3x+ = ( 5( 4 ( 3( + = 48 ( ( ( 8x + 14x 4= = 56 ( x+ ( x = (( + ( 4( = 56 e x x+ = x x x ( 6x 10x ( 9x 15 = + + x( 3x 5 3( 3x 5 ( 3x 5( x 3 = = ( x x+ = = 1 ( 3x 5( x 3 = ( 3( 5 ( ( 3 = 1 ( MHR Principles of Mathematics 10 Solutions 47
48 f 5x + 18x+ 9= 5x + 15x+ 3x+ 9 ( 5x 15x ( 3x 9 = x( x 3 3( x 3 ( x 3( 5x 3 = = + + ( ( 5x + 18x+ 9= = 65 ( x+ 3( 5x+ 3 = (( + 3 ( 5( + 3 = 65 The results are the same because the expressions are equivalent. Chapter 5 Section 5 Question 8 Page 46 Answers may vary. For example: a n = 17 or n = 8 x + 17n+ 16 = x+ 16 x+ 1 ( ( ( ( x n x x = b n = 8 or n = 0 3y + 8y+ 5= 3y + 5y+ 3y+ 5 ( 3y 5y ( 3y 5 = y( 3y 5 1( 3y 5 ( 3y 5( y 1 = = + + y + y+ = y + y+ y ( 3y 15y ( 5y 5 = y( y 5 5( y 5 ( y 5( 3y 5 = = + + c n = 13 or n = 3 6a + 13ab+ 7b = 6a + 6ab+ 7ab+ 7b ( ( = 6a + 6ab + 7ab+ 7b 6a( a b 7b( a b ( a b( 6a 7b = = + + a + ab+ b = a + ab+ ab+ b ( ( = 6a + 1ab + ab+ 7b 3a( a 7b b( a 7b ( a 7b( 3a b = = MHR Principles of Mathematics 10 Solutions
49 Chapter 5 Section 5 Question 9 Page 46 Answers may vary. For example: a k = 44 or k = 8 36m + 8m 44 = 4 9m + m 11 = m + m m ( m m ( m = m( m ( m ( m ( m = = m + m = m + m = m + m m ( m m ( m = m( m ( m ( m ( m = = b k = 4 or k = 60 18y 4 y+ 4 = 6 3y 7 y+ 4 = y y y ( y y ( y y( y ( y ( y ( y = = y y = y y = y y+ y = ( y y ( y = y( y ( y ( y ( y = = MHR Principles of Mathematics 10 Solutions 49
50 c k = 56 or k = p 7 pq+ 16q = 8 7 p 9 pq+ q = 8 7p 7pq pq+ q = 8 ( 7p 7pq ( pq q + + = 8 7p( p q q( p q = 8( p q( 7p q 81p 7 pq+ 16q = 81p 36 pq 36 pq+ 16q = 81p 36 pq + 36 pq + 16q ( ( 9p( 9p 4q 4q( 9p 4q ( 9p 4q( 9p 4q ( 9p 4q = = = Chapter 5 Section 5 Question 10 Page 46 If there are two integers whose product is a c and whose sum is b, then ax + bx + c can be factored over the integers. Chapter 5 Section 5 Question 11 Page 46 It is easier to factor ax + bx + c if a and c are prime numbers because there are fewer factors to check. Chapter 5 Section 5 Question 1 Page 47 a x + x = x + x x ( 6x 16x ( 3x 8 = + + ( ( ( 3x 8( x 1 = x 3x x+ 8 = + The length is 3x + 8 and the width is x 1. b P = ( 3x+ 8 + ( x 1 = ( 3( ( ( 10 1 = 114 A= x + x ( 10 ( 10 = = 7 If x = 10 cm, the perimeter is 114 cm and the area is 7 cm. 50 MHR Principles of Mathematics 10 Solutions
51 Chapter 5 Section 5 Question 13 Page 47 h = t + t ( t t ( t t t ( t t ( t = = = t( t 5 ( t 5 ( t 5( 5t = + = + The rocket hits the ground at t = 5, or 5 s. Chapter 5 Section 5 Question 14 Page 47 a r = 0.008( p 3000( p 1000 b The range must have positive values. This occurs for 1000 p c The maximum occurs for a value of p halfway between 1000 and 3000, or 000. Chapter 5 Section 5 Question 15 Page 47 R = x x = x x 360 = x + 18x 0x 360 = ( x 18x ( 0x = = x( x ( x ( x ( x There is more than one possible answer. Examples: Number sold: 0 x, price per jacket: 36 + x Number sold: 40 x, price per jacket: 18 + x Chapter 5 Section 5 Question 16 Page 47 Solutions for Achievement Checks are shown in the Teacher s Resource. MHR Principles of Mathematics 10 Solutions 51
52 Chapter 5 Section 5 Question 17 Page 47 a b c = x x x x x 4 ( 5x 15x ( 3x 9 5x ( x 3 3( x 3 ( x 3( 5x 3 = = = + + 7x 13x y + 6y = 7x 7x y 6x y + 6y ( 7 7 ( 6 6 7x ( x y 6y ( x y ( x y ( 7x 6y = x xy + xy + y 4 4 = = 6x + 13x y 8y = 6x + 16x y 3x y 8y ( ( ( ( 3 ( 3x 3 3 8y ( x 3 y = x + xy + xy y = x 3x + 8y y 3x + 8y = + 6 d 10m 7m n 1n = 10m 15m n + 8m n 1n ( ( ( ( 3 ( m 3 3n ( 5m 4n = m m n + m n n = 5m m 3n + 4n m 3n = + Chapter 5 Section 5 Question 18 Page 47 a ( x a ( x a ( x a ( x a ( x a = = x+ a + x+ a + x+ a + 1 = x+ a x+ a x+ a + 1 ( ( ( ( ( ( ( x a 1 ( x a 1 ( x a 1( x a 1 = = b ( x b ( x b ( x b ( x b ( x b = ( x b ( x b ( x b = ( x b ( x b 1 ( x b = ( x b ( x b ( x b 1( x b = = MHR Principles of Mathematics 10 Solutions
53 Chapter 5 Section 5 Question 19 Page 47 a = x x x x x ( 8x 14x ( 4x 7 = + + ( ( ( 4x 7( x 1 = x 4x x+ 7 = + Answers may vary. The shape could be a rectangle with dimensions (x 1 and (4x + 7, a parallelogram with base (x 1 and height (4x + 7, or a triangle with base (4x and height (4x + 7, or base (x 1 and height (8x b 4x 1x y+ 9xy = x( 4x 1xy+ 9y = x( 4x 6xy 6xy+ 9y = ( + ( + x 4x 6xy 6xy 9y = x x x 3y 3y x 3y = x x y x y ( ( ( 3 ( 3 ( 3 = x x y The shape is a square-based prism with side length (x 3y and height x. MHR Principles of Mathematics 10 Solutions 53
54 Chapter 5 Section 6 Factor a Perfect Square Trinomial and a Difference of Squares Chapter 5 Section 6 Question 1 Page 53 Use the pattern for a difference of squares. ( ( ( a x 16 = x 4 b = x+ 4 x 4 y ( y ( y ( 100 = 10 = + 10 y 10 c 9k 36= 9( k 4 ( k = 9 = 9( k + ( k d 4a 11= ( a 11 ( a ( = + 11 a 11 ( w ( w ( e f 36w 49 = 6 7 = w 7 ( ( ( ( p ( p ( 144 p 1 = 1 1 = p 1 ( g 16n 5 = 4n 5 h 100g 81 = 10g 9 = 4n+ 5 4n 5 = ( 10g+ 9( 10g 9 Chapter 5 Section 6 Question Page 53 Use the pattern for a difference of squares. ( ( h 5d = ( h ( 5d = ( m+ 7n( m 7n = ( h+ 5d( h 5d a m 49n = m 7n b ( ( c( c 100 9c = 10 3c d = c 169a 49b = ( 13a ( 7b = ( 13a+ 7b( 13a 7b e 5x 36y = ( 5x ( 6y ( ( g 16 8s = ( 81 s = 5x + 6y 5x 6y ( s = 9 = 9+ 9 ( s( s f 16c 9d = ( 4c ( 3d ( ( = 4c+ 3d 4c 3d h 75h 7g = 3( 5h 9g ( h ( g = = 35h+ 3g 5h 3g ( ( 54 MHR Principles of Mathematics 10 Solutions
55 Chapter 5 Section 6 Question 3 Page 53 Use the appropriate perfect square trinomial pattern. ( ( ( ( a x + 1x+ 36 = x + x b k + 18k+ 81 = k + k ( x 6 = + ( ( ( ( ( k 9 = + ( ( ( ( c y 6y+ 9= y y d ( y 3 = ( ( ( ( e x + 0x+ 100 = x + x f ( x 10 = + ( ( ( ( m 14m+ 49 = m m ( m 7 = ( ( ( ( ( 8 r 64 16r+ r = 8 8 r + r = Chapter 5 Section 6 Question 4 Page 53 Use the appropriate perfect square trinomial pattern. ( ( ( ( ( c 3 a 4c + 1c+ 9= c + c b 16k 8k + 1 = 4k 4k = + ( ( ( ( ( 4k 1 = ( ( ( ( c 5x + 70x+ 49 = 5x + 5x d ( 5x 7 = + e 100c 180c+ 81 = 10c 10c f ( ( ( ( ( 10c 9 = ( ( ( ( 9y 30y+ 5= 3y 3y ( 3y 5 = ( ( ( ( y+ 64y = y + 8y ( 5 8y = + Chapter 5 Section 6 Question 5 Page 54 a y is not squared. b 107 ( 6( 9 c 10 is not a perfect square. d The expression is a sum of squares, not a difference of squares. MHR Principles of Mathematics 10 Solutions 55
56 Chapter 5 Section 6 Question 6 Page 54 a 4x + 8xy + 49y = ( x + ( x( 7y + ( 7y ( x 7y = + b 9k 4k + 16m = ( 3k ( 3k( 4m + ( 4m ( 3k 4m = c d 5 p + 60 pq+ 144 q cannot be factored 9y 7 x cannot be factored e a 8ab+ 98b = ( a 14ab+ 49b ( a ( a( b ( b = ( a b = 7 f 196n 144m = 4( 49n 36m ( n ( m = = 47 ( n 6m( 7n+ 6m g 5x + 70xy+ 14 y cannot be factored h 100 f 10 fg+ 36g = 4( 5 f 30 fg+ 9g ( f ( f ( g ( g = ( f g = i 400 p 900 pq = 100 p( 4 p 9q ( ( = 100 p p 3q = 100 p( p+ 3q( p 3q 56 MHR Principles of Mathematics 10 Solutions
57 Chapter 5 Section 6 Question 7 Page 54 a ( ( A= x+ 5 x 3 b A= ( x+ 5 ( x 3 = 4x + 0x+ 5 x + 6x 9 = x + x = x + x+ x ( 3x 4x ( x 16 = x( x 8 ( x 8 ( x 8( 3x = = + + Chapter 5 Section 6 Question 8 Page 54 a b = or b = b b = 0 or b = 0 y + y+ 11 = ( y+ 11 4x + 0x+ 5= x+ 5 y y y ( + 11 = 11 c b = 4 or b = 4 d b = 5 ( = n np p n p ( = 3 7 n np p n p ( ( 4x 0x+ 5= x 5 w w w ( = + 5 e b = 5 f b = 11 or b = 11 81m 90m+ 5 = ( 9m 5 16 x 88xy+ 11y = ( 4x 11y = ( 4x + ( 11y Chapter 5 Section 6 Question 9 Page 54 Answers may vary. For example: a k = 4 or k = 9 m 4n = ( m+ n( m n m 9n = ( m+ 3n( m 3n b k = 1 or k = 5 x 9= x+ 3 x 3 ( ( ( ( 5x 9 = 5x+ 3 5x 3 c k = 16 or k = 5 49c 16 = 7c+ 4 7c 4 ( ( ( ( 49c 5 = 7c+ 5 7c 5 MHR Principles of Mathematics 10 Solutions 57
58 Chapter 5 Section 6 Question 10 Page 54 a 9a b 4abcd + 16c d = ( 3ab ( 3ab( 4cd + ( 4cd ( 3ab 4cd = b 5 ( x+ 5 = 15 ( x+ 5 = 15 + ( x ( x+ 5 = ( 0 + x( 10 x 3c+ 3c = 3c+ + 3c 3c+ 3c = 6c 4 c ( ( ( ( ( ( ( ( = 4c d 4x + 6x+ 9 cannot be factored Chapter 5 Section 6 Question 11 Page 54 ( 9x + 30x+ 5= 3x+ 5 This is a perfect square. The figure could be a square, or a parallelogram whose base is equal to its height. Chapter 5 Section 6 Question 1 Page 54 3 a x x + x = x( x x+ 1 ( ( ( 1 ( 1 = x x x + = x x ( 1 The height is x. The length and width are both x 1. b The box is a square-based rectangular prism, so the top and bottom are squares with area (x 1 and the four sides are rectangles with area x(x MHR Principles of Mathematics 10 Solutions
59 Chapter 5 Section 6 Question 13 Page 54 a Middle: ( x ( + x 1 Bottom: ( x ( + 5 x+ b Middle: ( ( x + x 1 = 4x + 8x+ 4 4x + 4x 1 Bottom: ( ( = 1x + 3 ( x = x+ 5 x+ = 4x + 0x+ 5 4x 8x 4 c Middle: 34 ( x + 1 = 34 ( ( = 63 Bottom: 34 ( x + 7 = 34 ( (5 + 7 = 1x + 1 ( x = = 81 The exposed area of the middle layer is 63 cm. The exposed area of the bottom layer is 81 cm. Chapter 5 Section 6 Question 14 Page 54 a A= r r+ π 14π 49π ( r r = π ( r = π 7 The decrease in radius was 7 cm. πr πr 14πr+ 49π = πr πr + 14πr 49π b ( = 14πr 49π The decrease in area was (14 πr 49π cm. Chapter 5 Section 6 Question 15 Page 55 x 1= ( x+ 1( x 1 ( x 1 = ( x 1( x 1 The two expressions are not the same. MHR Principles of Mathematics 10 Solutions 59
60 Chapter 5 Section 6 Question 16 Page 55 y x x = ( x = The coordinates of the vertex are (, 0. Chapter 5 Section 6 Question 17 Page 55 a = ( ( = 6( 4 = 104 c = ( ( = 195( 1 = 195 b 37 7 = ( ( 37 7 = 64( 10 = 640 d 8 = ( 8 + ( 8 = 50( 6 = 300 Chapter 5 Section 6 Question 18 Page 55 = a s ( n b s ( n = + + = n 6n 9 = + + n 6n 5 ( n 5( n 1 = + + c s ( n = ( 10 = = n s ( 5( 1 ( 10 ( 0 s = n+ n+ = = 165 There are 165 shaded squares on the 10th diagram. d Answers will vary. Chapter 5 Section 6 Question 19 Page 55 3 V = 4πx + 0πx + 5πx = πx 4x + 0x+ 5 ( ( x = πx + 5 The figure could be a square-based prism with height πx and base side length x + 5 or a cylinder with radius x + 5 and height x. 60 MHR Principles of Mathematics 10 Solutions
61 Chapter 5 Section 6 Question 0 Page 55 a ( x 4 16= ( x ( x 4 4 b ( x ( x ( x = ( x( x 8 = ( x = c ( 5 3 ( x y = x + y x y d k 8k + 16= ( k 4 = ( k + ( k e a 6 0a ( a = + f 4 4 y x y x y x = y x y x y x = Chapter 5 Section 6 Question 1 Page 55 a k = 7 or k = 7 ( ( 4 81x + 7x + 16 = 9x x 7x + 16 = 9x 4 = ( 3x+ ( 3x b k = 0 or k = y + 0y z + 5z = y + 5z ( ( = 5 y y z z y z MHR Principles of Mathematics 10 Solutions 61
62 Chapter 5 Section 6 Question Page 55 a b Answers may vary. For example: x 1 is one of the factors of each of the expressions and the number of terms in the other factor is equal to the degree of the original expression. The terms in the other factor form a sum where the coefficient of each of the terms is one and the terms are the sum of the descending degrees of the variable starting with 1 less than the original expression. The factored form of x 4 1 does not appear to follow the pattern. When expanded, the last two terms of this factored form result in the expression x 3 + x + x + 1, which does follow the pattern c The CAS verifies that x 6 1 follows the pattern. Chapter 5 Section 6 Question 3 Page 55 3 x x x 4 x x 4x x 4x + + = a ( ( 3 = x b m 3 64 = ( m 4( m + 4m+ 16 c 3 6 ( ( 4 7 y 15z = 3y 5z 9y + 15yz + 5z Chapter 5 Section 6 Question 4 Page 55 a ( ( 8 a+ a a+ = a a + a+ a a = a b 6 3 ( ( 4 k + 16e = k + 6e k 6k e+ 36e c 343q r 4 = ( 7q 4 + 9r 8 ( 49q 8 63q 4 r r 16 6 MHR Principles of Mathematics 10 Solutions
63 Chapter 5 Section 6 Question 5 Page 55 4 a ( a+ b = ( a+ b ( a+ b ( a ab b ( a ab b = = a a b a b a b a b ab a b ab b = a + 4a b+ 6a b + 4ab + b b 81x 4 16x 3 y + 16x y 96xy y 4 = ( 3x y 4 Chapter 5 Section 6 Question 6 Page 55 ( a b = a ab+ b = 9 Answer D = + a b ab ( = 15 3 MHR Principles of Mathematics 10 Solutions 63
64 Chapter 5 Review Chapter 5 Review Question 1 Page 56 ( ( a x+ 5 x+ 8 = x + 8x+ 5x+ 4 b = x + x x + 3y x 6y = x 6xy + 3xy 18y c ( ( = x 3xy 18y d ( ( 5a 6b a+ 9b = 10a + 45ab 1ab 54b = 10a + 33ab 54b 0 ( ( Chapter 5 Review Question Page 56 a ( k + ( k 7 = ( k 7k + k 14 = ( k 5k 14 = k + k b w( w 7v( w 3v = w( w 3wv 7wv+ 1v = w( w 10wv+ 1v = w 10w v+ 1wv 3 c 7x ( 7x + 3y( 3x + 9 y = 7x ( 1x + 63xy + 9xy + 7 y = 7x( 1x + 7xy+ 7y = 147x + 504x y+ 189xy 3 y+ 1 y+ 8 + y 8 y+ 1 = y + 8y+ y+ 8+ y + y 8y 8 d ( ( ( ( = + y y x 1 x 4 = x 4x x+4 = x x+ 5 4 e 4 x 6 4x x+ 7 11x 4 = 4 8x 10x 4x x 44x+ 77x 8 ( ( ( ( ( ( = 4( 8x 34x ( 11x + 33x = x + x + x + x = x + x MHR Principles of Mathematics 10 Solutions
65 Chapter 5 Review Question 3 Page 56 ( 9 7( A = x x+ + x = x x x = x + 16x Chapter 5 Review Question 4 Page 56 a b Chapter 5 Review Question 5 Page 56 Use the appropriate pattern for squaring a binomial. a ( ( x+ 6 = x + ( x( 6 + ( 6 b ( k + 8 = k + k = x + x ( ( ( ( c ( p+ 7 = p + p d ( = p + p ( ( ( ( = k + k r = ( r ( r( + ( = r r+ 4 4 ( ( ( ( e ( e 9 = e e f ( = e e ( ( ( ( q 0 = q q = q q MHR Principles of Mathematics 10 Solutions 65
66 Chapter 5 Review Question 6 Page 56 Use the appropriate pattern for the product of a sum and a difference. a ( b+ 6( b 6 = ( b ( 6 b ( a 7 ( a+ 7 = ( a ( 7 = b 36 c ( y+ 1 ( y 1 = ( y ( 1 d ( x 15 ( x+ 15 = ( x ( 15 = y 144 e ( e 10 ( e+ 10 = ( e ( 10 f ( x+ 6( x 6 = ( x ( 6 = e 100 Chapter 5 Review Question 7 Page 56 Use the appropriate pattern for squaring a binomial. ( ( ( ( ( a y+ 4x = y + y 4x + 4x b ( = y + 8xy+ 16x = x = a = x 5 ( ( ( ( 7m n = 7m 7m n + n = 49m 14mn+ n ( ( ( ( c ( c+ 9d = c + c 9d + 9d d = 4c + 36cd + 81d ( ( ( ( 5x+ 7y 5x 7y = 5x 7y ( x y = 5 49 = 50x + 98y e ( 3a 8c ( 3a+ 8c = ( 3a ( 8c f ( 5x 8y( 5x+ 8y = ( 5x ( 8y = 9a 64c ( 5x 64 y = = 5x + 64 y 66 MHR Principles of Mathematics 10 Solutions
67 Chapter 5 Review Question 8 Page 56 a x + 9x= x( x+ 9 b 3x + x = x( 3x+1 Chapter 5 Review Question 9 Page 56 + = ( + 11xy 9xz = x( 11y 9z a 1y 4z 1 y z b c c 3 c c( c 3 d + = + 4k 8 k = 4k( 1 k Chapter 5 Review Question 10 Page 56 a 4m + 1m+ 3m+ 9= ( 4m + 1m + ( 3m+ 9 4m( m 3 3( m 3 ( m 3( 4m 3 = = + + b 9k 6k + 6k 4= ( 9k 6k + ( 6k 4 3k( 3k ( 3k ( 3k ( 3k = + = + c 8x + 16x 5x 10= ( 8x + 16x + ( 5x 10 8x( x 5( x ( x ( 8x 5 = + + = + MHR Principles of Mathematics 10 Solutions 67
68 d 16x 1xy 1xy + 9 y = ( 16x 1xy + ( 1xy + 9 y 4x( 4x 3y 3y( 4x 3y ( 4x 3y( 4x 3y ( 4x 3y = = = Chapter 5 Review Question 11 Page 56 + = ( + ( a 8m 16m 4 4 m 4m 1 b 18c 3 + 4c 8c+ 6 = 9c 3 + 1c 4c+ 3 c ( 15m mn+ 66mn = m 15m n+ 66n d ax z az + axz = az ( x z + x Chapter 5 Review Question 1 Page 56 Length 10x + 5x, width 1. Length x + x, width 5. Length 10x + 5, width x. Length x + 1, width 5x. 68 MHR Principles of Mathematics 10 Solutions
69 Chapter 5 Review Question 13 Page 56 x + 9x+ 14= x+ x+ 7 a ( ( x + 11x+ 18 = x+ x+ 9 b ( ( c x + 4x+ 4= ( x+ ( x+ MHR Principles of Mathematics 10 Solutions 69
70 Chapter 5 Review Question 14 Page 56 + = ( ( x 8x+ 15= ( x 3( x 5 a c 17c 7 c 9 c 8 b + = ( ( x + 3x 10= ( x+ 5( x c z 14z 33 z 11 z 3 d e x + 8x 9= ( x+ 9( x 1 f x x 8= ( x 4( x+ Chapter 5 Review Question 15 Page 57 a y x x = 3 18 = ( x 6( x+ 3 b The x-intercepts are 3 and 6. c 3+ 6 = 1.5 The axis of symmetry is x = 1.5. y = x 3x 18 = 1.5 ( = 0.5 The vertex is (1.5, MHR Principles of Mathematics 10 Solutions
71 Chapter 5 Review Question 16 Page 57 a x + 7x+ 6= x + 4x+ 3x+ 6 b ( x 4x ( 3x 6 = x( x 3( x ( x ( x 3 = = + + c 6a 3a+ 15= 6a 18a 5a+ 15 d ( 6a 18a ( 5a 15 = + + 6a( a 3 5( a 3 ( a 3( 6a 5 = = y + y+ = y + y+ y+ ( 6y 7y ( y 9 = y( y 9 1( y 9 ( y 9( 3y 1 = = b b+ = b b b+ ( 4b 4b ( b 1 = + + 4bb ( 1 ( b 1 ( b 1( 4b 1 = = e 1m + 0m 8 = 4( 3m + 5m = m + m m ( m m ( m = m( m ( m ( m ( m = = f 14k 31k 10 = 14k 35k + 4k 10 ( 14k 35k ( 4k 10 = + 7k( k 5 ( k 5 ( k 5( 7k = + = + Chapter 5 Review Question 17 Page 57 a b 8x + xy 15y = 8x + 1xy 10xy 15y ( ( = 8x + 1xy + 10xy 15y 4x( x 3y 5y( x 3y ( x 3y( 4x 5y = + + = + 5c 4cd + 9 d is not factorable c 1m + 13mn+ 3n = 1m + 9mn+ 4mn+ 3n ( ( = 1m + 9mn + 4mn+ 3n 3m( 4m 3n n( 4m 3n ( 4m 3n( 3m n = = + + d w 9wx 8 x is not factorable MHR Principles of Mathematics 10 Solutions 71
72 e 4x + 6xy 9 y = 3( 8x + xy 3y = 3( 8x + 6xy 4xy 3y = ( + + ( 3 8x 6xy 4xy 3y ( ( ( x y( x y = 3 x 4x+ 3y y 4x+ 3y = f 9g + 4g 10 is not factorable Chapter 5 Review Question 18 Page 57 a 8 15 A= x + x = x + x x ( 8x 1x ( 10x 15 = + + 4x( x 3 5( x 3 ( x 3( 4x 5 = + + = + The length is 4x 5, and the width is x + 3. b P = ( x+ 3 + ( 4x 5 = ( ( ( 4( 1 5 = 140 A= x + x 8 15 ( 1 ( = = 1161 The perimeter is 140 cm and the area is 1161 cm. Chapter 5 Review Question 19 Page 57 ( ( ( a x 49 = x 7 b = x+ 7 x 7 y ( y ( y ( 11 = 11 = + 11 y 11 ( ( k ( c 4k 9= k 3 d a = a = + 3 k 3 e 9w 5x = 3w 5x f ( ( ( ( = 3w+ 5x 3w 5x ( ( a = = 16( 1+ 3a( 1 3a 1 81p = 1 ( 9p = ( 1+ 9p( 1 9p 7 MHR Principles of Mathematics 10 Solutions
73 Chapter 5 Review Question 0 Page 57 a x + 14x+ 49 = ( x + ( x( 7 + ( 7 ( x 7 = + b k + 8k + 16= ( k + ( k( 4 + ( 4 ( k 4 = + c y 10y+ 5 = ( y ( y( 5 + ( 5 ( y 5 = d 5y 70y+ 49 = ( 5y ( 5y( 7 + ( 7 ( 5y 7 = e 36c 108c+ 81 = 9( 4c 1c+ 9 ( c ( c( ( = ( c = 9 3 f y+ 64y = ( 11 + ( 11( 8y + ( 8y ( 11 8y = + Chapter 5 Review Question 1 Page 57 a k = 10 or k = 10 ( 5y + 10y+ 144 = 5y+ 1 ( 5y 10y+ 144 = 5y 1 b k = 49 ( 9x 4x+ 49= 3x 7 MHR Principles of Mathematics 10 Solutions 73
74 Chapter 5 Review Question Page 57 a 9w x 4wxyz + 16y z = ( 3wx ( 3wx( 4yz + ( 4yz ( 3wx 4yz = b 65 ( y 5 = 5 ( y 5 = 5 + ( y 5 5 ( y 5 = ( 0 + y( 30 y 4 4 c 144a 499 b is not factorable d 5x + 30x+ 4 is not factorable 74 MHR Principles of Mathematics 10 Solutions
75 Chapter 5 Chapter Test Chapter 5 Chapter Test Question 1 Page 58 x+ 3 x+ 3 = x + 9x+ 9 a ( ( x+ 3 x+ 4 = x + 7x+ 1 b ( ( Chapter 5 Chapter Test Question Page 58 4x 3x 5y 8z 1x 0x y 3x 3 + = + z a ( m m m+ m m + = m m + m m + m b ( ( = m 7m 1m 9 MHR Principles of Mathematics 10 Solutions 75
76 Chapter 5 Chapter Test Question 3 Page 58 y+ 5 y+ 9 = y + 9y+ 5y+ 4 a ( ( = y + y b ( ( 4x 7 3x+ = 1x + 8x 1x 14 = c ( 6k + 1 ( 6k 1 = ( 6k ( 1 d ( w 8 = ( w ( w( 8 + ( 8 = 36k 1 ( ( ( ( e ( 4c+ 5d = 4c + 4c 5d + 5d = 16c + 40cd + 5d = w w f ( x 4( x 7 5( 8x 9( 8x+ 9 = ( x 7x 4x+ 8 5( 64x 81 = ( x 11x+ 8 5( 64x = x x+ x = x x+ Chapter 5 Chapter Test Question 4 Page 58 a d = 0.006( s+ 1 ( s s = = s + s x 13x 14 b d = 0.006( s+ 1 ( 60 = =.36 d = s + s ( ( = =.36 Both forms give the same result, a stopping distance of.36 m. Chapter 5 Chapter Test Question 5 Page 58 a 9de + 6de 3 = 3de ( 3e+ d b 15 pqr 3 5pqr pqr= 5 pqr( 3pr 5pq + 1 c 5( x+ 6 ( x+ 6 = ( x+ 6( 3 d 16x + 8x 6x 3 = ( 16x + 8x + ( 6x 3 ( ( ( x 1( 8x 3 = 8x x+ 1 3 x+ 1 = + 76 MHR Principles of Mathematics 10 Solutions
77 Chapter 5 Chapter Test Question 6 Page 58 a SA = 4x( 3x ( 3x + 4 b SA = 4x( 3x ( 3x + 4 ( = x + x+ x + x = x + x+ x + x = x + x+ c SA = x + x ( x x ( x x x ( x x ( x = = = x( x ( x ( x ( x = = Chapter 5 Chapter Test Question 7 Page 58 a x + 11x+ 4 = ( x+ 3( x+ 8 b y 15y+ 56 = ( y 7( y 8 ( ( c n n 90 = n 10 n+ 9 d x 14x + 49 = x x ( h ( h ( e f d d h 100 = 10 = + 10 h 10 ( ( ( ( ( = x = d + d = d + 8 ( ( ( ( ( MHR Principles of Mathematics 10 Solutions 77
78 Chapter 5 Chapter Test Question 8 Page 58 a 3k + 1km 36m = 3( k + 4km 1m = 3 k + 6km km 1m ( ( = 3 k + 6km + km 1m k( k m m( k m ( k m( k m = = b y + y+ = y + y+ y+ ( 8y 16y ( 3y 6 = y( y 3( y ( y ( 8y 3 = = + + c 9w 4w+ 7= 9w 1w 3w+ 7 d ( 9w 1w ( 3w 7 = + + 3w( 3w 7 ( 3w 7 ( 3w 7( 3w 1 = = ( ( ( ( 5a + 60a+ 36 = 5a + 5a ( 5a 6 = + e 11w 144 = ( 11w 1 ( w ( = w 1 f 10x 7xy 6y = 10x 1xy+ 5xy 6y ( ( = 10x 1xy + 5xy 6y x( 5x 6y y( 5x 6y ( 5x 6y( x y = + = + Chapter 5 Chapter Test Question 9 Page 58 If there are two integers whose product is 9 18 and whose sum is 10, then 9x factored over the integers. 10x + 18 can be Chapter 5 Chapter Test Question 10 Page 58 x + 13x 30 = x+ 15 x a ( ( The length is x + 15, and the width is x. b The smallest integer value of x for which this area expression makes sense is x = MHR Principles of Mathematics 10 Solutions
79 Chapter 5 Chapter Test Question 11 Page 59 a k = 13 or k = 13 ( 36x + 13x+ 11 = 6x+ 11 ( 36x 13x+ 11 = 6x 11 b k = 16 ( 49d 56d + 16 = 7d 4 c k = 36 ( = 5 6 x xy y x y d k = 5 ( = a ab b a b Chapter 5 Chapter Test Question 1 Page 59 a ( 9 ( 5( A= x+ x+ x 5 b ( 9 ( 5( A= x+ x+ x = ( x 5 x 18x 81 x 5 = 18x = c ( ( ( A= x+ 9 x+ 5 x 5 ( ( ( = = 3 ( x ( 9( 53 A= = 7 + = 3 The result is the same, 3 square units, for both expressions because the expressions are equivalent. MHR Principles of Mathematics 10 Solutions 79
80 Chapter 5 Chapter Test Question 13 Page 59 = + 6 a y ( x ( x x = = x + x = x + x+ b y = x + 4x+ 70 = ( x + 1x+ 35 ( x ( x = c The three equations represent the same parabola. They result in the same graph. Chapter 5 Chapter Test Question 14 Page 59 3 a 9x 30x + 5x= x( 9x 30x+ 5 ( 3x 5 = x The height is x. The side length of the square base is 3x 5. b The prism is a square-based prism. The top and bottom are squares with side length 3x 5 and area (3x 5. The four sides are rectangles with width 3x 5, height x, and area x(3x 5. Chapter 5 Chapter Test Question 15 Page 59 Answers may vary. For example: a k = 4 or k = 9 4m 5= ( m+ 5( m 5 9m 5= 3m+ 5 3m 5 ( ( b k = 1 or k = 5 16d 1 = 4d + 1 4d 1 ( ( ( ( c k = 9 or k = 16 a 9b = ( a+ 3b( a 3b a 16b = a+ 4b a 4b 16d 5 = 4d + 5 4d 5 ( ( 80 MHR Principles of Mathematics 10 Solutions
81 Chapter 5 Chapter Test Question 16 Page 59 a = ( ( = 195 b = ( ( = 53 c 5 48 = ( ( 5 48 = 400 Chapter 5 Chapter Test Question 17 Page 59 a The total number of squares, s, in the nth diagram is s = 4n. b The number of shaded squares, S, in the nth diagram is S = n+ 3. c The number of unshaded squares, u, in the nth diagram is u = n n 4 3 d e u = n n 4 3 4n 4n 3n 3 = + ( 4n 4n ( 3n 3 = + 4n( n 1 3( n 1 ( n 1( 4n 3 = + = + u = n n 4 3 ( 15 ( 15 = 4 3 = 88 ( 1( 4 3 (( 15 1 ( 4( 15 3 u = n n+ = + = 88 Both forms of the formula give the same results for the 15th diagram. Chapter 5 Chapter Test Question 18 Page 59 Solutions for Achievement Checks are shown in the Teacher s Resource. MHR Principles of Mathematics 10 Solutions 81
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
By reversing the rules for multiplication of binomials from Section 4.6, we get rules for factoring polynomials in certain forms.
 SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
SECTION 5.4 Special Factoring Techniques 317 5.4 Special Factoring Techniques OBJECTIVES 1 Factor a difference of squares. 2 Factor a perfect square trinomial. 3 Factor a difference of cubes. 4 Factor
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
1.1 Practice Worksheet
 Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
How To Solve Factoring Problems
 05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
6706_PM10SB_C4_CO_pp192-193.qxd 5/8/09 9:53 AM Page 192 192 NEL
 92 NEL Chapter 4 Factoring Algebraic Epressions GOALS You will be able to Determine the greatest common factor in an algebraic epression and use it to write the epression as a product Recognize different
92 NEL Chapter 4 Factoring Algebraic Epressions GOALS You will be able to Determine the greatest common factor in an algebraic epression and use it to write the epression as a product Recognize different
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
5.1 FACTORING OUT COMMON FACTORS
 C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
C H A P T E R 5 Factoring he sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. T Today, skydiving is a popular sport around the world.
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Algebra II A Final Exam
 Algebra II A Final Exam Multiple Choice Identify the choice that best completes the statement or answers the question. Evaluate the expression for the given value of the variable(s). 1. ; x = 4 a. 34 b.
Algebra II A Final Exam Multiple Choice Identify the choice that best completes the statement or answers the question. Evaluate the expression for the given value of the variable(s). 1. ; x = 4 a. 34 b.
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
Algebra 1 Chapter 08 review
 Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
Name: Class: Date: ID: A Algebra 1 Chapter 08 review Multiple Choice Identify the choice that best completes the statement or answers the question. Simplify the difference. 1. (4w 2 4w 8) (2w 2 + 3w 6)
SOL Warm-Up Graphing Calculator Active
 A.2a (a) Using laws of exponents to simplify monomial expressions and ratios of monomial expressions 1. Which expression is equivalent to (5x 2 )(4x 5 )? A 9x 7 B 9x 10 C 20x 7 D 20x 10 2. Which expression
A.2a (a) Using laws of exponents to simplify monomial expressions and ratios of monomial expressions 1. Which expression is equivalent to (5x 2 )(4x 5 )? A 9x 7 B 9x 10 C 20x 7 D 20x 10 2. Which expression
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
How To Factor By Gcf In Algebra 1.5
 7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
Sect 6.7 - Solving Equations Using the Zero Product Rule
 Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
Math 0980 Chapter Objectives. Chapter 1: Introduction to Algebra: The Integers.
 Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Math 0980 Chapter Objectives Chapter 1: Introduction to Algebra: The Integers. 1. Identify the place value of a digit. 2. Write a number in words or digits. 3. Write positive and negative numbers used
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Factors and Products
 CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
The majority of college students hold credit cards. According to the Nellie May
 CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
CHAPTER 6 Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6. Factoring Trinomials of the Form b c 6.3 Factoring Trinomials of the Form a b c and Perfect Square Trinomials
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c
 Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
In this section, you will develop a method to change a quadratic equation written as a sum into its product form (also called its factored form).
 CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
CHAPTER 8 In Chapter 4, you used a web to organize the connections you found between each of the different representations of lines. These connections enabled you to use any representation (such as a graph,
Algebra Cheat Sheets
 Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Sheets Algebra Cheat Sheets provide you with a tool for teaching your students note-taking, problem-solving, and organizational skills in the context of algebra lessons. These sheets teach the concepts
Factoring Methods. Example 1: 2x + 2 2 * x + 2 * 1 2(x + 1)
 Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
Factoring Methods When you are trying to factor a polynomial, there are three general steps you want to follow: 1. See if there is a Greatest Common Factor 2. See if you can Factor by Grouping 3. See if
WEDNESDAY, 2 MAY 1.30 PM 2.25 PM. 3 Full credit will be given only where the solution contains appropriate working.
 C 500/1/01 NATIONAL QUALIFICATIONS 01 WEDNESDAY, MAY 1.0 PM.5 PM MATHEMATICS STANDARD GRADE Credit Level Paper 1 (Non-calculator) 1 You may NOT use a calculator. Answer as many questions as you can. Full
C 500/1/01 NATIONAL QUALIFICATIONS 01 WEDNESDAY, MAY 1.0 PM.5 PM MATHEMATICS STANDARD GRADE Credit Level Paper 1 (Non-calculator) 1 You may NOT use a calculator. Answer as many questions as you can. Full
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
Simplifying Algebraic Fractions
 5. Simplifying Algebraic Fractions 5. OBJECTIVES. Find the GCF for two monomials and simplify a fraction 2. Find the GCF for two polynomials and simplify a fraction Much of our work with algebraic fractions
5. Simplifying Algebraic Fractions 5. OBJECTIVES. Find the GCF for two monomials and simplify a fraction 2. Find the GCF for two polynomials and simplify a fraction Much of our work with algebraic fractions
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
Higher Education Math Placement
 Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
Higher Education Math Placement Placement Assessment Problem Types 1. Whole Numbers, Fractions, and Decimals 1.1 Operations with Whole Numbers Addition with carry Subtraction with borrowing Multiplication
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
A Systematic Approach to Factoring
 A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
A Systematic Approach to Factoring Step 1 Count the number of terms. (Remember****Knowing the number of terms will allow you to eliminate unnecessary tools.) Step 2 Is there a greatest common factor? Tool
Factoring Algebra- Chapter 8B Assignment Sheet
 Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Name: Factoring Algebra- Chapter 8B Assignment Sheet Date Section Learning Targets Assignment Tues 2/17 Find the prime factorization of an integer Find the greatest common factor (GCF) for a set of monomials.
Factoring. 472 Chapter 9 Factoring
 Factoring Lesson 9- Find the prime factorizations of integers and monomials. Lesson 9- Find the greatest common factors (GCF) for sets of integers and monomials. Lessons 9-2 through 9-6 Factor polynomials.
Factoring Lesson 9- Find the prime factorizations of integers and monomials. Lesson 9- Find the greatest common factors (GCF) for sets of integers and monomials. Lessons 9-2 through 9-6 Factor polynomials.
FACTORING QUADRATICS 8.1.1 and 8.1.2
 FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
Vocabulary Words and Definitions for Algebra
 Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Factoring Special Polynomials
 6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
6.6 Factoring Special Polynomials 6.6 OBJECTIVES 1. Factor the difference of two squares 2. Factor the sum or difference of two cubes In this section, we will look at several special polynomials. These
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Math 10C. Course: Polynomial Products and Factors. Unit of Study: Step 1: Identify the Outcomes to Address. Guiding Questions:
 Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
Course: Unit of Study: Math 10C Polynomial Products and Factors Step 1: Identify the Outcomes to Address Guiding Questions: What do I want my students to learn? What can they currently understand and do?
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation
 CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
CM2202: Scientific Computing and Multimedia Applications General Maths: 2. Algebra - Factorisation Prof. David Marshall School of Computer Science & Informatics Factorisation Factorisation is a way of
Sect 6.1 - Greatest Common Factor and Factoring by Grouping
 Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Sect 6.1 - Greatest Common Factor and Factoring by Grouping Our goal in this chapter is to solve non-linear equations by breaking them down into a series of linear equations that we can solve. To do this,
Factoring Flow Chart
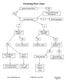 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
7-6. Choosing a Factoring Model. Extension: Factoring Polynomials with More Than One Variable IN T RO DUC E T EACH. Standards for Mathematical Content
 7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
Topic: Special Products and Factors Subtopic: Rules on finding factors of polynomials
 Quarter I: Special Products and Factors and Quadratic Equations Topic: Special Products and Factors Subtopic: Rules on finding factors of polynomials Time Frame: 20 days Time Frame: 3 days Content Standard:
Quarter I: Special Products and Factors and Quadratic Equations Topic: Special Products and Factors Subtopic: Rules on finding factors of polynomials Time Frame: 20 days Time Frame: 3 days Content Standard:
Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any.
 Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
Algebra 2 - Chapter Prerequisites Vocabulary Copy in your notebook: Add an example of each term with the symbols used in algebra 2 if there are any. P1 p. 1 1. counting(natural) numbers - {1,2,3,4,...}
MTH 092 College Algebra Essex County College Division of Mathematics Sample Review Questions 1 Created January 17, 2006
 MTH 092 College Algebra Essex County College Division of Mathematics Sample Review Questions Created January 7, 2006 Math 092, Elementary Algebra, covers the mathematical content listed below. In order
MTH 092 College Algebra Essex County College Division of Mathematics Sample Review Questions Created January 7, 2006 Math 092, Elementary Algebra, covers the mathematical content listed below. In order
MA107 Precalculus Algebra Exam 2 Review Solutions
 MA107 Precalculus Algebra Exam 2 Review Solutions February 24, 2008 1. The following demand equation models the number of units sold, x, of a product as a function of price, p. x = 4p + 200 a. Please write
MA107 Precalculus Algebra Exam 2 Review Solutions February 24, 2008 1. The following demand equation models the number of units sold, x, of a product as a function of price, p. x = 4p + 200 a. Please write
Polynomials and Factoring
 7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
7.6 Polynomials and Factoring Basic Terminology A term, or monomial, is defined to be a number, a variable, or a product of numbers and variables. A polynomial is a term or a finite sum or difference of
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Factoring Polynomials
 Factoring Polynomials 8A Factoring Methods 8-1 Factors and Greatest Common Factors Lab Model Factoring 8-2 Factoring by GCF Lab Model Factorization of Trinomials 8-3 Factoring x 2 + bx + c 8-4 Factoring
Factoring Polynomials 8A Factoring Methods 8-1 Factors and Greatest Common Factors Lab Model Factoring 8-2 Factoring by GCF Lab Model Factorization of Trinomials 8-3 Factoring x 2 + bx + c 8-4 Factoring
Introduction Assignment
 PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
6.1 The Greatest Common Factor; Factoring by Grouping
 386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
386 CHAPTER 6 Factoring and Applications 6.1 The Greatest Common Factor; Factoring by Grouping OBJECTIVES 1 Find the greatest common factor of a list of terms. 2 Factor out the greatest common factor.
10 7, 8. 2. 6x + 30x + 36 SOLUTION: 8-9 Perfect Squares. The first term is not a perfect square. So, 6x + 30x + 36 is not a perfect square trinomial.
 Squares Determine whether each trinomial is a perfect square trinomial. Write yes or no. If so, factor it. 1.5x + 60x + 36 SOLUTION: The first term is a perfect square. 5x = (5x) The last term is a perfect
Squares Determine whether each trinomial is a perfect square trinomial. Write yes or no. If so, factor it. 1.5x + 60x + 36 SOLUTION: The first term is a perfect square. 5x = (5x) The last term is a perfect
1.3. Maximum or Minimum of a Quadratic Function. Investigate A
 < P1-6 photo of a large arched bridge, similar to the one on page 292 or p 360-361of the fish book> Maximum or Minimum of a Quadratic Function 1.3 Some bridge arches are defined by quadratic functions.
< P1-6 photo of a large arched bridge, similar to the one on page 292 or p 360-361of the fish book> Maximum or Minimum of a Quadratic Function 1.3 Some bridge arches are defined by quadratic functions.
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
BEGINNING ALGEBRA ACKNOWLEDMENTS
 BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
Operations with Algebraic Expressions: Multiplication of Polynomials
 Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
Operations with Algebraic Expressions: Multiplication of Polynomials The product of a monomial x monomial To multiply a monomial times a monomial, multiply the coefficients and add the on powers with the
VOLUME of Rectangular Prisms Volume is the measure of occupied by a solid region.
 Math 6 NOTES 7.5 Name VOLUME of Rectangular Prisms Volume is the measure of occupied by a solid region. **The formula for the volume of a rectangular prism is:** l = length w = width h = height Study Tip:
Math 6 NOTES 7.5 Name VOLUME of Rectangular Prisms Volume is the measure of occupied by a solid region. **The formula for the volume of a rectangular prism is:** l = length w = width h = height Study Tip:
CRLS Mathematics Department Algebra I Curriculum Map/Pacing Guide
 Curriculum Map/Pacing Guide page 1 of 14 Quarter I start (CP & HN) 170 96 Unit 1: Number Sense and Operations 24 11 Totals Always Include 2 blocks for Review & Test Operating with Real Numbers: How are
Curriculum Map/Pacing Guide page 1 of 14 Quarter I start (CP & HN) 170 96 Unit 1: Number Sense and Operations 24 11 Totals Always Include 2 blocks for Review & Test Operating with Real Numbers: How are
Polynomial. Functions. 6A Operations with Polynomials. 6B Applying Polynomial. Functions. You can use polynomials to predict the shape of containers.
 Polynomial Functions 6A Operations with Polynomials 6-1 Polynomials 6- Multiplying Polynomials 6-3 Dividing Polynomials Lab Explore the Sum and Difference of Two Cubes 6-4 Factoring Polynomials 6B Applying
Polynomial Functions 6A Operations with Polynomials 6-1 Polynomials 6- Multiplying Polynomials 6-3 Dividing Polynomials Lab Explore the Sum and Difference of Two Cubes 6-4 Factoring Polynomials 6B Applying
Wednesday 15 January 2014 Morning Time: 2 hours
 Write your name here Surname Other names Pearson Edexcel Certificate Pearson Edexcel International GCSE Mathematics A Paper 4H Centre Number Wednesday 15 January 2014 Morning Time: 2 hours Candidate Number
Write your name here Surname Other names Pearson Edexcel Certificate Pearson Edexcel International GCSE Mathematics A Paper 4H Centre Number Wednesday 15 January 2014 Morning Time: 2 hours Candidate Number
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III
 Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Alum Rock Elementary Union School District Algebra I Study Guide for Benchmark III Name Date Adding and Subtracting Polynomials Algebra Standard 10.0 A polynomial is a sum of one ore more monomials. Polynomial
Factoring. Key Vocabulary
 8 Factoring Find the prime factorization of integers and monomials. Factor polynomials. Use the Zero Product Property to solve equations. Key Vocabulary factored form (p. 41) perfect square trinomials
8 Factoring Find the prime factorization of integers and monomials. Factor polynomials. Use the Zero Product Property to solve equations. Key Vocabulary factored form (p. 41) perfect square trinomials
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Ministry of Education. The Ontario Curriculum. Mathematics. Mathematics Transfer Course, Grade 9, Applied to Academic
 Ministry of Education The Ontario Curriculum Mathematics Mathematics Transfer Course, Grade 9, Applied to Academic 2 0 0 6 Contents Introduction....................................................... 2
Ministry of Education The Ontario Curriculum Mathematics Mathematics Transfer Course, Grade 9, Applied to Academic 2 0 0 6 Contents Introduction....................................................... 2
Polynomial Equations and Factoring
 7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
Section 1. Finding Common Terms
 Worksheet 2.1 Factors of Algebraic Expressions Section 1 Finding Common Terms In worksheet 1.2 we talked about factors of whole numbers. Remember, if a b = ab then a is a factor of ab and b is a factor
Worksheet 2.1 Factors of Algebraic Expressions Section 1 Finding Common Terms In worksheet 1.2 we talked about factors of whole numbers. Remember, if a b = ab then a is a factor of ab and b is a factor
Expression. Variable Equation Polynomial Monomial Add. Area. Volume Surface Space Length Width. Probability. Chance Random Likely Possibility Odds
 Isosceles Triangle Congruent Leg Side Expression Equation Polynomial Monomial Radical Square Root Check Times Itself Function Relation One Domain Range Area Volume Surface Space Length Width Quantitative
Isosceles Triangle Congruent Leg Side Expression Equation Polynomial Monomial Radical Square Root Check Times Itself Function Relation One Domain Range Area Volume Surface Space Length Width Quantitative
General Certificate of Secondary Education January 2014. Mathematics Unit T3 (With calculator) Higher Tier [GMT31] FRIDAY 10 JANUARY, 9.15am 11.
![General Certificate of Secondary Education January 2014. Mathematics Unit T3 (With calculator) Higher Tier [GMT31] FRIDAY 10 JANUARY, 9.15am 11. General Certificate of Secondary Education January 2014. Mathematics Unit T3 (With calculator) Higher Tier [GMT31] FRIDAY 10 JANUARY, 9.15am 11.](/thumbs/40/20949623.jpg) Centre Number 71 Candidate Number General Certificate of Secondary Education January 2014 Mathematics Unit T3 (With calculator) Higher Tier [GMT31] MV18 FRIDAY 10 JANUARY, 9.15am 11.15 am TIME 2 hours,
Centre Number 71 Candidate Number General Certificate of Secondary Education January 2014 Mathematics Unit T3 (With calculator) Higher Tier [GMT31] MV18 FRIDAY 10 JANUARY, 9.15am 11.15 am TIME 2 hours,
Calculating Area, Perimeter and Volume
 Calculating Area, Perimeter and Volume You will be given a formula table to complete your math assessment; however, we strongly recommend that you memorize the following formulae which will be used regularly
Calculating Area, Perimeter and Volume You will be given a formula table to complete your math assessment; however, we strongly recommend that you memorize the following formulae which will be used regularly
MATH 21. College Algebra 1 Lecture Notes
 MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
Florida Math 0028. Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper
 Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Florida Math 0028 Correlation of the ALEKS course Florida Math 0028 to the Florida Mathematics Competencies - Upper Exponents & Polynomials MDECU1: Applies the order of operations to evaluate algebraic
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
MATH 60 NOTEBOOK CERTIFICATIONS
 MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
CIRCUMFERENCE AND AREA OF A CIRCLE
 CIRCUMFERENCE AND AREA OF A CIRCLE 1. AC and BD are two perpendicular diameters of a circle with centre O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take = 3.14) 2. In the given
CIRCUMFERENCE AND AREA OF A CIRCLE 1. AC and BD are two perpendicular diameters of a circle with centre O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take = 3.14) 2. In the given
Algebra 1 Course Title
 Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
Algebra 1 Course Title Course- wide 1. What patterns and methods are being used? Course- wide 1. Students will be adept at solving and graphing linear and quadratic equations 2. Students will be adept
