Frequency Response of BJT & JFET
|
|
|
- Shauna Sherman
- 7 years ago
- Views:
Transcription
1 Alexandria High Institute for Engineering & Technology Frequency Response of BJT & JFET Course ECE241- Chapter (2) Sameh Selim )1)
2 Logarithms To clarify the relationship between the variables of a logarithmic function, consider the mathematical equations: b is the base, x the power. If b = 10 and x = 2, a = b x = (10) 2 = 100 but x = log b a = log = 2 For the electrical/electronics industry, the base in the logarithmic equation is limited to 10 and the number e = Common logarithms: logarithms taken to the base 10. Natural logarithms: logarithms taken to the base e. The two are related by In calculators, the common logarithm is denoted by "log" key and the natural logarithm by the "ln" key. Example 1: Using the calculator, determine the logarithm of the following numbers to the indicated base: a) Log b) log e e 3 c) log d) log e e -1 )2)
3 Example 2: Using the calculator, determine the logarithm of the following numbers: a) Log b) log e 64 c) log d) log N.B. the logarithm of a number does not increase in the same linear fashion as the number. The following table shows how the logarithm of a number increases only as the exponent of the number. If the antilogarithm of a number is desired, the 10 x or e x calculator functions are employed. Example 3: Using a calculator, determine the antilogarithm of the following expressions: a) 1.6 = log 10 a. b) 0.04 = log e a. Some properties of common logarithms: )3)
4 Example 4: Using calculator, determine the logarithm of the following numbers: a) log 10 (0.5) b) ( ) c) ( ) The use of log scales can significantly expand the range of variation of a particular variable on the graph. The semilog scale graph paper appears as in Figure below: )4)
5 DECIBELS The term "bel" (B) (derived from Alexander Graham Bell) was defined by the following equation to relate power levels P 1 and P 2 Practically, so the decibel (db) was defined such that: For a specified terminal (output) power (P 2 ) there must be a reference power level (P 1 ). The reference level is generally accepted to be 1mW, with an associated resistance of 600 (the characteristic impedance of audio transmission lines). There exists a second equation for decibels. For the system shown, V i equal to some value V1,. If V i is changed to some other level, V 2, then. To determine the resulting difference in decibels between the power levels, One of the advantages of the logarithmic relationship is the manner in which it can be applied to cascaded stages. )5)
6 For example, the magnitude of the overall voltage gain of cascaded system is given by Applying the proper logarithmic relationship results in In words, the equation states that the decibel gain of cascaded system is simply the sum of the decibel gain of each stage, i.e. Example 5: Find the magnitude gain corresponding to a decibel gain of 100. Check Example 6: The I/p power to a device is 10,000 W at a voltage of 1000 V. The O/P power is 500 W, while the o/p impedance is 20. a) Find the power gain in decibels. ( db ) b) Find the voltage gain in decibels. ( - 20 db ) c) Explain why parts (a) and (b) agree or disagree.( Ri = 100 Ro) Example 7: An amplifier rated at 40-W O/P is connected to a 10- speaker. a) Calculate the I/P power required for full power O/P if the power gain is 25 db. ( mw) b) c) Calculate the I/P voltage for rated O/P if the amplifier voltage gain is 40 db. ( 200 mv ) )6)
7 General Frequency considerations The magnitudes of the gain response of an RC coupled amplifier system is provided in the following Figure. Note that the horizontal scale is a logarithmic scale to permit a plot extending from the low- to the high-frequency regions. There is a band of frequencies in which the magnitude of the gain is either equal or relatively close to the midband value. To fix the frequency boundaries of relatively high gain, A vmid was chosen to be the gain at the cutoff levels. The corresponding frequencies f 1 and f 2 are generally called the corner, cutoff, break, or half-power frequencies. The multiplier was chosen because at this level the O/P power is half the midband power O/P, that is, at midfrequencies, and at the half-power frequencies, and P OHPF = 0.5 P omid (16) The bandwidth (or passband) of the system is determined by f 1 and f 2, that is, Bandwidth (BW) = f 2 f 1 (17) )7)
8 For applications of communications nature (audio, video), a decibel plot of the voltage gain vs frequency is more useful than that appearing in the above Figure: the curve is generally normalized as in the following Figure. In this Figure, the gain at each frequency is divided by the midband value. Obviously the midband value is then 1 as indicated. At halfpower frequencies, the resulting level is =. A decibel plot can now be obtained by applying At midband frequencies, 20 log 10 1 = 0, and at the cutoff frequencies, 20 log 10 = -3 db. Both values are clearly indicated in the resulting decibel plot, as shown in the following Figure, Most amplifiers introduce a 180 o phase shift between I/P and O/P signals. In fact, this is the case only in the midband region. At low frequencies, there is a phase shift such that V o lags V i by an increased angle. At high frequencies, the phase shift will drop below 180 o. the following Figure is a standard phase plot for an RC coupled amplifier. )8)
9 Low Frequency Analysis-Bode Plot: In the low-frequency region of the single-stage BJT or FET amplifier, it is the R-C combination formed by the network capacitors C c, C E and C s and the network resistive parameters that determine the cutoff frequencies. The series RC combination, as shown, and the development of a procedure that will result in a plot of frequency response with minimum of time and effort. At high frequencies, and the short-circuit equivalent can be substituted for the capacitor. The result is that V o V i at high frequencies. At f = 0 Hz, and the open-circuit approximation can be applied, with the result that V o = 0 V. Between the two extremes, the ratio Av = V o /V i will vary as shown in )9)
10 the following Figure. As the frequency increases, the capacitive reactance decreases and more of the input voltage appears across the O/P terminals. The O/P and I/P voltages are related by the voltage-divider rule as With magnitude of V o determined by For the special case where X C = R, And The level of which is indicated in on Figure above. In other words, at the frequency of which X C = R, the O/P will be 70.7% of the I/P for the RC network shown before. The frequency at which this occurs is determined from and in terms of logs, )11)
11 While at Av = Vo/Vi = 1 or Vo = Vi (the maximum value) If the gain equation is written as For the magnitude when f = f 1 In logarithmic form, the gain in db is For frequencies For where f f1 or (f1/f) 2 1, the equation above can be approximated by And finally, )11)
12 Ignoring the condition f f1 for the moment, a plot of the last equation on a frequency log scale will yield a result of a very useful nature for future decibel plots. The piecewise linear plot of the asymptotes and associated breakpoints is called a Bode Plot of magnitude vs frequency. The piecewise linear plot of the asymptotes and associated breakpoints is called a Bode plot of the magnitude versus frequency. Notes: A change in frequency by a factor of 2, i.e. one octave, results in 6-dB change in ratio, as shown by the gain change from f 1 /2 to f 1. A change in frequency by a factor of 10, i.e. one decade, results in 20- db change in ratio, as shown by the gain change from f 1 /10 to f 1. )12)
13 Steps for Bode plot: 1) Find f1 from the circuit parameters. 2) Sketch 2 asymptotes: one along the 0-dB and the other drawn thro' f1 sloped at 6 db/octave or 20 db/decade. 3) Find the 3-dB point corresponding to f1 and sketch the curve. Example 8: For the network shown in Figure: 1. Determine the break frequency. 2. Sketch the asymptotes and locate the -3 db point. 3. Sketch the frequency response curve. The Frequency response of the gain A v (db) for the R-C circuit is shown in Figure. The gain at any frequency can be determined from the frequency plot in the following manner: )13)
14 Check: Av(dB) = -3 db, Av = 0.707, and Av(dB) = - 1 db, (at f = 2f 1 ), Av = The phase angle is determined from f f 1, = 90 o f 1 = 100 f, = 89.4 o f = f 1, = 45 o f f 1, = 0 o f = 100 f 1, = o The phase response for the R-C circuit is shown. Low-Frequency Response (BJT) Amplifier In the analysis of the voltage-divider BJT, it will simply be necessary to find the appropriate equivalent resistance for the RC combination. Capacitors C s, C c, C E will determine the low-frequency response. We will examine the impact of each independently. Effect of Cs: the general form of the R-C configuration is established by the network of the following Figure. The total resistance is R s + R i. )14)
15 The cutoff frequency: At mid or high frequencies: The reactance of the capacitor will be short circuit approximate. The voltage V i is related to V s by: At f Ls, the voltage V i will be 70.7% of the value determined by this eqn., assuming that C s is the only capacitive element controlling the low frequency response. The ac equivalent for the i/p section of BJT amplifier: The value of R i is determined by: R i = R 1 //R 2 // r e The voltage V i applied to the i/p of the active device can be calculated using the voltage-divider rule: Effect of C C : Since the coupling capacitor is normally connected between the O/P of the active device and the applied load, the R-C configuration that determines the low cutoff frequency due to C C appears in the following Figure. The total series resistance is now R O + R L and the cutoff frequency due to C C is determined by: ( ) )15)
16 Ignoring the effects of C S and C E the O/P voltage V o will be 70.7% of its midband value at f LC. For the network of the loaded BJT amplifier, the ac equivalent network for the O/P section with V i = 0 V appears in the following Figure. The resulting value of R o in the equation of f LC is then simply R o = R C //r o Effect of C E : To determine f LE, the network seen by C E must be determined as shown in the Figure below. Once the level of Re is established, the cutoff frequency due to CE can be determined using the following equation: For the BJT network, the ac equivalent as seen by C E appears in the following Figure. The value of R e is therefore determined by Where ( ) The effect of C E on the gain is best described by recalling that the gain for the configuration )16)
17 of the shown Figure is given by: The maximum gain is obviously available where R E is zero ohms. The higher f L will be the predominant factor in determining the lowfrequency response for the complete system. Example: For the network shown in Figure with the following parameters: Cs = 10 F, CE = 20 F, Cc = 1 F, Rs = 1 K, R1 = 40 K, R2 = 10 K, RE = 2 K, Rc = 4 K, RL = 2.2 K, = 100, ro =, Vcc = 20 V a) Determine r e b) Find A Vmid = V o /V i c) Calculate Z i. d) Find A Vmid = V o /V s. e) Determine f Ls, f Lc, and f LE. f) Determine the lower cutoff frequency. g) Sketch the asymptotes of the Bode plot defined by the cutoff frequencies. h) Sketch the low-frequency response for the amplifier using results of (f). a) Determine re for dc conditions: R E = (100)(2 K ) = 200 K >> 10 R 2 = 100 K, check V B = 4 V, I E = 1.65 ma, re )17)
18 And r e = 100 (15.76 ) = 1576 = K b) Midband gain, check -90 c) = 40K//10K//1.576K 1.32 K d) From the Figure shown: So that ( )( ) e) Effect of C s R i = R 1 //R 2 // r e, check Ri = 1.32 K Effect of C C ( ), check 6.86 Hz ( ), check Hz Effect of C E = 1 K// 40 K // 10 K = K ( ) = ( )( )( ) 327 Hz f) f L = 327 Hz )18)
19 g), h) The low frequency plot for the network: Low-Frequency Response (FET) Amplifier The analysis is quite similar to that of the BJT amplifier. There are again capacitors C G, C C, and C S. The following Figure is used to establish the fundamental equations. Effect of C G : The ac equivalent network for the coupling capacitor between the source and the active device is shown in the following Figure. The cutoff frequency determined by CG will be: ( ) For the above network, )19)
20 Typically R G >> R sig and the lower cutoff frequency will be determined primarily by R G and C G. Effect of C C : For the coupling capacitor between the active device and the load the network of following Figure will result. The resulting cutoff frequency is For the given network, ( ) Effect of C S : For the source capacitor C S the resistance level of importance is defined by the following Figure. The cutoff frequency will be defined by For the above network, the resulting value of R eq ( ) ( ) Which for r d becomes Example: (a) Determine the lower cutoff frequency for the network of the above Fig, using the following parameters: C G = 0.01 F, C C = 0.5 F, C s = 2 F R sig = 10 k, R G = 1 M, R D = 4.7 k, R s = 1 k, R L = 2.2 k, g m = 2 ms I DSS = 8 ma, V P = -4 V, r d =, V DD = 20 V. (b) Sketch the frequency response using Bode plot. )21)
21 (a) Effect of C G : Using R sig =10 K, R i = R G = 1 M, check f LG 15.8 Hz Effect of C C : Using R O = R D //r d = 4.7 K, R L = 2.2 K, check f LC Hz Effect of C C : Using R eq = R S //(1/g m ), check R eq = ,and f Ls = Hz (b) The midband gain is determined by: ( ), check A Vmid -3. Using the midband gain to normalize the response will result in the frequency plot of Figure. )21)
22 Miller Effect Capacitance: In high-frequency region, the capacitive elements of importance are the inter-electrode (between terminals) capacitances internal to the active device and the wiring capacitance between leads of the network. For inverting amplifiers, the I/P and O/P capacitance is increased by a capacitance level sensitive to the inter-electrode capacitance between the I/P and O/P terminals of the device and the gain of the amplifier. In Figure, this "feedback" capacitance is defined by C f. Miller I/P Capacitance: Applying KCL: I i = I 1 + I 2 Using Ohm's law: Substituting, we obtain Establishing the equivalent network shows that the I/P impedance includes R i with the addition of a feedback capacitor magnified by the )22)
23 gain of the amplifier. In general the Miller effect I/P capacitance is defined by C Mi = (1 - A v )C f This shows that: For any inverting amplifier, the I/P capacitance will be increased by a Miller effect capacitance sensitive to the gain of the amplifier and the inter-electrode (parasitic) capacitance between the I/P and O/P terminals of the active device. The reason for the constraint that the amplifier be of the inverting type is now more apparent when you examine the equation of C MI. A positive A v would result in a negative capacitance (for A v > 1). Miller O/P Capacitance: Applying KCL: I o = I 1 + I 2 Using Ohm's law: The resistance R o is usually sufficiently large to permit ignoring I 1,, substituting V i = V o /A v will result in Or Resulting in the Miller O/P capacitance: ( ) )23)
24 For the usual situation where A v >> 1, this equation reduces to C MO = C f High-Frequency Response (BJT) Amplifier: Network Parameters: In the high-frequency region, the RC network of concern has the configuration appearing in Figure, the general form of A v : ( ) This results in a magnitude plot that drops off at 6 db/ octave with increasing frequency. The high-frequency model for the network of the following Figure appears in the next Figure. (BJT network with capacitors that affect the high frequency response) )24)
25 In fact, most specification sheets provide levels of C be and C bc and do not include C ce. Determining the Thevenin equivalent circuit for the I/P and O/P networks of the above Figure will result in the configuration of the following Figures. For the I/P network, the -3 db frequency is defined by With And ( ) At very high frequencies, the effect of C i is to reduce the total impedance of the parallel combination of R 1, R 2, Ri and C i, which results in a reduced level of voltage across C i, a reduction in I b, and gain of the system. )25)
26 For the O/P network, And At very high frequencies, C o will decrease reducing the total impedance of the O/P parallel branches of the equivalent model. The net result is that V o will also decline toward zero as the reactance X C becomes smaller. The frequencies f Hi and f Ho will each define a -6 db/octave asymptote. )26)
27 Example For the network shown in the Figure with the following parameters: R s = 1 K, R 1 = 40 K, R 2 = 10 K, R E = 2 K, R C = 4 K, R L = 2.2 K, C S = 10 F, C C = 1 F, C E = 20 F, C be = 36 pf, C bc = 4 pf, C Ce = 1 pf, C Wi = 6 pf, C Wo = 8 pf, = 100, r o =, V CC = 20 V. a) Find the I/P resistance R i b) Find the voltage gain A vmid. c) Determine the Thevenin equivalent I/P resistance R thi. d) Determine the Thevenin equivalent O/P resistance R tho. e) Find the input capacitance C i. f) Find the output capacitor C o. g) Determine f Hi and f Ho. a) Get V B, check V B = 4 V, get r e = r e = K, R i = R 1 //R 2 // r e, check Ri = 1.32 K b), check -90 c) R thi = R s // R 1 // R 2 // R i, check K d) R tho = R C // R L, check R tho = K )27)
28 e) ( ), check C i = 406 pf f) = 8 pf + 1 pf + [1 (-1/90)]4 pf = pf g), check f Hi = KHz h), check f Ho = 8.6 MHz In general, the lowest of the upper-cutoff frequencies defines a maximum possible bandwidth for the system. )28)
29 High-Frequency Response FET Amplifier The shown network is an inverting amplifier, so Miller effect capacitance will appear in the high-frequency ac equivalent network. Thevenin's i/p circuit Thevenin's o/p circuit For the i/p circuit f Hi = 1/2 R thi C i R thi = R sig //R G C i = C wi + C gs + C Mi C Mi = (1 A v )C gd For the o/p circuit f Ho = 1/2 R tho C o R tho = R D //R L //r d C o = C wo + C ds + C Mo C Mo = (1 1/A v )C gd )29)
30 Example: Determine the high cutoff frequency for the network of the above Fig, using the following parameters: C G = 0.01 F, C C = 0.5 F, C s = 2 F R sig = 10 k, R G = 1 M, R D = 4.7 k, R s = 1 k, R L = 2.2 k, g m = 2 ms I DSS = 8 ma, V P = -4 V, r d =, V DD = 20 V. Cgd = 2 pf, Cgs = 4 pf, Cds = 0.5 pf, Cwi = 5 pf, Cwo = 6 pf. A v = -g m (R D //R L ), check A v = -3. R thi = R sig //R G = 9.9 K. C i = C wi + C gs + (1-A v )C gd, check = 17 pf. f Hi = 1/(2 R thi C i ) = KHz R tho = R D //R L 1.5 K C o = C wo + C ds + C MO, check = 9.17 pf f Ho = 1/(2 )(1.5K )(9.17pF) = MHz From which it is noticed that the i/p capacitance with its Miller capacitance will determine the upper cutoff frequency. )31)
S-DOMAIN ANALYSIS: POLES, ZEROS, AND BODE PLOTS
 S-DOMAIN ANAYSIS: POES, ZEROS, AND BODE POTS The main objectiveis to find amplifier voltage gain as a transfer function of the complex frequency s. In this s-domain analysis a capacitance С is replaced
S-DOMAIN ANAYSIS: POES, ZEROS, AND BODE POTS The main objectiveis to find amplifier voltage gain as a transfer function of the complex frequency s. In this s-domain analysis a capacitance С is replaced
11: AUDIO AMPLIFIER I. INTRODUCTION
 11: AUDIO AMPLIFIER I. INTRODUCTION The properties of an amplifying circuit using an op-amp depend primarily on the characteristics of the feedback network rather than on those of the op-amp itself. A
11: AUDIO AMPLIFIER I. INTRODUCTION The properties of an amplifying circuit using an op-amp depend primarily on the characteristics of the feedback network rather than on those of the op-amp itself. A
Common Base BJT Amplifier Common Collector BJT Amplifier
 Common Base BJT Amplifier Common Collector BJT Amplifier Common Collector (Emitter Follower) Configuration Common Base Configuration Small Signal Analysis Design Example Amplifier Input and Output Impedances
Common Base BJT Amplifier Common Collector BJT Amplifier Common Collector (Emitter Follower) Configuration Common Base Configuration Small Signal Analysis Design Example Amplifier Input and Output Impedances
Common Emitter BJT Amplifier Design Current Mirror Design
 Common Emitter BJT Amplifier Design Current Mirror Design 1 Some Random Observations Conditions for stabilized voltage source biasing Emitter resistance, R E, is needed. Base voltage source will have finite
Common Emitter BJT Amplifier Design Current Mirror Design 1 Some Random Observations Conditions for stabilized voltage source biasing Emitter resistance, R E, is needed. Base voltage source will have finite
Chapter 12: The Operational Amplifier
 Chapter 12: The Operational Amplifier 12.1: Introduction to Operational Amplifier (Op-Amp) Operational amplifiers (op-amps) are very high gain dc coupled amplifiers with differential inputs; they are used
Chapter 12: The Operational Amplifier 12.1: Introduction to Operational Amplifier (Op-Amp) Operational amplifiers (op-amps) are very high gain dc coupled amplifiers with differential inputs; they are used
LAB 12: ACTIVE FILTERS
 A. INTRODUCTION LAB 12: ACTIVE FILTERS After last week s encounter with op- amps we will use them to build active filters. B. ABOUT FILTERS An electric filter is a frequency-selecting circuit designed
A. INTRODUCTION LAB 12: ACTIVE FILTERS After last week s encounter with op- amps we will use them to build active filters. B. ABOUT FILTERS An electric filter is a frequency-selecting circuit designed
Frequency Response of Filters
 School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 2 Frequency Response of Filters 1 Introduction Objectives To
School of Engineering Department of Electrical and Computer Engineering 332:224 Principles of Electrical Engineering II Laboratory Experiment 2 Frequency Response of Filters 1 Introduction Objectives To
SERIES-PARALLEL DC CIRCUITS
 Name: Date: Course and Section: Instructor: EXPERIMENT 1 SERIES-PARALLEL DC CIRCUITS OBJECTIVES 1. Test the theoretical analysis of series-parallel networks through direct measurements. 2. Improve skills
Name: Date: Course and Section: Instructor: EXPERIMENT 1 SERIES-PARALLEL DC CIRCUITS OBJECTIVES 1. Test the theoretical analysis of series-parallel networks through direct measurements. 2. Improve skills
TWO PORT NETWORKS h-parameter BJT MODEL
 TWO PORT NETWORKS h-parameter BJT MODEL The circuit of the basic two port network is shown on the right. Depending on the application, it may be used in a number of different ways to develop different
TWO PORT NETWORKS h-parameter BJT MODEL The circuit of the basic two port network is shown on the right. Depending on the application, it may be used in a number of different ways to develop different
Lecture 23: Common Emitter Amplifier Frequency Response. Miller s Theorem.
 Whites, EE 320 ecture 23 Page 1 of 17 ecture 23: Common Emitter mplifier Frequency Response. Miller s Theorem. We ll use the high frequency model for the BJT we developed the previous lecture and compute
Whites, EE 320 ecture 23 Page 1 of 17 ecture 23: Common Emitter mplifier Frequency Response. Miller s Theorem. We ll use the high frequency model for the BJT we developed the previous lecture and compute
Transistor Amplifiers
 Physics 3330 Experiment #7 Fall 1999 Transistor Amplifiers Purpose The aim of this experiment is to develop a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must accept input
Physics 3330 Experiment #7 Fall 1999 Transistor Amplifiers Purpose The aim of this experiment is to develop a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must accept input
Understanding Power Impedance Supply for Optimum Decoupling
 Introduction Noise in power supplies is not only caused by the power supply itself, but also the load s interaction with the power supply (i.e. dynamic loads, switching, etc.). To lower load induced noise,
Introduction Noise in power supplies is not only caused by the power supply itself, but also the load s interaction with the power supply (i.e. dynamic loads, switching, etc.). To lower load induced noise,
CHAPTER 6 Frequency Response, Bode Plots, and Resonance
 ELECTRICAL CHAPTER 6 Frequency Response, Bode Plots, and Resonance 1. State the fundamental concepts of Fourier analysis. 2. Determine the output of a filter for a given input consisting of sinusoidal
ELECTRICAL CHAPTER 6 Frequency Response, Bode Plots, and Resonance 1. State the fundamental concepts of Fourier analysis. 2. Determine the output of a filter for a given input consisting of sinusoidal
LABORATORY 2 THE DIFFERENTIAL AMPLIFIER
 LABORATORY 2 THE DIFFERENTIAL AMPLIFIER OBJECTIVES 1. To understand how to amplify weak (small) signals in the presence of noise. 1. To understand how a differential amplifier rejects noise and common
LABORATORY 2 THE DIFFERENTIAL AMPLIFIER OBJECTIVES 1. To understand how to amplify weak (small) signals in the presence of noise. 1. To understand how a differential amplifier rejects noise and common
Unit/Standard Number. High School Graduation Years 2010, 2011 and 2012
 1 Secondary Task List 100 SAFETY 101 Demonstrate an understanding of State and School safety regulations. 102 Practice safety techniques for electronics work. 103 Demonstrate an understanding of proper
1 Secondary Task List 100 SAFETY 101 Demonstrate an understanding of State and School safety regulations. 102 Practice safety techniques for electronics work. 103 Demonstrate an understanding of proper
Common-Emitter Amplifier
 Common-Emitter Amplifier A. Before We Start As the title of this lab says, this lab is about designing a Common-Emitter Amplifier, and this in this stage of the lab course is premature, in my opinion,
Common-Emitter Amplifier A. Before We Start As the title of this lab says, this lab is about designing a Common-Emitter Amplifier, and this in this stage of the lab course is premature, in my opinion,
CIRCUITS LABORATORY EXPERIMENT 3. AC Circuit Analysis
 CIRCUITS LABORATORY EXPERIMENT 3 AC Circuit Analysis 3.1 Introduction The steady-state behavior of circuits energized by sinusoidal sources is an important area of study for several reasons. First, the
CIRCUITS LABORATORY EXPERIMENT 3 AC Circuit Analysis 3.1 Introduction The steady-state behavior of circuits energized by sinusoidal sources is an important area of study for several reasons. First, the
30. Bode Plots. Introduction
 0. Bode Plots Introduction Each of the circuits in this problem set is represented by a magnitude Bode plot. The network function provides a connection between the Bode plot and the circuit. To solve these
0. Bode Plots Introduction Each of the circuits in this problem set is represented by a magnitude Bode plot. The network function provides a connection between the Bode plot and the circuit. To solve these
Fig6-22 CB configuration. Z i [6-54] Z o [6-55] A v [6-56] Assuming R E >> r e. A i [6-57]
![Fig6-22 CB configuration. Z i [6-54] Z o [6-55] A v [6-56] Assuming R E >> r e. A i [6-57] Fig6-22 CB configuration. Z i [6-54] Z o [6-55] A v [6-56] Assuming R E >> r e. A i [6-57]](/thumbs/40/21338705.jpg) Common-Base Configuration (CB) The CB configuration having a low input and high output impedance and a current gain less than 1, the voltage gain can be quite large, r o in MΩ so that ignored in parallel
Common-Base Configuration (CB) The CB configuration having a low input and high output impedance and a current gain less than 1, the voltage gain can be quite large, r o in MΩ so that ignored in parallel
Laboratory 4: Feedback and Compensation
 Laboratory 4: Feedback and Compensation To be performed during Week 9 (Oct. 20-24) and Week 10 (Oct. 27-31) Due Week 11 (Nov. 3-7) 1 Pre-Lab This Pre-Lab should be completed before attending your regular
Laboratory 4: Feedback and Compensation To be performed during Week 9 (Oct. 20-24) and Week 10 (Oct. 27-31) Due Week 11 (Nov. 3-7) 1 Pre-Lab This Pre-Lab should be completed before attending your regular
Experiment EB1: FET Amplifier Frequency Response
 EEE106 Electronics II: : FET Amplifier Frequency Response earng Outcome O4: Analyze the operation of JFET, MOSFET and BJT amplifiers and switchg circuits 1.0 Apparatus Equipment required Components required
EEE106 Electronics II: : FET Amplifier Frequency Response earng Outcome O4: Analyze the operation of JFET, MOSFET and BJT amplifiers and switchg circuits 1.0 Apparatus Equipment required Components required
Chapter 10. RC Circuits ISU EE. C.Y. Lee
 Chapter 10 RC Circuits Objectives Describe the relationship between current and voltage in an RC circuit Determine impedance and phase angle in a series RC circuit Analyze a series RC circuit Determine
Chapter 10 RC Circuits Objectives Describe the relationship between current and voltage in an RC circuit Determine impedance and phase angle in a series RC circuit Analyze a series RC circuit Determine
BJT AC Analysis 1 of 38. The r e Transistor model. Remind Q-poiint re = 26mv/IE
 BJT AC Analysis 1 of 38 The r e Transistor model Remind Q-poiint re = 26mv/IE BJT AC Analysis 2 of 38 Three amplifier configurations, Common Emitter Common Collector (Emitter Follower) Common Base BJT
BJT AC Analysis 1 of 38 The r e Transistor model Remind Q-poiint re = 26mv/IE BJT AC Analysis 2 of 38 Three amplifier configurations, Common Emitter Common Collector (Emitter Follower) Common Base BJT
Lecture 24: Oscillators. Clapp Oscillator. VFO Startup
 Whites, EE 322 Lecture 24 Page 1 of 10 Lecture 24: Oscillators. Clapp Oscillator. VFO Startup Oscillators are circuits that produce periodic output voltages, such as sinusoids. They accomplish this feat
Whites, EE 322 Lecture 24 Page 1 of 10 Lecture 24: Oscillators. Clapp Oscillator. VFO Startup Oscillators are circuits that produce periodic output voltages, such as sinusoids. They accomplish this feat
COMMON-SOURCE JFET AMPLIFIER
 EXPERIMENT 04 Objectives: Theory: 1. To evaluate the common-source amplifier using the small signal equivalent model. 2. To learn what effects the voltage gain. A self-biased n-channel JFET with an AC
EXPERIMENT 04 Objectives: Theory: 1. To evaluate the common-source amplifier using the small signal equivalent model. 2. To learn what effects the voltage gain. A self-biased n-channel JFET with an AC
Bode Diagrams of Transfer Functions and Impedances ECEN 2260 Supplementary Notes R. W. Erickson
 Bode Diagrams of Transfer Functions and Impedances ECEN 2260 Supplementary Notes. W. Erickson In the design of a signal processing network, control system, or other analog system, it is usually necessary
Bode Diagrams of Transfer Functions and Impedances ECEN 2260 Supplementary Notes. W. Erickson In the design of a signal processing network, control system, or other analog system, it is usually necessary
PIEZO FILTERS INTRODUCTION
 For more than two decades, ceramic filter technology has been instrumental in the proliferation of solid state electronics. A view of the future reveals that even greater expectations will be placed on
For more than two decades, ceramic filter technology has been instrumental in the proliferation of solid state electronics. A view of the future reveals that even greater expectations will be placed on
Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor)
 Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor) Concept: circuits Time: 30 m SW Interface: 750 Windows file: RLC.SWS EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage
Experiment #11: LRC Circuit (Power Amplifier, Voltage Sensor) Concept: circuits Time: 30 m SW Interface: 750 Windows file: RLC.SWS EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage
Measurement of Capacitance
 Measurement of Capacitance Pre-Lab Questions Page Name: Class: Roster Number: Instructor:. A capacitor is used to store. 2. What is the SI unit for capacitance? 3. A capacitor basically consists of two
Measurement of Capacitance Pre-Lab Questions Page Name: Class: Roster Number: Instructor:. A capacitor is used to store. 2. What is the SI unit for capacitance? 3. A capacitor basically consists of two
Transistor Characteristics and Single Transistor Amplifier Sept. 8, 1997
 Physics 623 Transistor Characteristics and Single Transistor Amplifier Sept. 8, 1997 1 Purpose To measure and understand the common emitter transistor characteristic curves. To use the base current gain
Physics 623 Transistor Characteristics and Single Transistor Amplifier Sept. 8, 1997 1 Purpose To measure and understand the common emitter transistor characteristic curves. To use the base current gain
Impedance Matching and Matching Networks. Valentin Todorow, December, 2009
 Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Impedance Matching and Matching Networks Valentin Todorow, December, 2009 RF for Plasma Processing - Definition of RF What is RF? The IEEE Standard Dictionary of Electrical and Electronics Terms defines
Basic Electronics Prof. Dr. Chitralekha Mahanta Department of Electronics and Communication Engineering Indian Institute of Technology, Guwahati
 Basic Electronics Prof. Dr. Chitralekha Mahanta Department of Electronics and Communication Engineering Indian Institute of Technology, Guwahati Module: 2 Bipolar Junction Transistors Lecture-2 Transistor
Basic Electronics Prof. Dr. Chitralekha Mahanta Department of Electronics and Communication Engineering Indian Institute of Technology, Guwahati Module: 2 Bipolar Junction Transistors Lecture-2 Transistor
Homework Assignment 03
 Question 1 (2 points each unless noted otherwise) Homework Assignment 03 1. A 9-V dc power supply generates 10 W in a resistor. What peak-to-peak amplitude should an ac source have to generate the same
Question 1 (2 points each unless noted otherwise) Homework Assignment 03 1. A 9-V dc power supply generates 10 W in a resistor. What peak-to-peak amplitude should an ac source have to generate the same
Physics 623 Transistor Characteristics and Single Transistor Amplifier Sept. 13, 2006
 Physics 623 Transistor Characteristics and Single Transistor Amplifier Sept. 13, 2006 1 Purpose To measure and understand the common emitter transistor characteristic curves. To use the base current gain
Physics 623 Transistor Characteristics and Single Transistor Amplifier Sept. 13, 2006 1 Purpose To measure and understand the common emitter transistor characteristic curves. To use the base current gain
ε: Voltage output of Signal Generator (also called the Source voltage or Applied
 Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Experiment #10: LR & RC Circuits Frequency Response EQUIPMENT NEEDED Science Workshop Interface Power Amplifier (2) Voltage Sensor graph paper (optional) (3) Patch Cords Decade resistor, capacitor, and
Ver 3537 E1.1 Analysis of Circuits (2014) E1.1 Circuit Analysis. Problem Sheet 1 (Lectures 1 & 2)
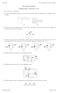 Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
Ver 3537 E. Analysis of Circuits () Key: [A]= easy... [E]=hard E. Circuit Analysis Problem Sheet (Lectures & ). [A] One of the following circuits is a series circuit and the other is a parallel circuit.
Bipolar Transistor Amplifiers
 Physics 3330 Experiment #7 Fall 2005 Bipolar Transistor Amplifiers Purpose The aim of this experiment is to construct a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must
Physics 3330 Experiment #7 Fall 2005 Bipolar Transistor Amplifiers Purpose The aim of this experiment is to construct a bipolar transistor amplifier with a voltage gain of minus 25. The amplifier must
CHAPTER 10 OPERATIONAL-AMPLIFIER CIRCUITS
 CHAPTER 10 OPERATIONAL-AMPLIFIER CIRCUITS Chapter Outline 10.1 The Two-Stage CMOS Op Amp 10.2 The Folded-Cascode CMOS Op Amp 10.3 The 741 Op-Amp Circuit 10.4 DC Analysis of the 741 10.5 Small-Signal Analysis
CHAPTER 10 OPERATIONAL-AMPLIFIER CIRCUITS Chapter Outline 10.1 The Two-Stage CMOS Op Amp 10.2 The Folded-Cascode CMOS Op Amp 10.3 The 741 Op-Amp Circuit 10.4 DC Analysis of the 741 10.5 Small-Signal Analysis
RLC Resonant Circuits
 C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
C esonant Circuits Andrew McHutchon April 20, 203 Capacitors and Inductors There is a lot of inconsistency when it comes to dealing with reactances of complex components. The format followed in this document
Noise Specs Confusing
 Noise Specs Confusing It s really all very simple once you understand it Then here s the inside story on noise for those of us who haven t been designing low noise amplifiers for ten years You hear all
Noise Specs Confusing It s really all very simple once you understand it Then here s the inside story on noise for those of us who haven t been designing low noise amplifiers for ten years You hear all
Design of a TL431-Based Controller for a Flyback Converter
 Design of a TL431-Based Controller for a Flyback Converter Dr. John Schönberger Plexim GmbH Technoparkstrasse 1 8005 Zürich 1 Introduction The TL431 is a reference voltage source that is commonly used
Design of a TL431-Based Controller for a Flyback Converter Dr. John Schönberger Plexim GmbH Technoparkstrasse 1 8005 Zürich 1 Introduction The TL431 is a reference voltage source that is commonly used
School of Engineering Department of Electrical and Computer Engineering
 1 School of Engineering Department of Electrical and Computer Engineering 332:223 Principles of Electrical Engineering I Laboratory Experiment #4 Title: Operational Amplifiers 1 Introduction Objectives
1 School of Engineering Department of Electrical and Computer Engineering 332:223 Principles of Electrical Engineering I Laboratory Experiment #4 Title: Operational Amplifiers 1 Introduction Objectives
Chapter 16. Active Filter Design Techniques. Excerpted from Op Amps for Everyone. Literature Number SLOA088. Literature Number: SLOD006A
 hapter 16 Active Filter Design Techniques Literature Number SLOA088 Excerpted from Op Amps for Everyone Literature Number: SLOD006A hapter 16 Active Filter Design Techniques Thomas Kugelstadt 16.1 Introduction
hapter 16 Active Filter Design Techniques Literature Number SLOA088 Excerpted from Op Amps for Everyone Literature Number: SLOD006A hapter 16 Active Filter Design Techniques Thomas Kugelstadt 16.1 Introduction
UNIVERSITY OF CALIFORNIA AT BERKELEY College of Engineering Department of Electrical Engineering and Computer Sciences. EE105 Lab Experiments
 UNIVERSITY OF CALIFORNIA AT BERKELEY College of Engineering Department of Electrical Engineering and Computer Sciences EE15 Lab Experiments Bode Plot Tutorial Contents 1 Introduction 1 2 Bode Plots Basics
UNIVERSITY OF CALIFORNIA AT BERKELEY College of Engineering Department of Electrical Engineering and Computer Sciences EE15 Lab Experiments Bode Plot Tutorial Contents 1 Introduction 1 2 Bode Plots Basics
Designing Stable Compensation Networks for Single Phase Voltage Mode Buck Regulators
 Designing Stable Compensation Networks for Single Phase Voltage Mode Buck Regulators Technical Brief December 3 TB47. Author: Doug Mattingly Assumptions This Technical Brief makes the following assumptions:.
Designing Stable Compensation Networks for Single Phase Voltage Mode Buck Regulators Technical Brief December 3 TB47. Author: Doug Mattingly Assumptions This Technical Brief makes the following assumptions:.
Amplifier Teaching Aid
 Amplifier Teaching Aid Table of Contents Amplifier Teaching Aid...1 Preface...1 Introduction...1 Lesson 1 Semiconductor Review...2 Lesson Plan...2 Worksheet No. 1...7 Experiment No. 1...7 Lesson 2 Bipolar
Amplifier Teaching Aid Table of Contents Amplifier Teaching Aid...1 Preface...1 Introduction...1 Lesson 1 Semiconductor Review...2 Lesson Plan...2 Worksheet No. 1...7 Experiment No. 1...7 Lesson 2 Bipolar
Since any real component also has loss due to the resistive component, the average power dissipated is 2 2R
 Quality factor, Q Reactive components such as capacitors and inductors are often described with a figure of merit called Q. While it can be defined in many ways, it s most fundamental description is: Q
Quality factor, Q Reactive components such as capacitors and inductors are often described with a figure of merit called Q. While it can be defined in many ways, it s most fundamental description is: Q
Technical Note #3. Error Amplifier Design and Applications. Introduction
 Technical Note #3 Error Amplifier Design and Applications Introduction All regulating power supplies require some sort of closed-loop control to force the output to match the desired value. Both digital
Technical Note #3 Error Amplifier Design and Applications Introduction All regulating power supplies require some sort of closed-loop control to force the output to match the desired value. Both digital
BJT Amplifier Circuits
 JT Amplifier ircuits As we have developed different models for D signals (simple large-signal model) and A signals (small-signal model), analysis of JT circuits follows these steps: D biasing analysis:
JT Amplifier ircuits As we have developed different models for D signals (simple large-signal model) and A signals (small-signal model), analysis of JT circuits follows these steps: D biasing analysis:
LM 358 Op Amp. If you have small signals and need a more useful reading we could amplify it using the op amp, this is commonly used in sensors.
 LM 358 Op Amp S k i l l L e v e l : I n t e r m e d i a t e OVERVIEW The LM 358 is a duel single supply operational amplifier. As it is a single supply it eliminates the need for a duel power supply, thus
LM 358 Op Amp S k i l l L e v e l : I n t e r m e d i a t e OVERVIEW The LM 358 is a duel single supply operational amplifier. As it is a single supply it eliminates the need for a duel power supply, thus
The 2N3393 Bipolar Junction Transistor
 The 2N3393 Bipolar Junction Transistor Common-Emitter Amplifier Aaron Prust Abstract The bipolar junction transistor (BJT) is a non-linear electronic device which can be used for amplification and switching.
The 2N3393 Bipolar Junction Transistor Common-Emitter Amplifier Aaron Prust Abstract The bipolar junction transistor (BJT) is a non-linear electronic device which can be used for amplification and switching.
AN105. Introduction: The Nature of VCRs. Resistance Properties of FETs
 Introduction: The Nature of s A voltage-controlled resistor () may be defined as a three-terminal variable resistor where the resistance value between two of the terminals is controlled by a voltage potential
Introduction: The Nature of s A voltage-controlled resistor () may be defined as a three-terminal variable resistor where the resistance value between two of the terminals is controlled by a voltage potential
BJT AC Analysis. by Kenneth A. Kuhn Oct. 20, 2001, rev Aug. 31, 2008
 by Kenneth A. Kuhn Oct. 20, 2001, rev Aug. 31, 2008 Introduction This note will discuss AC analysis using the beta, re transistor model shown in Figure 1 for the three types of amplifiers: common-emitter,
by Kenneth A. Kuhn Oct. 20, 2001, rev Aug. 31, 2008 Introduction This note will discuss AC analysis using the beta, re transistor model shown in Figure 1 for the three types of amplifiers: common-emitter,
Op amp DC error characteristics and the effect on high-precision applications
 Op amp DC error characteristics and the effect on high-precision applications Srudeep Patil, Member of Technical Staff, Maxim Integrated - January 01, 2014 This article discusses the DC limitations of
Op amp DC error characteristics and the effect on high-precision applications Srudeep Patil, Member of Technical Staff, Maxim Integrated - January 01, 2014 This article discusses the DC limitations of
Inductors in AC Circuits
 Inductors in AC Circuits Name Section Resistors, inductors, and capacitors all have the effect of modifying the size of the current in an AC circuit and the time at which the current reaches its maximum
Inductors in AC Circuits Name Section Resistors, inductors, and capacitors all have the effect of modifying the size of the current in an AC circuit and the time at which the current reaches its maximum
Application of network analyzer in measuring the performance functions of power supply
 J Indian Inst Sci, July Aug 2006, 86, 315 325 Indian Institute of Science Application of network analyzer in measuring the performance functions of power supply B SWAMINATHAN* AND V RAMANARAYANAN Power
J Indian Inst Sci, July Aug 2006, 86, 315 325 Indian Institute of Science Application of network analyzer in measuring the performance functions of power supply B SWAMINATHAN* AND V RAMANARAYANAN Power
BJT Amplifier Circuits
 JT Amplifier ircuits As we have developed different models for D signals (simple large-signal model) and A signals (small-signal model), analysis of JT circuits follows these steps: D biasing analysis:
JT Amplifier ircuits As we have developed different models for D signals (simple large-signal model) and A signals (small-signal model), analysis of JT circuits follows these steps: D biasing analysis:
BIASING OF CONSTANT CURRENT MMIC AMPLIFIERS (e.g., ERA SERIES) (AN-60-010)
 BIASING OF CONSTANT CURRENT MMIC AMPLIFIERS (e.g., ERA SERIES) (AN-60-010) Introduction The Mini-Circuits family of microwave monolithic integrated circuit (MMIC) Darlington amplifiers offers the RF designer
BIASING OF CONSTANT CURRENT MMIC AMPLIFIERS (e.g., ERA SERIES) (AN-60-010) Introduction The Mini-Circuits family of microwave monolithic integrated circuit (MMIC) Darlington amplifiers offers the RF designer
Sophomore Physics Laboratory (PH005/105)
 CALIFORNIA INSTITUTE OF TECHNOLOGY PHYSICS MATHEMATICS AND ASTRONOMY DIVISION Sophomore Physics Laboratory (PH5/15) Analog Electronics Active Filters Copyright c Virgínio de Oliveira Sannibale, 23 (Revision
CALIFORNIA INSTITUTE OF TECHNOLOGY PHYSICS MATHEMATICS AND ASTRONOMY DIVISION Sophomore Physics Laboratory (PH5/15) Analog Electronics Active Filters Copyright c Virgínio de Oliveira Sannibale, 23 (Revision
Op-Amp Simulation EE/CS 5720/6720. Read Chapter 5 in Johns & Martin before you begin this assignment.
 Op-Amp Simulation EE/CS 5720/6720 Read Chapter 5 in Johns & Martin before you begin this assignment. This assignment will take you through the simulation and basic characterization of a simple operational
Op-Amp Simulation EE/CS 5720/6720 Read Chapter 5 in Johns & Martin before you begin this assignment. This assignment will take you through the simulation and basic characterization of a simple operational
Basic Op Amp Circuits
 Basic Op Amp ircuits Manuel Toledo INEL 5205 Instrumentation August 3, 2008 Introduction The operational amplifier (op amp or OA for short) is perhaps the most important building block for the design of
Basic Op Amp ircuits Manuel Toledo INEL 5205 Instrumentation August 3, 2008 Introduction The operational amplifier (op amp or OA for short) is perhaps the most important building block for the design of
PHYSICS 360 - LAB #2 Passive Low-pass and High-pass Filter Circuits and Integrator and Differentiator Circuits
 PHYSICS 360 - LAB #2 Passie Low-pass and High-pass Filter Circuits and Integrator and Differentiator Circuits Objectie: Study the behaior of low-pass and high-pass filters. Study the differentiator and
PHYSICS 360 - LAB #2 Passie Low-pass and High-pass Filter Circuits and Integrator and Differentiator Circuits Objectie: Study the behaior of low-pass and high-pass filters. Study the differentiator and
BJT Characteristics and Amplifiers
 BJT Characteristics and Amplifiers Matthew Beckler beck0778@umn.edu EE2002 Lab Section 003 April 2, 2006 Abstract As a basic component in amplifier design, the properties of the Bipolar Junction Transistor
BJT Characteristics and Amplifiers Matthew Beckler beck0778@umn.edu EE2002 Lab Section 003 April 2, 2006 Abstract As a basic component in amplifier design, the properties of the Bipolar Junction Transistor
A Low-Cost, Single Coupling Capacitor Configuration for Stereo Headphone Amplifiers
 Application Report SLOA043 - December 1999 A Low-Cost, Single Coupling Capacitor Configuration for Stereo Headphone Amplifiers Shawn Workman AAP Precision Analog ABSTRACT This application report compares
Application Report SLOA043 - December 1999 A Low-Cost, Single Coupling Capacitor Configuration for Stereo Headphone Amplifiers Shawn Workman AAP Precision Analog ABSTRACT This application report compares
Lab #9: AC Steady State Analysis
 Theory & Introduction Lab #9: AC Steady State Analysis Goals for Lab #9 The main goal for lab 9 is to make the students familar with AC steady state analysis, db scale and the NI ELVIS frequency analyzer.
Theory & Introduction Lab #9: AC Steady State Analysis Goals for Lab #9 The main goal for lab 9 is to make the students familar with AC steady state analysis, db scale and the NI ELVIS frequency analyzer.
Engineering Sciences 22 Systems Summer 2004
 Engineering Sciences 22 Systems Summer 24 BODE PLOTS A Bode plot is a standard format for plotting frequency response of LTI systems. Becoming familiar with this format is useful because: 1. It is a standard
Engineering Sciences 22 Systems Summer 24 BODE PLOTS A Bode plot is a standard format for plotting frequency response of LTI systems. Becoming familiar with this format is useful because: 1. It is a standard
RLC Series Resonance
 RLC Series Resonance 11EM Object: The purpose of this laboratory activity is to study resonance in a resistor-inductor-capacitor (RLC) circuit by examining the current through the circuit as a function
RLC Series Resonance 11EM Object: The purpose of this laboratory activity is to study resonance in a resistor-inductor-capacitor (RLC) circuit by examining the current through the circuit as a function
TL082 Wide Bandwidth Dual JFET Input Operational Amplifier
 TL082 Wide Bandwidth Dual JFET Input Operational Amplifier General Description These devices are low cost high speed dual JFET input operational amplifiers with an internally trimmed input offset voltage
TL082 Wide Bandwidth Dual JFET Input Operational Amplifier General Description These devices are low cost high speed dual JFET input operational amplifiers with an internally trimmed input offset voltage
MAS.836 HOW TO BIAS AN OP-AMP
 MAS.836 HOW TO BIAS AN OP-AMP Op-Amp Circuits: Bias, in an electronic circuit, describes the steady state operating characteristics with no signal being applied. In an op-amp circuit, the operating characteristic
MAS.836 HOW TO BIAS AN OP-AMP Op-Amp Circuits: Bias, in an electronic circuit, describes the steady state operating characteristics with no signal being applied. In an op-amp circuit, the operating characteristic
Reading: HH Sections 4.11 4.13, 4.19 4.20 (pgs. 189-212, 222 224)
 6 OP AMPS II 6 Op Amps II In the previous lab, you explored several applications of op amps. In this exercise, you will look at some of their limitations. You will also examine the op amp integrator and
6 OP AMPS II 6 Op Amps II In the previous lab, you explored several applications of op amps. In this exercise, you will look at some of their limitations. You will also examine the op amp integrator and
Bipolar Junction Transistors
 Bipolar Junction Transistors Physical Structure & Symbols NPN Emitter (E) n-type Emitter region p-type Base region n-type Collector region Collector (C) B C Emitter-base junction (EBJ) Base (B) (a) Collector-base
Bipolar Junction Transistors Physical Structure & Symbols NPN Emitter (E) n-type Emitter region p-type Base region n-type Collector region Collector (C) B C Emitter-base junction (EBJ) Base (B) (a) Collector-base
Chapter 19 Operational Amplifiers
 Chapter 19 Operational Amplifiers The operational amplifier, or op-amp, is a basic building block of modern electronics. Op-amps date back to the early days of vacuum tubes, but they only became common
Chapter 19 Operational Amplifiers The operational amplifier, or op-amp, is a basic building block of modern electronics. Op-amps date back to the early days of vacuum tubes, but they only became common
Application Report SLVA051
 Application Report November 998 Mixed-Signal Products SLVA05 ltage Feedback Vs Current Feedback Op Amps Application Report James Karki Literature Number: SLVA05 November 998 Printed on Recycled Paper IMPORTANT
Application Report November 998 Mixed-Signal Products SLVA05 ltage Feedback Vs Current Feedback Op Amps Application Report James Karki Literature Number: SLVA05 November 998 Printed on Recycled Paper IMPORTANT
AN1991. Audio decibel level detector with meter driver
 Rev. 2.1 20 March 2015 Application note Document information Info Keywords Abstract Content SA604A, LM358, RSSI, cellular radio The SA604A can provide a logarithmic response proportional to the input signal
Rev. 2.1 20 March 2015 Application note Document information Info Keywords Abstract Content SA604A, LM358, RSSI, cellular radio The SA604A can provide a logarithmic response proportional to the input signal
See Horenstein 4.3 and 4.4
 EE 462: Laboratory # 4 DC Power Supply Circuits Using Diodes by Drs. A.V. Radun and K.D. Donohue (2/14/07) Department of Electrical and Computer Engineering University of Kentucky Lexington, KY 40506 Updated
EE 462: Laboratory # 4 DC Power Supply Circuits Using Diodes by Drs. A.V. Radun and K.D. Donohue (2/14/07) Department of Electrical and Computer Engineering University of Kentucky Lexington, KY 40506 Updated
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT
 EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA UNIT 5 - ELECTRICAL AND ELECTRONIC PRINCIPLES NQF LEVEL 3 OUTCOME 4 - ALTERNATING CURRENT 4 Understand single-phase alternating current (ac) theory Single phase AC
Circuits with inductors and alternating currents. Chapter 20 #45, 46, 47, 49
 Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
Circuits with inductors and alternating currents Chapter 20 #45, 46, 47, 49 RL circuits Ch. 20 (last section) Symbol for inductor looks like a spring. An inductor is a circuit element that has a large
www.jameco.com 1-800-831-4242
 Distributed by: www.jameco.com 1-800-831-4242 The content and copyrights of the attached material are the property of its owner. LF411 Low Offset, Low Drift JFET Input Operational Amplifier General Description
Distributed by: www.jameco.com 1-800-831-4242 The content and copyrights of the attached material are the property of its owner. LF411 Low Offset, Low Drift JFET Input Operational Amplifier General Description
TL074 TL074A - TL074B
 A B LOW NOISE JFET QUAD OPERATIONAL AMPLIFIERS WIDE COMMONMODE (UP TO V + CC ) AND DIFFERENTIAL VOLTAGE RANGE LOW INPUT BIAS AND OFFSET CURRENT LOW NOISE e n = 15nV/ Hz (typ) OUTPUT SHORTCIRCUIT PROTECTION
A B LOW NOISE JFET QUAD OPERATIONAL AMPLIFIERS WIDE COMMONMODE (UP TO V + CC ) AND DIFFERENTIAL VOLTAGE RANGE LOW INPUT BIAS AND OFFSET CURRENT LOW NOISE e n = 15nV/ Hz (typ) OUTPUT SHORTCIRCUIT PROTECTION
OPERATIONAL AMPLIFIERS
 INTRODUCTION OPERATIONAL AMPLIFIERS The student will be introduced to the application and analysis of operational amplifiers in this laboratory experiment. The student will apply circuit analysis techniques
INTRODUCTION OPERATIONAL AMPLIFIERS The student will be introduced to the application and analysis of operational amplifiers in this laboratory experiment. The student will apply circuit analysis techniques
Kit 106. 50 Watt Audio Amplifier
 Kit 106 50 Watt Audio Amplifier T his kit is based on an amazing IC amplifier module from ST Electronics, the TDA7294 It is intended for use as a high quality audio class AB amplifier in hi-fi applications
Kit 106 50 Watt Audio Amplifier T his kit is based on an amazing IC amplifier module from ST Electronics, the TDA7294 It is intended for use as a high quality audio class AB amplifier in hi-fi applications
2.161 Signal Processing: Continuous and Discrete Fall 2008
 MT OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 00 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS
MT OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 00 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS
Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models
 EE Modul 1: Electric Circuits Theory Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models EE Modul 1: Electric Circuits Theory Current, Voltage, Impedance Ohm
EE Modul 1: Electric Circuits Theory Basic Laws Circuit Theorems Methods of Network Analysis Non-Linear Devices and Simulation Models EE Modul 1: Electric Circuits Theory Current, Voltage, Impedance Ohm
*For stability of the feedback loop, the differential gain must vary as
 ECE137a Lab project 3 You will first be designing and building an op-amp. The op-amp will then be configured as a narrow-band amplifier for amplification of voice signals in a public address system. Part
ECE137a Lab project 3 You will first be designing and building an op-amp. The op-amp will then be configured as a narrow-band amplifier for amplification of voice signals in a public address system. Part
2 Port Parameters I 1. ECE145A/218A Notes Set #4 1. Two-ways of describing device: A. Equivalent - Circuit-Model
 ECE45A/8A Notes et #4 Port Parameters Two-ways of describing device: A. Equivalent - Circuit-Model Physically based Includes bias dependence Includes frequency dependence Includes size dependence - scalability
ECE45A/8A Notes et #4 Port Parameters Two-ways of describing device: A. Equivalent - Circuit-Model Physically based Includes bias dependence Includes frequency dependence Includes size dependence - scalability
AZ i Z s + Z i. [V s +(V ts + V n + I n Z s )] (1)
![AZ i Z s + Z i. [V s +(V ts + V n + I n Z s )] (1) AZ i Z s + Z i. [V s +(V ts + V n + I n Z s )] (1)](/thumbs/25/6038461.jpg) Euivalent Noise Input Voltage Figure shows the amplifier noise model with a Thévenin input source, where V s is the source voltage, Z s = s + jx s isthesourceimpedance,v ts is the thermal noise voltage
Euivalent Noise Input Voltage Figure shows the amplifier noise model with a Thévenin input source, where V s is the source voltage, Z s = s + jx s isthesourceimpedance,v ts is the thermal noise voltage
Lab 7: Operational Amplifiers Part I
 Lab 7: Operational Amplifiers Part I Objectives The objective of this lab is to study operational amplifier (op amp) and its applications. We will be simulating and building some basic op amp circuits,
Lab 7: Operational Amplifiers Part I Objectives The objective of this lab is to study operational amplifier (op amp) and its applications. We will be simulating and building some basic op amp circuits,
Objective. To design and simulate a cascode amplifier circuit using bipolar transistors.
 ascode Amplifier Design. Objective. o design and simulate a cascode amplifier circuit using bipolar transistors. Assignment description he cascode amplifier utilises the advantage of the common-emitter
ascode Amplifier Design. Objective. o design and simulate a cascode amplifier circuit using bipolar transistors. Assignment description he cascode amplifier utilises the advantage of the common-emitter
TL084 TL084A - TL084B
 A B GENERAL PURPOSE JFET QUAD OPERATIONAL AMPLIFIERS WIDE COMMONMODE (UP TO V + CC ) AND DIFFERENTIAL VOLTAGE RANGE LOW INPUT BIAS AND OFFSET CURRENT OUTPUT SHORTCIRCUIT PROTECTION HIGH INPUT IMPEDANCE
A B GENERAL PURPOSE JFET QUAD OPERATIONAL AMPLIFIERS WIDE COMMONMODE (UP TO V + CC ) AND DIFFERENTIAL VOLTAGE RANGE LOW INPUT BIAS AND OFFSET CURRENT OUTPUT SHORTCIRCUIT PROTECTION HIGH INPUT IMPEDANCE
Lecture 24. Inductance and Switching Power Supplies (how your solar charger voltage converter works)
 Lecture 24 Inductance and Switching Power Supplies (how your solar charger voltage converter works) Copyright 2014 by Mark Horowitz 1 Roadmap: How Does This Work? 2 Processor Board 3 More Detailed Roadmap
Lecture 24 Inductance and Switching Power Supplies (how your solar charger voltage converter works) Copyright 2014 by Mark Horowitz 1 Roadmap: How Does This Work? 2 Processor Board 3 More Detailed Roadmap
Lecture 060 Push-Pull Output Stages (1/11/04) Page 060-1. ECE 6412 - Analog Integrated Circuits and Systems II P.E. Allen - 2002
 Lecture 060 PushPull Output Stages (1/11/04) Page 0601 LECTURE 060 PUSHPULL OUTPUT STAGES (READING: GHLM 362384, AH 226229) Objective The objective of this presentation is: Show how to design stages that
Lecture 060 PushPull Output Stages (1/11/04) Page 0601 LECTURE 060 PUSHPULL OUTPUT STAGES (READING: GHLM 362384, AH 226229) Objective The objective of this presentation is: Show how to design stages that
= (0.400 A) (4.80 V) = 1.92 W = (0.400 A) (7.20 V) = 2.88 W
 Physics 2220 Module 06 Homework 0. What are the magnitude and direction of the current in the 8 Ω resister in the figure? Assume the current is moving clockwise. Then use Kirchhoff's second rule: 3.00
Physics 2220 Module 06 Homework 0. What are the magnitude and direction of the current in the 8 Ω resister in the figure? Assume the current is moving clockwise. Then use Kirchhoff's second rule: 3.00
AN-837 APPLICATION NOTE
 APPLICATION NOTE One Technology Way P.O. Box 916 Norwood, MA 262-916, U.S.A. Tel: 781.329.47 Fax: 781.461.3113 www.analog.com DDS-Based Clock Jitter Performance vs. DAC Reconstruction Filter Performance
APPLICATION NOTE One Technology Way P.O. Box 916 Norwood, MA 262-916, U.S.A. Tel: 781.329.47 Fax: 781.461.3113 www.analog.com DDS-Based Clock Jitter Performance vs. DAC Reconstruction Filter Performance
S-Parameters and Related Quantities Sam Wetterlin 10/20/09
 S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
S-Parameters and Related Quantities Sam Wetterlin 10/20/09 Basic Concept of S-Parameters S-Parameters are a type of network parameter, based on the concept of scattering. The more familiar network parameters
RGB for ZX Spectrum 128, +2, +2A, +3
 RGB for ZX Spectrum 128, +2, +2A, +3 Introduction... 2 Video Circuitry... 3 Audio Circuitry... 8 Lead Wiring... 9 Testing The Lead... 11 Spectrum +2A/+3 RGB Differences... 12 Circuitry Calculations...
RGB for ZX Spectrum 128, +2, +2A, +3 Introduction... 2 Video Circuitry... 3 Audio Circuitry... 8 Lead Wiring... 9 Testing The Lead... 11 Spectrum +2A/+3 RGB Differences... 12 Circuitry Calculations...
The basic cascode amplifier consists of an input common-emitter (CE) configuration driving an output common-base (CB), as shown above.
 Cascode Amplifiers by Dennis L. Feucht Two-transistor combinations, such as the Darlington configuration, provide advantages over single-transistor amplifier stages. Another two-transistor combination
Cascode Amplifiers by Dennis L. Feucht Two-transistor combinations, such as the Darlington configuration, provide advantages over single-transistor amplifier stages. Another two-transistor combination
Dependent Sources: Introduction and analysis of circuits containing dependent sources.
 Dependent Sources: Introduction and analysis of circuits containing dependent sources. So far we have explored timeindependent (resistive) elements that are also linear. We have seen that two terminal
Dependent Sources: Introduction and analysis of circuits containing dependent sources. So far we have explored timeindependent (resistive) elements that are also linear. We have seen that two terminal
EXPERIMENT NUMBER 5 BASIC OSCILLOSCOPE OPERATIONS
 1 EXPERIMENT NUMBER 5 BASIC OSCILLOSCOPE OPERATIONS The oscilloscope is the most versatile and most important tool in this lab and is probably the best tool an electrical engineer uses. This outline guides
1 EXPERIMENT NUMBER 5 BASIC OSCILLOSCOPE OPERATIONS The oscilloscope is the most versatile and most important tool in this lab and is probably the best tool an electrical engineer uses. This outline guides
