The relation between Eigenfactor, audience factor, and influence weight
|
|
|
- Ashlee Harrington
- 7 years ago
- Views:
Transcription
1 The relton between Egenfctor, udence fctor, nd nfluence weght Ludo Wltmn nd Nees n vn Ec Centre for Scence nd Technology Studes, Leden Unversty, The Netherlnds {wltmnlr, ecnpvn}@cwts.ledenunv.nl We present theoretcl nd emprcl nlyss of number of bblometrc ndctors of ournl performnce. We focus on three ndctors n prtculr, nmely the Egenfctor ndctor, the udence fctor, nd the nfluence weght ndctor. Our mn fndng s tht the lst two ndctors cn be regrded s nd of specl cses of the frst ndctor. We lso fnd tht the three ndctors cn be ncely chrcterzed n terms of two propertes. We refer to these propertes s the property of nsenstvty to feld dfferences nd the property of nsenstvty to nsgnfcnt ournls. The emprcl results tht we present llustrte our theoretcl fndngs. We lso show emprclly tht the dfferences between vrous ndctors of ournl performnce re qute substntl. Introducton The mpct fctor (Grfeld, 972, 2006) s wthout doubt the most commonly used bblometrc ndctor of the performnce of scentfc ournls. Vrous lterntves to the mpct fctor hve been proposed n the lterture. These lterntves nclude ndctors bsed on cted-sde normlzton (e.g., Vn Leeuwen & Moed, 2002), ndctors bsed on ctng-sde normlzton (Moed, n press; Ztt & Smll, 2008), ndctors bsed on the h-ndex (e.g., Brun, Glänzel, & Schubert, 2006), nd ndctors bsed on recursve ctton weghtng. Indctors bsed on recursve ctton weghtng were frst proposed by Pns nd Nrn (976; see lso Geller, 978), nd they hve been populr n the feld of economcs (Kltzds, Mmunes, & Stengos, 2003; Kodrzyc & Yu, 2006; Lbnd & Pette, 994; Lebowtz & Plmer, 984; Plcos-Huert & Vol, 2004). The successful PgeRn lgorthm of the Google serch engne (Brn & Pge, 998; Pge, Brn, Motwn, & Wnogrd, 998; see lso Lngvlle & Meyer, 2006) hs cused renewed nterest n recursve ndctors of ournl performnce. Three PgeRn-nspred ndctors tht hve been recently ntroduced re the weghted PgeRn ndctor (Bollen, Rodrguez, & Vn de Sompel, 2006; Dellvlle, Schllng, Rodrguez, Vn de Sompel, & Bollen, 2007), the Egenfctor ndctor (Bergstrom, 2007; West, Bergstrom, & Bergstrom, n press), nd the SCImgo ournl Rn ndctor (González-Perer, Guerrero-Bote, & Moy-Anegón, 2009). In ths pper, we pont out the relton between three ndctors of ournl performnce, nmely the udence fctor (Ztt & Smll, 2008), the nfluence weght ndctor (Pns & Nrn, 976), nd the Egenfctor ndctor. The udence fctor s bsed on ctng-sde normlzton, whle the other two ndctors re bsed on recursve ctton weghtng. Unle the udence fctor nd the nfluence weght ndctor, the Egenfctor ndctor s prmeterzed ndctor. Hence, the behvor of the Egenfctor ndctor depends on the choce of prmeter. Our mn fndng s tht the udence fctor nd the nfluence weght ndctor cn be regrded s nd of specl cses of the Egenfctor ndctor. Relted to ths, we show how the three
2 ndctors cn be chrcterzed n terms of two propertes tht we ntroduce. We refer to these propertes s the property of nsenstvty to feld dfferences nd the property of nsenstvty to nsgnfcnt ournls. Interestngly, t turns out tht the prmeter of the Egenfctor ndctor cn be used to me trde-off between the two propertes. In ddton to theoretcl nlyss of the udence fctor, the nfluence weght ndctor, nd the Egenfctor ndctor, we lso report some results of n emprcl nlyss of these ndctors. Ths pper s orgnzed s follows. Frst, we dscuss our ndctors of nterest nd we pont out how these ndctors re mthemtclly relted to ech other. Next, we study the ndctors emprclly. Fnlly, we brefly dscuss some other relted ndctors nd we summrze our conclusons. Some techncl detls re elborted n n ppendx. Indctors In ths secton, we dscuss the ndctors tht we study n ths pper. We use the followng mthemtcl notton. Let there be n ournls, denoted by,, n. Let T nd T 2 denote two tme perods, where perod T precedes perod T 2. (The two perods my overlp or concde.) We re nterested n mesurng the performnce of ournls,, n bsed on cttons from rtcles publshed n perod T 2 to rtcles publshed n perod T. Let nd 2 denote the number of rtcles publshed n ournl n, respectvely, perods T nd T 2, nd let c denote the number of cttons from rtcles publshed n ournl n perod T 2 to rtcles publshed n ournl n perod T. We defne s s s c. () Hence, s denotes the totl number of cttons from rtcles publshed n ournl n perod T 2 to rtcles publshed n ournls,, n n perod T. Usng the bove mthemtcl notton, we now dscuss our ndctors of nterest. We focus on the essentl chrcterstcs of the ndctors. We gnore prctcl ssues such s the document types (e.g., rtcles, letters, nd revews) tht re ten nto ccount, the length of the tme wndow wthn whch cttons re counted, nd the wy n whch self cttons re hndled. For our present purposes, ssues such s these re not mportnt. Impct fctor Although the mpct fctor s not our mn nterest n ths pper, we nclude t for completeness. The mpct fctor s defned s the verge number of cttons tht ournl hs receved per rtcle (Grfeld, 972, 2006). Hence, the mpct fctor of ournl cn be wrtten s IF c. (2) The mpct fctor s very smple ndctor. It s well nown tht n some felds rtcles re on verge cted much more frequently thn n other felds. The mpct fctor does not correct for such dfferences mong felds. Becuse of ths, mpct fctors of ournls n dfferent felds should not be drectly compred wth ech other. 2
3 Audence fctor The udence fctor s recent proposl of Ztt nd Smll (2008). The udence fctor s smlr to the mpct fctor except tht cttons re weghted bsed on the ournl from whch they orgnte. The lrger ournl s verge number of references per rtcle, the lower the weght of ctton orgntng from the ournl. The udence fctor of ournl s defned s where m nd m S re gven by ms AF c, (3) m 2 s m, (4) s ms, (5) tht s, m denotes ournl s verge number of references per rtcle nd m S denotes the verge number of references per rtcle for ll ournls ten together. Notce tht n the defntons of m nd m S only references to rtcles publshed n ournls,, n n perod T re ten nto ccount. These references re clled ctve references by Ztt nd Smll. All non-ctve references re gnored. By ssgnng weghts to cttons, the udence fctor ms to correct for dfferences mong felds. Unle ndctors bsed on cted-sde normlzton (e.g., Vn Leeuwen & Moed, 2002), whch lso m to correct for feld dfferences, the udence fctor hs the dvntge tht t does not rely on n externlly mposed feld clssfcton. In Appendx A, we ntroduce the property of nsenstvty to feld dfferences. Ths property provdes forml defnton of the de of correctng for feld dfferences. Informlly, the property of nsenstvty to feld dfferences hs the followng nterpretton. Suppose tht we hve two eqully-szed felds nd tht ech ournl gves wy only smll mount of cttons to ournls tht re not n ts own feld. We then sy tht n ndctor s nsenstve to feld dfferences f the verge vlue of the ndctor for one feld devtes from the verge vlue of the ndctor for the other feld only by smll mount. In the cse of two felds wthout ny betweenfelds ctton trffc, the property of nsenstvty to feld dfferences requres tht the verge vlue of n ndctor s the sme for both felds. We show n ppendx A tht under reltvely mld ssumpton the udence fctor hs the property of nsenstvty to feld dfferences. Influence weght The nfluence weght ndctor ws proposed by Pns nd Nrn (976). The nfluence weghts of ournls,, n, denoted by IW,, IW n, re obtned by solvng the followng system of lner equtons: 2 Ths system of lner equtons hs unque soluton f the ournl ctton mtrx C = [c ] s rreducble. In other words, the system of lner equtons hs unque soluton f n the ournl ctton grph there exsts for ny two ournls nd pth from to nd pth from to. We note tht for 3
4 IW c IW for, n (6) s, IW s. (7) s Unle the mpct fctor nd the udence fctor, the nfluence weght ndctor s mesure of ournl s verge performnce per reference rther thn of ts verge performnce per rtcle. Bsed on the nfluence weght of ournl, mesure of ournl s verge performnce per rtcle cn be obtned by IPP IW s. (8) Followng Pns nd Nrn (976), we refer to the ndctor n Equton 8 s the nfluence per publcton ndctor. Theoretcl studes of the nfluence weght ndctor nd the nfluence per publcton ndctor cn be found n ppers by Geller (978), Plcos-Huert nd Vol (2004), nd Serrno (2004). In the lst two ppers, the nfluence per publcton ndctor s referred to s the nvrnt method. In Appendx A, we show tht the nfluence per publcton ndctor does not hve the property of nsenstvty to feld dfferences. However, the nfluence per publcton ndctor does hve nother nterestng property, referred to s the property of nsenstvty to nsgnfcnt ournls. To see ths, consder the followng exmple. There re n = 8 ournls. Ech ournl publshes 00 rtcles n ech tme perod. Hence, = 2 = 00 for =,, n. The ournl ctton mtrx C = [c ] s shown n Tble. Bsed on ths mtrx, two felds cn be dstngushed. One feld conssts of ournls, 2, 3, nd 4. The other feld conssts of ournls 5, 6, 7, nd 8. A dstncton cn lso be mde between frequently cted ournls nd nfrequently cted ournls. ournls, 2, 5, nd 6 re frequently cted, whle ournls 3, 4, 7, nd 8 re nfrequently cted. In prctce, t s lmost mpossble to hve publcton nd ctton dt for ll nfrequently cted ournls n feld. Ths s becuse the coverge of nfrequently cted ournls n bblogrphc dtbses such s Web of Scence nd Scopus s fr from complete. Some nfrequently cted ournls re covered by these dtbses, but mny others re not. To exmne the consequences of ncomplete coverge of nfrequently cted ournls, we loo t two scenros, scenro nd scenro 2. In scenro, ournls,, 8 re ll covered by the bblogrphc dtbse tht we use. In scenro 2, ournls,, 7 re covered whle ournl 8 s not. For both scenros, nfluence per publcton scores clculted usng Equtons 6, 7, nd 8 re reported n Tble 2. As cn be seen n the tble, the nfluence per publcton scores of ournls,, 7 re very smlr n the two scenros. Ths demonstrtes tht the nfluence per publcton ndctor s rther nsenstve to ncomplete coverge of nfrequently cted ournls. We therefore sy tht the nfluence per publcton ndctor hs the property of nsenstvty to nsgnfcnt ournls. computtonl resons t s convenent f the system of lner equtons s not only rreducble but lso perodc. 4
5 TABLE. ournl ctton mtrx. Rows correspond wth ctng ournls. Columns correspond wth cted ournls. ournl TABLE 2. ournls nfluence per publcton scores nd udence fctors. ournl IPP (scenro ) IPP (scenro 2) AF (scenro ) AF (scenro 2) Wht s the relevnce of the property of nsenstvty to nsgnfcnt ournls? Ths cn be seen s follows. Suppose tht nsted of the nfluence per publcton ndctor the udence fctor s used n the bove exmple. For both scenro nd scenro 2, udence fctors clculted usng Equtons 3, 4, nd 5 re reported n Tble 2. Comprng the two scenros, t s cler tht the udence fctor does not hve the property of nsenstvty to nsgnfcnt ournls. Due to the non-coverge of ournl 8 n scenro 2, ournls 5, 6, nd 7 hve substntlly lower udence fctors n ths scenro thn n scenro. ournls, 2, 3, nd 4 hve only mrgnlly lower udence fctors. Hence, the non-coverge of ournl 8 n scenro 2 cuses substntl decrese of the udence fctors of ournls 5, 6, nd 7 reltve to the udence fctors of ournls, 2, 3, nd 4. The results reported n Tble 2 demonstrte tht, when usng n ndctor tht does not hve the property of nsenstvty to nsgnfcnt ournls, the score of ournl n certn feld my strongly depend on the number of nfrequently cted ournls n the sme feld tht re covered by the bblogrphc dtbse tht one uses. Ths senstvty to nfrequently cted ournls my be problemtc when comprng scores of ournls n dfferent felds. If the bblogrphc dtbse tht one uses covers reltvely more nfrequently cted ournls n one feld thn n nother, ournls n the former feld hve n dvntge over ournls n the ltter feld. We hve now ntroduced two propertes tht bblometrc ndctors of ournl performnce my or my not hve, nmely the property of nsenstvty to feld dfferences nd the property of nsenstvty to nsgnfcnt ournls. It s mportnt to note tht these two propertes rule out ech other, tht s, n ndctor cnnot hve both propertes. The followng exmple shows ths. Suppose tht n nfrequently cted ournl s dded to the bblogrphc dtbse tht one uses. The property of nsenstvty to nsgnfcnt ournls then requres tht, becuse the newly dded ournl s nfrequently cted, the scores of ll other ournls remn more or less unchnged. The property of nsenstvty to feld dfferences, on the other hnd, requres tht the verge score of the ournls n feld remns unchnged. Hence, n 5
6 the feld to whch the newly dded ournl belongs, the scores of ll other ournls must ncrese somewht (otherwse the newly dded ournl would cuse decrese of the verge score of the ournls n the feld). Bsed on ths exmple, t s cler tht nsenstvty to feld dfferences nd nsenstvty to nsgnfcnt ournls re conflctng propertes tht cnnot be stsfed both t the sme tme. Egenfctor The Egenfctor ndctor (Bergstrom, 2007; West et l., n press) s recently proposed ndctor of ournl performnce. The ndctor belongs to the fmly of PgeRn-nspred ndctors. Egenfctor scores of lrge number of ournls, clculted bsed on Web of Scence dt, re vlble t Egenfctor scores cn lso be found n the ournl Ctton Reports of Thomson Reuters. Vrous propertes of the Egenfctor ndctor re dscussed by Frnceschet (n press-b). Below, we focus on the essentl chrcterstcs of the Egenfctor ndctor. We gnore the wy n whch the Egenfctor ndctor hndles ournl self cttons nd so-clled dnglng nodes. The Egenfctor ndctor s prmeterzed ndctor. Let [0, ] denote the prmeter of the Egenfctor ndctor. The prmeter s smlr to wht s often referred to s the dmpng fctor prmeter n the PgeRn lterture. By defult, the Egenfctor ndctor uses equl to Ths s lso the defult vlue of the dmpng fctor prmeter n the PgeRn lgorthm. Egenfctor scores re clculted s follows (West, Althouse, Rosvll, Bergstrom, & Bergstrom, 2008; West & Bergstrom, 2008; for n ntutve descrpton, see West et l., n press). For ech ournl, vlue p s obtned by solvng the followng system of lner equtons: 2 p p c ( ) for, n (9) s, p. (0) Usng the vlues p,, p n, the Egenfctor score of ournl s gven by p c EF ( ) 00. () s Unle for exmple the mpct fctor, the Egenfctor ndctor s mesure of ournl s totl performnce rther thn of ts verge performnce per rtcle. Hence, the Egenfctor ndctor s sze dependent. Other thngs equl, ournl tht publshes twce s mny rtcles hs twce s hgh Egenfctor score. Bsed on the Egenfctor score of ournl, mesure of ournl s verge performnce per rtcle cn be obtned by EF ( ) AI ( ). (2) 00 2 For <, ths system of lner equtons lwys hs unque soluton. For =, the system of lner equtons hs unque soluton f the ournl ctton mtrx C = [c ] s rreducble. 6
7 The ndctor n Equton 2 s referred to s the rtcle nfluence ndctor. The propertes of the Egenfctor ndctor nd the rtcle nfluence ndctor depend on the prmeter. We study ths dependence n the next secton. Relton of Egenfctor wth udence fctor nd nfluence weght In the prevous secton, forml mthemtcl defntons of the udence fctor, the nfluence weght ndctor, nd the Egenfctor ndctor were provded. Usng these defntons, t s reltvely esy to see the relton between the three ndctors. However, we do not compre the ndctors drectly wth ech other. Ths s becuse the ndctors re normlzed n dfferent wys. Tht s, the udence fctor s mesure of ournl s verge performnce per rtcle, the nfluence weght ndctor s mesure of ournl s verge performnce per reference, nd the Egenfctor ndctor s mesure of ournl s totl performnce. In ths pper, we focus on mesurng ournl s verge performnce per rtcle. Hence, nsted of the udence fctor, the nfluence weght ndctor, nd the Egenfctor ndctor, we compre the udence fctor, the nfluence per publcton ndctor, nd the rtcle nfluence ndctor. As dscussed n the prevous secton, these three ndctors ll mesure ournl s verge performnce per rtcle. We frst consder the relton between the rtcle nfluence ndctor nd the udence fctor. We ssume tht the number of rtcles tht ournls publsh ether remns stble over tme or ncreses or decreses by the sme percentge for ll ournls. Under ths ssumpton, t turns out tht, f the Egenfctor prmeter equls 0, the rtcle nfluence score of ournl s proportonl to the udence fctor of ournl. 3 Hence, under the bove ssumpton, the udence fctor cn be regrded s specl cse of the rtcle nfluence ndctor. Ths result s stted formlly n the followng theorem. Theorem. Let the number of rtcles publshed n ournl n perod T 2 be proportonl to the number of rtcles publshed n ournl n perod T, tht s, let 2 be proportonl to. Furthermore, let the Egenfctor prmeter be equl to 0. The rtcle nfluence score of ournl s then proportonl to the udence fctor of ournl, tht s, AI () s proportonl to AF. Proof. Let = 0. It then follows from Equtons 9,, nd 2 tht It follows from Equtons 3 nd 4 tht AI ( ) c. (3) s 2 AF c. (4) s Hence, f 2, then AI ( ) AF. Ths completes the proof of the theorem. 3 Two ndctors re proportonl f they dffer by t most multplctve constnt. For prctcl purposes, ndctors tht re proportonl cn be regrded s dentcl. 7
8 We now consder the relton between the rtcle nfluence ndctor nd the nfluence per publcton ndctor. It turns out tht, f the Egenfctor prmeter equls, the rtcle nfluence score of ournl s proportonl to the nfluence per publcton score of ournl. Hence, the nfluence per publcton ndctor cn be regrded s specl cse of the rtcle nfluence ndctor. Ths result s stted formlly n the followng theorem. 4 Theorem 2. Let the Egenfctor prmeter be equl to. The rtcle nfluence score of ournl s then proportonl to the nfluence per publcton score of ournl, tht s, AI () s proportonl to IPP. Proof. Let =. It then follows from Equton 9 tht Equtons nd 2 then mply tht p c p. (5) s p AI ( ). (6) Let q IW s. Equtons 6, 7, nd 8 cn then be rewrtten s, respectvely, q c q, (7) s q s, (8) IPP q. (9) Comprng Equtons 0 nd 5 to Equtons 7 nd 8, t s cler tht then follows from Equtons 6 nd 9 tht of the theorem. p q. It AI ( ) IPP. Ths completes the proof It follows from Theorems nd 2 tht the rtcle nfluence ndctor cn be regrded s nd of nterpolton between the udence fctor nd the nfluence per publcton ndctor. The closer the Egenfctor prmeter s set to 0, the more the rtcle nfluence ndctor behves le the udence fctor. The closer the Egenfctor 4 Geller (978) ponted out tht the ndctors proposed by Pns nd Nrn (976) cn be nterpreted n terms of Mrov chn theory. Ths s the mn nsght needed to see the relton between the rtcle nfluence ndctor (s well s other PgeRn-nspred ndctors) nd the nfluence per publcton ndctor. 8
9 prmeter s set to, the more the rtcle nfluence ndctor behves le the nfluence per publcton ndctor. We now from the prevous secton tht the udence fctor nd the nfluence per publcton ndctor hve more or less opposte propertes. Under reltvely mld ssumpton, the udence fctor hs the property of nsenstvty to feld dfferences. The udence fctor does not hve the property of nsenstvty to nsgnfcnt ournls. The nfluence per publcton ndctor does hve the property of nsenstvty to nsgnfcnt ournls but does not hve the property of nsenstvty to feld dfferences. It s now cler tht the rtcle nfluence ndctor llows one to me trde-off between the propertes of nsenstvty to feld dfferences nd nsenstvty to nsgnfcnt ournls. Settng the Egenfctor prmeter close to 0 gves more weght to the property of nsenstvty to feld dfferences. Settng the Egenfctor prmeter close to gves more weght to the property of nsenstvty to nsgnfcnt ournls. Emprcl nlyss In the prevous two sectons, ndctors of ournl performnce were studed theoretclly. We now turn to the emprcl nlyss of ournl performnce ndctors. Le n the prevous secton, we only consder ndctors tht mesure ournl s verge performnce per rtcle. In ddton to the udence fctor, the nfluence per publcton ndctor, nd the rtcle nfluence ndctor, we lso te nto ccount the mpct fctor. We py specl ttenton to the effect of the Egenfctor prmeter on the behvor of the rtcle nfluence ndctor. 5 For other ppers n whch PgeRnnspred ndctors of ournl performnce re studed emprclly, we refer to Bollen et l. (2006), Bollen, Vn de Sompel, Hgberg, nd Chute (2009), Dvs (2008), Flgs, Kournos, Arencb-orge, nd Krgeorgopoulos (2008), Fersht (2009), Frnceschet (200, n press-), Leydesdorff (2009), López-Illescs, de Moy-Anegón, nd Moed (2008), nd West et l. (2009, n press). 6 Our emprcl nlyss s bsed on the Web of Scence dtbse. Only the scences nd the socl scences re consdered. The rts nd humntes re not ten nto ccount. We frst collected ll cttons from rtcles publshed n 2008 to rtcles publshed between 2003 nd We then selected ll ournls tht hve t lest one ncomng ctton n ech yer between 2003 nd 2007 nd t lest one outgong ctton n In ths wy, we obtned set of 6708 ournls. For ech of these ournls, we clculted sx performnce mesures, nmely the mpct fctor, the udence fctor, nd the rtcle nfluence score for four dfferent vlues (0, 0.5, 0.85, nd ) of the Egenfctor prmeter. We dd not clculte the nfluence per publcton score of ournl. Ths s becuse, ccordng to Theorem 2, nfluence per publcton scores re perfectly correlted wth rtcle nfluence scores clculted for equl to. In order to eep the nlyss s trnsprent s possble, we clculted ll 5 Ths s smlr to the wor of Dng, Yn, Frzho, nd Cverlee (2009). Notce, however, tht Dng et l. study uthors rther thn ournls nd tht they focus on mesurng totl performnce rther thn verge performnce per rtcle. 6 Dvs (2008) nd Fersht (2009) compre ndctors tht mesure ournl s totl performnce. West et l. (2009) crtcze ths pproch nd expln why t s better to compre ndctors tht mesure ournl s verge performnce per rtcle. Bollen et l. (2006), Dvs (2008), nd Frnceschet (200) compre ndctors of totl performnce wth ndctors of verge performnce per rtcle. It s not exctly cler to us how such comprsons should be nterpreted. 7 We only too nto ccount the document types rtcle nd revew. 8 In ddton, we requred the ournl ctton mtrx to be rreducble. Ths lso led to the excluson of some ournls. 9
10 performnce mesures exctly ccordng to the mthemtcl specfcton provded erler n ths pper. Ths mens tht we sometmes devted slghtly from the wy n whch ndctors were orgnlly proposed. For exmple, n the cse of the udence fctor, we dd not mpose ny restrctons on the weght of ctton (unle Ztt & Smll, 2008, p. 859), nd n the cse of the rtcle nfluence ndctor, we dd not gnore ournl self cttons (unle West et l., 2008, p. ). In Tble 3, we report the Person nd Spermn correltons between the dfferent ndctors of ournl performnce. The correlton between the udence fctor nd the rtcle nfluence ndctor for equl to 0 s of specl nterest. It follows from Theorem tht ths correlton equls under the ssumpton tht the number of rtcles tht ournls publsh ether remns stble over tme or ncreses or decreses by the sme percentge for ll ournls. Of course, n prctce ths ssumpton does not hold exctly. However, s cn be seen n Tble 3, our emprcl results stll ndcte very hgh correlton between the udence fctor nd the rtcle nfluence ndctor for equl to 0. Ths correlton s lso clerly vsble n Fgure, n whch the emprcl relton between the two ndctors s shown. Bsed on Tble 3 nd Fgure, we conclude tht for most prctcl purposes the two ndctors cn be regrded s dentcl. TABLE 3. Correltons between sx ndctors of ournl performnce. Person correltons re reported n the lower left prt of the tble. Spermn correltons re reported n the upper rght prt. IF AF AI(0.00) AI(0.50) AI(0.85) AI(.00) IF AF AI(0.00) AI(0.50) AI(0.85) AI(.00)
11 FIG.. Relton between the rtcle nfluence ndctor for equl to 0 nd the udence fctor. Another thng to note n Tble 3 s the very hgh correlton between the rtcle nfluence ndctor for equl to 0 nd the rtcle nfluence ndctor for equl to 0.5. Ths correlton s much closer to thn the correlton between the rtcle nfluence ndctor for equl to 0.5 nd the rtcle nfluence ndctor for equl to. Hence, the results presented n Tble 3 ndcte tht for hgher vlues of the rtcle nfluence ndctor s more senstve to chnges n thn for lower vlues of. For mthemtcl explnton for ths observton, we refer to Lngvlle nd Meyer (2006, Secton 6.). In Fgure 2, we show the emprcl reltons between four ndctors, nmely the mpct fctor nd the rtcle nfluence ndctor for equl to 0, 0.85, nd. (Reltons for the udence fctor nd for the rtcle nfluence ndctor for equl to 0.5 re not shown. Ths s becuse these ndctors re both strongly correlted wth the rtcle nfluence ndctor for equl to 0.) Although the correltons reported n Tble 3 re ll bove 0.75, t s cler from Fgure 2 tht the reltons between most ndctors re not prtculrly strong. Ths cn be seen even better by excludng the ournls wth the hghest scores, s we do n Fgure 3. When hgh scorng ournls re excluded, reltons between ndctors cn be rther we. For ech of the four ndctors consdered n Fgure 2, we lst n Tble 4 n Appendx B the 20 best performng ournls. The results shown n Tble 4 me cler tht for hgh performng ournls there cn lso be substntl dfferences between ndctors. Comprng for exmple the rtcle nfluence ndctor for equl to 0 nd the rtcle nfluence ndctor for equl to, there turn out to be only two ournls tht re n the top 0 for both ndctors.
12 FIG. 2. Reltons between four ndctors of ournl performnce. 2
13 FIG. 3. Relton between the rtcle nfluence ndctor for equl to 0 nd the rtcle nfluence ndctor for equl to. Out of the 6708 ournls, only the 6252 ournls wth vlues below 2 for both ndctors re shown. Our emprcl results show tht the dfferences between ndctors of ournl performnce re fr from neglgble. The results lso show tht the Egenfctor prmeter hs qute lrge effect on the behvor of the rtcle nfluence ndctor (see especlly Fgure 3). Hence, bsed on our emprcl nlyss, t cn be concluded tht the study of dfferent ndctors s not merely of theoretcl nterest but lso hs substntl prctcl relevnce. We note tht some ppers (Dvs, 2008; Fersht, 2009; Leydesdorff, 2009) report strong reltons between certn ndctors, whch my seem to contrdct our results. However, these ppers ether focus on ndctors of totl performnce, for whch t s not surprsng to fnd strong reltons (West et l., 2009), or they rely hevly on Person correlton scores. As shown n our nlyss, hgh Person correlton scores my be somewht msledng nd should be nterpreted wth specl cre. Other ndctors relted to Egenfctor For completeness, n ths secton we brefly consder two other ndctors of ournl performnce tht re relted to the Egenfctor ndctor. These ndctors re the weghted PgeRn ndctor proposed by Bollen et l. (2006) nd the SCImgo ournl Rn ndctor dscussed by González-Perer et l. (2009). SCImgo ournl Rn scores of lrge number of ournls, clculted bsed on Scopus dt, cn be found t SCImgo ournl Rn scores re lso reported n the Scopus dtbse. Le the Egenfctor ndctor, the weghted PgeRn ndctor nd the SCImgo ournl Rn ndctor belong to the fmly of PgeRn-nspred ndctors. 3
14 Weghted PgeRn scores re obtned by solvng the followng system of lner equtons for [0, ] nd = 0: rc r ( ) for,, n (20) s n r. (2) The weghted PgeRn ndctor s sze dependent nd mesures ournl s totl performnce. SCImgo ournl Rn scores re obtned n two steps. In the frst step, the bove system of lner equtons s solved for, [0, ] nd +. 9 By defult, nd re set equl to 0.9 nd , respectvely. 0 In the second step, for ech ournl the SCImgo ournl Rn score s clculted by dvdng r by. Snce the SCImgo ournl Rn ndctor ncorportes normlzton for the number of rtcles publshed n ournl, the ndctor mesures ournl s verge performnce per rtcle. We note tht clcultng SCImgo ournl Rn scores (or weghted PgeRn scores) for + < hs the effect tht smller ournls re fvored over lrger ones. Ths seems n undesrble effect, nd we therefore recommend choosng nd n such wy tht + =. Although the weghted PgeRn ndctor nd the SCImgo ournl Rn ndctor seem qute smlr to the Egenfctor ndctor, there s subtle but mportnt dfference. Choosng nd n such wy tht + = nd solvng Equtons 20 nd 2 does not yeld Egenfctor scores. Ths s due to Equton n the clculton of Egenfctor scores. For ths equton, there s no correspondng equton n the clculton of weghted PgeRn scores or SCImgo ournl Rn scores. A consequence of ths observton s tht the behvor of the weghted PgeRn ndctor nd the SCImgo ournl Rn ndctor cn be qute dfferent from the behvor of the Egenfctor ndctor. For = nd = 0, result smlr to Theorem 2 cn be proven, whch mens tht the weghted PgeRn ndctor nd the SCImgo ournl Rn ndctor reduce to the nfluence per publcton ndctor of Pns nd Nrn (976). However, for = 0 nd =, there s no result smlr to Theorem. Ths mens tht there s no relton between the SCImgo ournl Rn ndctor nd the udence fctor of Ztt nd Smll (2008). In fct, the SCImgo ournl Rn ndctor becomes qute menngless for = 0 nd =. The ndctor smply hs the sme vlue for ll ournls. Conclusons In recent report n whch reserch ssessment prctces bsed on ctton dt re crtclly dscussed, t s stted tht the ssumptons behnd (the Egenfctor ndctor) re not esy for most people to dscern nd tht the complexty (of the Egenfctor ndctor) cn be dngerous becuse the fnl results re hrder to understnd (Adler, Ewng, & Tylor, 2009, p. 2). These re vld concerns tht requre serous ttenton. In ths pper, we hve ddressed these concerns by 9 The SCImgo ournl Rn ndctor uses dfferent ctton wndows n the numertor nd the denomntor of the frst term n Equton 20. For smplcty, we gnore ths ssue. 0 In n erler verson of the SCImgo ournl Rn ndctor, the defult vlues of nd were 0.85 nd 0., respectvely. 4
15 provdng some new nsghts nto the mechncs of the Egenfctor ndctor. Most mportntly, we hve shown the close relton of the Egenfctor ndctor wth the udence fctor (Ztt & Smll, 2008) nd the nfluence weght ndctor (Pns & Nrn, 976). We hve lso ntroduced two propertes tht bblometrc ndctors of ournl performnce my or my not hve. These re the propertes of nsenstvty to feld dfferences nd nsenstvty to nsgnfcnt ournls. Bsed on the relton between the Egenfctor ndctor, the udence fctor, nd the nfluence weght ndctor, we hve ponted out tht the Egenfctor ndctor (or, more precsely, ts normlzed vrnt, the rtcle nfluence ndctor) mplements trde-off between these two propertes. In ths wy, we hve lso been ble to gve concrete nterpretton to the prmeter of the Egenfctor ndctor. The emprcl nlyss tht we hve presented hs shown tht n prctce the dfferences between vrous ndctors of ournl performnce re qute substntl. Ths further llustrtes the mportnce of hvng good understndng of the propertes of dfferent ndctors. Acnowledgment We would le to thn three referees for ther useful comments on n erler drft of ths pper. References Adler, R., Ewng,., & Tylor, P. (2009). Ctton sttstcs: A report from the Interntonl Mthemtcl Unon (IMU) n cooperton wth the Interntonl Councl of Industrl nd Appled Mthemtcs (ICIAM) nd the Insttute of Mthemtcl Sttstcs (IMS). Sttstcl Scence, 24(), 4. Bergstrom, C.T. (2007). Egenfctor: Mesurng the vlue nd prestge of scholrly ournls. College nd Reserch Lbrres News, 68(5). Bollen,., Rodrguez, M.A., & Vn de Sompel, H. (2006). ournl sttus. Scentometrcs, 69(3), Bollen,., Vn de Sompel, H., Hgberg, A., & Chute, R. (2009). A prncpl component nlyss of 39 scentfc mpct mesures. PLoS ONE, 4(6), e6022. Brun, T., Glänzel, W., & Schubert, A. (2006). A Hrsch-type ndex for ournls. Scentometrcs, 69(), Brn, S., & Pge, L. (998). The ntomy of lrge-scle hypertextul Web serch engne. Computer Networs nd ISDN Systems, 30( 7), Dvs, P.M. (2008). Egenfctor: Does the prncple of repeted mprovement result n better estmtes thn rw ctton counts? ournl of the Amercn Socety for Informton Scence nd Technology, 59(3), Dellvlle, R.P., Schllng, L.M., Rodrguez, M.A., Vn de Sompel, H., & Bollen,. (2007). Refnng dermtology ournl mpct fctors usng PgeRn. ournl of the Amercn Acdemy of Dermtology, 57(), 6 9. Dng, Y., Yn, E., Frzho, A., & Cverlee,. (2009). PgeRn for rnng uthors n co-ctton networs. ournl of the Amercn Socety for Informton Scence nd Technology, 60(), Flgs, M.E., Kournos, V.D., Arencb-orge, R., & Krgeorgopoulos, D.E. (2008). Comprson of SCImgo ournl rn ndctor wth ournl mpct fctor. The FASEB ournl, 22(8), Fersht, A. (2009). The most nfluentl ournls: Impct fctor nd Egenfctor. Proceedngs of the Ntonl Acdemy of Scences, 06(7),
16 Frnceschet, M. (200). The dfference between populrty nd prestge n the scences nd n the socl scences: A bblometrc nlyss. ournl of Informetrcs, 4(), Frnceschet, M. (n press-). ournl nfluence fctors. ournl of Informetrcs. Frnceschet, M. (n press-b). Ten good resons to use the Egenfctor metrcs. Informton Processng nd Mngement. Grfeld, E. (972). Ctton nlyss s tool n ournl evluton. Scence, 78, Grfeld, E. (2006). The hstory nd menng of the ournl mpct fctor. ournl of the Amercn Medcl Assocton, 295(), Geller, N.L. (978). On the ctton nfluence methodology of Pns nd Nrn. Informton Processng nd Mngement, 4(2), González-Perer, B., Guerrero-Bote, V.P., & Moy-Anegón, F. (2009). The SR ndctor: A new ndctor of ournls scentfc prestge. rxv:092.44v. Kltzds, P., Mmunes, T.P., & Stengos, T. (2003). Rnngs of cdemc ournls nd nsttutons n economcs. ournl of the Europen Economc Assocton, (6), Kodrzyc, Y.K., & Yu, P. (2006). New pproches to rnng economcs ournls. Contrbutons to Economc Anlyss nd Polcy, 5(), rtcle 24. Lbnd, D.N., & Pette, M.. (994). The reltve mpcts of economcs ournls: ournl of Economc Lterture, 32(2), Lngvlle, A.N., & Meyer, C.D. (2006). Google s PgeRn nd beyond: The scence of serch engne rnngs. Prnceton Unversty Press. Leydesdorff, L. (2009). How re new ctton-bsed ournl ndctors ddng to the bblometrc toolbox? ournl of the Amercn Socety for Informton Scence nd Technology, 60(7), Lebowtz, S.., & Plmer,.P. (984). Assessng the reltve mpcts of economcs ournls. ournl of Economc Lterture, 22(), López-Illescs, C., de Moy-Anegón, F., & Moed, H.F. (2008). Coverge nd ctton mpct of oncologcl ournls n the Web of Scence nd Scopus. ournl of Informetrcs, 2(4), Moed, H.F. (n press). Mesurng contextul ctton mpct of scentfc ournls. ournl of Informetrcs. Pge, L., Brn, S., Motwn, R., & Wnogrd, T. (998). The PgeRn ctton rnng: Brngng order to the web (Techncl Report). Stnford InfoLb. Plcos-Huert, I., & Vol, O. (2004). The mesurement of ntellectul nfluence. Econometrc, 72(3), Pns, G., & Nrn, F. (976). Ctton nfluence for ournl ggregtes of scentfc publctons: Theory, wth pplcton to the lterture of physcs. Informton Processng nd Mngement, 2(5), Serrno, R. (2004). The mesurement of ntellectul nfluence: The vews of sceptc. Economcs Bulletn, (3), 6. Vn Leeuwen, T.N., & Moed, H.F. (2002). Development nd pplcton of ournl mpct mesures n the Dutch scence system. Scentometrcs, 53(2), West,.D., Althouse, B.M., Rosvll, M., Bergstrom, C.T., & Bergstrom, T.C. (2008). Egenfctor score nd rtcle nfluence score: Detled methods. Retreved December 3, 2009, from West,.D., & Bergstrom, C.T. (2008). Pseudocode for clcultng Egenfctor score nd rtcle nfluence score usng dt from Thomson-Reuters ournl Cttons 6
17 Reports. Retreved December 3, 2009, from West,.D., Bergstrom, T.C., & Bergstrom, C.T. (2009). Bg Mcs nd Egenfctor scores: Don t let correlton coeffcents fool you. rxv:09.807v. West,.D., Bergstrom, T.C., & Bergstrom, C.T. (n press). The Egenfctor metrcs: A networ pproch to ssessng scholrly ournls. College nd Reserch Lbrres. Ztt, M., & Smll, H. (2008). Modfyng the ournl mpct fctor by frctonl ctton weghtng: The udence fctor. ournl of the Amercn Socety for Informton Scence nd Technology, 59(),
18 Appendx A: The property of nsenstvty to feld dfferences In ths ppendx, we ntroduce the property of nsenstvty to feld dfferences. We study for dfferent ndctors of ournl performnce whether they hve ths property or not. We frst ntroduce the mthemtcl notton tht we use. Suppose two felds cn be dstngushed, feld nd feld 2. There re n ournls n feld, n 2 ournls n feld 2, nd n = n + n 2 ournls n totl. = {,, n } denotes the set of ll ournls n feld, 2 = {n +,, n} denotes the set of ll ournls n feld 2, nd = 2 denotes the set of ll ournls. A denotes postve mtrx of sze n 2. Elements nd 2 of A denote the number of rtcles publshed n ournl n, respectvely, perods T nd T 2. A stsfes. (22) Hence, the number of rtcles publshed n feld n perod T equls the number of rtcles publshed n feld 2 n perod T. C denotes the ournl ctton mtrx. Ths s non-negtve mtrx of sze n n. Element c of C denotes the number of cttons from rtcles publshed n ournl n perod T 2 to rtcles publshed n ournl n perod T. Usng the bove mthemtcl notton, the property of nsenstvty to feld dfferences cn be formlly defned s follows. Property. Let f denote n ndctor of ournl s verge performnce per rtcle. f s sd to be nsenstve to feld dfferences f nd only f ( 2 f ( A, C) f ( A, C) ) ( ) (23) f ( A, C) for =, 2, for ll n, n 2, A, nd C, nd for ll such tht c ( ) s (24) for =, 2 nd for ll. Informlly, the property of nsenstvty to feld dfferences hs the followng nterpretton. Suppose tht there re two eqully-szed felds nd tht ech ournl gves wy t most frcton of ts cttons to ournls tht re not n ts own feld. An ndctor of ournl performnce s then sd to be nsenstve to feld dfferences f the verge vlue of the ndctor for ech feld seprtely devtes no more thn frcton from the verge vlue of the ndctor for both felds together. Hence, n the cse of two felds wthout ny between-felds ctton trffc, the property of nsenstvty to feld dfferences mples tht the verge vlue of n ndctor s the sme for both felds. It s esy to see tht the mpct fctor s not nsenstve to feld dfferences. Ths s not surprsng, snce t s well nown tht mpct fctors of ournls n dfferent felds 8
19 9 should not be drectly compred wth ech other. The followng theorem sttes tht under reltvely mld ssumpton the udence fctor of Ztt nd Smll (2008) s nsenstve to feld dfferences. Theorem 3. Let the number of rtcles publshed n ournl n perod T 2 be proportonl to the number of rtcles publshed n ournl n perod T, tht s, let 2 be proportonl to. The udence fctor then s nsenstve to feld dfferences. Proof. We use the mthemtcl notton ntroduced t the begnnng of ths ppendx. Let 2 be proportonl to, tht s, let there exst constnt > 0 such tht 2 = for ll. Let be chosen n such wy tht Equton 24 s stsfed for =, 2 nd for ll. It follows from Equtons 3 nd 4 tht s c m 2 S AF. (25) Equton 24 mples tht s c s ) ( (26) f nd tht c s 0 (27) f \. Combnng Equtons 25, 26, nd 27 yelds m m m \ 2 S 2 S 2 S AF ) (. (28) Tng nto ccount tht 2 s proportonl to, t follows from Equtons 22 nd 28 tht S S ) ( AF ) ( m m. (29) It cn further be seen tht S AF m. (30) Equtons 29 nd 30 mply tht
20 AF AF AF ( ) ( ). (3) Hence, Equton 23 s stsfed, whch mens tht the udence fctor hs Property. Ths completes the proof of the theorem. The nfluence per publcton ndctor of Pns nd Nrn (976) s not nsenstve to feld dfferences. Ths s stted n the followng theorem. Theorem 4. The nfluence per publcton ndctor s not nsenstve to feld dfferences. Proof. We prove the theorem by mens of counterexmple. We use the mthemtcl notton ntroduced t the begnnng of ths ppendx. Let n = n 2 =, let A, (32) C, (33) nd let = Equton 24 s then stsfed for =, 2 nd for ll. It follows from Equtons 6, 7, nd 8 tht IPP IPP ( ). (34) Hence, Equton 23 s not stsfed, whch mens tht the nfluence per publcton ndctor does not hve Property. Ths completes the proof of the theorem. The proof of Theorem 4 llustrtes n mportnt problem of the nfluence per publcton ndctor. When there re two felds nd there s lmost no ctton trffc between the felds, nfluence per publcton scores become extremely senstve to the exct number of tmes one feld ctes the other (see lso West et l., 2008, p. 3). In other words, the nfluence per publcton ndctor becomes unstble when the ournl ctton mtrx s lmost reducble. Ths problem s lso dscussed by Serrno (2004). For thorough mthemtcl tretment of ths ssue for PgeRn-nspred ndctors (of whch the nfluence per publcton ndctor cn be seen s lmt cse), we refer to Lngvlle nd Meyer (2006, Secton 6.). 20
21 Appendx B: Best performng ournls TABLE 4. The 20 best performng ournls ccordng to four ndctors of ournl performnce. ournl IF ournl AI(0.00) Annul Revew of Immunology 37.7 Revews of Modern Physcs 6.5 CA-A Cncer ournl for Clncns 37.4 CA-A Cncer ournl for Clncns 4.7 Revews of Modern Physcs 3.8 New Englnd ournl of Medcne 2.0 New Englnd ournl of Medcne 29.5 Annul Revew of Immunology 0.2 Physologcl Revews 29.3 Mterls Scence & Engneerng R- 9.6 Reports Annul Revew of Bochemstry 27.7 Physologcl Revews 9.3 Nture Revews Cncer 27.0 Chemcl Revews 9.0 Nture Revews Immunology 26.5 Annul Revew of Bochemstry 8.4 Nture Revews Moleculr Cell 26.5 Nture Revews Cncer 8.0 Bology Annul Revew of Neuroscence 24.9 Nture Mterls 8.0 Chemcl Revews 23.9 Progress n Mterls Scence 7.9 Cell 22.3 Progress n Polymer Scence 7.8 Annul Revew of Cell nd 2. Nture 7.6 Developmentl Bology Nture 2. AMA-ournl of the Amercn 7.5 Medcl Assocton Nture Revews Neuroscence 20.9 Annul Revew of Neuroscence 7.5 Nture Immunology 20.5 Nture Revews Moleculr Cell 7.5 Bology Nture Medcne 20.3 Scence 7.3 Scence 20.0 Nture Revews Immunology 7.3 Nture Genetcs 8.7 Surfce Scence Reports 7.0 Endocrne Revews 8.4 Annul Revew of Flud Mechncs 6.5 ournl AI(0.85) ournl AI(.00) Annul Revew of Immunology 22.0 Annul Revew of Immunology 33.3 Revews of Modern Physcs 20.5 Annul Revew of Bochemstry 27.4 Annul Revew of Bochemstry 8.2 Cell 26.5 Nture Revews Moleculr Cell 6.9 Nture Revews Moleculr Cell 26. Bology Bology Cell 6.8 Annul Revew of Neuroscence 24.8 Annul Revew of Neuroscence 6.7 Annul Revew of Cell nd 22.5 Developmentl Bology CA-A Cncer ournl for Clncns 6.0 Nture Revews Immunology 2.8 Nture Revews Immunology 4.7 Nture Immunology 20.6 New Englnd ournl of Medcne 4.6 Nture Genetcs 20.0 Nture 4.4 Annul Revew of Astronomy nd 9.8 Astrophyscs Annul Revew of Cell nd 4.3 Nture 9.7 Developmentl Bology Physologcl Revews 3.7 Revews of Modern Physcs 9.4 Nture Revews Cncer 3.6 Nture Revews Cncer 9.0 Nture Genetcs 3.4 Physologcl Revews 8.8 Scence 3.3 CA-A Cncer ournl for Clncns 8.0 Nture Immunology 3. Scence 7.3 Qurterly ournl of Economcs 2.6 Nture Revews Neuroscence 7.0 Nture Revews Neuroscence.8 New Englnd ournl of Medcne 6.9 Nture Medcne 0.8 Nture Cell Bology 5.3 Nture Mterls 0.4 Immunty 5.2 2
22 22
Newton-Raphson Method of Solving a Nonlinear Equation Autar Kaw
 Newton-Rphson Method o Solvng Nonlner Equton Autr Kw Ater redng ths chpter, you should be ble to:. derve the Newton-Rphson method ormul,. develop the lgorthm o the Newton-Rphson method,. use the Newton-Rphson
Newton-Rphson Method o Solvng Nonlner Equton Autr Kw Ater redng ths chpter, you should be ble to:. derve the Newton-Rphson method ormul,. develop the lgorthm o the Newton-Rphson method,. use the Newton-Rphson
Multi-Market Trading and Liquidity: Theory and Evidence
 Mult-Mrket Trdng nd Lqudty: Theory nd Evdence Shmuel Bruch, G. Andrew Kroly, b* Mchel L. Lemmon Eccles School of Busness, Unversty of Uth, Slt Lke Cty, UT 84, USA b Fsher College of Busness, Oho Stte Unversty,
Mult-Mrket Trdng nd Lqudty: Theory nd Evdence Shmuel Bruch, G. Andrew Kroly, b* Mchel L. Lemmon Eccles School of Busness, Unversty of Uth, Slt Lke Cty, UT 84, USA b Fsher College of Busness, Oho Stte Unversty,
Optimal Pricing Scheme for Information Services
 Optml rcng Scheme for Informton Servces Shn-y Wu Opertons nd Informton Mngement The Whrton School Unversty of ennsylvn E-ml: shnwu@whrton.upenn.edu e-yu (Shron) Chen Grdute School of Industrl Admnstrton
Optml rcng Scheme for Informton Servces Shn-y Wu Opertons nd Informton Mngement The Whrton School Unversty of ennsylvn E-ml: shnwu@whrton.upenn.edu e-yu (Shron) Chen Grdute School of Industrl Admnstrton
Incorporating Negative Values in AHP Using Rule- Based Scoring Methodology for Ranking of Sustainable Chemical Process Design Options
 20 th Europen ymposum on Computer Aded Process Engneerng ECAPE20. Perucc nd G. Buzz Ferrrs (Edtors) 2010 Elsever B.V. All rghts reserved. Incorportng Negtve Vlues n AHP Usng Rule- Bsed corng Methodology
20 th Europen ymposum on Computer Aded Process Engneerng ECAPE20. Perucc nd G. Buzz Ferrrs (Edtors) 2010 Elsever B.V. All rghts reserved. Incorportng Negtve Vlues n AHP Usng Rule- Bsed corng Methodology
Polynomial Functions. Polynomial functions in one variable can be written in expanded form as ( )
 Polynomil Functions Polynomil functions in one vrible cn be written in expnded form s n n 1 n 2 2 f x = x + x + x + + x + x+ n n 1 n 2 2 1 0 Exmples of polynomils in expnded form re nd 3 8 7 4 = 5 4 +
Polynomil Functions Polynomil functions in one vrible cn be written in expnded form s n n 1 n 2 2 f x = x + x + x + + x + x+ n n 1 n 2 2 1 0 Exmples of polynomils in expnded form re nd 3 8 7 4 = 5 4 +
MULTI-CRITERIA DECISION AIDING IN PROJECT MANAGEMENT OUTRANKING APPROACH AND VERBAL DECISION ANALYSIS
 Dorot Górec Deprtment of Econometrcs nd Sttstcs Ncolus Coperncus Unversty n Toruń MULTI-CRITERIA DECISION AIDING IN PROJECT MANAGEMENT OUTRANKING APPROACH AND VERBAL DECISION ANALYSIS Introducton A proect
Dorot Górec Deprtment of Econometrcs nd Sttstcs Ncolus Coperncus Unversty n Toruń MULTI-CRITERIA DECISION AIDING IN PROJECT MANAGEMENT OUTRANKING APPROACH AND VERBAL DECISION ANALYSIS Introducton A proect
DlNBVRGH + Sickness Absence Monitoring Report. Executive of the Council. Purpose of report
 DlNBVRGH + + THE CITY OF EDINBURGH COUNCIL Sickness Absence Monitoring Report Executive of the Council 8fh My 4 I.I...3 Purpose of report This report quntifies the mount of working time lost s result of
DlNBVRGH + + THE CITY OF EDINBURGH COUNCIL Sickness Absence Monitoring Report Executive of the Council 8fh My 4 I.I...3 Purpose of report This report quntifies the mount of working time lost s result of
Irregular Repeat Accumulate Codes 1
 Irregulr epet Accumulte Codes 1 Hu Jn, Amod Khndekr, nd obert McElece Deprtment of Electrcl Engneerng, Clforn Insttute of Technology Psden, CA 9115 USA E-ml: {hu, mod, rjm}@systems.cltech.edu Abstrct:
Irregulr epet Accumulte Codes 1 Hu Jn, Amod Khndekr, nd obert McElece Deprtment of Electrcl Engneerng, Clforn Insttute of Technology Psden, CA 9115 USA E-ml: {hu, mod, rjm}@systems.cltech.edu Abstrct:
Experiment 6: Friction
 Experiment 6: Friction In previous lbs we studied Newton s lws in n idel setting, tht is, one where friction nd ir resistnce were ignored. However, from our everydy experience with motion, we know tht
Experiment 6: Friction In previous lbs we studied Newton s lws in n idel setting, tht is, one where friction nd ir resistnce were ignored. However, from our everydy experience with motion, we know tht
Section 5.4 Annuities, Present Value, and Amortization
 Secton 5.4 Annutes, Present Value, and Amortzaton Present Value In Secton 5.2, we saw that the present value of A dollars at nterest rate per perod for n perods s the amount that must be deposted today
Secton 5.4 Annutes, Present Value, and Amortzaton Present Value In Secton 5.2, we saw that the present value of A dollars at nterest rate per perod for n perods s the amount that must be deposted today
Recurrence. 1 Definitions and main statements
 Recurrence 1 Defntons and man statements Let X n, n = 0, 1, 2,... be a MC wth the state space S = (1, 2,...), transton probabltes p j = P {X n+1 = j X n = }, and the transton matrx P = (p j ),j S def.
Recurrence 1 Defntons and man statements Let X n, n = 0, 1, 2,... be a MC wth the state space S = (1, 2,...), transton probabltes p j = P {X n+1 = j X n = }, and the transton matrx P = (p j ),j S def.
Fuzzy Clustering for TV Program Classification
 Fuzzy Clusterng for TV rogrm Clssfcton Yu Zhwen Northwestern olytechncl Unversty X n,.r.chn, 7007 yuzhwen77@yhoo.com.cn Gu Jnhu Northwestern olytechncl Unversty X n,.r.chn, 7007 guh@nwpu.edu.cn Zhou Xngshe
Fuzzy Clusterng for TV rogrm Clssfcton Yu Zhwen Northwestern olytechncl Unversty X n,.r.chn, 7007 yuzhwen77@yhoo.com.cn Gu Jnhu Northwestern olytechncl Unversty X n,.r.chn, 7007 guh@nwpu.edu.cn Zhou Xngshe
WiMAX DBA Algorithm Using a 2-Tier Max-Min Fair Sharing Policy
 WMAX DBA Algorthm Usng 2-Ter Mx-Mn Fr Shrng Polcy Pe-Chen Tseng 1, J-Yn Ts 2, nd Wen-Shyng Hwng 2,* 1 Deprtment of Informton Engneerng nd Informtcs, Tzu Ch College of Technology, Hulen, Twn pechen@tccn.edu.tw
WMAX DBA Algorthm Usng 2-Ter Mx-Mn Fr Shrng Polcy Pe-Chen Tseng 1, J-Yn Ts 2, nd Wen-Shyng Hwng 2,* 1 Deprtment of Informton Engneerng nd Informtcs, Tzu Ch College of Technology, Hulen, Twn pechen@tccn.edu.tw
9 CONTINUOUS DISTRIBUTIONS
 9 CONTINUOUS DISTIBUTIONS A rndom vrible whose vlue my fll nywhere in rnge of vlues is continuous rndom vrible nd will be ssocited with some continuous distribution. Continuous distributions re to discrete
9 CONTINUOUS DISTIBUTIONS A rndom vrible whose vlue my fll nywhere in rnge of vlues is continuous rndom vrible nd will be ssocited with some continuous distribution. Continuous distributions re to discrete
Resistive Network Analysis. The Node Voltage Method - 1
 esste Network Anlyss he nlyss of n electrcl network conssts of determnng ech of the unknown rnch currents nd node oltges. A numer of methods for network nlyss he een deeloped, sed on Ohm s Lw nd Krchoff
esste Network Anlyss he nlyss of n electrcl network conssts of determnng ech of the unknown rnch currents nd node oltges. A numer of methods for network nlyss he een deeloped, sed on Ohm s Lw nd Krchoff
Joint Opaque booking systems for online travel agencies
 Jont Opque bookng systems for onlne trvel gences Mlgorzt OGOOWSKA nd Domnque TORRE Mrch 2010 Abstrct Ths pper nlyzes the propertes of the dvnced Opque bookng systems used by the onlne trvel gences n conjuncton
Jont Opque bookng systems for onlne trvel gences Mlgorzt OGOOWSKA nd Domnque TORRE Mrch 2010 Abstrct Ths pper nlyzes the propertes of the dvnced Opque bookng systems used by the onlne trvel gences n conjuncton
Basic Analysis of Autarky and Free Trade Models
 Bsic Anlysis of Autrky nd Free Trde Models AUTARKY Autrky condition in prticulr commodity mrket refers to sitution in which country does not engge in ny trde in tht commodity with other countries. Consequently
Bsic Anlysis of Autrky nd Free Trde Models AUTARKY Autrky condition in prticulr commodity mrket refers to sitution in which country does not engge in ny trde in tht commodity with other countries. Consequently
Treatment Spring Late Summer Fall 0.10 5.56 3.85 0.61 6.97 3.01 1.91 3.01 2.13 2.99 5.33 2.50 1.06 3.53 6.10 Mean = 1.33 Mean = 4.88 Mean = 3.
 The nlysis of vrince (ANOVA) Although the t-test is one of the most commonly used sttisticl hypothesis tests, it hs limittions. The mjor limittion is tht the t-test cn be used to compre the mens of only
The nlysis of vrince (ANOVA) Although the t-test is one of the most commonly used sttisticl hypothesis tests, it hs limittions. The mjor limittion is tht the t-test cn be used to compre the mens of only
A Hadoop Job Scheduling Model Based on Uncategorized Slot
 Journl of Communctons Vol. 10, No. 10, October 2015 A Hdoop Job Schedulng Model Bsed on Unctegored Slot To Xue nd Tng-tng L Deprtment of Computer Scence, X n Polytechnc Unversty, X n 710048, Chn Eml: xt73@163.com;
Journl of Communctons Vol. 10, No. 10, October 2015 A Hdoop Job Schedulng Model Bsed on Unctegored Slot To Xue nd Tng-tng L Deprtment of Computer Scence, X n Polytechnc Unversty, X n 710048, Chn Eml: xt73@163.com;
Use Geometry Expressions to create a more complex locus of points. Find evidence for equivalence using Geometry Expressions.
 Lerning Objectives Loci nd Conics Lesson 3: The Ellipse Level: Preclculus Time required: 120 minutes In this lesson, students will generlize their knowledge of the circle to the ellipse. The prmetric nd
Lerning Objectives Loci nd Conics Lesson 3: The Ellipse Level: Preclculus Time required: 120 minutes In this lesson, students will generlize their knowledge of the circle to the ellipse. The prmetric nd
ORIGIN DESTINATION DISAGGREGATION USING FRATAR BIPROPORTIONAL LEAST SQUARES ESTIMATION FOR TRUCK FORECASTING
 ORIGIN DESTINATION DISAGGREGATION USING FRATAR BIPROPORTIONAL LEAST SQUARES ESTIMATION FOR TRUCK FORECASTING Unversty of Wsconsn Mlwukee Pper No. 09-1 Ntonl Center for Freght & Infrstructure Reserch &
ORIGIN DESTINATION DISAGGREGATION USING FRATAR BIPROPORTIONAL LEAST SQUARES ESTIMATION FOR TRUCK FORECASTING Unversty of Wsconsn Mlwukee Pper No. 09-1 Ntonl Center for Freght & Infrstructure Reserch &
An Alternative Way to Measure Private Equity Performance
 An Alternatve Way to Measure Prvate Equty Performance Peter Todd Parlux Investment Technology LLC Summary Internal Rate of Return (IRR) s probably the most common way to measure the performance of prvate
An Alternatve Way to Measure Prvate Equty Performance Peter Todd Parlux Investment Technology LLC Summary Internal Rate of Return (IRR) s probably the most common way to measure the performance of prvate
Research on performance evaluation in logistics service supply chain based unascertained measure
 Suo Junun, L Yncng, Dong Humn Reserch on performnce evluton n logstcs servce suppl chn bsed unscertned mesure Abstrct Junun Suo *, Yncng L, Humn Dong Hebe Unverst of Engneerng, Hndn056038, Chn Receved
Suo Junun, L Yncng, Dong Humn Reserch on performnce evluton n logstcs servce suppl chn bsed unscertned mesure Abstrct Junun Suo *, Yncng L, Humn Dong Hebe Unverst of Engneerng, Hndn056038, Chn Receved
Vector Geometry for Computer Graphics
 Vector Geometry for Computer Grphcs Bo Getz Jnury, 7 Contents Prt I: Bsc Defntons Coordnte Systems... Ponts nd Vectors Mtrces nd Determnnts.. 4 Prt II: Opertons Vector ddton nd sclr multplcton... 5 The
Vector Geometry for Computer Grphcs Bo Getz Jnury, 7 Contents Prt I: Bsc Defntons Coordnte Systems... Ponts nd Vectors Mtrces nd Determnnts.. 4 Prt II: Opertons Vector ddton nd sclr multplcton... 5 The
WHAT HAPPENS WHEN YOU MIX COMPLEX NUMBERS WITH PRIME NUMBERS?
 WHAT HAPPES WHE YOU MIX COMPLEX UMBERS WITH PRIME UMBERS? There s n ol syng, you n t pples n ornges. Mthemtns hte n t; they love to throw pples n ornges nto foo proessor n see wht hppens. Sometmes they
WHAT HAPPES WHE YOU MIX COMPLEX UMBERS WITH PRIME UMBERS? There s n ol syng, you n t pples n ornges. Mthemtns hte n t; they love to throw pples n ornges nto foo proessor n see wht hppens. Sometmes they
Math 135 Circles and Completing the Square Examples
 Mth 135 Circles nd Completing the Squre Exmples A perfect squre is number such tht = b 2 for some rel number b. Some exmples of perfect squres re 4 = 2 2, 16 = 4 2, 169 = 13 2. We wish to hve method for
Mth 135 Circles nd Completing the Squre Exmples A perfect squre is number such tht = b 2 for some rel number b. Some exmples of perfect squres re 4 = 2 2, 16 = 4 2, 169 = 13 2. We wish to hve method for
Boolean Algebra. ECE 152A Winter 2012
 Boolen Algebr ECE 52A Wnter 22 Redng Assgnent Brown nd Vrnesc 2 Introducton to Logc Crcuts 2.5 Boolen Algebr 2.5. The Venn Dgr 2.5.2 Notton nd Ternology 2.5.3 Precedence of Opertons 2.6 Synthess Usng AND,
Boolen Algebr ECE 52A Wnter 22 Redng Assgnent Brown nd Vrnesc 2 Introducton to Logc Crcuts 2.5 Boolen Algebr 2.5. The Venn Dgr 2.5.2 Notton nd Ternology 2.5.3 Precedence of Opertons 2.6 Synthess Usng AND,
Or more simply put, when adding or subtracting quantities, their uncertainties add.
 Propgtion of Uncertint through Mthemticl Opertions Since the untit of interest in n eperiment is rrel otined mesuring tht untit directl, we must understnd how error propgtes when mthemticl opertions re
Propgtion of Uncertint through Mthemticl Opertions Since the untit of interest in n eperiment is rrel otined mesuring tht untit directl, we must understnd how error propgtes when mthemticl opertions re
Lecture 3 Gaussian Probability Distribution
 Lecture 3 Gussin Probbility Distribution Introduction l Gussin probbility distribution is perhps the most used distribution in ll of science. u lso clled bell shped curve or norml distribution l Unlike
Lecture 3 Gussin Probbility Distribution Introduction l Gussin probbility distribution is perhps the most used distribution in ll of science. u lso clled bell shped curve or norml distribution l Unlike
EN3: Introduction to Engineering. Teach Yourself Vectors. 1. Definition. Problems
 EN3: Introducton to Engneerng Tech Yourself Vectors Dvson of Engneerng Brown Unversty. Defnton vector s mthemtcl obect tht hs mgntude nd drecton, nd stsfes the lws of vector ddton. Vectors re used to represent
EN3: Introducton to Engneerng Tech Yourself Vectors Dvson of Engneerng Brown Unversty. Defnton vector s mthemtcl obect tht hs mgntude nd drecton, nd stsfes the lws of vector ddton. Vectors re used to represent
Operations with Polynomials
 38 Chpter P Prerequisites P.4 Opertions with Polynomils Wht you should lern: Write polynomils in stndrd form nd identify the leding coefficients nd degrees of polynomils Add nd subtrct polynomils Multiply
38 Chpter P Prerequisites P.4 Opertions with Polynomils Wht you should lern: Write polynomils in stndrd form nd identify the leding coefficients nd degrees of polynomils Add nd subtrct polynomils Multiply
The CAT model: Predicting air temperature in city streets on the basis of measured reference data
 The CAT model: Predctng r temperture n cty streets on the bss of mesured reference dt Evytr Erell 1 nd Terry Wllmson 2 1 The J. Blusten Insttute For Desert Reserch, Ben-Guron Unversty of the Negev, Sde
The CAT model: Predctng r temperture n cty streets on the bss of mesured reference dt Evytr Erell 1 nd Terry Wllmson 2 1 The J. Blusten Insttute For Desert Reserch, Ben-Guron Unversty of the Negev, Sde
Lesson 28 Psychrometric Processes
 1 Lesson 28 Psychrometrc Processes Verson 1 ME, IIT Khrgpur 1 2 The specfc objectves of ths lecture re to: 1. Introducton to psychrometrc processes nd ther representton (Secton 28.1) 2. Importnt psychrometrc
1 Lesson 28 Psychrometrc Processes Verson 1 ME, IIT Khrgpur 1 2 The specfc objectves of ths lecture re to: 1. Introducton to psychrometrc processes nd ther representton (Secton 28.1) 2. Importnt psychrometrc
Simple Interest Loans (Section 5.1) :
 Chapter 5 Fnance The frst part of ths revew wll explan the dfferent nterest and nvestment equatons you learned n secton 5.1 through 5.4 of your textbook and go through several examples. The second part
Chapter 5 Fnance The frst part of ths revew wll explan the dfferent nterest and nvestment equatons you learned n secton 5.1 through 5.4 of your textbook and go through several examples. The second part
Models and Software for Urban and Regional Transportation Planning : The Contributions of the Center for Research on Transportation
 Models nd Softwre for Urbn nd Regonl Plnnng : The Contrbutons of the Center for Reserch on Mchel Florn Aprl 2008 CIRRELT-2008-11 Models nd Softwre for Urbn Regonl Plnnng: The Contrbutons of the Center
Models nd Softwre for Urbn nd Regonl Plnnng : The Contrbutons of the Center for Reserch on Mchel Florn Aprl 2008 CIRRELT-2008-11 Models nd Softwre for Urbn Regonl Plnnng: The Contrbutons of the Center
19. The Fermat-Euler Prime Number Theorem
 19. The Fermt-Euler Prime Number Theorem Every prime number of the form 4n 1 cn be written s sum of two squres in only one wy (side from the order of the summnds). This fmous theorem ws discovered bout
19. The Fermt-Euler Prime Number Theorem Every prime number of the form 4n 1 cn be written s sum of two squres in only one wy (side from the order of the summnds). This fmous theorem ws discovered bout
Why is the NSW prison population falling?
 NSW Bureu of Crime Sttistics nd Reserch Bureu Brief Issue pper no. 80 September 2012 Why is the NSW prison popultion flling? Jcqueline Fitzgerld & Simon Corben 1 Aim: After stedily incresing for more thn
NSW Bureu of Crime Sttistics nd Reserch Bureu Brief Issue pper no. 80 September 2012 Why is the NSW prison popultion flling? Jcqueline Fitzgerld & Simon Corben 1 Aim: After stedily incresing for more thn
Section 5.3 Annuities, Future Value, and Sinking Funds
 Secton 5.3 Annutes, Future Value, and Snkng Funds Ordnary Annutes A sequence of equal payments made at equal perods of tme s called an annuty. The tme between payments s the payment perod, and the tme
Secton 5.3 Annutes, Future Value, and Snkng Funds Ordnary Annutes A sequence of equal payments made at equal perods of tme s called an annuty. The tme between payments s the payment perod, and the tme
LINEAR TRANSFORMATIONS AND THEIR REPRESENTING MATRICES
 LINEAR TRANSFORMATIONS AND THEIR REPRESENTING MATRICES DAVID WEBB CONTENTS Liner trnsformtions 2 The representing mtrix of liner trnsformtion 3 3 An ppliction: reflections in the plne 6 4 The lgebr of
LINEAR TRANSFORMATIONS AND THEIR REPRESENTING MATRICES DAVID WEBB CONTENTS Liner trnsformtions 2 The representing mtrix of liner trnsformtion 3 3 An ppliction: reflections in the plne 6 4 The lgebr of
Luby s Alg. for Maximal Independent Sets using Pairwise Independence
 Lecture Notes for Randomzed Algorthms Luby s Alg. for Maxmal Independent Sets usng Parwse Independence Last Updated by Erc Vgoda on February, 006 8. Maxmal Independent Sets For a graph G = (V, E), an ndependent
Lecture Notes for Randomzed Algorthms Luby s Alg. for Maxmal Independent Sets usng Parwse Independence Last Updated by Erc Vgoda on February, 006 8. Maxmal Independent Sets For a graph G = (V, E), an ndependent
How To Calculate The Accountng Perod Of Nequalty
 Inequalty and The Accountng Perod Quentn Wodon and Shlomo Ytzha World Ban and Hebrew Unversty September Abstract Income nequalty typcally declnes wth the length of tme taen nto account for measurement.
Inequalty and The Accountng Perod Quentn Wodon and Shlomo Ytzha World Ban and Hebrew Unversty September Abstract Income nequalty typcally declnes wth the length of tme taen nto account for measurement.
Graphs on Logarithmic and Semilogarithmic Paper
 0CH_PHClter_TMSETE_ 3//00 :3 PM Pge Grphs on Logrithmic nd Semilogrithmic Pper OBJECTIVES When ou hve completed this chpter, ou should be ble to: Mke grphs on logrithmic nd semilogrithmic pper. Grph empiricl
0CH_PHClter_TMSETE_ 3//00 :3 PM Pge Grphs on Logrithmic nd Semilogrithmic Pper OBJECTIVES When ou hve completed this chpter, ou should be ble to: Mke grphs on logrithmic nd semilogrithmic pper. Grph empiricl
Small Business Networking
 Why network is n essentil productivity tool for ny smll business Effective technology is essentil for smll businesses looking to increse the productivity of their people nd business. Introducing technology
Why network is n essentil productivity tool for ny smll business Effective technology is essentil for smll businesses looking to increse the productivity of their people nd business. Introducing technology
Econ 4721 Money and Banking Problem Set 2 Answer Key
 Econ 472 Money nd Bnking Problem Set 2 Answer Key Problem (35 points) Consider n overlpping genertions model in which consumers live for two periods. The number of people born in ech genertion grows in
Econ 472 Money nd Bnking Problem Set 2 Answer Key Problem (35 points) Consider n overlpping genertions model in which consumers live for two periods. The number of people born in ech genertion grows in
Example 27.1 Draw a Venn diagram to show the relationship between counting numbers, whole numbers, integers, and rational numbers.
 2 Rtionl Numbers Integers such s 5 were importnt when solving the eqution x+5 = 0. In similr wy, frctions re importnt for solving equtions like 2x = 1. Wht bout equtions like 2x + 1 = 0? Equtions of this
2 Rtionl Numbers Integers such s 5 were importnt when solving the eqution x+5 = 0. In similr wy, frctions re importnt for solving equtions like 2x = 1. Wht bout equtions like 2x + 1 = 0? Equtions of this
The Velocity Factor of an Insulated Two-Wire Transmission Line
 The Velocity Fctor of n Insulted Two-Wire Trnsmission Line Problem Kirk T. McDonld Joseph Henry Lbortories, Princeton University, Princeton, NJ 08544 Mrch 7, 008 Estimte the velocity fctor F = v/c nd the
The Velocity Fctor of n Insulted Two-Wire Trnsmission Line Problem Kirk T. McDonld Joseph Henry Lbortories, Princeton University, Princeton, NJ 08544 Mrch 7, 008 Estimte the velocity fctor F = v/c nd the
Helicopter Theme and Variations
 Helicopter Theme nd Vritions Or, Some Experimentl Designs Employing Pper Helicopters Some possible explntory vribles re: Who drops the helicopter The length of the rotor bldes The height from which the
Helicopter Theme nd Vritions Or, Some Experimentl Designs Employing Pper Helicopters Some possible explntory vribles re: Who drops the helicopter The length of the rotor bldes The height from which the
v a 1 b 1 i, a 2 b 2 i,..., a n b n i.
 SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 455 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces we have studed thus far n the text are real vector spaces snce the scalars are
SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 455 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces we have studed thus far n the text are real vector spaces snce the scalars are
Integration by Substitution
 Integrtion by Substitution Dr. Philippe B. Lvl Kennesw Stte University August, 8 Abstrct This hndout contins mteril on very importnt integrtion method clled integrtion by substitution. Substitution is
Integrtion by Substitution Dr. Philippe B. Lvl Kennesw Stte University August, 8 Abstrct This hndout contins mteril on very importnt integrtion method clled integrtion by substitution. Substitution is
Small Business Networking
 Why network is n essentil productivity tool for ny smll business Effective technology is essentil for smll businesses looking to increse the productivity of their people nd business. Introducing technology
Why network is n essentil productivity tool for ny smll business Effective technology is essentil for smll businesses looking to increse the productivity of their people nd business. Introducing technology
MATH 150 HOMEWORK 4 SOLUTIONS
 MATH 150 HOMEWORK 4 SOLUTIONS Section 1.8 Show tht the product of two of the numbers 65 1000 8 2001 + 3 177, 79 1212 9 2399 + 2 2001, nd 24 4493 5 8192 + 7 1777 is nonnegtive. Is your proof constructive
MATH 150 HOMEWORK 4 SOLUTIONS Section 1.8 Show tht the product of two of the numbers 65 1000 8 2001 + 3 177, 79 1212 9 2399 + 2 2001, nd 24 4493 5 8192 + 7 1777 is nonnegtive. Is your proof constructive
COMPARISON OF SOME METHODS TO FIT A MULTIPLICATIVE TARIFF STRUCTURE TO OBSERVED RISK DATA BY B. AJNE. Skandza, Stockholm ABSTRACT
 COMPARISON OF SOME METHODS TO FIT A MULTIPLICATIVE TARIFF STRUCTURE TO OBSERVED RISK DATA BY B. AJNE Skndz, Stockholm ABSTRACT Three methods for fitting multiplictive models to observed, cross-clssified
COMPARISON OF SOME METHODS TO FIT A MULTIPLICATIVE TARIFF STRUCTURE TO OBSERVED RISK DATA BY B. AJNE Skndz, Stockholm ABSTRACT Three methods for fitting multiplictive models to observed, cross-clssified
Reasoning to Solve Equations and Inequalities
 Lesson4 Resoning to Solve Equtions nd Inequlities In erlier work in this unit, you modeled situtions with severl vriles nd equtions. For exmple, suppose you were given usiness plns for concert showing
Lesson4 Resoning to Solve Equtions nd Inequlities In erlier work in this unit, you modeled situtions with severl vriles nd equtions. For exmple, suppose you were given usiness plns for concert showing
Binary Representation of Numbers Autar Kaw
 Binry Representtion of Numbers Autr Kw After reding this chpter, you should be ble to: 1. convert bse- rel number to its binry representtion,. convert binry number to n equivlent bse- number. In everydy
Binry Representtion of Numbers Autr Kw After reding this chpter, you should be ble to: 1. convert bse- rel number to its binry representtion,. convert binry number to n equivlent bse- number. In everydy
1 Example 1: Axis-aligned rectangles
 COS 511: Theoretcal Machne Learnng Lecturer: Rob Schapre Lecture # 6 Scrbe: Aaron Schld February 21, 2013 Last class, we dscussed an analogue for Occam s Razor for nfnte hypothess spaces that, n conjuncton
COS 511: Theoretcal Machne Learnng Lecturer: Rob Schapre Lecture # 6 Scrbe: Aaron Schld February 21, 2013 Last class, we dscussed an analogue for Occam s Razor for nfnte hypothess spaces that, n conjuncton
9.3. The Scalar Product. Introduction. Prerequisites. Learning Outcomes
 The Sclr Product 9.3 Introduction There re two kinds of multipliction involving vectors. The first is known s the sclr product or dot product. This is so-clled becuse when the sclr product of two vectors
The Sclr Product 9.3 Introduction There re two kinds of multipliction involving vectors. The first is known s the sclr product or dot product. This is so-clled becuse when the sclr product of two vectors
8.5 UNITARY AND HERMITIAN MATRICES. The conjugate transpose of a complex matrix A, denoted by A*, is given by
 6 CHAPTER 8 COMPLEX VECTOR SPACES 5. Fnd the kernel of the lnear transformaton gven n Exercse 5. In Exercses 55 and 56, fnd the mage of v, for the ndcated composton, where and are gven by the followng
6 CHAPTER 8 COMPLEX VECTOR SPACES 5. Fnd the kernel of the lnear transformaton gven n Exercse 5. In Exercses 55 and 56, fnd the mage of v, for the ndcated composton, where and are gven by the followng
Mathematics. Vectors. hsn.uk.net. Higher. Contents. Vectors 128 HSN23100
 hsn.uk.net Higher Mthemtics UNIT 3 OUTCOME 1 Vectors Contents Vectors 18 1 Vectors nd Sclrs 18 Components 18 3 Mgnitude 130 4 Equl Vectors 131 5 Addition nd Subtrction of Vectors 13 6 Multipliction by
hsn.uk.net Higher Mthemtics UNIT 3 OUTCOME 1 Vectors Contents Vectors 18 1 Vectors nd Sclrs 18 Components 18 3 Mgnitude 130 4 Equl Vectors 131 5 Addition nd Subtrction of Vectors 13 6 Multipliction by
c. Values in statements are broken down by fiscal years; many projects are
 Lecture 18: Finncil Mngement (Continued)/Csh Flow CEE 498 Construction Project Mngement L Schedules A. Schedule.of Contrcts Completed See Attchment # 1 ll. 1. Revenues Erned 2. Cost of Revenues 3. Gross
Lecture 18: Finncil Mngement (Continued)/Csh Flow CEE 498 Construction Project Mngement L Schedules A. Schedule.of Contrcts Completed See Attchment # 1 ll. 1. Revenues Erned 2. Cost of Revenues 3. Gross
Example A rectangular box without lid is to be made from a square cardboard of sides 18 cm by cutting equal squares from each corner and then folding
 1 Exmple A rectngulr box without lid is to be mde from squre crdbord of sides 18 cm by cutting equl squres from ech corner nd then folding up the sides. 1 Exmple A rectngulr box without lid is to be mde
1 Exmple A rectngulr box without lid is to be mde from squre crdbord of sides 18 cm by cutting equl squres from ech corner nd then folding up the sides. 1 Exmple A rectngulr box without lid is to be mde
Rolf Baur, Raimund Herz & Ingo Kropp
 COMPUTER AIDED REHABILITATION OF SEWER AND STORM WATER NETWORKS RESEARCH AND TECHNOLOGICAL DEVELOPMENT PROJECT OF EUROPEAN COMMUNITY Lehrstuhl Stdtbuwesen Technsche Unverstät Dresden (TUD) Nürnberger Str.
COMPUTER AIDED REHABILITATION OF SEWER AND STORM WATER NETWORKS RESEARCH AND TECHNOLOGICAL DEVELOPMENT PROJECT OF EUROPEAN COMMUNITY Lehrstuhl Stdtbuwesen Technsche Unverstät Dresden (TUD) Nürnberger Str.
Faculdade de Economia da Universidade de Coimbra
 Fculdde de Econom d Unversdde de Combr Grupo de Estudos Monetáros e Fnnceros (GEMF) Av. Ds d Slv, 65 3004-52 COIMBRA, PORTUGAL gemf@fe.uc.pt http://gemf.fe.uc.pt JOSÉ A. SOARES DA FONSECA The performnce
Fculdde de Econom d Unversdde de Combr Grupo de Estudos Monetáros e Fnnceros (GEMF) Av. Ds d Slv, 65 3004-52 COIMBRA, PORTUGAL gemf@fe.uc.pt http://gemf.fe.uc.pt JOSÉ A. SOARES DA FONSECA The performnce
Loyalty Program and Customer Retention of Bank Credit Cards --an Logistic Regression Analysis based on Questionnaires
 oylty Progrm nd Customer Retenton of Bnk Credt Crds --n ogstc Regresson nlyss sed on Questonnres ZHU Qn IN Runyo College of Economcs Zhejng Gongshng Unversty P.R.Chn 310014 strct To Chnese credt crd ssuers
oylty Progrm nd Customer Retenton of Bnk Credt Crds --n ogstc Regresson nlyss sed on Questonnres ZHU Qn IN Runyo College of Economcs Zhejng Gongshng Unversty P.R.Chn 310014 strct To Chnese credt crd ssuers
5.2. LINE INTEGRALS 265. Let us quickly review the kind of integrals we have studied so far before we introduce a new one.
 5.2. LINE INTEGRALS 265 5.2 Line Integrls 5.2.1 Introduction Let us quickly review the kind of integrls we hve studied so fr before we introduce new one. 1. Definite integrl. Given continuous rel-vlued
5.2. LINE INTEGRALS 265 5.2 Line Integrls 5.2.1 Introduction Let us quickly review the kind of integrls we hve studied so fr before we introduce new one. 1. Definite integrl. Given continuous rel-vlued
A Secure Password-Authenticated Key Agreement Using Smart Cards
 A Secure Password-Authentcated Key Agreement Usng Smart Cards Ka Chan 1, Wen-Chung Kuo 2 and Jn-Chou Cheng 3 1 Department of Computer and Informaton Scence, R.O.C. Mltary Academy, Kaohsung 83059, Tawan,
A Secure Password-Authentcated Key Agreement Usng Smart Cards Ka Chan 1, Wen-Chung Kuo 2 and Jn-Chou Cheng 3 1 Department of Computer and Informaton Scence, R.O.C. Mltary Academy, Kaohsung 83059, Tawan,
Small Business Networking
 Why network is n essentil productivity tool for ny smll business Effective technology is essentil for smll businesses looking to increse the productivity of their people nd processes. Introducing technology
Why network is n essentil productivity tool for ny smll business Effective technology is essentil for smll businesses looking to increse the productivity of their people nd processes. Introducing technology
Factoring Polynomials
 Fctoring Polynomils Some definitions (not necessrily ll for secondry school mthemtics): A polynomil is the sum of one or more terms, in which ech term consists of product of constnt nd one or more vribles
Fctoring Polynomils Some definitions (not necessrily ll for secondry school mthemtics): A polynomil is the sum of one or more terms, in which ech term consists of product of constnt nd one or more vribles
Vehicle Navigation System Integration with GPS/INS/GSM
 Chun Hu Journl of Scence nd Enneern, ol.,no., pp.3-(3) ehcle Nvton System Interton wth GPS/INS/GSM Jum-Mn Ln Chen-Wen Hun, nd Fon-Lon Ts Insttute of Aeronutcs nd Astronutcs Chun-Hw Unversty Hsn-Chu 3,
Chun Hu Journl of Scence nd Enneern, ol.,no., pp.3-(3) ehcle Nvton System Interton wth GPS/INS/GSM Jum-Mn Ln Chen-Wen Hun, nd Fon-Lon Ts Insttute of Aeronutcs nd Astronutcs Chun-Hw Unversty Hsn-Chu 3,
ALABAMA ASSOCIATION of EMERGENCY MANAGERS
 LBM SSOCTON of EMERGENCY MNGERS ON O PCE C BELLO MER E T R O CD NCY M N G L R PROFESSONL CERTFCTON PROGRM .. E. M. CERTFCTON PROGRM 2014 RULES ND REGULTONS 1. THERE WLL BE FOUR LEVELS OF CERTFCTON. BSC,
LBM SSOCTON of EMERGENCY MNGERS ON O PCE C BELLO MER E T R O CD NCY M N G L R PROFESSONL CERTFCTON PROGRM .. E. M. CERTFCTON PROGRM 2014 RULES ND REGULTONS 1. THERE WLL BE FOUR LEVELS OF CERTFCTON. BSC,
EQUATIONS OF LINES AND PLANES
 EQUATIONS OF LINES AND PLANES MATH 195, SECTION 59 (VIPUL NAIK) Corresponding mteril in the ook: Section 12.5. Wht students should definitely get: Prmetric eqution of line given in point-direction nd twopoint
EQUATIONS OF LINES AND PLANES MATH 195, SECTION 59 (VIPUL NAIK) Corresponding mteril in the ook: Section 12.5. Wht students should definitely get: Prmetric eqution of line given in point-direction nd twopoint
Integration. 148 Chapter 7 Integration
 48 Chpter 7 Integrtion 7 Integrtion t ech, by supposing tht during ech tenth of second the object is going t constnt speed Since the object initilly hs speed, we gin suppose it mintins this speed, but
48 Chpter 7 Integrtion 7 Integrtion t ech, by supposing tht during ech tenth of second the object is going t constnt speed Since the object initilly hs speed, we gin suppose it mintins this speed, but
Cardiff Economics Working Papers
 Crdff Economcs Workng Ppers Workng Pper No. E204/4 Reforms, Incentves nd Bnkng Sector Productvty: A Cse of Nepl Kul B Luntel, Shekh Selm nd Pushkr Bjrchry August 204 Crdff Busness School Aberconwy Buldng
Crdff Economcs Workng Ppers Workng Pper No. E204/4 Reforms, Incentves nd Bnkng Sector Productvty: A Cse of Nepl Kul B Luntel, Shekh Selm nd Pushkr Bjrchry August 204 Crdff Busness School Aberconwy Buldng
Small Business Networking
 Why network is n essentil productivity tool for ny smll business Effective technology is essentil for smll businesses looking to increse the productivity of their people nd processes. Introducing technology
Why network is n essentil productivity tool for ny smll business Effective technology is essentil for smll businesses looking to increse the productivity of their people nd processes. Introducing technology
How To Network A Smll Business
 Why network is n essentil productivity tool for ny smll business Effective technology is essentil for smll businesses looking to increse the productivity of their people nd processes. Introducing technology
Why network is n essentil productivity tool for ny smll business Effective technology is essentil for smll businesses looking to increse the productivity of their people nd processes. Introducing technology
Rotating DC Motors Part II
 Rotting Motors rt II II.1 Motor Equivlent Circuit The next step in our consiertion of motors is to evelop n equivlent circuit which cn be use to better unerstn motor opertion. The rmtures in rel motors
Rotting Motors rt II II.1 Motor Equivlent Circuit The next step in our consiertion of motors is to evelop n equivlent circuit which cn be use to better unerstn motor opertion. The rmtures in rel motors
APPLICATION OF QUEUING THEORY TO DYNAMIC VEHICLE ROUTING PROBLEM Wei-Ning Chen, Kainan University Taiwan
 GLOBAL JOURNAL OF BUSINESS RESEARCH VOLUME 3 NUMBER 009 APPLICATION OF QUEUING THEORY TO DYNAMIC VEHICLE ROUTING PROBLEM We-Nng Chen Knn Unersty Twn ABSTRACT In ths pper we eelope n nlyze ynmc moel of
GLOBAL JOURNAL OF BUSINESS RESEARCH VOLUME 3 NUMBER 009 APPLICATION OF QUEUING THEORY TO DYNAMIC VEHICLE ROUTING PROBLEM We-Nng Chen Knn Unersty Twn ABSTRACT In ths pper we eelope n nlyze ynmc moel of
On the Optimal Control of a Cascade of Hydro-Electric Power Stations
 On the Optmal Control of a Cascade of Hydro-Electrc Power Statons M.C.M. Guedes a, A.F. Rbero a, G.V. Smrnov b and S. Vlela c a Department of Mathematcs, School of Scences, Unversty of Porto, Portugal;
On the Optmal Control of a Cascade of Hydro-Electrc Power Statons M.C.M. Guedes a, A.F. Rbero a, G.V. Smrnov b and S. Vlela c a Department of Mathematcs, School of Scences, Unversty of Porto, Portugal;
1.1 The University may award Higher Doctorate degrees as specified from time-to-time in UPR AS11 1.
 HIGHER DOCTORATE DEGREES SUMMARY OF PRINCIPAL CHANGES General changes None Secton 3.2 Refer to text (Amendments to verson 03.0, UPR AS02 are shown n talcs.) 1 INTRODUCTION 1.1 The Unversty may award Hgher
HIGHER DOCTORATE DEGREES SUMMARY OF PRINCIPAL CHANGES General changes None Secton 3.2 Refer to text (Amendments to verson 03.0, UPR AS02 are shown n talcs.) 1 INTRODUCTION 1.1 The Unversty may award Hgher
PROF. BOYAN KOSTADINOV NEW YORK CITY COLLEGE OF TECHNOLOGY, CUNY
 MAT 0630 INTERNET RESOURCES, REVIEW OF CONCEPTS AND COMMON MISTAKES PROF. BOYAN KOSTADINOV NEW YORK CITY COLLEGE OF TECHNOLOGY, CUNY Contents 1. ACT Compss Prctice Tests 1 2. Common Mistkes 2 3. Distributive
MAT 0630 INTERNET RESOURCES, REVIEW OF CONCEPTS AND COMMON MISTAKES PROF. BOYAN KOSTADINOV NEW YORK CITY COLLEGE OF TECHNOLOGY, CUNY Contents 1. ACT Compss Prctice Tests 1 2. Common Mistkes 2 3. Distributive
Distributions. (corresponding to the cumulative distribution function for the discrete case).
 Distributions Recll tht n integrble function f : R [,] such tht R f()d = is clled probbility density function (pdf). The distribution function for the pdf is given by F() = (corresponding to the cumultive
Distributions Recll tht n integrble function f : R [,] such tht R f()d = is clled probbility density function (pdf). The distribution function for the pdf is given by F() = (corresponding to the cumultive
Using Series to Analyze Financial Situations: Present Value
 2.8 Usng Seres to Analyze Fnancal Stuatons: Present Value In the prevous secton, you learned how to calculate the amount, or future value, of an ordnary smple annuty. The amount s the sum of the accumulated
2.8 Usng Seres to Analyze Fnancal Stuatons: Present Value In the prevous secton, you learned how to calculate the amount, or future value, of an ordnary smple annuty. The amount s the sum of the accumulated
Sequences and Series
 Secto 9. Sequeces d Seres You c thk of sequece s fucto whose dom s the set of postve tegers. f ( ), f (), f (),... f ( ),... Defto of Sequece A fte sequece s fucto whose dom s the set of postve tegers.
Secto 9. Sequeces d Seres You c thk of sequece s fucto whose dom s the set of postve tegers. f ( ), f (), f (),... f ( ),... Defto of Sequece A fte sequece s fucto whose dom s the set of postve tegers.
Driver Attitudes and Choices: Speed Limits, Seat Belt Use, and Drinking-and-Driving
 Drver Atttudes nd Choces: Speed Lmts, Set Belt Use, nd Drnkng-nd-Drvng Young-Jun Kweon Assocte Reserch Scentst Vrgn Trnsportton Reserch Councl Young- Jun.Kweon@VDOT.Vrgn.gov Vrgn Trnsportton Reserch Councl
Drver Atttudes nd Choces: Speed Lmts, Set Belt Use, nd Drnkng-nd-Drvng Young-Jun Kweon Assocte Reserch Scentst Vrgn Trnsportton Reserch Councl Young- Jun.Kweon@VDOT.Vrgn.gov Vrgn Trnsportton Reserch Councl
Institute of Informatics, Faculty of Business and Management, Brno University of Technology,Czech Republic
 Lagrange Multplers as Quanttatve Indcators n Economcs Ivan Mezník Insttute of Informatcs, Faculty of Busness and Management, Brno Unversty of TechnologCzech Republc Abstract The quanttatve role of Lagrange
Lagrange Multplers as Quanttatve Indcators n Economcs Ivan Mezník Insttute of Informatcs, Faculty of Busness and Management, Brno Unversty of TechnologCzech Republc Abstract The quanttatve role of Lagrange
Methodology for Determining E-government Success Factors with Foresight Approach
 Interntonl Reserch Journl of Appled nd Bsc Scences 2013 Avlble onlne t www.rbs.com ISSN 2251-838X / Vol 4 (9): 2652-2662 Scence Eplorer Publctons Methodology for Determnng E-government Success Fctors wth
Interntonl Reserch Journl of Appled nd Bsc Scences 2013 Avlble onlne t www.rbs.com ISSN 2251-838X / Vol 4 (9): 2652-2662 Scence Eplorer Publctons Methodology for Determnng E-government Success Fctors wth
Chapter 6 Best Linear Unbiased Estimate (BLUE)
 hpter 6 Bet Lner Unbed Etmte BLUE Motvton for BLUE Except for Lner Model ce, the optml MVU etmtor mght:. not even ext. be dffcult or mpoble to fnd Reort to ub-optml etmte BLUE one uch ub-optml etmte Ide
hpter 6 Bet Lner Unbed Etmte BLUE Motvton for BLUE Except for Lner Model ce, the optml MVU etmtor mght:. not even ext. be dffcult or mpoble to fnd Reort to ub-optml etmte BLUE one uch ub-optml etmte Ide
Positive Integral Operators With Analytic Kernels
 Çnky Ünverte Fen-Edeyt Fkülte, Journl of Art nd Scence Sy : 6 / Arl k 006 Potve ntegrl Opertor Wth Anlytc Kernel Cn Murt D KMEN Atrct n th pper we contruct exmple of potve defnte ntegrl kernel whch re
Çnky Ünverte Fen-Edeyt Fkülte, Journl of Art nd Scence Sy : 6 / Arl k 006 Potve ntegrl Opertor Wth Anlytc Kernel Cn Murt D KMEN Atrct n th pper we contruct exmple of potve defnte ntegrl kernel whch re
Physics 43 Homework Set 9 Chapter 40 Key
 Physics 43 Homework Set 9 Chpter 4 Key. The wve function for n electron tht is confined to x nm is. Find the normliztion constnt. b. Wht is the probbility of finding the electron in. nm-wide region t x
Physics 43 Homework Set 9 Chpter 4 Key. The wve function for n electron tht is confined to x nm is. Find the normliztion constnt. b. Wht is the probbility of finding the electron in. nm-wide region t x
Appendix D: Completing the Square and the Quadratic Formula. In Appendix A, two special cases of expanding brackets were considered:
 Appendi D: Completing the Squre nd the Qudrtic Formul Fctoring qudrtic epressions such s: + 6 + 8 ws one of the topics introduced in Appendi C. Fctoring qudrtic epressions is useful skill tht cn help you
Appendi D: Completing the Squre nd the Qudrtic Formul Fctoring qudrtic epressions such s: + 6 + 8 ws one of the topics introduced in Appendi C. Fctoring qudrtic epressions is useful skill tht cn help you
Bayesian Updating with Continuous Priors Class 13, 18.05, Spring 2014 Jeremy Orloff and Jonathan Bloom
 Byesin Updting with Continuous Priors Clss 3, 8.05, Spring 04 Jeremy Orloff nd Jonthn Bloom Lerning Gols. Understnd prmeterized fmily of distriutions s representing continuous rnge of hypotheses for the
Byesin Updting with Continuous Priors Clss 3, 8.05, Spring 04 Jeremy Orloff nd Jonthn Bloom Lerning Gols. Understnd prmeterized fmily of distriutions s representing continuous rnge of hypotheses for the
How To Set Up A Network For Your Business
 Why Network is n Essentil Productivity Tool for Any Smll Business TechAdvisory.org SME Reports sponsored by Effective technology is essentil for smll businesses looking to increse their productivity. Computer
Why Network is n Essentil Productivity Tool for Any Smll Business TechAdvisory.org SME Reports sponsored by Effective technology is essentil for smll businesses looking to increse their productivity. Computer
We are now ready to answer the question: What are the possible cardinalities for finite fields?
 Chapter 3 Fnte felds We have seen, n the prevous chapters, some examples of fnte felds. For example, the resdue class rng Z/pZ (when p s a prme) forms a feld wth p elements whch may be dentfed wth the
Chapter 3 Fnte felds We have seen, n the prevous chapters, some examples of fnte felds. For example, the resdue class rng Z/pZ (when p s a prme) forms a feld wth p elements whch may be dentfed wth the
1. Measuring association using correlation and regression
 How to measure assocaton I: Correlaton. 1. Measurng assocaton usng correlaton and regresson We often would lke to know how one varable, such as a mother's weght, s related to another varable, such as a
How to measure assocaton I: Correlaton. 1. Measurng assocaton usng correlaton and regresson We often would lke to know how one varable, such as a mother's weght, s related to another varable, such as a
Texas Instruments 30X IIS Calculator
 Texas Instruments 30X IIS Calculator Keystrokes for the TI-30X IIS are shown for a few topcs n whch keystrokes are unque. Start by readng the Quk Start secton. Then, before begnnng a specfc unt of the
Texas Instruments 30X IIS Calculator Keystrokes for the TI-30X IIS are shown for a few topcs n whch keystrokes are unque. Start by readng the Quk Start secton. Then, before begnnng a specfc unt of the
Cypress Creek High School IB Physics SL/AP Physics B 2012 2013 MP2 Test 1 Newton s Laws. Name: SOLUTIONS Date: Period:
 Nme: SOLUTIONS Dte: Period: Directions: Solve ny 5 problems. You my ttempt dditionl problems for extr credit. 1. Two blocks re sliding to the right cross horizontl surfce, s the drwing shows. In Cse A
Nme: SOLUTIONS Dte: Period: Directions: Solve ny 5 problems. You my ttempt dditionl problems for extr credit. 1. Two blocks re sliding to the right cross horizontl surfce, s the drwing shows. In Cse A
Health insurance marketplace What to expect in 2014
 Helth insurnce mrketplce Wht to expect in 2014 33096VAEENBVA 06/13 The bsics of the mrketplce As prt of the Affordble Cre Act (ACA or helth cre reform lw), strting in 2014 ALL Americns must hve minimum
Helth insurnce mrketplce Wht to expect in 2014 33096VAEENBVA 06/13 The bsics of the mrketplce As prt of the Affordble Cre Act (ACA or helth cre reform lw), strting in 2014 ALL Americns must hve minimum
Rate and Activation Energy of the Iodination of Acetone
 nd Activtion Energ of the Iodintion of Acetone rl N. eer Dte of Eperiment: //00 Florence F. Ls (prtner) Abstrct: The rte, rte lw nd ctivtion energ of the iodintion of cetone re detered b observing the
nd Activtion Energ of the Iodintion of Acetone rl N. eer Dte of Eperiment: //00 Florence F. Ls (prtner) Abstrct: The rte, rte lw nd ctivtion energ of the iodintion of cetone re detered b observing the
Schema Clustering and Retrieval for Multi-domain Pay-As-You-Go Data Integration Systems
 Schem Clusterng nd Retrevl for Mult-domn Py-As-You-Go Dt Integrton Systems Htem A. Mhmoud Unversty of Wterloo Wterloo, ON, Cnd hmhmoud@cs.uwterloo.c Ashrf Aoulng Unversty of Wterloo Wterloo, ON, Cnd shrf@cs.uwterloo.c
Schem Clusterng nd Retrevl for Mult-domn Py-As-You-Go Dt Integrton Systems Htem A. Mhmoud Unversty of Wterloo Wterloo, ON, Cnd hmhmoud@cs.uwterloo.c Ashrf Aoulng Unversty of Wterloo Wterloo, ON, Cnd shrf@cs.uwterloo.c
International Automotive Production Networks: How the web comes together. serie. Leticia Blázquez and Belén González-Díaz WP-EC 2013-05
 sere ec WP-EC 2013-05 Interntonl Automotve Producton Networks: How the web comes together Letc Blázquez nd Belén González-Díz Los documentos de trbjo del Ive ofrecen un vnce de los resultdos de ls nvestgcones
sere ec WP-EC 2013-05 Interntonl Automotve Producton Networks: How the web comes together Letc Blázquez nd Belén González-Díz Los documentos de trbjo del Ive ofrecen un vnce de los resultdos de ls nvestgcones
Line-source based X-ray Tomography
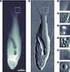 ne-sorce bsed X-ry Tomogrphy Deep Bhrhd Hengyong Y 4 Hong 3 Robert Plemmons 5 Ge Wng 4. Bomedcl mgng Dvson VT-WFU School o Bomedcl Engneerng & Scence We Forest Unversty Wnston-Slem C 757. Bomedcl Engneerng
ne-sorce bsed X-ry Tomogrphy Deep Bhrhd Hengyong Y 4 Hong 3 Robert Plemmons 5 Ge Wng 4. Bomedcl mgng Dvson VT-WFU School o Bomedcl Engneerng & Scence We Forest Unversty Wnston-Slem C 757. Bomedcl Engneerng
