OCTAL, BINARY, AND HEXADECIMAL NUMBERS
|
|
|
- Ruth Bruce
- 7 years ago
- Views:
Transcription
1 OCTAL, BINARY, AND HEXADECIMAL NUMBERS A: REVIEW - DECIMAL or BASE 10 NUMBERS When we see a number like 2,578 we know the 2 counts for more than the 7, even though 7 is a larger number than 2. The reason the 2 counts for more than the 7 is because in our number system, the Hindu-Arabic numeral system, place value is more important than the size of the individual digit. When we talk about decimal numbers, we are not just talking about numbers that have a decimal point, like For now, any base 10 number will be referred to as a decimal number, and vice versa. In base 10, there are 10 different digits that can occupy a column. They are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. If there are more than 9 items, we must represent that value using 2 or more digits. Back to the number: 2,578. The 8 is in the ones column, and 1 can be written as The 7 is in the tens column, and 10 can be written as The 5 is in the hundreds column, and 100 can be written as The 2 is in the thousands column, and 1000 can be written as Notice that the value of each column can be written as a power of 10. B: OCTAL or BASE 8 NUMBERS In octal there are only 8 different digits that can occupy a single column. They are 0, 1, 2, 3, 4, 5, 6, and 7. In base 10 there is no single digit to represent the number 10. In base 8 there is no single digit to represent the number 8 or 9. If there are more than 7 items, we must represent that value using 2 or more digits. Given the number: 33, The 2 is in the ones column, and 1 can be written as 8 0. The 6 is in the eights column, and 8 can be written as 8 1. The 4 is in the eight times eight, or 64s column, and 64 can be written as 8 2. The 3 is in the eight times eight times eight, or 512s column, and 512 can be written as 8 3. Converting an Octal Number into a Decimal Number Suppose I have the number above: 33, (Notice that there is a subscript after the number indicating that this is a base 8 number. In most cases, if there is no subscript you can assume the given number is base 10. Sometime a subscript of 10 is used to avoid confusion.) To convert the number 33, we look at what each digit represents. The 3 is the number of 512s we have: 3 * 512 = 1,536 The 4 is the number of 64s we have: 4 * 64 = 256 The 6 is the number of 8s we have: 6 * 8 = 48 The 2 is the number of 1s we have: 2 * 1 = 2 Adding up the far right column, we get: 1,842 So, 33, = 11,
2 Converting a Decimal Number into an Octal Number Given the number 307, how can that decimal number be converted into an octal number? The process is relatively straightforward. Look at the 4 digits from the previous octal number: 33, Going from left to right, the four columns represent the number of 512s, 64s, 8s, and 1s present. To begin the conversion of 307, we start by asking How many 512s are there in 307? There aren t any, so we will write down the digit zero, just as a place-holder. -> 0xxx Next, we ask How many 64s are there in 307? There are 4. The 4 in the 64s column accounted for 256. Subtract 256 from 307, to get 51 remaining. Next, we ask How many 8s are there in 51? There are 6. The 6 in the 8s column accounted for 48. Subtract from 48 from 51, to get 3 remaining. -> 04xx -> 046x There are three 1s left, so our final answer is: -> 0463 So, = C: BINARY or BASE 2 NUMBERS Binary numbers may look odd at first because they consist of zeroes and ones, and nothing else. Some typical binary numbers are: or or 10 or Given the number Let s identify the value of each of the ones. Going from right to left (or least significant to most significant): There is a 1 in the 1s column, and 1 can be written as 2 0. There is a 1 in the 2s column, and 2 can be written as 2 1. There is a 1 in the two times two, or 4s column, and 4 can be written as 2 2. There is a 0 in the two times two times two, or 8s column, and 8 can be written as 2 3. There is a 1 in the two times two times two times two, or 16s column, and 16 can be written as 2 4. Converting a Binary Number into a Decimal Number Suppose I have the number from above: To convert the number we look at what each binary digit represents and add up the total. There is a 1 in the 16s column: 1 * 16 = 16 There is a 0 in the 8s column: 0 * 8 = 0 There is a 1 in the 4s column: 1 * 4 = 4 There is a 1 in the 2s column: 1 * 2 = 2 There is a 1 in the 1s column: 1 * 1 = 1 Adding up the far right column, we get: 23 So, =
3 Converting a Decimal Number into a Binary Number The process of converting a decimal number into a binary number uses the same steps we saw previously when going from decimal to octal, with different numbers. Let s begin by identifying what each column represents in a binary number. Going from right to left, or smallest to largest, the columns are the 1s, 2s, 4s, 8s, 16s, 32s, 64s, 128s, 256s, 512s, and 1024s. (These numbers are simply the powers of 2, starting at zero.) To convert 487 into binary, we start by asking How many 1024s are there in 487? (Note: 1024 is the 11 th column, and 2 10 equals 1024.) There aren t any, so write down a zero as a place-holder. Next, we ask How many 512s are there in 487? There are 0. How many 256s are there in 487? There is 1. -> 0xxxxxxxxxx -> 00xxxxxxxxx -> 001xxxxxxxx Subtract 256 from 487 to get 231 remaining. How many 128s are there in 231? There is 1. -> 0011xxxxxxx Subtract 128 from 231 to get 103 remaining. How many 64s are there in 103? There is 1. -> 00111xxxxxx Subtract 64 from 103 to get 39 remaining. How many 32s are there in 39? There is 1. -> xxxxx Subtract 32 from 39 to get 7 remaining. How many 16s are there in 7? None. How many 8s are there in 7? None. How many 4s are there in 7? There is 1. -> xxxx -> xxx -> xx Subtract 4 from 7 to get 3 remaining. How many 2s are there in 3? There is 1. -> x Subtract 2 from 3 to get 1 remaining. Finally, there is 1 one left. -> So, =
4 D: HEXADECIMAL or BASE 16 NUMBERS Saving the strangest for last, hexadecimal numbers look very weird at first. With a little bit of work you will see that they behave like octal and binary numbers. In decimal there are 10 different digits that can occupy a column. They are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. In octal there are only 8 different digits that can occupy a column. They are 0, 1, 2, 3, 4, 5, 6, and 7. In binary there are only 2 different digits that can occupy a column. They are 0 and 1. In hexadecimal there are 16 different digits that can occupy a column. We start with the 10 digits most familiar to us: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. But we need 6 more digits, so we will use letters, namely A, B, C, D, E, and F. Hold up one hand and count your fingers. In base 10, you have 5. In base 8, you also have 5. In base 2, you have 101! And in our new base 16, you still have 5. Now count the fingers on both of your hands. In decimal you have 10 fingers. In octal you have 12 fingers. In binary you have 1010 fingers. In base 16, you have A fingers. Basically, in base 16 we must be able to represent 10, 11, 12, 13, 14, and 15 items using a single digit. So we let AA 16 = 10, BB 16 = 11, CC 16 = 12, DD 16 = 13, EE 16 = 14, and FF 16 = 15. A couple of interesting hexadecimal numbers are DDDDDDDD 16 and BBBBBBBB 16 Given the number: The D (or 13) is in the 1s column, and 1 can be written as The A (or 10) is in the 16s column, and 16 can be written as The 3 is in the sixteen times sixteen, or 256s column, and 256 can be written as Converting a Hexadecimal Number into a Decimal Number Suppose I have the number from above: To convert the number we look at what each digit represents. The 3 is the number of 256s we have: 3 * 256 = 768 The A is the number of 16s we have: 10 * 16 = 160 The D is the number of 1s we have: 13 * 1 = 13 Adding up the far right column, we get: 941 So, =
5 Converting a Decimal Number into a Hexadecimal Number Like before, we look at each column, see what value it represents, and then determine how many whole times the column value goes into the number we have left. Let s convert the decimal number 747 into a hexadecimal number. The process is similar to what we did for octal and binary numbers, except that the columns represent different values. In base 16, the first four column values are: 16 0 = 1, 16 1 = 16, 16 2 = 256, and 16 3 = How many 4096s are there in 747? None. How many 256s are there in 747? There are 2. Subtract 2 times 256 from 747, to get 235 remaining. How many 16s are there in 235? There are 14. To represent 14 in one digit we use the number E. The E in the 16s column accounted for 224 = 14*16. Subtract from 224 from 235, to get 11 remaining. -> 0xxx -> 02xx -> 02Ex To represent 11 in one digit we use the number B. -> 02EB So, = Homework: (Do this on a separate piece of paper.) 1. Convert the following Octal Numbers into Decimal Numbers: a b c d. 1,362 8 e. 3, Convert the following Decimal Numbers into Octal Numbers: a. 29 b. 67 c. 130 d. 609 e Convert the following Binary Numbers into Decimal Numbers: a b c d e Convert the following Decimal Numbers into Binary Numbers: a. 7 b. 33 c. 140 d. 299 e Convert the following Hexadecimal Numbers into Decimal Numbers: a. 1BB 16 b. B2 16 c. ABC 16 d. 101F 16 e. 3AED Convert the following Decimal Numbers into Hexadecimal Numbers: a. 17 b. 50 c. 239 d e. 10,958
Everything you wanted to know about using Hexadecimal and Octal Numbers in Visual Basic 6
 Everything you wanted to know about using Hexadecimal and Octal Numbers in Visual Basic 6 Number Systems No course on programming would be complete without a discussion of the Hexadecimal (Hex) number
Everything you wanted to know about using Hexadecimal and Octal Numbers in Visual Basic 6 Number Systems No course on programming would be complete without a discussion of the Hexadecimal (Hex) number
2 Number Systems. Source: Foundations of Computer Science Cengage Learning. Objectives After studying this chapter, the student should be able to:
 2 Number Systems 2.1 Source: Foundations of Computer Science Cengage Learning Objectives After studying this chapter, the student should be able to: Understand the concept of number systems. Distinguish
2 Number Systems 2.1 Source: Foundations of Computer Science Cengage Learning Objectives After studying this chapter, the student should be able to: Understand the concept of number systems. Distinguish
6 The Hindu-Arabic System (800 BC)
 6 The Hindu-Arabic System (800 BC) Today the most universally used system of numeration is the Hindu-Arabic system, also known as the decimal system or base ten system. The system was named for the Indian
6 The Hindu-Arabic System (800 BC) Today the most universally used system of numeration is the Hindu-Arabic system, also known as the decimal system or base ten system. The system was named for the Indian
Section 1.4 Place Value Systems of Numeration in Other Bases
 Section.4 Place Value Systems of Numeration in Other Bases Other Bases The Hindu-Arabic system that is used in most of the world today is a positional value system with a base of ten. The simplest reason
Section.4 Place Value Systems of Numeration in Other Bases Other Bases The Hindu-Arabic system that is used in most of the world today is a positional value system with a base of ten. The simplest reason
The Subnet Training Guide
 The Subnet Training Guide A Step By Step Guide on Understanding and Solving Subnetting Problems by Brendan Choi v25 easysubnetcom The Subnet Training Guide v25 easysubnetcom Chapter 1 Understanding IP
The Subnet Training Guide A Step By Step Guide on Understanding and Solving Subnetting Problems by Brendan Choi v25 easysubnetcom The Subnet Training Guide v25 easysubnetcom Chapter 1 Understanding IP
NUMBER SYSTEMS. 1.1 Introduction
 NUMBER SYSTEMS 1.1 Introduction There are several number systems which we normally use, such as decimal, binary, octal, hexadecimal, etc. Amongst them we are most familiar with the decimal number system.
NUMBER SYSTEMS 1.1 Introduction There are several number systems which we normally use, such as decimal, binary, octal, hexadecimal, etc. Amongst them we are most familiar with the decimal number system.
MEP Y9 Practice Book A
 1 Base Arithmetic 1.1 Binary Numbers We normally work with numbers in base 10. In this section we consider numbers in base 2, often called binary numbers. In base 10 we use the digits 0, 1, 2, 3, 4, 5,
1 Base Arithmetic 1.1 Binary Numbers We normally work with numbers in base 10. In this section we consider numbers in base 2, often called binary numbers. In base 10 we use the digits 0, 1, 2, 3, 4, 5,
Base Conversion written by Cathy Saxton
 Base Conversion written by Cathy Saxton 1. Base 10 In base 10, the digits, from right to left, specify the 1 s, 10 s, 100 s, 1000 s, etc. These are powers of 10 (10 x ): 10 0 = 1, 10 1 = 10, 10 2 = 100,
Base Conversion written by Cathy Saxton 1. Base 10 In base 10, the digits, from right to left, specify the 1 s, 10 s, 100 s, 1000 s, etc. These are powers of 10 (10 x ): 10 0 = 1, 10 1 = 10, 10 2 = 100,
Binary Numbers. Binary Octal Hexadecimal
 Binary Numbers Binary Octal Hexadecimal Binary Numbers COUNTING SYSTEMS UNLIMITED... Since you have been using the 10 different digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 all your life, you may wonder how
Binary Numbers Binary Octal Hexadecimal Binary Numbers COUNTING SYSTEMS UNLIMITED... Since you have been using the 10 different digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 all your life, you may wonder how
NUMBER SYSTEMS. William Stallings
 NUMBER SYSTEMS William Stallings The Decimal System... The Binary System...3 Converting between Binary and Decimal...3 Integers...4 Fractions...5 Hexadecimal Notation...6 This document available at WilliamStallings.com/StudentSupport.html
NUMBER SYSTEMS William Stallings The Decimal System... The Binary System...3 Converting between Binary and Decimal...3 Integers...4 Fractions...5 Hexadecimal Notation...6 This document available at WilliamStallings.com/StudentSupport.html
Unsigned Conversions from Decimal or to Decimal and other Number Systems
 Page 1 of 5 Unsigned Conversions from Decimal or to Decimal and other Number Systems In all digital design, analysis, troubleshooting, and repair you will be working with binary numbers (or base 2). It
Page 1 of 5 Unsigned Conversions from Decimal or to Decimal and other Number Systems In all digital design, analysis, troubleshooting, and repair you will be working with binary numbers (or base 2). It
CS321. Introduction to Numerical Methods
 CS3 Introduction to Numerical Methods Lecture Number Representations and Errors Professor Jun Zhang Department of Computer Science University of Kentucky Lexington, KY 40506-0633 August 7, 05 Number in
CS3 Introduction to Numerical Methods Lecture Number Representations and Errors Professor Jun Zhang Department of Computer Science University of Kentucky Lexington, KY 40506-0633 August 7, 05 Number in
Goals. Unary Numbers. Decimal Numbers. 3,148 is. 1000 s 100 s 10 s 1 s. Number Bases 1/12/2009. COMP370 Intro to Computer Architecture 1
 Number Bases //9 Goals Numbers Understand binary and hexadecimal numbers Be able to convert between number bases Understand binary fractions COMP37 Introduction to Computer Architecture Unary Numbers Decimal
Number Bases //9 Goals Numbers Understand binary and hexadecimal numbers Be able to convert between number bases Understand binary fractions COMP37 Introduction to Computer Architecture Unary Numbers Decimal
THE BINARY NUMBER SYSTEM
 THE BINARY NUMBER SYSTEM Dr. Robert P. Webber, Longwood University Our civilization uses the base 10 or decimal place value system. Each digit in a number represents a power of 10. For example, 365.42
THE BINARY NUMBER SYSTEM Dr. Robert P. Webber, Longwood University Our civilization uses the base 10 or decimal place value system. Each digit in a number represents a power of 10. For example, 365.42
EE 261 Introduction to Logic Circuits. Module #2 Number Systems
 EE 261 Introduction to Logic Circuits Module #2 Number Systems Topics A. Number System Formation B. Base Conversions C. Binary Arithmetic D. Signed Numbers E. Signed Arithmetic F. Binary Codes Textbook
EE 261 Introduction to Logic Circuits Module #2 Number Systems Topics A. Number System Formation B. Base Conversions C. Binary Arithmetic D. Signed Numbers E. Signed Arithmetic F. Binary Codes Textbook
Number Conversions Dr. Sarita Agarwal (Acharya Narendra Dev College,University of Delhi)
 Conversions Dr. Sarita Agarwal (Acharya Narendra Dev College,University of Delhi) INTRODUCTION System- A number system defines a set of values to represent quantity. We talk about the number of people
Conversions Dr. Sarita Agarwal (Acharya Narendra Dev College,University of Delhi) INTRODUCTION System- A number system defines a set of values to represent quantity. We talk about the number of people
6 3 4 9 = 6 10 + 3 10 + 4 10 + 9 10
 Lesson The Binary Number System. Why Binary? The number system that you are familiar with, that you use every day, is the decimal number system, also commonly referred to as the base- system. When you
Lesson The Binary Number System. Why Binary? The number system that you are familiar with, that you use every day, is the decimal number system, also commonly referred to as the base- system. When you
Chapter 7 Lab - Decimal, Binary, Octal, Hexadecimal Numbering Systems
 Chapter 7 Lab - Decimal, Binary, Octal, Hexadecimal Numbering Systems This assignment is designed to familiarize you with different numbering systems, specifically: binary, octal, hexadecimal (and decimal)
Chapter 7 Lab - Decimal, Binary, Octal, Hexadecimal Numbering Systems This assignment is designed to familiarize you with different numbering systems, specifically: binary, octal, hexadecimal (and decimal)
Numeration systems. Resources and methods for learning about these subjects (list a few here, in preparation for your research):
 Numeration systems This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Numeration systems This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
2011, The McGraw-Hill Companies, Inc. Chapter 3
 Chapter 3 3.1 Decimal System The radix or base of a number system determines the total number of different symbols or digits used by that system. The decimal system has a base of 10 with the digits 0 through
Chapter 3 3.1 Decimal System The radix or base of a number system determines the total number of different symbols or digits used by that system. The decimal system has a base of 10 with the digits 0 through
I Have...Who Has... Multiplication Game
 How to play the game: Distribute the cards randomly to your students. Some students may get more than one card. Select a student to begin by reading their card aloud. (example: 35. who has 4x4?) 35 4 x
How to play the game: Distribute the cards randomly to your students. Some students may get more than one card. Select a student to begin by reading their card aloud. (example: 35. who has 4x4?) 35 4 x
Number Systems and Radix Conversion
 Number Systems and Radix Conversion Sanjay Rajopadhye, Colorado State University 1 Introduction These notes for CS 270 describe polynomial number systems. The material is not in the textbook, but will
Number Systems and Radix Conversion Sanjay Rajopadhye, Colorado State University 1 Introduction These notes for CS 270 describe polynomial number systems. The material is not in the textbook, but will
The string of digits 101101 in the binary number system represents the quantity
 Data Representation Section 3.1 Data Types Registers contain either data or control information Control information is a bit or group of bits used to specify the sequence of command signals needed for
Data Representation Section 3.1 Data Types Registers contain either data or control information Control information is a bit or group of bits used to specify the sequence of command signals needed for
Decimal to Binary Conversion
 Decimal to Binary Conversion A tool that makes the conversion of decimal values to binary values simple is the following table. The first row is created by counting right to left from one to eight, for
Decimal to Binary Conversion A tool that makes the conversion of decimal values to binary values simple is the following table. The first row is created by counting right to left from one to eight, for
plc numbers - 13.1 Encoded values; BCD and ASCII Error detection; parity, gray code and checksums
 plc numbers - 3. Topics: Number bases; binary, octal, decimal, hexadecimal Binary calculations; s compliments, addition, subtraction and Boolean operations Encoded values; BCD and ASCII Error detection;
plc numbers - 3. Topics: Number bases; binary, octal, decimal, hexadecimal Binary calculations; s compliments, addition, subtraction and Boolean operations Encoded values; BCD and ASCII Error detection;
Useful Number Systems
 Useful Number Systems Decimal Base = 10 Digit Set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Binary Base = 2 Digit Set = {0, 1} Octal Base = 8 = 2 3 Digit Set = {0, 1, 2, 3, 4, 5, 6, 7} Hexadecimal Base = 16 = 2
Useful Number Systems Decimal Base = 10 Digit Set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Binary Base = 2 Digit Set = {0, 1} Octal Base = 8 = 2 3 Digit Set = {0, 1, 2, 3, 4, 5, 6, 7} Hexadecimal Base = 16 = 2
Lecture 2. Binary and Hexadecimal Numbers
 Lecture 2 Binary and Hexadecimal Numbers Purpose: Review binary and hexadecimal number representations Convert directly from one base to another base Review addition and subtraction in binary representations
Lecture 2 Binary and Hexadecimal Numbers Purpose: Review binary and hexadecimal number representations Convert directly from one base to another base Review addition and subtraction in binary representations
Computer Science 281 Binary and Hexadecimal Review
 Computer Science 281 Binary and Hexadecimal Review 1 The Binary Number System Computers store everything, both instructions and data, by using many, many transistors, each of which can be in one of two
Computer Science 281 Binary and Hexadecimal Review 1 The Binary Number System Computers store everything, both instructions and data, by using many, many transistors, each of which can be in one of two
Primes. Name Period Number Theory
 Primes Name Period A Prime Number is a whole number whose only factors are 1 and itself. To find all of the prime numbers between 1 and 100, complete the following exercise: 1. Cross out 1 by Shading in
Primes Name Period A Prime Number is a whole number whose only factors are 1 and itself. To find all of the prime numbers between 1 and 100, complete the following exercise: 1. Cross out 1 by Shading in
CSI 333 Lecture 1 Number Systems
 CSI 333 Lecture 1 Number Systems 1 1 / 23 Basics of Number Systems Ref: Appendix C of Deitel & Deitel. Weighted Positional Notation: 192 = 2 10 0 + 9 10 1 + 1 10 2 General: Digit sequence : d n 1 d n 2...
CSI 333 Lecture 1 Number Systems 1 1 / 23 Basics of Number Systems Ref: Appendix C of Deitel & Deitel. Weighted Positional Notation: 192 = 2 10 0 + 9 10 1 + 1 10 2 General: Digit sequence : d n 1 d n 2...
Number of bits needed to address hosts 8
 Advanced Subnetting Example 1: Your ISP has assigned you a Class C network address of 198.47.212.0. You have 3 networks in your company with the largest containing 134 hosts. You need to figure out if
Advanced Subnetting Example 1: Your ISP has assigned you a Class C network address of 198.47.212.0. You have 3 networks in your company with the largest containing 134 hosts. You need to figure out if
Positional Numbering System
 APPENDIX B Positional Numbering System A positional numbering system uses a set of symbols. The value that each symbol represents, however, depends on its face value and its place value, the value associated
APPENDIX B Positional Numbering System A positional numbering system uses a set of symbols. The value that each symbol represents, however, depends on its face value and its place value, the value associated
Decimals and other fractions
 Chapter 2 Decimals and other fractions How to deal with the bits and pieces When drugs come from the manufacturer they are in doses to suit most adult patients. However, many of your patients will be very
Chapter 2 Decimals and other fractions How to deal with the bits and pieces When drugs come from the manufacturer they are in doses to suit most adult patients. However, many of your patients will be very
COMPSCI 210. Binary Fractions. Agenda & Reading
 COMPSCI 21 Binary Fractions Agenda & Reading Topics: Fractions Binary Octal Hexadecimal Binary -> Octal, Hex Octal -> Binary, Hex Decimal -> Octal, Hex Hex -> Binary, Octal Animation: BinFrac.htm Example
COMPSCI 21 Binary Fractions Agenda & Reading Topics: Fractions Binary Octal Hexadecimal Binary -> Octal, Hex Octal -> Binary, Hex Decimal -> Octal, Hex Hex -> Binary, Octal Animation: BinFrac.htm Example
Oct: 50 8 = 6 (r = 2) 6 8 = 0 (r = 6) Writing the remainders in reverse order we get: (50) 10 = (62) 8
 ECE Department Summer LECTURE #5: Number Systems EEL : Digital Logic and Computer Systems Based on lecture notes by Dr. Eric M. Schwartz Decimal Number System: -Our standard number system is base, also
ECE Department Summer LECTURE #5: Number Systems EEL : Digital Logic and Computer Systems Based on lecture notes by Dr. Eric M. Schwartz Decimal Number System: -Our standard number system is base, also
Smart Meters Programme Schedule 2.6. (Insurance) (CSP North version)
 Smart Meters Programme Schedule 2.6 (Insurance) (CSP North version) Schedule 2.6 (Insurance) (CSP North version) Amendment History Version Date Status v.1 Signature Date Execution Copy 1. INSURANCE COVENANTS
Smart Meters Programme Schedule 2.6 (Insurance) (CSP North version) Schedule 2.6 (Insurance) (CSP North version) Amendment History Version Date Status v.1 Signature Date Execution Copy 1. INSURANCE COVENANTS
Chapter 19 Network Layer: Logical Addressing 19.1
 Chapter 19 Network Layer: Logical Addressing 19.1 Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. 19-1 IPv4 ADDRESSES An IPv4 address is a 32-bit address that
Chapter 19 Network Layer: Logical Addressing 19.1 Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. 19-1 IPv4 ADDRESSES An IPv4 address is a 32-bit address that
January 20, 2009 GEORGE W. WRIGHT VICE PRESIDENT, INFORMATION TECHNOLOGY OPERATIONS
 January 20, 2009 GEORGE W. WRIGHT VICE PRESIDENT, INFORMATION TECHNOLOGY OPERATIONS SUBJECT: Audit Report Service Continuity at the Information Technology and (Report Number ) This report presents the
January 20, 2009 GEORGE W. WRIGHT VICE PRESIDENT, INFORMATION TECHNOLOGY OPERATIONS SUBJECT: Audit Report Service Continuity at the Information Technology and (Report Number ) This report presents the
NUMBER SYSTEMS APPENDIX D. You will learn about the following in this appendix:
 APPENDIX D NUMBER SYSTEMS You will learn about the following in this appendix: The four important number systems in computing binary, octal, decimal, and hexadecimal. A number system converter program
APPENDIX D NUMBER SYSTEMS You will learn about the following in this appendix: The four important number systems in computing binary, octal, decimal, and hexadecimal. A number system converter program
NETWORK ADMINISTRATION
 NETWORK ADMINISTRATION INTRODUCTION The PressureMAP software provides users who have access to an Ethernet network supporting TCP/IP with the ability to remotely log into the MAP System via a network connection,
NETWORK ADMINISTRATION INTRODUCTION The PressureMAP software provides users who have access to an Ethernet network supporting TCP/IP with the ability to remotely log into the MAP System via a network connection,
Concepts in IP Addressing...
 3 Concepts in IP Addressing Terms You ll Need to Understand: Binary Hexadecimal Decimal Octet IP address Subnet Mask Subnet Host Increment Techniques You ll Need to Master: Identifying Address Class and
3 Concepts in IP Addressing Terms You ll Need to Understand: Binary Hexadecimal Decimal Octet IP address Subnet Mask Subnet Host Increment Techniques You ll Need to Master: Identifying Address Class and
HERNANDEZ & ASSOCIATES, P.C.
 Christine M. Hernández, Esq. HERNANDEZ & ASSOCIATES, P.C. Attorney for Respondent 1724 Vine Street Denver, Colorado 80206 Telephone: (303 623-1122 Facsimile: (303 893-6116 UNITED STATES DEPARTMENT OF JUSTICE
Christine M. Hernández, Esq. HERNANDEZ & ASSOCIATES, P.C. Attorney for Respondent 1724 Vine Street Denver, Colorado 80206 Telephone: (303 623-1122 Facsimile: (303 893-6116 UNITED STATES DEPARTMENT OF JUSTICE
UNDERSTANDING SMS: Practitioner s Basics
 UNDERSTANDING SMS: Practitioner s Basics Michael Harrington, CFCE, EnCE It is estimated that in 2006, 72% of all mobile phone users world wide were active users of SMS or text messaging. In European countries
UNDERSTANDING SMS: Practitioner s Basics Michael Harrington, CFCE, EnCE It is estimated that in 2006, 72% of all mobile phone users world wide were active users of SMS or text messaging. In European countries
Chapter 2. Binary Values and Number Systems
 Chapter 2 Binary Values and Number Systems Numbers Natural numbers, a.k.a. positive integers Zero and any number obtained by repeatedly adding one to it. Examples: 100, 0, 45645, 32 Negative numbers A
Chapter 2 Binary Values and Number Systems Numbers Natural numbers, a.k.a. positive integers Zero and any number obtained by repeatedly adding one to it. Examples: 100, 0, 45645, 32 Negative numbers A
NEXT. Tools of the Participant Portal: Scientific Reports & Deliverables
 NEXT Tools of the Participant Portal: Scientific Reports & Deliverables Scientific Reporting and Deliverables: Terminology Scientific Reporting: Standardised format & always due at the end of Reporting
NEXT Tools of the Participant Portal: Scientific Reports & Deliverables Scientific Reporting and Deliverables: Terminology Scientific Reporting: Standardised format & always due at the end of Reporting
IP Subnetting Colin Weaver, ITdojo
 IP Subnetting Colin Weaver, ITdojo Note: This document assumes that subnet zero is NOT used. For a description of subnet-zero, go here (http://www.cisco.com/warp/public/105/40.html). Subnetting IP networks
IP Subnetting Colin Weaver, ITdojo Note: This document assumes that subnet zero is NOT used. For a description of subnet-zero, go here (http://www.cisco.com/warp/public/105/40.html). Subnetting IP networks
Grade 6 Math Circles. Binary and Beyond
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 The Decimal System Grade 6 Math Circles October 15/16, 2013 Binary and Beyond The cool reality is that we learn to count in only one of many possible number
Faculty of Mathematics Waterloo, Ontario N2L 3G1 The Decimal System Grade 6 Math Circles October 15/16, 2013 Binary and Beyond The cool reality is that we learn to count in only one of many possible number
Accuplacer Arithmetic Study Guide
 Accuplacer Arithmetic Study Guide Section One: Terms Numerator: The number on top of a fraction which tells how many parts you have. Denominator: The number on the bottom of a fraction which tells how
Accuplacer Arithmetic Study Guide Section One: Terms Numerator: The number on top of a fraction which tells how many parts you have. Denominator: The number on the bottom of a fraction which tells how
Subnetting Examples. There are three types of subnetting examples I will show in this document:
 Subnetting Examples There are three types of subnetting examples I will show in this document: 1) Subnetting when given a required number of networks 2) Subnetting when given a required number of clients
Subnetting Examples There are three types of subnetting examples I will show in this document: 1) Subnetting when given a required number of networks 2) Subnetting when given a required number of clients
Subnetting Study Guide
 Subnetting Study Guide by Boson Software, LLC An octet is a binary number of 8 bits, with the lowest possible number being 00000000 and the highest possible number being 11111111, or 28. The binary number
Subnetting Study Guide by Boson Software, LLC An octet is a binary number of 8 bits, with the lowest possible number being 00000000 and the highest possible number being 11111111, or 28. The binary number
The Hexadecimal Number System and Memory Addressing
 APPENDIX C The Hexadecimal Number System and Memory Addressing U nderstanding the number system and the coding system that computers use to store data and communicate with each other is fundamental to
APPENDIX C The Hexadecimal Number System and Memory Addressing U nderstanding the number system and the coding system that computers use to store data and communicate with each other is fundamental to
Digital System Design Prof. D Roychoudhry Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur
 Digital System Design Prof. D Roychoudhry Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur Lecture - 04 Digital Logic II May, I before starting the today s lecture
Digital System Design Prof. D Roychoudhry Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur Lecture - 04 Digital Logic II May, I before starting the today s lecture
TCP/IP Cheat Sheet. A Free Study Guide by Boson Software, LLC
 boson_logo_tcpip.pdf 9/23/2010 11:28:19 AM TCP/IP Cheat Sheet A Free Study Guide by Boson Software, LLC Table 1 Address Class Summary Class s Hosts per Range of Network IDs (First Octet) Class A 126 16,777,214
boson_logo_tcpip.pdf 9/23/2010 11:28:19 AM TCP/IP Cheat Sheet A Free Study Guide by Boson Software, LLC Table 1 Address Class Summary Class s Hosts per Range of Network IDs (First Octet) Class A 126 16,777,214
Chapter 5. Binary, octal and hexadecimal numbers
 Chapter 5. Binary, octal and hexadecimal numbers A place to look for some of this material is the Wikipedia page http://en.wikipedia.org/wiki/binary_numeral_system#counting_in_binary Another place that
Chapter 5. Binary, octal and hexadecimal numbers A place to look for some of this material is the Wikipedia page http://en.wikipedia.org/wiki/binary_numeral_system#counting_in_binary Another place that
Systems I: Computer Organization and Architecture
 Systems I: Computer Organization and Architecture Lecture 2: Number Systems and Arithmetic Number Systems - Base The number system that we use is base : 734 = + 7 + 3 + 4 = x + 7x + 3x + 4x = x 3 + 7x
Systems I: Computer Organization and Architecture Lecture 2: Number Systems and Arithmetic Number Systems - Base The number system that we use is base : 734 = + 7 + 3 + 4 = x + 7x + 3x + 4x = x 3 + 7x
Style Guide for the Applied Dissertation
 Style Guide for the Applied Dissertation August 2009 The Style Guide for the Applied Dissertation describes the required format and style for applied dissertations at the Fischler School of Education and
Style Guide for the Applied Dissertation August 2009 The Style Guide for the Applied Dissertation describes the required format and style for applied dissertations at the Fischler School of Education and
Levent EREN levent.eren@ieu.edu.tr A-306 Office Phone:488-9882 INTRODUCTION TO DIGITAL LOGIC
 Levent EREN levent.eren@ieu.edu.tr A-306 Office Phone:488-9882 1 Number Systems Representation Positive radix, positional number systems A number with radix r is represented by a string of digits: A n
Levent EREN levent.eren@ieu.edu.tr A-306 Office Phone:488-9882 1 Number Systems Representation Positive radix, positional number systems A number with radix r is represented by a string of digits: A n
Solution for Homework 2
 Solution for Homework 2 Problem 1 a. What is the minimum number of bits that are required to uniquely represent the characters of English alphabet? (Consider upper case characters alone) The number of
Solution for Homework 2 Problem 1 a. What is the minimum number of bits that are required to uniquely represent the characters of English alphabet? (Consider upper case characters alone) The number of
Scilab Textbook Companion for Digital Electronics: An Introduction To Theory And Practice by W. H. Gothmann 1
 Scilab Textbook Companion for Digital Electronics: An Introduction To Theory And Practice by W. H. Gothmann 1 Created by Aritra Ray B.Tech Electronics Engineering NIT-DURGAPUR College Teacher Prof. Sabyasachi
Scilab Textbook Companion for Digital Electronics: An Introduction To Theory And Practice by W. H. Gothmann 1 Created by Aritra Ray B.Tech Electronics Engineering NIT-DURGAPUR College Teacher Prof. Sabyasachi
Decimal Number (base 10) Binary Number (base 2)
 LECTURE 5. BINARY COUNTER Before starting with counters there is some vital information that needs to be understood. The most important is the fact that since the outputs of a digital chip can only be
LECTURE 5. BINARY COUNTER Before starting with counters there is some vital information that needs to be understood. The most important is the fact that since the outputs of a digital chip can only be
Machine Architecture and Number Systems. Major Computer Components. Schematic Diagram of a Computer. The CPU. The Bus. Main Memory.
 1 Topics Machine Architecture and Number Systems Major Computer Components Bits, Bytes, and Words The Decimal Number System The Binary Number System Converting from Decimal to Binary Major Computer Components
1 Topics Machine Architecture and Number Systems Major Computer Components Bits, Bytes, and Words The Decimal Number System The Binary Number System Converting from Decimal to Binary Major Computer Components
Roman Numerals. Symbol Decimal Value I One (1) V Five (5) X Ten (10) L Fifty (50) C Hundred (100) D Five Hundred (500) M Thousand (1000)
 Roman Numerals Pre-requisite: Number System, Addition and Subtraction. Target Audience: Standard V to Standard VII. In Syllabus Standard V. Revision Standard VI & VII. Symbol Decimal Value I One (1) V
Roman Numerals Pre-requisite: Number System, Addition and Subtraction. Target Audience: Standard V to Standard VII. In Syllabus Standard V. Revision Standard VI & VII. Symbol Decimal Value I One (1) V
A Step towards an Easy Interconversion of Various Number Systems
 A towards an Easy Interconversion of Various Number Systems Shahid Latif, Rahat Ullah, Hamid Jan Department of Computer Science and Information Technology Sarhad University of Science and Information Technology
A towards an Easy Interconversion of Various Number Systems Shahid Latif, Rahat Ullah, Hamid Jan Department of Computer Science and Information Technology Sarhad University of Science and Information Technology
Introduction to Computer & Information Systems
 Introduction to Computer & Information Systems Binnur Kurt kurt@ce.itu.edu.tr Istanbul Technical University Computer Engineering Department Copyleft 2005 1 Version 0.1 About the Lecturer BSc İTÜ, Computer
Introduction to Computer & Information Systems Binnur Kurt kurt@ce.itu.edu.tr Istanbul Technical University Computer Engineering Department Copyleft 2005 1 Version 0.1 About the Lecturer BSc İTÜ, Computer
Binary Adders: Half Adders and Full Adders
 Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
1 3 7 5. 2 3 1 6. The pattern going to the right or the left from the decimal point is the same but there are two big differences:
 Review of Place Values in Decimal Numbers A decimal number includes a decimal point and digit(s) to the right of the decimal point. Saying a decimal number aloud is very similar to saying a whole number
Review of Place Values in Decimal Numbers A decimal number includes a decimal point and digit(s) to the right of the decimal point. Saying a decimal number aloud is very similar to saying a whole number
COMP 250 Fall 2012 lecture 2 binary representations Sept. 11, 2012
 Binary numbers The reason humans represent numbers using decimal (the ten digits from 0,1,... 9) is that we have ten fingers. There is no other reason than that. There is nothing special otherwise about
Binary numbers The reason humans represent numbers using decimal (the ten digits from 0,1,... 9) is that we have ten fingers. There is no other reason than that. There is nothing special otherwise about
CPEN 214 - Digital Logic Design Binary Systems
 CPEN 4 - Digital Logic Design Binary Systems C. Gerousis Digital Design 3 rd Ed., Mano Prentice Hall Digital vs. Analog An analog system has continuous range of values A mercury thermometer Vinyl records
CPEN 4 - Digital Logic Design Binary Systems C. Gerousis Digital Design 3 rd Ed., Mano Prentice Hall Digital vs. Analog An analog system has continuous range of values A mercury thermometer Vinyl records
4.3 TABLE 3 TABLE 4. 1342 five 1 125 3 25 4 5 2 1 125 75 20 2 222.
 .3 Conversion Between Number Bases 169.3 Conversion Between Number Bases Although the numeration systems discussed in the opening section were all base ten, other bases have occurred historically. For
.3 Conversion Between Number Bases 169.3 Conversion Between Number Bases Although the numeration systems discussed in the opening section were all base ten, other bases have occurred historically. For
Lecture 11: Number Systems
 Lecture 11: Number Systems Numeric Data Fixed point Integers (12, 345, 20567 etc) Real fractions (23.45, 23., 0.145 etc.) Floating point such as 23. 45 e 12 Basically an exponent representation Any number
Lecture 11: Number Systems Numeric Data Fixed point Integers (12, 345, 20567 etc) Real fractions (23.45, 23., 0.145 etc.) Floating point such as 23. 45 e 12 Basically an exponent representation Any number
NCTM Content Standard/National Science Education Standard
 Title: BASE-ic Space Travel Brief Overview: This unit introduces the concepts of bases and exponents (or powers) in order to gain a deeper understanding of place value. Students will assume the role of
Title: BASE-ic Space Travel Brief Overview: This unit introduces the concepts of bases and exponents (or powers) in order to gain a deeper understanding of place value. Students will assume the role of
Binary, Hexadecimal, Octal, and BCD Numbers
 23CH_PHCalter_TMSETE_949118 23/2/2007 1:37 PM Page 1 Binary, Hexadecimal, Octal, and BCD Numbers OBJECTIVES When you have completed this chapter, you should be able to: Convert between binary and decimal
23CH_PHCalter_TMSETE_949118 23/2/2007 1:37 PM Page 1 Binary, Hexadecimal, Octal, and BCD Numbers OBJECTIVES When you have completed this chapter, you should be able to: Convert between binary and decimal
Probability and Expected Value
 Probability and Expected Value This handout provides an introduction to probability and expected value. Some of you may already be familiar with some of these topics. Probability and expected value are
Probability and Expected Value This handout provides an introduction to probability and expected value. Some of you may already be familiar with some of these topics. Probability and expected value are
CDA 3200 Digital Systems. Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012
 CDA 3200 Digital Systems Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012 Outline Data Representation Binary Codes Why 6-3-1-1 and Excess-3? Data Representation (1/2) Each numbering
CDA 3200 Digital Systems Instructor: Dr. Janusz Zalewski Developed by: Dr. Dahai Guo Spring 2012 Outline Data Representation Binary Codes Why 6-3-1-1 and Excess-3? Data Representation (1/2) Each numbering
Prerequisite knowledge Students should have a good understanding of how our decimal number system works as well as understand place value.
 CSP Number Systems Mrs., GA Lesson Overview Learning Objectives and Evidence Statements 2.1.2 Explain how binary sequences are used to represent digital data. [P5] Prerequisite knowledge Students should
CSP Number Systems Mrs., GA Lesson Overview Learning Objectives and Evidence Statements 2.1.2 Explain how binary sequences are used to represent digital data. [P5] Prerequisite knowledge Students should
Capital Investment in Health Report of the Department of Health. Overview and Priorities
 Capital Investment in Health Report of the Department of Health Overview and Priorities Introduction The attached report, which can be read in conjunction with the HSE Capital Plan 2011-2015 1, seeks to
Capital Investment in Health Report of the Department of Health Overview and Priorities Introduction The attached report, which can be read in conjunction with the HSE Capital Plan 2011-2015 1, seeks to
Pre-Algebra Lecture 6
 Pre-Algebra Lecture 6 Today we will discuss Decimals and Percentages. Outline: 1. Decimals 2. Ordering Decimals 3. Rounding Decimals 4. Adding and subtracting Decimals 5. Multiplying and Dividing Decimals
Pre-Algebra Lecture 6 Today we will discuss Decimals and Percentages. Outline: 1. Decimals 2. Ordering Decimals 3. Rounding Decimals 4. Adding and subtracting Decimals 5. Multiplying and Dividing Decimals
3. Convert a number from one number system to another
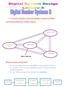 3. Convert a number from one number system to another Conversion between number bases: Hexa (16) Decimal (10) Binary (2) Octal (8) More Interest Way we need conversion? We need decimal system for real
3. Convert a number from one number system to another Conversion between number bases: Hexa (16) Decimal (10) Binary (2) Octal (8) More Interest Way we need conversion? We need decimal system for real
Advanced Topics: IP Subnetting A WHITE PAPER PREPARED FOR ASPE TECHNOLOGY. www.aspetech.com toll-free: 877-800-5221
 Advanced Topics: IP Subnetting A WHITE PAPER PREPARED FOR ASPE TECHNOLOGY www.aspetech.com toll-free: 877-800-5221 Advanced Topics IP Subnetting It is almost impossible to lay out an IP network without
Advanced Topics: IP Subnetting A WHITE PAPER PREPARED FOR ASPE TECHNOLOGY www.aspetech.com toll-free: 877-800-5221 Advanced Topics IP Subnetting It is almost impossible to lay out an IP network without
Binary Representation. Number Systems. Base 10, Base 2, Base 16. Positional Notation. Conversion of Any Base to Decimal.
 Binary Representation The basis of all digital data is binary representation. Binary - means two 1, 0 True, False Hot, Cold On, Off We must be able to handle more than just values for real world problems
Binary Representation The basis of all digital data is binary representation. Binary - means two 1, 0 True, False Hot, Cold On, Off We must be able to handle more than just values for real world problems
LSN 2 Number Systems. ECT 224 Digital Computer Fundamentals. Department of Engineering Technology
 LSN 2 Number Systems Department of Engineering Technology LSN 2 Decimal Number System Decimal number system has 10 digits (0-9) Base 10 weighting system... 10 5 10 4 10 3 10 2 10 1 10 0. 10-1 10-2 10-3
LSN 2 Number Systems Department of Engineering Technology LSN 2 Decimal Number System Decimal number system has 10 digits (0-9) Base 10 weighting system... 10 5 10 4 10 3 10 2 10 1 10 0. 10-1 10-2 10-3
COMBINATIONAL CIRCUITS
 COMBINATIONAL CIRCUITS http://www.tutorialspoint.com/computer_logical_organization/combinational_circuits.htm Copyright tutorialspoint.com Combinational circuit is a circuit in which we combine the different
COMBINATIONAL CIRCUITS http://www.tutorialspoint.com/computer_logical_organization/combinational_circuits.htm Copyright tutorialspoint.com Combinational circuit is a circuit in which we combine the different
Welcome to Math 19500 Video Lessons. Stanley Ocken. Department of Mathematics The City College of New York Fall 2013
 Welcome to Math 19500 Video Lessons Prof. Department of Mathematics The City College of New York Fall 2013 An important feature of the following Beamer slide presentations is that you, the reader, move
Welcome to Math 19500 Video Lessons Prof. Department of Mathematics The City College of New York Fall 2013 An important feature of the following Beamer slide presentations is that you, the reader, move
Chapter Binary, Octal, Decimal, and Hexadecimal Calculations
 Chapter 5 Binary, Octal, Decimal, and Hexadecimal Calculations This calculator is capable of performing the following operations involving different number systems. Number system conversion Arithmetic
Chapter 5 Binary, Octal, Decimal, and Hexadecimal Calculations This calculator is capable of performing the following operations involving different number systems. Number system conversion Arithmetic
Cyber Security Workshop Encryption Reference Manual
 Cyber Security Workshop Encryption Reference Manual May 2015 Basic Concepts in Encoding and Encryption Binary Encoding Examples Encryption Cipher Examples 1 P a g e Encoding Concepts Binary Encoding Basics
Cyber Security Workshop Encryption Reference Manual May 2015 Basic Concepts in Encoding and Encryption Binary Encoding Examples Encryption Cipher Examples 1 P a g e Encoding Concepts Binary Encoding Basics
3-17 15-25 5 15-10 25 3-2 5 0. 1b) since the remainder is 0 I need to factor the numerator. Synthetic division tells me this is true
 Section 5.2 solutions #1-10: a) Perform the division using synthetic division. b) if the remainder is 0 use the result to completely factor the dividend (this is the numerator or the polynomial to the
Section 5.2 solutions #1-10: a) Perform the division using synthetic division. b) if the remainder is 0 use the result to completely factor the dividend (this is the numerator or the polynomial to the
Xxxxxxxxxxxxxxxx Xxxxxxxxxxxxxxxx
 DEPARTMENT OF THE TREASURY INTERNAL REVENUE SERVICE WASHINGTON, D.C. 20224 201432038 TAX EXEMPT AND GOVERNMENT ENTITIES DIVISION MAY 1 5 2014 Uniform Issue List: 408.03-00 Legend: Taxpayer A IRA X IRAY
DEPARTMENT OF THE TREASURY INTERNAL REVENUE SERVICE WASHINGTON, D.C. 20224 201432038 TAX EXEMPT AND GOVERNMENT ENTITIES DIVISION MAY 1 5 2014 Uniform Issue List: 408.03-00 Legend: Taxpayer A IRA X IRAY
Today. Binary addition Representing negative numbers. Andrew H. Fagg: Embedded Real- Time Systems: Binary Arithmetic
 Today Binary addition Representing negative numbers 2 Binary Addition Consider the following binary numbers: 0 0 1 0 0 1 1 0 0 0 1 0 1 0 1 1 How do we add these numbers? 3 Binary Addition 0 0 1 0 0 1 1
Today Binary addition Representing negative numbers 2 Binary Addition Consider the following binary numbers: 0 0 1 0 0 1 1 0 0 0 1 0 1 0 1 1 How do we add these numbers? 3 Binary Addition 0 0 1 0 0 1 1
Number and codes in digital systems
 Number and codes in digital systems Decimal Numbers You are familiar with the decimal number system because you use them everyday. But their weighted structure is not understood. In the decimal number
Number and codes in digital systems Decimal Numbers You are familiar with the decimal number system because you use them everyday. But their weighted structure is not understood. In the decimal number
PAUL VOGEL MANAGING DIRECTOR, GLOBAL BUSINESS AND SENIOR VICE PRESIDENT
 February 12, 2008 GEORGE W. WRIGHT ACTING VICE PRESIDENT, CHIEF TECHNOLOGY OFFICER SUSAN M. PLONKEY VICE PRESIDENT, CUSTOMER SERVICE PAUL VOGEL MANAGING DIRECTOR, GLOBAL BUSINESS AND SENIOR VICE PRESIDENT
February 12, 2008 GEORGE W. WRIGHT ACTING VICE PRESIDENT, CHIEF TECHNOLOGY OFFICER SUSAN M. PLONKEY VICE PRESIDENT, CUSTOMER SERVICE PAUL VOGEL MANAGING DIRECTOR, GLOBAL BUSINESS AND SENIOR VICE PRESIDENT
Binary Representation
 Binary Representation The basis of all digital data is binary representation. Binary - means two 1, 0 True, False Hot, Cold On, Off We must tbe able to handle more than just values for real world problems
Binary Representation The basis of all digital data is binary representation. Binary - means two 1, 0 True, False Hot, Cold On, Off We must tbe able to handle more than just values for real world problems
Calculating Loan Payments
 IN THIS CHAPTER Calculating Loan Payments...............1 Calculating Principal Payments...........4 Working with Future Value...............7 Using the Present Value Function..........9 Calculating Interest
IN THIS CHAPTER Calculating Loan Payments...............1 Calculating Principal Payments...........4 Working with Future Value...............7 Using the Present Value Function..........9 Calculating Interest
Digital Design. Assoc. Prof. Dr. Berna Örs Yalçın
 Digital Design Assoc. Prof. Dr. Berna Örs Yalçın Istanbul Technical University Faculty of Electrical and Electronics Engineering Office Number: 2318 E-mail: siddika.ors@itu.edu.tr Grading 1st Midterm -
Digital Design Assoc. Prof. Dr. Berna Örs Yalçın Istanbul Technical University Faculty of Electrical and Electronics Engineering Office Number: 2318 E-mail: siddika.ors@itu.edu.tr Grading 1st Midterm -
Chapter 1. Binary, octal and hexadecimal numbers
 Chapter 1. Binary, octal and hexadecimal numbers This material is covered in the books: Nelson Magor Cooke et al, Basic mathematics for electronics (7th edition), Glencoe, Lake Forest, Ill., 1992. [Hamilton
Chapter 1. Binary, octal and hexadecimal numbers This material is covered in the books: Nelson Magor Cooke et al, Basic mathematics for electronics (7th edition), Glencoe, Lake Forest, Ill., 1992. [Hamilton
We Are HERE! Subne\ng
 TELE 302 Network Design Lecture 21 Addressing Strategies Source: McCabe 12.1 ~ 12.4 Jeremiah Deng TELE Programme, University of Otago, 2013 We Are HERE! Requirements analysis Flow Analysis Logical Design
TELE 302 Network Design Lecture 21 Addressing Strategies Source: McCabe 12.1 ~ 12.4 Jeremiah Deng TELE Programme, University of Otago, 2013 We Are HERE! Requirements analysis Flow Analysis Logical Design
Background Information on Exponentials and Logarithms
 Background Information on Eponentials and Logarithms Since the treatment of the decay of radioactive nuclei is inetricably linked to the mathematics of eponentials and logarithms, it is important that
Background Information on Eponentials and Logarithms Since the treatment of the decay of radioactive nuclei is inetricably linked to the mathematics of eponentials and logarithms, it is important that
How To Set The Sensor On A Powerpoint 3.5 (Powerpoint) On A Blackberry 2.5A (Powerplant) On An Iphone Or Ipad (Powerplant) On The Blackberry 3.2 (
 VMBGPOD Touch panel with Oled display for VELBUS system 1 Binairy format: bits Description
VMBGPOD Touch panel with Oled display for VELBUS system 1 Binairy format: bits Description
5.4 Solving Percent Problems Using the Percent Equation
 5. Solving Percent Problems Using the Percent Equation In this section we will develop and use a more algebraic equation approach to solving percent equations. Recall the percent proportion from the last
5. Solving Percent Problems Using the Percent Equation In this section we will develop and use a more algebraic equation approach to solving percent equations. Recall the percent proportion from the last
APPENDIX B. Routers route based on the network number. The router that delivers the data packet to the correct destination host uses the host ID.
 APPENDIX B IP Subnetting IP Addressing Routers route based on the network number. The router that delivers the data packet to the correct destination host uses the host ID. IP Classes An IP address is
APPENDIX B IP Subnetting IP Addressing Routers route based on the network number. The router that delivers the data packet to the correct destination host uses the host ID. IP Classes An IP address is
Digital codes. Resources and methods for learning about these subjects (list a few here, in preparation for your research):
 Digital codes This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Digital codes This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
