Lecture 6: Polygon rendering and OpenGL
|
|
|
- Samuel Pearson
- 7 years ago
- Views:
Transcription
1 Lecture 6: Polygon rendering and OpenGL 3-Dimensional Objects Bounded by Planar Surfaces (Facets) Y 4 8 Z X NUMERICAL TOPOLOGICAL DATA DATA Points Lines Faces 1. [0,0,0] 1. 1>>2 1,2,4,4 2. [2,0,0] 2. 1>>4 1,4,8,5 3. [2,2,0] 3. 1>>5 &c 4. [0,2,0] 4. 3>>4 &c 5. 3>>2 &c Diagram 1: Representing 3D objects A planar facet is defined by an ordered set of 3D vertices, lying on one plane, which form a closed polygon, (straight lines are drawn from each vertex to the following one with the last vertex connected to the first). The data describing a facet are of two types. First, there is the numerical data which is a list of 3D points, (3*N numbers for N points), and secondly, there is the topological data which describes which points are connected to form edges of the facet. For the cube shown in Diagram 1 we need 24 real numbers for the numerical data, 24 integers to store the line topology, and 24 integers to store the face topology. We will also need to maintain the number of lines and faces in the figure, and the number of edges per face. All this could be done using static structures (arrays), alternatively, if we start with abstract data types that express the structure of three dimensional objects, we may define the following data types (Diagram 2): Face 1 Face 2 Face 3 Object &c. Edge 1 Edge 2 Edge 3 Edge 4 P1 P2 &c. &c. P2 P3 P3 P4 P4 P1 Diagram 2 Possible Organisation for Graphical Data ordinate=x,y,z; Point = array[ordinate] of real; Edge = record start, finish: Point; end ; Edgelist = record thisedge: Edge ; nextedge: ^Edgelist; end ; Facetlist = record thisfacet: ^Edgelist; nextfacet:^facetlist; end ; Object=^Facetlist; It should be noted that redundancy exists in this case, since edges which belong to two facets are duplicated, and vertices which belong to three edges appear three times. However, when a large number of objects are processed, redundancy of data may help the speed. Later on in this lecture we will see other examples where this is true. What is OpenGL? OpenGL is a software library which creates an interface to graphics hardware. The OpenGL library provides an interface to the graphics hardware at the lowest level. Many graphics applications or graphics packages provide an interface to the graphics hardware at a much higher level and are built on top of OpenGL. Examples are packages such as OpenInventor or VTK. OpenGL is not a
2 general purpose graphics system. Instead, OpenGL is a polygon-based rendering system which supports a small number of geometric primitives for creating models: points, lines and polygons. Application or high-level graphics library OpenGL Utility Library (GLU) OpenGL Extension (GLX, WGL) OpenGL Utility Toolkit (GLUT) OpenGL Library (GL) Graphics hardware Figure 1: Overview of the OpenGL API OpenGL is hardware and operating system independent. It is up to the underlying implementation of the OpenGL system to decide how to implement the OpenGL functionality. On some platforms, the implementation may use accelerated hardware for rendering while on other platforms the implementation may use only software for rendering. OpenGL is available for operating systems like Windows 98/NT, Linux and Unix and for a wide variety of programming languages such as C, C++, Ada, Fortran and Java. The functionality of the OpenGL library is extended by a number of related libraries: The OpenGL utility library (GLU) contains several convenience routines which are implemented in terms of lower-level OpenGL commands. These include routines for setting up viewing transformations. The OpenGL Utility Toolkit (GLUT), a window system independent toolkit for writing OpenGL programs, implements a simple windowing application programming interface for OpenGL. GLUT makes it considerably easier to learn about and to explore OpenGL programming. In addition it provides a portable application programming interface (API) which facilitates writing a single OpenGL program that works on window systems such as Microsoft Windows and X Window System environments. Finally, each window system has a specific library that extends OpenGL functionality on that platform. For the X Window System, the OpenGL extension is called GLX. For Microsoft Windows, the OpenGL extension is called WGL. OpenGL Command Syntax All OpenGL commands use the prefix gl before the command name. Similarly, the OpenGL related libraries GLU and GLUT use the prefix glu and glut before the command name. For example, to define a vertex at position (1.0, 2.0, 0) the OpenGL command is: glvertex3f(1.0, 2.0, 0.0); In addition, the suffix 3f after the command name specifies the number of arguments and their type. In the example above, the last letter indicates the data type of the arguments (float in this case), while the preceding number indicates the number of arguments expected (3 in this case). Other
3 possible data types include bytes (suffix b), short integers (suffix s), long integers (suffix i), and doubles (suffix d). Most OpenGL arguments are available for different number and types of arguments. For example, the effect of the command glvertex2i(1, 2); is equivalent to the command above, except that it expects only two arguments whose type is int. OpenGL State Machine OpenGL is a state machine. OpenGL can be put into various states (or modes) that remain in effect until they are changed. The state encapsulates control for operations like transformations, rendering, lighting, shading and texture mapping. For example color is a state variable. By setting the color to red with command glcolor3f(1.0, 0.0, 0.0); the state of the variable color is set to red and all objects are drawn in this color until the current color is set to another color. Many other state variables can be enabled with the commands glenable() and gldisable(). OpenGL Rendering Pipeline In OpenGL the different processing stages define the OpenGL rendering pipeline (shown in Figure 2). At the beginning of this pipeline are either vertex data (describing points, lines, and polygons) or pixel data (bitmaps, pixmaps). The rendering pipeline is slightly different for vertex and pixel data. In the following, the rendering pipeline for vertex data is described in more detail. All geometric data has to be represented by vertices. However, it is common in computer graphics to model curves and surfaces by representing them in a parametric form, i.e. using control points. These representations are compact and easy to modify and store. Before such curves and surfaces can be rendered, they have to be transformed to vertices. Evaluators provide ways of deriving vertex data including their spatial coordinates, texture coordinates and surface normals from these parametric representations. The vertex data is then passed to the next stage during which per-vertex operations are carried out. In this stage vertices are transformed from their world coordinates to their screen coordinates. If texture-mapping is enabled, the texture coordinates of vertices are calculated. If lighting is enabled, the lighting for each vertex is calculated using its transformed position and surface normal, the light source position, as well as other lighting information. The next stage for vertex data is the primitive assembly during which vertex data may be clipped according to the shape of the viewing volume. For point data, clipping may be achieved by accepting or rejecting vertices. For line and polygon data, clipping may introduce new vertices depending on how a line or polygon is clipped. During the rasterization stage, both geometric data and pixel data are converted to fragments where each fragment corresponds to a pixel in the framebuffer. In this step, parameters such as line pattern and width are taken into account. Furthermore, calculations necessary for antialiasing are carried out. At the end of this step each fragment has an associated value for its color and depth.
4 Vertex data Evaluators Per-vertex operations and primitive assembly Display list Rasterization Per-fragment operations Pixel data Pixel operations Texture assembly Framebuffer Figure 2: Order of operations in the OpenGL rendering pipeline In the final stage, so-called per-fragment operations are performed. Before anything is drawn into the framebuffer, series of operations are performed to modify or delete fragments. For example, fragments may be passed through a number of tests including the depth-buffer test (which eliminates hidden surfaces using a z-buffer algorithm). If a fragment fails the test, it is not processed any further. Finally, other operations such as blending or dithering may be performed. At the end of this step, the processed fragments are drawn into the framebuffer. OpenGL Drawing Primitives OpenGL supports a number geometric primitives for drawing. All geometric primitives are described in terms of vertices. Each vertex is represented as the three coordinates (x, y, z) of a 3D point and can be used to define the endpoints of line segments or the corners of polygons. Note that internally OpenGL uses homogeneous coordinates so that each vertex is actually represented by four coordinates (x, y, z, w). If w is different from zero, these coordinates correspond to the Euclidean point (x/w, y/w, z/w). Since vertices can be used to define different geometric primitives such as points, lines and polygons, the type of geometric primitive associated with the vertex data has to be defined explicitly. For example, the following two code segments can be used to draw a polygon or a set of points: glbegin(gl_polygon); glvertex3f(0.0, 0.0, 0.0); glvertex3f(0.0, 3.0, 0.0); glvertex3f(4.0, 3.0, 0.0); glvertex3f(5.0, 1.5, 0.0); glvertex3f(4.0, 0.0, 0.0);
5 glend(); glbegin(gl_points); glvertex3f(0.0, 0.0, 0.0); glvertex3f(0.0, 3.0, 0.0); glvertex3f(4.0, 3.0, 0.0); glvertex3f(5.0, 1.5, 0.0); glvertex3f(4.0, 0.0, 0.0); glend(); An example of the output of the two code segments is shown in Figure 3. In addition to these two geometric primitives, OpenGL defines eight further geometric primitives shown in Figure 4. These include unconnected line segments (GL_LINES), connected line segments (GL_LINE_STRIP), triangles (GL_TRIANGLES), triangle strips (GL_TRIANGLE_STRIP), and fans (GL_TRIANGLE_FAN) as well as quadrilaterals (GL_QUADS) and quadrilaterals strips (GL_QUAD_STRIP). Quadrilaterals are four sided polygons. In addition to defining the coordinates of each vertex (using glvertex()), one can also define additional data for each vertex such as its color (using glcolor()), its normal (using glnormal()) and its texture coordinates (using gltexcoord()). Figure 3: Drawing a polygon or a set of points
6 GL_POINTS GL_LINES GL_LINE_STRIP GL_LINE_LOOP GL_TRIANGLES GL_TRIANGLE_STRIP GL_TRIANGLE_FAN GL_QUADS GL_POLYGON Figure 4: Different geometric primitives In general, polygons can be very complicated and slow to draw so that many high performance graphics systems like OpenGL make some strong assumptions on valid polygons. First, the edges of the polygon cannot intersect (i.e. the polygon must be simple). Second, polygons cannot have indentations (i.e. the polygon must be convex). In the real-world, the surfaces of objects consist often of non-simple or non-convex polygons. However, since all non-simple or non-convex polygons can be described as unions of simple, convex polygons, the problem does not arise in practice. For example, to draw non-convex polygons, one can subdivide them into convex polygons, i.e. triangles. Finally, the polygons must be planar, i.e. the vertices of a polygon must lie in a plane. Non-planar polygons are not allowed since after various transformations they may project to non-simple or non-convex polygons. OpenGL Viewing In order to render geometric primitives, OpenGL requires the definition of a number of transformations which determine the relationship between world, model, camera and screen coordinates. In OpenGL, the viewing, modelling, and projection transformations are specified by 4 x 4 matrices. The first matrix is the modelview matrix which transforms object coordinates into eye coordinates. In the next step, OpenGL applies the projection matrix to yield clipped coordinates. At this point, normalized device coordinates are obtained by perspective division, that means coordinates in the form (x, y, z, w) are normalised to yield (x/w, y/w, z/w, 1). Finally, window coordinates are obtained by applying the viewport transformation.
7 World coordinates Window coordinates Modelview transformation Perspective transformation Clip coordinates Perspective division Camera coordinates Normalised device Viewport coordinates transformation Figure 5: Transformtions in OpenGL The easiest way to set up the viewing transformation is to use the function glulookat(): void glulookat(float eyex, float eyey, float eyez, float focalx, float focaly, float focalz, float upx, float upy, float upz); Here the desired viewpoint is specified by eyex, eyey and eyez. The focalx, focaly and focalz arguments specify the focal point along the line of sight while the upx, upy and upz arguments specify the direction which is up. OpenGL supports perspective and orthographic (parallel) projection transformations. In order to define a perspective transformation, a viewing frustum must be defined. This viewing frustum forms a truncated pyramid which encapsulates the viewing volume (the part of the world which is visible). In this truncated pyramid the base corresponds to the front clipping plane while the apex corresponds to the back clipping plane. The easiest way to set up the perspective projection transformation is to use the function gluperspective(): void gluperspective(float fovy, float aspect, float near, float far); The meaning of the parameters of the function gluperspective() is illustrated in Figure 6: The parameter fovy specifies the angle of the field of view while the aspect defines the aspect ratio of the viewing frustum, i.e. its width divided by its height. The near and far values denote the distance of the viewpoint to the front and back clipping planes. As mentioned it is also possible to set up a parallel (or orthographic) projection transformation using the function glortho: glortho(double left, double right, double bottom, double top, double near, double far); The meaning of the parameters of the function glortho() is illustrated in Figure 7.
8 y w h θ near far x aspect = w / h z Figure 6: Specifying the perspective projection transformation using gluperspective top left far right towards the viewpoint near bottom Figure 7: Specifying the parallel projection transformation using glortho
OpenGL & Delphi. Max Kleiner. http://max.kleiner.com/download/openssl_opengl.pdf 1/22
 OpenGL & Delphi Max Kleiner http://max.kleiner.com/download/openssl_opengl.pdf 1/22 OpenGL http://www.opengl.org Evolution of Graphics Assembler (demo pascalspeed.exe) 2D 3D Animation, Simulation (Terrain_delphi.exe)
OpenGL & Delphi Max Kleiner http://max.kleiner.com/download/openssl_opengl.pdf 1/22 OpenGL http://www.opengl.org Evolution of Graphics Assembler (demo pascalspeed.exe) 2D 3D Animation, Simulation (Terrain_delphi.exe)
Image Processing and Computer Graphics. Rendering Pipeline. Matthias Teschner. Computer Science Department University of Freiburg
 Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
Image Processing and Computer Graphics Rendering Pipeline Matthias Teschner Computer Science Department University of Freiburg Outline introduction rendering pipeline vertex processing primitive processing
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Sample Exam Questions 2007
 Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Monash University Clayton s School of Information Technology CSE3313 Computer Graphics Questions 2007 INSTRUCTIONS: Answer all questions. Spend approximately 1 minute per mark. Question 1 30 Marks Total
Aston University. School of Engineering & Applied Science
 CS2150 Aston University School of Engineering & Applied Science CS2150: Computer Graphics January Examinations 2010 Date: XXX Time: XXX Instructions to Candidates: 1. Answer Question ONE and any other
CS2150 Aston University School of Engineering & Applied Science CS2150: Computer Graphics January Examinations 2010 Date: XXX Time: XXX Instructions to Candidates: 1. Answer Question ONE and any other
Computer Graphics. Anders Hast
 Computer Graphics Anders Hast Who am I?! 5 years in Industry after graduation, 2 years as high school teacher.! 1996 Teacher, University of Gävle! 2004 PhD, Computerised Image Processing " Computer Graphics!
Computer Graphics Anders Hast Who am I?! 5 years in Industry after graduation, 2 years as high school teacher.! 1996 Teacher, University of Gävle! 2004 PhD, Computerised Image Processing " Computer Graphics!
Graphics Input Primitives. 5. Input Devices Introduction to OpenGL. String Choice/Selection Valuator
 4ICT10 Computer Graphics and Virtual Reality 5. Input Devices Introduction to OpenGL Dr Ann McNamara String Choice/Selection Valuator Graphics Input Primitives Locator coordinate pair x,y Pick required
4ICT10 Computer Graphics and Virtual Reality 5. Input Devices Introduction to OpenGL Dr Ann McNamara String Choice/Selection Valuator Graphics Input Primitives Locator coordinate pair x,y Pick required
CSE 564: Visualization. GPU Programming (First Steps) GPU Generations. Klaus Mueller. Computer Science Department Stony Brook University
 GPU Generations CSE 564: Visualization GPU Programming (First Steps) Klaus Mueller Computer Science Department Stony Brook University For the labs, 4th generation is desirable Graphics Hardware Pipeline
GPU Generations CSE 564: Visualization GPU Programming (First Steps) Klaus Mueller Computer Science Department Stony Brook University For the labs, 4th generation is desirable Graphics Hardware Pipeline
Android and OpenGL. Android Smartphone Programming. Matthias Keil. University of Freiburg
 Android and OpenGL Android Smartphone Programming Matthias Keil Institute for Computer Science Faculty of Engineering 16. Dezember 2013 Outline 1 OpenGL Introduction 2 Displaying Graphics 3 Interaction
Android and OpenGL Android Smartphone Programming Matthias Keil Institute for Computer Science Faculty of Engineering 16. Dezember 2013 Outline 1 OpenGL Introduction 2 Displaying Graphics 3 Interaction
2: Introducing image synthesis. Some orientation how did we get here? Graphics system architecture Overview of OpenGL / GLU / GLUT
 COMP27112 Computer Graphics and Image Processing 2: Introducing image synthesis Toby.Howard@manchester.ac.uk 1 Introduction In these notes we ll cover: Some orientation how did we get here? Graphics system
COMP27112 Computer Graphics and Image Processing 2: Introducing image synthesis Toby.Howard@manchester.ac.uk 1 Introduction In these notes we ll cover: Some orientation how did we get here? Graphics system
A Short Introduction to Computer Graphics
 A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
A Short Introduction to Computer Graphics Frédo Durand MIT Laboratory for Computer Science 1 Introduction Chapter I: Basics Although computer graphics is a vast field that encompasses almost any graphical
Introduction to Computer Graphics
 Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 torsten@sfu.ca www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
Introduction to Computer Graphics Torsten Möller TASC 8021 778-782-2215 torsten@sfu.ca www.cs.sfu.ca/~torsten Today What is computer graphics? Contents of this course Syllabus Overview of course topics
4BA6 - Topic 4 Dr. Steven Collins. Chap. 5 3D Viewing and Projections
 4BA6 - Topic 4 Dr. Steven Collins Chap. 5 3D Viewing and Projections References Computer graphics: principles & practice, Fole, vandam, Feiner, Hughes, S-LEN 5.644 M23*;-6 (has a good appendix on linear
4BA6 - Topic 4 Dr. Steven Collins Chap. 5 3D Viewing and Projections References Computer graphics: principles & practice, Fole, vandam, Feiner, Hughes, S-LEN 5.644 M23*;-6 (has a good appendix on linear
Transformations in the pipeline
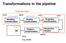 Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
Transformations in the pipeline gltranslatef() Modeling transformation ModelView Matrix OCS WCS glulookat() VCS CCS Viewing transformation Projection transformation DCS Viewport transformation (e.g. pixels)
Introduction to Computer Graphics Techniques and Applications. Hong Qin Center for Visual Computing (CVC) Stony Brook University
 Introduction to Computer Graphics Techniques and Applications Hong Qin Center for Visual Computing (CVC) Stony Brook University Presentation Outline What is computer graphics? 3D graphics pipeline Programming
Introduction to Computer Graphics Techniques and Applications Hong Qin Center for Visual Computing (CVC) Stony Brook University Presentation Outline What is computer graphics? 3D graphics pipeline Programming
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
CS 4204 Computer Graphics 3D views and projection Adapted from notes by Yong Cao 1 Overview of 3D rendering Modeling: *Define object in local coordinates *Place object in world coordinates (modeling transformation)
Realtime 3D Computer Graphics Virtual Reality
 Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
Realtime 3D Computer Graphics Virtual Realit Viewing and projection Classical and General Viewing Transformation Pipeline CPU Pol. DL Pixel Per Vertex Texture Raster Frag FB object ee clip normalized device
3D Viewing. Chapter 7. Projections. 3D clipping. OpenGL viewing functions and clipping planes
 3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
3D Viewing Chapter 7 Projections 3D clipping OpenGL viewing functions and clipping planes 1 Projections Parallel Perspective Coordinates are transformed along parallel lines Relative sizes are preserved
Scan-Line Fill. Scan-Line Algorithm. Sort by scan line Fill each span vertex order generated by vertex list
 Scan-Line Fill Can also fill by maintaining a data structure of all intersections of polygons with scan lines Sort by scan line Fill each span vertex order generated by vertex list desired order Scan-Line
Scan-Line Fill Can also fill by maintaining a data structure of all intersections of polygons with scan lines Sort by scan line Fill each span vertex order generated by vertex list desired order Scan-Line
Graphics Pipeline in a Nutshell
 Graphics Pipeline in a Nutshell How do we create a rendering such as this? CS334 Spring 2008 Design the scene (technical drawing in wireframe ) Apply perspective transformations to the scene geometry for
Graphics Pipeline in a Nutshell How do we create a rendering such as this? CS334 Spring 2008 Design the scene (technical drawing in wireframe ) Apply perspective transformations to the scene geometry for
INTRODUCTION TO RENDERING TECHNIQUES
 INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
INTRODUCTION TO RENDERING TECHNIQUES 22 Mar. 212 Yanir Kleiman What is 3D Graphics? Why 3D? Draw one frame at a time Model only once X 24 frames per second Color / texture only once 15, frames for a feature
The Design of the OpenGL Graphics Interface
 The Design of the OpenGL Graphics Interface Mark Segal Kurt Akeley Silicon Graphics Computer Systems 2011 N. Shoreline Blvd., Mountain View, CA 94039 Abstract OpenGL is an emerging graphics standard that
The Design of the OpenGL Graphics Interface Mark Segal Kurt Akeley Silicon Graphics Computer Systems 2011 N. Shoreline Blvd., Mountain View, CA 94039 Abstract OpenGL is an emerging graphics standard that
Lecture Notes, CEng 477
 Computer Graphics Hardware and Software Lecture Notes, CEng 477 What is Computer Graphics? Different things in different contexts: pictures, scenes that are generated by a computer. tools used to make
Computer Graphics Hardware and Software Lecture Notes, CEng 477 What is Computer Graphics? Different things in different contexts: pictures, scenes that are generated by a computer. tools used to make
CMSC 427 Computer Graphics 1
 CMSC 427 Computer Graphics 1 David M. Mount Department of Computer Science University of Maryland Fall 2010 1 Copyright, David M. Mount, 2010, Dept. of Computer Science, University of Maryland, College
CMSC 427 Computer Graphics 1 David M. Mount Department of Computer Science University of Maryland Fall 2010 1 Copyright, David M. Mount, 2010, Dept. of Computer Science, University of Maryland, College
Silverlight for Windows Embedded Graphics and Rendering Pipeline 1
 Silverlight for Windows Embedded Graphics and Rendering Pipeline 1 Silverlight for Windows Embedded Graphics and Rendering Pipeline Windows Embedded Compact 7 Technical Article Writers: David Franklin,
Silverlight for Windows Embedded Graphics and Rendering Pipeline 1 Silverlight for Windows Embedded Graphics and Rendering Pipeline Windows Embedded Compact 7 Technical Article Writers: David Franklin,
2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION
 2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION A world-coordinate area selected for display is called a window. An area on a display device to which a window is mapped is called a viewport. The window
2.3 WINDOW-TO-VIEWPORT COORDINATE TRANSFORMATION A world-coordinate area selected for display is called a window. An area on a display device to which a window is mapped is called a viewport. The window
How To Draw A Billiards Ball In Gta 3D With Texture Mapping (Gta 3) On A Computer Or 2D Or Gta 2D (Gt) On Your Computer Or Computer Or Your Computer (Or Your Computer)
 Pool Billiard An OpenGL-based billiard simulation Stefan HUBER Kamran SAFDAR Andreas SCHRÖCKER Fachbereich Computerwissenschaften Universität Salzburg June 10, 2009 S. Huber, K. Safdar, A. Schröcker: Pool
Pool Billiard An OpenGL-based billiard simulation Stefan HUBER Kamran SAFDAR Andreas SCHRÖCKER Fachbereich Computerwissenschaften Universität Salzburg June 10, 2009 S. Huber, K. Safdar, A. Schröcker: Pool
Computer Graphics Hardware An Overview
 Computer Graphics Hardware An Overview Graphics System Monitor Input devices CPU/Memory GPU Raster Graphics System Raster: An array of picture elements Based on raster-scan TV technology The screen (and
Computer Graphics Hardware An Overview Graphics System Monitor Input devices CPU/Memory GPU Raster Graphics System Raster: An array of picture elements Based on raster-scan TV technology The screen (and
Visualization of 2D Domains
 Visualization of 2D Domains This part of the visualization package is intended to supply a simple graphical interface for 2- dimensional finite element data structures. Furthermore, it is used as the low
Visualization of 2D Domains This part of the visualization package is intended to supply a simple graphical interface for 2- dimensional finite element data structures. Furthermore, it is used as the low
L20: GPU Architecture and Models
 L20: GPU Architecture and Models scribe(s): Abdul Khalifa 20.1 Overview GPUs (Graphics Processing Units) are large parallel structure of processing cores capable of rendering graphics efficiently on displays.
L20: GPU Architecture and Models scribe(s): Abdul Khalifa 20.1 Overview GPUs (Graphics Processing Units) are large parallel structure of processing cores capable of rendering graphics efficiently on displays.
The OpenGL R Graphics System: A Specification (Version 3.3 (Core Profile) - March 11, 2010)
 The OpenGL R Graphics System: A Specification (Version 3.3 (Core Profile) - March 11, 2010) Mark Segal Kurt Akeley Editor (version 1.1): Chris Frazier Editor (versions 1.2-3.3): Jon Leech Editor (version
The OpenGL R Graphics System: A Specification (Version 3.3 (Core Profile) - March 11, 2010) Mark Segal Kurt Akeley Editor (version 1.1): Chris Frazier Editor (versions 1.2-3.3): Jon Leech Editor (version
SOEM 024: Computer Aided Design. E. Rozos
 SOEM 024: Computer Aided Design E. Rozos 3D Design with AutoCAD 2002 Isometric Drawings 3D coordinates, views Wire-frame 3D modelling, extruding Primitive objects Boolean operators Terminology Boolean
SOEM 024: Computer Aided Design E. Rozos 3D Design with AutoCAD 2002 Isometric Drawings 3D coordinates, views Wire-frame 3D modelling, extruding Primitive objects Boolean operators Terminology Boolean
Masters of Science in Software & Information Systems
 Masters of Science in Software & Information Systems To be developed and delivered in conjunction with Regis University, School for Professional Studies Graphics Programming December, 2005 1 Table of Contents
Masters of Science in Software & Information Systems To be developed and delivered in conjunction with Regis University, School for Professional Studies Graphics Programming December, 2005 1 Table of Contents
H.Calculating Normal Vectors
 Appendix H H.Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use the OpenGL lighting facility, which is described in Chapter
Appendix H H.Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use the OpenGL lighting facility, which is described in Chapter
Interaction. Triangles (Clarification) Choice of Programming Language. Display Lists. The CPU-GPU bus. CSCI 480 Computer Graphics Lecture 3
 CSCI 480 Computer Graphics Lecture 3 Triangles (Clarification) Interaction January 18, 2012 Jernej Barbic University of Southern California http://www-bcf.usc.edu/~jbarbic/cs480-s12/ [Angel Ch. 3] 1 Can
CSCI 480 Computer Graphics Lecture 3 Triangles (Clarification) Interaction January 18, 2012 Jernej Barbic University of Southern California http://www-bcf.usc.edu/~jbarbic/cs480-s12/ [Angel Ch. 3] 1 Can
Angle - a figure formed by two rays or two line segments with a common endpoint called the vertex of the angle; angles are measured in degrees
 Angle - a figure formed by two rays or two line segments with a common endpoint called the vertex of the angle; angles are measured in degrees Apex in a pyramid or cone, the vertex opposite the base; in
Angle - a figure formed by two rays or two line segments with a common endpoint called the vertex of the angle; angles are measured in degrees Apex in a pyramid or cone, the vertex opposite the base; in
Computer Graphics CS 543 Lecture 12 (Part 1) Curves. Prof Emmanuel Agu. Computer Science Dept. Worcester Polytechnic Institute (WPI)
 Computer Graphics CS 54 Lecture 1 (Part 1) Curves Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) So Far Dealt with straight lines and flat surfaces Real world objects include
Computer Graphics CS 54 Lecture 1 (Part 1) Curves Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) So Far Dealt with straight lines and flat surfaces Real world objects include
B2.53-R3: COMPUTER GRAPHICS. NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions.
 B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
B2.53-R3: COMPUTER GRAPHICS NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF ANSWER
OpenGL Shading Language Course. Chapter 5 Appendix. By Jacobo Rodriguez Villar jacobo.rodriguez@typhoonlabs.com
 OpenGL Shading Language Course Chapter 5 Appendix By Jacobo Rodriguez Villar jacobo.rodriguez@typhoonlabs.com TyphoonLabs GLSL Course 1/1 APPENDIX INDEX Using GLSL Shaders Within OpenGL Applications 2
OpenGL Shading Language Course Chapter 5 Appendix By Jacobo Rodriguez Villar jacobo.rodriguez@typhoonlabs.com TyphoonLabs GLSL Course 1/1 APPENDIX INDEX Using GLSL Shaders Within OpenGL Applications 2
Computational Geometry. Lecture 1: Introduction and Convex Hulls
 Lecture 1: Introduction and convex hulls 1 Geometry: points, lines,... Plane (two-dimensional), R 2 Space (three-dimensional), R 3 Space (higher-dimensional), R d A point in the plane, 3-dimensional space,
Lecture 1: Introduction and convex hulls 1 Geometry: points, lines,... Plane (two-dimensional), R 2 Space (three-dimensional), R 3 Space (higher-dimensional), R d A point in the plane, 3-dimensional space,
Arrangements And Duality
 Arrangements And Duality 3.1 Introduction 3 Point configurations are tbe most basic structure we study in computational geometry. But what about configurations of more complicated shapes? For example,
Arrangements And Duality 3.1 Introduction 3 Point configurations are tbe most basic structure we study in computational geometry. But what about configurations of more complicated shapes? For example,
Visualizing Data: Scalable Interactivity
 Visualizing Data: Scalable Interactivity The best data visualizations illustrate hidden information and structure contained in a data set. As access to large data sets has grown, so has the need for interactive
Visualizing Data: Scalable Interactivity The best data visualizations illustrate hidden information and structure contained in a data set. As access to large data sets has grown, so has the need for interactive
Introduction to GPGPU. Tiziano Diamanti t.diamanti@cineca.it
 t.diamanti@cineca.it Agenda From GPUs to GPGPUs GPGPU architecture CUDA programming model Perspective projection Vectors that connect the vanishing point to every point of the 3D model will intersecate
t.diamanti@cineca.it Agenda From GPUs to GPGPUs GPGPU architecture CUDA programming model Perspective projection Vectors that connect the vanishing point to every point of the 3D model will intersecate
Interactive visualization of multi-dimensional data in R using OpenGL
 Interactive visualization of multi-dimensional data in R using OpenGL 6-Monats-Arbeit im Rahmen der Prüfung für Diplom-Wirtschaftsinformatiker an der Universität Göttingen vorgelegt am 09.10.2002 von Daniel
Interactive visualization of multi-dimensional data in R using OpenGL 6-Monats-Arbeit im Rahmen der Prüfung für Diplom-Wirtschaftsinformatiker an der Universität Göttingen vorgelegt am 09.10.2002 von Daniel
12-1 Representations of Three-Dimensional Figures
 Connect the dots on the isometric dot paper to represent the edges of the solid. Shade the tops of 12-1 Representations of Three-Dimensional Figures Use isometric dot paper to sketch each prism. 1. triangular
Connect the dots on the isometric dot paper to represent the edges of the solid. Shade the tops of 12-1 Representations of Three-Dimensional Figures Use isometric dot paper to sketch each prism. 1. triangular
Beginning Android 4. Games Development. Mario Zechner. Robert Green
 Beginning Android 4 Games Development Mario Zechner Robert Green Contents Contents at a Glance About the Authors Acknowledgments Introduction iv xii xiii xiv Chapter 1: Android, the New Kid on the Block...
Beginning Android 4 Games Development Mario Zechner Robert Green Contents Contents at a Glance About the Authors Acknowledgments Introduction iv xii xiii xiv Chapter 1: Android, the New Kid on the Block...
Geometry Chapter 1. 1.1 Point (pt) 1.1 Coplanar (1.1) 1.1 Space (1.1) 1.2 Line Segment (seg) 1.2 Measure of a Segment
 Geometry Chapter 1 Section Term 1.1 Point (pt) Definition A location. It is drawn as a dot, and named with a capital letter. It has no shape or size. undefined term 1.1 Line A line is made up of points
Geometry Chapter 1 Section Term 1.1 Point (pt) Definition A location. It is drawn as a dot, and named with a capital letter. It has no shape or size. undefined term 1.1 Line A line is made up of points
ME 111: Engineering Drawing
 ME 111: Engineering Drawing Lecture # 14 (10/10/2011) Development of Surfaces http://www.iitg.ernet.in/arindam.dey/me111.htm http://www.iitg.ernet.in/rkbc/me111.htm http://shilloi.iitg.ernet.in/~psr/ Indian
ME 111: Engineering Drawing Lecture # 14 (10/10/2011) Development of Surfaces http://www.iitg.ernet.in/arindam.dey/me111.htm http://www.iitg.ernet.in/rkbc/me111.htm http://shilloi.iitg.ernet.in/~psr/ Indian
An introduction to 3D draughting & solid modelling using AutoCAD
 An introduction to 3D draughting & solid modelling using AutoCAD Faculty of Technology University of Plymouth Drake Circus Plymouth PL4 8AA These notes are to be used in conjunction with the AutoCAD software
An introduction to 3D draughting & solid modelling using AutoCAD Faculty of Technology University of Plymouth Drake Circus Plymouth PL4 8AA These notes are to be used in conjunction with the AutoCAD software
CMSC 427 Computer Graphics 1
 CMSC 427 Computer Graphics 1 David M. Mount Department of Computer Science University of Maryland Spring 2004 1 Copyright, David M. Mount, 2004, Dept. of Computer Science, University of Maryland, College
CMSC 427 Computer Graphics 1 David M. Mount Department of Computer Science University of Maryland Spring 2004 1 Copyright, David M. Mount, 2004, Dept. of Computer Science, University of Maryland, College
Computer Applications in Textile Engineering. Computer Applications in Textile Engineering
 3. Computer Graphics Sungmin Kim http://latam.jnu.ac.kr Computer Graphics Definition Introduction Research field related to the activities that includes graphics as input and output Importance Interactive
3. Computer Graphics Sungmin Kim http://latam.jnu.ac.kr Computer Graphics Definition Introduction Research field related to the activities that includes graphics as input and output Importance Interactive
Algebra Geometry Glossary. 90 angle
 lgebra Geometry Glossary 1) acute angle an angle less than 90 acute angle 90 angle 2) acute triangle a triangle where all angles are less than 90 3) adjacent angles angles that share a common leg Example:
lgebra Geometry Glossary 1) acute angle an angle less than 90 acute angle 90 angle 2) acute triangle a triangle where all angles are less than 90 3) adjacent angles angles that share a common leg Example:
Intersection of a Line and a Convex. Hull of Points Cloud
 Applied Mathematical Sciences, Vol. 7, 213, no. 13, 5139-5149 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.12988/ams.213.37372 Intersection of a Line and a Convex Hull of Points Cloud R. P. Koptelov
Applied Mathematical Sciences, Vol. 7, 213, no. 13, 5139-5149 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.12988/ams.213.37372 Intersection of a Line and a Convex Hull of Points Cloud R. P. Koptelov
How To Draw In Autocad
 DXF Import and Export for EASE 4.0 Page 1 of 9 DXF Import and Export for EASE 4.0 Bruce C. Olson, Dr. Waldemar Richert ADA Copyright 2002 Acoustic Design Ahnert EASE 4.0 allows both the import and export
DXF Import and Export for EASE 4.0 Page 1 of 9 DXF Import and Export for EASE 4.0 Bruce C. Olson, Dr. Waldemar Richert ADA Copyright 2002 Acoustic Design Ahnert EASE 4.0 allows both the import and export
Introduzione ad OpenGL
 Introduzione ad OpenGL Cosa è OpenGL E una interfaccia so8ware all hardware grafico, rendering API Indipendente dal sistema di windowing Indipendente dal sistema operabvo Evoluzione di OpenGL Viene gesbta
Introduzione ad OpenGL Cosa è OpenGL E una interfaccia so8ware all hardware grafico, rendering API Indipendente dal sistema di windowing Indipendente dal sistema operabvo Evoluzione di OpenGL Viene gesbta
Triangle Scan Conversion using 2D Homogeneous Coordinates
 Triangle Scan Conversion using 2D Homogeneous Coordinates Marc Olano 1 Trey Greer 2 University of North Carolina Hewlett-Packard ABSTRACT We present a new triangle scan conversion algorithm that works
Triangle Scan Conversion using 2D Homogeneous Coordinates Marc Olano 1 Trey Greer 2 University of North Carolina Hewlett-Packard ABSTRACT We present a new triangle scan conversion algorithm that works
We can display an object on a monitor screen in three different computer-model forms: Wireframe model Surface Model Solid model
 CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
Triangulation by Ear Clipping
 Triangulation by Ear Clipping David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: November 18, 2002 Last Modified: August 16, 2015 Contents
Triangulation by Ear Clipping David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: November 18, 2002 Last Modified: August 16, 2015 Contents
Largest Fixed-Aspect, Axis-Aligned Rectangle
 Largest Fixed-Aspect, Axis-Aligned Rectangle David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: February 21, 2004 Last Modified: February
Largest Fixed-Aspect, Axis-Aligned Rectangle David Eberly Geometric Tools, LLC http://www.geometrictools.com/ Copyright c 1998-2016. All Rights Reserved. Created: February 21, 2004 Last Modified: February
Pre-Algebra 2008. Academic Content Standards Grade Eight Ohio. Number, Number Sense and Operations Standard. Number and Number Systems
 Academic Content Standards Grade Eight Ohio Pre-Algebra 2008 STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express large numbers and small
Academic Content Standards Grade Eight Ohio Pre-Algebra 2008 STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express large numbers and small
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 2D and 3D Transformations Doug Bowman Adapted from notes by Yong Cao Virginia Tech 1 Transformations What are they? changing something to something else via rules mathematics:
CS 4204 Computer Graphics 2D and 3D Transformations Doug Bowman Adapted from notes by Yong Cao Virginia Tech 1 Transformations What are they? changing something to something else via rules mathematics:
COMP175: Computer Graphics. Lecture 1 Introduction and Display Technologies
 COMP175: Computer Graphics Lecture 1 Introduction and Display Technologies Course mechanics Number: COMP 175-01, Fall 2009 Meetings: TR 1:30-2:45pm Instructor: Sara Su (sarasu@cs.tufts.edu) TA: Matt Menke
COMP175: Computer Graphics Lecture 1 Introduction and Display Technologies Course mechanics Number: COMP 175-01, Fall 2009 Meetings: TR 1:30-2:45pm Instructor: Sara Su (sarasu@cs.tufts.edu) TA: Matt Menke
Number Sense and Operations
 Number Sense and Operations representing as they: 6.N.1 6.N.2 6.N.3 6.N.4 6.N.5 6.N.6 6.N.7 6.N.8 6.N.9 6.N.10 6.N.11 6.N.12 6.N.13. 6.N.14 6.N.15 Demonstrate an understanding of positive integer exponents
Number Sense and Operations representing as they: 6.N.1 6.N.2 6.N.3 6.N.4 6.N.5 6.N.6 6.N.7 6.N.8 6.N.9 6.N.10 6.N.11 6.N.12 6.N.13. 6.N.14 6.N.15 Demonstrate an understanding of positive integer exponents
MMGD0203 Multimedia Design MMGD0203 MULTIMEDIA DESIGN. Chapter 3 Graphics and Animations
 MMGD0203 MULTIMEDIA DESIGN Chapter 3 Graphics and Animations 1 Topics: Definition of Graphics Why use Graphics? Graphics Categories Graphics Qualities File Formats Types of Graphics Graphic File Size Introduction
MMGD0203 MULTIMEDIA DESIGN Chapter 3 Graphics and Animations 1 Topics: Definition of Graphics Why use Graphics? Graphics Categories Graphics Qualities File Formats Types of Graphics Graphic File Size Introduction
Computer Graphics. Introduction. Computer graphics. What is computer graphics? Yung-Yu Chuang
 Introduction Computer Graphics Instructor: Yung-Yu Chuang ( 莊 永 裕 ) E-mail: c@csie.ntu.edu.tw Office: CSIE 527 Grading: a MatchMove project Computer Science ce & Information o Technolog og Yung-Yu Chuang
Introduction Computer Graphics Instructor: Yung-Yu Chuang ( 莊 永 裕 ) E-mail: c@csie.ntu.edu.tw Office: CSIE 527 Grading: a MatchMove project Computer Science ce & Information o Technolog og Yung-Yu Chuang
3D graphic acceleration history and architecture
 3D graphic acceleration history and architecture 2003-2016 Josef Pelikán, Jan Horáček CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ GPU architecture 2016 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca
3D graphic acceleration history and architecture 2003-2016 Josef Pelikán, Jan Horáček CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ GPU architecture 2016 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca
A JAVA-BASED MULTI-PARTICIPANT 3D GRAPHICS APPLICATION INTERFACE USING JAVAGL 1 AND JAVANL 2
 A JAVA-BASED MULTI-PARTICIPANT 3D GRAPHICS APPLICATION INTERFACE USING JAVAGL 1 AND JAVANL 2 Bing-Yu Chen and Ming Ouhyoung Communications and Multimedia Laboratory, Department of Comer Science and Information
A JAVA-BASED MULTI-PARTICIPANT 3D GRAPHICS APPLICATION INTERFACE USING JAVAGL 1 AND JAVANL 2 Bing-Yu Chen and Ming Ouhyoung Communications and Multimedia Laboratory, Department of Comer Science and Information
Understand the Sketcher workbench of CATIA V5.
 Chapter 1 Drawing Sketches in Learning Objectives the Sketcher Workbench-I After completing this chapter you will be able to: Understand the Sketcher workbench of CATIA V5. Start a new file in the Part
Chapter 1 Drawing Sketches in Learning Objectives the Sketcher Workbench-I After completing this chapter you will be able to: Understand the Sketcher workbench of CATIA V5. Start a new file in the Part
MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem
 MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem David L. Finn November 30th, 2004 In the next few days, we will introduce some of the basic problems in geometric modelling, and
MA 323 Geometric Modelling Course Notes: Day 02 Model Construction Problem David L. Finn November 30th, 2004 In the next few days, we will introduce some of the basic problems in geometric modelling, and
Interactive Computer Graphics
 Interactive Computer Graphics A Top-Down Approach Using OpenGL FIFTH EDITION EDWARD ANGEL UNIVERSITY OF NEW MEXICO PEARSON Addison Wesley Boston San Francisco New York London Toronto Sydney Tokyo Singapore
Interactive Computer Graphics A Top-Down Approach Using OpenGL FIFTH EDITION EDWARD ANGEL UNIVERSITY OF NEW MEXICO PEARSON Addison Wesley Boston San Francisco New York London Toronto Sydney Tokyo Singapore
Freehand Sketching. Sections
 3 Freehand Sketching Sections 3.1 Why Freehand Sketches? 3.2 Freehand Sketching Fundamentals 3.3 Basic Freehand Sketching 3.4 Advanced Freehand Sketching Key Terms Objectives Explain why freehand sketching
3 Freehand Sketching Sections 3.1 Why Freehand Sketches? 3.2 Freehand Sketching Fundamentals 3.3 Basic Freehand Sketching 3.4 Advanced Freehand Sketching Key Terms Objectives Explain why freehand sketching
Institution : Majmaah University. Academic Department : College of Science at AzZulfi. Programme : Computer Science and Information Course :
 Institution : Majmaah University. Academic Department : College of Science at AzZulfi. Programme : Computer Science and Information Course : Computer Graphics (CSI-425) Course Coordinator : Mr. ISSA ALSMADI
Institution : Majmaah University. Academic Department : College of Science at AzZulfi. Programme : Computer Science and Information Course : Computer Graphics (CSI-425) Course Coordinator : Mr. ISSA ALSMADI
VALLIAMMAI ENGNIEERING COLLEGE SRM Nagar, Kattankulathur 603203.
 VALLIAMMAI ENGNIEERING COLLEGE SRM Nagar, Kattankulathur 603203. DEPARTMENT OF COMPUTER SCIENCE AND ENGINEERING Year & Semester : III Year, V Semester Section : CSE - 1 & 2 Subject Code : CS6504 Subject
VALLIAMMAI ENGNIEERING COLLEGE SRM Nagar, Kattankulathur 603203. DEPARTMENT OF COMPUTER SCIENCE AND ENGINEERING Year & Semester : III Year, V Semester Section : CSE - 1 & 2 Subject Code : CS6504 Subject
Lecture 9: Geometric map transformations. Cartographic Transformations
 Cartographic Transformations Analytical and Computer Cartography Lecture 9: Geometric Map Transformations Attribute Data (e.g. classification) Locational properties (e.g. projection) Graphics (e.g. symbolization)
Cartographic Transformations Analytical and Computer Cartography Lecture 9: Geometric Map Transformations Attribute Data (e.g. classification) Locational properties (e.g. projection) Graphics (e.g. symbolization)
An Introduction to. Graphics Programming
 An Introduction to Graphics Programming with Tutorial and Reference Manual Toby Howard School of Computer Science University of Manchester V3.3, January 13, 2010 Contents 1 About this manual 1 1.1 How
An Introduction to Graphics Programming with Tutorial and Reference Manual Toby Howard School of Computer Science University of Manchester V3.3, January 13, 2010 Contents 1 About this manual 1 1.1 How
Reflection and Refraction
 Equipment Reflection and Refraction Acrylic block set, plane-concave-convex universal mirror, cork board, cork board stand, pins, flashlight, protractor, ruler, mirror worksheet, rectangular block worksheet,
Equipment Reflection and Refraction Acrylic block set, plane-concave-convex universal mirror, cork board, cork board stand, pins, flashlight, protractor, ruler, mirror worksheet, rectangular block worksheet,
Intermediate Tutorials Modeling - Trees. 3d studio max. 3d studio max. Tree Modeling. 1.2206 2006 Matthew D'Onofrio Page 1 of 12
 3d studio max Tree Modeling Techniques and Principles 1.2206 2006 Matthew D'Onofrio Page 1 of 12 Modeling Trees Tree Modeling Techniques and Principles The era of sprites and cylinders-for-trunks has passed
3d studio max Tree Modeling Techniques and Principles 1.2206 2006 Matthew D'Onofrio Page 1 of 12 Modeling Trees Tree Modeling Techniques and Principles The era of sprites and cylinders-for-trunks has passed
Blender Notes. Introduction to Digital Modelling and Animation in Design Blender Tutorial - week 9 The Game Engine
 Blender Notes Introduction to Digital Modelling and Animation in Design Blender Tutorial - week 9 The Game Engine The Blender Game Engine This week we will have an introduction to the Game Engine build
Blender Notes Introduction to Digital Modelling and Animation in Design Blender Tutorial - week 9 The Game Engine The Blender Game Engine This week we will have an introduction to the Game Engine build
GPU(Graphics Processing Unit) with a Focus on Nvidia GeForce 6 Series. By: Binesh Tuladhar Clay Smith
 GPU(Graphics Processing Unit) with a Focus on Nvidia GeForce 6 Series By: Binesh Tuladhar Clay Smith Overview History of GPU s GPU Definition Classical Graphics Pipeline Geforce 6 Series Architecture Vertex
GPU(Graphics Processing Unit) with a Focus on Nvidia GeForce 6 Series By: Binesh Tuladhar Clay Smith Overview History of GPU s GPU Definition Classical Graphics Pipeline Geforce 6 Series Architecture Vertex
COMP-557: Fundamentals of Computer Graphics McGill University, Fall 2010
 COMP-557: Fundamentals of Computer Graphics McGill University, Fall 2010 Class times 2:25 PM - 3:55 PM Mondays and Wednesdays Lecture room Trottier Building 2120 Instructor Paul Kry, kry@cs.mcgill.ca Course
COMP-557: Fundamentals of Computer Graphics McGill University, Fall 2010 Class times 2:25 PM - 3:55 PM Mondays and Wednesdays Lecture room Trottier Building 2120 Instructor Paul Kry, kry@cs.mcgill.ca Course
Chapter 2 - Graphics Programming with JOGL
 Chapter 2 - Graphics Programming with JOGL Graphics Software: Classification and History JOGL Hello World Program 2D Coordinate Systems in JOGL Dealing with Window Reshaping 3D Coordinate Systems in JOGL
Chapter 2 - Graphics Programming with JOGL Graphics Software: Classification and History JOGL Hello World Program 2D Coordinate Systems in JOGL Dealing with Window Reshaping 3D Coordinate Systems in JOGL
Algebra 1 2008. Academic Content Standards Grade Eight and Grade Nine Ohio. Grade Eight. Number, Number Sense and Operations Standard
 Academic Content Standards Grade Eight and Grade Nine Ohio Algebra 1 2008 Grade Eight STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express
Academic Content Standards Grade Eight and Grade Nine Ohio Algebra 1 2008 Grade Eight STANDARDS Number, Number Sense and Operations Standard Number and Number Systems 1. Use scientific notation to express
SketchUp Instructions
 SketchUp Instructions Every architect needs to know how to use SketchUp! SketchUp is free from Google just Google it and download to your computer. You can do just about anything with it, but it is especially
SketchUp Instructions Every architect needs to know how to use SketchUp! SketchUp is free from Google just Google it and download to your computer. You can do just about anything with it, but it is especially
COMPARISON OF TWO DIFFERENT SURFACES FOR 3D MODEL ABSTRACTION IN SUPPORT OF REMOTE SENSING SIMULATIONS BACKGROUND
 COMPARISON OF TWO DIFFERENT SURFACES FOR 3D MODEL ABSTRACTION IN SUPPORT OF REMOTE SENSING SIMULATIONS Paul Pope, Ph.D. Doug Ranken Los Alamos National Laboratory Los Alamos, New Mexico 87545 papope@lanl.gov
COMPARISON OF TWO DIFFERENT SURFACES FOR 3D MODEL ABSTRACTION IN SUPPORT OF REMOTE SENSING SIMULATIONS Paul Pope, Ph.D. Doug Ranken Los Alamos National Laboratory Los Alamos, New Mexico 87545 papope@lanl.gov
Computer Graphics Labs
 Computer Graphics Labs Abel J. P. Gomes LAB. 2 Department of Computer Science and Engineering University of Beira Interior Portugal 2011 Copyright 2009-2011 All rights reserved. LAB. 2 1. Learning goals
Computer Graphics Labs Abel J. P. Gomes LAB. 2 Department of Computer Science and Engineering University of Beira Interior Portugal 2011 Copyright 2009-2011 All rights reserved. LAB. 2 1. Learning goals
Fixplot Instruction Manual. (data plotting program)
 Fixplot Instruction Manual (data plotting program) MANUAL VERSION2 2004 1 1. Introduction The Fixplot program is a component program of Eyenal that allows the user to plot eye position data collected with
Fixplot Instruction Manual (data plotting program) MANUAL VERSION2 2004 1 1. Introduction The Fixplot program is a component program of Eyenal that allows the user to plot eye position data collected with
SolidWorks Implementation Guides. Sketching Concepts
 SolidWorks Implementation Guides Sketching Concepts Sketching in SolidWorks is the basis for creating features. Features are the basis for creating parts, which can be put together into assemblies. Sketch
SolidWorks Implementation Guides Sketching Concepts Sketching in SolidWorks is the basis for creating features. Features are the basis for creating parts, which can be put together into assemblies. Sketch
Activity Set 4. Trainer Guide
 Geometry and Measurement of Solid Figures Activity Set 4 Trainer Guide Mid_SGe_04_TG Copyright by the McGraw-Hill Companies McGraw-Hill Professional Development GEOMETRY AND MEASUREMENT OF SOLID FIGURES
Geometry and Measurement of Solid Figures Activity Set 4 Trainer Guide Mid_SGe_04_TG Copyright by the McGraw-Hill Companies McGraw-Hill Professional Development GEOMETRY AND MEASUREMENT OF SOLID FIGURES
GUI GRAPHICS AND USER INTERFACES. Welcome to GUI! Mechanics. Mihail Gaianu 26/02/2014 1
 Welcome to GUI! Mechanics 26/02/2014 1 Requirements Info If you don t know C++, you CAN take this class additional time investment required early on GUI Java to C++ transition tutorial on course website
Welcome to GUI! Mechanics 26/02/2014 1 Requirements Info If you don t know C++, you CAN take this class additional time investment required early on GUI Java to C++ transition tutorial on course website
COMPUTER GRAPHICS IMPORTANT QUESTION AND ANSWERS. Computer graphics
 Computer graphics 1. Define Computer graphics. Computer graphics remains one of the most existing and rapidly growing computer fields. Computer graphics may be defined as a pictorial representation or
Computer graphics 1. Define Computer graphics. Computer graphics remains one of the most existing and rapidly growing computer fields. Computer graphics may be defined as a pictorial representation or
Introduction to Computer Graphics. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012
 CSE 167: Introduction to Computer Graphics Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012 Today Course organization Course overview 2 Course Staff Instructor Jürgen Schulze,
CSE 167: Introduction to Computer Graphics Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012 Today Course organization Course overview 2 Course Staff Instructor Jürgen Schulze,
3D Math Overview and 3D Graphics Foundations
 Freescale Semiconductor Application Note Document Number: AN4132 Rev. 0, 05/2010 3D Math Overview and 3D Graphics Foundations by Multimedia Applications Division Freescale Semiconductor, Inc. Austin, TX
Freescale Semiconductor Application Note Document Number: AN4132 Rev. 0, 05/2010 3D Math Overview and 3D Graphics Foundations by Multimedia Applications Division Freescale Semiconductor, Inc. Austin, TX
Adobe Illustrator CS5 Part 1: Introduction to Illustrator
 CALIFORNIA STATE UNIVERSITY, LOS ANGELES INFORMATION TECHNOLOGY SERVICES Adobe Illustrator CS5 Part 1: Introduction to Illustrator Summer 2011, Version 1.0 Table of Contents Introduction...2 Downloading
CALIFORNIA STATE UNIVERSITY, LOS ANGELES INFORMATION TECHNOLOGY SERVICES Adobe Illustrator CS5 Part 1: Introduction to Illustrator Summer 2011, Version 1.0 Table of Contents Introduction...2 Downloading
OpenGL Performance Tuning
 OpenGL Performance Tuning Evan Hart ATI Pipeline slides courtesy John Spitzer - NVIDIA Overview What to look for in tuning How it relates to the graphics pipeline Modern areas of interest Vertex Buffer
OpenGL Performance Tuning Evan Hart ATI Pipeline slides courtesy John Spitzer - NVIDIA Overview What to look for in tuning How it relates to the graphics pipeline Modern areas of interest Vertex Buffer
Glencoe. correlated to SOUTH CAROLINA MATH CURRICULUM STANDARDS GRADE 6 3-3, 5-8 8-4, 8-7 1-6, 4-9
 Glencoe correlated to SOUTH CAROLINA MATH CURRICULUM STANDARDS GRADE 6 STANDARDS 6-8 Number and Operations (NO) Standard I. Understand numbers, ways of representing numbers, relationships among numbers,
Glencoe correlated to SOUTH CAROLINA MATH CURRICULUM STANDARDS GRADE 6 STANDARDS 6-8 Number and Operations (NO) Standard I. Understand numbers, ways of representing numbers, relationships among numbers,
Native code in Android Quad Detection
 Native code in Android Quad Detection 21 July 2013 This document provides information on how to build and run native (C/C++) code in Android platform using Android NDK and then use its scope to auto capture
Native code in Android Quad Detection 21 July 2013 This document provides information on how to build and run native (C/C++) code in Android platform using Android NDK and then use its scope to auto capture
AutoCAD i 3D Samordningsmodell Tips og Triks for tegning i 3D med AutoCAD
 AutoCAD i 3D Samordningsmodell Tips og Triks for tegning i 3D med AutoCAD Tesfaye Kebede Vianova systems AutoCAD 3D AutoCAD - 3D Samordningsmodell - Course Contents - New Features 3D AutoCAD 2013 - Sheet
AutoCAD i 3D Samordningsmodell Tips og Triks for tegning i 3D med AutoCAD Tesfaye Kebede Vianova systems AutoCAD 3D AutoCAD - 3D Samordningsmodell - Course Contents - New Features 3D AutoCAD 2013 - Sheet
TABLE OF CONTENTS. INTRODUCTION... 5 Advance Concrete... 5 Where to find information?... 6 INSTALLATION... 7 STARTING ADVANCE CONCRETE...
 Starting Guide TABLE OF CONTENTS INTRODUCTION... 5 Advance Concrete... 5 Where to find information?... 6 INSTALLATION... 7 STARTING ADVANCE CONCRETE... 7 ADVANCE CONCRETE USER INTERFACE... 7 Other important
Starting Guide TABLE OF CONTENTS INTRODUCTION... 5 Advance Concrete... 5 Where to find information?... 6 INSTALLATION... 7 STARTING ADVANCE CONCRETE... 7 ADVANCE CONCRETE USER INTERFACE... 7 Other important
Blender addons ESRI Shapefile import/export and georeferenced raster import
 Blender addons ESRI Shapefile import/export and georeferenced raster import This blender addon is a collection of 4 tools: ESRI Shapefile importer - Import point, pointz, polyline, polylinez, polygon,
Blender addons ESRI Shapefile import/export and georeferenced raster import This blender addon is a collection of 4 tools: ESRI Shapefile importer - Import point, pointz, polyline, polylinez, polygon,
2013 Getting Started Guide
 2013 Getting Started Guide The contents of this guide and accompanying exercises were originally created by Nemetschek Vectorworks, Inc. Vectorworks Fundamentals Getting Started Guide Created using: Vectorworks
2013 Getting Started Guide The contents of this guide and accompanying exercises were originally created by Nemetschek Vectorworks, Inc. Vectorworks Fundamentals Getting Started Guide Created using: Vectorworks
