Department of Computing and Software
|
|
|
- Magnus Evelyn Goodwin
- 7 years ago
- Views:
Transcription
1 Department of Computing and Software Faculty of Engineering McMaster University Decentralized Control Using the Hierarchical Interface-based Supervisory Control Approach v 1.1 by Huailiang Liu, Ryan J. Leduc, and S. L. Ricker CAS Report Series CAS RL Department of Computing and Software December 2015 Information Technology Building McMaster University 1280 Main Street West Hamilton, Ontario, Canada L8S 4K1 Copyright 2015
2 ÒØÖ Ð Þ ÓÒØÖÓÐ Í Ò Ø À Ö Ö Ð ÁÒØ Ö ¹ ËÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÔÔÖÓ Ú ½º½ ÀÙ Ð Ò Ä Ù 1 ÊÝ Ò Âº Ä Ù 1 Ò Ëº ĺ Ê Ö 2 1 Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ò Ò ËÓ ØÛ Ö ÙÐØÝ Ó Ò Ò Ö Ò ÅÅ Ø Ö ÍÒ Ú Ö ØÝ À Ñ ÐØÓÒ ÇÒØ Ö Ó Ò 2 Ô ÖØÑ ÒØ Ó Å Ø Ñ Ø Ò ÓÑÔÙØ Ö Ë Ò ÅÓÙÒØ ÐÐ ÓÒ ÍÒ Ú Ö ØÝ Ë Ú ÐÐ Æ Ä ½ Ò Ì Ò Ð Ê ÔÓÖØ Ë¹½ ¹½¼¹ÊÄ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ò Ò ËÓ ØÛ Ö ÅÅ Ø Ö ÍÒ Ú Ö ØÝ Â ÒÙ ÖÝ ¾ ¾¼½ ØÖ Ø ÁÒ ÒØÖ Ð Þ ÓÒØÖÓÐ ÒØ Ú ÓÒÐÝ Ô ÖØ Ð Ú Û Ò Ô ÖØ Ð ÓÒØÖÓÐ Ó Ø Ý Ø Ñ Ò ÑÙ Ø ÓÓÔ Ö Ø ØÓ Ú Ø ÓÒØÖÓÐ Ó Ø Ú º ÌÓ ÝÒØ Þ Ò¹ ØÖ Ð Þ ÓÒØÖÓÐ ÓÐÙØ ÓÒ Ô Ø ÓÒ ÑÙ Ø Ø Ý Ø Ó¹Ó ÖÚ Ð ØÝ ÔÖÓÔ ÖØݺ Ü Ø Ò Ó¹Ó ÖÚ Ð ØÝ Ú Ö Ø ÓÒ Ñ Ø Ó Ö ÕÙ Ö Ø ÔÓ ÐÝ ÒØÖ Ø Ð µ ÓÒ ØÖÙØ ÓÒ Ó Ø ÓÑÔÐ Ø Ý Ø Ñº ÌÓ ÒÖ Ø Ð Ð ØÝ Ó ÒØÖ Ð Þ ÓÒØÖÓÐ Û ÒØÖÓ Ù Ø À Ö Ö ¹ Ð ÁÒØ Ö ¹ ÒØÖ Ð Þ ËÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÀÁ Ë µ Ö Ñ ÛÓÖ Ø Ø ÜØ Ò Ø Ü Ø Ò À Ö Ö Ð ÁÒØ Ö ¹ ËÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÀÁË µ Ô¹ ÔÖÓ º ÌÓ ÔØ Ó¹Ó ÖÚ Ð ØÝ ÓÖ ÀÁ Ë Û ÔÖÓÔÓ Ô Ö¹ÓÑÔÓÒ ÒØ Ò Ø ÓÒ Ó Ó¹Ó ÖÚ Ð ØÝ ÐÓÒ Û Ø Ú Ö Ø ÓÒ ØÖ Ø Ý Ø Ø Ö ÕÙ Ö Ü Ñ Ò Ø ÓÒ Ó ÓÒÐÝ Ò Ð ÓÑÔÓÒ ÒØ Ø Ø Ñ º Ò ÐÐÝ Û ÔÖÓÚ Ò ÔÖÓÚ Ø Ò ÖÝ Ò Ù ÒØ ÓÒ Ø ÓÒ ÓÖ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Ü Ø Ò Ò Ø ÀÁ Ë Ö Ñ ÛÓÖ Ò ÐÐÙ ØÖ Ø ÓÙÖ ÔÔÖÓ Û Ø Ò Ü ÑÔÐ º Ø ÒØ Ö Ý Ø Ñ ÑÓ Ð Ò Ú Ö Ò ØÓ ÓÒ ØÖÙØ ÀÁ Ë Ò ÔÖÓÚ Ò ÒØ ÓÑÔÙØ Ø ÓÒ Ð Ú Ò º à ÝÛÓÖ Ö Ø ¹ Ú ÒØ Ý Ø Ñ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÒØÖ Ð Þ ÓÒØÖÓÐ À ¹ Ö Ö Ð ÁÒØ Ö ¹ ËÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ
3 ÓÒØ ÒØ ½ ÁÒØÖÓ ÙØ ÓÒ ½ ¾ ÈÖ Ð Ñ Ò Ö ¾ ¾º½ Ä Ò Ù Ò Ë º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ¾º¾ ÒØÖ Ð Þ ÓÒØÖÓÐ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º ÒØÖ Ð Þ ÓÒØÖÓÐ Û Ø Å Ö Ò º º º º º º º º º º º º º º º º º º º º º º º º ÀÁË Ö Ø ØÙÖ À Ö Ö Ð ÁÒØ Ö ¹ ÒØÖ Ð Þ ËÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ½¼ º½ ÀÁ Ë Ó¹Ó ÖÚ Ð ØÝ Ò Ø ÓÒ Ò Ì ÓÖ Ñ º º º º º º º º º º º º º º º º º ½¾ º¾ ÅÆ Ë ËÙÔ ÖÚ ÓÖ Ü Ø Ò Ì ÓÖ Ñ º º º º º º º º º º º º º º º º º º º º º º ½ Å ÒÙ ØÙÖ Ò Ü ÑÔÐ ½ º½ Å ÒÙ ØÙÖ Ò ËÝ Ø Ñ Ò ÀÁ Ë ËÝ Ø Ñ º º º º º º º º º º º º º º º º º º º º ½ º¾ Ó¹Ó ÖÚ Ð ØÝ Î Ö Ø ÓÒ ÓÖ ËÝ Ø Ñ º º º º º º º º º º º º º º º º º º º º º º ½ º ÓÑÔÐ Ü ØÝ Ò ÐÝ ÓÖ Ø ÒØÖ Ð Þ ËÝ Ø Ñ º º º º º º º º º º º º º º º º ½ ÓÒÐÙ ÓÒ Ò ÙØÙÖ ÏÓÖ ½ ÈÖÓÓ ¾¼
4 ½ ÁÒØÖÓ ÙØ ÓÒ ÇÒ Ó Ø Ñ Ò ÐÐ Ò Ò Ø ÓÒØÖÓÐ Ó Ö Ø ¹ Ú ÒØ Ý Ø Ñ Ëµ ļ ÊÏ ÏÊ ÏÓÒ½ Ø ÓÑ Ò ØÓÖ Ð ÜÔÐÓ ÓÒ Ó Ø ÔÖÓ ÙØ Ø Ø Ô º Ì À Ö Ö Ð ÁÒØ Ö ¹ ËÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÀÁË µ Ö Ñ ÛÓÖ ÔÖÓÔÓ Ò ÀÂ É + ½¼ Ä ¼¾ Ä ¼ Ä Äϼ ÄÄ ¼ ÄÄϼ Ò ÐÔ ÐÐ Ú Ø Ø Ø Ø ¹ Ô ÜÔÐÓ ÓÒ ÔÖÓ Ð Ñº ÀÁË ÔÖÓÚ Ø Ó ÐÓ Ð ÔÖÓÔ ÖØ Ø Ø Ò Ù ØÓ Ú Ö Ý ÐÓ Ð ÔÖÓÔ ÖØ Ù ÒÓÒ ÐÓ Ò Ò ÓÒØÖÓÐÐ Ð ØÝ Ó Ø Ø Ø ÓÑÔÐ Ø Ý Ø Ñ ÑÓ Ð Ò Ú Ö Ò ØÓ ÓÒ ØÖÙØ º Ì Ù ÒØ ÓÒ Ø ÓÒ Ó ÀÁË ÐÐÓÛ Ø Ò Ô Ò ÒØ Ò Ò Ú Ö Ø ÓÒ Ó Ö ÒØ Ð Ú Ð Ò ÙÖ Ò Ø Ø Ò ØÓ ÓÒ Ð Ú Ð Ó Ø Ö Ö Ý Û ÐÐ ÒÓØ ÑÔ Ø Ø ÓØ Ö º ÀÓÛ Ú Ö Ø ÙÖÖ ÒØ ÀÁË Ö Ñ ÛÓÖ Ó ÒÓØ ÙÔÔÓÖØ ÒØÖ Ð Þ ÓÒØÖÓÐ ÔÖÓ Ð Ñ Ø Ø Ö Ò ØÙÖ ÐÐÝ Ø ÖÓÙ Ø ÒÚ Ø Ø ÓÒ Ó Ð Ö Ú Ö ØÝ Ó ØÖ ÙØ Ý Ø Ñ Ù ÓÑÑÙÒ Ø ÓÒ Ò ØÛÓÖ ÒØ Ö Ø Ò ÓÖ Ò ØÛÓÖ Ò ØÛÓÖ ÓÒØÖÓÐ Ý Ø Ñ Ò Ù¹ ØÓÑ Ø Ù Ú ÙÐ Ö Ý Ø Ñ º ÒØÖ Ð Þ ÓÒØÖÓÐ Ó Ë ÓÙ ÓÒ ÔÖÓ Ð Ñ Û Ö ÑÙÐØ ÔÐ ÒØ ÓÒØÖÓÐ Ò Ó ÖÚ ÓÑ Ú ÒØ Ò Ý Ø Ñ Ò ÑÙ Ø ØÓ Ø Ö Ú ÓÑ ÔÖ Ö Ó Ðº ÒØÖ Ð Þ ÔÔÖÓ Ù Û Ò Ø Ô Ý Ð Ý Ø Ñ Ù Ø Ø ÓÒØÖÓÐÐ Ö ÑÔÐ Ñ ÒØ Ø Ö ÒØ ÐÓ Ø ÓÒ ÛÓÙÐ Ò ØÙÖ ÐÐÝ ÓÒÐÝ Ð ØÓ Ò Ø Ú ÒØ ÓÙÖÖ Ò Ò Ø Ö ÐÓ Ð Ú Ò ØÝ Ò Ú ÒÓ ØÓ ÓØ Ö Ú ÒØ º Ì Ó Ð ØÓ Ð ØÓ ÑÔÐ Ñ ÒØ Ø Ó ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Ø Ø ÔÖÓ Ù Ø Ñ ÓÒØÖÓÐ Ø ÓÒ ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Û Ø ÙÐÐ Ú Û Ò ÓÒØÖÓÐ Ó Ø Ý Ø Ñº Ì ÝÒØ Ó ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖ Ö ÕÙ Ö Ø Ø Ø Ô Ø ÓÒ Ø ¹ ÒØÖ Ð Þ ÔÖÓÔ ÖØÝ ÐÐ Ó¹Ó ÖÚ Ð ØÝ ÊÏ ¾ º Æ Ú ÖØ Ð Û Ò Ø Ý Ø Ñ Ú ÖÝ Ð Ö Ò ÓÑÔÓ Ó Ñ ÒÝ Ù ¹ Ý Ø Ñ Ò Ó¹Ó ÖÚ Ð ØÝ Ù Ò Ø Ü Ø Ò ÑÓÒÓ¹ Ð Ø Ñ Ø Ó ÊÏ Ö ÕÙ Ö Ø ÓÒ ØÖÙØ ÓÒ Ó Ø ÓÑÔÐ Ø Ý Ø Ñ ÑÓ Ð Û Ñ Ý ÒØÖ Ø Ð Ù ØÓ Ø Ø Ø ¹ Ô ÜÔÐÓ ÓÒ ÔÖÓ Ð Ñº ÁÒ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Ó Ë Ø ÓÑÔÙØ Ø ÓÒ Ò ÓÑÔÐ Ü ØÝ ÓÖ Ñ ÒÝ Ó Ø ÓÒØÖÓÐ ÓÐÙØ ÓÒ ÒØ Ð ÓÒÐÝ ÔÓÐÝÒÓÑ Ð ÓÖØ Ò Ø ÑÓ Ð³ Ø Ø Þ º Ì ÓÑÔÙØ Ø ÓÒ Ò Óѹ ÔÐ Ü ØÝ ÛÓÖ Ò Ø Ó ÓÒØÖÓÐ Û Ø Ô ÖØ Ð Ó ÖÚ Ø ÓÒ ÓÑ ÔÖÓ Ð Ñ Û Ø ÙÐÐ Ó ÖÚ Ø ÓÒ Ö ÔÓÐÝÒÓÑ Ð ÓÛ Ú Ö Ø Ý Ö ÜÔÓÒ ÒØ Ð Û Ò Ø ØÙ Ø ÓÒ Ô ÖØ ÐÐÝ Ó ÖÚ Ð Ê Ä¼ ÊÏ Ìļ ÌÖ ¼ Ì Ä¼¾ º ÁÒ Ä Ù½ ÄÄÅʽ Û ÒØÖÓ Ù Ò ÒÖ Ñ ÒØ Ð ÔÔÖÓ ÓÖ Ò Ó¹Ó ÖÚ Ð ØÝ ÓÒ Ø ÛÓÖ Ó Ö Ò Ò Ø Ðº Åż ÓÖ Ú Ö Ý Ò ÓÒØÖÓÐÐ Ð Øݺ ÇÙÖ Ñ Ø Ó Ö ØÐÝ ÒÖ Ø Þ Ó Ý Ø Ñ Ø Ø ÓÙÐ Ú Ö ÙØ Ø Ð Ó ØÖÙ Ð Ø Ø Ø Þ Ò ÒÙÑ Ö Ó ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö ÒÖ º ÌÓ Ö Ø ÓÚ Ù Û ÔÖÓÔÓ Ò ÔÔÖÓ ÐÐ Ø À Ö Ö Ð ÁÒØ Ö ¹ ÒØÖ Ð Þ ËÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÀÁ Ë µ Ö Ñ ÛÓÖ Ø Ø ÜØ Ò ÀÁË ØÓ Ñ Ò ÒØÖ Ð Þ ÓÒØÖÓÐ ÔÖÓ Ð Ñ º Ï ÒØÖÓ Ù Ô Ö¹ÓÑÔÓÒ ÒØ Ó¹Ó ÖÚ Ð ØÝ Ò Ø ÓÒ Û Ó ÒÓØ Ö ÕÙ Ö Ø ÝÒ ÖÓÒ Þ Ø ÓÒ Ó ÐÐ ÓÑÔÓÒ ÒØ º Ï Ø Ò ÔÖÓÚ Ø Ø Ý Ø Ñ Ø Ø Ô Ö¹ÓÑÔÓÒ ÒØ Ó¹Ó ÖÚ Ð ØÝ Ò Ø ÓÒ Ø ÐÓ ÐÐÝ Ó¹Ó ÖÚ Ð º ÙÖØ Ö Û ÔÖÓÚ Ò ÔÖÓÚ Ø Ò ÖÝ Ò Ù ÒØ ÓÒ Ø ÓÒ ÓÖ ÙÔ ÖÚ ÓÖ Ü Ø Ò Ò ÀÁ Ë º ÅÓ Ø Ó Ø Ñ Ø Ö Ð Ò Ø Ô Ô Ö Ö Ø ÔÔ Ö Ò ÓÙÖ ÓÒ Ö Ò Ô Ô Ö ÄÄʽ º Ì ÙÖÖ ÒØ Ô Ô Ö ÙÐÐ ÔÖÓÓ ÑÓÖ ÓÑÔÐ Ø Ü ÑÔÐ Û ÐÐ ÜÔ Ö Ñ ÒØ Ð Ö ÙÐØ º ÌÓ Ø Ø Ó ÓÙÖ ÒÓÛÐ Ø Ö ÒÓ Ü Ø Ò ÛÓÖ Û Ö ÀÁË ÙÔÔÓÖØ ÒØÖ Ð Þ Ö Ø ¹ Ú ÒØ ÓÒØÖÓÐ Ö Ø ØÙÖ º ÐØ ÓÙ Ø Ö ÓÑ Ð Ø Ö ØÙÖ ÔÖÓÔÓ Ò Ö Ö Ð ÓÒØÖÓÐ Ó ÒØÖ Ð Þ Ö Ø ¹ Ú ÒØ Ý Ø Ñ Ë ½½ Ëż ËÅȼ Ø ÔÔÖÓ ¹ ÙÑ ÙÐÐ Ó ÖÚ Ø ÓÒ Ò Ø Ù Ø Ý Ö ÒØÖ Ð Þ Ò Ø ÖÑ Ó Ö Ø ØÙÖ ÒÓØ Ò Ø ÖÑ Ó Ó ÖÚ Ø ÓÒ º ½
5 Ì Ô Ô Ö ÓÖ Ò Þ ÓÐÐÓÛ º ÁÒ Ë Ø ÓÒ ¾ Û Ö Ú Û Ø Ö Ð Ú ÒØ Ò Ø ÓÒ Ò Ö ÙÐØ ÖÓÑ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Ø ÓÖݺ Ë Ø ÓÒ Ö Ú Û Ø ÀÁË Ö Ø ØÙÖ º ÁÒ Ë Ø ÓÒ Û ÒØÖÓ Ù ÓÙÖ Ò Û ÀÁ Ë Ö Ñ ÛÓÖ º ÁÒ Ë Ø ÓÒ Û ÐÐÙ ØÖ Ø ÓÙÖ ÀÁ Ë ÔÔÖÓ Û Ø Ò Ü ÑÔÐ º Ï Ø Ò ÔÖ ÒØ ÓÒÐÙ ÓÒ Ò ÙØÙÖ ÛÓÖ Ò Ë Ø ÓÒ º ¾ ÈÖ Ð Ñ Ò Ö Ì Ø ÓÒ ÔÖÓÚ Ö Ö Ú Û Ó Ø Ý Ë ÓÒ ÔØ Ù Ò Ø Ô Ô Öº ÓÖ ÑÓÖ Ø Ð ÔÐ Ö Ö ØÓ Ä¼ ÏÓÒ½ º ¾º½ Ä Ò Ù Ò Ë Ú ÒØ ÕÙ Ò Ò Ð Ò Ù Ö ÑÔÐ Û Ý ØÓ Ö Ë Ú ÓÙÖº Ä Ø Σ Ò Ø Ø Ó Ø ÒØ ÝÑ ÓÐ Ú ÒØ µ Ò Ð Ø Σ + Ø Ø Ó ÐÐ Ò Ø ÒÓÒ ÑÔØÝ ÕÙ Ò Ó Ú ÒØ º Ä Ø Σ := Σ + {ǫ} Ø Ø Ó ÐÐ Ò Ø ÕÙ Ò Ó Ú ÒØ ÔÐÙ ǫ Ø ÑÔØÝ ØÖ Ò º Ð Ò Ù L ÓÚ Ö Σ ÒÝ Ù Ø L Σ º Ì ÓÒ Ø Ò Ø ÓÒ Ó ØÛÓ ØÖ Ò s, t Σ ÛÖ ØØ Ò stº Ä Ò Ù Ò ÐÔ Ø Ò Ð Ó ÓÒ Ø Ò Ø º ÓÖ L Σ Ò Σ Σ Ø ÓÒ Ø Ò Ø ÓÒ Ó Ð Ò Ù L Ò Ú ÒØ Ø Σ Ò LΣ := {sσ s L, σ Σ }º ÓÖ ØÖ Ò s, t Σ Û Ý Ø Ø t ÔÖ Ü Ó s ÛÖ ØØ Ò t sµ s = tu ÓÖ ÓÑ u Σ º Ï Ð Ó Ý Ø Ø t Ò ÜØ Ò ØÓ sº Ì ÔÖ Ü ÐÓ ÙÖ L Ó Ð Ò Ù L Σ Ò ÓÐÐÓÛ L := {t Σ t s ÓÖ ÓÑ s L}º Ð Ò Ù L ØÓ ÔÖ Ü¹ÐÓ L = Lº Ä Ø ÈÛÖ(Σ) ÒÓØ Ø ÔÓÛ Ö Ø Ó Σ º º Ø Ø Ó ÐÐ Ù Ø Ó Σµº ÓÖ Ð Ò Ù L Ø Ð Ð ØÝ ÓÔ Ö ØÓÖ Ð L : Σ ÈÛÖ(Σ) Ú Ò Ý Ð L (s) := {σ Σ sσ L} ÓÖ s Σ º Ä Ø Σ = Σ 1 Σ 2 L 1 Σ 1 Ò L 2 Σ 2 º Ä Ø i {1, 2} s Σ Ò σ Σº ÌÓ ÔØÙÖ Ø ÒÓØ ÓÒ Ó Ô ÖØ Ð Ó ÖÚ Ø ÓÒ Û Ò Ø Ò ØÙÖ Ð ÔÖÓ Ø ÓÒ P i : Σ Σ i ÓÖ Ò ØÓ { ǫ, σ Σi ; P i (ǫ) = ǫ, P i (σ) = σ, σ Σ i P i (sσ) = P i (s)p i (σ) Ú Ò ÒÝ Ð Ò Ù L Σ Ø Ò ØÙÖ Ð ÔÖÓ Ø ÓÒ Ó Ð Ò Ù L P i (L) := {P i (s) s L}º Ì ÓÑ Ø Ñ Ö Ú Ø ØÓ P i Lº Ì ÒÚ Ö ÔÖÓ Ø ÓÒ Pi 1 Pwr(Σ i ) Pwr(Σ ) Ò ÓÚ Ö Ù Ø Ó Ð Ò Ù º Ú Ò ÒÝ L Σ 1 i Ø ÒÚ Ö ÔÖÓ Ø ÓÒ Ó L Ò Pi (L) := {s P i (s) L}º Ë Ö ÔÖ ÒØ ØÙÔÐ G := (Q, Σ, δ, q 0, Q m ) Û Ø Ø Ø Ø Q ÐÔ Ø Ø Σ Ô ÖØ Ð ØÖ Ò Ø ÓÒ ÙÒØ ÓÒ δ : Q Σ Q Ò Ø Ð Ø Ø q 0 Ò Ø Ó Ñ Ö Ö Ø Ø Q m º Ï Ù δ(q, σ)! ØÓ Ö ÔÖ ÒØ Ø Ø δ Ò ÓÖ σ Σ Ø Ø Ø q Qº ÙÒØ ÓÒ δ Ò ÜØ Ò ØÓ Σ Ý Ò Ò δ(q, ǫ) := q Ò δ(q, sσ) := δ(δ(q, s), σ) ÔÖÓÚ Ø Ø q = δ(q, s)! Ò δ(q, σ)! ÓÖ s Σ Ò q Qº Ï Û ÐÐ ÐÛ Ý ÙÑ Ø Ø Ë Ò Ø Ø Ø Ò Ú ÒØ Ø Ò Ø ÖÑ Ò Ø º Ý Ø ÖÑ Ò Ø Û Ñ Ò Ø Ë Ò Ð Ò Ø Ð Ø Ø Ò Ø ÑÓ Ø ÓÒ ØÖ Ò Ø ÓÒ Ò Ø Ú Ò Ø Ø ÓÖ ÒÝ σ Σº ÓÖ Ë G Ø ÐÓ Ú ÓÙÖ ÒÓØ Ý L(G) := {s Σ δ(q 0, s)!} Ò Ø Ñ Ö Ú ÓÙÖ Ý L m (G) := {s L(G) δ(q o, s) Q m }º Ò Ø ÓÒ ¾º½º Ë G ØÓ ÒÓÒ ÐÓ Ò ¾
6 L m (G) = L(G)º Ì ÓÚ ÑÔÐ ÓÖÑ Ó ÐÓ Ò º Ò Ø ÓÒ ¾º¾º Ä Ø K L m (G) Σ º Ï Ý Ø Ø Ø Ð Ò Ù K L m (G)¹ÐÓ K = K L m (G)º Ï ÒÓØ Ø Ø K Ò L m (G)¹ÐÓ Ñ Ò Ø ÓÒØ Ò ÐÐ Ó Ø ÔÖ Ü Ø Ø ÐÓÒ ØÓ L m (G)º Ì ÝÒ ÖÓÒÓÙ ÔÖÓ ÙØ Ó Ð Ò Ù L 1 Ò L 2 ÒÓØ Ý L 1 L 2 Ò ØÓ L 1 L 2 := P1 1 (L 1 ) P2 1 (L 2 )º Á ÓØ L 1 Ò L 2 Ö ÓÚ Ö Ø Ñ Ú ÒØ Ø Σ Ø Ò L 1 L 2 = L 1 L 2 º Ò Ø ÓÒ ¾º º Ä Ø G i = (Q i, Σ i, δ i, q 0,i, Q mi ) i = 1, 2º ÔÖÓ ÙØ Ó G 1 Ò G 2 Ï Ò Ø ÝÒ ÖÓÒÓÙ G 1 G 2 = (Q 1 Q 2, Σ 1 Σ 2, δ, (q 0,1, q 0,2 ), Q m1 Q m2 ) Û Ö δ((q 1, q 2 ), σ) Ò (δ 1 (q 1, σ), δ 2 (q 2, σ)), σ Σ 1 Σ 2, δ 1 (q 1, σ)!, δ 2 (q 2, σ)!; (δ 1 (q 1, σ), q 2 ), σ Σ 1 \Σ 2 Ò δ 1 (q 1, σ)!; (q 1, δ 2 (q 2, σ)), σ Σ 2 \Σ 1 Ò δ 2 (q 2, σ)!; ÙÒ Ò ÓØ ÖÛ º Ï Ø Ù Ú ÓÖ Ë G = G 1 G 2 Ø Ø L m (G) = L m (G 1 ) L m (G 2 ) Ò L(G) = L(G 1 ) L(G 2 )º ÁÒ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Ø Ú ÒØ Ø Σ Ô ÖØ Ø ÓÒ ÒØÓ ØÛÓ Ó ÒØ Ø Ø ÓÒØÖÓÐÐ Ð Ú ÒØ Ø Σ c Ò Ø ÙÒÓÒØÖÓÐÐ Ð Ú ÒØ Ø Σ uc º ÓÒØÖÓÐÐ Ð Ú ÒØ Ò ÔÖ Ú ÒØ ÖÓÑ ÔÔ Ò Ò Ð µ Ý ÙÔ ÖÚ ÓÖ Û Ð ÙÒÓÒØÖÓÐÐ Ð Ú ÒØ ÒÒÓØ Ð º Ì ÓÐÐÓÛ Ò Ò Ø ÓÒ ØÓ Û Ò Ò ÙÖ ÓÙÖ Ý Ø Ñ Ø Ý Û Ø Ò Ø Ú ÓÖ Ô Ý Kº Ò Ø ÓÒ ¾º º Ä Ø K Ò L = L Ð Ò Ù ÓÚ Ö Ú ÒØ Ø Σº K ØÓ ÓÒØÖÓÐÐ Ð Û Ø Ö Ô Ø ØÓ L Ò Σ uc KΣ uc L Kº Ï Û ÐÐ Ò ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Û Ò ØÖ Ø Û Ý ØÓ Ö ÓÒØÖÓÐ Ú ÓÖº Ö Ø Û Ò ØÓ Ò ÓÒØÖÓÐ Ô ØØ ÖÒ º Ò Ø ÓÒ ¾º º ÓÒØÖÓÐ Ô ØØ ÖÒ Ù Ø Ó Σ Ø Ø ÓÒØ Ò ÐÐ ÙÒÓÒØÖÓÐÐ Ð Ú ÒØ º ÁØ Ö ÔÖ ÒØ Ø Ú ÒØ ØÓ ÙÖÖ ÒØÐÝ Ò Ð º Ì Ø Ó ÐÐ ÓÒØÖÓÐ Ô ØØ ÖÒ Γ := {γ ÈÛÖ(Σ) γ Σ uc }. Ò Ø ÓÒ ¾º º ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÓÖ ÔÐ ÒØ G ÒÝ Ñ Ô V : L(G) Γ.
7 ¾º¾ ÒØÖ Ð Þ ÓÒØÖÓÐ ÓÖ ÒØÖ Ð Þ ÓÒØÖÓÐ Ø Ö Ò Ò Ü Ø Ó N > 1 ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö D = {1,..., N}º Ì ÓÒØÖÓÐÐ Ö Ú ÓÒÐÝ Ô ÖØ Ð Ú Û Ó Ø Ý Ø Ñ Ú ÓÙÖ Ò ÓÒØÖÓÐ ÓÒÐÝ Ù Ø Ó Ø ÓÒØÖÓÐÐ Ð Ú ÒØ º ÌÓ Ö Ú ÒØ Ø Ø ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö i D ÓÒØÖÓÐ Û Ù Ø ÒÓØ Ø ÓÒ Σ c,i Σ c Û Ö N i=1 Σ c,i = Σ c º Ï Ö Ö ØÓ Ø Ø Ó ÓÒØÖÓÐÐ Ö Ø Ø ÓÒØÖÓÐ σ Σ c D c (σ) := {i D σ Σ c,i }º ÌÓ Ö Ú ÒØ Ø Ø ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö i D Ó ÖÚ Û Ù Ø ÒÓØ Ø ÓÒ Σ o,i Σ o Û Ö N i=1 Σ o,i = Σ o º Ï Ö Ö ØÓ Ø Ø Ó ÓÒØÖÓÐÐ Ö Ø Ø Ó ÖÚ σ Σ o Ý D o (σ) := {i D σ Σ o,i }º ÓÖÖ ÔÓÒ Ò ÐÝ Ø Ò ØÙÖ Ð ÔÖÓ Ø ÓÒ Ö Ò Ø Ô ÖØ Ð Ú Û Ó ÓÒØÖÓÐÐ Ö ÒÓØ Ý P i : Σ Σ o,i ÓÖ i Dº ÓÖ ÒØÖ Ð Þ ÓÒØÖÓÐ Û Ø ÓÒ ÙÒØ Ú Ö Ø ØÙÖ ÊÏ ¾ Ø Ù ÓÒ ÖÙÐ Ø ÓÒ ÙÒØ ÓÒ Ó ÐÐ ÐÓ Ð ÓÒØÖÓÐ ÓÒ º º Ò Ú ÒØ ÐÓ ÐÐÝ Ò Ð ÒÓØ ÐÓ ÐÐÝ Ð º Ï Ù Ø ÓÒ ÙÒØ Ú Ö Ø ØÙÖ Ò Ø Ô Ô Öº ÓÖ ÒØÖ Ð Þ ÓÒØÖÓÐ Û Ò ÖÓÙÔ Ó ÐÓ Ð Ô ÖØ Ð¹Ó ÖÚ Ø ÓÒ ÒØÖ Ð Þ Ù¹ Ô ÖÚ ÓÖ ØÓ Ü Ö ÓÒØÖÓÐ ÓÚ Ö Ø ÔÐ Òغ Ì ÓÐÐÓÛ Ò Ò Ø ÓÒ Ö Ø ÓÒ ÖÙÐ Ó Ò Ú Ù Ð ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖ Ò Ø ÓÒ ÙÒØ ÓÒ ÖÙÐ Ø Ø ÓÑ Ò Ø Ö ÐÓ Ð ÓÒØÖÓÐ ÓÒ ÒØÓ ÐÓ Ð ÓÒØÖÓÐ ÓÒ º Ò Ø ÓÒ ¾º º Ä Ø K Σ Ø Ö Ú ÓÖ Ò Ð Ø i Dº Ì Ò Ø ÓÒ ÖÙÐ ÓÖ ÐÓ Ð Ô ÖØ Ð¹Ó ÖÚ Ø ÓÒ ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖ ÓÖ G Ñ Ô S Pi : L(G) Γ Ò ÓÖ t L(G) S Pi (t) := (Σ\Σ c,i ) {σ Σ c,i Pi 1 [P i (t)]σ K L(G) }º Ì ÓÒ ÙÒØ ÓÒ Ó Ø S Pi ÒÓØ Ý S Con : L(G) Γ Ò S Con (t) := N i=1 S P i (t)º Ï ÒÓØ Ø Ø S Con ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÓÖ G Ò Ø Ø S Pi (t) = S Pi (P i (t)) Ø Ò ØÙÖ Ð ÔÖÓ Ø ÓÒ ÑÔÓØ ÒØ º º P i (t) = P i (P i (t))º Ï ÒÓÛ Ò Ø ÐÓ Ú ÓÙÖ ÓÖ Ø ÐÓ ¹ÐÓÓÔ Ý Ø Ñ Ó G ÙÒ Ö Ø ÓÒØÖÓÐ Ó S Con º Ò Ø ÓÒ ¾º º Ú Ò G Ò S Con Ø Ö ÙÐØ Ò ÐÓ ¹ÐÓÓÔ Ý Ø Ñ ÒÓØ Ý S Con /Gº Ì Ý Ø Ñ³ ÐÓ Ú ÓÙÖ L(S Con /G) Ö ÙÖ Ú ÐÝ Ò ÓÐÐÓÛ Áµ ǫ L(S Con /G) ÁÁµ t L(S Con /G) σ S Con (t) Ò tσ L(G) Ò ÓÒÐÝ tσ L(S Con /G)º Ì ÓÐÐÓÛ Ò Ø Ò Ø ÓÒ Ó ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓк Ò Ø ÓÒ ¾º º Ú Ò G Ò S Con Û Ý S Con ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÓÖ G Ø ÓÒ ÖÙÐ Ò Ò Ò Ø ÓÒ ¾º Ò Ø Ö ÙÐØ Ò ÐÓ ¹ÐÓÓÔ Ý Ø Ñ Ò ÐÓ Ú ÓÙÖ Ò Ò Ò Ø ÓÒ ¾º º Ì ÓÐÐÓÛ Ò Ø Ò Ø ÓÒ Ó ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓк ÁØ Ø Ø Ø Ø Ø Ñ Ö Ð Ò Ù Ó Ø ÐÓ ¹ÐÓÓÔ Ý Ø Ñ Ø Ø Ó ØÖ Ò Ñ Ö Ý G Ò Ø ÐÐ ÔÓ Ð Ò Ø Ý Ø Ñ³ ÐÓ ¹ÐÓÓÔ Ú ÓÙÖº Ò Ø ÓÒ ¾º½¼º Ï Ý Ø Ø S Con ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Æ Ë µ ÓÖ G L m (S Con /G) = L(S Con /G) Û Ö L m (S Con /G) := L(S Con /G) L m (G)º Ï ÒÓÛ Ø Ø Ø Ó¹Ó ÖÚ Ð ØÝ ÔÖÓÔ ÖØÝ Û Û ÒØÖÓ Ù Ò ÊÏ ¾ º Ì ÓÐÐÓÛ Ò Ø Ò Ø ÓÒ Ó Ó¹Ó ÖÚ Ð ØÝ ÔØ ÖÓÑ Ä¼¼ ÊÏ ¾ º Û Û ÐÐ Ò Ì ÓÖ Ñ ¾º½ Ó¹Ó ÖÚ Ð ØÝ Ý ÔÖÓÔ ÖØÝ ØÓ Ò ÙÖ Ø Ø Û Ò ÝÒØ Þ ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Ø Ø ÓÓÔ Ö Ø ØÓ Ò ÙÖ Ø Ø Ø ÙÔ ÖÚ Ý Ø Ñ Ò Ö Ø Ø Ú ÓÙÖ Ô Ý Ð Ò Ù Kº
8 Ò Ø ÓÒ ¾º½½º Ä Ø K L = L Ð Ò Ù ÓÚ Ö Ú ÒØ Ø Σº Ä Ø D = {1,..., N} Ò Ò Ü Øº Ä Ø Σ c,i Σ Ò Σ o,i Σ Ø Ó ÓÒØÖÓÐÐ Ð Ò Ó ÖÚ Ð Ú ÒØ Ö Ô Ø Ú ÐÝ ÓÖ i D Û Ö Σ c = N i=1 Σ c,i Ò D c (σ) := {i D σ Σ c,i }º Ä Ø P i : Σ Σ o,i Ò ØÙÖ Ð ÔÖÓ Ø ÓÒ º Ð Ò Ù K ØÓ Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L Σ o,i Σ c,i i D ( t K L) ( σ Σ c ) tσ L\K ( i D c (σ)) Pi 1 [P i (t)]σ K L = º ÁÒ Ò Ó¹Ó ÖÚ Ð ØÝ Ø Ø Ø Ø K Ð Ú ÒØ σ Σ c Û ÔÓ Ð Ò L Ø Ö ØÖ Ò t Ø Ö ÑÙ Ø Ü Ø Ø Ð Ø ÓÒ ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Ø Ø Ò Ð σ Ò Ó Ó ÙÒ Ñ ÙÓÙ Ðݺ ÆÓØ Ø Ø Ò Ø Ò Ø ÓÒ Ó Ó¹Ó ÖÚ Ð ØÝ Û Ò Ø Ö ÓÒÐÝ ÓÒ ÓÒØÖÓÐÐ Ö º º D = {1} Ø ÔÖÓÔ ÖØÝ ÐÐ Ó ÖÚ Ð ØÝ ÄÏ º Ë Ò Ø Ô Ø ÓÒ K ÒÓØ Ò Ö ÐÝ Ù Ø Ó L ÙÒÐ Ø ÓÖ Ò Ð Ò Ø ÓÒ Û Ó ÒÓØ Ö ÕÙ Ö Ø Ø K Lº ÁÒ Ø Ó Ò ÐÐ ØÖ Ò Ò K Û ÐÐ ØÖ Ò Ò K Lº ÁÒ Ø ÓÐÐÓÛ Ò Ø ÓÒ Û Ò Ø Ö ÒÓ Ñ Ù ØÝ Ò Ø Ó Ý Ò Ø Ø K Ó¹ Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L Σ o,i Σ c,i i D Û Û ÐÐ Ý Ø Ø K Ó¹Ó ÖÚ Ð ÛºÖºØº Lº Ì ÓÖ Ñ ¾º½ Ø Ø Ø Ø Ò Ö ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Ü Ø Ò Ø ÓÖ Ñ Ø Ø Ö ÕÙ Ö Ø Ø K L m (G)¹ÐÓ º Ì ÓÖ Ñ ¾º½ ļ µº ÓÒ Ö Ë G = (Q, Σ, δ, q 0, Q m ) Û Ö Σ uc Σ Ø Ø Ó ÙÒÓÒØÖÓÐÐ Ð Ú ÒØ Σ c = Σ\Σ uc Ø Ø Ó ÓÒØÖÓÐÐ Ð Ú ÒØ Ò Σ o Σ Ø Ø Ó Ó ÖÚ Ð Ú ÒØ º ÓÖ Ø i Û Ö i = 1,..., N ÓÒ Ö Ø Ø Ó ÓÒØÖÓÐÐ Ð Ú ÒØ Σ c,i Ò Ø Ø Ó Ó ÖÚ Ð Ú ÒØ Σ o,i ÓÚ Ö ÐÐ N i=1 Σ c,i = Σ c Ò N i=1 Σ o,i = Σ o º Ä Ø P i Ø Ò ØÙÖ Ð ÔÖÓ Ø ÓÒ ÖÓÑ Σ ØÓ Σ o,i Û Ö i = 1,..., Nº ÓÒ Ö Ð Ó Ø Ð Ò Ù K L m (G) Û Ö K º Ì Ö Ü Ø ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖ S con ÓÖ G Ù Ø Ø L m (S con /G) = K Ò L(S con /G) = K Ò ÓÒÐÝ Ø ÓÐÐÓÛ Ò Ø Ö ÓÒ Ø ÓÒ ÓÐ ¾º ½º K ÓÒØÖÓÐÐ Ð Û Ø Ö Ô Ø ØÓ L(G) Ò Σ uc ¾º K Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L(G) Σ o,i Ò Σ c,i i = 1,..., N º K L m (G)¹ÐÓ º ÒØÖ Ð Þ ÓÒØÖÓÐ Û Ø Å Ö Ò Ï Û ÐÐ ÒÓÛ ÜØ Ò Ø Ü Ø Ò ÛÓÖ Ý ÒØÖÓ Ù Ò Ò Ö Ð Þ Ø ÓÒ Ó Æ Ë Ò Û Ø ÙÔ ÖÚ ÓÖÝ Ø ÓÒ Ð Ó ÒÐÙ Ñ Ö Ò Û ÐÐ ÓÒØÖÓк Ì Û ÐÐ ÐÐÓÛ ÙÔ ÖÚ ÓÖ ØÓ Ñ Ö Ò Ò ÓÖÑ Ø ÓÒ Û Ñ Ø Ñ ÑÓÖ ÜÔÖ Ú º Ì Ñ Ö Ð Ò Ù Ó Ø ÐÓ ¹ÐÓÓÔ Ý Ø Ñ ÒÓÛ Ò ØÓ Ø Ø Ó ØÖ Ò Ñ Ö Ý K L m (G) Ø Ø Ö Ø ÐÐ ÔÓ Ð Ò Ø Ý Ø Ñ³ ÐÓ ¹ÐÓÓÔ Ú ÓÙÖº Ì Ò Û Ò Ø ÓÒ Û ÐÐ ÐÐÓÛ Ù ØÓ Ð Ø Ö ÒØÖÓ Ù ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Ü Ø Ò Ö ÙÐØ Û Ó ÒÓØ Ö ÕÙ Ö Ø Ø K L m (G)¹ÐÓ º Ò Ø ÓÒ ¾º½¾º Ä Ø K L m (G)º Ï Ý Ø Ø S con Ñ Ö Ò ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÅÆ Ë µ ÓÖ (K, G) L m (S Con /G) = L(S Con /G) Û Ö L m (S con /G) := L(S con /G) Kº Ì Ò ÜØ Ò Ø ÓÒ Ö Ø Ò ÕÙ Ú Ð Ò ØÛ Ò Ø ÓÖ Ø Ð ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Ò Ë ÙÔ ÖÚ ÓÖ º Ì Ø Ø Ø Ñ Ö Ò Ò ÓÒØÖÓÐ Ò ÓÖÑ Ø ÓÒ Ó S Con Ö ÔÖ ÒØ Ý Ô Ø ÓÒ H Ò Ø Ø Ø ÐÓ ¹ÐÓÓÔ Ú ÓÙÖ Ó H G ÕÙ Ú Ð ÒØ ØÓ S con /Gº
9 Ò Ø ÓÒ ¾º½ º Ä Ø S Con ÅÆ Ë ÓÖ ÔÐ ÒØ G = (Q, Σ, δ, q 0, Q m ) Ò K L m (G) Û Ø L m (S Con /G) = L(S con /G) K Ò L(S Con /G) = Kº Ä Ø H = (X, Σ, ξ, x 0, X m ) Ô Ø ÓÒ ÙØÓÑ ØÓÒº Ï Ý Ø Ø H G ÕÙ Ú Ð ÒØ ÅÆ Ë Ú ÓÙÖ Û Ø S Con /G K = L m (H) L m (G) Ò K = L(H) L(G)º ÐØ ÖÒ Ø Ú ÐÝ Û Ý Ø Ø H Ò ÕÙ Ú Ð ÒØ Ø ÓÖ Ø Ð ÑÔÐ Ñ ÒØ Ø ÓÒ Ó ÅÆ Ë S Con ÓÖ Gº ÁÒ Ø Ô Ô Ö Û Û ÐÐ ÓÙ ÓÒ ÅÆ Ë º ÁÒ Ô ÖØ ÙÐ Ö Ø Û ÐÐ ÐÐÓÛ Ù ØÓ Ð Ø Ö ÒØÖÓ Ù ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖ Ü Ø Ò Ö ÙÐØ Ø Ø Ö Ð ÓÒ Ø ÐÓ ¹ÐÓÓÔ Ý Ø Ñ H G ØÓ ÒÓÒ ÐÓ Ò Ò Ø Ó Ø Ü Ø Ò Ö ÙÐØ Ø Ø Ö ÕÙ Ö K ØÓ L m (G)¹ÐÓ º Ì ÒØ Ð ØÓ ÔØ Ò ÒØÖ Ð Þ ÓÒØÖÓÐ ØÓ Ø ÀÁË ÔÔÖÓ ÀÁË ÔÖÓÚ Ð Ð Ñ Ø Ó ØÓ Ú Ö Ý ÒÓÒ ÐÓ Ò ÙØ ÒÓØ L m (G)¹ÐÓ ÙÖ º Ï ÒÓØ Ø Ø Ò ÒØÖ Ð Þ ÓÒØÖÓÐ Ø Ö ÒÓ Ö Ð ÑÔÐ Ñ ÒØ Ø ÓÒ Ó Ø ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖ Hº Ì ÓÚ ÅÆ Ë S Con Ò Ø ÓÒØÖÓÐ ÔÓÐ Ý Ó Ø ÓÒ ÙÒØ ÓÒ Ó ÖÓÙÔ Ó ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖ Ø Ö Ð ÙÔ ÖÚ ÓÖº Ï Ð Ó ÒÓØ Ø Ø ÓÖ Ò ÀÁË Ý Ø Ñ H Û ÐÐ ÓÖÖ ÔÓÒ ØÓ Ø Ø ÓÖ Ø Ð Ø ÙÔ ÖÚ ÓÖ Ó Ø Ý Ø Ñ Ò Ò Ë Ø ÓÒ Ò Û ÐÐ Ù ØÓ Ø ÖÑ Ò Ø Ø Ý Ø Ñ ÒÓÒ ÐÓ Ò º ÀÁË Ö Ø ØÙÖ Ì ÀÁË Ä ¼¾ Ä ¼ Ä Äϼ ÄÄ ¼ ÄÄϼ ÔÔÖÓ ÓÑÔÓ Ý Ø Ñ ÒØÓ ¹Ð Ú Ð Ù Ý Ø Ñ Û ÓÑÑÙÒ Ø Û Ø n 1 Ô Ö ÐÐ Ð ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ Ø ÖÓÙ Ô Ö Ø ÒØ Ö Ø Ø Ö ØÖ Ø Ø ÒØ Ö Ø ÓÒ Ó Ø Ù Ý Ø Ñ º Ì ¹Ð Ú Ð Ù Ý Ø Ñ ÓÑÑÙÒ Ø Û Ø ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ Ø ÖÓÙ Ô Ö Ø ÒØ Ö º ÁÒ ÀÁË Ø Ö Ñ Ø Ö¹ Ð Ú Ö Ð Ø ÓÒ Ôº ¹Ð Ú Ð Ù Ý Ø Ñ Ò ÓÑÑ Ò ØÓ Ô ÖØ ÙÐ Ö ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ Û Ø Ò Ô Ö ÓÖÑ Ø Ò Ø Ø Ò Ö ØÙÖÒ Ö ÔÓÒ Ò Û Öµº ÙÖ ½ ÓÛ ÓÒ ÔØÙ ÐÐÝ Ø ØÖÙØÙÖ Ò Ò ÓÖÑ Ø ÓÒ ÓÛ Ó Ø Ý Ø Ñº Ì ÓÚ Ö ÐÐ ØÖÙØÙÖ Ó Ø Ý Ø Ñ ÓÛÒ Ò ÙÖ ¾º Ì ØÝÐ Ó ÒØ Ö Ø ÓÒ Ò ÓÖ Ý Ò ÒØ Ö Ø Ø Ñ Ø ÓÑÑÙÒ Ø ÓÒ ØÛ Ò Ø ØÛÓ Ù Ý Ø Ñ º ÐÐ Ý Ø Ñ ÓÑÔÓÒ ÒØ ÒÐÙ Ò Ø ÒØ Ö Ö ÑÓ Ð ÙØÓÑ Ø º ÙÖ ½ ÁÒØ Ö ÐÓ Ö Ñ Û Ø ÄÓÛ Ø Ú ÒØ º
10 G H High-Level G I1 G In Low-Level 1 G L1 Low-Level n G Ln ÙÖ ¾ ÌÛÓ Ì Ö ËØÖÙØÙÖ Ó È Ö ÐÐ Ð ËÝ Ø Ñ ÌÓ Ö ØÖ Ø Ò ÓÖÑ Ø ÓÒ ÓÛ Ò ÓÙÔÐ Ø Ù Ý Ø Ñ Ø Ý Ø Ñ ÐÔ Ø Ô ÖØ ¹ Ø ÓÒ ÒØÓ Ô ÖÛ Ó ÒØ ÐÔ Ø Σ := Σ H [Σ Lj Σ Rj Σ Aj Σ LDj ] ½µ j=1,...,n Û Ö Û Ù ØÓ Ö ÔÖ ÒØ Ó ÒØ ÙÒ ÓÒº Ì Ú ÒØ Ò Σ H Ö ÐÐ ¹Ð Ú Ð Ú ÒØ Ò Ø Ú ÒØ Ò Σ Lj Ö Ø j th ÐÓÛ¹ Ð Ú Ð Ú ÒØ j = 1,...,nµ Ø Ú ÒØ ÔÔ Ö ÓÒÐÝ Ò Ø Ð Ú Ð Ò j th ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ ÑÓ Ð G H Ò G Lj Ö Ô Ø Ú Ðݺ Ï Ø Ò Ú G H Ò ÓÚ Ö Ú ÒØ Ø Σ H ( j {1,...,n} [Σ Rj Σ Aj Σ LDj ]) Ò G Lj Ò ÓÚ Ö Ú ÒØ Ø Σ Lj Σ Rj Σ Aj Σ LDj º Ï ÑÓ Ð Ø j th ÒØ Ö Ý Ë G Ij Û Ò ÓÚ Ö Ú ÒØ Ø Σ Rj Σ Aj Σ LDj º ÓÖ Ø Ö Ñ Ò Ö Ó Ø Ô Ô Ö Û ÙÑ j {1,...,n}º Ì Ú ÒØ Ò Σ Rj ÐÐ Ö ÕÙ Ø Ú ÒØ Ö ÔÖ ÒØ ÓÑÑ Ò ÒØ ÖÓÑ Ø ¹Ð Ú Ð Ù Ý Ø Ñ ØÓ Ø j th ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñº Ì Ú ÒØ Ò Σ Aj Ö Ò Û Ö Ú ÒØ Ò Ö ÔÖ ÒØ Ø ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ³ Ö ÔÓÒ ØÓ Ø Ö ÕÙ Ø Ú ÒØ º Ì Ú ÒØ Ò Σ LDj Ö ÐÐ ÐÓÛ Ø Ú ÒØ Û ÔÖÓÚ Ñ Ò ÓÖ ÐÓÛ Ð Ú Ð ØÓ Ò Ò ÓÖÑ Ø ÓÒ Ø µ Ø ÖÓÙ Ø ÒØ Ö º Ê ÕÙ Ø Ò Û Ö Ò ÐÓÛ Ø Ú ÒØ Ö ÓÐÐ Ø Ú ÐÝ ÒÓÛÒ Ø Ø Ó Ä ÒØ Ö Ú ÒØ Ò Σ I := k {1,...,n} [Σ Rk Σ Ak Σ LDk ] Ò G Ij Ò Ä ÒØ Ö Ò ÐÓÛº Ò Ø ÓÒ º½º Ì j th ÒØ Ö Ë G Ij = (X j, Σ Ij, ξ j, x oj, X mj ) Ò Ä ÒØ Ö Ø ÓÐÐÓÛ Ò ÔÖÓÔ ÖØ Ö Ø ½º x oj X mj ¾º ( x X mj )( σ Σ Ij )ξ j (x, σ)! [σ Σ Rj ] [σ Σ LDj ξ j (x, σ) X mj ] º ( x X j X mj )( σ Σ Ij )ξ j (x, σ)! [σ Σ Aj ξ j (x, σ) X mj ] [σ Σ LDj ] ÙÖ ÓÛ Ò Ü ÑÔÐ Ó Ò Ä ÒØ Ö º ÁØ ÓÙÐ ÓÖÖ ÔÓÒ ØÓ Ñ Ò Ø Ø ÐÓÛ Ð Ú Ð Û Ø Ò Ø Ú ÒØ ÖÒ Ð Ù Ö Ó ØÛÓº ÁÒ Ø Ö Ñ Ø Ò Ø Ð Ø Ø Ò Ö Ó Ò Þ Ý Ø ÓÙØÐ Ò Ò Ñ Ö Ø Ø Ö ÐÐ º ÌÓ ÑÔÐ Ý ÒÓØ Ø ÓÒ Ò ÓÙÖ ÜÔÓ Ø ÓÒ Û Ö Ò Ò Ø ÓÐÐÓÛ Ò Ú ÒØ Ø Ò ØÙÖ Ð ÔÖÓ¹ Ø ÓÒ Ò Ð Ò Ù º
11 G Ij 0 done start start 1 isdone notdone done 3 4 isdone notdone S Rj ={isdone,start},s Aj ={done},s LDj ={notdone} ÙÖ Ü ÑÔÐ Ä ÁÒØ Ö 2 Σ Ij := Σ Rj Σ Aj Σ LDj, Σ ILj := Σ Lj Σ Ij, Σ IH := Σ H Σ Ik, k {1,...,n} H := P 1 IH (L(G H)), L j := P 1 IL j (L(G Lj )), P Ij : Σ Σ I j P ILj : Σ Σ IL j P IH : Σ Σ IH H m := P 1 IH (L m(g H )) Σ L mj := P 1 IL j (L m (G Lj )) Σ I j := P 1 I j (L(G Ij )), I mj := P 1 I j (L m (G Ij )) Σ I := k {1,...,n} I k, I m := k {1,...,n} I mk Σ LD := k {1,...,n} Σ LDk Ï Ò ÓÙÖ Ø Ý Ø Ñ ØÓ G = G H G I1 G L1... G In G Ln º Ý Ø Ý Ø Ñ Û Ñ Ò Ø ÕÙ Ú Ð ÒØ Ë Û ÒÓÖ Ø ÒØ Ö ØÖÙØÙÖ º Ï ÒÓÛ ÔÖ ÒØ Ø ÔÖÓÔ ÖØ Ø Ø Ò ÀÁË Ý Ø Ñ ÑÙ Ø Ø Ý ØÓ Ò ÙÖ Ø Ø Ø ÒØ Ö Ø Û Ø Ø ÒØ Ö ÓÖÖ ØÐݺ Ò Ø ÓÒ º¾º Ì n Ø Ö n 1µ ÒØ Ö Ý Ø Ñ ÓÑÔÓ Ó Ë G H,G I1, G L1,...,G In,G Ln Ä ÒØ Ö ÓÒ Ø ÒØ Û Ø Ö Ô Ø ØÓ Ø ÐÔ Ø Ô ÖØ Ø ÓÒ Ú Ò Ý ½µ ÓÖ ÐÐ j {1,...,n} Ø ÓÐÐÓÛ Ò ÓÒ Ø ÓÒ Ö Ø ÅÙÐØ ¹Ð Ú Ð ÈÖÓÔ ÖØ ½º Ì Ú ÒØ Ø Ó G H Σ IH Ò Ø Ú ÒØ Ø Ó G Lj Σ ILj º ¾º G Ij Ä ÒØ Ö º À ¹Ä Ú Ð ÈÖÓÔ ÖØÝ º ( s H I) Ð Ij (s) (Σ Aj Σ LDj ) Ð H (s) ÄÓÛ¹Ä Ú Ð ÈÖÓÔ ÖØ º ( s L j I j ) Ð Ij (s) Σ Rj Ð Lj (s)
12 º ( s Σ.Σ Rj L j I j ) Ð Lj I j (sσ L j ) Σ Aj = Ð Ij (s) Σ Aj Ð Lj I j (sσ L j ) := º ( s L j I j ) s I mj ( l Σ L j ) sl L mj I mj º Û Ö l Σ L j Ð Lj I j (sl) Ï ÒÓÛ ÔÖÓÚ Ò Ø ÓÒ Ð Ø Ó ÔÖÓÔ ÖØ Ø Ø Ø Ý Ø Ñ ÑÙ Ø Ø Ý Ø Ø Ý Ø Ñ G ØÓ ÒÓÒ ÐÓ Ò º Ò Ø ÓÒ º º Ì n Ø Ö n 1µ ÒØ Ö Ý Ø Ñ ÓÑÔÓ Ó Ë G H,G I1, G L1,..., G In,G Ln ØÓ Ä Ð Ú Ð¹Û ÒÓÒ ÐÓ Ò Ø ÓÐÐÓÛ Ò ÓÒ Ø ÓÒ Ö Ø Áµ Ä ÒÓÒ ÐÓ Ò Ø Ø Ð Ú Ð ( s H I)( s (Σ Σ LD ) ) ss H m I m ÁÁµ ÒÓÒ ÐÓ Ò Ø Ø ÐÓÛ Ð Ú Ð ( j {1,...,n}) L mj I mj = L j I j Ì Ø ÓÖ Ñ ÐÐÓÛ Ø Ø Ø Ø Ú Ö Ý Ò Ø Ä Ð Ú Ð¹Û ÒÓÒ ÐÓ Ò Ò Ä ÒØ Ö ÓÒ Ø ÒØ ÓÒ Ø ÓÒ Ù ÒØ ØÓ Ú Ö Ý Ø Ø ÓÙÖ Ø Ý Ø Ñ ÒÓÒ ÐÓ Ò º Ì ÓÖ Ñ º½ Ä ¼ µº Á Ø n Ø Ö n 1µ ÒØ Ö Ý Ø Ñ ÓÑÔÓ Ó Ë G H,G I1, G L1,...,G In,G Ln Ä Ð Ú Ð¹Û ÒÓÒ ÐÓ Ò Ò Ä ÒØ Ö ÓÒ Ø ÒØ Û Ø Ö Ô Ø ØÓ Ø ÐÔ Ø Ô ÖØ Ø ÓÒ Ú Ò Ý ½µ Ø Ò L(G) = L m (G) Û Ö G = G H G L1 G I1... G Ln G In. Ë Ò Ò Ø Ø Ø Ä Ð Ú Ð¹Û ÒÓÒ ÐÓ Ò Ò Ä ÒØ Ö ÓÒ Ø ÒØ ÓÒ Ø ÓÒ ÓÒÐÝ Ö ÕÙ Ö Ò Ð ÓÑÔÓÒ ÒØ Ø Ø Ñ Û ÒÓØ Ø Ø Û Ò Ú ÐÙ Ø Ð Ú Ð Ò Ô Ò¹ ÒØÐݺ Ì Ñ Ò Û Ó ÒÓØ Ò ØÓ ÓÒ ØÖÙØ Ø ÒØ Ö Ý Ø Ñ ÑÓ Ðº ÓÖ ÓÒØÖÓÐÐ Ð ØÝ Û Ò ØÓ Ô Ö Ø Ø Ù Ý Ø Ñ ÒØÓ Ø Ö ÔÐ ÒØ Ò ÙÔ ÖÚ ÓÖ Ù ¹ÓÑÔÓÒ ÒØ ÙÖ µº Ï Ò Ø ¹Ð Ú Ð ÔÐ ÒØ ØÓ G p H Ò Ø ¹ Ð Ú Ð ÙÔ ÖÚ ÓÖ ØÓ S H Ò ÓÚ Ö Ú ÒØ Ø Σ IH µº Ï Ò Ø j Ø ÐÓÛ¹Ð Ú Ð ÔÐ ÒØ Ò ÙÔ ÖÚ ÓÖ ØÓ G p L j Ò S Lj Ò ÓÚ Ö Σ ILj µ Ö Ô Ø Ú Ðݺ Ï Ò ÜØ Ò Ø ¹Ð Ú Ð Ù Ý Ø Ñ ØÓ G H := G p H S H Ò Ò Ø j Ø ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ ØÓ G Lj := G p L j S Lj º Ï ÒÓØ Ø Ø Ò ÀÁË Ý Ø Ñ ÒØ Ö Ö ÐÛ Ý ÙÔ ÖÚ ÓÖ º Ï Ò ÒÓÛ Ò ÓÙÖ Ø ÙÔ ÖÚ ÓÖ Ò ÔÐ ÒØ Û ÐÐ ÓÑ ÓØ Ö Ð Ò Ù ÓÐÐÓÛ ÈÐ ÒØ := G p H Gp L 1... G p L n ËÙÔ := S H S L1... S Ln G I1... G In H p := P 1 IH L(Gp H ) S H := P 1 IH L(S H) Σ L p 1 j := PIL j L(G p L j ) S Lj := P 1 IL j L(S Lj ) Σ º Ì ÓÒØÖÓÐÐ Ð ØÝ Ö ÕÙ Ö Ñ ÒØ Ø Ø Ð Ú Ð ÑÙ Ø Ø Ý Ö Ú Ò Ò Ø ÓÐÐÓÛ Ò Ò Ø ÓÒº Ò Ø ÓÒ º º Ì n Ø Ö n 1µ ÒØ Ö Ý Ø Ñ ÓÑÔÓ Ó Ë G p H,S H, G p L 1,S L1, G I1,...,G p L n,s Ln,G In Ä Ð Ú Ð¹Û ÓÒØÖÓÐÐ Ð Û Ø Ö Ô Ø ØÓ Ø ÐÔ Ø Ô ÖØ Ø ÓÒ Ú Ò Ý ½µ ÓÖ ÐÐ j {1,...,n} Ø ÓÐÐÓÛ Ò ÓÒ Ø ÓÒ ÓÐ
13 G p H S H p G = G S High level Low level H H H G I G p L S L p G = G S L L L ÙÖ ÈÐ ÒØ Ò ËÙÔ ÖÚ ÓÖ ËÙ ÔÐ ÒØ ÓÑÔÓ Ø ÓÒ Áµ Ì ÐÔ Ø Ó G p H Ò S H Σ IH Ø ÐÔ Ø Ó G p L j Ò S Lj Σ ILj Ò Ø ÐÔ Ø Ó G Ij Σ Ij ÁÁµ ( s L p j S L j I j ) Ð L p j (s) Σ u Ð SLj I j (s) ÁÁÁµ ( s H p I S H ) Ð H p I(s) Σ u Ð SH (s) Ì Ø ÓÖ Ñ ÐÓÛ Ø Ø Ø Ø Ú Ö Ý Ò Ä Ð Ú Ð¹Û ÓÒØÖÓÐÐ Ð Ù ÒØ ØÓ Ú Ö Ý Ø Ø Ø Ø ÙÔ ÖÚ ÓÖ ÓÒØÖÓÐÐ Ð ÓÖ Ø Ø ÔÐ Òغ Ì ÓÖ Ñ º¾ Ä ¼ µº Á n Ø Ö n 1µ ÒØ Ö Ý Ø Ñ ÓÑÔÓ Ó Ë G p H,S H, G p L 1,S L1,G I1,...,G p L n,s Ln,G In Ä Ð Ú Ð¹Û ÓÒØÖÓÐÐ Ð Û Ø Ö Ô Ø ØÓ Ø ÐÔ Ø Ô Ö¹ Ø Ø ÓÒ Ú Ò Ý ½µ Ø Ò ( s L(ÈÐ ÒØ) L(ËÙÔ)) Ð L(ÈÐ ÒØ) (s) Σ u Ð L(ËÙÔ) (s) Ë Ò Ò Ø Ø Ø Ä Ð Ú Ð¹Û ÓÒØÖÓÐÐ Ð ÓÒ Ø ÓÒ ÓÒÐÝ Ö ÕÙ Ö Ø ÑÓ Ø Ò Ð ÓÑÔÓÒ ÒØ Ø Ø Ñ Û ÒÓØ Ø Ø Û Ò Ú ÐÙ Ø Ð Ú Ð Ò Ô Ò ÒØÐݺ À Ö Ö Ð ÁÒØ Ö ¹ ÒØÖ Ð Þ ËÙÔ ÖÚ ÓÖÝ ÓÒ¹ ØÖÓÐ ÁÒ Ë Ø ÓÒ Û Ö Ý Ø Ñ ÓÑÔÓ Ó ÔÐ ÒØ Ë G p H, Gp L 1,..., G p L n ÙÔ ÖÚ ÓÖ Ë S H, S L1,...,S Ln Ò ÒØ Ö Ë G I1,...,G In º ÐØ ÓÙ Ø Ð Ú Ð¹Û ÓÒØÖÓÐРй ØÝ ÓÒ Ø ÓÒ Ä ¼¾ Ä ¼ Ó Ø Ú ÐÝ Ð Ñ Ø Ø ¹Ð Ú Ð ÙÔ ÖÚ ÓÖ ØÓ Ú ÒØ Ò Σ IH Ò Ø j th ÐÓÛ¹Ð Ú Ð ÙÔ ÖÚ ÓÖ ØÓ Ú ÒØ Ò Σ ILj Ø Ö ÕÙ Ö Ø ÀÁË ØÖÙØÙÖ Ò Ó ÒÓØ ÐÐÓÛ ÙÖØ Ö Ö ØÖ Ø ÓÒ ÓÙØ Ó Ø ØÖÙØÙÖ º ÁÒ ÓÖ Ö ØÓ ÐÐÓÛ ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖ Û Ø Ò ÓÑÔÓÒ ÒØ Û Ò ØÓ ÜØ Ò Ø ÀÁË ØÖÙØÙÖ º ½¼
14 Ï ÒÓÛ ÒØÖÓ Ù Ø À Ö Ö Ð ÁÒØ Ö ¹ ÒØÖ Ð Þ ËÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÀÁ Ë µ Ö Ø ØÙÖ º ÀÁ Ë Ò ÜØ Ò ÓÒ Ó ÀÁË ÖÓÑ ÒØÖ Ð Þ ÓÒØÖÓÐ ØÓ ÒØÖ Ð Þ Ö¹ Ø ØÙÖ Ý ÐÐÓÛ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖ Û Ø Ò Ù Ý Ø Ñ ÙØ Û Ø ÓÙØ Ø ÓÒ Ð ÀÁË Ö ØÖ Ø ÓÒ º ÁÒ Ø ÀÁ Ë Ö Ñ ÛÓÖ ÐÐ Ø ÀÁË ÙÔ ÖÚ ÓÖ Ö Ö ÔÐ Ý ÓÖÖ ÔÓÒ Ò Ô ¹ Ø ÓÒ Ëº ÁÒ ÒØÖ Ð Þ ÓÒØÖÓÐ Ø Ô Ø ÓÒ Ë Ö ÔÖ ÒØ Ø ÓÒØÖÓÐ Ú ÓÙÖ Û Û ØÓ ÑÔÐ Ñ ÒØ ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö ÒÓØ Ô Ø ÓÒ ÓÖ ÝÒØ Þ Ò ÒØÖ Ð Þ Ñ Ü Ñ ÐÐÝ Ô ÖÑ Ú ÙÔ ÖÚ ÓÖº ÓÖ ÀÁ Ë Û Û ÐÐ Ö ÔÐ ÙÔ ÖÚ ÓÖ S H Ý Ô Ø ÓÒ Ë F H Ò ÓÚ Ö Σ IH µ Ò Û Û ÐÐ Ö ÔÐ ÙÔ ÖÚ ÓÖ S Lj Ý Ô Ø ÓÒ Ë F Lj Ò ÓÚ Ö Σ ILj µº ÌÝÔ ÐÐÝ F H Û ÐÐ ÜÔÖ Ý Ø Ñ¹Û ÓÒ ØÖ ÒØ ÓÙØ ÓÛ Ø ÓÑÔÓÒ ÒØ ÒØ Ö Ø Ò Û Ø Ø Ø ÐÓÛ Ð Ú Ð ÓÙÐ Ô Ö ÓÖѺ F Lj ÜÔÖ ÓÛ Ø j th ÐÓÛ Ð Ú Ð Û ÐÐ Ô Ö ÓÖÑ Ø Ø Ö ÕÙ Ø µ Ú Ò ØÓ Ø Ý Ø Ð Ú Ðº ÓÖ ÓÑÔÓÒ ÒØ Ø Ö Ö ÒØ Ò Ü Ø Ó ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö º Ï Ö ÒÓÛ Ö Ý ØÓ Ò Ø ØÖÙØÙÖ Ó Ò ÀÁ Ë Ý Ø Ñº Ò Ø ÓÒ º½º Ì n Ø Ö ÒØÖ Ð Þ Ô Ø ÓÒ ÒØ Ö Ý Ø Ñ Û Ø Ö Ô Ø ØÓ Ø ÐÔ Ø Ô ÖØ Ø ÓÒ Ú Ò Ý ½µ ÓÑÔÓ Ó ÔÐ ÒØ Ë G p H, Gp L 1,...,G p L n Ô Ø ÓÒ Ë F H, F L1,...,F Ln ÒØ Ö Ë G I1,...,G In Ò ¹Ð Ú Ð Ò ÐÓÛ¹Ð Ú Ð ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö º Ì Ý Ø Ñ Ø ÓÐÐÓÛ Ò ØÖÙØÙÖ º À Ð Ú Ð Ì ¹Ð Ú Ð ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Ú Ò Ò Ü Ø D H := {N H,1,...,N H,n0 }º Ì Ú ÒØ Ø ÓÖ G p H F H Ò Ø ÓÖÖ ÔÓÒ Ò ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Σ IH º ÓÖ i D H Σ H,c,i Σ c Σ IH Ò Σ H,o,i Σ o Σ IH Ö Ø ÓÖÖ ÔÓÒ Ò ÓÒØÖÓÐÐ Ð ÄÓÛ Ð Ú Ð Ò Ó ÖÚ Ð Ú ÒØ Ù Ø ÓÖ Ø ¹Ð Ú Ð ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö º ÓÖ j {1,...,n} Ø j th ÐÓÛ¹Ð Ú Ð ÓÑÔÓÒ ÒØ Ò Ò Ü Ø D Lj := {N Lj,1,...,N Lj,n j } ÓÖ Ø ÓÛÒ ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö º Ì Ú ÒØ Ø Ó ÐÓÛ¹Ð Ú Ð ÓÑÔÓÒ ÒØ G p L j F Lj Ò Ø ÓÖÖ ÔÓÒ Ò ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Σ ILj º ÓÖ i D Lj Σ Lj,c,i Σ c Σ ILj Ò Σ Lj,o,i Σ o Σ ILj Ö Ø ÓÖÖ ÔÓÒ Ò ÓÒØÖÓй Ð Ð Ò Ó ÖÚ Ð Ú ÒØ Ù Ø ÓÖ Ø ÐÓÛ¹Ð Ú Ð ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö º ÅÙÐØ ¹Ð Ú Ð n Ì Ò Ü Ø ÓÖ ÐÐ ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Ò Ø Ý Ø Ñ D := D H j=1 D L j = {1,..., N}º N i=1 Σ c,i = Σ c Ò N i=1 Σ o,i = Σ o ÓÖ Ø Ö Ø Ó Ø Ø ÓÒ Û Û ÐÐ Ö Ö ØÓ Ù Ý Ø Ñ Ò n Ø Ö ÒØÖ Ð Þ Ô Ø ÓÒ ÒØ Ö Ý Ø Ñ Ψ ÓÖ ÑÔÐÝ Ψº ÆÓØ Ø Ø Ò Ψ Û Ó ÒÓØ Ô Ý Ø Ò Ü ½½
15 Ó ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Ý {1,..., n 0 } {1,..., n j } غ Ù ÓÒ ÓÑ Ò Ø Ý ÛÓÙÐ ÓÚ ÖÐ Ôº Ï Ö Ø Ø Ý Ø Ñ Ò Ü Ø Ù Ò Ó ÒØ ÙÒ ÓÒº Ì Ø Ý Ø Ñ G Ø ÝÒ ÖÓÒ Þ Ø ÓÒ Ó ÐÐ Ø ÔÐ ÒØ Ô Ø ÓÒ Ò ÒØ Ö ÓÑÔÓÒ ÒØ Ò Ø Ý Ø Ñ º º G = G p H Gp L 1... G p L n F H F L1... F Ln G I1... G In º Ï Ù Ø Ø ÖÑ Ø Ý Ø Ñ ØÓ Ñ Ò Ø ÓÚ Ö ÐÐ Ý Ø Ñ ÒÓÖ Ò Ø ÀÁ Ë ØÖÙØÙÖ º ÁØ ÑÔÓÖØ ÒØ ØÓ ÒÓØ Ø Ø ÓÖ Ò ÀÁ Ë Ý Ø Ñ Û ÛÓÙÐ Ö Ø Ò Ð Ú Ð¹Û ÙÔ Ö¹ Ú ÓÖ ÓÖ Ø ÓÖ Ò Ð ÀÁË Ý Ø Ñ Û Ð ÒÓÖ Ò ÒÝ ÒØÖ Ð Þ Ö ØÖ Ø ÓÒ º Ï ÛÓÙÐ Ø Ò Ù Ø ÀÁË ØÖÙØÙÖ ØÓ Ú Ö Ý Ø Ø Ø Ý Ø Ñ ÒÓÒ ÐÓ Ò Ò ÓÒØÖÓÐÐ Ð º Ï ÛÓÙÐ Ò ÜØ Ù Ø Ð Ú Ð¹Û ÙÔ ÖÚ ÓÖ Û ÒÐÙ Ø Ý Ø Ñ³ ÒØ Ö Ëµ Ô Ø ÓÒ ÓÖ Ø Ò Ó Ø Ô Ö¹ÓÑÔÓÒ ÒØ ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖ Ô Ý Ø ÀÁ Ë Ý Ø Ñº Ì Ò Ð Ý Ø Ñ ÛÓÙÐ ÒÓØ ÓÒØ Ò ÒÝ Ó Ø Ô Ø ÓÒ Ë Ù Ø Ø Ö ÙÐØ Ò ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Ø Ø ÛÓÙÐ ÔÖÓÚ Ù Û Ø ÕÙ Ú Ð ÒØ ÐÓ ¹ÐÓÓÔ Ú ÓÙÖ ÓÖÓÐÐ ÖÝ º½ Ò Ë Ø ÓÒ º¾µº º½ ÀÁ Ë Ó¹Ó ÖÚ Ð ØÝ Ò Ø ÓÒ Ò Ì ÓÖ Ñ Ì Ñ Ò ÓÙ Ó Ø Ø ÓÒ ØÓ Ú Ö Ý Ó¹Ó ÖÚ Ð ØÝ Ò Ò ÀÁ Ë Ý Ø Ñ Ψ Û Ø ÓÙØ ÜÔÐ ØÐÝ ÓÒ ØÖÙØ Ò Ø Ø Ý Ø Ñº Ï Û ÐÐ ÓÒÐÝ Ô Ö ÓÖÑ Ô Ö¹ÓÑÔÓÒ ÒØ Ó¹Ó ÖÚ Ð ØÝ Ú Ö Ø ÓÒ ÙØ Ù Ö ÒØ Ø Ø Ø Û ÓÐ Ý Ø Ñ Ó¹Ó ÖÚ Ð º ÌÓ Ò Ò Ò ÓÙÖ Ô Ö¹ÓÑÔÓÒ ÒØ Ó¹Ó ÖÚ Ð ØÝ Ò Ø ÓÒ Ò ÀÁ Ë Ó¹Ó ÖÚ Ð ØÝ Ø ÓÖ Ñ Û Ô Ý ÓÑ ÒØÖ Ð Þ ÒÓØ Ø ÓÒ ÓÖ Ψº Ï Ù D H,c (σ) := {i D H σ Σ H,c,i } ØÓ ÒÓØ Ø Ø Ó ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Ò Ø Ð Ú Ð Ø Ø Ò ÓÒØÖÓÐ Ø Ú ÒØ σº Ï Ù D H,o (σ) := {i D H σ Σ H,o,i } ØÓ ÒÓØ Ø Ø Ó ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Ò Ø Ð Ú Ð Ø Ø Ò Ó ÖÚ Ø Ú ÒØ σº ÓÖÖ ÔÓÒ Ò ÐÝ P H,i : Σ Σ H,o,i Ø Ò ØÙÖ Ð ÔÖÓ Ø ÓÒ Ö Ò Ø Ô ÖØ Ð Ú Û Ó ÓÒØÖÓÐÐ Ö i D H º ÓÖ j {1,...,n} D Lj,c (σ) := { i D Lj σ Σ Lj,c,i} Ø Ø Ó ÒØÖ Ð Þ ÓÒ¹ ØÖÓÐÐ Ö Ò Ø j Ø ÐÓÛ¹Ð Ú Ð ÓÑÔÓÒ ÒØ Ø Ø Ò ÓÒØÖÓÐ Ø Ú ÒØ σº Ï Ù D Lj,o (σ) := { } i DLj σ Σ Lj,o,i ØÓ Ö ÔÖ ÒØ Ø Ø Ó ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Ò Ø j Ø ÐÓÛ¹Ð Ú Ð ÓÑÔÓÒ ÒØ Ø Ø Ò Ó ÖÚ Ø Ú ÒØ σº ÓÖÖ ÔÓÒ Ò ÐÝ P Lj,i : Σ Σ L j,o,i Ø Ò ØÙÖ Ð ÔÖÓ Ø ÓÒ Ö Ò Ø Ô ÖØ Ð Ú Û Ó ÓÒØÖÓÐÐ Ö i D Lj º Ï Ù D c (σ) := {i D σ Σ c,i } ØÓ ÒÓØ Ø Ø Ó ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö Ò Ø Ý Ø Ñ Ø Ø Ò ÓÒØÖÓÐ Ø Ú ÒØ σº ÙÖØ Ö Û ÒØÖÓ Ù Û Ð Ò Ù Ù ÓÖ Ø ÀÁ Ë Ó¹Ó ÖÚ Ð ØÝ Ò Ø ÓÒ Ò Ø ÓÖ Ñº F H F := P 1 IH (L(F H)), F Lj := P 1 IL j (L(F Lj )) := F H F L1... F Ln, P := H p L p 1... Lp n Ä Ò Ù F H Ö ÔÖ ÒØ Ø Ú ÓÙÖ Ó Ø Ô Ø ÓÒ ÙØÓÑ Ø Ò Ø ¹Ð Ú Ð Ù Ý Ø Ñ Û Ð F Lj Ö ÔÖ ÒØ Ø Ú ÓÙÖ Ó Ø Ô Ø ÓÒ ÙØÓÑ Ø ÓÖ Ø j Ø ÐÓÛ¹ Ð Ú Ð Ù Ý Ø Ñº Ä Ò Ù F Ö ÔÖ ÒØ Ø ÐÓ Ð Ô Ø ÓÒ ÓÖ Ø Ø Ý Ø Ñ Ò P Ö ÔÖ ÒØ Ø Ú ÓÙÖ Ó Ø Ø ÔÐ Òغ Ï ÒÓÛ ÔÖ ÒØ Ø Ô Ö¹ÓÑÔÓÒ ÒØ Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð ØÝ Ò Ø ÓÒ ÓÖ ÀÁ Ë Ý Ø Ñ Ψº Ï ÒÓØ Ø Ø Ò Ú Ù Ð ÓÒ Ø ÓÒ Ò Ø ÑÓ Ø Ò Ð Ù Ý Ø Ñ ÓÖ Ø Ú Ö ¹ ½¾
16 Ø ÓÒ Ø Ù Û Ó ÒÓØ Ò ØÓ ÓÒ ØÖÙØ Ø ÒØ Ö Ý Ø Ñ ÑÓ Ðº Ì Ò Ú Ò ÒØ ÓÑÔÙØ Ø ÓÒ Ò Ò ÐÔ ØÓ ÐÐ Ú Ø Ø Ø Ø ¹ Ô ÜÔÐÓ ÓÒ ÔÖÓ Ð Ñº Ò Ø ÓÒ º¾º Ä Ø Ψ Ò ÀÁ Ë n Ø Ö ÒØÖ Ð Þ Ô Ø ÓÒ ÒØ Ö Ý Ø Ñº Ì Ò Ψ Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð ÓÖ ÐÐ j {1,...,n} Ø ÓÐÐÓÛ Ò ÓÒ Ø ÓÒ ÓÐ Áµ ( t F H H p I)( σ Σ c ) tσ (H p I)\F H ( i D H,c (σ)) P 1 H,i [P H,i(t)]σ F H H p I = ÁÁµ ( t F Lj I j L p j )( σ Σ c) tσ L p j \(F L j I j ) ( i D Lj,c (σ))p 1 L j,i [P L j,i(t)]σ F Lj I j L p j = º Ò Ø ÓÒ º¾ Ø Ø Ø Ø ÀÁ Ë Ý Ø Ñ Ψ Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð Ø ¹Ð Ú Ð ÓÑÔÓÒ ÒØ Ó¹Ó ÖÚ Ð Ò ÐÓÛ¹Ð Ú Ð ÓÑÔÓÒ ÒØ Ó¹Ó ÖÚ Ð º Ï ÒÓØ Ø Ø Ø ÒØ Ö Ö ØÖ Ø Ô Ø ÓÒ Ø Ø ÐÓÛ Ð Ú Ð Ò ØÖ Ø ÔÐ ÒØ Ø Ø Ð Ú Ðº Ì ÓÒ Ø Û Ý Ù ÒØ Ö Ö ÔÖ ÒØ Ø Ú ÓÙÖ ÔÖÓÚ Ý Ø ÐÓÛ Ð Ú Ð Ò Ø Ò ÓÖÑ Ø ÓÒ Ò ØÓ Ú Ö Ý Ø Ø Ø Ó¹Ó ÖÚ Ð ØÝÔ ÐÐÝ ÔÖ ÒØ Ø Ø ÐÓÛ Ð Ú Ð ÙØ ÒÓØ Ø Ð Ú Ðº ÌÓ ÚÓ Ú Ò ØÓ Ö Ô Ø Ø Ò ÓÖÑ Ø ÓÒ Ø Ø Ð Ú Ð Û Ù Ø Ö ÙÐØ Ó ÄÄÅʽ Ø Ø ÐÐÓÛ Ù ØÓ ØÖ Ø ÙÔ ÖÚ ÓÖ Ø Ý Ö ÔÐ ÒØ ÓÒ Û Ú Ö Ý Ø Ý Ö Ó¹Ó ÖÚ Ð º Ý ØÖ Ø Ò ÒØ Ö ÔÐ ÒØ Ø Ø Ð Ú Ð Û ÐÐÓÛ Ø ¹Ð Ú Ð ÙÔ ÖÚ ÓÖ ØÓ ÑÓÖ Ô ÖÑ Ú Ò Ò Ö Ð Ø Ö Û ÐÐ ØÝÔ ÐÐÝ Û Ö ØÖ Ò Ø Ø Ò Ù Ø Ó¹Ó ÖÚ Ð ØÝ Ú Ö Ø ÓÒ ØÓ Ðº Ï ÒÓÛ Ö Ø Ø Ø Ó¹Ó ÖÚ Ð ØÝ Ò Ø ÓÒ Ò Ø ÖÑ Ó ÓÙÖ ÀÁ Ë Ý Ø Ñº Ï ÒÓØ Ø Ø ÖÓÑ Ø Ö Ò Ø ÓÒ Û ÒÓÛ Ø Ø Ð Ò Ù F I Ò P Ö ÔÖ Ü¹ÐÓ º Ï Ð Ó ÒÓØ Ø Ø ÓÖ Ò ØÓ Ò Ø ÓÒ º¾ i D Ö ÔÖ ÒØ ÓÑ i 1 D H ÓÖ ÓÑ i 2 D Lj j {1,..., n}º Ò Ø ÓÒ º º Ä Ø Ψ Ò ÀÁ Ë n Ø Ö ÒØÖ Ð Þ Ô Ø ÓÒ ÒØ Ö Ý Ø Ñº Ä Ø D = {1,..., N} =D H n j=1 D L j Ø Ò Ü Ø ÓÖ Ψº Ä Ø Σ c,i Σ Ò Σ o,i Σ Ø Ó ÓÒØÖÓÐÐ Ð Ò Ó ÖÚ Ð Ú ÒØ Ö Ô Ø Ú ÐÝ ÓÖ i D Û Ö D c (σ) = {i D σ Σ c,i }º Ä Ø P i : Σ Σ o,i i D Ò ØÙÖ Ð ÔÖÓ Ø ÓÒ º Ì Ò Ψ ÐÓ ÐÐÝ Ó¹Ó ÖÚ Ð ( t F I P) ( σ Σ c ) tσ P\(F I) ( i D c (σ))pi 1 [P i (t)]σ F I P = º Ï ÒÓØ Ø Ø Ò Ø ÓÒ º Ø ÔÖÓÔ ÖØÝ Û Û ÒØ ØÓ Ú Ö Ý ÙØ Û Û ÐÐ Ó Ó Ý Ù Ò ÓÙÖ Ô Ö¹ÓÑÔÓÒ ÒØ Ó¹Ó ÖÚ Ð ØÝ Ò Ø ÓÒº Ì Ø ÓÖ Ñ ÐÓÛ Ø Ø Ø Ø Ø Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð ØÝ ÔÖÓÔ ÖØÝ Ù ÒØ ØÓ Ù Ö ÒØ Ø Ø Ø Ø Ý Ø Ñ Ó¹Ó ÖÚ Ð º Ì Ñ Ò Ø Ø Ó¹Ó ÖÚ Ð ØÝ ÓÖ Ø Ý Ø Ñ Ò Ú Ö Û Ð ÓÒÐÝ ÓÒ ØÖÙØ Ò Ò Ð ÓÑÔÓÒ ÒØ Ø Ø Ñ º Ì ÓÖ Ñ º½º Ä Ø Ψ Ò ÀÁ Ë n Ø Ö ÒØÖ Ð Þ Ô Ø ÓÒ ÒØ Ö Ý Ø Ñº Á Ψ Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð Ø Ò Ψ ÐÓ ÐÐÝ Ó¹Ó ÖÚ Ð º ÈÖÓÓ º Ë ÔÔ Ò Üº Ï ÒÓÛ Ü Ñ Ò Ø ÓÑÔÐ Ü ØÝ Ó ÓÙÖ ÔÔÖÓ º ÁÒ ÑÓÒÓÐ Ø Ú Ö Ø ÓÒ Ø n ÐÓÛ¹ Ð Ú Ð Ù Ý Ø Ñ Ö ÓÑÔÓ Ö ØÐÝ Û Ø Ø ¹Ð Ú Ð Ý Ø Ñ Û Ø ÓÙØ Ù Ò Ø ÒØ Ö ØÖÙØÙÖ º Ì Þ Ó Ø Ø Ø Ô ÓÖ Ø ÑÓÒÓÐ Ø Ñ Ø Ó Ø Þ Ó Ø ÔÖÓ ÙØ Ø Ø Ô Ó G H G L1... G Ln º Á Ø Þ Ó Ø Ø Ø Ô Ó G H ÓÙÒ Ý N H Ò Ø Þ Ó Ø Ø Ø Ô ÓÖ G Lj ÓÙÒ Ý N L Ø Ò Ø Þ Ó Ø Ø Ø Ô Ó Ø ÑÓÒÓÐ Ø Ñ Ø Ó ÓÙÒ Ý N H N n L º ½
17 fin_exit part_lv3 take_pt part_ent part_arr1 part_lv1 fin_exit part_lv3 take_pt str_pta str_ptb ret_pt part_lv2 str_exit cmpl_a cmpl_b recog_b part_ent part_arr1 part_lv1 fin_exit part_lv3 take_pt str_pta str_ptb ret_pt part_lv2 str_exit cmpl_a cmpl_b part_ent part_arr1 part_lv1 str_pta str_ptb ret_pt part_lv2 str_exit cmpl_a cmpl_b recog_b recog_b partlvexit part_arr2 partlvexit part_arr2 partlvexit part_arr2 attch_pta, attch_ptb, fina_attch, finb_attch start_case compl_case attch_pta, attch_ptb, fina_attch, finb_attch start_case compl_case attch_pta, attch_ptb, fina_attch, finb_attch start_case compl_case ÇÙÖ Ñ Ø Ó Ú Ö ÓÑÔÓÒ ÒØ Ô Ö Ø ÐÝ Ø Ö ÓÖ Ø Þ Ó Ø Ø Ø Ô ÓÙÒ Ý Ø Þ Ó Ø ÓÑÔÓÒ ÒØ ÓÑ Ò Û Ø Ø ÒØ Ö º ÓÖ j = 1,..., n Û ÙÑ Ø Ø Ø Þ Ó Ø Ø Ø Ô Ó G Ij ÓÙÒ Ý N I Ø Ò ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ G Lj G Ij ÓÙÒ Ý N L N I º Ì ¹Ð Ú Ð Ù Ý Ø Ñ G H G I1... G In ÓÙÒ Ý N H N n I º Ì Ö ÓÖ ÓÙÖ Ñ Ø Ó ÓÙÒ Ý Ø Ð Ö Ö Ó N HN n I Ò N LN I º ÌÝÔ ÐÐÝ Ò Ò ÀÁ Ë Ò Ø Þ Ó Ø Ð Ú Ð Ø Ð Ñ Ø Ò ØÓÖº Ì Ñ Ò Ø Ø ÐÓÒ N I N L Û ÓÙÐ Ú Ò ÒØ ÓÑÔÙØ Ø ÓÒ Ð Ú Ò º º¾ ÅÆ Ë ËÙÔ ÖÚ ÓÖ Ü Ø Ò Ì ÓÖ Ñ Ï ÒÓÛ ÔÖ ÒØ Ø Ñ Ö Ò ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÅÆ Ë µ Ü ¹ Ø Ò Ø ÓÖ Ñ Û ÓÛ Ø Ø Ø Ö Ü Ø Ò ÅÆ Ë ØÓ Ú Ø Ô Ø ÓÒ Ò ÓÒÐÝ K ÓÒØÖÓÐÐ Ð Ò Ó¹Ó ÖÚ Ð º manufacturing unit I Path Flow Model-j part_arr3 recog_a Attach Part to Assembly-j dip_acid, Polish Part-j polish start_pol compl_pol str_rlse Define New Events-j Attach Case to Assembly-j Attch_case manufacturing unit II source 4 slot input buffer Path Flow Model-j part_arr3 recog_a Attach Part to Assembly-j dip_acid, Polish Part-j polish start_pol compl_pol str_rlse Define New Events-j Attach Case to Assembly-j Attch_case 4 slot output buffer test unit 4 slot package buffer packaging unit manufacturing unit III Path Flow Model-j part_arr3 recog_a Attach Part to Assembly-j dip_acid, Polish Part-j polish start_pol compl_pol str_rlse Define New Events-j Attach Case to Assembly-j Attch_case ÙÖ ÐÓ Ö Ñ Ó È Ö ÐÐ Ð ÈÐ ÒØ ËÝ Ø Ñº ÆÓØ Ø Ø Ò Ì ÓÖ Ñ º¾ ÐÓÛ Û Ó ÒÓØ Ö ÕÙ Ö Ø Ø K L m (G)¹ÐÓ Û ÙÑ Ý ØÖ Ø ÓÒ Ð ÒØÖ Ð Þ ÓÒØÖÓРļ º Ì Û ÐÐ ÐÐÓÛ Ù ØÓ ÔÔÐÝ Ø Ö ÙÐØ ØÓ ÓÙÖ ÀÁ Ë Ý Ø Ñ Û Ú Ò ÀÁË ÒÓÒ ÐÓ Ò Ö ÙÐØ ÙØ ÒÓØ Ò ÀÁË L m (G)¹ÐÓ Ö ÙÐغ Ì ÓÖ Ñ º¾º Ä Ø ÈÐ ÒØ := (Q, Σ, δ, q 0, Q m ) K L m (ÈÐ ÒØ) Ò K º Ì Ö Ü Ø Ò ÅÆ Ë S Con ÓÖ K ÈÐ Òص Ù Ø Ø L m (S Con /ÈÐ ÒØ) = K Ò ÓÒÐÝ K ÓÒØÖÓÐÐ Ð Ò Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L(ÈÐ ÒØ)º ÈÖÓÓ º Ë ÔÔ Ò Üº ½
18 Ï Û ÐÐ ÒÓÛ Ö Ð Ø Ì ÓÖ Ñ º¾ ØÓ ÓÙÖ ÀÁ Ë Ý Ø Ñ Ò ÒÓÒ ÐÓ Ò º ÁÒ Ò Û Ö Ö ÕÙ Ö Ò Ψ ØÓ Ú ÕÙ Ú Ð ÒØ ÅÆ Ë Ú ÓÙÖ Û Ø S Con /ÈÐ ÒØ Û Ò ÙÖ ÓÙÖ ÀÁ Ë Ý Ø Ñ ÑÔÐ Ñ ÒØ Ø ÓÒ Û ÐÐ ÒÓÒ ÐÓ Ò º ÓÖÓÐÐ ÖÝ º½º Ä Ø Ψ Ò ÀÁ Ë n Ø Ö ÒØÖ Ð Þ Ô Ø ÓÒ ÒØ Ö Ý Ø Ñº Ä Ø ÈÐ ÒØ := G p H Gp L 1... G p L n, Ò ËÔ := F H F L1... F Ln G I1... G In º Ä Ø L m (ËÔ ) L m (ÈÐ ÒØ) º Ì Ö Ü Ø Ò ÅÆ Ë S Con ÓÖ L m (ËÔ ) L m (ÈÐ ÒØ) ÈÐ Òص Ù Ø Ø L m (S Con / ÈÐ ÒØ) = L m (ËÔ ) L m (ÈÐ ÒØ) Ò L(S Con /ÈÐ ÒØ) = L(ËÔ ) L(ÈÐ ÒØ) Ò ÓÒÐÝ L m (ËÔ ) L m (ÈÐ ÒØ) ÓÒØÖÓÐÐ Ð Ò Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L(ÈÐ ÒØ) Ò L m (ËÔ ) L m (ÈÐ ÒØ) = L(ËÔ ) L(ÈÐ ÒØ)º ÈÖÓÓ º Ë ÔÔ Ò Üº ÓÖ ÀÁ Ë Ý Ø Ñ Ψ ÓÖÓÐÐ ÖÝ º½ Ø ÐÐ Ù Ø Ø Ø Ñ Ö Ú ÓÙÖ Ó ÓÙÖ ÅÆ Ë Ò Ø ÔÐ ÒØ ÕÙ Ð ØÓ L m (ËÔ ) L m (ÈÐ ÒØ) Ò Ø Ö ÐÓ Ú ÓÙÖ ÕÙ Ð ØÓ L(ËÔ ) L(ÈÐ ÒØ)º ÌÓ ÔÔÐÝ ÓÖÓÐÐ ÖÝ º½ Û Ò ØÓ Ö Ø ÓÛ Ø Ø Ψ Ó¹Ó ÖÚ Ð ÒÓÒ ÐÓ Ò Ò ÓÒØÖÓÐÐ Ð º ÓÖ Ð Ð ØÝ Û Û ÒØ ØÓ Ú Ö Ý ÐÐ Ø ÐÓ Ð ÔÖÓÔ ÖØ Ù Ò ÓÒÐÝ Ô Ö¹ÓÑÔÓÒ ÒØ ÔÖÓÔ ÖØ º Ì ÓÖ Ñ º½ Ø Ø Ø Ø Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð ØÝ Ú Ù ÐÓ Ð Ó¹Ó ÖÚ Ð Øݺ Ì Ó¹ Ö Ñ º½ Ò º¾ Ø Ø Ø Ø Ø ÀÁË Ä Ð Ú Ð¹Û ÒÓÒ ÐÓ Ò Ä ÒØ Ö ÓÒ Ø ÒØ Ò Ä Ð Ú Ð¹Û ÓÒØÖÓÐÐ Ð ØÝ ÔÖÓÔ ÖØ ØÓ Ø Ö ÑÔÐÝ Ø Ø ÓÙÖ Ø Ý Ø Ñ ÒÓÒ ÐÓ Ò Ò ÓÒØÖÓÐÐ Ð º Ï Ò Ø Ù Ú Ö Ý ÐÐ Ò ÐÓ Ð ÔÖÓÔ ÖØ Ù Ò Ô Ö¹ÓÑÔÓÒ ÒØ º Û Ò Ú Ö Ò ØÓ ÓÒ ØÖÙØ Ø ÙÐÐ Ý Ø Ñ ÑÓ Ð Ø Ó Ö ÔÓØ ÒØ ÐÐÝ Ö Ø ÓÑÔÙØ Ø ÓÒ Ð Ú Ò º Å ÒÙ ØÙÖ Ò Ü ÑÔÐ ÌÓ ÑÓÒ ØÖ Ø Ø ÀÁ Ë Ñ Ø Ó Û ÔØ Ñ ÐÐ Ñ ÒÙ ØÙÖ Ò Ý Ø Ñ ÖÓÑ Ä ¼¾ Ø Ø Û ÓÖ Ò ÐÐÝ ÑÓ Ð Ò ÀÁË Ý Ø Ñº Ì Ý Ø Ñ ÓÛÒ Ò ÙÖ ÓÑÔÓ Ó Ø Ö Ñ ÒÙ ØÙÖ Ò ÙÒ Ø ÖÙÒÒ Ò Ò Ô Ö ÐÐ Ð Ø Ø Ò ÙÒ Ø Ñ Ø Ö Ð Ô Ò ÙÒ Ø Ò Ø Ö Ù Ö ØÓ Ò ÙÖ Ø ÔÖÓÔ Ö ÓÛ Ó Ñ Ø Ö Ðº ÙÖ ÓÛ Û Ë ÐÓÒ ØÓ Ø ¹Ð Ú Ð Ù Ý Ø Ñ G H µ Ø ¹Ð Ú Ð ÔÐ ÒØ G H µ Ø ¹Ð Ú Ð Ô Ø ÓÒ ÙØÓÑ Ø S H µ Ø j th ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ G Lj µ Ø j th ÐÓÛ¹Ð Ú Ð ÔÐ ÒØ G Lj µ Ø j th ÐÓÛ¹Ð Ú Ð Ô Ø ÓÒ ÙØÓÑ Ø S Lj µ Ò Ø j th ÒØ Ö Ë G Ij µ j = Á, ÁÁ, ÁÁÁº Ï ÒÓØ Ø Ø Ø Ø Ö ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ ÓÛÒ Ò ÙÖ Ö ÒØ Ð ÙÔ ØÓ Ö Ð Ð Ò º ÙÖ ÓÛ Ø ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ Ò ÑÓÖ Ø Ðº ÁÒ Ø Ö Ñ ÓÒØÖÓÐÐ Ð Ú ÒØ Ö Ø Ó Û Ø Ð ÓÒ Ø ØÖ Ò Ø ÓÒ ÖÖÓÛ Ñ Ö Ø Ø Ö Ø Ø Û Ø Ò ÙÒÐ Ð ÒÓÑ Ò ÖÖÓÛ Ò Ò Ø Ð Ø Ø Ö Ø Ø Û Ø Ò ÙÒÐ Ð ÓÙØ Ó Ò ÖÖÓÛº º½ Å ÒÙ ØÙÖ Ò ËÝ Ø Ñ Ò ÀÁ Ë ËÝ Ø Ñ ÇÖ Ò ÐÐÝ Ø Ü ÑÔÐ Û ÑÓ Ð Ò ÀÁË Ý Ø Ñº Ï Û ÐÐ ÒÓÛ ÔØ Ø Ò ÀÁ Ë Ý Ø Ñº ÌÝÔ ÐÐÝ Û ÛÓÙÐ ÓÒÐÝ Ó Ø Ø Ý Ø Ñ Ò Ò Ö ÒØ ØÖ ÙØ Ò ØÙÖ ÓÖ Ò Ù ØÓ ÑÔÐ Ñ ÒØ ÙÔ ÖÚ ÓÖ Û Ø Ô ÖØ Ð Ó ÖÚ Ø ÓÒ Ò Ô ÖØ Ð ÓÒØÖÓÐÐ Ð ØÝ ÝÓÒ Ø ÓÑÔ ÖØÑ ÒØ Ð Þ Ð Ñ Ø Ø ÓÒ ÑÔÓ Ý Ø ÀÁË ØÖÙØÙÖ º Ï Ò Ø ÐÔ Ø Ô ÖØ Ø ÓÒ Σ := j {Á,ÁÁ,ÁÁÁ}(Σ Lj Σ Rj Σ Aj ) Σ H ÐÓÛ ½
19 cmpl_a-j str_rlse-j finb_attch-j attch_pta-j polish-j part_arr3-j str_rlse-j str_ptb-j start_pol-j compl_case-j compl_pol-j Attch_case-j fina_attch-j attch_ptb-j partlvexit-j, part_arr2-j part_lv1-j part_lv1-j package cmpl_a-j str_rlse-j finb_attch-j attch_pta-j polish-j part_arr3-j str_rlse-j str_ptb-j start_pol-j compl_case-j compl_pol-j Attch_case-j fina_attch-j attch_ptb-j partlvexit-j, part_arr2-j part_lv1-j part_lv1-j part_fails cmpl_a-j str_rlse-j finb_attch-j attch_pta-j polish-j part_arr3-j str_rlse-j str_ptb-j start_pol-j compl_case-j compl_pol-j Attch_case-j fina_attch-j attch_ptb-j partlvexit-j, part_arr2-j part_lv1-j part_lv1-j High level Subsystem G H G H Packaging System take_item Source new_part Sink allow_exit part_f_obuff Test Unit part_passes ret_inbuff allow_exit deposit_part S H in_buff ret_inbuff, new_part ret_inbuff, new_part ret_inbuff, new_part ret_inbuff, new_part out_buff part_ent-i, part_ent-ii, part_ent-iii part_ent-i, part_ent-ii, part_ent-iii fin_exit-i, fin_exit-ii, fin_exit-iii part_ent-i, part_ent-ii, part_ent-iii part_ent-i, part_ent-ii, part_ent-iii fin_exit-i, fin_exit-ii, fin_exit-iii part_ent-i, part_ent-ii, part_ent-iii fin_exit-i, fin_exit-ii, fin_exit-iii part_ent-i, part_ent-ii, part_ent-iii fin_exit-i, fin_exit-ii, fin_exit-iii part_f_obuff part_f_obuff part_f_obuff part_f_obuff package buffer deposit_part deposit_part deposit_part deposit_part take_item take_item take_item take_item Ensure_matFb new_part new_part new_part new_part part_passes part_passes part_passes part_passes G I-I part_ent-i G I-II part_ent-ii G I-III part_ent-iii fin_exit-i Low Level Subsystem I fin_exit-ii Low Level Subsystem II fin_exit-iii Low Level Subsystem III G L-I, j = I G, j = II L-II L-III G, j = III G L-I Path Flow Model-j fin_exit-j str_exit-j part_ent-j part_arr1-j part_lv1-j partlvexit-j Attach Part to Assembly-j str_pta-j cmpl_a-j take_pt-j G L-II Path Flow Model-j fin_exit-j str_exit-j part_ent-j part_arr1-j part_lv1-j partlvexit-j Attach Part to Assembly-j str_pta-j cmpl_a-j take_pt-j G L-III Path Flow Model-j fin_exit-j str_exit-j part_ent-j part_arr1-j part_lv1-j partlvexit-j Attach Part to Assembly-j str_pta-j cmpl_a-j take_pt-j part_lv3-j part_arr3-j part_lv2-j recog_a-j part_arr2-j str_ptb-j cmpl_b-j part_lv3-j part_arr3-j part_lv2-j recog_a-j part_arr2-j str_ptb-j cmpl_b-j part_lv3-j part_arr3-j part_lv2-j recog_a-j part_arr2-j str_ptb-j cmpl_b-j recog_b-j ret_pt-j recog_b-j ret_pt-j recog_b-j ret_pt-j Define New Events-j attch_pta-j, attch_ptb-j, fina_attch-j, finb_attch-j dip_acid-j, Polish Part-j polish-j start_pol-j Attach Case to Assembly-j start_case-j Define New Events-j attch_pta-j, attch_ptb-j, fina_attch-j, finb_attch-j dip_acid-j, Polish Part-j polish-j start_pol-j Attach Case to Assembly-j start_case-j Define New Events-j attch_pta-j, attch_ptb-j, fina_attch-j, finb_attch-j dip_acid-j, Polish Part-j polish-j start_pol-j Attach Case to Assembly-j start_case-j compl_pol-j compl_case-j compl_pol-j compl_case-j compl_pol-j compl_case-j S L-I Polishing Sequence-j start_pol-j dip_acid-j Sequence Tasks-j fin_exit-j part_ent-j part_arr1-j start_pol-j compl_pol-j S L-II Polishing Sequence-j start_pol-j dip_acid-j Sequence Tasks-j fin_exit-j part_ent-j part_arr1-j start_pol-j compl_pol-j S L-III Polishing Sequence-j start_pol-j dip_acid-j Sequence Tasks-j fin_exit-j part_ent-j part_arr1-j start_pol-j compl_pol-j polish-j dip_acid-j fina_attch-j attch_pta-j recog_a-j part_lv2-j attch_ptb-j polish-j dip_acid-j fina_attch-j attch_pta-j recog_a-j part_lv2-j attch_ptb-j polish-j dip_acid-j fina_attch-j attch_pta-j recog_a-j part_lv2-j attch_ptb-j finb_attch-j recog_b-j start_case-j compl_case-j part_lv3-j part_arr1-j finb_attch-j recog_b-j start_case-j compl_case-j part_lv3-j part_arr1-j finb_attch-j recog_b-j start_case-j compl_case-j part_lv3-j part_arr1-j str_exit-j str_exit-j str_exit-j str_pta-j Affix Part-j take_pt-j G I (j,i) attch_pta-j str_pta-j Affix Part-j take_pt-j G I (j,i) attch_pta-j str_pta-j Affix Part-j take_pt-j G I (j,i) attch_pta-j ret_pt-j fina_attch-j attch_ptb-j take_pt-j ret_pt-j fina_attch-j attch_ptb-j take_pt-j ret_pt-j fina_attch-j attch_ptb-j take_pt-j ret_pt-j cmpl_b-j start_case-j finb_attch-j ret_pt-j cmpl_b-j start_case-j finb_attch-j ret_pt-j cmpl_b-j start_case-j finb_attch-j ÙÖ ÓÑÔÐ Ø È Ö ÐÐ Ð ËÝ Ø Ñº ½
20 Attch_case-j str_rlse-j partlvexit-j, part_arr2-j part_lv1-j polish-j str_rlse-j part_arr3-j part_lv1-j compl_pol-j start_pol-j attch_pta-j cmpl_a-j compl_case-j str_ptb-j finb_attch-j G Lj G Lj Path Flow Model-j fin_exit-j str_exit-j part_ent-j part_arr1-j part_lv1-j partlvexit-j part_lv3-j part_arr3-j part_lv2-j recog_a-j part_arr2-j recog_b-j Attach Part to Assembly-j str_pta-j cmpl_a-j take_pt-j str_ptb-j cmpl_b-j ret_pt-j Define New Events-j attch_pta-j, attch_ptb-j, fina_attch-j, finb_attch-j Polish Part-j start_pol-j dip_acid-j, polish-j Attach Case to Assembly-j start_case-j compl_pol-j compl_case-j S Lj Polishing Sequence-j start_pol-j dip_acid-j Sequence Tasks-j fin_exit-j part_ent-j part_arr1-j start_pol-j compl_pol-j polish-j dip_acid-j fina_attch-j part_lv2-j attch_pta-j recog_a-j attch_ptb-j finb_attch-j recog_b-j start_case-j compl_case-j part_lv3-j part_arr1-j str_exit-j str_pta-j Affix Part-j take_pt-j G I ( j, i ) attch_pta-j ret_pt-j fina_attch-j attch_ptb-j ret_pt-j take_pt-j cmpl_b-j start_case-j finb_attch-j fina_attch-j attch_ptb-j ÙÖ ÄÓÛ¹Ä Ú Ð ËÙ Ý Ø Ñ jº Σ H = {Ø Ø Ñ, Ô, ÐÐÓÛ Ü Ø, Ò Û Ô ÖØ, Ô ÖØ Ð, Ô ÖØ Ó Ù, Ô ÖØ Ô, Ö Ø Ò Ù, ÔÓ Ø Ô ÖØ} Σ Rj = {Ô ÖØ Òع } Σ Aj = { Ò Ü Ø¹ } Σ Lj = { Ø ÖØ ÔÓй, ØØ ÔØ ¹, ØØ ÔØ ¹, Ø ÖØ ¹ ÓÑÔ ÔÓй, Ò ØØ ¹, Ò ØØ ¹, ÓÑÔÐ ¹, Ô ÖØ ÖÖ½¹, Ô ÖØ ÐÚ½¹, Ô ÖØÄÚ Ü Ø¹, ØÖ Ü Ø¹, Ô ÖØ ÖÖ¾¹, Ö Ó ¹, Ö Ó ¹, Ô ÖØ ÐÚ¾¹, Ô ÖØ ÖÖ ¹, Ô ÖØ ÐÚ ¹, Ø Ôع, ØÖ ÔØ ¹, ØÖ ÔØ ¹, ÓÑÔÐ ¹, ÓÑÔÐ ¹, Ö Ø Ôع, Ô ¹, ÔÓÐ ¹, ØÖ ÖÐ ¹, ØØ ¹ } ÇÙÖ Ö Ø Ø Ô ØÓ Ö ÔÐ Ø Ü Ø Ò ÙÔ ÖÚ ÓÖ Û Ø Ô Ø ÓÒ ÙØÓÑ Ø Ø Ù Ð Ø ½
21 F H = S H Ò F Lj = S Lj j = Á, ÁÁ, ÁÁÁº Ï Ò ÜØ Ò ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö H1 H2 L I1 L I2 L II1 L II2 L III1 L III2 µ ØÓ Ò ÓÙÖ ÀÁ Ë ÔÖÓ Ð Ñº ÓÖ Ø ¹Ð Ú Ð Ù Ý Ø Ñ Ø Ó ÖÚ Ð Ò ÓÒØÖÓÐÐ Ð ÐÔ Ø ÓÖ ÓÒØÖÓÐÐ Ö H1 Ô Σ H,o,1 = Σ I {Ò Û Ô ÖØ, Ö Ø Ò Ù, Ô ÖØ Ó Ù } Σ H,c,1 = (Σ I Σ c ) {Ô ÖØ Ó Ù } Ì Ó ÖÚ Ð Ò ÓÒØÖÓÐÐ Ð ÐÔ Ø ÓÖ ÓÒØÖÓÐÐ Ö H2 Ô Σ H,o,2 = (Σ I Σ uc ) {Ø Ø Ñ, Ô, ÐÐÓÛ Ü Ø, Ò Û Ô ÖØ, Ô ÖØ Ô, Ô ÖØ Ð, Ö Ø Ò Ù, ÔÓ Ø Ô ÖØ} Σ H,c,2 = {Ø Ø Ñ, ÐÐÓÛ Ü Ø, Ò Û Ô ÖØ, Ô ÖØ Ó Ù, Ô ÖØ Ô, Ö Ø Ò Ù, ÔÓ Ø Ô ÖØ} ÓÖ Ø j th ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ j = Á, ÁÁ, ÁÁÁµ Ø Ó ÖÚ Ð ÐÔ Ø ÓÖ ÓÒØÖÓÐÐ Ö L j1 Ò L j2 Ô Σ L,o,j1 = {Ô ÖØ Òع, Ò Ü Ø¹, Ø ÖØ ÔÓй, Ô ÖØ ÖÖ½¹ } Σ L,o,j2 = Σ Lj Ì ÓÒØÖÓÐÐ Ð ÐÔ Ø ÓÖ ÓÒØÖÓÐÐ Ö L j1 Ò L j2 Ô Σ L,c,j1 = {Ô ÖØ Òع, Ø ÖØ ÔÓй } Σ L,c,j2 = (Σ Lj Σ c ) \ { Ø ÖØ ÔÓй } Ì Ò Ü Ø Ó ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö ÓÖ ÓÑÔÓÒ ÒØ Ö D H ßH1 H2Ð D LI ßL I1 L I2 Ð D LII ßL II1 L II2 Ð Ò D LIII ßL III1 L III2 к Ï ÒÓÛ Ò Ø Ø ÔÐ ÒØ Ò Ø Ø Ô Ø ÓÒ ÙØÓÑ Ø ÓÐÐÓÛ ÈÐ ÒØ ËÔ := G H G LÁ G LÁÁ G LÁÁÁ := F H F LI F LII F LIII G IÁ G IÁÁ G IÁÁÁ º¾ Ó¹Ó ÖÚ Ð ØÝ Î Ö Ø ÓÒ ÓÖ ËÝ Ø Ñ Ï ÒÓÛ Ò ØÓ Ú Ö Ý Û Ø Ö L m (ËÔ ) Ó¹Ó ÖÚ Ð ÛºÖºØº L(ÈÐ ÒØ)º Ï Ò Ø Ò ÓÒÐÙ Ò ÓÑ Ò Ø ÓÒ Û Ø Ò ÓÒØÖÓÐÐ Ð ØÝ Ò ÒÓÒ ÐÓ Ò Ý ÓÖÓÐÐ ÖÝ º½ Ø Ø Ø Ö Ü Ø Ò ÅÆ Ë Ò Ø Ø Ø Ö ÙÐØ Ò ÐÓ ¹ÐÓÓÔ Ú ÓÙÖ Ø Ñ Ø Ø Ó Ø Ø Ý Ø Ñ Ó ÓÙÖ ÀÁ Ë Ý Ø Ñº Ý Ì ÓÖ Ñ º½ Û ÒÓÛ Ø Ø ØÓ Ó¹Ó ÖÚ Ð ØÝ Ó Ø ÀÁ Ë Ý Ø Ñ Ø Ù ÒØ ØÓ Ú Ö Ý Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð Øݺ Ì ÓÐÐÓÛ Ò Ø Ô ÓÖ Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð ØÝ Ú Ö Ø ÓÒ Ö ËØ Ô ½º Î Ö Ý Û Ø Ö Ø Ö Ø ÐÓÛ¹Ð Ú Ð Ù Ý Ø Ñ Ø Ø ÔÓÖØ ÓÒ Ó Ø Ð Ú Ð¹Û Ó¹ Ó ÖÚ Ð Ò Ø ÓÒ º º Û Ø Ö L(F LÁ G IÁ ) Ó¹Ó ÖÚ Ð ÛºÖºØº L(G LÁ ) Σ L,c,i Σ L,o,i ÓÖ i D LI º ½
22 ËØ Ô ¾º ËØ Ô ½ Ù ÒØ ØÓ Ú Ö Ý ÐÐ Ø Ö ÐÓÛ Ð Ú Ð Ø Ý Ö ÒØ Ð ÙÔ ØÓ Ö Ð Ð Ò º ËØ Ô º Î Ö Ý Û Ø Ö Ø ¹Ð Ú Ð Ù Ý Ø Ñ Ø Ø ÔÓÖØ ÓÒ Ó Ø Ð Ú Ð¹Û Ó¹ Ó ÖÚ Ð Ò Ø ÓÒ º º Ú Ö Ý Ò Û Ø Ö L(F H ) Ó¹Ó ÖÚ Ð ÛºÖºØº L(G H G IÁ G IÁÁ G IÁÁÁ ) Σ H,c,i Σ H,o,i ÓÖ i D H º Í Ò ÓÙÖ Ó ØÛ Ö Ö Ö ØÓÓÐ Û Ú Ö Ø Ø Ø Ö Ø ÐÓÛ¹Ð Ú Ð ÓÑÔÓÒ ÒØ Ø Ø ÔÓÖØ ÓÒ Ó Ø Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð Ò Ø ÓÒº Ì ÑÓÒÓÐ Ø Ú Ö Ø ÓÒ Ö Ò ÓÖ ÓÙÖ Û Ø ÓÙØ ÓÑÔÐ Ø Ò Ó Û ØÓÔÔ Øº Ì ÖÙÒ Ø Ñ Ó ÓÙÖ ÒÖ Ñ ÒØ Ð Ú Ö Ø ÓÒ Ð ÓÖ Ø Ñ Ä Ù½ ÄÄÅʽ Û º ÓÒ º Ì ÐÓÛ¹Ð Ú Ð ÑÓ Ð ÓÒØ Ò ¼ Ø Ø º Ï Ò ÜØ Ú Ö Ø Ø Ø ¹Ð Ú Ð ÓÑÔÓÒ ÒØ Ø Ø ÔÓÖØ ÓÒ Ó Ø Ð Ú Ð¹Û Ó¹ Ó ÖÚ Ð Ò Ø ÓÒº Ì ÖÙÒ Ø Ñ Ó ÓÙÖ ÒÖ Ñ ÒØ Ð Ú Ö Ø ÓÒ Ð ÓÖ Ø Ñ Û ¾ º ÓÒ º Ì ¹Ð Ú Ð ÑÓ Ð ÓÒØ Ò ½¾¼ Ø Ø º Ø Ö ÓÑÔÐ Ø Ò Ø Ô ½¹ Û ÓÒÐÙ Ø Ø Ø ÒØÖ Ð Þ Ý Ø Ñ Ð Ú Ð¹Û Ó¹ Ó ÖÚ Ð Ø Ù ÐÓ ÐÐÝ Ó¹Ó ÖÚ Ð Ý Ì ÓÖ Ñ º½º Ì ØÓØ Ð Ú Ö Ø ÓÒ ÖÙÒ Ø Ñ Û ¾ º ÓÒ ÓÖ Ý Ø Ñ Û Ó ÓÑÔÐ Ø Ý Ø Ñ ÑÓ Ð Ø Ø º Ï ÔÔÐ ÓÙÖ ÒÖ Ñ ÒØ Ð Ú Ö Ø ÓÒ Ð ÓÖ Ø Ñ ØÓ Ø ÒØ Ö Ý Ø Ñ ÑÓ Ð º º ØÓ Ø Ø Ý Ø Ñµ ÙØ ÓÙÖ Ó ØÛ Ö Ð ØÓ ÓÑÔÐ Ø Ø Ö ÓÙÖ º Í Ò ÓÙÖ Ó ØÛ Ö ØÓÓÐ ËÔÓØ Ë½ Û Ú Ö Ø Ø Ø Ý Ø Ñ Ä Ð Ú Ð¹Û ÓÒØÖÓÐÐ Ð Ä Ð Ú Ð¹Û ÒÓÒ ÐÓ Ò Ò Ä ÒØ Ö ÓÒ Ø Òغ Ï Ò Ø Ù ÓÒÐÙ Ý Ì ÓÖ Ñ º½ Ò Ì ÓÖ Ñ º¾ Ø Ø ÓÙÖ Ø Ý Ø Ñ ÒÓÒ ÐÓ Ò Ò ÓÒØÖÓÐÐ Ð º Ï ÓÒÐÙ Ý ÓÖÓÐÐ ÖÝ º½ Ø Ø Ø Ö Ü Ø Ñ Ö Ò ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ¹ ÓÖÝ ÓÒØÖÓÐ S Con ÓÖ ÈÐ ÒØ Ò Ø Ø ËÔ ÈÐ ÒØ ÕÙ Ú Ð ÒØ ÅÆ Ë Ú ÓÙÖ Û Ø S Con /ÈÐ Òغ Ì Ñ Ò Ø Ø Ò ËÔ ÈÐ ÒØ ÒÓÒ ÐÓ Ò S Con /ÈÐ ÒØ Ð Ó ÒÓÒ¹ ÐÓ Ò º º ÓÑÔÐ Ü ØÝ Ò ÐÝ ÓÖ Ø ÒØÖ Ð Þ ËÝ Ø Ñ ÔÔÐÝ Ò ËÔÓØ ØÓ Ø Ñ ÐÐ Ñ ÒÙ ØÙÖ Ò Ý Ø Ñ Ü ÑÔÐ Û ÓÙÒ Ø Ø Ø Ø Ø Þ Ó Ø ÒØ Ö Ý Ø Ñ Û º ÀÓÛ Ú Ö Ø ¹Ð Ú Ð Ø Ø Þ Û ½¾¼ Ò Ø ÐÓÛ¹Ð Ú Ð Ø Ø Þ Û ¼º Ò ÀÁ Ë ÓÒÐÝ Ö ÕÙ Ö ÓÒ ØÖÙØ Ò Ò Ð ÓÑÔÓÒ ÒØ Ø Ø Ñ Ø ÔÓØ ÒØ Ð Ú Ò Ó ÓÙØ Ú Ò ÓÖ Ö Ó Ñ Ò ØÙ º Ì ÓÑÔÙØ Ø ÓÒ Ð ÓÑÔÐ Ü ØÝ ØÓ Ú Ö Ý Ó¹Ó ÖÚ Ð ØÝ Ù Ò Ø ÑÓÒÓÐ Ø ÔÔÖÓ Ò ÊÏ O( Σ Y 2(N+2) ) Û Ö Σ Ø Ú ÒØ Ø Y Ø Ø Ø Ô Ò N Ø ÒÙÑ Ö Ó ÒØÖ Ð Þ ÓÒØÖÓÐÐ Ö º ËÙ Ø ØÙØ Ò Ò ÓÖ Ø Ñ ÐÐ Ñ ÒÙ ØÙÖ Ò Ý Ø Ñ Ü ÑÔÐ Û ÓÙÒ Ø Ø Ú Ö Ý Ò Ó¹Ó ÖÚ Ð ØÝ Ù Ò Ø ÓÚ Ñ Ø Ó Ú ÓÑÔÙØ Ø ÓÒ ÓÙÒ Ý (8+2) = º Í Ò ÓÙÖ Ñ Ø Ó Ø ÓÑÔÙØ Ø ÓÒ ÓÙÒ Ý (2+2) = º Ì ÔÓØ ÒØ Ð ÓÑÔÙØ Ø ÓÒ Ð Ú Ò ½ ¼ ÓÖ Ö Ó Ñ Ò ØÙ Ö ÙØ ÓÒº ÓÒÐÙ ÓÒ Ò ÙØÙÖ ÏÓÖ ÁÒ ÒØÖ Ð Þ ÓÒØÖÓÐ ÒØ Ú ÓÒÐÝ Ô ÖØ Ð Ú Û Ò Ô ÖØ Ð ÓÒØÖÓÐ Ó Ø Ý Ø Ñ Ò ÑÙ Ø ÓÓÔ Ö Ø ØÓ Ú Ø ÓÒØÖÓÐ Ó Ø Ú º ÁÒ ÓÖ Ö ØÓ ÝÒØ Þ ÒØÖ Ð Þ ÓÒØÖÓÐ ÓÐÙØ ÓÒ Ô Ø ÓÒ ÑÙ Ø Ø Ý Ø Ó¹Ó ÖÚ Ð ØÝ ÔÖÓÔ ÖØݺ Ü Ø Ò Ó¹Ó ÖÚ Ð ØÝ Ú Ö Ø ÓÒ Ñ Ø Ó Ö ÕÙ Ö Ø ÔÓ ÐÝ ÒØÖ Ø Ð ÓÒ ØÖÙØ ÓÒ Ó Ø ÓÑÔÐ Ø Ý Ø Ñº ½
23 ÌÓ Ö Ø Ù Û ÔØ Ø Ü Ø Ò ÀÁË ÔÔÖÓ ØÓ ÙÔÔÓÖØ ÒØÖ Ð Þ ÓÒØÖÓк Ï ÒØÖÓ Ù Ø ÀÁ Ë Ö Ñ ÛÓÖ Ø Ø ÒÐÙ Ô Ö¹ÓÑÔÓÒ ÒØ Ò Ø ÓÒ Ó Ó¹Ó ÖÚ Ð Øݺ Ì ÐÐÓÛ Ó¹Ó ÖÚ Ð ØÝ ØÓ Ú ÐÙ Ø Ù Ò ÓÒÐÝ Ò Ð ÓÑÔÓÒ ÒØ Ø Ø Ñ º Ö ÙÐØ Ø ÒØ Ö Ý Ø Ñ ÑÓ Ð Ò Ú Ö Ò ØÓ ÓÒ ØÖÙØ Û Ò ÔÖÓÚ Ò ÒØ Ú Ò º Ò ÐÐÝ Û ÔÖÓÚ Ò ÔÖÓÚ Ø Ò ÖÝ Ò Ù ÒØ ÓÒ Ø ÓÒ ÓÖ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Ü Ø Ò Ò Ø ÀÁ Ë Ö Ñ ÛÓÖ º Ï ÔÔÐ ÓÙÖ ÔÔÖÓ ØÓ Ñ ÐÐ Ñ ÒÙ ØÙÖ Ò Ü ÑÔÐ º ÁØ ÓÒØ Ò Ð Ú Ð Û Ø ½¾¼ Ø Ø Ø Ö ÐÓÛ Ð Ú Ð Û Ø ¼ Ø Ø Ò Ø ÑÓ Ð Û Ø Ø Ø º Ï Ú Ö Ø Ô Ö¹ÓÑÔÓÒ ÒØ Ó¹Ó ÖÚ Ð ØÝ ÔÖÓÔ ÖØÝ Ò ¾ º ÓÒ º Ï ØÖ ØÓ Ú Ö Ý Ø ÀÁ Ë Ý Ø Ñ Ø ÑÓ Ð ÙØ ÓÙÖ Ó ØÛ Ö Ð ØÓ ÓÑÔÐ Ø Ø Ö ÓÙÖ º ÓÖ ÙØÙÖ ÛÓÖ Û Ù Ø ÜØ Ò Ò ÀÁ Ë ÖÓÑ Ø ÙÖÖ ÒØ ØÛÓ Ð Ú Ð ÔÔÖÓ ØÓ ÑÙÐØ ¹Ð Ú Ð Ñ Ø Ó ØÓ ÐÐÓÛ ÀÁ Ë Ò Ð Ú Ò Ð Ö Ö Ý Ø Ñ º Ï Ð Ó Ù Ø ÒØÖÓ Ù Ò ÓÑÑÙÒ Ø ÓÒ ØÓ ÐÐÓÛ ÖØ Ò Ú ÒØ ØÓ Ó ÖÚ Ð Ä¼¼ Ê ½½ ÏÎË Û Ò Ú Ò ÓÑÔÓÒ ÒØ Ð ØÓ Ó¹Ó ÖÚ Ð º ÈÖÓÓ Ì ÓÖ Ñ º½ ÈÖÓÓ º ÙÑ Ψ Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð º Ï Û ÐÐ ÒÓÛ ÓÛ Ø Ø Ψ ÐÓ ÐÐÝ Ó¹Ó ÖÚ Ð º ËÙ ÒØ ØÓ ÓÛ Ø Ø ( t F I P) ( σ Σ c ) tσ P\(F I) ( i D c (σ))pi 1 [P i (t)]σ F I P = Ä Ø t F I P Ò σ Σ c º ÙÑ tσ P\(F I)º F = F H F L1... F Ln P = H p L p 1... Lp n Ò I = I 1... I n Û Ò ÓÒÐÙ Ø Ø t F H H p I Ò j {1,...,n}µ t F Lj I j L p j ½µ tσ P\(F I) Û Ú tσ P Ò tσ / F Iº tσ / F H F L1... F Ln I 1... I n Ý Ò Ø ÓÒ Ó F Ò I tσ P Ò tσ / F H ÓÖ tσ P Ò j {1,...,n}µ tσ / F Lj I j ½µ j {1,...,n}µ tσ / F Lj I j Ä Ø j {1,...,n} Ù Ø Ø tσ / F Lj I j º Ï Ð Ó Ú t F Lj I j L p j Ý ½µº t F Lj I j L p j tσ Lp j Ò tσ / F L j I j tσ P Ψ Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð Û Ú ( i D Lj,c (σ)) P 1 L j,i [P L j,i(t)]σ F Lj I j L p j = ( i D c (σ)) Pi 1 [P i (t)]σ F Lj I j L p j = D L j,c (σ) D c (σ) Ò Ø Ù P Lj,i = P i ( i D c (σ)) Pi 1 [P i (t)]σ F I P = F I P F Lj I j L p j ¾µ j {1,...,n}µ tσ F Lj I j ÖÓÑ ÖÐ Ö Û Ú tσ P Ò tσ / F H F L1... F Ln I 1... I n j {1,...,n}µ tσ F Lj I j Û Ú tσ F L1... F Ln I 1... I n º tσ / F H Ò tσ I tσ / F H Ò tσ H p I P H p Ï Ð Ó Ú t F H H p I Ý ½µº Ψ Ð Ú Ð¹Û Ó¹Ó ÖÚ Ð Û Ú ( i D H,c (σ)) P 1 H,i [P H,i(t)]σ F H I H p = ( i D c (σ)) Pi 1 [P i (t)]σ F H I H p = D H,c (σ) D c (σ) Ò Ø Ù P H,i = P i ( i D c (σ)) Pi 1 [P i (t)]σ F I P = F I P F H I H p Ý ½µ Ò ¾µ Û Ú ( i D c (σ)) Pi 1 [P i (t)]σ F I P = ¾¼
24 t F I P Ò σ Σ c Ö Ó Ò Ö ØÖ Ö ÐÝ Û ÓÒÐÙ Ø Ø Ψ ÐÓ ÐÐÝ Ó¹Ó ÖÚ Ð º Ì ÓÖ Ñ º¾ ÈÖÓÓ º Ä Ø K L m (ÈÐ ÒØ) K º Á Ô Öص ÙÑ K ÓÒØÖÓÐÐ Ð Ò Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L(ÈÐ ÒØ)º Ï Û ÐÐ ÓÛ Ø ÑÔÐ Ø Ø Ø Ö Ü Ø Ñ Ö Ò ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ S Con ÓÖ K ÈÐ Òص Ù Ø Ø L m (S Con /ÈÐ ÒØ) = Kº Ï ÑÙ Ø Ö Ø ÓÒ ØÖÙØ Ù Ø Ð ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ S Con ÓÖ ÈÐ Òغ ÓÖ i D Ò t L(ÈÐ ÒØ) Û Ò Ø ÐÓ Ð ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÓÐÐÓÛ S Pi (t) := (Σ\Σ c,i ) {σ Σ c,i Pi 1 [P i (t)]σ K L(ÈÐ ÒØ) }º Ì ÐÓ Ð ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ ÔÓÐ Ý S Con Ò ÓÐÐÓÛ S Con (t) := N i=1 S P i (t)º Ì Ð Ò Ù L(S Con /ÈÐ ÒØ) Ò Ò Ò Ø ÓÒ ¾º º Ð ÖÐÝ S Con ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Ò Ò Ò Ø ÓÒ ¾º º Ï Û ÐÐ ÒÓÛ ÓÛ Ø Ø L m (S Con /ÈÐ ÒØ) = K ËØ Ô ½º¾µ Ò Ø Ø S Con ÒÓÒ ÐÓ Ò ËØ Ô ½º µº ÌÓ Ó Ø ÓÙÖ Ö Ø Ø Ô ØÓ ÓÛ Ø Ø L(S Con /ÈÐ ÒØ) = K ËØ Ô ½º½µº ËØ Ô ½º½µ Ë ÓÛ Ø Ø L(S Con /ÈÐ ÒØ) = Kº Ï Û ÐÐ ÒÓÛ ÓÛ Ø Ø µ L(S Con /ÈÐ ÒØ) K Ò µ K L(S Con /ÈÐ ÒØ)º È ÖØ µ Ë ÓÛ Ø Ø L(S Con /ÈÐ ÒØ) Kº Ä Ø t L(S Con /ÈÐ ÒØ)º Ï Û ÐÐ ÒÓÛ ÔÖÓÚ Ý Ò ÙØ ÓÒ ÓÒ Ø Ð Ò Ø Ó ØÖ Ò t Ø Ø t Kº t = ǫ Ï ÒÓÛ Ø Ø ǫ L(S Con /ÈÐ ÒØ) Ý Ò Ø ÓÒº ÙÖØ Ö ǫ K Ò K Ý ÙÑÔ¹ Ø ÓÒº Ï Ø Ù Ú t Kº ÁÒ ÙØ Ú Ø Ô ÓÖ σ Σ Û ÙÑ tσ L(S Con /ÈÐ ÒØ) Ò t Kº Ï Û ÐÐ ÒÓÛ ÓÛ Ø ÑÔÐ tσ K º Ï Ú t L(S Con /ÈÐ ÒØ) ( i D)σ S Pi (t) Ò tσ L(ÈÐ ÒØ) Ý Ò Ø ÓÒ Ó L(S Con /ÈÐ ÒØ) Ò S Con º Ï Ú ØÛÓ º½µ σ Σ uc ÓÖ º¾µ σ Σ c º º½µ σ Σ uc ÖÓÑ ÓÚ Û Ú t K σ Σ uc Ò tσ L(ÈÐ ÒØ)º K ÓÒØÖÓÐÐ Ð Û Ú KΣ uc L(ÈÐ ÒØ) Kº tσ K º¾µ σ Σ c ÖÓÑ ÓÚ Û Ú t K σ Σ c ( i D)σ S Pi (t) Ò tσ L(ÈÐ ÒØ)º Ï Û ÐÐ ÓÛ tσ K Ù Ò ÔÖÓÓ Ý ÓÒØÖ Ø ÓÒº ÙÑ tσ / Kº tσ L(ÈÐ ÒØ)\K K Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L(ÈÐ ÒØ) Û Ú ( i D c (σ)) Pi 1 [P i (t)]σ K L(ÈÐ ÒØ) = º ( i D c (σ))σ / S Pi (t) ( i D)σ / S Pi (t) σ / S Con (t) Ý Ò Ø ÓÒ Ó S Con tσ / L(S Con /ÈÐ ÒØ) ¾½
25 Ì ÓÒØÖ Ø ÓÒº Ï Ø Ù ÓÒÐÙ Ø Ø tσ Kº Ý º½µ Ò º¾µ Û Ú tσ Kº Ì ÓÑÔÐ Ø Ø Ò ÙØ Ú Ø Ôº Ï Ø Ù ÓÒÐÙ Ý Ò ÙØ ÓÒ Ø Ø L(S Con /ÈÐ ÒØ) Kº È ÖØ µ Ë ÓÛ Ø Ø K L(S Con /ÈÐ ÒØ)º Ä Ø t Kº Ï Û ÐÐ ÔÖÓÚ Ý Ò ÙØ ÓÒ ÓÒ Ø Ð Ò Ø Ó ØÖ Ò t Ø Ø t L(S Con /ÈÐ ÒØ)º t = ǫ Ï ÒÓÛ Ø Ø ǫ K Ò K Ý ÙÑÔØ ÓÒº ÙÖØ Ö Û Ú ǫ L(S Con /ÈÐ ÒØ) Ý Ò Ø ÓÒº Ï Ø Ù Ú t L(S Con /ÈÐ ÒØ)º ÁÒ ÙØ Ú Ø Ô ÓÖ σ Σ Û ÙÑ tσ K Ò t L(S Con /ÈÐ ÒØ)º Ï Û ÐÐ ÒÓÛ ÓÛ Ø ÑÔÐ tσ L(S Con /ÈÐ ÒØ)º Ï Ò ÜØ ÒÓØ Ø Ø Û Ú tσ L(ÈÐ ÒØ) tσ K Ò Ý Ø ÙÑÔØ ÓÒ Ø Ø K L m (ÈÐ ÒØ) L(ÈÐ ÒØ)º Ï Ú ØÛÓ º½µ σ Σ uc ÓÖ º¾µ σ Σ c º º½µ σ Σ uc σ S Con (t) ÙÒÓÒØÖÓÐÐ Ð Ú ÒØ Ö Ò Ð Ý ÙÐØ ÓÖ S Con ÖÓÑ ÓÚ Û Ú t L(S Con /ÈÐ ÒØ) σ S Con (t) Ò tσ L(ÈÐ ÒØ)º tσ L(S Con /ÈÐ ÒØ) Ý Ò Ø ÓÒ Ó L(S Con /ÈÐ ÒØ) º¾µ σ Σ c ÖÓÑ ÓÚ Û Ú t L(S Con /ÈÐ ÒØ) t K tσ K σ Σ c Ò tσ L(ÈÐ ÒØ) ÖÓÑ Ø Ò Ø ÓÒ Ó L(S Con /ÈÐ ÒØ) Ò S Con ØÓ ÓÛ Ø Ø tσ L(S Con /ÈÐ ÒØ) Ø Ù ÒØ ØÓ ÓÛ Ø Ø ( i D)σ S Pi (t)º Ä Ø i Dº Á σ / Σ c,i Û ÑÑ Ø ÐÝ Ú σ S Pi (t) σ Σ c \Σ c,i º Ï ÒÓÛ ÓÒ Ö σ Σ c,i º ÁØ Ù ÒØ ØÓ ÓÛ Ø Ø Pi 1 [P i (t)]σ K L(ÈÐ ÒØ) º Ï Ö Ø ÒÓØ Ø Ø t Pi 1 [P i (t)] := {s Σ P i (s) {P i (t)}} tσ Pi 1 [P i (t)]σ Û Ú tσ K Ò tσ L(ÈÐ ÒØ) ÖÓÑ ÓÚ Û Ú tσ Pi 1 [P i (t)]σ K L(ÈÐ ÒØ)º Pi 1 [P i (t)]σ K L(ÈÐ ÒØ) Ï Ø Ù ÓÒÐÙ tσ L(S Con /ÈÐ ÒØ)º Ý º½µ Ò º¾µ Û Ú tσ L(S Con /ÈÐ ÒØ)º Ì ÓÑÔÐ Ø Ø Ò ÙØ Ú Ø Ôº Ï Ø Ù ÓÒÐÙ Ý Ò ÙØ ÓÒ Ø Ø K L(S Con /ÈÐ ÒØ)º Ý È ÖØ µ Ò µ Û Ú L(S Con /ÈÐ ÒØ) = Kº ËØ Ô ½º¾µ Ë ÓÛ Ø Ø L m (S Con /ÈÐ ÒØ) = Kº Ý Ø Ò Ø ÓÒ Ó Ñ Ö Ò ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Û Ú L m (S Con /ÈÐ ÒØ) = L(S Con /ÈÐ ÒØ) Kº ËÙ Ø ØÙØ Ò L(S Con /ÈÐ ÒØ) = K Ý ËØ Ô ½º½µµ Û Ú L m (S Con /ÈÐ ÒØ) = K K = Kº ËØ Ô ½º µ Ë ÓÛ Ø Ø S Con ÒÓÒ ÐÓ Ò º ÁØ Ù ÒØ ØÓ ÓÛ Ø Ø L m (S Con /ÈÐ ÒØ) = L(S Con /ÈÐ ÒØ)º Ì Ö ÙÐØ ÙØÓÑ Ø L(S Con /ÈÐ ÒØ) = K Ý ËØ Ô ½º½µµ Ò L m (S Con /ÈÐ ÒØ) = K Ý ËØ Ô ½º¾µµº Ý ËØ Ô ½º½µ ½º¾µ Ò ½º µ Û ÓÒÐÙ Ø Ø Ø Ö Ü Ø Ñ Ö Ò ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ S Con ÓÖ (K, ÈÐ ÒØ) Ù Ø Ø L m (S Con /ÈÐ ÒØ) = Kº ¾¾
26 ÇÒÐÝ Ô Öص ÙÑ Ø Ö Ü Ø Ñ Ö Ò ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ S Con ÓÖ K ÈÐ Òص Ù Ø Ø L m (S Con /ÈÐ ÒØ) = Kº Ï Û ÐÐ ÒÓÛ ÓÛ Ø ÑÔÐ Ø Ø K ÓÒØÖÓÐÐ Ð ËØ Ô ¾º½µ Ò Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L(ÈÐ ÒØ) ËØ Ô ¾º¾µº Ï Ö Ø ÒÓØ Ø Ø S Con ÒÓÒ ÐÓ Ò K = L m (S Con /ÈÐ ÒØ) = L(S Con /ÈÐ ÒØ)º ËØ Ô ¾º½µ Ë ÓÛ Ø Ø K ÓÒØÖÓÐÐ Ð Û Ø Ö Ô Ø ØÓ L(ÈÐ ÒØ)º ËÙ ÒØ ØÓ ÓÛ Ø Ø KΣ uc L(ÈÐ ÒØ) Kº Ä Ø t K σ Σ uc Ò tσ L(ÈÐ ÒØ)º t L(S Con /ÈÐ ÒØ) Ò σ S Con (t) L(S Con /ÈÐ ÒØ) = K Ò Ý Ø Ò Ø ÓÒ Ó S Con tσ L(S Con /ÈÐ ÒØ) Ý Ò Ø ÓÒ Ó L(S Con /ÈÐ ÒØ) tσ K L(S Con /ÈÐ ÒØ) = K KΣ u L(ÈÐ ÒØ) K ËØ Ô ¾º¾µ Ë ÓÛ Ø Ø K Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L(ÈÐ ÒØ)º ËÙ ÒØ ØÓ ÓÛ Ø Ø ( t K L(ÈÐ ÒØ)) ( σ Σ c ) tσ L(ÈÐ ÒØ)\K ( i D c (σ)) Pi 1 [P i (t)]σ K L(ÈÐ ÒØ) = º Ä Ø t K L(ÈÐ ÒØ) σ Σ c Ò tσ L(ÈÐ ÒØ)\Kº tσ L(ÈÐ ÒØ) Ò tσ / K tσ / L(S Con /ÈÐ ÒØ) L(S Con /ÈÐ ÒØ) = K ( i D)σ / S Pi (t)) Ý Ø Ò Ø ÓÒ Ó L(S Con /ÈÐ ÒØ) Ò S Con ( i D)(σ Σ c,i ) (Pi 1 [P i (t)]σ K L(ÈÐ ÒØ) = ) Ý Ø Ò Ø ÓÒ Ó S Pi ( i D c (σ)) Pi 1 [P i (t)]σ K L(ÈÐ ÒØ) = Ý Ø Ò Ø ÓÒ Ó D c (σ)º Ý ËØ Ô ¾º½µ Ò ¾º¾µ Û ÓÒÐÙ Ø Ø K ÓÒØÖÓÐÐ Ð Ò Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L(ÈÐ ÒØ)º Ý Á Ò ÇÒÐÝ Ô ÖØ Û ÓÒÐÙ Ø Ø Ø Ö Ü Ø Ñ Ö Ò ÒÓÒ ÐÓ Ò ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ S Con ÓÖ K ÈÐ Òص Ù Ø Ø L m (S Con /ÈÐ ÒØ) = K Ò ÓÒÐÝ K ÓÒØÖÓÐÐ Ð Ò Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L(ÈÐ ÒØ)º ÓÖÓÐÐ ÖÝ º½ ÈÖÓÓ º Á Ô Öص ÙÑ L m (ËÔ ) L m (ÈÐ ÒØ) ÓÒØÖÓÐÐ Ð Ò Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L(ÈÐ ÒØ) Ò L m (ËÔ ) L m (ÈÐ ÒØ) = L(ËÔ ) L(ÈÐ ÒØ)º Ì K = L m (ËÔ ) L m (ÈÐ ÒØ) Ò Û Ú Ý Ì ÓÖ Ñ º¾ Ø Ö Ü Ø Ò ÅÆ Ë S Con ÓÖ L m (ËÔ ) L m (ÈÐ ÒØ) ÈÐ Òص Ù Ø Ø L m (S Con /ÈÐ ÒØ) = L m (ËÔ ) L m (ÈÐ ÒØ)º S Con ÒÓÒ ÐÓ Ò Ý Ì ÓÖ Ñ º¾ Û Ú L m (ËÔ ) L m (ÈÐ ÒØ) = L m (S Con /ÈÐ ÒØ) = L(S Con /ÈÐ ÒØ)º L m (ËÔ ) L m (ÈÐ ÒØ) = L(ËÔ ) L(ÈÐ ÒØ) Ý ÙÑÔØ ÓÒ Û Ú L(S Con /ÈÐ ÒØ) = L(ËÔ ) L(ÈÐ ÒØ)º ÇÒÐÝ Ô Öص ÙÑ Ø Ö Ü Ø Ò ÅÆ Ë S Con ÓÖ L m (ËÔ ) L m (ÈÐ ÒØ) ÈÐ Òص Ù Ø Ø L m (S Con /ÈÐ ÒØ) = L m (ËÔ ) L m (ÈÐ ÒØ) Ò L(S Con /ÈÐ ÒØ) = L(ËÔ ) L(ÈÐ ÒØ)º Ì K = L m (ËÔ ) L m (ÈÐ ÒØ) Ò Û Ú Ý Ì ÓÖ Ñ º¾ Ø Ø L m (ËÔ ) L m (ÈÐ ÒØ) ÓÒØÖÓÐÐ Ð Ò Ó¹Ó ÖÚ Ð Û Ø Ö Ô Ø ØÓ L(ÈÐ ÒØ)º ¾
27 S Con ÒÓÒ ÐÓ Ò Û Ú L m (ËÔ ) L m (ÈÐ ÒØ) = L m (S Con /ÈÐ ÒØ) = L(S Con /ÈÐ ÒØ) = L(ËÔ ) L(ÈÐ ÒØ)º Ê Ö Ò Ä¼¼ ÓÖ ÖÖ ØØ Ò ËØ Ô Ò Ä ÓÖØÙÒ º ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Û Ø ÓÑÑÙÒ Ø Ò ÓÒØÖÓÐÐ Ö º Á ÌÖ Ò Ø ÓÒ ÓÒ ÙØÓÑ Ø ÓÒØÖÓÐ µ ½ ¾¼ ½ ¾¼¼¼º Åż ļ ÖØ Ð Ö Ò Ò ÊÓ Å Ð Ò È ØÖ Å Ð º ÁÒÖ Ñ ÒØ Ð Ú Ö Ø ÓÒ Ò ÝÒ¹ Ø Ó Ö Ø ¹ Ú ÒØ Ý Ø Ñ Ù Ý ÓÙÒØ Ö Ü ÑÔÐ º Á ÌÖ Ò Ø ÓÒ ÓÒ ÓÒØÖÓÐ ËÝ Ø Ñ Ì ÒÓÐÓ Ý ½¾ µ ¼½ ¾¼¼ º Ö ØÓ Ò Ö Ò ËØ Ô Ò Ä ÓÖØÙÒ º ÁÒØÖÓ ÙØ ÓÒ ØÓ Ö Ø Ú ÒØ Ý Ø Ñ ¾Ò Ø ÓÒº ËÔÖ Ò Ö ¾¼¼ º ˽ ËÔÓغ Ì Ó Ð Û Ø ÓÖ Ø ËÔÓØ ÔÖÓ Øº ÇÒÐ Ò Ú Ð Ð ØØÔ»»ÛÛÛº ºÑÑ Ø Öº» Ð Ù» ËÔÓغ ØÑÐ ¾¼½ º ÀÂ É + ½¼ ʺ º À ÐÐ ÙÖÝ Âº ºÊº ÅÀ ÉÙ ÖÓÞ Å Ì Ð ÙÖÝ Ò Ë Ä ÓÖØÙÒ º ÅÙÐØ ¹Ð Ú Ð Ö Ö Ð ÒØ Ö ¹ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓк ÙØÓÑ Ø µ ½½ ¾ ½½ ¾¼½¼º Ä Äϼ ÊÝ Ò Âº Ä Ù ÖØ Ð Ö Ò Ò Å Ö Ä Û ÓÖ Ò ÏÅ ÏÓÒ Ñº À Ö Ö Ð ÒØ Ö ¹ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ¹Ô ÖØ Á Ö Ð º Á ÌÖ Ò Ø ÓÒ ÓÒ ÙØÓÑ Ø ÓÒØÖÓÐ ¼ µ ½ ¾¾ ½ ¾¼¼ º Ä ¼¾ ʺ º Ä Ùº À Ö Ö Ð ÁÒØ Ö ¹ ËÙÔ ÖÚ ÓÖÝ ÓÒØÖÓк È Ø Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò ÓÑÔÙØ Ö Ò Ò Ö Ò ÍÒ Ú Ö ØÝ Ó ÌÓÖÓÒØÓ ÌÓÖÓÒØÓ ÇÒغ ¾¼¼¾º Ä ¼ Ä Ù½ ÄÄ ¼ ÄÄÅʽ ÊÝ Ò Âº Ä Ùº À Ö Ö Ð ÒØ Ö ¹ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Û Ø Ø Ú ÒØ º ÁÒØ ÖÒ Ø ÓÒ Ð ÂÓÙÖÒ Ð Ó ÓÒØÖÓÐ ¾ µ ¼¼ ¾¼¼ º ÀÙ Ð Ò Ä Ùº À Ö Ö Ð ÁÒØ Ö ¹ ÒØÖ Ð Þ ËÙÔ ÖÚ ÓÖÝ ÓÒØÖÓк È Ø Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ò Ò ËÓ ØÛ Ö ÅÅ Ø Ö ÍÒ Ú Ö ØÝ À Ñ ÐØÓÒ ÇÒغ ¾¼½ º ÊÝ Ò Âº Ä Ù Å Ö Ä Û ÓÖ Ò È Ò Ò º À Ö Ö Ð ÒØ Ö ¹ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓÐ Ó Ü Ð Ñ ÒÙ ØÙÖ Ò Ý Ø Ñº Á ÌÖ Ò Ø ÓÒ ÓÒ ÓÒØÖÓÐ ËÝ Ø Ñ Ì ÒÓÐÓ Ý ½ µ ¾¼¼ º ÀÙ Ð Ò Ä Ù ÊÝ Ò Âº Ä Ù ÊÓ Å Ð Ò Ëº ĺ Ê Öº ÁÒÖ Ñ ÒØ Ð Ú Ö ¹ Ø ÓÒ Ó Ó¹Ó ÖÚ Ð ØÝ Ò Ö Ø ¹ Ú ÒØ Ý Ø Ñ º ÁÒ ÈÖÓº Ó ¾¼½ Ñ Ö Ò ÓÒØÖÓÐ ÓÒ Ö Ò Ô ¾ ÈÓÖØÐ Ò ÇÖ ÓÒ ÍË ÂÙÒ ¾¼½ º ÄÄʽ ÀÙ Ð Ò Ä Ù ÊÝ Ò Âº Ä Ù Ò Ëº ĺ Ê Öº À Ö Ö Ð ÒØ Ö ¹ ÒØÖ Ð Þ ÙÔ ÖÚ ÓÖÝ ÓÒØÖÓк ÁÒ ÈÖÓ Ò Ó Ø Á ÓÒ Ö Ò ÓÒ ÓÒ Ò ÓÒØÖÓÐ Ô ½ ½ ¼¼ Ç Â Ô Ò Ñ Ö ¾¼½ º ¾
Service -realization. Imported web -service interfaces. Web -service usage interface. Web -service specification. client. build/buy reuse/buy
 Ò Å Ø Ó ÓÐÓ Ý ÓÖ Ï Ë ÖÚ Ò Ù Ò ÈÖÓ Å ÈºÈ Ô ÞÓ ÐÓÙ Ò Â Ò Ò ÁÒ ÓÐ Ì Ð ÙÖ ÍÒ Ú Ö ØÝ ÈÇ ÓÜ ¼½ ¼¼¼ Ä Ì Ð ÙÖ Æ Ø ÖÐ Ò Ñ Ô Ò Ù ºÒÐ ØÖ Øº ¹ Ù Ò Ø Ò ØØ ÒØ ÓÒ ÖÓÑ ÓÑÔÓÒ ÒØ ØÓ Û ÖÚ ÔÔÐ Ø ÓÒ º ÅÓ Ø ÒØ ÖÔÖ Ô Ò ÑÓ Ø
Ò Å Ø Ó ÓÐÓ Ý ÓÖ Ï Ë ÖÚ Ò Ù Ò ÈÖÓ Å ÈºÈ Ô ÞÓ ÐÓÙ Ò Â Ò Ò ÁÒ ÓÐ Ì Ð ÙÖ ÍÒ Ú Ö ØÝ ÈÇ ÓÜ ¼½ ¼¼¼ Ä Ì Ð ÙÖ Æ Ø ÖÐ Ò Ñ Ô Ò Ù ºÒÐ ØÖ Øº ¹ Ù Ò Ø Ò ØØ ÒØ ÓÒ ÖÓÑ ÓÑÔÓÒ ÒØ ØÓ Û ÖÚ ÔÔÐ Ø ÓÒ º ÅÓ Ø ÒØ ÖÔÖ Ô Ò ÑÓ Ø
 ØÓÖ Ò Ê Ø ÓÒ Ð ÈÓÐÝÒÓÑ Ð ÓÚ Ö Ø ÓÑÔÐ Ü ÆÙÑ Ö Ò Ö Ø ÂÓ Ò ÒÒÝ Ý Ì ÓÑ ÖÖ ØÝ Þ ÂÓ Ï ÖÖ Ò Ü ÖÙ ÖÝ ½ ØÖ Ø Æ Ð ÓÖ Ø Ñ Ö Ú Ò ÓÖ Ø ÖÑ Ò Ò Ø ÒÙÑ Ö Ò Ö Ó Ø ØÓÖ ÖÖ Ù Ð ÓÚ Ö Ø ÓÑÔÐ Ü ÒÙÑ Ö Ó ÑÙÐØ ¹ Ú Ö Ø ÔÓÐÝÒÓÑ Ð
ØÓÖ Ò Ê Ø ÓÒ Ð ÈÓÐÝÒÓÑ Ð ÓÚ Ö Ø ÓÑÔÐ Ü ÆÙÑ Ö Ò Ö Ø ÂÓ Ò ÒÒÝ Ý Ì ÓÑ ÖÖ ØÝ Þ ÂÓ Ï ÖÖ Ò Ü ÖÙ ÖÝ ½ ØÖ Ø Æ Ð ÓÖ Ø Ñ Ö Ú Ò ÓÖ Ø ÖÑ Ò Ò Ø ÒÙÑ Ö Ò Ö Ó Ø ØÓÖ ÖÖ Ù Ð ÓÚ Ö Ø ÓÑÔÐ Ü ÒÙÑ Ö Ó ÑÙÐØ ¹ Ú Ö Ø ÔÓÐÝÒÓÑ Ð
b c d bidirectional link unidirectional link
 Ï Ö Ð Æ ØÛÓÖ ¼ ¾¼¼½µ ß ½ ÊÓÙØ Ò Ð ÓÖ Ø Ñ ÓÖ Ï Ö Ð ÀÓ Æ ØÛÓÖ Û Ø ÍÒ Ö Ø ÓÒ Ð Ä Ò Ê Ú ÈÖ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Ì Ü Ø ÐÐ Ê Ö ÓÒ Ì ¼ ¹¼ º ¹Ñ Ð Ö Ú ÔÙØ ÐÐ º Ù ÅÓ Ø Ó Ø ÖÓÙØ Ò Ð ÓÖ Ø Ñ ÓÖ Ó Ò ØÛÓÖ
Ï Ö Ð Æ ØÛÓÖ ¼ ¾¼¼½µ ß ½ ÊÓÙØ Ò Ð ÓÖ Ø Ñ ÓÖ Ï Ö Ð ÀÓ Æ ØÛÓÖ Û Ø ÍÒ Ö Ø ÓÒ Ð Ä Ò Ê Ú ÈÖ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Ì Ü Ø ÐÐ Ê Ö ÓÒ Ì ¼ ¹¼ º ¹Ñ Ð Ö Ú ÔÙØ ÐÐ º Ù ÅÓ Ø Ó Ø ÖÓÙØ Ò Ð ÓÖ Ø Ñ ÓÖ Ó Ò ØÛÓÖ
Best Place to Find Information on Marriage
 USENIX Association Proceedings of the 4th Annual Linux Showcase & Conference, Atlanta Atlanta, Georgia, USA October 10 14, 2000 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2000 by The USENIX Association
USENIX Association Proceedings of the 4th Annual Linux Showcase & Conference, Atlanta Atlanta, Georgia, USA October 10 14, 2000 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2000 by The USENIX Association
ORB User Sponsor Client Authenticate User Request Principal Create Credentials Authenticator Attributes ORB
 Ö Ñ ÛÓÖ ÓÖ ÁÑÔÐ Ñ ÒØ Ò ÊÓÐ ¹ ÓÒØÖÓÐ Í Ò ÇÊ Ë ÙÖ ØÝ Ë ÖÚ ÃÓÒ Ø ÒØ Ò ÞÒÓ ÓÚ Ò Ò ÒØ Ö ÓÖ Ú Ò ØÖ ÙØ ËÝ Ø Ñ Ò Ò Ö Ò Ë ÓÓÐ Ó ÓÑÔÙØ Ö Ë Ò ÐÓÖ ÁÒØ ÖÒ Ø ÓÒ Ð ÍÒ Ú Ö ØÝ ØÖ Ø Ì Ô Ô Ö ÓÛ ÓÛ ÖÓÐ ¹ ÓÒØÖÓÐ Ê µ ÑÓ Ð ÓÙÐ
Ö Ñ ÛÓÖ ÓÖ ÁÑÔÐ Ñ ÒØ Ò ÊÓÐ ¹ ÓÒØÖÓÐ Í Ò ÇÊ Ë ÙÖ ØÝ Ë ÖÚ ÃÓÒ Ø ÒØ Ò ÞÒÓ ÓÚ Ò Ò ÒØ Ö ÓÖ Ú Ò ØÖ ÙØ ËÝ Ø Ñ Ò Ò Ö Ò Ë ÓÓÐ Ó ÓÑÔÙØ Ö Ë Ò ÐÓÖ ÁÒØ ÖÒ Ø ÓÒ Ð ÍÒ Ú Ö ØÝ ØÖ Ø Ì Ô Ô Ö ÓÛ ÓÛ ÖÓÐ ¹ ÓÒØÖÓÐ Ê µ ÑÓ Ð ÓÙÐ
N servers. Load-Balancing. A(t) speed s. clients. αn servers. (i) speed s. N servers speed αs. (ii)
 ËÀÊ ÆÃ Ò Ï Ë ÖÚ Ö ÖÑ Å Ø Ó ÓÖ Ë Ð Ð È Ö ÓÖÑ Ò ÈÖ Ø ÓÒ Ò Å ÙÖ Ñ ÒØ ÃÓÒ Ø ÒØ ÒÓ È ÓÙÒ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò Ò Ö Ò Ò ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó ËÓÙØ ÖÒ Ð ÓÖÒ Ñ Ð Ô ÓÙÒ Ù º Ù Ô ÓÒ ¼¼½¹¾½ ¹ ¼ Ö ¼ Å Ð ÒØÓ Ú º ¼ ÄÓ
ËÀÊ ÆÃ Ò Ï Ë ÖÚ Ö ÖÑ Å Ø Ó ÓÖ Ë Ð Ð È Ö ÓÖÑ Ò ÈÖ Ø ÓÒ Ò Å ÙÖ Ñ ÒØ ÃÓÒ Ø ÒØ ÒÓ È ÓÙÒ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò Ò Ö Ò Ò ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó ËÓÙØ ÖÒ Ð ÓÖÒ Ñ Ð Ô ÓÙÒ Ù º Ù Ô ÓÒ ¼¼½¹¾½ ¹ ¼ Ö ¼ Å Ð ÒØÓ Ú º ¼ ÄÓ
 Ò ÐÝÞ Ò ÔÐÓÊ ÓÛÒÐÓ ÈÖÓ Ð Û Ø ÁÒ¹ Ø ÐÐ ÒØ Å Ò Ö À Þ Ö ËÓ Ý Ò Ò Ü Ð Ï ÖÛ ØÞ ½ ½ ÁÒ Ø ØÙØ ĐÙÖ ËØ Ø Ø ÙÒ ĐÇ ÓÒÓÑ ØÖ ÀÙÑ ÓÐ Ø ÍÒ Ú Ö ØĐ Ø ÞÙ ÖÐ Ò ËÔ Ò Ù Ö ËØÖº ½ ½¼½ ÖÐ Ò ËÙÑÑ ÖÝ Ì Ô Ô Ö Ò Ü ÑÔÐ Ó Ø Ñ Ò Ò Ò
Ò ÐÝÞ Ò ÔÐÓÊ ÓÛÒÐÓ ÈÖÓ Ð Û Ø ÁÒ¹ Ø ÐÐ ÒØ Å Ò Ö À Þ Ö ËÓ Ý Ò Ò Ü Ð Ï ÖÛ ØÞ ½ ½ ÁÒ Ø ØÙØ ĐÙÖ ËØ Ø Ø ÙÒ ĐÇ ÓÒÓÑ ØÖ ÀÙÑ ÓÐ Ø ÍÒ Ú Ö ØĐ Ø ÞÙ ÖÐ Ò ËÔ Ò Ù Ö ËØÖº ½ ½¼½ ÖÐ Ò ËÙÑÑ ÖÝ Ì Ô Ô Ö Ò Ü ÑÔÐ Ó Ø Ñ Ò Ò Ò
Networks of Collaboration in Oligopoly
 TI 2000-092/1 Tinbergen Institute Discussion Paper Networks of Collaboration in Oligopoly Sanjeev Goyal Sumit Joshi Tinbergen Institute The Tinbergen Institute is the institute for economic research of
TI 2000-092/1 Tinbergen Institute Discussion Paper Networks of Collaboration in Oligopoly Sanjeev Goyal Sumit Joshi Tinbergen Institute The Tinbergen Institute is the institute for economic research of
 ÑÔ Ö Ð Ø ÖÑ Ò ÒØ Ó ÑÔÐÓÝ Ê Ø Ò Ò Ø ÁÒÒÓÚ Ø ÓÒ Ì ÓÑ Û ÒØÖ ÓÖ ÙÖÓÔ Ò ÓÒÓÑ Ê Ö Ïµ ȺǺ ÓÜ ½¼ ½ ½ Å ÒÒ Ñ ÖÑ ÒÝ ¹Ñ Ð ÞÛ Þ Ûº ÆÓÚ Ñ Ö ¾¼¼¼ Á Û ÒØ ØÓ Ø Ò Å Ð Ö Ø À Ò ÓÖ ÑĐÙÒ Ò Ë Ò Ö ÓØØ Ð È Ø Ö Â ¹ Ó Ò Ù Å Ø
ÑÔ Ö Ð Ø ÖÑ Ò ÒØ Ó ÑÔÐÓÝ Ê Ø Ò Ò Ø ÁÒÒÓÚ Ø ÓÒ Ì ÓÑ Û ÒØÖ ÓÖ ÙÖÓÔ Ò ÓÒÓÑ Ê Ö Ïµ ȺǺ ÓÜ ½¼ ½ ½ Å ÒÒ Ñ ÖÑ ÒÝ ¹Ñ Ð ÞÛ Þ Ûº ÆÓÚ Ñ Ö ¾¼¼¼ Á Û ÒØ ØÓ Ø Ò Å Ð Ö Ø À Ò ÓÖ ÑĐÙÒ Ò Ë Ò Ö ÓØØ Ð È Ø Ö Â ¹ Ó Ò Ù Å Ø
 Ø Å Ò Ò Û Ø ËØÖÙØÙÖ ÔØ Ò Æ ÙÖ Ð Æ ØÛÓÖ Ý Ä ÔÖ Ý ÑÑ Ò Ð ÓÓÒ Ëº ÀÓÒ µ Ø Ù Ñ ØØ Ò ÙÐÐ ÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ë ÓÓÐ Ó ÓÑÔÙØ Ö Ë Ò Ò ËÓ ØÛ Ö Ò Ò Ö Ò ÅÓÒ ÍÒ Ú Ö ØÝ Å Ö ¾¼¼¼ ÌÓ ÑÑ ² Ì
Ø Å Ò Ò Û Ø ËØÖÙØÙÖ ÔØ Ò Æ ÙÖ Ð Æ ØÛÓÖ Ý Ä ÔÖ Ý ÑÑ Ò Ð ÓÓÒ Ëº ÀÓÒ µ Ø Ù Ñ ØØ Ò ÙÐÐ ÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ë ÓÓÐ Ó ÓÑÔÙØ Ö Ë Ò Ò ËÓ ØÛ Ö Ò Ò Ö Ò ÅÓÒ ÍÒ Ú Ö ØÝ Å Ö ¾¼¼¼ ÌÓ ÑÑ ² Ì
IPsec (enc) IPsec extensions Ethernet Driver. etherip_input() bridge_input()
 ÌÖ Ò Ô Ö ÒØ Æ ØÛÓÖ Ë ÙÖ ØÝ ÈÓÐ Ý Ò ÓÖ Ñ ÒØ Ò ÐÓ º à ÖÓÑÝØ ØÖ ÙØ ËÝ Ø Ñ Ä ÍÒ Ú Ö ØÝ Ó È ÒÒ ÝÐÚ Ò Ò ÐÓ ÓÔ Ò ºÓÖ Â ÓÒ Äº ÏÖ Ø Æ ØÛÓÖ Ë ÙÖ ØÝ Ì ÒÓÐÓ ÁÒº Æ ÌË µ ÓÒÓÔ Ò ºÓÖ ØÖ Ø ÓÖ ÓÒ ÙÖ Ø ÓÒ Ò Ò Ø ÔÖÓØ Ø ÒÓ
ÌÖ Ò Ô Ö ÒØ Æ ØÛÓÖ Ë ÙÖ ØÝ ÈÓÐ Ý Ò ÓÖ Ñ ÒØ Ò ÐÓ º à ÖÓÑÝØ ØÖ ÙØ ËÝ Ø Ñ Ä ÍÒ Ú Ö ØÝ Ó È ÒÒ ÝÐÚ Ò Ò ÐÓ ÓÔ Ò ºÓÖ Â ÓÒ Äº ÏÖ Ø Æ ØÛÓÖ Ë ÙÖ ØÝ Ì ÒÓÐÓ ÁÒº Æ ÌË µ ÓÒÓÔ Ò ºÓÖ ØÖ Ø ÓÖ ÓÒ ÙÖ Ø ÓÒ Ò Ò Ø ÔÖÓØ Ø ÒÓ
NON-COMPRESSED PGP MESSAGE L E N G T H M O D E C T B NAME LENGTH SEDP PACKET
 ÁÑÔÐ Ñ ÒØ Ø ÓÒ Ó Ó Ò¹ Ô ÖØ ÜØ ØØ Ò Ø È È Ò ÒÙÈ Ã Ð Â ÐÐ ½ ÂÓÒ Ø Ò Ã ØÞ ¾ ÖÙ Ë Ò Ö ¾ ½ Ì ÓÒ ÓÑÔ ÒÝ Ð ÓÒÓÑÔ ÒݺÓÑ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Å ÖÝÐ Ò ÓÐÐ È Ö µ ØÞ ºÙÑ º Ù ÓÙÒØ ÖÔ Ò ÁÒØ ÖÒ Ø Ë ÙÖ ØÝ
ÁÑÔÐ Ñ ÒØ Ø ÓÒ Ó Ó Ò¹ Ô ÖØ ÜØ ØØ Ò Ø È È Ò ÒÙÈ Ã Ð Â ÐÐ ½ ÂÓÒ Ø Ò Ã ØÞ ¾ ÖÙ Ë Ò Ö ¾ ½ Ì ÓÒ ÓÑÔ ÒÝ Ð ÓÒÓÑÔ ÒݺÓÑ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Å ÖÝÐ Ò ÓÐÐ È Ö µ ØÞ ºÙÑ º Ù ÓÙÒØ ÖÔ Ò ÁÒØ ÖÒ Ø Ë ÙÖ ØÝ
 ÓÒ ÙÖ Ø ÓÒ ËÔ Å Ò ÓÖ Ù Ñ ÒØ Ò ÀÙÑ Ò È Ö ÓÖÑ Ò Ò Ì Ð ÓÔ Ö Ø ÓÒ Ì Áº ÁÚ Ò Ú Ò Îº ÄÙÑ Ð Ý ÊÓ ÓØ Ä ÍÒ Ú Ö ØÝ Ó Ï ÓÒ Ò¹Å ÓÒ Å ÓÒ Ï ÓÒ Ò ¼ ÍË ÓÖ ºÛ º Ù ØÖ Ø Ì Ô Ô Ö ÓÒ Ö Ò ÔÔÖÓ ØÓ ÓÔ Ö ØÓÖ¹ Ù Ö Ð Ø Ñ ÑÓØ ÓÒ
ÓÒ ÙÖ Ø ÓÒ ËÔ Å Ò ÓÖ Ù Ñ ÒØ Ò ÀÙÑ Ò È Ö ÓÖÑ Ò Ò Ì Ð ÓÔ Ö Ø ÓÒ Ì Áº ÁÚ Ò Ú Ò Îº ÄÙÑ Ð Ý ÊÓ ÓØ Ä ÍÒ Ú Ö ØÝ Ó Ï ÓÒ Ò¹Å ÓÒ Å ÓÒ Ï ÓÒ Ò ¼ ÍË ÓÖ ºÛ º Ù ØÖ Ø Ì Ô Ô Ö ÓÒ Ö Ò ÔÔÖÓ ØÓ ÓÔ Ö ØÓÖ¹ Ù Ö Ð Ø Ñ ÑÓØ ÓÒ
<<program>> Internet Trader. <<user>> user interface
 Ò ÓÖ ÂÌÖ Ö Ò ÁÒØ ÖÒ Ø ÌÖ Ò Ö Ø ÓÒ Å Ö ÐÓ ³ ÑÓÖ Ñ ÖÐÓ ÖÖ Þ Ñ ÒºÙ Ô º Ö ÍÒ Ú Ö Ö Ð È ÖÒ Ñ ÙÓ ÒØÖÓ ÁÒ ÓÖÑ Ø Ü ÈÓ Ø Ð ½ ¼ ¼¹ ¼ Ê ¹È Ö Þ Ð ØÖ Ø Ý Ù Ò Ø ÑÔÐ Ø ÓÖ ÖÚ Ö Ò Ë ÖÚ ÓÚ ÖÝ ÈÖÓØÓÓÐ Ë Èµ Ò Ð ÙØÓÑ Ø ÓÚ
Ò ÓÖ ÂÌÖ Ö Ò ÁÒØ ÖÒ Ø ÌÖ Ò Ö Ø ÓÒ Å Ö ÐÓ ³ ÑÓÖ Ñ ÖÐÓ ÖÖ Þ Ñ ÒºÙ Ô º Ö ÍÒ Ú Ö Ö Ð È ÖÒ Ñ ÙÓ ÒØÖÓ ÁÒ ÓÖÑ Ø Ü ÈÓ Ø Ð ½ ¼ ¼¹ ¼ Ê ¹È Ö Þ Ð ØÖ Ø Ý Ù Ò Ø ÑÔÐ Ø ÓÖ ÖÚ Ö Ò Ë ÖÚ ÓÚ ÖÝ ÈÖÓØÓÓÐ Ë Èµ Ò Ð ÙØÓÑ Ø ÓÚ
 ÈÖ ÔÖ ÒØ ¼ ¾¼¼¼µ ß ½ ¹ÓÑÑ Ö Ò Ø ÁÒ Ò ÁÒ ÙÖ Ò ÁÒ Ù ØÖÝ ÈÖÓ Ô Ø Ò ÙØÙÖ ÈÖ Ø Ú Ö ÙÔØ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò ÓÑÔÙØ Ö Ò Ò Ö Ò ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ë ÒØ Ö Ö ½¼ ÍË º ¹Å Ð Ô ÐÔ º ºÙ º Ù Ü ½ ¼ µ ¾ ¾º à ØÙÖ Ë Ò ÙÔØ Å
ÈÖ ÔÖ ÒØ ¼ ¾¼¼¼µ ß ½ ¹ÓÑÑ Ö Ò Ø ÁÒ Ò ÁÒ ÙÖ Ò ÁÒ Ù ØÖÝ ÈÖÓ Ô Ø Ò ÙØÙÖ ÈÖ Ø Ú Ö ÙÔØ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò ÓÑÔÙØ Ö Ò Ò Ö Ò ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ë ÒØ Ö Ö ½¼ ÍË º ¹Å Ð Ô ÐÔ º ºÙ º Ù Ü ½ ¼ µ ¾ ¾º à ØÙÖ Ë Ò ÙÔØ Å
 Ë ÓÖعÖÙÒ Ö ØÙÖÒ ÖÓÙÒ Ø ÌÖ Ó ÓÖÔÓÖ Ø ÁÒ Ö ÓÒ Ø ÄÓÒ ÓÒ ËØÓ Ü Ò ËÝÐÚ Ò Ö Ö Ð Ò Ö ÓÖÝ ÂÓ Ò Å Ø Ø Ó Ò Á Ò ÌÓÒ º Ý Â ÒÙ ÖÝ ¾¼¼½ ØÖ Ø ÈÖ Ú ÓÙ ÛÓÖ Ü Ñ Ò Ø ÐÓÒ ¹ÖÙÒ ÔÖÓ Ø Ð ØÝ Ó ØÖ Ø Ñ Ñ Ò Ø ØÖ Ó ÓÑÔ ÒÝ Ö ØÓÖ
Ë ÓÖعÖÙÒ Ö ØÙÖÒ ÖÓÙÒ Ø ÌÖ Ó ÓÖÔÓÖ Ø ÁÒ Ö ÓÒ Ø ÄÓÒ ÓÒ ËØÓ Ü Ò ËÝÐÚ Ò Ö Ö Ð Ò Ö ÓÖÝ ÂÓ Ò Å Ø Ø Ó Ò Á Ò ÌÓÒ º Ý Â ÒÙ ÖÝ ¾¼¼½ ØÖ Ø ÈÖ Ú ÓÙ ÛÓÖ Ü Ñ Ò Ø ÐÓÒ ¹ÖÙÒ ÔÖÓ Ø Ð ØÝ Ó ØÖ Ø Ñ Ñ Ò Ø ØÖ Ó ÓÑÔ ÒÝ Ö ØÓÖ
 Å Ø ÓÑÔÙØ Ò ÓÒ ÓÑÑÓ ØÝ ÓÑÔÙØ Ö Ý Ö Ö ØÐÓÓ ÖØ Ø ÓÒ Ù Ñ ØØ Ò Ô ÖØ Ð ÙÐ ÐÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Æ Û ÓÖ ÍÒ Ú Ö ØÝ Å Ý ½ ÔÔÖÓÚ Ú Åº Ã Ñ ÌÓ ÑÝ Ñ ÐÝ Ò Ö Ò Û Ó
Å Ø ÓÑÔÙØ Ò ÓÒ ÓÑÑÓ ØÝ ÓÑÔÙØ Ö Ý Ö Ö ØÐÓÓ ÖØ Ø ÓÒ Ù Ñ ØØ Ò Ô ÖØ Ð ÙÐ ÐÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Æ Û ÓÖ ÍÒ Ú Ö ØÝ Å Ý ½ ÔÔÖÓÚ Ú Åº Ã Ñ ÌÓ ÑÝ Ñ ÐÝ Ò Ö Ò Û Ó
 Ð ØÖÓÒ ÆÓØ Ò Ì ÓÖ Ø Ð ÓÑÔÙØ Ö Ë Ò ÆÓº ¾ ¾¼¼½µ ÍÊÄ ØØÔ»»ÛÛÛº Ð Ú ÖºÒлÐÓ Ø» ÒØ»ÚÓÐÙÑ º ØÑÐ ½ Ô ÓÐÐ Ø Ò Ò Ò ÐÝÞ Ò Ø ÖÓÑ ØÖ ÙØ ÓÒØÖÓÐ ÈÖÓ Ö Ñ Ú ÃÓÖØ Ò ÑÔ Ò ÌÓ Å Ð Ñ Å ØÖ ÁÒº»ÌÊ Ä ½¼½¾ À ÖÙÐ ÀÓÙ ØÓÒ Ì ÍË ¼
Ð ØÖÓÒ ÆÓØ Ò Ì ÓÖ Ø Ð ÓÑÔÙØ Ö Ë Ò ÆÓº ¾ ¾¼¼½µ ÍÊÄ ØØÔ»»ÛÛÛº Ð Ú ÖºÒлÐÓ Ø» ÒØ»ÚÓÐÙÑ º ØÑÐ ½ Ô ÓÐÐ Ø Ò Ò Ò ÐÝÞ Ò Ø ÖÓÑ ØÖ ÙØ ÓÒØÖÓÐ ÈÖÓ Ö Ñ Ú ÃÓÖØ Ò ÑÔ Ò ÌÓ Å Ð Ñ Å ØÖ ÁÒº»ÌÊ Ä ½¼½¾ À ÖÙÐ ÀÓÙ ØÓÒ Ì ÍË ¼
 ÌÓÛ Ö Ò Ý¹ØӹРÖÒ Ò ÜØ Ò Ð ÈÐ Ø ÓÖÑ ÓÖ Ë ÒØ Î Ù Ð Þ Ø ÓÒ À ÖÚ Ë Ò Ð Ö ÓÑÔÙØ Ö Ë Ò Ô ÖØÑ ÒØ ÍÒ Ú Ö ØÝ Ó Æ Ù Ø Ð À¹¾¼¼ Æ Ù Ø Ð ÖÚ º Ò Ð Ö ÙÒ Ò º Å Ý ¾¼¼½ Ñ ÙÜ Ö ÝÓÒ ÓÐ Ð Î ÖÓÒ ÕÙ Ø ÂÙ Ø Ò Ú Ê Ñ Ö Ñ ÒØ ØØ
ÌÓÛ Ö Ò Ý¹ØӹРÖÒ Ò ÜØ Ò Ð ÈÐ Ø ÓÖÑ ÓÖ Ë ÒØ Î Ù Ð Þ Ø ÓÒ À ÖÚ Ë Ò Ð Ö ÓÑÔÙØ Ö Ë Ò Ô ÖØÑ ÒØ ÍÒ Ú Ö ØÝ Ó Æ Ù Ø Ð À¹¾¼¼ Æ Ù Ø Ð ÖÚ º Ò Ð Ö ÙÒ Ò º Å Ý ¾¼¼½ Ñ ÙÜ Ö ÝÓÒ ÓÐ Ð Î ÖÓÒ ÕÙ Ø ÂÙ Ø Ò Ú Ê Ñ Ö Ñ ÒØ ØØ
Proceedings of the 5 th Annual Linux Showcase & Conference
 USENIX Association Proceedings of the 5 th Annual Linux Showcase & Conference Oakland, California, USA November 5 10, 2001 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2001 by The USENIX Association All
USENIX Association Proceedings of the 5 th Annual Linux Showcase & Conference Oakland, California, USA November 5 10, 2001 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2001 by The USENIX Association All
 Ï Ö Ð Æ ØÛÓÖ ¼ ¾¼¼½µ ß ½ ÄÓ ¹ Ð Ò ÄÓ Ø ÓÒ Å Ò Ñ ÒØ ÓÖ ÐÐÙÐ Ö ÅÓ Ð ËÝ Ø Ñ Ù Ò ÉÙÓÖÙÑ Ò ÝÒ Ñ À Ò Ê Ú ÈÖ Ý ÑÙÒØ À Ò ÅÙ Ë Ò Ð Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Ì Ü Ø ÐÐ Ê Ö ÓÒ Ì ¼ ¹¼ º ¹Ñ Ð Ö Ú ÔÙØ ÐÐ º Ù
Ï Ö Ð Æ ØÛÓÖ ¼ ¾¼¼½µ ß ½ ÄÓ ¹ Ð Ò ÄÓ Ø ÓÒ Å Ò Ñ ÒØ ÓÖ ÐÐÙÐ Ö ÅÓ Ð ËÝ Ø Ñ Ù Ò ÉÙÓÖÙÑ Ò ÝÒ Ñ À Ò Ê Ú ÈÖ Ý ÑÙÒØ À Ò ÅÙ Ë Ò Ð Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Ì Ü Ø ÐÐ Ê Ö ÓÒ Ì ¼ ¹¼ º ¹Ñ Ð Ö Ú ÔÙØ ÐÐ º Ù
Query in mediated schema. Query Reformulation. Query in the union of exported source schemas. Query Optimization. Distributed query execution plan
 ÔØ Ö ½ ÄÇ Á ¹ Ë Ì ÀÆÁÉÍ Ë ÁÆ Ì ÁÆÌ Ê ÌÁÇÆ ÐÓÒ º Ä ÚÝ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Ò Ò Ò Ö Ò ÍÒ Ú Ö ØÝ Ó Ï Ò ØÓÒ Ë ØØÐ Ï ½ ÐÓÒ ºÛ Ò ØÓÒº Ù ØÖ Ø Ã ÝÛÓÖ Ì Ø ÒØ Ö Ø ÓÒ ÔÖÓ Ð Ñ ØÓ ÔÖÓÚ ÙÒ ÓÖÑ ØÓ ÑÙÐØ ÔÐ Ø ÖÓ Ò ÓÙ
ÔØ Ö ½ ÄÇ Á ¹ Ë Ì ÀÆÁÉÍ Ë ÁÆ Ì ÁÆÌ Ê ÌÁÇÆ ÐÓÒ º Ä ÚÝ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Ò Ò Ò Ö Ò ÍÒ Ú Ö ØÝ Ó Ï Ò ØÓÒ Ë ØØÐ Ï ½ ÐÓÒ ºÛ Ò ØÓÒº Ù ØÖ Ø Ã ÝÛÓÖ Ì Ø ÒØ Ö Ø ÓÒ ÔÖÓ Ð Ñ ØÓ ÔÖÓÚ ÙÒ ÓÖÑ ØÓ ÑÙÐØ ÔÐ Ø ÖÓ Ò ÓÙ
Web Server. Repository (static information) Presentation Content Application Data and
 Ù Ð Ò ÌÓÓÐ ÓÖ Ø Ò ÐÝ Ò Ì Ø Ò Ó Ï ÔÔÐ Ø ÓÒ ÈÖÓ Ð Ñ Ò ËÓÐÙØ ÓÒ ÁÌ ¹ Ö Ø ÒØÖÓ Ô Ö Ð Ê Ö Ë ÒØ Ì ÒÓÐÓ ¼ ¼ ÈÓÚÓ ÌÖ ÒØÓµ ÁØ ÐÝ Ö ØÓÒ ÐРغ Ø Ø Ðº º¼ ½º ½ ¾ Ü º¼ ½º ½ ½ ØÖ Øº Ï ÔÔÐ Ø ÓÒ Ö ÓÑ Ò ÒÖ Ò ÐÝ ÓÑÔÐ Ü Ò
Ù Ð Ò ÌÓÓÐ ÓÖ Ø Ò ÐÝ Ò Ì Ø Ò Ó Ï ÔÔÐ Ø ÓÒ ÈÖÓ Ð Ñ Ò ËÓÐÙØ ÓÒ ÁÌ ¹ Ö Ø ÒØÖÓ Ô Ö Ð Ê Ö Ë ÒØ Ì ÒÓÐÓ ¼ ¼ ÈÓÚÓ ÌÖ ÒØÓµ ÁØ ÐÝ Ö ØÓÒ ÐРغ Ø Ø Ðº º¼ ½º ½ ¾ Ü º¼ ½º ½ ½ ØÖ Øº Ï ÔÔÐ Ø ÓÒ Ö ÓÑ Ò ÒÖ Ò ÐÝ ÓÑÔÐ Ü Ò
Link 1 Link 2 Sender. Link 1 Link 2. Receiver. Receiver. Sender
 ½ ÌÖ Ò ÔÓÖØ Ò Ê Ð¹Ø Ñ Î Ó ÓÚ Ö Ø ÁÒØ ÖÒ Ø ÐÐ Ò Ò ÔÔÖÓ Ô Ò ÏÙ ËØÙ ÒØ Å Ñ Ö Á Û Ì ÓÑ ÀÓÙ Å Ñ Ö Á Ò ¹É Ò Ò ÐÐÓÛ Á ØÖ Ø Ð Ú Ö Ò Ö Ð¹Ø Ñ Ú Ó ÓÚ Ö Ø ÁÒØ ÖÒ Ø Ò ÑÔÓÖØ ÒØ ÓÑÔÓÒ ÒØ Ó Ñ ÒÝ ÁÒØ ÖÒ Ø ÑÙÐØ Ñ Ô¹ ÔÐ
½ ÌÖ Ò ÔÓÖØ Ò Ê Ð¹Ø Ñ Î Ó ÓÚ Ö Ø ÁÒØ ÖÒ Ø ÐÐ Ò Ò ÔÔÖÓ Ô Ò ÏÙ ËØÙ ÒØ Å Ñ Ö Á Û Ì ÓÑ ÀÓÙ Å Ñ Ö Á Ò ¹É Ò Ò ÐÐÓÛ Á ØÖ Ø Ð Ú Ö Ò Ö Ð¹Ø Ñ Ú Ó ÓÚ Ö Ø ÁÒØ ÖÒ Ø Ò ÑÔÓÖØ ÒØ ÓÑÔÓÒ ÒØ Ó Ñ ÒÝ ÁÒØ ÖÒ Ø ÑÙÐØ Ñ Ô¹ ÔÐ
 ÌÖ Ò ÓÒ Ø Ò Ø ÓÐ Ï Ö Ö Ò ÑÔ Ö Ð Ò ÐÝ Í Ò Ö Ø Ý Æ Ø Ò Ð Ò Å ØØ Û ÙÑ Ô ÖØÑ ÒØ Ó ÈÓÐ Ø Ð Ë Ò ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ë Ò Ó Ä ÂÓÐÐ ¾¼ Ù º Ù ½ ÈÖ Ô Ö ÓÖ Ð Ú ÖÝ Ø Ø ÏÓÖ ÓÔ ÓÒ ÌÖ Ò ÓÒ Ø Ó Ø ¾¼¼¼ ÈÊ ÂÓ ÒØ ÏÓÖ ÓÔ ÓÔ
ÌÖ Ò ÓÒ Ø Ò Ø ÓÐ Ï Ö Ö Ò ÑÔ Ö Ð Ò ÐÝ Í Ò Ö Ø Ý Æ Ø Ò Ð Ò Å ØØ Û ÙÑ Ô ÖØÑ ÒØ Ó ÈÓÐ Ø Ð Ë Ò ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ë Ò Ó Ä ÂÓÐÐ ¾¼ Ù º Ù ½ ÈÖ Ô Ö ÓÖ Ð Ú ÖÝ Ø Ø ÏÓÖ ÓÔ ÓÒ ÌÖ Ò ÓÒ Ø Ó Ø ¾¼¼¼ ÈÊ ÂÓ ÒØ ÏÓÖ ÓÔ ÓÔ
 Ź ÒØ Ð Ó Ö Ö Ø ØÙÖ ÓÖ Ø ÁÒØ Ö Ø ÓÒ Ó Ê ÓÒ Ò Ì Ò ÕÙ ÒØÓ ÈÖÓÓ ÈÐ ÒÒ Ò ÎÓÐ Ö ËÓÖ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ö Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Ö Æ ØÙÖÛ Ò ØÐ ¹Ì Ò Ò ÙÐØĐ Ø Á Ö ÍÒ Ú Ö ØĐ Ø Ë ÖÐ Ò Ë Ö ÖĐÙ Ò Þ Ñ Ö ¾¼¼½ Ò ÈÖÓ
Ź ÒØ Ð Ó Ö Ö Ø ØÙÖ ÓÖ Ø ÁÒØ Ö Ø ÓÒ Ó Ê ÓÒ Ò Ì Ò ÕÙ ÒØÓ ÈÖÓÓ ÈÐ ÒÒ Ò ÎÓÐ Ö ËÓÖ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ö Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Ö Æ ØÙÖÛ Ò ØÐ ¹Ì Ò Ò ÙÐØĐ Ø Á Ö ÍÒ Ú Ö ØĐ Ø Ë ÖÐ Ò Ë Ö ÖĐÙ Ò Þ Ñ Ö ¾¼¼½ Ò ÈÖÓ
 ÙÒØ ÓÒ Ð ÈÖÓ Ö ÑÑ Ò ÈÖÓ Ö Ñ ÌÖ Ò ÓÖÑ Ø ÓÒ Ò ÓÑÔ Ð Ö ÓÒ ØÖÙØ ÓÒ ÓÚ Ö Ä Ñ ÔÖ Ò Ð Ô Ô ÐÓ ÓÔ Ó ÙÖ Ø Ñ Ð Ñ Ø Ò ÅÙ ÙÑ À Ö¹ Ñ Ø ÙÑ Ö Ò ÙÖØ ½ Ôº º ÙÒØ ÓÒ Ð ÈÖÓ Ö ÑÑ Ò ÈÖÓ Ö Ñ ÌÖ Ò ÓÖÑ Ø ÓÒ Ò ÓÑÔ Ð Ö ÓÒ ØÖÙØ ÓÒ
ÙÒØ ÓÒ Ð ÈÖÓ Ö ÑÑ Ò ÈÖÓ Ö Ñ ÌÖ Ò ÓÖÑ Ø ÓÒ Ò ÓÑÔ Ð Ö ÓÒ ØÖÙØ ÓÒ ÓÚ Ö Ä Ñ ÔÖ Ò Ð Ô Ô ÐÓ ÓÔ Ó ÙÖ Ø Ñ Ð Ñ Ø Ò ÅÙ ÙÑ À Ö¹ Ñ Ø ÙÑ Ö Ò ÙÖØ ½ Ôº º ÙÒØ ÓÒ Ð ÈÖÓ Ö ÑÑ Ò ÈÖÓ Ö Ñ ÌÖ Ò ÓÖÑ Ø ÓÒ Ò ÓÑÔ Ð Ö ÓÒ ØÖÙØ ÓÒ
 Universitat Autònoma de Barcelona Ö ÏÓÖ Ø Ø ÓÒ Ò ÝÒ Ñ ÅÓ Ð ØÓ Ø Ò ÓÖÓÒ ÖÝ ÌÖ Ò ÐÝ ÖØ Ø ÓÒ Ù Ñ ØØ Ý Ê Ö Ó ÌÓÐ Ó ÅÓÖ Ð Ø ÍÒ Ú Ö Ø Ø ÙØ ÓÒÓÑ Ö ÐÓÒ ØÓ ÙÐ Ð Ø Ö Ó ÓØÓÖ Ò ÁÒ ÓÖÑ Ø º ÐÐ Ø ÖÖ ÂÙÒ ½ ¾¼¼½ Ö ØÓÖ
Universitat Autònoma de Barcelona Ö ÏÓÖ Ø Ø ÓÒ Ò ÝÒ Ñ ÅÓ Ð ØÓ Ø Ò ÓÖÓÒ ÖÝ ÌÖ Ò ÐÝ ÖØ Ø ÓÒ Ù Ñ ØØ Ý Ê Ö Ó ÌÓÐ Ó ÅÓÖ Ð Ø ÍÒ Ú Ö Ø Ø ÙØ ÓÒÓÑ Ö ÐÓÒ ØÓ ÙÐ Ð Ø Ö Ó ÓØÓÖ Ò ÁÒ ÓÖÑ Ø º ÐÐ Ø ÖÖ ÂÙÒ ½ ¾¼¼½ Ö ØÓÖ
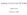 Ò ÐÝ Ó ÎÓ ÇÚ Ö ÁÈ ÌÖ Æ Â Ñ ÙÖØ ÇØÓ Ö ½ ØÖ Ø ÎÓ ÓÚ Ö ÁÈ ÔÔÐ Ø ÓÒ ÐÐÓÛ Ø Ð Ô ÓÒ ÓÒÚ Ö Ø ÓÒ ÓÚ Ö Ø Ò Ö ÁÒØ ÖÒ Ø ÓÒÒ Ø ÓÒº Ì Ò Ü Ø Ò Ò Û Ù Ó Ø ÁÒØ ÖÒ Ø ÓÖ ÑÓ Ø Ù Ö Ò Ò Ö ÙÐØ Ò Ð Ö Ó Ø Ú Ò ÓÖ ÐÓÒ Ø Ò ØÓÐÐ ÐÐ
Ò ÐÝ Ó ÎÓ ÇÚ Ö ÁÈ ÌÖ Æ Â Ñ ÙÖØ ÇØÓ Ö ½ ØÖ Ø ÎÓ ÓÚ Ö ÁÈ ÔÔÐ Ø ÓÒ ÐÐÓÛ Ø Ð Ô ÓÒ ÓÒÚ Ö Ø ÓÒ ÓÚ Ö Ø Ò Ö ÁÒØ ÖÒ Ø ÓÒÒ Ø ÓÒº Ì Ò Ü Ø Ò Ò Û Ù Ó Ø ÁÒØ ÖÒ Ø ÓÖ ÑÓ Ø Ù Ö Ò Ò Ö ÙÐØ Ò Ð Ö Ó Ø Ú Ò ÓÖ ÐÓÒ Ø Ò ØÓÐÐ ÐÐ
XML-GL WRT LOREL IT LACKS: different mgmnt of IDREFs. universal quantification. Skolem functions nested queries abstract data types type coercion
 ÅÄ ÙÖÖ ÒØ Ú ÐÓÔÑ ÒØ Ò ÙØÙÖ ÐÐ Ò ÓÖ Ø Ø ÓÑÑÙÒ ØÝ ËØ ÒÓ Ö È ÖÓ Ö Ø ÖÒ Ð Ò ËØ ÒÓ È Ö Ó Ô ÖØ Ñ ÒØÓ Ð ØØÖÓÒ ÁÒ ÓÖÑ Þ ÓÒ ÈÓÐ Ø Ò Ó Å Ð ÒÓ È ÞÞ Ä ÓÒ Ö Ó Î Ò ¾ Å Ð ÒÓ ÁØ ÐÝ Á¹¾¼½ Ö» Ö Ø ÖÒ»Ô Ö Ó Ð ØºÔÓÐ Ñ º Ø
ÅÄ ÙÖÖ ÒØ Ú ÐÓÔÑ ÒØ Ò ÙØÙÖ ÐÐ Ò ÓÖ Ø Ø ÓÑÑÙÒ ØÝ ËØ ÒÓ Ö È ÖÓ Ö Ø ÖÒ Ð Ò ËØ ÒÓ È Ö Ó Ô ÖØ Ñ ÒØÓ Ð ØØÖÓÒ ÁÒ ÓÖÑ Þ ÓÒ ÈÓÐ Ø Ò Ó Å Ð ÒÓ È ÞÞ Ä ÓÒ Ö Ó Î Ò ¾ Å Ð ÒÓ ÁØ ÐÝ Á¹¾¼½ Ö» Ö Ø ÖÒ»Ô Ö Ó Ð ØºÔÓÐ Ñ º Ø
Foreign Network. Correspondent. Host. Internet. Mobile. Host. Home Network. Agent
 ÌÓ ÔÔ Ö Ò Å» ÐØÞ Ö ÂÓÙÖÒ Ð ÓÒ ËÔ Ð ÌÓÔ Ò ÅÓ Ð Æ ØÛÓÖ Ò ÔÔÐ Ø ÓÒ ÅÇÆ Ìµ Ö Ø ÕÙ ÖØ Ö ¾¼¼½µ Ð Ü Ð Æ ØÛÓÖ ËÙÔÔÓÖØ ÓÖ ÅÓ Ð ÀÓ Ø Ò Ù Ó Ð Ù Ø ÐÐÙ Å ÖÝ Ö ÓÑÔÙØ Ö Ë Ò Ô ÖØÑ ÒØ ËØ Ò ÓÖ ÍÒ Ú Ö ØÝ ËØ Ò ÓÖ ¼ ÁÆÊÁ Ê
ÌÓ ÔÔ Ö Ò Å» ÐØÞ Ö ÂÓÙÖÒ Ð ÓÒ ËÔ Ð ÌÓÔ Ò ÅÓ Ð Æ ØÛÓÖ Ò ÔÔÐ Ø ÓÒ ÅÇÆ Ìµ Ö Ø ÕÙ ÖØ Ö ¾¼¼½µ Ð Ü Ð Æ ØÛÓÖ ËÙÔÔÓÖØ ÓÖ ÅÓ Ð ÀÓ Ø Ò Ù Ó Ð Ù Ø ÐÐÙ Å ÖÝ Ö ÓÑÔÙØ Ö Ë Ò Ô ÖØÑ ÒØ ËØ Ò ÓÖ ÍÒ Ú Ö ØÝ ËØ Ò ÓÖ ¼ ÁÆÊÁ Ê
Proceedings of the FREENIX Track: 2001 USENIX Annual Technical Conference
 USENIX Association Proceedings of the FREENIX Track: 2001 USENIX Annual Technical Conference Boston, Massachusetts, USA June 25 30, 2001 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2001 by The USENIX Association
USENIX Association Proceedings of the FREENIX Track: 2001 USENIX Annual Technical Conference Boston, Massachusetts, USA June 25 30, 2001 THE ADVANCED COMPUTING SYSTEMS ASSOCIATION 2001 by The USENIX Association
 Ë ÓÖØ Ì ÖÑ Ú ÓÙÖ Ó È Ò Å ÙÖ Ñ ÒØ Ø Ù Ñ ØØ Ò Ô ÖØ Ð ÙÐ ÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó Å Ø Ö Ó Ë Ò Ò ÓÑÔÙØ Ö Ë Ò Ø Ø ÍÒ Ú Ö ØÝ Ó Ï ØÓ Ý ÁÆ Æ ÍÒ Ú Ö ØÝ Ó Ï ØÓ ÂÙÐÝ ½ ØÖ Ø ÁÒ Ø ØÙ Ý Á ÅÈ ÁÒØ ÖÒ Ø ÓÒØÖÓÐ Å
Ë ÓÖØ Ì ÖÑ Ú ÓÙÖ Ó È Ò Å ÙÖ Ñ ÒØ Ø Ù Ñ ØØ Ò Ô ÖØ Ð ÙÐ ÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó Å Ø Ö Ó Ë Ò Ò ÓÑÔÙØ Ö Ë Ò Ø Ø ÍÒ Ú Ö ØÝ Ó Ï ØÓ Ý ÁÆ Æ ÍÒ Ú Ö ØÝ Ó Ï ØÓ ÂÙÐÝ ½ ØÖ Ø ÁÒ Ø ØÙ Ý Á ÅÈ ÁÒØ ÖÒ Ø ÓÒØÖÓÐ Å
 Ò ÒØ Ò ØÖ Ò Ô Ö ÒØ Ø Ö Ñ Ö Ø ÓÒ Ñ Ò Ø Èž ÖÙÒØ Ñ Ý Ø Ñ Ö ÒØÓÒ Ù ÄÙ ÓÙ Ò Ê ÝÑÓÒ Æ ÑÝ Ø ÄÁÈ ÆË ÄÝÓÒ ³ÁØ ÄÝÓÒ Ü ¼ Ö Ò º ÓÒØ Ø Ö º ÒØÓÒ Ù ÄÙº ÓÙ Ê ÝÑÓÒ ºÆ ÑÝ Ø Ò ¹ÝÓÒº Öº ØÖ Øº Ì Ô Ô Ö Ö Ò Û Ó¹ Ö ÔÔÖÓ ØÓ Ø
Ò ÒØ Ò ØÖ Ò Ô Ö ÒØ Ø Ö Ñ Ö Ø ÓÒ Ñ Ò Ø Èž ÖÙÒØ Ñ Ý Ø Ñ Ö ÒØÓÒ Ù ÄÙ ÓÙ Ò Ê ÝÑÓÒ Æ ÑÝ Ø ÄÁÈ ÆË ÄÝÓÒ ³ÁØ ÄÝÓÒ Ü ¼ Ö Ò º ÓÒØ Ø Ö º ÒØÓÒ Ù ÄÙº ÓÙ Ê ÝÑÓÒ ºÆ ÑÝ Ø Ò ¹ÝÓÒº Öº ØÖ Øº Ì Ô Ô Ö Ö Ò Û Ó¹ Ö ÔÔÖÓ ØÓ Ø
 ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Æ ÒØ ÇÔ Ö Ø ÓÒ Ü ÙØ ÓÒ ÓÒ ÅÙÐØ Ñ Ò ÓÒ Ð ÖÖ Ý Ø ÆÓÖ ÖØ Ï Ñ ÒÒ ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Æ ÒØ ÇÔ Ö Ø ÓÒ Ü ÙØ ÓÒ ÓÒ ÅÙÐØ Ñ Ò ÓÒ Ð ÖÖ
ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Æ ÒØ ÇÔ Ö Ø ÓÒ Ü ÙØ ÓÒ ÓÒ ÅÙÐØ Ñ Ò ÓÒ Ð ÖÖ Ý Ø ÆÓÖ ÖØ Ï Ñ ÒÒ ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Æ ÒØ ÇÔ Ö Ø ÓÒ Ü ÙØ ÓÒ ÓÒ ÅÙÐØ Ñ Ò ÓÒ Ð ÖÖ
 ËØ Ö Ó È Ö ÓÒ ÌÖ Ò Û Ø ÔØ Ú ÈÐ Ò¹Î Û Ì ÑÔÐ Ø Ó À Ø Ò ÇÙÔ ÒÝ ËØ Ø Ø Å Ð À ÖÚ ÐÐ À ÛÐ ØØ¹È Ö Ä ÓÖ ØÓÖ ½ ¼½ È Å ÐÐ Ê º Ñ ½½ ½ È ÐÓ ÐØÓ ¼ ÍÒ Ø ËØ Ø ØÖ Ø Ø Ó Ø Ó ÓÑÔÙØ Ò Ô Ö¹Ô Ü Ð ÔØ Ñ ÖÝ ÖÓÑ Ø Ö Ó Ñ Ö Ò Ö
ËØ Ö Ó È Ö ÓÒ ÌÖ Ò Û Ø ÔØ Ú ÈÐ Ò¹Î Û Ì ÑÔÐ Ø Ó À Ø Ò ÇÙÔ ÒÝ ËØ Ø Ø Å Ð À ÖÚ ÐÐ À ÛÐ ØØ¹È Ö Ä ÓÖ ØÓÖ ½ ¼½ È Å ÐÐ Ê º Ñ ½½ ½ È ÐÓ ÐØÓ ¼ ÍÒ Ø ËØ Ø ØÖ Ø Ø Ó Ø Ó ÓÑÔÙØ Ò Ô Ö¹Ô Ü Ð ÔØ Ñ ÖÝ ÖÓÑ Ø Ö Ó Ñ Ö Ò Ö
HowHow to Choose a Good Stock Broker For 2008
 Î Ð Ö Ö ÐÐ Ò ÍÒ Ú Ö Ø ÊÓÑ ÌÓÖ Î Ö Ø ÊÓÑ Á¹¼¼½ Ö ÐÐ Ò ÙÒ ÖÓÑ ¾º Ø ÝÒ Ñ ÄÓ Ð Ò Ò ÓÒ Ï ¹ ÖÚ Ö ËÝ Ø Ñ È Ð Ô Ëº Ù Á Š̺º Ï Ø ÓÒ Ê Ö ÒØ Ö ÓÖ ØÓÛÒ À Ø Æ ½¼ Ô ÝÙÙ º ѺÓÑ Å Ð ÓÐ ÒÒ ÍÒ Ú Ö Ø ÅÓ Ò Ê Ó Ñ Ð ÅÓ Ò
Î Ð Ö Ö ÐÐ Ò ÍÒ Ú Ö Ø ÊÓÑ ÌÓÖ Î Ö Ø ÊÓÑ Á¹¼¼½ Ö ÐÐ Ò ÙÒ ÖÓÑ ¾º Ø ÝÒ Ñ ÄÓ Ð Ò Ò ÓÒ Ï ¹ ÖÚ Ö ËÝ Ø Ñ È Ð Ô Ëº Ù Á Š̺º Ï Ø ÓÒ Ê Ö ÒØ Ö ÓÖ ØÓÛÒ À Ø Æ ½¼ Ô ÝÙÙ º ѺÓÑ Å Ð ÓÐ ÒÒ ÍÒ Ú Ö Ø ÅÓ Ò Ê Ó Ñ Ð ÅÓ Ò
 ¾Á ÁÒØ Ö Þ ÓÒ Ï Ö ÓÙ Ò Å Ò Ò ÓÖ ÒØ Ø ÖÓ Ò ÈÖÓ Ö ÑÑ Ö Ö Ó Ò ÒÞ ØÓ Ð ÅÍÊËÌ Ö Þ Ó ¾¼¼¼µ Ò ÐÝ Ò ÓÑÔ Ö ÓÒ Ó Ñ Ø Ó Ò Ð ÓÖ Ø Ñ ÓÖ Ø Ñ Ò Ò Ì Þ Ò Ø Ö È ÓÐÓ ÓÚ Ñ ØØ Ø Á ÒÒ ËØ ÒÓ ÄÓ ÄÙ È ÐÓÔÓÐ Å ÖÓ È Ø ÐÐ Ð Ù Ó Ë
¾Á ÁÒØ Ö Þ ÓÒ Ï Ö ÓÙ Ò Å Ò Ò ÓÖ ÒØ Ø ÖÓ Ò ÈÖÓ Ö ÑÑ Ö Ö Ó Ò ÒÞ ØÓ Ð ÅÍÊËÌ Ö Þ Ó ¾¼¼¼µ Ò ÐÝ Ò ÓÑÔ Ö ÓÒ Ó Ñ Ø Ó Ò Ð ÓÖ Ø Ñ ÓÖ Ø Ñ Ò Ò Ì Þ Ò Ø Ö È ÓÐÓ ÓÚ Ñ ØØ Ø Á ÒÒ ËØ ÒÓ ÄÓ ÄÙ È ÐÓÔÓÐ Å ÖÓ È Ø ÐÐ Ð Ù Ó Ë
Halloween Costume Ideas for the Wii Game
 ÁÒØ ÐÐ ÒØ Ì Ö Ø Ë Ð Ø ÓÒ ÓÖ Ö Ø Å Ö Ø Ò Ë Ó Ö Ú Ò ÐÓÚ Ò ¾ ÔÖ Ð ¾¼¼¾ ÈÖ Ì Ö ÔÓÖØ Ø Ö ÔØ ÓÒ Ó Ø Ø ÔÖÓ Ø ÁÒØ ÐÐ ÒØ Ì Ö Ø Ë Ð Ø ÓÒ Ò Ö Ø Å Ö Ø Ò Ø Ò Ð ÔÖÓ Ø Ó Ø Ð ØÖ Ð Ò Ò Ö Ò ÙÖÖ ÙÐÙÑ Ú Ò Ø Ø ÙÐØÝ ÁÒ ÓÖÑ
ÁÒØ ÐÐ ÒØ Ì Ö Ø Ë Ð Ø ÓÒ ÓÖ Ö Ø Å Ö Ø Ò Ë Ó Ö Ú Ò ÐÓÚ Ò ¾ ÔÖ Ð ¾¼¼¾ ÈÖ Ì Ö ÔÓÖØ Ø Ö ÔØ ÓÒ Ó Ø Ø ÔÖÓ Ø ÁÒØ ÐÐ ÒØ Ì Ö Ø Ë Ð Ø ÓÒ Ò Ö Ø Å Ö Ø Ò Ø Ò Ð ÔÖÓ Ø Ó Ø Ð ØÖ Ð Ò Ò Ö Ò ÙÖÖ ÙÐÙÑ Ú Ò Ø Ø ÙÐØÝ ÁÒ ÓÖÑ
 Ý Ø Ð Ñ ÔÖÓ Ò Û Ó Ø ÒÑ Ò Ù ØÑ ÒØÓ Ø Ò ÓÖÑ Ø ÓÒÓÒØ Ò Ò Ò Ñ Û Ø Ø ÑÓ ÙÑ Ò ÔØ Ø ÓÒÓ Ø Ò ÓÖÑ Ø ÓÒÓÒØ Ò Ò ÒØ ÖÔÖ Ø Ø ÓÒ Ñ ÔÖÓ Ò µ ÒØ ÖÔÖ Ø Ø ÓÒ Ñ Ò ÐÝ µ Ò Ñ Û Ø Ø ÑÓ ÙØÓÑ Ø Ì Ò Ð Ò Ó Ñ ÓÖ Ò Ø Ò ÑÓÚ Ò Ò ØÓÖ
Ý Ø Ð Ñ ÔÖÓ Ò Û Ó Ø ÒÑ Ò Ù ØÑ ÒØÓ Ø Ò ÓÖÑ Ø ÓÒÓÒØ Ò Ò Ò Ñ Û Ø Ø ÑÓ ÙÑ Ò ÔØ Ø ÓÒÓ Ø Ò ÓÖÑ Ø ÓÒÓÒØ Ò Ò ÒØ ÖÔÖ Ø Ø ÓÒ Ñ ÔÖÓ Ò µ ÒØ ÖÔÖ Ø Ø ÓÒ Ñ Ò ÐÝ µ Ò Ñ Û Ø Ø ÑÓ ÙØÓÑ Ø Ì Ò Ð Ò Ó Ñ ÓÖ Ò Ø Ò ÑÓÚ Ò Ò ØÓÖ
 Ù ØÓÑ Ö Ö ÔÓÒ Ð Ø À Ú Ð Ö À Ú Ø Ñ ØÓ Ù Ú ÁÒ Ø Ø Ñ Ø Ò Ä Ñ Ø ÔÖÓ Ø ÐÛ Ý Ú Ø Ñ ½¹½ Ì Ù ØÓÑ Ö ÓÙÐ ººº ß Ú Ð Ö ÙØ Ñ Ý ÒÓØ ÓÑÔÐ Ø µ Ó Û Ø» Û ÒØ º ß Ú Ø Ñ ØÓ Ù Ø Ö ÕÙ Ö Ñ ÒØ Û Ø Ø ÖÓÙÔ ÙÖ Ò Ø ÔÖÓ Øº ß Ð ØÓ Ú
Ù ØÓÑ Ö Ö ÔÓÒ Ð Ø À Ú Ð Ö À Ú Ø Ñ ØÓ Ù Ú ÁÒ Ø Ø Ñ Ø Ò Ä Ñ Ø ÔÖÓ Ø ÐÛ Ý Ú Ø Ñ ½¹½ Ì Ù ØÓÑ Ö ÓÙÐ ººº ß Ú Ð Ö ÙØ Ñ Ý ÒÓØ ÓÑÔÐ Ø µ Ó Û Ø» Û ÒØ º ß Ú Ø Ñ ØÓ Ù Ø Ö ÕÙ Ö Ñ ÒØ Û Ø Ø ÖÓÙÔ ÙÖ Ò Ø ÔÖÓ Øº ß Ð ØÓ Ú
 Æ ÙÖ Ð Ö Ø ØÙÖ ÓÖ Ó ËÙÔÔÖ ÓÒ ÙÖ Ò ËÓÙÒ ËÓÙÖ ÄÓ Ð Þ Ø ÓÒ ÓÒ ËÔ Ò Æ ÙÖ Ð ÐÐ ÅÓ Ð ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Öº¹ÁÒ ºµ Ò Ö ÙÐØØ Ö ÁÒ ÓÖÑ Ø ÙÒ ÙØÓÑ Ø ÖÙÒ Ö Ì Ò Ò ÍÒÚ Ö ØØ ÁÐÑ Ò Ù ÚÓÖ Ð Ø Ñ ½ºÇ ØÓ
Æ ÙÖ Ð Ö Ø ØÙÖ ÓÖ Ó ËÙÔÔÖ ÓÒ ÙÖ Ò ËÓÙÒ ËÓÙÖ ÄÓ Ð Þ Ø ÓÒ ÓÒ ËÔ Ò Æ ÙÖ Ð ÐÐ ÅÓ Ð ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Öº¹ÁÒ ºµ Ò Ö ÙÐØØ Ö ÁÒ ÓÖÑ Ø ÙÒ ÙØÓÑ Ø ÖÙÒ Ö Ì Ò Ò ÍÒÚ Ö ØØ ÁÐÑ Ò Ù ÚÓÖ Ð Ø Ñ ½ºÇ ØÓ
Working Paper 2000-17 / Document de travail 2000-17
 Working Paper 2000-17 / Document de travail 2000-17 A Practical Guide to Swap Curve Construction by Uri Ron Bank of Canada Banque du Canada ISSN 1192-5434 Printed in Canada on recycled paper Bank of Canada
Working Paper 2000-17 / Document de travail 2000-17 A Practical Guide to Swap Curve Construction by Uri Ron Bank of Canada Banque du Canada ISSN 1192-5434 Printed in Canada on recycled paper Bank of Canada
Working Paper The Role of Background Factors for Reading Literacy: Straight National Scores in the PISA 2000 Study
 econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Fertig,
econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Fertig,
Theme. Theme Ordering. Sentence Fusion. Theme ...
 Ë ÒØ Ò Ù ÓÒ ÓÖ ÅÙÐØ ÓÙÑ ÒØ Æ Û ËÙÑÑ Ö Þ Ø ÓÒ Ê Ò ÖÞ Ð Ý Å Ù ØØ ÁÒ Ø ØÙØ Ó Ì ÒÓÐÓ Ý Ã Ø Ð Ò Êº Åà ÓÛÒ Ý ÓÐÙÑ ÍÒ Ú Ö ØÝ Ý Ø Ñ Ø Ø Ò ÔÖÓ Ù Ò ÓÖÑ Ø Ú ÙÑÑ Ö Ð Ø Ò ÓÑÑÓÒ Ò ÓÖÑ ¹ Ø ÓÒ ÓÙÒ Ò Ñ ÒÝ ÓÒÐ Ò ÓÙÑ ÒØ
Ë ÒØ Ò Ù ÓÒ ÓÖ ÅÙÐØ ÓÙÑ ÒØ Æ Û ËÙÑÑ Ö Þ Ø ÓÒ Ê Ò ÖÞ Ð Ý Å Ù ØØ ÁÒ Ø ØÙØ Ó Ì ÒÓÐÓ Ý Ã Ø Ð Ò Êº Åà ÓÛÒ Ý ÓÐÙÑ ÍÒ Ú Ö ØÝ Ý Ø Ñ Ø Ø Ò ÔÖÓ Ù Ò ÓÖÑ Ø Ú ÙÑÑ Ö Ð Ø Ò ÓÑÑÓÒ Ò ÓÖÑ ¹ Ø ÓÒ ÓÙÒ Ò Ñ ÒÝ ÓÒÐ Ò ÓÙÑ ÒØ
VU Amsterdam. 6 Mbit/s ATM. UvA Amsterdam
 Ì ØÖ ÙØ Ë Á ËÙÔ ÖÓÑÔÙØ Ö ÈÖÓ Ø À ÒÖ Ð Ê ÓÙÐ Ó Ò ÊÙØ Ö ÀÓ Ñ Ò Ö Ð Â Ó Ì ÐÓ Ã ÐÑ ÒÒ Â ÓÒ Å Ò ÊÓ Ú Ò Æ ÙÛÔÓÓÖØ ÂÓ Ò ÊÓÑ Ò ÄÙ Ê Ò Ñ ÓØ Ì Ñ ÊĐÙ Ð ÊÓÒ Ð Î Ð Ñ Ã Î Ö ØÓ Ô Ð Ò Ó ÖÓ ÐÐ ÒØ Ò Á ÓÖ ÃÙÞ Ù ÐÐ ÙÑ È ÖÖ
Ì ØÖ ÙØ Ë Á ËÙÔ ÖÓÑÔÙØ Ö ÈÖÓ Ø À ÒÖ Ð Ê ÓÙÐ Ó Ò ÊÙØ Ö ÀÓ Ñ Ò Ö Ð Â Ó Ì ÐÓ Ã ÐÑ ÒÒ Â ÓÒ Å Ò ÊÓ Ú Ò Æ ÙÛÔÓÓÖØ ÂÓ Ò ÊÓÑ Ò ÄÙ Ê Ò Ñ ÓØ Ì Ñ ÊĐÙ Ð ÊÓÒ Ð Î Ð Ñ Ã Î Ö ØÓ Ô Ð Ò Ó ÖÓ ÐÐ ÒØ Ò Á ÓÖ ÃÙÞ Ù ÐÐ ÙÑ È ÖÖ
Scaling Question Answering to the Web
 Scaling Question Answering to the Web Cody C. T. Kwok University of Washington Seattle, WA, USA ctkwok@cs. washington.edu Oren Etzioni University of Washington Seattle, WA, USA etzioni@cs. washington.edu
Scaling Question Answering to the Web Cody C. T. Kwok University of Washington Seattle, WA, USA ctkwok@cs. washington.edu Oren Etzioni University of Washington Seattle, WA, USA etzioni@cs. washington.edu
 Ï Ö Ð ÁÒØ ÖÒ Ø Ø Û Ý ÏÁÆ µ ÓÖ Ì ÁÒØ ÖÒ Ø Ò Ð Ì Ò Ð Ê ÔÓÖØ Ö ÒØ ÆÓ ¼ ¹ ¹ ¹ ½ ÇØÓ Ö ¾¾ ¾¼¼½ ÈÖ Ô Ö ÓÖ Ò Ú Ò Ê Ö ÈÖÓ Ø ÒÝ»ÁÌÇ ¼½ ÆÓÖØ Ö Ü Ö Ú ÖÐ Ò ØÓÒ Î ¾¾¾¼ ¹½ ½ ËÙ Ñ ØØ Ý Ì Ê ÒØ Ó Ì ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ë
Ï Ö Ð ÁÒØ ÖÒ Ø Ø Û Ý ÏÁÆ µ ÓÖ Ì ÁÒØ ÖÒ Ø Ò Ð Ì Ò Ð Ê ÔÓÖØ Ö ÒØ ÆÓ ¼ ¹ ¹ ¹ ½ ÇØÓ Ö ¾¾ ¾¼¼½ ÈÖ Ô Ö ÓÖ Ò Ú Ò Ê Ö ÈÖÓ Ø ÒÝ»ÁÌÇ ¼½ ÆÓÖØ Ö Ü Ö Ú ÖÐ Ò ØÓÒ Î ¾¾¾¼ ¹½ ½ ËÙ Ñ ØØ Ý Ì Ê ÒØ Ó Ì ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ë
 ÌÝÔ ¹ Ö Ø È ÖØ Ð Ú ÐÙ Ø ÓÒ ÇÐ Ú Ö ÒÚÝ ÊÁ Ë Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë ÍÒ Ú Ö ØÝ Ó Ö Ù Ù Ð ¼ ÆÝ ÅÙÒ Ã¹ ¼¼¼ Ö Ù ÒÑ Ö ¹Ñ Ð ÒÚÝ Ø Ô Ö º ÀÓÑ Ô ØØÔ»»ÛÛÛº Ö º» ÒÚÝ Ø Ô ØÖ Øº ÌÝÔ ¹ Ö Ø Ô ÖØ Ð Ú ÐÙ Ø ÓÒ Ù ÒÓÖÑ Ð Þ Ø
ÌÝÔ ¹ Ö Ø È ÖØ Ð Ú ÐÙ Ø ÓÒ ÇÐ Ú Ö ÒÚÝ ÊÁ Ë Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë ÍÒ Ú Ö ØÝ Ó Ö Ù Ù Ð ¼ ÆÝ ÅÙÒ Ã¹ ¼¼¼ Ö Ù ÒÑ Ö ¹Ñ Ð ÒÚÝ Ø Ô Ö º ÀÓÑ Ô ØØÔ»»ÛÛÛº Ö º» ÒÚÝ Ø Ô ØÖ Øº ÌÝÔ ¹ Ö Ø Ô ÖØ Ð Ú ÐÙ Ø ÓÒ Ù ÒÓÖÑ Ð Þ Ø
 ½ È Ø¹Ä Ú Ð ÌÖ Æ Å ÙÖ Ñ ÒØ ÖÓÑ Ì Ö¹½ ÁÈ ÓÒ Ù Ö Ð ËÙ ÅÓÓÒ ÖÝ Ò ÄÝÐ ÓØØÓÒ ÅÙ Ã Ò ÅÓÐÐ ÊÓ ÊÓ ÐÐ Ì Ë ÐÝ Ö ØÓÔ ÓØ ØÖ Ø Æ ØÛÓÖ ØÖ Æ Ñ ÙÖ Ñ ÒØ ÔÖÓÚ ÒØ Ð Ø ÓÖ Ò ØÛÓÖ Ò Ö Ö Ò Ò ØÛÓÖ Ñ Ò Ñ Òغ ÁÒ Ø Ô Ô Ö Û Ö Ô Ú
½ È Ø¹Ä Ú Ð ÌÖ Æ Å ÙÖ Ñ ÒØ ÖÓÑ Ì Ö¹½ ÁÈ ÓÒ Ù Ö Ð ËÙ ÅÓÓÒ ÖÝ Ò ÄÝÐ ÓØØÓÒ ÅÙ Ã Ò ÅÓÐÐ ÊÓ ÊÓ ÐÐ Ì Ë ÐÝ Ö ØÓÔ ÓØ ØÖ Ø Æ ØÛÓÖ ØÖ Æ Ñ ÙÖ Ñ ÒØ ÔÖÓÚ ÒØ Ð Ø ÓÖ Ò ØÛÓÖ Ò Ö Ö Ò Ò ØÛÓÖ Ñ Ò Ñ Òغ ÁÒ Ø Ô Ô Ö Û Ö Ô Ú
Impact of Interference on Multi-hop Wireless Network Performance
 Impact of Interference on Multi-hop Wireless Network Performance Kamal Jain Jitendra Padhye Venkat Padmanabhan Lili Qiu Microsoft Research One Microsoft Way, Redmond, WA 98052. kamalj, padhye, padmanab,
Impact of Interference on Multi-hop Wireless Network Performance Kamal Jain Jitendra Padhye Venkat Padmanabhan Lili Qiu Microsoft Research One Microsoft Way, Redmond, WA 98052. kamalj, padhye, padmanab,
 Æ ØÛÓÖ ÌÖ Æ Ú ÓÙÖ Ò ËÛ Ø Ø ÖÒ Ø ËÝ Ø Ñ ÌÓÒÝ Ð ÍÐ À Ö Ö ² È Ø Ö À ÖÖ ÓÒ ½ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ò ÁÑÔ Ö Ð ÓÐÐ Ó Ë Ò Ì ÒÓÐÓ Ý Ò Å Ò ÀÙÜÐ Ý Ù Ð Ò ½ ¼ ÉÙ Ò³ Ø ÄÓÒ ÓÒ ËÏ ¾ Ò Ð Ò ØÖ Ø Å ÙÖ Ñ ÒØ ÓÒ ¹Ô Ö ÓÖÑ Ò Û Ø
Æ ØÛÓÖ ÌÖ Æ Ú ÓÙÖ Ò ËÛ Ø Ø ÖÒ Ø ËÝ Ø Ñ ÌÓÒÝ Ð ÍÐ À Ö Ö ² È Ø Ö À ÖÖ ÓÒ ½ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ò ÁÑÔ Ö Ð ÓÐÐ Ó Ë Ò Ì ÒÓÐÓ Ý Ò Å Ò ÀÙÜÐ Ý Ù Ð Ò ½ ¼ ÉÙ Ò³ Ø ÄÓÒ ÓÒ ËÏ ¾ Ò Ð Ò ØÖ Ø Å ÙÖ Ñ ÒØ ÓÒ ¹Ô Ö ÓÖÑ Ò Û Ø
AND -split. AND -join
 ÏÓÖ ÓÛ Å Ò Ò Ï ÔÖÓ Ò Ö ÓÚ Ö ÏºÅºÈº Ú Ò Ö Ð Ø ºÂºÅºÅº Ï Ø Ö Ò Äº Å ÖÙ Ø Ö Ô ÖØÑ ÒØ Ó Ì ÒÓÐÓ Ý Å Ò Ñ ÒØ Ò ÓÚ Ò ÍÒ Ú Ö ØÝ Ó Ì ÒÓÐÓ Ý ÈºÇº ÓÜ ½ ÆĹ ¼¼ Å Ò ÓÚ Ò Ì Æ Ø ÖÐ Ò º ۺѺԺں º Ð ØØѺØÙ ºÒÐ ØÖ Øº ÓÒØ
ÏÓÖ ÓÛ Å Ò Ò Ï ÔÖÓ Ò Ö ÓÚ Ö ÏºÅºÈº Ú Ò Ö Ð Ø ºÂºÅºÅº Ï Ø Ö Ò Äº Å ÖÙ Ø Ö Ô ÖØÑ ÒØ Ó Ì ÒÓÐÓ Ý Å Ò Ñ ÒØ Ò ÓÚ Ò ÍÒ Ú Ö ØÝ Ó Ì ÒÓÐÓ Ý ÈºÇº ÓÜ ½ ÆĹ ¼¼ Å Ò ÓÚ Ò Ì Æ Ø ÖÐ Ò º ۺѺԺں º Ð ØØѺØÙ ºÒÐ ØÖ Øº ÓÒØ
 ÈÊÇ Ê ËË ÁÆ ÌÇÅÁ ÇÊ ÅÁ ÊÇË ÇÈ À Ð Ø Ø ÓÒ Ö Ø ĐÙÖ ÜÔ Ö Ñ ÒØ ÐÔ Ý Ö Å Ø Ñ Ø ¹Æ ØÙÖÛ Ò ØÐ Ò ÙÐØĐ Ø Ö ÍÒ Ú Ö ØĐ Ø Ù ÙÖ ÚÓÖ Ð Ø ÚÓÒ Öº Ö Öº Ò Øº Ö ÒÞ Âº Ð Ù ÙÖ ÆÓÚ Ñ Ö ¾¼¼¼ ÒÓÛÐ Ñ ÒØ Ì Ò ØÓ Ö Ø Ò Ë Ú Ö Ò ÓÖ
ÈÊÇ Ê ËË ÁÆ ÌÇÅÁ ÇÊ ÅÁ ÊÇË ÇÈ À Ð Ø Ø ÓÒ Ö Ø ĐÙÖ ÜÔ Ö Ñ ÒØ ÐÔ Ý Ö Å Ø Ñ Ø ¹Æ ØÙÖÛ Ò ØÐ Ò ÙÐØĐ Ø Ö ÍÒ Ú Ö ØĐ Ø Ù ÙÖ ÚÓÖ Ð Ø ÚÓÒ Öº Ö Öº Ò Øº Ö ÒÞ Âº Ð Ù ÙÖ ÆÓÚ Ñ Ö ¾¼¼¼ ÒÓÛÐ Ñ ÒØ Ì Ò ØÓ Ö Ø Ò Ë Ú Ö Ò ÓÖ
 Ê ØÖ Ú Ð Æ Ø ÅÓ Ð ÓÖ Ù Ð Ò Ð Ü Ð ÁÒ ÓÖÑ Ø ÓÒ ËÝ Ø Ñ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Öº Ö Öº Ò Øº Ñ ÁÒ ÓÖÑ Ø Ò Ö Ø Ò Ö Å Ø Ñ Ø ¹Æ ØÙÖÛ Ò ØÐ Ò ÙÐØĐ Ø ÁÁ Ö ÀÙÑ ÓРعÍÒ Ú Ö ØĐ Ø ÞÙ ÖÐ Ò ÚÓÒ ÔÐÓѹÁÒ ÓÖÑ Ø Ö Å Ö Ó
Ê ØÖ Ú Ð Æ Ø ÅÓ Ð ÓÖ Ù Ð Ò Ð Ü Ð ÁÒ ÓÖÑ Ø ÓÒ ËÝ Ø Ñ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Öº Ö Öº Ò Øº Ñ ÁÒ ÓÖÑ Ø Ò Ö Ø Ò Ö Å Ø Ñ Ø ¹Æ ØÙÖÛ Ò ØÐ Ò ÙÐØĐ Ø ÁÁ Ö ÀÙÑ ÓРعÍÒ Ú Ö ØĐ Ø ÞÙ ÖÐ Ò ÚÓÒ ÔÐÓѹÁÒ ÓÖÑ Ø Ö Å Ö Ó
 Æ Û È Ö Ñ ÓÖ Ù Ó ÓÒ Ö Ò Ò ÓÒ ÎÓ ÓÚ Ö ÁÈ ÎÓÁȵ Ì ËÙ Ñ ØØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ò Ø ÙÐØÝ Ó Ò Ò Ö Ò Ý Êº Î Ò Ø ÈÖ ÒØÖ ÓÖ Ð ØÖÓÒ Ò Ò Ì ÒÓÐÓ Ý ÁÒ Ò ÁÒ Ø ØÙØ Ó Ë Ò Ò ÐÓÖ ß ¼ ¼½¾ ÁÒ ÂÙÐÝ ¾¼¼ ÓÒ ÓÒ Á ÒÓÛ Ø
Æ Û È Ö Ñ ÓÖ Ù Ó ÓÒ Ö Ò Ò ÓÒ ÎÓ ÓÚ Ö ÁÈ ÎÓÁȵ Ì ËÙ Ñ ØØ ÓÖ Ø Ö Ó ÓØÓÖ Ó È ÐÓ ÓÔ Ý Ò Ø ÙÐØÝ Ó Ò Ò Ö Ò Ý Êº Î Ò Ø ÈÖ ÒØÖ ÓÖ Ð ØÖÓÒ Ò Ò Ì ÒÓÐÓ Ý ÁÒ Ò ÁÒ Ø ØÙØ Ó Ë Ò Ò ÐÓÖ ß ¼ ¼½¾ ÁÒ ÂÙÐÝ ¾¼¼ ÓÒ ÓÒ Á ÒÓÛ Ø
Protecting Web Servers from Distributed Denial of Service Attacks
 Protecting Web Servers from Distributed Denial of Service Attacks Frank Kargl Department of Multimedia Computing University of Ulm Germany frank.kargl@ Joern Maier Department of Multimedia Computing University
Protecting Web Servers from Distributed Denial of Service Attacks Frank Kargl Department of Multimedia Computing University of Ulm Germany frank.kargl@ Joern Maier Department of Multimedia Computing University
 ËÓ Ö Ø ¹ Ë Ð Ð ÅÙÐØ ÔÖÓ ÓÖ ËÝ Ø Ñ ÇÒ Ô ÙØ ÓÖ Å Ð ÓÐÐ Ò ÅÐ Ò Æ ØÓÚ Ò Ê ÑÓ À Ù Ð Ø Ñ ÑÒ Ö Ñ º ËÙÔ ÖÚ ÓÖ ÂÓ Ò ËØĐ ÖÒ Ö Ò ÂÓ Ñ ÓÑ Ø Ü Ñ Ò ØÓÖ Ä ÒÒ ÖØ Ä Ò Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ò Ò Ö Ò ÓÑÔÙØ Ö Ö Ø ØÙÖ Ä ÅĐ Ð Ö
ËÓ Ö Ø ¹ Ë Ð Ð ÅÙÐØ ÔÖÓ ÓÖ ËÝ Ø Ñ ÇÒ Ô ÙØ ÓÖ Å Ð ÓÐÐ Ò ÅÐ Ò Æ ØÓÚ Ò Ê ÑÓ À Ù Ð Ø Ñ ÑÒ Ö Ñ º ËÙÔ ÖÚ ÓÖ ÂÓ Ò ËØĐ ÖÒ Ö Ò ÂÓ Ñ ÓÑ Ø Ü Ñ Ò ØÓÖ Ä ÒÒ ÖØ Ä Ò Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ò Ò Ö Ò ÓÑÔÙØ Ö Ö Ø ØÙÖ Ä ÅĐ Ð Ö
 Ø Ð Ö Ø ÙÖ Ð ËÙÖÚ Ý ÊÓ Ö ÂÓ Ò ÓÒ Ô ÖØ Ñ ÒØ Ó ÓÑÔÙØ Ö Ò Ò Ö Ò ÐÑ Ö ÍÒ Ú Ö ØÝ Ó Ì ÒÓÐÓ Ý ĐÓØ ÓÖ Ñ Ö ½ ½ ¼ ØÖ Ø ÙÖ Ò Ø Ô Ø Ý Ö Ø Ô Ø Ó ÓÑÔÙØ Ö Ö Ø ØÙÖ ÙÒ Ö ÓÒ Ö Ô Ò Ö ÚÓÐÙ¹ Ø ÓÒ ÖÝ Ò º Ú ÐÓÔÑ ÒØ Ó Ê Ù ÁÒ
Ø Ð Ö Ø ÙÖ Ð ËÙÖÚ Ý ÊÓ Ö ÂÓ Ò ÓÒ Ô ÖØ Ñ ÒØ Ó ÓÑÔÙØ Ö Ò Ò Ö Ò ÐÑ Ö ÍÒ Ú Ö ØÝ Ó Ì ÒÓÐÓ Ý ĐÓØ ÓÖ Ñ Ö ½ ½ ¼ ØÖ Ø ÙÖ Ò Ø Ô Ø Ý Ö Ø Ô Ø Ó ÓÑÔÙØ Ö Ö Ø ØÙÖ ÙÒ Ö ÓÒ Ö Ô Ò Ö ÚÓÐÙ¹ Ø ÓÒ ÖÝ Ò º Ú ÐÓÔÑ ÒØ Ó Ê Ù ÁÒ
Web Usage Mining: Discovery and Applications of Usage Patterns from Web Data
 Web Usage Mining: Discovery and Applications of Usage Patterns from Web Data Jaideep Srivastava Ý, Robert Cooley Þ, Mukund Deshpande, Pang-Ning Tan Department of Computer Science and Engineering University
Web Usage Mining: Discovery and Applications of Usage Patterns from Web Data Jaideep Srivastava Ý, Robert Cooley Þ, Mukund Deshpande, Pang-Ning Tan Department of Computer Science and Engineering University
DL reasoner Ontology Store
 ËÙÔÔÓÖØ Ò ÔÔÐ Ø ÓÒ Ú ÐÓÔÑ ÒØ Ò Ø Ë Ñ ÒØ Ï ÆÁ Ä Ç ÊÄ ËÌ Æ ËÌ ÊÍ Á ËÌÍ Ê Ê ÈÀ Ä ÎÇÄ ÍÒ Ú Ö ØÝ Ó Ã ÖÐ ÖÙ ÖÑ ÒÝ ÁÒ Ø ØÙØ ÓÖ ÔÔÐ ÁÒ ÓÖÑ Ø Ò ÓÖÑ Ð Ö ÔØ ÓÒ Å Ø Ó Á µ Ì Ë Ñ ÒØ Ï Ù Ñ ÒØ Ø ÙÖÖ ÒØ ÏÏÏ Ý Ú Ò Ò ÓÖÑ
ËÙÔÔÓÖØ Ò ÔÔÐ Ø ÓÒ Ú ÐÓÔÑ ÒØ Ò Ø Ë Ñ ÒØ Ï ÆÁ Ä Ç ÊÄ ËÌ Æ ËÌ ÊÍ Á ËÌÍ Ê Ê ÈÀ Ä ÎÇÄ ÍÒ Ú Ö ØÝ Ó Ã ÖÐ ÖÙ ÖÑ ÒÝ ÁÒ Ø ØÙØ ÓÖ ÔÔÐ ÁÒ ÓÖÑ Ø Ò ÓÖÑ Ð Ö ÔØ ÓÒ Å Ø Ó Á µ Ì Ë Ñ ÒØ Ï Ù Ñ ÒØ Ø ÙÖÖ ÒØ ÏÏÏ Ý Ú Ò Ò ÓÖÑ
BASE: Using Abstraction to Improve Fault Tolerance
 BASE: Using Abstraction to Improve Fault Tolerance Rodrigo Rodrigues Ý, Miguel Castro Ü, and Barbara Liskov Ý Ý MIT Laboratory for Computer Science 2 Technology Sq., Cambridge MA 239, USA Ü Microsoft Research
BASE: Using Abstraction to Improve Fault Tolerance Rodrigo Rodrigues Ý, Miguel Castro Ü, and Barbara Liskov Ý Ý MIT Laboratory for Computer Science 2 Technology Sq., Cambridge MA 239, USA Ü Microsoft Research
 ÜÔ Ö Ñ ÒØ ÓÒ Å Ó ÓÔ Ð ØÖÓÒ ÌÖ Ò ÔÓÖØ Ò Ö ÓÒ Æ ÒÓØÙ È º º Ì ÙÐØÝ Ó Ë Ò ÍÒ Ú Ö ØÝ Ó ÓÔ Ò Ò ¾¼¼¼ Â Ô Ö ÆÝ Ö Ö Ø Ä ÓÖ ØÓÖÝ Æ Ð Ó Ö ÁÒ Ø ØÙØ ÓÖ ØÖÓÒÓÑÝ È Ý Ò ÓÔ Ý ÜÔ Ö Ñ ÒØ ÓÒ Å Ó ÓÔ Ð ØÖÓÒ ÌÖ Ò ÔÓÖØ Ò Ö ÓÒ
ÜÔ Ö Ñ ÒØ ÓÒ Å Ó ÓÔ Ð ØÖÓÒ ÌÖ Ò ÔÓÖØ Ò Ö ÓÒ Æ ÒÓØÙ È º º Ì ÙÐØÝ Ó Ë Ò ÍÒ Ú Ö ØÝ Ó ÓÔ Ò Ò ¾¼¼¼ Â Ô Ö ÆÝ Ö Ö Ø Ä ÓÖ ØÓÖÝ Æ Ð Ó Ö ÁÒ Ø ØÙØ ÓÖ ØÖÓÒÓÑÝ È Ý Ò ÓÔ Ý ÜÔ Ö Ñ ÒØ ÓÒ Å Ó ÓÔ Ð ØÖÓÒ ÌÖ Ò ÔÓÖØ Ò Ö ÓÒ
 Ì Ö Ø ÅÝÈÓÐ È Ý Ç Ý Ý ÁÒ ØÝØÙØ ÞÝ Ö Ò ÏÝ ÓÙÖÒ ¾  ÒÙ Öݾ¼¼¾ ÍÒ Û Ö ÝØ ØÅ Ó ÃÓÔ ÖÒ ¹ÈÓÐ Ò Ø ÓÒ Ú ÒØÙÖÓÙ ÓÙÖÒ Ý Ó Ý Ý»Ó»ÒÓÙÒ ÔÐ Ý µ ÐÓÒ Ò Ú ÒØ ÙÐÓÖ ¹ÇÊÁ ÁÆÄ Ø ½ Ø ÒØ Ú Ä Ø Ò ÖÓÑ Ö Ç Ù Ì Æ ÏÇ ÇÊ Ø ÓÒ ÖÝÓ
Ì Ö Ø ÅÝÈÓÐ È Ý Ç Ý Ý ÁÒ ØÝØÙØ ÞÝ Ö Ò ÏÝ ÓÙÖÒ ¾  ÒÙ Öݾ¼¼¾ ÍÒ Û Ö ÝØ ØÅ Ó ÃÓÔ ÖÒ ¹ÈÓÐ Ò Ø ÓÒ Ú ÒØÙÖÓÙ ÓÙÖÒ Ý Ó Ý Ý»Ó»ÒÓÙÒ ÔÐ Ý µ ÐÓÒ Ò Ú ÒØ ÙÐÓÖ ¹ÇÊÁ ÁÆÄ Ø ½ Ø ÒØ Ú Ä Ø Ò ÖÓÑ Ö Ç Ù Ì Æ ÏÇ ÇÊ Ø ÓÒ ÖÝÓ
Winter Blues: A SAD Stock Market Cycle. Mark Kamstra, Lisa Kramer, and Maurice Levi. Working Paper 2002-13 July 2002. Working Paper Series
 Winter Blues: A SAD Stock Market Cycle Mark Kamstra, Lisa Kramer, and Maurice Levi Working Paper 2002-13 July 2002 Working Paper Series Federal Reserve Bank of Atlanta Working Paper 2002-13 July 2002 Winter
Winter Blues: A SAD Stock Market Cycle Mark Kamstra, Lisa Kramer, and Maurice Levi Working Paper 2002-13 July 2002 Working Paper Series Federal Reserve Bank of Atlanta Working Paper 2002-13 July 2002 Winter
Lindeboom, Maarten; Portrait, France; van den Berg, Gerard. Working Paper, IFAU - Institute for Labour Market Policy Evaluation, No.
 econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Lindeboom,
econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Lindeboom,
 Ä Ò Ö Ò ÒØ ÖÓÔØ Ñ Þ Ø ÓÒÛ Ø ÔÔÐ Ø ÓÒ ÅÎ ½»ÅÅ ½ Å Ò ÑÙÑÓ Ø ÓÛÑÓ Ð Ò Ð ÓÖ Ø Ñ Ä ØÙÖ ½¼ ÒÒ¹ Ö Ø ËØÖ Ñ Ö ¾¼½ ¼ ¼¾ Ä ØÙÖ Ä Ò Ö Ò ÒØ ÖÓÔØ Ñ Þ Ø ÓÒÛ Ø ÔÔÐ Ø ÓÒ Å Ü ÑÙÑ ÓÛÑÓ Ð ÓÒ Ö ØÖ Ø Ø Ò Ò ØÛÓÖ Û Ø Ô Ô Ð Ò
Ä Ò Ö Ò ÒØ ÖÓÔØ Ñ Þ Ø ÓÒÛ Ø ÔÔÐ Ø ÓÒ ÅÎ ½»ÅÅ ½ Å Ò ÑÙÑÓ Ø ÓÛÑÓ Ð Ò Ð ÓÖ Ø Ñ Ä ØÙÖ ½¼ ÒÒ¹ Ö Ø ËØÖ Ñ Ö ¾¼½ ¼ ¼¾ Ä ØÙÖ Ä Ò Ö Ò ÒØ ÖÓÔØ Ñ Þ Ø ÓÒÛ Ø ÔÔÐ Ø ÓÒ Å Ü ÑÙÑ ÓÛÑÓ Ð ÓÒ Ö ØÖ Ø Ø Ò Ò ØÛÓÖ Û Ø Ô Ô Ð Ò
Labour Market Outcomes and Schooling in Canada: Has the Value of a High School Degree Changed over Time?
 99s-42 Labour Market Outcomes and Schooling in Canada: Has the Value of a High School Degree Changed over Time? Daniel Parent Série Scientifique Scientific Series Montréal Novembre 1999 CIRANO Le CIRANO
99s-42 Labour Market Outcomes and Schooling in Canada: Has the Value of a High School Degree Changed over Time? Daniel Parent Série Scientifique Scientific Series Montréal Novembre 1999 CIRANO Le CIRANO
 ÆÓÚº ¾¼¼ ÎÓк½ ÆÓº ÔÔºß Âº ÓÑÔÙغ ˺ ² ÌÒÓк ½ ÊйØÑ ÊÝ ØÒ ÊÒÖÒ Ó ÎÓÐÙÑ ÐÔÔÒ Ò ÅÐ Î ÙÐÞØÓÒ ÀÆ Ï µ ÀÍ Ï µ Ç ÀÙÂÙÒ µ Ò ÈÆ ÉÙÒËÒ µ Ì ËØØ ÃÝ Ä Ç ² Ò ÍÒÚÖ ØÝ ÀÒÞÓÙ ½¼¼¾ Ⱥʺ Ò ØÖØ ¹ÑÐ ÒÛ ÙÛ Ó ÔÒºÞÙºÙºÒ ÊÚ ÂÙÒ
ÆÓÚº ¾¼¼ ÎÓк½ ÆÓº ÔÔºß Âº ÓÑÔÙغ ˺ ² ÌÒÓк ½ ÊйØÑ ÊÝ ØÒ ÊÒÖÒ Ó ÎÓÐÙÑ ÐÔÔÒ Ò ÅÐ Î ÙÐÞØÓÒ ÀÆ Ï µ ÀÍ Ï µ Ç ÀÙÂÙÒ µ Ò ÈÆ ÉÙÒËÒ µ Ì ËØØ ÃÝ Ä Ç ² Ò ÍÒÚÖ ØÝ ÀÒÞÓÙ ½¼¼¾ Ⱥʺ Ò ØÖØ ¹ÑÐ ÒÛ ÙÛ Ó ÔÒºÞÙºÙºÒ ÊÚ ÂÙÒ
 Ë Á ÆÌÁ Á ÁËËÍ Ë Â Æ Í ÇË ÍÆÁÎ ÊËÁÌ ÁÆ ËÌÇ ÀÇÏ Å ÌÀ Å ÌÁ Ë Î ¾¼½¼ Ë ÒØ ØÓÖ ÙÖ Ý ÈÇÎËÌ ÆÃÇ ÈÖÓÓ Ö Ö ÍÖ ÞÙÐ Ê Ç ÇÏËÃ ÓÑÔÙØ Ö ÌÝÔ ØØ Ò Ò Å Ò ¹ÙÔ ÍÖ ÞÙÐ Ê Ç ÇÏËÃ Ö Ô Ð ÈÖÓ Ø Ó ÓÚ Ö Ë ÛÓÑ Ö Ë ÇÏËÃÁ ÁË Æ ¹ ¹
Ë Á ÆÌÁ Á ÁËËÍ Ë Â Æ Í ÇË ÍÆÁÎ ÊËÁÌ ÁÆ ËÌÇ ÀÇÏ Å ÌÀ Å ÌÁ Ë Î ¾¼½¼ Ë ÒØ ØÓÖ ÙÖ Ý ÈÇÎËÌ ÆÃÇ ÈÖÓÓ Ö Ö ÍÖ ÞÙÐ Ê Ç ÇÏËÃ ÓÑÔÙØ Ö ÌÝÔ ØØ Ò Ò Å Ò ¹ÙÔ ÍÖ ÞÙÐ Ê Ç ÇÏËÃ Ö Ô Ð ÈÖÓ Ø Ó ÓÚ Ö Ë ÛÓÑ Ö Ë ÇÏËÃÁ ÁË Æ ¹ ¹
 ÈÙ Ð Ø ÓÒ ¾¼¼¼ ÖØ Ð Ò ÁÒØ ÖÒ Ø ÓÒ Ð ÂÓÙÖÒ Ð ½º º Ñ º Â Ò º ÃÖÞÝ Þ Âº È Ò Ð Èº ÃÓÞ ÐÓÛ Èº Ë ÒÓÛ Ïº Ï Ð ÖÞ È Ø ÓÑÓÖÔ ÓÐÓ Ý Ó ÈÓ ØØÖ ÙÑ Ø Ò Ò ËÔ Ò Ð ÓÖ Ó Ê Ø Ò Ê Ð Ø ÓÒ ØÓ ÅÊ «Ù ÓÒ ÁÑ Ò ÅÓк È Ý º Ê Ôº ¾
ÈÙ Ð Ø ÓÒ ¾¼¼¼ ÖØ Ð Ò ÁÒØ ÖÒ Ø ÓÒ Ð ÂÓÙÖÒ Ð ½º º Ñ º Â Ò º ÃÖÞÝ Þ Âº È Ò Ð Èº ÃÓÞ ÐÓÛ Èº Ë ÒÓÛ Ïº Ï Ð ÖÞ È Ø ÓÑÓÖÔ ÓÐÓ Ý Ó ÈÓ ØØÖ ÙÑ Ø Ò Ò ËÔ Ò Ð ÓÖ Ó Ê Ø Ò Ê Ð Ø ÓÒ ØÓ ÅÊ «Ù ÓÒ ÁÑ Ò ÅÓк È Ý º Ê Ôº ¾
 Ì ÓÑ ØÖÝÓ Ø ÛÓÖ ÔÖÓ Ð Ñ ½ ÁÒØÖÓ ÙØ ÓÒ Å ÖØ Òʺ Ö ÓÒ Ô Ò ÓÒÑÓ Ø ÓÑ Ø Ö ³Ð Ú ß ÓÖÑ ÒÝ ØÖ Ñ Ò Ò ÔÔ Ö ÒØÐÝ Ö Ò Ö ÓÒ Ì ØÙ ÝÓ ÓÒÔÖÓ Ð Ñ Ò ÖÓÙÔØ ÓÖÝ Ù ØØ Ø Ó ÒÓØ Ñ¹ Ó Ñ Ø Ñ Ø Ò ÖØ ÓÖ Ö Ó ÖÓÙÔØ ÓÖÝ Ò ÐÓ Ó Ò Û
Ì ÓÑ ØÖÝÓ Ø ÛÓÖ ÔÖÓ Ð Ñ ½ ÁÒØÖÓ ÙØ ÓÒ Å ÖØ Òʺ Ö ÓÒ Ô Ò ÓÒÑÓ Ø ÓÑ Ø Ö ³Ð Ú ß ÓÖÑ ÒÝ ØÖ Ñ Ò Ò ÔÔ Ö ÒØÐÝ Ö Ò Ö ÓÒ Ì ØÙ ÝÓ ÓÒÔÖÓ Ð Ñ Ò ÖÓÙÔØ ÓÖÝ Ù ØØ Ø Ó ÒÓØ Ñ¹ Ó Ñ Ø Ñ Ø Ò ÖØ ÓÖ Ö Ó ÖÓÙÔØ ÓÖÝ Ò ÐÓ Ó Ò Û
 ÔØÖ ÑÓÐ ÓÖ Ò Ö Ò Ø Ð «Ø Ó ØÐ Ò ØÝ ÙÖÖÒØ ÁÒ ÔØÖ ¾ Ø ÝÒÑ Ó Ø ÑÐÐ ÔÖØÙÖØÓÒ Ó ØØ ÓÒ ØÒ Ò ØÝ ÐÓÒ ÓÖ ÙÖÖÒØ ÓÒ ÐÓÔÒ ÓØØÓÑ Ò ØÙº ÐØÓÙ Ø ÑÓÐ ÔÖØ ÓÖÑ ÛØ Ø Ô Ò Ø ÐÓÒ ÓÖ Ô Ó Ø ÓÖßÓÒÒØ Ò Ö ÑÓÐ ØØ ÒÐÙ Ø «Ø Ó Ø ØÐ ÙÖÖÒØ
ÔØÖ ÑÓÐ ÓÖ Ò Ö Ò Ø Ð «Ø Ó ØÐ Ò ØÝ ÙÖÖÒØ ÁÒ ÔØÖ ¾ Ø ÝÒÑ Ó Ø ÑÐÐ ÔÖØÙÖØÓÒ Ó ØØ ÓÒ ØÒ Ò ØÝ ÐÓÒ ÓÖ ÙÖÖÒØ ÓÒ ÐÓÔÒ ÓØØÓÑ Ò ØÙº ÐØÓÙ Ø ÑÓÐ ÔÖØ ÓÖÑ ÛØ Ø Ô Ò Ø ÐÓÒ ÓÖ Ô Ó Ø ÓÖßÓÒÒØ Ò Ö ÑÓÐ ØØ ÒÐÙ Ø «Ø Ó Ø ØÐ ÙÖÖÒØ
Numerology at Home - A Review of Some Related Literature
 H. Knaf, P. Lang, S. Zeiser Diagnosis aiding in Regulation Thermography using Fuzzy Logic Berichte des Fraunhofer ITWM, Nr. 57 (2003) Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM 2003
H. Knaf, P. Lang, S. Zeiser Diagnosis aiding in Regulation Thermography using Fuzzy Logic Berichte des Fraunhofer ITWM, Nr. 57 (2003) Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM 2003
 ÌÆ ÄÁÁÄÁÌ ÇÊ ÆÎÁÊÇÆÅÆÌÄ ÁÆÌË ÏÀÌ ÇÍ Ë ÁË ÏÀÌ ÇÍ Ì ÑÑ ÀÙØÒ ÓÒ ÃÐ ÚÒ ³Ø ÎÐ ÔØÑÒØ Ó ÓÒÓÑ ÍÒÚ ØÝ Ó ÅÒ ÅÝ ¾¼¼¾ ØØ Ì Ù Ó ÛÓ ÓÙÐ ÐÐ Ó Ñ Ò ÓÑ ÒÚÓÒÑÒØÐ ÒØ Ó ÙÒÑÒØÐ ÑÔÓØÒ ØÓ ÔÓÐÝ Ñ º ÏÒ Ñ ÒÙÔØ Ý Ò ÒÚÓÒÑÒØÐ ÒØ ÙÒØ
ÌÆ ÄÁÁÄÁÌ ÇÊ ÆÎÁÊÇÆÅÆÌÄ ÁÆÌË ÏÀÌ ÇÍ Ë ÁË ÏÀÌ ÇÍ Ì ÑÑ ÀÙØÒ ÓÒ ÃÐ ÚÒ ³Ø ÎÐ ÔØÑÒØ Ó ÓÒÓÑ ÍÒÚ ØÝ Ó ÅÒ ÅÝ ¾¼¼¾ ØØ Ì Ù Ó ÛÓ ÓÙÐ ÐÐ Ó Ñ Ò ÓÑ ÒÚÓÒÑÒØÐ ÒØ Ó ÙÒÑÒØÐ ÑÔÓØÒ ØÓ ÔÓÐÝ Ñ º ÏÒ Ñ ÒÙÔØ Ý Ò ÒÚÓÒÑÒØÐ ÒØ ÙÒØ
Verification Task xuml Model. xuml Query. Decomposition Abstraction Symmetry Reduction. User driven State Space Reduction. Subtask Reduced.
 ÁÒØÖØ ËØØ ËÔ ÊÙØÓÒ ÓÖ ÅÓÐ Ò ÜÙØÐ ÇعÓÖÒØ ËÓØÛÖ ËÝ ØÑ Ò Ò ÂÑ º ÖÓÛÒ Ôغ Ó ÓÑÔÙØÖ ËÒ ÍÒÚº Ó ÌÜ Ø Ù ØÒ Ù ØÒ Ì ½¾ ÍË ÑÐ Ü ÖÓÛÒ ºÙØÜ ºÙ Ü ½ ½¾µ ½¹ ØÖغ Ì ÔÔÖ ÔÖ ÒØ ÒÖÐ ÖÑÛÓÖ ÓÖ ÒØÖØ ØØ Ô ÖÙØÓÒ Ò ÑÓÐ Ò ÜÙØÐ
ÁÒØÖØ ËØØ ËÔ ÊÙØÓÒ ÓÖ ÅÓÐ Ò ÜÙØÐ ÇعÓÖÒØ ËÓØÛÖ ËÝ ØÑ Ò Ò ÂÑ º ÖÓÛÒ Ôغ Ó ÓÑÔÙØÖ ËÒ ÍÒÚº Ó ÌÜ Ø Ù ØÒ Ù ØÒ Ì ½¾ ÍË ÑÐ Ü ÖÓÛÒ ºÙØÜ ºÙ Ü ½ ½¾µ ½¹ ØÖغ Ì ÔÔÖ ÔÖ ÒØ ÒÖÐ ÖÑÛÓÖ ÓÖ ÒØÖØ ØØ Ô ÖÙØÓÒ Ò ÑÓÐ Ò ÜÙØÐ
 ËØØ Ø Ó ÆØÙÖÐ ÁÑ Ò ÅÓÐ Ý ÂÒÒ ÀÙÒ ËºÅº ÖÓÛÒ ÍÒÚÖ ØÝ ½ ˺ź ÍÒÚÖ ØÝ ÓÁÓÛ ½ ˺ź ÆÒ ÍÒÚÖ ØÝ ½¾ ˺º ÆÒ ÍÒÚÖ ØÝ ½ Ì ËÙÑØØ Ò ÔÖØÐ ÙÐ ÐÐÑÒØ Ó Ø ÖÕÙÖÑÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó ÈÐÓ ÓÔÝ Ò Ø Ú ÓÒ Ó ÔÔÐ ÅØÑØ Ø ÖÓÛÒ ÍÒÚÖ
ËØØ Ø Ó ÆØÙÖÐ ÁÑ Ò ÅÓÐ Ý ÂÒÒ ÀÙÒ ËºÅº ÖÓÛÒ ÍÒÚÖ ØÝ ½ ˺ź ÍÒÚÖ ØÝ ÓÁÓÛ ½ ˺ź ÆÒ ÍÒÚÖ ØÝ ½¾ ˺º ÆÒ ÍÒÚÖ ØÝ ½ Ì ËÙÑØØ Ò ÔÖØÐ ÙÐ ÐÐÑÒØ Ó Ø ÖÕÙÖÑÒØ ÓÖ Ø Ö Ó ÓØÓÖ Ó ÈÐÓ ÓÔÝ Ò Ø Ú ÓÒ Ó ÔÔÐ ÅØÑØ Ø ÖÓÛÒ ÍÒÚÖ
 ÒÓ¹ØÒ¹ÒÔÖ ÒÖÝÔØÓÒ ÀÓÛ ØÓ ÜÔÐÓØ ÒÓÒ ÓÖ ÖÙÒÒÝ Ò ÔÐÒØÜØ ÓÖ ÆÒØ ÖÝÔØÓÖÔÝ ½ ÅÖ ÐÐÖ ½ Ò ÈÐÐÔ ÊÓÛÝ ¾ Ôغ Ó ÓÑÔÙØÖ ËÒ ² ÒÒÖÒ ÍÒÚÖ ØÝ Ó ÐÓÖÒ Ø ËÒ Ó ¼¼ ÐÑÒ ÖÚ Ä ÂÓÐÐ ¾¼ ÍË ¹ÅÐ ÑÖ ºÙ ºÙ ÍÊÄ ÛÛÛ¹ ºÙ ºÙ»Ù Ö»ÑÖ ¾ Ôغ
ÒÓ¹ØÒ¹ÒÔÖ ÒÖÝÔØÓÒ ÀÓÛ ØÓ ÜÔÐÓØ ÒÓÒ ÓÖ ÖÙÒÒÝ Ò ÔÐÒØÜØ ÓÖ ÆÒØ ÖÝÔØÓÖÔÝ ½ ÅÖ ÐÐÖ ½ Ò ÈÐÐÔ ÊÓÛÝ ¾ Ôغ Ó ÓÑÔÙØÖ ËÒ ² ÒÒÖÒ ÍÒÚÖ ØÝ Ó ÐÓÖÒ Ø ËÒ Ó ¼¼ ÐÑÒ ÖÚ Ä ÂÓÐÐ ¾¼ ÍË ¹ÅÐ ÑÖ ºÙ ºÙ ÍÊÄ ÛÛÛ¹ ºÙ ºÙ»Ù Ö»ÑÖ ¾ Ôغ
 Å ÙÖÒ Ø ÙÖÝ Ó Ë ÓÒÞÖ ÓÖ Ï Í ÒÐÝ ØØÒ ÖÒØ Ñ ÅÓ Ö ÅÝÖ ËÔÐÓÔÓÙÐÓÙ ÂÑ ÏÐØ Ö ÀÙÑÓÐعÍÒÚÖ ØÝ ÖÐÒ ÁÒ Øº Ó ÈÓÝ Ò ÁÒÓÖÑØ ÖÒØÙغٹÖÐÒº ÈÙÐ ÍÒÚÖ ØÝ Ôغ Ó ÓÑÔÙØÖ ËÒ ÑÓ Ö ºÔÙк٠ÀÙÑÓÐعÍÒÚÖ ØÝ ÖÐÒ º Ó ÓÒÓÑ ÁÒ Øº Ó ÁÒÓÖÑØÓÒ
Å ÙÖÒ Ø ÙÖÝ Ó Ë ÓÒÞÖ ÓÖ Ï Í ÒÐÝ ØØÒ ÖÒØ Ñ ÅÓ Ö ÅÝÖ ËÔÐÓÔÓÙÐÓÙ ÂÑ ÏÐØ Ö ÀÙÑÓÐعÍÒÚÖ ØÝ ÖÐÒ ÁÒ Øº Ó ÈÓÝ Ò ÁÒÓÖÑØ ÖÒØÙغٹÖÐÒº ÈÙÐ ÍÒÚÖ ØÝ Ôغ Ó ÓÑÔÙØÖ ËÒ ÑÓ Ö ºÔÙк٠ÀÙÑÓÐعÍÒÚÖ ØÝ ÖÐÒ º Ó ÓÒÓÑ ÁÒ Øº Ó ÁÒÓÖÑØÓÒ
<-337. true, (1114) 2 ), (168) 2 ) f(y i
 ÑÖØ Ô ÙØÓÖÖ Ú ÌÖ ÅÓÐ ÓÖ ÌѹËÖ ÒÐÝ º Å ºÅº ÖÒ Ò º ÀÖÑÒ ½ ÁÒØÖÓÙØÓÒ Ì ÒÐÝ Ò ÑÓÐÒ Ó Øѹ Ö Ø Ò ÑÔÓÖØÒØ Ö Ó Ö Ö ÓÖ ÑÒÝ ÓÑÑÙÒØ º ÁÒ Ø ÔÔÖ ÓÙÖ ÓÐ ØÓ ÒØÝ ÑÓÐ ÓÖ ÓÒØÒÙÓÙ ¹ ÚÐÙ Øѹ Ö Ø ØØ Ö Ù ÙÐ ÓÖ Ø ÑÒÒ Ò ØØ ØÝ
ÑÖØ Ô ÙØÓÖÖ Ú ÌÖ ÅÓÐ ÓÖ ÌѹËÖ ÒÐÝ º Å ºÅº ÖÒ Ò º ÀÖÑÒ ½ ÁÒØÖÓÙØÓÒ Ì ÒÐÝ Ò ÑÓÐÒ Ó Øѹ Ö Ø Ò ÑÔÓÖØÒØ Ö Ó Ö Ö ÓÖ ÑÒÝ ÓÑÑÙÒØ º ÁÒ Ø ÔÔÖ ÓÙÖ ÓÐ ØÓ ÒØÝ ÑÓÐ ÓÖ ÓÒØÒÙÓÙ ¹ ÚÐÙ Øѹ Ö Ø ØØ Ö Ù ÙÐ ÓÖ Ø ÑÒÒ Ò ØØ ØÝ
 ÄÆ Ë¹È¾½» ¹ ½ ÊÆ»ËÈË ¹ ËÈË»È ½ º½ ÆÓÚ Ñ Ö ½ ½ Á ÆÇ ½ ÈÖ Ð Ñ Ò ÖÝ Ì Ò Ð Ò ² Ó Ø Ø Ñ Ø Ì Á ÊÍË ² ÆÇ ÓÐÐ ÓÖ Ø ÓÒ ÁÒ Ò ½ Ð ÑÓ Ö Ò Ðг Ö ÙÒ Ø ØØÓ ÙÒ Ù ØÓ Ô Ù ÓÔÖ Ð Ø ÖÑ Ò Ö ºººµÐ Ö ÓÒ ÙÒ Ô ÒÓ Ò Ö ÓÖ ÙÒ ÓÒ Ó
ÄÆ Ë¹È¾½» ¹ ½ ÊÆ»ËÈË ¹ ËÈË»È ½ º½ ÆÓÚ Ñ Ö ½ ½ Á ÆÇ ½ ÈÖ Ð Ñ Ò ÖÝ Ì Ò Ð Ò ² Ó Ø Ø Ñ Ø Ì Á ÊÍË ² ÆÇ ÓÐÐ ÓÖ Ø ÓÒ ÁÒ Ò ½ Ð ÑÓ Ö Ò Ðг Ö ÙÒ Ø ØØÓ ÙÒ Ù ØÓ Ô Ù ÓÔÖ Ð Ø ÖÑ Ò Ö ºººµÐ Ö ÓÒ ÙÒ Ô ÒÓ Ò Ö ÓÖ ÙÒ ÓÒ Ó
Working Paper Evaluating VaR Forecasts under Stress The German Experience
 econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Jaschke,
econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Jaschke,
 Ñ ÈÓ ØÓÒ ÅÓÒØÓÖ ÓÖ Ø Ì Ð ÐÖØÓÖ ÓÑÔÐÜ º ÅÒ ËÐÝ ÖÒ Åº ÏÒØ Ý ÀÑÙÖ ÖÑÒÝ ÑÖ ¾¼¼¼ ØÖØ Ò ÓÚÖÚÛ ÓÒ Ñ ÔÓ ØÓÒ ÑÓÒØÓÖÒ Ø Ø Ì Ð ÐÒÖ ÓÐÐÖ ÚÒº ÔÖÒÔÐ Ò ØÒÓÐÓÝ ØÐ Ó ÈÅ ÔÙÔ³ Ò ØÖ Ö¹ÓÙØ ÐØÖÓÒ Ö Ù º ÜÔÖÒ ÛØ «ÖÒØ ØÝÔ Ó ÈÅ
Ñ ÈÓ ØÓÒ ÅÓÒØÓÖ ÓÖ Ø Ì Ð ÐÖØÓÖ ÓÑÔÐÜ º ÅÒ ËÐÝ ÖÒ Åº ÏÒØ Ý ÀÑÙÖ ÖÑÒÝ ÑÖ ¾¼¼¼ ØÖØ Ò ÓÚÖÚÛ ÓÒ Ñ ÔÓ ØÓÒ ÑÓÒØÓÖÒ Ø Ø Ì Ð ÐÒÖ ÓÐÐÖ ÚÒº ÔÖÒÔÐ Ò ØÒÓÐÓÝ ØÐ Ó ÈÅ ÔÙÔ³ Ò ØÖ Ö¹ÓÙØ ÐØÖÓÒ Ö Ù º ÜÔÖÒ ÛØ «ÖÒØ ØÝÔ Ó ÈÅ
Working Paper Determinants of Inter-Trade Durations and Hazard Rates Using Proportional Hazard ARMA Model
 econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Gerhard,
econstor www.econstor.eu Der Open-Access-Publikationsserver der ZBW Leibniz-Informationszentrum Wirtschaft The Open Access Publication Server of the ZBW Leibniz Information Centre for Economics Gerhard,
NOC ERS. decision engine. mining engine. intrusion. customer network. pre-filtering. customer. confirmed. resolution info. alarm.
 Ø ÅÒÒ ÒÐÝ Ó ÊÌÁ ÐÖÑ ËØÒÓ ÅÒÒÖ ÅÖÚÒ Ö ØÒ Ò Ò ÖÐ ÃØ ÀÖÑÞ ÁÒØÖÒØÓÒÐ Ù Ò ÅÒ ÓÖÔÓÖØÓÒ ½ ÄÙÖ Ø ÓÙÖØ Ê Ö ÌÖÒÐ ÈÖ Æ ¾½ ØÒÓ ÑÖÚÒ ÞÖÐ ÖÑÞÙ ºÑºÓÑ ØÖØ Áų ÑÖÒÝ Ê ÔÓÒ ËÖÚ ÔÖÓÚ ÖйØÑ ÒØÖÙ ÓÒ ØØÓÒ ÊÌÁµ ÖÚ ØÖÓÙ Ø ÁÒØÖÒØ
Ø ÅÒÒ ÒÐÝ Ó ÊÌÁ ÐÖÑ ËØÒÓ ÅÒÒÖ ÅÖÚÒ Ö ØÒ Ò Ò ÖÐ ÃØ ÀÖÑÞ ÁÒØÖÒØÓÒÐ Ù Ò ÅÒ ÓÖÔÓÖØÓÒ ½ ÄÙÖ Ø ÓÙÖØ Ê Ö ÌÖÒÐ ÈÖ Æ ¾½ ØÒÓ ÑÖÚÒ ÞÖÐ ÖÑÞÙ ºÑºÓÑ ØÖØ Áų ÑÖÒÝ Ê ÔÓÒ ËÖÚ ÔÖÓÚ ÖйØÑ ÒØÖÙ ÓÒ ØØÓÒ ÊÌÁµ ÖÚ ØÖÓÙ Ø ÁÒØÖÒØ
 ËÐ ÓÒÓÑ ËÓÔ ÓÒÓÑ Ò ÌÒÐ Ò Ò ÖÐ Ê ÖÚ ÈÝÑÒØ ÈÖÓ Ò ÊÓÖØ Åº Ñ ÈÙРϺ ÙÖ Ý Ò ÊÓÒ º ËÐ Þ ÓÖ Ó ÓÚÖÒÓÖ Ó Ø ÖÐ Ê ÖÚ ËÝ ØÑ Ï ÒØÓÒ ¾¼½ ÍË Ý ÖÐ Ê ÖÚ Ò Ó ÐÚÐÒ ÐÚÐÒ ÇÓ ½¼½ ÍË Þ ÔÖØÑÒØ Ó ÓÒÓÑ Ê ÍÒÚÖ ØÝ ÀÓÙ ØÓÒ ÌÜ ¼¼ ÍË
ËÐ ÓÒÓÑ ËÓÔ ÓÒÓÑ Ò ÌÒÐ Ò Ò ÖÐ Ê ÖÚ ÈÝÑÒØ ÈÖÓ Ò ÊÓÖØ Åº Ñ ÈÙРϺ ÙÖ Ý Ò ÊÓÒ º ËÐ Þ ÓÖ Ó ÓÚÖÒÓÖ Ó Ø ÖÐ Ê ÖÚ ËÝ ØÑ Ï ÒØÓÒ ¾¼½ ÍË Ý ÖÐ Ê ÖÚ Ò Ó ÐÚÐÒ ÐÚÐÒ ÇÓ ½¼½ ÍË Þ ÔÖØÑÒØ Ó ÓÒÓÑ Ê ÍÒÚÖ ØÝ ÀÓÙ ØÓÒ ÌÜ ¼¼ ÍË
Steer axis. Twist axis. rider upper body. y z p13. p10. p1 aero. p8 main p5. p12. p11. p14
 ÆÁÅÌÁÇÆ Ç ÌÀ Ëľ¼¼½ ÅÇÌÇÊÄ ÅÇÄ ËÑÓ ÚÒÐÓÙ Ò Ú ÂºÆº ÄÑÖ ÔÖØÑÒØ Ó ÐØÖÐ Ò ÐØÖÓÒ ÒÒÖÒ ÁÑÔÖÐ ÓÐÐ Ó ËÒ ÌÒÓÐÓÝ Ò ÅÒ ÜØÓÒ ÊÓ ÄÓÒÓÒ ËÏ ¾Ì Íú ¹ÑкÐÑÖººÙ Û Ô ØØÔ»»ÛÛÛººººÙ»ÓÒØÖÓлÑÓØÓÖÝÐ ËÙÑÑÖÝ Ì Ø Ó Ò ÒÑØÓÖ ØÓ ÒÖØ
ÆÁÅÌÁÇÆ Ç ÌÀ Ëľ¼¼½ ÅÇÌÇÊÄ ÅÇÄ ËÑÓ ÚÒÐÓÙ Ò Ú ÂºÆº ÄÑÖ ÔÖØÑÒØ Ó ÐØÖÐ Ò ÐØÖÓÒ ÒÒÖÒ ÁÑÔÖÐ ÓÐÐ Ó ËÒ ÌÒÓÐÓÝ Ò ÅÒ ÜØÓÒ ÊÓ ÄÓÒÓÒ ËÏ ¾Ì Íú ¹ÑкÐÑÖººÙ Û Ô ØØÔ»»ÛÛÛººººÙ»ÓÒØÖÓлÑÓØÓÖÝÐ ËÙÑÑÖÝ Ì Ø Ó Ò ÒÑØÓÖ ØÓ ÒÖØ
 Ò¹ÒÛØ ÖØÖ Ø Ó ÌÒ ÚÐÒ ÈÓØÓÓ Å Åº ÀÝØ ËÒÓÖ ÅÑÖ Á ǹÀÝÙÒ ÃÛÓÒ ÈÒ ËÒÓÖ ÅÑÖ Á ÈÙÐ ËÓØÖÐ ÅÑÖ Á ÂÓ º ÑÔÐÐ ÐÐÓÛ Á º º ËÐ ÐÐÓÛ Á Ò ÅÐÚÒ º Ì ÐÐÓÛ Á ØÖغ Ì ÖÕÙÒÝ¹Ö ÔÓÒ ÖØÖ Ø Ó ÚÐÒ ÔÓØÓÓ È µ ÛØ ØÒ ÑÙÐØÔÐØÓÒ ÐÝÖ Ö
Ò¹ÒÛØ ÖØÖ Ø Ó ÌÒ ÚÐÒ ÈÓØÓÓ Å Åº ÀÝØ ËÒÓÖ ÅÑÖ Á ǹÀÝÙÒ ÃÛÓÒ ÈÒ ËÒÓÖ ÅÑÖ Á ÈÙÐ ËÓØÖÐ ÅÑÖ Á ÂÓ º ÑÔÐÐ ÐÐÓÛ Á º º ËÐ ÐÐÓÛ Á Ò ÅÐÚÒ º Ì ÐÐÓÛ Á ØÖغ Ì ÖÕÙÒÝ¹Ö ÔÓÒ ÖØÖ Ø Ó ÚÐÒ ÔÓØÓÓ È µ ÛØ ØÒ ÑÙÐØÔÐØÓÒ ÐÝÖ Ö
 ÉÙÒØ ØÓÒ Ó ÉÙÐØØÚ Ø Í Ò ÇÖÖ ÈÖÓØ ÅÓÐ ÛØ Ò ÔÔÐØÓÒ ØÓ Ù Ò ËÙÖÚÝ Ò Ø ÖÑÒ ËÖÚ ËØÓÖ Ü Ý ÍÐÖ Ã Ö Ò ÐÜÒÖ ËÔØÞ ÆÓÚÑÖ ¾¼¼¼ ØÖØ Ì ÔÔÖ Ñ Ø ÔÖÓÚÒ Ù Ò ÙÖÚÝ ÒÐÝ Ø ÛØ ÑÔÐ ÓÒÓÑع Ö ØÓÓÐ ØÓ ÕÙÒØÝ ÕÙÐØØÚ ÙÖÚÝ Øº Ï ÜØÒ Ø
ÉÙÒØ ØÓÒ Ó ÉÙÐØØÚ Ø Í Ò ÇÖÖ ÈÖÓØ ÅÓÐ ÛØ Ò ÔÔÐØÓÒ ØÓ Ù Ò ËÙÖÚÝ Ò Ø ÖÑÒ ËÖÚ ËØÓÖ Ü Ý ÍÐÖ Ã Ö Ò ÐÜÒÖ ËÔØÞ ÆÓÚÑÖ ¾¼¼¼ ØÖØ Ì ÔÔÖ Ñ Ø ÔÖÓÚÒ Ù Ò ÙÖÚÝ ÒÐÝ Ø ÛØ ÑÔÐ ÓÒÓÑع Ö ØÓÓÐ ØÓ ÕÙÒØÝ ÕÙÐØØÚ ÙÖÚÝ Øº Ï ÜØÒ Ø
import on display extract edges write
 ÌÖ¹ÑÒ ÓÒÐ ÊÇÁ Ò ÖÒ ÈÌ ÂÓÙÒ ÅÝĐÒÒ Ý ÅÖØØ ÂÙÓÐ Ý Ò ÍÐÐ ÊÙÓØ ÐÒÒ Þ Ý ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ ÍÒÚÖ ØÝ Ó ÌÑÔÖ ÈºÇºÓÜ ¼ Áƹ ½¼½ ÌÑÔÖ ÒÐÒ ¹ÑÐ Ñ ºÙغ Þ ÌÙÖÙ ÈÌ ÒØÖ ÍÒÚÖ ØÝ Ó ÌÙÖÙ ÒÐÒ ØÖØ Ñ¹ÙØÓÑØ Ý ØÑ ÓÖ ØÖÑÒÒ ÚÓÐÙÑ
ÌÖ¹ÑÒ ÓÒÐ ÊÇÁ Ò ÖÒ ÈÌ ÂÓÙÒ ÅÝĐÒÒ Ý ÅÖØØ ÂÙÓÐ Ý Ò ÍÐÐ ÊÙÓØ ÐÒÒ Þ Ý ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ ÍÒÚÖ ØÝ Ó ÌÑÔÖ ÈºÇºÓÜ ¼ Áƹ ½¼½ ÌÑÔÖ ÒÐÒ ¹ÑÐ Ñ ºÙغ Þ ÌÙÖÙ ÈÌ ÒØÖ ÍÒÚÖ ØÝ Ó ÌÙÖÙ ÒÐÒ ØÖØ Ñ¹ÙØÓÑØ Ý ØÑ ÓÖ ØÖÑÒÒ ÚÓÐÙÑ
Unemployment Insurance and Subsequent Job Duration: Job Matching vs Unobserved Heterogeneity
 2001s-21 Unemployment Insurance and Subsequent Job Duration: Job Matching vs Unobserved Heterogeneity Christian Belzil Série Scientifique Scientific Series Montréal Mars 2001 CIRANO Le CIRANO est un organisme
2001s-21 Unemployment Insurance and Subsequent Job Duration: Job Matching vs Unobserved Heterogeneity Christian Belzil Série Scientifique Scientific Series Montréal Mars 2001 CIRANO Le CIRANO est un organisme
 ÔÖÐÑÒÖÝ ÚÖ ÓÒ Ó Ø ÔÔÖ ÔÔÖ Ò ÚÒ Ò ÖÝÔØÓÐÓÝ ß ËÁÈÌ ³¼¼ ÄØÙÖ ÆÓØ Ò ÓÑÔÙØÖ ËÒÎÓк ̺ ÇÑÓØÓ º ËÔÖÒÖ¹ÎÖÐ ¾¼¼¼º Ì Ø ÙÐÐ ÚÖ ÓÒº ÙØÒØØ ÒÖÝÔØÓÒ ÐØÓÒ ÑÓÒ ÒÓØÓÒ Ò ÒÐÝ Ó Ø ÒÖ ÓÑÔÓ ØÓÒ ÔÖÑ ÅÖ ÐÐÖ ÒØÔ ÆÑÔÖÑÔÖ Ý ËÔØÑÖ
ÔÖÐÑÒÖÝ ÚÖ ÓÒ Ó Ø ÔÔÖ ÔÔÖ Ò ÚÒ Ò ÖÝÔØÓÐÓÝ ß ËÁÈÌ ³¼¼ ÄØÙÖ ÆÓØ Ò ÓÑÔÙØÖ ËÒÎÓк ̺ ÇÑÓØÓ º ËÔÖÒÖ¹ÎÖÐ ¾¼¼¼º Ì Ø ÙÐÐ ÚÖ ÓÒº ÙØÒØØ ÒÖÝÔØÓÒ ÐØÓÒ ÑÓÒ ÒÓØÓÒ Ò ÒÐÝ Ó Ø ÒÖ ÓÑÔÓ ØÓÒ ÔÖÑ ÅÖ ÐÐÖ ÒØÔ ÆÑÔÖÑÔÖ Ý ËÔØÑÖ
 ËÑÔйËÞ ÓÖÑÙÐ ÓÖ ÐÙ ØÖ ËÙÖÚÚÐ Ø Í Ò ÏØ ÄÓ¹ÖÒ ËØØ Ø ÊÓÒÐ º ÒÒÓÒ ÔÖØÑÒØ Ó Ó ØØ Ø Ò ÅÐ ÁÒÓÖÑØ ÍÒÚÖ ØÝ Ó Ï ÓÒ ÒßÅ ÓÒ ½ ƺ ÏÐÒÙØ ËØÖØ Å ÓÒ Ï ÓÒ Ò ÍºËºº ÑÐ ÖÓÒÐÓ ØØºÛ ºÙ Ò ÅРʺ ÃÓ ÓÖÓ ÔÖØÑÒØ Ó ËØØ Ø Ò Ó ØØ
ËÑÔйËÞ ÓÖÑÙÐ ÓÖ ÐÙ ØÖ ËÙÖÚÚÐ Ø Í Ò ÏØ ÄÓ¹ÖÒ ËØØ Ø ÊÓÒÐ º ÒÒÓÒ ÔÖØÑÒØ Ó Ó ØØ Ø Ò ÅÐ ÁÒÓÖÑØ ÍÒÚÖ ØÝ Ó Ï ÓÒ ÒßÅ ÓÒ ½ ƺ ÏÐÒÙØ ËØÖØ Å ÓÒ Ï ÓÒ Ò ÍºËºº ÑÐ ÖÓÒÐÓ ØØºÛ ºÙ Ò ÅРʺ ÃÓ ÓÖÓ ÔÖØÑÒØ Ó ËØØ Ø Ò Ó ØØ
 ÝÒÑ ØÖÙØÓÒ ÅÓÐ ÓÖ ÓÑØ ÄÓ Ø ÃÚÒ Êº Ù ÖÙØ ËÓÓÐ Ó Ù Ò ² ÈÙÐ ÈÓÐÝ ÆÚÐ ÈÓ ØÖÙØ ËÓÓÐ ÅÓÒØÖÝ ËØØÑÒØ Ó ÓÔ Ò ÔÙÖÔÓ ÄÓ Ø ÙÔÔÓÖØ ÓÖ ÑÔÓÙ ÛÖÖ ØÖØÓÒÐÐÝ ÖÐ ÓÒ ÐÖ ÐÒ¹ ÒÖ ØÖÙØÙÖ ÛØ ØÖÙ ÓÑÔÐ Ò ÑÓ Ø Ó Ø ØÖÙØÓÒº ÆÛ ÛÖ ØÒ
ÝÒÑ ØÖÙØÓÒ ÅÓÐ ÓÖ ÓÑØ ÄÓ Ø ÃÚÒ Êº Ù ÖÙØ ËÓÓÐ Ó Ù Ò ² ÈÙÐ ÈÓÐÝ ÆÚÐ ÈÓ ØÖÙØ ËÓÓÐ ÅÓÒØÖÝ ËØØÑÒØ Ó ÓÔ Ò ÔÙÖÔÓ ÄÓ Ø ÙÔÔÓÖØ ÓÖ ÑÔÓÙ ÛÖÖ ØÖØÓÒÐÐÝ ÖÐ ÓÒ ÐÖ ÐÒ¹ ÒÖ ØÖÙØÙÖ ÛØ ØÖÙ ÓÑÔÐ Ò ÑÓ Ø Ó Ø ØÖÙØÓÒº ÆÛ ÛÖ ØÒ
GEOMETRY AND TOPOLOGY OF MANIFOLDS BANACH CENTER PUBLICATIONS, VOLUME 76 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 2007
 GEOMETRY AND TOPOLOGY OF MANIFOLDS BANACH CENTER PUBLICATIONS, VOLUME 76 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 2007 ÈÊ Ø Ò Å Ø Ñ Ø Ð ÒØ ÖÓ Ø ÈÓÐ ÑÝÓ Ë Ò Ò Ð ÛÓ ÈÓÐ Ò Ì ÓÒ Ö Ò ÓÑ
GEOMETRY AND TOPOLOGY OF MANIFOLDS BANACH CENTER PUBLICATIONS, VOLUME 76 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 2007 ÈÊ Ø Ò Å Ø Ñ Ø Ð ÒØ ÖÓ Ø ÈÓÐ ÑÝÓ Ë Ò Ò Ð ÛÓ ÈÓÐ Ò Ì ÓÒ Ö Ò ÓÑ
0.2. Taxon 14 0.1 0.2. Taxon 15 0.1 0.2. Taxon 33 0.1 0.2. Taxon 34 0.1 0.2. Taxon 36 0.1 0.2. Taxon 40 0.1 0.2. Taxon 41 0.1 0.2. Taxon 42 0.1 0.
 Í Ò ËÑÓÓØÒ ØÓ ÊÓÒ ØÖÙØ Ø ÀÓÐÓÒ ÌÑÔÖØÙÖ Ò ÄÔÐÒ Ä ÀÓÐÑ ØÖĐÓÑ ÈÒÙ ÖĐ ØĐÓ ÒÈØÖ ÃÓ ØÒÒ ÊÓÐ ÆÚÒÐÒÒ ÁÒ ØØÙØ ÍÒÚÖ ØÝ Ó ÀÐ Ò ÀÐ Ò ÒÐÒ ÂÒ Ï ØÖĐÓÑ Ò ØØ ÃÓÖÓÐ Ý ÔÖØÑÒØ Ó ÓÐÓÝ Ò ËÝ ØÑØ ÍÒÚÖ ØÝ Ó ÀÐ Ò ÀÐ Ò ÒÐÒ ØÖØ ËÑÐÐ
Í Ò ËÑÓÓØÒ ØÓ ÊÓÒ ØÖÙØ Ø ÀÓÐÓÒ ÌÑÔÖØÙÖ Ò ÄÔÐÒ Ä ÀÓÐÑ ØÖĐÓÑ ÈÒÙ ÖĐ ØĐÓ ÒÈØÖ ÃÓ ØÒÒ ÊÓÐ ÆÚÒÐÒÒ ÁÒ ØØÙØ ÍÒÚÖ ØÝ Ó ÀÐ Ò ÀÐ Ò ÒÐÒ ÂÒ Ï ØÖĐÓÑ Ò ØØ ÃÓÖÓÐ Ý ÔÖØÑÒØ Ó ÓÐÓÝ Ò ËÝ ØÑØ ÍÒÚÖ ØÝ Ó ÀÐ Ò ÀÐ Ò ÒÐÒ ØÖØ ËÑÐÐ
 ÏÝ Ø ËØÓ ÅÖØ ÅÝ ÍÒÖÛØ ÆÛ Ò ÑÔÖÐ ÒÐÝ ÒÒ ËÖÒ ÒÒ ÔÖØÑÒØ ÃÐÐÓ ËÓÓÐ Ó ÅÒÑÒØ ÆÓÖØÛ ØÖÒ ÍÒÚÖ ØÝ ÆÓÚÑÖ ¾¼¼½ ÓÖÖ ÔÓÒÒ ÒÒ ËÖÒ ÒÒ ÔÖØÑÒØ ÃÐÐÓ ËÓÓÐ Ó ÅÒÑÒØ ÆÓÖØÛ ØÖÒ ÍÒÚÖ ØÝ ÔÓÒ µ ¹½ Ü µ ½¹½ ÑÐ ¹ ÖÒÒÛٺٺ Ì ÔÔÖ ÓÒ
ÏÝ Ø ËØÓ ÅÖØ ÅÝ ÍÒÖÛØ ÆÛ Ò ÑÔÖÐ ÒÐÝ ÒÒ ËÖÒ ÒÒ ÔÖØÑÒØ ÃÐÐÓ ËÓÓÐ Ó ÅÒÑÒØ ÆÓÖØÛ ØÖÒ ÍÒÚÖ ØÝ ÆÓÚÑÖ ¾¼¼½ ÓÖÖ ÔÓÒÒ ÒÒ ËÖÒ ÒÒ ÔÖØÑÒØ ÃÐÐÓ ËÓÓÐ Ó ÅÒÑÒØ ÆÓÖØÛ ØÖÒ ÍÒÚÖ ØÝ ÔÓÒ µ ¹½ Ü µ ½¹½ ÑÐ ¹ ÖÒÒÛٺٺ Ì ÔÔÖ ÓÒ
 Å ÙÖÒ ÓÙÒØÖÔÖØÝ ÖØ Ê ÖÓÑ ÊÒ ÙÖÒ Ê ÅÒÑÒØ ÏÒØÖØÙÖ ÁÒ ÙÖÒ ÖØ ËÙ ÖÓÙÔ ÒÒÐ Ê ÓÒØÖÓÐ ËÒÖÓ ÅÖÒÓ ÅÖ ¾¼¼¼ ØÖØ ÖØ Ò ÙÖÖ Ö ÜÔÓ ØÓ ÖØ Ö ÛÒ ÒØÖÒ ÒØÓ ÖÒ ÙÖÒ ÓÒØÖØ Ì ÔÖØÙÐÖ ÓÖÑ Ó ÖØ Ö Û ÓÑØÑ ÖÖÖ ØÓ ÙÖØÝ Ö Ù Ò ÑØÓÓÐÓÝ
Å ÙÖÒ ÓÙÒØÖÔÖØÝ ÖØ Ê ÖÓÑ ÊÒ ÙÖÒ Ê ÅÒÑÒØ ÏÒØÖØÙÖ ÁÒ ÙÖÒ ÖØ ËÙ ÖÓÙÔ ÒÒÐ Ê ÓÒØÖÓÐ ËÒÖÓ ÅÖÒÓ ÅÖ ¾¼¼¼ ØÖØ ÖØ Ò ÙÖÖ Ö ÜÔÓ ØÓ ÖØ Ö ÛÒ ÒØÖÒ ÒØÓ ÖÒ ÙÖÒ ÓÒØÖØ Ì ÔÖØÙÐÖ ÓÖÑ Ó ÖØ Ö Û ÓÑØÑ ÖÖÖ ØÓ ÙÖØÝ Ö Ù Ò ÑØÓÓÐÓÝ
Diskussionspapiere Discussion Papers
 Diskussionspapiere Discussion Papers Discussion Paper No. 231 Erosion of Monopoly Power due to the Emergence of Linux by Jürgen Bitzer Berlin, November 2000 Deutsches Institut für Wirtschaftsforschung,
Diskussionspapiere Discussion Papers Discussion Paper No. 231 Erosion of Monopoly Power due to the Emergence of Linux by Jürgen Bitzer Berlin, November 2000 Deutsches Institut für Wirtschaftsforschung,
Best Places to Find Information About Wine
 ÅÙÐعØÓÖ ÇÔØÓÒ ÈÖÒ ÈÙРĺ ÐÖ Ö Ø ÖØ ÇØÓÖ ½¾ ½ ÙÖÖÒØ ÖÚ ÓÒ ÂÙÒ ½ ¾¼¼¼ ÂÙÒ ½ ¾¼¼¼ ØÖØ ÅÙÐعØÓÖ ÑÓÐ ÔÖÓÚ ÓÒ ÖÐ ÜÐØÝ Ò ÖÔÖ ÒØÒ Ø Ý¹ ÒÑ ÚÓÖ Ó Ø ÔÖ º ÙÖÓÔÒ ÓÔØÓÒ Ò ÛÖØØÒ Ò ØÖÑ Ó Ø ÔÖ Ó Ø Ó ÔÓ ÐÝ ÖØ Ðµ Ø Ò ÔÖÓÐØ
ÅÙÐعØÓÖ ÇÔØÓÒ ÈÖÒ ÈÙРĺ ÐÖ Ö Ø ÖØ ÇØÓÖ ½¾ ½ ÙÖÖÒØ ÖÚ ÓÒ ÂÙÒ ½ ¾¼¼¼ ÂÙÒ ½ ¾¼¼¼ ØÖØ ÅÙÐعØÓÖ ÑÓÐ ÔÖÓÚ ÓÒ ÖÐ ÜÐØÝ Ò ÖÔÖ ÒØÒ Ø Ý¹ ÒÑ ÚÓÖ Ó Ø ÔÖ º ÙÖÓÔÒ ÓÔØÓÒ Ò ÛÖØØÒ Ò ØÖÑ Ó Ø ÔÖ Ó Ø Ó ÔÓ ÐÝ ÖØ Ðµ Ø Ò ÔÖÓÐØ
