Introduction to FORM. Jos Vermaseren. Part 5 Miscellaneous topics Gamma matrices
|
|
|
- Blanche Bridges
- 8 years ago
- Views:
Transcription
1 Introduction to FORM Jos Vermaseren Part 5 Miscellaneous topics Gamma matrices
2 The next examples concern power series expansions. Substituting one series into another can cost much time if this is not done carefully. In the example below we want to substitute the power series for e y 1 into the power series for ln(1 + x). The whole should result in x if all goes well. First let us be brutish about it: #define N "7" Symbol i, x(: N ), y(: N ); Local ln = -sum_(i,1, N, sign_(i)/i*y^i);.sort On Statistics; id y = sum_(i,1, N,x^i*invfac_(i)); Print; Time = 4.65 sec Generated terms = 127 ln Terms in output = 1 Bytes used = 18 ln = x;
3 We see here that the declarations of x and y have a direct power cutoff. This is not so relevant for y, but it is for x. If we don t do this we obtain: #define N "7" Symbol i, x, y(: N ); Local ln = -sum_(i,1, N, sign_(i)/i*y^i);.sort On Statistics; id y = sum_(i,1, N,x^i*invfac_(i)); Print; Time = 6.63 sec Generated terms = ln Terms in output = 43 Bytes used = 998 ln = x /40320*x^ / *x^49; This shows that most generated terms are the terms that we throw away. Even when terms are thrown away rather quickly, they still need some time. Hence it is even better to become a bit more careful about what we generate and try to avoid the generation of terms that we don t need.
4 Next we use the expansion x x(1 + x 2 (1 + x 3 (1 + x (1 + )))) 4 in a slow way to take advantage of the elimination of powers that are too high. Try to verify that this is indeed what the next program does. #define N "50" On Statistics; Symbol i, x(: N ), y(: N ); Local ln = -sum_(i,1, N, sign_(i)/i*x^i); id x = x*y; #do i = 2, N +1 id y = 1 + x*y/ i ; #enddo Print; Time = sec Generated terms = ln Terms in output = 1 Bytes used = 18 ln = x;
5 Even though the above program is already much faster, it can be faster yet by sorting after each step in the expansion. #define N "50" On Statistics; Symbol i, x(: N ), y(: N ); Local X = -sum_(i,1, N, sign_(i)/i*x^i); id x = x*y; #do i = 2, N +1 id y = 1 + x*y/ i ;.sort:step i ; #enddo Print; ********Lots of statistics suppressed*****try this yourself Time = 0.11 sec Generated terms = 1 X Terms in output = 1 Bytes used = 18 X = x;
6 Of course one cannot always use such a nice expansion as the telescope expansion for the exponential. In that case one should just feed the proper coefficients one at a time. This is not much of an extra complication. We just need some extra features of FORM. Let us first look at the bracket statement: Symbols a,b,c; Local F = (a+b+c)^3; Bracket b; Print; F = + b * ( 3*c^2 + 6*a*c + 3*a^2 ) + b^2 * ( 3*c + 3*a ) + b^3 * ( 1 ) + c^3 + 3*a*c^2 + 3*a^2*c + a^3; We see that FORM has introduced brackets for which powers of b are taken outside, and all other objects are inside the brackets. One can specify many objects in a bracket statement, provided they are symbols, vectors, functions, tensors or dotproducts. The bracket for which nothing is outside is always printed last and the parentheses are omitted.
7 There is an option with the brackets for which the outside is printed but the contents are represented only by a mentioning of how many terms there are: Symbols a,b,c; Local F = (a+b+c)^3; Bracket b; Print[]; F = + b * ( 3 terms ) + b^2 * ( 2 terms ) + b^3 * ( 1 term ) + 1 * ( 4 terms ); This becomes rather handy when we just need to be the structure of an output and there are very many terms.
8 Symbols a,x,c; Local F = (a+x+c)^2+x; Bracket x;.sort Local G = F[x]^2-4*F[1]*F[x^2]; Print G; G = 1 + 4*c + 4*a; In this example we use the contents of the brackets of the expression F. This is done by attaching a pair of braces with the outside of the bracket we are interested in between them. It is possible to use $-variables between the braces, but in this context we will skip that.
9 Let us now return to our power series substitutions. First we define two power series expansions: #define N "10" Symbols i,x(: N ),y(: N ); Local F1 = sum_(i,1, N,x^i/i^2); Local F2 = sum_(i,1, N,y^i/i^3*sign_(i)); Print; F1 = x + 1/4*x^2 + 1/9*x^3 + 1/16*x^4 + 1/25*x^5 + 1/36*x^6 + 1/49*x^7 + 1/64*x^8 + 1/81*x^9 + 1/100*x^10; F2 = - y + 1/8*y^2-1/27*y^3 + 1/64*y^4-1/125*y^5 + 1/216*y^6-1/343*y^7 + 1/512*y^8-1/729*y^9 + 1/1000*y^10; We want to replace x in the first expansion by F2. How to proceed?
10 Bracket y;.sort Hide F2; id x = x*y; #do i = 1, N id x = F2[y^ i ]+x*y;.sort #enddo Print; F1 = - y + 3/8*y^2-91/432*y^ /6912*y^ / *y^ / *y^ / *y^ / *y^ / *y^ / *y^10; We have here the new feature Hide which tells FORM to put F2 in a special place in which it is not operated upon and its special bracket structure is preserved. To make F2 active again one can use the Unhide statement (see manual).
11 Another very useful feature of FORM are the tables. A table is a very special function with automatic substitution rules. Tables must have table elements and must be at least one dimensional. The elements are indicated by numbers. Tables can also be non-commuting. We will only commuting tables in the examples. Let us look at an example:
12 Symbols a,x,n; Table t1(0:2); Fill t1(0) = 1+a; Fill t1(1) = 2+a^2; Fill t1(2) = 3+a^3; * Local F = x+x^2+x^3; Print "<1> %t"; id x^n? = x^n*t1(n-1); Print " <2> %t"; Print; Bracket x; The table is declared as one dimensional, running from zero to two. We fill the elements with a fill statement. One can use normal formula s in the RHS. Don t use however $-variables or previously defined expressions! We included some print statements to see what happens.
13 <1> + x <2> + x <2> + a*x <1> + x^2 <2> + 2*x^2 <2> + a^2*x^2 <1> + x^3 <2> + 3*x^3 <2> + a^3*x^3 F = + x * ( 1 + a ) + x^2 * ( 2 + a^2 ) + x^3 * ( 3 + a^3 ); As one can see, the table elements of t1 are substituted immediately when they occur. But what happens when an element is asked for that doesn t exist?
14 Symbols a,x,n; Table t1(0:2); Fill t1(0) = 1+a; Fill t1(1) = 2+a^2; Fill t1(2) = 3+a^3; Local F = x+x^2+x^3; id x^n? = x^n*t1(n); Print; Bracket x; F = + x * ( 2 + a^2 ) + x^2 * ( 3 + a^3 ) + x^3 * ( t1(3) ); We see that the element number 3 is outside the table and/or has not been defined and hence is left untouched.
15 It is possible to specify that the program should be more strict and give an error message or a warning when either the table hasn t been filled completely or elements are used that are not inside the boundaries: Symbols a,x,n; Table,check,t1(0:2); Fill t1(0) = 1+a; Fill t1(1) = 2+a^2; Fill t1(2) = 3+a^3; Local F = x+x^2+x^3; id x^n? = x^n*t1(n); Print; Bracket x; Table boundary check. Argument 1 t1(3) The option strict tells FORM to give an error message when there are undefined elements.
16 Tables can also have arguments. Just as in regular functions there will only be a match when also the arguments match. These arguments can have wildcards: Symbols a,b,x,y,n,ep; Table t1(0:2,a?); Fill t1(0) = 1+a*ep; Fill t1(1) = 2+a*ep+a^2*ep^2; Fill t1(2) = 3+2*a*ep+a^2*ep^2+a^3*ep^3; Local F1 = x+x^2+x^3; Local F2 = x+x^2+x^3; if ( expression(f1) ) id x^n? = x^n*t1(n-1,y); if ( expression(f2) ) id x^n? = x^n*t1(n-1,n); Print +f; Bracket x; We see here the wildcard a? in the declaration of t1. In the fill statements we don t have to specify the a?, but we can use the a in the RHS. Then we use y in the table in F1 and n in F2. Notice that n have a value.
17 F1 = + x * ( 1 + y*ep ) + x^2 * ( 2 + y*ep + y^2*ep^2 ) + x^3 * ( 3 + 2*y*ep + y^2*ep^2 + y^3*ep^3 ); F2 = + x * ( 1 + ep ) + x^2 * ( 2 + 2*ep + 4*ep^2 ) + x^3 * ( 3 + 6*ep + 9*ep^2 + 27*ep^3 );
18 There is a second type of tables, called the sparse tables. In their case we just specify the dimension and no space for the elements is reserved in advance. The values however are not restricted to a range (just to the short integers which is either 2 15 to on 32 bits systems or 2 31 to on 64 bits systems). One may wonder why we need the first type of tables at all. The sparse tables can handle all types anyway. The difference lies in the speed at which table elements can be identified. In the case of sparse tables FORM has to do a lookup in the list of defined elements. This is not nearly as fast as looking up an array element. And undefined table elements have FORM checking quite frequently. Finally we will construct an example in which we generate the table elements in a less trivial construction, using $-variables.
19 Notice that each time $dummy is defined (in the preprocessor) the previous table elements are already known. The RHS of $dummy is directly expanded. #define MAX "6" #define NMAX "10" Symbols x,n,m,ep(: MAX ); Table,sparse,tp(1,m?); Fill tp(0) = 1; #do i = 1, NMAX #$dummy = tp( i -1,m)*( i +ep*m); Fill tp( i ) = $dummy ; #enddo Local F = x^2+x^8; id x^n? = x^n*tp(n,1/n); Bracket x; Print;
20 Time = 0.00 sec Generated terms = 10 F Terms in output = 10 Bytes used = 154 F = + x^2 * ( 2 + 3/2*ep + 1/4*ep^2 ) + x^8 * ( *ep /16*ep^ /128*ep^ /4096*ep^ /4096*ep^ /131072*ep^6 ); As one can see, the elements must have been expanded already, or we would have generated much more than the 10 terms that are mentioned.
21 The next topic concerns particle physics specific features. People who are not interested in this can safely skip this section.
22 For computations in particle physics FORM is equipped with Dirac gamma matrices. These are defined as g_. Actually g can indicate a whole string of gamma matrices. The first argument is an index (or a short number). After that follow the indices of the string of gamma matrices as in g_(1,mu1,mu2,mu3,mu4) = γ µ 1γ µ 2γ µ 3γ µ 4. There are special notations: g (n) is the unit matrix in string n. g5 (n) is the γ 5 matrix in string n. g6 (n) is 1 + γ 5 in string n. g7 (n) is 1 γ 5 in string n. To indicate the last three inside a string one can use 5, 6 or 7 as in g_(1,mu1,7_,mu2,mu3,mu4). Let us calculate a simple reaction: e e + µ µ + in QED. If we take all particles massless and assume that the e has momentum k 1, e + has k 2, µ has p 1 and µ + has p 2 we have k 1 p 1 k 2 p 2
23 Vectors k1, k2, p1, p2; Symbols s, t, u, e; Indices mu, nu, rho, sigma; Local M2 = * electron line e^2 * g_(1, k2, rho, k1, sigma) * * photon propagator d_(rho,mu) * d_(sigma,nu) / s^2 * * muon spin line e^2 * g_(2, p1, mu, p2, nu) ; Trace4,1; Trace4,2; Bracket e, s; Print;.sort
24 M2 = + s^-2*e^4 * ( 32*k1.p1*k2.p2 + 32*k1.p2*k2.p1 ); id k1.k2 = s/2; id p1.p2 = s/2; id k1.p1 = -t/2; id k2.p2 = -t/2; id k1.p2 = -u/2; id k2.p1 = -u/2; Bracket e, s; Print; M2 = + s^-2*e^4 * ( 8*t^2 + 8*u^2 );
25 Of course the interesting command here is the Trace4 command. The Trace4,1; statement causes the taking of the trace of the combination of all gamma matrices that have the spinline 1. In principle gamma matrices of different spinlines commute, so that should not give a problem. Things are a bit more complicated when the spinline is an index. In that case we have not yet fixed the spinline and hence they cannot commute under normal circumstances. However, once we say for instance Trace4,n; it is assumed that all gamma matrices with spinline n commute with all other gamma matrices (or other functions). The specification Trace4 means that the trace is taken in 4 dimensions. In that case FORM knows some tricks that are specific to 4 dimensions. Like Chisholm identities to pull some traces together: Vectors k1, k2, p1, p2; Indices mu, nu, rho, sigma; Local M2 = g_(1, k2, mu, k1, nu) * g_(2, p1, mu, p2, nu) ; Trace4,1; Print; Time = 0.00 sec Generated terms = 2 M2 Terms in output = 2 Bytes used = 50 M2 = 2*g_(2,p1,k1,nu,k2,p2,nu) + 2*g_(2,p1,k2,nu,k1,p2,nu);
26 The Chisholm identity that FORM uses is γ µ Tr[γ µ S] = 2(S + S R ) in which S is a string of gamma matrices with an odd number of matrices (γ 5 counts for an even number of matrices). S R is the reversed string. This relation can be used to combine traces with common indices. The complete trace algorithms are explained in the manual. It also explains about the Tracen statement for traces in n dimensions. Next we look at the reaction e e + τ τ + udν µ µ. We assume that all particles have a mass. The program could look like: p 1 p 2 The program could look like: q 1 q 2 p 7 (ν τ ) p 8 (µ ) p 6 (ν µ ) p 3 (ν τ ) p 5 (d) p 4 (u)
27 Vectors p1,...,p8,q,q1,q2; Indices m1,m2,m3,n1,n2,n3; Symbol emass, tmass, mass3,...,mass8,s; On Statistics; Local F = * * The incoming e- e+ pair. Momenta p1, p2 * (g_(1,p2)-emass)*g_(1,m1)* (g_(1,p1)+emass)*g_(1,n1)* * * The tau line. tau- is q1, tau+ is q2 *
28 (g_(2,p3)+mass3)*g_(2,m2)*g7_(2)* (g_(2,q1)+tmass)*g_(2,m1)* (-g_(2,q2)+tmass)* g_(2,m3)*g7_(2)*(g_(2,p6)-mass6)* g_(2,n3)*g7_(2)*(-g_(2,q2)+tmass)*g_(2,n1)* (g_(2,q1)+tmass)*g_(2,n2)*g7_(2)* * * The u d-bar pair. p4 is u, p5 is d-bar * (g_(3,p4)+mass4)*g_(3,m2)*g7_(3)* (g_(3,p5)-mass5)*g_(3,n2)*g7_(3)* * * The nu-bar mu pair. p7 is nu_bar, p8 is mu * (g_(4,p7)+mass7)*g_(4,m3)*g7_(4)* (g_(4,p8)-mass8)*g_(4,n3)*g7_(4)
29 * * Finally some normalization * /2^16; trace4,4; trace4,3; trace4,2; trace4,1;.sort Time = 0.01 sec Generated terms = 164 F Terms in output = 27 Bytes used = 1246 id q1.q1 = tmass^2; id q2.q2 = tmass^2; id p1.p2 = s/2-emass^2; id q1.q2 = s/2-tmass^2; print +s;
30 Time = 0.07 sec Generated terms = 35 F Terms in output = 24 Bytes used = 840 F = + 4*p1.p5*p2.p7*p3.p4*p6.p8*tmass^2*s - 8*p1.p5*p2.q2*p3.p4*p6.p8*p7.q1*tmass^2-8*p1.p5*p2.q2*p3.p4*p6.p8*p7.q2*tmass^2 + 4*p1.p7*p2.p5*p3.p4*p6.p8*tmass^2*s - 8*p1.p7*p2.q1*p3.p4*p5.q1*p6.p8*tmass^2-8*p1.p7*p2.q1*p3.p4*p5.q2*p6.p8*tmass^2-8*p1.q1*p2.p7*p3.p4*p5.q1*p6.p8*tmass^2-8*p1.q1*p2.p7*p3.p4*p5.q2*p6.p8*tmass^2 + 8*p1.q1*p2.q2*p3.p4*p5.p7*p6.p8*tmass^2 + 16*p1.q1*p2.q2*p3.p4*p5.q1*p6.p8*p7.q2-8*p1.q2*p2.p5*p3.p4*p6.p8*p7.q1*tmass^2-8*p1.q2*p2.p5*p3.p4*p6.p8*p7.q2*tmass^2
31 + 8*p1.q2*p2.q1*p3.p4*p5.p7*p6.p8*tmass^2 + 16*p1.q2*p2.q1*p3.p4*p5.q1*p6.p8*p7.q2 + 4*p3.p4*p5.p7*p6.p8*emass^2*tmass^2*s - 2*p3.p4*p5.p7*p6.p8*tmass^2*s^2 + 4*p3.p4*p5.p7*p6.p8*tmass^4*s - 8*p3.p4*p5.q1*p6.p8*p7.q1*emass^2*tmass^2-8*p3.p4*p5.q1*p6.p8*p7.q2*emass^2*tmass^2 + 8*p3.p4*p5.q1*p6.p8*p7.q2*emass^2*s + 4*p3.p4*p5.q1*p6.p8*p7.q2*tmass^2*s - 8*p3.p4*p5.q2*p6.p8*p7.q1*emass^2*tmass^2 + 4*p3.p4*p5.q2*p6.p8*p7.q1*tmass^2*s - 8*p3.p4*p5.q2*p6.p8*p7.q2*emass^2*tmass^2 ; Notice that the number of terms generated is rather modest ad that all masses of the decay products drop out. What happens if we don t apply tricks like the Chisholm identity? This is an option in the Trace4 statement:
32 trace4,nocontract,4; trace4,nocontract,3; trace4,nocontract,2; trace4,nocontract,1;.sort Time = 0.55 sec Generated terms = F Terms in output = 6891 Bytes used = Contract,0;.sort Time = 0.61 sec Generated terms = F Terms in output = 4223 Bytes used = id q1.q1 = tmass^2; id q2.q2 = tmass^2; id p1.p2 = s/2-emass^2; id q1.q2 = s/2-tmass^2;
33 if ( count(e_,1) ) Multiply x; Bracket x; print[]; Time = 0.63 sec Generated terms = 5528 F Terms in output = 4343 Bytes used = F = + x * ( 1307 terms ) + 1 * ( 3036 terms ); We see that there are 1307 terms with a Levi-Civita tensor in it. And lots of terms without. Is this indeed the same answer as we obtained before? Yes! But it is very difficult to prove it. It involves identities like the Schouten identity that we derived before. The only known systematic way to prove that they are equal is to write both expressions out in vector components. This is very messy.
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
A Concrete Introduction. to the Abstract Concepts. of Integers and Algebra using Algebra Tiles
 A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
Bits Superposition Quantum Parallelism
 7-Qubit Quantum Computer Typical Ion Oscillations in a Trap Bits Qubits vs Each qubit can represent both a or at the same time! This phenomenon is known as Superposition. It leads to Quantum Parallelism
7-Qubit Quantum Computer Typical Ion Oscillations in a Trap Bits Qubits vs Each qubit can represent both a or at the same time! This phenomenon is known as Superposition. It leads to Quantum Parallelism
NSM100 Introduction to Algebra Chapter 5 Notes Factoring
 Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Section 5.1 Greatest Common Factor (GCF) and Factoring by Grouping Greatest Common Factor for a polynomial is the largest monomial that divides (is a factor of) each term of the polynomial. GCF is the
Notes on Factoring. MA 206 Kurt Bryan
 The General Approach Notes on Factoring MA 26 Kurt Bryan Suppose I hand you n, a 2 digit integer and tell you that n is composite, with smallest prime factor around 5 digits. Finding a nontrivial factor
The General Approach Notes on Factoring MA 26 Kurt Bryan Suppose I hand you n, a 2 digit integer and tell you that n is composite, with smallest prime factor around 5 digits. Finding a nontrivial factor
9.4. The Scalar Product. Introduction. Prerequisites. Learning Style. Learning Outcomes
 The Scalar Product 9.4 Introduction There are two kinds of multiplication involving vectors. The first is known as the scalar product or dot product. This is so-called because when the scalar product of
The Scalar Product 9.4 Introduction There are two kinds of multiplication involving vectors. The first is known as the scalar product or dot product. This is so-called because when the scalar product of
Welcome to Math 19500 Video Lessons. Stanley Ocken. Department of Mathematics The City College of New York Fall 2013
 Welcome to Math 19500 Video Lessons Prof. Department of Mathematics The City College of New York Fall 2013 An important feature of the following Beamer slide presentations is that you, the reader, move
Welcome to Math 19500 Video Lessons Prof. Department of Mathematics The City College of New York Fall 2013 An important feature of the following Beamer slide presentations is that you, the reader, move
Algebra Unpacked Content For the new Common Core standards that will be effective in all North Carolina schools in the 2012-13 school year.
 This document is designed to help North Carolina educators teach the Common Core (Standard Course of Study). NCDPI staff are continually updating and improving these tools to better serve teachers. Algebra
This document is designed to help North Carolina educators teach the Common Core (Standard Course of Study). NCDPI staff are continually updating and improving these tools to better serve teachers. Algebra
3.2 The Factor Theorem and The Remainder Theorem
 3. The Factor Theorem and The Remainder Theorem 57 3. The Factor Theorem and The Remainder Theorem Suppose we wish to find the zeros of f(x) = x 3 + 4x 5x 4. Setting f(x) = 0 results in the polynomial
3. The Factor Theorem and The Remainder Theorem 57 3. The Factor Theorem and The Remainder Theorem Suppose we wish to find the zeros of f(x) = x 3 + 4x 5x 4. Setting f(x) = 0 results in the polynomial
Chapter 17. Orthogonal Matrices and Symmetries of Space
 Chapter 17. Orthogonal Matrices and Symmetries of Space Take a random matrix, say 1 3 A = 4 5 6, 7 8 9 and compare the lengths of e 1 and Ae 1. The vector e 1 has length 1, while Ae 1 = (1, 4, 7) has length
Chapter 17. Orthogonal Matrices and Symmetries of Space Take a random matrix, say 1 3 A = 4 5 6, 7 8 9 and compare the lengths of e 1 and Ae 1. The vector e 1 has length 1, while Ae 1 = (1, 4, 7) has length
Equations Involving Lines and Planes Standard equations for lines in space
 Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
Equations Involving Lines and Planes In this section we will collect various important formulas regarding equations of lines and planes in three dimensional space Reminder regarding notation: any quantity
Operation Count; Numerical Linear Algebra
 10 Operation Count; Numerical Linear Algebra 10.1 Introduction Many computations are limited simply by the sheer number of required additions, multiplications, or function evaluations. If floating-point
10 Operation Count; Numerical Linear Algebra 10.1 Introduction Many computations are limited simply by the sheer number of required additions, multiplications, or function evaluations. If floating-point
Year 9 set 1 Mathematics notes, to accompany the 9H book.
 Part 1: Year 9 set 1 Mathematics notes, to accompany the 9H book. equations 1. (p.1), 1.6 (p. 44), 4.6 (p.196) sequences 3. (p.115) Pupils use the Elmwood Press Essential Maths book by David Raymer (9H
Part 1: Year 9 set 1 Mathematics notes, to accompany the 9H book. equations 1. (p.1), 1.6 (p. 44), 4.6 (p.196) sequences 3. (p.115) Pupils use the Elmwood Press Essential Maths book by David Raymer (9H
Vectors 2. The METRIC Project, Imperial College. Imperial College of Science Technology and Medicine, 1996.
 Vectors 2 The METRIC Project, Imperial College. Imperial College of Science Technology and Medicine, 1996. Launch Mathematica. Type
Vectors 2 The METRIC Project, Imperial College. Imperial College of Science Technology and Medicine, 1996. Launch Mathematica. Type
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B. KITCHENS
 December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
December 4, 2013 MATH 171 BASIC LINEAR ALGEBRA B KITCHENS The equation 1 Lines in two-dimensional space (1) 2x y = 3 describes a line in two-dimensional space The coefficients of x and y in the equation
PGR Computing Programming Skills
 PGR Computing Programming Skills Dr. I. Hawke 2008 1 Introduction The purpose of computing is to do something faster, more efficiently and more reliably than you could as a human do it. One obvious point
PGR Computing Programming Skills Dr. I. Hawke 2008 1 Introduction The purpose of computing is to do something faster, more efficiently and more reliably than you could as a human do it. One obvious point
BX in ( u, v) basis in two ways. On the one hand, AN = u+
 1. Let f(x) = 1 x +1. Find f (6) () (the value of the sixth derivative of the function f(x) at zero). Answer: 7. We expand the given function into a Taylor series at the point x = : f(x) = 1 x + x 4 x
1. Let f(x) = 1 x +1. Find f (6) () (the value of the sixth derivative of the function f(x) at zero). Answer: 7. We expand the given function into a Taylor series at the point x = : f(x) = 1 x + x 4 x
Taylor and Maclaurin Series
 Taylor and Maclaurin Series In the preceding section we were able to find power series representations for a certain restricted class of functions. Here we investigate more general problems: Which functions
Taylor and Maclaurin Series In the preceding section we were able to find power series representations for a certain restricted class of functions. Here we investigate more general problems: Which functions
Some facts about polynomials modulo m (Full proof of the Fingerprinting Theorem)
 Some facts about polynomials modulo m (Full proof of the Fingerprinting Theorem) In order to understand the details of the Fingerprinting Theorem on fingerprints of different texts from Chapter 19 of the
Some facts about polynomials modulo m (Full proof of the Fingerprinting Theorem) In order to understand the details of the Fingerprinting Theorem on fingerprints of different texts from Chapter 19 of the
Question 2: How do you solve a matrix equation using the matrix inverse?
 Question : How do you solve a matrix equation using the matrix inverse? In the previous question, we wrote systems of equations as a matrix equation AX B. In this format, the matrix A contains the coefficients
Question : How do you solve a matrix equation using the matrix inverse? In the previous question, we wrote systems of equations as a matrix equation AX B. In this format, the matrix A contains the coefficients
Mathematics for Computer Science/Software Engineering. Notes for the course MSM1F3 Dr. R. A. Wilson
 Mathematics for Computer Science/Software Engineering Notes for the course MSM1F3 Dr. R. A. Wilson October 1996 Chapter 1 Logic Lecture no. 1. We introduce the concept of a proposition, which is a statement
Mathematics for Computer Science/Software Engineering Notes for the course MSM1F3 Dr. R. A. Wilson October 1996 Chapter 1 Logic Lecture no. 1. We introduce the concept of a proposition, which is a statement
Linear Algebra Notes for Marsden and Tromba Vector Calculus
 Linear Algebra Notes for Marsden and Tromba Vector Calculus n-dimensional Euclidean Space and Matrices Definition of n space As was learned in Math b, a point in Euclidean three space can be thought of
Linear Algebra Notes for Marsden and Tromba Vector Calculus n-dimensional Euclidean Space and Matrices Definition of n space As was learned in Math b, a point in Euclidean three space can be thought of
15.062 Data Mining: Algorithms and Applications Matrix Math Review
 .6 Data Mining: Algorithms and Applications Matrix Math Review The purpose of this document is to give a brief review of selected linear algebra concepts that will be useful for the course and to develop
.6 Data Mining: Algorithms and Applications Matrix Math Review The purpose of this document is to give a brief review of selected linear algebra concepts that will be useful for the course and to develop
2 Integrating Both Sides
 2 Integrating Both Sides So far, the only general method we have for solving differential equations involves equations of the form y = f(x), where f(x) is any function of x. The solution to such an equation
2 Integrating Both Sides So far, the only general method we have for solving differential equations involves equations of the form y = f(x), where f(x) is any function of x. The solution to such an equation
AMATH 352 Lecture 3 MATLAB Tutorial Starting MATLAB Entering Variables
 AMATH 352 Lecture 3 MATLAB Tutorial MATLAB (short for MATrix LABoratory) is a very useful piece of software for numerical analysis. It provides an environment for computation and the visualization. Learning
AMATH 352 Lecture 3 MATLAB Tutorial MATLAB (short for MATrix LABoratory) is a very useful piece of software for numerical analysis. It provides an environment for computation and the visualization. Learning
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
Factorising quadratics
 Factorising quadratics An essential skill in many applications is the ability to factorise quadratic expressions. In this unit you will see that this can be thought of as reversing the process used to
Factorising quadratics An essential skill in many applications is the ability to factorise quadratic expressions. In this unit you will see that this can be thought of as reversing the process used to
Cryptography and Network Security. Prof. D. Mukhopadhyay. Department of Computer Science and Engineering. Indian Institute of Technology, Kharagpur
 Cryptography and Network Security Prof. D. Mukhopadhyay Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur Module No. # 01 Lecture No. # 12 Block Cipher Standards
Cryptography and Network Security Prof. D. Mukhopadhyay Department of Computer Science and Engineering Indian Institute of Technology, Kharagpur Module No. # 01 Lecture No. # 12 Block Cipher Standards
Boolean Algebra Part 1
 Boolean Algebra Part 1 Page 1 Boolean Algebra Objectives Understand Basic Boolean Algebra Relate Boolean Algebra to Logic Networks Prove Laws using Truth Tables Understand and Use First Basic Theorems
Boolean Algebra Part 1 Page 1 Boolean Algebra Objectives Understand Basic Boolean Algebra Relate Boolean Algebra to Logic Networks Prove Laws using Truth Tables Understand and Use First Basic Theorems
State of Stress at Point
 State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
Algebraic expressions are a combination of numbers and variables. Here are examples of some basic algebraic expressions.
 Page 1 of 13 Review of Linear Expressions and Equations Skills involving linear equations can be divided into the following groups: Simplifying algebraic expressions. Linear expressions. Solving linear
Page 1 of 13 Review of Linear Expressions and Equations Skills involving linear equations can be divided into the following groups: Simplifying algebraic expressions. Linear expressions. Solving linear
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
1.6 The Order of Operations
 1.6 The Order of Operations Contents: Operations Grouping Symbols The Order of Operations Exponents and Negative Numbers Negative Square Roots Square Root of a Negative Number Order of Operations and Negative
1.6 The Order of Operations Contents: Operations Grouping Symbols The Order of Operations Exponents and Negative Numbers Negative Square Roots Square Root of a Negative Number Order of Operations and Negative
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
Lecture 16. Newton s Second Law for Rotation. Moment of Inertia. Angular momentum. Cutnell+Johnson: 9.4, 9.6
 Lecture 16 Newton s Second Law for Rotation Moment of Inertia Angular momentum Cutnell+Johnson: 9.4, 9.6 Newton s Second Law for Rotation Newton s second law says how a net force causes an acceleration.
Lecture 16 Newton s Second Law for Rotation Moment of Inertia Angular momentum Cutnell+Johnson: 9.4, 9.6 Newton s Second Law for Rotation Newton s second law says how a net force causes an acceleration.
1 Sets and Set Notation.
 LINEAR ALGEBRA MATH 27.6 SPRING 23 (COHEN) LECTURE NOTES Sets and Set Notation. Definition (Naive Definition of a Set). A set is any collection of objects, called the elements of that set. We will most
LINEAR ALGEBRA MATH 27.6 SPRING 23 (COHEN) LECTURE NOTES Sets and Set Notation. Definition (Naive Definition of a Set). A set is any collection of objects, called the elements of that set. We will most
Chapter 7: Additional Topics
 Chapter 7: Additional Topics In this chapter we ll briefly cover selected advanced topics in fortran programming. All the topics come in handy to add extra functionality to programs, but the feature you
Chapter 7: Additional Topics In this chapter we ll briefly cover selected advanced topics in fortran programming. All the topics come in handy to add extra functionality to programs, but the feature you
COLLEGE ALGEBRA. Paul Dawkins
 COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
COLLEGE ALGEBRA Paul Dawkins Table of Contents Preface... iii Outline... iv Preliminaries... Introduction... Integer Exponents... Rational Exponents... 9 Real Exponents...5 Radicals...6 Polynomials...5
3.2 Sources, Sinks, Saddles, and Spirals
 3.2. Sources, Sinks, Saddles, and Spirals 6 3.2 Sources, Sinks, Saddles, and Spirals The pictures in this section show solutions to Ay 00 C By 0 C Cy D 0. These are linear equations with constant coefficients
3.2. Sources, Sinks, Saddles, and Spirals 6 3.2 Sources, Sinks, Saddles, and Spirals The pictures in this section show solutions to Ay 00 C By 0 C Cy D 0. These are linear equations with constant coefficients
Factoring Flow Chart
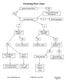 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
BEGINNING ALGEBRA ACKNOWLEDMENTS
 BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
Algebra I Vocabulary Cards
 Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
Algebra I Vocabulary Cards Table of Contents Expressions and Operations Natural Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers Absolute Value Order of Operations Expression
REVIEW EXERCISES DAVID J LOWRY
 REVIEW EXERCISES DAVID J LOWRY Contents 1. Introduction 1 2. Elementary Functions 1 2.1. Factoring and Solving Quadratics 1 2.2. Polynomial Inequalities 3 2.3. Rational Functions 4 2.4. Exponentials and
REVIEW EXERCISES DAVID J LOWRY Contents 1. Introduction 1 2. Elementary Functions 1 2.1. Factoring and Solving Quadratics 1 2.2. Polynomial Inequalities 3 2.3. Rational Functions 4 2.4. Exponentials and
Matrices 2. Solving Square Systems of Linear Equations; Inverse Matrices
 Matrices 2. Solving Square Systems of Linear Equations; Inverse Matrices Solving square systems of linear equations; inverse matrices. Linear algebra is essentially about solving systems of linear equations,
Matrices 2. Solving Square Systems of Linear Equations; Inverse Matrices Solving square systems of linear equations; inverse matrices. Linear algebra is essentially about solving systems of linear equations,
3.3. Solving Polynomial Equations. Introduction. Prerequisites. Learning Outcomes
 Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Solving Polynomial Equations 3.3 Introduction Linear and quadratic equations, dealt within Sections 3.1 and 3.2, are members of a class of equations, called polynomial equations. These have the general
Orthogonal Projections
 Orthogonal Projections and Reflections (with exercises) by D. Klain Version.. Corrections and comments are welcome! Orthogonal Projections Let X,..., X k be a family of linearly independent (column) vectors
Orthogonal Projections and Reflections (with exercises) by D. Klain Version.. Corrections and comments are welcome! Orthogonal Projections Let X,..., X k be a family of linearly independent (column) vectors
Notes on Determinant
 ENGG2012B Advanced Engineering Mathematics Notes on Determinant Lecturer: Kenneth Shum Lecture 9-18/02/2013 The determinant of a system of linear equations determines whether the solution is unique, without
ENGG2012B Advanced Engineering Mathematics Notes on Determinant Lecturer: Kenneth Shum Lecture 9-18/02/2013 The determinant of a system of linear equations determines whether the solution is unique, without
2.3. Finding polynomial functions. An Introduction:
 2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
2.3. Finding polynomial functions. An Introduction: As is usually the case when learning a new concept in mathematics, the new concept is the reverse of the previous one. Remember how you first learned
Math 55: Discrete Mathematics
 Math 55: Discrete Mathematics UC Berkeley, Spring 2012 Homework # 9, due Wednesday, April 11 8.1.5 How many ways are there to pay a bill of 17 pesos using a currency with coins of values of 1 peso, 2 pesos,
Math 55: Discrete Mathematics UC Berkeley, Spring 2012 Homework # 9, due Wednesday, April 11 8.1.5 How many ways are there to pay a bill of 17 pesos using a currency with coins of values of 1 peso, 2 pesos,
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Chapter 9. Systems of Linear Equations
 Chapter 9. Systems of Linear Equations 9.1. Solve Systems of Linear Equations by Graphing KYOTE Standards: CR 21; CA 13 In this section we discuss how to solve systems of two linear equations in two variables
Chapter 9. Systems of Linear Equations 9.1. Solve Systems of Linear Equations by Graphing KYOTE Standards: CR 21; CA 13 In this section we discuss how to solve systems of two linear equations in two variables
DETERMINANTS TERRY A. LORING
 DETERMINANTS TERRY A. LORING 1. Determinants: a Row Operation By-Product The determinant is best understood in terms of row operations, in my opinion. Most books start by defining the determinant via formulas
DETERMINANTS TERRY A. LORING 1. Determinants: a Row Operation By-Product The determinant is best understood in terms of row operations, in my opinion. Most books start by defining the determinant via formulas
Summation Algebra. x i
 2 Summation Algebra In the next 3 chapters, we deal with the very basic results in summation algebra, descriptive statistics, and matrix algebra that are prerequisites for the study of SEM theory. You
2 Summation Algebra In the next 3 chapters, we deal with the very basic results in summation algebra, descriptive statistics, and matrix algebra that are prerequisites for the study of SEM theory. You
Adding vectors We can do arithmetic with vectors. We ll start with vector addition and related operations. Suppose you have two vectors
 1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
1 Chapter 13. VECTORS IN THREE DIMENSIONAL SPACE Let s begin with some names and notation for things: R is the set (collection) of real numbers. We write x R to mean that x is a real number. A real number
SECTION 2.5: FINDING ZEROS OF POLYNOMIAL FUNCTIONS
 SECTION 2.5: FINDING ZEROS OF POLYNOMIAL FUNCTIONS Assume f ( x) is a nonconstant polynomial with real coefficients written in standard form. PART A: TECHNIQUES WE HAVE ALREADY SEEN Refer to: Notes 1.31
SECTION 2.5: FINDING ZEROS OF POLYNOMIAL FUNCTIONS Assume f ( x) is a nonconstant polynomial with real coefficients written in standard form. PART A: TECHNIQUES WE HAVE ALREADY SEEN Refer to: Notes 1.31
Lecture 8. Generating a non-uniform probability distribution
 Discrete outcomes Lecture 8 Generating a non-uniform probability distribution Last week we discussed generating a non-uniform probability distribution for the case of finite discrete outcomes. An algorithm
Discrete outcomes Lecture 8 Generating a non-uniform probability distribution Last week we discussed generating a non-uniform probability distribution for the case of finite discrete outcomes. An algorithm
Electrochemical Kinetics ( Ref. :Bard and Faulkner, Oldham and Myland, Liebhafsky and Cairns) R f = k f * C A (2) R b = k b * C B (3)
 Electrochemical Kinetics ( Ref. :Bard and Faulkner, Oldham and Myland, Liebhafsky and Cairns) 1. Background Consider the reaction given below: A B (1) If k f and k b are the rate constants of the forward
Electrochemical Kinetics ( Ref. :Bard and Faulkner, Oldham and Myland, Liebhafsky and Cairns) 1. Background Consider the reaction given below: A B (1) If k f and k b are the rate constants of the forward
Student Outcomes. Lesson Notes. Classwork. Discussion (10 minutes)
 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 5 8 Student Outcomes Students know the definition of a number raised to a negative exponent. Students simplify and write equivalent expressions that contain
NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 5 8 Student Outcomes Students know the definition of a number raised to a negative exponent. Students simplify and write equivalent expressions that contain
2.2 Separable Equations
 2.2 Separable Equations 73 2.2 Separable Equations An equation y = f(x, y) is called separable provided algebraic operations, usually multiplication, division and factorization, allow it to be written
2.2 Separable Equations 73 2.2 Separable Equations An equation y = f(x, y) is called separable provided algebraic operations, usually multiplication, division and factorization, allow it to be written
Linear Programming Notes V Problem Transformations
 Linear Programming Notes V Problem Transformations 1 Introduction Any linear programming problem can be rewritten in either of two standard forms. In the first form, the objective is to maximize, the material
Linear Programming Notes V Problem Transformations 1 Introduction Any linear programming problem can be rewritten in either of two standard forms. In the first form, the objective is to maximize, the material
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
University of Lille I PC first year list of exercises n 7. Review
 University of Lille I PC first year list of exercises n 7 Review Exercise Solve the following systems in 4 different ways (by substitution, by the Gauss method, by inverting the matrix of coefficients
University of Lille I PC first year list of exercises n 7 Review Exercise Solve the following systems in 4 different ways (by substitution, by the Gauss method, by inverting the matrix of coefficients
1.5. Factorisation. Introduction. Prerequisites. Learning Outcomes. Learning Style
 Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Factorisation 1.5 Introduction In Block 4 we showed the way in which brackets were removed from algebraic expressions. Factorisation, which can be considered as the reverse of this process, is dealt with
Fractions Practice: Answers
 Click on the links below to jump directly to the relevant section Fractions Practice: Answers Percents Practice: Answers Ratios Practice: Answers Proportions Practice: Answers Graphing Practice: Answers
Click on the links below to jump directly to the relevant section Fractions Practice: Answers Percents Practice: Answers Ratios Practice: Answers Proportions Practice: Answers Graphing Practice: Answers
Solutions to Problems in Goldstein, Classical Mechanics, Second Edition. Chapter 7
 Solutions to Problems in Goldstein, Classical Mechanics, Second Edition Homer Reid April 21, 2002 Chapter 7 Problem 7.2 Obtain the Lorentz transformation in which the velocity is at an infinitesimal angle
Solutions to Problems in Goldstein, Classical Mechanics, Second Edition Homer Reid April 21, 2002 Chapter 7 Problem 7.2 Obtain the Lorentz transformation in which the velocity is at an infinitesimal angle
Methods for Finding Bases
 Methods for Finding Bases Bases for the subspaces of a matrix Row-reduction methods can be used to find bases. Let us now look at an example illustrating how to obtain bases for the row space, null space,
Methods for Finding Bases Bases for the subspaces of a matrix Row-reduction methods can be used to find bases. Let us now look at an example illustrating how to obtain bases for the row space, null space,
Multi scale random field simulation program
 Multi scale random field simulation program 1.15. 2010 (Updated 12.22.2010) Andrew Seifried, Stanford University Introduction This is a supporting document for the series of Matlab scripts used to perform
Multi scale random field simulation program 1.15. 2010 (Updated 12.22.2010) Andrew Seifried, Stanford University Introduction This is a supporting document for the series of Matlab scripts used to perform
FURTHER VECTORS (MEI)
 Mathematics Revision Guides Further Vectors (MEI) (column notation) Page of MK HOME TUITION Mathematics Revision Guides Level: AS / A Level - MEI OCR MEI: C FURTHER VECTORS (MEI) Version : Date: -9-7 Mathematics
Mathematics Revision Guides Further Vectors (MEI) (column notation) Page of MK HOME TUITION Mathematics Revision Guides Level: AS / A Level - MEI OCR MEI: C FURTHER VECTORS (MEI) Version : Date: -9-7 Mathematics
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Math 1050 Khan Academy Extra Credit Algebra Assignment
 Math 1050 Khan Academy Extra Credit Algebra Assignment KhanAcademy.org offers over 2,700 instructional videos, including hundreds of videos teaching algebra concepts, and corresponding problem sets. In
Math 1050 Khan Academy Extra Credit Algebra Assignment KhanAcademy.org offers over 2,700 instructional videos, including hundreds of videos teaching algebra concepts, and corresponding problem sets. In
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
5.3 The Cross Product in R 3
 53 The Cross Product in R 3 Definition 531 Let u = [u 1, u 2, u 3 ] and v = [v 1, v 2, v 3 ] Then the vector given by [u 2 v 3 u 3 v 2, u 3 v 1 u 1 v 3, u 1 v 2 u 2 v 1 ] is called the cross product (or
53 The Cross Product in R 3 Definition 531 Let u = [u 1, u 2, u 3 ] and v = [v 1, v 2, v 3 ] Then the vector given by [u 2 v 3 u 3 v 2, u 3 v 1 u 1 v 3, u 1 v 2 u 2 v 1 ] is called the cross product (or
Binary Multiplication
 Binary Multiplication Q: How do we multiply two numbers? eg. 12, 345 6, 789 111105 987600 8641500 + 74070000 83, 810, 205 10111 10101 10111 00000 1011100 0000000 + 101110000 111100011 Pad, multiply and
Binary Multiplication Q: How do we multiply two numbers? eg. 12, 345 6, 789 111105 987600 8641500 + 74070000 83, 810, 205 10111 10101 10111 00000 1011100 0000000 + 101110000 111100011 Pad, multiply and
Factoring Algorithms
 Institutionen för Informationsteknologi Lunds Tekniska Högskola Department of Information Technology Lund University Cryptology - Project 1 Factoring Algorithms The purpose of this project is to understand
Institutionen för Informationsteknologi Lunds Tekniska Högskola Department of Information Technology Lund University Cryptology - Project 1 Factoring Algorithms The purpose of this project is to understand
PUTNAM TRAINING POLYNOMIALS. Exercises 1. Find a polynomial with integral coefficients whose zeros include 2 + 5.
 PUTNAM TRAINING POLYNOMIALS (Last updated: November 17, 2015) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
PUTNAM TRAINING POLYNOMIALS (Last updated: November 17, 2015) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
NOTES ON LINEAR TRANSFORMATIONS
 NOTES ON LINEAR TRANSFORMATIONS Definition 1. Let V and W be vector spaces. A function T : V W is a linear transformation from V to W if the following two properties hold. i T v + v = T v + T v for all
NOTES ON LINEAR TRANSFORMATIONS Definition 1. Let V and W be vector spaces. A function T : V W is a linear transformation from V to W if the following two properties hold. i T v + v = T v + T v for all
CD-ROM Appendix E: Matlab
 CD-ROM Appendix E: Matlab Susan A. Fugett Matlab version 7 or 6.5 is a very powerful tool useful for many kinds of mathematical tasks. For the purposes of this text, however, Matlab 7 or 6.5 will be used
CD-ROM Appendix E: Matlab Susan A. Fugett Matlab version 7 or 6.5 is a very powerful tool useful for many kinds of mathematical tasks. For the purposes of this text, however, Matlab 7 or 6.5 will be used
The Quantum Harmonic Oscillator Stephen Webb
 The Quantum Harmonic Oscillator Stephen Webb The Importance of the Harmonic Oscillator The quantum harmonic oscillator holds a unique importance in quantum mechanics, as it is both one of the few problems
The Quantum Harmonic Oscillator Stephen Webb The Importance of the Harmonic Oscillator The quantum harmonic oscillator holds a unique importance in quantum mechanics, as it is both one of the few problems
9 MATRICES AND TRANSFORMATIONS
 9 MATRICES AND TRANSFORMATIONS Chapter 9 Matrices and Transformations Objectives After studying this chapter you should be able to handle matrix (and vector) algebra with confidence, and understand the
9 MATRICES AND TRANSFORMATIONS Chapter 9 Matrices and Transformations Objectives After studying this chapter you should be able to handle matrix (and vector) algebra with confidence, and understand the
AP Physics 1 and 2 Lab Investigations
 AP Physics 1 and 2 Lab Investigations Student Guide to Data Analysis New York, NY. College Board, Advanced Placement, Advanced Placement Program, AP, AP Central, and the acorn logo are registered trademarks
AP Physics 1 and 2 Lab Investigations Student Guide to Data Analysis New York, NY. College Board, Advanced Placement, Advanced Placement Program, AP, AP Central, and the acorn logo are registered trademarks
How To Factor By Gcf In Algebra 1.5
 7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
9.2 Summation Notation
 9. Summation Notation 66 9. Summation Notation In the previous section, we introduced sequences and now we shall present notation and theorems concerning the sum of terms of a sequence. We begin with a
9. Summation Notation 66 9. Summation Notation In the previous section, we introduced sequences and now we shall present notation and theorems concerning the sum of terms of a sequence. We begin with a
Discuss the size of the instance for the minimum spanning tree problem.
 3.1 Algorithm complexity The algorithms A, B are given. The former has complexity O(n 2 ), the latter O(2 n ), where n is the size of the instance. Let n A 0 be the size of the largest instance that can
3.1 Algorithm complexity The algorithms A, B are given. The former has complexity O(n 2 ), the latter O(2 n ), where n is the size of the instance. Let n A 0 be the size of the largest instance that can
Factoring A Quadratic Polynomial
 Factoring A Quadratic Polynomial If we multiply two binomials together, the result is a quadratic polynomial: This multiplication is pretty straightforward, using the distributive property of multiplication
Factoring A Quadratic Polynomial If we multiply two binomials together, the result is a quadratic polynomial: This multiplication is pretty straightforward, using the distributive property of multiplication
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
Revised Version of Chapter 23. We learned long ago how to solve linear congruences. ax c (mod m)
 Chapter 23 Squares Modulo p Revised Version of Chapter 23 We learned long ago how to solve linear congruences ax c (mod m) (see Chapter 8). It s now time to take the plunge and move on to quadratic equations.
Chapter 23 Squares Modulo p Revised Version of Chapter 23 We learned long ago how to solve linear congruences ax c (mod m) (see Chapter 8). It s now time to take the plunge and move on to quadratic equations.
Vieta s Formulas and the Identity Theorem
 Vieta s Formulas and the Identity Theorem This worksheet will work through the material from our class on 3/21/2013 with some examples that should help you with the homework The topic of our discussion
Vieta s Formulas and the Identity Theorem This worksheet will work through the material from our class on 3/21/2013 with some examples that should help you with the homework The topic of our discussion
Lecture Notes on Polynomials
 Lecture Notes on Polynomials Arne Jensen Department of Mathematical Sciences Aalborg University c 008 Introduction These lecture notes give a very short introduction to polynomials with real and complex
Lecture Notes on Polynomials Arne Jensen Department of Mathematical Sciences Aalborg University c 008 Introduction These lecture notes give a very short introduction to polynomials with real and complex
Reading 13 : Finite State Automata and Regular Expressions
 CS/Math 24: Introduction to Discrete Mathematics Fall 25 Reading 3 : Finite State Automata and Regular Expressions Instructors: Beck Hasti, Gautam Prakriya In this reading we study a mathematical model
CS/Math 24: Introduction to Discrete Mathematics Fall 25 Reading 3 : Finite State Automata and Regular Expressions Instructors: Beck Hasti, Gautam Prakriya In this reading we study a mathematical model
Vector Notation: AB represents the vector from point A to point B on a graph. The vector can be computed by B A.
 1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
1 Linear Transformations Prepared by: Robin Michelle King A transformation of an object is a change in position or dimension (or both) of the object. The resulting object after the transformation is called
6.6 Factoring Strategy
 456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
456 CHAPTER 6. FACTORING 6.6 Factoring Strategy When you are concentrating on factoring problems of a single type, after doing a few you tend to get into a rhythm, and the remainder of the exercises, because
Vocabulary Words and Definitions for Algebra
 Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Name: Period: Vocabulary Words and s for Algebra Absolute Value Additive Inverse Algebraic Expression Ascending Order Associative Property Axis of Symmetry Base Binomial Coefficient Combine Like Terms
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Lecture 2 Matrix Operations
 Lecture 2 Matrix Operations transpose, sum & difference, scalar multiplication matrix multiplication, matrix-vector product matrix inverse 2 1 Matrix transpose transpose of m n matrix A, denoted A T or
Lecture 2 Matrix Operations transpose, sum & difference, scalar multiplication matrix multiplication, matrix-vector product matrix inverse 2 1 Matrix transpose transpose of m n matrix A, denoted A T or
To give it a definition, an implicit function of x and y is simply any relationship that takes the form:
 2 Implicit function theorems and applications 21 Implicit functions The implicit function theorem is one of the most useful single tools you ll meet this year After a while, it will be second nature to
2 Implicit function theorems and applications 21 Implicit functions The implicit function theorem is one of the most useful single tools you ll meet this year After a while, it will be second nature to
1 Introduction. Linear Programming. Questions. A general optimization problem is of the form: choose x to. max f(x) subject to x S. where.
 Introduction Linear Programming Neil Laws TT 00 A general optimization problem is of the form: choose x to maximise f(x) subject to x S where x = (x,..., x n ) T, f : R n R is the objective function, S
Introduction Linear Programming Neil Laws TT 00 A general optimization problem is of the form: choose x to maximise f(x) subject to x S where x = (x,..., x n ) T, f : R n R is the objective function, S
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS
 MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS Systems of Equations and Matrices Representation of a linear system The general system of m equations in n unknowns can be written a x + a 2 x 2 + + a n x n b a
MATRIX ALGEBRA AND SYSTEMS OF EQUATIONS Systems of Equations and Matrices Representation of a linear system The general system of m equations in n unknowns can be written a x + a 2 x 2 + + a n x n b a
Derivative Approximation by Finite Differences
 Derivative Approximation by Finite Differences David Eberly Geometric Tools, LLC http://wwwgeometrictoolscom/ Copyright c 998-26 All Rights Reserved Created: May 3, 2 Last Modified: April 25, 25 Contents
Derivative Approximation by Finite Differences David Eberly Geometric Tools, LLC http://wwwgeometrictoolscom/ Copyright c 998-26 All Rights Reserved Created: May 3, 2 Last Modified: April 25, 25 Contents
