|
|
|
- Bertram Gibson
- 9 years ago
- Views:
Transcription
1 RadiativeHeatingandCooling incircumstellarenvelopes Dipl.-Phys.PeterWoitke ausberlin von zurerlangungdesakademischengrades dertechnischenuniversitatberlin VomFachbereich04(Physik) DoktorderNaturwissenschaften(Dr.rer.nat.) genehmigtedissertation Berlin1997 D83
2 Promotionsausschu Vorsitzender:Prof.Dr.D.Zimmermann Berichter: TagdermundlichenPrufung: Prof.Dr.E.Sedlmayr Priv.Doz.Dr.J.P.Kaufmann
3 HatmaninnereRuhe,dannentstehtGelassenheit. Weiman,womaninnehaltenmu,entstehtgeistigeFestigkeit. HatmanGelassenheit,dannentstehtbesonnenesNachdenken. GibtesgeistigeFestigkeit,dannentstehtinnereRuhe. GibtesbesonnenesNachdenken,sokommtdasGelingen. (Konfuzius,BuchderRiten)
4
5 Zusammenfassung KleineFestkorperpartikelvoneinerGroebiszuetwa1mbildenaufdenersten Blickeineunbedeutende,eherstorendeKomponentederMaterieinunseremKosmos.Genauerbetrachtetkommtdiesen"Staubteilchen\jedocheinegrundsatzliche Bedeutungzu.AufgrundihrergroenWirkungsquerschnittefurdieWechselwirkung mitverantwortlichfurdenkosmischenkreislaufunddiechemischeevolutionder scheneigenschaftendesgasesinderinterstellarenmaterieundsindohnezweifel Universums.Siebeeinussenwesentlichdiedynamischen,thermischenundchemi- mitlichtpragensieinganzentscheidenderweisedaserscheinungsbilddesheutigen Materie.MankannohneUbertreibungsagen,daesohnedieExistenzderStaubteilchenwederdieErde,nochdenMenschen,javielleichtnichteinmaldieSonnmodynamischeBedingungen.NebenhohenDichtensindinsbesondereniedrige,aber gebenwurde. DieBildungdieserStaubteilchenausderGasphaseerfordertrelativspezischether- nichtzuniedrigetemperaturenunterhalbdersublimationstemperaturdesbetrachtetenfestkorpermaterialserforderlich.diesevoraussetzungistabsolutzwingend. demzufolgegeltendiemassivenwindedieserobjektealshauptproduktionsstatten soliegendiesevorallemindenzirkumstellarenhullenvonkuhlenriesensternenvor; FragtmannachderExistenzsolcherBedingungeninastrophysikalischenObjekten, desstaubesimuniversum.beiriesensternenmiteektivtemperaturenunterhalb vonetwa3000kistdermechanismusderstaubbildungunddesmassenverlustes nichtzuletztdurchdiearbeitenderberlinerarbeitsgruppevonprof.dr.sedlmayr durchabsorptions{undstreuprozessedenimpulsdesstrahlungsfeldesteilweise MolekulzumFestkorperzuermoglichen.DieentstehendenStaubteilchennehmen erreichtdasgastemperaturen,dieniedriggenugsind,umdenphasenubergangvom hinreichendverstanden:beigenugendgroenradialenabstandenvomstern aufundgebendiesendurchstoeandasgasweiter.dieserimpulseintragtreibt denstellarenwind. NebendiesenSternengibteseineReihevonweiterenstaubbildendenObjekten. InsbesondereexistierteinezahlenmaigeherunbedeutendeKlassevonRCoronae deckenkonnen,sodadieserfurdasbloeaugefurmonateoderjahrevomhimmel zurbildungvonriesigenstaubwolken,diedengesamtensternvorubergehendver- diesenobjektenkommtesinunvorhersagbarenzeitlichenabstandenimmerwieder Borealis(RCB)Sternen,diesichnichtrechtindasobigeBildeinordnenlassen.Bei zuverschwindenscheint1.beobachtungenlegennahe,daderstaubbildungsproze undnovae{explosionenvor. 1Ahnliche,wennauchnichtderartspektakulareBeobachtungenliegenfurWolf{Rayet{Sterne i
6 ii beidiesensternenineinerentfernungvonnureinigenwenigensternradienstattndenmu,obwohldiercb{sterneeektivtemperaturenvonetwa7000kbesitzen, diealsoheierundvielleuchtkraftigeralsdiesonnesind.dievorliegendearbeit ZUSAMMENFASSUNG nimmtdiesebeobachtungsergebnisseernst. dungindernahediesersternemitdenublichentheorienerklaren?setztmandie durchdiercb{sterneaufeineharteprobegestelltwerden:latsichdiestaubbilfernungenvomsternsehrhohetemperaturen,sodadiestaubbildungstheorien GangigeMethodenzurTemperaturbestimmungergebeninsogeringenradialenEnt- KannesinderNahevonheienSternenzuthermodynamischenBedingungenkom- Temperaturenalserwartetherrschen. GultigkeitderTheorienvoraus,somussenentwederdieBeobachtungenfalschsein, men,diestaubbildungsprozessezulassen?angeregtdurchdiesefragestellungunter- oderesmussenindernahediesersterne zumindestzeitweilig vielniedrigere suchtdievorliegendearbeitdenthermischenzustanddunnergaseunterdemein- uvonstellarenstrahlungsfeldern.eshandeltsichhierbeizunachstumallgemeine (nichtrcb{spezische),grundlegendestudien.einemethodezurzeitabhangigen TemperaturbestimmungvonGaseninzirkumstellarenHullenwirdentwickelt,die ModellrechnungeninzukunftigenArbeitenverwendetwerdenkann. vonvornhereinsokonzipiertist,dasiealselementarerbestandteilvonkomplexeren DasthermodynamischeKonzeptdieserMethodeberuhtaufeinernon{LTEBeschreibungdesGases,inderjedocheineGeschichtsabhangigkeitderKonzentrationendenetischesGleichgewicht(\steadystate")vorausgesetzt.Eswirdgezeigt,dadiesgangevonAtomenundeinfachgeladenenIonen,Vibrations{undRotationsuber- DiefolgendenradiativeProzessewerdenindieserArbeitberucksichtigt:Linienuber- vonh2,gebunden{frei{ubergangevonatomenausdemgrundzustandund(im gangevonpolarendiatomischenbzw.linearenmolekulen,quadrupol{ubergange MolekuleundderBesetzungsdichtenvernachlassigtwird.Stattdessenwirdeinki- AnnahmeeinegewohnlichethermodynamischeBeschreibungdesGaseszulat. sorptionsprozesseprozeitaufnimmtbzw.durchemissionsprozesseverliert.diera- diativenheiz{undkuhlratenbildensomitdiegrundlagezurthermodynamischen ModellierungdesGases. radiativenheiz{undkuhlraten,d.h.diewarmemengen,diedasgasdurchabziationsprozesseundfrei{frei{ubergange.dieseprozesseergebenindersummedie FallevonWassersto)ausangeregtenelektronischenNiveaus,fernerPhotodisso- dasichdieradiativenheiz{undkuhlratenausgleichen(strahlungsgleichgewicht). renhullenvonrcb{sternenbestimmt.diesezustandezeichnensichdadurchaus, ZunachstwerdendiestabilenGleichgewichtszustandedesGasesindenzirkumstella- DreiAnwendungenderentwickeltenMethodewerdenvorgestellt: Eswirdjedochfestgestellt,dadasStrahlungsgleichgewichteinezwarnotwendige, Gasesdarstellt.UntergegebenenDruck{undStrahlungsfeldbedingungenkonnen mehrerelosungenexistieren,d.h.eineraumlichekoexistenzvonheien,atomaren abernichthinreichendebedingungzurberechnungdesthermischenzustanddes
7 Phasennebenkalten,molekularenPhasenerscheintprinzipiellmoglich("thermische ZUSAMMENFASSUNG iii Bifurkationen\). DerRelaxationsprozedesGaseszumStrahlungsgleichgewichtwirdindenzirkum- StowellenureinhinreichenddichtesGasinderLageist,denStrahlungsgleichgewichtszustandnacheinigerZeitwiederzuerreichen.BeiTeilchendichten<108cm tendesgaseshinterstowellendiskutiert,diedurcheinepulsationdeszentralensternsverursachtwerden.esergibtsich,danachderpassageeinersolchestellarenhullenvonc{sternenuntersucht.hierbeiwirdinsbesonderedasverhal- SchlielichwirddaszeitabhangigethermischeVerhaltendesGasesindenzirkum- diesersternhullenverliert. StrahlungsgleichgewichtesihrebestimmendeBedeutungfurdieTemperaturstruktur verhaltsichdasgaszunehmendadiabatisch,sodaschlielichdiebedingungdes einembestimmtendichtebereichkanndabeidasgasdurcheinen2{stufen{proze, riodischesituationstudiert,inderdasgasindernahedessternsfortlaufenddurch Stowellenerhitztundkomprimiertwird,undinderZwischenzeitreexpandiert.In stellarenhullenvonpulsierendenrcb{sternengenaueruntersucht.eswirdeinepe- bestehendausradiativerkuhlunggefolgtvonadiabatischerexpansion,temperaturenerreichen,dieweitunterhalbderstrahlungsgleichgewichtstemperaturliegen. SchonbeiradialenAbstandenvonetwa1:5 3RtretenhierbeizeitweiligTemperaturenunterhalbvon1500Kauf,abhangigvonderStowellengeschwindigkeit.Diese DievorliegendeArbeitenthaltsomitgrundlegendeErkenntnisseuberdasthermodynamischeVerhaltenderGaseinzirkumstellarenHullen.Neue,alternativeWege VerdunklungsereignissedieserObjekteauslostwerdenkonnten. NahederRCB{SternedurchStowellenverursachtwird,wodurchdiespektakularen ArbeitstelltdaherdieHypotheseauf,dadieKondensationvonRuteilcheninder zurstaubbildungwerdenaufgezeigt.
8 iv
9 Abstract presentincircumstellarenvelopes. radiationelds.onthebasisofasteady{statenon{ltedescription,theradiative Thisthesisinvestigatesthethermalstateofdilutedgasesbeingexposedtostellar Thefollowingradiativeprocessesareexamined:linetransitionsofneutralandsingly ionizedatoms,vibrationalandrotationaltransitionsofpolardiatomicandlinear heatingandcoolingratesofthegasaredetermined,consideringthetypicaldensities Athermodynamicdescriptionofthegasisdevelopedwhichallowsforatime{ photodissociationandfree{freetransitions. theelectronicgroundstatesand(incaseofhydrogen)fromexcitedelectroniclevels, molecules,respectively,quadrupoletransitionsofh2,bound{freetransitionsfrom dependentdeterminationofthetemperaturestructureinthecircumstellarenvelopes stellarenvelopesofrcoronaeborealis(rcb)stars.itisfoundthatthecondition modelcalculations.threeapplicationsofthisdescriptionarepresented: First,thestableradiativeequilibriumstatesofthegasarecalculatedforthecircum- ofcoolandwarmstarsandcanbeincludedintomorecomplex,e.g.hydrodynamic, andradiationeld.thus,aspatialcoexistenceofhot,atomicandcool,molecular gas.morethanonetemperaturesolutionmayexistforxedconditionsofpressure ofradiativeequilibriumisnotsucientinordertodeterminethetemperatureofthe Second,therelaxationprocesstowardsradiativeequilibriumisstudiedinthecircumstellarenvelopesofC{stars.Thecharacterofthethermalrelaxationbehind propagatingshockwaves,whicharecausedbyapulsationofthecentralstar,is phasesisprincipallyconceivable(\thermalbifurcations"). discussed.itisfoundthatthegasmustbesucientlydenseinordertobecapable toreestablishradiativeequilibriumafterthepassageofsuchshocks.fordensities nallytheconditionofradiativeequilibriumloosesitssignicanceconcerningthe determinationofthetemperaturestructure. <108cm 3,thebehaviorofthegasbecomesmoreandmoreadiabatic,sothat Third,thetime{dependentbehaviorofthegasinthecircumstellarenvelopesof thegasisfoundtoundergoatwo{stepcoolingprocess,consistingofradiativecoolingathightemperaturesfollowedbyadiabaticexpansionatlowtemperatures.in atmospheresisdeveloped,wherethegasisperiodicallyheatedandcompressedby shockwavesandre{expandsbetweentheshocks.withinadistinctdensityinterval pulsatingrcbstarsisinvestigatedmoredetailed.amodelforshocklevitated atradialdistancesassmallas1:5 3R,despiteofthehigheectivetemperaturesof peraturesbelow1500k(farbelowthevaluesexpectedfromradiativeequilibrium) thiscaseaconsiderablesupercoolingofthegasoccurs,temporarilyproducingtem- closetorcbstarsiscausedbyshockwaves,whichmighttriggerthespectacular thesestars.thus,thisthesisstatesthehypothesisthattheonsetofdustformation declineevents. v
10 Contents Zusammenfassung Abstract vi ListofFigures ListofSymbols xiv x 1Introduction ListofTables xv 1.1The ModelsofDustFormation:::::::::::::::::::::::: Importance of for 1.2CriticalCommentsontheUsualMethodofTemperatureDetermination2 1.3ThePuzzleofDustFormationaroundRCBStars::::::::::: 1 1.5AimandStructureofthisWork:::::::::::::::::::::13 1.4RequirementsforDierentApproachesofTemperatureDetermination11 6 2TheThermodynamicConcept 2.1FirstLawofThermodynamicsandEquationofState:::::::::17 2.2LTEandNon{LTE:::::::::::::::::::::::::::: RadiativeHeatingandCooling 2.3SteadyState::::::::::::::::::::::::::::::::20 3.1Bound{BoundTransitions:::::::::::::::::::::::: EscapeProbabilityMethodforanN{Level{Systemwithout DiscussionoftheApplicabilityofSobolevTheory:: NumericalIterationScheme::::::::::::::27 Continuum:::::::::::::::::::::::::::: RotationalTransitionsofLinearPolarMolecules:::::::: LinesofAtomsandIons::::::::::::::::::::: AnExemplaryTwo{Level{Atom:::::::::::29 vi
11 3.1.4VibrationalTransitionsofDiatomicPolarMolecules:::::: Fast,ApproximateMethod:::::::::::::: RotationalHeatingandCoolingbyCO:::::::: VibrationalHeatingandCoolingbyCO:::::::40 3.2Bound{FreeTransitions::::::::::::::::::::::::: QuadrupoleTransitionsofH2:::::::::::::::::: Fast,ApproximateMethod:::::::::::::: TheRateEquationsforanN{LevelSystemwithContinuum: OtherNeutralAtoms::::::::::::::::::::::: TheH{Atom::::::::::::::::::::::::::: Fast,ApproximateMethod::::::::::::::46 3.3PhotodissociationandRadiativeAssociation::::::::::::::53 3.4Free{FreeTransitions:::::::::::::::::::::::::::58 3.5OverviewoftheConsideredRadiativeProcesses:::::::::::: TheH Heating/CoolingRate::::::::::::::::::55 4TheCalculationoftheEquationofState 3.6FurtherHeatingandCoolingProcesses:::::::::::::::::61 4.2CalculationoftheInternalEnergy::::::::::::::::::::67 4.1CalculationoftheParticleConcentrations:::::::::::::::65 5ThermalBifurcationsintheCircumstellarEnvelopesofRCBStars71 5.1TheModel::::::::::::::::::::::::::::::::: DenitionoftheRadiativeEquilibriumGasTemperature:::72 5.2Results::::::::::::::::::::::::::::::::::: ApproximationoftheRadiationField:::::::::::::: ElementAbundances::::::::::::::::::::::: DegreeofIonization::::::::::::::::::::::: RadiativeEquilibriumTemperatureSolutions::::::::: RadiativeHeatingandCoolingRates:::::::::::::: Chemistry:::::::::::::::::::::::::::::74 6RadiativeCoolingTimeScalesintheCircumstellarEnvelopesof 5.3Discussion:::::::::::::::::::::::::::::::::83 C{Stars 6.1TheModel:::::::::::::::::::::::::::::::::86 85 vii
12 6.1.3ApproximationoftheRadiationField:::::::::::::: ElementAbundances::::::::::::::::::::::: DenitionoftheRadiativeCoolingTimeScale:::::::::86 6.2Results::::::::::::::::::::::::::::::::::: CompositionoftheGas::::::::::::::::::::: LocalVelocityGradient::::::::::::::::::::: InternalEnergy:::::::::::::::::::::::::: TheRadiativeCoolingTimeScaleandtheRoleoftheVarious 6.2.4DependenceontheRadiationField::::::::::::::: DependenceontheVelocityGradient::::::::::::::94 HeatingandCoolingProcesses::::::::::::::::: ComparisontoAnalyticalHeating/CoolingFunctions::::: ResultsoftheComparison::::::::::::::: LTEHeating/CoolingFunction:::::::::::: Bowen'sHeating/CoolingFunction::::::::::95 7Shock{InducedCondensationaroundRCBStars 6.3Discussion::::::::::::::::::::::::::::::::: TheTransitionfromIsothermaltoAdiabaticShocks:::::98 7.1TheModel:AFixed,PeriodicallyShockedFluidElementinaConstantRadiationField::::::::::::::::::::::::::: Re{ExpansionPhases::::::::::::::::::::::: ShockTransitions::::::::::::::::::::::::: Thermodynamics::::::::::::::::::::::::: TheModelingProcedure::::::::::::::::::::: Results::::::::::::::::::::::::::::::::::: ExaminedRangeofParameters::::::::::::::::: OverviewofIntroducedParameters::::::::::::::: CyclicVariationsinthePeriodicallyShockedFluidElements: PreconditionsforCarbonNucleation:::::::::::::: DependenceonShockVelocity:::::::::::::::::: DependenceonDensity:::::::::::::::::::::: Discussion::::::::::::::::::::::::::::::::: AdvantagesoftheModel::::::::::::::::::::: DependenceonRadialDistance::::::::::::::::: InterpretationsofObservationswithRegardtotheModel:: Criticism::::::::::::::::::::::::::::::120 viii
13 ACurrentStatusofRCBResearch 8Conclusions A.1GeneralObservations:::::::::::::::::::::::::::127 A.2ObservationsDuringtheDeclineEvents::::::::::::::::129 A.3Models:::::::::::::::::::::::::::::::::::132 A.3.1HistoricalModels:::::::::::::::::::::::::132 A.3.2ModelCalculations::::::::::::::::::::::::132 References A.3.3EmpiricalModels:::::::::::::::::::::::::134 Danksagung 136 Lebenslauf ix
14 ListofSymbols symboldescription Aul Einsteincoecientforspontaneousemission unit page Blu BulB frequencyintegratedplanckfunction rotationalconstant ergs 1cm 2 B Einsteincoecientforabsorption Einsteincoecientforstimulatedemission Planckfunction ergs 1cm 2Hz 1 erg 1cm2s Cul D0mol Ea Clu ratecoecientforcollisionalexcitation ratecoecientforcollisionalde{excitation activationenergyofachemicalreaction Eel Eion Etrans Ediss Erot totaldissociationpotentialenergy totalelectronicexcitationenergy totalionicpotentialenergy Evib totalrotationalexcitationenergy Eul totaltranslationalenergy totalvibrationalexcitationenergy energydierencebetweenupperandlowerstate 67 fg Iinc J() freeenthalpyofformationatstandardpressure incidentcontinuousintensityfromdirection p ergs 1cm 2Hz 1str 1 54 Jcont J meanspectralintensity frequencyintegratedmeanintensity 25 ul rotationalquantumnumber continuousmeanintensityatlinecenter Jul J lineaveragedcontinuousmeanintensity ergs 1cm 2Hz 1 ul formingpervolumeandpersecond nucleationrate,i.e.thenumberofseedparticles solidangle cm 3s temperature{independentratecoecientforcollisionalde{excitation cm3s 1 32 epe simpliedmeanescapeprobability totalnetradiativeheatingfunction ergs 1cm 3 { meanescapeprobability Qbf bqrad bqdust ofdustgrains totalnetradiativeheatingratepermass totalnetheatingratepermassduetopresence ergs 1g 1 Qrad netradiativeheatingfunctionduetobound{free netradiativeheatingfunctionduetofree{free 22 transitions ergs 1cm 3 45 x 58
15 Qvib Qchem symboldescription Qrot rotationalnetheatingfunction vibrationalnetheatingfunction unit page Rrad chemicalreaction netradiativeheatingfunctionofaphoto{ ergs 1cm 3 37 Rij stellarradius 41 S totalratecoecientfortransitioni!j 54 SLul supersaturationratioofthegaswithrespectto linesourcefunction graphite ergs 1cm 2Hz 1 { Si(Tg) TM Sahafunctionofleveli temperature cm 3 Trot vibrationaltransitionmoment [cgs] 45 Tbb rotationalexcitationtemperature vibrationalexcitationtemperature blackbodytemperature Te Tg Trad TRE eectivestellartemperature uniquekinetictemperatureofthegas radiationtemperature 17 4 VWg radiativeequilibriumtemperature specicvolume1= cm3g 1 K 22 ZII Zrot dilutionfactor partitionfunctionofansinglyionizedatom 45 Zvib amu rotationalpartitionfunction vibrationalpartitionfunction atomicmassunitmc12=12 g 36 3 i bi i(tg) atm standardatmosphericpressure1: photo{recombinationcoecienttoleveli departurecoecientfromltebi=ni=ni dyncm 2 cm 3s 1 39 c ratecoecientforcollisionalionizationfromlevel i cm3s 1 46 e speedoflight cms jul El internalenergyofthegas elementabundancebynumber gasemissioncoecient ergs 1cm 3Hz 1str 1 ergg 1,18 25 frot gl;gu dimensionlessmeanintensityatul 66 ul numberofrotationaldegreesoffreedom statisticalweightsoflowerandupperlevel ratecoecientforcollisionalde{excitation cm3s 1 { hhhiabs hhiem Planck'sconstant enthalpypermassunith=e+p= h=(2) ergg 1 ergs 25 k meanabsorbedphotonenergy 70 kf meanemittedphotonenergy 39 kr Boltzmannconstant ratecoecientofaforwardchemicalreaction ergk 1 47 B ratecoecientofareversechemicalreaction gasabsorptioncoecient depends 54 J mel Planckmeanabsorptioncoecient intensitymeanabsorptioncoecient wavelength massofneutralatomofelementel cm 1 3 xi g 662
16 symboldescription me mred;i electronmass unit page D eredspeciesandcollisionpartneri reducedmassforcollisionsbetweentheconsid- cos g{ 45 n dipolemomentofamolecule [cgs] ni nl particledensityinlte,chemicalequilibrium 25 nu populationofleveli 35 levelpopulationofthelowerlevel 50 nel levelpopulationoftheupperlevel 24 n<h> at II totalneutralatomparticledensity singlyionizedatomparticledensity 25 n<he> totaldensityofh-nucleiinallionic,atomicand molecularformsh=(pelelmel)) 66 ncr totalheliumparticledensityinatomicorionized 29 nthick population criticaldensity(n<h>{value)forthermal 74 ne eects criticaldensity(n<h>{value)foropticaldepths electrondensity 31 ithr nmol nsp totalparticledensityofmoleculemol totalparticledensityofonespecies cm 3 32 ul 36! thresholdfrequencyforphotoionization!mol linecenterfrequency eigenfrequencyoftheharmonicoscillator pj j-thvibrationaleigenfrequencyofamolecule gaspressure Hz 67 ul(;) p psat prolefunctionoftheconsideredtransition standardpressure vaporpressureofneutralatomsoverthebulk material dyncm 2 Hz sel r radialdistancetothecenterofthestar massdensityofthegas gcm 3 25 f() mol mentel stoichiometriccoecientofmoleculemolforele- StefanBoltzmannconstant ergcm 2K bf i() photodissociationcrosssection totalcrosssectionforrotationalde{excitation bound{freeabsorptioncrosssectionfromleveli cm cool es ul meansobolevopticaldepth radiativeheating/coolingtimescale s anglebetweentheconsideredrayandtheradial characteristic direction 26 transitions temperature of vibrational K v1 dv dl vibrationalquantumnumber hydrodynamicgasvelocity terminalwindvelocity localmeanvelocitygradient kms 1 cms 1 { xii 28 26
17 ListofFigures 1.1Possibleradiativeequilibriumtemperaturesoverdilutionfactorina 1.3TemperaturestructureinhydrodynamicmodelsusingLTE{cooling:12 1.2SketchofanRCrBdeclineevent.:::::::::::::::::::: Planck{typeradiationeld:::::::::::::::::::::::: Temperaturestructureinhydrodynamicmodelsusing2{cooling:::12 3.2Temperaturedependenceofthelinecoolingrate::::::::::::30 3.1Thecoolingratepermassofanexemplarytwo{level{atom::::::30 2.1Thepoolsanduxesofenergyinthegas::::::::::::::::19 3.5VibrationalcoolingrateandexcitationtemperatureofCO::::::40 3.4RotationalcoolingrateandexcitationtemperatureofCO:::::::37 3.3Dependencyofthelinecoolingrateontheradiationeld:::::::30 3.6ThequadrupolecoolingrateofH2::::::::::::::::::::43 3.8Thebound{freeplusbound{boundcoolingrateofhydrogeninthe 3.7Thebound{freeplusbound{boundcoolingrateofhydrogeninthe casewithcontinuousradiationeld:::::::::::::::::::49 casewithoutcontinuousradiationeld::::::::::::::::: Thebound{freeandfree{freecoolingratesofH withoutcontinuous 3.9Detailsofthehydrogencoolingrate:::::::::::::::::: Thebound{freeandfree{freecoolingratesofH withcontinuous 5.1ElementabundancesofRCoronaeBorealis::::::::::::::: Overviewoftheconsideredheatingandcoolingprocesses:::::::60 radiationeld:::::::::::::::::::::::::::::::57 5.2Heating/coolingratesasfunctionofthegastemperature:::::::77 5.3ThermalbifurcationsinRCBenvelopesforp=102and100dyncm 2 5.4ThermalbifurcationsinRCBenvelopesforp=10 2and10 4dyncm ThermalbifurcationsinRCBenvelopesforp=10 6and10 8dyncm Thecomposition,theinternalenergyandthenetheatingfunctionof thegasasfunctionoftemperatureanddensity:::::::::::::89 xiii
18 6.4RadiativecoolingtimescalesforC{starenvelopesinthecaseJ= 6.3MostecientcoolingprocessreferringtoFig.6.2:::::::::::92 6.2RadiativecoolingtimescalesforC{starenvelopesforthecaseJ=0:92 6.6Radiativecoolingtimescalescalculatedfromtheanalyticalheating/coolingfunctionproposedbyBowen(1988)::::::::::::96 6.5MostecientcoolingprocessreferringtoFig.6.4:::::::::::93 B(3000K)::::::::::::::::::::::::::::::::93 7.1Ballistictrajectoriesofxeduidelementsintheenvelopeofapulsatingstar::::::::::::::::::::::::::::::::: RadiativecoolingtimescalecalculatedfromLTE:::::::::::96 7.2Schematicdescriptionofthethermodynamicprocessesoccurringina 7.3Timevariationsofthethermodynamicstatevariablesinaxed,periodicallyshocked,circumstellaruidelement:::::::::::::110 xeduidelementofthecseofapulsatingstar::::::::::: Detailsoftheperiodictimevariations:::::::::::::::::: Cyclicvariationsofdensityandtemperatureinxeduidelements: Minimumgastemperaturesandthepossibilityofcarbonnucleation tooccurataradialdistanceofr=2r:::::::::::::::::117 xiv
19 ListofTables 1.1Observationalandtheoreticalconstraintsonthenucleationdistance 3.2Vibrationalandrotationalheatingandcooling:consideredspecies 3.1Atomiclineheatingandcooling:consideredspeciesandtransitions:33 inrcbenvelopes:::::::::::::::::::::::::::::10 3.3Bound{freeheatingandcooling:consideredspeciesandatomicdata:53 3.4Overviewoffurtherheatingandcoolingprocesses:::::::::::62 andmoleculardata::::::::::::::::::::::::::::35 5.1AbundantmoleculesinthecircumstellarenvelopesofRCBstars:::74 5.2Importantheating/coolingprocessesforRCBabundances:::::::76 4.1Moleculardataforthedeterminationoftheinternalenergy::::::69 7.1Resultsoftheshock{inducedcondensationmodelasfunctionofradial distanceandshockvelocity::::::::::::::::::::::::118 xv
20 xvi
21 Chapter1 Introduction 1.1 ModelsofDustFormation TheImportanceofTemperatureDeterminationfor Comparedtotheusualorganizationalformsofmatterinspacelikestarsandthe interstellarmedium(ism),thereareremarkableandexceptionalthermodynamic starissucientlycoolthatitsradiationelddoesnotionizethesurroundingcse, tomassloss stillhigherbyordersofmagnitudethanintheism.ifthecentral byordersofmagnitudethanintheinteriorandtheatmospheresofstars,but due conditionsinextendedcircumstellarenvelopes(cses).here,thedensitiesarelower energybarriersduringtheirformation. temperaturescanexist,whichareononehandlowenoughtoensurethestability ofcomplexchemicalstructures,butontheotherhandhighenoughtobridgethe Therefore,thecircumstellarenvelopesofcoolstarsareacosmiclaboratory,where space.thehighdensitiescombinedwithlow,butnottoolow,temperaturesprovide largeamountsofcomplexchemicalandphysicalprocessescanoccur.theseprocessesareoffundamentalimportancefortheevolutionofmatter,especiallyfor almostidealpreconditionsforcondensationprocesses. thetransitionfrommoleculestodustgrains,i.e.theprimaryformationofsolidsin nomenalikenovaeandsupernovae,shockwavesinthemostdensepartsoftheism BesidestheCSEsofcoolstarsonlyafewclassesofastrophysicalobjectsareknown (probablyconnectedwithstarformation)orcometimpactsonplanets.therefore, whichshowsimilarthermodynamicconditions.thesearetherareexplosivepheistenceofdustparticlesisofgreatestimportancefortheappearanceofthepresent particles(dustgrains)inspace.theseparticlesarecarriedintotheismbystellar windsandnallycanbeobservedeverywhereintheuniverse.thisubiquitousex- thecsesofcoolstarsaresupposedtobethemainproductionsitesofsmallsolid nallytotheformationofseedanddustparticles,showsuchastrongtemperature Thechemicalreactions,whichsuccessivelyleadtoincreasingcomplexityingasesand lastbutnotleast,alsofortheexistenceoflife,includingmankind. universe,forthecirculationofmatter,fortheformationofstarsandplanetsand, smalltemperaturewindowofafewhundreddegreesbelowthesublimationtemper- dependencethatevenslighttemperaturedeviationscanchangetheformationrates byordersofmagnitude.therefore,eectivenucleationisgenerallyrestrictedtoa 1
22 atureofthesolidmaterial,whichistobeconsidered1.thusitisimmediatelyclear 2 CHAPTER1.INTRODUCTION ontheproperdeterminationofthetemperatureinthemedium.questionableor thattheresultsoftheoreticalmodelcalculationsofdustformationcriticallydepend insucientmethodsfortemperaturedeterminationcaneasilyinducesevereerrors intheresultsofsuchcalculations. Forthemodelingandtheunderstandingofdustformationfromthegas Howprofoundisourknowledgeofthetruethermodynamicstateofthegases(especiallytheirtemperature)inastrophysicalobjects?Inexceptionalcasesadirect thegasisabsolutelyrequired. phase,themostpreciseinformationaboutthethermodynamicstateof determinationofthetemperaturestraticationfromobservationsoftheobjects mightbepossible.however,theoreticalmethodsareusuallyrequiredwhichmay stillsuerfromlargeintrinsicuncertainties(seenextsection).astonishingly,most expenditureforthetheoreticaltemperaturedeterminationoftenseemstobeinadequatecomparedtothedetailedtreatmentofthechemistryanddustformation modelcalculationsconcerningdustformationincoolstellarenvelopesuserather simpleandnotveryreliablemethodsfortemperaturedetermination.atleast,the Thesequestionsgetevenmoreimportant,whenthegaselementsaresubjectto processesinsuchinvestigations. Howreliablearethoseresults?Inthiswaynewpotentialsites(e.g.closetohot dynamicprocesseswhichdirectlyaecttheinternalenergyofthegas.forinstance, inshockwaves,intheheatingbymagneto{acousticwavesorduringfastexpansions accompaniedbyadiabaticcooling.whichtemperaturedoesoneuseinsuchcases? 1.2 stars)fordustformationnotpreviouslyconsideredmightbediscovered. ThetemperaturestructureinextendedCSEsisusuallycalculatedbymeansof CriticalCommentsontheUsualMethodofTemperatureDetermination thesolutionofaradiativetransfer.assumingthatsolelyradiativeprocessesare equilibrium(re),wherethetotalamountofabsorbedradiativeenergyislocally balancedbythetotalamountofemittedradiativeenergyeverywhereintheenvelope. importantfortheheatingandcoolingofthegas,thegaswillrelaxtoradiative ThemeaningofthephysicalquantitiesisexplainedintheListofSymbolsonpagex. Incaseoflocalthermodynamicequilibrium(LTE),theemissivitycanbeeliminated RE: 4ZJd=4Zd (1.1) bymeansofkirchho'slaw=b(t): 1Thisstatementreferstoboththe\classical"andkinetictreatmentoftheproblem. LTE: ZJd=ZB(TRE)d (1.2)
23 1.2THEUSUALMETHODOFTEMPERATUREDETERMINATION Inordertoarriveatashortnotation,appropriatemeansoftheabsorptioncoecient 3 thetemperatureofthegasinradiativeequilibriumcanbeexpressedby (JandB)canbedenedsuchthatEq.(1.2)simpliestoJJ=BB(TRE)and AsfarastheassumptionsofREandLTEareappropriate,Eq.(1.3)togetherwith TRE4=J asolutionoftheradiativetransferdeterminesthepropertemperaturestructurein BJ: cases,wherethegasissucientlycoolformoleculeformation.consideringthe ofthekeyproblemsinastrophysicsandaverydiculttask,especiallyinthose calculationofthegasabsorptioncoecients.thiscalculation,however,isone theconsideredastrophysicalobject.theuncertaintyofthismethodlieswithinthe andbound{freetransitionsintheuvmaybeimportant.inprinciple,allthese rangingfromthenearirtothemicro{wavespectralregion.furthermoreelectronic gaswithasolarelementalcomposition,overabillionoflinetransitionsareknown H2Omolecule,forexample,whichisoneofthemostabundantspeciesinacool Therefore,duetothelackofknowledgeoftheexactfrequencydependencyof, shiftsduetohydrodynamicvelocitiesandselfshieldingcomeintoplay. questionsconcerningtheindividuallineprolesandtheeectscausedbydoppler transitionmustbetakenintoaccountforapropercalculationof.additional thesimplifyingassumptionj=bisoftenmade.inthiscasewehavej=b,which givestheblackbodytemperature grey: T4 const.j=bishenceforthcalledthe\quasi{greyassumption".inthefollowing, Alternatively,Eq.(1.4)canbederiveddirectlyfromEq.(1.2)byassuming= bb=j: theintrinsicuncertaintyofthisapproximationfortheresultingtemperaturestructureisexplored.first,eq.(1.4)obviouslyhasalwaysexactlyonetemperaturesolutionforagivenj,whereaseq.(1.3)mayhavetwoormorestablesolutions,because thefractionj=bcanbetemperature{dependentitself.thereby,thequasi{grey assumptionignoresthepossibilityofthermalbifurcations,whichwewillencounter matedbyconsideringtheextremecaseofa{function laterinthiswork. Themaximumeectcausedbytruefrequency{dependentabsorptioncanbeesti- radiativeprocesswhichdominatestheheatingandcoolingofthegasandwhichhas Thiscaseisnotasarticialasitmightrstappear,becausethereisoftenonespecial =0( 0): (1.5) acertaincharacteristicwavelength.weconsidertheeectsinadilutedplanckeld oftype J=WB(Trad); (1.6)
24 whichisausefulapproximationoftheradiationeldifthegaselementmainly 4 CHAPTER1.INTRODUCTION receiveslightfromadistantblackbodysource.inasphericallysymmetric,optically thincsewithtrad=tewendthedilutionfactortobe Allain(1996)hasshownthatevenforanopticallythickCSEEq.(1.6)stillprovides W(r)=120@1 s1 R2 areasonablettotheresultsoffrequency{dependentradiativetransfercalculations r21a: (1.7) (Winters1994).Ingeneral,theparameterTradissmallerthanTeandWislarger comparedtoeq.(1.7).fortheassumedwendwb0(trad)=b0(tre)or whichcanbecomparedtotheblackbodytemperaturegivenbyeq.(1.4) TRE=h0 k,ln 1+1Wexph0 ktrad 1!; (1.8) Figure1.1depictstheresultsforsomearbitrarilychosencentralwavelengths0= c=0.first,iftheradiationeldisnotdiluted(w=1),theretemperaturealways Tbb=W1=4Trad: (1.9) star)thefrequencydependencyofismeaninglessfortheresultingtemperature, equalstrad.inthiscase(typicalforthedeepatmosphereandtheinteriorofthe whichmakesthetemperaturedeterminationveryreliable. Fartheroutintheenvelope,however,whereW<1,awidespreadofpossible temperaturesolutionsexistdependingonthecentralwavelength(notethelogarithmicscalingofthetemperatureaxis).thepossiblesolutionsliebetweentheuv{ limith0maxfktrad;ktg(tuv=trad)andtheir{limith0minfktrad;ktg (TIR=WTrad).TheblackbodytemperatureTbb(cf.Eq.1.9)isjustonesolutionin thefrequencydependencyof.forexampleatr=2r,theresultis620k,ifthe interactionbetweenmatterandradiationeldmainlytakesplaceat0=10m,but Thetheoreticallydeterminedtemperaturestructureisthereforeverysensiblefor between,concerningaspecialtypeoffrequencydependencyof. is1920k,if0=1m: Ifwecomparethesevaluestothesmalltemperaturewindow,whereecientdust condensationmaytakeplace,itisobviousthatanuncertaintyconcerningthefrequencydependencyofasconsideredabovecaneasilychangethetemperaturesto r=2r: 0=(1:::10)m)TRE=( )K valueswellaboveorwellbelowpossiblecondensation,respectively.let'sgenerously thegasphasemayoccur.thecorrespondingradiusintervalsrcondintheoptically assumetcond=( )kforthetemperature,whereecientnucleationfrom thinlimitarethengivenby Tcond=( )K: 0=10m)rcond=(1:1:::1:35)R 0=1m grey )rcond=(11:5:::135)r )rcond=(2:7:::5:5)r
25 1.2THEUSUALMETHODOFTEMPERATUREDETERMINATION 5 Figure1.1:RadiativeequilibriumtemperaturesoverdilutionfactorWinaPlanck{type betweentheuvandtheir-limit,wherethecentralwavelength(seelabelsonsolidcurves) accordingtoeq.(1.7).theshadedregionindicatestherangeofpossibleretemperatures radiationeldwithtrad=3000k(cf.eq.1.6)accordingtoa{function{typegasabsorptioncoecient.theradiusaxisbelongstotheopticalthinlimit(pureradialdilution) issmallandlarge,respectively.thedashedlineshowstheblackbodytemperature.
26 TheseestimatesclearlyindicatethattheassumptionJ=Bhasadecisiveinuence 6 CHAPTER1.INTRODUCTION Alotofsimplifyingorevenunphysicalassumptionshavebeenmadeinthissection, ofdustformationinthecircumstellarenvelopesofcoolstars. sothatthecalculatednumbersaremeaningless.however,whatisimportantisthe onthecalculatedtemperaturestructurewithsevereconsequencesforthemodeling becomequestionable,whichisanothertopicofthiswork.moredetailedstudieson by1000k.theresultsareevenlessreliable,iftheassumptionsofreandlte cleartrendsintheresults.uncertaintiesconcerningthefrequencydependencyof theimportantheatingandcoolingprocessesarerequiredtotackletheproblemof caneasilychangetheresultsofthetheoreticallydeterminedtemperaturestructure tantandwhicharethecorrespondingrates?rememberingthestrongtemperature dependencyofnucleationfromthegasphase,suchinvestigationscanleadtoanew anddistincttheoreticalviewondustformationincses. theoreticaltemperaturedeterminationincses.whichspectralregionsareimpor- AnexampletotheaboveconclusioncanpossiblybefoundintheCSEsofRCoronae Borealisstars. 1.3 ThePuzzleofDustFormationaroundRCBStars knowntobeabout6thmagnitude,hadsuddenlydisappearedfromthesky.thestar remainedinvisibleforseveralmonthsandnallyrecoveredslowly.inthefollowing the25thbrighteststarinthenorthernconstellationcoronaeborealis,previously Morethantwocenturiesago,theGermanastronomerEduardPigottdiscoveredthat hisarticleonthisremarkablestarexactly200yearsago(pigott1797),whichestablishedanewclassofobjects theclassofirregularvariablestars.rcoronae years,pigottobservedsimilardisappearancesatirregularintervals.hepublished withinafewweeks,andtheeye{catchingshapeofthelightcurve,alwaysattracted muchinterestandfascinationintheastrophysicalcommunity.theuniquenessand (RCB)typedeclineeventswithdecreasesinvisualbrightnessofupto8magnitudes Borealisbecameitsrstmember.Sincethen,theunpredictableRCoronaeBorealis distinctivenessofthisextremetypeofvariabilityincontrasttothebroadvarietyof morecompleteobservationaldatahavebeencollectedcoveringthercbdecline Overtheyears,muchobservationaleortshavebeenundertakenandmoreand oneuniquephysicalmechanismwhichtriggersalltheevents. stellarparametersamongthercbstarsimmediatelysuggeststhattheremustbe Inspiteofthecompletenessandthequalityofobservationaldata,ourunderstanding observationsisoutlinedinappendixa. prehensivedatasetforthisextremetypeofstellarvariability.asummaryofthe events:photometry,spectroscopyandpolarimetry.theseobservationsformacom- ofthephysicalprocessescausingthercbdeclineeventsisstillratherpoor.since Loreta's(1934)andO'Keefe's(1939)basicsuggestionthatthedeclineeventsare causedbythesuddenoccurrenceofdustsomewhereinthelineofsighttowardsthe
27 1.3.THEPUZZLEOFDUSTFORMATIONAROUNDRCBSTARS 7 chromosphere? R CrB star stellar pulsation R cond =? ~7000 K ~10 4 L shock waves zone of possible nucleation t 0 t 1 dust growth & cloud formation & cloud acceleration t 2 radial dilution decline event visual brightness interpretation.inthiscase,thestellarparameters,thepulsationofthestar,theoccurrenceofshockwavesanddustcloudsandtheshapeofthelight-curvearesupportedby Figure1.2:Sketchofthephysicalprocesses,thegeometryandthetimeevolutionofan RCBdeclineevent.Avisualizationlikethisisalwaysamixtureofobservationalfactsand t 0 t 1 t 2 time ofthiswork. observations.thegeometryofthescenarioandthenucleationzonerefertothehypothesis
28 observer,theprogressduringthelastsixdecadesconcerningaphysicalexplanation 8 CHAPTER1.INTRODUCTION ofthephenomenonhasbeenslow.themostfavorablepicturetodayisthatclouds thestellarlight.inthelatephasesofadecline,thedustcloudmovesoutwardand Ifthedustcloudformsinthelineofsightitsuccessivelyeclipsesthestarandblocks radiallyacceleratedbyradiationpressureinrandomdirectionsawayfromthestar. ofcarbondustoccasionallyformfromthegasphaseneartothestar,whicharethen dispersesduetoradialdilution.thestarslowlyreturnstonormallight.thisoverall actuallycondensesisnowgenerallyaccepted. theearlyphasesofadecline,thephysicsandchemistryofthedeclinephase,the picture(sketchedinfig.1.2)andthefactthatitissomeformofcarbondustwhich thecircumstellarenvelopeetc.,arestillcontroversial.especiallysoarethephysical Allfurtherdetails,however,e.g.thedistanceofthedustcloudstothestarin survivalofthedustcloudsclosetothestar,thedynamicbehaviorofdustcloudsin reasonsfortheoccasionalonsetofdustformationandfortheformationofdust cloudsratherthansphericaldustshells.thus,thewholephenomenonisstillwaiting foraconvincingexplanation. OnekeytowardsabetterunderstandingoftheRCBdeclineeventsisgivenbythe radialdistancetothestellarphotosphere,wherefreshcarbondustcondensesfrom thegasphase.bymeansofareliabledeterminationofthisquantity,manyofthe proposedmodelsandscenarioscouldberuledoutimmediately.thedistanceto stellarradius,anangularresolutionof510 4arc-secondswouldberequired. RCrBisabout1000pcandinordertodetectadustcloudwithadiameterofone controversialquantitycannotbeobserveddirectly.however,thereexistsomeindirectobservationalcluesonthenucleationdistances,indicatingthatdustformation occursratherclosetothephotosphere: Temporalevolutionofemissionlines:Duringatypicaldeclineevent,arich Therefore,accordingtothepresentstateofobservationaltechniquesthishighly quentlycoverstheregionsresponsibleforthelineemissions.inthiscase,thedust (seeappendixa).itisnaturaltosuggestthattheexpandingdustcloudsubse- temporalevolutionofthreedistinguishableclassesofemissionlinescanbeobserved \chromospheric"emissionlinespectrumappears,similartoasolareclipse.aspecial cloudmustformbelowtheseregions.additionally,theemissionlinesareapparently Correspondingobservationalestimatesclaimanucleationdistanceof1:5 2R lesspolarizedthanthecontinuum(seeappendixa),whichsupportsthisscenario. absorptionlineshavebeendetectedjustinthebeginningofadecline(seeappendixa).sincesuchblueshiftsareonlyseeninthecontextofdeclineevents, (Claytonetal:1992). Dustaccelerationtimescale:Inmanycasesstronglyblueshifted(>200kms 1) onlypossibleratherclosetothestar,wheretheradiationuxissucientlyintense Accelerationstovelocitiesofafewhundredkm/swithinafewweeks,however,are (Whitneyetal:1993),yieldingnucleationdistancesof4 6R(Goeres1996). radiationpressureondustseemstoberesponsiblefortheaccelerationofthegas.
29 1.3.THEPUZZLEOFDUSTFORMATIONAROUNDRCBSTARS Declinetimescale:Theinitialdeclinephasetypicallylastsafewweeks.Ifthe 9 changesofthebrightnessandthespectraobservedduringthisphasearecausedby stellardisk,thedustcloudmustbelocatedclosetothestar(claytonetal:1992). anopticallythickdustcloud,radiallyexpandingandsubsequentlyobscuringthe Onlyinthiscase,thetangentialprojectionsofthemeasuredradialvelocitiescanbe aslargeasonestellarradiusperweek.fromthisargument,feast(1997)estimates Dustdilutiontimescale:Therecoveryphaseinlatedeclineissupposedtobe aconsequenceofthedustcloudmovingawayfromthestarataconstantvelocity theinitialradialdistanceofthedustcloudtobe2r. whileradiallydiluting.bysimultaneousmeasurementoftheexpansionvelocity(via absorptionlineblueshifts)andthegradientoflightincrease,anabsolutedistanceof thecloudcanbederived,compatiblewithnucleationdistancesof4 7R(Goeres thedeclinescanbeusedtoestimatetheangularcoverageofasingledustcloud 1996). IRuxconstancy:ThefactthattheIRuxesonlyshowminorchangesduring cloudmusthaveatleastthesizeofthestellardiskinordertooccultthestar,leads (Forrestetal:1972).Thesemi{coneangletogetherwiththeconditionthatsucha providesanestimateforthenucleationdistanceof2:5 6R(Goeresetal:1996). toaminimumdistanceofthedustcloudsatthebeginningofthedeclines,which (e.g.pugach1977,lawsonetal:1992).forsuchacorrelation,aphysicalconnection betweenthephotosphereofthestarandthecondensationzonewithaconstanttime individualobjectsthatthedeclineeventsalwaysbeginatxedpulsationphases Pulsationphasecorrelation:Thereissomeobservationalevidenceforcertain delayisrequired.thecloserthecondensationzonetothestar,themoreplausible thistypeofconnectionappears.thecharacterofthisargumentisonlyqualitative. theclearcommontendencyoftheobservationalndingsisthatdustcondensation Althoughatleastoneweaklinkcanbefoundineverychainoftheabovearguments, inrcbenvelopesinfactoccursfairlyclosetothephotosphereofthestar. Accordingtoallknowntheories(classicalnucleationtheory,chemicalpathwaycalculationsorthemodelingofchemicalreactionnetworks)theformationofasolid seemtocontradictthebasicsofdustformationtheory. Thesmallnucleationdistancesderivedfromobservationsatrstsight conditionspresentincsesforallhightemperaturecondensates(includinggraphite eredsolidmaterial.thisyieldslowertemperaturesthan2000kunderthedensity bodydemandstemperatureswellbelowthesublimationtemperatureoftheconsid- andsic).consideringthetypicalchemicalconditionspresentintheenvelopesof onlypresentoutsideabout11rforte=7000k.furthermore,ifweaskforthe InstandardmodelsforCSEs(cf.lastsection),suchtemperatureconditionsare (Goeres&Sedlmayr1992). RCBstars,temperaturesbelow1500Kareinevitablyrequiredforcarbonnucleation
30 Table1.1:ObservationalandtheoreticalconstraintsonthenucleationdistanceinRCB 10 CHAPTER1.INTRODUCTION envelopes.distancesaregiveninunitsofstellarradii. temporalevolutionandpolarimetryofchromospheric observations theory dustaccelerationtimescale emissionlines 1:5 2 declinetimescale dustdilutiontimescale 4 6 IRuxconstancy 2: sucientlylowgastemperaturefornucleation >11 pulsationphasecorrelation (close) sucientlylowdusttemperatureforduststability>20 minimumdistancerequiredtoassurethestabilityofsmallcarbondustparticlesin anopticallythinstellarradiationeld,theresultisabout20rforte=7000k (Fadeyev1988).InthecaseofhotRCBstarswitheectivetemperaturesupto TosummarizeTable1.1,twocontradictorypointsofviewcanbedistinguished.On formationappearstobeevenmoreserious K,onederivesdistancesaslargeas50Randsotheproblemofnearbydust onehand,theobservationalastronomersarguefordustformationneartothestaron thebasisofseveralsupporting,independentscienticndings.ontheotherhand, ofthepresentunderstandingofthercbtypedeclineevents.onceoneacceptsthat theoreticalmodelsfordustformationpredictlargenucleationdistancesasaconsequenceofthermodynamicconstraints.thisobviousconictbetweentheoryand dustformationoccursclosetothestar,asindicatedbyobservations,thereareonly observationtracesthroughthewholeliteratureandconstitutesthecentralproblem (i)therearefundamentalerrorsinthecurrentdustformationtheory.carbondust canbeformedfromthegasphasealreadyattemperaturesof Kas twowaysoutofthisdilemma: presentat2raccordingtothestandardmodelsofcses. thecontextofmorecarefulmethodsforthetemperaturedetermination,takinginto conventionaltheoriesondustformationareapplicable,buthavetobediscussedin orytorcbenvelopesconcerningthetemperaturedeterminationofthegas.the (ii)thereisamistakeinthepreviousapplicationsofstandarddustformationthe- accountthedynamicconditionsinthecsesofrcbstars. AllRCBstarsmeasuredthusfarseemtobepulsatingvariables(Lawson&Kilkenny 1996).Thepulsationperiodsareoftheorderof40daysandtheradialvelocity variationsatthephotosphererangefromabout3kms 1to20kms 1(cf.AppendixA).Thestellarpulsationcreatesshockwaves,whichfurthersteepenupin
31 theatmosphereandpropagateintothecse(e.g.bowen1988,fleischeretal:1992). 1.4REQUIREMENTSFORDIFFERENTAPPROACHES 11 strongdeviationsfromreinthegasphase.if,however,oneofthethreeusual orlessperiodicalcompressionandre{expansionofthegas,bothofwhichmaycause timeagain.theshocksdissipatemechanicalenergyandfurthermoreinitiateamore Consequently,axeduidelementintheenvelopeishitbyshockwavestimeand doned,theradialrangeofnucleationdistancesprescribedbyobservationscould easilyopenup. assumptionsfortemperaturedetermination(re,lte,greygasopacities)isaban- 1.4 turedetermination RequirementsforDierentApproachesofTempera- Themostpromisingscienticmethodtogaininsightintothecomplexprocesses equationswhichareintegratedintime.besideshydro-andthermodynamics,these gas,wherethephysicalinteractionsareformulatedintermsofordinarydierential tions.thebasisofthesemodelsisahydro-andthermodynamicdescriptionofthe ofastrophysicalobjectsisthemodelingbyfulltime{dependentcomputersimula- modelsmayincluderadiativetransfer,chemistryanddustformation,accordingto putermodelscanhelptobuildupahigherlevelofcompletenessinscience. amongtheseprocessescanbecomethemaintopicofexamination.therefore,com- thechosendegreeofapproximation.thereby,allthenecessaryphysicalandchemicalprocessescanbeinvestigatedsimultaneously,sothatjustthecomplexinterplay However,theresultsofthisrathernewmethodofscienticcomputingcannotbe toabstractandtosimplify.inthiscontext,the\best"descriptionofaphysical processunderinvestigationisnotnecessarilythemostaccurateanddetailedone betterthanourphysicalunderstandingofthebasicprocessesinvolvedandourability processwhileusingtheleastamountofresources.suchadescriptionmustbe butadescription,whichcorrectlydescribesthemostimportantfeaturesofthe Mirasandlong{periodvariablesontheAGBandRCBstars,CepheidsandRVTauri ConcerningthetemperaturedeterminationintheCSEsofpulsatingstars(suchas partoftheinvestigationsofastrophysicalobjects. sucientlysimpleinordertobeincludedinmorecomplexmodelcalculationsas cannotbeobtainedbymeansofradiativetransfercalculationsalone. pulsationcallsforatime{dependenttreatmentofthethermodynamics.asargued above,strongdeviationsfromremayoccurandthegastemperaturestructure starsneartotheinstabilitystrip)thepresenceofshockwavescausedbythestellar transfer,usingthebasicassumptionsofre,lteandgreygasopacitiesasdescribedinsect.1.2,whichdeterminestheinstantaneousre{temperaturestructureculatedasfollows.bowen(1988)rstcarriesoutafrequencyintegratedradiative Fleischeretal:1992,Feuchtingeretal:1993),thegastemperaturestructureiscal- Accordingtothepresentstateofapproximationinsuchmodels(Bowen1988, Secondly,hecalculatesthecurrentgastemperaturebyassumingalocalrelaxation
32 12 CHAPTER1.INTRODUCTION Figure1.3:TemperaturestructureadoptedfromFeuchtingeretal:(1993). logradius[cm] Figure1.4:AdoptedfromBowen(1988) case,assumingthatthegasinstantaneouslyrelaxestoreeverywhereintheenvelope.applyingradiationhydrodynamics,feuchtingeretal:(1993)useanapproach, towardreataniterate.fleischeretal:(1992)considertheisothermallimiting Qrad,isanimportantingredient.QradvanishesinREandotherwisedeterminesthe timescaleforrelaxationtowardre. namicsinthesemodels,thetotalnetheatingrateduetoradiativegainsandlosses, whichissimilartobowen's,butmoreconsistent.inordertotreatthethermody- ConcerningthecalculationofQradinthemodelscitedabove,crucialassumptions havebeenmade(lteor,incontrast,qrad/2),yieldingsimpleanalyticalexpressionsforqrad.butdependingonwhichoftheseassumptionsisapplied,thperaturesusuallyveryclosetothere{temperaturestructureexceptforsomethin gastemperaturestructureturnsouttobequitedierent.intheltecase,the gastemperaturepeaksatthelocationsoftheshockfronts(cf.fig.1.3).incontrast,atsmalldensitiesintheqrad/2case,ratherbroadregionsofenhanced gastemperaturesbehindtheshocksareproduced,almostentirelydecoupledfrom there{temperaturestructure(cf.fig.1.4).theseresultsaretypicalexamplesfor ofthesemodelcalculations,e.g.themasslossrate,andeventhemodelstability ter,respectively.theresultinggastemperaturestructureaectsallotherresults shockwavesofpredominantly\isothermal"orpredominantly\adiabatic"charac- (Wood1979).Animportantfeedbackbetweenthegastemperaturestructureand thedynamicsoftheseenvelopesisgivenbythecondensationofseedparticlesfrom thegasphase(nucleation),whichisverysensitivetothegastemperature.ittriggers calculatedradiativeheating/coolingratesareveryecient,resultingingastem- ConsideringthedeterminationofQradinotherastrophysicalenvironmentsextensivemodelcalculationshavebeenmadeforstationaryplane-parallelshocks,e.g.in duetoradiationpressureondustgrains(fleischeretal:1991). thefurtherevolutionofthedustcomponentandhencetheaccelerationofthegas
33 theinterstellarmedium,whereallphysicalpropertiesarepurelydeterminedbythe 1.5.AIMANDSTRUCTUREOFTHISWORK 13 distancefromtheshockfront,butarenotexplicitlytime{dependent(hollenbach& McKee1979,Fox&Wood1985,Hollenbach&McKee1989,Gillet&Lafon1989, Neufeld&Hollenbach1994).Thissituationallowsforaveryaccuratephysicaldescription,includingnon{LTEionization,non{equilibriumchemistryandradiative modelsforpulsatingstarsforessentiallytworeasons.first,theshocksintheenvelopesofpulsatingstarsarenotstationary(e.g.axeduidelementwillstartto transfer.however,thisschemecannotbeeasilyappliedtothetime{dependent re{expandafterithasbeencompressedbyanpropagatingshockasopposedtothe stationarysituation)andsecond,thedetaileddescriptiongiveninthepaperscited models,atleastatthepresentstateofcomputerspeed. aboveismuchtooelaboratetobeincludedwithintime{dependenthydrodynamic radiativetrapping.ontheotherhand,itmustbesucientlysimpletobeincluded accountimportantfeaturessuchasthenon{ltepopulationofexcitedstatesor mustbephysicallybasedontherelevantheatingandcoolingprocesses,takinginto Thus,thereisagreatneedforarealisticcalculationofQrad.Ontheonehand,it intime{dependenthydrodynamicmodels. Thebasicaimofthisworkistogainmoretheoreticalinsightsonthetemperature 1.5 structureofcircumstellarenvelopes,especiallythoseofpulsatingstars,whereshock AimandStructureofthisWork oreticaltemperaturedeterminationinagivenradiationeld radiationtransfer wavespropagatethroughtheenvelopes.thisworkfocusesontheproblemofthe- calculationsareexplicitlynotconsideredandarenotperformed. sityrangetypicalforcses.however,thereisdetailedknowledgeavailableatboth 1014cm 3.Precedingstudiesintheliteratureareusuallynotapplicableinthisden- Forthispurpose,theradiativeheatingandcoolingofthegasincircumstellarenvelopesisinvestigatedfromtheverybeginning,examiningdensitiesfrom105to extremesofthisdensityinterval.forlargedensities,extensivecalculationsofgas thenetradiativeheatingrate.atlowdensities,theimportantradiativeheating absorptioncoecientsinstellaratmospheresexistwhich,incaseoflte,determine andcoolingprocessesareknownfromstudiesofinterstellarcloudsandinterstellar shockwaves.thisworkderivesadvantagesfrombothandintendstoclosethegap dynamicmodelcalculations.thepossibilityofafastandproperinclusionofthe Duetothetime{dependentconditionspresentinCSEsofpulsatingstars,thedeterminationofthetemperaturestraticationmustinvolvetime{dependenthydro- betweenthesedensitylimits. calculatedheatingandcoolingratesintohydrodynamicmodelsisanessentialconstraintfortheseinvestigations.itistheaimofthisworktolaythefoundationsfonamicmodelcalculations. amorereliabletreatmentofthetime{dependentthermodynamicsinsuchhydrody-
34 Althoughdustformationisrarelydiscussedinthisworkexplicitly,theworkisguided 14 CHAPTER1.INTRODUCTION bythecertaintythattheformationofsolidsincsesrequireslargedensitiesand veryspecialtemperatureconditions.thequestion,whichalwaysstandsbehindthe investigationsandisthebasicmotivationforthisworkis: Theworkisorganizedasfollows: Whereintheenvelopesuchthermodynamicconditionsmayoccur? LTE. thermodynamics.thelevelofapproximationforthisworkisxedandtheinternal Chapter2describesthebasicconceptforthetreatmentofthetime{dependent Chapter3containsthecalculationsofthevariousheatingandcoolingratesconsideringarbitraryradiationelds.Computationalmethodsaredevelopedwhich energyofthegasisdenedaccordingtothebasicassumptionofsteady{statenon{ andofh2;linetransitionsofneutralatomsandions;bound{freetransitions;free{ processesisinvestigated:rotationalandro{vibrationaltransitionsofpolarmolecules Duetothewidetemperaturerangetobeconsidered,avarietyofdierentradiative includetheimportanteectsofnon{lteandofopticalthicknessinspectrallines. freetransitionsandphotochemicalreactions.specialattentionispaidtowhichkind completesthetheoreticalpartofthiswork. eredsofar,butmightbeoffurtherinterestfortheheatingandcoolingofthegas, correspondingrates.ashortlistofradiativeprocesses,whichhavenotbeenconsid- ofatomicandmoleculardatahastobeknownforareliabledeterminationofthe ofthegasaredeterminedfromtheelementabundancesi,themassdensityofthe technicaldetailsofthecalculationofthevariousparticleconcentrationsandthe internalenergyofthegasareexplained.theparticleconcentrationsandthestate Chapter4outlinessomecommonfeaturesforthefollowingapplications.The gas,itstemperaturetg,andthecontinuousradiationeldj. Inthefollowingchapters,threeapplicationsofthetheoreticalmethodsarepresented: riummaynotbeunique,butcanhavetwoormorestabletemperaturesolutions. tionsinthecsesofrcbstars.itisshownthattheconditionofradiativeequilib- These\thermalbifurcations",inprinciple,allowforaspatialcoexistenceofhotand Chapter5examinesthetopologyoftheradiativeequilibriumtemperaturesolu- coolphasesinthecircumstellarenvelope. sityandtemperature.theimportanceofthedierentheating/coolingprocesses foracarbon{enrichedgastypicalforc{starsarecalculatedasfunctionofgasden- responsetopropagatingshockwaves.forthispurpose,radiativecoolingtimescales Chapter6investigatestherelaxationtowardsradiativeequilibrium,especiallyin isdiscussedandthemostecientprocessinthevariousdensityandtemperature
35 1.5.AIMANDSTRUCTUREOFTHISWORK regionsisdetermined.theresultsofthecoolingtimescalesarecomparedtothose 15 derivedfromformerlyappliedanalyticalheating/coolingfunctionsinpreviousresearch.thecharacterofthethermalrelaxationofthegasafterthepassageofshock wavesisdiscussed,providingnewfueltothecontroversyaboutwhethertheshocks incsesbehavepredominantly\isothermally"or\adiabatically". Chapter7againconsidersRCBstars.Aphysicalmechanismispresented,which envelopesofpulsatingrcbstars.amodelforxeduidelements,whichare periodicallyhitbystrongshockwavesproducedbythestellarpulsation,isdeveloped maybeessentialfortheoccasionalonsetofdustformationinthecircumstellar elements,areinvestigated.accordingtothismodel,thepreconditionsforeective carbonnucleationmaybetemporarilypresentquiteneartothephotosphereofa andthethermalenergybalance,thechemistryandthenucleationinsuchuid pulsatingrcbstar,despitetheirhigheectivetemperatures.thus,thisworkmight bridgethegapbetweenobservationsandtheoryconcerningrcbstarsasoutlined insect.1.3. Chapter8summarizestheresultsandpresentstheconclusionsofthiswork. thefascinatingclassofrcbstarsandsummarizespreviousmodels.thisappendix AppendixAgivesanoverviewofthecurrentstatusofobservationalknowledgeon providesanimportantbackgroundfortheinvestigationsinchapter5and7.
36 16
37 Chapter2 Thischapterintendstostatethebasicassumptionsofthisworkandtoclarifythe TheThermodynamicConcept distributionofthegasatrestisassumedtobegivenbyauniquemaxwelliandistribution,characterizedbyasinglekinetictemperature,whichishenceforthcalledthe Thecentralphysicalquantityofthisworkisthetemperatureofthegas.Thevelocity meaningofsometermsfrequentlyused. whichdistributethetotaltranslationalenergypresentamongthegasparticles.the sponsiblefortherelaxationtowardsthemaxwelliandistributionareelasticcollisions dierentkindsofparticles(e.g.electronsandatoms)areneglected.theprocessesre- \gastemperature"anddenotedbytg.dierencesinthekinetictemperaturesof correspondingrelaxationtimescaleisassumedtobeconsiderablyshorterthanany othertimescaleinherentinthephysicalsystemunderinvestigation.withregard tothisrelaxation,themostcriticalprocessistheequalizationofthetranslational theconclusionthattheexistenceofauniquemaxwelliancansafelybeassumed. Mihalas(1984,seep.29andp.387foramorecomprehensivediscussion)arriveat energiesbetweenlightandheavyparticles,becauseoftheinecientenergytransferratesofsuchcollisions.forconditionsinstellaratmospheres,mihalas&weibeterminationbasedontherstlawofthermodynamics Theaimofthisworkistodevelopatime{dependentmethodfortemperaturede- 2.1 FirstLawofThermodynamicsandEquationofState ofheattransferedtothegasq(countedpositiveforgains)plustheworkdoneto Equation(2.1)statesthatthechangeofinternalenergydEisgivenbytheamount de=q+w: thegasw(countedpositivewhenthesurroundingsdeliverworktothegas). Howarethegastemperatureandtheinternalenergyrelatedtoeachother?Theanswerofthisquestionsseemstobetrivial(givenbythewell{knowncaloricequationof state),butinfactdeservessomefurtherdiscussionfordilutedgasesunderastrophysicalconditions.besidesthetranslationaldegreesoffreedom,arealgas{consisting ofneutralatoms,electrons,ionsandmolecules{hasadditionalpossibilitiestostore energy,whicharehenceforthcalled\thepoolsofenergy".thepopulationofexcited 17
38 electronic,vibrationalandrotationalstatesrepresentsuchpools.furthermore,energyisstoredinpotentialformaccordingtothebindingforcesbetweenelectrons andatoms(ionizationpotential)andbetweentheconstitutingatomsofmolecules 18 CHAPTER2.THETHERMODYNAMICCONCEPT (dissociationpotential).consequently,theinternalenergyofthegasisdenedas ThedetailsoftheevaluationofthevariousenergytermsarestatedinChapter4 e=1etrans+eion+ediss+eel+evib+erot (Eq.4.1{4.6).IncaseofLocalThermodynamicEquilibrium(LTE),therelationship (2.2) degreeofionization,theconcentrationofthemoleculesandthepopulationofthe betweenthegastemperaturetgandtheinternalenergyeiswell{dened.the excitedlevelscanbedeterminedbymeansofsahaequations,thelawofmassaction andboltzmanndistributions,respectively.allenergytermsineq.(2.2)canbe ofanysuitablesetoftwolocalstatevariables. calculatedstraightforwardly,yieldinge=e(;tg)or,moregenerally,easfunction cessesalterthestateofthegasinvariousways.figure2.1sketchesthissituation. 2.2 ConsideringthedilutedgasesinCSEs,however,LTEisnotvalid.Radiativepro- LTEandNon{LTE Thegasisrepresentedbythebiggreybox,containingtheinternalpoolsofenergy. Thegasinteractswiththeradiationeldviatheexchangeofphotonsandwiththe arrowonthel.h.sinthegureandthegasmayexchangeheatwithitssurroundings freedomofthegas.workcanbedonetothegasw= pdvasindicatedbythe dustcomponent,e.g.viainelasticcollisions.atthesametime,internalprocesses (notshown).examplesforthesuchprocessesareheatconduction,viscousprocesses (greyarrows)redistributethetotalinternalenergyamongthevariousdegreesof andshockdissipation. TheradiativeprocessesgenerallydrivethegasawayfromLTE1,whereastheinternalprocesses(processesnotinvolvingphotonsordustgrains,thatis)drivethizationfollowedbyradiativerecombinationortheabsorptionofaphotonfollowed thetranslationalenergypoolisindirect,sotospeak,becauseatransmittingstate isinvolved.usually,atwo{stepprocessisrequired,forexampleacollisionalion- gastowardlte.ingeneral,theenergytransportbetweentheradiationeldand Thus,anon{LTEtreatmentforthedilutedgasesinCSEsisrequired.Balancing stateofthegascannotbecalculatedbythermodynamicconsiderations. bycollisionalde{excitation2.thesetransmittingstates(e.g.theexcitedelectronic thegainsandlossesbyallcollisional,radiativeandchemicalprocesses,thechange statesoftheatoms)areconsiderablyaectedbytheradiationeldandhence,the areusuallylessimportant,e.g.free{freeemission(bremsstrahlung). 1ExceptforthecasethattheradiationeldexactlyequalsaPlanckianofthegastemperature. 2Directlinksbetweentheradiationledandthetranslationalenergypooldoalsoexist,but
39 2.2.LTEANDNON{LTE 19 ionization electronic excitation radiation p dv translation vibrational excitation dust dissociation rotational excitation nation;bound{bound,free{free,vibrationalandrotationalemission/absorption; photodissociation/radiativeassociation.blackdashedarrowsshowenergyexchangeratesbetweendustandgas(viacollisionsandsurfacechemicalreactions). orparticlecreation/destruction,respectively.dottedgreyarrowsshowadditional Fullgreyarrowsrepresent\internal"energyuxesviacollisional(de-)excitation uxesviaphotons.fromtoptobottom:photoionization/radiativerecombi- Figure2.1:Thepoolsanduxesofenergy.Blackfullarrowsindicateenergy statesviachemicalreactions. examplesofinternalenergyuxesnotexplicitlyconsideredinthiswork,suchas pumpingbyuorescence,ro{vibrationalpumpingortheexcitationofvibrational
40 oftheparticledensitynjiofchemicalspeciesiinquantumstatejcanbeexpressed 20 CHAPTER2.THETHERMODYNAMICCONCEPT by(e.g.mihalas&weibelmihalas1984,p.389) d(nji=) dt =X fklg6=fijg nlkrl!j k!i njix DiusionprocessesareneglectedinEq.(2.3)andd=dtdenotestheLagrangian fklg6=fijg Rj!l i!k: (2.3) coecientrj!l derivativewithrespecttotime,consideringacomoving-movingframe.therate processeswhichdestroyaparticleofspeciesiinstatejandcreateaparticleof specieskinstatel.forsimplecollisional,absorptionoremissionprocesseswehave i=k.forchemicalprocesses(i6=k),thequantumindicesjandlusuallyrefertothe i!k[hz]denotesthetotalrateofallcollisional,radiativeandchemical groundstate.theratecoecientsmaycontainfurtherparticledensities(collision partnersorchemicalreactants)ortheradiationeldj,dependingonwhichtype ofprocessisconsidered.theratecoecientswillbequantiedinchapter Ifthegasisexposedtostaticouterconditions(radiationeld,propertiesofthe dustcomponent,volumeetc.),thegaswillrelaxtowardsasteadystate3,i.e.the SteadyState concentrationsofallspeciesinallquantumstatesbecometime{independent d(nji=) calculatedbysolvingthecoupledalgebraicequationsoftypeeq.(2.3)forallspecies Incaseofasteadystatethel.h.sofEq.(2.3)vanishes.Theparticledensitiescanbe dt =0: (2.4) andstatesunderinvestigation.theresultsaretime{independentandcanformally beexpressedby Therefore,inadditiontothetwolocalstatevariablessucientinLTE,theradiation Consequently,thecaloricequationofstate(2.2)ofthegaswritesase=e(;Tg;J). nji=nji(;tg;j); (2.5) eldoccursasadditionalexternalparameterforthedeterminationoftheparticle densitiesandtheequationofstate4;5.theresultingsteadystateofcoursediers Jdisappears. internal(e.g.collisional)processesdominate,lteisvalidandthedependencyon fromlteingeneral.inthelimitingcaseoflargedensities,however,wherethe ofthesteadystate,whichisthemeanlocalvelocitygradientdv 3Othertermsusedintheliteratureare\kineticequilibrium"or\statisticalequilibrium". However,theinuenceofthisparameterissmall. thecalculationoftheratecoecientsforbound{boundtransitionsconcerningopticallythicklines. 5TheinuenceofthedustcomponentonthestateofthegasisneglectedinEq.(2.5) 4InChapter3itwillbestatedthatanotherexternalparameterentersintothedetermination dl.thisparameterisinvolvedin
41 2.3.STEADYSTATE 21 Theconditionofastaticenvironmentcanberelaxedtosomeextendconcerning thosetime{dependentsituationswherethechangesoftheouterconditionsoccur slowly.inthiscasethegasrapidlyaccommodatestothevaryingenvironment.this workassumesthatthisaccommodationinfactoccursinstantaneously: Theinternalrelaxationofthegastowardsteadystateisassumedtooccur onashorttimescalecomparedtothechangesoftheouterconditions. Inthiscase,acaloricequationofstateexists,asstatedabove,althoughthegasis notinlte.athermodynamicdescriptionofthegasisappropriate6.ofcourse,the 6Consideringtheexcitedelectronicstatesofatomsandions,therelaxationtimescaleisgivenby theradiativelifetimesofthelevelsatsmalldensitiesandisevenshorteratlargedensities.allowed electronictransitionshaveradiativelifetimesoftypically10 8s,butactuallytheslowestratewithin thelevelsystemdecidesupontherelaxationtimetowardacompletesteadystate,whichcanbe aslargeas102sforthemeta{stablelevelsincludedinthiswork.theradiativelifetimesofthe vibrationalandrotationallevelsofpolardiatomicmoleculesarefoundtobetypically s. Thesetimescalesaretobecomparedtotypicalhydrodynamictimescales,whichfortheCSEs ofpulsatingstarsareapproximatelygivenbyonepulsationperiod,whichisabout107sformiras and106sforrcbstars.hence,therelaxationoftheelectronic,vibrationalandrotationalstates canbeassumedtobefast. Consideringtherelaxationtowardsionizationequilibrium(balancebetweenionizationandrecombinationrates),thecorrespondingtimescalesareverydierent.Ifphotoionizationdominates, e.g.consideringthecasej=b(7000k),therelaxationtimescalesarefoundtobe s forallatomsunderinvestigation,independentofdensityandtemperature.ifcollisionalionization dominates,therelaxationtimescalestronglydependsonthedensity.inthecasej=b(3000k) therelaxationlasts104satadensityof1013cm 3,106sat109cm 3and109sat105cm 3, concerninglowtemperatures.ifthetemperatureishighenoughtocauseconsiderablecollisional ionization,therelaxationtimescalebecomesmuchshorter.hence,therelaxationofthedegree ofionizationisfastinthosecases,whereisitimportantforthecalculationoftheradiativeheating/coolingrates,butcanexceedthehydrodynamictimescalesotherwise. Thechemicalprocessesusuallyintroducethelargesttimescalestothegas(disregardingdust formationprocesses).thechemicalrelaxationtimescalescanindeedexceedhydrodynamictime scalesincses(e.g.becketal:1992).however,thechemicalprocessesthemselvesdonotprovide rstorderradiativeheatingandcoolingrates themostimportantheatingandcoolingprocesses usuallyinvolvethedegreesoffreedomdiscussedabove,whichcanbeassumedtobepopulated accordingtoasteadystate. Thus,onehastoconcludethattherelaxationofthegasinCSEstowardsitssteadysteadymay notalwaysbecomplete.afulltime{dependentnon{lteapproachwouldberequiredforamore accuratemodelingofthegas.inthiscase,therstlawofthermodynamicshastobeappliedtothe translationalenergyalonee=etrans=.acaloricequationofstatedoesnotexistintheusualsense orbecomesobsolete.onehastodeterminetheinternalenergydistributionprocessesinthiscase, e.g.howmuchtranslationalenergyisconsumedorliberatedduringachemicalreaction.atime{ dependenttreatmentofionizationandchemistrywithinhydrodynamicmodelsseemstobeoutof question,atleastatthecurrentstateofcomputerspeed.thiswouldintroducealargenumberof new(sti)dierentialequationstotheusualsetofhydrodynamicequationstobesolved,which requiresmuchmorecomputationaleorts.however,thepossibilitytoincludetheresultsofthis workintosuchcalculationsisregardedasessential,concerningfutureinvestigations.therefore, theassumptionofasteadystateismadenevertheless.itrepresentsanappropriatecompromise betweenaccuracyandexpense:itaccountsforthemostimportantnon{lteeects,butkeeps thingssimpleenoughforathermodynamicdescriptioncompatibletohydrodynamiccalculations. Forafurtherdiscussionofthistopic,seeMihalas&WeibelMihalas(1984,p.386{396)
42 particledensitiescanonlybedetermined,iftheradiationeldisknown;thatis, 22 CHAPTER2.THETHERMODYNAMICCONCEPT eventuallymodiedbydustinthecse,whichisalsoconsideredas\external". strongspectrallines.theradiationeldismainlyprovidedbyexternalsources, thecircumstellarenvelopesareopticallythinbydenition,maybeexceptforsome thereareasmanynewexternalparametersasarerequiredtospecifyj.however, much,responsiblefortheradiationeld.therefore,thenon{lteradiativetransfer calculationsconcerningthedustcomponent.thegasitselfisnot,oratleastnot Therefore,itseemsappropriatetoprescribetheradiationeldinCSEs(e.g.bya problemdecouplesincses(incontrasttothesituationinstellaratmospheres)and radiallydilutedphotosphericradiationeld)ortousetheresultsofradiativetransfer thethermodynamicbehaviorofthegascanbestudiedintheproposedway. TherstlawofthermodynamicsEq.(2.1)isfurtherspecializedinthefollowing. Accordingtothedenitionoftheinternalenergy(cf.Eq.2.2),theinternalenergy transferratesdonotcauseanyheatingorcooling,sincetheyonlytransferenergy eldandthedust,thatis)tothegas.letbqraddenotethetotalnetheatingrate givenbythesumofenergyuxesfromtheremainingexternalpools(theradiation fromoneinternalpooltoanother(cf.fig.2.1).thenetheatingratebq=q=dtis ofdustgrains.disregardingotherheating/coolingmechanismsasheatconduction, convectionandviscousprocesses,whichareusuallynegligibleatthelowdensities perunitmassandtimeduetoradiativeprocesses,whichisgiventheamountof netabsorbedphotonenergy,andbqdustthetotalnetheatingcausedbythepresence incses,therstlawofthermodynamicswrites pisthegaspressureandv=1=thespecicvolume.thegastemperaturecanbe de dt= pdv regardedasanimplicitresultofthesolutionofeq.(2.6),inferredfromthecaloric dt+bqrad+bqdust; (2.6) stateofthegasisdetermined.thenetradiativeheatingratebqradisakindofuseful equationofstate. byproductofthesecalculations. ThemaintaskofthefollowingChapter3willbetoquantifyalltheimportant Asaconsequenceofthesteady{stateassumption,theinternalenergyandthenet internalandexternalrates,asfaraspossible.bymeansoftheserates,thesteady parametricspecicationofj.thus,itisguaranteedthattheproposedtime{ tabulatebqradandeasfunctionoftwostatevariables,sayandtg,andasuitable arereadilyavailableinhydrodynamicmodelcalculations.itishencepossibleto heatingfunctionareentirelydeterminedbymeansoflocalphysicalquantities,which modelcalculationswithregardtofutureinvestigations. dependentmethodoftemperaturedeterminationcanbeincludedinhydrodynamic
43 Chapter3 RadiativeHeatingandCooling requiresaquantitativeanalysisofallradiativeprocessesoccurringintheconsidered istheinvestigationofthemostimportantheatingandcoolingprocesses,mainly uidelement adicultandprincipallyinnitetask.whatisfeasible,however, Thedeterminationofthetotalradiativeheating/coolingrateofthegasinCSEs relyingontheexperienceofprecedingstudies. Fromstellaratmospherecalculationsitisgenerallyknown,thatbound{freetran- onlyasecond{order{eectinthiscontext1.inpredominantlyneutralstellaratmospheres,thebound{freetransitionsofh areimportant.belowabout3500ksorptioncoecient(e.g.unsold1968)andhencefortheheatingandcoolingofthe gas.theadditionalconsiderationoflinetransitions(\lineblanketed"models)is sitionusuallyaretheprimarycausefortheshapeandthemagnitudeoftheab- theirelectronicbands,vibrationalandrotationalspectra,especiallythosemolecules moleculesenterintocompetitionandsoondominatetheabsorptioncoecientby Concerninginterstellarconditions,Hollenbach&McKee(1979,1989)pointedout thatforbiddenne{structurelines,meta-stabletransitionsandsomelow{lyingper- withpermanentdipolemoment(jrgensen1994). tenprovidethedominantcoolingmechanismforashockednon{moleculargas.if mittedlinetransitionsofthevariousneutralandsinglyionizedmetalatomsof- present,polarmoleculescontributebytheirlargeamountofallowedvibrationaland rotationallinetransitions.bound{freetransitions(mainlyofhydrogen),lyand HareimportantattemperaturesT>8000K,especiallyforlargedensities. ing/coolingratesforcses.ageneraltheoreticaldescriptionmustbedeveloped coolingprocessesmentionedaboveinordertounifythepictureofimportantheat- whichisapplicabletoboth,stellaratmospheresaswellasinterstellardensityconditions. Reviewingtheseexperiences,itisimportanttotackleatleastalltheheatingand processisalwaysdiscussedsimultaneously,whichisdierentfromotherapproaches concerninginterstellarmatter(e.g.spitzer1978),wheretheheatingandcooling Inthefollowingthenetheatingrateofoneparticularradiativeprocessanditsreverse spectrallines theeectsoflinesinamovingmediummaybelargerbyordersofmagnitude ratesareusuallydiscussedstrictlyapart. 1Thisstatementreferstoastaticatmosphere,whereselfshieldingdiminishestheinuenceof 23
44 Bound{BoundTransitions CHAPTER3.RADIATIVEHEATINGANDCOOLING systemofboundstatesispresented.themethodisapplicabletolinetransitionsof methodforthecalculationoftheheating/coolingrateofanarbitraryn{level{ Themostbasicformofinteractionbetweenmatterandradiationeldisgivenby atomsandions,tovibrationalandrotationaltransitionsofmoleculesandalsoto theabsorptionandemissionoflinephotons.inthissection,ageneraltheoretical quadrupoletransitionsofh2.ithasthefollowingfeatures: a)thecalculationofthelevelpopulationisperformedundertheassumptionof atomictransitions. thedensityconditionspresentincircumstellarenvelopes,especiallyforallowed steady-statenon{lte.itisabsolutelynecessarytoconsidernon{lteunder b)comparedtointerstellarconditions,thehighdensitiesencounteredincircumstellarenvelopesmaycauselargeopticaldepthsinthelines,whichsignicantly changetheheating/coolingratesduetoradiativetrapping.theseeectsare c)sincepropagatingshockwavesmaybepresentinthecircumstellarenvelopes ofpulsatingstars,largevelocitygradientsoccur.incontrasttosteady,plane{ tackledbyapplyinganescapeprobabilitymethod. incaseofsphericalsymmetry. asoutlinedbyhollenbach&mckee(1979).thisworkusesthesobolevtheory tryoftheowrequiresadierentmethodtocalculatetheescapeprobabilities parallelshocks(e.g.intheism),theexplicittime{dependenceandthegeome- d)lineabsorptioniscompletelytakenintoaccount.theintensecontinuous radiationeldincircumstellarenvelopeschangesthecoolingratessignicantly 3.1.1EscapeProbabilityMethodforanN{Level{SystemwithoutContinuum andcaninfactleadtonetlineheating incontrasttointerstellarconditions. isthetotalrateofenergywhichistransferredto/fromtheradiationeldvialine AnatomicormolecularN{levelsystemisconsidered.Thequantitytobedetermined statisticalequationsaregivenby emission/absorption.thistotalenergytransferrateiscalculatedintwosteps. First,thelevelpopulationsniarecalculatedbymeansofthestatisticalequations (\steadystatenon{lte")andsecondly,theenergytransferrateisdetermined.the andcanbesolvedtogetherwiththeequationfortheconservationofthetotalparticle nixj6=irij=xj6=injrji; (3.1) densityoftheconsideredspeciesnsp=pini.theratecoecientsaredenedby
45 3.1.BOUND{BOUNDTRANSITIONS Rlu=BluJul+Clu; Rul=Aul+BulJul+Cul (3.2) (3.3) 25 whereuandllabelanupperandlowerlevel,respectively.theratecoecients forstimulatedemissionbulandabsorptionblucanbecalculatedfromthosefor excitationculbyapplyingadetailedbalancerelation: spontaneousemissionaulbyapplyingtheeinsteinrelations.similarly,therate coecientsforcollisionalexcitationclucanbecalculatedfromthoseforcollisional Blu=gu Bul= 2h3ulAul glbul c2 (3.4) Clu=gu glculexp( Eul=kTg) (3.5) Thefrequencyintegratedmeanintensity Jul=1 (3.6) asknown),butismodiedbylineemissionandabsorptionintheconsideredresonanceregionitself,whichbecomesimportantforopticallythicklines.anexact isnotsolelygivenbytheincidentcontinuousintensitiesiinc 4ZZul(;)I()dd ()(whichareregarded (3.7) diativetransfercalculationsinthemovingmedium,whichgoesfarbeyondthescope ofthiswork.fortunately,thereareapproximateescapeprobabilitytechniquesavailable,whichcanaccountforthemostimportantresonanceeects.thisworkusesthe solutionofthisproblemcanonlybeachievedbyfrequencydependentnon{ltera- foradetaileddescriptionseewoitke1992)2: Sobolevapproximationinthecaseofsphericalsymmetry(e.g.Puls&Hummer1988, Jcont ul Jul=Pe =1 4ZIinc uljcont ul+(1 Pe ul()d ul)slul (3.9) (3.8) SLul=2h3ul c2 gunl glnu 1! 1 Pe ul=1 4Z1 exp S ul() ul()d (3.11) (3.10) dvk dl()=1 2vr+2@v S ul()=c3aul 83ul gu glnl nu!dvk dl() (3.13) (3.12) ignoringradiationtransfereectsintheconsideredresonanceregionitself. Pe continuousmeanintensityatlinecenterfrequencycausedbyincidentradiation ulisthemeanescapeprobabilityandslulthelinesourcefunction.jcont 2AdiscussionoftheapplicabilityofSobolevtheorytotheshockedenvelopesofpulsatingstars ulisthe isgivenonp.28.
46 26 Jcont ul,inprinciple,resultsfromthecalculationofacontinuousradiativetransfer CHAPTER3.RADIATIVEHEATINGANDCOOLING (withouttheconsideredline).forsimplicity,theincidentintensitiesareassumedto ineq.(3.11):anappropriatemeanvelocitygradientddv inordertoavoidtheelaborateandtime{consumingintegrationoverthesolidangle beisotropicineq.(3.8)3.s dvk dlthevelocitygradientonaconsideredray.thefollowingapproximationisused ulistheso{calledsobolevopticaldepthofthelineand probabilitiesarecalculatedaccordingto 1=2 0 1vr (3.14) es ul=c3aul 83ul gu glnl nu!*dv dl+ 1 (3.16) (3.15) epe ul=1 exp es es ul() andreachesamaximumvalueof33%aroundpe0:5.dierentowgeometriesand TheerrorofthisprocedurevanishesforthetwoimportantcasesPe!0andPe!1 ; (3.17) forddv caseswithvanishingvelocitygradientscanbetackledbyusingdierentexpressions toeliminatetheunknownlinesourcefunctionsslul.itisstraightforwardtoshow Forthenumericalsolutionofthestatisticalequations(3.1)itisveryadvantageous dleineq.(3.14)assummarizedinneufeld&kaufman(1993). that nuaul+(nubul nlblu)jul=nuaulepe =AulePeul 1 Jcont SLul! nu(1+jul) nlgu ul gljul! (3.19) (3.18) combinedintothefollowingsetofeectiveratecoecients localcontinuousradiationeld.bymeansofeq.(3.19)allaboveequationscanbe wherejul=c2=(2h3ul)jcont erul=aulepe ulisadimensionlessquantitywhichcharacterizesthe erlu=gu gl AulePe ul(1+jul)+cul uljul+culexp Eul ktg!: (3.21) (3.20) ofrij,wherethelinesourcefunctionsdonotappearanymore. ThelevelpopulationscannowbecalculatedbysolvingEq.(3.1)witheRijinstead eectoftheincidentintensitiesisproportionaltotheescapeprobabilityinthatparticulardirection, wherethevelocitygradientissmallerorlargerthanthemeanvelocitygradient,respectively:the toeq.(3.8),iftheconsidereduidelementmainlyreceivesthelightfromaparticulardirection, 3Strictlyspeaking,theinuenceofincidentcontinuousradiationincreasesordecreasescompared butthe(isotropic)re-emissionisproportionaltothemeanescapeprobability.
47 3.1.BOUND{BOUNDTRANSITIONS Finally,afterhavingdeterminedthelevelpopulations,thenetheatingratecan 27 readilybecalculatedeitherfrom Qcoll=XlXu>lEulCul nu nlgu glexp Eul ktg! orbymultiplyingtheradiativerateineq.(3.18)by Eulandsummingupthe (3.22) contributionsfromalltransitions: Qrad=XlXu>lEulnuAulePe ul Jcont SLul 1! =XlXu>lEulAulePe ul nlgu gljul nu(1+jul)! ul (3.24) (3.23) thegainsandlossesfromthetranslationalandtheradiativepool(theonlyconsideredsourceterms)balanceeachother(cf.fig.2.1).thisequalitydemonstratesthe Bothexpressionsareequivalentandmustyieldthesameresult(Qcoll=Qrad),since physicalmeaningofthebasicassumptionofsteadystate:afastrelaxationofthe isassured.equation(3.23)showsthemodicationsfromtheusualexpression degreeofexcitationoftheconsideredspeciesisassumedsuch,thatqcoll=qrad PEulnuAulcausedbyopticalthicknessandincidentcontinuousradiation(note howeverthatthelevelpopulationsarealsoaected). probabilitiesdependonthelevelpopulations.inmostcases,adirect{iteration Thesolutionofthestatisticalequationsstillrequiresaniteration,sincetheescape NumericalIterationScheme eld{conditions,wherex(it)meansquantityxatiterationstepit: convergesrapidly,buttherearealsocasesinwhichthisprocedurefails.thefollowingscheme,whichmaybecalledadecelerated{iteration,convergesforall consideredmodelatomsunderallconsidereddensity{,temperature{andradiation 1.PuteS 2.CalculateeRul(it)andeRlu(it)accordingtoEqs.(3.20)and(3.21). 3.Determinenj(it)fromthestatisticalequations(3.1). ul(0)=0;epe ul(0)=1;qrad(0)= CalculateQcoll(it)andQrad(it)accordingtoEqs.(3.22)and(3.24). 8.CalculateePe 7.PuteS 5.Dene=j1 Qrad(it)=Qrad(it 1)j. 6.CalculateeS ul(it)=es ulaccordingtoeq.(3.16). 9.Gobacktostep2unless< ul(it)fromeq.(3.17). ul(it 1)+[eS ul es ul(it 1)]exp( maxf0;(it 30)=10g). 10.TakeQradasnalresult,ifthepopulationisclosetoLTE otherwise almostequallylargenumbers.) relyonqcoll(toavoidtheerrorsproducedbythesubtractionoflarge,
48 28 Thetotallineheating/coolingratedependsonthefollowingphysicalparameters: CHAPTER3.RADIATIVEHEATINGANDCOOLING Theparticledensityoftheconsideredspeciesnsp,theparticledensitiesofthecollisionpartners,thegastemperatureTg,thecontinuousbackgroundradiationeld Thefollowingatomicormoleculardataarerequired:thestatisticalweightsgiand energieseioftheconsideredlevels,theeinsteincoecientsforspontaneousemission Jcont ulandthelocalmeanvelocitygradientddv Aulandtheratecoecientsforcollisionalde{excitationCul(Tg)(wheretheparticle dle. toarbitraryconditionsofdensity,temperatureandradiationeldandcanbeapplied ofthetotallineheating/coolingrateofanarbitraryn{level{system.itisapplicable Thepresentedmethodisanuniversalandrapidlyconvergingtoolforthecalculation densitiesofthecollisionpartnersenterintothecalculation). makessense DiscussionoftheApplicabilityofSobolevTheory toavarietyofowgeometries,asfarastheinvolvedescapeprobabilityconcept TheapplicationofSobolevtheorytotheshockedenvelopesofpulsatingstarsrequires somecriticalremarks: 1)Sobolevtheoryisapplicableonlyincaseoflargevelocitygradients,where thesizesoftheresonanceregions(whereanemittedlinephotoncanstillbe re-absorbed)aresmallcomparedtotypicalscaleheightsoftheenvelope.in caseofthermalbroadening,thisconditioncanbewrittenas Ddv vthmax(dln dle Regardingtheresultsoftime{dependentmodelsfortheenvelopesoflong{ dr;dlnt dr;dlnnsp periodicvariablestars(bowen1988,fleischer1994),thisconditionseemsto dr;:::): (3.25) bejustevenfullled.thethermalvelocitiesareafewkms 1,themean velocitygradient(cf.eq.3.14)istypically5to50kms 1=Randthescale frontsinthepost{shockregions,wherethetemperaturegradientscanbefairly height(ther.h.s.ofeq.3.25)istypically1r.problemscanoccurveryclose tothestar,wherethescaleheightcanbemuchsmaller,andclosetoshock 2)Duetothestrictdivisionbetweenconsideredlineandcontinuum,lineoverlaps large. areanintrinsicproblemofsobolevtheory.thesobolevtheoryrequiresthat theemittedlinephotonsofoneparticulartransitioncannotbere-absorbedby anyotherlinetransitionanywhereelseintheenvelope: v1c< l.h.s.ofeq.3.26)isabout10 4forAGB{stars,whichisusuallymuchsmaller Themaximumrelativeshiftofthelinesduetohydrodynamicvelocities(the (3.26)
49 3.1.BOUND{BOUNDTRANSITIONS thantherelativespacingoftheconsideredspectrallines(ther.h.s.ofeq.3.26, 29 whereisthefrequencydierenceoftwoconsideredlines).thiscondition wherether.h.s.ofeq.(3.26)isgivenby2hb=h!210 3(cf.Sect.3.1.4). Buteveninthiscase,condition(3.26)remainsvalid.Problemscanoccurin becomesmoreseriousforthevibrationalbandsofdiatomicpolarmolecules, 3)Theproblemofnon{monotonicvelocitygradientsinthesaw{toothlikevelocityeldsofCSEsofpulsatingstarscoupledwiththequestionofthedierence betweenlocalandglobalescapeisignored.thereby,theradiativeheating electronicbandsofmolecules,wherethespacingoftheindividuallinesiseven morenarroworinverynarrowspacedatomicmultiplets. 4)Closetothelocationofavelocitydiscontinuity(causedbyashockfront),most ofe.g.onepost{shocklayerbylineemissionsfromthepost{shockregionof anothershockwaveisneglectedinthiswork. coolingofotherwiseopticallythicklinesincreases,whichmaybeimportant justforthehotemittingpost{shockregionsdirectlybehindshockwaves. Therefore,largerescapeprobabilitiescanoccurinthiscaseandtheradiative ofthedisturbingabsorberaremissinginthedirectionsacrossthediscontinuity. Theadvantagesofthepresentedescapeprobabilitymethod,however,clearlyoutweightheseshort{comings.Aslongasnobetterandcomparablesimplemethodsare available,thesobolevtheoryisjusttheappropriatecompromisebetweensimplicity andaccuracyofthephysicaldescription.usingthistheory,theresultsoftheline heating/coolingratesareentirelydeterminedbylocalphysicalproperties(whichare availableinhydrodynamicmodels),stillincludingthemostimportantlinetransfer completely,whichwouldinducemuchlargererrors AnExemplaryTwo{Level{Atom eects.theonlyrealalternativewouldbetoignoreopticaldeptheectsofthelines Inordertodemonstratethebasicfeaturesofthelineheating/coolingfunctions,an exemplarytwo{level{atomisexamined.thefollowing(typical)atomicparameters andphysicalconditionsareconsidered: g1=g0;e=k=10000k;a10=10 2Hz;C10=n<H>10 10Hzcm3 Theresultinglineheating/coolingratepermassQrad=asfunctionofthetotal nh:nh2:nhe:nsp=1:0:0:1:10 4;*dv dl+=20kms 1 hydrogenparticledensityn<h>isdepictedinfig.3.1forthecaseofnegligiblecontinuousradiationeldjcont=0.theguredemonstratesthefundamentaldensity{ 500R sitiesncrandnthick,whicharedenedbelow: dependingontherelationbetweenthedensityofthegasn<h>andtwocriticalden- dependenceofthetwo{levelcoolingrate.threedierentcasescanbedistinguished,
50 30 CHAPTER3.RADIATIVEHEATINGANDCOOLING I II III Figure3.1:Thecoolingrate(fulllines,leftaxis)andtheexcitationtemperature, denedbyktexc=eul=ln((gunl)=(glnu)),inunitsoftg(dashedlines,rightaxis) ofanexemplarytwo{level{atominthecaseofnegligiblecontinuousradiationeld Jcont =0. Figure3.2:Thetemperaturedependence 1010cm 3andJcont ofthelinecoolingratepermassforn<h>= catepointsalreadydepictedinfig.3.1. =0.Fullcirclesindi-Figure3.3:Thedependencyoftheline coolingratepermassontheradiationeld forn<h>=1010cm 3andTg=2000K.
51 3.1.BOUND{BOUNDTRANSITIONS I.n<H>>nthick:Thelineisopticallythickandthecoolingrateislimitedby 31 thelocalsurroundings.lteisvalid.inthelimitingcasen<h>!1the escapeprobabilityscalesaspe!1=s/ 1.Thereby,Qradbecomesdensity{ radiativetrapping,whereonlyafractionoftheemittedlinephotonscanescape II.ncr<n<H><nthick:Theatomisthermallypopulated(LTE)andthelineis independent. III.n<H><ncr:Theatomispopulatedsub{thermally(non{LTE)andthecooling opticallythin.thecoolingrateissimplygivenbythethermalrateofemitted rateislimitedbytherateofenergytransferredfromthegasviacollisions, photons,leadingtoqrad/. ncrdenotestheusualcriticaldensityforthermalpopulationandnthickcorresponds isfollowedbyspontaneousemission. whichyieldsqrad/2.inthelimitingcasen<h>!0,eachexcitingcollision tos=1.thecriticaldensitiesaredenedby nthick=8 ncr= C10=n<H> A10g0 A10 g110 c3*dv dl+n<h> nsp : (3.28) (3.27) ase.g.incaseofthelargeeinsteincoecientsofallowedtransitions,thecooling Insomecases,thetwocriticaldensitieswilloverlap(ncr>nthick).Ifthishappens, ratedirectlychangesfromtheqrad/2totheqrad=constbehavior. hence,forecientlinecooling4.afurtherincreaseofthetemperaturedoesnot temperatureofabouttg>e=5kisrequiredforecientcollisionalexcitationand, Figure3.2showsthe\freezingout"oftheconcerneddegreeoffreedom.Aminimum increasethecoolingratemuch.however,sinceatthesametimeothercoolinglines temperature{dependenceisuniqueforalldensities:theqrad(n<h>)-curveissimply enterintocompetitionandbecomemuchmoreecient,theconsideredspectral shiftedup-anddownwardsinfig.3.1accordingtothattemperature{dependence. densityandtemperatureconditionsinordertobeanecientcoolant.thedepicted linegetslessimportantincomparison.hence,aspectrallinerequiresveryspecial heatinginthecaseofintensecontinuousradiationeldsasshowninfig.3.3.this Linetransitionscancausenetcoolingofthegas,butcaninfactalsocausenet resultisstraightforward,butfundamentallydierentfromtheexperiencewithinterstellarmatter,wherethecontinuousradiationeldmaybeneglectedandwhereline transitionsgenerallycauseradiativecooling.equation(3.23)expressesthelinear dependencyshowninfig.3.3. Allthediscusseddependenciesofthetwo{levellineheating/coolingfunctionare concerningamulti{level{atom. outlinedinthiswork. quitegeneralandapproximatelyapplyalsototheotherheating/coolingmechanisms 4However,theconsideredlinecanstillbeinterestingforradiativeheatingasfarasEl<kTg
52 LinesofAtomsandIons CHAPTER3.RADIATIVEHEATINGANDCOOLING envelopes,theselectionofspeciesandlinesiscrucial.theselectiondependsonthe consideredelementalabundancesandontheconsidereddensityandtemperature conditions.asarguedabove,oneshouldespeciallyincludeavarietyoflineswith Forageneraldiscussionoftheimportanceoflineheatingandcoolingincircumstellar atomicdata(especiallythecollisionrates)canbeproblematic.theselectionoflines inthisworkismainlybasedontheexperienceofhollenbach&mckee(1989).since theirworkrelatestointerstellarconditions,mainlythefew,low{lyinglevelsofthe dierenteulvalues(dierentspectralregions).furthermore,theavailabilityof Incaseoflargerdensities,wherethepopulationisgenerallyclosertoLTE,more moreabundantatomsandionsaretakenintoaccount. linesenterintocompetitionandthechosenselectionmaybeinsucient.especially tobeimportantsolelyatsmalldensities,atroublesomeexpansionofthelinelist oftransitionstobeconsidered).however,sincespectrallineshavegenerallyproven important(whichimmediatelycausestroublesduetotherapidlyincreasingnumber forhighgastemperatures,eventhepopulationofveryhigh{lyinglevelsmaybecome dominateatlargerdensitiesanyway. Therefore,onlyafewfurtherlines,whichsatisfytheconditions wouldberatherfruitless,becausethebound{freeheatingandcoolingrateswill largeelementalabundance, neutralorsinglyionized, lowexcitationenergyel, havebeenadditionallyincluded,especiallyfrommendoza(1983)andthereferences collisionaldataavailable largeaul,dierenteulvaluesand therein.thecompletenessofthemodelatomsisanothernecessarypreconditionfor non{lteinvestigations.if,forexample,atransitionwiththeprincipalquantum numberjump9!5looksinteresting,allthe55transitionsuptolevels9shouldbe takenintoaccount.table3.1summarizestheselectionofspeciesandlinetransitions inthiswork,comprising15speciesand85lines.thelistincludesmostoftheexisting lowerthan10 4)andwithneutralHatoms: withfreeelectrons(whichareusuallydominantunlessthedegreeofionizationis Theratesforcollisionalde-excitationareassumedtobegivenbythecollisionrates low{lyingenergylevelsoftheconsideredspecies. Cul(Tg)=neeul(Tg)+nHHul(Tg) xul(tg)=xultg=trefxul (3.29) ThecollisionalratesareoftenrepresentedasEq.(3.30),sothatforonecollisionrate usuallytwoparameters(ul,andul)aretobecollectedforelectronsandh{atoms. ThereareoftendierenttsfordierenttemperatureregimesTref.
53 3.1.BOUND{BOUNDTRANSITIONS Table3.1:Atomiclineheatingandcooling:consideredspeciesandtransitions33 H Levels(1) ul[m](2) n=1,n=2,n= ,0.1025,0.656 Ref. He+n=1,n=2,n=3,n=4,n= ,0.0256,0.0243,0.0237, 11S,23S,21S,23P0,21P0 1.56,1.08,0.887,3.56,2.06, ,0.0601,0.0591,0.0584, ,0.122,0.109, 4 C 3P0,3P1,3P ,0.321, ,229.9, C+ 3P,1D2,1S ,0.462,0.873 N 2P1=2,2P3=2 2P,4P N+ 4S3=2,2D,2P 0.520,0.347,1.04 O 0.656,0.306,0.576 O+ 3P2,3P1,3P0 3P,1D2,1S0 63.1,44.2, ,0.297, S3=2,2D5=2,2D3= ,0.372,508 Si+ 3P0,3P1,3P2 3P,1D2,1S ,44.8, ,0.653,1.10 S 2P1=2,2P3=2 2P,4P 3P2,3P1,3P ,17.4,56.6 S+ 3P,1D2,1S0 4S3=2,2D3=2,2D5=2,2P1=2,2P3=20.673,0.672,0.408,0.407,314.5, 1.10,0.459, ,1.029,1.037,1.032, D4,5D3,5D2 24.0,14.2, Fe+ 5D4,5F5,5F4 6D9=2,6D7=2,6D5=2 1.44,1.36, ,15.0,35.4 (1):Levelsarelistedintheorderofenergy(rstlevel=groundlevel).Levelswithout 6D9=2,4F9=2,4F7=2,4D7=2 5.34,4.12,1.26,17.9,1.64,1.80 (2):Orderoftransitions:1!0fortwo-level-atoms,1!0,2!0,2!1forthree-levelatoms,1!0,2!0,3!0,2!1,3!1,3!2forfour-level-atoms,1!0,2!0, lowerindexaremultipletswhicharetreatedassinglelevels. 3 5:Luttermoser&Johnson(1992) 4:Mendoza(1983)andreferencestherein,Hul=10 12cm3s 1isassumed 3:Hollenbach&McKee(1989)andreferencestherein 3!0,4!0,2!1,3!1,4!1,3!2,4!2,4!3forve-level-atoms. 6:EinsteincoecientsfromMihalas(1978),collisionalde-excitationratesfrom Mihalas&Stone(1968)
54 34 Inconclusion,theselectionoflineshasbeenperformedinviewoftheimportancefor CHAPTER3.RADIATIVEHEATINGANDCOOLING (usuallyclosetothephotosphereofthestar)wherethedensityislarge.incontrast, however,refertoanopticaldepth1,i.e.toaparticularshellofthecse wouldprobablysuggesttoconsiderthoselines,whichcanbeseen.theselines, thegas notfromtheobservationalpointofview.atrstsight,anastronomer ceedsaccordingtothemethodsoutlinedinsect eachrowintable3.1 thelineslistedintable3.1maynotevenoccurinthestellarspectra. sultsroughlyareasuperpositionofseveraltwo{level{typefunctionsasdepicted Thecalculationofthevariouslineheating/coolingfunctionsstraightforwardlypro- morecomplex,sincethepopulationofthelowerlevelchangesandtheupperlevel infig.3.1.thebehavioroflineswithlargerexcitationenergy,however,isusually istherebyconsideredasclosedmulti{level{systemwithprowni=nsp.there- canbepumpedbyanothertransitionetc.inarealphysicalsituation,theconcentrationsofthecarriersofthelinesnsp=n<h>additionallydependonthetemperature, thedensityandtheradiationeld.thesameoccursfortheelectronconcentration, whichisofcrucialimportanceforthecollisionrates. theradiativeenergyexchange.especiallythero{vibrationaltransitionsofabundantpolarmoleculeshaveproventobeimportantunderinterstellarconditions Assoonasmoleculesbecomeabundantinthegasphase,theyusuallydominate (e.g.neufeld&kaufman1993),intheatmospheresofcoolstarsandeveninthe mentofmoleculesinradiativetransferarisesfromthelargenumberoflinetransitions outeratmosphereofthesun(e.g.ayres1981).thegeneralproblemofthetreat- tobeconsidered.fornon{lteinvestigations,ahugeamountofmoleculardatahas tobecollected(individualradiativelifetimes,collisionratesetc.).thisprocedureis 3.1.3RotationalTransitionsofLinearPolarMolecules troscopicdetails,butinthetotaleectofmoleculesfortheradiativeheatingand nately,therearesomeapproximateanalyticalexpressionsavailableforcertaintypes ofmolecules(e.g.diatomicmolecules).sincewearenotinterestedinanyspec- onlyfeasibleforaveryfewwell{knownmoleculesandsubsetsoftransitions.fortu- coolingofthegas,theseanalyticalapproximationsarejustappropriate. Concerningtherotationaltransitionsoflinearpolarmolecules,thebasicmodelofa rigidrotatorprovidesthestatisticalweightsgjandenergiesejofthelevels.the EinsteincoecientsforthealloweddipoletransitionswithselectionruleJ!J 1 (forspontaneousemission)canbederivedfromtherotationalconstantbandthe dipolemomentd(chin&weaver1984).theratesforcollisionalde-excitationcul areadoptedfromhollenbach&mckee(1979) AJ!J 1=644 EJ=J(J+1)hB gj=2j+1 3hJ!J 1 (3.32) (3.31) c 32D2J+1 J (3.33)
55 3.1.BOUND{BOUNDTRANSITIONS Cul=0glhB ktgexp El ktgxinivth;i (3.34) 35 malvelocityand0isthetotalcollisionalcrosssection,whichisusuallyestimated wherej!j 1=2JBisthefrequencyofthetransition,vth;ithemostprobablether- vth;i=q8ktg=mred;i; (3.35) momentd,whichcanbetakenfromvariousmoleculardatatables,e.g.landolt{ arethetotalcollisionalcrosssection0,therotationalconstantbandthedipole Themoleculardatarequiredforthecalculationoftherotationalheating/coolingrate tobe10 15cm2. sideredmoleculesinthiswork. Bornstein(Hellwege1982).Table3.2summarizesthesemoleculardataofthecon- Table3.2:Vibrationalandrotationalheatingandcooling:considered Species(3)[K]1=10[Hz]B[MHz]D[D]0[cm2] speciesandmoleculardata OH CO HCN C2H CH C2N SiC {(1) 2.3 { SiO SiN SiS (1):Thevibrationalheating/coolingfunctionofthismoleculecannotbe CS (2) treatedaccordingtosect.3.1.4,sinceitisnotdiatomic (2):Estimated.Thecorrespondingnetvibrationalheatingfunction,however,isnotsignicantlyaectedbythechoiceofthisparameter (cf.sect.3.1.4). consideredinthiswork.inthecasec>o,wateritisalmostabsent (3):Sinceonlyapplicationsforcarbon{enrichedcasesaremade,H2Oisnot Thecalculationoftherotationalheating/coolingfunctioncanbeperformedsimilarlytothelastparagraph.Insteadofsolvingthestatisticalequations(3.1)forall fromthegasphase. consideredrotationallevelpopulationsnj,however(whichwouldalsobepossible, buttooelaborateforourpurpose),iusethefollowingapproximatemethodproposed
56 36 bykrugeretal:(1994).therotationalstatesareassumedtobepopulatedaccording CHAPTER3.RADIATIVEHEATINGANDCOOLING toaboltzmann{distributionwithayetunknownrotationalexcitationtemperature Trot: Zrot=kTrot nj=nmolgj hb Zrotexp EJ ktrot (3.37) (3.36) overtherotationalstatesineq.(3.22)byintegrals,itcanbeshownthatthetotal rateofcollisionalenergytransfersimpliesto BymeansofEqs.(3.31),(3.32),(3.34),(3.36)and(3.37)andbyreplacingthesums Therotationaltemperatureisfoundbyiteration,untilthebothresultsforQcoll Qcoll=0nmolk(Trot Tg)Xinivth;i: (3.38) intheindividuallines,istherebycarriedoutovertherstjmax=(7ktrot=hb)1=2 (typically102)rotationalstatesbypl;u!pjmax heatingrateaccordingtoeq.(3.24),whichproperlyincludestheopticaldeptheects andqradfromeqs.(3.38)and(3.24)areequal.theevaluationoftheradiativenet 97%ofthetotalthermalemissionrateintheopticallythinlimit. J=1(u=J;l=J 1),yieldingabout RotationalHeatingandCoolingbyCO Forexample,therotationalheatingcoolingfunctionofCOisbrieydiscussed,which outlinedintable3.2andthefollowingphysicalconditionsareconsidered: isofspecialimportanceduetoitslargeabundance.themoleculardataofcoare Figure3.4depictstheresultsforthecaseJcont nh:nh2:nhe:nco=0:1:0:2:10 3;*dv =0.Thedensity{dependenceofthe dl+=20kms 1=500R (withthecriticaldensitiesncr106cm 3andnthick109cm 3forCO,cf.Eqs.3.41 and3.42below).duetotheincreasingpopulationofthehigherrotationallevels andthesmallerradiativelifetimesoftheselevels,however,therotationalcooling rotationalcoolingfunctionisgenerallysimilartoatwo{level{typecoolingfunction Fast,ApproximateMethod functionscalesasqrot/t2g,whichisdierentfromatwo{level{typecoolingfunction. upperresultscanbeused,ifthecontinuousradiationeldinthemicro{wavespectral (e.g.forthemodelcalculationsinchapter7).insuchcases,thefollowingttothe calculationoftherotationalheating/coolingfunctionsmaybetootimeexpensive Forcertainapplications,eventherathersimplemethoddescribedaboveforthe
57 3.1.BOUND{BOUNDTRANSITIONS 37 Jcont Figure3.4:RotationalcoolingrateandexcitationtemperatureofCOincase regiontslikejcont =0.Arrowsindicatethetrendforincreasinggastemperature. WB(Trad)W2kTrad(=c)2(Rayleigh{Jeansapproximation): Qrot;LTE=102442DB2 Qrot=Qrot;LTE n<h>+1+n<h> ncr nthick! 1 3c3h2 nmolk2tgwtrad Tg (3.39) ncr=102442db2ktg 3h2c30vth (3.40) nthick=0:08ktg 2DB*dv dl+n<h> nmol ; (3.42) (3.41) centrationsofthecollisionpartners.consideringtypicalastrophysicalrelevant molecules,thecriticaldensitiesforthermalpopulationoftherotationalstatesncr wherevth=n 1 rangebetweenabout105cm 3(e.g.SiS)and108cm 3(e.g.HCN). <H>Pinivth;iisthemeanthermalvelocitywithrespecttothecon- beanalyticallyderivedfromeq.(3.23).equation(3.40)expressesthedependencies atthecriticaldensities,<10%elsewhere).qrot;lteistherotationalheating/cooling functionincaseoflte(trot=tg)andvanishingopticaldepths(epe Equation(3.39)isaveryusefultformulawithacceptableaccuracy(error<35% oftherotationalheating/coolingfunctionuponthetemperatureandtheradiation ul=1),whichcan
58 38 eld.astherotationalfrequenciesarelocatedinthemicro{wavespectralregion CHAPTER3.RADIATIVEHEATINGANDCOOLING (cf.their{limitinfig.1.1).theoppositecaseismuchmoreprobable:therotationaltransitionswillalmostalwayscausenetradiativecooling.accordingto occursincasewtrad>tgwhichseemsunlikelytooccurincircumstellarenvelopes (h1!0=k=2hb=k5:5kforco),radiativeheatingviarotationalpumpingsolely thecomparativelyweaktemperature{dependence,rotationalheating/coolingisespeciallysignicantatlowgastemperatures.therelevanceofaconsideredmolecule scalesasnmol2db2,whichisimportantforthechoiceofthemoleculestobetaken intoaccount. ing/coolingmechanismforthegas.thevibrationalspectraofpolyatomicmolecules Theallowedvibrationaltransitionsofpolarmoleculesalsoprovideaneectiveheat VibrationalTransitionsofDiatomicPolarMolecules arealreadyrathercomplex,sothatnoclosedanalyticalexpressionsforthemeanradiativelifetimesandthecollisionratesareknown.therefore,thisworkrestrictsto thevibrationaltransitionsofdiatomicpolarmoleculeswithselectionrulesv!v 1 heating/coolingbypolyatomicmoleculesprobablyisasecond{order{eect5.the themostabundantpolarmoleculesinthegasphase(e.g.co).thevibrational correspondingwavelengthstypicallyrangefrom4mto12m6. ;J!J1(forspontaneousemission).Fortunately,thesemoleculesareusually rotatorisapplied,whichissucientforthepurposeofthiswork. Forthelevelenergies,themostsimplemodelofaharmonicoscillatorandarigid J!J+1=v644 Ev;J=h!v+12+J(J+1)hB gv;j=gj (3.43) J!J+1!3(TM)2J+1 (\P{branch") (3.45) (3.44) Av!v 1 J!J 1=v644 3h v!v 1 J!J 1 c C10= 1 exp( =Tg)XiniexpBi AiT 1=3 ktg=1atm 2J+1 g(\r{branch") (3.47) (3.46) Ai=1:1610 3mred;i =h!=k 1amu1=24=3 (3.49) (3.48) Cvv0=(v v0)c10exp Bi=18:42+0:015Aimred;i (v v0 1)1:5=Tg 1amu1=4 1+1:5=Tg! (3.51) (3.50) 5AnexceptionistheH2Omoleculeincaseofanoxygenrichelementalcompositionofthegas. 6Notethatovertonetransitionsarenotconsideredhere(cf.discussioninSect.3.6).
59 3.1.BOUND{BOUNDTRANSITIONS visthevibrationalquantumnumber,!theeigenfrequencyoftheharmonicoscillator 39 andtmitstransitionmoment,whichisrelatedtothemeanradiativelifetimeof analyticalrepresentationoftherateofcollisionalde-excitationoftherstvibrational therstexcitedvibrationalstatevia1=10=a1!0 representationoftheeinsteincoecientsisadoptedfromnuth&donn(1981).the statec10istakenfrommillikan&white(1964).thelandau{tellercoecients J!J+1+A1!0 J!J 1.Theanalytical accordingtoeqs.(3.49)and(3.50).thecorrespondingcollisionalcrosssections systems"(diatomicmoleculeplusatomordiatomicmoleculeascollisionpartner) forvibrationalde-excitationaremuchlessthanthegeometriccrosssectionsofthe AiandBiaretobedeterminedbyexperimentsorcanbeestimatedfor\simple moleculesandshowastrongtemperature{dependence.thecollisionalde-excitation Equations(3.43){(3.51)formausefulsetofapproximateanalyticalexpressionsfor \surprisalanalysis"(elitzur1983). ratesforhigherquantumnumbersv>v0accordingtoeq.(3.51)areestimatedby therequiredmoleculardataintermsofafewbasicquantities,whicharetheeigenfrequency!,therotationalconstantbandthetransitionmomenttm(orthemean availableonlyforafewwell-knownmolecules(fromlaboratoryexperimentsorab caneasilybeobtainedfromvariousmoleculardatatables,whereasthelatteris lifetimeoftherstexcitedvibrationalstate10,respectively).thersttwodata Ofcourse,moreaccurateEinsteincoecientsandcollisionaldatacanbeusedfor to100hz.theobviousadvantageoftheanalyticalexpressionsaboveistheirbroad applicabilitytodiatomicpolarmolecules.thedisadvantageisthemodestaccuracy. initoquantummechanicalcalculations).typicalvaluesfor1=10rangefromabout1 ingtoboltzmanndistributions: Asinthelastsection,thero{vibrationalstatesareassumedtobepopulatedaccord- particularmolecules,ifavailable. Zvib= nv;j=nmolgj 1 exp( h!=ktvib) ZvibZrotexp 1 vh! ktvib J(J+1)hB ktrot! (3.53) (3.52) againfoundbyiteration,untiltheresultsforqradandqcollderivedfromeq.(3.24) andeq.(3.22)areequal.equation(3.22)istherebyevaluatedsolelyforthevitationalheating/coolingfunctionandthevibrationalexcitationtemperaturetvibis Therotationaltemperatureisconsideredasknownfromthecalculationofthero- l=fv 1;J1g),whichyields98%ofthetotalthermalemissionrateinthe rate.equation(3.24)isevaluatedaccordingtopl;u!pvmax brationalstatesandrestrictedtotherstvmax=1+6ktvib=h!vibrationallev- elspl;u!pvmax v=1pv 1 opticallythinlimit. v0=0(u=v;l=v0),yieldingabout99%ofthetotalcollisional v=1pjmax J=0(u=fv;Jg;
60 40 CHAPTER3.RADIATIVEHEATINGANDCOOLING Figure3.5:VibrationalcoolingrateandexcitationtemperatureofCOincase VibrationalHeatingandCoolingbyCO Jcont =0. tion.incaseofco,moreaccuratecollisionaldataareavailable:the1!0rate andtheconsideredvelocitygradientandgasabundancesaregiveninthelastsec- ofthecomoleculeiscalculated.themoleculardataforcoaregivenintable3.2 Inordertoillustratetheoutlinedprocedure,thevibrationalheating/coolingfunction seehollenbach&mckee1989).landau{tellercoecientshavebeenexplicitlymeasuredfortheco{hecollisions(millikan&white1964). Figure3.5depictstheresultsforthecaseJcont &Hollenbach1994)andforcollisionswithH2moleculesfromRosenbergetal:(1971, coecientsforcollisionswithhatomsaretakenfromglassgold(1993,seeneufeld essentiallyisatwo{level{typecoolingfunctionandconsequentlyshowsallthefeaturesdiscussedinsect thehighervibrationallevelsv2areusually =0.Thevibrationalcoolingrate notverysignicant.accordingtothelargeeinsteincoecientsofthevibrational transitions,themaximumpossibleemissionrateintheopticallythinltecase Qrad/2totheQrad=constcaseataboutn0cr1011:5cm 3forCO.Thebasicslope sitions.consequently,thevibrationalcoolingfunctiondirectlychangesfromthe isneverrealized,becausetheemissionislimitedeitherbyinsucientcollisional pumpingorbyradiativetrapping,whichisthetypicalbehaviorofallowedtran- ofthetemperature{dependenceisthesameasdepictedinfig.3.2,althoughfor
61 3.1.BOUND{BOUNDTRANSITIONS temperaturestg>,thehighervibrationallevelscausesomemodications.the 41 vibrationalband. tedphotonsarespreadamongthenestructureofthep{andr{branchofthe sensibilityofthevibrationalheating/coolingtoopticalthickness,sincetheemit- maindierencetoanordinarytwo{level{typecoolingfunctionarisesfromtheweak Fast,ApproximateMethod assumedthatthebackgroundradiationeldisconstantoverthevibrationalband andequalsjcont formulaisdesigned,whichcanbeappliedintime{criticalmodelcalculations.itis Similartotherotationalheating/coolingfunctionintheprevioussection,afastt 1!0:Qvib=Qvib;LTE Qvib;LTE=nmol n<h>+1+n<h> ncr nthick! 1 exp(=tg) 1 h! B1!0(Tg) 1! Jcont (3.54) ncr=n<h> 10C10 (3.55) nthick=26:410*dv dl+ktg hb h! hc!3n<h> nmol (3.56) n0cr=pncrnthick (3.58) (3.57) occursincasejcont elsewhere.thedependencyofthevibrationalheating/coolingfunctionontheradiationeldisexpressedbyeq.(3.55),oncemoreindicatingthatradiativeheating Theaccuracyofformula(3.54)isabout35%atn<H>n0crandbetterthan10% exchangerateincaseoflte(tvib=tg)andnegligibleopticaldepths(epe Althoughthismaximumpossiblerateisusuallynotrealized(seeabove),itscales theresultsasformulatedineq.(3.54).asfarasncr>nthicksisvalid,thevibrational >Bandradiativecoolingotherwise.Qvib;LTEistheenergy heating/coolingrateisalmostentirelyindependentfromthemeanlifetime10.this ul=1). ingtypicalvaluesfor10andc10fordiatomicpolarmoleculesandgastemperatures diatomicpolarmolecules,forwhichthe10{valuesarenotexactlyknown.consider K,thecriticaldensitiesforthermalexcitationofthevibrationalstates allowsforthedeterminationofthevibrationalheating/coolingratesalsoofthose ncrareoftheorder cm 3,whichduetoradiativetrappingareusually signicantlyreduced(ncr!n0cr)byupto4ordersofmagnitude7.consideringthe extremelytemperature{dependentandthevibrationalenergiesofthereactantsmaybeinvolved. rotationalstates).chemicalreactionsmightbeaectedbytheseeects,sincemanyreactionsare polarmoleculescanbeexpectedincircumstellarenvelopes(incontrasttothepopulationofthe 7Consequently,strongnon{LTEeectsconcerningthepopulationofthevibrationalstatesof presentedbycherchneetal:(1992). grainsintheseenvelopes.arstapproachtohandlereactantsofdierenttemperatureshasbeen Thissituationmayhavesevereconsequencesforthechemistryandalsoforthenucleationofdust
62 42 mostlyrealizedcaseqvib/2,theimportanceofamolecularspeciesunderexaminationconcerningitscontributiontothetotalheating/coolingofthegasscalesas CHAPTER3.RADIATIVEHEATINGANDCOOLING nmolh!c10. betweenthegasandtheradiationeld,becausethesemoleculeshaveextremely 3.1.5QuadrupoleTransitionsofH2 Unpolarmoleculesmayusuallybeneglectedconsideringthetotalenergyexchange smallradiativetransitionprobabilities.theh2molecule,however,maybesucientlyabundantinordertocompensateforthis.itsro{vibrationalquadrupole Theradiativeheating/coolingfunctionofH2iscalculatedanalogouslytoSect transitionsareknowntobesignicantinwarminterstellarcloudsandarelocated roughlybetween1mand25m. Sect Thelevelenergiesarederivedfromthespectroscopicconstants tionprobabilitiesmustbeused,whichmeansamuchlargerexpensecomparedto Sincenoanalyticalexpressionsareavailable,anextensivelistofindividualtransi- E(v;J)=hcwev+12 wexev+122+bvj(j+1) DeJ2(J+1)2 we=4401:2;xe=121:33;bv=60:853 3:062v+12;De=0:0471[cm 1] (3.59) asgivenbyhuber&herzberg(1979)andtheeinsteincoecientsforspontaneous emissionofthe(forbidden)ro{vibrationalquadrupoletransitionsv!v0;j! vibrationaltransitions). Thecollisionalvibrationalde-excitationrates1!0forH{atomsandH2{molecules fj 2;J;J+2garetakenfromTurneretal:(1977),wherealltransitionswithv5 areadoptedfromlepp&shull(1983)andreferencestherein.thoseforhe{atoms andj20aretakenintoaccount(comprising114purerotationaland898ro{ Eq.(3.51).Thecollisional(de{)excitationoftherotationalstatesisnotconsidered collisionalratesforthehighervibrationalstatesareagainestimatedaccordingto areestimatedaccordingtoeq.(3.47)withahe=145:5andbhe=20:77.the approximationisreliable,unlessthegasdensityislowerthan105cm 3. indetailhere instead,therotationaltemperatureofh2isassumedtoequal thegastemperature.accordingtothecalculationsoflepp&shull(1983),this IftheopticaldepthsinthelinesareneglectedasassumedintheworkofLepp&Shull (1983),theirresultscanbereproducedwithinamaximumfactorof2(generally 105cm 3,provingthatthepresentedmethodincludingtheintroductionofexcitationtemperaturesworksproperly.Figure3.6showstheresultsoncemoreforthe casejcont =0,nH:nH2:nHe=0:1:0:2andDdv muchbetter)forallconsideredgastemperaturesandfordensitieslargerthan opticallythick.thevibrationalcoolingrateismoreimportantforhightemperatures(tg>1000k)andhighdensities,whereitexceedstherotationalcoolingrate densitiesunlessn<h>>1012cm 3,whereeventhequadrupoletransitionsbecome totheassumptiontrot=tg,therotationalcoolingrateisproportionaltoforall dle=20kms 1=500R.According
63 3.1.BOUND{BOUNDTRANSITIONS 43 coolingrate(thinfulllines),therotationalcoolingrate(dottedlines,leftaxis) Jcont Figure3.6:Thetotalquadrupolecoolingrate(thickfulllines),thevibrational andthevibrationalexcitationtemperature(dashedlines,rightaxis)ofh2incase byaboutoneorderofmagnitude.thecriticaldensityforthermalpopulationofthe =0. vibrationalstatesoftheh2moleculestronglydependsonthegastemperatureand rangesfrom106to1010cm 3. ThetotalcontributionofH2heatingandcoolingroughlystaysproportionaltothe typicalforforbiddenlines.incomparisontootherheating/coolingrates,which anaccuracyofaboutoneorderofmagnitude).thisbehaviorisanaturalconsequencefromthelowtransitionprobabilitiesofthequadrupoletransitions,andis gasdensityoverthewholeconsidereddensityrangeofcircumstellarenvelopes(with decreaseasqrad/2forsmalldensities,theh2quadrupoleheating/coolingisespeciallysignicantatlowdensity(e.g.interstellar)conditions.
64 Bound{FreeTransitions CHAPTER3.RADIATIVEHEATINGANDCOOLING Bound{freetransitions(photoionisationandradiativerecombination)generallyprovideimportantheatingandcoolingratesassoonasconsiderablefractionalionization i)astronguvradiationeldispresentwhichcausesboth,photoionisation andnetradiativeheatingofthegas.thiscaseisgenerallyrealizedinthe ispresentinthegas,whichoccursinthefollowingtwocases: ii)thegasisdenseandhot,sothatcollisionalionizationcausesconsiderable overwhelmingpartoftheism(exceptforthedenseandshieldedmolecular fractionalionization.hightemperatures(>8000kforhydrogen)areusuallyrequiredforeectivecollisionalionizationwhich,followedbyradiative clouds),wheretheinterstellaruvradiationeldinteractswiththegas. dependontherelationbetweenthegastemperatureandthepresentuvradiationeld,seebelow).thecompetitiveprocessesofcollisionalionization recombination,preferablycausesnetcoolingofthegas(thedetails,however, andthree{bodyrecombinationarefurthermoreresponsibleforkeepingtheionizationequilibriumclosetolteinstellaratmospheres.inreturn,thelarge ConsideringthephysicalconditionsinCSEs,largefractionalionizationespecially radiativeheatingandcoolingofthegasase.g.intheatmospheresofhotstars. bound{freeopacitiesinthecaseofltecontroltheradiativetransferandthe beexpected. TheconditionsinthepredominantlyneutralCSEsofcool(e.g.AGB)starsdo alreadysucientlyintensetocauseconsiderablebound{freeradiativeheatingcan occursaroundwarmandhotstars,wherethephotosphericuvradiationeldis generallynotfavorlargebound{freeheating/coolingrates.thereare,however, importantexceptionsfromthisrule:first,ifchromosphericactivityispresent, interstellaruvradiationeldcanpenetrateintotheconsideredlayerofthecse,it radiativeheatingbybound{freetransitionsofthegascanbeeective.second,ifthe followedbyradiativerecombinationcanbeanimportantcoolingprocesses. thehotpost{shockgaslayersinthecsesofpulsatingstars,collisionalionization willcauseconsiderablefractionalionizationandradiativeheating.third,concerning 3.2.1TheRateEquationsforanN{LevelSystemwithContinuum ined.besidesthebound{boundprocessesdiscussedbefore,theprocessesofpho- (denotedby\ii")fortherstionizedstateoftheconsideredspeciesisexamtoionisation,radiativerecombination,collisionalexcitationandthree{bodyrecombinationaretakenintoaccount.analogouslytosect.3.1.1thelevelpopulations AlevelsystemconsistingofNboundelectronicstatesplusoneadditionallevel n1;n2;:::;nn;niiarederivedfromthestatisticalequations(3.1),assumingthatthe netproductionratesofallconsideredstatesvanish(steady{statenon{lte).this
65 3.2.BOUND{FREETRANSITIONS assumptionismorerestrictiveinthissection,becausethetimescaleforrelaxation 45 circumstances(e.g.inthecaseoflowfractionalionization)andmightexceedother, e.g.hydrodynamictimescales.furthermore,thelevelsystemisassumedtobe paredtothetimescalesforrelaxationoftheexcitedboundstatesundercertain towardsionizationequilibrium(niipiriii=piniriii)canbemuchlargercom- \closed"inthesensethatotherprocesses,whichmightprovideadditionalsource termsfortheparticledensitiesoftheneutralandsinglyionizedatoms(e.g.chemical Theratecoecientsforthebound{boundtransitionsaregivenbyEqs.(3.20)and reactions,chargeexchangereactions)areneglected. (3.21),whereasthoseforthebound{freetransitionsareformulatedaccordingto Mihalas(1978): RiII=41 ithrj Zhbf RIIi= ne i()d+nei(tg) (3.60) Si(Tg) 0 B@41 ithr Z 22 Si(Tg)=2ZII gi(2mektg)1:5 c2+j h!exp h ktgbf i()d+nei(tg)1ca(3.61) ilabelsaboundstate,bf h3 exp i ktg! i()isthebound{freeabsorptioncrosssectionandi(tg) (3.62) theratecoecientforcollisionalionization(weonlyconsidercollisionswithelectrons Thetotalradiativeheating/coolingfunctionofsuchamulti{levelsystemcomprisescontributionsfrombound{boundtransitions,whicharecalculatedaccording toeq.(3.24)andfrombound{freetransitions: Qbf rad=4nxi=11 ithr ZniJ niine Si(Tg)2h3 partitionfunctionoftheionizedstate. i=hthecorrespondingthresholdfrequency,si(tg)thesahafunctionandziithe here).iistheenergydierencebetweenthei-thlevelandthecontinuum,ithr= Itisimportanttonotethattheevaluationoftheradiativeheating/coolingratedependsonthedenitionoftheinternalenergy.Inthiswork,thetotalabsorbed/emitted photonenergyiscalculatedandtheionizationenergiesioccuraspotentialsinthe thiscase,nointernalionizationpotentialsareconsidered,butanadditionalfactor internalenergy(cf.eq.2.2).concerningotherpublications,theradiativeheating andcoolingratesoccasionallyrefertothepooloftranslationalenergyalone.in c2+jexp h ktg!bf i()d (3.63) functionzii,onlybf (h i)=happearsineq.(3.63),describingthegainorlossofpuretranslational energy. Besidesthedataforthelevelenergiesi,thestatisticalweightsgiandthepartition i()andi(tg)arerequiredforthecalculationofthebound{free
66 46 radiativeheating/coolingfunctions.theso{calledphoto{recombinationcoecients CHAPTER3.RADIATIVEHEATINGANDCOOLING Fortheactualsolutionoftheoutlinedsystemofequations,allintegralsareevaluated relationsforbound{freetransitions,whicharealreadyincludedineqs.(3.61,3.63). areprincipallynotneeded8,sincetheycanbededucedfromtheeinstein{milne boundtransitions,wherethesameprocedureasoutlinedinsect isapplied. includingniirequiresan(inner)iterationoftheescapeprobabilitiesofthebound{ Thesystemofequationsiswell{denedforgiventotalparticledensitynsp=nII+ numerically.thesolutionofthestatisticalequations(3.1)forthelevelpopulations Pni,giventemperatureTg,givenradiationeldJandgivenelectrondensityne. conservationne=pnii,comprisingallionsunderconsideration,whichinreturn Another(outer)iterationisnecessarytoachievethephysicalconditionofcharge yieldstheelectrondensity. Accordingtotheoutlinedequations,thedegreeofionizationofthegasandthe bound{freeheating/coolingratesarecalculatedsimultaneously.opticaldepthseffectsarenotincludedconcerningthebound{freetransitions incontrasttothe bound{boundtransitionsdiscussedbefore,whereitwaspossibletoapplysobolev theory9.thisproblemcouldonlybehandledbymeansofnon{local(non{lte) assumethegastobeopticallythininthecontinuumandputj=jcont theradiativeheatingandcoolingofsinglegaselements,weignoretheseeects, radiativetransfercalculations.sincethebasicapproachofthisworkistodetermine,wherejcont Fast,ApproximateMethod isthecontinuousbackgroundradiationeld. cientsas ing/coolingfunctionscanbederivedbyintroducingthephoto{recombinationcoef- Ausefulandquiteilluminatingformforthegeneralbound{freeratesandheat- i(t)=4 Si(T)1 ithr22 Z ThesecondpartofEq.(3.64)providesacommontformula,wheretheparameters c2exp h ktbf i()daitbi (3.64) aiandbiareoccasionallystatedintheliterature.asfarasstimulatedbound{free emissioncanbeneglected(whichusuallyisaveryaccurateapproximationinthe UV10),therecombinationratescanbere-writtenas RIIi=nei(Tg)+ Si(Tg)i(Tg): n2e lations,seebelow. 8Thephoto{recombinationcoecients,however,areveryusefulforquick,approximatecalcu- (3.65) canbelocatedintheopticalorevenirspectralregion. drivethegastowardslte{ionizationalreadyatcomparativelysmallergasdensities. 10Note,however,thatthecorrespondingwavelengthsofrecombinationstohighlyexcitedstates 9Suchopticaldeptheectsareexpectedtoreducethebound{freeheating/coolingratesand
67 3.2.BOUND{FREETRANSITIONS IfthecontinuousradiationeldtslikeJWB(Trad)W2h3=c2exp( h ktrad) 47 thephoto{recombinationcoecient: (Wienapproximation),alsotheionizationratescanpartlybeexpressedintermsof thenetbound{freeheatingratethenreducesto Bydeterminingthederivative@i=@(1=kT)fromEq.(3.64),itcanbeshownthat RiII=WSi(Trad)i(Trad)+nei(Tg) (3.66) Qbf rad=nxi=1niwsi(trad)i(trad)hhiabs hhiem i i=i+(1:5+bi)ktg; =i+(1:5+bi)ktrad i niinei(tg)hhiem i (3.68) (3.67) Equation(3.67)isexactasfarastheupperconditionsarevalidandthederivative wherehhiabs=emisthemeanabsorbedandemittedphotonenergy,respectively. (3.69) dzii=dtcanbeneglected.thebigtechnicaladvantageofeqs.(3.65),(3.66)and parameters(aiandbi)havetobeknownforeachconsideredbound{freetransition. (3.67)isthatnointegralsoccurandthatinsteadofafunction(bf tonsequalsthenumberoffree{boundemittedphotons(asinthecaseofnegligible Equation(3.67)demonstratesthatevenifthenumberofbound{freeabsorbedpho- i())onlytwo collisionalionization),thenetrateoftransferredenergydoesusuallynotvanish,in contrasttoallbound{bound{typetransitionsdiscussedintheprevioussection.the energy.inthecaseofthermodynamicequilibrium,however,wherej=b(tg)and ni=niine=si,thenetbound{freeradiativeheatingrateaccordingtoeq.(3.63)or reasonlieswithintheintegrationovertheabsorbed/emittedphotonspectrum,since accordingtoeq.(3.67)isindeedzero asdemandedbydetailedbalance. themeanabsorbedphotonenergyusuallydiersfromthemeanemittedphoton Themostsimplecaseoccurs,ifsolelythegroundstateoftheneutralatomisconsideredandifthecollisionalionizationratesareneglected.Fromtheconditionof steadystaten1r1ii=niirii1itfollowsthatinthiscasethenetheating/coolingrate simpliesto (independentofthevalueofthedilutionfactorw),whichcorrespondstotheuv{ Inthiscase,radiativeheatingoccursforTrad>Tgandradiativecoolingotherwise Qbf rad=niine1(tg)1:5+b1k(trad Tg): (3.70) limitdepictedinfig.1.1.
68 TheH{AtomCHAPTER3.RADIATIVEHEATINGANDCOOLING However,thehigh{lyingenergylevelsofhydrogenmakeitalmostinaccessiblefor thetotaldegreeofionizationandtheradiativeheatingandcoolingofthegas. Accordingtoitsoverwhelmingabundance,hydrogenisalwaysimportantforboth, collisionalexcitationandcollisionalionizationatlowertemperatures,sothatthe andphysicalconditionsareconsidered: oftherstthreeboundlevelsandtheionizedstate11.thefollowingdataofhydrogen Fordemonstration,apurehydrogenplasmaisexaminedinthefollowing,consisting importanceofhydrogenismainlyrestrictedtohightemperatures. n=13:598ev=n2;gn=2n2;zii=1;bf n<h>=n1+n2+n3+nii;ne=nii;*dv dl+=20kms 1=500R n()=2:815(+29)gnii n53 whichareoftheorderofunity.thecollisionalionizationratecoecientsn(tg)are takenfromluttermoser&johnson(1992)andthereferencestherein.thehydrogen abbreviationx(y)=x10yincgs{units.gniiarethebound{freegauntfactors, Thebound{freeabsorptioncrosssectionsaretakenfromMihalas(1978)withthe bound{freetransitionsii!1(lyman{continuum),ii!2(balmer{continuum)and II!3(Paschen{continuum)arecalculatedbymeansoftheexactequationsgivenin Sect Thetreatmentofthehydrogenbound{boundtransitions2!1(Ly), Figures3.7and3.8showtheresultingtotal(bound{freeplusbound{bound)cooling 3!1(H)and3!2(H)hasbeendescribedinSect.3.1. ratesofhydrogen.twoguresarepresentedhere,sincethedegreeofionizationand plotsbefore. eld,whichischosentobezerointherstandtoequalaplanckianof3000kin thesecondgure.notethescalingofthey{axiswhichisdierentfromtheother theheating/coolingratesstronglydependonthecontinuousback{groundradiation heatingandcoolingisfoundtobeunimportantfortg<6000k.howeverforhigher gastemperatures,hydrogencoolingsoonbecomesecientandnallyhydrogen Comparedtothemagnitudeoftheheating/coolingratesdiscussedsofar,hydrogen providesthedominantcoolingrateofthegasattemperaturesabove8000k. Thistemperature{dependencyisaconsequenceofthehigh{lyingenergylevelsof temperatures. ThetotalhydrogencoolingrateisfoundtoscaleroughlyasQ/2,whichisan indicatorforstrongnon{lteeectsinthelevelpopulations12. hydrogen,whichcanbecollisionallyexcitedorionizedsolelyinthecaseofhighgas ofhydrogentotheelectrondensity. stellarenvironmentsfordescribingaccuratelyboththeemergenthspectrumandthecontribution 11Luttermoseretal:(1989)haveshownthatathree{levelmodelforhydrogenissucientincool Sect.3.1.Concerningthebound{freeheating/coolingfunctions,wehavenIIneSiniinLTE, whichaccordingtoeq.(3.63)alsoimpliesq/asfarashydrogenismostlyneutral. 12LTEwithoutopticaldeptheectsimpliesQ/forspectrallinesasalreadydiscussedin
69 3.2.BOUND{FREETRANSITIONS 49 Figure3.7:Thetotal(bound{freeplusbound{bound)hydrogencoolingrate (fulllines,leftaxis)andthedegreeofionization(dashedlines,rightaxis)inthe casewithoutcontinuousradiationeld. Figure3.8:SameasFig.3.7,butwithanunderlyingcontinuousradiationeld.
70 50 ThedegreeofionizationinFig.3.7showsastep{likebehavior.Thisisaneect CHAPTER3.RADIATIVEHEATINGANDCOOLING density,lyandforlargerdensitiesalsohbecomeopticallythick.consequently, causedbythevaryingopticaldepthsofthehydrogenlines:withincreasinggas theeectiveradiativebound{boundratesaccordingtoeqs.(3.20)and(3.21)becomenegligiblecomparedwiththecollisionalrates,forcingtheupperlevelofthdersofmagnitude,leadingtosuccessivelyenhancedelectronconcentrationsfrom consideredtransitiontoachievethermalpopulationwithrespecttothelowerlevel. Therefore,thecollisionalionizationratefromthatupperlevelisincreasedbyor- therighttotheleftinfig.3.7.infig.3.8,thisbehaviorissmearedout,sincethe ratesforphotoionisationenterintocompetition. ThehydrogennetcoolingratesinthecaseJ=B(3000K)depictedinFig.3.8 arefoundtobelargerthaninthecasej=0,sincephotoionisationproduces considerablyhigherelectronconcentrations,providingmorecollisionpartners13. Furtherdetailsconcerningtherelativecontributionsofthedierenttransitionsand thelevelpopulationsarepresentedinfig.3.9,consideringthecasetg=8000kand J=0.Theb{factorsfordeparturesfromLTEarecalculatedas ne= bi=ni=ni=nisi(tg)=n2 0:5+q0:25+n<H>(1=S1+1=S2+1=S3) e (3.72) (3.71) Hydrogenbound{freecoolingisfoundtodominateinhotdensemedia,whereas particulardensity,whichdependsontheconsideredgastemperatureandvelocity withincreasinggasdensity.thetransitionbetweenthesetwocasesoccursata emissioninhydrogenlinesdominatesthecoolingofahotthingas,whichisa straightforwardconsequenceoftheincreasingopticaldepthsinthehydrogenlines gradient.infig.3.9,thistransitiondensityisaboutn<h>=1010cm 3.Thebumps onthetotalcoolingratesdepictedinfig.3.7correspondtothesetransitions. TheLyman{continuumalwaysprovidesthemostimportantbound{freecooling outbyhollenbach&mckee(1989)andneufeld&hollenbach(1994),althoughly Lyisusuallythemostimportanthydrogencoolinglineashasalreadybeenpointed rate.therelativecontributionsoftheothercontinuawithrespecttothelyman{ isopticallythickforallconsidereddensities(epe continuumscaleas1=n3,whichcanbeanalyticallyderivedfromeq.(3.63). gradient).however,forlargedensities,hbecomesmoreecientthanly,because thehtransition(3!2)doesnotinvolvethegroundleveland,hence,isnotsomuch aectedbyopticalthickness.therefore,thereisinfactasmalldensity{interval, 210:5=n<H>forthechosenvelocity wherehisthemostecientcoolingprocess,alreadymoreimportantthanly areconstant,anincreaseofthebackgroundcontinuousradiationeldalwaysimpliesreducednet changeoftheconcentrationsofthecollisionpartners.iftheconcentrationofthecollisionpartners andstillmoreimportantthanbound{freetransitions(aroundn<h>=1010cm 3in coolingratesandnallycausesnetradiativeheating. 13Thisisdierentfromallcoolingratesdiscussedsofar,sincewehavenotyetconsidereda
71 3.2.BOUND{FREETRANSITIONS 51 Figure3.9:DetailsforthecaseTg=8000KandJ=0.Upperpanel:relativecontributionsofthedierentbound{boundandbound{freetransitions. Fig.3.9).Lyisalsoalwaysopticallythick(similartoLy)andhencealwaysmuch Lowerpanel:b{factorsforthehydrogenlevels. lessimportantthanh. ThelowerpanelofFig.3.9showsthegradualchangefromalmostLTE{ionization andlte{population(bn1)atlargedensitiestopronouncednon{lteconditionsat stateispopulatedhyper{thermally,whichisanimportantresultforthecsesofcool (providedthattrad<tgforaplanckeldj=b(trad)).consequently,theground bii{factorindicatesthatthedegreeofionizationofhydrogenisalwayssub{thermal smalldensities,causedbythedecreasingrelevanceofthecollisionalprocesses.the stars,sinceitkeepsthegaspredominantlyneutralalsoatfairlyhightemperatures Thepopulationsoftheexcitedhydrogenlevelsarecompletelydecoupledatsmall andlowdensities,wherehydrogenwouldbestronglyionizedaccordingtolte. thestronglydecreasingescapeprobabilitiesofthelinesphotons.ltepopulation densitiesandarethermallycoupledtothegroundstateforlargedensities,causedby ionization,however,extremelylargedensitiesarerequired(e.g.n<h>>1016cm 3 fortg=10000k),wherethethree{body{recombinationratesbecomerelevant. tothehigherexcitedlevels,nallyalsofortheionizedstate.forcompletelte{ isestablishedindirectionofincreasinggasdensitiessuccessivelyfromthelower
72 52 ThesituationinthecaseJ=B(3000K)isquitedierent.Here,thenetbound{free CHAPTER3.RADIATIVEHEATINGANDCOOLING coolingratesdominateovernetbound{boundcoolingratesunlessthegasdensityis smallerthan107cm 3forallconsideredtemperatures.Negativeandpositivenet contributionsfromthedierenttransitionsmayoccuratthesametime,although eective,whereasatsmalldensitieslydominates. thesumofallcontributionsalwaysresultsinanetcooling. Tosummarize,hydrogenismainlyanimportanthigh{temperaturecoolant,approximatelycontributingasQ/2.ForlargedensitiestheLyman{continuumismost 3.2.3OtherNeutralAtoms Concerningotheratomsthanhydrogen,solelytheelectronicgroundstatesofthe neutralatomsareconsideredinthisworkforpracticalreasons.furthermore,since recombinationratesandthebound{freeheating/coolingfunctions.theapproxiproximatemethodoutlinedonp.46canbeusedforthecalculationofthephoto{ allbound{freetransitionsfromthegroundstatesarelocatedintheuv,theap- theapplicationoftheapproximatemethodisratheraccurateandverypractical, sationcrosssectionsofthevariousmetalatomsfromschmutzler(1987).therefore, ableagreementwiththosecalculatedfromeq.(3.61),whenapplyingthephotoioni- matephoto{recombinationratesderivedfromeq.(3.65)arefoundtoshowreason- Theratesofcollisionalionizationaredeterminedfromtheanalyticalexpression givenbyallen(1973) sinceitavoidsthetime{consumingnumericalfrequencyintegrations. whereo1isthenumberofopticalelectronsoftheneutralatom.table3.3summarizes 1(Tg)=1:1( 8)o1qTg1=eV 2exp ktg!; 1 (3.73) thedatausedforthedeterminationofthethebound{freeheating/coolingrates. bound{freetransitionsareoncemoresummarized.themethodsareusedforthe andthecalculationofthebound{freeheatingandcoolingrates: determinationoftheelectronconcentration,theconcentrationsofthevariousions Attheendofthissection,theimportantfeaturesofthedevelopedmethodsforthe Ionizationequilibrium(steadystatenon{LTE)isassumedtodeterminethe photoionisationand{recombination,collisionalionizationandthree{body{ particledensitiesoftheconsideredatoms,ionsandelectrons.theratesof Acoupleofsimplifyingassumptionsareusedforotheratomsthanhydrogen. Hydrogenistreatedmoreaccurately,includingofthersttwoexcitedlevels. recombinationaretakenintoaccountforeachatom. Bound-freeopticaldepthseectsareignored.
73 3.3.PHOTODISSOCIATIONANDRADIATIVEASSOCIATION Table3.3:Bound{freeheatingandcooling:consideredspeciesandatomicdata53 Species1[eV](1)g(1) He Z(1;3) II 2.06(-10)-0.67 a(2) 1 b(2) 1 o(4) 1 NC (-10) (-10)-0.62 Mg OS (-10) (-10) Si (-10) (-10) (1):Allen(1973). Na Fe (-10) (-10)-0.69 (2):Beck(1993)andreferencestherein. 2 (3):Forsimplicity,thepartitionfunctionZIIisapproximatedbythe 1 (4):Thenumberof\optical"electronsisthenumberofelectronsin thelastoccupiedquantumstate statisticalweightofthegroundstateoftheionizedatom. densitiescanbereproduced. changefromalmostlteionizationatlargedensitiestonon{lteionizationatsmall Inconclusion,theoutlinedmethodsareapproximate,butsimpleandapplicableto thewiderangeofdensityconditionspresentincircumstellarenvelopes.thegradual 3.3 Radiativegainsandlossesofthegascanalsobecausedbychemicalreactions. Accordingtothedenitionoftheinternalenergyinthiswork(cf.Fig.2.1),solely PhotodissociationandRadiativeAssociation (photodissociationorradiativeassociation)contributetotheradiativeheatingor thosereactionswhichareaccompaniedbyanabsorptionoremissionofaphoton from3to8ev(exceptionsco:11.1evandn2:9.9ev),whichalreadygivesa cooling,respectively14. Thedissociationpotentialsofthemoleculesofastrophysicalinteresttypicallyrange about10ev,thedissociationenergiesaresubstantiallysmaller.thus,asfarashard rstimpressionoftheconcernedwavelengthregionoftheradiativeprocessesunderinvestigation.comparedtotypicalmolecularionizationpotentialsofmorethan energiesandmightbeconsideredasadditionalsourcetermsforthesepools,butdonotdirectly heating/coolingofthegaseveniftheyare\exothermic"or\endothermic".suchreactionsonly convertdissociationpotentialenergiesintotranslational,ro{vibrationalandelectronicexcitation 14Puregasphasereactions,whichdonotinvolvephotons,donotcontributetotheradiative aectthetotalinternalenergyofthegas.
74 54 UVradiationisabsent,photodissociationisexpectedtobemoreecientforthe CHAPTER3.RADIATIVEHEATINGANDCOOLING heatingofthegasthanphotoionisationinthemoleculardomainofcircumstellarenvelopes,evenifthecorrespondingphotocrosssectionsaresmaller.inthefollowing, aphoto{chemicalreactionofprototype isconsidered,whereaandblabelanatom,ion,moleculeorelectronandabthe AB+hkf *)kra+b (3.74) mostlyinitiatedbyabsorptioninelectronicbands(e.g.thelyman{andwerner{ andreversereaction,respectively.irrespectiveofthefactthatphotodissociationis correspondingcompositespecies.kfandkraretheratecoecientsoftheforward bandsofh2),whichareinprinciplenarrow{spacedbound{boundtransitions,the photodissociationcrosssectionsf()areassumedtobegiveninaquasi{continuous FromthedetailedbalanceconsiderationnABkfJ=B=nAnBkritisfound way kf=4zj hf()d: (3.75) kr(t)=nab nanbt4zb(t) hf()datexp Ea witheabeingtheactivationenergy.comingbacktotherstpart,nxistheparticle ThesecondpartofEq.(3.76)istheusualArrheniuslawforthebackwardreaction kt: bedeterminedbymeansofthelawofmassactionfromthecorrespondingfree enthalpyofformationatstandardpressurep densityofspeciesxinchemicalequilibrium,i.e.therstfractionineq.(3.76)can fg (T)=fG AB(T) fg A(T) fg B(T)<0 nanbt=kt nab p exp fg (T) kt (3.78) (3.77) Thecontributionofthephotochemicalreaction(3.74)tothetotalnetheatingfunctionofthegasisgivenby nxaretheactualparticledensities,whichinthiscontexthavetobedeterminedfrom Qchem rad=4z0@nabj nanbnab nanbtgb(tg)1af()d: (3.79) implythattheinvolvedmoleculehasbetoabundant). thosereactions,whichhavethelargestnetphoto{rates(thisdoesnotnecessarily thesteady{statesolutionofachemicalreactionnetwork.especiallyinterestingare dierentspeciestobeconsideredandthepooravailabilityofappropriatemolecular Thegeneralproblemofthetreatmentoftheseprocessesisthelargeamountof
75 3.3.PHOTODISSOCIATIONANDRADIATIVEASSOCIATION dataf()15.therefore,thesofaroutlinedequationsdonotlookverypromising, 55 approximatemethodforthebound{freetransitionsdiscussedinthelastsection.we assumethecontinuousradiationeldtotlikejwb(trad)andconsiderthe Thisproblemcanbeavoidedbythefollowingconsideration,analogouslytothe sincetheycansolelybeappliedtoaveryfew,well{knownmolecules(e.g.h2,co). casemaxfktg;ktradgd0ab<h,applyingwien'slawasbefore.bydierentiating Eq.(3.76)withrespectto1=kT,thefollowingexpressioncanbederived: hhiabs= fg (Trad)+Ea+( 1)kTrad Qchem rad=nabwkr(trad)nanb nabtrad hhiabs nanbkr(tg)hhiem hhiem= fg (Tg)+Ea+( 1)kTg (3.82) (3.81) (3.80) havetobeknown.theconsiderationsndthemeanabsorbedandemittedphoton sinceonlythegibbsenergiesfg andthearrheniuscoecientsa,andea photo{reactioncaneasilybeappliedtotheresultsofchemicalreactionnetworks, ComparedtoEq.(3.79),thisexpressionforthenetheatingrateofaconsidered energiestobeoforder fg +Ea ktd0ab+ea,i.e.themoleculedissociation energyplustheactivationenergyoftheradiativeassociationreaction.thenet associationforthethermalbalanceofthegasincses,the(steadystate)resultsof chemicalreactionnetworkcalculationsarerequiredprovidingthevariousconcentrationsofthespeciesunderexamination.suchinvestigationsgobeyondthescopeof thisworkandmustbelefttofutureinvestigations.however,animportantexample heatingratevanishesinthecaseofthermodynamicequilibrium,asexpected. Foracomprehensivediscussionoftheimportanceofphotodissociationandradiative isconsideredinthefollowingsection TheH Heating/CoolingRate ThenegativehydrogenionH showsexceptionallylargephoto{ratesincircumstellar atmospheresofwarmstarsasthesun.therefore,itisimportanttoconsiderthe envelopes(beck1993).itsbound{freeandfree{freetransitionsarefurthermore TheconcentrationofH incircumstellarenvelopesismostlycontrolledbythefollowingtworeactions(becketal:1992): H +h H +H kf;2 kf;1 *)kr;2 *)kr;1 H2+e : H+e (3.83) radiativeheatingandcoolingbyh inmoredetails. well{knowntobethemostsignicantcontributortothegasopacityinthestellar minestheratesandtheheating/coolingfunction diculttomeasureinlaboratoryexperiments. 15ConsideringthefrequencyintegrationinEq.(3.79),thesoftendoff()almostentirelydeter- (3.84)
76 56 Thus,theconcentrationofH insteadystate(\kineticequilibrium")isalways CHAPTER3.RADIATIVEHEATINGANDCOOLING proportionaltotheelectronconcentration: Reaction3.83(\H bound{free")istheprocesstobeconsideredfortheradiative nh =nenhkr;1+nh2kr;2 heatingandcoolingofthegas.theaboveoutlinedmethodsarestraightforwardly kf;1+nhkf;2 (3.85) ation.thereactionratecoecientskf;1andkr;1arecalculatedbymeansofthe \exact"eqs.(3.75)and(3.76),wherealabelsthehatom,btheelectronandab andradiativerecombinationratherthanasphotodissociationandradiativeassoci- applied,althoughthebound{freetransitionsofh areclassiedasphotoionisation thenegativeionh.thebound{freeabsorptioncrosssectionofh isinterpolated fromtablesgivenbywishart(1979).stimulatedrecombinationsaretreatedinlte, forsimplicity.theratecoecientsofthesecondreaction(3.84)aretakenas kf;2=1:35( 9)cm3s 1(Schmetekopfetal:1967) kr;2=nh nh nh2nekf;2: (3.87) (3.86) ionizationandphotoionisationofmetalatomswithlowionizationpotentials(na, ThenH densityiscalculatedafterwardsfromeq.(3.85)16.accordingly,collisional ne,nhandnh2aredeterminedbymeansofthemethodsoutlinedinchapter4. Consideringagasofsolarelementalabundances,therequiredparticledensities Mg,Fe,...)areimportantlow{temperatureelectrondonatorsandprovideelectron concentrationsofatleast10 5forTg>5000K,leadingtoconsiderableH particle andthefree-freeheating/coolingrateisdeterminedby18 densities17. TheradiativeheatingandcoolingbyH comprisesbound{freeandfree-freecontributions.thebound{freeheating/coolingrateiscalculatedaccordingtoeq.(3.79), Qrad(H )=Qbf Qrad(H )=4nHneZJ B(Tg)()d; rad(h )+Qrad(H ) (3.88) Stilley&Callaway(1970): wherethefree{freecrosssection()isttedonthedipolelengthcalculationsof (3.89) ()= 1:3727( 25) +4:3748( 10) 2:5993( 7)=Tg 2!1 exp( h 17Incontrast,theconsiderationofapurehydrogenplasmaleadstoasystematicunderestimation 16Thisisanapproximateprocedure,sinceitneglectsthefeedbackontheformerparticledensities. ktg)cm5 oftheh concentrationandheating/coolingrates:theresultingelectronconcentrationsare solelyrefertothethermalmotionofthegas. smallerinthiscase,especiallyaroundtg6000k,justwheretheheatingandcoolingofh turns outtobemostsignicant. 18Kirchho'slaw=B(Tg)isapplicabletofree{freetransitionsalsoinnon{LTE,sincethey
77 3.3.PHOTODISSOCIATIONANDRADIATIVEASSOCIATION 57 dashedlines,rightaxis)ofh inthecasewithoutcontinuousradiationeld. free{freecoolingrate(shortdashedlines,leftaxis)andtheconcentration(long Figure3.10:Thetotal(bound{free+free{free)coolingrate(fulllines),the Figure3.11:SameasFig.3.10,butwithunderlyingcontinuousradiationeld.
78 58 Figures3.10and3.11depicttheresultsforthetwocasesJ=0andJ=B(3000K). CHAPTER3.RADIATIVEHEATINGANDCOOLING foradensemedium,e.g.instellaratmospheres.thestep{likebehavioroftheh leastq/2.therefore,theradiativeheatingandcoolingofh isonlyimportant Inbothcases,theradiativecoolingrateofH scalesasq/nhne,whichimpliesat concentrationandtotalcoolingratesfortg=10000kandtg=8000kinfig.3.10 inthegures),hydrogenismostlylockedinh2,andtheconcentrationandthe metalswithlowionizationpotentials.forevenlowergastemperatures(notshown whereasforlowergastemperaturestheelectronconcentrationiscontrolledbythe correspondtothestep{likedegreeofionizationofhydrogen(cf.figs.3.7and3.8), heating/coolingratesofh rapidlyvanish. considerablysmallerduetothelargephotoionisationrateskf;1.however,sincethe radiativecoolingratesofh arerelatedtonhneandnottonh,thecoolingrates ThecalculatedH concentrationsforthecasej=b(3000k)(cf.fig.3.11)are elds(notshown),thebound{freetransitionseectivelydestroythenegativeion, belessimportantthanbound{freeheating/cooling.forevenmoreintenseradiation dierentelectronconcentrations.free{freeheating/coolingofh isalwaysfoundto remainsimilar.thedierencesbetweenfigs.3.10and3.11aremainlycausedbythe chemistry(atlargedensities)quicklyrestorestheh ions. temperatures,wheretheproductofelectronandatomichydrogendensityislarge. Inconclusion,H ismainlyanimportantcoolantforlargedensitiesandmedium sothatradiativeheatingbyh israrelyfoundtobesignicant only,ifanactive 3.4 Ifthegasisalmostfullyionizedandthedensityislarge(n<H>>1011cm 3),freefreeemission(Bremsstrahlung)becomesaneectivecoolingprocess.Weusethe Free{FreeTransitions Allen(1973)andinclude,forconsistency,thereverseprocessoffree{freeabsorption bymeansoftherelation=b(tg) ordinaryexpressionforfree{freeemissionforapartiallysinglyionizedgasgivenin (Tg)=5:44( 39)n2e qtgexp h ktg Qrad=4Z(Tg) B(Tg) 1!d: J (3.91) (3.90) diativeheating,iftheincidentradiationeldmainlyconsistsofirphotons,where otherradiativeheatingprocessesbecomeimpossible.however,thegasmustbe quently,free{freetransitionsprincipallyprovideoneoflastingpossibilitiesforra- Free{freetransitionsalwaysconcernthewholeelectromagneticspectrum.Conse- considerablyionized(qrad/n2e)forsuchheating.
79 3.5.OVERVIEWOFTHECONSIDEREDRADIATIVEPROCESSES OverviewoftheConsideredRadiativeProcesses 59 providearstimpressionoftheirneteectandtheirimportancefortheheating cretion.theshownspectralpositionsofthevariousradiativeprocessesalready Figure3.5summarizestheradiativeheating/coolingfunctionsconsideredinthis andcoolingofthegas.ingeneral,radiativeheatingoccursinthecasej>b(tg) work.towhatextendthisselectioniscomplete,mustbelefttothereader'sdis- andcoolingintheoppositecase19.forthedepictedcaseofadilutedplanck{type thermalrelaxationofthegastowardsradiativeequilibrium,thegastemperature radiationeld,theradiativeprocessesatshortwavelengths(bound{freetransitions, (vibrationalandrotationaltransitions,spectrallines)forcooling.consideringthe willtuneinsuchaway,thatthesegainsandlossesbalanceeachother.notethat spectrallines)areresponsibleforradiativeheatingandthoseatlongwavelengths theformationofmoleculesinthegasintensiestheinteractionbetweenmatterand quentlyleadingtolowerradiativeequilibriumtemperatures(thiseectcaninfact causethermalbifurcationsinthegasasdiscussedinchapter6). radiationeldatlongwavelengths,thusreinforcingradiativecoolingandconse- moreplacedtogether: Aspartofthissummary,theimportantfeaturesofthedevelopedmethodsareonce Allconsideredradiativeprocessesaretreatedinnon{LTE.Thenon{LTEdescriptionofthemoleculesisrestrictedtoindividualvibrationalandrotational Allcorrespondingreverseprocessesaretakenintoaccount,relyingondetailed state. excitationtemperatures.theheating/coolingratesarecalculatedinsteady{ atureandtheradiationeld.inthecasej=b(tg)(asinthermodynamic balanceconsiderations.consequently,eachconsideredpairofforwardand equilibrium),alldiscussednetheating/coolingratesvanish(qrad=0). caseactuallyoccursdependsuponaspecicrelationbetweenthegastemper- reverseprocesscanappearasbothnetradiativeheatingandcooling.which Theheating/coolingratesareformulatedforarbitraryradiationeldsJ.EspeciallysimpleexpressionsarederivedfordilutedPlanckeldsoftypeJ= Opticaldepthseectsareincludedforallbound{boundtypetransitionsand neglectedotherwise. WB(Trad)20. sourcefunctions(consideringe.g.atwo{level{atom)generallysatisfyj><s><b(tg). asfarastheconsideredheating/coolingprocessesmerelyrefertosuchregion. 19Theserelationsarenotexact,butusuallycorrectalsoinnon{LTE,sincethecorresponding 20ThetparametersWandTradcanbedierentfordierentspectralregions(e.g.UVandIR),
80 60 CHAPTER3.RADIATIVEHEATINGANDCOOLING H2ro{vib.quadrupole:ca.1 25m Balmercontinuum: Paschencontinuum: H bound{free: <0:365m free{freetransitions: allwavelengths <0:821m <1:65m Figure3.12:Overviewoftheconsideredheatingandcoolingprocesses.Thefull lineshowsanassumedcontinuousmeanintensityjaccordingtoeq.(1.6)with diativecoolingatlongwavelengths,respectively.thelowerpanelindicatesthe betweenmatterandradiationeld,favoringradiativeheatingatshortandra- W=0:029(r=3Rforpureradialdilution)andTrad=3000K.Thedashedline wavelengthregionsoftheconsideredheating/coolingprocesses. istheplanckfunctionfortg=1500k.thearrowsindicatetheenergyexchange
81 3.6.FURTHERHEATINGANDCOOLINGPROCESSES FurtherHeatingandCoolingProcesses 61 Thetheoreticalpartofthisworkceaseswithsomeremarksonthoseheatingand Ofcourse,theproperinclusionofallradiativeprocessesisprincipallydesirable.The constructionofsuchanutmost\complete"set,however,isalonglastingprocess andcannotbecarriedoutbyonesinglework.theselectionofheating/cooling coolingprocesseswhichhavenotbeentakenintoaccount. numberofprocesses(morespecies,morelines,etc.)ofthealreadyconsideredtypes ofprocesses,andsecond,totakeintoaccountfurthertypesofprocesses. Apurequantitativeextensionwillprobablynotleadtosubstantialchangescomparedtotheforthcomingresultsofthiswork,sincethemostpromisingcandidatesof eachconsideredtypeofprocessarealreadyincluded.whatmaybecrucial,however, aretheadditionaltypesofprocessesnotconsideredsofar,whichmightproveto functionsofthisworkmaybeextendedintwoways:first,toincludealarger theseobstaclesshallbexedinthissection. them,moreorlessserious,specicobstaclesoccurredwhichpreventasimplequantitativediscussionforthetimebeing.togetherwithsomevaluationsandremarks, beimportantundercertaincircumstances.astheauthorstartedtostudyafewof Table3.4listssomeinterestingcandidatesofdierenttypesofprocesses,theexpectedspectralregionofabsorbed/emittedphotons,theexpectedeectforthegasments,however,arenecessaryconcerningtheenergygainsandlossescausedbythe givenforreasonsofcompletenessandtoopenthediscussion.someadditionalcom- andsomecomments.extensiveexplanationsarenotincluded,astable3.4ismainly thefacedobstaclesforthedeterminationofthecorrespondingheating/coolingrates (e.g.fleischeretal:1992)andcannotbedeterminedbyanysteady{stateconsiderations.therefore,theheatingandcoolingprocessescausedbythepresenceofdusponent(hereespeciallythetotaldustsurface)shouldbetreatedtime{dependently Duetothelargetimescalesinvolvedinthedustformationprocess,thedustcom- presenceofdustgrains: Consequently,energytransferratesdirectlyoccurbycollisions.Thecorrespondingratescaneasilybeaddedtothetotalnetradiativeheatingrateofthegas,if Dustgrainsprovideasimilarexternalpoolastheradiationeld(seeFig.2.1). arenotexplicitlyincludedinthiswork. perature,driftvelocities,etc.)areavailable.theratesforthermalaccommoda- tion(energytransferviainelasticgas{dustcollisions)aregiven,forexample,in theappropriateinformationsaboutthedustcomponent(totalsurface,dusttemsionswithmovingdustgrainscausedbyradiationpressure)ingoldreich&scoville (1976)orinKrugeretal:(1994). Morediculttodeterminearetheheating/coolingratescausedbysurfacechemical Burke&Hollenbach(1983)andthosefordriftheating(energytransferviagascolli- reactions,whichprincipallyexchangealltypesofgasinternalenergies(especially dissociationandionizationpotentials)withthedustcomponent.verydetailed knowledgeaboutthesereactionsisrequired.
82 62 Table3.4:Overviewoffurtherheatingandcoolingprocessesnotexplicitlyconsideredin CHAPTER3.RADIATIVEHEATINGANDCOOLING processthiswork. spectral photodissociation severalev numberoftrans., (),concurring region (estimated) importantforwhat? obstacles comments electronic reactionchannelsand (2) molecules trans.of severalev rad.heatingin moleculardomain, maybeimportant counterbalanceforrot. andvib.cooling numberoftrans.,rad. lifetimes,coll.rates, lineoverlaps probablystrong non{lteeects: vib.trans. andsmallcoll.rates shortrad.lifetimes of (typically0:01 1s) polyatomic molecules 3 20m heatingandcoolingselectionrules,rad. lifetimes(analytical expressions),coll. rates unpolarpolyatomic vib. moleculesmaybecome overtone polarduring trans. 1 5m heatingandcoolingrad.lifetimes (analytical expressions) A{coes.aboutone magnitudesmaller thanforgroundtone vibration,(1) rot.trans. ofnon{linear molecules GHz lifetimes(analytical expressions) selectionrules,rad. trans. bf.trans. fromexcited (1) states severalev heatingandcooling, indirect (de{)excitationof boundlevels atoms (),completemodel trans.of bf.and. (2) negative ions, molecules several0.1ev heatingandcooling(),concurring reactionchannelsand rates (2) chemical reactions gasphase depends electronicandvib. levelsofreaction products,probably followedbyemission, indirectexcitationofreactionrates, i.e.cooling reactants reactionheats,energy distributionamong thevariousdegreesof freedomonthe dicult,cooling approximately proceedsonchemical bf.=bound{free,.=free{free,rad.=radiative,rot.=rotational,vib.=vibrational,a{ timescale coes.=einsteincoecientsforspontaneousemission(inverseoftheradiativelifetimes),coll. rates=collisionalde-excitationratecoecients,trans.=transitions,()=corresponding photocrosssections. (2)=seethesimple,approximatemethodsproposedinthiswork (1)=polyatomicmolecules(exceptforH2O)aregenerallylessabundantthandiatomic molecules(e.g.co)incses
83 3.6.FURTHERHEATINGANDCOOLINGPROCESSES Table3.4continuedfrompage62 63 process spectral region (estimated) importantforwhat? obstacles comments Raman scattering UVand optical moleculargasesby rad.heatingof inelasticscattering absolutecrosssections (Stokesand Anti-stokes)of individualmolecules, e.g.ofh2 forramanscatteringtoarbitrary wavelengths,however, crosssectionsare unpolarmoleculesand appliestopolarand dust: thermal accommodation dust:drift heatingandcooling accordingto small heating { temperaturedierence betweengasanddust ecientmechanism, dust:surface seekrugeretal:(1994) reactions { energies(heatingand dissociationpotential gainorlossof excitedreactants cooling),desorptionofreactionrates, (heating) reactionproducts reactionheats,energy distributionamong thevariousdegreesof freedomofthe dicult
84 64
85 Chapter4 TheCalculationoftheEquationofState physicsandthethermodynamicdescriptionofthegas.havingoncedetermined Thecalculationoftheequationofstateprovidesthebasiclinkbetweenthemicro- themicrophysicalquantities(theparticledensities)asfunctionofasuitableset goingbackintothedetailsofmicrophysics. modelingofthegascanbeperformedonahigher,thermodynamiclevelwithout propertiesofthegascanbedeterminedbymeansofstatisticalmethods.thus,the ofthermodynamicstatevariables(e.g.temperatureanddensity),allmacroscopic sidersasteadystate.consequently,twoadditionalexternalparametersenterinto and.aspointedoutinchapter2,thisworkdoesnotrelyonlte,butcon- ThischapterdescribestheassumptionsandthenumericaltechniquesusedtodeterminetheparticledensitiesandtheinternalenergyofthegasasfunctionofTg theusualthermodynamicdescription:theradiationeldjandthemeanvelocity gradientddv aresummarizedinthisseparatechapter. dle.sincethetechniquesarethesameforallfollowingapplications,they 4.1 Thebasisforthecalculationoftheparticleconcentrationsaretheelementabundances.Inthiswork,amixtureoftheelementsH,He,C,N,O,Na,Mg,Si,SandFe CalculationoftheParticleConcentrations isconsidered.sincedierenttypesofstarswithdierentabundancesareconsidered ions,electronsandmolecules: intheforthcomingapplications(c{stars,rcbstars),theassumedabundancesare statedseparately(cf.sect.5.1.2andsect.6.1.2).thefollowingbasicassumptions aremadeinordertocalculatethevariousparticledensitiesoftheneutralatoms, Neutralandsinglyionizedatomsaretakenintoconsideration.Theratiosbetweentheparticledensitiesofionsandneutralatomsarecalculatedbymeans (steadystatenon{lte),asdescribedinchapter3. toionization,-recombination,collisionalionizationand3-bodyrecombination ofthestatisticalequationseq.(3.1),takingintoaccounttheratesofpho- Forsimplicity,theratiosbetweentheparticledensitiesofmoleculesandneutralatomsarecalculatedaccordingtochemicalequilibrium1.Negativeions calculatingthesteadystatesolution(\kineticequilibrium")ofacompleteandreliablechemical 1Thisisofcourseasimplifyingassumption.Animprovementofthemodelmaybeachievedby 65
86 66 aretreatedlikemolecules(exceptforh,cf.sect.3.3.1).thechemistry CHAPTER4.THECALCULATIONOFTHEEQUATIONOFSTATE comprises130species(gail&sedlmayr1986),wheresomelargerpurecarbon moleculeshaveadditionallybeenincludedusingthethermo{chemicaldata {iterationtechniques,untiltheconservationofchargeandelementsisassured.the followingschemeisapplied,wherethequantities,tg,jandddv TheparticledensitiesarenallyfoundbymeansofnestedNewton{Raphsonand fromgoeres&sedlmayr(1992). 1. Estimatetheelectrondensityneandallneutralatomdensitiesinthe electronicgroundstatenel 0. dlearegiven: Performaninner{iterationforeachatomicspeciesinordertosolvethe coupledequationsforthelevelpopulationsandtheescapeprobabilities pendontg,jandne. Calculatethebound{freeandfree{boundratesRiIIandRIIi,whichde- 3a. (comparesect ),i.e.: 3b. Tg,J,theescapeprobabilitiesePe partners. DeterminethelevelpopulationsandtheionparticledensitiesnEl Calculatethebound{boundrateseRulandeRlu,whichdependon ulandthedensitiesofthecollision 3c. fromthestatisticalequations(3.1). populationsandthelocalvelocitygradientddv CalculatetheescapeprobabilitiesePe ulwhichdependonthelevel dle. II 3d. 4. calequilibriumaccordingtothetotalneutralatomdensitiesnel Calculatetheparticledensitiesofthemoleculesnmolbyassumingchemi- Gobacktostep3aunlesstheprocedurehasconverged. 5.Calculatethecurrenterrorsofchargeandelementconservation,i.e. gastemperaturetg. atandthe ~F(ne;nH0;:::;nFe 0)= 0 B@ PElElmEl nhat nhii PmolnmolsHmol H ne PElnEl II+Pmolnmolsemol 1CA 6.PerformoneNewton{Raphsoniterationstep,i.e.solveD~F~n=~Ffor PElElmEl nfe Fe at nfe. II PmolnmolsFe thecorrections~nandput~n!~n ~n,wherethecomponentsofthe mol 7.Gobacktostep2unlessallfurthercorrectionsbecomesmall= vector~nareshownastheargumentof~fintheupperequation. elementabundances,mostoftheimportantreactionchannelsprobablyinvolvetheabundantpure reactionratenetwork,which,however,goesbeyondthescopeofthiswork.concerningthercb j=e;h;:::;fefnj=njg< max carbonmolecules,whichareallradicalsandwhosereactionratesareonlypoorlyknown.
87 4.2.CALCULATIONOFTHEINTERNALENERGY Thesuccessfulconvergenceofthisiterationschemecriticallydependsonthequality 67 theelectrondensity)maydependontheescapeprobabilities,asdemonstratedfor areincluded.inthiscase,thedegreeofionizationofaconsideredatom(andhence {iteration(step3 3d)isnecessary,ifbound{freetransitionsfromexcitedlevels ofstep1,i.e.therstestimateoftheelectronandneutralatomdensities.theinner hydrogeninsect ifnosuchbound{freetransitionsareconsidered(asforall havingsolvedtheaboveiterationscheme.especiallyallexcitedstatesofionscan becalculatedafterwards,sinceonlytherstionizationstageistakenintoaccount. otherelementsthanhydrogeninthiswork),thesystemofequationsdecouplesand Thedescribedmethodyieldsallparticlesdensities,includingtheconsideredlevel thepopulationsofthemulti{levelatomswithoutcontinuumcanbedeterminedafter populations,asfunctionofthemassdensity,thegastemperaturetg,thecontinuousbackgroundradiationeldjandthevelocitygradientddv 4.2 CalculationoftheInternalEnergy dle. ingoncedeterminedtheparticledensitiesasoutlinedabove,theevaluationofthe internalenergyiscomparablesimpleandnotverytime{consuming. Fordynamicconsiderations,theproperdeterminationoftheinternalenergyisas Accordingtothedenitionoftheinternalenergyinthiswork(cf.Chapter2),the importantasthedeterminationoftheradiativeheatingandcoolingrates2.hav- electronic,vibrationalandrotationalexcitationenergies.thedierenttermsare internalenergycomprisesoftranslational,ionizationanddissociationpotentialand calculatedasfollows: Etrans=32nkTg Eion=XElnEl IIEl II+XElnEl IIIEl II+El III+::: (4.1) Ediss= XmolnmolD0mol (4.3) (4.2) Evib=XmolnmolXj Eel=Xi;jnijEij exph!mol gjh!mol jj (4.4) Erot=Xmolfmol 2nmolkTmol rot ktmol vib 1 : (4.6) (4.5) considere=fkt=(2)atthesametime.thedenitionsoftheinternalenergyandtheradiative heatingandcoolingratesrefertoeachother.forexample,theinternalenergyinthemolecular domainturnsouttobenegativeinthiswork. 2Warning:Oneshouldnottaketheradiativeheatingandcoolingratesoutofthisworkand
88 nisthetotalgasparticledensity(atoms+ions+electrons+molecules).ii=iii 68 CHAPTER4.THECALCULATIONOFTHEEQUATIONOFSTATE (measuredfromthevibrationalgroundstate),i.e.theenergyrequiredtototally dissociatethemoleculeintoitsconstitutingatomsat0k.bydenition,neutral forreasonsofcompleteness).d0molisthetotaldissociationpotentialofamolecule istheionizationpotentialoftherst/secondionizationstage(thelatteronlygiven atomshavezeropotentialenergies. nijistheparticledensityofspeciesiinthej-thexcitedelectronicstateandeij largerotationaltemperatures,whichissucientinthiscontext.frotisthenumber thecorrespondingenergydierencetoitselectronicgroundstate.!mol eigenfrequencyofamoleculeandgjthecorrespondingdegeneracy.equation(4.5) assumesindependent,harmonicoscillators.equation(4.6)istheclassicallimitfor j isthej-th ofrotationaldegreesoffreedom(2forlinearmolecules,3otherwise). Asfaraspossible,thevibrationalandrotationalexcitationtemperaturesTrotand Forthecalculationofthedissociationpotential,vibrationalandrotationalexcitation areassumedtoequalthegastemperature. Forthosemoleculeswhicharenotconsideredtherein,theexcitationtemperatures TvibarecalculatedbymeansofthemethodsoutlinedintheSects.3.1.3and mentabundances.additionaldatafortheionizationpotentialsel theselectedmoleculesandsummarizesthenecessarymoleculardata.theselection comprisesthemostabundantmoleculesinbothcases,c{starandrcbstarele- energies,onlytheabundantmoleculesmustbetakenintoaccount.table4.1lists electroniclevelsei;jcanbefoundinthetables3.1and3.3. theinternalenergyprovidethecaloricandthermalequationsofstateintheform Insummary,theoutlinedmethodsforthecalculationoftheparticledensitiesand IIandtheexcited p=p;tg;j;ddv e=e;tg;j;ddv dle=1(etrans+eion+ediss+eel+evib+erot) ne+xel(nel at+nel II)+Xmolnmol!kTg: (4.7) Asimilarexpressioncanbewrittenforthetotalradiativenetheatingrateofthe (4.8) densities,whichdependondensityandtemperature,theradiationeldandthe gas,whichiscalculatedaccordingtochapter3asfunctionofthevariousparticle velocitygradient Equations(4.7)to(4.9)denethethermodynamicsystemwhichisexaminedinthefollowingpartsofthiswork. dle: (4.9) Qrad=Qrad;Tg;J;Ddv independentstatevariablesissucienttodeterminethethermodynamicstateand TogetherwiththetwoexternalparametersJandDdv butotherusefulchoicescanbee.g.(p;),(p;tg)or(p;h),dependingontheproblem. henceallgasproperties.equations(4.7)to(4.9)areformulatedintermsof(;tg), dle,anysuitablesetoftwo
89 4.2.CALCULATIONOFTHEINTERNALENERGY 69 moleculed0mol[ev](1)!mol[1/cm]and(degeneracy)(2) Table4.1:Moleculardataforthedeterminationoftheinternalenergy. CO H (1) (1) frot C2H2 CH (1) (1),640.0(2),3220.0(1) CH (1),1973.8(1),3281.9(1),611.6(2),729.3(2) (1),1534.0(2),3018.7(3),1306.0(3) C (1) C (1),63.1(2),2040.0(1) C (1) 350.0(1),450.0(1),1088.0(1),1103.0(1),1431.0(1), (1),2344.0(1) 112.0(2),222.0(2),648.0(2),863.0(1),1632.0(1), 3 C (2),1206.0(1),1745.0(1),2132.0(1), 73.0(2),157.0(2),240.0(2),598.0(2),631.0(1), C (1),2376.0(1) 184.0(2),253.0(2),419.0(1),497.0(2),555.0(2), 2 N (2),1522.0(2),1971.0(2),2013.0(2) 568.0(2),577.0(1),661.0(1),690.0(2),946.0(1), (1) 3 C2N2 CN (1) (1),324.0(2),1050.8(1) HCN (1),846.0(1),2158.0(1),503.0(2),234.0(2) SiC (1),713.5(2),3311.5(1) Si2C (1),837.0(1),186.0(1) SiO (1),275.0(2),1600.0(1) 983.0(1) 3 SiS (1) 744.5(1) (1):ThetotaldissociationpotentialenergycanbedeterminedfromtheJANAFtables CS (1) (Chaseetal:1985)accordingtoD0mol=fH0(mol) PElsEl molfh0(el)at0k. 2 (2):ValuesfordiatomicmoleculesaretakenfromHuber&Herzberg(1979)accordingto ForthelargercarbonmoleculesC7andC10,thedissociationpotentialsaretaken fromabinitioquantummechanicalcalculations(\scaledbindingenergies"from!=!e 2!exe.ValuesforpolyatomicmoleculesfromChaseetal:(1985).Values Raghavachari&Binkley1987). therelationfvib=3n 5=3N 6forlinearandnon{linearmolecules,respectively. forc4,c5,c7andc10fromraghavachari&binkley(1987).thereadermayverify
90 Inpractice,suchdependenciesarecodedbynumericalinversion.Onecomputer 70 CHAPTER4.THECALCULATIONOFTHEEQUATIONOFSTATE valuesforandtgwhichyield(p;h)bynewton{raphsoniteration. above,yieldingthevaluesofallstatevariablesasfunctionof(;tg).ife.g.a formulationin(p;h)isneeded,anothercomputerroutinendsthecorresponding routinecarriesoutthedeterminationofthermodynamicstateofthegasasstated
91 Chapter5 ThermalBifurcationsinthe Asarstapplicationofthethermodynamicdescriptiondevelopedinthiswork,the CircumstellarEnvelopesofRCBStars topologyoftheradiativeequilibriumsolutionsisinvestigated. Radiativeequilibrium(RE)isdenedastheequalityofradiativegainsandlosses. anylong{termphysicallyrealizedsolutionmustbethermallystable,thecondition criterionforthethermalstabilityofgasesunderastrophysicalconditions1.since ductionandheatingbymagneto-acousticwavesorcosmicrays),reisthemain Supposingthatotherheatingandcoolingprocessesarenegligible(asheatcon- ofreprovidesthebasicequationforthedeterminationofthegastemperaturein thecaseofstaticconditions. However,asshowninthischapter,theconditionofREmaynotbeunique,but Muchmore1986),inlatetypestars(Kneer1983)andintheinterstellarmedium occurintheoutersolaratmosphere(ayres1981;muchmore&ulmschneider1985; canhavetwoormorestabletemperaturesolutions.thesemultiplesolutionsare (e.g.biermannetal:1972). commonlycalled\thermalbifurcations".thermalbifurcationsarewell{knownto mightberelatedtotheformationofdustintheseenvelopes,whichcausesthespectacularrcb{typedeclineevents(cf.sect.1.3andappendixa)tionofwhetherornotlow{temperaturesolutionsalreadyexistatsmallradialdis- ThischapterinvestigatesthecircumstellarenvelopesofRCBstars.Here,thequestancestothestarisofspecialscienticinterest.Theoccurrenceofsuchsolutions Themainintentionofthischapteristodemonstratethatthermalbifurcations,in Thetemperaturesofthesephasescaneasilydierbyseveralthousandsofdegrees. principle,canleadtodierent,coexistingphasesofthegasinpressureequilibrium. ThephenomenonofthermalbifurcationsisexpectedtooccurfrequentlyinallpartiallymoleculargasespressionalongaRE{trajectory,dp 1Asecondarycriterionforthermalstabilityisthatthegasmustoerresistanceagainstcom- dre>0.otherwise,thegasisunstableagainstcollapsing 71
92 72 TheModel CHAPTER5.THERMALBIFURCATIONSINRCBSTARS 5.1.1DenitionoftheRadiativeEquilibriumGasTemperature valuesofthegaspressurep,theradiationeldjandthemeanlocalvelocity eachotheraredetermined.theregastemperaturestre gradientddv Inthefollowingthegastemperatureswhereradiativeheatingandcoolingbalance dleaccordingto garecalculatedforgiven Equation(5.1)isanimplicitdenitionoftheREgastemperature,whichmayof Q radp;tre g;j;ddv coursebenon{unique.forstabilityonehastorequirethatthederivativeofqrad dle=0: evenmoreradiationandwillheatupfurther. g (<0, Thebifurcationpoints,wheresolutionsappearordisappear,satisfyEq.(5.1)and >0,unstableRE (5.2) havezerorstderivatives.theyonlyexistforcertainvaluesoftheotherparameters, e.g.forspecialradiationelds. TheelementabundancesoftheprototypestarRCoronaeBorealisareconsidered, 5.1.2ElementAbundances adoptingthevaluesfromcottrell&lambert(1982)2.rcbsarechemicallypeculiarstars,showingstronghydrogendeciencyandconsiderablecarbonenrichment (cf.appendixa).mgandneareassumedtohavethesolarabundancesgivenby workforallmodelswithregardtorcbstars. Allen(1973).Figure5.1summarizesthechoiceoftheelementabundancesinthis 2OtherRCBstarsshowconsiderable,individualdeviationsfromtheseabundances,especially Figure5.1:AssumedelementabundancesofRCoronaeBorealis forh:heandc:n:o(lambert&rao1994). 6 Na H S Si Al Fe Mg Ne 5 4 N 3 O C 2 1 He 0 log ε
93 5.2.RESULTS 5.1.3ApproximationoftheRadiationField 73 eldisused.theradiationeldisttedbyaradiallydilutedblackbodyeldof determinationoftheparticledensitiesandthecalculationoftheradiativeheating andcoolingrates.inthischapter,atwo{parameterapproximationoftheradiation Theradiationeldisanimportantingredientforthemodel,enteringintoboththe theeectivetemperatureteofthecentralstar estareneglected,i.e.thecseisassumedtobeopticallythin.teissettobe Absorptionbetweentheouteredgeofthephotosphereandthelocationofinter- J(r)=121 q1 R2=r2B(Te): (5.3) approximationreasonablytsthestellarspectrumintheopticalandirregionwith 7000K,whichisarepresentativevalueforthisclassofstars(cf.AppendixA).The amaximumdeviationofafactor1:5,butleadstosomewhattoohighintensities continuousuv{emissionsfromshockedgaslayersinthecircumstellarenvelopeand bethedominantsourceforradiationatallwavelengths chromosphericemissions, depthsinthestellaratmosphere.furthermore,thestellarphotosphereisassumedto for<300nm(asplundetal:1997),whichisaconsequenceofthelargeuvoptical regions,respectively,ascomparedtoeq.(5.3). nored.sucheectswouldenhancethemeanintensitiesintheuvandirspectral alsoir{emissionsfromextendedcircumstellardust{shells(cf.appendixa)areig- ofthercbapplicationsarestatedrst.inthefollowing,thetypicalfeaturesforthe 5.2 BeforestudyingthestructureoftheRE{solutions,someofthemicrophysicalresults Results ionizationandthechemistryofthegasaresummarizedandtheroleofthevarious heating/coolingprocessesisdiscussed.regardingtheabundances(cf.fig.5.1),the resultscandieralotfromthoseofahydrogen{richgaswithnearlysolarabundances asencounteredintheinterstellarmediumorforexampleintheatmospheresof AGB{stars DegreeofIonization Fractionalionizationusuallyturnsouttobelarge,irrespectiveofthegastemperature.Thisisaconsequenceofthelargeratesofphotoionizationaccordingtothe 30000K,wheretheratesofcollisionalionizationcomeintoplay.Consequently, thedegreeofionizationequalsalmost1fortg>30000kandisapproximatelygiven menthelium,however,ismostlyneutralunlessthegastemperatureislargerthan assumedradiationeldwithitsstronguvintensities.themostabundantele- carbonismainlypresentintheformofmoleculesandtheelectronsareprovidedby bythec/he{ratioatlowergastemperatures.atverylowtemperaturestg<1200k,
94 74 otherelements,mainlysiandmg.accordingtothesomewhatpoortoftheuv CHAPTER5.THERMALBIFURCATIONSINRCBSTARS partofthestellarspectrum,theseresultsarestillpreliminary3. Thecharacteroftheresultschangesforverylargedensities(n<He>>1014cm 3 tionrates.consequently,thedegreeofionizationsmoothlyreachestheresultsof eciencyofthevariouscollisionalprocesses,especiallythethree{bodyrecombinamosphericlayersofthestar,thestateofthegasisclosetolteduetothelarge or>10 9gcm 3orp>100dyncm 2).Forsuchdensities,aspresentintheat- Saha{ionizationwithincreasingdensities Chemistry Moleculesbecomeabundantinthegasphaseapproximatelybelowadividinglinein thegastemperature/density{planereachingfromtg4000katn<he>=1014cm 3 moleculestooccurarecoandn2. totg1500katn<he>=105cm 3.Withdecreasingtemperature,therst Elementsmostabundantmolecules(2) purecc2,c3,c4,c5,c7, Table5.1:AbundantmoleculesinthecircumstellarenvelopesofRCBstars(1) abundantmolecules(3) C/N O C10(monocyclicring),... N2,CN,C2N,C2N2 CO NCN,C4N2 NO,O2,CO2,C2O Si/S Mg H SiC2,Si2C,SiC,SiO,SiS,CS C2H,HCN,H2,C2H2 SiN,Si2,Si3,Si2N,SO,SN,S2 CH,OH,HN,HS,SiH,CH4,C2H4 (1):resultingfromequilibriumchemistrybasedontheelementabundancesgivenin Fe (atomic) MgO,MgN,MgS,MgH Fig.5.1fortherangen<He>=106:::1012cm 3andTg=800:::5000K FeO (3):moleculeswithmax (2):moleculeswithnmol=n<C>>10 6somewhereinthe(n<He>;Tg){plane Table5.1reviewsthemoreabundantmoleculesforthehydrogen{decientand moleculeiscomposedof. Elfnmol=n<El>g>10 10,whereElincludesallelementsthe carbon{richelementcompositionconsideredhere.thechemistryisdividedintothe followingsubgroups.themostabundantgroupcontainsthepurecarbonmolecules chemistry.oxygenismostlyblockedbytheformationofcoandconsequentlyall SeeGoeres&Sedlmayr(1992)formoredetailedinformationconcerningthecarbon gastemperaturetheconcentrationsofthemorecomplexcarbonmoleculesincrease. withsmallchains,whichareallradicals,andmonocyclicrings.withdecreasing othermoleculescontainingoxygenarenotabundant.especiallyh2oispractically forrcbstarsinfutureinvestigations. 3Asubstantialimprovementofthemodelmaybeachievedbyusingadetailedmodelspectrum
95 5.2.RESULTS absentfromthegasphase.thenextgrouparecompoundsformedoutofnitrogen 75 andcarbon.themostimportantnitrogenmolecule,however,isn2.furthermore, (exceptforsio).ironandmagnesiumbearingmoleculesareunimportant. formedoutoftheseelementsandtheabundantandunblockedelementscandn thereareseveralabundantsilicon,sulphurandhydrogenbearingmolecules,all 5.2.3RadiativeHeatingandCoolingRates Thequestionofimportantcontributorstotheheatingandcoolingofsuchspecial Ddv variousradiativeprocessesforatypicalchoiceoftheparameterste,r=rand case.table5.2summarizestheresultsofthisworkconcerningtheroleofthe gashastobeinvestigatedcarefully.noprecedingstudiesareavailableforthis therstlineofeachpanelintable5.2)increaseswithincreasinggastemperature bymanyordersofmagnitudeandmoderatelydecreaseswithdecreasingdensity. Theimportanceoftheindividualheatingandcoolingprocessesstronglydepends dle.theabsolutevalueofthetotalradiativeheating/coolingrate(asgivenin ontemperatureanddensity.usuallyonespecialradiativeprocessdominatesin acertaintemperature/densityregime.allbasicradiativeprocessesmaycause heatingorcoolingandchangethesignatdierenttemperatures,whichdependon theelectrondensity)averycomplexpictureappears,whichshowsthefollowing boththecarriersoftheheating/coolingratesandthecollisionpartners(especially oftheprocess(cf.fig.3.5).togetherwiththestronglyvaryingconcentrationof therelationbetweenjandthesourcefunctionatthecharacteristicwavelength features: Free{freeheating/coolingisimportantforlargedensities(n<He>>1012cm 3). Bound{freetransitions,mainlyofHeandC,providethemostimportant Theheating/coolingratesoflinetransitionscoverthewholetemperature/den- heating/coolingprocessatlargedensities(n<he>>1011cm 3),whereallthe bound{boundtypetransitionsareopticallythick. temperatures.themostimportantcontributorsarehe+,c+,n+,s+and ingofthegasfornottoolargedensities(n<he><1011cm 3)andnottoolow sity{planeandaregenerallyimportant.theydominatetheheatingandcool- Assoonaspolarmoleculesbecomeabundantinthegasphase,theirlargenumberofallowedtransitions(vibrationalandrotational)dominatestheradiative Fe+,becauseofthehighfractionalionizationinthemodel(cf.Sect.5.2.1). insect coplaystheoverwhelmingroleconcerningtheheatingandcoolingofthegasbymolecules,sinceitisthemostabundantpolarmoleculeby heatingandcoolingofthegas.thishappensbelowthedividinglinedescribed andsis.forlargerdensities(n<he>>1010cm 3)thevibrationaltransitions areimportant,whereasforsmallerdensitiesthepurerotationaltransitionsare approximatelytwoordersofmagnitude.furtherimportantmoleculesarecs moresignicant.
96 76 CHAPTER5.THERMALBIFURCATIONSINRCBSTARS Table5.2:Importantheating/coolingprocessesforRCBabundancesasfunctionoftemperatureTganddensityn<He>(1);(2).ParametersarechosenasTe=7000K,r=2Rand Ddv dle=10kms 1=R(3) K He-bf 1014cm 3 1:0(14) 1012cm cm 3 108cm 3 106cm 3 C-bf He-bf C-bf 1:0(12) HeII HeI He-bf 1:2(11) CII HeII HeI 3:3(9) CII HeII HeI 4:3(7) 20000K He-bf C-bf O-bf 5:3(10) He-bf C-bf O-bf 5:7(8) CII HeI SiII 8:1(8) CII HeI SiII 1:7(7) CII OII NII 3:5(5) 10000K C-bf O-bf 1:2(8) CII C-bf SiII 4:8(6) CII SiII NII 2:3(7) CII NII SII 4:7(5) CII NII OII 2:6(4) 6000K +C-bf +O-bf 1:9(6) +C-bf +O-bf 2:0(5) CII NII SiII 3:2(5) NII CII SII 1:7(4) NII OII FeII 2:7(3) 3000K +C-bf +2:1(7) CO-vib +C-bf 4:6(5) +CII+C-bf +O-bf +1:8(5) +CII+NII +SII +4:9(3) +SII+NII FeII +4:7(2) 1500K +Fe-bf +Si-bf+Mg-bf +7:3(4) CS-vib CO-vib+SiII 6:2(4) +CII+C-bf +SiII +5:6(4) CO-rot+CII +SII 7:2(3) CO-rot+SII +NII 5:1(3) 800K +Mg-bf +Fe-bf+Na-bf +1:8(4) +CO-vib +SiS-vib+SiII +2:6(4) +CO-vib +SiS-vib CO-rot +4:9(2) CO-rot+FeII HCN-rot 1:5(3) CO-rot+FeII +He-bf 1:0(3) 400K +Mg-bf +Fe-bf+Na-bf +2:7(4) +CO-vib+SiII +1:1(4) +SiS-vib+SiII +FeII +7:6(2) +FeII+CO-rot +SiII +4:0(2) +CO-rot+FeII +SiII +2:6(2) Eachpanelofthetablehastwoentries: (1)Therstlineistheresultingtotalnetradiativeheatingratepermassofthegas (2)Alistofthethreemostecientheating/coolingprocessesisstatedbelowinorder ofdecreasingabsolutenetrates: =cooling,+=heating,i=linesofneutral atom,ii=linesofionizedatom,=free{free,bf=bound{free,vib=vibrational, Qrad=[ergs 1g 1],whereX(Y)meansX10Y. (3)R=73Risassumedinthiscontext. rot=rotationaltransitions.
97 5.2.RESULTS dyncm 2(n<He>109:::21010cm 3),Te=7000K,r=3RandDdv Figure5.2:Heating/coolingratesasfunctionofthegastemperatureforp= 10kms 1=R.Thethickfulllineshowsthetotalnetheatingrate.Theother dashedanddottedlinesdepictthefree-freerateq,thetotalbound{freerate Qbf(allatoms/ions),thetotallineheating/coolingrateQLines(allatomsand dle= solutions. ions),thetotalvibrationalrateqvib(allmolecules)andthetotalrotationalrate Qrot(allmolecules).Thecirclesdenotestableradiativeequilibriumtemperature 5.2.4RadiativeEquilibriumTemperatureSolutions Thesolutionsoftheradiativeequilibriumproblemarerelatedtothechangesofsign Iwillbrieyexplorethereasonsforthesechangesofsigninthefollowing. ofthetotalnetradiativeheatingfunctionqradasafunctionofthegastemperature. Theheating/coolingratesasfunctionsofthegastemperatureareshowninFig.5.2 forasamplechoiceoftheparameters.thesumsoftheratesofallkindsofprocesses changethesignatdierenttemperatures.fortheparameterschoseninfig.5.2, (free-free,bound-free,lines,vibrationalandrotationaltransitions)aredepicted.for onends:bound{free7000k,spectrallines4800k,free-free615k,vibraingthedirectiontolowergastemperatures,thedierentprocessessubsequently sucientlyhightemperatures,allradiativeprocessescausenetcooling.consider-
98 78 tional575kandrotational200k.finally,forsucientlylowtemperatures,all CHAPTER5.THERMALBIFURCATIONSINRCBSTARS ishenceforthcalledthe\high{temperaturesolution".forthehightemperaturesin problem.consideringthedirectiontolowtemperatures,therstsolutiontooccur radiativeprocessescausenetheating. Fig.5.2,thelinetransitionsprovidethedominantheating/coolingprocess.Conse- Thus,therealwaysexistsatleastonestablesolutionfortheradiativeequilibrium ture,wherethetotallineheating/coolingrateqlineschangesitssign. quently,thehigh{temperaturesolution(4830k)isusuallyclosetothetempera- Thehigh{temperaturesolutionreferstoapredominantlymolecule{free, ThechangeofsignofQLinesiscausedbythetemperature{dependentcompeting QLinesforsmallandQbfforlargedensities,respectively. partiallyionizedgas.thetemperatureisxedbythechangeofsignof bination,andcollisionalionizationfollowedbyradiativerecombination4.ifmolecule citationfollowedbylineemission.thechangeofsignofqbfiscausedbythe competingprocessesofphotoionizationfollowedbycollisional(three{body)recom- processesoflineabsorptionfollowedbycollisionalde-excitation,andcollisionalex- betheonlysolutionandtheradiativeequilibriumproblemwouldbeunique. However,oncethegashasreachedasucientlylowtemperature,moleculesbecome formationwasnotpossibleinthegasphase,thehigh{temperaturesolutionwould locatedintheirandmicrowavespectralregion,entersintocompetitionwiththe abundant.theirlargenumberofallowedvibrationalandrotationaltransitions, otheratomictransitionswhichsubstantiallyincreasestheeciencyoftheinteraction temperaturesarerequiredtocauseachangeofsignofthemolecularheating/cooling faintnessofthecentralstaratthesewavelengths,assketchedinfig.3.5.muchlower betweenthegasandtheradiationeldatlongwavelengths.thereby,theappearance functions. ofmoleculescausesreinforcedcoolingforthepresentbecauseofthecomparable temperaturesolutionsresultfromanequilibriumbetweenatomicheating Theadditionaltemperaturesolutionsarecausedbythepresenceof andmolecularcooling.thelow{temperaturesolutionsarecausedbya molecules.twotypesofstablesolutionsarefound.themedium{ ForexampleinFig.5.2,onendsasecondstablesolutionat1900K,where theradiativeheatingbylinesandbound{freetransitionsisbalancedbyvibrational changeofsignofthedominantmolecularheating/coolingfunction. cooling.ataboutthethirdstablesolution(565k)thevibrationalheating/cooling superpositionofthenumeroustransitions. functionchangesitssign.additionalunstablesolutionsexistat2290kand 1440K. 4Strictlyspeaking,evenQbfandQLinesmaychangethesignmorethanonce,becauseofthe
99 5.2.RESULTS 79 p=10+2dyncm 2 p=100dyncm 2 Figure5.3:ThermalbifurcationsinRCBenvelopesforp=102dyncm 2(upper panel,n<he>1014:::51015cm 3)and100dyncm 2(lowerpanel,n<He> unstablesolutions,respectively.theradiusaxisbelongstotheopticalthinlimit 1012:::51013cm 3).TheradiativeequilibriumtemperaturesolutionsTRE shownversusdilutionfactorwinaplanck{typeradiationeldwithte=7000k andforhdv dli=10kms 1=R.Fullanddottedblacklinesindicatestableand gare bodytemperaturetbbarethesameasshownandexplainedinfig.1.1. (pureradialdilution)accordingtoeq.(1.7).theuv{andir-limitandtheblack
100 80 CHAPTER5.THERMALBIFURCATIONSINRCBSTARS p=10 2dyncm 2 p=10 4dyncm :::51011cm 3)and10 4dyncm 2(lowerpanel,n<He>108:::5109cm 3). Figure5.4:SameasFig.5.3,butforp=10 2dyncm 2(upperpanel,n<He>
101 5.2.RESULTS 81 p=10 6dyncm 2 p=10 8dyncm 2 Figure5.5:SameasFig.5.3,butforp=10 6dyncm 2(upperpanel,n<He> 106:::5107cm 3)and10 8dyncm 2(lowerpanel,n<He>104:::5105cm 3).
102 82 ThegeneraltopologyoftheradiativeequilibriumsolutionsisdepictedintheFigs.5.3 CHAPTER5.THERMALBIFURCATIONSINRCBSTARS dilutionaccordingtoeq.(1.7),butitsmeaningismoregeneral.wcharacterizes Thisfactorisrelatedtoadistinctradialdistanceinthecaseofpuregeometric to5.5.thetemperaturesolutionsareshownasfunctionofthedilutionfactorw. thestructureofthebifurcations.w=1togetherwithreimpliescompletethermodynamicequilibrium(te)accordingtotheconceptofthiswork:inthecase wherew=1theradiationeldisanon{dilutedplanck{eldj=b(trad)andthe thedeparturefromanequilibriumand,hence,isanappropriatevariabletostudy isdirectlybalancedbyitscorrespondingreverseprocess,whichcharacterizeste. (cf.chapter3),thisworkaccuratelydescribesthisbehavior. Sinceallreverseprocessesareincludedbymeansofdetailedbalanceconsiderations onlysolutionofreisgivenbytre g=trad.every(collisionalorphoto-)process AllcalculatedREtemperaturesolutionsarelocatedbetweentheIR{limit(TIR= Thermalbifurcationsarefoundtooccurunderthefollowingconditions: WTe)andtheUV{limit(TUV=Te),nicelyconrmingthesimpleresultsofSect.1.2 wherelteanda{typegasabsorptioncoecienthavebeenconsidered. 1)Ahigh{temperaturestablesolutionmustbepossible,i.e.aradiativeequilibriumstateofthegasmainlyconsistingofatomsandions5. 2)W<0:1(r>1:5R)isrequiredtomakepossibleamolecule{rich,low{ 3)p<1dyncm 2(n<He><1013cm 3)isrequiredtolimittheinuenceofthe temperaturesolutionasmotivatedbytheir{limit. notproduceadditionalsolutions. lowtemperatures(cf.table5.2)and,consequently,moleculeformationdoes rates.fortoolargedensities,qbfdominatestheheatingandcoolingevenfor bound{freeheating/coolingratescomparedtothemolecularheating/cooling and810kforp=10 2dyncm 2andW=0:05)candierbyseveralthousands dilutionfactor.thestabletemperaturesolutions(e.g.5220k,2000k,1220k simultaneoustemperaturesolutionsmayexist,dependingonthepressureandthe Undertheseconditions,thegasisalwaysfoundtobeatleastbi{stable.Upto4 ofdegrees,usuallyyieldingonehigh{temperature,atomicsolutionandoneormore whichcanbeseenbycomparisonofthefigs.5.3to5.5.thegeneraltendencyis low{temperature,molecularsolutions. AnotherresultofthemodelisthattheREgastemperaturesaredensity{dependent, thatathingastendstobecoolerthanadensegas,consideringthesamebranch comparedtothelatter,yieldinglowerretemperaturesaccordingtofig.1.1. ofsolution.thisiscausedbytheincreasingimportanceofspectrallinesandrotationaltransitionscomparedtobound{freeandvibrationaltransitionsfordecreasing density,respectively.theformertransitionshavelongercharacteristicwavelengths entersintothemolecularregimeanddisappears.onlyonelow{temperaturesolutionremainsin thiscase. W<0:01inFig.5.5.Inthiscasethe\high"{temperaturesolutiondropsbelow2000K,whereit 5Aviolationofthiscriterionoccursatsmallpressuresp<10 6dyncm 2andlargedilutions
103 5.3.DISCUSSION Discussion 83 mainlyconsistingofatomsandions.bothphasesareinradiativeequilibriumand ThecircumstellarenvelopesofRCBstarsshowamulti{stablecharacter.Coolgas phases,mainlyconsistingofmolecules,canprincipallycoexistbesideshotphases, reinforcedradiativecooling6.thegasthencoolsdowntomuchlowertemperatures, Themulti{stablecharacterofthegascausesakindof\coolingtrap".Oncethe gashasreachedasucientlylowtemperature,moleculesareformedwhichcause inpressurebalancewitheachother. untiltheheatingandcoolingbymoleculesaloneproducesanothersolutionofthe Thermalbifurcationsarefoundtooccurinalargerangeofexaminedparameters, concerningboththeradialdistancetothestarandthegaspressure.thesendings radiativeequilibriumproblemandstabilizesthelowtemperature. thermalbifurcationsareexpectedtooccurmainlyinthecsesofwarmstarswith indicatethattheoccurrenceofthermalbifurcationsisnotrestrictedtothecsesof Te>4500K,wheretheatomic,high{temperaturesolutionstillexists(cf.criterion1 RCBstars,butisacommonphenomenoninpartiallymoleculargases.However,the oftheitemlistonthepreviouspage). ConcerningtheCSEsofcoolstars(asC{andM{starsontheAGB),theradiative equilibriumgastemperaturesareexpectedtobemuchlowerthantheblack{body quently,thesolutionsoftheradiativeequilibriumproblemshouldbesimilarto temperatures.thegasinthesecircumstellarenvelopesismolecule{rich.conse- inthischapterisnotappropriateforthiscaseandtheresultscanbedierent. enshroudedandhenceopticallythick.theapproximationoftheradiationeldused Nevertheless,theconsequencesofthemulti{stablecharacterofthegasreachfar, thelow{temperaturesolutionsdiscussedabove.however,theseenvelopesaredust{ asf.kneer(1983)wroteinviewofthisinstability:\iconcludethatrestellar atmosphereswithte=5800kmaynotexist,inprinciple".iwouldnotgothat far,butconsiderforexampleagaselementwhichslowlymovesoutwardsinacse Thegastemperatureslowlydecreaseswithincreasingradialdistancedowntoabout consistsofatomsandionsaslongasthehigh{temperaturesolutionisrealized. oftheelementshallbeslow,sothatreremainsvalid.thegaselementmainly withatemperaturestructuresimilartothatdepictedinfig.5.5.themotion 2000K,untilsuddenly,atabout4RinFig.5.5,acertainamountofmoleculeshas beenformed,justsucienttodestabilizetheradiativeequilibrium.thegasthen quicklycoolsdowntowardsthesecond,low{temperaturesolutionat200k.the nalchemicalcompositionandtheamountofdustformedinthegaselementwill cruciallydependontherelationbetweenthechemicalandthecoolingtimescale duringthistransition.intheend,thechemistryfreezesoutanddustformation generaltheoreticalviewofthechemistryandthedustformationprocessesinstellar becomesimpossibleagain.ifthisscenarioprovestobetrueitwouldchangeour 6Howsuchasucientlylowtemperaturecanbereached,isleftopenforthepresent.
104 84 envelopesquitedramatically.othertopicsrelatedtothemulti{stablecharacterof CHAPTER5.THERMALBIFURCATIONSINRCBSTARS thegascouldbeinhomogeneities,cloudformationorahysteresis{likebehaviorof ityofreunderdynamicconditions.forexample,thelow{temperaturesolutions calculateradiativecoolingtimescales,whichgiveanimpressionontheapplicabil- thegasinthecsesofpulsatingstars. caneasilybedestabilizedbyadiabaticheating/coolingrates,whichdiminishesthe TheresultsofthischapterrefertotheassumptionofstaticRE.Chapter6will meaningofthelow{temperatureresultsofthischaptertosomeextent. theradiationeld.eachradiativeprocesswhichisadditionallytakenintoaccount dependsonthedetailsof(i)thechemistry,(ii)theheating/coolingfunctionsand(iii) areliabledeterminationofthegastemperatureisdicult.inthestaticcaseitreally Incontrasttothegeneralnding,thatthermalbifurcationsshouldoccurprincipally, theresultsofchapter7,aswillbediscussedtherein. maychangetheresultsfortre gsubstantially.thisisfundamentallydierentfrom
105 Chapter6 RadiativeCoolingTimeScalesinthe Thesecondapplicationofthethermodynamicmethodsdevelopedinthisworkinvestigatestherelaxationtowardsradiativeequilibrium.Agaselementinnon{RE isconsidered.theelement,beinghotterorcoolerthaninre,willconsequently radiateawayexcessinternalenergy(radiativecooling)orgainradiativeenergyby CircumstellarEnvelopesofC{Stars Thecharacterofthethermalbehaviorofthegasunderdynamicalconditionscan whichisdenedbelow. netabsorption(radiativeheating),respectively.thekeyquantitywhichdescribes theeciencyofthisrelaxationisthetimescaleforradiativecoolingorheating, thegasquasiinstantaneouslyrelaxestowardsreand,consequently,thecondition consideredprocess.iftheradiativecoolingtimescaleisshorterthantheothers, timescale")withtheotherhydrodynamicorchemicaltimescalesinvolvedinthe bediscussedbycomparingthistimescale(henceforthcalledthe\radiativecooling andmustbecalculatedtime{dependently. thantheothers,thetemperatureofthegasdependsonthehistoryoftheprocess ofrecanbeusedtodeterminethegastemperature.ifitiscomparableorlarger ConcerningthechemistryandthedustformationintheCSEsofpulsatingstars,the temperatureunderdynamicconditionsisinvestigated. Inthefollowing,theapplicabilityofREforthedeterminationofthegas characterofthethermalrelaxationofthegasinresponsetopropagatingshockwaves pulsatingstarsarehitbyshockwavestimeandtimeagain.theshocksdissipate whichsteepenuptoshockwavesintheatmosphereandpropagateintothecse isofspecialimportance.thepulsationintheinteriorofthestarproduceswaves, mechanicalenergyandheatupthegastoconsiderablyhightemperatures.thegas mustbeabletoradiateawaythisexcessinternalenergybeforethenextshockhits (e.g.bowen1988,fleischeretal:1992).thus,thegaselementsintheenvelopesof formation.infact,fromobservations,justtheoppositeconclusionscanbedrawn. chemicalanddustformationprocesses. Followingthisconsideration,onewouldexpectthestellarpulsationtohinderdust theelement.otherwise,itwillneverbecomesucientlycooltoallowforcomplex Manyofthedust{formingobjectsareknowntobepulsatingstars.Moreover,a 85
106 strongcorrelationbetweentheoccurrenceofanirexcess(indicatingdustformation) 86 CHAPTER6.RADIATIVECOOLINGTIMESCALESINC{STARS byobservations. stars(jura1986),i.e.stellarpulsationfavorsdustformation.therefore,anecient relaxationoftheshock{heatedgasincircumstellarenvelopesseemstobeconrmed andalightvariability(indicatingstellarpulsation)canbeobservedforlatetype ThischapterconsiderstheCSEsofpulsatingC{stars.ItpicksupthecontroversialquestionofwhethertheshocksintheseCSEsbehavepredominantly\isothermally"or\adiabatically"(moreinformationsaboutthiscontroversycanbefoundin Sect.1.4).Aclaricationofthisquestionisanimportantsteptowardstheprincipal understandingofdustformationinthecsesofpulsatingstars DenitionoftheRadiativeCoolingTimeScale TheModel Anarbitraryphysicalquantityyshallbeconsidered.Thetimeevolutionofyis assumedtobegivenbytherstorderordinarydierentialequation Theequilibriumvaluesofthephysicalquantityyareimplicitlydenedbyf(y)=0. dy dt=f(y): (6.1) timerequiredfortherelaxationist=y y Ifyistorelaxtowardequilibrium,i.e.y(t+t)y,therstorderestimateofthe FirstorderTaylorexpansionofEq.(6.1)intimeyieldsy(t+t)=y(t)+tf(y). Theradiativecoolingtimescaleisdenedanalogously,consideringpureradiative heating/coolingaccordingtode f(y): (6.2) cool;tg;j;ddv dle=e;tre dt=bqradwithbqrad=qrad= g;j;ddv bqrad;tg;j;ddv dle e;tg;j;ddv dle gisoneretemperaturesolutionasdenedinchapter5.apartfromtheproblemofremulti{stability,tre : (6.3) thermodynamicquantitiesandtg,thecontinuousbackgroundradiationeldj andthelocalvelocitygradientddv theentiredensity{andtemperature{rangeencounteredintheshockedenvelopesof gandtherebycoolarecompletelydeterminedbythe pulsatingc{stars. dle.inthefollowing,theaimistocalculatecoolfor
107 6.1.THEMODEL 6.1.2ElementAbundances 87 TheelementcompositionofC{starsisassumedtobesolarexceptforcarbon.The byc=o=1:7,whichaccordingtofrantsman&eglitis(1988)isarepresentative fromallen(1973).carbonisassumedtobeoverabundantwithrespecttooxygen TheabundanceofHeisassumedtobeHe=H=0:1andtheabundanceofMgistaken solarabundancesareadoptedfromlambert&rao(1994)andreferencestherein. valueforc{stars. FortheapplicationswithregardtoC{starsthemeanback{groundintensitiesare assumedtobegivenbyannon{dilutedplanckeld(w=1),thatis 6.1.3ApproximationoftheRadiationField Thisisdoneforthreereasons.First,theCSEsofC{starsaresupposedtobedust enshroudedandhencenotopticallythin.eq.(6.4)representsthelimitingcaseofan J=B(Trad): (6.4) opticallythickcse.second,theassumptionconsiderablysimpliestheevaluation ofthecoolingtimescaleasdenedabove.accordingtoeq.(6.4)thereisalways latterofcourserequiresmoredetailedknowledgeaboutj.theparametertradis todeterminecoolandnottondthespecictemperaturesolutionsofre.the well{denedaccordingtoeq.(6.3).third,thecalculationsareperformedinorder exactlyone(trivial)retemperaturesolutiongivenbytre g=trad.thereby,coolis assumedtovarybetween0and3000kforc{starenvelopes,considering3000kas remarkablysimilar(cf.sect.6.2.4).therefore,thechoiceoftheradiationeldis arepresentativevaluefortheeectivetemperaturesofthesestars.evenforthe notcrucialforthedeterminationofcool.chromosphericemissionsandcontinuous extremecasesj=0andj=b(3000k),theresultsforthecoolingtimescalesare emissionsfromshockedgaslayersinthecseareagainignored LocalVelocityGradient meanvelocitygradientddv theshockedenvelopesofcoolpulsatingstars(e.g.fig.1ofwintersetal:1994),the Regardingthetypicalsaw{tooth{likevelocitystructuresinmodelcalculationsfor fronts).therefore,thisparameterisxedandsettoddv throughoutthewholeconsideredcircumstellarshell(exceptfortheverythinshock characteristicvalueoftheorderofv1=rvaryingbyaboutoneorderofmagnitude dle,asdenedbyeq.(3.14),hasmoreorlessacertain inuenceofthisparameterissmall(cf.sect.6.2.5). dle=20kms 1=500R.The
108 Results CHAPTER6.RADIATIVECOOLINGTIMESCALESINC{STARS Beforediscussingtheresultsfortheradiativecoolingtimescales,someofthemicrophysicalresultsshallbestatedrst:thecompositionofthegas(degreeofionization 6.2.1CompositionoftheGas andchemistry),theinternalenergyandtheroleofthedierentradiativeprocesses. thegureshowscontourlinesoftheconcentrationsofh2ande inthetemperature/density{plane,indicatingwhetherthegasispredominantlymolecular,atomic ThecompositionofthegasisroughlydepictedinFig.6.1.Theupperpanelof orionized.thetwoextremecasesj=0andj=b(3000k)areconsideredonthe leftandrighthandsideoffig.6.1,respectively. Theresultingelectrondensityisveryimportantforthecalculationoftheradiative collisionpartner,alsoonthebound{boundcollisionrates.thedegreeofionization heating/coolingrates.ithasadecisiveinuenceonthebound{freeratesand,as processeslinearlydependonne(cf.eq.3.60and3.61),thedensity{dependence ofthegasisfoundtostronglydependontheradiationeld. cancelsoutandthecontourlinesarehorizontallinesonthelefthandsideoffig.6.1. whichismainlybalancedbyradiativerecombination.sincetheratesoftheboth InthecaseTrad=0,fractionalionizationissolelycausedbycollisionalionization, Thedeviationsfromstraightlinesathightemperaturesarecausedbycollisional thanadirectcollisionalexcitationh+e!h++2e (cf.sect.3.2.2).fractional ionizationisfoundtobenegligible(<10 5)forTg<5000KinthecaseJ=0. excitationfromexcitedstatesofhydrogen.forlargedensitiesatwo{stepcollisional processh+e!h+e andh+e!h++2e turnsouttobemoreecient importantthancollisionalionizationfortg<5000k.sincethephotoionizationrates izationpotentials(si,mg,fe,na)additionallyproducesfreeelectronsandismore aredensity{independent,buttheradiativerecombinationratesdodependonthe ForTrad=3000K(righthandside)photoionizationofmetalatomswithlowiontainedforlowtemperatures,dependingonthedensity1.Thus,fractionalionization isfoundtobemuchlargerthaninlteatlowtemperaturesforthisradiationeld. density,thecontourlinesareapproximatelyverticallinesfortg<5000konthe righthandsideoffig.6.1.adegreeofionizationaslargeas10 3to10 5isre- radiativerecombinationratesintheentiretemperature/density{planeunderin- Thethree{bodyrecombinationratesarefoundtobenegligiblecomparedtothe tionunlessthetemperatureisaslargeas>10000k.onlyforverylargedensities, (n<he>>1016cm 3)thecalculatedfractionalionizationofthegasapproachesLTE. vestigation.consequently,lte(saha){ionizationisneverachieved.forexam- ple,thegasremainspredominantlyneutralfortheradiationeldsunderexamina- andgraindrift,forexample. 1Suchdegreeofionizationisexpectedtocauseconsiderableeectswithregardtograincharge
109 6.2.RESULTS 89 Figure6.1:Thecomposition,theinternalenergyandthenetheatingfunctionofthegas (fulllines).themiddlediagramsshowthetotalinternalenergyofthegaseona linearscalerangingfromabout 1:4(12)to+1:3(13)erg/g.Thezero{lineisadditionally asfunctionoftemperatureanddensity.theupperdiagramsarecontourplotsoftheh2{ concentrationlog(nh2=n<h>)(dottedlines)andtheelectronconcentrationlog(ne=n<h>) shownasadashedlineandthesignofeisindicated.thelowerdiagramsshowthe AllcalculationaremadeforDdv considersthecasej=0,whereastherightcolumnconsidersthecasej=b(3000k). QradispositivebelowandnegativeabovethedashedTg=3000K{line.Theleftcolumn totalnetheatingfunctionofthegaslogjqrad=j[ergg 1s 1].Ontherighthandside, dle=20kms 1=500R.
110 Thechemicalcompositionofthegasiscalculatedbyassumingchemicalequilibrium 90 CHAPTER6.RADIATIVECOOLINGTIMESCALESINC{STARS theconcentrationsofthemoleculesarefoundtobeverysimilarcomparedtotheresultsofpreviousworksusingchemicalequilibrium.theresultsoftheapplicationof withrespecttotheneutralatomdensitiesinthiswork(cf.chapter4).consequently, entneutralatomdensitiesduetotheupperresultsconcerningtheionizationwhich (e.g.gail&sedlmayr1988).somemodicationsarecausedbythesomewhatdier- yieldsomewhatdierentmoleculeconcentrations(e.g.lesssiliconbearingmolecules chemicalequilibriumtoc{starsenvelopeshavethoroughlybeendescribedelsewhere linesintheupperpaneloffig.6.1. aresmall.theh2{concentration,forexample,isdepictedbythedottedcontour ifsiisstronglyionizedasinthecasetrad=3000k).however,thesemodications Thedeterminationoftheinternalenergyofthegasisanimportantingredientfor 6.2.2InternalEnergy dependenttreatmentofthermodynamics,forexampleinhydrodynamicmodels.it thecalculationofthecoolingtimescale.moreover,itisessentialforanytime{ providesthebasiclinkfromtheenergycontent,whichismodiedbyradiative heatingandcooling,tothetemperatureofthegas. ular,atomicandionizedstateofthegas.theregimesaredividedbyconsiderable Threedierentregimescanbedistinguishedwhichrefertothepredominantlymolec- plane.theinternalenergydiersalotfromthatofanidealgas(e=fkt=(2)). ThemiddlediagramsofFig.6.1depictcontourlinesofeinthetemperature/density{ gaswhilethetemperatureonlychangesgradually.withinonephase,theinternal energybarriersinbetween.inodertoovercomesuchabarrier(toperformaphase transition),aconsiderableamountofenergyistobeaddedortoberemovedfromthe tionenergy,arefoundtosignicantlycontributetothetotalinternalenergyofthe Allcomponentsoftheinternalenergy(cf.Eq.2.2),exceptfortheelectronicexcita- anidealgas.theinternalenergyalwaysincreasesmonotonicallywithtemperature. energyapproximatelydependslinearlyonthetemperature,closetothebehaviorof energyisnegativeinthemolecularregime).erotisabout0:57etransassoonash2 forhightemperatureswhereitreachesabout4etransat20000k.edissdominates theinternalenergyatlowtemperatures,about 59Etransat500K(theinternal gas,atleastinaparticularregionoftemperatureanddensity.eionisimportant thepopulationofthevibrationalstatesofthemoleculesisstronglyaectedbythe radiationeld.itsmaximumcontributionisfoundtobe0:07etransfortrad=0 and1:2etransfortrad=3000k.eelisfoundtobenegligible(<310 4Etrans). ismoreabundantthanh.thecontributionofevibdependsontrad,indicatingthat density.thedependenceontheradiationeldissignicant.theionicpotential Theinternalenergyofthegasisnotcompletelydeterminedbytemperatureand principallyalsopresent,butnegligible. sponsibleforthesedependences.thedependenceofeonthevelocitygradientis energyeionandthevibrationalexcitationenergyofmoleculesevibaremainlyre-
111 6.2.RESULTS 6.2.3TheRadiativeCoolingTimeScaleandtheRoleoftheVarious 91 Trad=0)andinFig.6.4(forTrad=3000K).Thedashedarrowswillbediscussedlater TheradiativecoolingtimescalesasfunctionofandTgaredepictedinFig.6.2(for HeatingandCoolingProcesses to10yearsforawarmandthingas.thecoolingtimescalestronglydepends Typicalvaluesforcoolarefoundtorangefrom10 2sforahotanddensegas radiativeheatingfunctionbqradisadditionallyshowninthelowerpaneloffig.6.1. (insect.6.2.7)andarenotofinterestforthepresent.forcompleteness,thenet onboththegastemperatureandthegasdensity.thetemperature{dependenceis foundtocomprise9ordersofmagnitudeatlargeand3ordersofmagnitudeatsmall isalsostrong,8ordersofmagnitudeathighand3ordersofmagnitudeatlower densities,consideringgastemperaturesof500:::20000k.thedensity{dependence gastemperaturesrequiredfortheecientexcitationoftheupperstates,bynon{ functions,whichareaectedbythevaryingparticleconcentrations,byminimum Thesedependencesresultfromasuperpositionofthedierentheatingandcooling temperatures,consideringdensitiesof104:::1014cm 3. LTEeectsandbyradiativetrapping.Ingeneral,adensegasheatsandcools toprovideareasonablettotheresults.thereareevencases,whereadensegas n<h>>1011cm 3.Inthisregion,allimportantradiativeheatingandcoolingrates moreecientlythanathingas.however,asimpleapproachlikeqrad/2fails areofbound{boundtransitiontypeandthetotalrateisstronglyreducedbythe heatsandcoolslessecientlythanathingas.thisoccursfortg<4000kand lowcontinuousradiationeldsandhighdensities,theheatingandcoolingofthe areuncertaininthisregion.forsucientlylowgastemperatures(tg<1500k), ofthestrengthbutofthenumberoflinestakenintoaccount.therefore,theresults largeopticaldepthsinthelines.theheating/coolingeciencyisnomoreaquestion gasispossiblycontrolledmostlybythepresenceofdustgrains(e.g.viathermal accommodation),sincedustformationcantakeplaceecientlyinthisregion. followingpictureappears: Themosteectiveheating/coolingprocessesarestatedintheFigs.6.3and6.5.The Forhightemperatures(Tg>6000:::10000K),hydrogencoolingdominates. tiesbound{freecoolingofhydrogenturnsouttobemoreimportantduetothe largeopticaldepthinthehydrogenlines.free{freecoolingisalsoimportant ForsmalldensitiescoolingbyLyandHisecient,whereasforlargedensi- Forintermediatetemperatures,thereisazoneofconsiderablesmallerheating/coolingrates,i.e.largercoolingtimescales.Inthiszone,thetemperature isalreadytoolowinordertoexcitetheh{atoms,butstilltoohighforcon- CIIandOII.Atverylargedensities(n<H>>1011:::1012cm 3),bound{free transitionsofh dominatetheradiativeheatingandcooling. ofneutralandsinglyionizedmetalatoms:ci,oi,sii,fei,feiiandalsosi, forhightemperaturesandlargedensities. siderablemoleculeconcentrations.theremainingradiativeprocessesarelines
112 92 CHAPTER6.RADIATIVECOOLINGTIMESCALESINC{STARS Figure6.2:Contourlinesoftheradiativecoolingtimescales(fulllines).The (isobar)coolingtrackwithamaximumradiativecoolingtimescaleofoneyear digitsonthecurveslabellogcool[days].thedashedarrowindicatesthecritical onthetrack.parameters:trad=0andddv dle=20kms 1=500R. H bf H I H bf C I Si I O I C I Fe I Fe II O I CO vib Figure6.3:MostecientcoolingprocessreferringtoFig.6.2(schematically, C 2 H rot rot=rotational,vib=vibrational,i=linesofneutralatom,ii=linesofionized HCN SiO vib H SiS vib CO rot atom,bf=bound{free). 2
113 6.2.RESULTS 93 established.notethatthecoolingtimescaleremainspositiveandsteady,al- thoughthenetradiativeheatingfunctionqradchangesitssignattg=3000k. Figure6.4:Contourlinesoflogcool[days]asinFig.6.2,butforTrad=3000K. ThecriticalcoolingtrackendsatTg=Trad,whereradiativeequilibriumisre- H bf CII H I H bf O I C I CO vib CO rot C 2 H rot Figure6.5:Mostecientheating/coolingprocessreferringtoFig.6.4. H 2 vib H 2 vib HCN rot H SiS vib 2 CS rot rot CO rot Fe II Fe II
114 94Forlowtemperatures(Tg<2000:::4000K,assoonasCOisabundant), CHAPTER6.RADIATIVECOOLINGTIMESCALESINC{STARS CNareimportant.Forsmalldensitiesrotationalheating/coolingdominates, rotationaltransitionsofco,sis,hcn,c2h,cs,h2andalsoofsioand polarmoleculesdominatetheradiativeheatingandcooling.vibrationaland vibrationalstates(cf.sect.3.1). whereasforlargedensitiesthevibrationalheating/coolingismoreimportant, asexpectedfromthelargercriticaldensitiesforthethermalpopulationofthe ThecoolingtimescaleasfunctionofJisexpectedtovarybetweenthevaluesshown inthefigs.6.2and6.4,supposedthat0jb(3000k)forc{starenvelopes DependenceontheRadiationField Theradiativecoolingtimescaleisfoundtobeonlymarginallyaectedbythechoice oftheradiationeld.themaximumdeviationbetweentheextremestrad=0and Trad=3000Kisfoundtobe2.4dex,whichoccursintheregioncontrolledbyH Forexample,atTg<3000KinFig.6.4,theradiativeprocesseschangefromcooling smaller.thestandarddeviationisfoundtobe0.6dex.thisisasurprisingresult. atlargedensitiesandwarmtemperatures.however,theusualdeviationismuch eciencyofradiativeheatingandcoolingisaninherentfeatureofthegas,mainly controlledbytemperatureanddensity. eciencythanthoseresponsibleforcooling.butthisturnsouttobewrong.the toheating.onewouldexpecttheprocessesresponsibleforheatingtohaveadierent assumedvalueof20kms 1=500R.SignicantdierencesareonlyfoundforTg< Thecalculationshavebeenrepeatedwiththeonetenthandtentimestheusually 6.2.5DependenceontheVelocityGradient careanywayasstatedinsect qradnevervariesmorethanlinearlywithddv 4000Kandn<H>>1011cm 3,wheretheevaluationofQradhastobetakenwith Forsmallerdensitiesorhighertemperaturesthedependenceismuchsmaller. dle. Inthefollowing,theresultsofthisworkarecomparedtopreviousanalyticalap ComparisontoAnalyticalHeating/CoolingFunctions temperaturestructures. proachestodeterminetheradiativeheatingandcoolingratesincircumstellaren- encesinthehydrodynamicmodelcalculationsconcerningforexampletheresulting velopes.aspointedoutinsect.1.4,theseapproachesleadtoconsiderabledier-
115 6.2.RESULTS Bowen'sHeating/CoolingFunction 95 bybowen(1988): Thefollowinganalyticexpressionofthenetradiativeheatingratehasbeenproposed BowenstrictlyassumesQrad/2throughoutthecircumstellarenvelope.Theheating/coolingprocesseswhichbehaveinsuchawayarelimitedbythecollisionalenergy 2C0(Trad Tg) (6.5) bqrad=3k onemightcalleq.(6.5)thestrictnon{lteheating/coolingrate.atemperature{ independentcoolingtimescaleisfurthermoreassumed.theparameterc0,reecting transferasinthelimitingcaseofsmalldensities(cf.sect ).consequently, rateiscalculatedasdescribedbybowen(1988),althoughseveralassumptionsare turescoolingbyemissioninlyisadditionallytakenintoaccount.thish{cooling involvedhere,whichwithregardtothisworkseemtobequestionable,asforexampletheassumptionofaconstant(density{independent)escapeprobabilityfor Ly. theradiativecoolingtimescale,ischosentobe10 5gscm 3.Forhighertempera LTEHeating/CoolingFunction bymeansoftheassumptionoflteb"=bb(tg): thegas,thefollowingexpressionforthenetradiativeheatingratecanbeobtained StartingfromtheexactexpressionbQrad=4RbJd 4Rb"d,wherebisthe trueabsorptioncrosssectionpermassandb"isthespectralemissivitypermassof bqrad=4bj(;tg)t4 rad bb(;tg)t4 g tionpermassofthegas.isthestefanboltzmannconstant.thisanalyticalform bj(;tg)istheintensity{meanandbb(;tg)theplanck{meanabsorptioncrosssec- (6.6) ofthenetradiativeheatingratehasbeenusedbyfeuchtingeretal:(1993),assuming eralrequiresverylargedensities(cf.chapter3).furthermore,ifoneuses'swhich collisionallypopulatedlevelsoftheconsideredatomsandmolecules,whichingen- Qrad/results.UsingEq.(6.6)meanstoassumethatallradiativeprocessesreferto aconstantgreygasabsorptioncrosssection.asfarasbisdensity{independent, callythin2.duetothelackofplanck{meanopacities,rosselandmeanopacitiesare usedinthefollowingforbothopacitiesineq.(6.6).therosselandmeanopacities examplethenumerouslinesofmolecules),theincludedlinesareassumedtobeopti- havebeencalculatedbyopacitysamplingmethodswithrespecttospectrallines(for ResultsoftheComparison br(;tg)areinterpolatedfromtablesprovidedbyscholz(scholz&tsuji1984). thelteheating/coolingfunctionaredepictedinthefigs.6.6and6.7,respectively. TheresultingradiativecoolingtimescalesaccordingtoBowen'sandaccordingto 2Infact,thesetwoassumptionscontradicteachother.
116 96 CHAPTER6.RADIATIVECOOLINGTIMESCALESINC{STARS ing/coolingfunctionproposedbybowen(1988).trad=3000kiscon- sidered. Figure6.6:logcool[days]calculatedfromtheanalyticalheat- Figure6.7:logcool[days]asintheuppergure,butcalculatedfrom thelte{heating/coolingfunction.nocriticalcoolingtrackexistshere, year. sincetheradiativecoolingtimescaleisalways(much)shorterthanone
117 6.2.RESULTS Inthiscontext,e=3kTg=(2)with=1:27amuisassumedforbothapproaches 97 muchagreementwiththeresultsobtainedinthiswork.bowen'sheating/cooling functionyieldsastrongdensitydependence(cool/ 1,verticalcontourlines), NeitherthecoolingtimescalesderivedfromBowen'snorfromtheLTErateshow underdiscussion.theseresultscanbecomparedtofig.6.4. ing/coolingratescalculatedinthiswork,bowen'srateusuallygivesmuchsmaller values(uptoafactorof10 6inthelow{density,low{temperatureregime),whereas coolingtimescales(roughlyhorizontalcontourlines).comparedtotheheat- whereasthelteheating/coolingfunctionyieldsmoreorlessdensity{independent density,high{temperatureregime).thebestthatcanbesaidisthatthecooling twoanalyticalformulae. timescalescalculatedinthisworkusuallyliebetweenthevaluesderivedfromthe thelterateusuallygivesmuchlargervalues(uptoafactorof106inthelow{ coolingmoredetailed,andsincehydrogencoolingisdominantathightemperatures paredtotheresultsofthiswork.asbowen'sratetosomeextenttreatshydrogen 8000K)Bowen'srategivesaboutthesameslopeandorderofmagnitudecom- Someroughagreementsarefound,nevertheless.Forhightemperatures(Tg> andcoolingforhightemperatures,anintermediateminimumforthepredominantly accordingtothiswork,thisagreementwastobeexpected.thelterateproduces ciencyinthemolecularregimeatlowtemperatures.bestagreementwiththelte asimilartemperature{dependenceasfoundinthiswork:veryeectiveheating atomicphaseatwarmtemperaturesandare{increaseoftheheating/coolinge- coolingtimescaleisfoundonthelefthandsideofthediagramsatlargedensities probably,itisbecause detailedagreementisnotachieved,notevenfortheselargedensities.thisdisagreementmightbecausedbymissingradiativeprocessesinthiswork.however,more (yieldingsimilarcoolingtimescaleswithinabout2ordersofmagnitude).however, ii)accordingtothiswork,thegasisstillfarfrombeinginlteatn<h>= i)rosselandmeansofhavebeenusedinsteadofplanckmeans, Insummary,bothanalyticalheating/coolingfunctionsyieldpooragreementwith iii)thelteheating/coolingfunctionneglectsopticaldepthsinthelines. and 1014cm 3(especiallywithregardtothedegreeofionization,cf.Fig.3.9), theresultsofthiswork.bowen'srateseemstounderestimateandthelterate stressesthenecessitytousemoredetailedmodelcalculationsfortheradiativeheatingandcooling.theproposedanalyticalfunctionsareinsucienttodescribethe seemstooverestimatetheheating/coolingeciencybyordersofmagnitude.this radiativeheatingandcoolinginthecircumstellarenvelopesofcoolstars.
118 6.2.7TheTransitionfromIsothermaltoAdiabaticShocks 98 CHAPTER6.RADIATIVECOOLINGTIMESCALESINC{STARS discussionofthecharacterofthethermalrelaxationbehindpropagatingshockwaves inthecircumstellarenvelopesofpulsatingstars. Thecalculatedradiativecoolingtimescalesofthisworkallowforaquantitative consistingofh+10%he).afterthepassageoftheshock,thegasradiatesawaythe Agaselementbeinghitbyastrongshockwaveofvelocityvsisalmostinstantaneouslyheateduptohightemperatures(11500K[vs=20kms 1]2foranidealgas excessinternalenergydissipatedbytheshock,i.e.itrelaxestore,inprinciple. P.Furthermore,thepropagatingshockwavesinitiateaconsiderablecompression However,consideringthemoreorlessperiodicallyshockedenvelopesofpulsating wavehitstheelement.thistimeisgivenbyaboutonestellarpulsationalperiod andre-expansionofthegasaccompaniedbyconsiderableadiabaticheating/cooling. stars,onlyalimitedtimeforthisrelaxationisavailable,beforethenextshock ThetimescaleoftheseprocessesisalsogivenbyP.Thus,therelationbetweenthe radiativecoolingtimescalecoolandthestellarpulsationalperiodpdeterminesthe characterofthethermalbehaviorofthegasinthecsesofpulsatingstars. IfcoolismuchsmallerthanP,thegasquicklyrelaxestoREbehindtheshocks. coolp,isothermalshocks Theadiabaticheating/coolingratesaremeaningless.REisestablishedintheoverwhelmingpartsofthecircumstellarenvelope,exceptforsomethintemperature temperaturestructureofthecsecanbecalculatedbyassumingre. peaksatthelocationoftheshockfronts(cf.fig.1.3).apartfromthesepeaks,the cool>p,adiabaticshocks (6.7) coolingadiabaticallyinthemeantime.thetemperaturestructuremustbecalculatedtime{dependently. Inanalogytothesituationinstationaryshocks(e.g.Neufeld&Hollenbach1994),an isobarcoolingtrackinthetemperature/density{planeisconsideredinthefollowing. coolingtimescalecoolonthetrack.theisobarcoolingtrackwithcool1yronthe track(henceforthcalledthe\criticalcoolingtrack")isdepictedinfig.6.2,fig.6.4 andalsoinfig.6.6asdashedgreyarrow,consideringoneyearasatypicalperiodof Thetotalcoolingtimealongsuchatrackisroughlygivenbythemaximumradiative sequently,thegassubsequentlyheatsupduetotheshocks(cf.fig.1.4),roughly radiateawaytheenergydissipatedbyoneshockwithinonepulsationalperiod.con- If,however,coolexceedsP,a\chromospheric"situationresults.Thegascannot isanestimateforthedividinglinebetweentheshocksofpredominantlyisothermal andpredominantlyadiabaticcharacter.gaselementswhichareshockedtotheleft meanparticlemassduetophasetransitions(cf.fig.6.1).thecriticalcoolingtrack pulsatingc{stars.thedeviationsfromastraightlinearecausedbychangesofthe ofthecriticalcoolingtrackscanreestablishrebeforethenextshockarrives thosewhichareshockedtotherightofthecriticalcoolingtrackwillbehitbythe nextshockbeforerecanbeachieved.
119 6.3.DISCUSSION Accordingtotheresultsofthiswork,atransitionofthecharacteroftheshockwaves 99 AroundTg5000Kthecoolinggaselementspendsmostofitstotalcoolingtime. frompredominantlyisothermaltopredominantlyadiabaticwithdecreasingdensity. istobeexpectedtooccuraroundpost{shockdensitiesof106:::108cm 3,changing Thecoolingtimescaleinthistemperatureregionisfoundtovaryby4 5orders ofmagnitudefortheentirerangeofconsidereddensities,whichis10ordersof nalanswertothesequestionscanonlybeobtainedbymeansoftime{dependent forisothermalshocks,densitiesaslargeas1010:::1012cm 3wouldberequired.A magnitude.therefore,asharptransitionisnotexpectedtooccur,ratheragradual hydrodynamicmodelcalculations. changeoverabroadrangeofdensities.forexample,ifcool<0:01pwasdemanded readyoccursat1011cm 3.TheLTEratepredictstheshockstobecloseto AccordingtoBowen'srate,thetransitionfromisothermaltoadiabaticshocksal- theisothermallimitingcaseforalldensities.thisexplainsthedierencesbetween themodelcalculationsofbowen(1988)andfeuchtingeretal:(1993)concerningthe 6.3 resultingtemperaturestructures. namicsinthemodelcalculationsforcoolstellarenvelopes,especiallyinthecase Theresultsofthischapterstronglysuggesttoincludetime{dependentthermody- Discussion previouslyusedarenotsucientinthiscontext. Atimescalediscussioncanbeperformedinordertoclarifywhetherornottheconditionofradiativeequilibrium(RE)canbeusedtodeterminethegastemperature. Bycomparingtheradiativecoolingtimescalecool,asdepictedintheFigs.6.2and culationoftherelevantheatingandcoolingrates.simpleanalyticalexpressions ofpulsatingstars.thebasisforthethermodynamicdescriptionisarealisticcal- 6.4,withtheothertimescalescontrollingthephysicalprocessunderconsideration, itcanbedecidedwhetherthetemperaturesmaybecalculatedfromradiativetransfercalculations(assumingre),orwhether,forinstance,asimpleadiabaticcooling lawismoreappropriate. Thegeneraltendencyoftheresultsobtainedinthisworkisthatthecondition determinationonthebasisofreisjustied.however,ingeneral,time{dependent tobeoftheorderofdays,sothatreisprobablyestablishedandatemperature Forthelargedensitiesclosetothestartheradiativecoolingtimescalesarefound ofrecanonlypartlybeusedinordertodeterminethetemperatureofthegas. beconsidered,themorequestionablethedeterminationofthetemperatureonthe eectsasadiabaticcoolingcanthroughoutbeimportant.thelowerthedensityto basisofrebecomes.forinstance,atn<h>107cm 3inthewarmatomicphase, theradiativecoolingtimescaleapproachestheorderofoneyear,alreadyclosetothe Concerningtheshockedenvelopesofpulsatingstars,thethermodynamicsshouldbe expansiontimescaleinstationarywindmodelsforc{stars(e.g.krugeretal:1994).
120 treatedtime{dependentlyandifonlyfortheexistenceoftheshockwaves.additionally,apartfromthelocationsoftheshockfronts,strongdeviationsfromreare 100 CHAPTER6.RADIATIVECOOLINGTIMESCALESINC{STARS toapproximatelyadiabatic. expectedtooccurroughlyatdensitiesn<h><108cm 3,connectedwiththegradual transitionofthecharacteroftheshocks,changingfromapproximatelyisothermal heatingandcoolingratescalculatedinthisworkintothetime{dependenthydrodynamicmodelcalculationscanbeachievedbytabulatingqradandtheinternal temperature{dependenceofthechemicalandthenucleationprocesses,pronounced energyeasfunctionsof,tgandfurtherparameterscharacterizingthelocalcontinuousradiationeldandthelocalmeanvelocitygradient.accordingtothestrong eectsareconceivable3.anothertopicwhichmightberelatedtotheresultsofthis formationprocessesareaectedistobeinvestigated.theproperinclusionofthe peraturestructuresofcoolstellarenvelopes.howfarthechemicalandthedust Time{dependentthermodynamiceectscancausesubstantialchangesinthetem- workistheformationofchromospheres. dynamicmodelingmayhavewithregardtodustformation. 3Thefollowingchapterwilldemonstratewhatsevereconsequencesatime{dependentthermo-
121 Chapter7 RCBStars Shock{InducedCondensationaround modynamicprocess.themostcomplexlevelincludedintheworkisachieved: Thethirdandlastapplicationinthisworkstudiesadistincttime{dependentther- ThecircumstellarenvelopesofpulsatingRCBstarsareconsidered.Athermodynamicdescriptionforxeduidelementswhichareperiodicallyhitbyshockwaves isdeveloped.astheshockscompressthegas,itre{expandsinthemeantimewhich time{dependentnon{lte(inthesteadystateapproximation)andnon{re. causesconsiderableadiabaticcooling.theinternalenergybalance,thetemperature requiredforsuchnucleation.thecalculationsprovideahypothesisforthephysical elementsareinvestigated.specialattentionispaidtotheminimumradialdistance causeofthespectacularrcbdeclineeventswhicharesupposedtobecausedby ofthegasandthepossibilityforeectivecarbonnucleationtooccurinsuchuid AppendixA. andthescienticmeaningofthesestudiesarefurtherdescribedinsect.1.3andin dustformationclosetotheserelativelyhotstars.theastronomicalbackground 7.1 mentinaconstantradiationfield TheModel:AFixed,PeriodicallyShockedFluidEle- Achosenuidelementinthecircumstellarenvelopeofapulsatingstaristime followsaroughlyballistictrajectory,whilecooling,chemicallyrelaxingandre{ Fleischeretal:1992,Feuchtingeretal:1993).Betweentheshocks,theuidelement Theshocksaccelerate,heat,chemicallyalterandcompressthegas(Bowen1988, andtimeagainhitbypropagatingshockwavescausedbythestellarpulsation. playofdierentphysicalprocessestakesplace:hydrodynamics,thermodynamics, expanding(gillet&lafon1983,bowen1988). Thus,theCSEsofpulsatingstarsareastrophysicalsiteswhereacomplexinter- thermodynamicconsequencesofthehydrodynamicsituationofperiodicallyshocked circumstellarshockwavesisaverychallengingworkwhichgoesfarbeyondthescope ofthisthesis.instead,themodelcalculationspresentedinthischapterstudythe chemistryanddustformations.acompletemodelingoftheseprocessesoccurringin gas.asimplegas{boxdescriptionsuitableforthethermodynamicinvestigationsis 101
122 r r(t) developedforthissituationwhich,accordingtoobservations,isapparentlycommon 102 CHAPTER7.SHOCK{INDUCEDCONDENSATIONINRCBSTARS amongthedust{formingobjects(jura1986). Thecircumstellarenvelopeisassumedtooscillateinaperiodicmanner1.Furthermore,masslossisneglected.Masslossleadstoanadditionaloutwardmovemencussedinthischapter,whichisthetemporalsupercoolingofthegasbelowitsRE{ Therefore,theneglectionofmasslosssystematicallyunderestimatestheeectdis- accompaniedbyadditionalexpansion,whichcausesadditionaladiabaticcooling. temperatureduringthephasesofre{expansion.accordingtotheseassumptions, theuidelementexactlyreturnstoitsstartingpoint(cf.fig.7.1)andallhydrodynamicandthermodynamicquantitiesvaryperiodicallyintimewiththepulsation asbeingtypicalfortheenvelopesofpulsatingstars. periodofthestar.wewillconcentrateonthismostsimplecase,whichisconsidered v s.t Figure7.1:Lagrangiantrajectories(schematically,upperpanel)anddistance r gravitationaldeceleration.there{expansionofthegasbetweentheshocksis inthelaboratoryframe.onaverage,theaccelerationbyshocksisbalancedby cumstellarenvelopeofapulsatingstarwithoutmassloss.vsistheshockvelocity betweentwoneighboringuidelements(lowerpanel)intheshock{levitatedcir- t causedbythephase{shiftoftheballistictrajectoriesaccordingtothegravitation TheperiodicsituationassketchedinFig.7.1canbedividedintotwophases:the ofthestar. shocktransitionandthere{expansionofthegas.bothprocessesareexaminedin thefollowinginorderndanappropriateprescriptionoftheperiodicboundary envelopeispossibleevenifthestellarpulsationisperfectlyperiodic. conditions,whichthegaselementsareexposedto. 1Fleischeretal:(1995)havepointedoutthatamulti-periodicorevenchaoticoscillationofthe
123 7.1.1ShockTransitions 7.1.THEMODEL 103 TheshocktransitionsaretreatedbyapplyingtheRankine{Hugoniotrelations(e.g. Landau{Lifschitz1959).Theshockfrontisconsideredasinnitesimallythinandthe magneticeldsandvanishingcontributionsoftheradiativeuxareassumed: actualtransitionprocessasinstantaneous.thejumpconditionsforaplane{parallel ofmass,momentumandenergyinacomovingframeoftheshockfront.negligible perpendicularshock(~v?tothefront)aregivenbytheequationsoftheconservation p1+1v21=p2+2v22 12v21+h1=12v22+h2 1v1=2v2 (7.1) Equations(7.1)relatethehydrodynamicandthermodynamicpropertiesoftheupstreamow(index1,\pre{shock")tothoseofthedownstreamow(index2,\post{ shock").h=e+p=istheenthalpyandetheinternalenergypermassofthegas. Togetherwiththeequationofstate(cf.Chapter4)thepost{shockquantitiescan theequationofstateisapplicableagain.thistimeisassumedtobesmallcompared passageoftheshockwave,whenthegashasjustrelaxedtoitssteadystate,sothat Strictlyspeaking,theso{denedpost{shockstatereferstoadenitetimeafterthe becalculatedfromthepre{shockthermodynamicstateandtheshockvelocityv1. ofequations(7.1)requiresaniteration.thefollowingsimpleiterationschemeis topulsationperiodpandtheradiativecoolingtimescale. appliedwhichisfoundtoconvergereliably: Duetothenon{trivialequationofstateinvolved,theactualsolutionofthesystem 1)Startwithacompressionratiooffour(v2=v1=4). 2)Puth2=h1+(v21 v2)=2andp2=p1+1v1(v1 v2). 4)Dene=j1 (2v2)=(1v1)j. 3)Calculatethepost{shockdensityaccordingtotheequation 5)Performoneiterationstepbyv2!0:1v2+0:9v11=2. ofstateintheform2=2p2;h2;j;ddv dle. TheradiationeldJ,thevelocitygradientDdv 6)Gobacktostep2unless<10 8. beequalonbothsidesofthefront(cf.sect.7.1.6). Theseparametersaresettoxedvaluesduringthecalculationsandareassumedto additionalparametersforthecalculationoftheequationofstate(cf.chapter4). dleandtheelementabundancesiare Thecalculatedcompressionratios2=1forstrongshocks(v1pre{shocksound Accordingtothetheoreticaldescriptionoutlined,thegasiscompletelydissociated bythedissociationandionizationpotentialenergytermsintheequationofstate. valuesrangefrom5to9,dependingontheshockvelocity.thiseectiscaused speed)arefoundtobelargerthanthemaximumvalueof4foranidealgas.typical
124 andpartiallyionizedbystrongshocks.sincethedissipatedshockenergyispartly 104 CHAPTER7.SHOCK{INDUCEDCONDENSATIONINRCBSTARS consumedinordertobreakthechemicalbondsandtoionizetheatoms,thepost{ valuesare20000kto70000kforshockvelocities20kms 1to50kms 1.Thepost{ massivehydrogen{decientgas. shockgastemperaturesarefoundtobelowercomparedtoanidealgas.typical shocktemperaturesarehighercomparedtoahydrogen{richgasbecauseofthemore Betweentheshocks,thechangeoftheinternalenergyofthegasiscalculatedviathe 7.1.2Re{ExpansionPhases rstlawofthermodynamics(cf.sect.7.1.3).inordertondanappropriatedescriptionofthere{expansionprocess,asuitablestatevariableischosen,whoseexplicit cannotbylimitedtosingleuidelementconsiderations.thefollowingapproachis consistentphysicaldescriptionwouldincludetime{dependenthydrodynamicsand time{dependencecanbeprescribed.ofcourse,thisisanapproximateprocedure.a adaptedtotheexperienceofhydrodynamicmodelcalculations. p1isthepre{shockandp2thepost{shockgaspressure(cf.eq.7.1),modthe p 1=(t)=p 1= 2 +p 1= 1 p 1= 2 tmodp modulofunctionandtheadiabaticindexofthegas,whichisassumedtobe5/3 P (7.2) ismotivatedasfollows: inthiscontext.themainideaofthisapproachistoassumethatthegaspressure (i)inthelimiting(adiabatic)caseofnegligibleradiativeheating/cooling,where monotonicallydecreasesbetweentheshockswithapower{lawintime.theapproach pv=const,thevolumevarieslikeasaw{toothfunctionintime V1isthepre{shockvolumeandVmintheminimumvolumeofaxeduidelement V(t)=Vmin+(V1 Vmin)tMODP duringoneperiodiccycle.vminequalsthepost{shockvolumev2intheadiabatic P : (7.3) Inthiscase,theLagrangiantrajectoriesr(t)aresecond{orderpolynomialsandthe readilyobtainedifthegasactuallybehavespurelyballisticassketchedinfig.7.1. dependenthydrodynamicmodelcalculations(e.g.bowen1988,seehisfig.4).itis case.equation(7.3)providesagoodttothevolumevariationsfoundintime{ theabsoluteradialdistance,theenclosedvolumev/r2risproportionaltor and,therefore,alsoasaw{toothfunction.ingeneral,takingintoaccountradiativeheatingandcooling,thecalculatedvolumevariationdoesnotdiermuchfrom Eq.(7.3)asdemonstratedinFig.7.3.ThemaindierenceisthatinthiscaseVmin distancebetweentwoneighboringuidelementsrvarieslikeasaw{toothfunctionsintime.supposedthattheamplitudeofradialmotionissmallcomparedto issmallerthanv2,whichwillbecomemoreclearinthenextparagraph.
125 (ii)accordingtoeq.(7.2)thegaspressurevariesonatimescaleofp.hence,fast 7.1.THEMODEL 105 thepassageofashockwave,wherethegasishotandcoolsveryeciently.this theuidelementcompressesbyfastcooling,whichespeciallyoccursshortlyafter radiativecoolingwithcoolpautomaticallyproceedsisobaricly.consequently, aboutafactor4isfollowedbyasubsequentpost{shockcompression,whichamounts 1979and1989,Neufeld&Hollenbach1994),wheretheinitialshockcompressionof uptoafactor100.thereasonforthisbehavioristhattheowissubsonicbehind matcheswellwiththeresultsofstationaryshockmodels(e.g.hollenbach&mckee thefront,sothatpressurebalancecanestablish.thecitedcalculationsshowthat astationaryow.therefore,againconsideringtheperiodicshocks,vminingeneral compressionbyradiativecooling2.thepost{shockcoolingusuallyproceedssofast, doesnotcoincidewithv2,butissubstantiallysmallerduetosubsequentpost{shock p=constisvalidwithin25%accuracyinthewholepost{shockregioninthecaseof (iii)accordingtotheassumptionthatthepressurevariationismonotonicallydecreasingbetweentheshocks,theamplitudeofpressurevariationisgivenbythejump thateq.(7.3)isstillagoodapproximationoftheresultingoverallvolumevariation. conditionseq.(7.1).thereisnoneedtointroduceadditionalfreeparametersin ordertodescribetheamplitudeofthecyclicvariationscausedbytheshocks.especiallyvminisaresultofthecalculations.ifthevolumewaschosentobeprescribed, Theresultsarenotmuchaectedbytheassumedslopeofthepressuretime{ dependence.additionalcalculationshavebeencarriedoutwithdierentvalues forandalsocalculationswherethevolumewaschosentobeprescribed(using onefreeparameter,thatisvmin,wouldbeadditionallyrequired. onlytheexistenceofaperiodicalperturbationoftheuidelementanditsamplitude (characterizedbytheshockvelocity)areapparentlyimportant. Eq.(7.3)withVminasadditionalfreeparameter).Theresultsareverysimilar 7.1.3Thermodynamics Thetimeevolutionoftheinternalenergyeoftheconsidereduidelementduring dynamics there{expansionphasesisstraightforwardlycalculatedviatherstlawofthermo- thespecicenthalpyh=e+p=andtosolveinstead Sincethegaspressureischosentobeprescribed,itismoreconvenienttoconsider de dt= pdv dt+bqrad: (7.4) Equation(7.5)issolvedbyimplicitnumericalintegrationwithadaptivestepsize dh dt=+vdp control.thekeyforthiscalculationisthedeterminationofthestateofthegasand dt+bqrad: thepressuregradientprovidesanon{negligiblehydrodynamicforce. 2Consequently,thetrajectoriesareinfactnotpurelyballistic.Inthehotpost{shockregions
126 thenetradiativeheating/coolingrateasfunctionofp,h,jandddv 106 CHAPTER7.SHOCK{INDUCEDCONDENSATIONINRCBSTARS calculations. andqradateveryinstantoftime,sothateq.(7.5)becomesanordinarydierential equation.thegastemperaturetgasfunctionoftimeisanimplicitresultofthese dlewhichyieldsv issketchedinfig.7.2.auidelementinthecseofapulsating(rcb)staris Aschematicdescriptionofthethermodynamicprocessesandthemodelingprocedure 7.1.4TheModelingProcedure considered.inphase1theelementishitbyapropagatingshockwave,whereitis heatedandcompressed(!v2).duringphase2itcoolsdownandfurthercompresses duetofast,approximatelyisobaricradiativecooling(!vmin).accordingtothe periodicityintheseenvelopes,thegaselementnallyre-expandsduringtherestof eachperiodicalcycleinphase3(!v1).thesethreephasesrepeatperiodically. thermodynamic processes model 1) shock solution of the transition jump conditions } 2) post shock cooling solution of dh dp ^ = V + Qrad dt dt for given p=p(t) 3) re expansion Figure7.2:Thethreeperiodicallyrepeatingphasesofshocktransition,post{ : heating heating(inphase3).thetheoreticaldescriptionoftheprocessesisoutlinedon shockcoolingandre{expansionforauidelementinthecircumstellarenvelope : radiative / cooling therighthandside ofapulsatingstar.wiggledarrowsindicatenetradiativecooling(inphase2)or : adiabatic cooling
127 Themodelsimulatestheseprocessesbysolvingtheshockjumpconditionsatthe 7.1.THEMODEL 107 mentbecomeperiodically.usually3to25periodsarerequiredinordertoachieve instantsoftimewheretheshockwaveshitthegaselementt2f0;1p;2p;:::gand bycalculatingtherstlawofthermodynamicsinthemeantime.thecalculations arecontinueduntilthevariationsofthethermodynamicquantitiesinthegasele- periodicity.indetail,thecalculationsproceedasfollows: 1)ChooseaxedradiationeldJ,axedvelocitygradientDdv 2)Ateveryfullperiod,solvethejumpconditionsEq.(7.1)forthepost{ arbitraryinitialenthalpyh1. shockvelocityv1andatxedpre{shockgaspressurep1.startwithan dle,axed 3)Considerthetimevariationofthegaspressureduringtheforthcoming shockstate(p2;h2). 4)Gobacktostep2,unlessallvariationshavebecomeperiodic. thalpyaccordingtoeq.(7.5),yielding(p1;h01)attheendofthisperiod. periodasexplicitlygivenaccordingtoeq.(7.2)andcalculatetheen- Thenal(periodic)resultsofthemodeldependonthefollowingparameters: 7.1.5OverviewofIntroducedParameters Twoparametersforthedescriptionofthebackgroundcontinuousradiationeld(Teandr=R,cf.Eq.5.3). Parametersforthecompositionandtheoveralldensityoftheconsidered Twoparametersforthestrengthandthefrequencyofthepropagating shockwaves(v1andp). Twoadditionalparameterswhoseeectsontheresultsaresmall,that gaselement(iandp1). isthelocalmeanvelocitygradientddv explicitpressuretime{dependenceduringre{expansion(cf.eq.7.2). dleandthepowerindexforthe 7.1.6ExaminedRangeofParameters Teandr=R:TheeectivetemperatureofthecentralRCBstarisassumedto be7000kthroughoutthischapter,whichapparentlyisarepresentativevaluefor beconstantduringthecalculations.incontrast,asignicantradialmotionofthe uidelement(assketchedinfig.7.1)isassumedtobesmallcomparedtor,so thatr=r,forsimplicity,isxed.thereby,themeanintensityjisassumedto thisclassofstars(lambert&rao1994).thevariationoftheradialpositionofthe areconsidered. furthercomplicationofthemodelofminorimportance.radialdistancesof1:5 5R uidelementwouldimplyanadditionaltime{dependenceofj,whichisregardedas
128 P:Thepulsationperiodisassumedtobe44days,whichisthevaluesuggestedby 108 CHAPTER7.SHOCK{INDUCEDCONDENSATIONINRCBSTARS Fernieetal:(1972)forRCrB.SinceotherRCBstarsshowverysimilarvaluesforP (cf.appendixa)thisparameterisalsoxedforthecalculations. willfurthermoredependontheconsideredradialdistance.time{dependentmodels v1:theshockvelocityisuncertain,maybedierentfordierentrcbstarsand developsomewherebelowthephotosphere,wherethevelocityvariationisusuallya fewkms 1.Theshocksconsiderablysteepenupaccordingtotheexponentialdensity 1992,Wintersetal:1994,Feuchtingeretal:1993)indicatethattheshocksbeginto forthecircumstellarenvelopesoflong{periodvariables(bowen1988,fleischeretal: gradientintheouteratmosphereandsoonreachshockvelocitiesof30kms 1(the shockvelocitycanapproximatelybeidentiedwiththeamplitudeofvelocityjumps occurringinthesemodels).atlargerradialdistances,thedensitygradientbecomes orevenalmostzero,dependingonthemodel.itisunclear,whethertheseresults smallerandtheshockvelocityusuallytendstodecreaseagain,leadingto10kms 1 canbeadoptedtorcbstars.largephotosphericvelocityvariationsof20km 1 (implyingshockvelocitiesof40kms 1)havebeenobservedforRYSgr,whichis thestrongestknownpulsatingrcbstar(cf.appendixa).thesemeasurements strongershockscanbeexpectedinthecse3.however,rysgrisanexceptional refertothelineformationregion,i.e.tothephotosphereofthestar.considerably case.otherrcbstarsshowradialvelocityvariationsofabout5to10kms 1, butnolinesplittingwhichisanindicatorforshockactivityinthephotosphere (AppendixA).ShockactivityintheCSEisprobablynotdirectlydetectable,at leastnotatmaximumlight(apartfromthedeclineevents),whenthestaristoo bright.therefore,thequestionsoftheexistenceofshockwavesinthecsesof RCBstarsandtheirvelocitiescannotbedecidedbyobservationsyet.Thiswork fromtheory.shockvelocitiesof20 50kms 1areconsidered. presupposesthepresenceofshockwavesinrcbstarenvelopes,since(i)rcbstars showconsiderableradialvelocityvariationsatthephotosphereand(ii)evensmall i:theelementalabundancesoftheprototypestarrcrbareadoptedfromcottrell& amplitudewavesareknowntosteepenuptoconsiderableshockwavesinthecse Lambert(1982),cf.Fig.5.1. increasingradialdistance,theactualdensitystructureofthecircumstellarenvelopes p1:thepre{shockpressureoftheuidelementsisvariedindependentlyofr=r. Althoughthemeangaspressurecanbeexpectedtomonotonicallydecreasewith comparedtoagbstarenvelopes.forshock{levitatedcsesassketchedinfig.7.1,v1gep ThegravitationalforceatthephotosphereofanRCBstarisabout30timeslargerthanthatof isagoodapproximation.geisthegravitationaldecelerationcorrectedforradiativeacceleration. 3ThefollowingtheoreticalconsiderationpointstolargershockvelocitiesinRCBstarenvelopes aboutafactorof10smaller,yieldingabout3timeslargershockvelocitiescomparedtoagbstars. If10kms 1isconsideredasatypicalvalueforAGBstars,valuesofabout30kms 1arededuced anagbstar(roughlyassumingequalstellarmassesandluminosities)andthepulsationperiod fortheenvelopesofrcbstars.
129 7.2.RESULTS 109 ofrcbstarsisnotknown.pre{shockgaspressuresof dyncm 2are considered. Themeanlocalvelocitygradientisnocrucialparametertothemodelandisassumed tobegivenbyddv dle=v1=r.thestellarradiusisassumedtober=73rinthis context(fernie1982).thepowerindexfortheprescriptionofthetime{dependence ofthegaspressureissetto=5= Results 7.2.1CyclicVariationsinthePeriodicallyShockedFluidElements Anexampleoftheresultsforthecyclicvariationsofthethermodynamicstate variablesinxed,periodicallyshocked,circumstellaruidelementsisdepictedin Fig.7.3.Therst3periodsafterperiodicityhasbeenachievedareplottedona lineartimescale.thepost{shockgastemperatureisfoundtobe24000kinthe consideredcase,whichisoutofthedepictedrange.duringtherst1:5%ofthe period(16hours)thegasecientlycoolsdownto10000k,whichcausesfurther compression.theshockcompressionfactoris6:2andthepost{shockcompression factoris2:0.anattempttodepictthedierencebetweentheshockandthepost{ shockcompressionismadeinthemiddlepanel,butonthislinearscalethetotal (shock+post{shock)compressionphaseappearslikeasingle,almostinstantaneous process.thegasapproximatelyre{expandsadiabaticallyafterthiscompression.a saw{toothlikebehaviorofthevolumeresults.thetemperaturereachestre gafter about10%oftheperiodandisclearlybelowtre g afterwards.hereandinthe remainderofthischaptertre gdenotestherststable\high{temperature"solution ofradiativeequilibriumasdenedinchapter5.tre g isdensity{dependentand hencenotconstant. Infact,thevalueofTRE gispracticallymeaninglessforthegasinthedepictedcase ofp1=1:610 5dyncm 2,whichcorrespondstoadensityvariationofn<He>= 6107:::7108cm 3.Thetime{dependenttemperatureofthegasisessentially determinedbytheshocktransitionandtheeciencyoftheradiativecoolingathigh{ temperaturesduringthepost{shockcoolingphase.thesetwophasesdeterminethe starttemperatureandthetotal(de{)compressionfactorfortheforthcomingphase ofre{expansionwhichproceedsapproximatelyadiabatically.reisneverrealized andcannotbeusedtodeterminethetemperatureofthegas. FurtherdetailsareshowninFig.7.4,wherethesamesettingoftheparameters isinvestigatedexceptforalargershockvelocityof50kms 1.Inthiscase,the post{shocktemperatureisfoundtobe64000kandtheshockandpost{shock compressionfactorsare8:4and11,respectively.allradiativeprocessescause netcoolingbehindtheshockandsincethecoolingtimescaleisasshortasinitially 100s,theuidelementveryquicklycoolsdownduetoradiativelosses.Within therst0:3%oftheperiod(3hours),thetemperaturedropsto8000k.
130 110 CHAPTER7.SHOCK{INDUCEDCONDENSATIONINRCBSTARS plottedfordistancer=2r,shockvelocityv1=20kms 1andpre{shockpressure specicvolumeandthegastemperature(calculated,middleandlowerpanel)is Figure7.3:Timevariationsinaxed,periodicallyshocked,circumstellaruid p1=1:610 5dyncm 2.Thedottedlinesinthemiddlepanelindicatethepre{ elementofanrcbstar.thegaspressure(assumed,upperpanel)andthe depictstheradiativeequilibriumgastemperature. shock,post{shockandminimumvolume.thedashedlineinthelowerpanel
131 7.2.RESULTS Duringthisphase,whichisplottedonalogarithmictimescaleinFig.7.4,the 111 panel.thetemperaturereachestre uidelementcompressesascanbeseenfromtheincreasingdensityintheupper theremainingtimeoftheperiod,theuidelementre-expandsbyatotalfactorof 92.Thisre-expansioncausesintenseadiabaticcoolingasindicatedbythecooling rateqadb=vdp=dtinfig.7.4,whichistheconcurringratefordh=dtineq.(7.5). gafter1%oftheperiod(10hours).during heatingfunctionqradchangesitssign(notethetwofoldlogarithmicy{axisinthe Consequently,thegastemperaturedecreasesbelowTRE Thedecisivepointforthethermalbehaviorofthisuidelementisreachednow.The lowerpaneloffig.7.4). gandthetotalnetradiative ofthegasissucientinordertoovercomethismaximum.iftheanswerisno,the adiabaticcoolingofthegasiscompensatedbynetradiativeheating,thecoolingof atatemperatureof3000k.thequestioniswhetherornottheadiabaticcooling pointisrelatedtotherstintermediatemaximumofqrad(tg)depictedinfig.5.2 Tg<TRE timeoftheperiod(atlowergastemperaturesjqradjisusuallysmallercomparedto thegasisstoppedandthere{expansionproceedsmoreorlessisothermally(with therstmaximum),andthere-expansionapproximatelyproceedsadiabatically. g).iftheanswerisyes,theadiabaticratedominatesduringtheremaining Thecharacterofthere{expansionprocess,beingeitherisothermaloradiinantlyneutral,atomicphaseofthegas(causedbylineandbound{free transitions)priortomoleculeformation4. abatic,isdecidedbytheeciencyoftheradiativeheatinginthepredom- Inthegure,theadiabaticcoolingexceedsthenetradiativeheatingrate(jQadbj> heating/coolingfunctionsenterintocompetition,andsoonbecomemoreimportant lineheating/coolingratehasbeendominating,nowthevibrationalandrotational coolenoughinordertoallowforconsiderablemoleculeformation.whilesofarthe jbqradj)and,thus,thecoolingofthegascontinues.subsequently,thegasbecomes thanqlines.sincethemolecularratescausenetradiativecoolingforthepresent, Qradagainchangesitssignandtheadiabaticcoolingofthegasisnallyeven process. duringthere{expansion,whichisplottedonalinearscaleinfig.7.4.consequently, supportedbynetradiativecooling.however,qadbremainsthemostimportantrate Thus,thegastemperatureislowerthaninradiativeequilibriumalmostallthetime. there{expansionwhichtakesabout99%oftheperiodapproximatelyisanadiabatic Thegastemperaturenallyreachesaminimumvalueof780Kandisbelow1500K discussedinthesect forabout60%oftheperiodatdensitiesn<he>=4108:::1:5108cm 3.These arethermodynamicconditionsfavorableforeectivecarbonnucleation,aswillbe excessinternalenergydissipatedbyashock,cf.sect Thisstatementreferstocaseswherethegasrstofalliscapabletoquicklyradiateawaythe
132 112 CHAPTER7.SHOCK{INDUCEDCONDENSATIONINRCBSTARS Figure7.4:Detailsofthetimevariationsinaxed,periodicallyshocked,circumstellar uidelementofanrcbstar.thex{axisisbrokeninthisplot.therst2%ofthe theheatingandcoolingrates,respectively.thethickfulllineshowsthetotalnetradiative andthetotalheliumparticledensity(dottedline).themiddleandlowerpaneldepict Theupperpanelshowsthegastemperature(fullline),theREtemperature(dashedline) periodaredepictedonalogarithmicscale,whereastheother98%areplottedlinearly. rateandtheotherthindottedanddashedlinesdepictpartialrates,thesesarethenet thethickdottedline.parameters:r=2r,v1=50kms 1andp1=1:610 5dyncm 2. sumsoftheradiativegains/lossescausedbytheindicatedtransitiontype(i.e.allbound{ freetransitions,allvibrationaltransitionsetc.).theadiabaticcoolingrateisdepictedby free{free,bound{free,atomicline,vibrationalandrotationalrates.thelatterratesarethe
133 7.2.RESULTS 113 Figure7.5:Cyclicvariationsofdensityandtemperatureinperiodicallyshocked uidelementsatr=2r.theelementsdierbydierentvaluesofthepre{shock v1=20kms 1andv1=50kms 1,respectively.Theshortdashedlinesindicate theshocktransitions.thelongdashedlineshowstheradiativeequilibriumgas gaspressure.thegrayandblackcyclesdepicttheresultsforshockvelocities 7.2.2DependenceonDensity temperature. pressurep1,whichxesthemeandensityofthegasduringtheperiodicvariations. Theresultsdiscussedsofarhavebeencalculatedforaparticularpre{shockgas shocksisquitedierentforotherdensities.thisdensity{dependenceisdepicted sity(cf.chapter6),thethermalbehaviorofthegasinresponsetotheperiodic infig.7.5,wheretheperiodicallyrepeatingthermodynamicprocessesappearas Sincetheeciencyoftheradiativeheating/coolingisstronglyaectedbytheden- counterclockwisecycles. withthepost{shockstate(uppercorner),thegaselementreachesre(leftcorner) aratedandanalmosttriangularcycleresults(seel.h.s.ofthegure).beginning Concerningverylargedensities,thethreephasessketchedinFig.7.2arewellsep-
134 within1%oftheperiodduetoecient,approximatelyisobaricradiativecooling.theslightdeparturefromastraightlineonthiscoolingtrackisrelatedto 114 CHAPTER7.SHOCK{INDUCEDCONDENSATIONINRCBSTARS expansion.therefore,thegastemperaturestaysclosetotre of2.sincethecouplingtoreisstrongatthesedensities,theadiabaticcooling therecombinationofhe,wherethemeangasparticleweightchangesbyafactor ratesarenegligiblecomparedtotheradiativeratesinthesubsequentphaseofre{ caseofisothermalshocks.forabout99%oftheperiod,theelementiscloseto uppercorneragain,etc.thetriangularcyclesaretypicalresultsforthelimiting leadingtotherightcorner.finally,theuidelementisshockedandjumpstothe gduringthisprocess duringtheoverwhelmingpartoftheperiod.however,thisprocedureisonlyfeasibleforlargedensities.roughlyspeaking,reisareliablecriterionfortemperature determinationfordensitiesn<he>>1011cm 3. RE.Therefore,theconditionofREcanbeusedtodeterminethegastemperature consequently,thegasneverapproachesre.onthecontrary,acorona{likesituation energydissipatedbyoneshockcannotberadiatedawayduringoneperiodand, results,wherethegasisheateduptoextremelyhightemperaturesduetotheenergy Ontheotherextreme,consideringthecaseofverysmalldensities,theexcessinternal dissipationofwaves.forexample,inthecycleonther.h.s.forv1=50kms 1,thegas Oncethegashasrecombined,itscoolingtimescalebecomesmuchlargerthanthe ispredominantlyionizedandalwayshotterthan20000k.thisbehavioristypical period. forthelimitingcaseofadiabaticshocks.theresultingperiodictracks(seer.h.s.of Concerninganintermediaterangeofdensities,theradiativeenergyexchangeis Fig.7.5)consistofshocktransition,Herecombinationandadiabaticre{expansion. downfarbelowtre coolingratesduringthephasesofre{expansion.inthiscasetheuidelementcools shocks,butisnottooecientinordertobemaintainbalancewiththeadiabatic ecientenoughinordertocauseafastrelaxationofthegastowardsreafterthe ofmoleculedissociationenergy. (mainlycoandc3),wherethefurthercoolingofthegasisdelayedbytheliberation adiabatictracksatthelowerpartoffig.7.5arecausedbymoleculeformation g asdiscussedinsect thesmallkinksonthealmost Asupercoolingofthegasoccurswithinadistinctdensity{intervalcaused byatwo{stepprocessofradiativecoolingathightemperaturesfollowed dependentcooling/heatingeciencyofthegas.regardingthebroadspectrumof Thedensity{dependencedepictedinFig.7.5isanaturalconsequenceofthedensity{ byadiabaticcoolingatlowtemperatures. ofapulsatingstarthedensityisjustappropriateforthiseect. densitiesencounteredincses,itseemsinevitablethatsomewhereintheenvelope
135 7.2.RESULTS 7.2.3DependenceonShockVelocity 115 arelargerforstrongshocks,implyinglargeradiabaticcoolingratesduringthephases mightbesurprising,butitisactuallystraightforward.thetotalcompressionratios butdoalsoallowforlowerminimumtemperatures.atrstsight,thisdependence Largershockvelocitiesv1producehighermaximumtemperaturesbehindtheshocks, oftheperturbation,causingbothup{anddownwarddeviationsfromre. ofre{expansion.theshockvelocitycanberegardedasameasurefortheamplitude 7.2.4PreconditionsforCarbonNucleation Inthefollowing,thepossibilityofeectivecarbonnucleationtotakeplaceinthese counteredincircumstellarenvelopes,thesizeofthecriticalclusterusuallyisassmall periodicallyshockeduidelementsisinvestigated5.consideringthedensitiesen- temperatureofmacroscopicdustparticles(the\dusttemperature").accordingto as10atoms.therefore,thechemicalreactionsinvolvedintheformationprocessof suchseedsareassumedtobecontrolledbythegastemperatureratherthanthere assumedradiationeld,macroscopicgrains(strictlyspeaking,graphitegrainsinthesmallparticle limitofmietheory)denitelyevaporateatthesmallradialdistancesunderinvestigation,because theirinternaltemperaturesaremuchtoohigh(fadeyev1988).incontrast,largemoleculesmight 5Theformationofmacroscopicdustgrainsisnotdiscussedinthiswork.Accordingtothe bestableprovidedthattheiropticalanduvabsorptionpropertiesarecomparablesmaller. onceadustcloudhasformed,theradiationowsaroundtheopticallythickregionandnewdust easilyincreasetheabsorptioncoecientofthegas/dustmixturebyafactorof105.therefore, tocausealocalreductionofthedusttemperature.thephasetransitionfromgastodustcan Absorptionbythedustitselfisapromisingcandidateinordertoblockotheradiationeldand Apparently,theformationofdustclosetothestarmustbeaccompaniedbysomekindofshielding. particlesmaycondenseandgrowintheshadowofthiscloud,whereasthegrainsattheinneredge ofthecloudtowardsthestarswillevaporate.aquasistablesituationmightbeconceivablewhere star.sphericaldustformationinadistinctradiallayercausesanincreaseofthedusttemperatures inthelayerswithintheshellviaback{warmingandhasalmostnoeectonthedusttemperature Incontrast,theformationofasphericaldustshellseemstobeabsolutelyimpossibleclosetothe thedustcloudsurvivesthestrongradiationeldviaself{shieldinginadynamicalsense. ratherthandustshellformationincaseswherethegasissucientlydenseandcoolfornucleation intheouterlayers,becausetheradiationuxisnotblocked,butjusttransmitted. Thus,aninstabilitycausedbydustformationpossiblyexistswhichfavorsdustcloudformation butastrongradiationeldhinderstheseedparticlestogrowfurther. starenvelopes.inordertoclarifythesequestions,atleast2dmodelcalculationsarerequired, Dicultquestionsareraisedbytheseconsiderations,whichmaybeimportantnotonlyforthe dustformationinrcbstarsbutforanyharshradiationeldenvironments,e.g.inwolf{rayet dustgrains.dustformationclosetothestarinanycasemustproceedviathisrststep. theformationofseedparticlesandleaveasidetheproblemofthethermalstabilityofmacroscopic ontherstnecessarystepconcerningthetransitionfromthegasphasetodustparticles,whichis challengingproblemwhichgoesfarbeyondthescopeofthiswork.therefore,iwillconcentrate whichmustincluderadiativetransferandtime{dependentdustformation/destruction avery
136 thisassumption,thesupersaturationratiosiscalculatedas 116 CHAPTER7.SHOCK{INDUCEDCONDENSATIONINRCBSTARS S=nCkTg isthevaporpressureofcarbonatomsoverthebulkmaterial(graphite)atgas wherencistheparticledensityofneutralcarbonatomsinthegasphaseandpsat psat(tg); (7.6) Figure7.6showsthisconditionandgivesanoverviewofallresultsconcerningthe temperature.anecessaryconditionforcarbonnucleationtotakeplaceiss>1. periodicallyshockeduidelementsatr=2r.theminimumgastemperature occurringinoneperiodiccycleisdepictedasafunctionofthemeanheliumparticle densityduringthecyclewhichisdenedas Figure7.6demonstratesthattheconditionsappropriateforeectivecarbonnucleationaretemporarilypresentintheperiodicallyshockeduidelements,concerning 0n<He>dt: (7.7) n<he>=1pzp adistinctdensity{intervalbracketedbyn<he>=107:3cm 3and109:3cm 3.Incontrast,dustformationisthermodynamicallyimpossibleatr=2R,ifthetemperature ofthegasisgivenbytre persecond,iscalculatedbyapplyingclassicalnucleationtheory(gailetal:1984). ThenucleationrateJ,whichisthenumberofseedparticlesformingpervolumeand librium(cf.chapter5). g,whichisthehigh{temperaturesolutionofradiativeequiestingdensity{interval,nucleationratesofj=n<he>=10 13:5:::10 15:5s 1occur, ThenucleationratesareplottedascontourlinesinFig.7.6.Consideringtheinter- ecientcarbonnucleationmaytakeplace. Thetotalgrowthtimeforaseedparticletoreachamacroscopicsize,say0:01m, elsfortheenvelopesoflong{periodvariables(fleischeretal:1992),indicatingthat whicharelargevaluescomparedtothoseexperiencedfromtime{dependentmod- thatdustgrowthispossible(cf.footnote5): ofcarbonlockedinco).thedusttemperatureisassumedtobesucientlylowso intoaccountallthermallyimpingingcarbonbearingspecies(exceptfortheamount canbeestimatedbyconsideringthethreedimensionalgrowthbyaccretion,taking V0=4=3a30isthemonomervolume(a0=1:2810 8cmforgraphite,Gailetal:1984), tot gr= V0(n<C> n<o>)vth 0:01m (7.8) sidered)andthestickingprobability.assuming=1,alowerlimitiscalculated fortheactualtotalgrowthtime. vth=qktg=(2mc)thethermalvelocity(whichisabitsmallerifmoleculesarecon- isoftheorderofafewweeks(feast1986).inanycase,thetotalgrowthtimemust regionshouldnotexceedthetimescaleoftheinitialdropofthelight{curve,which InordertocauseaRCBdeclineevent,thetotalgrowthtimeinthedustforming
137 7.2.RESULTS 117 meangasdensityduringthecyclefortwodierentshockvelocitiesasindicated. theminimumtemperaturesoccurringinoneperiodiccycleasfunctionofthe tooccurataradialdistanceofr=2r.thefulllinesandpointsdepict Figure7.6:Minimumgastemperaturesandthepossibilityofcarbonnucleation oftheguresketchesthecondensationregime,i.e.theregionoffavorable thermodynamicconditionsforcarbonnucleation.onlybelowthes=1{limit, thegasissupersaturatedwithrespecttographite.contourlinesofthelogarithm Thedashedlineistheradiativeequilibriumgastemperature.Thelowerpart onepulsationperiod. oftheclassicalnucleationratej[cm 3s 1]areplotted.Ontherightedge,the growthtimeforaseedparticletoreachthemacroscopicsizeof0:01mexceeds
138 notexceedthepulsationperiodofthestar.thisconditionisadditionallyshown 118 CHAPTER7.SHOCK{INDUCEDCONDENSATIONINRCBSTARS thegasoccurs. thisconditionisjustfullledwithinthedensity{interval,wherethesupercoolingof infig.7.6,constitutinganabsolutelowerlimitforthedensityinthedustforming region,whichcanberesponsibleforanrcbdeclineevent.asdepictedinfig.7.6, Thepredictionsofthemodelconcerningtheminimumradialdistancerequiredfor ecientcarbonnucleationareofspecialinterest.previousmodelingofdustformationinthecsesofrcbstarshassueredfromthenecessitytoconsiderratherlargtionstellusthatdustformationprobablyoccursmuchclosertothestar(cf.sect.1.3 Thedependenceoftheresultsofthismodelontheparameterr=Risdepictedin andappendixa). radialdistancesinordertoobtainsucientlylowtemperatures,whereasobserva DependenceonRadialDistance Table7.1,wheretheminimumoftheTg;min{curve(cf.Fig.7.6)isstatedintherst rowandtheintervalofmeanheliumparticledensitieswithtg;min(n<he>)<1500k isstatedinthesecondrow. Table7.1:Resultsasfunctionofradialdistanceandshockvelocity. r=1:5r v1=20kms K v1=50kms 1 r=2:0r 1950K (0:2:::6:5)108cm K r=3:0r(3:7:::13)108cm K { (0:2:::18)108cm 3 710K r=5:0r(2:3:::77)108cm 3(0:2:::650)108cm 3 950K (0:2:::69)108cm 3 500K 200K ismuchlessdistinctivethanexperiencedfromre.achangeoftheshockvelocity, thestar,theeasierlowtemperaturesappropriateforcarbonnucleationareachievable.however,intheexaminedcaseoftime{dependentnon{re,thisdependence Thegeneraltendencyoftheresultsisasexpected:thelargertheradialdistanceto forexample,caneasilycauseverydierentconditions.consideringthe20kms 1 shocks,gastemperatureslowerthan1500kareproducedforr>3r,whereasconcerningthe50kms 1shocks,evenlowergastemperaturesoccurforallconsidered radialdistances. interval,centeredaroundafew108cm 3inallconsideredcases.Theparticular temporalsupercoolingofthegasbehindshockwavesisonlypossiblewithinaspecial, Comparedtotheinuenceofr=R,thedensity{dependenceisveryselective.The narrowdensity{interval.thedeeperthetemperature{minimum,thewiderthis
139 7.3.DISCUSSION density{rangeisingoodagreementwiththeestimatespresentedbygoeres(1992) 119 forthedensityofthedustformingregionsintheenvelopesofrcbstars. Therefore,theinuenceofr=Rontheresultsislesspronouncedthantheinuence atradialdistancesassmallas1:5 3R.Strictlyspeaking,thisstatementrefersto notverydistinct.theessentialoutcomeofthismodelitthatshockwavesare principallycapabletoproducelowtemperaturesappropriateforcarbonnucleation ofv1andn<he>.thepredictedvaluesforthecondensationdistancearehence heatingandcompressionfollowedbyre{expansionissupposedtobeaninevitable, theinvestigatedcaseofperiodicshocks.however,sincethebasicprocessesofshock straightforwardconsequenceofcircumstellarshockwaves,iconclude: everasucientlystrongshockwaveencountersthosepartsofthecir- cumstellarenvelope,wherethegasdensityisjustappropriateforthe two{stepcoolingprocessdescribedinsect Favorablethermodynamicconditionsforcarbonnucleationoccur,when- pulsatingrcbstarshasbeeninvestigated.thecomplexinterplaybetweenshock{ 7.3 ThethermodynamicbehaviorofperiodicallyshockeduidelementsintheCSEsof Discussion gasdensityandthegastemperature,dependingontheshockvelocity. foundtooccurinthissituation,comprising1 2ordersofmagnitudesforboththe Largetime{variationsofthethermodynamicconditionsinxeduidelementsare heating,radiativeheatingandcoolingandadiabaticcoolinghasbeenexamined. Thecalculationsprovideahypothesisforthephysicalcauseoftheonsetofdust formationclosetoapulsatingrcbstar,connectedwiththequestionofthetrigger conditionsforcarbonnucleationarefoundtobetemporarilypresentclosetothe star,despiteofthehigheectivetemperaturesofthercbstars.thefollowing ofthercb{typedeclineevents.asaconsequenceofthepresenceofshockwaves, twobasicconditionsarerequiredinordertoallowforeectivecondensationclose thegasisusuallynotinre.inthetime{dependentnon{resituation,favorable toarbitraryshockwaves,nomatterhowtheshockwascreated. shockvelocitymustbelargerthanabout20kms 1.Theresultscanbegeneralized tothestar.thegasdensitymustbebracketedbyabout cm 3andthe overviewofpreviouslypublishedmodelscanbefoundinappendixa.ashort discussionofthepossiblelinkstoobservationscompletesthischapter. hand,andthemainpointsofcriticismontheotherhand.forcomparison,an InthefollowingIwillbrieysummarizetheadvantagesofthismodelontheone 7.3.1AdvantagesoftheModel 1)Theobviousattractionofthemodelisthatdustformationclosetothestar isexplainedfromphysics.themodelpredictsthattemperaturesaslowas
140 Kcanbepresentatradialdistancesassmallas2R.Accordingtothe CHAPTER7.SHOCK{INDUCEDCONDENSATIONINRCBSTARS 2)Thecondensationdistancesarefoundtobeassmallas1:5 3R,inagreementwiththevaluesinferredfromobservations(e.g.Claytonetal:1992, factmeansfavorableconditionsforcarbonnucleation. calculations,theseconditionslastformorethanhalfoftheperiodwhichin cf.sect.1.3).incontrast,noneofthepublishedmodelscanexplainthis 3)Thenarrowdensity{intervalnecessaryforthetwo{stepcoolingprocesscausing fundamentalfeatureofthedustformationinrcbenvelopesinaquantitative thelowtemperaturesagreeswithpreviousestimatesofthedensityinthenucleationzoneofrcbstars(goeres1992).thisagreementisnotself{evident. way. icalpropertyofthegas,whichistheradiativeheating/coolingeciency.this eciencydecreaseswithdecreasinggasdensityduetoincreasingnon{lte Thedensity{dependenceofthemodeliscausedbyacompletelydierentphys- 4)Thedependencyofthemodelontheeectivetemperatureofthestarissmall. PreliminarytestcalculationswithTe= Kyieldsimilarresults eects. phenomenonisreportedforavarietyofstarscomprisingeectivetemperatures occurat1:5rforashockvelocityof50kms 1.Thisinsensibilityofthe modelwithrespecttoteapparentlyagreeswithobservations,sincethercb asdepictedabove.evenforte=9000k,gastemperaturesbelow1000k pronouncedte{dependence. of K.Incontrast,allotherproposedphysicalmodelsexhibita 7.3.2Criticism 1)ShockactivityinthephotosphereofRCBstarsisonlyconrmedforone absorptionlinesplitting(cf.appendixa).therefore,thepresenceofshock wavesinrcbenvelopesisgenerallydoubted. velocityvariations,butnoshockactivityinthephotosphereasinferredfrom exceptionalobject,whichisrysgr.otherrcbstarsshowconsiderableradial circumstellarenvelopearerequired.adirectobservationofcircumstellarshock wavesisverydicult,duetocontrasteectswithregardtothebrightstar.a tothephotosphereofthestar,whereasinformationsabouttheconditionsinthe Comments:Thebasicproblemoftheaboveargumentisthattheobservationsrefer chancetoobservecircumstellarpropertiesmaybepresentduringtheearlyphases ofthedeclineevents.atthepresentstateofobservations,nopreciseinformations aboutcircumstellarshockactivityhavebeendeduced,atleastonecannotruleout dependingonthephotosphericdensitygradient.justinthosecases,wherethe knowntobecapabletosteepenuptoconsiderablystrongshockwavesinthecse, theory,evensmallamplitude(subsonic)wavesinthephotosphereofthestarare thepossibilitythatshockwavesareinfactpresentinallrcbstarsenvelopes.from initialradialpulsationissmall,thedensitygradientturnsouttobelarge,which ampliesthewaves.
141 7.3.DISCUSSION 2)RCBstarsshowsimilardeclineeventswithrespecttodeclinefrequency,time 121 scalesanddeclineamplitude,regardlessoftheirspecialpulsationproperties (e.g.theradialvelocityamplitudes).therefore,acausalconnectionbetween pulsationanddustformationseemssuspect. cumstellarshockwaves,sothatsomecorrelationsareexpected.fromobservations, substantial.inanycase,thepulsationofthestarshouldberesponsibleforthecir- thecommentsontheupperpointmayberepeated,butinfactthiscriticismismore Comments:Thisisthemostseriousobjectiontotheproposedmodel.Ofcourse, evidenceispoorconcerningthiscorrelation(cf.appendixa). ofthestar(cf.appendixa)wouldcontradicttheaboveargument,butobservational theoftenclaimedcorrelationbetweenthebeginofadeclineandthepulsationphase 3)Themodelatrstsightseemstosuggestdustshellformationratherthan dustcloudformation,asfarasasphericallysymmetricpulsationofthestaris considered.dustshellformation,however,canberuledoutfromobservations alwaysonlyaveryfew probablyjustone dustcloudperpulsationperiod clouds(cf.footnote5)isnotveryconvincing,atleastcannotexplainwhy (cf.appendixa).feast(1997)arguesthattheproposedinstabilitywhich survivesthedust{destroyingradiationeld. mightberesponsiblefora\fragmentation"oftheformingdustshellintodust Comments:Thisiscertainlyaweakpointofthemodel.However,themodelin becomesopticallythickduetodustformation,thebasicassumptionofopticalthinnessbreaksdownandtheradiationeldmustbecalculatedbymeansofthesolution whichinanycasemustbethestartingpointofthedeclineevents.oncethegas factdoesnotmakeanypredictionsofwhathappensaftertheonsetofnucleation. Itonlyintendstoshowhowtheonsetofnucleationispossibleneartothestar, ofa(non{local)radiativetransfer.itisprincipallynotpossibletomodeltheformationofacloudwithouttakingintoaccounttheimportantphysicalinteractiontency.atrivialwayoutistheprescriptionofanon{sphericalsituationpriorto dustformation.onecould,forexample,considerasuperpositionofnon{spherical inamore{dimensionalway.allmodelspublishedsofarsuerfromthisinconsis- presentedthermodynamicmethodsareofcourseapplicabletosuchprescribedsituations.however,inmypersonalopinion,suchassumptionsdonotreallyexplain anything.whatisnecessaryisthemodelingofthephysicalprocessofcloudforma- inhomogeneities.inbothcases,theconditionsfordustformationaredierentin neighboringuidelements,whichmightleadtotheformationofdustclouds.the shockwavesduetonon{radialpulsations,oronecouldprescribetheexistenceof tothestarisseriousandisnotrestrictedtotheproposedmodel. placepriortodustformation,orwhetherthecauseofcloudformationisrelatedto theprocessofdustformationitself.theproblemofthesurvivalofthedustclose tionfromapreviouslyhomogeneoussituation,nomatterwhetherthisprocesstakes 7.3.3InterpretationsofObservationswithRegardtotheModel 1)IftheRCBdeclineeventsareinfactcausedbyshock{inducedcondensation, density.thiscouldtosomeextentexplaintheprincipalsimilarityofthelight{ similarinitialthermodynamicconditionsofthegaswouldbepresentinthe nucleationzoneatthebeginningofalldeclines,concerningforinstancethegas
142 122curvesconcerninglightamplitudesandtimescalesinvolved,irrespectiveofthe CHAPTER7.SHOCK{INDUCEDCONDENSATIONINRCBSTARS widerangeofstellarpropertiesofrcbstarssuchaseectivetemperature, elementabundancesandpulsationproperties.themodelsuggeststhatthe 2)Accordingtothemodel,aformingdustcloudinthelineofsightwouldalwaysbelocatedbehindashockwave,whosehotpost{shockregionmightbe responsibleforsome\chromospheric"lineemissionsasobservedduringthe fartherout,theshockencounterslessandlessdensepartsofthecircumstellar earlydeclines.ifthentheentirecomplexofshockwaveanddustcloudmoves envelope,probablycausingafadingofthelineemissionsasthedeclinepro- andapartfromthestar. declineeventsarecausedbyadistinctphysicalprocessofthegasindependent aboutv1=2.theshock{inducedemissionlinesareexpectedtobesharpand outwards,leavingthepost{shockgaswithanoutwarddirectedvelocityof 10kms 1agreeswiththeproposedscenario,becausetheshockpropagates gresses.additionally,theobservedblue{shiftoftheemissionlinesoftypically unpolarized,inagreementwithobservations,becausethegasemitsundisturbedinfrontofthedust.therefore,themodelseemstogenerallyagree staticchromosphere. emissionslines,ifinterpretedasshockactivityratherthanasactivityfroma withthespectralpropertiesandthetime{evolutionoftheobservednarrow 3)Theproposedmechanismconstitutesacausalconnectionbetweenshockwaves ofthestaratmaximumlight(e.g.lawsonetal:1992),supposedthatthesmall theobservedcorrelationbetweenthebeginofadeclineandthepulsationphase rangeofthegasdensitiesnecessaryforthismechanismissolelypresentata anddustformationincircumstellarenvelopes,whichmightnaturallyexplain Insummary,theproposedmodelprovidesasolutiontothecentralproblemhowdust takeaparticulartimetoreachthisdistance. particularradialdistancetothestar,andsupposedthattheshocksalways condensationmayoccurclosetothestar,butiscertainlynotcapabletoprovidea fromobservations:temperatures,densities,radialdistancesandtimescales.it yieldsabouttherightconditionsfordustformationasinferredfromtheoryand completeexplanationofthepuzzleofthercbdeclineeventssofar.morecomplex apparentlybridgesagapbetweenthetheoryofdustformationontheonehand,and modelcalculationsarerequiredinordertoachievethisaim.thepresentmodel toincludethedevelopedthermodynamicmethodsintomorecomplexcalculations asakindofstartingpoint. bythecontroversyaboutthecondensationdistances.therefore,itseemspromising theobservationsofrcbstarsontheotherhand(cf.sect.1.3),whichismanifested Otherresults,whichareworthtobementioned,areasfollows.Thelow{temperature solutionsofrefoundinchapter5areneverfoundtoberealizedortohaveany eectontheresultsintheperiodicallyshockedsituation.oncetheadiabaticcooling theyaredenitelystrongerthantheremainingheating/coolingratesaroundthe ratesaresucientlystronginordertodestabilizethehigh{temperaturesolution,
143 7.3.DISCUSSION low{temperaturesolutions.similarly,thedetailsofthechemistry,theradiative 123 heatingandcoolingratesandthespectralpeculiaritiesofthebackgroundradiation thedensity{intervalappropriateforthetwo{stepcoolingprocessshiftsabit.hence, elddonotcauseprincipalchangesinthecyclicthermodynamicprocesses.what incontrasttotheresultsofthethermalbifurcationsdiscussedinchapter5,the resultsofthischapterhaveamuchmoregeneralmeaning. happens,forexample,ifanotherimportantheating/coolingrateisincluded,isthat eectivetemperature,thepulsationpropertiesofthestarandtheelementalabundances(e.g.thehdeciency)mightprovideanexplanationforthefact,thatthlarenvelopesofpulsatingstars notonlyinrcbenvelopes.theinuenceofthe Inprinciple,theeectdiscussedinthisworkisexpectedtooccurinallcircumstel- stellarparametersmustbefurtherinvestigated.especiallythedependencesonthe includingradiativetransferandatime{dependenttreatmentofthedustcomplex elingofthecircumstellarenvelopesofrcbstars.higherdimensionalcalculations dynamicmodelcalculationsarerequiredinordertoallowforamorerealisticmod- RCBphenomenonisrestrictedtoaspecialclassofobjects.Time{dependenthydro- dustgrainsclosetothestar,closelyrelatedtotheself{shieldingindustclouds. wouldberequiredinordertomodeltheformationanddestructionofmacroscopic
144 124
145 Chapter8 investigated.radiativeheatingandcoolingrateshavebeencalculatedconsideringthetypical(p;t){rangeandtheradiationeldspresentinthecircumstellar Conclusions Thethermalstateofdilutedgasesbeingsubjecttostellarradiationeldshasbeen temperatureofgasesunderstaticaswellasdynamicconditions.asanimportant Thesestudiesintendtolaythefoundationsfortheoreticalmethodstodeterminethe envelopes(cses)ofcoolandwarmstars. Theresultsofthisworkshowthatanon{LTEtreatmentoftheatomsandmolecules ingredient,suchmethodsmustbepartofanyfundamentalmodelingofcses,especiallywithregardtothesimulationofthechemicalanddustformationprocesses, isessentialinordertocalculatetheeciencyoftheradiativeheatingandcooling whichareknowntobestronglytemperature{dependent. processesincses.thepossibilitytoincludethecalculatedheatingandcooling ratesintomorecomplexcalculations(e.g.time{dependenthydrodynamicmodels) isalsoregardedasessential.apropercoupling,however,canbeachievedonlyif thebasicassumptionsarecompatible.therefore,acompromisemethodhasbeen proposedwherethestateofthegasiscalculatedbymeansoftheassumptionofa macroscopicpropertiesofthegasdonotdependonhistoryandcanbecalculated depthseectsofspectrallinesinsobolevapproximation.ontheotherhand,all populationoftheexcitedelectronic,vibrationalandrotationalstatesandoptical steadystate.ononehand,thismethodaccountsfornon{lteionization,non{lte models. Thus,athermodynamicdescriptionhasbeendeveloped,wherethestateofthegasis asfunctionoflocal,instantaneousphysicalquantities,whichareavailableinsuch gradientddv twoexternalparameterswhicharetheradiationeldjandthelocalmeanvelocity determinedbytwoindependentstatevariables,e.g.andtg(asusualinlte),plus processesbymeansofdetailedbalanceconsiderations. fulltime{dependentnon{lteapproach.itincludeslteasalimitingcase,which occursatlargedensities.thelatterisachievedbystrictlyincludingallreverse dle.themethodgoesonestepbeyondlte,butdoesnotrepresenta First,thetopologyofthesolutionsofradiativeequilibrium(RE)hasbeenexamined, Threeapplicationsofthismethodhavebeenpresented: ormorestabletemperaturesolutions.twodierenttypesofsolutionshavebeen consideringthecsesofrcoronaeborealis(rcb)stars.theresultsshowthat theconditionofre,i.e.theequalityofradiativegainsandlosses,canhavetwo identied:high{temperature,predominantlyatomicstatesandlow{temperature, 125
146 predominantlymolecularstates.themolecule{richstatesarefoundtobesubstantiallycoolerthanablackbodyinre.thisresultisstraightforward,inferredfrom 126 CHAPTER8.CONCLUSIONS sequencesforthechemistryandthedustformationintheseenvelopes.concerning thelargesensitivityofthemoleculesintheinfraredspectralregion.itisexpected thatthisresultisvalidincoolstellarenvelopesaswell,possiblywithimportantcon- additionallycomeintoplaywhichmeansthatinprincipleaspatialcoexistenceof thecsesofwarmstarswithte>4500k,thehigh{temperature,atomicsolutions iedforthecaseofc{starsenvelopes.comparisontotheothertimescalesinvolved Second,thetimescalesofradiativerelaxationprocessestowardsREhavebeenstud- inpressurebalancewitheachother(\thermalbifurcations"). high{temperatureandlow{temperaturegasphasesisconceivable,bothinreand scaleismuchshorterthantheothers,thecharacterofthethermodynamicprocessis oftemperaturedeterminationwhicharebasedonre.iftheradiativecoolingtime approximatelyisothermalandthetemperaturecanbecalculatedbymeansofre.in intheprocesstobemodeledyieldsacriterionfortheapplicabilityofthemethods theoppositecasethegasbehavesmoreorlessadiabatically.thethermalrelaxation creaseoftheeciencyoftheradiativeheatingandcoolingprocesses.consequently, ofsuchrelaxation.withdeceasingdensity,increasingnon{lteeectsleadtoade- densityhasbeenidentiedtobethekeyquantitywhichdecidesuponthecharacter ofthegasbehindcircumstellarshockwaveshasbeendiscussedaccordingly.thegas agradualchangeofthenatureoftheshocksisexpectedtooccuraround108cm 3, changingfrompredominantlyisothermaltopredominantlyadiabatic.theseresults toshock{levitatedatmospheresofpulsatingstars.largetime{variationsofthe stronglysuggesttoincludetime{dependentmethodsfortemperaturedetermination thermodynamicconditionsarefoundtooccurinsuchuidelements,comprising Third,amodelforperiodicallyshockeduidelementshasbeendeveloped,applicable intothemodelsoftheenvelopesofpulsatingstars. aftertheheatingandcompressionbyashockwave,thegasrstradiatesawaythe WithregardtoRCBstars,thefollowingeecthascometolight.Incertaincases 1 2ordersofmagnitudesinthestatevariables,dependentontheshockvelocity. excessinternalenergydissipatedbyashockwaveandthenre{expandsadiabatically. 1:5 3R,despiteofthehigheectivetemperaturesofthesestars.Suchconditions temporarilyoccurforshockvelocities20 50kms 1atradialdistancesassmallas Thistwo{stepcoolingprocesscanproducetemperaturessubstantiallylowerthanin REwithinadistinctdensityinterval.Temperaturesaslowas1000Karefoundto arefavorableforcarbonnucleation.thus,thepresentworkstatesthehypothesis larenvelopeshavebeenundertaken,providingnewinsightsandnewideasonthe Inconclusion,basicstudiesofthethermodynamicbehaviorofgasesincircumstel- mighttriggerthespectacularrcb{typedeclineevents. thattheonsetofdustcondensationclosetothestariscausedbyshockwaves,which processesleadingtodustformation.
147 AppendixA ThisappendixintendstogiveabriefoverviewonthecurrentstatusofRCBresearch, CurrentStatusofRCBResearch providinganimportantbackgroundfortheinvestigationsinchapter5and7.since thisclassofstarsshowssomanyinterestingaspectsinvariouselds,onlythetopics andintherecentreviewsoflambert&rao(1994)andclayton(1996). ThereadercanndfurtherinformationsinthediplomathesisofS.Friedrich(1995) whichprovidecluesonthedustformationandthedeclineeventsaresummarized. A.1 Classication:TheclassofRCBstarstodaycomprises32knownobjectsinour Galaxy(Lambert&Rao1994).Thisnumbervariesasaconsequenceofrecentobservationsandtheclassicationofsomeobjectsisstillunderdiscussion(Clayton 1996).Acertainvericationrequiresatleastthesuccessfulobservationofonede- GeneralObservations V854Cen,wasnotdiscoveredbefore19861.Themaincriterionforclassicationis ofrcbstarsisundoubtfullymuchlarger,probablybetween200and1000inthe Galaxy(Lawsonetal:1990).Forexample,thethirdbrightestRCBstaronthesky, clineevent,whichisquiteadicultobservationaltask.therefore,thetruenumber alsotheoccurrenceofsmall{scalevisualbrightnessvariations.rcbstarsaresingle theoccurrenceofthercb{typedeclineevents(cf.a.2:lightcurves).additional starsoftypicalspectraltypef{gibwithabsolutebrightnessesmv= 4to 5 varyinghydrogendeciencyamongtheobjectsof(logh=he= 0:3to 7:2),and criteriaareacarbonoverabundance(c=he=0:01to0:1)andaclearbutstrongly alsoextremevaluesfromabout4000kforwxcraandsapsuptoabout20000k (Feast1979),suggestingluminositiesofaboutL104L.Thestellarmassescanbe fordycenandv348sgroccur.comparedtothislargespreadofeectivetemperatures,thedeclineeventsoftheindividualrcbstarsshowaremarkablesimilarity (involvingdustformation),whichisapparentlynotverysensitivetotheeective intheirdeclinelightcurves,e.g.thedeclineamplitudesandtimescalesinvolved. temperatureofthestar. Therefore,auniquephysicalmechanismseemstoberesponsibleforalltheevents determinedbypulsationalmodels,yielding0:8 0:9M(Wei1987).Theeective temperaturestypicallyarete=( )k(lambert&rao1994).however, 1Thisisbecausethisobjectisindeclinemostofthetime. 127
148 128 Pulsations:Besidesthedeclineevents,allthoroughlyobservedRCBstarsshow AppendixA 0:1to0:4magforperiodsoftypically40days(Feast1990;Lawsonetal:1992; variationshaveadditionallybeendeducedfromthedoppler{shiftofphotospheric Lawson&Kilkenny1996).ForaconsiderablenumberofRCBstars,radialvelocity moreorlessperiodicalvisualbrightnessvariationswithamplitudesrangingfrom Thereareseveralcluesthatthepulsationshaveadirectfeedbackonthedynamicsandthechemistryoftheouteratmospheresofthesestars.ThemostextremceptionalcaseofRYSgr.Thevariationsofvelocityandbrightnessusuallyoccurin phase,suggestingthercbstarstobeirregularradialpulsators(lawsonetal:1990). absorptionlines,yieldingabout5to10kms 1andabout20kms 1fortheex- propagationofashockwavethroughtheatmosphereofthestar(lawson1986, Lawsonetal:1991).Furthermore,besidessomepermanentemissionlinesprobably pulsatorrysgrshowsphase{correlatedline{splitting,whichisinterpretedasthe ofchromosphericcharacter(e.g.cii1335a),thereoccurphase{correlatedemission featuresintheuv,whichmightbecausedbyshockheating.theequivalentwidths ofelectronicabsorptionbandsofc2(swan)andcn(violet),associatedwiththe MassLoss:ThequestionofwhetherornottheRCBstars besidestheoccasional caseofrcrb(claytonetal:1995). outeratmosphere,showaclearcorrelationwiththepulsationalphaseofthestarin thedeclines(cf.a.2:spectroscopy)areblue{shiftedbytypically10kms 1,which masslosseventsduetodustcloudformation undergoanunderlyingpermanent However,theseeectscanhardlybedistinguishedfromthedustandgasclouds, accordingtofeast(1990,1996)suggestsapermanentradiation{drivenmassloss. massloss,isundercontroversialdiscussion.thenarrowemissionlinesseenduring whichapparentlyarepresentoutofthelineofsightatanytimenearthestar RCBenvelopes,aclaricationofthisquestionwouldbedecisivelyimportant.In (cf.a.1:dustshells).forthetheoreticalunderstandingofthedustformationin amassivestellarwind,whichisnotdrivenbythedustitself,thedustformation mightbeasecondaryprocessandcouldoccurratherdistantfromthestar.in contrast,ifthereisnomassivewind,thedensitiesaretoolowanddustcannotform dustcloudformationeventsrangefrom10 6Myr 1(Feast1986)to10 7Myr 1 atlargedistances.estimatesforthemeanmasslossratesinferredfromthesumof 2 25m,irrespectivewhetherthestarisindeclineornot.Theexcesscanbetted (Claytonetal:1992). DustShells:TheinfraredphotometryofRCBstarsshowaclearexcessatabout byblackbody{curvesofcharacteristictemperatures600{900k(kilkenny&whittet 1984).Thisthermalemissionisobviouslycausedbythetotalamountofdustinthe Sge(Jurcsik1996),showingamoreorlesspermanentIRexcessafterthosedeclines,butnoexcess ofthelineofsight2;3.themeanradialdistancesofthese\dustshells"areestimated vicinityofthestar,whichhasbeenformedduringtheformerdeclineeventsorout before. 3Sincethesedustcloudshaveproventobeopticallythininlatedecline,itwouldactuallybe 2ThisinterpretationisstronglysupportedfromtheobservationoftheveryrstdeclinesofFG moreappropriatetottheexcessby(1=)b(t).
149 tobe10{90stellarradii(walker1985).recently,feastetal:(1997)publishedextensivelong{terminfraredphotometrydatafor12rcbstarsandconcludedthat A.2.OBSERVATIONSDURINGTHEDECLINEEVENTS 129 mass,increases.thisisanargumentinfavoroftheformationofhotdustcloseto themeandusttemperatureisincreasing,ifthel{ux,representingthetotaldust thereisevidenceforaspreadindusttemperaturesineachrcbshell,wherethe thestar.sincethelimitingvalueof1500kisconstantforallrcbstarsobserved, hottestcomponentsarealwayslimitedbyabout1500k4.feast(1997)arguesthat thecondensationtemperatureofcarbonpossiblyisthecontrollingfactorinallrcb envelopes.furthermore,anotherexcessinthefarir(60{100m)canbeobserved forseveralobjects(e.g.rcrbandsutau),whichpointstodistant,fossildustand StellarEvolution:ThepopularityoftheRCBstarsisalsocausedbytheirmysteriousorigin.SincetheRCBstarsaresorare,theymustbeeitheramanifestation Gillettetal:(1986),thelinearsizeoftheshellofRCrBisabout18arcmin(8pc)5. gasshells,probablyconnectedwiththeformerevolutionofthestar.accordingto infactatopicofrecentresearchonstellarevolution.themergingoftwowhite Twomajorevolutionaryscenarioshavebeenworkedoutduringthelast15years (Iben1983,Schonberner1986,Renzini1990),indicatingthattheRCBstarsare ofapeculiarsidepathofstellarevolution,oracommon,butrapidlyevolvingstage. dwarfs(doubledegenerate(dd)scenario)andthere{birthofanpost{agbstar Thesemodelsmakedierentpredictionsaboutthesurfaceelementalcomposition, agreementwithobservationsisstillratherpoor.lastbutnotleast,theveryfast thelifetimesofrcbstarsandtheirspatialdistributioninthegalaxy.however, asaconsequenceofalastthermalpulse(finalheliumshellflash(ff)scenario). evolutionoffgsge(kipper1996,jurcsik1993)acrossthehr{diagramduringthe lastcenturysuggeststhatthebirthofanewrcbstarhasactuallybeenobserved. LightCurves:Theindividuallightcurvesofthespectaculardeclineeventsare quitedierentinappearanceconcerningboththedierenteventsandthedierent A.2 ObservationsDuringtheDeclineEvents stars.nevertheless,theireye{catchingshapeissotypicalthattheyessentiallydene thenalrecoveryphasethereusuallyisaphaseoflow{levelchaoticlightvariation, fromdeepdeclinesusuallytakesmonthsoryears.betweentheinitialdecreaseand thevisualbrightnessoftypically3 6magwithinafewweeks,whereastherecovery thisclassofobjects.thelightcurvesofthercbstarsstartwithasuddendropin superimposingeachother,areoftenobserved,suggestingmultipledustformation events. lastingbetweenzeroandseveralyears(goeres&sedlmayr1992).multipleminima, colorvariations.theinitialdecreaseinlightalwaysappearsslightlyreddened.the ColorVariations:ThedeclineeventsofRCBstarsareaccompaniedbycomplex 4Ingoodagreementwiththecarboncondensationtemperature,cf.A.3:Goeres&Sedlmayr 5Ashugeastheangularsizeofthemoon.
150 130 lightthenmaybecomebluish(a\blue"declineaccordingtocottrelletal:1990)or AppendixA remainsreddened(a\red"decline).asthedeclineprogresses,astrongreddeningoc- (Alexanderetal:1972,Cottrelletal:1990).ThenallightincreaseapparentlyproceedsonauniquelineforallRCBstarswithslope+5intheV=(B V){diagramcurs,untilthelightnallyincreasesagainandthestarslowlyreachesitsusualbrightnessandcolor.ThesevariationsresultintypicalloopsintheV=(B V){diagram whichisanunusuallylargevaluecomparedtointerstellarreddening(cottrell1996), providingcluesonthenatureofthedust.thecauseofthebluinginearlydecline hasbeenproposedtobeanadditional,radialextended,hotterlightsourcethanthe staritself(pugach1991,claytonetal:1992),emittingat Amainlyin cloudradiiduringtheinitialformationand/orvaryingdistancesfromthelineof formoflineemission(asplund1995).this\chromosphere"initiallyisnot,orisat sightmightproduceredorbluedeclines. declinesmaybecausedbydierentcloudgeometriesduringthedeclines.varying leastmuchless,eclipsedbythedustcloud.thedierencebetweenredandblue havesmalleramplitudescomparedtotheopticalregion.asarule,theamplitudes IRObservations:Thelightvariationsintheinfraredregionsduringthedeclines decreasewithincreasingwavelengthandvanishesataboutthel{band(=3:6m), wouldbeexpectedifthedustwaspresentinasphericalsymmetricfashion.this wherethelightisalreadydominatedbythermaldustemission(e.g.feastetal:1997). Noanti{correlationbetweentheopticalandIRbrightnesshasbeenfound,which isthemainobservationalargumentfordustcloudformationratherthandustshell thestar. formation(forrestetal:1972).furthermore,thedustmassproducedinonedecline ExtinctionoftheDustParticles:ThepossibilitytoobservetheRCBstars apparentlyissmallcomparedtothetotalmassofthedustpresentinthevicinityof twice,uncoveredandcoveredbydust,allowsforadirectdeterminationoftheextinctioncurveofthematerialresponsibleforthedeclineevents.theresultsclearly aswellasthespecialappearanceofthisfeatureisdiscussedinvariouspublications caseofrcbstars(e.g.hechtetal:1984).thegeneralshapeoftheextinctioncurve positionofthewell{knowngraphite\bump"at2200aisshiftedto Ain indicatethecarbonaceouscharacterofthedustmaterial(/1=).however,the Maron1989,Wright1989,Drilling&Schonberner1989,Hecht1991,Jeery1995, concerningthenatureofthedustgrainsinrcbenvelopes(e.g.holmetal:1987, fullerenes).theonlyclearuniquetendencyinthesepapersseemstobetheunusual bon,\onion{like"structures,amorphouscarboncorescoveredbygraphitemantles, hydrogenatthesurfaceorunusuallatticeormicroscopicstructures(\glassy"car- Zubko1996).Manyinterpretationsarepossible.Unusualsizedistributions,no smallradiiofthedustparticles,typically50atomaximumvaluesofabout600a. Spectroscopy:Sofar,onlytwodeclineeventsofRCBstarshavebeencompletely monitoredasfunctionoftimebyopticalspectroscopy:the1967declineofrysgr (Alexanderetal:1972)andthe1988declineofRCrB(Cottrelletal:1990).However,fragmentaryspectraldataisavailableforseveraleventsofthethreebrightest
151 CurrentStatusofRCBResearch RCBstarsRCrB,RYSgrandV854Cen,coveringcertainphasesofthedeclines 131 Asplund1995).Thespectraindicateaspecialtimeevolution.Untilthebeginningof (e.g.lambertetal:1990,lawsonetal:1992,claytonetal:1992,rao&lambert1993, distinguishbetweenthreecomponents,namede1,e2andbl.mostoftheemission 1992)6.Astheintensityofthephotospheric(absorptionline)spectrumdecreases,a rich\chromospheric"emissionlinespectrumcomestolight.alexanderetal:(1972) adecline,nospectralchangeshavebeenreportedsofar(cottrelletal:1990,lawson (8eV)ofneutralorsinglyionizedmetalatoms,whichareblue-shiftedbytypically 10kms 1anddisappearaftersomeweeks.AsmallernumberofnarrowE2{emission linesoflowexcitationenergies(3ev),mainlymultiplettsofsciiandtiiiremain linebelongtotheclassofnarrow(50kms 1)E1{linesofhighexcitationenergy visiblefor50 150days.Asthedeclineprogresses,theopticalspectrummainly consistsofvebroad( kms 1),unshiftedBL{emissionlines:CaIIH&K, \chromospheric",althoughtheydonotlooklikethechromosphericemissionsofany absorptionlinespectrumre{appearsandsoondominatesthelightfromtheremainingemissionlines.thephysicalnatureoftheemissionlinesisusuallydescribedby NaIDandalineat3888A,probablyHeI(Feast1975).Finallythephotospheric absorptioncomponentscanbeobserved,especiallyblue{shiftedfeatureswithtypical velocitiesof200kms 1towardstheobserver.Thesecomponentsaresupposedto TheBL{linesusuallyshowamulti{componentstructure.Dierentemissionand otherstars(clayton1996). radiationpressure.hence,thesevelocitiescanbeassociatedwiththevelocitiesof thedustclouds. originatefromthegasdraggedalongwiththedustcloudsbeingacceleratedby region,havebeenreported.incontrast,theemissionlinesremainmoreorlessunpolarized(whitneyetal:1992).thephysicaleectcausingthepolarizationismainly allowforimportantconclusions.first,thedustisdistributednon{sphericallyand thescatteringoflightatthesurfacesofdustgrains7.therefore,theseobservations Polarization:Thelightduringthedeclinesgenerallyisstronglypolarized(Serkowski&Kruszewski1969,Coyne&Shawl1973,Standfordetal:1988,Emov1990).In thecontinuum,degreesofpolarizationupto14%,especiallyinthebluespectral ratherclosetothephotosphere. dustseemstoformbelowthelineemissionregions,suggestingdustformationoccurs forthelineemissions,atleastmuchlessthanthephotosphere.consequently,the second,thedustcloudcausingthedeclinedoesnoteclipsetheregionsresponsible declinestooccuratparticularpulsationalphasesofthestar(e.g.lawsonetal:1992). acausalconnectionbetweenthepulsationsandthedeclineevents.foratleast FurtherObservations:Severalobservationalcluescanbefoundwhichpointto Furthermore,themultipledropsofthelightcurveinthebeginningofthedecline twoobjects(rysgrandv854cen)thereissomeevidencefortheonsetofthe canbemade. 6Tocatchastarjustbeforeadecline,however,needsaveryluckymoment,sincenopredictions 7Possiblyatthesurfacesofotherdistantdustcloudsoutofthelineofsight.
152 132 eventsseemtooccurattimeintervalscorrespondingtotheperiodofthestar(feast AppendixA Finally,long{timevariationsofthedecline{activityhavebeenreported,actingon timescalesofafewthousandyears(menzies1986,feast1990).accordingtothe meantimebetweenthedeclines,isincreasingwithincreasinghydrogenabundance. 1996).AccordingtoJurcsik(1996),thedecline{activity,i.e.theinverseofthe personalopinionoftheauthor,theobservationsreviewedinthislastparagraphare lessstrikingthanthoseoutlinedbefore,stillleavingenoughroomforinterpretation. proachestomodelthercbdeclineeventshavebeencarriedoutsofar.themodest Comparedtothenumberandthequalityofobservations,onlyafewtheoreticalap- A.3 Models theoreticalapproachesandsolutions.aconsistent,physicaldescriptionoftheproblemobviouslymustcontain(i)adetailedcalculationofthermodynamics,chemistry activityofthetheoreticiansispossiblycausedbythecomplexityoftheprocesses anddustformation,(ii)asolutionofradiativetransferand(iii)amodelingofthe andthesomewhattroublesomegeometryinvolved.theseobstaclespreventsimple hydrodynamicsforthedust{enrichedgas.duetothecloudygeometryallthese keyproblemsofthedeclines,e.g.onthetriggerforthesuddenonsetofdustformation.ontheotherhand,severalempiricalmodelsprescribetheexistence,the Presently,thereareononehandafewtheoreticalworkswhichfocusoncertain Noneofthepublishedmodels includingthiswork satisfytheserequirements. investigationshavetobeworkedoutinmorethanonespatialdimension. consequencesandargueinfavororagainstcertainscenarios. geometryandthemovementofthedustinfrontofthestar,calculatetheobservable tionoccasionallyoccursinamassive,sphericalstellaroutow,whichcausesthe Loreta(1934)andO'Keefe(1939):Loreta(1934)assumesthatdustforma- A.3.1HistoricalModels declines.o'keefe(1939)agreeswithloreta'shypothesis,butproposesthatthe dustformsinejectedblobsofgas,similartosolarprotuberances.thesolidmatter proposedtocondenseisbelievedtobe\principallycarbon".bothmodelsassume thatdustformationtakesplaceratherdistantfromthestar,wherethetemperature modynamicconsiderations,o'keefederivescondensationtemperaturesof1360k, islowenoughtoallowforthephasetransition.basedonsomefundamentalther- declines,theprogresssincethenhasapparentlybeenratherslow. statements,whichuptodateprovidethebasicideafortheexplanationofthercb densities107cm 3anddistancesofabout8stellarradii.Reviewingtheseearly Wdowiak(1975):Giantconvectioncellsareproposedtobepresentatthesurfaces A.3.2ModelCalculations ofrcbstars.scalingtheobservationsofthegranulationandthesuper{granulation
153 CurrentStatusofRCBResearch ofthesuntogiantstardimensions,wdowiakarguesforconsiderablylowertemperaturesovercertainrestrictedareasofthestar.followinghisideas,thisfavorsdust thispictureandarguedthateventhesemi{regularvisuallightvariationsmightbe formationovertheseareas,followedbydustcloudejection.feast(1996)tookover 133 onlyqualitatively,asnocalculationsofthesuper{granulationhavebeencarriedout sphere,especiallyforhotrcbstars,aswdowiakstatedhimself.hisargumentis fewthousanddegreeslessmaynotbesucientfordustformationinthephoto- causedbythiseectratherthanbystellarpulsation.problemsremainasevena andtheformationofdusthasnotbeencalculated. Fadeyev(1983{1988):Y.Fadeyevwastherstwhoappliedclassicalnucleation theory,basedonthebulkmaterialdataforgraphite,tothecircumstellarenvelopes isprescribedast=t(r),andaradiallyexpandinguidelementisfollowedstarting ofrcbstars8.inhislatestmostadvancedwork(fadeyev1988),thetemperature atthesonicpointwithagiveninitialvelocity.accordingtotheassumptionsofan opticallythinradiationeld,greygasopacities,radiativeequilibriuminthegasand gasduetoradiationpressureondustgrainsyieldsabout150days.inhisearlier starandits(prescribed)masslossratearefound.theaccelerationtimescaleofthe includingthegreenhouseeectforamorphouscarbon,dustformationispossible works,atemporalenhancementofthegasdensitycausedbypropagatingshock outsideofabout20r.strongcorrelationswiththeeectivetemperatureofthe wavesarealsoconsidered.themodelprincipallyhasdicultiestoexplain(i)the dustformationinrcbstarsofdierenteectivetemperatures,(ii)thepre{existence ofamassivestellarwindand(iii)theoccurrenceofhighvelocityfeaturessoonafter thebeginningofadecline. ingconditionsinrcbenvelopes.thechemistryisdominatedbyamixtureofpure carbonmoleculesinaninertheliumgas,similarlytorecentlaboratoryexperiments thoroughlyinvestigatedthecarbonchemistryandthenucleationundertheprevail- Goeres&Sedlmayr(1992):Goeres(1992)andGoeres&Sedlmayr(1992)have concerningtheformationof\buckyballs"(c60).however,themainchemicalpathwaytotheformationofsootparticlesinvolvessmallcarbonchains,monocyclicrings (PACs).Fullerenesareproposedtoformasminorby{productsofthispathway.Gas andlargerdehydrogenized,curved,butnotclosedpolyaromaticcarbonmolecules temperaturesroughlybelow1500kareinevitablynecessaryforcarbonnucleation. ThemaingrowthspeciesistheabundantC3radical.Moleculedriftisproposedto triggerthefurthergrowthtolargermolecules.thedeclinesarecausedbydensity enhancementsduetosuperimposingshockwaveswhichoriginatefromnon{radial pulsations.thedescendingandtheascendingbranchesofthelightcurveareexplainedbyhydrostaticdustgrowthandradialdilutionataconstantoutowvelocity, thesameprincipalproblemsasabove. Asplund&Gustafsson(1996):Gustafsson&Asplund(1996)haveworkedout detailedatmospherecalculationsforhydrogendecientstars(static,planeparalrespectively.thegastemperatureisprescribedasinthemodeloffadeyev,causing 8...andpublishedhisresults.
154 134 lel,lte),usingaccuratelycalculated,line{blanketedabsorptioncoecients,which AppendixA heliumionizationzone(atross10).intheselayers,theradiativeacceleration surfacesofthestarsarebelowtheso{denededdingtonlimit( =grad=ggrav=1). However,radiativeinstabilitiesarepresentinthedeeperphotosphericlayersatthe yieldgoodagreementwiththeobservedspectra.accordingtothesemodels,the exceedsthegravitationaldeceleration >1which,accordingtotheirmodels,is layersareunstableagainstcompressionandoutwardaccelerationofgasblobs.as balancedbypressureinversions.asplund&gustafsson(1996)recognizethatsuch theyputforwardthemselves,thereasonforadeclineeventisproposedtobethe accelerationofsuchagasblobinthedeepphotosphereofthestar,followedbya supersonicinjectionthroughtheatmosphere,radiativecoolinganddustformation. Thus,thecauseoftheRCBdeclinesmightbefoundintheradialatmosphericstructureofthestaritself.Themodelseemstobepromising,butsofartheinvestigations Themodeldoesnotexplainthereasonfordustformationclosetothestar,itonly ofblobinjectionhavenotbeenperformed.dustformationhasnotbeencalculated. arerestrictedtohydrostaticconsiderations.hydrodynamicalmodelsfortheprocess A.3.3EmpiricalModels providesthenecessarydensityconditions. Humphreys&Ney(1974):Asecondarycoolstarwithanopticallythickdust envelopecausesthedeclineevents.suchbinarymodelshaveprincipalproblemsto Wingetal:(1972)andGrinin(1988):Orbitingdustcloudsfromtimetotime noobservationalevidenceforbinaryrcbstarshavebeenreportedsofar. explaintheasymmetryandthetruerandomnessofthelightcurves.furthermore, Keplerorbits. shouldbedrivenawayfromthestarduetoradiationpressureratherthandoing obscurethestar theproblemsarethesameasabove.moreover,thedustclouds approachhasvariedabit,butthemainidearemainstheexpansionofadustcloudof modelforthedustcloudevolutionwhichcausesthedeclines.overtheyears,the Pugach(1984{1994):Pugachandco{workershavedevelopedacomprehensive initiallyinnitesimalsmall,sphericaldustcloudwithagaussiandensityprole forthedierentcolorshavebeenperformedforthefollowinggeometry.amassive, homologouslyexpands(v=r=t)ataxedplacewithacertainosetfromthe constantmassataxedlocationinfrontofthestar.radiativetransfercalculations onwavelength.pugachshowedwithhiswork,thattheshapeofthelightcurve, additionallyemittedradiation,whichisnotaectedbythedustcloudbutdepends lineofsightinfrontofthestar.themodelintroducesthreeparameters:the andthecolorvariations,canbereproducedbythisscenario.nohydrodynamical totaldustmass,theosetfromthelineofsightandtheintensityofscatteredor of g(Pugach&Koval'chuk1994).Theshortcomingofthismodelisof movementofthecloudisneeded,nodustformationmustbeconsidered.itcanallbe explainedbypuregeometry.estimatesforthetotaldustcloudmassesyieldvalues
155 CurrentStatusofRCBResearch coursethatitdoesnotreallyexplainanything.theexistenceofthedustcloudis 135 Emov(1990):Spontaneouschangesoftheabsorptionpropertiesofapre{existing prescribedandthereasonforthehomologouscloudexpansionremainsmysterious. particles.themodelcantosomeextentdescribetheshapeofthelightcurveandthe ofsuchspecialdustisnotprovided. colorvariations,butareasonforthespontaneouschangesaswellastheexistence dustshellcausethedeclines,e.g.viaspontaneousalignmentofnon{sphericaldust FurtherModels:Manyfurthercommentsandestimatesarestatedintheliterature,e.g.Feast(1986,1996,1997),Alexanderetal:(1972),Forrestetal:(1971sultsinviewofsomead{hocassumedscenarios.Therefore,theydonotappear 1972).However,thesepublicationsmainlypresentobservationsanddiscussthere- asextra\models"inthisappendix.nevertheless,importantconclusionscanbe drawnfromtheseconsiderations.thestandardmodelinthesepublicationsclearly istheformationofdustcloudsneartothestar,followedbyradialexpansionand dilution.fromtheirobservationsofrcrb,forrestetal:(1972)concludedthatthe sizesofthedustcloudsandthedeclineactivitiesofrcbstarsareinagreementwith theformationofonedustcloudperpulsationalperiod. dustcloudcausingthe1972declineonlycoveredabout3%ofthesolidangle(correspondingtoasemiconeangleofabout20).accordingtofeast(1986),theangular
156 References Alexander,J.B.,Andrews,P.J.,Catchpole,R.M.,Feast,M.W., AspectroscopicandphotometricstudyofthepulsatingRCoronaeBorealis LloydEvans,T.,Menzies,J.W.,Wisse,P.N.J.,Wisse,M.(1972). Allain,T.(1996).Photodestructionandgrowthofinterstellarpolycyclicaromatichydrocarbons.Dissertation,TechnischeUniversitatBerlin,FRG. typevariablerysagittarii.mnras158,305{360. Asplund,M.(1995).SpectroscopyofRYSgrduringthe1993minimum. Allen,C.W.(1973).AstrophysicalQuantities.London:TheAthlonePress. Asplund,M.,Gustafsson,B.(1996).ArethedeclinesofRCoronaeBorealis A&A294,763{772. Asplund,M.,Gustafsson,B.,Kiselman,D.,Eriksson,K.(1997).Line- (Hrsg.),Hydrogen-DecientStars,pp.39{42.ASPConf.Ser.96. starscausedbysuper-eddingtonluminosities?inc.s.jeeryundu.heber Ayres,T.R.(1981).Thermalbifurcationinthesolarouteratmosphere. decientcarbonstars.a&a318(2),521{534. blanketedmodelatmospheresforrcornonaeborealisstarsandhydrogen- Beck,H.K.B.(1993).Ionization,ChemistryandDustFormationintheOut- ApJ244,1064{1071. Beck,H.K.B.,Gail,H.-P.,Henkel,R.,Sedlmayr,E.(1992).Chemistry owsofclassicalnovaeandredgiants.dissertation,technischeuniversitat, Berlin,FRG. Biermann,P.,Kippenhahn,R.,Tscharnuter,W.,Yorke,H.(1972). incircumstellarshells.i.chromosphericradiationeldsanddustformation inopticallythinshellsofm-giants.a&a265,626{642. Bowen,G.H.(1988).Dynamicalmodellingoflong-periodvariablestaratmospheres.ApJ329,299{317. PhaseTransitionintheInterstellarMedium.A&A19,113{122. Burke,J.R.,Hollenbach,D.J.(1983).TheGas{GrainInteractioninthe ChaseJr.,M.W.,Davies,C.A.,DowneyJr.,J.R.,Frurip,D.J.,Mc InterstellarMedium:ThermalAccommodationandTrapping.ApJ265,223{ InJ.Phys.Chem.Ref.Dat.,Vol.14Suppl.1.NationalBureauofStandards. Donald,R.A.,Syverud,A.N.(1985).JANAFThermochemicalTables. 136
157 Chin,G.,Weaver,H.A.(1984).VibrationalandrotationalexcitationofCO Cherchneff,I.,Barker,J.R.,Tielens,A.G.G.M.(1992).Polycyclic 269{287. AromaticHydrocarbonformationincarbon-richstellarenvelopes.ApJ401, Clayton,G.C.(1996).TheRCoronaeBorealisStars.PASP108,225{1996. Clayton,G.C.,Whitney,B.A.,Meade,M.R.,Babler,B.,Bjork- incomets:nonequilibriumcalculations.apj285,858{869. Clayton,G.C.,Whitney,B.A.,Stanford,S.A.,Drilling,J.S. man,k.s.,nordsieck,k.h.(1995).long-termspectroscopicandpo- larimetricmonitoringofrcoronaeborealisnearmaximumlight.pasp107, (1992).ObservationsofRCoronaeBorealisstarsindecline:Empiricalargumentsfordustformationnearthestellarsurface.ApJ397,652{ {426. Cottrell,P.L.(1996).RCoronaeBorealisstars:currentstatusoftheobservationaldata.InC.S.JeeryundU.Heber(Hrsg.),Hydrogen-Decient CoronaeBorealisandXXCamelopardalis.ApJ261,595{611. Stars,pp.13{25.ASPConf.Ser.96. Cottrell,P.L.,Lambert,D.L.(1982).ThechemicalcompositionofR Coyne,G.V.,Shawl,S.J.(1973).PolarimetryofRCoronaeBorealisat Cottrell,P.L.,Lawson,W.A.,Buchhorn,M.(1990).The1988decline ofrcoronaeborealis.mnras244,149{167. Drilling,J.S.,Schoenberner,D.(1989).Onthenatureofnewlyformed visuallightminimum.apj186,961{966. Efimov,Y.S.(1990).RCrBinthebrightnessminimumof1988/1989.SvA34, 247{254. dustaroundthehydrogen-decientstarv348sagittarii.apj343,l45{l48. Elitzur,M.(1983).Onvibrationalexcitationofinterstellarmolecules.ApJ266, Fadeyev,Y.A.(1983).GraphitegrainformationintheatmospheresofRCoronaeBorealisstars.Ap&SS95,357{ {613. Fadeyev,Y.A.(1986).TheoryofdustformationinRCoronaeBorealisstars. Fadeyev,Y.A.(1988).CarbondustformationinRCoronaeBorealisstars. Dordrecht,pp.441{451.D.ReidelPub.Comp. InK.Hungeretal.(Hrsg.),HydrogenDecientStarsandRelatedObjects, Feast,M.W.(1975).TheRCoronaeBorealistypevariables.InV.Sherwoodet al.(hrsg.),vaiablestarsandstellarevolution,pp.129.iausymp.67. MNRAS233,65{78. Feast,M.W.(1979)..InF.M.Batesonetal.(Hrsg.),ChangingTrendsin VariableStarReseach,pp.246.IAUColl.46.
158 Feast,M.W.(1990).TheperiodicitiesofRCoronaeBorealisstarsandtheir Feast,M.W.(1986).TheRCrBstarsandtheircircumstellarmaterial.In drecht,pp.151{161.d.reidelpub.comp. K.Hungeretal.(Hrsg.),HydrogenDecientStarsandRelatedObjects,Dor- Feast,M.W.(1996a).SomegeneralproblemsconcerningRCBstars.InC.S. shells.aspconf.ser.11,538{548. Feast,M.W.(1996b).Thepulsation,temperaturesandmetallicitiesofMira JeeryundU.Heber(Hrsg.),Hydrogen-DecientStars,pp.3{11.ASPConf. andsemiregularvariablesindierentstellarsystems.mnras278,11{21. Ser.96. Feast,M.W.(1997).TheRCoronaeBorealisstars{II.Furtherinferences Feast,M.W.,Cartner,B.S.,Roberts,G.,Catchpole,R.M.(1997). fromtheinfrareddata.mnras285(2),339{357. Fernie,J.D.(1982).RCoronaeBorealisnearmaximumlight.PASP94,172{ tions.mnras285(2),317{338. TheRCoronaeBorealisstars{I.Infraredphotometryandlong-termvaria- Fernie,J.D.,Sherwood,V.,DuPuy,D.L.(1972).Aphotometricstudy 176. Feuchtinger,M.U.,Dorfi,E.A.,Hofner,S.(1993).Radiationhydrodynamicsinatmospheresoflong{periodvariables.A&A273,513{523. ofselectedrcoronaeborealisvariables.apj172,383{390. Fleischer,A.J.,Gauger,A.,Sedlmayr,E.(1991).Generationofshocks Fleischer,A.J.,Gauger,A.,Sedlmayr,E.(1992).CircumstellarDust shellsaroundlong-periodvariables.i.dynamicalmodelsofc-starsincluding dustformation,growthandevaporation.a&a266,321{339. byradiationpressureonnewlyformedcircumstellardust.a&a242,l1{l4. Forrest,W.J.,Gillett,F.C.,Stein,W.A.(1971).VariabilityofradiationfromcircumstellargrainssurroundingRCoronaeBorealis.ApJ170, L29{L31. Fleischer,A.J.,Gauger,A.,Sedlmayr,E.(1995).CircumstellarDust mechanismcausedbydustformation.a&a297,543{555. shellsaroundlong-periodvariables.iii.instabilityduetoanexterior{ Forrest,W.J.,Gillett,F.C.,Stein,W.A.(1972).InfraredmeasurementsofRCoronaeBorealisthroughits1972marchejuneminimum.ApJ178icalmodels.ApJ297,455{475. L129{L132. Fox,M.W.,Wood,R.P.(1985).ShockwavesinMiravariables.II.Theoret- Frantsman,Y.L.,Eglitis,I.E.(1988).TheC/O{ratioinNstars: observationsandtheory.sva14,l109{l111.
159 Gail,H.-P.,Sedlmayr,E.(1986).Theprimarycondensationprocessfordust Friedrich,S.(1995).DiePhysikderRCrB-Sterne:Phanomenologieundihre KonsequenzenfurdieModellierung.Diplomarbeit,TechnischeUniversitat, Berlin,FRG. Gail,H.-P.,Sedlmayr,E.(1988).Dustformationinstellarwinds.IV.Heteromolecularcarbongrainformationandgrowth.A&A206,153{168. aroundlatem-typestars.a&a166,225{236. Gillet,D.;Lafon,J.-P.J.,David,P.(1989).Radiativeshocksinatomic Gillett,F.C.,Backman,D.E.,Beichman,C.,Neugebauer,G.(1986). andmolecularstellaratmospheres.iii.theshockwavevelocityproblemin ApJ310,842{852. IRASobservationsofRCoronaeBorealis-detectionandstudyofafossilshell. Mirastars.A&A220,185{196. Goeres,A.(1996).ChemistryandThermodynamicsoftheNucleationinRCrB Goeres,A.(1992).StaubbildungindenHullenvonKohlenstosternen:RCoronaeBorealis.Dissertation,Techn.Univ.Berlin,Berlin. Goeres,A.,Sedlmayr,E.(1992).TheenvelopesofRCoronaeBorealisstars. I.Aphysicalmodelofthedeclineeventsduetodustformation.A&A265, pp.69{81.aspconf.ser.96. starshells.inc.s.jeeryundu.heber(hrsg.),hydrogen-decientstars, Goldreich,P.,Scoville,N.(1976).OH-IRStars.I.Physicalpropertiesof 216{236. Grinin,V.P.(1988).Ontheblueemissionvisibleduringdeepminimaofyoung circumstellarenvelopes.apj205,144{154. Gustafsson,B.,Asplund,M.(1996).Modelatmospheresforcoolhydrogendecientcarbonstars.InC.S.JeeryundU.Heber(Hrsg.),Hydrogen{ irregularvariables.svalett.14,27{28. DecientStars,pp.27{38.ASPConf.Ser.96. Hecht,J.H.(1991).ThenatureofdustaroundRCoronaeBorealisstars: Hecht,J.H.,Holm,A.V.,Donn,B.,Wu,C.-C.(1984).Thedustaround isolatedamorphouscarbonorgraphitefractals?apj367,635{640. Hellwege,K.-H.(1982).Landolt-Bornstein:Numericaldataandfunctional Springer-Verlag. relationshipsinscienceandtechnology,bandii/14ofnewseries.berlin: RCoronaeBorealistypestars.ApJ280,228{234. Hollenbach,D.,McKee,F.(1989).Moleculeformationandinfraredemissioninfastinterstellarshocks.III.ResultsforJshocksinmolecularclouds. ApJ342,306{336. Hollenbach,D.,McKee,F.(1979).Moleculeformationandinfraredemission infastinterstellarshocks.i.physicalprocesses.apjs41,555{592.
160 Huber,K.P.,Herzberg,G.(1979).MolecularSpectraandMolecularStruc- Holm,A.V.,Wu,C.-C.,Hecht,J.,Donn,B.(1987).ThefadingofR ture,bandiv.constantsofdiatomicmolecules.vannostrandreinholdcom- pany. CoronaeBorealis.PASP99,497{508. Humphreys,R.M.,Ney,E.P.(1974).InfraredStarsinbinarysystems. Iben,I.J.,Kaler,J.B.,Truran,J.W.,Rezini,A.(1983).Ontheevolutionofthosenucleiofplanetarynebulaethatexperienceanalheliumshell ApJ190,339{347. Jeffery,C.S.(1995).Theultravioletpropertiesofcoolmaterialejectedby ash.apj264,605{612. Jrgensen,U.G.(Hrsg.)(1994).IAUColloquium146:MoleculesintheStellar Environment,Berlin.SpringerVerlag. hydrogen-decientstars.a&a299,135{143. Jurcsik,J.(1996).OntheInter-fadesPeriodsofRCrBTypeVariables.InC.S. Jura,M.(1986).TheRoleofdustinmasslossfromlate-typestars.Irishastr. JeeryundU.Heber(Hrsg.),Hydrogen-DecientStars,pp.96.ASPConf. J.17,322{330. Kilkenny,D.,Whittet,D.C.B.(1984).Infraredphotometryandbroadband Ser.96. Kneer,F.(1983).ApossibleexplanationoftheWilson-Bappurelationandthe chromosherictemperatureriseinlate-typestars.apj128,311{317. uxdistributionsofsouthernrcoronaeborealisstars.mnras208,25{33. Kruger,D.,Gauger,A.,Sedlmayr,E.(1994).Two{uidmodelsforstationarydust{drivenwinds.I.Momentumandenergybalance.A&A290,573{ 589. Lambert,D.L.,KameswaraRao,N.(1994).TheRCoronaeBorealisStars Lambert,D.L.,Rao,N.K.,Giridhar,S.(1990).HighresolutionspectroscopyofRCoronaeBorealisduringthe1988{1989minimum.JA&A11, {AFewMereFacts.JA&A15,47{67. Lawson,W.A.(1986).RYSgr:pulsationrelatedphenomenon.InK.Hungeret 475{490. Lawson,W.A.(1992).SpectroscopyoftheRCoronaeBorealisstarV854Cen 215.D.ReidelPub.Comp. al.(hrsg.),hydrogendecientstarsandrelatedobjects,dordrecht,pp.211{ Lawson,W.A.,Cottrell,P.L.,Clark,M.(1991).RadialvelocityvariationsoftheRCoronaeBorealisstarRYSgr.MNRAS251,687{692. throughadeclineonset.mnras258,33{36.
161 Lawson,W.A.,Cottrell,P.L.,Gilmore,A.C.,Kilmartin,P.M. Lawson,W.A.,Cottrell,P.L.,Kilmartin,P.M.,Gilmore,A.C. (1992).PredictingmasslosseventsinRCoronaeBorealis:declinesofV854 Cen.MNRAS256,339{348. Lawson,W.A.,Kilkenny,D.(1996).Theobservationalcharacterization (1990).Thephotometriccharacteristicsofcoolhydrogen-decientcarbon U.Heber(Hrsg.),Hydrogen-DecientStars,pp.349{360.ASPConf.Ser.96. ofhydrogen-decientcarbonstarsaspulsatingstars.inc.s.jeeryund stars.mnras247,91{117. Loreta,E.(1934).NotasullestellevariabiliRCoronidi.Astron.Nachr.254, Lepp,S.,Shull,M.(1983).TheKineticTheoryofH2Dissociation.ApJ270, 578{582. Luttermoser,D.G.,Johnson,H.R.(1992).Ionizationandexcitationin coolgiantstars,i.hydrogenandhelium.apj388,579{ Maron,N.(1989).PropertiesofthecircumstellargrainsinRCoronaeBorealis. Luttermoser,D.G.,Johnson,H.R.,Avrett,E.H.,Loeser,R.(1989). Ap&SS161,201{207. Chromosphericstructureofcoolcarbonstars.ApJ345,543{553. Mendoza,C.(1983).Compilationoftransitionprobabilities,electronexcitation Menzies,J.W.(1986).RYSgr:Canthetimeofthenextminimumbepredicted? PlanetryNebulae,Dordrecht,pp.154{172.D.ReidelPublishingCompany. ratecoecientsandphotoionizationcrosssections.ind.r.flower(hrsg.), Mihalas,D.(1978).StellarAtmospheres(2nded.).SanFrancisco:W.H.FreemanandCompany. Dordrecht,pp.207{210.D.ReidelPub.Comp. InK.Hungeretal.(Hrsg.),HydrogenDecientStarsandRelatedObjects, Mihalas,D.,WeibelMihalas,B.(1984).FoundationsofRadiationHydrodynamics.OxfordUniversityPress. Millikan,R.C.,White,D.R.(1964).Systematicsofvibrationalrelaxation. Muchmore,D.(1986).Non-uniquesolutionstothestellaratmosphereproblem. A&A155,172{174. J.Chem.Phys.39(4),3209{3213. Neufeld,D.A.,Hollenbach,D.J.(1994).Densemolecularshocksand Muchmore,D.,Ulmschneider,P.(1985).EectsofCOmoleculesonthe accretionontoprotostellardisks.apj428,170{185. outersolaratmosphere:atime{dependentapproach.apj142,393{400. Neufeld,D.A.,Kaufman,M.J.(1993).Radiativecoolingofwarmmolecular gas.apj418,263{272.
162 O'Keefe,J.A.(1939).RemarksonLoreta'sHypothesisconcerningRCoronae Nuth,A.N.,Donn,B.(1981).Vibrationaldisequilibriuminlowpressure Borealis.ApJ90,294{300. clouds.apj247,925{935. Pigott,E.(1797)..Philos.Trans.R.Soc.London1,133. Pugach,A.F.(1977).OntheconnectionbetweenpulsationsofRYSgrand Pugach,A.F.(1984).AmodeloftheRCoronaeBorealisphenomenon.SvA28, 1{3. thetotallightdeclines.inform.bull.variablestars1277(iaucommun.27), Pugach,A.F.(1990).InterpretationofphotometricobservationsofRCoronae Borealis.Lightcurves.SvA34,646{ {292. Pugach,A.F.(1992).InterpretationofphotometricobservationsofRCoronae Pugach,A.F.(1991).InterpretationofphotometricobservationsofRCoronae Borealis.Anoncentraleclipsebyaninhomogeneouscloud.SvA36,612{618. Borealis.Colorfeatures.SvA35,61{65. Pugach,A.F.,Koval'chuk,G.U.(1994).InterpretationofRCoronaeBo- Pugach,A.F.,Skarzhevskii,V.O.(1993).Interpretationofphotometric ports38,219{224. realisphotometricobervations:thesyntheticlightcurve.astronomyre- Puls,J.,Hummer,D.J.(1988).TheSobolevapproximationforthelineforce observationsofrcoronaeborealis.approximationtables.astronomyreports37,169{175. Raghavachari,K.,Binkley,J.S.(1987).Structure,stabilityandfragmentationofsmallcarbonclusters.J.Chem.Phys.87(4),2191{2197tinuumopacity.A&A191,87{98. andlinesourcefunctioninaspherically{symmetricalstellarwindwithcon- Rao,N.K.,Lambert,D.L.(1993).HighresolutionspectroscopyoftheR Renzini,A.(1990).EvolutionaryscenariosforRCrBstars.ASPConf.Ser.11, CoronaeBorealisstar,V854Centauri,duringadeepminimum.AJ105,1915{ 549{ Schmetekopf,A.L.,Fehsenfeld,F.C.,Ferguson,E.E.(1967).LaboratorymeasurementoftherateconstantforH +H!H2+e.ApJ148, Schmutzler,E.(1987).ZumthermischenZustanddunnerPlasmenunterdem EinubeliebigerPhotonenspektren.Dissertation,UniversitatBonn,Bonn, L155{L156. FRG.
163 Scholz,M.,Tsuji,T.(1984).Theeectsofsphericalextensionuponthephotosphericstructureandspectrumofredgiants:comparisonofMandCstars. Schonberner,D.(1986).EvolutionarystatusandoriginofextremelyhydrogenlatedObjects,Dordrecht,pp.471{480.D.ReidelPub.Comdecientstars.InK.Hungeretal.(Hrsg.),HydrogenDecientStarsandRe- A&A130,11{18. Serkowski,K.,Kruszewski,A.(1969).ChangesinpolarizationoftheRCrB Spizer,L.(1978).PhysicalProcessesintheInterstellarMedium.New{York:J. starrysgr.apj155,l15. Stanford,S.A.,CLayton,G.C.,Meade,M.R.,Nordsieck,K.H. (1988).RCoronaeBorealisdustejections:Apreferredplane?ApJ325,L9{ answhitney,b.a.,murison,m.a.,nook,m.a.,anderson,c.m. Wiley&Sons. Stilley,J.L.,Callaway,J.(1970).Free-freeabsorptioncoecientofthe negativehydrogenion.apj160,245{260. L12. Turner,J.,Kirby-Docken,K.,Dalgarno,A.(1977).TheQuadrupole Unsold,A.(1968).PhysikderSternatmospharen(2.Auageed.).Berlin,Heidelberg:Springer. 281{292. Vibration{RotationTransitionProbabilitiesofMolecularHydrogen.ApJS35, Walker,H.J.(1985).IRASphotometryofdustshellsaroundhydrogendecientstars.A&A152,58{62. Wdowiak,T.J.(1975).Coarsephotosphericconvectionandtheejectionofdust Whitney,B.A.,Balm,S.B.,Clayton,G.C.(1993).Dustformationin byrcoronaeborealis.apj198,l139{l140. Whitney,B.A.,Clayton,G.C.,Schulte-Ladbeck,R.E.,Meade, ASPConf.Ser.No.45. RCBstars.InD.Sasselov(Hrsg.),LuminousHighLatitudeStars,pp.115{122. Wing,R.F.,Baumert,J.H.,Strom,S.E.,Strom,K.M.(1972).Infrared tothegeometryofthedustandemission-lineregion.aj103,1652{1657. photometrieofrcrbduringitsrecentdecline.pasp84,646{647. M.R.(1992).SpectropolarimetryofV854Centauriatminimumlight:Clues Winters,J.M.,Fleischer,A.J.,Gauger,A.,Sedlmayr,E.(1994). Winters,J.M.(1994).Internalstructureandopticalappearanceofcircumstellardustshellsaroundcoolcarbongiants.Dissertation,TechnischeUniversitat, CircumstellarDustshellsaroundLong-periodVariables.II.Theoretical Berlin,FRG. Wishart,A.W.(1979).Thebound{freephoto-detachmentcross-sectionofH. MNRAS187,59p{60p. lightcurvesofc{stars.a&a290,623{633.
164 Wood,P.R.(1979).PulsationandmasslossinMiravariables.ApJ227,220{ Woitke,P.(1992).StaubbildunginderSupernova1987A.Diplomarbeit,TechnischeUniversitat,Berlin,FRG. Wright,E.L.(1989).FractaldustgrainsaroundRCoronaeBorealisstars Zubko,V.G.(1996).OntheinterpretationoftheextinctioncurvesofRCB stars.mnrasinpress,. ApJ346,L89{L91.
165 MeinenDank::: IchdankeihmfurdieFreiheit,dieermiraufmeinemwissenschaftlichenWegeinraumte, :::mochteichzunachstherrnprof.dr.sedlmayraussprechen.vonseinerunverwechelbarenartzudenkenhabeichundwerdeichhoentlichauchnochinzukunftviellernen. deresmirdurchunburokratischemanahmenermoglichte,andasinstitutfurastonomie undastrophysikzuruckzukehrenundhiermeinedissertationzubeenden. WeiterhindankeichHerrnPriv.Doz.Dr.KaufmannfurdieErstellungdesZweitgutachtens FurdieToleranz,dieHilfbereitschaftunddiefruchtbarenDiskussionenbeiderErstellung sowieherrnprof.dr.zimmermann,dersichbereiterklarthat,denprufungsvorsitzzu unddasvertrauen,dasermirtrotzzwischenzeitlicherdierenzenschenkte.erwares, michbeiholgerbeck,christianehelling,janmartinwintersundbeipetercottrell,die derarbeitmochteichallenmitgliederndesinstitutesdanken,insbesonderebedankeich ubernehmen. DanielKrugerhatganzwesentlichbeidernaturwissenschaftlichenKonzeptiondieserAr- unentgeltlichearbeitandenrechnerndesinstitutesdiesearbeiterstmoglichmachte. zurseitegestandenhaben.weiterhindankeichuwebolick,derdurchseinegrotenteils mirbeiderkorrekturderarbeitunddererledigungderprufungsformalitatentatkraftig chieren... unddeinekorrekturenbesondersbedanken vielleichtkannichmichdafurbaldrevanbeitmitgewirkt.diegrundideeerwuchsausseinerdiplomarbeit,aufdiewiederumandreasgaugereinuhatte.ichmochtemichbeidir,daniel,furdiezahlreichendiskussionen AchimGoeresdankeichvonHerzenfurdieBeratungnichtnurinfachlichenFragen.Neben meinearbeitodervielmehrmeinepersonzuunterstutzen.ichwerdenievergessen,wie hergab,ummeinendarauffolgendenkurzvortrageinzuleiten. einerartinnererseelenverwandschaftfuhleichbeiihmstetsdasaufrichtigebestreben, MeininnigsterDankgehortjedochDietrichEwert,vondessenHartnackigkeit,schierunendlicherEnergieundliebevollerZielstrebigkeitichnochviellernenwerde.IneinerZeit, ermuntert,meinearbeitfortzusetzen. eraufderinternationalentagunginbamberg(1995)seineneingeladenenvortragdafur alsichmitderastrophysikinnerlichfastschonabgeschlossenhatte,hatermichtaglich
166 Lebenslauf PeterWoitke PersonlicheDaten Alter:32Jahre Geburtsort:Berlin{Spandau Familienstand:ledig Anschrift:Schwendyweg6,13587Berlin Sept.1977{Dez.1983 Sept.1971{Juli1977 SchuleundStudium Apr.1984{Okt.1992 Astrid{Lindgren{GrundschuleinBerlin{Staaken Freiherr{vom{Stein{GymnasiuminBerlin{Spandau StudiumderPhysikanderTechnischenUniversitatBerlin ThemaderDiplomarbeit:"StaubbildunginderSupernova Jan.1984{Marz.1984 StudienbegleitendeTatigkeiten: IndustriepraktikumbeiderFirmaSiemens 1987A\,AbschlualsDiplom{Physiker Apr.1989{Marz.1992 Apr.1987{Feb.1989 KurseundPraktikainBionikundEvolutionsstrategie TutorimphysikalischenGrundpraktikum(Projektlabor) abnov.1992 furastronomieundastrophysikdertuberlinbei BeruicherWerdegang TatigkeitalswissenschaftlicherMitarbeiteramInstitut BetreuungvonSeminarvortragenundDiplomarbeiten ArbeitundMitarbeitanwissenschaftlichenPublikationen TeilnahmeaninternationalenTagungen(z.B.St.Louis,1994) Prof.Dr.E.SedlmayrmitdenAufgabenbereichen: Okt.1996{Jan.1997 derfirmabbjservisggmbh TatigkeitalsNetzwerk{AdministratorundInformatikerbei Sprachen: BesondereKenntnisse EDV: (Schulkenntnisse) Englisch(sicherinWortundSchrift),Franzosisch diverseerfahrungenmitpcs,workstationsundgrorechnernunterdos,windowsundunix.computersprachen: Programmen(Paradox5.0)sowiemitStandardsoftware{ C,C++,Fortran,GFA{Basic,PascalundAssembler.ErfahrungenmitPC{NetzwerkenunterNovel3.12,Datenbank{ Sport: ProduktenwieMS-WordundExcel. imvolleyball TatigkeitalsTrainervonHerren-undDamenmannschaften Berlin,den31.Juni1997
Schneps, Leila; Colmez, Coralie. Math on Trial : How Numbers Get Used and Abused in the Courtroom. New York, NY, USA: Basic Books, 2013. p i.
 New York, NY, USA: Basic Books, 2013. p i. http://site.ebrary.com/lib/mcgill/doc?id=10665296&ppg=2 New York, NY, USA: Basic Books, 2013. p ii. http://site.ebrary.com/lib/mcgill/doc?id=10665296&ppg=3 New
New York, NY, USA: Basic Books, 2013. p i. http://site.ebrary.com/lib/mcgill/doc?id=10665296&ppg=2 New York, NY, USA: Basic Books, 2013. p ii. http://site.ebrary.com/lib/mcgill/doc?id=10665296&ppg=3 New
San$Diego$Imperial$Counties$Region$of$Narcotics$Anonymous$ Western$Service$Learning$Days$$ XXX$Host$Committee!Guidelines$ $$
 SanDiegoImperialCountiesRegionofNarcoticsAnonymous WesternServiceLearningDays XXXHostCommitteeGuidelines I. Purpose ThepurposeoftheWesternServiceLearningDays(WSLD)XXXHostCommittee(HostCommittee)isto organize,coordinateandproducethewsldxxxeventwithinthe6weekperiodof3weekspriortotheendof
SanDiegoImperialCountiesRegionofNarcoticsAnonymous WesternServiceLearningDays XXXHostCommitteeGuidelines I. Purpose ThepurposeoftheWesternServiceLearningDays(WSLD)XXXHostCommittee(HostCommittee)isto organize,coordinateandproducethewsldxxxeventwithinthe6weekperiodof3weekspriortotheendof
Learn AX: A Beginner s Guide to Microsoft Dynamics AX. Managing Users and Role Based Security in Microsoft Dynamics AX 2012. Dynamics101 ACADEMY
 Learn AX: A Beginner s Guide to Microsoft Dynamics AX Managing Users and Role Based Security in Microsoft Dynamics AX 2012 About.com is a Rand Group Knowledge Center intended to provide our clients, and
Learn AX: A Beginner s Guide to Microsoft Dynamics AX Managing Users and Role Based Security in Microsoft Dynamics AX 2012 About.com is a Rand Group Knowledge Center intended to provide our clients, and
TITLE 9. HEALTH SERVICES CHAPTER 1. DEPARTMENT OF HEALTH SERVICES ADMINISTRATION ARTICLE 4. CODES AND STANDARDS REFERENCED
 TITLE 9. HEALTH SERVICES CHAPTER 1. DEPARTMENT OF HEALTH SERVICES ADMINISTRATION ARTICLE 4. CODES AND STANDARDS REFERENCED R9-1-412. Physical Plant Health and Safety Codes and Standards A. The following
TITLE 9. HEALTH SERVICES CHAPTER 1. DEPARTMENT OF HEALTH SERVICES ADMINISTRATION ARTICLE 4. CODES AND STANDARDS REFERENCED R9-1-412. Physical Plant Health and Safety Codes and Standards A. The following
1. Who can use Agent Portal? 2. What is the definition of an active agent? 3. How to access Agent portal? 4. How to login?
 1. Who can use Agent Portal? Any active agent who is associated with Future Generali Life Insurance Company Limited can logon to Agent Portal 2. What is the definition of an active agent? An agent, whose
1. Who can use Agent Portal? Any active agent who is associated with Future Generali Life Insurance Company Limited can logon to Agent Portal 2. What is the definition of an active agent? An agent, whose
How To Get A Financial Aid Award In Athena
 Athena Self-Service Walkthrough By the UGA Office of Student Financial Aid 220 Holmes/Hunter Academic Building Athens, GA 30602-6114 Phone: (706) 542-6147 Section 1 How to Find Out What is Needed by the
Athena Self-Service Walkthrough By the UGA Office of Student Financial Aid 220 Holmes/Hunter Academic Building Athens, GA 30602-6114 Phone: (706) 542-6147 Section 1 How to Find Out What is Needed by the
The following report presents financial data only. The full and binding version is available in Polish. K2 INTERNET S.A.
 The following report presents financial data only. The full and binding version is available in Polish. K2 INTERNET S.A. Annual Financial Statement of K2 Internet S.A. for the twelve-month period ended
The following report presents financial data only. The full and binding version is available in Polish. K2 INTERNET S.A. Annual Financial Statement of K2 Internet S.A. for the twelve-month period ended
Data Security at the KOKU
 I. After we proposed our project to the central registration office of the city of Hamburg, they accepted our request for transferring information from their birth records. Transfer of all contact details
I. After we proposed our project to the central registration office of the city of Hamburg, they accepted our request for transferring information from their birth records. Transfer of all contact details
Regulatory Story. RNS Number : 8343I. DCD Media PLC. 08 July 2013. TR-1: NOTIFICATION OF MAJOR INTEREST IN SHARES i
 1 of 7 25/11/2013 11:51 Regulatory Story Go to market news section Company TIDM Headline Released DCD Media PLC DCD Holding(s) in Company 15:19 08-Jul-2013 8343I15 RNS : 8343I DCD Media PLC 08 July 2013
1 of 7 25/11/2013 11:51 Regulatory Story Go to market news section Company TIDM Headline Released DCD Media PLC DCD Holding(s) in Company 15:19 08-Jul-2013 8343I15 RNS : 8343I DCD Media PLC 08 July 2013
1 of 7 31/10/2012 18:34
 Regulatory Story Go to market news section Company TIDM Headline Released Number Ironveld PLC IRON Holding(s) in Company 18:01 31-Oct-2012 0348Q18 RNS Number : 0348Q Ironveld PLC 31 October 2012 TR-1:
Regulatory Story Go to market news section Company TIDM Headline Released Number Ironveld PLC IRON Holding(s) in Company 18:01 31-Oct-2012 0348Q18 RNS Number : 0348Q Ironveld PLC 31 October 2012 TR-1:
Introduction to Windchill Projectlink 10.2
 Introduction to Windchill Projectlink 10.2 Overview Course Code Course Length TRN-4270 1 Day In this course, you will learn how to participate in and manage projects using Windchill ProjectLink 10.2. Emphasis
Introduction to Windchill Projectlink 10.2 Overview Course Code Course Length TRN-4270 1 Day In this course, you will learn how to participate in and manage projects using Windchill ProjectLink 10.2. Emphasis
The following report presents financial data only. The full and binding version is available in Polish. K2 INTERNET S.A.
 The following report presents financial data only. The full and binding version is available in Polish. K2 INTERNET S.A. Annual Financial Statement of K2 Internet S.A. for the twelve-month period ended
The following report presents financial data only. The full and binding version is available in Polish. K2 INTERNET S.A. Annual Financial Statement of K2 Internet S.A. for the twelve-month period ended
Declaration to be submitted by directors in the Applicant Company 1
 Form SNBFI/D1 Name of the Applicant Company: Declaration to be submitted by directors in the Applicant Company 1 1. Personal Details 1.1 Full name: 1.2 National Identity Card number: 1.3 Passport number:
Form SNBFI/D1 Name of the Applicant Company: Declaration to be submitted by directors in the Applicant Company 1 1. Personal Details 1.1 Full name: 1.2 National Identity Card number: 1.3 Passport number:
THE PSYCHOLOGY CLUB EASTERN CONNECTICUT STATE UNIVERSITY CONSTITUTION. Article I: Name. Article II: Purpose
 THE PSYCHOLOGY CLUB EASTERN CONNECTICUT STATE UNIVERSITY CONSTITUTION Article I: Name The name of this organization shall be called the Psychology Club of Eastern Connecticut State College. Article II:
THE PSYCHOLOGY CLUB EASTERN CONNECTICUT STATE UNIVERSITY CONSTITUTION Article I: Name The name of this organization shall be called the Psychology Club of Eastern Connecticut State College. Article II:
CHAPTER 5 Energy Efficient HVAC Design
 CHAPTER 5 Energy 5.1 Guideline 5.2 Mandatory clause 5.3 Technical notes #$$% #$$% #$$& ( ) +, (./ 5.3.1 on optimization of cooling load estimation %0 Table 5.3.1: Inside design conditions for airconditioned
CHAPTER 5 Energy 5.1 Guideline 5.2 Mandatory clause 5.3 Technical notes #$$% #$$% #$$& ( ) +, (./ 5.3.1 on optimization of cooling load estimation %0 Table 5.3.1: Inside design conditions for airconditioned
Life Insurance. Basic Life Insurance. Optional Life Insurance
 Life Insurance Basic Life Insurance PEIA fers active employees under age 65 a basic $10,000 decreasing term life insurance policy with accidental death and dismemberment (AD&D) benefits. The value this
Life Insurance Basic Life Insurance PEIA fers active employees under age 65 a basic $10,000 decreasing term life insurance policy with accidental death and dismemberment (AD&D) benefits. The value this
Workflow Administration of Windchill 10.2
 Workflow Administration of Windchill 10.2 Overview Course Code Course Length TRN-4339-T 2 Days In this course, you will learn about Windchill workflow features and how to design, configure, and test workflow
Workflow Administration of Windchill 10.2 Overview Course Code Course Length TRN-4339-T 2 Days In this course, you will learn about Windchill workflow features and how to design, configure, and test workflow
Hi iv. Declaration Certificate Acknowledgement Preface. List o f Table. List o f Figures. viii xvi xvii. 1.1 Introduction 1
 Declaration Certificate Acknowledgement Preface. List o f Table. List o f Figures Hi iv V viii xvi xvii Chapter 1 Introduction 1-13 1.1 Introduction 1 1.2 Statement of the Problem 3 1.2.1 Terms used in
Declaration Certificate Acknowledgement Preface. List o f Table. List o f Figures Hi iv V viii xvi xvii Chapter 1 Introduction 1-13 1.1 Introduction 1 1.2 Statement of the Problem 3 1.2.1 Terms used in
TABLE OF CONTENTS CHAPTER DESCRIPTION PAGE
 vii TABLE OF CONTENTS CHAPTER DESCRIPTION PAGE TITLE DECLARATION DEDICATION ACKNOWLEDGEMENT ABSTRACT ABSTRAK LIST OF CONTENTS LIST OF FIGURES LIST OF TABLES LIST OF APPENDICES i ii iii iv v vi vii xii
vii TABLE OF CONTENTS CHAPTER DESCRIPTION PAGE TITLE DECLARATION DEDICATION ACKNOWLEDGEMENT ABSTRACT ABSTRAK LIST OF CONTENTS LIST OF FIGURES LIST OF TABLES LIST OF APPENDICES i ii iii iv v vi vii xii
PG DIPLOMA IN GLOBAL STRATEGIC MANAGEMENT LIST OF BOOKS*
 PG DIPLOMA IN GLOBAL STRATEGIC MANAGEMENT LIST OF BOOKS* Paper I: INTERNATIONAL BUSINESS ENVIRONMENT Global Business Environment (ICMR Publication Textbook) [Ref. No: GBE 11 2K4 23] [ISBN: 81-7881-693-8]
PG DIPLOMA IN GLOBAL STRATEGIC MANAGEMENT LIST OF BOOKS* Paper I: INTERNATIONAL BUSINESS ENVIRONMENT Global Business Environment (ICMR Publication Textbook) [Ref. No: GBE 11 2K4 23] [ISBN: 81-7881-693-8]
Introduction. Acknowledgments Support & Feedback Preparing for the Exam. Chapter 1 Plan and deploy a server infrastructure 1
 Introduction Acknowledgments Support & Feedback Preparing for the Exam xv xvi xvii xviii Chapter 1 Plan and deploy a server infrastructure 1 Objective 1.1: Design an automated server installation strategy...1
Introduction Acknowledgments Support & Feedback Preparing for the Exam xv xvi xvii xviii Chapter 1 Plan and deploy a server infrastructure 1 Objective 1.1: Design an automated server installation strategy...1
1. Access your account Log in to your online account at http://service.ringcentral.com using your main Ring Central phone number and password.
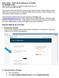 Ring Central Quick Set Up settings for GA Hotline For assistance call National Hotline Committee Chair [email protected] Ring Central Support (888) 898-4591 The purpose of this document is
Ring Central Quick Set Up settings for GA Hotline For assistance call National Hotline Committee Chair [email protected] Ring Central Support (888) 898-4591 The purpose of this document is
Contents. 1 Introduction. 2 Feature List. 3 Feature Interaction Matrix. 4 Feature Interactions
 1 Introduction 1.1 Purpose and Scope................................. 1 1 1.2 Organization..................................... 1 2 1.3 Requirements Notation............................... 1 2 1.4 Requirements
1 Introduction 1.1 Purpose and Scope................................. 1 1 1.2 Organization..................................... 1 2 1.3 Requirements Notation............................... 1 2 1.4 Requirements
BSTP SRF 81 Medical Emergency and Work Place Injury
 Page 1 of 5 Table of Contents I. PRINCIPLE (Purpose):...2 II. ROLE:...2 III. GLOSSARY, ABBREVIATIONS OR DEFINITIONS:...2 IV. INDICATIONS (Policy):...2 V. SPECIMENS (Samples):...2 VI. MATERIALS, REAGENTS,
Page 1 of 5 Table of Contents I. PRINCIPLE (Purpose):...2 II. ROLE:...2 III. GLOSSARY, ABBREVIATIONS OR DEFINITIONS:...2 IV. INDICATIONS (Policy):...2 V. SPECIMENS (Samples):...2 VI. MATERIALS, REAGENTS,
ISSUING THE AIR OPERATOR CERTIFICATE, OPERATIONS SPECIFICATIONS, AND COMPLETING THE CERTIFICATION REPORT
 ISSUING THE AIR OPERATOR CERTIFICATE, OPERATIONS SPECIFICATIONS, AND COMPLETING THE CERTIFICATION REPORT GUIDANCE MATERIAL FOR INSPECTORS CA AOC-017 AIR OPERATOR CERTIFICATION RECORD OF AMENDMENTS Amendment
ISSUING THE AIR OPERATOR CERTIFICATE, OPERATIONS SPECIFICATIONS, AND COMPLETING THE CERTIFICATION REPORT GUIDANCE MATERIAL FOR INSPECTORS CA AOC-017 AIR OPERATOR CERTIFICATION RECORD OF AMENDMENTS Amendment
NATIONAL UNIVERSITY OF SCIENCE AND TECHNOLOGY
 NATIONAL UNIVERSITY OF SCIENCE AND TECHNOLOGY FACULTY OF COMMERCE GENERAL MASTERS IN BUSINESS ADMINISTRATION MANAGERIAL ACCOUNTING GMB 562 FINAL EXAMINATION 11 DECEMBER 2003 TIME ALLOWED: 3 HOURS + 30
NATIONAL UNIVERSITY OF SCIENCE AND TECHNOLOGY FACULTY OF COMMERCE GENERAL MASTERS IN BUSINESS ADMINISTRATION MANAGERIAL ACCOUNTING GMB 562 FINAL EXAMINATION 11 DECEMBER 2003 TIME ALLOWED: 3 HOURS + 30
STATE UNIVERSITY OF NEW YORK COLLEGE OF TECHNOLOGY CANTON, NEW YORK COURSE OUTLINE JUST 201 CRITICAL ISSUES IN CRIMINAL JUSTICE
 STATE UNIVERSITY OF NEW YORK COLLEGE OF TECHNOLOGY CANTON, NEW YORK COURSE OUTLINE JUST 201 CRITICAL ISSUES IN CRIMINAL JUSTICE Prepared by: Dr. Brian K. Harte SCHOOL OF BUSINESS AND CRIMINAL JUSTICE Department
STATE UNIVERSITY OF NEW YORK COLLEGE OF TECHNOLOGY CANTON, NEW YORK COURSE OUTLINE JUST 201 CRITICAL ISSUES IN CRIMINAL JUSTICE Prepared by: Dr. Brian K. Harte SCHOOL OF BUSINESS AND CRIMINAL JUSTICE Department
vii TABLE OF CONTENTS CHAPTER TITLE PAGE DECLARATION DEDICATION ACKNOWLEDGEMENT ABSTRACT ABSTRAK
 vii TABLE OF CONTENTS CHAPTER TITLE PAGE DECLARATION DEDICATION ACKNOWLEDGEMENT ABSTRACT ABSTRAK TABLE OF CONTENTS LIST OF TABLES LIST OF FIGURES LIST OF ABBREVIATIONS LIST OF SYMBOLS LIST OF APPENDICES
vii TABLE OF CONTENTS CHAPTER TITLE PAGE DECLARATION DEDICATION ACKNOWLEDGEMENT ABSTRACT ABSTRAK TABLE OF CONTENTS LIST OF TABLES LIST OF FIGURES LIST OF ABBREVIATIONS LIST OF SYMBOLS LIST OF APPENDICES
FINAL JOINT PRETRIAL ORDER. This matter is before the Court on a Final Pretrial Conference pursuant to R. 4:25-1.
 SUPERIOR COURT OF NEW JERSEY MIDDLESEX COUNTY:LAW DIVISION Docket No. Plaintiff(s), v. Defendant(s). FINAL JOINT PRETRIAL ORDER This matter is before the Court on a Final Pretrial Conference pursuant to
SUPERIOR COURT OF NEW JERSEY MIDDLESEX COUNTY:LAW DIVISION Docket No. Plaintiff(s), v. Defendant(s). FINAL JOINT PRETRIAL ORDER This matter is before the Court on a Final Pretrial Conference pursuant to
COMPUTERS ORGANIZATION 2ND YEAR COMPUTE SCIENCE MANAGEMENT ENGINEERING JOSÉ GARCÍA RODRÍGUEZ JOSÉ ANTONIO SERRA PÉREZ
 COMPUTERS ORGANIZATION 2ND YEAR COMPUTE SCIENCE MANAGEMENT ENGINEERING UNIT 1 - INTRODUCTION JOSÉ GARCÍA RODRÍGUEZ JOSÉ ANTONIO SERRA PÉREZ Unit 1.MaNoTaS 1 Definitions (I) Description A computer is: A
COMPUTERS ORGANIZATION 2ND YEAR COMPUTE SCIENCE MANAGEMENT ENGINEERING UNIT 1 - INTRODUCTION JOSÉ GARCÍA RODRÍGUEZ JOSÉ ANTONIO SERRA PÉREZ Unit 1.MaNoTaS 1 Definitions (I) Description A computer is: A
The City of Philadelphia Department of Human Services. The Improving Outcomes for Children Initiative. Community Umbrella Agency Practice Guidelines
 Webelievethatacommunity neighborhoodapproachwithclearlydefinedrolesbetween countyandproviderstaffwillpositivelyimpactsafety,permanency,andwell being." Whatareweworkingtogethertoachieve? o Morechildrenandyouthmaintainedsafelyintheirownhomesandcommunities.
Webelievethatacommunity neighborhoodapproachwithclearlydefinedrolesbetween countyandproviderstaffwillpositivelyimpactsafety,permanency,andwell being." Whatareweworkingtogethertoachieve? o Morechildrenandyouthmaintainedsafelyintheirownhomesandcommunities.
An Enterprise Modeling Framework for Banks using. Algebraic Graph Transformation
 An Enterprise Modeling Framework for Banks using Algebraic Graph Transformation vorgelegt von Diplom-Wirtschaftsinformatiker Christoph Brandt aus Berlin-Lichterfelde von der Fakultät IV - Elektrotechnik
An Enterprise Modeling Framework for Banks using Algebraic Graph Transformation vorgelegt von Diplom-Wirtschaftsinformatiker Christoph Brandt aus Berlin-Lichterfelde von der Fakultät IV - Elektrotechnik
Nearshore IT Sourcing for Small- and Medium-Sized Enterprises: An Exploratory Study of Swiss SMEs Sourcing from Russia and Ukraine
 Nearshore IT Sourcing for Small- and Medium-Sized Enterprises: An Exploratory Study of Swiss SMEs Sourcing from Russia and Ukraine DISSERTATION of the University of St. Gallen, Graduate School of Business
Nearshore IT Sourcing for Small- and Medium-Sized Enterprises: An Exploratory Study of Swiss SMEs Sourcing from Russia and Ukraine DISSERTATION of the University of St. Gallen, Graduate School of Business
Consolidated Annual Report of the AB Capital Group for the financial year 2008/2009. covering the period from July 1, 2008 to June 30, 2009
 Consolidated Annual Report of the AB Capital Group for the financial year 2008/2009 covering the period from July 1, 2008 to June 30, 2009 Selected financial data converted to EUR SELECTED FINANCIAL DATA
Consolidated Annual Report of the AB Capital Group for the financial year 2008/2009 covering the period from July 1, 2008 to June 30, 2009 Selected financial data converted to EUR SELECTED FINANCIAL DATA
Department of International Trade at Feng Chia University Master s Program Requirements Policy
 Department of International Trade at Feng Chia University Master s Program Requirements Policy Revised and approved by the Department Affairs Committee on June 9 th, 2005 Revised and approved by the Department
Department of International Trade at Feng Chia University Master s Program Requirements Policy Revised and approved by the Department Affairs Committee on June 9 th, 2005 Revised and approved by the Department
THE FIRST SCHEDULE (See rule 7) Table I - FEES PAYABLE
 Number of entry On what payable Number of the relevant Form THE FIRST SCHEDULE (See rule 7) Table I - FEES PAYABLE Natural For e-filing Small entity, alone or with natural Others, alone or with natural
Number of entry On what payable Number of the relevant Form THE FIRST SCHEDULE (See rule 7) Table I - FEES PAYABLE Natural For e-filing Small entity, alone or with natural Others, alone or with natural
ReCap, ReCap Pro Features, and ReCap 360 Web Services FAQ
 ReCap, ReCap Pro Features, and ReCap 360 Web Services FAQ Autodesk Reality Solutions Group R e Cap FAQ 1 I. What are the ReCap Products and Services available today? - ReCap is Autodesk desktop application
ReCap, ReCap Pro Features, and ReCap 360 Web Services FAQ Autodesk Reality Solutions Group R e Cap FAQ 1 I. What are the ReCap Products and Services available today? - ReCap is Autodesk desktop application
TABLE OF CONTENTS CHAPTER TITLE PAGE
 viii TABLE OF CONTENTS CHAPTER TITLE PAGE TITLE PAGE DECLARATION DEDICATION ACKNOWLEDGEMENT ABSTRACT ABSTRAK TABLE OF CONTENTS LIST OF TABLES LIST OF FIGURES LIST OF APPENDICES I II III IV VI VII VIII
viii TABLE OF CONTENTS CHAPTER TITLE PAGE TITLE PAGE DECLARATION DEDICATION ACKNOWLEDGEMENT ABSTRACT ABSTRAK TABLE OF CONTENTS LIST OF TABLES LIST OF FIGURES LIST OF APPENDICES I II III IV VI VII VIII
EL PASO COUNTY DEPARTMENT OF HUMAN RESOURCES. Family and Medical Leave
 EL PASO COUNTY DEPARTMENT OF HUMAN RESOURCES Family and Medical Leave Revised Date: El Paso County shall provide eligible employees up to 12 weeks of unpaid leave per year for certain family and medical
EL PASO COUNTY DEPARTMENT OF HUMAN RESOURCES Family and Medical Leave Revised Date: El Paso County shall provide eligible employees up to 12 weeks of unpaid leave per year for certain family and medical
Impact of IT Outsourcing on Business & IT Alignment
 x Impact of IT Outsourcing on Business & IT Alignment Summary IT outsourcing does not matter from an alignment perspective This dissertation is the end result of over four years of research, and over fifteen
x Impact of IT Outsourcing on Business & IT Alignment Summary IT outsourcing does not matter from an alignment perspective This dissertation is the end result of over four years of research, and over fifteen
vii TABLE OF CONTENTS CHAPTER TITLE PAGE DECLARATION DEDICATION ACKNOWLEDGEMENT ABSTRACT ABSTRAK
 vii TABLE OF CONTENTS CHAPTER TITLE PAGE DECLARATION DEDICATION ACKNOWLEDGEMENT ABSTRACT ABSTRAK TABLE OF CONTENTS LIST OF TABLES LIST OF FIGURES LIST OF SYMBOLS / ABBREVIATIONS LIST OF APPENDICES ii iii
vii TABLE OF CONTENTS CHAPTER TITLE PAGE DECLARATION DEDICATION ACKNOWLEDGEMENT ABSTRACT ABSTRAK TABLE OF CONTENTS LIST OF TABLES LIST OF FIGURES LIST OF SYMBOLS / ABBREVIATIONS LIST OF APPENDICES ii iii
EIGHTH DIRECTIVE OF DEPUTY RECEIVER (IMPLEMENTING THE HOW/HWC PLAN OE LIQUIDATION)
 COMMONWEALTH OF VIRGINIA STATE CORPORATION COMMISSION COMMONWEALTH OF VIRGINIA at the Relation of the STATE CORPORATION COMMISSION, Applicant, v. CASE NO. INS-1994-00218 HOW INSURANCE COMPANY, A RISK RETENTION
COMMONWEALTH OF VIRGINIA STATE CORPORATION COMMISSION COMMONWEALTH OF VIRGINIA at the Relation of the STATE CORPORATION COMMISSION, Applicant, v. CASE NO. INS-1994-00218 HOW INSURANCE COMPANY, A RISK RETENTION
SITE PHOTOGRAPHS (GOOGLE EARTH): ROAD REHABILITATION Refer to Appendix B for a map of the viewpoint locations.
 469335: N7 Rehab BA Report_Appendix B5 Page i SITE PHOTOGRAPHS (GOOGLE EARTH): ROAD REHABILITATION Refer to Appendix B for a map of the viewpoint locations. R1 R1 R2 R2 Looking north with Okiep east of
469335: N7 Rehab BA Report_Appendix B5 Page i SITE PHOTOGRAPHS (GOOGLE EARTH): ROAD REHABILITATION Refer to Appendix B for a map of the viewpoint locations. R1 R1 R2 R2 Looking north with Okiep east of
Delivering Business Intelligence With Microsoft SQL Server 2005 or 2008 HDT922 Five Days
 or 2008 Five Days Prerequisites Students should have experience with any relational database management system as well as experience with data warehouses and star schemas. It would be helpful if students
or 2008 Five Days Prerequisites Students should have experience with any relational database management system as well as experience with data warehouses and star schemas. It would be helpful if students
Financial Management Practices
 RK. Jain Shveta Singh Surendra Singh Yadav Financial Management Practices An Empirical Study of Indian Corporates QA Springer Part I Background 1 Introduction 3 Objectives 4 Rationale 5 Research Methodology
RK. Jain Shveta Singh Surendra Singh Yadav Financial Management Practices An Empirical Study of Indian Corporates QA Springer Part I Background 1 Introduction 3 Objectives 4 Rationale 5 Research Methodology
THE PERFORMANCE MANAGEMENT GROUP LLC
 THE PERFORMANCE MANAGEMENT GROUP LLC ON-CAMPUS TRAINING: LEAN SIX SIGMA EXCELLENCE IN HEALTHCARE DELIVERY BLACK BELT CERTIFICATION Performance Improvement Training for the Healthcare Industry ABOUT THE
THE PERFORMANCE MANAGEMENT GROUP LLC ON-CAMPUS TRAINING: LEAN SIX SIGMA EXCELLENCE IN HEALTHCARE DELIVERY BLACK BELT CERTIFICATION Performance Improvement Training for the Healthcare Industry ABOUT THE
FLORIDA STATE COLLEGE AT JACKSONVILLE NON-COLLEGE CREDIT COURSE OUTLINE. Insurance Customer Service Representative
 Form 2B, Page 1 FLORIDA STATE COLLEGE AT JACKSONVILLE NON-COLLEGE CREDIT COURSE OUTLINE COURSE NUMBER: RMI 0093 COURSE TITLE: PREREQUISITE(S): COREQUISITE(S): Insurance Customer Service Representative
Form 2B, Page 1 FLORIDA STATE COLLEGE AT JACKSONVILLE NON-COLLEGE CREDIT COURSE OUTLINE COURSE NUMBER: RMI 0093 COURSE TITLE: PREREQUISITE(S): COREQUISITE(S): Insurance Customer Service Representative
B1 Project Management 100
 Assignment of points B1 Project Management 100 Requirements for Design Presentation Meetings and Proposal Submissions for Key to Project Management Design Presentation Meeting and Proposal Submissions
Assignment of points B1 Project Management 100 Requirements for Design Presentation Meetings and Proposal Submissions for Key to Project Management Design Presentation Meeting and Proposal Submissions
3 BUSINESS ACCOUNTING STANDARD,,INCOME STATEMENT I. GENERAL PROVISIONS
 APPROVED by Resolution No. 1 of 18 December 2003 of the Standards Board of the Public Establishment the Institute of Accounting of the Republic of Lithuania 3 BUSINESS ACCOUNTING STANDARD,,INCOME STATEMENT
APPROVED by Resolution No. 1 of 18 December 2003 of the Standards Board of the Public Establishment the Institute of Accounting of the Republic of Lithuania 3 BUSINESS ACCOUNTING STANDARD,,INCOME STATEMENT
BAHAUDDIN ZAKARIYA UNIVERSITY, MULTAN.
 BAHAUDDIN ZAKARIYA UNIVERSITY, MULTAN. RE-TENDER TENDER DOCUMENT For LAB EQUIPMENTS FOR THE INSTITUTE OF ADVANCED MATERIALS Last Date of Submission: 29.02.2016 BAHAUDDIN ZAKARIYA UNIVERSITY, MULTAN www.bzu.edu.pk
BAHAUDDIN ZAKARIYA UNIVERSITY, MULTAN. RE-TENDER TENDER DOCUMENT For LAB EQUIPMENTS FOR THE INSTITUTE OF ADVANCED MATERIALS Last Date of Submission: 29.02.2016 BAHAUDDIN ZAKARIYA UNIVERSITY, MULTAN www.bzu.edu.pk
Monthly Noteholder's Statement Synchrony Credit Card Master Note Trust Series 2012-6
 Monthly teholder's Statement Synchrony Credit Card Master te Trust Series 2012-6 Class A 1.3600% tes Class B 1.8300% tes Class C 2.6700% tes Pursuant to the Master Indenture, dated as of September 25,
Monthly teholder's Statement Synchrony Credit Card Master te Trust Series 2012-6 Class A 1.3600% tes Class B 1.8300% tes Class C 2.6700% tes Pursuant to the Master Indenture, dated as of September 25,
CLASS TEST GRADE 11. PHYSICAL SCIENCES: CHEMISTRY Test 6: Chemical change
 CLASS TEST GRADE PHYSICAL SCIENCES: CHEMISTRY Test 6: Chemical change MARKS: 45 TIME: hour INSTRUCTIONS AND INFORMATION. Answer ALL the questions. 2. You may use non-programmable calculators. 3. You may
CLASS TEST GRADE PHYSICAL SCIENCES: CHEMISTRY Test 6: Chemical change MARKS: 45 TIME: hour INSTRUCTIONS AND INFORMATION. Answer ALL the questions. 2. You may use non-programmable calculators. 3. You may
PART A: OVERVIEW...1 1. INTRODUCTION...1 2. APPLICABILITY...1 3. OBJECTIVE...1 PART B: LEGAL PROVISIONS...2 4. LEGAL PROVISIONS...
 PART A: OVERVIEW...1 1. INTRODUCTION...1 2. APPLICABILITY...1 3. OBJECTIVE...1 PART B: LEGAL PROVISIONS...2 4. LEGAL PROVISIONS...2 PART C: POLICY...2 5. SCOPE OF ACTIVITIES THAT CAN BE OUTSOURCED...2
PART A: OVERVIEW...1 1. INTRODUCTION...1 2. APPLICABILITY...1 3. OBJECTIVE...1 PART B: LEGAL PROVISIONS...2 4. LEGAL PROVISIONS...2 PART C: POLICY...2 5. SCOPE OF ACTIVITIES THAT CAN BE OUTSOURCED...2
Course Syllabus Business Intelligence and CRM Technologies
 Course Syllabus Business Intelligence and CRM Technologies August December 2014 IX Semester Rolando Gonzales I. General characteristics Name : Business Intelligence CRM Technologies Code : 06063 Requirement
Course Syllabus Business Intelligence and CRM Technologies August December 2014 IX Semester Rolando Gonzales I. General characteristics Name : Business Intelligence CRM Technologies Code : 06063 Requirement
Statement after the Act on Marriage Formation and Dissolution 11b concerning knowledge of Aliens Act rules on family reunification
 Statement after the Act on Marriage Formation and Dissolution 11b concerning knowledge of Aliens Act rules on family reunification Pursuant to section 9 (1) (a - d) a residence permit can be issued upon
Statement after the Act on Marriage Formation and Dissolution 11b concerning knowledge of Aliens Act rules on family reunification Pursuant to section 9 (1) (a - d) a residence permit can be issued upon
Solar Activity and Earth's Climate
 Rasmus E. Benestad Solar Activity and Earth's Climate Second Edition Published in association with Springer Praxis ids Publishing Publisl PRAXI Chichester, UK Contents Preface to the second edition Preface
Rasmus E. Benestad Solar Activity and Earth's Climate Second Edition Published in association with Springer Praxis ids Publishing Publisl PRAXI Chichester, UK Contents Preface to the second edition Preface
THE PERFORMANCE MANAGEMENT GROUP LLC
 THE PERFORMANCE MANAGEMENT GROUP LLC ONLINE TRAINING: LEAN SIX SIGMA SERVICE EXCELLENCE BLACK BELT CERTIFICATION Performance Improvement Training for Service Industries: Financial Services Telecommunications
THE PERFORMANCE MANAGEMENT GROUP LLC ONLINE TRAINING: LEAN SIX SIGMA SERVICE EXCELLENCE BLACK BELT CERTIFICATION Performance Improvement Training for Service Industries: Financial Services Telecommunications
Coronal expansion and solar wind
 Coronal expansion and solar wind The solar corona over the solar cycle Coronal and interplanetary temperatures Coronal expansion and solar wind acceleration Origin of solar wind in magnetic network Multi-fluid
Coronal expansion and solar wind The solar corona over the solar cycle Coronal and interplanetary temperatures Coronal expansion and solar wind acceleration Origin of solar wind in magnetic network Multi-fluid
Performance Objective Identification Worksheet
 Performance Objective Identification Worksheet INSTRUCTIONS For each of the performance objective identified, you must indicate by page and paragraph number the equivalent performance objective in your
Performance Objective Identification Worksheet INSTRUCTIONS For each of the performance objective identified, you must indicate by page and paragraph number the equivalent performance objective in your
2010 MegaPath Inc. All rights reserved. Confidential and Proprietary 2
 Polycom SIP Phones Base Configuration for MegaPath Duet Hosted Voice Service Contents Summary... 3 Configuration Settings Overview... 3 Restarting the Phone... 5 Rebooting the Phone... 6 Uploading Log
Polycom SIP Phones Base Configuration for MegaPath Duet Hosted Voice Service Contents Summary... 3 Configuration Settings Overview... 3 Restarting the Phone... 5 Rebooting the Phone... 6 Uploading Log
b) Discussion of Bid c) Voting (1) Results: Coastal Carolina wins B. State Communications Coordinator of the Year 1. Winthrop University
 South Carolina Organization for Residential Education 2015 SCORE Boardroom Minutes I. Call to order at 8:02 am II. Roll Call: Clemson, Coastal Carolina, College of Charleston, Winthrop University, University
South Carolina Organization for Residential Education 2015 SCORE Boardroom Minutes I. Call to order at 8:02 am II. Roll Call: Clemson, Coastal Carolina, College of Charleston, Winthrop University, University
INSURANCE IN. Historical Development, Present Status and Future. Challenges
 INSURANCE IN ETHIOPIA Historical Development, Present Status and Future Challenges Hailu Zeleke August 2007 TABLE OF CONTENTS PAGE ACKNOWLEDGEMENTS vi ACRONYMS vii INTRODUCTION viif CHARTER 1: RISK - MEANING
INSURANCE IN ETHIOPIA Historical Development, Present Status and Future Challenges Hailu Zeleke August 2007 TABLE OF CONTENTS PAGE ACKNOWLEDGEMENTS vi ACRONYMS vii INTRODUCTION viif CHARTER 1: RISK - MEANING
Business Administration of Windchill PDMLink 10.0
 Business Administration of Windchill PDMLink 10.0 Overview Course Code Course Length TRN-3160-T 3 Days After completing this course, you will be well prepared to set up and manage a basic Windchill PDMLink
Business Administration of Windchill PDMLink 10.0 Overview Course Code Course Length TRN-3160-T 3 Days After completing this course, you will be well prepared to set up and manage a basic Windchill PDMLink
Implementation Plan: Development of an asset and financial planning management. Australian Capital Territory
 Implementation Plan: Development of an asset and financial planning management framework for TAMS Australian Capital Territory NATIONAL PARTNERSHIP AGREEMENT TO SUPPORT LOCAL GOVERNMENT AND REGIONAL DEVELOPMENT
Implementation Plan: Development of an asset and financial planning management framework for TAMS Australian Capital Territory NATIONAL PARTNERSHIP AGREEMENT TO SUPPORT LOCAL GOVERNMENT AND REGIONAL DEVELOPMENT
(i) The program shall prepare candidates who are familiar with the historical foundations of gifted and talented education;
 Effective May 15, 2014 505-3-.90 GIFTED IN-FIELD EDUCATION ENDORSEMENT PROGRAM (1) Purpose. This rule states field-specific content standards for approving endorsement programs that prepare individuals
Effective May 15, 2014 505-3-.90 GIFTED IN-FIELD EDUCATION ENDORSEMENT PROGRAM (1) Purpose. This rule states field-specific content standards for approving endorsement programs that prepare individuals
Tennessee Wesleyan College Math 131 C Syllabus Spring 2016
 Tennessee Wesleyan College Math 131 C Syllabus Spring 2016 I. Course: College Algebra, M131 C Location: Durham 303 Days/Time: MWF 1100-1150 Credit hours: 3 II. III. IV. Instructor: Dr. David J. Ashe Office:
Tennessee Wesleyan College Math 131 C Syllabus Spring 2016 I. Course: College Algebra, M131 C Location: Durham 303 Days/Time: MWF 1100-1150 Credit hours: 3 II. III. IV. Instructor: Dr. David J. Ashe Office:
City of Georgetown. Cisco Unified Communications. Scope of Work
 Company Name Project Name Appendices City of Georgetown Cisco Unified Communications Scope of Work I. Overview The objective for this project is to assist the City of Georgetown with the upgrade of their
Company Name Project Name Appendices City of Georgetown Cisco Unified Communications Scope of Work I. Overview The objective for this project is to assist the City of Georgetown with the upgrade of their
EMC AND VIRTUSTREAM MAY 26, 2015. Copyright 2015 EMC Corporation. All rights reserved.
 EMC AND VIRTUSTREAM MAY 26, 2015 1 FORWARD-LOOKING STATEMENTS This presentation contains forward-looking statements as defined under the Federal Securities Laws. Actual results could differ materially
EMC AND VIRTUSTREAM MAY 26, 2015 1 FORWARD-LOOKING STATEMENTS This presentation contains forward-looking statements as defined under the Federal Securities Laws. Actual results could differ materially
Facility Online Manager
 Facility Online Manager Instruction for users FOM TM is an online accounting and instrument management software. This software can be used as a simple online scheduler for small research group, or as a
Facility Online Manager Instruction for users FOM TM is an online accounting and instrument management software. This software can be used as a simple online scheduler for small research group, or as a
In studying the Milky Way, we have a classic problem of not being able to see the forest for the trees.
 In studying the Milky Way, we have a classic problem of not being able to see the forest for the trees. A panoramic painting of the Milky Way as seen from Earth, done by Knut Lundmark in the 1940 s. The
In studying the Milky Way, we have a classic problem of not being able to see the forest for the trees. A panoramic painting of the Milky Way as seen from Earth, done by Knut Lundmark in the 1940 s. The
To define and explain different learning styles and learning strategies.
 Medical Billing and Coding Program Overview The Medical Billing and Coding program prepares students for entry-level employment as a medical billing and/or coding clerk. It discusses the fundamentals of
Medical Billing and Coding Program Overview The Medical Billing and Coding program prepares students for entry-level employment as a medical billing and/or coding clerk. It discusses the fundamentals of
Stratex International Plc ('Stratex' or 'the Company') Holdings in Company
 Regulatory Story Go to market news section Company TIDM Headline Released Stratex International PLC STI Holding(s) in Company 17:30 04-Feb-2010 7233G17 RNS : 7233G Stratex International PLC 04 February
Regulatory Story Go to market news section Company TIDM Headline Released Stratex International PLC STI Holding(s) in Company 17:30 04-Feb-2010 7233G17 RNS : 7233G Stratex International PLC 04 February
Final report SA-R of the AB S.A. company for the financial year 2009/2010. covering the period from 01-07-2009 to 30-06-2010
 Final report SA-R of the AB S.A. company for the financial year 2009/2010 covering the period from 01-07-2009 to 30-06-2010 Selected financial data translated into euro SELECTED FINANCIAL DATA in thous.
Final report SA-R of the AB S.A. company for the financial year 2009/2010 covering the period from 01-07-2009 to 30-06-2010 Selected financial data translated into euro SELECTED FINANCIAL DATA in thous.
CHAPTER 42A. Case management of certain personal injuries actions. 42A.1. (1) Subject to paragraph (3), this Chapter applies to actions
 CHAPTER 42A Case management of certain personal injuries actions Application and interpretation of this Chapter 42A.1. (1) Subject to paragraph (3), this Chapter applies to actions proceeding as ordinary
CHAPTER 42A Case management of certain personal injuries actions Application and interpretation of this Chapter 42A.1. (1) Subject to paragraph (3), this Chapter applies to actions proceeding as ordinary
Salary Scales. Shown on the following pages are the various salary scales in effect at the issuance of the Proposed Budget.
 SALARY SCALES D 1 Shown on the following pages are the various salary scales in effect at the issuance of the Proposed Budget. Pay Scale I, in effect for the period January 1, 2011 through December 31,
SALARY SCALES D 1 Shown on the following pages are the various salary scales in effect at the issuance of the Proposed Budget. Pay Scale I, in effect for the period January 1, 2011 through December 31,
NATHAN world map of natural hazards. 2011 version
 world map of natural hazards 2011 version World Map of Natural Hazards Geointelligence for your business A new name but the recipe for success is the same: In the 2011 version, we are offering both proven
world map of natural hazards 2011 version World Map of Natural Hazards Geointelligence for your business A new name but the recipe for success is the same: In the 2011 version, we are offering both proven
SOUTH DAKOTA STATE UNIVERSITY Policy and Procedure Manual
 Office/Contact: Graduate School Source: SDBOR Curriculum Definitions; SDBOR Policy 2:5; SDBOR Policy 2:8; SDBOR Policy 2:23; SDBOR Policy 2:29 Link: http://www.sdbor.edu/services/academics/aac/documents/curriculum-definitions_001.pdf;
Office/Contact: Graduate School Source: SDBOR Curriculum Definitions; SDBOR Policy 2:5; SDBOR Policy 2:8; SDBOR Policy 2:23; SDBOR Policy 2:29 Link: http://www.sdbor.edu/services/academics/aac/documents/curriculum-definitions_001.pdf;
Q2 FY2015 Consolidated Financial Results
 Q2 FY2015 Consolidated Financial Results (Three months ended September 30, 2015) Sony Corporation Q2 FY2015 Consolidated Results Q2 Q2 Change & operating revenue 1,901.5 1,892.7-0.5% Operating income -85.6
Q2 FY2015 Consolidated Financial Results (Three months ended September 30, 2015) Sony Corporation Q2 FY2015 Consolidated Results Q2 Q2 Change & operating revenue 1,901.5 1,892.7-0.5% Operating income -85.6
This Version Not For Distribution EMR/EHR
 This Version Not For Distribution EMR/EHR Cheng B Saw, Ph.D. Chair, Asian-Oceanic Affairs of AAPM Director - Physics, Northeast Radiation Oncology Centers President, CBSaw Publishing, LLC Harrisburg, PA,
This Version Not For Distribution EMR/EHR Cheng B Saw, Ph.D. Chair, Asian-Oceanic Affairs of AAPM Director - Physics, Northeast Radiation Oncology Centers President, CBSaw Publishing, LLC Harrisburg, PA,
Reading List for Choosing Your College Major Items listed below are available at Collin College Libraries.
 Reading List for Choosing Your College Major Items listed below are available at Collin College Libraries. 2003 Title: Great jobs for art majors Author: Camenson, Blythe. Publisher, Date: Chicago : VGM
Reading List for Choosing Your College Major Items listed below are available at Collin College Libraries. 2003 Title: Great jobs for art majors Author: Camenson, Blythe. Publisher, Date: Chicago : VGM
How To Write A Constitution Of The Gorgonia Law Honor Society
 The Constitution of the Georgia Law Honor Society Article I ADMINISTRATION AND PURPOSE Section 1. The Georgia Law Honor Society of Secondary Schools (hereinafter, The Georgia Law Honor Society) shall be
The Constitution of the Georgia Law Honor Society Article I ADMINISTRATION AND PURPOSE Section 1. The Georgia Law Honor Society of Secondary Schools (hereinafter, The Georgia Law Honor Society) shall be
Agenda item number: 5 FINANCE AND PERFORMANCE MANAGEMENT OVERVIEW AND SCRUTINY COMMITTEE FUTURE WORK PROGRAMME
 Agenda item number: 5 COMMITTEE FINANCE AND PERFORMANCE MANAGEMENT OVERVIEW AND SCRUTINY COMMITTEE DATE TUESDAY 17 JUNE 2003 TITLE OF REPORT RESPONSIBLE OFFICER FUTURE WORK PROGRAMME Ann Joyce, Head of
Agenda item number: 5 COMMITTEE FINANCE AND PERFORMANCE MANAGEMENT OVERVIEW AND SCRUTINY COMMITTEE DATE TUESDAY 17 JUNE 2003 TITLE OF REPORT RESPONSIBLE OFFICER FUTURE WORK PROGRAMME Ann Joyce, Head of
ANNEX ON FINANCIAL SERVICES
 1. Scope and Definition ANNEX ON FINANCIAL SERVICES This Annex applies to measures affecting the supply of financial services. Reference to the supply of a financial service in this Annex shall mean the
1. Scope and Definition ANNEX ON FINANCIAL SERVICES This Annex applies to measures affecting the supply of financial services. Reference to the supply of a financial service in this Annex shall mean the
Agenda Item #06-29 Effective Spring 2007 Eastern Illinois University Revised Course Proposal MGT 4500, Employee Staffing and Development
 Agenda Item #06-29 Effective Spring 2007 Eastern Illinois University Revised Course Proposal MGT 4500, Employee Staffing and Development 1. Catalog Description a. Course Number: MGT 4500 b. Title: Employee
Agenda Item #06-29 Effective Spring 2007 Eastern Illinois University Revised Course Proposal MGT 4500, Employee Staffing and Development 1. Catalog Description a. Course Number: MGT 4500 b. Title: Employee
"Charting the Course... MOC 20409 B Server Virtualization with Windows Hyper-V and System Center. Course Summary
 Description Course Summary This five day course will provide you with the knowledge and skills required to design and implement Microsoft Server solutions using Hyper-V and System. Objectives At the end
Description Course Summary This five day course will provide you with the knowledge and skills required to design and implement Microsoft Server solutions using Hyper-V and System. Objectives At the end
DataIntegrationwithXMLandSemanticWeb Technologies
 DataIntegrationwithXMLandSemanticWeb Technologies Athesispresented by RubénTous Submittedinpartialfullmentoftherequerimentsfor DoctorateinComputerScienceandDigitalCommunication thedegreeofdoctorofphilosophy
DataIntegrationwithXMLandSemanticWeb Technologies Athesispresented by RubénTous Submittedinpartialfullmentoftherequerimentsfor DoctorateinComputerScienceandDigitalCommunication thedegreeofdoctorofphilosophy
Proposal Form Professional Indemnity Insurance for Design Industry Firms and Consultants
 Proposal Form Professional Indemnity Insurance for Design Industry Firms and Consultants To assist with the completion of this Proposal Form, the following words will mean:- Principal is any equity/salaried
Proposal Form Professional Indemnity Insurance for Design Industry Firms and Consultants To assist with the completion of this Proposal Form, the following words will mean:- Principal is any equity/salaried
1.- L a m e j o r o p c ió n e s c l o na r e l d i s co ( s e e x p li c a r á d es p u é s ).
 PROCEDIMIENTO DE RECUPERACION Y COPIAS DE SEGURIDAD DEL CORTAFUEGOS LINUX P ar a p od e r re c u p e ra r nu e s t r o c o rt a f u e go s an t e un d es a s t r e ( r ot u r a d e l di s c o o d e l a
PROCEDIMIENTO DE RECUPERACION Y COPIAS DE SEGURIDAD DEL CORTAFUEGOS LINUX P ar a p od e r re c u p e ra r nu e s t r o c o rt a f u e go s an t e un d es a s t r e ( r ot u r a d e l di s c o o d e l a


