ESSENTIAL QUESTION How can you factor expressions of the form ax 2 + bx + c?
|
|
|
- Joanna Sutton
- 8 years ago
- Views:
Transcription
1 LESSON 15.3 Factoring ax 2 + bx + c A.SSE.2 Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you factor expressions of the form ax 2 + bx + c? Factoring a x 2 + bx + c where c > 0 When you factor a polynomial in the form ax 2 + bx + c, the result will be the product of two binomial factors, in the form ( x + )( x + ). The product of the two coefficients of x will be a, and the product of the two constant terms will be c. The sum of the products of the inner and outer terms will be bx. Math On the Spot EXAMPLE 1 A.SSE.2 A Factor 4 x x STEP 1 Factor out any common factors of 4, 26, and x x + 42 = 2(2 x x + 21) STEP 2 STEP 3 Make a table that lists the factor pairs for a and c. Find the value of b that results from each combination of factor pairs. a = 2 c = 21 1 and 2 1 and 21 (1)(21) + (2)(1) = 23 1 and 2 3 and 7 (1)(7) + (2)(3) = 13 1 and 2 7 and 3 (1)(3) + (2)(7) = 17 1 and 2 21 and 1 (1)(1) + (2)(21) = 43 Use the combination of factor pairs that yields the correct value of b to factor the polynomial. (1x + 3)(2x + 7) =(x + 3)(2x + 7) 4 x x + 42 = 2(x + 3)(2x + 7) 13 is the sum that you re looking for. B Factor 3 x 2-26x STEP 1 Factor out any common factors of 3, 26, and 35. 3, 26, and 35 share no common factors other than 1. Lesson
2 STEP 2 Make a table that lists the factor pairs for a and c. Find the value of b that results from each combination of factor pairs. My Notes a = 3 c = 35 1 and 3-1 and -35 (1)(-35) + (3)(-1) = 38 1 and 3-5 and -7 (1)(-7) + (3)(-5) = 22 1 and 3-7 and -5 (1)(-5) + (3)(-7) = 26 1 and 3-35 and -1 (1)(-1) + (3)(-35) = 106 STEP 3 Use the combination of factor pairs that yields the correct value of b to factor the polynomial. -26 is the sum that you re looking for. 3x 2-26x + 35 = (1x - 7)(3x - 5) = (x - 7)(3x - 5) REFLECT 1. Critical Thinking When factoring 3 x 2-26x + 35, why should both factors of c be negative? 2. What If? If none of the factor pairs for a and c result in the correct value for b, what do you know about the polynomial? YOUR TURN Factor each polynomial x 2-14x x x x 2-48x x x + 70 Personal Math Trainer Online Practice and Help x x x 2-165x Unit 4
3 Factoring a x 2 + bx + c where c < 0 When factoring ax 2 + bx + c, if the value of c is negative, you know that one of the factors of c must be negative and one must be positive. Apply what you already know about factoring trinomials to this new situation. EXAMPLE 2 A.SSE.2 Math On the Spot A Factor 6 x 2-21x STEP 1 Factor out any common factors of 6, 21, and x 2-21x - 45 = 3(2 x 2-7x - 15) STEP 2 Make a table that lists the factor pairs for a and c. Since c is negative, one factor will be positive and the other will be negative. a = 2 c = and 2 1 and -15 (1)(-15) + (2)(1) = 13 1 and 2 3 and -5 (1)(-5) + (2)(3) = 1 1 and 2 5 and -3 (1)(-3) + (2)(5) = 7 1 and 2 15 and -1 (1)(-1) + (2)(15) = 29 1 and 2-1 and 15 (1)(15) + (2)(-1) = 13 1 and 2-3 and 5 (1)(5) + (2)(-3) = 1 1 and 2-5 and 3 (1)(3) + (2)(-5) = 7 1 and 2-15 and 1 (1)(1) + (2)(-15) = 29-7 is the sum that you re looking for. STEP 3 Use the combination of factor pairs that yields the correct value of b to factor the polynomial. (1x - 5)(2x + 3) = (x - 5)(2x + 3) B Factor 4 x 2 + 4x x 2-21x - 45 = 3(x - 5)(2x + 3) STEP 1 Factor out any common factors for 4, 4, and 35. STEP 2 4, 4, and 35 share no common factors other than 1. Make a table that lists the factor pairs for a and c. Since c is negative, one factor will be positive and the other will be negative. Lesson
4 Math Talk Mathematical Practices How does the sign of c help you choose the correct factor pair for c? a = 4 c = and 4 1 and -35 (1)(-35) + (4)(1) = 31 1 and 4 5 and -7 (1)(-7) + (4)(5) = 13 1 and 4 7 and -5 (1)(-5) + (4)(7) = 23 1 and 4 35 and -1 (1)(-1) + (4)(35) = and 4-1 and 35 (1)(35) + (4)(-1) = 31 1 and 4-5 and 7 (1)(7) + (4)(-5) = 13 1 and 4-7 and 5 (1)(5) + (4)(-7) = 23 1 and 4-35 and 1 (1)(1) + (4)(-35) = and 2 1 and -35 (2)(-35) + (2)(1) = 68 2 and 2 5 and -7 (2)(-7) + (2)(5) = 4 2 and 2 7 and -5 (2)(-5) + (2)(7) = 4 2 and 2 35 and -1 (2)(-1) + (2)(35) = 68 STEP 3 Use the combination of factor pairs that yields the correct value of b to factor the polynomial. 4x 2 + 4x - 35 = (2x + 7)(2x - 5) 4 is the sum that you re looking for. REFLECT 9. What If? Suppose a is a negative number. What would be the first step in factoring ax 2 + bx + c? Explain. 10. Make a Conjecture Using the information in the tables in Example 2, make a conjecture about what happens to b when you swap the positions of the plus and minus signs in the binomial factors. YOUR TURN Personal Math Trainer Online Practice and Help Factor each polynomial x x x x Unit 4
5 Guided Practice 1. Factor 3 x x (Example1) Complete the table for all factors of a and c. a = 3 c = 12 1 and 3 1 and 12 (1)(12) + (3)(1) = 1 and 3 2 and (1)( ) + ( )(2) = 12 1 and 3 and (1)( ) + (3)( ) = 1 and 3 and (1)( ) + ( )(4) = 1 and 3 and (1)( ) + ( )( ) = 1 and 3 and 1 (1)(1) + ( )( ) = 37 The factored form of 3 x x + 12 is (x + )( x + ). 2. Factor 8 x 2-2x - 6. (Example 2) 8, -2, and -6 have a common factor of, so 8 x 2-2x - 6 = (4 x 2 - x - 3) Complete the table for all factors of a and c. a = 4 c = -3? 1 and 4 1 and -3 (1)(-3) + (4)(1) = 1 1 and 3 and (1)( ) + (4)( ) = 1 and and (1)( ) + ( )( ) = 1 and and (1)( ) + ( )( ) = 2 and and (2)( ) + ( )(1) = and 3 and (2)( ) + (2)(3) = 4 The factored form of 8 x 2-2x - 6 is (x - )(4x + ). ESSENTIAL QUESTION CHECK-IN 3. How can you factor expressions of the form ax 2 + bx + c? Lesson
6 Name Class Date 15.3 Independent Practice A.SSE.2, A.SSE.3 Factor each trinomial, if possible x x - 15 Personal Math Trainer Online Practice and Help 13. The area of a soccer field is (24x x + 100) m 2. The width of the field is (4x + 10) m. What is the length? 5. 6x 2-29x x x z z d 2 + 7d Find all the possible values of b such that 3x 2 + bx - 2 can be factored. 15. Write the polynomial modeled, and then factor it. 12x 2 4x -15x y 2-11y g g n 2 + 3n Representing Real-World Problems The attendance at a team s basketball game can be approximated with the polynomial 5x x + 285, where x is the number of wins the team had in the previous month. a. Factor the polynomial completely. 12. How is factoring a trinomial in the form ax 2 + bx + c similar to factoring a trinomial in the form x 2 + bx + c? How is it different? b. Estimate the attendance if the team won 4 games in the previous month. 17. Kyle stood on a bridge and threw a rock up and over the side. The height of the rock, in meters, can be approximated by -5t 2 + 5t + 24, where t is the time in seconds after Kyle threw it. Completely factor the expression. 546 Unit 4
7 18. A triangle has an area of 1_ 2 ( 4x x + 30) ft 2. If the base of the triangle is (x + 6) ft, find the height of the triangle. 19. Draw Conclusions If a polynomial in the form ax 2 + bx + c has a = b = c = 1, can the expression be factored? Explain. 20. Counterexamples Marc thinks the only time a polynomial in the form ax 2 + bx + c cannot be factored is when at least one of the values for a, b, or c is a prime number. Find a counterexample to Marc s statement. 21. Shruti has a rectangular picture frame with an area of 30x 2 + 5x - 75 cm 2. a. Find the width of the frame if the height is (3x + 5) cm. b. Find the width of the frame if the height is (2x - 3) cm. c. Find the width of the frame when the height is 5 cm. 22. Communicate Mathematical Ideas Has the expression (3x + 7)(6x + 3) been factored completely? Explain. 23. Explain the Error Luna performed the work shown below to factor the polynomial 24x x + 3. Explain her error, and find the correctly factored form. 24x x + 3 = 3( 8x 2 + 6x + 0) = 3( 8x 2 + 6x) = 3(2x)(4x + 3) Lesson
8 24. The length of Rebecca s rectangular garden was two times the width, w. Rebecca increased the length and width of the garden so that the area of the new garden is ( 2w 2 + 7w + 6) square yards. By how much did Rebecca increase the length and the width? 25. The height in feet above the ground of a football that has been thrown or kicked can be described by the expression - 16t 2 + vt + h where t is the time in seconds, v is the initial upward velocity in feet per second, and h is the initial height in feet. a. Write an expression for the height of a football at time t when the initial upward velocity is 20 feet per second and the initial height is 6 feet. b. Factor your expression from part a. c. Find the height of the football after 1 second. FOCUS ON HIGHER ORDER THINKING Work Area 26. Critical Thinking Is there a value of m that will make x 2 + mx + 80 factorable? If so, how many? Explain and give all the possible values. 27. Explain the Error Frank has factored the polynomial 12x 2 + 5x - 2 as (3x - 1)(4x + 2). Explain his error. Give the correct factorization. 28. Communicate Mathematical Ideas Can the polynomial 4x 2 + 0x - 25 be factored? Explain. 548 Unit 4
15.1 Factoring Polynomials
 LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
LESSON 15.1 Factoring Polynomials Use the structure of an expression to identify ways to rewrite it. Also A.SSE.3? ESSENTIAL QUESTION How can you use the greatest common factor to factor polynomials? EXPLORE
Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder).
 Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
Math 50, Chapter 8 (Page 1 of 20) 8.1 Common Factors Definitions 1. A factor of integer is an integer that will divide the given integer evenly (with no remainder). Find all the factors of a. 44 b. 32
6.3 FACTORING ax 2 bx c WITH a 1
 290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
290 (6 14) Chapter 6 Factoring e) What is the approximate maximum revenue? f) Use the accompanying graph to estimate the price at which the revenue is zero. y Revenue (thousands of dollars) 300 200 100
Sect 6.7 - Solving Equations Using the Zero Product Rule
 Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Sect 6.7 - Solving Equations Using the Zero Product Rule 116 Concept #1: Definition of a Quadratic Equation A quadratic equation is an equation that can be written in the form ax 2 + bx + c = 0 (referred
Factoring and Applications
 Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
Factoring and Applications What is a factor? The Greatest Common Factor (GCF) To factor a number means to write it as a product (multiplication). Therefore, in the problem 48 3, 4 and 8 are called the
FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c
 Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Tallahassee Community College 55 FACTORING TRINOMIALS IN THE FORM OF ax 2 + bx + c This kind of trinomial differs from the previous kind we have factored because the coefficient of x is no longer "1".
Factoring Trinomials using Algebra Tiles Student Activity
 Factoring Trinomials using Algebra Tiles Student Activity Materials: Algebra Tiles (student set) Worksheet: Factoring Trinomials using Algebra Tiles Algebra Tiles: Each algebra tile kits should contain
Factoring Trinomials using Algebra Tiles Student Activity Materials: Algebra Tiles (student set) Worksheet: Factoring Trinomials using Algebra Tiles Algebra Tiles: Each algebra tile kits should contain
Section 6.1 Factoring Expressions
 Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Section 6.1 Factoring Expressions The first method we will discuss, in solving polynomial equations, is the method of FACTORING. Before we jump into this process, you need to have some concept of what
Chapter R.4 Factoring Polynomials
 Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Chapter R.4 Factoring Polynomials Introduction to Factoring To factor an expression means to write the expression as a product of two or more factors. Sample Problem: Factor each expression. a. 15 b. x
Factor Polynomials Completely
 9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
9.8 Factor Polynomials Completely Before You factored polynomials. Now You will factor polynomials completely. Why? So you can model the height of a projectile, as in Ex. 71. Key Vocabulary factor by grouping
Factoring Quadratic Expressions
 Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring the trinomial ax 2 + bx + c when a = 1 A trinomial in the form x 2 + bx + c can be factored to equal (x + m)(x + n) when the product of m x n equals c and the sum of m + n equals b. (Note: the
Factoring. Factoring Monomials Monomials can often be factored in more than one way.
 Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Factoring Factoring is the reverse of multiplying. When we multiplied monomials or polynomials together, we got a new monomial or a string of monomials that were added (or subtracted) together. For example,
Name Intro to Algebra 2. Unit 1: Polynomials and Factoring
 Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
Name Intro to Algebra 2 Unit 1: Polynomials and Factoring Date Page Topic Homework 9/3 2 Polynomial Vocabulary No Homework 9/4 x In Class assignment None 9/5 3 Adding and Subtracting Polynomials Pg. 332
7.2 Quadratic Equations
 476 CHAPTER 7 Graphs, Equations, and Inequalities 7. Quadratic Equations Now Work the Are You Prepared? problems on page 48. OBJECTIVES 1 Solve Quadratic Equations by Factoring (p. 476) Solve Quadratic
476 CHAPTER 7 Graphs, Equations, and Inequalities 7. Quadratic Equations Now Work the Are You Prepared? problems on page 48. OBJECTIVES 1 Solve Quadratic Equations by Factoring (p. 476) Solve Quadratic
Factoring Polynomials
 Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring Polynomials Factoring Factoring is the process of writing a polynomial as the product of two or more polynomials. The factors of 6x 2 x 2 are 2x + 1 and 3x 2. In this section, we will be factoring
Factoring. 472 Chapter 9 Factoring
 Factoring Lesson 9- Find the prime factorizations of integers and monomials. Lesson 9- Find the greatest common factors (GCF) for sets of integers and monomials. Lessons 9-2 through 9-6 Factor polynomials.
Factoring Lesson 9- Find the prime factorizations of integers and monomials. Lesson 9- Find the greatest common factors (GCF) for sets of integers and monomials. Lessons 9-2 through 9-6 Factor polynomials.
Veterans Upward Bound Algebra I Concepts - Honors
 Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Veterans Upward Bound Algebra I Concepts - Honors Brenda Meery Kaitlyn Spong Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org Chapter 6. Factoring CHAPTER
Polynomial Equations and Factoring
 7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
7 Polynomial Equations and Factoring 7.1 Adding and Subtracting Polynomials 7.2 Multiplying Polynomials 7.3 Special Products of Polynomials 7.4 Dividing Polynomials 7.5 Solving Polynomial Equations in
Factoring Trinomials: The ac Method
 6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
6.7 Factoring Trinomials: The ac Method 6.7 OBJECTIVES 1. Use the ac test to determine whether a trinomial is factorable over the integers 2. Use the results of the ac test to factor a trinomial 3. For
1.3 Polynomials and Factoring
 1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
1.3 Polynomials and Factoring Polynomials Constant: a number, such as 5 or 27 Variable: a letter or symbol that represents a value. Term: a constant, variable, or the product or a constant and variable.
( ) FACTORING. x In this polynomial the only variable in common to all is x.
 FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
FACTORING Factoring is similar to breaking up a number into its multiples. For example, 10=5*. The multiples are 5 and. In a polynomial it is the same way, however, the procedure is somewhat more complicated
10 7, 8. 2. 6x + 30x + 36 SOLUTION: 8-9 Perfect Squares. The first term is not a perfect square. So, 6x + 30x + 36 is not a perfect square trinomial.
 Squares Determine whether each trinomial is a perfect square trinomial. Write yes or no. If so, factor it. 1.5x + 60x + 36 SOLUTION: The first term is a perfect square. 5x = (5x) The last term is a perfect
Squares Determine whether each trinomial is a perfect square trinomial. Write yes or no. If so, factor it. 1.5x + 60x + 36 SOLUTION: The first term is a perfect square. 5x = (5x) The last term is a perfect
Solving Quadratic Equations
 9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
9.3 Solving Quadratic Equations by Using the Quadratic Formula 9.3 OBJECTIVES 1. Solve a quadratic equation by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation
Factoring Polynomials
 Factoring Polynomials 8A Factoring Methods 8-1 Factors and Greatest Common Factors Lab Model Factoring 8-2 Factoring by GCF Lab Model Factorization of Trinomials 8-3 Factoring x 2 + bx + c 8-4 Factoring
Factoring Polynomials 8A Factoring Methods 8-1 Factors and Greatest Common Factors Lab Model Factoring 8-2 Factoring by GCF Lab Model Factorization of Trinomials 8-3 Factoring x 2 + bx + c 8-4 Factoring
Factors and Products
 CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
CHAPTER 3 Factors and Products What You ll Learn use different strategies to find factors and multiples of whole numbers identify prime factors and write the prime factorization of a number find square
1.3 Algebraic Expressions
 1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
1.3 Algebraic Expressions A polynomial is an expression of the form: a n x n + a n 1 x n 1 +... + a 2 x 2 + a 1 x + a 0 The numbers a 1, a 2,..., a n are called coefficients. Each of the separate parts,
VOLUME of Rectangular Prisms Volume is the measure of occupied by a solid region.
 Math 6 NOTES 7.5 Name VOLUME of Rectangular Prisms Volume is the measure of occupied by a solid region. **The formula for the volume of a rectangular prism is:** l = length w = width h = height Study Tip:
Math 6 NOTES 7.5 Name VOLUME of Rectangular Prisms Volume is the measure of occupied by a solid region. **The formula for the volume of a rectangular prism is:** l = length w = width h = height Study Tip:
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0).
 This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
This is Factoring and Solving by Factoring, chapter 6 from the book Beginning Algebra (index.html) (v. 1.0). This book is licensed under a Creative Commons by-nc-sa 3.0 (http://creativecommons.org/licenses/by-nc-sa/
1.1 Practice Worksheet
 Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
Math 1 MPS Instructor: Cheryl Jaeger Balm 1 1.1 Practice Worksheet 1. Write each English phrase as a mathematical expression. (a) Three less than twice a number (b) Four more than half of a number (c)
7-6. Choosing a Factoring Model. Extension: Factoring Polynomials with More Than One Variable IN T RO DUC E T EACH. Standards for Mathematical Content
 7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
7-6 Choosing a Factoring Model Extension: Factoring Polynomials with More Than One Variable Essential question: How can you factor polynomials with more than one variable? What is the connection between
How To Factor By Gcf In Algebra 1.5
 7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
7-2 Factoring by GCF Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up Simplify. 1. 2(w + 1) 2. 3x(x 2 4) 2w + 2 3x 3 12x Find the GCF of each pair of monomials. 3. 4h 2 and 6h 2h 4. 13p and 26p
1.3. Maximum or Minimum of a Quadratic Function. Investigate A
 < P1-6 photo of a large arched bridge, similar to the one on page 292 or p 360-361of the fish book> Maximum or Minimum of a Quadratic Function 1.3 Some bridge arches are defined by quadratic functions.
< P1-6 photo of a large arched bridge, similar to the one on page 292 or p 360-361of the fish book> Maximum or Minimum of a Quadratic Function 1.3 Some bridge arches are defined by quadratic functions.
6.1 Add & Subtract Polynomial Expression & Functions
 6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
6.1 Add & Subtract Polynomial Expression & Functions Objectives 1. Know the meaning of the words term, monomial, binomial, trinomial, polynomial, degree, coefficient, like terms, polynomial funciton, quardrtic
Factoring Polynomials
 Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring a Polynomial Expression Factoring a polynomial is expressing the polynomial as a product of two or more factors. Simply stated, it is somewhat the reverse process of multiplying. To factor polynomials,
Factoring. Key Vocabulary
 8 Factoring Find the prime factorization of integers and monomials. Factor polynomials. Use the Zero Product Property to solve equations. Key Vocabulary factored form (p. 41) perfect square trinomials
8 Factoring Find the prime factorization of integers and monomials. Factor polynomials. Use the Zero Product Property to solve equations. Key Vocabulary factored form (p. 41) perfect square trinomials
Math 25 Activity 6: Factoring Advanced
 Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
Instructor! Math 25 Activity 6: Factoring Advanced Last week we looked at greatest common factors and the basics of factoring out the GCF. In this second activity, we will discuss factoring more difficult
A. Factoring out the Greatest Common Factor.
 DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
DETAILED SOLUTIONS AND CONCEPTS - FACTORING POLYNOMIAL EXPRESSIONS Prepared by Ingrid Stewart, Ph.D., College of Southern Nevada Please Send Questions and Comments to ingrid.stewart@csn.edu. Thank you!
SPECIAL PRODUCTS AND FACTORS
 CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
CHAPTER 442 11 CHAPTER TABLE OF CONTENTS 11-1 Factors and Factoring 11-2 Common Monomial Factors 11-3 The Square of a Monomial 11-4 Multiplying the Sum and the Difference of Two Terms 11-5 Factoring the
Using the ac Method to Factor
 4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
4.6 Using the ac Method to Factor 4.6 OBJECTIVES 1. Use the ac test to determine factorability 2. Use the results of the ac test 3. Completely factor a trinomial In Sections 4.2 and 4.3 we used the trial-and-error
MATH 90 CHAPTER 6 Name:.
 MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
MATH 90 CHAPTER 6 Name:. 6.1 GCF and Factoring by Groups Need To Know Definitions How to factor by GCF How to factor by groups The Greatest Common Factor Factoring means to write a number as product. a
expression is written horizontally. The Last terms ((2)( 4)) because they are the last terms of the two polynomials. This is called the FOIL method.
 A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
A polynomial of degree n (in one variable, with real coefficients) is an expression of the form: a n x n + a n 1 x n 1 + a n 2 x n 2 + + a 2 x 2 + a 1 x + a 0 where a n, a n 1, a n 2, a 2, a 1, a 0 are
BEGINNING ALGEBRA ACKNOWLEDMENTS
 BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
BEGINNING ALGEBRA The Nursing Department of Labouré College requested the Department of Academic Planning and Support Services to help with mathematics preparatory materials for its Bachelor of Science
x 4-1 = (x²)² - (1)² = (x² + 1) (x² - 1) = (x² + 1) (x - 1) (x + 1)
 Factoring Polynomials EXAMPLES STEP 1 : Greatest Common Factor GCF Factor out the greatest common factor. 6x³ + 12x²y = 6x² (x + 2y) 5x - 5 = 5 (x - 1) 7x² + 2y² = 1 (7x² + 2y²) 2x (x - 3) - (x - 3) =
Factoring Polynomials EXAMPLES STEP 1 : Greatest Common Factor GCF Factor out the greatest common factor. 6x³ + 12x²y = 6x² (x + 2y) 5x - 5 = 5 (x - 1) 7x² + 2y² = 1 (7x² + 2y²) 2x (x - 3) - (x - 3) =
Tool 1. Greatest Common Factor (GCF)
 Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
Chapter 4: Factoring Review Tool 1 Greatest Common Factor (GCF) This is a very important tool. You must try to factor out the GCF first in every problem. Some problems do not have a GCF but many do. When
How To Solve Factoring Problems
 05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
05-W4801-AM1.qxd 8/19/08 8:45 PM Page 241 Factoring, Solving Equations, and Problem Solving 5 5.1 Factoring by Using the Distributive Property 5.2 Factoring the Difference of Two Squares 5.3 Factoring
Factor and Solve Polynomial Equations. In Chapter 4, you learned how to factor the following types of quadratic expressions.
 5.4 Factor and Solve Polynomial Equations Before You factored and solved quadratic equations. Now You will factor and solve other polynomial equations. Why? So you can find dimensions of archaeological
5.4 Factor and Solve Polynomial Equations Before You factored and solved quadratic equations. Now You will factor and solve other polynomial equations. Why? So you can find dimensions of archaeological
called and explain why it cannot be factored with algebra tiles? and explain why it cannot be factored with algebra tiles?
 Factoring Reporting Category Topic Expressions and Operations Factoring polynomials Primary SOL A.2c The student will perform operations on polynomials, including factoring completely first- and second-degree
Factoring Reporting Category Topic Expressions and Operations Factoring polynomials Primary SOL A.2c The student will perform operations on polynomials, including factoring completely first- and second-degree
MATH 21. College Algebra 1 Lecture Notes
 MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
MATH 21 College Algebra 1 Lecture Notes MATH 21 3.6 Factoring Review College Algebra 1 Factoring and Foiling 1. (a + b) 2 = a 2 + 2ab + b 2. 2. (a b) 2 = a 2 2ab + b 2. 3. (a + b)(a b) = a 2 b 2. 4. (a
Section 2.5 Average Rate of Change
 Section.5 Average Rate of Change Suppose that the revenue realized on the sale of a company s product can be modeled by the function R( x) 600x 0.3x, where x is the number of units sold and R( x ) is given
Section.5 Average Rate of Change Suppose that the revenue realized on the sale of a company s product can be modeled by the function R( x) 600x 0.3x, where x is the number of units sold and R( x ) is given
Factoring Polynomials
 UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
UNIT 11 Factoring Polynomials You can use polynomials to describe framing for art. 396 Unit 11 factoring polynomials A polynomial is an expression that has variables that represent numbers. A number can
Mathematics Placement
 Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Mathematics Placement The ACT COMPASS math test is a self-adaptive test, which potentially tests students within four different levels of math including pre-algebra, algebra, college algebra, and trigonometry.
Polynomials. Key Terms. quadratic equation parabola conjugates trinomial. polynomial coefficient degree monomial binomial GCF
 Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
Polynomials 5 5.1 Addition and Subtraction of Polynomials and Polynomial Functions 5.2 Multiplication of Polynomials 5.3 Division of Polynomials Problem Recognition Exercises Operations on Polynomials
In algebra, factor by rewriting a polynomial as a product of lower-degree polynomials
 Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
Algebra 2 Notes SOL AII.1 Factoring Polynomials Mrs. Grieser Name: Date: Block: Factoring Review Factor: rewrite a number or expression as a product of primes; e.g. 6 = 2 3 In algebra, factor by rewriting
AIP Factoring Practice/Help
 The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
The following pages include many problems to practice factoring skills. There are also several activities with examples to help you with factoring if you feel like you are not proficient with it. There
Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results
 Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results Unit Title: Quadratic Expressions & Equations Course: Algebra I Unit 8 - Quadratic Expressions & Equations Brief Summary of Unit: At
Wentzville School District Algebra 1: Unit 8 Stage 1 Desired Results Unit Title: Quadratic Expressions & Equations Course: Algebra I Unit 8 - Quadratic Expressions & Equations Brief Summary of Unit: At
Algebra 2 PreAP. Name Period
 Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for completing
Introduction Assignment
 PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
PRE-CALCULUS 11 Introduction Assignment Welcome to PREC 11! This assignment will help you review some topics from a previous math course and introduce you to some of the topics that you ll be studying
QUADRATIC EQUATIONS EXPECTED BACKGROUND KNOWLEDGE
 MODULE - 1 Quadratic Equations 6 QUADRATIC EQUATIONS In this lesson, you will study aout quadratic equations. You will learn to identify quadratic equations from a collection of given equations and write
MODULE - 1 Quadratic Equations 6 QUADRATIC EQUATIONS In this lesson, you will study aout quadratic equations. You will learn to identify quadratic equations from a collection of given equations and write
4.4 Factoring ax 2 + bx + c
 4.4 Factoring ax 2 + bx + c From the last section, we now know a trinomial should factor as two binomials. With this in mind, we need to look at how to factor a trinomial when the leading coefficient is
4.4 Factoring ax 2 + bx + c From the last section, we now know a trinomial should factor as two binomials. With this in mind, we need to look at how to factor a trinomial when the leading coefficient is
FACTORING ax 2 bx c. Factoring Trinomials with Leading Coefficient 1
 5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
5.7 Factoring ax 2 bx c (5-49) 305 5.7 FACTORING ax 2 bx c In this section In Section 5.5 you learned to factor certain special polynomials. In this section you will learn to factor general quadratic polynomials.
Factoring (pp. 1 of 4)
 Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring (pp. 1 of 4) Algebra Review Try these items from middle school math. A) What numbers are the factors of 4? B) Write down the prime factorization of 7. C) 6 Simplify 48 using the greatest common
Factoring Polynomials
 Factoring Polynomials 8A Factoring Methods 8-1 Factors and Greatest Common Factors Lab Model Factorization by GCF 8-2 Factoring by GCF Lab Model Factorization of x 2 + bx + c 8-3 Factoring x 2 + bx + c
Factoring Polynomials 8A Factoring Methods 8-1 Factors and Greatest Common Factors Lab Model Factorization by GCF 8-2 Factoring by GCF Lab Model Factorization of x 2 + bx + c 8-3 Factoring x 2 + bx + c
Factoring Flow Chart
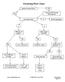 Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
Factoring Flow Chart greatest common factor? YES NO factor out GCF leaving GCF(quotient) how many terms? 4+ factor by grouping 2 3 difference of squares? perfect square trinomial? YES YES NO NO a 2 -b
A.3. Polynomials and Factoring. Polynomials. What you should learn. Definition of a Polynomial in x. Why you should learn it
 Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Appendi A.3 Polynomials and Factoring A23 A.3 Polynomials and Factoring What you should learn Write polynomials in standard form. Add,subtract,and multiply polynomials. Use special products to multiply
Factoring Guidelines. Greatest Common Factor Two Terms Three Terms Four Terms. 2008 Shirley Radai
 Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
Factoring Guidelines Greatest Common Factor Two Terms Three Terms Four Terms 008 Shirley Radai Greatest Common Factor 008 Shirley Radai Factoring by Finding the Greatest Common Factor Always check for
We start with the basic operations on polynomials, that is adding, subtracting, and multiplying.
 R. Polnomials In this section we want to review all that we know about polnomials. We start with the basic operations on polnomials, that is adding, subtracting, and multipling. Recall, to add subtract
R. Polnomials In this section we want to review all that we know about polnomials. We start with the basic operations on polnomials, that is adding, subtracting, and multipling. Recall, to add subtract
Polynomial Degree and Finite Differences
 CONDENSED LESSON 7.1 Polynomial Degree and Finite Differences In this lesson you will learn the terminology associated with polynomials use the finite differences method to determine the degree of a polynomial
CONDENSED LESSON 7.1 Polynomial Degree and Finite Differences In this lesson you will learn the terminology associated with polynomials use the finite differences method to determine the degree of a polynomial
Factoring Polynomials and Solving Quadratic Equations
 Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Factoring Polynomials and Solving Quadratic Equations Math Tutorial Lab Special Topic Factoring Factoring Binomials Remember that a binomial is just a polynomial with two terms. Some examples include 2x+3
Answer Key for California State Standards: Algebra I
 Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
Algebra I: Symbolic reasoning and calculations with symbols are central in algebra. Through the study of algebra, a student develops an understanding of the symbolic language of mathematics and the sciences.
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c
 Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
Unit 7 Quadratic Relations of the Form y = ax 2 + bx + c Lesson Outline BIG PICTURE Students will: manipulate algebraic expressions, as needed to understand quadratic relations; identify characteristics
FACTORING OUT COMMON FACTORS
 278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
278 (6 2) Chapter 6 Factoring 6.1 FACTORING OUT COMMON FACTORS In this section Prime Factorization of Integers Greatest Common Factor Finding the Greatest Common Factor for Monomials Factoring Out the
MATH 60 NOTEBOOK CERTIFICATIONS
 MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
MATH 60 NOTEBOOK CERTIFICATIONS Chapter #1: Integers and Real Numbers 1.1a 1.1b 1.2 1.3 1.4 1.8 Chapter #2: Algebraic Expressions, Linear Equations, and Applications 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
Unit 3: Day 2: Factoring Polynomial Expressions
 Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
Unit 3: Day : Factoring Polynomial Expressions Minds On: 0 Action: 45 Consolidate:10 Total =75 min Learning Goals: Extend knowledge of factoring to factor cubic and quartic expressions that can be factored
Keystone National High School Placement Exam Math Level 1. Find the seventh term in the following sequence: 2, 6, 18, 54
 1. Find the seventh term in the following sequence: 2, 6, 18, 54 2. Write a numerical expression for the verbal phrase. sixteen minus twelve divided by six Answer: b) 1458 Answer: d) 16 12 6 3. Evaluate
1. Find the seventh term in the following sequence: 2, 6, 18, 54 2. Write a numerical expression for the verbal phrase. sixteen minus twelve divided by six Answer: b) 1458 Answer: d) 16 12 6 3. Evaluate
Review of Intermediate Algebra Content
 Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
Review of Intermediate Algebra Content Table of Contents Page Factoring GCF and Trinomials of the Form + b + c... Factoring Trinomials of the Form a + b + c... Factoring Perfect Square Trinomials... 6
Factoring a Difference of Two Squares. Factoring a Difference of Two Squares
 284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
284 (6 8) Chapter 6 Factoring 87. Tomato soup. The amount of metal S (in square inches) that it takes to make a can for tomato soup is a function of the radius r and height h: S 2 r 2 2 rh a) Rewrite this
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form
 ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
ALGEBRA 2: 4.1 Graph Quadratic Functions in Standard Form Goal Graph quadratic functions. VOCABULARY Quadratic function A function that can be written in the standard form y = ax 2 + bx+ c where a 0 Parabola
Summer Math Exercises. For students who are entering. Pre-Calculus
 Summer Math Eercises For students who are entering Pre-Calculus It has been discovered that idle students lose learning over the summer months. To help you succeed net fall and perhaps to help you learn
Summer Math Eercises For students who are entering Pre-Calculus It has been discovered that idle students lose learning over the summer months. To help you succeed net fall and perhaps to help you learn
Factoring Trinomials of the Form x 2 bx c
 4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
4.2 Factoring Trinomials of the Form x 2 bx c 4.2 OBJECTIVES 1. Factor a trinomial of the form x 2 bx c 2. Factor a trinomial containing a common factor NOTE The process used to factor here is frequently
6.4 Factoring Polynomials
 Name Class Date 6.4 Factoring Polynomials Essential Question: What are some ways to factor a polynomial, and how is factoring useful? Resource Locker Explore Analyzing a Visual Model for Polynomial Factorization
Name Class Date 6.4 Factoring Polynomials Essential Question: What are some ways to factor a polynomial, and how is factoring useful? Resource Locker Explore Analyzing a Visual Model for Polynomial Factorization
MATH 108 REVIEW TOPIC 10 Quadratic Equations. B. Solving Quadratics by Completing the Square
 Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
Math 108 T10-Review Topic 10 Page 1 MATH 108 REVIEW TOPIC 10 Quadratic Equations I. Finding Roots of a Quadratic Equation A. Factoring B. Quadratic Formula C. Taking Roots II. III. Guidelines for Finding
Learning Objectives 9.2. Media Run Times 9.3
 Unit 9 Table of Contents Unit 9: Factoring Video Overview Learning Objectives 9.2 Media Run Times 9.3 Instructor Notes 9.4 The Mathematics of Factoring Polynomials Teaching Tips: Conceptual Challenges
Unit 9 Table of Contents Unit 9: Factoring Video Overview Learning Objectives 9.2 Media Run Times 9.3 Instructor Notes 9.4 The Mathematics of Factoring Polynomials Teaching Tips: Conceptual Challenges
Greatest Common Factor (GCF) Factoring
 Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
Section 4 4: Greatest Common Factor (GCF) Factoring The last chapter introduced the distributive process. The distributive process takes a product of a monomial and a polynomial and changes the multiplication
FACTORING ax 2 bx c WITH a 1
 296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
296 (6 20) Chapter 6 Factoring 6.4 FACTORING a 2 b c WITH a 1 In this section The ac Method Trial and Error Factoring Completely In Section 6.3 we factored trinomials with a leading coefficient of 1. In
Section 3.1 Quadratic Functions and Models
 Section 3.1 Quadratic Functions and Models DEFINITION: A quadratic function is a function f of the form fx) = ax 2 +bx+c where a,b, and c are real numbers and a 0. Graphing Quadratic Functions Using the
Section 3.1 Quadratic Functions and Models DEFINITION: A quadratic function is a function f of the form fx) = ax 2 +bx+c where a,b, and c are real numbers and a 0. Graphing Quadratic Functions Using the
SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014))
 SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014)) There are so far 8 most common methods to solve quadratic equations in standard form ax² + bx + c = 0.
SOLVING QUADRATIC EQUATIONS BY THE NEW TRANSFORMING METHOD (By Nghi H Nguyen Updated Oct 28, 2014)) There are so far 8 most common methods to solve quadratic equations in standard form ax² + bx + c = 0.
FACTORING QUADRATICS 8.1.1 and 8.1.2
 FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
FACTORING QUADRATICS 8.1.1 and 8.1.2 Chapter 8 introduces students to quadratic equations. These equations can be written in the form of y = ax 2 + bx + c and, when graphed, produce a curve called a parabola.
Perimeter, Area, and Volume
 Perimeter, Area, and Volume Perimeter of Common Geometric Figures The perimeter of a geometric figure is defined as the distance around the outside of the figure. Perimeter is calculated by adding all
Perimeter, Area, and Volume Perimeter of Common Geometric Figures The perimeter of a geometric figure is defined as the distance around the outside of the figure. Perimeter is calculated by adding all
Solving Quadratic Equations by Factoring
 4.7 Solving Quadratic Equations by Factoring 4.7 OBJECTIVE 1. Solve quadratic equations by factoring The factoring techniques you have learned provide us with tools for solving equations that can be written
4.7 Solving Quadratic Equations by Factoring 4.7 OBJECTIVE 1. Solve quadratic equations by factoring The factoring techniques you have learned provide us with tools for solving equations that can be written
FACTORING QUADRATICS 8.1.1 through 8.1.4
 Chapter 8 FACTORING QUADRATICS 8.. through 8..4 Chapter 8 introduces students to rewriting quadratic epressions and solving quadratic equations. Quadratic functions are any function which can be rewritten
Chapter 8 FACTORING QUADRATICS 8.. through 8..4 Chapter 8 introduces students to rewriting quadratic epressions and solving quadratic equations. Quadratic functions are any function which can be rewritten
Introduction to Quadratic Functions
 Introduction to Quadratic Functions The St. Louis Gateway Arch was constructed from 1963 to 1965. It cost 13 million dollars to build..1 Up and Down or Down and Up Exploring Quadratic Functions...617.2
Introduction to Quadratic Functions The St. Louis Gateway Arch was constructed from 1963 to 1965. It cost 13 million dollars to build..1 Up and Down or Down and Up Exploring Quadratic Functions...617.2
Algebra II A Final Exam
 Algebra II A Final Exam Multiple Choice Identify the choice that best completes the statement or answers the question. Evaluate the expression for the given value of the variable(s). 1. ; x = 4 a. 34 b.
Algebra II A Final Exam Multiple Choice Identify the choice that best completes the statement or answers the question. Evaluate the expression for the given value of the variable(s). 1. ; x = 4 a. 34 b.
A Concrete Introduction. to the Abstract Concepts. of Integers and Algebra using Algebra Tiles
 A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
A Concrete Introduction to the Abstract Concepts of Integers and Algebra using Algebra Tiles Table of Contents Introduction... 1 page Integers 1: Introduction to Integers... 3 2: Working with Algebra Tiles...
Factoring Trinomials of the Form
 Section 4 6B: Factoring Trinomials of the Form A x 2 + Bx + C where A > 1 by The AC and Factor By Grouping Method Easy Trinomials: 1 x 2 + Bx + C The last section covered the topic of factoring second
Section 4 6B: Factoring Trinomials of the Form A x 2 + Bx + C where A > 1 by The AC and Factor By Grouping Method Easy Trinomials: 1 x 2 + Bx + C The last section covered the topic of factoring second
POLYNOMIALS and FACTORING
 POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
POLYNOMIALS and FACTORING Exponents ( days); 1. Evaluate exponential expressions. Use the product rule for exponents, 1. How do you remember the rules for exponents?. How do you decide which rule to use
MATH 10034 Fundamental Mathematics IV
 MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
MATH 0034 Fundamental Mathematics IV http://www.math.kent.edu/ebooks/0034/funmath4.pdf Department of Mathematical Sciences Kent State University January 2, 2009 ii Contents To the Instructor v Polynomials.
10.1. Solving Quadratic Equations. Investigation: Rocket Science CONDENSED
 CONDENSED L E S S O N 10.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations
CONDENSED L E S S O N 10.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations
FACTORING POLYNOMIALS
 296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
296 (5-40) Chapter 5 Exponents and Polynomials where a 2 is the area of the square base, b 2 is the area of the square top, and H is the distance from the base to the top. Find the volume of a truncated
