arxiv: v1 [gr-qc] 5 Aug 2009
|
|
|
- Dylan Wilkinson
- 8 years ago
- Views:
Transcription
1 A new numerical method to construct binary neutron star initial data arxiv: v1 [gr-qc] 5 Aug 009 Wolfgang Tichy Department of Physics, Florida Atlantic University, Boca Raton, FL 33431, USA Abstract. We present a new numerical method for the generation of binary neutron star initial data using a method along the lines of the the Wilson-Mathews or the closely related conformal thin sandwich approach. Our method uses six different computational domains, which include spatial infinity. Each domain has its own coordinates which are chosen such that the star surfaces always coincide with domain boundaries. These properties facilitate the imposition of boundary conditions. Since all our fields are smooth inside each domain, we are able to use an efficient pseudospectral method to solve the elliptic equations associated with the conformal thin sandwich approach. Currently we have implemented corotating configurations with arbitrary mass ratios, but an extension to arbitrary spins is possible. The main purpose of this paper is to introduce our new method and to test our code for several different configurations. PACS numbers: 04.5.dk, Db, Jd, Fk
2 A new numerical method to construct binary neutron star initial data 1. Introduction Currently several gravitational wave detectors such as LIGO [1, ], Virgo [3, 4] or GEO [5] are already operating, while several others are in the planning or construction phase [6]. One of the most promising sources for these detectors are the inspirals and mergers of binary neutron stars (NS). In order to make predictions about the final phase of such inspirals and mergers, fully non-linear numerical simulations of the Einstein Equations are required. To start such simulations initial data are needed. The emission of gravitational waves tends to circularize the orbits [7, 8]. Thus, during the inspiral, we expect the two NSs to be in quasicircular orbits around each other with a radius which shrinks on a timescale much larger than the orbital timescale. This means that the initial data should have an approximate helical Killing vector ξ µ. In addition, one would like to have the initial data in coordinates such that this approximate symmetry is manifest, i.e. the time evolution vector should lie along ξ µ, so that the time derivatives of the evolved quantities are minimized. In order to achieve these goals we use the Wilson-Mathews approach [9, 10], which is closely related to the conformal thin sandwich formalism [11]. The Wilson-Mathews approach approach has already been successfully used by several groups. Among them are results for corotating [1, 13, 14, 15] and irrotational [16, 17, 18, 19, 0] NS binaries with equal masses. One group has also produced results for unequal mass systems [1, ]. In this paper we present a new numerical method to construct initial data for binary NSs in corotating configurations for arbitrary mass ratios. The main focus is on the numerical method rather than on new physics. We describe an efficient implementation of this method with the SGRID code [3], discuss code tests, and compare with previous results. Throughout we will use units where G = c = 1. Later when we present numerical results we will use fully dimensionless units by setting κ in the polytropic equation of state to κ = G = c = 1. Latin indices such as i run from 1 to 3, while Greek indices such as µ run from 0 to 3. The paper is organized as follows. In Sec. we describe the General Relativistic equations that govern binary neutron stars described by perfect fluids. Sec. 3 describes our particular numerical implementation of these equations, followed by results for some particular configurations in Sec. 4. We conclude with a discussion of our method in Sec. 5.. Binary neutron stars in General Relativity In this section we describe the equations governing binary NSs in quasi circular orbits..1. ADM decomposition of Einstein s equations We use the Arnowitt-Deser-Misner (ADM) decomposition of Einstein s equations (see e.g. [4]) and write the line element ds = α dt + γ ij (dx i + β i )(dx j + β j ) (1)
3 A new numerical method to construct binary neutron star initial data 3 in terms of the lapse α, shift β i and the 3-metric γ ij. The extrinsic curvature is defined by K ij = 1 α ( tγ ij β γ ij ), () With these definitions Einstein s equations split into the evolution equations t γ ij = αk ij + β γ ij t K ij = α(r ij K il K l j + KK ij) D i D j α + β K ij 8πS ij + 4πγ ij (S ρ) (3) and the Hamiltonian and momentum constraint equations R K ij K ij + K = 16πρ D j (K ij γ ij K) = 8πj i. (4) Here R ij and R are the Ricci tensor and scalar computed from γ ij, D i is the derivative operator compatible with γ ij and all indices here are raised and lowered with the 3-metric γ ij. The source terms ρ, j i, S ij and S = γ ij S ij are projections of the stress-energy tensor T µν given by ρ j i = T µν n µ n ν = T µν n µ γ νi S ij = T µν γ µi γ νj (5) and correspond to the energy density, flux and stress-tensor. The vector n µ appearing here is the the 4-vector normal to a t = const slice... Decomposition of 3-metric and extrinsic curvature As in [9, 10] the 3-metric γ ij is decomposed into a conformal factor ψ and a conformal metric γ ij such that γ ij = ψ 4 γ ij. (6) The extrinsic curvature is split into its trace K and its tracefree part A ij by writing it as K ij = A ij γ ijk (7).3. Quasi equilibrium assumptions We now make some additional simplifying assumptions. First we assume that our binary is in an approximately circular orbit and that the stars are corotating. This implies the existence of an approximate helical Killing vector ξ µ. In a coordinate system where this helical symmetry is manifest and the time evolution vector lies along ξ µ, all time derivatives should approximately be zero. Here we only assume that the time derivative t γ ij of the conformal metric and the time derivative t K of the trace of the extrinsic
4 A new numerical method to construct binary neutron star initial data 4 curvature vanish. The former allows us to express the extrinsic curvature in terms of the shift and results in A ij = 1 ψ 4 α ( Lβ) ij, (8) where ( Lβ) ij = D i β j + D j β i 3 D k β k, (9) and D k is the derivative operator compatible with γ ij. The assumption t K = 0 together with the evolution equation of K (derived from Eq. (3)) implies ψ 5 [ D k Dk (αψ) α D k Dk ψ] = α(r + K) + β i Di K.4. Further simplifications and boundary conditions + 4πα(S 3ρ). (10) Next we also choose a maximal slice and thus K = 0, and assume that the conformal 3-metric is flat and given by [9, 10] γ ij = δ ij. This latter assumption merely simplifies our equations and could in principle be improved by e.g. choosing a post-newtonian expression for γ ij as in [5, 6]. Using Eq. (11) the Hamiltonian and momentum constraints in Eq. (4) and Eq. (10) simplify and we obtain D ψ = ψ5 3α ( LB) ij ( LB) ij πψ 5 ρ D j ( LB) ij = ( LB) ij Dj ln(αψ 6 ) + 16παψ 4 j i [ ] 7ψ D 4 (αψ) = αψ 3α ( LB) ij ( LB) ij + πψ 4 (ρ + S), where ( LB) ij = D i B j + D j B i 3 δij Dk B k, Di = i, and (11) (1) B i = β i + ωǫ ij3 (x j x j CM ). (13) Here x i CM denotes the center of mass position and ω is the orbital angular velocity, which we have chosen to lie along the z-direction. The elliptic equations (1) have to be solved subject to the boundary conditions lim ψ = 1, r at spatial infinity. lim r Bi = 0, lim αψ = 1. (14) r
5 A new numerical method to construct binary neutron star initial data 5.5. Matter equations We assume that the matter in both stars is a perfect fluid with a stress-energy tensor T µν = [ρ 0 (1 + ǫ) + P]u µ u ν + Pg µν. (15) Here ρ 0 is the mass density (which is proportional the number density of baryons), P is the pressure, ǫ is the internal energy density divided by ρ 0, u µ is the 4-velocity of the fluid and g µν is the spacetime metric. The matter variables in Eq.(5) are then ρ = α [ρ 0 (1 + ǫ) + P]u 0 u 0 P j i = α[ρ 0 (1 + ǫ) + P]u 0 u 0 (u i /u 0 + β i ) S ij = [ρ 0 (1 + ǫ) + P]u 0 u 0 (u i /u 0 + β i )(u j /u 0 + β j ) + Pγ ij (16) The fact that ν T µν = 0 yields the relativistic Euler equation [ρ 0 (1 + ǫ) + P]u ν ν u µ = (g µν + u µ u ν ) ν P, (17) which together with the continuity equation ν (ρ 0 u ν ) = 0 (18) governs the fluid. For corotating stars we can show that the continuity equation (18) is identically satisfied. Furthermore one can show that the Euler equation leads to (see e.g. problem in [7]) [ρ 0 (1 + ǫ) + P]d ln(u µ ξ µ ) = dp, (19) where ξ µ is the assumed helical Killing vector. With the help of the first law of thermodynamics (d[ρ 0 (1 + ǫ)] = [ρ 0 (1 + ǫ) + P]dρ 0 /ρ 0 ) this equation can be integrated to yield u µ ξ µ C 1/ ρ 0 = ρ 0 (1 + ǫ) + P, (0) where C 1/ are constants of integration for each star. We will later choose them such that the rest mass of each star has a prescribed value. In corotating coordinates and taking into account our conformally flat 3-metric, u µ ξ µ can be written as u µ ξ µ = 1/u 0 = [α ψ 4 δ ij β i β j ] 1/. (1) In order simplify the problem we assume a polytropic equation of state P = κρ 1+1/n 0. () It is then convenient to introduce the dimensionless ratio which we use to write q = P/ρ 0, (3) ρ 0 = κ n q n P = κ n q n+1 ǫ = nq. (4)
6 A new numerical method to construct binary neutron star initial data 6 3. Numerical method In order to construct binary NS initial data we have to solve the five elliptic equations in Eq. (1), with the matter terms given by Eqs. (16), (1) and (4). In addition, our data also have to satisfy Eq. (0), which can be expressed as q = 1 n + 1 ( C1/ u µ ξ µ 1 ) for each star. We will solve the whole set of equations by iterating over the following steps: (i) We first come up with an initial guess for q in each star, in practice we simply choose Tolman-Oppenheimer-Volkoff (TOV) solutions (see e.g. Chap. 3 in [4]) for each. (ii) Next we solve the 5 coupled elliptic equations (1) for this given q. (iii) Then we use Eq. (5) to update q in each star. The constants C 1/ in general have different values for each star. We adjust the value for each star such that it has a prescribed rest mass. After updating q we go back to step (ii) and iterate until all equations are satisfied up to a given tolerance Coordinates adapted to star surfaces Note that the matter is smooth inside the stars. However, at the surface (at q = 0), ρ 0, P and ǫ are not differentiable. This means that if we want to take advantage of a spectral method, the star surfaces should be domain boundaries. A difficulty with our iterative approach, however, is that each time we update q the matter distributions change, so that the stars change shape or even move. Hence the domain boundaries have to be changed as well. In order to address this problem we introduce several domains each with its own coordinates. These coordinates depend on two freely specifiable functions which will allow us to vary the location of the domain boundaries, so that we can always adapt our domains to the current star surfaces in each iteration. As in the initial data approaches in [8, 9] our aim was to introduce as few domains as possible. The coordinates we will use, are very similar to the ones introduced by Ansorg [30]. We place both stars on the x-axis and write down the necessary coordinate transformations in two steps. First we express the standard Cartesian coordinates as x = b [ ] 1 (X + R ) + 1 (X R ) [ ] 1 y = b (X + R ) 1 XR cosφ [ ] 1 z = b (X + R ) 1 XR sin φ, (6) where b is a parameter related to the distance between the stars, and X, R are functions of the new coordinates (A, B, φ) we will use in each domain. Note that spatial infinity is located at the point where X = R = 0 and that in order to cover all (x, y, z) it is sufficient the restrict X, R, φ to the ranges 0 X 1, 0 R 1 X and 0 φ π. In order to complete the coordinate transformation between the Cartesian (5)
7 A new numerical method to construct binary neutron star initial data 7 (x, y, z) and the new coordinates (A, B, φ), we now write down X and R as functions of (A, B, φ). Inside star1 we use X = (1 A){R[C + (B, φ)] BR[C + (1, φ)]} + B cos([1 A] arg[c + (1, φ)]) + (1 B)A R = (1 A){I[C + (B, φ)] BI[C + (1, φ)]} + B sin([1 A] arg[c + (1, φ)]), (7) where the strictly positive function σ + (B, φ) in ( ) C + (B, φ) = σ+ (B, φ) + iπb tanh 4 determines the shape of the star surface. The surface is always located at A = 0 but depending on the choice for σ + (B, φ) it will be at different (x, y, z), e.g. for σ + (B, φ) = const we will get a spherical surface in (x, y, z). Note that this star is located around x = b. Inside star we use a similar transformation given by X = (1 A){R[C (B, φ)] BR[C (1, φ)]} + B cos( π A + [1 A] arg[c (1, φ)]) R = (1 A){I[C (B, φ)] BI[C (1, φ)]} + B sin( π A + [1 A] arg[c (1, φ)]) + (1 B)A, where the strictly negative function σ (B, φ) in ( ) C (B, φ) = σ (B, φ) + iπb tanh 4 determines where the star surface (A = 0) is located in (x, y, z) coordinates. Star is located around x = b. Note that the A, B, φ coordinates are different inside each star, but in order to cover each star their ranges are 0 A 1, 0 B 1 and 0 φ π in each case. The outside of both stars is covered by two additional domains. The first one covers the region outside star1 for all positive x, while the second one covers the region outside star for all negative x. Both coordinate transformations can be written as X = (1 A){R[C ± (B, φ)] BR[C ± (1, φ)]} + B cos( π 4 A + [1 A] arg[c ±(1, φ)]) R = (1 A){I[C ± (B, φ)] BI[C ± (1, φ)]} (8) (9) (30) + B sin( π 4 A + [1 A] arg[c ±(1, φ)]), (31) where we use C + (B, φ) in the former and C (B, φ) in the latter. In each case the star surface is at A = 0 and spatial infinity is at (A, B) = (1, 0). Figure 1 shows the coordinate lines in z = 0 plane.
8 A new numerical method to construct binary neutron star initial data 8 Figure 1. The plot shows the lines of constant A and B in the xy-plane for b = 1.84, σ + (B, φ) = 1.51 and σ (B, φ) = 1.8. The two neutron stars are marked with NS1 and NS. In addition, the (x, y) positions of a few points are indicated. The coordinate singularities at A = 1 inside the stars are located at x = ±b. 3.. Spectral method In order to solve the elliptic equations (1) we use the SGRID code [3] which employs pseudospectral methods to accurately compute spatial derivatives. We use Chebyshev expansions in the A- and B-directions and Fourier expansions φ-direction. As collocation points we choose A l = 1 [ ( )] πl 1 cos n A 1 B j = 1 [ 1 cos ( πj n B 1 )] φ k = πk n φ, (3) where l, j, k are integers obeying 0 l < n A, 0 j < n B, 0 k < n φ. (33) The number n A, n A and n φ of collocation points in each direction is chosen to be equal in all four domains, to ensure that the grid points on the boundaries of two adjacent domains will be at the same (x, y, z) location. As in [3] will solve Eq. (1) as written down in Cartesian form and compute derivatives like x ψ using the chain rule: x ψ = A x Aψ + B x Bψ + φ x φψ. (34) Note that all points with with B = 0 or B = 1 lie along the x-axis, with x independent of φ. Hence along this axis we have the standard coordinate singularity of polar coordinates. Furthermore, all points with A = 1 in the interior of each star correspond to just one point on the x-axis. Thus there is an additional coordinate singularity at A = 1 inside each star. We have found that if we simply use the A, B, φ coordinates as described above we were not able to solve the elliptic equations (1). The culprit is the singularity at A = 1 inside each star. Near these points the Jacobian
9 A new numerical method to construct binary neutron star initial data 9 blows up so strongly that we cannot accurately compute derivatives using Eq. (34). This problem would also occur if we did use the exact same coordinates as proposed by Ansorg [30]. In [30] the problem is not addressed since for black holes one can use excision boundary conditions and does not need the inner domains. One way around this problem would be to construct different basis functions, which would have to be chosen such that they have vanishing B and φ derivatives at A = 1. However, then we would not be able to use Fast Fourier transforms anymore to compute derivatives. For this reason we have chosen a different approach. We simply restrict the range of A inside each star so that inside 0 A A max < 1. The collocation points in A inside the stars are then given by matrix (A,B,φ) (x,y,z) A l = A max [ 1 cos ( )] lπ. (35) n A 1 We typically choose A max = In this way we completely avoid the singularities at A = 1. Of course then, our inner domains do not cover the entire star interiors any more. Instead they leave out a small hole around A = 1. We simply cover this hole by placing two additional cubical domains inside each star. Each cube is chosen such that completely covers the hole (described by A max < A 1). In each cube we use standard Cartesian coordinates so that it overlaps with part of the inner domain covered by the A, B, φ coordinates. The collocation points inside each cube are then x l = x ( ) min x max lπ cos + x min + x max n c 1 y j = y ( ) min y max jπ cos + y min + y max n c 1 z k = z ( ) min z max kπ cos + z min + z max, n c 1 (36) where the minima and maxima x min, x max, y min, y max z min, z max are chosen such that the cube covers the hole, and where n c = 6 is typically sufficient, since the cubes are very small. Figure shows how a cube is fitted into star1. In order to numerically solve the elliptic equations in Eq. (1) we arrange the values of the fields ψ, B i and αψ at each grid point in a vector w. Since we solve for 5 fields, the dimension of this vector is five times the total number of grid points. In order to find a w that satisfies Eq. (1) we impose Eq. (1) at all interior grid points. At adjacent domain boundaries we impose the conditions that fields and their normal derivatives are equal on both sides. At infinity we impose Eq. (14). In the domains covered by the A, B, φ coordinates we impose the following regularity conditions along the x-axis: For k > 0 we demand while for k = 0 we impose Ψ(A l, B j, φ k ) = Ψ(A l, B j, φ 0 ), (37) s Ψ(A l, B j, φ 0 ) + s φ φ Ψ(A l, B j, φ 0 ) = 0. (38)
10 A new numerical method to construct binary neutron star initial data 10 Figure. In order to avoid the coordinate singularity at A = 1 inside the stars, we have restricted the range of A to 0 A The remaining space is filled with a small cube of length 0.016b. This figure is a blowup of the inside of NS1 in Fig. 1 where the small cubes are not visible. Here Ψ stands for either ψ, B i or αψ, and s = y + z is the distance from the x- axis. In order to deal with the cubes which overlap the A, B, φ covered domains inside each star, we impose the condition that the fields at points on the cube boundaries must be equal to the fields in the A, B, φ covered domain interpolated to these points. Correspondingly we also demand that the fields at points on the A = A max boundaries must equal to the fields in the cube interpolated to these points. This interpolation is done with our given spectral accuracy. To compute a field at a point that is not a collocation point, we first compute the spectral expansion coefficients from the field values at the collocation points in the domain of interest. To interpolate to any point in this domain we then compute the field value from a sum over coefficients times the basis functions evaluated at the point in question. This last interpolation step can be computationally expensive if we interpolate onto many points, while going between field values and collocation points can be done via Fast Fourier transforms and is thus not very expensive. Note, however, that in our case these interpolations are not too costly, because our cubical domains have only 6 3 grid points. Such a small number of points should always be sufficient because the cubic domains are so small so that all fields are nearly constant inside the cubes, e.g. on the scale of Fig. 1 the cubes are not visible. This is an advantage over the domain decomposition used in [31, 17] where interpolations are needed between domains with many more grid points. If we take all these conditions into account we obtain N = 4n A n B n φ +n 3 c non-linear equations of the form f m (w) = 0, m = 1,,..., N (39) for the N unknowns comprising the solution vector w. We solve this system of equations by a Newton-Raphson scheme. This scheme requires an initial guess, for which we simply use two TOV solutions in conformally flat isotropic coordinates. In order to solve the
11 A new numerical method to construct binary neutron star initial data 11 linearized equations f m (w) x n = f w n m (w) (40) in each Newton-Raphson step, we note that f m (w) contains spectral derivatives of w is sparse in the sense that it contains about 95% zeros. So in order to numerically solve the linearized Eq. (40) we use the sparse matrix solver UMFPACK [3, 33, 34, 35, 36]. in different directions, so that the N N matrix fm(w) w n 3.3. Iteration scheme As already mentioned solving the elliptic equations in Eq. (1) once is not enough. After each solve, we have to adjust q using Eq. (5). This adjustment presents the problem that the star surfaces (located at q = 0) change. Hence we have to also adjust σ + (B, φ) and σ (B, φ) in order to keep both star surfaces at A = 0. While this adjustment is not hard to implement, it incurs a high computational cost since adjusting σ + (B, φ) and σ (B, φ) amounts to changing our computational grid, and after each such adjustment we need to interpolate all relevant fields onto the new grid. In addition, the adjustment has to be carried out several times after each individual elliptic solve, since we were only able to achieve a stable iteration scheme if we pick the free constants C 1, C, ω and x CM as follows. Let us call the intersection points of the x-axis with the side of the star surface not facing the origin x out1 and x out (located at (A, B) = (0, 0)) for each star. We then determine ω and x CM by requiring that x out1 and x out remain constant. This task is accomplished by a root finder. In each iteration of this root finder C 1, C are adjusted such that the rest mass of each star remains constant (by another root finder). These root finders have to evaluate q and thus need to adjust the domain shapes several times. If we do not adjust ω and x CM we find that the stars drift around too much for the iterations to converge. Instead of x out1 and x out it is also possible to fix the points x max1 and x max where the maximum values of q occur. In addition, we have observed that once a new q is set the elliptic solve often overcorrects which again can result in an unstable iteration scheme. To overcome this problem we typically do not take the ψ, B i and αψ coming from solving Eq. (1) as our new fields. Rather, we take the average of this solution and the ψ, B i and αψ from the previous iteration step as our new fields. In this way ψ, B i and αψ change less from one iteration step to the next. 4. Results All the results presented in this section were computed for n = 1 polytopes (see Eq. ()) in units where κ = 1. In order to check that our SGRID code is working properly we have checked the convergence of the constraints. For these tests we have computed the constraints directly from Eq. (4) for different numbers of grid points. From Fig. 3 we see that
12 A new numerical method to construct binary neutron star initial data Hamiltonian constraint n Figure 3. The L -norm of the Hamiltonian constraint on the grid inside star 1 converges exponentially with the number of grid points n A = n B = n. The plot is for an equal mass binary with rest masses m 01 = m 0 = The star centers are located at x max1 = x max =.11, and n φ = 8 and n c = 6 are kept fixed. the Hamiltonian constraint converges exponentially with the number of grid points, as expected for a spectral method. The momentum constraints as well as t K converge to zero in a similar fashion. We have computed initial data for the configurations listed in table 1. Each configuration is described by the rest masses m 01 and m 0 of the two stars given by m 0i = ρ 0 u 0 αψ 6 d 3 x, i = {1, } (41) stari and the separation parameter b, which appears in the coordinate transformations and is approximately half the separation. For each configuration we have also computed the ADM mass and angular momentum given by and M ADM = ( ρ πα ( LB) ij ( LB) ij ) ψ 5 d 3 x (4) J ADM = [(x x CM )j y yj x ] ψ 10 d 3 x. (43) Our iterative scheme also yields the orbital angular velocity ω and the location of the center of mass x CM. Furthermore we list the maximum values of q in each star along the x-axis, together with their x-coordinates, and also the locations of the inner and outer edges of each star. We also show the distance d 1 between the stars and star diameters d 1/ defined by d 1 = x max1 x max and d 1/ = x out1/ x in1/. The equal mass configuration in table 1 is very close to configurations already computed by Baumgarte et al. [13] and also by Gourgoulhon et al. [17] and agrees with those to better than 1% (see Table II. in [17]). Note that our code has no problems handling unequal mass systems, as well as systems that are far apart. In addition, it is very memory efficient. A typical run with n A = n B = 18 points needs only about 80MB of memory. The initial data can thus be generated on ordinary PCs. On a.3ghz Linux PC it takes about 30
13 A new numerical method to construct binary neutron star initial data 13 m m b M ADM J ADM ω d d d x CM q max q max x in x max x out x in x max x out M ADM M ( κ0 κ ) n/ m 01 /M ADM m 0 /M ADM d 1 /M ADM d 1 /M ADM d /M ADM ωm ADM J ADM /MADM Table 1. Properties of initial data for different parameters m 01, m 0 and b. The numbers are first given in units of G = c = κ = 1. The total ADM mass M ADM is also given in solar masses where κ 0 = m and n = 1 (Note that κ n/ GM ADM /c is dimensionless). After that we also list some quantities in geometric units (G = c = 1) in terms of the total ADM mass. hours to push the Hamiltonian constraint down to 10 4 if we use n A = n B = 18 points. The main reason for the low memory footprint is that our spectral code needs only very few grid points to achieve the quoted accuracies. Figure 4 shows q in the xy-plane for a binary with rest masses m 01 = 0.14 and m 0 = We can see how the domain boundaries are adapted such that q is non-zero only in the inner domains. Note that q is the rest mass density for κ = n = 1. In Figs. 5 and 6 we show the conformal factor ψ and the largest shift component B y for the same configuration. Note that unlike q both are smooth (C 1 ) across the domain boundaries. In order to further verify our code we have performed a comparison with previous results from Taniguchi et al. [1]. In Figs. 7 and 8 we show how M ADM and J ADM vary as a function of ω for a binary with rest masses m 01 = and m 0 = As we can see our results (squares) approach the expected post-newtonian results (taken
14 A new numerical method to construct binary neutron star initial data q y x Figure 4. q in the xy-plane for a binary with rest masses m 01 = 0.14, m 0 = 0.06 and b = Psi y x Figure 5. Conformal factor ψ in the xy-plane for a binary with rest masses m 01 = 0.14 and m 0 = from [37, 5, 38, 39]) for point particles (dotted line) for small ω. At intermediate ω our results differ from point particle results and instead agree with previous results obtained by Taniguchi et al. [1]. Note that, while the agreement in M ADM does not look as good as for J ADM, the values for M ADM from both methods still agree to better than 0.05%. With our current code we can construct initial data only up to ω Beyond that point, already the first iteration of our elliptic solver fails. We suspect that our initial guess of simply using two spherical TOV stars with B i = 0 is not good enough for close configurations, and that the solver would succeed if we provided a guess that is closer to the true solution. Notice that while Taniguchi et al. [1] can extend their sequence to higher ω they also did not record a turning point in either curve for this configuration.
15 A new numerical method to construct binary neutron star initial data By y x Figure 6. Largest shift component B y in inertial coordinates for a binary with rest masses m 01 = 0.14 and m 0 = M ADM for m 01 =0.1461, m 0 =0.199 PN point particles Taniguchi et al. this work ω Figure 7. The ADM mass for a binary with rest masses m 01 = and m 0 = as a function of angular velocity in units of G = c = κ = 1. Shown are results for post--newtonian point particles (dotted line), values from previous work [1] (crosses), and results from our new code (squares). 5. Discussion The purpose of this paper is to introduce a new numerical method for the computation of binary neutron star initial data with the SGRID code [3]. The method uses six domains with different coordinate systems in each domain. The coordinates in four of these domains are closely related to the ones suggested in [30]. We have, however, added two extra domains with Cartesian coordinates to remove coordinate singularities. All our fields are C inside each domain. This allows us to use an efficient pseudo-spectral collocation method to solve the elliptic equations (1) associated with the initial data construction. Note that, we directly solve the 5 Eqs. (1), i.e. we do not split the
16 A new numerical method to construct binary neutron star initial data J ADM for m 01 =0.1461, m 0 =0.199 PN point particles Taniguchi et al. this work ω Figure 8. The ADM angular momentum for the same cases as in Fig. 7 in units of G = c = κ = 1. shift in the momentum constraint into a vector and a gradient of a scalar, which would introduce an additional elliptic equation. Thus we have one less equation to solve than in the original Wilson-Mathews approach [9, 10]. Since two of our domains extend to spatial infinity we are able to easily impose the boundary conditions in Eq. (14) without the need of any approximations such as Robin boundary conditions. At present we have only considered corotating configurations. The numerical method, however, could be easily extended to configurations with arbitrary spins, e.g. by following the approach in [0]. This approach involves the addition of one more elliptic equation for a velocity potential. The boundary conditions for this extra equation need to be imposed at the star surface, which is somewhat involved if one uses cubical domains as in [0]. We our new method, however, such boundary conditions can be easily imposed, since each star surface is a domain boundary. It is well known that the star surfaces of close configurations can develop cusps due to tidal forces [19, 17, 0]. We have not investigated this issue with our new method yet, because our elliptic solver currently fails already during the first step for close configurations. We suspect that we need an initial guess that is better than two spherical TOV stars with vanishing shift B i. We would like to point out, however, that our method should not have any additional problems with such cups if they occur only along the x-axis (the line connecting the two stars). The reason is that the σ ± (B, φ) which appear in the coordinate transformations and describe the star surfaces, can easily be chosen such that the domain boundaries have arbitrary cusps on the x-axis. Note that such cusp producing σ ± (B, φ) are themselves perfectly smooth in A, B, φ coordinates, so that we do not expect to loose spectral accuracy.
17 A new numerical method to construct binary neutron star initial data 17 Acknowledgments It is a pleasure to thank Pedro Marronetti for useful discussions about NS initial data. This work was supported by NSF grant PHY [1] B. Abbott et al. LIGO: The Laser Interferometer Gravitational-Wave Observatory arxiv: [gr-qc]. [] [3] F. Acernese et al. The Virgo 3 km interferometer for gravitational wave detection. J. Opt. A: Pure Appl. Opt., 10:064009, 008. [4] VIRGO - [5] [6] B. Schutz. Gravitational wave astronomy. Class. Quantum Grav., 16:A131 A156, [7] P. C. Peters and J. Mathews. Gravitational radiation from point masses in a Keplerian orbit. Phys. Rev., 131: , [8] P. C. Peters. Gravitational radiation and the motion of two point masses. Phys. Rev., 136:B14 B13, [9] J. R. Wilson and G. J. Mathews. Instabilities in close neutron star binaries. Phys. Rev. Lett., 75:4161, [10] J. R. Wilson, G. J. Mathews, and P. Marronetti. Relativistic Numerical Method for Close Neutron Star Binaries. Phys. Rev., D54: , [11] J. W. York. Conformal thin-sandwich data for the initial-value problem of general relativity. Phys. Rev. Lett., 8: , [1] T. W. Baumgarte, G. B. Cook, M. A. Scheel, S. L. Shapiro, and S. A. Teukolsky. Binary Neutron Stars in General Relativity: Quasi- Equilibrium Models. Phys. Rev. Lett., 79: , [13] T. W. Baumgarte, G. B. Cook, M. A. Scheel, S. L. Shapiro, and S. A. Teukolsky. General Relativistic Models of Binary Neutron Stars in Quasiequilibrium. Phys. Rev., D57: , [14] G. J. Mathews, P. Marronetti, and J. R. Wilson. Relativistic Hydrodynamics in Close Binary Systems: Analysis of Neutron-Star Collapse. Phys. Rev., D58:043003, [15] P. Marronetti, G. J. Mathews, and J. R. Wilson. Binary neutron star systems: From the Newtonian regime to the last stable orbit. Phys. Rev., D58:107503, [16] Silvano Bonazzola, Eric Gourgoulhon, and Jean-Alain Marck. Numerical models of irrotational binary neutron stars in general relativity. Phys. Rev. Lett., 8:89 895, [17] Eric Gourgoulhon, Philippe Grandclement, Keisuke Taniguchi, Jean-Alain Marck, and Silvano Bonazzola. Quasiequilibrium sequences of synchronized and irrotational binary neutron stars in general relativity. I. Method and tests. Phys. Rev., D63:06409, 001. [18] P. Marronetti, G. J. Mathews, and J. R. Wilson. Irrotational binary neutron stars in quasiequilibrium. Phys. Rev. D, 60:087301, [19] Koji Uryu and Yoshiharu Eriguchi. A new numerical method for constructing quasi-equilibrium sequences of irrotational binary neutron stars in general relativity. Phys. Rev., D61:1403, 000. [0] Pedro Marronetti and Stuart L. Shapiro. Relativistic models for binary neutron stars with arbitrary spins. Phys. Rev., D68:10404, 003. [1] Keisuke Taniguchi and Eric Gourgoulhon. Quasiequilibrium sequences of synchronized and irrotational binary neutron stars in general relativity. III: Identical and different mass stars with gamma =. Phys. Rev., D66:104019, 00. [] Keisuke Taniguchi and Eric Gourgoulhon. Various features of quasiequilibrium sequences of binary neutron stars in general relativity. Phys. Rev., D68:1405, 003. [3] Wolfgang Tichy. Black hole evolution with the bssn system by pseudo-spectral methods. Phys.
18 A new numerical method to construct binary neutron star initial data 18 Rev., D74:084005, 006. [4] C. W. Misner, K. S. Thorne, and J. A. Wheeler. Gravitation. W. H. Freeman, San Francisco, [5] Wolfgang Tichy, Bernd Brügmann, Manuela Campanelli, and Peter Diener. Binary black hole initial data for numerical general relativity based on post-newtonian data. Phys. Rev. D, 67:064008, 003. gr-qc/ [6] Bernard J. Kelly, Wolfgang Tichy, Manuela Campanelli, and Bernard F. Whiting. Black hole puncture initial data with realistic gravitational wave content. Phys. Rev., D76:04008, 007. [7] Alan P. Lightman, William H. Press, Richard H. Price, and Saul A. Teukolsky. Problem Book in Relativity and Gravitation. Princeton University Press, Princeton, NJ, [8] Marcus Ansorg, Bernd Brügmann, and Wolfgang Tichy. A single-domain spectral method for black hole puncture data. Phys. Rev. D, 70:064011, 004. [9] Marcus Ansorg. A double-domain spectral method for black hole excision data. Phys. Rev., D7:04018, 005. [30] Marcus Ansorg. Multi-Domain Spectral Method for Initial Data of Arbitrary Binaries in General Relativity. Class. Quant. Grav., 4:S1 S14, 007. [31] Silvano Bonazzola, Eric Gourgoulhon, and Jean-Alain Marck. Numerical approach for high precision 3-D relativistic star models. Phys. Rev., D58:10400, [3] Timothy A. Davis and Iain S. Duff. An unsymmetric-pattern multifrontal method for sparse LU factorization. SIAM J. Matrix Anal. Applic., 18(1): , [33] Timothy A. Davis and Iain S. Duff. A combined unifrontal/multifrontal method for unsymmetric sparse matrices. ACM Trans. Math. Softw., 5(1):1 0, [34] Timothy A. Davis. Algorithm 83: Umfpack v4.3 an unsymmetric-pattern multifrontal method. ACM Trans. Math. Softw., 30(): , 004. [35] Timothy A. Davis. A column pre-ordering strategy for the unsymmetric-pattern multifrontal method. ACM Trans. Math. Softw., 30(): , 004. [36] Timothy A. Davis. UMFPACK a sparse linear systems solver using the Unsymmetric MultiFrontal method: [37] G. Schäfer and N. Wex. Physics Lett. A, 174:196, [38] Wolfgang Tichy, Bernd Brügmann, and Pablo Laguna. Gauge conditions for binary black hole puncture data based on an approximate helical Killing vector. Phys. Rev. D, 68:064008, 003. [39] Wolfgang Tichy and Bernd Brügmann. Quasi-equilibrium binary black hole sequences for puncture data derived from helical killing vector conditions. Phys. Rev. D, 69:04006, 004.
Gravitational waves from neutron stars binaries: accuracy and tidal effects in the late inspiral S. Bernuzzi TPI-PAF FSU Jena / SFB-TR7
 Gravitational waves from neutron stars binaries: accuracy and tidal effects in the late inspiral S. Bernuzzi TPI-PAF FSU Jena / SFB-TR7 M. Thierfelder, SB, & B.Bruegmann, PRD 84 044012 (2011) SB, MT, &
Gravitational waves from neutron stars binaries: accuracy and tidal effects in the late inspiral S. Bernuzzi TPI-PAF FSU Jena / SFB-TR7 M. Thierfelder, SB, & B.Bruegmann, PRD 84 044012 (2011) SB, MT, &
Differential Relations for Fluid Flow. Acceleration field of a fluid. The differential equation of mass conservation
 Differential Relations for Fluid Flow In this approach, we apply our four basic conservation laws to an infinitesimally small control volume. The differential approach provides point by point details of
Differential Relations for Fluid Flow In this approach, we apply our four basic conservation laws to an infinitesimally small control volume. The differential approach provides point by point details of
Introduction to SME and Scattering Theory. Don Colladay. New College of Florida Sarasota, FL, 34243, U.S.A.
 June 2012 Introduction to SME and Scattering Theory Don Colladay New College of Florida Sarasota, FL, 34243, U.S.A. This lecture was given at the IUCSS summer school during June of 2012. It contains a
June 2012 Introduction to SME and Scattering Theory Don Colladay New College of Florida Sarasota, FL, 34243, U.S.A. This lecture was given at the IUCSS summer school during June of 2012. It contains a
Radiation reaction for inspiralling binary systems with spin-spin
 Radiation reaction for inspiralling binary systems with spin-spin coupling 1 Institute of Theoretical Physics, Friedrich-Schiller-University Jena December 3, 2007 1 H. Wang and C. M. Will, Phys. Rev. D,
Radiation reaction for inspiralling binary systems with spin-spin coupling 1 Institute of Theoretical Physics, Friedrich-Schiller-University Jena December 3, 2007 1 H. Wang and C. M. Will, Phys. Rev. D,
Figure 2.1: Center of mass of four points.
 Chapter 2 Bézier curves are named after their inventor, Dr. Pierre Bézier. Bézier was an engineer with the Renault car company and set out in the early 196 s to develop a curve formulation which would
Chapter 2 Bézier curves are named after their inventor, Dr. Pierre Bézier. Bézier was an engineer with the Renault car company and set out in the early 196 s to develop a curve formulation which would
= = GM. v 1 = Ωa 1 sin i.
 1 Binary Stars Consider a binary composed of two stars of masses M 1 and We define M = M 1 + and µ = M 1 /M If a 1 and a 2 are the mean distances of the stars from the center of mass, then M 1 a 1 = a
1 Binary Stars Consider a binary composed of two stars of masses M 1 and We define M = M 1 + and µ = M 1 /M If a 1 and a 2 are the mean distances of the stars from the center of mass, then M 1 a 1 = a
State of Stress at Point
 State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
State of Stress at Point Einstein Notation The basic idea of Einstein notation is that a covector and a vector can form a scalar: This is typically written as an explicit sum: According to this convention,
Introduction to spectral methods
 Introduction to spectral methods Eric Gourgoulhon Laboratoire de l Univers et de ses Théories (LUTH) CNRS / Observatoire de Paris Meudon, France Based on a collaboration with Silvano Bonazzola, Philippe
Introduction to spectral methods Eric Gourgoulhon Laboratoire de l Univers et de ses Théories (LUTH) CNRS / Observatoire de Paris Meudon, France Based on a collaboration with Silvano Bonazzola, Philippe
arxiv:gr-qc/0702038v1 7 Feb 2007
 A new spectral apparent horizon finder for 3D numerical relativity arxiv:gr-qc/0702038v1 7 Feb 2007 1. Introduction Lap-Ming Lin 1,2 and Jérôme Novak 2 1 Department of Physics and Institute of Theoretical
A new spectral apparent horizon finder for 3D numerical relativity arxiv:gr-qc/0702038v1 7 Feb 2007 1. Introduction Lap-Ming Lin 1,2 and Jérôme Novak 2 1 Department of Physics and Institute of Theoretical
Nonlinear Iterative Partial Least Squares Method
 Numerical Methods for Determining Principal Component Analysis Abstract Factors Béchu, S., Richard-Plouet, M., Fernandez, V., Walton, J., and Fairley, N. (2016) Developments in numerical treatments for
Numerical Methods for Determining Principal Component Analysis Abstract Factors Béchu, S., Richard-Plouet, M., Fernandez, V., Walton, J., and Fairley, N. (2016) Developments in numerical treatments for
Gravitational self-force in the ultra-relativistic regime Chad Galley, California Institute of Technology
 Gravitational self-force in the ultra-relativistic regime Chad Galley, California Institute of Technology with Rafael Porto (IAS) arxiv: 1302.4486 v2 soon! (with details) Capra16; Dublin, Ireland; July
Gravitational self-force in the ultra-relativistic regime Chad Galley, California Institute of Technology with Rafael Porto (IAS) arxiv: 1302.4486 v2 soon! (with details) Capra16; Dublin, Ireland; July
Chapter 2. Derivation of the Equations of Open Channel Flow. 2.1 General Considerations
 Chapter 2. Derivation of the Equations of Open Channel Flow 2.1 General Considerations Of interest is water flowing in a channel with a free surface, which is usually referred to as open channel flow.
Chapter 2. Derivation of the Equations of Open Channel Flow 2.1 General Considerations Of interest is water flowing in a channel with a free surface, which is usually referred to as open channel flow.
Testing dark matter halos using rotation curves and lensing
 Testing dark matter halos using rotation curves and lensing Darío Núñez Instituto de Ciencias Nucleares, UNAM Instituto Avanzado de Cosmología A. González, J. Cervantes, T. Matos Observational evidences
Testing dark matter halos using rotation curves and lensing Darío Núñez Instituto de Ciencias Nucleares, UNAM Instituto Avanzado de Cosmología A. González, J. Cervantes, T. Matos Observational evidences
Orbits of the Lennard-Jones Potential
 Orbits of the Lennard-Jones Potential Prashanth S. Venkataram July 28, 2012 1 Introduction The Lennard-Jones potential describes weak interactions between neutral atoms and molecules. Unlike the potentials
Orbits of the Lennard-Jones Potential Prashanth S. Venkataram July 28, 2012 1 Introduction The Lennard-Jones potential describes weak interactions between neutral atoms and molecules. Unlike the potentials
Specific Intensity. I ν =
 Specific Intensity Initial question: A number of active galactic nuclei display jets, that is, long, nearly linear, structures that can extend for hundreds of kiloparsecs. Many have two oppositely-directed
Specific Intensity Initial question: A number of active galactic nuclei display jets, that is, long, nearly linear, structures that can extend for hundreds of kiloparsecs. Many have two oppositely-directed
Lecture 2. Gravitational Waves from Binary Systems: Probes of the Universe. Historical importance of orbiting systems.
 Gravitational Waves Notes for Lectures at the Azores School on Observational Cosmology September 2011 B F Schutz Albert Einstein Institute (AEI), Potsdam, Germany http://www.aei.mpg.de, Bernard.Schutz@aei.mpg.de
Gravitational Waves Notes for Lectures at the Azores School on Observational Cosmology September 2011 B F Schutz Albert Einstein Institute (AEI), Potsdam, Germany http://www.aei.mpg.de, Bernard.Schutz@aei.mpg.de
We can display an object on a monitor screen in three different computer-model forms: Wireframe model Surface Model Solid model
 CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
CHAPTER 4 CURVES 4.1 Introduction In order to understand the significance of curves, we should look into the types of model representations that are used in geometric modeling. Curves play a very significant
Wolfgang Tichy. Address: Science & Engineering Building, Room 444 Physics Department Florida Atlantic University 777 Glades Road Boca Raton, FL 33431
 Wolfgang Tichy Address: Science & Engineering Building, Room 444 Physics Department Florida Atlantic University 777 Glades Road Boca Raton, FL 33431 Phone: (561) 318 0442 Fax: (561) 297 2662 E-Mail: wolf@fau.edu
Wolfgang Tichy Address: Science & Engineering Building, Room 444 Physics Department Florida Atlantic University 777 Glades Road Boca Raton, FL 33431 Phone: (561) 318 0442 Fax: (561) 297 2662 E-Mail: wolf@fau.edu
Lecture Notes to Accompany. Scientific Computing An Introductory Survey. by Michael T. Heath. Chapter 10
 Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Chapter 10 Boundary Value Problems for Ordinary Differential Equations Copyright c 2001. Reproduction
Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Chapter 10 Boundary Value Problems for Ordinary Differential Equations Copyright c 2001. Reproduction
INITIAL DATA FOR BLACK HOLE EVOLUTIONS
 INITIAL DATA FOR BLACK HOLE EVOLUTIONS A Dissertation Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy
INITIAL DATA FOR BLACK HOLE EVOLUTIONS A Dissertation Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy
Solving Simultaneous Equations and Matrices
 Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Solving Simultaneous Equations and Matrices The following represents a systematic investigation for the steps used to solve two simultaneous linear equations in two unknowns. The motivation for considering
Numerical Simulations of Black-Hole Spacetimes
 Numerical Simulations of Black-Hole Spacetimes Thesis by Tony Chu In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy California Institute of Technology Pasadena, California
Numerical Simulations of Black-Hole Spacetimes Thesis by Tony Chu In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy California Institute of Technology Pasadena, California
The Math Circle, Spring 2004
 The Math Circle, Spring 2004 (Talks by Gordon Ritter) What is Non-Euclidean Geometry? Most geometries on the plane R 2 are non-euclidean. Let s denote arc length. Then Euclidean geometry arises from the
The Math Circle, Spring 2004 (Talks by Gordon Ritter) What is Non-Euclidean Geometry? Most geometries on the plane R 2 are non-euclidean. Let s denote arc length. Then Euclidean geometry arises from the
11.1. Objectives. Component Form of a Vector. Component Form of a Vector. Component Form of a Vector. Vectors and the Geometry of Space
 11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
11 Vectors and the Geometry of Space 11.1 Vectors in the Plane Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. 2 Objectives! Write the component form of
Incorporating Internal Gradient and Restricted Diffusion Effects in Nuclear Magnetic Resonance Log Interpretation
 The Open-Access Journal for the Basic Principles of Diffusion Theory, Experiment and Application Incorporating Internal Gradient and Restricted Diffusion Effects in Nuclear Magnetic Resonance Log Interpretation
The Open-Access Journal for the Basic Principles of Diffusion Theory, Experiment and Application Incorporating Internal Gradient and Restricted Diffusion Effects in Nuclear Magnetic Resonance Log Interpretation
Lesson 3: Isothermal Hydrostatic Spheres. B68: a self-gravitating stable cloud. Hydrostatic self-gravitating spheres. P = "kt 2.
 Lesson 3: Isothermal Hydrostatic Spheres B68: a self-gravitating stable cloud Bok Globule Relatively isolated, hence not many external disturbances Though not main mode of star formation, their isolation
Lesson 3: Isothermal Hydrostatic Spheres B68: a self-gravitating stable cloud Bok Globule Relatively isolated, hence not many external disturbances Though not main mode of star formation, their isolation
Data Provided: A formula sheet and table of physical constants is attached to this paper. DARK MATTER AND THE UNIVERSE
 Data Provided: A formula sheet and table of physical constants is attached to this paper. DEPARTMENT OF PHYSICS AND ASTRONOMY Autumn Semester (2014-2015) DARK MATTER AND THE UNIVERSE 2 HOURS Answer question
Data Provided: A formula sheet and table of physical constants is attached to this paper. DEPARTMENT OF PHYSICS AND ASTRONOMY Autumn Semester (2014-2015) DARK MATTER AND THE UNIVERSE 2 HOURS Answer question
A QUICK GUIDE TO THE FORMULAS OF MULTIVARIABLE CALCULUS
 A QUIK GUIDE TO THE FOMULAS OF MULTIVAIABLE ALULUS ontents 1. Analytic Geometry 2 1.1. Definition of a Vector 2 1.2. Scalar Product 2 1.3. Properties of the Scalar Product 2 1.4. Length and Unit Vectors
A QUIK GUIDE TO THE FOMULAS OF MULTIVAIABLE ALULUS ontents 1. Analytic Geometry 2 1.1. Definition of a Vector 2 1.2. Scalar Product 2 1.3. Properties of the Scalar Product 2 1.4. Length and Unit Vectors
Mechanics 1: Conservation of Energy and Momentum
 Mechanics : Conservation of Energy and Momentum If a certain quantity associated with a system does not change in time. We say that it is conserved, and the system possesses a conservation law. Conservation
Mechanics : Conservation of Energy and Momentum If a certain quantity associated with a system does not change in time. We say that it is conserved, and the system possesses a conservation law. Conservation
arxiv:gr-qc/9409057v1 27 Sep 1994
 Gravitational Radiation from Nonaxisymmetric Instability in a Rotating Star J. L. Houser, J. M. Centrella, and S. C. Smith Department of Physics and Atmospheric Science, Drexel University, Philadelphia,
Gravitational Radiation from Nonaxisymmetric Instability in a Rotating Star J. L. Houser, J. M. Centrella, and S. C. Smith Department of Physics and Atmospheric Science, Drexel University, Philadelphia,
Orbital Dynamics with Maple (sll --- v1.0, February 2012)
 Orbital Dynamics with Maple (sll --- v1.0, February 2012) Kepler s Laws of Orbital Motion Orbital theory is one of the great triumphs mathematical astronomy. The first understanding of orbits was published
Orbital Dynamics with Maple (sll --- v1.0, February 2012) Kepler s Laws of Orbital Motion Orbital theory is one of the great triumphs mathematical astronomy. The first understanding of orbits was published
the points are called control points approximating curve
 Chapter 4 Spline Curves A spline curve is a mathematical representation for which it is easy to build an interface that will allow a user to design and control the shape of complex curves and surfaces.
Chapter 4 Spline Curves A spline curve is a mathematical representation for which it is easy to build an interface that will allow a user to design and control the shape of complex curves and surfaces.
Spectral Methods for Numerical Relativity
 Spectral Methods for Numerical Relativity Philippe Grandclement, Jérôme Novak To cite this version: Philippe Grandclement, Jérôme Novak. Spectral Methods for Numerical Relativity. This paper has bene submitted
Spectral Methods for Numerical Relativity Philippe Grandclement, Jérôme Novak To cite this version: Philippe Grandclement, Jérôme Novak. Spectral Methods for Numerical Relativity. This paper has bene submitted
Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows
 Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows 3.- 1 Basics: equations of continuum mechanics - balance equations for mass and momentum - balance equations for the energy and the chemical
Lecture 3 Fluid Dynamics and Balance Equa6ons for Reac6ng Flows 3.- 1 Basics: equations of continuum mechanics - balance equations for mass and momentum - balance equations for the energy and the chemical
Orbital Dynamics of Eccentric Compact Binaries
 Orbital Dynamics of Eccentric Compact Binaries Laboratoire Univers et Théories Observatoire de Paris / CNRS Collaborators: S. Akcay, L. Barack, N. Sago, N. Warburton Phys. Rev. D 91 124014 (2015), arxiv:1503.01374
Orbital Dynamics of Eccentric Compact Binaries Laboratoire Univers et Théories Observatoire de Paris / CNRS Collaborators: S. Akcay, L. Barack, N. Sago, N. Warburton Phys. Rev. D 91 124014 (2015), arxiv:1503.01374
1 3 4 = 8i + 20j 13k. x + w. y + w
 ) Find the point of intersection of the lines x = t +, y = 3t + 4, z = 4t + 5, and x = 6s + 3, y = 5s +, z = 4s + 9, and then find the plane containing these two lines. Solution. Solve the system of equations
) Find the point of intersection of the lines x = t +, y = 3t + 4, z = 4t + 5, and x = 6s + 3, y = 5s +, z = 4s + 9, and then find the plane containing these two lines. Solution. Solve the system of equations
Practice Final Math 122 Spring 12 Instructor: Jeff Lang
 Practice Final Math Spring Instructor: Jeff Lang. Find the limit of the sequence a n = ln (n 5) ln (3n + 8). A) ln ( ) 3 B) ln C) ln ( ) 3 D) does not exist. Find the limit of the sequence a n = (ln n)6
Practice Final Math Spring Instructor: Jeff Lang. Find the limit of the sequence a n = ln (n 5) ln (3n + 8). A) ln ( ) 3 B) ln C) ln ( ) 3 D) does not exist. Find the limit of the sequence a n = (ln n)6
The Basics of FEA Procedure
 CHAPTER 2 The Basics of FEA Procedure 2.1 Introduction This chapter discusses the spring element, especially for the purpose of introducing various concepts involved in use of the FEA technique. A spring
CHAPTER 2 The Basics of FEA Procedure 2.1 Introduction This chapter discusses the spring element, especially for the purpose of introducing various concepts involved in use of the FEA technique. A spring
Elasticity Theory Basics
 G22.3033-002: Topics in Computer Graphics: Lecture #7 Geometric Modeling New York University Elasticity Theory Basics Lecture #7: 20 October 2003 Lecturer: Denis Zorin Scribe: Adrian Secord, Yotam Gingold
G22.3033-002: Topics in Computer Graphics: Lecture #7 Geometric Modeling New York University Elasticity Theory Basics Lecture #7: 20 October 2003 Lecturer: Denis Zorin Scribe: Adrian Secord, Yotam Gingold
arxiv:1405.3693v1 [gr-qc] 14 May 2014
![arxiv:1405.3693v1 [gr-qc] 14 May 2014 arxiv:1405.3693v1 [gr-qc] 14 May 2014](/thumbs/27/11758962.jpg) International Journal of Modern Physics D c World Scientific Publishing Company arxiv:1405.3693v1 [gr-qc] 14 May 2014 Key Elements of Robustness in Binary Black Hole Evolutions using Spectral Methods Béla
International Journal of Modern Physics D c World Scientific Publishing Company arxiv:1405.3693v1 [gr-qc] 14 May 2014 Key Elements of Robustness in Binary Black Hole Evolutions using Spectral Methods Béla
The Fourth International DERIVE-TI92/89 Conference Liverpool, U.K., 12-15 July 2000. Derive 5: The Easiest... Just Got Better!
 The Fourth International DERIVE-TI9/89 Conference Liverpool, U.K., -5 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de technologie supérieure 00, rue Notre-Dame Ouest Montréal
The Fourth International DERIVE-TI9/89 Conference Liverpool, U.K., -5 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de technologie supérieure 00, rue Notre-Dame Ouest Montréal
Chapter 22: Electric Flux and Gauss s Law
 22.1 ntroduction We have seen in chapter 21 that determining the electric field of a continuous charge distribution can become very complicated for some charge distributions. t would be desirable if we
22.1 ntroduction We have seen in chapter 21 that determining the electric field of a continuous charge distribution can become very complicated for some charge distributions. t would be desirable if we
Contents. Microfluidics - Jens Ducrée Physics: Navier-Stokes Equation 1
 Contents 1. Introduction 2. Fluids 3. Physics of Microfluidic Systems 4. Microfabrication Technologies 5. Flow Control 6. Micropumps 7. Sensors 8. Ink-Jet Technology 9. Liquid Handling 10.Microarrays 11.Microreactors
Contents 1. Introduction 2. Fluids 3. Physics of Microfluidic Systems 4. Microfabrication Technologies 5. Flow Control 6. Micropumps 7. Sensors 8. Ink-Jet Technology 9. Liquid Handling 10.Microarrays 11.Microreactors
Two vectors are equal if they have the same length and direction. They do not
 Vectors define vectors Some physical quantities, such as temperature, length, and mass, can be specified by a single number called a scalar. Other physical quantities, such as force and velocity, must
Vectors define vectors Some physical quantities, such as temperature, length, and mass, can be specified by a single number called a scalar. Other physical quantities, such as force and velocity, must
Neutron stars as laboratories for exotic physics
 Ian Jones Neutron stars as laboratories for exotic physics 1/20 Neutron stars as laboratories for exotic physics Ian Jones D.I.Jones@soton.ac.uk General Relativity Group, Southampton University Context
Ian Jones Neutron stars as laboratories for exotic physics 1/20 Neutron stars as laboratories for exotic physics Ian Jones D.I.Jones@soton.ac.uk General Relativity Group, Southampton University Context
DIRECT ORBITAL DYNAMICS: USING INDEPENDENT ORBITAL TERMS TO TREAT BODIES AS ORBITING EACH OTHER DIRECTLY WHILE IN MOTION
 1 DIRECT ORBITAL DYNAMICS: USING INDEPENDENT ORBITAL TERMS TO TREAT BODIES AS ORBITING EACH OTHER DIRECTLY WHILE IN MOTION Daniel S. Orton email: dsorton1@gmail.com Abstract: There are many longstanding
1 DIRECT ORBITAL DYNAMICS: USING INDEPENDENT ORBITAL TERMS TO TREAT BODIES AS ORBITING EACH OTHER DIRECTLY WHILE IN MOTION Daniel S. Orton email: dsorton1@gmail.com Abstract: There are many longstanding
Notes on Elastic and Inelastic Collisions
 Notes on Elastic and Inelastic Collisions In any collision of 2 bodies, their net momentus conserved. That is, the net momentum vector of the bodies just after the collision is the same as it was just
Notes on Elastic and Inelastic Collisions In any collision of 2 bodies, their net momentus conserved. That is, the net momentum vector of the bodies just after the collision is the same as it was just
Structure formation in modified gravity models
 Structure formation in modified gravity models Kazuya Koyama Institute of Cosmology and Gravitation University of Portsmouth Dark energy v modified gravity Is cosmology probing the breakdown of general
Structure formation in modified gravity models Kazuya Koyama Institute of Cosmology and Gravitation University of Portsmouth Dark energy v modified gravity Is cosmology probing the breakdown of general
AP Physics 1 and 2 Lab Investigations
 AP Physics 1 and 2 Lab Investigations Student Guide to Data Analysis New York, NY. College Board, Advanced Placement, Advanced Placement Program, AP, AP Central, and the acorn logo are registered trademarks
AP Physics 1 and 2 Lab Investigations Student Guide to Data Analysis New York, NY. College Board, Advanced Placement, Advanced Placement Program, AP, AP Central, and the acorn logo are registered trademarks
L 2 : x = s + 1, y = s, z = 4s + 4. 3. Suppose that C has coordinates (x, y, z). Then from the vector equality AC = BD, one has
 The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
The line L through the points A and B is parallel to the vector AB = 3, 2, and has parametric equations x = 3t + 2, y = 2t +, z = t Therefore, the intersection point of the line with the plane should satisfy:
White Dwarf Properties and the Degenerate Electron Gas
 White Dwarf Properties and the Degenerate Electron Gas Nicholas Rowell April 10, 2008 Contents 1 Introduction 2 1.1 Discovery....................................... 2 1.2 Survey Techniques..................................
White Dwarf Properties and the Degenerate Electron Gas Nicholas Rowell April 10, 2008 Contents 1 Introduction 2 1.1 Discovery....................................... 2 1.2 Survey Techniques..................................
DYNAMICS OF GALAXIES
 DYNAMICS OF GALAXIES 2. and stellar orbits Piet van der Kruit Kapteyn Astronomical Institute University of Groningen the Netherlands Winter 2008/9 and stellar orbits Contents Range of timescales Two-body
DYNAMICS OF GALAXIES 2. and stellar orbits Piet van der Kruit Kapteyn Astronomical Institute University of Groningen the Netherlands Winter 2008/9 and stellar orbits Contents Range of timescales Two-body
Steady Heat Conduction
 Steady Heat Conduction In thermodynamics, we considered the amount of heat transfer as a system undergoes a process from one equilibrium state to another. hermodynamics gives no indication of how long
Steady Heat Conduction In thermodynamics, we considered the amount of heat transfer as a system undergoes a process from one equilibrium state to another. hermodynamics gives no indication of how long
Advanced CFD Methods 1
 Advanced CFD Methods 1 Prof. Patrick Jenny, FS 2014 Date: 15.08.14, Time: 13:00, Student: Federico Danieli Summary The exam took place in Prof. Jenny s office, with his assistant taking notes on the answers.
Advanced CFD Methods 1 Prof. Patrick Jenny, FS 2014 Date: 15.08.14, Time: 13:00, Student: Federico Danieli Summary The exam took place in Prof. Jenny s office, with his assistant taking notes on the answers.
Figure 1.1 Vector A and Vector F
 CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
CHAPTER I VECTOR QUANTITIES Quantities are anything which can be measured, and stated with number. Quantities in physics are divided into two types; scalar and vector quantities. Scalar quantities have
Electromagnetism Laws and Equations
 Electromagnetism Laws and Equations Andrew McHutchon Michaelmas 203 Contents Electrostatics. Electric E- and D-fields............................................. Electrostatic Force............................................2
Electromagnetism Laws and Equations Andrew McHutchon Michaelmas 203 Contents Electrostatics. Electric E- and D-fields............................................. Electrostatic Force............................................2
Module 1 : Conduction. Lecture 5 : 1D conduction example problems. 2D conduction
 Module 1 : Conduction Lecture 5 : 1D conduction example problems. 2D conduction Objectives In this class: An example of optimization for insulation thickness is solved. The 1D conduction is considered
Module 1 : Conduction Lecture 5 : 1D conduction example problems. 2D conduction Objectives In this class: An example of optimization for insulation thickness is solved. The 1D conduction is considered
Neutron Stars. How were neutron stars discovered? The first neutron star was discovered by 24-year-old graduate student Jocelyn Bell in 1967.
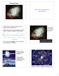 Neutron Stars How were neutron stars discovered? The first neutron star was discovered by 24-year-old graduate student Jocelyn Bell in 1967. Using a radio telescope she noticed regular pulses of radio
Neutron Stars How were neutron stars discovered? The first neutron star was discovered by 24-year-old graduate student Jocelyn Bell in 1967. Using a radio telescope she noticed regular pulses of radio
Sound. References: L.D. Landau & E.M. Lifshitz: Fluid Mechanics, Chapter VIII F. Shu: The Physics of Astrophysics, Vol. 2, Gas Dynamics, Chapter 8
 References: Sound L.D. Landau & E.M. Lifshitz: Fluid Mechanics, Chapter VIII F. Shu: The Physics of Astrophysics, Vol., Gas Dynamics, Chapter 8 1 Speed of sound The phenomenon of sound waves is one that
References: Sound L.D. Landau & E.M. Lifshitz: Fluid Mechanics, Chapter VIII F. Shu: The Physics of Astrophysics, Vol., Gas Dynamics, Chapter 8 1 Speed of sound The phenomenon of sound waves is one that
Derive 5: The Easiest... Just Got Better!
 Liverpool John Moores University, 1-15 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de Technologie Supérieure, Canada Email; mbeaudin@seg.etsmtl.ca 1. Introduction Engineering
Liverpool John Moores University, 1-15 July 000 Derive 5: The Easiest... Just Got Better! Michel Beaudin École de Technologie Supérieure, Canada Email; mbeaudin@seg.etsmtl.ca 1. Introduction Engineering
arxiv:1603.01211v1 [quant-ph] 3 Mar 2016
![arxiv:1603.01211v1 [quant-ph] 3 Mar 2016 arxiv:1603.01211v1 [quant-ph] 3 Mar 2016](/thumbs/40/21474653.jpg) Classical and Quantum Mechanical Motion in Magnetic Fields J. Franklin and K. Cole Newton Department of Physics, Reed College, Portland, Oregon 970, USA Abstract We study the motion of a particle in a
Classical and Quantum Mechanical Motion in Magnetic Fields J. Franklin and K. Cole Newton Department of Physics, Reed College, Portland, Oregon 970, USA Abstract We study the motion of a particle in a
The Essence of Gravitational Waves and Energy
 The Essence of Gravitational Waves and Energy F. I. Cooperstock Department of Physics and Astronomy University of Victoria P.O. Box 3055, Victoria, B.C. V8W 3P6 (Canada) March 26, 2015 Abstract We discuss
The Essence of Gravitational Waves and Energy F. I. Cooperstock Department of Physics and Astronomy University of Victoria P.O. Box 3055, Victoria, B.C. V8W 3P6 (Canada) March 26, 2015 Abstract We discuss
Some Comments on the Derivative of a Vector with applications to angular momentum and curvature. E. L. Lady (October 18, 2000)
 Some Comments on the Derivative of a Vector with applications to angular momentum and curvature E. L. Lady (October 18, 2000) Finding the formula in polar coordinates for the angular momentum of a moving
Some Comments on the Derivative of a Vector with applications to angular momentum and curvature E. L. Lady (October 18, 2000) Finding the formula in polar coordinates for the angular momentum of a moving
MASTER OF SCIENCE IN PHYSICS MASTER OF SCIENCES IN PHYSICS (MS PHYS) (LIST OF COURSES BY SEMESTER, THESIS OPTION)
 MASTER OF SCIENCE IN PHYSICS Admission Requirements 1. Possession of a BS degree from a reputable institution or, for non-physics majors, a GPA of 2.5 or better in at least 15 units in the following advanced
MASTER OF SCIENCE IN PHYSICS Admission Requirements 1. Possession of a BS degree from a reputable institution or, for non-physics majors, a GPA of 2.5 or better in at least 15 units in the following advanced
1 Determinants and the Solvability of Linear Systems
 1 Determinants and the Solvability of Linear Systems In the last section we learned how to use Gaussian elimination to solve linear systems of n equations in n unknowns The section completely side-stepped
1 Determinants and the Solvability of Linear Systems In the last section we learned how to use Gaussian elimination to solve linear systems of n equations in n unknowns The section completely side-stepped
Discrete mechanics, optimal control and formation flying spacecraft
 Discrete mechanics, optimal control and formation flying spacecraft Oliver Junge Center for Mathematics Munich University of Technology joint work with Jerrold E. Marsden and Sina Ober-Blöbaum partially
Discrete mechanics, optimal control and formation flying spacecraft Oliver Junge Center for Mathematics Munich University of Technology joint work with Jerrold E. Marsden and Sina Ober-Blöbaum partially
Orbital Dynamics in Terms of Spacetime Angular Momentum
 Chapter 4 Orbital Dynamics in Terms of Spacetime Angular Momentum by Myron W. Evans 1 and H. Eckardt 2 Alpha Institute for Advanced Study (AIAS) (www.aias.us, www.atomicprecision.com) Abstract Planar orbital
Chapter 4 Orbital Dynamics in Terms of Spacetime Angular Momentum by Myron W. Evans 1 and H. Eckardt 2 Alpha Institute for Advanced Study (AIAS) (www.aias.us, www.atomicprecision.com) Abstract Planar orbital
Orbital Mechanics. Angular Momentum
 Orbital Mechanics The objects that orbit earth have only a few forces acting on them, the largest being the gravitational pull from the earth. The trajectories that satellites or rockets follow are largely
Orbital Mechanics The objects that orbit earth have only a few forces acting on them, the largest being the gravitational pull from the earth. The trajectories that satellites or rockets follow are largely
The Two-Body Problem
 The Two-Body Problem Abstract In my short essay on Kepler s laws of planetary motion and Newton s law of universal gravitation, the trajectory of one massive object near another was shown to be a conic
The Two-Body Problem Abstract In my short essay on Kepler s laws of planetary motion and Newton s law of universal gravitation, the trajectory of one massive object near another was shown to be a conic
Poisson Equation Solver Parallelisation for Particle-in-Cell Model
 WDS'14 Proceedings of Contributed Papers Physics, 233 237, 214. ISBN 978-8-7378-276-4 MATFYZPRESS Poisson Equation Solver Parallelisation for Particle-in-Cell Model A. Podolník, 1,2 M. Komm, 1 R. Dejarnac,
WDS'14 Proceedings of Contributed Papers Physics, 233 237, 214. ISBN 978-8-7378-276-4 MATFYZPRESS Poisson Equation Solver Parallelisation for Particle-in-Cell Model A. Podolník, 1,2 M. Komm, 1 R. Dejarnac,
6 J - vector electric current density (A/m2 )
 Determination of Antenna Radiation Fields Using Potential Functions Sources of Antenna Radiation Fields 6 J - vector electric current density (A/m2 ) M - vector magnetic current density (V/m 2 ) Some problems
Determination of Antenna Radiation Fields Using Potential Functions Sources of Antenna Radiation Fields 6 J - vector electric current density (A/m2 ) M - vector magnetic current density (V/m 2 ) Some problems
Euclidean quantum gravity revisited
 Institute for Gravitation and the Cosmos, Pennsylvania State University 15 June 2009 Eastern Gravity Meeting, Rochester Institute of Technology Based on: First-order action and Euclidean quantum gravity,
Institute for Gravitation and the Cosmos, Pennsylvania State University 15 June 2009 Eastern Gravity Meeting, Rochester Institute of Technology Based on: First-order action and Euclidean quantum gravity,
On Motion of Robot End-Effector using the Curvature Theory of Timelike Ruled Surfaces with Timelike Directrix
 Malaysian Journal of Mathematical Sciences 8(2): 89-204 (204) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Journal homepage: http://einspem.upm.edu.my/journal On Motion of Robot End-Effector using the Curvature
Malaysian Journal of Mathematical Sciences 8(2): 89-204 (204) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Journal homepage: http://einspem.upm.edu.my/journal On Motion of Robot End-Effector using the Curvature
MODULE VII LARGE BODY WAVE DIFFRACTION
 MODULE VII LARGE BODY WAVE DIFFRACTION 1.0 INTRODUCTION In the wave-structure interaction problems, it is classical to divide into two major classification: slender body interaction and large body interaction.
MODULE VII LARGE BODY WAVE DIFFRACTION 1.0 INTRODUCTION In the wave-structure interaction problems, it is classical to divide into two major classification: slender body interaction and large body interaction.
Continuous Groups, Lie Groups, and Lie Algebras
 Chapter 7 Continuous Groups, Lie Groups, and Lie Algebras Zeno was concerned with three problems... These are the problem of the infinitesimal, the infinite, and continuity... Bertrand Russell The groups
Chapter 7 Continuous Groups, Lie Groups, and Lie Algebras Zeno was concerned with three problems... These are the problem of the infinitesimal, the infinite, and continuity... Bertrand Russell The groups
Chapter 9 Unitary Groups and SU(N)
 Chapter 9 Unitary Groups and SU(N) The irreducible representations of SO(3) are appropriate for describing the degeneracies of states of quantum mechanical systems which have rotational symmetry in three
Chapter 9 Unitary Groups and SU(N) The irreducible representations of SO(3) are appropriate for describing the degeneracies of states of quantum mechanical systems which have rotational symmetry in three
Dynamics. Basilio Bona. DAUIN-Politecnico di Torino. Basilio Bona (DAUIN-Politecnico di Torino) Dynamics 2009 1 / 30
 Dynamics Basilio Bona DAUIN-Politecnico di Torino 2009 Basilio Bona (DAUIN-Politecnico di Torino) Dynamics 2009 1 / 30 Dynamics - Introduction In order to determine the dynamics of a manipulator, it is
Dynamics Basilio Bona DAUIN-Politecnico di Torino 2009 Basilio Bona (DAUIN-Politecnico di Torino) Dynamics 2009 1 / 30 Dynamics - Introduction In order to determine the dynamics of a manipulator, it is
Lecture L22-2D Rigid Body Dynamics: Work and Energy
 J. Peraire, S. Widnall 6.07 Dynamics Fall 008 Version.0 Lecture L - D Rigid Body Dynamics: Work and Energy In this lecture, we will revisit the principle of work and energy introduced in lecture L-3 for
J. Peraire, S. Widnall 6.07 Dynamics Fall 008 Version.0 Lecture L - D Rigid Body Dynamics: Work and Energy In this lecture, we will revisit the principle of work and energy introduced in lecture L-3 for
Notes: Most of the material in this chapter is taken from Young and Freedman, Chap. 13.
 Chapter 5. Gravitation Notes: Most of the material in this chapter is taken from Young and Freedman, Chap. 13. 5.1 Newton s Law of Gravitation We have already studied the effects of gravity through the
Chapter 5. Gravitation Notes: Most of the material in this chapter is taken from Young and Freedman, Chap. 13. 5.1 Newton s Law of Gravitation We have already studied the effects of gravity through the
Level Set Framework, Signed Distance Function, and Various Tools
 Level Set Framework Geometry and Calculus Tools Level Set Framework,, and Various Tools Spencer Department of Mathematics Brigham Young University Image Processing Seminar (Week 3), 2010 Level Set Framework
Level Set Framework Geometry and Calculus Tools Level Set Framework,, and Various Tools Spencer Department of Mathematics Brigham Young University Image Processing Seminar (Week 3), 2010 Level Set Framework
Metrics on SO(3) and Inverse Kinematics
 Mathematical Foundations of Computer Graphics and Vision Metrics on SO(3) and Inverse Kinematics Luca Ballan Institute of Visual Computing Optimization on Manifolds Descent approach d is a ascent direction
Mathematical Foundations of Computer Graphics and Vision Metrics on SO(3) and Inverse Kinematics Luca Ballan Institute of Visual Computing Optimization on Manifolds Descent approach d is a ascent direction
Name Class Date. true
 Exercises 131 The Falling Apple (page 233) 1 Describe the legend of Newton s discovery that gravity extends throughout the universe According to legend, Newton saw an apple fall from a tree and realized
Exercises 131 The Falling Apple (page 233) 1 Describe the legend of Newton s discovery that gravity extends throughout the universe According to legend, Newton saw an apple fall from a tree and realized
Central configuration in the planar n + 1 body problem with generalized forces.
 Monografías de la Real Academia de Ciencias de Zaragoza. 28: 1 8, (2006). Central configuration in the planar n + 1 body problem with generalized forces. M. Arribas, A. Elipe Grupo de Mecánica Espacial.
Monografías de la Real Academia de Ciencias de Zaragoza. 28: 1 8, (2006). Central configuration in the planar n + 1 body problem with generalized forces. M. Arribas, A. Elipe Grupo de Mecánica Espacial.
Chapter 22 The Hamiltonian and Lagrangian densities. from my book: Understanding Relativistic Quantum Field Theory. Hans de Vries
 Chapter 22 The Hamiltonian and Lagrangian densities from my book: Understanding Relativistic Quantum Field Theory Hans de Vries January 2, 2009 2 Chapter Contents 22 The Hamiltonian and Lagrangian densities
Chapter 22 The Hamiltonian and Lagrangian densities from my book: Understanding Relativistic Quantum Field Theory Hans de Vries January 2, 2009 2 Chapter Contents 22 The Hamiltonian and Lagrangian densities
Fundamentals of grain boundaries and grain boundary migration
 1. Fundamentals of grain boundaries and grain boundary migration 1.1. Introduction The properties of crystalline metallic materials are determined by their deviation from a perfect crystal lattice, which
1. Fundamentals of grain boundaries and grain boundary migration 1.1. Introduction The properties of crystalline metallic materials are determined by their deviation from a perfect crystal lattice, which
Variational approach to restore point-like and curve-like singularities in imaging
 Variational approach to restore point-like and curve-like singularities in imaging Daniele Graziani joint work with Gilles Aubert and Laure Blanc-Féraud Roma 12/06/2012 Daniele Graziani (Roma) 12/06/2012
Variational approach to restore point-like and curve-like singularities in imaging Daniele Graziani joint work with Gilles Aubert and Laure Blanc-Féraud Roma 12/06/2012 Daniele Graziani (Roma) 12/06/2012
Vector Spaces; the Space R n
 Vector Spaces; the Space R n Vector Spaces A vector space (over the real numbers) is a set V of mathematical entities, called vectors, U, V, W, etc, in which an addition operation + is defined and in which
Vector Spaces; the Space R n Vector Spaces A vector space (over the real numbers) is a set V of mathematical entities, called vectors, U, V, W, etc, in which an addition operation + is defined and in which
Chapter 11 Equilibrium
 11.1 The First Condition of Equilibrium The first condition of equilibrium deals with the forces that cause possible translations of a body. The simplest way to define the translational equilibrium of
11.1 The First Condition of Equilibrium The first condition of equilibrium deals with the forces that cause possible translations of a body. The simplest way to define the translational equilibrium of
1 Lecture 3: Operators in Quantum Mechanics
 1 Lecture 3: Operators in Quantum Mechanics 1.1 Basic notions of operator algebra. In the previous lectures we have met operators: ˆx and ˆp = i h they are called fundamental operators. Many operators
1 Lecture 3: Operators in Quantum Mechanics 1.1 Basic notions of operator algebra. In the previous lectures we have met operators: ˆx and ˆp = i h they are called fundamental operators. Many operators
The Einstein field equations
 The Einstein field equations Part I: the right-hand side Atle Hahn GFM, Universidade de Lisboa Lisbon, 21st January 2010 Contents: 1 Einstein field equations: overview 2 Special relativity: review 3 Classical
The Einstein field equations Part I: the right-hand side Atle Hahn GFM, Universidade de Lisboa Lisbon, 21st January 2010 Contents: 1 Einstein field equations: overview 2 Special relativity: review 3 Classical
Vector and Matrix Norms
 Chapter 1 Vector and Matrix Norms 11 Vector Spaces Let F be a field (such as the real numbers, R, or complex numbers, C) with elements called scalars A Vector Space, V, over the field F is a non-empty
Chapter 1 Vector and Matrix Norms 11 Vector Spaces Let F be a field (such as the real numbers, R, or complex numbers, C) with elements called scalars A Vector Space, V, over the field F is a non-empty
Physics 9e/Cutnell. correlated to the. College Board AP Physics 1 Course Objectives
 Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Physics 9e/Cutnell correlated to the College Board AP Physics 1 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring
Gravitomagnetism and complex orbit dynamics of spinning compact objects around a massive black hole
 Gravitomagnetism and complex orbit dynamics of spinning compact objects around a massive black hole Kinwah Wu Mullard Space Science Laboratory University College London United Kingdom kw@mssl.ucl.ac.uk
Gravitomagnetism and complex orbit dynamics of spinning compact objects around a massive black hole Kinwah Wu Mullard Space Science Laboratory University College London United Kingdom kw@mssl.ucl.ac.uk
Dynamics of Iain M. Banks Orbitals. Richard Kennaway. 12 October 2005
 Dynamics of Iain M. Banks Orbitals Richard Kennaway 12 October 2005 Note This is a draft in progress, and as such may contain errors. Please do not cite this without permission. 1 The problem An Orbital
Dynamics of Iain M. Banks Orbitals Richard Kennaway 12 October 2005 Note This is a draft in progress, and as such may contain errors. Please do not cite this without permission. 1 The problem An Orbital
Numerical Analysis Lecture Notes
 Numerical Analysis Lecture Notes Peter J. Olver 5. Inner Products and Norms The norm of a vector is a measure of its size. Besides the familiar Euclidean norm based on the dot product, there are a number
Numerical Analysis Lecture Notes Peter J. Olver 5. Inner Products and Norms The norm of a vector is a measure of its size. Besides the familiar Euclidean norm based on the dot product, there are a number
Motion of a Leaky Tank Car
 1 Problem Motion of a Leaky Tank Car Kirk T. McDonald Joseph Henry Laboratories, Princeton University, Princeton, NJ 8544 (December 4, 1989; updated October 1, 214) Describe the motion of a tank car initially
1 Problem Motion of a Leaky Tank Car Kirk T. McDonald Joseph Henry Laboratories, Princeton University, Princeton, NJ 8544 (December 4, 1989; updated October 1, 214) Describe the motion of a tank car initially
Computer Graphics. Geometric Modeling. Page 1. Copyright Gotsman, Elber, Barequet, Karni, Sheffer Computer Science - Technion. An Example.
 An Example 2 3 4 Outline Objective: Develop methods and algorithms to mathematically model shape of real world objects Categories: Wire-Frame Representation Object is represented as as a set of points
An Example 2 3 4 Outline Objective: Develop methods and algorithms to mathematically model shape of real world objects Categories: Wire-Frame Representation Object is represented as as a set of points
How Gravitational Forces arise from Curvature
 How Gravitational Forces arise from Curvature 1. Introduction: Extremal ging and the Equivalence Principle These notes supplement Chapter 3 of EBH (Exploring Black Holes by Taylor and Wheeler). They elaborate
How Gravitational Forces arise from Curvature 1. Introduction: Extremal ging and the Equivalence Principle These notes supplement Chapter 3 of EBH (Exploring Black Holes by Taylor and Wheeler). They elaborate
How To Understand General Relativity
 Chapter S3 Spacetime and Gravity What are the major ideas of special relativity? Spacetime Special relativity showed that space and time are not absolute Instead they are inextricably linked in a four-dimensional
Chapter S3 Spacetime and Gravity What are the major ideas of special relativity? Spacetime Special relativity showed that space and time are not absolute Instead they are inextricably linked in a four-dimensional
